KGANCDA: predicting circRNA-disease associations based on knowledge graph attention network Free

The brief information of the datasets

Dataset	circRNA	Disease	lncRNA	miRNA	circRNA-disease	circRNA-miRNA	miRNA-disease	lncRNA-disease	lncRNA-miRNA
Dataset1	514	62	573	564	647	756	732	1066	308
Dataset2	330	79	297	245	346	146	106	528	241

Dataset	circRNA	Disease	lncRNA	miRNA	circRNA-disease	circRNA-miRNA	miRNA-disease	lncRNA-disease	lncRNA-miRNA
Dataset1	514	62	573	564	647	756	732	1066	308
Dataset2	330	79	297	245	346	146	106	528	241

Table 1

The brief information of the datasets

Dataset	circRNA	Disease	lncRNA	miRNA	circRNA-disease	circRNA-miRNA	miRNA-disease	lncRNA-disease	lncRNA-miRNA
Dataset1	514	62	573	564	647	756	732	1066	308
Dataset2	330	79	297	245	346	146	106	528	241

Dataset	circRNA	Disease	lncRNA	miRNA	circRNA-disease	circRNA-miRNA	miRNA-disease	lncRNA-disease	lncRNA-miRNA
Dataset1	514	62	573	564	647	756	732	1066	308
Dataset2	330	79	297	245	346	146	106	528	241

Figure 1

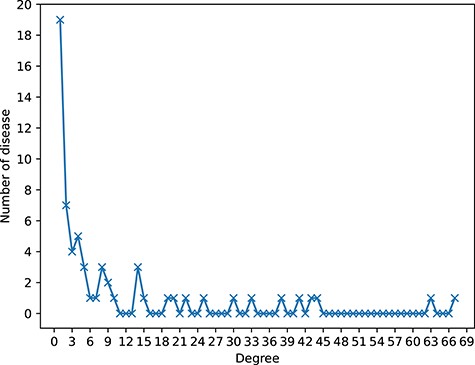
The sparsity of circRNA-disease associations of dataset1. The horizontal axis (Degree) represents the number of related circRNAs of each disease. The longitudinal axis (Number of disease) represents the number of diseases with corresponding degree. For example, there are 19 diseases that only have association with one circRNA.

Figure 2

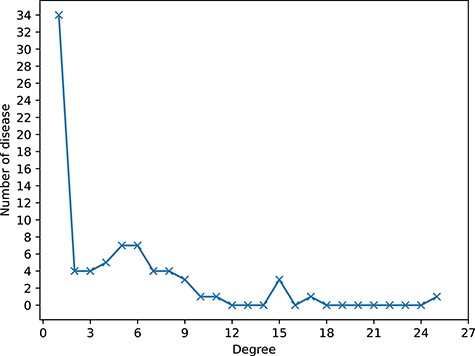
The sparsity of circRNA-disease associations of dataset2. The horizontal axis (Degree) represents the number of related circRNAs of each disease. The longitudinal axis (Number of disease) represents the number of diseases with corresponding degree. For example, there are 34 diseases that only have association with one circRNA.

Knowledge graph

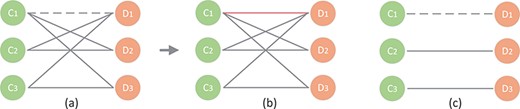
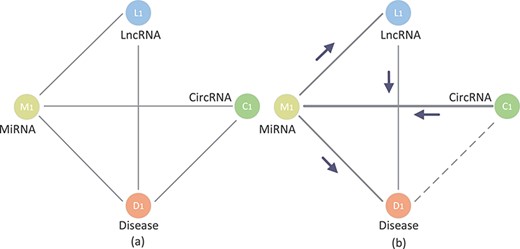
As shown in Figure 3A, there are two sets: circRNA (C₁, C₂ and C₃) and disease (D₁, D₂ and D₃), which are represented as green circles and orange circles, respectively. Taking C₁ as an example, C₁ directly links to three disease nodes (D₁, D₂ and D₃). Supposing that the association C₁–D₁ is the potential association that needs to be predicted. Based on the hypothesis that similar circRNAs tend to be related with similar diseases [27, 36, 37], many traditional methods may find that C₂ and C₃ are similar to C₁. Because C₂ and C₃ are associated with D₁, the prediction score of the association C₁–D₁ is higher than other candidate associations. However, as shown in Figure 3C, the association data are sparse in circRNA-disease association network and C₁ is usually not similar with any circRNAs. Thus, the performance of these methods only based on low-level interaction information is limited. However, it can be found from Figure 4 that the knowledge graph of circRNA-disease contains more kinds of entities and associations. Besides the low-order association information, the embeddings of it will contain high-order neighbor information. Supposing that the C₁–D₁ is the potential association that needs to be predicted. It can be found that circRNA C₁ is related with miRNA M₁ and lncRNAs L₁, and these nodes are related with the candidate disease D₁. After repeatedly propagating in knowledge graph attention network, the embedding of circRNA C₁ will contain neighbor information from miRNA, lncRNA, etc. Therefore, the method based on knowledge graph can effectively predict potential association C₁–D₁.

Figure 3

A toy example of traditional method.

Figure 4

The example of circRNA-disease knowledge graph.

The knowledge graph of circRNA-disease is formulated as G|$=(V,E)$|⁠, where V represents the various entities (circRNA, disease, lncRNA and miRNA) and E denotes the edge set (the associations among entities). The form of knowledge graph could be presented as entity-relation-entity triples |$T=(h,r,t)$|⁠, where |$h,t\in V$| denote entities (circRNA, disease, miRNA and lncRNA) and |$r\in E$| denotes the relationships between entities.

$$\begin{equation} S\left(h,r,t\right)={\left\Vert{W}_1{V}_h+{V}_r-{W}_1{V}_t\right\Vert}_2^2 \end{equation}$$

(1)

where |${V}_h,{V}_t\in{R}^a$| and |${V}_r\in{R}^k$| denote the embeddings of head entities, tail entities and association entities, respectively. a represents the embedding size of the tail entity and the head entity. |${W}_1\in{R}^{k\times a}$| denotes the transformation matrix which projects the representations of each entity into the same space. Furthermore, a set of false triples are constructed and represented as |$(h,r,{t}^{\prime})$|⁠, where |${t}^{\prime }$| is replaced by any valid entity randomly. The target is to enlarge the difference between true triple score and false triple score. Therefore, the loss function is defined as follows:

$$\begin{equation} {L}_1=\sum_{h,r,t,{t}^{\prime}\in \Omega}-\ln sigmoid\left(S\left(h,r,{t}^{\prime}\right)-S\left(h,r,t\right)\right) \end{equation}$$

(2)

$$\begin{equation} \Omega =T\cup F \end{equation}$$

(3)

where |$(h,r,t)\in T$| denotes positive triple set and |$(h,r,{t}^{\prime})\in F$| denotes false negative triple set.

Graph attention network

Graph attention mechanism

An entity h could be involved in multiple triples. Therefore, there are many neighbors of entity h. To discriminate the importance of different neighbors [38], an attentional mechanism is designed in here. All triples of entity h are represented as |${N}_h=\{(h,r,t)|h,t\in V,r\in E\}$|⁠, where t denotes all neighbors of entity h in the graph. We use |${V}_{N_h}$| to represent the embeddings of entity h after aggregating all neighbors. The aggregation formula is defined as follows:

$$\begin{equation} {V}_{N_h}=\sum_{\left(h,r,t\right)\in{N}_h}a\left(h,r,t\right){V}_t \end{equation}$$

(4)

where |${V}_t$| represents the neighbor tail embeddings. |$a(h,r,t)$| denotes the attention weight of each neighbor, which decides the amount of information propagated from neighbors. The relational attention |$a(h,r,t)$| is defined as follows:

$$\begin{equation} a\left(h,r,t\right)={\left({W}_1{V}_t\right)}^T\mathit{\tanh}\left(\left({W}_1{V}_h+{V}_r\right)\right) \end{equation}$$

(5)

where |${V}_h$| represents the embeddings of head entities. The activation function is set as tanh [39]. Then, the coefficient of all entities connected with entity h is normalized by the softmax function:

$$\begin{equation} a\left(h,r,t\right)=\frac{\exp \left(a\left(h,r,t\right)\right)}{\sum_{\left(h,{r}^{\prime },{t}^{\prime}\right)\in{N}_h}\exp \left(a\left(h,{r}^{\prime },{t}^{\prime}\right)\right)} \end{equation}$$

(6)

Aggregation information from neighbors

To aggregate neighbors’ information and update each entity’s embeddings, the aggregation function |$f({V}_h,{V}_{N_h})$| is defined as follows:

$$\begin{equation} f\left({V}_h,{V}_{N_h}\right)= LeakyReLU\left({W}_2\left({V}_h+{V}_{N_h}\right)\right) \end{equation}$$

(7)

where |${W}_2\in{R}^{d^{\prime}\times d}$| represents transformation matrix.|${d}^{\prime }$| represents the transformation size.

After aggregating 1st order neighbors, each entity contain the neighbor information from their one-hop neighbors. Then more propagation layers are stacked to explore high-order neighbor information from multi-hop neighbors. Specifically, by stacking l-th layer, the embeddings of each entity will contain the information from their l-hop neighbors. The embedding vector of the entity h is defined as follows:

$$\begin{equation} {V}_h^{(l)}=f\left({V}_h^{\left(l-1\right)},{V}_{N_h}^{\left(l-1\right)}\right) \end{equation}$$

(8)

$$\begin{equation} {V}_{N_h}^{\left(l-1\right)}=\sum_{\left(h,r,t\right)\in{N}_h}a\left(h,r,t\right){V}_t^{\left(l-1\right)} \end{equation}$$

(9)

where |${V}_h^{(l-1)} and\ {V}_{N_h}^{(l-1)}$| represent the embeddings of entity h and the embeddings of neighbors in (l−1)-th layer, respectively. |${V}_t^{(l-1)}$| represents the tail entities connected with entity h, of which the embeddings contain the information from its (l−1)-hop neighbors.

Prediction and optimization

Multiple layer perceptron

After propagating in graph attention layers, the embeddings of each entity are obtained. Considering a circRNA C_i (or a disease D_j), the embedding of circRNA C_i in l-th layers is |${v}_i^{(l)}$| (the embedding of disease D_j in l-th layer is |${v}_j^{(l)}$|⁠). Then, by concatenating embeddings of each layer, the final representation of C_i (D_j) is defined as follows:

$$\begin{equation} {V}_{c_i}={v}_i^{(0)}\left\Vert \cdots \right\Vert{v}_i^{(l)} \end{equation}$$

(10)

$$\begin{equation} {V}_{d_j}={v}_j^{(0)}\left\Vert \cdots \right\Vert{v}_j^{(l)} \end{equation}$$

(11)

where |$\Vert$| represents the catenation operator. Moreover, |${V}_{c_i}$| and |${V}_{d_j}$| are connected as the embedding of the circRNA-disease association and the multilayer perceptron is employed on the embedding, which is represented as follows:

$$\begin{equation} {\hat{y}}_{ij}={W}^l{\sigma}^l\left({W}^{l-1}{\sigma}^{l-1}\left(\dots{\left( {W}^{1} {\left({V}_{c_i}\Vert{V}_{d_j}\right)}+{b}^{1}\right)}\dots \right)+{b}^{l-1}\right)+{b}^l \end{equation}$$

(12)

where |${W}^l$| and |${b}^l$| represent the learnable weight matrix and the bias in multilayer perceptron, respectively. |${\sigma}^l$| represents the activation function in l-th layer. The ReLU [40] is selected as the activation function in hidden layers. To control the output values in range of 0 to 1, sigmoid is used in the output layer.

Loss function

To optimize the parameters of the model, the loss function of graph attention neural network is defined as follows:

$$\begin{equation} {L}_2=\!\!\sum_{\begin{array}{c}\left(i,j\right)\in P\\{}\left({i}^{\prime },{j}^{\prime}\right)\in N\end{array}}\!\!-\ln sigmoid\left({\hat{y}}_{ij}-{\hat{y}}_{i^{\prime }{j}^{\prime }}\right) \end{equation}$$

(13)

where P and N denote the positive samples and negative samples, respectively. During the process of optimization, the prediction scores of positive samples and negative samples will be discriminated. The positive samples will be assigned a higher prediction value than the negative ones.

To construct an end-to-end model, the final loss function is defined by combining Equations (2) and (13):

$$\begin{align} L =&\sum_{h,r,t,{t}^{\prime}\in \Omega}-\ln sigmoid\left(S\left(h,r,{t}^{\prime}\right)-S\left(h,r,t\right)\right)\nonumber\\&+\sum_{\begin{array}{c}\left(i,j\right)\in P\\{}\left({i}^{\prime },{j}^{\prime}\right)\in N\end{array}}-\ln sigmoid\left({\hat{y}}_{ij}-{\hat{y}}_{i^{\prime }{j}^{\prime }}\right)+\lambda{\left\Vert \alpha \right\Vert}_2^2 \end{align}$$

(14)

where |$\lambda$| is the regularization parameter to avoid overfitting. |$\alpha$| denotes all parameters including |${W_1}^{(l)}$|⁠, |${W_2}^{(l)}$| and |${W}^l$|⁠, |$l\in \{1,2,3,\dots \}$|⁠.

As shown in Figure 5, KGANCDA mainly contains three parts: dataset collection, circRNA-disease knowledge graph and graph attention neural network. Specifically, it collects multiple entities and relationships from public databases [31–35]. The new knowledge graph is constructed based on the collected datasets. Then, the graph neural network is designed to obtain the embeddings of each entity. After propagating in the graph attention neural network, the embeddings of each entity contain information from their multi-hop neighbors. Furthermore, the attention mechanism is utilized to improve the quality of the embeddings by aggregating information of each neighbor based on the importance of them. Furthermore, the designed multilayer perceptron is employed on the embeddings of each pair of circRNA-disease association and the prediction scores are obtained.

Figure 5

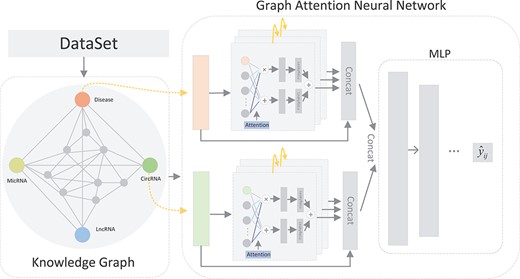
The flowchart of KGANCDA.

Experiments and results

Evaluation metrics

In this paper, the 5-fold cross validation is used to evaluate the performance of the model. In the 5-fold cross validation, all samples are divided into five sub-datasets. Then, each sub-data set is selected as the test sample in turn and other four sub-datasets are regarded as training samples. The final results are average values of the five times experiments. Furthermore, the scores of unknown samples and test samples are sorted in descending order. The receiver operating curve (ROC) is plotted by calculating the true positive rate (TPR) and the false positive rate (FPR) with different thresholds. Finally, the area under the curve (AUC) is computed to evaluate the performance of model. The TPR and FPR are defined as follows

$$\begin{equation} TPR=\frac{TP}{TP+ FN} \end{equation}$$

(15)

$$\begin{equation} FPR=\frac{FP}{FP+ TN} \end{equation}$$

(16)

where TP and TN denote the number of correctly identified associations from positive samples and negative samples, respectively. FP and FN represent the number of false identified associations from positive samples and negative samples, respectively. In addition, the area under the precision-recall curve (AUPR), F1-score, accuracy, precision and recall are used to evaluate the performance of method, which are defined as follows

$$\begin{equation} F1\_ score=\frac{2 TP}{2 TP+ FP+ FN} \end{equation}$$

(17)

$$\begin{equation} Acc=\frac{TP+ TN}{TP+ TN+ FP+ FN} \end{equation}$$

(18)

$$\begin{equation} Pre=\frac{TP}{TP+ FP} \end{equation}$$

(19)

$$\begin{equation} Rec=\frac{TP}{TP+ FN} \end{equation}$$

(20)

Five-fold cross validation

To verify the performance of KGANCDA, we compare it with six state-of-the-art models including RWR [18], DMFCDA [37], GCNCDA [30], KATZHCDA [15], DWNN-RLS [41] and CD-LNLP [42]. All models are compared in the same experiment settings, and the parameters of compared model are best parameters as they recommended. As shown in Figure 6, the AUC of KGANCDA achieves average value 0.8714 on dataset1, which is better than other six state-of-the-art methods on dataset1 (RWR: 0.7046, DMFCDA: 0.5715, GCNCDA: 0.7468, KATZHCDA: 0.6994, DWNN-RLS: 0.5797, CD-LNLP: 0.6933). The result of dataset2 is shown in Figure 7 that the AUC of KGANCDA achieves average value 0.8847, which outperforms the other methods (RWR: 0.8487, DMFCDA: 0.6001, GCNCDA: 0.7084, KATZHCDA: 0.7946, DWNN-RLS: 0.7674, CD-LNLP: 0.8034). As Figure 8 shows, it can be found that the average AUPR value of KGANCDA is 0.0907 on dataset1, which is superior to the other methods (RWR: 0.0086, DMFCDA: 0.0045, GCNCDA: 0.0095, KATZHCDA: 0.0122, DWNN-RLS: 0.0050, CD-LNLP: 0.0080). Moreover, it is shown in Figure 9 that the average AUPR of KGANCDA is 0.0237 on dataset2, which is better than the other methods (RWR: 0.0115, DMFCDA: 0.0032, GCNCDA: 0.0048, KATZHCDA: 0.0097, DWNN-RLS: 0.0069, CD-LNLP: 0.0088). Figures 10 and 11 show the number of correctly identified circRNA-disease associations in 5-fold cross validation on dataset1 and dataset2, respectively. As Figures 10 and 11 show, due to the sparsity of the circRNA-disease association, the performance of the other methods is limited. However, KGANCDA can identify more associations of circRNA-disease (67, 79, 90 pairs of associations identified successfully in top-10, top-20 and top-50 on dataset1 and 24, 29, 47 in top-10, top-20 and top-50 on dataset2, respectively). The reason may be that miRNAs and lncRNAs in knowledge graph can provide high-order neighbor information to the embeddings of circRNAs and diseases, which help to improve the performance of the model. The correctly predicted specific circRNA-disease associations of all methods are recorded in Supplementary Files S4 for dataset1 (https://github.com/lanbiolab/KGANCDA/blob/main/Additional%20Files) and S5 for dataset2 (https://github.com/lanbiolab/KGANCDA/blob/main/Additional%20Files). In addition, the values of other performance metrics are listed in Table 2 (including accuracy, precision, recall and F1_score, KGANCDA obtained 0.4943, 0.0154, 0.8731, 0.0272 on dataset1 and 0.4953, 0.0084, 0.8867, 0.0157 on dataset2, respectively.). These results indicate that KGANCDA outperforms other state-of-the-art methods.

Figure 6

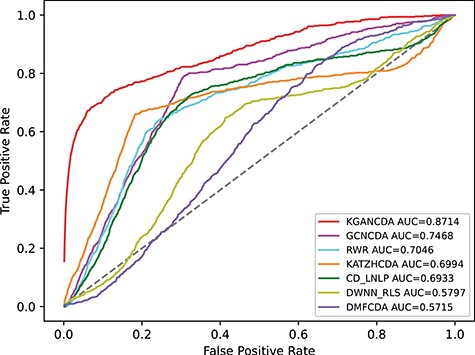
The performance comparison of KGANCDA, RWR, DMFCDA, GCNCDA, KATZHCDA, DWNN-RLS and CD-LNLP in term of AUC value on dataset1.

Figure 7

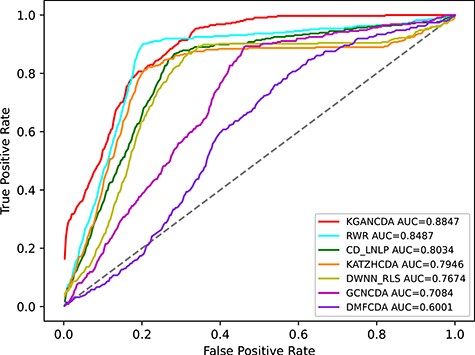
The performance comparison of KGANCDA, RWR, DMFCDA, GCNCDA, KATZHCDA, DWNN-RLS and CD-LNLP in term of AUC value on dataset2.

Figure 8

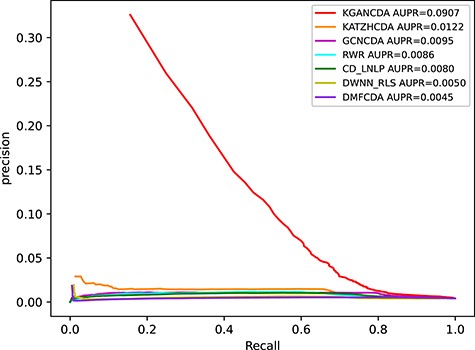
The performance comparison of KGANCDA, RWR, DMFCDA, GCNCDA, KATZHCDA, DWNN-RLS and CD-LNLP in term of AUPR value on dataset1.

Figure 9

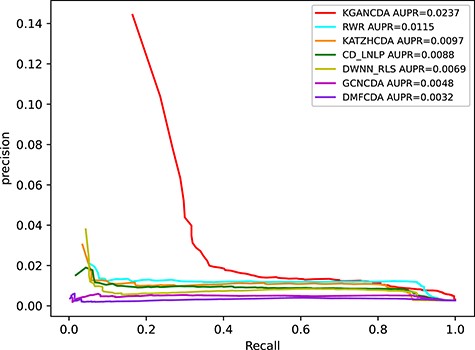
The performance comparison of KGANCDA, RWR, DMFCDA, GCNCDA, KATZHCDA, DWNN-RLS and CD-LNLP in term of AUPR value on dataset2.

Figure 10

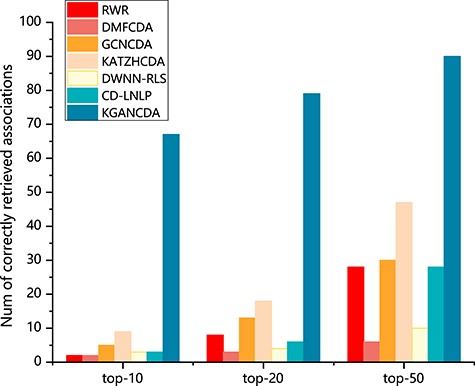
The number of correctly identified circRNA-disease associations of all methods on dataset 1 based on 5-fold cross validation.

Figure 11

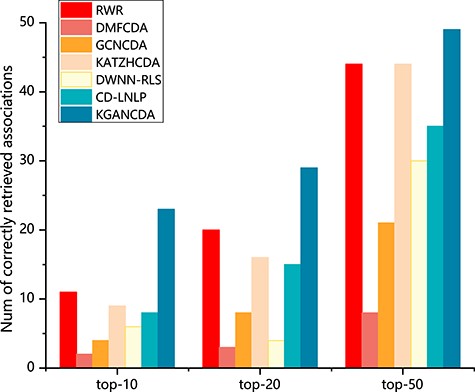
The number of correctly identified circRNA-disease associations of all methods on dataset 2 based on 5-fold cross validation.

Table 2

Comparison of methods on two datasets based on 5-fold cross validation

	Methods	Acc	Pre	Rec	F1_score
Dataset1	RWR	0.4929	0.0068	0.7094	0.0134
	DMFCDA	0.4936	0.0044	0.5637	0.0085
	GCNCDA	0.4933	0.0074	0.7509	0.0144
	KATZHCDA	0.4929	0.0081	0.7041	0.0154
	DWNN-RLS	0.4919	0.0049	0.5870	0.0095
	CD-LNLP	0.4928	0.0066	0.6982	0.0130
	KGANCDA	0.4942	0.0151	0.8682	0.0267
Dataset2	RWR	0.4951	0.0066	0.8509	0.0127
	DMFCDA	0.5040	0.0031	0.5953	0.0062
	GCNCDA	0.4944	0.0042	0.7125	0.0083
	KATZHCDA	0.4948	0.0060	0.7974	0.0117
	DWNN-RLS	0.4947	0.0053	0.7706	0.0103
	CD-LNLP	0.4949	0.0058	0.8062	0.0112
	KGANCDA	0.4953	0.0084	0.8867	0.0157

	Methods	Acc	Pre	Rec	F1_score
Dataset1	RWR	0.4929	0.0068	0.7094	0.0134
	DMFCDA	0.4936	0.0044	0.5637	0.0085
	GCNCDA	0.4933	0.0074	0.7509	0.0144
	KATZHCDA	0.4929	0.0081	0.7041	0.0154
	DWNN-RLS	0.4919	0.0049	0.5870	0.0095
	CD-LNLP	0.4928	0.0066	0.6982	0.0130
	KGANCDA	0.4942	0.0151	0.8682	0.0267
Dataset2	RWR	0.4951	0.0066	0.8509	0.0127
	DMFCDA	0.5040	0.0031	0.5953	0.0062
	GCNCDA	0.4944	0.0042	0.7125	0.0083
	KATZHCDA	0.4948	0.0060	0.7974	0.0117
	DWNN-RLS	0.4947	0.0053	0.7706	0.0103
	CD-LNLP	0.4949	0.0058	0.8062	0.0112
	KGANCDA	0.4953	0.0084	0.8867	0.0157

Table 2

Comparison of methods on two datasets based on 5-fold cross validation

	Methods	Acc	Pre	Rec	F1_score
Dataset1	RWR	0.4929	0.0068	0.7094	0.0134
	DMFCDA	0.4936	0.0044	0.5637	0.0085
	GCNCDA	0.4933	0.0074	0.7509	0.0144
	KATZHCDA	0.4929	0.0081	0.7041	0.0154
	DWNN-RLS	0.4919	0.0049	0.5870	0.0095
	CD-LNLP	0.4928	0.0066	0.6982	0.0130
	KGANCDA	0.4942	0.0151	0.8682	0.0267
Dataset2	RWR	0.4951	0.0066	0.8509	0.0127
	DMFCDA	0.5040	0.0031	0.5953	0.0062
	GCNCDA	0.4944	0.0042	0.7125	0.0083
	KATZHCDA	0.4948	0.0060	0.7974	0.0117
	DWNN-RLS	0.4947	0.0053	0.7706	0.0103
	CD-LNLP	0.4949	0.0058	0.8062	0.0112
	KGANCDA	0.4953	0.0084	0.8867	0.0157

	Methods	Acc	Pre	Rec	F1_score
Dataset1	RWR	0.4929	0.0068	0.7094	0.0134
	DMFCDA	0.4936	0.0044	0.5637	0.0085
	GCNCDA	0.4933	0.0074	0.7509	0.0144
	KATZHCDA	0.4929	0.0081	0.7041	0.0154
	DWNN-RLS	0.4919	0.0049	0.5870	0.0095
	CD-LNLP	0.4928	0.0066	0.6982	0.0130
	KGANCDA	0.4942	0.0151	0.8682	0.0267
Dataset2	RWR	0.4951	0.0066	0.8509	0.0127
	DMFCDA	0.5040	0.0031	0.5953	0.0062
	GCNCDA	0.4944	0.0042	0.7125	0.0083
	KATZHCDA	0.4948	0.0060	0.7974	0.0117
	DWNN-RLS	0.4947	0.0053	0.7706	0.0103
	CD-LNLP	0.4949	0.0058	0.8062	0.0112
	KGANCDA	0.4953	0.0084	0.8867	0.0157

The effect of different components in KGANCDA

Ablation study

To validate the effectiveness of different modules (circRNA-disease knowledge graph and knowledge graph attention mechanism), we remove them in turn and analysis the effectiveness of them. We remove the knowledge graph and initialize embeddings randomly (named KGANCDA/−kg) and the attention mechanism (named KGANCDA/−att), respectively. The AUC and AUPR of different models are shown in Figures 12 and 13, respectively. We have following findings:

The performance of KGANCDA is superior to KGANCDA/−kg, which illustrates that knowledge graph could enrich information of embeddings and help to improve the accuracy of prediction.
KGANCDA outperforms than KGANCDA/−att, which demonstrates that distinguishing the importance of the information from different neighbors could help to improve the quality of embeddings.

Figure 12

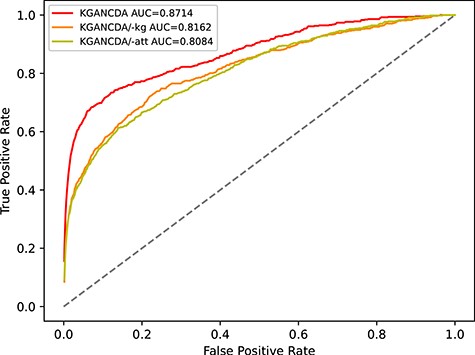
The performance comparison of KGANCDA, KGANCDA/−kg, KGANCDA/−att in term of AUC value based on 5-fold cross validation on dataset1.

Figure 13

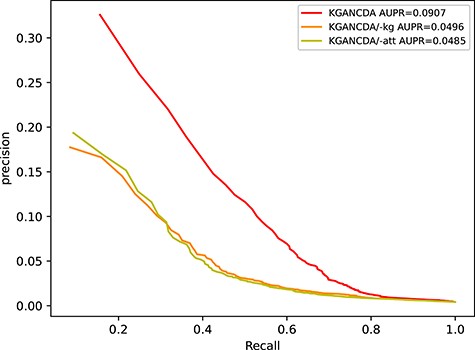
The performance comparison of KGANCDA, KGANCDA/−kg, KGANCDA/−att in term of AUPR value based on 5-fold cross validation on dataset1.

The effect of different knowledge graph (KG) embedding

To evaluate the effectiveness of different KG embedding, the transR [67], transE [43] and tranH [44] are chosen to compare under the same experiment settings. TransE is a base model, which is used widely due to its robustness. The score function of TransE is defined as

$$\begin{equation} S\left(h,r,t\right)=\left\Vert{V}_h+{V}_r-{V}_t\right\Vert \end{equation}$$

(21)

where |${V}_h$|⁠, |${V}_r$|⁠, |${V}_t\in{R}^a$|⁠, |$a$| is the embedding of entities. TransH is proposed to address the problem that the head entity embeddings generated by transE are similar, which limits the performance of the model. The score function of transH is defined as

$$\begin{equation} S\left(h,r,t\right)={\left\Vert{V}_{h_{\perp }}+{V}_r-{V}_{t_{\perp }}\right\Vert}_2^2 \end{equation}$$

(22)

$$\begin{equation} {V}_{h_{\perp }}={V}_h-{w}_r^T{V}_h{w}_r \end{equation}$$

(23)

$$\begin{equation} {V}_{t_{\perp }}={V}_t-{w}_r^T{V}_t{w}_r \end{equation}$$

(24)

$$\begin{equation} {\left\Vert{W}_r\right\Vert}_2 = 1 \end{equation}$$

(25)

where |${w}_r\in{R}^d$| denotes a normal vector of the relation-specific hyperplane, d denotes the embedding dimension. |${V}_{h_{\perp }}$| and |${V}_{t_{\perp }}$| are the vectors after projecting |${V}_h$| and |${V}_t$| on the relation-specific hyperplane. The models with transR, transE and transH are named as KGANCDA/transR, KGANCDA/transE and KGANCDA/transH, respectively. The results are shown in Figure 14. Here is our observation:

KGANCDA/transR outperforms KGANCDA/transE and KGANCDA/transH. It demonstrates that embeddings generated by transR are better than other two models. This inspires us to explore more knowledge graph models that can extract high-quality embeddings from multisource associations in the future works.

Figure 14

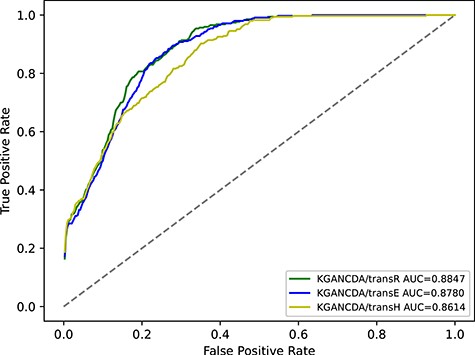
The performance comparison of KGANCDA/transE, KGANCDA/transH and KGANCDA/transR in term of AUC value on dataset2.

The effect of propagation layer and aggregation function

The effect of propagation layers

To evaluate the effectiveness of different propagation layers, we tested different layers of KGANCDA. The number of layers is in the range of 1 to 5. The models with different layers are named with corresponding numbers. For example, the KGANCDA with 1 propagation layer is named KGANCDA_1. The results are shown in Figure 15. We have the following observations:

With the increase of propagation layers, the performance is gradually improved. The AUC of KGANCDA_2 and KGANCDA_3 is significantly superior to KGANCDA_1. It demonstrates that the information from multi-order neighbors is captured by stacking multilayers of KGANCDA. It also illustrates that the embeddings containing high-order information could help to explore circRNA-disease associations. Specifically, as the example mentioned in Figure 4, the potential circRNA-disease associations could be retrieved based on multiple paths such as CircRNA-MiRNA-Disease or CircRNA-MiRNA-LncRNA-Disease rather than depending on traditional methods in Figure 3.
It can be found that the performance of KGANCDA_4 reaches the ceiling and the AUC value of KGANCDA_5 drops, which indicates that it is sufficient to consider 4-hop neighbors for each entity. For an entity, information from multiple layers may introduce noise into the embeddings.

Figure 15

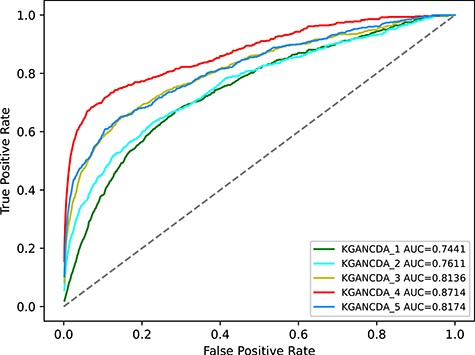
Average AUC value on different number of propagation layers in KGANCDA on dataset1.

The effect of aggregation functions

To demonstrate the effectiveness of the aggregation function, we compare it with aggregation function. In the function, |${V}_h$| and |${V}_{N_h}$| are concatenated. Then, it applies a nonlinear activation function and the final embeddings are obtained. The function is defined as

$$\begin{equation} {f}_{CONCAT}\left({V}_h,{V}_{N_h}\right)= LeakyReLU\left({W}_3\left({V}_h\Vert{V}_{N_h}\right)\right) \end{equation}$$

(26)

where |${W}_3\in{R}^{d^{\prime}\times 2d}$| is a weight matrix.

In here, we compare different aggregation functions (ADD aggregation function used in KGANCDA, Concatenation aggregation function). The model with concatenation functions is named KGANCDA_Concat. The result is shown in Figure 16. It can be found that the KGANCDA outperforms than the KGANCDA_Concat, which represents that the features are interacted fully in our methods. Therefore, it could conclude that the feature interaction is important in the information aggregation phase, which helps improve the performance of the method.

Figure 16

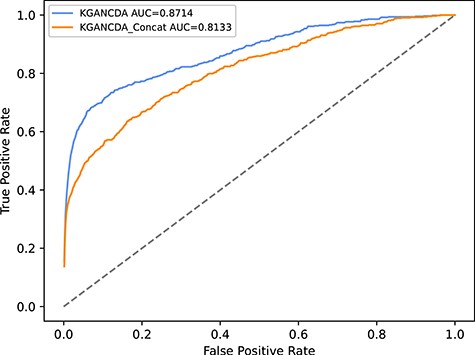
The performance of different combination functions of KGANCDA on dataset1.

Parameters setting

In KGANCDA, the Xavier initializer [45] is implemented to initialize all parameters and the parameters are optimized by Adam [46]. The training epochs are set as 150 and the batch size is fixed at 20. The learning rate is set to 0.0001. The |$\lambda$| is set as |${10}^{-5}$| and we use 0.1 dropout ratio following each layer in KGANCDA. Following the recommendation of Hu et al. [47], the dimensions of propagation layers are designed as a tower structure. As shown in Figure 17, the effect of different dimensions is compared and the structure with four layer (512–256–128-64) is selected in KGANCDA.

Figure 17

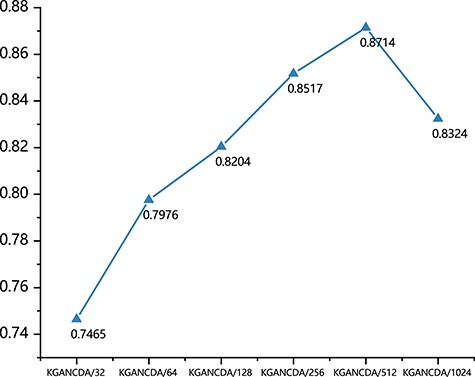
The effect of different dimensions of embeddings of KGANCDA on dataset1.

For MLP part, the four-layer structure (2944–736–184-1) is designed to obtain the affinity scores of each pair of circRNA-disease associations. The negative samples are randomly selected. To investigate the effect of the number of negative samples and training epochs, we change different ratio of negative samples and different epochs from 1:2 to 1:15 and from 20 to 150, respectively. After repeated experiments, it could be concluded that the performance is best if the ratio of negative samples is set as 1:4 and the epoch is set as 60.

Case study

To further verify the capability of KGANCDA to predict potential circRNA-disease associations, case study is implemented on colorectal cancer. Colorectal cancer is the second lethal cancer worldwide [48]. According to the static, it is the second most common cause of cancer death in United States [49]. Identifying circRNA related with colorectal cancer may help the diagnosis and treatment. Specifically, all known associations are trained in the proposed model. Then all unknown associations are predicted by the model. The top-15 predicted circRNAs of colorectal cancer are listed in Table 3.

Table 3

The top 15 predicted results of colorectal cancer-related circRNAs based on KGANCDA on dataset1

Rank	CircRNA	Evidence
1	circZFR	unknown
2	hsa_circ_0001649	PMID:29421663
3	hsa_circ_0009910	unknown
4	circRBM23	unknown
5	hsa_circ_0005273	PMID:31973707
6	hsa_circ_0080145	unknown
7	circ-ANAPC7	unknown
8	circ-ABCB10	PMID:33902207
9	hsa_circ_0000799	unknown
10	circHIPK3	PMID:29549306
11	circMTO1	PMID:30556859
12	circCCDC66	PMID:33125087
13	cicRNA_100876	PMID:33275225
14	hsa_circRNA_103809	PMID:30249393
15	circAGFG1	PMID:32681092

Rank	CircRNA	Evidence
1	circZFR	unknown
2	hsa_circ_0001649	PMID:29421663
3	hsa_circ_0009910	unknown
4	circRBM23	unknown
5	hsa_circ_0005273	PMID:31973707
6	hsa_circ_0080145	unknown
7	circ-ANAPC7	unknown
8	circ-ABCB10	PMID:33902207
9	hsa_circ_0000799	unknown
10	circHIPK3	PMID:29549306
11	circMTO1	PMID:30556859
12	circCCDC66	PMID:33125087
13	cicRNA_100876	PMID:33275225
14	hsa_circRNA_103809	PMID:30249393
15	circAGFG1	PMID:32681092

Table 3

The top 15 predicted results of colorectal cancer-related circRNAs based on KGANCDA on dataset1

Rank	CircRNA	Evidence
1	circZFR	unknown
2	hsa_circ_0001649	PMID:29421663
3	hsa_circ_0009910	unknown
4	circRBM23	unknown
5	hsa_circ_0005273	PMID:31973707
6	hsa_circ_0080145	unknown
7	circ-ANAPC7	unknown
8	circ-ABCB10	PMID:33902207
9	hsa_circ_0000799	unknown
10	circHIPK3	PMID:29549306
11	circMTO1	PMID:30556859
12	circCCDC66	PMID:33125087
13	cicRNA_100876	PMID:33275225
14	hsa_circRNA_103809	PMID:30249393
15	circAGFG1	PMID:32681092

Rank	CircRNA	Evidence
1	circZFR	unknown
2	hsa_circ_0001649	PMID:29421663
3	hsa_circ_0009910	unknown
4	circRBM23	unknown
5	hsa_circ_0005273	PMID:31973707
6	hsa_circ_0080145	unknown
7	circ-ANAPC7	unknown
8	circ-ABCB10	PMID:33902207
9	hsa_circ_0000799	unknown
10	circHIPK3	PMID:29549306
11	circMTO1	PMID:30556859
12	circCCDC66	PMID:33125087
13	cicRNA_100876	PMID:33275225
14	hsa_circRNA_103809	PMID:30249393
15	circAGFG1	PMID:32681092

It can be found that 9 of 15 circRNAs (hsa_circ_0001649, hsa_circ_0005273, circ-ABCB10, circHIPK3, circMTO1, circCCDC66, circRNA_100876, has_circRNA_103809, circAGFG1) are confirmed by recent literature. The hsa_ circ_0001649 ranked at top 2 locates at chr6:146209155–14216113, which is related with gastric carcinoma growth [50] and stromal cell invasion in endometriosis [51]. It has been proved that the expression level in colorectal cancer is significantly lower than the normal tissues by using qRT-PCRs [52]. The hsa_circ_0005273 ranked at top 5 is located at chr8:141710989–141716304. Previous research has demonstrated that hsa_circ_0005273 is related with the proliferation and migration of bladder cancer [53]. Recent study has shown that hsa_circ_0005273 is positively associated with tumor growth and metastasis in colorectal cancer [54]. The circ-ABCB10 ranked at top 8 is located at chr1:2296659–229678118. It can upregulate the expression of miR-277 to inhibit the proliferation, migration, invasion and growth of subcutaneous xenografts and increase the radiosensitivity of SW480 cells [55]. It demonstrates that circHIPK3 located at chr11:33307958–33309057 can promote the growth and metastasis of colorectal cancer by sponging miR-7 [56]. In addition, circHIPK3 is demonstrated to be associated with many diseases, such as gliomas [57], bladder cancer [58], epithelial ovarian cancer [59]. The QRT-PCR shows that the expression of circMTO1 ranked at top 11 is significantly decreased in colorectal cancer tissues. It can promote colorectal cancer progression via activating Wnt/β-catenin signaling pathway [60]. In addition, circMTO1 is also related with bladder cancer [61]. The circCCDC66 ranked at top 12 locates at chr3:56626997–56628056, which has been proved that it can promote the development of colorectal cancer cells via regulation of miR-3140/autophagy [62]. The circRNA_100876 ranked at top 13 is located at chr11:71668272–71671937. It has been demonstrated that circRNA_100876 is abnormally overexpressed in colorectal cancer tissues and cell lines. The inhibition of circRNA_100876 can reduce the invasion ability of colorectal cancer cell [63]. It has been verified that hsa_circRNA_103809 ranked at top 14 can regulate the expression of miR-532-3p and FOXO4 by using qRT-PCR, western bolt and other experiments. The has_circRNA_103809 is significantly downregulated in colorectal cancer tissues [64]. The circAGFG1 ranked at top 15 has been found that it significantly suppresses cell proliferation, migration, invasion in colorectal cancer cell [65]. In addition, the circAGFG1 is found to be associated with triple-negative breast cancer in previous research [66]. Although other associations are not verified by the current study, it deserves biologists to further study by using experimental method.

Conclusion

More and more studies demonstrate that the circRNA is related with many diseases and can be regarded as the biomarkers of diagnosis and treatment of the disease. In recent years, many computational methods are proposed to predict circRNA-disease associations. However, many methods only depend on low-order interaction information, and the performance is limited due to the sparse interaction data. In this paper, we propose a new method, KGANCDA, to identify circRNA-disease associations based on knowledge graph attention network. Besides low-order neighbor information, KGANCDA can capture high-order neighbor information from multisource associations, which alleviates the limitation of data sparsity. In addition, a knowledge graph attention mechanism is used to improve the quality of the embeddings by distinguishing the importance of information from each entity’s neighbors. Finally, a multilayer perceptron is used to predict latent associations based on the embeddings of circRNA and disease. To verify the effectiveness of our model, we compare KGANCDA with six state-of-the-art methods (RWR, DMFCDA, GCNCDA, KATZHCDA, DWNN-RLS and CD-LNLP) based on 5-fold cross validation. In addition, the case study demonstrates that KGANCDA is an effective tool to predict circRNA-disease associations. The reasons of KGANCDA outperforms the other methods are concluded as following: (1) the miRNAs and lncRNAs in knowledge graph provide many high-order neighbor information to the embeddings of circRNAs and diseases, which help improve the performance of the model. (2) The knowledge graph attention network can improve the quality of the embeddings by aggregating neighbor information from multipath and distinguish the importance of them, which alleviate the problem of data sparsity.

In the future research, we will integrate more kinds of biological data and explore more methods that can extract high-quality embeddings of circRNA and disease [68–71].

Key Points

It has been proved that circRNAs have close associations with many diseases. Therefore, predicting potential circRNA-disease associations contributes to diagnose and treatment of diseases.
We collect multiple association data (circRNA, disease, lncRNA and miRNA) from several public databases. Based on these association data, two knowledge graphs (cancer and non-cancer) are constructed. All data and code are released for further research.
We propose a new computational model (KGANCDA) based on knowledge graph attention network to predict CircRNA-Disease Associations. Besides low-order neighbor information, our method can capture high-order neighbor information from multisource neighbor information, which can alleviate the problem of data sparsity. To the best of our knowledge, this is the first work to apply knowledge graph attention network to predict circRNA-disease association.
The experimental results of benchmark datasets demonstrate that it outperforms than other state-of-the-art methods. Moreover, the case study shows that it is an effective tool for predicting potential circRNA-disease associations.

Funding

National Natural Science Foundation of China (grant nos 62072124, 61963004 and 61972185), the Natural Science Foundation of Guangxi (grant nos 2021GXNSFAA075041 and 2018GXNSFBA281193), the Science and Technology Base and Talent Special Project of Guangxi (grant no. AD20159044), the Shenzhen Science and Technology Program (grant no. KQTD20200820113106007), the Hunan Provincial Science and Technology Program (grant no. 2018WK4001).

Wei Lan received the PhD in computer science from Central South University, China, in 2016. Currently, he is a lecturer in School of Computer, Electronic and Information in the Guangxi University, Nanning, China. His current research interests include bioinformatics and machine learning.

Yi Dong received the BS degree in computer science from Hubei University of Technology, China, in 2019. He is currently an MSc student in computer science and technology, Guangxi University from 2019. His research interests include bioinformatics and deep learning.

Qingfeng Chen received the PhD degree in computer science from the University of Technology Sydney in 2004. He is currently a professor and the director of the bioinformatics team of the State Key Laboratory for Conservation and Utilization of Subtropical Agro-Bioresources at Guangxi University, China. His research interests include bioinformatics, data mining and artificial intelligence.

Ruiqing Zheng received the PhD in computer science from Central South University, China, in 2021. He is currently a lecturer at School of Computer Science and Engineering, Central South University, China. His current research areas are single data analysis and gene regulatory network construction.

Jin Liu received the PhD in computer science from Central South University, China, in 2017. He is currently an association professor at School of Computer Science and Engineering, Central South University, China. His current research interests include machine learning, medical image analysis, bioinformatics and related applications.

Yi Pan received his PhD degree in computer science from the University of Pittsburgh, USA, in 1991. He is the dean and a professor in the School of Computer Science and Control Engineering, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, China. His current research interests include bioinformatics, big data, machine learning, cloud computing and wireless networks.

Yi-Ping Phoebe Chen received the PhD in computer science from the University of Queensland. She is a professor and chair of the Department of Computer Science and Computer Engineering at La Trobe University, Australia. Her research interests include bioinformatics, data mining and multimedia.

References

1.

Jeck

WR

,

Sharpless

NE

.

Detecting and characterizing circular RNAs

.

Nat Biotechnol

2014

;

32

(

5

):

453

–

61

.

2.

Lan

W

,

Dong

Y

,

Chen

QF

, et al.

IGNSCDA: predicting CircRNA-disease associations based on improved graph convolutional network and negative sampling

.

IEEE/ACM Transac Comput Biol Bioinform

2021

;

99

(

9

):

1

–

1

.

3.

Lu

WY

.

Roles of the circular RNA circ-Foxo3 in breast cancer progression

.

Cell Cycle

2017

;

16

(

7

):

589

–

90

.

4.

Panda

AC

,

De

S

,

Grammatikakis

I

, et al.

High-purity circular RNA isolation method (RPAD) reveals vast collection of intronic circRNAs

.

Nucleic Acids Res

2017

;

45

(

12

):

e116

.

5.

Xu

S

,

Zhou

L

,

Ponnusamy

M

, et al.

A comprehensive review of circRNA: from purification and identification to disease marker potential

.

PeerJ

2018

;

2018

(

6

):

e5503

.

6.

Fanale

D

,

Taverna

S

,

Russo

A

, et al.

Circular RNA in exosomes

.

Circular RNAs

2018

;

1087

:

109

–

17

.

7.

Sanger

HL

,

Klotz

G

,

Riesner

D

, et al.

Viroids are single-stranded covalently closed circular RNA molecules existing as highly base-paired rod-like structures

.

Proc Natl Acad Sci

1976

;

73

(

11

):

3852

–

6

.

8.

Lan

W

,

Wang

J

,

Li

M

, et al.

Predicting microRNA-disease associations based on improved microRNA and disease similarities

.

IEEE/ACM Trans Comput Biol Bioinform

2018

;

15

(

6

):

1774

–

82

.

9.

Patop

IL

,

Wüst

S

,

Kadener

S

.

Past, present, and future of circRNAs

.

EMBO J

2019

;

38

(

16

):

e100836

.

10.

Lan

W

,

Wang

J

,

Li

M

, et al.

Computational approaches for prioritizing candidate disease genes based on PPI networks

.

Tsinghua Sci Technol

2015

;

20

(

5

):

500

–

12

.

11.

Lei

X

,

Mudiyanselage

TB

,

Zhang

Y

, et al.

A comprehensive survey on computational methods of non-coding RNA and disease association prediction

.

Brief Bioinform

2021

;

22

(

4

):

bbaa350

.

12.

Lan

W

,

Li

M

,

Zhao

K

, et al.

LDAP: a web server for lncRNA-disease association prediction

.

Bioinformatics

2017

;

33

(

3

):

458

–

60

.

13.

Liang

G

,

Ling

Y

,

Mehrpour

M

, et al.

Autophagy-associated circRNA circCDYL augments autophagy and promotes breast cancer progression

.

Mol Cancer

2020

;

19

(

1

):

1

–

16

.

14.

Zheng

X

,

Huang

M

,

Xing

L

, et al.

The circRNA circSEPT9 mediated by E2F1 and EIF4A3 facilitates the carcinogenesis and development of triple-negative breast cancer

.

Mol Cancer

2020

;

19

(

1

):

1

–

22

.

15.

Fan

C

,

Lei

X

,

Wu

FX

.

Prediction of CircRNA-disease associations using KATZ model based on heterogeneous networks

.

Int J Biol Sci

2018

;

14

(

14

):

1950

.

16.

Deng

L

,

Zhang

W

,

Shi

Y

, et al.

Fusion of multiple heterogeneous networks for predicting circRNA-disease associations

.

Sci Rep

2019

;

9

(

1

):

1

–

10

.

17.

Zhao

Q

,

Yang

Y

,

Ren

G

, et al.

Integrating bipartite network projection and KATZ measure to identify novel CircRNA-disease associations

.

IEEE Trans Nanobioscience

2019

;

18

(

4

):

578

–

84

.

18.

Vural

H

,

Kaya

M

,

Alhajj

R

. A model based on random walk with restart to predict circRNA-disease associations on heterogeneous network. In:

Proceedings of the 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining

.

New York, USA

:

Vancouver, ACM

,

2019

. p.

929

–

32

.

19.

Li

G

,

Luo

J

,

Wang

D

, et al.

Potential circRNA-disease association prediction using DeepWalk and network consistency projection

.

J Biomed Inform

2020

;

2020

(

112

):

103624

.

20.

Ge

E

,

Yang

Y

,

Gang

M

, et al.

Predicting human disease-associated circRNAs based on locality-constrained linear coding

.

Genomics

2020

;

112

(

2

):

1335

–

42

.

21.

Zhang

Y

,

Lei

X

,

Fang

Z

.

CircRNA-disease associations prediction based on metapath2vec++ and matrix factorization

.

Big Data Mining Analyt

2020

;

3

(

4

):

280

–

91

.

22.

Wei

H

,

Liu

B

.

iCircDA-MF: identification of circRNA-disease associations based on matrix factorization

.

Brief Bioinform

2020

;

21

(

4

):

1356

–

67

.

23.

Xiao

Q

,

Luo

J

,

Dai

J

.

Computational prediction of human disease-associated circRNAs based on manifold regularization learning framework

.

IEEE J Biomed Health Inform

2019

;

23

(

6

):

2661

–

9

.

24.

Xiao

Q

,

Zhong

J

,

Tang

X

, et al.

iCDA-CMG: identifying circRNA-disease associations by federating multi-similarity fusion and collective matrix completion

.

Mol Genet

2021

;

296

(

1

):

223

–

33

.

25.

Wang

L

,

You

ZH

,

Huang

YA

, et al.

An efficient approach based on multi-sources information to predict circRNA-disease associations using deep convolutional neural network

.

Bioinformatics

2020

;

36

(

13

):

4038

–

46

.

26.

Fan

C

,

Lei

X

,

Pan

Y

.

Prioritizing CircRNA-disease associations with convolutional neural network based on multiple similarity feature fusion

.

Front Genet

2020

;

2020

(

11

):

1042

.

27.

Lu

C

,

Zeng

M

,

Wu

FX

, et al.

Improving circRNA-disease association prediction by sequence and ontology representations with convolutional and recurrent neural networks

.

Bioinformatics

2020

;

36

(

24

):

5656

–

64

.

10.1109/TCYB.2020.3022852

28.

Deepthi

K

,

Jereesh

AS

.

Inferring potential circRNA-disease associations via deep autoencoder-based classification

.

Mol Diagn Ther

2021

;

25

(

1

):

87

–

97

.

29.

Wang

L

,

You

ZH

,

Li

JQ

, et al.

IMS-CDA: prediction of circRNA-disease associations from the integration of multisource similarity information with deep stacked autoencoder model

.

IEEE Transac Cybern

2020

.

.

30.

Wang

L

,

You

ZH

,

Li

YM

, et al.

GCNCDA: a new method for predicting circRNA-disease associations based on graph convolutional network algorithm

.

PLoS Comput Biol

2020

;

16

(

5

):

e1007568

.

31.

Lan

W

,

Zhu

M

,

Chen

Q

, et al.

CircR2Cancer: a manually curated database of associations between circRNAs and cancers

.

Database

2020

;

2020

(

(2020)

):

baaa085

.

32.

Miao

YR

,

Liu

W

,

Zhang

Q

, et al.

lncRNASNP2: an updated database of functional SNPs and mutations in human and mouse lncRNAs

.

Nucleic Acids Res

2017

;

46

(

D1

):

D276

–

80

.

33.

Chen

G

,

Wang

Z

,

Wang

D

, et al.

LncRNADisease: a database for long-non-coding RNA-associated diseases

.

Nucleic Acids Res

2012

;

41

(

D1

):

D983

–

6

.

34.

Rophina

M

,

Sharma

D

,

Poojary

M

, et al.

Circad: a comprehensive manually curated resource of circular RNA associated with diseases

.

Database

2020

;

2020

(

(2020)

):

baaa019

.

35.

Zhao

Z

,

Wang

K

,

Wu

F

, et al.

circRNA disease: a manually curated database of experimentally supported circRNA-disease associations

.

Cell Death

2018

;

9

(

5

):

1

–

2

.

36.

Lan

W

,

Huang

L

,

Lai

D

, et al.

Identifying interactions between long noncoding RNAs and diseases based on computational methods

.

Comput Syst Biol

2018

;

1754

:

205

–

21

.

37.

Zeng

M

,

Zhang

F

,

FangXiang

W

, et al.

Deep matrix factorization improves prediction of human circRNA-disease associations

.

IEEE J Biomed Health Inform

2020

;

25

(

3

):

891

–

9

.

. doi.org/10.1016/j.neucom. 2020.09.094.

38.

Lan

W

,

Wu

X

,

Chen

Q

, et al.

GANLDA: graph attention network for lncRNA-disease associations prediction

.

Neurocomputing

2021

39.

Wang

X

,

He

X

, Cao Y et al. Kgat: knowledge graph attention network for recommendation. In:

Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining

.

New York, USA: Alaska, ACM

,

2019

. p.

950

–

8

.

40.

Glorot

X

,

Bordes

A

,

Bengio

Y

. Deep sparse rectifier neural networks. In:

Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics

. MIT, Cambridge, USA: Fort Lauderdale,

2011

.

p. 315–23

.

41.

Yan

C

,

Wang

J

,

Wu

FX

.

DWNN-RLS: regularized least squares method for predicting circRNA-disease associations

.

BMC Bioinformatics

2018

;

19

(

19

):

73

–

81

.

42.

Zhang

W

,

Yu

C

,

Wang

X

, et al.

Predicting CircRNA-disease associations through linear neighborhood label propagation method

.

IEEE Access

2019

;

2019

(

7

):

83474

–

83

.

43.

Bordes

A

,

Usunier

N

,

Garcia-Duran

A

, et al.

Translating embeddings for modeling multi-relational data

.

Adv Neural Inform Process Syst

2013

;

26

:

2787

–

95

.

44.

Wang

Z

,

Zhang

J

,

Feng

J

, et al. Knowledge graph embedding by translating on hyperplanes.

Proc AAAI Conf Artificial Intell

2014

;

28

(

1

):

1112

–

9

.

45.

Glorot

X

,

Bengio

Y

. Understanding the difficulty of training deep feedforward neural networks. In:

Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics

. MIT, Cambridge, USA: Sardinia,

2010

, p.

249

–

56

.

46.

Kingma

DP

,

Ba

J

.

Adam: a method for stochastic optimization

.

arXiv preprint arXiv:14126980

2014

.

47.

Hu

B

,

Shi

C

,

Zhao

WX

, et al. Leveraging meta-path based context for top-n recommendation with a neural co-attention model.

In: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining

.

London, New York, USA

:

ACM

,

2018

. p.

1531

–

40

.

48.

Xie

YH

,

Chen

YX

,

Fang

JY

.

Comprehensive review of targeted therapy for colorectal cancer

.

Signal Transduct Target Ther

2020

;

5

(

1

):

1

–

30

.

49.

Siegel

RL

,

Miller

KD

,

Goding Sauer

A

, et al.

Colorectal cancer statistics, 2020

.

CA Cancer J Clin

2020

;

70

(

3

):

145

–

64

.

50.

Sun

H

,

Wang

Q

,

Yuan

G

, et al.

Hsa_circ_0001649 restrains gastric carcinoma growth and metastasis by downregulation of miR-20a

.

J Clin Lab Anal

2020

;

34

(

6

):e23235.

51.

Li

Q

,

Li

N

,

Liu

H

, et al.

Estrogen-decreased hsa_circ_0001649 promotes stromal cell invasion in endometriosis

.

Reproduction

2020

;

160

(

4

):

511

–

9

.

52.

Ji

W

,

Qiu

C

,

Wang

M

, et al.

Hsa_circ_0001649: a circular RNA and potential novel biomarker for colorectal cancer

.

Biochem Biophys Res Commun

2018

;

497

(

1

):

122

–

6

.

53.

Zhong

Z

,

Lv

M

,

Chen

J

.

Screening differential circular RNA expression profiles reveals the regulatory role of circTCF25-miR-103a-3p/miR-107-CDK6 pathway in bladder carcinoma

.

Sci Rep

2016

;

6

(

1

):

1

–

12

.

54.

Yang

H

,

Li

X

,

Meng

Q

, et al.

CircPTK2 (hsa_circ_0005273) as a novel therapeutic target for metastatic colorectal cancer

.

Mol Cancer

2020

;

19

(

1

):

1

–

15

.

55.

Xie

Y

,

Liu

J

,

Li

J

, et al.

Effects of silencing circRNA ABCB10 expression on biological properties of colorectal cancer cells

.

Zhonghua Zhong Liu Za Zhi

2021

;

43

(

4

):

449

–

56

.

56.

Zeng

K

,

Chen

X

,

Xu

M

, et al.

CircHIPK3 promotes colorectal cancer growth and metastasis by sponging miR-7

.

Cell Death Dis

2018

;

9

(

4

):

1

–

15

.

57.

Jin

P

,

Huang

Y

,

Zhu

P

, et al.

CircRNA circHIPK3 serves as a prognostic marker to promote glioma progression by regulating miR-654/IGF2BP3 signaling

.

Biochem Biophys Res Commun

2018

;

503

(

3

):

1570

–

4

.

58.

Li

Y

,

Zheng

F

,

Xiao

X

, et al.

Circ HIPK 3 sponges miR-558 to suppress heparanase expression in bladder cancer cells

.

EMBO Rep

2017

;

18

(

9

):

1646

–

59

.

59.

Liu

N

,

Zhang

J

,

Zhang

L

, et al.

CircHIPK3 is upregulated and predicts a poor prognosis in epithelial ovarian cancer

.

Eur Rev Med Pharmacol Sci

2018

;

22

(

12

):

3713

–

8

.

60.

Ge

Z

,

Li

L

,

Wang

C

, et al.

CircMTO1 inhibits cell proliferation and invasion by regulating Wnt/beta-catenin signaling pathway in colorectal cancer

.

Eur Rev Med Pharmacol Sci

2018

;

22

(

23

):

8203

–

9

.

61.

Li

Y

,

Wan

B

,

Liu

L

, et al.

Circular RNA circMTO1 suppresses bladder cancer metastasis by sponging miR-221 and inhibiting epithelial-to-mesenchymal transition

.

Biochem Biophys Res Commun

2019

;

508

(

4

):

991

–

6

.

62.

Feng

J

,

Li

Z

,

Li

L

, et al.

Hypoxia-induced circCCDC66 promotes the tumorigenesis of colorectal cancer via the miR-3140/autophagy pathway

.

Int J Mol Med

2020

;

46

(

6

):

1973

–

82

.

63.

Zhou

G

,

Huang

D

,

Sun

Z

, et al.

Characteristics and prognostic significance of circRNA-100876 in patients with colorectal cancer

.

Eur Rev Med Pharmacol Sci

2020

;

24

(

22

):

11587

–

93

.

64.

Bian

L

,

Zhi

X

,

Ma

L

, et al.

Hsa_circRNA_103809 regulated the cell proliferation and migration in colorectal cancer via miR-532–3p/FOXO4 axis

.

Biochem Biophys Res Commun

2018

;

505

(

2

):

346

–

52

.

65.

Zhang

L

,

Dong

X

,

Yan

B

, et al.

CircAGFG1 drives metastasis and stemness in colorectal cancer by modulating YY1/CTNNB1

.

Cell Death Dis

2020

;

11

(

7

):

1

–

15

.

66.

Yang

R

,

Xing

L

,

Zheng

X

, et al.

The circRNA circAGFG1 acts as a sponge of miR-195-5p to promote triple-negative breast cancer progression through regulating CCNE1 expression

.

Mol Cancer

2019

;

18

(

1

):

1

–

19

.

67.

Lin

Y

,

Liu

Z

,

Sun

M

, et al. Learning entity and relation embeddings for knowledge graph completion.

Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence

. AAAI, Menlo Park, USA: Austin,

2015

. p.

2181

–

7

.

68.

Chen

Q

,

Lai

D

,

Lan

W

, et al.

ILDMSF: inferring associations between long non-coding RNA and disease based on multi-similarity fusion

.

IEEE/ACM Trans Comput Biol Bioinform

2021

;

18

(

3

):

1106

–

12

.

69.

Fan

Z

,

Lei

X

, et al.

Prediction of miRNA-circRNA associations based on K-NN multi-label with random walk restart on a heterogeneous network

.

Big Data Mining Analyt

2019

;

2

(

4

):

248

–

72

.

10.1109/TCBB.2020.3034910

70.

Lan

W

,

Lai

D

,

Chen

Q

, et al.

LDICDL: LncRNA-disease association identification based on collaborative deep learning

.

IEEE/ACM Trans Comput Biol Bioinform

2020

.

.

71.

Lan

W

,

Wang

J

,

Li

M

, et al.

Predicting drug–target interaction using positive-unlabeled learning

.

Neurocomputing

2016

;

206

:

50

–

7

.