Drug-pathway association prediction: from experimental results to computational models

List of databases and web serves

Database or web sever	Function	URL
DrugBank	Provide drug, drug interaction, drug action and drug-target information	http://www.drugbank.ca/
CTD	Provide high-throughput predicted associations between chemicals and pathways	http://ctd.mdibl.org/
CMap	Provide gene expression data of five human cancer cell lines both before and after the treatments of bioactive small molecules	https://portals.broadinstitute.org/cmap/
CancerResource	Provide drug-related information and low-throughput validated drug-pathway associations	http://bioinformatics.charite.de/care
CellMiner	Provide gene expression data and drug sensitivity data of cancer cell lines	http://discover.nci.nih.gov/cellminer
CancerDR	Provide pharmacological profiling data of drugs across different cancer cell lines	http://crdd.osdd.net/raghava/cancerdr/
ChemBank	Provide molecular descriptors and compound information	http://chembank.broadinstitute.org/
ChEMBL	Provide the assessment of distribution, in vivo absorption, metabolism, toxicity and excretion properties information for great number of drug-like bioactive compounds	https://www.ebi.ac.uk/chembldb
TTD	Provide comprehensive information of the clinical trial drugs and drug-pathway associations	http://bidd.nus.edu.sg/group/ttd/ttd.asp
KEGG pathway	Provide some low-throughput validated drug-pathway associations	https://www.genome.jp/kegg/pathway.html
Pathway Commons	Provide the biological pathway data collected from multiple organism	http://www.pathwaycommons.org/

Database or web sever	Function	URL
DrugBank	Provide drug, drug interaction, drug action and drug-target information	http://www.drugbank.ca/
CTD	Provide high-throughput predicted associations between chemicals and pathways	http://ctd.mdibl.org/
CMap	Provide gene expression data of five human cancer cell lines both before and after the treatments of bioactive small molecules	https://portals.broadinstitute.org/cmap/
CancerResource	Provide drug-related information and low-throughput validated drug-pathway associations	http://bioinformatics.charite.de/care
CellMiner	Provide gene expression data and drug sensitivity data of cancer cell lines	http://discover.nci.nih.gov/cellminer
CancerDR	Provide pharmacological profiling data of drugs across different cancer cell lines	http://crdd.osdd.net/raghava/cancerdr/
ChemBank	Provide molecular descriptors and compound information	http://chembank.broadinstitute.org/
ChEMBL	Provide the assessment of distribution, in vivo absorption, metabolism, toxicity and excretion properties information for great number of drug-like bioactive compounds	https://www.ebi.ac.uk/chembldb
TTD	Provide comprehensive information of the clinical trial drugs and drug-pathway associations	http://bidd.nus.edu.sg/group/ttd/ttd.asp
KEGG pathway	Provide some low-throughput validated drug-pathway associations	https://www.genome.jp/kegg/pathway.html
Pathway Commons	Provide the biological pathway data collected from multiple organism	http://www.pathwaycommons.org/

Table 1

(https://portals.broadinstitute.org/cmap/)

List of databases and web serves

Database or web sever	Function	URL
DrugBank	Provide drug, drug interaction, drug action and drug-target information	http://www.drugbank.ca/
CTD	Provide high-throughput predicted associations between chemicals and pathways	http://ctd.mdibl.org/
CMap	Provide gene expression data of five human cancer cell lines both before and after the treatments of bioactive small molecules	https://portals.broadinstitute.org/cmap/
CancerResource	Provide drug-related information and low-throughput validated drug-pathway associations	http://bioinformatics.charite.de/care
CellMiner	Provide gene expression data and drug sensitivity data of cancer cell lines	http://discover.nci.nih.gov/cellminer
CancerDR	Provide pharmacological profiling data of drugs across different cancer cell lines	http://crdd.osdd.net/raghava/cancerdr/
ChemBank	Provide molecular descriptors and compound information	http://chembank.broadinstitute.org/
ChEMBL	Provide the assessment of distribution, in vivo absorption, metabolism, toxicity and excretion properties information for great number of drug-like bioactive compounds	https://www.ebi.ac.uk/chembldb
TTD	Provide comprehensive information of the clinical trial drugs and drug-pathway associations	http://bidd.nus.edu.sg/group/ttd/ttd.asp
KEGG pathway	Provide some low-throughput validated drug-pathway associations	https://www.genome.jp/kegg/pathway.html
Pathway Commons	Provide the biological pathway data collected from multiple organism	http://www.pathwaycommons.org/

Database or web sever	Function	URL
DrugBank	Provide drug, drug interaction, drug action and drug-target information	http://www.drugbank.ca/
CTD	Provide high-throughput predicted associations between chemicals and pathways	http://ctd.mdibl.org/
CMap	Provide gene expression data of five human cancer cell lines both before and after the treatments of bioactive small molecules	https://portals.broadinstitute.org/cmap/
CancerResource	Provide drug-related information and low-throughput validated drug-pathway associations	http://bioinformatics.charite.de/care
CellMiner	Provide gene expression data and drug sensitivity data of cancer cell lines	http://discover.nci.nih.gov/cellminer
CancerDR	Provide pharmacological profiling data of drugs across different cancer cell lines	http://crdd.osdd.net/raghava/cancerdr/
ChemBank	Provide molecular descriptors and compound information	http://chembank.broadinstitute.org/
ChEMBL	Provide the assessment of distribution, in vivo absorption, metabolism, toxicity and excretion properties information for great number of drug-like bioactive compounds	https://www.ebi.ac.uk/chembldb
TTD	Provide comprehensive information of the clinical trial drugs and drug-pathway associations	http://bidd.nus.edu.sg/group/ttd/ttd.asp
KEGG pathway	Provide some low-throughput validated drug-pathway associations	https://www.genome.jp/kegg/pathway.html
Pathway Commons	Provide the biological pathway data collected from multiple organism	http://www.pathwaycommons.org/

DrugBank

(http://www.drugbank.ca)

DrugBank is a comprehensive, freely available database including detailed drug, drug interaction, drug action and drug-target information about FDA-approved drugs [30]. This information could be used to calculate drug similarity or construct drug feature vector in the process of drug-pathway association prediction. Up to now, this database has been updated to DrugBank 5.0 version [30]. There are total 2385 approved (FDA, Health Canada, EMA, etc.) drugs.

CTD

(http://ctd.mdibl.org)

CTD is a public database that provides curated interactions between chemicals, genes, phenotypes, environmental exposures and diseases [22]. It also contains a list of pathways that are statistically enriched among the genes that interact with an invested chemical. The files about chemical-pathway enriched associations can be downloaded from the website of http://ctdbase.org/downloads/#chempathwaysenriched. These associations between chemicals and pathways are high-throughput predicted by computing the significance of enrichment between pathways and the genes that interact with a chemical through the hypergeometric distribution. Researchers can employ these associations as validation information for drug-pathway association prediction models. However, the type and mechanism of chemical-pathway enriched associations are unknown due to the fact that they are only predicted associations.

Connectivity map (CMap)

CMap is a project that provides a collection of genome-wide transcriptional expression data from five human cancer cell lines both before and after the treatments of bioactive small molecules [31]. There are 7056 Affymetrix microarrays, in which 6100 arrays are obtained from cell lines treated by small molecules and the rest are control samples. The microarray data can be obtained from http://www.broadinstitute.org/cmap/cel_file_chunks.jsp. The genes expression data both before and after small molecules’ treatments can be used to analyze associations between small molecule drugs and pathways. In fact, some previous study has employed this data to predict potential drug-pathway associations [32].

CancerResource

(http://bioinformatics.charite.de/care)

CancerResource is a freely available database without registration. It includes more than 2000 cancer cell lines and drug sensitivity data under the treatment with about 50,000 drugs as well as 91,000 drug-target interactions [23]. The drug related data would contribute to mining drug related information in the problem of drug-pathway association prediction. In addition, compounds and target genes are projected onto cancer-associated pathways to better understand how drug-target interactions are beneficial for cancer treatment. Thus, CancerResource contains some cancer related pathway-drug associations which are low-throughput validated. There are both positive correlation and negative correlation types in these associations. Actually, CancerResource has been used to validate predicted drug-pathway associations in previous study [33].

CellMiner

(http://discover.nci.nih.gov/cellminer)

CellMiner is the first online database resource which integrates the data of molecular profile based on 60 diverse human cancer cell lines (the NCI-60) [34]. The data contains RNA expression, DNA methylation, DNA fingerprinting, sequence mutation, as well as treatment response to more than 100,000 compounds. The gene expression data and drug sensitivity data of cancer cell lines in CellMiner can be utilized to predict potential drug-pathway associations [35].

Cancer drug resistance database (CancerDR)

(http://crdd.osdd.net/raghava/cancerdr/)

It is important to know which drug is effective for a particular cancer type. The database of CancerDR provides the pharmacological profiling data involving 952 cancer cell lines and 148 anti-cancer drugs in which the number of FDA approved drugs, clinical trials drugs and experimental drugs are 36, 48 and 64, respectively [36]. The pharmacological profiling data may be useful for inferring associations between drugs and cancer related pathways.

ChemBank

(http://chembank.broadinstitute.org/)

ChemBank is a public database including freely available data derived from small molecules and small-molecule screens [37]. The ChemBank database is made up of 95 tables divided into seven logical parts representing molecular descriptors, compound information, assay results, assay metadata, ontological association, biological finding and user information. During the data collection phase of drug-pathway association prediction, researchers can search small molecule drug-related information from the ChemBank database to calculate the similarity of small molecule drugs or characterize small molecule characteristics.

ChEMBL

(https://www.ebi.ac.uk/chembldb)

The open database of ChEMBL provides the assessment of distribution, in vivo absorption, metabolism, toxicity and excretion properties information for great number of drug-like bioactive compounds [38]. Currently, the database collects 5.4 million bioactivity measurements for more than 1 million compounds from the primary published literature. ChEMBL contains abundant information about drug-like bioactive compounds, which could provide the important guarantee for potential drug-pathway association prediction.

TTD

(http://bidd.nus.edu.sg/group/ttd/ttd.asp)

TTD is a useful database for facilitating the drug discovery [29]. The database provided comprehensive information of the clinical trial drugs and their targets based on extensive drug discovery efforts. Besides, TTD database contained known low-throughput validated drug-pathway associations which can be used for drug-pathway prediction. Among the drug-pathway associations, there are both positive correlation and negative correlation types.

KEGG Pathway

(https://www.genome.jp/kegg/pathway.html)

KEGG Pathway database is the main database in KEGG [24]. The database contains manually drawn KEGG reference pathway and organism-specific pathway maps. There were 496 manually drawn KEGG reference pathways, which were divided into six categories. Besides, each pathway has a brief summary of the biological processes shown in the pathway map and the drugs would be listed if the pathway has associated drugs. In this database, if pathway contains drug targets, this pathway is considered to be associated with the drug. Thus, KEGG pathway database is widely used in many calculation models [33, 35, 39] for drug-pathway association prediction since it can provide some low-throughput validated drug-pathway associations. Besides, there are both positive correlation and negative correlation types in these associations.

Table 2

List of different types of computational methods

Model type	Model names	Model feature
Bayesian spare factor-based models	iFad and FacPad	Drug-pathway association prediction problem was described by linear model and collapsed Gibbs sampling algorithm was employed for the Bayesian inference.
Matrix decomposition-based models	iPaD, L_2,1-iPaD, L₁L_2,1-iPaD and IGMF	Both drug sensitivity and gene expression data were decomposed and drug-pathway association prediction problem was transformed as regularized optimization problem.
Other machine learning-based models	Drug-pathway association prediction via multiple feature fusion, RGRF, LSA-PU-KNN and Pathway-based LDA	Different kinds of data were integrated as features to represent drug and pathway and different classifiers were utilized to train prediction model based on training samples.

Model type	Model names	Model feature
Bayesian spare factor-based models	iFad and FacPad	Drug-pathway association prediction problem was described by linear model and collapsed Gibbs sampling algorithm was employed for the Bayesian inference.
Matrix decomposition-based models	iPaD, L_2,1-iPaD, L₁L_2,1-iPaD and IGMF	Both drug sensitivity and gene expression data were decomposed and drug-pathway association prediction problem was transformed as regularized optimization problem.
Other machine learning-based models	Drug-pathway association prediction via multiple feature fusion, RGRF, LSA-PU-KNN and Pathway-based LDA	Different kinds of data were integrated as features to represent drug and pathway and different classifiers were utilized to train prediction model based on training samples.

Table 2

(http://www.pathwaycommons.org/)

List of different types of computational methods

Model type	Model names	Model feature
Bayesian spare factor-based models	iFad and FacPad	Drug-pathway association prediction problem was described by linear model and collapsed Gibbs sampling algorithm was employed for the Bayesian inference.
Matrix decomposition-based models	iPaD, L_2,1-iPaD, L₁L_2,1-iPaD and IGMF	Both drug sensitivity and gene expression data were decomposed and drug-pathway association prediction problem was transformed as regularized optimization problem.
Other machine learning-based models	Drug-pathway association prediction via multiple feature fusion, RGRF, LSA-PU-KNN and Pathway-based LDA	Different kinds of data were integrated as features to represent drug and pathway and different classifiers were utilized to train prediction model based on training samples.

Model type	Model names	Model feature
Bayesian spare factor-based models	iFad and FacPad	Drug-pathway association prediction problem was described by linear model and collapsed Gibbs sampling algorithm was employed for the Bayesian inference.
Matrix decomposition-based models	iPaD, L_2,1-iPaD, L₁L_2,1-iPaD and IGMF	Both drug sensitivity and gene expression data were decomposed and drug-pathway association prediction problem was transformed as regularized optimization problem.
Other machine learning-based models	Drug-pathway association prediction via multiple feature fusion, RGRF, LSA-PU-KNN and Pathway-based LDA	Different kinds of data were integrated as features to represent drug and pathway and different classifiers were utilized to train prediction model based on training samples.

Pathway Commons

Pathway Commons is a web resource providing the biological pathway data collected from multiple organisms [40]. The data include transport and catalysis events, complex assembly, biochemical reactions and physical interactions involving DNA, RNA, proteins, small molecules and complexes. There were over 1400 pathways and 687,000 interactions. Researchers could search pathway related information from Pathway Commons during the data collection phase of drug-pathway association prediction.

Computational Models

Since the idea of one drug-one target limits the research and development of new drug, pathway-based strategy of drug discovery received the attention of researchers. On the one hand, seeking drug-pathway associations by biological experiments is time-consuming and laborious. On the other hand, biological experiments and next-generation sequencing have accumulated a mass of data, such as gene expression profiles, drug sensitivity profiles, drug-pathway associations and so on. Thus, some computational models were developed to infer potential drug-pathway associations based on biological data about drugs and pathways. In this section, we will introduce these prediction models.

A series of machine learning algorithms have been employed to identify potential associations between drugs and pathways. These algorithms can be further divided into Bayesian spare factor-based, matrix decomposition-based and other machine learning methods (See Table 2). In both Bayesian spare factor-based and matrix decomposition-based methods, the data of gene transcription profiles or drug sensitivity profiles of different human cell lines or both were utilized to infer drug-pathway associations. In Bayesian spare factor-based methods, association prediction problem was described by linear model, while matrix decomposition-based methods usually transformed the problem as regularized optimization models. Besides, in other machine learning based models, different kinds of data, such as drug chemical structure, pathway-related genes expression and known drug-pathway associations were integrated as features to represent drug and pathway. Then, different classifiers can be utilized to train prediction model based on training samples. In the following, we would introduce these three classes of machine learning-based methods for drug-pathway association prediction.

Bayesian spare factor-based models

iFad

Ma et al. [33] established a Bayesian sparse factor analysis model named iFad to infer potential drug-pathway associations by analyzing the gene expression and drug sensitivity data measured under different human cancer cell lines (See Figure 1). iFad considers that the gene expression level and the drug sensitivity of cell lines are associated with the pathway activity level X via the following linear models:

$$\begin{equation} {\displaystyle \begin{array}{l}{Y}_1={W}_1X+{\Sigma}_1,{\Sigma}_1\sim N\left(0,{\psi}_1\right),{\psi}_1=\mathit{\operatorname{diag}}\left\{{\tau}_{g1}^{-1}\right\}\\[4pt] {}{Y}_2={W}_2X+{\Sigma}_2,{\Sigma}_2\sim N\left(0,{\psi}_2\right),{\psi}_2=\mathit{\operatorname{diag}}\left\{{\tau}_{g2}^{-1}\right\}\\{}{X}_{k,j}\sim Normal\left(0,1\right)\\{}{\tau}_{g1}\sim Gamma\left({\alpha}_1,{\beta}_1\right),{g}_1=1,2,...{G}_1\\{}{\tau}_{g2}\sim Gamma\left({\alpha}_2,{\beta}_2\right),{g}_2=1,2,...{G}_2\end{array}} \end{equation}$$

(1)

where the matrix W₁ describes the regulating direction and intensity of the pathway activities under the gene expression level, while the matrix W₂ denotes the regulating direction and intensity of the pathway activities under the drug sensitivity. Besides, the matrices of Y₁ and Y₂ are employed to denote the gene expression level and drug sensitivity data. The potential factor activity matrix X is enjoyed together in two feature spaces of gene expression and drug sensitivity. Each element in the matrix X is supposed to obey the standard normal distribution. Furthermore, the variables G₁ and G₂ represent the number of genes and drugs. Additionally, |${\Sigma}_1$| and |${\Sigma}_2$| denote the noise data with mean 0 and diagonal covariance matrices |${\varPsi}_1$| and |${\varPsi}_2$|⁠. The precision |${\tau}_{g_1}$| (for the g₁th gene) and |${\tau}_{g_2}$| (for the g₂th drug) are formulated utilizing a Gamma prior with shape parameters |${\alpha}_1$|⁠, |${\alpha}_2$| and rate parameters |${\beta}_1$|⁠, |${\beta}_2$|⁠.

Figure 1

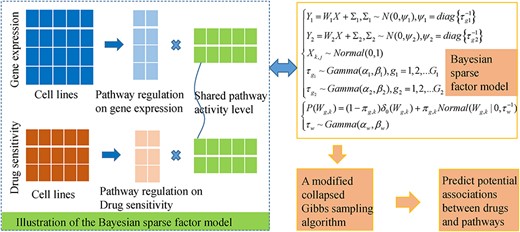
The flowchart of a Bayesian sparse factor analysis model of iFad to infer potential drug-pathway associations by analyzing the gene expression and drug sensitivity datasets measured under different human cancer cell lines.

The spike-and-slab mixture prior was employed for the factor loading matrix W₁ and W₂ [41].

$$\begin{equation} {\displaystyle \begin{array}{l}P\left({W}_{g,k}\right)=\left(1-{\pi}_{g,k}\right){\delta}_0\left({W}_{g,k}\right)+{\pi}_{g,k} Normal\left({W}_{g,k}|0,{\tau}_w^{-1}\right)\\{}{\tau}_w\sim Gamma\left({\alpha}_w,{\beta}_w\right)\end{array}} \end{equation}$$

(2)

where the variable g denotes drug g or gene g and the variable k represents pathway k. Besides, |${\delta}_0$| is the Dirac delta function denoting the unit point mass at zero and |${\pi}_{k,g}$| represented the prior probability that |${W}_{g,k}$| is non-zero. If |${W}_{g,k}$| is non-zero, it was supposed to obey a normal distribution with mean 0 and precision |${\tau}_w$|⁠. The precision |${\tau}_w$| was supposed to follow a Gamma prior. Besides, an auxiliary indicator variable |${Z}_{g,k}$| was employed to enable the calculation of posterior probabilities. Since |${W}_1,{Z}_1,{L}_1,{\pi}_1$| and |${W}_2,{Z}_2,{L}_2,{\pi}_2$| have similar formats, the general formula was described as follows:

$$\begin{equation} P\left({Z}_{g,k}=1\right)={\pi}_{g,k}=\left\{\kern-6pt{\displaystyle \begin{array}{ll}{\eta}_0,& \mathrm{if}\;{L}_{g,k}=0\\{}1-{\eta}_1,& \mathrm{if}\;{L}_{g,k}=1\end{array}}\right. \end{equation}$$

(3)

where |$P({Z}_{g,k}=1)$| denotes the priori probability of |${Z}_{g,k}=1$|⁠. The parameters |${\eta}_0$| and |${\eta}_1$| are user-specific parameters. In this way, known association matrices L₁ and L₂ are utilized to induce the sparsity structure of the factor loading matrices W₁ and W₂. After this setting, they can obtain the prior probability of different components of the model, together with the complete joint posterior probability. Based on the real data of NCI-60 dataset, the mission of iFad lies in the underlying of posterior probability of |${Z}_2=1$| which indicates associations between drugs and pathways. In this study, a modified collapsed Gibbs sampling was employed to estimate parameters for iFad.

FacPad

Ma et al. [32] proposed another Bayesian sparse factor model named FacPad to infer pathways responsive to treatments. Different from iFad which jointly analyze two matrices, FacPad was constructed for the analysis of only one matrix Y with the size of G rows and J columns, which denotes the genome-wide transcriptional response based on different treatments. G and J represents the number of genes and treatments respectively. Each treatment corresponds a given drug at a specific dosage under a stipulated time. Thus, the number of treatments is usually lager than the number of drugs. Firstly, the description of the Bayesian sparse factor model is as follows:

$$\begin{equation} {\displaystyle \begin{array}{l}Y= WX+E,{E}_{\cdot, j}\sim N\left(0,\varSigma \right)\\{}\Sigma =\mathit{\operatorname{diag}}\left\{{\tau}_1^{-1},{\tau}_2^{-1},...,{\tau}_g^{-1},...,{\tau}_G^{-1}\right\}\\{}{X}_{k,j}\sim Normal\left(0,1\right)\\{}{\tau}_g\sim Gamma\left({\alpha}_g,{\beta}_g\right),g=1,2,...G\\{}{W}_{g,k}=\left\{\kern-5pt\begin{array}{ll}0,& \mathrm{if}\;{L}_{g,k}=0\\{}N\left(0,{\tau}_w^{-1}\right),& \mathrm{if}\;{L}_{g,k}=1\end{array}\right.\\{}{\tau}_w\sim Gamma\left({\alpha}_w,{\beta}_w\right)\end{array}} \end{equation}$$

(4)

where W is the factor loading matrix revealing the strength of gene-pathway associations. Besides, each non-zero element in |$W$| follows a normal prior with mean 0 and precision |${\tau}_w$|⁠. The matrix L denotes the prior information of pathway structure with the size of G rows and K columns. K represents the number of pathways used in present study. In addition, |${L}_{g,k}$| is equal to 1 if the pathway k contains the gene g, otherwise 0. Furthermore, X is a latent factor matrix whose element denotes the treatment response under a certain pathway. E is noisy matrix. Then, an improved collapsed Gibbs sampling method [42] is employed to approximate the parameters in FacPad model. Finally, the solution of X can be obtained after estimating the parameter in the last step and the elements in the matrix X can reflect the association scores between pathways and drug treatments. By encoding pathways as potential factors, FacPad naturally combines previous knowledge of gene-pathway associations to help infer drug targets. However, running this program requires relatively good computing resources.

Figure 2

The flowchart of iPaD for inferring drug-pathway associations using the data of gene transcription and drug sensitivity profiles of human cell lines.

Matrix decomposition-based models

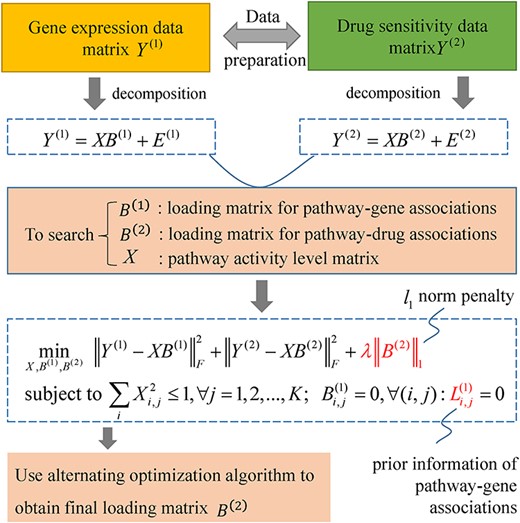
iPaD

Li et al. [35] proposed an integrative Penalized Matrix Decomposition (iPaD) method to infer drug-pathway associations using the data of gene transcription and drug sensitivity profiles of human cell lines (See Figure 2). In their method, |${Y}^{(1)}\in{\mathrm{R}}^{N\times{G}^{(1)}}$| and |${Y}^{(2)}\in{\mathrm{R}}^{N\times{G}^{(2)}}$| represent the gene transcription and drug sensitivity profiles, respectively. The variables |$N,{G}^{(1)},{G}^{(2)}$| denote the number of human cancer cell lines, genes and drugs. |$X\in{\mathrm{R}}^{N\times K}$| stand for the activity levels of all the K pathways among N cell lines. |${B}^{(1)}$| and |${B}^{(2)}$| were employed to represent the pathway-gene association and pathway-drug association matrices, respectively. The matrices of |${Y}^{(1)}$| and |${Y}^{(2)}$| can be decomposed as follows:

$$\begin{equation} {\displaystyle \begin{array}{l}{Y}^{(1)}=X{B}^{(1)}+{E}^{(1)}\\{}{Y}^{(2)}=X{B}^{(2)}+{E}^{(2)}\end{array}} \end{equation}$$

(5)

where |${E}^{(1)}$| and |${E}^{(2)}$| denote residuals. In order to seek out the solution of |$X$|⁠, |${B}^{(1)}$| and |${B}^{(2)}$|⁠, they transformed the Eq. (5) into a bi-convex optimization problem as follows:

$$\begin{equation} {\displaystyle \begin{array}{l}\underset{X,{B}^{(1)},{B}^{(2)}}{\min }{\left\Vert{Y}^{(1)}-X{B}^{(1)}\right\Vert}_F^2+{\left\Vert{Y}^{(2)}-X{B}^{(2)}\right\Vert}_F^2+\lambda{\left\Vert{B}^{(2)}\right\Vert}_1\\{}\mathrm{subject}\ \mathrm{to}\;\sum \limits_i{X}_{i,j}^2,\forall j=1,2,...,K\\{}\kern4em {B}_{i,j}^{(1)}=0,\forall \left(i,j\right)\in \left\{\left(i,j\right)|{L}_{i,j}^{(1)}=0\right\}\end{array}} \end{equation}$$

(6)

where |${\Vert \Vert}_1$| denotes the L₁-norm, i.e., |${\left\Vert{B}^{(2)}\right\Vert}_1={\sum}_i{\sum}_j\mid{B}_{i,j}^{(2)}\mid$|⁠. Usually, the known gene-pathway associations are complete and accurate. |${L}^{(1)}\in{\left\{0,1\right\}}^{K\times{G}^1}$|⁠, an indicator matrix, is utilized to reveal the prior knowledge about gene-pathway associations. Besides, |${\left\Vert{Y}^{(1)}-X{B}^{(1)}\right\Vert}_F^2+{\left\Vert{Y}^{(2)}-X{B}^{(2)}\right\Vert}_F^2$| is the sum of squared residuals. Moreover, the matrix |${B}^{(2)}$| should be sparse since a pathway is usually related with a few drugs and vice versa. |$\lambda{\left\Vert{B}^{(2)}\right\Vert}_1$| is utilized to achieve sparse solutions of |${B}^{(2)}$| since the L₁-norm can produce sparsity. Finally, they employed an optimization algorithm to find the solution of |$X$|⁠, |${B}^{(1)}$| and |${B}^{(2)}$|⁠. Among them |${B}^{(2)}$| was used to indicate drug-pathway associations. In iPaD, the bi-convex optimization problem can be solved efficiently. Besides, there is only one parameter easily determined through cross-validation.

L_2,1-iPaD

Liu et al. [39] developed a computational method named L_2,1-iPaD to infer drug-pathway associations. The previous method of iPaD used the L₁-norm penalty on the regularization term. However, the sparsity produced by lasso-type penalties is too dispersive, that is, the zero elements in the solution of drug-pathway association matrix are too dispersive. The L_2,1-norm of a matrix is the sum of L₂-norm of each row of the matrix. Thus, in L_2,1-iPaD, L_2,1-norm penalty was employed to replace the L₁-norm penalty since it can produce row sparsity. The optimization model of L_2,1-iPaD can be described as follows:

$$\begin{equation} {\displaystyle \begin{array}{l}\underset{X,{B}^{(1)},{B}^{(2)}}{\min}\;{\left\Vert{Y}^{(1)}-X{B}^{(1)}\right\Vert}_F^2+{\left\Vert{Y}^{(2)}-X{B}^{(2)}\right\Vert}_F^2+\lambda{\left\Vert{B}^{(2)}\right\Vert}_{2,1}\\{}\mathrm{subject}\ \mathrm{to}\;\sum \limits_i{X}_{i,j}^2\le 1,\forall j=1,2,...,K\\{}\kern4.6em {B}_{i,j}^{(1)}=0,\forall \left(i,j\right)\in \left\{\left(i,j\right)|{L}_{i,j}^{(1)}=0\right\}\end{array}} \end{equation}$$

(7)

where the matrices of |${Y}^{(1)}$| and |${Y}^{(2)}$| represent the gene transcription and drug sensitivity profiles, respectively. Besides, |$X$| stands for the activity levels of pathways in cell lines. In addition, |${B}^{(1)}$| and |${B}^{(2)}$| represent the pathway-gene association and pathway-drug association matrices, respectively. Furthermore, |${\left\Vert\;\right\Vert}_{2,1}$| denotes the L_2,1-norm, i.e., |${\left\Vert W\right\Vert}_{2,1}={\sum}_{i=1}^m\;\sqrt{\sum_{j=1}^d\;{W}_{i,j}^2}$|⁠. Similarly to iPaD, alternating optimization algorithm was employed to solve the optimization model of L_2,1-iPaD.

L₁L_2,1-iPaD

Wang et al. [43] constructed another calculation model of L₁L_2,1-iPaD to identify drug-pathway associations. Different from previous methods of iPaD and L_2,1-iPaD, the authors aim to enhance the sparsity of the matrix |${B}^{(2)}$|⁠. Therefore, they consider the sum of the L₁-norm and L_2,1-norm penalties as the regularization term in the objective function as follows:

$$\begin{equation}\kern-1pc {\displaystyle \begin{array}{l}\underset{X,{B}^{(1)},{B}^{(2)}}{\min }{\left\Vert{Y}^{(1)}-X{B}^{(1)}\right\Vert}_F^2+{\left\Vert{Y}^{(2)}-X{B}^{(2)}\right\Vert}_F^2+{\lambda}_1{\left\Vert{B}^{(2)}\right\Vert}_1+{\lambda}_2{\left\Vert{B}^{(2)}\right\Vert}_{2,1}\\{}\mathrm{subject}\ \mathrm{to}\;\sum \limits_i{X}_{i,j}^2\le 1,\forall j=1,2,...,K\\{}\kern4.12em {B}_{i,j}^{(1)}=0,\forall \left(i,j\right)\in \left\{\left(i,j\right)|{H}_{i,j}^{(1)}=0\right\}\end{array}} \end{equation}$$

(8)

where |${\lambda}_1$| and |${\lambda}_2$| are two adjustable parameters, which are employed to control the sparsity of the matrix B⁽²⁾. As the |${\lambda}_1$| and |${\lambda}_2$| increase, the sparsity of the matrix B⁽²⁾ would increase. The matrices |${Y}^{(1)}$| and |${Y}^{(2)}$| represent the drug sensitivity data and gene expression data. Besides, the matrix |$X$| represents the pathway activity level. Moreover, the matrix |${H}^{(1)}$| denotes the prior information of gene-pathway associations. The solution of the pathway activity level matrix X, drug-gene association matrix |${B}^{(1)}$| and drug-pathway association matrix |${B}^{(2)}$| can be obtained after solving the Eq. (8) by alternating optimization algorithm. Then, the matrix |${B}^{(2)}$| is utilized to indicate the associations between drugs and pathways.

IGMF

Dai et al. [44] developed a novel method named Integrative Graph regularized Matrix Factorization (IGMF) for drug-pathway association prediction. Firstly, similar to the iPaD method, IGMF decomposed the matrices |${Y}^{(1)}$| and |${Y}^{(2)}$| which represent transcription data and drug sensitivity data as follows:

$$\begin{equation} {\displaystyle \begin{array}{l}{Y}^{(1)}=U{V}^{(1)}+{E}^{(1)}\\{}{Y}^{(2)}=U{V}^{(2)}+{E}^{(2)}\end{array}} \end{equation}$$

(9)

where U denotes the cell line-pathway association matrix. Besides, the matrices V⁽¹⁾ and V⁽²⁾ represent the pathway-gene associations and pathway-drug associations. In addition, E⁽¹⁾ and E⁽²⁾ represent the residual errors. Secondly, the manifold learning is employed to detect the internal geometry of data. The matrix N denotes the p-nearest neighbor graph for the pathway similarity matrix W.

$$\begin{equation} {N}_{uv}=\left\{\kern-6pt{\displaystyle \begin{array}{ll}1,& u\in{N}_p(v)\;\mathrm{or}\;v\in{N}_p(u)\\{}0,& \mathrm{otherwise}\end{array}}\right. \end{equation}$$

(10)

where |${N}_p(v)\;\mathrm{and}\;{N}_p(u)$| denotes the p-nearest neighbors of pathway u and v based on pathway similarity. The matrix N can indicate the intrinsic information of original data. Let |${W}_{u,v}^{\ast }={N}_{uv}{W}_{uv}$|⁠, D is a diagonal matrix with |${D}_{uu}={\sum}_{v=1}^n{W}_{u,v}^{\ast }$|⁠, and |$L=D-{W}_{u,v}^{\ast }$| denotes the graph Laplacians matrix. Under this setting, the integrative analysis model can be formulated as follows:

$$\begin{equation} {\displaystyle \begin{array}{l}\underset{U,{V}^{(1)},{V}^{(2)}}{\min }{\left\Vert{Y}^{(1)}-U{V}^{(1)}\right\Vert}_F^2+{\left\Vert{Y}^{(2)}-U{V}^{(2)}\right\Vert}_F^2+ \lambda Tr(({V^{(2)}})^{T}\ LV^{(2)}) +\beta{\left\Vert{V}^{(2)}\right\Vert}_1\\{}\mathrm{subject}\ \mathrm{to}\;\sum \limits_i{U}_{i,j}^{(2)}\le 1,\forall j=1,2,...,K\\{}\kern4.12em {V}_{i,j}^{(1)}=0,\forall \left(i,j\right)\in \left\{\left(i,j\right)|{L}_{i,j}^{(1)}=0\right\}\end{array}} \end{equation}$$

(11)

where the parameters |$\lambda$| and |$\beta$| are utilized to regulate the smoothness and the sparsity of the pathway-drug matrix. Besides, |${L}^{(1)}$| is the prior pathway-gene association matrix. Finally, V⁽²⁾ can be used to indicate potential drug-pathway associations when the formula (11) is solved by alternating optimization algorithm. IGMF introduced manifold learning via graph regularization constraint to inspect intrinsic geometry of the data, while the previous models of iPaD, L_2,1-iPaD and L₁ L_2,1-iPaD only considered the fact that drug-pathway association is spare.

Other machine learning-based models

Drug-pathway association prediction via multiple feature fusion

Song et al. [45] predicted drug-pathway associations via multiple feature fusion (See Figure 3). In their study, the drug features are divided into drug chemical structure similarity features and molecular functional-groups features. Besides, the pathway features are divided into expression level features of pathway related genes, expression variation features of pathway related genes and pathway similarity features based on pathway-related genes. Moreover, three different machine learning methods including the Gaussian Interaction Profiles (GIP) kernels method, Bipartite Local Models method (BLM) and Graph-based Semi-Supervised Learning method (GBSSL) are utilized to infer drug-pathway associations, respectively. We introduced the details of these three algorithms as follows.

Figure 3

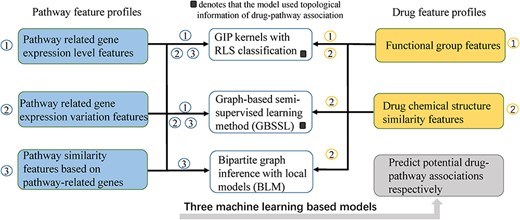
The flowchart of drug-pathway association prediction via multiple feature fusion.

GIP kernels with RLS classification

GIP along with the Regularized Least Squares (RLS) method [45] has been successfully used to infer drug-target interactions [46]. In present study, they first computed the GIP kernels for drugs ( |${K}_{GIP,d}$| ) and pathways ( |${K}_{GIP,p}$| )

$$\begin{equation} {K}_{GIP,d}\left({d}_i,{d}_j\right)=\exp \left(-{\gamma}_d{\left\Vert I{P}_{d_i}-I{P}_{d_j}\right\Vert}^2\right) \end{equation}$$

(12)

where |$I{P}_{d_i}$| ( |$I{P}_{d_j}$| ) is a binary vector denoting the associations between drug |${d}_i$| ( |${d}_j$| ) and each pathway. The parameter |${\gamma}_d$| regulates the kernel bandwidth, which can be calculated as follows:

$$\begin{equation} {\gamma}_d={\gamma}_d^{\ast }/\left(\frac{1}{n_d}\sum \limits_{i=1}^{n_d}{\left\Vert I{P}_{d_i}\right\Vert}^2\right) \end{equation}$$

(13)

where |${\gamma}_d^{\ast }$| was set as 1. The variable |${n}_d$| denotes the number of drugs. In a similar way, |${K}_{GIP,p}\Big({p}_i,{p}_j\Big)$| can be computed for pathway |${p}_i$| and |${p}_j$|⁠. Then |${K}_d$| and |${K}_p$| are used to denote the feature data of drug and pathway.

$$\begin{equation} {K}_d=\left({K}_{GIP},{S}_d,{F}_d\right) \end{equation}$$

(14)

$$\begin{equation} {K}_p=\left({K}_{GIP,p},{A}_p,{V}_p,{S}_p\right) \end{equation}$$

(15)

where the matrix |${S}_d$| denotes drug chemical structure similarity and the matrix |${F}_d$| denotes molecular functional-groups feature of drug. Besides, the matrices |${A}_p$| and |${V}_p$| represent the pathway related gene expression level and variation. In addition, the matrix |${S}_p$| denotes the pathway similarity based on pathway-related genes. Then, based on these biological data, RLS-avg function was utilized to predict drug-pathway associations as follows:

$$\begin{equation} \hat{Y}=\frac{\left({K}_d{\left({K}_d+\sigma I\right)}^{-1}Y\right)+{\left({K}_p{\left({K}_p+\sigma I\right)}^{-1}{Y}^T\right)}^T}{2} \end{equation}$$

(16)

where |$Y$| denotes initial drug-pathway association matrix and |$\hat{Y}$| denotes the inferred drug-pathway association score matrix. Besides, |$\sigma$| is a regularized parameter and I is an identity matrix.

Graph-based semi-supervised learning method (GBSSL)

GBSSL is a semi-supervised learning method [45] that uses all labeled and unlabeled drug-pathway pairs as input data. After carrying out GBSSL, the labels of unlabeled samples can be inferred. Firstly, GBSSL utilized a graph to denote the samples. In the graph, each node represents a drug-pathway pair and the edges were weighted by the matrix W. The node i and j would be connected if |${W}_{ij}$| is greater than zero, otherwise they are not connected. The matrix W is defined as follows:

$$\begin{equation} {W}_{ij}=\left\{\kern-6pt{\displaystyle \begin{array}{ll}\exp\;\left(-\frac{{\left\Vert{x}_i-{x}_j\right\Vert}^2}{\sigma^2}\right)& if\;i\ne j\\{}0& if\;i=j\end{array}}\right. \end{equation}$$

(17)

where |$\sigma$| is a length scale hyper parameter. Besides, |${x}_i$| and |${x}_j$| represent the feature vector of the i-th and j-th sample. In this method, the matrices |${S}_d$|⁠, |${A}_p$|⁠, |${V}_p$| and |${S}_p$| as well as topology information of drug-pathway associations, combined to denote the feature vectors of drug-pathway samples, are the same as that in the above model of GIP kernels with RLS classification. Secondly, the matrix |$S={D}^{-1/2}W{D}^{-1/2}$| can be defined where D is a diagonal matrix and |${D}_{i,i}=\sum_{j=1}^n{W}_{i,j}$|⁠. The variable n represents the number of all drug-pathway pairs. Besides, the |$n\times 2$| matrix Y denotes the initial labels of all samples where the label of known drug-pathway association is (1,0) and the label of unknown drug-pathway pair is (0,1). In addition, the |$n\times 2$| matrix F is employed to denote the scores of drug-pathway pairs. If |${F}_{i,1}\ge{F}_{i,2}$|⁠, the i-th drug-pathway pair would be labeled with (1,0); otherwise the pair would be labeled with (0,1). The matrix F can be obtained by the following iterative formula:

$$\begin{equation} F\left(t+1\right)=\alpha SF(t)+\left(1-\alpha \right)Y \end{equation}$$

(18)

where the parameter |$\alpha$| is used to control the closeness between |$F(t+1)$| and |$F(t)$|⁠. Let the matrix |${F}^{\ast }$| denotes the limit of |$\{F(t)\}$|⁠.

$$\begin{equation} {\displaystyle \begin{array}{l}{F}^{\ast }=\underset{t\to \infty }{\lim } \ F(t)\\{}\kern1.36em =\underset{{\mathrm{t}}\to \infty }{\lim}({\alpha }S)^{{t-1}}\ Y+\left(1-\alpha \right)\underset{t\to \infty }{\lim }\sum_{i=0}^{t-1}{\left(\alpha S\right)}^iY\end{array}} \end{equation}$$

(19)

Finally, The final prediction result can be denoted by the matrix |${F}^{\ast }$| and |${F}^{\ast }={(I-\alpha S)}^{-1}Y$|⁠.

Bipartite local models method (BLM)

BLM, utilized to infer drug-pathway associations [45], is a supervised method [47, 48]. Firstly, for each given drug, the local classifier of Support Vector Machine (SVM) was employed to predict drug-associated pathways. Then, for each pathway, SVM was also utilized to predict pathway-associated drugs. Finally, each drug-pathway pair obtained two prediction scores and the maximum was selected to denote the prediction score of this drug-pathway pair. In this model the drug chemical structure similarity matrix |${S}_d$| and the pathway similarity matrix |${S}_p$| based on pathway-related genes were used to denote drugs and pathways, respectively. Different from GIP kernels method and GBSSL, the topological information of drug-pathway association is not utilized as feature profile in this model.

Above three prediction models used different feature profiles to predict drug-pathway associations. One limitation of these methods is that all the pathways or drugs must have known associations.

RGRF

Song et al. [49] developed an improved Rotation Forest named RGRF (Relief and GBSSL-based Rotation Forest) to infer potential associations between compounds and pathways (See Figure 4). Rotation Forest algorithm is an ensemble learning method by integrating multiple independently trained classifiers based on decision tree. Rotation Forest algorithm mainly includes two parts. The first part is feature extraction. The feature set is randomly split into n subset and then the Principal Component Analysis (PCA) method is utilized to extract features for each subset. Then, the new features of n subsets are combined to establish new feature set. The second part is constructing classifiers. In Rotation Forest, the base classifier is decision tree. RGRF algorithm improved Rotation Forest in two points as follows. Firstly, Relief method [50], widely employed as a feature-weighting algorithm based on instance learning, was selected to replace PCA method as the projection filter. Secondly, considering semi-supervised method generally obtained better performance compared with supervised method when working on the dataset in which unlabeled samples are far more than labeled samples, they employed GBSSL instead of decision trees as the base classifier [51]. In present study, they integrated drug chemical structure similarity, drug mode of active similarity and genomic-based similarity of pathway as features to denote compound-pathway pairs. However, the information about pathways is not abundant yet.

Figure 4

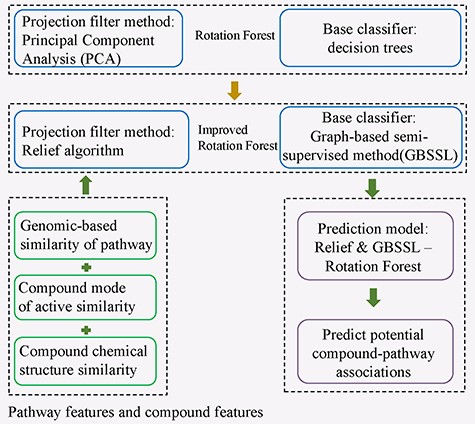
The flowchart of an improved Rotation Forest ensemble learning method of RGRF to infer potential associations between compounds and pathways.

LSA-PU-KNN

Chen et al. [52] proposed a disease-combined LSA (latent semantic analysis)-PU (positive-unlabeled)-KNN (k nearest neighbors) framework to predict potential drug-pathway associations (See Figure 5). First, they combined drug-drug similarity features, drug-disease associations, pathway-pathway similarity features, pathway-diseases associations and pathway related gene expression features as feature vector to denote the drug-pathway pair. Second, LSA was utilized to cut down the dimension of feature vectors. LSA utilizes a singular value decomposition (SVD) to obtain a low-dimensional feature matrix. The matrix F is used to denote the feature vectors of drug-pathway samples with the size of m rows and n columns. The variables m and n denote the number of samples and the dimension of feature vector. Then the SVD of the matrix F is as follows:

$$\begin{equation} F=\sum \limits_{i=1}^{\mathit{\operatorname{rank}}(F)}{\sigma}_i{u}_i{v}_i= U\varSigma{V}^T \end{equation}$$

(20)

where |${\sigma}_i$| represents the i-th singular value of the matrix F. Besides, the vectors |${u}_i$| and |${v}_i$| denotes the left and right singular vector of the i-th singular value of the matrix F. Besides, U and V are the left and right singular matrix, respectively. |$\varSigma$| is a diagonal matrix and |${\varSigma}_{ii}={\sigma}_i$|⁠. Then, they selected the top-t singular values to obtain a t-dimensional matrix |${F}^{\prime }$| as follows:

$$\begin{equation} {F}^{\prime }={U}^{\prime }{\varSigma}^{\prime }{V^{\prime}}^T \end{equation}$$

(21)

where the diagonal elements of |${\varSigma}^{\prime }$| are the top-t singular respectively. |${U}^{\prime }$| and |${V}^{\prime }$| is the corresponding left and right singular matrix. Therefore, the high-dimensional feature matrix F is transformed as the matrix |${F}^{\prime }$| with the size of m rows and t columns. In LSA method, the variable t is choose according to the energy concentration ratio. Finally, they used a PU-KNN algorithm to infer drug-pathway associations. Specifically, they constructed positive sample set |${P}_0$| and unlabeled sample set |${U}_0$|⁠. The size of the two sample sets is the same. Then they extract reliable negative samples RN, likely positive samples LP and likely negative samples LN through the method used in previous study [53]. The sample in LP (or LN) has a weight which denotes the probability that the sample is positive (or negative). Next, given a test drug-pathway pair |$t{}_1$| and its k nearest neighbors |${D}_k$| from unlabeled sample set |${U}_0$|⁠. The associated probability of |$t{}_1$| can be calculated as follows:

$$\begin{equation} P\left({t}_1=1\right)=\frac{\sum \limits_{d_i\in{D}_K}P\left({d}_i=1\right)}{K} \end{equation}$$

(22)

where |${t}_1=1$| denotes that |$t{}_1$| is associated pair and |${d}_i$| is a sample in the |${D}_k$|⁠. LSA-PU-KNN constructed the drug-disease-pathway networks and combined multiple features, which made the data more comprehensive. Besides, PU learning algorithm solved the class-imbalance problem.

Figure 5

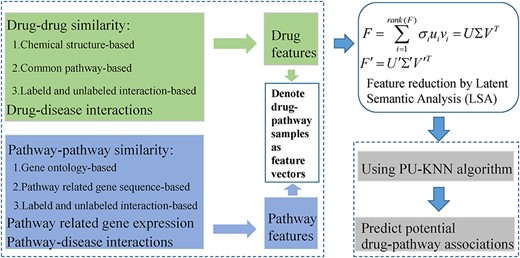
The flowchart of a disease-combined LSA-PU-KNN framework to predict potential drug-pathway associations.

Pathway-based LDA

Naruemon et al. [54] proposed a pathway-based Latent Dirichlet allocation (LDA) method to infer pathway responsiveness under drug treatment. LDA, a generative probabilistic model, belong to unsupervised learning algorithm based the basic idea that the document comes from a set of topics, while the topic is composed of multiple words. In this study, authors make an analogy between the drug-pathway-gene associations and document-topic-word associations. Firstly, they transformed the differential expression level of a gene before and after drug treatment into a positive integer with an appropriate scaling. Then, the positive integer is regarded as the number of appearance of a word in a document. Then, for a series of drugs with information of transformed differential gene expression levels and gene-pathway associations, a collapsed Gibbs sample algorithm was utilized to infer the parameters of the pathway-based LDA model [55]. Finally, given a new drug d, the learned model in the last step can be used to infer the pathway responsiveness |${\theta}_d$| under the new drug treatment.

$$\begin{equation} {\theta}_d=\left({a}_1,{a}_2,...,{a}_T\right) \end{equation}$$

(23)

where |${\theta}_d$| is a T-dimensional vector. The varibale T is the number of all pathways in this study. Besides, the element |${a}_T$| denotes the association probability between the T-th pathway and the drug d.

Methods of algorithm evaluation

Effective calculation models would provide reliable predictive results for further experimental validation, which would accelerate the progress of identification of drug-pathway associations and further promote pathway-based drug research and development. Therefore, evaluating the predictive performance of different algorithms is necessary. In this section, we introduced several methods of algorithm evaluation.

Permutation Test

In the several matrix decomposition-based drug-pathway association prediction models [35, 39, 43, 44], permutation test was employed to assess the predictive performance of these prediction models. More specifically, the gene expression profile matrix |${Y}^{(1)}$| and drug sensitivity matrix |${Y}^{(2)}$| as well as some priori information are the input of models. After implementing predictive algorithm based on these input data, the drug-pathway association matrix |${B}^{(2)}$| can be obtained. Actually, if the element |${B}_{i,j}^{(2)}$| is nonzero, the corresponding pair between i-th drug and j-th pathway is considered as potential association predicted by the predictive model. Then, the permutation test is utilized to estimate the significance of the identified drug-pathway association. The first step of the permutation test is shuffling the rows of the matrix |${Y}^{(2)}$|⁠. It’s worth noting that both gene expression profile matrix |${Y}^{(1)}$| and drug sensitivity matrix |${Y}^{(2)}$| are input data of drug-pathway association prediction models, but researchers only care about potential drug-pathway association. Thus, the matrix |${Y}^{(1)}$| should be not changed in the permutation test. Next, the new drug-pathway association matrix |${B}^{(2)^{\ast }}$| can be obtained by implementing algorithm with the new matrix |${Y}^{(2)^{\ast }}$|⁠. Finally, the p-value of each element in the matrix |${B}^{(2)}$| is computed as follows:

$$\begin{equation} {P}_{i,j}=\frac{\sum_{t=1}^TI\left(\left|{B}_{i,j}^{(2)^{\ast }(t)}\right|\ge \left|{B}_{i,j}^{(2)}\right|\right)}{T} \end{equation}$$

(24)

where |$T$| denotes the number of permutation test. Besides, |${B}_{i,j}^{(2)}$| denotes association score between the i-th drug and j-th pathway when the input data of algorithm is original data. In addition, |${B}_{i,j}^{(2)^{\ast }(t)}$| represents the association score between the i-th drug and j-th pathway in the t-th permutation. If |$\left| {B}_{i,j}^{(2)^{\ast }(t)}\right| \ge \left| {B}_{i,j}^{(2)}\right|$|⁠, |$I\left(\left|{B}_{i,j}^{(2)^{\ast }(t)}\right|\ge \left|{B}_{i,j}^{(2)}\right|\right)$| in the numerator of Eq. (24) is equal to 1, otherwise 0. |${P}_{i,j}$| denotes the p-value of this drug-pathway pair. The p-value is used to estimate the significance of the element in the matrix |${B}^{(2)}$| and the smaller the p-value, the stronger of the significance of the inferred drug-pathway association.

Recall enhancement

The measurement of recall enhancement [56] was utilized to check whether the predicted drug-pathway associations with higher association scores are reliable associations [54]. To be specific, in the first step, all predicted potential drug-pathway associations are ranked according to their association scores in a descending order. |$T{P}_k\;\mathrm{and}\;F{P}_k$| denote the number of true positives and false positives among the top-k drug-pathway associations, respectively. Second, all predicted potential associations are randomly ranked. |$Random\_T{P}_k\;\mathrm{and}\; Random\_F{P}_k$| represent the number of true positives and false positives among the top-k drug-pathway associations. It’s worth noting that drug-pathway associations recorded in some databases (KEGG pathway, CTD, CancerResource and so on) are not comprehensive. Thus, researchers should validate the top-k drug-pathway associations by referring to multiple databases. Then, they can calculate the fold enrichment of true positive drug-pathway associations ( |$FE\_T{P}_k$| ) and fold enrichment of false positive drug-pathway associations ( |$FE\_F{P}_k$| ) by investigating the number of true positives and false positives among top-k associations ranked in the manner of the first and second step respectively as follows:

$$\begin{equation} FE\_T{P}_k=\frac{T{P}_k}{Random\_T{P}_k} \end{equation}$$

(25)

$$\begin{equation} FE\_F{P}_k=\frac{F{P}_k}{Random\_F{P}_k} \end{equation}$$

(26)

It is worth noting that the true positive associations mean that they are validated by known database or experimental literature. We expect that |$FE\_T{P}_k$| is lager and |$FE\_F{P}_k$| is small.

Furthermore, they also evaluated the predictive performance for individual drug. To begin with, for each drug d, the prediction associated-pathways are ordered according to their association scores in a descending order. Then they computed an average precision (AP) of top-M ranks by using the known association information in the validated set as follows:

$$\begin{equation} AP=\frac{\sum_{m=1}^M\left({P}_m\times{l}_m\right)}{N} \end{equation}$$

(27)

$$\begin{equation} {P}_m=\frac{n_m}{m} \end{equation}$$

(28)

where |${l}_m$| is equal to 1 if the pathway at rank m is confirmed to be associated with investigated drug and 0 otherwise. Besides, |${n}_m$| denotes the number of confirmed pathways based on validated set of the top-m ranks. The variable |$N$| represents the number of confirmed pathways among the top-M pathways. Obviously, the higher value of |$AP$| is expected.

K-fold cross validation

K-fold cross validation is widely used to evaluate the performance of prediction model especially machine learning-based models [3, 57, 58]. The procedure of K-fold cross validation can be executed as follows. First, all drug-pathway associations are divided into K subsets. Then, each subset is left out as test set in turn, while the remaining K-1 subsets are used as training set. It is worth noting that K is usually set as 5 or 10. After implementing K-fold cross validation for prediction models, there are several common measurements often employed to estimate the predictive performance, namely Sensitivity (SN), Specificity (SP), Matthews correlation coefficient (MCC), Accuracy (ACC), Precision and Recall as follows:

$$\begin{equation} SN=\frac{TP}{TP+ FN} \end{equation}$$

(29)

$$\begin{equation} SP=\frac{TN}{TP+ FP} \end{equation}$$

(30)

$$\begin{equation} MCC=\frac{TP\times TN- FP\times FN}{\sqrt{\left( TP+ FP\right)\left( TP+ FN\right)\left( TN+ FP\right)\left( TN+ FN\right)}} \end{equation}$$

(31)

$$\begin{equation} ACC=\frac{TP+ TN}{TP+ FP+ TN+ FN} \end{equation}$$

(32)

$$\begin{equation} \Pr \mathrm{ecision}=\frac{TP}{TP+ FP} \end{equation}$$

(33)

$$\begin{equation} \operatorname{Re}\mathrm{call}=\frac{TP}{TP+ FN} \end{equation}$$

(34)

where TP, TN, FP and FN denote the number of true positive samples, true negative samples, false positive samples and false negative samples predicted by computational model in the test sample set, respectively. Besides, the receiver operating characteristic (ROC) curve is drawn by plotting the true positive rate (TPR, sensitivity) against the false positive rate (FPR, 1-specificity) with different thresholds. Then the area under the ROC curve (AUC) can be obtained after drawing ROC curve and the higher AUC prediction model achieves, the better predictive performance prediction model is. Similarly, the area under precision-recall (PR) curve (AUPR) can be obtained after drawing PR curve by plotting the Precision against the Recall with different thresholds. The higher AUPR would demonstrate the better performance of calculation model.

Discussion and conclusion

The progress of drug research and development provides security for the treatment of human diseases. Many complex diseases have been overcome after discovering novel effective drugs. Different from new drug development, some researchers proposed the idea of drug repositioning. They expect to mine the novel applications of old drugs and realize the treatment for new disease using these old drugs, which can provide new treatment strategy for human diseases to some extent. However, there are many complex diseases especially cancer lacking of effective drugs and therapeutic schedule. Moreover, most of chemotherapy drugs have various side effects. Therefore, in order to overcome the trouble mentioned above, the research and development of novel drug is still necessary. However, progress in the drug development is relatively slow. Traditional drug discovery usually follows the strategy of one drug-one target. Recently, more and more scholars are paying attention to the importance of pathways in drug discovery since many studies have demonstrated the associations between drugs and pathways. The pathway-based drug discovery provides a new idea for the research and development of drug, but exploring the associations between drugs and pathways is time consuming and expensive by biological experiments. Actually, there are various type of data about drugs and pathway accumulated in the process of research of drugs and pathways, such as known drug-pathway associations, drug sensitivity profile, pathway related gene expression information and so on. Thus, effective computational methods are expected to predict new drug-pathway association using these accumulated data.

In this article, we first introduced the status of drugs and drug research and development. Then, we described the relationship between drug and pathway, because pathways play an important role in drug discovery. Next, we listed some databases and web servers about drugs and drug-pathway associations for the convenience of researchers. In addition, we described some state-of-the-art computational methods for drug-pathway association inferring and divided them into several classes, namely matrix decomposition-based methods, Bayesian sparse factor-based methods and other machine learning-based methods. Finally, we introduced several evaluation methods for estimating the predictive performance of prediction models. In the following, we will summarize the advantages and the limitations of these computational methods and provide an outlook about the future development of drug-pathway association prediction and identification.

Two Bayesian spare factor-based models for drug-pathway association prediction introduced in this review have a common idea that drug-pathway associations can be predicted by searching the latent factor. With this idea, two statistical frameworks were established and a modified collapsed Gibbs sampling algorithm was employed for the Bayesian inference. Some advantages contribute to their predictive performance. The first advantage of Bayesian spare factor-based model is that the model can analyze both single type of data and multiple types of data. Secondly, a Bayesian framework could integrate the prior pathway knowledge into the model, such as known gene-pathway associations and drug-pathway associations. Finally, Bayesian spare factor-based models explicitly consider the sparse nature of the drug-pathway associations. On the other hand, there are also some limitations in the Bayesian factor-based models. First, a larger number of parameters need to be estimated. Second, the Bayesian factor-based models require relatively good computational resource.

Four matrix decomposition-based methods introduced in this review jointly analyze drug sensitivity and gene expression data to infer drug-pathway associations. The first advantage of the matrix decomposition-based methods is that they could mine the shared latent factor of various kinds of biological data and further identify the potential associations between drugs and pathways. Thus, matrix decomposition-based method may be an appropriate choice with increasing high throughput data. Besides, they transformed the problem of matrix decomposition into an optimization problem and introduced different penalty term. The optimization problem can be solved by scalable bi-convex optimization algorithm, which greatly improve the computational efficiency of the model. Another advantage of these matrix decomposition-based methods is that there are only one or two parameters in the models. Thus, parameter selection is relatively easy. On the contrary, there are also some limitations in these matrix decomposition-based methods. First, the purpose of the several methods is to seek out the loading matrix for drug-pathway associations. If the element in the loading matrix is nonzero, the corresponding drug-pathway pair is considered as associated pair. Besides, the more important elements are considered to become non-zeros earlier than the less important ones when updating loading matrix by alternating optimization algorithm. However, the loading matrix could not reflect the associated probability of drug-pathway pairs. Second, there are only few differences among the existing matrix decomposition-based methods for drug-pathway association prediction. To be specific, the iPaD takes the L₁-norm penalty on the regularization term, while the L_2,1-iPaD uses the L_2,1-norm penalty to replace of L₁-norm penalty. Besides, the L₁L_2,1-iPaD utilizes the sum of L₁-norm penalty and L_2,1-norm penalty as the regularization term. Moreover, IGMF employs L₁-norm penalty together with graph regularization. Finally, the several matrix decomposition-based models do not use the prior information about drug-pathway associations when they were used to predict potential drug-pathway associations based on the CCLE dataset, which may reduce the predictive accuracy to some extent. In the future, more and more drug-pathway associations will be discovered, so making full use the prior information of drug-pathway associations is important for prediction models.

As for other machine learning-based models, multiple feature data and known drug-pathway associations are used to train prediction model. Various types of data of drugs and pathways, such as drug chemical structure, drug functional groups, pathway related gene expression profile and so on, can be processed and integrated as features to represent drug-pathway samples as feature vectors. Thus, making full use of different kinds of data is an advantage of these machine learning-based models. Besides, effective feature reduction or selection methods, such as Relief and LSA methods mentioned above, would benefit for distinguishing associated drug-pathway pairs form unassociated pairs. Of course, there are also some limitations in these machine learning-based models. First, the parameters are hard to select. Second, prediction bias may be produced in these models since some drugs (or pathways) have more associated pathways (or drugs). Third, in the supervised machine learning model, for example BLM, both positive samples (associated drug-pathway pairs) and negative samples (unassociated drug-pathway pairs) are necessary to construct the training sample set. However, it is difficult to obtain negative samples since unassociated drug-pathway pairs are hard to collect. Actually, the real data about drug-pathway pairs consist of known associated drug-pathway pair and unlabeled drug-pathway pairs. In addition, the number of known associated pairs is far less than the number unlabeled pairs. Dealing with the class-imbalance samples, semi-supervised machine learning method, such as GBSSL, shows better performance than supervised method. Besides, semi-supervised methods don’t need negative samples. In addition, different machine learning algorithms have their own advantages and disadvantages and single classifier may not perform well. Therefore, we could take the idea of ensemble learning by integrating multiple types of classifiers to construct prediction model. In addition, it is important to select appropriate machine learning algorithm to establish classifier when facing different datasets.

Since pathway-based drug discovery would be a valuable strategy to design novel drugs for overcoming complex diseases, the researchers tried to utilize both experimental and computational methods to replenish the knowledge base about drugs, pathways and drug-pathway associations. As we know, biological experiment is convincing in revealing the mechanisms of drugs and pathways as well as drug-pathway associations. However, biological experiments take much time and cost. Thus, some computational methods were proposed to infer potential drug-pathway associations. However, the number of current computational methods is far from enough and more effective calculation models are expected. When using calculation method to predict drug-pathway associations, the data collection and processing is an important step. Nowadays, the data of drugs is relatively sufficient. However, the data of pathways is insufficient. Thus, some computational methods only use the pathway related gene expression data. From this perspective, more work should be devoted to collect useful data about pathways in the future. Besides, network based methods have been successfully utilized in many fields such as miRNA-disease association prediction [59–62], small molecule-miRNA association identification [63–66], drug-target interaction prediction [67, 68], long non-coding RNA-disease association prediction [58, 69, 70] and so on. Random walk or various propagation algorithms [71, 72] are employed in the problem of association prediction. With the development of experimental technology in the research of drugs and pathways, more and more data would be accumulated. Network-based method could make full use of different kinds of data to construct heterogeneous network and further efficiently predict potential associations, which would improve the predictive accuracy. Currently, there are hardly no network-based method proposed to identify drug-pathway associations. Therefore, it should arouse our attention to consider how to establish drug-pathway heterogeneous network and develop effective network based algorithms for drug-pathway association prediction in the future.

What’s more, the goal of calculation models is inferring reliable drug-pathway associations for further experimental validation. Thus, the predictive algorithms should be packaged into auxiliary tools for the convenience of biologists. We believe that combination of experimental and computational approaches would promote the development of drug-pathway association identification and pathway-based drug discovery. Drug-pathway association prediction plays an important role in the drug research and development. Besides, there is a close relationship between drug-pathway association prediction, drug-target interaction prediction and drug response prediction. Firstly, the drug-target interaction prediction and drug-pathway association prediction by computational methods could accelerate the progress of drug research and development which provides security for the treatment of human diseases, while drug response prediction could promote the development of precision therapy since it can predict drug response for different patients by analyzing individual genomic signatures or other features. Therefore, drug-pathway association prediction, drug-target interaction prediction and drug response prediction can all promote the advancement of human medical health. Secondly, drug-target interaction prediction is benefit for drug-pathway association prediction. Besides, both drug-target interaction prediction and drug-pathway association prediction are useful for drug response prediction. Actually, some other significant studies also contributed to the drug research and development. For example, adverse drug reactions (ADRs) lead to the failure of many drug candidates. Thus, investigating associations between pathways and ADRs is crucial and some methods had been proposed to explore ADR-pathway associations [73, 74]. Therefore, pathway-ADR association inferring can be a future direction for the pathway-based drug discovery. Besides, drug repositioning is also a hot topic in the field of drug research. In previous study [75], researchers constructed the hybrid network using gene-centric and drug-centric data under given pathological context, respectively. They utilized a calculation model of NetWalk to score drugs based on gene-centric data or do a reverse analysis to score genes and pathways. The scores can reflect the association between drug (gene or pathway) and the given pathological context. In this way, they could find the potential drugs as well as novel drug targets for different pathological contexts. Thus, how to use drug-pathway associations to solve the problem of drug reposition is also an important research direction in the future. Finally, drug combination is a promising strategy for overcoming drug resistance and treating complex diseases. In previous study, Chen et al. [76] developed a calculation method named as NLLSS for inferring potential synergistic drug combinations through integrating the information of drug chemical structures, known synergistic drug combinations as well as drug-target interactions. As mentioned in the drug-pathway association section, pathways play an important role in many complex diseases and closely associated with drugs. Therefore, it would be a future direction for synergistic drug combination prediction by introducing the information of drug-pathway associations.

Key Points

The pathway-based drug discovery provides a new strategy for the research and development of drug.
Identifying drug-pathway associations is a key step in the pathway-based drug discovery.
We introduced some publicly accessible databases and web servers about drug and drug-pathway association.
Computational models have proposed to predict potential drug-pathway associations for further experimental validation, which can save much time and cost.
Computational models were divided into three classes, namely matrix decomposition-based, Bayesian sparse factor-based and other machine learning-based model.
We introduced several methods of algorithm evaluation to estimate the predictive performance of calculation models.
The advantages and limitations of computational models were discussed.

Funding

XC was supported by National Natural Science Foundation of China under Grant No. 61972399.

Chun-Chun Wang is a PhD student of School of Information and Control Engineering, China University of Mining and Technology. His research interests include bioinformatics, complex network algorithm, and machine learning.

Yan Zhao is a PhD student of School of Information and Control Engineering, China University of Mining and Technology. His research interests include bioinformatics, complex network algorithm, and machine learning.

Xing Chen, PhD, is a professor of School of Information and Control Engineering, China University of Mining and Technology. He is also the Founding Director of Institute of Bioinformatics, China University of Mining and Technology. His research interests include bioinformatics, complex network algorithm, and machine learning.

References

1.

Mullard

A

.

2018 FDA drug approvals

.

Nat Rev Drug Discov

2019

;

18

:

85

–

9

.

2.

Paul

SM

,

Mytelka

DS

,

Dunwiddie

CT

, et al.

How to improve R&D productivity: the pharmaceutical industry's grand challenge

.

Nat Rev Drug Discov

2010

;

9

:

203

–

14

.

3.

Chen

X

,

Yan

CC

,

Zhang

X

, et al.

Drug-target interaction prediction: databases, web servers and computational models

.

Brief Bioinform

2016

;

17

:

696

–

712

.

4.

Mailankody

S

,

Prasad

V

.

Five years of cancer drug approvals: innovation, efficacy, and costs

.

JAMA Oncol

2015

;

1

:

539

–

540.e535

.

5.

Experts in Chronic Myeloid Leukemia. The price of drugs for chronic myeloid leukemia (CML) is a ref lection of the unsustainable prices of cancer drugs: from the perspective of a large group of CML experts

.

Blood

2013

;

121

:

4439

–

42

.

Crossref

PubMed

6.

Sanger

F

.

Sequences, sequences, and sequences

.

Annu Rev Biochem

1988

;

57

:

1

–

29

.

7.

Sanger

F

,

Air

GM

,

Barrell

BG

, et al.

Nucleotide sequence of bacteriophage φX174 DNA

.

Nature

1977

;

265

:

687

.

8.

Scannell

JW

,

Blanckley

A

,

Boldon

H

, et al.

Diagnosing the decline in pharmaceutical R&D efficiency

.

Nat Rev Drug Discov

2012

;

11

:

191

–

200

.

9.

Hyman

DM

,

Taylor

BS

,

Baselga

J

.

Implementing genome-driven oncology

.

Cell

2017

;

168

:

584

–

99

.

10.

Geysen

HM

,

Schoenen

F

,

Wagner

D

, et al.

Combinatorial compound libraries for drug discovery: an ongoing challenge

.

Nat Rev Drug Discov

2003

;

2

:

222

–

30

.

11.

Hogan

JC

, Jr.

Combinatorial chemistry in drug discovery

.

Nat Biotechnol

1997

;

15

:

328

–

30

.

12.

Hopkins

AL

.

Network pharmacology: the next paradigm in drug discovery

.

Nat Chem Biol

2008

;

4

:

682

–

90

.

13.

Lindsay

MA

.

Finding new drug targets in the 21st century

.

Drug Discov Today

2005

;

10

:

1683

–

7

.

14.

Neuzillet

C

,

Tijeras-Raballand

A

,

Cohen

R

, et al.

Targeting the TGFbeta pathway for cancer therapy

.

Pharmacol Ther

2015

;

147

:

22

–

31

.

15.

Akhurst

RJ

,

Hata

A

.

Targeting the TGFbeta signalling pathway in disease

.

Nat Rev Drug Discov

2012

;

11

:

790

–

811

.

16.

Rahimifard

M

,

Maqbool

F

,

Moeini-Nodeh

S

, et al.

Targeting the TLR4 signaling pathway by polyphenols: a novel therapeutic strategy for neuroinflammation

.

Ageing Res Rev

2017

;

36

:

11

–

9

.

17.

Thomas

C

,

Pellicciari

R

,

Pruzanski

M

, et al.

Targeting bile-acid signalling for metabolic diseases

.

Nat Rev Drug Discov

2008

;

7

:

678

–

93

.

18.

Rudin

CM

,

Hann

CL

,

Laterra

J

, et al.

Treatment of medulloblastoma with hedgehog pathway inhibitor GDC-0449

.

N Engl J Med

2009

;

361

:

1173

–

8

.

19.

Wilhelm

SM

,

Carter

C

,

Tang

L

, et al.

BAY 43-9006 exhibits broad spectrum oral antitumor activity and targets the RAF/MEK/ERK pathway and receptor tyrosine kinases involved in tumor progression and angiogenesis

.

Cancer Res

2004

;

64

:

7099

–

109

.

20.

Speciale

A

,

Anwar

S

,

Canali

R

, et al.

Cyanidin-3-O-glucoside counters the response to TNF-alpha of endothelial cells by activating Nrf2 pathway

.

Mol Nutr Food Res

2013

;

57

:

1979

–

87

.

21.

Ma

H

,

Zhao

H

.

Drug target inference through pathway analysis of genomics data

.

Adv Drug Deliv Rev

2013

;

65

:

966

–

72

.

22.

Davis

AP

,

Grondin

CJ

,

Johnson

RJ

, et al.

The comparative Toxicogenomics database: update 2019

.

Nucleic Acids Res

2019

;

47

:

D948

–

d954

.

23.

Gohlke

BO

,

Nickel

J

,

Otto

R

, et al.

CancerResource–updated database of cancer-relevant proteins, mutations and interacting drugs

.

Nucleic Acids Res

2016

;

44

:

D932

–

7

.

24.

Kanehisa

M

,

Furumichi

M

,

Tanabe

M

, et al.

KEGG: new perspectives on genomes, pathways, diseases and drugs

.

Nucleic Acids Res

2017

;

45

:

D353

–

d361

.

25.

Zhao

S

,

Iyengar

R

.

Systems pharmacology: network analysis to identify multiscale mechanisms of drug action

.

Annu Rev Pharmacol Toxicol

2012

;

52

:

505

–

21

.

26.

Giuliano

KA

,

Haskins

JR

,

Taylor

DL

.

Advances in high content screening for drug discovery

.

Assay Drug Dev Technol

2003

;

1

:

565

–

77

.

27.

Hughes

JE

.

Genomic technologies in drug discovery and development

.

Drug Discov Today

1999

;

4

:

6

.

28.

Ulrich

R

,

Friend

SH

.

Toxicogenomics and drug discovery: will new technologies help us produce better drugs?

Nat Rev Drug Discov

2002

;

1

:

84

–

8

.

29.

Yang

H

,

Qin

C

,

Li

YH

, et al.

Therapeutic target database update 2016: enriched resource for bench to clinical drug target and targeted pathway information

.

Nucleic Acids Res

2016

;

44

:

D1069

–

74

.

30.

Wishart

DS

,

Feunang

YD

,

Guo

AC

, et al.

DrugBank 5.0: a major update to the DrugBank database for 2018

.

Nucleic Acids Res

2018

;

46

:

D1074

–

d1082

.

31.

Lamb

J

,

Crawford

ED

,

Peck

D

, et al.

The connectivity map: using gene-expression signatures to connect small molecules, genes, and disease

.

Science

2006

;

313

:

1929

–

35

.

32.

Ma

H

,

Zhao

H

.

FacPad: Bayesian sparse factor modeling for the inference of pathways responsive to drug treatment

.

Bioinformatics

2012

;

28

:

2662

–

70

.

33.

Ma

H

,

Zhao

H

.

iFad: an integrative factor analysis model for drug-pathway association inference

.

Bioinformatics

2012

;

28

:

1911

–

8

.

34.

Shankavaram

UT

,

Varma

S

,

Kane

D

, et al.

CellMiner: a relational database and query tool for the NCI-60 cancer cell lines

.

BMC Genomics

2009

;

10

:

277

.

35.

Li

C

,

Yang

C

,

Hather

G

, et al.

Efficient drug-pathway association analysis via integrative penalized matrix decomposition

.

IEEE/ACM Trans Comput Biol Bioinform

2016

;

13

:

531

–

40

.

36.

Kumar

R

,

Chaudhary

K

,

Gupta

S

, et al.

CancerDR: cancer drug resistance database

.

Sci Rep

2013

;

3

:

1445

.

37.

Seiler

KP

,

George

GA

,

Happ

MP

, et al.

ChemBank: a small-molecule screening and cheminformatics resource database

.

Nucleic Acids Res

2008

;

36

:

D351

–

9

.

38.

Gaulton

A

,

Bellis

LJ

,

Bento

AP

, et al.

ChEMBL: a large-scale bioactivity database for drug discovery

.

Nucleic Acids Res

2012

;

40

:

D1100

–

7

.

39.

Liu

JX

,

Wang

DQ

,

Zheng

CH

, et al.

Identifying drug-pathway association pairs based on L2,1-integrative penalized matrix decomposition

.

BMC Syst Biol

2017

;

11

:

119

.

40.

Cerami

EG

,

Gross

BE

,

Demir

E

, et al.

Pathway commons, a web resource for biological pathway data

.

Nucleic Acids Res

2011

;

39

:

D685

–

90

.

41.

Bernardo

J

,

Bayarri

M

,

Berger

J

, et al.

Bayesian factor regression models in the “large p, small n” paradigm

.

Bayesian statistics

2003

;

7

:

733

–

42

.

42.

Pournara

I

,

Wernisch

L

.

Factor analysis for gene regulatory networks and transcription factor activity profiles

.

BMC Bioinformatics

2007

;

8

:

61

.

43.

Wang

DQ

,

Gao

YL

,

Liu

JX

, et al.

Identifying drug-pathway association pairs based on L1L2,1-integrative penalized matrix decomposition

.

Oncotarget

2017

;

8

:

48075

–

85

.

44.

Dai

LY

,

Zheng

CH

,

Liu

JX

, et al.

Integrative graph regularized matrix factorization for drug-pathway associations analysis

.

Comput Biol Chem

2019

;

78

:

474

–

80

.

45.

Song

M

,

Yan

Y

,

Jiang

Z

.

Drug-pathway interaction prediction via multiple feature fusion

.

Mol Biosyst

2014

;

10

:

2907

–

13

.

46.

van

Laarhoven

T

,

Nabuurs

SB

,

Marchiori

E

.

Gaussian interaction profile kernels for predicting drug-target interaction

.

Bioinformatics

2011

;

27

:

3036

–

43

.

47.

Bleakley

K

,

Yamanishi

Y

.

Supervised prediction of drug-target interactions using bipartite local models

.

Bioinformatics

2009

;

25

:

2397

–

403

.

48.

Yamanishi

Y

,

Araki

M

,

Gutteridge

A

, et al.

Prediction of drug-target interaction networks from the integration of chemical and genomic spaces

.

Bioinformatics

2008

;

24

:

i232

–

40

.

49.

Song

M

,

Jiang

Z

.

Inferring association between compound and pathway with an improved ensemble learning method

.

Mol Inform

2015

;

34

:

753

–

60

.

50.

Kira

K

,

Rendell

L

.

Proceedings of the ninth international workshop on Machine learning

,

1992

.

51.

Yu

W

,

Yan

Y

,

Liu

Q

, et al.

Predicting drug-target interaction networks of human diseases based on multiple feature information

.

Pharmacogenomics

2013

;

14

:

1701

–

7

.

52.

Chen

X

,

Wu

QF

,

Yan

GY

.

RKNNMDA: ranking-based KNN for MiRNA-disease association prediction

.

RNA Biol

2017

;

14

:

952

–

62

.

53.

Yang

P

,

Li

X-L

,

Mei

J-P

, et al.

Positive-unlabeled learning for disease gene identification

.

Bioinformatics

2012

;

28

:

2640

–

7

.

54.

Pratanwanich

N

,

Lio

P

.

Exploring the complexity of pathway-drug relationships using latent Dirichlet allocation

.

Comput Biol Chem

2014

;

53

:

144

–

52

.

55.

Griffiths

TL

,

Steyvers

M

.

Finding scientific topics

.

Proc Natl Acad Sci U S A

2004

;

101

:

5228

–

35

.

56.

Zhou

T

,

Kuscsik

Z

,

Liu

JG

, et al.

Solving the apparent diversity-accuracy dilemma of recommender systems

.

Proc Natl Acad Sci U S A

2010

;

107

:

4511

–

5

.

57.

Chen

X

,

Xie

D

,

Zhao

Q

, et al.

MicroRNAs and complex diseases: from experimental results to computational models

.

Brief Bioinform

2019

;

20

:

515

–

39

.

58.

Chen

X

,

Yan

CC

,

Zhang

X

, et al.

Long non-coding RNAs and complex diseases: from experimental results to computational models

.

Brief Bioinform

2017

;

18

:

558

–

76

.

PubMed

59.

Xuan

P

,

Han

K

,

Guo

Y

, et al.

Prediction of potential disease-associated microRNAs based on random walk

.

Bioinformatics

2015

;

31

:

1805

–

15

.

60.

Chen

X

,

Xie

D

,

Wang

L

, et al.

BNPMDA: bipartite network projection for MiRNA-disease association prediction

.

Bioinformatics

2018

;

34

:

3178

–

86

.

61.

You

ZH

,

Huang

ZA

,

Zhu

Z

, et al.

PBMDA: a novel and effective path-based computational model for miRNA-disease association prediction

.

PLoS Comput Biol

2017

;

13

:

e1005455

.

62.

Chen

X

,

Zhou

Z

,

Zhao

Y

.

ELLPMDA: ensemble learning and link prediction for miRNA-disease association prediction

.

RNA Biol

2018

;

15

:

807

–

18

.

63.

Qu

J

,

Chen

X

,

Sun

YZ

, et al.

Inferring potential small molecule-miRNA association based on triple layer heterogeneous network

.

J Chem

2018

;

10

:

30

.

Crossref

64.

Lv

Y

,

Wang

S

,

Meng

F

, et al.

Identifying novel associations between small molecules and miRNAs based on integrated molecular networks

.

Bioinformatics

2015

;

31

:

3638

–

44

.

65.

Chen

X

,

Guan

N-N

,

Sun

Y-Z

, et al.

MicroRNA-small molecule association identification: from experimental results to computational models

.

Brief Bioinform

2020

;

21

:

47

–

61

.

66.

Qu

J

,

Chen

X

,

Sun

YZ

, et al.

In Silico prediction of small molecule-miRNA associations based on the HeteSim algorithm

.

Mol Ther Nucleic Acids

2019

;

14

:

274

–

86

.

67.

Campillos

M

,

Kuhn

M

,

Gavin

AC

, et al.

Drug target identification using side-effect similarity

.

Science

2008

;

321

:

263

–

6

.

68.

Chen

X

,

Liu

MX

,

Yan

GY

.

Drug-target interaction prediction by random walk on the heterogeneous network

.

Mol Biosyst

2012

;

8

:

1970

–

8

.

69.

Chen

X

.

Predicting lncRNA-disease associations and constructing lncRNA functional similarity network based on the information of miRNA

.

Sci Rep

2015

;

5

:

13186

.

70.

Chen

X

.

KATZLDA: KATZ measure for the lncRNA-disease association prediction

.

Sci Rep

2015

;

5

:

16840

.

71.

Chen

X

,

Zhang

DH

,

You

ZH

.

A heterogeneous label propagation approach to explore the potential associations between miRNA and disease

.

J Transl Med

2018

;

16

:

348

.

72.

Lotfi Shahreza

M

,

Ghadiri

N

,

Mousavi

SR

, et al.

Heter-LP: a heterogeneous label propagation algorithm and its application in drug repositioning

.

J Biomed Inform

2017

;

68

:

167

–

83

.

73.

Chen

X

,

Wang

Y

,

Wang

P

, et al.

Systematic analysis of the associations between adverse drug reactions and pathways

.

Biomed Res Int

2015

;

2015

:

670949

.

PubMed