-
PDF
- Split View
-
Views
-
Cite
Cite
Abukari Mohammed Yakubu, Yi-Ping Phoebe Chen, Ensuring privacy and security of genomic data and functionalities, Briefings in Bioinformatics, Volume 21, Issue 2, March 2020, Pages 511–526, https://doi.org/10.1093/bib/bbz013
Close - Share Icon Share
Abstract
In recent times, the reduced cost of DNA sequencing has resulted in a plethora of genomic data that is being used to advance biomedical research and improve clinical procedures and healthcare delivery. These advances are revolutionizing areas in genome-wide association studies (GWASs), diagnostic testing, personalized medicine and drug discovery. This, however, comes with security and privacy challenges as the human genome is sensitive in nature and uniquely identifies an individual. In this article, we discuss the genome privacy problem and review relevant privacy attacks, classified into identity tracing, attribute disclosure and completion attacks, which have been used to breach the privacy of an individual. We then classify state-of-the-art genomic privacy-preserving solutions based on their application and computational domains (genomic aggregation, GWASs and statistical analysis, sequence comparison and genetic testing) that have been proposed to mitigate these attacks and compare them in terms of their underlining cryptographic primitives, security goals and complexities—computation and transmission overheads. Finally, we identify and discuss the open issues, research challenges and future directions in the field of genomic privacy. We believe this article will provide researchers with the current trends and insights on the importance and challenges of privacy and security issues in the area of genomics.
Introduction
The acquisition of genetic samples has become ubiquitous and is increasing in recent times due to the decrease in sequencing cost. These data are shared in public databases, biobanks and repositories (e.g. UK biobank [1] and the 1000 Genomes Project [2]) to assist researchers and clinicians to advance biomedical research to better understand the structures and functionalities of biological data—DNA, RNA and proteins. This advancement in research will, amongst many other things, broaden the use and applications of genetic testing in areas such as (i) paternity testing—to determine whether two individuals are parent and child, (ii) diagnostic testing—to diagnose whether an individual is affected by a certain disease and (iii) pharmacogenetic testing—in personalized medicine to tailor treatment for an individual and the development of efficient drugs and therapies.
Despite these benefits, there are still serious concerns about the security and privacy of genomic data in storage, sharing, in transit and during computation. Donors of DNA samples sometimes ask questions such as: ‘How is my genetic data stored? Who has access to it? What security measures are in place to protect my privacy?’ These concerns are born out of the fact that
i In Australia, genetic data is collected and used to drive the agenda of the Australian Genomics Health Alliance in genomic medicine [3].
ii A new bill moving through the US congress, if passed, will allow companies to have access to their employee’s genetic data by requiring them to undergo genetic testing or they will be fined thousands of dollars [4].
iii In the UK, the National Health Service has proposed a genetic database where the DNA of babies will be sequenced at birth. [5].
The human genome is special and has certain characteristics such as being unique, it does not change much over an individual’s lifetime, it is non-revocable, it reflects ethnic heritage, is correlated between relatives and can identify predisposition to diseases that makes it a vast collection of sensitive information and prone to privacy risk and attacks [6]. As a result of these sensitive properties, there are ethical regulations on how genomic data should be shared. Federal laws in countries such Australia, Canada, USA and UK prohibit health insurance companies and employers from discriminating against people based on genetic information. However, there are still loopholes in these laws, for instance, in some states in the US, this law does not apply to companies providing disability, life or long-term care insurance [7]. Furthermore, companies still discriminate without openly stating their reasons for doing so [8]. This is however different in the EU with the new General Data Protection Regulation law where the use of personal data has been restricted to the purpose for which it was collected [9]. For instance, this prohibits processing of direct-to-consumer (DTC) data for other purposes such as insurance without consent from individuals. Examples of such discriminations are (i) an employer denying an employee a promotion because his DNA reveals that his skill set does not match the job profile and (ii) an insurance company declining coverage for an individual based on his inclination to certain health conditions (e.g. breast cancer, sickle cell anemia and other Mendelian diseases) revealed from his DNA. Another privacy risk is compromising kinship privacy. This occurs when leaking an individual’s genome gives away some genetic information about his close relatives due to DNA correlation amongst individuals from the same family [10–12]. One of the paramount implications this has is that people are skeptical about privacy issues related to genomic data and reluctant to participate in genetic testing programs which is crucial in helping researchers learn the structure and functions of the human genome for the advancement of areas in biomedical science such as personalized medicine. This is a global problem, not just a one-country issue. Thus, there is the need for the privacy, security and confidentiality of genomic data to be protected at storage and during computation. Genomic privacy is a multidisciplinary area and to address these issues, policymakers, and cryptographic and bioinformatics research communities are collaborating to enact policies and design secure frameworks that are yet to sufficiently address security goals and computational issues specific to genomic practical use-cases.
Related surveys and articles on genomic privacy, each with a different focus and contribution, have discussed the privacy and security issues facing genomic data and surveyed proposed migration techniques (cryptographic and non-cryptographic). Techniques applicable for comprising and breaching the privacy of genomic data and mitigation methods have been reviewed in [13]. Another article also discussed the genome privacy problem, privacy attacks and mitigation strategies [6]. This study further presented (i) an opinion poll from the biomedical community and (ii) a framework in the context of health care, biomedical research, legal and forensics and DTC services, for the security and privacy of genomic data. Privacy and security problems for sharing, storing and computing on genomic data with related query and output privacy guarantees are presented in [14], and techniques applicable to addressing these problems are reviewed. A categorization of genome privacy problems and their solutions based on sequence alignment and querying private and public genomic databases is presented in [15]. Other surveys have focused on discussing genomic privacy within a specific jurisdiction. For instance, a study discussed the technical and ethical aspects of genomic privacy focused on data sharing for biomedical research in the United States [16]. A recent study proposed a methodology for the categorization of privacy techniques which is then used as a basis for evaluation and critical analysis of challenges confronting the genomic privacy community [17]. In contrast to these useful surveys, our article focuses on (i) inspired by the categorization of privacy breaching techniques presented in [13], we discuss the adversarial goal, background knowledge and inference technique required for each class of attack as presented in Table 1 and (ii) driven from as Table 3, we evaluate and compare privacy-preserving techniques applicable to mitigating these attacks in terms of their security goals (confidentiality, integrity, query privacy, output privacy and adversarial model) and complexities (computation and transmission overheads) that is not addressed in previous surveys. The evaluation criteria (security goals and complexities) we use in this article, we believe are essential in determining the scalability and feasibility of a genomic privacy-preserving technique in a real-life setting. In summary, the goals of this article are as follows:
i We present an overview of current privacy attacks on genomic data and discuss the adversarial background information, inference techniques and predictions required to compromise the privacy of an individual in each attack category.
ii We discuss and compare cryptographic primitives and how their native overheads, strengths and weakness can influence the design of genomic privacy techniques.
iii We classify genomic privacy-preserving techniques based on their biomedical, clinical and research use-cases into genomic aggregation, genome-wide association studies (GWASs) and statistical analysis, sequence comparison and genetic testing, and present a comparative analysis using their underlining cryptographic primitives, security goals and complexities (computation and transmission overheads).
iv We also discuss the challenges, research gaps and future directions in the field of genomic privacy and highlight why they should be addressed.
| Work . | Adversary goal . | Adversary background knowledge . | IT . | IC . |
|---|---|---|---|---|
| Identity tracing attacks | ||||
| Sweeney et al., 2013 [18] | Re-identify participants of the personal genome project | Victim’s demographic data | Demographic data matching | M |
| Gymrek et al., 2013 [19] | Triangulate identity from surnames and Y chromosomes | Victim’s surname, Y-chromosome haplotypes and demographic data | Statistical hypothesis testing | M |
| Shringarpure and Bustamante, 2015 [20] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, SFS of the population in the beacon | Likelihood-ratio test | L |
| Raisaro et al., 2017 [21] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, AFs in the beacon | Likelihood-ratio test | L |
| von Thenen et al., 2018 [22] | Re-identify an individual within a data set in a beacon | VCF files of people from the victim’s population, corresponding MAF and LD and high-order correlation | High-order Markov chain model | H |
| Erlich et al., 2018 [23] | Re-identify an individual by long-range familial search | Victim’s genotype, familial relations, demographic data (location, age and sex) | DNA matching, search space pruning | L |
| Attribute disclosure attacks | ||||
| Homer et al., 2008 [24] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: large set of SNPs (> 10 000) | Statistical testing, distance measure | M |
| Fredrikson et al., 2014 [25] | Infer sensitive genetic markers of an individual from a warfarin dosage pharmacogenetic model | Warfarin dose predicting model, victim’s demographic data and dosage | Model inversion | M |
| Humbert et al., 2015 [26] | Predict an individual’s predisposition to Alzheimer’s disease | Victim’s anonymized genotype and phenotype, SNP-trait association | Statistical methods based on SNP correlation | M |
| Cai et al., 2015 [27] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: small set of SNPs (> 25) | Data mining and matching techniques, deterministic proofs of study inclusion | L |
| Lippert et al., 2017 [28] | Predict an individual’s traits for re-identification | Victim’s genotype and phenotypes | Machine learning methods | H |
| Completion attacks | ||||
| Kong et al., 2008 [29] | Infer haplotypes of ungenotyped individuals from their relatives genetic information | Family members pedigree structure, genotypes (LD between haplotypes) | Genotype imputation, haplotype sharing graph | H |
| Humbert et al., 2013 [10] | Infer an individual’s genotype from their relatives genomes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) | Belief propagation, factor graph | L |
| Humbert et al., 2017 [11] | Infer an individual’s genotype from their relatives genomes and phenotypes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) and phenotypes | Belief propagation, factor graph | L |
| Deznabi et al., 2017 [30] | Reconstruct missing parts of an individual’s genotype | Pedigree structure, victim’s partial genotype (high order correlation between SNPs) and phenotypes | Belief propagation, factor graph | M |
| He et al., 2018 [31] | Predict the genotypes and traits of individuals based on publicly available genome data and traits released by individuals or their relatives | Genotypes and phenotypes of the victim and relatives, and SNP-trait association from GWAS | Belief propagation, factor graph | L |
| Work . | Adversary goal . | Adversary background knowledge . | IT . | IC . |
|---|---|---|---|---|
| Identity tracing attacks | ||||
| Sweeney et al., 2013 [18] | Re-identify participants of the personal genome project | Victim’s demographic data | Demographic data matching | M |
| Gymrek et al., 2013 [19] | Triangulate identity from surnames and Y chromosomes | Victim’s surname, Y-chromosome haplotypes and demographic data | Statistical hypothesis testing | M |
| Shringarpure and Bustamante, 2015 [20] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, SFS of the population in the beacon | Likelihood-ratio test | L |
| Raisaro et al., 2017 [21] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, AFs in the beacon | Likelihood-ratio test | L |
| von Thenen et al., 2018 [22] | Re-identify an individual within a data set in a beacon | VCF files of people from the victim’s population, corresponding MAF and LD and high-order correlation | High-order Markov chain model | H |
| Erlich et al., 2018 [23] | Re-identify an individual by long-range familial search | Victim’s genotype, familial relations, demographic data (location, age and sex) | DNA matching, search space pruning | L |
| Attribute disclosure attacks | ||||
| Homer et al., 2008 [24] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: large set of SNPs (> 10 000) | Statistical testing, distance measure | M |
| Fredrikson et al., 2014 [25] | Infer sensitive genetic markers of an individual from a warfarin dosage pharmacogenetic model | Warfarin dose predicting model, victim’s demographic data and dosage | Model inversion | M |
| Humbert et al., 2015 [26] | Predict an individual’s predisposition to Alzheimer’s disease | Victim’s anonymized genotype and phenotype, SNP-trait association | Statistical methods based on SNP correlation | M |
| Cai et al., 2015 [27] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: small set of SNPs (> 25) | Data mining and matching techniques, deterministic proofs of study inclusion | L |
| Lippert et al., 2017 [28] | Predict an individual’s traits for re-identification | Victim’s genotype and phenotypes | Machine learning methods | H |
| Completion attacks | ||||
| Kong et al., 2008 [29] | Infer haplotypes of ungenotyped individuals from their relatives genetic information | Family members pedigree structure, genotypes (LD between haplotypes) | Genotype imputation, haplotype sharing graph | H |
| Humbert et al., 2013 [10] | Infer an individual’s genotype from their relatives genomes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) | Belief propagation, factor graph | L |
| Humbert et al., 2017 [11] | Infer an individual’s genotype from their relatives genomes and phenotypes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) and phenotypes | Belief propagation, factor graph | L |
| Deznabi et al., 2017 [30] | Reconstruct missing parts of an individual’s genotype | Pedigree structure, victim’s partial genotype (high order correlation between SNPs) and phenotypes | Belief propagation, factor graph | M |
| He et al., 2018 [31] | Predict the genotypes and traits of individuals based on publicly available genome data and traits released by individuals or their relatives | Genotypes and phenotypes of the victim and relatives, and SNP-trait association from GWAS | Belief propagation, factor graph | L |
Notations: H: High; IT: Inference technique; IC: Inference complexity; L: Low; LRT: Likelihood-ratio test; M: Medium; SFS: Site frequency spectrumWe measure the inference complexity (level of hardness to perform) of a technique as a function of the genetic and prior knowledge of the adversary, amount of data processing and molecular techniques involved [13]. Inference technique is of low complexity if adversary has genetic knowledge, adequate prior knowledge with low data processing. Medium complexity techniques require genetic knowledge, adequate prior knowledge and medium data processing. High complexity techniques also require genetic knowledge, adequate/little prior knowledge and large-scale data processing
| Work . | Adversary goal . | Adversary background knowledge . | IT . | IC . |
|---|---|---|---|---|
| Identity tracing attacks | ||||
| Sweeney et al., 2013 [18] | Re-identify participants of the personal genome project | Victim’s demographic data | Demographic data matching | M |
| Gymrek et al., 2013 [19] | Triangulate identity from surnames and Y chromosomes | Victim’s surname, Y-chromosome haplotypes and demographic data | Statistical hypothesis testing | M |
| Shringarpure and Bustamante, 2015 [20] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, SFS of the population in the beacon | Likelihood-ratio test | L |
| Raisaro et al., 2017 [21] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, AFs in the beacon | Likelihood-ratio test | L |
| von Thenen et al., 2018 [22] | Re-identify an individual within a data set in a beacon | VCF files of people from the victim’s population, corresponding MAF and LD and high-order correlation | High-order Markov chain model | H |
| Erlich et al., 2018 [23] | Re-identify an individual by long-range familial search | Victim’s genotype, familial relations, demographic data (location, age and sex) | DNA matching, search space pruning | L |
| Attribute disclosure attacks | ||||
| Homer et al., 2008 [24] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: large set of SNPs (> 10 000) | Statistical testing, distance measure | M |
| Fredrikson et al., 2014 [25] | Infer sensitive genetic markers of an individual from a warfarin dosage pharmacogenetic model | Warfarin dose predicting model, victim’s demographic data and dosage | Model inversion | M |
| Humbert et al., 2015 [26] | Predict an individual’s predisposition to Alzheimer’s disease | Victim’s anonymized genotype and phenotype, SNP-trait association | Statistical methods based on SNP correlation | M |
| Cai et al., 2015 [27] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: small set of SNPs (> 25) | Data mining and matching techniques, deterministic proofs of study inclusion | L |
| Lippert et al., 2017 [28] | Predict an individual’s traits for re-identification | Victim’s genotype and phenotypes | Machine learning methods | H |
| Completion attacks | ||||
| Kong et al., 2008 [29] | Infer haplotypes of ungenotyped individuals from their relatives genetic information | Family members pedigree structure, genotypes (LD between haplotypes) | Genotype imputation, haplotype sharing graph | H |
| Humbert et al., 2013 [10] | Infer an individual’s genotype from their relatives genomes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) | Belief propagation, factor graph | L |
| Humbert et al., 2017 [11] | Infer an individual’s genotype from their relatives genomes and phenotypes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) and phenotypes | Belief propagation, factor graph | L |
| Deznabi et al., 2017 [30] | Reconstruct missing parts of an individual’s genotype | Pedigree structure, victim’s partial genotype (high order correlation between SNPs) and phenotypes | Belief propagation, factor graph | M |
| He et al., 2018 [31] | Predict the genotypes and traits of individuals based on publicly available genome data and traits released by individuals or their relatives | Genotypes and phenotypes of the victim and relatives, and SNP-trait association from GWAS | Belief propagation, factor graph | L |
| Work . | Adversary goal . | Adversary background knowledge . | IT . | IC . |
|---|---|---|---|---|
| Identity tracing attacks | ||||
| Sweeney et al., 2013 [18] | Re-identify participants of the personal genome project | Victim’s demographic data | Demographic data matching | M |
| Gymrek et al., 2013 [19] | Triangulate identity from surnames and Y chromosomes | Victim’s surname, Y-chromosome haplotypes and demographic data | Statistical hypothesis testing | M |
| Shringarpure and Bustamante, 2015 [20] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, SFS of the population in the beacon | Likelihood-ratio test | L |
| Raisaro et al., 2017 [21] | Re-identifying individuals and their relatives within a beacon | VCF file of the victim’s genome, # of individuals in the beacon, AFs in the beacon | Likelihood-ratio test | L |
| von Thenen et al., 2018 [22] | Re-identify an individual within a data set in a beacon | VCF files of people from the victim’s population, corresponding MAF and LD and high-order correlation | High-order Markov chain model | H |
| Erlich et al., 2018 [23] | Re-identify an individual by long-range familial search | Victim’s genotype, familial relations, demographic data (location, age and sex) | DNA matching, search space pruning | L |
| Attribute disclosure attacks | ||||
| Homer et al., 2008 [24] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: large set of SNPs (> 10 000) | Statistical testing, distance measure | M |
| Fredrikson et al., 2014 [25] | Infer sensitive genetic markers of an individual from a warfarin dosage pharmacogenetic model | Warfarin dose predicting model, victim’s demographic data and dosage | Model inversion | M |
| Humbert et al., 2015 [26] | Predict an individual’s predisposition to Alzheimer’s disease | Victim’s anonymized genotype and phenotype, SNP-trait association | Statistical methods based on SNP correlation | M |
| Cai et al., 2015 [27] | Determine the presence of an individual in a GWAS | Victim’s SNP profile, GWAS statistics: small set of SNPs (> 25) | Data mining and matching techniques, deterministic proofs of study inclusion | L |
| Lippert et al., 2017 [28] | Predict an individual’s traits for re-identification | Victim’s genotype and phenotypes | Machine learning methods | H |
| Completion attacks | ||||
| Kong et al., 2008 [29] | Infer haplotypes of ungenotyped individuals from their relatives genetic information | Family members pedigree structure, genotypes (LD between haplotypes) | Genotype imputation, haplotype sharing graph | H |
| Humbert et al., 2013 [10] | Infer an individual’s genotype from their relatives genomes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) | Belief propagation, factor graph | L |
| Humbert et al., 2017 [11] | Infer an individual’s genotype from their relatives genomes and phenotypes | Family members familial relationships, genotypes (LD between SNPs, Minor allele frequencies) and phenotypes | Belief propagation, factor graph | L |
| Deznabi et al., 2017 [30] | Reconstruct missing parts of an individual’s genotype | Pedigree structure, victim’s partial genotype (high order correlation between SNPs) and phenotypes | Belief propagation, factor graph | M |
| He et al., 2018 [31] | Predict the genotypes and traits of individuals based on publicly available genome data and traits released by individuals or their relatives | Genotypes and phenotypes of the victim and relatives, and SNP-trait association from GWAS | Belief propagation, factor graph | L |
Notations: H: High; IT: Inference technique; IC: Inference complexity; L: Low; LRT: Likelihood-ratio test; M: Medium; SFS: Site frequency spectrumWe measure the inference complexity (level of hardness to perform) of a technique as a function of the genetic and prior knowledge of the adversary, amount of data processing and molecular techniques involved [13]. Inference technique is of low complexity if adversary has genetic knowledge, adequate prior knowledge with low data processing. Medium complexity techniques require genetic knowledge, adequate prior knowledge and medium data processing. High complexity techniques also require genetic knowledge, adequate/little prior knowledge and large-scale data processing
| . | . | . | Overheads . | . | . | |||
|---|---|---|---|---|---|---|---|---|
| Technique . | Operations . | HR . | Comp . | Comm . | Storage . | AL . | Advantages . | Limitations . |
| DP [38] | Any operations | Any CPU | M | L | M | H | Provides privacy of individual data within a statistical database, supports any mathematical operation, provides privacy against a computationally unbounded adversary | High accuracy losses, degraded data utility |
| HE [42] | Addition and multiplication | Any CPU | H | M | H | M | Allows computation over encrypted data, provides at most semantic security, ensures input and output privacy of data | Computationally expensive, restricted to addition and multiplication operations, cipher-blow up problems leading to higher storage cost |
| SMC [43] | Boolean operations | Any CPU | M | H | M | M | Allows private computation over multiple parties, provides unconditionally or information-theoretic security, ensures input privacy of data | High data transmission cost, scalability issues |
| SCH [44] | Any operations | Cryptographic coprocessor | L | L | L | L | Efficient computation and communication with negligible accuracy losses, supports any mathematical operation, provides security against malicious adversary, ensures integrity of data | Restricted in memory size which depends on hardware and OS |
| . | . | . | Overheads . | . | . | |||
|---|---|---|---|---|---|---|---|---|
| Technique . | Operations . | HR . | Comp . | Comm . | Storage . | AL . | Advantages . | Limitations . |
| DP [38] | Any operations | Any CPU | M | L | M | H | Provides privacy of individual data within a statistical database, supports any mathematical operation, provides privacy against a computationally unbounded adversary | High accuracy losses, degraded data utility |
| HE [42] | Addition and multiplication | Any CPU | H | M | H | M | Allows computation over encrypted data, provides at most semantic security, ensures input and output privacy of data | Computationally expensive, restricted to addition and multiplication operations, cipher-blow up problems leading to higher storage cost |
| SMC [43] | Boolean operations | Any CPU | M | H | M | M | Allows private computation over multiple parties, provides unconditionally or information-theoretic security, ensures input privacy of data | High data transmission cost, scalability issues |
| SCH [44] | Any operations | Cryptographic coprocessor | L | L | L | L | Efficient computation and communication with negligible accuracy losses, supports any mathematical operation, provides security against malicious adversary, ensures integrity of data | Restricted in memory size which depends on hardware and OS |
Notations: AL: Accuracy loss; Comp: Computation; Comm: Communication; DP: Differential privacy; HE: Homomorphic encryption; HR: Hardware requirement; H: High; L: Low; M: Medium; SMC: Secure multi-party computation; SCH: Secure cryptographic hardware;
| . | . | . | Overheads . | . | . | |||
|---|---|---|---|---|---|---|---|---|
| Technique . | Operations . | HR . | Comp . | Comm . | Storage . | AL . | Advantages . | Limitations . |
| DP [38] | Any operations | Any CPU | M | L | M | H | Provides privacy of individual data within a statistical database, supports any mathematical operation, provides privacy against a computationally unbounded adversary | High accuracy losses, degraded data utility |
| HE [42] | Addition and multiplication | Any CPU | H | M | H | M | Allows computation over encrypted data, provides at most semantic security, ensures input and output privacy of data | Computationally expensive, restricted to addition and multiplication operations, cipher-blow up problems leading to higher storage cost |
| SMC [43] | Boolean operations | Any CPU | M | H | M | M | Allows private computation over multiple parties, provides unconditionally or information-theoretic security, ensures input privacy of data | High data transmission cost, scalability issues |
| SCH [44] | Any operations | Cryptographic coprocessor | L | L | L | L | Efficient computation and communication with negligible accuracy losses, supports any mathematical operation, provides security against malicious adversary, ensures integrity of data | Restricted in memory size which depends on hardware and OS |
| . | . | . | Overheads . | . | . | |||
|---|---|---|---|---|---|---|---|---|
| Technique . | Operations . | HR . | Comp . | Comm . | Storage . | AL . | Advantages . | Limitations . |
| DP [38] | Any operations | Any CPU | M | L | M | H | Provides privacy of individual data within a statistical database, supports any mathematical operation, provides privacy against a computationally unbounded adversary | High accuracy losses, degraded data utility |
| HE [42] | Addition and multiplication | Any CPU | H | M | H | M | Allows computation over encrypted data, provides at most semantic security, ensures input and output privacy of data | Computationally expensive, restricted to addition and multiplication operations, cipher-blow up problems leading to higher storage cost |
| SMC [43] | Boolean operations | Any CPU | M | H | M | M | Allows private computation over multiple parties, provides unconditionally or information-theoretic security, ensures input privacy of data | High data transmission cost, scalability issues |
| SCH [44] | Any operations | Cryptographic coprocessor | L | L | L | L | Efficient computation and communication with negligible accuracy losses, supports any mathematical operation, provides security against malicious adversary, ensures integrity of data | Restricted in memory size which depends on hardware and OS |
Notations: AL: Accuracy loss; Comp: Computation; Comm: Communication; DP: Differential privacy; HE: Homomorphic encryption; HR: Hardware requirement; H: High; L: Low; M: Medium; SMC: Secure multi-party computation; SCH: Secure cryptographic hardware;
| Category . | Scheme . | Architecture . | Cryptographic primitive . | Security . | Efficiency . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| C . | I . | QP . | OP . | AM . | Comp Complexity . | Comm Complexity . | ||||
| Genomic aggregation | Kantarcioglu et al., 2008 [64] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)\textrm {Q}$| | |$O(1)$| |
| Canim et al., 2012 [65] | SO | SCP, AES(CTR mode) | ⬤ | ⬤ | ⃝ | ⬤ | MA | |$O(n/b)\textrm {SE} +O(r)\textrm {Q}$| | |$O(1)$| | |
| Ghasemi et al., 2017 [66] | SO | Paillier encryption | ⬤|$^{\dagger }$| | ⃝ | ⬤ | ⬤ | SH | – | – | |
| Nassar et al., 2017 [67] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(r)\textrm {Q}$| | |$O(1)$| | |
| Hasan et al., 2018 [68] | SO | Paillier encryption, GC | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nk)\textrm {PK} + O(nr)\textrm {BT} + O(\delta )\textrm {Q}$| | |$O(1)$| | |
| GWAS and statistical analysis | Kamm et al., 2013 [70] | SC | SMC, OT, SS | ⬤ | ⃝ | – | ⬤ | SH | |$\gamma (O(n)\textrm {FC} + O(n)\textrm {TE})$| | |$O(\gamma )$| |
| Tramer et al., 2015 [69] | – | DP | ⬤ | ⃝ | – | ⬤ | WA | – | – | |
| Huang et al., 2017 [41] | SO, SC | SMC, GC, DP | ⬤ | ⃝ | – | ⬤ | SH | |$O(nlog^2n)\textrm {OS} + O(n)\textrm {OD}$| | |$O(n)$| | |
| Sadat et al., 2018 [57] | SC | Paillier encryption, SGX | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)$| | |$O(d)O(1)$| | |
| Dan et al., 2018 [71] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PCA}$| | |$O(n)$| | |
| Cho et al., 2018 [49] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(p+n)\textrm {PCA}$| | |$O(p+n)$| | |
| Sequence comparison | Atallah and Li, 2005 [72] | SO | SMC, OT, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PK} + O(n^2)\textrm {CM}$| | |$O(\sigma n^2)$| |
| Jha et al., 2008 [73] | SC | SMC, OT, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤|$^{\dagger }$| | SH | |$O(n^2/\phi ^2)\textrm {CM}$| | |$O(n^2/\phi ^2)$| | |
| Wang et al., 2009b [46] | SC | SMC, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤ | SH | |$O(\rho n^3)\textrm {CM}$| | |$O(\rho n^3)$| | |
| Xu et al., 2014 [54] | SO | AES, HMAC, FPGA | ⬤ | ⬤ | – | – | MA | |$O(n/b)\textrm {SE} + O(1)\textrm {H} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Wang et al., 2017a [78] | SO | Predicate encryption | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {Enc} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Sousa et al., 2017 [77] | SO | SHE, AES, hash | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n/b)\textrm {SE}+O(n)\textrm {H}+O(n)\textrm {Q}$| | |$O(1)$| | |
| Asharov et al., 2017 [74] | SC | GC, OT, SS | ⃝ | ⃝ | ⬤ | – | SH | – | – | |
| Mahdi et al., 2018 [76] | SO | GC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(\Omega )SK + O(nr)BT + O(r)Q$| | |$O(1)$| | |
| Wang and Zhang, 2018 [79] | SO | AOPE, Hash | ⬤ | ⃝ | – | – | SH | |$O(1)\textrm {Enc} + O(logv)\textrm {Dec} +O(n^2)\textrm {CM}$| | |$O(1)$| | |
| Genetic Testing | Troncoso-Pastoriza et al., 2007 [80] | SC | Paillier encryption, SS, OT | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nq\sigma )\textrm {PK} + O(n\sigma )\textrm {MP}$| | |$O(n(q+ \sigma ))$| |
| Bruekers et al., 2008 [48] | SC | SMC, hash, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(nk)\textrm {PK} +O(n-t)\textrm {CM}$| | |$O(n^{t})\textrm {IT};O(n^{t+1}) [\textrm {PT,AT}]$| | |
| McLaren et al., 2016 [81] | SO | Paillier encryption, SMC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {PK} + O(n/b)\textrm {SE}$| + |$O(n)\textrm {CM} + O(n)\textrm {MP}$| | |$O(m)$| | |
| Jagadeesh et al., 2017 [62] | SO, SC | SMC, OT, GC | ⬤ | ⃝ | – | ⬤|$^{\dagger }$| | SH | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | |
| Blanton and Bayatbabolghani, 2017 [47] | SC | SMC, Hash, OT | ⬤ | ⬤ | – | – | SH | |$O(n)\textrm {CM} + O(n)\textrm {H}$| | |$O(n)$| | |
| Chen et al., 2017 [56] | SO | SGX, AES-GCMElliptic Curve DS | ⬤ | ⬤ | ⬤ | – | MA | |$O(n/b)\textrm {SE} + O(r)\textrm {H}$| + |$O(1)\textrm {Q}$| | |$O(1)$| | |
| Category . | Scheme . | Architecture . | Cryptographic primitive . | Security . | Efficiency . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| C . | I . | QP . | OP . | AM . | Comp Complexity . | Comm Complexity . | ||||
| Genomic aggregation | Kantarcioglu et al., 2008 [64] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)\textrm {Q}$| | |$O(1)$| |
| Canim et al., 2012 [65] | SO | SCP, AES(CTR mode) | ⬤ | ⬤ | ⃝ | ⬤ | MA | |$O(n/b)\textrm {SE} +O(r)\textrm {Q}$| | |$O(1)$| | |
| Ghasemi et al., 2017 [66] | SO | Paillier encryption | ⬤|$^{\dagger }$| | ⃝ | ⬤ | ⬤ | SH | – | – | |
| Nassar et al., 2017 [67] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(r)\textrm {Q}$| | |$O(1)$| | |
| Hasan et al., 2018 [68] | SO | Paillier encryption, GC | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nk)\textrm {PK} + O(nr)\textrm {BT} + O(\delta )\textrm {Q}$| | |$O(1)$| | |
| GWAS and statistical analysis | Kamm et al., 2013 [70] | SC | SMC, OT, SS | ⬤ | ⃝ | – | ⬤ | SH | |$\gamma (O(n)\textrm {FC} + O(n)\textrm {TE})$| | |$O(\gamma )$| |
| Tramer et al., 2015 [69] | – | DP | ⬤ | ⃝ | – | ⬤ | WA | – | – | |
| Huang et al., 2017 [41] | SO, SC | SMC, GC, DP | ⬤ | ⃝ | – | ⬤ | SH | |$O(nlog^2n)\textrm {OS} + O(n)\textrm {OD}$| | |$O(n)$| | |
| Sadat et al., 2018 [57] | SC | Paillier encryption, SGX | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)$| | |$O(d)O(1)$| | |
| Dan et al., 2018 [71] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PCA}$| | |$O(n)$| | |
| Cho et al., 2018 [49] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(p+n)\textrm {PCA}$| | |$O(p+n)$| | |
| Sequence comparison | Atallah and Li, 2005 [72] | SO | SMC, OT, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PK} + O(n^2)\textrm {CM}$| | |$O(\sigma n^2)$| |
| Jha et al., 2008 [73] | SC | SMC, OT, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤|$^{\dagger }$| | SH | |$O(n^2/\phi ^2)\textrm {CM}$| | |$O(n^2/\phi ^2)$| | |
| Wang et al., 2009b [46] | SC | SMC, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤ | SH | |$O(\rho n^3)\textrm {CM}$| | |$O(\rho n^3)$| | |
| Xu et al., 2014 [54] | SO | AES, HMAC, FPGA | ⬤ | ⬤ | – | – | MA | |$O(n/b)\textrm {SE} + O(1)\textrm {H} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Wang et al., 2017a [78] | SO | Predicate encryption | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {Enc} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Sousa et al., 2017 [77] | SO | SHE, AES, hash | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n/b)\textrm {SE}+O(n)\textrm {H}+O(n)\textrm {Q}$| | |$O(1)$| | |
| Asharov et al., 2017 [74] | SC | GC, OT, SS | ⃝ | ⃝ | ⬤ | – | SH | – | – | |
| Mahdi et al., 2018 [76] | SO | GC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(\Omega )SK + O(nr)BT + O(r)Q$| | |$O(1)$| | |
| Wang and Zhang, 2018 [79] | SO | AOPE, Hash | ⬤ | ⃝ | – | – | SH | |$O(1)\textrm {Enc} + O(logv)\textrm {Dec} +O(n^2)\textrm {CM}$| | |$O(1)$| | |
| Genetic Testing | Troncoso-Pastoriza et al., 2007 [80] | SC | Paillier encryption, SS, OT | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nq\sigma )\textrm {PK} + O(n\sigma )\textrm {MP}$| | |$O(n(q+ \sigma ))$| |
| Bruekers et al., 2008 [48] | SC | SMC, hash, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(nk)\textrm {PK} +O(n-t)\textrm {CM}$| | |$O(n^{t})\textrm {IT};O(n^{t+1}) [\textrm {PT,AT}]$| | |
| McLaren et al., 2016 [81] | SO | Paillier encryption, SMC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {PK} + O(n/b)\textrm {SE}$| + |$O(n)\textrm {CM} + O(n)\textrm {MP}$| | |$O(m)$| | |
| Jagadeesh et al., 2017 [62] | SO, SC | SMC, OT, GC | ⬤ | ⃝ | – | ⬤|$^{\dagger }$| | SH | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | |
| Blanton and Bayatbabolghani, 2017 [47] | SC | SMC, Hash, OT | ⬤ | ⬤ | – | – | SH | |$O(n)\textrm {CM} + O(n)\textrm {H}$| | |$O(n)$| | |
| Chen et al., 2017 [56] | SO | SGX, AES-GCMElliptic Curve DS | ⬤ | ⬤ | ⬤ | – | MA | |$O(n/b)\textrm {SE} + O(r)\textrm {H}$| + |$O(1)\textrm {Q}$| | |$O(1)$| | |
Notations: & AES: Advanced encryption standard; AM: Adversarial Model; AOPE: Additive order preserving encryption; AT: Ancestry test; BT: Building tree operation; |$b$|: Data block size used in AES; C: Confidentiality; Comp: Computation; Comm: Communication; CM: Sequence comparison operation; DP: Differential privacy; Dec: Decryption function; |$d$|: number of data owners; Enc: Encryption function; FC: Allele frequency counting; FPGA: Field-programmable gate array; GC: Garbled circuit; H: Hash operation; HE: Homomorphic encryption; I: Integrity; IT: Identity test; |$m$|: # of iterations in an interactive protocol; MA: Malicious; Max: Maximum operation; MP: Muliplication operation; |$n$|: Sequence length; OT: Oblivious transfer; OS: Oblivious sorting; OD: Oblivious de-duplication; P1,2,3: Protocol 1,2, 3; |$p$|: # of study participants; PCA: Principal component analysis; PK: Public key encryption operation; PT: Paternity test; Q: Genomic query operation; |$q$|: # of finite automata state; QP: Query Privacy; |$r$|: # of records in genomic dataset; SE: Symmetric key encryption operation; SM: Semi-honest; SMC: Secure multi-party computation; SHE: Somewhat homomorphic encryption; SS: Secret sharing; SO: Secure outsourcing; SC: Secure collaboration; TE: GWAS test evaluation; |$t$|: # of tolerable matching errors; |$v$|: maximum plaintext value; WA: Weak adversary; |$\delta$|: depth of index tree; |$\Omega$|: # of tree nodes; |$\gamma$|: # of secret shares
| Category . | Scheme . | Architecture . | Cryptographic primitive . | Security . | Efficiency . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| C . | I . | QP . | OP . | AM . | Comp Complexity . | Comm Complexity . | ||||
| Genomic aggregation | Kantarcioglu et al., 2008 [64] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)\textrm {Q}$| | |$O(1)$| |
| Canim et al., 2012 [65] | SO | SCP, AES(CTR mode) | ⬤ | ⬤ | ⃝ | ⬤ | MA | |$O(n/b)\textrm {SE} +O(r)\textrm {Q}$| | |$O(1)$| | |
| Ghasemi et al., 2017 [66] | SO | Paillier encryption | ⬤|$^{\dagger }$| | ⃝ | ⬤ | ⬤ | SH | – | – | |
| Nassar et al., 2017 [67] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(r)\textrm {Q}$| | |$O(1)$| | |
| Hasan et al., 2018 [68] | SO | Paillier encryption, GC | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nk)\textrm {PK} + O(nr)\textrm {BT} + O(\delta )\textrm {Q}$| | |$O(1)$| | |
| GWAS and statistical analysis | Kamm et al., 2013 [70] | SC | SMC, OT, SS | ⬤ | ⃝ | – | ⬤ | SH | |$\gamma (O(n)\textrm {FC} + O(n)\textrm {TE})$| | |$O(\gamma )$| |
| Tramer et al., 2015 [69] | – | DP | ⬤ | ⃝ | – | ⬤ | WA | – | – | |
| Huang et al., 2017 [41] | SO, SC | SMC, GC, DP | ⬤ | ⃝ | – | ⬤ | SH | |$O(nlog^2n)\textrm {OS} + O(n)\textrm {OD}$| | |$O(n)$| | |
| Sadat et al., 2018 [57] | SC | Paillier encryption, SGX | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)$| | |$O(d)O(1)$| | |
| Dan et al., 2018 [71] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PCA}$| | |$O(n)$| | |
| Cho et al., 2018 [49] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(p+n)\textrm {PCA}$| | |$O(p+n)$| | |
| Sequence comparison | Atallah and Li, 2005 [72] | SO | SMC, OT, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PK} + O(n^2)\textrm {CM}$| | |$O(\sigma n^2)$| |
| Jha et al., 2008 [73] | SC | SMC, OT, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤|$^{\dagger }$| | SH | |$O(n^2/\phi ^2)\textrm {CM}$| | |$O(n^2/\phi ^2)$| | |
| Wang et al., 2009b [46] | SC | SMC, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤ | SH | |$O(\rho n^3)\textrm {CM}$| | |$O(\rho n^3)$| | |
| Xu et al., 2014 [54] | SO | AES, HMAC, FPGA | ⬤ | ⬤ | – | – | MA | |$O(n/b)\textrm {SE} + O(1)\textrm {H} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Wang et al., 2017a [78] | SO | Predicate encryption | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {Enc} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Sousa et al., 2017 [77] | SO | SHE, AES, hash | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n/b)\textrm {SE}+O(n)\textrm {H}+O(n)\textrm {Q}$| | |$O(1)$| | |
| Asharov et al., 2017 [74] | SC | GC, OT, SS | ⃝ | ⃝ | ⬤ | – | SH | – | – | |
| Mahdi et al., 2018 [76] | SO | GC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(\Omega )SK + O(nr)BT + O(r)Q$| | |$O(1)$| | |
| Wang and Zhang, 2018 [79] | SO | AOPE, Hash | ⬤ | ⃝ | – | – | SH | |$O(1)\textrm {Enc} + O(logv)\textrm {Dec} +O(n^2)\textrm {CM}$| | |$O(1)$| | |
| Genetic Testing | Troncoso-Pastoriza et al., 2007 [80] | SC | Paillier encryption, SS, OT | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nq\sigma )\textrm {PK} + O(n\sigma )\textrm {MP}$| | |$O(n(q+ \sigma ))$| |
| Bruekers et al., 2008 [48] | SC | SMC, hash, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(nk)\textrm {PK} +O(n-t)\textrm {CM}$| | |$O(n^{t})\textrm {IT};O(n^{t+1}) [\textrm {PT,AT}]$| | |
| McLaren et al., 2016 [81] | SO | Paillier encryption, SMC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {PK} + O(n/b)\textrm {SE}$| + |$O(n)\textrm {CM} + O(n)\textrm {MP}$| | |$O(m)$| | |
| Jagadeesh et al., 2017 [62] | SO, SC | SMC, OT, GC | ⬤ | ⃝ | – | ⬤|$^{\dagger }$| | SH | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | |
| Blanton and Bayatbabolghani, 2017 [47] | SC | SMC, Hash, OT | ⬤ | ⬤ | – | – | SH | |$O(n)\textrm {CM} + O(n)\textrm {H}$| | |$O(n)$| | |
| Chen et al., 2017 [56] | SO | SGX, AES-GCMElliptic Curve DS | ⬤ | ⬤ | ⬤ | – | MA | |$O(n/b)\textrm {SE} + O(r)\textrm {H}$| + |$O(1)\textrm {Q}$| | |$O(1)$| | |
| Category . | Scheme . | Architecture . | Cryptographic primitive . | Security . | Efficiency . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| C . | I . | QP . | OP . | AM . | Comp Complexity . | Comm Complexity . | ||||
| Genomic aggregation | Kantarcioglu et al., 2008 [64] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)\textrm {Q}$| | |$O(1)$| |
| Canim et al., 2012 [65] | SO | SCP, AES(CTR mode) | ⬤ | ⬤ | ⃝ | ⬤ | MA | |$O(n/b)\textrm {SE} +O(r)\textrm {Q}$| | |$O(1)$| | |
| Ghasemi et al., 2017 [66] | SO | Paillier encryption | ⬤|$^{\dagger }$| | ⃝ | ⬤ | ⬤ | SH | – | – | |
| Nassar et al., 2017 [67] | SO | Paillier encryption | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(r)\textrm {Q}$| | |$O(1)$| | |
| Hasan et al., 2018 [68] | SO | Paillier encryption, GC | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nk)\textrm {PK} + O(nr)\textrm {BT} + O(\delta )\textrm {Q}$| | |$O(1)$| | |
| GWAS and statistical analysis | Kamm et al., 2013 [70] | SC | SMC, OT, SS | ⬤ | ⃝ | – | ⬤ | SH | |$\gamma (O(n)\textrm {FC} + O(n)\textrm {TE})$| | |$O(\gamma )$| |
| Tramer et al., 2015 [69] | – | DP | ⬤ | ⃝ | – | ⬤ | WA | – | – | |
| Huang et al., 2017 [41] | SO, SC | SMC, GC, DP | ⬤ | ⃝ | – | ⬤ | SH | |$O(nlog^2n)\textrm {OS} + O(n)\textrm {OD}$| | |$O(n)$| | |
| Sadat et al., 2018 [57] | SC | Paillier encryption, SGX | ⬤ | ⃝ | ⃝ | ⬤ | SH | |$O(nk)\textrm {PK}+O(n)$| | |$O(d)O(1)$| | |
| Dan et al., 2018 [71] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PCA}$| | |$O(n)$| | |
| Cho et al., 2018 [49] | SC | SMC, SS | ⬤ | ⃝ | – | ⬤ | SH | |$O(p+n)\textrm {PCA}$| | |$O(p+n)$| | |
| Sequence comparison | Atallah and Li, 2005 [72] | SO | SMC, OT, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(n^2)\textrm {PK} + O(n^2)\textrm {CM}$| | |$O(\sigma n^2)$| |
| Jha et al., 2008 [73] | SC | SMC, OT, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤|$^{\dagger }$| | SH | |$O(n^2/\phi ^2)\textrm {CM}$| | |$O(n^2/\phi ^2)$| | |
| Wang et al., 2009b [46] | SC | SMC, GC | ⬤|$^{\dagger }$| | ⃝ | – | ⬤ | SH | |$O(\rho n^3)\textrm {CM}$| | |$O(\rho n^3)$| | |
| Xu et al., 2014 [54] | SO | AES, HMAC, FPGA | ⬤ | ⬤ | – | – | MA | |$O(n/b)\textrm {SE} + O(1)\textrm {H} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Wang et al., 2017a [78] | SO | Predicate encryption | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {Enc} + O(n)\textrm {Q}$| | |$O(1)$| | |
| Sousa et al., 2017 [77] | SO | SHE, AES, hash | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n/b)\textrm {SE}+O(n)\textrm {H}+O(n)\textrm {Q}$| | |$O(1)$| | |
| Asharov et al., 2017 [74] | SC | GC, OT, SS | ⃝ | ⃝ | ⬤ | – | SH | – | – | |
| Mahdi et al., 2018 [76] | SO | GC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(\Omega )SK + O(nr)BT + O(r)Q$| | |$O(1)$| | |
| Wang and Zhang, 2018 [79] | SO | AOPE, Hash | ⬤ | ⃝ | – | – | SH | |$O(1)\textrm {Enc} + O(logv)\textrm {Dec} +O(n^2)\textrm {CM}$| | |$O(1)$| | |
| Genetic Testing | Troncoso-Pastoriza et al., 2007 [80] | SC | Paillier encryption, SS, OT | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(nq\sigma )\textrm {PK} + O(n\sigma )\textrm {MP}$| | |$O(n(q+ \sigma ))$| |
| Bruekers et al., 2008 [48] | SC | SMC, hash, HE | ⬤ | ⃝ | – | ⬤ | SH | |$O(nk)\textrm {PK} +O(n-t)\textrm {CM}$| | |$O(n^{t})\textrm {IT};O(n^{t+1}) [\textrm {PT,AT}]$| | |
| McLaren et al., 2016 [81] | SO | Paillier encryption, SMC, AES | ⬤ | ⃝ | ⬤ | ⬤ | SH | |$O(n)\textrm {PK} + O(n/b)\textrm {SE}$| + |$O(n)\textrm {CM} + O(n)\textrm {MP}$| | |$O(m)$| | |
| Jagadeesh et al., 2017 [62] | SO, SC | SMC, OT, GC | ⬤ | ⃝ | – | ⬤|$^{\dagger }$| | SH | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | P1. Max: |$O(logp)$| P2. Diff: |$O(logp)$| P3. CM: |$O(n)$| | |
| Blanton and Bayatbabolghani, 2017 [47] | SC | SMC, Hash, OT | ⬤ | ⬤ | – | – | SH | |$O(n)\textrm {CM} + O(n)\textrm {H}$| | |$O(n)$| | |
| Chen et al., 2017 [56] | SO | SGX, AES-GCMElliptic Curve DS | ⬤ | ⬤ | ⬤ | – | MA | |$O(n/b)\textrm {SE} + O(r)\textrm {H}$| + |$O(1)\textrm {Q}$| | |$O(1)$| | |
Notations: & AES: Advanced encryption standard; AM: Adversarial Model; AOPE: Additive order preserving encryption; AT: Ancestry test; BT: Building tree operation; |$b$|: Data block size used in AES; C: Confidentiality; Comp: Computation; Comm: Communication; CM: Sequence comparison operation; DP: Differential privacy; Dec: Decryption function; |$d$|: number of data owners; Enc: Encryption function; FC: Allele frequency counting; FPGA: Field-programmable gate array; GC: Garbled circuit; H: Hash operation; HE: Homomorphic encryption; I: Integrity; IT: Identity test; |$m$|: # of iterations in an interactive protocol; MA: Malicious; Max: Maximum operation; MP: Muliplication operation; |$n$|: Sequence length; OT: Oblivious transfer; OS: Oblivious sorting; OD: Oblivious de-duplication; P1,2,3: Protocol 1,2, 3; |$p$|: # of study participants; PCA: Principal component analysis; PK: Public key encryption operation; PT: Paternity test; Q: Genomic query operation; |$q$|: # of finite automata state; QP: Query Privacy; |$r$|: # of records in genomic dataset; SE: Symmetric key encryption operation; SM: Semi-honest; SMC: Secure multi-party computation; SHE: Somewhat homomorphic encryption; SS: Secret sharing; SO: Secure outsourcing; SC: Secure collaboration; TE: GWAS test evaluation; |$t$|: # of tolerable matching errors; |$v$|: maximum plaintext value; WA: Weak adversary; |$\delta$|: depth of index tree; |$\Omega$|: # of tree nodes; |$\gamma$|: # of secret shares
The remainder of this paper is organized as follows: Privacy attacks on genomic data presents the most relevant current privacy attacks on genomic data which are categorized into identity tracing, attribute disclosure and completion attacks. Cryptographic primitives and System model and architecture discuss the cryptographic building blocks and security goals and systems architecture employed in protecting genomic data, respectively. Secure techniques for genomic data surveys state-of-the-art genomic privacy-preserving solutions and compares them in terms of application domain and complexities—computation and transmission. Open issues and challenges in genomic privacy research domain are presented in Open issues and challenges and the work is concluded in Conclusion.
Privacy attacks on genomic data
The privacy risk presented in the introduction of this paper together with some real-life privacy comprising scenarios on genomic data discussed in [6] have motivated the cryptographic and bioinformatic research community to dedicate an area of research with the aim of better understanding the privacy risks related to genomic data. In this area, researchers quantify privacy loss and explore attacks on genomic data by modeling attacker behaviors as they would have occurred in real life. A privacy attack occurs when an adversary compromises the privacy of an individual by exploiting sensitive information inferred from his/her DNA for purposes such as personal gain, blackmail, to alter evidence in the case of forensics to be used in the court of law or some other dubious reasons. The adversary in this context uses public information (e.g. genomic and phenotypic data, demographic data, genealogy and family pedigree) gathered from genome-sharing websites (e.g. PatientsLikeMe and OpenSNP) and online social networks (OSNs) to (i) triangulate the identity of an individual, (ii) infer sensitive attributes such as disease and drug abuse or (iii) reconstruct an individual’s genetic sequence from partially available DNA data. In the rest of this section, we briefly discuss privacy attacks on genomic data which we categorize into the three most relevant attack types—identity tracing attacks, attribute disclosure attacks and completion attacks. We present the current state-of-the-art attacks on the privacy and security of genomic data in Table 1 and represent a taxonomy of the attacks in Figure 1 that depicts the background information and techniques required to launch each attack. In this and coming sections, we use ‘victim’ to refer to the individual whose genome is comprised and ‘adversary’ to indicate the individual carrying out the attack.
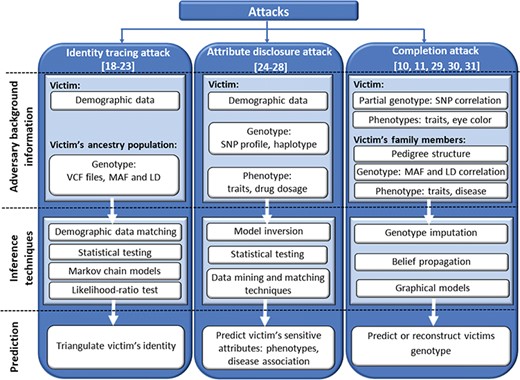
Taxonomy of genomic privacy attacks. A typical genomic privacy attack (identity tracings, attribute disclosure and completion attacks) involves three steps. First, the adversary acquires background information about the victim and his/her family members if required. The adversary then applies inference techniques and finally predicts the identity or disease associations of the victim.
Identity tracing attacks
An identity tracing attack occurs when an adversary obtains an anonymized or de-identified DNA and identifies the owner by using publicly available quasi-identifiers (age, sex, surname, zip code, etc.) obtained from social media or public record search portals such as PeopleSmart and FindOutTheTruth [13]. This was demonstrated in a study where participants of the Personal Genome Project were re-identified using demographic data—birth dates, sex, zip code [18]. Another study discovered that an adversary can infer surnames from Y chromosomes acquired from genealogical websites, e.g. Ysearch (www.ysearch.org) and SMGF (www.smgf.org) [19]. These surnames were then combined with other types of metadata, such as age and state, to triangulate the identity of the victim.
Amongst their goals to drive the agenda for secure genomic data sharing, the global alliance for genomics and health (GA4GH), which creates policies and standards for the secure sharing of genomic data, initiated a project called beacon. A beacon is a web service that allows institutions to implement and securely share genetic data and answer queries such as ‘Do you have an allele at a specific position in a genome?’ and respond with a ‘Yes’ or ‘No’ [32]. The security goal of the beacon is to make it difficult for an adversary to re-identify an individual within a data set. However, recent studies have demonstrated that beacons are more vulnerable than expected and have highlighted the severity of the genomic privacy risk [20, 22]. These studies launched an attack to re-identify an individual by querying the beacon and inferring the results and alleles at certain positions. A recent study [21] further examined the risk associated with beacons and the attack proposed in [20]. This study proposed an attack that considers an adversary with some background knowledge about the allele frequencies (AFs) in the targeted beacon and as a result yields a higher re-identification power than [20]. In addition to re-identification, data sets with disease(s) associations make it possible to infer the victim’s disease status. In forensics, crime solving has been enhanced by identifying and tracing suspects via distant familial relatives. The suspect’s distant genetic relatives are acquired by looking up his genome-wide profile against a public third-party consumer genealogy service provider such as GEDmatch. A recent study demonstrated that such techniques could be exploited by an adversary to comprise the privacy of an individual by using demographic information such as location, age and sex [23].
Attribute disclosure attacks
The goal of the adversary in attribute disclosure attacks is to predict sensitive attributes of the victim, such as phenotypes, disease association and drug abuse. In this attack, the DNA sample of the victim is known and the adversary matches it against public genetic study databases or published GWAS results and statistics [13].
Summary statistics have long been thought to conceal the identity and associated phenotypes of GWAS participants. However, research within the past decade has proved this notion to be incorrect. One of the first work to demonstrate vulnerabilities in aggregate statistics showed that an adversary with access to the victim’s SNP profile can infer the presence of the victim in a case group of a GWAS study from AFs of a large set of single-nucleotide polymorphisms (SNPs). A recent study in this line of research also exploited summary statistics by using AFs to determine an individual’s presence in a GWAS and hence their disease status [27]. This study also showed that an adversary can yield higher prediction confidence with a smaller set of SNPs (|$>25$| SNPs) as opposed to past studies [24, 33] which required large amounts of SNP data (|$>10\thinspace 000$| SNPs and |$>200$| SNPs) to make a prediction. In addition to exploiting GWAS statistics for disease prediction, visible phenotypic traits such as eye color can be linked to public genomic databases to re-identify an individual’s genotype and subsequently infer disease associations. This was proven in a study where researchers used visible phenotypic traits to infer an individual’s predisposition to Alzheimer’s disease [26]. In another study, authors proposed a technique for predicting multiple phenotypic traits (face, voice, age, height, weight, BMI, eye color and skin color) from whole genome sequenced (WGS) data [28]. These predictions (combination of multiple DNA-based predictive models) were later used to re-identify individuals from a subset of their study cohort with good accuracies reported. However, these findings received criticisms from fellow researchers in the field. An example of such critiques argued that face structure inference is driven by population averages and not from trait-specific markers [34]. They further demonstrated a base-line re-identification procedure with similar accuracy as [28] that relies on low dimensional demographic information: age, sex and self-reported ethnicity that are expected to be available to the adversary as opposed to some phenotypic data (high-dimensional trait) used in [28] which might not be available to the adversary.
In a personalized medicine application where machine learning models (pharmacogenetic models) are trained to predict warfarin dosage, researchers have proven that sensitive information leaked by the models can be used to launch an attack to infer the sensitive genetic markers of an individual as well as some demographic data—age, race, height and weight [25].
Completion attacks
Completion attack is the application of techniques such as genotype imputation to reconstruct the victim’s genetic information from partially available DNA data or a family member’s DNA sequence [13, 35]. Studies have demonstrated that this attack is commonly used to breach kin privacy where the privacy of the victim is comprised by exploiting the genetic information of his family members obtained from public online resources: OSNs, genome-sharing websites (e.g. OpenSNP, 23andMe and PatientsLikeMe) and genealogical data repositories [10]. This is possible because of the high correlation of genomic data between family members that leads to interdependent privacy risks. This has been demonstrated in a study where by observing the genome of an individual, it is possible to reconstruct the genomes of relatives using statistical relationships (pairwise correlation) between DNA sequences [10]. An extension to this work improved the inference power by adding additional background information of the relatives phenotypes [11]. Another study [30] to improve the inference attack in [10] considered complex correlation in the genome as opposed to pairwise correlation used in [10]. In addition to the aforementioned reconstruction attacks, a recent study also predicted the victim’s genotypes and phenotypes [31]. This technique, however, yielded low computation complexity as compared to previous studies.
The above discussed attacks have relied on SNP correlations for inference, however, it is possible to reconstruct a victim’s genome by observing identical regions of the DNA sequence between his relatives. In a study to demonstrate this haplotypes for individuals who are not genotyped are identified by observing DNA regions that are identical by descent between their close and distant relatives [29].
Cryptographic primitives
Cryptographic primitives are low-level cryptographic algorithms used to build cryptographic systems to provide information security. There are several primitives in the cryptographic literature; however, in this section we discuss only those that are relevant and have been used to secure genomic data for storage and computation. Categorization of these techniques are illustrated in Figure 2. In this and coming sections, we use ‘efficiency’ to refer to computation and communication complexities.

Categorization of cryptographic primitives applied in literature to secure genomic data.
Differential privacy (DP)
where |$\varepsilon$| is the privacy parameter which in most cases is achieved by adding random noise to the output |$S$|. The addition of noise reduces the accuracy of the computation. As a result, there is often a trade-off between the privacy and utility (useful outputs) of the data. In applications where GWAS is used to understand the correlation between genetic regions (loci) and drug response/reactions for the purpose of advancing pharmacogenomics, accuracy is critical and should not be compromised [39]. Recent studies have discussed ways to approach this trade-off to yield near accurate results [40, 41]. However, the issue of accuracy is still an active research area and there is still a need to find the right balance between computational efficiency, privacy loss and the statistical utility of perturbed P-values, |$\chi ^2$|-statistics, MAFs etc.
Homomorphic encryption (HE)
An encryption scheme can be homomorphic on addition or multiplication depending on whether |$\circ _{p}$| is the addition or multiplication operator. Based on the operations that can be computed of their encrypted data, HE techniques can be categorized into (i) partially HE—allows either addition or multiplication, (ii) somewhat HE—allows both addition and multiplication but limited in number of computation times and (iii) fully HE—supports both addition and multiplication for unlimited number of computations. A detailed discussion on these categories is beyond the scope of this article and can be found at [42]. In preserving the privacy of genomic data, HE is useful when data owners want to outsource their data to a public cloud while allowing certain computations such as paternity tests and disease risk tests to be carried out on encrypted SNPs, haplotypes or short tandem repeats (STRs).
Secure multi-party computation (SMC)
SMC is used in a setting where multiple parties |$P_{1}, P_{2},..., P_{n}$| need to collaborate to compute a function |$f(.)$| on their data |$D_{1}, D_{2},..., D_{n}$| while keeping them private except for the computation result |$f(D_{1}, D_{2},..., D_{n})$|.
The most popular way of implementing SMC is using garbled circuit (GC) which was first introduced by Yao [45]. The GC implementation expresses the function |$f(.)$| as a Boolean circuit (a collection of gates) where computation is performed for each gate that involves multiple rounds of communication between parties. Generally speaking, this protocol is expensive in communication for genomic data which often has millions of nucleotides, i.e. the number of iterations is linear to the sequence length. SMC-based privacy-preserving techniques for processing genomic data usually employ a two-party computation case to tackle simple tasks such as sequence comparisons, genetic testing and GWASs, yet they have not been able to get around the complexity issues [41, 46, 47]. Other efficient implementations of SMC have used HEs and secret sharing in place of the expensive GC computations [48, 49].
Secure cryptographic hardware (SCH)
SCH uses hardware to complement software for data encryption and protection. It is most often implemented as part of the processors instruction set and comes in the form of cryptographic coprocessors, accelerators, chip cards, smart cards etc. The following are well-known implementation of SCH:
Software Guard Extensions (SGX) [50, 51]: SGX was introduced in 2015 by Intel as an extension to its 6th generation of core microprocessors. It allows an application to execute code and protect data within its own trusted execution environment —a secure container called an enclave. Contents of the enclave are sealed and protected against external software such as malicious software (privileged malware) and privileged software (virtual machine monitors, BIOS or operating systems).
ARM TrustZone [52]: TrustZone is a security extension provided by ARM in some of their processors (ARM1176, Cortex-A series, v8-M architecture) which creates two environments (a secure world and non-secure world) that can run simultaneously on a single core. The secure world provides confidentiality and integrity to high-value code and data such as cryptographic operations.
IBM cryptographic coprocessor [44]: This is a hardware security module consisting of a microprocessor, memory, special cryptographic hardware and a random number generator contained in a tamper resistant box. It provides a secure environment where data and cryptographic functions are processed and sealed from the rest of the server.
Field-programmable gate array (FPGA) [53]: FPGA is a re-programmable integrated circuit that allows customers to tailor it to their needs. Similar to the SGX and IBM cryptographic coprocessor, FPGAs also have the capability of isolating the computation from the rest of the server.
Using SCH comes with benefits such as (i) it is more efficient than traditional cryptographic methods, (ii) it can compute any arbitrary function as opposed to HE techniques which are limited to addition and multiplication and (iii) it is tamper resistant. Due to these advantages, they have been used to implement efficient and tamper-resistant secure genomic techniques [54–57]. They are, however, restricted in memory size especially for processing genomic data with millions of nucleotides.
Choosing the right cryptographic primitives
The selection of an encryption technique to protect the privacy of genomic data is vital in determining the scalability and feasibility of an application. The criteria for selection depends on a number of factors such as overheads (computation and communication) incurred by the cryptosystem, arithmetic operations and computational task supported by the encryption technique (e.g. linear operations are supported by HE, whilst comparison operations can be accomplished with SMC), the genomic application use-case, the security requirements and threat model for the given scenario. It is noteworthy to mention that one or more encryption techniques can be combined to complement each other in a given framework. For instance, (i) in a genetic testing application where disease markers are tested and compared against encrypted genomes, HE is used for linear computation on encrypted data whilst SMC is utilized for comparisons [48] and (ii) DP has been combined with SMC to hide GWAS participants for the secure computation of meta-analysis [41]. We present a comparison of the various cryptographic primitives discussed in this Section in Table 2. We compare their overhead in terms of (i) computation time: the time taken to encrypt and decrypt a genome sequence [58], (ii) communication overhead: the amount of data bits transferred between parties in the cryptographic protocol [58], (iii) storage overhead: storage overhead or blowup is estimated as the difference in size between the encrypted data and its original plaintext version [58]. In designing techniques to protect genomic data, storage overhead needs to be minimized as the size of a human sequenced genome can be approximately 200GB depending on the coverage, number of reads and read length. Most encryption schemes, after converting data from plaintext to ciphertext increase the size of the ciphertext and as such, the resulting encrypted genome requires more space (|$>200$|GB) than its plaintext version. This is as a result of using larger encryption keys within a Galois field (finite field) and (iv) accuracy loss: the percentage of error margin between the results of plaintext genomic computations and its secure version [58], i.e. |$\frac {e}{G(D)}\times 100$|, where |$e$| is the error margin and |$G(D)$| is the plaintext genomic computation function on sequence data |$D$|. In DP applications, the amount of accuracy loss is dependent on the privacy parameter |$\varepsilon$| in Equation 3.1. Smaller |$\varepsilon$| means higher accuracy loss (higher noise variance) and stronger privacy and vice versa. This often depends on trade-off between data privacy and utility. There are techniques on minimizing accuracy loss in DP. This however is a broad area and outside the scope of this article. We refer the reader to [38, 59]. Table 2 also presents the operations they support, the hardware requirement for their implementation and some limitations. We believe this will assist researchers in choosing the right cryptographic primitive/s when securing genomic data.
System model and architecture
In this section, we discuss the architectural framework types and models applicable to protecting genomic data.
System architecture
In the genomic privacy literature, secure genomic techniques are built based on either of the following architectural or system models [60, 61].
Secure outsourcing: In this architecture, as shown in Figure 3, the data owner (e.g. a hospital or a research facility) is limited in resources and wants to securely outsource the storage and computation of genomic data to a third-party cloud (e.g. Google Genomics) while making data available to other stakeholders such as pharmaceutical companies and research labaratories. HE is mostly used in this architectural framework where computation is performed on encrypted data in the cloud.

System architectures adopted for protecting genomic data. (Left) Secure outsourcing: data owner delegates storage and computation of genomic data to an untrusted third party. Step 1—data owner (DO) acquires encryption keys from a trusted authority (TA). The role of TA could be played by NIH. Step 2—DO encrypts genomic data with the keys and transits it to the cloud for storage and computation. Steps 3, 4—at any point in time, a data user (DU) such as a researcher or pharmaceutical company can submit a query request to the cloud, for example, to query some biomarkers for a specific disease. The cloud then processes the query on the encrypted genomic data and sends back an encrypted result. Step 5—finally, DU decrypts the results with the keys acquired from the TA. (Middle) Secure collaboration: this figure shows the application of SMC to facilitate the joint computation of genomic data. Multiple DOs encrypt their data and send them to centralized or distributed computation servers where genomic data processing such as GWAS is performed. DOs learn nothing about each other’s data except for the computation results. (Right) Privacy attack scenario: this is a typical attack case which can be carry out on either secure outsourcing or collaboration scenario depending on the amount of information leakage or compromised security parameters. Step 1—DO encrypts or anonymizes data and sends it to a public server for storage. Steps 2, 3, 4, 5—the adversary acquires anonymized DNA or leaked information from the public storage and de-anonymizes it with a combination of metadata inferences plus some other inferences and statistical techniques. Steps 6, 7, 8—with the re-identified DNA, the adversary is capable of performing further statistical techniques coupled with lookups against a public data set of GWAS results or SNP-trait association to predict the disease status of the compromised victim.
Secure collaboration: Here multiple genomic data owners (e.g. hospitals, health institutions, research institutions and laboratories) want to jointly perform a function on their private data |$D_{1}, D_{2},..., D_{n}$| while keeping them hidden from each other as depicted in Figure 3. For instance, a research institution might want to perform a GWAS association test across multiple genomic data sets under different security jurisdictions. The main cryptographic primitive employed in this architectural setting is SMC.
Whilst we have stated the most commonly used cryptographic technique used under each model, it is important to note that depending on the use-case and application goals any cryptographic technique can be used under either models. For instance, (i) for a use-case to secure GWAS aggregate statistics DP has been employed under both models [41] and (ii) for a malicious setting SCH has been used [56]. It is also worth mentioning that both models can be combined into one framework to complement each other and not necessarily as standalones [62].
Security model and requirements
A security model and requirements is a set assumptions and standards used as guidelines by researchers to design secure frameworks. In this subsection, we discuss the commonly used security guidelines adopted by the genomic privacy research community for modeling secure frameworks.
Threat model
Threat models are used to describe the behavior of adversaries in a privacy-preserving framework. In genomic privacy and other privacy-preserving techniques, adversarial behaviors are categorized into semi-honest and malicious behaviors.
Semi-honest model: This model is the most commonly adopted threat behavior for designing secure genomic techniques. It describes a security setting where parties faithfully follow the protocol specifications, meaning that they correctly carry out the computation and return correct results to the client [63]. They, however, try to learn sensitive information by observing computation and output results. For example, DTC genetic testing service providers such as 23andMe and color genomics will carry out the test (e.g. genealogy, ancestry or disease risk test) faithfully, but might try to learn additional information about the test participant by observing their SNP or STR profiles.
Malicious model: This model addresses a more realistic security setting than the semi-honest behavior as parties can deviate from the protocol specifications to learn sensitive information [63]. An adversary in this threat environment can tamper with the genomic computation by injecting false data or returning false results to the client. Protocols that address this model provides more security but are generally more expensive than those build for semi-honest only [48]. This is as result of using other techniques such as zero-knowledge proofs to ensure that parties in the protocol don’t behave maliciously.
Security guarantees
In addition to systems architecture and threat models, a secure framework should achieve certain security goals and guarantees. This is mainly more application specific and for secure genomic techniques, the following guarantees ought to be achieved.
Confidentiality: The genomic data should not be revealed to unauthorized parties.
Integrity: The data owner or client should be able to verify any tampering done to the genomic data by an adversary.
Query privacy: This ensures that query content sent to genomic data sets or biobanks is not learnt by unauthorized parties. This is useful in genetic testing and personalized medicine setting where pharmaceutical companies want to query a public genomic data set while at the same time keeping the content of their proprietary test query private.
Output privacy: The output of a genomic computation should not be revealed to any party other the intended recipient or the client.
Secure techniques for genomic data
In this section, we survey the techniques that have been proposed to (i) mitigate the attacks discussed in Privacy attacks ongenomic data, and (ii) protect the privacy and security of the human genome during storage and computation. For better organization and clarity, we group these techniques by their application domain—genomic aggregation, GWAS and statistical analysis, sequence comparison and genomic testing. Finally, we compare and evaluate them based on their security goals and complexities in terms of computation and communication.
Secure genomic aggregation
Aggregate operations (e.g. SNP or allele counts, frequencies, etc.) on large genomic data sets are the fundamental building blocks for genomic analysis such as GWASs, disease susceptibility tests and paternity test. For instance, a count query is used in disease susceptibility to test for rare variants (biomarkers) within a patient’s DNA sequence and GWAS applies statistical analysis to AFs to study gene–disease associations. These operations present an opportunity for genomic data sets from multiple sources and different jurisdictions, which otherwise cannot be shared on a common repository due to privacy issues, to be represented in the form of summary statistics often utilized by GWASs.
Several techniques in the literature have been proposed for the secure aggregation of genomic data. One of the very first work to demonstrate this proposed a technique to privately compute count queries on a genome data set to ascertain which records meet a certain query predicate of genotypes and phenotypes [64]. This study used two third-party servers (one for data storage and the other to manage the cryptographic keys) and HE to allow data owners to encrypt their DNA data before uploading them to the data storage server. The limitations of this technique are 2-fold: (i) computational cost incurred from encrypting the whole genomic database with HE, and (ii) the query response time is slow due to the binary encoding scheme used to represent the DNA sequences and the query coupled with multiple rounds of communication between the two third-party servers. In a bid to address limitation 1, a recent study proposed the use of a symmetric key encryption scheme (Advanced Encryption Standard in CTR mode) which is less costly than HE [65]. This study further optimized their solution to achieve less communication rounds by using only one third-party server with a secure cryptographic coprocessor (SCP) as opposed to the two servers used in [64]. Such a technique leverages the tamper-resistant feature of the SCP to address a malicious security model where the internal memory of the server is erased if tampering is detected. It is important to note that though an SCP addresses the security challenges in a realistic adversarial setting (malicious adversary), it is still limited in memory size and computation power. Another recent study [66] on addressing the computational cost issues of [64] proposed a trade-off between security and efficiency in that instead of encrypting the whole database to achieve stronger security as in [64], they partially encrypted the database whiles improving efficiency. Security and privacy of genome data in this model is achieved by partially encrypting the genome database, permuting genome sequences columns and inserting fake records to disassociate relationship between genomic sequence and sensitive attribute (e.g. disease). While it is vulnerable to Homer et al.’s attack [24], privacy is preserved under a semi-honest cloud model. Improving the query response time from limitation 2 has been proposed by recent studies [67, 68]. While [67] utilizes an efficient encoding technique for DNA sequences which makes it possible to represent a richer set of queries, [68] proposes a tree-based indexing technique for the efficient execution of queries. Furthermore, [68] guarantees data, query and output privacy as opposed to a previous studies [64, 65] in the same lines which only provided data and query privacy.
Secure GWAS and statistical analysis
GWAS is an approach used by researchers to evaluate the correlation between genetic regions (loci) such as SNPs and traits such as diseases between two sets of research groups—the case and control groups. This has, over the past few years, proven to be instrumental in enabling researchers to discern the genetic variations that drive common and complex diseases such as diabetes and cancers, and in doing so, is laying the groundwork for personalized medicine. For this goal to be realized, large amounts of genomic data from different sources and studies need to be analyzed. This has so far been hindered by privacy issues related to sharing genomic data for GWAS. The genomic privacy research community has been actively investigating new ways to carry out GWAS securely while protecting the privacy of the study participants. Popular statistical methods such as linkage disequilibrium, Hardy–Weinberg equilibrium, Cochran–Armitage test for trend and Fisher’s exact test used in association tests have already been implemented securely [57].
The application of differential privacy for releasing GWAS statistics (MAFs, |$\chi ^2$|-statistics, P-values etc.) without comprising the privacy of participants especially the attack discovered by [24] is a well-known area in genomic privacy [6]. One of the key focus of work in this area is to find a better trade-off between data utility and the privacy of GWAS participants. A study in this direction proposed a relaxation to the adversarial settings of DP to achieve a higher utility while at the same time protecting membership disclosure [69]. Genotype and phenotype data used in GWAS, in most cases, are stored across multiple biobanks in different locations. Securing GWAS analysis in such distributed environments is vital in in-cooperating private data from different sources without privacy leaks. This was presented in a study where data (genotype and phenotype) are securely aggregated from multiple data collectors and secretly shared amongst computation servers [70]. Researchers can then submit analysis request to these servers where SMC is used to process shares and output a result.
In GWAS, it is a common practice for researchers to perform meta-analysis which allows them to combine summary statistics from multiple studies and from different geo-locations to increase statistical power and reduce false-positives in their results. It is a well-established fact that these summary statistics are prone to inference attacks if not protected. This has been demonstrated in a recent study where researchers propose an SMC and differential privacy-based quality control procedures for meta-analysis [41]. The key focus of this work is to protect summary statistics while at the same time securely checking for studies with quality issues in the meta-analysis pipeline. This protocol, however, suffers from the computation and communication overheads of SMC-based protocols. Apart from GWAS quality control procedures, another recent study proposed a privacy-preserving technique to correct population stratification (i.e. to account for false-positive associations introduced by population structure) in GWAS by securely running PCA with SMC [71].
For large-scale GWAS of millions of individuals and about 10K SNPs, the secure evaluation of statistical analysis such as principal component analysis (PCA) using SMC based on HE requires over 30 years of computation time while the GC-based approach incurs a communication overhead of roughly 190 PB, which is not feasible. A recent work [49] proposed a technique to reduce these overheads to a number of days for computation and 36 TB of data transfer. This technique uses SMC driven by secret sharing to facilitate GWAS quality control, population stratification analysis (based on PCA) and association tests while preserving the confidentially of participants.
Research on secure GWAS is still in its infant stage and further investigation with other cryptographic primitives and statistical methods such as logistic regression will be required for the quantification of privacy, test accuracy and efficiencies within various GWAS stages (i.e. pre and post-GWAS, quality control and population stratification). In particular, what trade-off between privacy and utility in differential privacy will be optimal for a given GWAS association test and what cryptosystems will give near accurate results as that obtained from carrying out GWAS in cleartext domain.
Secure sequence comparison and matching
Sequence comparison is one of the most fundamental techniques to analyze DNA sequences for similarity or homology. This is often achieved by aligning sequences to evaluate the optimal cost of insertions, deletions and substitutions of nucleobases (A, C, G and T). Well-known sequence comparison methods such as dynamic programming methods (Smith–Waterman and Needleman–Wunsch algorithms), word methods (BLAST and FASTA) and their variants have been implemented securely by the cryptographic research community to protect the privacy of DNA donors. An example of such work proposed an SMC-based technique for pairwise sequence comparison using dynamic programming (Smith–Waterman algorithm) [72, 73]. Both studies presented a setting where two parties can compute the edit distance between their sequences such that neither party learns anything about the private sequence of the other except the comparison result.
The use of edit distance for sequence comparison has seen applications in clinical setting such as similar patient querying. This is useful where matching patients with similar genomic sequence helps inform a medical doctor of possible diagnoses and effective treatment options. Despite its usefulness, edit distance between two sequences is quadratic in time complexity. A recent study in this direction approximated the edit distance problem for querying similar patients [74]. Their approximation is based on partitioning sequences (database sequences and query sequence) into blocks according to a public reference sequence. Edit distance between these blocks are then precomputed and parties in the protocol apply GC to securely compute shares which are then summed locally to retrieve the approximate edit distance. This approximation method, however, leaks information about patients who are not supposed be to reveal by the exact computation of edit distance. Other related studies in the same line are [75, 76]. Whiles [75] also suffers from an information leakage, [76] provides privacy guarantees for the genomic data, the query and the computation output.
Dynamic programming methods are computationally costly especially for a whole-genome comparison. For privacy-preserving implementations, such overheads will always add up to the complexities inherent in the underlining cryptographic primitive, consequently rendering the application impractical. One way of dealing with such complexity is breaking the computation problem down so that more costly operations can be executed on high-end servers. This has been shown in a study where researchers proposed a dynamic programming technique in an SMC setting. The study decomposed the computation problem based on the sensitivity level of the genome data using program specialization by exploiting the fact that |$99.5\%$| of human genomes are similar and therefore not sensitive [46]. This allowed the data owner to perform computation on the sensitive parts of the sequence while the third-party environment processes the rest of the sequence (non-sensitive nucleotides). Another approach to avoid the computation-intensive operations that come with dynamic programming is to opt for efficient comparison methods (e.g. BLAST and FASTA). One such study focused on securing BLAST algorithm by proposing a technique to securely outsource computation of DNA read-mapping to the cloud environment [54]. This study made use of secure hardware with FPGAs, on the cloud to seal computation and prevent sensitive information leakage to the rest of the server thereby protecting the DNA sequence.
The limitations of SMC and HE techniques such as scalability issues due to multiple communication rounds and introducing significant storage cost, respectively, are major roadblocks confronting the practical usability of secure sequence comparison frameworks in real-world clinical settings. Finding workarounds or solutions to these challenges together with the development of techniques to protect sequence search patterns will be a huge step. A recent study aimed at solving these challenges, proposed the use of private information retrieval techniques with HE to run queries over encrypted genomic variants based on some comparison predicates [77]. This technique yields a faster query response time as opposed to implementation versions of sequence comparison solely based on HE. Another recent study went about the scalability issues discussed above by using a modified version of the predicate encryption (PE) scheme as opposed to SMC. This study addressed a sequence comparison privacy use-case in personalized medicine where genetic testing is used to diagnose and treat an individual [78].
The majority of privacy-preserving genomic techniques that involve two or more third-party servers assume a security requirement of non-colluding servers. This means third-party servers can collude to break the security of the system. A recent study sought to address this by proposing a collusion-resistant approach to securely outsource dynamic programming-based sequence comparison to a single cloud server thereby dismissing the non-colluding requirement [79]. The technique utilizes additive order preserving encryption (AOPE algorithm) that is homomorphic on addition and preserves the numerical order of plaintext values thereby allowing the cloud to run comparison on encrypted genome sequences.
Though sequence comparison is amongst the widely covered areas in the implementation of privacy-preserving genomic techniques, most of them are built on SMC primitives which is complex in bandwidth. Other primitives, such as lattice-based or fully HEs to support arbitrary sequence comparison operations on ciphertexts are yet to be explored. Also, adversarial models based on assumptions of semi-honest and non-colluding parties should be adopted for a more practical and realistic setting of a malicious adversary.
Secure genetic/genomic testing
Genetic testing is the examination of variations in chromosomes, genes and proteins between an individual’s genome and some biomarkers to determine certain disease risk, parentage, genealogy, etc. There are several genetic test types used for different purposes. These test are often performed on SNPs or the WGS. To the best of our knowledge, only disease susceptibility, identity, paternity, genealogical and compatibility tests have been implemented securely to preserve genome privacy.
One of the very first studies to secure a genetic test adapted finite automata to securely run DNA queries to determine an individual’s disease risk [80]. The query is formulated as a regular expression and is run obliviously on the DNA sequence to check for disease markers. This study used secret sharing HE and oblivious transfer in an interactive protocol to ensure that both the query and the genome data were kept private. Most recent work has reduced the disease susceptibility testing and diagnosis problem to a secure two-party case where parties use interaction protocols to test for the presence of mutations and rare variants [62, 81]. The focus of [81] is to predict HIV-related cases, while [62] adopting frequency-based clinical genetics to propose three different protocols to diagnose patients with monogenic disorders.
In addition to securing the disease risk test, other studies have proposed cryptographic protocols for paternity, identity and ancestry tests. One such work presents a secure technique based on homomorphic Paillier encryption to match DNA profiles (STRs) from two parties to conduct paternity, identity and ancestry tests [48]. The secure matching problem is accomplished by constructing polynomials over the input STRs which are kept private and yields zero if there is match. Another work proposes the use of GCs in a two-party setting (SMC based) to securely evaluate (i) paternity tests over STRs from a parent and child, and (ii) genetic compatibility tests between partners to determine the risk of passing certain Mendelian-inherited diseases to their children [47]. Again, STRs are kept private from parties in the SMC protocol. However, the genetic compatibility test in this work leaks the disease which is being tested. This information leakage might be exploited by an adversary.
All the aforementioned secure genetic testing techniques are based on SMC, HE or a combination of both. SMC and HE-based techniques are known to have scalability issues due to overheads in storage, computation and communication, which makes them difficult to adopt for practical use over large scale genomic data or the full human genome [6]. A recent study proposed the use of SCH as an alternative to SMC and HE to implement a secure scalable practical genetic testing system [56]. This technique enabled the efficient and secure outsourcing of storage and genetic testing to an untrusted cloud environment for the purposes of disease diagnosis and personalized medicine. The secure hardware in the cloud is based on Intel’s SGX that provides a secure computation unit (enclave) where the genetic testing functions are executed. Despite the fact that SCH-based techniques are more scalable than SMC and HEs, they are limited in memory size (e.g. a single SGX machine is limited to 128 MB) which is crucial when processing large volumes of genomic data. The application of SGX to secure genomic computation is still new and further investigations will be required to establish its vulnerabilities, limitations and mitigation strategies for attacks including side-channel and in-memory attacks.
Though not directly related to genomic testing, the beacon service provides an opportunity for researchers to query a beacon network for the presence of an allele. This not only promotes data sharing but also facilitates research in areas of identifying disease markers for genomic testing. The re-identification attack by [20] on beacons as discussed in Identity tracing attacks has raised awareness on the need to protect beacon services. A recent study proposed two differentially private techniques, eliminating random positions and randomization of response, to protect a beacon [82]. Both methods are based on introducing inaccuracies to conceal the presence of an individual in a beacon database. Another study proposed a flipping strategy to optimize the trade-off between the utility and the privacy of the beacon service [83]. In this study, the discriminative power for each SNP in the database is calculated, and the top |$k$| SNPs with the greatest power are flipped. We, however, do not include these techniques in Table 2 as they are solely based on randomization and data perturbation techniques. The goal of Table 2 is to compare cryptographic techniques for protecting genomic data.
Comparison and evaluation of secure genomic techniques
Secure genomic computation techniques are evaluated using the following two criteria: (1) security guarantees achieved by the system as discussed in Security model and requirements and (2) the efficiency of the technique in terms of computation and communication overheads. We compare the secure genomic techniques surveyed in this section using these criteria and present them in Table 3 which we believe will give researchers an insight into the security goals and overheads incurred by the cryptosystems already proposed in the literature on specific genomic computation areas.
Security: We evaluate and compare security guarantees in the table using symbols (i) :⬤ security guarantee is met as per definition in Security guarantees, (ii) ⬤|$^{\dagger }$|: security guarantee is met as per definition in Security guarantees, however with some information leakage. For instance, schemes with security bounded to the message (genome sequence) distribution or genome sequence length is leak during SMC protocol, (iii) ⃝: security guarantee not met and (iv) –: security guarantee not available or not applicable to the framework as per the authors definition of their security goals. The prime security goal of any secure genomic technique is to provide confidentiality where a probabilistic polynomial time adversary has negligible probability of breaking the scheme. This has so far been provided by all the schemes surveyed in this section. However, there are a number of ways an adversary can infer confidential genomic information without necessarily breaking the encryption system, for example, by observing the information leaked during computation or from the output, or using the attack techniques presented in Table 1. Incorporating integrity checks into secure systems is one approach to detect adversarial tampering aimed at learning sensitive information. Very few techniques in genomic privacy have adapted SCH which has tamper detection built into its coprocessors for integrity checking [54, 56, 65]. Other than SCH, coming up with genomic tamper-resistant techniques has been challenging either because it is difficult to achieve or it incurs extra computation cost which might render the system impractical. This leaves an unexplored area in the genomic privacy domain to design techniques that provide a security guarantee of integrity.
Efficiency: For fairness of the comparison between schemes, we evaluate efficiencies using asymptotic complexity (Big |$O$| notation) for (i) computation complexity as a function of the time it takes to encrypt/decrypt and perform the task such as sequence comparison and run queries on the genomic sequence and (ii) communication complexity in terms of the number of computation rounds (iterations) between parties in the protocol. For instance, techniques based on SMC and OT involve multiple interactions between parties in order to compute a function and as such, incur a communication complexity linear to the length of the genome sequence (i.e. |$\propto n$|). From Table 3, it is evident that secure hardware-based techniques [54, 56, 65] have the least computation cost which is linear to the genome sequence length (|$n$|) and communication in constant time of |$O(1)$|, whereas HE-based techniques [72, 80] incur the most computation cost as a result of ciphertext expansions during encryption (i.e. encryption within a modular field with some exponentiation operation which is known to be more costly than other arithmetic operations– addition and multiplication) with security parameters chosen to provide stronger security requirements. In the case of an outsourced genomic storage model, this ciphertext expansion will increase data storage size and cost on third-party servers hosted by cloud providers (e.g. AWS, Google and Microsoft). It has been shown that privacy-preserving techniques for sequence comparison has scalability issues such as communication overhead that is linear to the sequence length (n) and number of parties in the protocol [72]. SMC techniques based on HE [72] incur excessive computation cost whilst those based on GC [46, 73] yield communication burdens. Loosely speaking, a better approach to yield efficiency in SMC would be to adopt secret sharing as applied in the work in [49].
It is important to note that the underlining genomic computation which is been protected plays a vital role in estimating the efficiency of a secure framework. For example, the computation cost inherent to dynamic programming algorithms such as Smith–Waterman and Needleman–Wunsch for sequence comparison are quadratic (|$<O(n^3)$|) and as such when implemented in a secure domain will result in even higher overheads as is evident from the techniques [46, 72, 73] in Table 3.
Open issues and challenges
In this section, we summarize the open issues and challenges in designing techniques for securing genomic data and processing.
Gap between current approaches and their applicability: Work still needs to done to transition techniques for secure genomic processing from theory to practice. The majority of techniques in the literature are impractical for a real-world human genome that is several sequences long. For the most part, it is the result of the underling cryptographic system used. It is noteworthy to emphasize that there is no one cryptographic primitive which is best suited to protect genomic data for computation and storage. Any cryptosystem can be used. However, employing efficient versions of a cryptosystem and understanding whether it is applicable for a given genomic application area will be the first step towards achieving real-world feasible frameworks. For instance, SMC has been combined with differential privacy to solve privacy issues in GWAS [41], whereas HE and SMC have been used to complement each other to provide better efficiency and security guarantees in genetic testing and personalized medicine where biomarkers and test queries might be proprietary to test providers or pharmaceutical companies [81]. Despite these advances, more studies are still required to evaluate the performance of genomic applications in real-world privacy-preserving settings.
Tradeoff between security and efficiency: Security comes at the cost of efficiency. This means the more secure a scheme is, the lower its efficiency. Cryptographic systems have different ways of tuning encryption parameters for stronger security such as using large key sizes, large prime numbers in a modular ring and increasing the difficulty of a mathematical problem (e.g. computing discrete logarithms). The more these techniques are tuned for stronger security guarantees, the more overheads they incur and the less efficient the framework becomes. Hence, a secure genomic framework should be designed taking into consideration the tradeoff between the security required by the application and its efficiency.
Accuracy loss: There is always a price to pay for implementing privacy-preserving techniques. One of these is accuracy loss which is the margin of error between a secure implementation and its plaintext version. In genomic application processing, accuracy is critical and this error margin needs to be evaluated to estimate the impact it might have on clinical decisions for diagnostic testing or research results in GWAS. Current secure genomic techniques in the literature fail to address this, as a result, there is no measure of the impact they might have in a real clinical setting. Future solutions should be designed to address accuracy with the goal of achieving negligible accuracy losses.
Personalized medicine and beyond: Advances in personalized medicine are beginning to use techniques such as artificial intelligence (AI) to classify mutations that contribute to diseases such as tumor growth, for example, classifying mutations in the BRCA1 and BRCA2 gene for breast cancer. These techniques are instrumental in the realization of personalized medicine and the transformation of health care delivery, and they are already being applied by companies in the industry such as Deep Genomics [84] and Atomwise [85]. However, protecting the privacy of patients remains the most critical issue with the commercialization of personalized medicine. Thus, designing secure AI models for personalized medicine whilst preserving the privacy of patients will be an interesting direction to explore.
Conclusion
The advancement of genome sequencing techniques is driving the ease of access and the collection of genomic data for storage, sharing and processing. This comes with increasing security and privacy concerns which are yet to be sufficiently addressed for purposes such as health care delivery, research and DTC services. In this article, we explored and surveyed the relevant work on privacy attacks and privacy-preserving techniques for genomic data. An adversary is always exploring new ways to comprise the privacy of an individual via his/her DNA sample for personal gain, blackmail or some other dubious reasons. As a result, further research is required to propose techniques to thwart these attacks not just in theory but in the practical application to real-life settings as well. We believe the comparison of secure genomic techniques based on computation and communication overheads and the future directions provided in this article will serve as a guide for the genomic privacy researcher to achieve this goal.
The sensitive nature of the human genome raises privacy and security concerns for the storage and computation of genomic data.
Current privacy attacks on genomic data classified into the most relevant attack types—identity tracing, attribute disclosure and completion attacks.
State-of-the-art techniques to secure and protect the privacy of genomic data. Comparison of these techniques in terms their security goals and complexities—computation and transmission overheads.
Discuss and highlight challenges, research gaps and future directions in the field of genomic privacy.
Mohammed Yakubu Abukari is a PhD student at the Department of Computer Science and Information Technology, La Trobe University. His research interests include computer security in bioinformatics and multimedia processing.
Yi-Ping Phoebe Chen, is a professor of the Department of Computer Science and Information Technology, La Trobe University. Her research interests include bioinformatics, multimedia technologies and knowledge discovery.
References


