-
PDF
- Split View
-
Views
-
Cite
Cite
Chunfa Tong, Lianying Shen, Yafei Lv, Zhong Wang, Xiaoling Wang, Sisi Feng, Xin Li, Yihan Sui, Xiaoming Pang, Rongling Wu, Structural mapping: how to study the genetic architecture of a phenotypic trait through its formation mechanism, Briefings in Bioinformatics, Volume 15, Issue 1, January 2014, Pages 43–53, https://doi.org/10.1093/bib/bbs067
Close - Share Icon Share
Abstract
Traditional approaches for genetic mapping are to simply associate the genotypes of a quantitative trait locus (QTL) with the phenotypic variation of a complex trait. A more mechanistic strategy has emerged to dissect the trait phenotype into its structural components and map specific QTLs that control the mechanistic and structural formation of a complex trait. We describe and assess such a strategy, called structural mapping, by integrating the internal structural basis of trait formation into a QTL mapping framework. Electrical impedance spectroscopy (EIS) has been instrumental for describing the structural components of a phenotypic trait and their interactions. By building robust mathematical models on circuit EIS data and embedding these models within a mixture model-based likelihood for QTL mapping, structural mapping implements the EM algorithm to obtain maximum likelihood estimates of QTL genotype-specific EIS parameters. The uniqueness of structural mapping is to make it possible to test a number of hypotheses about the pattern of the genetic control of structural components. We validated structural mapping by analyzing an EIS data collected for QTL mapping of frost hardiness in a controlled cross of jujube trees. The statistical properties of parameter estimates were examined by simulation studies. Structural mapping can be a powerful alternative for genetic mapping of complex traits by taking account into the biological and physical mechanisms underlying their formation.
INTRODUCTION
The final phenotype of a trait is the consequence of interactions of its internal and external structures and processes [1, 2]. It is such a phenotype that forms the features of an organism, allowing it to survive and interact with its environment. A central theme of biology is to study the intimate association of the phenotype’s structure or form and its function or activity [3]. Structure is the basic component of the phenotype that can be understood at the molecule, cell or tissue level, whereas function refers to the capacity of how different structures are used. In order to identify the function of a phenotype, therefore, we first need to understand how the shape and properties of a structure determine its functions [4, 5].
Traditional approaches for mapping quantitative trait loci (QTLs) that control a phenotype do not consider the structural basis of the phenotype, thus failing to relate the structure of the phenotype with its function. The genetic mapping of complex traits can be improved through the dissection of the phenotypes into the underlying structural components. By measuring the structure of organic and inorganic materials, electrical impedance spectroscopy (EIS) has been increasingly used to study the function and properties of biological issues [3, 6–11]. The EIS method is based on the physical principle that the signal of alternating current (AC) will change in its amplitude and phase when it passes through a tissue, arising from the polarization and relaxation of the tissue. Based on those changes, the impedance of the tissue that is composed of a real (resistance) and an imaginary part (reactance) in a complex plane can be determined. When the real and imaginary part is measured at different frequencies, an impedance spectrum is observed [9]. Because the proportion of the AC passing through the tissue depends on its frequency and the tissue properties, such as plasma membranes, cell volumes and intra and extracellular conductivities, the electrical impedance of the tissue at a series of frequencies provides information about the cell population.
It has been observed that intracellular resistance is highly correlated with physiological and pathological variables of tissues, such as frost hardiness [8, 9] and cancer risk [3, 10], through changes in cellular features and processes. With a proper equivalent electrical model, it is possible to study the tissue properties according to the changes in the parameters of the model [12]. In this article, we describe and assess a computational model—structural mapping—for mapping specific QTLs that determine the function of complex traits using EIS parameters that quantify tissue properties. In the EIS analysis, a number of robust mathematical models have been established to describe the dynamic properties of impedance through the tissue [7, 13, 14]. These models are integrated with genetic mapping derived to map dynamic QTLs [15–17], characterizing the genetic effects of QTLs on the trait by testing the mathematical parameters. Structural mapping is shown to be powerful for mapping internal structural properties of phenotypic formation and can be used to study the genetic control mechanisms of structural–functional relationships that pervade the kingdom of biology.
MODEL
EIS modeling
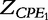 and
and 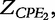 respectively. According to Macdonald [13], the impedance of the constant phase elements (CPEs) is expressed as:
respectively. According to Macdonald [13], the impedance of the constant phase elements (CPEs) is expressed as: 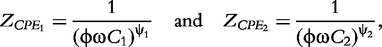
![Schematic determination of the distributed model parameters (double-DCE) of an impedance spectrum of a tissue (shown by open diamond). Real part of impedance on x-axis and imaginary part of impedance on y-axis (A). Frequency increases from right (80 Hz) to left (1 MHz). The two circles represent the two arcs of the spectrum. DCE1 and DCE2 are distributed circuit elements composed of constant phase elements (CPE) in parallel with resistors (B). Resistances (R, R1 and R2) of the equivalent model are obtained according to the intersections of the circles with x-axis. The centre of the circles is below x-axis—‘depressed center’ defined by parameters ψ1 andψ2. Relaxation times τ1 and τ2 are obtained from the apex of the circles. ZCPE1 and ZCPE2 are impedances of constant phase elements. Adapted from Repo et al. [9].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/bib/15/1/10.1093/bib/bbs067/2/m_bbs067f1p.jpeg?Expires=1749352497&Signature=F3MKgCZvbKvEyU8GrFp76WknTYlLrX2hNUqXm2ImGOvbHzrrChZZFP1PSEuc-xafK0XmXUW5dI73eK6FAgjL5vwV63sarezn9UT9welTrV8TUlvlySbMYxhUNpPX77XHd4GJzlF57ONt4iyj91mjH0K2BPZ4XFurPQTDuXc6XY1aX1lt39wsJmjJzEPAHBSJ0ulie3vvx12ukGTTjO-6CYp6hmEahOxmTgpgD6PJhp-Y9b3A~bk50FuZFFdfMUkKDH~o8HSYYPIIRDwfLhEN1xmvmWpsMQBUd2no5k~39q1ljn8DOoQXI0zVG8jL9YBrqIjXRSM-Y-NG810KqO4ilQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Schematic determination of the distributed model parameters (double-DCE) of an impedance spectrum of a tissue (shown by open diamond). Real part of impedance on x-axis and imaginary part of impedance on y-axis (A). Frequency increases from right (80 Hz) to left (1 MHz). The two circles represent the two arcs of the spectrum. DCE1 and DCE2 are distributed circuit elements composed of constant phase elements (CPE) in parallel with resistors (B). Resistances (R, R1 and R2) of the equivalent model are obtained according to the intersections of the circles with x-axis. The centre of the circles is below x-axis—‘depressed center’ defined by parameters ψ1 andψ2. Relaxation times τ1 and τ2 are obtained from the apex of the circles. ZCPE1 and ZCPE2 are impedances of constant phase elements. Adapted from Repo et al. [9].
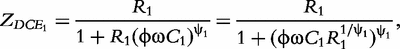
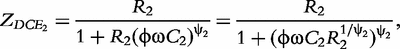
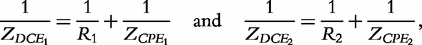
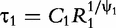 and
and 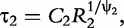 which are two relaxation times of the DCEs, we have:
which are two relaxation times of the DCEs, we have: 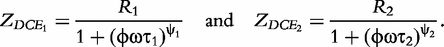
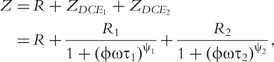
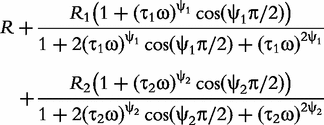
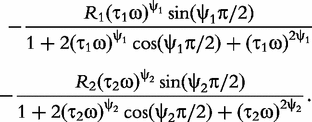
In sum, the double-DCE model contains three resistances (R, R1 and R2), two relaxation times (τ1 and τ2) and two distribution coefficients (ψ1 and ψ2) of the relaxation times. Mathematical interpretations of all these parameters are diagrammed in Figure 1.
Regression model
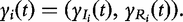 Structural mapping integrates the double-DCE (1) into a statistical model for QTL mapping, expressed as:
Structural mapping integrates the double-DCE (1) into a statistical model for QTL mapping, expressed as: 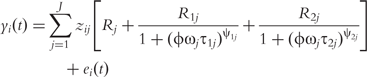
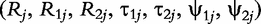 are a set of EIS parameters for QTL genotype j; and ei(t) is a residual error distributed as a complex normal distribution with mean 0 and variance σ2. The complex vector
are a set of EIS parameters for QTL genotype j; and ei(t) is a residual error distributed as a complex normal distribution with mean 0 and variance σ2. The complex vector 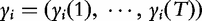 can be divided into two T-dimensional subvectors, one for the real part and the other for the imaginary part. For simplicity, we assume that the two parts are not correlated, but each part follows a multivariate normal distribution. Therefore, the phenotype vector yi(t) has the structure of covariance matrix, expressed as:
can be divided into two T-dimensional subvectors, one for the real part and the other for the imaginary part. For simplicity, we assume that the two parts are not correlated, but each part follows a multivariate normal distribution. Therefore, the phenotype vector yi(t) has the structure of covariance matrix, expressed as: 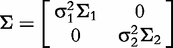
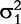 and
and 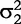 are the variances of real and imaginary parts, respectively; and Σ1 and Σ2 are the corresponding correlation matrices. There are many approaches which can model the covariance structure. Here, the first-order autoregressive [AR(1)] model is used, i.e.
are the variances of real and imaginary parts, respectively; and Σ1 and Σ2 are the corresponding correlation matrices. There are many approaches which can model the covariance structure. Here, the first-order autoregressive [AR(1)] model is used, i.e. 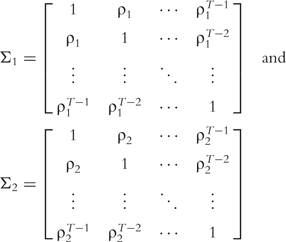
Mixture model
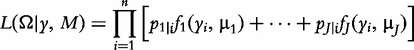
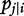 is the conditional probability of QTL genotype j, conditional on the genotypes of the two flanking markers of progeny i [18]; and
is the conditional probability of QTL genotype j, conditional on the genotypes of the two flanking markers of progeny i [18]; and 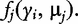 is a probability density function of multivariate complex normal distribution expressed as:
is a probability density function of multivariate complex normal distribution expressed as: 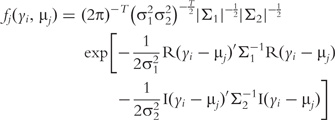
 and
and 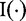 stand for the real and imaginary parts of a complex vector, respectively.
stand for the real and imaginary parts of a complex vector, respectively.Parameter estimation
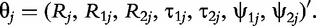 for QTL genotype j and use the first-order Taylor expansion to approximate μj by:
for QTL genotype j and use the first-order Taylor expansion to approximate μj by: 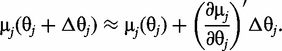
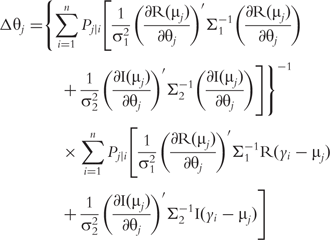
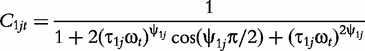
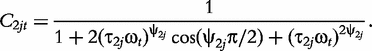
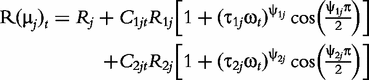
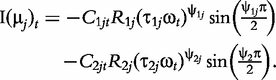
The derivatives of the tth element of R(μj) and I(μj) with respective to parameters Rj, R1j, τ1j, ψ1j, R2j, τ2j and ψ2j can be obtained, which are shown in Box 1. By solving the equations, we obtain the estimates of the EIS parameters for different QTL genotypes.
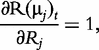
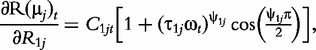
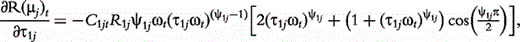
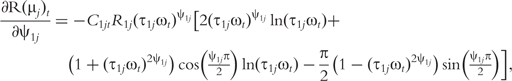
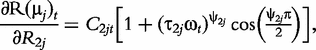
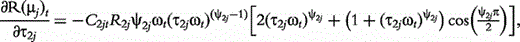
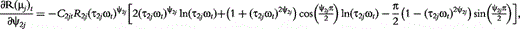
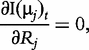
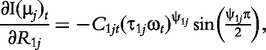
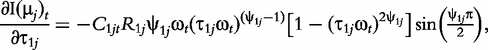
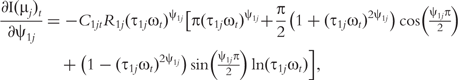
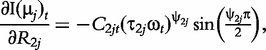

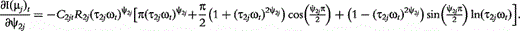
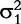 and
and  given the other parameters, as:
given the other parameters, as: 
In the E-step, a posterior probability of progeny i that has a QTL genotype j is calculated as Equation (9). In the M-step, the parameters are estimated by Equations (9) and (10). This procedure is repeated until the iterative value of each parameter converges. The SEs of the MLEs can be estimated by using the inverse of the Fisher information matrix.
Hypothesis tests
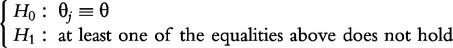
where  and
and  denote the MLEs of the unknown parameters under the H0 and H1, respectively. If a high peak of LR profiles exceeds a critical threshold, then a QTL that controls the curve of the electrical impedance on the complex plane is asserted to exist in a marker interval. The genome-wide critical threshold is determined by performing permutation tests [19].
denote the MLEs of the unknown parameters under the H0 and H1, respectively. If a high peak of LR profiles exceeds a critical threshold, then a QTL that controls the curve of the electrical impedance on the complex plane is asserted to exist in a marker interval. The genome-wide critical threshold is determined by performing permutation tests [19].
The merit of the model also lies in the test of a number of physiologically meaningful properties of tissues. Each of the equivalent circuit EIS parameters contained within a distributed model of the tissues [1] has a particular biological mean. For example, the relaxation times, τ1 and τ2, describe the peak of the high-frequency arc of the impedance spectrum, which are highly correlated with frost hardiness, and ψ1 and ψ2 are the distribution coefficients of the relaxation times.
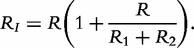
It is interesting to test how the QTLs detected control each of these parameters by formulating the null hypothesis,

 and
and  respectively, for
respectively, for  The LR test statistics are calculated to compare against the critical values for the significance determination.
The LR test statistics are calculated to compare against the critical values for the significance determination.
RESULTS
Worked example
We described a statistical model for structural mapping that capitalizes on the capacity of the EIS device to quantify the biological and physiochemical features of a tissue by an equivalent electrical circuit analysis [9]. To validate the ability of structural mapping to map a phenotypic trait from its structural underpinnings, we implemented the algorithm to analyze a mapping data collected from a controlled cross between two heterozygous parents in Chinese jujube (Zizyphus jujuba Mill.) [20]. A male tree Dongzao (Z. jujuba Mill, cv: Dongzao) was pollinated to a female tree Linyilizao (Z. jujuba Mill, cv: Linyilizao) to generate a full-sib family. A mapping population of 150 individuals from this family was established by genotyping 423 molecular markers to construct two parent-specific linkage maps. Thus, a pseudo-test backcross design is used for QTL mapping [21]. Part of the mapping population (86 hybrids) were measured for EIS at 31 different frequencies (300 Hz to 4 MHz) with a dual trace oscilloscope using shoots under a range of temperatures (–4 to 20°C). Electrical impedance was displayed as real (resistive component) and imaginative (capacitive reactance component) parts.
Figure 2 illustrates Cole–Cole impedance plots that describe the imaginary versus real complex plane for these hybrids. Here, the imaginary part of the complex impedance of the stems under study is plotted against the real part, each curve being a function of the frequency characterized by one hybrid. The imaginary part changes with the part par in a hyperbolic manner. The impedance spectra of each hybrid can be viewed as an equivalent circuit with two DCEs. The variation of Cole–Cole impedance plots among different hybrids increases dramatically with increasing frequency, implying a possible involvement of QTLs for electrical impedance spectra.
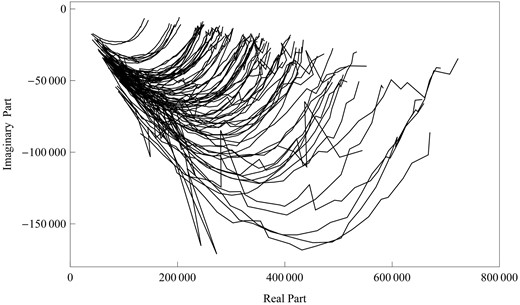
Cole–Cole plots for 86 mapping hybrids in Chinese jujube trees, composed of the imaginary part and real part.
To ensure its homoscedasticity over frequency, both the real and imaginary data are log-transformed. By scanning for the existence of QTLs in the genome, we calculated LRs at every two 2 cM through the linkage map, obtaining an LR profile against the genome position. To simplify calculations, we used a single-DCE model which takes the first two terms of model (1). Several significant QTLs were detected to affect electrical impedance spectra at the chromosome- and genome-wide level, but only one at the genome-wide level detected on the female-based linkage map is reported here for the demonstration of the new model (Figure 3). At this QTL, two different genotypes each are described by a group of EIS parameters (R, R1, τ1, ψ1). As shown in Figure 4, the two QTL genotypes display different patterns of EIS curves, suggesting the impact of this QTL on structural components of shoots.
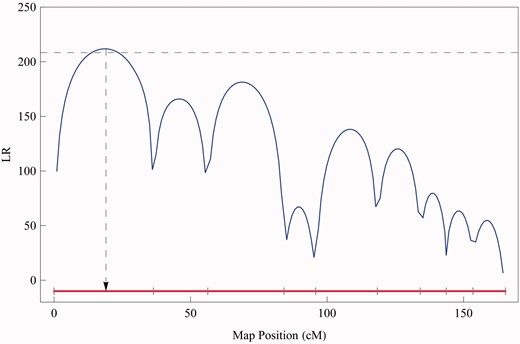
The LR profile of QTL search over a linkage group. The genome-wide critical threshold is indicated by the dash horizontal line. The LR peak corresponds to the MLE of the QTL position indicated by a of the arrowed dash vertical line. The positions of markers are indicated at ticks at x-axis.

Two different curves (indicated by thick lines) for a QTL detected to affect EIS curves at the genome-wide 5% significance level. The gray curves are raw data for 86 progeny.
The EIS parameters through recalculation can be used to describe extracellular and intracellular resistances of a tissue which are related to its physiological properties such as frost hardiness. We test whether the QTL detected using our model affects extracellular and intracellular resistances of the stems of Chinese jujube. This QTL is found to display highly significant effects on both types of cellular resistance (P < 0.001). According to previous studies in tree physiology [8, 9], these two types of resistance are highly associated with frost hardiness. Our mapping population allows the distinction of two QTL-genotype groups of Chinese jujube hybrids based on the posterior probabilities of QTL genotypes given marker genotypes [18]. It is found that these two genotypes differ highly significantly in frost hardiness of jujube hybrids (P < 0.001), suggesting that results of QTL mapping with EIS can be used to diagnose the performance of trees to tolerate and resist to coldness.
Simulation
We performed a simulation study to evaluate the precision of parameter estimates, the power of structural mapping and its false positive rates using EIS data. The simulation mimics the real example analyzed above by assuming a 100-cM long linkage group with 11 equidistant markers in a backcross population. A putative QTL is assumed to be located at 46 cM from the first marker of the group. Different heritabilities (H2 = 0.1, 0.4) and various sample sizes (n = 100, 200) are considered. Estimated values of the parameters from the new model are tabulated in Table 1, in a comparison with their true values used to simulate the data. It can be seen that the model provides reasonably good estimates of the model parameters, even with a modest heritability (0.1) and sample size (100). When the sample size increases to 200, the model can surely well estimate all the parameters. At a small heritability and sample size, the model displays reasonably high power for QTL detection (0.80) and low FRP (0.06). These features can improve further when a heritability and/or sample size increases.
Means of the QTL position and MLEs of the parameters for two QTL genotypes in a pseudo-test backcross design of different sample sizes (n) under different heritabilities (H2), calculated from 200 simulation replicates. The root of mean squares errors of the estimate of each parameter is in parentheses
| Parameter . | True value . | n = 100 . | n = 200 . | ||
|---|---|---|---|---|---|
| . | . | H2 = 0.1 . | H2 = 0.4 . | H2 = 0.1 . | H2 = 0.4 . |
| QTL position | 46 | 45.95 (1.67) | 45.89 (1.64) | 46.02 (1.17) | 45.94 (1.27) |
| R1 | 14 288.2 | 14 371 (1468) | 14 150 (598) | 14 326 (1010) | 14 130 (465) |
| R11 | 132 114 | 131 453 (9543) | 131 654 (3775) | 130 699 (6574) | 131 778 (2764) |
| τ1 | 3.137 | 3.189 (0.135) | 3.148 (0.063) | 3.195 (0.099) | 3.146 (0.040) |
| ψ1 | 0.5256 | 0.526 (0.008) | 0.525 (0.004) | 0.526 (0.006) | 0.525 (0.003) |
| R2 | 14 109 | 13 089 (1334) | 13 963 (557) | 13 092 (883) | 13 875 (419) |
| R12 | 181 502 | 182 249 (13 212) | 182 735 (5410) | 182 150 (8646) | 182 304 (3818) |
| τ2 | 6.862 | 7.225 (0.287) | 6.946 (0.117) | 7.240 (0.198) | 6.962 (0.081) |
| ψ1 | 0.5489 | 0.539 (0.007) | 0.547 (0.003) | 0.539 (0.005) | 0.546 (0.002) |
| ρ1 | 0.9994 | 0.999 | 0.999 | 0.999 | 0.999 |
| ρ2 | 0.9930 | 0.993 | 0.993 | 0.993 | 0.992 |
 | 0.229 | 0.223 (0.033) | 0.224 (0.025) | ||
 | 0.263 | 0.279 (0.046) | 0.279 (0.038) | ||
 | 0.046 | 0.045 (0.006) | 0.045 (0.005) | ||
 | 0.053 | 0.053 (0.007) | 0.05 (0.005) | ||
| Parameter . | True value . | n = 100 . | n = 200 . | ||
|---|---|---|---|---|---|
| . | . | H2 = 0.1 . | H2 = 0.4 . | H2 = 0.1 . | H2 = 0.4 . |
| QTL position | 46 | 45.95 (1.67) | 45.89 (1.64) | 46.02 (1.17) | 45.94 (1.27) |
| R1 | 14 288.2 | 14 371 (1468) | 14 150 (598) | 14 326 (1010) | 14 130 (465) |
| R11 | 132 114 | 131 453 (9543) | 131 654 (3775) | 130 699 (6574) | 131 778 (2764) |
| τ1 | 3.137 | 3.189 (0.135) | 3.148 (0.063) | 3.195 (0.099) | 3.146 (0.040) |
| ψ1 | 0.5256 | 0.526 (0.008) | 0.525 (0.004) | 0.526 (0.006) | 0.525 (0.003) |
| R2 | 14 109 | 13 089 (1334) | 13 963 (557) | 13 092 (883) | 13 875 (419) |
| R12 | 181 502 | 182 249 (13 212) | 182 735 (5410) | 182 150 (8646) | 182 304 (3818) |
| τ2 | 6.862 | 7.225 (0.287) | 6.946 (0.117) | 7.240 (0.198) | 6.962 (0.081) |
| ψ1 | 0.5489 | 0.539 (0.007) | 0.547 (0.003) | 0.539 (0.005) | 0.546 (0.002) |
| ρ1 | 0.9994 | 0.999 | 0.999 | 0.999 | 0.999 |
| ρ2 | 0.9930 | 0.993 | 0.993 | 0.993 | 0.992 |
 | 0.229 | 0.223 (0.033) | 0.224 (0.025) | ||
 | 0.263 | 0.279 (0.046) | 0.279 (0.038) | ||
 | 0.046 | 0.045 (0.006) | 0.045 (0.005) | ||
 | 0.053 | 0.053 (0.007) | 0.05 (0.005) | ||
The parameters include three types: (i) the position of QTL, (ii) QTL effects specified by genotype-specific DCE parameters and (iii) AR(1) parameters.
Means of the QTL position and MLEs of the parameters for two QTL genotypes in a pseudo-test backcross design of different sample sizes (n) under different heritabilities (H2), calculated from 200 simulation replicates. The root of mean squares errors of the estimate of each parameter is in parentheses
| Parameter . | True value . | n = 100 . | n = 200 . | ||
|---|---|---|---|---|---|
| . | . | H2 = 0.1 . | H2 = 0.4 . | H2 = 0.1 . | H2 = 0.4 . |
| QTL position | 46 | 45.95 (1.67) | 45.89 (1.64) | 46.02 (1.17) | 45.94 (1.27) |
| R1 | 14 288.2 | 14 371 (1468) | 14 150 (598) | 14 326 (1010) | 14 130 (465) |
| R11 | 132 114 | 131 453 (9543) | 131 654 (3775) | 130 699 (6574) | 131 778 (2764) |
| τ1 | 3.137 | 3.189 (0.135) | 3.148 (0.063) | 3.195 (0.099) | 3.146 (0.040) |
| ψ1 | 0.5256 | 0.526 (0.008) | 0.525 (0.004) | 0.526 (0.006) | 0.525 (0.003) |
| R2 | 14 109 | 13 089 (1334) | 13 963 (557) | 13 092 (883) | 13 875 (419) |
| R12 | 181 502 | 182 249 (13 212) | 182 735 (5410) | 182 150 (8646) | 182 304 (3818) |
| τ2 | 6.862 | 7.225 (0.287) | 6.946 (0.117) | 7.240 (0.198) | 6.962 (0.081) |
| ψ1 | 0.5489 | 0.539 (0.007) | 0.547 (0.003) | 0.539 (0.005) | 0.546 (0.002) |
| ρ1 | 0.9994 | 0.999 | 0.999 | 0.999 | 0.999 |
| ρ2 | 0.9930 | 0.993 | 0.993 | 0.993 | 0.992 |
 | 0.229 | 0.223 (0.033) | 0.224 (0.025) | ||
 | 0.263 | 0.279 (0.046) | 0.279 (0.038) | ||
 | 0.046 | 0.045 (0.006) | 0.045 (0.005) | ||
 | 0.053 | 0.053 (0.007) | 0.05 (0.005) | ||
| Parameter . | True value . | n = 100 . | n = 200 . | ||
|---|---|---|---|---|---|
| . | . | H2 = 0.1 . | H2 = 0.4 . | H2 = 0.1 . | H2 = 0.4 . |
| QTL position | 46 | 45.95 (1.67) | 45.89 (1.64) | 46.02 (1.17) | 45.94 (1.27) |
| R1 | 14 288.2 | 14 371 (1468) | 14 150 (598) | 14 326 (1010) | 14 130 (465) |
| R11 | 132 114 | 131 453 (9543) | 131 654 (3775) | 130 699 (6574) | 131 778 (2764) |
| τ1 | 3.137 | 3.189 (0.135) | 3.148 (0.063) | 3.195 (0.099) | 3.146 (0.040) |
| ψ1 | 0.5256 | 0.526 (0.008) | 0.525 (0.004) | 0.526 (0.006) | 0.525 (0.003) |
| R2 | 14 109 | 13 089 (1334) | 13 963 (557) | 13 092 (883) | 13 875 (419) |
| R12 | 181 502 | 182 249 (13 212) | 182 735 (5410) | 182 150 (8646) | 182 304 (3818) |
| τ2 | 6.862 | 7.225 (0.287) | 6.946 (0.117) | 7.240 (0.198) | 6.962 (0.081) |
| ψ1 | 0.5489 | 0.539 (0.007) | 0.547 (0.003) | 0.539 (0.005) | 0.546 (0.002) |
| ρ1 | 0.9994 | 0.999 | 0.999 | 0.999 | 0.999 |
| ρ2 | 0.9930 | 0.993 | 0.993 | 0.993 | 0.992 |
 | 0.229 | 0.223 (0.033) | 0.224 (0.025) | ||
 | 0.263 | 0.279 (0.046) | 0.279 (0.038) | ||
 | 0.046 | 0.045 (0.006) | 0.045 (0.005) | ||
 | 0.053 | 0.053 (0.007) | 0.05 (0.005) | ||
The parameters include three types: (i) the position of QTL, (ii) QTL effects specified by genotype-specific DCE parameters and (iii) AR(1) parameters.
DISCUSSION
The electrical properties of tissues in a range of frequencies are associated with the cellular components and the dimensions, internal structure and arrangements of the constituent cells [3]. Therefore, tissues with different cellular structures will produce impedance spectra characteristic of these issues. By analyzing electrical properties of biological tissues, we can better understand their structure and function. More recently, EIS has been increasingly used to study the electrical impedance of various tissues over a frequency range and determine their frequency-dependent electric and dielectric behavior [3, 6–11], providing scientific guidance for prognosis, diagnosis and prevention. The use of impedance spectroscopy electrical characterization is a novel approach to comprehend the genetic architecture of phenotypic traits underlying pathology and complex diseases.
We described a computational model for structural mapping by taking into account the structural components of phenotypic traits using EIS information. Structural mapping incorporates the electrical properties of phenotypic formation into a genetic mapping framework by which the genetic control of complex traits can be studied from a mechanistic perspective. Structural mapping was used to analyze a mapping data collected for an experimental cross of outcrossing tree species, Chinese jujube. Significant QTLs were detected to affect the complex impedance of shoots, some of which were also detected by mapping frost hardiness [20]. Because there is a strong correlation between intracellular resistance and frost hardiness [8, 9], the detection of pleiotropic QTLs for these two traits can well confirm the validation of our model. The simulation study by mimicking the real example provides a justification of statistical properties of the model.
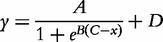
Genetic mapping of complex traits has been thought to be one of the most difficult tasks in genetic research, owing to the multifactorial etiology of trait control.
Traditional approaches for genetic mapping dissect the phenotype of a trait into its genetic components at the molecular level, neglecting the mechanistic details of trait formation.
Structural analysis reveals the formation of a phenotype from its mechanistic and structural properties. By integrating it with genetic mapping, we describe and assess a mapping strategy called structural mapping, which can better elucidate the genetic machineries of trait formation and development.
FUNDING
This work is partially supported by Special Fund for Forestry Scientific Research in the Public Interest (No. 201004017); NSF/IOS-0923975; Changjiang Scholars Award and ‘Thousand-Person Plan’ Award.


