-
PDF
- Split View
-
Views
-
Cite
Cite
Talea Cornelius, Katelyn Gettens, Amy A. Gorin, Dyadic Dynamics in a Randomized Weight Loss Intervention, Annals of Behavioral Medicine, Volume 50, Issue 4, August 2016, Pages 506–515, https://doi.org/10.1007/s12160-016-9778-8
Close - Share Icon Share
Abstract
Despite health and economic burdens associated with overweight and obesity, long-term weight loss intervention efforts have been largely unsuccessful. Observations that weight status tends to cluster in social groups, and findings showing “ripple” effects of weight change within social clusters, raise questions about the impact of social relationships on weight loss.
Through a reanalysis of data from a randomized weight loss intervention, this study compared dyadic dynamics in intervention participants and in-home partners.
Over the course of 18 months, data was collected from 201 pairs enrolled in either behavioral weight loss treatment (BWL) or treatment including partners and providing items to facilitate healthy choices at home (BWL + H). Using a dyadic growth curve model, covariance between baseline BMI, BMI change trajectories, and starting BMI and BMI trajectory for both the self and the other were examined.
There were strong indicators of dependence in the data. Baseline BMI was positively correlated for both treatment groups. In the BWL + H condition, BMI change trajectories were positively correlated. In the BWL condition, this reversed: Change trajectories were negatively correlated. Additionally, partner BMI and primary participant BMI change were positively correlated, indicating that a heavier partner at baseline related to less weight loss.
Social relationships exert a significant influence on weight loss outcomes. Depending on the intervention group, these influences may help (BWL + H) or hinder (BWL). It may be that home intervention changed social support and interaction in important ways and that these effects could be effectively harnessed to implement more effective interventions (NCT00200330).
Overweight and obesity remain widely recognized as one of the predominant healthcare concerns in the USA [1–3]. Recent reports indicate that 69 % of adults and 17 % of youth are now living with overweight or obesity [4]. No states in the USA have obesity prevalence rates below 20 %, and 18 states are within the 30–35 % prevalence range. Estimates project that obesity rates will exceed 44 % in every state in the USA by the year 2030 [5]. Overweight and obesity also place individuals at higher risk for many serious health conditions, including all causes of morbidity and mortality, heart disease, stroke, type 2 diabetes, and certain types of cancer [2]. The economic, medical, and social costs of overweight and obesity are well documented and are predicted to increase by $48–66 billion per year by 2030 [6, 7].
Despite the significant health and economic challenges associated with overweight and obesity, behavioral interventions have not been as successful as desired, particularly in promoting successful, long-term weight loss maintenance [8]. To address these challenges, researchers have searched for new ways to maximize treatment efficacy, harnessing the impact of environmental, social, and interpersonal influences on weight loss and maintenance processes. One promising area is targeting pairs, or dyads, as a unit of analysis and intervention. This study analyzed patterns of social influence in weight change in a sample of dyads in a randomized weight loss intervention. The impact of treatment condition on dyadic dynamics was also explored.
Background
Weight and weight-related behaviors have been found to cluster within social contexts. If a person has social relationships with others who are overweight, that person is likely to be overweight as well [9–13]. Researchers have begun exploring the possibility that intervening in social contexts may allow for weight loss treatment effects to also spread through social contact, both maximizing health benefits and minimizing costs. A randomized clinical trial conducted by Gorin et al. [14] found this “ripple” effect. Untreated spouses of weight loss intervention participants lost a clinically significant amount of weight over the course of 12 months, with the more intensive intervention maximizing weight loss in spouses. Further, changes in eating behavior (e.g., lower fat intake) and in-home food cues (e.g., food availability) were related to spouse weight loss, indicating that these benefits might spread via behavioral modeling or common environmental exposure.
In an analysis of intervention data specifically examining the effects of partner behavior on weight loss outcomes, Schierberl Scherr et al. [15] found that spouses of weight loss treatment participants were affected by changes in the participant's fat and energy intake. The inverse was not true (i.e., participants were not affected by spouse behavior change). There was a significant interaction between primary participant change in energy intake and treatment condition such that if primary participant had a high reduction in energy intake, treatment group did not impact their partner's weight loss. However, for primary participants with low reductions in energy intake, their partner lost more weight when in the condition that involved partners in treatment [15]. This indicates that, when uninvolved in treatment, partners might benefit from participant behavior change—when partners are involved in treatment, main effects of treatment may take precedence.
Other intervention studies have found similar effects. For example, overweight wives of husbands in a dietary weight loss intervention have been found to lose weight with only minimal treatment involvement [16]. Rossini et al. [17] reported positive changes toward a healthier diet and weight loss among overweight family members of participants in a CBT weight loss program [17]. Researchers have also worked to disentangle the effects of a healthy presence (i.e., a normal weight partner) versus a healthy change (i.e., a partner who changes behavior and loses weight). Conceptualizing this as “changing alone” or “changing together,” Jackson, Steptoe, and Wardle [18] found that having a normal BMI partner did not increase a person's odds of losing weight. In contrast, someone with an overweight or obese partner who lost weight was three times more likely to lose weight themselves. This speaks to the power of changing together and leads to further questions about reciprocal effects of weight loss within dyads over time.
Targeting dyads may not be more effective for all intervention participants. In a study comparing standard weight loss treatment and a treatment involving partners and intervening in the home, Gorin et al. [19] found that male participants lost more weight in the standard condition. In contrast, female participants benefitted more in the home intervention condition. Thus, when considering dyadic processes in intervention design, it is important to also consider individual treatment outcomes.
Purpose
We aim to build on previous findings regarding social processes in weight loss, using dyadic growth curve analysis. This analysis accounts for nonindependence between dyad members—a statistical assumption necessary for nondyadic models—and allows for a meaningful examination of covariance within dyads—the interdependence between dyad members [20]. We can then conduct a more fine-grained analysis of dyadic processes. Specifically, we will be able to examine similarities between members in initial BMI and change in BMI over time, as well as the relationship between a person's starting BMI, their own BMI change, and the BMI change of their partner. In other words, does the rate of weight loss for one partner predict weight loss for the other? And, do these effects work in both directions (i.e., does a weight loss intervention participant influence their partner, and does a partner influence a weight loss intervention participant?). To our knowledge, no studies have directly tested covariance between change slopes within dyads over time. We will also examine the effects of either standard treatment or treatment including partner participation and home intervention on these dyadic dynamics. A deeper understanding of these dyadic dynamics could lend insight to factors that contribute to ripple effects in weight loss treatment, and allow future interventions to more effectively harness these dynamics to maximize health benefits for both treatment enrollees and their in-home partners.
Methods
Data from a weight loss intervention were reanalyzed [19], with a specific focus on decomposing and examining interdependence within dyads. Because the original outcomes study found differences in weight loss by condition between male and female participants, interactions with sex were included in the statistical model. This was intended as a replication of the original findings with a different analysis, with a primary goal of examining the effect of treatment condition on dyadic processes, and a secondary goal of considering individual treatment effects and dyadic processes simultaneously.
Participants
Participants were 201 overweight and obese individuals enrolled in the Lifestyle Eating and Activity Program (LEAP) weight loss trial and their in-home partners, recruited through media advertising and direct mailing in the Providence, Rhode Island area [19]. Primary participants expressed interest in enrollment and nominated an in-home partner to complete study procedures with them. Both primary participants and partners completed informed consent prior to study initiation. The majority of participant–partner dyads were spouses (67.2 %), followed by parent–adult child pairs (17.4 %), significant others (10 %), other relatives (3.0 %), and roommates (2.5 %). Individuals eligible for LEAP were 21–70 years old, had a body mass index (BMI) between 25 and 50 kg/m2, and had a household member willing to participate in the study as a support partner. Partners had to reside in the same home as primary participants, be between 15 and 70 years old, and have a BMI between 25 and 70 kg/m2. Individuals were excluded if they or their partner reported a heart condition, chest pain, loss of consciousness, being unable to walk two blocks without stopping, current participation in another weight loss program and/or taking weight loss medication, current pregnancy or planning to become pregnant in the 18 months, or any condition in the judgment of the research team that made it unlikely that the individual would complete the study protocol (e.g., geographical relocation or substance abuse). Individuals endorsing joint problems, prescription medication usage, or other conditions that could limit exercise were required to obtain written physician consent to participate.
Intervention
Participants were randomized to standard behavioral weight loss treatment (BWL) or BWL plus home environment changes (BWL + H). Both groups met weekly for 6 months and bi-monthly for 12 months. In the BWL group, only primary participants received treatment consisting of a standard calorie and fat-restricted diet (e.g., 1200–1800 kcals/day and 30 % fat, depending on initial weight) and a gradual increase in physical activity until participants reached >200 min of moderate-intensity physical activity per week. Standard treatment also included training in behavioral weight loss skills such as self-monitoring, goal setting, cognitive restructuring, problem solving, and, later in the program, weight loss maintenance strategies. Participants were encouraged to share information regarding behavioral weight loss strategies with their partners, although partners were untreated. The BWL + H condition aimed to target the individual plus the physical and social cues within their homes. BWL + H participants and their partners were given items to facilitate healthy choices in their homes (e.g., exercise equipment, portion plates, and motivational posters) and attended standard treatment together. Additionally, BWL + H aimed to modify the type and amount of food consumed, the availability of exercise equipment, and sedentary activities, and create positive models for healthy eating and exercise in the home by including partners in treatment (for further details on the full intervention, see the original paper [19]). Groups met weekly for 6 months followed by bi-weekly meetings for 12 months and were led by interventionists with a master's or doctoral degree in nutrition, exercise physiology, or behavioral psychology. All study procedures were reviewed and approved by The Miriam Hospital's Institutional Review Board.
Data Analysis
Percent body weight change is the customary unit of analysis in weight loss interventions; however, for the current analysis, BMI was used. Using percent body weight would start every participant at 0 % lost, discarding important information and variance in the intercept, and would not make sense for this analysis. For standard analysis of weight loss outcomes, see the original paper [19].
Because dyads could be meaningfully distinguished by primary participant versus partner status, change in BMI over time was estimated using a distinguishable dyadic growth curve model. A distinguishable dyadic growth curve model provides separate estimates of both fixed effects (e.g., average predicted baseline BMI and predicted BMI change slope), as well as random effects (e.g., amount of variance not explained by fixed effects, such as variance in starting BMI) for primary participants and partners. This model also accounts for dependence in data both over time (autocorrelation; a person's BMI is likely to be related to itself across time points) and within dyads (dyad members are likely to have similar BMI). It also allows for meaningful explorations of covariance both within individuals (e.g., starting BMI as it relates to BMI change over time) and within dyads (e.g., relationship between primary and partner change in BMI over time). Errors, or observed deviations of an individual's actual BMI from their predicted BMI slope, are also able to be examined within dyads. For example, it can be determined if there is a relationship between one dyad member losing more (or less) weight than predicted and the other dyad member losing more (or less) weight than predicted.
Fixed effects are reported; however, the random effects are of primary interest in this analysis. All models were estimated using the mixed linear function in SPSS for multilevel modeling [21], and restricted maximum likelihood estimation (REML); variances and correlations were estimated using an unstructured correlation matrix. Indices of model fit were obtained by running identical models maximum likelihood estimation (ML) to allow for comparison of changes in fit due to fixed effects.
Results
Data from 201 dyads was collected at four time points: 0, 6, 12, and 18 months. Time was centered at baseline and coded so that each unit represented a 6-month change. The intercept can thus be interpreted as average BMI at baseline, and the slope for time can be interpreted as average BMI change over the span of 6 months. SPSS syntax can be seen in Appendix.
Descriptive Statistics
Of the 201 dyads, 99 were randomized to BWL, and 102 were randomized to BWL + H. Primary participants (NFemale = 157; NMale = 44) had an average BMI of 36.42 at baseline (SD = 6.14), and a mean age of 48.93 (SD = 10.46); partners (NFemale = 94; NMale = 107) had an average BMI of 32.95 at baseline (SD = 5.88), and a mean age of 47.84 (SD = 13.08).
All 201 primary participants provided BMI at baseline, 198 at 6 months, 180 at 12 months, and 185 at 18 months. In total, 170 provided data across all four time points. Primary participants with complete data were less likely to be in the BWL condition, B = −1.08, p = .01, were older, B = .05, p < .01, had more years of education, B = 1.02, p < .001, and were less likely to be Hispanic, B = −1.24, p = .04. All 201 partners provided BMI at baseline, 190 at 6 months, 175 at 12 months, and 182 at 18 months, with 165 providing data at all time points. Partners with complete data were less likely to be in the BWL condition, B = −1.53, p < .001, were less likely to be female, B = −.85, p = .03, and were older, B = .05, p = .001. All dyads were retained for analysis; the flexibility inherent in growth curve modeling allows for the estimation of a change trajectory even when there are different numbers of observations for each case [22].
Unconditional Model
In the first model, participant status (a within dyads variable, i.e., all dyads had both a primary participant and a partner, dummy coded, 0 = primary, 1 = partner), time, and the interaction between status and time were entered. The deviance (−2 log likelihood) for the model was 7162.66, and the model had 17 parameters. This is an unconditional growth curve with different intercepts and slopes for primary participants and partners. Primary participants had, on average, a predicted BMI of 35.47 at baseline, B = 35.74, t(199.96) = 84.10, p < .001. Partners’ predicted BMI was significantly lower at baseline, B = −3.30, t(199.72) = 6.39, p < .001. There was also an effect of time for primary participants, such that, over the course of a 6-month step, BMI decreased by −.69 on average, B = −.69, t(184.60) = 7.60, p < .001. Partners experienced decreases .21 smaller in BMI over time, B = .21, t(171.17) = 2.19, p = .03.
Conditional Model
The conditional model included participant status, time, treatment condition, sex, and all interactions. The deviance for this model was 7132.36 and had 29 parameters. This model was a significant improvement over the unconditional model, χ2(12) = 30.30, p < .01. The four-way interaction between time, status, condition, and sex was significant, B = −1.38, t(373.02) = 2.73, p < .01. Simple slopes analysis was conducted to unpack two-way interactions and main effects of time for each type of participant. There was significant BMI loss over time for all participants (the change for partner males in standard treatment trended towards significance; see Table 1).
| . | Primary participants . | Partners . | ||||||
|---|---|---|---|---|---|---|---|---|
| Female . | Male . | Female . | Male . | |||||
| B . | t . | B . | t . | B . | t . | B . | t . | |
| Home environment | −.81 | 5.89** | −.72 | 2.85** | −.71 | 5.75** | −.64 | 5.87** |
| Standard | −.32 | 2.21* | −1.52 | 5.45** | −.34 | 2.54* | −.19 | 1.67+ |
| . | Primary participants . | Partners . | ||||||
|---|---|---|---|---|---|---|---|---|
| Female . | Male . | Female . | Male . | |||||
| B . | t . | B . | t . | B . | t . | B . | t . | |
| Home environment | −.81 | 5.89** | −.72 | 2.85** | −.71 | 5.75** | −.64 | 5.87** |
| Standard | −.32 | 2.21* | −1.52 | 5.45** | −.34 | 2.54* | −.19 | 1.67+ |
(+p < .1,
p < .05,
p < .01)
| . | Primary participants . | Partners . | ||||||
|---|---|---|---|---|---|---|---|---|
| Female . | Male . | Female . | Male . | |||||
| B . | t . | B . | t . | B . | t . | B . | t . | |
| Home environment | −.81 | 5.89** | −.72 | 2.85** | −.71 | 5.75** | −.64 | 5.87** |
| Standard | −.32 | 2.21* | −1.52 | 5.45** | −.34 | 2.54* | −.19 | 1.67+ |
| . | Primary participants . | Partners . | ||||||
|---|---|---|---|---|---|---|---|---|
| Female . | Male . | Female . | Male . | |||||
| B . | t . | B . | t . | B . | t . | B . | t . | |
| Home environment | −.81 | 5.89** | −.72 | 2.85** | −.71 | 5.75** | −.64 | 5.87** |
| Standard | −.32 | 2.21* | −1.52 | 5.45** | −.34 | 2.54* | −.19 | 1.67+ |
(+p < .1,
p < .05,
p < .01)
BMI change for primary participants in the home environment condition did not differ by sex, B = −.09, t(190.26) = .32, p = .75; however, it did differ by sex in the standard treatment, B = 1.20, t(201.73) = 3.82, p < .001 (males lost more weight than females). For partners, BMI change did not differ by sex in either the home environment or standard conditions, B = −.06, t(77.86) = .38, p = .71, and B = −.15, t(93.09) = .85, p = .40, respectively. Predicted weight loss trajectories are displayed in Fig. 1. There was some indication of nonlinearity in the data, such that weight loss tapered off over time. For reasons of interpretability, the quadratic term for time is not reported here. When the quadratic term was included, the direction and significance of the remaining coefficients were unaltered.
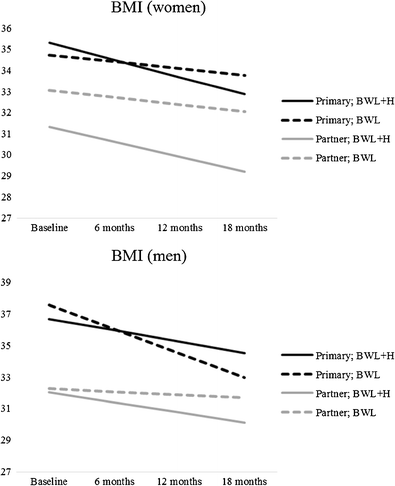
Male Participants
Primary male participants differed in weight loss based on treatment, B = −.81, t(213.15) = 2.15, p = .03, losing more weight in the standard condition. In contrast, male partners lost more weight in the home environment condition, B = −.45, t(86.03) = 2.83, p < .01. As such, in the home environment condition, weight loss for male partners did not differ from male primary participants, B = .07, t(233.17) = .25, p = .80, whereas primary males lost more in the standard treatment than male partners, B = −1.33, t(167.97) = 4.39, p < .001.
Female Participants
Female participants differed in weight loss based on treatment—this was true for primary participants, B = .48, t(127.57) = 2.41, p = .02, as well as partners, B = .36, t(96.03) = 2.02, p < .05. Both primary and partners lost more weight in the home environment condition. In the home environment condition, weight loss for female partners did not differ from female primary participants B = .10, t(222.50) = .57, p = .57; this was also true in the standard treatment, B = −.02, t(106.55) = .10, p = .92.
Final Model
To ensure accurate reporting of variance and covariance components, we ran a final model including the quadratic term for time, as well as the interaction between participant status and the quadratic term for time (keeping this term distinguishable between primary participants and partners). The deviance for this model was 6837.62 with 31 parameters, and improved model fit significantly, χ2(2) = 294.74, p < .01.
Actor–Partner Correlations
In the final model, there was a significant amount of error variance for both primary participants (1.47, p < .001) and partners (1.54, p < .001). The partial ICC (a measure of dependence in the data—or the correlation between primary and partner errors around predicted slopes) was positive and significant, r = .51, p < .001. This indicates that, if a primary participant had a BMI higher (or lower) than expected based on their predicted change slope, their partner also had a higher (or lower) than expected BMI. In other words, BMI was significantly associated within dyads across time. Correlations and variances are displayed in Table 2. The correlation between variance in starting BMI was significant and positive, r = .21, p < .01, showing that pairs tended to have similar BMIs at the beginning of the study. Stated otherwise, if one person had a higher than predicted starting BMI, the other dyad member tended to have a higher BMI as well. The correlation between variance in the rate of change for primary participants and their partner's initial BMI was also positive and significant, r = .21, p = .02, indicating that primary participants who had partners with a higher initial BMI tended to have attenuated decrease in BMI change. There was a trend toward a correlation between variance in the rate of change for partners and primary initial BMI, r = .20, p = .07. This may suggest a similar relationship for partners, such that a heavier primary participant tended to reduce BMI loss over time for partners. Interestingly, variance in individual initial BMI did not correlate with variation in BMI change for either primary participants, r = −.08, p = .34, or partners, r = .07, p = .52. Seemingly, the starting BMI of the other dyad member is related to rate of BMI change over time, but one's own starting BMI is not. Finally, the correlation of the BMI change slope between primary participant and partners was not significant, r = .09, p = .47.
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 34.57** | |||
| Partner intercept | .21** | 31.39** | ||
| Primary slope | −.08 | .21* | 1.22** | |
| Partner slope | .20+ | .07 | .09 | .33** |
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 34.57** | |||
| Partner intercept | .21** | 31.39** | ||
| Primary slope | −.08 | .21* | 1.22** | |
| Partner slope | .20+ | .07 | .09 | .33** |
Variances are on the diagonal; correlations of error variance are off-diagonal (+p < .1, *p < .05, **p < .01)
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 34.57** | |||
| Partner intercept | .21** | 31.39** | ||
| Primary slope | −.08 | .21* | 1.22** | |
| Partner slope | .20+ | .07 | .09 | .33** |
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 34.57** | |||
| Partner intercept | .21** | 31.39** | ||
| Primary slope | −.08 | .21* | 1.22** | |
| Partner slope | .20+ | .07 | .09 | .33** |
Variances are on the diagonal; correlations of error variance are off-diagonal (+p < .1, *p < .05, **p < .01)
The BWL + H treatment intervened with both primary participants and their partners. This could have altered dyadic dynamics, leading to different forms of influence in the different treatment groups. This is akin to an interaction, where variance components are dependent upon treatment condition. To better understand these relationships and their implications, we broke the dataset into two groups and re-examined the variance–covariance matrices.
BWL + H Actor–Partner Correlations
The variance and error correlations are displayed in Table 3. There was a significant amount of error variance for primary participants (1.50, p < .001) and partners (1.45, p < .001). The correlation between errors was positive and significant, r = .57, p < .001. Of specific interest, only two significant error correlations were found. One was for baseline BMI, r = .25, p = .01, mirroring the results for the full sample. The other was for slope variance. This estimate was positive and significant, r = .37, p < .01, indicating a positive relationship between predicted participant and partner weight loss trajectories. Stated otherwise, if one dyad member had a steeper predicted weight loss trajectory, the other dyad member also tended to have a steeper predicted weight loss trajectory. The correlations between other baseline BMI and own BMI change slope were both nonsignificant.
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 35.81** | |||
| Partner intercept | .25* | 34.16** | ||
| Primary slope | −.11 | .07 | 1.30** | |
| Partner slope | .18 | .14 | .37** | .38** |
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 35.81** | |||
| Partner intercept | .25* | 34.16** | ||
| Primary slope | −.11 | .07 | 1.30** | |
| Partner slope | .18 | .14 | .37** | .38** |
Variances are on the diagonal; correlations of error variance are off-diagonal (+p < .1, *p < .05, **p < .01)
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 35.81** | |||
| Partner intercept | .25* | 34.16** | ||
| Primary slope | −.11 | .07 | 1.30** | |
| Partner slope | .18 | .14 | .37** | .38** |
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 35.81** | |||
| Partner intercept | .25* | 34.16** | ||
| Primary slope | −.11 | .07 | 1.30** | |
| Partner slope | .18 | .14 | .37** | .38** |
Variances are on the diagonal; correlations of error variance are off-diagonal (+p < .1, *p < .05, **p < .01)
BWL Actor–Partner Correlations
The variance and error correlations are displayed in Table 4. There was a significant amount of error variance for primary participants (1.43, p < .001) and partners (1.11, p < .001). The correlation between errors was positive and significant, r = .47, p < .001. In this subsample, there was a trend toward a relationship between variance in baseline BMI for primary participants and partners, r = .17, p < .10. Although the correlation between variance in primary participant baseline BMI and partner slope was not significant, the correlation between partner baseline BMI and primary participant BMI slope was positive and significant, r = .42, p < .001, indicating that primary participants who had partners with a higher initial BMI tended to have attenuated decrease in BMI change. Finally, the correlation between primary participant and partner slope variance was negative and significant, r = −.38, p = .02, indicating a negative relationship between predicted participant and partner weight loss trajectories. Stated otherwise, if one dyad member had a steeper predicted weight loss trajectory, the other dyad member tended to have a shallower predicted weight loss trajectory.
Variances and correlations of error variances for BWL (standard) treatment group
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 33.27** | |||
| Partner intercept | .17+ | 29.52** | ||
| Primary slope | −.03 | .42** | 1.16** | |
| Partner slope | .13 | −.22 | −.38* | .54** |
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 33.27** | |||
| Partner intercept | .17+ | 29.52** | ||
| Primary slope | −.03 | .42** | 1.16** | |
| Partner slope | .13 | −.22 | −.38* | .54** |
Variances are on the diagonal; correlations of error variance are off-diagonal (+p < .1, *p < .05, **p < .01)
Variances and correlations of error variances for BWL (standard) treatment group
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 33.27** | |||
| Partner intercept | .17+ | 29.52** | ||
| Primary slope | −.03 | .42** | 1.16** | |
| Partner slope | .13 | −.22 | −.38* | .54** |
| . | Primary intercept . | Partner intercept . | Primary slope . | Partner slope . |
|---|---|---|---|---|
| Primary intercept | 33.27** | |||
| Partner intercept | .17+ | 29.52** | ||
| Primary slope | −.03 | .42** | 1.16** | |
| Partner slope | .13 | −.22 | −.38* | .54** |
Variances are on the diagonal; correlations of error variance are off-diagonal (+p < .1, *p < .05, **p < .01)
Analyses were repeated with the 90 dyads in the BWL + H condition and 69 dyads in the BWL where both dyad members provided weight data across all four time points. In both cases, variance–covariance components mirrored results from the full sample. The correlation between predicted weight loss trajectories was somewhat attenuated in the BWL condition, r = −.25, p = .14, and the correlation between primary participant BMI and partner weight loss trajectory was positive and significant, r = .33, p = .02.
Conclusions
Our findings expand on previous research showing a significant influence of partners on weight loss outcomes. Using dyadic growth curve analyses we were able to distinguish between important sources of within-person effects, or the relationship between starting BMI and BMI loss over time, as well as influence within dyads, including similarities in starting BMI, similarities in change over time, and the influence of partner starting BMI on one's own BMI change over time. Notable findings include strong indicators of nonindependence, relationships between primary and partner baseline BMI and change slopes, and the influence of partner baseline BMI on primary participant weight loss.
As indicated by significant, strong positive error correlations, there was considerable nonindependence in the data. That is, if one dyad member was heavier (or lighter) than predicted at a given time point, the other dyad member was also heavier (or lighter). This shows that there is a dynamic within the dyad leading to similarities in weight change over time not accounted for by the predictors in the model. There are numerous possible explanations for this effect, which could range from shared personality traits within dyads to shared environmental exposure, home stress, etc. It is also important to note that, with this different analysis, findings for weight loss outcomes and sex differences in treatment effectiveness replicate those reported in the original paper [19].
The significant covariance in initial BMI replicates findings that BMI clusters within social contacts [9–13]. This does not answer the questions of why, however. It is possible that this could occur due to social influence processes prior to data collection, that it could occur due to homophily and selection effects (i.e., choosing to form relationships with people who are similar to you; [23, 24]), or some combination of both.
The observation that starting BMI of a partner can be related to the BMI change of a primary participant is novel. As indicated by a positive correlation between partner starting BMI and primary participant BMI change in the standard condition, if the partner had a higher starting BMI, participants lost less weight over the course of the study. There are a number of reasons this could have occurred. It may be that a heavier other was used as a basis for social comparison, and, as such, comparison to a higher BMI referent led to acceptance of higher weight in general, and, subsequently, less weight loss. This parallels the observation that, as referent group body weight increases on average, so does misclassification of overweight status as normal [25]. This finding also supports general observations of weight clustering. Because obesity has been found to “spread” through social contact [9], it may be that an upward pull was active in the standard treatment: The influence of a present, heavy other has generally been found to lead to an increase in weight. Possibilities leading to this effect include initial presence of more high-fat foods or fewer exercise cues, such that a greater change would need to occur to cue more weight loss behaviors. It may be that the home intervention in the BWL + H condition affected the presence of food or exercise cues associated with a heavier partner, thus removing their influence over the course of the study. This would indicate that restructuring an environment can positively impact weight loss within dyads. It may also be that the BWL + H condition otherwise affected partner dynamics through inclusion of the partner in treatment, combating the detrimental effect on weight loss associated with having a heavier partner. This would indicate that partner supports can positively impact weight loss within dyads. These possibilities are speculative, however, and are beyond the scope of this paper. They should be explicitly tested in future research. Studies attempting to separate home and partner support dynamics would be especially informative. Whatever the reason, the fact that partner initial BMI has a significant effect on an individual's own weight loss trajectory speaks to the importance of dyadic influence, particularly when considering one's own starting BMI does not.
The relationship between predicted BMI change slopes within dyads was revealed to be complex, and varied between treatment conditions. It is likely that the BWL + H intervention, which targeted both dyad members and intervened in the home, altered the dyadic dynamics. Within the BWL + H group, a moderate–strong correlation indicated that change trajectories were similar. If one dyad member lost more weight, the other member did as well. Within the BWL group, the opposite occurred. BMI slopes were negatively correlated, such that, if one dyad member had a steeper weight loss trajectory, the other member had a trajectory that was more shallow. It is possible that the BWL + H treatment created a more collaborative environment, where dyad members looked to each other to encourage and support each other's weight loss. It is also possible that the home intervention similarly affected the weight loss for both dyad members, creating similarities in weight loss trajectories. Again, studies attempting to separate the effects of these two factors would be clinically relevant. The reason for the negative correlation between slopes in the BWL group, however, is unclear. Previous findings from Gorin et al. [26] and Powers et al. [27] highlight the importance of autonomy support and communication styles among partners to promote successful weight management [26, 27]. It is possible that the type and level of perceived support within a dyad is influenced when the intervention involves unequal involvement. Untreated partners may feel distanced from the weight loss process, negatively impacting dyadic communication and support patterns. Alternatively, partner involvement could bolster helpful dyadic support processes, allowing partners to work together to succeed.
Although the BWL + H treatment condition showed promise for maximizing and harnessing dyadic processes, this must be considered in light of the finding that primary male participants benefitted more from standard treatment. Intervening in a social or home environment context may have the potential to facilitate dyadic weight loss processes; however, main effects of treatment should not be ignored. Potential negative effects of a more involved intervention must be considered in tandem with potential benefits. Future studies should follow up on these possibilities. For example, it may be that longer-term dyadic support processes are more effective at promoting weight loss maintenance, and benefits initially associated with standard treatment for males become nonsignificant.
There were a number of limitations in this study. Due to the complexity of the model, we did not include the quadratic term for time when interpreting the main fixed effects. However, this was not the main purpose of the study, and we did include the quadratic term when interpreting variance and covariances to avoid specification errors. Notably, when including the quadratic term, the other regression coefficients were unaltered.
Additionally, due to low numbers of dyads in some relationship categories, we did not include interactions with different relationship types. However, when restricted to the 69 married couples in BWL and the 66 married couples in BWL + H, the subgroup analyses of error correlations mirrored results from all relationship types.
Although this study provides insights into dynamics occurring within dyads during weight loss, there is a considerable amount of unexplained interdependence in weight loss outcomes, and the factors influencing dyadic dynamics are unclear. Future studies should be designed to explore specific components of an intervention that can harness dyadic dynamics to promote weight loss. This might take the form of examining intervention components that change correlations between partners in terms of weight loss, protecting weight loss participants from negative influence of overweight partners and promoting effective dyadic communication strategies, or working to understand what other factors in the home or in a relationship might affect these dynamics. A deeper understanding of social dynamics in weight loss could contribute to the development of effective interventions that can elicit positive changes in other household members, which could in turn promote weight loss maintenance, improve intervention dissemination, and minimize costs.
Traditional individual-focused weight loss approaches that emphasize personal choices and willpower fail to consider the larger social and environmental contexts in which people function, an aspect of weight management that has been identified as a critical consideration if we hope to improve weight loss maintenance outcomes [26, 28]. Indeed, recent weight loss interventions have begun to target dyads (e.g., [29, 30]), indicating that steps are being taken toward greater understanding of specific environmental and social supports to facilitate weight loss and lay a foundation for longer-term weight loss maintenance.
This study indicates a significant influence of partners on weight loss outcomes for participants in a weight loss intervention. These dynamics varied between treatment groups. In standard treatment (BWL), partner BMI at baseline related to a shallower BMI change trajectory over time, and dyadic weight loss trajectories were negatively correlated. In an enhanced treatment that included partners and intervened in the home (BWL + H), partners’ weight loss trajectory related to primary participant weight loss: If the partner lost more weight, the primary participant did as well. Our findings highlight the influence of social and larger environmental contexts on weight management and further elucidate the necessity of interventions targeting dyadic and interpersonal factors of health behavior change. Novel approaches, both statistical and clinical, that closely examine the intricacies of dyadic health behavior change are critical in unraveling the complex dynamics that occur within social relationships to affect important health outcomes and promote improved long-term weight management.
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.
Appendix
*Unconditional growth model
**REML
MIXED BMI_A WITH Primary_A Partner_A CBMI_P CTime GROUP_BL Primary_Partner_BL_A SEX_0_1_A
/CRITERIA = CIN(95) MXITER(100) MXSTEP(65) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0,
ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED = Primary_Partner_BL_A CTime Primary_Partner_BL_A*CTime | SSTYPE(3)
/METHOD = REML
/PRINT = SOLUTION TESTCOV
/RANDOM = Primary_A Partner_A Primary_A*CTime Partner_A*CTime | SUBJECT(CoupleID) COVTYPE(UNR)
/REPEATED = Primary_Partner_BL_A | SUBJECT(CoupleID*CTime) COVTYPE(CSH).
**ML for chi square comparison
MIXED BMI_A WITH Primary_A Partner_A CBMI_P CTime GROUP_BL Primary_Partner_BL_A SEX_0_1_A
/CRITERIA = CIN(95) MXITER(100) MXSTEP(65) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0,
ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED = Primary_Partner_BL_A CTime Primary_Partner_BL_A*CTime | SSTYPE(3)
/METHOD = ML
/PRINT = SOLUTION TESTCOV
/RANDOM = Primary_A Partner_A Primary_A*CTime Partner_A*CTime | SUBJECT(CoupleID) COVTYPE(UNR)
/REPEATED = Primary_Partner_BL_A | SUBJECT(CoupleID*CTime) COVTYPE(CSH).
*Conditional Model
**REML
MIXED BMI_A WITH Primary_A Partner_A CBMI_P CTime GROUP_BL Primary_Partner_BL_A SEX_0_1_A
/CRITERIA = CIN(95) MXITER(100) MXSTEP(65) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0,
ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED = GROUP_BL CTime SEX_0_1_A Primary_Partner_BL_A CTime*GROUP_BL CTime*Primary_Partner_BL_A
CTime*SEX_0_1_A GROUP_BL*Primary_Partner_BL_A GROUP_BL*SEX_0_1_A Primary_Partner_BL_A*SEX_0_1_A
CTime*GROUP_BL*Primary_Partner_BL_A CTime*GROUP_BL*SEX_0_1_A CTime*Primary_Partner_BL_A*SEX_0_1_A
GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A*CTime | SSTYPE(3)
/METHOD = REML
/PRINT = SOLUTION TESTCOV
/RANDOM = Primary_A Partner_A Primary_A*CTime Partner_A*CTime | SUBJECT(CoupleID) COVTYPE(UNR)
/REPEATED = Primary_Partner_BL_A | SUBJECT(CoupleID*CTime) COVTYPE(CSH).
**ML
MIXED BMI_A WITH Primary_A Partner_A CBMI_P CTime GROUP_BL Primary_Partner_BL_A SEX_0_1_A
/CRITERIA = CIN(95) MXITER(100) MXSTEP(65) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0,
ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED = GROUP_BL CTime SEX_0_1_A Primary_Partner_BL_A CTime*GROUP_BL CTime*Primary_Partner_BL_A
CTime*SEX_0_1_A GROUP_BL*Primary_Partner_BL_A GROUP_BL*SEX_0_1_A Primary_Partner_BL_A*SEX_0_1_A
CTime*GROUP_BL*Primary_Partner_BL_A CTime*GROUP_BL*SEX_0_1_A CTime*Primary_Partner_BL_A*SEX_0_1_A
GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A*CTime | SSTYPE(3)
/METHOD = ML
/PRINT = SOLUTION TESTCOV
/RANDOM = Primary_A Partner_A Primary_A*CTime Partner_A*CTime | SUBJECT(CoupleID) COVTYPE(UNR)
/REPEATED = Primary_Partner_BL_A | SUBJECT(CoupleID*CTime) COVTYPE(CSH).
*Final Model
**REML
MIXED BMI_A WITH Primary_A Partner_A CBMI_P CTime GROUP_BL Primary_Partner_BL_A SEX_0_1_A CTimeSq
/CRITERIA = CIN(95) MXITER(100) MXSTEP(65) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0,
ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED = GROUP_BL CTime Primary_Partner_BL_A SEX_0_1_A CTimeSq CTime*GROUP_BL
CTime*Primary_Partner_BL_A CTime*SEX_0_1_A CTimeSq*Primary_Partner_BL_A
GROUP_BL*Primary_Partner_BL_A GROUP_BL*SEX_0_1_A Primary_Partner_BL_A*SEX_0_1_A
CTime*GROUP_BL*Primary_Partner_BL_A CTime*GROUP_BL*SEX_0_1_A CTime*Primary_Partner_BL_A*SEX_0_1_A
GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A
CTime*GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A | SSTYPE(3)
/METHOD = REML
/PRINT = SOLUTION TESTCOV
/RANDOM = Primary_A Partner_A Primary_A*CTime Partner_A*CTime | SUBJECT(CoupleID) COVTYPE(UNR)
/REPEATED = Primary_Partner_BL_A | SUBJECT(CoupleID*CTime) COVTYPE(CSH).
**ML
MIXED BMI_A WITH Primary_A Partner_A CBMI_P CTime GROUP_BL Primary_Partner_BL_A SEX_0_1_A CTimeSq
/CRITERIA = CIN(95) MXITER(100) MXSTEP(65) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0,
ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED = GROUP_BL CTime Primary_Partner_BL_A SEX_0_1_A CTimeSq CTime*GROUP_BL
CTime*Primary_Partner_BL_A CTime*SEX_0_1_A CTimeSq*Primary_Partner_BL_A
GROUP_BL*Primary_Partner_BL_A GROUP_BL*SEX_0_1_A Primary_Partner_BL_A*SEX_0_1_A
CTime*GROUP_BL*Primary_Partner_BL_A CTime*GROUP_BL*SEX_0_1_A CTime*Primary_Partner_BL_A*SEX_0_1_A
GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A
CTime*GROUP_BL*Primary_Partner_BL_A*SEX_0_1_A | SSTYPE(3)
/METHOD = ML
/PRINT = SOLUTION TESTCOV
/RANDOM = Primary_A Partner_A Primary_A*CTime Partner_A*CTime | SUBJECT(CoupleID) COVTYPE(UNR)
/REPEATED = Primary_Partner_BL_A | SUBJECT(CoupleID*CTime) COVTYPE(CSH).
*Split by condition - quadratic
MIXED BMI_A WITH Primary_A Partner_A CBMI_P CTime Primary_Partner_BL_A SEX_0_1_A CTimeSq
/CRITERIA = CIN(95) MXITER(100) MXSTEP(65) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0,
ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED = CTime Primary_Partner_BL_A SEX_0_1_A CTimeSq
CTime*Primary_Partner_BL_A CTime*SEX_0_1_A CTimeSq*Primary_Partner_BL_A Primary_Partner_BL_A*SEX_0_1_A
CTime*Primary_Partner_BL_A*SEX_0_1_A | SSTYPE(3)
/METHOD = REML
/PRINT = SOLUTION TESTCOV
/RANDOM = Primary_A Partner_A Primary_A*CTime Partner_A*CTime | SUBJECT(CoupleID) COVTYPE(UNR)
/REPEATED = Primary_Partner_BL_A | SUBJECT(CoupleID*CTime) COVTYPE(CSH).
Footnotes
Funding The original study was funded by NHLBI (HL77082).
References
Author notes
Authors’ Statement of Conflict of Interest and Adherence to Ethical Standards
Talea Cornelius is funded on an NIH T-32 training grant. Katelyn Gettens is funded on an NIH grant (HL125157). Amy Gorin has received external grant funding from NIH, NHLBI (R21 HL125157; R01 HL77082), NICHD (R21 HD073966; R21 HD065185), Weight Watchers, NIAAA (R01AA021471), NIDDK (R01DK092374; U01 DK067861; R01 DK 57413; DK066787 S1), NINR (R01 NR07960), Science Applications International Corporation, Community Health Network of Connecticut, Aetna Foundation, National Cancer Institute, National Library of Medicine, and Obesity Society New Investigator Grant, and has consulted on NHLBI grants (R01 HL090864; R01 HL118208), NIDDK grants (R03 DK095959), NICHD grants (K23 HD057957), and NIMHD grants (R03 MH083987). She holds a secondary appointment as adjunct assistant professor at Brown Medical School in Providence, RI. She has also served as co-chair for the Society of Behavioral Medicine, Obesity and Eating Disorders Special Interest Group, and as a consultant for the Obesity Program at Connecticut Children's Medical Center, in Hartford, CT. All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.
All participants provided informed consent. Procedures were approved by the Miriam Hospital Institutional Review Board.



