-
PDF
- Split View
-
Views
-
Cite
Cite
Brice Corgnet, Roberto Hernán-González, Praveen Kujal, David Porter, The Effect of Earned Versus House Money on Price Bubble Formation in Experimental Asset Markets, Review of Finance, Volume 19, Issue 4, July 2015, Pages 1455–1488, https://doi.org/10.1093/rof/rfu031
Close - Share Icon Share
Abstract
Does house money exacerbate price bubbles? We compare house money asset market experiments with an earned money treatment where initial portfolios are constructed from a real effort task. Bubbles occur; however, trading volumes and earnings dispersion are significantly higher with house money. We investigate the role of cognitive ability in accounting for the differences in earnings distribution across treatments by using the cognitive reflection test (CRT). Low CRT subjects earned less than high CRT subjects. Low CRT subjects were net purchasers (sellers) of shares when the price was above (below) fundamental value. The opposite was true for high CRT subjects.
1. Introduction
Do individuals make different economic decisions when they use their own money (“earned money”) compared to when they do not (“house money”)? Evidence of a “house money effect” was found by Thaler and Johnson (1990) in a lottery choice experiment. They found that subjects were more likely to exhibit risk-seeking behavior in the presence of a prior gain. This result raised the question about the robustness of experimental results where subjects make decisions using house money.
The effect of house money has been examined in bargaining and income redistribution experiments. When money is earned, subjects tend to recognize merit and divide money among subjects according to their respective contributions (Hoffman and Spitzer, 1985; Konow, 2000; Oxoby and Spraggon, 2008). In ultimatum games when money is not earned, merit does not play a role and subjects are more likely to share the initial endowment equally (Güth, Schmittberger, and Schwarze, 1982; Güth and Tietz, 1988).1 But Cherry, Frykblom, and Shogren (2002) show that, in a dictator game, 95% of the dictators follow game-theoretic predictions by not transferring any amount to the other player when they earned their wealth. Reinstein and Reiner (2012) obtain similar findings in a charitable giving game. In these studies, subjects earn money prior to deciding upon the allocation of the outcome by answering a quiz (Cherry, Frykblom, and Shogren, 2002; Oxoby and Spraggon, 2008), playing a simple hash mark game (Hoffman and Spitzer, 1985), adding numbers (Reinstein and Reiner, 2012), or stuffing and folding envelopes (Konow, 2000). On the other hand, Cherry, Kroll, and Shogren (2005) find no evidence of the house money effect in voluntary contribution games. The variability of results across different games suggests that the effect may also be specific to the environment being tested.
Even though most of the previously mentioned research provides evidence of a house money effect in bargaining games, it is not clear how these results extend to market games of exchange.
1.1 HOUSE MONEY VERSUS EARNED MONEY IN ASSET MARKETS
It is well known that prices in experimental asset markets do not follow the theoretical prediction and bubbles are commonly observed with inexperienced subjects (Smith, Suchanek, and Williams, 1988). Experimental asset markets are characterized by persistent (average) price deviation from fundamental value in early periods, with prices significantly above fundamental as the market progresses and then a crash to fundamental value at the end. The question we address is whether the use of house money to endow initial portfolios of cash and shares to subjects encourages the “mispricing” found in experimental asset markets.
Specifically, we investigate whether traders behave differently when they earn their starting endowment (“Earned Money treatment”) than when they do not (“House Money baseline”) in experimental asset markets with price bubbles and crashes. Asset market bubbles have been found to be robust to treatments variations such as short selling, capacity to buy on margin, brokerage fees, limit price change rules (King et al., 1993; Porter and Smith, 1994) and assets generating certain dividends (Porter and Smith, 1995). Further, even though the introduction of futures markets may reduce bubble amplitude, it does not affect their duration (Porter and Smith, 1995). Nevertheless, a complete set of futures (one for each of the fifteen periods) seems to eliminate bubbles (Noussair and Tucker, 2006). Interestingly, bubbles tend to disappear with twice-experienced subjects even when experienced and inexperienced traders are mixed (Dufwenberg, Lindqvist, and Moore, 2005). However, bubbles may still be observed among twice-experienced traders when the market environment is modified by increasing liquidity and dividend uncertainty (Hussam, Porter, and Smith, 2008). The existence of bubbles has been partly ascribed to subjects’ irrational behaviors (Lei, Noussair, and Plott, 2001). The authors find evidence of systematic errors in decision making accompanying bubbles. Traders engage in unprofitable transactions at prices above the maximum possible or below the minimum possible dividend stream.
The asset market environment is a good candidate to study the house money effect as it is characterized by systematic deviations of market prices from fundamental values in contradiction to the equilibrium predictions obtained in market-clearing models (Tirole, 1982). In that context, we may wonder whether the house money effect can account for part of the discrepancy between the fundamental value of the asset and the prices observed in the laboratory. Earlier research on the house money effect offers little guidance to our current study as it mostly examines bargaining games and aims at studying the role of house money on distributive preferences. Market experiments differ considerably from these settings as they do not involve concerns for distributive preferences. The only work that contemplates the potential effect of house money in a market environment was conducted by Ang, Diavatopoulos, Schwarz (2010). The authors conducted experimental asset markets (as a robustness check) in which subjects played with their own money. No significant differences were found between the house money and the own money cases. Besides natural concerns with a possible selection bias, the authors’ results should be interpreted with caution as they conducted only two experimental sessions with subjects’ own money. This small sample follows from the fact that the primary goal of the authors was to assess the emergence of bubbles under different compensation schemes, wealth and supply constraints, as well as the effect of the relative risk aversion of traders rather than studying the house money effect per se.
In order to study the effect of earned money in experimental asset markets, we recruited subjects for a two-part experiment. In the first part, subjects had to perform a 2 hour real effort task that consisted in developing a database for a research institute. All subjects earned the same amount in this part and were told that their money was carried over for the experiment which will be realized in the second part.2 In the second part, which took place after 3 days, subjects participated in a standard experimental asset market with certain dividends (Smith, Suchanek, and Williams, 1988; Porter and Smith, 1995). The value of each subject’s initial portfolio composed of both cash and shares was exactly equal to the fixed payment earned from the first-day task ($31.5).3
Our main findings are that bubbles were similar in the house and earned money treatments. However, relative to the house money treatment, transaction volumes were 31% lower in the earned money treatment. One of the direct effects of reduced transactions is that the dispersion of earnings was more pronounced in the house money compared with earned money treatment. We investigate earnings dispersion further by categorizing subjects according to their performance on the cognitive reflection test (CRT) (Frederick, 2005).4 We find that subjects with low CRT scores were net purchasers (sellers) of shares when the price was above (below) fundamental value while the opposite was true for subjects with high CRT scores. As a result, high CRT subjects earned more money on average than the initial value of their portfolio while low CRT subjects earned less. This result was true for both the house and earned money treatments.
2. Experimental Design and Hypothesis
2.1 PROCEDURE
One hundred and eighty subjects from a major university participated in the house money (henceforth HM) and earned money (henceforth EM) treatments.
2.1.a The HM treatment
In the baseline HM treatment, subjects only participated in the asset market experiment for which they were endowed with a portfolio of cash and shares worth $31.50 from the experimenter (house money). The HM experiments were conducted as standard asset market experiments (Smith, Suchanek, and Williams, 1988). Nine subjects each participated in a fifteen period asset market. Our only departure from the standard structure was that the dividend was certain (Porter and Smith, 1995). This was dictated by the design requirement of the EM treatment where we wanted to ensure that subjects did not see their earned money being put to risk. A certain dividend guaranteed that if the subjects simply held on to their shares and cash endowment they would finish the market experiment with the amount of money they had previously earned.
2.1.b The EM treatment
Subjects in the EM treatment were told that they will be participating in an experiment that has two parts (Table I) with the second part taking place 3 days after the first part. Subjects were told that they will be performing a task related to a database for a research institute in the first part and that the amount earned in the task, $31.50, will be carried over to the second part.5 They were also informed that they would be paid in cash for the entire experiment at the end of the second part. Including the 2-day show-up fees subjects earned, on average, $51.50.6 As a result, in the EM treatment final earnings were partially coming from show-up fees which were not earned by subjects. The show-up fee, however, could not be used for trading and, as such, differed from the endowment subjects receive in standard experimental asset markets. In that respect, our treatment is one of earned endowment. We did not have subjects earn their show-up fees because the IRB rules at the laboratory where the studies were conducted require that subjects cannot be recruited without being paid a show-up fee (or their show-up fee being put at risk).7
| First day—task . | Second day—asset market . |
|---|---|
|
|
| First day—task . | Second day—asset market . |
|---|---|
|
|
| First day—task . | Second day—asset market . |
|---|---|
|
|
| First day—task . | Second day—asset market . |
|---|---|
|
|
In the first part of the experiment, subjects performed a task requiring (real) effort of 2 h. The task performed by the subjects was intended to resemble as closely as possible a short-term job.8 We ensured that subjects were aware of the economic significance of their work task by explicitly stating in the instructions that the database to be developed was going to be used by a research institute (which was indeed the case). In order to stress the difference between a standard laboratory experiment and the work task (in the EM treatment), we conducted the two parts, that is the work task and the experimental asset market, on two separate days.9
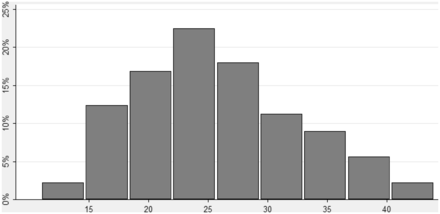
In our work task, subjects had to search and download academic articles into a file folder with the objective of building a database. Subjects had to search on JSTOR for the articles, download them and copy them into a file folder. If they could not copy any article then they had to state the exact reason as to why it was not downloaded.10 All subjects were paid the same fixed wage of $31.50 for the task irrespective of the effort made. This was done to ensure that the starting endowment for all the subjects was the same in the asset market experiment. Subjects were told in the instructions (see Appendix B) that they were “expected to search a minimum of 20 articles in a JSTOR database and download them to a personal folder with their name (that will be identified later)”. A great majority of subjects (83%) were able to download twenty articles or more.11 On average (median) subjects downloaded 25.4 (25.0) articles, with the maximum number of articles being 44 and the minimum being 11 (see Figure 1 for a histogram of the number of downloaded articles).
In the second part, the subjects participated in an asset market experiment (Table I). Each experiment had nine subjects. Each asset earned a fixed dividend of 24 cents in each period and lasted for fifteen periods. Subjects started the experiment with four, five, or six shares and had cash endowments of 1,710, 1,350, or 990 cents, respectively. The total value of the endowment equaled $31.50 dollars for all subjects, which is exactly equal to the money they earned in the prior task. Subjects were told several times that their earnings will be used in the asset market experiment. For example, subjects were informed explicitly that:
(i) Before participating in this experiment, you earned $31.50 by working on the database for the research institute during 2 hours. This full amount of cash will be used to pay for your initial portfolio in the current experiment.
We provided each subject with detailed calculations regarding the value of their initial portfolio which was composed of both cash and shares (see Instructions page 3 in Appendix C). We then clarified the link between the work task completed in the first part of the experiment and the initial portfolio endowment.
(ii) Notice that the value of your initial portfolio corresponds to the earnings in the 2 hours you spent working on the database.
Point (ii) was further repeated in the experimental summary at the end of the instructions where subjects were told that the initial value of their portfolio ($31.50) corresponded to the earnings they obtained in the work task 3 days ago. This was done to ensure that the subjects knew that they were playing with the amount they earned in the earlier task. We summarize our experimental design in Table II.
| Treatment . | Number of subjects per sessions . | Number of sessions . |
|---|---|---|
| House Money Baseline | 9 | 10 |
| Earned Money Treatment | 9 | 10 |
| Treatment . | Number of subjects per sessions . | Number of sessions . |
|---|---|---|
| House Money Baseline | 9 | 10 |
| Earned Money Treatment | 9 | 10 |
| Treatment . | Number of subjects per sessions . | Number of sessions . |
|---|---|---|
| House Money Baseline | 9 | 10 |
| Earned Money Treatment | 9 | 10 |
| Treatment . | Number of subjects per sessions . | Number of sessions . |
|---|---|---|
| House Money Baseline | 9 | 10 |
| Earned Money Treatment | 9 | 10 |
2.1.c CRT
To complement our analysis of the effect of earned money on individual behavior, we collected data regarding subjects’ cognitive ability at the end of each experimental session. We used the CRT as a measure of cognitive ability (Frederick, 2005). The CRT has been found to correlate with general measures of intelligence as well as different aspects of individual decision making such as risk and time preferences (Frederick, 2005; Oechssler, Roider, and Schmitz, 2009) and levels of reasoning (Brañas-Garza, García-Muñoz, and Hernán-González, 2012). The CRT consists of the following three questions:
A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?
If it takes five machines 5 min to make five widgets, how long would it take 100 machines to make 100 widgets?
In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?
The CRT score corresponds to the total number of correct answers and varies from 0 to 3.
2.2 HYPOTHESIS
Bubbles in experimental asset markets are characterized in many dimensions such as price deviations from fundamental value, duration, and trade volume. If house money has an effect it will be manifested in changes in these measures. It seems natural to suppose (and as suggested by Thaler and Johnson, 1990) that subjects might engage in greater speculative behavior when they have none of their own money at stake and that this speculative behavior will likely result in higher trading volumes and mispricing. If, as Lei, Noussair, and Plott (2001) and Kirchler, Huber, and Stüockl (2012) suggest, bubbles are a manifestation of some underlying confusion about the market environment, then earned money should have no effect. Given this, we examine the following null hypothesis in our experiments.
Hypothesis:Earned money will have no effect on the characteristics of price bubbles.
3. Results
We use different measures of bubbles considered in the literature in order to check for differences between treatments and also to compare with results reported by other authors. We consider the following measures of bubbles:12
Amplitude: measures the trough-to-peak change in asset value relative to its fundamental value. This is measured as, A = Max{: t = 1 … 15} − Min{ : t = 1 … 15}. Where, Pt is the average market price in period t, ft is the fundamental value of the asset in period t, and E is the expected dividend value over the life of the asset.
- Duration: measures the length, in periods, in which there is an observed increase in market prices relative to the fundamental value of the asset. Formally, duration is defined as:
Haessel-R2 (Walter W. Haessel, 1978): measures goodness-of-fit between observed (mean prices) and fundamental values. It is appropriate, since the fundamental values are exogenously given. Haessel-R2 tends to 1 as trading prices tend to fundamental values.
- Normalized average price deviation (NAV): sums up the absolute deviation between the average price and the fundamental value for each of the fifteen periods. It is defined as follows:
- Normalized absolute price deviation (NAP): as defined in Haruvy and Noussair (2006), NAP measures the per-share aggregate overvaluation (or undervaluation), relative to the fundamental value of the asset in a given period and is defined as:where, Pk is the price of the k-th transaction in the experiment, 45 the total number of shares, 100 is a normalization scalar, and fk is the fundamental value of the asset when the k-th transaction takes place. Large values of NAP reflect volumetric deviations from fundamentals. This measure is similar to the normalized average price deviation. However, NAV does not depend on the number of trades and can then be used to compare the extent of mispricing in sessions with different levels of trading volumes.
- Turnover: measures the volume of share transactions relative to the number of shares on issue in the market:where, T is the number of trading periods, is the number of transactions in period t and 45 is the total number of shares in the market which in our case is equal to 45.
3.1 BUBBLE CHARACTERISTICS
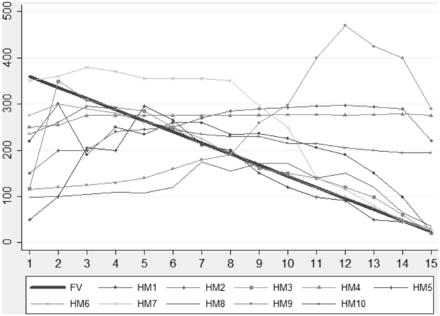
In Figure 2, we plot per period median price for each session in the HM treatment. Interestingly, although prices always start below the fundamental value, in three of our sessions average prices keep close to the fundamental value for most of the periods. Table III reports bubble measures for each session.
Average bubble measures for different treatments
aMann–Whitney–Wilcoxon test.
| Treatment . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Turnover . |
|---|---|---|---|---|---|---|---|
| House money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 7.98 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 5.38 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 4.96 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 8.31 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3.98 | |
| Earned Money | 1 | 0.46 | 6 | 0.82 | 29 | 1.5 | 3.0 |
| 2 | 0.60 | 4 | 0.80 | 37 | 1.3 | 2.9 | |
| 3 | 0.84 | 5 | 0.53 | 69 | 1.8 | 3.0 | |
| 4 | 0.52 | 8 | 0.92 | 81 | 2.8 | 2.5 | |
| 5 | 0.74 | 4 | 0.61 | 27 | 2.0 | 5.8 | |
| 6 | 1.13 | 12 | 0.69 | 116 | 9.2 | 8.8 | |
| 7 | 0.53 | 7 | 0.79 | 40 | 3.3 | 5.2 | |
| 8 | 0.24 | 2 | 0.97 | 12 | 1.0 | 4.8 | |
| 9 | 0.39 | 7 | 0.84 | 37 | 2.7 | 5.5 | |
| 10 | 0.56 | 5 | 0.88 | 29 | 2.1 | 4.0 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 6.4 | |
| Earned Money | Average | 0.60 | 6 | 0.78 | 48 | 2.8 | 4. 6 |
| Median | 0.55 | 6 | 0.81 | 37 | 2.1 | 4.4 | |
| MWWa (p-values) | 0.13 | 0.21 | 0.13 | 0.13 | 0.01 | 0.07 | |
| Treatment . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Turnover . |
|---|---|---|---|---|---|---|---|
| House money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 7.98 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 5.38 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 4.96 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 8.31 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3.98 | |
| Earned Money | 1 | 0.46 | 6 | 0.82 | 29 | 1.5 | 3.0 |
| 2 | 0.60 | 4 | 0.80 | 37 | 1.3 | 2.9 | |
| 3 | 0.84 | 5 | 0.53 | 69 | 1.8 | 3.0 | |
| 4 | 0.52 | 8 | 0.92 | 81 | 2.8 | 2.5 | |
| 5 | 0.74 | 4 | 0.61 | 27 | 2.0 | 5.8 | |
| 6 | 1.13 | 12 | 0.69 | 116 | 9.2 | 8.8 | |
| 7 | 0.53 | 7 | 0.79 | 40 | 3.3 | 5.2 | |
| 8 | 0.24 | 2 | 0.97 | 12 | 1.0 | 4.8 | |
| 9 | 0.39 | 7 | 0.84 | 37 | 2.7 | 5.5 | |
| 10 | 0.56 | 5 | 0.88 | 29 | 2.1 | 4.0 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 6.4 | |
| Earned Money | Average | 0.60 | 6 | 0.78 | 48 | 2.8 | 4. 6 |
| Median | 0.55 | 6 | 0.81 | 37 | 2.1 | 4.4 | |
| MWWa (p-values) | 0.13 | 0.21 | 0.13 | 0.13 | 0.01 | 0.07 | |
Average bubble measures for different treatments
aMann–Whitney–Wilcoxon test.
| Treatment . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Turnover . |
|---|---|---|---|---|---|---|---|
| House money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 7.98 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 5.38 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 4.96 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 8.31 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3.98 | |
| Earned Money | 1 | 0.46 | 6 | 0.82 | 29 | 1.5 | 3.0 |
| 2 | 0.60 | 4 | 0.80 | 37 | 1.3 | 2.9 | |
| 3 | 0.84 | 5 | 0.53 | 69 | 1.8 | 3.0 | |
| 4 | 0.52 | 8 | 0.92 | 81 | 2.8 | 2.5 | |
| 5 | 0.74 | 4 | 0.61 | 27 | 2.0 | 5.8 | |
| 6 | 1.13 | 12 | 0.69 | 116 | 9.2 | 8.8 | |
| 7 | 0.53 | 7 | 0.79 | 40 | 3.3 | 5.2 | |
| 8 | 0.24 | 2 | 0.97 | 12 | 1.0 | 4.8 | |
| 9 | 0.39 | 7 | 0.84 | 37 | 2.7 | 5.5 | |
| 10 | 0.56 | 5 | 0.88 | 29 | 2.1 | 4.0 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 6.4 | |
| Earned Money | Average | 0.60 | 6 | 0.78 | 48 | 2.8 | 4. 6 |
| Median | 0.55 | 6 | 0.81 | 37 | 2.1 | 4.4 | |
| MWWa (p-values) | 0.13 | 0.21 | 0.13 | 0.13 | 0.01 | 0.07 | |
| Treatment . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Turnover . |
|---|---|---|---|---|---|---|---|
| House money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 7.98 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 5.38 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 4.96 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 8.31 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3.98 | |
| Earned Money | 1 | 0.46 | 6 | 0.82 | 29 | 1.5 | 3.0 |
| 2 | 0.60 | 4 | 0.80 | 37 | 1.3 | 2.9 | |
| 3 | 0.84 | 5 | 0.53 | 69 | 1.8 | 3.0 | |
| 4 | 0.52 | 8 | 0.92 | 81 | 2.8 | 2.5 | |
| 5 | 0.74 | 4 | 0.61 | 27 | 2.0 | 5.8 | |
| 6 | 1.13 | 12 | 0.69 | 116 | 9.2 | 8.8 | |
| 7 | 0.53 | 7 | 0.79 | 40 | 3.3 | 5.2 | |
| 8 | 0.24 | 2 | 0.97 | 12 | 1.0 | 4.8 | |
| 9 | 0.39 | 7 | 0.84 | 37 | 2.7 | 5.5 | |
| 10 | 0.56 | 5 | 0.88 | 29 | 2.1 | 4.0 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 6.4 | |
| Earned Money | Average | 0.60 | 6 | 0.78 | 48 | 2.8 | 4. 6 |
| Median | 0.55 | 6 | 0.81 | 37 | 2.1 | 4.4 | |
| MWWa (p-values) | 0.13 | 0.21 | 0.13 | 0.13 | 0.01 | 0.07 | |
We confirm the results of Porter and Smith (1995) by not identifying significant differences in bubble measures when comparing experimental asset markets with certain dividends versus markets with asset markets with uncertain dividends.13 We perform a comparison of different bubble measures for treatments with randomly drawn dividends and inexperienced subjects against our HM experiments (see Table AI in Appendix A). We find that bubble measures do not differ significantly from those obtained in the HM treatment when considering standard significance levels.14
Figure 3 shows per-period median price for the EM treatment. Though differing in magnitudes, bubbles form in 6 out of 10 cases in the HM treatment and in 5 out of 10 cases in the EM treatment. From Figures 2 and 3, one can see significant mispricing in both the house money and the EM treatments. We reject the equality of all bubbles measures between the HM and EM treatments using a multivariate test (p = 0.38).15
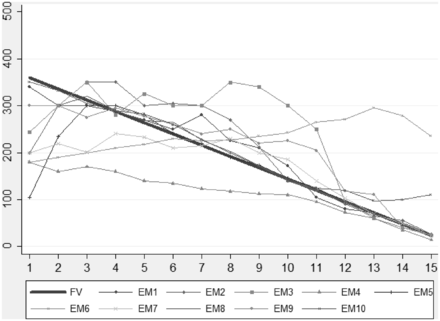
Looking at each bubble measure separately (Table III), we observe no significant differences between the house money and the EM treatment except for NAP (p = 0.01) and turnover (p = 0.07). A lower NAP tells us that relative to the HM experiments, and considering all transactions, prices in the EM treatment were closer to the fundamental value. Average trading volumes are 31% lower in the EM treatment compared with the HM treatment. Note that NAP is, by definition, closely linked to trading volumes. NAP automatically increases with an increase in the number of transactions K as long as transactions are completed at prices that are not exactly equal to fundamental values. The fact that the measures of mispricing that are not affected by trading volumes, such as NAV and Haessel-R2 values, do not differ across treatments suggests that there are no significant differences in the pattern of prices across treatments. We conclude that the difference in the NAP measure across treatments is mostly driven by differences in trading volumes. We summarize our findings as follows.
Result 1:We find that the earned money treatment has no significant effect on asset mispricing, but has a significant effect on measures of trading volume.
Finally, we investigate the distribution of subjects’ earnings across treatments. Figure 4 below shows a histogram of subjects’ earnings at the end of the experiment for each treatment.16
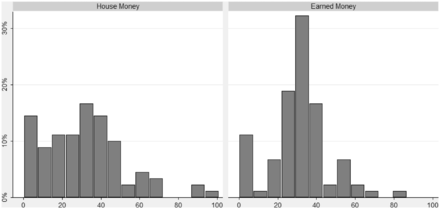
We observe that the dispersion of earnings, measured by their standard deviation and the Gini coefficient, is significantly greater in the HM treatment than in the EM treatment (Table IV). Note that a crucial element in explaining differences in earnings dispersion across treatments is the difference in trading volumes (K) between the earned money and the HM treatment.17 Interestingly, we find that earnings dispersion by session, measured by the standard error of subject’s earnings, is highly correlated with trading volumes (Spearman’s ρ = 0.697, p = 0.03 and ρ = 0.746, p = 0.01 for the HM and EM treatments, respectively).18
| Treatment . | Session . | Standard error . | Gini coefficient . |
|---|---|---|---|
| House Money | 1 | 28.64 | 0.45 |
| 2 | 32.61 | 0.53 | |
| 3 | 20.55 | 0.34 | |
| 4 | 17.88 | 0.30 | |
| 5 | 21.68 | 0.36 | |
| 6 | 26.73 | 0.41 | |
| 7 | 13.24 | 0.20 | |
| 8 | 14.59 | 0.25 | |
| 9 | 23.26 | 0.39 | |
| 10 | 12.56 | 0.21 | |
| Earned Money | 1 | 14.90 | 0.23 |
| 2 | 11.37 | 0.19 | |
| 3 | 7.04 | 0.10 | |
| 4 | 7.91 | 0.13 | |
| 5 | 15.44 | 0.24 | |
| 6 | 24.34 | 0.39 | |
| 7 | 23.55 | 0.39 | |
| 8 | 9.03 | 0.15 | |
| 9 | 17.79 | 0.27 | |
| 10 | 18.71 | 0.30 | |
| House Money | Average | 21.17 | 0.35 |
| Median | 21.11 | 0.35 | |
| Earned Money | Average | 15.01 | 0.24 |
| Median | 15.17 | 0.23 | |
| MWWa (p-values) | 0.08 | 0.05 | |
| Treatment . | Session . | Standard error . | Gini coefficient . |
|---|---|---|---|
| House Money | 1 | 28.64 | 0.45 |
| 2 | 32.61 | 0.53 | |
| 3 | 20.55 | 0.34 | |
| 4 | 17.88 | 0.30 | |
| 5 | 21.68 | 0.36 | |
| 6 | 26.73 | 0.41 | |
| 7 | 13.24 | 0.20 | |
| 8 | 14.59 | 0.25 | |
| 9 | 23.26 | 0.39 | |
| 10 | 12.56 | 0.21 | |
| Earned Money | 1 | 14.90 | 0.23 |
| 2 | 11.37 | 0.19 | |
| 3 | 7.04 | 0.10 | |
| 4 | 7.91 | 0.13 | |
| 5 | 15.44 | 0.24 | |
| 6 | 24.34 | 0.39 | |
| 7 | 23.55 | 0.39 | |
| 8 | 9.03 | 0.15 | |
| 9 | 17.79 | 0.27 | |
| 10 | 18.71 | 0.30 | |
| House Money | Average | 21.17 | 0.35 |
| Median | 21.11 | 0.35 | |
| Earned Money | Average | 15.01 | 0.24 |
| Median | 15.17 | 0.23 | |
| MWWa (p-values) | 0.08 | 0.05 | |
| Treatment . | Session . | Standard error . | Gini coefficient . |
|---|---|---|---|
| House Money | 1 | 28.64 | 0.45 |
| 2 | 32.61 | 0.53 | |
| 3 | 20.55 | 0.34 | |
| 4 | 17.88 | 0.30 | |
| 5 | 21.68 | 0.36 | |
| 6 | 26.73 | 0.41 | |
| 7 | 13.24 | 0.20 | |
| 8 | 14.59 | 0.25 | |
| 9 | 23.26 | 0.39 | |
| 10 | 12.56 | 0.21 | |
| Earned Money | 1 | 14.90 | 0.23 |
| 2 | 11.37 | 0.19 | |
| 3 | 7.04 | 0.10 | |
| 4 | 7.91 | 0.13 | |
| 5 | 15.44 | 0.24 | |
| 6 | 24.34 | 0.39 | |
| 7 | 23.55 | 0.39 | |
| 8 | 9.03 | 0.15 | |
| 9 | 17.79 | 0.27 | |
| 10 | 18.71 | 0.30 | |
| House Money | Average | 21.17 | 0.35 |
| Median | 21.11 | 0.35 | |
| Earned Money | Average | 15.01 | 0.24 |
| Median | 15.17 | 0.23 | |
| MWWa (p-values) | 0.08 | 0.05 | |
| Treatment . | Session . | Standard error . | Gini coefficient . |
|---|---|---|---|
| House Money | 1 | 28.64 | 0.45 |
| 2 | 32.61 | 0.53 | |
| 3 | 20.55 | 0.34 | |
| 4 | 17.88 | 0.30 | |
| 5 | 21.68 | 0.36 | |
| 6 | 26.73 | 0.41 | |
| 7 | 13.24 | 0.20 | |
| 8 | 14.59 | 0.25 | |
| 9 | 23.26 | 0.39 | |
| 10 | 12.56 | 0.21 | |
| Earned Money | 1 | 14.90 | 0.23 |
| 2 | 11.37 | 0.19 | |
| 3 | 7.04 | 0.10 | |
| 4 | 7.91 | 0.13 | |
| 5 | 15.44 | 0.24 | |
| 6 | 24.34 | 0.39 | |
| 7 | 23.55 | 0.39 | |
| 8 | 9.03 | 0.15 | |
| 9 | 17.79 | 0.27 | |
| 10 | 18.71 | 0.30 | |
| House Money | Average | 21.17 | 0.35 |
| Median | 21.11 | 0.35 | |
| Earned Money | Average | 15.01 | 0.24 |
| Median | 15.17 | 0.23 | |
| MWWa (p-values) | 0.08 | 0.05 | |
Our findings regarding earnings dispersion are summarized as follows.
Result 2:Compared with the house money treatment, earnings dispersion is significantly lower in the earned money treatment.
In the next section, we examine the correlation between CRT scores and individual trader behavior.
3.2 CRT CORRELATES
The CRT scores provide one, among other possible, measures of subjects’ cognitive skills (Frederick, 2005) which can be used to sort subjects accordingly. Table V provides subject score (0, 1, 2, 3) on the CRT and its relationship with subjects’ earnings across treatments.
Baseline treatment—mean (median) earnings
[Number of observations].
aMann–Whitney–Wilcoxon test. This test reports the comparison of subjects’ earnings with CRT = 0 and subjects with CRT > 0.
| CRT . | 0 . | 1 . | 2 . | 3 . | >0 . | MWWa (p-values) . |
|---|---|---|---|---|---|---|
| House Money | $ 22.31 | $ 35.71 | $ 30.45 | $ 49.29 | $ 37.08 | 0.0012 |
| ($ 22.12) | ($ 35.21) | ($ 32.33) | ($ 40.75) | ($ 35.57) | ||
| [34] | [24] | [19] | [13] | [56] | ||
| Earned Money | $ 25.07 | $ 33.53 | $ 31.98 | $ 35.19 | $ 33.71 | 0.0021 |
| ($23.49) | ($ 34.88) | ($ 31.64) | ($ 35.83) | ($ 34.34) | ||
| [23] | [27] | [17] | [23] | [67] | ||
| CRT . | 0 . | 1 . | 2 . | 3 . | >0 . | MWWa (p-values) . |
|---|---|---|---|---|---|---|
| House Money | $ 22.31 | $ 35.71 | $ 30.45 | $ 49.29 | $ 37.08 | 0.0012 |
| ($ 22.12) | ($ 35.21) | ($ 32.33) | ($ 40.75) | ($ 35.57) | ||
| [34] | [24] | [19] | [13] | [56] | ||
| Earned Money | $ 25.07 | $ 33.53 | $ 31.98 | $ 35.19 | $ 33.71 | 0.0021 |
| ($23.49) | ($ 34.88) | ($ 31.64) | ($ 35.83) | ($ 34.34) | ||
| [23] | [27] | [17] | [23] | [67] | ||
Baseline treatment—mean (median) earnings
[Number of observations].
aMann–Whitney–Wilcoxon test. This test reports the comparison of subjects’ earnings with CRT = 0 and subjects with CRT > 0.
| CRT . | 0 . | 1 . | 2 . | 3 . | >0 . | MWWa (p-values) . |
|---|---|---|---|---|---|---|
| House Money | $ 22.31 | $ 35.71 | $ 30.45 | $ 49.29 | $ 37.08 | 0.0012 |
| ($ 22.12) | ($ 35.21) | ($ 32.33) | ($ 40.75) | ($ 35.57) | ||
| [34] | [24] | [19] | [13] | [56] | ||
| Earned Money | $ 25.07 | $ 33.53 | $ 31.98 | $ 35.19 | $ 33.71 | 0.0021 |
| ($23.49) | ($ 34.88) | ($ 31.64) | ($ 35.83) | ($ 34.34) | ||
| [23] | [27] | [17] | [23] | [67] | ||
| CRT . | 0 . | 1 . | 2 . | 3 . | >0 . | MWWa (p-values) . |
|---|---|---|---|---|---|---|
| House Money | $ 22.31 | $ 35.71 | $ 30.45 | $ 49.29 | $ 37.08 | 0.0012 |
| ($ 22.12) | ($ 35.21) | ($ 32.33) | ($ 40.75) | ($ 35.57) | ||
| [34] | [24] | [19] | [13] | [56] | ||
| Earned Money | $ 25.07 | $ 33.53 | $ 31.98 | $ 35.19 | $ 33.71 | 0.0021 |
| ($23.49) | ($ 34.88) | ($ 31.64) | ($ 35.83) | ($ 34.34) | ||
| [23] | [27] | [17] | [23] | [67] | ||
In Table V, we compare earnings for subjects with a CRT score of zero with earnings for subjects with scores greater than zero (last column).19 With house money, subjects with a CRT score of zero earn on average $22.31, which is 40% less than the subjects who have positive CRT scores ($37.08, MWW, p = 0.0012). This result also holds for the treatment with earned money (MWW, p = 0.0021). However, this difference in earnings across subjects with different CRT scores is lower when subjects use their own money (EM treatment). In particular, the earnings of subjects with a CRT score of zero were 12% larger in the EM treatment compared with the HM treatment while the earnings of subjects with a positive CRT score were 9% lower (MWW, p = 0.5692 and p = 0.4553, respectively). In addition, subjects with a CRT score of three earned 120.9% more than those with a score of zero in the HM treatment (MWW, p < 0.001), whereas the difference in earnings between these subjects was only equal to 40.4% in the EM treatment (MWW, p < 0.001).
In Figure 5, we show subjects’ average portfolio value at the end of each period by CRT score. From the very beginning, subjects with a higher CRT score earn more money and this difference increases over time. Interestingly, HM subjects earning differences across CRT scores are even larger. Under EM, subjects with a higher CRT score cannot take full advantage of subjects with low scores.20
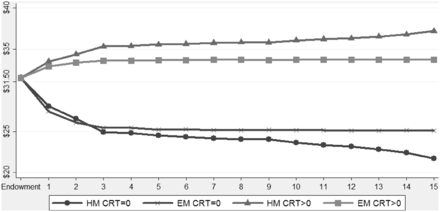
We summarize our results regarding CRT scores and earnings as follows.
Result 3: Subjects with positive CRT scores earn significantly more than subjects with a zero CRT score. Differences in earnings across subjects with different CRT scores are significantly more pronounced in the house money treatment than in the earned money treatment.
This result is in line with the recent work of Cueva and Rustichini (2012) according to which subjects with high cognitive skills measured with non-verbal IQ tend to outperform subjects with low cognitive skills.
Now, we study trading patterns in more detail to uncover some of the possible reasons for the observed differences in subjects’ earnings. In particular, we study whether subjects were net buyers or net sellers of the asset when the price was lower or higher than the fundamental value of the asset. We compute the number of net purchases per period as the number of purchases minus the number of sales of an individual for that period. Table VI presents the results of a panel data, with random effects and clusters by session, of the net number of purchases on a dummy variable capturing CRT scores (CRTd) and on the difference between the average period price and the fundamental value relative to the fundamental value (). We show that subjects with a CRT score of zero are net buyers (sellers) when the asset price is above (below) the fundamental value since the coefficient associated with the variable () is positive and significant. Note that this result is statistically significant for the HM treatment, whereas it is only marginally so in the EM treatment. Subjects with a CRT score greater than zero are net buyers (sellers) when the asset price is below (above) the fundamental value since the coefficient associated with the variable [] is negative and significant. This finding is particularly interesting as it shows that high CRT subjects may be feeding the bubble in the early stages of the experiment and get out of it before it crashes. Further, the effect of CRT score on net purchases is more pronounced in the HM treatment than in the EM treatment.
Subjects’ number of net purchases by period
CRTd = 0 if subject’s CRT = 0 and 1 otherwise. is the (session) average price of period t. FVt is the fundamental value of period t.
*p < 0.10, **p < 0.05, and ***p < 0.01.
| Variables . | House Money . | Earned Money . |
|---|---|---|
| Constant | 0.0689 | −0.1282* |
| −0.1001 | 0.1716* | |
| 0.0765** | 0.0689* | |
| −0.1358** | −0.1144** | |
| R2 | 0.0053 | 0.0021 |
| Wald chi2 | 9.02** | 7.04* |
| −0.0593** | −0.0455** | |
| Variables . | House Money . | Earned Money . |
|---|---|---|
| Constant | 0.0689 | −0.1282* |
| −0.1001 | 0.1716* | |
| 0.0765** | 0.0689* | |
| −0.1358** | −0.1144** | |
| R2 | 0.0053 | 0.0021 |
| Wald chi2 | 9.02** | 7.04* |
| −0.0593** | −0.0455** | |
Subjects’ number of net purchases by period
CRTd = 0 if subject’s CRT = 0 and 1 otherwise. is the (session) average price of period t. FVt is the fundamental value of period t.
*p < 0.10, **p < 0.05, and ***p < 0.01.
| Variables . | House Money . | Earned Money . |
|---|---|---|
| Constant | 0.0689 | −0.1282* |
| −0.1001 | 0.1716* | |
| 0.0765** | 0.0689* | |
| −0.1358** | −0.1144** | |
| R2 | 0.0053 | 0.0021 |
| Wald chi2 | 9.02** | 7.04* |
| −0.0593** | −0.0455** | |
| Variables . | House Money . | Earned Money . |
|---|---|---|
| Constant | 0.0689 | −0.1282* |
| −0.1001 | 0.1716* | |
| 0.0765** | 0.0689* | |
| −0.1358** | −0.1144** | |
| R2 | 0.0053 | 0.0021 |
| Wald chi2 | 9.02** | 7.04* |
| −0.0593** | −0.0455** | |
Our findings regarding trading patterns across subjects with different CRT scores are summarized as follows:21
Result 4: Subjects with positive CRT scores buy (sell) shares when the asset price is below (above) the fundamental value. Subjects with a zero CRT score behave in the opposite manner.
This result means that in our asset market experiments, which is a zero-sum game, there is a transfer of earnings from subjects with low CRT scores to subjects with high CRT scores. High CRT subjects purchase shares in the early periods, when prices are below the fundamental value and sell those shares when the prices exceed the fundamental value (see left panel of Figure 6). This transfer of wealth is less pronounced in the EM treatment (see right panel of Figure 6).
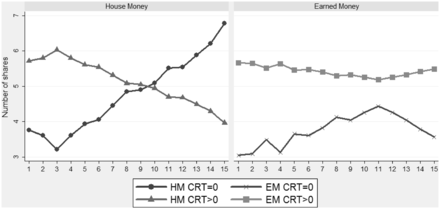
Average number of shares held at the end of the period by CRT score and across periods for house money (on the left panel) and for earned money (on the right panel).
4. Conclusion
In this article, we have studied the house money effect in an experimental asset market with bubbles and crashes. We found that even though bubbles still occurred in the EM treatment, trading volumes were significantly reduced. The reduction in trading volumes implied a significant decrease in the dispersion of subjects’ earnings in the EM treatment compared with house money.
We investigated earnings dispersion by categorizing subjects according to their cognitive ability which was measured using the CRT. We found that subjects with lower CRT scores were net purchasers (sellers) of shares when the price was above (below) fundamental value while the opposite was true for subjects with higher CRT scores. Consequently, high CRT subjects earned more money on average than the initial value of their portfolio while low CRT subjects earned less. This result was true for both the house and EM treatments.
Our main conclusion is that there is indeed a house money effect in experimental asset markets. The house money effect manifests itself in trading volume that subsequently affects earnings dispersion. Bubbles, however, are maintained and we find no differences between our two treatments, or comparing our results with other experiments with uncertain dividends. We take a preliminary step by studying individual behavior in asset markets as reflected by the well-known CRT. We use the CRT to sort subject behavior in asset markets and find that cognitive abilities, as reflected by the CRT, do seem to matter. Individuals with a high CRT score feed the bubble in the early stages and get out of it in later periods. Further research needs to be done to better understand the link between cognitive abilities and bubble formation in experimental asset markets.
Our findings also shed light on the ongoing discussion regarding excessive trading in financial markets where average mutual-fund turnover has increased from 15% in the 1950s to around 100% in 2011 (Edelen, Evans, and Kadlec, 2013). This excessive trading which could be explained by investors’ overconfidence and urge to “do something” (Dow and Gorton, 1997; Odean, 1999) could be tamed by redesigning incentive packages of fund managers. For example, a proportion of their base salary could be automatically invested in their clients’ portfolio.
Appendix A: Comparison with other studies
Bubble measures in our HM treatment and those reported by Corgnet et al. (2010) are not significantly different when using a multivariate test (p = 0.21).22
Average bubble measures for related studiesa
aAll of them are studies with the same number of periods (15) and traders (9). Data obtained from Corgnet, Kujal, and Porter (2010).
| . | Amplitude . | Duration . | NAV . | NAP . |
|---|---|---|---|---|
| House Money | 0.84 | 8.2 | 6.4 | 82.7 |
| Corgnet, Kujal, and Porter (2010) | 1.26 | 10.3 | 11.2 | 130 |
| Smith, Van Boening, and Wellford (2000) | 1.39 | – | 5.5 | – |
| Porter and Smith (1995) | 1.53 | 10.1 | – | – |
| King et al. (1993) | 1.61 | 9.5 | 11.8 | – |
| Smith, Suchanek, and Williams (1988) | 1.24 | 10.2 | 5.7 | – |
| . | Amplitude . | Duration . | NAV . | NAP . |
|---|---|---|---|---|
| House Money | 0.84 | 8.2 | 6.4 | 82.7 |
| Corgnet, Kujal, and Porter (2010) | 1.26 | 10.3 | 11.2 | 130 |
| Smith, Van Boening, and Wellford (2000) | 1.39 | – | 5.5 | – |
| Porter and Smith (1995) | 1.53 | 10.1 | – | – |
| King et al. (1993) | 1.61 | 9.5 | 11.8 | – |
| Smith, Suchanek, and Williams (1988) | 1.24 | 10.2 | 5.7 | – |
Average bubble measures for related studiesa
aAll of them are studies with the same number of periods (15) and traders (9). Data obtained from Corgnet, Kujal, and Porter (2010).
| . | Amplitude . | Duration . | NAV . | NAP . |
|---|---|---|---|---|
| House Money | 0.84 | 8.2 | 6.4 | 82.7 |
| Corgnet, Kujal, and Porter (2010) | 1.26 | 10.3 | 11.2 | 130 |
| Smith, Van Boening, and Wellford (2000) | 1.39 | – | 5.5 | – |
| Porter and Smith (1995) | 1.53 | 10.1 | – | – |
| King et al. (1993) | 1.61 | 9.5 | 11.8 | – |
| Smith, Suchanek, and Williams (1988) | 1.24 | 10.2 | 5.7 | – |
| . | Amplitude . | Duration . | NAV . | NAP . |
|---|---|---|---|---|
| House Money | 0.84 | 8.2 | 6.4 | 82.7 |
| Corgnet, Kujal, and Porter (2010) | 1.26 | 10.3 | 11.2 | 130 |
| Smith, Van Boening, and Wellford (2000) | 1.39 | – | 5.5 | – |
| Porter and Smith (1995) | 1.53 | 10.1 | – | – |
| King et al. (1993) | 1.61 | 9.5 | 11.8 | – |
| Smith, Suchanek, and Williams (1988) | 1.24 | 10.2 | 5.7 | – |
Average bubble measures comparing HM treatment and Corgnet, Kujal, and Porter (2010)’s baseline sessions with random dividend
aMWW stands for the Mann–Whitney–Wilcoxon test.
| . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Upward trend . | Num transactions . | Turnover . |
|---|---|---|---|---|---|---|---|---|---|
| House Money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 3 | 334 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 11 | 473 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 2 | 194 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 9 | 355 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4 | 220 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 1 | 359 | 8.0 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 2 | 342 | 5.4 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 6 | 223 | 5.0 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 11 | 374 | 8.3 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3 | 179 | 4.0 | |
| Corgnet et al. | N11 | 1.08 | 9 | 0.33 | 119 | 10.9 | 5 | 121 | 5.5 |
| N21 | 1.37 | 12 | 0.10 | 137 | 9.5 | 9 | 132 | 6.0 | |
| N31 | 1.33 | 5 | 0.59 | 134 | 13.2 | 5 | 143 | 6.5 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 5 | 295 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 4 | 288 | 6.4 | |
| Corgnet et al. | Average | 1.26 | 9 | 0.34 | 130 | 11.2 | 6 | 132 | 6.0 |
| Median | 1.33 | 9 | 0.33 | 134 | 10.9 | 5 | 132 | 6.0 | |
| MWWa (p-values) | 0.06 | 0.87 | 0.13 | 0.06 | 0.13 | 0.44 | – | >0.99 | |
| . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Upward trend . | Num transactions . | Turnover . |
|---|---|---|---|---|---|---|---|---|---|
| House Money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 3 | 334 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 11 | 473 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 2 | 194 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 9 | 355 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4 | 220 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 1 | 359 | 8.0 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 2 | 342 | 5.4 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 6 | 223 | 5.0 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 11 | 374 | 8.3 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3 | 179 | 4.0 | |
| Corgnet et al. | N11 | 1.08 | 9 | 0.33 | 119 | 10.9 | 5 | 121 | 5.5 |
| N21 | 1.37 | 12 | 0.10 | 137 | 9.5 | 9 | 132 | 6.0 | |
| N31 | 1.33 | 5 | 0.59 | 134 | 13.2 | 5 | 143 | 6.5 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 5 | 295 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 4 | 288 | 6.4 | |
| Corgnet et al. | Average | 1.26 | 9 | 0.34 | 130 | 11.2 | 6 | 132 | 6.0 |
| Median | 1.33 | 9 | 0.33 | 134 | 10.9 | 5 | 132 | 6.0 | |
| MWWa (p-values) | 0.06 | 0.87 | 0.13 | 0.06 | 0.13 | 0.44 | – | >0.99 | |
Average bubble measures comparing HM treatment and Corgnet, Kujal, and Porter (2010)’s baseline sessions with random dividend
aMWW stands for the Mann–Whitney–Wilcoxon test.
| . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Upward trend . | Num transactions . | Turnover . |
|---|---|---|---|---|---|---|---|---|---|
| House Money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 3 | 334 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 11 | 473 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 2 | 194 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 9 | 355 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4 | 220 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 1 | 359 | 8.0 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 2 | 342 | 5.4 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 6 | 223 | 5.0 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 11 | 374 | 8.3 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3 | 179 | 4.0 | |
| Corgnet et al. | N11 | 1.08 | 9 | 0.33 | 119 | 10.9 | 5 | 121 | 5.5 |
| N21 | 1.37 | 12 | 0.10 | 137 | 9.5 | 9 | 132 | 6.0 | |
| N31 | 1.33 | 5 | 0.59 | 134 | 13.2 | 5 | 143 | 6.5 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 5 | 295 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 4 | 288 | 6.4 | |
| Corgnet et al. | Average | 1.26 | 9 | 0.34 | 130 | 11.2 | 6 | 132 | 6.0 |
| Median | 1.33 | 9 | 0.33 | 134 | 10.9 | 5 | 132 | 6.0 | |
| MWWa (p-values) | 0.06 | 0.87 | 0.13 | 0.06 | 0.13 | 0.44 | – | >0.99 | |
| . | Session . | Amplitude . | Duration . | Haessel-R2 . | NAV . | NAP . | Upward trend . | Num transactions . | Turnover . |
|---|---|---|---|---|---|---|---|---|---|
| House Money | 1 | 0.58 | 9 | 0.65 | 59 | 4.7 | 3 | 334 | 7.4 |
| 2 | 1.19 | 13 | 0.38 | 130 | 13.4 | 11 | 473 | 10.5 | |
| 3 | 0.53 | 3 | 0.82 | 25 | 2.1 | 2 | 194 | 4.3 | |
| 4 | 1.05 | 14 | 0.48 | 116 | 7.7 | 9 | 355 | 7.9 | |
| 5 | 0.85 | 4 | 0.35 | 53 | 4.7 | 4 | 220 | 4.9 | |
| 6 | 0.28 | 5 | 0.95 | 19 | 3.1 | 1 | 359 | 8.0 | |
| 7 | 0.49 | 7 | 0.81 | 66 | 3.0 | 2 | 342 | 5.4 | |
| 8 | 0.90 | 6 | 0.00 | 95 | 8.1 | 6 | 223 | 5.0 | |
| 9 | 1.73 | 11 | 0.72 | 194 | 14.7 | 11 | 374 | 8.3 | |
| 10 | 0.76 | 10 | 0.84 | 70 | 2.5 | 3 | 179 | 4.0 | |
| Corgnet et al. | N11 | 1.08 | 9 | 0.33 | 119 | 10.9 | 5 | 121 | 5.5 |
| N21 | 1.37 | 12 | 0.10 | 137 | 9.5 | 9 | 132 | 6.0 | |
| N31 | 1.33 | 5 | 0.59 | 134 | 13.2 | 5 | 143 | 6.5 | |
| House Money | Average | 0.84 | 8 | 0.60 | 83 | 6.4 | 5 | 295 | 6.7 |
| Median | 0.80 | 8 | 0.68 | 68 | 4.7 | 4 | 288 | 6.4 | |
| Corgnet et al. | Average | 1.26 | 9 | 0.34 | 130 | 11.2 | 6 | 132 | 6.0 |
| Median | 1.33 | 9 | 0.33 | 134 | 10.9 | 5 | 132 | 6.0 | |
| MWWa (p-values) | 0.06 | 0.87 | 0.13 | 0.06 | 0.13 | 0.44 | – | >0.99 | |
Appendix B: Instructions Part I (Task)
Instructions:
This is a study in decision-making. Funding for this project has been provided by several funding agencies.
You will be taking part in an experiment that consists of two parts. In the first part, you will be required to perform a task related to a Research Institute database.
The amount earned in the first task is credited to your account and will be used in the second part. In the second part, you will be participating in an economic experiment.
The amount you will earn in the first task will be carried over to the experiment you will take part in the second part. You will be paid IN CASH for the entire experiment at the end of the second part that will take place at the end of this week.
Today’s Task:
In this part you will be performing a task for a Research Institute database.
You have a list of academic articles on your desk.
You are expected to search a minimum of 20 articles in a JSTOR database and download them to a folder (that will be identified later).
You will be credited $31.50 for this task.
Where to save the articles?
Please, right click on the mouse and create a new folder on the desktop.
Please, name the folder now using your own complete name.
You will be saving the articles into this folder.
How to save an article?
For example, the article:
– Edward L. Glaeser, David I. Laibson, Jose A. Scheinkman, Christine L. Soutter, 2000, Measuring Trust, The Quarterly Journal of Economics, 115, 811–846.
Go to, http://www.jstor.org/
Then select Economics.
Type in the name of the journal, e.g., “Quarterly Journal of Economics”
Go to the corresponding year and page numbers
Click on the article and save it to your folder.
How do I download the article from JSTOR?
Once you find the article you will find a screen similar to the one below
– click on View pdf on the right hand side.

Then click on proceed to pdf.

Then right-click on the article to save as in your folder in the format mentioned earlier.

Format of the saved article
Author1&Author2_TitleofPaper_JournalInitialsYear.pdf
For example, the article:
– Edward L. Glaeser, David I. Laibson, Jose A. Scheinkman, Christine L. Soutter, 2000, Measuring Trust, The Quarterly Journal of Economics, 115, 811–846.
Will be saved as, Glaeser&Laibson&Scheinkman&Soutter_Measuring Trust_ QJE2000.pdf
Note: Journal initials are the first letters of the journal title.
– For example, for Quarterly Journal of Economics the initials are QJE, for Economic Journal the initials are EJ, for American Economic Review the initials are AER etc …
What if you do not find the article on JSTOR?
Move on to the next article on the list.
Please state on the handout that the article was not available.
What if the journal is not available on JSTOR?
State on the handout that the journal is not available on JSTOR and move on to the next article on your list.
Please make sure that all articles are saved using the naming format we provide above.
Appendix C: Instructions Part II (Asset Markets)
INSTRUCTIONS (1/14)
This is an experiment in market decision making. You will be paid in cash for your participation at the end of the experiment. Different participants may earn different amounts. What you earn depends on your decisions and the decisions of others.
[(Only EM treatment) Before participating in this experiment, you earned $31.50 by working on the ESI database during 2 hours. This full amount of cash will be used to pay for your initial portfolio in the current experiment.]
The experiment will take place through computer terminals at which you are seated. If you have any questions during the instruction round, raise your hand and a monitor will come by to answer your question. If any difficulties arise after the experiment has begun, raise your hand, and someone will assist you.
INSTRUCTIONS (2/14)
In this experiment you will be able to buy and sell a commodity, called Shares, from one another.
At the start of the experiment, every participant will be given some Cash and Shares.
The shares last for EXACTLY 15 periods of trading. After each trading period the share will earn a dividend of 24 cents. Thus, if you had a share at the end of period 1, you would get a return of 24 cents for that period.
If you held a share from period 1 until the end of period 15, then that share would return to you a total of $3.60 (15 × 24 cents) over the 15 periods. Similarly, if you bought a share in period 2 and held it from period 2 until the 15th period, the accumulated dividends would be $3.36 (14 × 24 cents).
INSTRUCTIONS (3/14)23
INSTRUCTIONS (4/14)
During every period, traders can buy or sell shares from one another by making offers to buy or to sell.
Every time a trade is made, it will be shown as a dark GREEN dot in the graph located on the left of the lower part of your screen. Transactions are also listed on the Market Book located on the right of the graph. If you buy a share (or somebody sold it to you), the cell in the Market Book will be shown in light BLUE. The cell will be shown in RED if you sell a share (or somebody buys it from you). The cells that are shown without colors correspond to transactions in which you are not involved either as a buyer or as a seller.
INSTRUCTIONS (5/14)
To enter a new order to buy or to sell a share, type in the price at which you would like to buy, or sell, in the appropriate Add order to Buy box or Add order to Sell box. Click the Add order to Buy or Add order to Sell button to submit your order.
INSTRUCTIONS (6/14)
Every time someone posts an order to buy a share, it will be added to the list of best orders to buy (in the BLUE quadrant). This list shows only the best FOUR orders. Every time someone makes an offer to sell a share, it will be added to the list of the best orders to sell (in the RED quadrant). This list shows only the best FOUR orders.
The orders to buy will be listed from the highest price to the lowest price, while the orders to sell will be listed from the lowest price to the highest price.
Your own orders in this list will be highlighted in ORANGE. For example, you have just posted an order to sell at a price equal to 202 and this corresponds to the third best order in the market (that is, the third lowest order to sell). This order will appear in the third place in the list of orders to sell.
INSTRUCTIONS (7/14)
To accept an existing order from another participant, click the Buy a share at or Sell at share at buttons located on the right of the list of orders to sell and orders to buy, respectively. The list of orders to buy shows you the four highest orders to buy that are currently available on the market, while the list of orders to sell shows you the four lowest orders to sell. By clicking on the Buy a share at button, you buy at the listed price of 104 in the current example; by clicking on the Sell at share at button, you sell at the listed price of 96 in the current example. Your own existing orders to buy or sell are highlighted in ORANGE.
In the situation illustrated in the following screen shot, the best order to sell corresponds to a price of 104 (the lowest value in the list of orders to sell). This is the price at which you can currently buy the share. The best order to buy corresponds to a price of 96 (the highest value in the list of orders to buy since this is the only order to buy currently available). This is the price at which you can currently sell the share.

INSTRUCTIONS (8/14)
Whenever you enter new orders to buy, or sell, you will have those orders listed in a table below the list of orders to buy and sell. By double clicking on any cell in the table, you can cancel your own orders.
INSTRUCTIONS (9/14)
At the end of every period, each share will pay a dividend of 24 cents. The dividend for each period will appear in the Dividends Table.
The earned dividends (for shares) of each period will be added to the cash account of the holder.
The number of your shares will change, only when you buy, or sell, shares.
Notice that you cannot place orders to buy for an amount that is greater than your current Cash. The information regarding the remaining cash available to buy is displayed in the box below your current Cash. Also, you cannot place more orders to sell shares than the Number of shares you currently hold. The information regarding the remaining shares available to sell is displayed below your current Number of shares.

INSTRUCTIONS (10/14)
During a period and each time you place an order or complete a transaction a message will appear in the box above the dividends table. This message box provides indications on whether your order or transaction has been completed successfully. For example, if you attempt to buy a share at a price that is higher than your current cash holdings, a message will appear in the box stating that you do not have sufficient cash to buy this share.

INSTRUCTIONS (11/14)
An example:
Suppose you have 5 shares and 150 in Cash at the start of a period, and you make one transaction during the period purchasing a share for 110 cents within the period, and the dividend for the period is 24 cents, then:
Your Cash holdings will increase by 34 cents (Dividends of 24 times 6 shares minus a purchase at 110). Your new cash holding will thus be 150 + 34 = 184 cents.
Your share holdings will increase from 5 to 6 units.
INSTRUCTIONS (12/14)
Another example:
At the end of the previous period, you had 4 shares and 242 in Cash.
Suppose in the next period you make two transactions. You sell one share for 130 and another share for 110, and the dividend for the period is 24, then:
Your Cash holdings will increase by 288 cents (Dividends of 24 times 2 shares plus sales of 130 plus 110). Your new cash holding will thus be 242 + 288 = 530 cents.
Your share holdings will, however, decrease from 4 to 2 units.
INSTRUCTIONS (13/14)
This experiment will last for 15 periods. Each period will last for several minutes. The remaining time (in seconds) will appear on the top of your screen.

When the time is about to expire, the color will change to RED.

We will have a short practice period to allow you to become familiar with entering orders and making trades.
INSTRUCTIONS SUMMARY (14/14)
You will be given an initial amount of Cash and Shares.
Every share generates a dividend of 24 cents at the end of each of 15 trading periods.
You can submit orders to BUY shares and orders to SELL shares.
You make trades by buying at the current lowest order to sell or selling at the current highest order to buy.
The market lasts for 15 periods. At the end of period 15, there will be one last dividend draw. After that the share expires and is worth nothing to you.
The initial value of your portfolio is equal to $31.50 (=990 cents + 6 shares × $3.60).24[(Only EM treatment) This amount corresponds to the earnings you obtained in the 2 hours you spent working on the ESI database.]
Click “Ready” to start the experiment.
* The authors acknowledge financial support from grant [ECO2012/00103/001] from the Spanish Ministry of Education.
1 Note that despite extensive evidence of an effect of earned money on the allocation of joint outcomes, Rutstrom and Williams (2000) report no significant differences in allocations whether endowments were earned or randomly generated.
2 Further, we made no promises in terms of a safety net that subjects would be able to recover the money from the experiment (as in Clark (2002)).
3 In addition, subjects were paid a $10 show-up fee for each appearance.
4 This 3-min questionnaire was administered while subjects waited for their payments at the end of the experiment. As is common in this literature, the CRT was not incentivized.
5 See Appendix B for instructions.
6 The show-up fee was $10 each day. A high show-up fee was used in this treatment to ensure that subjects who participated in the first day experiment would come back for the second. This was indeed the case for all subjects but one.
7 In addition, recruiting subjects who would accept to earn their show-up fees may create selection effects possibly attracting a high proportion of risk lovers and overconfident subjects.
8 This task is similar to that in Falk and Ichino (2006) where recruited students folded papers and stuffed envelopes to prepare the mailing of a questionnaire study for the University of Zurich.
9 Also, the monitors who were in charge of supervising subjects in the work task were different from the experimenters conducting the second part of the experiment. This constant supervision also helped to avoid shirking behavior from subjects.
10 The most common reason for an article not being downloaded was lack of availability due to different restrictions on download permissions.
11 After having run all the experiments, we noticed that one subject in one session participated in the asset market experiment without having attended the first day. Excluding this session from the analysis does not affect the results of the article.
13 We compare our results (with certain dividends) with the results of Corgnet, Kujal, and Porter (2010) (uncertain dividends).
14 We use a multivariate test comparing all bubble measures in our study and in Corgnet, Kujal, and Porter (2010). We report a p-value of 0.21. When comparing each bubble measure separately (see Table A2 in Appendix A), we report marginally significant differences for amplitude and NAP between our house money treatment and the baseline treatment in Corgnet, Kujal, and Porter (2010).
15 We used command sr.loc.test in R to do these spatial rank tests of multivariate location. We obtained similar values using a Hotelling’s T2 test (p = 0.41).
16 We obtain a positive but not significant correlation between subject’s performance in the task (number of articles downloaded) and either their CRT score (Spearman’s ρ = 0.1013, p = 0.36) or their earnings in the asset market experiment (Spearman’s ρ = 0.1087, p = 0.31). We also ran a regression of the number of articles downloaded controlling for subjects’ earnings and CRT score (or a dummy that takes value 1 for positive CRT scores, and zero otherwise) and found that all the coefficients were not significantly different from zero (all p’s > 0.38).
17 The variance of earnings increases in K. Indeed, let us consider a market with two traders, each of them being endowed with the same amount of cash C. Let us call B the number of times trader 1 is buying the asset while S is the total number of times trader 1 is selling the asset. The variance of earnings can then be expressed as follows: where is the fundamental value of the asset when trader 1 buys (sells) the asset for the () times. Also, is the price of the asset when trader 1 buys (sells) the asset for the () times. Assuming that prices are independent and identically distributed random variables with variance σ2 then the variance of earnings is: (B + S)σ2 = Kσ2.
18 Similar values are found using Gini coefficients instead of standard deviations of subjects’ earnings (Spearman’s ρ = 0.649, p = 0.04 and ρ = 0.709, p = 0.02 for the HM and EM treatments, respectively).
19 The same procedure has been used in Brañas-Garza, García-Muñoz, and Hernán-González (2012). Our results are stronger if we compare the tails of the CRT scores distribution (subjects with 0 and 3 scores only).
20 For each treatment, we ran a panel data regression, with random effects and clusters by session, of subjects’ portfolio value on a dummy variable capturing CRT scores (CRTd which takes value one if the subject’s CRT is positive and value zero otherwise), period dummies, and the interaction effect. The portfolio value of subjects with positive CRT scores is significantly higher than those subjects with zero CRT scores. Interestingly, in the HM treatment the difference in the portfolio value increases over time, as the coefficients of the period dummies (with respect to the first period, omitted) are negative and decrease over time for subjects with zero CRT score, while they are positive and increase over time for subjects with positive CRT score (the coefficients of all the fifteen interaction terms, CRTd × Period, are significant, all p’s < 0.095). In the EM treatment, however, the difference in portfolio value by CRT remains constant across periods (no period dummy is significant, and the coefficients of all the fifteen interaction terms are not significant either, all p’s > 0.143).
21 We also studied differences in the total number of transactions for all treatments (and number of transactions by treatment across periods) by CRT score and did not find any significant differences (MWW, p = 0.923 and p = 0.410 in treatment HM and EM, respectively). This result holds across periods (MWW, most p’s > 0.164 for all periods and treatments, except for period 8 in the Earned Money treatment, p = 0.074).
22 We used command sr.loc.test in R to do these spatial rank tests of multivariate location. We obtained similar values using a Hotelling’s T2 test (p = 0.21).
23 This part of the instructions was specific to each subject’s initial portfolio. The initial endowment of cash and number of shares were 990, 1,350, or 1,710 cents and 6, 5, or 4 shares, respectively.
24 Again, this paragraph was specific to each subject’s initial portfolio.



