Skip to Main Content

Article Navigation

Journal Article

Irreducible compositions of degree two polynomials over finite fields have regular structure

Abstract

Let q be an odd prime power and D be the set of irreducible polynomials in $F_{q} [x]$ which can be written as a composition of degree two polynomials. In this paper, we prove that D has a natural regular structure by showing that there exists a finite automaton having D as accepted language. Our method is constructive.

1. Introduction

It has been of great interest in recent years the study of irreducible polynomials which can be written as composition of degree two polynomials (see for example [1, 2, 6, 8, 9, 11, 13, 14, 15–17]). Such polynomials are also used in other contexts, see for example Rafe Jones’ construction of irreducible polynomials reducible modulo every prime [15] or the proof of [3, Conjecture 1.2] in [5]. In this paper, we explain how the theory of this class of polynomials completely fits in a general context which allows the use of powerful machinery coming from the theory of finite automata (in characteristic different from 2). In fact, we show that some irreducibility questions over finite fields can be translated into automata theoretical ones (see Definition 3.6 and Theorem 3.8). As a side result, we also obtain that the set of irreducible polynomials which can be written as the composition of degree two polynomials is naturally endowed with a regular structure given by Theorem 3.11.

Let $F_{q}$ be a finite field of odd characteristic and let $S \subset F_{q} [x]$ be a set of monic degree two polynomials. In this paper, we consider the set $S$ to be an alphabet, and a word $f_{1} \dots f_{k} \in S^{*}$ corresponds to the composition $f_{1} ◦ \dots ◦ f_{k} \in F_{q} [x]$ ⁠. The empty word naturally corresponds to $x$ ⁠. Let $I \subset S^{*}$ be the language of words whose corresponding compositions are irreducible. Our goal is to show that $I$ is a regular language by providing an automaton that accepts it. The entire theory lifts to local fields under the assumption that the set $S$ is finite and none of its elements has discriminant in the maximal ideal of the local field.

2. Distinguished sets and freedom

We include in this section some elementary facts concerning the freedom of the monoid generated by a finite set of irreducible degree two polynomials. These results will be needed in Section 3. Each polynomial $f \in S$ can be uniquely written as $f = {(x - a_{f})}^{2} - b_{f}$ for some $a_{f}, b_{f} \in F_{q}$ ⁠. We define $D_{S} = {b_{f} : f \in S}$ to be the distinguished set of $S$ ⁠.

We denote by $S^{*}$ the set of words over the alphabet $S$ ⁠, so $S^{*}$ is the free monoid generated by the symbols in $S$ ⁠. Let $C_{S} \subseteq F_{q} [x]$ be the compositional monoid generated by $S$ ⁠, that is the smallest subset of $F_{q} [x]$ containing $S$ and $x$ which is closed by composition.

We will denote by $π$ the natural surjective morphism of monoids $S^{*} ⟶ C_{S}$ which maps a word $f_{1} f_{2} \dots f_{k} \in S^{*}$ to the composition $f_{1} ◦ f_{2} ◦ \dots ◦ f_{k} \in F_{q} [x]$ ⁠. Notice that, for an element $f \in S$ ⁠, we will denote by $f^{(n)}$ the $n$ -fold composition of $f$ with itself.

For

b \in D_{S}

⁠, we define

A_{b}

as the subset of all

a

in

F_{q}

such that there exists

f \in S

with

f = {(x - a)}^{2} - b

⁠. For any of the

A_{b}

⁠, we define the difference set

A_{b} - A_{b} = {a - a^{'} : a, a^{'} \in A_{b}} .

We can define a relation

\sim

on

S^{*}

by setting

u \sim w

if there exists

ℓ \in ⋃_{b \in D_{S}} (A_{b} - A_{b})

for which

π (u) + ℓ = π (w)

⁠. This relation is symmetric and reflexive but not transitive, unless

⋃_{b \in D_{S}} (A_{b} - A_{b})

is an additive subgroup of

F_{q}

⁠.

In this section, we provide a computable condition to establish whether $C_{S}$ is a free monoid, which will be needed later on.

Proposition 2.1

Let $u, v$ be words of $S^{*}$ of equal length $n \geq 1$ ⁠. Let $u^{'}, v^{'}$ be the $(n - 1)$ -suffixes of $u$ and $v$ ⁠, respectively. Then

$π (u) = π (v)$ implies $u^{'} \sim v^{'},$
$u \sim v$ if and only if $π (fu) = π (gv)$ for some $f, g \in S$ ⁠.

Proof

Let us first prove (i). Suppose

π (u) = π (v)

and let us write

π {(u) = (h_{1} - a)}^{2} - b = {(h_{2} - a^{'})}^{2} - b^{'} = π (v)

for

h_{1} = π (u^{'})

⁠,

h_{2} = π (v^{'})

⁠. Then we have

(h_{1} - a - h_{2} + a^{'}) (h_{1} + h_{2} - a - a^{'}) = b - b^{'}

⁠. Since

h_{1} + h_{2} - a - a^{'}

has positive degree, this forces

b = b^{'}

and

h_{1} - a - h_{2} + a^{'} = 0

⁠. Now it is clear that

a, a^{'} \in A_{b}

⁠, which implies

a^{'} - a \in A_{b} - A_{b}

⁠, and then

u^{'} \sim v^{'}

⁠.

Let us now prove (ii). If $u \sim v$ ⁠, by definition we have $π (u) - a = π (v) - a^{'}$ for $a - a^{'} \in A_{b} - A_{b}$ for some $b$ ⁠. Now, by squaring and subtracting $b$ on both sides of the equality we get $f (π (u)) = g (π (v))$ for some $f, g \in S$ ⁠, and hence $π (fu) = π (gv)$ ⁠. Vice versa, if there exists $f, g \in S$ such that $π (fu) = π (gv)$ ⁠, then (i) applies.□

Lemma 2.2

Let $u, v$ be words of $S^{*}$ of equal length $n \geq 1$ ⁠. If $∣ D_{S} ∣ = ∣ S ∣$ or $∣ D_{S} ∣ = 1$ ⁠, then we have that $u \sim v$ if and only if $π (u) = π (v)$ ⁠.

Proof

One direction is trivial: if $π (u) = π (v)$ ⁠, then $u \sim v$ ⁠. For the other direction, we look at the two cases separately.

In the case $∣ D_{S} ∣ = ∣ S ∣$ ⁠, it follows from $u \sim v$ that $π (u) - π (v) = c \in A_{b} - A_{b}$ for some $b \in D_{S}$ ⁠. However, $A_{b}$ consists of only one element, so $c = 0$ ⁠.

For the case $∣ D_{S} ∣ = 1$ ⁠, assume that $u \sim v$ ⁠, so $π (u) = π (v) + c$ for some $c \in F_{q}$ ⁠. Let $u^{'}, v^{'}$ be the $(n - 1)$ -suffixes of $u$ and $v$ ⁠. Then, since $∣ D_{S} ∣ = 1$ ⁠, we have that ${(π {(u^{'}) - a_{1})}^{2} - (π (v^{'}) - a_{2})}^{2} = c$ for some $a_{1}, a_{2} \in F_{q}$ ⁠. As $c$ is constant, this forces $(π (u^{'}) - a_{1}) - (π (v^{'}) - a_{2}) = 0$ ⁠, which in turn forces $c = 0$ and hence $π (u) = π (v)$ ⁠.□

The following proposition shows that the freedom of the monoid is ensured whenever $D_{S}$ is either maximal or minimal.

Proposition 2.3

If $∣ D_{S} ∣ = ∣ S ∣$ or $∣ D_{S} ∣ = 1$ ⁠, then $C_{S} ≅ S^{*}$ ⁠.

Proof

Clearly, a polynomial of degree two in $C_{S}$ cannot have two distinct writings in terms of compositions. Let $F$ be a polynomial in $C_{S}$ of minimal degree with two different writings, that is, such that $F = π (fu) = π (gv)$ for $f, g \in S$ and $u, v \in S^{*}$ of positive length. From $π (fu) = π (gv)$ ⁠, one deduces by Proposition 2.1 that $u \sim v$ ⁠. Lemma 2.2 now gives $π (u) = π (v)$ ⁠, which implies $u = v$ by the minimality of $F$ ⁠.□

Corollary 2.4

If $∣ S ∣ = 2$ then $C_{S} ≅ S^{*}$ ⁠.

Proof

Immediate by observing that $∣ D_{S} ∣ = 1$ or $∣ D_{S} ∣ = ∣ S ∣ = 2$ ⁠.□

3. An automaton for irreducible compositions

3.1. Capelli’s Lemma

In this subsection, we describe the basic tools needed to establish the main result. We start with a well-known result by Capelli, which gives a necessary and sufficient criterion to control the irreducibility of the composition of two polynomials.

Lemma 3.1 (Capelli’s Lemma)

Let $K$ be a field and $f, g \in K [x]$ polynomials. Let $β \in \bar{K}$ be a root of $g$ ⁠. Then, $g ◦ f$ is irreducible over $K$ if and only if $g$ is irreducible over $K$ and $f - β$ is irreducible over $K (β)$ ⁠.

We now use Capelli’s Lemma to produce a simple ancillary result which will help us in what follows.

Lemma 3.2

Let $g \in F_{q} [x]$ be monic and irreducible of even degree, and let $f = {(x - a_{f})}^{2} - b_{f} \in F_{q} [x]$ ⁠. Then, $g ◦ f$ is irreducible if and only if $g (- b_{f})$ is not a square in $F_{q}$ ⁠.

Proof

Let

d = \deg (g)

⁠, and let

β \in F_{q^{d}}

be a root of

g

⁠. According to Lemma 3.1,

g ◦ f

is irreducible over

F_{q}

if and only if

f - β

is irreducible over

F_{q^{d}}

⁠. Writing

f - β = {(x - a_{f})}^{2} - (b_{f} + β)

⁠, this is equivalent to

b_{f} + β

not being a square in

F_{q^{d}}

⁠. Let

N : F_{q^{d}} \to F_{q}

be the norm map. If

β_{1}, \dots, β_{d}

are the roots of

g

⁠, we have

N {(b_{f} + β) = \prod_{i = 1}^{d} (b_{f} + β_{i}) = (- 1)}^{d} \prod_{i = 1}^{d} ((- b_{f}) - β_{i}) = g (- b_{f}),

since

d

is even. Now we can conclude, since

b_{f} + β

is a non-square in

F_{q^{d}}

if and only if

N (b_{f} + β) = g (- b_{f})

is a non-square in

F_{q}

⁠.□

We are now ready to state one of the basic ingredients of the proof of the main theorem, which will allow us to ‘push’ irreducibility questions for compositions of degree two polynomials on a finite level.

Proposition 3.3

Let $f_{1}, \dots, f_{k} \in F_{q} [x]$ be monic polynomials of degree two. Write $f_{i} = {(x - a_{i})}^{2} - b_{i}$ for all $i$ ⁠. Then, $f_{1} ◦ \dots ◦ f_{k}$ is irreducible if and only if all of the following are non-squares in $F_{q}$ ⁠:

$b_{1}$
$f_{1} (- b_{2})$
$⋮$
$(f_{1} ◦ \dots ◦ f_{k - 1}) (- b_{k})$ ⁠.

Proof

Clearly, $f_{1}$ is irreducible if and only if $b_{1}$ is a non-square. The rest follows by inductive application of Lemma 3.2.□

3.2. Brief interlude on Automata Theory

In this subsection, we recall the basic results needed in the next section. For the definition of deterministic finite automaton (DFA) and non-deterministic finite automaton (NFA), we refer for example to [12, Chapter 2]. Since all the automata in the paper will have a finite set of states, we will often omit the word finite.

Let $Σ$ be a set of symbols (an alphabet) and $Σ^{*}$ be the set of words over $Σ$ ⁠, that is the free monoid generated by it. Let us recall that a subset $L$ of $S^{*}$ is called a language. Let · be the usual binary operation in $Σ^{*}$ (that is, concatenation of words) and $*$ be the unary operation on languages defined by $L \mapsto L^{*}$ where $L^{*}$ is the smallest submonoid of $Σ^{*}$ containing $L$ (in the context of languages, this operation is often called Kleene star).

A language is said to be regular if it is finite or can be expressed recursively starting from finite sets using the operations $\cup, \cdot,^{*}$ (see [12] for more details). The following fact is well known.

Theorem 3.4

A language is regular if and only if it is accepted by a DFA.

We will need the following fundamental results from the theory of Automata.

Theorem 3.5

If a language $L$ is accepted by a DFA or an NFA, then it is regular.

Roughly, the theorem above states that the accepted languages of NFAs do not generalize the notion of regular language.

We will also be using the notion of a partial deterministic finite automaton, which is the same as a DFA, except the transition function is actually a partial function. If, when reading a word, a required transition is not defined, the word is rejected. Clearly, a partial DFA is a special case of an NFA, so languages accepted by partial DFAs are also regular.

3.3. Putting all together: building the automaton

We first define a finite deterministic automaton $N = N (S)$ using the data contained in $S$ ⁠.

Definition 3.6

The states of the automaton $N (S)$ are given by the following:

A special start state $I$ ⁠. It is accepting.
For each $a \in F_{q}$ ⁠, we have a distinguished state $[a]$ ⁠. It is accepting if $- a$ is a non-square.
For each $a \in F_{q}$ ⁠, we have a state ${a}$ ⁠. It is accepting if $a$ is a non-square.

The transitions are as follows:

For each $f \in S$ ⁠, we have a transition $I \overset{f}{\to} [- b_{f}]$ ⁠.
For each $f \in S$ and each $a \in F_{q}$ ⁠, we have a transition $[a] \overset{f}{\to} {f (a)}$ ⁠.
For each $f \in S$ and each $a \in F_{q}$ ⁠, we have a transition ${a} \overset{f}{\to} {f (a)}$ ⁠.

Remark 3.7

The reason we distinguish between the states ${a}$ and $[a]$ is that they may be accepting at different times: ${a}$ accepts if $a$ is non-square, $[a]$ if $- a$ is non-square. In the case that $- 1$ is a square in $F_{q}$ ⁠, the two are equivalent and we can identify the two types of states.

Theorem 3.8

The language $I$ of irreducible compositions is regular.

Proof

Let $L$ be the regular language over the alphabet $S$ that is accepted by the automaton $N$ reading from right to left. It is easy to see that a single letter $f$ is in $L$ if and only if $b_{f}$ is nonsquare. Furthermore, a word $f_{1} \dots f_{k}$ ⁠, $k \geq 2$ ⁠, is in $L$ if and only if $(f_{1} ◦ \dots ◦ f_{k - 1}) (- b_{f_{k}})$ is nonsquare. By Proposition 3.3, it follows that the word $f_{1} \dots f_{k}$ corresponds to an irreducible polynomial if and only if each prefix $f_{1} \dots f_{l}$ ⁠, $l \leq k$ ⁠, lies in $L$ ⁠. In other words, $I$ is the language of all words whose every prefix is in $L$ ⁠.

We want to prove that $I$ is regular. To do so, let us first construct a non-deterministic automaton $U$ from $N$ by reversing all the arrows of $N$ and setting the start state of $N$ as final state of $U$ and the final states of $N$ as start states of $U$ ⁠. Observe that the accepted language of $U$ is again the language $L$ ⁠, this time reading from left to right as usual. Now we use subset construction (see for example [12, Section 2.3.5]) to generate a new deterministic automaton $V$ having the same accepted language as $U$ ⁠. Finally, we remove all non-accepting states from $V$ to obtain the partial automaton $M$ ⁠. It is easily seen that $M$ accepts exactly those words whose every prefix is accepted by $V$ ⁠, which as explained above is $I$ ⁠.□

Remark 3.9

Notice that the language accepted by the final automaton $M$ is prefix closed.

We now provide an example to see the theorem in action.

Example 3.10

As a simple example, consider the case $q = 5$ and $S = {f, g}$ with $f = x^{2} - 2$ and $g = {(x - 1)}^{2} - 3$ ⁠.

We first construct the interim automaton $N$ using the method described in Definition 3.6. Since $p \equiv 1 \mod 4$ ⁠, we can identify the nodes $[a]$ and ${a}$ ⁠. Note that we have removed the node ${0}$ since it is not reachable from $I$ ⁠. The result is seen in Fig. 1.

After performing the transformation described in the proof of Theorem 3.8 and cutting out all unreachable states, we end up with the simple partial automaton $M$ in Fig. 2. This shows that the irreducible compositions of $f$ and $g$ are precisely those of the form $f^{(n)}$ ⁠, $f^{(n)} ◦ g$ ⁠, $f^{(n)} ◦ g^{(2)}$ and $f^{(n)} ◦ g^{(2)} ◦ f$ for $n \geq 0$ ⁠.

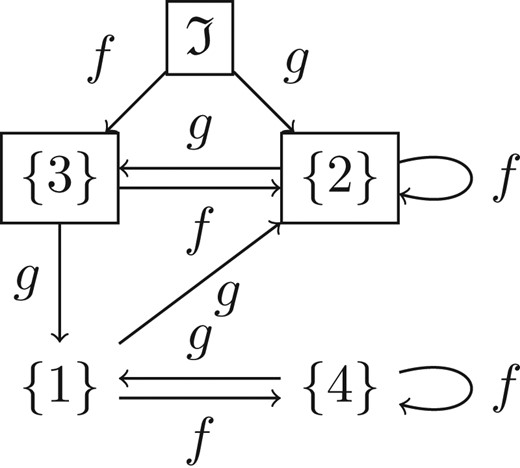
The interim automaton N for Example 3.10, coming from Definition 3.6. Boxed states are accepting.

Figure 1.

The interim automaton $N$ for Example 3.10, coming from Definition 3.6. Boxed states are accepting.

Open in new tab Download slide

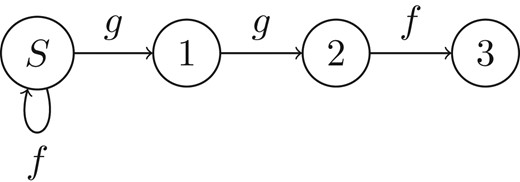
The automaton M accepting I for Example 3.10. All states are accepting.

Figure 2.

The automaton $M$ accepting $I$ for Example 3.10. All states are accepting.

Open in new tab Download slide

Using the machinery we developed in the rest of the paper, we describe an infinite set of primes of $F_{q} [x]$ having a finite regular structure.

Theorem 3.11

Let $F_{q}$ be a finite field of characteristic different from 2. The set of monic irreducible polynomials having coefficients in $F_{q}$ which can be written as a non-empty composition of degree 2 polynomials can be partitioned into a finite disjoint union $⨆_{a \in F_{q}} L_{a}$ in such a way that each $L_{a}$ is in natural bijection with the words of a regular language $L$ ⁠, which is independent of $a$ ⁠. In particular, the set of monic irreducible polynomials has a finite regular expression in terms of the elementary operations $\cup, \cdot,^{*}$ ⁠.

Proof

Let

D

be the set of monic irreducible polynomials in

F_{q} [x]

that can be written as non-empty composition of degree 2 polynomials. Let

S = {x^{2} - b : b \in F_{q}}

⁠. By Proposition 2.3,

C_{S}

is isomorphic to

S^{*}

⁠, so it is naturally embedded in

F_{q} [x]

⁠. Apply now Theorem 3.8 to obtain the regular language of irreducible polynomials

I

generated by

S

⁠, and let

L = I ⧹ {x}

⁠. Let

ψ_{a} : L ⟶ F_{q} [x]

be the shift map defined by

f (x) \mapsto f (x + a)

⁠. Let

L_{a} = ψ_{a} (L)

⁠. It is easy to observe that for any polynomial

f \in D

⁠, there exists

a \in F_{q}

such that

f (x - a)

can be written as an element of

C_{S}

⁠. This shows that

D = ⋃_{a \in F_{q}} L_{a} .

It remains to show that

L_{a} \cap L_{b} = \emptyset

if

a \neq b

⁠, the final result will follow immediately. We argue by induction on the length of the words in

L

(that is, the degree of the polynomials). Let

a, b \in F_{q}

with

a \neq b

such that there exist two words

v, w \in L

of minimal length

ℓ

such that

ψ_{a} (v) = ψ_{b} (w)

⁠. If

ℓ = 1

⁠, this is clearly impossible, so let us assume

ℓ > 1

⁠. We can write

f (v^{'} (x + a)) = g (w^{'} (x + b))

for some

f, g \in S

and

v^{'}, w^{'}

suffixes of

v

and

w

⁠, respectively. Therefore, for some

k, j \in F_{q}

⁠, we have

v^{'} {(x + a)}^{2} - w^{'} {(x + b)}^{2} = (v^{'} (x + a) - w^{'} (x + b)) (v^{'} (x + a) + w^{'} (x + b)) = k - j .

Since

v^{'}, w^{'}

are monic and the characteristic of

F_{q}

is different from 2, then the degree of the polynomial

(v^{'} (x + a) + w^{'} (x + b))

is greater than or equal to 2. This forces both

k = j

and

(v^{'} (x + a) - w^{'} (x + b)) = 0

⁠, which contradicts the minimality of

ℓ

⁠.□

Example 3.12

For an example demonstrating Theorem 3.11, take

q = 3

and

S = {f, g, h}

with

f = x^{2}

⁠,

g = x^{2} - 1

⁠,

h = x^{2} - 2

⁠. From Proposition 2.3,

C_{S}

is free and isomorphic to

S^{*}

⁠. Applying the construction, we get the automaton shown in Fig. 3. We see that the irreducible polynomials in

C_{S}

are exactly

x

⁠,

h

⁠,

h ◦ g ◦ f^{(n)}

for

n \geq 0

⁠, and

h^{(2)} ◦ k

for

k \in C_{S}

arbitrary (possibly the identity). Applying Theorem 3.11, it follows that the set of irreducible polynomials in

F_{3} [x]

that can be written as a non-empty composition of degree 2 polynomials is precisely

⋃_{a \in F_{3}} ({h (x + a)} \cup {h ◦ g ◦ f^{(n)} (x + a) : n \geq 0} \cup {h^{(2)} ◦ k (x + a) : k \in C_{S}}) .

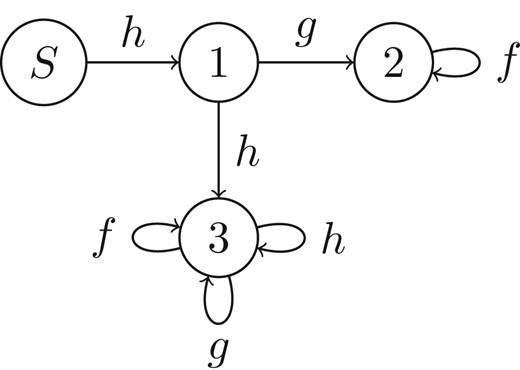
The automaton M accepting I for Example 3.12. All states are accepting.

Figure 3.

The automaton $M$ accepting $I$ for Example 3.12. All states are accepting.

Open in new tab Download slide

Let us now describe two implications of our result in the case in which $q$ is small compared with $n$ ⁠. Recall that the iterated logarithm of a positive real number $x$ ⁠, denoted by $\log^{*} x$ ⁠, is the number of times the logarithm function must be iteratively applied before the result is less than or equal to $1$ ⁠.

Corollary 3.13

For fixed $q$ ⁠, we can list all monic irreducible polynomials of degree $2^{n}$ which are compositions of degree 2 polynomials with complexity $O (q^{n} 2^{n} n 8^{\log^{*} (2^{n})})$ ⁠, where the implied constant depends only on $q$ ⁠.

Proof

First, we choose $S = {x^{2} - a : a \in F_{q}}$ and write down the automaton $M$ given by Theorem 3.8. The complexity of this step is $O (1)$ ⁠, where the implied constant clearly depends only on $q$ ⁠. Since the distinguished set is maximal, we can identify the polynomials $C_{S}$ and the words in $S^{*}$ ⁠. Now the construction is recursive: let $L_{0} (m)$ be the set of words of $S^{*}$ of length $m$ (so polynomials of degree $2^{m}$ ⁠). For any word $g \in L_{0} (m)$ and any $f \in S$ ⁠, check if the word $gf$ is accepted by the automaton $M$ ⁠: if it is, $gf$ is an element in $L_{0} (m + 1)$ ⁠. This check takes constant time for fixed $q$ if for each element of $L_{0} (m)$ we also store the state in which the automaton ends after reading it. As we observed in Remark 3.9, the language accepted by $M$ is prefix closed, so all the elements of $L_{0} (m + 1)$ can be constructed in this way. Then, constructing $L_{0} (m + 1)$ from $L_{0} (m)$ costs at most $O (q^{m + 1})$ ⁠.

It is elementary now to observe that

L_{0} (1)

can be easily constructed by selecting the irreducible degree 2 polynomials (again

O (1)

operations) and, therefore, that

L_{0} (n)

can be constructed in time at most

O (q^{n})

⁠. Using the proof of Theorem 3.11 directly, we know that the set

D (n)

of all irreducible polynomials of degree

2^{n}

which are compositions of degree 2 polynomials can be written as

D (n) = ⨆_{a \in F_{q}} L_{a} (n),

where

L_{a} (n) = {g (x + a) : g \in L_{0} (n)}

⁠.

In order to represent the elements of $D (n)$ by coefficients, we now need to evaluate the elements of $L_{0} (n)$ ⁠. For a single such element, if we evaluate it from inside out, this means squaring polynomials of degree $d = 1, 2, \dots, 2^{n - 1}$ and subtracting a constant each time. According to [10], such a squaring can be done in time $O (d \log (d) 8^{\log^{*} (d)})$ ⁠, the total time for each element hence being $O (2^{n} n 8^{\log^{*} (2^{n})})$ ⁠.□

Remark 3.14

The reader should notice that this is much quicker than listing such polynomials by using an irreducibility test. This would have in fact complexity $O (q^{n} 2^{n} n 8^{\log^{*} (2^{n})} I (2^{n}))$ ⁠, where $I (2^{n})$ is the cost of the chosen irreducibility test for a polynomial of degree $2^{n}$ ⁠. Again, the implied constant depends on the time of constructing the automaton, which just depends on the parameter $q$ ⁠.

Another interesting fact is that (again for fixed $q$ ⁠) we have an efficient deterministic algorithm to test irreducibility for polynomials which are a composition of degree two polynomials.

Corollary 3.15

Let $f$ be a polynomial of degree $2^{n}$ which is known to be a composition of monic degree two polynomials. Then $f$ can be tested for irreducibility in time $O (2^{n} n^{2} 8^{\log^{*} (2^{n})})$ ⁠, where the implied constant depends only on $q$ ⁠.

Proof

We need to write $f$ in the form $f = g_{1} ◦ g_{2} ◦ \dots ◦ g_{n} ◦ ℓ$ ⁠, where $g_{i} = x^{2} - a_{i}$ and $ℓ = x - b$ ⁠, with $a_{i}$ and $b$ in $F_{q}$ ⁠.

For this, suppose we have $F = G ◦ H$ with $G = x^{2} - a$ ⁠, where $a \in F_{q}$ ⁠, and $H$ is a polynomial of degree $d \geq 1$ ⁠. Assume $F$ is known, and we seek $G$ and $H$ ⁠. We apply the algorithm Univariate decomposition from [7, Section 2] with $r = 2$ ⁠. This gives us the unique $\tilde{G}$ of degree 2 and $\tilde{H}$ of degree $d$ with $\tilde{H} (0) = 0$ such that $F = \tilde{G} ◦ \tilde{H}$ ⁠. Clearly, setting $c = H (0)$ ⁠, we have $\tilde{H} = H - c$ and $\tilde{G} = G (x + c) = x^{2} + 2 cx + c^{2} - a$ ⁠. From this, it is easy to recover $c$ ⁠, $a$ ⁠, $G$ and $H$ ⁠. The algorithm Univariate decomposition takes time $O (d \log {(d)}^{2} 8^{\log^{*} (d)})$ ⁠, again using the multiplication algorithm from [10].

Applying this repeatedly to the $f$ from the theorem will find the decomposition $f = g_{1} ◦ g_{2} ◦ \dots ◦ g_{n} ◦ ℓ$ in $O (2^{n} n^{2} 8^{\log^{*} (2^{n})})$ time, which can then be checked for irreducibility with the automaton in time $O (n)$ ⁠. Again, for fixed $q$ ⁠, constructing the automaton has constant complexity, independently of the degree of the polynomial we are testing.□

Remark 3.16

For fixed $q$ ⁠, testing irreducibility for a polynomial of degree $2^{n}$ using for example Rabin’s test [18] with fast polynomial operations costs $O (n 4^{n})$ ⁠.

Remark 3.17

As we already mentioned, the whole point is that our algorithm is very efficient in the regime of small fixed $q$ and large $n$ ⁠. Let us nonetheless have a quick look at the complexity with regard to $q$ ⁠. If we follow the algorithm as described in Corollary 3.15 directly, the complexity appears to be exponential in $q$ ⁠. In particular, we can expect the subset construction step to take exponential time and space.

Fortunately, it is not in fact necessary to construct the entire automaton to execute the above algorithm. Instead, we can solely construct the interim automaton $N$ from Theorem 3.8. This takes $O (q^{2})$ field operations, and has to be done only once for each $q$ ⁠. Then, given the decomposition of the polynomial into $f_{1} ◦ \dots ◦ f_{n}$ we can run a word $f_{1} \dots f_{n}$ through $N$ directly as follows: define $S_{0}$ as the set of accepting states of $N$ ⁠. Then, for $i$ from $1$ to $n$ ⁠, let $S_{i}$ be the set of all states $t$ such that there is an $s \in S_{i - 1}$ and a transition $t \overset{f_{i}}{\to} s$ in $N$ ⁠. If at some point $S_{i}$ does not contain the initial state $I$ ⁠, we reject the word. Otherwise, we accept.

This method mirrors the reversal and subset construction from Theorem 3.8, except that only the parts that are actually used are computed. The complexity of this algorithm is easy to determine: when computing $S_{i}$ from $S_{i - 1}$ ⁠, we can iterate over all states $t$ of the automaton and check whether the unique outgoing transition labelled $f_{i}$ ends in $S_{i - 1}$ ⁠. Hence, each step takes only $O (q)$ field operations, for a total cost of $O (q^{2} + nq)$ ⁠. Since for small $q$ the quantity $2^{n} n^{2} 8^{\log^{*} (2^{n})}$ dominates $q^{2} + nq$ ⁠, the complexity in terms of $F_{q}$ -operations remains unchanged.

4. Irreducible compositions over local fields

In this final section, we will show how the results of the previous sections can be lifted, under some additional hypothesis, to polynomials over local fields. Let $K$ be a non-Archimedean local field with finite residue field $F_{q}$ of odd characteristic. Let $O_{K}$ be its ring of integers and $ϖ$ be a uniformizer. We will denote by $\tilde{\cdot}$ the reduction map $O_{K} [x] \to F_{q} [x]$ ⁠. Let us start by recalling the following lemma, which we state in a weaker form, sufficient for our purposes.

Lemma 4.1

Let

L

be any field and let

f, g \in L [x]

be monic polynomials with

f = {(x - a_{f})}^{2} - b_{f}

for some

a_{f}, b_{f} \in L

⁠. Then we have:

disc {(g ◦ f) = \pm disc (g)}^{2} \cdot 4^{\deg g} \cdot g (- b_{f}) .

Proof

See [14, Lemma 2.6].□

Theorem 4.2

Let $f_{1}, \dots, f_{k} \in O_{K} [x]$ be monic polynomials of degree 2 such that $ϖ ∤ disc (f_{1})$ ⁠. Then $f_{1} ◦ \dots ◦ f_{k}$ is irreducible in $K [x]$ if and only if $\tilde{f_{1}} ◦ \dots ◦ \tilde{f_{k}}$ is irreducible in $F_{q} [x]$ ⁠.

Proof

One direction is obvious, so let us assume that

f_{1} ◦ \dots ◦ f_{k}

is irreducible. For every

i = 1, \dots, k

⁠, let

f_{i} = {(x - a_{i})}^{2} - b_{i}

for some

a_{i}, b_{i} \in O_{K}

⁠. By Proposition 3.3, we need to show that the following elements are not squares:

$c_{1} ≔ \tilde{b_{1}}$
$c_{2} ≔ \tilde{f_{1}} (\tilde{- b_{2}})$
$⋮$
$c_{k} ≔ (\tilde{f_{1}} ◦ \dots ◦ \tilde{f_{k - 1}}) (\tilde{- b_{k}})$ ⁠.

First, suppose that

c_{t} = 0

for some

t \in {1, \dots, k}

⁠. This implies that

\tilde{f_{1}}

has a root, and since by hypothesis the discriminant of

\tilde{f_{1}}

is non-zero, by Hensel’s lemma we can lift such a root to a root of

f_{1}

⁠. But then

f_{1} ◦ \dots ◦ f_{k}

is clearly reducible, which is a contradiction. Thus we can assume that

c_{i} \neq 0

for all

i \in {1, \dots, k}

⁠. Now let

t \in {1, \dots, k}

be such that

c_{t}

is a non-zero square. By Proposition 3.3, this implies that

\tilde{f_{1}} ◦ \dots ◦ \tilde{f_{t}}

is reducible. On the other hand, applying Lemma 4.1 recursively and using the definition of the

c_{i}

’s we get that

disc (\tilde{f_{1}} ◦ \dots ◦ \tilde{f_{t}}) = u \cdot \prod_{i = 1}^{t} c_{i}^{2^{t - i}} \neq 0,

where

u

is an appropriate power of 2 (up to sign). This proves that

ϖ ∤ disc (f_{1} ◦ \dots ◦ f_{t})

and since

f_{1} ◦ \dots ◦ f_{t}

is irreducible by hypothesis, it defines an unramified extension of

K

⁠. It follows that

\tilde{f_{1}} ◦ \dots ◦ \tilde{f_{t}}

is irreducible (see for example [4, Chapter 7]), giving a contradiction.□

It is clear that the hypothesis that $ϖ ∤ disc (f_{1})$ is necessary for the claim to hold, since for example $x^{2} - ϖ$ is irreducible in $K [x]$ ⁠, while its reduction is reducible in $F_{q} [x]$ ⁠.

Given a finite set $S \subseteq O_{K} [x]$ of monic polynomials of degree two with unitary discriminant, Theorem 4.2 shows that irreducible compositions of the elements of $S$ correspond bijectively to irreducible compositions of the elements of $\tilde{S} \subseteq F_{q} [x]$ ⁠. Therefore, if we consider $S$ as an alphabet and $I$ is the language of irreducible compositions of the elements of $S$ ⁠, we deduce immediately the following corollary.

Corollary 4.3

The language $I$ is regular.

Proof

It is enough to apply Theorem 3.8 to the language of irreducible compositions of the elements of $\tilde{S}$ ⁠.□

The above corollary essentially states that the theory we developed in the rest of the paper lifts entirely to local fields, at least in the case in which the elements in $S$ have unitary discriminant. It would be interesting to understand what happens when this condition is not satisfied.

5. Further research

One of the natural questions arising from the results in the present paper is whether Theorem 3.11 can be generalized to higher degree polynomials. In fact any lift of such results to polynomials of degree three or more would be of great interest, in particular because the necessary and sufficient criterion by Boston and Jones [16] (and the subsequent results on the subject such as [1, 2, 6, 8, 11]) only exists in degree two. In the context of local fields, another interesting issue arising from Theorem 4.2 of this paper is the following: how can one include singular polynomials in the generating set $S$ ? In fact, the condition on the discriminant seems to be essential. Another question arising from these results is whether it is possible to explicitly compute the generating function of the language of irreducible compositions just in terms of the coefficient of the generating polynomials. It is indeed possible to compute such a function just in terms of the obtained automata, but this would drop most of the available information. In particular, it seems that the key ingredient to address this issue is to understand the structure of the finite submonoid of maps from $F_{q}$ to $F_{q}$ which can be written as composition of degree two polynomials. More generally, many of the questions and constructions which were related just to the compositions of a single polynomial, now seem to naturally arise in this more general context, were the rigidity of finite automata theory provides assistance.

Funding

The first author was supported by Swiss National Science Foundation Grant no. 168459. The second author is thankful to Swiss National Science Foundation Grant nos. 161757 and 171248.

Acknowledgements

The authors are thankful to the anonymous referee for his suggestions, which greatly improved the content and the readability of the paper. We are especially thankful for suggesting a reference which boiled down the complexity in Corollary 3.15 from $O (4^{n})$ to $O (2^{n} n^{2} 8^{\log^{*} (2^{n})})$ ⁠.

References

1

O.

Ahmadi

, A note on stable quadratic polynomials over fields of characteristic two.

2009

. https://arxiv.org/abs/0910.4556.

2

O.

Ahmadi

,

F.

Luca

,

A.

Ostafe

and

I. E.

Shparlinski

,

On stable quadratic polynomials

,

Glasg. Math. J.

54

(

2012

),

359

–

369

.

3

J. C.

Andrade

,

S. J.

Miller

,

K.

Pratt

and

M.-T.

Trinh

,

Special sets of primes in function fields

,

INTEGERS

13

(

2013

),

2

.

OpenURL Placeholder Text

4

J. W. S.

Cassels

,

Local fields, volume 3 of London Mathematical Society Student Texts

,

Cambridge University Press

,

Cambridge

,

1986

.

OpenURL Placeholder Text

5

A.

Ferraguti

and

G.

Micheli

,

On the existence of infinite, non-trivial F-sets

,

J. Number Theory

168

(

2016

),

1

–

12

.

6

A.

Ferraguti

,

G.

Micheli

and

R.

Schnyder

, On sets of irreducible polynomials closed by composition, (Eds.

S.

Duquesne

and

S.

Petkova-Nikova

),

Arithmetic of finite fields, volume 10064 of Lecture Notes in Computer Science

,

Springer

,

Cham

,

2016

,

77

–

83

.

OpenURL Placeholder Text

7

J.

von zur Gathen

,

Functional decomposition of polynomials: the tame case

,

J. Symbolic Comput.

9

(

1990

),

281

–

299

.

8

D.

Gomez

and

A. P.

Nicolás

,

An estimate on the number of stable quadratic polynomials

,

Finite Fields Appl.

16

(

2010

),

401

–

405

.

9

D.

Gómez-Pérez

,

L.

Mérai

and

I. E.

Shparlinski

, On the complexity of exact counting of dynamically irreducible polynomials.

2017

. https://arxiv.org/abs/1706.04392.

10

D.

Harvey

,

J.

Van Der Hoeven

and

G.

Lecerf

,

Faster polynomial multiplication over finite fields

,

J. ACM (JACM)

63

(

2017

),

52

.

11

D. R.

Heath-Brown

and

G.

Micheli

, Irreducible polynomials over finite fields produced by composition of quadratics. Revista Matemática Iberoamericana (to appear),

2017

. ArXiv preprint: https://arxiv.org/abs/1701.05031.

12

J. E.

Hopcroft

,

R.

Motwani

and

J. D.

Ullman

,

Introduction to Automata Theory, Languages, and Computation

,

Addison Wesley

,

Boston, MA

,

2001

.

OpenURL Placeholder Text

13

R.

Jones

,

Iterated galois towers, their associated martingales, and the p-adic mandelbrot set

,

Compos. Math.

143

(

2007

),

1108

–

1126

.

14

R.

Jones

,

The density of prime divisors in the arithmetic dynamics of quadratic polynomials

,

J. Lond. Math. Soc.

78

(

2008

),

523

–

544

.

15

R.

Jones

,

An iterative construction of irreducible polynomials reducible modulo every prime

,

J. Algebra

369

(

2012

),

114

–

128

.

16

R.

Jones

and

N.

Boston

,

Settled polynomials over finite fields

,

Proc. Am. Math. Soc.

140

(

2012

),

1849

–

1863

.

17

A.

Ostafe

and

I. E.

Shparlinski

,

On the length of critical orbits of stable quadratic polynomials

,

Proc. Am. Math. Soc.

138

(

2010

),

2653

–

2656

.

18

M. O.

Rabin

,

Probabilistic algorithms in finite fields

,

SIAM J. Comput.

9

(

1980

),

273

–

280

.

© The Author(s) 2018. Published by Oxford University Press. All rights reserved. For permissions, please e-mail: [email protected]

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Views

1,693

Altmetric

Total Views 1,693

1,286 Pageviews

407 PDF Downloads

Since 4/1/2018

Month:	Total Views:
April 2018	7
May 2018	12
June 2018	6
July 2018	9
August 2018	6
September 2018	12
October 2018	39
November 2018	8
December 2018	6
January 2019	3
February 2019	6
March 2019	23
April 2019	33
May 2019	37
June 2019	22
July 2019	18
August 2019	9
September 2019	15
October 2019	27
November 2019	27
December 2019	30
January 2020	15
February 2020	22
March 2020	19
April 2020	45
May 2020	23
June 2020	39
July 2020	27
August 2020	14
September 2020	32
October 2020	73
November 2020	29
December 2020	37
January 2021	25
February 2021	16
March 2021	28
April 2021	17
May 2021	28
June 2021	18
July 2021	16
August 2021	22
September 2021	28
October 2021	32
November 2021	30
December 2021	31
January 2022	19
February 2022	30
March 2022	16
April 2022	25
May 2022	19
June 2022	14
July 2022	12
August 2022	18
September 2022	18
October 2022	21
November 2022	19
December 2022	33
January 2023	28
February 2023	18
March 2023	12
April 2023	13
May 2023	17
June 2023	13
July 2023	16
August 2023	14
September 2023	19
October 2023	20
November 2023	24
December 2023	17
January 2024	32
February 2024	10
March 2024	10
April 2024	17
May 2024	13
June 2024	10
July 2024	14
August 2024	10
September 2024	8
October 2024	14
November 2024	6
December 2024	10
January 2025	10
February 2025	14
March 2025	32
April 2025	7