-
PDF
- Split View
-
Views
-
Cite
Cite
Luiz L Lopes, A closer look at the Yukawa interaction from a symmetry group perspective, Progress of Theoretical and Experimental Physics, Volume 2023, Issue 11, November 2023, 113D01, https://doi.org/10.1093/ptep/ptad129
Close - Share Icon Share
Abstract
I investigate the use of the SU(3) Clebsch–Gordan coefficients in light of the relations of completeness and closure. I show that in the case of αV = F/(F + D) ≠ 1, there is an additional interaction: the exchange of a ρ meson between a Λ and a Σ0 hyperon that only affects the symmetric coupling. I then calculate these additional coupling constants and show that this recovers the completeness and closure of the SU(3) Clebsch–Gordan coefficients for all values of αV. Besides, it increases the symmetry of the theory, now we can group the baryon octet into four doublets. Finally, I add the new coupling constants to study numerical results in the hyperon onset in dense nuclear matter assuming αV as a free parameter.
1. Introduction
The study of nuclear physics is almost a century old. And despite its senility, some techniques developed in the early years are still helpful today in describing strongly interacting matter. In 1935, H. Yukawa [1] proposed that the interaction between nucleons was mediated by an exchange of massive particles. Nowadays, such interaction is called a one-boson exchange, or Yukawa coupling [2], and it is expressed as the so-called Yukawa Lagrangian:
The theory of the strong force and the use of the Yukawa couplings underwent a great leap forward with the works of J. Schwinger [3] and especially with the elegant and imperative work of J. J. Sakurai [4]. Based on current conservations and local gauge invariance, Sakurai proposed a model that deals explicitly with baryon–baryon interaction via vector meson exchange. In such a model, the ω meson couples to the hypercharge while the ρ0 meson couples to the isospin.
With the development of symmetry group theories, Sakurai’s theory was relegated as just a particular case of the more powerful and well-accepted flavor SU(3) symmetry group theory [5–8]. However, with the onset of the more restrictive flavor-spin hybrid SU(6) group: SU(6) ⊃ SU(3) ⊗ SU(2), Sakurai’s theory was restored in its full glory; and again, the ω meson couples to the hypercharge and the ρ meson couples to the isospin [8–11].
Although the Yukawa coupling explicitly deals with baryon–baryon interaction via one-boson exchange, such interaction has proven extremely useful also in many-body theories. In 1974, J. D. Walecka applied the Yuakwa coupling to describe dense nuclear matter in mean field approximation (MFA) [12]. In this approach, the mesonic fields are replaced by their expected values and the nucleons do not interact with each other but instead, they behave like a free Fermi gas with a classical background field. The Walecka model and its extensions are today known as quantum hadrodynamics (QHD) [13] and they soon become a standard effective field theory to describe dense nuclear matter.
From the early 1990s on, the interest in studying neutron stars with exotic matter has increased significantly, and to reduce the huge uncertainties about the hyperon–meson coupling constants, the use of the SU(6) symmetry group became a standard approach and is widely used, even nowadays [14–21]. However, the discovery and confirmation of hypermassive neutron stars in the early 2010s have shaken our trust in SU(6) coupling constants. For instance, J0348+0432 with a mass range of 2.01 ± 0.04 M⊙ [22] and especially PSR J0740+6620, whose gravitational mass is 2.08 ± 0.07 M⊙ [23,24], bring great tension between the onset of energetically favorable hyperons and its well-known softening of the equation of state (EoS). This phenomenon is called the hyperon puzzle. Quickly, several authors realized that it was possible to reconcile massive neutron stars with hyperons in their core by partially breaking the SU(6) symmetry in favor of the less restrictive flavor SU(3) symmetry [25–39].
Although in the SU(3) the ρ0 meson does not necessarily couple directly to the isospin, its sign depends on the isospin projection [7,8]. This implies that the coupling of the ρ between the neutrons is the opposite of that between the protons. The same is true for the Ξ’s and for the Σ’s. Such behavior is summarized in Eq. (2):
Moreover, as one can correctly guess, the coupling constants between Λ’s and between Σ0’s are null:
once their isospin projection is zero.
When we are dealing with the Yukawa coupling (Eq. 1), especially in QHD, we usually assume that the Dirac field |$\bar{\psi }_B$| is the complex conjugate of the field ψB. From the SU(3) point of view, that is almost always true. Most of the gBBM is zero for crossed terms, i.e. if |$\bar{\psi }_B$| and ψB are not complex conjugates to each other.
The key point of the present work is that if we assume that |$\bar{\psi }_B$| and ψB are always complex conjugates to each other, the relation of completeness and closure of the SU(3) Clebsch–Gordan (CG) coefficients is violated if αV ≠ 1. This implies that, in this case, the set of coupling constants is incomplete. Indeed, there are crossed Yukawa couplings (sometimes called coupled channels):
that may in fact differ from zero. From the field theory point of view [3], Eq. (4) indicates that the Σ0 and the Λ interact with each other via ρ meson exchange. However, in the MFA, the Λ and the Σ0 now interact with the background field of the meson ρ. The strength of this interaction depends only on the coupling constant.
In this work, I calculate the crossed coupling constants from Eq. (4) by imposing that the Yukawa Lagrangian (Eq. 1) is invariant under the SU(3) flavor symmetry group and show that this crossed coupling contributes to the symmetric coupling while having no effect in the antisymmetric one. Therefore, it restores the relation of completeness and closure for the symmetric coupling, and as a consequence, for all values of αV. Thereafter, I explicitly add the crossed Yukawa terms to build a more complete QHD Lagrangian. Then, I calculate the new energy eigenvalues for the Λ and Σ0 hyperons. Finally, we see how the modified energy eigenvalues affect some of the microscopic and macroscopic properties in neutron stars and dense nuclear matter assuming αV as a free parameter.
2. The SU(3) group formalism
In the SU(3) symmetry group formalism (see Refs. [7–10,38] and the references therein for additional discussion), each eigenstate can be labeled as |N Y I I3〉, where N is the dimension of the representation, Y is the hypercharge, I is the total isospin, and I3 is the isospin projection. Assuming that the Yukawa coupling of the QHD (Eq. 1) is invariant under the SU(3) flavor symmetry group implies that its eigenstate is |0 0 0 0〉, or simply a unitary singlet.
The eigenstate of the ρ0 is |8 0 1 0〉. Therefore, in order to produce a Yukawa Lagrangian that is a unitary singlet, the direct product (|$\bar{\psi }_B~\otimes ~\psi _B$|) also must have the same eigenstate: |8 0 1 0〉. As the hypercharge and isospin projection are additive numbers, the simplest way to couple (|$\bar{\psi }_B~\otimes ~\psi _B$|) to result in |8 0 1 0〉 is to assume that |$\bar{\psi }_B$| and ψB are complex conjugates to each other. After that, we must couple the resulting |8 0 1 0〉 state to the ρ0 meson in order to obtain the unitary singlet: (|$\bar{\psi }_B~\otimes$| ψB) ⊗ ρ0 = |0 0 0 0〉. From the use of the Speiser method [7], there are two ways to couple (|$\bar{\psi }_B~\otimes ~\psi _B$|) to result in the |8 0 1 0〉 state: typically, antisymmetric and symmetric coupling. Therefore, the Yukawa Lagrangian of Eq. (1) can be rewritten as:
where g (g′) is the constant associated with the symmetric (antisymmetric) coupling, while C8 (|$C^{\prime }_8$|) is the SU(3) CG coefficient of the symmetric (antisymmetric) coupling to result in the |8 0 1 0〉 state. Furthermore, C1 is the CG coefficient to the product |$(\bar{\psi }_B \psi _B)\times \rho ^0$| to result in the unitary singlet. The SU(3) CG coefficients can be calculated from the isoscalar factors, as discussed in Ref. [7]. Once their values are well known, we use the tables presented in Ref. [40]. Explicitly, we have:
Nevertheless, the SU(3) CG coefficients, like their SU(2) counterparts (see, e.g. chapter 3 in Sakurai’s classical book [41]), must satisfy the relations of completeness and closure. In other words, we must have: |$\sum C^2_8 = \sum C^{\prime 2}_8 = \sum C^2_8 = 1$|. However, one can easily check that:
The results in Eq. (7) show us that the set of coupling constants presented in Eq. (6) are complete for the antisymmetric coupling (g′), but not complete for the symmetric one (g). There is some additional (|$\bar{\psi }_B~\otimes ~\psi _B$|) product that still results in the |8 0 1 0〉 state, but its components are not complex conjugates to each other. Indeed, the direct product |$\bar{\psi }_{\Sigma ^0}~\otimes ~\psi _\Lambda$|, as well as |$\bar{\psi }_{\Lambda }~\otimes ~\psi _{\Sigma ^0}$| produce an eigenstate |8 0 1 0〉. The coupling constants gΣΛρ and gΛΣρ can be calculated with the SU(3) CG coefficients:
As can be seen, these crossed couplings are only non-null in the symmetric coupling (g), as in the antisymmetric one (g′) the set was already complete. When we add these two additional coupling constants, we recover the relations of completeness and closure: |$\sum C^2_8 = \sum C^{\prime 2}_8 = \sum C^2_8 = 1$|, implying that we now have a complete set of coupling constants in agreement with the SU(3) group for both the antisymmetric and symmetric couplings. Moreover, as can be seen, unlike the cases of isospin doublets (as protons and neutrons; Ξ0 and Ξ−, etc.) the gΣΛρ and gΛΣρ are both positives and not opposite to each other as the ones in Eq. (2) are. Now, following Ref. [7] we introduce the coupling constants:
which results in:
Within the flavor SU(3) symmetry, we have in principle three free parameters: αV, the ratio z = g8/g1, and the mixing angle θV (see Refs. [8,29,38] for additional discussion). When we assume the SU(6) symmetry we have:
and the Sakurai proposals [4] are restored: the ρ meson couples to the isospin, therefore gΣΛρ = 0.
As αV = F/(F + D) is a weight factor for the contributions of the antisymmetric F (corresponding to {8′}) and the symmetric D (corresponding to {8}) couplings relative to each other, when we assume αV = 1, the symmetric couplings are neglected (g = 0), therefore SU(3) CG coefficients already form a complete set without the need of the |$g_{\Sigma ^0\Lambda \rho }$| coupling.
However, if αV ≠ 1, the symmetric coupling is also taken into account. Consequently, the gΣΛρ ≠ 0 and these interactions must be considered to account for the completeness of the theory. The now complete set of coupling constants in agreement with the SU(3) theory is presented in Table 1. These results are fully model-independent and can be applied to a diversity of calculations in future works. It is worth pointing out that αV = 1 is still a legitimate choice and was used to reproduce hyperon–nucleon scattering data [42]. The phenomenological necessity of the |$g_{\Lambda ^0\Sigma \rho }$| coupling in the context of the hyperon–nucleon scatterings remains unknown.
Complete set of baryon–vector mesons coupling constants for different values of αv, within the SU(3) symmetry group. These results are fully model-independent.
| . | αv . | |||
|---|---|---|---|---|
| . | 1.00 . | 0.75 . | 0.50 . | 0.25 . |
| gΛΛω/gNNω | 0.667 | 0.687 | 0.714 | 0.75 |
| gΣΣω/gNNω | 0.667 | 0.812 | 1.0 | 1.25 |
| gΞΞω/gNNω | 0.333 | 0.437 | 0.571 | 0.75 |
| gΛΛϕ/gNNω | −0.471 | −0.619 | −0.808 | −1.06 |
| gΣΣϕ/gNNω | −0.471 | −0.441 | −0.404 | −0.354 |
| gΞΞϕ/gNNω | −0.943 | −0.972 | −1.01 | −1.06 |
| gΛΛρ/gNNρ | 0.0 | 0.0 | 0.0 | 0.0 |
| gΣΣρ/gNNρ | 2.0 | 1.5 | 1.0 | 0.5 |
| gΞΞρ/gNNρ | 1.0 | 0.5 | 0.0 | −0.5 |
| |$g_{\Sigma ^0\Lambda \rho }/g_{NN\rho }$| | 0.0 | 0.288 | 0.577 | 0.866 |
| . | αv . | |||
|---|---|---|---|---|
| . | 1.00 . | 0.75 . | 0.50 . | 0.25 . |
| gΛΛω/gNNω | 0.667 | 0.687 | 0.714 | 0.75 |
| gΣΣω/gNNω | 0.667 | 0.812 | 1.0 | 1.25 |
| gΞΞω/gNNω | 0.333 | 0.437 | 0.571 | 0.75 |
| gΛΛϕ/gNNω | −0.471 | −0.619 | −0.808 | −1.06 |
| gΣΣϕ/gNNω | −0.471 | −0.441 | −0.404 | −0.354 |
| gΞΞϕ/gNNω | −0.943 | −0.972 | −1.01 | −1.06 |
| gΛΛρ/gNNρ | 0.0 | 0.0 | 0.0 | 0.0 |
| gΣΣρ/gNNρ | 2.0 | 1.5 | 1.0 | 0.5 |
| gΞΞρ/gNNρ | 1.0 | 0.5 | 0.0 | −0.5 |
| |$g_{\Sigma ^0\Lambda \rho }/g_{NN\rho }$| | 0.0 | 0.288 | 0.577 | 0.866 |
Complete set of baryon–vector mesons coupling constants for different values of αv, within the SU(3) symmetry group. These results are fully model-independent.
| . | αv . | |||
|---|---|---|---|---|
| . | 1.00 . | 0.75 . | 0.50 . | 0.25 . |
| gΛΛω/gNNω | 0.667 | 0.687 | 0.714 | 0.75 |
| gΣΣω/gNNω | 0.667 | 0.812 | 1.0 | 1.25 |
| gΞΞω/gNNω | 0.333 | 0.437 | 0.571 | 0.75 |
| gΛΛϕ/gNNω | −0.471 | −0.619 | −0.808 | −1.06 |
| gΣΣϕ/gNNω | −0.471 | −0.441 | −0.404 | −0.354 |
| gΞΞϕ/gNNω | −0.943 | −0.972 | −1.01 | −1.06 |
| gΛΛρ/gNNρ | 0.0 | 0.0 | 0.0 | 0.0 |
| gΣΣρ/gNNρ | 2.0 | 1.5 | 1.0 | 0.5 |
| gΞΞρ/gNNρ | 1.0 | 0.5 | 0.0 | −0.5 |
| |$g_{\Sigma ^0\Lambda \rho }/g_{NN\rho }$| | 0.0 | 0.288 | 0.577 | 0.866 |
| . | αv . | |||
|---|---|---|---|---|
| . | 1.00 . | 0.75 . | 0.50 . | 0.25 . |
| gΛΛω/gNNω | 0.667 | 0.687 | 0.714 | 0.75 |
| gΣΣω/gNNω | 0.667 | 0.812 | 1.0 | 1.25 |
| gΞΞω/gNNω | 0.333 | 0.437 | 0.571 | 0.75 |
| gΛΛϕ/gNNω | −0.471 | −0.619 | −0.808 | −1.06 |
| gΣΣϕ/gNNω | −0.471 | −0.441 | −0.404 | −0.354 |
| gΞΞϕ/gNNω | −0.943 | −0.972 | −1.01 | −1.06 |
| gΛΛρ/gNNρ | 0.0 | 0.0 | 0.0 | 0.0 |
| gΣΣρ/gNNρ | 2.0 | 1.5 | 1.0 | 0.5 |
| gΞΞρ/gNNρ | 1.0 | 0.5 | 0.0 | −0.5 |
| |$g_{\Sigma ^0\Lambda \rho }/g_{NN\rho }$| | 0.0 | 0.288 | 0.577 | 0.866 |
3. The QHD formalism and numerical results
I now study the effects of |$g_{\Sigma ^0\Lambda \rho }$| on dense nuclear matter for αV ≠ 1 and compare the results with those without this term.
I began by imposing chemical equilibrium and zero electric charge net, a situation expected in neutron star interiors, to investigate the influence of the crossed terms. Let us start with a classical QHD Lagrangian without crossed couplings. Its Lagrangian reads [27,38]:
in natural units. Additional discussion about the parameters and the formalism can be found in Refs. [12,13,27,31] and the references therein. The g’s in Eq. (12) have only two instead of three subscripts to make it clear that in this Lagrangian |$\bar{\psi }_B$| is always the complex conjugate of ψB. Applying Euler–Lagrange and the quantization rules we obtain the energy eigenvalues (which at T = 0 K is also the chemical potential). In MFA we have:
Now I add the coupled channels in the Lagrangian of Eq. (12):
where the 1/2 factor was added to keep the internal coherence with Eq. (12). When we apply Euler–Lagrange to the now-complete SU(3) Lagrangian, we see that the energy eigenvalue for all other six baryons is kept as in Eq. (13). For the Λ and the Σ0 we have two coupled equations:
However, as we already know the energy eigenvalue without the coupled channel, their inclusion is much easier in Hamiltonian formalism. The diagonal terms are the well-known unperturbed energy eigenvalues given by Eq. (13), while the crossed terms are off-diagonal. We have:
where |$|\psi _B \rangle = (\psi _\Lambda , \psi _\Sigma )$| and |$\Delta = 1/2(g_{\Sigma ^0\Lambda \rho })\rho _0$|. As we are dealing with a beta-stable matter, |$\mu _\Lambda = \mu _\Sigma$|, the new energy eigenvalues are (see, e.g. chapter 5 of Sakurai’s book [41] for a complete discussion):
Despite the energy eigenvalues from Eq. (17) being exact, the issue here is that the coupled channels lead us to mixed states [43]. In other words, the |$\psi _\Lambda$| and |$\psi _\Sigma$| are not eigenstates of the Hamiltonian of Eq. (16) anymore. Instead, we have a superposition [41,43]. However, as we have EB > >Δ in Eq. (16), and following Sakurai’s nomenclature [41], |$\psi _\Lambda$| and |$\psi _\Sigma$| are “almost good” eigenstates of Eq. (16). Therefore we can recognize E1 as the eigenvalue of the Λ, and E2 as the eigenvalue of the Σ0.
Reducing the coupled channel to MFA is not new. It was successfully used to account for the kaon interaction in nuclear medium in MFA (see, e.g. section 10.1 of Glendenning’s book [44] and the references therein), though such interaction is explicitly a coupled channel coming from the gNΛK and gNΣK couplings [45,46] (indeed, like the gΛΛρ, the gNNK is null [7]). It is also worth pointing out that the Λ–Σ interaction is supported by experimental data, in the so-called coherent Λ−Σ coupling [47,48]. Finally, the eigenvalues of the other six baryons are given by their usual expression, Eq. (13).
It is interesting to notice that when I calculated the |$g_{\Sigma ^0\Lambda \rho }$| and the |$g_{\Lambda \Sigma ^0\rho }$| coupling constants from the SU(3) CG coefficients, I showed that both have positive signs. However, as they are off-diagonal contributions, they ultimately contribute with opposite signs to the energy eigenvalues, as displayed in Eq. (17). So, for practical purposes, the (Σ0, Λ) forms a new isospin doubled, exactly like the (p,n), (Σ+, Σ−), and (Ξ0, Ξ−), with the coupling constants given by Table 1. The total EoS is given by [27]:
where B indicates baryon and l indicates leptons. The pressure is easily obtained by thermodynamic relations: p = ∑fμfnf − ϵ, where the sum runs over all the fermions and μf is the corresponding chemical potential.
To obtain numerical results, I consider αV a free parameter but use only αV = 0.25, which has the strongest influence of the |$g_{\Sigma ^0\Lambda \rho }$|, in order to not saturate the figures. Also, I use two different parametrizations, the eL3ωρ [38], that virtually fulfills every constraint of the symmetric nuclear matter, and the well-known and the widely used GM1 parametrization [49]. All parameters and predictions for the eL3ωρ are presented in Table I of Ref. [38], whereas the GM1 can be found in Table I of Ref. [31]. The coupling constants of the hyperons with the scalar meson are fixed to reproduce the hyperon potential depth values: |$U_\Lambda$| = −28 MeV and |$U_\Sigma$| = +30 MeV. For the |$U_\Xi$|, I chose |$U_\Xi$| = −18 MeV as suggested in Ref. [50] when I used the GM1 parametrization (which allows a direct comparison with the results presented in Ref. [31]), and chose |$U_\Xi$| = −4 MeV as suggested in Ref. [51] for the eL3ωρ parametrization (which allows a comparison with the results presented in Ref. [38]).
The reason I use two different parametrizations is that in the eL3ωρ there is a nonlinear coupling between the ω and ρ mesons, as introduced in the IUFSU model [52], whereas for the GM1 there isn’t. Such coupling influences the mass of the ρ meson, which ultimately affects the strength of the ρ field at high densities.
The particle population for the beta-stable matter at T = 0 K for αv = 0.25 is displayed in Fig. 1. We can see that the main effect of the |$g_{\Sigma ^0\Lambda \rho }$| coupling is to suppress the Λ onset, pushing it away to higher densities, whilst, at the same time, it favors the Ξ−. In the case of the eL3ωρ parametrization, the presence of the |$g_{\Sigma ^0\Lambda \rho }$| coupling pushes the Λ threshold from 0.4114 fm−3 to 0.4416 fm−3, whilst the Ξ− is drawn close, approaching from 0.5821 fm−3 to 0.5168 fm−3. This indicates an increase of around 10% in the density of the Λ and a decrease of around 10% in the density of the Ξ−. In the case of the GM1 parametrizations, the results are more extreme. The |$g_{\Sigma ^0\Lambda \rho }$| coupling not only suppresses the Λ threshold whilst favoring the Ξ−, but it exchanges their roles. Within it, the Ξ− is now the first hyperon to appear and becomes the most populous hyperon at higher densities. The Λ threshold is pushed away from 0.3264 fm−3 to 0.4405 fm−3; an increase of around 35%. On the other hand, the Ξ− is drawn close, approaching from 0.4079 fm−3 to 0.3655 fm−3, a decrease of around 10%.
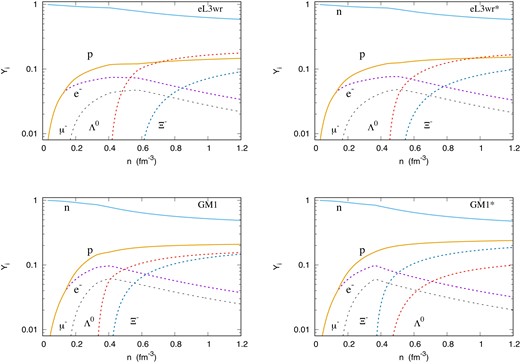
Particle population for the eL3ωρ and for the GM1. Results with (without) * indicate the presence (absence) of the |$g_{\Sigma ^0\Lambda \rho }$| coupling.
Now I use the EoS of the beta-stable electric neutral matter to solve the Tolman–Oppenheimer–Volkoff (TOV) equations [53]. For both parametrizations, I use the BPS EoS [54] for the outer crust and the BBP EoS [55] for the inner crust. I do not plot the EoS itself because the effects of the |$g_{\Sigma ^0\Lambda \rho }$| coupling are visually indistinguishable. The numerical results are presented in Fig. 2.
![Left: Neutron stars mass–radius relation for the eL3ωρ and the GM1 models. The solid (dotted) lines indicate the presence (absence) of the $g_{\Sigma ^0\Lambda \rho }$ coupling. The orange hatched area is the mass–radius uncertainty of the PSR J0740+6620 pulsar [24], and the blue hatched area is the intersection of two estimations from the Neutron star Interior Composition Explorer (NICER) for the 1.4M⊙ [56,57]. Right: Zoom in for M ≥ 2.0M⊙.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2023/11/10.1093_ptep_ptad129/2/m_ptad129fig2.jpeg?Expires=1750238719&Signature=USYHnLDL7acGQo-5MRf7eiWqm-xOv-0eGR83Pdy2uwcU1cUfJOSjn~AGNNdClylbrU8Fj4F7wClFzm63j62gyIpRrqTGL5wHoTA8-tdrC~pvzOgwDSjax6tDsLDQGbVBFeC1Cjli6z7KAjB9YZ4NF3tRvo9v2uvPRbHheKd5dqqT6c7BLtzCs3l4ftkuHIfSOx4bX9nhJJvyBDByyTLLrSTM-2zJcgA5m1WXnSR5PXq8jKKX0clSyfWUOk7vfYHh8etBWYE4JaLFgZaKJl5TsyoS24OjwojJ73Kdk8h9knRrm5GdyDA-GZvBDy7PCaAUIaW9KK~inN8KGDerwMss9Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Left: Neutron stars mass–radius relation for the eL3ωρ and the GM1 models. The solid (dotted) lines indicate the presence (absence) of the |$g_{\Sigma ^0\Lambda \rho }$| coupling. The orange hatched area is the mass–radius uncertainty of the PSR J0740+6620 pulsar [24], and the blue hatched area is the intersection of two estimations from the Neutron star Interior Composition Explorer (NICER) for the 1.4M⊙ [56,57]. Right: Zoom in for M ≥ 2.0M⊙.
We can also discuss some constraints related to neutron stars. Today, maybe the more important constraint is the undoubted existence of supermassive neutron stars. Using the NICER X-ray telescope, Ref. [24] was able to constrain the mass and the radius of PSR J0740+6620 in the range of M = 2.08 ± 0.07M⊙, and 11.41 km < R < 13.70 km, respectively. We plot this constraint as a hatched area in Fig. 2. As can be seen, both the eL3ωρ and GM1 models fulfill this constraint.
Other constraints are related to the radius and tidal parameter of the canonical 1.4 M⊙ star; however, they are still the subject of high debate about their true values. Recently, results obtained from Bayesian analysis indicate that the radius of the canonical star lies between 10.8 km and 13.2 km [58]; and 11.3 km to 13.5 km [59]; whilst results coming from the NICER X-ray telescope point out that R1.4 lies between 11.52 km and 13.85 km [56] and between 11.96 km and 14.26 km [57]. State-of-the-art theoretical results at low and high baryon density point to an upper limit of R1.4 < 13.6 km [60]. Finally, PREX2 results [61] indicate that the radius of the canonical star lies between 13.25 km < R1.4 < 14.26 km. I use the intersection between the two NICER results [56,57]: 11.96 km < R1.4 < 13.85 km, as a constraint for the canonical star.
In relation to the tidal parameter, an upper limit of 860 was found in Ref. [59]. A close limit, Λ1.4 < 800, was pointed out in Ref. [62]. In Ref. [58], an upper limit of 686 was deduced from Bayesian analysis. On the other hand, two mutually exclusive constraints are presented in Ref. [63], which proposed a limit between 70 < Λ1.4 < 580, and the PREX2 inferred values, whose limit lies between 642 < Λ1.4 < 955 [61]. As hyperons are not present at a 1.4 M⊙ star, we always have R1.4 = 12.82 km and Λ1.4 = 516 for the eL3ωρ, and R1.4 = 13.68 km and Λ1.4 = 696 for the GM1. Other results are presented in Table 2.
Some neutron star properties. Results with (without) * indicate the presence (absence) of the |$g_{\Sigma ^0\Lambda \rho }$| coupling.
| . | Mmax/M⊙ . | Hyp. at (fm−3) . | R2.0 (km) . |
|---|---|---|---|
| eL3ωρ | 2.202 | Λ at 0.4114 | 12.379 |
| eL3ωρ* | 2.206 | Λ at 0.4416 | 12.420 |
| GM1 | 2.208 | Λ at 0.3264 | 13.092 |
| GM1* | 2.223 | Ξ− at 0.3655 | 13.193 |
| . | Mmax/M⊙ . | Hyp. at (fm−3) . | R2.0 (km) . |
|---|---|---|---|
| eL3ωρ | 2.202 | Λ at 0.4114 | 12.379 |
| eL3ωρ* | 2.206 | Λ at 0.4416 | 12.420 |
| GM1 | 2.208 | Λ at 0.3264 | 13.092 |
| GM1* | 2.223 | Ξ− at 0.3655 | 13.193 |
Some neutron star properties. Results with (without) * indicate the presence (absence) of the |$g_{\Sigma ^0\Lambda \rho }$| coupling.
| . | Mmax/M⊙ . | Hyp. at (fm−3) . | R2.0 (km) . |
|---|---|---|---|
| eL3ωρ | 2.202 | Λ at 0.4114 | 12.379 |
| eL3ωρ* | 2.206 | Λ at 0.4416 | 12.420 |
| GM1 | 2.208 | Λ at 0.3264 | 13.092 |
| GM1* | 2.223 | Ξ− at 0.3655 | 13.193 |
| . | Mmax/M⊙ . | Hyp. at (fm−3) . | R2.0 (km) . |
|---|---|---|---|
| eL3ωρ | 2.202 | Λ at 0.4114 | 12.379 |
| eL3ωρ* | 2.206 | Λ at 0.4416 | 12.420 |
| GM1 | 2.208 | Λ at 0.3264 | 13.092 |
| GM1* | 2.223 | Ξ− at 0.3655 | 13.193 |
As can be seen, for massive neutron stars the influence of the |$g_{\Sigma ^0\Lambda \rho }$| coupling is very limited. The |$g_{\Sigma ^0\Lambda \rho }$| coupling causes a small increase of the maximum mass, as well as causing an increase of the radius for a fixed mass value. All these increments are about only 0.5%. This may sound a little disappointing but we must remember that no one could know how strong would be the influence of the |$g_{\Sigma ^0\Lambda \rho }$| until someone calculated its value.
The effect of the |$g_{\Sigma ^0\omega \rho }$| coupling is more evident when we consider a matter consisting of only neutrons and Λ’s. In Refs. [64,65] the authors study a liquid–gas-like phase transition within neutron-Λ matter. The neutron-Λ matter was also used to study spinodal instability in Ref. [66]. Moreover, the existence of a neutral bound state consisting of only neutrons and Λ’s was investigated in Refs. [67,68]. Here I follow Ref. [66] and use |$\mu _n =\mu _\Lambda$|. The EoS and the square of the speed of sound |$v_s^2 = \partial p/\partial \epsilon$| are displayed in Fig. 3.
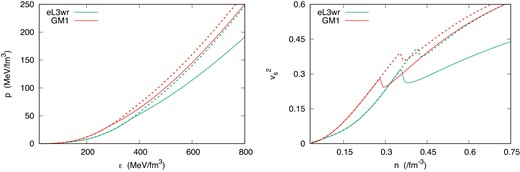
The EoS and the |$v_s^2$| for neutron-Λ matter. The dotted (solid) lines indicate the presence (absence) of the |$g_{\Sigma ^0\Lambda \rho }$| coupling.
As can be seen, the presence of the |$g_{\Sigma ^0\Lambda \rho }$| stiffens the EoS, as well as increases the speed of sound at high densities and pushes away the onset of the Λ. For the eL3ωρ the Λ threshold is pushed from 0.3634 fm−3 to 0.4164 fm−3, whereas within the GM1 parametrization the onset is pushed from 0.2819 fm−3 to 0.3586 fm−3. For the GM1 the increase of the density threshold is higher than 25%, whereas for the eL3ωρ it is around 15%.
Before I finish, I would like to mention that the applications of the |$g_{\Sigma ^0\Lambda \rho }$| are far beyond those presented in this work. For instance, it can potentially affect hypernuclei [47] energy levels, as well as hyperon–baryon scattering [42].
4. Conclusions
In this work, I investigate the use of the symmetry groups and the SU(3) CG coefficients to fix the coupling constants of the baryon octet with the vector meson in order to keep the Yukawa Lagrangian as a singlet for both the antisymmetric and symmetric couplings. The main results of the present work are summarized below:
I found that the current set of coupling constants for the SU(3) symmetry group does not satisfy the relations of completeness and closure for the symmetric coupling, whereas it was already complete for the antisymmetric one (αV = 1).
There are two additional Yukawa interactions related to the exchange of the neutral ρ meson between the Σ0 and the Λ hyperon. When these interactions are taken into account the relations of completeness and closure are restored.
Then I calculated the |$g_{\Sigma ^0\Lambda \rho }$| coupling constants within SU(3) and SU(6) symmetry groups. In SU(6) we have |$g_{\Sigma ^0\Lambda \rho }$| = 0, and Sakurai’s theory of strong interaction is restored [4]. Therefore, for the pure F-mode (αV = 1) the |$g_{\Sigma ^0\Lambda \rho }$| is not required to satisfy the SU(3) symmetry group. However, if αV ≠ 1, the gΣΛρ ≠ 0 and these interactions must be considered to account for the completeness of the theory. These results are fully model-independent.
The Λ–Σ interaction is supported by experimental data, in the so-called coherent Λ−Σ coupling [47,48].
In order to study the effects of the |$g_{\Sigma ^0\Lambda \rho }$| couplings, I added these crossed Yukawa couplings to the QHD model to study dense nuclear matter, on which αV is usually a free parameter.
I showed that these crossed terms enter as off-diagonal terms in the Hamiltonian. As a consequence, the coupling with the Λ and with the Σ0 present opposite signs, despite having the same CG coefficients.
I then obtained some numerical results for dense nuclear matter within two different parametrizations: the eL3ωρ [38] and the GM1 [49]. I showed that the |$g_{\Sigma ^0\Lambda \rho }$| coupling suppresses the Λ onset whilst favoring the Ξ− one. In the case of the GM1, this is enough to make the Ξ− the first hyperon to appear. In the case of massive neutron stars, the |$g_{\Sigma ^0\Lambda \rho }$| coupling causes a very small increase of the maximum masses and the radii for fixed masses (around 0.5%).
Finally, I studied a hadronic matter constituted by only neutrons and Λ’s. I showed that the |$g_{\Sigma ^0\Lambda \rho }$| coupling stiffens the EoS, and pushes the hyperon threshold to higher densities. It also affects the speed of sound.
Funding
Funding Open Access funding: SCOAP3.
Acknowledgement
The author was partially supported by CNPq Universal Grant No. 409029/2021-1.



