Abstract
In this article we study the thermodynamic phase transition of a regular Hayward-AdS black hole, by introducing a new order parameter, which is the potential conjugate to the magnetic charge arising from a non-linearly coupled electromagnetic field. We use Landau continuous phase transition theory to discuss the van der Waals-like critical phenomena of the black hole. The well-known interpretation of the phase transition of an AdS black hole as being a large and small black hole transition is re-interpreted as being a transition between a high-potential phase and a low-potential phase. The microstructure associated with this phase transition is studied using the Ruppeiner geometry. By investigating the behaviour of the Ruppeiner scalar curvature, we find that charged and uncharged (effective) molecules of the black hole have distinct microstructure, which is analogous to that of fermion and boson gas.
1. Introduction
In black hole physics, one of the most intriguing questions is whether a black hole has a microscopic structure. As Boltzmann said, “If you can heat it, it has microscopic structure”, which is one of the simplest and most elegant answers to this question. In the pioneering work of Hawking and Bekenstein [1–4] it was shown that a black hole is not only a gravity system but also a thermal system. A black hole possesses temperature and entropy, which are related to its surface gravity and event horizon area, respectively. As the black hole absorbs or emits matter, its Hawking temperature changes, which suggests that the black hole must have a microstructure. Inspired by this, several approaches have been developed to probe the microscopic origin of black hole thermodynamics [5–21]. Unlike a conventional thermodynamic system, where the macroscopic quantities are constructed from the microscopic knowledge of a system, the statistical investigation of a black hole is carried out in the reverse order. The microstructure of a black hole is scrutinized from its macroscopic thermodynamic quantities by studying the phase transitions.
Black holes exhibit a wide variety of phase transitions like those of ordinary thermodynamic systems. Particularly, phase transitions in an AdS background have been extensively studied in recent years. One of the crucial assumptions in these studies is that the cosmological constant is identified as the thermodynamic variable, pressure [22]. For a charged AdS black hole, the first-order (discontinuous) and second-order (continuous) phase transition traits are analytically similar to those of a van der Waals (vdW) fluid [23–25]. By studying these phase transitions, the microstructure of the black hole can be investigated through thermodynamic geometry methods. Ruppeiner geometry has proven to be quite useful and interesting in probing the interactions of a black hole from its macroscopic thermodynamic properties [26]. In this technique, a line element, which is the measure of the distance between two neighbouring fluctuation states, is defined in a appropriate parametric space [27]. The curvature scalar constructed using this line element is an indicator of the nature of the constituents of the system; a positive sign is used for the repulsive interactions and a negative sign for the attractive ones. The interpretation of this correspondence in black hole physics is adopted from the results obtained by the applications of Ruppeiner geometry in ordinary thermodynamic systems [28,29].
For a charged AdS black hole, choosing a parameter space with coordinates such as mass and pressure, the Ruppeiner curvature scalar can be written in terms of the molecular density of the black hole microstates [5]. Here, by introducing the concept of black hole molecules, the authors have studied the phase transition and the interaction between the black hole molecules in two distinct phases. The molecular number density measures the microscopic degrees of freedom, through the use of which the order parameter is constructed. However, recently it was shown that for an RN-AdS black hole the phase transition is regulated by the electric potential [8]. Black holes can exist in any of the three potential phases, namely, the high-potential phase, the low-potential phase and the neutral-potential phase. The neutral-potential phase of the black hole is analogous to the liquid–vapour coexistence phase found in a vdW system. The potential due to the charge $$Q$$
serves as the order parameter. The microscopic and phase transition study is carried out by using the Landau continuous phase transition theory. The influence of charge, the key entity in phase transition as it was conjectured, on the microstructure is investigated via Ruppeiner geometry. In this regard, one of the motivations for our research stems from the curiosity about the phase structure of the black holes which are composed of magnetic charges.
It is widely believed that, due to imperfections in classical theories of gravity, there exist spacetime singularities which may be remedied by considering quantum effects, which calls for a quantum theory of gravity. Since there is no conclusive theory for quantum gravity, the intuitive answers to these are given in the semi-classical regime. The first regular black hole model, which is free from a singularity, was proposed by Bardeen [30], where the singularity is replaced with a de Sitter core. Subsequent studies showed that a regular black hole could be realized as a solution of Einstein gravity coupled to a non-linear electrodynamics source, which is the charged version of a Bardeen black hole [31,32]. A regular black hole can also be interpreted as the gravitational field of a non-linear magnetic monopole. A different kind of regular solution was provided by Hayward [33]. Similar to the Bardeen solution, it is a degenerate configuration of the gravitational field of a non-linear magnetic monopole. The solution carries magnetic charges and a free integration constant.
It is more reasonable to rephrase the question we posed in the beginning as, “Does a black hole without a singularity have a microstructure?” In this work, we investigate the phase structure of regular Hayward black hole in an AdS background. The article is organized as follows. In Sect. 2, the phase transition is studied using the Landau theory of continuous phase transition, followed by probing the microstructure using Ruppeiner geometry in Sect. 3. Results are presented in Sect. 4.
2. Phase transition of regular Hayward black hole
2.1. Thermodynamics of the black hole
The action of Einstein gravity coupled to a nonlinear electromagnetic field in AdS spacetime background is [
34,
35]
In the above expression, the Lagrangian density
$$\mathcal{L}$$
is a function of
$$\mathcal{F}=F^{\mu \nu}F_{\mu \nu}$$
and the field strength of the vector field is
$$F=dA$$
. A Hayward class of solutions arises from the Lagrangian density,
where
$$\mu >0$$
is a dimensionless constant and
$$\alpha>0$$
has a dimension of length squared. The general static spherically symmetric solution is given by
where
$$d\Omega ^2=d\theta ^2+\sin \theta ^2d\phi ^2$$
and
$$Q_m$$
is the total magnetic charge of the black hole
In the AdS background, the function
$$f(r)$$
has the form
where
$$M_S$$
is the Schwarzchild mass and
$$g$$
is the free integration constant, which is related to magnetic charge as
The ADM (Arnowitt, Deser and Misner) mass can be read off from the asymptotic behaviour of the function
$$f(r)$$
and it has the following form,
The Schwarzchild mass
$$(M_S)$$
is the resultant of the nonlinear self interactions of the massless graviton. The other contribution,
$$M_{em}$$
, is associated with the nonlinear interaction between the graviton and the photon. The Hayward black hole solution corresponds to the case where
$$M_S=0$$
and
$$\mu=3$$
, which has the following metric function (henceforth we will take
$$M_{em}=M$$
):
The pressure
$$P$$
is related to the cosmological constant
$$\Lambda$$
, as
$$P=- \Lambda /8\pi$$
. The event horizon of this black hole is determined by the condition
$$f(r_+)=0$$
, through the use of which the explicit expression for mass
$$M$$
can be written. The Hawking temperature of the black hole, which is related to the surface gravity
$$\kappa$$
, is obtained as
With this temperature, we can write the first law of thermodynamics in the conventional form,
where
$$\Psi$$
is the conjugate potential for the magnetic charge
$$Q_m$$
,
$$\Pi$$
is conjugate to the parameter
$$\alpha$$
. The volume and entropy of the black hole have the following non-trivial profile:
Rearranging Eq. (
9) we have the equation of state,
The critical behaviour of a regular Hayward black hole can be studied by choosing a pair of conjugate variables like
$$(P{-}V)$$
or
$$(T{-}S)$$
. Choosing the pair
$$(P,V)$$
we have the Maxwell’s equal area law in the form
With Eq. (
14) and using corresponding expressions for
$$P_0(V_1)$$
and
$$P_0(V_2)$$
from the equation of state, we obtain
where
We have taken
$$ x=r_1/r_2$$
, where
$$r_1$$
and
$$r_2$$
are the black hole radii for first-order phase transition points.
$$x=1$$
gives critical values of temperature
$$T$$
and pressure
$$P$$
;
During the phase transition, the system undergoes a sudden change in its physical properties which is controlled by external thermodynamic variables. A familiar example in day-to-day life is the solid–liquid–gas transition due to a change in the temperature or pressure. A common feature of these transitions is that the order or symmetry of the system changes at the transition point. At the phase transition point of a black hole, there is a sudden change in the potential
$$\Psi$$
, which is controlled by the pressure and temperature. This indicates that the black hole microstructure is in different phases at different potentials. The two phases of the black hole with different symmetry and order are determined by the potentials
where
$$r_1$$
and
$$r_2$$
can be written in terms of
$$x$$
using Eq. (
15), and the critical value of the potential
$$\Psi _C$$
can be obtained by setting
$$x=1$$
. We define the following order parameter to characterize the phase transition:
The behaviour of the order parameter is shown in Fig. 1, where we have defined $$\chi=T/T_C$$
. We examine the mechanism of black hole phase transition from the perspective of black hole magnetic charge, since the conjugate potential of magnetic charge serves as the order parameter, using Landau theory.
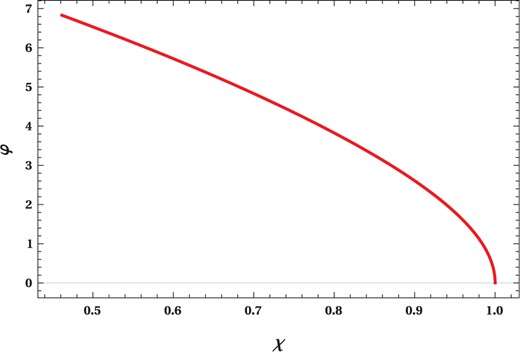
Fig. 1.
The order parameter vs reduced temperature $$(\varphi{-}\chi)$$
plot of a regular Hayward-AdS black hole.
2.2. Phase transition of the black hole
In Landau theory, a continuous phase transition is associated with a broken symmetry. In other words, the phase transition is the spontaneous breaking of the symmetry, where the system chooses one state during this. Landau realized that an approximate form for the free energy could be constructed without prior knowledge about the microscopic states. In this theory, it is always possible to ascertain an order parameter which vanishes on the high-temperature side of the phase transition and has a non-zero value on the low-temperature side of the phase transition. That is, in one phase, the order parameter has a non-zero value; in another phase, it vanishes. The order parameter describes the nature and extent of symmetry breaking. At the second-order phase transition, the order parameter grows continuously from the null value at the critical point. Since the order parameter approaches zero at the phase transition, one can Taylor-expand the free energy as a power series of the order parameter. The symmetries of the theory govern the form of this expansion.
The phase transition in a black hole system can also be characterized by the symmetry and order degrees as in a conventional thermodynamic system. In a black hole system, we can identify two phases with different potentials below the critical point (for $$T<T_C$$
). The system in a higher-potential phase $$\varphi _1$$
possesses a relatively ordered state with lower symmetry. This corresponds to a certain orientation of black hole molecules under the action of the strong potential $$\varphi _1$$
. In contrast, the system in a lower-potential state $$\varphi _2$$
possesses a relatively lower-order degree and a higher symmetry than the phase $$\varphi _1$$
. This is due to the weakened orientation of the black hole molecules. The black hole molecules will have a certain orientation for all the values of temperature below critical value $$T_C$$
. When the temperature is above the critical value ($$T>T_C$$
), the thermal motion of molecules increases and causes the black hole molecules to attain random orientation. The system now has a higher symmetry than all the states below the critical temperature. For the less symmetrical phase (below the critical temperature with higher-order), the order parameter $$\varphi$$
is non-zero. For the more symmetrical phase (above critical temperature with lower order), the order parameter $$\varphi$$
is zero.
Near the critical point
$$T_C$$
, the order parameter
$$\varphi$$
is small and hence the free energy can be expanded in terms of the order parameter. The symmetry of the system under the transformation
$$\Psi \rightleftharpoons -\Psi$$
removes the odd powers in that perturbation series;
where
$$G_0$$
is the Gibbs free energy at
$$\varphi (T)=0$$
, which describes the temperature dependence of the high-temperature phase near the critical point.
In Landau theory, it is presumed that
$$b>0$$
so that the free energy
$$G$$
has a minimum for finite values of the order parameter
$$\varphi$$
. For
$$a>0$$
, there is only one minimum at
$$\varphi =0$$
, which corresponds to the symmetrical phase (more symmetrical phase), whereas for
$$a<0$$
there are two minima with
$$\varphi\neq 0$$
in the unsymmetrical phase (less symmetrical phase). The transition point is governed by the condition of
$$a=0$$
. One of the assumptions of the theory is that
$$a(T)$$
has no singularity at the transition point, so it can be expanded in the neighbourhood of the critical point as integral powers of
$$(T-T_C)$$
. To the first order,
The coefficient
$$b(T)$$
may also be replaced by
$$b(T_C)=b$$
. The expansion of free energy, therefore, becomes
In the unsymmetrical phase, the dependence of the order parameter
$$\varphi$$
on the temperature near the critical point is determined by the condition that
$$G$$
, which is a function of
$$\varphi$$
, be a minimum. In a stable equilibrium state,
$$G(T)$$
has a vanishing first derivative and a positive second derivative:
The solutions of Eq. (
28) are
The solution $$\varphi =0$$
, when $$a>0$$
, renders a disordered state in the temperature range $$T>T_C$$
. The non-zero solution corresponds to the ordered state, where the configuration of the phases on the temperature scale depends on the sign of $$a_0$$
. For $$a_0>0$$
and $$a_0<0$$
, the ordered state corresponds to the temperatures $$T<T_C$$
and $$T>T_C$$
, respectively. From Eq. (30) we have $$\varphi \propto (T-T_C)^{1/2}$$
near the critical point, which gives the critical exponent $$\beta =1/2$$
.
Substituting these solutions (
30) back to the Eq. (
27), we get the reliance of free energy on the temperature near the phase transition point:
These solutions match at
$$T=T_C$$
, i.e., the free energy is continuous at the critical point. At constant pressure the total differential of the Gibbs free energy is
The expression for entropy is
This is the difference of entropy between the ordered and disordered states. If the entropy of the disordered phase is
$$S_0$$
, then that of the ordered phase will be
$$S_0+({a_0^2}/{b}) (T-T_C)$$
. The black hole entropy is also continuous at the phase transition point. The specific heat can be calculated as
The specific heat has a jump at the critical point,
From this it is clear that the heat capacity of the ordered state is greater than that of the disordered state. This expression also indicates that the critical exponent
$$\alpha$$
is zero. From Eq. (
27) and Eq. (
33), we have
which gives
Using Eq. (
30) gives two branches:
From this we can infer that the critical exponent
$$\gamma=1$$
. At the phase transition point
$$a=0$$
, therefore, from Eq. (
38) we can obtain the relation
which simply tells us that the critical exponent
$$\delta =3$$
.
3. Ruppeiner geometry and microstructure
Landau theory, being universal, does not give the phase structure of the system. However, the symmetry or order of degree of the system arises from the underlying microstructure. The parameters
$$a$$
and
$$b$$
in the theory are related to the system characteristics. However, they do not appear in the identification of critical exponents. This discrepancy persists even for a conventional thermodynamic system. This is because, in the continuous phase transition theory, the fluctuation of the order parameter is not considered near the transition point. This can be addressed by using a fluctuation theoretical tool, namely the Ruppeiner geometry. The black hole microstructure can be analyzed by studying the nature of the Ruppeiner curvature scalar
$$R$$
. The thermodynamic invariant curvature scalar
$$R$$
is calculated by using the definition in the Weinhold energy form [
36]
in the
$$(S,P)$$
parametric space. The exact expression for the curvature scalar is complicated. Using the earlier results (Eqns
15,
16 and
17) we obtain the curvature scalar for the two phases of the black hole. The obtained
$$R$$
is plotted against
$$\chi$$
to study the nature of the interaction between the black hole molecules (
Fig. 2). We also note that in the limit
$$g/r_+<<1$$
the Ruppeiner scalar takes the simple form
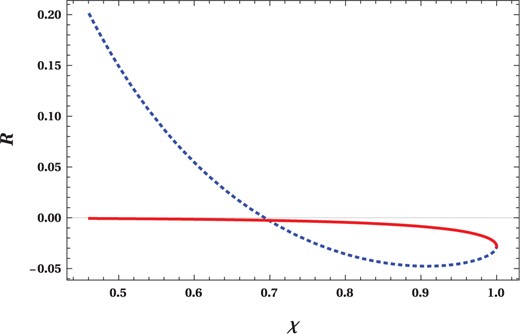
Fig. 2.
The Ruppeiner scalar curvature vs reduced temperature $$(R{-}\chi)$$
plot for a regular Hayward-AdS black hole. The blue dotted line and the red solid line correspond to $$R_1$$
and $$R_2$$
branches, respectively.
The behaviour of $$R$$
does not change in this approximation. This simply means that the correction to entropy in a regular black hole does not impact the nature of microscopic interactions. In a magnetically charged black hole, there are two distinct types of molecules; charged and uncharged, which contributes to the microscopic degrees of freedom of the entropy. The black hole phase transition can be seen as a manifestation of the phase structure of a two-fluid system with magnetically charged and uncharged molecules.
The ordered and disordered phase of the black hole can be attributed to the relative degree of freedom of the magnetically charged molecules. If the d.o.f. of charged molecules is $$N_g$$
and the total d.o.f the black hole is $$N$$
, the black hole can have three different situations depending on $$N_g/N$$
ratio. $$N_g/N=n_0$$
is moderately ordered, $$N_g/N>n_0$$
is highly ordered and $$N_g/N<n_0$$
is the less-ordered phase, due to the action of the magnetic potential $$\Psi$$
.
At a given temperature the magnetic potential corresponding to the $$R_1$$
(blue dotted line) and $$R_2$$
(red solid line) branches are different. Since $$\Psi _2 <\Psi _1$$
, $$R_2$$
represents the symmetric phase of the black hole where the molecules are in a disordered state. In other words, $$R_2$$
stands for the low-potential phase of the black hole. Therefore the $$R_2$$
branch always represents the situation $$N_g/N<n_0$$
, whereas the phases corresponding to $$R_1$$
have three different cases. The $$R_1>0$$
phase $$(N_g/N<n_0)$$
has less symmetry and higher order, $$R_1=0$$
phase $$(N_g/N=n_0)$$
has both moderate symmetry and order, and the $$R_1<0$$
phase $$(N_g/N>n_0)$$
has more symmetry and lower order.
4. Discussions
From several recent developments in the field of black hole thermodynamics, it is a well-established notion that black holes have microstructure like ordinary thermodynamic systems. Moreover, the degrees of freedom of these constituent black hole molecules is what counts towards the black hole entropy. The phase structure of these molecules entitles the thermodynamic and phase transition properties of the system. In this work, we have shown that the phase transition of a magnetically charged black hole is determined by the magnetic potential. However, this result is similar to that of an RN-AdS black hole where the key role is played by the electric potential [8]. The symmetry or the order degree of the regular black hole is governed by the magnetic potential. The changing symmetry results in different phases of the system, which is investigated using the Landau theory of continuous phase transition.
The statistical interpretation of the Ruppeiner scalar reveals the nature of the interaction of the black hole molecules. Under the limiting case $$g\rightarrow0$$
, we have $$R<0$$
, which corresponds to uncharged molecules. With the presence of charged molecules, $$R$$
tends to become positive. In the context of quantum gases, $$R<0$$
and $$R>0$$
results are obtained for fermion gas and boson gas, respectively [37,38]. For the regular Hayward black hole, magnetically charged molecules and uncharged molecules have different microstructures similar to fermion gas and boson gas.
However, in the case of anyon gas, the sign of $$R$$
tells us the average interaction between the constituents. Positive $$R$$
stands for repulsive, and negative $$R$$
corresponds to attractive interaction. Vanishing $$R$$
implies zero interaction. In this way, we can think that the black hole molecules have repulsive, attractive and zero interactions depending on the curvature scalar behaviour. Our research gives information about the microstructure of magnetically charged molecules which is similar to that of electrically charged molecules in an RN-AdS black hole. This phenomenological description will help us understand the exact microstructure of the black hole in future research, and similar investigation can be done for other non-singular black holes.
Acknowledgements
Authors N.K.A., A.R.C.L. and K.H. would like to thank U.G.C. Govt. of India for financial assistance under UGC-NET-SRF scheme.
References
[1]Hawking
S.W.
,
Commun. Math. Phys.
43
,
199
(
1975
);
46
,
206
(
1976
) [erratum]. ()
[2]Bekenstein
J. D.
,
Lett. Nuovo Cim.
4
,
737
(
1972
). ()
[3]Bekenstein
J. D.
,
Phys. Rev. D
7
,
2333
(
1973
). ()
[4]Bardeen
J. M.
, Carter
B.
, and Hawking
S. W.
,
Commun. Math. Phys.
31
,
161
(
1973
). ()
[14]Chabab
M.
, El Moumni
H.
, Iraoui
S.
, Masmar
K.
, and Zhizeh
S.
,
Int. J. Geom. Meth. Mod. Phys.
15
,
1850171
(
2018
) [
arXiv:1704.07720 [gr-qc]] [
Search inSPIRE]. ()
[28]Janyszek
H.
and Mrugaa
R.
,
J. Phys. A: Math. Gen.
23
,
467
(
1990
). ()
[29]Oshima
H.
, Obata
T.
, and Hara
H.
,
J. Phys. A: Math. Gen.
32
,
6373
(
1999
). ()
[30]Bardeen
J. M.
,
Proc Int. Conf. GR5
, p.
174
(
1968
).
[36]Weinhold
F.
,
J. Chem. Phys.
63
,
2479
(
1975
). ()
[37]Mirza
B.
and Mohammadzadeh
H.
,
Phys. Rev. E
78
,
021127
(
2008
). ()
[38]May
H.-O.
, Mausbach
P.
, and Ruppeiner
G.
,
Phys. Rev. E
88
,
032123
(
2013
). ()
© The Author(s) 2021. Published by Oxford University Press on behalf of the Physical Society of Japan.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (
http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided the original work is properly cited.
PDF





