-
PDF
- Split View
-
Views
-
Cite
Cite
Kiseki D Nakamura, Kentaro Miuchi, Shingo Kazama, Yutaro Shoji, Masahiro Ibe, Wakutaka Nakano, Detection capability of the Migdal effect for argon and xenon nuclei with position-sensitive gaseous detectors, Progress of Theoretical and Experimental Physics, Volume 2021, Issue 1, January 2021, 013C01, https://doi.org/10.1093/ptep/ptaa162
Close - Share Icon Share
Abstract
The Migdal effect is attracting interest because of the potential to enhance the sensitivities of direct dark matter searches to the low-mass region. In spite of its great importance, the Migdal effect has not been experimentally observed yet. A realistic experimental approach towards the first observation of the Migdal effect in the neutron scattering was studied with Monte Carlo simulations. In this study, the potential background rate was studied together with the event rate of the Migdal effect by a neutron source. It was found that a table-top-sized |$\sim (30~\mbox{cm})^3$| position-sensitive gaseous detector filled with argon or xenon target gas can detect characteristic signatures of the Migdal effect with sufficient rates (O(|$10^2\sim10^3$|) events per day). A simulation result of a simple experimental set-up showed two significant background sources, namely the intrinsic neutrons and the neutron-induced gamma-rays. It is found that the intrinsic neutron background rate for the argon gas is at an acceptable level and some future study of the reduction of the gamma-rays from the laboratory would make the observation of the Migdal effect possible. The background for the xenon gas, on the other hand, is found to be much more serious than for the argon gas. Future works on the isotope separation as well as the reduction of the gamma-rays from the detector and laboratory will be needed before the Migdal effect can be observed for the xenon gas case.
1. Introduction
Revealing the nature of the unidentified gravitational source in the universe, or dark matter, is one of the most important tasks in particle physics, astroparticle physics and cosmology. Weakly Interacting Massive Particles (WIMPs) are said to be one of the most attractive candidates and have been searched for for decades by various ways [1, 2]. In spite of these intensive searches for the “standard” WIMPs with a mass of a hundred GeV to several TeV, they have not been discovered yet. Although the interest and motivation for finding these standard WIMPs have not decreased [3], some experimental efforts to search for other types of dark matter candidates are being carried out. Among many types of other dark matter candidates [4, 5], lighter WIMPs are attracting interest and some experiments have investigated this new frontier [6–8].
Low-mass WIMPs are conventionally searched for with low-threshold WIMP detectors such as bolometers and “S2-only analysis” of two-phase liquid noble gas detectors. Recently, some groups reported the results and plans for light WIMP searches using an effect known as the Migdal effect [9–14], motivated by its recent reformulation [15] (see also Refs. [16, 17]).
The Migdal effect refers to the immediate excitation or ionization of the recoil atom at the standard nuclear recoil, which was first calculated in a different context by A. B. Migdal in 1941 [18]. A sudden change of the nuclear velocity caused by the recoil disturbs the electric potential of the atom. When its energy is absorbed by the surrounding electrons, the recoil atom is either excited or ionized. Then, the excited or ionized atom immediately de-excites through the X-ray transition, the Auger transition, or the Coster–Kronig transition, which deposits additional energy inside the detector. The probability of having the Migdal effect depends on the momentum transfer, but it is very suppressed in the case of light WIMPs.
These Migdal effects can even take place in a very low energy nuclear recoil where the recoil atoms are hardly detectable due to the poor ionization capability. Thus the Migdal effect effectively lowers the detection energy threshold of nuclear recoils and drastically improves the sensitivity of the low-mass WIMP searches. In spite of its great importance for the WIMP searches, the Migdal effect itself has not been observed experimentally yet. A realistic experimental approach, including potential background sources, towards the first observation of the Migdal effect is discussed in this paper.
2. Conceptual experimental design
As introduced in the previous section, the experimental observation of the Migdal effect itself is important for the low-mass WIMP searches. We hereby propose a method to detect the characteristic signature of the Migdal effect; a nuclear recoil with an additional electric signal. In order to detect the topology of these two signals, position-sensitive gaseous detectors were considered.
Among three possible reactions of the electric signals, we focused on the reaction associated with the emission of the characteristic X-rays so that the electric signal can be spatially separated from the nuclear recoils with an appropriate choice of the gas and its pressure. This “two-cluster” event topology can be used to select signals out of a huge amount of background events to claim a clear observation of the Migdal effect. Argon gas at 1 atm and xenon gas at 8 atm are chosen for this study so that the characteristic X-ray absorption length would be several centimeters.
Time projection chambers (TPCs) are widely-used position-sensitive gaseous detectors. Micro Pattern Gaseous Detectors (MPGDs) are well-studied readout devices for gaseous argon TPCs around the normal pressure. A typical three-dimensional spatial resolution of millimeters or less and an energy resolution of about |$30\%$| FWHM at 5.9 keV are realized [19, 20]. A readout system using the electroluminescence (EL) photons is developed for a high-pressure gaseous xenon detector [21]. The energy resolution of |$4\%$| at 30 keV has been demonstrated with the EL signal read by photon detectors with a pitch of 10 mm [21]. These detectors can realize energy thresholds of 1 keV for argon and 2 keV for xenon.
Detectors with a detection volume of |$(30~\mbox{cm})^3$| or larger are being used for some purposes[22, 23]. Considering these realistic detectors, we assume a detector with a detection volume of |$(30~\mbox{cm})^3$| with MPGD and EL readouts for the argon and xenon TPCs, respectively. The EL method is chosen for the xenon case because it has demonstrated a better performance in high-pressure xenon than MPGDs. The total numbers of the target nuclei for the argon and the xenon detectors are shown in Table 1.
Typical values of parameters for estimating the Migdal effect. The branching ratios for |$(n,l)=\rm 1s$| and |$q_{\rm e}=511\,{\rm eV}$| are shown. Details on the event cut are described in Sect. 3.2.
| Target gas . | Ar 1 atm |$(30\,\mbox{cm})^3$| . | Xe 8 atm |$(30\,\mbox{cm})^3$| . |
|---|---|---|
| Number of nuclei | |$7.26\times10^{23}$| | 5.81|$\times10^{24}$| |
| Cross-section for 565 keV neutron | 0.65 barn [24] | 6.0 barn [24] |
| Migdal branching | |$7.2\times10^{-5}$| [15] | |$4.6\times10^{-6}$| [15] |
| Fluorescence yield (K shell) | 0.14 [25] | 0.89 [26] |
| Scaling factor |$(q_{\rm e}^{\rm max}/511~\rm eV)^2$| | 2.92 [15] | 0.280 [15] |
| Event rate | 603 events per day | 975 events per day |
| Event rate (after cut 3) | 344 events per day | 361 events per day |
| Target gas . | Ar 1 atm |$(30\,\mbox{cm})^3$| . | Xe 8 atm |$(30\,\mbox{cm})^3$| . |
|---|---|---|
| Number of nuclei | |$7.26\times10^{23}$| | 5.81|$\times10^{24}$| |
| Cross-section for 565 keV neutron | 0.65 barn [24] | 6.0 barn [24] |
| Migdal branching | |$7.2\times10^{-5}$| [15] | |$4.6\times10^{-6}$| [15] |
| Fluorescence yield (K shell) | 0.14 [25] | 0.89 [26] |
| Scaling factor |$(q_{\rm e}^{\rm max}/511~\rm eV)^2$| | 2.92 [15] | 0.280 [15] |
| Event rate | 603 events per day | 975 events per day |
| Event rate (after cut 3) | 344 events per day | 361 events per day |
Typical values of parameters for estimating the Migdal effect. The branching ratios for |$(n,l)=\rm 1s$| and |$q_{\rm e}=511\,{\rm eV}$| are shown. Details on the event cut are described in Sect. 3.2.
| Target gas . | Ar 1 atm |$(30\,\mbox{cm})^3$| . | Xe 8 atm |$(30\,\mbox{cm})^3$| . |
|---|---|---|
| Number of nuclei | |$7.26\times10^{23}$| | 5.81|$\times10^{24}$| |
| Cross-section for 565 keV neutron | 0.65 barn [24] | 6.0 barn [24] |
| Migdal branching | |$7.2\times10^{-5}$| [15] | |$4.6\times10^{-6}$| [15] |
| Fluorescence yield (K shell) | 0.14 [25] | 0.89 [26] |
| Scaling factor |$(q_{\rm e}^{\rm max}/511~\rm eV)^2$| | 2.92 [15] | 0.280 [15] |
| Event rate | 603 events per day | 975 events per day |
| Event rate (after cut 3) | 344 events per day | 361 events per day |
| Target gas . | Ar 1 atm |$(30\,\mbox{cm})^3$| . | Xe 8 atm |$(30\,\mbox{cm})^3$| . |
|---|---|---|
| Number of nuclei | |$7.26\times10^{23}$| | 5.81|$\times10^{24}$| |
| Cross-section for 565 keV neutron | 0.65 barn [24] | 6.0 barn [24] |
| Migdal branching | |$7.2\times10^{-5}$| [15] | |$4.6\times10^{-6}$| [15] |
| Fluorescence yield (K shell) | 0.14 [25] | 0.89 [26] |
| Scaling factor |$(q_{\rm e}^{\rm max}/511~\rm eV)^2$| | 2.92 [15] | 0.280 [15] |
| Event rate | 603 events per day | 975 events per day |
| Event rate (after cut 3) | 344 events per day | 361 events per day |
There are various neutron sources potentially available for this experiment. In this study, a continuous neutron beam with an energy of 565 keV and a flux of |$1000~\mbox{cm}^{-2}~\mbox{s}^{-1}$| at 1 m is assumed. This is a realistic value for a |$\rm ^7Li(p,n)^7Be$| reaction at an irradiation facility in the National Institute of Advanced Industrial Science and Technology (AIST), Japan. The cross-sections of elastic scattering between 565-keV neutrons and the target nuclei are shown in Table 1. It should be noted that, in general, the higher the neutron energy, the greater the expected gamma-ray background rate from the detector and the laboratory materials. Thus we choose this energy as a typical neutron energy instead of more common sources like DT (deutron–triton) or DD (deutron–deutron) generators.
3. Signal
In this section, Migdal effect signals are discussed. First, an overview of the features of the Migdal effect including the expected event rate is given based on Ref. [15]. Then a more realistic MC simulation study on the detection possibility of the characteristic features of the Migdal effect is described.
3.1. Signal overview
Probabilities of the Migdal effects depend on the quantum numbers |$(n,l)$| of the associated electron. When an electron with a large principal quantum number (|$n$|) is involved, the probability of the Migdal effect is large but the additional electric energy is small because of the small binding energy. Observations of the Migdal effects with large principal quantum numbers, especially with |$n\geq 3$| for xenon, are important for further searches and possible discoveries of WIMPs [9]. However, the electric energies of these reactions are typically less than 1 keV and existing detectors are not suitable for a clear observation with a two-cluster topology. Therefore, |$(n,l)=(1,0)$| cases (1s, K shell) for both argon and xenon where additional electric energies can be detected with practical detectors are chosen for the first observation of the Migdal effect. The branching ratios of the Migdal effect for the |$(n,l)=(1,0)$| cases are listed in Table 1.
Figure 1 illustrates the reactions we expect to observe. The first reaction is the nuclear recoil (1) with a recoil energy of |$E_{\rm NR}$| and the Migdal effect (2). The orbital electron that receives energy by the Migdal effect transitions to another orbit or goes out of the atom. Since the probability of the latter process is several orders of magnitude higher than that of the former one, the latter process is studied in this paper. The recoil nuclei and the Migdal electron are detected as one cluster (cluster A). A de-excitation takes place following the emission of the Migdal electron. The de-excitation can be seen as a characteristic X-ray (3) or an Auger electron. Probabilities of de-excitation of K-shell hole by X-ray emission, or the fluorescence yield, are listed in Table 1. Characteristic X-ray can be detected at a distance of several centimeters with the detector condition we assume, such that a second cluster (cluster B) with a fixed energy (|$E_{\rm dex}$|) is expected. This topology information will provide us with a clear signal of the Migdal effect together with a powerful background rejection. Finally, multiple Auger electrons and de-excitation X-rays with a total energy of |$E_{\rm nl}-E_{\rm dex}$| are emitted for the energy conservation, where |$E_{\rm nl}$| is the binding energy of the |$(n,l)$| electron (4).
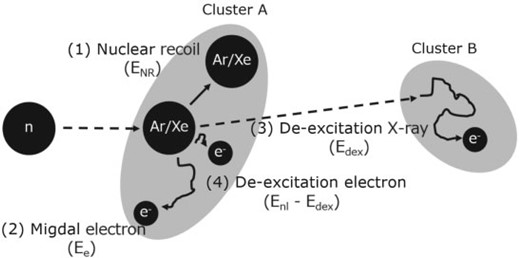
Schematic diagram of the reaction mechanism related to the Migdal effect.
Here |$m_{\rm n}$| is the neutron mass and |$E_{\rm n}$| is the neutron energy. It is seen that the scaling factor for argon is one order of magnitude larger than that for xenon because |$m_{\rm N}$| is smaller and |$E_{\rm NR}$| is consequently larger for a given energy of neutrons.
Expected event rates calculated for the experimental and physical conditions discussed so far are shown in the final row of Table 1. Here the event rates for the nuclear recoils associated with characteristic X-rays from the Migdal effect are shown. The rates [|$O(10^2\sim10^3)$| events per day] themselves, without the consideration of any backgrounds, are encouraging ones. In reality, the background rates without any reduction are much larger than these signal rates. It is one of the important points of this study to discuss a realistic method to discriminate background events with the event topologies, which will be discussed in Sect. 4.
It should be emphasized that our calculation and discussed measurement are only for the isolated atoms. For application to dark matter searches, it is also important to test the Migdal effect in the liquid medium.
3.2. Signal simulation
A simple calculation showed an encouraging signal event rate as an ideal case. A more realistic Geant4 [27] Monte Carlo (MC) simulation study was then performed.
Four particles, listed as (1)–(4) in the following, are generated for the MC simulation.
(1) A recoil nucleus with a recoil energy of |$E_{\rm NR}$| following the probability distribution discussed in Ref. [15] is generated. The position is homogeneously distributed in the detection volume. Here |$E_{\rm NR}$|, recoil angle |$\theta$| and the transition energy to the electron (|$\Delta E$|) have correlations as shown in Eq. (4.18) in Ref. [15].
(2) A Migdal electron with an energy |$E_{\rm e}=\Delta E - E_{\rm nl}$| is generated.
(3) A de-excitation X-ray with an energy |$E_{\rm dex}$| is generated. K|$_\alpha$| or K|$_\beta$| X-ray with known intensity ratio is generated with its characteristic energy.
(4) De-excitation electron with an energy |$E_{\rm nl}-E_{\rm dex}$| is generated.
The initial directions of the particles generated in (2)–(4) are isotropic.
Figures 2 and 3 show the results of the signal simulations for argon and xenon targets, respectively. The total energy spectra, energy spectra of the X-rays (cluster B) and the distributions of the distance between two clusters are shown in the left-hand, center, and right-hand panels, respectively. Here the events with any energy deposition within 1 cm from the wall are rejected (cut 1, fiducial cut) in order to reject the background charged particles; most of them are protons, from the wall of the detector. The second criteria for the event selection is to require two clusters with a distance larger than 1 cm (cut 2). A further requirement is that either cluster energy is in the characteristic X-ray energy region (cut 3, 3.2|$\,\pm\,$|2 keV for argon and 29.6|$\,\pm\,$|1.5 keV for xenon). Results before cut 3 are shown in Figs 2 and 3 in order to illustrate characteristic features of the Migdal effect events. Signal efficiencies after cut 1, cut 2, and cut 3 for the argon case are 86|$\%$|, 57|$\%$| and 57|$\%$|, respectively. Signal efficiencies after cut 1, cut 2, and cut 3 for the xenon case are 77|$\%$|, 46|$\%$| and 37|$\%$|, respectively. The inefficiency in cut 3 for the xenon case is caused by cutting K-|$\beta$| signals.
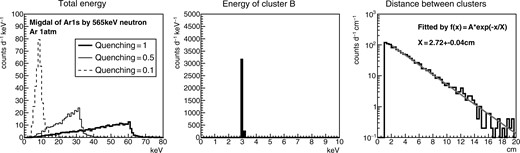
Signal MC simulation results with argon gas. The spectra of the total energy, energy spectra of cluster B, and the distributions of the distance between the two clusters are shown in the left-hand, center, and right-hand panels, respectively.
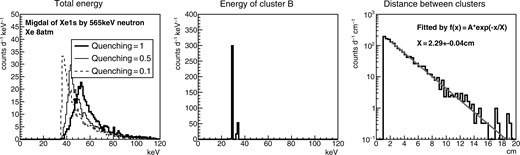
Signal MC simulation results with xenon gas. The spectra of the total energy, energy spectra of cluster B, and the distributions of the distance between two clusters are shown in the left-hand, center, and right-hand panels, respectively.
The left-hand plots show the quenching factor dependence of the total energy. Three cases, with quenching factors of 1, 0.5 and 0.1, are shown. The case of quenching = 1, where the recoil nuclei would show the same ionization efficiency with electrons, is shown as a reference. Since the quenching factor depends on the detector parameters such as the density of the medium, impurities and the electric field, it needs to be measured at an actual detector condition. The real quenching factors can be between 0.1 and 0.5, and thus energy spectra for these two cases are shown as references. The real spectrum would be expected somewhere between these two spectra. The effect of quenching appears more clearly in the spectrum with an argon target. This is because the nuclear recoil energy is larger than the energy of the characteristic X-ray. Hereafter our discussions will assume the case of quenching = 1, i.e. without considering the quenching. This will help us to understand the real recoil energy and can be certified since the event selections can be tuned with a measured quenching factor prior to the Migdal effect experiments.
In the center plots, it is seen that the energy spectra of cluster B make peaks, so that the background can be efficiently rejected by requiring two clusters with either one having the energy of the characteristic X-ray. It should be noted that the quenching factors need not be considered for the X-ray signals.
The distance distributions between two clusters shown in the right-hand plots have an exponential shape representing the absorption length of X-rays. The best-fitting curves shown with red lines are consistent with the ones for the expected absorption length (2.95 cm and 2.19 cm for argon and xenon, respectively). This shape would be a very good evidence of the Migdal effect, in contrast to the flat distribution for the neutron multiple scatterings or the distribution proportional to the square of the distance for accidental backgrounds.
4. Background
Background studies were carried out with Geant4 MC simulations. In this study, it turned out that there exist two significant background sources, namely the intrinsic neutrons and the neutron induced gamma-rays. An unavoidable intrinsic neutron background caused by the incident neutron on the target gas will be discussed first. Then, a gamma-ray background from the |$({\rm n}, \gamma)$| reaction in the chamber and the laboratory material will be evaluated.
4.1. Intrinsic neutron background
Nuclear recoils by the incident neutrons associated with another energy deposition will become unavoidable background events because their event topology would look like the Migdal signal events discussed in the previous section.
First, the accidental coincidence background where two independent nuclear recoils take place within a time resolution of the TPC (|$\sim 10~\mu\rm{s}$|) is studied. The probabilities of accidental coincidence within the whole detection volume of |$(30~\mbox{cm})^3$| are |$O(10^{-4})$| and |$O(10^{-2})$| for the argon and xenon targets, respectively. Additional |$O(10^{-2})$| reduction is expected since the typical distance between the two clusters of the Migdal event is within a few cm. For the argon case, the event rate is smaller than that of the Migdal signal. For the xenon case, the accidental coincidence can be rejected by requiring the energy of cluster B to be 30 keV since the maximum recoil energy is about 18 keV.
We then studied the background events created by interactions of neutrons and target nuclei, mainly multiple scatterings and inelastic scatterings, as an intrinsic background. The key parameters to reject these intrinsic backgrounds are the energy of the cluster B and the distance between two clusters, as shown in the center and right-hand panels of Fig. 2 and Fig. 3. The rate and the rejection efficiency of the background events were studied with the MC simulations. In order to study the pure effect of this intrinsic background, a detector with a gas-only target of |$(30~\mbox{cm})^3$| was prepared and irradiated with neutrons of the same energy (565 keV) as the signal study.
Figure 4 shows the total energy spectra obtained by the argon-target MC simulations. The spectrum without any cut is shown by the black filled histgram (cut 0). The spectrum after the fiducial cut, the same as the signal selection, is shown with the blue filled histogram (cut 1). Elastic scatterings make a dominant contribution below 60 keV. The background rate is found to decrease by about 4 orders of magnitude by requiring two clusters (cut 2, red filled histogram). The background rate above 60 keV is further decreased by requiring that either cluster energy is in the characteristic X-ray energy region (3.2|$\,\pm\,$|2 keV, cut 3). This is one of the advantages of using a position-sensitive gaseous detector. The spectrum of the final background sample is shown by the grey filled histogram. The energy spectrum of the Migdal events is shown by a black line for comparison. The background rate was found to be a few times larger than the signal rate with a similar energy spectrum. It should be noted that the energy resolution is not taken into account, which would make the discrimination of these two spectra difficult. Since the shape of the distance distribution is different between the signal and background, it is possible to detect the excess of the signal, which is a short distance, by fitting as shown in Fig. 5. Here the spectra of the background (cut 3), the signal and the sum of these two components are shown with red, blue and black lines, respectively. The remaining backgrounds of the intrinsic neutron are neutron multiple scattering events. The mean free path of the neutron and the argon nucleus is |$5.7\times 10^4$| cm and the shape of the distribution is determined by the detector size. The background distance distribution (blue) is in good agreement with the efficiency curve of detecting two clusters in a |$(28~\rm cm)^3$| volume. The cluster–distance distribution of the Migdal effect events is found to be steeper, showing a shorter absorption length of the characteristic X-ray. Therefore, the observation of the Migdal effect can be claimed by extracting the signal rate from the cluster–distance distribution.
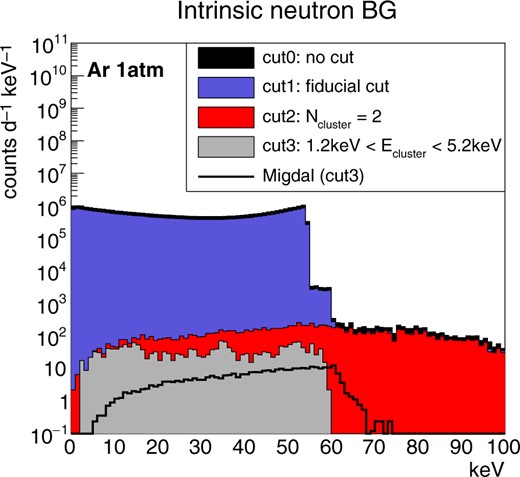
Simulated total energy spectra of the intrinsic neutron background events for the argon target. The black filled histogram is the raw energy spectrum. Blue, red, and gray histograms are those after cut 1, 2, and 3, respectively. The solid black line is the energy spectrum of the Migdal effect.
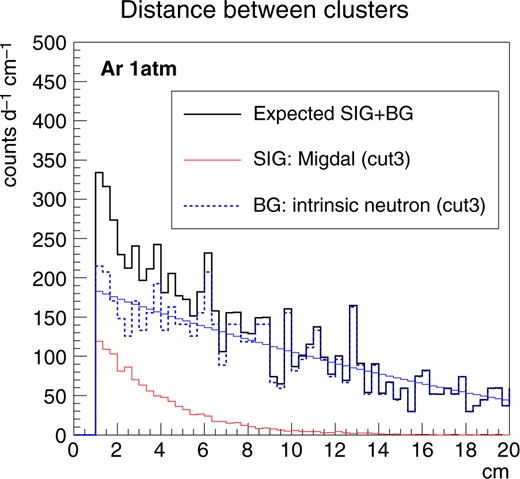
MC simulation results for the distance between two clusters for the argon target. Red, blue, and black histograms show the intrinsic neutron background events, signal events and the sum of these two components.
Figure 6 shows the total energy spectra obtained by the xenon-target MC simulations. The criteria for cuts 0 to 2 are the same as those for the argon-target case. Cut 3 requires that one of the clusters has the energy of the K|$\alpha$| X-rays of xenon, 29.6|$\,\pm\,$|1.5 keV. Here an realistic energy resolution of about 5% FWHM was assumed. The count rate of the Migdal effect is shown with a solid black line. The result shows a much higher background rate than that of the argon-target case. Distance distribution analysis is not demonstrated for the xenon-target case because the background rate is found to be much higher than the signals rate and the background events are also found to have X-rays of similar energy. The reason for the higher background rate can be explained by Fig. 7, which shows the isotope breakdown of the background energy spectrum. It is seen that the peak around 40–60 keV and the continuum component over 60 keV are due to |$\rm {}^{129}Xe$| (natural abundance 26.4 |$\%$|) which has an inelastic scattering associated with 40-keV or 120-keV |$\gamma$|-rays. These inelastic scatterings make two clusters, one by the nuclear recoil and another by the X-ray, and make the discrimination difficult even with the event topologies. The next-largest contribution is neutron capture reaction by |$\rm {}^{131}Xe$| (natural abundance 21.2 |$\%$|), which has an emission of 80-keV |$\gamma$|-rays. Although the contribution of |$\rm {}^{131}Xe$| is much smaller than that of |$\rm {}^{129}Xe$|, it is still larger than the count rate of the Migdal effect. The third contribution comes from |$\rm {}^{130}Xe$| (natural abundance 4.1 |$\%$|), which is associated with high-energy (|$\sim\,$|MeV) gamma-rays. Partial energy depositions of Compton-scattered electrons from these gamma-rays make the continuum component of the background spectrum. Other isotopes make the background less than the Migdal effect. Among the various isotopes, it is seen that |$\rm {}^{134}Xe$| and |$\rm {}^{136}Xe$|, which have natural abundances of 10.4 |$\%$| and 8.9 |$\%$|, make less background than the Migdal effect. In this MC study, the background contribution of |$\rm {}^{133}Xe$|, which is produced by the neutron capture of |$\rm {}^{132}Xe$| and emits 81 keV prompt gamma-rays, is not taken account because of a long half-life of 5.2 d. Since the rate is estimated to be around |$O(10^4)$| counts day|$^{-1}$|, it is necessary to apply an energy selection of |$<80$| keV or remove |$\rm {}^{132}Xe$| by isotope separation.
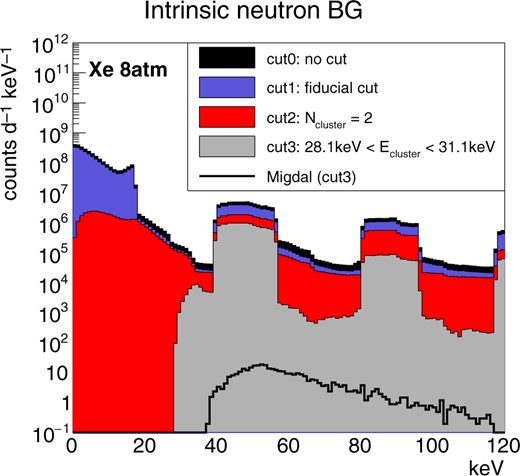
Simulated total energy spectra of the intrinsic neutron background events for the xenon target. The black filled histogram is the raw energy spectrum. Blue, red, and gray histograms are those after cut 1, 2, and 3, respectively. The black solid line is the energy spectrum of the Migdal effect.
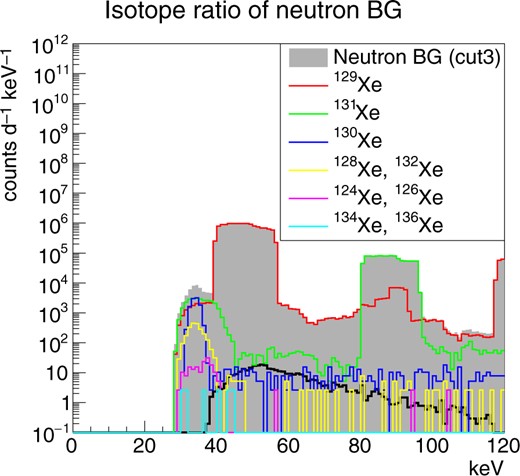
Isotope breakdown of the intrinsic neutron background events for the xenon target.
The possibility of observing the Migdal effect with xenon gas becomes realistic with an isotope enrichment of the isotopes larger than A = 133. More than four orders of reduction for |$\rm {}^{129}Xe$| and |$\rm {}^{131}Xe$| are required considering the original contributions of these isotopes to the background spectrum. With an additional energy selection between 60 keV and 80 keV, the Migdal effect can be observed with xenon gas.
4.2. Gamma-ray background
Neutrons interact with materials of the laboratory and the detector and generate gamma-rays via (n,|$\gamma$|) reactions. The production rates and the energies of gamma-ray backgrounds depend on the laboratory geometry and detector design. Here, typical gamma-ray backgrounds for a simplified geometry shown in Fig. 8 are studied. A stainless chamber with a thickness of 5 mm is implemented, enclosing a gas medium with a volume of |$(36~\rm cm)^3$|. The detection volume is kept the same as the one used in the signal simulation |$(30~\mbox{cm})^3$| while a 3-cm buffer is prepared for each plane. The neutron source is set at a position 1 m away from the detector center, the same condition as for the signal simulation. For the gamma-rays from the laboratory materials, neutrons from the (p,Li) reaction are generated in directions taking account of the energy and rate dependence. The energy-angle correlation is shown in Fig. 9. The detector is set at the center of a laboratory with a size of |$(11.5~\rm m)^3$|. An aluminum floor with an effective thickness of 7.8 mm is constructed 1 m below the detector center.
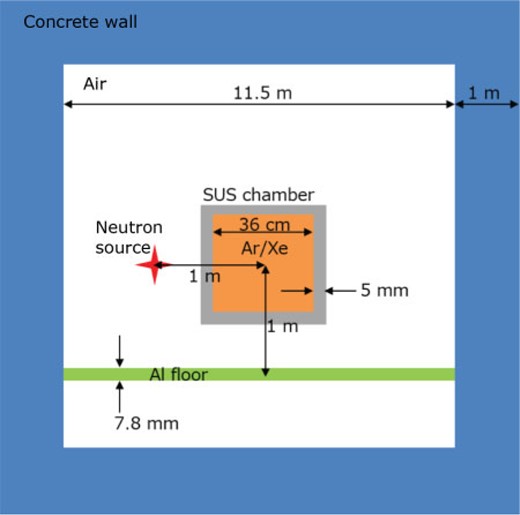
A geometry for the gamma-ray background MC simulation. The figure is not to scale.
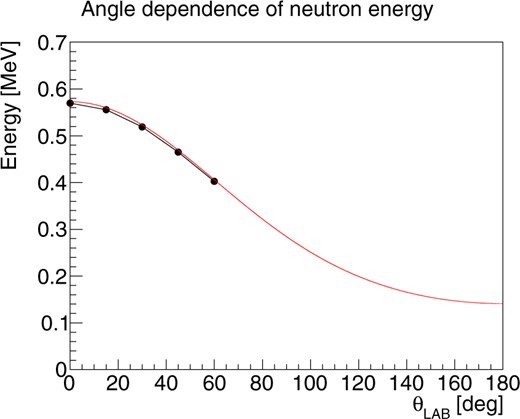
Angular dependence of neutron energy due to |$^7$|Li(p,n)|$^7$|Be reaction. Black dots are simulation results by AIST, red lines are calculation results from kinematics. The neutrons used to estimate the gamma-ray background due to the (n,|$\gamma$|) reaction with the structure were generated according to the red line.
The MC results are shown in Figs. 10–13. The selection criteria are the same as the ones used in the intrinsic neutron backgrounds. The gamma-ray backgrounds from the chamber material for the argon and xenon cases are shown in Fig. 10 and Fig. 11, respectively. The chamber has the gas medium inside so that these background spectra are the sum of the intrinsic neutron background and the gamma-ray background. The gamma-ray backgrounds from the chamber material are shown with green filled histograms for a better understanding. It is seen that the gamma-ray background rate is smaller than that of the intrinsic neutron background for the argon case. The gamma-ray background rate is also found to be smaller than that of the intrinsic neutron background but significantly larger than that of the Migdal signal for the xenon case. Possibilities to reduce the chamber background are discussed in Sect. 4.3.
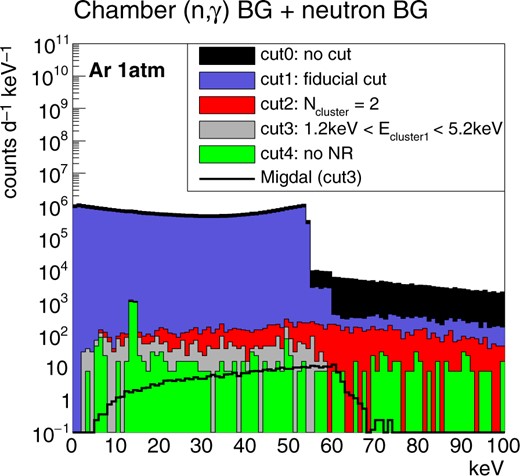
Results of the gamma-ray background MC simulation study. The energy spectra from the chamber material for the argon gas detector are shown. The colors are the same as the ones used in Fig. 4 with an additional green filled histogram (cut 4). At cut 4, we require the event including only the electron-recoil events, showing the gamma-ray background.
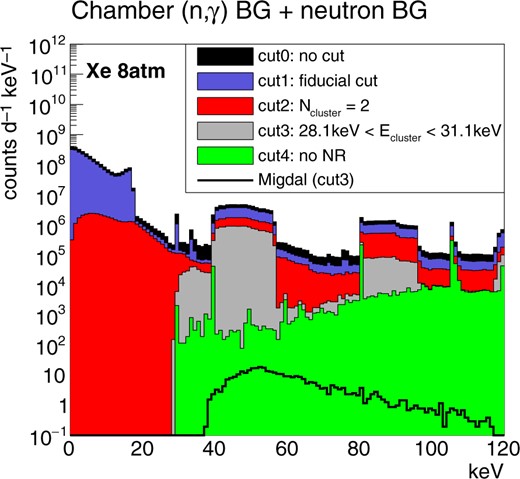
Results of the gamma-ray background MC simulation study. The energy spectra from the chamber material for the xenon gas detector are shown. The colors are the same as the ones used in Fig. 10.
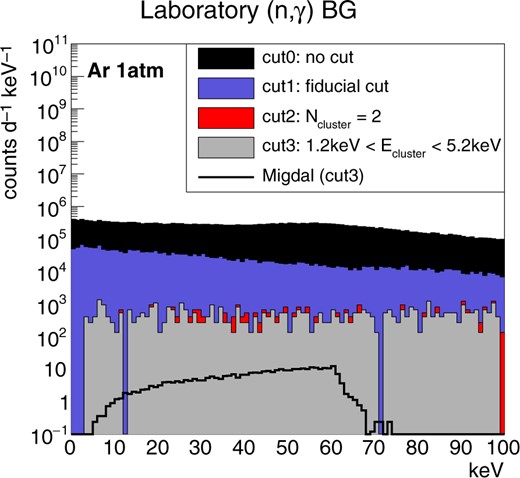
Results of the gamma-ray background MC simulation study. The energy spectra from the laboratory material for the argon gas detector are shown. The colors are the same as the ones used in Fig. 4
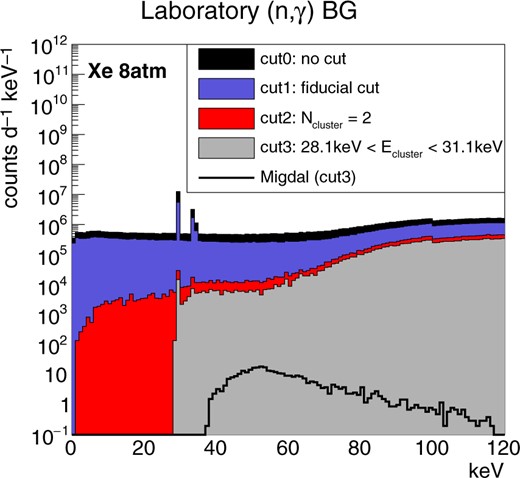
Results of the gamma-ray background MC simulation study. The energy spectra from the laboratory material for the xenon gas detector are shown. The colors are the same as the ones used in Fig. 6.
The gamma-ray background spectra from the laboratory material for the argon and xenon cases are shown in Fig. 12 and Fig. 13, respectively. (n,|$\gamma$|) reactions take place in the concrete and aluminum floor and the gamma-ray flux at the detector position is recorded. The gamma-rays are newly generated at the detector position to increase the statistics. The rate of the gamma-ray backgrounds from the laboratory is found to be much larger than that of the Migdal effect. These backgrounds need to be reduced at the generation point of the neutrons. Hydrocarbon and |$\rm^{10}B$| shieldings with a hole only in the detector direction can be set around the reaction point to reduce the number of neutrons reaching the laboratory materials. The gamma-rays from the laboratory can also be reduced using shieldings around the detector. It should be noted that these shieldings need to be designed with a good consideration of the laboratory geometry and neutron energy because the new material would provide new sources of gamma-ray background. With these shieldings, the gamma-ray background rates need to be reduced at least two orders of magnitude to observe the Migdal effect.
4.3. Discussion
The background study so far assumes a continuous (DC) neutron beam. It would be possible to reduce delayed or continuous background such as laboratory gamma-rays with a pulsed neutron beam. The effect of the background rejection with the pulsed neutron beam would depend on the time evolution of the background rate. One needs to have a good understanding of the neutron beam to estimate the background rejection by a pulsed beam. The gamma-ray background from the chamber can be reduced by designing a chamber with a smaller amount of material, like polyimide film, for the argon gas case because the gas pressure is at the normal pressure. For the xenon gas case, on the other hand, the chamber material cannot be reduced because of its high pressure. A self-shielding technique can be used instead, by increasing the detector volume and using the outer |$\sim\,$|10 cm as a veto region. Also, it may be effective to install a solid scintillator on the wall inside the chamber [28] as an active shielding. In this sense this study is giving a conservative estimation of the background rate.
The angular distribution of the Migdal electron from |$n=1$| follows |$\cos^2\theta_{N-e}$|, with |$\theta_{N-e}$| as the polar angle from the momentum of the recoil nucleus. Therefore, if the direction of the nucleus and the direction of the Migdal electron can be measured, the background can be reduced further. This effect would be valid even by measuring only the direction of the Migdal electron because the direction of the recoil nuclei is biased in the forward direction of the incoming neutron. The challenging point of this method is that the energy of the Migdal electrons is about 10 keV, resulting a track length of 2 mm and 1 mm in the argon and xenon gas, respectively. In the future, it would be interesting to be able to use the direction information of Migdal electrons by some breakthrough of the technology like emulsions, low-pressure gaseous detectors, or columnar recombination.
5. Conclusions
The possibility of the experimental observation of the Migdal effect in the neutron scattering with position sensitive gaseous detectors is studied. Some modes of the Migdal effects would have two clusters; one for the nuclear recoil and the other for the associated X-ray. Table-top-sized position-sensitive gaseous detectors |$\sim(30~\rm cm)^3$| filled with argon or xenon target gas are found to be capable of detecting sufficient rates [O(|$10^2\sim10^3$|) events per day] of these two-cluster Migdal events. Distributions of the distance between two clusters, representing the absorption length of the characteristic X-rays, would be strong evidence of the Migdal effect observation.
Two significant background sources, namely the intrinsic neutrons and the neutron induced gamma-rays, are found to exist. These background rates are found to be higher than the Migdal effect rates even with a relatively low-energy (565 keV) neutron source. It is found that the intrinsic neutron background rate for the argon gas is at an acceptable level and some future study for the reduction of the gamma-rays from the laboratory would make the observation of the Migdal effect possible. The background for the xenon gas, on the other hand, is found to be much more serious than for the argon gas. Future works on the isotope separation as well as the reduction of the gamma-rays from the detector and laboratory will be needed before the Migdal effect observation for xenon gas case.
Acknowledgements
This work was supported by KAKENHI Grant-in-Aids (18K13567, 26104005, 16H02189, 19H05806, 18H03697, 18H05542, 19H05810, 19H05805), ICRR Joint-Usage, I-CORE Program of the Israel Planning Budgeting Committee (grant No. 1937/12), World Premier International Research Center Initiative (WPI), MEXT, Japan.



