Formation of dynamically transversely trapping surfaces and the stretched hoop conjecture

Abstract

A dynamically transversely trapping surface (DTTS) is a new concept for an extension of a photon sphere that appropriately represents a strong gravity region and has close analogy with a trapped surface. We study formation of a marginally DTTS in time-symmetric, conformally flat initial data with two black holes, with a spindle-shaped source, and with a ring-shaped source, and clarify that |$\mathcal{C}\lesssim 6\pi GM$| describes the condition for the DTTS formation well, where |$\mathcal{C}$| is the circumference and |$M$| is the mass of the system. This indicates that an understanding analogous to the hoop conjecture for the horizon formation is possible. Exploring the ring system further, we find configurations where a marginally DTTS with the torus topology forms inside a marginally DTTS with the spherical topology, without being hidden by an apparent horizon. There also exist configurations where a marginally trapped surface with the torus topology forms inside a marginally trapped surface with the spherical topology, showing a further similarity between DTTSs and trapped surfaces.

1. Introduction

The recent observation of a black hole shadow [1] produced by a central massive object in the galaxy M87 significantly increased the importance of the concept of a photon sphere [2]. A photon sphere is a spherically symmetric surface on which circular orbits of photons exist, and in a Schwarzschild black hole, it is located at |$r=3GM$| where |$r$| is the areal radius, |$G$| is the Newtonian constant of gravitation, and |$M$| is the Arnowitt–Deser–Misner mass that represents the total energy of the black hole. The edge of a black hole shadow is primarily determined by the photon sphere, or its extension, the fundamental photon orbits [3]. Similarly to event/apparent horizons as extended concepts of |$r=2GM$| of a Schwarzschild spacetime, appropriately extended concepts of a photon sphere |$r=3GM$| would also significantly advance our understanding of spacetimes with strong gravity regions. Several extended concepts of a photon sphere have been proposed so far: a photon surface [4], a loosely trapped surface [5], a static/stationary transversely trapping surface (TTS) [6], a wandering set [7], a dynamically transversely trapping surface (DTTS) [8], and a quasi-local photon surface [9]. In this paper we focus attention on a DTTS proposed in our previous paper. A (marginally) DTTS is an analogous concept to a (marginally) trapped surface, appropriately represents a strong gravity region outside a horizon, and is easily calculated.

In our previous paper [8] we pointed out similarities between a (marginally) DTTS and a (marginally) trapped surface. Both surfaces are determined on a spacelike hypersurface and have similar gauge dependence properties. In time-symmetric initial data, the area |$A_0$| of a convex DTTS satisfies the Penrose-like inequality |$A_0\le 4\pi (3GM)^2$|⁠, similarly to the fact that the area |$A_{\rm AH}$| of an apparent horizon satisfies the Riemannian Penrose inequality |$A_{\rm AH}\le 4\pi (2GM)^2$| [10–12], which is a special case of the Penrose conjecture [13]. We explore the similarity between the two surfaces further in this paper, paying attention to the condition for the formation of the two kinds of surfaces. As the condition for the horizon formation, the hoop conjecture has been proposed by Thorne [14]:

Conjecture 1

Black holes with horizons form when and only when a mass |$M$| gets compacted into a region whose circumference in every direction is bounded by |$\mathcal{C}\lesssim 4\pi GM$|⁠.

Here, |$4\pi GM$| is the circumference of the horizon of a Schwarzschild black hole with a mass |$M$|⁠, i.e. |$2\pi (2GM)$|⁠. Although the hoop conjecture is loosely formulated, it is tested in many examples and the results basically support this conjecture [15–32]. One implication of this conjecture is that an apparent horizon which is arbitrarily long in one direction does not form. Similarly, the condition |$\mathcal{C}\lesssim 6\pi GM$| may be expected as the condition for the formation of a marginally DTTS, where |$6\pi GM$| is the circumference of a photon sphere of a Schwarzschild black hole with mass |$M$|⁠, i.e. |$2\pi (3GM)$|⁠.

The hoop conjecture is also related to topological properties of apparent horizons. In higher-dimensional spacetimes, it is known that horizons of stationary black holes can have nonspherical topologies like black strings or black rings [33,34]. This is understood from the fact that the hoop conjecture does not hold in higher-dimensional spacetimes. In Ref. [35], initial data with a spindle-shaped source in a five-dimensional spacetime are studied, and an apparent horizon which is arbitrarily long in one direction is shown to form (see also Refs. [36–42] for related studies). From the formation of an arbitrarily long apparent horizon, the formation of an apparent horizon with the topology |$S^1\times S^2$| is also expected by slightly bending and connecting the edges of a long apparent horizon. In fact, initial data with a ring-shaped source are also studied in Ref. [35], and an apparent horizon with the topology |$S^1\times S^2$| forms for a sufficiently large radius of the ring. Conversely, in four-dimensional spacetimes, since an apparent horizon cannot be long in one direction due to the hoop conjecture, an apparent horizon with the torus topology is not expected to form [29]. More precisely, even if a marginally trapped surface with the torus topology (a marginally trapped torus, hereafter) forms, it would be surrounded by a marginally trapped surface with the spherical topology (hereafter, a marginally trapped sphere). In fact, all existing examples of marginally trapped tori in asymptotically flat initial data are hidden by marginally trapped spheres [43,44].

Motivated by the above discussions, we study two issues in this paper. First, we examine whether the understanding that is analogous to the hoop conjecture is possible or not for the formation of a marginally DTTS with the spherical topology (hereafter, a marginally DTT sphere). For this purpose, we study time-symmetric conformally flat initial data with two black holes, with a spindle-shaped source, and with a ring-shaped source. In particular, we will show that a marginally DTT sphere that is arbitrarily long in one direction does not form in the spindle initial data. We also show that in all systems, the condition |$\mathcal{C}\lesssim 6\pi GM$| reasonably gives the necessary and sufficient conditions for the formation of (outermost) marginally DTT spheres. We will call this condition the stretched hoop conjecture.

Next, we study the formation of a marginally DTTS with the torus topology (hereafter, a marginally DTT torus) by studying the ring system in more detail. The stretched hoop conjecture indicates that if a marginally DTT torus forms, it would be located inside a marginally DTT sphere. In the ring system, it will be demonstrated that there is a parameter region where a marginally DTT torus forms, and a marginally DTT torus is always located inside a marginally DTT sphere at least in the ring system. Note that although we proved in our previous paper [8] that a convex DTTS must have the spherical topology, the formation of marginally DTT tori here does not contradict the theorem because they are not convex. Furthermore, we provide a further similarity between marginally DTTSs and marginally trapped surfaces by showing that there is a parameter region where a marginally trapped torus forms inside a marginally trapped sphere.

This paper is organized as follows. In the next section we briefly review the definition of a (marginally) DTTS and present the equations to solve for a marginally DTTS in time-symmetric initial data. In Sect. 3, we explain the setup of the three systems studied in this paper, i.e. two-black-hole initial data, spindle initial data, and ring initial data. The numerical method of solving for a marginally DTTS in these systems is also explained. In Sect. 4 we examine whether the understanding that is analogous to the hoop conjecture for horizon formation is possible or not for marginally DTT spheres. In Sect. 5 the formation of marginally DTT tori is examined in the ring system. Also, the formation of marginally trapped spheres/tori is examined to show the similarity between marginally DTTSs and marginally trapped surfaces. Section 6 is devoted to a summary and discussions. In Appendix A, the numerical method of solving for marginally DTT tori in the ring system is explained. In Appendix B, the formation of marginally DTT tori is studied approximately in the situation where the ring radius |$R$| is much smaller than |$GM$|⁠. Throughout the paper, we work in the framework of the theory of general relativity for four-dimensional spacetimes. We use units in which the speed of light is unity, |$c=1$|⁠, while the Newtonian constant of gravitation |$G$| is explicitly shown.

2. Dynamically transversely trapping surfaces

In this section we present a brief review of the definition of a (marginally) DTTS that was proposed in our previous paper [8]. The definition is given in Sect. 2.1, and useful formulae to solve for a marginally DTTS in time-symmetric initial data are presented in Sect. 2.2. We refer readers to our previous paper [8] for more detailed explanations and derivations.

2.1. Definition

Figure 1 depicts the configuration to be considered. Let us consider a spacelike hypersurface |$\Sigma$| with a future-directed unit normal |$n^a$| in a spacetime |$\mathcal{M}$| with a metric |$g_{ab}$|⁠. The induced metric and the extrinsic curvature of |$\Sigma$| are |$q_{ab}=g_{ab}+n_an_b$| and |$K_{ab} = (1/2)\pounds_n q_{ab}$|⁠, respectively, where |$\pounds$| is a Lie derivative with respect to |$\mathcal{M}$|⁠. A DTTS is a two-dimensional closed orientable surface |$\sigma_0$| in a spacelike hypersurface |$\Sigma$|⁠. The two-dimensional surface |$\sigma_0$| can be regarded as a surface in |$\Sigma$|⁠, and the outward unit normal to |$\sigma_0$| in this sense is denoted by |$\hat{r}^a$|⁠. The induced metric and the extrinsic curvature of |$\sigma_0$| (as a surface in |$\Sigma$|⁠) are |$h_{ab}=q_{ab}-\hat{r}_a\hat{r}_b$| and |$k_{ab} = (1/2){}^{(3)}\pounds_{\hat{r}}h_{ab}$|⁠, respectively, where |${}^{(3)}\pounds$| is a Lie derivative with respect to |$\Sigma$|⁠. We introduce a timelike hypersurface |$S$| in |$\mathcal{M}$|⁠, which intersects with |$\Sigma$| precisely at |$\sigma_0$|⁠. Denoting the outward unit normal to |$S$| as |$\bar{r}^a$|⁠, the induced metric and the extrinsic curvature of |$S$| are |$\bar{p}_{ab}=g_{ab}-\bar{r}_a\bar{r}_b$| and |$\bar{K}_{ab} = (1/2)\pounds_{\bar{r}}\bar{p}_{ab}$|⁠, respectively. The two-dimensional surface |$\sigma_0$| can be regarded as a surface in |$S$|⁠, and the future-directed unit normal to |$\sigma_0$| that is tangent to |$S$| is denoted by |$\bar{n}^a$|⁠. Note that the two hypersurfaces |$S$| and |$\Sigma$| are not necessarily orthogonal to each other, and hence |$\bar{r}^a$| and |$\bar{n}^a$| do not coincide with |$\hat{r}^a$| and |$n^a$| in general, respectively. The extrinsic curvature of |$\sigma_0$| as a surface in |$S$| is defined by |$\bar{k}_{ab} = (1/2){}^{(3)}\bar{\pounds}_{\bar{n}}h_{ab}$|⁠, where |${}^{(3)}\bar{\pounds}_{\bar{n}}$| is a Lie derivative associated with |$S$|⁠.

$Configuration to be considered. A two-dimensional closed surface $\sigma_0$ exists in a spacelike hypersurface $\Sigma$ of a spacetime $\mathcal{M}$. A timelike hypersurface $S$ intersects with $\Sigma$ precisely at $\sigma_0$. The notation is also indicated. See text and Ref. [8] for details.$

Fig. 1.

Configuration to be considered. A two-dimensional closed surface |$\sigma_0$| exists in a spacelike hypersurface |$\Sigma$| of a spacetime |$\mathcal{M}$|⁠. A timelike hypersurface |$S$| intersects with |$\Sigma$| precisely at |$\sigma_0$|⁠. The notation is also indicated. See text and Ref. [8] for details.

Open in new tab Download slide

With these notations, a DTTS is defined as follows:

Definition 1

Suppose |$\Sigma$| to be a smooth spacelike hypersurface of a spacetime |$\mathcal{M}$|⁠. A smooth closed orientable two-dimensional surface |$\sigma_0$| in |$\Sigma$| is a dynamically transversely trapping surface (DTTS) if and only if there exists a timelike hypersurface |$S$| in |$\mathcal{M}$| that intersects |$\Sigma$| precisely at |$\sigma_0$| and satisfies the following three conditions at arbitrary points on |$\sigma_0$|⁠:

$$\begin{eqnarray} \bar{k} = 0, &\quad& \textrm{(the momentarily non-expanding condition),} \label{momentarily-non-expanding-condition} \\ \end{eqnarray}$$

(1)

$$\begin{eqnarray} \mathrm{max}\big(\bar{K}_{ab}k^ak^b\big) = 0, &\quad& \textrm{(the marginally transversely trapping condition),} \label{marginally-transversely-trapping-condition} \\ \end{eqnarray}$$

(2)

$$\begin{eqnarray} {}^{(3)}\bar{\pounds}_{\bar{n}} \bar{k}\le 0, &\quad& \textrm{(the accelerated contraction condition),} \label{accelerated-contraction-condition} \end{eqnarray}$$

(3)

where |$k^a$| are arbitrary future-directed null vectors tangent to |$S$| and the quantity |$\pounds_{\bar{n}}\bar{k}$| is evaluated with a time coordinate in |$S$| whose lapse function is constant on |$\sigma_0$|⁠.

In Definition 1, we allow both non-self-intersecting and self-intersecting surfaces as DTTSs. In the case of marginally outer trapped surfaces (MOTS), self-intersection is allowed and explicit examples of self-intersecting MOTSs have been constructed in a numerical simulation of a two-black-hole collision [45]. In a similar manner, a self-intersecting DTTS may form. But in the explicit construction of marginally DTTSs in Sects. 4 and 5 in this paper, we focus on non-self-intersecting DTTSs for simplicity.

As an example, let us consider an |$r=\mathrm{const.}$| sphere |$\sigma_0$| on a |$t=\mathrm{const.}$| hypersurface in a Schwarzschild spacetime. The momentarily non-expanding condition of Eq. (1) means that we consider photons emitted with the initial condition |$dr/dt=0$| from |$\sigma_0$|⁠. Due to the spherical symmetry, the timelike hypersurface |$S$| satisfying the marginally transversely trapping condition of Eq. (2) is the one composed of worldlines of all photons, which corresponds to the photon surface [4]. Calculating the quantity |${}^{(3)}\bar{\pounds}_{\bar{n}} \bar{k}$|⁠, we find that an |$r=\mathrm{const.}$| sphere with |$r\le 3GM$| satisfies the accelerated contraction condition, while a surface with |$r>3GM$| does not satisfy it.

We define a dynamically transversely trapping region and a marginally DTTS with the following definition:

Definition 2

Consider a collection of all DTTSs such that any two of these DTTSs can be transformed to one another by continuous deformation without violating the three conditions of Eqs. (1)–(3). The region in which these DTTSs exist is said to be a dynamically transversely trapping region (or, more generally, one of the dynamically transversely trapping regions). If the outer boundary of a dynamically transversely trapping region satisfies

$$\begin{equation} \pounds_{\bar{n}} \bar{k}= 0, \label{Equation-for-marginally-DTTS} \end{equation}$$

(4)

it is said to be a marginally DTTS.

2.2. Time-symmetric case

Here, we briefly describe how to find a marginally DTTS in time-symmetric initial data. In this case, a timelike hypersurface |$S$| that intersects |$\Sigma$| orthogonally satisfies |$\bar{k}_{ab}=0$| at |$\sigma_0$|⁠, and thus satisfies the momentarily non-expanding condition, Eq. (1). Therefore, the relations |$\bar{r}^a=\hat{r}^a$| and |$\bar{n}^a=n^a$| hold, and the analysis is simplified. We span the coordinates in the neighborhood of |$\sigma_0$| so that the metric takes the form

$$\begin{equation} ds^2 = -\alpha^2dt^2 + \varphi^2 dr^2 + h_{ij}dx^idx^j + 2\gamma_{ri}drdx^i, \label{metric-neighborhood-of-sigma0} \end{equation}$$

(5)

where the spacelike hypersurface |$\Sigma$| is given by |$t=0$|⁠, the timelike hypersurface |$S$| is given by |$r=0$|⁠, and |$\alpha=\mathrm{const.}$| on |$\sigma_0$|⁠. The extrinsic curvature of |$S$| becomes

$$\begin{equation} \bar{K}_{ab}=-n_an_b\frac{{}^{(3)}\pounds_{\hat{r}}\alpha}{\alpha}+k_{ab}. \end{equation}$$

(6)

Since |$k_{ab}$| is symmetric, there exists an orthonormal basis |$(\mathbf{e}_1)_a$| and |$(\mathbf{e}_2)_a$| that diagonalizes |$k_{ab}$| as

$$\begin{equation} k_{ab} = k_{\rm 1}(\mathbf{e}_1)_a(\mathbf{e}_1)_b +k_{\rm 2}(\mathbf{e}_2)_a(\mathbf{e}_2)_b, \label{kab-diagonalized} \end{equation}$$

(7)

and we introduce

$$\begin{eqnarray} k_{\rm L} &=& \mathrm{max}(k_1,k_2), \label{def:k_L}\\ \end{eqnarray}$$

(8a)

$$\begin{eqnarray} k_{\rm S} &=& \mathrm{min}(k_1,k_2) \label{def:k_S} \end{eqnarray}$$

(8b)

for a later convenience. Then, the marginally transversely trapping condition of Eq. (2), is rewritten as

$$\begin{equation} k_{\rm L} = \frac{{}^{(3)}\pounds_{\hat{r}}\alpha}{\alpha}. \label{marginally-transversely-trapping-condition-time-symmetric} \end{equation}$$

(9)

By combining geometric equations, the following formula for |${}^{(3)}\bar{\pounds}_{n}\bar{k}$| is derived [8]:

$$\begin{equation} {}^{(3)}\bar{\pounds}_{n}\bar{k} = -\frac12{}^{(2)}R -8\pi GP_r +k\frac{{}^{(3)}\pounds_{\hat{r}}\alpha}{\alpha} +\frac12\big(k^2-k_{ab}k^{ab}\big), \label{Lie-derivative-bark-time-symmetric} \end{equation}$$

(10)

where |$P_{r}:=T_{ab}\hat{r}^a\hat{r}^b$| is the radial pressure, and the Einstein field equations |$G_{ab}=8\pi GT_{ab}$| have been assumed. By substituting Eq. (9) into Eq. (10) and requiring |${}^{(3)}\bar{\pounds}_{n}\bar{k}$| to be zero, we obtain the equation for marginally DTTSs:

$$\begin{equation} -\frac12{}^{(2)}R -8\pi GP_{r} + k_1k_2+(k_1+k_2)\mathrm{max}(k_1,k_2)=0, \label{Equation-for-a-marginally-DTTS-time-symmetric} \end{equation}$$

(11)

where the left-hand side is expressed only in terms of geometrical and physical quantities on |$\Sigma$|⁠. Since only vacuum initial data are considered in this paper, the radial pressure is set to be zero, |$P_{r}=0$|⁠, in what follows.

3. Setups and the equation for marginally DTTSs

In this section we describe the setups of the systems. The three systems to be investigated are explained one by one in Sect. 3.1. The methods of solving for marginally DTT spheres/tori are briefly commented on in Sect. 3.2.

3.1. Setups of the systems

In this paper we consider time-symmetric initial data with conformally flat structure,

$$\begin{equation} ds^2 = \varPsi^4(dx^2+dy^2+dz^2). \end{equation}$$

(12)

The Hamiltonian constraint for a vacuum spacetime becomes

$$\begin{equation} \bar{\nabla}^2\varPsi = 0, \end{equation}$$

(13)

where |$\bar{\nabla}^2$| denotes the flat-space Laplacian. We consider three kinds of solutions to this equation.

3.1.1. Two-black-hole initial data

The first one is a system of two black holes momentarily at rest,

$$\begin{equation} \varPsi = 1+\frac{GM}{4\sqrt{x^2+y^2+(z-z_0)^2}} +\frac{GM}{4\sqrt{x^2+y^2+(z+z_0)^2}}. \end{equation}$$

(14)

This is called the Brill–Lindquist initial data [46]. Although marginally DTTSs in this system have been studied in our previous paper, we examine the same system again from the viewpoint of the stretched hoop conjecture.

3.1.2. Spindle initial data

The second one is a system with a spindle source located at |$-L/2\le z\le L/2$| on the |$z$|-axis,

$$\begin{eqnarray} \varPsi &=& 1+\frac{GM}{2L}\int_{-L/2}^{L/2} \frac{d\zeta}{\sqrt{x^2+y^2+(z-\zeta)^2}}. \label{Psi-spindle-integral-form} \end{eqnarray}$$

(15)

After integration, we obtain

$$\begin{equation} \varPsi = 1+\frac{GM}{2L}\log\frac{r_+-z_+}{r_--z_-}, \end{equation}$$

(16)

with

$$\begin{eqnarray} z_\pm &:=& z \mp {L}/{2},\\ \end{eqnarray}$$

(17a)

$$\begin{eqnarray} r_\pm &:=& \sqrt{x^2+y^2+z_\pm^2}. \end{eqnarray}$$

(17b)

We study this system in order to examine to what extent a marginally DTTS can become long in one direction. The same system was studied from the viewpoint of the apparent horizon formation in Ref. [24].

3.1.3. Ring initial data

The third one is a system with a ring-shaped source located at a circle with radius |$R$| on the |$(x,y)$|-plane,

$$\begin{eqnarray} \varPsi &=& 1+\frac{GM}{4\pi} \int_{0}^{2\pi} \frac{d\zeta}{\sqrt{(x-R\cos\zeta)^2+(y-R\sin\zeta)^2+z^2}}. \label{Psi-ring-integral-form} \end{eqnarray}$$

(18)

Using the complete elliptic integral of the first kind,

$$\begin{equation} K(\kappa) = \int_0^{\pi/2}\frac{d\zeta}{\sqrt{1-\kappa^2\sin^2\zeta}} \qquad \textrm{with} \qquad \kappa := \sqrt{\frac{2b}{a+b}}, \end{equation}$$

(19)

the conformal factor is represented as

$$\begin{equation} \varPsi = 1+\frac{GM}{\pi\sqrt{a+b}}K(\kappa), \label{Psi-ring-final-form} \end{equation}$$

(20)

where |$a$| and |$b$| are defined by

$$\begin{eqnarray} a&:=& x^2+y^2+z^2+R^2,\\ \end{eqnarray}$$

(21a)

$$\begin{eqnarray} b&:=& 2R\sqrt{x^2+y^2}. \end{eqnarray}$$

(21b)

This system is chosen in order to examine to what extent a marginally DTTS can become oblate. Also, the formation of a marginally DTT/trapped torus is studied in this system. The same system was studied from the viewpoint of the apparent horizon formation in Ref. [24].

3.2. Method of solving for marginally DTTSs

We briefly describe how to solve for marginally DTT spheres in the three systems and to solve for marginally DTT/trapped tori in the ring system.

3.2.1. Marginally DTT spheres

In order to solve for marginally DTT spheres, it is convenient to introduce the spherical-polar coordinates |$(\tilde{r}, \tilde{\theta}, \phi)$| with

$$\begin{eqnarray} x &=& \tilde{r}\sin\tilde{\theta}\cos\phi,\\ \end{eqnarray}$$

(22a)

$$\begin{eqnarray} y &=& \tilde{r}\sin\tilde{\theta}\sin\phi,\\ \end{eqnarray}$$

(22b)

$$\begin{eqnarray} z &=& \tilde{r}\cos\tilde{\theta}. \end{eqnarray}$$

(22c)

From the axial symmetry, the conformal factor |$\varPsi$| depends only on |$\tilde{r}$| and |$\tilde{\theta}$|⁠. We parametrize a surface |$\sigma_0$| with the spherical topology as

$$\begin{equation} \tilde{r}=h(\tilde{\theta}). \label{sphere-parametrization} \end{equation}$$

(23)

The equations for marginally DTT spheres become second-order ordinary differential equations of |$h(\tilde{\theta})$|⁠. Those equations have been derived in order to study the Brill–Lindquist two-black-hole initial data in our previous paper [8], and the same equations presented in terms of the conformal factor |$\varPsi$| can be applied to spindle and ring initial data as well. Hence, we refer interested readers to Ref. [8] for the explicit forms of the equations and their derivation. Those equations are solved under the boundary conditions |$h^\prime=0$| at |$\tilde{\theta}=0$| and |$\pi/2$|⁠.

3.2.2. Marginally DTT/trapped tori

In order to study marginally DTT/trapped tori in the ring system, it is convenient to introduce the coordinates |$(\tilde{\rho}, \tilde{\xi}, \phi)$| by

$$\begin{eqnarray} x&=&(R+\tilde{\rho}\cos\tilde{\xi})\cos\phi,\\ \end{eqnarray}$$

(24a)

$$\begin{eqnarray} y&=&(R+\tilde{\rho}\cos\tilde{\xi})\sin\phi,\\ \end{eqnarray}$$

(24b)

$$\begin{eqnarray} z&=&\tilde{\rho}\sin\tilde{\xi}. \end{eqnarray}$$

(24c)

In these coordinates, the position of the ring is given by |$\tilde{\rho}=0$|⁠, and the metric becomes

$$\begin{equation} ds^2 = \varPsi^4\big[d\tilde{\rho}^2 + \tilde{\rho}^2d\tilde{\xi}^2 +(R+\tilde{\rho}\cos\tilde{\xi})^2d\phi^2\big]. \end{equation}$$

(25)

Parametrizing a toroidal surface |$\sigma_0$| by

$$\begin{equation} \tilde{\rho}=h(\tilde{\xi}), \label{parametrization-torus} \end{equation}$$

(26)

we perform the following coordinate transformations from |$(\tilde{\rho}, \tilde{\xi})$| to |$(\rho, \xi)$|⁠:

$$\begin{eqnarray} \tilde{\rho} &=& \rho+h(\xi), \label{coordinate-transformation-tilderho-rho-xi}\\ \end{eqnarray}$$

(27)

$$\begin{eqnarray} \tilde{\xi} &=& \xi-p(\rho,\xi), \label{coordinate-transformation-tildexi-rho-xi} \end{eqnarray}$$

(28)

in order to calculate the orthonormal components of the extrinsic curvature |$k_{ab}$|⁠, i.e. |$k_1$| and |$k_2$| defined in Eq. (7). In the new coordinates, the surface |$\sigma_0$| is given by |$\rho=0$|⁠, and we require |$\tilde{\xi}=\xi$| on the surface |$\sigma_0$|⁠, i.e. |$p(0,\xi)=0$|⁠. Then, the orthonormal basis on |$\sigma_0$| is introduced as

$$\begin{equation} \mathbf{e}_1=\varPsi^2\sqrt{h^{\prime 2}+h^2} \mathrm{d}\xi, \qquad \mathbf{e}_2=\varPsi^2(R+h\cos\xi) \mathrm{d}\phi. \label{orthonormal-basis-torus} \end{equation}$$

(29)

The formulae for |$k_1$| and |$k_2$| and the equations for marginally DTT/trapped tori are presented in Appendix A. Those equations are reduced to second-order ordinary differential equations for |$h(\tilde{\xi})$|⁠, and we numerically solve them under the boundary conditions |$h^\prime =0$| at |$\tilde{\xi} = 0$| and |$\pi$|⁠.

4. Stretched hoop conjecture

In this section we study whether the inequality |$\mathcal{C}\lesssim 6\pi GM$| gives the condition for the formation of outermost DTT spheres. In Sect. 4.1 we briefly review the trials to formulate precisely the hoop conjecture as previously discussed. In Sect. 4.2, after commenting on how to test the stretched hoop conjecture in this paper, we present the numerical results. We summarize the numerical results and discuss their implications in Sect. 4.3.

4.1. Description of the hoop conjecture

The hoop conjecture is loosely formulated, probably because its main purpose is to give an intuition for the condition for horizon formation. But when the hoop conjecture is tested, a more precise formulation is required, and efforts in such a direction have been made in several works [18,24].¹ The ambiguous points are whether the horizon is an apparent horizon or an event horizon, the definitions of the circumference |$\mathcal{C}$| and the mass |$M$|⁠, and the meaning of “|$\lesssim$|” (or, in which situations the hoop conjecture is regarded to hold). As for the concept of the horizon, most works adopt the apparent horizon, although there is also a study [27] that discussed the connection between event horizon formation and the hoop conjecture.

In the formulation by Flanagan [18], both the circumference and the mass are functions of a closed surface |$\sigma$|⁠, i.e. |$\mathcal{C}(\sigma)$| and |${M}_{\rm Q}(\sigma)$|⁠, and for each spacelike hypersurface the following quantity (say, the hoop parameter) is determined:

$$\begin{equation} \mathcal{H}_{\rm A} = \mathrm{min}\left[\frac{\mathcal{C}(\sigma)}{4\pi GM_{\rm Q}(\sigma)}\right]. \end{equation}$$

(30)

Several candidates for the definition |$\mathcal{C}(\sigma)$| are discussed in Refs. [18,24], and there does not seem to be a consensus. As for an axisymmetric surface |$\sigma$|⁠, the following definition seems to be widely accepted:

$$\begin{equation} \mathcal{C}(\sigma) = \mathrm{max}(\mathcal{C}_{\rm p},\ \mathcal{C}_{\rm e}), \label{Circumference-axisymmetric-case} \end{equation}$$

(31)

where |$\mathcal{C}_{\rm p}$| is the polar circumference that is twice the proper distance between the north and south poles, and |$\mathcal{C}_{\rm e}$| is the maximum length of closed azimuthal curves. See also Ref. [26] for the application of the definition of |$\mathcal{C}(\sigma)$| for non-axisymmetric surfaces proposed in Ref. [24].

The definition of the mass is also an open problem. Several negative arguments against the hoop conjecture were made by studying a static charged star [51–53], but it was pointed out that the evaluation of the mass was not appropriate because the energy of electric fields distributes outside of the surface on which the circumference is evaluated [18,54,55]. The problem is that local gravitational mass cannot be determined uniquely in general relativity, and there are many candidates for the “quasilocal mass” |$M_{\rm Q}(\sigma)$| associated with a surface |$\sigma$|⁠. In Refs. [25, 28] the hoop conjecture was tested using Penrose’s quasilocal mass [56] and Hawking’s quasilocal mass [57], respectively, and it was reported that the hoop conjecture holds better if the quasilocal definitions of masses are used rather than the ADM mass.² In systems where the amount of energy of matter or junk gravitational radiation outside |$\sigma$| is small, the hoop conjecture holds well with the ADM mass [15,24,26].

The criterion for the statement that the hoop conjecture holds (or does not hold) is also not very clear. The natural criterion would be as follows. Consider a collection of spacelike hypersurfaces, which may be a sequence of time evolution, or may be a set of initial data. If there are two values |$\mathcal{H}_{\rm A}^{\rm (S)}$| and |$\mathcal{H}_{\rm A}^{\rm (N)}$| such that the apparent horizon is present if |$\mathcal{H}_{\rm A}\le \mathcal{H}_{\rm A}^{\rm (S)}$| and is absent if |$\mathcal{H}_{\rm A}\ge \mathcal{H}_{\rm A}^{\rm (N)}$|⁠, the hoop conjecture is regarded to hold for that collection of hypersurfaces, because both the necessary and sufficient conditions for the apparent horizon formation are given in terms of |$\mathcal{H}_{\rm A}$|⁠. Although this criterion was explicitly stated in Ref. [28] for the first time, the existing works seem to have adopted this criterion implicitly.

4.2. Examination of the stretched hoop conjecture

We now turn our attention to the stretched hoop conjecture for the formation of outermost DTT spheres. Since we would like to examine whether |$\mathcal{C}\lesssim 6\pi GM$| gives the condition for the formation of DTTSs, we consider

$$\begin{equation} \mathcal{H}_{\rm D} = \mathrm{min} \left[\frac{\mathcal{C}(\sigma)}{6\pi GM_{\rm Q}(\sigma)}\right] \end{equation}$$

(32)

as the stretched hoop parameter to be studied. In this paper we adopt the ADM mass as the definition of mass, that is, |$M_{\rm Q}(\sigma)=M$| for arbitrary surfaces |$\sigma$|⁠, because the initial data are vacuum and no energy density of matter is present outside |$\sigma$|⁠. Furthermore, since the initial data are time symmetric and conformally flat, junk energy of gravitational waves is expected to be small. Then, the problem is reduced to finding the minimum value of |$\mathcal{C}(\sigma)$|⁠.

By virtue of the axial symmetry of the systems, we adopt Eq. (31) as the definition of the circumference. For prolate systems (i.e. the two-black-hole initial data and the spindle initial data), on the one hand, the minimum value of |$\mathcal{C}(\sigma)$| coincides with the minimum value of the polar circumference |$\mathcal{C}_{\rm p}(\sigma)$|⁠. Parametrizing the surface |$\sigma$| in the same manner as Eq. (23), the value of |$\mathcal{C}_{\rm p}$| is calculated from

$$\begin{equation} \mathcal{C}_{\rm p} = \int_0^{\pi}\varPsi^2 \sqrt{h^2+h^{\prime 2}}d\tilde{\theta}. \end{equation}$$

(33)

From the variational principle, the equation for |$h(\tilde{\theta})$| is derived as

$$\begin{equation} h^{\prime\prime}-2\left(\frac{\varPsi_{,\tilde{r}}}{\varPsi}+\frac{1}{h}\right)h^{\prime 2} -\left(2\frac{\varPsi_{,\tilde{r}}}{\varPsi}+\frac{1}{h}\right)h^2 +2\frac{\varPsi_{,\tilde{\theta}}}{\varPsi} \left(1+\frac{h^{\prime 2}}{h^2}\right)h^{\prime} =0. \label{Equation-Hoop-prolate} \end{equation}$$

(34)

The same equation is presented in Refs. [15,24]. For oblate systems (i.e. the ring initial data), on the other hand, the minimum value of |$\mathcal{C}(\sigma)$| coincides with the minimum circumference of circles |$\tilde{r}=\mathrm{const.}$| on the equatorial plane:

$$\begin{equation} \mathcal{C}_{\rm e} = \mathrm{min} \left[2\pi \tilde{r}\varPsi^2(\tilde{r},\pi/2)\right]. \end{equation}$$

(35)

The value of |$\tilde{r}$| at which |$\mathcal{C}_{\rm e}$| becomes minimal is determined by the equation |$\varPsi+2\tilde{r}\varPsi_{,\tilde{r}}=0$| on the equatorial plane. Below, we present the numerical results for the three systems, one by one.

4.2.1. Two-black-hole initial data

The marginally DTT spheres in two-black-hole systems have been calculated in our previous paper [8], and the (common) marginally DTT sphere that surrounds both black holes exists for |$z_0/GM\lesssim 1.1506$|⁠. A three-dimensional (3D) plot of the marginally DTT spheres for |$z_0/GM=1.1506$| is shown in Fig. 2, together with the shortest hoop that surrounds both black holes determined from Eq. (34). Figure 3 shows the behavior of the stretched hoop parameter |$\mathcal{H}_{\rm D}$| as a function of |$z_0/GM$|⁠. The stretched hoop parameter |$\mathcal{H}_{\rm D}$| is a monotonically increasing function of |$z_0/GM$|⁠, and if the relation |$\mathcal{H}_{\rm D}\le 0.9293$| (respectively, |$\mathcal{H}_{\rm D}\ge 0.9294$|⁠) holds, the (common) marginally DTT sphere is present (respectively, absent).

Fig. 2.

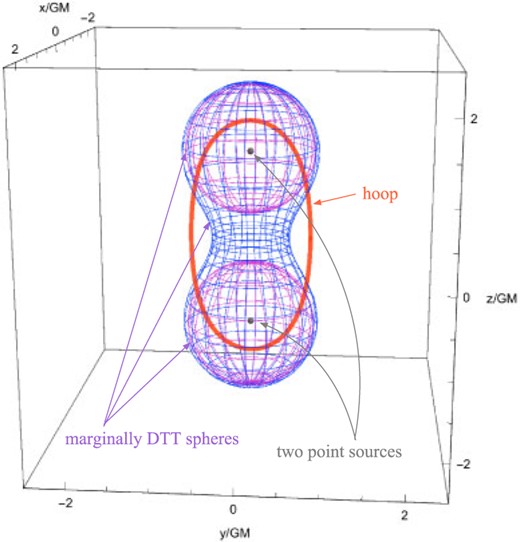
Three-dimensional plot of the marginally DTT spheres for |$z_0/GM=1.1506$| in the two-black-hole initial data. The shortest hoop that surrounds the system is also shown.

Open in new tab Download slide

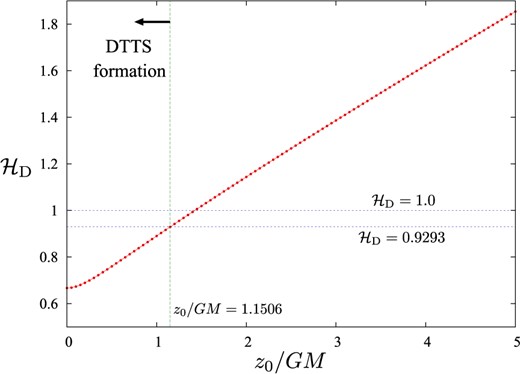
$The stretched hoop parameter $\mathcal{H}_{\rm D}$ as a function of $z_0/GM$ in the initial data of two black holes. The value $\mathcal{H}_{\rm D}=0.9293$ is indicated by a horizontal dashed line, and the marginally DTT sphere forms if $\mathcal{H}_{\rm D}\le 0.9293$ holds. The value $\mathcal{H}_{\rm D}=1.0$ is also indicated for comparison.$

Fig. 3.

The stretched hoop parameter |$\mathcal{H}_{\rm D}$| as a function of |$z_0/GM$| in the initial data of two black holes. The value |$\mathcal{H}_{\rm D}=0.9293$| is indicated by a horizontal dashed line, and the marginally DTT sphere forms if |$\mathcal{H}_{\rm D}\le 0.9293$| holds. The value |$\mathcal{H}_{\rm D}=1.0$| is also indicated for comparison.

Open in new tab Download slide

4.2.2. Spindle initial data

The left panel of Fig. 4 depicts marginally DTT spheres for values of |$L/GM$| from |$0.0$| to |$3.0$| at |$0.5$| intervals, and for |$3.4928$|⁠. As the value of |$L/GM$| is increased, the marginally DTT sphere becomes more prolate. For |$L/GM= 3.4928$|⁠, the marginally DTT sphere approximately degenerates with the inner boundary of the dynamically transversely trapping region (that is not plotted in Fig. 4), and they vanish for |$L/GM\ge 3.4929$|⁠. Therefore, a marginally DTT sphere cannot become arbitrarily long in the |$z$| direction. This result is similar to the apparent horizon formation in the same initial data studied in Ref. [24], while it is in contrast to the apparent horizon formation in the higher-dimensional version of these initial data where the apparent horizon can become arbitrarily long [35]. The right panel of Fig. 4 shows a 3D plot of the marginally DTT sphere for |$L/GM=3.4928$| together with the shortest hoop that surrounds the system.

$Marginally DTT spheres in the spindle initial data. Left panel: Sections of marginally DTT spheres with the $(x,z)$-plane for $L/GM=0.0$, $0.5$, $1.0$, $1.5$, $2.0$, $2.5$, $3.0$, and $3.4928$ in spindle systems. For $R/GM\ge 3.4929$, a marginally DTT sphere cannot be found. Right panel: 3D plot of the marginally DTT sphere for $L/GM=3.4928$. The shortest hoop that surrounds the system is also shown.$

Fig. 4.

Marginally DTT spheres in the spindle initial data. Left panel: Sections of marginally DTT spheres with the |$(x,z)$|-plane for |$L/GM=0.0$|⁠, |$0.5$|⁠, |$1.0$|⁠, |$1.5$|⁠, |$2.0$|⁠, |$2.5$|⁠, |$3.0$|⁠, and |$3.4928$| in spindle systems. For |$R/GM\ge 3.4929$|⁠, a marginally DTT sphere cannot be found. Right panel: 3D plot of the marginally DTT sphere for |$L/GM=3.4928$|⁠. The shortest hoop that surrounds the system is also shown.

Open in new tab Download slide

Figure 5 shows the behavior of the stretched hoop parameter |$\mathcal{H}_{\rm D}$| as a function of |$L/GM$|⁠. The stretched hoop parameter |$\mathcal{H}_{\rm D}$| is a monotonically increasing function of |$L/GM$|⁠, and if the relation |$\mathcal{H}_{\rm D}\le 0.9506$| (respectively, |$\mathcal{H}_{\rm D}\ge 0.9507$|⁠) holds, the marginally DTT sphere is present (respectively, absent).

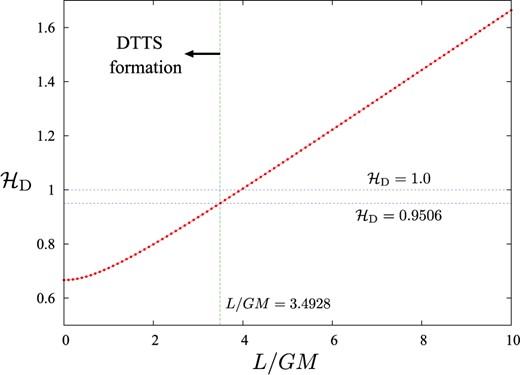
$The stretched hoop parameter $\mathcal{H}_{\rm D}$ as a function of $L/GM$ in the spindle initial data. The value $\mathcal{H}_{\rm D}=0.9506$ is indicated by a horizontal dashed line, and the marginally DTT sphere forms if $\mathcal{H}_{\rm D}\le 0.9506$ holds. The value $\mathcal{H}_{\rm D}=1.0$ is also indicated for comparison.$

Fig. 5.

The stretched hoop parameter |$\mathcal{H}_{\rm D}$| as a function of |$L/GM$| in the spindle initial data. The value |$\mathcal{H}_{\rm D}=0.9506$| is indicated by a horizontal dashed line, and the marginally DTT sphere forms if |$\mathcal{H}_{\rm D}\le 0.9506$| holds. The value |$\mathcal{H}_{\rm D}=1.0$| is also indicated for comparison.

Open in new tab Download slide

4.2.3. Ring initial data

The left panel of Fig. 6 depicts marginally DTT spheres for values of |$R/GM$| from |$0.0$| to |$1.0$| at |$0.2$| intervals, and for |$1.0943$|⁠. As the value of |$R/GM$| is increased, the marginally DTT sphere becomes more oblate. For |$R/GM= 1.0943$|⁠, the marginally DTT sphere approximately degenerates with the inner boundary of the dynamically transversely trapping region (that is not plotted in Fig. 6), and they vanish for |$R/GM\ge 1.0944$|⁠. The right panel of Fig. 6 shows a 3D plot of the marginally DTT sphere for |$R/GM=1.0943$| together with the shortest hoop that surrounds the system.

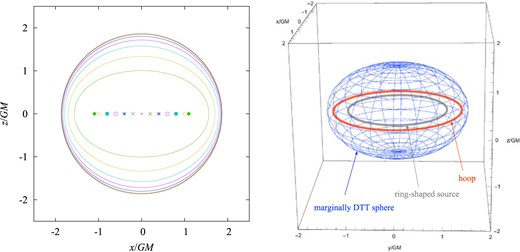
$Marginally DTT spheres in the ring initial data. Left panel: Sections of marginally DTT spheres with the $(x,z)$-plane for $R/GM=0.0$, $0.2$, $0.4$, $0.6$, $0.8$, $1.0$, and $1.0943$ in ring systems. For $R/GM\ge 1.0944$, a marginally DTT sphere cannot be found. Right panel: 3D plot of the marginally DTT sphere for $R/GM=1.0943$. The shortest hoop that surrounds the system is also shown.$

Fig. 6.

Marginally DTT spheres in the ring initial data. Left panel: Sections of marginally DTT spheres with the |$(x,z)$|-plane for |$R/GM=0.0$|⁠, |$0.2$|⁠, |$0.4$|⁠, |$0.6$|⁠, |$0.8$|⁠, |$1.0$|⁠, and |$1.0943$| in ring systems. For |$R/GM\ge 1.0944$|⁠, a marginally DTT sphere cannot be found. Right panel: 3D plot of the marginally DTT sphere for |$R/GM=1.0943$|⁠. The shortest hoop that surrounds the system is also shown.

Open in new tab Download slide

Figure 7 shows the behavior of the stretched hoop parameter |$\mathcal{H}_{\rm D}$| as a function of |$R/GM$|⁠. The stretched hoop parameter |$\mathcal{H}_{\rm D}$| is a monotonically increasing function of |$R/GM$|⁠, and if the relation |$\mathcal{H}_{\rm D}\le 0.9754$| (respectively, |$\mathcal{H}_{\rm D}\ge 0.9755$|⁠) holds, the marginally DTT sphere is present (respectively, absent).

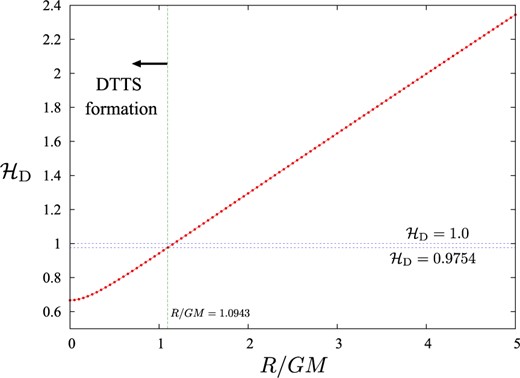
$The stretched hoop parameter $\mathcal{H}_{\rm D}$ as a function of $R/GM$ in the ring initial data. The value $\mathcal{H}_{\rm D}=0.9754$ is indicated by a horizontal dashed line, and the marginally DTT sphere forms if $\mathcal{H}_{\rm D}\le 0.9754$ holds. The value $\mathcal{H}_{\rm D}=1.0$ is also indicated for comparison.$

Fig. 7.

The stretched hoop parameter |$\mathcal{H}_{\rm D}$| as a function of |$R/GM$| in the ring initial data. The value |$\mathcal{H}_{\rm D}=0.9754$| is indicated by a horizontal dashed line, and the marginally DTT sphere forms if |$\mathcal{H}_{\rm D}\le 0.9754$| holds. The value |$\mathcal{H}_{\rm D}=1.0$| is also indicated for comparison.

Open in new tab Download slide

4.3. Summary of the numerical results

In each of the three systems, the region where the DTT sphere is present/absent can be specified by the values of |$\mathcal{H}_{\rm D}$|⁠. Putting the three results together, a marginally DTT sphere forms if |$\mathcal{H}_{\rm D}\le 0.9294$|⁠, and it does not form if |$\mathcal{H}_{\rm D}\ge 0.9755$|⁠. Therefore, the stretched hoop parameter |$\mathcal{H}_{\rm D}$| becomes an indicator for the formation of a marginally DTT sphere, at least in the systems studied in this paper. From this result, it would be fair to present the following stretched hoop conjecture:

Conjecture 2

Strong gravity regions with marginally DTT spheres form when and only when a mass |$M$| gets compacted into a region whose circumference in every direction is bounded by |$\mathcal{C}\lesssim 6\pi GM$|⁠.

The stretched hoop conjecture suggests that an arbitrarily long DTT sphere cannot form. As discussed in Sect. 1, this also indicates that a marginally DTT torus could not form, or even if it does form, it would be located inside a marginally DTT sphere. In the next section we investigate the ring system further, and show that there is a parameter region of |$R/GM$| where a marginally TTS torus actually forms inside a marginally TTS sphere.

5. Further examination of the ring system

As mentioned in Sect. 1, there is the possibility that DTT tori may form unless they are convex [more strictly, unless |$k_{\rm S}\ge -k_{\rm L}/3$| is satisfied, where |$k_{\rm S}$| and |$k_{\rm L}$| are defined in Eqs. (8a) and (8b)]. In Sect. 5.1, we will show that in a ring system there is a parameter region where a marginally DTT torus is actually present inside a marginally DTT sphere. In Sect. 5.2, we present the similarity between the two concepts of a DTTS and a trapped surface by showing that there are configurations where a marginally trapped torus forms inside a marginally trapped sphere in the same system.

5.1. Marginally DTT tori

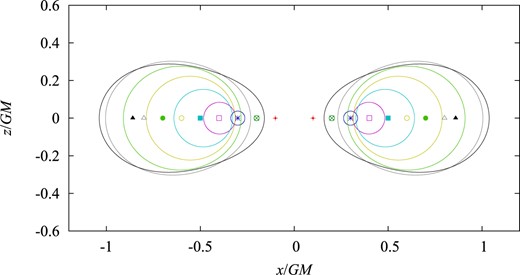
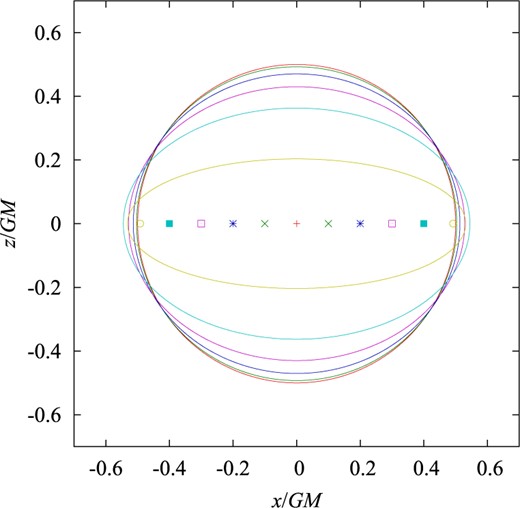
As a result of numerical survey, we have found that a marginally DTT torus actually exists in the parameter range |$0<R/GM\le 0.8598$|⁠. Figure 8 shows sections of a marginally DTT torus in the |$(x, z)$|-plane for values of |$R/GM$| from |$0.1$| to |$0.8$| at |$0.1$| intervals, and for |$0.8598$|⁠. No solution has been found for |$R/GM\ge 0.8599$|⁠. Since a marginally DTT sphere exists in the range |$R/GM\le 1.0943$|⁠, a marginally DTT torus is located inside a marginally DTT sphere. In Fig. 9, a marginally DTT torus and a marginally DTT sphere are plotted together for |$R/GM = 0.6$| (left panel), |$0.8598$| (middle panel), and |$1.0943$| (right panel).

$Sections of marginally DTT tori in ring systems with the $(x,z)$-plane for $R/GM=0.1$, $0.2$, $0.3$, $0.4$, $0.5$, $0.6$, $0.7$, $0.8$, and $0.8598$. For $R/GM\ge 0.8599$, a marginal DTT torus cannot be found.$

Fig. 8.

Sections of marginally DTT tori in ring systems with the |$(x,z)$|-plane for |$R/GM=0.1$|⁠, |$0.2$|⁠, |$0.3$|⁠, |$0.4$|⁠, |$0.5$|⁠, |$0.6$|⁠, |$0.7$|⁠, |$0.8$|⁠, and |$0.8598$|⁠. For |$R/GM\ge 0.8599$|⁠, a marginal DTT torus cannot be found.

Open in new tab Download slide

Fig. 9.

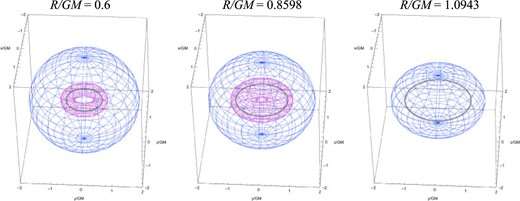
Three-dimensional plots of a marginally DTT sphere and a marginally DTT torus for |$R/GM=0.6$| (left panel), |$0.8598$| (middle panel), and |$1.0943$| (right panel).

Open in new tab Download slide

Since it has been proved that a DTTS must have spherical topology as long as |$k_{\rm S}\ge -k_{\rm L}/3$| [8], the obtained DTT tori must violate this inequality. Figure 10 plots the value of |$k_1$| (solid curves) and |$k_2$| (dashed curves) as functions of the angular coordinate |$\tilde{\xi}$| for |$R/GM=0.1$|⁠, |$0.4$|⁠, and |$0.8$|⁠. For all values of |$\tilde{\xi}$| the relation |$k_2<0<k_1$| is maintained, and thus the marginally DTT tori are not convex. Also, at least in the neighborhood of |$\tilde{\xi}=\pi$|⁠, the relation |$k_2\ge -k_1/3$| is violated. For |$R/GM\ll 1$|⁠, the relation |$k_1\approx -2k_2$| holds approximately.

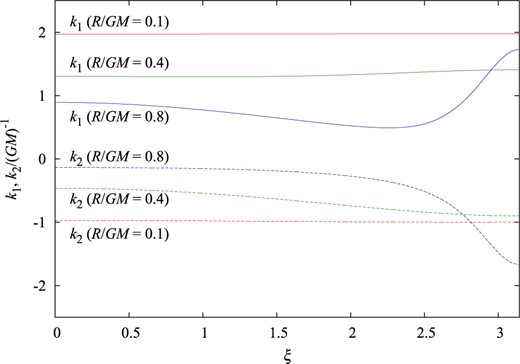
$The values of $k_1$ (solid lines) and $k_2$ (dashed lines) of marginally DTT tori as functions of the angular coordinate $\tilde{\xi}$ for $R/GM=0.1$, $0.4$, and $0.8$.$

Fig. 10.

The values of |$k_1$| (solid lines) and |$k_2$| (dashed lines) of marginally DTT tori as functions of the angular coordinate |$\tilde{\xi}$| for |$R/GM=0.1$|⁠, |$0.4$|⁠, and |$0.8$|⁠.

Open in new tab Download slide

The validity of these numerical results is checked as follows. Integrating Eq. (11) on a marginally DTTS, we have

$$\begin{equation} \Delta :=\int_{\sigma_0} k_1(k_1+2k_2)dA-2\pi\chi(\sigma_0) =0, \end{equation}$$

(36)

where |$\chi(\sigma_0)$| is the Euler characteristic, which is zero for a toroidal surface. The numerical value of |$\Delta$| deviates from zero due to numerical errors, and the error decreases as the numerical accuracy is systematically increased if the calculation is correct. By contrast, if there is a mistake somewhere, the value of |$\Delta$| does not decrease by this procedure. By increasing the number of grid points up to |$10^4$| and increasing the accuracy of the initial condition in the shooting method up to |$O(10^{-12})$|⁠, the typical value of |$\Delta$| is decreased to the order of |$10^{-10}$|⁠. This result supports the correctness of our numerical calculation. Also, as demonstrated in Appendix B, an approximate solution of a marginally DTT torus can be obtained for a small ring with |$R\ll GM$|⁠, and it is also consistent with our numerical results.

Figure 11 shows the area of the marginally DTT sphere and the marginally DTT torus normalized by the area of a photon sphere in a spherically symmetric case, |$A_0/4\pi(3GM)^2$|⁠, as functions of |$R/GM$|⁠. The area of the marginally DTT sphere is a monotonically decreasing function of |$R/GM$|⁠, and takes the value |$A_0/4\pi(3GM)^2\approx 0.7274$| at |$R/GM=1.0943$|⁠. Therefore, the area satisfies the Penrose-like inequality, |$A_0\le 4\pi (3GM)^2$|⁠. By contrast, the area of the marginally DTT torus does not show monotonic behavior. Also, in the limit |$R/GM\to 0$|⁠, the area becomes indefinitely large. This is because the condition |$k_{\rm S}\ge -k_{\rm L}/3$| is not satisfied on a marginally DTT torus, and hence the Penrose-like inequality proved in our previous paper [8] does not apply to it. Unfortunately, such a large DTT torus may not have important physical meaning because it is hidden inside an apparent horizon that forms for |$R/GM\lesssim 0.49203$|⁠. However, we would like to point out that there is a parameter region of |$R/GM$| where a marginally DTT torus exists without being hidden by an apparent horizon. Although we are not sure whether an event horizon that encloses marginally DTT torus exists or not in the present analysis of initial data, this result indicates that it may be possible to observe the positions where marginally DTT tori exist.

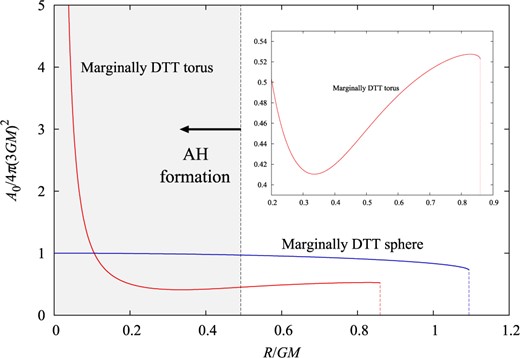
$The area $A_{0}$ of a marginally DTT sphere and that of a marginally DTT torus as functions of $R/GM$. The area is normalized by $4\pi (3GM)^2$. The parameter region $0\le R/GM\le 0.49203$ where an apparent horizon forms is indicated by shaded regions. The inset enlarges the behavior of $A_{0}/4\pi (3GM)^2$ for a marginally DTT torus in the domain $0.2\le R/GM\le 0.9$.$

Fig. 11.

The area |$A_{0}$| of a marginally DTT sphere and that of a marginally DTT torus as functions of |$R/GM$|⁠. The area is normalized by |$4\pi (3GM)^2$|⁠. The parameter region |$0\le R/GM\le 0.49203$| where an apparent horizon forms is indicated by shaded regions. The inset enlarges the behavior of |$A_{0}/4\pi (3GM)^2$| for a marginally DTT torus in the domain |$0.2\le R/GM\le 0.9$|⁠.

Open in new tab Download slide

5.2. Marginally trapped tori

In our previous paper [8] we compared marginally DTTSs and marginally trapped surfaces for the Brill–Lindquist initial data of two equal-mass black holes, and stressed the similarity between them. Here, we would like to proceed with similar analysis of the ring system. In particular, there are configurations where a marginally trapped torus forms inside a marginally trapped sphere. Although the formation of trapped tori has been reported in other systems [43,44], the trapped torus formation in the present system is reported for the first time, to the best of our knowledge.

Figure 12 depicts a marginally trapped sphere (that is, an apparent horizon and a minimal surface at the same time) for values of |$R/GM$| from |$0.1$| to |$0.4$| at |$0.1$| intervals, and for |$0.49203$|⁠. For |$R/GM= 0.49203$|⁠, the minimal surface approximately degenerates with an inside maximal surface, and they vanish for |$R/GM\ge 0.49204$|⁠.³

$Sections of marginally trapped spheres (apparent horizons and spherical minimal surfaces, at the same time) in ring systems with the $(x,z)$-plane for $R/GM=0.1$, $0.2$, $0.3$, $0.4$, and $0.49203$. For $R/GM\ge 0.49204$, a marginally trapped sphere cannot be found. Compare with Fig. 6.$

Fig. 12.

Sections of marginally trapped spheres (apparent horizons and spherical minimal surfaces, at the same time) in ring systems with the |$(x,z)$|-plane for |$R/GM=0.1$|⁠, |$0.2$|⁠, |$0.3$|⁠, |$0.4$|⁠, and |$0.49203$|⁠. For |$R/GM\ge 0.49204$|⁠, a marginally trapped sphere cannot be found. Compare with Fig. 6.

Open in new tab Download slide

Marginally trapped tori found in our numerical calculations are plotted in Fig. 13 for values of |$R/GM$| from |$0.05$| to |$0.40$| at |$0.05$| intervals, and for |$0.41413$|⁠. For |$R/GM\ge 0.41414$|⁠, a marginally trapped torus cannot be found. The marginally trapped torus is always located inside the marginally trapped sphere. In Fig. 14, the marginally trapped sphere and the marginally trapped torus are plotted together for |$R/GM=0.20$| (left panel), |$0.41413$| (middle panel), and |$0.49203$| (right panel). See also Appendix B for an approximate analysis for |$R\ll GM$| that supports the existence of the marginally trapped torus.

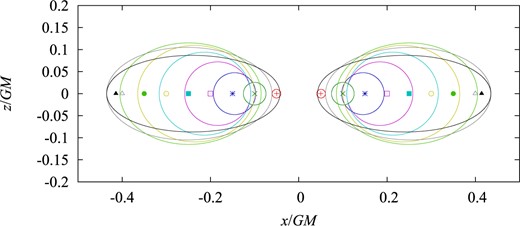
$Sections of marginally trapped tori (toroidal minimal surfaces, at the same time) in ring systems with the $(x,z)$-plane for $R/GM=0.05$, $0.10$, $0.15$, $0.20$, $0.25$, $0.30$, $0.35$, $0.40$, and $0.41413$. For $R/GM\ge 0.41414$, a marginally trapped torus cannot be found. Compare with Fig. 8.$

Fig. 13.

Sections of marginally trapped tori (toroidal minimal surfaces, at the same time) in ring systems with the |$(x,z)$|-plane for |$R/GM=0.05$|⁠, |$0.10$|⁠, |$0.15$|⁠, |$0.20$|⁠, |$0.25$|⁠, |$0.30$|⁠, |$0.35$|⁠, |$0.40$|⁠, and |$0.41413$|⁠. For |$R/GM\ge 0.41414$|⁠, a marginally trapped torus cannot be found. Compare with Fig. 8.

Open in new tab Download slide

Fig. 14.

Three-dimensional plots of a marginally trapped sphere and a marginally trapped torus for |$R/GM=0.20$| (left panel), |$0.41413$| (middle panel), and |$0.49203$| (right panel). Compare with Fig. 9.

Open in new tab Download slide

Figure 15 shows the area of the marginally trapped sphere and the marginally trapped torus normalized by the horizon area in the spherically symmetric case, |$A_{\rm min}/4\pi(2GM)^2$|⁠, as functions of |$R/GM$|⁠. The area of the sphere monotonically decreases as |$R/GM$| is increased, and takes the value |$A_{\rm min}/4\pi(2GM)^2\approx 0.9801$| at |$R/GM=0.49203$|⁠. The area of the torus is also a monotonically decreasing function of |$R/GM$|⁠, and it is always greater than one. As the value of |$R/GM$| decreases to zero, the area of the torus becomes unboundedly large. Note that this result does not contradict the existing proofs of the Riemannian Penrose inequality |$A_{\rm min}\le 4\pi (2GM)^2$| [10–12], because those proofs apply only to the outermost minimal surface, while in each of the present systems a toroidal minimal surface exists inside a spherical maximal surface, which, in turn, exists inside a spherical minimal surface.

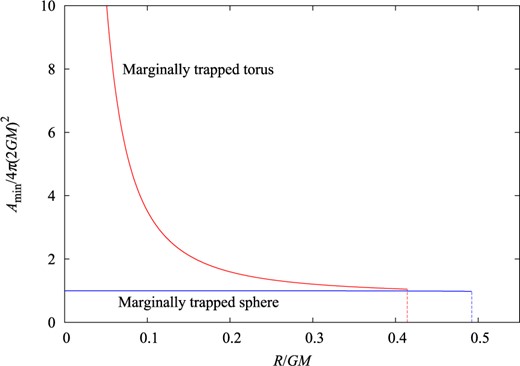
$The area $A_{\rm min}$ of a marginally trapped sphere and that of a marginally trapped torus (a spherical minimal surface and a toroidal minimal surface, at the same time, respectively) as functions of $R/GM$. The area is normalized by $4\pi (2GM)^2$.$

Fig. 15.

The area |$A_{\rm min}$| of a marginally trapped sphere and that of a marginally trapped torus (a spherical minimal surface and a toroidal minimal surface, at the same time, respectively) as functions of |$R/GM$|⁠. The area is normalized by |$4\pi (2GM)^2$|⁠.

Open in new tab Download slide

6. Summary and discussion

We have studied the formation of marginally DTTSs in time-symmetric, conformally flat initial data in order to examine whether they can be understood analogously to the hoop conjecture. Three kinds of systems have been studied, with two-black-hole initial data, spindle initial data, and ring initial data. In all systems, the condition |$\mathcal{C}\lesssim 6\pi GM$| approximately describes the formation of the (outermost) marginally DTT sphere, and we have proposed the stretched hoop conjecture for the formation of marginally DTT spheres in Sect. 4.3. Our results indicate that an arbitrarily long DTT sphere is unlikely to form.

It has also been shown that in the ring system there is a parameter region of the ring radius |$R$| where a marginally DTT torus forms. Such a marginally DTT torus is located inside a marginally DTT sphere, consistent with the expectation from the stretched hoop conjecture. Since there is a parameter region where a marginally DTT torus is not hidden inside an apparent horizon, marginally DTT tori may be observable. In addition, there is a parameter region of |$R$| where a marginally trapped torus forms inside a marginally trapped sphere. This provides a further example of the similarity between (marginally) DTTSs and (marginally) trapped surfaces.

The condition for the formation of marginally DTT tori is left as a remaining problem. We point out that the same statement should also hold for marginally trapped tori. Although one may expect that marginally DTT/trapped tori may form if matter is concentrated in a ring-shaped region, the existing works indicate that trapped tori form even in the initial data of a spherically symmetric star [44]. Although the authors of Ref. [44] discussed such a condition in terms of the binding energy of a star, how to apply that condition to the present ring system is unclear. Another remaining problem is that since a DTT torus has been shown to form, DTTSs with the topologies of double torus, triple torus, and so on may form as well. In order to clarify this, it is necessary to study non-axisymmetric initial data, which will be more difficult compared to the study in this paper.

The present paper answers one of the remaining problems listed in our previous paper [8]. Since a (marginally) DTTS is a new concept, there still remain a lot of issues to be clarified, i.e. the preparation of methods of solving for marginally DTTSs on non-time-symmetric initial data, the possible constraints from the presence of a DTTS on the global properties of a spacetime, the connection to a wandering set [7] that is the extension of a photon sphere defined from global point of view, and exploring the connection to observations. We hope to report on these in forthcoming papers.

Acknowledgements

H.Y. thanks Takeshi Chiba for helpful discussions in 2001. H.Y. is supported by Grant-in-Aid for Scientific Research (C) no. JP18K03654 from the Japan Society for the Promotion of Science (JSPS). K.I. is supported by JSPS Grant-in-Aid for Young Scientists (B) no. JP17K14281. T.S. is supported by Grant-in-Aid for Scientific Research (C) no. JP16K05344 from JSPS. K.I. and T.S. are also supported by Scientific Research (A) no. JP17H01091, and in part by JSPS Bilateral Joint Research Projects (JSPS-NFR collaboration) “String Axion Cosmology.” The work of H.Y. is partly supported by Osaka City University Advanced Mathematical Institute (MEXT Joint Usage/Research Center on Mathematics and Theoretical Physics).

Appendix A. Equations for marginally DTT/trapped tori in ring initial data

In this appendix we present the derivation of the equations for marginally DTT/trapped tori studied in Sects. 3.2.2 and 5. Through the coordinate transformations in Eqs. (27) and (28), the metric in the neighborhood of |$\sigma_0$| becomes

$$\begin{eqnarray} ds^2 & = & \varPsi^4\left[1+(\rho+h)^2p_{,\rho}^2\right]d\rho^2 \nonumber\\ && +\ \varPsi^4\left[h^{\prime 2}+(\rho+h)^2(1-p_{,\xi})^2\right]d\xi^2 \nonumber\\ && +\ 2\varPsi^4\left[h^{\prime}-(\rho+h)^2(1-p_{,\xi})p_{,\rho}\right]d\rho d\xi \nonumber\\ && +\ \varPsi^4\left[R+(\rho+h)\cos(\xi-p)\right]^2d\phi^2, \end{eqnarray}$$

(A.1)

and we require the coordinates |$(\rho, \xi, \phi)$| to be orthogonal, that is,

$$\begin{equation} h^{\prime}=(\rho+h)^2(1-p_{,\xi})p_{,\rho}. \end{equation}$$

(A.2)

In particular, this relation means that

$$\begin{equation} p_{,\rho} = \frac{h^\prime}{h^2}, \qquad p_{,\rho\xi} = \frac{h^{\prime\prime}}{h^2}-\frac{2h^{\prime 2}}{h^3} \end{equation}$$

(A.3)

on |$\sigma_0$|⁠. With respect to the orthonormal basis given by Eq. (29), the diagonalized orthonormal components of the extrinsic curvature defined in Eq. (7) are calculated from

$$\begin{align} k_{\xi\xi} = \frac{1}{2\varphi}\partial_\rho h_{\xi\xi}, \qquad & k_1=\frac{k_{\xi\xi}}{h_{\xi\xi}},\\ \end{align}$$

(A.4)

$$\begin{align} k_{\phi\phi} = \frac{1}{2\varphi}\partial_\rho h_{\phi\phi}, \qquad & k_2=\frac{k_{\phi\phi}}{h_{\phi\phi}}. \end{align}$$

(A.5)

The result is

$$\begin{eqnarray} k_1 &=& -\frac{h}{\varPsi^2(h^2+h^{\prime 2})^{3/2}}\left(h^{\prime\prime}+C\right), \label{k1-torus} \\ \end{eqnarray}$$

(A.6a)

$$\begin{eqnarray} k_2 &=& \frac{D}{\varPsi^2h\sqrt{h^2+h^{\prime 2}}}, \label{k2-torus} \end{eqnarray}$$

(A.6b)

with

$$\begin{eqnarray} C&=& -h-2\frac{h^{\prime 2}}{h} -2\left(\frac{\varPsi_{,\tilde{\rho}}}{\varPsi}-\frac{h^\prime}{h^2}\frac{\varPsi_{,\tilde{\xi}}}{\varPsi}\right) (h^2+h^{\prime 2}), \label{torus-C} \\ \end{eqnarray}$$

(A.7a)

$$\begin{eqnarray} D&=& \frac{h\cos\xi+h^\prime\sin\xi}{R+h\cos\xi}h +2\left(\frac{\varPsi_{,\tilde{\rho}}}{\varPsi}-\frac{h^\prime}{h^2}\frac{\varPsi_{,\tilde{\xi}}}{\varPsi}\right) h^2, \label{torus-D} \end{eqnarray}$$

(A.7b)

where the relation

$$\begin{equation} \varPsi_{,\rho} = \varPsi_{,\tilde{\rho}}-\frac{h^\prime}{h^2}\varPsi_{,\tilde{\xi}} \end{equation}$$

(A.8)

is used. The two-dimensional Ricci scalar |${}^{(2)}R$| on |$\sigma_0$| that appears in Eq. (11) is calculated as

$$\begin{equation} \frac12{}^{(2)}R = \frac{1}{\varPsi^4(h^2+h^{\prime 2})}(Ah^{\prime\prime}+B), \label{Ricci-scalar-torus} \end{equation}$$

(A.9)

with

$$\begin{align} A & =\frac{2h^\prime}{h^2+h^{\prime 2}} \frac{\varPsi_{,\tilde{\rho}}h^\prime +\varPsi_{,\tilde{\xi}}}{\varPsi} -2\frac{\varPsi_{,\tilde{\rho}}}{\varPsi} -\frac{h\cos\xi+h^\prime\sin\xi}{(R+h\cos\xi)(h^2+h^{\prime 2})}h, \label{torus-A} \\ \end{align}$$

(A.10a)

$$\begin{align} B & = 2\left(\frac{\varPsi_{,\tilde{\rho}}h^\prime +\varPsi_{,\tilde{\xi}}}{\varPsi}\right)^2 -\frac{2}{\varPsi}\left(\varPsi_{,\tilde{\rho}\tilde{\rho}}h^{\prime 2} +2\varPsi_{,\tilde{\rho}\tilde{\xi}}h^{\prime} +\varPsi_{,\tilde{\xi}\tilde{\xi}}\right) +\frac{h\cos\xi+h^\prime\sin\xi}{(R+h\cos\xi)(h^2+h^{\prime 2})} (h^2+2h^{\prime 2}) \nonumber \\ & \quad + \frac{2}{(R+h\cos\xi)(h^2+h^{\prime 2})} \frac{\varPsi_{,\tilde{\rho}}h^\prime +\varPsi_{,\tilde{\xi}}}{\varPsi} \left[h^3\sin\xi-h^{\prime 3}\cos\xi+hh^{\prime}(R+h^\prime \sin\xi)\right], \label{torus-B} \end{align}$$

(A.10b)

where the relations

$$\begin{eqnarray} \varPsi_{,\xi} &=& \varPsi_{,\tilde{\rho}}h^\prime+\varPsi_{,\tilde{\xi}}, \\ \end{eqnarray}$$

(A.11a)

$$\begin{eqnarray} \varPsi_{,\xi\xi}&=& \varPsi_{,\tilde{\rho}}h^{\prime\prime} +\varPsi_{,\tilde{\rho}\tilde{\rho}}h^{\prime 2} +2\varPsi_{,\tilde{\rho}\tilde{\xi}}h^{\prime} +\varPsi_{,\tilde{\xi}\tilde{\xi}} \end{eqnarray}$$

(A.11b)

are used. We now present the equations for marginally DTT/trapped tori in terms of |$h$|⁠, |$A$|⁠, |$B$|⁠, |$C$|⁠, and |$D$|⁠.

Appendix A.1. Marginally DTT tori with |$k_1\le k_2$|

$$\begin{equation} h^{\prime\prime} = \frac{-2CD+(D^2/h^2-B)(h^2+h^{\prime 2})}{2D+A(h^2+h^{\prime 2})}. \label{equation-prolate-case} \end{equation}$$

(A.12)

Appendix A.2. Marginally DTT tori with |$k_1\ge k_2$|

In the case |$k_1\ge k_2$|⁠, Eq. (11) becomes

$$\begin{multline} h^{\prime\prime} = -C + \frac{h^2+h^{\prime 2}}{h^2}\left[D+\frac12(h^2+h^{\prime 2})A\right] \\ \mp \frac{h^2+h^{\prime 2}}{h^2}\sqrt{\left[D+\frac12(h^2+h^{\prime 2})A\right]^2+h^2(B-AC)}. \label{equation-oblate-case} \end{multline}$$

(A.13)

This equation includes a double sign. In the case of marginally DTT spheres, it is possible to choose an appropriate sign by requiring the equation to be consistent with the presence of a photon sphere in the spherically symmetric case [8]. Since an appropriate sign cannot be chosen from such physical considerations in the toroidal case, we study the cases for both signs. As a result, a marginally trapped torus can be obtained for the minus sign of Eq. (A.13). For the plus sign, we could not obtain a solution satisfying the boundary conditions.

Appendix A.3. Marginally trapped tori

Since a marginally trapped surface coincides with a minimal surface in time-symmetric initial data, the equation for marginally trapped tori becomes |$k=k_1+k_2=0$|⁠. This is equivalent to

$$\begin{equation} h^{\prime\prime} = -C+\frac{h^2+h^{\prime 2}}{h^2}D. \end{equation}$$

(A.14)

Appendix B. Approximate analysis of marginally DTT/trapped tori

In this appendix we proceed with an approximate analysis of the marginally DTT/trapped tori in the ring initial data in order to provide evidence for their existence and support the numerical results in Sect. 5. We focus on the case |$GM\gg R$|⁠, for which our numerical results indicate that the radii of marginally DTT/trapped tori become much smaller compared to |$R$|⁠. For this reason, we consider the expanded form of |$h(\tilde{\xi})$| of Eq. (26) as

$$\begin{equation} h(\tilde{\xi}) = \rho_0+\sum_{n\ge 1}\rho_n\cos (n\tilde{\xi}), \end{equation}$$

(B.1)

and assume

$$\begin{equation} R \gg \rho_0\gg \rho_n \quad (n=1,2, \ldots). \end{equation}$$

(B.2)

$$\begin{equation} K(\kappa) = -\frac12\log(1-\kappa^2)+2\log 2+O((1-\kappa^2)\log(1-\kappa^2)), \end{equation}$$

(B.3)

which is derived using Mathematica.⁴ Here, |$1-\kappa^2$| is approximated as |$1-\kappa^2 \approx {\tilde{\rho}^2}/{4R^2}$|⁠, and then we have

$$\begin{equation} \varPsi \ \approx\ -\frac{GM}{2\pi R}\log\left(\frac{\tilde{\rho}}{8R}\right). \end{equation}$$

(B.4)

From the formulae presented in Appendix A, the two-dimensional Ricci scalar |${}^{(2)}R$| is ignored because |${}^{(2)}R\ll O(\varPsi^{-4}\rho_0^{-2})$| holds, where |$\varPsi^{-4}\rho_0^{-2}$| is the order of |$k_1^2$| and |$k_1k_2$|⁠. Equations (A.7a) and (A.7b) for |$C$| and |$D$|⁠, which are related to |$k_1$| and |$k_2$| through Eqs. (A.6a) and (A.6b), are approximated as

$$\begin{eqnarray} C&\approx& -h - 2\frac{\varPsi_{,\tilde{\rho}}}{\varPsi}h^2 \ \approx\ -\rho_0\left[1+\frac{2}{\log({\rho_0}/{8R})}\right], \\ \end{eqnarray}$$

(B.5)

$$\begin{eqnarray} D&\approx& 2\frac{\varPsi_{,\tilde{\rho}}}{\varPsi}h ^2 \ \approx\ \frac{2\rho_0}{\log({\rho_0}/{8R})}. \end{eqnarray}$$

(B.6)

We now solve for marginally DTT tori and marginally trapped tori.

Appendix B.1. Marginally DTT tori

$$\begin{equation} \rho_0 \ \approx\ 8\exp(-6) R \ \approx\ 0.01983\times R, \end{equation}$$

(B.7)

and hence a solution consistent with the assumption |$\rho_0\ll R$| is obtained. Let us compare this result with the numerically obtained data. For the parameter |$R/M = 1.0\times 10^{-3}$|⁠, the numerical result shows that the radius takes values in the range |$1.974\times 10^{-5} \lesssim h(\tilde{\xi})/M\lesssim 2.014\times 10^{-5}$| due to the angular dependence of |$h(\tilde{\xi})$|⁠. This is consistent with the radius from the approximation, |$\rho_0/M\approx 1.983\times 10^{-5}$|⁠.

Appendix B.1. Marginally trapped tori

The equation for marginally trapped tori is |$k_1+k_2=0$|⁠, and this is equivalent to |$C\approx D$|⁠. Solving this equation, we have

$$\begin{equation} \rho_0 = 8\exp(-4) R \ \approx\ 0.1465\times R. \end{equation}$$

(B.8)

Although the value of |$\rho_0/R$| is relatively large and the approximation may not be very good, let us proceed further. For the parameter |$R/M = 1.0\times 10^{-3}$|⁠, the numerical result shows that the radius takes values in the range |$1.359\times 10^{-4} \lesssim h(\tilde{\xi})/M\lesssim 1.570\times 10^{-4}$|⁠, which is consistent with the radius from the approximation, |$\rho_0/M\approx 1.465\times 10^{-4}$|⁠.

Footnotes

¹ See also Refs. [40, 47–49] for proposals on variants of the hoop conjecture. There is a debate on the proposal of Refs. [40,48,49]: see Ref. [50].

² See also Refs. [58,59] for studies on the hoop conjecture with the Brown–York quasilocal mass, |$M_{\rm BY}$| [60]. In this case, the hoop conjecture takes the form |$\mathcal{C}\lesssim 2\pi GM_{\rm BY}$| due to the property of the Brown–York mass.

³ In Ref. [24], the existence of an extremely oblate apparent horizon up to |$R/GM\lesssim 0.70$| is reported. In 2001, H.Y. privately communicated with Takeshi Chiba, one of the authors of Ref. [24], and we agreed that the extremely oblate apparent horizon could be a numerical artifact that appears when the resolution is not sufficient. We also agreed on the maximum value of |$R/GM$| for the existence of an apparent horizon.

⁴ We have also rigorously proved this relation through calculations by hand.

References

[1]

Akiyama

et al. [Event Horizon Telescope Collaboration],

Astrophys. J.

875

(

2019

) [arXiv:1906.11238 [astro-ph.GA]] [Search inSPIRE]. (

http://dx.doi.org/10.3847/2041-8213/ab0ec7

)

Month:	Total Views:
May 2020	78
June 2020	52
July 2020	63
August 2020	42
September 2020	20
October 2020	26
November 2020	22
December 2020	11
January 2021	21
February 2021	12
March 2021	18
April 2021	22
May 2021	10
June 2021	5
July 2021	18
August 2021	12
September 2021	5
October 2021	12
November 2021	6
December 2021	2
January 2022	11
February 2022	12
March 2022	5
April 2022	8
May 2022	10
June 2022	3
July 2022	12
August 2022	14
September 2022	20
October 2022	12
November 2022	5
December 2022	20
January 2023	17
February 2023	6
March 2023	2
April 2023	14
May 2023	7
June 2023	3
July 2023	5
August 2023	3

Article Contents

Formation of dynamically transversely trapping surfaces and the stretched hoop conjecture

Abstract

1. Introduction

2. Dynamically transversely trapping surfaces

2.1. Definition

2.2. Time-symmetric case

3. Setups and the equation for marginally DTTSs

3.1. Setups of the systems

3.1.1. Two-black-hole initial data

3.1.2. Spindle initial data

3.1.3. Ring initial data

3.2. Method of solving for marginally DTTSs

3.2.1. Marginally DTT spheres

3.2.2. Marginally DTT/trapped tori

4. Stretched hoop conjecture

4.1. Description of the hoop conjecture

4.2. Examination of the stretched hoop conjecture

4.2.1. Two-black-hole initial data

4.2.2. Spindle initial data

4.2.3. Ring initial data

4.3. Summary of the numerical results

5. Further examination of the ring system

5.1. Marginally DTT tori

5.2. Marginally trapped tori

6. Summary and discussion

Acknowledgements

Appendix A. Equations for marginally DTT/trapped tori in ring initial data

Appendix A.1. Marginally DTT tori with |$k_1\le k_2$|

Appendix A.2. Marginally DTT tori with |$k_1\ge k_2$|

Appendix A.3. Marginally trapped tori

Appendix B. Approximate analysis of marginally DTT/trapped tori

Appendix B.1. Marginally DTT tori

Appendix B.1. Marginally trapped tori

Footnotes

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only