-
PDF
- Split View
-
Views
-
Cite
Cite
C Watanabe, K Yanase, N Yoshinaga, Searching optimum equations of state of neutron star matter in strong magnetic fields with rotation, Progress of Theoretical and Experimental Physics, Volume 2020, Issue 10, October 2020, 103E04, https://doi.org/10.1093/ptep/ptaa134
Close - Share Icon Share
Abstract
Masses and radii of neutron stars are obtained in the presence of strong magnetic fields together with rotation. Mass-radius relations are calculated using 11 equations of state (EoSs: GM1, TM1-a, TM1-b, TM2|$\omega\rho$|-a, TM2|$\omega\rho$|-b, NL3-a, NL3-b, NL3|$\omega\rho$|-a, NL3|$\omega\rho$|-b, DDME2-a and DDME2-b) in relativistic mean field (RMF) theory. Obtained masses are over and around twice the solar mass (|$M_\odot$|) for all EoSs in the presence of strong magnetic fields of |$3 \times 10^{18}$| G at the center. For NL3|$\omega\rho$|-a and NL3|$\omega\rho$|-b EoSs, masses are more than |$M=2.17\,M_\odot$|(observed maximum mass: |$2.14\,M_\odot$|) even without magnetic fields. Rotational effects are found to be insignificant in any case, at least up to the Kepler frequency. Suitable EoSs are also selected concerning the constraint on the radius of a neutron star.
1. Introduction
The possible range of values for mass and radius of a neutron star has been one of the main themes in the study of neutron stars since their discovery. In 1939, Oppenheimer and Volkoff (and, independently, Tolman) applied the Einstein equation to a neutron star and calculated numerically its mass in a non-interacting, strongly degenerate relativistic gas of neutrons [1,2]. They calculated its mass to show that stable static neutron stars have a maximum mass |$M_{max} \sim 0.71\, M_\odot$|; the so-called the Oppenheimer–Volkoff mass limit. Cameron showed that the inclusion of the nuclear force can considerably stiffen the equation of state (EoS) [3]. This inclusion can increase the maximum mass of the Oppenheimer–Volkoff limit to about |$2M_\odot$|. The Brueckner–Bethe–Goldstone (BBG) theory, formulated in 1954–1965, is a successful application of field-theoretical methods to strongly interacting many-body systems. Strong repulsive nuclear forces (two-body or three-body) have been found to be necessary to explain maximum masses of neutron stars within the nucleon’s degrees of freedom. Recently, some advanced studies use microscopic EOSs based on the Brueckner–Hartree–Fock (BHF) many-body theory with realistic two- or three-body nucleonic forces [4,5] and also those EOSs based on lowest order constrained variational (LOCV) many-body theory [6].
Massive neutron stars can be easily described if neutron star matter consists of only nucleons and some varieties of leptons. However, hyperons should appear naturally in the high-density region of a neutron star, where its central density is several times higher than the nuclear saturation density. The appearance of hyperons softens the EoS of neutron star matter, and makes it difficult to explain the presence of the massive neutron stars with mass twice the solar mass |$M_\odot$|. This problem is referred to as the hyperon puzzle.
In 2010, the neutron star PSR J1614-2230 forming a binary system with a white dwarf was discovered, whose observed mass is |$1.97\pm 0.04\,M_\odot$| [7]. In 2013, the neutron star PSR J0348+0432 with a mass of |$2.01\pm 0.04\,M_\odot$| was observed, and the existence of neutron stars that have masses twice the solar mass is now established beyond doubt [8]. In a recent observation in 2019, the mass of the millisecond pulsar (MSP) J0740+6620 was measured to be |$2.14^{+ 0.10}_{- 0.09}\,M_\odot$| [9]. Such very heavy neutron stars impose a strong condition on EoSs. Furthermore, there exist strong magnetized neutron stars, called magnetars, which have a magnetic field of about |$2\times10^{15}$| G on the surface [10]. Thus, the mass of a neutron star should be explained in the presence of strong magnetic fields. In observations, a millisecond magnetar is considered as a target of the future gravitational wave detections [11,12]. Also, the short gamma-ray burst event GRB051221A is believed to be a millisecond magnetar [13].
In our previous study [14], the mass–radius relation (MR relation) of deformed neutron stars in the axially symmetric poloidal magnetic field was calculated. The MR relations were obtained by solving the Hartle equations [15–19], whereas those for spherical stars were obtained by the Tolman–Oppenheimer–Volkoff (TOV) equations. The anisotropic effects of the poloidal magnetic fields were found to be non-negligible for a strong magnetic field of more than |$3\times10^{18}$| G at the center of a neutron star. In the present study rotation is also considered in addition to the strong magnetic fields. In this study rotation makes a neutron star deformed, but unlike the previous study the deformation is only caused by rotation, not by strong magnetic fields.
Observed radii of neutron stars set a stringent condition on the EoS. The neutron star radius |$R$| now has an upper limit of |$R = 13.6\,$|km at |$M =1.4\, M_\odot$|, which is derived from the observation of the GW170817 gravitational wave event [20]. In this study, 11 EoSs— GM1 [21], TM1-a, TM1-b, TM2|$\omega\rho$|-a, TM2|$\omega\rho$|-b, NL3-a, NL3-b, NL3|$\omega\rho$|-a, NL3|$\omega\rho$|-b, DDME2-a and DDME2-b [22]— are employed, which include hyperons in addition to nucleons as components. The MR relations of the 11 EoSs are each compared with GM1 EoS as a reference. TM1 and TM2 are different concerning the slope parameter |$L$|, where |$L$| is closely related to the radius of a neutron star. The NL3 parametrization is fitted to the ground-state properties of both stable and unstable nuclei. This parametrization predicts very large, purely nucleonic neutron star maximum masses, but a symmetry energy slope parameter |$L$| is too large. Thus, we also consider the parametrization NL3|$\omega\rho$| with a softer density dependence of the symmetry energy due to the inclusion of the nonlinear |$\omega\rho$| term.
This paper is organized as follows. Section 2 provides the formulation of the relativistic mean field theory and basic properties of obtained EoSs. Section 3 gives the results of our study. Discussions are given in Sect. 4. Finally, a summary is given in Sect. 5.
2. Formulations
2.1. Equations of state
Here, |$ \boldsymbol{ \tau } / 2 $| represents the isospin operator and |$\sigma_{ \mu \nu } = { i }/{ 2 }\left[ \gamma_{ \mu }, \gamma_{ \nu } \right]$|, where |$\gamma_{ \mu }$| is the Dirac |$\gamma$| matrix. Characters in bold font represent isovector fields. The baryon octet |$\{p,n,\Lambda,\Sigma^{0},\Sigma^{\pm},\Xi^{0},\Xi^{-}\}$|, the electron (|$0.511$| MeV), the muon (|$105.7$| MeV), and the tauon (|$1777$| MeV) are considered for fermions [29]. For mesons, the scalar-meson |$\sigma$|, the vector-meson |$\omega$|, and the vector-isovector-meson |$\boldsymbol{\rho}$| with masses of |$m_{ \sigma } = 511.198$| MeV, |$m_{ \omega } = 783.0$| MeV, and |$m_{ \rho } = 770.0$| MeV, and hidden-strangeness mesons |$\sigma^{*}$| and |$\phi$|, with masses of |$m_{ \sigma^* } = 975$| MeV and |$m_{ \phi } = 1020$| MeV, are introduced. The coupling constants of nucleons with these mesons, |$g_{\sigma N}$|, |$g_{\omega N}$|, and |$g_{\rho N}$|, and some self-interactions among mesons are determined by fitting the physical quantities at the saturation density [21,23,24]. The obtained values are listed in Table 1.
| . | GM1 [21] . | TM1 [25] . | TM2|$\omega \rho$| [30] . | NL3 [31] . | NL3|$\omega \rho$| [32] . | DDME2 [33] . |
|---|---|---|---|---|---|---|
| |$g_{\sigma N}$| | 8.895 | 10.03 | 9.998 | 10.22 | 10.22 | 10.54 |
| |$g_{\omega N}$| | 10.61 | 12.61 | 12.50 | 12.87 | 12.87 | 13.02 |
| |$g_{\rho N}$| | 8.195 | 9.264 | 11.30 | 8.948 | 11.28 | 7.367 |
| |$b\times 10^{3}$| | 2.947 | 1.508 | 1.763 | 1.028 | 1.028 | 0 |
| |$c\times 10^{3}$| | -1.070 | 0.061 | -0.790 | -0.442 | -0.442 | 0 |
| |$\xi$| | 0 | 0.0169 | 0.0113 | 0 | 0 | 0 |
| |$\Lambda_{ \omega }$| | 0 | 0 | 0.03 | 0 | 0.03 | 0 |
| . | GM1 [21] . | TM1 [25] . | TM2|$\omega \rho$| [30] . | NL3 [31] . | NL3|$\omega \rho$| [32] . | DDME2 [33] . |
|---|---|---|---|---|---|---|
| |$g_{\sigma N}$| | 8.895 | 10.03 | 9.998 | 10.22 | 10.22 | 10.54 |
| |$g_{\omega N}$| | 10.61 | 12.61 | 12.50 | 12.87 | 12.87 | 13.02 |
| |$g_{\rho N}$| | 8.195 | 9.264 | 11.30 | 8.948 | 11.28 | 7.367 |
| |$b\times 10^{3}$| | 2.947 | 1.508 | 1.763 | 1.028 | 1.028 | 0 |
| |$c\times 10^{3}$| | -1.070 | 0.061 | -0.790 | -0.442 | -0.442 | 0 |
| |$\xi$| | 0 | 0.0169 | 0.0113 | 0 | 0 | 0 |
| |$\Lambda_{ \omega }$| | 0 | 0 | 0.03 | 0 | 0.03 | 0 |
| . | GM1 [21] . | TM1 [25] . | TM2|$\omega \rho$| [30] . | NL3 [31] . | NL3|$\omega \rho$| [32] . | DDME2 [33] . |
|---|---|---|---|---|---|---|
| |$g_{\sigma N}$| | 8.895 | 10.03 | 9.998 | 10.22 | 10.22 | 10.54 |
| |$g_{\omega N}$| | 10.61 | 12.61 | 12.50 | 12.87 | 12.87 | 13.02 |
| |$g_{\rho N}$| | 8.195 | 9.264 | 11.30 | 8.948 | 11.28 | 7.367 |
| |$b\times 10^{3}$| | 2.947 | 1.508 | 1.763 | 1.028 | 1.028 | 0 |
| |$c\times 10^{3}$| | -1.070 | 0.061 | -0.790 | -0.442 | -0.442 | 0 |
| |$\xi$| | 0 | 0.0169 | 0.0113 | 0 | 0 | 0 |
| |$\Lambda_{ \omega }$| | 0 | 0 | 0.03 | 0 | 0.03 | 0 |
| . | GM1 [21] . | TM1 [25] . | TM2|$\omega \rho$| [30] . | NL3 [31] . | NL3|$\omega \rho$| [32] . | DDME2 [33] . |
|---|---|---|---|---|---|---|
| |$g_{\sigma N}$| | 8.895 | 10.03 | 9.998 | 10.22 | 10.22 | 10.54 |
| |$g_{\omega N}$| | 10.61 | 12.61 | 12.50 | 12.87 | 12.87 | 13.02 |
| |$g_{\rho N}$| | 8.195 | 9.264 | 11.30 | 8.948 | 11.28 | 7.367 |
| |$b\times 10^{3}$| | 2.947 | 1.508 | 1.763 | 1.028 | 1.028 | 0 |
| |$c\times 10^{3}$| | -1.070 | 0.061 | -0.790 | -0.442 | -0.442 | 0 |
| |$\xi$| | 0 | 0.0169 | 0.0113 | 0 | 0 | 0 |
| |$\Lambda_{ \omega }$| | 0 | 0 | 0.03 | 0 | 0.03 | 0 |
In the b-parameter sets (TM1-b, TM2|$\omega \rho$|-b, NL3-b, NL3|$\omega\rho$|-b and DDME2-b), |$R_{ \omega \Lambda } = 1$| is adopted, which corresponds to a symmetry breaking of the SU(6) symmetry. The values of hyperon potentials in symmetric nuclear matter, |$U^{ N }_{ \Lambda } = - 30$| MeV, |$U^{ N }_{ \Sigma } = 0$| MeV, and |$U^{ N }_{ \Xi } = -14$| MeV [22] are used to determine the value of |$R_{\sigma h}$|. Thus, ratios of the |$\sigma$|–|$\Lambda$| coupling, the |$\sigma$|–|$\Sigma$| coupling and the |$\sigma$|–|$\Xi$| coupling in EoS parameter sets except GM1 are adopted as in Table 2.
Adopted ratios of |$\sigma$|–|$\Lambda$| coupling, |$\sigma$|–|$\Sigma$| coupling and |$\sigma$|–|$\Xi$| coupling in EoS parameter sets.
| EoS . | |$R_{ \sigma \Lambda}$| . | |$R_{ \sigma \Sigma}$| . | |$R_{ \sigma \Xi}$| . |
|---|---|---|---|
| TM1-a | 0.64 | 0.56 | 0.32 |
| TM1-b | 0.91 | 0.56 | 0.32 |
| TM2|$\omega \rho$|-a | 0.64 | 0.55 | 0.32 |
| TM2|$\omega \rho$|-b | 0.93 | 0.55 | 0.32 |
| NL3-a | 0.67 | 0.59 | 0.33 |
| NL3-b | 0.97 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-a | 0.67 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-b | 0.97 | 0.59 | 0.33 |
| DDME2-a | 0.69 | 0.60 | 0.34 |
| DDME2-b | 0.98 | 0.60 | 0.34 |
| EoS . | |$R_{ \sigma \Lambda}$| . | |$R_{ \sigma \Sigma}$| . | |$R_{ \sigma \Xi}$| . |
|---|---|---|---|
| TM1-a | 0.64 | 0.56 | 0.32 |
| TM1-b | 0.91 | 0.56 | 0.32 |
| TM2|$\omega \rho$|-a | 0.64 | 0.55 | 0.32 |
| TM2|$\omega \rho$|-b | 0.93 | 0.55 | 0.32 |
| NL3-a | 0.67 | 0.59 | 0.33 |
| NL3-b | 0.97 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-a | 0.67 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-b | 0.97 | 0.59 | 0.33 |
| DDME2-a | 0.69 | 0.60 | 0.34 |
| DDME2-b | 0.98 | 0.60 | 0.34 |
Adopted ratios of |$\sigma$|–|$\Lambda$| coupling, |$\sigma$|–|$\Sigma$| coupling and |$\sigma$|–|$\Xi$| coupling in EoS parameter sets.
| EoS . | |$R_{ \sigma \Lambda}$| . | |$R_{ \sigma \Sigma}$| . | |$R_{ \sigma \Xi}$| . |
|---|---|---|---|
| TM1-a | 0.64 | 0.56 | 0.32 |
| TM1-b | 0.91 | 0.56 | 0.32 |
| TM2|$\omega \rho$|-a | 0.64 | 0.55 | 0.32 |
| TM2|$\omega \rho$|-b | 0.93 | 0.55 | 0.32 |
| NL3-a | 0.67 | 0.59 | 0.33 |
| NL3-b | 0.97 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-a | 0.67 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-b | 0.97 | 0.59 | 0.33 |
| DDME2-a | 0.69 | 0.60 | 0.34 |
| DDME2-b | 0.98 | 0.60 | 0.34 |
| EoS . | |$R_{ \sigma \Lambda}$| . | |$R_{ \sigma \Sigma}$| . | |$R_{ \sigma \Xi}$| . |
|---|---|---|---|
| TM1-a | 0.64 | 0.56 | 0.32 |
| TM1-b | 0.91 | 0.56 | 0.32 |
| TM2|$\omega \rho$|-a | 0.64 | 0.55 | 0.32 |
| TM2|$\omega \rho$|-b | 0.93 | 0.55 | 0.32 |
| NL3-a | 0.67 | 0.59 | 0.33 |
| NL3-b | 0.97 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-a | 0.67 | 0.59 | 0.33 |
| NL3|$\omega \rho$|-b | 0.97 | 0.59 | 0.33 |
| DDME2-a | 0.69 | 0.60 | 0.34 |
| DDME2-b | 0.98 | 0.60 | 0.34 |
An empirical value of the binding energy in double-|$\Lambda$| hypernuclei |$\Delta B = 0.50$| MeV is employed for adjusting the coupling of |$\Lambda$| hyperon with the |$\sigma^{*}$| meson to get |$R_{\sigma^* \Lambda} = 1$| [22]. Due to the absence of information for the double-|$\Sigma$| and double-|$\Xi$| hypernuclei, the coupling of the |$\Sigma$| and |$\Xi$| hyperons with the |$\sigma^*$| meson are fixed to zero: |$R_{\sigma^* \Sigma} = R_{\sigma^* \Xi}=0$|.
Masses and charges of the baryon octet are given in Table 3. The experimental values of the anomalous magnetic moments (AMMs) defined by |$\kappa_{b}=\mu_{b}/\mu_{N}-\text{sgn}(q_{b})\,m_{p}/m_{b}$| for baryons are also given. Some of their nuclear properties as well as predictions for the neutron star maximum mass are presented in Table 4.
Baryon masses (|$m_{b}$|) in units of MeV, anomalous magnetic moments (|$\kappa_{b}$|), and electric charges (|$q_{b}$|) for the baryon octet. |$\kappa_{b}$| is defined as |$\kappa_{b}=\mu_{b}/\mu_{N}-\text{sgn}(q_{b})\,m_{p}/m_{b}$| where |$\mu_{N}$| is the nuclear magneton [29].
| . | |$p$| . | |$n$| . | |$\Lambda$| . | |$\Sigma^{+}$| . | |$\Sigma^{0}$| . | |$\Sigma^{-}$| . | |$\Xi^{0}$| . | |$\Xi^{-}$| . |
|---|---|---|---|---|---|---|---|---|
| |$m_{b}$| | |$938.3$| | |$939.6$| | |$1116$| | |$1189$| | |$1193$| | |$1197$| | |$1315$| | |$1322$| |
| |$\kappa_{b}$| | |$1.79$| | |$-1.91$| | |$-0.61$| | |$1.67$| | |$1.61$| | |$-0.38$| | |$-1.25$| | |$0.06$| |
| |$q_{b}$| | |$+1$| | |$0$| | |$0$| | |$+1$| | |$0$| | |$-1$| | |$0$| | |$-1$| |
| . | |$p$| . | |$n$| . | |$\Lambda$| . | |$\Sigma^{+}$| . | |$\Sigma^{0}$| . | |$\Sigma^{-}$| . | |$\Xi^{0}$| . | |$\Xi^{-}$| . |
|---|---|---|---|---|---|---|---|---|
| |$m_{b}$| | |$938.3$| | |$939.6$| | |$1116$| | |$1189$| | |$1193$| | |$1197$| | |$1315$| | |$1322$| |
| |$\kappa_{b}$| | |$1.79$| | |$-1.91$| | |$-0.61$| | |$1.67$| | |$1.61$| | |$-0.38$| | |$-1.25$| | |$0.06$| |
| |$q_{b}$| | |$+1$| | |$0$| | |$0$| | |$+1$| | |$0$| | |$-1$| | |$0$| | |$-1$| |
Baryon masses (|$m_{b}$|) in units of MeV, anomalous magnetic moments (|$\kappa_{b}$|), and electric charges (|$q_{b}$|) for the baryon octet. |$\kappa_{b}$| is defined as |$\kappa_{b}=\mu_{b}/\mu_{N}-\text{sgn}(q_{b})\,m_{p}/m_{b}$| where |$\mu_{N}$| is the nuclear magneton [29].
| . | |$p$| . | |$n$| . | |$\Lambda$| . | |$\Sigma^{+}$| . | |$\Sigma^{0}$| . | |$\Sigma^{-}$| . | |$\Xi^{0}$| . | |$\Xi^{-}$| . |
|---|---|---|---|---|---|---|---|---|
| |$m_{b}$| | |$938.3$| | |$939.6$| | |$1116$| | |$1189$| | |$1193$| | |$1197$| | |$1315$| | |$1322$| |
| |$\kappa_{b}$| | |$1.79$| | |$-1.91$| | |$-0.61$| | |$1.67$| | |$1.61$| | |$-0.38$| | |$-1.25$| | |$0.06$| |
| |$q_{b}$| | |$+1$| | |$0$| | |$0$| | |$+1$| | |$0$| | |$-1$| | |$0$| | |$-1$| |
| . | |$p$| . | |$n$| . | |$\Lambda$| . | |$\Sigma^{+}$| . | |$\Sigma^{0}$| . | |$\Sigma^{-}$| . | |$\Xi^{0}$| . | |$\Xi^{-}$| . |
|---|---|---|---|---|---|---|---|---|
| |$m_{b}$| | |$938.3$| | |$939.6$| | |$1116$| | |$1189$| | |$1193$| | |$1197$| | |$1315$| | |$1322$| |
| |$\kappa_{b}$| | |$1.79$| | |$-1.91$| | |$-0.61$| | |$1.67$| | |$1.61$| | |$-0.38$| | |$-1.25$| | |$0.06$| |
| |$q_{b}$| | |$+1$| | |$0$| | |$0$| | |$+1$| | |$0$| | |$-1$| | |$0$| | |$-1$| |
Nuclear properties at saturation number density [|$\rho$| (fm|$^{-3}$|)] predicted by 6 kinds of EoSs used in this study [22,34]: energy per nucleon [|$B/A$| (MeV)], incompressibility [|$K$| (MeV)], symmetry energy [|$J$| (MeV)], its slope parameter [|$L$| (MeV)], and curvature [|$K_{sym}$| (MeV)] at the saturation point of uniform symmetric nuclear matter [35].
| . | GM1 . | TM1 . | TM2|$\omega \rho$| . | NL3 . | NL3|$\omega \rho$| . | DDME2 . |
|---|---|---|---|---|---|---|
| |$\rho$| | 0.154 | 0.146 | 0.146 | 0.148 | 0.148 | 0.152 |
| |$B/A$| | -16.3 | -16.3 | -16.4 | -16.30 | -16.30 | -16.14 |
| |$K$| | 300.7 | 281.2 | 281.7 | 271.8 | 271.8 | 250.9 |
| |$J$| | 32.5 | 36.9 | 32.1 | 37.4 | 31.7 | 32.3 |
| |$L$| | 94.4 | 111.2 | 54.8 | 118.9 | 55.5 | 51.2 |
| |$K_{sym}$| | 18.1 | 33.8 | -70.5 | 101.6 | -7.6 | -87.1 |
| . | GM1 . | TM1 . | TM2|$\omega \rho$| . | NL3 . | NL3|$\omega \rho$| . | DDME2 . |
|---|---|---|---|---|---|---|
| |$\rho$| | 0.154 | 0.146 | 0.146 | 0.148 | 0.148 | 0.152 |
| |$B/A$| | -16.3 | -16.3 | -16.4 | -16.30 | -16.30 | -16.14 |
| |$K$| | 300.7 | 281.2 | 281.7 | 271.8 | 271.8 | 250.9 |
| |$J$| | 32.5 | 36.9 | 32.1 | 37.4 | 31.7 | 32.3 |
| |$L$| | 94.4 | 111.2 | 54.8 | 118.9 | 55.5 | 51.2 |
| |$K_{sym}$| | 18.1 | 33.8 | -70.5 | 101.6 | -7.6 | -87.1 |
Nuclear properties at saturation number density [|$\rho$| (fm|$^{-3}$|)] predicted by 6 kinds of EoSs used in this study [22,34]: energy per nucleon [|$B/A$| (MeV)], incompressibility [|$K$| (MeV)], symmetry energy [|$J$| (MeV)], its slope parameter [|$L$| (MeV)], and curvature [|$K_{sym}$| (MeV)] at the saturation point of uniform symmetric nuclear matter [35].
| . | GM1 . | TM1 . | TM2|$\omega \rho$| . | NL3 . | NL3|$\omega \rho$| . | DDME2 . |
|---|---|---|---|---|---|---|
| |$\rho$| | 0.154 | 0.146 | 0.146 | 0.148 | 0.148 | 0.152 |
| |$B/A$| | -16.3 | -16.3 | -16.4 | -16.30 | -16.30 | -16.14 |
| |$K$| | 300.7 | 281.2 | 281.7 | 271.8 | 271.8 | 250.9 |
| |$J$| | 32.5 | 36.9 | 32.1 | 37.4 | 31.7 | 32.3 |
| |$L$| | 94.4 | 111.2 | 54.8 | 118.9 | 55.5 | 51.2 |
| |$K_{sym}$| | 18.1 | 33.8 | -70.5 | 101.6 | -7.6 | -87.1 |
| . | GM1 . | TM1 . | TM2|$\omega \rho$| . | NL3 . | NL3|$\omega \rho$| . | DDME2 . |
|---|---|---|---|---|---|---|
| |$\rho$| | 0.154 | 0.146 | 0.146 | 0.148 | 0.148 | 0.152 |
| |$B/A$| | -16.3 | -16.3 | -16.4 | -16.30 | -16.30 | -16.14 |
| |$K$| | 300.7 | 281.2 | 281.7 | 271.8 | 271.8 | 250.9 |
| |$J$| | 32.5 | 36.9 | 32.1 | 37.4 | 31.7 | 32.3 |
| |$L$| | 94.4 | 111.2 | 54.8 | 118.9 | 55.5 | 51.2 |
| |$K_{sym}$| | 18.1 | 33.8 | -70.5 | 101.6 | -7.6 | -87.1 |
The RMF EoS is used to describe the denser region, where its number density is greater than the neutron drip density |$\rho_{\text{ND}}=2.51\times 10^{-4}\ \text{fm}^{-3}$|. The neutron drip density is predicted by the HFB-25 Brussels–Montreal nuclear mass model [36]. The neutron drip density might be changed in the presence of a strong magnetic field, but the MR relation of neutron stars is not so sensitive to the neutron drip density. In order to describe the lower-density region, the Baym–Pethick–Sutherland (BPS) EoS is used [37] with the atomic masses given in Ame2012 [38,39] and HFB-24 [40].
2.2. Magnetic fields
2.3. Hartle equations
3. Results
Figure 1 shows the total mass |$M$| (|$M_\odot$|) as a function of its radius (km) (MR relation) by solving the TOV equation without magnetic fields or rotation. The unstable region ([|$ {{\partial M\left( {{\varepsilon _c}} \right)}}]/{{\partial {\varepsilon _c}}} < 0 $|, where |$\varepsilon _c $| is the energy density at the center) is not shown for each EoS in the figure. It is seen that NL3-a, NL3-b, NL3|$\omega\rho$|-a, NL3|$\omega\rho$|-b, DDME2-a and DDME2-b EoSs surpass twice the solar mass. For each EoS, the maximum mass and the radius at |$M=1.4\,M_\odot$| are shown in Table 5.
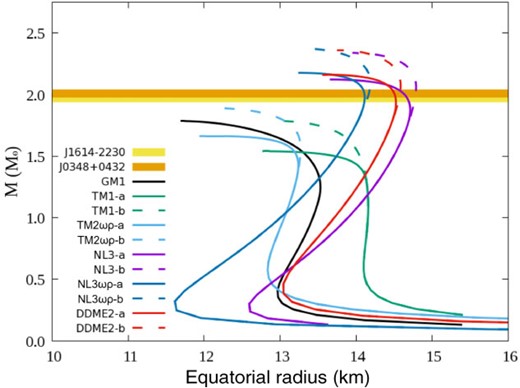
MR relations of 11 EoSs without magnetic fields or rotation. The unstable region in each EoS is not shown. The yellow solid line and orange solid line indicate pulsars PSR J1614-2230 and PSR J0348+0432, respectively. The colored lines represent the following: black (solid line); GM1 EoS, green (solid line); TM1-a EoS, green (dashed line); TM1-b EoS, light blue (solid line); TM2|$\omega \rho$|-a EoS, light blue (dashed line); TM2|$\omega \rho$|-b EoS, purple (solid line); NL3-a EoS, purple (dashed line); NL3-b EoS, dark blue (solid line); NL3|$\omega \rho$|-a EoS, dark blue (dashed line); NL3|$\omega \rho$|-b EoS, red (solid line); DDME2-a EoS, red (dashed line); DDME2-b EoS.
Maximum mass (|$M_{\rm{max}}$|) in units of |$M_\odot$| and radius (km) at |$M=1.4\,M_\odot$| (|$R_{1.4\,M_\odot}$|) for each EoS without magnetic fields or rotation.
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 1.784 | 13.49 |
| TM1-a | 1.540 | 14.07 |
| TM1-b | 1.787 | 14.10 |
| TM2|$\omega \rho$|-a | 1.663 | 13.24 |
| TM2|$\omega \rho$|-b | 1.891 | 13.23 |
| NL3-a | 2.122 | 14.35 |
| NL3-b | 2.336 | 14.35 |
| NL3|$\omega \rho$|-a | 2.175 | 13.49 |
| NL3|$\omega \rho$|-b | 2.372 | 13.49 |
| DDME2-a | 2.161 | 14.08 |
| DDME2-b | 2.360 | 14.08 |
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 1.784 | 13.49 |
| TM1-a | 1.540 | 14.07 |
| TM1-b | 1.787 | 14.10 |
| TM2|$\omega \rho$|-a | 1.663 | 13.24 |
| TM2|$\omega \rho$|-b | 1.891 | 13.23 |
| NL3-a | 2.122 | 14.35 |
| NL3-b | 2.336 | 14.35 |
| NL3|$\omega \rho$|-a | 2.175 | 13.49 |
| NL3|$\omega \rho$|-b | 2.372 | 13.49 |
| DDME2-a | 2.161 | 14.08 |
| DDME2-b | 2.360 | 14.08 |
Maximum mass (|$M_{\rm{max}}$|) in units of |$M_\odot$| and radius (km) at |$M=1.4\,M_\odot$| (|$R_{1.4\,M_\odot}$|) for each EoS without magnetic fields or rotation.
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 1.784 | 13.49 |
| TM1-a | 1.540 | 14.07 |
| TM1-b | 1.787 | 14.10 |
| TM2|$\omega \rho$|-a | 1.663 | 13.24 |
| TM2|$\omega \rho$|-b | 1.891 | 13.23 |
| NL3-a | 2.122 | 14.35 |
| NL3-b | 2.336 | 14.35 |
| NL3|$\omega \rho$|-a | 2.175 | 13.49 |
| NL3|$\omega \rho$|-b | 2.372 | 13.49 |
| DDME2-a | 2.161 | 14.08 |
| DDME2-b | 2.360 | 14.08 |
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 1.784 | 13.49 |
| TM1-a | 1.540 | 14.07 |
| TM1-b | 1.787 | 14.10 |
| TM2|$\omega \rho$|-a | 1.663 | 13.24 |
| TM2|$\omega \rho$|-b | 1.891 | 13.23 |
| NL3-a | 2.122 | 14.35 |
| NL3-b | 2.336 | 14.35 |
| NL3|$\omega \rho$|-a | 2.175 | 13.49 |
| NL3|$\omega \rho$|-b | 2.372 | 13.49 |
| DDME2-a | 2.161 | 14.08 |
| DDME2-b | 2.360 | 14.08 |
Maximum mass (|$M_{\rm{max}}$|) of a rotating neutron star in units of |$M_\odot$|, polar radius (|$R^p_{1.4\,M_\odot}$|) and equatorial radius (|$R^e_{1.4\,M_\odot}$|) at |$M=1.4\,M_\odot$|, and eccentricity (|$e$|), respectively, at |$\Omega=6\times10^{3}$| Hz (|$\Omega=0.02$| km|$^{-1}$| in gravitational units).
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 1.851 | 12.43 | 14.51 | 0.60 |
| TM1-a | 1.675 | 12.79 | 15.39 | 0.67 |
| TM1-b | 1.895 | 12.79 | 15.39 | 0.67 |
| TM2|$\omega \rho$|-a | 1.762 | 12.12 | 14.10 | 0.59 |
| TM2|$\omega \rho$|-b | 1.964 | 12.12 | 14.10 | 0.59 |
| NL3-a | 2.236 | 13.05 | 15.10 | 0.58 |
| NL3-b | 2.439 | 13.05 | 15.10 | 0.58 |
| NL3|$\omega \rho$|-a | 2.275 | 12.43 | 13.78 | 0.48 |
| NL3|$\omega \rho$|-b | 2.446 | 12.43 | 13.78 | 0.48 |
| DDME2-a | 2.273 | 13.06 | 15.05 | 0.57 |
| DDME2-b | 2.451 | 13.06 | 15.05 | 0.57 |
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 1.851 | 12.43 | 14.51 | 0.60 |
| TM1-a | 1.675 | 12.79 | 15.39 | 0.67 |
| TM1-b | 1.895 | 12.79 | 15.39 | 0.67 |
| TM2|$\omega \rho$|-a | 1.762 | 12.12 | 14.10 | 0.59 |
| TM2|$\omega \rho$|-b | 1.964 | 12.12 | 14.10 | 0.59 |
| NL3-a | 2.236 | 13.05 | 15.10 | 0.58 |
| NL3-b | 2.439 | 13.05 | 15.10 | 0.58 |
| NL3|$\omega \rho$|-a | 2.275 | 12.43 | 13.78 | 0.48 |
| NL3|$\omega \rho$|-b | 2.446 | 12.43 | 13.78 | 0.48 |
| DDME2-a | 2.273 | 13.06 | 15.05 | 0.57 |
| DDME2-b | 2.451 | 13.06 | 15.05 | 0.57 |
Maximum mass (|$M_{\rm{max}}$|) of a rotating neutron star in units of |$M_\odot$|, polar radius (|$R^p_{1.4\,M_\odot}$|) and equatorial radius (|$R^e_{1.4\,M_\odot}$|) at |$M=1.4\,M_\odot$|, and eccentricity (|$e$|), respectively, at |$\Omega=6\times10^{3}$| Hz (|$\Omega=0.02$| km|$^{-1}$| in gravitational units).
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 1.851 | 12.43 | 14.51 | 0.60 |
| TM1-a | 1.675 | 12.79 | 15.39 | 0.67 |
| TM1-b | 1.895 | 12.79 | 15.39 | 0.67 |
| TM2|$\omega \rho$|-a | 1.762 | 12.12 | 14.10 | 0.59 |
| TM2|$\omega \rho$|-b | 1.964 | 12.12 | 14.10 | 0.59 |
| NL3-a | 2.236 | 13.05 | 15.10 | 0.58 |
| NL3-b | 2.439 | 13.05 | 15.10 | 0.58 |
| NL3|$\omega \rho$|-a | 2.275 | 12.43 | 13.78 | 0.48 |
| NL3|$\omega \rho$|-b | 2.446 | 12.43 | 13.78 | 0.48 |
| DDME2-a | 2.273 | 13.06 | 15.05 | 0.57 |
| DDME2-b | 2.451 | 13.06 | 15.05 | 0.57 |
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 1.851 | 12.43 | 14.51 | 0.60 |
| TM1-a | 1.675 | 12.79 | 15.39 | 0.67 |
| TM1-b | 1.895 | 12.79 | 15.39 | 0.67 |
| TM2|$\omega \rho$|-a | 1.762 | 12.12 | 14.10 | 0.59 |
| TM2|$\omega \rho$|-b | 1.964 | 12.12 | 14.10 | 0.59 |
| NL3-a | 2.236 | 13.05 | 15.10 | 0.58 |
| NL3-b | 2.439 | 13.05 | 15.10 | 0.58 |
| NL3|$\omega \rho$|-a | 2.275 | 12.43 | 13.78 | 0.48 |
| NL3|$\omega \rho$|-b | 2.446 | 12.43 | 13.78 | 0.48 |
| DDME2-a | 2.273 | 13.06 | 15.05 | 0.57 |
| DDME2-b | 2.451 | 13.06 | 15.05 | 0.57 |
It is found that rotation has a small effect on mass even with the Kepler frequency (|$6\times10^{3}$| Hz).
Next, magnetic fields |$- { 1 }/{ 4 } F^{ \mu \nu } F_{ \mu \nu }$| in Eq. (5) are considered for the 11 EoSs by solving TOV equations in Eqs. (15) and (16). Figure 3 shows MR relations with magnetic fields. The magnetic field strength at the center is adopted as |$B_0 = 2.5 \times 10^{18}$| G. As shown in Fig. 3 and Table 7, GM1, TM1-b and TM2|$\omega\rho$|-b EoSs give masses greater than two solar masses. Moreover, considering the upper limit of |$R = 13.6$| km at 1.4 |$M_\odot$| [20], TM2|$\omega \rho$|-a and TM2|$\omega \rho$|-b EoSs are in the range of the observation with respect to radii. However, NL3-a, NL3-b, NL3|$\omega\rho$|-a, NL3|$\omega\rho$|-b, DDME2-a and DDME2-b EoSs are not in the range of the observation with respect to radius, but their masses surpass twice the two-solar-mass.
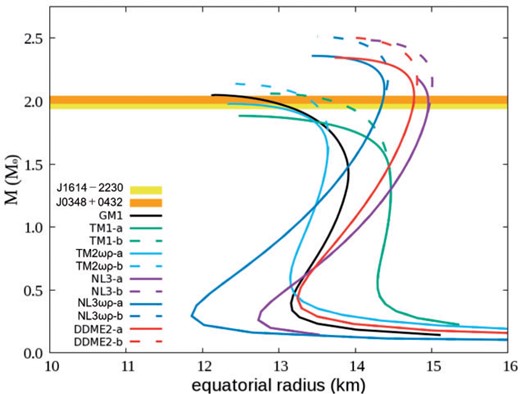
Same as Fig. 1, but with magnetic fields (|$B_0=2.5 \times 10^{18}$| G).
Same as Table 5, but with magnetic fields (|$B_0=2.5\times 10^{18}$| |$\rm{G}$|).
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.050 | 13.91 |
| TM1-a | 1.883 | 14.45 |
| TM1-b | 2.060 | 14.46 |
| TM2|$\omega \rho$|-a | 1.979 | 13.58 |
| TM2|$\omega \rho$|-b | 2.135 | 13.58 |
| NL3-a | 2.313 | 14.53 |
| NL3-b | 2.487 | 14.53 |
| NL3|$\omega \rho$|-a | 2.360 | 13.70 |
| NL3|$\omega \rho$|-b | 2.513 | 13.70 |
| DDME2-a | 2.345 | 14.50 |
| DDME2-b | 2.505 | 14.50 |
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.050 | 13.91 |
| TM1-a | 1.883 | 14.45 |
| TM1-b | 2.060 | 14.46 |
| TM2|$\omega \rho$|-a | 1.979 | 13.58 |
| TM2|$\omega \rho$|-b | 2.135 | 13.58 |
| NL3-a | 2.313 | 14.53 |
| NL3-b | 2.487 | 14.53 |
| NL3|$\omega \rho$|-a | 2.360 | 13.70 |
| NL3|$\omega \rho$|-b | 2.513 | 13.70 |
| DDME2-a | 2.345 | 14.50 |
| DDME2-b | 2.505 | 14.50 |
Same as Table 5, but with magnetic fields (|$B_0=2.5\times 10^{18}$| |$\rm{G}$|).
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.050 | 13.91 |
| TM1-a | 1.883 | 14.45 |
| TM1-b | 2.060 | 14.46 |
| TM2|$\omega \rho$|-a | 1.979 | 13.58 |
| TM2|$\omega \rho$|-b | 2.135 | 13.58 |
| NL3-a | 2.313 | 14.53 |
| NL3-b | 2.487 | 14.53 |
| NL3|$\omega \rho$|-a | 2.360 | 13.70 |
| NL3|$\omega \rho$|-b | 2.513 | 13.70 |
| DDME2-a | 2.345 | 14.50 |
| DDME2-b | 2.505 | 14.50 |
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.050 | 13.91 |
| TM1-a | 1.883 | 14.45 |
| TM1-b | 2.060 | 14.46 |
| TM2|$\omega \rho$|-a | 1.979 | 13.58 |
| TM2|$\omega \rho$|-b | 2.135 | 13.58 |
| NL3-a | 2.313 | 14.53 |
| NL3-b | 2.487 | 14.53 |
| NL3|$\omega \rho$|-a | 2.360 | 13.70 |
| NL3|$\omega \rho$|-b | 2.513 | 13.70 |
| DDME2-a | 2.345 | 14.50 |
| DDME2-b | 2.505 | 14.50 |
For the |$B_0=3\times10^{18}$| G case, the results are shown in Fig. 4 and Table 8. All EoSs except TM1-a give masses greater than two solar masses. However, considering the upper limit of |$R = 13.6\,$|km at |$1.4\,M_\odot$|, no EoS is in the range of the observation concerning radius. Therefore, the central magnetic field strength should be smaller than |$B_0=3\times10^{18}$| G.
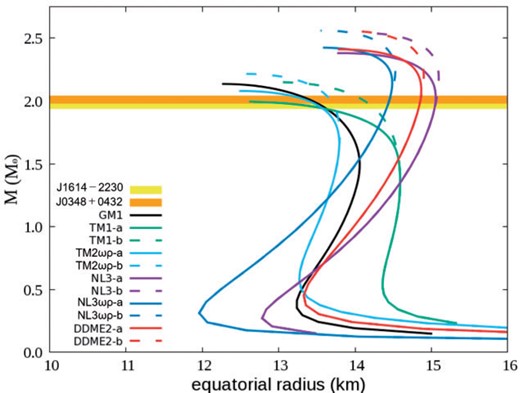
Same as Fig. 1, but with magnetic fields (|$B_0=3 \times 10^{18}$| G).
Same as Table 5, but with magnetic fields (|$B_0=3\times 10^{18}$| |$\rm{G}$|).
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.135 | 14.05 |
| TM1-a | 1.993 | 14.59 |
| TM1-b | 2.150 | 14.59 |
| TM2|$\omega \rho$|-a | 2.079 | 13.72 |
| TM2|$\omega \rho$|-b | 2.215 | 13.72 |
| NL3-a | 2.381 | 14.69 |
| NL3-b | 2.541 | 14.69 |
| NL3|$\omega \rho$|-a | 2.424 | 13.91 |
| NL3|$\omega \rho$|-b | 2.562 | 13.91 |
| DDME2-a | 2.410 | 14.44 |
| DDME2-b | 2.557 | 14.44 |
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.135 | 14.05 |
| TM1-a | 1.993 | 14.59 |
| TM1-b | 2.150 | 14.59 |
| TM2|$\omega \rho$|-a | 2.079 | 13.72 |
| TM2|$\omega \rho$|-b | 2.215 | 13.72 |
| NL3-a | 2.381 | 14.69 |
| NL3-b | 2.541 | 14.69 |
| NL3|$\omega \rho$|-a | 2.424 | 13.91 |
| NL3|$\omega \rho$|-b | 2.562 | 13.91 |
| DDME2-a | 2.410 | 14.44 |
| DDME2-b | 2.557 | 14.44 |
Same as Table 5, but with magnetic fields (|$B_0=3\times 10^{18}$| |$\rm{G}$|).
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.135 | 14.05 |
| TM1-a | 1.993 | 14.59 |
| TM1-b | 2.150 | 14.59 |
| TM2|$\omega \rho$|-a | 2.079 | 13.72 |
| TM2|$\omega \rho$|-b | 2.215 | 13.72 |
| NL3-a | 2.381 | 14.69 |
| NL3-b | 2.541 | 14.69 |
| NL3|$\omega \rho$|-a | 2.424 | 13.91 |
| NL3|$\omega \rho$|-b | 2.562 | 13.91 |
| DDME2-a | 2.410 | 14.44 |
| DDME2-b | 2.557 | 14.44 |
| EoS . | |$M_{\rm{max}}$| . | |$R_{1.4\,M_\odot}$| . |
|---|---|---|
| GM1 | 2.135 | 14.05 |
| TM1-a | 1.993 | 14.59 |
| TM1-b | 2.150 | 14.59 |
| TM2|$\omega \rho$|-a | 2.079 | 13.72 |
| TM2|$\omega \rho$|-b | 2.215 | 13.72 |
| NL3-a | 2.381 | 14.69 |
| NL3-b | 2.541 | 14.69 |
| NL3|$\omega \rho$|-a | 2.424 | 13.91 |
| NL3|$\omega \rho$|-b | 2.562 | 13.91 |
| DDME2-a | 2.410 | 14.44 |
| DDME2-b | 2.557 | 14.44 |
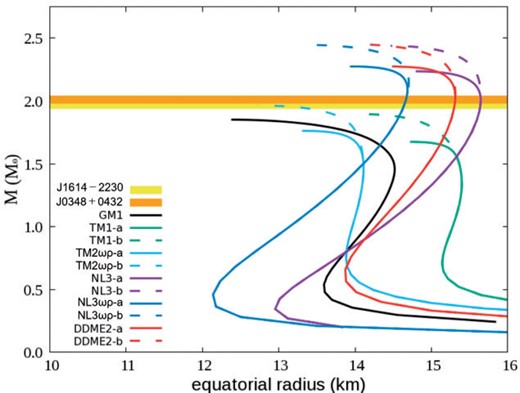
Finally, the MR relations are calculated in the presence of both rotation and magnetic fields. This case, with both rotation and magnetic fields, is considered here because of the emergency of a millisecond magnetar in the occasion of a neutron star merger [13]. The MR relations are shown in Fig. 5. Maximum masses of neutron stars, two kinds of radius and eccentricity with both rotation [|$\Omega=6\times10^{2}$| Hz (|$\Omega=0.002$| |$\rm{km}^{-1}$| in gravitational units)] and magnetic fields (|$B_0=2.5\times 10^{18}$| |$\rm{G}$|) are shown in Table 9.
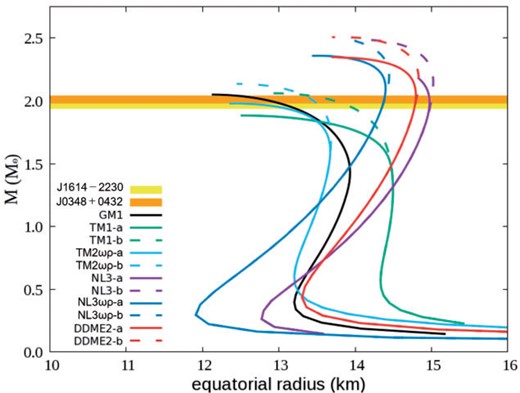
Same as Fig. 1, but with both rotation (|$\Omega=6\times10^{2}$| Hz) and magnetic fields (|$B_0=2.5\times10^{18}$| G).
Same as Table 6, but with both rotation (|$\Omega=6\times10^{2}$| Hz) and magnetic fields (|$B_0=2.5\times 10^{18}$| |$\rm{G}$|).
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 2.050 | 13.89 | 13.93 | 0.083 |
| TM1-a | 1.884 | 14.42 | 14.48 | 0.095 |
| TM1-b | 2.061 | 14.43 | 14.50 | 0.096 |
| TM2|$\omega \rho$|-a | 1.980 | 13.54 | 13.62 | 0.11 |
| TM2|$\omega \rho$|-b | 2.136 | 13.54 | 13.62 | 0.11 |
| NL3-a | 2.314 | 14.51 | 14.54 | 0.064 |
| NL3-b | 2.487 | 14.72 | 14.76 | 0.074 |
| NL3|$\omega \rho$|-a | 2.360 | 13.67 | 13.73 | 0.094 |
| NL3|$\omega \rho$|-b | 2.513 | 13.67 | 13.73 | 0.094 |
| DDME2-a | 2.346 | 14.23 | 14.31 | 0.11 |
| DDME2-b | 2.506 | 14.23 | 14.31 | 0.11 |
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 2.050 | 13.89 | 13.93 | 0.083 |
| TM1-a | 1.884 | 14.42 | 14.48 | 0.095 |
| TM1-b | 2.061 | 14.43 | 14.50 | 0.096 |
| TM2|$\omega \rho$|-a | 1.980 | 13.54 | 13.62 | 0.11 |
| TM2|$\omega \rho$|-b | 2.136 | 13.54 | 13.62 | 0.11 |
| NL3-a | 2.314 | 14.51 | 14.54 | 0.064 |
| NL3-b | 2.487 | 14.72 | 14.76 | 0.074 |
| NL3|$\omega \rho$|-a | 2.360 | 13.67 | 13.73 | 0.094 |
| NL3|$\omega \rho$|-b | 2.513 | 13.67 | 13.73 | 0.094 |
| DDME2-a | 2.346 | 14.23 | 14.31 | 0.11 |
| DDME2-b | 2.506 | 14.23 | 14.31 | 0.11 |
Same as Table 6, but with both rotation (|$\Omega=6\times10^{2}$| Hz) and magnetic fields (|$B_0=2.5\times 10^{18}$| |$\rm{G}$|).
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 2.050 | 13.89 | 13.93 | 0.083 |
| TM1-a | 1.884 | 14.42 | 14.48 | 0.095 |
| TM1-b | 2.061 | 14.43 | 14.50 | 0.096 |
| TM2|$\omega \rho$|-a | 1.980 | 13.54 | 13.62 | 0.11 |
| TM2|$\omega \rho$|-b | 2.136 | 13.54 | 13.62 | 0.11 |
| NL3-a | 2.314 | 14.51 | 14.54 | 0.064 |
| NL3-b | 2.487 | 14.72 | 14.76 | 0.074 |
| NL3|$\omega \rho$|-a | 2.360 | 13.67 | 13.73 | 0.094 |
| NL3|$\omega \rho$|-b | 2.513 | 13.67 | 13.73 | 0.094 |
| DDME2-a | 2.346 | 14.23 | 14.31 | 0.11 |
| DDME2-b | 2.506 | 14.23 | 14.31 | 0.11 |
| EoS . | |$M_{\rm{max}}$| . | |$R^p_{1.4\,M_\odot}$| . | |$R^e_{1.4\,M_\odot}$| . | |$e$| . |
|---|---|---|---|---|
| GM1 | 2.050 | 13.89 | 13.93 | 0.083 |
| TM1-a | 1.884 | 14.42 | 14.48 | 0.095 |
| TM1-b | 2.061 | 14.43 | 14.50 | 0.096 |
| TM2|$\omega \rho$|-a | 1.980 | 13.54 | 13.62 | 0.11 |
| TM2|$\omega \rho$|-b | 2.136 | 13.54 | 13.62 | 0.11 |
| NL3-a | 2.314 | 14.51 | 14.54 | 0.064 |
| NL3-b | 2.487 | 14.72 | 14.76 | 0.074 |
| NL3|$\omega \rho$|-a | 2.360 | 13.67 | 13.73 | 0.094 |
| NL3|$\omega \rho$|-b | 2.513 | 13.67 | 13.73 | 0.094 |
| DDME2-a | 2.346 | 14.23 | 14.31 | 0.11 |
| DDME2-b | 2.506 | 14.23 | 14.31 | 0.11 |
All 11 EoSs give masses greater than or around twice the solar mass in the presence of both rotation and magnetic fields. Again NL3-a, NL3-b, NL3|$\omega\rho$|-a, NL3|$\omega\rho$|-b, DDME2-a and DDME2-b EoSs surpass |$2.14\,M_\odot$| and meet the observation with respect to radius (|$R \leq 13.6\,$|km in |$1.4\,M_\odot$|).
4. Discussion
4.1. Rotation
Here we discuss how much rotation brings in the additional mass |$m_0$|. Here, TM2|$\omega\rho$|-b EoS is chosen for discussion. In Fig. 6, the maximum mass is expressed approximately as |$M/M_\odot=1.8932-3.619\times10^{-3}~\Omega+1.123\times10^{-3}~\Omega^2 $| up to the second order of |$\Omega$|, where the rotational frequency |$\Omega$| is given in units of Hz. If one wants to describe a neutron star with mass of |$2\,M_\odot$| only by rotation, one needs more than |$12000\,$|Hz frequency. However, the observed value of the maximum frequency is about |$700\,$|Hz (|$\Omega \sim 0.0015\,$|km|$^{-1}$| in gravitational units) so that |$\Omega = 12000\,$|Hz is unrealistic.
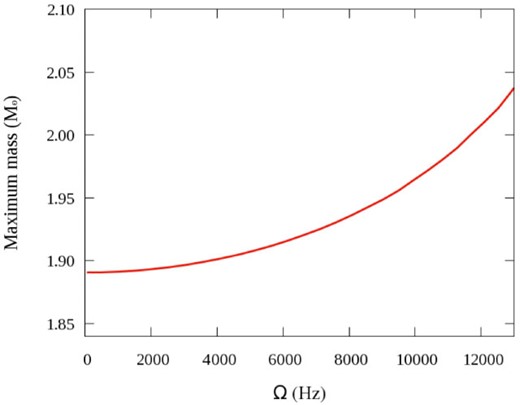
Frequency |$\Omega$| (Hz) versus maximum mass (|$M_\odot$|) for TM2|$\omega\rho$|-b EoS.
4.2. Two-solar-mass problem
In Sect. 3, MR relations have been calculated for the 11 EoSs. Calculated maximum masses of NL3-a, NL3-b, NL3|$\omega\rho$|-a, NL3|$\omega\rho$|-b, DDME2-a and DDME2-b EoSs are over twice the solar mass without magnetic fields. Masses calculated by GM1, TM1-b and TM2|$\omega\rho$|-b EoSs with strong magnetic fields (|$B_0 = 2.5 \times 10^{18}$| G) become over twice the solar mass. In Ref. [46], MR relations were calculated with magnetic fields of |$B_0 = 3.1 \times 10^{18}$| G. Using GM1 EoS, they obtained a mass of over twice the solar mass. Their results are consistent with ours.
4.3. Radius at |$1.4\,M_\odot$|
From the observation of the GW170817 gravitational wave event, the upper limit radius is |$13.6$| km [20] at |$M =1.4\, M_\odot$|. Also, another source reports the upper limit radius |$13.76$| km [47] at |$M =1.4\, M_\odot$|. The lower-limit radius was reported as |$10.68^{+0.15}_{-0.04}$| km [48] at |$M =1.6\, M_\odot$|. The upper limit of radius found by NICER observations is |$13.02^{+1.24}_{-1.06}\,$|km [49] at |$M=1.44^{+0.15}_{-0.14} \, M_\odot$|. The validity of each EoS in this respect is discussed here. The neutron star radii at |$1.4\,M_\odot$| are summarized in Table 10, which shows that radii predicted by TM1-a, TM1-b, NL3-a, NL3-b, DDME2-a and DDME2-b EoSs are over |$13.6\,$|km in any case. For the GM1 EoS, the radius becomes smaller than |$13.6$| km only in the case of no magnetic fields and no rotation. As for TM2|$\omega\rho$|-a and TM2|$\omega\rho$|-b EoSs, radii become smaller than |$13.6\,$|km in the case of no rotation. For NL3|$\omega\rho$|-a and NL3|$\omega\rho$|-b EoSs, radii are in the range of observation without magnetic fields or rotation.
Radius at |$M=1.4$| (|$M_\odot$|) for each EoS. |$R$| indicates radius without rotation or magnetic fields, |$R^e_{\rm{rot}}$| is the equator radius with rotation (|$6\times10^{3}$| Hz), |$R_{\rm{mag}}$| is the radius with magnetic fields (|$B_0=2.5\times10^{18}$| G), and |$R^e_{\rm{rot\&mag}}$| is the equator radius with both rotation (|$\Omega=6 \times 10^2$| Hz) and magnetic fields (|$B_0=2.5\times10^{18}$| G) for each EoS.
| EoS . | |$R$| . | |$R^e_{\rm{rot}}$| . | |$R_{\rm{mag}}$| . | |$R^e_{\rm{rot\&mag}}$| . |
|---|---|---|---|---|
| GM1 | 13.49 | 14.51 | 13.91 | 13.93 |
| TM1-a | 14.07 | 15.39 | 14.45 | 14.48 |
| TM1-b | 14.10 | 15.39 | 14.46 | 14.50 |
| TM2|$\omega \rho$|-a | 13.24 | 14.10 | 13.58 | 13.62 |
| TM2|$\omega \rho$|-b | 13.23 | 14.10 | 13.58 | 13.62 |
| NL3-a | 14.35 | 15.10 | 14.53 | 14.54 |
| NL3-b | 14.35 | 15.10 | 14.53 | 14.76 |
| NL3|$\omega \rho$|-a | 13.49 | 13.78 | 13.70 | 13.73 |
| NL3|$\omega \rho$|-b | 13.49 | 13.78 | 13.70 | 13.73 |
| DDME2-a | 14.08 | 15.05 | 14.50 | 14.31 |
| DDME2-b | 14.08 | 15.05 | 14.50 | 14.31 |
| EoS . | |$R$| . | |$R^e_{\rm{rot}}$| . | |$R_{\rm{mag}}$| . | |$R^e_{\rm{rot\&mag}}$| . |
|---|---|---|---|---|
| GM1 | 13.49 | 14.51 | 13.91 | 13.93 |
| TM1-a | 14.07 | 15.39 | 14.45 | 14.48 |
| TM1-b | 14.10 | 15.39 | 14.46 | 14.50 |
| TM2|$\omega \rho$|-a | 13.24 | 14.10 | 13.58 | 13.62 |
| TM2|$\omega \rho$|-b | 13.23 | 14.10 | 13.58 | 13.62 |
| NL3-a | 14.35 | 15.10 | 14.53 | 14.54 |
| NL3-b | 14.35 | 15.10 | 14.53 | 14.76 |
| NL3|$\omega \rho$|-a | 13.49 | 13.78 | 13.70 | 13.73 |
| NL3|$\omega \rho$|-b | 13.49 | 13.78 | 13.70 | 13.73 |
| DDME2-a | 14.08 | 15.05 | 14.50 | 14.31 |
| DDME2-b | 14.08 | 15.05 | 14.50 | 14.31 |
Radius at |$M=1.4$| (|$M_\odot$|) for each EoS. |$R$| indicates radius without rotation or magnetic fields, |$R^e_{\rm{rot}}$| is the equator radius with rotation (|$6\times10^{3}$| Hz), |$R_{\rm{mag}}$| is the radius with magnetic fields (|$B_0=2.5\times10^{18}$| G), and |$R^e_{\rm{rot\&mag}}$| is the equator radius with both rotation (|$\Omega=6 \times 10^2$| Hz) and magnetic fields (|$B_0=2.5\times10^{18}$| G) for each EoS.
| EoS . | |$R$| . | |$R^e_{\rm{rot}}$| . | |$R_{\rm{mag}}$| . | |$R^e_{\rm{rot\&mag}}$| . |
|---|---|---|---|---|
| GM1 | 13.49 | 14.51 | 13.91 | 13.93 |
| TM1-a | 14.07 | 15.39 | 14.45 | 14.48 |
| TM1-b | 14.10 | 15.39 | 14.46 | 14.50 |
| TM2|$\omega \rho$|-a | 13.24 | 14.10 | 13.58 | 13.62 |
| TM2|$\omega \rho$|-b | 13.23 | 14.10 | 13.58 | 13.62 |
| NL3-a | 14.35 | 15.10 | 14.53 | 14.54 |
| NL3-b | 14.35 | 15.10 | 14.53 | 14.76 |
| NL3|$\omega \rho$|-a | 13.49 | 13.78 | 13.70 | 13.73 |
| NL3|$\omega \rho$|-b | 13.49 | 13.78 | 13.70 | 13.73 |
| DDME2-a | 14.08 | 15.05 | 14.50 | 14.31 |
| DDME2-b | 14.08 | 15.05 | 14.50 | 14.31 |
| EoS . | |$R$| . | |$R^e_{\rm{rot}}$| . | |$R_{\rm{mag}}$| . | |$R^e_{\rm{rot\&mag}}$| . |
|---|---|---|---|---|
| GM1 | 13.49 | 14.51 | 13.91 | 13.93 |
| TM1-a | 14.07 | 15.39 | 14.45 | 14.48 |
| TM1-b | 14.10 | 15.39 | 14.46 | 14.50 |
| TM2|$\omega \rho$|-a | 13.24 | 14.10 | 13.58 | 13.62 |
| TM2|$\omega \rho$|-b | 13.23 | 14.10 | 13.58 | 13.62 |
| NL3-a | 14.35 | 15.10 | 14.53 | 14.54 |
| NL3-b | 14.35 | 15.10 | 14.53 | 14.76 |
| NL3|$\omega \rho$|-a | 13.49 | 13.78 | 13.70 | 13.73 |
| NL3|$\omega \rho$|-b | 13.49 | 13.78 | 13.70 | 13.73 |
| DDME2-a | 14.08 | 15.05 | 14.50 | 14.31 |
| DDME2-b | 14.08 | 15.05 | 14.50 | 14.31 |
Considering the observed maximum mass |$2.14\,M_\odot$| and the upper limit of the radius |$13.6\,$|km, NL3|$\omega\rho$|-a and NL3|$\omega\rho$|-b EoSs are the most suitable of the 11 EoSs and meet the requirements of observations. TM2|$\omega\rho$|-b EoS is also found to be nearly in the range of the observation, namely, |$M=2.2\,M_\odot$| and |$R=13.7$| km, with strong magnetic fields (|$3 \times 10^{18}$| G).
4.4. Particle populations of neutron star matter
The relative populations of baryons and leptons for TM2|$\omega\rho$|-b EoS without magnetic fields are shown as functions of baryon number density in Fig. 7. For baryons, populations of all octet baryons are shown. For leptons, populations of |$e^-$|, |$\mu^-$|, and |$\tau^-$| are shown, but the heavy lepton |$\tau^-$| does not appear in the figure. Figure 8 shows the populations of the baryons and leptons with the magnetic fields of |$B_0 = 2.5 \times 10^{18}\,$|G. In this case, populations of electrons, muons, |$\Sigma^-$| and |$\Sigma^+$| are staggering. The population of |$\Xi^+$| rises faster than that without magnetic fields. The uncharged particles |$\Sigma^0$| and |$\Lambda$| are not affected by the magnetic field. Again, there is no population of the heavy lepton |$\tau^-$| in the figure.
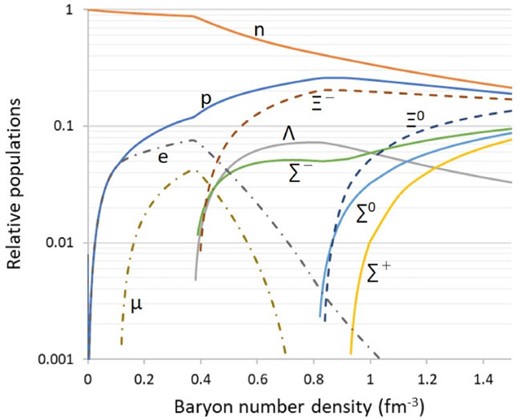
Particle populations as a function of baryon number density without magnetic fields.
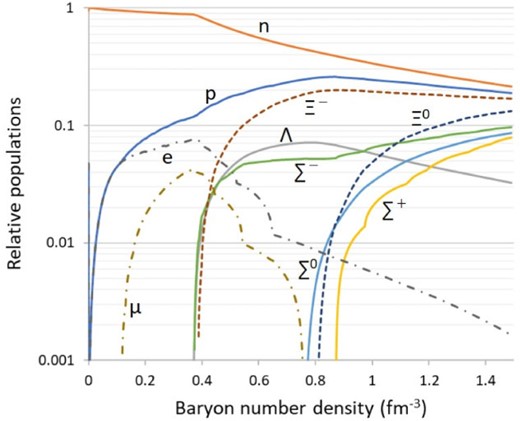
Same as Fig. 7, but with magnetic fields (|$B_0 = 2.5 \times 10^{18}$| G).
5. Summary
In this work the mass–radius relations have been calculated for magnetized and rotating neutron stars using 11 EoSs, which include hyperons in addition to nucleons as components. For NL3|$\omega\rho$|-a and NL3|$\omega\rho$|-b EoSs, masses over the observed maximum mass of |$2.14\,M_\odot$| are obtained and predicted radii are in the range of |$R \leq 13.6$| km at |$1.4\,M_\odot$| without rotation or magnetic fields. As for NL3-a, NL3-b, DDME2-a and DDME2-b EoSs, they surpass |$2.14\,M_\odot$| without rotation or magnetic fields. However, radii are not in the range of the observation of |$R \leq 13.6$| km at |$1.4\,M_\odot$|. For the TM1-b and TM2|$\omega \rho$|-b EoSs, masses more than |$2.14\,M_\odot$| are obtained in the strong magnetic field of |$3 \times 10^{18}$| G at the center. As for the GM1, TM1-b, TM2|$\omega\rho$|-a and TM2|$\omega \rho$|-b EoSs, masses over |$2\,M_\odot$| are obtained both with the strong magnetic field of |$2.5 \times 10^{18}$| G and in the rotation of |$6\times 10^{2}$| Hz. From the observed radius, the central magnetic field strength should be smaller than |$B_0=3\times10^{18}$| G.
Considering both the observed maximum mass |$2.14\,M_\odot$| and the upper limit of the radius from the gravitational wave event, two suitable EoSs (NL3|$\omega\rho$|-a and NL3|$\omega\rho$|-b) among the 11 are found to meet the requirements of observations. TM2|$\omega\rho$|-b EoS is also found to be nearly in the range of the observation, namely, |$M=2.2\,M_\odot$| and |$R=13.7$| km, with strong magnetic fields (|$3 \times 10^{18}$| G) at the center. This result also suggests that most EoSs need a stiffer matter in the core of a neutron star, such as quark matter.
In this work we have not considered the effects of the magnetic field on the crust EOS (BPS EOS). It is certain that the strength of the magnetic field affects electrons in the crust so that the radii of neutron stars might be substantially changed [50]. It is one of our future tasks to check how electrons in the circumstance of the strong magnetic fields affect the radius of a neutron star. Also, hyperon–quark hybrid stars with rotation or/and magnetic fields should be considered in the future.
Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (C) (Grants No. 20K03925) from the Japan Society for the Promotion of Science (JSPS).
Appendix A. Energy levels in a strong magnetic field
Appendix B. Hartle equations
From the above equations, 9 nonlinear equations are obtained (Eqs. B.5, B.9, B.13, B.15, B.17, B.18, B.19, B.20, and B.21) with respect to 9 variables (|$M$|, |$p_0$|, |$j$|, |$g$|, |$\varpi$|, |$\delta P_0$|, |$m_0$|, |$v_2$|, and |$h_2$|). The equations are solved from |$r = 0$|. The initial value of the central density is given as |$\varepsilon_c$| where |$\varepsilon_c=\varepsilon(r=0)$|. In addition, the pressure of the center |$p_c = p(\varepsilon_c)$| is determined from the equation of state. The initial value of other variables are 0 except for |$j$| and |$\varpi$|. Here the initial value of |$j$| is taken as 1.



