-
PDF
- Split View
-
Views
-
Cite
Cite
Sota Arakawa, Masaki Takemoto, Taishi Nakamoto, Geometrical structure and thermal conductivity of dust aggregates formed via ballistic cluster–cluster aggregation, Progress of Theoretical and Experimental Physics, Volume 2019, Issue 9, September 2019, 093E02, https://doi.org/10.1093/ptep/ptz102
Close - Share Icon Share
Abstract
We report on a theoretical study of the geometrical structure of porous dust aggregates formed via ballistic cluster–cluster aggregation (BCCA). We calculated the gyration radius |$R_{\rm gyr}$| and the graph-based geodesic radius |$R_{\rm geo}$| as a function of the number of constituent particles |$N$|. We found that |$R_{\rm gyr} / r_{0} \sim N^{0.531 \pm 0.011}$| and |$R_{\rm geo} / r_{0} \sim N^{0.710 \pm 0.013}$|, where |$r_{0}$| is the radius of the constituent particles. Furthermore, we defined two constants that characterize the geometrical structure of fractal aggregates: |$D_{\rm f}$| and |$\alpha$|. The definitions of |$D_{\rm f}$| and |$\alpha$| are |$N \sim {( R_{\rm gyr} / r_{0} )}^{D_{\rm f}}$| and |${R_{\rm geo}} / {r_{0}} \sim {\left( {R_{\rm gyr}} / {r_{0}} \right)}^{\alpha}$|, respectively. Our study revealed that |$D_{\rm f} \simeq 1.88$| and |$\alpha \simeq 1.34$| for the clusters of the BCCA.
In addition, we also studied the filling factor dependence of the thermal conductivity of statically compressed fractal aggregates. From this study we reveal that the thermal conductivity of statically compressed aggregates |$k$| is given by |$k \sim 2 k_{\rm mat} {( r_{\rm c} / r_{0} )} \phi^{(1 + \alpha) / (3 - D_{\rm f})}$|, where |$k_{\rm mat}$| is the material thermal conductivity, |$r_{\rm c}$| is the contact radius of the constituent particles, and |$\phi$| is the filling factor of the dust aggregates.
1. Introduction
The study of the aggregation of small dust particles into larger aggregates is crucial for understanding fundamental processes in astrophysics and geophysics. For example, the growth of aerosol or haze particles in the atmosphere causes scattering and absorption of the sunlight [e.g., 1]. In addition to this, aggregation of dust particles also occurs in the mineral clouds of exoplanets and hence understanding the fundamental processes involved in the formation process of dust aggregates in exoplanets is imperative in order to interpret the transmission spectra [e.g., 2,3]. In addition, aggregation of dust particles in the solar nebula is the first step towards the formation of the planets [e.g., 4–7], and the density evolution of dust aggregates is considered to be the key to understanding the evolution from nanometer- or micrometer-sized dust grains to kilometer-sized small bodies [e.g., 8–11]. The resulting aggregates frequently have a complex and fractal structure with an extremely low filling factor [e.g., 12–14]. Therefore, understanding the geometrical structure of these fractal aggregates and its influence on physical properties such as the thermal conductivity and the compressive strength is of immense current interest.
The thermal conductivity for porous dust aggregates composed of micron-sized |${\rm Si}{\rm O}_{2}$| glass grains has been obtained by several experimental studies [e.g., 15,16], and it is empirically known that the thermal conductivity is approximately proportional to the square of the filling factor [17–19]. However, a theoretical explanation of the dependence of thermal conductivity on the filling factor is still lacking.
In contrast to the thermal conductivity, the filling factor dependence of the tensile strength of porous dust aggregates is well understood [20]; it is evaluated from the fractal structure of dust aggregates and the maximum force required to separate two sticking particles. The compression strength would also be evaluated from the fractal structure of dust aggregates and the rolling energy needed to rotate a constituent particle around its connecting points [21].
In this paper we describe the geometrical structure of porous dust aggregates formed in astrophysical environments. We present the calculation of the gyration radius (which is defined in Sect. 2.1) and the graph-based geodesic radius (which is defined in Sect. 2.2) of porous dust aggregates. Subsequently, we present interpretations of the filling factor dependence of thermal conductivity on the geometrical structure, and we also confirm the validity of our theoretical understanding by comparing it with the result of direct numerical calculations in Sect. 3. Finally, in Sect. 4 we also present a modified interpretation of the filling factor dependence of compression strength and the average coordination number of dust aggregates.
2. Ballistic cluster–cluster aggregation
In the early stage of dust growth in astrophysical environments such as protoplanetary or circumplanetary disks, the collision velocity is sufficiently low to avoid collisional compaction, and collisions between similar-sized dust aggregates are dominant [e.g., 22,23]. Therefore, the shape of dust aggregates in astrophysical environments is expected to resemble the clusters of ballistic cluster–cluster aggregation (BCCA). BCCA clusters are formed by the sticking of two equal-sized BCCA clusters with no restructuring (see Fig. 3(a) of Ref. [24]). We prepare BCCA clusters using the following procedure: (1) prepare an aggregate composed of |$2^{i}$| particles (initially |$i = 0$|); (2) copy this aggregate and change the orientation of the copy randomly; (3) make a new aggregate composed of |$2^{i + 1}$| particles by ballistic sticking of these two aggregates with a randomly chosen offset; (4) continue the procedure (1)–(3). As shown in Fig. 1, a BCCA cluster has a highly porous structure. In this study we have assumed that all constituent particles (hereafter referred to as “monomers”) are spherical and have the same radius |$r_{0}$|.

Projection of a three-dimensional dust aggregate formed via ballistic cluster–cluster aggregation. The number of constituent particles is |$N = 2^{16} = 65536$|.
2.1. Gyration radius
We carried out 20 growth sequences of |$N$|-body simulations of BCCA as in previous studies [24,25]. We show the geometric mean of the gyration radius |$R_{\rm gyr}$| as a function of the number of monomers |$N$| in Fig. 2(a). We found that the gyration radius |$R_{\rm gyr}$| is given by

(a) Fitting of the gyration radius of BCCA clusters |$R_{\rm gyr}$| as a function of the number of monomers |$N$|. (b) Fitting of the graph-based geodesic radius of BCCA clusters |$R_{\rm geo}$| as a function of |$N$|. The circles represent the averaged data, with vertical error bars of twice the standard error. The dashed line is the best fit obtained with the weighted least-squares method.
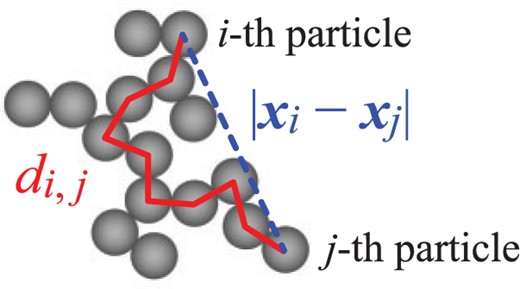
Schematic description of the distance between the |$i$|th and |$j$|th particles, |$| {\boldsymbol x}_{i} - {\boldsymbol x}_{j} |$|, and the graph geodesic between the |$i$|th and |$j$|th particles, |$d_{i,j}$|. It is clear that the graph geodesic |$d_{i,j}$| is larger than the distance |$| {\boldsymbol x}_{i} - {\boldsymbol x}_{j} |$|.
Therefore, we can calculate the filling factor of BCCA clusters from the number of monomers.
2.2. Graph-based geodesic radius
Granular materials and dust aggregates transmit compressive stresses via a network of force chains [e.g., 27]. Further, the chains of monomers also conduct heat [e.g., 28]. Therefore, understanding the chain structure within dust aggregates is essential, especially for the study of the mechanical and heat transfer properties. Here, we introduce the graph geodesic and graph-based geodesic radius. Figure 3 schematically illustrates a BCCA cluster. The distance between the |$i$|th and |$j$|th particles is |$| {\boldsymbol x}_{i} - {\boldsymbol x}_{j} |$|, and we define the graph geodesic between the |$i$|th and |$j$|th particles as |$d_{i,j}$| in Fig. 3. Considering the graph structure of a BCCA cluster, which is a tree (i.e. a connected acyclic graph), we can uniquely determine the graph geodesic |$d_{i,j}$|.
2.3. Bifractality of statically compressed BCCA clusters
In the early stage of dust growth, the fractal dimension of dust aggregates is |$D_{\rm f} \simeq 1.9$|. When the dust aggregates grow into centimeter-sized clusters, BCCA clusters are dynamically compressed by dust–dust collisions [e.g., 29] and/or statically compressed by the ram pressure of the disk gas [e.g., 30]. Although it depends on the physical properties of the disk and the monomers, the compression mechanism for icy aggregates composed of submicron-sized monomers in the minimum mass solar nebula [31,32] is static compression by ram pressure [30]. In this study we focus on the geometrical structure of statically compressed BCCA clusters.
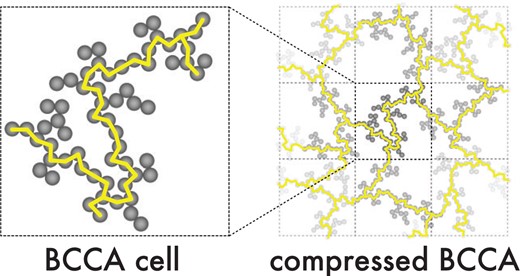
Schematic description of a BCCA cell in ancompressed BCCA cluster. The yellow lines represent the possible heat paths.
It is important to note that the geometrical structure of dynamically compressed BCCA clusters is also characterized by bifractality [e.g., 6]. The resulting fractal dimension is approximately 2.5 on a large scale, and it remains |$D_{\rm f}$| of BCCA on a small scale. Therefore, bifractality is a common characteristic of compressed BCCA clusters. We also hypothesize that this bifractality is a common structure for compressed fractal aggregates even when the initial cluster does not originate from BCCA but from other aggregation processes, for example diffusion-limited cluster aggregation [e.g., 33] or reaction-limited cluster aggregation [e.g., 34]. We will, however, need to confirm this hypothesis in the future.
3. Thermal conductivity
In this section we calculate the thermal conductivity of compressed BCCA clusters and demonstrate the manner in which the geometrical structure affects the thermal conductivity.
3.1. Methods
We calculate the thermal conductivity of compressed BCCA clusters composed of 16384 (|$= 2^{14}$|) monomers. The snapshots used in this study and in our previous study [19] are the same, and were prepared by Tatsuuma et al. [20]. The methods of the thermal conductivity calculation are described in our previous studies [18,19], and are briefly summarized here.
We also consider the series connection of dust aggregates in a cubic periodic boundary (see Fig. 5). It is expected that the series connection of dust aggregates would reduce the artificial effects of the boundary condition on the thermal conductivity calculations.
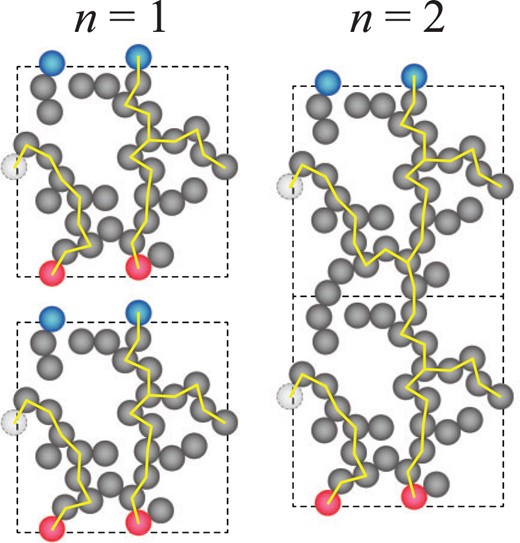
Schematic description of the series connection of dust aggregates in a cubic periodic boundary. The blue monomers are on the upper boundary and the reds are on the lower boundary; the yellow lines represent the heat paths. The series connection of dust aggregates would reduce the artificial effects of the boundary condition.
3.2. Filling factor dependence
Figure 6 shows the projection of a three-dimensional compressed BCCA cluster in a cubic periodic boundary. The blue monomers are on the upper boundary and the reds are on the lower boundary. The yellow monomers represent the heat paths and the grays are the non-contributing monomers. The filling factor of the aggregates is |$\phi = 10^{-1.5}$|. It is clear that not all monomers contribute to the heat transfer within the dust aggregate.

An example snapshot of a compressed BCCA cluster in a cubic periodic boundary. The blue monomers are on the upper boundary and the reds are on the lower boundary. The yellow monomers represent the heat paths and the grays are the non-contributing monomers. The filling factor of the aggregates is |$\phi = 10^{-1.5}$|.
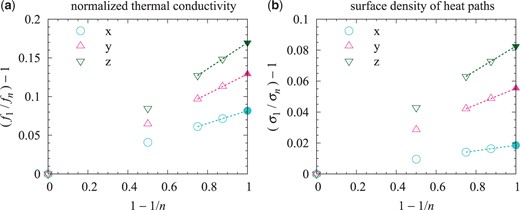
(a) Example calculation of |$f_{\infty}$| (filled marker) using |$f_{1}$|, |$f_{2}$|, |$f_{4}$|, and |$f_{8}$| (open markers). (b) Example calculation of |$\sigma_{\infty}$| (filled marker) by using |$\sigma_{1}$|, |$\sigma_{2}$|, |$\sigma_{4}$|, and |$\sigma_{8}$| (open markers). The aggregate used in this calculation is the same as in Fig. 6. We calculated |$f_{\infty}$| and |$\sigma_{\infty}$| from three directions (|$x$|, |$y$|, and |$z$|).
Figure 8(a) shows the normalized thermal conductivity for the limiting case of |$n \to \infty$|, |$f_{\infty}$|, as a function of the filling factor |$\phi$|. We used ten snapshot data points for each |$\phi$| obtained from different compression simulations [20] and calculated |$f_{\infty}$| from three directions. The circles represent the geometric mean of 30 calculation results of the temperature structure, with vertical error bars of twice the standard error. We found that |$f_{\infty}$| is given by
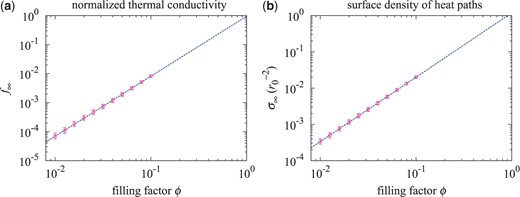
(a) Fitting of the normalized thermal conductivity for the limiting case of |$n \to \infty$|, |$f_{\infty}$|, as a function of the filling factor |$\phi$|. (b) Fitting of the surface density of heat paths for the limiting case of |$n \to \infty$|, |$\sigma_{\infty}$|, as a function of |$\phi$|. The circles represent the averaged data, with vertical error bars of twice the standard error. The dashed line is the best fit obtained from the weighted least-squares method.
3.3. Surface density of heat paths
We found that |$1.85 < D_{\rm f} < 1.92$| in Sect. 2.1; therefore, we obtain |$1.74 < {2 / {( 3 - D_{\rm f} )}} < 1.85$|. The range of |$2 / {( 3 - D_{\rm f} )}$| matches the numerical result, |$\sigma \sim \phi^{1.775 \pm 0.025} {r_{0}}^{-2}$|. This fact validates the assumption that |$\overline{\mathcal{N}}_{\rm path} \sim \mathcal{O} {( 1 )}$| for BCCA cells.
3.4. Understanding the filling factor dependence of the thermal conductivity
Here, we demonstrate the manner in which the filling factor dependence of the thermal conductivity is derived from the geometrical structure. For compressed BCCA clusters the fractal dimension is three on a large scale, then the thermal conductivity of compressed BCCA clusters should be the same as the thermal conductivity of BCCA cells.
The derived relation shows excellent coincidence with our numerical result, |$f \sim \phi^{2.068 \pm 0.034}$|.
4. Discussion
4.1. Reinterpretation of the filling factor dependence of the compressive strength
We can also derive the filling factor dependence of the compressive strength of compressed BCCA clusters from the geometrical structure. In this section we evaluate the compressive strength |$P_{\rm c}$| as Kataoka et al. [21] did.
This estimate was based on the assumption that the compression is accompanied by the rolling of a single pair of monomers in a BCCA cell. In this derivation, |$3 / {\left( 3 - D_{\rm f} \right)} \simeq 2.69$| and it might not reproduce their numerical results. Although our findings suggest that the |$\alpha$| parameter associated with the chain length plays a significant role in the compression of dust aggregates, further studies on the force distribution within compressed fractal aggregates are required.
4.2. Revisiting the average coordination number of compressed aggregates
The average coordination number (i.e. the average number of contacts per monomer) |$Z$| increases as an aggregate is compressed. Arakawa et al. [19] found that, for compressed BCCA clusters, the filling factor dependence of |$Z$| is given by |$Z = 2 + 9.38 \phi^{1.62}$|. Here, we derive this equation from the geometrical structure.
The compressive strength |$P_{\rm c}$| is also affected by the average coordination number |$Z$|. If |$Z \simeq 2$|, nearly all the monomers can roll when they are compressed. Therefore, the interparticle force is close to the rolling friction force and the compressive strength is given by Eq. (36). On the other hand, in the high-density region (|$\phi \gg 0.1$| and |$Z \gg 2$|) most of the particles cannot roll freely and the compressive strength is larger than the value evaluated for the case of |$Z \simeq 2$| [e.g., 38–41]. Thus, we expect that the compressive strength would be given by the sliding friction force in the high-density limit [40], although future studies are required to understand this in detail.
5. Summary
We have conducted numerical simulations of the BCCA of small dust particles and calculated the geometrical structure of the fractal dust aggregates. Additionally, we derived the filling factor dependence of the physical properties of porous dust aggregates. Our key findings are summarized as follows.
We calculated the gyration radius |$R_{\rm gyr}$| and the graph-based geodesic radius |$R_{\rm geo}$| as functions of the number of constituent particles |$N$|. We found that |$R_{\rm gyr} / r_{0} \sim N^{0.531 \pm 0.011}$| and |$R_{\rm geo} / r_{0} \sim N^{0.710 \pm 0.013}$|, where |$r_{0}$| is the radius of the constituent particles. Thereafter, we defined two constants which characterize the geometrical structure of fractal aggregates: |$D_{\rm f}$| and |$\alpha$|, as |$N \sim {( R_{\rm gyr} / r_{0} )}^{D_{\rm f}}$| and |${R_{\rm geo}} / {r_{0}} \sim {\left( {R_{\rm gyr}} / {r_{0}} \right)}^{\alpha}$|, respectively. We revealed that |$D_{\rm f} \simeq 1.88$| and |$\alpha \simeq 1.34$| for BCCA clusters.
Kataoka et al. [21] found that the geometrical structure of statically compressed BCCA clusters is characterized by bifractality. This structure evolution suggests that the static compression first reconstructs the fractal aggregate on a large scale because of the weak compressive strength on a large scale. Therefore, we can imagine that it is possible to understand the physical properties of statically compressed BCCA clusters from the geometrical structure of small BCCA clusters preserved in compressed aggregates (“BCCA cells”).
We investigated the filling factor dependence of the thermal conductivity of statically compressed aggregates. We found that the filling factor dependence can be interpreted from the geometrical structure of dust aggregates. The thermal conductivity of statically compressed aggregates |$k$| is given by |$k \sim 2 k_{\rm mat} {( r_{\rm c} / r_{0} )} \phi^{(1 + \alpha) / (3 - D_{\rm f})}$|, where |$k_{\rm mat}$| is the material thermal conductivity, |$r_{\rm c}$| is the contact radius of the constituent particles, and |$\phi$| is the filling factor of dust aggregates.
The compressive strength |$P_{\rm c}$| is also derived from the geometrical structure as |$P_{\rm c} \sim {( E_{\rm roll} / {r_{0}}^{3} )} \phi^{(2 + \alpha) / (3 - D_{\rm f})}$|, where |$E_{\rm roll}$| is the energy needed to rotate a monomer around its connection point by |$\pi/ 2$| rad. Our finding suggests that the |$\alpha$| parameter associated with the chain length plays a significant role in the compression of dust aggregates. In addition, the average coordination number |$Z$| is derived from the geometrical structure as |$Z = 2 + C \phi^{D_{\rm f} / (3 - D_{\rm f})}$|, where |$C \sim 9$| is the number of inter-cell contacts per BCCA cell.
Acknowledgements
We are grateful to Misako Tatsuuma, Akimasa Kataoka, and Hidekazu Tanaka for providing snapshots of compressed BCCA clusters and the simulation code for preparing BCCA clusters. We also thank Satoshi Okuzumi, Hiroaki Katsuragi, and Sin-iti Sirono for fruitful discussions and comments. S.A. is supported by a Grant-in-Aid for Japan Society for the Promotion of Science (JSPS) Research Fellow (JP17J06861). This work is supported by a JSPS KAKENHI grant (JP18K03721).



