-
PDF
- Split View
-
Views
-
Cite
Cite
Tomohiro Nakama, Jun’ichi Yokoyama, Reheating through the Higgs amplified by spinodal instabilities and gravitational creation of gravitons, Progress of Theoretical and Experimental Physics, Volume 2019, Issue 3, March 2019, 033E02, https://doi.org/10.1093/ptep/ptz014
Close - Share Icon Share
Abstract
It is shown that a positive non-minimal coupling of the Higgs field to gravity can solve the two problems in inflation models in which a post-inflationary universe is dominated by energy with a stiff equation of state such as kination, namely, overproduction of gravitons in the gravitational reheating scenario, and overproduction of curvature perturbation from Higgs condensation. Furthermore, we argue that the non-minimal coupling parameter can be constrained more stringently with the progress in observations of large-scale structure and cosmic microwave background.
1. Introduction
If the equation of state parameter |$w$| is larger than |$1/3$| after inflation (for a review of inflation, see, e.g., Ref. [1]), the energy density of the inflaton decreases more quickly than radiation. For instance, the universe can be dominated by the kinetic energy of the inflaton (kination) after k-inflation [2], G-inflation [3,4], or quintessential inflation [5], when |$w=1$| and the energy density decays as |$a^{-6}$| where |$a$| is the cosmic scale factor. A relatively large |$w$| may also be realized by an inflaton oscillating around a minimum of its potential if it is steeper than quartic [6].
In these models reheating is supposed to take place due to gravitational particle production. Since spinor and gauge fields are conformally invariant without mass terms, production of minimally coupled massless scalar fields has been discussed as a source of radiation in these models [6] and used in the literature [2,3,5]. Since each polarization mode of gravitons satisfies the same equation of motion to the linear order, they are produced twice as much as a massless minimally coupled scalar field. Hence, if this is the only mechanism of reheating after inflation, gravitons would be overproduced relative to radiation unless we introduce sufficiently many light bosons. Thus we should seek other sources of entropy after inflation.
One of the candidates is the standard Higgs field as it may acquire a condensation of long-wave quantum fluctuations, which are generated if it is minimally coupled to gravity so that its effective mass is much smaller than the Hubble parameter during inflation [7]. If it has a typical amplitude around the root-mean-square in the domain corresponding to our Universe, its energy density is of the same order of radiation energy created by gravitational particle production just after inflation [8]. However, since its amplitude remains constant until the Hubble parameter decreases to its effective mass, its energy density would surpass that of both the remnant inflaton and radiation created gravitationally. Hence the Universe is reheated by Higgs condensation, which mainly decays to gauge bosons [11,12]. It has been shown, however, that such a scenario does not yield sensible cosmology because the Higgs condensation has too large fluctuations that generate too large curvature perturbation [8].
In this paper we argue that if the Higgs field is non-minimally coupled to the scalar curvature, we can not only solve the overproduction problems of both curvature fluctuations and gravitons but also find interesting observational constraints due to relic gravitons. Indeed, if the Higgs field has a large enough positive non-minimal coupling such as the conformal coupling |$\xi=1/6$|, then it has a large enough effective mass |$m^2_{\rm eff}=\xi R =12\xi H^2$| during inflation and no long-wavelength perturbations are generated [9,13,32]. This additional mass term, however, becomes negative after inflation if |$w>1/3$| [13], and consequently it experiences spinodal instabilities [14,15] shortly after inflation, which determines the energy density of the Higgs field and hence its decay products. This can provide a more efficient source of reheating than gravitational particle production. Then the contribution of gravitons to the radiation can be sufficiently small depending on the value of the non-minimal coupling. Since the presence of graviton radiation affects the observed cosmic microwave background and the structures of the universe [16,17], this scenario can be probed by these observations and we can obtain constraints on the non-minimal coupling. See also Ref. [18] for a recent discussion on a different aspect of gravitational reheating.
The rest of the paper is organized as follows. In the next section, we introduce a simple model of a transition from a de Sitter phase to a kination, which we use as an example, and then discuss gravitational reheating and the creation of gravitons at the transition. Then we discuss spinodal instabilities of the Higgs at the transition in Sect. 3. It is convenient to express the energy density of gravitons as an effective, additional contribution to the number of neutrino species [16,17], which we denote by |$N_{\mathrm{eff,GW}}$|, to relate it to observations of the cosmic microwave background and the structures of the universe. We present this quantity for several combinations of parameter values in Sect. 4, with comparison to existing constraints and expected future sensitivities. We conclude in Sect. 5.
2. Gravitational reheating and production of gravitons
In order to discuss gravitational reheating, let us take the Hubble parameter to be constant during inflation with the scale factor |$a=\exp[H(t-t_0)]$|, where |$t_0$| is chosen to be the moment when the spacetime starts to deviate from de Sitter expansion toward the end of inflation. We denote the conformal time by |$\eta$|, and take |$\eta=\eta_0$| at |$t=t_0$|. Then, |$(\eta_0-\eta)H=a(t)^{-1}-1.$| Well before |$\eta_0$|, we have |$\eta\simeq-1/(aH). $| Let us consider the case in which the inflaton’s energy density, |$\rho_{\mathrm{inf}}$|, is dominated by its kinetic energy after inflation so that we find |$\rho_{\mathrm{inf}}\propto a^{-6}$|, and hence |$H(t)\propto a^{-3},\ a\propto t^{1/3}$|, and |$\eta\propto t^{2/3}\propto a^{2}.$|
Following Ref. [8] we introduce |$f(H\eta)\equiv a^2(\eta)$| and |$x=H\eta$|, and also normalize |$\eta$| so that |$H\eta_0=-1$|. Similarly to Ref. [8], we consider the following transition from a de Sitter phase to a kination:
The upper limit of the integration above, |$x$|, should be taken sufficiently larger than the end of the transition at |$x=-1+x_0$|. Numerical integrations revealed |$I\simeq 50x_0^{-0.262}$| at least for |$0.1<x_0<1$|. This radiation energy surpasses that of kination at |$a=a_{\mathrm{end}}\sqrt{32/3}\pi M_p/H\equiv a_R$| and the reheating temperature is given by |$T_R=M_p[90/\pi^2g_*(T_R)]^{1/4}(32\pi^2/3)^{-3/4}(\Lambda_{\mathrm{COBE}}/M_p)^2(r/0.01)=4\times 10^6(r/0.01)\,\mathrm{GeV} $| as a function of the tensor-to-scalar ratio |$r$|, where |$M_p=2.435\times 10^{18}\,\mathrm{GeV}$| is the reduced Planck mass, |$\Lambda_{{\mathrm{COBE}}}=2.54\times 10^{13}\,\mathrm{GeV}$|, and |$g_*(T_R)$| is set to 106.75 (see Ref. [18] for more details), if the Universe is reheated by a minimally coupled massless scalar field created gravitationally, instead of by the Higgs amplified by spinodal instabilities discussed in the next section.
Since the graviton satisfies the same equation of motion as a massless minimally coupled scalar field, its energy density is twice as large as that given by Eq. (3), reflecting their two polarization states [6]. This situation is in contradiction with the observations of the cosmic microwave background and large-scale structures of the Universe, and this problem can be circumvented by spinodal instabilities of the Higgs as discussed below.
3. Spinodal instabilities of the Higgs
It turns out that the |$\lambda$| term is unimportant for the parameter values that we consider for which the effect of created gravitons is (potentially) observable (see Table 1 in Sect. 4).
Examples of |$N_{\mathrm{eff,GW}}$| at the photon decoupling for several combinations of the model parameters |$(x_0,\xi,\lambda)$|. The reheating temperature is |$4\times 10^{6}N^{3/4}(r/0.01)\,\mathrm{GeV}$| (see the text for more details).
| |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . | |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . |
|---|---|---|---|---|---|
| (0.1,1,0.01) | 0.72 | 5 | (0.1,1,0.005) | 0.72 | 5 |
| (0.1,2,0.01) | 0.089 | 23 | (0.1,2,0.005) | 0.088 | 23 |
| (0.5,1,0.01) | 0.65 | 5 | (0.5,1,0.005) | 0.64 | 5 |
| (0.5,2,0.01) | 0.067 | 28 | (0.5,2,0.005) | 0.064 | 29 |
| |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . | |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . |
|---|---|---|---|---|---|
| (0.1,1,0.01) | 0.72 | 5 | (0.1,1,0.005) | 0.72 | 5 |
| (0.1,2,0.01) | 0.089 | 23 | (0.1,2,0.005) | 0.088 | 23 |
| (0.5,1,0.01) | 0.65 | 5 | (0.5,1,0.005) | 0.64 | 5 |
| (0.5,2,0.01) | 0.067 | 28 | (0.5,2,0.005) | 0.064 | 29 |
Examples of |$N_{\mathrm{eff,GW}}$| at the photon decoupling for several combinations of the model parameters |$(x_0,\xi,\lambda)$|. The reheating temperature is |$4\times 10^{6}N^{3/4}(r/0.01)\,\mathrm{GeV}$| (see the text for more details).
| |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . | |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . |
|---|---|---|---|---|---|
| (0.1,1,0.01) | 0.72 | 5 | (0.1,1,0.005) | 0.72 | 5 |
| (0.1,2,0.01) | 0.089 | 23 | (0.1,2,0.005) | 0.088 | 23 |
| (0.5,1,0.01) | 0.65 | 5 | (0.5,1,0.005) | 0.64 | 5 |
| (0.5,2,0.01) | 0.067 | 28 | (0.5,2,0.005) | 0.064 | 29 |
| |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . | |$(x_0,\xi,\lambda)$| . | |$N_{\mathrm{eff,GW}}$| . | |$N^{3/4}$| . |
|---|---|---|---|---|---|
| (0.1,1,0.01) | 0.72 | 5 | (0.1,1,0.005) | 0.72 | 5 |
| (0.1,2,0.01) | 0.089 | 23 | (0.1,2,0.005) | 0.088 | 23 |
| (0.5,1,0.01) | 0.65 | 5 | (0.5,1,0.005) | 0.64 | 5 |
| (0.5,2,0.01) | 0.067 | 28 | (0.5,2,0.005) | 0.064 | 29 |
We introduce the mode function |$\chi_k(\eta)$| by rewriting each Fourier mode as |$\chi(\boldsymbol{k},\eta)=\chi_k(\eta)a(\boldsymbol{k})+\chi_k^*(\eta)a^\dagger(\boldsymbol{k})$|, where |$a$| and |$a^\dagger$| satisfy |$[a(\boldsymbol{k}),a^\dagger(\boldsymbol{k}')]=\delta(\boldsymbol{k}-\boldsymbol{k}')$|.
During a de Sitter phase, |$R=12H^2$|, and shortly after |$\eta_0$|, |$R$| decreases rapidly to become negative. After taking a negative minimum value |$R_m$| at |$\eta=\eta_m$|, |$|R|$| decays rapidly (|$R\propto a^{-6}$|) during kination. The modes satisfying |$k^2\lesssim k_M^2\equiv -a^2(\eta_m)(\xi-1/6)R_m$| grow during a short interval after |$\eta_0$| due to the last term of Eq. (18). We use |$k_M$| as the upper limit of the |$k$|-integrations. First we solve for the time evolution of Higgs fluctuations in Fourier space solving Eq. (16), with the initial conditions provided using Eq. (19), at the moment sufficiently before the end of the de Sitter phase. To solve Eq. (17), the time evolution of the Ricci scalar is needed, which can be obtained using Eq. (2), assuming the model for a smooth transition from a de Sitter phase to a kination phase outlined in Eq. (1). The term |$\langle \chi^2\rangle$| in Eq. (18) can be computed using Eq. (8) at each time step. The energy density of the Higgs field well after spinodal instability terminates can then be determined using Eqs. (10), (11), (13), and (14). On the other hand, the energy density of gravitons generated at the transition can be calculated using Eq. (3) for the same transition model, noting that the numerical factor |$I$| there is determined by |$x_0$|, which specifies how sudden the transition is. The ratio between these two energy densities determines the observability of gravitational waves, as discussed in the next section.
The time evolution of the third and fourth terms of Eq. (18) is shown in Figs. 1 and 2, for |$(x_0,\xi,\lambda)=(0.5,1,0.01)$|. In this case, we find |$k_M\simeq 1.7 H$|, and these show that the self-interaction term is negligible even after the instability growth. The fourth term turns out to be |$\simeq -0.018 H^2$|, whereas the third term is |$\simeq 0.017 H^2$| at |$\eta=7H^{-1}$| when the latter saturates.
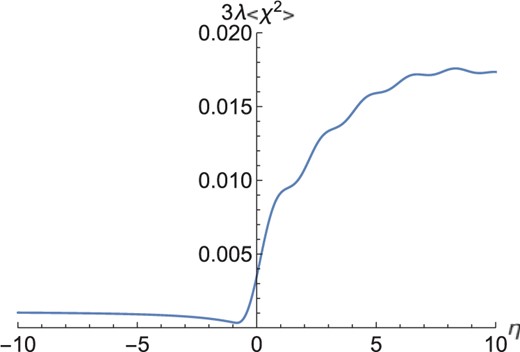
Time evolution of the third term of Eq. (18), for |$(x_0,\xi,\lambda)=(0.5,1,0.01)$| in the Hubble unit |$H=1$|.
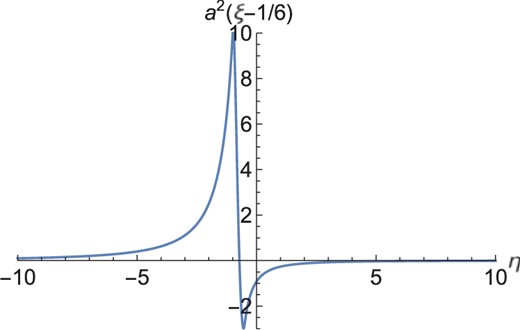
Time evolution of the fourth term of Eq. (18), for |$(x_0,\xi,\lambda)=(0.5,1,0.01)$| in the Hubble unit |$H=1$|.
4. The relation between the model parameters and |$N_{\mathrm{eff,GW}}$|
The prefactor here turns out to be 2.36 and 2.86 at the photon decoupling and the big bang nucleosynthesis, respectively.
Examples of |$N_{\mathrm{eff,GW}}$| at the photon decoupling for several combinations of the model parameters |$(x_0,\xi,\lambda)$| are shown in Table 1. Note that the result is independent of the energy scale of inflation because both |$\rho_{\mathrm{GW}}$| and |$\rho_{\mathrm{Higgs}}$| scale as |$H^4$|. The parameters of the numerical calculations include |$(d\eta,dk,\eta_i,k_m)$|, where |$d\eta$| (|$dk$|) is the interval for |$\eta$| (|$k$|), |$\eta_i$| is the initial moment of numerical integration and |$k_m$| is the minimum wavenumber. Table 1 was obtained for |$(d\eta,dk,\eta_i,k_m)$|=|$(0.01,0.01,-10,0.05)$| in units of the Hubble parameter during inflation, namely, taking |$H=1$|. We have obtained almost the same results for |$(d\eta,dk,\eta_i,k_m)=$||$(0.02,0.01,-10,0.1),$||$(0.01,0.02,-10,0.1),$||$(0.01,0.01,-20,0.1)$|, and |$(0.01,0.01,-10,0.1)$|. Making |$x_0$| smaller enhances both spinodal instabilities and gravitational particle production. Consequently, |$N_{\mathrm{eff,GW}}$| is not significantly altered by changing |$x_0$|. Increasing |$\xi$| enhances only spinodal instabilities, hence |$N_{\mathrm{eff,GW}}$| is smaller for larger |$\xi$|. Table 1 also shows that the self-interaction term is unimportant for the values of |$\xi$| yielding observable |$N_{\mathrm{eff,GW}}$|, as discussed in the previous section.
The energy density of the Higgs after spinodal instabilities is related to that of gravitons via |$\rho_{\mathrm{Higgs}}=(2.86/N_{\mathrm{eff,GW}})\rho_{\mathrm{GW}}=N\rho_r$| from Eq. (26), where |$\rho_r$| is the energy density of a minimally coupled massless scalar field created gravitationally provided in Sect. 2, |$N=5.72/N_{\mathrm{eff,GW}}$|, and |$N_{\mathrm{eff,GW}}$| is that at the photon decoupling. This means that the reheating temperature is higher by |$N^{3/4}$| from Ref. [18], relative to the reheating temperature given in Sect. 2. This factor |$N^{3/4}$| is also shown in Table 1.
The quantity |$N_{\mathrm{eff,GW}}$| can be constrained by observations of the cosmic microwave background and the structures of the universe [16,17]. Future observations of the cosmic microwave background, potentially reaching |$\sigma(N_{\mathrm{eff}})\sim 0.02$|–|$0.03$| [25], or 21 cm line radiation [26] would probe larger values of |$\xi$| for this reheating scenario. For comparison, there is a 95% C.L. upper limit on |$N_{\mathrm{eff}}^{\mathrm{(upper)}}$| of |$4.65$| from big bang nucleosynthesis [27,28]. There is also a 95% C.L. upper limit of 3.77 from Planck power spectra alone [29]. The dependence of |$N_{\mathrm{eff,GW}}$| on |$\xi$| is also shown in Fig. 3.
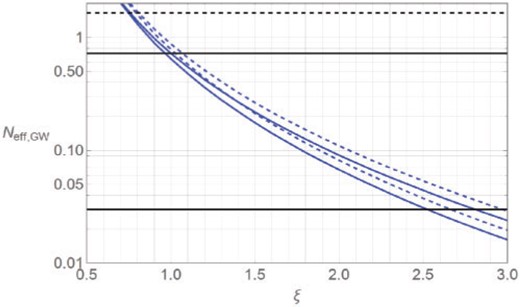
The dependence of |$N_{\mathrm{eff,GW}}$| at the photon decoupling (solid) and at the big bang nucleosynthesis (dashed) on the Higgs non-minimal coupling |$\xi$|. The parameter |$x_0$|, characterizing the rapidness of the transition from a de Sitter phase to a kination, is taken as 0.1 (upper) and 0.5 (lower), and |$\lambda=0.01$|. The horizontal lines from top to bottom show an upper limit from the abundance of the light elements |$(4.65-3=1.65)$|, the Planck satellite |$(3.77-3.046=0.724)$|, and an expected future limit of 0.03 (see the text for more detail).
5. Conclusion
In a class of inflation models in which inflation is followed by a kination, the universe is supposed to be reheated by gravitational particle production, which is rather inefficient with a relatively low reheating temperature. What is worse, gravitons are created twice as much as massless minimally coupled bosons, which cause problems in big bang nucleosynthesis, cosmic microwave background observation, and cosmic structure formation. Thus we need an additional reheating mechanism, which may be provided by the standard Higgs field. However, while condensation of long-wave fluctuations in the Higgs field acquired during inflation can provide an additional source of radiation, it also eventually causes too large curvature fluctuations, so that this scenario does not work, either [8].
In this situation, we have shown that both of these problems can be solved if the Higgs field is non-minimally coupled to the scalar curvature, and further shown that observations that probe extra graviton radiation can be used to constrain the value of the non-minimal coupling parameter |$\xi$| by expressing the energy density of gravitons as an effective additional contribution to the number of neutrino species, denoted by |$N_{\mathrm{eff,GW}}$|. It is determined by how rapid the transition from inflation to the next phase is (|$x_0$|), the Higgs non-minimal coupling to gravity |$\xi$|, and its self-coupling |$\lambda$|, but is independent of the energy scale of inflation. The values of |$N_{\mathrm{eff,GW}}$| for several combinations of these model parameters are presented in Table 1. It turns out that this quantity is mainly determined by |$\xi$|, with only weak dependence on |$x_0$|. It is hardly affected by changing |$\lambda$|, when |$\xi$| is not too large and hence |$N_{\mathrm{eff,GW}}$| can be observable. This indicates that spinodal instability is not so strong that the Higgs field does not reach the minimum of the potential.
Although the conformal coupling |$\xi=1/6$| is sufficient to suppress the long-wavelength fluctuation of Higgs condensation, the quantity |$N_{\mathrm{eff,GW}}$| is yet too large to be consistent with existing observations even for |$\xi\simeq 1$|, so that the graviton creation yields a more stringent lower bound on |$\xi$| than the curvature fluctuations generated from the Higgs field. In other words, future experiments would be able to probe larger values of |$\xi$|.
A few comments are in order. The requirement that the electroweak vacuum be stable [30–32] after the Higgs growth at the transition would provide additional constraints on this scenario, especially when |$\xi$| is large and the substantial spinodal instability is shut off by the self-interaction term, though they would depend on particle physics. Gravitational creation of gravitons can also be used to constrain reheating in modified gravity theories. While it is suppressed in |$R^2$| inflation [33,34], it constrains an |$f(R)$| scenario considered in Ref. [35]. Our conclusions would not be significantly altered by the inclusion of metric fluctuations, or by a different choice of frame [36]. Our limits are loosened by a late-time entropy production [37,38]. Such a possibility can be explored by a comparison of tensor modes on cosmic microwave background B-mode polarization scales and on the DECIGO band [39].
Though we have restricted our attention to gravitational radiation generated at the transition from a de Sitter phase to a kination phase, it would be worthwhile to mention gravitational wave frequency spectra |$\Omega_{\mathrm{GW}}(f)$| generated during inflation on different frequencies. The spectrum |$\Omega_{\mathrm{GW}}$| behaves as |$f^{-2}, f^{0}, f$| for modes that reenter the horizon during matter domination, radiation domination, and kination, respectively [40]. The amplitude of the plateau (|$\sim f^0$|) is roughly given as |$\rho_{\mathrm{c}}\Omega_{\mathrm{GW}}\sim f^2h(f)^2\sim f_{\mathrm{eq}}^2H^2(a_0/a_{\mathrm{eq}})^{-2}=f_{\mathrm{R}}^2H^2(a_0/a_{\mathrm{R}})^{-2}$|, noting that the initial amplitude is |$\sim H$| and it decays in proportion to the inverse of the scale factor after the reentry. Here, the subscript R denotes quantities at reheating. The amplitude at |$f=f_{\mathrm{K}}$|, the comoving frequency corresponding to the beginning of kination, is |$\rho_{\mathrm{c}}\Omega_{\mathrm{GW}}(f_{\mathrm{K}})\sim H^4(a_0/a_{\mathrm{K}})^{-4}$|, simply because the initial energy density |$\sim H^4$| is red-shifted from the moment of generation. If one considers cases where the Universe is reheated through a component created at the same time, the beginning of a kination, with energy density |$H^4$|, as in the scenario considered in this paper, then this amplitude just coincides with |$\rho_{\mathrm{rad},0}$|: |$\rho_{\mathrm{c}}\Omega_{\mathrm{GW}}(f_{\mathrm{K}})\sim \rho_{\mathrm{rad},0}$|. Furthermore, the frequency is |$f_{\mathrm{K}}=H(a_0/a_{\mathrm{K}})^{-1}\sim (c^5\rho_{\mathrm{rad},0}/h)^{1/4}\sim 10^{11}$| Hz. Hence, the location and height of the peak corresponding to the beginning of kination is independent of the Hubble parameter during inflation (see Fig. 4 of Ref. [40]). The energy density of gravitational waves corresponding to this peak is somewhat smaller than what we calculated in Sect. 2. Thus gravitons created from gravitational particle production impose more stringent constraints on |$\xi$| than tensor perturbations generated during inflation.
Note added in press
After we posted the original version of this paper in the arXiv, Dimopoulos and Markkanen posted a paper discussing a similar situation [41] there. They, however, considered a case in which |$\xi$| is much larger than in our case and the scalar field settles to the potential minimum immediately after the kination commences.
Acknowledgements
We thank Kohei Kamada and anonymous referees for helpful input. T.N. is also grateful to Teruaki Suyama and Marc Kamionkowski for useful discussions. T.N. was partially supported by Japan Society for the Promotion of Science (JSPS) Postdoctoral Fellowships for Research Abroad. J.Y. was supported by JSPS KAKENHI, Grant-in-Aid for Scientific Research 15H02082 and Grant-in-Aid for Scientific Research on Innovative Areas 15H05888.
Footnotes
1Here, the difference in the effective degrees of freedom defined in terms of the energy density |$g_*$| and the entropy density |$g_s$| is neglected, since it is always insignificant (|$g_*=3.363$| versus |$g_s=3.909$| after the annihilation of |$e^+e^-$| [22]). For simplicity, we set |$g_*=g_s=3.5$|, which would be a good approximation given the weak dependence on the degrees of freedom. At the time of the big bang nucleosynthesis, |$g_*=g_s=10.75$|.



