Abstract
In the present work, available experimental data up to high-spin states of |$^{119-126}$|Sn isotopes with different seniority (|$v$|), including |$v = 4$|, 5, 6, and 7, are interpreted with the shell model, by performing shell-model calculations in the 50–82 valence shell composed of |$1g_{7/2}$|, |$2d_{5/2}$|, |$1h_{11/2}$|, |$3s_{1/2}$|, and |$2d_{3/2}$| orbitals. The results are compared with the available experimental data. These states are described in terms of broken neutron pairs occupying the |$h_{11/2}$| orbital. Possible configurations of seniority isomers in these nuclei are discussed. The breaking of three neutron pairs is responsible for generating high-spin states. The isomeric states |$5^-$|, |$7^-$|, |$10^+$|, and |$15^-$| of even Sn isotopes, and isomeric states |$19/2^+$|, |$23/2^+$|, |$27/2^-$|, and |$35/2^+$| of odd Sn isotopes, are described in terms of different seniority. For even Sn isotopes, the isomeric states |$5^-$|, |$7^-$|, and |$10^+$| are due to seniority |$v = 2$|; the isomeric state |$15^-$| is due to seniority |$v = 4$|, and, in the case of odd Sn isotopes, the isomeric states |$19/2^+$|, |$23/2^+$|, and |$27/2^-$| are due to seniority |$v = 3$|, and the isomeric state |$35/2^+$| in |$^{123}$|Sn is due to seniority |$v = 5$|. These are maximally aligned spins, which involve successive pair breakings in the |$\nu (h_{11/2})$| orbital.
1. Introduction
The Sn region is an important region, in which many experimental and theoretical studies, such as identification of different isomeric states in Sn isotopes [1–9], Gamow–Teller decay of the doubly magic nucleus |$^{100}$|Sn [10], measurement of electromagnetic properties of different excited states [11], upcoming measurements for definite spin assignments [12], population of high-spin states [1], theoretical calculations of nuclear |$g$| factors [13], and ab initio study of lighter Sn isotopes [14], are going on. Recent studies report lowering of the |$\nu g_{7/2}$| orbital in comparison with the |$\nu d_{5/2}$| for |$^{101}$|Sn [15]. It is possible with direct spin assignments, together with magnetic moment measurements, to probe the wave function of the ground states of the |$^{101-107}$|Sn isotopes. This may help to accurately determine the ordering of the |$\nu d_{5/2}-\nu g_{7/2}$| orbitals.
The number of particles that are not in pairs coupled to angular momentum |$J = 0$| is known as seniority (|$v$|) [16]. There are several textbook examples where |$g_{9/2}$|, |$h_{11/2}$|, and |$i_{13/2}$| orbitals are responsible for generating high-spin seniority states. The |$g_{9/2}$| orbital is responsible for the |$10^+$| and |$12^+$| states in the case of |$^{94}$|Ru and |$^{96}$|Pd with configuration |$\pi g_{9/2}^4$| [17]. The |$\nu g_{9/2}^4$| configuration is responsible for the |$8^+$| state of seniority |$v=2$| in |$^{72}$|Ni and |$^{74}$|Ni [17]. The high-spin seniority states are due to the |$h_{11/2}$| orbital in the Sn region. The role of the |$i_{13/2}$| orbital in the 82–126 major shell region is crucial for the seniority |$v=4$| states. In the case of even |$^{200,202}$|Pb isotopes the seniority |$v=4$| states are |$16^+$| [|$\nu i_{13/2}^2 \nu f_{5/2}^2$|] and |$17^-,19^-$| [|$\nu i_{13/2}^3 \nu f_{5/2}^1$|] [18].
In the Sn region, the appearance of isomeric states in |$N=82$| isotones and |$Z=50$| isotopes is very common, in even isotopes |$10^+$|, and in odd isotopes |$27/2^-$|. The role of the |$h_{11/2}$| orbital is crucial for the investigation of these isomers within the shell model. There are three different experimental groups that are working to identify seniority isomers in the Sn isotopes. The Fotiades [19] group at LBNL, the Astier [1] group at Legnaro and the IRes-Strasbourg and Iskra group [2,3] at Argonne have done different experiments to populate isomeric states in odd and even Sn isotopes using fusion–fission reactions. The high-spin structure above the |$10^+$| isomers in |$^{118,120,122,124}$|Sn was reported by Fotiades et al. in Ref. [19]. More complete level schemes in odd and even Sn isotopes with |$A = 119$|–126 are populated in the |$^{12}$|C + |$^{238}$|U and |$^{18}$|O + |$^{208}$|Pb fusion–fission reactions reported by Astier et al. [1]. The aim of this experiment was to built high-spin states above the long-lived isomeric states lying around 4.5 MeV. The excited states above the |$v=2$| isomers have been populated in even |$^{118-128}$|Sn isotopes in the fusion–fission reaction [2], while excited states with seniority |$v= 3$|, 5, and 7 have been investigated in odd |$^{119-125}$|Sn isotopes [2]. In these experiments [1–3] for even |$^{120,122,124,126}$|Sn isotopes the isomeric states are |$10^+$|, |$5^-$|, |$7^-$|, and |$15^-$|, while for odd |$^{119,121,123,125}$|Sn isotopes they are |$27/2^-$|, |$19/2^+$|, and |$23/2^+$|. We show these isomeric states in Figs. 1and 2 for even and odd Sn isotopes, respectively. In these figures we also show the seniority of these different isomeric states. One of the important applications of the nuclear shell model is to identify states involving many identical nucleons in the same orbital; thus it is possible to identify high-spin states in Sn isotopes with the |$(\nu h_{11/2})^n$| configuration.
![Different isomeric states [1–3] for $^{120,122,124,126}$Sn isotopes.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f1.jpeg?Expires=1748188926&Signature=d7TQzWqZvwkZy2AeRrhsE0mGh5RB63G20uvJ6YAIGR0cklcVR69Nm7GdT95-e0tTLgXwHwe75QX6h2ugB3WiHKT4tbBfVI1my9vILwBtdiu7SBJgyPCJLEo1FYjxwmb5XpWTa4VTWJyGrmBB1wt1AEPykcRH5cheYqo3gcgMAOIPvBqmeC3Iys5wMtDzVmDNphC7qF5j~ykQh4W4ljXWpVHZC9ydqmam~RwWj2C1eP0zUeC82REkj268o4EW52-nzGMXqQQhfVeT0jbkl4Hsw-G0yZHQr4FRExHd9V2-TWW563qk-Qui1kA4OIPNUoB0WAGmRZKOJeeydVqqRf4uqg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![Different isomeric states for $^{119,121,123,125}$Sn isotopes [1–3].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f2.jpeg?Expires=1748188926&Signature=fo1seS70ysb391wxaDlZbLxTNno-VuLBqXkuQ1en6H~nsVB7A-WybvTFC0hXBYJJHygaHudDMe6FPoCKkNOpQ8MVFTRvwJe4rxN-ucRiEud3w9sdaSaFapI49K9laF~ZYbf-fzoWb6JpZyWU~rlxawC-NP6QAIFyl0twQDcJGjxcB6vaKU4NS7kSh7Pqfh~18xugwBpKvwLOwBzcmX7HD-2yPiZQ~pYLM30rcdHbauIgU8gJxg6FccVimMu0t-WJz8smGGgQVPsahdXZy8mBBMVKxnOgAM4isj-V3ev2707Nk-c~JPkrfVM8USczKAjOYhkGsyeNZBjId96OaqcZZw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Our focus is to explain different isomeric states in term of seniority as proposed by Astier et al. [1] and we report additional states in comparison to Refs. [2,3]. In Refs. [2,3], shell-model results for energy levels are reported only for selected states. Thus, the present work will add more information to the earlier shell-model results reported in Refs. [1–3] and our calculated values for different |$B(E2)$| transitions will be very useful for future experiments.
This work is organized as follows: a comprehensive comparison of shell-model results and experimental data is given in Sect. 2. Configurations of different isomeric states are shown in Sect. 3. In Sect. 4 a comparison of the calculated transition probabilities for isomeric states is given. Finally, concluding remarks are made in Sect. 5.
2. Shell-model Hamiltonian and model space
The shell-model calculations for the Sn isotopes have been performed in the full 50–82 valence shell composed of |$1g_{7/2}$|, |$2d_{5/2}$|, |$1h_{11/2}$|, |$3s_{1/2}$|, and |$2d_{3/2}$| orbitals without any truncation. We have performed calculations with the SN100PN interaction due to Brown et al. [20,21]. The residual two-body interaction was obtained from the CD-Bonn G-matrix within the so-called |$\hat{Q}$|-box folded-diagram theory and the further |$nn$| part was multiplied by a factor of 0.90 to improve the agreement with the experiment for |$^{130}$|Sn. The single-particle energies for the neutrons are |$-10.609$|, |$-10.289$|, |$-8.717$|, |$-8.694$|, and |$-8.816$| MeV for the |$1g_{7/2}$|, |$2d_{5/2}$|, |$2d_{3/2}$|, |$3s_{1/2}$|, and |$1h_{11/2}$| orbitals, respectively. The results shown in this work were obtained with the code Antoine [22]. In this region, we have previously reported shell-model results for the structural properties of some nuclei [23–30] using the SN100PN interaction.
2.1. Analysis of spectra of even isotopes of Sn
Since a |$^{100}$|Sn core is used in this work, neutron excitations are important among the 1|$g_{7/2}$|, 2|$d_{5/2}$|, 2|$d_{3/2}$|, 3|$s_{1/2}$|, and 1|$h_{11/2}$| orbitals for the |$^{119-126}$|Sn isotopes. The valence neutrons contribute in the structure of these nuclei because of the |$Z = 50$| shell closure. In this section we perform shell-model calculations for the even–even isotopes in the 50–82 shell, in order to describe the positive and negative parity levels of these nuclei. The even–even isotopes of Sn are discussed first. The odd isotopes |$^{119,121,123,125}$|Sn have been studied within the shell model in Ref. [2]. We sketch the results for the odd isotopes for completeness and comparison in Sect. 2.2, including some more recently measured states.
A comparison of the calculated spectrum of |$^{120}$|Sn with the experimental data is shown in Fig. 3. The calculated 2|$^+$| and 4|$^+$| levels are 67 keV lower and only 10 keV higher, respectively, than those in the experiment. Then, there are gaps both in the experiment and calculation (490 keV and 400 keV, respectively) between the 4|$^+$| and 6|$^+$| levels, the calculated one being less. In the calculation, the |$6^+$|, |$8^+$|, and |$10^+$| triple of the levels is slightly lower and more compressed than the experimental one. For the negative parity levels, the |$5^-$| and |$7^-$| levels are 118 keV and 95 keV higher, respectively, as compared to those of the experimental ones. The calculated |$9^-$| level is 537 keV lower than in the experiment. In the experiment the |$11^-$|, |$13^-$|, and |$15^-$| levels are almost equidistant, i.e., 253 keV and 241 keV away from each other.
![Comparison of experimental [1,2] and calculated excitation spectra using SN100PN interaction for $^{120}$Sn.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f3.jpeg?Expires=1748188926&Signature=y8okS21poxqpiz2~D9R5VzNPiQcYJ3Ov9C0zVVZMY2wBRrjqDbE-qQPHXudVmuFmShmVD4aFdqgf0X0j0mR1cXy2mZYkB6JPO7kephVkqeG~HGZyRNWSFY1660kurLK7cokRrwc9HGjje69q-lsp8LXMeeW4dI9s1yt5Q0GuBp8epPVXxV-D-uwDKbvhIq5N8m5qhcrdkwsWzEllmnqRhsikzVUPSqr9z29I1FcNamHPjNCLei2Hbbu1vo~pRLul0Dcv7g~V9mHfFKjQBkXv91~A1ac0q8uS3WjrDavHRagL-0cGKvC1ng9b4n9BSJXyvJOCyXKp5SLN54kcm7tDSQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
A comparison of the calculated values with the experimental data for |$^{122}$|Sn is shown in Fig. 4. Comparing Figs. 3 and 4 one can see that the positive parity spectrum of the |$^{122}$|Sn is very similar to that of |$^{120}$|Sn. The 2|$^+$| level is predicted 46 keV lower and 4|$^+$| level is only 26 keV higher than the experimental values, i.e., the values of the both energy levels are decreased with respect to the ground state as compared to those of |$^{120}$|Sn. The calculated positive parity levels of |$^{122}$|Sn are better described by shell-model calculation as compared to those of |$^{120}$|Sn. For the negative parity levels, the |$5^-$| and |$7^-$| levels are 85 and 73 keV higher, respectively, as compared to those of the experimental ones.
![Comparison of experimental [1,2] and calculated excitation spectra for $^{122}$Sn using SN100PN interaction.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f4.jpeg?Expires=1748188926&Signature=GRszvQPlWQMmr9rVolXFilthDYA8tA8KJCyKqZt726nc4B4e9QPxXW1PlbXz4OaGfIy7LJv~4Fer1cI2y257ZDcz7P2CptlO6ur1326vyFXGU8vS7vlTyidx0tvb4unPkYWdfaPa1qDpdAY0vmV5y7jA2sAyMvE4T4DJeVkgoU00LmKjshTSG7Dm34a0TxDU9J26nx5tg~vRuM5YXrZQTkn1ESiGtjQ10N1fD9p53NiTp~VxdHipYPcN3JIjd2QKXXzyuaOGPPJGUlZAp-0m0eghSqhhx~YKQ-yu8uZSnaqnfpJu0Sx2hyFt~Ibv9Q6AVFDhKcLMTWEStDL7sE051w__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
A comparison of the calculated values with the experimental data for |$^{124}$|Sn is shown in Fig. 5. As compared to |$^{122}$|Sn, in the calculation only the energy of the |$2^+$| level is increased to 3 keV and all other energies of the levels are decreased with respect to the ground state like in the experiment. The 2|$^+$| and 4|$^+$| levels are only 35 keV and 15 keV lower, respectively, than the experimental ones, which shows better agreement as compared to that of |$^{120,122}$|Sn. The values of the respective experimental and calculated energy gaps between the 4|$^+$| and 6|$^+$| levels are 352 keV and 339 keV. They are also in better agreement with the experiment than those for |$^{120,122}$|Sn. The |$6^+$|, |$8^+$|, and |$10^+$| triplet of the levels in the calculation is still slightly lower and more compressed than in the experiment: the differences in the values of the experimental |$6^+$| and |$8^+$|, and |$8^+$| and |$10^+$| levels are 124 and 79 keV, respectively, while the calculated values of these differences are 89 and 52 keV, respectively. The experimental difference between the |$6^+$| and |$8^+$| levels is decreased while the difference between the |$8^+$| and |$10^+$| levels is increased as compared to that of |$^{122}$|Sn. A reverse trend is seen in the differences of the calculated levels: the difference between the |$6^+$| and |$8^+$| level is increased, the difference between |$8^+$| and |$10^+$| is decreased as compared to that of |$^{122}$|Sn.
![Comparison of experimental [1,2] and calculated excitation spectra for $^{124}$Sn using SN100PN interaction.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f5.jpeg?Expires=1748188926&Signature=ZRE3eYfCTazH8X7SZJcvhtsZ6YhNN9VItp6~-F7erqjnMkR0p-RPh86kNIG0vVWYDmiKiEearYCSSiKKYYUzL6VRXCxWgGG4JTGdylWtYhuT~68QahCYEwg9RzDZ9eL5Wce3qTl4nuy6nkNYfnnpSkRbgRNsskIkhRoNz8yE0Bl0OPxW6yoPHBtkfOXJ7AhEnIG2i2hKlYCNU1xsCdix~KPZB96sd8Pe258ecQWZyL1JVGUuoqbcFAeOp5tXrBrGQibgxLxq9IY0NA0f3hDjVa78eY~ruhuBhMcNlN~WdK9uJoYK0mnfbjSahvkS86GgkX9nYhYxrjj-uBeXIFY5QA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
For the negative parity levels, the |$5^-$| and |$7^-$| levels are 56 and 62 keV higher, respectively, as compared to those of the experimental ones. For these two levels the calculations are clearly better than the |$^{120,122}$|Sn cases.
A comparison of the calculated values with the experimental data for |$^{126}$|Sn is shown in Fig. 6. The shell-model calculation predicts the energies of the 2|$^+$| and 4|$^+$| levels to be only 17 keV and 38 keV lower, respectively, than the experimental ones. This shows slightly better agreement as compared to that for |$^{124}$|Sn. The values of the gaps between 4|$^+$| and 6|$^+$| are 324 and 333 keV in the experiment and calculation, respectively. They are also in better agreement with the experiment than in |$^{120,122,124}$|Sn.
![Comparison of experimental [1,2] and calculated excitation spectra for $^{126}$Sn using SN100PN interaction.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f6.jpeg?Expires=1748188926&Signature=SGtNhlkLPLLAkp3Gb~cQVQ234wGgYreqg7wO2aY5FMaCBHA2UaGjO6TcZPlqa5vGMfOJXeVTP-xtqe4lBYpAhBJrgyfWJYx0B~JoFOmjxxnkMQ8FFRpJObx1flAc-VUEr-q~NrjUiuQ8D6adKkBDx9SM5u4mytNKUZMsn5NVC~uvmpRmYPIJFyTXuYAbBxzavLX1WYjFCbhiAw~6gsqqIQNW2assGh5gfOjbiOjePdjC2LHZJA~CvmhJx1xfXgbCpSJ2XXttJkGrkK4A-iiAApjYfu025OcMRD38o6NDvoGBd5VbhbsOe1cdLZhtACmg8y23tkbz5H6MrqN~Lny5Eg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
2.2. Analysis of spectra of odd isotopes of Sn
For the odd isotopes of Sn, unpaired neutron interchanges the position of the positive and negative parity bands as compared to the even-even isotopes. Calculation gives 11/2|$^{-}$| as the ground state for all the odd isotopes of Sn considered here. For |$^{121,123}$|Sn, in the experiment, the |$11/2^-$| level is slightly higher than the ground states of these nuclei.
For |$^{119}$|Sn, in Fig. 7 we present the calculation up to 35/2|$^-$| and 39/2|$^+$|. The calculation gives 11/2|$^-$| as the ground state of |$^{119}$|Sn, while in the experiment 11/2|$^-$| is the excited state with 89 keV energy.
![Comparison of experimental [1,3] and calculated excitation spectra for $^{119}$Sn using SN100PN interaction.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f7.jpeg?Expires=1748188926&Signature=4AgMa58EWbLpZsxVVltLNf-Rb0A-qIlfQc9vuN1e~IyrUTfvrfh4Ucif5AnBB~AT5uPsCDLOhrJYxB0pOY3EJVtDKkVFrqTJMpe1Z1fBi~QLFcUf1BZ1GrREyw6BoQ18uxjwbKyie4MQ6Ou-jpApAiiE~9q~GsMOIalzoTkpoJCrX0F5~gtt0B~GJngb2G-Pv-KCenR3zMw07eqbs7VMC9Pzk6WeALUXOV-849006t3SlJRZmJSgMbUmJylea5SjlQOuZdPyn90XSc3gMT4p2Id1TKc1WdwFBfvoEw~3~iWxMX73-MFNwZcMoNihgdLnsv6v-kAAwSO9FA6g7zODLw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The calculated values of the |$13/2^-$|, |$15/2^-$|, |$19/2^-$|, |$23/2^-$|, and |$27/2^-$| levels are 168 keV, 265 keV, 310 keV, 240 keV, and 285 keV lower than their respective experimental counterparts, though the calculated pattern of the |$^{119}$|Sn spectrum is very similar to the experimental one. The spectrum of |$^{121}$|Sn is given in Fig. 8. The calculation gives |$11/2^-$| as the ground state of |$^{121}$|Sn, while in the experiment the energy of this level is 6 keV.
![Comparison of experimental [1,3] and calculated excitation spectra for $^{121}$Sn using SN100PN interaction.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f8.jpeg?Expires=1748188926&Signature=UspE03UuwuF7Z5LCAw3W3mor4XB0VEOVjHEpLvMZGI~LFj9SEO4BLR0avmZfqgAQ4cmykDJ1MGGAO7DWtS4aMjZ-bfGK1QRHLwGFaHX10YR9FfzE9zCDJfjFaPjF1~yX6AUBTCzCE2unHB9~qKmIP69MYop7jCW3zQRf9lt2LFL2-IHmD-LkbEUYZmVS3iy15biCGPKmKGoyv0DvDyFf119TYKIyvA09Wyg59UwEypCNnG6cVZghS9PSCAQxIAJTbkS0IcJ~2fxK8lCbeLgCqiHA6KY0n3cSdxqxwzfTjsGv1WDebNCENBTaHDAa2geAwLs3xfVaJnZGCpABbkuYRA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The calculated values of the |$15/2^-$|, |$19/2^-_1$|, |$19/2^-_2$|, |$23/2^-$|, |$27/2^-$|, |$31/2^-_1$| levels are 143 keV, 101 keV, 161 keV, 66 keV, 116 keV, 213 keV lower than their experimental counterparts. The calculated |$29/2^-$| level is 203 keV higher than that of the experiment. Only the calculated value of this level is larger; otherwise the calculated pattern of the |$^{121}$|Sn spectrum is now similar to the experimental one up to the |$31/2^-_1$| level, while it was up to |$27/2^-$| in the case of |$^{119}$|Sn. More experimental data are available for the positive parity levels of |$^{121}$|Sn as compared to |$^{119}$|Sn. The calculated pattern is similar to the experimental one.
The spectrum of |$^{123}$|Sn is given in Fig. 9. Reaching the |$^{123}$|Sn isotope, one can see that both the calculated and experimental ground states are |$11/2^-$|, while for the |$^{119,121}$|Sn |$11/2^-$| experimental levels the energy values were 89 keV and 6 keV, respectively. By careful comparison of the experimental and calculated patterns it can be seen that the whole calculated negative parity spectrum is very similar to the experimental one, while the similarity was up to |$27/2^-$| and |$31/2^-$| for |$^{119,121}$|Sn, respectively. The calculated values of the |$15/2^-_1$|, |$19/2^-_1$|, |$23/2^-$|, |$27/2^-$|, |$31/2^-_1$| levels are 111 keV, 252 keV, 44 keV, 98 keV, 206 keV lower than their experimental counterparts, respectively, while the calculated |$13/2^-$|, |$19/2^-_2$|, |$31/2^-_2$|, |$35/2^-_2$|, |$39/2^-_1$|, |$39/2^-_2$| levels are 1 keV, 1 keV, 271 keV, 11 keV, 96 keV, 262 keV higher than the experimental ones. If one follows the pattern, |$39/2^-$| spin can be assigned to the experimental level at 5520 keV almost definitely according to the shell-model prediction. From these differences it is also seen that the agreement of the calculated values of the energy levels of |$^{123}$|Sn is much better than those of |$^{119,121}$|Sn. All negative and positive parity levels of |$^{123}$|Sn are better described as compared to |$^{119,121}$|Sn by the shell-model calculation.
![Comparison of experimental [1,3] and calculated excitation spectra for $^{123}$Sn using SN100PN interaction.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f9.jpeg?Expires=1748188926&Signature=uM94iR~Z9VGsgb0cTukTXqLnS7w5qIyHLsb1Dz8FUKYBQs~sDL3nCFh0Cm5S6-YvM1dtg-8vCYHw58hFLe1qN37DG1FJ4JahFjfPg2156YlRwEQD4vmVrVeT5-VeJSIQW-Rxpgx~QaA9BqconEb02OBCyEjJ~U4N9ADA-bE-0wTgZkQIyN44L9gRb6hm4jCQDGUsjc6y-zSoCVJeZOkWb5oox~z8XRggQH0kQw9c33axwHSSL39zbXE9hMdzesD2NuC~lD3lwZoEte22f4TZLQfln4iD53uVvmAQuXvmeF3NvNsRIm-MxFfnO4lSj4FiNec8fUXjJK~~7G5Q~xPElw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
As is seen from Fig. 10, both calculated and experimental ground states are |$11/2^-$| as for |$^{123}$|Sn. All respective positive and negative parity excited state energies are lower both in the experiment and calculation with respect to the ground state as compared to the |$^{119,121}$|Sn isotopes.
![Comparison of experimental [1,3] and calculated excitation spectra for $^{125}$Sn using SN100PN interaction.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2019/10/10.1093_ptep_ptz108/1/m_ptz108f10.jpeg?Expires=1748188926&Signature=2pM32m94BV2QC60qdFXZjJaj1CCTJfJRf9-U21DEa6~q2pBn7rFb7L-1Ib008CJXVF8vZOcq6KTIqjLwASqkZ-YVcessetJShNXF-EPC7ELbgGoBQ2GGmh7L3LGhU3pZMPdA0RYXC6AB03F8UBSdke-q9Vm7Z1U3bN0hOCuJGFcO1-velAbOJVYA4eKHuUE4lgKweBsEsyTzmSUFx59DbcXG68LsYVO5SKq~cH6nKPxdQk-kdtT3oNGRboHCs6RGT0HD3Kx7g7MbwhHLIjJlGhT0JKGg2I4VcyYdgX5zln5TOUy44YzDqRic~lxHcKWXWYrzAixcinKcTC6xp6K8HQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The similarity of the experimental and calculated patterns is kept. However, between the experimental |$(31/2)^-$| and |$(35/2)^-$| levels the second predicted |$31/2^-_2$| appears. The calculated |$39/2^-_1$| level is only 57 keV higher than the experimental one. In the calculation, below this level, there are the |$35/2_2^-$| and |$37/2^-_1$| levels; above this level, there are the |$37/2_2^-$| and |$39/2^-_2$| levels. The calculated values of the |$15/2^-$|, |$19/2^-_1$|, |$23/2^-$|, |$27/2^-$|, |$31/2^-$| levels are 94 keV, 135 keV, 60 keV, 108 keV, 126 keV lower than their experimental counterparts. The |$19/2^-_2$| and |$29/2^-$| levels are 158 keV, 109 keV higher than the experimental ones. From these differences it is also seen that the agreement of the calculated values of the energy levels of |$^{125}$|Sn is better than that of |$^{119,121,123}$|Sn.
3. Configuration of the isomeric states
|$^{119-126}$|Sn isotopes, which contain more than 68 neutrons, are good for studying high-spin states since they contain |$\nu (h_{11/2})^n$| with |$v=4,5,6$| and the high-spin states cannot be formed only by |$\nu s_{1/2}$| and |$\nu d_{3/2}$| orbitals themselves. In Ref. [1], the |$^{119-126}$|Sn isotopes were produced as fragments of binary fission induced by heavy ions. Among them, isomeric states have been established from the delayed coincidences between fission fragment detectors and the gamma array. Further experimental data are taken from Refs. [2,3]. All the observed states are treated in terms of broken neutron pairs occupying the |$\nu (h_{11/2})$| orbital. The configurations of high-spin states are due to the |$(\nu h_{11/2})^n$| or |$(\nu h_{11/2})^n$||$(\nu d_{3/2})^1$| ones.
Configurations of the isomeric states |$10^+$|, |$5^-$|, |$7^-$|, |$15^-$|, and |$19^-$| of even isotopes of Sn and |$27/2^-$|, |$19/2^+$|, and |$23/2^+$| odd isotopes, emerging from the current shell-model calculation, are given separately in Table 1. The seniorities given in this table are proposed in Ref. [1]. As is seen from Table 1, the percentage of the seniority isomer configurations increases by increasing the neutron number. This is because the role of the |$h_{11/2}$| orbital is dominant and the average occupancy of this orbital is increasing. The average occupancy of the |$h_{11/2}$| orbital is 5.17 in |$^{119}$|Sn and 7.79 in |$^{125}$|Sn. The wave functions are very fragmented; e.g., different configurations corresponding to the |$10^+$| state in |$^{120}$|Sn are shown in Table 2. The |$10^+$| states of all even isotopes and |$27/2^-$| states of all odd isotopes are formed by breaking pairs in a pure |$\nu (h_{11/2})$| orbital with |$v=2$| and |$v=3$|, respectively. The |$d_{3/2}$| and |$s_{1/2}$| orbitals also participate in the formation of other isomeric states of the Sn isotopes.
Configurations of isomeric states in |$^{119,120,121,122,123,124,125,126}$|Sn isotopes. The probability of the largest component of the configuration is given in the brackets.
| Spin | Seniority | |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn |
|---|---|---|---|---|---|
| |$10^+$| | |$v =2$||$(h_{11/2}^2)$| | |$g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [10.13%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [15.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{6}$| [18.64%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{8}$| [37.24%] |
| |$5^-$| | |$v =2$||$(h_{11/2}^1s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{5}$| [11.79%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{5}$| [12.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{7}$| [23.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{9}$| [27.67%] |
| |$7^-$| | |$v =2$||$(h_{11/2}^1d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [17.00%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [16.24%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [22.14%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$| [24.63%] |
| |$15^-$| | |$v =4$||$(h_{11/2}^3d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [27.60%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [23.21%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [28.76%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$|[30.86%] |
| Spin | Seniority | |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn |
| |$27/2^-$| | |$v = 3$||$(h_{11/2}^3)$| | |$g_{7/2}^8d_{5/2}^6h_{11/2}^{5}$| [13.80%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{5}$| [14.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{7}$| [19.86%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{7}$| [34.55%] |
| |$19/2^+$| | |$v = 3$||$(h_{11/2}^2s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{4}$| [11.77%] | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{6}$| [13.81%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{6}$| [17.74%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{8}$| [31.15%] |
| |$23/2^+$| | |$v = 3$||$(h_{11/2}^2d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{4}$| [18.49%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{6}$| [21.77%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{6}$| [20.19%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{8}$| [25.57%] |
| |$35/2^+$| | |$v = 5$||$(h_{11/2}^4d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^3s_{1/2}^2h_{11/2}^{4}$| [2.50%] |
| Spin | Seniority | |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn |
|---|---|---|---|---|---|
| |$10^+$| | |$v =2$||$(h_{11/2}^2)$| | |$g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [10.13%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [15.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{6}$| [18.64%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{8}$| [37.24%] |
| |$5^-$| | |$v =2$||$(h_{11/2}^1s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{5}$| [11.79%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{5}$| [12.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{7}$| [23.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{9}$| [27.67%] |
| |$7^-$| | |$v =2$||$(h_{11/2}^1d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [17.00%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [16.24%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [22.14%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$| [24.63%] |
| |$15^-$| | |$v =4$||$(h_{11/2}^3d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [27.60%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [23.21%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [28.76%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$|[30.86%] |
| Spin | Seniority | |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn |
| |$27/2^-$| | |$v = 3$||$(h_{11/2}^3)$| | |$g_{7/2}^8d_{5/2}^6h_{11/2}^{5}$| [13.80%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{5}$| [14.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{7}$| [19.86%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{7}$| [34.55%] |
| |$19/2^+$| | |$v = 3$||$(h_{11/2}^2s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{4}$| [11.77%] | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{6}$| [13.81%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{6}$| [17.74%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{8}$| [31.15%] |
| |$23/2^+$| | |$v = 3$||$(h_{11/2}^2d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{4}$| [18.49%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{6}$| [21.77%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{6}$| [20.19%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{8}$| [25.57%] |
| |$35/2^+$| | |$v = 5$||$(h_{11/2}^4d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^3s_{1/2}^2h_{11/2}^{4}$| [2.50%] |
Configurations of isomeric states in |$^{119,120,121,122,123,124,125,126}$|Sn isotopes. The probability of the largest component of the configuration is given in the brackets.
| Spin | Seniority | |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn |
|---|---|---|---|---|---|
| |$10^+$| | |$v =2$||$(h_{11/2}^2)$| | |$g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [10.13%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [15.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{6}$| [18.64%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{8}$| [37.24%] |
| |$5^-$| | |$v =2$||$(h_{11/2}^1s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{5}$| [11.79%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{5}$| [12.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{7}$| [23.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{9}$| [27.67%] |
| |$7^-$| | |$v =2$||$(h_{11/2}^1d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [17.00%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [16.24%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [22.14%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$| [24.63%] |
| |$15^-$| | |$v =4$||$(h_{11/2}^3d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [27.60%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [23.21%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [28.76%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$|[30.86%] |
| Spin | Seniority | |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn |
| |$27/2^-$| | |$v = 3$||$(h_{11/2}^3)$| | |$g_{7/2}^8d_{5/2}^6h_{11/2}^{5}$| [13.80%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{5}$| [14.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{7}$| [19.86%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{7}$| [34.55%] |
| |$19/2^+$| | |$v = 3$||$(h_{11/2}^2s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{4}$| [11.77%] | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{6}$| [13.81%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{6}$| [17.74%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{8}$| [31.15%] |
| |$23/2^+$| | |$v = 3$||$(h_{11/2}^2d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{4}$| [18.49%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{6}$| [21.77%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{6}$| [20.19%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{8}$| [25.57%] |
| |$35/2^+$| | |$v = 5$||$(h_{11/2}^4d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^3s_{1/2}^2h_{11/2}^{4}$| [2.50%] |
| Spin | Seniority | |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn |
|---|---|---|---|---|---|
| |$10^+$| | |$v =2$||$(h_{11/2}^2)$| | |$g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [10.13%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{6}$| [15.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{6}$| [18.64%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{8}$| [37.24%] |
| |$5^-$| | |$v =2$||$(h_{11/2}^1s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{5}$| [11.79%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{5}$| [12.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{7}$| [23.07%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{9}$| [27.67%] |
| |$7^-$| | |$v =2$||$(h_{11/2}^1d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [17.00%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [16.24%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [22.14%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$| [24.63%] |
| |$15^-$| | |$v =4$||$(h_{11/2}^3d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{5}$| [27.60%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}h_{11/2}^{7}$| [23.21%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{1}s_{1/2}^2h_{11/2}^{7}$| [28.76%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^{3}s_{1/2}^2h_{11/2}^{7}$|[30.86%] |
| Spin | Seniority | |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn |
| |$27/2^-$| | |$v = 3$||$(h_{11/2}^3)$| | |$g_{7/2}^8d_{5/2}^6h_{11/2}^{5}$| [13.80%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{5}$| [14.26%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^{7}$| [19.86%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^{7}$| [34.55%] |
| |$19/2^+$| | |$v = 3$||$(h_{11/2}^2s_{1/2}^1)$| | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{4}$| [11.77%] | |$g_{7/2}^8d_{5/2}^6s_{1/2}^1h_{11/2}^{6}$| [13.81%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{6}$| [17.74%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^2s_{1/2}^1h_{11/2}^{8}$| [31.15%] |
| |$23/2^+$| | |$v = 3$||$(h_{11/2}^2d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{4}$| [18.49%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1h_{11/2}^{6}$| [21.77%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{6}$| [20.19%] | |$g_{7/2}^8d_{5/2}^6d_{3/2}^1s_{1/2}^2h_{11/2}^{8}$| [25.57%] |
| |$35/2^+$| | |$v = 5$||$(h_{11/2}^4d_{3/2}^1)$| | |$g_{7/2}^8d_{5/2}^6d_{3/2}^3s_{1/2}^2h_{11/2}^{4}$| [2.50%] |
Probability of different configurations for the |$10^+$| state in |$^{120}$|Sn.
| Probability | Wave functions |
|---|---|
| 8.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^4)$| |
| 5.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6s_{1/2}^2h_{11/2}^4)$| |
| 9.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6h_{11/2}^6)$| |
| 3.1|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2$||$s_{1/2}^2h_{11/2}^4)$| |
| 6.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2h_{11/2}^6)$| |
| 4.0|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4s_{1/2}^2h_{11/2}^6)$| |
| 2.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4h_{11/2}^8)$| |
| 1.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^2d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^4h_{11/2}^4)$| |
| 4.7|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^4)$| |
| 10.1|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^6)$| |
| 4.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6s_{1/2}^2h_{11/2}^6)$| |
| 2.6|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6h_{11/2}^8)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^4h_{11/2}^6)$| |
| 4.5|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 2.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2h_{11/2}^8)$| |
| 1.4|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4s_{1/2}^2h_{11/2}^8)$| |
| 1.3|$\%$| | |$\nu(g_{7/2}^4d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| Probability | Wave functions |
|---|---|
| 8.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^4)$| |
| 5.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6s_{1/2}^2h_{11/2}^4)$| |
| 9.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6h_{11/2}^6)$| |
| 3.1|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2$||$s_{1/2}^2h_{11/2}^4)$| |
| 6.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2h_{11/2}^6)$| |
| 4.0|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4s_{1/2}^2h_{11/2}^6)$| |
| 2.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4h_{11/2}^8)$| |
| 1.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^2d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^4h_{11/2}^4)$| |
| 4.7|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^4)$| |
| 10.1|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^6)$| |
| 4.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6s_{1/2}^2h_{11/2}^6)$| |
| 2.6|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6h_{11/2}^8)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^4h_{11/2}^6)$| |
| 4.5|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 2.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2h_{11/2}^8)$| |
| 1.4|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4s_{1/2}^2h_{11/2}^8)$| |
| 1.3|$\%$| | |$\nu(g_{7/2}^4d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
Probability of different configurations for the |$10^+$| state in |$^{120}$|Sn.
| Probability | Wave functions |
|---|---|
| 8.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^4)$| |
| 5.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6s_{1/2}^2h_{11/2}^4)$| |
| 9.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6h_{11/2}^6)$| |
| 3.1|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2$||$s_{1/2}^2h_{11/2}^4)$| |
| 6.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2h_{11/2}^6)$| |
| 4.0|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4s_{1/2}^2h_{11/2}^6)$| |
| 2.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4h_{11/2}^8)$| |
| 1.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^2d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^4h_{11/2}^4)$| |
| 4.7|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^4)$| |
| 10.1|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^6)$| |
| 4.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6s_{1/2}^2h_{11/2}^6)$| |
| 2.6|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6h_{11/2}^8)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^4h_{11/2}^6)$| |
| 4.5|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 2.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2h_{11/2}^8)$| |
| 1.4|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4s_{1/2}^2h_{11/2}^8)$| |
| 1.3|$\%$| | |$\nu(g_{7/2}^4d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| Probability | Wave functions |
|---|---|
| 8.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6d_{3/2}^2h_{11/2}^4)$| |
| 5.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6s_{1/2}^2h_{11/2}^4)$| |
| 9.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^6h_{11/2}^6)$| |
| 3.1|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2$||$s_{1/2}^2h_{11/2}^4)$| |
| 6.6|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4d_{3/2}^2h_{11/2}^6)$| |
| 4.0|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4s_{1/2}^2h_{11/2}^6)$| |
| 2.4|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^4h_{11/2}^8)$| |
| 1.9|$\%$| | |$\nu(g_{7/2}^8d_{5/2}^2d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^4h_{11/2}^4)$| |
| 4.7|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^4)$| |
| 10.1|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6d_{3/2}^2h_{11/2}^6)$| |
| 4.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6s_{1/2}^2h_{11/2}^6)$| |
| 2.6|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^6h_{11/2}^8)$| |
| 1.8|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^4h_{11/2}^6)$| |
| 4.5|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
| 2.9|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4d_{3/2}^2h_{11/2}^8)$| |
| 1.4|$\%$| | |$\nu(g_{7/2}^6d_{5/2}^4s_{1/2}^2h_{11/2}^8)$| |
| 1.3|$\%$| | |$\nu(g_{7/2}^4d_{5/2}^6d_{3/2}^2s_{1/2}^2h_{11/2}^6)$| |
In the case of |$^{120,122,124,126}$|Sn isotopes the different seniority states occur due to maximally aligned spin, which involves successive pair breakings in the |$\nu (h_{11/2})$| orbital. For 10|$^+$||$(h_{11/2}^2)$|, there is one pair breaking of the |$h_{11/2}$| orbital; thus, the seniority is two (|$v =2$|); for |$5^-$||$(h_{11/2}^1s_{1/2}^1)$|, one unpaired neutron is in the |$h_{11/2}$| orbital and one neutron is in the |$s_{1/2}$| orbital; thus, the seniority is two (|$v =2$|); for |$7^-$||$(h_{11/2}^1d_{3/2}^1)$|, one unpaired neutron is in the |$h_{11/2}$| orbital and one neutron is in the |$d_{3/2}$| orbital; thus, the seniority is two (|$v =2$|); for |$15^-$||$(h_{11/2}^3d_{3/2}^1)$|, three unpaired neutrons are in the |$h_{11/2}$| orbital and one neutron is in the |$d_{3/2}$| orbital and the number of unpaired neutrons is four; thus, the seniority is four (|$v =4$|). For |$19^-$||$(h_{11/2}^5d_{3/2}^1)$|, five unpaired neutrons are in the |$h_{11/2}$| orbital and one neutron is in the |$d_{3/2}$| orbital; thus, the seniority is six (|$v = 6$|).
In the case of |$^{119,121,123,125}$|Sn isotopes the different seniority states occur due to maximally aligned spin, which involves successive pair breakings in the |$\nu (h_{11/2})$| orbital. For |$27/2^-$||$(h_{11/2}^3)$|, three unpaired neutrons are in the |$h_{11/2}$| orbital; thus, the seniority is three (|$v = 3)$|; for |$19/2^+$||$(h_{11/2}^2s_{1/2}^1)$|, two unpaired neutrons are in the |$h_{11/2}$| orbital and one neutron is in the |$s_{1/2}$| orbital; thus, the seniority is three (|$v = 3)$|; for |$23/2^+$||$(h_{11/2}^2d_{3/2}^1)$|, two unpaired neutrons are in the |$h_{11/2}$| orbital and one neutron is in the |$d_{3/2}$| orbital; thus, the seniority is three (|$v = 3)$|; for |$35/2^+$||$(h_{11/2}^4d_{3/2}^1)$|, four unpaired neutrons are in the |$h_{11/2}$| orbital and one neutron is in the |$d_{3/2}$| orbital; thus, the seniority is five (|$v = 5)$|. The seniority of the |$39/2^+$| state is seven (|$v=7$|). Here there are six unpaired neutrons in the |$h_{11/2}$| orbital and one neutron in the |$d_{3/2}$| orbital; the number of unpaired neutrons is seven and thus the seniority is seven (|$v = 7)$|.
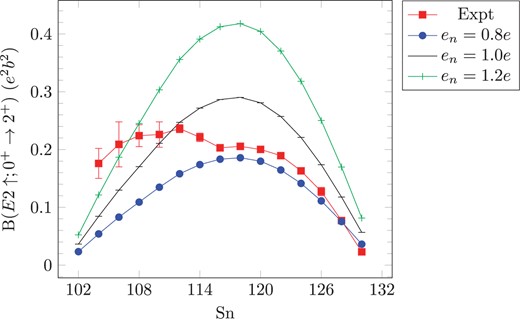
4. Transition probabilities
In Table 3, we show |$B(E2)$| transition probabilities of the isomeric states for |$^{119-126}$|Sn isotopes. These calculated values of |$E2$| transition probabilities are important for future experiments. After calculating |$B(E2; 0^+ \rightarrow 2^+)$| for heavier Sn isotopes, we have found that the calculated results show good agreement with experimental data with |$e_n=0.8e$| (see Fig. 11). Thus, for comparison, apart from the standard effective charge for neutron |$e_n=0.5e$|, we have also calculated |$B(E2)$| values with a second set of effective charge |$e_n=0.8e$|, although for high-spin states |$B(E2)$| values are very large with this effective charge. The SN100PN interaction results for energy levels are in reasonable agreement with the experimental data; however, the calculated results for |$B(E2)$| transitions are not in good agreement. This might be due to a deficiency in the wave functions rather than in the effective operator, because electromagnetic properties are sensitive to the detailed composition of the nuclear wave function.
Calculated |$B(E2)$| values for different transitions in |$e^2fm^4$| using |$e_n=0.5e$|, |$e_n=0.8e$| separated by “/”. Experimental data have been taken from Ref. [2].
| |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn | |||||
|---|---|---|---|---|---|---|---|---|
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$10^+ \rightarrow 8^+$| | NA | 0.69/1.50 | NA | 0.15/0.47 | NA | 3.46/8.75 | NA | 10.23/26.38 |
| |$15^- \rightarrow 13^-$| | 21(2) | 81.11/211.89 | 4.7(4) | 76.83/192.00 | 3.2(4) | 34.97/88.17 | 22(2) | 14.22/36.38 |
| |$7^- \rightarrow 5^-$| | NA | 28.23/74.92 | NA | 16.42/39.66 | NA | 4.94/11.59 | NA | 0.0013/0.003 |
| |$5^- \rightarrow 3^-$| | NA | 39.73/102.74 | NA | 45.86/118.79 | NA | 44.67/113.31 | NA | 21.18/53.74 |
| |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn | |||||
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$27/2^- \rightarrow 23/2^-$| | 73(7) | 21.09/57.52 | NA | 0.61/1.62 | NA | 12.86/32.81 | NA | 23.36/60.42 |
| |$23/2^+ \rightarrow 19/2^+$| | 6.7(8) | 59.12/149.82 | 1.8(2) | 52.17/133.33 | 0.22(3) | 25.31/43.15 | 5.4(7) | 6.95/21.99 |
| |$19/2^+ \rightarrow 15/2^+$| | NA | 0.09/0.91 | NA | 5.12/19.81 | 6.7(25) | 9.17/24.17 | 22(4) | 10.03/24.60 |
| |$35/2^+ \rightarrow 31/2^+$| | NA | 10.58/27.09 | NA | 58.41/149.52 | 109(29) | 0.391/1.003 | NA | 47.67/122.04 |
| |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn | |||||
|---|---|---|---|---|---|---|---|---|
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$10^+ \rightarrow 8^+$| | NA | 0.69/1.50 | NA | 0.15/0.47 | NA | 3.46/8.75 | NA | 10.23/26.38 |
| |$15^- \rightarrow 13^-$| | 21(2) | 81.11/211.89 | 4.7(4) | 76.83/192.00 | 3.2(4) | 34.97/88.17 | 22(2) | 14.22/36.38 |
| |$7^- \rightarrow 5^-$| | NA | 28.23/74.92 | NA | 16.42/39.66 | NA | 4.94/11.59 | NA | 0.0013/0.003 |
| |$5^- \rightarrow 3^-$| | NA | 39.73/102.74 | NA | 45.86/118.79 | NA | 44.67/113.31 | NA | 21.18/53.74 |
| |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn | |||||
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$27/2^- \rightarrow 23/2^-$| | 73(7) | 21.09/57.52 | NA | 0.61/1.62 | NA | 12.86/32.81 | NA | 23.36/60.42 |
| |$23/2^+ \rightarrow 19/2^+$| | 6.7(8) | 59.12/149.82 | 1.8(2) | 52.17/133.33 | 0.22(3) | 25.31/43.15 | 5.4(7) | 6.95/21.99 |
| |$19/2^+ \rightarrow 15/2^+$| | NA | 0.09/0.91 | NA | 5.12/19.81 | 6.7(25) | 9.17/24.17 | 22(4) | 10.03/24.60 |
| |$35/2^+ \rightarrow 31/2^+$| | NA | 10.58/27.09 | NA | 58.41/149.52 | 109(29) | 0.391/1.003 | NA | 47.67/122.04 |
Calculated |$B(E2)$| values for different transitions in |$e^2fm^4$| using |$e_n=0.5e$|, |$e_n=0.8e$| separated by “/”. Experimental data have been taken from Ref. [2].
| |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn | |||||
|---|---|---|---|---|---|---|---|---|
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$10^+ \rightarrow 8^+$| | NA | 0.69/1.50 | NA | 0.15/0.47 | NA | 3.46/8.75 | NA | 10.23/26.38 |
| |$15^- \rightarrow 13^-$| | 21(2) | 81.11/211.89 | 4.7(4) | 76.83/192.00 | 3.2(4) | 34.97/88.17 | 22(2) | 14.22/36.38 |
| |$7^- \rightarrow 5^-$| | NA | 28.23/74.92 | NA | 16.42/39.66 | NA | 4.94/11.59 | NA | 0.0013/0.003 |
| |$5^- \rightarrow 3^-$| | NA | 39.73/102.74 | NA | 45.86/118.79 | NA | 44.67/113.31 | NA | 21.18/53.74 |
| |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn | |||||
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$27/2^- \rightarrow 23/2^-$| | 73(7) | 21.09/57.52 | NA | 0.61/1.62 | NA | 12.86/32.81 | NA | 23.36/60.42 |
| |$23/2^+ \rightarrow 19/2^+$| | 6.7(8) | 59.12/149.82 | 1.8(2) | 52.17/133.33 | 0.22(3) | 25.31/43.15 | 5.4(7) | 6.95/21.99 |
| |$19/2^+ \rightarrow 15/2^+$| | NA | 0.09/0.91 | NA | 5.12/19.81 | 6.7(25) | 9.17/24.17 | 22(4) | 10.03/24.60 |
| |$35/2^+ \rightarrow 31/2^+$| | NA | 10.58/27.09 | NA | 58.41/149.52 | 109(29) | 0.391/1.003 | NA | 47.67/122.04 |
| |$^{120}$|Sn | |$^{122}$|Sn | |$^{124}$|Sn | |$^{126}$|Sn | |||||
|---|---|---|---|---|---|---|---|---|
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$10^+ \rightarrow 8^+$| | NA | 0.69/1.50 | NA | 0.15/0.47 | NA | 3.46/8.75 | NA | 10.23/26.38 |
| |$15^- \rightarrow 13^-$| | 21(2) | 81.11/211.89 | 4.7(4) | 76.83/192.00 | 3.2(4) | 34.97/88.17 | 22(2) | 14.22/36.38 |
| |$7^- \rightarrow 5^-$| | NA | 28.23/74.92 | NA | 16.42/39.66 | NA | 4.94/11.59 | NA | 0.0013/0.003 |
| |$5^- \rightarrow 3^-$| | NA | 39.73/102.74 | NA | 45.86/118.79 | NA | 44.67/113.31 | NA | 21.18/53.74 |
| |$^{119}$|Sn | |$^{121}$|Sn | |$^{123}$|Sn | |$^{125}$|Sn | |||||
| |${B(E2; i \rightarrow f}$|) | Expt. | SM | Expt. | SM | Expt. | SM | Expt. | SM |
| |$27/2^- \rightarrow 23/2^-$| | 73(7) | 21.09/57.52 | NA | 0.61/1.62 | NA | 12.86/32.81 | NA | 23.36/60.42 |
| |$23/2^+ \rightarrow 19/2^+$| | 6.7(8) | 59.12/149.82 | 1.8(2) | 52.17/133.33 | 0.22(3) | 25.31/43.15 | 5.4(7) | 6.95/21.99 |
| |$19/2^+ \rightarrow 15/2^+$| | NA | 0.09/0.91 | NA | 5.12/19.81 | 6.7(25) | 9.17/24.17 | 22(4) | 10.03/24.60 |
| |$35/2^+ \rightarrow 31/2^+$| | NA | 10.58/27.09 | NA | 58.41/149.52 | 109(29) | 0.391/1.003 | NA | 47.67/122.04 |
Shell-model results of |$B(E2)$| values for Sn isotopes.
In Fig. 12, we show amplitudes of the reduced transition probabilities for |$E2$| isomeric decay in Sn isotopes corresponding to isomeric states |$10^+$| and |$27/2^-$|. The |$10^+$| and |$8^+$| states are due to seniority two and the |$27/2^-$| and |$23/2^-$| states are due to seniority three. Thus a linear decrease in |$B(E2)$| values is obtained. The behavior of the |$\sqrt{B(E2;10^+ \rightarrow 8^+)}$| and |$\sqrt{B(E2;27/2^- \rightarrow 23/2^-)}$| transitions as a function of mass number (|$A$|) was used to determine the filling of the |$\nu h_{11/2}$| orbital. Since we have plotted the results in the same figure, we have multiplied by a factor of 0.264 for |$B(E2)$| values corresponding to the |$27/2^- \rightarrow 23/2^-$| transition; this comes from expressions for the |$v=2$| and |$v=3$| transitions as reported in Ref. [31] (for more details about the expressions please see this reference). The 0.264 factor is used to compensate coefficients of fractional parentage (c.f.p.) entering in the expression [32] of states with seniority |$v =3$| (for |$23/2^-$| and |$27/2^-$|) in comparison to states with seniority |$v =2$| (for |$8^+$| and |$10^+$|). The similar behavior of |$B(E2)$| values for the |$10^+ \rightarrow 8^+$| and |$27/2^- \rightarrow 23/2^-$| transitions occurs because the initial and final states have the same seniority with increasing neutron numbers.
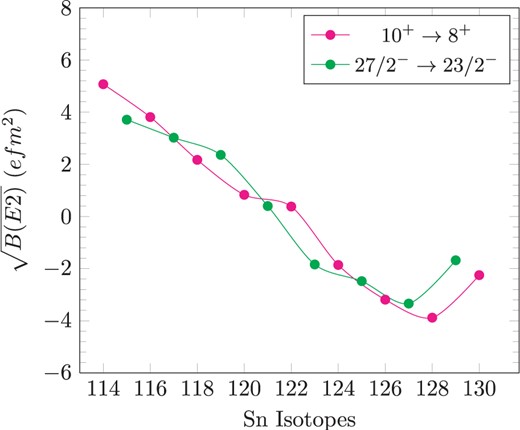
Shell-model results (with |$e_n=0.5e$|) for amplitudes of the reduced transition probabilities for |$E2$| isomeric decay in Sn isotopes. The |${B(E2;27/2^- \rightarrow 23/2^-)}$| values are multiplied by the factor 0.264.
5. Summary and conclusion
In the present work we have reported a comprehensive shell-model description of high-spin states in |$^{119-126}$|Sn isotopes. With the shell-model configurations of different high-spin states, we have analyzed different isomeric states in these nuclei. These states can be described in terms of several broken neutron pairs occupying the |$h_{11/2}$| orbital. The high-spin isomers in Sn isotopes are due to seniority |$(v) = 2$|, 3, 4, and 5. For the |$^{120,122,124,126}$|Sn isotopes, the seniority of isomeric states |$10^+$|, |$5^-$|, and |$7^-$| is two (|$v = 2$|); the seniority of isomeric state |$15^-$| is four (|$v = 4$|); the seniority of the |$19^-$| state is six (|$v = 6$|). For the |$^{119,121,123,125}$|Sn isotopes, the seniority of isomeric states |$19/2^+$|, |$23/2^+$|, and |$27/2^-$| is three (|$v = 3$|); the seniority of isomeric state |$35/2^+$| is five (|$v=5$|); the seniority of the |$39/2^+$| state is seven (|$v=7$|). The probability of different configurations is not so large but it increases with neutron number for heavier Sn isotopes. We have also reported |$B(E2)$| values for different transitions for |$^{120-126}$|Sn isotopes.
Acknowledgements
B.B. acknowledges financial support from MHRD (Govt. of India) for her Ph.D. thesis work. P.C.S. acknowledges the hospitality extended to him during his stay at Saitama University, Japan. M.J.E.’s work is partially supported by the Uzbekistan National Agency of Science and Technology (OT-F2-15). We would like to thank N. Yoshinaga and K. Yanase for useful discussions and initial collaboration in this work.
