-
PDF
- Split View
-
Views
-
Cite
Cite
H. Matsuno, N. Itagaki, T. Ichikawa, Y. Yoshida, Y. Kanada-En’yo, Effect of |$^{12}\mathrm{C}+\alpha$| clustering on the |$E0$| transition in |$^{16}\mathrm{O}$|, Progress of Theoretical and Experimental Physics, Volume 2017, Issue 6, June 2017, 063D01, https://doi.org/10.1093/ptep/ptx065
Close - Share Icon Share
Abstract
We investigate cluster structures and |$E0$| transitions of |$0^+$| states in |$^{16}$|O. In particular, we discuss the mixing effect of |$3\alpha$| and |$\alpha$| breaking components in the |$^{12}$|C cluster on the |$E0$| transitions. To this end, we perform a microscopic calculation including |$\alpha$| cluster and cluster-breaking model spaces. By analyzing the obtained results, we confirm that the |$0_2^+$| and |$0_3^+$| states of |$^{16}$|O are indeed the weak-coupling |$^{12}\mathrm{C}(0^+)+\alpha$| and |$^{12}\mathrm{C}(2^+)+\alpha$| cluster states, respectively. We find mainly two important mechanisms for reducing the |$E0$| transition: (i) the difference in intrinsic spin configurations between the initial and final states caused by the cluster breaking and (ii) the mixing of planar |$4\alpha$| configurations in the excited states. We show that the |$E0$| operator excites the initial (ground) state not to planar |$4\alpha$| configurations but predominantly to triangular pyramid |$4\alpha$| configurations. Thus, the mixture of the planar |$4\alpha$| configurations in the |$0_2^+$| state significantly reduces the |$E0$| transition matrix elements to this state. We conclude that the |$E0$| transitions tend to be enhanced by cluster states, but they are affected by various mechanisms originating in the detailed structures of the final states.
1. Introduction
The |$E0$| transition in heavy nuclei has been intensively studied to obtain information on nuclear matter properties because the giant monopole resonance energy is sensitive to incompressibility. In addition, it has also recently been discussed in relation to cluster structures of light nuclei [1,2]. If the system is composed of strongly bound subsystems called clusters and the intercluster potential is weak, the intercluster motion can be excited with a small amount of energy. Indeed, in light nuclei, it is known that cluster states appear in low-excitation-energy regions. Since the |$E0$| operator strongly excites the intercluster motion, those cluster states tend to have enhanced |$E0$| transitions and contribute to significant |$E0$| strengths in the low-energy region. Recently, strong |$E0$| transitions from the ground states have been discussed in relation to cluster structures for |$^{11}\mathrm{B}$| [1], |$^{12, 13}\mathrm{C}$| [2–4], and |$^{24}\mathrm{Mg}$|, etc. [5,6].
In |$^{16}\mathrm{O}$|, strong |$E0$| transitions from the ground state to the |$0_2^+$| (|$E_x=6.0494\,\mathrm{MeV}$|) and |$0_3^+$| (|$E_x=12.049\,\mathrm{MeV}$|) states have been observed. The measured |$E0$| matrix elements for the |$0_1^+\to0_2^+$| and |$0_1^+\to0_3^+$| transitions are |$3.55\pm0.21\,e\,\mathrm{fm}^2$| and |$4.03\pm0.09\,e\,\mathrm{fm}^2$|, respectively [7,8], and they correspond to about 3% and 8% of the energy-weighted sum rule [9]. In Ref. [10], it is suggested that the |$E0$| transition strengths in the low-excitation-energy region originate from the degree of freedom for cluster structure. The |$0_2^+$| state of |$^{16}\mathrm{O}$| is known to have a developed |$^{12}\mathrm{C}+\alpha$| cluster structure [11]. Based on the cluster approaches, the cluster structures and |$E0$| transitions of these low-lying |$0^+$| states have been theoretically explained in the frameworks of the orthogonality condition model (OCM) of |$^{12}\mathrm{C}+\alpha$| (|$^{12}\mathrm{C}+\alpha$| OCM) [12,13], that of |$4\alpha$| (|$4\alpha$| OCM) [10], and the antisymmetrized molecular dynamics (AMD) model with the generator coordinate method (GCM) of |$^{12}\mathrm{C}+\alpha$| [|$^{12}\mathrm{C(AMD)}+\alpha$| GCM] [14].
In this paper, we reanalyze the |$E0$| transitions from the ground state of |$^{16}\mathrm{O}$| to |$^{12}\mathrm{C}+\alpha$| cluster states while focusing on how the cluster structure contributes to the |$E0$| transitions. Particular attention is paid to the structure of the |$^{12}\mathrm{C}$| cluster part. In the ground and excited states of |$^{12}\mathrm{C}$|, |$3\alpha$| dynamics plays an essential role. So far, various |$3\alpha$| cluster models have been successfully introduced in describing the structure of |$^{12}\mathrm{C}$| [15]. However, since |$^{12}\mathrm{C}$| corresponds to the subclosure of spin–orbit attractive orbits (|$p_{3/2}$|), it has recently been pointed out that the cluster-breaking effect of |$3\alpha$|, i.e., the mixing of |$jj$|-coupling shell components, is important [16]; this is not taken into account in the conventional |$3\alpha$| cluster models. Therefore, it is expected that both the |$3\alpha$| cluster and |$jj$|-coupling components of the |$^{12}\mathrm{C}$| part are important in the |$^{12}\mathrm{C}+\alpha$| cluster states of |$^{16}\mathrm{O}$|. In the preceding works of Refs. [10,12,13] for |$^{16}\mathrm{O}$|, the effect of |$3\alpha$| cluster breaking in |$^{12}\mathrm{C}$| is missing. On the other hand, the treatment of |$3\alpha$| dynamics is insufficient in Ref. [14]. Also, the OCM adopted in Refs. [10,12,13] is a semi-microscopic model and the wave function is not fully antisymmetrized. Thus, it is worthwhile to introduce a microscopic model to discuss the possible effects of the mixing of |$3\alpha$|-breaking components on the |$E0$| transitions in |$^{16}\mathrm{O}$|.
The aim of this work is to clarify cluster structures and their contribution to the |$E0$| transitions in |$^{16}\mathrm{O}$| by taking into account both |$3\alpha$| dynamics and |$\alpha$| cluster breaking in the |$^{12}\mathrm{C}$| part in a microscopic framework. In addition, we clarify the mechanism for the existence of two strong |$E0$| transitions in the low-excitation-energy region of |$^{16}\mathrm{O}$|.
For this purpose, we prepare both a |$3\alpha$| cluster model space and a cluster-breaking model space for the |$^{12}\mathrm{C}$| part in a unified manner. To achieve this, we use the antisymmetrized quasi cluster model (AQCM) [17–21], which can easily describe the |$p_{3/2}$| subclosed configuration as well as |$3\alpha$| cluster wave functions by extending the cluster model. Note that the original AQCM can smoothly connect a cluster state to a |$jj$|-coupling shell state with one parameter. In this work, we adopt the AQCM description just to add the |$p_{3/2}$| subclosed configuration to |$3\alpha$| cluster wave functions of the |$^{12}\mathrm{C}$| part as done in Ref. [17].
This paper is organized as follows. We describe our formulation in this work in Sect. 2. The results and discussion are given in Sect. 3. Finally, we present our conclusion and outlook in Sect. 4.
2. Formulation
In this section, we describe the wave function of |$^{16}\mathrm{O}$| and the Hamiltonian in the present model.
2.1. Wave function
2.1.1. Single-particle wave function
The coordinate system is defined in the following way. The model used in this study consists of the |$^{12}\mathrm{C}(3\alpha)+\alpha$| and |$^{12}\mathrm{C}(p_{3/2})+\alpha$| model spaces. We place the |$^{12}\mathrm{C}$| cluster and the |$\alpha$| cluster on the |$z$| axis with a distance |$h$|. The center of mass of the whole system is set to the origin. For the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space, firstly, we describe the |$^{12}\mathrm{C}$| cluster with three |$\alpha$| clusters placed on the |$x$|–|$y$| plane in an equilateral triangle configuration with a side length |$R$|. Next, we consider the rotation of the |$^{12}\mathrm{C}$| cluster part with an angle |$\theta$|. In the present calculation, only 1D rotation is taken into account for the sake of simplicity. The |$^{12}\mathrm{C}(3\alpha)+\alpha$| configuration defined by parameters |$R$|, |$h$|, and |$\theta$| is schematically shown in Fig. 1. For the |$^{12}\mathrm{C}(p_{3/2})+\alpha$| model space, we describe the |$^{12}\mathrm{C}$| cluster with the |$p_{3/2}$| subclosed configuration by taking a small enough |$R$| value as |$R=0.1\,\mathrm{fm}$| and the dissolution parameter |$\varLambda=1$| in the AQCM parametrization for the three |$\alpha$| clusters, as done in Ref. [17]. Since the |$p_{3/2}$| subclosed state is spherical, we do not need to consider the rotational degree of freedom of the |$^{12}\mathrm{C}(p_{3/2})$| cluster.
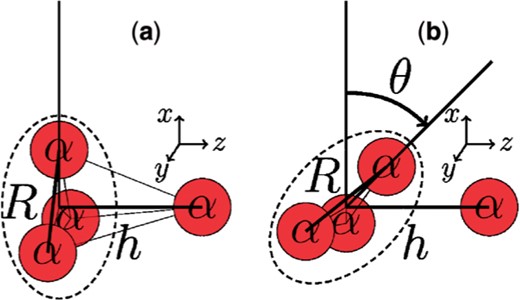
Schematic figure for the definitions of |$R$|, |$h$|, and |$\theta$|. The red spheres show the |$\alpha$| clusters. The left-hand panel (a) shows the |$\theta=0$| configuration and the right-hand panel (b) corresponds to |$\theta$| rotation of the |$^{12}\mathrm{C}$| cluster part.
2.1.2. Wave function of the total system
2.2. Squared overlap with |$^{12}\mathrm{C}+\alpha$| cluster wave function
2.3. Hamiltonian
3. Results and discussion
3.1. Energy levels and the features of each state
We first investigate the features of the obtained |$0^+$| states in |$^{16}\mathrm{O}$|. The obtained energy of the ground state is |$-127.5\,\mathrm{MeV}$|, which reproduces well the experimental value of |$-127.6\,\mathrm{MeV}$| [27]. In Table 1, we tabulate the obtained excitation energies, root mean square (r.m.s.) charge radii, and |$\alpha$| decay widths of the |$0_n^+$| (|$n=1,\ldots,4$|) states. The |$\alpha$| decay widths are calculated using the method shown in Ref. [28]. The |$\alpha$| decay widths |$\varGamma$| are determined as
Calculated excitation energies (|$E_x$|), r.m.s. charge radii (|$R_c$|), and |$\alpha$| decay widths (|$\varGamma$|). In the calculations of the charge radii, we use the charge radius of a proton with a value of |$0.887\, \mathrm{fm}$| [26]. The experimental charge radius of the |$0_1^+$| state is |$R_c=2.70\,\mathrm{fm}$| [26].
| State . | |$E_x$| (MeV) . | |$R_c$| (fm) . | |$\varGamma$| (MeV) . |
|---|---|---|---|
| |$0_1^+$| | |$\phantom{0}0.0$| | |$2.60$| | |
| |$0_2^+$| | |$17.0$| | |$2.92$| | |
| |$0_3^+$| | |$22.2$| | |$3.00$| | |$0.000\,17$| |
| |$0_4^+$| | |$24.6$| | |$3.15$| | |$0.55$| |
| State . | |$E_x$| (MeV) . | |$R_c$| (fm) . | |$\varGamma$| (MeV) . |
|---|---|---|---|
| |$0_1^+$| | |$\phantom{0}0.0$| | |$2.60$| | |
| |$0_2^+$| | |$17.0$| | |$2.92$| | |
| |$0_3^+$| | |$22.2$| | |$3.00$| | |$0.000\,17$| |
| |$0_4^+$| | |$24.6$| | |$3.15$| | |$0.55$| |
Calculated excitation energies (|$E_x$|), r.m.s. charge radii (|$R_c$|), and |$\alpha$| decay widths (|$\varGamma$|). In the calculations of the charge radii, we use the charge radius of a proton with a value of |$0.887\, \mathrm{fm}$| [26]. The experimental charge radius of the |$0_1^+$| state is |$R_c=2.70\,\mathrm{fm}$| [26].
| State . | |$E_x$| (MeV) . | |$R_c$| (fm) . | |$\varGamma$| (MeV) . |
|---|---|---|---|
| |$0_1^+$| | |$\phantom{0}0.0$| | |$2.60$| | |
| |$0_2^+$| | |$17.0$| | |$2.92$| | |
| |$0_3^+$| | |$22.2$| | |$3.00$| | |$0.000\,17$| |
| |$0_4^+$| | |$24.6$| | |$3.15$| | |$0.55$| |
| State . | |$E_x$| (MeV) . | |$R_c$| (fm) . | |$\varGamma$| (MeV) . |
|---|---|---|---|
| |$0_1^+$| | |$\phantom{0}0.0$| | |$2.60$| | |
| |$0_2^+$| | |$17.0$| | |$2.92$| | |
| |$0_3^+$| | |$22.2$| | |$3.00$| | |$0.000\,17$| |
| |$0_4^+$| | |$24.6$| | |$3.15$| | |$0.55$| |
![Energy levels of $0^+$ states obtained by this work (Present), the $^{12}\mathrm{C}+\alpha$ resonating group method (RGM) [30], $^{12}\mathrm{C}+\alpha$ GCM [31], $^{12}\mathrm{C}+\alpha$ OCM [12,13], $4\alpha$ OCM [10], and $^{12}\mathrm{C}$(AMD) $+\alpha$ GCM [14], together with the experimental one (Exp). The dashed line indicates $^{12}\mathrm{C}+\alpha$ threshold energy. Here, I, II, III, and IV denote the character of the states, whose dominant configurations are: I: closed $p$-shell structure, II: $^{12}\mathrm{C}(0^+)+\alpha$ cluster structure, III: $^{12}\mathrm{C}(2^+)+\alpha$ cluster structure, and IV: higher nodal behavior of $^{12}\mathrm{C}(0^+)+\alpha$ structure.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2017/6/10.1093_ptep_ptx065/1/m_ptx065F2.jpeg?Expires=1748190671&Signature=4FB81pBLbVSLil4Sf4q4GEcyE2N~k~t4EA-UyPmNWjpzfwcOU5upvYSdrTK0l~Daz2xjsbo7L-sxTbLcYfxYR9URyop~pUdQtNXTd8-AZiP5dREqj1FmJaxuK5f0JOk9pbgMEXwwKSOn6wRZCH6H2w33gy6H38HJnib~zP2dY1BvUQBq8Nrx54DxrEIsgbgVvmlP9kjgiHXxZJ4p21ZtrbTHwYCM02uZZE-6OI27gYz0LgQVOx~cnp-jcr0~K5tCtnRL3ZSoY-l0r2A6ClzaZBi0ckf1iF1RhAvs0B-SadUANe8cQB1josaWRGz0xUptWXTB~XoKohAND7V8~YrC8w__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Energy levels of |$0^+$| states obtained by this work (Present), the |$^{12}\mathrm{C}+\alpha$| resonating group method (RGM) [30], |$^{12}\mathrm{C}+\alpha$| GCM [31], |$^{12}\mathrm{C}+\alpha$| OCM [12,13], |$4\alpha$| OCM [10], and |$^{12}\mathrm{C}$|(AMD) |$+\alpha$| GCM [14], together with the experimental one (Exp). The dashed line indicates |$^{12}\mathrm{C}+\alpha$| threshold energy. Here, I, II, III, and IV denote the character of the states, whose dominant configurations are: I: closed |$p$|-shell structure, II: |$^{12}\mathrm{C}(0^+)+\alpha$| cluster structure, III: |$^{12}\mathrm{C}(2^+)+\alpha$| cluster structure, and IV: higher nodal behavior of |$^{12}\mathrm{C}(0^+)+\alpha$| structure.
Figures 3(a), (b), (c), and (d) show the |$[^{12}\mathrm{C}(0^+,2^+)+\alpha]_{0^+}$| cluster components in the obtained |$0^+_1$|, |$0^+_2$|, |$0^+_3$|, and |$0^+_4$| states, respectively, as a function of the intercluster distance |$h$|. The solid line with circles indicates the squared overlap between each obtained state and the |$^{12}$|C(0|$^+$|) + |$\alpha$| cluster wave function. The dotted line with open circles indicates that for the |$^{12}$|C(2|$^+$|) + |$\alpha$| cluster wave function. In the |$0_1^+$| state (Fig. 3(a)), the squared overlap shows a peak in the small |$h$| region (|$h\sim2\,\mathrm{fm}$|), indicating the compact structure of this state. Two components, |$[^{12}\mathrm{C}(0^+)+\alpha]_{0^+}$| and |$[^{12}\mathrm{C}(2^+)+\alpha]_{0^+}$|, show similar distributions, because |$[^{12}\mathrm{C}(0^+)+\alpha]_{0^+}$| and |$[^{12}\mathrm{C}(2^+)+\alpha]_{0^+}$| represent the same closed |$p$|-shell configuration at small relative distances. Figure 3(b) for the |$0_2^+$| state shows a dominant |$[^{12}\mathrm{C}(0^+)+\alpha]_{0^+}$| component with a peak around |$h=4\,\mathrm{fm}$| and the minor |$[^{12}\mathrm{C}(2^+)+\alpha]_{0^+}$| component, indicating that the |$0_2^+$| state has a developed |$[^{12}\mathrm{C}(0^+)+\alpha]_{0^+}$| structure. In contrast, the |$0_3^+$| state has a dominant |$[^{12}\mathrm{C}(2^+)+\alpha]_{0^+}$| component with a peak around |$h=4\,\mathrm{fm}$|, as shown in Fig. 3(c). This indicates that the |$0_3^+$| state has a developed |$[^{12}\mathrm{C}(2^+)+\alpha]_{0^+}$| structure. Figure 3(d) for the |$0_4^+$| state shows a higher nodal behavior of |$[^{12}\mathrm{C}(0^+)+\alpha]_{0^+}$| structure in this state. In the above analysis of the |$[^{12}\mathrm{C}(0^+,2^+)+\alpha]_{0^+}$| cluster components, we have confirmed that the |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states can be understood as weak-coupling |$^{12}\mathrm{C}+\alpha$| cluster states. The nature of each |$0^+$| state is consistent with the |$^{12}\mathrm{C}+\alpha$| OCM [12,13] and |$4\alpha$| OCM calculations [10]. Namely, the dominant cluster components and relative energies of the |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states are in good agreement with the results of Refs. [10,12,13].
![Squared overlap between the (a) $0_1^+$, (b) $0_2^+$, (c) $0_3^+$, and (d) $0_4^+$ states and the $^{12}\mathrm{C}(I^+)+\alpha$ cluster wave functions defined in Sect. 2.2. These values are calculated using Eq. (8). The solid line with circles indicates the squared overlap for the $[^{12}\mathrm{C}(0^+)+\alpha]_{0^+}$ wave function as a function of $h$. The dotted line with open circles indicates that for the $[^{12}\mathrm{C}(2^+)+\alpha]_{0^+}$ wave function.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ptep/2017/6/10.1093_ptep_ptx065/1/m_ptx065F3.jpeg?Expires=1748190671&Signature=NLf18GLhH7tkSX0ElEbK~G3jnL6NYH5~rOtcN2eEA~oBw0ddUZtVcoQGeiLhhGCBV1kNj0ffT2dqbfOFYHeeP2YTYL9Yv1J9XWPgrLih51s4jC4o3l5FvLAkUSbEyGn87cvnxx~mbFSPYf~Yr9vSr2ZF8iuE4kHlGIAMCDnRNOEwPC9zqMq-TqSfJJxyh4UMrR0J22ecnL-dtFsLTb3f9OxVmdv3ajeOOBJyICQgQmccVU-qDm4XMD3LR~-THGweVofQGdA7FinbunBdy2Bv6Ba5TFAiU~XVTR8R03s1vqQGdAsU~DNvno9ajD8GxDMNjXmwgriJD4rSmwFeWJla0g__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Squared overlap between the (a) |$0_1^+$|, (b) |$0_2^+$|, (c) |$0_3^+$|, and (d) |$0_4^+$| states and the |$^{12}\mathrm{C}(I^+)+\alpha$| cluster wave functions defined in Sect. 2.2. These values are calculated using Eq. (8). The solid line with circles indicates the squared overlap for the |$[^{12}\mathrm{C}(0^+)+\alpha]_{0^+}$| wave function as a function of |$h$|. The dotted line with open circles indicates that for the |$[^{12}\mathrm{C}(2^+)+\alpha]_{0^+}$| wave function.
3.2. |$E0$| transition matrix element
In Table 2, the obtained |$E0$| transition matrix elements from |$0_1^+$| to |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| are tabulated with the available experimental data and also theoretical values of other calculations. In this work, remarkable |$E0$| transitions to the |$0_2^+$| and |$0_3^+$| states are obtained because of the developed cluster structures of these states. However, we somewhat overestimate their matrix elements compared to the experimental |$E0$|. It could be possible that this overestimate is concerned with the |$E0$| transition of the |$^{12}\mathrm{C}$| part. In our model, 3|$\alpha$| breathing excitation of |$^{12}\mathrm{C}$| is included and this mode enhances |$E0$| transitions. This overestimation could come from the weaker binding problem for the |$^{12}\mathrm{C}$| part. In the present calculation, the interaction parameters are adjusted to the |$^{16}\mathrm{O}$| binding energy, but they underestimate the |$^{12}\mathrm{C}$| binding energy. This is a well known problem of density-independent two-body effective interactions. The weaker binding of |$^{12}\mathrm{C}$| may cause overestimation of monopole excitations in the |$^{12}\mathrm{C}$| subsystem, which could enhance the |$E0$| transitions of |$^{16}\mathrm{O}$|. If we suppress contributions from the monopole excitations of |$^{12}\mathrm{C}$| by hand, we get a better result for the |$E0$| matrix elements of |$^{16}\mathrm{O}$|. Indeed, when we truncate our model space with |$R =2$|, |$3$|, and |$4\,\mathrm{fm}$|, i.e., calculate only within |$^{12}\mathrm{C}(3\alpha)+\alpha$| with |$R = 1\,\mathrm{fm}$| and |$^{12}\mathrm{C}(p_{3/2})+\alpha$|, the |$E0$| matrix elements for the |$0_1^+\to0_2^+$| and |$0_1^+\to0_3^+$| transitions are reduced to |$3.85\,e\, \mathrm{fm}^2$| and |$4.27\,e\,\mathrm{fm}^2$|, respectively. The |$E0$| transition matrix elements from |$0_1^+$| to |$0_2^+$| and to |$0_3^+$| are smaller in the previous research (|$^{12}\mathrm{C}+\alpha$| OCM calculation, |$4\alpha$| OCM calculation, and |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha$| GCM calculation) than those of our results. In the |$4\alpha$| OCM calculation, |$^{12}\mathrm{C}$| is bound from the |$3\alpha$| threshold more correctly than in our calculation. In the |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha$| GCM calculation, the |$^{12}\mathrm{C}$| part is described by only three important configurations. In both cases, the excitation of the |$^{12}\mathrm{C}$| part is more suppressed in comparison to our result, and that may reduce the |$E0$| transition.
|$E0$| transition matrix elements from the |$0_1^+$| to |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states calculated with the present AQCM, |$^{12}\mathrm{C}+\alpha$| OCM [12,13], |$4\alpha$| OCM [10], and |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha\ \mathrm{GCM}$| [14]. Experimental data (Exp) are taken from Refs. [7,8].
| |$(e\,\mathrm{fm^2})$| . | AQCM . | |$^{12}\mathrm{C}+\alpha$| OCM . | |$4\alpha$| OCM . | |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha\ \mathrm{GCM}$| . | Exp . |
|---|---|---|---|---|---|
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$3.88$| | |$3.9$| | |$4.0$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.50$| | |$2.4$| | |$3.5$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$-$| | |$2.4$| | |$6.0$| | No data |
| |$(e\,\mathrm{fm^2})$| . | AQCM . | |$^{12}\mathrm{C}+\alpha$| OCM . | |$4\alpha$| OCM . | |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha\ \mathrm{GCM}$| . | Exp . |
|---|---|---|---|---|---|
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$3.88$| | |$3.9$| | |$4.0$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.50$| | |$2.4$| | |$3.5$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$-$| | |$2.4$| | |$6.0$| | No data |
|$E0$| transition matrix elements from the |$0_1^+$| to |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states calculated with the present AQCM, |$^{12}\mathrm{C}+\alpha$| OCM [12,13], |$4\alpha$| OCM [10], and |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha\ \mathrm{GCM}$| [14]. Experimental data (Exp) are taken from Refs. [7,8].
| |$(e\,\mathrm{fm^2})$| . | AQCM . | |$^{12}\mathrm{C}+\alpha$| OCM . | |$4\alpha$| OCM . | |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha\ \mathrm{GCM}$| . | Exp . |
|---|---|---|---|---|---|
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$3.88$| | |$3.9$| | |$4.0$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.50$| | |$2.4$| | |$3.5$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$-$| | |$2.4$| | |$6.0$| | No data |
| |$(e\,\mathrm{fm^2})$| . | AQCM . | |$^{12}\mathrm{C}+\alpha$| OCM . | |$4\alpha$| OCM . | |$^{12}\mathrm{C}(\mathrm{AMD})+\alpha\ \mathrm{GCM}$| . | Exp . |
|---|---|---|---|---|---|
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$3.88$| | |$3.9$| | |$4.0$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.50$| | |$2.4$| | |$3.5$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$-$| | |$2.4$| | |$6.0$| | No data |
3.3. Mixing effect of |$p_{3/2}$| and rotation effect for |$^{12}\mathrm{C}$|
In this subsection, we discuss in detail how the |$E0$| transitions are affected by cluster structures, in particular, the |$^{12}\mathrm{C}$| cluster structure. We consider the mixing effect of the |$p_{3/2}$| subclosed configuration and rotation effect of |$3\alpha$| in the |$^{12}\mathrm{C}$| part. In the full model space of the present calculation, these effects are already taken into account, but we perform additional calculations within truncated model spaces in order to investigate individually each contribution to the |$E0$| transition strengths.
As mentioned later, the triangular pyramid configurations (Fig. 4(a)) are most important for the |$E0$| transitions. However, the configurations for which the |$^{12}\mathrm{C}$| part is rotating (Fig. 4(b)) are necessary for describing the weak-coupling states. In addition, mixing of the |$^{12}\mathrm{C}(p_{3/2})$| configuration (Fig. 4(c)) is important for the |$^{12}\mathrm{C}$| cluster part. As a consequence, although the |$E0$| transition from the ground state to the triangular pyramid configurations (Fig. 4(a)) is originally large, by introducing more configurations, the |$E0$| transition from the ground state to the final states becomes weaker.
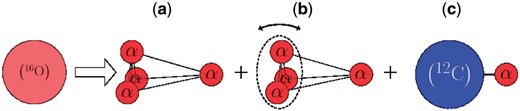
Schematic figure for the three typical configurations introduced in our calculation: (a) triangular pyramid configuration, (b) configuration in which the |$^{12}\mathrm{C}$| part is rotating, and (c) |$^{12}\mathrm{C}(p_{3/2})+\alpha$| configuration. The small red spheres, blue sphere, and large red sphere show the |$\alpha$| clusters, |$^{12}\mathrm{C}$| cluster, and the closed |$p$|-shell configuration of |$^{16}\mathrm{O}$|, respectively.
3.3.1. Mixing effect of the |$p_{3/2}$| subclosed configuration for |$^{12}\mathrm{C}$|
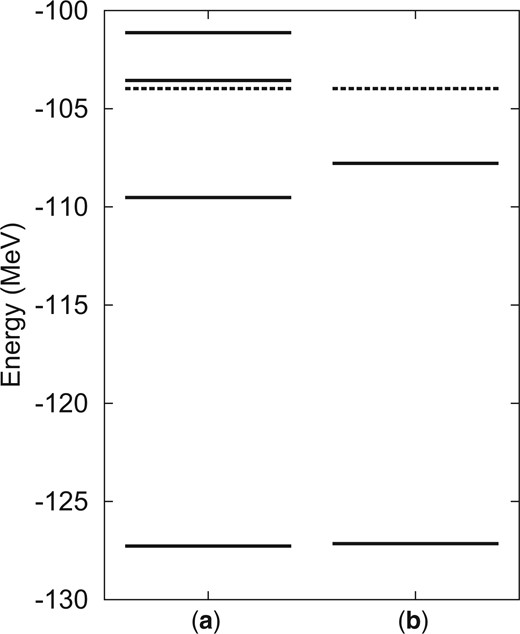
To investigate the mixing effect of the |$p_{3/2}$| subclosed configuration of the |$^{12}\mathrm{C}$| cluster, we calculate the energies and |$E0$| transitions within the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space by truncating the |$^{12}\mathrm{C}(p_{3/2})+\alpha$| bases, and compare them with those calculated in the full model space. The energy levels of the two calculations are compared in Fig. 5. The ground-state energy in the full model space (Fig. 5(a)) and that in the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space (Fig. 5(b)) are almost unchanged. This is because the ground state dominantly has a doubly closed shell configuration in both the full and |$^{12}\mathrm{C}(3\alpha)+\alpha$| model spaces. However, the |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states obtained in the full model space are 1–2|$\,\mathrm{MeV}$| lower than those in the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space because of the spin–orbit potential energy gain caused by the mixing of the |$p_{3/2}$| subclosed configuration.
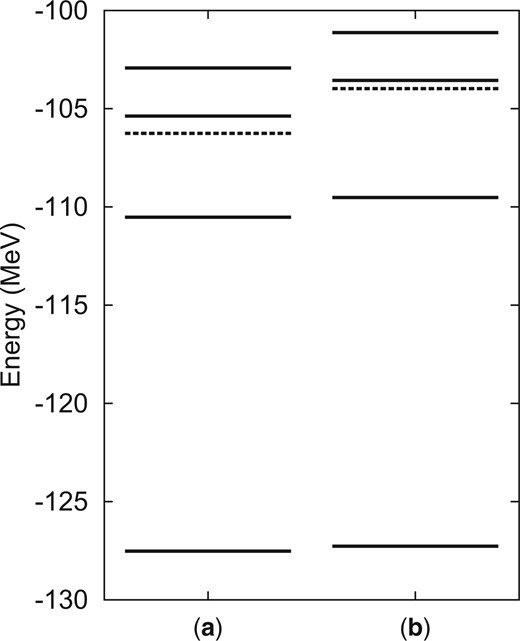
Energy levels of |$0^+$| states obtained in (a) the full model space and (b) only the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space. The dashed lines indicate the |$^{12}\mathrm{C}+\alpha$| threshold in each model space.
The mixing of the |$p_{3/2}$| subclosed configuration also affects the |$E0$| transitions. We show the |$E0$| transition matrix elements of two calculations in Table 3. |$M(E0; 0_1^+\to0_2^+)=6.92\,e\,\mathrm{fm^2}$| in the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space is slightly larger than the value, |$6.03\,e\,\mathrm{fm^2}$|, in the full model space. This indicates that the mixing of the |$p_{3/2}$| subclosed component for |$^{12}\mathrm{C}$| reduces the |$E0$| transition matrix element from |$0_1^+$| to |$0_2^+$| by 13%. This reduction can be understood by a difference in the spin configuration between the initial and final states. The initial ground state has a dominant |$p$| closed configuration with zero intrinsic spin |$(S=0)$|. However, the |$p_{3/2}$| subclosed component of the |$^{12}\mathrm{C}+\alpha$| cluster structure in the final |$0_2^+$| state makes a nonzero intrinsic spin |$(S\ne 0)$| contribution because of the |$3\alpha$| cluster breaking of the |$^{12}\mathrm{C}$| cluster. Since the |$E0$| transition operator does not change the intrinsic spin configuration, the |$E0$| transition between two states that have different spin configurations is suppressed. This is the reason why the mixing of |$^{12}\mathrm{C}(p_{3/2})+\alpha$| in the final state reduces the |$E0$| transition from the ground state. This reduction mechanism does not occur in the calculation of the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space, in which the |$3\alpha$| cluster breaking is omitted and excited |$0^+$| states of |$^{16}\mathrm{O}$| always have the same |$S=0$| configuration as that of the initial |$0^+_1$| state. Unlike the |$0_2^+$| state, the |$E0$| transition matrix element from the |$0_1^+$| to |$0_3^+$| state is enhanced by the mixing of |$^{12}\mathrm{C}(p_{3/2})+\alpha$| configurations to the model space. The reason for this is that the change in the wave function of |$0_2^+$| affects the transition to |$0_3^+$| through the orthogonality condition. If the |$^{12}\mathrm{C}(p_{3/2})+\alpha$| configuration is mixed, the wave function of the |$0_3^+$| state changes, and the components of the original |$0_2^+$| states, which enhance the |$E0$| transition, contribute to the |$0_3^+$| state (as we discuss shortly, triangular pyramid configurations are especially important). The squared overlap between |$0_3^+$| obtained including |$^{12}\mathrm{C}(p_{3/2})+\alpha$| and |$0_3^+$| obtained without |$^{12}\mathrm{C}(p_{3/2})+\alpha$| is |$0.67$|, and, in return, the squared overlap between |$0_3^+$| obtained including |$^{12}\mathrm{C}(p_{3/2})+\alpha$| and |$0_2^+$| obtained without |$^{12}\mathrm{C}(p_{3/2})+\alpha$| is |$0.09$|. Thus, the |$0_2^+$| component obtained by the |$^{12}\mathrm{C}(3\alpha)+\alpha$| configuration gets into a new |$0_3^+$| state calculated with the |$^{12}$|C(|$p_{3/2}$|)+|$\alpha$| configuration.
| . | full . | |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$6.92$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.98$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$1.99$| | No data |
| . | full . | |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$6.92$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.98$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$1.99$| | No data |
| . | full . | |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$6.92$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.98$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$1.99$| | No data |
| . | full . | |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$6.92$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$3.98$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$1.99$| | No data |
3.3.2. Rotation effect of the |$^{12}\mathrm{C}$| cluster
We here discuss the rotation effect of the |$^{12}\mathrm{C}(3\alpha)$| cluster on the |$E0$| transition strength. Note that the rotation of the |$^{12}\mathrm{C}$| cluster is equivalent to the |$\alpha$| cluster rotation around the |$^{12}\mathrm{C}$| cluster in an angular momentum projected state. To this end, we calculate the |$E0$| transition matrix elements from the ground state to each GCM basis state with the |$^{12}\mathrm{C}(3\alpha)+\alpha$| configuration. The obtained results are shown in Fig. 6. In the calculations, the length |$R$| between |$\alpha$| clusters (see Fig. 1) is taken as |$R=2\,\mathrm{fm}$|, and the |$h$| and |$\theta$| dependences are considered. By defining the |$^{12}\mathrm{C}(3\alpha)+\alpha$| configuration with |$R=2\,\mathrm{fm}$|, |$h$|, and |$\theta$| as |$|h,\theta\rangle$|, we calculate the |$E0$| transition matrix elements |$|\langle\overline{h,\theta}|\hat M(E0) |0_1^+\rangle|$| for the component orthogonal to the ground state,
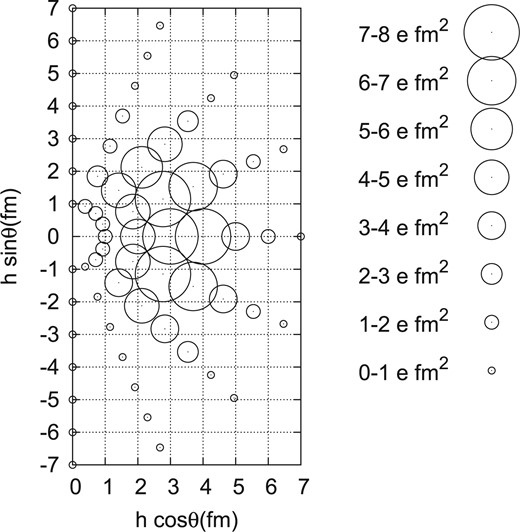
Distribution of |$E0$| transition matrix elements from the ground state to GCM basis states in |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space. The centers of the circles indicate the positions of the |$\alpha$| cluster against the |$^{12}\mathrm{C}(3\alpha)$| cluster in the body-fixed frame. The length |$R$| (see Fig. 1) is taken as |$R=2\,\mathrm{fm}$|. The GCM basis states are projected to be orthogonal to the ground state. The circle sizes represent the values of the monopole transition matrix elements.
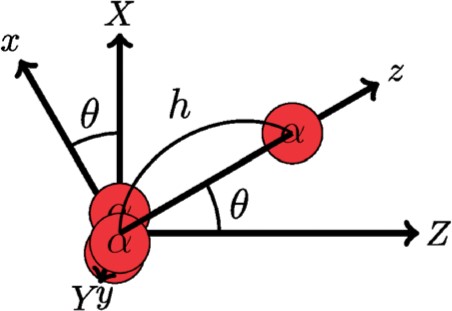
Schematic figure for the parameters |$h$| and |$\theta$| in the body-fixed |$XYZ$| frame of the |$^{12}\mathrm{C}(3\alpha)$| cluster. The red spheres show the |$\alpha$| clusters. The parameter |$\theta$| is identical to that defined in Fig. 1 because the |$XYZ$| frame can be transformed to the |$xyz$| frame in Fig. 1.
Figures 8(a) and (b) show the energy levels calculated with and without rotation, respectively. The energies of the ground states in the two calculations are found to be almost identical. This is because the ground state dominantly has a simple doubly closed shell configuration. However, the number of excited states around the threshold energy calculated with the |$\theta=0$| model space (without rotation) is smaller than that of the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space (with rotation). The |$0_2^+$| state obtained with the |$\theta=0$| model space fragments into some states by the rotation of the |$^{12}\mathrm{C}(3\alpha)$| cluster. In Table 4, we also tabulate the |$E0$| transition matrix elements from the |$0_1^+$| to |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states calculated with and without rotation. In the case of the |$\theta=0$| model space (without rotation), |$M(E0; 0_1^+\to0_2^+)$| is equal to |$7.93\,e\,\mathrm{fm^2}$|. This is larger than the value of |$6.92\,e\,\mathrm{fm^2}$| for the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space (with rotation). By the rotation effect, the |$E0$| transition strength fragments into some states, which reduces the |$E0$| transition to the |$0_2^+$| state.
Energy levels of |$0^+$| states obtained in the (a) |$^{12}\mathrm{C}(3\alpha)+\alpha$| and (b) |$\theta=0$| basis model spaces. The dashed lines indicate the |$^{12}\mathrm{C}+\alpha$| threshold in each calculation.
| . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.92$| | |$7.93$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$3.98$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.99$| | |$-$| | No data |
| . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.92$| | |$7.93$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$3.98$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.99$| | |$-$| | No data |
| . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.92$| | |$7.93$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$3.98$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.99$| | |$-$| | No data |
| . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . |
|---|---|---|---|
| |$(e\,\mathrm{fm^2})$| . | model space . | model space . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.92$| | |$7.93$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$3.98$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.99$| | |$-$| | No data |
The present analysis with and without rotation indicates that the rotation of the oblate |$^{12}\mathrm{C}(3\alpha)$| cluster significantly contributes to the features of the |$0_2^+$| state. This means that the mixing of planar |$4\alpha$| configurations to triangular pyramid |$4\alpha$| configurations occurs in the |$0_2^+$| state. Many cluster-model calculations show the predominant |$^{12}\mathrm{C}(0^+)+\alpha$| component in the |$0_2^+$| state [10,12–14], which is consistent with mixing of the planar and triangular pyramid |$4\alpha$| configurations in terms of the strong-coupling picture. The predominant planar square |$4\alpha$| structure of the |$0_2^+$| state is also supported by the recent ab initio calculation with chiral nuclear effective field theory [32].
3.4. Interaction dependence
In this subsection, we discuss how the energies and |$E0$| transitions of |$^{16}\mathrm{O}$| change when the adopted interaction is different. The basic features already discussed are not affected by the change. We investigate the cases when either the central part or spin–orbit part of the interaction is modified. For the central part, we investigate the case that |$M$| in Eq. (10) is changed from |$0.62$| to |$0.6$|. Although the width parameter |$b$| (|$\nu$|) in Eq. (1) is different, |$M=0.6$| is used in Ref. [25] to reproduce the |$\alpha+\alpha$| scattering phase shift. For the spin–orbit part, we investigate the case |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$| in Eq. (11).
In Tables 5 and 6, we tabulate |$0^+$| energies and |$E0$| transition matrix elements from the |$0_1^+$| to |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states in the full model space, |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space, and |$\theta=0$| basis model space (defined in the preceding subsection) with (I) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, (II) |$M=0.6$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, and (III) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$|. Here (I) is the original interaction, and (II) and (III) are introduced in Sects. 3.4.1 and 3.4.2, respectively.
|$0^+$| energies in the full model space, |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space, and |$\theta=0$| basis model space with (I) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, (II) |$M=0.6$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, and (III) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$|.
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | ||||
|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | ||||
| |$(\mathrm{MeV})$| . | I . | II . | III . | I . | II . | I . | II . |
| |$0_1^+$| | |$-127.5$| | |$-137.9$| | |$-128.2$| | |$-127.3$| | |$-137.7$| | |$-127.1$| | |$-137.5$| |
| |$0_2^+$| | |$-110.5$| | |$-118.7$| | |$-117.1$| | |$-109.5$| | |$-117.2$| | |$-107.8$| | |$-115.9$| |
| |$0_3^+$| | |$-105.4$| | |$-113.4$| | |$-110.6$| | |$-103.6$| | |$-111.1$| | |$-$| | |$-$| |
| |$0_4^+$| | |$-102.9$| | |$-110.4$| | |$-107.7$| | |$-101.1$| | |$-107.8$| | |$-$| | |$-$| |
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | ||||
|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | ||||
| |$(\mathrm{MeV})$| . | I . | II . | III . | I . | II . | I . | II . |
| |$0_1^+$| | |$-127.5$| | |$-137.9$| | |$-128.2$| | |$-127.3$| | |$-137.7$| | |$-127.1$| | |$-137.5$| |
| |$0_2^+$| | |$-110.5$| | |$-118.7$| | |$-117.1$| | |$-109.5$| | |$-117.2$| | |$-107.8$| | |$-115.9$| |
| |$0_3^+$| | |$-105.4$| | |$-113.4$| | |$-110.6$| | |$-103.6$| | |$-111.1$| | |$-$| | |$-$| |
| |$0_4^+$| | |$-102.9$| | |$-110.4$| | |$-107.7$| | |$-101.1$| | |$-107.8$| | |$-$| | |$-$| |
|$0^+$| energies in the full model space, |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space, and |$\theta=0$| basis model space with (I) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, (II) |$M=0.6$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, and (III) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$|.
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | ||||
|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | ||||
| |$(\mathrm{MeV})$| . | I . | II . | III . | I . | II . | I . | II . |
| |$0_1^+$| | |$-127.5$| | |$-137.9$| | |$-128.2$| | |$-127.3$| | |$-137.7$| | |$-127.1$| | |$-137.5$| |
| |$0_2^+$| | |$-110.5$| | |$-118.7$| | |$-117.1$| | |$-109.5$| | |$-117.2$| | |$-107.8$| | |$-115.9$| |
| |$0_3^+$| | |$-105.4$| | |$-113.4$| | |$-110.6$| | |$-103.6$| | |$-111.1$| | |$-$| | |$-$| |
| |$0_4^+$| | |$-102.9$| | |$-110.4$| | |$-107.7$| | |$-101.1$| | |$-107.8$| | |$-$| | |$-$| |
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | ||||
|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | ||||
| |$(\mathrm{MeV})$| . | I . | II . | III . | I . | II . | I . | II . |
| |$0_1^+$| | |$-127.5$| | |$-137.9$| | |$-128.2$| | |$-127.3$| | |$-137.7$| | |$-127.1$| | |$-137.5$| |
| |$0_2^+$| | |$-110.5$| | |$-118.7$| | |$-117.1$| | |$-109.5$| | |$-117.2$| | |$-107.8$| | |$-115.9$| |
| |$0_3^+$| | |$-105.4$| | |$-113.4$| | |$-110.6$| | |$-103.6$| | |$-111.1$| | |$-$| | |$-$| |
| |$0_4^+$| | |$-102.9$| | |$-110.4$| | |$-107.7$| | |$-101.1$| | |$-107.8$| | |$-$| | |$-$| |
|$E0$| transition matrix elements from the |$0_1^+$| to |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states in the full model space, |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space, and |$\theta=0$| basis model space with (I) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, (II) |$M=0.6$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, and (III) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$|. The experimental data (Exp) are taken from Refs. [7,8].
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . | ||||
|---|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | . | ||||
| |$(e\,\mathrm{fm^2})$| . | I . | II . | III . | I . | II . | I . | II . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$5.29$| | |$3.57$| | |$6.92$| | |$6.53$| | |$7.93$| | |$7.29$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$5.32$| | |$0.96$| | |$3.98$| | |$3.99$| | |$-$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$0.73$| | |$6.73$| | |$1.99$| | |$0.54$| | |$-$| | |$-$| | No data |
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . | ||||
|---|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | . | ||||
| |$(e\,\mathrm{fm^2})$| . | I . | II . | III . | I . | II . | I . | II . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$5.29$| | |$3.57$| | |$6.92$| | |$6.53$| | |$7.93$| | |$7.29$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$5.32$| | |$0.96$| | |$3.98$| | |$3.99$| | |$-$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$0.73$| | |$6.73$| | |$1.99$| | |$0.54$| | |$-$| | |$-$| | No data |
|$E0$| transition matrix elements from the |$0_1^+$| to |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states in the full model space, |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space, and |$\theta=0$| basis model space with (I) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, (II) |$M=0.6$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|, and (III) |$M=0.62$|, |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$|. The experimental data (Exp) are taken from Refs. [7,8].
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . | ||||
|---|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | . | ||||
| |$(e\,\mathrm{fm^2})$| . | I . | II . | III . | I . | II . | I . | II . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$5.29$| | |$3.57$| | |$6.92$| | |$6.53$| | |$7.93$| | |$7.29$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$5.32$| | |$0.96$| | |$3.98$| | |$3.99$| | |$-$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$0.73$| | |$6.73$| | |$1.99$| | |$0.54$| | |$-$| | |$-$| | No data |
| . | In full . | In |$^{12}\mathrm{C}(3\alpha)+\alpha$| . | In |$\theta=0$| basis . | . | ||||
|---|---|---|---|---|---|---|---|---|
| . | model space . | model space . | model space . | . | ||||
| |$(e\,\mathrm{fm^2})$| . | I . | II . | III . | I . | II . | I . | II . | Exp . |
| |$M(E0; 0_1^+\to0_2^+)$| | |$6.03$| | |$5.29$| | |$3.57$| | |$6.92$| | |$6.53$| | |$7.93$| | |$7.29$| | |$3.55\pm0.21$| |
| |$M(E0; 0_1^+\to0_3^+)$| | |$5.02$| | |$5.32$| | |$0.96$| | |$3.98$| | |$3.99$| | |$-$| | |$-$| | |$4.03\pm0.09$| |
| |$M(E0; 0_1^+\to0_4^+)$| | |$1.54$| | |$0.73$| | |$6.73$| | |$1.99$| | |$0.54$| | |$-$| | |$-$| | No data |
3.4.1. |$M$| dependence of the central force
We change the Majorana parameter |$M$| and use the interaction set (II). Using the parameter |$M=0.6$|, as shown in Table 5, the central interaction becomes more attractive and the |$0_1^+$| state is much overbound (|$-137.9\,\mathrm{MeV}$|) compared with the experimental one (|$-127.6\,\mathrm{MeV}$|) [27], and excited states appear around the |$^{12}\mathrm{C}+\alpha$| threshold.
As shown in Table 6, we note that the |$E0$| transition from the |$0_1^+$| to |$0_2^+$| states in the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space (|$6.53\,e\,\mathrm{fm^2}$|) is larger than that in the full model space (|$5.29\,e\,\mathrm{fm^2}$|) in the case of set II. This tendency is not changed in comparison to that of the original interaction (“I” in Table 6). Also, the |$E0$| transition from the |$0_1^+$| to |$0_2^+$| states in the |$\theta=0$| basis model space (|$7.29\,e\,\mathrm{fm^2}$|) is larger than that in the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space (|$6.53\,e\,\mathrm{fm^2}$|), as in previous subsections. Furthermore, the |$E0$| transition from the |$0_1^+$| to |$0_3^+$| states in |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space (|$3.99\,e\,\mathrm{fm^2}$|) is smaller than that in the full model space (|$5.32\,e\,\mathrm{fm^2}$|). This tendency is also unchanged in comparison to that of the original interaction.
3.4.2. Spin–orbit interaction dependence
Next we investigate the case of the spin–orbit interaction getting stronger. We adopt the interaction set (III), |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$| in Eq. (11), while |$M$| is returned to the original value, |$M=0.62$|. Since the spin–orbit force does not affect |$\alpha$| cluster states, the results within the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space and |$\theta=0$| model space are unchanged. Here, we show the results within the full model space with |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$| and discuss the relation to the results with |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|.
As shown in Table 5, the energy of |$0_1^+$| (|$-128.2\,\mathrm{MeV}$|) is almost unchanged from that obtained with the original interaction (|$-127.5\,\mathrm{MeV}$|) but the |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| are much lower. This is because the |$0_1^+$| state has an almost closed |$p$|-shell configuration and is not affected by the spin–orbit force, but the |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states have |$^{12}\mathrm{C}+\alpha$| configurations; in particular, the |$^{12}\mathrm{C}$| part contains not only |$3\alpha$| configurations but also |$\alpha$|-breaking configurations, and the strong spin–orbit force makes their levels lower. Note that the structures of the |$0_3^+$| and |$0_4^+$| states in the case of |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$| are exchanged in comparison to the case of |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$|. As shown in Table 6, the |$E0$| transition from the |$0_1^+$| to |$0_2^+$| state (|$3.57\,e\,\mathrm{fm^2}$|) is smaller than that with the original interaction (|$6.03\,e\,\mathrm{fm^2}$|), because the strong spin–orbit force increases the |$^{12}\mathrm{C}(p_{3/2})+\alpha$| configuration in the |$0_2^+$| state. Needless to say, this is smaller than that obtained only within the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model space (|$6.92\,e\,\mathrm{fm^2}$|), where the spin–orbit interaction does not contribute. Note that the |$E0$| transition from the |$0_1^+$| to |$0_4^+$| states with |$V_\mathrm{LS1}=-V_\mathrm{LS2}=3000\,\mathrm{MeV}$| (III) should be compared with that from the |$0_1^+$| to |$0_3^+$| states with |$V_\mathrm{LS1}=-V_\mathrm{LS2}=2000\,\mathrm{MeV}$| (I) as their structures are exchanged.
4. Conclusion
We have investigated the |$0^+$| energy levels and |$E0$| transitions in |$^{16}\mathrm{O}$| with a microscopic model including both four |$\alpha$| cluster and cluster-breaking model spaces. The order of the |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| energies and their intervals are consistent with the previous semi-microscopic calculations, although the energy of the ground state is much overbound from the |$^{12}\mathrm{C}+\alpha$| threshold. The |$0_2^+$|, |$0_3^+$|, and |$0_4^+$| states are understood as weak-coupling cluster states dominantly having |$^{12}\mathrm{C}(0^+)+\alpha$|, |$^{12}\mathrm{C}(2^+)+\alpha$|, and higher nodal |$^{12}\mathrm{C}(0^+)+\alpha$| cluster features, respectively. For the |$E0$| transition, we found two states with strong |$E0$| transitions from the ground state in the low-energy region. However, the obtained |$E0$| transition matrix elements from the |$0_1^+$| to |$0_2^+$| and |$0_3^+$| states are slightly larger than the experimental data. This overestimation could come from the weaker binding of the |$^{12}\mathrm{C}$| part. The interaction is adjusted to reproduce the |$^{16}\mathrm{O}$| binding energy, and this gives underbinding for |$^{12}\mathrm{C}$|, which is a known problem of density-independent two-body effective interactions. The weaker binding of |$^{12}\mathrm{C}$| causes the overestimation of the monopole excitations in the |$^{12}\mathrm{C}$| subsystem. Indeed, when we truncate our model space for the |$^{12}\mathrm{C}$| part, these |$E0$| matrix elements agree with the experimental data. We have confirmed that the |$E0$| transition is affected by details of cluster structures.
In this work, we focused on the structure of the |$^{12}\mathrm{C}$| cluster part. For this purpose, we compared the full model-space calculation with the |$^{12}\mathrm{C}(3\alpha)+\alpha$| calculation (no mixing of the |$^{12}\mathrm{C}(p_{3/2})+\alpha$| configuration). The energies of excited states in the low-energy region obtained by the full model-space calculation are slightly lower than those obtained by the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model-space calculation because of the spin–orbit potential energy gain caused by the mixing of the |$p_{3/2}$| subclosed configuration. The mixing of the |$p_{3/2}$| subclosed configuration for |$^{12}\mathrm{C}$| affects the |$E0$| transition from the ground state; the mixing reduces the |$E0$| transition matrix element from the |$0_1^+$| to |$0_2^+$| states of |$^{16}\mathrm{O}$|. This reduction can be easily understood by the difference in the intrinsic spin structure between the |$^{12}\mathrm{C}(3\alpha)+\alpha$| and |$^{12}\mathrm{C}(p_{3/2})+\alpha$| cluster states, because the |$E0$| operator does not change the intrinsic spin configuration.
We also discussed the rotation effect of the |$^{12}\mathrm{C}(3\alpha)$| cluster by comparing the results of the |$^{12}\mathrm{C}(3\alpha)+\alpha$| model (with rotation) and those of a triangular pyramid model (without rotation). Although the triangular pyramid bases are most important for the |$E0$| transitions, planar bases are necessary for describing the weak-coupling states in the low-energy region. The |$0_2^+$| state obtained with the triangular pyramid model space fragments into some states by the rotation effect of the |$^{12}\mathrm{C}$| cluster, and the mixing of the planar |$4\alpha$| configurations reduces the |$E0$| transition from the ground state. The reduction, i.e., fragmentation mechanism of the |$E0$| transition strength by the rotation effect of the cluster in |$^{16}\textrm{O}$| is consistent with that in |$^{10}\textrm{Be}$| and |$^{14}\textrm{C}$| discussed in Refs. [22,33]. Since the |$E0$| operator excites only the radial degree of freedom, the “doorway state” directly excited from the ground state by the |$E0$| operator should have a similar ground-state geometry. The doorway-state component is fragmented into a couple of cluster states by the coupling of the intercluster motion with the rotation degree of freedom of clusters. As a result, the |$E0$| transition strength is also fragmented in energy spectra. This is a general feature of |$E0$| transition strengths for cluster states containing a deformed cluster. Furthermore, we investigated the interaction dependence of these features. We confirmed that these features are hardly affected by changing the strength of the spin–orbit interaction and Majorana exchange parameter of the central interaction. We conclude that the |$E0$| transition characterizes the clustering of the final states, but this is influenced by various mechanisms related to the detailed structures of the final states.
Acknowledgement
The authors are grateful for use of the computer facility at the Yukawa Institute for Theoretical Physics, Kyoto University. This work was supported by JSPS KAKENHI Grant Numbers 716143900002 (N.I.), 15K05078 (T.I.), and 26400270 (Y.K.-E.).



