Scalar one-loop four-point Feynman integrals with complex internal masses

In parallel and orthogonal space [11,12], which is spanned by external momenta, the Feynman integral is obtained:

\begin{matrix} D_{0} & = & 2 \int_{- \infty}^{\infty} d l_{0} d l_{1} d l_{2} \int_{0}^{\infty} d l_{⊥} \frac{1}{P_{1} P_{2} P_{3} P_{4}} . \end{matrix}

(6)

Let us define the momenta |$q_i =\sum\limits_{j=1}^i p_j$| for |$i, j=1,2, \ldots,4$|⁠. One arrives at the case of at least one time-like momentum, |$p_i^2>0$| for |$i=1,2,\ldots, 4$|⁠, e.g., |$p_1^2>0$|⁠. Working in the rest frame of |$p_1$|⁠, one has

\begin{matrix} q_{1} & = & (q_{10}, 0, 0, 0), \end{matrix}

(7)

\begin{matrix} q_{2} & = & (q_{20}, q_{21}, 0, 0), \end{matrix}

(8)

\begin{matrix} q_{3} & = & (q_{30}, q_{31}, q_{32}, 0), \end{matrix}

(9)

\begin{matrix} q_{4} & = & 0. \end{matrix}

(10)

In the complex mass scheme, the internal masses take the form

\begin{matrix} m_{k}^{2} & = & m_{0 k}^{2} - i m_{0 k} Γ_{k}; \end{matrix}

(11)

|$\Gamma_{k}\geqslant 0$| are decay widths of unstable particles |$k = 1,2, \ldots, 4$|⁠.

The Feynman integral is then written explicitly as

\begin{matrix} D_{0} & = & 2 \int_{- \infty}^{\infty} d l_{0} d l_{1} d l_{2} \int_{0}^{\infty} d l_{⊥} \times \\ \times \frac{1}{[(l_{0} + q_{10})^{2} - l_{1}^{2} - l_{2}^{2} - l_{⊥}^{2} - m_{1}^{2} + i ρ] [(l_{0} + q_{20})^{2} - (l_{1} + q_{21})^{2} - l_{2}^{2} - l_{⊥}^{2} - m_{2}^{2} + i ρ]} \\ \times \frac{1}{[(l_{0} + q_{30})^{2} - (l_{1} + q_{31})^{2} - (l_{2} + q_{32})^{2} - l_{⊥}^{2} - m_{3}^{2} + i ρ] [l_{0}^{2} - l_{1}^{2} - l_{2}^{2} - l_{⊥}^{2} - m_{4}^{2} + i ρ]} . \end{matrix}

(12)

Partitioning the integrand into the form

\begin{matrix} \frac{1}{P_{1} P_{2} P_{3} P_{4}} & = & \frac{1}{P_{1} (P_{2} - P_{1}) (P_{3} - P_{1}) (P_{4} - P_{1})} + \frac{1}{P_{2} (P_{1} - P_{2}) (P_{3} - P_{2}) (P_{4} - P_{2})} \\ + \frac{1}{P_{3} (P_{1} - P_{3}) (P_{2} - P_{3}) (P_{4} - P_{3})} + \frac{1}{P_{4} (P_{1} - P_{4}) (P_{2} - P_{4}) (P_{3} - P_{4})} \\ = & \sum_{k = 1}^{4} \frac{1}{P_{k} \prod_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}} (P_{l} - P_{k})}, \end{matrix}

(13)

we then make a shift on |$P_k$| by |$l_i\longrightarrow l_i+q_{ki}$| for |$k=1,2,\ldots,4$| and |$i=0,1,\ldots, 3$|⁠; the resulting equation reads

\begin{matrix} D_{0} & = & 2 \sum_{k = 1}^{4} \int_{- \infty}^{\infty} d l_{0} d l_{1} d l_{2} \int_{0}^{\infty} d l_{⊥} \times \\ \times \frac{1}{[l_{0}^{2} - l_{1}^{2} - l_{2}^{2} - l_{⊥}^{2} - m_{k}^{2} + i ρ]} \frac{1}{\prod_{\begin{matrix} l = 1 \\ k \neq l \end{matrix}}^{4} [a_{l k} l_{0} + b_{l k} l_{1} + c_{l k} l_{2} + d_{l k}]} . \end{matrix}

(14)

We have already introduced the following kinematic variables:

\begin{matrix} a_{l k} = 2 (q_{l 0} - q_{k 0}), & b_{l k} = - 2 (q_{l 1} - q_{k 1}), \\ c_{l k} = - 2 (q_{l 2} - q_{k 2}), & d_{l k} = (q_{l} - q_{k})^{2} - (m_{l}^{2} - m_{k}^{2}) . \end{matrix}

(15)

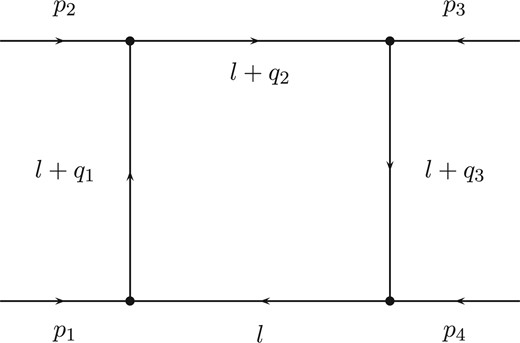
It is important to note that the kinematic variables |$a_{lk}, b_{lk}, c_{lk} \in \mathbb{R}$| and |$ d_{lk}\in \mathbb{C}$|⁠. In the following subsections, we are going to calculate this integral.

2.1. Linearization and |$l_0$|-integration

To integrate over |$l_0$|⁠, we first linearize |$l_0$| by applying a transform as

\begin{matrix} \begin{matrix} l_{0} = x + z, & l_{1} = y, \\ l_{2} = x, & l_{⊥} = t; \end{matrix} \end{matrix}

(16)

then the Jacobian of this transformation is |$ |J|=\Big|\dfrac{\partial(l_0,l_1,l_2,l_{\perp})}{\partial(z,y,x,t)}\Big|=1$|⁠. We arrive at

\begin{matrix} D_{0} & = & 2 \sum_{k = 1}^{4} \int_{- \infty}^{\infty} d x d y \int_{- \infty}^{\infty} d z \int_{0}^{\infty} d t F (x, y, z, t), \end{matrix}

(17)

with the integrand corresponding to

\begin{matrix} F (x, y, z, t) & = & \frac{1}{[2 x z - z^{2} - y^{2} - t^{2} - m_{k}^{2} + i ρ] \prod_{\begin{matrix} l = 1 \\ k \neq l \end{matrix}}^{4} [a_{l k} z + b_{l k} y + A C_{l k} x + d_{l k}]} . \end{matrix}

(18)

In this integrand, we have already used new variables:

\begin{matrix} A C_{l k} = a_{l k} + c_{l k} \in R . \end{matrix}

(19)

The integrand now depends linearly on |$x$|⁠. Thus, the |$x$|-integration will be taken easily by applying the residue theorem. For this purpose, one should first analyze the |$x$|-poles of this integrand. These poles are

\begin{matrix} x_{l} & = & - [\frac{a_{l k}}{A C_{l k}} z + \frac{b_{l k}}{A C_{l k}} y + \frac{d_{l k}}{A C_{l k}}], \end{matrix}

(20)

\begin{matrix} x_{0} & = & \frac{z^{2} + y^{2} + t^{2} + m_{k}^{2} - i ρ}{2 z} . \end{matrix}

(21)

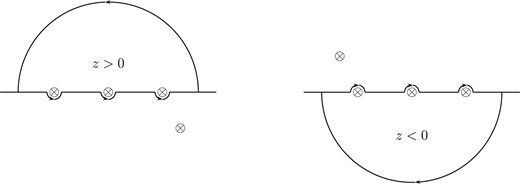
We realize that |$\mathrm{Im}\left(\dfrac{z^2+y^2+t^2+m_k^2-i \rho}{2z} \right) =- \dfrac{m_{0k} \Gamma_{k} +\rho}{2z}$|⁠, which depends on the sign of |$z$|⁠. The location of |$x_0$| in the |$x$|-complex plane will be determined by the sign of |$z$|⁠; see Fig. 2 for more details. We should therefore rewrite |$D_0$| as follows:

Fig. 2.

The contour integration in the |$x$|-plane.

\begin{matrix} D_{0} = D_{0}^{+} + D_{0}^{-}, \end{matrix}

(22)

with

\begin{matrix} D_{0}^{+} & = & 2 \sum_{k = 1}^{4} \int_{- \infty}^{\infty} d x d y \int_{0}^{\infty} d z \int_{0}^{\infty} d t F (x, y, z, t), \end{matrix}

(23)

\begin{matrix} D_{0}^{-} & = & 2 \sum_{k = 1}^{4} \int_{- \infty}^{\infty} d x d y \int_{- \infty}^{0} d z \int_{0}^{\infty} d t F (x, y, z, t) . \end{matrix}

(24)

By closing the integration contour over the upper |$x$| plane when |$z>0$| and vice versa, as shown in Fig. 2, and then applying the residue theorem, the resulting equation then reads

\begin{matrix} D_{0}^{+} & = & 2 π i \sum_{k = 1}^{4} \sum_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}}^{4} \frac{1}{A C_{l k}} \int_{- \infty}^{\infty} d y \int_{0}^{\infty} d z \int_{0}^{\infty} d t \frac{1}{\prod_{\begin{matrix} m = 1 \\ m \neq l \\ l \neq k \end{matrix}} (A_{m l k} z + B_{m l k} y + C_{m l k})} \\ \times \frac{f_{l k} (1 - δ (A C_{l k}))}{[(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} - \frac{2 b_{l k}}{A C_{l k}} y z - \frac{2 d_{l k}}{A C_{l k}} z - y^{2} - t^{2} - m_{k}^{2} + i ρ]}, \end{matrix}

(25)

and

\begin{matrix} D_{0}^{-} & = & - 2 π i \sum_{k = 1}^{4} \sum_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}}^{4} \frac{1}{A C_{l k}} \int_{- \infty}^{\infty} d y \int_{- \infty}^{0} d z \int_{0}^{\infty} d t \frac{1}{\prod_{\begin{matrix} m = 1 \\ m \neq l, k \end{matrix}} (A_{m l k} z + B_{m l k} y + C_{m l k})} \\ \times \frac{f_{l k}^{-} (1 - δ (A C_{l k}))}{[(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} - \frac{2 b_{l k}}{A C_{l k}} y z - \frac{2 d_{l k}}{A C_{l k}} z - y^{2} - t^{2} - m_{k}^{2} + i ρ]} . \end{matrix}

(26)

The |$ f_{lk}$| and |$ f_{lk}^{-}$| functions indicate the residue contributions from the |$x$|-poles in Eq. (20). These functions are defined as

\begin{matrix} f_{l k} = {\begin{matrix} 0, & if Im (- \frac{d_{l k}}{A C_{l k}}) < 0; \\ 1, & if Im (- \frac{d_{l k}}{A C_{l k}}) = 0; \\ 2, & if Im (- \frac{d_{l k}}{A C_{l k}}) > 0. \end{matrix} and f_{l k}^{-} = {\begin{matrix} 0, & if Im (- \frac{d_{l k}}{A C_{l k}}) > 0; \\ 1, & if Im (- \frac{d_{l k}}{A C_{l k}}) = 0; \\ 2, & if Im (- \frac{d_{l k}}{A C_{l k}}) < 0. \end{matrix} \end{matrix}

(27)

The new kinematic variables introduced in this step are listed as follows:

\begin{matrix} A_{m l k} & = & a_{m k} - \frac{a_{l k}}{A C_{l k}} A C_{m k}, \end{matrix}

(28)

\begin{matrix} B_{m l k} & = & b_{m k} - \frac{b_{l k}}{A C_{l k}} A C_{m k}, \end{matrix}

(29)

\begin{matrix} C_{m l k} & = & d_{m k} - \frac{d_{l k}}{A C_{l k}} A C_{m k} . \end{matrix}

(30)

The delta function is defined as

δ (A C_{l k}) = {\begin{matrix} 0, & if A C_{l k} \neq 0; \\ 1, & if A C_{l k} = 0. \end{matrix}

(31)

It is important to note that |$A_{mlk}, B_{mlk} \in \mathbb{R}$|⁠, and |$C_{mlk}\in \mathbb{C}$|⁠. Combined with the definition of |$f_{lk}$| and |$ f_{lk}^{-}$| in Eq. (27), we verify easily that

\begin{matrix} I m [(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} - \frac{2 b_{l k}}{A C_{l k}} y z - \frac{2 d_{l k}}{A C_{l k}} z - y^{2} - t^{2} - m_{k}^{2} + i ρ] > 0. \end{matrix}

(32)

2.2. The |$y$|-integration

We are now going to evaluate the threefold integrals introduced in the previous subsection; see Eqs. (25) and (26). In order to work out the |$y$|-integration, one has to linearize |$y$| by using the Euler shift |$t\rightarrow t+y$|⁠. However, we realize that the terms proportional to |$t^2$| and |$y^2$| in the integrand have the same sign. One can first make |$t^2$| and |$y^2$| have opposite signs by applying a complex rotation in the |$t$|-plane.

The integrand written in terms of |$t$| has two poles, which are

\begin{matrix} t_{1, 2} = \pm \sqrt{(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} - \frac{2 b_{l k}}{A C_{l k}} y z - \frac{2 d_{l k}}{A C_{l k}} z - y^{2} - m_{k}^{2} + i ρ} . \end{matrix}

(33)

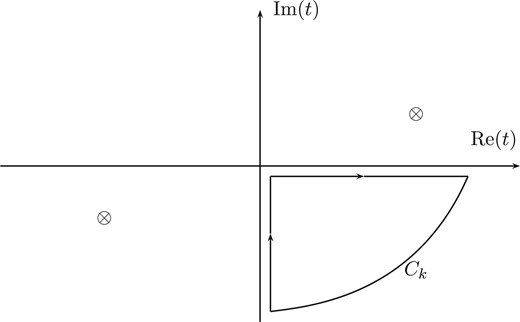
Because of Eq. (32), we find that |$t_{1,2}$| are located in the first and third quarters of the |$t$|-complex plane, as described in Fig. 3. Because of this, one should choose the integration contour on the fourth quarter of the |$t$|-complex plane, as in Fig. 3. There are no residua of |$t$|-poles that contribute to the |$t$|-integration contour. We therefore derive the following relation:

Fig. 3.

|$t$|-rotation.

\begin{matrix} \int_{0}^{\infty} d t = \frac{1}{2} \int_{- \infty}^{\infty} d t = - \int_{- i \infty}^{0} d t = - \frac{1}{2} \int_{- i \infty}^{i \infty} d t . \end{matrix}

(34)

We now apply the relation in Eq. (34). One then performs the rotation, e.g., |$t\longrightarrow it$|⁠. The resulting equations read

\begin{matrix} D_{0}^{+} & = & π \sum_{k = 1}^{4} \sum_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}}^{4} \frac{1}{A C_{l k}} \int_{- \infty}^{\infty} d y \int_{0}^{\infty} d z \int_{- \infty}^{\infty} d t \frac{1}{\prod_{\begin{matrix} m = 1 \\ m \neq l, k \end{matrix}} (A_{m l k} z + B_{m l k} y + C_{m l k})} \\ \frac{f_{l k} (1 - δ (A C_{l k}))}{[(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} - \frac{2 b_{l k}}{A C_{l k}} y z - \frac{2 d_{l k}}{A C_{l k}} z - y^{2} + t^{2} - m_{k}^{2} + i ρ]}, \end{matrix}

(35)

\begin{matrix} D_{0}^{-} & = & - π \sum_{k = 1}^{4} \sum_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}}^{4} \frac{1}{A C_{l k}} \int_{- \infty}^{\infty} d y \int_{- \infty}^{0} d z \int_{- \infty}^{\infty} d t \frac{1}{\prod_{\begin{matrix} m = 1 \\ m \neq l, k \end{matrix}} (A_{m l k} z + B_{m l k} y + C_{m l k})} \\ \frac{f_{l k}^{-} (1 - δ (A C_{l k}))}{[(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} - \frac{2 b_{l k}}{A C_{l k}} y z - \frac{2 d_{l k}}{A C_{l k}} z - y^{2} + t^{2} - m_{k}^{2} + i ρ]} . \end{matrix}

(36)

After obtaining the opposite signs for |$t^2$| and |$y^2$| in these integrands, we proceed with the linearization of |$y$| by performing the above Euler transformation, or |$t\rightarrow t+y$|⁠. We arrive at

\begin{matrix} D_{0}^{+} & = & + π \sum_{k = 1}^{4} \sum_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}}^{4} \frac{1}{A C_{l k}} \int_{- \infty}^{\infty} d y \int_{0}^{\infty} d z \int_{- \infty}^{\infty} d t \frac{1}{\prod_{\begin{matrix} m = 1 \\ m \neq l, k \end{matrix}} (A_{m l k} z + B_{m l k} y + C_{m l k})} \\ \times \frac{f_{l k} (1 - δ (A C_{l k}))}{[(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} + 2 (t - \frac{b_{l k}}{A C_{l k}} z) y - \frac{2 d_{l k}}{A C_{l k}} z + t^{2} - m_{k}^{2} + i ρ]}, \end{matrix}

(37)

\begin{matrix} D_{0}^{-} & = & - π \sum_{k = 1}^{4} \sum_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}}^{4} \frac{1}{A C_{l k}} \int_{- \infty}^{\infty} d y \int_{- \infty}^{0} d z \int_{- \infty}^{\infty} d t \frac{1}{\prod_{\begin{matrix} m = 1 \\ m \neq l, k \end{matrix}} (A_{m l k} z + B_{m l k} y + C_{m l k})} \\ \times \frac{f_{l k}^{-} (1 - δ (A C_{l k}))}{[(1 - \frac{2 a_{l k}}{A C_{l k}}) z^{2} + 2 (t - \frac{b_{l k}}{A C_{l k}} z) y - \frac{2 d_{l k}}{A C_{l k}} z + t^{2} - m_{k}^{2} + i ρ]} . \end{matrix}

(38)

The |$y$|-integration will be taken by using the residue theorem. The locations of the |$y$|-poles are more complicated than in the case of |$x$|-integration. According to Eqs. (37) and (38), combined with Eq. (32), it is easy to check that the imaginary parts of the |$y$|-poles in these integrands are

\begin{matrix} Im (\frac{\frac{2 d_{l k}}{A C_{l k}} z + m_{k}^{2} - i ρ}{t - \frac{b_{l k}}{A C_{l k}} z}), \end{matrix}

(39)

which depend on the sign of |$t-\frac{b_{lk}}{AC_{lk}}z$|⁠. Similar to the |$x$|-integration, we should cut the integration of |$t$| into two segments |$t \geqslant \alpha_{lk}z$| and |$t\leqslant \alpha_{lk}z$| with |$\alpha_{lk}=\frac{b_{lk}}{AC_{lk}} $|⁠. The imaginary parts of the remaining poles, which are the roots of the following equation:

\begin{matrix} A_{m l k} z + B_{m l k} y + C_{m l k} = 0, \end{matrix}

(40)

become more complicated. They then contribute to the residua of the integrations taken.

Closing the contour on the upper plane of |$y$| if |$t \geqslant \alpha_{lk}z$| and vice versa, one takes into account the residua of the |$y$|-poles in Eq. (40). Finally, we arrive at

\begin{matrix} D_{0} & = & D_{0}^{+ +} + D_{0}^{+ -} + D_{0}^{- +} + D_{0}^{- -}, \end{matrix}

(41)

with

\begin{matrix} D_{0}^{+ +} & = & + i π^{2} \sum_{\begin{matrix} m, l, k = 1 \\ l \neq k \neq m \end{matrix}}^{4} \frac{(1 - δ (A C_{l k})) (1 - δ (B_{m l k}))}{A C_{l k} (A_{n l k} B_{m l k} - A_{m l k} B_{n l k})} \int_{0}^{\infty} d z \int_{α_{l k} z}^{\infty} d t f_{l k} g_{m l k} I_{n m l k}^{'} (z, t), \end{matrix}

(42)

\begin{matrix} D_{0}^{+ -} & = & - i π^{2} \sum_{\begin{matrix} m, l, k = 1 \\ l \neq k \neq m \end{matrix}}^{4} \frac{(1 - δ (A C_{l k})) (1 - δ (B_{m l k}))}{A C_{l k} (A_{n l k} B_{m l k} - A_{m l k} B_{n l k})} \int_{0}^{\infty} d z \int_{- \infty}^{α_{l k} z} d t f_{l k} g_{m l k}^{-} I_{n m l k}^{'} (z, t), \end{matrix}

(43)

\begin{matrix} D_{0}^{- +} & = & - i π^{2} \sum_{\begin{matrix} m, l, k = 1 \\ l \neq k \neq m \end{matrix}}^{4} \frac{(1 - δ (A C_{l k})) (1 - δ (B_{m l k}))}{A C_{l k} (A_{n l k} B_{m l k} - A_{m l k} B_{n l k})} \int_{- \infty}^{0} d z \int_{α_{l k} z}^{\infty} d t f_{l k}^{-} g_{m l k} I_{n m l k}^{'} (z, t), \end{matrix}

(44)

\begin{matrix} D_{0}^{- -} & = & + i π^{2} \sum_{\begin{matrix} m, l, k = 1 \\ l \neq k \neq m \end{matrix}}^{4} \frac{(1 - δ (A C_{l k})) (1 - δ (B_{m l k}))}{A C_{l k} (A_{n l k} B_{m l k} - A_{m l k} B_{n l k})} \int_{- \infty}^{0} d z \int_{- \infty}^{α_{l k} z} d t f_{l k}^{-} g_{m l k}^{-} I_{n m l k}^{'} (z, t), \end{matrix}

(45)

and the integrand

\begin{matrix} I_{n m l k}^{'} (z, t) & = & \frac{1}{[z + F_{n m l k}] [D_{m l k}^{'} z^{2} - 2 \frac{A_{m l k}}{B_{m l k}} z t - 2 \frac{C_{m l k}}{B_{m l k}} t + E_{m l k}^{'} z + t^{2} - m_{k}^{2} + i ρ]} . \end{matrix}

(46)

We have already introduced the following kinematic variables:

\begin{matrix} F_{n m l k} & = & \frac{C_{n l k} B_{m l k} - B_{n l k} C_{m l k}}{A_{n l k} B_{m l k} - B_{n l k} A_{m l k}}, \end{matrix}

(47)

\begin{matrix} D_{m l k}^{'} & = & 1 - \frac{2 a_{l k}}{A C_{l k}} + 2 \frac{b_{l k}}{A C_{l k}} \frac{A_{m l k}}{B_{m l k}}, \end{matrix}

(48)

\begin{matrix} E_{m l k}^{'} & = & - 2 (\frac{d_{l k}}{A C_{l k}} - \frac{b_{l k}}{A C_{l k}} \frac{C_{m l k}}{B_{m l k}}) . \end{matrix}

(49)

The |$g_{mlk}$| and |$g^-_{mlk}$| functions will indicate the locations of the |$y$|-poles in Eq. (40) that contributed to the integrations. They are defined as

\begin{matrix} g_{m l k} = {\begin{matrix} 0, & if I m (- \frac{C_{m l k}}{B_{m l k}}) < 0; \\ 1, & if I m (- \frac{C_{m l k}}{B_{m l k}}) = 0; \\ 2, & if I m (- \frac{C_{m l k}}{B_{m l k}}) > 0; \end{matrix} and g_{m l k}^{-} = {\begin{matrix} 0, & if I m (- \frac{C_{m l k}}{B_{m l k}}) > 0; \\ 1, & if I m (- \frac{C_{m l k}}{B_{m l k}}) = 0; \\ 2, & if I m (- \frac{C_{m l k}}{B_{m l k}}) < 0. \end{matrix} \end{matrix}

(50)

We now make a shift |$t\longrightarrow t'=t-\alpha_{lk}z$|⁠. The Jacobian of this shift is |$1$| and the |$t$|-integrals change the border to |$[0, \pm \infty]$|⁠. The resulting equations read

\begin{matrix} D_{0}^{+ +} & = & + i π^{2} ⨁_{n m l k} \int_{0}^{\infty} d z \int_{0}^{\infty} d t f_{l k} g_{m l k} I_{n m l k} (z, t), \end{matrix}

(51)

\begin{matrix} D_{0}^{+ -} & = & - i π^{2} ⨁_{n m l k} \int_{0}^{\infty} d z \int_{- \infty}^{0} d t f_{l k} g_{m l k}^{-} I_{n m l k} (z, t), \end{matrix}

(52)

\begin{matrix} D_{0}^{- +} & = & - i π^{2} ⨁_{n m l k} \int_{- \infty}^{0} d z \int_{0}^{\infty} d t f_{l k}^{-} g_{m l k} I_{n m l k} (z, t), \end{matrix}

(53)

\begin{matrix} D_{0}^{- -} & = & + i π^{2} ⨁_{n m l k} \int_{- \infty}^{0} d z \int_{- \infty}^{0} d t f_{l k}^{-} g_{m l k}^{-} I_{n m l k} (z, t), \end{matrix}

(54)

with the new notations

\begin{matrix} ⨁_{n m l k} & = & \sum_{\begin{matrix} k = 1 \end{matrix}}^{4} \sum_{\begin{matrix} l = 1 \\ l \neq k \end{matrix}}^{4} \sum_{\begin{matrix} m = 1 \\ m \neq l \\ m \neq k \end{matrix}}^{4} \frac{1}{A C_{l k} (A_{n l k} B_{m l k} - A_{m l k} B_{n l k})} [1 - δ (A C_{l k})] [1 - δ (B_{m l k})], \\ I_{n m l k} (z, t) & = & \frac{1}{[z + F_{n m l k}] [D_{m l k} z^{2} - 2 (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) z t - 2 \frac{C_{m l k}}{B_{m l k}} t - 2 \frac{d_{l k}}{A C_{l k}} z + t^{2} - m_{k}^{2} + i ρ]}, \end{matrix}

(55)

where

\begin{matrix} D_{m l k} & = & 1 - \frac{2 α_{l k}}{A C_{l k}} + \frac{b_{l k}^{2}}{A C_{l k}^{2}} = - 4 \frac{(q_{l} - q_{k})^{2}}{A C_{l k}^{2}}, \\ F_{n m l k} & = & \frac{C_{n l k} B_{m l k} - B_{n l k} C_{m l k}}{A_{n l k} B_{m l k} - B_{n l k} A_{m l k}} . \end{matrix}

(56)

We note that |$D_{mlk}\in \mathbb{R}$| and |$F_{nmlk}\in \mathbb{C}$|⁠.

With the definitions of |$f_{kl}, f^-_{kl}$| in Eq. (27) and |$g_{mlk},g^-_{mlk}$| in Eq. (50), one again confirms that

\begin{matrix} I m [D_{m l k} z^{2} - 2 (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) z t - 2 \frac{C_{m l k}}{B_{m l k}} t - 2 \frac{d_{l k}}{A C_{l k}} z + t^{2} - m_{k}^{2} + i ρ] > 0. \end{matrix}

(57)

We have just arrived at the twofold integrations. In the following subsections, we will present the approach to calculating these integrals (51)–(54) in detail.

2.3. The |$t$|-integration

To linearize |$t$|⁠, we perform a shift

\begin{matrix} z = z^{'} + β_{m l k} t^{'} & z^{'} = \frac{z - β_{m l k} t}{1 - β_{m l k} φ_{m l k}}, \\ ⟹ \\ t = t^{'} + φ_{m l k} z^{'} & t^{'} = \frac{t - φ_{m l k}, z}{1 - β_{m l k} φ_{m l k}} . \end{matrix}

(58)

The Jacobian of this shift is

\begin{matrix} J = | 1 - β_{m l k} φ_{m l k} | . \end{matrix}

(59)

To remove the quadratic term of |$t$|⁠, we have to choose |$\beta_{mlk}$| as the roots of the equation

\begin{matrix} D_{m l k} β_{m l k}^{2} - 2 (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) β_{m l k} + 1 = 0, \end{matrix}

(60)

or these roots are written explicitly as

\begin{matrix} β_{m l k}^{(1, 2)} = \frac{(\frac{A_{m l k}}{B_{m l k}} - α_{l k}) \pm \sqrt{{(\frac{A_{m l k}}{B_{m l k}} - α_{l k})}^{2} - D_{m l k}}}{D_{m l k}} . \end{matrix}

(61)

With this, the integrand written in terms of |$t$| depends linearly on |$t$|⁠, which is

I_{n m l k} (z, t) = \frac{1}{[z + β_{m l k} t + F_{n m l k}] [Q_{m l k} t + P_{m l k} t z + E_{m l k} z + Z_{m l k} z^{2} - m_{k}^{2} + i ϱ]},

(62)

with

\begin{matrix} Q_{m l k} & = & - 2 (\frac{C_{m l k}}{B_{m l k}} + \frac{d_{l k}}{A C_{l k}} β_{m l k}), \end{matrix}

(63)

\begin{matrix} P_{m l k} & = & - 2 [(\frac{A_{m l k}}{B_{m l k}} - α_{l k}) (1 + β_{m l k} φ_{m l k}) - D_{m l k} β_{m l k} - φ_{m l k}], \end{matrix}

(64)

\begin{matrix} E_{m l k} & = & - 2 (\frac{d_{l k}}{A C_{l k}} + \frac{C_{m l k}}{B_{m l k}} φ_{m l k}), \end{matrix}

(65)

\begin{matrix} Z_{m l k} & = & D_{m l k} - 2 (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) φ_{m l k} + φ_{m l k}^{2}, \end{matrix}

(66)

\begin{matrix} D_{m l k} & = & - 4 \frac{(q_{l} - q_{k})^{2}}{A C_{l k}^{2}}, \end{matrix}

(67)

\begin{matrix} F_{n m l k} & = & \frac{C_{n l k} B_{m l k} - B_{n l k} C_{m l k}}{A_{n l k} B_{m l k} - B_{n l k} A_{m l k}} . \end{matrix}

(68)

We will choose |$\varphi_{mlk}$| as the root of the equation |$Z_{mlk}=0$|⁠,

\begin{matrix} φ_{m l k}^{2} - 2 (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) φ_{m l k} + D_{m l k} = 0, \end{matrix}

(69)

or their solutions are given by

\begin{matrix} φ_{m l k}^{(1, 2)} = (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) \pm \sqrt{{(\frac{A_{m l k}}{B_{m l k}} - α_{l k})}^{2} - D_{m l k}} . \end{matrix}

(70)

We note that the final result of |$D_0$| is independent of the parameters |$\varphi_{mlk}$| and |$\beta_{mlk}$|⁠. Without loss of generality, we choose |$\varphi_{mlk}=\varphi_{mlk}^{(1)}$| and |$\beta_{mlk}=\beta_{mlk}^{(1)}$| in the following calculation. In this case, we have

\begin{matrix} P_{m l k} = - 4 [{(\frac{A_{m l k}}{B_{m l k}} - α_{l k})}^{2} - D_{m l k}] β_{m l k} . \end{matrix}

(71)

The relations between |$D_{mlk}$| and the external momenta are shown in Table 1.

Table 1.

|$D_{mlk}$| given in terms of external momenta.

|$l=1,k=2$|

|$q_1-q_2=-p_2$|

|$D_{m12}=-4\frac{p_2^2}{AC_{lk}^2}$|

|$l=1,k=3$|

|$q_1-q_3=-p_2-p_3$|

|$D_{m13}=-4\frac{(p_2+p_3)^2}{AC_{lk}^2}$|

|$l=1,k=4$|

|$q_1-q_4=p_1$|

|$D_{m14}=-4\frac{p_1^2}{AC_{lk}^2}$|

|$l=2,k=3$|

|$q_2-q_3=-p_3$|

|$D_{m23}=-4\frac{p_3^2}{AC_{lk}^2}$|

|$l=2,k=4$|

|$q_2-q_4=p_1+p_2$|

|$D_{m24}=-4\frac{(p_1+p_2)^2}{AC_{lk}^2}$|

|$l=3,k=4$|

|$q_3-q_4=-p_4$|

|$D_{m34}=-4\frac{p_4^2}{AC_{lk}^2} $|

To follow the calculation easily, we would like to omit the index for the kinematic variables that appear in Eq. (62) in the rest of this paper.

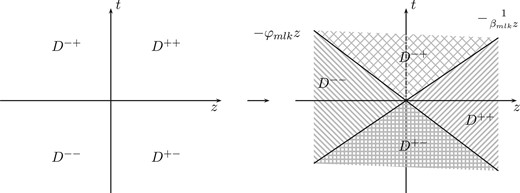
2.3.1. In the case of |$D_{mlk} <0$|

In this case, |$\beta_{mlk} \leqslant 0$| and |$\varphi_{mlk}\geqslant 0$|⁠. The integration region now looks like Fig. 4.

Fig. 4.

The integration region.

To integrate over |$t$|⁠, one first splits the integrations written in terms of |$t$| as follows:

\begin{matrix} D^{+ +} & ⟶ & \int_{0}^{\infty} d z \int_{- φ_{m l k} z}^{- 1 / β_{m l k} z} d t = \int_{0}^{\infty} d z \int_{- φ_{m l k} z}^{\infty} d t - \int_{0}^{\infty} d z \int_{- 1 / β_{m l k} z}^{\infty} d t, \\ D^{+ -} & ⟶ & \int_{0}^{\infty} d z \int_{- \infty}^{- φ_{m l k} z} d t - \int_{- \infty}^{0} d z \int_{- \infty}^{- 1 / β_{m l k} z} d t, \\ D^{- +} & ⟶ & \int_{0}^{\infty} d z \int_{- 1 / β_{m l k} z}^{\infty} d t + \int_{- \infty}^{0} d z \int_{- φ_{m l k} z}^{\infty} d t, \\ D^{- -} & ⟶ & \int_{- \infty}^{0} d z \int_{- 1 / β_{m l k} z}^{- φ_{m l k} z} d t = \int_{- \infty}^{0} d z \int_{- 1 / β_{m l k} z}^{\infty} d t - \int_{- \infty}^{0} d z \int_{- φ_{m l k} z}^{\infty} d t . \end{matrix}

We next rewrite the |$t$|-integrand in the form of

\begin{matrix} I_{n m l k} (t, z) & = & \frac{1}{β (Q + P z)} \frac{1}{[\frac{E z - m_{k}^{2} + i ϱ}{Q + P z} - \frac{F + z}{β}]} {\frac{1}{t + \frac{F + z}{β}} - \frac{1}{t + \frac{E z - m_{k}^{2} + i ϱ}{Q + P z}}} . \end{matrix}

(72)

We are going to apply Eq. (A8) for calculating the |$t$|-integrations. In order to use Eq. (A8), the integrand |$\mathcal{I}_{nmlk}(t, z) $| must have no poles in real |$t$|-axes. However, in the case of real masses, |$F_{nmlk}$| are real, and so |$\mathcal{I}_{nmlk}(t, z)$| may have poles in negative real |$t$|-axes. To treat this problem, we make |$F_{nmlk}\rightarrow F_{nmlk}+i\rho'$| with |$\rho'\geqslant 0$|⁠. The final result is obtained by taking |$\rho'\rightarrow 0$|⁠. Using the master integral (A8), one gets

\begin{matrix} \int_{- \infty}^{σ z} d t I_{n m l k} (t, z) & = & \frac{1}{β (Q + P z)} \frac{1}{[\frac{E z - m_{k}^{2} + i ϱ}{Q + P z} - \frac{F + z}{β}]} {\ln (- \frac{(1 + β σ) z + F}{β}) \\ - \ln (- \frac{P σ z^{2} + (E + Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}, \end{matrix}

(73)

and

\begin{matrix} \int_{σ z}^{\infty} d t I_{n m l k} (t, z) & = & \frac{1}{β (Q + P z)} \frac{1}{[\frac{E z - m_{k}^{2} + i ϱ}{Q + P z} - \frac{F + z}{β}]} {- \ln (\frac{(1 + β σ) z + F}{β}) \\ + \ln (\frac{P σ z^{2} + (E + Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}, \end{matrix}

(74)

where |$\sigma$| will be |$-\varphi_{mlk}$| or |$-\frac{1}{\beta_{mlk}}$|⁠.

With the help of Eqs. (73) and (74), one obtains

\begin{matrix} \frac{D^{+ +}}{i π^{2}} & = & ⨁_{n m l k} f_{l k} g_{m l k} \int_{0}^{\infty} d z {\int_{- φ z}^{\infty} d t - \int_{- 1 / β z}^{\infty} d t} I_{n m l k} (t, z) \\ = & ⨁_{n m l k} f_{l k} g_{m l k} \int_{0}^{\infty} d z G (z) {- \ln (\frac{(1 - β φ) z + F}{β}) + \ln (\frac{F}{β}) \\ + \ln (\frac{- P φ z^{2} + (E - Q φ) z - m_{k}^{2} + i ϱ}{Q + P z}) \\ - \ln (\frac{- \frac{P}{β} z^{2} + (E - \frac{Q}{β}) z - m_{k}^{2} + i ϱ}{Q + P z})}; \end{matrix}

(75)

\begin{matrix} \frac{D^{+ -}}{i π^{2}} & = & - ⨁_{n m l k} f_{l k} g_{m l k}^{-} {\int_{0}^{\infty} d z \int_{- \infty}^{- φ z} d t + \int_{- \infty}^{0} d z \int_{- \infty}^{- 1 / β z} d t} I_{n m l k} (t, z) \\ = & - ⨁_{n m l k} f_{l k} g_{m l k}^{-} {\int_{0}^{\infty} d z G (z) [\ln (- \frac{(1 - β φ) z + F}{β}) \\ - \ln (- \frac{- P φ z^{2} + (E - Q φ) z - m_{k}^{2} + i ϱ}{Q + P z})] + \\ \int_{- \infty}^{0} d z G (z) [\ln (- \frac{F}{β}) - \ln (- \frac{- \frac{P}{β} z^{2} + (E - \frac{Q}{β}) z - m_{k}^{2} + i ϱ}{Q + P z})]}; \end{matrix}

(76)

\begin{matrix} \frac{D^{- +}}{i π^{2}} & = & - ⨁_{n m l k} f_{l k}^{-} g_{m l k} {\int_{0}^{\infty} d z \int_{- 1 / β z}^{\infty} d t + \int_{- \infty}^{0} d z \int_{- φ z}^{\infty} d t} I_{n m l k} (t, z) \\ = & - ⨁_{n m l k} f_{l k}^{-} g_{m l k} {\int_{0}^{\infty} d z G (z) [- \ln (\frac{F}{β}) + \ln (\frac{- \frac{P}{β} z^{2} + (E - \frac{Q}{β}) z - m_{k}^{2} + i ϱ}{Q + P z})] + \\ \int_{- \infty}^{0} d z G (z) [- \ln (\frac{(1 - β φ) z + F}{β}) + \ln (\frac{- P φ z^{2} + (E - Q φ) z - m_{k}^{2} + i ϱ}{Q + P z})]}; \end{matrix}

(77)

\begin{matrix} \frac{D^{- -}}{i π^{2}} & = & ⨁_{n m l k} f_{l k}^{-} g_{m l k}^{-} \int_{- \infty}^{0} d z {\int_{- 1 / β z}^{\infty} d t - \int_{- φ z}^{\infty} d t} I_{n m l k} (t, z) \\ = & ⨁_{n m l k} f_{l k}^{-} g_{m l k}^{-} \int_{- \infty}^{0} d z G (z) {- \ln (\frac{F}{β}) + \ln (\frac{- \frac{P}{β} z^{2} + (E - \frac{Q}{β}) z - m_{k}^{2} + i ϱ}{Q + P z}) \\ + \ln (\frac{(1 - β φ) z + F}{β}) - \ln (\frac{- P φ z^{2} + (E - Q φ) z - m_{k}^{2} + i ϱ}{Q + P z})} . \end{matrix}

(78)

Here the |$G(z)$| function is given by

\begin{matrix} G (z) = \frac{1}{β (E z - m_{k}^{2} + i ρ) - (Q + P z) (F + z)} . \end{matrix}

(79)

\begin{matrix} \frac{D_{0}}{i π^{2}} & = & \sum_{k = 1}^{4} \sum_{\begin{matrix} l = 1 \\ k \neq l \end{matrix}}^{4} \sum_{\begin{matrix} m = 1 \\ m \neq l \\ m \neq k \end{matrix}}^{4} \frac{(1 - δ_{l k} (A C_{l k})) (1 - δ_{l k} (B_{m l k}))}{A C_{l k} (B_{m l k} A_{n l k} - B_{n l k} A_{m l k})} | 1 - β_{m l k} φ_{m l k} | \times \\ \times [\int_{0}^{\infty} d z G (z) {(f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (\frac{F}{β}) \\ - f_{l k} g_{m l k} \ln (\frac{(1 - β φ) z + F}{β}) - f_{l k} g_{m l k}^{-} \ln (- \frac{(1 - β φ) z + F}{β}) \\ - (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (\frac{- \frac{P}{β} z^{2} + (E - \frac{Q}{β}) z - m_{k}^{2} + i ϱ}{Q + P z}) \\ + f_{l k} g_{m l k} \ln (\frac{- P φ z^{2} + (E - Q φ) z - m_{k}^{2} + i ϱ}{Q + P z}) \\ + f_{l k} g_{m l k}^{-} \ln (- \frac{- P φ z^{2} + (E - Q φ) z - m_{k}^{2} + i ϱ}{Q + P z})} \\ + \int_{- \infty}^{0} d z G (z) {- f_{l k}^{-} g_{m l k}^{-} \ln (\frac{F}{β}) - f_{l k} g_{m l k}^{-} \ln (- \frac{F}{β}) \\ + (f_{l k}^{-} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}) \ln (\frac{(1 - β φ) z + F}{β}) \\ + f_{l k}^{-} g_{m l k}^{-} \ln (\frac{- \frac{P}{β} z^{2} + (E - \frac{Q}{β}) z - m_{k}^{2} + i ϱ}{Q + P z}) \\ + f_{l k} g_{m l k}^{-} \ln (- \frac{- \frac{P}{β} z^{2} + (E - \frac{Q}{β}) z - m_{k}^{2} + i ϱ}{Q + P z}) \\ - (f_{l k}^{-} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}) \ln (\frac{- P φ z^{2} + (E - Q φ) z - m_{k}^{2} + i ϱ}{Q + P z})}] . \end{matrix}

(80)

In the next steps, we are now going to calculate the |$z$|-integrals. We realize that

\begin{matrix} I m (E_{m l k} - Q_{m l k} φ_{m l k}) = {\begin{matrix} \geq 0, & with + +, + -; \\ \leq 0 & with - +, - -; \end{matrix} \end{matrix}

(81)

and

\begin{matrix} I m (E_{m l k} - \frac{Q_{m l k}}{β_{m l k}}) = {\begin{matrix} \geq 0, & with + +, + -; \\ \leq 0 & with - +, - -, \end{matrix} \end{matrix}

(82)

where we use the notations |$++,+-, \ldots, -$|⁠, which correspond to the appearance of |$f_{lk}g_{mlk},f_{lk}g_{mlk}^-, \ldots, f_{lk}^-g_{mlk}^-$| in the formulae mentioned.

From Eqs. (81) and (82), we also confirm that

\begin{matrix} Im (P σ z^{2} + (E + Q σ) z - m_{k}^{2} + i ρ) \geq 0 \end{matrix}

(83)

with |$\sigma=-\varphi_{mlk}$| or |$\sigma=-1/\beta_{mlk}$|⁠.

From Eq. (71), we realize that |$P_{mlk}$| is nonzero real in the case |$D_{mlk}<0.$| We rewrite |$ G(z)$| as follows:

\begin{matrix} G (z) & = & \frac{1}{- P (z - T_{1}) (z - T_{2})}, \end{matrix}

(84)

with

\begin{matrix} T_{1} & = & \frac{(Q + P F - β E)}{- 2 P} + \frac{\sqrt{(Q + P F - β E)^{2} - 4 P (Q F + β m_{k}^{2} - i β ρ)}}{- 2 P}, \end{matrix}

(85)

\begin{matrix} T_{2} & = & \frac{(Q + P F - β E)}{- 2 P} - \frac{\sqrt{(Q + P F - β E)^{2} - 4 P (Q F + β m_{k}^{2} - i β ρ)}}{- 2 P} . \end{matrix}

(86)

Defining the arguments of the logarithmic functions are

\begin{matrix} S (σ, z) & = & P σ z^{2} + (E + Q σ) z - m_{k}^{2} + i ρ \\ = & P σ (z - Z_{1 σ}) (z - Z_{2 σ}), \end{matrix}

(87)

with

\begin{matrix} Z_{1 φ} & = & \frac{(E - Q φ) + \sqrt{(E - Q φ)^{2} - 4 P φ (m_{k}^{2} - i ρ)}}{2 P φ}, \end{matrix}

(88)

\begin{matrix} Z_{2 φ} & = & \frac{(E - Q φ) - \sqrt{(E - Q φ)^{2} - 4 P φ (m_{k}^{2} - i ρ)}}{2 P φ}, \end{matrix}

(89)

\begin{matrix} Z_{1 β} & = & \frac{(E - \frac{Q}{β}) + \sqrt{(E - \frac{Q}{β})^{2} - 4 \frac{P}{β} (m_{k}^{2} - i ρ)}}{\frac{2 P}{β}}, \end{matrix}

(90)

\begin{matrix} Z_{2 β} & = & \frac{(E - \frac{Q}{β}) - \sqrt{(E - \frac{Q}{β})^{2} - 4 \frac{P}{β} (m_{k}^{2} - i ρ)}}{\frac{2 P}{β}} . \end{matrix}

(91)

In order to perform the |$z$|-integrals, we decompose the logarithmic functions in the |$z$|-integrands, as in Eq. (A1). In particular, one has

\begin{matrix} \ln (\frac{S (σ, z)}{P z + Q}) & = & \ln (P σ z - P σ Z_{1 σ}) + \ln (z - Z_{2 σ}) - \ln (P z + Q) \\ + 2 π i θ [Im (P σ Z_{1 σ})] θ [Im (Z_{2 σ})] - 2 π i θ [- Im (Q)] θ [- Im (\frac{S (σ, z)}{P z + Q})], \end{matrix}

(92)

and

\begin{matrix} \ln (\frac{- S (σ, z)}{P z + Q}) & = & \ln (- P σ z + P σ Z_{1 σ}) + \ln (z - Z_{2 σ}) - \ln (P z + Q) \\ - 2 π i θ [Im (P σ Z_{1 σ})] θ [- Im (Z_{2 σ})] + 2 π i θ [Im (Q)] θ [- Im (\frac{S (σ, z)}{P z + Q})] . \end{matrix}

(93)

By determining that |$\text{Im}\left(\pm\dfrac{S(\sigma,z)}{Pz+Q}\right)$| is independent of |$\sigma$| and using Eqs. (92) and (93), |$D_0$| can be presented in the form

\begin{matrix} \frac{D_{0}}{i π^{2}} & = & ⨁_{n m l k} \int_{0}^{\infty} d z G (z) {Ω_{n m l k}^{+} - f_{l k} g_{m l k} \ln (\frac{1 - β φ}{β} z + \frac{F}{β}) \\ - f_{l k} g_{m l k}^{-} \ln (\frac{- (1 - β φ)}{β} z - \frac{F}{β}) - (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (\frac{- P z}{β} + \frac{P Z_{1 β}}{β}) \\ - (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (z - Z_{2 β}) + f_{l k} g_{m l k} \ln (- P φ z + P φ Z_{1 φ}) \\ + f_{l k} g_{m l k} \ln (z - Z_{2 φ}) + f_{l k} g_{m l k}^{-} \ln (P φ z - P φ Z_{1 φ}) \\ + f_{l k} g_{m l k}^{-} \ln (z - Z_{2 φ}) + (f_{l k}^{-} g_{m l k} - f_{l k} g_{m l k}^{-}) \ln (P z + Q)} \\ + ⨁_{n m l k} \int_{- \infty}^{0} d z G (z) {Ω_{n m k}^{-} + f_{l k}^{-} g_{m l k}^{-} \ln (z - Z_{2 β}) \\ + f_{l k} g_{m l k}^{-} \ln (\frac{P z}{β} - \frac{P Z_{1 β}}{β}) + (f_{l k}^{-} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}) \ln (\frac{1 - β φ}{β} z + \frac{F}{β}) \\ + f_{l k}^{-} g_{m l k}^{-} \ln (\frac{- P z}{β} + \frac{P Z_{1 β}}{β}) - (f_{l k}^{-} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}) \ln (- P φ z + P φ Z_{1 φ}) \\ + f^{-} g^{-} \ln (z - Z_{2 β}) + (f_{l k}^{-} g_{m l k} - f_{l k} g_{m l k}^{-}) \ln (P z + Q) \\ - (f_{l k}^{-} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}) \ln (z - Z_{2 φ})} \\ + 2 π i ⨁_{n m l k} (f_{l k} g_{m l k}^{-} θ [Im (Q)] + f_{l k}^{-} g_{m l k} θ [- Im (Q)]) \int_{- \infty}^{\infty} d z G (z) θ [- Im (\frac{S (σ, z)}{P z + Q})] . \end{matrix}

(94)

We first emphasize that |$\ln(Pz+Q) $| might have poles in negative real axes in the real mass cases. However, in these cases, |$f_{lk}=f_{lk}^-=1$| and |$g_{mlk}=g_{mlk}^-=1$|⁠. As a result, one checks that |$(\,f^{-}_{lk}g_{mlk}^{-} -f_{lk}g_{mlk}) \ln(Pz+Q)=0$|⁠. Thus we do not need to make |$Q\longrightarrow Q+i\rho'$| as in the |$F_{nmlk}$| case. Secondly, the |$z$|-integrals are now split into three basic integrals:

\begin{matrix} \int_{0}^{\infty} G (z) d z; \int_{0}^{\infty} \ln (a z + b) G (z) d z; \int_{- \infty}^{\infty} θ [- Im (\frac{S (σ, z)}{P z + Q})] G (z) d z . \end{matrix}

These integrals are calculated in concrete terms in the appendix.

2.3.2. In the case of |$0<D_{mlk}\leqslant \left(\frac{A_{mlk}}{B_{mlk}}-\alpha_{lk}\right)^2$| and |$\frac{A_{mlk}}{B_{mlk}}-\alpha_{lk} < 0$|

In this case, we have

\begin{matrix} β_{m l k} & = \frac{(\frac{A_{m l k}}{B_{m l k}} - α_{l k}) + \sqrt{{(\frac{A_{m l k}}{B_{m l k}} - α_{l k})}^{2} - D_{m l k}}}{D_{m l k}} < 0, \end{matrix}

(95)

\begin{matrix} φ_{m l k} & = (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) + \sqrt{{(\frac{A_{m l k}}{B_{m l k}} - α_{l k})}^{2} - D_{m l k}} < 0. \end{matrix}

(96)

It is easy to check that |$-\varphi_{mlk}-(-\frac{1}{\beta_{mlk}}) = -\sqrt{\left(\frac{A_{mlk}}{B_{mlk}}-\alpha_{lk}\right)^2-D_{mlk}}\leqslant0$|⁠. Therefore, the integration region now looks like Fig. 5. In this case, the integration region of |$D_0$| is similar to the |$D_{mlk}<0$| case. As a result, the analytical calculation of |$D_0$| in this case is the same as that in the case of |$D_{mlk}<0$|⁠.

Fig. 5.

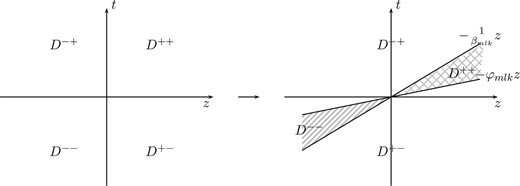
The integration region.

2.3.3. In the case of |$0<D_{mlk}\leqslant \left(\frac{A_{mlk}}{B_{mlk}}-\alpha_{lk}\right)^2$| and |$\frac{A_{mlk}}{B_{mlk}}-\alpha_{lk}> 0$|

In this case, |$\beta_{mlk}$| and |$\varphi_{mlk}$| are positive and we confirm that

\begin{matrix} (- φ_{m l k}) - (- \frac{1}{β_{m l k}}) = - \sqrt{{(\frac{A_{m l k}}{B_{m l k}} - α_{l k})}^{2} - D_{m l k}} ⩽ 0. \end{matrix}

(97)

Therefore, the integration region now looks like Fig. 6.

Fig. 6.

The integration region.

Applying the same procedure, |$D_0$| reads

\begin{matrix} \frac{D_{0}}{i π^{2}} & = & ⨁_{n m l k} \int_{0}^{\infty} d z G (z) {Θ_{n m l k} + f_{l k}^{-} g_{m l k} \ln (\frac{1 - β φ}{β} z + \frac{F}{β}) \\ + f_{l k}^{-} g_{m l k}^{-} \ln (- \frac{1 - β φ}{β} z - \frac{F}{β}) - f_{l k}^{-} g_{m l k} \ln (- P φ z + P φ Z_{1 σ}) \\ - f_{l k}^{-} g_{m l k}^{-} \ln (P φ z - P φ Z_{1 σ}) + (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (- \frac{P}{β} z + \frac{P}{β} Z_{1 β}) \\ - (f_{l k}^{-} g_{m l k} + f_{l k}^{-} g_{m l k}^{-}) \ln (z - Z_{2 φ}) + (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (z - Z_{2 β}) \\ + (f_{l k}^{-} g_{m l k}^{-} - f_{l k} g_{m l k}) \ln (P z + Q)} \\ + ⨁_{n m l k} \int_{- \infty}^{0} d z G (z) {Θ_{n m l k}^{-} - (f_{l k} g_{m l k}^{-} + f_{l k} g_{m l k}) \ln (\frac{(1 - β φ)}{β} z + \frac{F}{β}) \\ - f_{l k} g_{m l k}^{-} \ln (- \frac{P}{β} z + \frac{P}{β} Z_{1 β}) - f_{l k}^{-} g_{m l k}^{-} \ln (\frac{P}{β} z - \frac{P}{β} Z_{1 β}) \\ + (f_{l k} g_{m l k} + f_{l k} g_{m l k}^{-}) \ln (- P φ z + P φ Z_{1 φ}) - (f_{l k} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}^{-}) \ln (z - Z_{2 β}) \\ + (f_{l k} g_{m l k} + f_{l k} g_{m l k}^{-}) \ln (z - Z_{2 φ}) + (f_{l k}^{-} g_{m l k}^{-} - f_{l k} g_{m l k}) \ln (P z + Q)} \\ - 2 π i ⨁_{n m l k} (f_{l k} g_{m l k} θ [- Im (Q)] + f_{l k}^{-} g_{m l k}^{-} θ [Im (Q)]) \int_{- \infty}^{\infty} θ [- Im (\frac{S (σ, z)}{P z + Q})] G (z) d z, \end{matrix}

(98)

where the new kinematic variables introduced in this formula are

\begin{matrix} Θ_{n m l k} & = & - (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (\frac{F}{β}) - 2 π i f_{l k}^{-} g_{m l k} θ [- Im (P φ Z_{1 φ})] θ [Im (Z_{2 φ})] \\ + 2 π i f_{l k}^{-} g_{m l k}^{-} θ [- Im (P φ Z_{1 φ})] θ [- Im (Z_{2 φ})] \\ + 2 π i (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) θ [Im (- \frac{P Z_{1 β}}{β})] θ [Im (Z_{2 β})], \end{matrix}

(99)

and

\begin{matrix} Θ_{n m l k}^{-} & = & f_{l k} g_{m l k}^{-} \ln (\frac{F}{β}) + f_{l k}^{-} g_{m l k}^{-} \ln (- \frac{F}{β}) - 2 π i f_{l k} g_{m l k}^{-} θ [- Im (\frac{P Z_{1 β}}{β})] θ [Im (Z_{1 β})] \\ + 2 π i f_{l k}^{-} g_{m l k}^{-} θ [- Im (\frac{P Z_{1 β}}{β})] θ [- Im (Z_{1 β})] \\ + 2 π i (f_{l k} g_{m l k} + f_{l k} g_{m l k}^{-}) θ [- Im (P φ Z_{1 φ})] θ [Im (Z_{2 φ})] . \end{matrix}

(100)

The last integrals written in terms of |$z$| will be evaluated by means of the basic integrals presented in the appendix.

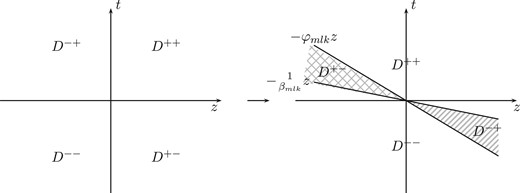
2.3.4. In the case of |$D_{mlk} > \left(\frac{A_{mlk}}{B_{mlk}}-\alpha_{lk}\right)^2$|

From Eq. (80), each term relating to the following integral will be presented as

\begin{matrix} T_{12}^{+} & = & C_{σ} \int_{0}^{\infty} \frac{\ln (\frac{- P σ z^{2} + (E - Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}{(z - T_{1}) (z - T_{2})} d z \\ = & \frac{C_{σ}}{T_{1} - T_{2}} \int_{0}^{\infty} {\frac{\ln (\frac{- P σ z^{2} + (E - Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}{z - T_{1}} d z - \frac{\ln (\frac{- P σ z^{2} + (E - Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}{z - T_{2}} d z} \\ = & \frac{C_{σ}}{T_{1} - T_{2}} \int_{0}^{\infty} {\frac{\ln (\frac{- P σ z^{2} + (E - Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}{z - T_{1}} d z - \frac{\ln (\frac{- P σ T_{1}^{2} + (E - Q σ) T_{1} - m_{k}^{2} + i ϱ}{Q + P T_{1}})}{z - T_{1}} d z} \\ + \frac{C_{σ}}{T_{2} - T_{1}} \int_{0}^{\infty} {\frac{\ln (\frac{- P σ z^{2} + (E - Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}{z - T_{2}} d z - \frac{\ln (\frac{- P σ T_{2}^{2} + (E - Q σ) T_{2} - m_{k}^{2} + i ϱ}{Q + P T_{2}})}{z - T_{2}} d z} \\ + \frac{C_{σ}}{T_{1} - T_{2}} \sum_{i = 1}^{2} \int_{0}^{\infty} \frac{\ln (\frac{- P σ T_{i}^{2} + (E - Q σ) T_{i} - m_{k}^{2} + i ϱ}{Q + P T_{i}})}{z - T_{i}} d z, \end{matrix}

(101)

where |$C_{\sigma}$| are coefficients in front of the mentioned integrals. We also apply the same trick for each term relating to

\begin{matrix} T_{12}^{-} & = & C_{σ} \int_{- \infty}^{0} \frac{\ln (\frac{- P σ z^{2} + (E - Q σ) z - m_{k}^{2} + i ϱ}{Q + P z})}{(z - T_{1}) (z - T_{2})} d z, \end{matrix}

(102)

\begin{matrix} T_{0}^{+} & = & C_{σ} \int_{0}^{\infty} \frac{\ln (\pm \frac{(1 - β φ) z + F}{β})}{(z - T_{1}) (z - T_{2})} d z, \end{matrix}

(103)

\begin{matrix} T_{0}^{-} & = & C_{σ} \int_{- \infty}^{0} \frac{\ln (\pm \frac{(1 - β φ) z + F}{β})}{(z - T_{1}) (z - T_{2})} d z . \end{matrix}

(104)

We have already added to |$D_0$| the extra terms, the sum of which is up to zero. These extra terms will contribute to the residue of the |$z$|-poles when |$\beta_{mlk}, \varphi_{mlk}$| become complex.

2.3.5. In the case of |$D_{mlk}=0$|

In this case, the integrands of |$D_{0}^{++}$|⁠, |$D_{0}^{+-}$|⁠, |$D_{0}^{-+}$|⁠, and |$D_{0}^{-}$| have the form

\begin{matrix} I (z, t) & = & \frac{1}{[z + F_{n n l k}] [- 2 (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) z t - 2 \frac{C_{m l k}}{B_{m l k}} t - 2 \frac{d_{l k}}{A C_{l k}} z + t^{2} - m_{k}^{2} + i ρ]} \end{matrix}

(105)

\begin{matrix} = & \frac{1}{[z + F_{n n l k}] [(K_{m l k} t + M_{m l k}) z + L_{m l k} t + t^{2} - m_{k}^{2} + i ρ]}, \end{matrix}

(106)

where new kinematic variables are introduced:

\begin{matrix} K_{m l k} & = & - 2 (\frac{A_{m l k}}{B_{m l k}} - α_{l k}) \in R, \end{matrix}

(107)

\begin{matrix} L_{m l k} & = & - 2 \frac{C_{m l k}}{B_{m l k}} \in C, \end{matrix}

(108)

\begin{matrix} M_{m l k} & = & - 2 \frac{d_{l k}}{A C_{l k}} \in C . \end{matrix}

(109)

Instead of linearizing |$t$|⁠, we are going to calculate the |$z$|-integrals directly. The resulting equations read

\begin{matrix} \int_{0}^{\infty} d z I (z, t) & = & H (t) [\ln (F_{n m l k}) - \ln (\frac{t^{2} + L_{m l k} t - m_{k}^{2} + i ρ}{K_{m l k} t + M_{m l k}})], \end{matrix}

(110)

\begin{matrix} \int_{- \infty}^{0} d z I (z, t) & = & - H (t) [\ln (- F_{n m l k}) - \ln (- \frac{t^{2} + L_{m l k} t - m_{k}^{2} + i ρ}{K_{m l k} t + M_{m l k}})] . \end{matrix}

(111)

|$ \mathcal{H}(t)$| is defined as

\begin{matrix} H (t) & = & \frac{1}{- t^{2} + (K_{m l k} F_{n m l k} - L_{m l k}) t + M_{m l k} F_{n m l k} + m_{k}^{2} - i ρ} \\ = & - \frac{1}{(t - W_{n m l k}^{(1)}) (t - W_{n m l k}^{(2)})}, \end{matrix}

(112)

where |$ W_{nmlk}^{(1,2)}$| are given by

\begin{matrix} W_{n m l k}^{(1, 2)} = \frac{K_{m l k} F_{n m l k} - L_{m l k} \pm \sqrt{(K_{m l k} F_{n m l k} - L_{m l k})^{2} + 4 (K_{m l k} F_{n m l k} + m_{k}^{2} - i ρ)}}{2} . \end{matrix}

(113)

Finally, one gets

\begin{matrix} D_{0}^{+ +} & = & + i π^{2} ⨁_{n m l k} \int_{0}^{\infty} d t f_{l k} g_{m l k} H (t) {\ln (F_{n m l k}) - \ln (\frac{t^{2} + L_{m l k} t - m_{k}^{2} + i ρ}{K_{m l k} t + M_{m l k}})}, \end{matrix}

(114)

\begin{matrix} D_{0}^{+ -} & = & - i π^{2} ⨁_{n m l k} \int_{- \infty}^{0} d t f_{l k} g_{m l k}^{-} H (t) {\ln (F_{n m l k}) - \ln (\frac{t^{2} + L_{m l k} t - m_{k}^{2} + i ρ}{K_{m l k} t + M_{m l k}})}, \end{matrix}

(115)

\begin{matrix} D_{0}^{- +} & = & + i π^{2} ⨁_{n m l k} \int_{0}^{\infty} d t f_{l k}^{-} g_{m l k} H (t) {\ln (- F_{n m l k}) - \ln (- \frac{t^{2} + L_{m l k} t - m_{k}^{2} + i ρ}{K_{m l k} t + M_{m l k}})}, \end{matrix}

(116)

\begin{matrix} D_{0}^{- -} & = & - i π^{2} ⨁_{n m l k} \int_{- \infty}^{0} d t f_{l k}^{-} g_{m l k}^{-} H (t) {\ln (- F_{n m l k}) - \ln (- \frac{t^{2} + L_{m l k} t - m_{k}^{2} + i ρ}{K_{m l k} t + M_{m l k}})} . \end{matrix}

(117)

It is easy to confirm that

\begin{matrix} Im (L_{m l k}) = {\begin{matrix} \geq 0, & for + +, - +, \\ \leq 0 & for + -, - -, \end{matrix} and Im (M_{m l k}) = {\begin{matrix} \geq 0, & for + +, + -, \\ \leq 0 & for - +, - - . \end{matrix} \end{matrix}

(118)

Moreover, one also verifies that

\begin{matrix} Im [t^{2} + L_{m l k} t - m_{k}^{2} + i ρ] > 0 and Im [K_{m l k} t + M_{m l k}] > 0, \end{matrix}

(119)

noting that |$X(t)$| is the second-order polynomial written in terms of |$t$| in the argument of the logarithmic functions. In detail, it is

\begin{matrix} X (t) = t^{2} + L_{m l k} t - m_{k}^{2} + i ρ = (t - X_{m l k}^{(1)}) (t - X_{m l k}^{(2)}), \end{matrix}

(120)

with

\begin{matrix} X_{m l k}^{(1, 2)} = \frac{- L_{m l k} \pm \sqrt{L_{m l k}^{2} - 4 (- m_{k}^{2} + i ρ)}}{2} . \end{matrix}

(121)

Because |$\text{Im}(X(t))$| and |$\text{Im}(K_{mlk}t+M_{mlk})$| have the same sign, the logarithmic functions are decomposed as follows:

\begin{matrix} \ln (\pm \frac{X (t)}{K_{m l k} t + M_{m l k}}) & = & \ln [\pm X (t)] - \ln (K_{m l k} t + M_{m l k}), \end{matrix}

(122)

and

\begin{matrix} \ln [X (t)] & = & \ln (t - X_{m l k}^{(1)}) + \ln (t - X_{m l k}^{(2)}) + 2 π i θ [Im (X_{m l k}^{(1)})] θ [Im (X_{m l k}^{(2)})], \\ \ln [- X (t)] & = & \ln (- t + X_{m l k}^{(1)}) + \ln (t - X_{m l k}^{(2)}) - 2 π i θ [Im (X_{m l k}^{(1)})] θ [- Im (X_{m l k}^{(2)})] . \end{matrix}

(123)

Finally, we arrive at

\begin{matrix} \frac{D_{0}}{i π^{2}} & = & ⨁_{n m l k} \int_{0}^{\infty} d t H (t) {χ_{n m l k}^{+} - f_{l k} g_{m l k} \ln (t - X_{m l k}^{(1)}) - f_{l k}^{-} g_{m l k} \ln (- t + X_{m l k}^{(1)}) \\ - (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (t - X_{m l k}^{(2)}) - (f_{l k} g_{m l k} + f_{l k}^{-} g_{m l k}) \ln (K_{m l k} t + M_{m l k})} \\ - ⨁_{n m l k} \int_{- \infty}^{0} d t H (t) {χ_{n m l k}^{-} - f_{l k} g_{m l k}^{-} \ln (t - X_{m l k}^{(1)}) - f_{l k}^{-} g_{m l k}^{-} \ln (- t + X_{m l k}^{(1)}) \\ - (f_{l k} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}^{-}) \ln (t - X_{m l k}^{(2)}) - (f_{l k} g_{m l k}^{-} + f_{l k}^{-} g_{m l k}^{-}) \ln (K_{m l k} t + M_{m l k})}, \end{matrix}

(124)

where the new kinematic variables are given by

\begin{matrix} χ_{n m l k}^{+} & = & f_{l k} g_{m l k} \ln (F_{n m l k}) + f_{l k}^{-} g_{m l k} \ln (- F_{n m l k}) - 2 π i f_{l k} g_{m l k} θ [Im (X_{m l k}^{(1)})] θ [Im (X_{m l k}^{(2)})] \\ + 2 π i f_{l k}^{-} g_{m l k} θ [Im (X_{m l k}^{(1)})] θ [- Im (X_{m l k}^{(2)})], \end{matrix}

(125)

\begin{matrix} χ_{n m l k}^{-} & = & f_{l k} g_{m l k}^{-} \ln (F_{n m l k}) + f_{l k}^{-} g_{m l k}^{-} \ln (- F_{n m l k}) - 2 π i f_{l k} g_{m l k}^{-} θ [Im (X_{m l k}^{(1)})] θ [Im (X_{m l k}^{(2)})] \\ + 2 π i f_{l k}^{-} g_{m l k}^{-} θ [Im (X_{m l k}^{(1)})] θ [- Im (X_{m l k}^{(2)})] . \end{matrix}

(126)

The remaining integrals (written in terms of |$t$|⁠) will be integrated by using the basic integrals, which are described in the appendix.

In the next step, we will extend this work for evaluating tensor one-loop four-point functions with complex internal masses. In the parallel and orthogonal space [11,12,23], a tensor one-loop |$N$|-point integral with rank |$M$| can be decomposed as

\begin{matrix} T_{μ_{1} μ_{2} \dots μ_{M}}^{N} = (- 1)^{\frac{p_{⊥}}{2}} \frac{{(g_{μ_{1} μ_{2}} \dots g_{μ_{p_{⊥}} - 1} g_{μ_{p_{⊥}}})}_{sym}}{K} T^{(p_{0}, p_{1}, \dots, p_{⊥})}, \end{matrix}

(127)

with

\begin{matrix} K = {\begin{matrix} \prod_{i = 0}^{(p_{⊥} - 2) / 2} (n - J + 2 i), & if p_{⊥} \neq 0, \\ 1, & if p_{⊥} = 0, \end{matrix} \end{matrix}

(128)

where the space-time dimension is |$n$| and |$J$| is the number of parallel dimensions (spanned by the external momenta). The tensor coefficients (form factors) are given by

\begin{matrix} T_{N}^{p_{0}, p_{1} \dots p_{⊥}} & = & \frac{2 π^{\frac{n - J}{2}}}{Γ (\frac{n - J}{2})} \int_{- \infty}^{\infty} d l_{0} d l_{1} \dots d l_{J - 1} \int_{0}^{\infty} l_{⊥}^{n - J - 1} d l_{⊥} \frac{l_{0}^{p_{0}} l_{1}^{p_{1}} \dots l_{J - 1}^{p_{J - 1}} l_{⊥}^{p_{⊥}}}{P_{1} P_{2} \dots P_{N}} . \end{matrix}

(129)

The traditional tensor reduction for one-loop integrals was proposed by Passarino and Veltman [4] and later developed by Denner and Dittmaier [5]. In these schemes, the form factors will be obtained by contracting the Minkowski metric (⁠|$g_{\mu\nu}$|⁠) and external momenta into the tensor integrals. At this stage, we have to solve a system of linear equations where the Gram determinants appear in the denominator. If the Gram determinants vanish or become very small, the reduction method will break or spoil the numerical stability (this is called the Gram determinant problem). The framework in this paper can be extended to calculate the form factors (or tensor one-loop integrals) directly. This will be the subject of a future publication (K. H. Phan, manuscript in preparation). It therefore provides a new approach to solve the Gram determinant problem analytically.

3. Numerical checks

The calculation has been implemented into a C|$++$| program called ONELOOP4PT.CPP. In this program, the function uses the de facto input parameters of LoopTools. The syntax of the new function is as follows:

\begin{matrix} ONELOOP4PT (p_{1}^{2}, p_{2}^{2}, p_{3}^{2}, p_{4}^{2}, s, t, m_{1}^{2}, m_{2}^{2}, m_{3}^{2}, m_{4}^{2}, ρ), \end{matrix}

(130)

with |$s = (p_1+p_2)^2$| and |$t = (p_2+p_3)^2$|⁠.

In this section, we are going to check the program with LoopTools version |$2.12$| [22] (called LoopTools v.|$2.12$|⁠). In Tables 2 and 3, we check ONELOOP4PT.CPP with LoopTools in real and complex masses respectively. The input parameters are presented in these tables. One finds a good agreement between this work and LoopTools in all cases.

Table 2.

In the case of |$(m_1^2,m_2^2,m_3^2,m_4^2)=(10, 20,30,40)$|⁠, and |$ \rho=10^{-30}.$|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)\;$\|	This work LoopTools v.\|$2.12$\|
\|$(10,50,10,70, 170, 10)$\|	\|$-1.221\,979\,771\,717\,3585\times 10^{-4}+2.009\,833\,708\,713\,9847\times 10^{-3}\; i$\|
	\|$-1.221\,979\,769\,699\,2298\times 10^{-4}+2.009\,833\,709\,284\,3695\times 10^{-3}\; i$\|
\|$(10,50,10,70, 170, -10)$\|	\|$-1.486\,716\,266\,289\,6689\times 10^{-4}+1.697\,624\,355\,415\,6623\times 10^{-3}\; i$\|
	\|$-1.486\,716\,266\,482\,8184\times 10^{-4}+1.697\,624\,355\,242\,6918\times 10^{-3}\;i$\|
\|$(10,-50,10,-70, 170, 10)$\|	\|$\;\;\;3.351\,965\,931\,200\,3411\times10^{-4} + 2.912\,362\,010\,029\,4989\times 10^{-4}\; i$\|
	\|$\;\;\;3.351\,965\,931\,227\,0943\times 10^{-4} + 2.912\,362\,011\,787\,9053\times 10^{-4}\; i$\|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)\;$\|	This work LoopTools v.\|$2.12$\|
\|$(10,50,10,70, 170, 10)$\|	\|$-1.221\,979\,771\,717\,3585\times 10^{-4}+2.009\,833\,708\,713\,9847\times 10^{-3}\; i$\|
	\|$-1.221\,979\,769\,699\,2298\times 10^{-4}+2.009\,833\,709\,284\,3695\times 10^{-3}\; i$\|
\|$(10,50,10,70, 170, -10)$\|	\|$-1.486\,716\,266\,289\,6689\times 10^{-4}+1.697\,624\,355\,415\,6623\times 10^{-3}\; i$\|
	\|$-1.486\,716\,266\,482\,8184\times 10^{-4}+1.697\,624\,355\,242\,6918\times 10^{-3}\;i$\|
\|$(10,-50,10,-70, 170, 10)$\|	\|$\;\;\;3.351\,965\,931\,200\,3411\times10^{-4} + 2.912\,362\,010\,029\,4989\times 10^{-4}\; i$\|
	\|$\;\;\;3.351\,965\,931\,227\,0943\times 10^{-4} + 2.912\,362\,011\,787\,9053\times 10^{-4}\; i$\|

Table 2.

In the case of |$(m_1^2,m_2^2,m_3^2,m_4^2)=(10, 20,30,40)$|⁠, and |$ \rho=10^{-30}.$|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)\;$\|	This work LoopTools v.\|$2.12$\|
\|$(10,50,10,70, 170, 10)$\|	\|$-1.221\,979\,771\,717\,3585\times 10^{-4}+2.009\,833\,708\,713\,9847\times 10^{-3}\; i$\|
	\|$-1.221\,979\,769\,699\,2298\times 10^{-4}+2.009\,833\,709\,284\,3695\times 10^{-3}\; i$\|
\|$(10,50,10,70, 170, -10)$\|	\|$-1.486\,716\,266\,289\,6689\times 10^{-4}+1.697\,624\,355\,415\,6623\times 10^{-3}\; i$\|
	\|$-1.486\,716\,266\,482\,8184\times 10^{-4}+1.697\,624\,355\,242\,6918\times 10^{-3}\;i$\|
\|$(10,-50,10,-70, 170, 10)$\|	\|$\;\;\;3.351\,965\,931\,200\,3411\times10^{-4} + 2.912\,362\,010\,029\,4989\times 10^{-4}\; i$\|
	\|$\;\;\;3.351\,965\,931\,227\,0943\times 10^{-4} + 2.912\,362\,011\,787\,9053\times 10^{-4}\; i$\|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)\;$\|	This work LoopTools v.\|$2.12$\|
\|$(10,50,10,70, 170, 10)$\|	\|$-1.221\,979\,771\,717\,3585\times 10^{-4}+2.009\,833\,708\,713\,9847\times 10^{-3}\; i$\|
	\|$-1.221\,979\,769\,699\,2298\times 10^{-4}+2.009\,833\,709\,284\,3695\times 10^{-3}\; i$\|
\|$(10,50,10,70, 170, -10)$\|	\|$-1.486\,716\,266\,289\,6689\times 10^{-4}+1.697\,624\,355\,415\,6623\times 10^{-3}\; i$\|
	\|$-1.486\,716\,266\,482\,8184\times 10^{-4}+1.697\,624\,355\,242\,6918\times 10^{-3}\;i$\|
\|$(10,-50,10,-70, 170, 10)$\|	\|$\;\;\;3.351\,965\,931\,200\,3411\times10^{-4} + 2.912\,362\,010\,029\,4989\times 10^{-4}\; i$\|
	\|$\;\;\;3.351\,965\,931\,227\,0943\times 10^{-4} + 2.912\,362\,011\,787\,9053\times 10^{-4}\; i$\|

Table 3.

In the case of |$m_1^2=10-5i,m_2^2=20-2i, m_3^2=30-3i, m_4^2=40-4i$|⁠, and |$ \rho=10^{-30}.$|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)$\|	(This work) \|$\times 10^{-4}$\| (LoopTools v.\|$2.12$\|)\|$\times 10^{-4}$\|
\|$(10,60,10,90,200,10)$\|	\|$-7.675\,495\,827\,590\,1917+ 7.936\,923\,630\,833\,591\,22\; i$\|
	\|$ -7.675\,495\,827\,590\,2069+ 7.936\,923\,630\,833\,577\,94\; i $\|
\|$(10,60,-10,90,200,10)$\|	\|$ -6.221\,361\,528\,827\,8696+ 8.202\,897\,883\,235\,273\,71\; i$\|
	\|$ -6.221\,361\,528\,827\,8837 + 8.202\,897\,883\,235\,259\,00\; i$\|
\|$(10,-60,-10,-90,200,-10)$\|	\|$\;\;\;1.531\,845\,524\,366\,8001 + 2.561\,867\,870\,169\,164\,87\; i$\|
	\|$\;\;\;1.531\,845\,524\,366\,7963 + 2.561\,867\,870\,169\,158\,70\; i$\|
\|$(10,60,0,0,200,-10)$\|	\|$-3.349\,931\,574\,662\,3337 + 6.178\,621\,892\,720\,976\,45\; i$\|
	\|$-3.349\,931\,574\,662\,3217 + 6.178\,621\,892\,720\,981\,60\; i$\|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)$\|	(This work) \|$\times 10^{-4}$\| (LoopTools v.\|$2.12$\|)\|$\times 10^{-4}$\|
\|$(10,60,10,90,200,10)$\|	\|$-7.675\,495\,827\,590\,1917+ 7.936\,923\,630\,833\,591\,22\; i$\|
	\|$ -7.675\,495\,827\,590\,2069+ 7.936\,923\,630\,833\,577\,94\; i $\|
\|$(10,60,-10,90,200,10)$\|	\|$ -6.221\,361\,528\,827\,8696+ 8.202\,897\,883\,235\,273\,71\; i$\|
	\|$ -6.221\,361\,528\,827\,8837 + 8.202\,897\,883\,235\,259\,00\; i$\|
\|$(10,-60,-10,-90,200,-10)$\|	\|$\;\;\;1.531\,845\,524\,366\,8001 + 2.561\,867\,870\,169\,164\,87\; i$\|
	\|$\;\;\;1.531\,845\,524\,366\,7963 + 2.561\,867\,870\,169\,158\,70\; i$\|
\|$(10,60,0,0,200,-10)$\|	\|$-3.349\,931\,574\,662\,3337 + 6.178\,621\,892\,720\,976\,45\; i$\|
	\|$-3.349\,931\,574\,662\,3217 + 6.178\,621\,892\,720\,981\,60\; i$\|

Table 3.

In the case of |$m_1^2=10-5i,m_2^2=20-2i, m_3^2=30-3i, m_4^2=40-4i$|⁠, and |$ \rho=10^{-30}.$|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)$\|	(This work) \|$\times 10^{-4}$\| (LoopTools v.\|$2.12$\|)\|$\times 10^{-4}$\|
\|$(10,60,10,90,200,10)$\|	\|$-7.675\,495\,827\,590\,1917+ 7.936\,923\,630\,833\,591\,22\; i$\|
	\|$ -7.675\,495\,827\,590\,2069+ 7.936\,923\,630\,833\,577\,94\; i $\|
\|$(10,60,-10,90,200,10)$\|	\|$ -6.221\,361\,528\,827\,8696+ 8.202\,897\,883\,235\,273\,71\; i$\|
	\|$ -6.221\,361\,528\,827\,8837 + 8.202\,897\,883\,235\,259\,00\; i$\|
\|$(10,-60,-10,-90,200,-10)$\|	\|$\;\;\;1.531\,845\,524\,366\,8001 + 2.561\,867\,870\,169\,164\,87\; i$\|
	\|$\;\;\;1.531\,845\,524\,366\,7963 + 2.561\,867\,870\,169\,158\,70\; i$\|
\|$(10,60,0,0,200,-10)$\|	\|$-3.349\,931\,574\,662\,3337 + 6.178\,621\,892\,720\,976\,45\; i$\|
	\|$-3.349\,931\,574\,662\,3217 + 6.178\,621\,892\,720\,981\,60\; i$\|

\|$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)$\|	(This work) \|$\times 10^{-4}$\| (LoopTools v.\|$2.12$\|)\|$\times 10^{-4}$\|
\|$(10,60,10,90,200,10)$\|	\|$-7.675\,495\,827\,590\,1917+ 7.936\,923\,630\,833\,591\,22\; i$\|
	\|$ -7.675\,495\,827\,590\,2069+ 7.936\,923\,630\,833\,577\,94\; i $\|
\|$(10,60,-10,90,200,10)$\|	\|$ -6.221\,361\,528\,827\,8696+ 8.202\,897\,883\,235\,273\,71\; i$\|
	\|$ -6.221\,361\,528\,827\,8837 + 8.202\,897\,883\,235\,259\,00\; i$\|
\|$(10,-60,-10,-90,200,-10)$\|	\|$\;\;\;1.531\,845\,524\,366\,8001 + 2.561\,867\,870\,169\,164\,87\; i$\|
	\|$\;\;\;1.531\,845\,524\,366\,7963 + 2.561\,867\,870\,169\,158\,70\; i$\|
\|$(10,60,0,0,200,-10)$\|	\|$-3.349\,931\,574\,662\,3337 + 6.178\,621\,892\,720\,976\,45\; i$\|
	\|$-3.349\,931\,574\,662\,3217 + 6.178\,621\,892\,720\,981\,60\; i$\|

In Table 4, we compare the results generated by ONELOOP4PT.CPP with LoopTools by changing the value of |$m_3^2$|⁠. The other input parameters are fixed as follows: |$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)=(10, -60,-10,-90,200,-10)$| and |$(m_1^2,m_2^2,m_4^2)=(10-5i,20-2i,40-4i)$|⁠, and |$ \rho=10^{-30}.$| One again finds a good agreement between the results computed from this work and LoopTools in all cases of |$m_3^2$|⁠.

Table 4.

In the case of |$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)=(10, -60,-10,-90,200,-10)$| and |$(m_1^2,m_2^2,m_4^2)=(10-5i,20-2i,40-4i)$|⁠, and |$ \rho=10^{-30}.$|

\|$m_3^{2}$\|	This work LoopTools v.\|$2.12$\|
\|$10-3i$\|	\|$ 2.225\,160\,881\,981\,8614\times 10^{-4}+3.603\,281\,499\,379\,6746\times 10^{-4}\; i$\|
	\|$2.225\,160\,881\,981\,8662\times 10^{-4}+3.603\,281\,499\,379\,6724\times 10^{-4}\; i$\|
\|$100-3i$\|	\|$ 8.345\,421\,685\,133\,3892\times 10^{-5}+1.392\,861\,635\,442\,8907\times 10^{-4}\; i$\|
	\|$ 8.345\,421\,685\,133\,4176\times 10^{-5}+1.392\,861\,635\,442\,8922\times 10^{-4}\; i$\|
\|$1000 -3i$\|	\|$1.558\,129\,882\,600\,2613\times 10^{-5}+2.240\,482\,177\,961\,2569\times 10^{-5}\; i$\|
	\|$1.558\,129\,882\,600\,2624\times 10^{-5}+2.240\,482\,177\,961\,2618\times 10^{-5}\;i$\|
\|$100\,000 -3i$\|	\|$1.830\,817\,081\,036\,1346\times 10^{-6}+2.415\,245\,966\,391\,0780\times 10^{-6}\; i$\|
	\|$1.830\,817\,081\,036\,1369\times 10^{-6}+2.415\,245\,966\,391\,0805\times 10^{-6}\; i$\|

\|$m_3^{2}$\|	This work LoopTools v.\|$2.12$\|
\|$10-3i$\|	\|$ 2.225\,160\,881\,981\,8614\times 10^{-4}+3.603\,281\,499\,379\,6746\times 10^{-4}\; i$\|
	\|$2.225\,160\,881\,981\,8662\times 10^{-4}+3.603\,281\,499\,379\,6724\times 10^{-4}\; i$\|
\|$100-3i$\|	\|$ 8.345\,421\,685\,133\,3892\times 10^{-5}+1.392\,861\,635\,442\,8907\times 10^{-4}\; i$\|
	\|$ 8.345\,421\,685\,133\,4176\times 10^{-5}+1.392\,861\,635\,442\,8922\times 10^{-4}\; i$\|
\|$1000 -3i$\|	\|$1.558\,129\,882\,600\,2613\times 10^{-5}+2.240\,482\,177\,961\,2569\times 10^{-5}\; i$\|
	\|$1.558\,129\,882\,600\,2624\times 10^{-5}+2.240\,482\,177\,961\,2618\times 10^{-5}\;i$\|
\|$100\,000 -3i$\|	\|$1.830\,817\,081\,036\,1346\times 10^{-6}+2.415\,245\,966\,391\,0780\times 10^{-6}\; i$\|
	\|$1.830\,817\,081\,036\,1369\times 10^{-6}+2.415\,245\,966\,391\,0805\times 10^{-6}\; i$\|

Table 4.

In the case of |$(p_1^{2}, p_2^2, p_3^2, p_4^2, s, t)=(10, -60,-10,-90,200,-10)$| and |$(m_1^2,m_2^2,m_4^2)=(10-5i,20-2i,40-4i)$|⁠, and |$ \rho=10^{-30}.$|

\|$m_3^{2}$\|	This work LoopTools v.\|$2.12$\|
\|$10-3i$\|	\|$ 2.225\,160\,881\,981\,8614\times 10^{-4}+3.603\,281\,499\,379\,6746\times 10^{-4}\; i$\|
	\|$2.225\,160\,881\,981\,8662\times 10^{-4}+3.603\,281\,499\,379\,6724\times 10^{-4}\; i$\|
\|$100-3i$\|	\|$ 8.345\,421\,685\,133\,3892\times 10^{-5}+1.392\,861\,635\,442\,8907\times 10^{-4}\; i$\|
	\|$ 8.345\,421\,685\,133\,4176\times 10^{-5}+1.392\,861\,635\,442\,8922\times 10^{-4}\; i$\|
\|$1000 -3i$\|	\|$1.558\,129\,882\,600\,2613\times 10^{-5}+2.240\,482\,177\,961\,2569\times 10^{-5}\; i$\|
	\|$1.558\,129\,882\,600\,2624\times 10^{-5}+2.240\,482\,177\,961\,2618\times 10^{-5}\;i$\|
\|$100\,000 -3i$\|	\|$1.830\,817\,081\,036\,1346\times 10^{-6}+2.415\,245\,966\,391\,0780\times 10^{-6}\; i$\|
	\|$1.830\,817\,081\,036\,1369\times 10^{-6}+2.415\,245\,966\,391\,0805\times 10^{-6}\; i$\|

\|$m_3^{2}$\|	This work LoopTools v.\|$2.12$\|
\|$10-3i$\|	\|$ 2.225\,160\,881\,981\,8614\times 10^{-4}+3.603\,281\,499\,379\,6746\times 10^{-4}\; i$\|
	\|$2.225\,160\,881\,981\,8662\times 10^{-4}+3.603\,281\,499\,379\,6724\times 10^{-4}\; i$\|
\|$100-3i$\|	\|$ 8.345\,421\,685\,133\,3892\times 10^{-5}+1.392\,861\,635\,442\,8907\times 10^{-4}\; i$\|
	\|$ 8.345\,421\,685\,133\,4176\times 10^{-5}+1.392\,861\,635\,442\,8922\times 10^{-4}\; i$\|
\|$1000 -3i$\|	\|$1.558\,129\,882\,600\,2613\times 10^{-5}+2.240\,482\,177\,961\,2569\times 10^{-5}\; i$\|
	\|$1.558\,129\,882\,600\,2624\times 10^{-5}+2.240\,482\,177\,961\,2618\times 10^{-5}\;i$\|
\|$100\,000 -3i$\|	\|$1.830\,817\,081\,036\,1346\times 10^{-6}+2.415\,245\,966\,391\,0780\times 10^{-6}\; i$\|
	\|$1.830\,817\,081\,036\,1369\times 10^{-6}+2.415\,245\,966\,391\,0805\times 10^{-6}\; i$\|

4. Conclusions

In this paper, we have presented the analytic solution for scalar one-loop four-point integrals with real and complex internal masses. This method can be extended to calculate tensor integrals directly. It may provide a new way to solve the inverse determinant problem analytically. In the numerical checks, we compared this work with LoopTools. We found a good agreement between the results generated from this work and those from LoopTools. In future work, we will use this method to evaluate tensor one-loop four-point integrals.

Acknowledgements

This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.01-2016.33. The author is also grateful to Chau Thien Nhan for reading the manuscript and to all members of the Theoretical Physics Department, University of Science Ho Chi Minh City for fruitful discussions. K. H. Phan is grateful to Dr Do Hoang Son for fruitful discussions and his contribution to this work.

Funding

Open Access funding: SCOAP|$^3$|⁠.

Appendix

In this appendix, we present several useful formulae. The first one we mention is

\begin{matrix} \ln (a b) & = & \ln (a) + \ln (b) + η (a, b), \end{matrix}

(A1)

\begin{matrix} \ln (\frac{a}{b}) & = & \ln (a) - \ln (b) + η (a, \frac{1}{b}), \end{matrix}

(A2)

where the eta function is defined as

\begin{matrix} η (a, b) & = & 2 π i {θ [- Im (a)] θ [- Im (b)] θ [Im (a b)] - θ [Im (a)] θ [Im (b)] θ [- Im (a b)]} . \end{matrix}

(A3)

Let us consider |$f(z)$| as a rational function with |$\lim\limits_{z\rightarrow \infty}f(z)=0$| and no poles on the negative real |$z$|-axes; |$z_k$| are poles of |$f(z)$|⁠. By closing the integration contour as in Fig. A1, one can derive the following relation:

\begin{matrix} \oint f (z) \ln (z) d z & = & 2 i π \sum_{k} R es {f (z) \ln (z); z_{k}} \end{matrix}

(A4)

\begin{matrix} = & {\int_{- \infty}^{0} + \int_{0}^{- \infty} + \int_{Γ_{k}} + \int_{C_{k}}} f (z) \ln (z) d z \end{matrix}

(A5)

\begin{matrix} = & \int_{- \infty}^{0} f (x) \ln (x) d x + \int_{0}^{- \infty} f (x e^{- 2 i π}) (\ln (x) - 2 i π) d x \end{matrix}

(A6)

\begin{matrix} = & 2 i π \int_{- \infty}^{0} f (z) d z . \end{matrix}

(A7)

Fig. A1.

The integration contour.

http://dx.doi.org/10.1016/0550-3213(79)90234-7

We then arrive at the relation

\begin{matrix} \int_{- \infty}^{a} f (z) d z & = & + \sum_{k} R es {f (z) \ln (z - a); z_{k}} = \int_{- a}^{\infty} f (- z) d z . \end{matrix}

(A8)

We consider three basic integrals in the following paragraphs.

|$\underline{\mathrm{Basic\,\,\,integral}\,I:}$|⁠: The basic integral |$I$| is defined as
$\begin{matrix} R_{1} (x, y) = \int_{0}^{\infty} \frac{1}{(z + x) (z + y)} d z = \frac{\ln (x) - \ln (y)}{x - y}, \end{matrix}$
(A9)
with |$x,y\in \mathbb{C}$|⁠.
|$\underline{\mathrm{Basic\,\,\,integral}\,II:}$|⁠: The basic integral |$II$| is
$\begin{matrix} R_{2} (r, x, y) = \int_{0}^{\infty} \frac{\ln (1 + r z)}{(z + x) (z + y)} d z & = & - \frac{1}{x - y} [{Li}_{2} (1 - r x) - {Li}_{2} (1 - r y)] \\ - \frac{1}{x - y} [η (x, r) \ln (1 - r x) - η (y, r) \ln (1 - r y)], \end{matrix}$
(A10)
with |$r, x,y\in \mathbb{C}$|⁠.
|$\underline{\mathrm{Basic\,\,\,integral}\,III:}$|⁠: The basic integral |$III$| has the form
$\begin{matrix} R_{3} & = & \int_{- \infty}^{\infty} d z G (z) θ [Im (\frac{S (σ, z)}{P z + Q})], \end{matrix}$
(A11)
with |$G(z)$| and |$S(\sigma,z) $| being defined in Eqs. (79) and (87) respectively. We know that |$\text{Im} \left(\frac{ S(\sigma,z)}{Pz+Q}\right)$| is independent of |$\sigma$|⁠; we can then expand the integrand as
$\begin{matrix} \int_{- \infty}^{\infty} d z G (z) θ [Im (\frac{S (σ, z)}{P z + Q})] & = & \int_{- \infty}^{\infty} d z G (z) θ [A_{0} z^{2} + B_{0} z + C_{0}], \end{matrix}$
(A12)
where |$A_0, B_0, C_0$| are given by
$\begin{matrix} A_{0} & = & P Im (E), \end{matrix}$
(A13)
$\begin{matrix} B_{0} & = & P Γ_{k} + ρ P + Re(Q)Im (E) - Im (Q) Re (E), \end{matrix}$
(A14)
$\begin{matrix} C_{0} & = & Im (Q) Re (m_{k}^{2}) + Re (Q) (Γ_{k} + ρ) . \end{matrix}$
(A15)
For |$ \text{Im}\Bigg(\dfrac{ S(\sigma,z)}{Pz_0+Q}\Bigg) \geq 0$| in the region |$\Omega \subset \mathbb{R}$|⁠, one then has
$\begin{matrix} \int_{- \infty}^{\infty} d z G (z) θ [Im (\frac{S (σ, z)}{P z + Q})] & = & \int_{Ω} d z G (z) . \end{matrix}$
The integral on the right-hand side of this equation can be reduced to basic integral |$I$|⁠.

References

[1]

ATLAS Collaboration

, arXiv:1307.7292 [hep-ex] [Search inSPIRE].

[2]

CMS Collaboration

, arXiv:1307.7135 [hep-ex] [Search inSPIRE].

[3]

Baer

et al. arXiv:1306.6352 [hep-ph] [Search inSPIRE].

[4]

Passarino

and

Veltman

M. J. G.

Nucl. Phys. B

160

151

(

1979

). (

)

http://dx.doi.org/10.1016/j.nuclphysb.2005.11.007

[5]

Denner

and

Dittmaier

Nucl. Phys. B

734

(

2006

) [arXiv:hep-ph/0509141] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.nuclphysb.2005.06.033

[6]

Denner

Dittmaier

Roth

and

Wieders

L. H.

Nucl. Phys. B

724

247

(

2005

) [arXiv:hep-ph/0505042] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/0550-3213(79)90605-9

[7]

’t Hooft

and

Veltman

M. J. G.

Nucl. Phys. B

153

365

(

1979

). (

)

http://dx.doi.org/10.1016/0550-3213(91)90011-L

[8]

Denner

Nierste

and

Scharf

Nucl. Phys. B

367

637

(

1991

). (

)

http://dx.doi.org/10.1016/j.cpc.2009.07.012

[9]

Nhung

D. T.

and

Ninh

L. D.

Comput. Phys. Commun.

180

2258

(

2009

) [arXiv:0902.0325 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.nuclphysb.2010.11.002

[10]

Denner

and

Dittmaier

Nucl. Phys. B

844

199

(

2011

) [arXiv:1005.2076 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1007/BF01559496

[11]

Kreimer

Z. Phys. C

667

(

1992

). (

)

http://dx.doi.org/10.1142/S0217751X93000758

[12]

Kreimer

Int. J. Mod. Phys. A

1797

(

1993

). (

)

http://dx.doi.org/10.1007/BF01621031

[13]

Franzkowski

Dissertation

(

University of Mainz, 1997

[14]

van Oldenborgh

G. J.

and

Vermaseren

J. A. M.

Z. Phys. C

425

(

1990

). (

)

http://dx.doi.org/10.1088/1126-6708/2008/02/002

[15]

Ellis

R. K.

and

Zanderighi

J. High Energy Phys.

0802

002

(

2008

) [arXiv:0712.1851 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2011.06.011

[16]

van Hameren

Comput. Phys. Commun.

182

2427

(

2011

) [arXiv:1007.4716 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2009.06.024

[17]

Binoth

Guillet

J.-P.

Heinrich

Pilon

and

Reiter

Comput. Phys. Commun.

180

2317

(

2009

) [arXiv:0810.0992 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2011.05.015

[18]

Cullen

Guillet

J. P.

Heinrich

Kleinschmidt

Pilon

Reiter

and

Rodgers

Comput. Phys. Commun.

182

2276

(

2011

) [arXiv:1101.5595 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2014.03.009

[19]

Guillet

J. P.

Heinrich

and

von Soden-Fraunhofen

J. F.

Comput. Phys. Commun.

185

1828

(

2014

) [arXiv:1312.3887 [hep-ph]] [Search inSPIRE]. (

)

https://doi.org/10.1016/0370-2693(93)90469-X

[20]

Bern

Dixon

L. J.

and

Kosower

D. A.

Phys. Lett. B

302

299

(

1993

); (

)

318

649

(

1993

) [erratum] [arXiv:hep-ph/9212308] [Search inSPIRE]. (

http://dx.doi.org/10.1016/0370-2693(93)90400-C

)

http://dx.doi.org/10.1007/s100520100675

[21]

Duplancic

and

Nizic

Eur. Phys. J. C

357

(

2001

) [arXiv:hep-ph/0006249] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/S0010-4655(98)00173-8

[22]

Hahn

and

Perez-Victoria

Comput. Phys. Commun.

118

153

(

1999

) [arXiv:hep-ph/9807565] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/S0010-4655(02)00158-3

[23]

Bauer

and

H. S.

Comput. Phys. Commun.

144

154

(

2002

) [arXiv:hep-ph/0102231] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.nuclphysbps.2008.09.123

[24]

Berger

C. F.

Bern

Dixon

L. J.

Febres Cordero

Forde

Ita

Kosower

D. A.

and

Maitre

Nucl. Phys. Proc. Suppl.

183

313

(

2008

) [arXiv:0807.3705 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1088/1126-6708/2008/03/042

[25]

Ossola

Papadopoulos

C. G.

and

Pittau

J. High Energy Phys.

0803

042

(

2008

) [arXiv:0711.3596 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2016.07.033

[26]

Carrazza

Ellis

R. K.

and

Zanderighi

Comput. Phys. Commun.

209

134

(

2016

) [arXiv:1605.03181 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2016.10.013

[27]

Actis

Denner

Hofer

Lang

J. N.

Scharf

and

Uccirati

arXiv:1605.01090 [hep-ph] [Search inSPIRE].

[28]

Denner

Dittmaier

and

Hofer

Comput. Phys. Commun.

212

220

(

2017

) [arXiv:1604.06792 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1142/S0217751X08040263

[29]

Heinrich

Int. J. Mod. Phys. A

1457

(

2008

) [arXiv:0803.4177 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2012.09.020

[30]

Borowka

Carter

and

Heinrich

Comput. Phys. Commun.

184

396

(

2013

) [arXiv:1204.4152 [hep-ph]] [Search inSPIRE]. (

)

http://dx.doi.org/10.1016/j.cpc.2015.05.022

[31]

Borowka

Heinrich

Jones

S. P.

Kerner

Schlenk

and

Zirke

Comput. Phys. Commun.

196

470

(

2015

) [arXiv:1502.06595 [hep-ph]] [Search inSPIRE]. (

)

https://www.researchgate.net/publication/51938482_Numerical_Approach_to_Calculation_of_Feynman_Loop_Integrals

[32]

Borowka

Heinrich

Jahn

Jones

S. P.

Kerner

Schlenk

and

Zirke

arXiv:1703.09692 [hep-ph] [Search inSPIRE].

[33]

Yuasa

Ishikawa

Kurihara

Fujimoto

Shimizu

Hamaguchi

de Doncker

and

Kato

PoS CPP

2010

017

(

2010

) [arXiv:1109.4213 [hep-ph]] [Search inSPIRE]. (

)

[34]

Gluza

Kajda

and

Riemann

Comput. Phys. Commun.

177

879

(

2007

) [arXiv:0704.2423 [hep-ph]] [Search inSPIRE]. (

http://dx.doi.org/10.1016/j.cpc.2007.07.001

)