Performance evaluation of a klystron beam focusing system with anisotropic ferrite magnet Open Access

1. Introduction

The International Linear Collider (ILC) is an electron–positron collider for high-energy physics with a center-of-mass energy up to 500 GeV. In order to achieve the final energy, the ILC should be equipped with more than 16,000 accelerating cavities to accelerate electrons and positrons [1]. Something of the order of 1000 klystrons are also needed to feed the radio frequency (RF) power to the cavities. For example, the Distributed RF Scheme (DRFS), one of the RF power feed schemes formerly proposed for ILC, utilizes 8000 medium-power klystrons [2]. Due to the large number of klystron units, even a low failure rate of each component could increase the load of maintenance work and limit the availability of the facility.

For DRFS, the reliability of the klystron itself is estimated to be fairly high because of its relatively low output power (800 kW per klystron). In addition to the high reliability of the klystron itself, that of the whole system is also important. The klystron beam focusing system is one of the key components in the whole system. In fact, according to KEK injector operating statistics covering ten years in the 2000s, failures in the focusing solenoids was the most frequent reason for exchanging klystron assemblies [3].

Focusing systems with permanent magnets for klystrons have been developed in some accelerator laboratories. In the SLAC two-mile linear accelerator [4] and the Photon Factory linac in KEK [5], focusing systems with Alnico magnets were developed and utilized for accelerator operation. However, both laboratories have discontinued them and have employed solenoid coils as the klystron beam focusing system. The main reason for this was the complexity of the field tuning. The magnetic fields generated by the magnets in these laboratories were tuned by partial magnetization and/or demagnetization of the Alnico magnets, or attaching magnetic material shims such as iron bars. Since the Alnico magnets have low coercivity, magnetization of the magnets could be degraded irreversibly by peripheral magnetic fields and magnetic materials. Therefore, the same focusing field could not be reproduced even if the magnets were assembled in the same positions.

Because the number of magnet systems in the ILC klystron is quite large, they must be cost effective and be easy to tune. This paper reports on the development of a prototype focusing magnet with ferrite magnets for the ILC DRFS klystron and the result of a performance evaluation of the focusing magnet by way of both experimental and numerical studies. It should be noted that the technical design report (TDR) for the ILC adopts the Distributed Klystron Scheme (DKS) using the multi-beam klystron (MBK) instead of the DRFS mainly because of the higher efficiency after discussions during the GDE (global design effort) for ILC. Needless to say, a similar technique is also applicable to DKS.

The main purpose of this study is to prove that focusing systems with permanent magnets can replace electromagnets with similar performance (power conversion efficiency and peak power). This paper consists of six sections. In Sect. 2, the conceptual design of the magnet is briefly presented. Section 3 describes the design process for the prototype magnet and the result of performance estimation using simulation. In Sect. 4, the result of a power test with the prototype magnet is presented. In Sect. 5, the effect of asymmetric fields and error fields on output power is discussed. In Sect. 6, a brief summary is presented.

2. Conceptual design of focusing system

In this section, the conceptual design of our focusing system with permanent magnets is briefly described. A detailed description can be found in Ref. [6]. Anisotropic ferrite is chosen as the magnetic material based on the following reasons:

• High-enough remanent field: The remanent field of anisotropic ferrite is about 4 kG. Since the required magnetic field to focus an electron beam in the DRFS klystron is up to 1 kG, the ferrite magnet can generate a magnetic field with sufficient magnitude.

• High coercivity: Because anisotropic ferrite magnets have high coercivity, demagnetization is not anticipated by peripheral magnetic fields.

• Lower cost: The material cost of ferrite is lower than other materials such as neodymium magnets, because a ferrite magnet is composed of iron oxide.

The focusing field is unidirectional along the beam axis, in contrast to the periodic permanent magnet (PPM) configuration [7]. Then the field distribution can be the same as the field generated by a solenoid coil except for the reverse fields in the exterior regions. The unidirectional field distribution can avoid damage to the klystron tube wall due to beam loss [8] caused by the energy stop-band on the electron beam transmission. In order to generate the required magnetic field with a smaller amount of ferrite material, the magnets are configured in a quasi-Halbach dipole configuration [9]. In this configuration, the assembled magnets can be classified into three sections: top, middle, and bottom. The middle section consists of magnets with the easy axis parallel to the beam axis, and magnetized in the opposite direction of the magnetic field on the beam axis. These magnets surround the klystron body and the position of the magnets should be as close as possible so as to generate the focusing field at the klystron tube efficiently. The magnets at the top and bottom sections have the easy axis in radial directions. These magnets and the iron yoke form return paths for the magnetic fields. The configuration also contributes to reduce the stray magnetic field outside the system and to prevent field distortion due to disturbance caused by magnetic materials in the vicinity of the system. The magnet configuration and the magnetic field flux distribution calculated by PANDIRA [10] are shown in Fig. 1. The magnets are divided into a number of segments and each segment is movable independently. By virtue of this segmentation and movability, magnets can be set near the klystron tube after the insertion of the tube to the focusing alcove. The placement of the magnets near the tube can reduce the required volume of magnets to generate the focusing field. Local tuning of the magnetic field can also be realized by fine positioning of the segments. This tuning scheme has good reproducibility of the magnetic field, because ferrite magnets with the same magnet positions generate the same magnetic field owing to the high coercivity of ferrite magnets. Also, the scheme is a much easier process compared with the early studies where the field distributions were tuned by cumbersome tuning methods [5], as stated in the introduction.

Fig. 1.

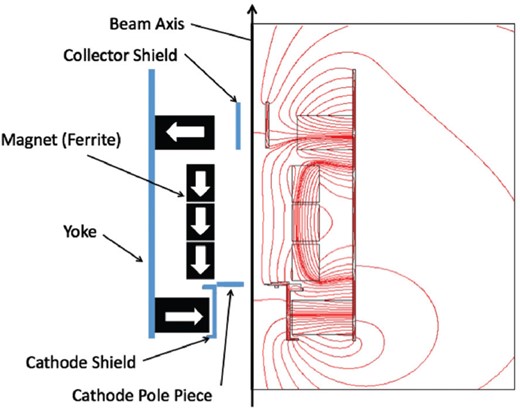
Configuration of magnets (left side of the figure). The calculated field distribution is shown to the right.

Open in new tabDownload slide

3. Design of prototype model

To evaluate the performance of the focusing system described in Sect. 2, a prototype was designed for DRFS klystrons. The klystron assumed to be used in DRFS was an E37501 (a modulating anode klystron, frequency: 1.3 GHz, nominal output power: 800 kW) manufactured by Toshiba Electron Tube & Devices Co., Ltd. A modulating anode embedded in the klystron makes the radius of the high-voltage insulator around the cathode part large, which requires a large outer radius of the oil tank, and hence inflates the magnet volume for that part. RADIA 4.29 [11–13] was used for the magnetic field design. After the fabrication cost estimation, the basic dimensions of the ferrite piece was chosen as $150 mm×100 mm$ cross section and 25.4 mm thickness. The optimized result of the magnet and yoke configuration is shown in Fig. 2. The properties of each magnet are described in Ref. [6]. The magnets are designed to avoid interference with the cooling pipes and the RF input port on the klystron outer wall. The fields in the cathode region were shielded by the oil tank, whose cylinder is made of ferromagnetic iron. All magnets except for the bottom section are segmented into two-fold symmetric shapes and each segment can be moved individually. By moving the positions of the magnets, the field distribution in the beam drift region can be adjusted. All magnets with two-fold symmetry can evacuate from the central region to make the space to insert the klystron from the top [see Fig. 2(b) and (d)]. The two-fold segmentation breaks the axisymmetry and generates multipole field components starting from a quadrupole component. The effects of the multipole components on the beam are discussed later. The tuned field distribution for efficient beam focusing is shown in Fig. 3. In this figure, the vertical axis is normalized by the maximum value of the magnetic field distribution. For the following discussions, the positions of the cathode, input cavity, and output cavity are indicated by $zcathode$⁠, $zinput$⁠, and $zoutput$⁠, respectively. Compared with the field generated by the electromagnet (EM) in Fig. 3, the permanent magnet (PM) field has ripples in the beam drift region. These ripples were caused by longitudinal segmentation of the magnets. To estimate the effect on beam focusing, the beam envelope was calculated as cylindrically symmetric problems by the DGUN code [15]. Comparing the beam envelopes for the PM focusing and the EM focusing (Fig. 4), the difference between two envelopes is not significant, which suggests that such ripples can be neglected for a klystron design.

Fig. 2.

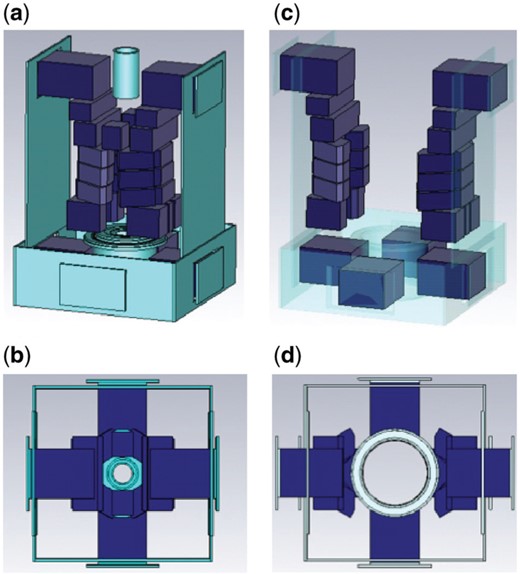
Designed configurations of magnets and iron yoke. (a) Magnets positioned for beam operation. (b) Top view of the location of the magnets illustrated in (a). (c) Magnet positions for klystron installation. All the magnets with two-fold symmetry can evacuate from the central region to make the space to insert the klystron from the top. (d) Top view of the magnets illustrated in (c). The space of the center region is cleared for the insertion of the klystron tube into the focusing alcove.

Open in new tabDownload slide

Fig. 3.

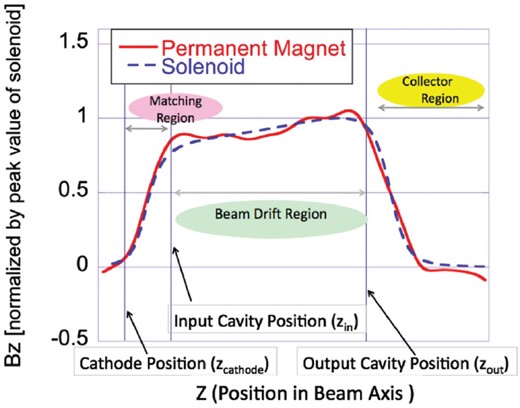
Magnetic field distribution along the beam axis. The electron beam from the cathode is accelerated and matched to the Brillouin flow optics in the matching region and is transported through the beam drift region. It finally goes into the collector region to be damped.

Open in new tabDownload slide

Fig. 4.

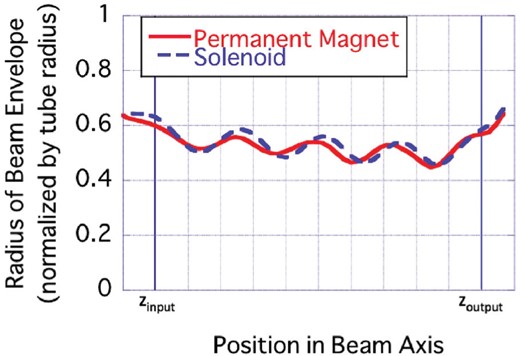
Beam envelopes calculated by 2.5-dimensional simulation with DGUN.

Open in new tabDownload slide

Multipole components of magnetic fields in the transverse planes are also generated because the distribution of magnets is not azimuthally symmetric. The dominant component is quadrupole, and the strength of the quadrupole component reaches $20 G cm−1$ (see Fig. 12). Higher-order components such as an octupole component also exist, but their magnitudes are less than one tenth of the quadrupole component in the beam region. Quadrupole fields deform a circular beam into an elliptical beam [15]. In the case of our magnet system, electron beams are magnetically confined and rotate around the center of the beam (Brillouin flow). Therefore, the effect of the quadrupole field is not simple. To evaluate the electron distribution in the beam propagation from the cathode to the collector, three-dimensional beam tracking simulation was performed with CST Particle Studio. Figure 5 shows the calculated beam profiles at several points along the beam axis. From the results, while the beam profile became elliptical during beam propagation in the quadrupole component field, all the particles reached the collector without hitting the tube wall. Beam simulations with RF modulation were also performed with PIC (particle-in-cell) simulation and no beam loss was observed in any beam slices.

Fig. 5.

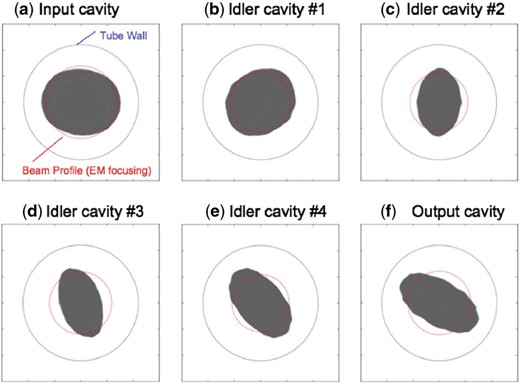
Beam profiles at cavity positions calculated by three-dimensional simulation with CST Particle Studio.

Open in new tabDownload slide

4. Test with prototype magnet

4.1. Fabrication of prototype magnet

Based on the design described in Sect. 3, the prototype magnet was fabricated. The magnet pieces shaped from $150 mm×100 mm×25.4 mm$ ferrite ingots to the designed shapes were glued together with acrylic cured resin. Then, each glued segment was also glued on an iron plate or an aluminum block. All the magnets were supported by these metallic structures. Pictures of the fabricated prototype are shown in Fig. 6. The magnets could be moved as designed for the klystron insertion and the field tuning. The typical accuracy of the magnet position alignment is less than 1 mm.

Fig. 6.

Fabricated prototype magnet. (Top) Klystron insertion mode: magnets are retracted toward the outer sides, making the space to let the cathode assembly part go through, which is the thickest part of the klystron. (Bottom) Klystron operating mode; magnets are moved to the designed position to generate the proper focusing field.

Open in new tabDownload slide

In the field tuning process, the magnetic field distributions ${Bx(z),By(z),Bz(z)}$ on the beam axis were measured with a three-axis Hall probe (Senis 3MH3). After some iterative processes of tuning by adjusting magnet positions, the longitudinal field distribution could be adjusted to the designed one within a 2% error in the beam drift region. The field in the matching region (see Fig. 3) was more precisely adjusted to suppress ripples of the beam envelope. The typical transverse field distribution is shown in Fig. 7. The transverse fields were caused by residual positioning errors of the magnets in the tuning process, mechanical errors in the magnet shapes, and magnetization errors in the fabrication process. Careful field tuning can make this transverse field less than 10 G (corresponding to 1% magnitude compared with the longitudinal magnetic field). This magnitude (fraction) of the transverse magnetic field on the beam axis was comparable to that of the focusing system developed at SLAC [16].

Fig. 7.

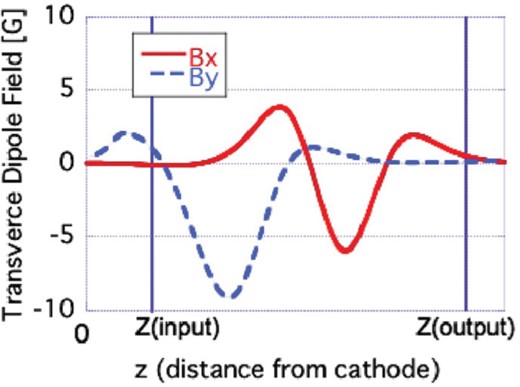
Typical measured transverse (dipole) magnetic fields along the beam axis.

Open in new tabDownload slide

The displacement of the beam center can be estimated with an assumption that electrons follow the magnetic flux lines. The displacement of the flux line $Δr$ at the position $z$ can be estimated by integrating the flux line angle (⁠$Btransverse/Bz$⁠) from the beam axis. Using these facts, the beam displacements in the $x$ and $y$ directions can be derived in a first-order approximation as follows.

The $x$-component of the transverse field can be described as

$Btransverse,x(x,y,z)=Bx(z)+xrBr(r,z),$

(1)

where $r=x2+y2$ is displacement from the beam axis, $Bx(z)$ is the $x$-component of the dipole field on the axis, and $Br(r,z)$ is the azimuthally symmetric field component at a distance $r$ from the axis. Using the condition div $B=0$⁠, $Br(r,z)$ can be derived from the longitudinal field component on the axis as

$Br(r,z)=−12∂Bz(z)∂zr.$

(2)

Hereby, the displacement of the beam center $Δr$ can be calculated as

$Δx(z)=∫zcathodezBx(ξ)+Δx(ξ)Δr(ξ)Br(Δr(ξ),ξ)Bz(ξ)dξ,$

(3)

$Δy(z)=∫zcathodezBy(ξ)+Δy(ξ)Δr(ξ)Br(Δr(ξ),ξ)Bz(ξ)dξ,$

(4)

$Δr(z)=Δx(z)2+Δy(z)2,$

(5)

where $Δx$ and $Δy$ are the displacements of the beam center in the $x$ and $y$ directions, respectively. The calculated result of the displacement of the beam center due to the transverse magnetic field estimated by Eqs. (2)–(5) is shown in Fig. 8, together with the result from CST Particle Studio. Although the space charge effects are neglected in the first-order estimate, the estimated beam displacement gives a rough guess close to the result with CST, which reduces a lot the effort and computation time required. The reason for the discrepancy should be non-linear effects due to space charges and beam–wall interactions.

Fig. 8.

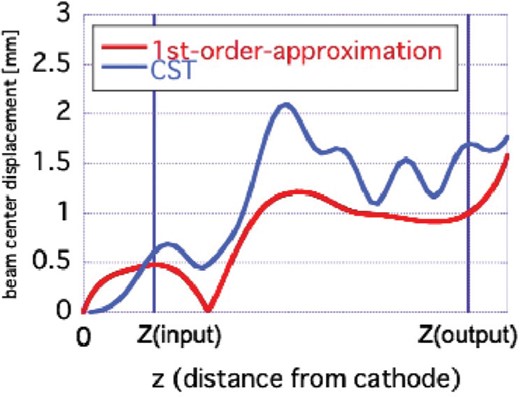
The estimated beam-center displacement due to the transverse magnetic field (see Fig. 7). Both the calculated result of the first-order approximation and the result from a massive simulation with CST Particle Studio are presented.

Open in new tabDownload slide

4.2. Klystron power test

A klystron power test was performed in the summer of 2015 at KEK STF (Superconducting rf Test Facility), where the development of a 40 MeV superconducting test accelerator and ILC-type cryomodules were ongoing at the same time. A 1 MW dummy load was connected. A modulator at the STF building in KEK supplied the power for the klystron, including heater power, cathode high voltage, and modulating anode pulse. A preliminary result of the power test was presented in Ref. [6]. In the initial stage of the experiment, a diode test was carried out. In this test, no RF power was fed to the input cavity and the beam was just transported to the collector. The cathode voltage was set between 45 kV and 67.5 kV, and the modulating anode voltage at beam extraction was 0.26 times the cathode voltage. The measured perveance of the extracted beam was $1.29±0.03[μA V−3/2]$⁠. This value is the same as the result using the solenoid (⁠$1.29±0.04[μA V−3/2]$⁠). Since the perveance is determined only by the gun geometry, it is reasonable. Then, the measured result suggested that an extracted beam condition similar to that with EM focusing could be achieved. During the beam extraction test, the temperature rise of the cooling water for the klystron body was monitored, and no significant temperature rise was detected. These results suggested that the amount of electron loss on the klystron tube body was ignorable and our prototype magnets had sufficient beam transport efficiency.

Then, the test with RF excitation was carried out. The RF input–output characterization was measured at several cathode voltages. The result is shown in Fig. 9. At 65.8 kV cathode voltage, the saturated output power reached $798±8 kW$⁠. Because the required output power per klystron for DRFS is 800 kW, the system with permanent magnet focusing had enough capability to produce the RF power.

Fig. 9.

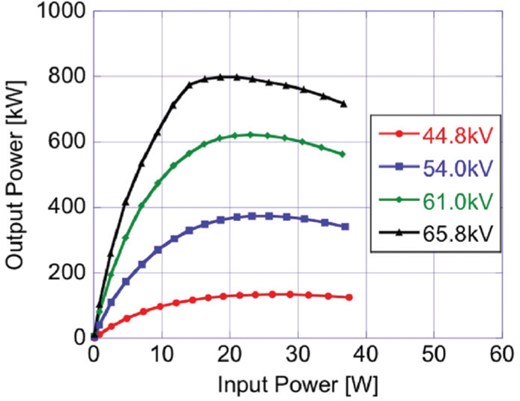
The output RF power of the DRFS klystron with permanent magnet focusing as a function of input RF power at four cathode voltages.

Open in new tabDownload slide

Fig. 10.

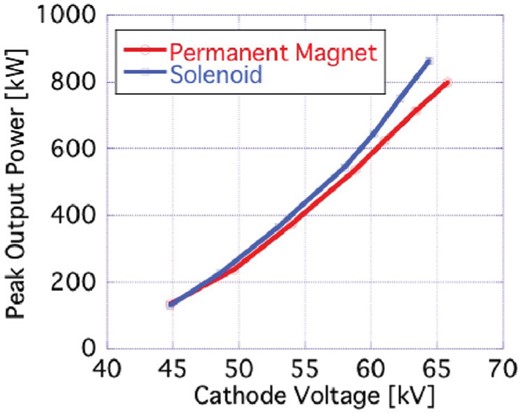
The results of the power test. Output RF power is shown as a function of the cathode voltage with permanent magnet focusing and solenoid focusing.

Open in new tabDownload slide

5. Discussion

5.1. Output power compared with solenoid focusing

Since the prototype system was designed to have a similar axial magnetic field distribution to the solenoid, output power with the PM focusing system was estimated as the same degree as the output power with EM focusing. For comparison, the saturated output power measurement was also performed with an electromagnet. The results for both PM focusing and EM focusing are shown in Fig. 11. The output power with the EM focusing is slightly larger than that with PM focusing by about 10%. For production of 5.6 kW RF average power (nominal parameter for DRFS; 800 kW peak RF power with 5 Hz repetition rate and 1.5 ms pulse duration), the required average beam power is about 9.6 kW (59% efficiency for beam-to-RF energy conversion) with the solenoid magnet and 10.5 kW (54% efficiency) with the prototype permanent magnet. Because the solenoid magnet continuously consumes 1.2 kW power, the total power consumption of the klystron system with the EM focusing system exceeds that with the prototype PM focusing system, which shows that PM focusing has an advantage from the viewpoint of the total power consumption. The power conversion efficiency of the klystron tube with an improved PM focusing system should be improved to at least the same as the EM focusing, and the required power from wall plug would be reduced. If such an improved PM focusing system can be developed, the total saved power in the total facility will be 9.6 MW in DRFS since the number of klystrons is about 8000.

Fig. 11.

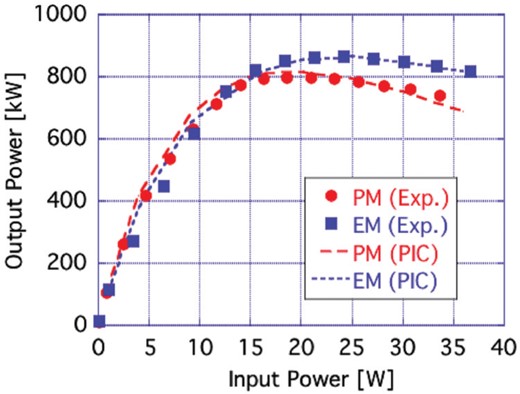
The input–output characteristic both measured in the power test and calculated with PIC (particle-in-cell) simulation.

Open in new tabDownload slide

The main reason for the discrepancy in output power between the PM focusing and the EM focusing is considered to be beam deformation and displacement due to the small multipole field components. Beam deformation and displacement leads to asymmetric distribution of the particles and may cause excitation of higher-order modes in the cavities such as TM110 and TM210 modes. The kick due to the higher-order modes and dipole magnetic field might cause beam loss and decrease output power. However, a significant temperature rise of the tube outer wall was not observed, indicating that there were no beam losses in the klystron tube during the power test. The deformation of the beam decreases the clearance between the beam envelope and the tube wall (including cavity iris), and pushes up the global coupling factors between the beam and the cavities, which represents a coupling factor averaged over all the electrons in the beam (see Appendix).

The calculated value of the global coupling factor $M$ focused by the PM without dipole error was about 1% larger than the EM focusing. As the beams propagate through the tube, beams with larger energy modulation would result in larger density modulation and larger RF current of the beam. Since the cavities in the klystron are designed and tuned for a beam focused with EM focusing, an electron beam with a larger beam–cavity coupling factor tends to be longitudinally over-focused at the output cavity. According to the one-dimensional klystron simulation, while a small increase of less than 1.2% relative to the global coupling factor value for the EM focusing leads to an increase of the output power, a larger increase of the global coupling factor causes a decrease in the output power. Therefore, with perturbation on the global coupling factor larger than 1.2%, the maximum bunching efficiency and the induced RF current in the output cavity decrease compared with EM focusing. With PM focusing with a dipole error, the perturbation of the global coupling factor was larger than 2% and expected output power is less than with EM focusing.

To evaluate the effects of the beam displacements and deformations, three-dimensional PIC (particle-in-cell) simulations with CST Particle Studio were also performed. In the simulation, the excited voltages of higher-order modes were less than those of the fundamental mode by two orders of magnitude. In addition, any beam loss in the beam drift region was not observed in the simulations. The simulation results showed the tendency of changing the output power with the PM focusing compared with the EM focusing as predicted from the one-dimensional simulation discussed above. The calculated output power with the EM focusing (case-0) was $865±5 kW$⁠. This result is consistent with the experimental result. The calculated output power with the PM focusing without dipole field component (case-1; with quadrupole field) was $874±6 kW$⁠. With the dipole field shown in Fig. 7, the peak output power with the PM focusing (case-2; with both the dipole and the quadrupole field components) was calculated as $809±7 kW$ (the output power was decreased to $95%±2%$ of that with the EM focusing). These results suggested that the dipole fields in the prototype PM focusing system reduce the output power. In order to evaluate the effect of quadrupole components, we carried out a beam simulation in the EM focusing system on which the dipole component is superposed (case-3; with dipole field). While the system is not a real one, the output power was estimated at $875±5 kW$⁠. These simulation results can be summarized as follows: either the dipole field or the quadrupole field component slightly enhances the output power, and the existence of both dipole and quadrupole field components reduces the output power. Therefore, it is suggested that the reduction of the output power in case-2 was due to not only the dipole component, but the sum effect of the dipole and quadrupole field components. The reduction of the output power is supposed to be caused by the excess of the beam–cavity coupling due to the beam center displacement and the beam deformation. In Fig. 11, the input–output characteristics both measured in the power test and calculated by the PIC simulations are presented. In the PIC simulations, the induced voltages of idler cavities (⁠$Vcavity$⁠) were also monitored (see Table 1). The calculated results shows that all the induced voltages with the PM focusing are larger than those with the EM focusing, which indicates that the former case has larger global coupling factors than the latter.

5.2. Suppression of the transverse field

As discussed in the previous subsection, the beam-to-RF power conversion efficiency was supposed to be deteriorated by the transverse multipole magnetic field on the klystron designed for axisymmetric field focusing. After the completion of the allowed experiment time in the busy STF schedule, improvements to the focusing system were studied. To recover the output power, the multipole field components have to be suppressed. The transversal segmentation of the magnets with a higher symmetry would result in fewer multipole components. The magnet configuration with two-fold axial symmetry about the beam axis generates the quadrupole components, which was not supposed to have much effect on the efficiency at the design stage. It should be noted that the construction of a more highly symmetric structure leads to more difficulty in the magnet position alignment and complexity of the mechanical support of the magnets. Considering the above-mentioned situation, and the fabrication and the assembling cost, a transverse field suppressor is favored rather than the modification of the magnet structure in a fancy way.

Although the multipole field suppressor can be realized either by active methods, such as correction coils, or by passive methods such as additional magnetic materials, the passive methods have the advantage of higher reliability. Passive field suppression can be achieved by installing a transverse field filter with anisotropic macroscopic permeability, where the relative permeability in the longitudinal direction is close to unity and those in transverse directions are sufficiently larger than 1. A filter with such an anisotropic permeability can be realized by sparsely stacked rings made of soft-magnetic material such as silicon steel sheets. For our permanent magnet system, the inner radii of the rings can touch the klystron outer wall (60 mm) and the outer radii are 70 mm, while the thickness of the rings is 0.5 mm. For evaluation of the suppression capability of the transverse field, magnetic fields were calculated with CST EM studio. From the calculated results with various ring intervals, a ring train with 12 mm spacing could suppress the multipole field component most efficiently without a significant reduction of longitudinal magnetic field component. With 12 mm interval rings, the quadrupole field is suppressed down to less than 1/5 (see Fig. 12). The calculated transverse dipole field was also reduced to less than 1/2 of the field without the filter. While the transverse multipole field components were suppressed efficiently, the effect of installing the rings on the longitudinal field components around the axis was less than 1% (⁠$<0.5mm/12mm$⁠).

Fig. 12.

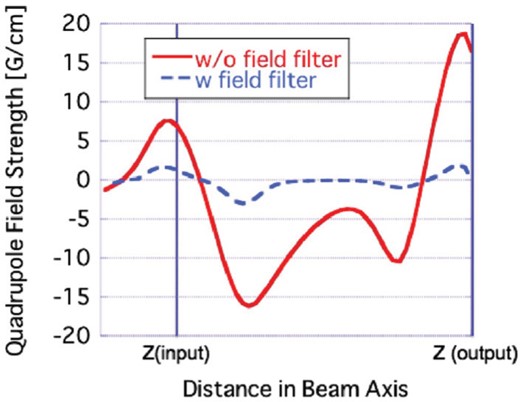
Transverse quadrupole magnetic field calculated with CST EM studio. The transverse field filter reduces the quadrupole field to less than 20% of the field without the filter.

Open in new tabDownload slide

PIC simulation results with the filter showed the improvement of the output power. The calculated output power with the filter-installed PM focusing was $875±5 kW$⁠. The output power becomes almost the same as that with the EM focusing case. A PIC simulation including the magnet imperfections with the field filter showed no output power reduction. These results indicate that such a filter effectively reduces the transverse multipole components.

6. Conclusion

Klystron beam focusing systems with permanent magnets are well suited to large accelerator facilities such as future linear colliders to enhance their reliability and reduce costs. Even the prototype system with the ferrite magnets for 1.3 GHz, 800 kW klystrons exhibits performance almost the same as with EM focusing. This PM focusing system could not be optimized because of the limited trial and experiment time. To reduce the fabrication costs, anisotropic ferrite was adopted as the magnetic material and the magnets were designed to be pushed in after the klystron tube insertion to the focusing alcove. The movable magnet feature could also be usable for the field tuning process. The technologies adopted in the prototype system can be applied to other klystrons such as the multi-beam klystron for ILC. Furthermore, by mitigating the effects of the transverse magnetic field, the focusing system with permanent magnets can also reduce the power consumption in the accelerator facilities.

Acknowledgements

This work was supported by the Collaborative Research Program of the Institute for Chemical Research, Kyoto University (grant # 2016-10). The authors thank Mr. Y. Okubo at Toshiba Electron Tubes & Devices Co., Ltd. for giving us the klystron data and for the fruitful discussions on the klystron, and thank Dr. H. Hayano at KEK for his continuous encouragement and fruitful comments. The authors also thank Dr. S. Fukuda, Dr. S. Michizono, and Dr. T. Matsumoto at KEK for their support in executing the klystron power test. The experimental results presented in this paper could not have been acquired without their help.

A ppendix. Beam–cavity coupling factor

References