The possibility of the condensation of excitations with non-zero momentum in rectilinearly moving and rotating superfluid bosonic and fermionic (with Cooper pairing) media is considered in terms of a phenomenological order-parameter functional at zero and non-zero temperature. The results might be applicable to the description of bosonic systems like superfluid , ultracold atomic Bose gases, charged pion and kaon condensates in rotating neutron stars, and various superconducting fermionic systems with pairing, like proton and color-superconducting components in compact stars, metallic superconductors, and neutral fermionic systems with pairing, like the neutron component in compact stars and ultracold atomic Fermi gases. The order parameters of the “mother” condensate in the superfluid and the new condensate of excitations, corresponding energy gains, critical temperatures, and critical velocities are found.
1. Introduction
The possibility of the condensation of rotons in superfluid helium (He-II) moving in a capillary at zero temperature with a flow velocity exceeding the Landau critical velocity was suggested in Ref. [1]. In Ref. [2], the condensation of excitations with non-zero momentum in various relativistic and non-relativistic cold media moving with velocity exceeding was studied further with the help of the effective Lagrangian for the complex scalar field, which describes Bose excitations in the medium. The Landau critical velocity is determined by the minimum of at finite momentum , where is a branch of the spectrum of Bose excitations. Possible manifestations of the phenomenon in the bulk of He-II, rotating neutron stars with and without pion condensate, nuclei at high angular momentum, and heavy-ion collisions were discussed. A similar effect can also occur in a normal Fermi liquid with a zero-sound branch in the spectrum of particle–hole excitations [3,4]. When the velocity of the Fermi liquid exceeds the Landau critical velocity related to this branch, the number of excitations should grow exponentially with time and in the course of their interactions they may form a Bose condensate with a finite momentum. This possibility was studied in Ref. [3] for a moving Fermi liquid at finite temperature. Various consequences of the phenomenon in application to nuclear systems were announced. In Ref. [5], the results of Ref. [1] for He-II in a capillary were extended to He-II in a bulk. The condensation of excitations in cold atomic Bose gases moving with a flow velocity exceeding was considered in Ref. [6]. The role of a Bose condensate of zero-sound-like excitations with non-zero momentum in the description of the stability of modes in rapidly rotating pulsars was discussed in Ref. [7].
Below, we study the possibility of the condensation of excitations in a state with non-zero momentum in moving media in the presence of a superfluid subsystem. The systems of interest are neutral bosonic superfluids, such as superfluid , cf. [1,8–11], cold Bose atomic gases, cf. [6,12–14], inhomogeneous condensates in neutron stars, cf. [15,16], charged bosonic superfluids like and and condensates with in neutron stars, cf. [2,15–17], and various Fermi systems with Cooper pairing, like the neutron superfluid in neutron star interiors, cf. [18], cold Fermi atomic gases, cf. [19], neutron gas in neutron star crusts, cf. [20], or charged superfluids, as paired protons in neutron star interiors, cf. [18], paired quarks in color-superconducting regions of hybrid stars, cf. [21], and paired electrons in metallic superconductors, cf. [22,23].
The key idea of the phenomenon is the following [1,2]: When a medium moves as a whole with respect to a laboratory frame with a velocity higher than , it may become energetically favorable to transfer part of its momentum from particles of the moving medium to a Bose condensate of excitations (CoE) with a non-zero momentum . This would happen if the spectrum of excitations is soft in some region of momenta. References [1,6] studied the condensation of excitations at assuming the conservation of flow velocity. Alternatively, we consider systems with other conditions, assuming the conservation of momentum (or angular momentum for rotating systems) as in Ref. [2]. We consider bosonic and fermionic superfluid systems moving initially with a flow velocity above both for and (the latter case has not yet been considered in the mentioned references), taking into account a back reaction of the CoE on the “mother” condensate of the superfluid.
The work is organized as follows. In Sect. 2, we construct the phenomenological order-parameter functional for the description of the CoE coupled with the mother condensate in the superfluid moving linearly with a flow velocity exceeding . Section 3 is devoted to a description of cold moving superfluids. Section 4 studies peculiarities of the two-fluid motion in warm superfluids in the presence of a CoE. In Sect. 5, we discuss a particular role of vortices. Some numerical estimates valid for fermion superfluids in the BCS limit and for He-II are performed in Sect. 6. Section 7 describes the CoE in rotating systems with application to rapidly rotating pulsars. Section 8 contains concluding remarks.
2. Order-parameter functional for moving fluid
In the spirit of the Landau phenomenological theory of a second-order phase transition, the free-energy density of a superfluid subsystem in its rest frame can be expanded in the order parameter
for temperatures
, where
is the critical temperature of the second-order phase transition [
9,
10]:
Here,
,
, and
are phenomenological parameters depending on the temperature, so that
vanishes at
. When applied to superconductors, the functional (
1) is known in the literature as the Ginzburg–Landau model [
9], while for the case of superfluid
it is called the Ginzburg–Pitaevskii model. The phenomenological description of cold weakly interacting Bose gases was performed by Gross and Pitaevskii [
9]. As pointed out in Ref. [
10], the expansion in the order parameter is a primary feature in Landau's phase transition theory, whereas an expansion in powers of
is a secondary assumption. Therefore, we will use the functional (
1) for all
.
For , the coefficients and can be expanded as [10] and , and is usually assumed to be constant, . Within the mean-field approximation from the Taylor expansion of in , it follows that , . The width of the fluctuation region, wherein the mean-field approximation is not applicable, is evaluated with the help of the Ginzburg [10] and Ginzburg–Levanyuk [24,25] criteria. For ordinary metallic superconductors the fluctuation region proves to be usually very narrow and the mean-field approximation then holds for almost any temperature below , except for a tiny vicinity of . Thus, for , neglecting the mentioned narrow fluctuation region, one may use , . For He-II, fluctuations prove to be important for all temperatures below , cf. [10]. Using the experimental fact that the specific heat of He-II has no power divergence at , we get and , which coincides with phenomenological findings [10].
Consider a system at a finite temperature consisting of normal and superfluid parts undergoing rectilinear motion parallel to a wall. The wall singles out the laboratory frame with respect to which the motion is defined. Interactions between particles in normal fluid may lead to the creation of excitations. The mechanisms of excitation production depend on the specifics of problems, and will be discussed below in Sects. 4, 5, and 7.
We assume that the superfluid moves with an initial velocity with respect to the wall, and additionally the excitations can carry some net momentum, , with respect to the superfluid. Then one can define an average velocity of the excitations with respect to the superfluid component . With respect to the wall, the excitations have the average velocity . The motion of the superfluid as a whole with velocity relative to the reference frame of the wall can be described by introducing the phase of the condensate field with
We can write the variational functional for the condensate field in the standard form of the two-fluid model [
11]:
The density of the superfluid component, which determines the amplitude of the condensate field
, is related to the normal component
by the relation
where
is the mass of the pair for systems with pairing, and the mass of a boson in bosonic superfluids, e.g., the mass of the
atom in case of the He-II. The quantity
in Eq. (
2) stands for a binding free-energy density of the normal subsystem in its rest frame, which explicit form is not of interest here. The first term in (
2) can be hidden in
as a phase of the condensate field. For the case when the normal component rests,
, i.e., the superfluid moves with the velocity
, the minimization of the functional (
2) gives
and, hence, the critical temperature decreases with a velocity increase as
[
26] and vanishes at
. In reality, the superfluid flow
becomes unstable with
even at the smaller velocity
, determined from the condition
, see [
27–
29]. In general,
is smaller than
[
27], and for small
one finds [
10,
27]
. Thus, for a flow in a narrow pipe, in the equilibrium state with
and hence
, the CoE would not appear since the mother condensate is already destroyed for
. Therefore, in further discussion we assume that
. Situations in which the latter condition is fulfilled will be discussed later in the text. In the case
of interest, the finite value of
implies only a redefinition of the critical temperature
. Thereby, to simplify further notations we put
. The generalization is straightforward. Then the free-energy density functional of the system moving with velocity
with respect to the wall is\break given by
The equilibrium volume-averaged value of the condensate is then given by Eq. (
4), and the volume-averaged density of the normal component,
, is related to the averaged total density of the fluid,
, as
. The equilibrium value of the volume-averaged free-energy density (we shall call it an “in”-state) is
When the speed of the flow
exceeds the Landau critical velocity,
on top of the mother condensate
there may appear in the fluid a CoE
[
1,
2,
6] with the frequency
and momentum
calculated in the rest frame of the superfluid, where, as we have assumed, the ratio
has a minimum at
. For He-II, the spectrum
is the standard phonon–roton spectrum, normalized as
for small
. In the case of straightforward motion, following the symmetry arguments, we may choose the simplest form of the CoE order parameter depending on the time
and the coordinate
as
with a constant amplitude
for the homogeneous system that we consider.
For the description of the CoE with the given frequency
, the functional (
1) must be supplemented by the functional
involving higher-gradient terms so that the variation of the Fourier transform of the full functional reproduces the excitation frequency
and the self-interaction parameters of the CoE free-energy density functional:
For example, in Ref. [
6] these parameters were estimated for cold weakly interacting Bose gases. The explicit structure of
is not important for our study as we use the phenomenological parameters
, and
.
We suppose that, when the CoE is formed (we shall call it a “fin”-state), the initial momentum density is redistributed between the fluid and the CoE:
Here,
is the momentum density carried by the CoE in the rest frame of the superfluid,
is the resulting momentum density carried by the CoE in the laboratory frame, and the first term,
, is the resulting momentum density carried by the superfluid in the laboratory frame. So, the CoE necessarily moves in the laboratory frame.
In the presence of the CoE, the resulting order parameter
is the sum of the mother condensate,
, and the CoE,
,
. The volume-averaged free-energy density of the system with the CoE,
, can be written as
where
is the energy of the excitation including the mean-field potential,
. Now, using the momentum conservation (
8) we express
through
and get for the change of the averaged free-energy density associated with the CoE,
where we put
. We now apply the functional (
10) to superfluids for
and
.
3. Cold superfluid
3.1. Bosonic system
At
the whole medium is superfluid and the amplitudes of the condensates are constrained by the spatially averaged particle number density,
In the presence of the CoE the density begins spatially oscillating around its averaged value. For a weak condensate, i.e.,
, we find perturbatively
The density modulation was predicted in [
1] and reproduced in the numerical simulation of the supercritical flow in He-II using a realistic density functional [
5].
Replacing Eq. (
11) in (
10) and putting
, we find the change of the spatially averaged energy density of the system because of the appearance of the CoE,
,
where
,
,
,
are considered above coefficients taken now for
. Minimizing this functional with respect to
, we obtain
From (
8) we find that because of the CoE with
the flow is decelerated to the velocity
The volume-averaged energy gain due to the appearance of the CoE is
If
, one has
. As we estimate below in the cases of He-II and the BCS weak coupling, the parameter
and
.
As follows from Eq. (
16), the CoE appears in a second-order phase transition since
but
. The amplitude of the CoE (
14) grows with the velocity, whereas the amplitude of the mother condensate decreases. The value
vanishes when
, the second critical velocity, at which
according to Eq. (
11). The value
is evaluated from (
14) as
When the mother condensate disappears at
, the excitation spectrum is cardinally reconstructed, and the superfluidity destruction occurs as a first-order phase transition. We assume that for
the excitation spectrum has no low-lying local minimum at a finite momentum. Then the amplitude
jumps from
to 0 and
jumps from
to 0 at
.
3.2. Fermionic system
As shown in Refs. [
19,
20,
30], in fermionic systems with pairing there may exist bosonic modes with suitable spectra, supporting quasiparticle excitations with energy
and momentum
, where
is the pairing gap computed in the rest frame of the superfluid; see Fig. 2 in [
19], and Fig. 4 in [
20]. For these modes, the Landau critical velocity is
and for
there is a chance for the condensation of the bosonic excitations as we considered above.
Besides bosonic excitations there exist fermionic ones with spectrum
. Stemming from the breakup of Cooper pairs, the fermionic excitations are produced pairwise and the corresponding (fermion) Landau critical velocity is
. The latter expression reduces to [
31]
We see that, up to a small correction of the order of
,
. More accurately, we get
.
For
, the fermionic excitations are produced near the wall and move, therefore, with respect to the superfluid with the velocity
.
1 Hence, the change of the energy density due to the Cooper pair breaking can be calculated as
Expanding this integral for velocities
close to the critical velocity
, we find
being valid for
. Since the critical velocity
is slightly smaller than
, Eq. (
20) wins over Eq. (
16) for
, but already for the velocities
the formation of the CoE becomes energetically more favorable than the pair breaking. Although the above estimates are applicable only for
, there is another argument in favor of the condensation of bosonic excitations. In a system in which the normal component (fermionic excitations) moves relative to superfluid with the velocity
, the pairing gap decreases (the Rogers–Bardeen effect [
32]). In the case under consideration, a superfluid moves with the velocity
relative to the wall. Excitations are produced near the wall, and the pairing gap decreases, being determined by the equation [
33]
For
this equation has the solution
With the subsequent growth of
(for
) the gap continues to decrease and, as follows from Eq. (
21), it vanishes at
, see [
33]. Since in the presence of the CoE the final velocity of the flow is
and the gap does not change, the additional gain in the energy density due to the formation of the condensate of bosonic excitations compared to the pair breaking without the CoE formation is
where [
9]
. For
, by substituting Eq. (
22) in Eq. (
23) and rewriting
, we easily find
For
one has
, and, as follows from Eq. (
23), the gain in the energy density because of the CoE compared to the full destruction of the pairing would be
.
Thus we can conclude that the creation of the condensate of bosonic excitations with finite momentum in moving cold fermionic systems with pairing leading to a reduction of the flow velocity is energetically more profitable than the breaking of Cooper pairs and the decrease of the pairing gap.
4. Warm superfluid, two-fluid motion
Only for a very low
can the normal component be neglected. For a higher temperature, the normal subsystem serves as a reservoir of particles for the formation of the mother and daughter condensates, whose amplitudes are now to be chosen by minimization of the free energy of the system. Therefore, minimizing (
10), we now vary
and
independently and find
where
. The quantity
stands for the renormalized critical temperature, which depends now on the flow velocity, and
stands for the second critical velocity depending on
. The condition
implies the relation between
and
:
The solution of this equation for the velocity,
, increases with the decreasing temperature, and the solution for the temperature,
, decreases with increasing
. At
or
we have
but
, and for
or for
the condensate
vanishes, as for
the spectrum of excitations does not contain a suitable low-lying branch. Thus, the superfluidity is destroyed at
or
in a first-order phase transition.
From Eqs. (
8) and (
25) we find for
and
the resulting velocity of the flow.
similar to Eq. (
15) obtained above for
. If
, one has
, and
for
.
Substituting the order parameters from Eq. (
25) to Eq. (
10), we find for the averaged free-energy density gain owing to the appearance of the CoE
for
. Thus, for
the free energy decreases owing to the appearance of the CoE with
in the presence of the non-vanishing mother condensate. The value of
is to be found from the minimization of Eq. (
28). As
, the momentum
gets renormalized and differs now from the value corresponding to the minimum of
. As for
, for
the CoE appears at
in a second-order phase transition but it disappears at
in a first-order phase transition with jumps from
to 0.
At finite temperature the dynamics of the CoE amplitude can be determined from the equation [
34]
where
is the formation rate of the CoE. In the theory of non-equilibrium superconductors this equation is known as the time-dependent Ginzburg–Landau equation. Note that the dynamics following this equation is different from that which follows from the Gross–Pitaevskii equation describing a weakly non-ideal Bose gas in an external field. It is determined by the time dependence of the potential. We emphasize that the above consideration assumes that the formation rate
of the CoE is faster than the deceleration rate
of the normal subsystem. The former time
is of microscopic origin, whereas
might be very large as it is caused by the friction force between the normal component and the wall. For rotating compact stars,
is determined by the decay of a star magnetic field yielding
yrs [
18] for magnetic fields below
G. Thus, the CoE has enough time to develop in such cases.
When a fluid flowing with at is cooled down to , it consists of four components: the normal excitations, the superfluid, the vortices, and the CoE, all moving rigidly with (if ). If the system is then rapidly re-heated to , the superfluid component, the vortices, and the CoE vanish and the remaining normal fluid consists of two fractions: one still moving with , owing to conservation of the momentum, and the other one, originating from the melted CoE, with mass equal to , moving with a higher velocity until a new equilibrium is established. This may show one possibility for how one could identify the formation of the CoE experimentally.
Note that for fermion superfluids at after the CoE is formed, the flow velocity , for (the estimate is done for ), and hence the Cooper pair breaking does not occur, whereas the condensate of Bose excitations is preserved.
5. Vortices
Above, we focused our consideration on the cases where either the vortices are absent (as in a narrow capillary [1]) or they leave the system (in open systems), or the presence of vortices supports a common rigid motion of the normal and superfluid components [22] (e.g., as in systems with charged components [35], or in rotating systems, like neutron stars [18]).
In the case of He-II moving in a narrow capillary, vortices do not appear—see [1,5]. For rectilinearly moving superfluids in extended geometry there may appear excitations of the type of vortex rings and other structures [36]. The energy of the ring is estimated [10,11] as , and the momentum is , where is the radius of the vortex ring and is the coherence length, , as estimated above. Thus, is the Landau critical velocity for the vortex production, where in the absence of impurities is of the order of the transverse size of the system. For a system of distributed impurities moving together with the fluid, is the typical distance between the defects. Vortices are pinned to the impurities and move together with them and the superfluid. In an open clean system at the vortex rings are pushed to infinity by Magnus and Iordanskii forces. Note that for spatially extended systems the value is lower than the Landau critical velocity . A flow moving with velocity for may be considered as metastable, since the vortex creation probability is hindered by a large potential barrier and formation of a vortex takes a long time [37,38]. The vortex production rate increases strongly, however, when approaches [37,38]. For motion in a pipe, the vortices are captured by the pipe wall, forming after a while a stationary subsystem in the frame of the walls. Periodic solitonic solutions of the Gross–Pitaevskii equation were studied in [39]. This situation might be rather similar to that of a mother condensate moving in a periodic potential, produced by the spatial variations of the CoE order parameter [6]. Since in exterior regions of the vortices the superfluidity persists, our consideration of the condensation of excitations for is applicable. Note that in He-II under a high external pressure decreases and at some conditions becomes lower than , see [40], and in the interval there are no vortices but the CoE may appear.
In superconducting systems vortices, if formed, are involved in a common motion with the superconducting subsystem due to the appearance of a tiny London field [35] distributed throughout the medium that supports the condition .
In rotating superfluids, vortices appear at rotation frequency , where for the spherical system is the size of the system (transversal size for the cylindrical system), and their number grows with an increase of . When the density of vortices becomes sufficiently large, they form a lattice, cf. [22], thereby forcing the superfluid and normal components to move as a rigid body, i.e. with .
6. Estimates for fermionic and bosonic superfluids
We now apply the expressions derived in the previous sections to several practical cases.
6.1. Fermionic superfluid
Consider a fermion system with the singlet pairing. In the weak-coupling (BCS) approximation the parameters of the functional (
1) can be extracted from the microscopic theory [
9]:
where
stands for the effective fermion mass (
in the weak-coupling limit),
is the particle number density, and the fermion chemical potential is
. The function
is the Riemann
-function, and
. With the BCS parameters we have
and the pairing gap
; see [
23].
With parameters (31) we estimate and where . We see that if one gets , since the latter inequality is reduced to the inequality , which is well satisfied. In this limit, given by Eq. (25) gets the same form as Eq. (14). The resulting flow velocity after condensation of excitations, (27), is lower than but close to it.
Since for the BCS case we have
,
, Eq. (
26) for the new critical temperature is easily solved, for
:
In the last equality we put
. We also estimate the maximal second critical velocity as
.
6.2. Bosonic superfluid: He-II
We turn now to the bosonic superfluid, He-II. In He-II there exists a branch of the phonon–roton excitations [
9,
10]. The typical energy of the rotonic excitations
at the roton minimum
depends on the pressure and temperature. According to [
41], for the saturated vapor pressure
at
and
at
, and
in the whole temperature interval. Other parameters of He-II at the saturated vapor pressure are [
10]:
and
, with the helium atom mass
. The parametrization holds for
, but for rough estimates can be used up to
. For instance, using Eq. (
1) we evaluate the He-II mass-density as
, which is of the order of the experimental value
at
.
Taking into account that we deal with the rotonic excitation,
i.e.,
and
, we estimate
Taking from [
1] that
, and assuming
, we again estimate
.
Using the results of [
41],
dependence can be fitted with 99% accuracy as
where
. Using
, we evaluate condensate amplitudes and the final flow velocity as functions of temperature and depict them in
Fig. 1. The CoE appears at
in a second-order phase transition. For
, the amplitude of the condensate
(
) increases (decreases) linearly with
. The closer
is to
, the steeper the change of the condensate amplitudes. The final velocity of the flow, which sets in after the appearance of the CoE, decreases with increasing~
. With
,
, the renormalized critical temperature determined by Eq. (
26) is
for
. The mother condensate
vanishes when
reaches the value
, which depends on the temperature as
. At
the superfluidity disappears in a first-order phase transition. The corresponding energy release can be estimated from (
29) as
, where
is the specific heat jump at
[
10].
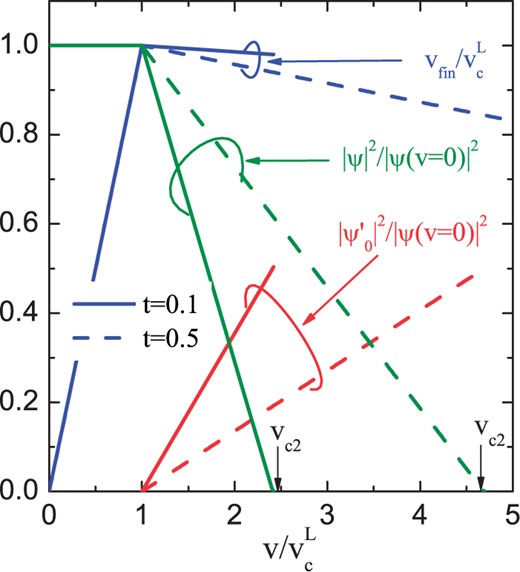
Figure 1.
Condensate amplitudes and , Eq. (25), and the final flow velocity , Eq. (27), in superfluid plotted as functions of the flow velocity for various temperatures. Vertical arrows indicate . Velocities are scaled by the values of the Landau critical velocities and , and the condensates are normalized to the condensate amplitude in the superfluid at rest.
7. Rotating superfluids: pulsars
The novel phase with the CoE may also exist in rotating systems. Here, excitations can be generated because of the rotation. Now we should use angular momentum conservation instead of momentum conservation. Also, the structure of the order parameter is more complicated than the plane wave. For the cylindrical geometry a probing CoE function can be taken in the form [
2]
where
and
are polar coordinates and
and
are variational parameters. The value of the critical angular velocity for the appearance of the first vortices,
, proves to be very low for systems of large size
, e.g. like neutron stars. With these modifications, the results obtained above for motion with constant
continue to hold.
In the inner crust and in a part of the core of a neutron star, protons and neutrons are paired in the state owing to attractive and interactions, cf. [18]. In denser regions of the star interior the pairing disappears, but neutrons might be paired in the state. The charged superfluid component should co-rotate with the normal matter. This, as we have mentioned, is due to the appearance of a tiny magnetic field (London effect) in the whole volume of the superfluid; () is the proton mass (charge) [35]. This tiny field, being for the most rapidly rotating pulsars, has no influence on parameters of the star and can be neglected.
With a typical neutron star radius , and for typical for the pairing, we estimate . For the neutron star contains arrays of neutron vortices with regions of superfluidity in between them, and the star rotates as a rigid body. The vortices would completely overlap only if reached the unrealistically large value . The most rapidly rotating pulsar PSR J1748-2446ad has the angular velocity 4500 Hz [42]. The value of the critical angular velocity for the formation of the CoE in neutron star matter is for the pairing gap and at the nucleon density , where is the density of the atomic nucleus, and is the speed of light. The superfluidity will coexist with the CoE and the array of vortices until the rotation frequency reaches the value , at which both the CoE and the superfluidity disappear completely. From Eq. (26) with the BCS parameters we estimate .
There are many other millisecond pulsars in low-mass X-ray binaries of a typical age . Thus, in the detected rapidly rotating pulsars the CoE might coexist with superfluidity, which would also affect their hydrodynamical description [43–45]. A possible influence of the CoE on the window of the r-mode instability in the millisecond pulsars was recently studied by us in [7]. Also, a CoE may appear in the presence of a charged pion condensate with a finite momentum in massive neutron stars [17]—see a discussion of an additional slowing down of the pulsar which may arise owing to the presence of the condensation in [2]. In massive neutron stars there may also exist and/or condensates with finite momentum, cf. [15,16]. A similar effect to that on a charged pion condensate may exist on and condensates. Another interesting issue is the possibility of the formation of CoEs in color-superconducting regions of rotating hybrid stars. Various CoEs may arise there since pairing gaps between quarks of different colors and flavors may have essentially different values, e.g. in 2SC, 2SC + X, color spin locking, and other possible phases, see [46].
8. Conclusion
In this paper we studied the possibility of the condensation of excitations with , when a superfluid initially flows with respect to a wall with a velocity larger than the Landau critical velocity . Differing from Refs. [1,5,6], which studied bosonic superfluid systems for at a fixed velocity , we considered this phenomenon for bosonic and fermionic superfluid systems both for and at the conserving momentum for rectilinear motion (at the conserving angular momentum for a rotation). In the presence of the CoE the final velocity of the superfluid becomes less than . Also, compared to Refs. [1,2,5] we incorporated the interaction between the CoE and the “mother” condensate of the superfluid. We studied the case of , when the normal component can be neglected, and the case of higher , when it serves as a reservoir of particles affecting the formation of the mother condensate and CoE. The latter case was not previously described in the literature.
At finite temperatures we first studied systems where the superfluid and normal components move with respect to each other with a relative velocity (the average velocity of excitations with respect to the superfluid component), and then focused on the case of . Note that at finite the mother condensate may exist only for very low values of (much less than the Landau critical velocity). In rotating superfluids vortices form a lattice and the system rotates as a rigid body. Also, charged subsystems are forced to move as a whole owing to the London force. These are conditions when indeed one can put .
A back reaction of the CoE on the mother condensate proves to be important both for and for . We found that the CoE appears in a second-order phase transition at and the condensate amplitude grows linearly with increasing velocity. Simultaneously, the mother condensate decreases and vanishes at , then the superfluidity is destroyed in a first-order phase transition with an energy release. For the resulting flow velocity is .
We found that for cold fermion systems with pairing the creation of the condensate of bosonic excitations with finite momentum, leading to a reduction of the flow velocity up to the value of the Landau critical velocity , is energetically more profitable than the breaking of Cooper pairs appearing for () and the decrease of the pairing gap (except the case when the initial velocity is in a narrow vicinity of the critical point). To the best of our knowledge the possibility of condensation of bosonic excitations with finite momentum in moving fermionic systems with pairing has not yet been considered in the literature. For fermion superfluids at , after the CoE is formed the flow velocity becomes less than and the Cooper pair breaking does not occur, whereas the condensate of Bose excitations is preserved. The CoE appears in the second-order phase transition. The mother condensate decreases and vanishes at , then the superfluidity is destroyed in a first-order phase transition with an energy release.
We discussed condensation of Bose excitations in rotating superfluids, such as pulsars, and showed that in the existing most rapidly rotating millisecond pulsars superfluidity might coexist with the CoE.
Acknowledgements
We thank M. Yu. Kagan for detailed discussion of the results. The work was supported by the Ministry of Education and Science of the Russian Federation (Basic part), by Slovak Grant No. VEGA-1/0469/15, and by “NewCompStar,” COST Action MP1304.
References
[1]Pitaevskii
L. P.
JETP Lett.
39
,
511
(
1984
).
[2]Voskresensky
D. N.
JETP
77
,
917
(
1993
).
[3]Voskresensky
D. N.
Phys. Lett. B
358
,
1
(
1995
).
[4]Kolomeitsev
E. E.
Voskresensky
D. N.
Eur. Phys. J. A
52
,
362
(
2016
).
[5]Ancilotto
F.
Dalfovo
F.
Pitaevskii
L. P.
Toigo
F.
Phys. Rev. B
71
,
104530
(
2005
).
[6]Baym
G.
Pethick
C. J.
Phys. Rev. A
86
,
023602
(
2012
).
[7]Kolomeitsev
E. E.
Voskresensky
D. N.
Phys. Rev. C
91
,
025805
(
2015
).
[8]Melnikovsky
L. A.
Phys. Rev. B
84
,
024525
(
2011
).
[9]Lifshitz
E. M.
Pitaevskii
L. P.
Statistical Physics, Part Two
(
Pergamon Press
,
Oxford
,
1980
).
[10]Ginsburg
V. L.
Sobyanin
A. A.
Sov. Phys. Usp.
19
,
773
(
1977
).
[11]Khalatnikov
I. M.
An Introduction to the Theory of Superfluidity
(
Benjamin
,
New York
,
1965
).
[12]Shammass
I.
Rinott
S.
Berkovitz
A.
Schley
R.
Steinhauer
J.
Phys. Rev. Lett.
109
,
195301
(
2012
).
[13]Ha
L.-Ch.
Clark
L. W.
Parker
C. V.
Anderson
B. M.
Chin
Ch.
Phys. Rev. Lett.
114
,
055301
(
2015
).
[14]Khamehchi
M. A.
Zhang
Y.
Hamner
C.
Busch
Th.
Engels
P.
Phys. Rev. A
90
,
063624
(
2014
).
[15]Kolomeitsev
E. E.
Kämpfer
B.
Voskresensky
D. N.
Nucl. Phys. A
588
,
889
(
1995
).
[16]Kolomeitsev
E. E.
Voskresensky
D. N.
Phys. Rev. C
68
,
015803
(
2003
).
[17]Migdal
A. B.
Saperstein
E. E.
Troitsky
M. A.
Voskresensky
D. N.
Phys. Rept.
192
,
179
(
1990
).
[18]Shapiro
S.
Teukolsky
S. A.
Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects
(
Wiley
,
New York
,
1983
).
[19]Combescot
R.
Kagan
M. Yu.
Stringari
S.
Phys. Rev. A
74
,
042717
(
2006
).
[20]Martin
N.
Urban
M.
Phys. Rev. C
90
,
065805
(
2014
).
[21]Bailin
D.
Love
A.
Phys. Rept.
107
,
325
(
1984
).
[22]Tilley
D. R.
Tilley
J.
Superfluidity and Superconductivity
(
IoP Publishing
,
Bristol
,
1990
).
[23]Abrikosov
A. A.
Fundamentals of the Theory of Metals
(
North Holland
,
Amsterdam
,
1988
).
[24]Ginzburg
V. L.
Levanyuk
A. P.
J. Phys. Chem. Solids
6
,
51
(
1958
).
[25]Levanyuk
A. P.
Zh. Eksp. Teor. Fiz.
36
,
810
(
1959
) [Sov. Phys. JETP
9
,
571
(
1960
)].
[26]Amit
D. J.
Phys. Lett. A
26
,
466
(
1968
).
[27]Kramer
L.
Phys. Rev.
179
,
149
(
1969
).
[28]Andreev
A. F.
Melnikovsky
L. A.
Physica C
404
,
34
(
2004
).
[29]Andreev
A. F.
Melnikovsky
L. A.
J. Low. Temp. Phys.
135
,
411
(
2004
).
[30]Kulik
I. O.
Entin-Wohlman
O.
Orbach
R.
J. Low Temp. Phys.
43
,
591
(
1981
).
[31]Castin
Y.
Ferrier-Barbut
I.
Salomon
C.
Comptes Rendus Phys.
16
,
241
(
2015
) [arXiv:1408.1326 [cond-mat.quant-gas]] [Search
inSPIRE].
[32]Bardeen
J.
Rev. Mod. Phys.
34
,
667
(
1962
).
[33]Zagoskin
A. M.
Quantum Theory of Many-Body Systems
(
Springer
,
New York
,
1998
), p.
182
.
[34]Lifshiz
E. M.
Pitaevskii
L. P.
Physical Kinetics
(
Pergamon Press
,
Oxford
,
1981
).
[35]Sauls
J.
Ögelman
H.
van den Heuvel
E. P. J.
Timing Neutron Stars
, (
Kluwer Academic Publishers
,
Dordrecht
,
1989
), pp.
457
.
[36]Andreev
A. F.
Kagan
M. Yu.
Sov. Phys. JETP
59
,
318
(
1984
).
[37]Iordansky
S. V.
Sov. Phys. JETP
21
,
467
(
1965
).
[38]Langer
J. S.
Fisher
M. E.
Phys. Rev. Lett.
19
,
560
(
1967
).
[39]Tsuzuki
T.
J. Low Temp. Phys.
4
,
441
(
1971
).
[40]McClintock
P. V. E.
Bowley
R. M.
Halperin
W. P.
The Landau critical velocity
, in
Progress in Low Temperature Physics
(
Elsevier Sci. B.V.
,
Amsterdam
,
1995
), Vol.
XIV
.
[41]Brooks
J. S.
Donnelly
J.
J. Phys. Chem.
6
,
51
(
1977
).
[43]Andreev
A. F.
Lifshitz
I. M.
Sov. Phys. JETP
29
,
1107
(
1969
).
[44]Andreev
A. F.
Bashkin
E. P.
Sov. Phys. JETP
42
,
164
(
1976
).
[45]Bashkin
E. P.
Meyerovich
A. E.
Adv. Phys.
30
,
1
(
1981
).
[46]Blaschke
D.
Grigorian
H.
Voskresensky
D. N.
Astron. Astrophys.
368
,
561
(
2001
).
© The Author(s) 2017. Published by Oxford University Press on behalf of the Physical Society of Japan.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (
http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided the original work is properly cited.
PDF




