-
PDF
- Split View
-
Views
-
Cite
Cite
Yugo Abe, Takeo Inami, Yoshiharu Kawamura, Yoji Koyama, Inflation from radion gauge-Higgs potential at Planck scale, Progress of Theoretical and Experimental Physics, Volume 2015, Issue 9, September 2015, 093B03, https://doi.org/10.1093/ptep/ptv110
Close - Share Icon Share
Abstract
We study whether inflation is realized based on the radion gauge-Higgs potential obtained from the one-loop calculation in five-dimensional gravity coupled to a |$U(1)$| gauge theory. We show that the gauge-Higgs can give rise to inflation in accord with the astrophysical data and the radion plays a role in fixing the values of physical parameters. We clarify the reason why the radion dominated inflation and the hybrid inflation cannot occur in our framework.
1. Introduction
It is believed that the universe has evolved into the present one as a result of a rapid expansion called “inflation” in its very early stage. The well-known difficulties in the standard big-bang model are solved by the slow-roll inflation scenario [1, 2]. Furthermore, recent accurate measurements have confirmed the predictions of a flat universe with a nearly scale-invariant density perturbation [3].
A large remaining problem is to explore the origin of inflation or to disclose the identity of a scalar particle called the “inflaton.” The following requirements can be imposed on the model as clues to a solution: The inflaton should be the inevitable product of a theory at a high-energy scale. The potential of inflaton should be stable against various corrections. Concretely, there should be no fine tuning among parameters receiving quantum corrections and no sensitivity to gravitational corrections.
On a four-dimensional (4D) space-time, no model has yet solved the problem completely. In most models, the inflaton is an ad hoc particle introduced by hand, and the stability of the potential is threatened by radiative and gravitational corrections relating non-renormalizable terms suppressed by the power of the Planck mass because the inflaton takes a larger value than the Planck mass, and such corrections cannot be controlled without powerful symmetries and/or mechanisms.
Effective field theories on a higher-dimensional space-time provide a possible solution to the problem. Some scalar fields exist inevitably as parts of ingredients in the theory and are massless at the tree level. The scalar potential can be induced radiatively and stabilized by local symmetries. Typical ones are the extranatural inflation model [4, 5] and the radion inflation model [6]. In the former model, a scalar field called the “gauge-Higgs” appears from the extra-dimensional component(s) of the gauge field. It becomes dynamical degrees of freedom called the Wilson line phase and its value is fixed by quantum corrections [7]. In the latter model, a scalar field called the “radion” originates from the extra-dimensional component(s) of the graviton, and its vacuum expectation value (VEV) is related to the size of the extra space.
Recently, the effective potential with respect to both the radion and the gauge-Higgs has been derived at the one-loop level upon the |$S^1$| compactification, from gravity theory coupled to a |$U(1)$| gauge boson and matter fermions on a five-dimensional (5D) space-time [8]. We refer to the potential as the “radion gauge-Higgs potential.” It is interesting to investigate whether it works as the inflaton potential and what features exist in such a coexisting system.
In this article, we study whether the slow-roll inflation is realized compatible with the astrophysical data, based on the radion gauge-Higgs potential. In the analysis, we pay attention to which particle can play the role of inflaton and the magnitude of the physical parameters.
The content of our article is as follows. In the next section, we explain the radion gauge-Higgs potential and constraints on the inflaton potential. In Sect. 3, we study the gauge-Higgs inflation after focusing on a candidate inflaton. It will be shown that the inflation can be achieved in our framework. In the last section, we give conclusions and discussions.
2. Setup
2.1. Radion gauge-Higgs potential
It is an attractive idea that the structure and evolution of our 4D space-time might be deeply linked to the dynamics of quantities relating to an extra space. The |$V(\chi ,\varphi )$| must describe the physics around the Planck scale if the magnitude of |$L_{\rm phys}^{-1}$|, |$m_{\rm phys}$|, and/or |$\mu _{\rm phys}$| can be comparable to the reduced Planck mass |$M_{G}$| (|$\equiv (8\pi G)^{-1/2} = 2.4 \times 10^{18}$| GeV). There are nearly flat domains around the minimum of |$V(\chi ,\varphi )$|. Hence it is reasonable to expect that the radion gauge-Higgs potential plays the role of inflaton potential.
2.2. Constraints on inflaton potential
3. Analysis
3.1. Candidate inflaton
Let us guess the inflaton |$\phi $| under the assumption that |$V(x, \theta )$| is the inflaton potential. There are several possibilities: (a) |$\phi $| is a mixture of |$x$| and |$\theta $|; (b) |$\phi $| is |$x$| or |$\theta $|. In the hybrid inflation scenario [11], there is a field called “waterfall” |$\omega $| other than |$\phi $|. The role of |$\omega $| is to terminate the inflation induced by |$\phi $|, through the fall into the minimum of |$V$|.
The |$\epsilon $| (|$\eta $|) can be given by a linear combination of |$\epsilon _{\chi '}$|, |$\epsilon _{\varphi }$|, and |$\epsilon _{\chi '\varphi }$| (|$\eta _{\chi '}$|, |$\eta _{\varphi }$|, and |$\eta _{\chi '\varphi }$|) locally on the space of scalar fields. From (16)–(18), we see that the slow-roll conditions are fulfilled if and only if |$\varphi $| dominantly contributes to |$\epsilon $| and |$\eta $|, i.e., |$\epsilon \simeq \epsilon _{\varphi }$| and |$\eta \simeq \eta _{\varphi }$|, and |$f$| is much bigger than |$M_G$|. In this way, the gauge-Higgs is a candidate inflaton, while the radion fails to be.
In the case with |$f \gg M_G$|, the value of |$V$| changes rapidly in the direction of |$\chi '$| because |$|\partial V/\partial \chi '| \gg |\partial V/\partial \varphi |$|. Then, in the first stage, |$\chi '$| is moving toward the region where |$\partial V/\partial \chi ' \simeq 0$|, but |$\chi '$| cannot play the role of inflaton, in this period, because |$\epsilon _{\chi '} = O(1)$| and |$\eta _{\chi '} = O(1)$| except for a narrow region near |$\langle \chi ' \rangle $|. Hence the hybrid inflation cannot occur in our model.
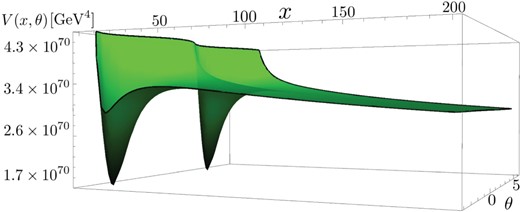
The value of |$r_V$| is sensitive to that of |$r_m (= \mu /m)$|, and |$r_m$| is restricted to |$r_m \lesssim 0.3$| for |$r_V \lesssim O(10^{-2})$|. In other words, the shape of |$V$| changes drastically depending on the value of |$r_{m}$|. As a reference, typical configurations of |$V(x,\theta )$| are described in Figs. 1 and 2. Note that the direction of the |$x$|-axis is zoomed out. We take the following values for the parameters: |$r_m=1.0$|, |$L=6\times 10^{-20}\,{\rm GeV}^{-1}$|, and |$m=5.1\times 10^{18}\,{\rm GeV}$| in Fig. 1, and |$r_m=0.1$|, |$L=6\times 10^{-20}\,{\rm GeV}^{-1}$|, and |$m=5.1\times 10^{18}\,{\rm GeV}$| in Fig. 2. As seen from these figures, the values of both |$V$| and |$x(\theta )$| satisfying |$\partial V/\partial x = 0$| change rapidly depending on |$\theta $| for |$r_m = 1.0$|, and the values of |$V$| and |$x(\theta )$| are almost independent of |$\theta $| for |$r_m = 0.1$|.

3.2. Gauge-Higgs dominated inflation
We investigate whether the gauge-Higgs dominated inflation (an extension of the extranatural inflation) is realized based on |$V(x, \theta )$|. We study the case with |$c_{1}=4$|, |$c_{2}=1$|, and |$r_m = 0.3$|. The reason we choose |$r_m = 0.3$| is that the magnitude of |$L^{-1}_{\rm phys}$|, |$m_{\rm phys}$|, and |$\mu _{\rm phys}$| can be larger than the reduced Planck mass if |$r_m$| is smaller than |$0.3$|. Although the leading term (|$k=1$|) in |$V(x, \theta )$| is known to be a good approximation to |$V$| itself, we carry out the numerical analysis including the next-to-leading term (|$k=2$|) because it contributes dominantly to the second derivative of the potential with respect to |$\varphi $| (the slow-roll parameter |$\eta $|) around |$\theta =\pi /2$|.1
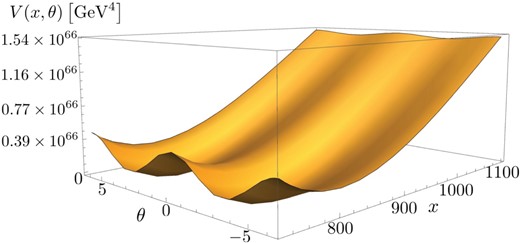
The potential |$V(x,\theta )$| for |$L= 6 \times 10^{-20}\,{\rm GeV}^{-1}$| and |$m=5.1\times 10^{18}\,{\rm GeV}$|.
Next, we impose the following conditions on the parameters in order to limit the range of |$L$|:
The value of the 4D gauge coupling constant |$g_{4}$| is less than unity, in order to make the analysis based on perturbation trustworthy.
- The physical fermion masses |$m_{\rm phys}$| and |$\mu _{\rm phys}$| are smaller than the 5D reduced Planck mass |$M_{G_5}$| defined bywhere |$G_{5}$| is the 5D Newton constant. From the perspective of 5D theory, |$M_{G_{5}}$| would be more fundamental than the 4D one.(28)\begin{equation} M_{G_{5}}\equiv \sqrt[3]{\frac{1}{8\pi G_{5}}}= \sqrt[3]{\frac{1}{8\pi LG}}, \end{equation}
The allowed values of physical parameters for |$f=10M_G$| and |$r_m=\mu /m=0.3$|.
| Values of physical parameters . |
|---|
| |$L_{\rm phys}^{-1} =1.2 \times 10^{17}\sim 6.2 \times 10^{17}\,{\rm GeV}$| |
| |$m_{\rm phys}\simeq 9.3\times 10^{17}\,{\rm GeV}$| |
| |$\langle \chi '\rangle =9.7 \times 10^{17}\sim 1.1\times 10^{19}\,{\rm GeV}$| |
| |$\mu _{\rm phys} \simeq 2.8\times 10^{17}\,{\rm GeV}$| |
| |$M_{\varphi } \simeq 1.5\times 10^{13}\,{\rm GeV}$| |
| |$M_{\chi '} \simeq 6.7\times 10^{15}\,{\rm GeV}$| |
| |$g_{4}= 0.007 \sim 0.9$| |
| |$M_{G_{5}}=9.9\times 10^{17}\sim 4.9\times 10^{18}\,{\rm GeV}$| |
| |$r \simeq 0.10$| |
| Values of physical parameters . |
|---|
| |$L_{\rm phys}^{-1} =1.2 \times 10^{17}\sim 6.2 \times 10^{17}\,{\rm GeV}$| |
| |$m_{\rm phys}\simeq 9.3\times 10^{17}\,{\rm GeV}$| |
| |$\langle \chi '\rangle =9.7 \times 10^{17}\sim 1.1\times 10^{19}\,{\rm GeV}$| |
| |$\mu _{\rm phys} \simeq 2.8\times 10^{17}\,{\rm GeV}$| |
| |$M_{\varphi } \simeq 1.5\times 10^{13}\,{\rm GeV}$| |
| |$M_{\chi '} \simeq 6.7\times 10^{15}\,{\rm GeV}$| |
| |$g_{4}= 0.007 \sim 0.9$| |
| |$M_{G_{5}}=9.9\times 10^{17}\sim 4.9\times 10^{18}\,{\rm GeV}$| |
| |$r \simeq 0.10$| |
The allowed values of physical parameters for |$f=10M_G$| and |$r_m=\mu /m=0.3$|.
| Values of physical parameters . |
|---|
| |$L_{\rm phys}^{-1} =1.2 \times 10^{17}\sim 6.2 \times 10^{17}\,{\rm GeV}$| |
| |$m_{\rm phys}\simeq 9.3\times 10^{17}\,{\rm GeV}$| |
| |$\langle \chi '\rangle =9.7 \times 10^{17}\sim 1.1\times 10^{19}\,{\rm GeV}$| |
| |$\mu _{\rm phys} \simeq 2.8\times 10^{17}\,{\rm GeV}$| |
| |$M_{\varphi } \simeq 1.5\times 10^{13}\,{\rm GeV}$| |
| |$M_{\chi '} \simeq 6.7\times 10^{15}\,{\rm GeV}$| |
| |$g_{4}= 0.007 \sim 0.9$| |
| |$M_{G_{5}}=9.9\times 10^{17}\sim 4.9\times 10^{18}\,{\rm GeV}$| |
| |$r \simeq 0.10$| |
| Values of physical parameters . |
|---|
| |$L_{\rm phys}^{-1} =1.2 \times 10^{17}\sim 6.2 \times 10^{17}\,{\rm GeV}$| |
| |$m_{\rm phys}\simeq 9.3\times 10^{17}\,{\rm GeV}$| |
| |$\langle \chi '\rangle =9.7 \times 10^{17}\sim 1.1\times 10^{19}\,{\rm GeV}$| |
| |$\mu _{\rm phys} \simeq 2.8\times 10^{17}\,{\rm GeV}$| |
| |$M_{\varphi } \simeq 1.5\times 10^{13}\,{\rm GeV}$| |
| |$M_{\chi '} \simeq 6.7\times 10^{15}\,{\rm GeV}$| |
| |$g_{4}= 0.007 \sim 0.9$| |
| |$M_{G_{5}}=9.9\times 10^{17}\sim 4.9\times 10^{18}\,{\rm GeV}$| |
| |$r \simeq 0.10$| |
The tensor-to-scalar ratio (7) is evaluated as |$r \simeq 0.10$|. It is within the range of the observational upper bound, |$r<0.12$| [3], but still large enough to be testable by future observations.
From the above analysis, it is confirmed that the gauge-Higgs has the properties required for the inflaton and gauge-Higgs dominated inflation can be achieved not so unnaturally.
4. Conclusion and discussion
Using the radion gauge-Higgs potential obtained from one-loop corrections in the 5D gravity theory coupled to a |$U(1)$| gauge boson and matter fermions, we have found that the gauge-Higgs |$\varphi $| can give rise to a large-field inflation in accord with the astrophysical data. In contrast, it is difficult to realize the inflation dominated by the radion |$\chi '$|, because the slow-roll conditions cannot be fulfilled except for a narrow region satisfying |$\partial V/\partial \chi ' \simeq 0$|. Furthermore, the hybrid inflation scenario is not achieved in our model where |$\chi '$| is moving toward the minimum of the potential in the first stage.
Based on the gauge-Higgs dominated inflation scenario, we have determined the values of parameters using constraints on the inflaton potential. Some of these are different from those in specific gauge-Higgs inflation models [4, 5], and this is mainly due to the difference in setup. Our model contains gravity and physical parameters such as the 4D gauge coupling constant |$g_4$|, the size of extra space |$L_{\rm phys}$|, and the fermion masses |$m_{\rm phys}$| and |$\mu _{\rm phys}$| are multiplied by some power of |$\langle \chi \rangle $|. Even if the parameter |$f$| is trans-Planckian, i.e., |$f > M_G$|, |$g_4$| can be as large as the standard model gauge coupling constants at the grand unified scale. This is due to the fact that |$g_4$| is proportional to |$\langle \chi \rangle ^{1/3}$| and |$\chi $| can take a pretty large VEV. In this case, the size of |$L_{\rm phys}^{-1}$|, |$m_{\rm phys}$|, and |$\mu _{\rm phys}$| can be below the 5D reduced Planck mass. As seen from the fact that |$\varphi $| works as the inflaton, |$\varphi $| acquires mass of |$O(10^{13})$| GeV through radiative corrections. Other massive particles are much heavier than |$\varphi $|. The masses of the first KK modes and the fermion zero modes are of |$O(10^{17})$| GeV, and the radion mass is of |$O(10^{15})$| GeV. Because the value of the radion stays almost constant in the region with |$\partial V/\partial \chi ' \simeq 0$|, the physical size of the extra dimension has been almost stabilized at the initial time of inflation and |$V(\langle \chi ' \rangle , \varphi )$| is effectively treated as the inflaton potential.
Our model is left with problems concerning parameters. The first one is a common problem in inflation models: how the inflaton can take a suitable initial value to realize inflation compatible with observation. Because our potential has |$\chi '$| and |$\varphi $|, it can be traded for the initial-value problem of |$\chi '$| that is our future work. The second one is to determine the value of |$f$| without using constraints on the inflation potential. It is necessary to fix |$g_4$| and |$\langle \chi \rangle $|. The value of |$g_4$| can be obtained by the VEV of some scalar field such as the dilaton and/or the moduli. It would be efficient to extend our system by incorporating such scalar fields. The magnitude of |$\langle \chi \rangle $| strongly depends on the ratio of fermion masses |$r_m = \mu /m$|. For smaller |$r_m$|, larger |$\langle \chi \rangle $| is obtained. It would be important to explore the origin of massive fermions. The last one is how our results are reliable after receiving gravitational corrections, which are uncontrollable at present.
Furthermore, the effective field theory at the Planck scale has not yet been known. In our model, the values of several parameters can be of the order of the Planck mass and the field value of the gauge-Higgs is above the Planck scale. This result could indicate that the quantum theory of gravity such as string theory is necessary to understand the mechanism of inflation more properly. Using it, there is a possibility that gravitational corrections are controlled and our analyses are justified. In string theory construction of inflation models, the type of axion inflation is extensively studied (e.g., see [13]) for large-field inflation. We note that our effective potential is generated through the perturbative loop corrections and the origin of inflaton(s) is different from that in axion inflation models, though some of the properties of the inflaton potential, especially the periodicity, are shared. It would be interesting to study the inflation based on the effective potential relating several scalar fields such as the dilaton, the moduli (including the radion), and the gauge-Higgs in the framework of string theory.
Funding
Open Access funding: SCOAP3.
Acknowledgements
This work is supported in part by funding from the Nagano Society for The Promotion of Science (Y.A.), scientific grants from the Ministry of Education, Culture, Sports, Science and Technology under Grant Nos. 21244036 and 20012487 (T.I.), Grant Nos. 21244036 and 22540272 (Y. Kawamura), and the National Center for Theoretical Science (NCTS) and the grant 101-2112-M-007-021-MY3 of the Ministry of Science and Technology of Taiwan (Y. Koyama). Y.A. benefited greatly from his visit to the National Taiwan University. He wishes to thank Professor Ho for giving him the opportunity to visit. T.I. wishes to thank CTS of NTU for partial support.
If one considers the running of the spectral index that corresponds to third and higher derivatives of the potential with respect to the inflaton, the higher-order terms (|$k>2$|) are necessary to evaluate it correctly [12].
We drop the infinite part of |$a$| and show only the finite part. We need a fine tuning to determine |$a$|, and this is the sort of fine-tuning problem known as the cosmological constant problem.



