Multiple point principle of the Standard Model with scalar singlet dark matter and right-handed neutrinos

Abstract

We consider the multiple point principle of the Standard Model with scalar singlet dark matter (DM) and three heavy right-handed neutrinos at the scale where the beta function |$\beta _{\lambda }$| of the effective Higgs self-coupling |$\lambda _{\rm eff}$| becomes zero. We do a two-loop analysis and find that the top quark mass |$M_{t}$| and the Higgs portal coupling |$\kappa$| are strongly related to each other. One of the good points of this model is that a larger |$M_{t}({\gtrsim }171\,{\rm GeV})$| is allowed. This fact is consistent with the recent experimental value |$M_{t}=173.34 \pm 0.76$|GeV [ATLAS, CDF, CMS, and D0 Collaborations, arXiv:1403.4427 [hep-ex]], which corresponds to the DM mass |$769\,{\rm GeV}\leq m_{\rm DM} \leq 1053$| GeV.

1. Introduction

The discovery of the Higgs-like particle and its mass [1, 2] is a very meaningful result for the Standard Model (SM). It suggests that the Higgs potential can be stable up to the Planck scale |$M_{\rm pl}$| and also that both the Higgs self-coupling |$\lambda$| and its beta function |$\beta _{\lambda }$| become very small around the Planck scale. This fact has attracted much attention, and there are many works trying to find its physical meaning [3–20].

One interesting and meaningful study is to consider how the physics beyond the SM affects such a criticality. For example, recently there has been a two-loop analysis of the Higgs portal |$Z_{2}$| scalar model [21]. In this model, the SM singlet scalar is a dark matter (DM) candidate, and it is found that its mass can be predicted to be |$400\,{\rm GeV} \lt m_{\rm DM} \lt 470\,{\rm GeV}$| from the requirement that |$\lambda$| and |$\beta _{\lambda }$| simultaneously become zero at |$10^{17}$|GeV; this is usually called the multiple point principle (MPP) [3–5].

In this paper, we study the MPP of the next minimal extension of the SM, namely, besides the Higgs portal |$Z_{2}$| scalar, we include SM singlet heavy right-handed neutrinos [19, 22, 23]. The MPP of this model at the (reduced) Planck scale |$M_{{\rm pl}}$| has already been investigated in Ref. [19]. There, by using the two-loop beta functions and the tree-level Higgs potential, they concluded that |$m_{{\rm DM}}$| and the heavy Majorana mass |$M_{\rm R}$| of the right-handed neutrino should be

\[8.5\,(8.0)\times 10^{2}\,{\rm GeV}\leq m_{{\rm DM}}\leq 1.4\,(1.2)\times 10^{3}\,{\rm GeV},\]

(1)

\[6.3\,(5.5)\times 10^{13}\,{\rm GeV}\leq M_{\rm R}\leq 1.6\,(1.2)\times 10^{14}\,{\rm GeV},\]

(2)

within |$172.6\,{\rm GeV}\leq M_{t}\leq 174.1\,{\rm GeV}$|⁠. The different points in this paper are as follows: Although, within the renormalizable Lagrangian, there are also two scalar couplings in this model (see Eq. (12)), we focus on |$\lambda$| (and |$\beta _{\lambda }$|⁠) in this paper.¹ The existence of heavy right-handed neutrinos is naturally needed if we try to explain the light neutrino masses by the seesaw mechanism. Thus, this model is phenomenologically interesting because it can explain both DM and the light neutrino masses.

We consider the MPP at the scale where |$\beta _{\lambda }$| becomes zero. Namely, we do not fix the MPP scale at |$M_{{\rm pl}}$|⁠. As a result, the condition |$\beta _{\lambda }=0$| does not reduce the degrees of freedom of the parameters.
In addition to the two-loop beta functions, we also calculate the one-loop effective potential.
We fix |$M_{\rm R}$| to |$10^{13}$|GeV, and include the Yukawa coupling |$Y_{\rm R}$| between the |$Z_{2}$| scalar and the right-handed neutrinos.

This paper is organized as follows. In Sect. 2, we review the MPP of the pure SM for the later discussion. In Sect. 3, we give a two-loop analysis of the SM with the scalar singlet DM and three right-handed neutrinos. In Sect. 4, a summary is given.

2. Preliminary: Multiple point principle of SM

In the SM, the one-loop effective potential in the Landau gauge is given by

\[V_{{\rm eff}}(\phi ,\mu )=V_{{\rm tree}}(\phi ,\mu ) +V^{{\rm SM}}_{{\rm 1\,loop}}(\phi ,\mu ),\]

(3)

where

\[V_{{\rm tree}}(\phi ,\mu ):=e^{4\Gamma (\phi )}\frac {\lambda (\mu )}{4}\phi ^{4},\]

(4)

\begin{align}V_{{\rm 1\,loop}}(\phi )&:=e^{4\Gamma (\phi )}\left \{-6\cdot \frac {M_{t}(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \frac {M_{t}^{2}(\phi )}{\mu ^{2}}\right ) -\frac {3}{2}+2\Gamma (\phi )\right ] \right . \\ &\quad +3\cdot \frac {M_{W}(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \frac {M_{W}^{2}(\phi )}{\mu ^{2}}\right ) -\frac {5}{6}+2\Gamma (\phi )\right ] \\ &\quad \left . +3\cdot \frac {M_{Z}(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \frac {M_{Z}^{2}(\phi )}{\mu ^{2}}\right ) -\frac {5}{6}+2\Gamma (\phi )\right ] \right \},\end{align}

(5)

\[M_{t}(\phi ) =\frac {y_{t}(\mu )}{\sqrt {2}}\phi ,\quad M_{W}(\phi )=\frac {g_{2}(\mu )}{2}\phi ,\quad M_{Z}=\frac {\sqrt {g_{2}^{2}(\mu )+g_{{\rm Y}}^{2}(\mu )}}{2}\phi .\]

(6)

Here, |$\mu$| is the renormalization scale, |$\Gamma (\phi )$| is the wave function renormalization, and |$\lambda (\mu )$|⁠, |$y_{t}(\mu )$|⁠, |$g_{2}(\mu )$|⁠, and |$g_{Y}(\mu )$| are the renormalized couplings.² By using these results, the effective Higgs self-coupling |$\lambda _{{\rm eff}}(\phi ,\mu )$| can be defined as

\[V_{{\rm eff}}(\phi ,\mu ):=\frac {\lambda _{{\rm eff}}(\phi ,\mu )}{4}\phi ^{4}.\]

(7)

To minimize the contribution of |$V^{{\rm SM}}_{{\rm 1\,loop}}(\phi ,\mu )$|⁠, we set |$\phi =\mu$| in the following discussion.

The left panel of Fig. 1 shows |$\lambda _{{\rm eff}}(\phi )$| as a function of |$\phi$|⁠. For the initial values, we have used the numerical results of Ref. [24], and the Higgs mass is fixed at

\[M_{h}=125.15\,{\rm GeV}.\]

(8)

We use Eq. (8) as a typical value in the following discussion. The band corresponds to |$95{\%}$| CL deviation of the top quark pole mass |$M_{t}$|⁠. For the 1|$\sigma$| level, this is given by [25]

\[M_{t}=171.2\pm 2.4\,{\rm GeV}.\]

(9)

If we assume that all the other parameters of the SM except for |$M_{t}$| are fixed, we can find the scale |$\Lambda _{\beta }$| where |$\beta _{\lambda _{{\rm eff}}}$| becomes zero as a function of |$M_{t}$|⁠. Here, |$\beta _{\lambda _{{\rm eff}}}$| means

\[\beta _{\lambda _{{\rm eff}}}(\phi ):=\frac {d\lambda _{{\rm eff}}(\phi )}{d\log \phi }.\]

(10)

The right panel of Fig. 1 shows |$\Lambda _{\beta }$| as a function of |$M_{t}$|⁠. The MPP requires that |$\lambda _{{\rm eff}}(\Lambda _{\beta })$| should become zero, and predicts

\[M_{t}=170.9\,{\rm GeV}.\]

(11)

This is the MPP of the pure SM. In the next section, we discuss the MPP of the SM with the scalar singlet DM and three right-handed neutrinos.

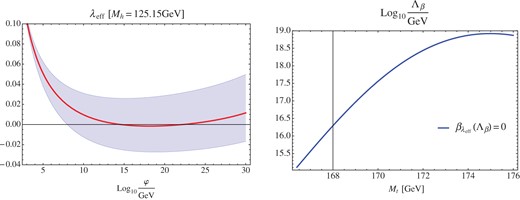
$Left: the running effective Higgs self-coupling $\lambda _{{\rm eff}}$ as a function of the Higgs field $\phi$. The blue band corresponds to $95{\%}$ confidence level (CL) deviation of the top quark pole mass $M_{t}$. Right: the scale $\Lambda _{\beta }$ where $\beta _{\lambda _{{\rm eff}}}$ becomes zero as a function of $M_{t}$.$

Fig. 1.

Left: the running effective Higgs self-coupling |$\lambda _{{\rm eff}}$| as a function of the Higgs field |$\phi$|⁠. The blue band corresponds to |$95{\%}$| confidence level (CL) deviation of the top quark pole mass |$M_{t}$|⁠. Right: the scale |$\Lambda _{\beta }$| where |$\beta _{\lambda _{{\rm eff}}}$| becomes zero as a function of |$M_{t}$|⁠.

Open in new tab Download slide

3. MPP of the SM with scalar singlet dark matter and right-handed neutrinos

We consider the following renormalizable Lagrangian:

\begin{align} {\mathcal {L}}&={\mathcal {L}}_{{\rm SM}}+ \frac {1}{2}\partial _{\mu }S\partial ^{\mu }S-\frac {m_{{\rm DM}}^{2}}{2}S^{2}-\frac {\kappa }{2}S^{2}H^{\dagger }H-\frac {\lambda _{{\rm DM}}}{4!}S^{4}+ \sum _{j=1}^{3}\bar {\nu }_{{\rm R}j}i\gamma ^{\mu }\partial _{\mu }\nu _{{\rm R}j}\\ &\quad -\sum _{i,j}\left ( y_{\nu ij}\bar {L}_{i}H^{\dagger }\nu _{{\rm R}j}+ {\rm h.c}\right ) -\sum _{i,j}\left ( M_{{\rm R}ij}+ \frac {Y_{{\rm R}ij}}{\sqrt {2}}S\right ) \bar {\nu }_{{\rm R}i}^{c}\nu _{{\rm R}j}. \end{align}

(12)

Here, |$H$| is the Higgs field, |$S$| is the SM singlet real scalar field, |$m_{{\rm DM}}$| is its mass, |$\nu _{{\rm R}i}$| are right-handed neutrinos, |$M_{{\rm R}ij}$| are their Majorana masses, and |$(Y_{{\rm R}ij},y_{\nu ij})$| are the Yukawa couplings. For simplicity, we assume that |$M_{{\rm R}ij}$|⁠, |$Y_{{\rm R}ij}$|⁠, and |$y_{\nu ij}$| are diagonalized, and also that they are respectively equal for the three generations. In this case, Eq. (12) becomes

\begin{align} {\mathcal {L}}&={\mathcal {L}}_{{\rm SM}}+ \frac {1}{2}\partial _{\mu }S\partial ^{\mu }S-\frac {m_{{\rm DM}}^{2}}{2}S^{2}-\frac {\kappa }{2}S^{2}H^{\dagger }H-\frac {\lambda _{{\rm DM}}}{4!}S^{4}+ \sum _{i=1}^{3}\bar {\nu }_{{\rm R}i}i\gamma ^{\mu }\partial _{\mu }\nu _{{\rm R}i}\\ &\quad -y_{\nu }\sum _{i=1}^{3}\left ( \bar {L}_{i}H^{\dagger }\nu _{{\rm R}i}+ {\rm h.c}\right ) -\sum _{i=1}^{3}\left ( M_{\rm R}+ \frac {Y_{\rm R}}{\sqrt {2}}S\right ) \bar {\nu }_{{\rm R}i}^{c}\nu _{{\rm R}i}. \end{align}

(13)

Thus, including the top mass |$M_{t}$|⁠, there are seven unknown parameters,

\[M_{t},\quad m_{{\rm DM}},\quad \kappa ,\quad \lambda _{{\rm DM}},\quad y_{\nu },\quad M_{\rm R},\quad Y_{\rm R},\]

(14)

in this model. In the following discussion, to distinguish the initial values of these parameters at |$\mu =M_{t}$| from their running couplings, we use the subscript 0 for their initial values, like |$\kappa _{0}$|⁠, except for |$M_{t}$|⁠. Because |$S$| is the candidate for the DM, |$m_{{\rm DM}}$| and |$\kappa$| must satisfy some relation such that they can explain the observed energy density [27]:

\[\Omega _{{\rm DM}}h^{2}:=\frac {\rho _{{\rm DM}}h^{2}}{\rho _{{\rm tot}}}= 0.1196 \pm 0.0031\,(68{\%}\ {\rm CL}).\]

(15)

For |$m_{{\rm DM}}\gtrsim M_{h}$|⁠, this relation is approximately given by [28]

\[\log _{10}\kappa \simeq -3.63+1.04 \log _{10}\left ( \frac {m_{{\rm DM}}}{{\rm GeV}}\right ) .\]

(16)

Moreover, if we assume that the neutrino mass is |$0.1$| eV, |$y_{\nu }$| and |$M_{\rm R}$| must satisfy

\[-\frac {M_{\rm R}}{2}\left ( 1-\sqrt {1+ \frac {2y_{\nu }^{2}v_{h}^{2}}{M_{\rm R}^{2}}}\right ) \simeq \frac {y_{\nu }^{2}v_{h}^{2}}{2M_{\rm R}}=0.1~{\rm eV},\]

(17)

where |$v_{h}$| is the Higgs expectation value. This is the usual relation of the seesaw mechanism. In the following discussion, we choose |$M_{\rm R}=10^{13}$|GeV, so |$y_{\nu }$| is fixed by Eq. (17). As a result, four of the seven parameters remain free; they are

\[M_{t},\quad \kappa ,\quad \lambda _{{\rm DM}},\quad {\rm and}\quad Y_{\rm R}.\]

(18)

To discuss how the effective couplings behave at the high-energy scale, we must know the renormalization group equations (RGEs) of this model. Their results are presented in Appendix A. Here, note that the contributions from the heavy right-handed neutrinos should be taken into account at the scale where |$\mu \geq M_{\rm R}$|⁠. The one-loop effective potential of the Higgs field is given by

\[V_{{\rm 1\,loop}}(\phi ,\mu ):=\left \{\begin {array}{ll}V^{{\rm SM}}_{{\rm 1\,loop}}(\phi )+ \dfrac {M_{{\rm DM}}(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \dfrac {M_{{\rm DM}}(\phi )^{2}}{\mu ^{2}}\right ) -\dfrac {3}{2}\right ] -6\cdot \dfrac {M^{-}_{\nu }(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \dfrac {M^{-}_{\nu }(\phi )^{2}}{\mu ^{2}}\right ) -\dfrac {3}{2}\right ] \\ \quad ({\rm for}\ \phi \lt M_{\rm R}),\\ V^{{\rm SM}}_{{\rm 1\,loop}}(\phi )+ \dfrac {M_{{\rm DM}}(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \dfrac {M_{{\rm DM}}(\phi )^{2}}{\mu ^{2}}\right ) -\dfrac {3}{2}\right ] -6\cdot \dfrac {M^{-}_{\nu }(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \dfrac {M^{-}_{\nu }(\phi )^{2}}{\mu ^{2}}\right ) -\dfrac {3}{2}\right ] \\ \quad -6\cdot \dfrac {M^{+ }_{\nu }(\phi )^{4}}{64\pi ^{2}}\left [ \log \left ( \dfrac {M^{+ }_{\nu }(\phi )^{2}}{\mu ^{2}}\right ) -\dfrac {3}{2}\right ] \quad ({\rm for}\ \phi >M_{\rm R}), \end {array}\right .\]

(19)

where

\[M_{{\rm DM}}(\phi ):=\sqrt {e^{2\Gamma (\phi )}\frac {\kappa \phi ^{2}}{2}+m^{2}_{{\rm DM}}},\quad M_{\nu }^{\pm }(\phi ):=\frac {M_{\rm R}}{2}\left ( 1\pm \sqrt {1+ \frac {2y_{\nu }^{2}e^{2\Gamma (\phi )}\phi ^{2}}{M_{\rm R}^{2}}}\right ) .\]

(20)

In these expressions, we have put |$S=0$| because we now focus on the MPP of the Higgs sector.³ Furthermore, we can neglect |$m_{{\rm DM}}$| in Eq. (20) because its effect is very small when |$\phi \gg m_{{\rm DM}}$|⁠. As in Sect. 2, we set |$\phi =\mu$|⁠, and define the effective Higgs self-coupling |$\lambda _{{\rm eff}}$| as

\[\lambda _{{\rm eff}}(\phi ):=\frac {4}{\phi ^{4}}V(\phi )=\frac {4}{\phi ^{4}}\left ( V_{{\rm tree}}(\phi )+V_{{\rm 1\,loop}}(\phi )\right ) .\]

(21)

Figure 2 shows |$\lambda _{{\rm eff}}(\phi )$| for various values of the parameters. Here, the typical values are chosen to be

\[\lambda _{{\rm DM}0}=0.2,\quad \kappa _{0}=0.2,\quad Y_{\rm R0}=0.2.\]

(22)

One can see that |$\lambda _{{\rm eff}}$| depends mainly on |$M_{t}$| and |$\kappa _{0}$|⁠, and hardly on |$\lambda _{{\rm DM}0}$| and |$Y_{\rm R0}$|⁠. This is because |$\lambda _{{\rm DM}}$| does not appear in |$\beta _{\lambda }$| and |$Y_{\rm R}$| appears at the two-loop level (see Eq. (A7) in Appendix A). Therefore, by fixing |$\lambda _{{\rm DM}}$| and |$Y_{\rm R}$|⁠, we can relate |$M_{t}$| and |$\kappa _{0}$| from the MPP.

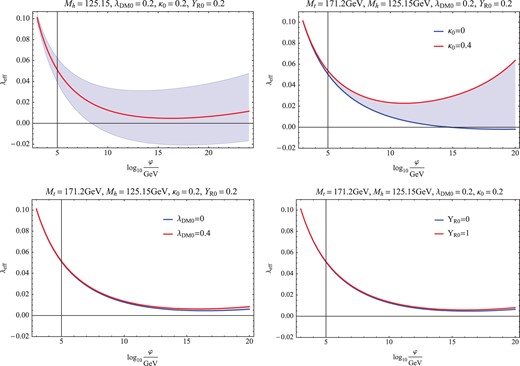
$The running effective Higgs self-coupling $\lambda _{{\rm eff}}$ as a function of $\phi$. The upper left (right) panel shows the $M_{t}\,(\kappa _{0})$ dependence. For $M_{t}$, the blue band corresponds to 95${\%}$ CL deviation from $171.2$GeV. The lower left (right) panel shows the $\lambda _{{\rm DM}0}$$(Y_{\rm R0})$ dependence.$

Fig. 2.

The running effective Higgs self-coupling |$\lambda _{{\rm eff}}$| as a function of |$\phi$|⁠. The upper left (right) panel shows the |$M_{t}\,(\kappa _{0})$| dependence. For |$M_{t}$|⁠, the blue band corresponds to 95|${\%}$| CL deviation from |$171.2$|GeV. The lower left (right) panel shows the |$\lambda _{{\rm DM}0}$||$(Y_{\rm R0})$| dependence.

Open in new tab Download slide

By the same procedure of Sect. 2, we can calculate the scale |$\Lambda _{\beta }$| where |$\beta _{\lambda _{{\rm eff}}}$| becomes zero, and obtain |$\lambda _{{\rm eff}}(\Lambda _{\beta })$| as a function of |$M_{t}$| and |$\kappa _{0}$|⁠. Figure 3 shows the results. In the upper (lower) panels, |$Y_{\rm R0}$| is fixed to |$0.2$||$(0.7)$|⁠. The difference between the left and right panels is whether the tree- or one-loop-level potential is used. The parameter regions where |$\lambda _{{\rm eff}}(\Lambda _{\beta })\lt 0$| and |$\lambda _{{\rm DM}}(\Lambda _{\beta })\lt 0$| are filled, respectively, with blue and red. Both of them are excluded from the stability of the potentials. The MPP predicts that |$M_{t}$| and |$\kappa _{0}$| should exist on the green contour. One of the good points of this model is that a larger |$M_{t}$| is allowed, unlike in the SM. This is consistent with the recent experimental value [26],

\[M_{t}=173.34\pm 0.76\,{\rm GeV},\]

(23)

which corresponds to the DM mass (see Eq. (16)),

\[769\,{\rm GeV}\leq m_{{\rm DM}}\leq 1053\,{\rm GeV}.\]

(24)

Two comments are needed.

The contours that represent |$\Lambda _{\beta }=10^{16}$|GeV, |$10^{17}$|GeV, and |$10^{18}$|GeV are also shown in Fig. 3 by red, blue, and orange, respectively. Thus, a larger |$M_{t}$| (such as Eq. (23)) means that, in this model, the MPP of the Higgs potential occurs at the relatively low-energy scale (⁠|${\lesssim }10^{16}$|GeV).
As is seen from the lower panels of Fig. 3, we can also require |$\lambda _{{\rm DM}}(\Lambda _{\beta })=0$| in addition to |$\lambda _{{\rm eff}}(\lambda _{\beta })=0$|⁠. Because |$\kappa _{0}$| and |$Y_{\rm R0}$| appear in the one-loop part of |$\beta _{\lambda _{{\rm DM}}}$|⁠, we can obtain a further relation between them by |$\lambda _{{\rm DM}}(\Lambda _{\beta })=0$|⁠. Although one might think that the one remaining parameter can be determined by |$\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })=0$|⁠, we have checked that it is difficult to satisfy |$\lambda _{{\rm DM}}(\Lambda _{\beta }) = \beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })=0$| simultaneously. See Appendix B for more details.

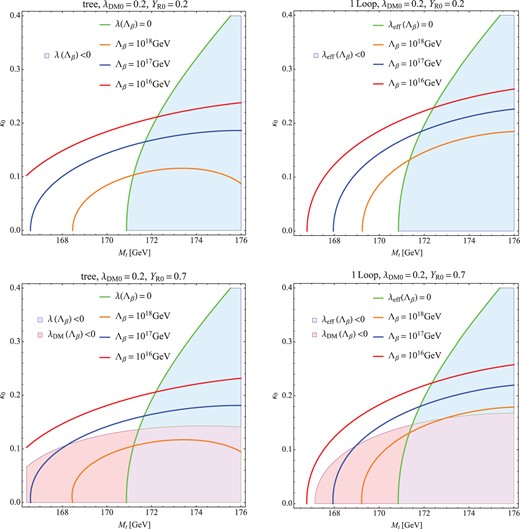
$The parameter dependences of $\lambda _{{\rm eff}}(\Lambda _{\beta })$. Here, $\lambda _{{\rm DM}0}$ is fixed at 0.2, and $Y_{\rm R0}$ is fixed at $0.2~(0.7)$ in the upper (lower) panels. The left (right) panels show the calculations by using the tree- (one-loop-) level potential. The green lines show the prediction by the MPP. The contours that represent $\Lambda _{\beta }=10^{16}$GeV, $10^{17}$GeV, and $10^{18}$GeV are also shown by red, blue, and orange, respectively.$

Fig. 3.

The parameter dependences of |$\lambda _{{\rm eff}}(\Lambda _{\beta })$|⁠. Here, |$\lambda _{{\rm DM}0}$| is fixed at 0.2, and |$Y_{\rm R0}$| is fixed at |$0.2~(0.7)$| in the upper (lower) panels. The left (right) panels show the calculations by using the tree- (one-loop-) level potential. The green lines show the prediction by the MPP. The contours that represent |$\Lambda _{\beta }=10^{16}$|GeV, |$10^{17}$|GeV, and |$10^{18}$|GeV are also shown by red, blue, and orange, respectively.

Open in new tab Download slide

4. Summary

We have discussed the MPP of the SM with scalar singlet DM and right-handed neutrinos. We have found that |$\lambda _{{\rm eff}}$| and |$\beta _{\lambda _{{\rm eff}}}$| can simultaneously become zero within a reasonable parameter region. The MPP predicts a strong relation between the portal coupling |$\kappa$| and the top mass |$M_{t}$|⁠. Unlike the pure SM, a larger |$M_{t}$| is allowed in this model, which is favorable for the recent experimental values [25, 26]:

\[M_{t}=173.34 \pm 0.76\,{\rm GeV}.\]

(25)

Although we have found that the MPP can be satisfied for the Higgs potential, it is difficult to realize the exact flatness of the scalar potential at some high-energy scale |$\Lambda$|⁠:

\[\lambda (\Lambda )=\beta _{\lambda }(\Lambda )=\lambda _{{\rm DM}}(\Lambda )=\beta _{\lambda _{{\rm DM}}}(\Lambda )=\kappa (\Lambda )=\beta _{\kappa }(\Lambda )=0;\]

(26)

see Appendix B for details. It would be interesting to consider a generalization of this model in such a way that the MPP can be realized for whole scalar fields.

Funding

Open Access funding: SCOAP³.

Acknowledgements

We thank Hikaru Kawai, Yuta Hamada, and Koji Tsumura for valuable discussions.

Appendix A. Two-loop renormalization group equations

The two-loop RGEs where the Lagrangian is given by Eq. (13) are as follows:⁴

\[\frac {dg_{Y}}{dt} =\frac {1}{(4\pi )^{2}}\frac {41}{6}g_{Y}^{3}+ \frac {g_{Y}^{3}}{(4\pi )^{4}}\left ( \frac {199}{18}g_{Y}^{2}+ \frac {9}{2}g_{2}^{2}+ \frac {44}{3}g_{3}^{2}-\frac {17}{6}y_{t}^{2}-\frac {3}{2}y_{\nu }^{2}\right ) ,\]

(A1)

\[\frac {dg_{2}}{dt} =-\frac {1}{(4\pi )^{2}}\frac {19}{6}g_{2}^{3}+ \frac {g_{2}^{3}}{(4\pi )^{4}}\left ( \frac {3}{2}g_{Y}^{2}+ \frac {35}{6}g_{2}^{2}+12g_{3}^{2}-\frac {3}{2}\left ( y_{t}^{2}+y_{\nu }^{2}\right ) \right ) ,\]

(A2)

\[\frac {dg_{3}}{dt} =-\frac {7}{(4\pi )^{2}}g_{3}^{3}+ \frac {g_{3}^{3}}{(4\pi )^{4}}\left ( \frac {11}{6}g_{Y}^{2}+ \frac {9}{2}g_{2}^{2}-26g_{3}^{2}-2y_{t}^{2}\right ) , \]

(A3)

\begin{align}\frac {dy_{t}}{dt}&=\frac {y_{t}}{(4\pi )^{2}}\left ( \frac {9}{2}y_{t}^{2}+3y_{\nu }^{2}-\frac {17}{12}g_{Y}^{2}-\frac {9}{4}g_{2}^{2}-8g_{3}^{2}\right ) \\ &\quad + \frac {y_{t}}{(4\pi )^{4}}\Biggl \{-12y_{t}^{4}-\frac {27}{4}y_{\nu }^{4}-\frac {27}{4}y_{t}^{2}y_{\nu }^{2}-\frac {9}{8}Y_{\rm R}^{2}y_{\nu }^{2}+6\lambda ^{2}+ \frac {1}{4}\kappa ^{2}-12\lambda y_{t}^{2}\\ &\quad +g_{Y}^{2}\left ( \frac {131}{16}y_{t}^{2}+ \frac {15}{8}y_{\nu }^{2}\right ) +g_{2}^{2}\left ( \frac {225}{16}y_{t}^{2}+ \frac {45}{8}y_{\nu }^{2}\right ) +36g_{3}^{2}y_{t}^{2}+ \frac {1187}{216}g_{Y}^{4}\\ &\quad -\frac {23}{4}g_{2}^{4}-108g_{3}^{4}-\frac {3}{4}g_{Y}^{2}g_{2}^{2}+9g_{2}^{2}g_{3}^{2}+ \frac {19}{9}g_{3}^{2}g_{Y}^{2}\Biggl \},\end{align}

(A4)

\begin{align}\frac {dy_{\nu }}{dt}&=\frac {y_{\nu }}{(4\pi )^{2}}\left ( \frac {9}{2}y_{\nu }^{2}+3y_{t}^{2}+ \frac {1}{4}Y_{\rm R}^{2}-\frac {3}{4}g_{Y}^{2}-\frac {9}{4}g_{2}^{2}\right ) \\ &\quad + \frac {y_{\nu }}{(4\pi )^{4}}\Biggl \{-12y_{\nu }^{4}-\frac {27}{4}y_{t}^{4}-\frac {19}{32}Y_{\rm R}^{4}-y_{\nu }^{2}\left ( \frac {27}{4}y_{t}^{2}+ \frac {21}{16}Y_{\rm R}^{2}\right ) +6\lambda ^{2}+ \frac {1}{4}\kappa ^{2}\\ &\quad -12\lambda y_{\nu }^{2} - \kappa Y_{\rm R}^{2} +g_{Y}^{2}\left ( \frac {123}{16}y_{\nu }^{2}+ \frac {85}{24}y_{t}^{2}+ \frac {9}{16}Y_{\rm R}^{2}\right ) +g_{2}^{2}\left ( \frac {225}{16}y_{\nu }^{2}+ \frac {45}{8}y_{t}^{2}+ \frac {27}{16}Y_{\rm R}^{2}\right ) \\ &\quad +20g_{3}^{2}y_{t}^{2}+ \frac {35}{24}g_{Y}^{4}-\frac {23}{4}g_{2}^{4}-\frac {9}{4}g_{Y}^{2}g_{2}^{2}\Biggl \},\end{align}

(A5)

\begin{align}\frac {dY_{\rm R}}{dt}&=\frac {Y_{\rm R}}{(4\pi )^{2}}\left ( 3Y_{\rm R}^{2}+2y_{\nu }^{2}\right ) + \frac {Y_{\rm R}}{(4\pi )^{4}}\Biggl \{-\frac {81}{16}Y_{\rm R}^{4}-\frac {27}{4}Y_{\rm R}^{2}y_{\nu }^{2}-9y_{t}^{2}y_{\nu }^{2}-\frac {27}{2}y_{\nu }^{4}\\ &\quad -\lambda _{{\rm DM}}Y_{\rm R}^{2}-8\kappa y_{\nu }^{2}-\frac {1}{4}g_{Y}^{2}y_{\nu }^{2}-\frac {3}{4}g_{2}^{2}y_{\nu }^{2}\Biggl \},\end{align}

(A6)

\begin{align}\frac {d\lambda }{dt}&=\frac {1}{(4\pi )^{2}}\left ( \lambda \left ( 24 \lambda -9 g_{2}^2-3 g_{Y}^2 +12 y_{\nu }^2+12 y_{t}^2\right ) + \frac {3}{4} g_{2}^2 g_{Y}^2+ \frac {9 g_{2}^4}{8}\right . \\ &\quad \left . + \frac {3 g_{Y}^4}{8}+ \frac {\kappa ^2}{2}-6y_{\nu }^4-6 y_{t}^4\right ) + \frac {1}{(4\pi )^{4}} \Biggl \{-2\kappa ^{3}-5\kappa ^{2}\lambda -312\lambda ^{3}+36\lambda ^{2}\left ( g_{Y}^{2}+3g_{2}^{2}\right ) \\ &\quad + \lambda \left ( \frac {629}{24}g_{Y}^{4}+ \frac {39}{4}g_{2}^{2}g_{Y}^{2}-\frac {73}{8}g_{2}^{4}\right ) + \frac {305}{16}g_{2}^{6}-\frac {289}{48}g_{Y}^{2}g_{2}^{4}-\frac {559}{48}g_{Y}^{4}g_{2} ^{2}+ \frac {379}{48}g_{Y}^{6}\\ &\quad -32g_{3}^{2}y_{t}^{4}-\frac {8}{3}g_{Y}^{2}y_{t}^{4}-\frac {9}{4}g_{2}^{4}\left ( y_{t}^{2}+y_{\nu }^{2}\right ) + \lambda y_{t}^{2}\left ( \frac {85}{6}g_{Y}^{2}+ \frac {45}{2}g_{2}^{2}+80g_{3}^{2}\right ) \\ &\quad + \lambda y_{\nu }^{2}\left ( \frac {15}{2}g_{Y}^{2}+ \frac {45}{2}g_{2}^{2}\right ) +g_{Y}^{2}y_{t}^{2}\left ( -\frac {19}{4}g_{Y}^{2}+ \frac {21}{2}g_{2}^{2}\right ) -g_{Y}^{2}y_{\nu }^{2}\left ( \frac {3}{4}g_{Y}^{2}+ \frac {3}{2}g_{2}^{2}\right ) \\ &\quad -144\lambda ^{2}\left ( y_{t}^{2}+y_{\nu }^{2}\right ) -3\lambda \left ( y_{t}^{4}+y_{\nu }^{4}+ \frac {3}{2}Y_{\rm R}^{2}y_{\nu }^{2}\right ) +30\left ( y_{t}^{6}+y_{\nu }^{6}+ \frac {1}{5}Y_{\rm R}^{2}y_{\nu }^{4}\right ) -\frac {3}{2}Y_{\rm R}^{2}\kappa ^{2}\Biggl \},\end{align}

(A7)

\begin{align}\frac {d\lambda _{{\rm DM}}}{dt}&=\frac {1}{(4\pi )^{2}}\left ( 3\lambda _{{\rm DM}}^{2}+12\kappa ^{2}+6\lambda _{{\rm DM}}Y_{\rm R}^{2}-18Y_{\rm R}^{4}\right ) \\ &\quad + \frac {1}{(4\pi )^{4}}\Biggl \{-\frac {17}{3}\lambda _{{\rm DM}}^{3}-20\kappa ^{2}\lambda _{{\rm DM}}-48\kappa ^{3}-72\left ( y_{t}^{2}+y_{\nu }^{2}\right ) \kappa ^{2}+24\left ( g_{Y}^{2}+3g_{2}^{2}\right ) \kappa ^{2}\\ &\quad +72Y_{\rm R}^{4}\left ( Y_{\rm R}^{2}+y_{\nu }^{2}\right ) + \lambda _{{\rm DM}}Y_{\rm R}^{2}\left ( \frac {21}{2}Y_{\rm R}^{2}-18y_{\nu }^{2}\right ) -9Y_{\rm R}^{2}\lambda _{{\rm DM}}^{2}\Biggl \}, \end{align}

(A8)

\begin{align}\frac {d\kappa }{dt}&=\frac {1}{(4\pi )^{2}}\left ( 4\kappa ^{2}+12\kappa \lambda + \kappa \lambda _{{\rm DM}}+3\kappa \left ( 2y_{t}^{2}+2y_{\nu }^{2}+Y_{\rm R}^{2}\right ) -\frac {3}{2}\kappa \left ( g_{Y}^{2}+3g_{2}^{2}\right ) -12Y_{\rm R}^{2}y_{\nu }^{2}\right ) \\ &\quad + \frac {\kappa }{(4\pi )^{4}}\Biggl \{-\frac {21}{2}\kappa ^{2}-72\kappa \lambda -60\lambda ^{2}-6\kappa \lambda _{{\rm DM}}-\frac {5}{6}\lambda _{{\rm DM}}^{2}-\left ( y_{t}^{2}+y_{\nu }^{2}\right ) \left ( 12\kappa +72\lambda \right ) \\ &\quad -3Y_{\rm R}^{2}\left ( 2\kappa + \lambda _{{\rm DM}}\right ) -\frac {27}{2}y_{t}^{4}-\frac {27}{2}y_{\nu }^{4}-\frac {3}{4}Y_{\rm R}^{4}+ \frac {51}{4}Y_{\rm R}^{2}y_{\nu }^{2}+g_{Y}^{2}\left ( \kappa +24\lambda \right ) +3g_{2}^{2}\left ( \kappa +24\lambda \right ) \\ &\quad +y_{t}^{2}\left ( \frac {85}{12}g_{Y}^{2}+ \frac {45}{4}g_{2}^{2}+40g_{3}^{2}\right ) +y_{\nu }^{2}\left ( \frac {15}{4}g_{Y}^{2}+ \frac {45}{4}g_{2}^{2}\right ) + \frac {557}{48}g_{Y}^{4}-\frac {145}{16}g_{2}^{4}+ \frac {15}{8}g_{Y}^{2}g_{2}^{2}\Biggl \}\\ &\quad + \frac {Y_{\rm R}^{2}y_{\nu }^{2}}{(4\pi )^{4}}\Biggl \{\frac {3}{2}\left ( g_{Y}^{2}+3g_{2}^{2}\right ) +27Y_{\rm R}^{2}+66y_{\nu }^{2}\Biggl \},\end{align}

(A9)

\[\frac {d\Gamma }{dt} =\frac {1}{(4\pi )^{2}}\left ( \frac {9}{4}g_{2}^{2}+ \frac {3}{4}g_{Y}^{2}-3y_{t}^{2}-3y_{\nu }^{2}\right ) .\]

(A10)

Appendix B. Is an exact flat potential possible?

One question is whether the MPP can be realized exactly, namely, if

\[\lambda (\Lambda _{\beta })=\beta _{\lambda }(\Lambda _{\beta })=\lambda _{{\rm DM}}(\Lambda _{\beta })=\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })=\kappa (\Lambda _{\beta })=\beta _{\kappa }(\Lambda _{\beta })=0\]

(B1)

is possible or not. Here, for simplicity, we also define |$\Lambda _{\beta }$| as the scale where |$\beta _{\lambda }$| becomes zero. To discuss this possibility, it is qualitatively enough to consider one-loop RGEs. One can easily understand that it is impossible to realize Eq. (B1) as follows: even if |$\lambda (\Lambda _{\beta })$|⁠, |$\beta _{\lambda }(\Lambda _{\beta })$|⁠, |$\lambda _{{\rm DM}}(\Lambda _{\beta })$|⁠, and |$\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })$| become simultaneously zero, we cannot make |$\kappa (\Lambda _{\beta })$| zero because the one-loop part of |$\beta _{\lambda _{{\rm DM}}}$| at |$\Lambda _{\beta }$| becomes

\[\beta _{\lambda _{{\rm DM}}}|_{\Lambda _{\beta }}=\frac {1}{(4\pi )^{2}}\left ( 12\kappa ^{2}-18Y_{\rm R}^{4}\right ) ,\]

(B2)

and we need |$\kappa (\Lambda _{\beta })\neq 0$| to satisfy |$\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })=0$|⁠.⁵ Furthermore, it is also difficult even to satisfy |$\lambda _{{\rm DM}}(\Lambda _{\beta })=\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })=0$| simultaneously; see Fig. B1. This shows the contours such that |$\lambda _{{\rm DM}}(\Lambda _{\beta })$| and |$\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })$| become zero, respectively. Here, we have used two-loop RGEs. One can see that the two contours do not intersect.

$The blue (red) lines show the contours where $\beta _{\lambda _{{\rm DM}}}(\lambda _{{\rm DM}})(\Lambda _{\beta })=0$. The left (right) panel is the $M_{t}=170~(176)$GeV case. Here, note that, if $\kappa _{0}\gtrsim 0.3$, $\Lambda _{\beta }$ becomes less than $M_{\rm R}=10^{13}$GeV, and there is no solution of $\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })=0$ because the one-loop part of $\beta _{\lambda _{{\rm DM}}}$ is always positive when $\mu \leq M_{\rm R}$.$

Fig. B1.

The blue (red) lines show the contours where |$\beta _{\lambda _{{\rm DM}}}(\lambda _{{\rm DM}})(\Lambda _{\beta })=0$|⁠. The left (right) panel is the |$M_{t}=170~(176)$|GeV case. Here, note that, if |$\kappa _{0}\gtrsim 0.3$|⁠, |$\Lambda _{\beta }$| becomes less than |$M_{\rm R}=10^{13}$|GeV, and there is no solution of |$\beta _{\lambda _{{\rm DM}}}(\Lambda _{\beta })=0$| because the one-loop part of |$\beta _{\lambda _{{\rm DM}}}$| is always positive when |$\mu \leq M_{\rm R}$|⁠.

Open in new tab Download slide

It is difficult to realize the MPP of the other scalar couplings simultaneously in addition to |$\lambda$|⁠. This is discussed in Appendix B.

For the beta functions of the SM, see, e.g., Refs. [21, 24, 29]. Alternatively, we can reproduce them by using the results in Appendix A.

Of course, we can consider the MPP of the DM sector. We study such a situation in Appendix B.

The calculations in this appendix are based on Refs. [30–32], and our results are in agreement with the recent result [23] when there is only one right-handed neutrino and |$Y_{\rm R}=0$|⁠.

Typically, a non-zero positive |$Y_{\rm R0}$| is needed to make |$\beta _{\lambda _{{\rm DM}}}$| negative. As a result, |$Y_{\rm R}(\Lambda _{\beta })$| is non-zero because the one-loop part of |$\beta _{Y_{\rm R}}$| is always positive.

References

Aad

et al.

[ATLAS Collaboration]

Phys. Lett. B

716

(

2012

) [

arXiv

[hep-ex]

] [

Search inSPIRE

10.1016/j.physletb.2012.08.020

Crossref

Search ADS

Chatrchyan

et al.

[CMS Collaboration]

Phys. Lett. B

716

(

2012

) [

arXiv

[hep-ex]

] [

Search inSPIRE

10.1016/j.physletb.2012.08.021

Crossref

Search ADS

Froggatt

C. D.

Nielsen

H. B.

Phys. Lett. B

368

(

1996

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1016/0370-2693(95)01480-2

Crossref

Search ADS

Froggatt

C. D.

Nielsen

H. B.

Takanishi

Phys. Rev. D

113014

(

2001

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1103/PhysRevD.64.113014

Crossref

Search ADS

Nielsen

H. B.

, [

arXiv

[hep-ph]

] [

Search inSPIRE

Shaposhnikov

Wetterich

Phys. Lett. B

683

196

(

2010

) [

arXiv

[hep-th]

] [

Search inSPIRE

10.1016/j.physletb.2009.12.022

Crossref

Search ADS

Meissner

K. A.

Nicolai

Phys. Lett. B

660

260

(

2008

) [

arXiv

[hep-th]

] [

Search inSPIRE

10.1016/j.physletb.2007.12.035

Crossref

Search ADS

Khoze

V. V.

McCabe

J. High Energy Phys.

1408

026

(

2014

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1007/JHEP08(2014)026

Crossref

Search ADS

Kawai

Okada

Prog. Theor. Phys.

127

689

(

2012

) [

arXiv

[hep-th]

] [

Kawai

Int. J. Mod. Phys. A

1340001

(

2013

10.1142/S0217751X13400010

Crossref

Search ADS

Hamada

Kawai

Kawana

Int. J. Mod. Phys. A

1450099

(

2014

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1142/S0217751X14500997

Crossref

Search ADS

Hamada

Kawai

Kawana

, [

arXiv

[hep-ph]

] [

Search inSPIRE

Hamada

Kawai

Oda

K. y.

Prog. Theor. Exp. Phys.

2014

023B02

(

2014

) [

arXiv

[hep-ph]

] [

Hamada

Kawai

Oda

K. y.

Park

S. C.

Phys. Rev. Lett.

112

241301

(

2014

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1103/PhysRevLett.112.241301

Crossref

Search ADS

PubMed

Hamada

Kawai

Oda

K. y.

Park

S. C.

, [

arXiv

[hep-ph]

] [

Search inSPIRE

Hamada

Oda

K. y.

Takahashi

, [

arXiv

[hep-ph]

] [

Search inSPIRE

Kawamura

Prog. Theor. Exp. Phys.

2013

113B04

(

2013

) [

arXiv

[hep-ph]

] [

Meissner

K. A.

Nicolai

Phys. Lett. B

648

312

(

2007

) [

arXiv

[hep-th]

] [

Search inSPIRE

10.1016/j.physletb.2007.03.023

Crossref

Search ADS

Haba

Ishida

Kaneta

Takahashi

Phys. Rev. D

036006

(

2014

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1103/PhysRevD.90.036006

Crossref

Search ADS

Iso

Orikasa

Prog. Theor. Exp. Phys.

2013

023B08

(

2013

) [

arXiv

[hep-ph]

] [

Search inSPIRE

Hamada

Kawai

Oda

K. y.

J. High Energy Phys.

1407

026

(

2014

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1007/JHEP07(2014)026

Crossref

Search ADS

Haba

Takahashi

Phys. Rev. D

115009

(

2014

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1103/PhysRevD.89.115009

Crossref

Search ADS

Haba

Ishida

Takahashi

, [

arXiv

[hep-ph]

] [

Search inSPIRE

Buttazzo

Degrassi

Giardino

P. P.

Giudice

G. F.

Sala

Salvio

Strumia

J. High Energy Phys.

1312

089

(

2013

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1007/JHEP12(2013)089

Crossref

Search ADS

Moch

et al. , [

arXiv

[hep-ph]

] [

Search inSPIRE

ATLAS, CDF, CMS, and D0 Collaborations

, [

arXiv

[hep-ex]

] [

Search inSPIRE

Ade

P. A. R.

et al.

[Planck Collaboration]

Astron. Astrophys.

(

2014

) [

arXiv

[astro-ph.CO]

] [

Search inSPIRE

Cline

J. M.

Kainulainen

Scott

Weniger

Phys. Rev. D

055025

(

2013

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1103/PhysRevD.88.055025

Crossref

Search ADS

Hamada

Kawai

Oda

K. y.

Phys. Rev. D

053009

(

2013

) [

arXiv

[hep-ph]

] [

Search inSPIRE

10.1103/PhysRevD.87.053009

Crossref

Search ADS

Machacek

M. E.

Vaughn

M. T.

Nucl. Phys. B

222

(

1983

10.1016/0550-3213(83)90610-7

Crossref

Search ADS

Machacek

M. E.

Vaughn

M. T.

Nucl. Phys. B

236

221

(

1984

10.1016/0550-3213(84)90533-9

Crossref

Search ADS

Machacek

M. E.

Vaughn

M. T.

Nucl. Phys. B

249

(

1985

10.1016/0550-3213(85)90040-9

Crossref

Search ADS

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.Funded by SCOAP3

Download all slides

Month:	Total Views:
January 2017	8
February 2017	3
March 2017	5
July 2017	1
August 2017	4
October 2017	2
November 2017	2
December 2017	8
January 2018	5
February 2018	4
March 2018	11
April 2018	5
May 2018	2
June 2018	7
July 2018	14
August 2018	5
September 2018	3
October 2018	2
November 2018	12
December 2018	3
January 2019	6
February 2019	5
March 2019	10
April 2019	8
May 2019	13
June 2019	3
July 2019	11
August 2019	5
September 2019	10
October 2019	7
November 2019	8
December 2019	7
January 2020	11
February 2020	9
March 2020	4
April 2020	5
May 2020	3
June 2020	4
July 2020	1
August 2020	6
September 2020	4
October 2020	5
November 2020	8
December 2020	3
January 2021	1
February 2021	6
March 2021	4
April 2021	5
May 2021	4
June 2021	2
July 2021	3
August 2021	3
September 2021	2
October 2021	3
November 2021	8
December 2021	2
January 2022	5
February 2022	2
March 2022	3
April 2022	5
May 2022	2
June 2022	1
July 2022	7
August 2022	8
September 2022	8
October 2022	11
November 2022	3
December 2022	6
January 2023	9
February 2023	1
March 2023	1
April 2023	4
May 2023	4
July 2023	2
August 2023	2
September 2023	2
October 2023	5
November 2023	1
December 2023	3
January 2024	10
February 2024	5
March 2024	8
April 2024	8
May 2024	4
June 2024	12
July 2024	7
August 2024	5
September 2024	2
October 2024	4
November 2024	6
December 2024	2
January 2025	6
February 2025	3
March 2025	5
April 2025	4
May 2025	1

Article Contents

Multiple point principle of the Standard Model with scalar singlet dark matter and right-handed neutrinos

Abstract

1. Introduction

2. Preliminary: Multiple point principle of SM

3. MPP of the SM with scalar singlet dark matter and right-handed neutrinos

4. Summary

Funding

Acknowledgements

Appendix A. Two-loop renormalization group equations

Appendix B. Is an exact flat potential possible?

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Multiple point principle of the Standard Model with scalar singlet dark matter and right-handed neutrinos Open Access

Abstract

1. Introduction

2. Preliminary: Multiple point principle of SM

3. MPP of the SM with scalar singlet dark matter and right-handed neutrinos

4. Summary

Funding

Acknowledgements

Appendix A. Two-loop renormalization group equations

Appendix B. Is an exact flat potential possible?

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Multiple point principle of the Standard Model with scalar singlet dark matter and right-handed neutrinos