Entanglement of local operators in large-N conformal field theories

Abstract

In this paper, we study Renyi and von Neumann entanglement entropy of excited states created by local operators in large-|$N$| (or large-central-charge) conformal field theories (CFTs). First we point out that a naive large-|$N$| expansion can break down for the von Neumann entanglement entropy, while it does not for the Renyi entanglement entropy. This happens even for the excited states in free Yang–Mills theories. Next, we analyze strongly coupled large-|$N$| CFTs from both the field-theoretic and holographic viewpoints. We find that the Renyi entanglement entropy of the excited state, produced by a local operator, grows logarithmically under its time evolution and its coefficient is proportional to the conformal dimension of the local operator.

1. Introduction

The entanglement entropy (EE) and its generalization, called the Renyi entanglement entropy (REE), have been actively studied recently as a useful tool to understand quantum many-body systems and quantum field theories, as well as gravitational theories. In quantum systems, they play a role of good quantum order parameters that characterize the degrees of freedom hidden in various ground states. In particular, they also reveal essential properties in conformal field theories (CFTs) [1, 2] and topological field theories [3, 4]. One main advantage of considering entanglement entropy is that it offers us a geometrical interpretation of many basic properties of quantum systems. Indeed, this becomes manifest in the holographic entanglement entropy (HEE) [5–9] when we apply the AdS/CFT correspondence [10] or, more generally, the holographic principle [11–13].

To define the entanglement entropy, we divide the total space into two subregions |$A$| and |$B$| so that the total Hilbert space is factorized |$\mathcal {H} = \mathcal {H}_A \otimes \mathcal {H}_B$|⁠. We define the reduced density matrix |$\rho _A$| with respect to subsystem |$A$| from the original density matrix |$\rho$| by tracing out |$\mathcal {H}_B$| such that |$\rho _A = {\rm Tr}_{\mathcal {H}_B}\rho$|⁠. The |$n$|th Renyi entanglement entropy (REE) for subsystem |$A$| is defined by

\[S^{(n)}_A = \frac {\log {\rm Tr}[(\rho _A)^n]}{1- n }.\]

(1)

The (von Neumann) entanglement entropy (EE) is defined as the |$n \rightarrow 1$| limit:

\[S^{(1)}_A = -{\rm Tr}[\rho _A \log \rho _A].\]

(2)

So far, most works on entanglement entropy have focused on Renyi entanglement entropies for ground states. The main purpose of this paper is to offer a general picture of entanglement entropy for a simple class of excited states that are obtained by acting local operators on the vacua in CFTs. The studies for such local operator excitations were initiated in a slightly different setup in Ref. [14] and then Ref. [15]. We will pursue the latter approach in this paper. We are interested in the difference of |$S^{(n)}_A$| between the excited state and the ground state, denoted by |$\Delta S^{(n)}_A$|⁠. We choose subsystem |$A$| to be half of the total space. Recently, analytical calculations of |$\Delta S^{(n)}_A$| have been performed for massless free scalar fields in Refs. [15, 16] and rational 2D CFTs [17]. In the latter paper, it was proven that |$\Delta S^{(n)}_A$| coincides with the quantity called quantum dimension of the primary operator. The present paper will start with a brief review of these previous results so that readers can understand the whole picture.

However, these previous results were obtained in CFTs that do not have tractable holographic duals via AdS/CFT. Therefore, the main purpose of this work is to consider large-|$N$| gauge theories or large-|$c$| CFTs as they can possibly have holographic duals. We will perform both field-theoretic and holographic analyses and explain how they are consistent with each other. In particular, we would like to understand how the large-|$N$| limit affects the calculations of entanglement entropy. We will find that the behavior of von Neumann entanglement entropy |$(n=1)$| is rather different from that of Renyi entanglement entropy |$(n>1)$| with respect to the large-|$N$| scaling in our examples. Note that such a difference does not usually occur for ground states of CFTs, where both von Neumann and Renyi entropies scale as |$c\sim N^2$|⁠. Furthermore, in strongly coupled and large-|$N$| CFTs, our holographic and field-theoretic calculations suggest that more complicated subtlety appears in the |$n\rightarrow 1$| limit. At the same time we will find a new behavior of the time evolution of Renyi entanglement entropy that is peculiar to strongly coupled large-|$N$| CFTs.

To motivate our work further, note that a universal relation similar to the first law of thermodynamics, called the first-law-like relation [18–26], has been identified for an excited state produced by a small perturbation.¹ However, we cannot apply this to our problem as we choose subsystem |$A$| to be half of the total space and thus its size is much larger than the length scale of the excitation.

We would also like to mention that there are other classes of excited states that have been studied well, called quantum quenches [34, 35]. Refer to, e.g., Refs. [36–48] for their holographic dual calculations. Since quantum quenches are triggered by sudden changes of Hamiltonian, they generate infinitely many operators acting on the vacua. Therefore, we can say that our local operator excitations are milder and more elementary, though some computation techniques are common to both. One more interesting class will be excited states with energy fluxes. These are holographically dual to plane wave geometries and have been studied in Refs. [49–51].

This paper is organized as follows: In Sect 2 we will review the calculations of (Renyi) entanglement entropy of local operator excited states with a few pedagogical examples. In addition, we will present a brief analysis of the energy density of our excited states. In Sect. 3, we will study (Renyi) entanglement entropy of local operator excited states in a large-|$N$| free Yang–Mills theory. In Sect. 4, we will study the same entanglement entropy in 2D CFTs with a large central charge. In addition, we will give a review of previous results in rational 2D CFTs. In Sect. 5, we will perform a holographic computation of the Renyi entanglement entropy of the local operator excited states. In Sect. 6, we briefly mention a holographic result of von Neumann entanglement entropy for these excited states. In Sect. 7 we will summarize our results. In Appendix A, we present the details of calculations of |$2n$|-point functions in large-|$c$| 2D CFTs. In Appendix B, we give some details of geodesic calculations, used for the holographic analysis of Renyi entropy. In Appendix C, we present details of the direct computation of Renyi entropy of excited states in the free Yang–Mills theory.

2. Renyi entanglement entropy of local operator excited states

Here we give a brief review of replica method calculations of the (Renyi) entanglement entropy of local operator excited states following Refs. [15, 16] (see also Refs. [17, 52, 53]). For a basic construction of the replica method in quantum field theories refer to e.g. Ref. [2].

Consider a QFT in |$d$|-dimensional flat spacetime |$R^{1,d-1}$|⁠, whose time and |$d-1$|-dimensional space are denoted by |$t$| and |$x^i\ (i = 1, 2, \ldots , d - 1)$|⁠. We focus on an excited state |$|\Psi _O\rangle$| defined by acting a local operator |$O(\tau , x^i)$| on the vacuum state |$|0\rangle$| at a point |$x^i$| and time |$t = 0$| in a given QFT: |$|\Psi _O\rangle = O(0,x^i)|0\rangle$|⁠. Its time evolution under the Hamiltonian |$H$| is described by

\[|\Psi _O(t)\rangle = \sqrt {\mathcal {N}}\cdot e^{-iHt}e^{-\epsilon H}O(0,x^i)|0\rangle ,\]

(3)

where |$\mathcal {N}$| is a normalization and an infinitesimal parameter |$\epsilon$| is the regularization of the ultraviolet behavior of the local operator, which, as we will see later in Sect. 2.3, makes the energy of this excited state finite.

Now we choose the location of insertion of the local operator |$O$| to be

\[x^1 = -l(<0),\ (x^2, x^3, \ldots , x^{d-1}) = {\bf{x}},\]

(4)

at the time |$t = 0$|⁠. The final result does not depend on the choice of the vector |${\bf{x}}$| owing to the translational invariance.

We would like to compute the (Renyi) entanglement entropy |$S^{(n)}_A$| defined by (1) in the replica method (see e.g. Ref. [2]), performing the Euclidean continuation |$\tau = it$|⁠. To define the (Renyi) entanglement entropy, we choose subsystem |$A$| to be the half space |$x_1>0$|⁠. It is useful to introduce a complex coordinate as follows:

\[w = x^1 +i\tau , \quad \bar {w} = x^1 - i\tau .\]

(5)

The density matrix at real time |$t$| for the locally excited states (3) is written as

\[\begin {array}{rl} \rho (t) &= \mathcal {N}\cdot e^{-iHt}e^{-\epsilon H}O(0,x^i)|0\rangle \langle 0|O^{\dagger }(0, x^i)e^{-\epsilon H}e^{iHt} \\ &= \mathcal {N}\cdot O(w_2, \bar {w_2}, {\bf{x}})|0\rangle \langle 0| {O}^{\dagger }(w_1, \bar {w}_1, {\bf{x}}), \end {array}\]

(6)

where the normalization factor |$\mathcal {N}$| is determined by the condition |$\hbox {Tr}\rho (t) = 1$|⁠. Here we also defined

\[w_1 = i(\epsilon - it) - l, w_2 = -i(\epsilon +it) - l,\]

(7)

\[\bar {w}_1 = -i(\epsilon - it) - l, \quad \bar {w}_2 = i(\epsilon +it) - l.\]

(8)

Throughout the computation we treat |$\epsilon \pm it$| as purely real numbers until the end of the calculations as in Refs. [16, 34, 44].

Now, if we define |$\Delta S^{(n)}_A$| by subtracting the ground state result from |$S^{(n)}_A$|⁠, then |$\Delta S^{(n)}_A$| is computed as

\[\Delta S_A^{(n)} = \frac {1}{1 - n} \log \left (\frac {{\rm Tr} \rho _A^n}{{\rm Tr} (\rho ^{(0)}_{A})^n}\right ),\]

(9)

where |$\rho ^{(0)}_A$| is the ground state reduced density matrix.

By thinking of the path-integral description, as usual in the replica method, |$\Delta S_A^{(n)}$| can be expressed in terms of the correlation functions of an operator that excites the state [15, 16]:

\[\begin {array}{rl} \Delta S_A^{(n)} &= \frac {1}{1 - n}\left (\log \frac {Z_n}{Z^{(0)}_n} - n\log \frac {Z_1}{Z^{(0)}_1}\right ) \\ &= \frac {1}{1 - n} \left (\log {\left \langle O^{\dagger }(w_1, \bar {w}_1, {\bf{x}})O(w_2, \bar {w}_2, {\bf{x}})\cdots O(w_{2n}, \bar {w}_{2n}, {\bf{x}}) \right \rangle }_{\Sigma _n}\right ) \\ &\quad - \frac {n}{1-n} \left (\log {\left \langle O^{\dagger }(w_1, \bar {w}_1, {\bf{x}})O(w_2, \bar {w}_2, {\bf{x}})\right \rangle }_{\Sigma _1}\right ), \end {array}\]

(10)

where |$Z_n$| and |$Z^{(0)}_n$| corresponds to the partition functions on |$\Sigma _n$| such that |${\rm Tr} \rho _A^n = \frac {Z_n}{(Z_1)^n}$| and |${\rm Tr} (\rho ^{(0)}_{A})^n = \frac {Z^{(0)}_n}{(Z^{(0)}_1)^n}$|⁠. The |$n$|-sheeted |$d$|-dimensional space |$\Sigma _n$| is given by Fig. 1, where |$2n$| operators |$O$| and |$O^{\dagger }$| are located periodically as

\[w_{2k+1} = e^{2\pi ik} \cdot w_1, \quad w_{2k+2} = e^{2\pi ik}\cdot w_2.\]

(11)

The geometry of |$\Sigma _n$| is obtained by pasting |$n$| copies of the flat space |$R^{d}(=\Sigma _1)$| such that the angle at the origin |$w = \bar {w} = 0$| is extended from |$2\pi$| to |$2\pi n$|⁠. In other words, the metric of |$\Sigma _n$| is simply given by introducing the polar coordinate as |$w = \rho e^{i\theta }$|⁠:

\[ds^2 = d\rho ^2 + \rho ^2 d\theta ^2 + \sum _{i=2}^{d-1} (dx_i)^2,\]

(12)

with |$0 \leq \theta \leq 2\pi n$| and |$0 \leq \rho <\infty$|⁠.

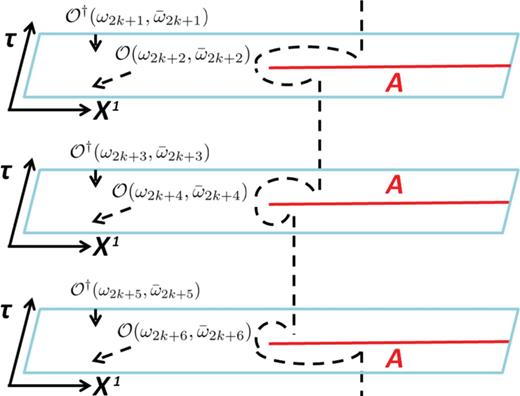
$The $n$-sheeted geometry $\Sigma _n$, constructed by gluing subsystem $A$ on a sheet to another subsystem $A$ on other sheet.$

Fig. 1.

The |$n$|-sheeted geometry |$\Sigma _n$|⁠, constructed by gluing subsystem |$A$| on a sheet to another subsystem |$A$| on other sheet.

Open in new tab Download slide

2.1. Free massless scalar field in four dimensions

As an example, consider a free massless scalar field |$\phi$| in four dimensions [15, 16]. We would like to briefly review the real time evolution of the Renyi entropy for the states excited by acting |$\phi$| on the ground state (see Ref. [16] for more details). The density matrix for such a state is defined by

\[\rho (t) = \mathcal {N}\cdot \phi (w_2, \bar {w}_2, {\bf{x}})\left |0\right \rangle \left \langle 0\right |\phi (w_1, \bar {w}_1, {\bf{x}}).\]

(13)

\[G_n(r, s, \theta , \theta ', {\bf{x}}, {\bf{x}}') = \frac {1}{4n\pi ^2 r s (a-a^{-1})} \frac {a^{\frac {1}{n}} - a^{-\frac {1}{n}}}{a^{\frac {1}{n}} +a^{-\frac {1}{n}}-2\cos {\frac {\theta -\theta '}{n}}},\]

(14)

where |$a$| is defined by

\[\frac {a}{1+a^2} = \frac {r s}{\left |{\bf{x}} - {\bf{x}}'\right |^2+r^2+s^2}.\]

(15)

Then we perform an analytic continuation (7) and (8) to study the real time evolution.

\[{\left \langle \phi (w_1, \bar {w}_1, {\bf{x}}) \phi (w_2, \bar {w}_2, {\bf{x}})\right \rangle }_{\Sigma _1} = \frac {1}{16\pi ^2 \epsilon ^2}.\]

(16)

In this way, we can evaluate the Renyi entanglement entropy for the locally excited states (13) by the replica method. Below we would like to show the final results for |$n=2$| and |$n=3$|⁠:

\[\Delta S^{(2)}_A = \left\{ \begin {array}{ll}0 &0 <t <l, \\ \log 2 - \log \left [1 + \dfrac {l^2}{t^2}\right ] &t \ge l, \\ \end {array}\right .\]

(17)

and

\[\Delta S^{(3)}_A = \left\{ \begin {array}{ll}0 &0 <t <l, \\ -\dfrac {1}{2} \log \left [\dfrac {1}{4} + \dfrac {3 l^2}{4 t^2}\right ] &t \ge l. \end {array}\right .\]

(18)

The time evolution of these Renyi entropies is plotted in Fig. 2.

$The plots of $\Delta S^{(2)}_A$ (green) and $\Delta S^{(3)}_A$ (blue) as functions of the time $t$ in the $\epsilon \rightarrow 0$ limit (we chose $l=10$). The red horizontal corresponds to the late time value $\log {2}$.$

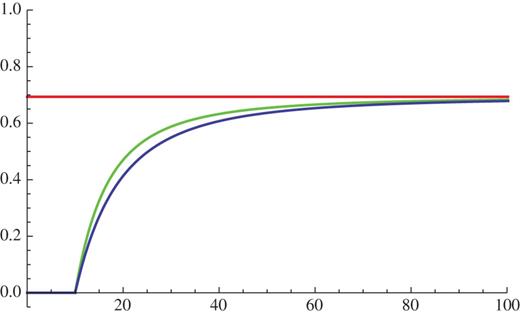
Fig. 2.

The plots of |$\Delta S^{(2)}_A$| (green) and |$\Delta S^{(3)}_A$| (blue) as functions of the time |$t$| in the |$\epsilon \rightarrow 0$| limit (we chose |$l=10$|⁠). The red horizontal corresponds to the late time value |$\log {2}$|⁠.

Open in new tab Download slide

In the |$\epsilon \rightarrow 0$| limit and at late time, the final value of the second and third Renyi entanglement entropies is given by

\[\Delta S^{(2)}_A \rightarrow \log 2, \quad \Delta S^{(3)}_A \rightarrow \log 2.\]

(19)

Moreover, we can prove the same result |$\Delta S^{(n)}_A$| for any |$n$| [16]. This entropy |$\log 2$| coincides with that of an Einstein-Podolsky-Rosen (EPR) state (maximally entangled state of two spins). Indeed, we can explain this in terms of an entangled pair. We decompose |$\phi$| to the left-moving mode and the right-moving mode,

\[\phi = \phi _L + \phi _R.\]

(20)

After taking into account the normalization, the locally excited state is expressed by

\[\left | \Psi _\phi \right \rangle = \frac {1}{\sqrt {2}}\phi _L {\left |0\right \rangle }_L \otimes {\left |0\right \rangle }_R + \frac {1}{\sqrt {2}} {\left |0\right \rangle }_L\otimes \phi _R {\left |0\right \rangle }_R.\]

(21)

Thus this expression (21) manifestly shows that the excited state at late time becomes an EPR state [15, 16]. This is because the division of the total space into two halves |$A$| and |$B$| implies that, in the late time limit |$t \rightarrow \infty$|⁠, two parts of the entangled pair propagate in opposite (left and right) directions.

More generally, if we consider an excited state obtained by acting |$\phi ^k$| on the ground state, it can be written as

\[\left |\Psi _{\phi ^k}\right \rangle = \frac {1}{2^{\frac {k}{2}}}\sum ^{k}_{m=0}\sqrt {_k C_m}{\left |m\right \rangle }_A \otimes {\left |k-m\right \rangle }_B,\]

(22)

where |$_k C_m=\frac {k!}{m!(k-m)!}$|⁠. From this expression, it is straightforward to evaluate the finite value of |$\Delta S^{(n)}_A$| at late time. In Ref. [16], it was proved that this evaluation precisely matches that obtained from the replica calculation (10).

2.2. 2D CFTs and free scalar example

As another simple example, let us consider 2D CFTs and study the replica calculations in explicit examples. We focus on an excited state that is defined by acting a primary operator |$O$| on the vacuum |$|0\rangle$| in a given 2D CFT. The (chiral) conformal dimension of this operator is defined as |$\Delta _O$|⁠. We employ the Euclidean formulation and introduce the complex coordinate

\[(w,\bar {w}) = (x +i\tau , x - i\tau )\]

(23)

on |$R^2$| such that |$\tau$| and |$x$| are the Euclidean time and the space, respectively. We insert the primary operator |$O$| at |$x=-l<0$| and consider its real time evolution from time |$0$| to |$t$| under the Hamiltonian |$H$|⁠. This process is described by the following density matrix:

\[\begin {array}{rl} \rho (t) &= \mathcal {N} \cdot e^{-iHt}e^{-\epsilon H}O(-l)|0\rangle \langle 0|O^{\dagger }(-l)e^{-\epsilon H}e^{iHt} \\ &= \mathcal {N} \cdot O(w_2, \bar {w}_2)|0\rangle \langle 0| O^{\dagger }(w_1, \bar {w}_1), \end {array}\]

(24)

where the normalization factor |$\mathcal {N}$| is again determined by the normalization condition |$\hbox {Tr}\rho (t) = 1$|⁠. Note that (24) is simply the 2D version of (6) and we defined |$w_1$| and |$w_2$| as in (7) and (8). An infinitesimal positive parameter |$\epsilon$| is again an ultraviolet regularization and we treat |$\epsilon \pm it$| as purely real numbers until the end of the calculations as in Refs. [16, 34, 44].

To calculate |$\Delta S^{(n)}_A$|⁠, we employ the replica method in the path-integral formalism that we explained in the previous subsection. We choose subsystem |$A$| to be an interval |$0\leq x\leq L$| at |$\tau =0$|⁠. The replica method calculation involves the partition function on a |$n$|-sheeted Riemann surface |$\Sigma _n$| with |$2n$| operators |$O$| and its conjugate. In the end, we find that |$\Delta S_A^{(n)}$| can be computed as

\[\begin {array}{rl} \Delta S_A^{(n)} &= \frac {1}{1-n} \Biggl [\!\log {\left \langle {O}^{\dagger }_a(w_l,\bar {w}_1)O(w_2,\bar {w}_2) \cdots O(w_{2n},\bar {w}_{2n})\right \rangle }_{\Sigma _n} \\ &\quad - n\log {\left \langle {O}^{\dagger }(w_l,\bar {w}_1)O(w_2,\bar {w}_2)\right \rangle }_{\Sigma _1}\!\!\Biggr ] \end {array}\]

(25)

where |$(w_{2k+1}, w_{2k+2})$| for |$k = 1, 2, \ldots , n - 1$| are |$n-1$| replicas of |$(w_1,w_2)$| in the |$k$|th sheet of |$\Sigma _n$|⁠. The first term in the second line is given by a |$2n$|-point correlation function on |$\Sigma _n$|⁠. The second term is a two-point function on |$\Sigma _1=R^2$| and we normalized this such that

\[\langle O^{\dagger }(w_1,\bar {w}_1)O(w_2,\bar {w}_2)\rangle _{\Sigma _1} = |w_{12}|^{-4\Delta _O} = (2\epsilon )^{-4\Delta _O},\]

(26)

which is equal to |$\mathcal {N}^{-1}$|⁠.

Now we would like to focus on the second Renyi entropy |$\Delta S^{(2)}_A$|⁠. Please refer to Ref. [17] for more details. Let us apply the conformal transformation:

\[w/(w - L) = z^n,\]

(27)

which maps |$\Sigma _n$| into |$\Sigma _1$|⁠. By employing (7) and (8) with |$n=2$|⁠, we find that |$(z_i, \bar {z}_i)$| are given by

\[\begin {array}{rl} z_1 &= -z_3 = \sqrt {(l - t - i \epsilon )/(l +L - t - i \epsilon )}, \\ z_2 &= -z_4 = \sqrt {(l - t +i \epsilon )/(l +L - t +i \epsilon )}. \end {array}\]

(28)

Moreover, the cross-ratios are |$z = z_{12}z_{34}/(z_{13}z_{24})$|⁠, |$\bar {z} = \bar {z}_{12}\bar {z}_{34}/(\bar {z}_{13}\bar {z}_{24})$|⁠, where |$z_{i j} = z_i - z_j$|⁠. Consider now the behavior of |$(z, \bar {z})$| in the limit |$\epsilon \rightarrow 0$|⁠. When |$0 <t <l$| or |$t >L +l$|⁠, one can show that |$(z, \bar {z}) \rightarrow (0,0)$| as

\[z \simeq \frac {L^2\epsilon ^2}{4(l - t)^2 (L +l - t)^2}, \quad \bar {z} \simeq \frac {L^2\epsilon ^2}{4(l+t)^2(L+l+t)^2}.\]

(29)

In the other case |$l <t <L +l$|⁠, we find that |$(z, \bar {z}) \rightarrow (1, 0)$|⁠:

\[z \simeq 1 - \frac {L^2 \epsilon ^2}{4(l-t)^2(L+l-t)^2}, \quad \bar {z}\simeq \frac {L^2\epsilon ^2}{4(l+t)^2(L+l+t)^2}.\]

(30)

Though the limit |$(z,\bar {z}) \rightarrow (1,0)$| does not satisfy the complex conjugation, it inevitably arises due to the analytical continuation of |$t$|⁠.

Owing to the conformal symmetry, the four-point function on |$\Sigma _1$| can be written as

\[\begin {array}{rl} &\langle O^{\dagger }(z_1, \bar {z}_1)O(z_2, \bar {z}_2) O^{\dagger }(z_3, \bar {z}_3) O(z_4, \bar {z}_4)\rangle _{\Sigma _1} \\ &\quad = |z_{13}z_{24}|^{-4\Delta _O} \cdot G(z,\bar {z}). \end {array}\]

(31)

Applying the conformal map (27), we obtain the four-point function on |$\Sigma _2$|⁠:

\[\begin {array}{rl} &\langle O^{\dagger }(w_1,\bar {w}_1)O(w_2,\bar {w}_2)O^{\dagger }(w_3,\bar {w}_3)O(w_4,\bar {w}_4)\rangle _{\Sigma _n} \\ &\quad = \prod _{i=1}^{4}\left |dw_i/dz_i\right |^{-2 \Delta _O } \langle O^{\dagger }(z_1,\bar {z}_1)O(z_2,\bar {z}_2)O^{\dagger }(z_3, \bar {z}_3)O(z_4,\bar {z}_4)\rangle _{\Sigma _1} \\ &\quad = (4L)^{-8\Delta _O} \left |(z_1^2 - 1) (z_2^2 - 1)/(z_1z_2) \right |^{8\Delta _O} \cdot G(z,\bar {z}). \end {array}\]

(32)

Using this and (26), the relevant ratio that we need to compute |$\Delta S^{(2)}_A$| is expressed as

\[\begin {array}{rl} &\frac {\langle O^{\dagger }(w_1, \bar {w}_1)O(w_2, \bar {w}_2)O^{\dagger }(w_3, \bar {w}_3)O(w_4, \bar {w}_4) \rangle _{\Sigma _n}}{\left (\langle O^{\dagger }(w_1, \bar {w}_1)O(w_2, \bar {w}_2)\rangle _{\Sigma _1}\right )^2} \\ &\quad = |z|^{4\Delta _O}|1 - z|^{4\Delta _O} \cdot G(z,\bar {z}). \end {array}\]

(33)

For example, consider a |$c = 1$| CFT defined by a massless free scalar |$\phi$|⁠. Let us choose operators

\[O_1 = e^{\frac {i}{2} \phi },\ \ \ O_2=(e^{\frac {i}{2} \phi } +e^{-\frac {i}{2} \phi })/\sqrt {2},\]

(34)

which have a common conformal dimension |$\Delta _1 = \Delta _2 = \frac {1}{8}$|⁠. The functions |$G(z, \bar {z})$| for |$O_1$| and |$O_2$| can be computed as follows:

\[\begin {array}{rl} G_1(z, \bar {z}) &= 1/\sqrt {\left | z \right | \left | 1 - z \right |}, \\ G_2(z, \bar {z}) &= (|z| +1 + |1 - z|)\cdot G_1(z, \bar {z})/2, \end {array}\]

(35)

respectively. It is obvious that for the operator |$O_1$| the Renyi entropy vanishes at all times |$\Delta S^{(2)}_A = 0$|⁠. For |$O_2$|⁠, taking into account the two periods (29) and (30), we get

\[\Delta S^{(2)}_A = \left\{ \begin {array}{ll}0 &\left (0 <t <l, \ {\rm or}\ \ t >l +L\right ), \\ \log 2 &\left (l <t <l +L\right ). \end {array}\right .\]

(36)

Now let us give a heuristic interpretation of these results in the |$c=1$| CFT. First of all, it is clear that we will always get the trivial result |$\Delta S^{(n)}_A$| for the time |$0<t<l$| and |$t>l+L$| [17] (we will review this proof in Sect. 4.1). This is because the local operator creates an entangled pair(s) at |$x=-l$| and each half of the pairs propagates in the opposite direction at the speed of light. However, for the times |$0<t<l$| and |$t>l+L$|⁠, all of them are inside subsystem |$B$|⁠. Therefore they do not contribute to the quantum entanglement between |$A$| and |$B$|⁠.

On the other hand, during the time |$l<t<t+L$|⁠, |$\Delta S^{(n)}_A$| can be non-trivial because half of the entangled pairs are situated in |$A$| and the other half are in |$B$|⁠. The ones in |$A$| (and |$B$|⁠) consist of the right-moving (and left-moving) mode, respectively.

Now we obtain the trivial result for |$O_1$| even during the time |$l<t<t+L$|⁠. This is because the excited state |$e^{\frac {i}{2}\phi }|0\rangle$| can be regarded as a direct product state

\[e^{\frac {i}{2}\phi _L}|0\rangle _L\otimes e^{\frac {i}{2}\phi _R}|0\rangle _R,\]

(37)

in the left-moving (⁠|$L$|⁠: chiral) and right-moving (⁠|$R$|⁠: anti-chiral) sector [44]. This is, of course, not an entangled state. In contrast, |$O_2$| creates a maximally entangled state (or equally EPR state):

\[\frac {1}{\sqrt {2}}\left (e^{\frac {i}{2}\phi _L}|0\rangle _L\otimes e^{\frac {i}{2}\phi _R}|0\rangle _R +e^{-\frac {i}{2}\phi _L}|0\rangle _L \otimes e^{-\frac {i}{2}\phi _R}|0\rangle _R\right ),\]

(38)

which produces the Renyi entanglement entropy |$\log 2$| for any |$n$|⁠. This explains the behavior (36).

We will continue the analysis of |$\Delta S^{(n)}_A$| in general cases including large-central-charge CFTs in Sect. 4.

2.3. Analysis of energy density

Before we go on, we would like to briefly comment on the behavior of energy density |$T_{tt}$|⁠. For simplicity, consider a 2D CFT on the 2D Euclidean flat space |$R^2=\Sigma _1$| and employ the coordinate |$(w,\bar {w})=(x+i\tau ,x-i\tau )$| defined in the previous subsection. We create an excited state by inserting a primary operator |$O$| at |$x=-l<0$| so that the time evolution of the density matrix looks like (24).

In this setup, the energy density of this excited state at |$(z,\bar {z}) = (x,x)$| after the time |$t$| can be found as

\[\begin {array}{rl} \langle T_{tt}\rangle &= \frac {\langle O^\dagger (w_2,\bar {w}_2)T_{tt}(x,x)O(w_1,\bar {w}_1)\rangle }{\langle O^\dagger (w_2,\bar {w}_2)O(w_1,\bar {w}_1)\rangle } \\ &= \Delta _O \epsilon ^2\left [\frac {1}{\left ((x+l-t)^2+ \epsilon ^2\right )^2} + \frac {1}{\left ((x+l+t)^2+ \epsilon ^2\right )^2}\right ], \end {array}\]

(39)

where |$(w_i, \bar {w}_i)$| have already been defined in (7) and (8).

\[\Delta E_A=\int _{x\in A} dx T_{tt}(x)\sim \frac {\Delta _O}{\epsilon },\]

(40)

up to an overall factor. This gets divergent in the point-like limit |$\epsilon \rightarrow 0$|⁠.

One may think that it will be useful if we can find any direct relation between the excitation energy and the entanglement entropy growth. In particular cases, such a relation is known and is called the first-law-like relation. Here the first law means a linear relation between the change of entanglement entropy |$\Delta S^{(1)}_A$| and that of energy |$\Delta E_A=\int _{x\in A} dx^d T_{tt}(x)$| or energy density |$\Delta T_{tt}$| in subsystem |$A$|⁠. The first-law-like relation was first found in Ref. [18] by using the holographic entanglement entropy [5–9] for any choice of subsystem |$A$|⁠, assuming translational invariance. This relation is expressed as follows:

\[\Delta E_A\simeq T_{A}\cdot \Delta S^{(1)}_A,\]

(41)

where the “effective temperature” |$T_{A}$| scales like |$T_A=\frac {C_A}{L}$| using the linear size |$L$| of subsystem |$A$|⁠. The coefficient |$C_A$| depends on the shape of |$A$|⁠. We can apply this formula only for small excitations such that |$L^{d+1}T_{tt}\ll 1$|⁠. Refer also to Refs. [21–26] for more holographic calculations.

Remarkably, this was extended to general inhomogeneous cases in Refs. [19, 20] by employing the analysis of conformal transformation [54]. When subsystem |$A$| is given by a round ball |$|x|\leq L/2$| with the radius |$L/2$|⁠, the relation

\[\Delta S^{(1)}_A\simeq \int _{|x|\leq L/2} dx^d \left (\frac {L^2/4-|x|^2}{L}\right ) T_{tt}(x)\]

(42)

was shown for small excitations in any |$d+1$|-dimensional CFT, even without assuming holography.

Therefore, one might think that we may compute |$\Delta S^{(1)}_A$| from the energy increase by using this first-law-like relation. However, this is not the case, as we explain below. Indeed, when |$l - L/2 <t <l +L/2$|⁠, the right-hand side of (42) can be estimated as follows:

\[\int _{|x|\leq L/2} dx \left (\frac {L^2/4-|x|^2}{L}\right ) T_{tt}(x)\sim \frac {\Delta _O (L^2/4-(t-l)^2)}{L\epsilon }.\]

(43)

up to an overall factor.

If we naively apply the first law (42), we will be in trouble because |$\Delta S^{(1)}_A$| gets divergent in the |$\epsilon \rightarrow 0$| limit. This contradicts the fact that, in 2D rational CFTs [17], |$\Delta S^{(1)}_A$| should be equal to the log of the quantum dimension that is finite. Indeed, we can easily see why the first law (42) breaks down, because the energy |$\Delta E_A$| gets divergent as in (40) and thus should not be regarded as a small excitation². Nevertheless, we would like to mention that, if we keep |$\epsilon$| large, then we can apply the first law because the energy density gets very small, although we are not interested in such a situation in this paper.

3. Excited states in large-|$N$| free Yang–Mills

Here we would like to compute the |$n$|th Renyi entanglement entropy in free |$U(N)$| gauge theory in four dimensions. We are interested in excited states that are obtained by acting the following gauge-invariant local operators:

\[{\rm Tr} \mathcal {Z}^J ={\rm Tr} (\phi _1+i\phi _2)^J,\]

(44)

on the vacuum. Here |$\phi _{1}$| and |$\phi _2$| represent two real massless scalar fields in |$R^{1,3}$|⁠, which belongs to the adjoint representation. In this work we assume that |$J\sim O(1)$|⁠, but it will be an interesting future problem to repeat our analysis for operators with large |$J$| (of the order of some powers of |$N$|⁠).

3.1. Replica method calculations

In the large-|$N$| limit, the leading contributions come from only disconnected planar diagrams. Then the two-point function on |$\Sigma _n$| is approximated by³

\[\left \langle {\it{Tr}} \mathcal {Z}^J(w, \bar {w},{\bf{x}}) {\it{Tr}} \bar {\mathcal {Z}}^J(w', \bar {w}', {\bf{x}}')\right \rangle = {\it{JN}}^{J} (G_{n})^J + (1/N\ {\rm corrections}),\]

(45)

where the Green function |$G_n$| is defined by (14) in Sect. 2.

In the large-|$N$| limit, the |$2n$|-point function in the replica formula (10) is at most |$\mathcal {O}(N^{J n})$|⁠. Various disconnected diagrams of planar diagrams can contribute to the |$2n$|-point function of |$Tr \mathcal {Z}^J$|⁠. However, we can show that only two disconnected diagrams, which are depicted in Fig. 3 (for an |$n=4$| example), can contribute to |$\Delta S^{(n)}_A$| in the limit |$\epsilon \rightarrow 0$|⁠, as pointed out in Ref. [16].

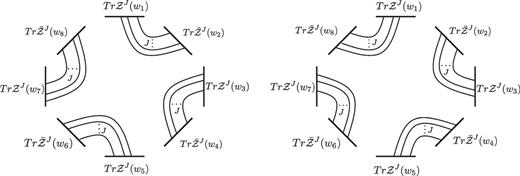
$The two dominant diagrams for the $4$th Renyi entanglement entropy $\Delta S^{(4)}_A$ in the large-$N$ and $\epsilon \rightarrow 0$ limits.$

Fig. 3.

The two dominant diagrams for the |$4$|th Renyi entanglement entropy |$\Delta S^{(4)}_A$| in the large-|$N$| and |$\epsilon \rightarrow 0$| limits.

Open in new tab Download slide

One of them corresponds to the product of the propagators between two points on the same sheet (remember Fig. 1). Another one is the product of the propagators between |$w_{2k}$| and |$w_{2k+1}$|⁠, where |$k$| runs from |$1$| to |$n$|⁠.

In this way, the leading term of |$\Delta S^{(n)}_A$| is computed as

\[\Delta S^{(n)}_A = \left\{ \begin {array}{ll}0 &t <l, \\ \dfrac {\log {\left [\frac {J^n N^{n J} \left (\frac {l+t}{32 \pi ^2 t \epsilon ^2}\right )^{n J} +J^n N^{n J}\left (\frac {-l+t}{32 \pi ^2 t \epsilon ^2}\right )^{n J}}{J^n N^{n J}\left (\frac {1}{16 \pi ^2 \epsilon ^2}\right )^{n J}}\right ]}}{1-n} = -\dfrac {\log {\left [2^{-J n} \left (\left (1-\frac {l}{t}\right )^{J n} + \left (\frac {l+t}{t}\right )^{J n}\right )\right ]}}{-1 +n} &t \ge l. \end {array}\right .\]

(46)

Moreover, if we take the late time limit |$t \rightarrow \infty$|⁠, the final value of Renyi entropy is given by

\[\Delta S^{(n)}_A = \frac {(J n-1) \log {2}}{n-1}.\]

(47)

The time evolution of |$\Delta S^{(2)}_A$| for |$J=3$| is plotted in Fig. 4. We immediately notice that |$\Delta S^{(n)}$| diverges in the von Neumann entropy limit |$n=1$|⁠. As we explain later by using a different method, this problem occurs because we ignore the higher-order terms in the large-|$N$| expansion, which becomes important only in the |$n=1$| limit. We can find from this observation that we can trust the leading-order result (46) iff |$n >1$|⁠.

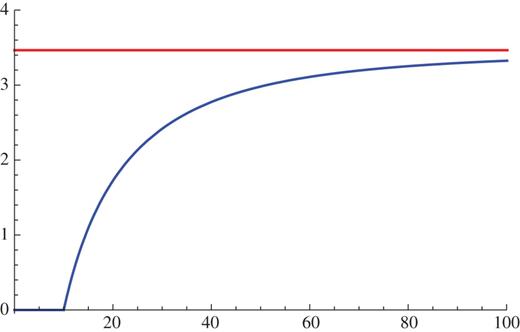
$Plot of $\Delta S^{(2)}_A$ (blue) as a function of $t$ in the $\epsilon \rightarrow 0$ limit. Here we chose $l=10$, $n=2$, and $J=3$. The red line corresponds to the late time value $5\log {2}$.$

Fig. 4.

Plot of |$\Delta S^{(2)}_A$| (blue) as a function of |$t$| in the |$\epsilon \rightarrow 0$| limit. Here we chose |$l=10$|⁠, |$n=2$|⁠, and |$J=3$|⁠. The red line corresponds to the late time value |$5\log {2}$|⁠.

Open in new tab Download slide

3.2. Left–right decomposition and entangled pair interpretation

There is another method to compute the late time limit of |$\Delta S^{(n)}_A$| by using the structures of excited states [15, 16]. We can regard an excited state produced by a local operator in a CFT as a combination of creation operators acting on the left-moving vacuum |$|0\rangle _L$| and the right-moving one |$|0\rangle _R$| in the product Hilbert space |$\mathcal {H}_L\otimes \mathcal {H}_R$|⁠. Thus, when we insert the local operator, this creates an entangled pair and each half of the pair will propagate in the left or right direction. At late time, one of them will be in subsystem |$A$| and the other in subsystem |$B$|⁠. Thus the excited state will have a non-trivial quantum entanglement at late time. Therefore, we can compute the Renyi entropy |$\Delta S^{(n)}_A$| directly from the reduced density matrix obtained by tracing out the left-moving (or right-moving) part.

In this section, we apply this analysis to our trace operators (44) built out of matrices in 4D CFTs with the |$U(N)$| gauge group. By decomposing the |$U(N)$| scalar field |$\phi$| into the left- and right-moving modes as in (20), we can express our excited states as follows:

\[\left |\Psi _{{\rm Tr}[\phi ^J]}\right \rangle \equiv {\rm Tr}\left [(\phi _L+ \phi _R)^J\right ]\left |0_L\right \rangle \left |0_R\right \rangle ,\]

(48)

where we take |$\phi _{L/R}$| to be |$N\times N$| matrices with the Wick contraction rule

\[\langle \left (\phi _A\right )^\alpha _\beta \left (\phi _B\right )^\mu _\nu \rangle = \delta _{AB}\,\delta ^\alpha _\nu \delta ^\mu _\beta , \quad A,B\in {\{ }L,R{\} }.\]

(49)

The corresponding density matrix in |$\mathcal {H}_{L}\otimes \mathcal {H}_R$| space is

\[\rho _{L\cup R} = \left | \Psi _{{\rm Tr}[\phi ^J]} \right \rangle \left \langle \Psi _{{\rm Tr}[\phi ^J]}\right |.\]

(50)

We can then trace over |$\mathcal {H}_L$| and, using the replica method, evaluate the Renyi entropy of |$\rho _R={\rm Tr}_L\left (\rho _{L\cup R}\right )$| as

\[\Delta S^{(n)}_R=\frac {1}{1-n}\log {\rm Tr} \rho ^n_R.\]

(51)

As a warm up, consider the |$J=1$| case in which the excited state is simply

\[\left | \Psi _{{\rm Tr}[\phi ]}\right \rangle \propto \left (\left | {\rm Tr}(\phi _L)\right \rangle \left | 0_R \right \rangle + \left | 0_L \right \rangle \left | {\rm Tr}(\phi _R) \right \rangle \right ).\]

(52)

The orthonormal basis in |$\mathcal {H}_L$| (also |$\mathcal {H}_R$|⁠) has two normalized states, the vacuum and a state obtained by acting with a single trace,

\[\left\{ \left | 0_{L}\right \rangle , \frac {1}{\sqrt {N}} \left | {\rm Tr}(\phi _{L}) \right \rangle \right\} ,\]

(53)

where the normalization of the single trace state can be deduced from (49). Tracing over |$\mathcal {H}_L$| gives the reduced density matrix in |$\mathcal {H}_R$|

\[\rho _R = \frac {1}{2}\left | 0 \right \rangle \left \langle 0 \right | + \frac {1}{2N}\left | {\rm Tr}(\phi _{R}) \right \rangle \left \langle {\rm Tr}(\phi _{R})\right |,\]

(54)

which after normalization to |${\rm Tr} (\rho ) = 1$| becomes |$\rho _R = {\text {diag}}\left (\frac {1}{2}, \frac {1}{2}\right )$|⁠. Finally, the |$n$|th Renyi entanglement entropy for the state excited by |${\rm Tr}(\phi )$| is given by

\[\Delta S^{(n)}_R = \frac {1}{1-n}\log \left (2^{1-n}\right ) = \log (2).\]

(55)

It is easy to see that |$\left | \Psi _{{\rm Tr}[\phi ]} \right \rangle$| in |$\mathcal {H}_L\otimes \mathcal {H}_R$| is equivalent to the EPR state; therefore, all the Renyi entropies are equal to |$\log 2$|⁠, which is the entropy of the maximally entangled state. Note that this result is the same as the |$N=1$| case reviewed in Sect. 2.1. This is simply because we can treat |${\rm Tr}[\phi ]$| as a single real scalar field by diagonalizing the Hamiltonian of the system.

The situation becomes more interesting once we consider the traces of products of matrices. For |$J=2$|⁠, the excited state is given by

\[\left | \Psi _{{\rm Tr}[\phi ^2]} \right \rangle \propto \left | {\rm Tr}\phi ^2_L \right \rangle \left | 0_R \right \rangle + \left | 0_L \right \rangle \left | {\rm Tr}\phi ^2_R \right \rangle +2\sum ^{N}_{\alpha ,\beta =1}\left | \left (\phi _L\right )^\alpha _\beta \right \rangle \left | \left (\phi _R\right )^\beta _\alpha \right \rangle ,\]

(56)

where in the third term we explicitly wrote the indices in |${\rm Tr}(\phi _L\phi _R)\left | 0_L \right \rangle \left | 0_R \right \rangle$|⁠.

The Hilbert space |$\mathcal {H}_L$| consists of the vacuum, the state obtained by the action of |${\rm Tr}(\phi ^2_L)$|⁠, and the |$N^2$| states |$\left | \left (\phi _L\right )^{\alpha }_\beta \right \rangle$|⁠, all with appropriate normalizations. Tracing out |$\mathcal {H}_L$| and normalizing gives the reduced density matrix in |$\mathcal {H}_R$|⁠:

\[\rho _R = \hbox {diag}\left (\frac {1}{4}, \frac {1}{4}, \frac {\vec {1}}{2N^2}\right ),\]

(57)

where |$\vec {1}$| is the |$N^2$|-dimensional unit vector. Using the replica trick, we again obtain the |$n$|th Renyi entropies

\[\Delta S^{(n)}_R = \frac {1}{1-n}\log \left (2^{1-2n}+ \frac {1}{2^nN^{2(n-1)}}\right ).\]

(58)

Notice now the striking difference between Renyi entropies with |$n\ge 2$| and the von Neumann entropy for |$n=1$|⁠. For |$n\ge 2$| and large |$N$|⁠, we can simply neglect the |$1/N$| corrections and the leading result is

\[\Delta S^{(n\ge 2)}_R\simeq \frac {2n-1}{n-1}\cdot \log 2.\]

(59)

This perfectly matches with (47) obtained in the large-|$N$| limit using free-field Wick contractions.

However, in the limit |$n = 1$|⁠, the von Neumann entropy is equal to

\[\Delta S^{(1)}_R = \log \left (2\sqrt {2}N\right ),\]

(60)

\[{\rm Tr} \rho ^n_R=2^{1-Jn} + \frac {(J-1)J^n}{2^{Jn}N^{2(n-1)}}+O(1/N^{4(n-1)})\]

(61)

and the Renyi entropies⁵

\[\Delta S^{(n)}_R \sim \frac {J\,n-1}{n-1}\log 2\]

(62)

perfectly match the leading order of the replica calculation (47). It is also interesting to point that the min-entropy |$(n\rightarrow \infty )$| shows a universal behavior

\[\Delta S^{(\infty )}_R \sim J\log 2.\]

(63)

For the von Neumann entropy, we cannot neglect the |$1/N$| corrections and we need to take into account other terms that can contribute as |$n\rightarrow 1$|⁠. Nevertherless, we can again estimate it as

\[\Delta S^{(1)}_R\sim J\log N,\]

(64)

up to a certain |$O(1)$| constant.

It is intriguing that we observe the |$\log N$| entropy only for the von Neumann entropy. The scalar field is |$N\times N$| matrix-valued and its almost maximally entangled state can produce the |$\log N$| entropy. Furthermore, since there are |$J$| scalar operators in Tr|$[\phi ^J]$|⁠, then we can easily understand (64). However, a lesson we learned here is that this naive argument cannot be applied to the Renyi entropies. If we roughly regard |$n$| as the inverse temperature, we might say that the result of von Neumann entropy |$n=1$| looks “deconfined”, while those for Renyi entropies |$n=2,3,\ldots$| looks “confined” as the former corresponds to a higher temperature than the latter. We hope to understand this “transition”-like behavior better in our future work.

4. 2D CFT at large |$c$|

Now we turn to 2D CFTs (2D CFTs) having in mind the AdS|$_3/$|CFT|$_2$| correspondence. We will follow the formulation explained in Sect. 2.2. In order to have the possibility of a classical gravity dual, we are interested in taking the large-|$c$| limit, where |$c$| is the central charge of a CFT.

4.1. General arguments

The function |$G(z,\bar {z})$| defined in (31) is the essential part of the four-point function. Owing to the holomorphic/anti-holomorphic factorization, this function can be written as a sum of conformal blocks [67]:

\[G(z,\bar {z})=\sum _{b}(C^{b}_{OO^\dagger })^2F_O(b|z)\bar {F}_O(b|\bar {z}).\]

(65)

The index |$b$| corresponds to each |$\phi _b$| of all Virasoro primary fields; note that they are decomposed into left-moving (chiral) and right-moving (anti-chiral) primary fields. Thus we can write |$b$| as |$(b_L,b_R)$|⁠, corresponding to |$\phi _b(z,\bar {z})=\phi _{b_L}(z)\phi _{b_R}(\bar {z})$|⁠. We assume that the summation over |$b$| is a discrete sum, as is true in typical AdS/CFT examples.

How to take this summation of |$b=(b_L,b_R)$| depends on the spectrum of 2D CFT that we consider. One simple class of CFTs, such as rational CFTs, is defined by the diagonal sum |$b_L=b_R(\equiv a)$|⁠, where the total Hilbert space is given by

\[\mathcal {H}=\oplus _{a}\left (\mathcal {H}^{(a)}_{L}\otimes \mathcal {H}^{(a)}_{R}\right ).\]

(66)

However, in general, this is not the case because there are generators other than the Virasoro operators. For example, if we consider the current algebra or equally the WZW model, (66) is correct only if we regard the index |$a$| as that for all primary fields of current algebra instead of Virasoro algebra.

\[F_O(b|z)\rightarrow z^{\Delta _b-2\Delta _O},\]

(67)

where |$\Delta _b$| is the conformal dimension of the primary operator labeled |$b$| (called |$\phi _b$|⁠). The factor |$C^{b}_{OO^\dagger }$| is the coefficient of the normalized three-point function |$\langle OO^\dagger \phi _b\rangle$|⁠.

First we consider the time |$0<t<l$| or |$t>l+L$|⁠, where localized excitations that are generated at |$x=-l$| and propagate in opposite directions at the speed of light are outside of subsystem |$A$|⁠. This means that the entangled pairs are both in region |$B$|⁠. Therefore we expect that there is no entanglement generation between |$A$| and |$B$|⁠, as we already mentioned in Sect. 2.2. Indeed, we can obtain from (29) that in the |$\epsilon \rightarrow 0$| limit we have |$(z,\bar {z})\rightarrow (0,0)$| and |$G(z,\bar {z})\simeq |z|^{-4\Delta _O}$|⁠, as the dominant contribution arises when |$\phi _b$| coincides with the identity operator |$\phi _0=I$|⁠. Thus (33) leads to |$\Delta S^{(2)}_A=0$|⁠, as expected.

4.2. Rational 2D CFTs

Before we start the large-|$c$| analysis, we would like to briefly review the results in rational CFTs obtained in Ref. [17]. This is useful because they provide an instructive example where we can compute |$\Delta S^{(n)}_A$| both analytically and exactly. In rational CFTs the summation over |$b$| is a finite sum and we can choose the Hilbert space structure given by (66).

In rational CFTs, we can employ the properties of the fusion transformation, which exchanges |$z_2$| with |$z_4$| (or equally |$z$| with |$1-z$|⁠) given by

\[F_O(b|1-z)=\sum _{d}F_{bd}[O]\cdot F_O(d|z),\]

(68)

where the coefficients |$F_{bd}[O]$| are constants, which are called fusion matrices [68–70]. Thus by using (67), in the limit |$(z,\bar {z})\rightarrow (1,0)$|⁠, the conformal block is reduced to the contribution from the vacuum sector:

\[G(z,\bar {z})\simeq F_{00}[O]\cdot (1-z)^{-2\Delta _O}\bar {z}^{-2\Delta _O},\]

(69)

where we employed the fact that |$C^{0}_{OO}=1$|⁠.

Therefore we find the following expression from (33):

\[\Delta S^{(2)}_A=-\log F_{00}[O]=\log d_O,\]

(70)

where |$d_O=1/F_{00}[O]$| is called the quantum dimension [68–70] and is related to the S-matrix of the modular transformation by

\[d_O=S_{0O}/S_{00}.\]

(71)

4.3. Large-|$c$| limit

Now we move on to the large-|$c$| limit of 2D CFTs. We are interested in the time period |$l<t<L+l$|⁠, where we expect non-trivial results, corresponding to the limit |$(z,\bar {z})\rightarrow (1,0)$| as explained in (30). We will keep only the leading order of |$\frac {\Delta _O}{c}(\ll 1)$| expansion. We will discuss subleading corrections in Sect. 4.5 later.

Since we are motivated by the AdS/CFT, we are interested in those CFTs with gravity duals. Therefore we would like to assume the existence of a gap in the spectrum such that the density of states |$d(\Delta )$| behaves like |$d(\Delta )\sim O(1)$| for |$\Delta <O(c)$|⁠. This corresponds to the threshold where AdS black holes appear. Moreover, in the summation of conformal blocks (65) we can ignore the contributions from intermediate states with large conformal dimension |$\Delta _b\sim O(c)$|⁠, as their conformal blocks are exponentially suppressed in the large-|$c$| limit [72, 73].

These arguments are parallel with Ref. [73], where the ground state entanglement entropy in the large-|$c$| limit was analyzed. However, note that, in that paper, the large-|$c$| limit was taken with |$\frac {\Delta _O}{c}$| kept finite because the correlation functions of twist operators were computed. In our case, the operator |$O$| expresses the excitation above the vacuum and we do not need any twist operators as we employed the conformal map to describe the replicated Riemann surface |$\Sigma _2$|⁠.

In our large-|$c$| limit |$\frac {\Delta _O}{c},\frac {\Delta _b}{c}\ll 1$|⁠, we have the following simple and universal expression of the vacuum conformal block [72, 76]:

\[F_O(b|z)\simeq z^{\Delta _b-2\Delta _O}\cdot {}_2F_1(\Delta _b,\Delta _b,2\Delta _b,z),\]

(72)

where |${}_2F_1(a,b,c,z)$| is the hypergeometric function. This shows that for any |$\Delta _b\ll c$| the conformal block |$F_O(b|z)$| can only possess at most a logarithmic singularity |$\sim \log (1-z)$| in the limit |$z\rightarrow 1$|⁠.

However, to perform a complete analysis of the large-|$c$| limit, we need to know the structure of Hilbert space to deal with the summation over |$b$| in (65). Since this is in general too complicated, we would like to approximate it only by the contribution from the vacuum conformal block:

\[G(z,\bar {z})\simeq F_O(0|z)\bar {F}_O(0|\bar {z}).\]

(73)

This argument is clearly justified for the diagonal Hilbert space structure (66) in the limit |$(z,\bar {z})\rightarrow (1,0)$|⁠, though in general AdS/CFT examples we cannot expect this. This is because in this limit we have |$\bar {F}_O(0|\bar {z})\simeq \bar {z}^{\Delta _b-2\Delta _O}$|⁠, which gives the dominant contribution if |$\Delta _b=0$|⁠.

Moreover, we would like to argue that this approximation can be applied to examples with gravity duals.⁶ This is because we can set |$b_R=0$| in the limit |$\bar {z}\rightarrow 0$| and because the summation over |$b_L$| just multiplies some factor that is not exponentially large with respect to the central charge.

In the language of AdS/CFT correspondence, this approximation (73) corresponds to ignoring backreactions of local excitations to supergravity fields in the bulk AdS. We will confirm this explicitly in the next section.

Under this approximation (73), we can simply evaluate |$G(z,\bar {z})$| as follows:

\[\lim _{(z,\bar {z})\rightarrow (1,0)}G(z,\bar {z})\simeq \bar {z}^{-2\Delta _O}.\]

(74)

By using (33) and (30), this leads to the following second Renyi entropy when |$l<t<L+l$|⁠:

\[\begin {array}{rl} \Delta S^{(2)}_A&= -\log (1-z)^{2\Delta _O},\\ &= 4\Delta _O\cdot \log \left [\frac {2(t-l)(L+l-t)}{L\epsilon }\right ]. \end {array}\]

(75)

In the limit |$l\ll t\ll L$| we obtain

\[\Delta S^{(2)}_A\simeq 4\Delta _O\cdot \log \frac {2t}{\epsilon }=2\hat {\Delta }_O\cdot \log \frac {2t}{\epsilon }.\]

(76)

Remember that |$\Delta _O$| is the chiral conformal dimension and it is related to the usual conformal dimension |$\hat {\Delta }_O$| (common in the definition in higher dimensions) via |$\hat {\Delta }_O=2\Delta _O$|⁠.

However, we have to be careful with the large-|$c$| approximation (72) that we employed. Note that the bootstrap equation

\[G(z,\bar {z})=G(1-z,1-\bar {z}),\]

(77)

\[F_O(b|z)\simeq \frac {1}{D^b_O}\cdot (1-z)^{-2\Delta _O}+ \cdots , \quad (z\rightarrow 1),\]

(78)

where |$D^b_O$| is a certain constant. The relation (77) requires

\[\sum _{b_L,b_R}\frac {(C^{b}_{OO^\dagger })^2}{D^{b_L}_O\cdot D^{b_R}_O}=1.\]

(79)

These are indeed true in the fusion relation (68) in rational CFTs and, in this case, |$D^0_{O}$| coincides with the quantum dimension |$d_O$|⁠. Since this term is missing in the large-|$c$| approximation (72) and also in perturbative corrections, which will be discussed in Sect. 4.5, we can speculate that it should come from non-perturbative corrections like |$\frac {1}{D^b_O}\sim \exp (-c^{a})$| (⁠|$a$| is a certain positive constant) and thus |$D^b_O$| are expected to be very large |$D^b_O\rightarrow \infty$| in the limit |$c\rightarrow \infty$|⁠.⁷ In other words, the large-|$c$| approximation (72) will break down if |$z$| is very close to |$1$| such as |$z\sim (D^b_O)^{-\frac {1}{2\Delta _O}}$|⁠.

If we take into account (78), we find the following behavior of |$\Delta S^{(2)}_A$| (we took the limit |$L\rightarrow \infty$|⁠):

\[\Delta S^{(2)}_A = \left\{ \begin {array}{ll}4\Delta _O\cdot \log \frac {2(t-l)}{\epsilon } &\left (\epsilon \ll t-l\ll (D^0_O)^{\frac {1}{4\Delta _O}}\epsilon \right ), \\ \log D^0_O & \left (t-l\gg (D^0_O)^{\frac {1}{4\Delta _O}}\epsilon \right ). \end {array}\right ..\]

(80)

In this way we found a logarithmic time evolution in an intermediate process. Note that this is typical only for the large-|$c$| limit. Indeed, if we look at the previous examples of rational CFTs or free CFTs, we find |$D^0_O\sim O(1)$| and thus the logarithmic period disappears. In the next section, we will reproduce the same logarithmic behavior from the gravity side of AdS/CFT and will show that similar results can be obtained even in higher dimensions. It will be a very intriguing future problem to evaluate |$D^0_O$| in some concrete models of 2D CFTs with gravity duals.

4.4. Equivalence to free-field Wick contractions

To generalize the previous analysis of the logarithmic behavior to |$\Delta S^{(n)}_A$| for any |$n$|⁠, it is useful to note that our large-|$c$| approximation is equivalent to the computations of |$2n$|-point functions on |$\Sigma _n$| using “(free-field) Wick contractions”. For simplicity let us take the entangling region in this section to be the half line (⁠|$L\rightarrow \infty$| in previous sections), and use the map from |$\Sigma _1$| to |$\Sigma _n$|⁠:

\[w(z)=z^n.\]

(81)

We can find the two-point function of operators |$O(w_i,\bar {w}_i)$| on |$\Sigma _n$|⁠:

\[\langle O^\dagger (w_1,\bar {w}_1)O(w_2,\bar {w}_2)\rangle _{\Sigma _n}=n^{-4\Delta _O}|w_1w_2|^{\frac {2\Delta _O(1-n)} {n}}|w^{1/n}_1-w^{1/n}_2|^{-4\Delta _O}.\]

(82)

Moreover, it can be shown (see (129)) that the ratio of the two-point function on |$\Sigma _n$| to the two-point function on |$\Sigma _1$| at late time is given by

\[\frac {\langle O^\dagger (w_1,\bar {w}_1)O(w_2,\bar {w}_2)\rangle _{\Sigma _n}}{\langle O^\dagger (w_1,\bar {w}_1)O(w_2,\bar {w}_2)\rangle _{\Sigma _1}}\simeq \left (\frac {\epsilon }{n\sin \left (\frac {\pi }{n}\right )t}\right )^{2\Delta _O}.\]

(83)

Using the fact that leading divergent contribution to the correlation function comes from two types of Wick contractions as in the arguments in Sect. 3.1, we get at late time

\[\frac {\langle O^{\dagger }(w_1,\bar {w}_1)O(w_{2},\bar {w}_{2})\cdots O^{\dagger }(w_{2n-1},\bar {w}_{2n-1})O(w_{2n},\bar {w}_{2n})\rangle _{\Sigma _n}}{\left (\langle O^\dagger (w_1,\bar {w}_1)O(w_2,\bar {w}_2)\rangle _{\Sigma _1}\right )^n}\simeq 2\left (\frac {\epsilon }{n\sin \left (\frac {\pi }{n}\right )t}\right )^{2n\Delta _O}.\]

(84)

That leads to the |$n$|th Renyi entropy

\[\Delta S^{(n)}_A\simeq \frac {1}{1-n}\log \left [2\left (\frac {\epsilon } {n\sin \left (\frac {\pi }{n}\right )t}\right )^{2n\Delta _O}\right ] =\frac {2n\Delta _O}{n-1}\log \left (\frac {n\sin \left (\frac {\pi }{n}\right )t}{\epsilon }\right )-\frac {1}{n-1}\log 2.\]

(85)

Setting |$n=2$|⁠, we recover the logarithmic behavior at large |$c$| (76).

However, the same caution should be offered as previously. If we take |$\epsilon \rightarrow 0$| strictly, our large-|$c$| approximation breaks down. In other words, if |$t$| gets very large such that |$t\gg (D^{0}_O)^{\frac {1}{4\Delta _O}}$|⁠, the logarithmic growth will be terminated and |$\Delta S^{(n)}_A$| approaches some constant of order |$\log D^{0}_O$| as in (80).

Before we proceed, it is useful to rewrite the ratio of the two-point functions on |$\Sigma _n$| and |$\Sigma _1$| in terms of coordinates |$w=e^{\phi +i\tau /R}$|⁠. We will later compare it with the same ratio obtained holographically using geodesics in a topological black hole. In |${\{ }\tau ,\phi {\} }$| coordinates we have

\[\begin {array}{rl} |w_1w_2|^{\frac {n-1}{n}}&= e^{\phi _1+ \phi _2-\frac {\phi _1+ \phi _2}{n}}\\ |w^{1/n}_1-w^{1/n}_2|^2&= e^{\frac {\phi _1+ \phi _2}{n}}\,2 \left (\cosh \left (\frac {\Delta \phi }{n}\right )-\cos \left (\frac {\Delta \tau }{nR}\right )\right ). \end {array}\]

(86)

Therefore, we can simplify the ratio to

\[\frac {\langle O^\dagger (w_1,\bar {w}_1)O(w_2,\bar {w}_2)\rangle _{\Sigma _n}}{\langle O^\dagger (w_1,\bar {w}_1)O(w_2,\bar {w}_2)\rangle _{\Sigma _1}} =\left (\frac {\cosh \left (\Delta \phi \right ) -\cos \left (\frac {\Delta \tau }{R}\right )} {n^2\left (\cosh \left (\frac {\Delta \phi }{n}\right ) -\cos \left (\frac {\Delta \tau }{n\,R}\right )\right )}\right )^{2\Delta _O}.\]

(87)

4.5. |$\Delta /c$| corrections

In the previous subsections we assumed the factorization of the four-point function in the strict large-|$c$| limit that is equivalent to Wick contractions. Here we will elaborate further on this limit and consider the subleading correction to large |$c$| by including only the Virasoro conformal block from the identity operator as in (73). See the details in Appendix A and Ref. [77] for a pedagogical review of the direct approach to Virasoro blocks.

Let us start with |$n=2$| Renyi entropy and later we will generalize this analysis for higher |$n$|⁠. Using the replica method, in order to evaluate |$\Delta S^{(2)}_A$| for operator |$O$| with (chiral) conformal dimension |$\Delta _O$|⁠, we need to compute the 4-point correlator of |$O$| on |$\Sigma _2$|⁠. Using the conformal map |$w(z)$| from the complex plane to |$\Sigma _n$| we have

\[\langle O^\dagger (w_1,\bar {w}_1)\cdots O(w_4,\bar {w}_4)\rangle _{\Sigma _2}=\left (\prod ^4_{i=1}\left |\frac {dw_i}{dz_i}\right |^{-2\Delta _O}\right )\langle O^\dagger (z_1,\bar {z}_1)\cdots O(z_4,\bar {z}_4)\rangle _{\Sigma _1}.\]

(88)

Focus now on the four-point function on |$\Sigma _1$| and evaluate it using the Virasoro decomposition of the conformal block. More precisely, we can rewrite it in terms of the three-point functions by inserting, after the second operator, the identity that is a sum over projectors to all states corresponding to the operators of the theory and their descendants. Performing the computation this way requires specific details of the CFT and is very complicated. However, in the limit that we are interested in, the large central charge but finite |$\Delta ^2_O/c$|⁠, the contribution to the four-point function of the primaries in a 2D CFT⁸ from the identity is given by [77]

\[\langle O^\dagger (z_1,\bar {z}_1)\cdots O(z_4,\bar {z}_4)\rangle _{\Sigma _1}\simeq \langle O^\dagger (z_1,\bar {z}_1)O(z_2,\bar {z}_2)\rangle _{\Sigma _1} \langle O^\dagger (z_3,\bar {z}_3)O(z_4,\bar {z}_4)\rangle _{\Sigma _1}\mathcal {V}_0(z)\bar {\mathcal {V}}_0(\bar {z}),\]

(89)

where the vacuum conformal blocks |$\mathcal {V}_0(z)$| and |$\bar {\mathcal {V}}_0(\bar {z})$| at large |$c$| are the following functions of the conformal cross-ratios:

\[\mathcal {V}_0(z)=\exp \left (\frac {2\Delta ^2_O}{c}z^2_2F_1(2,2;4;z)\right ),\qquad \bar {\mathcal {V}}_0(\bar {z})=\exp \left (\frac {2\Delta ^2_O}{c}\bar {z}^2_2F_1(2,2;4;\bar {z})\right ).\]

(90)

This result is sufficient to obtain |$\Delta _O/c$| corrections to our late time limit |$(z,\bar {z})\rightarrow (1,0)$| of the Renyi entropies. Namely, plugging back to (88), we can write the correction to the large-|$c$| factorization of the four-point correlator as

\[\begin {array}{rl} &\langle O^\dagger (w_1,\bar {w}_1) \cdots O(w_4,\bar {w}_4)\rangle _{\Sigma _2}\\ &\quad =\langle O^\dagger (z_1,\bar {z}_1)O(z_2,\bar {z}_2)\rangle _{\Sigma _2} \langle O^\dagger (z_3,\bar {z}_3)O(z_4,\bar {z}_4)\rangle _{\Sigma _2}\mathcal {V}_0(z)\bar {\mathcal {V}}_0(\bar {z})+ \cdots , \end {array}\]

(91)

where the ellipsis stand for contributions from operators with higher conformal dimensions.

Recall that, at late time |$(z,\bar {z})\rightarrow (1,0)$| and |$l\ll t(\ll L)$|⁠, we find from (30) that

\[1-z\simeq \left (\frac {\epsilon }{2t}\right )^2.\]

(92)

After writing the hypergeometric functions in terms of the logarithm

\[\frac {2\Delta ^2_O}{c}\,z^2_2F_1(2,2;4;z)=-\frac {24\Delta ^2_O}{c}-\frac {12\Delta ^2_O}{c}\frac {2-z}{z}\log (1-z)\]

(93)

one can check that at late time the contribution from the |$\bar {\mathcal {V}}_0(0)$| is just |$1$|⁠. Finally inserting (92) gives us the scaling of |$\Delta S^{(2)}_A$| at late time

\[\Delta S^{(2)}_A=4\Delta _O\left (1-\frac {6\Delta _O}{c}\right )\log \left (\frac {2t}{\epsilon }\right )+ \frac {24\Delta ^2_O}{c}+ \cdots .\]

(94)

As we can see, the correction from the vacuum conformal block only changes the coefficient of the logarithmic growth for the late time second Renyi entropy.

The above analysis can be generalized to a |$2n$|-point functions at large |$c$| (see Appendix A). The correlator can be written as

\[\langle O^\dagger (w_1,\bar {w}_1)\cdots O(w_{2n},\bar {w}_{2n})\rangle _{\Sigma _2}=\left (\prod ^{n}_{i=1}\langle O^\dagger (w_{2i-1},\bar {w}_{2i-1})O^\dagger (w_{2i},\bar {w}_{2i})\rangle _{\Sigma _2}\right ) \mathcal {V}_0(Z_{2n})\bar {\mathcal {V}}_0(\bar {Z}_{2n}),\]

(95)

where the conformal blocks are again given by (90) but the cross-ratios are in |${\{ }z_1,z_2,z_{2n-1},z_{2n}{\} }$|⁠:

\[Z_{2n}=\frac {(z_1-z_2)(z_{2n-1}-z_{2n})}{(z_1-z_{2n-1})(z_2-z_{2n})},\qquad \bar {Z}_{2n}=\frac {(\bar {z}_1-\bar {z}_2)(\bar {z}_{2n-1}-\bar {z}_{2n})}{(\bar {z}_1-\bar {z}_{2n-1})(\bar {z}_2-\bar {z}_{2n})}.\]

(96)

Using the late time scaling of |$z$|'s derived in Ref. [17] we can show that at late time

\[1-Z_{2n}\simeq \left (\frac {\epsilon }{n\sin \left (\frac {\pi }{n}\right )\,t}\right )^2, \qquad \bar {Z}_{2n}\rightarrow 0,\]

(97)

and combining all together we have the corrected |$n$|th Renyi entropy

\[\Delta S^{(n)}_A=\frac {2n\Delta _O}{n-1}\left (1-\frac {12\Delta _O}{n\,c}\right )\log \left (\frac {n\sin \left (\frac {\pi }{n}\right )t}{\epsilon }\right )+ \frac {24\Delta ^2_O}{c(n-1)}+ \cdots .\]

(98)

This clearly shows that the logarithmic behavior at late time persists for all the Renyi entropies |$n\ge 2$| once we include the contribution from the identity.

5. Holographic analysis of Renyi entanglement entropy

The AdS/CFT duality allows us to compute observables in conformal field theory from dual string theory. In the classical gravity regime of strings, which usually corresponds to a particular corner of the CFT parameter space, observables like correlation functions of primary operators can be computed by evaluating the supergravity action on the classical solution for the field dual to the operator under consideration [78, 79].

In our CFT analysis of (Renyi) entanglement entropies, we tried to be as general as possible and considered a large class of field theories in two dimensions at large |$c$| or higher dimensions at large |$N$|⁠. In two dimensions, our main object in the replica construction of the |$n$|th Renyi entropy was the |$2n$|-point function of operators |$O(w_i,\bar {w}_i)$| on the |$n$| copies of the complex plane |$(\Sigma _n)$|⁠. In principle, if we knew the holographic dictionary for all the 2D CFTs on |$\Sigma _n$|⁠, we could compute the |$2n$|-point function holographically using, e.g., Witten diagrams. This is of course far from reality and we will be able to perform only a modest step in this direction. Namely, we will approximate the |$2n$|-point function on |$\Sigma _n$| by a product of two-point functions computed using the geodesic approximation in a Euclidean AdS topological black hole by employing the coordinate transformation found in Ref. [54]. This corresponds to the leading term in the large-|$N$| limit. As we learned from the field-theoretic analysis, there are subtle problems with the leading-term large-|$N$| approximation in the late time limit and |$n\rightarrow 1$|⁠. In this section, we will ignore these issues and address them again in the final section.

The topological black hole, as we will review below, has an asymptotic boundary given by |$S^1\times H^{d-1}$| where |$H^{d-1}$| is a |$d-1$|-hyperbolic plane (Euclidean AdS|$_{d-1}$|⁠). We can identify it with |$\Sigma _n$| up to a conformal factor [54]. Then, similarly to Ref. [80], we assume that the two-point functions of the bulk fields |$\Phi _\Delta$| dual to operators |$O(x)$| with (sufficiently large) dimension |$\Delta$| can be computed semi-classically:

\[\langle \Phi _\Delta (x)\Phi _\Delta (x')\rangle \sim e^{-\frac {\Delta }{R}\,L(\gamma ) },\]

(99)

where |$\gamma$| is the geodesic between the operator's insertion points that we schematically denoted |$x$| and |$x'$|⁠. Our approximation should be valid for a general class of CFTs at large central charge |$c$|⁠. We further refer to Ref. [81] for a discussion on the validity and subtleties of (99).

In the formulas below we will no longer use the |$\Phi _\Delta$| since they do not play any role in our general derivations. Instead, we identify the holographic result for the two-point function on |$\Sigma _n$| with the exponent of the geodesic length as

\[\langle O^\dagger (x)O(x')\rangle _{hol}\sim e^{-\frac {2\Delta _O}{R}\,L^{(n)}}.\]

(100)

Let us now review a few basic facts about topological black holes and proceed with the computation of the geodesic lengths.

5.1. Topological black holes in AdS

The Euclidean topological black hole in AdS|$_{d+1}$| is given by the metric [82]

\[ds^2=f(r)d\tau ^2+ \frac {dr^2}{f(r)}+r^2\frac {d\zeta ^2+dx_idx_i}{\zeta ^2}\]

(101)

where

\[f(r)=-1-\frac {\mu }{r^{d-2}}+ \frac {r^2}{R^2}.\]

(102)

It will be convenient to redefine the hyperbolic coordinate |$\phi =\log \zeta$| so that the metric becomes

\[ds^2=f(r)d\tau ^2+ \frac {dr^2}{f(r)}+r^2d\phi ^2+r^2e^{-2\phi }dx^2_i.\]

(103)

This is an example of an asymptotically AdS black hole with a negatively curved horizon. The name “topological” comes from the fact that in four dimensions one can use the isometry of the hyperbolic plane |$H^2$| and obtain a black hole with a horizon of an arbitrary topology. Similar properties of these solutions can be demonstrated in higher dimensions but we will not need or use them here.

Topological black holes have a temperature that depends on |$d$| and the horizon radius |$r_+ $|⁠,

\[\beta ^{-1}=T_{H}=\frac {d\, r^2_+ -(d-2)R^2}{4\pi R^2 r_+ },\]

(104)

\[\beta =2\pi n R\]

(105)

and, as a result, the boundary will consist of CFT|$_d$| on |$\Sigma _n$|⁠. From this condition, we can also find |$\mu$| as a function of |$n$| and |$d$|⁠. It is given by

\[|\mu (d,n)|=R^{d-2}\left (\frac {1}{d\,n}+ \sqrt {1-\frac {2}{d} + \frac {1}{d^2\,n^2}}\right )^{d-2}\left (1-\left (\frac {1}{d\,n}+ \sqrt {1-\frac {2}{d}+ \frac {1}{d^2\,n^2}}\right )^2\right ),\]

(106)

and, since we will set |$x_i$| to constant in (103), it will be our main parameter capturing the dependence on the dimensions and periodicity |$n$|⁠. For the clarity of our formulas, we define more compactly

\[|\mu (d,n)|\equiv R^{d-2}F_{(d,n)}.\]

(107)

It is important to notice that, for |$n=1$|⁠, |$\mu (d,1)$| vanishes. The opposite limit of |$n\rightarrow \infty$| corresponds to the extremal black hole with a degenerate horizon.

Last but not least, in order to keep contact with the CFT results and conventions of Ref. [15], we recall that, for |$\mu =0$| and |$x_i={\text {const}}$|⁠, metric (103) can be mapped into AdS|$_{d+1}$| in Poincaré coordinates,

\[ds^2=R^2\frac {dT^2+dY^2+dx_i^2+dZ^2}{Z^2},\]

(108)

by setting

\[\begin {array}{rl} Y-iT&= \sqrt {1-\frac {R^2}{r^2}}e^{\phi -i\tau /R},\\ Y+iT&= \sqrt {1-\frac {R^2}{r^2}}e^{\phi +i\tau /R}, \\ Z&= \frac {R}{r}e^{\phi }. \end {array}\]

(109)

By taking the asymptotic limit of this map we can find the relation to the polar coordinates on the plane |$w=r\,e^{i\theta }$|⁠:

\[r=e^{\phi },\qquad \theta =\frac {\tau }{R}.\]

(110)

It is clear from this map that the space |$(T,Y,x)$| precisely describe the |$n$|-sheeted space |$\Sigma _n$| as the periodicity of |$\tau$| is |$2\pi nR$|⁠.

This brief summary of the topological black hole should suffice for our further analysis and we will proceed directly with computation of the geodesic length in the background (103). More details and further references can be found in Ref. [82].

5.2. Geodesic length

Let us start with the general metric (103) and set all the |$x_i={\rm const}$|⁠. As a result, the dependence on |$d$| and the periodicity |$n$| is fully captured by |$|\mu (d,n)|$|⁠. We will compute the length of the geodesic |$\left (\tau (r),\phi (r)\right )$| between the end-points |$(\tau _i,\phi _i)$| and |$(\tau _f,\phi _f)$| located at the boundary |$r=r_\Lambda$|⁠. The geodesic extends into the bulk and has a turning point at |$r=r_{\ast }$|⁠. This way, the length is twice the length from the boundary to the turning point and it is given by

\[\frac {L}{2}=\int ^{r_\Lambda }_{r_{\ast }}\sqrt {f(r)\tau '^2+ \frac {1}{f(r)}+r^2\phi '^2}\,dr\equiv \int ^{r_\Lambda }_{r_{\ast }}\mathcal {L}\,dr.\]

(111)

The functional depends neither on |$\tau$| nor |$\phi$| so the equations of motion are just the two conservation laws

\[\frac {f(r)\tau '}{\mathcal {L}}=C_1\qquad \qquad \frac {r^2\phi '}{\mathcal {L}}=C_2\]

(112)

where |$C_{1}$| and |$C_2$| are arbitrary constants. These two ordinary differential equations can be simplified to

\[\frac {d\tau }{dr} = \frac {C_1 r}{f(r)\sqrt {f(r)(r^2-C^2_2)-r^2C^2_1}}\]

(113)

\[\frac {d\phi }{dr} = \frac {C_2}{r\sqrt {f(r)(r^2-C^2_2)-r^2C^2_1}}.\]

(114)

We can further relate |$C_1$| to |$C_2$| and |$r_{\ast }$|⁠. Namely, at the turning point, both derivatives |$\tau '$| and |$\phi '$| diverge so the denominator on the right-hand side of (114) must vanish at |$r=r_{\ast }$|⁠. That leads to the relation

\[C^2_1=\frac {f(r_{\ast })(r^2_{\ast }-C^2_2)}{r^2_{\ast }}.\]

(115)

Finally, we can insert this into (114) and, since both |$\tau$| and |$\phi$| should be finite, we incorporate the boundary conditions at |$\infty$| in the usual manner. The procedure yields our main integrals,

\[\Delta \tau \equiv \tau _f-\tau _i = 2\int ^{\infty }_{r_{\ast }}\frac {r\sqrt {f(r_{\ast })(r^2_{\ast }-C^2_2)}\,dr}{f(r)\sqrt {f(r)r^2_{\ast }(r^2-C^2_2)-f(r_{\ast })r^2(r^2_{\ast }-C^2_2)}}\]

(116)

\[\Delta \phi \equiv \phi _f-\phi _i = 2\int ^{\infty }_{r_{\ast }}\frac {C_2r_{\ast }\,dr}{r\sqrt {f(r)r^2_{\ast }(r^2-C^2_2)-f(r_{\ast })r^2(r^2_{\ast }-C^2_2)}},\]

(117)

as well as the the length,

\[\frac {L}{2}=\int ^{r_\Lambda }_{r_{\ast }}\frac {r_{\ast }\,r\,dr}{\sqrt {f(r)r^2_{\ast }(r^2-C^2_2)-f(r_{\ast })r^2(r^2_{\ast }-C^2_2)}}.\]

(118)

From this point we have to proceed with specific values of |$d$| and |$n$|⁠.

5.3. Analysis in AdS|$_3/$|CFT|$_2$|

We will begin with the simplest case that can be solved analytically, the |$d=2$| that corresponds to the AdS|$_3$|/CFT|$_2$| setup. Strictly speaking, there are no topological black holes in |$d=2$| but we can always consider metric (103) with |$d=2$| and identify integer |$n$| of the periodicity with the number of copies of the dual CFT. For |$d=2$| we have

\[\mu =\frac {1}{n^2}-1,\qquad \qquad r_+ =\frac {R}{n}.\]

(119)

Integrals (117) can be performed analytically and are equal to

\[\begin {array}{rl} \frac {\Delta \tau }{R}&=2n\arctan \left (\frac {R}{nr_{\ast }}\sqrt {\frac {r^2_{\ast }-C^2_2}{r^2_{\ast }-r^2_+ }}\right )\\ \Delta \phi &=2n\,{\rm arctanh}\left (\frac {RC_2}{n\,r^2_{\ast }}\right ). \end {array}\]

(120)

Similarly, for large cut-off |$r_\Lambda$|⁠, the length is given by

\[\frac {L}{2R}=\int ^{r_{\Lambda }}_{r_{\ast }}\frac {r\,dr}{\sqrt {(r^2-r^2_{\ast })\left (r^2-\frac {r^2_+C^2_2}{r^2_{\ast }}\right )}} \simeq \log \left (\frac {2r_\Lambda }{\sqrt {r^2_{\ast }-\frac {R^2C^2_2}{n^2r^2_{\ast }}}}\right ).\]

(121)

We can easily invert (120) and find |$C_2$| and |$r_{\ast }$| as functions of |$\Delta \phi$| and |$\Delta \tau$|⁠. Inserting them into the length gives

\[\frac {L}{2R}=\log \left (\frac {nr_\Lambda }{R}\sqrt {2\cosh \left (\frac {\Delta \phi }{n}\right ) -2\cos \left (\frac {\Delta \tau }{nR}\right )}\right ).\]

(122)

Now we will use the standard semi-classical prescription for computing the propagator in a CFT using holography. Namely, the two-point function of operators with (large) dimension |$\Delta$| is equal to the exponent of the action of a massive particle with mass |$m\sim \Delta$| evaluated on the particle's geodesic with boundary conditions determined by the insertion points of operators in the CFT. Assuming that such an approximation holds for our setup as well, the two-point function of operators with dimension |$\Delta =2\Delta _O$| in |$n$| copies of CFT|$_2$| (⁠|$\Sigma _n$|⁠) can be approximated by the exponent of the geodesic length in the topological black hole:

\[e^{-\frac {2\Delta _O}{R} L^{(n)}}=\left (\frac {1}{\frac {2n^2\,r^2_\Lambda }{R^2}\left (\cosh \left (\frac {\Delta \phi }{n}\right ) -\cos \left (\frac {\Delta \tau }{n\,R}\right )\right )}\right )^{2\Delta _O}.\]

(123)

By construction, when computing |$\Delta S^{(n)}_A$| at late time, we are mostly interested in the ratio of the two-point function on |$\Sigma _n$| to the two-point function on |$\Sigma _1$|⁠. The relevant object will then be

\[e^{-\frac {2\Delta _O}{R}\left (L^{(n)}-L^{(1)}\right )}=\left (\frac {\cosh \left (\Delta \phi \right ) -\cos \left (\frac {\Delta \tau }{R}\right )}{n^2\left (\cosh \left (\frac {\Delta \phi }{n}\right )-\cos \left (\frac {\Delta \tau }{n\,R}\right )\right )}\right )^{2\Delta _O}.\]

(124)

One can verify that this ratio perfectly matches the CFT|$_2$| result (87) computed using a conformal map.

\[\begin {array}{rl} \cos \left (\frac {\tau _1-\tau _2}{R}\right )&=\frac {l^2-\epsilon ^2-t^2}{\sqrt {(l^2-t^2+ \epsilon ^2)^2+4\epsilon ^2t^2}}\\ \cosh \left (\phi _1-\phi _2\right )&=\frac {l^2+ \epsilon ^2-t^2}{\sqrt {(l^2-t^2+ \epsilon ^2)^2+4\epsilon ^2t^2}} \end {array}\]

(125)

and in the late time limit |$(t\gg l \gg \epsilon )$| we have

\[\cos \frac {\Delta \tau }{R} =-1+O(t^{-4})\]

(126)

\[\cosh \Delta \phi =-1+ \frac {2\epsilon ^2}{t^2}+O(t^{-4}).\]

(127)

In terms of |$\tau$| and |$\phi$|⁠, that corresponds to

\[\frac {\Delta \tau }{R}=\pi +O(t^{-2}),\qquad \Delta \phi =i\left (\pi -\frac {2\epsilon }{t}\right )+O(t^{-2}).\]

(128)

In our solutions (120), the late time limit can be extracted by first analytically continuing |$C_2\rightarrow i |C_2|$| and then taking |$r_{\ast }$| very large while keeping |$\beta =\frac {R |C_2|}{r^2_{\ast }}$| fixed but also large. Since all the transverse directions in (103) are fixed to constant, we take this as the universal late time limit in any dimensions |$d$|⁠.

In the late time limit the ratio (124) becomes

\[e^{-\frac {2\Delta _O}{R}\left (L^{(n)}-L^{(1)}\right )}=\left (\frac {\epsilon }{n\sin \left (\frac {\pi }{n}\right )t}\right )^{2\Delta _O}.\]

(129)

Then, the leading contribution (the shortest length) to the |$2n$|-point correlator comes from two possible Wick contractions (remember Fig. 3): namely, the first, in which we contract the pairs of operators on the same sheet, and the second, when the operator on the |$i$|th sheet is contracted with the operator on sheet |$i+1$| (the operator on the |$n$|th sheet is contracted with the operator on sheet |$i=1$|⁠). As a result, using the holographic ratio (129), we obtain the late time limit of the Renyi entropy:

\[\Delta S^{(n)}_A\simeq \frac {1}{1-n}\log \left [2\left (\frac {\epsilon }{n\sin \left (\frac {\pi }{n}\right )t} \right )^{2n\Delta _O}\right ].\]

(130)

More explicitly, e.g. for |$n=2$| in |$d=2$|⁠, we have

\[\Delta S^{(2)}_A=4\Delta _O\log \left (\frac {2t}{\epsilon }\right )-\log 2.\]

(131)

Our holographic results (130) perfectly agree with our 2D CFT results (85) in the large-|$c$| limit. This confirms that our large-|$c$| approximation, studied in Sect. 4, corresponds to the dual gravity calculation with the geodesic approximation, which ignores all backreactions of the massive particle in the AdS.

5.4. Analysis in higher dimensions

For higher |$d$| the integrals become more complicated and the analytical answer seems very hard to obtain (inverting |$C_2$| and |$r_{\ast }$|⁠). However, we can still extract the late time answer (⁠|$t \gg l$| but still smaller than |$\infty$|⁠) for |$\Delta S^{(n)}_A$|⁠. Here we briefly describe the procedure and state the main results; more details can be found in Appendix B.

Analyzing the geodesic lengths in |$d\ge 2$| (see Appendix B for details), one can check that at late time |$\Delta S^{(n)}_A$| has the same divergent behavior,

\[\Delta S^{(n)}_A\simeq \frac {4n\Delta }{d(n-1)}\log \left (\frac {F_{(d,n)}\,t}{2\,\epsilon }\right )+C_{(n,d)}-\frac {1}{n-1}\log 2,\]

(132)

where |$C_{(n,d)}$| is some non-universal constant and |$F_{(d,n)}$| was defined in (107). Note that higher Renyi entropies all behave similarly and, e.g., in the extremal limit we get the min-entropy

\[\Delta S^{(\infty )}_A\simeq \frac {4\Delta }{d}\log \left (\frac {t}{\epsilon }\right ).\]

(133)

6. Holographic analysis of von Neumann entanglement entropy

In the previous section, we holographically evaluated the Renyi entanglement entropy in the replica method by employing the heavy particle geodesic approximation of two-point functions in AdS/CFT. However, this approximation, which keeps only the leading term in the large-|$N$| expansion, is valid for |$n>1$| and we cannot obtain any reliable result for the von Neumann entanglement entropy |$n=1$|⁠. Obviously, one way to deal with this problem is to take into account the backreactions in our topological black hole analysis by computing directly the Witten diagrams for the holographic |$2n$|-point functions as in Refs. [78, 79]. Unfortunately this requires rather complicated analysis and we do not want to pursue it here. Moreover, our previous large-|$c$| analysis in 2D CFT suggests that we may need to incorporate non-perturbative corrections of quantum gravity to get sensible results in this limit.

Therefore, we would like to consider some other holographic calculations for |$n=1$|⁠. Indeed, the holographic entanglement entropy [5–9] offers another method to compute von Neumann entanglement entropy without referring to the Renyi entropy. In this calculation, we prepare a (time-dependent) gravity background dual to the excited state defined by a local operator in CFT and compute the extremal surface area.

Actually we would like to point out that the holographic entanglement entropy for the excited state by a local operator coincides with the calculation done in the previous paper [44]. In Ref. [44], the gravity dual is obtained by a heavy falling particle (with mass |$m$|⁠) in AdS and the holographic entanglement entropy has been computed by taking into account gravity backreactions analytically. Thus this backreacted geometry offers the gravity dual of the excited state by a local operator with conformal dimension |$\Delta \simeq mR$|⁠. Indeed, we can confirm that the holographic stress energy tensor in this gravity background precisely reproduces (39) for the AdS|$_3/$|CFT|$_2$| setup. For a large mass |$m$| such that |$\Delta \sim O(N^2)=O(c)$|⁠, we will be able to regard it as a version of local quench as it causes a very large excitation, as argued in Ref. [44]. We are interested in the opposite case |$\Delta \ll c$|⁠.

Let us focus on the AdS|$_3/$|CFT|$_2$| case so that we get analytical results. In the construction of Ref. [44], the regularization parameter⁹|$\epsilon$| appears as a parameter of the trajectory of the falling massive particle: |$z=\sqrt {t^2+ \epsilon ^2}$| in the Poincaré AdS|$_3$| space |$ds^2=R^2\left (\frac {dz^2-dt^2+dx^2}{z^2}\right )$|⁠. Then, when subsystem |$A$| is given by a half line |$x>0$| and we insert the local operator at |$(t,x)=(0,-l)$|⁠, the final result of time evolution of holographic entanglement entropy looks as follows [44]:

\[\begin {array}{rl} & \Delta S^{(1)}_A=0 \ \ (t<l), \\ & \Delta S^{(1)}_A\simeq \frac {c}{6}\log \frac {t}{\epsilon }+ \frac {c}{6}\log \frac {\Delta }{c} \ \ \left (t\gg l\right ). \end {array}\]

(134)

Firstly we note that the slope of the logarithmic time evolution is given by a constant of the CFT, i.e., the central charge |$c$|⁠. However, if we take the |$\Delta \rightarrow 0$| limit, we get |$\Delta S^{(1)}_A=0$| for any time because the logarithmic region is pushed into the infinite late time and disappears, as expected.

Even though the logarithmic behavior also occurs in our previous holographic analysis of Renyi entanglement entropy in terms of |$2n$|-point functions, the coefficient of the logarithmic term |$\log t/\epsilon$| is given by |$\frac {2n\Delta }{n-1}$| (130). This gets divergent in the von Neumann limit |$n\rightarrow 1$|⁠, where the approximation by the large-|$N$| limit breaks down, as we mentioned. It is possible to speculate that the regularization of this divergence comes from summing over non-perturbative corrections of the large-|$N$| expansion and that this gives the finite gradient proportional to the central charge |$c$|⁠, as we will discuss in the next section. It will be a very important future problem to study this issue closely.

7. Summary and discussions

In this paper we studied the Renyi and von Neumann entanglement entropy of excited states produced by local operators in large-|$N$| (or equally large-|$c$|⁠) CFTs with holographic duals. The Renyi entanglement entropy growth |$\Delta S^{(n)}_A$| can be computed from a |$2n$|-point correlation function. We did both field-theoretic and holographic analyses in various dimensions. We mainly chose subsystem |$A$| to be simply the half space.

Firstly, we studied these quantities in free CFTs. In particular, we analyzed the scalar operator in a free |$U(N)$| Yang–Mills theory in four dimensions. We found that the Renyi and von Neumann entanglement entropies both grow monotonically in time and eventually approach finite constants |$\Delta S^{(n)}_A$|⁠. We computed them analytically and exactly. We also found that the Renyi entanglement entropy |$n>1$| always scales like |$\Delta S^{(n)}_A\simeq \frac {Jn-1}{n-1}\log 2$| as in (47), where |$J$| is the number of scalar fields in the local operator or equally its conformal dimension. However, in the von Neumann entropy limit |$n\rightarrow 1$|⁠, we immediately find that this gets divergent. This is because the large-|$N$| expansion breaks down and we have to sum over many terms, where we cannot ignore the connected diagrams even for the dominant contributions. In other words, some of the subleading terms scale as some powers of |$N^{1-n}$|⁠, which can be ignored only when |$n>1$|⁠. By taking these contributions into account, we find that the von Neumann entanglement entropy scales like |$\Delta S^{(1)}_A\sim J\log N$|⁠, which has the logarithmic enhancement. This result is consistent with the intuitive argument that, since the scalar field is an |$N\times N$| matrix, each scalar field should produce |$\sim \log N^2$| entanglement entropy. Our analysis reveals an intriguing phenomenon where the Renyi and von Neumann entanglement entropies behave differently. As a consequence, we have to be very careful when we take the von Neumann entropy limit |$n\rightarrow 1$| for excited states.

Next, as another main result of this paper, we analyzed these entropies in strongly coupled and large-|$N$| CFTs so that they have classical gravity duals via the AdS/CFT. We did this analysis for 2D CFTs in the large-|$c$| limit. Then, we pursued two holographic computations: one was the geodesic approximation of correlation functions in the replica calculations of Renyi entanglement entropy. The other was the analysis of von Neumann entanglement entropy using the holographic entanglement entropy, which is essentially the same as the earlier work [44]. Below we would like to summarize the main part of our results schematically.

Generally within our analysis, being weakly coupled or strongly coupled, the growth of entanglement entropy |$\Delta S^{(n)}_A$| behaves as follows (assuming the limit |$t\gg l\gg \epsilon$|⁠, where we can suppress |$l$| dependence):

\[\begin {array}{rl} \Delta S^{(n)}_A&=-\frac {1}{n-1}\log {\frac {\langle O^{\dagger }O \!\cdots \! O^{\dagger } O \rangle _{\Sigma _n}}{\left (\langle O^{\dagger } O \rangle _{\Sigma _1}\right )^n}} \\ &\simeq -\frac {1}{n-1}\log \left [\frac {1}{D_n}+ \mu _n\cdot \left (\frac {\epsilon }{t}\right )^{\nu _n}\right ]. \end {array}\]

(135)

Here, |$D_n(>0),\nu _n(>0)$| and |$\mu _n$| are |$n$|-dependent constants. Since the |$2n$|-point function is reduced to the two-point function at |$n=1$|⁠, we obtain the relation

\[\frac {1}{D_1}+ \mu _1\cdot \left (\frac {\epsilon }{t}\right )^{\nu _1}=1.\]

(136)

In our free-field theory example of the 4D |$U(N)$| scalar field, for the Renyi entanglement entropy |$n\geq 2$|⁠, we found

\[D_n=2^{Jn-1}+O(N^{-2}),\]

(137)

while |$\mu _n=O(2^{-Jn})$| and |$\nu _n=O(1)$|⁠. If we take the von Neumann limit |$n\rightarrow 1$| we cannot ignore the subleading terms of large-|$N$| expansion in (137) as we mentioned. However, once we take this into account, the late time limit |$t\rightarrow \infty$| is smoothly taken and we obtain a finite entropy. A similar behavior is true for the rational CFTs in two dimensions, where |$D_n$| is given by the quantum dimension |$d_O$| of the primary operator |$O$| as |$D_n=(d_O)^{n-1}$| [17] and therefore |$\Delta S^{(n)}_A$| approaches the same value |$\log d_O$| for any |$n$| in the late time limit |$t\rightarrow \infty$|⁠. It is also helpful to note that, in these examples, there is no time range where the second term in (135), which is time-dependent, becomes dominant over the first term |$1/D_n$|⁠. In other words, we cannot find logarithmic increases of |$\Delta S^{(n)}_A$| in the above examples.

On the other hand, our holographic analysis of strongly coupled large-|$N$| CFTs in |$d$| dimensions lead to the following behavior for an operator with the conformal dimension |$\Delta$|⁠:

\[\nu _n\simeq \frac {4n\Delta }{d}+O\left (\frac {\Delta ^2}{c}\right ),\]

(138)

\[D_n\sim e^{b_n\cdot N^{a_n}},\]

(139)

where |$a_n$| and |$b_n$| are positive constants. This of course corresponds to a non-perturbative contribution in the large-|$N$| expansion. In our holographic and field-theoretic arguments, it was very difficult to compute this non-perturbative term |$D_n$|⁠. However, since we expect that it is very large, we find that there is a long time period where |$\Delta S^{(n)}_A$| grows logarithmically with time as

\[\Delta S^{(n)}_A\simeq \frac {\nu _n}{n-1}\log \frac {t}{\epsilon },\]

(140)

as in (80). It is intriguing to note that this logarithmic growth is peculiar to strongly coupled large-|$N$| CFTs. At late time limit |$t\rightarrow \infty$|⁠, |$\Delta S^{(n)}_A$| approaches¹⁰ a constant |$\frac {1}{n-1}\log D_n$|⁠.

The von Neumann limit |$n\rightarrow 1$| is subtler in strongly coupled large-|$N$| CFTs than that in free-field CFTs. The leading-order results (138) and (140) already tell us that |$\Delta S^{(n)}_A$| gets divergent at |$n=1$| and thus this says that the large-|$N$| expansion will break down again. On the other hand, our holographic result (134) based on the holographic entanglement entropy [44] implies the following behavior:

\[\nu _n=(n-1)\cdot \nu +O\left ((n-1)^2\right ),\]

(141)

where |$\nu$| should satisfy

\[\mu _1\nu =\frac {c}{6}.\]

(142)

Moreover, the relation (136) leads to

\[\frac {1}{D_1}+ \mu _1=1.\]

(143)

These suggest that |$\nu \sim O(c)$| and this is possible only if we assume non-perturbative terms in (138).

This von Neumann entanglement entropy grows logarithmically |$\Delta S^{(1)}_A\simeq \frac {c}{6}\log \frac {t}{\epsilon }$| even in the late time limit. This looks similar to the local quantum quenches [35]. However, notice the difference that in our setup we consider a single local operator excitation and that it is much simpler than the one for local quenches, which are triggered by a sudden change of Hamiltonian at a particular point and which produce infinitely many operators. In this way, the results for the strongly coupled large-|$N$| CFTs look different from those for free CFTs. Therefore, it is an important future problem to confirm our prediction for strongly coupled CFTs and understand both the |$n\rightarrow 1$| limit and the late time limit |$t\rightarrow \infty$| in more detail.

Funding

Open Access funding: SCOAP³.

Acknowledgements

We would like to thank Sumit Das, Roberto Emparan, Stefano Giusto, Vishnu Jejjala, Tokiro Numasawa, Hesam Soltanpanahi, Rodolfo Russo, and Kento Watanabe for comments and useful discussions, and especially Sylvain Ribault for detailed explanations of a large central charge limit of 2D CFTs. P.C. and M.N. are supported by a JSPS fellowship. T.T. is supported by a JSPS Grant-in-Aid for Scientific Research (B) No. 25287058 and by a JSPS Grant-in-Aid for Challenging Exploratory Research No. 24654057. T.T. is also supported by the World Premier International Research Center Initiative (WPI Initiative) from the Japan Ministry of Education, Culture, Sports, Science and Technology (MEXT).

Appendix A. |$2n$|-point correlators at large |$c$|

In this appendix we briefly summarize the analysis of Ref. [77] on direct computation of the vacuum Virasoro conformal blocks at large central charge. We also generalize the large-|$c$| results to |$2n$|-point functions and outline the derivation of formula (95) from the main text.

Let us start with the four-point correlator of primary operators in a 2D CFT at large central charge. We can insert into the correlator the identity, i.e., a sum over projectors on states corresponding to all the operators of the theory and their descendants. Schematically we have

\[\langle O^\dagger (z_1,\bar {z}_1)\cdots O(z_4,\bar {z}_4)\rangle _{\Sigma _1} =\sum _{\alpha _h,\bar {\alpha }_{\bar {h}}}\langle O^\dagger (z_1,\bar {z}_1)O(z_2,\bar {z}_2) \left | \alpha _h,\bar {\alpha }_{\bar {h}} \right \rangle \left \langle \bar {\alpha }_{\bar {h}},\alpha _h \right | O^\dagger (z_3,\bar {z}_3)O(z_4,\bar {z}_4)\rangle _{\Sigma _1},\]

(A1)

where |$\alpha _h$| (⁠|$\bar {\alpha }_{\bar {h}}$|⁠) stands for all operators of dimension |$h$||$(\bar {h})$| and their descendants.

\[\left | \alpha _0 \right \rangle =\frac {L^{k_1}_{-m_1}\cdots L^{k_p}_{-m_p}\left | 0 \right \rangle }{\sqrt {\mathcal {N}_{{\{ }m_i,k_i{\} }}}}\]

(A2)

where |$k_1+ \cdots +k_p=k$|⁠, |$m_1>\cdots >m_p$|⁠, and the creation operators |$L_{-m}$|⁠, with |$m\ge 2$|⁠, are the generators of the Virasoro algebra

\[[L_m,L_{n}]=(m-n)L_{m+n}+ \frac {c}{12}m(m^2-1)\delta _{m,-n}.\]

(A3)

First, one can easily check that |$k$|-graviton states are orthogonal only at large |$c$|⁠; the overlap between states with different numbers of |$L_{-m}$| can be neglected at large |$c$|⁠. Moreover, applying (A3), one can also show that the leading large-|$c$| contribution to the norm of the state with |$k$|-gravitons is given by

\[\mathcal {N}_{{\{ }m_i,k_i{\} }}\sim \left (\frac {c}{12}\right )^k\prod ^{p}_{i=1} k_i!m^{k_i}_i(m^2_i-1)^{k_i}.\]

(A4)

As shown in Ref. [77], using (A3) as well as the commutation relation for generators |$L_{-m}$| with primary operators

\[[L_{\pm m},O(z_i,\bar {z}_i)]=\left (\Delta _O(1\pm m)z^{\pm m}_i+z^{1\pm m}_i\partial _{z_i}\right )O(z_i,\bar {z}_i)\]

(A5)

after summing over all |$k$|-graviton contributions we get the large-|$c$| part of the four-point function that comes from the identity operator

\[\langle O^\dagger (z_1,\bar {z}_1)\cdots O(z_4,\bar {z}_4)\rangle _{\Sigma _1}\sim \langle O^\dagger (z_1,\bar {z}_1)O(z_2,\bar {z}_2)\rangle _{\Sigma _1} \langle O^\dagger (z_3,\bar {z}_3)O(z_4,\bar {z}_4)\rangle _{\Sigma _1}\mathcal {V}_0(z)\bar {\mathcal {V}}_0(\bar {z}),\]

(A6)

where the vacuum conformal blocks at large |$c$| are given by exponentials of the single graviton contribution (see Ref. [77] for the detailed derivation)

\[\mathcal {V}_0(z)=\exp \left (\frac {2\Delta ^2_O}{c}z^2_2F_1(2,2;4;z)\right ),\qquad \bar {\mathcal {V}}_0(\bar {z})=\exp \left (\frac {2\Delta ^2_O}{c}\bar {z}^2_2F_1(2,2;4;\bar {z})\right ),\]

(A7)

where |$z$| and |$\bar {z}$| are the conformal cross-ratios constructed from |${\{ }z_1,z_2,z_3,z_4{\} }$|⁠.

Their analysis can be extended for our purposes to the |$2n$|-point correlator of the primary fields satisfying (A5). Let us first look at the contribution from a single graviton |$L_{-m}$| (holomorphic part). To keep our formulas compact we label the operators by their position |$O_i\equiv O(z_i,\bar {z}_i)$|⁠. We insert the |$n-1$| projection operators after each pair of operators:

\[\begin {array}{rl} G^{(k=1)}_{2n}&\equiv \sum ^{\infty }_{{\{ }m{\} }=2}\mathcal {N}_{{\{ }m{\} }}\langle O_{1}O_{2}L_{-m_1}\rangle \langle L_{m_1}O_3O_4L_{-m_2}\rangle \cdots \\ &\quad \langle L_{m_{n-2}}O_{2n-3}O_{2n-2}L_{-m_{n-1}}\rangle \langle L_{m_{n-1}}O_{2n-1}O_{2n}\rangle , \end {array}\]

(A8)

where the norm is given by

\[\mathcal {N}_{{\{ }m{\} }}=\left (\frac {12}{c}\right )^{n-1}\,\prod ^{n-1}_{k=1}\frac {1}{m_k(m^2_k-1)}.\]

(A9)

The building blocks in (A8) can again be computed at large |$c$| using (A3) and (A5). The three-point functions are

\[\begin {array}{rl} \langle O_{i}O_jL_{-m}\rangle &=\Delta _O\left ((m-1)(z^{-m}_i+z^{-m}_j)+ \frac {2}{z_{ij}}(z^{1-m}_i-z^{1-m}_j)\right )\langle O_{i}O_j\rangle \\ \langle L_{m}O_{i}O_j\rangle &=\Delta _O\left ((m+1)(z^{m}_i+z^{m}_j)-\frac {2}{z_{ij}}(z^{1+m}_i-z^{1+m}_j)\right )\langle O_{i}O_j\rangle \end {array}\]

(A10)

and the four-point functions with |$L_n$|⁠, |$n\ge 2$| and |$L_{-m}$|⁠, |$m\ge 2$| are explicitly given by

\[\begin {array}{rl} \langle L_n O_{i} O_{j} L_{-m}\rangle &=\langle [L_n,O_i]O_j L_{-m}\rangle + \langle O_i[L_n,O_j] L_{-m}\rangle + \langle O_{i}O_j [L_n,L_{-m}]\rangle \\ &=\sum _{k={\{ }i,j{\} }}\left (\Delta _O(1+n)z^{n}_k+z^{1+n}_k\partial _{z_k}\right )\langle O_{i}O_jL_{-m}\rangle \\ & \quad + \langle O_{i}O_j [L_n,L_{-m}]\rangle . \end {array}\]

(A11)

Notice that the last term is equal to

\[\langle O_{i}O_j [L_n,L_{-m}]\rangle =(n+m)\langle O_{i}O_j L_{n-m}\rangle + \frac {c}{12}n(n^2-1)\delta _{n,m}\langle O_{i}O_j\rangle .\]

(A12)

It is then clear that at large |$c$|

\[\langle L_n O_{i} O_{j} L_{-m}\rangle \sim \frac {c}{12}n(n^2-1)\delta _{n,m}\langle O_{i}O_j\rangle .\]

(A13)

Inserting this into |$G^{(k=1)}_{2n}$| yields

\[\begin {array}{rl} G^{(k=1)}_{2n}&\sim \prod ^{n-1}_{i=2}\langle O_{2i-1}O_{2i}\rangle \sum ^{\infty }_{{\{ }m{\} }=2}\mathcal {N}_{{\{ }m{\} }}\!\left (\prod ^{n-2}_{l=1}\frac {c}{12}m_l(m^2_l-1)\delta _{m_l,m_{l+1}}\!\right )\!\langle O_{1}O_{2}L_{-m_1}\rangle \langle L_{m_{n-1}}O_{2n-1}O_{2n}\rangle \\ &=\left (\prod ^{n-1}_{i=2}\langle O_{2i-1}O_{2i}\rangle \right ) \frac {12}{c}\sum ^{\infty }_{m_{1}=2}\frac {1}{m_{1}(m^2_{1}-1)}\langle O_{1}O_{2}L_{-m_{1}}\rangle \langle L_{m_{1}}O_{2n-1}O_{2n}\rangle \\ &=\left (\prod ^{n}_{i=1}\langle O_{2i-1}O_{2i}\rangle \right ) \mathcal {V}^{(k=1)}_0(Z_{2n}) \end {array}\]

(A14)

where the conformal block is

\[\mathcal {V}^{(k=1)}_0(Z_{2n})=\frac {2\Delta ^2_O}{c}Z^2_{2n}\,_2F_1(2,2;4;Z_{2n})\]

(A15)

and |$Z_{2n}$| is the conformal cross-ratio constructed from |${\{ }z_1,z_2,z_{2n-1},z_{2n}{\} }$|⁠. Notice that the contribution from all the four-point functions is such that it precisely cancels the |$(n-2)$| norms and at the end we only have a single factor of |$\Delta ^2_O/c$|⁠. All the other contributions would be suppressed by higher powers of |$1/c$|⁠.

Taking into account also the anti-holomorphic part, we have the contribution from a single graviton:

\[G^{(k=1)}_{2n}= \left (\prod ^{n}_{i=1}\langle O_{2i-1}O_{2i}\rangle \right ) \mathcal {V}^{(k=1)}_0(Z_{2n})\bar {\mathcal {V}}^{(k=1)}_0(\bar {Z}_{2n})+ \cdots .\]

(A16)

Now, the leading |$c$| contribution from |$k$|-graviton states must be the one that cancels the “maximal” number of the norms with powers of |$c^{k}$|⁠. This is precisely the contribution with the same structure of |$L$| on both sides of the four-point functions and is proportional to the product of |$\delta _{m,n}$|⁠. Finally, summing up all the |$k$|-graviton contributions and noticing that the contribution of each of the |$k$|-gravitons commutes with each other [77] we get the exponentiation of the single graviton answer (95) at large |$c$|⁠.

Appendix B. Geodesic length in |$d>2$|

For |$d>2$| the integrals (117) become much more complicated and even though for |$d=3,4$| one can still integrate them to known elliptic functions, inverting them to find |$C_2$| and |$r_{\ast }$| becomes a formidable task. Nevertheless, in order to extract the geodesic length at late time, we can just expand the integrals for large |$r_{\ast }$| and find the answer to an arbitrary order of precision. Let us carefully go through the analysis in |$d=3$|⁠. The relevant denominator that appears in the integrals (117) is given by

\[Den_3(x)=\frac {r^6_{\ast }(x-1)pol_3(x)}{R^2\,x}\]

(B1)

where

\[\begin {array}{rl} pol_3(x)&=x^4+x^3+x^2\left (\frac {|C_2|^2R^2}{r^4_{\ast }}-\frac {|\mu |R^2}{r^3_{\ast }}-\frac {|\mu ||C_2|^2R^2}{r^5_{\ast }}\right )\\ &\quad +x\left (\frac {|C_2|^2R^2}{r^4_{\ast }}-\frac {|\mu ||C_2|^2R^2}{r^5_{\ast }}\right )-\frac {|\mu ||C_2|^2R^2}{r^5_{\ast }}. \end {array}\]

(B2)

\[\beta =\frac {R |C_2|}{r^2_{\ast }},\]

(B3)

expand the integrals

\[|\Delta \phi | =2\beta \int ^{\infty }_{1}\frac {dx}{\sqrt {x(x-1)pol_3(x)}}\]

(B4)

\[\frac {\Delta \tau }{R} =2\beta \int ^{\infty }_1\frac {\sqrt {1+ \frac {R^2}{\beta ^2r^2_{\ast }}}\sqrt {1-\frac {R^2}{r^2_{\ast }}+ \frac {|\mu |R^2}{r^3_{\ast }}}x^{5/2}dx}{\left (x^3-\frac {R^2}{r^2_{\ast }}x+ \frac {|\mu |R^2}{r^3_{\ast }}\right )\sqrt {(x-1)pol_3(x)}}\]

(B5)

to order |$r^{-3}_{\ast }$|⁠, and integrate. The answer reads

\[\begin {array}{rl} \pi -\frac {2\epsilon }{t} = |\Delta \phi | &= \pi -\frac {2}{\beta }+ \frac {2}{3\beta ^3}+ \frac {2|\mu |}{r_{\ast }}-\frac {2|\mu |}{r_{\ast }\beta }+ \frac {15\pi -16}{16}\frac {|\mu |^2}{r^2_{\ast }}\\ &\quad -\frac {3|\mu |}{2r_{\ast }\beta ^2}-\frac {2|\mu |^2}{\beta r^2_{\ast }}+ \left (\frac {61}{12}-\frac {15\pi }{16}\right )\frac {|\mu |^3}{r^3_{\ast }}+O(\varepsilon ^4) \end {array}\]

(B6)

\[\begin {array}{rl}\pi = \frac {\Delta \tau }{R} &= \pi -\frac {2}{\beta }+ \frac {2}{3\beta ^3}+ \frac {2|\mu |}{r_{\ast }}-\frac {2|\mu |}{r_{\ast }\beta }+ \frac {15\pi -16}{16}\frac {|\mu |^2}{r^2_{\ast }}\\ &\quad -\frac {3|\mu |}{2r_{\ast }\beta ^2}+ \frac {R^2}{r^2_{\ast }\beta }-\frac {2|\mu |^2}{r^2_{\ast }\beta }+ \frac {R^2|\mu |}{3r^3_{\ast }}+ \left (\frac {61}{12}-\frac {15\pi }{16}\right )\frac {|\mu |^3}{r^3_{\ast }}+O(\varepsilon ^4), \end {array}\]

(B7)

where we denote |$\varepsilon =|\mu |/r_{\ast }$|⁠. Once we subtract the two equations we get a relation between the parameters:

\[\frac {2\epsilon }{t}=\frac {R^2}{r^2_{\ast }\beta }+ \frac {R^2|\mu |}{3r^3_{\ast }}.\]

(B8)

This algorithm can be repeated for any |$d$| and we have verified that in |$d$| dimensions the relation becomes

\[\frac {2\epsilon }{t}\sim \frac {R^2}{r^2_{\ast }\beta }+ \lambda _{d}\frac {R^2|\mu |}{r^d_{\ast }},\]

(B9)

where |$\lambda _d$| is some |$O(1)$| number that depends on |$d$|⁠.

Now comes the crucial observation: in order for the terms on the right-hand side of this equation to be of the same order (as we assume in our expansion) we must have

\[\beta \sim \alpha _d \frac {r^{d-2}_{\ast }}{|\mu |}\]

(B10)

where |$\alpha _d$| is some |$O(1)$| number. Then

\[\frac {2\epsilon }{t}\sim \frac {R^2|\mu |}{r^d_{\ast }}\left (\frac {1}{\alpha _d}+ \lambda _d\right )\equiv c_d\frac {R^2|\mu |}{r^d_{\ast }}\]

(B11)

where in |$d$| dimensions we have |${\rm dim}(|\mu |)=d-2$|⁠.

Finally, from (118), we get the length of the geodesic to the leading order in |$\beta$|⁠:

\[\frac {L^{(n)}_{12}}{2R}\sim \log \left (\frac {2r_\Lambda }{r_{\ast }\beta }\right ) =\log \left (\frac {2r_\Lambda |\mu (n)|}{\alpha _d\, r^{d-1}_{\ast }}\right ),\]

(B12)

which after using (B11) gives the late time propagator in |$d$| dimensions:

\[e^{-\frac {2\Delta _O}{R} L^{(n)}_{12}}\sim \left (\frac {\alpha _dR^{\frac {d-2}{d}}} {\frac {2r_\Lambda }{R}|\mu |^{\frac {1}{d}}} \left (\frac {2\epsilon }{c_dt}\right )^{\frac {1}{d}-1}\right )^{4\Delta _O}.\]

(B13)

This leads to the leading-order contribution to |$\Delta S^{(n)}_A$| (132).

Appendix C. Higher |$J$| operators

In this appendix we present some details of the direct computation of |$\Delta S^{(n)}_R$|⁠. We have carried them out up to length 5 but already for |$J=3$| one can see the subtleties and understand the general procedure behind the computation. For |$J=3$| we expand the operator |${\rm Tr}(\phi ^3)$| into left- and right-moving parts:

\[\left | \psi _3 \right \rangle =\left | {\rm Tr}\phi ^3_L \right \rangle \left | 0_R \right \rangle + \left | 0_L \right \rangle \left | {\rm Tr}\phi ^3_R \right \rangle +3\sum ^{N}_{\alpha ,\beta =1}\left | \left (\phi ^2_L\right )^\alpha _\beta \right \rangle \left | \left (\phi _R\right )^\beta _\alpha \right \rangle +3\sum ^{N}_{\alpha ,\beta =1} \left | \left (\phi _L\right )^\alpha _\beta \right \rangle \left | \left (\phi ^2_R\right )^\beta _\alpha \right \rangle ,\]

(C1)

where we again write explicitly the summation over indices in traces that contain both |$\phi _L$| and |$\phi _R$|⁠. The orthonormal basis should be given by

\[\left\{ \left | 0_{L} \right \rangle ,\frac {1}{\sqrt {3N(N^2+1)}}\left | {\rm Tr}(\phi ^3_{L}) \right \rangle , \left | \left (\phi _{L}\right )^\alpha _\beta \right \rangle ,\mathcal {N}_{\alpha ,\beta } \left | \left (\phi ^2_{L}\right )^\alpha _\beta \right \rangle \right\} .\]

(C2)

However, note that the scalar product for two of the last states with different indices is

\[\left \langle \left (\phi ^2_{L}\right )^a_b\right |\left .\left (\phi ^2_{L}\right )^c_d\right \rangle =N\,\delta ^a_d\delta ^c_b+ \delta ^a_b\delta ^c_d\]

(C3)

so these states are orthogonal only at large |$N$|⁠. Let us then focus on |$n\ge 2$| and proceed assuming large |$N$| (for finite |$N$| we should probably work with Schur polynomials instead of traces; see Refs. [83–88] for the appropriate technology for |$U(N)$| and other classical gauge groups) with basis

\[\left\{ \left | 0_{L} \right \rangle ,\frac {1}{\sqrt {3N^3}}\left | {\rm Tr}(\phi ^3_{L}) \right \rangle ,\left | \left (\phi _{L}\right )^\alpha _\beta \right \rangle ,\frac {1}{\sqrt {N}}\left | \left (\phi ^2_{L}\right )^\alpha _\beta \right \rangle \right\} .\]

(C4)

After normalization the reduced density matrix becomes

\[\rho _R={\text {diag}}\left (\frac {1}{8},\frac {1}{8},\frac {9\times \vec {1}}{24N^2},\frac {9\times \vec {1}}{24N^2}\right )\]

(C5)

and

\[{\rm Tr}(\rho ^n_R)=\frac {2}{8^n}+ \frac {2\cdot 9^n N^2}{(24)^nN^{2n}}=2^{1-3n}+ \frac {2\,3^{n}}{2^{3n}N^{2(n-1)}}.\]

(C6)

This way the large-|$N$| Renyi entropy for |$J=3$| becomes

\[\Delta S^{(n)}_{R}=\frac {3n-1}{n-1}\log 2;\]

(C7)

hence, we get a perfect agreement with (47). Note again that |$1/N$| corrections contain powers of |$n-1$| and hence they will contribute to von Neumann entropy at |$n=1$|⁠.

Refer also to Refs. [27–33] for recent studies on the connections between the Einstein equation and fundamental constraints satisfied by the entanglement entropy (such as the first-law-like relation or its generalizations).

See Ref. [71] for a similar conclusion in a time-independent setup.

Here we ignore the difference between |$SU(N)$| and |$U(N)$| gauge theory, as we take the large-|$N$| limit.

Note that this breakdown occurs because we neglect connected planar diagrams. A similar breakdown of perturbation theory has been observed in a wide range of examples of calculating von Neumann entanglement entropy under relevant operator perturbations. This was pointed out in a specific example in Ref. [55] (see Eqs. (2.43) and (2.44) in that paper), which typically leads to logarithmic contributions. For recent progress of analysis of entanglement entropy in the presence of operator perturbations, refer to e.g. Refs. [56–66].

Even though we assumed |$J\sim O(1)$|⁠, it is interesting to note that the second term becomes important once |$J\sim N^{2\frac {n-1}{n+1}}$|⁠.

Note that we cannot apply this argument to theory without gravity duals. For example, consider the free CFT defined by |$c$| free massless scalar fields |$\phi _1,\phi _2,\ldots ,\phi _c$|⁠. Let us focus on the operator |$O=e^{ip\phi _1}$| for any |$p$|⁠. This clearly has the vanishing entropy |$\Delta S^{(2)}_A=0$| and this does not agree with our later results, e.g. (76). In such free CFTs there is no gap in the spectrum and we need to sum up so many conformal blocks.

If we focus on the modes |$b$| corresponding to the large conformal dimension |$\Delta _b\gg c$|⁠, we can apply Cardy's formula [74, 75] to estimate the number of primaries in the large-|$c$| limit. This is because we can ignore the difference between the numbers of primaries and those with their descendants in the large-|$c$| limit. This leads to the approximation of the density of states: |$d(\Delta )\sim e^{2p\sqrt {c\Delta }}$|⁠, where |$p>0$| is a certain |$O(1)$| constant. If we naively assume that the normalized three-point functions are all |$O(1)$|⁠, then the bootstrap constraint (79) leads to the estimation that |$D^{b}_O \gtrsim e^{p\sqrt {c\Delta _b}}$| for |$\Delta _b\gg c$|⁠. Therefore, for the state |$\phi _b$| with a small conformal dimension |$\Delta _b\ll c$|⁠, we expect |$D^{b}_O \gtrsim e^{p'c}$| with another |$O(1)$| constant |$p'(>0)$|⁠. This is indeed exponentially large in the large-|$c$| limit.

We assume that we can take the large-|$c$| limit.

Please note that in Ref. [44] this parameter |$\epsilon$| is written as |$\alpha$|⁠.

However, notice that from our computations in this paper we cannot completely deny the possibility that |$D_n$| is infinitely large such that |$\frac {1}{D_n}=0$| precisely, though physically this may look unusual. If this happens, even in the late time limit |$t\rightarrow \infty$|⁠, the Renyi entanglement entropy grows logarithmically and does not approach a constant. On the other hand, our previous rough argument in footnote 5, and its generalization to any |$n$| following [17], give the estimation |$D_n\gtrsim e^{p_n(n-1)c}$|⁠, where |$p_n$| is a positive |$O(1)$| constant. If this is true, both Renyi and von Neumann entanglement entropies approach finite constants |$\Delta S^{(n)}_A\gtrsim O(c)$| in the late time limit |$t\rightarrow \infty$|⁠. It is a very important future problem to examine this issue more closely.

Projection operators are tensor products of the holomorphic and anti-holomorphic parts so we treat explicitly only the holomorphic contribution and simply multiply the answer by the anti-holomorphic counterpart.

References

Holzhey

Larsen

Wilczek

Nucl. Phys. B

424

443

(

1994

) [

Month:	Total Views:
January 2017	12
February 2017	6
March 2017	6
August 2017	6
September 2017	2
October 2017	3
November 2017	3
December 2017	10
January 2018	6
February 2018	8
March 2018	16
April 2018	27
May 2018	36
June 2018	7
July 2018	14
August 2018	7
September 2018	12
October 2018	10
November 2018	10
December 2018	14
January 2019	7
February 2019	9
March 2019	12
April 2019	12
May 2019	10
June 2019	9
July 2019	6
August 2019	17
September 2019	12
October 2019	9
November 2019	12
December 2019	9
January 2020	16
February 2020	17
March 2020	6
April 2020	12
May 2020	5
June 2020	6
July 2020	12
August 2020	10

Article Contents

Entanglement of local operators in large-N conformal field theories Open Access

Abstract

1. Introduction

2. Renyi entanglement entropy of local operator excited states

2.1. Free massless scalar field in four dimensions

2.2. 2D CFTs and free scalar example

2.3. Analysis of energy density

3. Excited states in large-|$N$| free Yang–Mills

3.1. Replica method calculations

3.2. Left–right decomposition and entangled pair interpretation

4. 2D CFT at large |$c$|

4.1. General arguments

4.2. Rational 2D CFTs

4.3. Large-|$c$| limit

4.4. Equivalence to free-field Wick contractions

4.5. |$\Delta /c$| corrections

5. Holographic analysis of Renyi entanglement entropy

5.1. Topological black holes in AdS

5.2. Geodesic length

5.3. Analysis in AdS|$_3/$|CFT|$_2$|

5.4. Analysis in higher dimensions

6. Holographic analysis of von Neumann entanglement entropy

7. Summary and discussions

Funding

Acknowledgements

Appendix A. |$2n$|-point correlators at large |$c$|

Appendix B. Geodesic length in |$d>2$|

Appendix C. Higher |$J$| operators

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Entanglement of local operators in large-N conformal field theories