Gravitational radiation from an axion cloud around a black hole: Superradiant phase

Abstract

Motivated by the possible existence of string axions with ultralight masses, we study gravitational radiation from an axion cloud around a rotating black hole (BH). The axion cloud extracts the rotation energy of the BH by superradiant instability, while it loses energy through the emission of gravitational waves (GWs). In this paper, GWs are treated as perturbations on a fixed background spacetime to derive the energy emission rate. We give an analytic approximate formula for the case where the axion Compton wavelength is much larger than the BH radius, and then present numerical results without approximation. The energy loss rate of the axion cloud through GW emission turns out to be smaller than the energy gain rate of the axion cloud by superradiant instability until nonlinear self-interactions of axions become important. In particular, an axion bosenova must happen at the last stage of superradiant instability.

1. Introduction

Within a few years, the ground-based detectors Advanced LIGO, Advanced VIRGO, and KAGRA are expected to begin operation with sufficiently high sensitivity to detect gravitational wave (GW) signals from binary mergers of black holes (BHs) or neutron stars. We will have a very exciting era of general relativity, and much interesting science will be done. One interesting possibility is finding signals from unknown sources or effects of unestablished hypothetical theories.

Do we have a possibility of detecting signals from string theory through GW detectors? Naïvely, it seems difficult because the effects of string theory are expected to appear at very high energy scales (e.g., the string scale). However, the authors of Refs. [1,2] answered “Maybe yes,” if there are string axions with ultralight masses. Since string theories (or M-theory) require our spacetime to have 10 or 11 dimensions, the extra dimensions beyond four have to be compactified. Then, the extra dimensions have dynamical degrees of freedom to change their shape and size which are called moduli, and they effectively behave as fields in our four-dimensional spacetime. One of the moduli will be the QCD axion. We can also expect the existence of other pseudoscalar fields with ultralight masses, called string axions, whose expected number is typically from 10 to 100. The allowed mass range is from |$10^{-10}$| eV to |$10^{-33}$| eV, and further below. Depending on their masses, they cause a variety of phenomena that could be observed in the context of cosmophysics (⁠|$=$| cosmology and astrophysics). This is called the axiverse scenario (see also Ref. [3] for an overview).

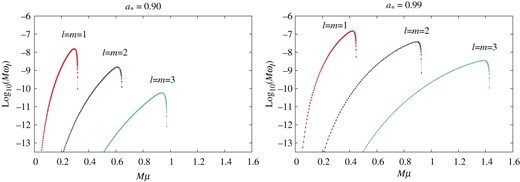
$Imaginary part $M\omega _{{\mathrm {I}}}$ of bound state eigenfrequency as functions of $M\mu $ for the BH rotation parameter $a_*=0.90$ (left) and $0.99$ (right). The results for the modes $\ell =m=1$, $2$, and $3$ are shown.$

Fig. 1.

Imaginary part |$M\omega _{{\mathrm {I}}}$| of bound state eigenfrequency as functions of |$M\mu $| for the BH rotation parameter |$a_*=0.90$| (left) and |$0.99$| (right). The results for the modes |$\ell =m=1$|⁠, |$2$|⁠, and |$3$| are shown.

Open in new tab Download slide

Suppose one of the string axions has mass |$\mu \sim 10^{-10}$| eV. The Compton wavelength |$1/\mu $| is comparable to the radius of a BH with solar mass |$M\sim M_{\odot }$| (throughout this paper, we use the units |$c=G=\hbar = 1$|⁠). Then, around a rotating solar-mass BH, there appears an unstable quasi-bound-state mode whose amplitude grows exponentially through the extraction of the BH rotation energy. This instability is called superradiant instability. Due to this instability, an axion cloud is formed around the BH from quantum zero-point oscillations even if we start from vacuum. Assuming the behavior of the scalar field to be |$\Phi \propto {\mathrm {e}}^{-{\mathrm { i}}\omega t}$|⁠, the growth rate has been calculated by approximate methods [4–6] and by numerical methods [7–9] by solving the frequency-domain eigenvalue problem (see also Ref. [10] for a related issue and Ref. [11] for recent simulations of the same system including gravitational backreaction).¹ There, eigenfrequencies with complex values, |$\omega = \omega _{{\mathrm {R}}}+{\mathrm { i}}\omega _{{\mathrm { I}}}$|⁠, are obtained, and a quasibound state is unstable if |$\omega _{{\mathrm {I}}}$| is positive. The maximum growth rate has been found to be |$M\omega _{{\mathrm {I}}}\sim 10^{-7}$|⁠, and the corresponding time scale to be around |$10^{7} M$|⁠, which is much longer than |$M$| (see Fig. 1). But this time scale is about |$1$| minute for |$M=M_{\odot }$|⁠. Even for |$M\omega _{{\mathrm {I}}} \sim 10^{-12}$|⁠, the time scale is about |$1$| day. Therefore, for a wide range of parameters, the time scale of the superradiant instability is much shorter than the observation period of the ground-based GW detectors.

The axion cloud becomes denser and denser as the superradiant instability proceeds, and two effects gradually become important. One is nonlinear self-interaction, and the other is the GW emission. Here, the nonlinear self-interaction comes from the potential of the axion field |$\Phi $|⁠, which is assumed to have the standard form |$V = f_{{\mathrm {a}}}^2\mu ^2[1-\cos (\Phi /f_{{\rm a}})]$| in the present paper, where |$f_{{\mathrm {a}}}$| is the axion decay constant. In our previous paper [12], we numerically simulated the time evolution of an axion field obeying the sine–Gordon equation in the Kerr background spacetime. The result is that the nonlinear self-interaction leads to “axion bosenova,” which shares some features with the bosenova observed in experiments [15] on Bose–Einstein condensates. The bosenova is characterized by the termination of superradiant instability and the gradual infall of positive energy from the axion cloud into the BH. The bosenova happens when the energy |$E_{{\mathrm {a}}}$| of the axion cloud becomes |$E_{{\rm a}}/M\approx 1600(f_{{\mathrm {a}}}/M_{{\mathrm { p}}})^2$|⁠, where |$M_{{\mathrm {p}}}$| is the Planck mass. If |$f_{{\mathrm {a}}}$| corresponds to the GUT scale, |$f_{{\mathrm {a}}}=10^{16}$| GeV, the bosenova happens when the axion cloud acquires 0.16% energy of the BH mass.

In the same paper, Ref. [12], we also gave an order estimate of the amplitude of GWs emitted during the bosenova, and found a possibility of detecting signals from the bosenova if it happens around a BH near the solar system (say, within 1 kpc). This motivates us to study GWs from the bosenova in more detail. However, before doing that, we have to study GW emission before the bosenova, i.e., in the superradiant phase. The reason is as follows. The axion cloud obtains energy by extraction of the BH's rotation energy, while it loses energy by emission of GWs. The energy extraction rate |${\mathrm {d}}E_{{\mathrm { a}}}/{\rm d}t$| is related to the superradiant growth rate as

\begin{equation}\label{eq1} \frac{{\rm d}E_{{\rm a}}}{{\rm d}t} = 2\omega_{{\rm I}} E_{{\rm a}}, \end{equation}

(1)

and is therefore proportional to |$(E_{{\mathrm {a}}}/M)$|⁠. On the other hand, the energy loss rate by the GW emission (i.e., the radiation rate) is |${\mathrm {d}}E_{\mathrm { GW}}/{\mathrm { d}}t \propto (E_{{\mathrm { a}}}/M)^2$|⁠. This is because the perturbation equation indicates that the GW amplitude is proportional to |$E_{{\mathrm {a}}}$|⁠, and the energy flux is proportional to the squared amplitude of GWs. For this reason, |${\mathrm {d}}E_{{\rm a}}/{\mathrm { d}}t$| is larger than |${\mathrm {d}}E_{\mathrm { GW}}/{\mathrm { d}}t$| when |$E_{{\mathrm {a}}}$| is sufficiently small. But there is a possibility that |${\mathrm {d}}E_{\mathrm { GW}}/{\mathrm { d}}t$| may catch up with |${\mathrm {d}}E_{{\mathrm { a}}}/{\mathrm { d}}t$| as |$E_{{\mathrm {a}}}$| is increased. If this is the case, all of the extracted energy from the BH is converted into GWs, and the growth of the axion cloud stops. Then, bosenova does not happen and the GW emission stays at a level undetectable by GW experiments in the near future. The GW emission rate in the linear growth phase also gives us the lower bound on the expected GW fluxes from potential sources. Therefore, the study of GWs in the superradiant phase is important.

Approximate estimates of GW emissions from the BH–axion system were previously given by Arvanitaki et al. in Refs. [1,2]. There, the GW radiation from a huge gravitational atom in Newton potential was considered for the case |$M\mu \ll 1$|⁠. Two GW emission processes were pointed out. One is radiation by level transitions of the axion cloud as a gravitational atom. This process occurs when the wavefunction of the axion cloud is given by the superposition of two or more levels of bound eigenstates, and GWs of frequencies identical to the energy differences of the levels are radiated. The other is the annihilation of two axions. This can happen even for an axion cloud occupying just one bound-state level, and GWs with the frequency |$2\omega $| are emitted, where |$\omega $| is the (real part of) the axion bound-state frequency. For both processes, Arvanitaki et al. derived approximate formulas for the GW radiation rates and concluded that the radiation rates are sufficiently small to allow the growth of the axion cloud by superradiant instability until the occurrence of a bosenova.

In this paper, we consider the situation where approximately all of the axion particles occupy one bound-state level. Because the GW radiation by level transition is subdominant in such a situation, we focus on the two-axion annihilation process. We push forward the study of Ref. [2] on this process in two respects. First, since the approximate analysis in Ref. [2] was limited to the case where the two axions to be annihilated are at the |$2p$| level (i.e., |$\ell =m=1$| and |$n_{{\mathrm {r}}}=0$|⁠), we extend to more general cases of |$\ell =m\ge 1$| and |$n_{{\mathrm {r}}}\ge 0$|⁠. Next, we perform numerical calculations of the GW emission in the Kerr background for general values of |$M\mu $|⁠. This is certainly necessary because the superradiant instability for the modes |$\ell =m=2$| and |$3$| becomes effective when |$M\mu \sim 1$|⁠, where the approximation |$M\mu \ll 1$| breaks down. Similarly to Ref. [2], the analysis is done within the classical approximation.

This paper is organized as follows. In the next section, we describe the general strategy and derive formulas that are used in the subsequent two sections. In Sect. 3, we give an approximate formula for the energy loss rate in the case |$M\mu \ll 1$|⁠. In this case, the flat spacetime can be adopted as the background spacetime, and we call this approximation the “flat approximation.” In Sect. 4, we explain the numerical method for the general value of |$M\mu $|⁠, where the Kerr spacetime is adopted as the background spacetime. Section 5 is devoted to the conclusion. In Appendix A, we describe technical details for computing axion quasi-bound states around a Kerr BH numerically. In Appendix B, we sketch the derivation of the GW radiation rate presented in Sect. 3.

2. General strategy

In this section, we briefly summarize the basic features of the superradiant growth of an axion cloud around a rotating BH and the methods for evaluating the GW radiation rate from this system.

2.1 Superradiant bound states of an axion field

\begin{align} {\mathrm{d}}s^2 &= -\frac{\Delta - a^2\sin^2\theta}{\Sigma}{\rm d}t^2 -\frac{4Mar \ \sin^2\theta}{\Sigma}{\rm d}t{\rm d}\varphi\notag\\ &\quad +\left[\frac{(r^2+a^2)^2-\Delta a^2\sin^2\theta}{\Sigma}\right] \sin^2\theta {\rm d}\varphi^2 +\frac{\Sigma}{\Delta}{\rm d}r^2 +\Sigma {\rm d}\theta^2,\end{align}

(2a)

with

\begin{equation}\label{eq2b} \Sigma = r^2+a^2\cos^2\theta, \qquad \Delta = r^2+a^2-2Mr. \end{equation}

(2b)

The event horizon is located at |$r_+=M+\sqrt {M^2-a^2}$| and it rotates with the angular velocity |$\Omega _{{\mathrm {H}}} = a/(r_+^2+a^2)$| as seen by observers at spatial infinity.

We consider a real scalar field |$\Phi $| in the Kerr spacetime. Here, |$\Phi $| is treated as a test field and its gravitational backreaction is neglected. Because we study the situation much before the bosenova, the effect of the nonlinear self-interaction is less important. For this reason, we ignore the nonlinear term and assume |$\Phi $| to satisfy the massive Klein–Gordon equation

\begin{equation} \nabla^2\Phi - \mu^2\Phi =0.\label{eq3} \end{equation}

(3)

In the Kerr spacetime, the separation of variables of the field |$\Phi $| is possible as

\begin{equation} \Phi = \Re\hat{\Phi}, \quad\hat{\Phi} ={\mathrm{e}}^{-{\rm i}\omega t}R_{\ell m}^{~\omega \mu}(r)S_{\ell m}^{~\omega \mu}(\theta){\rm e}^{{\rm i}m\phi}.\label{eq4} \end{equation}

(4)

Throughout the paper, |$\hat {f}$| indicates the complexified quantity of a real function |$f$|⁠, i.e., |$f=\Re \hat {f}$|⁠. In the following, we denote |$R=R_{\ell m}^{~\omega \mu }(r)$| and |$S=S_{\ell m}^{~\omega \mu }(\theta)$| for simplicity. See Appendix A for the equations that |$S(\theta)$| and |$R(r)$| satisfy.

The superradiant instability occurs only for quasi-bound states. Such a quasi-bound state is obtained by assuming the field to decay at infinity and to be ingoing at the horizon. The procedure is similar to the calculation of the bound states of a hydrogen atom in quantum mechanics. In the case of the hydrogen atom, one imposes the wave function to decay at infinity and to be regular at the origin. Then, the energy levels are discretized. In the same manner, the frequency |$\omega $| is discretized in the case of the BH–axion system. Since there is an ingoing flux at the horizon, the frequency |$\omega $| becomes complex, |$\omega = \omega _{{\mathrm {R}}} + {\mathrm { i}}\omega _{{\rm I}}$|⁠. The imaginary part gives the exponential behavior: the field decays for |$\omega _{{\mathrm {I}}}<0$| and grows for |$\omega _{{\mathrm {I}}}>0$|⁠. In the case |$\omega _{{\rm I}}>0$|⁠, the bound state is unstable, and this happens when the superradiance condition |$\omega _{{\mathrm {R}}}<m\Omega _{{\rm H}}$| is satisfied. Physically, the instability happens because the energy density in the neighborhood of the BH horizon becomes negative for |$\omega _{{\rm R}}<m\Omega _{{\mathrm {H}}}$|⁠, and negative energy falls into the horizon. Then, due to energy conservation, the amplitude of the outside field becomes larger. This is the superradiant instability.

Approximate solutions for superradiant bound states were constructed in the parameter region |$M\mu \ll 1$| by the matched asymptotic expansion (MAE) method [4], and in the parameter region |$M\mu \gg 1$| by the WKB method [5]. The solution in the MAE method is closely related to our analysis in Sect. 3. In this method, two approximate solutions are constructed in a near-horizon region and in a distant region, and they are matched in the overlapping region where both approximations are valid. The equation in the distant region is identical to the Schrödinger equation for a hydrogen atom except that the electric potential |$-e^2/r$| is replaced by the Newton potential |$-M\mu /r$|⁠. Therefore, the BH–axion system can be regarded as a huge gravitational atom, which is characterized by the angular quantum numbers |$(\ell , m)$| and the radial quantum number |$n_{{\mathrm {r}}}=0, 1, 2, \ldots $|

In the parameter range |$M\mu \sim 1$|⁠, numerical calculations are required to determine the bound-state levels. Such analyses have been done by several authors [7–9]. In Ref. [9], a detailed analysis was reported using the continued fraction method developed by Leaver [16]. We also reproduced a consistent result using our independent code—see Appendix A for technical details. For a quasi-bound state, the real part |$\omega _{{\mathrm {R}}}$| of the eigenfrequency is smaller than the mass |$\mu $|⁠. The difference between the two quantities, |$\mu -\omega _{{\rm R}}$|⁠, can be interpreted as the binding energy due to gravitational interaction, and typically the binding energy |$\mu -\omega _{{\mathrm {R}}}$| is found to be much smaller compared to the mass |$\mu $|⁠. Figure 1 shows the numerical results for the imaginary part |$M\omega _{{\mathrm {I}}}$| of the eigenfrequency as functions of |$M\mu $| for the BH rotation parameter |$a_*=0.90$| and |$0.99$|⁠. The results for the modes |$\ell = m = 1, 2,$| and |$3$| and |$n_{{\mathrm {r}}}=0$| are shown. The unstable range of |$M\mu $| becomes larger as |$m$| is increased because of the superradiance condition |$\mu \approx \omega _{{\mathrm {R}}}<m\Omega _{{\mathrm { H}}}$|⁠. The peak value of |$M\omega _{{\mathrm {I}}}$| becomes smaller as |$\ell =m$| is increased and as |$a_*$| is decreased.

Figure 2 shows an example of the radial profile of |$R$| for the bound-state solution with |$\ell =m=1$| (the left panel) and the corresponding configuration in the equatorial plane (the right panel). The system parameters are adopted to be |$M\mu =0.40$| and |$a_*=0.99$|⁠. The function |$R$| is shown as a function of the tortoise coordinate |$r_*$| defined by

\begin{equation} {\mathrm{d}}r_* = \frac{r^2+a^2}{\Delta} {\rm d}r.\label{eq5} \end{equation}

(5)

Figure 3 shows the same information for the mode with |$\ell = m = 2$| and the system parameter |$M\mu =0.89$|⁠. In these two figures, we chose the modes which are reduced to gravitational atoms with the radial quantum number |$n_{{\mathrm {r}}}=0$| for |$M\mu \ll 1$|⁠. For these modes, the field |$\Phi $| has one maximum and one minimum for |$\ell = m = 1$|⁠, and two maxima and two minima for |$\ell = m = 2$| in the equatorial planes (i.e., right panels) outside of the ergoregion. In the left panels, ingoing waves which behave as |$R\sim {\mathrm {e}}^{-{\mathrm { i}}(\omega -m\Omega _{{\mathrm { H}}})r_*}$| can be seen. These waves carry negative energy density into the BH. In Sect. 4, we use these numerical solutions for mode functions of the quasi-bound states as the source term of GWs.

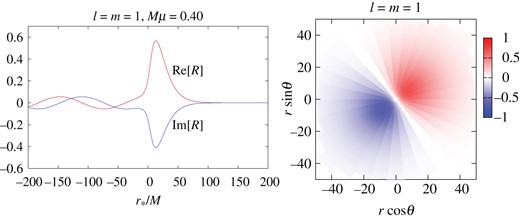
$Left panel: Radial function $R$ of the axion quasi-bound state as a function of the tortoise coordinate $r_*/M$ for $\ell = m = 1$, $M\mu = 0.40$, and the BH rotation parameter $a_*=0.99$. Right panel: The configuration in the equatorial plane $\theta =\pi /2$. There is one maximum and one minimum.$

Fig. 2.

Left panel: Radial function |$R$| of the axion quasi-bound state as a function of the tortoise coordinate |$r_*/M$| for |$\ell = m = 1$|⁠, |$M\mu = 0.40$|⁠, and the BH rotation parameter |$a_*=0.99$|⁠. Right panel: The configuration in the equatorial plane |$\theta =\pi /2$|⁠. There is one maximum and one minimum.

Open in new tab Download slide

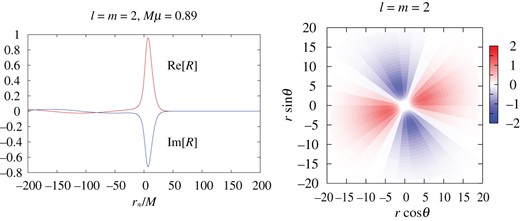
$As Fig. 2 but for $\ell = m = 2$ and $M\mu = 0.89$. We can see two maxima and two minima in the right panel.$

Fig. 3.

As Fig. 2 but for |$\ell = m = 2$| and |$M\mu = 0.89$|⁠. We can see two maxima and two minima in the right panel.

Open in new tab Download slide

2.2 GWs from an axion cloud

The energy–momentum tensor of the axion field is

\begin{equation} T_{\mu\nu} = T_{\mu\nu}(\Phi,\Phi),\label{eq6} \end{equation}

(6)

where |$T_{\mu \nu }(A,B)$| is defined as

\begin{equation} T_{\mu\nu}(A,B) = \nabla_\mu A \nabla_\nu B-\frac12 g_{\mu\nu}\left(\nabla_\rho A\nabla^\rho B+\mu^2 AB\right).\label{eq7} \end{equation}

(7)

We study GWs generated by this energy–momentum tensor |$T_{\mu \nu }$|⁠. For this purpose, we consider the perturbation

\begin{equation}\label{eq8} \tilde{g}_{\mu\nu} = g_{\mu\nu} + h_{\mu\nu}, \end{equation}

(8)

where |$\tilde {g}_{\mu \nu }$| is the spacetime metric, |$g_{\mu \nu }$| is the background Kerr metric, and |$h_{\mu \nu }$| is a small perturbation. We introduce |${\psi }_{\mu \nu }$| by

\begin{equation}\label{eq9} {\psi}^{\mu}_{~\nu} = h^{\mu}_{~\nu}-\frac12 \delta^\mu_{~\nu}h^{\rho}_{~\rho}. \end{equation}

(9)

Then, in the de Donder gauge

\begin{equation}\label{eq10} \nabla^{\nu}{\psi}_{\mu\nu} = 0, \end{equation}

(10)

the Einstein equations for |${\psi }_{\mu \nu }$| become

\begin{equation} \Delta_{{\mathrm{L}}} {\psi}_{\mu\nu} = 16\pi T_{\mu\nu},\label{eq11} \end{equation}

(11)

where |$\Delta _{{\mathrm { L}}}$| is the Lichnerowicz operator that reduces in the vacuum case to

\begin{equation} \Delta_{{\mathrm{L}}} \varphi_{\mu\nu} = -\nabla^2\varphi_{\mu\nu} -2R_{\mu ~ \nu}^{~\rho~\sigma}\varphi_{\rho\sigma}.\label{eq12} \end{equation}

(12)

Equation (11) can be rewritten as an equation for |$h_{\mu \nu }$|⁠,

\begin{equation} \Delta_{{\mathrm{L}}} {h}_{\mu\nu}=16\pi \left(T_{\mu\nu}-\frac{1}{2} T^{\rho}_{~\rho}g_{\mu\nu}\right).\label{eq13} \end{equation}

(13)

Here, we introduce one approximation. The field |$\Phi $| is proportional to |${\mathrm {e}}^{\omega _{{\mathrm { I}}} t}$| by the superradiant instability, and the energy–momentum tensor gradually grows larger. However, the time scale of the instability is very long, |$\gtrsim 10^7M$|⁠, and its effect on the GW flux must be small. For this reason, we ignore the imaginary part |$\omega _{{\mathrm {I}}}$| and calculate GWs from an oscillating source without exponential growth. This also means that we ignore the ingoing flux of the field |$\Phi $| to the BH horizon.

In addition to this, there is another subtlety. Originally, the superradiant unstable mode for |$\Phi $| is obtained as a complex function |$\hat \Phi $| proportional to |${\rm e}^{-{\mathrm {i}}\omega t + {\mathrm { i}}m\phi }$|⁠. Then, the energy–momentum tensor should be estimated by using its real part |$\Phi =\Re {\hat \Phi }$| as

\begin{equation} T_{\mu\nu}(\Phi,\Phi) =\frac14 \left[T_{\mu\nu}(\hat\Phi,\hat\Phi) + T_{\mu\nu}(\hat\Phi^*,\hat\Phi^*) +2T_{\mu\nu}(\hat\Phi,\hat\Phi^*)\right],\label{eq14} \end{equation}

(14)

where |$z^*$| denotes the complex conjugate of |$z$|⁠. Clearly, the left-hand side of Eq. (14) is not the real part of |$T(\hat \Phi ,\hat \Phi)/2$| when |$\hat {\Phi }$| are the sum of several oscillating modes proportional to |${\rm e}^{-{\mathrm {i}}(2\omega)t + {\mathrm { i}}(2m)\phi }$|⁠, because of the presence of the term |$T(\hat \Phi ,\hat \Phi ^*)$|⁠. In fact, this term can be interpreted as the source for the GW emission by level transition [2]. However, for a monochromatic eigenmode of |$\Phi $|⁠, the stationary terms corresponding to |$T(\hat \Phi ,\hat \Phi ^*)$| generate only stationary perturbations |$h_{\mu \nu }$|⁠, and we are not interested in such perturbations. Hence, we neglect this contribution and focus on GWs generated by the oscillating terms of Eq. (14). For this purpose, it is convenient to introduce the complexified energy–momentum tensor |$\hat {T}$| defined by

\begin{equation}\label{eq15} T_{\mu\nu}(\Phi,\Phi) = \Re(\hat{T}_{\mu\nu})\quad \hbox{with} \quad\hat{T}_{\mu\nu}=(1/2)T_{\mu\nu}(\hat\Phi,\hat\Phi). \end{equation}

(15)

Since |$\hat {T}$| is proportional to |${\mathrm {e}}^{-2{\rm i}\omega t+2{\mathrm { i}}m\phi }$|⁠, the frequency |$\tilde {\omega }$| and the azimuthal quantum number |$\tilde {m}$| of GWs satisfy

\begin{equation} \tilde{\omega} = 2\omega, \qquad \tilde{m} = 2m.\label{eq16} \end{equation}

(16)

Hereafter, tilde indicates a quantity for GWs.

Once a solution for the mode function is given, the GW radiation rate toward null infinity can be calculated by

\begin{equation} \frac{{\mathrm{d}}E^{\rm (out)}_{\rm GW}}{{\rm d}t} = \frac{1}{32\pi} \int_{r=r_{\rm out}} g^{\mu\rho}g^{\nu\sigma} \dot{h}_{\mu\nu}^{{\rm TT}} \dot{h}^{{\rm TT}}_{\rho\sigma} {\rm d}S,\label{eq17} \end{equation}

(17)

where |$\dot {h}_{\mu \nu }^{{\rm TT}}$| denotes the time derivative of a metric perturbation in the transverse-traceless (TT) gauge, and |${\mathrm {d}}S$| is the area element of the 2-surface in a distant region specified by |$t$| and |$r=r_{\mathrm {out}}$|⁠. Here, the conditions for the TT gauge are

\begin{equation}\label{eq18} \nabla^\mu h^{{\rm TT}}_{\mu\nu}=0\quad{\rm and}\quad g^{\mu\nu} h^{{\rm TT}}_{\mu\nu}=0, \end{equation}

(18)

and the existence of the TT gauge has been shown for a vacuum perturbation of a vacuum spacetime (e.g., p. 186 of Ref. [17]). On the other hand, the formula for the energy flux |${\mathrm {d}}E_{\rm GW}^{\rm (bh)}/{\rm d}t$| absorbed by the horizon of a Kerr BH is derived in Ref. [18] in terms of the Newman–Penrose quantity |$\psi _0$| or |$\psi _4$|⁠. A consistent formula is found using the Isaacson effective energy–momentum tensor for high-frequency GWs in Ref. [19]. In this paper, we do not explicitly calculate the GW energy flux across the horizon for the following reason: In Refs. [18,19], |${\mathrm {d}}E_{\rm GW}^{\rm (bh)}/{\rm d}t$| has been shown to be proportional to |$\tilde {\omega }-\tilde {m}\Omega _{{\rm H}}$|⁠. As stated in Eqs. (16), the frequency and the azimuthal quantum number of GWs satisfy |$\tilde {\omega }=2\omega $| and |$\tilde {m}=2m$|⁠. Then, if the axion cloud satisfies the superradiance condition |$\omega <m\Omega _{{\mathrm {H}}}$|⁠, emitted GWs also satisfy the superradiance condition |$\tilde {\omega }<\tilde {m}\Omega _{{\mathrm {H}}}$|⁠. Therefore, the GW energy flux to the horizon is negative, |${{\mathrm {d}}E_{\rm GW}^{\rm (bh)}}/{{\rm d}t}<0$|⁠, and hence, the total radiation rate is

\begin{equation}\label{eq19} \frac{{\rm d}E_{\rm GW}}{{\rm d}t}=\frac{{\rm d}E_{\rm GW}^{\rm (out)}}{{\rm d}t}+\frac{{\rm d}E_{\rm GW}^{\rm (bh)}}{{\rm d}t} <\frac{{\rm d}E_{\rm GW}^{\rm (out)}}{{\rm d}t}. \end{equation}

(19)

This means that |${{\mathrm {d}}E_{\rm GW}^{\rm (out)}}/{{\rm d}t}$| gives the upper bound of the total energy loss rate |${{\mathrm {d}}E_{\mathrm { GW}}}/{{\mathrm { d}}t}$| of the axion cloud due to GW emission, and if |${{\mathrm {d}}E_{\rm GW}^{\rm (out)}}/{{\rm d}t}$| is smaller than the energy extraction rate |${\rm d}E_{{\mathrm {a}}}/{\mathrm { d}}t$| of the axion cloud, we can safely declare that the GW emission does not stop the growth of the axion cloud by consuming all the energy extracted from the BH by the superradiant instability.

In order to estimate the GW emission rate toward null infinity with the aid of the formula (17), in principle, we have to solve Eq. (11) first and then find a gauge transformation that puts the solution into the TT gauge. However, this is a rather intricate task. Therefore, we adopt the following different method.

First, we pay attention to the fact that the solution |$h_{\mu \nu }$| of Eq. (13) satisfies the vacuum Einstein equations outside the finite source region. Therefore, it is related to the homogeneous out-mode solutions²|$\hat {u}^{(\tilde {j})}_{\mu \nu }$| at future null infinity |$\mathscr {I}^+$| as

\begin{equation} \hat{h}_{\mu\nu} = \sum_{\tilde{j}}C_{\tilde{j}}\hat{u}^{(\tilde{j})}_{\mu\nu} \quad {\mathrm{at}} \quad \mathscr{I}^+.\label{eq20} \end{equation}

(20)

Here, we introduce a complex metric perturbation |$\hat {h}_{\mu \nu }\propto {\rm e}^{-{\rm i}\tilde {\omega }t+{\rm i}\tilde {m}\phi }$| with |$h_{\mu \nu } =\Re [\hat {h}_{\mu \nu }]$| as before, and |$\tilde {j}$| indicates the collection of indexes to specify each mode, i.e. the angular quantum numbers |$\tilde {\ell }$| and |$\tilde {m}$| and the “polarization state” |$P=\pm 1$| (in the definition of Chrzanowski [19]). The out-mode |$\hat {u}^{(\tilde {j})}_{\mu \nu }$| is a solution to the homogeneous equation

\begin{equation}\label{eq21} \Delta_{{\mathrm{L}}} \hat{u}^{(\tilde{j})}_{\mu\nu} = 0 \end{equation}

(21)

satisfying the boundary condition of vanishing flux across the future horizon |$\mathscr {H}^+$| (i.e., the absence of ingoing waves at |$r_*\to -\infty $|⁠). Therefore, |$\hat {u}^{(\tilde {j})}_{\mu \nu }$| represents the process such that incoming waves and outcoming waves travel from past null infinity |$\mathscr {I}^-$| and the past horizon |$\mathscr {H}^-$|⁠, respectively, and all waves become outgoing waves to future null infinity |$\mathscr {I}^+$|⁠. Note that in Eq. (20), |$\hat {u}^{(\tilde {j})}_{\mu \nu }$| indicates only outgoing waves to future null infinity |$\mathscr {I}^+$| (incoming waves from |$\mathscr {I}^-$| are not included). Since we consider monochromatic waves, the out-mode solutions |$\hat {u}^{(\tilde {j})}_{\mu \nu }$| are also in proportion to |${\mathrm {e}}^{-{\rm i}\tilde {\omega }t+{\rm i}\tilde {m}\phi }$|⁠. By a gauge transformation, the perturbation can be expressed in the TT gauge, in which |$\hat {h}_{\mu \nu }^{\rm TT}$| can be expanded in terms of |$\hat {u}^{(\tilde {j}) {\rm TT}}_{\mu \nu }$| with the same expansion coefficients |$C_{\tilde {j}}$|⁠. By inserting this expansion in the TT gauge into (17), we obtain

\begin{equation} \left\langle \frac{{\mathrm{d}}E^{\rm (out)}_{\rm GW}}{{\rm d}t} \right \rangle = \frac{1}{64\pi}\sum_{\tilde{j}}\tilde{\omega}^2\left|C_{\tilde{j}}\right|^2 J_{\tilde{j}}\label{eq22} \end{equation}

(22)

with

\begin{equation} J_{\tilde{j}}=\int g^{\mu\rho}g^{\nu\sigma}\hat{u}_{\mu\nu}^{(\tilde{j}){\rm TT}} \hat{u}^{*(\tilde{j}){\rm TT}}_{\rho\sigma}{\rm d}S,\label{eq23} \end{equation}

(23)

where |$\left \langle X \right \rangle $| implies the time average over a time sufficiently larger than |$1/\tilde \omega $|⁠. Here, since this formula for |$J_{\tilde {j}}$| is an expression at future null infinity, just the contribution of outgoing waves has to be taken into account: We must not include the contribution of incoming waves of |$\hat {u}_{\mu \nu }^{(\tilde {j}){\mathrm {TT}}}$| in this formula.

Next, we determine |$C_{\tilde {j}}$|⁠. First, we apply Green's theorem to the identity

\begin{equation}\label{eq24} \nabla_\rho\left(\hat{u}^{*(\tilde{j}){\mathrm{TT}}}_{\mu\nu}\nabla^\rho \hat{h}^{\mu\nu} -\hat{h}^{\mu\nu}\nabla^\rho \hat{u}^{*(\tilde{j}){\rm TT}}_{\mu\nu}\right) =-16\pi \hat{u}^{*(\tilde{j}){\rm TT}}_{\mu\nu}\hat{T}^{\mu\nu} \end{equation}

(24)

to obtain

\begin{equation} \int_{\partial D}\left(\hat{u}^{*(\tilde{j}){\rm TT}}_{\mu\nu}\nabla^\rho \hat{h}^{\mu\nu} -\hat{h}^{\mu\nu}\nabla^\rho \hat{u}^{*(\tilde{j}){\rm TT}}_{\mu\nu}\right) n_\rho {\rm d}\Sigma =-16\pi \int_D\hat{u}^{*(\tilde{j}){\rm TT}}_{\mu\nu}\hat{T}^{\mu\nu}\sqrt{-g}{\rm d}^4x,\label{eq25} \end{equation}

(25)

where |${\mathrm { d}}\Sigma $| and |$\sqrt {-g}{\mathrm {d}}^4x$| are the 3-volume and 4-volume elements of |$\partial D$| and |$D$|⁠, respectively, and |$n_\rho $| is the unit normal to |$\partial D$|⁠. This relation holds for an arbitrary domain |$D$|⁠. Let us adopt as |$D$| the domain surrounded by |$t=t_0$| and |$t=t_0+\Delta t$|⁠, |$r=r_{\mathrm {out}}$|⁠, and |$r=r_{\mathrm {in}}$|⁠. Here, |$r=r_{\mathrm {out}}$| is located at a sufficiently far position from the axion cloud, and |$r=r_{\mathrm {in}}$| is located close to the horizon.

In the left-hand side of the relation (25), the surface integrals at |$t=t_0$| and |$t=t_0+\Delta t$| remain finite and we can safely neglect their contribution if we take a sufficiently large |$\Delta t$|⁠. Then, both sides of this relation are proportional to |$\Delta t$|⁠. Besides, because of the boundary condition for |${u}^{*(\tilde {j}){\mathrm {TT}}}_{\mu \nu }$| imposed at the future horizon (i.e., |${u}^{*(\tilde {j}){\mathrm {TT}}}_{\mu \nu }$| include only outgoing waves), the surface integral at |$r=r_{\mathrm {in}}$| vanishes. Hence, we have

\begin{equation} -16\pi\langle u^{(\tilde{j}){\rm TT}}, T\rangle =\int_{r=r_{\rm out}} \left(\hat{u}^{*(\tilde{j}){\rm TT}}_{\mu\nu}\partial_{r} \hat{h}^{\mu\nu} -\hat{h}^{\mu\nu}\partial_{r} \hat{u}^{*(\tilde{j}){\rm TT}}_{\mu\nu}\right) {\rm d}S, \label{eq26} \end{equation}

(26)

where the “inner product” of |${u}_{\mu \nu }$| and |${T}_{\mu \nu }$| is defined as

\begin{equation} \langle {u}, {T}\rangle =\frac{1}{\Delta t}\int_{t_0}^{t_0+\Delta t}{\mathrm{d}}t \int \hat{u}_{\mu\nu}\hat{T}^{\mu\nu}\sqrt{-g}{\rm d}r{\rm d}\theta {\rm d}\phi. \label{eq27} \end{equation}

(27)

Note that because |$u^{\rm TT}_{t\mu }\approx u^{\rm TT}_{r\mu }\approx 0$|⁠, only the angular component |$h_{IJ}$| (⁠|$I,J=\theta ,\phi $|⁠) appear in the right-hand side of Eq. (26). From this, it follows that the right-hand side is invariant under the gauge transformation |$h_{IJ}\rightarrow h_{IJ}+ \delta h_{IJ}$| with |$\delta h_{IJ} = \nabla _{I} \xi _{J} + \nabla _{J}\xi _{I}$|⁠. This implies that |$h_{\mu \nu }^{\rm }$| can be replaced by its counterpart in the TT gauge, |$h^{\mathrm {TT}}_{\mu \nu }$|⁠. Hence, substituting the expansion formula (20) in the TT gauge into the right-hand side of Eq. (26), we obtain

\begin{equation} C_{\tilde{j}}=8\pi {\rm i} \frac{ \left\langle {u}^{(\tilde{j}){\rm TT}},T \right\rangle} {\tilde{\omega} J_{\tilde{j}}},\label{eq28} \end{equation}

(28)

where we used the fact that outgoing waves of |$\hat {u}_{\mu \nu }^{(\tilde {j}){\mathrm {TT}}}$| behave as |$\sim {\mathrm {e}}^{-{\rm i}\tilde {\omega }(t-r)}/r$| for large |$r$|⁠. Note here that although the homogeneous out-mode solution also includes incoming waves |$\sim {\mathrm {e}}^{-{\rm i}\tilde {\omega }(t+r)}/r$|⁠, those terms have canceled out because |$\hat {h}_{\mu \nu }$| represents purely outgoing waves. This is the reason why the right-hand side of Eq. (26) can be expressed only in terms of the quantities of outgoing waves as |$2{\rm i}\tilde {\omega }C_{\tilde {j}}J_{\tilde {j}}$|⁠.

Furthermore, in spite of the fact that the relation (26) was derived assuming the TT gauge conditions, the inner product |$\langle {u}^{(\tilde {j}){\rm TT}},{T}\rangle $| is invariant under the gauge transformation |$\hat {u}_{\mu \nu }^{{\mathrm {TT}}}\to \hat {u}_{\mu \nu }= \hat {u}_{\mu \nu }^{{\rm TT}}+\delta \hat {u}_{\mu \nu }$| with |$\delta \hat {u}_{\mu \nu } = \nabla _{\mu }\xi _{\nu } + \nabla _{\nu }\xi _{\mu }$| because |$\langle \delta u,T\rangle =0$| holds. This can be shown by rewriting the integral of |$(\nabla _{\mu }\xi _{\nu })T^{\mu \nu } = \nabla _{\mu }(T^{\mu \nu }\xi _{\nu })$| in the domain |$D$| into the surface terms by the Gauss law and using the absence of the energy flux at the boundaries |$r=r_{\mathrm {in}}$| and |$r_{\mathrm {out}}$|⁠. Therefore, the inner product |$\langle \hat {u}^{(\tilde {j})},{T}\rangle $| can be calculated without taking special care of the gauge choice, and it is sufficient to find a solution |$u^{(\tilde {j})}_{\mu \nu }$| satisfying the TT gauge condition only at future null infinity. In the Kerr background, we can explicitly construct such out-mode solutions, as we will see later.

Substituting Eq. (28) in an arbitrary gauge into Eq. (22), the energy emission rate is given by

\begin{equation} \left\langle \frac{{\mathrm{d}}E^{\rm (out)}_{\rm GW}}{{\rm d}t} \right \rangle = \pi \sum_{\tilde{j}} \frac{\left|\langle u^{(\tilde{j})},T\rangle\right|^2} {J_{\tilde{j}}},\label{eq29} \end{equation}

(29)

with |$J_{\tilde {j}}$| defined in Eq. (23).

2.3 Methods for calculating the energy emission rate

In order to evaluate the radiation rate using Eq. (29), we have to calculate the homogeneous solution |$\hat {u}_{\mu \nu }$| for a gravitational perturbation and perform the integration of the inner product |$\langle u, T\rangle $|⁠. Also, the values of |$J_{\tilde {j}}$| have to be calculated. We explain the methods for calculating these quantities.

2.3.1 Homogeneous GWs

We use the Teukolsky formalism [21] in order to calculate the homogeneous solution of a gravitational perturbation of the Kerr spacetime. By setting |$M=a=0$|⁠, this formalism can also be applied to a perturbation for a flat spacetime studied in the next section. The Teukolsky formalism realizes the separation of the variables |$(t, r, \theta , \phi)$| of the perturbative equations using the Newman–Penrose formalism [22]. In the Teukolsky formalism, the Kinnersley null tetrads are adopted:

\begin{equation} l^\mu = \frac{1}{\Delta}\left(r^2+a^2, \ 1, \ 0, \ a \right)\end{equation}

(30a)

\begin{equation} n^\mu = \frac{1}{2\Sigma}\left(r^2+a^2, \ -\Delta, \ 0, \ a\right)\end{equation}

(30b)

\begin{equation} m^\mu = \frac{1}{\sqrt{2}(r+{\mathrm{i}}a\cos\theta)}\left({\rm i}a\sin\theta, \ 0, \ 1, \ \frac{{\rm i}}{\sin\theta}\right).\end{equation}

(30c)

In terms of these tetrads, the metric (2a) of the Kerr spacetime is

\begin{equation}\label{eq31} g_{\mu\nu} = -l_\mu n_\nu - n_\mu l_\nu + m_\mu m^*_\nu + m_\nu m^*_\mu. \end{equation}

(31)

The equations for the Newman–Penrose quantities |$\psi _0$| and |$\rho ^{-4}\psi _4$| are given by

\begin{align} &\left[\frac{(r^2+a^2)^2}{\Delta}-a^2\sin^2\theta\right] \frac{\partial^2\psi}{\partial t^2} +\frac{4Mar}{\Delta}\frac{\partial^2\psi}{\partial t\partial\phi} +\left[\frac{a^2}{\Delta}-\frac{1}{\sin^2\theta}\right] \frac{\partial^2\psi}{\partial\phi^2}\notag\\ &\quad -\Delta^{-s}\frac{\partial }{\partial r} \left(\Delta^{s+1}\frac{{\mathrm{d}}\psi}{{\rm d}r}\right) -\frac{1}{\sin\theta}\frac{\partial}{\partial\theta} \left(\sin\theta\frac{\partial\psi}{\partial\theta}\right) -2s\left[ \frac{a(r-M)}{\Delta}+\frac{{\rm i}\cos\theta}{\sin^2\theta} \right]\frac{\partial\psi}{\partial\phi}\notag\\ &\quad -2s\left[ \frac{M(r^2-a^2)}{\Delta}-r-{\rm i}a\cos\theta \right] \frac{\partial\psi}{\partial t} +(s^2\cot^2\theta-s)\psi = 0, \label{eq32} \end{align}

(32)

with |$s=\pm 2$|⁠, respectively. Here, the energy–momentum tensor is set to be zero because we need to generate homogeneous solutions. By writing |$\psi = {\mathrm {e}}^{-{\rm i}\tilde {\omega }t}{\rm e}^{{\rm i}\tilde {m}\phi } {}_sR_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(r) {}_sS_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(\theta)$|⁠, the Teukolsky equation (32) is separated as

\begin{equation} \Delta^{-s}\frac{{\rm d}}{{\rm d}r}\left(\Delta^{s+1} \frac{{\rm d}{}_sR_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}}{{\rm d}r}\right) +\left[\frac{\tilde{K}^2-2{\rm i}s(r-M)\tilde{K}}{\Delta}+4{\rm i}s\tilde{\omega} r-\lambda\right] {}_sR_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}=0,\label{eq33}\end{equation}

(33)

\begin{align} &\frac{1}{\sin\theta}\frac{{\rm d}}{{\rm d}\theta} \left(\sin\theta\frac{{\rm d}{}_sS_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}}{{\rm d}\theta} \right)+\left(a^2\tilde{\omega}^2\cos^2\theta -\frac{\tilde{m}^2}{\sin^2\theta} -2a\tilde{\omega} s\cos\theta\right.\notag\\ &\quad -\left.\frac{2\tilde{m}s\cos\theta}{\sin^2\theta} -s^2\cot^2\theta +s+{}_sA_{\tilde{\ell} \tilde{m}} \right){}_sS_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}=0,\label{eq34} \end{align}

(34)

where

\begin{equation}\label{eq35} \tilde{K}=(r^2+a^2)\tilde{\omega} - a\tilde{m}, \quad \lambda = {}_{s}A_{\tilde{\ell}\tilde{m}}+a^2\tilde{\omega}^2-2a\tilde{m}\tilde{\omega}. \end{equation}

(35)

The function |${}_sS_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(\theta){\rm e}^{{\mathrm {i}}\tilde {m}\phi }$| is called a spin-weighted spheroidal harmonic, and |${}_sA_{\tilde {\ell }\tilde {m}}$| is its eigenvalue. For a spherically symmetric spacetime, the spin-weighted spheroidal harmonics reduce to the spin-weighted spherical harmonics

\begin{align} {}_sY_{\tilde{\ell}\tilde{m}}(\theta,\phi) &= {\mathrm{e}}^{{\rm i}\tilde{m}\phi} \sqrt{\frac {(\tilde{\ell}+\tilde{m})!(\tilde{\ell}-\tilde{m})!} {(\tilde{\ell}+s)!(\tilde{\ell}-s)!} \frac{2\tilde{\ell}+1}{4\pi} } \sin^{2\tilde{\ell}}(\theta/2)\notag\\ &\quad \times \sum_{r=0}^{\tilde{\ell}-s}\left(\begin{matrix} \tilde{\ell}-s\\ r \end{matrix}\right) \left(\begin{matrix} \tilde{\ell}+s\\ r+s-\tilde{m} \end{matrix}\right) (-1)^{\tilde{\ell}-r-s+\tilde{m}}\cot^{2r+s-\tilde{m}}(\theta/2),\label{eq36} \end{align}

(36)

with |${}_sA_{\tilde {\ell }\tilde {m}}=\tilde {\ell }(\tilde {\ell }+1)-s(s+1)$|⁠. Here, we followed the convention given in the Appendix of Ref. [23] that has been widely used in recent years.³ For nonzero real values of |$a\tilde {\omega }$|⁠, we fix the phase by requiring that |${}_sS_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(\theta)$| remain a real function, and adopt the standard normalization condition |$\int |{}_sS_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(\theta)|^2 \sin \theta {\mathrm {d}}\theta = 1/2\pi $|⁠. For a Kerr spacetime, we have to generate |${}_sS_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(\theta)$| and |${}_sA_{\tilde {\ell }\tilde {m}}$| by numerical calculation or by approximate formulas. The method is explained in Sect. 4.1.

As explained in Sect. 2.2, we calculate only the GW radiation rate toward infinity, |${\mathrm {d}}E_{\rm GW}^{\rm (out)}/{\rm d}t$|⁠, that gives the upper bound on the total radiation rate. In order to evaluate this quantity, we need to generate the out-mode solution |$\hat {u}_{\mu \nu }$| for a gravitational perturbation of a Kerr spacetime. The asymptotic behavior of |$R$| for the out-mode is

\begin{equation}\label{eq37} {}_sR_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}\sim \begin{cases} \displaystyle {\mathrm{e}}^{{\rm i}(\tilde{\omega}-\tilde{m}\Omega_{{\rm H}})r_*} & (r_*\to -\infty),\\ \displaystyle Z_{\rm in}\frac{{\rm e}^{-{\rm i}\tilde{\omega}r_*}}{r} + Z_{\rm out}\frac{{\rm e}^{{\rm i}\tilde{\omega} r_*}}{r^{2s+1}} & (r_*\to +\infty), \end{cases} \end{equation}

(37)

where |$r_*$| is the tortoise coordinate defined in Eq. (5). Here, the first line gives outcoming waves from the past horizon |$\mathscr {H}^+$|⁠, while the second line is the superposition of incoming waves from past null infinity |$\mathscr {I}^-$| and outgoing waves to future null infinity |$\mathscr {I}^+$|⁠. In this paper, we choose |$s=+2$| for a technical reason that is explained in Sect. 4.1.

Once the functions |${}_{+2}R(r)$| and |${}_{\pm 2}S(\theta)$| are obtained, the next step is to reconstruct the metric perturbation |$\hat {u}_{\mu \nu }$| from the Teukolsky functions. The function |$\psi _0$| or |$\psi _4$| is known to completely determine the metric perturbation [25]. Intuitively, this is because |$\psi _0$| or |$\psi _4$| is a gauge-invariant quantity, and its real and imaginary parts correspond to the two degrees of freedom of GWs. The explicit formula was derived by Cohen and Kegeles [26,27] and Chrzanowski [19], under some assumptions, and its complete proof was given by Wald [28]. Here, we adopt the following metric formula given by Chrzanowski in the outgoing radiation gauge |$\hat {u}_{\mu \nu }n^\nu = \hat {u}_{\nu }^{~\nu } =0$|⁠:⁴

\begin{align} \hat{u}_{\mu\nu}(\tilde{\ell}, \tilde{m}, {\tilde{\omega}}, P) &=\left(-n_\mu n_\nu\mathcal{A} -m_\mu m_\nu\mathcal{B} +n_{(\mu}m_{\nu)}\mathcal{C}\right) {}_{+2}R_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}(r) {}_{-2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}(\theta) {\mathrm{e}}^{{\rm i}\tilde{m}\phi-{\rm i}\tilde{\omega}t}\notag\\ &\quad +P\left(-n_\mu n_\nu\mathcal{A}^* -m^*_\mu m^*_\nu\mathcal{B}^* +n_{(\mu}m^*_{\nu)}\mathcal{C}^* \right) {}_{+2}R_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}(r) {}_{+2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}(\theta) {\rm e}^{{\rm i}\tilde{m}\phi-{\rm i}\tilde{\omega}t}, \label{eq38} \end{align}

(38)

where |$\mathcal {A}$|⁠, |$\mathcal {B}$|⁠, and |$\mathcal {C}$| are operators

\begin{equation}\mathcal{A} =\rho^{* -4}(\delta-3\alpha^*-\beta+5\pi^*)(\delta - 4\alpha^* + \pi^*),\end{equation}

(39a)

\begin{equation}\mathcal{B} =\rho^{* -4}(\Delta + 5\mu^* - 3\gamma^* + \gamma)(\Delta + \mu^*-4\gamma^*),\end{equation}

(39b)

\begin{align} \mathcal{C} &=\rho^{* -4}\left[(\delta + 5\pi^*+\beta - 3\alpha^* + \tau)(\Delta + \mu^*-4\gamma^*)\right.\notag\\ &\quad +\left.(\Delta + 5\mu^*-\mu-3\gamma^*-\gamma)(\delta - 4\alpha^*+\pi^*)\right]. \end{align}

(39c)

Here, |$\alpha $|⁠, |$\beta $|⁠, |$\gamma $|⁠, |$\mu $|⁠, and |$\pi $| are the Newman–Penrose variables [22] (see [21] for expressions in the Kinnersley tetrad), and |$\Delta = n^\mu \nabla _\mu $|⁠, |$\delta = m^\mu \nabla _\mu $|⁠. The polarization-state parameter |$P$| takes a value |$+1$| or |$-1$|⁠, and the perturbations with |$P=\pm 1$| are reduced to the even-type and odd-type perturbations of a Schwarzschild spacetime in the nonrotating case, |$a_*=0$|⁠, respectively [30,31] (or the scalar and vector modes in [32]).

In order to calculate |$J$| defined in Eq. (23), we need the behavior of outgoing waves of |$\hat {u}_{IJ}$| in the TT gauge. For outgoing waves in Eq. (37), the outgoing radiation gauge agrees with the TT gauge at the distant region |$r\gg M$|⁠:

\begin{equation}\label{eq40} \hat{u}_{IJ} \approx \frac{Z_{\mathrm{out}}}{2}\tilde{\omega}^2 \frac{{\rm e}^{-{\rm i}\tilde{\omega} (t-r)}}{r} \times \begin{cases} r^2\mathbb{S}_{IJ} & (P=+1),\\ r^2\mathbb{V}_{IJ} & (P=-1). \end{cases} \end{equation}

(40)

Here, we wrote only the |$I,J=\theta , \phi $| components because the other components are subdominant. The explicit formulas for |$\mathbb {S}_{IJ}$| and |$\mathbb {V}_{IJ}$| are

\begin{equation}\mathbb{S}_{IJ} ={\mathrm{e}}^{{\rm i}\tilde{m}\phi}\left(\begin{matrix} {}_{-2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}+{}_{+2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}} &{\rm i}\sin\theta ({}_{-2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}-{}_{+2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}})\\ *&-\sin^2\theta ({}_{-2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}+{}_{+2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}) \end{matrix}\right),\end{equation}

(41a)

\begin{equation} \mathbb{V}_{IJ} = {\rm e}^{{\rm i}\tilde{m}\phi}\left(\begin{matrix} {}_{-2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}-{}_{+2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}} & {\rm i}\sin\theta ({}_{-2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}} +{}_{+2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}})\\ *&-\sin^2\theta ({}_{-2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}} -{}_{+2}S_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}}) \end{matrix}\right).\end{equation}

(41b)

Note that in the case of a spherically symmetric spacetime, these tensors |$\mathbb {S}_{IJ}$| and |$\mathbb {V}_{IJ}$| are identical to those given in Ref. [32] for the transverse-traceless part of gravitational perturbation except for overall factors. For this asymptotic form of |$\hat {u}_{\mu \nu }$|⁠, the value of |$J$| defined in Eq. (23) is calculated as

\begin{equation}\label{eq42} J = 2\left|Z_{\mathrm{out}}\right|^2\tilde{\omega}^4 \end{equation}

(42)

for both |$P=\pm 1$|⁠. Substituting Eq. (42) into the formula for the radiation rate (29), we have

\begin{equation} \frac{{\mathrm{d}}E_{\rm GW}}{{\rm d}t} = \frac{\pi}{2} \left|\frac{\langle u, T\rangle}{Z_{\rm out}}\right|^2 \tilde{\omega}^{-4}.\label{eq43} \end{equation}

(43)

2.3.2 Energy–momentum tensor

Once the out-mode GW solution |$u_{\mu \nu }$| and the value of |$Z_{\mathrm {out}}$| are obtained, we can calculate the inner product using the energy–momentum tensor (6). Because the homogeneous solution |$\hat {u}_{\mu \nu }$| of Eq. (38) is spanned only by |$n_\mu n_\nu $|⁠, |$n_{(\mu }m_{\nu)}$|⁠, |$n_{(\mu }m^*_{\nu)}$|⁠, |$m_\mu m_\nu $|⁠, and |$m^*_\mu m^*_\nu $|⁠, the terms proportional to |$g_{\mu \nu }$| do not contribute to generation of GWs. For this reason, we only consider |$\hat {T}^{\prime }_{\mu \nu } = (1/2)\nabla _{\mu }\hat {\Phi }\nabla _{\nu }\hat {\Phi }$|⁠, and the components necessary for our calculation are

\begin{equation} \hat{T}^{\prime\mu\nu}n_{\mu}n_{\nu} = \frac{{\mathrm{e}}^{-2{\rm i}\omega t}{\rm e}^{2{\rm i}m\phi}}{8\Sigma^2} \left[{\rm i}KR+\Delta R_{,r}\right]^2S^2,\end{equation}

(44a)

\begin{equation} \hat{T}^{\prime\mu\nu}m_{\mu}m_{\nu} = \frac{{\rm e}^{-2{\rm i}\omega t}{\rm e}^{2{\rm i}m\phi}}{4(r+{\rm i}a\cos\theta)^2} \left[S_{,\theta}+\left(a\omega\sin\theta-\frac{m}{\sin\theta}\right)S\right]^2 R^2,\end{equation}

(44b)

\begin{equation} \hat{T}^{\prime\mu\nu}m^{*}_{\mu}m^{*}_{\nu} = \frac{{\rm e}^{-2{\rm i}\omega t}{\rm e}^{2{\rm i}m\phi}}{4(r-{\rm i}a\cos\theta)^2} \left[S_{,\theta}-\left(a\omega\sin\theta-\frac{m}{\sin\theta}\right)S\right]^2 R^2, \end{equation}

(44c)

\begin{equation} \hat{T}^{\prime\mu\nu}n_{\mu}m_{\nu} = \frac{-{\rm e}^{-2{\rm i}\omega t}{\rm e}^{2{\rm i}m\phi}}{4\sqrt{2}\Sigma (r+{\rm i}a\cos\theta)} \left[{\rm i}KR+\Delta R_{,r}\right] \left[S_{,\theta}+\left(a\omega\sin\theta-\frac{m}{\sin\theta}\right)S\right] SR,\label{eq44d}\end{equation}

(44d)

\begin{equation} \hat{T}^{\prime\mu\nu}n_{\mu}m^{*}_{\nu} = \frac{-{\rm e}^{-2{\rm i}\omega t}{\rm e}^{2{\rm i}m\phi}}{4\sqrt{2}\Sigma (r-{\rm i}a\cos\theta)} \left[{\rm i}KR+\Delta R_{,r}\right] \left[S_{,\theta}-\left(a\omega\sin\theta-\frac{m}{\sin\theta}\right)S\right] SR,\end{equation}

(44e)

with |$K=(r^2+a^2)\omega - am$|⁠.

In the following two sections, we apply this formalism to the analytic approximation in the flat background spacetime and fully numerical calculations in the Kerr background spacetime, respectively.

3. Gravitational radiation in the flat approximation

In this section, we derive approximate formulas for the GW radiation rate in the case |$M\mu \ll 1$|⁠. In this case, most of the axion cloud distributes in a region far from the BH. Detweiler [4] constructed an approximate solution by the MAE method for this case. As stated earlier, the outer solution agrees with the wave function of a hydrogen atom. The solution is

\begin{equation} \hat{\Phi} = -\frac{\sqrt{2E_{{\mathrm{a}}}}}{\omega}(2k)^{3/2} \sqrt{\frac{(n-\ell-1)!}{2n(n+\ell)!}} {\rm e}^{-{\rm i}\omega t} {\rm e}^{-kr}(2kr)^\ell L_{n-\ell-1}^{2\ell+1}(2kr)Y_{\ell m}(\theta,\phi).\label{eq45} \end{equation}

(45)

Here, |$L_{n-\ell -1}^{2\ell +1}(x)$| represents the Laguerre polynomial, and |$k$| is defined by

\begin{equation} k=\sqrt{\mu^2-\omega^2}.\label{eq46} \end{equation}

(46)

The value of |$k$| is discretized as

\begin{equation}\label{eq47} k = \frac{M\mu^2}{n}, \end{equation}

(47)

where |$n=1,2,\ldots $| is the principal quantum number defined by

\begin{equation}\label{eq48} n:=\ell + 1 + n_{{\mathrm{r}}} \end{equation}

(48)

with the radial quantum number |$n_{{\mathrm { r}}}=0,1,2,\ldots $|⁠. Note that the gravitational analogue of the Bohr radius is given by |$a_0=1/M\mu ^2 = n/k$|⁠. In Eq. (45), we added the extra factor |$\sqrt {2E_{{\mathrm {a}}}}/\omega $| compared to the standard wavefunction of a hydrogen atom in order to normalize the axion field so that

\begin{equation}\label{eq49} E_{{\rm a}} = \int T_{tt}r^2{\rm d}r{\rm d}\Omega \end{equation}

(49)

is satisfied, where |${\mathrm {d}}\Omega = \sin \theta {\rm d}\theta {\rm d}\phi $|⁠. We ignore the near-horizon solution because it is small and gives a minor contribution to the generation of GWs. In this approximation, the axion field is bounded by the Newton potential |$-M\mu /r$|⁠, and the spacetime is approximately flat. For this reason, we approximate the background metric |$g_{\mu \nu }$| as the flat spacetime metric |$\eta _{\mu \nu }$| in calculating the homogeneous GW solution and the inner product |$\langle u,T\rangle $|⁠. We call this approximation the flat approximation. In this flat approximation, we replace |$g_{\mu \nu }$| of the energy–momentum tensor (6) by |$\eta _{\mu \nu }$|⁠, and raise and lower the tensor indices |$\mu , \nu $| by |$\eta _{\mu \nu }$|⁠.

Here, we point out a potential problem in this approximate method. The approximate solution (45) for the axion field satisfies the equation

\begin{equation}\label{eq50} \eta^{\mu\nu}\partial_\mu\partial_\nu\Phi- \mu^2\Phi = -\frac{2kn}{r}\Phi. \end{equation}

(50)

The right-hand side comes from the Newton potential or, in other words, the contribution from the static perturbation generated by the BH mass |$M$|⁠. On the other hand, in calculating the homogeneous GWs and the inner product, we completely ignore the background curvature and use the flat metric |$\eta _{\mu \nu }$|⁠. As a result, we have

\begin{equation}\label{eq51} \partial_\mu T^{\mu\nu} = -\frac{kn}{r}\partial^\nu\Phi^2, \end{equation}

(51)

and the conservation of the energy and momentum is weakly violated. Because of this, if we adopt the gauge transformation |$\delta u_{\mu \nu }=\partial _\mu \xi _\nu +\partial _\nu \xi _\mu $|⁠, we have

\begin{equation}\label{eq52} \langle \delta u, T\rangle=\frac{1}{\Delta t}\int\frac{kn}{r}\xi^\mu\partial_\mu\Phi^2\sqrt{-g}{\mathrm{d}}^4x, \end{equation}

(52)

and therefore the gauge invariance of the inner product is not guaranteed. For this reason, we have to check carefully to what extent the “error” in Eq. (52) can be large. We will come back to this point in the last part of this section.

3.1 Solution to Teukolsky equation

In the flat spacetime, the radial Teukolsky equation becomes

\begin{equation}\label{eq53} \frac{{\rm d}^2{}_{s}R_{\tilde{\ell}\tilde{m}}}{{\rm d}\tilde{r}^2} + \frac{2s+2}{\tilde{r}}\frac{{\rm d}{}_{s}R_{\tilde{\ell}\tilde{m}}}{{\rm d}\tilde{r}} +\left[1+\frac{2{\rm i}s}{\tilde{r}}-\frac{(\tilde{\ell}-s)(\tilde{\ell}+s+1)}{\tilde{r}^2}\right] {}_{s}R_{\tilde{\ell}\tilde{m}}=0. \end{equation}

(53)

Here, the rescaled radial coordinate |$\tilde {r}=\tilde {\omega }r$| is introduced. This equation can be solved analytically. Choosing |$s=+2$|⁠, the general solution is given as

\begin{equation}\label{eq54} {}_{+2}R_{\tilde{\ell}\tilde{m}} = A {\mathrm{e}}^{-{\rm i}\tilde{r}}\tilde{r}^{\tilde{\ell}-2}U(\tilde{\ell}-1,2\tilde{\ell}+2,2{\rm i}\tilde{r}) +B {\rm e}^{-{\rm i}\tilde{r}}\tilde{r}^{\tilde{\ell}-2}F(\tilde{\ell}-1,2\tilde{\ell}+2,2{\rm i}\tilde{r}), \end{equation}

(54)

where |$F$| and |$U$| denote the confluent hypergeometric functions of the first and second kinds, respectively. We choose the integral constants to be |$A=0$|⁠, |$B=1$|⁠;

\begin{equation}\label{eq55} {}_{+2}R_{\tilde{\ell}\tilde{m}}={\mathrm{e}}^{-{\rm i}\tilde{r}}\tilde{r}^{\tilde{\ell}-2}F(\tilde{\ell}-1,2\tilde{\ell}+2,2{\rm i}\tilde{r}), \end{equation}

(55)

so that the radial function becomes regular at the origin, |$\tilde {r}=0$|⁠. The asymptotic behavior at large |$\tilde {r}$| is

\begin{equation}\label{eq56} {}_{+2}R_{\tilde{\ell}\tilde{m}}\approx \frac{\Gamma(2\tilde{\ell}+2)}{(2{\mathrm{i}})^{\tilde{\ell}+3}\Gamma(\tilde{\ell}-1)} \frac{{\rm e}^{{\rm i}\tilde{r}}}{\tilde{r}^5} +\frac{\Gamma(2\tilde{\ell}+2)}{(-2{\rm i})^{\tilde{\ell}-1}\Gamma(\tilde{\ell}+3)} \frac{{\rm e}^{-{\rm i}\tilde{r}}}{\tilde{r}}. \end{equation}

(56)

Here, the first term represents outgoing waves. From this asymptotic behavior, the coefficient |$Z_{\mathrm { out}}$| for the asymptotic outgoing waves in Eq. (37) is read to be

\begin{equation} Z_{\mathrm{out}}=\frac{\Gamma(2\tilde{\ell}+2)}{(2{\rm i})^{\tilde{\ell}+3}\Gamma(\tilde{\ell}-1)}\tilde{\omega}^{-5}.\label{eq57} \end{equation}

(57)

3.2 Energy emission rate

The remaining task is to obtain the homogeneous solution |$\hat {u}^{(\tilde {j})}_{\mu \nu }$| and calculate the integral |$\langle u^{(\tilde {j})}, T\rangle $|⁠, where the index |$(\tilde {j})$| is a shorthand for |$(\tilde {\ell },\tilde {m}, P)$| to label each GW mode as noted in Sect. 2.2. Since the calculation of the inner product is rather tedious, we sketch the calculations in Appendix B, and just present the results here. It is convenient to discuss the results for the odd-type GWs (⁠|$P=-1$|⁠) and for the even-type GWs (⁠|$P=+1$|⁠) separately.

3.2.1 Odd-type perturbation

In the case of odd-type perturbation, |$P=-1$|⁠, the inner product |$\langle u,T\rangle $| vanishes after integration with respect to the angular coordinates |$(\theta , \phi)$|⁠. Therefore, we find that GWs of the odd-type modes are not radiated in our BH–axion system in the flat approximation. This is a natural result because the oscillating part of the energy–momentum tensor of the axion cloud has just the even-type mode. The stationary part of the energy–momentum tensor generates the odd-type perturbation that corresponds to the gravitational angular momentum, and this part has been ignored in our analysis.

3.2.2 Even-type perturbation

We now discuss the case of even-type perturbation, |$P=+1$|⁠. Here, we assume the axion cloud to be in the mode |$\ell = m$| for simplicity. Then, it turns out that only GWs of the mode |$\tilde {\ell }=\tilde {m}=2\ell $| are radiated, and the energy radiation rate is given by

\begin{equation} \frac{{\mathrm{d}}E_{\rm GW}}{{\rm d}t} =C_{n\ell} \left(\frac{E_{{\rm a}}}{M}\right)^2(\mu M)^{Q_{\ell}}, \end{equation}

(58a)

where

\begin{equation} Q_{\ell} = 4\ell+10,\label{eq58b} \end{equation}

(58b)

and

\begin{equation} C_{n\ell}=\frac{16^{\ell+1}\ell(2\ell-1)\Gamma(2\ell-1)^2\Gamma(\ell+n+1)^2} {n^{4\ell+8}(\ell+1)\Gamma(\ell+1)^4\Gamma(4\ell+3)\Gamma(n-\ell)^2}.\end{equation}

(58c)

Table 1 summarizes the values of |$C_{n\ell }$| and |$Q_{\ell }$| and the radiated GW mode |$(\tilde {\ell }, \tilde {m})$| for several axion modes.

Table 1.

Open in new tab

Approximate values of |$C_{n\ell }$|⁠, values of |$Q_{\ell }$|⁠, and the emitted GW mode |$(\tilde {\ell }, \tilde {m})$| for several axion cloud modes |$(n, \ell , m)$|⁠.

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

Table 1.

Open in new tab

Approximate values of |$C_{n\ell }$|⁠, values of |$Q_{\ell }$|⁠, and the emitted GW mode |$(\tilde {\ell }, \tilde {m})$| for several axion cloud modes |$(n, \ell , m)$|⁠.

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

3.3 Comparison with the superradiant growth rate

Here, we compare the GW radiation rate with the energy extraction rate of the axion cloud by the superradiant instability. For the situation |$M\mu \ll 1$|⁠, an approximate formula for the growth rate by the instability has been derived by Detweiler [4] with the MAE method. The approximate growth rate is given by

\begin{align}\label{eq59} M\omega_{{\mathrm{I}}} &= (M\mu)^{4\ell+5}(ma_*-2\mu r_+) \frac{2^{4\ell+2}(n+\ell)!}{n^{2\ell+4}(n-\ell-1)!} \left[\frac{\ell!}{(2\ell+1)!(2\ell)!}\right]^2\notag\\ &\quad\times\prod_{j=1}^{\ell}\left[(1-a_*^2)j^2+(ma_*-2\mu r_+)^2\right]. \end{align}

(59)

Note that the definition of |$n$| in Ref. [4] is different from ours: it corresponds to our radial quantum number |$n_{{\mathrm {r}}}$|⁠. With this |$\omega _{{\mathrm {I}}}$|⁠, the energy extraction rate by the superradiant instability is given by Eq. (1). Because the energy extraction rate and the GW radiation rate are proportional to |$(M\mu)^{4\ell + 5}$| and |$(M\mu)^{Q_\ell }$| with |$Q_\ell =4\ell +10$|⁠, respectively, the GW radiation rate has a higher power of |$(M\mu)$|⁠. Since our approximation holds for |$M\mu \ll 1$|⁠, the GW radiation rate is expected to be much smaller than the energy extraction.

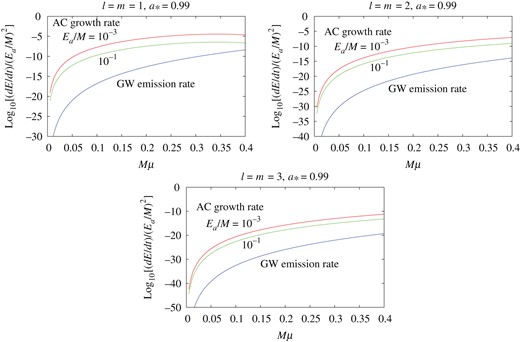
$The GW radiation rate normalized by $(E_{{\mathrm {a}}}/M)^2$ as functions of $M\mu $ in the flat approximation. The cases of the axion cloud in the mode $\ell = m = 1$, $2$, and $3$, and $n_{{\mathrm {r}}}=0$, are shown for the BH rotation parameter $a_*=0.99$. The energy extraction rates of the axion cloud are also plotted for the two cases $E_{{\mathrm {a}}}/M=10^{-3}$ and $10^{-1}$ for comparison. In all cases, the energy extraction rate is larger than the GW radiation rate.$

Fig. 4.

The GW radiation rate normalized by |$(E_{{\mathrm {a}}}/M)^2$| as functions of |$M\mu $| in the flat approximation. The cases of the axion cloud in the mode |$\ell = m = 1$|⁠, |$2$|⁠, and |$3$|⁠, and |$n_{{\mathrm {r}}}=0$|⁠, are shown for the BH rotation parameter |$a_*=0.99$|⁠. The energy extraction rates of the axion cloud are also plotted for the two cases |$E_{{\mathrm {a}}}/M=10^{-3}$| and |$10^{-1}$| for comparison. In all cases, the energy extraction rate is larger than the GW radiation rate.

Open in new tab Download slide

Figure 4 shows the GW radiation rate |${\rm d}E_{\mathrm {GW}}/{\mathrm { d}}t$| and the energy extraction rate |${\rm d}E_{{\mathrm {a}}}/dt$| by the superradiant instability normalized by |$(E_{{\mathrm {a}}}/M)^2$| as functions of |$M\mu $| for |$\ell =m=1$|⁠, |$2$|⁠, and |$3$|⁠. The BH rotation parameter is fixed to be |$a_*=0.99$|⁠, and we show the two cases where the energy of the axion cloud is |$E_{{\mathrm {a}}}/M\sim 10^{-3}$| and |$10^{-1}$|⁠. These two values correspond to the energies when the bosenova happens for the choice of the decay constant |$f_{{\mathrm {a}}}=10^{16}$| and |$10^{17}$| GeV, respectively [12]. The figure shows that the energy extraction rate is much larger. For other values of the BH rotation parameter |$a_*$|⁠, we have found that the result does not change in the region where the superradiant instability works effectively. Therefore, in the region |$M\mu \ll 1$|⁠, the GW radiation rate is smaller than the energy extraction rate, and the GW emission does not hinder the growth of the axion cloud by the superradiant instability for a wide range of system parameters.

3.4 Reliability of the flat approximation

Now, we discuss the problem of the gauge dependence of the inner product in the flat approximation, Eq. (52). Here, we consider the gauge transformation |$\delta u$| of |$u$| generated by a vector field |$\xi ^\mu \propto {\rm e}^{-{\mathrm {i}}\tilde {\omega }t}$|⁠. Since |$\delta u\sim \omega \xi $| and |$\partial _t\Phi ^2\sim \omega \Phi ^2$|⁠, we have

\begin{equation}\label{eq60} \langle \delta u,T\rangle \sim \frac{\beta\omega^2}{\Delta t} \int \delta u\frac{\Phi^2}{\tilde{r}}\sqrt{-g}{\mathrm{d}}^4x. \end{equation}

(60)

Here, we have introduced the small parameter |$\beta :=k/\omega \approx \mu M/n$|⁠. On the other hand, since the order of the |$tt$| component of the energy–momentum tensor is |$T_{tt}\sim \omega ^2 \Phi ^2$|⁠, readers may expect that |$\langle u,T\rangle \sim ({\omega ^2}/{\Delta t}) \int u{\Phi ^2}\sqrt {-g}{\mathrm {d}}^4x$|⁠, and thus |$\langle \delta u,T\rangle \sim \beta \langle u,T\rangle \ll \langle u, T\rangle $|⁠. However, this is incorrect because the leading-order terms with respect to |$\beta $| cancel out in the calculation of |$\langle u,T\rangle $| as explained just before Eq. (34) in Appendix B. The fact is that because of this cancellation,

\begin{equation}\label{eq61} \langle u,T\rangle \sim \frac{\beta\omega^2}{\Delta t}\int u\Phi^2\sqrt{-g}{\mathrm{d}}^4x, \end{equation}

(61)

and therefore |$\langle u, T\rangle \sim \langle \delta u, T\rangle $|⁠. The change in the inner product caused by the gauge transformation contributes to the leading order of |$\langle u, T\rangle $|⁠. Although this problem of the gauge dependence would be solved by introducing the static perturbation from a flat spacetime that corresponds to the Newton potential, the analytic calculation will become much more difficult in such an analysis.

From the observations above, the value of the coefficients |$C_{n\ell }$| of Eq. (58c) is not reliable and may be changed by a factor. In fact, we also calculated the inner product |$\langle u, T\rangle $| using the gauge-invariant formalism for perturbations in spherically symmetric spacetimes in general dimensions [32] in the radiation gauge |$u_{0\mu }=u^{\mu }_{~\mu }=0$| and found that the prefactor |$C_{n\ell }$| for the radiation formula (58a) for the even-type mode differs from Eq. (58c) by a factor of |$(\ell -1)^2/4$| (although the result for the odd-type mode is unchanged). However, we would like to stress that the power dependence on |$(\mu M)$| must not be changed by the gauge choice: we can trust the power |$Q_{\ell }$| of |$(\mu M)$| given by Eq. (58b). We will confirm this statement in the fully numerical calculation in the Kerr background spacetime in the next section.

Note that this gauge dependence just appears in the case of the flat approximation. In the full numerical calculations in the Kerr background below, the gauge invariance of the inner product is guaranteed because the energy conservation |$\nabla _\mu T^{\mu \nu }=0$| is fully satisfied.

4. Gravitational radiation in Kerr background

In this section, we explain the numerical method of computing the GW radiation rate from an axion cloud in the Kerr background spacetime and present the numerical results. This analysis can be applied for the range of the system parameter |$M\mu \sim 1$|⁠.

4.1 Numerical method

The numerical method of calculating the axion bound state |$\hat {\Phi }={\mathrm {e}}^{-{\rm i}\omega t}{\rm e}^{{\rm i}m\phi }R(r)S(\theta)$| was already explained in Sect. 2.1. The bound-state frequency and the radial function |$R(r)$| are obtained by the continued fraction method. The angular function |$S(\theta)$| is approximately calculated with an expansion formula |$S(\theta) = \sum _i S^{(i)}{c}_{0}^{i}$| with |${c}_{0}^2 = -a^2k^2$| up to the sixth order for each |$(\ell , m)$|—see Appendix A for details. Once these functions are obtained, the necessary components of the energy–momentum tensor are calculated with Eqs. (44a)–(44e).

In order to generate the homogeneous solutions |$u^{(\tilde {j})}_{\mu \nu }$|⁠, we first calculate the functions and quantities that appear in the Teukolsky function—the spin-weighted spheroidal harmonics |${}_sS_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(\theta){\rm e}^{{\mathrm {i}}\tilde {m}\phi }$| and its eigenvalue |${}_sA_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}$|⁠, and the radial function |${}_sR_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(r)$|⁠.

For the eigenvalue |${}_sA_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}$|⁠, we adopt the approximate formula for small |$\tilde {c}:=a\tilde {\omega }$| given in Refs. [33,34] that is applicable for arbitrary values of |$(s, \tilde {\ell }, \tilde {m})$|⁠. This approximate formula is given in the form of the series expansion with respect to |$\tilde {c}=a\tilde {\omega }$| up to the sixth order. Since approximate formulas for the functions |${}_sS_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}$| have not been given in the existing literature, we have derived the series expansion |${}_sS(\theta) = \sum _{i}{}_sS^{(i)}\tilde {c}^i$| up to the sixth order for each value of |$(s, \tilde {\ell }, \tilde {m})$|⁠. The reason why we use the approximate formula is that regularization at poles is necessary when we calculate the metric from the Teukolsky functions. This regularization procedure is much more difficult for numerically generated data.

The radial function |${}_{+2}R_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(r_*)$| was numerically generated using the fourth-order Runge–Kutta method starting from |$r_*=-200$| to outward up to |$r_*/M = 1000$| or |$4000$| depending on the situation. Here, we choose |$s=+2$| for the following reason. In order to construct the out-mode solution, we have to generate solutions without ingoing waves that behave as |${}_{s}R_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }} \sim \Delta ^{-s}{\mathrm {e}}^{-{\rm i}(\tilde {\omega }-\tilde {m}\Omega _{{\rm H}})r_*}$| near the horizon. If we choose |$s=-2$|⁠, the amplitude of ingoing waves is an exponentially increasing function of |$r_*$|⁠, and therefore a small numerical error easily grows large to give a large amount of spurious ingoing waves in solving the equation from a near-horizon position to the outward direction. Conversely, in the case of |$s=+2$|⁠, the amplitude of ingoing waves is an exponentially decreasing function, and a numerical error stays small to give a well-behaved solution. In other words, the out-mode solution is a numerical attractor for |$s=+2$|⁠.

In order to calculate the radiation rate, we have to determine the value of |$Z_{\mathrm {out}}$| from the numerical data. This is done by fitting the numerical data with the asymptotic expansion formula of the form

\begin{equation}\label{eq62} {}_{+2}R_{\tilde{\ell}\tilde{m}}^{~\tilde{\omega}} \approx Z_{\rm in}\frac{{\rm e}^{-{\rm i}\tilde{\omega} r}}{r^{1+2M\tilde{\omega} {\rm i}}} \left[1 + \frac{A_1}{r} + \cdots + \frac{A_5}{r^5} \right] +Z_{\rm out}\frac{{\rm e}^{{\rm i}\tilde{\omega} r}}{r^{5-2M\tilde{\omega} {\rm i}}} \left[1 + \frac{B_1}{r} + \frac{B_2}{r^2} \right]. \end{equation}

(62)

Here, the coefficients |$A_1,\ldots ,A_5$| and |$B_1, B_2$| are determined from the asymptotic expansion of the radial Teukolsky equation (33), and the fitting parameters are |$Z_{\mathrm {in}}$| and |$Z_{\mathrm {out}}$|⁠. Although the amplitude of outgoing waves decays more rapidly compared to that of incoming waves at large |$r$|⁠, the value of |$Z_{\mathrm {out}}$| can be evaluated fairly accurately by increasing the numerical accuracy of |${}_{+2}R_{\tilde {\ell }\tilde {m}}^{~\tilde {\omega }}(r)$|⁠. The fit was done in the range |$100\le r_*/M\le 300$|⁠, because the numerical noise increases as the value of |$r_*/M$| is further increased.

$GW energy radiation rates for the modes $(\tilde {\ell }, \tilde {m}) = (2,2)$ (), $(3,2)$ (), $(4,2)$ (), and $(5,2)$ () from the axion cloud in the $(\ell , m) = (1,1)$ mode as functions of $M\mu $ in the cases of $a_*=0.00$, $0.50$, $0.90$, and $0.99$. The result for the flat approximation is shown by a dashed curve in the figure of $a_*=0.00$, and the vertical lines indicate the border of the superradiant instability for each $a_*$.$

Fig. 5.

GW energy radiation rates for the modes |$(\tilde {\ell }, \tilde {m}) = (2,2)$| (⁠ formula ⁠), |$(3,2)$| (⁠ formula ⁠), |$(4,2)$| (⁠ formula ⁠), and |$(5,2)$| (⁠ formula ⁠) from the axion cloud in the |$(\ell , m) = (1,1)$| mode as functions of |$M\mu $| in the cases of |$a_*=0.00$|⁠, |$0.50$|⁠, |$0.90$|⁠, and |$0.99$|⁠. The result for the flat approximation is shown by a dashed curve in the figure of |$a_*=0.00$|⁠, and the vertical lines indicate the border of the superradiant instability for each |$a_*$|⁠.

Open in new tab Download slide

4.2 General properties

The modes of radiated GWs can be restricted by the symmetry properties of the (spin-weighted) spheroidal harmonics. Assuming that the axion cloud is in the mode |$\ell = m$|⁠, we have

\begin{equation}\label{eq63} S_{\ell m}(\theta) = S_{\ell m}(\pi-\theta). \end{equation}

(63)

On the other hand, the spin-weighted spheroidal harmonics for the even azimuthal quantum number |$\tilde {m}=2m$| satisfies

\begin{equation}\label{eq64} {}_{+2}S_{\tilde{\ell} \tilde{m}}^{~\tilde{\omega}}(\theta) = (-1)^{\tilde{\ell}} {}_{-2}S_{\tilde{\ell} \tilde{m}}^{~\tilde{\omega}}(\pi-\theta) \end{equation}

(64)

under the convention in this paper described in Sect. 2.3.1. From these properties, the angular integration of |$\langle u,T\rangle $| becomes zero when |$P=(-1)^{\tilde {\ell }+1}$|⁠. Therefore, the radiated GW modes are limited to the ones satisfying |$P=(-1)^{\tilde {\ell }}$|⁠. For the “even-type” perturbations |$(P=+1)$|⁠, the GW modes with the quantum numbers |$\tilde {\ell }-\tilde {m}=0, 2, 4,\ldots $| are radiated, and for the “odd-type” perturbations |$(P=-1)$|⁠, those with the quantum numbers |$\tilde {\ell }-\tilde {m} =1, 3, 5,\ldots $| are radiated.

In the flat approximation in the previous section, all vector modes (⁠|$P=-1$|⁠) vanished. But in the case of the rotating Kerr background, our numerical data show that the |$P=-1$| modes are nonzero as we see below. The reason can be understood by considering the slow rotation case. The effect of the BH rotation is given by the odd-type perturbation, and the coupling between the even-type axion distribution and the odd-type rotation becomes the source for the odd-type GWs at the second order.

4.3 Numerical results

Now we show the numerical results.

4.3.1 |$\ell =m=1$|

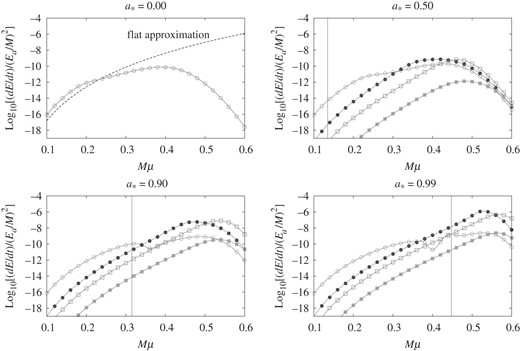
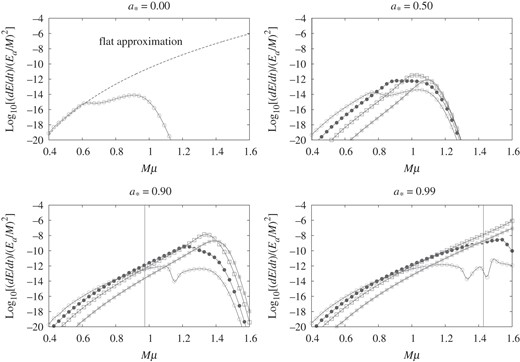
We begin with the results for the axion cloud in the |$\ell = m = 1$| mode that is reduced to the gravitational atom with a vanishing radial quantum number |$n_{{\mathrm {r}}}=0$| for |$M\mu \ll 1$|⁠. Figure 5 shows the GW radiation rates |${\mathrm {d}}E_{\rm GW}^{(\tilde {\ell }\tilde {m})}/{\rm d}t$| normalized by |$(E_{{\mathrm {a}}}/M)^2$| for the modes |$(\tilde {\ell }, \tilde {m})=(2,2)$| (circles, ⁠), |$(3,2)$| (black circles, ⁠), |$(4,2)$| (squares, ⁠), and |$(5,2)$| (black squares, ⁠) as functions of |$M\mu $| for |$a_*=0.00$|⁠, |$0.50$|⁠, |$0.90$|⁠, and |$0.99$|⁠. Since GWs in the modes |$P=(-1)^{\tilde {\ell }+1}$| are not emitted, as discussed in Sect. 4.2, we just present the results for the modes |$P=(-1)^{\tilde {\ell }}$|⁠. In the panel of |$a_*=0.00$|⁠, only the mode |$(\tilde {\ell }, \tilde {m})=(2,2)$| is shown because other modes become zero for the same reason as the flat approximation. However, as the value of |$a_*$| is increased, the contribution of other modes becomes important. In fact, there are regions where the modes |$(\tilde {\ell }, \tilde {m})=(3,2)$| or |$(4,2)$| become dominant.

In each panel of |$a_*=0.50$|⁠, |$0.90$|⁠, and |$0.99$|⁠, the vertical line indicates the threshold of the superradiant instability. On the left-hand side of the line, the axion cloud grows by superradiant instability, at least if the GW emission is neglected. On the right-hand side, no superradiant instability occurs, and the axion cloud, even if it were produced by some mechanism, would simply shrink gradually due to infall into the BH. We find the general tendency such that the radiation rate decreases for very large |$M\mu $|⁠. The reason is as follows. In the superradiant regime, there is always a potential minimum of the axion field and the quasi-bound state is formed. Although this potential minimum also exists for |$M\mu $| not much larger than the threshold, it disappears at some point as |$M\mu $| is further increased. In such a situation, the field cannot form a bound state and it just falls into the horizon. Then, the field is concentrated near the horizon and the GW emission becomes inefficient, because the redshift effect becomes more and more significant as |$M\mu $| increases further. The GW radiation rate decreases rapidly with |$M\mu $|⁠.

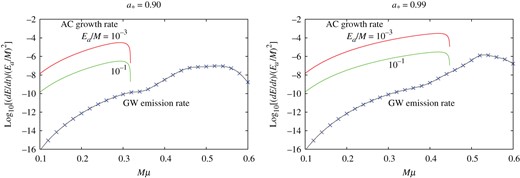
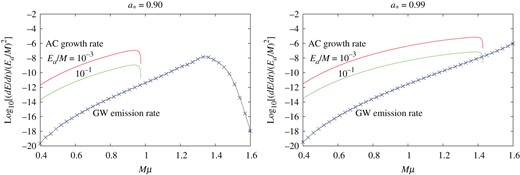
$Total GW energy emission rate from the axion cloud in the $(\ell , m) = (1,1)$ mode and the energy extraction rate of the axion cloud for the cases of $E_{{\mathrm {a}}}/M=10^{-3}$ and $10^{-1}$ as functions of $M\mu $. The cases of the BH rotation parameter $a_*=0.90$ (left) and $0.99$ (right) are shown. The total GW energy emission rate is evaluated by summing the first four GW modes $\tilde {\ell } = 2$, $3$, $4$, and $5$. The energy extraction rate is larger in all cases.$

Fig. 6.

Total GW energy emission rate from the axion cloud in the |$(\ell , m) = (1,1)$| mode and the energy extraction rate of the axion cloud for the cases of |$E_{{\mathrm {a}}}/M=10^{-3}$| and |$10^{-1}$| as functions of |$M\mu $|⁠. The cases of the BH rotation parameter |$a_*=0.90$| (left) and |$0.99$| (right) are shown. The total GW energy emission rate is evaluated by summing the first four GW modes |$\tilde {\ell } = 2$|⁠, |$3$|⁠, |$4$|⁠, and |$5$|⁠. The energy extraction rate is larger in all cases.

Open in new tab Download slide

In the panel of |$a_*=0.00$|⁠, the result of the flat approximation is also shown. For a small value of |$M\mu $|⁠, our numerical data obey the same power dependence on |$M\mu $| as the approximate formula |${\mathrm {d}}E_{{\mathrm { GW}}}/{\rm d}t\propto (M\mu)^{14}$|⁠. There is a shift by a constant factor from the curve of the approximate formula, because the value of |$C_{n\ell }$| includes the error by a factor as discussed in Sect. 3.4.

Figure 6 compares the total GW radiation rate |${\mathrm {d}}E_{\mathrm { GW}}/{\mathrm { d}}t$| and the energy extraction rate |${\mathrm {d}}E_{\mathrm { a}}/{\mathrm { d}}t$| normalized with |$(E_{{\rm a}}/M)^2$| as functions of |$M\mu $| for |$a_*=0.90$| and |$a_*=0.99$|⁠. Here, the total GW emission rate is approximated by the sum of the GW radiation rates for the first four modes with respect to |$\tilde {\ell }$|⁠,

\begin{equation}\label{eq65} \frac{{\mathrm{d}}E_{\rm GW}}{{\rm d}t} \approx\sum_{\tilde{\ell}=\tilde{m}}^{\tilde{m}+3} \frac{{\rm d}E_{\rm GW}^{(\tilde{\ell}\tilde{m})}}{{\rm d}t}. \end{equation}

(65)

Since the power dependence on |$(E_{{\mathrm { a}}}/M)$| of the two rates are different from each other, we have to specify this value to compare them. As we have done in the flat approximation, we consider the two cases |$E_{{\mathrm {a}}}/M=10^{-3}$| and |$10^{-1}$|⁠. Each curve of the energy extraction rate crosses the curve of the GW radiation rate at the point where the former curve suddenly drops near the threshold of the superradiant instability. Therefore, the GW emission scarcely affects the growth of the axion cloud due to the superradiant instability.

4.3.2 |$\ell =m=2$|

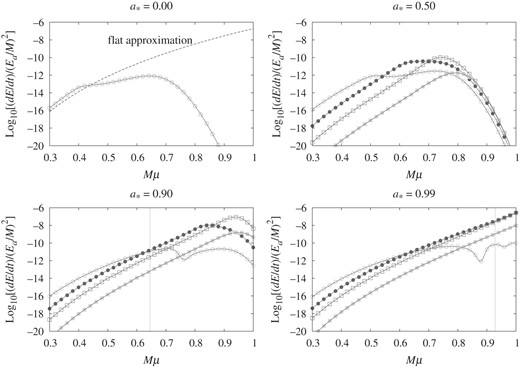
We turn our attention to the results for the axion cloud in the |$\ell = m = 2$| mode with the radial quantum number |$n_{{\mathrm {r}}}=0$|⁠. Figure 7 shows the radiation rates |${\mathrm {d}}E_{\rm GW}^{(\tilde {\ell }\tilde {m})}/{\rm d}t$| normalized with |$(E_{{\mathrm {a}}}/M)^2$| for the GW modes |$(\tilde {\ell }, \tilde {m})=(4,4)$| (circles, ⁠), |$(5,4)$| (black circles, ⁠), |$(6,4)$| (squares, ⁠), and |$(7,4)$| (black squares, ⁠) as functions of |$M\mu $| for |$a_*=0.00$|⁠, |$0.50$|⁠, |$0.90$|⁠, and |$0.99$|⁠. Similarly to the case |$\ell = m= 1$|⁠, only the mode |$(\tilde {\ell }, \tilde {m})=(4,4)$| is radiated in the case of |$a_*=0.00$|⁠. But as the value of |$a_*$| is increased, the contribution of other modes becomes important, and there are regions where the modes |$(\tilde {\ell }, \tilde {m})=(5,4)$| or |$(6,4)$| become dominant. Again, the effect of nonlinearity with respect to |$M\mu $| tends to suppress the GW radiation rate. Similarly to the case of |$\ell =m=1$|⁠, the numerical data (shown in the panel of |$a_*=0.00$|⁠) have the same power dependence |${\mathrm {d}}E_{\rm GW}/{\mathrm { d}}t \propto (M\mu)^{18}$| as the result of the flat approximation for |$M\mu \ll 1$|⁠.

$As Fig. 5 for the GW modes $(\tilde {\ell }, \tilde {m}) = (4,4)$ (), $(5,4)$ (), $(6,4)$ (), and $(7,4)$ () from the axion cloud in the $\ell = m = 2$ mode.$

Fig. 7.

As Fig. 5 for the GW modes |$(\tilde {\ell }, \tilde {m}) = (4,4)$| (⁠ formula ⁠), |$(5,4)$| (⁠ formula ⁠), |$(6,4)$| (⁠ formula ⁠), and |$(7,4)$| (⁠ formula ⁠) from the axion cloud in the |$\ell = m = 2$| mode.

Open in new tab Download slide

Figure 8 compares the total GW radiation rate with the energy extraction rate as functions of |$M\mu $| for |$a_*=0.90$| and |$0.99$|⁠. Here, the total GW radiation rate is approximated by the sum of the GW radiation rates for the first four modes with respect to |$\tilde {\ell }$|⁠, and the curves of the energy extraction rate for the cases |$E_{{\rm a}}/M=10^{-3}$| and |$10^{-1}$| are shown. Similarly to the case |$\ell = m = 1$|⁠, the GW radiation rate is much smaller than the energy extraction rate except for a very small region near the threshold of the superradiant instability. Therefore, the GW emission scarcely affects the growth of the axion cloud due to the superradiant instability also in the case |$\ell = m = 2$|⁠.

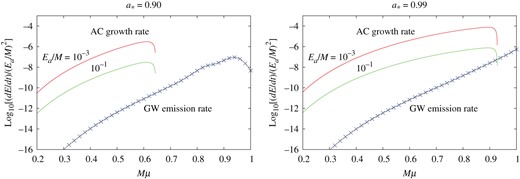
$As Fig. 6 but for the axion cloud in the $\ell = m = 2$ mode. The total GW energy radiation rate is evaluated by summing the first four GW modes $\ell = 4$, $5$, $6$, and $7$.$

Fig. 8.

As Fig. 6 but for the axion cloud in the |$\ell = m = 2$| mode. The total GW energy radiation rate is evaluated by summing the first four GW modes |$\ell = 4$|⁠, |$5$|⁠, |$6$|⁠, and |$7$|⁠.

Open in new tab Download slide

4.3.3 |$\ell =m=3$|

Finally, we show the results for the axion cloud in the |$\ell = m = 3$| mode with the radial quantum number |$n_{{\rm r}}=0$|⁠. Figure 9 shows the radiation rates |${\rm d}E_{\mathrm {GW}}^{(\tilde {\ell }\tilde {m})}/{\rm d}t$| normalized by |$(E_{{\mathrm {a}}}/M)^2$| for the GW modes |$(\tilde {\ell }, \tilde {m})=(6,6)$| (circles, ⁠), |$(7,6)$| (black circles, ⁠), |$(8,6)$| (squares, ⁠), and |$(9,6)$| (black squares, ⁠) as functions of |$M\mu $| for |$a_*=0.00$|⁠, |$0.50$|⁠, |$0.90$|⁠, and |$0.99$|⁠. The general features are same as the previous two cases. Although only the mode |$(\tilde {\ell }, \tilde {m})=(6,6)$| is radiated in the nonrotating case, the contribution of other modes becomes important as the value of |$a_*$| is increased. The GW radiation is suppressed for a very large value of |$M\mu $|⁠. In this case, the numerical data coincide well with the flat approximation for |$M\mu \ll 1$|⁠, as shown in the panel of |$a_*=0.00$|⁠.

$As Fig. 5 but for the GW modes $(\tilde {\ell }, \tilde {m}) = (6,6)$ (), $(7,6)$ (), $(8,6)$ (), and $(9,6)$ () from the axion cloud in the $\ell = m = 3$ mode.$

Fig. 9.

As Fig. 5 but for the GW modes |$(\tilde {\ell }, \tilde {m}) = (6,6)$| (⁠ formula ⁠), |$(7,6)$| (⁠ formula ⁠), |$(8,6)$| (⁠ formula ⁠), and |$(9,6)$| (⁠ formula ⁠) from the axion cloud in the |$\ell = m = 3$| mode.

Open in new tab Download slide

Figure 10 compares the total GW radiation rate (approximated by the sum of the radiation rates for the first four modes with respect to |$\tilde {\ell }$|⁠) and the energy extraction rates for |$E_{{\mathrm {a}}}/M=10^{-3}$| and |$10^{-1}$| as functions of |$M\mu $| for |$a_*=0.90$| and |$0.99$|⁠. Again, the GW radiation rate is much smaller than the energy extraction rate except for a very small region near the threshold of the superradiant instability.

$As Fig. 6 but for the axion cloud in the $\ell = m = 3$ mode. The total GW energy emission rate is evaluated by summing the first four GW modes $\ell = 6$, $7$, $8$, and $9$.$

Fig. 10.

As Fig. 6 but for the axion cloud in the |$\ell = m = 3$| mode. The total GW energy emission rate is evaluated by summing the first four GW modes |$\ell = 6$|⁠, |$7$|⁠, |$8$|⁠, and |$9$|⁠.

Open in new tab Download slide

4.4 Summary of the numerical result

We have calculated the GW radiation rates to infinity, |${\mathrm {d}}E_{\rm GW}^{\rm (out)}/{\rm d}t$|⁠, as functions of |$M\mu $| from the axion clouds in the modes |$\ell = m = 1$|⁠, |$2$|⁠, and |$3$|⁠. Our numerical data have the same power dependence as the flat approximation for small values of |$M\mu $|⁠. We compared the numerical results of |${\mathrm {d}}E_{\rm GW}/{\mathrm { d}}t$| with the energy extraction rates |${\rm d}E_{{\mathrm {a}}}/{\mathrm { d}}t$| of the axion cloud. The value of |${\mathrm {d}}E_{\rm GW}^{\rm (out)}/{\rm d}t$| is much smaller than |${\mathrm {d}}E_{{\mathrm { a}}}/{\mathrm { d}}t$| for both the cases |$E_{{\mathrm {a}}}/M=10^{-3}$| and |$10^{-1}$|⁠. Therefore, similarly to the flat approximation, the axion cloud also grows by the superradiant instability until the effect of the nonlinear self-interaction becomes important when the background spacetime is adopted to be a rotating Kerr BH spacetime.

5. Conclusion

In this paper, we have studied GW emissions from an axion cloud in the superradiant phase around a rotating BH by combining analytic methods and numerical calculations. First, for |$M \mu \ll 1$| for which the Newtonian approximation is good, we have derived the analytic formula (58a)–(58c) in the flat spacetime approximation. This formula can be translated into the expression for the observed nondimensional GW amplitude |$h$| as

\begin{equation} h \sim C^{\mathrm{N}} \alpha_g^{2\ell+4} \left(\frac{G M}{d c^2}\right) \left(\frac{E_a}{Mc^2}\right); \quad C^{\rm N}=\sqrt{2C_{n\ell}}, \label{eq66} \end{equation}

(66)

with |$C_{n\ell }$| given in Table 1, where |$d$| is the distance to the source from us, |$\alpha _g$| is defined by

\begin{equation}\label{eq67} \alpha_g = \frac{\mu M}{M_{\mathrm{pl}}^2}, \end{equation}

(67)

and we have recovered |$G$| and |$c$|⁠.

This formula cannot be used when |$\alpha _g$| becomes of the order of unity, because the axion cloud approaches the BH horizon and relativistic effects become significant. Therefore, for the parameter range |$\alpha _g \sim 1$|⁠, we have computed the GW emission rate from the axion cloud corresponding to the modes |$\ell = m = 1$|⁠, |$2$|⁠, and |$3$| by solving the perturbation of the Kerr background spacetime numerically. As shown in Figs. 5, 7, and 9, the results of the numerical calculations indicate that the GW emission rate for each GW mode deviates from the above analytic formula when |$\alpha _g$| approaches unity, and rapidly decreases beyond some critical value of |$\alpha _g$| due to relativistic effects. This critical value of |$\alpha _g$| depends on the angular momentum parameter |$a_*=J/M^2$| and the quantum number |$\ell $| characterizing the superradiant mode of the cloud, and increases with |$a_*$| and |$\ell $|⁠. Interestingly, up to this critical value, the above analytic formula reproduces the numerical results rather well when |$a_*$| is large if the energy emission rates of all modes are summed up, although the deviation becomes significant at larger |$\alpha _g$| for |$a_*\ll 1$|⁠.

These GW emission rates were compared with the energy extraction rate by the superradiant instability. When the axion decay constant is in the range |$f_{{\rm a}}=10^{16}$|–|$10^{17}\,{\mathrm {GeV}}$| [12] and the angular momentum is in the range |$a_*=0.90$|–|$0.99$|⁠, we have found that the GW emission rate is much smaller than the energy extraction rate except for a small region near the threshold of superradiant instability, as illustrated in Figs. 4, 6, 8, and 10. Therefore, the GW emission does not hinder the growth of the axion cloud through the superradiant instability for a wide range of the system parameters.

In our previous paper [12], we simulated the time evolution of an axion field around a Kerr BH taking account of nonlinear self-interaction, and showed that “axion bosenova” happens as the result of superradiant instability. Our results in this paper indicate that we do not have to change this picture even if we take into account the backreaction of the GW emission from the axion cloud. Since the GW emission rate is sufficiently low, the superradiant instability continues until the bosenova happens by nonlinear self-interaction.

Because we can safely declare that bosenova happens, our next task is to calculate the GW emission during bosenova. In our previous paper [12], we gave a preliminary estimation of the emission rate by the quadrupole formula. The result can be expressed as

\begin{equation}\label{eq68} h \simeq C^{\mathrm{Q}} (\ell+1)^2\alpha_g^{-4}\left(\frac{M}{T_{\rm BN}}\right)^{2} \left(\frac{\Delta E_{{\rm a}}}{E_{{\rm a}}}\right) \left(\frac{G M}{dc^2}\right) \left(\frac{E_{{\rm a}}}{Mc^2}\right), \end{equation}

(68)

where |$C^{\mathrm { Q}}$| is a nondimensional constant of order one. |$T_{\mathrm {BN}}$| and |$\Delta E_{{\mathrm {a}}}$| are the typical time scale and the change in the axion cloud energy during the bosenova collapse, respectively. If we adopt |$T_{\rm BN}$| as the largest time scale of the bosenova |$\approx (50$|–|$500)M$| in which the axion cloud energy |$\Delta E_{{\mathrm {a}}}\approx (0.05$|–|$0.2) E_{{\mathrm {a}}}$| falls into the BH as observed in our simulation, the value of |$h$| becomes smaller than that of the superradiant phase (67) by a factor of |$10$|–|$100$|⁠. In fact, our estimate was that if bosenova happens around the BH candidate, Cygnus X-1, GWs emitted in that process may not be detectable even with advanced GW detectors. However, in our simulation [12], it was also found that there are other shorter characteristic time scales for oscillations of the axion cloud in the radial direction |$\sim 20M$| in the bosenova phenomena. The fluctuations of the axion cloud with such time scales may generate GWs that are detectable by the advanced GW detectors, and therefore simulations of bosenova phenomena including the gravitational perturbation should be necessary in order to clarify this point.

In the present paper, we have studied the case in which only a single mode grows by superradiance. In realistic situations, however, there may exist several unstable modes. Although the instability growth rates for them are largely different, the amplitudes of all of them can become large simultaneously if the instability growth times are all shorter than the age of the BH. Then, GW emissions in the superradiant phase will be more complicated because the emitted GWs will be the superposition of those from the two-axion annihilation processes in several bound-state levels and from the process of axion level transitions. This multi-level occupation will also make the bosenova collapse and the associated GW emissions much more complicated. Further, we should also carefully estimate the detectability of GW emissions in the superradiant phase because it lasts for a much longer time than the bosenova collapse. Clearly, GW emissions in such realistic situations can be correctly evaluated only by combining the method developed in the present paper and the numerical simulations of bosenova in our previous paper [12]. This program is now in progress.

Acknowledgements

H.Y. thanks Masato Nozawa, Takahiro Tanaka, Yasumichi Sano, Misao Sasaki, and Kouji Nakamura for helpful comments. This work is supported by the Grant-in-Aid for Scientific Research (A) (22244030) from Japan Society for the Promotion of Science (JSPS).

Appendix A. Numerical construction of axion bound states

In this appendix, we present details of the numerical construction of the quasibound state of an axion cloud.

A.1 Equation

Assuming the form of Eq. (4), |$\hat {\Phi } = {\rm e}^{-{\mathrm {i}}\omega t}R(r)S(\theta){\rm e}^{{\rm i}m\phi }$|⁠, the massive Klein–Gordon equation (3) in the Kerr background spacetime with the metric (2a) is reduced to the following two separated equations:

\begin{equation} \frac{{\rm d}}{{\rm d}r}\Delta \frac{{\rm d}R}{{\rm d}r} +\left[\frac{K^2}{\Delta} -\lambda_{\ell m} -\mu^2r^2\right]R=0, \label{eqA1} \end{equation}

(A1)

\begin{equation} \frac{1}{\sin\theta} \frac{{\rm d}}{{\rm d}\theta}\sin\theta\frac{{\rm d}S}{{\rm d}\theta} +\left[ -k^2a^2\cos^2\theta-\frac{m^2}{\sin^2\theta}+A_{\ell m} \right]S=0, \label{eqA2} \end{equation}

(A2)

where the definition of |$k$| is the same as Eq. (46), |$k=\sqrt {\mu ^2-\omega ^2}$|⁠, and

\begin{equation}\label{eqA3} K=(r^2+a^2)\omega-am, \quad \lambda_{\ell m}=A_{\ell m}+a^2\omega^2-2am\omega. \end{equation}

(A3)

The angular equation (A2) is identical to the equation for the spin-weighted spheroidal harmonics (34) with |$s=0$| if we replace |$a^2\tilde {\omega }^2$| with |$-k^2a^2$|⁠.

A.2 Angular eigenvalues and angular eigenfunctions

The eigenvalue |$A_{\ell m}$| has to be evaluated approximately or numerically for |$a_*\neq 0$|⁠. In this paper, we use the approximate formula derived by Seidel [33] (see also [34]). Setting |$c_0^2=-k^2a^2$|⁠, Seidel's approximate formula is given in the series with respect to |$c_0$| up to the sixth order:

\begin{equation}\label{eqA4} A_{\ell m} \approx A^{(0)}_{\ell m} + A^{(2)}_{\ell m} c_0^2 + A^{(4)}_{\ell m}c_0^4 + A^{(6)}_{\ell m}c_0^6. \end{equation}

(A4)

The zeroth-order term is |$A^{(0)}_{\ell m}=\ell (\ell +1)$|⁠. The formulas for |$A^{(i)}$| have been given for general |$\ell $| and |$m$| (or more generally for any spins |$s$|⁠). This gives a fairly good approximation.

As for the angular function |$S=S_{\ell m}(c_0;\theta)$|⁠, we could not find an approximate formula for general values of |$\ell $| and |$m$| in existing studies. For this reason, we derived expansion formulas |$S_{\ell m}(c_0;\theta)$| with respect to |$c_0$| up to the sixth order for the values of |$(\ell , m)$| necessary for our purpose. For |$\ell =m>0$|⁠, the expansion formula can be expressed as

\begin{equation}\label{eqA5} S_{\ell m} \approx B \sin^\ell \theta \left(1+a^{(2)}\cos^2\theta +a^{(4)}\cos^4\theta +a^{(6)}\cos^6\theta \right). \end{equation}

(A5)

Here, |$B$|⁠, |$a^{(2)}$|⁠, |$a^{(4)}$|⁠, and |$a^{(6)}$| are polynomials of |$c_0$|⁠. The coefficients |$a^{(i)}$| are defined from the angular equation (A2) order by order, and the value of |$B$| is determined from the normalization condition |$\int |S_{\ell m}(c_0;\theta)|^2 \sin \theta {\mathrm {d}}\theta = 1/2\pi $|⁠.

A.3 Continued fraction method

The next task is to determine the eigenvalue for |$\omega $| that corresponds to the quasi-bound state. The asymptotic behavior of |$R(r)$| at infinity satisfying the decaying condition is

\begin{equation}\label{eqA6} R\sim r^{-1+\frac{M(2\omega^2-\mu^2)}{k}}{\mathrm{e}}^{-kr}, \end{equation}

(A6)

where we assumed |$\Re k>0$|⁠. On the other hand, the behavior in the neighborhood of the horizon satisfying the ingoing condition is given as

\begin{equation}\label{eqA7} R\sim {\mathrm{e}}^{- {\rm i}(\omega-m\Omega_{{\rm H}})r_*}, \end{equation}

(A7)

with the tortoise coordinate |$r_*$| defined in Eq. (5) and the angular velocity |$\Omega _{{\mathrm {H}}} = a/(r_+^2+a^2)$| of the Kerr BH. Dolan [9] assumed that the radial function is expressed by the following infinite series:

\begin{equation} R(r) = (r-r_+)^{-{\rm i}\sigma}(r-r_-)^{{\rm i}\sigma + \chi-1} {\rm e}^{-kr}\sum_{n=0}^{\infty}a_n\left(\frac{r-r_+}{r-r_-}\right)^n,\label{eqA8} \end{equation}

(A8)

where |$r_\pm =M\pm b$| with |$b=\sqrt {M^2-a^2}$|⁠, and

\begin{equation}\label{eqA9} \sigma = \frac{2Mr_+}{r_+-r_-}(\omega-m\Omega_{{\mathrm{H}}}),\quad \chi=\frac{M(2\omega^2-\mu^2)}{k}. \end{equation}

(A9)

Assuming that the series are convergent, the formula (A8) satisfies the boundary conditions above. Substituting the formula (A8) into the radial equation (A1), we obtain the three-term recurrence relation

\begin{equation} a_1=-\frac{\beta_0}{\alpha_0}a_0, \end{equation}

(A10a)

\begin{equation} \alpha_na_{n+1}+\beta_na_n+\gamma_{n}a_{n-1}=0, \end{equation}

(A10b)

where

\begin{equation} {\alpha}_n = (n+1)[n+1-2{\rm i}\sigma] \end{equation}

(A11a)

\begin{equation} {\beta}_n = -2n^2 + 2n\left[-1+2{\rm i}\sigma - 2bk -\frac{M}{k}(\mu^2-2\omega^2)\right]+{\beta}_0, \end{equation}

(A11b)

\begin{equation} {\gamma}_n = (n-1)\left[ n+1 -2{\rm i}\sigma - \frac{2M}{k}(2\omega^2-\mu^2)\right]+{\gamma}_1, \end{equation}

(A11c)

with

\begin{align} {\beta}_0 &= a^2k^2 - 2M(M+b)(\mu^2-2\omega^2) +4M^2\omega^2- (1-2{\rm i}M\omega)\left[1+\frac{{\rm i}}{b}(am-2M^2\omega)\right]\notag\\ &\quad +\left[ -2k-\frac{M}{bk}(\mu^2-2\omega^2) \right] \left[b(1-2{\rm i}M\omega)+{\rm i}(am-2M^2\omega) \right]-A_{\ell m}, \end{align}

(A12a)

\begin{align} {\gamma}_1 &= \frac{M^2(\mu^2-2\omega^2)^2}{k^2} -\frac{{\rm i}M(\mu^2-2\omega^2)}{bk}\left[-am+2M^2\omega+2{\rm i}b(1-{\rm i}M\omega)\right]\notag\\ &\quad +(1-2{\rm i}M\omega)\left[1+\frac{{\rm i}}{b}(am-2M^2\omega)\right].\label{eqA12b} \end{align}

(A12b)

Although these formulas are apparently different from the ones presented in Ref. [9], we have checked that they exactly agree. From the three-term recurrence relations (A10a) and (A10b), we obtain the following relation of the continued fraction:

\begin{equation}\label{eqA13} 0=\beta_0-\frac{\alpha_0\gamma_1}{\beta_1-} \frac{\alpha_1\gamma_2}{\beta_2-} \frac{\alpha_2\gamma_3}{\beta_3-}\cdots. \end{equation}

(A13)

This gives the equations for |$\omega $|⁠, and we solved numerically using the Newton method. Typically, we took account of the first 1000 terms of the recurrence relation (i.e., we assumed |$a_n=0$| for |$n\ge 1000$|⁠). The result is presented in Fig. 1.

A.4 Radial function

Once the eigenfrequency |$\omega $| for the quasi-bound state is determined, we can numerically calculate the sequence of numbers |$a_n$| using the recurrence relations (A10a) and (A10b). Then, using the formula (A8), the radial function |$R(r)$| is generated. Some examples can be found in Figs. 2 and 3.

Appendix B. Inner product in the flat approximation

In Sect. 3, we presented the formula for the gravitational radiation rate. The radiation rate vanishes for the odd-type modes, and is given by Eqs. (58a)–(58c) for the even-type modes. These results are derived from Eqs. (43) and (57) after calculating |$\langle u, T\rangle $|⁠. In this section, we sketch the calculation of this inner product |$\langle u, T\rangle $|⁠.

For simplicity, we denote the radial function and spin-weighted spherical harmonics for the Teukolsky function as |$\tilde {R}:= {}_{+2}R_{\tilde {\ell }\tilde {m}}(r)$| and |${}_{s}\tilde {Y} := {}_{s}Y_{\tilde {\ell }\tilde {m}}(\theta ,\phi)$|⁠, respectively. On the other hand, |$R=R_{\ell m}(r)$| and |$Y:=Y_{\ell m}(\theta ,\phi)$| represent the radial function and spherical harmonics for the axion field.

Because the background spactime is assumed to be flat, the Kinnersley tetrad and the Newman–Penrose variables become

\begin{equation}\label{eqB1} \ell^\mu = (1,1,0,0), \quad n^\mu = (1/2, -1/2, 0, 0), \quad m^\mu = (0,0,1,{\mathrm{i}}/\sin\theta)/\sqrt{2}r, \end{equation}

(B1)

and

\begin{equation}\label{eqB2} \rho = -1/r, \quad \beta=-\alpha=\cot\theta/2\sqrt{2}r, \quad \mu = -1/2r, \quad \pi = \tau = \gamma=0. \end{equation}

(B2)

Then, the functions appearing in the Chrzanowski formula (38) are calculated as

\begin{equation} \mathcal{A}\left(\tilde{R}~{}_{-2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\right)=\frac{\tilde{r}^2}{2\tilde{\omega}^2}\tilde{R}\ \eth\eth{}_{-2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t} \end{equation}

(B3a)

\begin{equation} \mathcal{A}^*\left(\tilde{R}~{}_{+2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\right) =\frac{\tilde{r}^2}{2\tilde{\omega}^2}\tilde{R}\ \eth^*\eth^*{}_{+2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\end{equation}

(B3b)

\begin{equation}\mathcal{B}\left(\tilde{R}~{}_{-2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\right) =\frac{\tilde{r}^4}{4\tilde{\omega}^2} \left[2{\rm i}\tilde{R}_{,\tilde{r}} +\left(-2+\frac{2{\rm i}}{\tilde{r}}+\frac{\tilde{\ell}^2+\tilde{\ell}-2}{\tilde{r}^2}\right)\tilde{R} \right]{}_{-2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t} \end{equation}

(B3c)

\begin{equation} \mathcal{B}^*\left(\tilde{R}~{}_{+2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\right) =\frac{\tilde{r}^4}{4\tilde{\omega}^2} \left[2{\rm i}\tilde{R}_{,\tilde{r}} +\left(-2+\frac{2{\rm i}}{\tilde{r}}+\frac{\tilde{\ell}^2+\tilde{\ell}-2}{\tilde{r}^2}\right)\tilde{R} \right]{}_{+2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t} \end{equation}

(B3d)

\begin{equation} \mathcal{C} \left(\tilde{R}~{}_{-2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\right) = \frac{\tilde{r}^3}{\sqrt{2}\tilde{\omega}^2} \left({\rm i}\tilde{R}+\tilde{R}_{,\tilde{r}}+\frac{2}{\tilde{r}}\tilde{R}\right)\ \eth{}_{-2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\end{equation}

(B3e)

\begin{equation} \mathcal{C}^* \left(\tilde{R}~{}_{+2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}\right) = \frac{\tilde{r}^3}{\sqrt{2}\tilde{\omega}^2} \left({\rm i}\tilde{R}+\tilde{R}_{,\tilde{r}}+\frac{2}{\tilde{r}}\tilde{R}\right)\ \eth^*{}_{+2}\tilde{Y}{\rm e}^{-{\rm i}\tilde{\omega}t}. \end{equation}

(B3f)

On the other hand, the necessary components of the energy–momentum tensor, Eqs. (44a)–(44e), become

\begin{equation} \hat{T}_{\mu\nu}m^\mu m^\nu =\frac{\tilde{\omega}^2}{4\tilde{r}^2}R^2 \left(\eth Y\right)^2{\rm e}^{-2{\rm i}\omega t},\end{equation}

(B4a)

\begin{equation} \hat{T}_{\mu\nu}m^{*\mu} m^{* \nu} =\frac{\tilde{\omega}^2}{4\tilde{r}^2}R^2 \left(\eth^* Y\right)^2{\rm e}^{-2{\rm i}\omega t},\end{equation}

(B4b)

\begin{equation}\hat{T}_{\mu\nu}n^\mu n^\nu =\frac{\tilde{\omega}^2}{8}\left(\frac{{\rm i}}{2}R+R_{,\tilde{r}}\right)^2Y^2{\rm e}^{-2{\rm i}\omega t},\end{equation}

(B4c)

\begin{equation}\hat{T}_{\mu\nu}n^\mu m^\nu =\frac{\tilde{\omega}^2}{4\sqrt{2}\tilde{r}}\left(\frac{{\rm i}}{2}R+R_{,\tilde{r}}\right)R\left(\eth Y\right)Y{\rm e}^{-2{\rm i}\omega t},\end{equation}

(B4d)

\begin{equation}\hat{T}_{\mu\nu}n^{\mu} m^{* \nu} =\frac{\tilde{\omega}^2}{4\sqrt{2}\tilde{r}}\left(\frac{{\rm i}}{2}R+R_{,\tilde{r}}\right)R\left(\eth^* Y\right)Y{\rm e}^{-2{\rm i}\omega t}.\end{equation}

(B4e)

Here, we used the standard definition for the “eth” operators [23], |$\eth $| and |$\eth ^*$|⁠, which act on the spin-weighted spherical harmonics as

\begin{equation} \eth \left({}_sY_{\tilde{\ell}\tilde{m}}\right) :=-\left(\partial_\theta+\frac{{\mathrm{i}}}{\sin\theta}-s\cot\theta\right){}_{s}Y_{\tilde{\ell}\tilde{m}},\end{equation}

(B5a)

\begin{equation} \eth^* \left({}_sY_{\tilde{\ell}\tilde{m}}\right) :=-\left(\partial_\theta-\frac{{\rm i}}{\sin\theta}+s\cot\theta\right){}_{s}Y_{\tilde{\ell}\tilde{m}}. \end{equation}

(B5b)

It is worth noting the following useful formulas [23] in order to carry out the angular integrations below:

\begin{equation} \eth \left({}_sY_{\tilde{\ell}\tilde{m}}\right) =+\sqrt{(\tilde{\ell}-s)(\tilde{\ell}+s+1)}{}_{s+1}Y_{\tilde{\ell}\tilde{m}},\end{equation}

(6a)

\begin{equation} \eth^* \left({}_sY_{\tilde{\ell}\tilde{m}}\right) =-\sqrt{(\tilde{\ell}+s)(\tilde{\ell}-s+1)}{}_{s-1}Y_{\tilde{\ell}\tilde{m}}. \end{equation}

(6b)

B.1 Odd-type modes

\begin{equation} \int \left[(\eth^*{}_{-2}\tilde{Y})^*(\eth^*Y)Y-(\eth^*{}_{+2}\tilde{Y})^*(\eth Y)Y\right]{\mathrm{d}}\Omega=0,\end{equation}

(B7a)

\begin{equation}\int \left[({}_{-2}\tilde{Y})^*(\eth^*Y)^2-({}_{+2}\tilde{Y})^*(\eth Y)^2\right]{\rm d}\Omega=0,\end{equation}

(B7b)

\begin{equation} \int \left[(\eth\eth{}_{-2}\tilde{Y})^*Y^2-(\eth^*\eth^*{}_{+2}\tilde{Y})^*Y^2\right]{\rm d}\Omega=0. \end{equation}

(B7c)

Since all the angular integrals become zero, we have |$\langle u, T\rangle = 0$|⁠. Therefore, odd-type GWs are not radiated.

B.2 Even-type modes

\begin{equation} \int \left[(\eth^*{}_{-2}\tilde{Y})^*(\eth^*Y)Y +(\eth^*{}_{+2}\tilde{Y})^*(\eth Y)Y\right]{\mathrm{d}}\Omega = -I_{\Omega}\sqrt{(\tilde{\ell}-1)\tilde{\ell}(\tilde{\ell}+1)(\tilde{\ell}+2)},\end{equation}

(B8a)

\begin{equation} \int \left[({}_{-2}\tilde{Y})^*(\eth^*Y)^2 +({}_{+2}\tilde{Y})^*(\eth Y)^2\right]{\rm d}\Omega = {2\ell(\ell+1)}I_{\Omega} \sqrt{\frac{\tilde{\ell}(\tilde{\ell}+1)}{(\tilde{\ell}-1)(\tilde{\ell}+2)}},\end{equation}

(B8b)

\begin{equation} \int \left[(\eth\eth{}_{-2}\tilde{Y})^*Y^2 +(\eth^*\eth^*{}_{+2}\tilde{Y})^*Y^2\right]{\rm d}\Omega = 2I_{\Omega} \sqrt{(\tilde{\ell}-1)\tilde{\ell}(\tilde{\ell}+1)(\tilde{\ell}+2)}, \end{equation}

(B8c)

where we introduced the definition

\begin{equation}\label{eqB9} I_\Omega = \int \left({}_{0}Y_{\tilde{\ell}\tilde{m}}\right)^* \left(Y_{\ell m}\right)^2{\rm d}\Omega. \end{equation}

(B9)

Hereafter, we assume the axion cloud to be in the |$\ell = m $| mode. In this setup, the integral |$I_\Omega $| becomes nonzero if and only if |$\tilde {\ell } =\tilde {m}= 2\ell $|⁠, and its analytic expression for these mode parameters is

\begin{equation} I_{\Omega} = \frac{\Gamma(2\ell+2)\sqrt{\Gamma(4\ell+2)}} {4^{2\ell+1}\left[\Gamma(\ell+1)\right]^2\Gamma(2\ell+3/2)}. \label{eqB10} \end{equation}

(B10)

After integrating |$\hat {u}^*_{ab}\hat {T}^{ab}$| with respect to the angular variables |$(\theta ,\phi)$|⁠, we have

\begin{align}\label{eqB11} \int \hat{u}^*_{ab}\hat{T}^{ab}{\mathrm{d}}\Omega &= \frac{I_{\Omega}}{16} \sqrt{(\tilde{\ell}-1)\tilde{\ell}(\tilde{\ell}+1)(\tilde{\ell}+2)}\notag\\ &\quad \times\left\{ -\frac{2\ell(\ell+1)\tilde{r}^2}{(\tilde{\ell}-1)(\tilde{\ell}+2)} \left[-2{\rm i}\tilde{R}^*_{,\tilde{r}} +\left(-2-\frac{2{\rm i}}{\tilde{r}}+\frac{\tilde{\ell^2}+\tilde{\ell}-2}{\tilde{r}^2}\right) \tilde{R}^*\right]R^2 \right.\notag\\ &\quad -\left.2\tilde{r}^2\tilde{R}^*\left(\frac{{\rm i}}{2}R+R_{,\tilde{r}}\right)^2 +\tilde{r}^2\left(2{\rm i}\tilde{R}^*-2\tilde{R}^*_{,\tilde{r}}-\frac{4}{\tilde{r}}\tilde{R^*}\right) \left(\frac{{\rm i}}{2}R+R_{,\tilde{r}}\right)R \right\}. \end{align}

(B11)

Now, we multiply the volume element in the radial direction |$r^2 {\rm d}r = \tilde {\omega }^{-3}\tilde {r}^2 {\rm d}\tilde {r}$| and perform the integration. Integrating by parts and rewriting with the equation for the radial function of the axion field |$R$|⁠,

\begin{equation}\label{eqB12} R_{,\tilde{r}\tilde{r}}+\frac{2}{\tilde{r}}R_{,\tilde{r}} +\left[-\frac{\beta^2}{4}+\frac{\ell(\ell+1)}{\tilde{r}^2} -\frac{n\beta}{\tilde{r}} \right]R=0, \end{equation}

(B12)

where |$\beta $| is a small parameter |$\beta :=k/\omega \approx \mu M/n$|⁠, we have

\begin{align} \langle u,T\rangle&\approx \frac{I_{\Omega}}{16}\tilde{\omega}^{-3} \sqrt{(\tilde{\ell}-1)\tilde{\ell}(\tilde{\ell}+1)(\tilde{\ell}+2)}\notag\\ &\quad\times \int \tilde{R}^* \tilde{r}^4 \left\{\left[\frac{2\ell+1}{2(2\ell-1)}-\frac{2(\ell+1)}{2\ell-1}\frac{{\rm i}}{\tilde{r}}\right]R^2 -\frac{2{\mathrm{i}}}{2\ell-1} RR_{,\tilde{r}} -\frac{2n\beta}{\tilde{r}}R \right\}{\rm d}\tilde{r}. \label{eqB13} \end{align}

(B13)

\begin{align} R&=A{\mathrm{e}}^{-y}\left[(kr)^{\ell}+q(kr)^{\ell+1}+\cdots\right]\nonumber\\ &=A{\rm e}^{-(\beta/2)\tilde{r}}\left(\frac{\beta}{2}\right)^{\ell}\left[\tilde{r}^{\ell}+\frac{q\beta}{2} \tilde{r}^{\ell+1}+\cdots\right] \label{eqB14} \end{align}

(B14)

with

\begin{equation} A = -\frac{\sqrt{2E_{{\rm a}}}}{\omega}(2k)^{3/2}\sqrt{\frac{(n-\ell-1)!}{2n(n+\ell)!}}\frac{2^\ell(n+\ell)!}{(n-\ell-1)!(2\ell+1)!},\label{eqB15}\end{equation}

(B15)

\begin{equation} q =\frac{\ell-n+1}{\ell+1}.\label{eqB16} \end{equation}

(B16)

Substituting Eq. (B14) into Eq. (B13), we have

\begin{align}\label{eqB17} \langle u,T\rangle &=\frac{I_\Omega}{16}\tilde{\omega}^{-3} \sqrt{(\tilde{\ell}-1)\tilde{\ell}(\tilde{\ell}+1)(\tilde{\ell}+2)}A^2 \left(\frac{\beta}{2}\right)^{2\ell} \left\{\frac{2\ell+1}{2(2\ell-1)}f^{(1)}(\beta) - \frac{2(2\ell+1){\rm i}}{2\ell-1}f^{(0)}(\beta)\right.\notag\\ &\quad +\left. \frac{(2\ell+1)q}{2(2\ell-1)} \beta f^{(2)}(\beta) + \frac{[1-(4\ell+3)q]{\rm i}}{2\ell-1} \beta f^{(1)}(\beta) - 2n\beta f^{(0)}(\beta) \right\}, \end{align}

(B17)

where we defined the formula

\begin{equation}\label{eqB18} f^{(N)}(\beta) := \int_0^{\infty}\tilde{R}^*\tilde{r}^{2\ell+3+N}{\rm e}^{-\beta \tilde{r}}{\rm d}\tilde{r}. \end{equation}

(B18)

The integration of |$f^{(0)}$| can be performed analytically as

\begin{align} f^{(0)}&=\frac{\Gamma(4\ell+2)}{(\beta-{\mathrm{i}})^{4\ell+2}} \left[1+\frac{4}{(\beta-{\rm i})^2}\right]^{1/2-\ell} \exp\left[-{\rm i}(2\ell-1)\arctan\left(\frac{2}{\beta-{\rm i}}\right)\right]\nonumber\\ &= \Gamma(4\ell+2) \left[1-4{\rm i}\beta -(2\ell+9)\beta^2+\cdots\right],\label{eqB19} \end{align}

(B19)

and |$f^{(N)}$| with |$N>0$| are given by differentiating |$f^{(0)}$| as

\begin{equation}\label{eqB20} f^{(N)} = (-1)^{N}\frac{{\mathrm{d}}^Nf^{(0)}}{{\rm d}\beta^N}. \end{equation}

(B20)

Substituting these formulas, we find that the terms of |$O(\beta ^{2\ell })$| cancel out. Therefore, the order of the inner product becomes |$O(\beta ^{2\ell +1})$|⁠, and the final result is

\begin{equation}\label{eqB21} \langle u,T\rangle =\frac{I_\Omega}{8}\tilde{\omega}^{-3} \sqrt{(\tilde{\ell}-1)\tilde{\ell}(\tilde{\ell}+1)(\tilde{\ell}+2)}A^2 \frac{n}{\ell+1}\Gamma(4\ell+2)\left(\frac{\beta}{2}\right)^{2\ell+1}. \end{equation}

(B21)

Substituting this formula with Eqs. (B10), (B15), and (57) into Eq. (43), we find the formula for the GW energy emission rate, Eqs. (58a)–(58c).

The growth rate was also reproduced in a time-domain simulation by our code for a special case [12], and more systematic analyses of very long time evolutions were reported by Dolan [13]. See also [14] for earlier work.

The homogeneous GWs are classified into four independent modes: in-, out-, up-, and down-modes depending on the boundary conditions at future and past null infinity |$\mathscr {I}^+$| and |$\mathscr {I}^-$| and the future and past horizons |$\mathscr {H}^+$| and |$\mathscr {H}^-$| (see, e.g., p. 93 of Ref. [20]).

There is arbitrariness in the phase choice in the spin-weighted spherical/spheroidal harmonics that depends on authors, and our choice is different from that of Ref. [24]. We thank the referee of this paper for pointing this out.

The authors of Ref. [29] derived an apparently different formula and claimed that Chrzanowski's formula includes typos. However, we have checked that both the formulas lead to the same result.

References

Arvanitaki

Dimopoulos

Dubovsky

Kaloper

March-Russell

Phys. Rev. D

123530

(

2010

10.1103/PhysRevD.81.123530

Crossref

Search ADS

Arvanitaki

Dubovsky

Phys. Rev. D

044026

(

2011

10.1103/PhysRevD.83.044026

Crossref

Search ADS

Kodama

Yoshino

Int. J. Mod. Phys. Conf. Ser.

(

2012

10.1142/S2010194512004199

Crossref

Search ADS

Detweiler

S. L.

Phys. Rev. D

2323

(

1980

10.1103/PhysRevD.22.2323

Crossref

Search ADS

Zouros

T. J. M.

Eardley

D. M.

Ann. Phys. (N.Y.)

118

139

(

1979

10.1016/0003-4916(79)90237-9

Crossref

Search ADS

Rosa

J. G.

J. High Energy Phys.

1006

015

(

2010

10.1007/JHEP06(2010)015

Crossref

Search ADS

Furuhashi

Nambu

Prog. Theor. Phys.

112

983

(

2004

10.1143/PTP.112.983

Crossref

Search ADS

Cardoso

Yoshida

J. High Energy Phys.

0507

009

(

2005

10.1088/1126-6708/2005/07/009

Crossref

Search ADS

Dolan

S. R.

Phys. Rev. D

084001

(

2007

10.1103/PhysRevD.76.084001

Crossref

Search ADS

Rosa

J. G.

J. High Energy Phys.

1302

014

(

2013

10.1007/JHEP02(2013)014

Crossref

Search ADS

Okawa

Witek

Cardoso

arXiv

[gr-qc].

Yoshino

Kodama

Prog. Theor. Phys.

128

153

(

2012

10.1143/PTP.128.153

Crossref

Search ADS

Dolan

S. R.

124026

(

2013

Strafuss

M. J.

Khanna

Phys. Rev. D

024034

(

2005

10.1103/PhysRevD.71.024034

Crossref

Search ADS

Donley

E. A.

Claussen

N. R.

Cornish

S. L.

Roberts

J. L.

Cornell

E. A.

Wieman

C. E.

Nature

412

295

(

2001

Leaver

E. W.

Proc. R. Soc. London A

402

1985

(285)

Wald

General Relativity

(

The University of Chicago Press

Chicago

1984

Teukolsky

S. A.

Astrophys. J.

193

443

(

1974

10.1086/153180

Crossref

Search ADS

Chrzanowski

P. L.

Phys. Rev. D

2042

(

1975

10.1103/PhysRevD.11.2042

Crossref

Search ADS

Frolov

V. P.

Novikov

I. D.

Black Hole Physics: Basic Concepts and New Developments

(

Kluwer Academic Publishers

Dordrecht and Boston

1998

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Teukolsky

S. A.

Astrophys. J.

185

635

(

1973

10.1086/152444

Crossref

Search ADS

Newman

Penrose

J. Math. Phys. (N.Y.)

566

(

1962

10.1063/1.1724257

Crossref

Search ADS

Zaldarriaga

Seljak

Phys. Rev. D

1830

(

1997

10.1103/PhysRevD.55.1830

Crossref

Search ADS

Press

W. H.

Teukolsky

S. A.

Astrophys. J.

185

649

(

1973

10.1086/152445

Crossref

Search ADS

Wald

R. M.

J. Math. Phys.

1453

(

1973

10.1063/1.1666203

Crossref

Search ADS

Cohen

J. M.

Kegeles

L. S.

Phys. Rev. D

1070

(

1974

10.1103/PhysRevD.10.1070

Crossref

Search ADS

Cohen

J. M.

Kegeles

L. S.

Phys. Lett. A

(

1975

10.1016/0375-9601(75)90583-6

Crossref

Search ADS

Wald

R. M.

Phys. Rev. Lett.

203

(

1978

10.1103/PhysRevLett.41.203

Crossref

Search ADS

Dias

O. J. C.

Reall

H. S.

Santos

J. E.

J. High Energy Phys.

0908

101

(

2009

10.1088/1126-6708/2009/08/101

Crossref

Search ADS

Regge

Wheeler

J. A.

Phys. Rev.

108

1063

(

1957

10.1103/PhysRev.108.1063

Crossref

Search ADS

Zerilli

F. J.

Phys. Rev. D

2141

(

1970

10.1103/PhysRevD.2.2141

Crossref

Search ADS

Kodama

Ishibashi

Prog. Theor. Phys.

110

701

(

2003

10.1143/PTP.110.701

Crossref

Search ADS

Seidel

Class. Quant. Grav.

1057

(

1989

10.1088/0264-9381/6/7/012

Crossref

Search ADS

Berti

Cardoso

Casals

Phys. Rev. D

024013

(

2006

);

73, 109902 (2006). [erratum]

10.1103/PhysRevD.73.024013

Crossref

Search ADS

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download all slides

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

Axion mode \|$(n,\ell ,m)$\|	Atomic orbital	\|$C_{n\ell }$\|	\|$Q_{\ell }$\|	GW mode \|$(\tilde {\ell },\tilde {m})$\|
\|$(2, 1, 1)$\|	2p	\|$1.56\times 10^{-3}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 1, 1)$\|	3p	\|$1.93\times 10^{-4}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(4, 1, 1)$\|	4p	\|$3.81\times 10^{-5}$\|	\|$14$\|	\|$(2, 2)$\|
\|$(3, 2, 2)$\|	3d	\|$1.89\times 10^{-7}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 2, 2)$\|	4d	\|$6.81\times 10^{-8}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(5, 2, 2)$\|	5d	\|$2.35\times 10^{-9}$\|	\|$18$\|	\|$(4, 4)$\|
\|$(4, 3, 3)$\|	4f	\|$2.89\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 3, 3)$\|	5f	\|$2.14\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(6, 3, 3)$\|	6f	\|$1.13\times 10^{-11}$\|	\|$22$\|	\|$(6, 6)$\|
\|$(5, 4, 4)$\|	5g	\|$3.17\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(6, 4, 4)$\|	6g	\|$3.98\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|
\|$(7, 4, 4)$\|	7g	\|$2.97\times 10^{-15}$\|	\|$26$\|	\|$(8, 8)$\|

Month:	Total Views:
November 2016	1
January 2017	72
February 2017	5
March 2017	3
April 2017	4
May 2017	5
June 2017	6
July 2017	9
August 2017	8
September 2017	11
October 2017	8
November 2017	10
December 2017	28
January 2018	12
February 2018	23
March 2018	25
April 2018	20
May 2018	19
June 2018	19
July 2018	24
August 2018	7
September 2018	21
October 2018	14
November 2018	15
December 2018	23
January 2019	20
February 2019	19
March 2019	26
April 2019	27
May 2019	32
June 2019	16
July 2019	28
August 2019	31
September 2019	18
October 2019	29
November 2019	27
December 2019	6
January 2020	25
February 2020	20
March 2020	10
April 2020	9
May 2020	6
June 2020	21
July 2020	14
August 2020	9
September 2020	23
October 2020	14
November 2020	19
December 2020	33
January 2021	4
February 2021	11
March 2021	20
April 2021	12
May 2021	7
June 2021	31
July 2021	20
August 2021	24
September 2021	23
October 2021	30
November 2021	27
December 2021	24
January 2022	16
February 2022	32
March 2022	19
April 2022	30
May 2022	35
June 2022	32
July 2022	46
August 2022	17
September 2022	17
October 2022	16
November 2022	19
December 2022	27
January 2023	23
February 2023	12
March 2023	30
April 2023	18
May 2023	20
June 2023	15
July 2023	23
August 2023	24
September 2023	23
October 2023	16
November 2023	35
December 2023	35
January 2024	47
February 2024	34
March 2024	38
April 2024	58
May 2024	21
June 2024	30
July 2024	34
August 2024	18
September 2024	33
October 2024	19
November 2024	19
December 2024	27
January 2025	28
February 2025	20
March 2025	37
April 2025	53
May 2025	12

Article Contents

Gravitational radiation from an axion cloud around a black hole: Superradiant phase Open Access

Abstract

1. Introduction

2. General strategy

2.1 Superradiant bound states of an axion field

2.2 GWs from an axion cloud

2.3 Methods for calculating the energy emission rate

2.3.1 Homogeneous GWs

2.3.2 Energy–momentum tensor

3. Gravitational radiation in the flat approximation

3.1 Solution to Teukolsky equation

3.2 Energy emission rate

3.2.1 Odd-type perturbation

3.2.2 Even-type perturbation

3.3 Comparison with the superradiant growth rate

3.4 Reliability of the flat approximation

4. Gravitational radiation in Kerr background

4.1 Numerical method

4.2 General properties

4.3 Numerical results

4.3.1 |$\ell =m=1$|

4.3.2 |$\ell =m=2$|

4.3.3 |$\ell =m=3$|

4.4 Summary of the numerical result

5. Conclusion

Acknowledgements

Appendix A. Numerical construction of axion bound states

A.1 Equation

A.2 Angular eigenvalues and angular eigenfunctions

A.3 Continued fraction method

A.4 Radial function

Appendix B. Inner product in the flat approximation

B.1 Odd-type modes

B.2 Even-type modes

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Gravitational radiation from an axion cloud around a black hole: Superradiant phase