Influence of plasma density on associated electrical elements of an ion sheath

Abstract

An attempt is made to theoretically estimate the values of electrical elements such as capacitance, resistance, and inductance for an ion sheath using experimental parameters. Quantitative estimations of the L, C and R components as a function of plasma density are analyzed for argon plasma at a particular electron temperature. The magnitude of the estimated grid bias approaches the real value for higher values of a correction factor.

1. Introduction

The basics of plasma sheath interaction physics have various roles to play in fundamental research of confined plasmas [1–3] and in the development of plasma-based technology in industrial applications. The physical understanding of boundary wall–plasma interaction processes has become a subject of fundamental importance both for basic [4,5] and applied interest [6]. The boundary wall modifies the plasma particle distributions in such a way that a thin layer of natural non-neutral plasma called a Debye sheath or ion sheath [7].

The richness (or excess) of positive or negative charges in this non-neutral layer formed in the vicinity of the biased electrode depends upon the polarity of the applied potential with respect to the bulk plasma. In the case of a highly negatively biased electrode or wall, a positive space-charge-limited sheath current is observable at the wall, which is normally described by the well-known Child–Langmuir law [8].

It is an established fact that the positive ion-rich sheath (in the Child limit) is equivalent to a series electrical circuit consisting of resistance (R), inductance (L), and capacitance (C) as the circuit elements under the diode-like ion sheath approximation in the presence of low frequency oscillation, but the oscillation frequency must be lower than the ion plasma frequency.

The physical origin of the sheath capacitance could be the formation of a localized positive space charge layer to shield the negative wall potential, and the origin of the sheath resistance could be associated with the ions in motion, which have to overcome the potential barrier to pass through the positive space charge layer. The physical origin of the sheath inductance is not clearly mentioned in literature, but it may be caused by some kind of ion fluctuation.

Prakash et al. studied the variation of these electrical components as a function of applied grid bias [9]. In the present work, we have theoretically estimated the frequency of oscillations for different densities of argon plasma at a constant electron temperature. The electrical components such as resistance, capacitance, and inductance for an ion sheath are estimated for a particular surface area at a fixed grid bias. The required plasma parameters are taken from an experiment performed in a double plasma (DP) device [10]. The sheath components are analyzed as a function of plasma density with few approximations.

2. Theory and estimation

For the theoretical estimation of sheath components, we have used experimental data from the work of Popa and Schrittwieser [11]. They performed an experiment in a DP device producing plasma only in the source chamber and using the target chamber as collector. Plasma leaked through the negatively biased (⁠|${V}_{{\mathrm {G}}}$|⁠) separating grid from source into target. The target chamber plasma was mainly a diffusion plasma [12]. The source chamber was at ground potential and the target chamber was either positively or negatively biased with respect to ground. The plasma potential in the target chamber changed almost linearly with the applied bias (⁠|${V}_{{\rm T}}$|⁠), which created a difference in plasma potential between source and target chambers, which was referred to as bi-potential asymmetry. When a positive space charge layer formed around the grid, low frequency instability was observed in the positively biased target chamber. The frequency of oscillation arises due to the asymmetric potential structure between the two plasma chambers.

For physical visualization, the source and target chambers along with the bias voltage applied to the grid (⁠|${V}_{{\mathrm {G}}}$|⁠) and the target chamber (⁠|${V}_{{\mathrm {T}}}$|⁠) are shown schematically in Fig. 1(a). The detail of the experimental setup is available in Ref. [11]. The asymmetric bi-potential structure produced in the system is also shown schematically in Fig. 1(b).

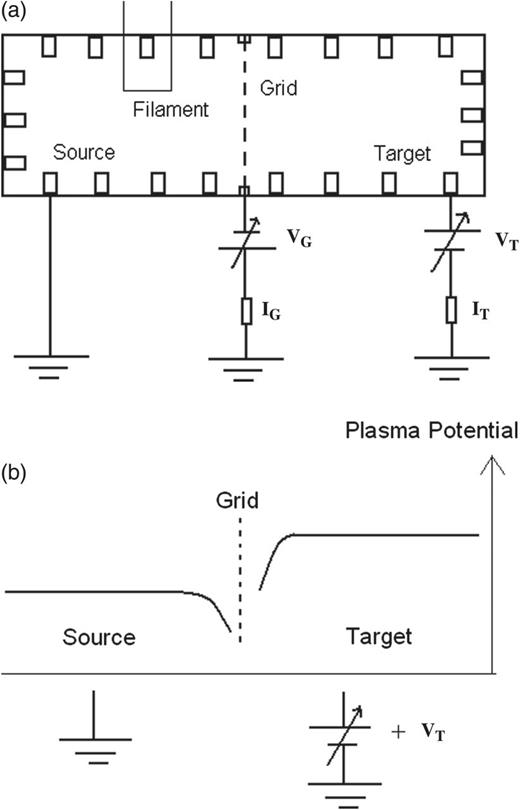
$(a): Schematic diagram of a DP device showing source chamber, target chamber, and grid. The presence of filament indicates that plasma is solely produced in the source chamber. ${V}_{\mathrm {G}}$ and ${V}_{{\mathrm {T}}}$ are the grid and target chamber bias, respectively. ${\mathrm {I}}_{\mathrm { G}}$ and $\hbox {I}_{{\mathrm {T}}}$ represent the grid and target chamber currents, respectively. (b): The difference in plasma potential in the source and target chambers caused by the target chamber bias ${V}_{{\mathrm {T}}}$.$

Fig. 1.

(a): Schematic diagram of a DP device showing source chamber, target chamber, and grid. The presence of filament indicates that plasma is solely produced in the source chamber. |${V}_{\mathrm {G}}$| and |${V}_{{\mathrm {T}}}$| are the grid and target chamber bias, respectively. |${\mathrm {I}}_{\mathrm { G}}$| and |$\hbox {I}_{{\mathrm {T}}}$| represent the grid and target chamber currents, respectively. (b): The difference in plasma potential in the source and target chambers caused by the target chamber bias |${V}_{{\mathrm {T}}}$|⁠.

Open in new tab Download slide

Popa and Schrittwieser experimentally verified the theoretical relation between ion bounce frequency (⁠|$f$|⁠), plasma density (⁠|$n$|⁠), and grid bias voltage (⁠|${V}_{{\mathrm {G}}}$|⁠); at an effective electron temperature of 2.9 eV in argon plasma this can be expressed as

\begin{equation}\label{eq1} f^{2}=1.2\times 10^{-2}(n/V_{{\rm G}}^{1/2}). \end{equation}

(1)

The detailed derivation of the above equation is given in Ref. [11]. In deriving Eq. (1), the electron temperature is assumed to be constant and the presence of impurity in the system is neglected.

According to the experiment referred to here, |$f$| is the frequency observed in the target (diffusion) chamber and |$n$| is the plasma density of the source (discharge) chamber of the DP device.

The electrical components of an ion sheath derived by Rosa are based on the solution of Poisson's equation under a collisionless Child sheath approximation for low frequency fluctuations [13]. The expressions for resistance, capacitance, and inductance as derived by Rosa are as follows:

\begin{equation} R_{{\mathrm{sh}}} = (c_{{\rm s}}\tau^{2}_{\rm io}\lambda^{2}/12\varepsilon_{0})\label{eq2}\end{equation}

(2)

\begin{equation} C_{{\rm sh}} = (1+\lambda^{2}/6) (\varepsilon_{0}/\chi_{0})\label{eq3}\end{equation}

(3)

\begin{equation} L_{{\rm sh}} = -(c_{{\rm s}}\tau^{3}_{\rm io}\lambda^{2}/40\varepsilon_{0}).\label{eq4} \end{equation}

(4)

Here, |$\varepsilon _{0}$| is the vacuum permitivity, |$c_{{\rm s}}$| is the ion acoustic speed, |$\lambda =\omega _{{\rm pi}}\tau _{{\mathrm {io}}}$|⁠, where |$\omega _{{\mathrm {pi}}}$| is the ion plasma oscillation frequency and |$\tau _{{\mathrm {io}}}$| is the ion transit time through the sheath.

The equilibrium sheath width |$\chi _{0}$| (here denoted by |$d$|⁠) is expressed in terms of the ion transit time |$\tau _{{\mathrm {io}}}$| and ion acoustic speed |$c_{\mathrm {s}}$| as

\begin{equation}\label{eq5} \chi_{0}=d=(1+\lambda^{2}/6) c_{\rm s}\tau_{\rm io}. \end{equation}

(5)

The ion transit time |$\tau _{\mathrm {io}}$| is correlated with the applied grid bias voltage |$V_{{\mathrm {G}}}$| as [14,15]

\begin{equation}\label{eq6} \textit{eV}_{{\rm G}}/T_{{\rm e}} = (1+\lambda^{2}/4)\lambda^{2}/2. \end{equation}

(6)

Here, |$e$| is the electronic charge and |$T_{{\mathrm {e}}}$| is the electron temperature.

From Eq. (6), we can write

\begin{equation}\label{eq7} \lambda^{2}=2[-1+(1+2\textit{eV}_{\rm G}/T_{\rm e})^{1/2}]. \end{equation}

(7)

Equations (2), (3), and (4) can also be expressed in the following forms [14]:

\begin{equation} R_{{\rm sh}}=\lambda^{2}d^{2}/[12\varepsilon_{0}Ac_{{\rm s}}(1+\lambda^{2}/6)^{2}]\label{eq8} \end{equation}

(8)

\begin{equation} C_{{\rm sh}}= \varepsilon_{0}(1+\lambda^{2}/6)A/d\label{eq9}\end{equation}

(9)

\begin{equation} L_{{\rm sh}}= -\lambda ^{2}d^{3}/[40\varepsilon_{0}A c^{2}_{{\rm s}}(1 + \lambda^{2}/6)^{3}].\label{eq10} \end{equation}

(10)

The surface area of the grid (⁠|$A$|⁠) can be approximated by the cross section of the machine for low grid transparency.

Equation (8) can be modified in the following form,

\begin{equation}\label{eq11} R_{{\mathrm{sh}}}= R_{0}D^{2}, \end{equation}

(11)

where

\begin{equation}\label{eq12} R_{0}= \lambda^{2}\lambda^{2}_{{\rm De}}/[12\varepsilon_{0}A c_{{\rm s}}(1+\lambda^{2}/6)^{2}]. \end{equation}

(12)

Here, |$D = d/\lambda _{{\mathrm { De}}}$| and |$\lambda _{{\mathrm {De}}} =(\varepsilon _{0}T_{\mathrm { e}}/\textit {ne}^{2})^{1/2}$| defines the Debye length.

Similarly, under a flat surface approximation, Equation (9) can be modified in the following form:

\begin{equation}\label{eq13} C_{{\rm sh}} = C_{0}/D, \end{equation}

(13)

where

\begin{equation}\label{eq14} C_{0} =\varepsilon_{0}[(1+\lambda^{2}/6)A/\lambda_{{\rm De}}]K. \end{equation}

(14)

Here, |$K$| represents the correction factor to accommodate the effect of the non-neutral plasma medium on the sheath equivalent capacitance [14,16].

Similarly, |$L_{\mathrm {sh}}$| from (10) can be expressed as

\begin{equation}\label{eq15} L_{{\rm sh}}=-L_{0}D^{3}, \end{equation}

(15)

where

\begin{equation}\label{eq16} L_{0}=-\lambda^{2}\lambda^{3}_{{\rm De}}/[40\varepsilon_{0}A c^{2}_{{\rm s}}(1+\lambda^{2}/6)^{3}]. \end{equation}

(16)

The total charge on the sheath equivalent plane capacitor plate is given by

\begin{equation}\label{eq17} Q_{\rm sh}=enAd, \end{equation}

(17)

which can also be expressed as

\begin{equation}\label{eq18} Q_{\rm sh}= Q_{0}D \end{equation}

(18)

where

\begin{equation}\label{eq19} Q_{0}=enA\lambda_{\rm De}. \end{equation}

(19)

Using these elements, the e.m.f. (⁠|$E$|⁠) of the circuit, which drives the current through the circuit, can be expressed as

\begin{equation}\label{eq20} E\approx V_{{\mathrm{G}}}= R_{0}\textit{ID}^{2}+V_{0}D^{2}. \end{equation}

(20)

This e.m.f. can be approximated by the grid bias voltage (⁠|$E \approx V_{\mathrm { G}}$|⁠). Here, |$V_{0}=Q_{0}/C_{0}$|⁠, and |$I$| is the child sheath current. The equivalent circuit is shown in Fig. 2. Here, |$I$| is replaced by grid current |$I_{\mathrm {G}}$|⁠.

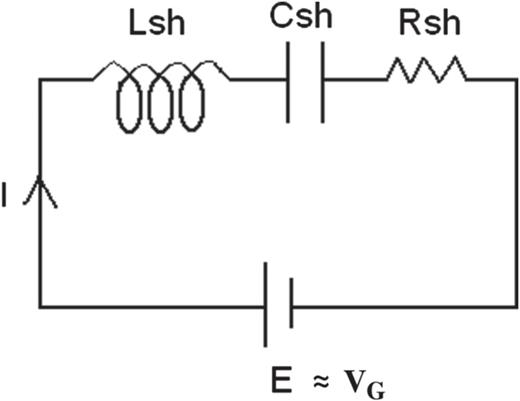
$Schematic diagram of the sheath equivalent series LCR circuit. $L_{\mathrm {sh}}$, $C_{\mathrm {sh}}$, $R_{\mathrm {sh}}$, and $E$ denote the sheath associated inductance, capacitance, resistance, and e.m.f., respectively. $I$ denotes the Child current flowing through the circuit.$

Fig. 2.

Schematic diagram of the sheath equivalent series LCR circuit. |$L_{\mathrm {sh}}$|⁠, |$C_{\mathrm {sh}}$|⁠, |$R_{\mathrm {sh}}$|⁠, and |$E$| denote the sheath associated inductance, capacitance, resistance, and e.m.f., respectively. |$I$| denotes the Child current flowing through the circuit.

Open in new tab Download slide

Equation (20) can be expressed introducing the correction factor |$K$| as

\begin{equation}\label{eq21} V_{\mathrm{G}} = R_{0}I_{\rm G}D^{2}+(1/K)[(\textit{en}\lambda^{2}_{{\rm De}})/\varepsilon_{0}(1+\lambda^{2}/6)]D^{2}. \end{equation}

(21)

We can express the grid current |$I_{\mathrm { G}}$| with the help of the well-known Child's law [17]:

\begin{equation} I_{\mathrm{G}} = (4/9)\varepsilon_{0}A(2e/m_{i})^{1/2}V_{\rm G}^{3/2}d^{-2}\label{eq22}\end{equation}

(22)

\begin{equation} I_{\rm G} = I_{\rm C}/D^{2},\label{eq23} \end{equation}

(23)

where

\begin{equation}\label{eq24} I_{\rm C} = (4/9)\varepsilon_{0}A(2e/m_{i})^{1/2}V_{\rm G}^{3/2}\lambda^{-2}_{\rm De}. \end{equation}

(24)

We have seen that for estimation of the sheath components one must know the plasma parameters such as density and electron temperature. We have used Eq. (1) to estimate the frequency of oscillations for different plasma densities at a constant grid bias |$V_{\mathrm { G}}$| obtained from Ref. [11]. Generally, the electron temperature changes with the change in discharge voltage, but in the experiment referred to here the electron temperature was very weakly dependent on the discharge current, in most cases in the range 2.8–3 eV, so they took a constant value of 2.9 eV.

Although Popa and Schrittwieser estimated plasma density by a different technique, we have used the density recorded by the Langmuir probe because it is the most simple and commonly used diagnostic tool.

The plasma parameters taken from Ref. [11] are shown in Table 1. The diameter of the machine was 0.44 m, which is approximated to be the diameter of the grid because of its low transparency (77 lines per centimeter), and hence the area |$A$| is approximately 0.152 m|$^{2}$|⁠.

Table 1.

Open in new tab

Plasma density and electron temperature from Ref. [11].

Discharge current (mA)	Plasma density from Langmuir probe \|$n\,(10^{14}\,m^{-3})$\|	Effective electron temperature \|$T_{\mathrm {e}}$\| (eV)
60	1.6	2.9
120	3.1
180	4.5
240	5.9
300	7.5

Discharge current (mA)	Plasma density from Langmuir probe \|$n\,(10^{14}\,m^{-3})$\|	Effective electron temperature \|$T_{\mathrm {e}}$\| (eV)
60	1.6	2.9
120	3.1
180	4.5
240	5.9
300	7.5

Table 1.

Open in new tab

Plasma density and electron temperature from Ref. [11].

Discharge current (mA)	Plasma density from Langmuir probe \|$n\,(10^{14}\,m^{-3})$\|	Effective electron temperature \|$T_{\mathrm {e}}$\| (eV)
60	1.6	2.9
120	3.1
180	4.5
240	5.9
300	7.5

Discharge current (mA)	Plasma density from Langmuir probe \|$n\,(10^{14}\,m^{-3})$\|	Effective electron temperature \|$T_{\mathrm {e}}$\| (eV)
60	1.6	2.9
120	3.1
180	4.5
240	5.9
300	7.5

Again, the estimated frequency of oscillation (⁠|$f$|⁠) is found to be inversely proportional to the estimated sheath width (⁠|$d$|⁠), as can be seen from Figs. 3 and 4. The frequency of oscillation (⁠|$f$|⁠) and sheath width (⁠|$d$|⁠) are estimated using equation (1) and (5) respectively.

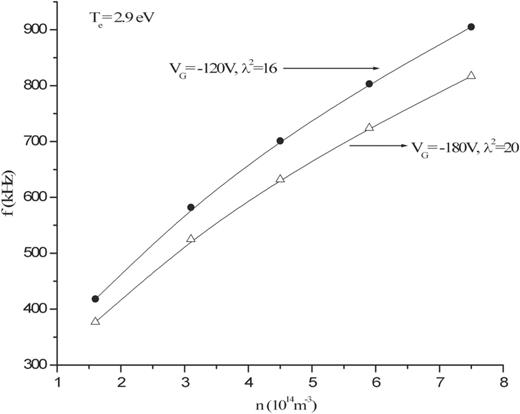
$The variation of the estimated frequency ($f$) at different plasma densities ($n$) for fixed $V_{{\mathrm {G}}}=-120$ V and $-$180 V at $T_{{\mathrm {e}}}=2.9$ eV.$

Fig. 3.

The variation of the estimated frequency (⁠|$f$|⁠) at different plasma densities (⁠|$n$|⁠) for fixed |$V_{{\mathrm {G}}}=-120$| V and |$-$|180 V at |$T_{{\mathrm {e}}}=2.9$| eV.

Open in new tab Download slide

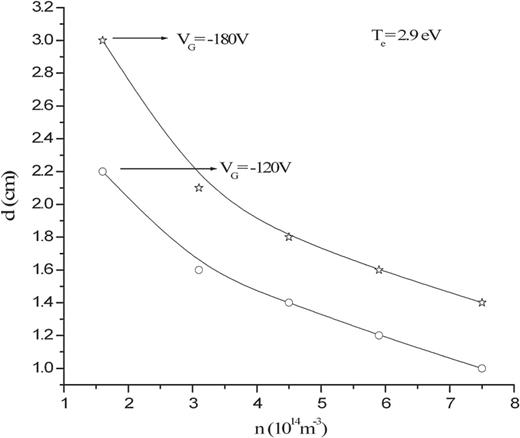
$The variation of the estimated sheath thickness ($d$) at different plasma densities ($n$) for fixed $V_{{\mathrm {G}}}=-120$ V and $-$180 V at $T_{{\mathrm {e}}}=2.9$ eV.$

Fig. 4.

The variation of the estimated sheath thickness (⁠|$d$|⁠) at different plasma densities (⁠|$n$|⁠) for fixed |$V_{{\mathrm {G}}}=-120$| V and |$-$|180 V at |$T_{{\mathrm {e}}}=2.9$| eV.

Open in new tab Download slide

In such a case, the ion transit time through the sheath is approximated by the inverse of the frequency of oscillation [18,19],

\begin{equation}\label{eq25} f = {t_{\rm io}}^{-1}. \end{equation}

(25)

The frequencies of oscillation (⁠|$f$|⁠), ion plasma frequency (⁠|$\omega _{{\mathrm {ip}}}=2\pi f_{{\mathrm { ip}}}$|⁠), ion transit time (⁠|$\tau _{\mathrm {io}}$|⁠), and |$\lambda ^{2}$|⁠, which are calculated for different plasma densities at a constant electron temperature of 2.9 eV are shown in Table 2.

Table 2.

Open in new tab

The frequency of oscillation (⁠|$f$|⁠), ion plasma frequency (⁠|$\omega _{ip}$|⁠), ion transit time (⁠|$\tau _{\mathrm {io}}$|⁠), and |$\lambda ^{2}$|⁠, calculated for different plasma densities for |$V_{{\mathrm {G}}}=-120$| V. The effective electron temperature 2.9 eV is considered.

Plasma density \|$n\, (10^{14}\,\hbox {m}^{-3})$\|	\|$f$\| (kHz)	\|$\tau _{\mathrm {io}}$\| (⁠\|$\mu $\|s)	\|$\omega _{{\mathrm {pi}}}$\| (MHz)	\|$c_{\mathrm {s}}$\| (10\|$^{3}$\| m/s)	Grid area \|$A\, (m^{2})$\|	\|$\lambda ^{2}$\|	\|$d$\| (cm)	\|$f/f_{{\mathrm {ip}}}$\|	\|$\lambda _{\mathrm {De}}$\| (cm)	\|$D=d/\lambda _{\mathrm {De}}$\|
1.6	418	2.4	2.68	2.6	0.152	16	2.2	0.9	0.1	\|$\approx $\|22
3.1	582	1.7	3.74			16	1.6	0.9	0.07	22
4.5	701	1.4	4.5			16	1.3	0.9	0.059	22
5.9	803	1.2	5.16			16	1.1	0.9	0.052	22
7.5	905	1.1	5.82			16	1	0.9	0.046	22

Plasma density \|$n\, (10^{14}\,\hbox {m}^{-3})$\|	\|$f$\| (kHz)	\|$\tau _{\mathrm {io}}$\| (⁠\|$\mu $\|s)	\|$\omega _{{\mathrm {pi}}}$\| (MHz)	\|$c_{\mathrm {s}}$\| (10\|$^{3}$\| m/s)	Grid area \|$A\, (m^{2})$\|	\|$\lambda ^{2}$\|	\|$d$\| (cm)	\|$f/f_{{\mathrm {ip}}}$\|	\|$\lambda _{\mathrm {De}}$\| (cm)	\|$D=d/\lambda _{\mathrm {De}}$\|
1.6	418	2.4	2.68	2.6	0.152	16	2.2	0.9	0.1	\|$\approx $\|22
3.1	582	1.7	3.74			16	1.6	0.9	0.07	22
4.5	701	1.4	4.5			16	1.3	0.9	0.059	22
5.9	803	1.2	5.16			16	1.1	0.9	0.052	22
7.5	905	1.1	5.82			16	1	0.9	0.046	22

Table 2.

Open in new tab

Plasma density \|$n\, (10^{14}\,\hbox {m}^{-3})$\|	\|$f$\| (kHz)	\|$\tau _{\mathrm {io}}$\| (⁠\|$\mu $\|s)	\|$\omega _{{\mathrm {pi}}}$\| (MHz)	\|$c_{\mathrm {s}}$\| (10\|$^{3}$\| m/s)	Grid area \|$A\, (m^{2})$\|	\|$\lambda ^{2}$\|	\|$d$\| (cm)	\|$f/f_{{\mathrm {ip}}}$\|	\|$\lambda _{\mathrm {De}}$\| (cm)	\|$D=d/\lambda _{\mathrm {De}}$\|
1.6	418	2.4	2.68	2.6	0.152	16	2.2	0.9	0.1	\|$\approx $\|22
3.1	582	1.7	3.74			16	1.6	0.9	0.07	22
4.5	701	1.4	4.5			16	1.3	0.9	0.059	22
5.9	803	1.2	5.16			16	1.1	0.9	0.052	22
7.5	905	1.1	5.82			16	1	0.9	0.046	22

Plasma density \|$n\, (10^{14}\,\hbox {m}^{-3})$\|	\|$f$\| (kHz)	\|$\tau _{\mathrm {io}}$\| (⁠\|$\mu $\|s)	\|$\omega _{{\mathrm {pi}}}$\| (MHz)	\|$c_{\mathrm {s}}$\| (10\|$^{3}$\| m/s)	Grid area \|$A\, (m^{2})$\|	\|$\lambda ^{2}$\|	\|$d$\| (cm)	\|$f/f_{{\mathrm {ip}}}$\|	\|$\lambda _{\mathrm {De}}$\| (cm)	\|$D=d/\lambda _{\mathrm {De}}$\|
1.6	418	2.4	2.68	2.6	0.152	16	2.2	0.9	0.1	\|$\approx $\|22
3.1	582	1.7	3.74			16	1.6	0.9	0.07	22
4.5	701	1.4	4.5			16	1.3	0.9	0.059	22
5.9	803	1.2	5.16			16	1.1	0.9	0.052	22
7.5	905	1.1	5.82			16	1	0.9	0.046	22

It is found that the estimated frequency of oscillation |$f$| increases with the increase in plasma density for a fixed grid bias voltage. The frequency has a lower value for higher negative values of |$V_{\mathrm {G}}$|⁠. This is shown in Fig. 3. The ratio |$f/f_{{\mathrm {ip}}}$| (⁠|$\approx $|0.9) remains constant. The ratio |$f/f_{{\mathrm {ip}}} <1$| suggests that the frequency of oscillation is always less than the ion plasma frequency. In such a case, the ion current across the sheath is at all times in equilibrium with the applied voltage and is often assumed to obey Child's law for a space-charge-limited current.

The sheath widths (⁠|$d$|⁠) obtained from relation (5) for different densities are plotted for two different grid bias voltages in Fig. 4. As usual, the sheath thickness was found to contract with the increase in density, and the sheath thickness was found to be greater for higher negative values of |$V_{{\mathrm {G}}}$|⁠.

The values of |$R_{\mathrm {sh}}$| are calculated for different densities (frequency) using Eqs. (11) and (12). The estimated value of the sheath resistance was found to be of the order of |$10^{4}\Omega $|⁠. The resistance decreases with the increase in plasma density and its value is higher for more negative values of |$V_{\mathrm {G}}$|⁠. The variation of estimated sheath resistance with density is shown in Fig. 5.

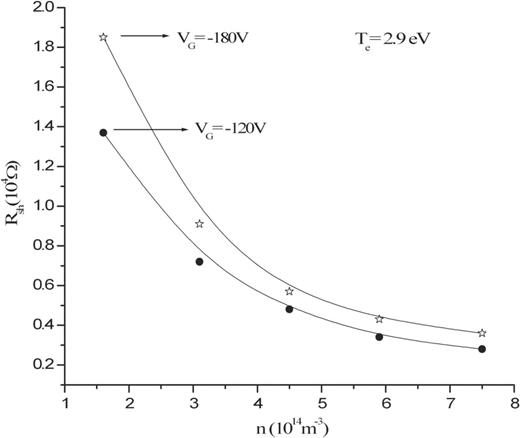
$The variation of the estimated sheath resistance ($R_{\mathrm {sh}}$) at different plasma densities ($n$) for fixed $V_{{\mathrm {G}}}=-120$ V and $-$180 V at $T_{{\mathrm {e}}}=2.9$ eV.$

Fig. 5.

The variation of the estimated sheath resistance (⁠|$R_{\mathrm {sh}}$|⁠) at different plasma densities (⁠|$n$|⁠) for fixed |$V_{{\mathrm {G}}}=-120$| V and |$-$|180 V at |$T_{{\mathrm {e}}}=2.9$| eV.

Open in new tab Download slide

The sheath capacitance at different densities was estimated using Eqs. (13) and (14), and was found to increase with the increase in plasma density. The estimated values of sheath capacitance lie in the range of |$10^{-10}$| Farad. The magnitude of the sheath capacitance decreases with increasing negative values of |$V_{\mathrm {G}}$|⁠. The variation of estimated sheath capacitance with density is shown in Fig. 6.

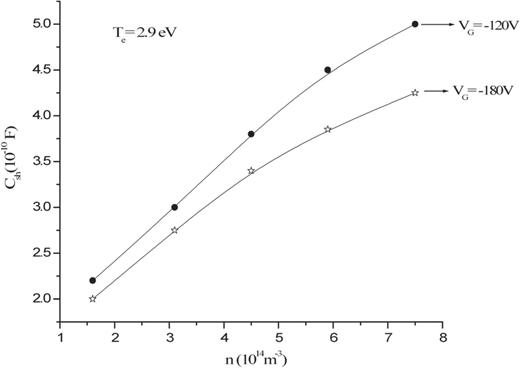
$The variation of the estimated sheath capacitance ($C_{\mathrm {sh}}$) at different plasma densities ($n$) for fixed $V_{{\mathrm {G}}}=-120$ V and $-$180 V at $T_{{\mathrm {e}}}=2.9$ eV.$

Fig. 6.

The variation of the estimated sheath capacitance (⁠|$C_{\mathrm {sh}}$|⁠) at different plasma densities (⁠|$n$|⁠) for fixed |$V_{{\mathrm {G}}}=-120$| V and |$-$|180 V at |$T_{{\mathrm {e}}}=2.9$| eV.

Open in new tab Download slide

The sheath inductance at different densities was estimated using Eqs. (15) and (16). The negative values of the sheath inductance were found to decrease with an increase in plasma density. The sheath inductance possesses higher negative values for more negative |$V_{\mathrm {G}}$|⁠. The estimated values of sheath inductance lie in the range of 10|$^{-3}$| Henry. The variation of estimated sheath inductance with density is shown in Fig. 7.

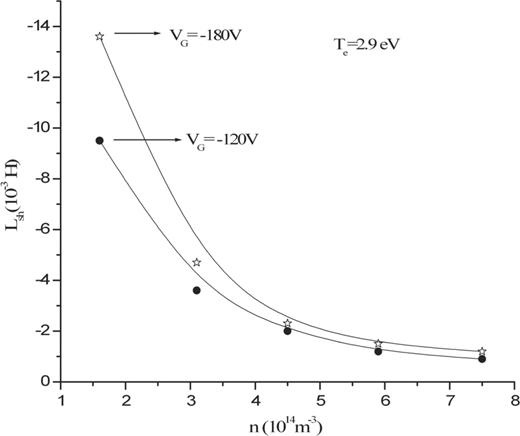
$The variation of the estimated inductance ($L_{\mathrm {sh}}$) at different plasma densities for fixed $V_{{\mathrm {G}}}=-120$ V and $-$180 V at $T_{{\mathrm {e}}}=2.9$ eV.$

Fig. 7.

The variation of the estimated inductance (⁠|$L_{\mathrm {sh}}$|⁠) at different plasma densities for fixed |$V_{{\mathrm {G}}}=-120$| V and |$-$|180 V at |$T_{{\mathrm {e}}}=2.9$| eV.

Open in new tab Download slide

In order to check the reasonableness of the values for the estimated sheath capacitance, we assumed a parallel plate capacitor, which is supposed to form between the positive ion space charge layer and the negatively biased grid. The capacitance of such a capacitor is given by

\begin{equation}\label{eq26} C=\varepsilon_{0}A/d. \end{equation}

(26)

The sheath capacitance values obtained from relations (13) and (14) were compared with the parallel plate capacitance given by (26) and found to be of the same order.

Further, we can say that the sheath capacitance also behaves like a varactor diode. In such a diode, capacitance is inversely proportional to the thickness of the depletion region. Similarly, we have found that the estimated sheath capacitance is also inversely proportional to sheath thickness. In Fig. 8, the variation of sheath capacitance with sheath thickness is shown. Wood studied this behavior of ion sheaths using a variable capacitor model [20].

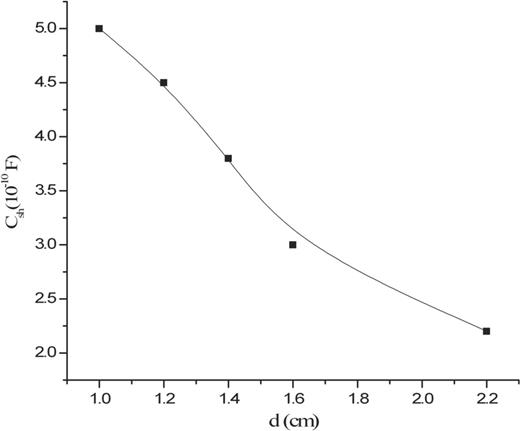
$The variation of the estimated sheath capacitance ($C_{\mathrm {sh}}$) with sheath thickness ($d$).$

Fig. 8.

The variation of the estimated sheath capacitance (⁠|$C_{\mathrm {sh}}$|⁠) with sheath thickness (⁠|$d$|⁠).

Open in new tab Download slide

The total charge in the sheath obtained from relations (18) and (19) was also found to increase with the increase in density, as shown in Fig. 9. For higher negative grid voltages, the value of the charge is found to be more. The estimated values of charge were found to lie in the range of 10|$^{-7}$| Coulomb.

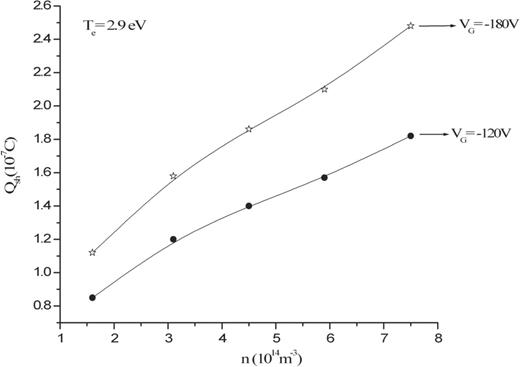
$The variation of the estimated charge in the sheath ($Q_{\mathrm {sh}}$) at different plasma densities ($n$) for fixed $V_{{\mathrm {G}}}=-120$ V and $-$180 V at $T_{{\mathrm {e}}}=2.9$ eV.$

Fig. 9.

The variation of the estimated charge in the sheath (⁠|$Q_{\mathrm {sh}}$|⁠) at different plasma densities (⁠|$n$|⁠) for fixed |$V_{{\mathrm {G}}}=-120$| V and |$-$|180 V at |$T_{{\mathrm {e}}}=2.9$| eV.

Open in new tab Download slide

The grid current |$I_{\mathrm {G}}$| at different plasma densities (sheath widths) are estimated using relations (23) and (24). The estimated grid current |$I_{\mathrm {G}}$| appeared in the range of mA, which is in agreement with the experimental values (Fig. 2(a) of Ref. [11]). The variations of |$I_{\mathrm {G}}$| for different plasma densities are plotted in Fig. 10.

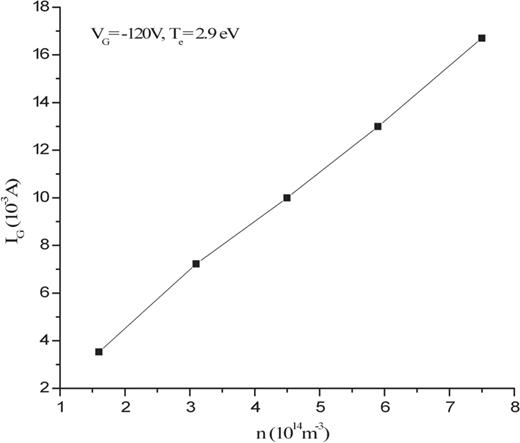
$The variation of the estimated grid current ($I_{\mathrm {G}}$) at different plasma densities ($n$) for fixed $V_{\mathrm {G}}=-120$ V at $T_{{\mathrm {e}}}= 2.9$ eV.$

Fig. 10.

The variation of the estimated grid current (⁠|$I_{\mathrm {G}}$|⁠) at different plasma densities (⁠|$n$|⁠) for fixed |$V_{\mathrm {G}}=-120$| V at |$T_{{\mathrm {e}}}= 2.9$| eV.

Open in new tab Download slide

Finally, to examine the reasonableness of the values of |$R_{\mathrm {sh}}$|⁠, |$C_{\mathrm {sh}}$|⁠, |$Q_{\mathrm {sh}}$|⁠, and |$I_{\rm G}$| we have used relation (21) to get the approximate value of the grid bias |$V_{\mathrm {G}}$|⁠.

Considering different values of the correction factor |$K=2$|⁠, 3, 4, and 5, the approximate values of the grid bias |$V_{\mathrm {G}}$| were estimated. In Table 3, values of the estimated grid bias from relation (21) for different values of |$K$| at different plasma densities are shown. For |$K=2$|⁠, the estimated value of the grid bias was found to be twice the magnitude of the grid bias (⁠|$-$|120 V) used in the theoretical estimations, but as value of |$K$| increased, the estimated |$V_{\mathrm {G}}$| approached the magnitude of the assumed value, and at |$K=5$| both are nearly equal.

Table 3.

Open in new tab

The estimated grid bias voltage at different plasma densities at |$V_{{\mathrm {G}}}=-120$| V for different values of |$K$|⁠.

Plasma density \|$n\,(10^{14}\,\hbox {m}^{-3})$\|	\|$I_{\mathrm {G}}\,(10^{-3}A)$\|	For \|$K=2\ V_{\mathrm {G}}$\| from Eq. (21)	For \|$K=3$\|\|$V_{\mathrm {G}}\,(V)$\|	For \|$K=4$\|\|$V_{{\mathrm {G}}}\,(V)$\|	For \|$K=5$\|\|$V_{{\mathrm {G}}}\,(V)$\|
1.6	3.5	\|$\approx $\|240	\|$\approx $\|176	\|$\approx $\|144	\|$\approx $\|124
3.1	7.2	240	176	144	124
4.5	10	240	176	144	124
5.9	13	240	176	144	124
7.5	16.7	240	176	144	124

Plasma density \|$n\,(10^{14}\,\hbox {m}^{-3})$\|	\|$I_{\mathrm {G}}\,(10^{-3}A)$\|	For \|$K=2\ V_{\mathrm {G}}$\| from Eq. (21)	For \|$K=3$\|\|$V_{\mathrm {G}}\,(V)$\|	For \|$K=4$\|\|$V_{{\mathrm {G}}}\,(V)$\|	For \|$K=5$\|\|$V_{{\mathrm {G}}}\,(V)$\|
1.6	3.5	\|$\approx $\|240	\|$\approx $\|176	\|$\approx $\|144	\|$\approx $\|124
3.1	7.2	240	176	144	124
4.5	10	240	176	144	124
5.9	13	240	176	144	124
7.5	16.7	240	176	144	124

Table 3.

Open in new tab

The estimated grid bias voltage at different plasma densities at |$V_{{\mathrm {G}}}=-120$| V for different values of |$K$|⁠.

Plasma density \|$n\,(10^{14}\,\hbox {m}^{-3})$\|	\|$I_{\mathrm {G}}\,(10^{-3}A)$\|	For \|$K=2\ V_{\mathrm {G}}$\| from Eq. (21)	For \|$K=3$\|\|$V_{\mathrm {G}}\,(V)$\|	For \|$K=4$\|\|$V_{{\mathrm {G}}}\,(V)$\|	For \|$K=5$\|\|$V_{{\mathrm {G}}}\,(V)$\|
1.6	3.5	\|$\approx $\|240	\|$\approx $\|176	\|$\approx $\|144	\|$\approx $\|124
3.1	7.2	240	176	144	124
4.5	10	240	176	144	124
5.9	13	240	176	144	124
7.5	16.7	240	176	144	124

Plasma density \|$n\,(10^{14}\,\hbox {m}^{-3})$\|	\|$I_{\mathrm {G}}\,(10^{-3}A)$\|	For \|$K=2\ V_{\mathrm {G}}$\| from Eq. (21)	For \|$K=3$\|\|$V_{\mathrm {G}}\,(V)$\|	For \|$K=4$\|\|$V_{{\mathrm {G}}}\,(V)$\|	For \|$K=5$\|\|$V_{{\mathrm {G}}}\,(V)$\|
1.6	3.5	\|$\approx $\|240	\|$\approx $\|176	\|$\approx $\|144	\|$\approx $\|124
3.1	7.2	240	176	144	124
4.5	10	240	176	144	124
5.9	13	240	176	144	124
7.5	16.7	240	176	144	124

As expected, the estimated |$V_{\mathrm {G}}$| was found to be independent of plasma density, as shown in Fig. 11.

$The values of grid bias voltage $V_{\mathrm {G}}$ estimated from Eq. (21) for different values of correction factor $K$.$

Fig. 11.

The values of grid bias voltage |$V_{\mathrm {G}}$| estimated from Eq. (21) for different values of correction factor |$K$|⁠.

Open in new tab Download slide

Although there is no answer as to how to make the correct choice of |$K$| values, it is mentioned in the literature that for lower grid potentials, |$K=3$| seems to be more reasonable for close agreement of theoretical estimations with experimental findings [14].

3. Conclusion

The electrical components of an ion sheath were estimated by a simple analytical approach from experimental parameters. We have used formulae found in the literature to estimate these components as functions of argon plasma density. The plasma density was in the range of |$10^{14}\,\hbox {m}^{-3}$| and effective electron temperature was 2.9 eV. The estimated frequency of oscillation was in the range of few hundreds of kHz, which is below the ion plasma frequency.

The value of |$R_{\mathrm {sh}}$| was in the 10|$^{3}$| ohm range, |$C_{\mathrm {sh}}$| was in the 10|$^{-10}$| Farad range, and |$L_{\rm sh}$| was in the 10|$^{-3}$| Henry range. For a fixed grid bias voltage, the sheath resistance and inductance decrease with an increase in density, but sheath capacitance increases.

In the case of both resistance and inductance, the value was higher for higher negative values of |$V_{\mathrm {G}}$|⁠, but in the case of sheath capacitance, the value is higher for lower negative values of |$V_{\mathrm {G}}$|⁠. The magnitude of the estimated grid bias approached the real value (⁠|$-$|120 V, assumed for theoretical estimations) as the value of |$K$| increased, and at |$K=5$| both were nearly equal.

This present study was undertaken for argon plasma having a grid area of 0.152 m|$^{2}$|⁠, considering a constant electron temperature, and neglecting the presence of any impurity in the system. It can be extended to different grid areas for plasmas produced by any gas.

References

Tongs

Langmuir

Phys. Rev.

876

(

1929

Month:	Total Views:
December 2016	1
January 2017	15
February 2017	2
May 2017	1
August 2017	1
October 2017	1
December 2017	10
January 2018	8
February 2018	15
March 2018	14
April 2018	16
May 2018	5
June 2018	6
July 2018	12
August 2018	4
September 2018	9
October 2018	3
November 2018	6
December 2018	4
January 2019	5
February 2019	12
March 2019	8
April 2019	8
May 2019	9
June 2019	2
July 2019	6
August 2019	8
September 2019	11
October 2019	5
November 2019	11
December 2019	8
January 2020	7
February 2020	7
March 2020	4
April 2020	1
May 2020	3
June 2020	2
July 2020	3
August 2020	6
September 2020	2

Article Contents

Influence of plasma density on associated electrical elements of an ion sheath Open Access

Abstract

1. Introduction

2. Theory and estimation

3. Conclusion

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Influence of plasma density on associated electrical elements of an ion sheath