-
PDF
- Split View
-
Views
-
Cite
Cite
H. Nakada, K. Sugiura, Predicting magic numbers of nuclei with semi-realistic nucleon–nucleon interactions, Progress of Theoretical and Experimental Physics, Volume 2014, Issue 3, March 2014, 033D02, https://doi.org/10.1093/ptep/ptu027
Close - Share Icon Share
Abstract
Magic numbers are predicted in a wide range of the nuclear chart by self-consistent mean-field calculations with the M3Y-P6 and P7 semi-realistic |$NN$| interactions. The magic numbers are identified by vanishing pair correlations in the spherical Hartree–Fock–Bogolyubov regime. We also identify submagic numbers when the energy gain due to the pairing is sufficiently small. It is found that the results with M3Y-P6 correspond well to the known data, apart from a few exceptions. For some of the magic or submagic numbers, the prediction differs from that with the Gogny-D1S or D1M interaction. The roles of the tensor force and the spin–isospin channel originating from the one-pion exchange potential are investigated in the |$Z$|- or |$N$|-dependence of the shell gap.
1. Introduction
Shell structure is a fundamental concept in nuclear physics, and is well described by constituent nucleons moving inside the nuclear mean field (MF) almost independently. A large energy gap between the single-particle (s.p.) orbits in the spherically symmetric MF produces a magic number, i.e. relative stability of nuclei having a specific proton (|$Z$|) or neutron number (|$N$|), manifesting the shell structure. It has been shown by experiments using radioactive beams that the shell structure, and therefore the magic numbers, may depend on |$Z$| and |$N$| [1]. The magic numbers of nuclei are important in understanding the origin of matter, since elements were synthesized via nuclear reactions that should be greatly influenced by the stability of the relevant nuclei. For instance, several peaks in the abundance of elements correspond to the magic numbers of |$N$|. The magic numbers of nuclei could also be responsible for the existence limit of superheavy elements that have not yet been observed.
For the |$Z$|- and |$N$|-dependence of the shell structure, which is sometimes called shell evolution [2], several possible mechanisms have been pointed out. Since the height of the centrifugal barrier depends on the orbital angular momentum |$\ell $| of the s.p. orbits, the s.p. energies of the loosely bound orbits may have significant |$\ell $|-dependence, possibly influencing the shell evolution [3]. However, there has been no clear evidence that the |$\ell $|-dependence of the s.p. energies gives rise to the appearance or disappearance of magic numbers. On the other hand, the roles of specific channels in the effective nucleonic interaction have been argued. It has been clarified that tensor channels are important in shell evolution [4–6]. The central spin–isospin channel of the nucleon–nucleon (|$NN$|) interaction has also been considered [7]. In addition to the |$NN$| interaction, the roles of the three-nucleon (|$NNN$|) interaction have been investigated [8].
While the significance of the tensor force in shell evolution has been clarified qualitatively in Ref. [4], the effects of specific channels on magic numbers should be assessed carefully, because in practice magic numbers emerge via the interplay between various channels. One of the authors (H.N.) has developed M3Y-type semi-realistic |$NN$| interactions in a series of articles [9–12]. By applying the numerical methods of Refs. [13–15], self-consistent Hartree–Fock (HF) and Hartree–Fock–Bogolyubov (HFB) calculations have been implemented with the semi-realistic interactions. Since the interactions explicitly include the tensor force with a realistic origin and have a reasonable nature on the central spin–isospin channel, the MF approaches employing the semi-realistic interactions provide us with a suitable framework for investigating the magic numbers in a wide range of the nuclear chart. A good example is the s.p. level inversion observed from |$^{40}$|Ca to |$^{48}$|Ca, which is reproduced remarkably well by the M3Y-type interactions including the realistic tensor force [6]. Note also that the numerical methods of Refs. [13–15] have the ability to handle loosely bound orbitals. The MF calculations with semi-realistic interactions have been implemented to investigate the shell structure in neutron-rich Ca and Ni nuclei [5]. In this paper we extensively apply the spherical MF approaches with semi-realistic interactions, particularly the parameter sets M3Y-P6 and P7 [12], and predict magic numbers in a wide range of the nuclear chart, from relatively light to heavy nuclei, including nuclei far off the |$\beta $| stability line. As discarded in the conventional MF approaches, tensor-force effects are one of the current hot topics in nuclear structure physics. We investigate the effects of the tensor force and those of the spin–isospin channel by comparing the results to those with the Gogny-D1S [16] and D1M [17] interactions.
2. Effective Hamiltonian
3. Identification of magic and submagic numbers
The definition of magic numbers is not necessarily clear. Experimentally, they have been identified by relative stability; e.g. mass irregularity, kink in the separation energies, and high excitation energies. From the theoretical viewpoint, the magic nature, which is called “magicity”, is linked to the quenching of many-body correlations. Typically, the spherical HF solution is expected to give a good approximation for the doubly magic nuclei. The nuclei having either magic |$Z$| or |$N$| are usually spherical. For spherical nuclei, the pairing among like nucleons provides a dominant correlation beyond the HF. We shall therefore identify magic numbers (and submagic numbers) by comparing the spherical HF and HFB results for even–even nuclei.
The quadrupole deformation can be another source that breaks magicity. However, both the pair excitation and the quadrupole deformation are driven by the quenching of the shell gap in most cases, although the strength of the residual interaction associated with the individual correlation is relevant as well. Thus the sizable pair correlation within the spherical HFB could also be a measure of the quadrupole deformation. Conversely, when we view magicity breaking via the pairing in this study, it does not necessarily indicate that the breakdown takes place due to the pair correlation in reality. The present work will give an informative overview of the distribution of magic numbers over the nuclear chart. Although a more precise investigation taking into account the deformation degrees of freedom (d.o.f.) is desirable, we leave this for future work, as it needs intensive calculations.
The magic numbers |$Z=2,8,20,28,50,82$| and |$N=2,8,20,28,50,82,126$| have been established around the |$\beta $| stability line. These numbers are kept magic in a certain region, but it has been clarified by experiments that the |$N=8,20,28$| magicity is eroded far off the |$\beta $| stability line. As will be shown in Sect. 4, |$N=184$| can also be a good magic number, insensitive to |$Z$|. We first implement the HF and HFB calculations for even–even nuclei along these numbers. If we find a good candidate for another magic number, we additionally carry out calculations around it. Since the validity of the MF approaches could be questioned in very light nuclei and it is difficult to collect experimental data for extremely heavy nuclei, we restrict our calculations to the nuclei having |$8\leq Z\leq 126$| and |$N\leq 200$|.
From the spherical HFB results, we identify |$Z$| (|$N$|) as magic when the proton (neutron) pair correlation vanishes. We recognize the vanishing pair correlation through the proton (neutron) pair energy |$E_p^{\mathrm {pair}}$| (|$E_n^{\mathrm {pair}}$|), i.e. the energy contributed by the proton (neutron) pairing tensor in the HFB state. There are certain cases in which the pair correlation survives, but the HF and the HFB energies, which are denoted by |$E_{\rm HF}$| and |$E_{{\mathrm {HFB}}}$|, are very close. In these nuclei, correlation effects are suppressed, resulting in, e.g., high excitation energy. Such suppression takes place particularly when either |$Z$| or |$N$| is a good magic number, as has been pointed out for |$^{68}$|Ni [5] and |$^{146}$|Gd [22]. We therefore identify |$Z$| (|$N$|) as submagic if |$E_{\mathrm {HF}}-E_{{\mathrm { HFB}}}$| is smaller than a certain value |$\lambda _{\mathrm {sub}}$| for |$N = \hbox {magic}$| (|$Z = \hbox {magic}$|) nuclei. We adopt |$\lambda _{\mathrm {sub}}=0.5\,{\mathrm { MeV}}$| and |$0.8\,{\mathrm {MeV}}$| in the calculations below, independent of |$A$|. Comparison of the results using different |$\lambda _{\mathrm {sub}}$| values will show how sensitive (or insensitive) they are to |$\lambda _{\mathrm {sub}}$|.
There could be disputes over the above criterion for magic and submagic numbers. It is true that the criterion, based solely on spherical MF calculations, is not complete. We may find the influence of quadrupole deformation by comparing the current D1S results to those of the comprehensive deformed HFB calculations [23]. However, previous studies have suggested [5] that the semi-realistic interactions often give a simple picture for the appearance and disappearance of magicity, in good connection to the shell structure under spherical symmetry. Indeed, prediction of magicity with the semi-realistic interactions is in harmony with the known data. Moreover, since quadrupole deformation may quench magicity but cannot enhance it, the prediction within the spherical MF regime is useful in selecting candidates and in giving an overview of how the magic numbers can distribute over the nuclear chart.
Magicity has been studied from kinks in the two-proton (|$S_{2p}$|) or two-neutron separation energies (|$S_{2n}$|) in several works [24,25]. Although |$S_{2p}$| and |$S_{2n}$| are calculable within the spherical HFB calculations, it is not straightforward to draw a quantitative measure for magicity from |$S_{2p}$| and |$S_{2n}$| that is applicable to a wide range of the nuclear chart. We here comment that the magic and submagic numbers shown below, which are identified from the criterion given above, are compatible with the kinks in the calculated |$S_{2p}$| or |$S_{2n}$|.
4. Predicting magic and submagic numbers
We now show the prediction for magic and submagic numbers, which are identified by the criterion given in Sect. 3. For the HF and HFB calculations, we have used the methods developed in Ref. [14] with the basis functions of Ref. [15]. The s.p. bases up to |$\ell =\ell _{\mathrm {max}}+2$|, where |$\ell _{\mathrm {max}}$| is the highest |$\ell $| of the occupied level in the HF configuration for each nucleus, should be included to handle the pair correlation appropriately [14]. We use the |$\ell \leq 7$| bases for the |$N<82$| nuclei, the |$\ell \leq 8$| bases for the |$82\leq N< 126$| nuclei, and the |$\ell \leq 9$| bases for the |$N\geq 126$| nuclei in the HFB. No additional approximations are imposed, by explicitly treating the exchange and the pairing terms of |$V_{\rm Coul}$| [26–28] as well as the |$2$|-body term of |$H_{{\mathrm {c.m.}}}$|.
4.1 Overview of magic and submagic numbers
To illustrate how we identify magic and submagic numbers, we show |$E_n^{\mathrm {pair}}$| and |$E_{\mathrm {HF}}-E_{{\mathrm { HFB}}}$| for the O isotopes calculated with D1M and M3Y-P6 in Fig. 1, and likewise for the |$N=28$| isotones in Fig. 2.
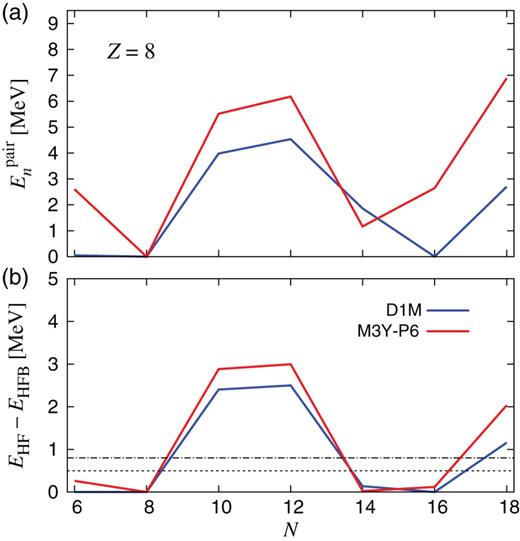
(a) |$E_n^{\mathrm {pair}}$| and (b) |$E_{\mathrm {HF}}-E_{{\mathrm { HFB}}}$| in the |$Z=8$| nuclei. The blue and red lines represent the results with the D1M and M3Y-P6 interactions, respectively. In (b), the |$\lambda _{\mathrm {sub}}$| values (|$0.5\,{\mathrm {MeV}}$| and |$0.8\,{\mathrm {MeV}}$|) are shown by the thin dotted and dot-dashed lines.

(a) |$E_p^{\mathrm {pair}}$| (|$E_n^{\mathrm {pair}}$|) and (b) |$E_{\mathrm {HF}}-E_{{\mathrm { HFB}}}$| in the |$N=28$| nuclei. In (a) |$E_n^{\mathrm {pair}}$| is represented by the dotted line and |$E_p^{\mathrm {pair}}$| by the solid lines. The color legend is the same as in Fig. 1.
In the O isotopes we always have |$E_p^{\mathrm {pair}}=0$| and therefore |$Z=8$| is regarded as magic. Because |$E_n^{\rm pair}$| vanishes at |$N=8$|, |$^{16}$|O is a good doubly magic nucleus. We find that |$E_n^{\mathrm {pair}}$| also vanishes at |$N=16$| with the D1M interaction, indicating that |$N=16$| is a magic number at |$^{24}$|O. With the M3Y-P6 interaction, |$E_n^{\mathrm {pair}}$| does not fully vanish though relatively small. The suppression of the neutron pairing is confirmed in |$E_{\mathrm {HF}}-E_{{\mathrm { HFB}}}$|, and we consider that |$N=16$| is submagic at |$^{24}$|O in the M3Y-P6 result. Analogously, |$N=14$| is submagic both with D1M and M3Y-P6.
In Fig. 2, |$E_n^{\mathrm {pair}}$| as well as |$E_p^{\rm pair}$| are presented for the |$N=28$| isotones. We remark that non-vanishing |$E_n^{\mathrm {pair}}$| are obtained in the |$Z\leq 14$| region with the M3Y-P6 interaction. The same holds with M3Y-P7, but is not shown. This well corresponds to the observed breakdown of the |$N=28$| magicity in this region. At |$^{42}$|Si, |$E_{\mathrm {HF}}-E_{{\mathrm { HFB}}}$| is less than |$0.8\,{\mathrm {MeV}}$|. However, deformation may be driven because neither |$Z$| nor |$N$| is magic. For this reason we do not regard |$N=28$| to be submagic at |$^{42}$|Si, although deformed MF calculations are required for full justification. In contrast, when we apply D1M, |$Z=14$| is magic and |$N=28$| remains submagic at |$^{42}$|Si, although the |$N=28$| magicity is lost at |$^{40}$|Mg.
The |$N=28$| magicity holds in |$Z\geq 16$|. We do not find quenching of the proton pairing in this region, except at the normal magic numbers |$Z=20$| and |$28$|.
We search for magic and submagic numbers in this manner in a wide range of the nuclear chart, applying the spherical HF and HFB calculations. The prediction with the M3Y-P6 and P7 semi-realistic interactions is summarized in Figs. 3 and 4. For comparison, the prediction with D1M is displayed in Fig. 5. We shall take a close look at these results, along with the result with D1S, in the subsequent subsections. The boundaries in Figs. 3–5 for the nuclei having magic Z or N represent position of the drip lines obtained from the spherical HFB calculations. For open-shell nuclei the boundaries are somewhat arbitrary, not representing reliable drip lines, because we have not taken into account deformation in the present work.
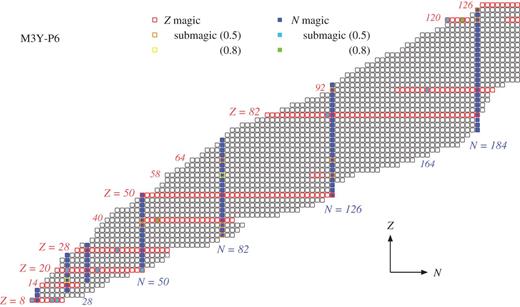
Chart showing magic numbers predicted with the M3Y-P6 interaction. Individual boxes correspond to even–even nuclei. Magic (submagic) |$Z$| are represented by boxes with a red (orange or yellow) outline, and magic (submagic) |$N$| by blue (skyblue or green) filled boxes. The |$\lambda _{\mathrm {sub}}$| values for the submagic numbers (in MeV) are as parenthesized.
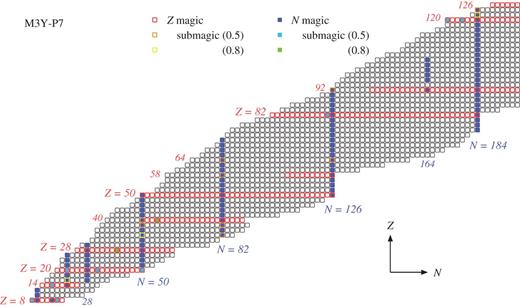
Chart showing magic numbers predicted with the M3Y-P7 interaction. See Fig. 3 for legend.
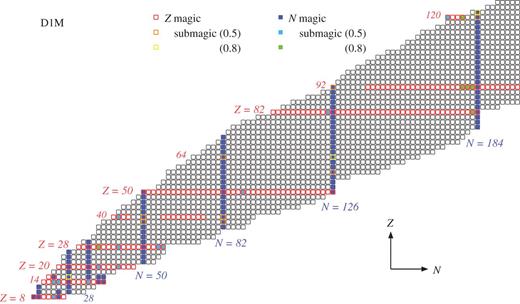
Chart showing magic numbers predicted with the D1M interaction. See Fig. 3 for legend.
4.2 |$N=6$|, |$14$|, and |$16$|
The |$N=16$| magicity at |$^{24}$|O observed in the experiments [3] is more or less reproduced by any of the four interactions: magic in the Gogny interactions (D1S and D1M) and submagic in the M3Y-P6 and P7 interactions. The |$N=16$| magicity is extended to |$Z=10$| with D1M and even to |$Z=14$| with D1S. We find that |$N=14$| as well as |$N=6$| behave as magic or submagic in the O nuclei, as seen in Fig. 1.
4.3 |$N=20$| and |$28$|
It is remarked that the |$N=20$| magicity is lost at |$Z=10$| with M3Y-P6 and at |$Z=10,12$| with M3Y-P7, though not with D1M. This reminds us of the experimentally established “island of inversion”. The usual interpretation of the island of inversion is as deformation around |$N=20$| for the |$Z\lesssim 12$| nuclei [29,30], but the possibility of a large fluctuation in the pairing has also been suggested [31]. Although the present calculation does not tell us the mechanism, it is interesting to see that the loss of the magicity is well described with M3Y-P7, and partially with M3Y-P6.
Another notable point is that |$N=20$| becomes submagic at |$^{40}$|Ca, rather than magic, with M3Y-P6 and M3Y-P7. This point should be further investigated in the near future.
As already argued in relation to Fig. 2, the |$N=28$| magicity is lost in |$N\leq 14$| in the M3Y-P6 and P7 results, while only in |$N\leq 12$| in the D1S and D1M results, although quadrupole deformation has been shown to emerge at |$^{42}$|Si in the deformed HFB calculation with D1S [23].
4.4 |$N=32$|, |$34$|, and |$40$|
Although |$N=32$| and |$34$| are magic for the Si and S isotopes with D1M (and |$N=34$| with D1S), this prediction is not supported with the semi-realistic M3Y-P6 and P7 interactions. Irrespective of the interactions, |$N=32$| is submagic at |$^{52}$|Ca owing to the closure of the |$n1p_{3/2}$| orbit, as is consistent with the experimental data [32]. However, the |$N=32$| magicity is not found at |$^{60}$|Ni with M3Y-P6 and P7, although it is kept with D1S and D1M. The origin of the |$Z$|- and interaction-dependence of the |$N=32$| magicity will be discussed in Sect. 5. The recently suggested magicity of |$N=34$| at |$^{54}$|Ca [33] is not seen in Figs. 3–5.
The submagic nature of |$N=40$| at |$^{68}$|Ni, which is again compatible with the data [34], is reproduced by all the interactions. On the other hand, the |$N=40$| magicity is lost at |$^{60}$|Ca in the M3Y-P6 and P7 results, while it is preserved in the D1S and D1M results. The |$N=40$| magicity also depends on the interactions at |$^{80}$|Zr, to which we shall return in Sect. 4.10.
4.5 |$N=50$|, |$56$|, and |$58$|
We do not find a loss of the |$N=50$| magicity except at |$^{70}$|Ca. It is noted that |$N=50$| is indicated to be submagic at |$^{70}$|Ca, rather than magic, with the M3Y-P6 and P7 interactions. The |$^{70}$|Ca nucleus is not bound within the spherical HFB with D1S and D1M.
We find that |$N=56$| is submagic at |$^{96}$|Zr except with D1M because of the |$n1d_{5/2}$| closure, corresponding well to the high first excitation energy in the measurements [35]. In the D1S and D1M results |$N=56$| and |$58$| are submagic in the Ni isotopes. Although the submagic nature of |$N=58$| at |$^{86}$|Ni has been argued using M3Y-P5 in Ref. [5], the magicity is not apparent in the M3Y-P6 and P7 results.
4.6 |$N=82$|, |$90$|, |$124$|, and |$126$|
The magicity of |$N=82$| and |$N=126$| is maintained in the whole region of |$Z$|. |$N=90$|
is predicted to be submagic with D1S and D1M at |$^{140}$|Sn because the |$n1f_{7/2}$| orbit is fully occupied, but not with M3Y-P6 and P7. |$N=124$| becomes submagic at |$^{206}$|Pb with all the interactions, having the |$(n2p_{1/2})^{-2}$| configuration.
4.7 |$N=164$|, |$184$|, and in between
|$N=164$| becomes magic with M3Y-P7 at |$^{256}$|U and submagic with M3Y-P6 because of the occupation of the |$n0i_{11/2}$|, |$n1g_{9/2}$|, and |$n0j_{15/2}$| orbits, while it does not with the D1S and D1M interactions. The |$N=164$| magicity is developed in the M3Y-P7 results, also occurring in |$96\leq Z \leq 104$|. The neutron numbers |$N=178$|, |$180$|, and |$182$| are classified as submagic for the U nuclei with D1M, but not with the M3Y-P6 and P7 interactions. The |$N=178$| magicity is connected to the occupation of |$n1g_{7/2}$| and |$n2d_{5/2}$|, and |$N=182$| to the additional occupation of |$n2d_{3/2}$|, leaving |$n3s_{1/2}$| unoccupied. However, |$N=180$| is not connected to the subshell closure. The pair correlation seems to become small partly because of the large mass number and the small degeneracy of the relevant orbitals. This problem in the D1M result could be alleviated if we introduce |$A$|-dependence in |$\lambda _{\rm sub}$|, though it is not needed for M3Y-P6.
Along with |$Z=120$| isotopes, |$N=172$| and |$178$| become submagic with all the interactions. With D1S, |$^{292}120$| is even a doubly magic nucleus and |$N=182$| is also submagic. |$N=184$|
is a good magic number for all the bound nuclei, with any of the interactions employed in the present work, whereas the deformed HFB calculations with D1S suggest instability against fission in |$Z\geq 104$| [23].
4.8 |$Z=14$| and |$16$|
Having |$Z=14$| and |$N=20$|, |$^{34}$|Si is predicted to be doubly magic with any of the four interactions, as has been argued in connection to the proton bubble structure [6]. |$Z=14$| stays as a magic number in the results with the D1S and D1M interactions. In contrast, it is not a magic number in |$N\geq 26$| with M3Y-P6 and P7, nor at |$N=14$| with M3Y-P6. The stiffness of the |$Z=14$| core seems relevant to where the |$N=28$| magicity is broken, which has been argued in Sect. 4.3.
All the interactions indicate that |$Z=16$| is weakly submagic at |$^{36}$|S. With the D1M interaction |$Z=16$| becomes magic at |$N=12$| and |$14$| (also at |$N=16$| with D1S), while it is not with the M3Y-P6 and P7 interactions.
4.9 |$Z=20$| and |$28$|
In the present study, |$Z=20$| and |$28$| remain as magic numbers in the whole region of |$N$|, irrespective of the effective interactions. As pointed out in Ref. [5], the persistence of the |$Z=28$| magicity around |$^{78}$|Ni is in contrast to the argument in Ref. [4], although the realistic tensor force is included in M3Y-P6 and P7. This difference occurs because magic numbers are a result of the interplay among various interaction channels, even though the tensor force plays a significant role.
4.10 |$Z=34$|, |$38$|, and |$40$|
The |$Z=38$| and |$40$| magicity has been known to be enhanced along the |$N=50$| isotones. This nature is well described, with both |$Z$| staying submagic.
We find that |$Z=34$| is submagic with M3Y-P6 and P7 at |$N=82$| while |$^{116}$|Se is unbound with D1S and D1M. |$Z=38$| is predicted to be submagic with all of the four interactions at |$^{120}$|Sr.
The Zr isotopes have been known to exhibit remarkable |$N$|-dependence in their structure. While |$^{90}$|Zr is close to doubly magic, the Zr nuclei are deformed in |$60\leq N\lesssim 70$| as well as in |$N\approx 40$|. We find that the current results for the Zr isotopes significantly depend on the interactions. Although |$Z=40$| is magic in |$38\leq N\leq 46$| with D1M (in |$38\leq N\leq 48$| with D1S), this magicity is broken with M3Y-P6 and P7, which is consistent with the experimental data. As a typical example, |$^{80}$|Zr is doubly magic with the Gogny interactions, while both |$Z$| and |$N$| lose magicity with the M3Y-P6 and P7 interactions. The observed energy levels show that |$^{80}$|Zr is deformed and never doubly magic. The deformed HFB does not solve this problem of the D1S interaction [23].
In the present work using the spherical MF calculations, |$Z=40$| is indicated to be magic in |$60\lesssim N\lesssim 70$|, with any of the four interactions. This is contradictory to the recent experiments [36]. It is desirable to implement deformed MF calculations, particularly those using the semi-realistic interactions.
The |$^{122}$|Zr nucleus is doubly magic in the M3Y-P6 and P7 results, and is close to doubly magic with the submagic nature of |$Z=40$| in the Gogny results.
4.11 |$Z=50$|, |$58$|, and |$64$|
We predict no breakdown of the |$Z=50$| magicity in the present calculations. However, deformation has been suggested for neutron-rich Sn nuclei in the previous calculations; e.g. for |$98\leq N\leq 110$| in the calculations with D1S [23] and similarly in the relativistic MF calculations [37]. Further study is desirable by applying the M3Y-P6 and P7 interactions to the deformed MF calculations.
All the current interactions reproduce the submagic nature of |$Z=64$| at |$^{146}$|Gd, which has long been investigated (e.g. Ref. [22]). We also find that |$Z=58$| becomes submagic at |$^{140}$|Ce with M3Y-P6 and P7, though not with D1S and D1M. The measured first excitation energy is slightly higher in |$^{140}$|Ce [38] than in the surrounding |$N=82$| isotones |$^{138}$|Ba and |$^{142}$|Nd.
Irrespective of the interactions, we see a certain magicity of |$Z=58$| at |$^{184}$|Ce (magic with M3Y-P7 and submagic with the others), and of |$Z=64$| at |$^{190}$|Gd (submagic with any of the interactions). |$Z=58$| becomes magic in |$118\leq N\leq 122$| with M3Y-P6 and in |$108\leq N\leq 126$| with M3Y-P7, though not in the D1S and D1M results.
4.12 |$Z=82$| and |$92$|
Within the spherical MF calculations, the Pb nuclei are bound up to |$N=184$| with all the interactions, and the last bound nucleus |$^{266}$|Pb is predicted to be a good doubly magic nucleus. Since quadrupole deformation has been predicted to take place in |$144\leq N\leq 166$| by the deformed HFB calculations with D1S [23], stability against deformation should be further investigated in future studies.
The |$Z=92$| number gains a certain magicity, behaving as submagic at |$^{218}$|U. While |$Z=92$| is not fully closed in the neutron-deficient region, it is predicted to be magic in |$N\gtrsim 150$| in the present work. This magicity is stronger in the D1S, D1M, and M3Y-P7 results, even holding at |$^{238}$|U, which is known as a deformed nucleus [39], in contrast to the M3Y-P6 result in which |$Z=92$| is not magic up to |$N=150$|. It should be mentioned that deformed ground states have been predicted by the deformed HFB calculations with D1S in |$N\lesssim 170$| except |$N \approx 126$| [23].
4.13 |$Z=120$|, |$124$|, and |$126$|
The proton magic numbers beyond |$Z=100$| have attracted interest, in connection to the superheavy nuclei in the so-called “island of stability”. Although |$Z=114$| has been considered a candidate for a magic number, the present work does not support this, irrespective of the interactions. On the other hand, |$Z=120$| may behave as a magic number. We see that |$Z=120$| is magic in |$N\leq 178$| with any of the four interactions. In the M3Y-P7 result the |$Z=120$| magicity extends to |$N=200$|, and in the M3Y-P6 result it disappears at |$N=180$| but revives at |$N=196$|, apart from its submagic nature at |$N=184$|. The |$Z=120$| magicity is also predicted in |$N\leq 182$| and |$N\geq 194$| with D1S. In the D1M result the |$Z=120$| magicity is lost in |$N\geq 180$|, despite its submagic nature at |$N=184$|. |$Z=124$|
is predicted to be submagic at |$N=184$| with D1S, M3Y-P6, and P7, and unbound within the spherical HFB with D1M. |$Z=126$| is a good magic number with D1S, M3Y-P6, and M3Y-P7, but not with D1M. It is commented that the fission d.o.f. may arise in the |$Z\gtrsim 120$| nuclei [23].
5. Effects of tensor and OPEP-central channels
As mentioned in Sect. 1, the tensor force |$v^{({\mathrm {TN}})}$| in the |$NN$| interaction affects the shell structure to a significant degree. The central spin–isospin channel, whose dominant part is |$v_{\rm OPEP}^{({\mathrm {C}})}$|, may cooperatively contribute to the shell evolution in certain cases [10]. In this section we investigate the roles of |$v^{({\mathrm {TN}})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| in some detail, by analyzing the spherical HF results. Since these channels are explicitly contained in M3Y-P6 and P7 but not in D1S and D1M, comparison among these results will be useful in assessing the effects of |$v^{({\mathrm {TN}})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$|.
We here comment on the difference in the magicity between M3Y-P6 and P7, which is found mainly in the heavier mass region in Figs. 3 and 4. As the |$v^{({\rm TN})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| channels are identical between them, it is not obvious what the main source of the difference between M3Y-P6 and P7 is. Although these two parameter sets yield different neutron-matter energies at high densities, it is not likely that this significantly influences the magicity of nuclei. The strength of |$v^{({\mathrm {LS}})}$|, which is slightly stronger in M3Y-P7 than in M3Y-P6, does not account for all the visible difference between Figs. 3 and 4.
5.1 |$N=16$|, |$32$|, and |$40$|
While |$N=16$| behaves as magic or submagic at |$^{24}$|O irrespective of the effective interactions, its magicity depends on the interactions for larger |$Z$|, i.e. near the |$\beta $| stability line. The shell gap |$\Delta \varepsilon _n(0d_{3/2}-1s_{1/2})$| is relevant to the |$N=16$| magicity. In Ref. [10] we showed that |$v^{({\mathrm {TN}})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| give the |$Z$|-dependence by using the older parameter set M3Y-P5. Analogous results are obtained with the present parameters M3Y-P6 and P7, which we do not repeat here.
The |$N=32$| magicity is basically determined by |$\Delta \varepsilon _n(0f_{5/2}\hbox {--}1p_{3/2})$| or |$\Delta \varepsilon _n(1p_{1/2}\hbox {--}1p_{3/2})$|. As mentioned in Sect. 4, |$N=32$| is submagic at |$^{52}$|Ca but not at |$^{60}$|Ni with the M3Y-P6 and P7 interactions. We have found that |$N=40$| is submagic at |$^{68}$|Ni but not at |$^{60}$|Ca in the M3Y results, though submagic at both nuclei in the Gogny results. The highest occupied neutron orbits are |$1p_{1/2}$| at |$^{68}$|Ni and |$0f_{5/2}$| at |$^{60}$|Ca. The strong |$Z$|-dependence of |$\Delta \varepsilon _n(0g_{9/2}\hbox {--}0f_{5/2})$| due to |$v^{({\mathrm {TN}})}$| is important to the erosion of the |$N=40$| magicity at |$^{60}$|Ca. The role of |$v^{({\mathrm {TN}})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| in the |$N=32$| and |$40$| magicity has already been presented in Ref. [5] by employing M3Y-P5. The essential points do not change with M3Y-P6 and P7.
5.2 |$N=56$|
From Figs. 3–5 we have found that the submagic nature of |$N=56$| at |$^{96}$|Zr is well accounted for with M3Y-P6 and P7, but not with D1M. We present the relevant s.p. energy difference |$\Delta \varepsilon _n(0g_{7/2}\hbox {--}1d_{5/2})$| in Fig. 6, for D1M and M3Y-P6. It is found that |$\Delta \varepsilon _n$| strongly depends on |$Z$| in the M3Y-P6 result, as |$p0g_{9/2}$| is occupied in |$40\leq Z\leq 50$|. This |$Z$|-dependence produces the relatively large gap at |$^{96}$|Zr. The M3Y-P6 result also suggests that |$n1d_{5/2}$| and |$n0g_{7/2}$| are nearly degenerate around |$^{106}$|Sn, compatible with the observed levels in |$^{105,107}$|Sn [40,41].
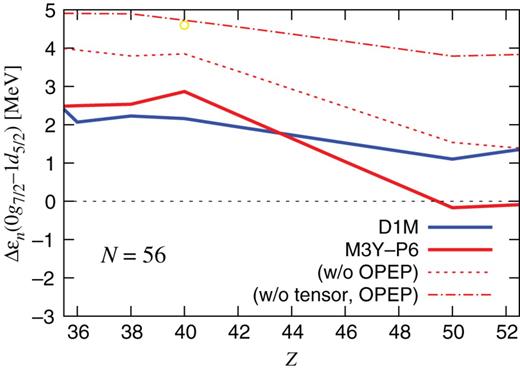
|$\Delta \varepsilon _n(0g_{7/2}\hbox {--}1d_{5/2})$| in the |$N=56$| nuclei. Blue and red solid lines are the results with D1M and M3Y-P6, respectively. The yellow circle in the top part of the figure indicates that |$N=56$| is submagic at |$Z=40$| in Fig. 3 (i.e. the M3Y-P6 result). The thin red dotted and dot-dashed lines are obtained by subtracting the contributions of |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\mathrm {TN}})}$| from the M3Y-P6 result; see text for details.
In order to clarify the effects of |$v_{\mathrm {OPEP}}^{({\rm C})}$| and |$v^{({\mathrm {TN}})}$| on the |$Z$|-dependence of the shell gap, |$\Delta \varepsilon _n-\Delta \varepsilon _n^{({\rm OPEP})}$| is plotted by the thin red dotted line and |$\Delta \varepsilon _n-\Delta \varepsilon _n^{({\mathrm {OPEP}})} -\Delta \varepsilon _n^{({\mathrm { TN}})}$| by the thin red dot-dashed line in Fig. 6. The difference between the red solid line and the red dotted line corresponds to |$\Delta \varepsilon _n^{({\rm OPEP})}(0g_{7/2}\hbox {--}1d_{5/2})$|, representing the effects of |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$|, and the difference between the red dotted line and the red dot-dashed line to |$\Delta \varepsilon _n^{({\rm TN})}(0g_{7/2}\hbox {--}1d_{5/2})$|, showing the effects of |$v^{({\mathrm {TN}})}$|. It is found that the difference in the s.p. energies depends only weakly on |$Z$| as long as we do not have contributions from |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\mathrm {TN}})}$|, both from the D1M result and the M3Y-P6 result of |$\Delta \varepsilon _n-\Delta \varepsilon _n^{({\mathrm {OPEP}})} -\Delta \varepsilon _n^{({\mathrm { TN}})}$|, which are almost parallel to each other. Such similarity in the slope was seen in the Ca isotopes in Ref. [6]. It is reasonable to conclude that |$v^{({\mathrm {TN}})}$| and |$v_{\rm OPEP}^{({\mathrm {C}})}$| are responsible for the |$Z$|-dependence.
5.3 |$N=164$|
As shown in Figs. 3–5, |$N=164$| becomes a submagic number with M3Y-P6 and a magic number with M3Y-P7 at |$^{256}$|U, although it is not with the D1S and D1M interactions. The |$N=164$| shell gap is primarily determined by |$\Delta \varepsilon _n(1g_{7/2}\hbox {--}0j_{15/2})$|, and is also relevant to |$\Delta \varepsilon _n(2d_{5/2}\hbox {--}0j_{15/2})$|. These s.p. energy differences are shown for D1M and M3Y-P6 in Fig. 7. We find an enhancement of the gap at |$Z=92$| in the M3Y-P6 case, which is regarded as the origin of the magicity. We do not have a similar |$Z$|-dependence in the D1M result.
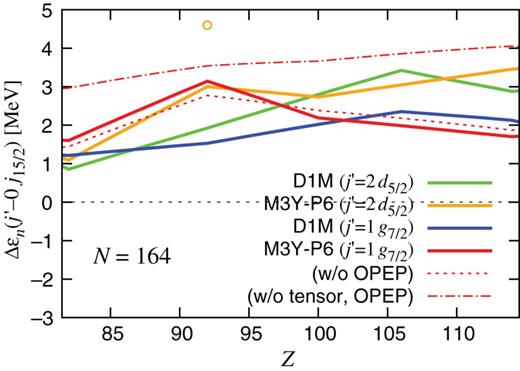
|$\Delta \varepsilon _n(j'\hbox {--}0j_{15/2})$| (|$j'=2d_{5/2}$| or |$1g_{7/2}$|) in the |$N=164$| nuclei. The green (orange) solid line is for |$j'=2d_{5/2}$| calculated with D1M (M3Y-P6), and the blue (red) solid line is for |$j'=1g_{7/2}$| with D1M (M3Y-P6). |$N=164$| is submagic at |$Z=92$| in Fig. 3, which is indicated by the orange circle in the top part of the figure. We have no other magicity in Fig. 3 or in Fig. 5 (i.e. the D1M result). In the results represented by the thin red dotted and dot-dashed lines, the contributions of |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\mathrm {TN}})}$| are subtracted from |$\Delta \varepsilon _n(1g_{7/2}\hbox {--}0j_{15/2})$| with M3Y-P6.
For |$\Delta \varepsilon _n(1g_{7/2}\hbox {--}0j_{15/2})$|, the M3Y-P6 result of |$\Delta \varepsilon _n-\Delta \varepsilon _n^{({\mathrm {OPEP}})}$| (the thin red dotted line) and |$\Delta \varepsilon _n-\Delta \varepsilon _n^{({\mathrm {OPEP}})} -\Delta \varepsilon _n^{({\mathrm { TN}})}$| (the thin red dot-dashed line) is plotted in Fig. 7. We find that |$\Delta \varepsilon _n(1g_{7/2}\hbox {--}0j_{15/2})$| is insensitive to |$Z$| in the D1M result and in the M3Y-P6 result without the contributions of |$v_{\mathrm {OPEP}}^{({\rm C})}$| and |$v^{({\mathrm {TN}})}$|. It is clarified that the |$N=164$| magicity emerges primarily by |$v^{({\mathrm {TN}})}$| and complementarily by |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$|.
5.4 |$Z=14$|
We have shown in Figs. 3–5 that |$Z=14$| behaves as a good magic number for all |$N$| with D1M, while its magicity depends on |$N$| with M3Y-P6 and P7. The relevant s.p. energy differences |$\Delta \varepsilon _p(1s_{1/2}\hbox {--}0d_{5/2})$| and |$\Delta \varepsilon _p(0d_{3/2}\hbox {--}0d_{5/2})$| with D1M and M3Y-P6 are presented in Fig. 8. It is noted that, while |$n0d_{3/2}$| is higher than |$n1s_{1/2}$| for all |$N$| in the D1M result, |$n0d_{3/2}$| comes down so that the level sequence could be inverted in |$N\geq 26$| in the M3Y-P6 result. The breakdown of the |$Z=14$| magicity at |$N\approx 28$| with M3Y-P6 seems linked to this behavior of |$n0d_{3/2}$|.
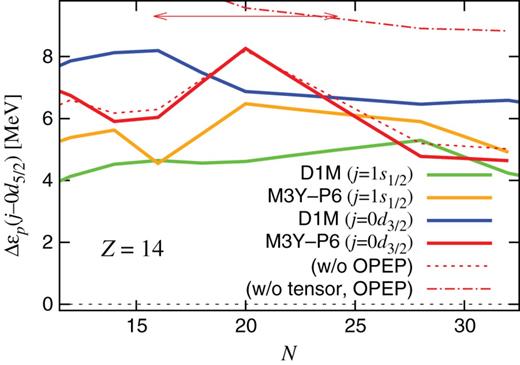
|$\Delta \varepsilon _p(j\hbox {--}0d_{5/2})$| (|$j=1s_{1/2}$| or |$0d_{3/2}$|) in the |$Z=14$| nuclei. The green (orange) solid line is for |$j=1s_{1/2}$| calculated with D1M (M3Y-P6), and the blue (red) solid line is for |$j=0d_{3/2}$| with D1M (M3Y-P6). The region where |$Z=14$| is magic in Fig. 3 is shown by the red arrow in the top part of the figure, while, in Fig. 5, |$Z=14$| is magic for all |$N$|. |$\Delta \varepsilon _p(0d_{3/2}\hbox {--}0d_{5/2})$| after subtracting the |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\mathrm {TN}})}$| contributions from the M3Y-P6 result are displayed by thin red dotted and dot-dashed lines.
The effects of |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\rm TN})}$| on |$\Delta \varepsilon _p(0d_{3/2}\hbox {--}0d_{5/2})$| are investigated via |$\Delta \varepsilon _p-\Delta \varepsilon _p^{({\mathrm {OPEP}})}$| and |$\Delta \varepsilon _p-\Delta \varepsilon _p^{({\mathrm {OPEP}})} -\Delta \varepsilon _p^{({\mathrm { TN}})}$| in Fig. 8. After the contributions of |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\mathrm {TN}})}$| are subtracted, |$\Delta \varepsilon _p(0d_{3/2}\hbox {--}0d_{5/2})$| with M3Y-P6 does not have strong |$N$|-dependence in |$20\leq N\leq 28$|, becoming almost parallel to the corresponding D1M result. We confirm that the strong |$N$|-dependence of |$\Delta \varepsilon _p(0d_{3/2}\hbox {--}0d_{5/2})$| from |$N=20$| to |$28$| predominantly originates in |$v^{({\rm TN})}$|, aided by a subsidiary contribution from |$v_{\rm OPEP}^{({\mathrm {C}})}$|.
5.5 |$Z=40$|
The s.p. energy difference relevant to the |$Z=40$| magicity is |$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$|. We compare the |$N$|-dependence of |$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| between D1M and M3Y-P6 in Fig. 9.
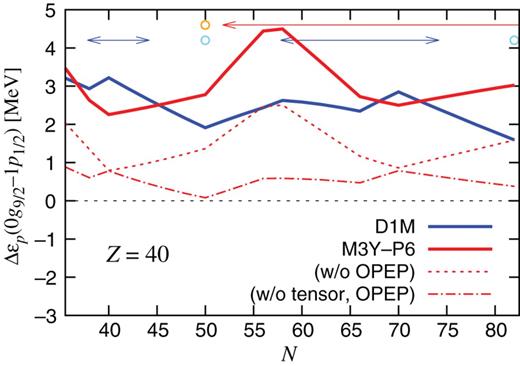
|$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| in the |$Z=40$| nuclei. The blue and red solid lines are the results with D1M and M3Y-P6, respectively. For the latter, the thin red dotted and dot-dashed lines represent the effects of |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\mathrm {TN}})}$| as in Fig. 6. The region where |$Z=40$| is magic in Fig. 5 (Fig. 3) is shown by the blue (red) arrows, and submagic by the skyblue (orange) circles in the top part of the figure.
We find opposite trends between the D1M and the M3Y-P6 results on |$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| in |$40\leq N\leq 50$| as |$n0g_{9/2}$| is occupied, and in |$70\leq N\leq 82$| as |$n0h_{11/2}$| is occupied. In addition, the rising tendency of |$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| at |$50\leq N\leq 56$| in the M3Y-P6 result is not conspicuous with D1M. It is notable that, after the contributions of |$v_{\rm OPEP}^{({\mathrm {C}})}$| and |$v^{({\mathrm {TN}})}$| are subtracted, the M3Y-P6 result becomes almost parallel to that of D1M. In contrast, once |$v^{({\mathrm {TN}})}$| is set in, the s.p. energy difference has quite similar |$N$|-dependence to the full result. This clarifies the significance of |$v^{({\mathrm {TN}})}$| in the |$N$|-dependence of the shell gap at |$Z=40$|. The relatively small |$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| at |$N=40$| contributes to the loss of the |$Z=40$| magicity around |$^{80}$|Zr seen in Fig. 3, and the relatively large |$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| at |$N=82$| to the persistence of the magicity around |$^{122}$|Zr. The large |$\Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| at |$N\approx 60$| prevents the |$Z=40$| magicity from being broken within the spherical HFB. It will be an interesting future subject to see whether and how the observed deformation at |$60\leq N\lesssim 70$| is accounted for, under the sizable shell gap caused by |$v^{({\mathrm {TN}})}$|.
5.6 |$Z=58$|
The |$Z=58$| magicity in the neutron-rich region of |$N\gtrsim 110$| occurs because of the |$p0g_{7/2}$| occupation, to which the energy difference |$\Delta \varepsilon _p(1d_{5/2}\hbox {--}0g_{7/2})$| is relevant. However, when comparing |$\Delta \varepsilon _p(1d_{5/2}\hbox {--}0g_{7/2})$| between D1M and M3Y-P6, it should be noted that |$n0i_{13/2}$| lies lower than |$n2p_{3/2}$| in the spherical HF calculation with M3Y-P6 in |$100\leq N\leq 120$|, while these two orbits are inverted with D1M except at |$^{172}$|Ce. We therefore show |$\Delta \varepsilon _p(1d_{5/2}\hbox {--}0g_{7/2})$| with D1M, in which the s.p. levels are filled in the same order as in the M3Y-P6 case, by the blue dashed line in Fig. 10. If the neutron occupation is taken to be similar, |$\Delta \varepsilon _p(1d_{5/2}\hbox {--}0g_{7/2})$| with M3Y-P6 after removing the |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| and |$v^{({\mathrm {TN}})}$| contributions is almost parallel to |$\Delta \varepsilon _p(1d_{5/2}\hbox {--}0g_{7/2})$| with D1M. As seen in Fig. 10, |$v^{({\mathrm {TN}})}$| gives rise to large |$\Delta \varepsilon _p(1d_{5/2}\hbox {--}0g_{7/2})$| at |$N\approx 114$|, with a cooperative effect of |$v_{\rm OPEP}^{({\mathrm {C}})}$|. Although its degree depends on other channels of the interactions, as recognized by comparing Figs. 3 and 4, it is expected that the |$Z=58$| magicity is enhanced in |$N\gtrsim 110$| because of |$v^{({\mathrm {TN}})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$|.
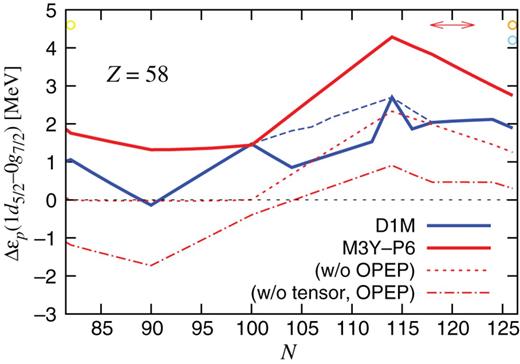
|$\Delta \varepsilon _p(1d_{5/2}\hbox {--}0g_{7/2})$| in the |$Z=58$| nuclei. The blue dashed line is obtained with D1M by filling the s.p. levels in the same order as in the M3Y-P6 result. The red arrow and orange and yellow circles at the top of the figure correspond to the magic and submagic numbers in Fig. 3, and the skyblue circle to the submagic number in Fig. 5. See Fig. 6 for other conventions.
5.7 Assessment of tensor-force and OPEP effects
To quantify the |$Z$|- or |$N$|-dependence of the shell gap, we consider the double difference of the s.p. energies |$\delta \Delta \varepsilon _{\tau _z}(j_2\hbox {--}j_1)$| (|$\tau _z=p,n$|): |$\Delta \varepsilon _{\tau _z}(j_2\hbox {--}j_1)$| at a certain nuclide |$(Z_b,N_b)$| relative to that at a reference nuclide |$(Z_a,N_a)$|. The reference nuclides are chosen so that they are comparatively close to the |$\beta $| stability line. We can then view the contributions of |$v^{({\mathrm {TN}})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| on |$\delta \Delta \varepsilon _{\tau _z}(j_2\hbox {--}j_1)$| through the corresponding quantities |$\delta \Delta \varepsilon ^{({\rm TN})}_{\tau _z}(j_2\hbox {--}j_1)$| and |$\delta \Delta \varepsilon ^{({\rm OPEP})}_{\tau _z}(j_2\hbox {--}j_1)$|. Figure 11 summarizes the effects of |$v^{({\mathrm {TN}})}$| and |$v_{\rm OPEP}^{({\mathrm {C}})}$| on |$\delta \Delta \varepsilon _{\tau _z}(j_2\hbox {--}j_1)$| in the HF results with the M3Y-P6 interaction, by selecting the nuclei at which |$v^{({\mathrm {TN}})}$| affects the magic numbers. We find that |$\delta \Delta \varepsilon ^{({\rm OPEP})}_{\tau _z}(j_2\hbox {--}j_1)$| usually has the same sign but that it does not exceed |$\delta \Delta \varepsilon ^{({\rm TN})}_{\tau _z}(j_2\hbox {--}j_1)$| as long as it is sizable, although it should not be discarded in many cases.
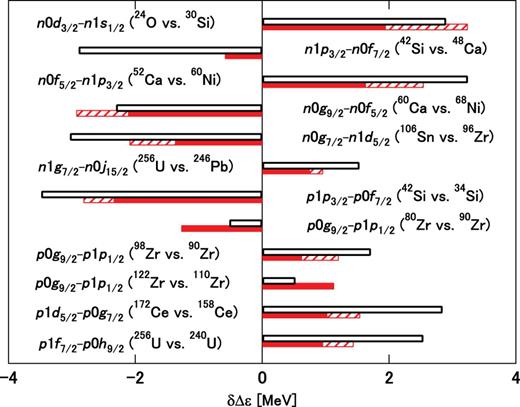
Difference between the shell gaps for two members of isotopes or isotones |$\delta \Delta \varepsilon _{\tau _z}(j_2\hbox {--}j_1)$| (open bars), with the contributions of |$v^{({\mathrm {TN}})}$| (red filled bars) and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| (red hatched bars) to it, obtained from the HF results with M3Y-P6. See text for details.
We look at some of the individual results in Fig. 11 for illustration. The |$\Delta \varepsilon _n(0d_{3/2}\hbox {--}1s_{1/2})$| value at |$^{24}$|O relative to that at |$^{30}$|Si is shown in the top row of Fig. 11. This seems to account for the |$N=16$| magicity at |$^{24}$|O. We obtain |$\delta \Delta \varepsilon _n(0d_{3/2}\hbox {--}1s_{1/2}) =2.9\,{\mathrm {MeV}}$| with M3Y-P6, which means that the |$N=16$| shell gap is larger at |$^{24}$|O than at |$^{30}$|Si by |$2.9\,{\mathrm {MeV}}$|. Since |$\delta \Delta \varepsilon ^{({\rm TN})}_n(0d_{3/2}\hbox {--} 1s_{1/2})=2.0\,{\mathrm {MeV}}$| and |$\delta \Delta \varepsilon ^{({\rm OPEP})}_n(0d_{3/2}\hbox {--}1s_{1/2}) =1.3\,{\mathrm {MeV}}$|, it is difficult to obtain the enhancement of the shell gap without |$v^{({\mathrm {TN}})}$| and |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$|. The gap could even be reduced from |$^{30}$|Si to |$^{24}$|O without them.
In the second row of Fig. 11, |$\delta \Delta \varepsilon _n(1p_{3/2}\hbox {--}0f_{7/2})$| obtained as |$\Delta \varepsilon _n(1p_{3/2}\hbox {--}0f_{7/2})$| at |$^{42}$|Si relative to that at |$^{48}$|Ca is presented. The negative value of |$\delta \Delta \varepsilon _n(1p_{3/2}\hbox {--}0f_{7/2})$| indicates quenching of the |$N=28$| shell gap at |$^{42}$|Si. However, |$v^{({\mathrm {TN}})}$| gives only |$-0.6\,{\mathrm {MeV}}$| to the full |$\delta \Delta \varepsilon _n(1p_{3/2}\hbox {--}0f_{7/2})\,(=-2.9\,{\rm MeV})$|, and the |$v_{\mathrm {OPEP}}^{({\mathrm { C}})}$| contribution is small but positive (not visible in Fig. 11). Though the |$v^{({\mathrm {TN}})}$| effect should not be ignored in describing the |$N=28$| shell erosion, it is not necessarily dominant.
We next discuss |$\delta \Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| evaluated for |$^{80}$|Zr relative to |$^{90}$|Zr. We have |$-0.5\,{\mathrm {MeV}}$| in the full M3Y-P6 result, while |$\delta \Delta \varepsilon ^{({\rm TN})}_p(0g_{9/2}\hbox {--}1p_{1/2}) =-1.3\,{\mathrm {MeV}}$|. Namely, the sign of |$\delta \Delta \varepsilon _p(0g_{9/2}\hbox {--}1p_{1/2})$| is inverted owing to |$v^{({\mathrm {TN}})}$|, which could be crucial in the erosion of the |$Z=40$| magicity at |$N\approx 40$|. Sign inversion due to |$v^{({\mathrm {TN}})}$| is also found in the comparison between |$^{122}$|Zr and |$^{110}$|Zr, which could be important to the persistence of the |$N=82$| magicity around |$^{122}$|Zr.
Several points about the tensor-force and OPEP effects are confirmed from Fig. 11:
The tensor force often plays a significant role in the |$Z$|- or |$N$|-dependence of the shell gap, accounting for the appearance and disappearance of magicity.
The central spin–isospin channel from the OPEP tends to enhance the tensor-force effect. Strong |$Z$|- or |$N$|-dependence of the shell gap often coincides with their cooperative contribution.
These effects appear strongly when an orbit having high |$\ell $| is occupied.
6. Conclusion
We predict magic and submagic numbers in a wide range of the nuclear chart from spherical mean-field calculations with the M3Y-P6 and P7 semi-realistic |$NN$| interactions, which contain the tensor force from the |$G$|-matrix as well as the central spin–isospin channel from the OPEP. The magic numbers are identified by vanishing pair correlations in the HFB results, and the submagic numbers by small differences between the HFB and the HF energies. Although deformation degrees of freedom are not explicitly taken into account, the semi-realistic interactions describe the erosion of |$N=20$| and |$28$| magicity in the proton-deficient region, as well as the emergence of |$N=16$| and |$32$| magicity. In addition to the known magic numbers, possible magicity at |$N=40$|, |$56$|, |$90$|, |$124$|, |$172$|, |$178$|, |$164$|, |$184$| and |$Z=14$|, |$16$|, |$34$|, |$38$|, |$40$|, |$58$|, |$64$|, |$92$|, |$120$|, |$124$|, |$126$| has been argued, in comparison with similar predictions obtained from the Gogny D1S and D1M interactions. The prediction with M3Y-P6 does not contradict the known data, except at |$^{32}$|Mg and the Zr isotopes with |$60\leq N\lesssim 70$|. Although calculations including the deformation degrees of freedom are needed for complete understanding of the magic numbers, this work will be useful in selecting candidates for the magic numbers and in giving an overview of how the magic numbers can distribute over the nuclear chart.
By analyzing the shell gaps in the HF results, the roles of the tensor force and of the central spin–isospin channel from the OPEP are investigated. It is confirmed that the tensor force often plays a significant role in the |$Z$|- or |$N$|-dependence of the shall gap, accounting for the appearance and disappearance of magicity, and the central spin–isospin channel tends to enhance the tensor-force effect. The present results are qualitatively consistent with Refs. [4,7], although quantitative aspects should not be underestimated because they make a difference in certain cases.
It will be interesting to study the effects of deformation on the magicity with semi-realistic interactions, and to investigate whether and how the discrepancy between the current results and the data for several nuclei could be resolved.
Acknowledgements
The authors are grateful to T. Inakura for discussions and his assistance in drawing the figures. This work is financially supported by a Grant-in-Aid for Scientific Research (C), Nos. 22540266 and 25400245, by the Japan Society for the Promotion of Science, and by a Grant-in-Aid for Scientific Research on Innovative Areas, No. 24105008, by The Ministry of Education, Culture, Sports, Science and Technology, Japan. Numerical calculations were performed on the HITAC SR16000s at the Institute of Management and Information Technologies in Chiba University, at the Yukawa Institute for Theoretical Physics in Kyoto University, at the Information Technology Center in University of Tokyo, and at the Information Initiative Center in Hokkaido University.



