-
PDF
- Split View
-
Views
-
Cite
Cite
Takumi Iritani, Hideo Suganuma, Lattice QCD analysis of the Polyakov loop in terms of Dirac eigenmodes, Progress of Theoretical and Experimental Physics, Volume 2014, Issue 3, March 2014, 033B03, https://doi.org/10.1093/ptep/ptu030
Close - Share Icon Share
Abstract
Using the Dirac mode expansion method, which keeps gauge invariance, we analyze the Polyakov loop in terms of the Dirac modes in SU(3) quenched lattice QCD in both confined and deconfined phases. First, to investigate the direct correspondence between confinement and chiral symmetry breaking, we remove low-lying Dirac modes from the confined vacuum generated by lattice QCD. In this system without low-lying Dirac modes, while the chiral condensate |$\langle \bar {q} q\rangle $| is extremely reduced, we find that the Polyakov loop is almost zero and |$Z_3$| center symmetry is unbroken, which indicates quark confinement. We also investigate the removal of ultraviolet (UV) Dirac modes, and find that the Polyakov loop is almost zero. Second, we deal with the deconfined phase above |$T_{{\mathrm {c}}}$|, and find that the behaviors of the Polyakov loop and |$Z_3$| symmetry are not changed without low-lying or UV Dirac modes. Finally, we develop a new method to remove low-lying Dirac modes from the Polyakov loop for a larger lattice of |$12^3 \times 4$| at finite temperature, and find almost the same results. These results suggest that each eigenmode has information about confinement, i.e., the “seed” of confinement is distributed in a wider region of the Dirac eigenmodes, unlike chiral symmetry breaking, and there is no direct correspondence between confinement and chiral symmetry breaking through Dirac eigenmodes.
1. Introduction
Quantum chromodynamics (QCD) has been established as the fundamental theory of the strong interaction. However, its non-perturbative phenomena such as color confinement and chiral symmetry breaking [1,2] are not yet fully understood. It is an intriguing subject to clarify the relation between these non-perturbative phenomena [3–29]. As for possible evidence on the close relation between confinement and chiral symmetry breaking, lattice QCD calculations have shown almost simultaneous chiral and deconfinement transitions at finite temperature and in finite volume [30–32]. Actually, at the quenched level, the deconfinement phase transition is of the first order, and both the Polyakov loop |$\langle L_P \rangle $| and the chiral condensate |$\langle \bar qq \rangle $| jump at the same critical temperature |$T_{{\mathrm {c}}}$| [30]. (Note that the chiral condensate and the hadron masses can be calculated from the quark propagator even at the quenched level [30].)
In the presence of dynamical quarks, the thermal phase transition of QCD is modified depending on the quark mass. In the chiral limit of |$N_f=3$|, chiral transition is of the first order [30–32]. For the two light u,d-quarks and relatively heavy s-quark of |$N_f = 2+1$|, lattice QCD shows crossover at finite temperature, and hence, to be strict, there is no definite critical temperature [31–35]. Also in this case, the near coincidence of the two peak positions of the Polyakov loop susceptibility and the chiral susceptibility suggests a close relation between confinement and chiral symmetry breaking in QCD [31,32], although several lattice QCD studies reported a slightly higher peak position for the Polyakov loop susceptibility than that of the light-quark chiral susceptibility [34,35]. In the case of QCD-like theory with adjoint representation fermions, however, two phase transitions of deconfinement and chiral restoration occur at two distinct temperatures [36–39].
In the dual-superconductor picture [40–42], the confinement is discussed in terms of the magnetic monopole which appears as the topological object in the maximally Abelian (MA) gauge [5,6,43–52]. By removing magnetic monopoles from the QCD vacuum, both confinement and chiral symmetry breaking are simultaneously lost, as shown in lattice QCD [5,6]. This fact suggests that both phenomena are related via magnetic monopoles. Similar results are also obtained by removing center vortices from the QCD vacuum in the maximal center gauge in lattice QCD [12,13]. However, it is not sufficient to prove the direct relationship, since removing such topological objects might be too fatal for most non-perturbative QCD phenomena [18–20].
On the other hand, the Dirac operator is directly related to chiral symmetry breaking. As shown in the Banks–Casher relation, the chiral condensate |$\langle \bar {q}q \rangle $| is proportional to the Dirac zero-mode density [53], and chiral symmetry restoration is observed as a spectral gap of eigenmodes. Therefore, in order to clarify correspondence between chiral symmetry breaking and confinement, it is a promising approach to investigate confinement in terms of the Dirac eigenmodes [7–11,13–29].
In Gattringer's formula [7], the Polyakov loop can be expressed by the sum of Dirac spectra with twisted boundary condition on the lattice [7–11]. In our previous studies, we formulated a gauge-invariant Dirac mode expansion method in lattice QCD, and analyzed the contribution of Dirac modes to the Wilson loop, the interquark potential, and the Polyakov loop [18–29]. In contrast to chiral symmetry breaking, these studies indicate that the low-lying Dirac eigenmodes are not relevant for confinement properties such as the area law of the Wilson loop, the linear confining potential, and the zero expectation value of the Polyakov loop [18–29]. It is also reported that hadrons still remain as bound states even without chiral symmetry breaking by removing low-lying Dirac modes [15–17].
In this paper, we perform a detailed analysis of the Polyakov loop in terms of Dirac eigenmodes, using the gauge-invariant Dirac mode expansion method [18–21]. In fact, we remove low-lying or high Dirac modes from the QCD vacuum generated by lattice QCD, and then calculate the IR/UV-cut Polyakov loop in both confined and deconfined phases to investigate the contribution of the removed Dirac modes to the confinement. We also discuss the temperature dependence of the IR/UV-cut Polyakov loop. For the Polyakov loop, unlike the Wilson loop, we can develop a practical calculation after removing the low-lying Dirac modes by a reformulation with respect to the removed IR Dirac mode space, which enables us to calculate with larger lattices.
The organization of this paper is as follows. In Sect. 2, we briefly review the Dirac mode expansion method in lattice QCD, and formulate the Dirac mode projected Polyakov loop. In Sect. 3, we show the lattice QCD results of the Dirac mode projected Polyakov loop in both confined and deconfined phases at finite temperature. In Sect. 4, we propose a new method to calculate the Polyakov loop without IR Dirac modes in a larger volume at finite temperature, by reformulation with respect to the removed IR Dirac mode space. Section 5 will be devoted to summary.
2. Formalism
In this section, we review the Dirac mode expansion method in lattice QCD [18–29], which is a gauge-invariant expansion with the Dirac eigenmode. We also formulate the Polyakov loop in the operator formalism of lattice QCD, and the Dirac mode projected Polyakov loop [21–23].
2.1 Dirac mode expansion method in lattice QCD
Here, we use a similar philosophy to clarify the importance of monopoles by removing them from the QCD vacuum [5,6,47,48]. So far, by removing the monopoles from the gauge configuration generated by lattice QCD in the MA gauge and by checking its effect, several studies have shown the important role of monopoles to the nonperturbative phenomena such as confinement [30,47], chiral symmetry breaking [5,6], and instantons [48].
Note that, instead of the Dirac mode basis, one can expand the link variable operator with an arbitrary eigenmode basis of an appropriate operator in QCD. For example, it would also be interesting to analyze the QCD phenomena in terms of the eigenmodes of the covariant Laplacian operator |$D^2 = D^\mu D^\mu $| [54] and the Faddeev–Popov operator |$M = - \partial _i D_i$| in the Coulomb gauge [55–60].
We also note that the low-lying Dirac mode is closely related to instantons. By filtering ultraviolet eigenmodes, instanton-like structure is clearly revealed without cooling or smearing techniques [62,63]. In fact, Dirac eigenfunctions are useful probes to investigate the topological structure of the QCD vacuum.
2.2 Polyakov loop operator and its Dirac mode projection
3. Lattice QCD results
We study the Polyakov loop and the |$Z_3$| center symmetry in terms of the Dirac mode in SU(3) lattice QCD at the quenched level, using the standard plaquette action and the ordinary periodic boundary condition. We adopt the jackknife method to estimate the statistical error.
In this section, we calculate full eigenmodes of the Dirac operator using LAPACK [64], and perform the Dirac mode removal from the nonperturbative vacuum generated by lattice QCD calculations. We investigate the Polyakov loop without the specific Dirac modes, showing the full figure of the Dirac spectrum. To reduce the computational cost, we utilize the Kogut–Susskind (KS) formalism [21]. However, to obtain the full Dirac eigenmodes, the reduced computational cost is still quite large, so we take relatively small lattices, |$6^4$| and |$6^3 \times 4$|. The calculation with a larger lattice of |$12^3 \times 4$| will be discussed in Sect. 4.
3.1 Dirac mode projected Polyakov loop in the confined phase
In this subsection, we mainly analyze the contribution of the low-lying Dirac modes to the Polyakov loop in the confined phase below |$T_{{\mathrm {c}}}$|.
Below |$T_{{\mathrm {c}}}$|, the expectation value of the Polyakov loop |$\langle L_P\rangle $| is very small, and would be exactly zero in infinite volume. Then, one may simply consider that any part of zero is zero and any type of filtering leaves zero unchanged. However, this is not correct. For example, after the filtering of the monopole removal in the MA gauge, the Polyakov loop has a non-zero expectation value in the remaining system called the photon part, even at low temperatures [5]. Similarly, the confinement property is lost by the removal of center vortices in the maximal center gauge [65–67], or by cutting off the infrared-momentum gluons in the Landau gauge [68,69]. We also comment on the other filtering of smearing and cooling methods, which are popular techniques to remove quantum fluctuations [30]. Using these methods, the low-lying Dirac eigenmode density is reduced [70], and the confinement property will be lost after many iterations of the cooling. These filtering operations actually change the Polyakov loop from zero even at low temperatures. In fact, after some filtering, it is nontrivial whether the system keeps |$\langle L_P\rangle =0$| or not.
Here, we consider an interesting filtering of the Dirac mode projection, introduced in the previous section. We use the periodic |$6^4$| lattice with |$\beta = 5.6$| at the quenched level. The lattice spacing |$a$| is found to be about |$0.25$| fm [18–21], which is determined so as to reproduce the string tension |$\sigma = 0.89$| GeV fm|$^{-1}$| [71,72]. If one regards this system as the finite temperature system, the temperature is estimated as |$T = 1/(N_t a) \simeq 0.13$| GeV.
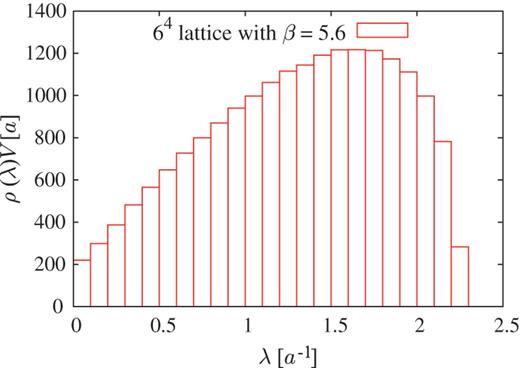
The Dirac spectral density |$\rho (\lambda)$| on a |$6^4$| lattice with |$\beta = 5.6$|, i.e., |$a \simeq 0.25$| fm. Because |$\rho (-\lambda)=\rho (\lambda)$|, only the positive region of |$\lambda $| is shown. The bin width is taken as |$\Delta \lambda = 0.1a^{-1}$|. The total number of eigenmodes is |$6^4 \times 3 = 3888$|.
Figure 2 is a scatter plot of the original (no Dirac mode cut) Polyakov loop |$\langle L_P \rangle $| for 50 gauge configurations. As shown in Fig. 2, |$\langle L_P \rangle $| is almost zero, and |$Z_3$| center symmetry is unbroken.
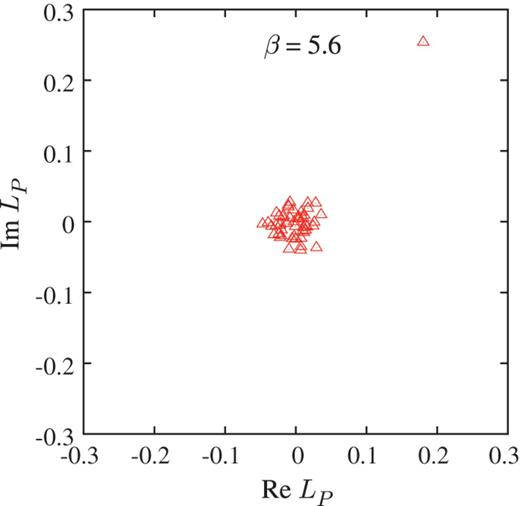
Scatter plot of the Polyakov loop |$\langle L_P \rangle $| in the confined phase on the periodic lattice of |$6^4$| and |$\beta = 5.6$|, i.e., |$a \simeq 0.25$| fm.
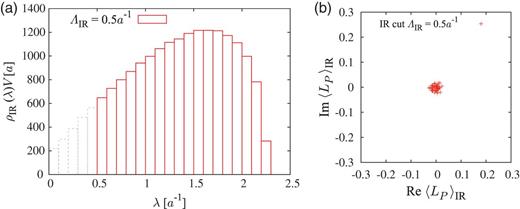
(a) The IR-cut Dirac spectral density |$\rho _{\rm IR}(\lambda)\equiv \rho (\lambda)\theta (|\lambda |-\Lambda _{\mathrm {IR}})$|, and (b) the IR-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR}}$| on the periodic lattice of |$6^4$| at |$\beta = 5.6$| for the IR-cut of |$\Lambda _{\mathrm {IR}} = 0.5a^{-1}$|.
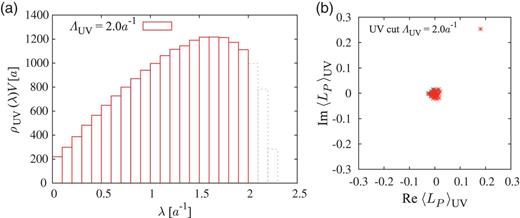
(a) The UV-cut Dirac spectral density |$\rho _{\rm UV}(\lambda)\equiv \rho (\lambda)\theta (\Lambda _{\rm UV}-|\lambda |)$|, and (b) the UV-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {UV}}$| on the periodic lattice of |$6^4$| at |$\beta = 5.6$| for |$\Lambda _{\mathrm {UV}} = 2.0a^{-1}$|.
Thus, in both cuts of low-lying Dirac modes in Fig. 3(b) and high modes in Fig. 4(b), the Polyakov loop |$\langle L_P\rangle _{\mathrm {IR/UV}}$| is almost zero, which means that the system remains in the confined phase. In fact, we find “Dirac mode insensitivity” to the Polyakov loop or the confinement property. We also examine the removal of intermediate (IM) Dirac modes from the Polyakov loop in the confined phase in Appendix A, and find similar Dirac mode insensitivity. It suggests that each eigenmode has the information of confinement, and the Polyakov loop is not affected by the removal of any eigenvalue region. Therefore, we consider that there is no direct correspondence between the Dirac eigenmodes and the Polyakov loop in the confined phase. This Dirac mode insensitivity to confinement is consistent with the previous Wilson loop analysis [18–21].
3.2 Dirac mode projected Polyakov loop in the deconfined phase
Next, we investigate the Polyakov loop in the deconfined phase at high temperature. Here, we use a periodic lattice of |$6^3 \times 4$| at |$\beta = 6.0$|, which corresponds to |$a \simeq 0.10$| fm and |$T \equiv 1/(N_ta) \simeq 0.5$| GeV.
As shown in Fig. 5, the Polyakov loop has non-zero expectation values as |$\langle L_P \rangle \neq 0$|, and shows |$Z_3$| center group structure on the complex plane. This behavior means the deconfined and center symmetry broken phase.
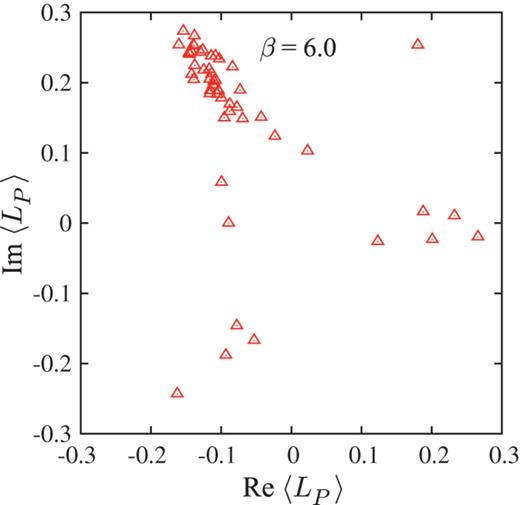
Scatter plot of the Polyakov loop |$L_P$| in the deconfined phase on the periodic lattice of |$6^3 \times 4$| at |$\beta = 6.0$|, corresponding to |$a \simeq 0.10$| fm and |$T \equiv 1/(N_ta) \simeq 0.5$| GeV.
To begin with, we investigate the difference in the Dirac spectral density |$\rho (\lambda)$| between the confined and the deconfined phases. Figure 6 shows the Dirac spectral density in the deconfined phase at high temperature on |$6^3 \times 4$| at |$\beta = 6.0$|, i.e., |$T \simeq 0.5$| GeV. For comparison, we also add the spectrum density in the confined phase at low temperature on |$6^3 \times 4$| at |$\beta = 5.6$|, i.e., |$a \simeq 0.25$| fm and |$T = 1/(N_ta) \simeq 0.2$| GeV, below the critical temperature |$T_{{\mathrm {c}}} \simeq 0.26$| GeV at the quenched level. In both phases, the total number of eigenmodes is |$6^3 \times 4 \times 3 = 2592$|. As shown in Fig. 6, the low-lying Dirac eigenmodes are suppressed in the high-temperature phase, which leads to the chiral restoration.
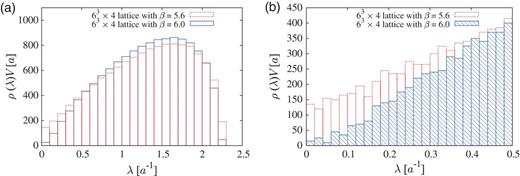
The Dirac spectrum density |$\rho (\lambda)$| in confined phase (|$\beta = 5.6$|) and deconfined phase (|$\beta = 6.0$|) on a |$6^3 \times 4$| lattice. (a) The comparison on full spectral densities. (b) The comparison on low-lying spectral densities.
We show the Dirac mode projected Polyakov loop |$\langle L_P\rangle _{\mathrm {IR/UV}}$| at |$\Lambda _{\mathrm {IR}} = 0.5a^{-1}$| and |$\Lambda _{\mathrm {UV}} = 2.0a^{-1}$| in Figs. 7(a) and (b), respectively. These mode cuts correspond to removing about 200 modes from the full eigenmodes, and a trivial reduction (or normalization) factor for the IR/UV-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR/UV}}$| appears.
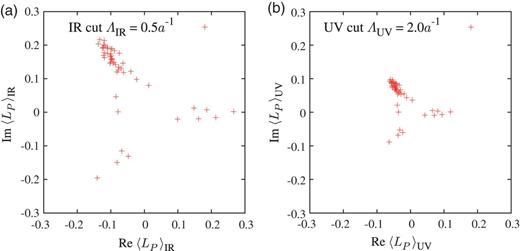
Scatter plot of the IR/UV-cut Polyakov loop in the deconfined phase on the periodic lattice of |$6^3 \times 4$| at |$\beta = 6.0$|, i.e., |$a \simeq 0.10$| fm and |$T \equiv 1/(N_ta) \simeq 0.5$| GeV. (a) |$\langle L_P\rangle _{\rm IR}$| in the case of the IR Dirac mode cut of |$\Lambda _{\rm IR} = 0.5a^{-1}$|. (b) |$\langle L_P\rangle _{\mathrm {UV}}$| in the case of the UV Dirac mode cut of |$\Lambda _{\mathrm {UV}} = 2.0a^{-1}$|. According to the mode cut, a constant reduction factor appears.
As shown in Fig. 7, both IR/UV-cut Polyakov loops |$\langle L_P\rangle _{\mathrm {IR/UV}}$| are non-zero and show the characteristic |$Z_3$| structure, similar to the original Polyakov loop |$\langle L_P \rangle $|. This suggests Dirac mode insensitivity in the deconfined phase also. In Appendix A, we show the IM-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IM}}$| in the deconfined phase, and find similar results.
We also note that the absolute value of the UV-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {UV}}$| is smaller than that of the IR-cut one |$\langle L_P\rangle _{\mathrm {IR}}$| in each gauge configuration, as shown in Fig. 7, in spite of almost the same number of removed IR/UV modes. In fact, as the quantitative effect to the Polyakov loop, the contribution of UV Dirac modes is larger than that of IR Dirac modes [8], although the deconfinement nature indicated by the non-zero Polyakov loop does not change by the removal of either IR or UV Dirac modes.
Thus, the Polyakov loop behavior and the |$Z_3$| center symmetry are rather insensitive to the removal of the Dirac modes in the IR, IM, or UV regions in both confined and deconfined phases. Therefore, we conclude that there is no clear correspondence between the Dirac modes and the Polyakov loop in both confined and deconfined phases.
3.3 Temperature dependence of the Dirac mode projected Polyakov loop
So far, we have analyzed the role of the Dirac mode to the Polyakov loop in both confined and deconfined phases. In this subsection, we consider the temperature dependence of the Polyakov loop in terms of the Dirac mode by varying the lattice parameter |$\beta $| at fixed |$N_t$|. Here, we use |$6^3 \times 4$| lattice with |$\beta = 5.4 \sim 6.0$|.
Figure 8 shows the |$\beta $| dependence of the absolute value of the IR-cut Polyakov loop |$\langle |L_P^{\mathrm {IR}}| \rangle $| with the low-lying cut (|$\Lambda _{\mathrm {IR}} = 0.5a^{-1},1.0a^{-1}$|), and the UV-cut Polyakov loop |$\langle | L_P^{\mathrm {UV}}|\rangle $| with the UV cut (|$\Lambda _{\mathrm {UV}} = 2.0a^{-1}, 1.7a^{-1}$|). The numbers of the removed Dirac modes for |$\Lambda _{\mathrm {IR}} = 0.5a^{-1}$| and |$1.0a^{-1}$| are approximately equal to |$\Lambda _{\mathrm {UV}} = 2.0a^{-1}$| and |$1.7a^{-1}$|, respectively. For comparison, we also add the original Polyakov loop |$ \langle | L_P | \rangle $|, which shows the deconfinement phase transition around |$\beta = 5.6 \sim 5.7$|.
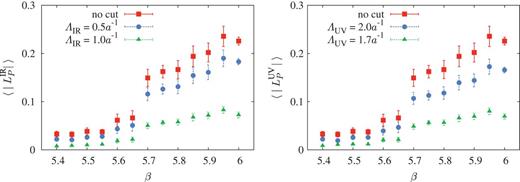
The |$\beta $| dependence of the IR/UV-cut Polyakov loop |$\langle | L_P^{\mathrm {IR/UV}}|\rangle $| on a |$6^3 \times 4$| lattice. (a) |$\langle |L_P^{\mathrm {IR}}|\rangle $| for the IR Dirac mode cut of |$\Lambda _{\mathrm {IR}} = 0.5a^{-1}$| and |$1.0a^{-1}$|. (b) |$\langle | L_P^{\mathrm {UV}}|\rangle $| for the UV cut of |$\Lambda _{\mathrm {UV}} = 2.0a^{-1}$| and |$1.7a^{-1}$|. According to the mode cut, a reduction factor for |$\langle L_P\rangle _{\mathrm {IR/UV}}$| appears.
As shown in Fig. 8, both IR-cut and UV-cut Polyakov loops |$\langle | L_P^{\mathrm {IR/UV}}|\rangle $| show almost the same |$\beta $| dependence as the original |$\langle |L_P|\rangle $|, apart from a normalization factor. Thus, we find again no direct connection between the Polyakov loop properties and the Dirac eigenmodes. This result is consistent with the similar analysis for the Wilson loop using the Dirac mode expansion method. Even after removing IR/UV Dirac modes, the Wilson loop |$\langle W \rangle _{\rm IR/UV}$| exhibits the area law with the same slope, i.e., the confining force |$\sigma $| [18–21].
Figure 9 shows the IR-cut chiral condensate |$\langle \bar {q}q \rangle _{\mathrm {IR}}$| with |$\Lambda _{\mathrm {IR}} = 0.5a^{-1}$|, and the UV-cut chiral condensate |$\langle \bar {q}q \rangle _{\mathrm {UV}}$| with |$\Lambda _{\mathrm {UV}} = 2.0a^{-1}$|, as a function of |$\beta $|. Here, the current quark mass is taken as |$m = 0.01a^{-1}$|. For comparison, we also add the original (no Dirac mode cut) chiral condensate |$\langle \bar {q}q \rangle $|. The chiral phase transition occurs around |$\beta = 5.6 \sim 5.7$|, which coincides with the deconfinement transition indicated by the Polyakov loop in Fig. 8. The chiral condensate is almost unchanged by the UV-mode cut as |$\langle \bar {q}q \rangle _{\mathrm {UV}} \simeq \langle \bar {q}q \rangle $|. On the other hand, the chiral condensate is drastically changed and becomes almost zero as |$\langle \bar {q}q \rangle _{\rm IR}\simeq 0$| by the IR Dirac mode cut in the whole region of |$\beta $|. This clearly shows the essential role of the low-lying Dirac modes to the chiral condensate. However, the Polyakov loop behavior is insensitive to the Dirac mode, as shown in Fig. 8.
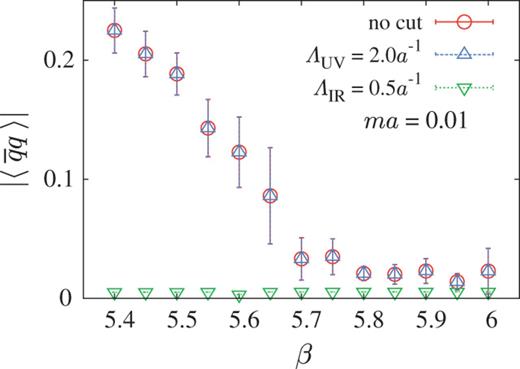
The |$\beta $| dependence of the chiral condensate |$\langle \bar {q}q \rangle _{{\mathrm {IR}}/{\rm UV}}$| after removing IR/UV Dirac modes on a |$6^4 \times 4$| lattice. For comparison, we add the original (no Dirac mode cut) condensate |$\langle \bar {q}q \rangle $|, which almost coincides with |$\langle \bar {q}q \rangle _{{\mathrm {UV}}}$|.
4. A new method to remove low-lying Dirac modes from Polyakov loop for large lattices
In this section, as a convenient formalism, we propose a new method to remove low-lying Dirac modes from the Polyakov loop without evaluating full Dirac modes. Here, we consider the removal of a small number of low-lying Dirac modes, since only these modes are responsible for chiral symmetry breaking. For the Polyakov loop, unlike the Wilson loop, we can easily perform its practical calculation after removing the low-lying Dirac modes, by reformulation with respect to the removed IR Dirac mode space, which enables us to calculate with larger lattices.
As a numerical problem, it costs huge computational power to obtain the full eigenmodes of the large matrix |$\mathbb{\textit{D}}$|, and thus our analysis was restricted to relatively small lattices in the previous section. However, in usual eigenvalue problems, e.g., in quantum mechanics, one often needs only a small number of low-lying eigenmodes, and there are several useful algorithms such as the Lanczos method to evaluate only low-lying eigenmodes, without performing full diagonalization of the matrix.
4.1 Reformulation of IR Dirac mode subtraction
Thus, using Eqs. (40) and (45), we can perform the actual calculation of the IR Dirac mode cut Polyakov loop |$\langle L_P \rangle _{\mathrm {IR}}$|, with only the IR matrix elements on the low-lying Dirac modes. In this method, we do not need full diagonalization of the Dirac operator, and hence the calculation cost is considerably reduced.
In principle, we can generalize this method for larger temporal-size lattices and Wilson loop analysis, although the number of terms becomes larger in these cases.
4.2 Lattice QCD analysis of IR Dirac mode contribution to Polyakov loop
Before applying this method to larger-volume lattice calculations, we investigate the IR Dirac mode contribution to the Polyakov loop, |$L_P^{(i)}$| defined in Eqs. (41)|$\sim $|(44), on the periodic lattice of |$6^3 \times 4$| at |$\beta = 6.0$|, which corresponds to the deconfined phase.
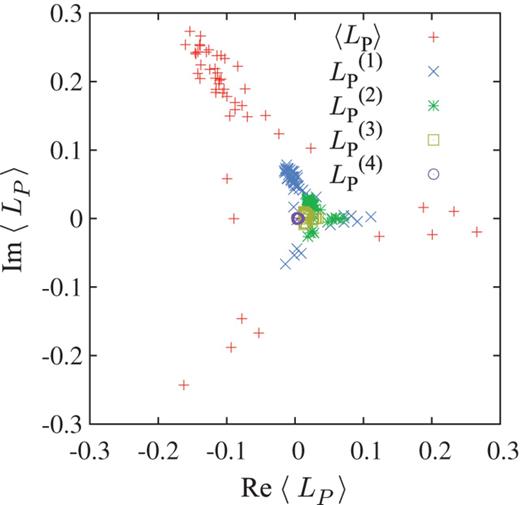
IR Dirac mode contributions to the Polyakov loop, |$L_P^{(1)}$|, |$L_P^{(2)}$|, |$L_P^{(3)}$|, and |$L_P^{(4)}$| defined in Eqs. (41)|$\sim $|(44), in the case of |$\Lambda _{\mathrm {IR}} = 0.5a^{-1}$|, in the deconfined phase on the periodic lattice of |$6^3 \times 4$| at |$\beta = 6.0$|. For comparison, the original Polyakov loop |$\langle L_P \rangle $| is added.
4.3 Lattice QCD result for a larger-volume lattice
Now, we show the lattice QCD result for the Polyakov loop after removing low-lying Dirac modes from the confined phase on a larger periodic lattice. Figure 11 shows the scatter plot of the IR-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR}}$| on the quenched lattice of |$12^3 \times 4$| at |$\beta =5.6$|, i.e., |$a \simeq $| 0.25 fm and |$T = 1/(N_ta) \simeq 0.2$| GeV below |$T_{{\mathrm {c}}}\simeq 0.26$| GeV, using 50 gauge configurations. For comparison, the original (no-cut) Polyakov loop |$\langle L_P \rangle $| is also shown in Fig. 11. Here, we use ARPACK [73] to calculate the low-lying Dirac eigenmodes. For the IR cut parameter we use |$\Lambda _{\mathrm {IR}}= 0.08a^{-1}$|, which corresponds to the removal of about 180 low-lying Dirac modes from the total of 20 736 modes. In this case, the IR-cut quark condensate |$\langle \bar qq\rangle _{\rm IR}$| is reduced to only about 7%, i.e., |$\langle \bar qq\rangle _{\mathrm {IR}}/\langle \bar qq\rangle \simeq 0.07$|, around the physical current quark mass of |$m \simeq 0.006a^{-1} \simeq $| 5 MeV.
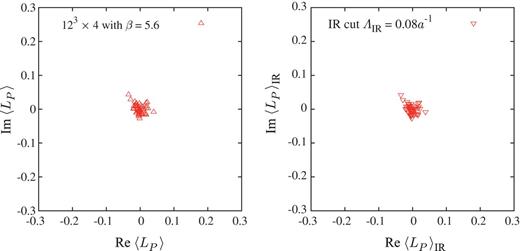
The Polyakov loop |$\langle L_P\rangle $| (left) and the IR Dirac mode cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR}}$| (right) with |$\Lambda _{\mathrm {IR}} \simeq 0.08a^{-1}$| on a |$12^3 \times 4$| lattice at |$\beta = 5.6$| (confinement phase).
Note again that the IR-cut Polyakov loop is almost zero as |$\langle L_P\rangle _{\mathrm {IR}} \simeq 0$| and the |$Z_3$| center symmetry is kept, that is, the confinement is still realized, even without the low-lying Dirac modes, which are essential for chiral symmetry breaking.
Next, we show the removal of low-lying Dirac modes from the deconfined phase on a larger periodic lattice. Figure 12 shows the IR-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR}}$| together with |$\langle L_P \rangle $| on |$12^3 \times 4$| at |$\beta =5.7$|, i.e., |$a \simeq $| 0.186 fm [71,72] and |$T\equiv 1/(N_ta)\simeq $| 0.27 GeV above |$T_{{\mathrm {c}}}$|, using 50 gauge configurations. We use |$\Lambda _{\mathrm {IR}}= 0.08a^{-1}$|, which corresponds to the removal of about 120 low-lying Dirac modes from the total of 20 736 modes. In this case, we find |$\langle L_P\rangle _{\mathrm {IR}}\simeq \langle L_P \rangle $| for each gauge configuration, and observe almost no effect from the IR Dirac mode removal for the Polyakov loop.
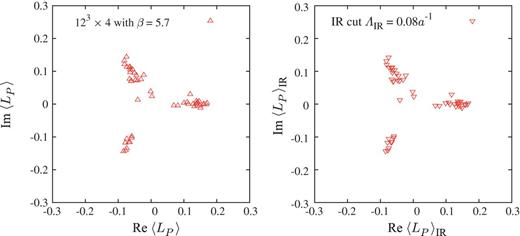
The Polyakov loop |$\langle L_P\rangle $| (left) and the IR Dirac mode cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR}}$| (right) with |$\Lambda _{\mathrm {IR}} \simeq 0.08a^{-1}$| on a |$12^3 \times 4$| lattice at |$\beta = 5.7$| (deconfinement phase).
Thus, for both confined and deconfined phases, the Polyakov loop behavior is almost unchanged by removing the low-lying Dirac modes, in terms of the zero/non-zero expectation value and the |$Z_3$| center symmetry. In fact, we find again the IR Dirac mode insensitivity to the Polyakov loop or the confinement property, this time for the larger-volume lattice.
5. Summary and concluding remarks
In this paper, we have investigated the direct correspondence between the Polyakov loop and the Dirac eigenmodes in a gauge-invariant manner in SU(3) lattice QCD at the quenched level in both confined and deconfined phases. Based on the Dirac mode expansion method, we have removed the essential ingredient of chiral symmetry breaking from the Polyakov loop.
In the confined phase, we have found that the IR-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR}}$| is still almost zero even without low-lying Dirac eigenmodes. As shown in the Banks–Casher relation, these low-lying modes are essential for chiral symmetry breaking. This result indicates that the system still remains in the confined phase after the effective restoration of chiral symmetry. We have also analyzed the role of high (UV) Dirac modes, and have found that the UV-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {UV}}$| is also zero. These results indicate that there is no definite Dirac mode region relevant for the Polyakov loop behavior; in fact, each Dirac eigenmode seems to feel that the system is in the confined phase.
This Dirac mode insensitivity to the confinement is consistent with the previous Wilson loop analysis with Dirac mode expansion in Refs. [18–21], where the Wilson loop shows an area law and linear confining potential is almost unchanged even without low-lying or high Dirac eigenmodes. These results are also consistent with the existence of hadrons as bound states without low-lying Dirac modes [15–17]. Also, Gattringer's formula suggests that the existence of Dirac zero modes does not seem to contribute to the Polyakov loop [7].
Next, we have analyzed the Polyakov loop in the deconfined phase at high temperature, where the Polyakov loop |$\langle L_P \rangle $| has a non-zero expectation value, and its value distributes in the |$Z_3$| direction in the complex plane. We have found that both IR-cut and UV-cut Polyakov loops |$\langle L_P\rangle _{\mathrm {IR/UV}}$| have the same properties of non-zero expectation value and |$Z_3$| symmetry breaking.
We have also investigated the temperature dependence of the IR/UV-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR/UV}}$|, and have found that |$\langle L_P\rangle _{\mathrm {IR/UV}}$| shows almost the same temperature dependence as the original Polyakov loop |$\langle L_P \rangle $|, while the IR-cut chiral condensate |$\langle \bar qq \rangle _{\mathrm {IR}}$| becomes almost zero even below |$T_{{\mathrm {c}}}$|, after removing the low-lying Dirac modes.
Finally, we have developed a new method to calculate the IR-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IR}}$| in a larger volume at finite temperature, by reformulation with respect to the removed IR Dirac mode space, and have found again the IR Dirac mode insensitivity to both the Polyakov loop and the confinement property on a larger lattice of |$12^3\times 4$|.
These lattice QCD results and related studies [15–21,24–29] suggest that each eigenmode has the information of confinement/deconfinement, i.e., the “seed” of confinement is distributed in a wider region of the Dirac eigenmodes. We consider that there is no direct connection between color confinement and chiral symmetry breaking through the Dirac eigenmodes. In fact, a one-to-one correspondence does not hold between confinement and chiral symmetry breaking in QCD, and their appearance can be different in QCD. This mismatch may suggest richer QCD phenomena and richer structures in QCD phase diagrams. It would be interesting to proceed to full QCD and investigate dynamical quark effects in our framework. It would also be interesting to search the relevant modes only for color confinement but irrelevant for chiral symmetry breaking [74].
Funding
Open Access funding: SCOAP3.
Acknowledgements
The authors thank Shinya Gongyo for his contribution to the early stage of this study. This work is in part supported by the Grant for Scientific Research [(C) No. 23540306, Priority Areas “New Hadrons” (E01:21105006)] and a Grant-in-Aid for JSPS Fellows [No. 23-752] from the Ministry of Education, Culture, Science and Technology (MEXT) of Japan. The lattice QCD calculations were performed on the NEC-SX8R and NEC-SX9 at Osaka University.
Appendix A. Intermediate Dirac mode removal for Polyakov loop
Figures A1 and A2 show the IM-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IM}}$| on the periodic lattice of |$6^4$| at |$\beta = 5.6$| in the confined phase, and that of |$6^3 \times 4$| at |$\beta = 6.0$| in the deconfined phase, respectively. Here, we remove the IM modes of |$0.5-1.0[a^{-1}]$|, |$1.0-1.5[a^{-1}]$|, and |$1.5-2.0[a^{-1}]$|, respectively.
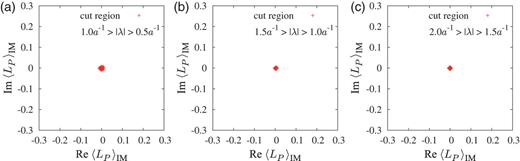
The IM-cut Polyakov loop on the periodic lattice of |$6^4$| at |$\beta = 5.6$| in the confined phase. The cut region of the Dirac mode is (a) |$|\lambda | \in (0.5a^{-1},1.0a^{-1})$|, (b) |$|\lambda | \in (1.0a^{-1},1.5a^{-1})$|, and (c) |$|\lambda | \in (1.5a^{-1},2.0a^{-1})$|, respectively.
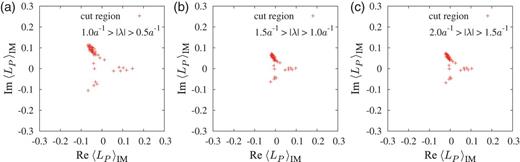
The IM-cut Polyakov loop on the periodic lattice of |$6^3 \times 4$| at |$\beta = 6.0$| in the deconfined phase. The cut region of the Dirac mode is (a) |$|\lambda | \in (0.5a^{-1},1.0a^{-1})$|, (b) |$|\lambda | \in (1.0a^{-1},1.5a^{-1})$|, and (c) |$|\lambda | \in (1.5a^{-1},2.0a^{-1})$|, respectively.
In the confined phase, the IM-cut Polyakov loop |$\langle L_P\rangle _{\mathrm {IM}}$| is almost zero, and |$\langle L_P\rangle _{\mathrm {IM}}$| has non-zero expectation value in the deconfined phase. These Dirac mode insensitivities are similar to the case of IR/UV-cut Polyakov loops.



