Local stability analysis of the azimuthal magnetorotational instability of ideal MHD flows

Abstract

A local stability analysis is carried out of axisymmetric rotating flows of a perfectly conducting fluid, subjected to an external azimuthal magnetic field |$B_{\theta }$| to non-axisymmetric as well as axisymmetric perturbations. We use the Hain–Lüst equation, capable of dealing with perturbations over a wide range of the axial wavenumber |$k$|⁠, which supplements the previous results of |$|k| \to \infty$| [G. I. Ogilvie and J. E. Pringle, Mon. Not. R. Astron. Soc. 279, 152 (1996)]. When the magnetic field is sufficiently weak, instability occurs for |$Ro=r \Omega '/(2\Omega )<Ro_c$| with |$Ro_c$| close to zero, with the maximum growth rate given by the Oort |$A$|-value |$|Ro|$|⁠, where |$\Omega (r)$| is the angular velocity of the rotating flow as a function only of |$r$|⁠, the distance from the axis of symmetry, and the prime designates the derivative in |$r$|⁠. As the magnetic field is increased, the flow becomes unstable to waves of long axial wavelength for a finite range of |$Ro$| around |$0$| when |$Rb=r^2 (B_{\theta }/r)'/(2B_{\theta })<-1/4$| with growth rate proportional to |$|B_{\theta }|$|⁠, giving unstable rotating flows under the current-free background magnetic field.

1. Introduction

Since the rediscovery of Velikhov and Chandrasekhar's result [1, 2] by Balbus and Hawley [3], the magnetorotational instability (MRI) has attracted great attention as a plausible mechanism for triggering turbulence in the flow of an accretion disk, for promoting outward transport of angular momentum while matter accretes to the center. There is a well known Rayleigh's criterion for the stability of a rotating flow of circular streamlines [4]. Given the angular velocity |$\Omega (r)$| as a function only of the distance |$r$| from the rotation axis, define the local Rossby number by |$Ro={\frac {1}{2}}{d} \log \Omega /{d} \log r=r\Omega '/(2\Omega )$| [5, 6]. Here the prime designates the derivative with respect to |$r$|⁠. In terms of the epicyclic frequency |$\kappa ^2=(\Omega ^2 r^4)'/r^3$|⁠, it is expressed as |$Ro=\kappa ^2/(4\Omega ^2)-1$|⁠. If |$\kappa ^2\geq 0$| or |$Ro\geq -1$| everywhere, such a rotating flow is linearly stable against axisymmetric disturbances [4, 6]. For an accretion disk, the angular velocity could satisfy the Keplerian law: |$\Omega (r)^2r=-\nabla \Phi ;\ \Phi =1/r$|⁠, for which |$Ro=-3/4$|⁠. Rayleigh's criterion may suggest that Keplerian rotation |$\Omega \propto r^{-3/2}$| is hydrodynamically stable.

The magnetic field parallel to the rotation axis drastically alters the stability characteristics. If the axial magnetic field is applied, however weak it is, a rotating flow suffers from instability if |$Ro <0$| [1, 2], implying that an accretion disk with Keplerian flow is unstable. We refer to this instability as the standard magnetorotational instability (SMRI). The maximum growth rate at a local portion was found to be |$3 |\Omega |/4$| for a Keplerian rotation [7]. For a general rotating flow of differential rotation |$\Omega (r)$| satisfying |$Ro <0$|⁠, the most unstable local instability mode of the SMRI is the axisymmetric one, with the maximum growth rate being |$\nu _A/\Omega ={\frac {1}{2}}|{d} \log \Omega /{d} \log r|$|⁠, the Oort |$A$|-value [7]. A distinguishing feature is that this growth rate is independent of the applied field strength.

When the magnetic field is frozen into the fluid, the differential rotation of the flow generates the azimuthal component of the magnetic field once the magnetic field acquires the radial component, which is possibly created by perturbing the axial field [8, 9]. Hence, it is worthwhile to look into the stability of a rotating flow applied by the azimuthal magnetic field and by a combination of the azimuthal and the axial magnetic field. The instability of the former case is called the azimuthal MRI or the AMRI, and the latter is called the helical MRI or the HMRI [5]. The HMRI has been extensively studied for a fluid of very low conductivity, called the inductionless limit [5, 10], because this is relevant to the experimental setting of using a liquid metal of very low conductivity [11]. Recently, an elaborate analysis has also been carried out for the AMRI in the regime of very low conductivity [12, 13].

For the perfectly conducting case, the AMRI and the HMRI to 3D disturbances of short wavelength were both examined numerically by Balbus and Hawley [8]. They showed the occurrence of the instability by conducting a numerical computation of linearized equations simplified by leaving out, by physical intuition, terms that appeared to be less important when the spatial variation of the basic magnetic field was slow. But they did not give the values of the growth rate or the parameter region for instability. Define the magnetic Rossby number |$Rb=r^2 (B_{\theta }/r)'/(2B_{\theta })$| [17]. Ogilvie and Pringle [14] addressed 3D AMRI by not only short-wavelength but also global analyses. By the former analysis, they showed that, in the limit of the axial wavenumber |$k\rightarrow \infty$|⁠, the maximum growth rate approaches the Oort |$A$|-value in the weak-field regime, while, in the same limit, the instability occurs for magnetic Rossby number |$Rb>-3/4$| in the strong-field regime. But the critical Rossby number in the weak-field regime and the growth rate in the strong-field regime are untouched. We point out that the traditional treatment of the short-wave stability analysis is liable to miss some terms if a WKB form of the solution is substituted at an early stage. The missing terms are indispensable to the analysis of disturbance with finite values of |$k$|⁠. A careful approach to escape from such a pitfall is first to deduce a differential equation for a single component of the displacement field, and thereafter to substitute the WKB form of the solution into the resulting equation. For a circular symmetric flow, the equation for the radial displacement field is known as the Hain–Lüst equation [15, 16]. In this paper, we resort to the Hain–Lüst equation, as augmented with the terms of the basic flow, in its full form, for the AMRI to non-axisymmetric as well as axisymmetric disturbances. With this equation at hand, we are capable of exploring the local instability over a wide range of |$k$|⁠. The formulation will be made in Sect. 2. Section 3 shows that this approach restores the known results of the axisymmetric SMRI and the axisymmetric AMRI.

We shall show in Sect. 4 that, when the steady imposed azimuthal magnetic field |$B_{\theta }(r)$| is sufficiently weak, the flow of the Rossby number |$Ro=r \Omega '/(2\Omega )<Ro_c$| is unstable with the critical Rossby number close to zero |$Ro_c\approx 0$|⁠, being dependent on |$B_{\theta }(r)$| and |$Rb$|⁠, in an analogous way to the SMRI. But the situation is totally altered as |$B_{\theta }(r)$| is increased, as detailed in Sect. 5. For |$Rb>-3/4$|⁠, the wave of |$k \to \infty$| is excited [14] and is likely to become dominant for |$Rb>-1/\sqrt {8}$|⁠, and, for |$Rb<-1/4$|⁠, the wave of |$k =0$| is excited and is likely to become dominant for |$Rb<-1/\sqrt {8}$|⁠. In either case, the modes of the lowest azimuthal wavenumbers |$m=0$| and |$m=1$| are the fastest growing. The instability mode of |$k =0$| is admitted in a limited range of |$Ro$| around |$Ro=0$|⁠, whereas the instability mode of |$k \to \infty$| is admitted for all the values of |$Ro$|⁠, implying the remarkable fact that there is no critical value of |$Ro$|⁠. Moreover, we shall establish that the maximum growth rate is proportional to |$|B_{\theta }|$| and can exceed the Oort |$A$|-value. The last section (Sect. 6) is devoted to a summary and conclusions.

2. Short-wavelength stability analysis

We consider a circular symmetric flow of an incompressible inviscid fluid with infinite electric conductivity, subjected to a steady external magnetic field, and the linear stability of a localized disturbance along one of the streamlines. We assume that the radial wavelength is very small compared with the radius |$r$| of the streamline, being a type of WKB approximation. We introduce global cylindrical coordinates |$(r, \theta , z)$| with the |$z$|-axis lying on the symmetric axis. The basic state is a rotating flow in equilibrium, with the angular velocity |$\Omega (r)$|⁠, subject to a magnetic field having the azimuthal and axial components |$B_{\theta }(r)=r\mu (r)$| and |$B_z$|⁠.

\[{\boldsymbol{{{U}}}}=r\Omega (r){\boldsymbol{{{e}}}}_{\theta },\ {\boldsymbol{{{B}}}}=r\mu (r){\boldsymbol{{{e}}}}_{\theta }+B_z{\boldsymbol{{{e}}}}_z,\]

(1)

where |${\boldsymbol{{{e}}}}_{\theta }$| and |${\boldsymbol{{{e}}}}_z$| are the unit vectors in the azimuthal and axial directions, respectively. After the second half of Sect. 3, we focus on the azimuthal field.

The linearized equations of the momentum and the induction equations for disturbance |$\tilde {{\boldsymbol{{{u}}}}}$|⁠, |$\tilde {{\boldsymbol{{{B}}}}}$|⁠, and |$\tilde {p}$| are

\[\frac {\partial \tilde {{\boldsymbol{{{u}}}}} }{\partial t}+ (\tilde {{\boldsymbol{{{u}}}}}\cdot \nabla ){\boldsymbol{{{U}}}}+ ({\boldsymbol{{{U}}}}\cdot \nabla )\tilde {{\boldsymbol{{{u}}}}} =-\frac {1}{\rho }(\nabla \tilde {p})+ \frac {1}{\rho \mu _0}(\tilde {{\boldsymbol{{{B}}}}}\cdot \nabla ){\boldsymbol{{{B}}}}+ \frac {1}{\rho \mu _0}({\boldsymbol{{{B}}}}\cdot \nabla )\tilde {{\boldsymbol{{{B}}}}},\]

(2)

\[\frac {\partial \tilde {{\boldsymbol{{{B}}}}} }{\partial t} =\nabla \times ({\boldsymbol{{{u}}}} \times \tilde {{\boldsymbol{{{B}}}}})+ \nabla \times (\tilde {{\boldsymbol{{{u}}}}} \times {\boldsymbol{{{B}}}}),\]

(3)

\[\nabla \cdot \tilde {{\boldsymbol{{{u}}}}} =0,\]

(4)

\[\nabla \cdot \tilde {{\boldsymbol{{{B}}}}} =0,\]

(5)

where |$\mu _0$| is the magnetic permeability and the density |$\rho$| is assumed to be constant. The last equation is the solenoidal property of the magnetic field. The first step is to assume the disturbances |$\tilde {{\boldsymbol{{{u}}}}}$|⁠, |$\tilde {{\boldsymbol{{{B}}}}}$|⁠, and |$\tilde {p}$| in the normal-mode form |$\exp [\lambda t+i(m\theta +k z)]$|⁠. Then the linearized equations (2)–(5) combine into matrix form for |$\boldsymbol {\xi }=(\tilde {u_r},\ \tilde {u_\theta },\ \tilde {u_z},\ \tilde {B_r},\ \tilde {B_\theta },\ \tilde {B_z},\ \tilde {p})$| as

\[{{\mathsf{M}}}\boldsymbol {\xi } = 0,\]

(6)

where

\[{\mathsf{M}}=\displaystyle \left (\begin {matrix}\displaystyle \tilde {\lambda } &\displaystyle -2\Omega &\displaystyle 0 &\displaystyle -\frac {iF}{\rho \mu _0}&\displaystyle \frac {2\mu }{\rho \mu _0}&\displaystyle 0&\displaystyle \frac {1}{\rho }\frac {d}{d r} \\ \displaystyle 2\Omega +r\frac {d\Omega }{dr}& \displaystyle \tilde {\lambda }&\displaystyle 0&\displaystyle -\left (2\mu +r\frac {d\mu }{dr}\right )&\displaystyle -\frac {iF}{\rho \mu _0}&\displaystyle 0& \displaystyle \frac {1}{r\rho } im \\ \displaystyle 0&\displaystyle 0 &\displaystyle \tilde {\lambda } &\displaystyle 0&\displaystyle 0&\displaystyle -\frac {iF}{\rho \mu _0}& \displaystyle \frac {1}{\rho } ik \\ \displaystyle -iF&0&0&\displaystyle \tilde {\lambda }&0&0&0 \\ \displaystyle r\frac {d\mu }{dr}&\displaystyle -iF&0&\displaystyle -r\frac {d\Omega }{dr}&\displaystyle \tilde {\lambda }&0&0\\ 0&0&\displaystyle -iF&0&0&\displaystyle \tilde {\lambda }&0\\ \displaystyle \frac {1}{r}+ \frac {d}{dr}&\displaystyle \frac {im}{r}&ik&0&0&0&0\\ 0&0&0&\displaystyle \frac {1}{r}+ \frac {d}{dr}&\displaystyle \frac {im}{r} &ik &0 \end {matrix}\right ),\]

(7)

with |$\tilde {\lambda }=\displaystyle \lambda +im\Omega$| and |$F=m\mu +B_zk$|⁠.

We can rule out, from (6), the disturbance magnetic field to obtain representations for |$\tilde {{\boldsymbol{{{u}}}}}$| in terms of |$\tilde {p}$| and its derivative as

\[\tilde {u_r}+ \frac {1}{E \rho } \left (\tilde {\lambda }+ \frac {F^2}{\tilde {\lambda }\rho \mu _0} \right ) \frac {{d} \tilde {p}}{{d} r}+ \frac {im}{E\rho r}\left (2\Omega -\frac {2i\mu F}{\tilde {\lambda }\rho \mu _0} \right )\tilde {p}=0,\]

(8)

\[\begin {align} \tilde {u_\theta } &- \frac {1}{E\rho } \left [2\Omega + \left (1+ \frac {F^2}{\tilde {\lambda }^2\rho \mu _0} \right ) r\frac {{d} \Omega }{{d} r} -\frac {2i\mu F}{\tilde {\lambda }\rho \mu _0} \right ] \frac {{d} \tilde {p}}{{d} r} \\ & + \frac {im}{Er\rho }\left (\tilde {\lambda }+ \frac {F^2}{\tilde {\lambda }\rho \mu _0}+ \frac {2i\mu F}{\tilde {\lambda }^2\rho \mu _0}r \frac {{d} \Omega }{{d} r} -\frac {2\mu }{\tilde {\lambda }\rho \mu _0}r\frac {{d} \mu }{{d} r} \right ) \tilde {p}=0, \end {align}\]

(9)

\[\displaystyle \tilde {u_z}+ \frac {ik}{\rho \left (\tilde {\lambda }+F^2/(\tilde {\lambda }\rho \mu _0)\right )}\tilde {p}=0,\]

(10)

where

\[\begin {align} E& = \left (\tilde {\lambda }+ \frac {F^2}{\tilde {\lambda }\rho \mu _0} \right )^2 + \frac {2\mu r}{\tilde {\lambda }\rho \mu _0} \left (\tilde {\lambda }+ \frac {F^2}{\tilde {\lambda }\rho \mu _0}\right ) \left (\frac {i F}{\tilde {\lambda }}\frac {{d} \Omega }{{d} r} -\frac {{d} \mu }{{d} r} \right ) \\ & \quad +2 \left [2\Omega + \left (1+ \frac {F^2}{\tilde {\lambda }^2\rho \mu _0} \right ) r\frac {{d} \Omega }{{d} r} -\frac {2i\mu F}{\tilde {\lambda }\rho \mu _0} \right ] \left (\Omega - \frac {i\mu F}{\tilde {\lambda }\rho \mu _0} \right ). \end {align}\]

(11)

Substitution of (8)–(10) into the continuity equation (4) then gives rise to a second-order differential equation of |$\tilde {p}$|⁠:

\[\begin {align} & \left (\frac {1}{r}+ \frac {{d} }{{d} r}\right )\left [\left (\tilde {\lambda }+ \frac {F^2}{\tilde {\lambda }\rho \mu _0} \right )\frac {1}{E}\frac {{d} \tilde {p}}{{d} r}+ \frac {2im}{rE}\left (\Omega -\frac {i\mu F}{\tilde {\lambda }\rho \mu _0}\right )\tilde {p}\right ] \\ &\quad -\frac {im}{rE}\left\{\left [2\Omega + \left (1+ \frac {F^2}{\tilde {\lambda }^2\rho \mu _0} \right ) r\frac {{d} \Omega }{{d} r} -\frac {2i\mu F}{\tilde {\lambda }\rho \mu _0} \right ]\frac {{d} \tilde {p}}{{d} r} \right.\\ &\quad \left. -\frac {im}{r}\left (\tilde {\lambda }+ \frac {F^2}{\tilde {\lambda }\rho \mu _0}+ \frac {2ir \mu F}{\tilde {\lambda }^2\rho \mu _0}\frac {{d} \Omega }{{d} r} -\frac {2r\mu }{\tilde {\lambda }\rho \mu _0}\frac {{d} \mu }{{d} r} \right )\tilde {p}\right\}-\frac {k^2}{ \tilde {\lambda }+F^2/(\tilde {\lambda }\rho \mu _0) }\tilde {p}=0. \end {align}\]

(12)

We introduce a new variable |$\chi =-ru_r/\tilde {\lambda }$| associated with the radial Lagrangian displacement [15]. Equation (8) expresses |$\chi$| in terms of |$\tilde {p}$| and |${d} \tilde {p}/{d} r$|⁠. Next, by taking differentiation, with respect to |$r$|⁠, of (8) after multiplication by |$r$|⁠, we relate |${d} \chi /{d} r$| with |$\tilde {p}$|⁠, |${d} \tilde {p}/{d} r$|⁠, and |${d}^2 \tilde {p}/{d} r^2$|⁠, the last of which is eliminated with the aid of (12). By using (8) again to further eliminate |${d} \tilde {p}/{d} r$|⁠, we are led to

\[\frac {\rho }{h^2r}\left (\tilde {\lambda }^2+ \frac {F^2}{\rho \mu _0}\right )\frac {{d} \chi }{{d} r}-\frac {2im\rho }{h^2r^2}\left ( \Omega \tilde {\lambda }-\frac {i\mu F}{\rho \mu _0}\right )\chi =\tilde {p}.\]

(13)

Substitution of (13) for |$\tilde {p}$| into (8) gives rise to

\[\frac {{d}}{{d} r}\left (f\frac {{d} \chi }{{d} r} \right )=g\chi ,\]

(14)

where, by use of the definition |$h^2=m^2/r^2+k^2$|⁠,

\[\begin {align} f &= \frac {1}{h^2r}\left (\tilde {\lambda }^2+ \frac {F^2}{\rho \mu _0} \right ), \\ g & = \frac {{d}}{{d} r}\left [{\frac {2im}{h^2r^2}} \left (\Omega \tilde {\lambda }-\frac {i\mu F}{\rho \mu _0}\right ) \right ] + \frac {1}{r}\left (\tilde {\lambda }^2+ \frac {F^2}{\rho \mu _0} \right ) + \frac {{d} \Omega ^2}{{d} r}- \frac {1}{\rho \mu _0}\frac {{d} \mu ^2}{{d} r} \\ & \quad + \frac {4k^2\left (\Omega \tilde {\lambda }- \mu iF/(\rho \mu _0) \right )^2} {h^2 r(\tilde {\lambda }^2+F^2/(\rho \mu _0))}.\end {align}\]

This is none other than the Hain–Lüst equation [16], as extended to accommodate the effect of a rotating flow. We seek the solution of (14) in the WKB approximation. For this purpose, we substitute into (14) the form |$\chi (r)=p(r)\exp [i\int q(r){d} r]$| with the constraint that the radial wavelength |$2\pi /q$| is assumed to be much shorter than the characteristic length |$L$|⁠, a measure for radial inhomogeneity, namely, |$qL\gg 1$|⁠. Neglecting the second-order terms in |$qL\gg 1$|⁠, the dispersion relation is gained from (14) as |$\displaystyle q^2=-g/f$|⁠, producing

\[\begin {align} & (h^2+q^2)\left (\tilde {\lambda }^2+ \frac {F^2}{\rho \mu _0} \right )^2 +4k^2\left (\Omega \tilde {\lambda }-\frac {i\mu F}{\rho \mu _0} \right )^2 \\ & \qquad +4h^2 \left [{\frac {im r}{2}}\frac {{d}}{{d} r}\left (\frac {\Omega \tilde {\lambda }-\frac {i\mu F}{\rho \mu _0}}{h^2r^2}\right ) + \Omega ^2Ro-\frac {\mu ^2}{\rho \mu _0}Rb \right ] \left (\tilde {\lambda }^2+ \frac {F^2}{\rho \mu _0} \right )=0, \end {align}\]

(15)

where we have introduced the Rossby number |$Ro$| [5, 6] and the magnetic Rossby number |$Rb$| [17] by

\[Ro=\frac {1}{2}\frac {r}{\Omega }\frac {{d} \Omega }{{d} r},\quad Rb=\frac {1}{2}\frac {r}{\mu }\frac {{d} \mu }{{d} r}.\]

(16)

Appendix A rearranges (15) into a polynomial equation in |$\lambda$|⁠.

3. Axisymmetric perturbations

For the standard MRI (SMRI), i.e., for |${\boldsymbol{{{B}}}}=B_z{\boldsymbol{{{e}}}}_z$| with |$B_{\theta }$| left out, the maximum growth rate is the Oort |$A$|-value |$\nu _A/\Omega ={\frac {1}{2}}|{d} \log \Omega /{d} \log r|=|Ro|$| [7], which is attained at |$m=0$|⁠, the radial wavenumber |$q=0$| and the axial wavenumber |$k$| satisfying |$\omega _{A}/\Omega =\pm \sqrt {1-\kappa ^4/(16\Omega ^4)}$|⁠, with |$\omega _{A}=k B_z/\sqrt {\rho \mu _0}$| and |$\kappa$| being the epicyclic frequency [8, 9]. At the outset, we shall confirm that our approach of using (14) restores this well known result.

For the SMRI, the dispersion relation (15) simplifies, when |$m=0$|⁠, to

\[\frac {\lambda ^2}{\Omega ^2} +Ro \left ( \frac {\lambda ^2}{\Omega ^2}+ \frac {\omega _{A}^2}{\Omega ^2} \right ) + {\frac {1}{4\alpha ^2}}\left ( \frac {\lambda ^2}{\Omega ^2} + \frac {\omega _{A}^2}{\Omega ^2} \right )^2=0,\]

(17)

where |$\alpha =k/\sqrt {q^2+k^2}$|⁠. We read off from (17), limited to |$\lambda =0$|⁠, the stability boundary as

\[Ro_c=- {\frac {\omega _{A}^2}{4\alpha ^2 \Omega ^2}}(<0),\quad \mbox {or } \frac {\omega _A}{\Omega }=0.\]

(18)

As the magnetic field |$\sqrt {k^2+q^2}B_z\rightarrow 0$|⁠, the above representation |$Ro_c \rightarrow 0$|⁠, and the Velikhov–Chandrasekhar paradox [1, 2], a glamor of the MRI, is retrieved. We note in passing that this paradox was resolved by taking account of the electric resistivity and the viscosity [6, 18]. The eigenvalue |$\lambda$|⁠, the root of (17), is

\[\frac {\lambda }{\Omega } =\pm \sqrt {\alpha ^2Ro^2 -\left (|\alpha | \mp \sqrt {\alpha ^2(1+Ro)^2 + \left (\frac {\omega _A}{\Omega }\right )^2} \right )^2 }.\]

(19)

The growth rate |${\rm Re}[\lambda ]$|⁠, the real part of |$\lambda$|⁠, reaches the maximum value |$|\alpha Ro|$| at |$(\omega _A/\Omega )^2=\alpha ^2[1-(1+Ro)^2]$|⁠, among which the maximum growth rate |$\nu _{\rm A}/\Omega =|Ro|$|⁠, being the Oort |$A$|-value, is attained at |$|\alpha |=1$|⁠. It should be borne in mind that the Oort |$A$|-value is realizable only when |$-2<Ro<0$| as required by |$(\omega _{\rm A}/\Omega )^2>0$| with |$k$| a disposable parameter. For a Keplerian rotation (⁠|$Ro=-3/4$|⁠), |$\nu _{\rm A}=3|\Omega |/4$| when |$\omega _A=\pm \sqrt {15}\Omega /4$| in accord with Ref. [8].

The critical wavenumber for the instability is read off from (18) to be |$\omega _A/\Omega =\pm \sqrt {-4Ro}$|⁠, meaning that the instability is invited when |$\omega _A/\Omega \in (-\sqrt {-4Ro}, 0)\cup (0,\sqrt {-4Ro})$|⁠. For the SMRI, the most unstable mode is likely to be axisymmetric. The axisymmetric mode is tractable since the eigenvalues |$\lambda$| are either real or pure imaginary, whereas for a non-axisymmetric perturbation, the eigenvalues are complex, being less analytically tractable.

Next, we turn to the azimuthal MRI (AMRI), for which the magnetic field has an azimuthal component |${\boldsymbol{{{B}}}}=r\mu (r){\boldsymbol{{{e}}}}_{\theta }$| only. For the axisymmetric case (⁠|$m=0$|⁠), the growth rate calculated from (15) is

\[\lambda =\pm 2 \Omega \alpha \sqrt {-1 -Ro +Rb\, \omega _{A\theta }^2/\Omega ^2},\quad \lambda =0,\]

(20)

where |$\omega _{A\theta }=\mu /\sqrt {\rho \mu _0},$| and |$\lambda =0$| is a double root. The instability region is |$Ro<Rb\,\omega _{A\theta }^2/\Omega ^2-1$|⁠, i.e., the critical Rossby number |$Ro_c=Rb\, \omega _{A\theta }^2/\Omega ^2-1$|⁠, which recovers Michael's criterion [19] (see also Refs. [2, 20]). Recently, this criterion has been extended to include the viscosity and the electric resistivity [13]. In case of |$Rb\,\omega _{A\theta }=0$|⁠, the criterion reduces to that of Rayleigh's centrifugal instability; when either magnetic field or the magnetic shear vanishes, the Keplerian flow is stable. The magnetic shear acts to either lower (⁠|$Rb<0$|⁠) or to raise (⁠|$Rb>0$|⁠) the critical Rossby number for the axisymmetric mode. In view of (20), for a Keplerian flow (⁠|$Ro=-3/4$|⁠), the instability occurs for |$Rb\,\omega _{A\theta }^2/\Omega ^2>1/4$|⁠. Either increase of |$Rb$| on the side of |$Rb>0$| or |$\omega _{A\theta }^2$| increases the growth rate.

4. Non-axisymmetric perturbations: overview

The inclusion of non-axisymmetric perturbations (⁠|$m\neq 0$|⁠) supplies the rich characteristics of the AMRI. In order to gain an insight into the 3D AMRI, we start with a stability analysis for the motionless state and then proceed to the case of a very weak magnetic field. The former corresponds to the strong-field limit.

By trial and error of numerical calculation, it is probable that the maximum growth rate is attained in the limit of |$k\rightarrow \infty$|⁠. The dispersion relation (15) reduces, in the limit of |$k^2+q^2 \rightarrow \infty$|⁠, to

\[4 (\tilde {\lambda } \Omega - i m \omega _{A\theta }^2)^2 + {\frac {1}{\alpha ^2}}(\tilde {\lambda }^2 +m^2 \omega _{A\theta }^2)^2 + (\tilde {\lambda }^2 +m^2 \omega _{A\theta }^2) (4 \Omega ^2 Ro - 4 Rb\,\omega _{A\theta }^2)=0.\]

(21)

Equation (21), which is valid for a strong magnetic field as well, was derived by Ogilvie and Pringle [14], and coincides with the dispersion relation of Ref. [13] if the viscous and resistive terms are dropped off.

For the motionless state (⁠|$\Omega \equiv 0$|⁠), the roots |$\lambda$| of (21) are written out explicitly in compact form as

\[\lambda =\pm \sqrt {-m^2+2\alpha ^2 Rb\pm 2\alpha \sqrt {m^2+ \alpha ^2 Rb^2}}\, \omega _{A\theta }.\]

(22)

One of the roots (22) becomes positive, signifying instability, when |$2|\alpha | \sqrt {m^2+ \alpha ^2Rb^2}>m^2-2\alpha ^2 Rb.$| For an axisymmetric perturbation (⁠|$m=0$|⁠), the instability criterion is |$Rb>0$|⁠. For non-axisymmetric perturbations, this condition is superseded by |$Rb>m^2/(4\alpha ^2)-1$|⁠. A glance at (22) shows that the growth rate is zero for |$\alpha =0$|⁠. When |$m$| exhausts all the integers and |$\alpha$| exhausts all the real numbers contained in the range of |$0<|\alpha | \leq 1$|⁠, the magnetic Rossby number |$Rb>-3/4$| is the widest possible |$Rb$| range for instability [14]. This condition coincides with the necessary condition for the instability, in the limit of |$|k| \to \infty$|⁠, derived in a wider context by Newcomb's energy principle [12, 22], which takes the form

\[-r p' >{\frac {1}{2\mu _0}} m^2 {\boldsymbol{{{B}}}}^2,\]

(23)

where |$p'={d} p/{d} r$| [15]. Substituting |${\boldsymbol{{{B}}}}(r)=B_{\theta }(r) {\boldsymbol{{{e}}}}_{\theta }$| into the equilibrium condition |$\boldsymbol {0}=-\nabla p+ (\nabla \times {\boldsymbol{{{B}}}})\times {\boldsymbol{{{B}}}}/\mu _0,$| we have |$p'=-B_{\theta }/(\mu _0 r) (r B_{\theta })'$|⁠. As noted in Ref. [15], (23) is not valid for the axisymmetric case |$m=0$|⁠, for which (23) is replaced by Suydam's criterion for the local interchange condition. As a consequence, |$m=\pm 1$| in (23) provides the maximum possible range for instability, and this condition is exactly |$Rb>-3/4$|⁠.

The maximum growth rate is found by rewriting (22) as

\[\lambda =\pm \sqrt {\alpha ^2(Rb+1)^2- \left (\sqrt {m^2+ \alpha ^2Rb^2} \mp \alpha \right )^2 }\, \omega _{A\theta }.\]

(24)

Since |$m$| takes integral values but |$\alpha$| is confined to the range |$0<|\alpha | \leq 1$|⁠, the maximum of |$\lambda$| is attained either at |$m=0$| or |$m=\pm 1$|⁠. When |$Rb$| is larger than 3/4, the maximum is |$\lambda _{\rm max}=2\sqrt {Rb} |\omega _{A\theta }|$| attained at |$m=0$| and |$|\alpha |=1$|⁠. For |$-3/4 <Rb \leq 3/4$|⁠, the maximum is attained at |$m= \pm 1$| with its value |$\lambda _{\rm max}=\sqrt {-1+2 Rb+2\sqrt {1+Rb^2}}|\omega _{A\theta }|$|⁠.

For comparison, we look into the case of |$k=0$|⁠. The dispersion relation (15) reduces to

\[\begin {align} &\left (\tilde {\lambda }^2+m^2 \omega _{A\theta }^2\right ) \left[\left (q^2+ \frac {m^2}{r^2}\right )(\tilde {\lambda }^2+m^2 \omega _{A\theta }^2)+ \frac {4m^2}{r^2} (\Omega ^2 Ro +Rb\,\omega _{A\theta }^2)\right. \\ & \quad \left. + \frac {4im\Omega Ro}{r^2}(\lambda +2im\Omega )\right ]=0. \end {align}\]

(25)

For the motionless state |$(\Omega \equiv 0)$|⁠, the eigenvalues are

\[\lambda = \left\{ \begin {array}{l}\displaystyle \pm \frac {m\omega _{A\theta }}{\sqrt {m^2 +q^2 r^2 }} \sqrt { -4Rb-m^2- q^2 r^2 }, \\ \pm im \omega _{A\theta }. \end {array}\right .\]

(26)

The criterion for instability is read off, from (26), as

\[Rb<-\frac {m^2+q^2 r^2 }{4}\leq -\frac {1}{4}\]

(27)

with the maximum value of growth rate

\[\lambda = |\omega _{A\theta }|\sqrt { -4Rb-1 }\]

(28)

attained at |$m=\pm 1$| and |$q=0$|⁠. The instability relevant to the current-free magnetic field |${\boldsymbol{{{B}}}}_\theta (r)\propto 1/r$| (⁠|$Rb=-1$|⁠) is this mode rather than that of |$k\rightarrow \infty$|⁠. The growth rate is proportional to |$|\omega _{A\theta }|$|⁠.

It is instructive to look into the eigenvalues and eigenfunctions of waves, of |$k\rightarrow \infty$|⁠, on a rotating flow with no external magnetic field. For a non-axisymmetric perturbation |$m\neq 0$| and simultaneously in the presence of a rotational flow with angular velocity |$\Omega \neq 0$|⁠, the energy principle is difficult to apply, and we appeal to the WKB method by restricting it to short-wavelength perturbations. In the absence of a magnetic field (⁠|$\omega _{A\theta }\equiv 0$|⁠), (21) has roots |$\lambda _{1,2}/\Omega =-i m \pm 2\alpha \sqrt {-(1 +Ro)}$| and |$\lambda _{3,4}/\Omega =-i m$|⁠. The latter pertain to the mode characterized by the advection of the disturbance magnetic field frozen into the local rotating flow. The root |$\lambda _{1,2}$| pertains to the inertial wave or the Kelvin wave [23]. Its frequency |$\omega _{1,2}$| as defined by |$\lambda _{1,2}=-i\omega _{1,2}$| is given by |$\omega _{1,2}=m \mp 2\alpha \sqrt {1+Ro}.$| This distinction between |$\lambda _{1,2}$| and |$\lambda _{3,4}$| manifests itself by constructing the eigenfunction |$\boldsymbol {\xi }$| of (6). For simplicity, we take |$Ro=0$|⁠, |$\alpha =1$|⁠, and |$|m| \ll |k|$|⁠. The eigenfunctions corresponding to |$\lambda _{1,2}=-i(m \mp 2)$| are |$\boldsymbol {\xi }_{1,2}=(\mp i, 1, 0,0,0,0,0)$|⁠, and those corresponding to |$\lambda _{3,4}=-i\omega _{3,4}$| are |$\boldsymbol {\xi }_3=(0,0,0,1,0,0,0)$| and |$\boldsymbol {\xi }_4=(0,0,0,0,1,0,0)$|⁠. It is simply the disturbance magnetic field |$\boldsymbol {\xi }_{3,4}$| that is advected by the fluid (⁠|$\omega _{3,4}=m$|⁠). For a uniform rotation (⁠|$Ro=0$|⁠), the frequency |$\omega _{1,2}=m \mp 2\alpha$| is confined to |$-2\leq \omega _1\leq 0$| (upper sign) and |$0\leq \omega _2\leq 2$| (lower sign) [24]. The parameter |$\alpha$| plays the role of a counter for the radial nodal structure, with |$|\alpha |=1$|⁠, or |$|q/k| \ll 1$|⁠, corresponding to a simple structure and with |$|\alpha |\ll 1$|⁠, or |$|q/k| \gg 1$|⁠, corresponding to a highly fine radial structure. The mode with eigenfrequency |$\omega _1$|⁠, being smaller than |$m \Omega$|⁠, is called the retrograde mode, while that with eigenfrequency |$\omega _2$|⁠, being larger than |$m \Omega$|⁠, is called the cograde mode [23]. Alternatively, from the viewpoint of the way approaching the limiting frequency |$m$| for |$\alpha =0$|⁠, |$\omega _1$| and |$\omega _2$| are referred to as the Sturmian and the anti-Sturmian, respectively [16]. There is no growing perturbation unless |$Ro<-1$|⁠. This implies that the same criterion as Rayleigh's one for the centrifugal instability applies to the non-axisymmetric perturbations too. Figure 1 depicts |${\rm Re}[\lambda ]$| (left) and |${\rm Im}[\lambda ]=-\omega$| (right) of the eigenvalue for the helical perturbation |$m=1$| with the simplest nodal structure |$\alpha =1$| when no external magnetic field is applied (⁠|$\omega _{A\theta } \equiv 0$|⁠).

$The growth rate ${\rm Re}[\lambda ]$ (left) and the frequency ${\rm Im}[\lambda ]=-\omega$ (right) of the perturbation of $m=1$ and $\alpha =1$ in the absence of the external magnetic field ($\omega _{A\theta }\equiv 0$ and consequently $Rb=0$).$

Fig. 1.

The growth rate |${\rm Re}[\lambda ]$| (left) and the frequency |${\rm Im}[\lambda ]=-\omega$| (right) of the perturbation of |$m=1$| and |$\alpha =1$| in the absence of the external magnetic field (⁠|$\omega _{A\theta }\equiv 0$| and consequently |$Rb=0$|⁠).

Open in new tab Download slide

We are now ready to inquire into how a weak azimuthal magnetic field deforms the above dispersion relation. When |$\omega _{A\theta }\neq 0$|⁠, but with |$|\omega _{A\theta }/\Omega |\ll 1$|⁠, the expression for the eigenvalue can be expanded to second order in a small parameter |$\omega _{A\theta }/\Omega$| as, unless |$|\alpha | \ll 1$|⁠,

\[{\frac {\lambda _{1,2}}{\Omega }} \approx \left\{ \begin {array}{ll} -i m \pm 2|\alpha | \sqrt {-(1 +Ro)}-{\frac {1}{1+Ro}}\left ( i m \pm Rb|\alpha | \sqrt {-(1 +Ro)}\right. &\\ \quad \left. \pm \displaystyle{\frac {m^2}{4|\alpha |}} {\frac {2+Ro}{\sqrt {-(1 +Ro)}}} \right ) \left ({\frac {\omega _{A\theta }}{\Omega }} \right )^2 &(Ro \neq -1), \\ -im \pm \sqrt {{\frac {2\alpha m \omega _{A\theta }}{\Omega }}} +i {\frac {\alpha \omega _{A\theta }}{\Omega }} \pm {\frac {\alpha ^2-m^2+ \alpha ^2 Rb}{2\sqrt {2\alpha m}}} \left ({\frac {\omega _{A\theta }}{\Omega }} \right )^{3/2} &(Ro =-1), \\ \end {array}\right .\]

(29)

\[{\frac {\lambda _{3,4}}{\Omega }} \approx \left\{ \begin {array}{ll}-i m\pm m \sqrt {\frac {Ro}{-(1+Ro)}}{\frac {\omega _{A\theta }}{\Omega }}+ {\frac {im}{1+Ro} }\left ({\frac {\omega _{A\theta }}{\Omega }} \right )^2 &(Ro \neq -1, 0), \\ -im \pm i\sqrt {{\frac {2\alpha m \omega _{A\theta }}{\Omega }}} -i {\frac {\alpha \omega _{A\theta }}{\Omega }} \mp i {\frac {\alpha ^2-m^2+ \alpha ^2 Rb}{2\sqrt {2\alpha m}}} \left ({\frac {\omega _{A\theta }}{\Omega }} \right )^{3/2} &(Ro =-1), \\ -i m +m \left (i \mp \sqrt {Rb-m^2/(4\alpha ^2)} \right ) \left ({\frac {\omega _{A\theta }}{\Omega }} \right )^2 &(Ro=0), \end {array}\right .\]

(30)

where the double-sign corresponds in the same order, and the upper sign corresponds to |$\lambda _1$| and |$\lambda _3$|⁠, and the lower sign corresponds to |$\lambda _2$| and |$\lambda _4$|⁠. For both |$\lambda _{1,2}$| and |$\lambda _{3,4}$|⁠, the first expansions are singular at |$Ro=-1$|⁠, where a separate treatment is necessary. For the expansion at |$Ro=-1$|⁠, we have ignored the terms of |$O\left ( (\omega _{A\theta }/\Omega )^2\right )$|⁠. For |$\lambda _{3,4}$|⁠, the first expansion for |$Ro\neq -1, 0$| of (30) is invalidated in the limit of |$Ro \rightarrow 0$| as well, because the coefficient of the third term |$(\omega _{A\theta }/\Omega )^3$| is proportional to |$Ro^{-1/2}$|⁠, which diverges in the limit |$Ro \rightarrow 0$|⁠. This singularity requires a separate treatment for the case of |$Ro=0$| and the resulting expression is the third expression of (30). The branches |$\lambda _{1,2}$| of the inertial waves, subjected to the azimuthal magnetic field, are called the fast magneto-Coriolis (MC) waves. The branches |$\lambda _{3,4}$| are called the slow magneto-Coriolis (MC) waves [6]. In case of |$|\alpha | \ll 1$|⁠, (29) and (30) give way to

\[{\frac {\lambda _{1,2}}{\Omega }} \approx -i m \left (1+ {\frac {\omega _{A\theta }}{\Omega }} \right ) \pm i\left (1+ {\frac {\omega _{A\theta }}{\Omega }} \right ) |\alpha | +O(\alpha ^2),\]

(31)

\[{\frac {\lambda _{3,4}}{\Omega }} \approx -i m \left (1- {\frac {\omega _{A\theta }}{\Omega }} \right ) \pm i\left (1- {\frac {\omega _{A\theta }}{\Omega }} \right ) |\alpha | +O(\alpha ^2).\]

(32)

By applying the magnetic field, the frequency |$m$| degenerate at |$\alpha =0$| is split into |$m(1\pm \omega _{A\theta }/\Omega )$|⁠. In the limit of |$|\alpha |\rightarrow 0$|⁠, the frequency defined via |$\lambda _{1,2}=-i\omega _{1,2}$| of the fast MC waves degenerates to |$m(\Omega + \omega _{A\theta })$| with |$\omega _1$| (upper sign) approaching from below and |$\omega _2$| (lower sign) from above, and that of the slow MC waves, stemming from the frozen-in advection, degenerates to |$m(\Omega -\omega _{A\theta })$| with |$\omega _3$| (upper sign) approaching from below and |$\omega _4$| (lower sign) from above. For this reason, the fast and slow MC waves may refer to the forward and backward modes, with the upper sign Sturmian and the lower sign anti-Sturmian [16].

The first expansion of (30) suggests that the instability occurs when |$Ro \stackrel {<}{\sim }0$|⁠. This property is reminiscent of the SMRI for which the critical Rossby number (18) is close to but less than zero if the resistivity is zero [6]. The situation is slightly different for the AMRI. The first part of (30) becomes invalid at |$Ro=0$|⁠, to which the third expansion of (30) applies. The third part implies that, when |$Rb >m^2/(4\alpha ^2) \geq m^2/4$| by varying |$|\alpha | \in (0, 1]$|⁠, |$Ro_c>0$|⁠, but otherwise, |$Ro_c\leq 0$|⁠. In the following, we determine |$Ro_c$|⁠.

It turns out that |$Ro_c$| is very small. Near |$Ro_c \approx 0$|⁠, we seek the eigenvalues of the slow MC wave in a power series in the small parameter |$\omega _{A\theta }/\Omega$|⁠, and, in keeping, we represent |$Ro$| in a power series in |$\omega _{A\theta }/\Omega$|⁠. The result for the slow MC wave is

\[{\frac {\lambda _{3,4}}{\Omega }}\approx -im +m \left (i \pm \sqrt {Rb-Ro_2 -m^2/(4\alpha ^2)} \right )\left ({\frac {\omega _{A\theta }}{\Omega }} \right )^2,\]

(33)

for |$0<|\alpha |\leq 1$| and |$Ro = Ro_2 \left (\omega _{A\theta }/\Omega \right )^2 + \cdots .$| It follows from (33) that the slow MC wave is amplified when |$Ro_2<Rb-m^2/(4\alpha ^2).$| For small values of |$\left (\omega _{A\theta }/\Omega \right )^2$|⁠, the AMRI is caused when approximately

\[Ro <\left (Rb-{\frac {m^2}{4\alpha ^2}} \right ) \left ({\frac {\omega _{A\theta }}{\Omega }} \right )^2 \leq Ro_c\approx \left (Rb-{\frac {1}{4}} \right ) \left ({\frac {\omega _{A\theta }}{\Omega }} \right )^2.\]

(34)

Figure 2 shows the growth rate (left) and the frequency (right) for |$\omega _{A\theta }/\Omega =0.5$|⁠. The other para-meters |$m=1$|⁠, |$\alpha =1$|⁠, and |$Rb=0$| are the same as in Fig. 1. For this choice of the parameters, |$Ro_c=-1/16$|⁠. It is observed that the instability is driven when the frequencies |$\omega _3$| and |$\omega _4$| of the slow MC wave (⁠|$=$| backward wave) collide at around |$\omega =m=1$| at the critical value |$Ro_c$|⁠. To clarify the source for the instability, the positive values of the asymptotic formulas |${\rm Re}[\lambda _{1,2}/\Omega ]$| and |${\rm Re}[\lambda _{3,4}/\Omega ]$| provided by the first equations of (29) and (30) respectively are superposed, with long-dashed lines, on the left panel of Fig. 2. For |$Ro>-1$|⁠, the instability originates from the slow MC waves, but, for |$Ro<-1$|⁠, the dominant role in the instability is played by the fast MC waves. At the dividing point |$Ro=-1$|⁠, the flow is necessarily unstable; for |$\alpha m \omega _{A\theta }/\Omega >0$|⁠, |${\rm Re}[\lambda _{1,2}]\neq 0$| as is seen from the second part of (29) and the fast MC wave is amplified, but, for |$\alpha m \omega _{A\theta }/\Omega <0$|⁠, the slow MC wave is amplified, with the growth rate given by |$|{\rm Re}[\lambda _{3,4}]|$|⁠, the real part of the second expression of (30).

$The growth rate ${\rm Re}[\lambda ]$ (left) and the frequency ${\rm Im}[\lambda ]=-\omega$ (right) of the perturbation of $m=1$ and $\alpha =1$ for $\omega _{A\theta }/\Omega =0.5$. The magnetic shear is $Rb=0$. The long-dashed lines (left) show the positive real part of the first part of (29) for $Ro<-1$ and that of (30) for $-1<Ro<0$.$

Fig. 2.

The growth rate |${\rm Re}[\lambda ]$| (left) and the frequency |${\rm Im}[\lambda ]=-\omega$| (right) of the perturbation of |$m=1$| and |$\alpha =1$| for |$\omega _{A\theta }/\Omega =0.5$|⁠. The magnetic shear is |$Rb=0$|⁠. The long-dashed lines (left) show the positive real part of the first part of (29) for |$Ro<-1$| and that of (30) for |$-1<Ro<0$|⁠.

Open in new tab Download slide

Here we point out that, unlike the axisymmetric SMRI, the axisymmetric AMRI is of the fast MC-wave origin. The growth rate of the axisymmetric AMRI, the left values of (20) in the limit of |$k\rightarrow \infty$|⁠, has a link with the first part of (29) specialized to |$m=0$|⁠. For the fast MC wave, the critical Rossby number |$Ro_c$| is close to |$-1$| when |$|\omega _{A\theta }/\Omega | \ll 1$|⁠, being consistent with the argument of Sect. 3. In contrast, the eigenvalues (30) of the slow MC wave become zero for |$m=0$|⁠, in agreement with the second values of (20), which does not contribute to the axisymmetric AMRI. For the AMRI, the slow MC wave, raising the critical value to |$Ro_c\approx 0$|⁠, close to Velikhov–Chandrasekhar's value for the SMRI, is intrinsic to non-axisymmetric perturbations.

Given a small value of |$|\omega _{A\theta }/\Omega |$|⁠, the maximum growth rate increases with |$|m|$|⁠. Interestingly, the maximum growth rate approaches, as |$|m|$| is increased, the same value as that of the SMRI as found by Ogilvie and Pringle [14]. Figure 3 displays the growth rate |$\nu =\rm {Re}[\lambda _{3,4}]$| as functions of the Alfvén frequency |$\omega _{A\theta }$| with azimuthal wavenumbers |$m=1$|⁠, |$5$|⁠, and |$10$| for |$Ro=-3/4$| and |$Rb=-1$|⁠. Since the system is Hamiltonian, to each damping perturbation (⁠|$\nu <0$|⁠) corresponds the growing perturbation (⁠|$\nu >0$|⁠) and therefore we display only the solution with positive real part |$\nu$|⁠. The change of the sign of |$Rb$|⁠, namely, the choice of |$Rb=1$|⁠, does not change the growth rate much. We observe from Fig. 3 that, as |$m$| increases, the maximum growth rate approaches |$3|\Omega |/4$|⁠, though the width of the instability band in |$\omega _{A\theta }/\Omega$| is narrowed with |$m$|⁠. Indeed, by taking |$m \omega _{A\theta }^2=0$| and |$Rb \omega _{A\theta }^2=0$| in (21) as a limit of small values of |$|\omega _{A\theta }/\Omega |$| while maintaining |$|m \omega _{A\theta }/\Omega |$| finite, we can show that the maximum growth rate happens to coincides with the Oort |$A$|-value |$\nu _{\rm A}/|\Omega |=|Ro|$|⁠. In this limit, (21) is solved for |$\tilde {\lambda }$|⁠, yielding

\[{\frac {\lambda }{\Omega }} =-im \pm \sqrt {\alpha ^2 Ro^2-\left ( \sqrt {\left (m {\frac {\omega _{A\theta }}{\Omega }} \right )^2 + \alpha ^2(1+Ro)^2}\mp \alpha \right )^2}.\]

(35)

The growth rate |$\nu =|{\rm Re}[\lambda ]|$| takes the maximum value close to |$|\alpha Ro|$| when |$\sqrt {\left (m\omega _{A\theta }/\Omega \right )^2 + \alpha ^2(1+Ro)^2} =|\alpha |,$| or at |$m \approx \pm (\Omega /\omega _{A\theta })\alpha \sqrt {1-(1+Ro)^2}$|⁠. Actually, |$m$| should be an integer closest to the right-hand side. By varying |$\alpha$|⁠, the maximum value among the above is close to the Oort |$A$|-value |$\nu _{\rm A}/|\Omega |=|Ro|$| at |$\alpha =\pm 1$| [7]. The instability window is found from (35) as |$\alpha ^2Ro^2>\left (\sqrt {\left (m\omega _{A\theta }/\Omega \right )^2 + \alpha ^2(1+Ro)^2}-|\alpha |\right )^2.$| The instability takes place for |$0<|\omega _{A\theta }/\Omega | <2\sqrt {|\alpha Ro|}/|m|,$| whose upper bound |$2\sqrt {|Ro|}/|m|$| is reached at |$|\alpha |=1$|⁠. The width of the instability band is narrowed with |$|m|$| being inversely proportional to |$|m|$|⁠, as is confirmed from Fig. 3.

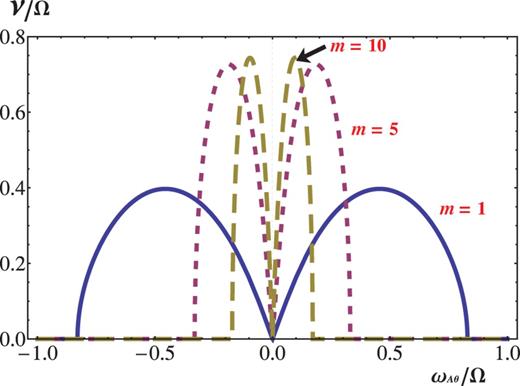
$The growth rate, in the limit $k\rightarrow \infty$ with $\alpha =1$ fixed, of the non-axisymmetric AMRI versus $\omega _{A\theta }/\Omega$, in the range of small values, for different azimuthal wavenumbers $m=1$ (solid line), 5 (dashed line), and 10 (long-dashed line) for $Ro=-3/4$, a Keplerian rotation. The magnetic Rossby number is $Rb=-1$.$

Fig. 3.

The growth rate, in the limit |$k\rightarrow \infty$| with |$\alpha =1$| fixed, of the non-axisymmetric AMRI versus |$\omega _{A\theta }/\Omega$|⁠, in the range of small values, for different azimuthal wavenumbers |$m=1$| (solid line), 5 (dashed line), and 10 (long-dashed line) for |$Ro=-3/4$|⁠, a Keplerian rotation. The magnetic Rossby number is |$Rb=-1$|⁠.

Open in new tab Download slide

The AMRI shares common features with the SMRI in that the instability occurs for |$Ro <Ro_c \approx 0$| no matter how weak the external magnetic field may be, when it is applied, and the maximum growth rate is |$|Ro|$|⁠, regardless of the strength of the external field. This resemblance holds true as far as |$|\omega _{A\theta }/\Omega | \ll 1$|⁠. However, a distinctive behavior manifests itself when the azimuthal magnetic field |$B_{\theta }$| is intensified to the level |$|\omega _{A\theta }/\Omega |=O(1)$|⁠, as will be described in the subsequent section.

5. Non-axisymmetric perturbations: strong external field

This section is concerned with the case of |$|\omega _{A\theta }/\Omega | \sim 1$|⁠. The previous investigation of |$|k| \to \infty$| [14] showed that a purely magnetic instability is excited when |$Rb>-3/4$|⁠. Both cases |$Ro<0$| and |$Ro\geq 0$| entail this instability, or, put another way, there is no critical Rossby number. But this mode subsides as |$Rb$| is decreased and dies down at |$Rb=-3/4$|⁠. Another unstable mode of |$k=0$| is born at |$Rb=-1/4$|⁠, develops as |$Rb$| is decreased, and surpasses the mode of |$|k| \to \infty$| for |$Rb \leq -1/\sqrt {8}$|⁠. The instability mode of |$k=0$| is confined to a finite range in |$Ro$| centered on |$Ro=0$|⁠, |$Ro^2 <(|Rb|-1/4)(\omega _{A\theta }/\Omega )^2$| for |$-1/2 \leq Rb <-1/4$|⁠, and |$Ro^2<Rb^2(\omega _{A\theta }/\Omega )^2$| for |$Rb <-1/2$|⁠. We should keep in mind the results of the previous section that, for small values of |$|\omega _{A\theta }/\Omega |$|⁠, the unstable mode of |$|k| \to \infty$| prevails for the entire range of |$Rb$|⁠, though restricted to |$Ro <Ro_c$|⁠, with |$Ro_c$| depending on |$Rb$| as given by (34).

The numerical calculation for |$m=1$|⁠, for instance, shows that, for |$Rb>0$|⁠, the maximum growth rate is taken in the limit of |$k\rightarrow \infty$| and that the maximum value overshoots the Oort |$A$|-value |$\nu _{\rm A}$| when |$|\omega _{a\theta }|$| and |$Rb$| are increased. In the limit of |$k \rightarrow \infty$| with fixed |$\alpha$|⁠, the asymptotics of the growth rate for |$|\omega _{A\theta }/\Omega | \gg 1$| is deduced with ease by manipulating the expansion of (21) in |$\Omega /\omega _{A\theta }$|⁠, up to |$O(1)$|⁠, as

\[{\frac {\lambda _{1,2}}{\Omega }} \approx \pm \sqrt {2\alpha ^2Rb-m^2+2|\alpha | \sqrt {m^2+ \alpha ^2Rb^2} }{\frac {\omega _{A\theta }}{\Omega }} -im\left (1-{\frac {|\alpha |}{\sqrt {m^2+ \alpha ^2Rb^2}}} \right ),\]

(36)

\[{\frac {\lambda _{3,4}}{\Omega }} \approx \pm \sqrt {2\alpha ^2Rb-m^2-2|\alpha | \sqrt {m^2+ \alpha ^2Rb^2}}{\frac {\omega _{A\theta }}{\Omega }} -im\left (1+ {\frac {|\alpha |}{\sqrt {m^2+ \alpha ^2Rb^2}}}\right ).\]

(37)

The parameter |$Ro$| resides only in higher-order terms in |$\Omega /\omega _{A\theta }$|⁠. Both sides of |$Ro<0$| and |$Ro\geq 0$| entail the instability, as opposed to the case of small values of |$|\omega _{A\theta }/\Omega |$|⁠. When |$Rb>0$|⁠, (36) and (37) are reduced, if specialized to |$m=0$|⁠, to the large |$\omega _{A\theta }/|\Omega |$| asymptotics of the left and right parts of (20). Unlike the case of |$|\omega _{A\theta }/\Omega | \ll 1$|⁠, the unstable mode is necessarily the fast MC wave (⁠|$\lambda _{1,2}$|⁠) regardless of the value of |$Ro$|⁠. When |$Rb<0$|⁠, the roles of |$\lambda _{1,2}$| and |$\lambda _{3,4}$| are exchanged. The growth rate is proportional to |$\omega _{A\theta }/\Omega$|⁠. The maximum value of the growth rate |$\nu _{1,2}={\rm Re}[\lambda _{1,2}]$| with respect to |$m$| and |$\alpha$| is evaluated by rewriting (36) into

\[{\frac {\nu _{1,2}}{\Omega }} \approx \pm \sqrt {\alpha ^2(Rb+1)^2 -\left (\sqrt {m^2+ \alpha ^2 Rb^2}-|\alpha | \right )^2 }{\frac {\omega _{A\theta }}{\Omega }}.\]

(38)

For an integer |$m$| and |$0<|\alpha | \leq 1$|⁠, this is real when |$Rb\geq m^2/(4\alpha ^2)-1\geq -3/4$||$(m \neq 0)$| and |$Rb\geq 0$||$(m=0)$|⁠. The maximum value is taken at |$|\alpha |=1$|⁠, and at |$m=0$| for |$Rb\geq 3/4$|⁠, but at |$|m|=1$| for |$-3/4<Rb<3/4$|⁠, with the maximum values

\[{\frac {\nu _{\rm max}}{\Omega }} \approx \left\{ \begin {array}{ll}2\sqrt {Rb} |\omega _{A\theta }/\Omega | & (Rb\geq 3/4), \\ \sqrt {2Rb-1+2 \sqrt {1+Rb^2} }|\omega _{A\theta }/\Omega | & (-3/4<Rb<3/4). \end {array}\right .\]

(39)

This value decreases to zero as |$Rb$| decreases to |$-3/4$|⁠.

Figure 4 shows the growth rate, for |$m=1$| in the limit of |$k \to \infty$|⁠, over a wide range of the Alfvén frequency |$\omega _{A\theta }/\Omega$| and for typical values of |$Rb$| (⁠|$=0,\ 1,\ 5$|⁠) in the range of |$Rb>-3/4$|⁠. The flow is Keplerian (⁠|$Ro<0$|⁠). Figure 5 is the counterpart for positive |$Ro (=1)$|⁠. The difference lies in the neighborhood of the origin |$(\omega _{A\theta }/\Omega , \nu /\Omega )=(0,0)$|⁠. The critical condition (34), if rearranged, implies that, for |$Rb>1/4$|⁠, the unstable mode of |$|k| \rightarrow \infty$| is excited for |$(\omega _{A\theta }/\Omega )^2>Ro/(Rb-1/4)$|⁠, though the validity is limited to |$|\omega _{A\theta }/\Omega | \ll 1$|⁠. Figure 5 for |$Ro>0$| exhibits the disappearance of instability in a finite range in |$|\omega _{A\theta }/\Omega |$|⁠, being wider for a smaller value of |$Rb$| (⁠|$>1/4$|⁠). For instance, the |$k \rightarrow \infty$| mode arises at |$\omega _{A\theta }/\Omega \approx 0.48$| for |$Ro=1$| and |$Rb=5$|⁠, for which |$\sqrt {Ro/(Rb-1/4)}\approx 0.4588$|⁠.

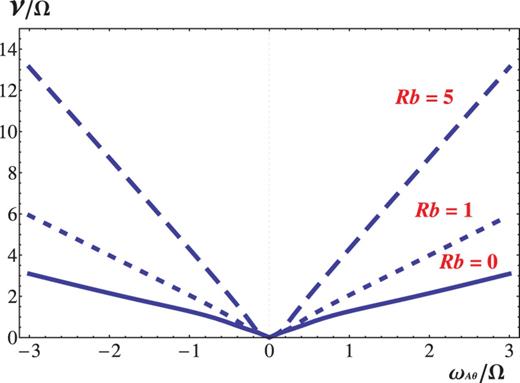
$The growth rate, for $m=1$ and $k\rightarrow \infty$ with fixed $\alpha =1$, of the non-axisymmetric AMRI over a wide range of $\omega _{A\theta }/\Omega$ for negative $Ro=-3/4$ and different non-negative magnetic Rossby numbers $Rb$: $Rb=0$ (solid line), 1 (dashed line), and 5 (long-dashed line).$

Fig. 4.

The growth rate, for |$m=1$| and |$k\rightarrow \infty$| with fixed |$\alpha =1$|⁠, of the non-axisymmetric AMRI over a wide range of |$\omega _{A\theta }/\Omega$| for negative |$Ro=-3/4$| and different non-negative magnetic Rossby numbers |$Rb$|⁠: |$Rb=0$| (solid line), 1 (dashed line), and 5 (long-dashed line).

Open in new tab Download slide

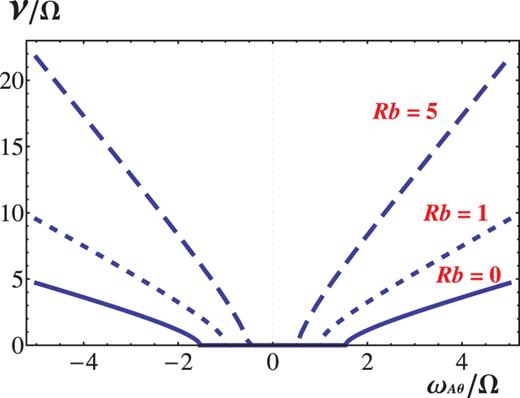
$The growth rate, for $m=1$ and $k\rightarrow \infty$, of the non-axisymmetric AMRI over a wide range of $\omega _{A\theta }/\Omega$ for positive $Ro=1$ and different non-negative $Rb$: $Rb=0$ (solid line), 1 (dashed line), 5 (long-dashed line).$

Fig. 5.

The growth rate, for |$m=1$| and |$k\rightarrow \infty$|⁠, of the non-axisymmetric AMRI over a wide range of |$\omega _{A\theta }/\Omega$| for positive |$Ro=1$| and different non-negative |$Rb$|⁠: |$Rb=0$| (solid line), 1 (dashed line), 5 (long-dashed line).

Open in new tab Download slide

An unstable mode of the other extreme |$k\rightarrow 0$| is seeded at |$Rb=-1/4$|⁠, is strengthened and becomes dominant as |$Rb$| is decreased on the side of |$Rb<0$| and |$|\omega _{A\theta }/\Omega |\sim 1$|⁠. In this limit, the dispersion relation (15) admits its roots in a tidy form as

\[\begin {align} {\frac {\lambda }{\Omega }}&= \frac {-i m(m^2 +q^2 r^2 +2 Ro)\pm m \sqrt { (-4Rb-m^2- q^2 r^2) (m^2 +q^2 r^2) (\omega _{A\theta }/\Omega )^2- 4 Ro^2}} {m^2 +q^2 r^2}, \\ {\frac {\lambda }{\Omega }}&= -im \left (1 \pm {\frac {\omega _{A\theta }}{\Omega }}\right ). \end {align}\]

(40)

\[{\frac {\nu }{\Omega }}= \pm {\frac {m}{m^2 +q^2 r^2}} \sqrt {\left [4Rb^2-(m^2+q^2r^2+2Rb)^2 \right ] \left ({\frac {\omega _{A\theta }}{\Omega }} \right )^2- 4 Ro^2}.\]

(41)

It follows from (41) that the sign of |$Ro$| is irrelevant to the growth rate, The instability occurs in a finite range in |$Ro$| centered on |$Ro=0$|⁠. Noting that the realizability of |$m^2+q^2r^2+2Rb=0$| for |$m\neq 0$| is confined to |$Rb \leq -1/2$|⁠, the maximum width of the instability band is obtained, for |$-1/2 \leq Rb<-1/4$|⁠, by taking |$|m|=1$| and |$q=0$|⁠, with the instability range |$Ro^2<(|Rb|-1/4) (\omega _{A\theta }/\Omega )^2.$| For |$Rb<-1/2$|⁠, the instability range is |$Ro^2<Rb^2 (\omega _{A\theta }/\Omega )^2,$| and the large-magnetic-field asymptotics of the growth rate |$\nu$| is obtained from (41) as

\[{\frac {\nu }{\Omega }}\approx \sqrt {{\frac {4|Rb|}{m^2+q^2 r^2}}-1} \left |{\frac {m\omega _{A\theta }}{\Omega }} \right | \leq \sqrt {4|Rb|-1}\left |{\frac {\omega _{A\theta }}{\Omega }} \right |,\]

(42)

with the upper bound taken at |$q=0$| and |$|m|=1$|⁠. Comparison with (39) shows that the instability mode of |$k=0$| prevails over that of |$|k|\rightarrow \infty$| for approximately |$Rb \leq -1/\sqrt {8}$|⁠.

The condition |$1 \leq m^2+q^2 r^2<-4Rb$|⁠, under restriction of |$m\neq 0$|⁠, for the existence of the unstable mode of |$k=0$| signifies that the value of |$|Rb|$| limits the range of |$|m|$| for instability. For instance, |$Rb=-1$| admits only |$m=\pm 1$| for instability. To have an idea of the instability parameters for the case of |$Rb<-1/4$| and |$|\omega _{A\theta }/\Omega | \sim 1$|⁠, we show in Fig. 6 the instability region, in the space of |$(m, Ro)$|⁠, of the |$k=0$| wave, for a Keplerian flow (⁠|$Ro=-3/4$|⁠). The left panel of Fig. 6 fixes |$Rb=-1$| and varies the values of |$|\omega _{A\theta }/\Omega |$|⁠. The right panel fixes |$|\omega _{A\theta }/\Omega |=1$| and varies the values of |$Rb$|⁠. The gray region indicates the set of parameters for which the AMRI occurs, colored darker gray as the parameter value is increased. Figure 6 shows that the increase of |$|\omega _{A\theta }(r)/\Omega |$| and/or |$|Rb|$| enlarges the instability range in |$Ro$|⁠, though limited to the case of |$Rb<-1/4$| with |$|\omega _{A\theta }/\Omega | \sim 1$|⁠. The left figure confirms that |$Rb$| determines the range of azimuthal wavenumber |$m$| for the instability. The right figure shows that increasing |$|Rb|$| results in widening of the instability range both in |$Ro$| and |$m$|⁠.

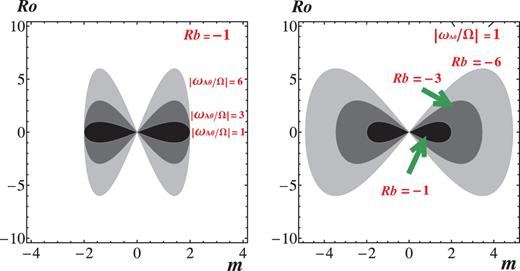
$The instability region of the non-axisymmetric wave of $k=0$ for $Rb<-1/4$. The flow is Keplerian ($Ro=-3/4$). The left figure fixes $Rb=-1$ and depicts the instability region with increasing $|\omega _{A\theta }(r)/\Omega |$ from dark gray to light gray. The right figure fixes $|\omega _{A\theta }(r)/\Omega |=1$ and depicts the instability region with increasing $|Rb|$ from dark gray to light gray.$

Fig. 6.

The instability region of the non-axisymmetric wave of |$k=0$| for |$Rb<-1/4$|⁠. The flow is Keplerian (⁠|$Ro=-3/4$|⁠). The left figure fixes |$Rb=-1$| and depicts the instability region with increasing |$|\omega _{A\theta }(r)/\Omega |$| from dark gray to light gray. The right figure fixes |$|\omega _{A\theta }(r)/\Omega |=1$| and depicts the instability region with increasing |$|Rb|$| from dark gray to light gray.

Open in new tab Download slide

For |$Rb\geq -1/\sqrt {8}$|⁠, the shortest waves (⁠|$k \to \infty$|⁠) dominate over the long waves (⁠|$k =0$|⁠) for |$|\omega _{A\theta }/\Omega | \sim 1$|⁠, and the transition of behavior from the regime of |$|\omega _{A\theta }/\Omega | \ll 1$| to the regime of |$|\omega _{A\theta }/\Omega | \sim 1$| is displayed in a single figure, Fig. 4 for the case of |$Ro\leq 0$| and Fig. 5 for the case of |$Ro>0$|⁠. A distinctive feature of Fig. 5 arises around the origin |$(\omega _{A\theta }/\Omega , \nu /\Omega ) =(0,0)$|⁠, where the instability disappears in a finite range of |$\omega _{A\theta }/\Omega$| with its width depending on |$Rb$|⁠. Notably, the maximum growth rate increases, beyond the Oort |$A$|-value, indefinitely with |$|\omega _{A\theta }/\Omega |$| linearly in it.

On the other hand, a smooth transition may not be expected from the regime of |$|\omega _{A\theta }/\Omega | \ll 1$| to that of |$|\omega _{A\theta }/\Omega | \sim 1$|⁠, when |$Rb<-1/\sqrt {8}$|⁠, because the maximum growth rate occurs in the short-wave limit (⁠|$k \to \infty$|⁠) for |$|\omega _{A\theta }/\Omega | \ll 1$|⁠, but in the long-wave limit for |$|\omega _{A\theta }/\Omega | \sim 1$|⁠. With a choice of |$Ro=-3/4$| and |$Rb=-1/2$|⁠, Fig. 7 shows the maximum growth rate of |$m=1$| mode, in the limit of |$k \to \infty$| and in the opposite limit |$k \rightarrow 0$| simultaneously. For the former, the maximum occurs at |$|\alpha |=1$| and for the latter, the maximum occurs at |$q=0$|⁠, being mathematically equivalent to each other. As argued above, because |$Rb<-1/\sqrt {8}$|⁠, the mode of |$k \to 0$| overweighs that of |$k \to \infty$| in the regime of |$|\omega _{A\theta }/\Omega | \sim 1$|⁠. The maximum growth rate of the former increases without bound in proportion to |$|\omega _{A\theta }/\Omega |$|⁠. The instability mode of |$k=0$|⁠, being admitted only for |$|\omega _{A\theta }/\Omega |>|Ro/Rb|=|Ro|/\sqrt {|Rb|-1/4}=3/2$| when |$Rb=-1/2$|⁠, is excluded in the regimes of |$|\omega _{A\theta }/\Omega | \ll 1$|⁠.

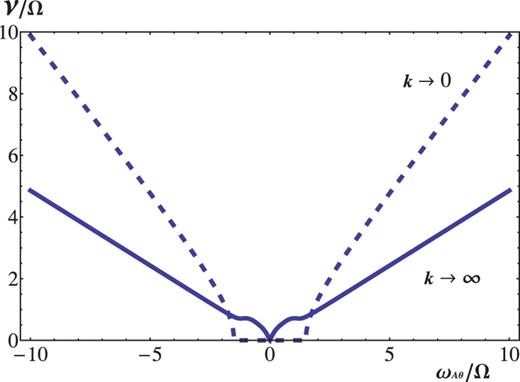
$The crossover of the most unstable mode of $m=1$ from the regime of $|\omega _{A\theta }/\Omega | \ll 1$ to that of $|\omega _{A\theta }/\Omega | \sim 1$ in the case of $Rb=-1/2$. The maximum growth rate occurs at $k \to \infty$ (solid line) in the former regime but at $k=0$ in the latter (dashed line), and they are simultaneously shown as a function of $\omega _{A\theta }/\Omega$. The flow is Keplerian ($Ro=-3/4$). In both limits, the maxima are taken at $|\alpha |=1$.$

Fig. 7.

The crossover of the most unstable mode of |$m=1$| from the regime of |$|\omega _{A\theta }/\Omega | \ll 1$| to that of |$|\omega _{A\theta }/\Omega | \sim 1$| in the case of |$Rb=-1/2$|⁠. The maximum growth rate occurs at |$k \to \infty$| (solid line) in the former regime but at |$k=0$| in the latter (dashed line), and they are simultaneously shown as a function of |$\omega _{A\theta }/\Omega$|⁠. The flow is Keplerian (⁠|$Ro=-3/4$|⁠). In both limits, the maxima are taken at |$|\alpha |=1$|⁠.

Open in new tab Download slide

Figure 8 chooses |$Rb=-1$|⁠, with the other parameters being unchanged. The regime |$|\omega _{A\theta }/\Omega | \ll 1$| accommodates the instability modes of |$|k|\rightarrow \infty$| with |$|m|\geq 2$| as well with the overall maximum growth rate being close to the Oort |$A$|-value, as illustrated by Fig. 3. In the regime |$|\omega _{A\theta }/\Omega | \sim 1$|⁠, the instability mode of |$k\rightarrow \infty$| disappears because |$Rb \leq -3/4$|⁠. The maximum growth rate for |$k\rightarrow \infty$| corresponds to |$|\alpha |=1$|⁠. But this is not the case with the wave of |$k=0$|⁠. Near the critical point |$|\omega _{A\theta }/\Omega |=|Ro/Rb|=3/4$|⁠, the most unstable mode has |$|qr|=1$| in favor of |$m^2+q^2r^2+2Rb=0.$| As |$|\omega _{A\theta }/\Omega |$| is increased, |$|qr|$| decreases monotonically to zero, as is seen from (42). In between, the maximum is taken at an intermediate value of |$qr$|⁠. On the whole, for |$|\omega _{A\theta }/\Omega | \stackrel {>}{\sim } 0.8$| approximately, the mode of |$k=0$| prevails over that of |$k \to \infty$|⁠.

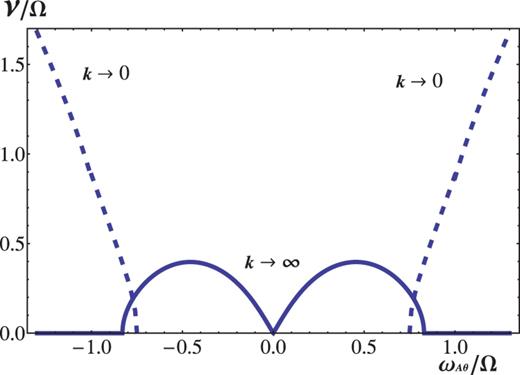
$The crossover of the most unstable mode of $m=1$ from the regime of $|\omega _{A\theta }/\Omega | \ll 1$ to that of $|\omega _{A\theta }/\Omega | \sim 1$ in the case of $Rb=-1$ for a Keplerian flow ($Ro=-3/4$). For the limit of $k=0$, $|qr|=1$ at the critical point $\omega _{A\theta }/\Omega =3/4$ and $|qr|$ decreases, with $\omega _{A\theta }/\Omega$, to zero along the graph.$

Fig. 8.

The crossover of the most unstable mode of |$m=1$| from the regime of |$|\omega _{A\theta }/\Omega | \ll 1$| to that of |$|\omega _{A\theta }/\Omega | \sim 1$| in the case of |$Rb=-1$| for a Keplerian flow (⁠|$Ro=-3/4$|⁠). For the limit of |$k=0$|⁠, |$|qr|=1$| at the critical point |$\omega _{A\theta }/\Omega =3/4$| and |$|qr|$| decreases, with |$\omega _{A\theta }/\Omega$|⁠, to zero along the graph.

Open in new tab Download slide

For |$Ro=-3/4$| and |$Rb=-1$|⁠, we show in Fig. 9 the growth rate |$\nu$| as a function of the radial wavenumber |$qr$|⁠. The maximum growth rate is found with ease to be |$\nu _{\rm max}/|\Omega |=\sqrt {7}/3$|⁠, which is attained at |$q=1/\sqrt {8}$|⁠. This value is larger than the Oort |$A$|-value |$\nu _{\rm A}/|\Omega |=3/4$|⁠.

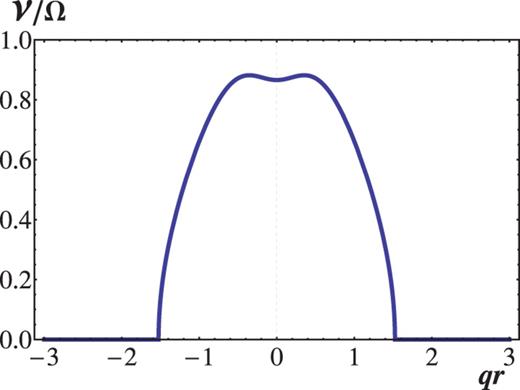
$The growth rate of the non-axisymmetric wave of $m=1$ and $k\rightarrow 0$, versus $q r$ with $q$ being the radial wavenumber, for $Rb=-1$ and $\omega _{A\theta }/\Omega =1$. The flow is Keplerian ($Ro=-3/4$). The maximum growth rate is $\nu _{\rm max}=\sqrt {7}\Omega /3$ taken at $qr=\pm 1/\sqrt {8}$.$

Fig. 9.

The growth rate of the non-axisymmetric wave of |$m=1$| and |$k\rightarrow 0$|⁠, versus |$q r$| with |$q$| being the radial wavenumber, for |$Rb=-1$| and |$\omega _{A\theta }/\Omega =1$|⁠. The flow is Keplerian (⁠|$Ro=-3/4$|⁠). The maximum growth rate is |$\nu _{\rm max}=\sqrt {7}\Omega /3$| taken at |$qr=\pm 1/\sqrt {8}$|⁠.

Open in new tab Download slide

6. Discussions

We have explored the AMRI of a perfectly conducting fluid to non-axisymmetric as well as axisymmetric perturbations of short wavelengths, based on the Hain–Lüst equation (14) augmented with the terms originating from a background flow of differential rotation. The present investigation is capable of dealing with a rotating flow of arbitrary angular velocity profile |$\Omega (r)$|⁠. The advantage of using the Hain–Lüst equation is that the risk of dropping off the terms with radial derivatives can be avoided. If we substitute the WKB ansatz |$\boldsymbol {\xi } \propto \exp [i\int q(r){d} r]$|⁠, at an earlier stage, into (6) say, the derivative in |$r$| is replaced by multiplication |$i q$|⁠, and after this stage, the operation of radial derivative |$iq={d}/{d} r$| is liable to be inactive, though it should be. It is safer to keep all the derivative terms to the very last stage where we apply the short-wavelength approximation. Retaining all the relevant terms has disclosed richer aspects of the AMRI to non-axisymmetric perturbations than known ones (cf. Ref. [8]).

Given |$Rb$|⁠, for small values of |$|\omega _{A\theta }/\Omega |$|⁠, a rotating flow is unstable to non-axisymmetric perturbations of |$|k|\rightarrow \infty$| if |$Ro<(Rb-1/4)(\omega _{A\theta }/\Omega )^2$| as dictated by (34). It is found that the maximum growth rate is the Oort |$A$|-value |$|Ro|$| [14]. For |$|\omega _{A\theta }/\Omega | \sim 1$|⁠, the situation is changed. When |$Rb>-3/4$|⁠, the rotating flow is unstable to perturbations of |$|k|\rightarrow \infty$| in the whole range of |$Ro$|⁠. But the mode of |$|k|\rightarrow \infty$| subsides as |$Rb$| is decreased and disappears at |$Rb=-3/4$|⁠. Another unstable mode of |$k=0$| emerges at |$Rb=-1/4$|⁠, develops as |$Rb$| is decreased, and surpasses the mode of |$|k| \to \infty$| for |$Rb \leq -1/\sqrt {8}$|⁠. The instability mode of |$k=0$| is confined to a finite range in |$Ro$| centered on |$Ro=0$|⁠, |$Ro^2 <(|Rb|-1/4)(\omega _{A\theta }/\Omega )^2$| for |$-1/2 \leq Rb <-1/4$|⁠, and |$Ro^2<Rb^2(\omega _{A\theta }/\Omega )^2$| for |$Rb <-1/2$|⁠, as derived from (41). The behavior, over the whole range of |$\omega _{A\theta }/\Omega$|⁠, of the modes of |$m=1$| and |$|k|\rightarrow \infty$| and of |$m=1$| and |$k=0$| is summarized as follows. For |$Ro<0$| and |$Rb <-3/4$|⁠, the mode of |$|k|\rightarrow \infty$| is confined approximately to |$0<|\omega _{A\theta }/\Omega |<\sqrt {|Ro|/(|Rb|+1/4)}$|⁠, as is read off from (34). The unstable mode of |$k=0$| exists for |$|\omega _{A\theta }/\Omega |>|Ro/Rb|$| when |$Ro <-1/2$|⁠, and for |$|\omega _{A\theta }/\Omega |>|Ro|/\sqrt {|Rb|-1/4}$| when |$-1/2\leq Ro <-1/4$|⁠. The overall behavior for |$Ro<0$| and |$Rb<-3/4$| looks like Fig. 8. For |$Rb>-3/4$|⁠, the mode of |$|k|\rightarrow \infty$| extends to the entire range of |$\omega _{A\theta }/\Omega$|⁠, and for |$-3/4<Rb<-1/\sqrt {8}$|⁠, the graph looks like Fig. 7. For |$Ro<0$| and |$Rb>-1/\sqrt {8}$|⁠, the mode of |$|k|\rightarrow \infty$| predominates over the mode of |$k=0$| over the entire range of |$\omega _{A\theta }/\Omega$|⁠. For |$Rb\geq -1/4$|⁠, the mode of |$k=0$| disappears. The asymptotic behavior at large values of |$|\omega _{A\theta }/\Omega |$| is common for all values of |$Ro$| and is given by (39). At small values of |$|\omega _{A\theta }/\Omega |$|⁠, the mode of |$|k|\rightarrow \infty$| is confined to |$0<|\omega _{A\theta }/\Omega |<\sqrt {|Ro/(Rb-1/4)|}$| for |$-1/4<Rb<1/4$| and |$Ro<0$|⁠. This branch is absent for |$Ro\geq 0$|⁠. For |$Rb>1/4$|⁠, this branch exists for |$|\omega _{A\theta }/\Omega |>\sqrt {Ro/(Rb-1/4)}$|⁠. As a whole, for |$Rb>-1/4$|⁠, the graph looks like Fig. 4 for |$Ro<0$| and like Fig. 5 for |$Ro>0$|⁠. It is remarkable that the growth rate exceeds the Oort |$A$|-value by increasing |$|\omega _{A\theta }/\Omega |$|⁠.

This is not the end of story. We have exclusively explored the unstable modes in the two extremes, |$|k|\rightarrow \infty$| and |$k=0$|⁠, as either of the two is likely to be dominant. However, a detailed examination shows that there are cases that, given |$Ro$| and |$Rb$|⁠, the mode of the largest growth rate occurs at an intermediate value of |$k$|⁠. For instance, given a Keplerian rotation (⁠|$Ro=-3/4$|⁠), for |$|\omega _{A\theta }/\Omega |\ll 1$| and fixing |$m=1$| and |$q=0$|⁠, the most unstable mode occurs at an intermediate value of |$k$| when |$Rb \stackrel {<}{\sim }-17.5$|⁠. Furthermore, the transition of the behavior from |$|\omega _{A\theta }/\Omega | \ll 1$| to that of |$|\omega _{A\theta }/\Omega | \sim 1$| calls for elaboration.

It is probable that these properties, in particular, the non-existence of a critical Rossby number for large values of |$Rb$| (⁠|$Rb>-3/4$| for the AMRI) may carry over to the helical MRI (HMRI), for which both the axial and azimuthal magnetic fields are externally imposed. From a practical viewpoint, the inductionless limit is worth pursuing, since the laboratory experiments on using a liquid metal, such as PROMISE (Potsdam ROssendorf Magnetic InStability Experiment) [11], belong to this regime. In the previous papers on AMRI [13] and HMRI [17] for the inductionless limit, the condition for non-existence of the critical Rossby number is obtained as |$Rb>-1/2$|⁠.

Care should be taken with the most unstable mode of |$k=0$| and |$q=0$|⁠, which is dominant |$|\omega _{A\theta }/\Omega |\sim 1$| for |$Rb<-1/\sqrt {8}$|⁠. This mode may lie outside the range of validity of the WKB approximation to short-wavelength waves. Moreover, the perturbation of large |$m$| invites the action of the viscous and/or resistive cut-off. To draw a definite conclusion on the AMRI or HMRI to non-axisymmetric perturbations, global modal analyses are indispensable. Also, for the purpose of the global stability analyses, the Hain–Lüst equation provides us with a sound basis [21]. The determination of the maximum growth rate for the AMRI and the HMRI is left for a future investigation.

Acknowledgement

We are grateful to Oleg N. Kirillov for his invaluable guidance with the MRI. R.Z. was supported by a Ph.D. Studentship from the China Scholarship Council. Y.F. was supported in part by a Grant-in-Aid for Scientific Research from the Japan Society for the Promotion of Science (Grant No. 24540407).

Appendix A. Dispersion relation (15)

The dispersion relation (15) can be rewritten as

\[\lambda ^4+ib_1\lambda ^3+a_2\lambda ^2+ib_3\lambda +a_4=0,\]

(A1)

where

\[\begin {align} b_1&= 4 m \Omega \left(1+ \frac {Roh^2-k^2}{h^2(h^2 +q^2)r^2}\right), \notag \\ a_2&= 2 \left (F_1^2 - 3 m^2 \Omega ^2\right )+ \frac {4h^2}{h^2+q^2}\left(\Omega ^2Ro - Rb \omega _{A\theta }^2\right)+ \frac {4k^2\Omega ^2}{k^2+q^2} \notag \\ & \quad + \frac {4 m}{h^2 (h^2 +q^2) r^2} \left\{k^2 (3 m \Omega ^2 - F_1 \omega _{A\theta }) +h^2 [Rb \omega _{A\theta }(F_1 +m \omega _{A\theta })-4 m \Omega ^2 Ro]\right\}, \notag \\ b_3&= 4 m \Omega \left (F_1^2 - m^2 \Omega ^2\right )+ \frac { 8 m \Omega h^2}{h^2+q^2}\left(\Omega ^2 Ro - Rb \omega _{A\theta }^2\right)+ \frac {8 \Omega k^2}{k^2+q^2}\left(m \Omega ^2 - F_1 \omega _{A\theta }\right)\notag \\ & \quad + \frac {4 m \Omega }{h^2 (h^2 +q^2) r^2} \left(F_1^2 (h^2 Ro-k^2) - 2 F_1 m (k^2 - h^2 Rb) \omega _{A\theta } \right. \notag \\ & \quad \left. +m^2 \left [3 k^2 \Omega ^2 +h^2 \left (2 Rb \omega _{A\theta }^2-5 \Omega ^2 Ro \right )\right ]\right), \notag \\ a_4&= \left (F_1^2 - m^2 \Omega ^2\right )^2+ \frac { 4 h^2}{h^2+q^2} \left[\left (F_1^2 - m^2 \Omega ^2\right ) \left (\Omega ^2 Ro - Rb \omega _{A\theta }^2\right )-\frac {k^2}{h^2}\left (m \Omega ^2 - F_1 \omega _{A\theta }\right )^2\right] \notag \\ & \quad + \frac {4 m (F_1^2 - m^2 \Omega ^2)}{h^2 (h^2 +q^2) r^2}\left[k^2 \left (m \Omega ^2 - F_1 \omega _{A\theta }\right ) +h^2 \left (F_1 Rb \omega _{A\theta }-2 m \Omega ^2 Ro +m Rb \omega _{A\theta }^2\right )\right], \notag \end {align}\]

supplemented by the Alfvén frequencies |$\omega _{A\theta }=\mu /\sqrt {\rho \mu _0}$| and |$\omega _{A}=k B_z/\sqrt {\rho \mu _0}$|⁠, and |$F_1= m \omega _{A\theta } + \omega _{A}=F/\sqrt {\rho \mu _0}$|⁠.

References

Velikhov

JETP

1398

(

1959

)

Chandrasekhar

Proc. Nat. Acad. Sci.

253

(

1960

Month:	Total Views:
January 2017	13
February 2017	4
March 2017	1
April 2017	3
June 2017	3
July 2017	1
August 2017	3
September 2017	3
November 2017	1
December 2017	19
January 2018	8
February 2018	18
March 2018	18
April 2018	14
May 2018	5
June 2018	10
July 2018	11
August 2018	13
September 2018	15
October 2018	7
November 2018	8
December 2018	4
January 2019	7
February 2019	8
March 2019	10
April 2019	12
May 2019	12
June 2019	5
July 2019	7
August 2019	10
September 2019	22
October 2019	68
November 2019	15
December 2019	12
January 2020	18
February 2020	11
March 2020	5
April 2020	5
May 2020	7
June 2020	4

Article Contents

Local stability analysis of the azimuthal magnetorotational instability of ideal MHD flows Open Access

Abstract

1. Introduction

2. Short-wavelength stability analysis

3. Axisymmetric perturbations

4. Non-axisymmetric perturbations: overview

5. Non-axisymmetric perturbations: strong external field

6. Discussions

Acknowledgement

Appendix A. Dispersion relation (15)

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Local stability analysis of the azimuthal magnetorotational instability of ideal MHD flows