Abstract
A pseudo su(1,1)-algebra is formulated as a possible deformation of the Cooper pair in the su(2)-algebraic many-fermion system. With the aid of this algebra, it is possible to describe the behavior of individual fermions which are generated as the result of interaction with the external environment. The form presented in this paper is a generalization of a certain simple case developed recently by the authors. The basic idea follows the su(1,1) algebra in the Schwinger boson representation for treating energy transfer between the harmonic oscillator and the external environment. The Hamiltonian is given following the idea of phase space doubling in the thermo-field dynamics formalism, and the time-dependent variational method is applied to this Hamiltonian. Its trial state is constructed in the frame deformed from the BCS-Bogoliubov approach to superconductivity. Several numerical results are shown.
1. Introduction
It may be hardly necessary to mention, but the BCS-Bogoliubov approach to superconductivity has made a central contribution to the study of nuclear structure theory. The orthogonal set in this approach is determined through two steps. At the first step, the state |$|\phi _B)$| given in the following plays the leading part: (1.1a)(1.1b) Here, Γ, z, |$\widetilde {S}_+$| and |$|0)$| denote the normalization constant, complex parameter, the Cooper pair creation and the fermion vacuum, respectively. Including |$\widetilde {S}_-$| and |$\widetilde {S}_0$|, the set |$(\widetilde {S}_{\pm ,0})$| forms the su(2) algebra. Clearly, |$|\phi _B)$| is the state with zero seniority, but it is not an eigenstate of the fermion-number operator and plays the role of the quasiparticle vacuum. At the second step, the states with nonzero seniority are constructed by operating the quasiparticles on |$|\phi _B)$| in the appropriate manner. On the other hand, the Cooper pair can be treated by the conventional technique of the su(2) algebra. The orthogonal set in this approach is also determined through two steps. The first is to construct the minimum weight state |$|m)$|, which does not contain any Cooper pair: (1.2) Therefore, |$|m)$| is not necessarily the state with zero seniority. The second is to construct the states orthogonal to |$|m)$| by operating on |$\widetilde {S}_+$| in the appropriate manner. The description above tells us that, for the two approaches, the orthogonal set is constructed in opposite orders. Therefore, without any argument, it may not be concluded that they are equivalent to each other.
\begin{equation} |\phi_B) = \frac{1}{\sqrt{\Gamma}}\exp \left(z\widetilde{S}_+\right)| 0),\label{eq1.1a} \end{equation}
\begin{equation} \Gamma=(1+|z|^2)^{2\Omega_0}.\label{eq1.1b} \end{equation}
\begin{equation} \widetilde{S}_-|m)=0.\label{eq1.2} \end{equation}
In response to the above-mentioned situation, the authors recently proposed a certain idea [1]. In this idea, the quasiparticle in the framework of the conservation of the fermion number, which is called the “quasiparticle”, was introduced. Through the medium of this operator, it was shown that both are equivalent to each other in a certain sense. Further, in the paper following Ref. [1], the present authors discussed another role of the “quasiparticle”, which leads to the idea of deformation of the Cooper pair [2]. Hereafter, this paper will be referred to as (A). Any state |$| \phi)$| with zero seniority, including |$| \phi _B)$|, obeys the condition (A.13), which is strongly related to the “quasiparticle”. This condition does not lead to fixing the form of |$| \phi)$| automatically, so a new condition additional to the condition (A.13) is required. If the condition (A.17) for |$| \phi)$|, namely |$\widetilde {S}_-| \phi)=z(\Omega _0-\widetilde {S}_0)| \phi)$|, is added, we obtain |$| \phi _B)$|. In (A), we treated the case of the condition (A.18), namely |$\widetilde {S}_-| \phi)=z \left [(\Omega _0-\widetilde {S}_0)(\Omega _0+\widetilde {S}_0+1)\right ]^{\frac {1}{2}}| \phi)$|, in detail. In this case, |$| \phi)$| is obtained in the form (1.3a)(1.3b) Here, |$\widetilde {\mathcal {T}}_+$| is an operator factorized in the product of |$\widetilde {S}_+$| and a certain operator. The definition of |$\widetilde {\mathcal {T}}_+$| including |$\widetilde {\mathcal {T}}_-$| and |$\widetilde {\mathcal {T}}_0$| is given in the relation (A.36). The commutation relations among |$\widetilde {\mathcal {T}}_{\pm ,0}$|, which are shown in the relation (A.39), suggest that, in spite of considering the su(2)-algebraic many-fermion model, the set |$(\widetilde {\mathcal {T}}_{\pm ,0})$| resembles the su(1,1) algebra in behavior. The form (1.3b) is given explicitly in the relation (A.25).
\begin{equation} | \phi)=\frac{1}{\sqrt{\Gamma}}\exp\left(z\widetilde{\mathcal{T}}_+\right)| 0),\label{eq1.3a}\end{equation}
\begin{equation} \Gamma=\sum_{n=0}^{2\Omega_0}(|z|^2)^n.\label{eq1.3b} \end{equation}
It is well known that, with the use of two kinds of boson operators, the su(2) and the su(1,1) algebra, the generators of which are denoted as |$\hat {S}_{\pm ,0}$| and |$\hat {T}_{\pm ,0}$|, respectively, can be formulated. They are called the Schwinger boson representations [3]. For these two algebras, we prepare two boson spaces: (1) the space constructed under a fixed magnitude of the su(2)-spin, |$s(=0, 1/2, 1, \ldots , s_{\mathrm {max}})$|, and (2) the space constructed under a fixed magnitude of the su(1,1)-spin, |$t(=1/2, 1, 3/2, \ldots , \infty)$|. Following the idea of the boson mapping [4], any operator in space (1) can be mapped into space (2). In space (1), we can find the set |$(\hat {\mathcal {T}}_{\pm ,0})$|, which obeys (1.4) Naturally, the set |$(\hat {\mathcal {T}}_{\pm ,0})$| shows su(1,1)-like behavior and it is called the pseudo-su(1,1) algebra by the present authors [5]. In (A), we presented a concrete expression for |$(\widetilde {\mathcal {T}}_{\pm ,0})$| which corresponds to |$(\hat {\mathcal {T}}_{\pm ,0})$| with |$t=1/2$|. On the other hand, we know that the mixed-mode boson coherent state constructed by |$(\hat {T}_{\pm ,0})$| enables us to describe the “damped and amplified harmonic oscillation” in the frame of the conservative form. Through this description, we can understand the energy transfer between the harmonic oscillator and the external environment. Further, by regarding the mixed-mode boson coherent state as the statistically mixed state, thermal effects in time evolution are described with some interesting results [5–7]. Therefore, with the aid of the set |$(\hat {\mathcal {T}}_{\pm ,0})$|, it may also be possible to describe the boson behavior under consideration. Its examples are found in the pairing and the Lipkin model in the Holstein–Primakoff-type boson realization [8,9]. The results were shown in Ref. [5]. A primitive form of the above idea is the phase space doubling introduced in the thermo field dynamics formalism [10]. However, it is impossible in the framework of the set |$(\hat {\mathcal {T}}_{\pm ,0})$| to investigate the behavior of individual fermions. The form given in (A) may be useful for this problem, but, as is clear from the form (1.3), the case of the state |$| \phi)$| with nonzero seniority cannot be treated in the frame of (A).
\begin{equation} \hat{\mathcal{T}}_{\pm,0} \stackrel{\textrm{(mapped)}}{\longrightarrow} \hat{T}_{\pm,0}.\label{eq1.4} \end{equation}
This paper aims at two targets. First is to generalize the pseudo-su(1,1) algebra with zero seniority to the case with nonzero seniority. Second is to apply the generalized form to a concrete many-fermion system. The su(2) algebra in the many-fermion model is characterized by s and |$s_0$|; for a given s, |$s_0=-s, -s+1, \ldots , s-1, s$|. The su(1,1) algebra in the Schwinger boson representation is characterized by t and |$t_0$|; for a given t, |$t_0=t, t+1, \ldots , \infty $|. The pseudo-su(1,1) algebra in the Schwinger boson representation, which is abbreviated to |$B_{ps}$|-form, is a possible deformation of the su(1,1) algebra and, therefore, it should be characterized at least by |$(t, t_0)$|. However, we are now considering the pseudo-su(1,1) algebra, which is a possible deformation of the Cooper pair in the su(2)-algebraic many-fermion model. Hereafter, we will abbreviate it to |$F_{ps}$|-form. One of main problems for the first target is how to import |$(t,t_0)$| in the |$B_{ps}$|-form into the |$F_{ps}$|-form characterized by |$(s, s_0)$|. Following an idea developed in this paper, we have (1.5) Of course, a form generalized from |$| \phi)$| as shown in the relation (1.3) can be presented. This form also contains the complex parameter z and the normalization constant Γ, which is a function of |$x=|z|^2$|. Another problem with the first target is how to calculate Γ for the range |$0 \leq x < \infty $|. As a possible application of the |$F_{ps}$|-form, we adopt the following scheme: Under the time-dependent variational method for a given Hamiltonian expressed in terms of |$(\widetilde {\mathcal {T}}_{\pm ,0})$|, we investigate the time evolution of the system. The trial state is |$| \phi)$|, and then our problem is reduced to finding the time dependence of z. For the above task, we must calculate the expectation values of |$\widetilde {\mathcal {T}}_{\pm ,0}$|. Naturally, Γ appears in the expectation values. However, Γ is a complicated polynomial in x and it may be impossible to handle it in a consolidated fashion for the whole range. If dividing the whole range into the two, |$0\leq x \leq \gamma $| and |$\gamma \leq x <\infty $|, Γ becomes approximate, but simple for each range, and very accurate. Here, |$\gamma $| denotes a certain constant.
\begin{equation} \widetilde{S}_{\pm,0} \stackrel{\textrm{(deformed)}}{\longrightarrow} \widetilde{\mathcal{T}}_{\pm,0}.\label{eq1.5} \end{equation}
For the second target, we must prepare a model for the application. The model is a non-interacting many-fermion system in one single-particle level, which we will call the intrinsic system. The reason we investigate such a simple model comes from the su(1,1) algebra in the Schwinger boson representation. As was already mentioned, this algebra helps us to describe the harmonic oscillator interacting with the external environment. If we follow the thermo-field dynamics formalism, we prepare a new degree of freedom for an auxiliary harmonic oscillator for the environment, that is, phase space doubling. Further, as the interaction between both degrees of freedom, the form which is proportional to |$(\hat {T}_+-\hat {T}_-)$| is adopted. Our present scheme follows the above. Our problem is to describe the above-mentioned intrinsic system interacting with the external environment. For this aim, we introduce an auxiliary many-fermion system and, as the interaction between both systems, we adopt the form proportional to |$(\widetilde {\mathcal {T}}_+-\widetilde {\mathcal {T}}_-)$|. To the above Hamiltonian, we apply the time-dependent variational method. The trial state is of the form generalized from |$| \phi)$| shown in the relation (1.3) and the variational parameters are z and |$z^*$| contained in this state. Through the variation, we obtain certain differential equations for |$\dot {z}$| and |$\dot {z}^*$|. By solving them appropriately, including approximation, we can arrive at a certain type of the time evolution. According to the result, the intrinsic system shows rather complicated cyclic behavior. One cycle can be represented in terms of a chain of different functions for the time: linear, sinh and sin types. This point is essentially different from the result obtained in the su(1,1)-algebraic boson model which permits an infinite boson number. This case does not show any cyclic behavior. The above description may be quite natural, because the present model is a form of the su(2)-algebraic fermion model in which the Pauli principle works.
In next section, after recapitulating the su(1,1)-algebraic boson model presented by Schwinger, a pseudo-su(1,1) algebra is formulated as a possible deformation of the Schwinger boson representation, in which the maximum weight state is introduced. In Sect. 3, a possible pseudo-su(1,1) algebra as a deformation of the Cooper pair is formulated in the frame of the su(2)-algebraic many-fermion model. Section 4 is devoted to giving conditions under which the two pseudo-su(1,1) algebras are equivalent to each other, mainly by paying attention to the quantum numbers for the orthogonal sets of both algebras. In Sect. 5, the generalization from |$| \phi)$| shown in the relation (1.3) is presented. Explicit expressions of the normalization constant Γ and the expectation value of the fermion number operator |$N$| are given. Since Γ and |$N$| have complicated forms, approximate expressions are presented in Sect. 6 in each of the two regions. In Sect. 7, a simple many-fermion model obeying the pseudo-su(1,1) algebra is presented for the application of the idea developed in Sects. 2–6. Sections 8, 9, and 10 are devoted to discussing various properties of Γ, i.e., |$N$| in the approximate forms given in Sect. 6. In Sect. 11, following the scheme mentioned in Sect. 7, some concrete results are presented and it is shown that one cycle consists of a chain of the three different functions for the time. Finally, in Sect. 12, some concluding remarks, including future problems, are given.
2. The su(1,1) algebra in the Schwinger boson representation and its deformation – pseudo-su(1,1) algebra
With the use of two kinds of boson operators |$(\hat {a}, \hat {a}^*$|) and (|$\hat {b}, \hat {b}^*$|), the Schwinger boson representation of the su(1,1) algebra can be formulated. This algebra is composed of three operators which are denoted as |$\hat {T}_{\pm ,0}$|. They obey the relations (2.1)(2.2) The Casimir operator, which is denoted as |$\hat {\boldsymbol {T}}^2$|, and its properties are given by (2.3)(2.4) The Schwinger boson representation is presented in the form (2.5) The eigenstate of |$\hat {\boldsymbol {T}}^2$| and |$\hat {T}_0$| with the eigenvalues |$t(t-1)$| and |$t_0$|, respectively, which is constructed on the minimum weight state |$| t \rangle $|, is expressed in terms of the following form: (2.6) Here, t and |$t_0$| obey (2.7) Of course, |$| t \rangle $| is given in the form (2.8) The state |$| t \rangle $| satisfies the relation (2.9) Concerning the state |$| t \rangle $|, we must give a small comment. The state |$(\sqrt {(2t-1)!})(\hat {a}^*)^{2t-1}| 0 \rangle $| also satisfies the relation (2.9), and it is orthogonal to |$| t \rangle $|. This indicates that we have two types for the minimum weight states, which should be discriminated by the quantum number additional to t. We omit this discrimination, and in this paper we will adopt the form (2.8). The above is an outline of the su(1,1) algebra in the Schwinger boson representation.
\begin{equation} \hat{T}_0^*=\hat{T}_0,\quad \hat{T}_{\pm}^*=\hat{T}_{\mp},\label{eq2.1}\end{equation}
\begin{equation} [\hat{T}_+, \hat{T}_-]=-2\hat{T}_0, \quad [\hat{T}_0, \hat{T}_{\pm}]=\pm\hat{T}_{\pm}.\label{eq2.2} \end{equation}
\begin{equation} \hat{\boldsymbol{T}}^2=\hat{T}_0^2-\frac{1}{2}\left(\hat{T}_-\hat{T}_++\hat{T}_+\hat{T}_-\right) =\hat{T}_0\left(\hat{T}_0\mp 1\right)-\hat{T}_{\pm}\hat{T}_{\mp},\label{eq2.3}\end{equation}
\begin{equation} [\hat{T}_{\pm,0}, \hat{\boldsymbol{T}}^2]=0.\label{eq2.4} \end{equation}
\begin{equation} \hat{T}_+=\hat{a}^*\hat{b}^*, \quad \hat{T}_-=\hat{b}\hat{a}, \quad \hat{T}_0=\frac{1}{2}(\hat{a}^*\hat{a}+\hat{b}^*\hat{b})+\frac{1}{2}.\label{eq2.5} \end{equation}
\begin{equation} | t,t_0 \rangle= \left[\frac{(2t-1)!}{(t_0-t)!(t_0+t-1)!}\right]^{\frac{1}{2}}\left(\hat{T}_+\right)^{t_0-t}| {t} \rangle, \quad (\langle {t,t_0} |t,t_0\rangle=1).\label{eq2.6} \end{equation}
\begin{equation} t=1/2,\enspace 1,\enspace 3/2, \ldots, \infty, \qquad t_0=t,\enspace t+1,\enspace t+2, \ldots,\infty.\label{eq2.7} \end{equation}
\begin{equation} | t \rangle=\left(\sqrt{(2t-1)!}\right)^{-1}(\hat{b}^*)^{2t-1}| 0 \rangle , \quad \left(| t=1/2 \rangle=| 0 \rangle\right).\label{eq2.8} \end{equation}
\begin{equation} \hat{T}_-| t \rangle=0, \qquad \hat{T}_0| t \rangle=t| t \rangle .\label{eq2.9} \end{equation}
Since we are considering a boson system, no upper limit exists for the values of t and |$t_0$|. In other words, the terminal states do not exist, as can be seen in the relation (2.7). As a possible variation, we will consider the case where the terminal state exists for |$t_0$|: (2.10) The reason for investigating this case will be mentioned in Sect. 3 in relation to the su(2)-algebraic many-fermion model. In the space specified by the relation (2.10), we introduce three operators defined as (2.11) Here, |$\epsilon $| denotes an infinitesimal positive parameter, which plays a role in avoiding the vanishing denominator. Successive operation of |$\hat {\mathcal {T}}_+$| gives us the following: (2.12a)(2.12b)(2.13) Therefore, the present boson space spanned by the orthogonal set (2.6) is divided into two subspaces and we are interested in the subspace governed by the relation (2.12), in which |$(\hat {\mathcal {T}}_+)^{t_m-t}| t \rangle $| is the terminal state. In this subspace, the commutation relations for |$\hat {\mathcal {T}}_{\pm ,0}$| are given in the form (2.14)(2.15) We also have the relation (2.16) Again, we note the following relation: (2.17) The operation of |$\hat {\mathcal {T}}_+$| in the present subspace is essentially the same as that of |$\hat {T}_+$|. We call the set |$(\hat {\mathcal {T}}_{\pm ,0}$|) the pseudo-su(1,1) algebra. It contains the positive parameter |$t_m$|. For practical purposes, we must find the condition for fixing the value of |$t_m$|. The relation (2.12a) suggests that we may be permitted to call the terminal state the maximum weight state.
\begin{equation} t_0=t,\enspace t+1,\ldots, t_m-1,\enspace t_m.\label{eq2.10} \end{equation}
\begin{equation} \hat{\mathcal{T}}_+=\hat{T}_+ \left[\frac{t_m-\hat{T}_0}{t_m-\hat{T}_0+\epsilon}\right]^{\frac{1}{2}}, \quad \hat{\mathcal{T}}_-= \left[\frac{t_m-\hat{T}_0}{t_m-\hat{T}_0+\epsilon}\right]^{\frac{1}{2}}\hat{T}_-, \quad \hat{\mathcal{T}}_0=\hat{T}_0.\label{eq2.11} \end{equation}
\begin{equation} \hat{\mathcal{T}}_+\cdot\left(\hat{\mathcal{T}}_+\right)^{t_0-t}| t \rangle= \left(\hat{T}_+\right)^{t_0+1-t}| t \rangle\quad {\mathrm{for}}\quad t_0=t,\enspace t+1, \ldots, t_m-2,\enspace t_m-1,\label{eq2.12a} \end{equation}
\begin{equation} \hat{\mathcal{T}}_+\cdot\left(\hat{\mathcal{T}}_+\right)^{t_m-t}| t \rangle=0,\label{eq2.12b} \end{equation}
\begin{equation} \hat{\mathcal{T}}_+\cdot\left(\hat{\mathcal{T}}_+\right)^{t_0-t}| {t} \rangle= \left(\hat{T}_+\right)^{t_0+1-t}| t \rangle\quad {\rm for}\quad t_0=t_m+1,\ t_m+2, \ldots .\label{eq2.13} \end{equation}
\begin{equation} [\hat{\mathcal{T}}_+ , \hat{\mathcal{T}}_-]=-2\hat{\mathcal{T}}_0 +(t_m+t)(t_m-t+1)| {t,t_m} \rangle\langle {t,t_m} |,\label{eq2.14} \end{equation}
\begin{equation} [\hat{\mathcal{T}}_0, \hat{\mathcal{T}}_{\pm}]=\pm\hat{\mathcal{T}}_{\pm}.\label{eq2.15} \end{equation}
\begin{align} \hat{\boldsymbol{\mathcal{T}}}^2 &= \hat{\mathcal{T}}_0^2-\frac{1}{2}\left(\hat{\mathcal{T}}_-\hat{\mathcal{T}}_++\hat{\mathcal{T}}_+\hat{\mathcal{T}}_-\right)\nonumber\\ &=t(t-1)+\frac{1}{2}(t_m+t)(t_m-t+1)| t,t_m \rangle\langle t,t_m |.\label{eq2.16} \end{align}
\begin{equation} \left(\hat{\mathcal{T}}_+\right)^{t_0-t}| t \rangle =\left(\hat{T}_+\right)^{t_0-t}| t \rangle\quad {\mathrm{for}}\quad t_0=t, t+1,\ldots, t_m-1, t_m.\label{eq2.17} \end{equation}
3. An su(2)-algebraic many-fermion model – pseudo-su(1,1) algebra
In Sect. 2, we presented the pseudo-su(1,1) algebra as a possible deformation of the su(1,1) algebra. In this section, we will formulate the pseudo-su(1,1) algebra in the su(2)-algebraic many-fermion model, which was promised in (A). First, we will give an outline of the present many-fermion model. The constituents are confined in |$4\Omega _0$| single-particle states, where |$\Omega _0$| denotes integer or half-integer. Since |$4\Omega _0$| is an even number, all single-particle states are divided into equal parts P and |$\overline {P}$|. Therefore, as a partner, each single-particle state belonging to P can find a single-particle state in |$\overline {P}$|. We express the partner of the state α belonging to P as |$\bar {\alpha }$|, and fermion operators in α and |$\bar {\alpha }$| are denoted as |$(\tilde {c}_{\alpha }, \tilde {c}_{\alpha }^*$|) and |$(\tilde {c}_{\bar {\alpha }},\tilde {c}_{\bar {\alpha }}^*)$|, respectively. As the generators |$\widetilde {S}_{\pm ,0}$|, we adopt the following form: (3.1) The symbol |$s_{\alpha }$| denotes the real number satisfying |$s_{\alpha }^2=1$|. The sum |$\sum _{\alpha }$||$(\sum _{\bar {\alpha }}$|) is carried out in all single-particle states in P (|$\overline {P}$|), and we have |$\sum _{\alpha }1=2\Omega _0 (\sum _{\bar {\alpha }}1=2\Omega _0$|). The operators |$\widetilde {S}_{\pm ,0}$| form the su(2) algebra obeying the relations (3.2)(3.3) The Casimir operator, which is denoted as |$\widetilde {\boldsymbol {S}}^2$|, and its property are given by (3.4)(3.5) The eigenstate of |$\widetilde {\boldsymbol {S}}^2$| and |$\widetilde {S}_0$| with the eigenvalues |$s(s+1)$| and |$s_0$|, respectively, is expressed in the form (3.6) Here, s and |$s_0$| obey (3.7) The state |$| s)$| denotes the minimum weight state satisfying (3.8) Since |$| s)$| is given in a many-fermion system, it depends on not only s but also the quantum numbers additional to s, and recently we presented an idea on how to construct |$| s)$| in an explicit form [11,12]. Later, we will sketch it. Needless to say, the operator |$\widetilde {S}_+\ (\widetilde {S}_-)$| plays the role of creation (annihilation) of the Cooper pair.
\begin{align} \widetilde{S}_+&=\sum_{\alpha}s_{\alpha}\widetilde{c}_{\alpha}^*\tilde{c}_{\bar{\alpha}}^*, \quad \widetilde{S}_-=\sum_{\alpha}s_{\alpha}\widetilde{c}_{\bar{\alpha}}\tilde{c}_{\alpha}, \nonumber\\ \widetilde{S}_0&=\frac{1}{2}\widetilde{N}-\Omega_0 , \quad \widetilde{N}=\sum_{\alpha}(\widetilde{c}_{\alpha}^*\tilde{c}_{\alpha} +\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\bar{\alpha}}).\label{eq3.1} \end{align}
\begin{equation} \widetilde{S}_0^*=\widetilde{S}_0 , \quad \widetilde{S}_{\pm}^*=\widetilde{S}_{\mp} ,\label{eq3.2} \end{equation}
\begin{equation}[\widetilde{S}_+ , \widetilde{S}_-]=2\widetilde{S}_0 , \quad [\widetilde{S}_0 , \widetilde{S}_{\pm} ]=\pm\widetilde{S}_{\pm} .\label{eq3.3} \end{equation}
\begin{equation} \widetilde{\boldsymbol{S}}^2=\widetilde{S}_0^2+\frac{1}{2}\left(\widetilde{S}_-\widetilde{S}_+ +\widetilde{S}_+\widetilde{S}_-\right) =\widetilde{S}_0\left(\widetilde{S}_0\mp 1\right)+\widetilde{S}_{\pm}\widetilde{S}_{\mp},\label{eq3.4} \end{equation}
\begin{equation} [\widetilde{S}_{\pm,0}, \widetilde{\boldsymbol{S}}^2]=0.\label{eq3.5} \end{equation}
\begin{equation} | s,s_0)= \left[\frac{(s-s_0)!}{(2s)!(s+s_0)!}\right]^{\frac{1}{2}}\left(\widetilde{S}_+\right)^{s+s_0}| s) , \quad \left((s,s_0 |s,s_0)=1\right).\label{eq3.6} \end{equation}
\begin{equation} s=0,\enspace 1/2,\enspace 1,\ldots, \Omega_0, \quad s_0=-s,\enspace -s+1, \ldots, s-1,\enspace s .\label{eq3.7} \end{equation}
\begin{equation}\label{eq3.8} \widetilde{S}_-| s)=0, \quad \widetilde{S}_0| s)=-s| s). \end{equation}
As a possible deformation of |$\widetilde {S}_{\pm ,0}$|, i.e., deformation of the Cooper pair, we introduce three operators in the space spanned by the set (3.6). They are expressed in the form (3.9) Here, |$\epsilon $| denotes an infinitesimal positive parameter. The form (3.9) contains the positive parameter |$t'$|, and in (A) we considered the case |$t'=1/2$| for |$s=\Omega _0$|. The commutation relations for |$\widetilde {\mathcal {T}}_{\pm ,0}$| are given in the form (3.10)(3.11) The operator |$\widetilde {\boldsymbol {\mathcal {T}}}^2$| is expressed as (3.12) From the comparison of the relations (3.10)–(3.12) with the relations (2.14)–(2.16), we can understand that the set |$(\widetilde {\mathcal {T}}_{\pm ,0})$| also forms the pseudo-su(1,1) algebra. Successive operation of |$\widetilde {\mathcal {T}}_+$| on the state |$| s)$| gives us (3.13a)(3.13b) The relation (3.13b) tells us that |$(\widetilde {\mathcal {T}}_+)^{2s}| s)$| is the maximum weight state. Further, we have (3.14) The relation (3.14) suggests that, in order to describe the su(2)-algebraic model, it may be enough to treat the model in the orthogonal set |$\{(\widetilde {S}_+)^{s+s_0}| s)\}$|. In spite of this fact, we describe it in the orthogonal set |$\{(\widetilde {\mathcal {T}}_+)^{s+s_0}| s)\}$|. The reason will become clear in Sect. 5. It must also be noted that |$\{(\widetilde {\mathcal {T}}_+)^{s+s_0}| {s}); s_0=-s, -s+1,\ldots , s\}$| corresponds to |$\{(\hat {\mathcal {T}}_+)^{t_0-t}| {t} \rangle ; t_0=t,t+1,\ldots , t_m\}$|, which is defined in the relation (2.12).
\begin{equation} \widetilde{\mathcal{T}}_+=\widetilde{S}_+ \left[\frac{s+\widetilde{S}_0+2t'}{s-\widetilde{S}_0+\epsilon}\right]^{\frac{1}{2}}, \quad \widetilde{\mathcal{T}}_-= \left[\frac{s+\widetilde{S}_0+2t'}{s-\widetilde{S}_0+\epsilon}\right]^{\frac{1}{2}}\widetilde{S}_- , \quad \widetilde{\mathcal{T}}_0=s+\widetilde{S}_0+t'.\label{eq3.9} \end{equation}
\begin{equation} [\widetilde{\mathcal{T}}_+ , \widetilde{\mathcal{T}}_-]=-2\widetilde{\mathcal{T}}_0 +(2s+2t')(2s+1)| s,s)(s,s | , \label{eq3.10}\end{equation}
\begin{equation} [\widetilde{\mathcal{T}}_0, \widetilde{\mathcal{T}}_{\pm}]=\pm\widetilde{\mathcal{T}}_{\pm}.\label{eq3.11} \end{equation}
\begin{align} \widetilde{\boldsymbol{\mathcal{T}}}^2 &= \widetilde{\mathcal{T}}_0^2-\frac{1}{2}\left(\widetilde{\mathcal{T}}_-\widetilde{\mathcal{T}}_++\widetilde{\mathcal{T}}_+\widetilde{\mathcal{T}}_-\right)\nonumber\\ &=t'(t'-1)+\frac{1}{2}(2s+2t')(2s+1)| s,s)(s,s |.\label{eq3.12} \end{align}
\begin{equation} \widetilde{\mathcal{T}}_+\cdot\left(\widetilde{\mathcal{T}}_+\right)^{s+s_0}| s) =\left(\widetilde{\mathcal{T}}_+\right)^{s+s_0+1}| s)\quad {\mathrm{for}}\quad s_0=-s, -s+s,\ldots, s-1, \label{eq3.13a}\end{equation}
\begin{equation} \widetilde{\mathcal{T}}_+\cdot\left(\widetilde{\mathcal{T}}_+\right)^{2s}| s)=0.\label{eq3.13b} \end{equation}
\begin{equation} \left(\widetilde{\mathcal{T}}_+\right)^{s+s_0}| s) = \left[\frac{(2t'-1+s+s_0)!}{(2t'-1)!}\frac{(s-s_0)!}{(2s)!}\right]^{\frac{1}{2}}\left(\widetilde{S}_+\right)^{s+s_0}| s).\label{eq3.14} \end{equation}
4. Condition for the equivalence of two pseudo-su(1,1) algebras
In last two sections, we derived the pseudo-su(1,1) algebra from two algebraic models: (1) the su(1,1) algebra in the Schwinger boson representation, and (2) the su(2) algebra in the many-fermion system. As was mentioned in Sect. 1, we call these the Bps- and Fps-form, respectively. Three quantities t, |$t_0$|, and |$t_m$| characterize the Bps-form. In these three, t and |$t_0$| indicate the quantum numbers for the su(1,1) algebra itself and, in particular, t determines the irreducible representation. The quantity |$t_m$| is an artificial parameter introduced from the outside for defining the maximum weight state of the Bps-form. On the other hand, the Fps-form is characterized by four quantities, s, |$s_0$|, |$\Omega _0$|, and |$t'$|. The quantities s and |$s_0$| indicate the quantum numbers for the su(2) algebra itself, and s determines the irreducible representation. The existence of the maximum weight state is guaranteed by |$\Omega _0$|. The quantity |$t'$| is an artificial parameter introduced for constructing the Fps-form.
With this in mind, let us search for the condition which makes Bps- and Fps-form equivalent to each other. For this aim, we require the following correspondence: (4.1) Here, |$|\!| {t,t_0} \rangle $| and |$|\!| s,s_0)$| are given as (4.2a)(4.2b) If the correspondence (4.1) is permitted, the number of the states in (4.2a) should be equal to that of the states in (4.2b): (4.3) Since |$|\!| t,t_m \rangle $| corresponds to |$|\!| s,s)$|, the relations (2.14) and (3.10) should lead to (4.4) Then, with the use of the relation (4.3), we have (4.5) The eigenvalues of |$\hat {\mathcal {T}}_0$| and |$\widetilde {\mathcal {T}}_0$| for |$|\!| {t,t_0} \rangle $| and |$|\!| s,s_0)$| are given by |$t_0$| and |$s+s_0+t'$|, respectively, and they should be equal to each other: (4.6) The cases |$s_0=-s$| and |$s_0=s$| correspond to the cases |$t_0=t$| and |$t_0=t_m$|, respectively, and they lead to |$t_m=2s+t'$|. They are consistent with the relations (4.5) and (4.3).
\begin{equation} |\!| {t,t_0} \rangle\sim |\!| s,s_0).\label{eq4.1} \end{equation}
\begin{equation} |\!| t,t_0 \rangle=\left(\hat{\mathcal{T}}_+\right)^{t_0-t}| t \rangle , \quad (t_0=t, t+1,\ldots, t_m-1, t_m),\label{eq4.2a} \end{equation}
\begin{equation} |\!| {s,s_0})=\left(\widetilde{\mathcal{T}}_+\right)^{s+s_0}| s) , \quad (s_0=-s, -s+1,\ldots, s-1, s).\label{eq4.2b} \end{equation}
\begin{equation} t_m-t+1=2s+1, \quad {\mathrm{i.e.,}}\quad t_m-t=2s.\label{eq4.3} \end{equation}
\begin{equation} (t_m+t)(t_m-t+1)=(2s+2t')(2s+1).\label{eq4.4} \end{equation}
\begin{equation}\label{eq4.5} t=t' . \end{equation}
\begin{equation} t_0=s+s_0+t'.\label{eq4.6} \end{equation}
The above result is summarized as follows: (4.7) We can see that t, |$t_0$|, and |$t_m$| which characterize the |$B_{ps}$|-form are expressed in terms of the s, |$s_0$|, and |$t'$| characterizing the |$F_{ps}$|-form. However, usually, the su(2)-algebraic many-fermion model contains two quantum numbers apart from |$\Omega _0$|, which determines the framework of the model. As was already mentioned, |$t'$| is introduced as an artificial parameter and t determines the irreducible representation of the su(1,1) algebra. Therefore, |$t'$| may be a function of |$\Omega _0$| and s, which determine the framework of the irreducible representation of the su(2) algebra. As an example, in this paper we will adopt the following form: (4.8) If |$t=1/2$|, s is equal to |$\Omega _0$|, and we investigated this case in (A). The forms (4.7) and (4.8) give us the relation (4.9)
\begin{equation} t=t', \quad t_0=s+s_0+t', \quad t_m=2s+t'.\label{eq4.7} \end{equation}
\begin{equation} t'=\Omega_0+\frac{1}{2}-s\ (=t), \quad {\mathrm{i.e.,}}\quad s+t=\Omega_0+\frac{1}{2}.\label{eq4.8} \end{equation}
\begin{equation} t=t'=\Omega_0+\frac{1}{2}-s, \quad t_0=\Omega_0+\frac{1}{2}+s_0, \quad t_m=\Omega_0+\frac{1}{2}+s.\label{eq4.9} \end{equation}
The final task of this section is to examine the validity of the relation (4.8). For this examination, the detailed structure of the state |$| s)$| must be investigated in relation to the state |$| t \rangle $|. Concerning the construction of the minimum weight state for the present su(2)-algebraic model, the present authors recently presented an idea with the aid of which the minimum weight state can be determined methodically [11,12]. Following this idea, we will consider the present problem. First, we introduce the following su(2) generators: (4.10) The generators |$\widetilde {R}_{\pm ,0}$| satisfy the relation (4.11) The relation (4.11) suggests that the minimum weight state exists not only for |$(\widetilde {S}_{\pm ,0})$| but also |$(\widetilde {R}_{\pm ,0})$|, denoted by |$| m_0)$|: (4.12) The definitions of |$\widetilde {S}_-$|, |$\widetilde {R}_-$|, |$\widetilde {S}_0$|, and |$\widetilde {R}_0$| give us the following form: (4.13) It should be noted that |$| m_0)$| is composed of only the fermion creation operators belonging to |$\overline {P}$|, and symbolically we express |$| m_0)$| in the form (4.14) Here, |$\tilde {c}_{\overline {P}}^*$| and |$2r$| denote any of the |$\tilde {c}_{\bar {\alpha }}^*$| and the number of |$\tilde {c}_{\overline {P}}^*$|, respectively. The operation of |$\widetilde {S}_0$| on |$| m_0)$| leads us to (4.15) If |$| m_0)$| is adopted as |$| s)$|, we have (4.16) We can see that |$2r$| denotes the seniority number. Further, with the use of the raising operator, |$\widetilde {R}_+$|, and a certain scalar operator for the su(2) algebra |$(\widetilde {R}_{\pm ,0})$|, |$\widetilde {\mathcal {P}}^*$|, the minimum weight state |$| m)$| is obtained in the form |$| m)=\widetilde {\mathcal {P}}^*\cdot (\widetilde {R}_+)^{r+r_0}| m_0)$|. The above is our idea as presented in Ref. [2].
\begin{equation} \widetilde{R}_+=\sum_{\alpha}\tilde{c}_{\alpha}^*\tilde{c}_{\bar{\alpha}}, \quad \widetilde{R}_-=\sum_{\alpha}\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\alpha}, \quad \widetilde{R}_0=\frac{1}{2}\sum_{\alpha}(\tilde{c}_{\alpha}^*\tilde{c}_{\alpha} -\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\bar{\alpha}}).\label{eq4.10} \end{equation}
\begin{equation} [{\mathrm{any\ of}}\ \widetilde{R}_{\pm,0}, {\rm any\ of}\ \widetilde{S}_{\pm,0}]=0.\label{eq4.11} \end{equation}
\begin{align} \widetilde{S}_-| m_0)&=0, \quad \widetilde{R}_-| m_0)=0, \nonumber\\ \widetilde{S}_0| m_0)&=-s| m_0), \quad \widetilde{R}_0| m_0)=-r| m_0).\label{eq4.12} \end{align}
\begin{equation}\label{eq4.13} | m_0) = \begin{cases} | 0) & (r=0), \\ \displaystyle \prod_{i=1}^{2r}\tilde{c}_{\bar{\alpha}_i}^*| 0) & (r=1/2, 1, 3/2,\ldots, \Omega_0). \end{cases} \end{equation}
\begin{equation} | m_0)=(\tilde{c}_{\overline{P}}^*)^{2r}| 0).\label{eq4.14} \end{equation}
\begin{equation} \widetilde{S}_0| m_0) =\left(\frac{1}{2}\sum_{\alpha}(\tilde{c}_{\alpha}^*\tilde{c}_{\alpha}+\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\bar{\alpha}}) -\Omega_0\right)| m_0) =-(\Omega_0-r)| m_0).\label{eq4.15} \end{equation}
\begin{equation} s=\Omega_0-r.\label{eq4.16} \end{equation}
In Sect. 7, we will investigate the present pseudo-su(1,1) algebra under the idea of phase space doubling in the thermo-field dynamics formalism. With this aim, it is enough to adopt |$| m_0)$| as the minimum weight state for the su(2) algebra |$(\widetilde {S}_{\pm ,0})$|. In other words, if we adopt the form |$| m)=\widetilde {\mathcal {P}}^*(\widetilde {R}_+)^{r+r_0}| m_0)$|, the present pseudo-su(1,1) algebra becomes powerless for the idea of the phase space doubling. Under the above argument, let us consider the correspondence of |$| t \rangle $| with |$| s)$|. As for |$| s)$|, we adopt the form |$| r)\!)=(\tilde {c}_{\overline {P}}^*)^{2r}| 0) (r=\Omega _0-s)$|: (4.17) Of course, the following correspondence may be permitted: (4.18) Concerning |$| t \rangle $| and |$| s)$||$(=| r)\!))$|, we have (4.19) Therefore, the following correspondence is obtained: (4.20) Thus, the relation (4.17) leads us to (4.21) The above is nothing but the relation (4.8). The operators |$\widetilde {\mathcal {T}}_{\pm ,0}$| can be summarized in the form (4.22) Thus, we can finish the task.
\begin{equation} | t \rangle=(\hat{b}^*)^{2t-1}| 0 \rangle \sim | s)=(\tilde{c}_{\overline{P}}^*)^{2r}| 0).\label{eq4.17} \end{equation}
\begin{equation} | 0 \rangle\ \sim\ | 0).\label{eq4.18} \end{equation}
\begin{equation} \hat{b}^*| t \rangle=| t+1/2 \rangle , \quad \tilde{c}_{\overline{P}}^*| r)\!)=| r+1/2)\!).\label{eq4.19} \end{equation}
\begin{equation} (\hat{b}^*)^\nu| {0} \rangle \sim (\tilde{c}_{\overline{P}}^*)^{\nu}| 0)\quad {\mathrm{for}}\quad \nu=0,\ 1,\ 2,\ldots .\label{eq4.20} \end{equation}
\begin{equation} 2t-1=2r, \quad {\rm i.e.,}\quad 2t-1=2(\Omega_0-s).\label{eq4.21} \end{equation}
\begin{align} \widetilde{\mathcal{T}}_+&=\widetilde{S}_+ \left[\frac{\Omega_0+\frac{1}{2}+t+\widetilde{S}_0}{\Omega_0+\frac{1}{2}-t-\widetilde{S}_0+\epsilon}\right]^{\frac{1}{2}}, \quad \widetilde{\mathcal{T}}_-= \left[\frac{\Omega_0+\frac{1}{2}+t+\widetilde{S}_0}{\Omega_0+\frac{1}{2}-t-\widetilde{S}_0+\epsilon}\right]^{\frac{1}{2}}\widetilde{S}_-,\nonumber\\ \widetilde{\mathcal{T}}_0&=\Omega_0+\frac{1}{2}+\widetilde{S}_0.\label{eq4.22} \end{align}
We know that the Cooper pair in the BCS-Bogoliubov theory can be described by |$\widetilde {S}_{\pm }$|, and the set |$(\widetilde {S}_{\pm ,0})$| forms the su(2) algebra. On the other hand, |$\widetilde {\mathcal {T}}_{\pm }$| can be regarded as a possible deformation of the Cooper pair which still belongs to the category of the su(2) algebra. If we notice that the relation (2.11) represents a possible deformation of the su(1,1) algebra, our algebra, which we call the pseudo-su(1,1) algebra, may be expected to be useful for treating physical problems different from the superconductivity and its related problem.
5. A possible fermion number non-conserving state in the su(2)-algebraic model
In (A), we investigated the fermion number non-conserving state shown in the form (5.1) Here, Γ and z denote the normalization |$((\phi | \phi)=1)$| and complex parameter, respectively. The state (5.1) is an example of the deformation of the BCS-Bogoliubov state. In this section, we will develop its generalization to the case |$t>1/2$|, i.e., |$s<\Omega _0$|: (5.2) The state (5.2) can be expanded to (5.3) For the convenience of the treatment, we formulate in the |$B_{ps}$|-frame. Then, |$| \phi)$| corresponds to |$| \phi \rangle $| given as (5.4) Using relation (4.9), |$2s$| and |$(t_m-t)$| can be expressed in the relation (5.5) The normalization constant Γ can be expressed as a function of a new variable x (|$=|z|^2)$| in the form (5.6) Here, (5.7) Of course, the relations (5.6) and (5.7) are useful in the cases |$x\sim 0$| and |$x\rightarrow \infty $|, respectively. First, we will discuss the relation to the su(1,1)-algebraic model. It is noted that |$\Gamma _t(x)$| can be rewritten in the form (5.8) For this rewriting, we used the formula (5.9) i.e., (5.10)(5.11) If |$2\Omega _0-(2t-1)\rightarrow \infty $|, the expression (5.6) is an infinite series which is convergent for |$x<1$|: (5.12) The form (5.12) corresponds to the case of the su(1,1)-algebraic model, and at |$x=1$| it diverges. However, the form (5.6) is a finite series defined in the range |$0\leq x <\infty $| and, of course, at |$x=1$|, it is finite. This can be shown explicitly in the form (5.13) The form (5.13) can be derived from the relation (5.8) through the relation (5.14) The relation (5.13) gives us the finite value at |$x=1$|: (5.15) We have shown four expressions for |$\Gamma _t(x)$|. It may be necessary to put each expression to its proper use. Through the state |$| \phi \rangle $| (or |$| \phi)$|), we can learn the difference between the su(1,1)- and the pseudo-su(1,1)-algebraic models.
\begin{equation}\label{eq5.1} | \phi)=\frac{1}{\sqrt{\Gamma}}\exp\left(z\widetilde{\mathcal{T}}_+\right)| \Omega_0) \quad {\mathrm{for}}\quad t=1/2,\ {\rm i.e.,}\ s=\Omega_0. \end{equation}
\begin{equation} | \phi)=\frac{1}{\sqrt{\Gamma}}\exp\left(z\widetilde{\mathcal{T}}_+\right)| s).\label{eq5.2} \end{equation}
\begin{equation} | \phi)=\frac{1}{\sqrt{\Gamma}}\sum_{n=0}^{2s}\frac{z^n}{n!}\left(\widetilde{\mathcal{T}}_+\right)^n| s) .\label{eq5.3} \end{equation}
\begin{equation} | \phi \rangle=\frac{1}{\sqrt{\Gamma}}\sum_{n=0}^{t_m-t}\frac{z^n}{n!}\left(\hat{T}_+\right)^{n}| t \rangle, \quad (\langle \phi |\phi\rangle=1).\label{eq5.4} \end{equation}
\begin{equation} 2s=t_m-t=2\Omega_0-(2t-1) .\label{eq5.5} \end{equation}
\begin{equation} {\mathrm{(i)}}\quad \Gamma=\Gamma_t(x)=\sum_{n=0}^{2\Omega_0-(2t-1)}x^n \left(\begin{matrix} 2t-1+n \\ 2t-1 \end{matrix} \right) =1+2tx+\cdots , \quad (0\leq x < \infty).\label{eq5.6} \end{equation}
$\left (\begin {matrix} 2t-1+n \\ 2t-1 \end {matrix} \right)$
denotes the binomial coefficient, and for deriving the above form the orthogonal set (2.6) is used. We will treat Γ in various values of t and, hereafter, Γ is denoted as |$\Gamma _t(x)$|. The function |$\Gamma _t(x)$| is a polynomial for x, the degree of which is |$2\Omega _0-(2t-1)$| and all the coefficients of |$x^n\ (n=1,2,\ldots , 2\Omega _0-(2t-1))$| are positive. Therefore, we have another expression: \begin{align} {\mathrm{(ii)}}\quad \Gamma_t(x) &= \left(\begin{matrix} 2\Omega_0 \\ 2t-1 \end{matrix} \right) x^{2\Omega_0-(2t-1)}\sum_{n=0}^{2\Omega_0-(2t-1)}\left(\frac{1}{x}\right)^n \left(\begin{matrix} 2\Omega_0-n \\ 2t-1 \end{matrix}\right) \left(\begin{matrix} 2\Omega_0 \\ 2t-1 \end{matrix}\right)^{-1}\nonumber\\ &= \left(\begin{matrix} 2\Omega_0 \\ 2t-1 \end{matrix} \right) x^{2\Omega_0-(2t-1)} \left[1+\frac{1}{x}\cdot\left(\frac{2\Omega_0-(2t-1)}{2\Omega_0}\right)+\cdots \right].\label{eq5.7} \end{align}
\begin{equation} {\mathrm{(iii)}}\quad \Gamma_t(x)=\frac{1}{(1-x)^{2t}}\left[ 1-x^{2\Omega_0+1}\sum_{n=0}^{2t-1}\left(\frac{1-x}{x}\right)^n \left(\begin{matrix} 2\Omega_0+1\\ n \end{matrix} \right)\right].\label{eq5.8} \end{equation}
\begin{equation} \Gamma_t(x)=\frac{1}{2t-1}\frac{\mathrm{d}}{\mathrm{d}x}\Gamma_{t-1/2}(x)\quad {\rm for}\quad t>1/2,\label{eq5.9} \end{equation}
\begin{equation} \Gamma_t(x)=\frac{1}{(2t-1)!}\left(\frac{\mathrm{d}}{\mathrm{d}x}\right)^{2t-1}\Gamma_{1/2}(x)\quad {\rm for}\quad t\geq 1/2,\label{eq5.10} \end{equation}
\begin{equation}\Gamma_{1/2}(x)=\sum_{n=0}^{2\Omega_0}x^n=\frac{1-x^{2\Omega_0+1}}{1-x}.\label{eq5.11} \end{equation}
\begin{equation} \Gamma_t(x)=\frac{1}{(1-x)^{2t}} \quad (0\leq x <1).\label{eq5.12} \end{equation}
\begin{equation} {\mathrm{(iv)}}\quad \Gamma_t(x)=x^{2\Omega_0-(2t-1)}\sum_{n=0}^{2\Omega_0-(2t-1)}\left(\frac{1-x}{x}\right)^n \left(\begin{matrix} 2\Omega_0+1\\ 2t+n \end{matrix} \right).\label{eq5.13} \end{equation}
\begin{equation} \sum_{n=0}^{2t-1}\left(\frac{1-x}{x}\right)^n \left(\begin{matrix} 2\Omega_0+1\\ n \end{matrix} \right) = \frac{1}{x^{2\Omega_0+1}}-\sum_{n=2t}^{2\Omega_0+1}\left(\frac{1-x}{x}\right)^n \left(\begin{matrix} 2\Omega_0+1\\ n \end{matrix} \right).\label{eq5.14} \end{equation}
\begin{equation}\label{eq5.15} \Gamma_t(x=1)=\left(\begin{matrix} 2\Omega_0+1\\ 2t \end{matrix} \right). \end{equation}
Next, we will consider the expectation value of the fermion number operator |$\widetilde {N}$| for the state |$| \phi)$|, which also depends on t and x. With this aim, the following relation is useful: (5.16) Then, in the |$B_{ps}$|-form, we have the relation (5.17)(5.18) For the four forms of |$\Gamma _t(x)$|, |$\Lambda _t(x)$| can be expressed in the form (5.19)(5.20)(5.21)(5.22) The forms (i)′ and (ii)′ are suitable for investigating the cases |$x\sim 0$| and |$x\rightarrow \infty $|: (5.23b)(5.23b) The form (iv)|${}'$| is suited to the case |$x\sim 1$|: (5.24) The form (iii)|${}'$| is related to the su(1,1)-algebraic model: (5.25) The relation (5.17) gives us the expectation value of |$\widetilde {N}$|, denoted by |$N$|. The typical three cases are as follows: (5.26a)(5.26b)(5.26c) We can see that at |$t=1/2$|, the above result is reduced to that in (A). The relation (4.21) tells us that the number |$(2t-1)$| indicates the seniority number. Therefore, |$(2t-1)$| fermions belonging to |$\overline {P}$| cannot contribute to the fermion pair |$\widetilde {S}_+$||$(\widetilde {S}_-)$| and, thus, |$(2t-1)$| single-particle states are not available for the formation of the fermion pair. In this sense, the result (5.26) is quite natural. The result (5.26) tells us that the case |$x=1$| corresponds to the intermediate situation between the cases |$x=0$| and |$x\rightarrow \infty $|. Figure 1 shows various cases for t in the case |$\Omega _0=19/2$|. In the range |$0\leq x \lesssim 2$|, the slopes are steep; after |$x\sim 2$|, the slopes become gentle. More precisely, as t increases, the point where the slope becomes gentle approaches |$x=0$|. This feature can be read in the result (5.26).
\begin{equation} \widetilde{\mathcal{T}}_0=s+\widetilde{S}_0+t=\frac{\widetilde{N}}{2}+\frac{1}{2}, \quad{\mathrm{i.e.,}}\quad \widetilde{N}=2\widetilde{\mathcal{T}}_0-1.\label{eq5.16} \end{equation}
\begin{align} N&=2\langle \phi |\hat{\mathcal{T}}_0| \phi \rangle-1= 2\langle \phi |\hat{T}_0| \phi \rangle-1=2\mathcal{T}_0-1\nonumber\\ &=2t-1+2\Lambda_t(x),\label{eq5.17}\end{align}
\begin{equation} \Lambda_t(x)=x\cdot\frac{\frac{\mathrm{d}\Gamma_t(x)}{\mathrm{d}x}}{\Gamma_t(x)}= \frac{tx\Gamma_{t+1/2}(x)}{\Gamma_{t}(x)}.\label{eq5.18} \end{equation}
\begin{equation} {\mathrm{(i)'}}\quad \Lambda_t(x)=\frac{\displaystyle \sum_{n=1}^{2\Omega_0-(2t-1)}nx^n \left(\begin{matrix} 2t-1+n \\ 2t-1 \end{matrix}\right)}{\displaystyle 1+\sum_{n=1}^{2\Omega_0-(2t-1)}x^n \left(\begin{matrix} 2t-1+n \\ 2t-1 \end{matrix}\right)},\label{eq5.19}\end{equation}
\begin{align} {\rm (ii)'}\quad \Lambda_t(x) &=2\Omega_0-(2t-1)\nonumber\\ &\quad - \frac{\displaystyle \sum_{n=1}^{2\Omega_0-(2t-1)}n\left(\frac{1}{x}\right)^n \left(\begin{matrix} 2\Omega_0-n \\ 2t-1 \end{matrix}\right) \left(\begin{matrix} 2\Omega_0 \\ 2t-1 \end{matrix}\right)^{-1} }{\displaystyle 1+\sum_{n=1}^{2\Omega_0-(2t-1)}\left(\frac{1}{x}\right)^n \left(\begin{matrix} 2\Omega_0-n \\ 2t-1 \end{matrix}\right) \left(\begin{matrix} 2\Omega_0 \\ 2t-1 \end{matrix}\right)^{-1}},\label{eq5.20}\end{align}
\begin{equation} {\rm (iii)'}\quad \Lambda_t(x)=\frac{\displaystyle \frac{2tx}{1-x}-((2\Omega_0+1)-(2t-1))x^{2\Omega_0+1} \left(\frac{1-x}{x}\right)^{2t-1} \left(\begin{matrix} 2\Omega_0+1 \\ 2t-1 \end{matrix}\right)} {\displaystyle 1-x^{2\Omega_0+1}\sum_{n=1}^{2t-1} \left(\frac{1-x}{x}\right)^n \left(\begin{matrix} 2\Omega_0+n \\ n \end{matrix}\right)},\label{eq5.21}\end{equation}
\begin{align} {\rm (iv)'}\quad \Lambda_t(x)&=\frac{2t}{2t+1}(2\Omega_0-(2t-1))\nonumber\\ &\quad \times \frac{\displaystyle 1+\sum_{n=1}^{2\Omega_0-2t}\left(\frac{1-x}{x}\right)^n \left(\begin{matrix} 2\Omega_0+1 \\ 2t+1+n \end{matrix}\right) \left(\begin{matrix} 2\Omega_0+1 \\ 2t+1 \end{matrix}\right)^{-1} }{\displaystyle 1+\sum_{n=1}^{2\Omega_0-(2t-1)}\left(\frac{1-x}{x}\right)^n \left(\begin{matrix} 2\Omega_0+1 \\ 2t+n \end{matrix}\right) \left(\begin{matrix} 2\Omega_0+1 \\ 2t \end{matrix}\right)^{-1}}.\label{eq5.22} \end{align}
\begin{equation} \Lambda_t(x)=2t(x+\cdots) \quad (x\sim 0),\label{eq5.23a} \end{equation}
\begin{equation} \Lambda_t(x)=(2\Omega_0-(2t-1))\left(1-\frac{1}{2\Omega_0}\cdot\frac{1}{x}+\cdots \right) \quad (x\rightarrow \infty).\label{eq5.23b} \end{equation}
\begin{equation} \Lambda_t(x)=\frac{2t}{2t+1}(2\Omega_0-(2t-1))\left(1+\frac{\Omega_0+1}{(t+1)(2t+1)}(x-1)+\cdots \right).\label{eq5.24} \end{equation}
\begin{equation}\label{eq5.25} \Lambda_t(x)=\frac{2tx}{1-x} \quad \left((2\Omega_0+1)-(2t-1)\rightarrow \infty \right). \end{equation}
\begin{equation} N=2t-1 \quad (x=0),\label{eq5.26a} \end{equation}
\begin{align} N&=2t-1+2\left(\frac{2t}{2t+1}\right)(2\Omega_0-(2t-1))\nonumber\\ &=\left(\frac{2t}{2t+1}\right)\cdot 4\Omega_0 -\left(\frac{2t-1}{2t+1}\right)\cdot (2t-1) \quad (x=1),\label{eq5.26b} \end{align}
\begin{equation} N=2t-1+2(2\Omega_0-(2t-1)) =4\Omega_0-(2t-1)\quad (x\rightarrow \infty).\label{eq5.26c} \end{equation}
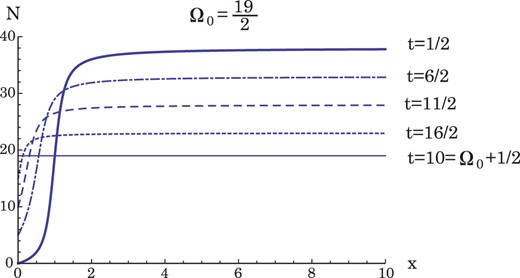
Fig. 1.
The figure shows |$N$| as a function of x with various t for the case |$\Omega _0=19/2$|. The solid, dash-dotted, dashed, and dotted curves represent the cases |$t=1/2$|, 3, |$11/2$|, and 8, respectively. The thin line represents the case |$t=\Omega _0+1/2\ (=10)$|.
In the |$B_{ps}$|-form framework, the expectation value |$\mathcal {T}_+=({\phi } |\widetilde {\mathcal {T}}_+| {\phi })$| is given in the form (5.27) It is noted that |$\mathcal {T}_+$| is expressed in terms of the product of |$z^*$| and the function of |$x\, (=|z|^2)$|, |$\Lambda _t(x)/x$|. In order to get a transparent understanding for |$\mathcal {T}_+$|, we introduce a new parameter |$(y, y^*)$|: (5.28) Then, |$\mathcal {T}_+$| is expressed as (5.29) After lengthy calculation, we have the relation (5.30)(5.31) Then, |$\mathcal {T}_{\pm }$| can be expressed as (5.32) The expectation value |$N$| is expressed in the form (5.33) With the use of the relation (5.17), |$\mathcal {T}_0$| is of the form (5.34) If |$Y$| given in the relation (5.31) can be neglected, the set |$(\mathcal {T}_{\pm ,0})$| reduces to the classical counterpart of the set of the su(1,1) generator |$\hat {T}_{\pm ,0}$|, namely, it is the classical counterpart of the Holstein–Primakoff representation. It should be noted that |$(y, y^*)$| is the canonical variable in the boson type. The above feature of the su(1,1) algebra was discussed in detail by the present authors with Kuriyama in Ref. [5].
\begin{align}\label{eq5.27} \mathcal{T}_+&=\langle \phi |\hat{\mathcal{T}}_+| \phi \rangle=\langle \phi |\hat{T}_+| \phi \rangle\nonumber\\ &=z^*\cdot\frac{1}{\Gamma}\sum_{n=0}^{2\Omega_0-(2t-1)}nx^{n-1} \left(\begin{matrix} 2t-1+n \\ n \end{matrix} \right) \nonumber\\ &=z^*\cdot \frac{1}{x}\Lambda_t(x). \end{align}
\begin{equation} y=z\sqrt{\frac{\Lambda}{x}}=\frac{z}{|z|}\sqrt{\Lambda}, \quad {\mathrm{i.e.,}}\qquad \Lambda=y^*y.\label{eq5.28} \end{equation}
\begin{equation} \mathcal{T}_+=y^*\sqrt{\frac{\Lambda}{x}}.\label{eq5.29} \end{equation}
\begin{equation} \frac{\Lambda}{x}=2t+y^*y-Y,\label{eq5.30}\end{equation}
\begin{equation} Y=\frac{\displaystyle 2tx^{2\Omega_0+1} \left[\left(\frac{1-x}{x}\right)^{2t} \left(\begin{matrix} 2\Omega_0+1 \\ 2t \end{matrix}\right) -\sum_{n=1}^{2t-1} \left(\frac{1-x}{x}\right)^{n} \left(\begin{matrix} 2\Omega_0+n \\ n \end{matrix}\right)\right]} {\displaystyle 1-x^{2\Omega_0+1}\sum_{n=1}^{2t-1} \left(\frac{1-x}{x}\right)^{n} \left(\begin{matrix} 2\Omega_0+n \\ n \end{matrix}\right)}.\quad \label{eq5.31} \end{equation}
\begin{equation} \mathcal{T}_+=y^*\cdot\sqrt{2t+y^*y-Y}, \quad \mathcal{T}_-=\sqrt{2t+y^*y-Y}\cdot y.\label{eq5.32} \end{equation}
\begin{equation} N=(2t-1)+2y^*y.\label{eq5.33} \end{equation}
\begin{equation} \mathcal{T}_0=t+y^*y.\label{eq5.34} \end{equation}
6. Approximate expression for the expectation value of the fermion number operator
In Sect. 5, we gave the expectation value of |$\widetilde {N}$| for |$| \phi)$|. The result is too complicated to use for practical purposes. Therefore, we must find an approximate expression which is fit for this purpose. As was already mentioned, roughly speaking, in the region where x is sufficiently large, |$N$| changes gently, but in the region |$x \lesssim 2$|, especially |$x \lesssim 1$|, it changes steeply. Therefore, it may be impossible to give an approximate expression of |$N$| in terms of a well-behaved simple function of x in the whole range |$0\leq x <\infty $|, but, if the range is limited, it may be possible. Judging from the behavior shown in Fig. 1, it may be natural to divide the whole range into two: (1) |$0\leq x \leq \gamma _t$| and (2) |$\gamma _t\leq x <\infty $|. Here, we conjecture that |$\gamma _t$| is given in the form (6.1) Later, we will give an interpretation of the relation (6.1). We treat the ranges (1) and (2) separately.
\begin{equation} \gamma_t=\frac{2\Omega_0-(2t-1)}{2\Omega_0}=1-\frac{2t-1}{2\Omega_0} (\leq 1).\label{eq6.1} \end{equation}
First, we introduce the following function for the approximate expression of |$\Gamma _t(x)$|, which is denoted as |$\Gamma _t^a(x)$|: (6.2) Here, α and |$\beta $| are real parameters which will be determined later. For the form (6.2), we have the following relation: (6.3a)(6.3b) The forms (6.2) are reduced to the forms (5.6) and (5.7) if |$x\sim 0$| and |$x\rightarrow \infty $|, respectively. From the above consideration, it may be understandable that |$\Gamma _t^a(x)$| is a possible approximation of |$\Gamma _t(x)$|. The functions |$(1-\alpha x)$| and |$(1-\beta /x)$| should not have the points which make |$1-\alpha x=0$| and |$1-\beta /x=0$| in the ranges |$0\leq x \leq \gamma _t$| and |$\gamma _t \leq x < \infty $|, respectively. These situations are realized under the condition (6.4)
\begin{equation} \Gamma_t(x) = \begin{cases} \displaystyle \left(\frac{1}{1-\alpha x}\right)^{\frac{2t}{\alpha}} \left(=\Gamma_t^{a_1}(x)\right) & {\mathrm{for\ range\ (1)}} \\ \displaystyle \left(\begin{matrix} 2\Omega_0 \\ 2t-1 \end{matrix} \right) \left[x^{2\Omega_0}\left(\frac{1}{1-\frac{\beta}{x}}\right)^{\frac{1}{2\Omega_0\beta}}\right]^{2\Omega_0-(2t-1)} \!\!\!\!\!\! \left(=\Gamma_t^{a_2}(x)\right) & {\rm for\ range\ (2)}. \end{cases}\label{eq6.2} \end{equation}
\begin{equation} \Gamma_t^{a_1}(x)=1+2tx+\cdots \quad (\alpha x <1),\label{eq6.3a}\end{equation}
\begin{equation} \Gamma_t^{a_2}(x) =\left(\begin{matrix} 2\Omega_0 \\ 2t-1 \end{matrix}\right) x^{2\Omega_0-(2t-1)}\left(1+\frac{2\Omega_0-(2t-1)}{2\Omega_0}\frac{1}{x}+\cdots \right) \quad \left(\frac{\beta}{x}<1\right).\label{eq6.3b} \end{equation}
\begin{equation} \alpha < \frac{1}{\gamma_t}, \quad \beta <\gamma_t.\label{eq6.4} \end{equation}
Through the relation (5.18), we define the approximate form of |$\Lambda _t(x)$| as follows: (6.5) We require the condition that the functions (6.5) should connect with each other smoothly at |$x=\gamma _t$|: (6.6a)(6.6b)
\begin{equation}\label{eq6.5} \Lambda_t^{a}(x)=\frac{x\frac{\mathrm{d}\Gamma_t^a(x)}{\mathrm{d}x}}{\Gamma_t^a(x)} =\begin{cases} \displaystyle \frac{2tx}{1-\alpha x} & {\mathrm{for}}\quad 0\leq x \leq \gamma_t,\\ \displaystyle (2\Omega_0-(2t-1))\left(1-\frac{1}{2\Omega_0(x-\beta)}\right) & {\rm for}\quad \gamma_t\leq x < \infty. \end{cases} \end{equation}
\begin{equation} \frac{2t\gamma_t}{1-\alpha \gamma_t}=(2\Omega_0-(2t-1))\left(1-\frac{1}{2\Omega_0(\gamma_t-\beta)}\right),\label{eq6.6a} \end{equation}
\begin{equation} \frac{2t}{(1-\alpha \gamma_t)^2}=\frac{2\Omega_0-(2t-1)}{2\Omega_0(\gamma_t-\beta)^2}.\label{eq6.6b} \end{equation}
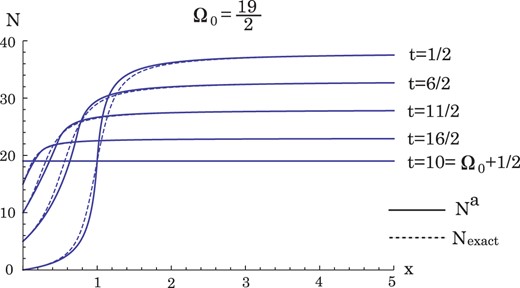
Fig. 2.
The figure shows |$N^a$| as a function of x with various t for the case |$\Omega _0=19/2$|. The solid curves represent |$N^a$| and, for comparison, the exact |$N$| are depicted. It is noted that the horizontal scale is different from that of Fig. 1.
The condition (6.6) determines α and |$\beta $| in the form (6.7a)(6.7b) We can see that α and |$\beta $| depend on t, and therefore, hereafter, we express α and |$\beta $| as |$\alpha _t$| and |$\beta _t$|. Clearly, they satisfy the condition (6.4). The approximate expression of |$N$|, |$N^a$|, is given by (6.8) Figure 2 shows several concrete cases, together with |$N$| shown in the relation (5.17). We can see that the agreement is rather good. Next, we discuss the typical three cases |$x=0$|, |$x=1$|, and |$x\rightarrow \infty $|. The cases |$x=0$| and |$x\rightarrow \infty $| agree with the exact results shown in the relations (5.26a) and (5.26c), because these two cases are constructed so as to reproduce the exact results. The case |$x=1$| is expressed in the form (6.9) The exact result (5.26b) can be expressed as (6.10) The cases |$2t=1$| and |$2\Omega _0$| agree with the exact results, but in the other cases, disagreement with the exact one is not so much as imagined.
\begin{equation} \alpha=\frac{1}{\gamma_t}\left(1-\frac{1}{2\Omega_0}\sqrt{\frac{2t}{\gamma_t}}-\frac{2t}{2\Omega_0}\right) (=\alpha_t),\label{eq6.7a} \end{equation}
\begin{equation} \beta=\gamma_t\left(1-\frac{1}{2\Omega_0}\sqrt{\frac{2t}{\gamma_t}}-\frac{1}{2\Omega_0 \gamma_t}\right) (=\beta_t).\label{eq6.7b} \end{equation}
\begin{equation} N^a=2t-1+2\Lambda_t^a(x).\label{eq6.8} \end{equation}
\begin{equation}\label{eq6.9} N^a=2t-1+2\left(1-\frac{1}{(2t+1)+\left(\left[2t\left(1-\frac{2t-1}{2\Omega_0}\right)\right]^{\frac{1}{2}}-1\right)}\right) (2\Omega_0-(2t-1)). \end{equation}
\begin{equation}\label{eq6.10} N=2t-1+2\left(1-\frac{1}{2t+1}\right)(2\Omega_0-(2t-1)). \end{equation}
Let us discuss the quantity |$\gamma _t$| which was introduced in the opening paragraph of this section. First, for |$t=1/2$|, we note the following relation: (6.11) With the use of the formulae (i)|${}'$| and (ii)|${}'$|, we can prove this relation. In (A), we also gave the relation (6.11). This relation tells us that if |$\Lambda _{1/2}$| for |$0\leq x \leq 1$| is given, we are able to obtain |$\Lambda _{1/2}$| for |$1\leq x <\infty $|, and vice versa. From the above argument, the range |$0\leq x < \infty $| is divided by |$x=1$|: (1) |$0\leq x \leq 1$| and (2) |$1\leq x <\infty $|. In the case |$2\Omega _0-(2t-1)=0$|, i.e., |$t=\Omega _0+1/2$|, |$\Lambda _{t=\Omega _0+1/2}=0$| and the range |$0\leq x<\infty $| is formally divided by |$x=0$|: (1) |$x=0$| and (2) |$0\leq x < \infty $|. Combining the above two extreme cases with the behavior of |$N (=2t-1+2\Lambda)$| shown in Fig. 1, we conjecture that the range |$0\leq x <\infty $| is divided by |$x=\gamma _t=(2\Omega _0-(2t-1))/(2\Omega _0)$|: (1) |$0\leq x \leq \gamma _t$| and (2) |$\gamma _t \leq x<\infty $|. The parameter |$\gamma _t$| is the ratio of the number of single-particle states in |$\overline {P}$| which can contribute to the fermion pair formation to the total number of the single-particle states in |$\overline {P}$|. Therefore, if |$\gamma _t$| is near to 1, the possibility for fermion pair formation is large, and vice versa. The above is the interpretation of the conjecture for |$\gamma _t$|.
\begin{equation}\label{eq6.11} \Lambda_{1/2}(x)+\Lambda_{1/2}\left(\frac{1}{x}\right)=2\Omega_0. \end{equation}
In the framework of our approximation, we generalized the relation (6.11), which can be rewritten as (6.12) If |$1\leq x <\infty $|, we have |$0\leq 1/x \leq 1$|, i.e., |$x\cdot (1/x)=1$|. We generalize the relation (6.12) to the case of arbitrary values of t. If |$\gamma _t\leq x <\infty $|, |$\gamma _t^2/x$| obeys the inequality |$0\leq \gamma _t^2/x \leq \gamma _t$|, i.e., |$x\cdot (\gamma _t^2/x)=\gamma _t^2$|. Of course, if |$t=1/2$|, we have |$x\cdot (1/x)=1$|. Then the relation (6.5) for |$0\leq x\leq \gamma _t$| gives (6.13) The relation (6.13) leads to (6.14) Therefore, the relation (6.5) for |$\gamma _t\leq x<\infty $| can be rewritten as (6.15) With the use of the explicit expressions of |$\alpha _t$| and |$\beta _t$| given in the relation (6.7), we have the following: (6.16) If |$\Lambda _t^{a_1}$| is given, |$\Lambda _t^{a_2}$| is obtained by the relation (6.16). In the case |$t=1/2$|, |$\Lambda _{1/2}^{a_2}(x)$| is expressed as (6.17) Also, in the case |$t=\Omega _0+1/2$|, i.e., |$2\Omega _0-(2t-1)=0$|, we have (6.18) In the exact case for |$t>1/2$|, numerically, the relation corresponding to the relation (6.16) may be presented, but, in analytical form, it may be impossible.
\begin{equation} \Lambda_{1/2}(x)=2\Omega_0-\Lambda_{1/2}\left(\frac{1}{x}\right).\label{eq6.12} \end{equation}
\begin{equation} \Lambda_t^{a_1}\left(\frac{\gamma_t^2}{x}\right) =\frac{2t\cdot\frac{\gamma_t^2}{x}}{1-\alpha_t\cdot\frac{\gamma_t^2}{x}}, \quad {\mathrm{i.e.,}}\quad \frac{\gamma_t^2}{x}=\frac{\Lambda_t^{a_1}\left(\frac{\gamma_t^2}{x}\right)}{\alpha_t\Lambda_t^{a_1}\left(\frac{\gamma_t^2}{x}\right)+2t}.\label{eq6.13} \end{equation}
\begin{equation} x=\gamma_t^2\left(\alpha_t+\frac{2t}{\Lambda_t^{a_1}\left(\frac{\gamma_t^2}{x}\right)}\right) \quad (\gamma_t\leq x<\infty).\label{eq6.14} \end{equation}
\begin{align}\label{eq6.15} \Lambda_t^{a_2}(x) &= 2\Omega_0 \gamma_t\left(1-\frac{1}{2\Omega_0(x-\beta_t)}\right)\nonumber\\ &=2\Omega_0 \gamma_t\Biggl(1-\frac{1}{2\Omega_0\Bigl[\gamma_t^2\Bigl(\alpha_t+\frac{2t}{\Lambda_t^{a_1}\left(\frac{\gamma_t^2}{x}\right)}\Bigl) -\beta_t\Bigl]}\Biggl). \end{align}
\begin{equation} \Lambda_t^{a_2}(x)=2\Omega_0 \gamma_t\left(1-\frac{\Lambda_t^{a_1}\left(\frac{\gamma_t^2}{x}\right)}{(1-2t\gamma_t)\Lambda_t^{a_1}\left(\frac{\gamma_t^2}{x}\right)+2t\cdot 2\Omega_0} \right).\label{eq6.16} \end{equation}
\begin{equation} \Lambda_{1/2}^{a_2}(x)=2\Omega_0-\Lambda_{1/2}^{a_1}\left(\frac{1}{x}\right).\label{eq6.17} \end{equation}
\begin{equation} \Lambda_{t=\Omega_0+1/2}^{a_2}(x)=0.\label{eq6.18} \end{equation}
Finally, we will investigate the parameters |$\alpha _t$| and |$\beta _t$| given in the relations (6.7a) and (6.7b), respectively. Both relations can be rewritten as (6.19a)(6.19b) The above expressions tell us (6.20) In the su(1,1)-algebraic model we have |$\alpha _t=1$|, which is realized in the case with |$\Omega _0\rightarrow \infty $| and finite values of t. However, in our present model, |$\Omega _0$| and t are finite and |$\alpha _t$| should obey the condition (6.20). We do not know any model related to |$\beta _t$|, and thus any comparison is impossible. Since |$\alpha _t$| is decreasing for |$2t$|, the maximum value of |$\alpha _t$| is given as (6.21) At the point |$2t=2t^0$|, which will be discussed later, |$\alpha _t$| vanishes |$(\alpha _{t^0}=0$|). After |$\alpha _{t^0}=0$|, |$\alpha _t$| can change to |$-\infty $|: (6.22) The quantity |$\Lambda _t^{a_1}(x)$| in the range |$\alpha _{1/2}>\alpha _t >0$| is of the type similar to that of the su(1,1)-algebraic model: |$\Lambda _t^{a_1}(x)=2tx/(1-|\alpha _t| x)$|. At |$\alpha _{t^0}=0$|, |$\Lambda _t^{a_1}(x)=2t^0x$| and in the range |$0>\alpha _t >-\infty $|, |$\Lambda _t^{a_1}(x)=2tx/(1+|\alpha _t|x)$|. If |$2\Omega _0$| and |$2t$| can change continuously, |$\alpha _t=0$| itself has its own meaning. But, they are integers, and we treat |$\alpha _t=0$| as an auxiliary condition. This leads us to a certain cubic equation for |$2t$| with one real solution, given as (6.23a) The expression (6.23a) is approximated in the form (6.23b) As is conjectured in relation (6.23), |$2t^0$| cannot be expected to be integer. Therefore, two integers |$2t^+$| and |$2t^-$| (|$t^+<t^-$|) which are the nearest to |$2t^0$| must be searched: |$\alpha _t>0$| for |$1\leq 2t\leq 2t^+$| and |$\alpha _t<0$| for |$2t^-\leq 2t\leq 2\Omega _0+1$|. For this searching, the relation (6.23) is useful. For example, in the case |$2\Omega _0=19$|, the relations (6.23a) and (6.23b) give us |$2t^0 \sim 13.0235$| and 13.0562, respectively and, therefore, |$2t^+=13$| and |$2t^-=14$|. For these, we have |$\alpha _{t^+}=8.5460\times 10^{-3}\ (>0)$| and |$\alpha _{t^-}=-0.2764\ (<0)$|. The treatment of |$\beta _t$| is rather simple. As is clear from the relation (6.19b), the maximum value of |$\beta _t$| is also given in the case |$t=1/2$|: (6.24) Then, gradually decreasing, at the point |$2t=2\Omega _0-2$|, |$\beta _{\Omega _0-1}$| is given as (6.25) At the point |$2t=2\Omega _0-1$|, |$\beta _{\Omega _0-1/2}$| is given as (6.26) At the terminal points |$2t=2\Omega _0$| and |$2\Omega _0+1$|, we have (6.27) We can see that the sign of |$\beta _t$| changes between |$2t=2\Omega _0-2$| and |$2\Omega _0-1$|. The point which satisfies |$\beta _t=0$| is given at |$2t=2t^0{}'$|, shown as (6.28)
\begin{equation} \alpha_t=1-\frac{1}{2\Omega_0-(2t-1)}\left(\left[\frac{2\Omega_0\cdot 2t}{2\Omega_0-(2t-1)}\right]^{\frac{1}{2}}+1\right),\label{eq6.19a} \end{equation}
\begin{equation} \beta_t=1-\frac{1}{2\Omega_0}\left(2t+ \left[\frac{2t}{2\Omega_0}(2\Omega_0-(2t-1))\right]^{\frac{1}{2}}\right).\label{eq6.19b} \end{equation}
\begin{equation}\label{eq6.20} \alpha_t < 1, \quad \beta_t < 1. \end{equation}
\begin{equation} \alpha_{1/2}=1-\frac{1}{\Omega_0}, \quad \gamma_{1/2}=1.\label{eq6.21} \end{equation}
\begin{equation} \alpha_{\Omega_0}=-2\Omega_0\ \left(\gamma_{\Omega_0}=\frac{1}{2\Omega_0}\right), \quad \alpha_{\Omega_0+1/2}\rightarrow -\infty\quad (\gamma_{\Omega_0+1/2}=0).\label{eq6.22} \end{equation}
\begin{align}\label{eq6.23a} 2t^0&=2\Omega_0+\frac{1}{3}-(2\Omega_0)^{\frac{2}{3}}\left[ \left(\frac{1}{2}(A+B)\right)^{\frac{1}{3}}- \left(\frac{1}{2}(A-B)\right)^{\frac{1}{3}}\right],\nonumber\\ A&= \left[\left(1-\frac{5}{54\Omega_0}\right)\left(1+\frac{1}{2\Omega_0}\right)\right]^{\frac{1}{2}}, \quad B=1+\frac{1}{6\Omega_0}-\frac{1}{54\Omega_0^2}. \end{align}
\begin{equation}\label{eq6.23b} 2t^0=2\Omega_0-(2\Omega_0)^{\frac{2}{3}}+\frac{1}{3}(2\Omega_0)^{\frac{1}{3}}+\frac{1}{3} -\frac{10}{81}(2\Omega_0)^{-\frac{1}{3}}. \end{equation}
\begin{equation} \beta_{1/2}=1-\frac{1}{\Omega_0}.\label{eq6.24} \end{equation}
\begin{equation} \beta_{\Omega_0-1}=\frac{1}{\Omega_0}\left(1-\frac{1}{2} \left[3\left(1-\frac{1}{2\Omega_0}\right)\right]^{\frac{1}{2}}\right) (>0) .\label{eq6.25} \end{equation}
\begin{equation} \beta_{\Omega_0-1/2}=-\frac{1}{2\Omega_0}\left(\left[2-\frac{1}{\Omega_0}\right]^{\frac{1}{2}}-1\right) (<0) .\label{eq6.26} \end{equation}
\begin{equation}\label{eq6.27} \beta_{\Omega_0}=\beta_{\Omega_0+1/2}=-\frac{1}{2\Omega_0}. \end{equation}
\begin{equation}\label{eq6.28} 2t^0{}'=2\Omega_0- \frac{2\Omega_0-1+2\Omega_0 \left(5+\frac{1}{\Omega_0}+\frac{1}{4\Omega_0^2}\right)^{\frac{1}{2}}}{2(2\Omega_0+1)}. \end{equation}
7. A simple example of a many-fermion model obeying the pseudo-su(1,1) algebra
In next three sections, we intend to discuss an example of the application of the idea developed so far. This section will be devoted to presenting a simple many-fermion model aimed at the application. As an illustrative example of our idea, first, we give a short summary of the “damped and amplified oscillator”. The starting Hamiltonian is the simplest, i.e., the harmonic oscillator: (7.1) Here, |$(\hat {b}, \hat {b}^*)$| denotes the boson operator. As an auxiliary degree of freedom for the “damping and amplifying”, new boson |$(\hat {a}, \hat {a}^*)$| is introduced. The Hamiltonian for |$(\hat {a}, \hat {a}^*)$| is also the harmonic oscillator type: (7.2) Further, as for the interaction between both degrees of freedom, the following form is adopted: (7.3) The idea presented in Ref. [6,7] is to adopt the Hamiltonian (7.4)
\begin{equation}\label{eq7.1} \hat{H}_b=\omega\hat{b}^*\hat{b} \quad (\omega; {\mathrm{frequency}}). \end{equation}
\begin{equation}\label{eq7.2} \hat{H}_a=\omega\hat{a}^*\hat{a}. \end{equation}
\begin{equation} \hat{V}_{ab}=-\mathrm{i}\gamma(\hat{a}^*\hat{b}^*-\hat{b}\hat{a}) \quad (\gamma \ ; \ {\mathrm{constant}}).\label{eq7.3} \end{equation}
\begin{equation}\label{eq7.4} \hat{H}=\hat{H}_b-\hat{H}_a+\hat{V}_{ba}. \end{equation}
By treating |$\hat {H}$| appropriately, we can describe the “damped and amplified oscillation” in a conservative form. It should be noted that, for the Hamiltonian (7.4), the form |$(\hat {H}_b+\hat {H}_a+\hat {V}_{ba})$| is not adopted. It shows that the Hamiltonian (7.4) is not the energy of the entire system, but the generator for time evolution. This is a significant feature of this approach. With the use of |$\hat {T}_{\pm }$| defined in the relation (2.5), |$\hat {H}$| can be expressed as (7.5) Here, |$\hat {T}$| is defined as (7.6a)(7.6b) By using the mixed-mode coherent states for the su(1,1) algebra, the present authors, with Kuriyama, have extensively investigated the Hamiltonian (7.5) and its variations [5].
\begin{equation} \hat{H}=2\omega\left(\hat{T}-\frac{1}{2}\right)-\mathrm{i}\gamma\left(\hat{T}_+-\hat{T}_-\right).\label{eq7.5} \end{equation}
\begin{equation} \hat{T}=-\frac{1}{2}(\hat{a}^*\hat{a}-\hat{b}^*\hat{b})+\frac{1}{2},\label{eq7.6a} \end{equation}
\begin{equation} \hat{\boldsymbol{T}}^2=\hat{T}\left(\hat{T}-1\right), \quad [\hat{T}_{\pm,0}, \hat{T}]=0.\label{eq7.6b} \end{equation}
The above illustrative example teaches us the following: In order to treat the system such as the “damped and amplified oscillator” in an isolated system, so-called phase space doubling is required. The idea of phase space doubling occupies the main part of the thermo-field dynamics formalism [10]. Then, the original intrinsic oscillator expressed in terms of the boson |$(\hat {b}, \hat {b}^*)$| and the “external environment” expressed in terms of the boson |$(\hat {a}, \hat {a}^*)$| appear. The interaction between both systems is introduced. We will apply the above consideration to a simple many-fermion system.
We make the following translation into the fermion system: (7.7)(7.8)(7.9) Here, |$\widetilde {\mathcal {T}}$| is introduced in the relation (4.10), and the relation (4.11) suggests the relation |$[\widetilde {\mathcal {T}},\, \widetilde {\mathcal {T}}_{\pm }]=0$|. Under the above translation, our Hamiltonian is expressed in the form (7.10) It may be clear that we have the translation (7.11) The original intrinsic Hamiltonian |$\widetilde {H}_{\overline {P}}$| may be the simplest in many-fermion systems, and our aim is to describe this system in the “external environment”. The Hamiltonian (7.10) was set up under an idea analogous to that in the case (7.5). However, it may be permitted to regard the Hamiltonian (7.10) as the energy of the entire system. Concerning this point, we will discuss the possibility in Sect. 11. It may be important to see that the conventional pairing Hamiltonian and the present one are expressed in terms of the su(2) generators, |$\widetilde {S}_{\pm ,0}$|, but, differently from the former, the latter does not commute with the total fermion number operator. In this sense, the use of the state (1.1) for the variational treatment in the pairing Hamiltonian is justified by the symmetry breaking. On the other hand, the use of the state (5.1) (or (5.2)) may be natural as a possible trial state for the variation without any comment such as the symmetry breaking.
\begin{equation} (\hat{b}, \hat{b}^*)\rightarrow (\tilde{c}_{\bar{\alpha}}, \tilde{c}_{\bar{\alpha}}^*), \quad (\hat{a}, \hat{a}^*)\rightarrow (\tilde{c}_{\alpha}, \tilde{c}_{\alpha}^*),\label{eq7.7}\end{equation}
\begin{equation} (\hat{T}-\frac{1}{2}\rightarrow \widetilde{\mathcal{T}}=-\frac{1}{2}\sum_{\alpha} (\tilde{c}_{\alpha}^*\tilde{c}_{\alpha}-\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\bar{\alpha}})\, (=-\widetilde{R}_0), \quad \hat{T}_{\pm}\rightarrow \widetilde{\mathcal{T}}_{\pm},\label{eq7.8} \end{equation}
\begin{equation} \omega\, ({\mathrm{frequency}}) \rightarrow \varepsilon\, (\hbox{single-particle energy}).\label{eq7.9} \end{equation}
\begin{equation} \widetilde{H}=2\varepsilon \widetilde{\mathcal{T}}-\mathrm{i}\gamma\left(\widetilde{\mathcal{T}}_+-\widetilde{\mathcal{T}}_-\right).\label{eq7.10} \end{equation}
\begin{equation} \hat{H}_b\rightarrow \widetilde{H}_{\overline{P}}=\varepsilon\widetilde{N}_{\overline{P}}, \quad \widetilde{N}_{\overline{P}}=\sum_{\alpha}\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\bar{\alpha}}, \quad \hat{H}_a\rightarrow \widetilde{H}_P=\varepsilon\widetilde{N}_P, \quad \widetilde{N}_P=\sum_{\alpha}\tilde{c}_{\alpha}^*\tilde{c}_{\alpha}.\label{eq7.11} \end{equation}
Our basic idea is to describe the Hamiltonian (7.10) in the framework of the time-dependent variational method: (7.12) Here, the state |$| \phi)$| is used for the trial state of the variation. In order to avoid confusion between the time variable and the quantum number t, we will use |$\tau $| for the time variable. For the relation (7.12), the following are useful: (7.13)(7.14) Here, |$\mathcal {T}_{\pm }$| is given in the relation (5.27) and |$\mathcal {H}$| is defined as (7.15) Then, the relations (7.12)–(7.14) give us (7.16) For the relation (7.16), |$\mathcal {H}$| is adopted in the following form: (7.17) Under the Hamiltonian (7.17), the relation (7.16) is reduced to the differential equation (7.18) Here, |$\Lambda _t'(x)$| denotes the derivative of |$\Lambda _t(x)$| with respect to x.
\begin{equation}\label{eq7.12} \delta\int (\phi |\mathrm{i}\partial_{\tau}-\widetilde{H}| \phi)\mathrm{d}\tau=0. \end{equation}
\begin{equation} \delta \int (\phi |\mathrm{i}\partial_{\tau}| \phi)\mathrm{d}\tau = \frac{\mathrm{i}}{2}\int\left(\delta z^*\cdot \dot{z}-\delta z\cdot \dot{z}^*\right) \left(\frac{\partial \mathcal{T}_+}{\partial z^*}+\frac{\partial \mathcal{T}_-}{\partial z}\right)\mathrm{d}\tau ,\label{eq7.13} \end{equation}
\begin{equation} \delta \int (\phi |\widetilde{H}| \phi)\mathrm{d}\tau = \int\left(\delta z^*\frac{\partial \mathcal{H}}{\partial z^*} +\delta z\frac{\partial \mathcal{H}}{\partial z}\right)\mathrm{d}\tau .\label{eq7.14} \end{equation}
\begin{equation}\label{eq7.15} \mathcal{H}=\mathcal{H}(z^*,z)=(\phi |\widetilde{H}{| \phi)}. \end{equation}
\begin{equation} \mathrm{i}\dot{z}\frac{1}{2} \left(\frac{\partial \mathcal{T}_+}{\partial z^*}+\frac{\partial \mathcal{T}_-}{\partial z}\right) =\frac{\partial \mathcal{H}}{\partial z^*}, \quad -\mathrm{i}\dot{z}^*\frac{1}{2} \left(\frac{\partial \mathcal{T}_+}{\partial z^*}+\frac{\partial \mathcal{T}_-}{\partial z}\right) =\frac{\partial \mathcal{H}}{\partial z}.\label{eq7.16} \end{equation}
\begin{equation} \mathcal{H}=\varepsilon(2t-1)-\mathrm{i}\gamma\left(\mathcal{T}_+-\mathcal{T}_-\right) =\varepsilon(2t-1)-\gamma\cdot \mathrm{i}(z^*-z)\frac{\Lambda_t(x)}{x}.\label{eq7.17} \end{equation}
\begin{equation} \dot{z}=-\gamma\left[ 1-\frac{z^2}{x}\left(1-\frac{\Lambda_t(x)}{x\Lambda'_t(x)}\right) \right], \quad \dot{z}^*=-\gamma\left[ 1-\frac{z^{*2}}{x}\left(1-\frac{\Lambda_t(x)}{x\Lambda'_t(x)}\right)\right].\label{eq7.18} \end{equation}
The relation (7.18) forms our basic framework for describing the time evolution. In order to give the physical interpretation of the relation (7.18), we examine the case |$\Lambda _t^{a_1}(x)$|. In this case, the relation (7.18) becomes (7.19) If z is expressed as |$z=u+\mathrm {i}v$| (u, v: real), we have (7.20) If we eliminate v from the relation (7.20), the following equation is derived: (7.21) If the relation (7.21) is interpreted in Newton mechanics, a mass point with mass 1 moves in the one-dimensional space under the external force |$4\gamma ^2\alpha _t^2 u(1/\alpha _t -u^2)$| and the velocity-dependent force |$6\alpha _t u\dot {u}$|. The force |$4\gamma ^2\alpha _t^2 u(1/\alpha _t -u^2)$| is expressed in terms of the potential energy |$V(u)$|: (7.22) The cases |$\alpha _t>0$| and |$\alpha _t<0$| correspond to double well-like and single well-like potentials, respectively, and the case |$\alpha _t=0$| to no external force. The existence of the velocity-dependent force suggests that our model enables us to describe the dissipation phenomena in the many-fermion system. If we can solve the equation of motion (7.21), u can be determined as a function of |$\tau $| and the second expression in (7.20) gives us the following form: (7.23) Here, we omitted the initial condition for u and v. Thus, we are able to obtain |$u(\tau)$| and |$v(\tau)$| and, then, x is determined as a function of |$\tau $|: (7.24) The case |$\Lambda _t^{a_2}(x)$| is not so simple as the case |$\Lambda _t^{a_1}(x)$|, because, in classical mechanics, we cannot find any simple example analogous to this case. The above is an outline of our model, which is discussed in the following sections.
\begin{equation} \dot{z}=-\gamma(1-\alpha_t z^2), \quad \dot{z}^*=-\gamma(1-\alpha_t z^*{}^2).\label{eq7.19} \end{equation}
\begin{equation} \dot{u}=-\gamma(1-\alpha_t u^2+\alpha_t v^2), \quad \dot{v}=2\gamma\alpha_t uv.\label{eq7.20} \end{equation}
\begin{equation} {\ddot u}=4\gamma^2\alpha_t^2 u\left(\frac{1}{\alpha_t}-u^2\right)+6\alpha_t u\dot{u}.\label{eq7.21} \end{equation}
\begin{equation}\label{eq7.22} 4\gamma^2\alpha_t^2 u\left(\frac{1}{\alpha_t}-u^2\right) =-\frac{\mathrm{d}V(u)}{\mathrm{d}u}, \quad V(u)=-4\gamma^2\left(\frac{1}{2}\alpha_t u^2 -\frac{1}{4}\alpha_t^2 u^4\right). \end{equation}
\begin{equation} v(\tau)=\mathrm{e}^{2\gamma\alpha_t\int^{\tau}u(\tau')\mathrm{d}\tau'}.\label{eq7.23} \end{equation}
\begin{equation} x(\tau)=u(\tau)^2+v(\tau)^2 .\label{eq7.24} \end{equation}
Finally, we give the expectation values of |$\widetilde {N}_{\overline {P}}$| and |$\widetilde {N}_{P}$| for |$| \phi)$|, |$N_{\overline {P}}$| and |$N_P$|: (7.25a)(7.25b) The expectation value of |$\widetilde {N}(=\widetilde {N}_{\overline {P}}+\widetilde {N}_P)$| is given as |$N=(2t-1+\Lambda _t(x))+\Lambda _t(x)$|, and it is nothing but the result (5.17).
\begin{equation} N_{\overline{P}}=2t-1+\Lambda_t(x),\label{eq7.25a} \end{equation}
\begin{equation}N_P=\Lambda_t(x).\label{eq7.25b} \end{equation}
8. Various properties of |$\Lambda _t^{a_1}(x)$| for describing its time dependence
Let us investigate various properties of |$\Lambda _t^{a_1}(x)$|. First, we notice that the present system is of two dimensions and, therefore, there exist two constants of motion. One is the quantum number t and the second, which will be denoted as |$\kappa $|, is given through the relation (8.1) This may be self-evident, because |$\mathcal {H}$| itself, shown in the relation (7.17), is a constant of motion. If z is expressed in the form |$z=u+\mathrm {i}v$|, we have (8.2) The relation (8.1) leads to (8.3) Inversely, x can be expressed as a function of y: (8.4) Then, u can be given in the form (8.5) The sign |$+$| or |$-$| may be chosen appropriately. Later, we will discuss this problem. As is clear in the above argument, |$(u,v)$| and also x are functions of y. Since |$u^2 \geq 0$|, the relation (8.5) gives us the inequality (8.6) The inequality (8.6) suggests that the value of y cannot vary freely. We will apply the above scheme to the cases |$\Lambda _t^{a_1}(x)$|.
\begin{equation}\label{eq8.1} \mathrm{i}(z^*-z)\frac{\Lambda_t(x)}{x}=2\kappa . \end{equation}
\begin{equation} \mathrm{i}(z^*-z)=2v .\label{eq8.2} \end{equation}
\begin{equation} v=\frac{\kappa}{y}, \quad y=\frac{\Lambda_t(x)}{x}, \quad (x=|z|^2=u^2+v^2, \quad y\geq 0).\label{eq8.3} \end{equation}
\begin{equation} x=f_t(y).\label{eq8.4} \end{equation}
\begin{equation} u=\pm\sqrt{x-v^2}=\pm \frac{1}{y} \left(y^2 f_t(y)-\kappa^2\right)^{\frac{1}{2}}.\label{eq8.5} \end{equation}
\begin{equation} y^2 f_t(y) \geq \kappa^2 .\label{eq8.6} \end{equation}
For the case |$\Lambda _t(x)/x=\Lambda _t^{a_1}(x)/x=2t/(1-\alpha _t x)$|, we have (8.7) The relation (8.7) is applicable in the range |$0\leq x \leq \gamma _t$|. This point will be discussed further in Sect. 10. Thus, the inequality (8.6) is reduced to (8.8) i.e., (8.9)(8.10)
\begin{equation} x=f_t(y)=\frac{1}{\alpha_t}\left(1-\frac{2t}{y}\right),\quad {\mathrm{i.e.,}}\quad \Lambda_t^{a_1}(x)=\frac{1}{\alpha_t}(y-2t).\label{eq8.7} \end{equation}
\begin{equation} \frac{1}{\alpha_t}\cdot y(y-2t)\geq \kappa^2,\label{eq8.8} \end{equation}
\begin{align} w&= \begin{cases} +y(y-2t)\geq \rho^2, &\quad (\alpha_t >0) \\ -y(y-2t)\geq \rho^2, &\quad (\alpha_t <0) \end{cases}\label{eq8.9}\end{align}
\begin{equation}\rho=\sqrt{|\alpha_t|}\kappa.\label{eq8.10} \end{equation}
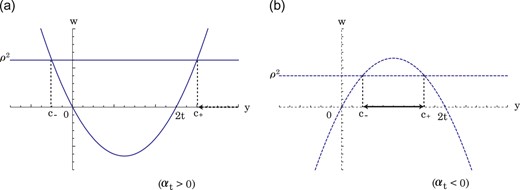
Fig. 3.
The figures show the inequality in (8.9) schematically with |$\Omega _0=19/2$|: (a) |$t=5/2$|, then |$\alpha _t\approx 0.766\, (>0)$|; (b) |$t=15/2$|, then |$\alpha _t \approx -0.710\, (<0)$|.
The behavior of the relation (8.9) is depicted in Fig. 3. In Fig. 3, we can find the following restriction to y: (8.11a)(8.11b) Here, |$c_{\pm }$| denote solutions of the quadratic equations (8.12a)(8.12b) The above equation is obtained by equating both sides of the inequality (8.9). Therefore, with the use of new variable |$\chi $|, y can be parametrized in the form (8.13a)(8.13b) In Sect. 11, we will discriminate between the former (8.13a) and the latter (8.13b) in terms of the notations |$y_+$| and |$y_-$|. With the use of Eq. (8.13), u and v can be expressed as follows: (8.14)(8.15) By substituting Eq. (8.13) into the relation (8.7), x can be expressed in terms of |$\cosh \chi $| and |$\cos \chi $|. Then we can express |$\Lambda _t^{a_1}(x)=2tx/(1-\alpha _t x)$| as a function of |$\cosh \chi $| and |$\cos \chi $|.
\begin{equation} y\geq c_+, \quad {\mathrm{i.e.}}\quad y\geq \frac{1}{2}(c_+ +c_-)+\frac{1}{2}(c_+-c_-), \quad (\alpha_t>0)\label{eq8.11a} \end{equation}
\begin{equation} c_- \leq y \leq c_+, \quad {\rm i.e.,}\quad \frac{1}{2}(c_+ +c_-)-\frac{1}{2}(c_+-c_-)\leq y \leq \frac{1}{2}(c_+ +c_-)+\frac{1}{2}(c_+-c_-) \quad (\alpha_t<0).\label{eq8.11b} \end{equation}
\begin{equation} y^2-2ty-\rho^2=0 \quad (\alpha_t>0),\label{eq8.12a} \end{equation}
\begin{equation} -y^2+2ty-\rho^2=0 \quad (\alpha_t<0).\label{eq8.12b} \end{equation}
\begin{equation} y=\frac{1}{2}(c_+ +c_-)+\frac{1}{2}(c_+-c_-)\cosh \chi \quad (\alpha_t>0),\label{eq8.13a} \end{equation}
\begin{equation} y= \frac{1}{2}(c_+ +c_-)+\frac{1}{2}(c_+-c_-)\cos \chi \quad (\alpha_t<0).\label{eq8.13b} \end{equation}
\begin{align} u&=\begin{cases} \displaystyle \pm \frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{1}{y}\sqrt{(y-c_+)(y-c_-)} =\pm\frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{1}{y}\cdot\frac{1}{2}(c_+-c_-)|\sinh \chi|, \ (\alpha_t>0) \displaystyle \pm \frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{1}{y}\sqrt{(c_+ -y)(y-c_-)} =\pm\frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{1}{y}\cdot\frac{1}{2}(c_+-c_-)|\sin \chi|, \ (\alpha_t < 0) \end{cases}\label{eq8.14} \end{align}
\begin{equation} v=\frac{1}{\sqrt{|\alpha_t|}}\cdot \frac{\rho}{y}. \quad (\alpha_t \neq 0)\label{eq8.15} \end{equation}
Since Eq. (8.12) gives us the solutions |$c_{\pm }=t\pm \sqrt {t^2+\rho ^2}$| for |$\alpha _t>0$| and |$c_{\pm }=t\pm \sqrt {t^2-\rho ^2}$| for |$\alpha _t <0$|, the relation (8.13) can be expressed as (8.16) Then u and v are obtained in the form (8.17) We can express z as a function of |$\rho $| and |$\chi $|. The quantity x is obtained in the form (8.18a)(8.18b) Thus, we have the following form for |$\Lambda _t^{a_1}(x)$|: (8.19a)(8.19b) It may be necessary for determining the time dependence of |$\Lambda _t^{a_1}(x)$| to investigate the behavior of |$\chi $| over time.
\begin{equation} y=\begin{cases} t+\sqrt{t^2+\rho^2}\cosh \chi &\quad (\alpha_t>0), \\ t+\sqrt{t^2-\rho^2}\cos \chi &\quad (\alpha_t <0). \end{cases}\label{eq8.16} \end{equation}
\begin{equation} u=\begin{cases} \displaystyle \pm\frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{\sqrt{t^2+\rho^2}|\sinh \chi|}{t+\sqrt{t^2+\rho^2}\cosh \chi} \displaystyle \pm\frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{\sqrt{t^2-\rho^2}|\sin \chi|}{t+\sqrt{t^2-\rho^2}\cos \chi} \end{cases}\!\!\!,\quad v= \begin{cases} \displaystyle \frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{\rho}{t+\sqrt{t^2+\rho^2}\cosh \chi} & (\alpha_t>0), \displaystyle \frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{\rho}{t+\sqrt{t^2-\rho^2}\cos \chi} & (\alpha_t<0). \end{cases}\label{eq8.17} \end{equation}
\begin{equation} x = \frac{1}{\alpha_t}\cdot\frac{\sqrt{t^2+\rho^2}\cosh \chi-t}{\sqrt{t^2+\rho^2}\cosh \chi+t} \quad (\alpha_t>0),\label{eq8.18a} \end{equation}
\begin{equation} x = \frac{1}{\alpha_t}\cdot\frac{\sqrt{t^2-\rho^2}\cos \chi-t}{\sqrt{t^2-\rho^2}\cos \chi+t} \quad (\alpha_t<0).\label{eq8.18b} \end{equation}
\begin{equation} \Lambda_t^{a_1}(x)= \frac{1}{\alpha_t}(\sqrt{t^2+\rho^2}\cosh \chi -t) \quad (\alpha_t>0),\label{eq8.19a}\end{equation}
\begin{equation}\Lambda_t^{a_1}(x)= \frac{1}{\alpha_t}(\sqrt{t^2-\rho^2}\cos \chi -t) \quad (\alpha_t<0).\label{eq8.19b} \end{equation}
The starting variables for describing the present model are u and v. As is shown in relations (8.14) and (8.15), the new variables are |$\rho $| and |$\chi $|. Depending on |$\alpha _t>0$| and |$\alpha _t<0$|, the connections to |$(u, v)$| are different from each other. However, |$\rho $| is a constant of motion and |$\mathcal {H}$| can be expressed as (8.20) Therefore, the time dependence of |$(u, v)$| is given through y, which is a function of |$\chi $|. First, we notice the relation (8.21) Here, we used relation (7.19). With the use of the relation (8.21), we have |$\dot {y}$| in the following form: (8.22) i.e., (8.23) On the other hand, the relation (8.13) gives us |$\dot {y}$| in the form (8.24) Combining the relations (8.23) and (8.24), |$\dot {\chi }$| is obtained: (8.25a)(8.25b) Our final aim is to present the time dependence of |$\Lambda _t^{a_1}(x)$|, which is also a function of y. The quantity y contains |$\cosh \chi $| or |$\cos \chi $|. As can be seen in the relation (8.25), |$\chi $| is given in the following two cases: (8.26a)(8.26b) Here, |$\pm \chi _{\pm }^0$| denote the initial values of |$\chi _{\pm }$| (|$\tau =0$|). Then, we have (8.27) If |$\chi _+^0=\chi _-^0$|, case (ii) is nothing but case (i). The case |$\cos \chi $| is also in the same situation as the above. The above argument suggests that it may be enough to adopt the case (i): (8.28) The above argument gives us the time dependence of |$\Lambda _t^{a_1}(x)$|. Further, this procedure suggests the following form for u: (8.29a)(8.29b)
\begin{equation} \mathcal{H}=\varepsilon (2t-1)-\frac{2\gamma}{\sqrt{|\alpha_t|}}\cdot\rho, \quad \dot{\rho}=0.\label{eq8.20} \end{equation}
\begin{equation}\label{eq8.21} \dot{x}=\dot{z}^*z+z^*\dot{z}=-2\gamma(1-\alpha_t x)\cdot u . \end{equation}
\begin{equation}\label{eq8.22} \dot{y}=\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\Lambda_t^{a_1}(x)}{x}\right)\cdot\dot{x}=-2\gamma\alpha_t y\cdot u, \end{equation}
\begin{equation} \dot{y}= \begin{cases} \displaystyle \mp 2\gamma\sqrt{|\alpha_t|}\cdot\frac{1}{2}(c_+-c_-)|\sinh \chi| & \quad (\alpha_t>0), \displaystyle \mp 2\gamma\sqrt{|\alpha_t|}\cdot\frac{1}{2}(c_+-c_-)|\sin \chi| & \quad (\alpha_t<0). \end{cases}\label{eq8.23} \end{equation}
\begin{equation}\label{eq8.24} \dot{y}= \begin{cases} \displaystyle +\frac{1}{2}(c_+-c_-)\sinh \chi\cdot \dot{\chi} & \quad (\alpha_t>0), \displaystyle -\frac{1}{2}(c_+-c_-)\sin \chi\cdot\dot{\chi} & \quad (\alpha_t<0). \end{cases} \end{equation}
\begin{align} \dot{\chi}&=\mp 2\gamma\sqrt{|\alpha_t|}\cdot\frac{|\sinh \chi|}{\sinh \chi} = \begin{cases} \mp 2\gamma\sqrt{|\alpha_t|} & \quad {\mathrm{for}} \ \chi>0 \\ \pm 2\gamma\sqrt{|\alpha_t|} & \quad {\rm for} \ \chi<0 \end{cases}\quad (\alpha_t>0),\label{eq8.25a}\\\end{align}
\begin{align} \dot{\chi}&=\pm 2\gamma\sqrt{|\alpha_t|}\cdot\frac{|\sin \chi|}{\sin \chi} = \begin{cases} \pm 2\gamma\sqrt{|\alpha_t|} & \quad {\rm for} \ \chi>0 \\ \mp 2\gamma\sqrt{|\alpha_t|} & \quad {\rm for} \ \chi<0 \end{cases}\quad (\alpha_t<0).\label{eq8.25b} \end{align}
\begin{equation} {\mathrm{(i)}}\quad \chi =\chi_+=+2\gamma\sqrt{|\alpha_t|}\cdot \tau +\chi_+^0,\label{eq8.26a}\end{equation}
\begin{equation} {\rm (ii)}\quad \chi =\chi_-=-2\gamma\sqrt{|\alpha_t|}\cdot \tau -\chi_-^0.\label{eq8.26b} \end{equation}
\begin{equation} \cosh \chi_+=\cosh (2\gamma\sqrt{|\alpha_t|}\cdot\tau+\chi_+^0), \quad \cosh \chi_-=\cosh (2\gamma\sqrt{|\alpha_t|}\cdot\tau+\chi_-^0).\label{eq8.27} \end{equation}
\begin{equation} \dot{\chi}=+2\gamma\sqrt{|\alpha_t|}, \quad{\mathrm{i.e.,}}\quad \chi=2\gamma\sqrt{|\alpha_t|}\cdot \tau+\chi^0 \quad (\chi^0\, : \, {\rm constant}).\label{eq8.28} \end{equation}
\begin{equation} u=\frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{\sqrt{t^2+\rho^2}\sinh \chi}{t+\sqrt{t^2+\rho^2}\cosh \chi} \quad (\alpha_t>0),\label{eq8.29a} \end{equation}
\begin{equation} u=\frac{1}{\sqrt{|\alpha_t|}}\cdot\frac{\sqrt{t^2-\rho^2}\sin \chi}{t+\sqrt{t^2-\rho^2}\cos \chi} \quad (\alpha_t<0).\label{eq8.29b} \end{equation}
9. Various properties of |$\Lambda _t^{a_2}(x)$| for describing its time-dependence – general arguments
The aim of this section is to formulate the case |$\Lambda _t^{a_2}(x)$|. In order to make the discussion in parallel to the case |$\Lambda _t^{a_1}(x)$|, it may be inconvenient for formulating the case |$\Lambda _t^{a_2}(x)$| to use the variables z, |$z^*$|, and x used in the case |$\Lambda _t^{a_1}(x)$|. The three variables are denoted by |$z'$|, |$z'{}^*$|, and |$x'$|, respectively: (9.1) In the new notations for the variables, the relations (7.17) and (7.18) are expressed as (9.2)(9.3) We redefine z, |$z^*$|, and x in the following form: (9.4) In the new variables, we have (9.5) It may be important to see that the range for x is the same as that in the case |$\Lambda _t^{a_1}(x)$|.
\begin{equation} z\rightarrow z', \quad z^*\rightarrow z'{}^*, \quad x\rightarrow x', \quad {\mathrm{i.e.,}}\quad x'=|z'|^2.\label{eq9.1} \end{equation}
\begin{equation} \mathcal{H}=\varepsilon(2t-1)-\gamma\cdot \mathrm{i}(z'{}^*-z')\frac{\Lambda_t^{a_2}(x')}{x'},\label{eq9.2} \end{equation}
\begin{equation}\dot{z}'=-\gamma\left[ 1-\frac{z'{}^2}{x'}\left(1-\frac{\Lambda_t^{a_2}(x')}{x'\Lambda_t^{a_2}{}'(x')}\right)\right] , \quad \dot{z}'{}^*=-\gamma\left[ 1-\frac{z'{}^{*2}}{x'}\left(1-\frac{\Lambda_t^{a_2}(x')}{x'\Lambda_t^{a_2}{}'(x')}\right)\right].\label{eq9.3} \end{equation}
\begin{equation} z=\frac{\gamma_t}{z'{}^*} , \quad z^*=\frac{\gamma_t}{z'}, \quad x=|z|^2=\frac{\gamma_t^2}{x'} .\label{eq9.4} \end{equation}
\begin{equation}\label{eq9.5} \gamma_t \leq x' < \infty \longrightarrow 0\leq x \leq \gamma_t . \end{equation}
With the use of the new variables, |$\mathcal {H}$| can be rewritten as (9.6)(9.7) The relations (8.1)–(8.3) are reduced to (9.8)(9.9)(9.10) The function |$x=f_t(y')$| in the present case is given by (9.11) We can treat u in the present case under the same idea as that of the case |$\Lambda _t^{a_1}(x)$|. Since |$u^2=x-v^2 \geq 0$|, we have the following inequality: (9.12) i.e., (9.13)(9.14)
\begin{equation} \mathcal{H}=\varepsilon (2t-1)-\gamma\cdot \mathrm{i}(z^*-z)\frac{\Lambda_t^{a_2}(\frac{\gamma_t^2}{x})}{\gamma_t},\label{eq9.6} \end{equation}
\begin{equation}\frac{\Lambda_t^{a_2}\left(\frac{\gamma_t^2}{x}\right)}{\gamma_t}=2\Omega_0 \left(\frac{\gamma_t^2-\left(\beta_t+\frac{1}{2\Omega_0}\right)x}{\gamma_t^2-\beta_t x}\right). \label{eq9.7} \end{equation}
\begin{gather} \mathrm{i}(z^*-z)\frac{\Lambda_t^{a_2}\left(\frac{\gamma_t^2}{x}\right)}{\gamma_t}=2\kappa ,\label{eq9.8} \end{gather}
\begin{gather} \mathrm{i}(z^*-z)=2v ,\label{eq9.9} \end{gather}
\begin{gather} v=\frac{\kappa}{y'}, \quad y'=\frac{\Lambda_t^{a_2}\left(\frac{\gamma_t^2}{x}\right)}{\gamma_t}.\label{eq9.10} \end{gather}
\begin{equation} x=f_t(y')=\frac{\gamma_t^2(2\Omega_0-y')}{\beta_t(2\Omega_0-y')+1}.\label{eq9.11} \end{equation}
\begin{equation} \frac{\gamma_t^2}{\beta_t}\cdot\frac{y'{}^2(y'-2\Omega_0)}{y'-\left(2\Omega_0+\frac{1}{\beta_t}\right)} \geq \kappa^2,\label{eq9.12} \end{equation}
\begin{align} w'&= \begin{cases} \displaystyle +\frac{y'{}^2(y'-2\Omega_0)}{y'-\left(2\Omega_0+\frac{1}{|\beta_t|}\right)} \geq \sigma^2 &\quad (\beta_t >0), \\ \displaystyle -\frac{y'{}^2(y'-2\Omega_0)}{y'-\left(2\Omega_0-\frac{1}{|\beta_t|}\right)} \geq \sigma^2 &\quad (\beta_t <0), \end{cases}\label{eq9.13} \end{align}
\begin{equation} \sigma=\frac{\sqrt{|\beta_t|}}{\gamma_t}\kappa , \qquad \dot{\sigma}=0 .\label{eq9.14} \end{equation}
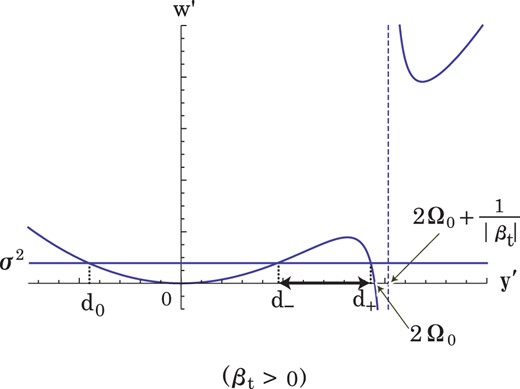
Fig. 4.
The behavior of the relation (9.13) for |$\beta _t>0$| is depicted. Here, |$\Omega _0=19/2$| and |$t=5/2$| are adopted, which lead to |$\beta _t=(14-15/\sqrt {57})/19 \approx 0.632\, (>0)$|.
The case |$\gamma _t=0$| appears in |$2t-1=2\Omega _0$| and, later, we will consider this case. The behavior of the relation (9.13) for |$\beta _t>0$| is depicted in Fig. 4. In Fig. 4, we can find out the relation (9.15) Therefore, the same idea as that shown in relation (8.13) for |$\alpha _t<0$| can be adopted: (9.16a) Here, |$\psi $| denotes a new parameter and, later, the explicit forms of |$d_{\pm ,0}$| will be shown. In order to treat the |$\beta _t<0$|, some comments are necessary. As was shown in the relations (6.26) and (6.27), in the present case |$\beta _t<0$| appears only in the three cases: Later, we will consider case (iii) separately. Cases (i) and (ii) give us |$2\Omega _0-1/|\beta _t|<0$| and |$2\Omega _0-1/|\beta _t|=0$|, respectively. The behavior of the relation (9.13) for |$\beta _t<0$| is depicted in Fig. 5(a) and (b), separately. We can see that the parametrization of the above case is the same as shown in relation (9.16a): (9.16b) In Sect. 11, we will discriminate between the former (9.16a) and the latter (9.16b) in terms of the notations |$y'_+$| and |$y'_-$|.
\begin{equation}\label{eq9.15} d_- \leq y' \leq d_t, \quad {\mathrm{i.e.,}}\quad \frac{1}{2}(d_++d_-)-\frac{1}{2}(d_+-d_-) \leq y' \leq \frac{1}{2}(d_++d_-)+\frac{1}{2}(d_+-d_-). \end{equation}
\begin{equation} y'=\frac{1}{2}(d_++d_-)+\frac{1}{2}(d_+-d_-)\cos \psi \quad (\beta_t>0).\label{eq9.16a} \end{equation}
\begin{align} {\mathrm{(i)}}\quad t&=\Omega_0-\frac{1}{2}\ \left(\beta_{\Omega_0-1/2}=-\frac{1}{2\Omega_0} \left(\frac{1-\frac{1}{\Omega_0}}{\left[2-\frac{1}{\Omega_0}\right]^{\frac{1}{2}}+1} \right) , \quad \gamma_{\Omega_0-1/2}=\frac{1}{\Omega_0}\right) ,\nonumber\\ {\rm (ii)}\quad t&=\Omega_0\ \left(\beta_{\Omega_0}=-\frac{1}{2\Omega_0} , \quad \gamma_{\Omega_0}=\frac{1}{2\Omega_0}\right),\nonumber\\ {\rm (iii)}\quad t&=\Omega_0+\frac{1}{2}\ \left(\beta_{\Omega_0+1/2}=-\frac{1}{2\Omega_0} , \quad \gamma_{\Omega_0+1/2}=0\right).\nonumber \end{align}
\begin{equation} y'=\frac{1}{2}(d_++d_-)+\frac{1}{2}(d_+-d_-)\cos \psi \quad (\beta_t<0).\label{eq9.16b} \end{equation}
Fig. 5.
The behavior of the relation (9.13) for |$\beta _t<0$| is depicted in the cases (a) |$2\Omega _0-1/|\beta _t|<0$| and (b) |$2\Omega _0-1/|\beta _t|=0$|, separately. Here, in (a), |$\Omega _0=19/2$| and |$t=18/2$| are adopted which lead to |$\beta _t=(1-6/\sqrt {19})/19 \approx -0.0198\ (<0)$| and |$2\Omega _0-1/|\beta _t|\approx -31.466\ (<0)$|. In (b), |$\Omega _0=19/2$| and |$t=19/2$| are adopted which lead to |$\beta _t=-1/19\ (<0)$| and |$2\Omega _0-1/|\beta _t|=0$|.
By equating both sides of the relation (9.13), we derive the following cubic equation: (9.17a)(9.17b) Three real solutions of Eq. (9.17) give us |$d_{\pm ,0}$|: (9.18a)(9.18b) Here, |$\theta $| (|$0\leq \theta \leq \pi $|) denotes a parameter which satisfies (9.19a)(9.19b)(9.19c) The relations (6.26) and (6.27) support the inequality (9.19c). The above three quantities |$d_{\pm ,0}$| satisfy (9.20) With the use of relation (9.18), we have the following expression: (9.21a)(9.21b) By substituting the above result (9.21) into the relation (9.16), we are able to obtain |$y'$| as a function of |$\cos \psi $|.
\begin{equation} y'{}^3-2\Omega_0 y'{}^2-\sigma^2y'+\sigma^2\left(2\Omega_0+\frac{1}{|\beta_t|}\right)=0 \quad (\beta_t>0),\label{eq9.17a} \end{equation}
\begin{equation} -y'{}^3+2\Omega_0 y'{}^2-\sigma^2y'+\sigma^2\left(2\Omega_0-\frac{1}{|\beta_t|}\right)=0 \quad (\beta_t<0).\label{eq9.17b} \end{equation}
\begin{align} d_+&=\frac{2}{3}\left(\Omega_0+\sqrt{4\Omega_0^2+3\sigma^2}\cos\frac{\theta}{3}\right), \nonumber\\ d_-&=\frac{2}{3}\left(\Omega_0-\sqrt{4\Omega_0^2+3\sigma^2}\cos\left(\frac{\theta+\pi}{3}\right)\right) , \nonumber\\ d_0&=\frac{2}{3}\left(\Omega_0-\sqrt{4\Omega_0^2+3\sigma^2}\cos\left(\frac{\theta-\pi}{3}\right)\right) \quad (\beta_t>0),\label{eq9.18a} \end{align}
\begin{align} d_+&=\frac{2}{3}\left(\Omega_0+\sqrt{4\Omega_0^2-3\sigma^2}\cos\frac{\theta}{3}\right), \nonumber\\ d_-&=\frac{2}{3}\left(\Omega_0-\sqrt{4\Omega_0^2-3\sigma^2}\cos\left(\frac{\theta+\pi}{3}\right)\right), \nonumber\\ d_0&=\frac{2}{3}\left(\Omega_0-\sqrt{4\Omega_0^2-3\sigma^2}\cos\left(\frac{\theta-\pi}{3}\right)\right) \quad (\beta_t<0).\label{eq9.18b} \end{align}
\begin{equation} \cos \theta =\frac{8\Omega_0^3-9\left(\frac{3}{2|\beta_t|}+2\Omega_0\right)\sigma^2} {\left(\sqrt{4\Omega_0^2+3\sigma^2}\right)^3}\qquad {\mathrm{for}}\quad \beta_t>0,\label{eq9.19a} \end{equation}
\begin{equation} \cos \theta =\frac{8\Omega_0^3-9\left(\frac{3}{2|\beta_t|}-2\Omega_0\right)\sigma^2} {\left(\sqrt{4\Omega_0^2-3\sigma^2}\right)^3}\qquad {\rm for}\quad \beta_t<0, \label{eq9.19b} \end{equation}
\begin{equation} \frac{3}{2|\beta_t|}-2\Omega_0 >0 \qquad {\rm for}\quad \beta_t<0 .\label{eq9.19c} \end{equation}
\begin{equation} d_++d_-+d_0=2\Omega_0.\label{eq9.20} \end{equation}
\begin{align} \frac{1}{2}(d_++d_-)&=\frac{1}{3}\left(2\Omega_0+\sqrt{4\Omega_0^2+3\sigma^2}\cos \left(\frac{\pi-\theta}{3}\right)\right) ,\nonumber\\ \frac{1}{2}(d_+-d_-)&=\frac{1}{\sqrt{3}}\sqrt{4\Omega_0^2+3\sigma^2}\sin \left(\frac{\pi-\theta}{3}\right)\quad (\beta_t>0),\label{eq9.21a} \end{align}
\begin{align} \frac{1}{2}(d_++d_-)&=\frac{1}{3}\left(2\Omega_0+\sqrt{4\Omega_0^2-3\sigma^2}\cos \left(\frac{\pi-\theta}{3}\right)\right),\nonumber\\ \frac{1}{2}(d_+-d_-)&=\frac{1}{\sqrt{3}} \sqrt{4\Omega_0^2-3\sigma^2}\sin \left(\frac{\pi-\theta}{3}\right)\quad (\beta_t<0).\label{eq9.21b} \end{align}
With the use of |$y'$|, we have the expressions for |$x'$| and |$\Lambda _t^{a_2}(x')$| in the form (9.22)(9.23) The relation (9.22) is applicable in the range |$\gamma _t \leq x' < \infty $|; this point will be discussed in Sect. 10. In the relation (9.16), |$y'$| is given as a function of |$\cos \psi $|. Therefore, if the time dependence of |$\psi $| is determined, we have the time dependence of |$\Lambda _t^{a_2}(x')$|. Concerning this point, we can see that in the case |$\gamma _t=0$|, |$\Lambda _t^{a_2}(x')$| vanishes. This is quite natural and the reason is simple: The case |$\gamma _t=0$| gives us the relation |$2t-1=2\Omega _0$| and the relations (4.21) and (5.17) suggest that this case corresponds to the maximum seniority number, that is, there does not exist the possibility of the creation of the Cooper pair.
\begin{equation} x'=\frac{\gamma_t^2}{x}=\beta_t+\frac{1}{2\Omega_0-y'},\label{eq9.22} \end{equation}
\begin{equation} \Lambda_t^{a_2}(x')=\Lambda_t^{a_2}\left(\frac{\gamma_t^2}{x}\right)=\gamma_t y' .\label{eq9.23} \end{equation}
Let us investigate the time dependence of |$\psi $|. The basic idea is the same as that in the case |$\Lambda _t^{a_1}(x)$|. First, we notice that the relation (9.3) can be rewritten as follows: (9.24) Here, of course, |$x'=\gamma _t^2/x$|. Then, we can calculate |$\dot {x}$|: (9.25) Similar to the case of |$\Lambda _t^{a_1}(x)$|, u is obtained in the form (9.26) Here, it is noted that in the case |$2\Omega _0-1/|\beta _t|=0$|, |$d_0=0$| and it corresponds to the situation shown in Fig. 5(b). The relations (9.10) and (9.25) lead to the following form for |$\dot {y}'$|: (9.27) By substituting the quantity u shown in the relation (9.26), |$\dot {y}'$| is obtained. On the other hand, the result (9.16) gives us (9.28) Equating the expressions (9.27) and (9.28) and treating the double sign |$\pm $| in the same way as in the case |$\Lambda _t^{a_1}(x)$|, we obtain |$\dot {\psi }$| in the following form: (9.29) Here, we used the relation (9.20). By solving the differential equation (9.29), we obtain |$\psi $| as a function of |$\tau $|. But, in spite of simple form, the exact solution may be impossible to obtain in analytical form except for the following two cases: (1) |$d_+=d_-$| for |$\beta _t >0$| and |$\beta _t < 0$|, and (2) |$\Omega _0-(3/2)\cdot d_0=1/|\beta _t|-(\Omega _0+d_0/2)$|. Case (2) corresponds to Fig. 5(b). Therefore, we must search for a reasonable approximation for the solution.
\begin{equation} \dot{z}=\frac{\gamma}{\gamma_t}\left[z^2-x\left(1-\frac{\Lambda_t^{a_2}(x')}{x'\Lambda_t^{a_2}{}'(x')}\right)\right],\quad \dot{z}^*=\frac{\gamma}{\gamma_t}\left[z^{*2}-x\left(1-\frac{\Lambda_t^{a_2}(x')}{x'\Lambda_t^{a_2}{}'(x')}\right)\right].\label{eq9.24} \end{equation}
\begin{equation} \dot{x}=\dot{z}^* z+z^*\dot{z} =2\gamma\cdot\frac{x^2}{\gamma_t^3}\cdot\frac{\Lambda_t^{a_2}(x')}{\Lambda_t^{a_2}{}'(x')}\cdot u .\label{eq9.25} \end{equation}
\begin{equation} u= \begin{cases} \displaystyle \pm\frac{\gamma_t}{\sqrt{|\beta_t|}}\cdot\frac{1}{y'} \sqrt{(d_+-y')(y'-d_-)}\cdot \left(\frac{y'-d_0}{(2\Omega_0+\frac{1}{|\beta_t|})-y'}\right)^{\frac{1}{2}} & \quad (\beta_t>0), \\ \displaystyle \pm\frac{\gamma_t}{\sqrt{|\beta_t|}}\cdot\frac{1}{y'} \sqrt{(d_+-y')(y'-d_-)}\cdot \left(\frac{y'-d_0}{y'-(2\Omega_0-\frac{1}{|\beta_t|})}\right)^{\frac{1}{2}} & \quad (\beta_t<0). \end{cases}\label{eq9.26} \end{equation}
\begin{equation} \dot{y}'=-\frac{2\gamma}{\gamma_t}y'\cdot u .\label{eq9.27} \end{equation}
\begin{equation} \dot{y}'=-\frac{1}{2}(d_+-d_-)\sin \psi \cdot \dot{\psi} .\label{eq9.28} \end{equation}
\begin{equation} \dot{\psi}= \begin{cases} \displaystyle \frac{2\gamma}{\sqrt{|\beta_t|}} \left(\frac{(\Omega_0-\frac{3}{2}d_0)+\frac{1}{2}(d_+-d_-)\cos \psi} {\frac{1}{|\beta_t|}+(\Omega_0+\frac{1}{2}d_0)-\frac{1}{2}(d_+-d_-)\cos \psi}\right)^{\frac{1}{2}} &\quad (\beta_t>0), \\ \displaystyle \frac{2\gamma}{\sqrt{|\beta_t|}} \left(\frac{(\Omega_0-\frac{3}{2}d_0)+\frac{1}{2}(d_+-d_-)\cos \psi} {\frac{1}{|\beta_t|}-(\Omega_0+\frac{1}{2}d_0)+\frac{1}{2}(d_+-d_-)\cos \psi}\right)^{\frac{1}{2}} &\quad (\beta_t<0). \end{cases}\label{eq9.29} \end{equation}
010. Various properties of |$\Lambda _t^{a_2}(x)$| for describing its time-dependence – procedure for the application
Let us consider a guide to the approximation for the differential equation (9.29). We start in rewriting this equation: (10.1a)(10.1b) Here, |$\mathcal {J}$|, |$A_{\pm }$|, and |$B$| are defined as (10.2a) Using relation (9.20) and Figs. 4 and 5, we can show that |$A_{\pm }$| and |$B$| obey the inequality (10.2b) The expression (10.1) can be regarded as the total energy |$E_{\pm }$| with the kinetic energy |$\mathcal {J}\dot {\psi }^2/2$| and the potential energy |$V_{\pm }(\psi)$|. With the aid of the inequality (10.2b), we can prove the following relation: (10.3) Therefore, if the angle variable |$\psi $| changes continuously in the range |$-\infty < \psi < \infty $|, the present case can be understood in terms of rotational motion with moment of inertia |$\mathcal {J}$| and periodically changing angular velocity. However, in the present case, |$\psi $| does not change continuously, because the original variable |$x'$| changes in the range |$\gamma _t \leq x' <\infty $| and the other x in the range |$0 \leq x \leq \gamma _t$|. The relation (9.22) suggests that for certain angles, denoted as |$\psi ^c$|, the variable |$\psi $| should obey the condition (10.4) This means that any result derived from the relation (10.1) in the range |$-1\leq \cos \psi \leq \cos \psi ^c$| is meaningless. This range is treated in relation to the variable |$\chi $| discussed in Sect. 8. In this sense, the quantity |$\cos \psi ^c$| plays an essential role in our treatment. Including the value of |$\cos \psi ^c$|, the detail will be considered in Sect. 11. This is illustrated in Fig. 6 for the range |$-\pi \lesssim \psi \lesssim \pi $|. The longitudinal axis represents |$v_{\pm }(\psi)$| defined as (10.5a)(10.5b) Hereafter, we will treat the angle |$\psi $| in the range (10.6)
\begin{equation} \frac{1}{2}\mathcal{J}\dot{\psi}^2+V_+(\psi)=E_+ , \quad V_+(\psi)=-\frac{A_++B}{A_+-\cos\psi} , \quad E_+=-1 \ (\beta_t>0),\label{eq10.1a}\end{equation}
\begin{equation} \frac{1}{2}\mathcal{J}\dot{\psi}^2+V_-(\psi)=E_- , \quad V_-(\psi)=+\frac{A_--B}{A_-+\cos\psi} , \quad E_-=+1 \ (\beta_t<0).\label{eq10.1b} \end{equation}
\begin{equation} \mathcal{J}=\frac{|\beta_t|}{2\gamma^2}, \quad A_{\pm}=\frac{\frac{2}{|\beta_t|}\pm (2\Omega_0+d_0)}{d_+-d_-}, \quad B=\frac{2\Omega_0-3d_0}{d_+-d_-}.\label{eq10.2a} \end{equation}
\begin{equation} A_{\pm}>1, \quad B>1, \quad A_->B.\label{eq10.2b} \end{equation}
\begin{equation} V_{\pm}(\psi)<E_{\pm} \quad (-1 \leq \cos\psi \leq 1).\label{eq10.3} \end{equation}
\begin{equation} \cos\psi^c \leq \cos \psi \leq 1 .\label{eq10.4} \end{equation}
\begin{equation} v_{\pm}(\psi)=\mp\frac{1}{A_{\pm}\mp \cos\psi}, \quad v_{\pm}(-\psi)=v_{\pm}(\psi) .\label{eq10.5a} \end{equation}
\begin{equation} v_{\pm}(\psi)=\mp\frac{1}{A_{\pm}\mp \cos \psi},\quad v_{\pm}(-\psi)=v_{\pm}(\psi) .\label{eq10.5b} \end{equation}
\begin{equation} -\pi \leq \psi \leq \pi .\label{eq10.6} \end{equation}
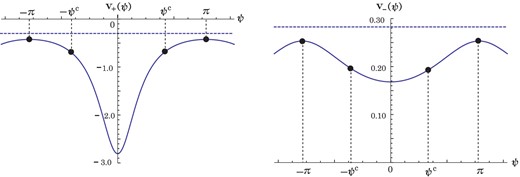
Fig. 6.
The figure shows |$v_{\pm }(\psi)$| as function of |$\psi $| in the range |$-\pi \leq \psi \leq \pi $|. The horizontal dotted line corresponds to |$E_{\pm }/(A_{\pm }\pm B)$||$(E_{\pm }=\mp 1)$|.
Let us present an idea for the approximation of |$v_{\pm }(\psi)$|, which will be adopted in this paper. Needless to say, we seek a possible approximation in the range (10.7) But, for the time being, forgetting the range (10.7), |$\psi $| is treated in the range (10.6). The behavior of |$v_{\pm }(\psi)$| is illustrated in Fig. 6. In order to understand this behavior more precisely, we take up the first and the second derivative of |$v_{\pm }(\psi)$| for |$\psi $|, |$v_{\pm }'(\psi)$|, and |$v''_{\pm }(\psi)$|: (10.8a)(10.8b) Since |$V_{\pm }(\psi)$| represents the potential energy, the force |$F_{\pm }(\psi)$| acting on the present system is given in the form (10.9)
\begin{equation} -\psi^c \leq \psi \leq \psi^c, \quad 0 \leq \psi^c \leq \pi .\label{eq10.7} \end{equation}
\begin{equation} v_{\pm}'(\psi)=\frac{\sin \psi}{(A_{\pm}\mp \cos\psi)^2} ,\label{eq10.8a} \end{equation}
\begin{equation} v_{\pm}''(\psi)=\pm \frac{\cos^2\psi \pm A_{\pm}\cos\psi -2}{(A_{\pm}\mp \cos \psi)^3} .\label{eq10.8b} \end{equation}
\begin{equation} F_{\pm}(\psi)=-\frac{\mathrm{d}V_{\pm}(\psi)}{\mathrm{d}\psi}=-(A_{\pm}\pm B)\cdot v_{\pm}'(\psi) .\label{eq10.9} \end{equation}
Fig. 7.
The figure shows |$v'_{\pm }(\psi)$| as function of |$\psi $| in the range |$0 \leq \psi \leq \pi $|.
Therefore, we can learn the characteristics of |$F_{\pm }(\psi)$| through |$v_{\pm }'(\psi)$|. Since |$F_{\pm }(-\psi)$|, i.e., |$v_{\pm }'(-\psi)=-v_{\pm }'(\psi)$|, it may be enough to investigate |$v_{\pm }'(\psi)$| in the range |$0\leq \psi \leq \pi $|. Its behavior is shown in Fig. 7. The angle |$\psi ^d$| gives us the maximum value of |$v_{\pm }'(\psi)$| and its value is determined by |$v_{\pm }''(\psi)=0$|: (10.10) The flectional point of |$v_{\pm }(\psi)$| is given by |$\psi ^d$| and we have the following:
\begin{equation} \cos\psi^d=\pm\frac{1}{2}\left(\sqrt{A_{\pm}^2+8}-A_{\pm}\right).\label{eq10.10} \end{equation}
|$v_{\pm }'(\psi)$| is increasing in the range |$\psi < \psi ^d$|,
|$v_{\pm }'(\psi)$| is decreasing in the range |$\psi >\psi ^d$|.
The above two cases and the relation |$F_{\pm }(-\psi)=F_{\pm }(\psi)$| teach us that the force under consideration is attractive for the point, the center of the force and as |$|\psi |$| increases, the strength of the force increases in case (i) and decreases in case (ii). This indicates that the property of the force is transformed at |$\psi =\psi ^d$|. The above is a distinctive feature of |$F_{\pm }(\psi)$|. With this feature in mind, we consider the approximation of |$v_{\pm }(\psi)$| through |$v_{\pm }'(\psi)$|.
In order to obtain the idea, first, we must introduce the angle |$\psi ^c$| into the above argument. In the case |$v_+'(\psi)$|, we have two possibilities, which are illustrated in Fig. 8. As is clear from the relation (10.7), the force |$F_+(\psi)$| has its meaning for the solid curve OC. Our idea may be the simplest and it is summarized as follows: (a) In the case (a), the curves OD and DC are replaced with the straight lines OD and DC. (b) In the case (b), the curve OC is replaced with the straight line OC. The above scheme is also applicable to the case |$v_-'(\psi)$|. It should be noted that the above approximation preserves the distinctive feature of |$F_{\pm }(\psi)$| already mentioned, and the values of |$v_{\pm }'(\psi)$| at |$\psi =0$|, |$\psi ^d$|, and |$\psi ^c$|. By adopting the symbol |$v_{\pm }^a(\psi)$| for the approximate form of |$v_{\pm }(\psi)$|, the above idea is formulated as follows: (10.11a)(10.11b)(10.12)
\begin{equation} {\mathrm{(a)}}\quad v_{\pm}^{a}{}'(\psi) = -w_{\pm}^{cd}\cdot(\psi-\psi^c) +v_{\pm}'(\psi^c) \quad \left(w_{\pm}^{cd}=-\frac{v_{\pm}'(\psi^c)-v_{\pm}'(\psi^d)}{\psi^c-\psi^d}\right)\quad {\rm (DC)},\label{eq10.11a}\end{equation}
\begin{equation} v_{\pm}^{a}{}'(\psi) =w_{\pm}^d\cdot\psi \quad \left(w_{\pm}^d=\frac{v_{\pm}'(\psi^d)}{\psi^d}\right)\quad {\rm (OD)},\label{eq10.11b} \end{equation}
\begin{equation} {\rm (b)}\quad v_{\pm}^a{}'(\psi)=w_{\pm}^c\cdot\psi \quad\left(w_{\pm}^c=\frac{v_{\pm}'(\psi^c)}{\psi^c}\right)\quad {\rm (OC)}.\label{eq10.12} \end{equation}
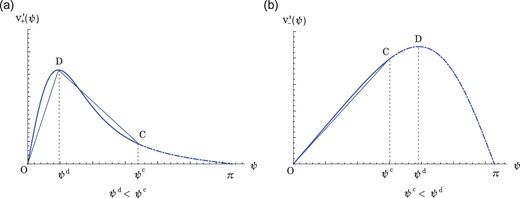
Fig. 8.
The figure shows |$v'_{\pm }(\psi)$| as function of |$\psi $| in the range |$0 \leq \psi \leq \pi $|. The solid curves and dot-dashed curves represent the exact results. The thin lines represent the approximate ones. (a) The parameters are taken as |$\kappa =-15/2$|, |$t=5/2$|, and |$\Omega _0=19/2$|. Here, |$\alpha _t\approx 0.7656\ (>0) $| and |$\beta _t\approx 0.6323\ (>0)$| are derived. Also, |$A_+\approx 1.3564$|, |$\psi ^c\approx 1.7123$|, and |$\psi ^d\approx 0.4729$| are obtained. (b) The parameters are taken as |$\kappa =-1$|, |$t=18/2$|, and |$\Omega _0=19/2$|. In this parameter set, |$\alpha _t\approx -6.0384\ (<0) $| and |$\beta _t\approx -0.0198\ (<0)$| are derived. Here, |$A_-\approx 4.9493$|, |$\psi ^c\approx 1.4877$|, and |$\psi ^d\approx 1.9558$| are obtained.
Naturally, the relations (10.11) and (10.12) give us (10.13) By integrating the relations (10.11) and (10.12), we are able to obtain the approximate form of |$v_{\pm }(\psi)$|, |$v_{\pm }^a(\psi)$|.
\begin{equation} v_{\pm}^a{}'(0)=v_{\pm}'(0) , \quad v_{\pm}^a{}'(\psi^d)=v_{\pm}'(\psi^d) , \quad v_{\pm}^a{}'(\psi^c)=v_{\pm}'(\psi^c) .\label{eq10.13} \end{equation}
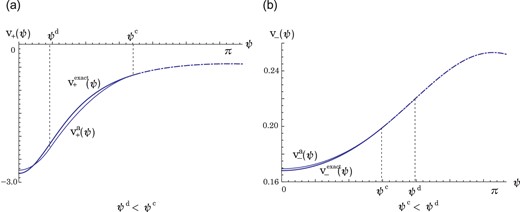
Fig. 9.
The figure shows |$v_{\pm }(\psi)$| as function of |$\psi $| in the range |$0 \leq \psi \leq \pi $|. The solid and dot-dashed curves represent the exact results. The thin curves represent the approximate ones. The parameters are the same ones used in Fig. 8.
For the integration, we require the condition (10.14) As was already mentioned, the angle |$\psi ^c$| plays the role of the doorway to the range treated by |$\chi $|. Therefore, for obtaining |$v_{\pm }^a(\psi)$|, consideration of the behavior of |$v_{\pm }(\psi)$| at |$\psi =\pm \psi ^c$| and the neighboring region should be prior to any other region. The above consideration suggests the condition (10.14). By integrating (10.11a) under the condition (10.14), we have the following expression for |$v_{\pm }^a(\psi)$|: (10.15a) If we require that, at |$\psi =\psi ^d$|, the value of |$v_{\pm }^a(\psi)$| from the side OD agrees with that from the side DC for the relation of (10.11b), we obtain the expression (10.15b) The above requirement may be acceptable, because the present system conserves the energy. For case (b), the condition (10.12) gives us the following expression: (10.16) By replacing |$\psi $| with |$-\psi $|, we have expressions in the range |$-\psi ^c\leq \psi \leq 0$|. Thus, we have obtained the approximate expressions of |$v_{\pm }(\psi)$| in our scheme. It should be noted that, owing to the approximation, we are forced to have |$v_{\pm }^a(0)\neq v_{\pm }(0)$|, and |$v_{\pm }^a(\psi ^d)\neq v_{\pm }(\psi ^d)$|. In Fig. 9, the solid and dot-dashed curves represent the exact |$v_{\pm }(\psi)$|. Under the idea formulated by (10.11)–(10.13), the approximate |$v_{\pm }^a(\psi)$| are obtained and are shown by thin curves. Figure 9 shows that the |$v_{\pm }^a(\psi)$| represent a good approximation for the exact result in the range |$-\psi ^c \leq \psi \leq \psi ^c$| under consideration.
\begin{equation} v_{\pm}^a(\psi^c)=v_{\pm}(\psi^c) .\label{eq10.14} \end{equation}
\begin{equation} v_{\pm}^a(\psi) = -\frac{1}{2}w_{\pm}^{cd}\cdot (\psi-\psi^c)^2 +v_{\pm}'(\psi^c)\cdot(\psi-\psi^c)+v_{\pm}(\psi^c)\ {\mathrm{(DC)}}.\label{eq10.15a} \end{equation}
\begin{equation} v_{\pm}^a(\psi)=\frac{1}{2}w_{\pm}^d\cdot(\psi^2-\psi^d{}^2) -\frac{1}{2}(v_{\pm}'(\psi^c)+v_{\pm}'(\psi^d))\cdot(\psi^c-\psi^d)+v_{\pm}(\psi^c) \ {\mathrm{(OD)}}.\label{eq10.15b} \end{equation}
\begin{equation} v_{\pm}^a(\psi)=\frac{1}{2}w_{\pm}^c(\psi^2-\psi^c{}^2) +v_{\pm}(\psi^c) \quad {\rm (OC)}.\label{eq10.16} \end{equation}
Finally, we will sketch the approximate solution of |$\psi $| as a function of |$\tau $|. The relation (10.1) leads us to the following approximate expression for |$\dot {\psi }$|: (10.17) For |$v_{\pm }^a(\psi)$|, the relations (10.15) and (10.16) must be used. As can be seen in the forms (10.15) and (10.16), the potential energy is expressed as a quadratic function of |$\psi $|. For the coefficients of |$\psi ^2$|, we have the inequalities (10.18) Therefore, |$\psi $| can be simply expressed in the form (10.19a)(10.19b) Then, our problem is reduced to determining the coefficients |$(\mathcal {A}_h, \omega _h,\alpha _h,\mathcal {B}_h)$| and |$(\mathcal {A}_n, \omega _n,\alpha _n,\mathcal {B}_n)$|. In next section, some examples will be given.
\begin{equation} \dot{\psi}= \left[\frac{2}{\mathcal{J}}(E_{\pm}-(A_{\pm}\pm B)v_{\pm}^a(\psi))\right]^{\frac{1}{2}}.\label{eq10.17} \end{equation}
\begin{equation} w_{\pm}^{cd}> 0 , \quad w_{\pm}^d > 0 , \quad w_{\pm}^c >0 .\label{eq10.18} \end{equation}
\begin{equation} \psi(\tau)=\psi_h(\tau)=\mathcal{A}_h\sinh (\omega_h\tau+\alpha_h)+\mathcal{B}_h \quad {\mathrm{(CD)}},\label{eq10.19a} \end{equation}
\begin{equation} \psi(\tau)=\psi_n(\tau)=\mathcal{A}_n\sin (\omega_n\tau+\alpha_n)+\mathcal{B}_n \quad {\rm (OD),\ (OC)}.\label{eq10.19b} \end{equation}
11. Discussion
One of the aims of this paper is to describe a simple many-fermion model obeying the pseudo-su(1,1) algebra in terms of the time-dependent variational method. In this description, the function |$\Lambda _t(x)$| plays a central role. For its original form, we adopted an approximate form which consists of two parts: |$\Lambda _t^{a_1}(x)$| for |$0\leq x \leq \gamma _t$| and |$\Lambda _t^{a_2}(x')$| for |$\gamma _t \leq x' <\infty $|. Treating both parts independently in Sects. 8 and 9, we derived various features induced by these two functions. Therefore, it is inevitable to investigate the connection between the results derived from the two forms. To this end, it may be convenient to discuss the connection under four categories, although they are correlated with one another.
The first is related to constants of motion. We have already mentioned that t is one of them, i.e., common to the two parts. The others are |$\rho $| in the range |$0\leq x \leq \gamma _t$| and |$\sigma $| in the range |$\gamma _t \leq x' < \infty $|, shown in the relations (8.10) and (9.14), respectively. They are not independent of each other. By eliminating |$\kappa $| in both relations, we have (11.1a) As is clear from Figs. 3(b), 4 and 5, |$\rho ^2$| and |$\sigma ^2$| have maximum values. On the other hand, Fig. 3(a) shows that in this case, formally, |$\rho ^2$| is permitted to become |$\infty $|. However, relation (11.1) teaches us that, in this case, the maximum value also exists, because |$\sigma ^2$| has a maximum value. For example, in the case |$\beta _t >0$|, the maximum value of |$\sigma ^2$|, |$(\sigma ^2)_{\mathrm {max}}$|, is given by (11.1b) Here, |$d_m$| denotes the value of |$y'$| which makes |$w'$| in the relation (9.13) the maximum.
\begin{equation} \sigma=\frac{1}{\gamma_t}\sqrt{\frac{|\beta_t|}{|\alpha_t|}}\cdot \rho , \quad {\mathrm{i.e.,}}\quad \sigma^2=\frac{1}{\gamma_t^2}\cdot \frac{|\beta_t|}{|\alpha_t|}\cdot \rho^2 .\label{eq11.1a} \end{equation}
\begin{equation} (\sigma^2)_{\rm max}=\frac{d_m^2(d_m-2\Omega_0)}{d_m-\left(2\Omega_0+\frac{1}{\beta_t}\right)},\quad d_m=2\Omega_0\left(1-\frac{2}{3+\sqrt{9+16\Omega_0|\beta_t|}}\right).\label{eq11.1b} \end{equation}
The ranges covered by x and |$x'$| are |$0\leq x \leq \gamma _t$| and |$\gamma _t \leq x' < \infty $|, respectively. The second category is related to these ranges. Relations (8.7) and (9.22) lead to the following inequalities: (11.2a)(11.2b) The inequality (11.2a) gives us (11.3)(11.4) Also, the inequality (11.2b) gives us (11.5) For the derivation of the inequalities (11.4) and (11.5), we used the relation (6.7). It should be noted that although |$y_+$| contains |$\cosh \chi $|, it should be finite.
\begin{equation} 0 \leq \frac{1}{\alpha_t}\left(1-\frac{2t}{y}\right) \leq \gamma_t ,\label{eq11.2a} \end{equation}
\begin{equation} \gamma_t \leq \beta_t+\frac{1}{2\Omega_0-y'} < \infty .\label{eq11.2b} \end{equation}
\begin{gather} 2t \leq y_+ \leq 2\Omega_0\left(1-\frac{1}{1+\sqrt{2t\gamma_t}}\right),\label{eq11.3} \end{gather}
\begin{gather} 2\Omega_0\left(1-\frac{1}{1+\sqrt{2t\gamma_t}}\right) \leq y_- \leq 2t . \label{eq11.4} \end{gather}
\begin{equation} 2\Omega_0\left(1-\frac{1}{1+\sqrt{2t\gamma_t}}\right) \leq y_{\pm}' \leq 2t .\label{eq11.5} \end{equation}
At the point |$x=x'=\gamma _t$|, y connects to |$y'$|. As was shown in the relations (6.19) and (6.28), y and |$y'$| consist of |$y_{\pm }$| and |$y_{\pm }'$|, respectively. Therefore, it is necessary to investigate, for example, if |$y_+$| can connect to |$y'$| or not. The third category is concerned with the above. Formally, we can find four combinations between y and |$y'$|: |$(y_+, y_+')$|, |$(y_+, y'_-)$|, |$(y_-, y'_+)$|, and |$(y_-, y'_-)$|. The relations from (6.19) to (6.28) with their interpretations lead us to the following three cases: (11.6a)(11.6b)(11.6c) If the relation |$\alpha _t < \beta _t$| is noticed, the above three cases may be understandable. The cases (i), (ii), and (iii) correspond to the combinations |$(y_+, y'_+)$|, |$(y_-, y_+')$|, and |$(y_-, y_-')$|, respectively. Therefore, |$y_+$| cannot connect with |$y_-'$|.
\begin{equation} {\mathrm{(i)}}\quad {\rm if}\quad \frac{1}{2}\leq t < t^0 , \quad 0 < \alpha_t \leq \beta_t , \quad ({\rm in\ the\ case}\ t=1/2,\ \alpha_t=\beta_t)\label{eq11.6a} \end{equation}
\begin{equation} {\rm (ii)}\quad {\rm if}\quad t^0 < t < t^0{}' , \quad \alpha_t < 0 < \beta_t , \label{eq11.6b} \end{equation}
\begin{equation} {\rm (iii)}\quad {\rm if}\quad t^0{}' < t \leq \Omega_0+\frac{1}{2} , \quad \alpha_t < \beta_t < 0 .\label{eq11.6c} \end{equation}
For the above three combinations, we show the maximum values of the squares of the constants of motion |$\kappa ^2$| introduced in the relation (8.1). The conditions |$c_+-c_-=0$| and |$d_+-d_-=0$| give us the maximum values |$\kappa _m^{(i)2}$||$(i=1, 2, 3, 4)$| for the cases (1), (2), (3), and (4) related to Figs. 3(a), 3(b), 4, and 5, respectively. With the use of these conditions, we obtain the following results: (11.7a)(11.7b)(11.7c)(11.7d) For the combination |$(y_+, y_+')$|, we choose the smaller value of |$\kappa _m^2$|, i.e., |$\kappa _m^{(3)2}$|. For the combination |$(y_-, y_+')$| and |$(y_-, y_-')$|, we choose the smaller values of |$\kappa _m^2$| for each case; |${\mathrm {min}}\{ \kappa _m^{(2)2}, \kappa _m^{(3)2}\}$| and |${\mathrm {min}}\{ \kappa _m^{(2)2}, \kappa _m^{(4)2}\}$|, respectively.
\begin{equation} {\mathrm{(1)}}\quad \kappa_m^{(1)}{}^2 \rightarrow \infty \quad (y_+;\ {\rm Fig. \,3(a)}),\label{eq11.7a} \end{equation}
\begin{equation} {\rm (2)}\quad \kappa_m^{(2)}{}^2 = \frac{t^2}{|\alpha_t|} \quad (y_-;\ {\rm Fig.\,3(b)}),\label{eq11.7b} \end{equation}
\begin{equation} {\rm (3)}\quad \kappa_m^{(3)}{}^2 = \frac{\gamma_t^2}{|\beta_t|}\cdot\frac{16\Omega_0^3}{9(4\Omega_0+\frac{3}{|\beta_t|})} \quad (y_+';\ {\rm Fig. 4}),\label{eq11.7c}\end{equation}
\begin{equation} {\rm (4)}\quad \kappa_m^{(4)}{}^2 = \frac{\gamma_t^2}{|\beta_t|}\cdot\frac{4\Omega_0^2}{3} \quad (y_-';\ {\rm Fig.\,5}).\label{eq11.7d} \end{equation}
The fourth category is related to giving the explicit expression of the connection. First, let us notice again that |$\Lambda _t^{a_1}(x)$| and |$\Lambda _t^{a_2}(x')$| should connect with each other smoothly at |$x=x'=\gamma _t$|: (11.8) The explicit expression of the relation (11.8) is presented in the relation (6.6). The first relation (11.8) and the definition of y and |$y'$| in (8.3) and (9.10) lead to (11.9) Here, |$(y)_t$| and |$(y')_t$| denote the values of y and |$y'$| at the point |$x=x'=\gamma _t$|, respectively, and, with the use of the relation (6.7), |$y_t$| is given by (11.10) The above is the connection between the results derived from the two forms.
\begin{equation} \Lambda_t^{a_1}(\gamma_t)=\Lambda_t^{a_2}(\gamma_t) , \quad \Lambda_t^{a_1}{}'(\gamma_t)=\Lambda_t^{a_2}{}'(\gamma_t) .\label{eq11.8} \end{equation}
\begin{equation} (y)_t=(y')_t\ (=y_t) .\label{eq11.9} \end{equation}
\begin{equation} y_t=2\Omega_0\left(1-\frac{1}{1+\sqrt{2t\gamma_t}}\right) .\label{eq11.10} \end{equation}
Our final task is to investigate the time evolution of |$\Lambda _t$| in the approximate form, |$\Lambda _t^a$|. The path of the evolution is illustrated in Fig. 10. The lines SC and CT correspond to |$\Lambda _t^{a_1}=(y-2t)/\alpha _t$| and |$\Lambda _t^{a_2}=\gamma _t y'$|, respectively. Here, y and |$y'$| are given in the relations (8.13) and (9.16), respectively. They depend on two constants of motion, t and |$\kappa $|. It is noted that |$\Lambda _t^a$| has minimum and maximum values which correspond to |$y=c_+$| and |$y'=d_+$|, respectively. At the point C, |$\Lambda _t^a$| changes from |$\Lambda _t^{a_1}$| to |$\Lambda _t^{a_2}$|, i.e., from y to |$y'$|, and vice versa. The dependence of |$\Lambda _t^a$| on the time |$\tau $| may be periodic. One cycle consists of four paths (S|$\rightarrow $|C, C|$\rightarrow $|T, T|$\rightarrow $|C, C|$\rightarrow $|S), which is shown in Fig. 10.
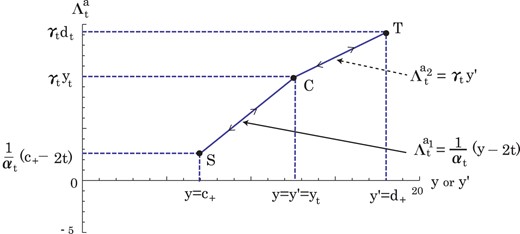
Fig. 10.
The path of the evolution is illustrated in the case of |$\Omega _0=19/2$| and |$t=5/2$|.
With the use of the relation (11.9) with (8.13) and (9.16), we have the following relations: (11.11)(11.12) Here, |$\chi ^c$| and |$\psi ^c$| denote the values of |$\chi $| and |$\psi $| at the point C, respectively. It can be seen that if |$\chi ^c$| and |$\psi ^c$| are positive, |$-\chi ^c$| and |$-\psi ^c$| also satisfy the relations (11.11) and (11.12), respectively. The angle |$\psi ^c$| is nothing but that introduced in Sect. 10. On the other hand, |$\chi $| and |$\psi $| are equal to 0 at the point S and the point T, respectively. The above consideration permits us to choose |$\chi $| and |$\psi $| including the signs of |$\chi ^c$| and |$\psi ^c$| in the form shown in Fig. 11. For the cycle (S|$\rightarrow $|C|$\rightarrow $|T|$\rightarrow $|C|$'$|(=C)|$\rightarrow $|S), it may be enough to regard |$\dot {\chi }$| and |$\dot {\psi }$| as positive, |$\dot {\chi }>0$| and |$\dot {\psi }>0$|, at any position except the point S with |$\dot {\chi }=0$| and the point T with |$\dot {\psi }=0$|. It is easily verified by |$\sinh \chi =\sin \chi =\sin \psi =0$| for |$\chi =\psi =0$|. The time derivatives |$\dot {\chi }$| and |$\dot {\psi }$| are given in the relations (8.28) and (10.17), respectively. We already mentioned that there are three cases for the combinations at the point C: |$(y_+,y'_+)$|, |$(y_+,y'_-)$|, and |$(y_-,y'_-)$|. If applying this rule to the present cycle, we obtain the following three cases:
\begin{equation} \cosh \chi^c=\frac{y_t-\frac{1}{2}(c_++c_-)}{\frac{1}{2}(c_+-c_-)}\enspace (\alpha_t>0) , \quad \cos \chi^c=\frac{y_t-\frac{1}{2}(c_++c_-)}{\frac{1}{2}(c_+-c_-)}\enspace (\alpha_t<0), \quad\label{eq11.11} \end{equation}
\begin{equation} \cos\psi^c=\frac{y_t-\frac{1}{2}(d_++d_-)}{\frac{1}{2}(d_+-d_-)}\quad (\beta_t>0 , \beta_t<0) .\label{eq11.12} \end{equation}
\begin{align} &{\mathrm{(i)}}\ \ \ \alpha_t>0\quad ({\rm S}\rightarrow {\rm C})\ , \qquad \beta_t>0\quad ({\rm C}\rightarrow {\rm T}\rightarrow {\rm C'(=C)})\ , \qquad \alpha_t>0\quad ({\rm C'}\rightarrow {\rm S})\ , \nonumber\\ &{\rm (ii)}\ \ \alpha_t>0\quad ({\rm S}\rightarrow {\rm C})\ , \qquad \beta_t<0\quad ({\rm C}\rightarrow {\rm T}\rightarrow {\rm C'(=C)})\ , \qquad \alpha_t>0\quad ({\rm C'}\rightarrow {\rm S})\ , \nonumber\\ &{\rm (iii)}\ \alpha_t<0\quad ({\rm S}\rightarrow {\rm C})\ , \qquad \beta_t<0\quad ({\rm C}\rightarrow {\rm T}\rightarrow {\rm C'(=C)})\ , \qquad \alpha_t<0\quad ({\rm C'}\rightarrow {\rm S})\ . \nonumber \end{align}
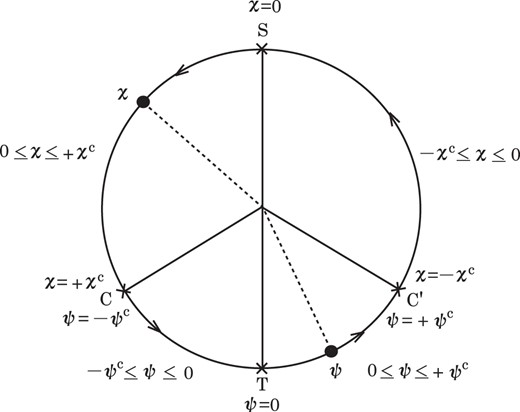
Fig. 11.
The values of |$\chi $| and |$\psi $| on each point are shown.
We take up the case where the cycle starts from the point S, that is, the initial condition is given by |$\chi ^0=0$| at |$\tau ^0=0$|. Here, |$\chi ^0$| and |$\tau ^0$| appear in the relation (8.28). In order to demonstrate our idea, we present several results derived in case (i) with |$\psi ^c >\psi ^d$|. In this case, there exists the flectional point D specified by |$\psi =\pm \psi ^d$| between C and T, and also between T and C′. Then, the path (C|$\rightarrow $|T|$\rightarrow $|C′(=C)) is decomposed into three: C|$\rightarrow $|D, D|$\rightarrow $|T, and T|$\rightarrow $|D|$'$|(=D). We discriminate between D and D|$'$| by the condition (|$\psi _D=-\psi ^d$|, |$\psi _{D'}=\psi ^d$|). General solutions of the paths (S|$\rightarrow $|C, C|$'\rightarrow $|S), (C|$\rightarrow $|D, D|$'\rightarrow $|C|$'$|) and (D|$\rightarrow $|T, T|$\rightarrow $|D′) are given by the relations (8.28), (10.19a), and (10.19b), respectively. The parameters |$(\omega _h, \mathcal {A}_h)$| and |$(\omega _n, \mathcal {A}_n)$| contained in the relation (10.19) are obtained in the form (11.13a)(11.13b)
\begin{equation} \omega_h = \left(\frac{A_++B}{\mathcal{J}}\cdot w_+^{cd}\right)^{\frac{1}{2}} ,\label{eq11.13a} \end{equation}
\begin{equation} \mathcal{A}_h= \left[\frac{2}{w_+^{cd}}\left(\frac{E_+}{A_++B}-v_+(\psi^c)\right) -\left(\frac{v_+'(\psi^c)}{w_+^{cd}}\right)^2\right]^{\frac{1}{2}}, \label{eq11.13b} \end{equation}
\begin{equation} \omega_n=\left(\frac{A_++B}{\mathcal{J}}\cdot w_+^{d}\right)^{\frac{1}{2}},\label{eq11.14a} \end{equation}
\begin{equation} \mathcal{A}_n= \left[\frac{2}{w_+^{d}}\left(\frac{E_+}{A_++B}-v_+(\psi^c)\right) +{\psi^{d}}^2+\frac{1}{w_+^d}\left(v_+'(\psi^c)+v_+'(\psi^d)\right) \left(\psi^c-\psi^d\right)\right]^{\frac{1}{2}}.\label{eq11.14b} \end{equation}
Let |$\tau ^C$|, |$\tau ^D$|, |$\tau ^T$|, |$\tau ^{D'}$|, |$\tau ^{C'}$| and |$\tau ^S$| denote the arrival, i.e., departure times at the points C, D, T, D|$'$|, C|$'$|, and S, respectively, after the cycle starts from S at the time |$\tau ^0=0$|. Then these times obey the following condition: (11.15) Under the condition (11.15), we can determine |$(\alpha _h, \mathcal {B}_h)$| and |$(\alpha _n, \mathcal {B}_n)$|, and |$\chi (\tau)$| and |$\psi (\tau)$| for each path are given in the following form: (11.16a)(11.16b)(11.16c)(11.16d)(11.16e)(11.16f) In connection with the relations (7.21) and (7.22), it was suggested that our model enables us to describe the dissipation phenomena in the many-fermion system. The paths (1) and (6) correspond to this suggestion. It indicates that this dissipation cannot be observed at any time. The condition (11.15) also gives us the time intervals for the paths: (11.17a)(11.17b)(11.17c) The results (11.17a)–(11.17c) give us |$\tau ^C$|, etc. For example, we have (11.18a)(11.18b)
\begin{equation} \begin{array}{ll} (1)\ \chi(0)=0, \quad \chi(\tau^C)=\chi^c, & (2)\ \psi_h(\tau^C)=-\psi^c, \quad \psi_h(\tau^D)=-\psi^d, \\ (3)\ \psi_n(\tau^D)=-\psi^d, \quad \psi_n(\tau^T)=0, & (4)\ \psi_n(\tau^T)=0, \quad \psi_n(\tau^{D'})=\psi^d, \\ (5)\ \psi_h(\tau^{D'})=\psi^d, \quad \psi_h(\tau^{C'})=\psi^c, & (6)\ \chi(\tau^{C'})=-\chi^c, \quad \chi(\tau^S)=0. \end{array} \label{eq11.15} \end{equation}
\begin{equation} (1)\ {\mathrm{S}}\rightarrow{\rm C}\ ; \ \chi(\tau)=2\gamma\sqrt{|\alpha_t|} \cdot\tau\ \quad (0\leq \tau \leq \tau^C), \label{eq11.16a} \end{equation}
\begin{equation} (2)\ {\rm C}\rightarrow{\rm D}\ ; \ \psi(\tau)=\mathcal{A}_h\sinh\left[\omega_h (\tau-\tau^C)+\sinh^{-1}\left(\frac{v_+'(\psi^c)}{\mathcal{A}_h w_+^{cd}}\right)\right] -\frac{v_+'(\psi^c)}{w_+^{cd}}-\psi^{c} (\tau^C\leq \tau \leq \tau^D), \label{eq11.16b} \end{equation}
\begin{equation} (3)\ {\rm D}\rightarrow{\rm T}\ ; \ \psi(\tau)=\mathcal{A}_n\sin\left[\omega_n (\tau-\tau^D)-\sin^{-1}\left(\frac{\psi^d}{\mathcal{A}_n}\right)\right]\ \quad (\tau^D \leq \tau \leq \tau^T), \label{eq11.16c} \end{equation}
\begin{equation} (4)\ {\rm T}\rightarrow{\rm D'}\ ; \ \psi(\tau)=\mathcal{A}_n\sin\left[\omega_n (\tau-\tau^T)\right]\ \quad (\tau^T \leq \tau \leq \tau^{D'}), \label{eq11.16d} \end{equation}
\begin{align} &(5)\ {\rm D'}\rightarrow{\rm C'}\ ; \ \psi(\tau)=\mathcal{A}_h\sinh\left[\omega_h (\tau-\tau^{D'})-\sinh^{-1}\left(\frac{1}{\mathcal{A}_h}\left(\psi^c-\psi^d+\frac{v_+'(\psi^c)}{w_+^{cd}}\right)\right)\right] \nonumber\\ &\qquad\qquad\qquad\qquad\qquad +\left(\psi^c-\psi^d+\frac{v_+'(\psi^c)}{w_+^{cd}}\right)+\psi^d\ \quad (\tau^{D'}\leq \tau \leq \tau^{C'}), \label{eq11.16e} \end{align}
\begin{equation} (6)\ {\rm C'}\rightarrow{\rm S}\ ; \ \chi(\tau)=2\gamma\sqrt{|\alpha_t|}\cdot(\tau-\tau^{C'})-\chi^c\ \quad (\tau^{C'} \leq \tau \leq \tau^S). \label{eq11.16f} \end{equation}
\begin{equation} \tau^S-\tau^{C'}= \tau^C=\frac{\chi^c}{2\gamma\sqrt{|\alpha_t|}},\label{eq11.17a} \end{equation}
\begin{align} \tau^{C'}-\tau^{D'}&= \tau^D-\tau^C\nonumber\\ &=\frac{1}{\omega_h}\left\{ \sinh^{-1}\left[\frac{1}{\mathcal{A}_h}\left(\psi^c-\psi^d+\frac{v'_+(\psi^c)}{w_+^{cd}}\right)\right]- \sinh^{-1}\left(\frac{v'_+(\psi^c)}{\mathcal{A}_h w_+^{cd}}\right)\right\}, \label{eq11.17b} \end{align}
\begin{align} \tau^{D'}-\tau^T&= \tau^T-\tau^D\nonumber\\ &=\frac{1}{\omega_n}\sin^{-1}\left(\frac{\psi^d}{\mathcal{A}_n}\right) .\label{eq11.17c} \end{align}
\begin{equation} \tau^S=2\tau^T ,\label{eq11.18a} \end{equation}
\begin{align}\tau^T&=\frac{\chi^c}{2\gamma\sqrt{|\alpha_t|}}+\frac{1}{\omega_h} \left\{ \sinh^{-1}\left[\frac{1}{\mathcal{A}_h}\left(\psi^c-\psi^d+\frac{v'_+(\psi^c)}{w_+^{cd}}\right)\right]- \sinh^{-1}\left(\frac{v'_+(\psi^c)}{\mathcal{A}_h w_+^{cd}}\right)\right\}\nonumber\\ &\quad +\frac{1}{\omega_n}\sin^{-1}\left(\frac{\psi^d}{\mathcal{A}_n}\right) .\label{eq11.18b} \end{align}
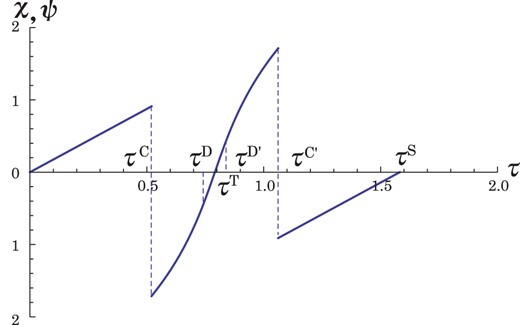
Fig. 12.
The behavior of |$\chi (\tau)$| and |$\psi (\tau)$| in one cycle. Here, the same parameters as those used in Fig. 8(a) are adopted.
The time |$\tau ^S$| is nothing but the period of the cycle. Figure 12 illustrates how |$\chi (\tau)$| and |$\psi (\tau)$| behave in one cycle. Here, in the regions of |$\tau \leq \tau ^C$| and |$\tau \geq \tau ^{C'}$|, |$\chi (\tau)$| is shown and is a linear function with respect to time |$\tau $|. In the region of |$\tau ^C \leq \tau \leq \tau ^{C'}$|, |$\psi (\tau)$| is used, and from |$\tau ^C$| to |$\tau ^T$|, |$\psi (\tau)$| is changed from a |$\sinh $|-type to a |$\sin $|-type function, and vice versa from |$\tau ^T$| to |$\tau ^{C'}$|. Our main interest is concerned with the energy of the intrinsic system expressed in the form (11.19) Here, |$\widetilde {H}_{\overline {P}}$| and |$N_{\overline {P}}$| are given in the relations (7.11) and (7.25), respectively, and, therefore, it may be enough for the understanding of |$E_b$| to consider |$N_{\overline {P}}$| (|$\varepsilon =1$|). In Fig. 13, the result is shown as a function of |$\tau $| under the approximation developed in Sects. 8–10 with the same parameters as those used in Fig. 8(a). In the region of |$\tau \leq \tau ^C$| and |$\tau \geq \tau ^{C'}$|, |$x\leq \gamma _t$| is satisfied where |$\Lambda _t^{a_1}(x)$| is used as the approximation of |$\Lambda _t(x)$|. In the region of |$\tau ^C \leq \tau \leq \tau ^{C'}$|, |$\Lambda _t^{a_2}(x)$| is used in the approximation of |$\Lambda _t(x)$|. It is seen that, in one cycle, the energy flows into the intrinsic system from the external environment from time 0 to |$\tau ^T$| and vice versa from |$\tau ^T$| to |$\tau ^S$|.
\begin{equation} E_b\equiv(\phi |\widetilde{H}_{\overline{P}}| \phi) =\varepsilon N_{\overline{P}} .\label{eq11.19} \end{equation}
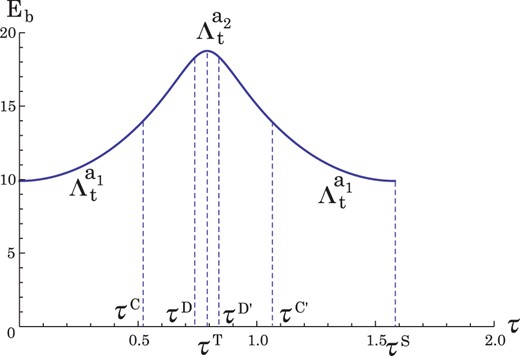
Fig. 13.
The approximate energy of the intrinsic system, |$\langle \widetilde {H}_{\overline {P}}\rangle =\varepsilon N_{\overline {P}}$|, is shown as a function of time |$\tau $| under the same parameter set as those used in Fig. 8(a).
We will discuss some problems related to the result shown in Fig. 13. The energy |$E_b$| shows periodic behavior for time |$\tau $|. Such behavior cannot be expected in the su(1,1)-algebraic model, in which, following the |$\cosh $|-type change, |$E_b$| increases or decreases. Since our model belongs to the su(2)-algebraic model, the periodic behavior appears. In Fig. 13, we can see that the minimum and the maximum values exist in |$E_b$|. We consider these two values for the case |$(\alpha _t > 0, \beta _t >0)$| in a rather general form. The relation (8.13a) teaches us that if |$\chi =0$|, y becomes the minimum, i.e., |$y_{\mathrm {min}}=c_+$|. Then, with the aid of expression (8.7), we have (11.20) On the other hand, the relation (9.16a) gives us the maximum value of |$y'$|, if |$\psi =0$|, i.e., |$y'_{\rm max}=d_+$|. Then, the relation (9.23) gives us (11.21) Of course, |$d_+$| is a solution of the cubic equation (9.17a) and we use a possible approximate solution: (11.22) Here, |$d_m$| is given in the relation (11.1b). In the cases |$\sigma ^2=0$| and |$(\sigma ^2)_{\mathrm {max}}$|, the solution (11.22) is exact. With the aid of the relation (7.25a), |$(E_b)_{\mathrm {min}}$| and |$(E_b)_{\rm max}$| are expressed as follows: (11.23a)(11.23b) In the case |$\rho ^2=0$|, |$(E_b)_{\mathrm {min}}=2t-1$| and, as |$\rho ^2$| increases, |$(E_b)_{\mathrm {min}}$| increases. Conversely, in the case |$\sigma ^2=0$|, |$(E_b)_{\rm max}=2\Omega _0$| and, as |$\sigma ^2$| increases, |$(E_b)_{\rm max}$| decreases. For the case |$(2\Omega _0=19,\ 2t=5,\ 2\kappa =-15)$|, we have |$(E_b)_{\mathrm {min}}=9.9072$| and |$(E_b)_{\mathrm {max}}=18.7569$|, which is very near to |$(E_b)_{\mathrm {max}}=18.7562$| calculated under the exact solution of the cubic equation (9.17a). This result may support the validity of the approximate form (11.22).
\begin{equation}\label{eq11.20} \left(\Lambda_t^{a_1}\right)_{\rm min} =\frac{1}{\alpha_t}(y_{\rm min}-2t)=\frac{1}{\alpha_t}(c_+-2t) =\frac{\rho^2}{\alpha_t}\cdot\frac{1}{t+\sqrt{t^2+\rho^2}} . \end{equation}
\begin{equation} \left(\Lambda_t^{a_2}\right)_{\mathrm{max}} =\gamma_t y'_{\rm max}=\gamma_t d_+ .\label{eq11.21} \end{equation}
\begin{equation} d_+=2\Omega_0\left(1-\frac{\sigma^2}{2\Omega_0|\beta_t|}\cdot \frac{2}{4\Omega_0^2-\sigma^2+ \left[(4\Omega_0^2-\sigma^2)^2-\frac{4\sigma^2(2\Omega_0+d_m)}{|\beta_t|}\right]^{\frac{1}{2}}}\right) .\label{eq11.22} \end{equation}
\begin{equation} (E_b)_{\mathrm{min}}=2t-1+\frac{\rho^2}{\alpha_t}\cdot \frac{1}{t+\sqrt{t^2+\rho^2}},\label{eq11.23a}\end{equation}
\begin{equation} E_b)_{\rm max}=2\Omega_0- \frac{\sigma^2}{|\beta_t|}\cdot \frac{2\gamma_t}{4\Omega_0^2-\sigma^2+ \left[(4\Omega_0^2-\sigma^2)^2-\frac{4\sigma^2(2\Omega_0+d_m)}{|\beta_t|}\right]^{\frac{1}{2}}}.\label{eq11.23b} \end{equation}
Next, on the basis of the above argument, we investigate the trial state (5.3) which leads us to |$(E_b)_{\rm min}$| and |$(E_b)_{\mathrm {max}}$|. In the ranges |$0 \leq x \leq \gamma _t$| and |$\gamma _t \leq x' < \infty $|, the state (5.3) contains the parameters |$z\ (x=|z|^2)$| and |$z'\ (x'=|z'|^2)$|, respectively. Here, the relation (9.1) should be noted. In the range |$0 \leq x \leq \gamma _t$|, we note the relation (8.18a) and, then, the value of x at |$\chi =0$| is the minimum: (11.24) The function |$x_{\mathrm { min}}(\rho ^2)$| is increasing for |$\rho ^2$| with |$x_{\mathrm {min}}(\rho ^2=0)=0$|, i.e., |$z=0$|. Therefore, the state |$| {\phi })$| corresponding to |$z=0$| is the minimum weight state (4.13), |$| {m_0})$|, which contains |$(2t-1)$| fermions only in |$\overline {P}\ (N_{\overline {P}}=2t-1,\ N_P=0)$|. In the range |$\gamma _t \leq x' < \infty $|, we note the relation (9.22) and the value of |$x'$| at |$\psi =0$| is the maximum: (11.25) Here, we used the approximate expression (11.22) for |$d_+$|. The function |$x'_{\mathrm {max}}(\sigma ^2)$| is decreasing for |$\sigma ^2$| with |$x'_{\rm max}(\sigma ^2=0)\rightarrow \infty $|, i.e., |$z'\rightarrow \infty $|. Therefore, the state |$| {\phi })$| corresponding to |$z'\rightarrow \infty $| is |$\left (\widetilde {\mathcal {T}}_+\right)^{2\Omega _0-(2t-1)}| {m_0})\ (2s=2\Omega _0-(2t-1))$| which contains the maximum number of fermions permitted by the seniority coupling scheme (|$N_{\overline {P}}=2\Omega _0,\ N_P=2\Omega _0-(2t-1)$|). From the above argument, it may be clear that as |$\kappa ^2$| increases from |$\kappa ^2=0$|, |$\rho ^2$| and |$\sigma ^2$| also increase from |$\rho ^2=\sigma ^2=0$| and |$(E_b)_{\mathrm {min}}$| and |$(E_b)_{\rm max}$| become larger than |$(2t-1)$| and smaller than |$2\Omega _0$|, respectively. If, at |$\tau =0$|, the cycle starts at the point S with |$(E_b)_{\mathrm {min}}$|, it passes the critical points C and D and at |$\tau =\tau ^T$| arrives at T. Although the points C and D are introduced under the approximation adopted in this paper, they play an essential role for treating the present model in a well-known simple mathematical form.
\begin{equation} x_{\mathrm{min}}=\frac{1}{\alpha_t}\cdot \frac{\sqrt{t^2+\rho^2}-t}{\sqrt{t^2+\rho^2}+t}\, (=x_{\rm min}(\rho^2)).\label{eq11.24} \end{equation}
\begin{align} x'_{\mathrm{max}} &= |\beta_t|+\frac{1}{2\Omega_0-y'_{\rm max}}=|\beta_t|+\frac{1}{2\Omega_0-d_+} \nonumber\\ &= \frac{|\beta_t|}{\sigma^2}\left(4\Omega_0^2+ \left[(4\Omega_0^2-\sigma^2)^2-\frac{4\sigma^2(2\Omega_0+d_m)}{|\beta_t|}\right]^{\frac{1}{2}} \right)\ (=x'_{\rm max}(\sigma^2)).\label{eq11.25} \end{align}
The above is a basic part which our simple many-fermion model produces under the pseudo-su(1,1) algebra.
12. Concluding remarks
In this section, we will give some remarks on the Hamiltonian (7.10). This Hamiltonian was set up under the correspondences (7.7)–(7.9). The original boson Hamiltonian (7.5) is a generator for time evolution and does not represent the energy of the entire system. It aims at the description of the “damped and amplified harmonic oscillator”. By regarding the mixed-mode boson coherent state as a statistically mixed state, we can describe the harmonic oscillator at finite temperature, which will be shown in the relation (12.6). In this sense, the above-mentioned description provides us a possible entrance to the problems related to finite temperature. The Hamiltonian (7.10) can be regarded as the fermion version of the harmonic oscillator in the su(1,1) algebra in the Schwinger boson representation. Nevertheless, it may be possible to treat the Hamiltonian (7.10) as the energy of the entire system, as was already mentioned in Sect. 7. In order to confirm this conjecture, we reexamine the correspondences (7.7)–(7.9).
Let us start with the relation (7.9). The frequency |$\omega $| is positive, but the single-particle energy |$\varepsilon $| is not always positive. Therefore, instead of the relation (7.11), it is permissible to set up the following form: (12.1) The form (12.1) suggests that the system under consideration is nothing but a many-fermion system in two single-particle levels, |$\overline {P}$| and P, with the level distance |$2|\varepsilon |$|. If the relation (12.1) is admitted, |$\widetilde {H}$| represents the energy of the entire system. From this point of view, the state |$| \phi)$| is not the statistically mixed state, but the trial state of the time-dependent variation for |$\widetilde {H}$| as the energy of the entire system. Therefore, the results obtained in this paper present the information provided by |$| \phi)$| as a statistically pure state.
\begin{equation}\label{eq12.1} \widetilde{H}_{\overline{P}}=\varepsilon\sum_{\alpha}\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\bar{\alpha}}, \quad \widetilde{H}_{P}=\varepsilon\sum_{\alpha}\tilde{c}_{\alpha}^*\tilde{c}_{\alpha}, \quad \widetilde{H}_{\overline{P}}+\widetilde{H}_P=2\varepsilon \widetilde{\mathcal{T}}. \end{equation}
Next, we reexamine the correspondence (7.7) and (7.8). First, we notice the following: If the vacuum changes appropriately, the fermion creation operator becomes the annihilation operator, that is, if |$| 0)\!)=\tilde {c}^*| {0})\ (\tilde {c}| 0)=0)$|, |$\tilde {c}^*| 0)\!)=0$|. In the case of the boson operator, we cannot find such a situation. If we note the above fact, the following correspondence may be also permitted: (12.2) Then, for |$(\hat {T}-1/2)$|, we have (12.3) The correspondence (12.2) suggests that the set |$(\widetilde {S}_{\pm ,0})$| is replaced with the set |$(\widetilde {R}_{\pm ,0})$|. Then, another type of pseudo-su(1,1) algebra can be defined in the form (12.4) The Hamiltonian in this case is expressed as (12.5) It may be clear that the above does not correspond to the deformation of the Cooper pair. It corresponds to the deformation of the density-type fermion pair. The Hamiltonian (12.5) is applicable to the case where the single-particle energy of the level P is equal to that of |$\overline {P}$|.
\begin{equation}\label{eq12.2} (\hat{b}, \hat{b}^*) \rightarrow (s_{\alpha}\tilde{c}_{\bar{\alpha}}^*, s_{\alpha}\tilde{c}_{\bar{\alpha}}), \quad (\hat{a}, \hat{a}^*) \rightarrow (\tilde{c}_{\alpha}, \tilde{c}_{\alpha}^*) . \end{equation}
\begin{align}\label{eq12.3} \hat{T}-\frac{1}{2}\rightarrow \stackrel{\tiny\circ} {\mathcal{T}} &= -\frac{1}{2}\sum_{\alpha}(\tilde{c}_{\alpha}^*\tilde{c}_{\alpha} -s_{\alpha}\tilde{c}_{\bar{\alpha}}s_{\alpha}\tilde{c}_{\bar{\alpha}}^*) \nonumber\\ &=-\frac{1}{2}\sum_{\alpha}(\tilde{c}_{\alpha}^*\tilde{c}_{\alpha} +\tilde{c}_{\bar{\alpha}}^*\tilde{c}_{\bar{\alpha}})+\Omega_0. \end{align}
\begin{align} {\stackrel{\tiny\circ}{\mathcal{T}}}_+&=\widetilde{R}_+ \left(\frac{\Omega_0+\frac{1}{2}+t+\widetilde{R}_0}{\Omega_0+\frac{1}{2}-t-\widetilde{R}_0+\epsilon}\right)^{\frac{1}{2}}, \quad {\stackrel{\tiny\circ} {\mathcal{T}}}_-= \left(\frac{\Omega_0+\frac{1}{2}+t+\widetilde{R}_0}{\Omega_0+\frac{1}{2}-t-\widetilde{R}_0+\epsilon}\right)^{\frac{1}{2}}\widetilde{R}_-, \nonumber\\ {\stackrel{\tiny\circ} {\mathcal{T}}}_0 &=\Omega_0+\frac{1}{2}+\widetilde{R}_0.\label{eq12.4} \end{align}
\begin{equation} \stackrel{\tiny\circ} {H}=2\varepsilon\stackrel{\tiny\circ} {\mathcal{T}}-\mathrm{i}\gamma\left(\stackrel{\tiny\circ} {\mathcal{T}}_+-\stackrel{\tiny\circ} {\mathcal{T}}_-\right) .\label{eq12.5} \end{equation}
Finally, we must mention two problems to be solved in the near future. By regarding the mixed-mode boson coherent state as the statistically mixed state, the expectation value of |$\hat {H}_b=\omega \hat {b}^*\hat {b}$| is given by (12.6) The first and second terms represent the energy at the low temperature limit and the energy coming from the thermal fluctuation in the Bose distribution, respectively [5–7]. One of the future problems is to investigate the thermal effect such as is shown in the relation (12.6) by regarding the state |$| \phi)$| as the statistically mixed state for |$\widetilde {H}_{\overline {P}} =\varepsilon \sum _{\alpha }\tilde {c}_{\bar {\alpha }}^*\tilde {c}_{\bar {\alpha }}$|. In this case, our concern is to examine if the Fermi distribution appears or not. The second problem is related to the Hamiltonians |$\widetilde {H}_{\overline {P}}$| and |$\widetilde {H}_{P}$|. They are on a level with |$\hat {H}_b$| and |$\hat {H}_a$|. In Ref. [5], we can find some examples extended from |$\hat {H}_b$| and |$\hat {H}_a$|. The future task is to also investigate the cases extended from |$\widetilde {H}_{\overline {P}}$| and |$\widetilde {H}_P$|. The above two are our future problems to be solved.
\begin{equation} \langle \hat{H}_b\rangle \sim \omega\cdot (2t-1)+\omega\cdot \frac{1}{\mathrm{e}^{\omega \beta}-1} \quad (\beta=(k_B T)^{-1}).\label{eq12.6} \end{equation}
Acknowledgements
One of the authors (Y.T.) is partially supported by a Grant-in-Aid of Scientific Research (No. 23540311) from the Ministry of Education, Culture, Sports, Science, and Technology in Japan.
References
1
Tsue Y.Providência C.da Providência J, Yamamura M.
Prog. Theor. Phys.
128
, 693
(2012
) 2
Tsue Y.Providência C.da Providência J, Yamamura M.
Prog. Theor. Phys.
128
, 717
(2012
) 3 (
, Schwinger J.
On angular momentum
. In Quantum Theory of Angular Momentum
, eds Biedenharn
L.
Van Dam
H.
Academic Press
, New York
, 1965
), p. 229
.4
Marumori T.Yamamura M., Tokunaga A.
Prog. Theor. Phys.
31
, 1009
(1964
) 5
Kuriyama A.da Providência JTsue Y., Yamamura M.
Prog. Theor. Phys. Suppl.
141
, 113
(2001
) 6
Celeghini E.Rasetti M., Vitiello G.
Ann. Phys. (N.Y.)
215
, 156
(1992
) 7
Tsue Y.Kuriyama A., Yamamura M.
Prog. Theor. Phys.
91
, 469
(1994
) 8
9
Pang S.C.Klein A., Dreizler R.M.
Ann. Phys. (N.Y.)
49
, 477
(1968
) 10
Umezawa H.Matsumoto H., Tachiki M.
Thermo Field Dynamics and Condensed States
(North Holland
, Amsterdam
, 1982
).11
Tsue Y.Providência C.da Providência J, Yamamura M.
Prog. Theor. Phys.
127
, 117
(2012
) 12
Tsue Y.Providência C.da Providência J, Yamamura M.
Prog. Theor. Phys.
127
, 303
(2012
) Author notes
†
These authors contributed equally to this work.
© The Author(s) 2013. Published by Oxford University Press on behalf of the Physical Society of Japan.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
