High-Impact Research from Philosophia Mathematica
Explore a collection of the most read and most cited articles making an impact in Philosophia Mathematica published within the past two years. This collection will be continuously updated with the journal's leading articles so be sure to revisit periodically to see what is being read and cited.
Also discover the articles being discussed the most on digital media by exploring this Altmetric report pulling the most discussed articles from the past year.
Most cited
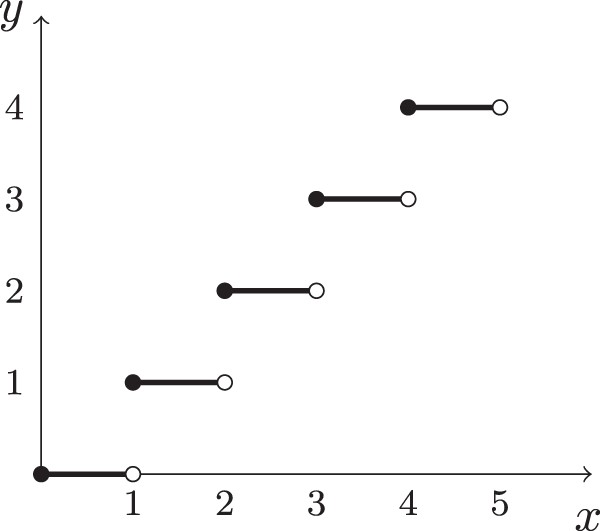I examine the classical idea of ‘algorithm’ as a sequential, step-by-step, deterministic procedure ( i.e. , the idea of ‘algorithm’ that was already in use by the 1930s), with respect to three themes, its relation to the notion of an ‘effective procedure’, its different roles and uses in logic, computer science, and ...
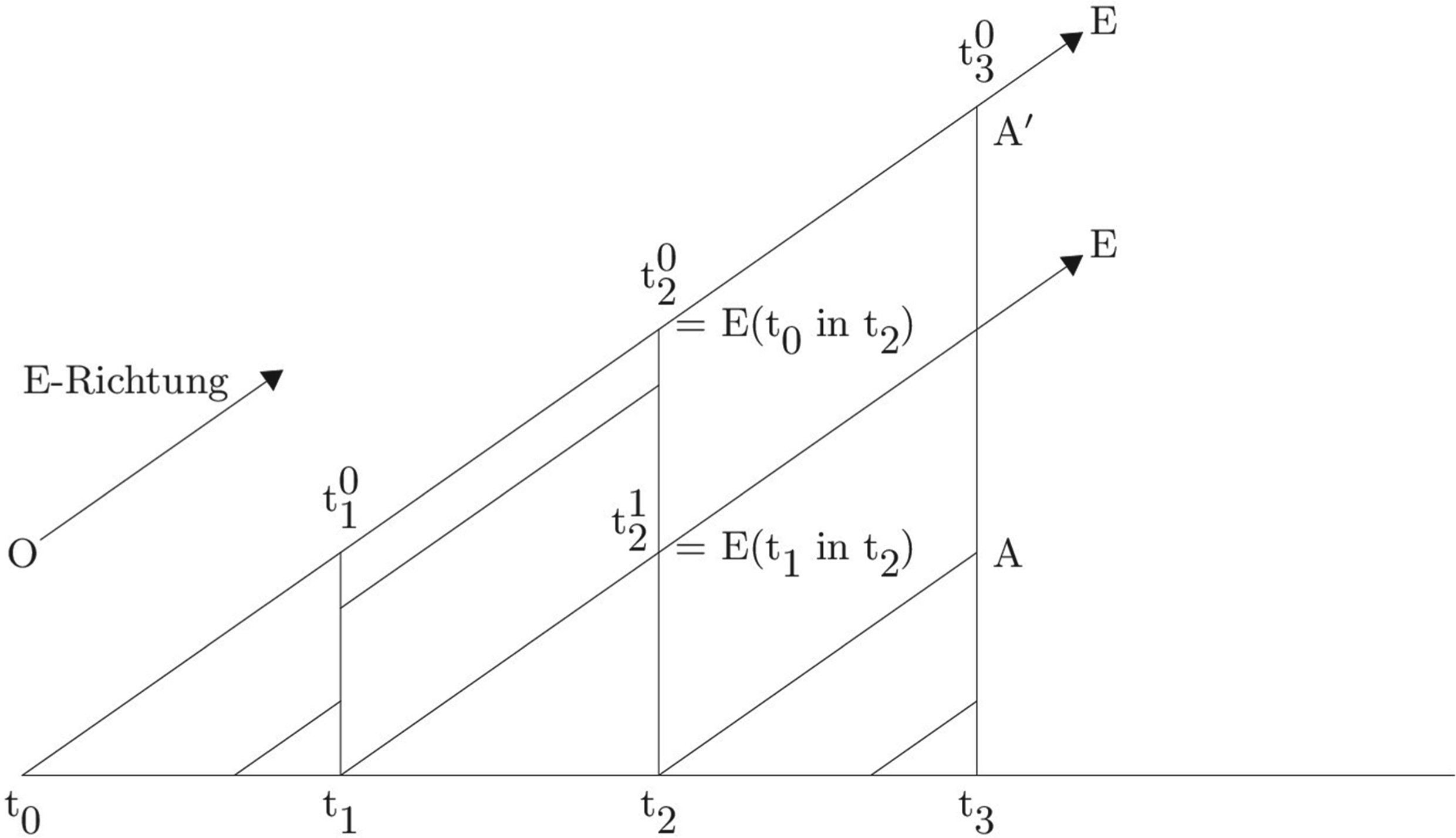Brouwer’s view on induction has relatively recently been characterised as one on which it is not only intuitive (as expected) but functional, by van Dalen. He claims that Brouwer’s ‘Ur-intuition’ also yields the recursor. Appealing to Husserl’s phenomenology, I offer an analysis of Brouwer’s view that supports this ...
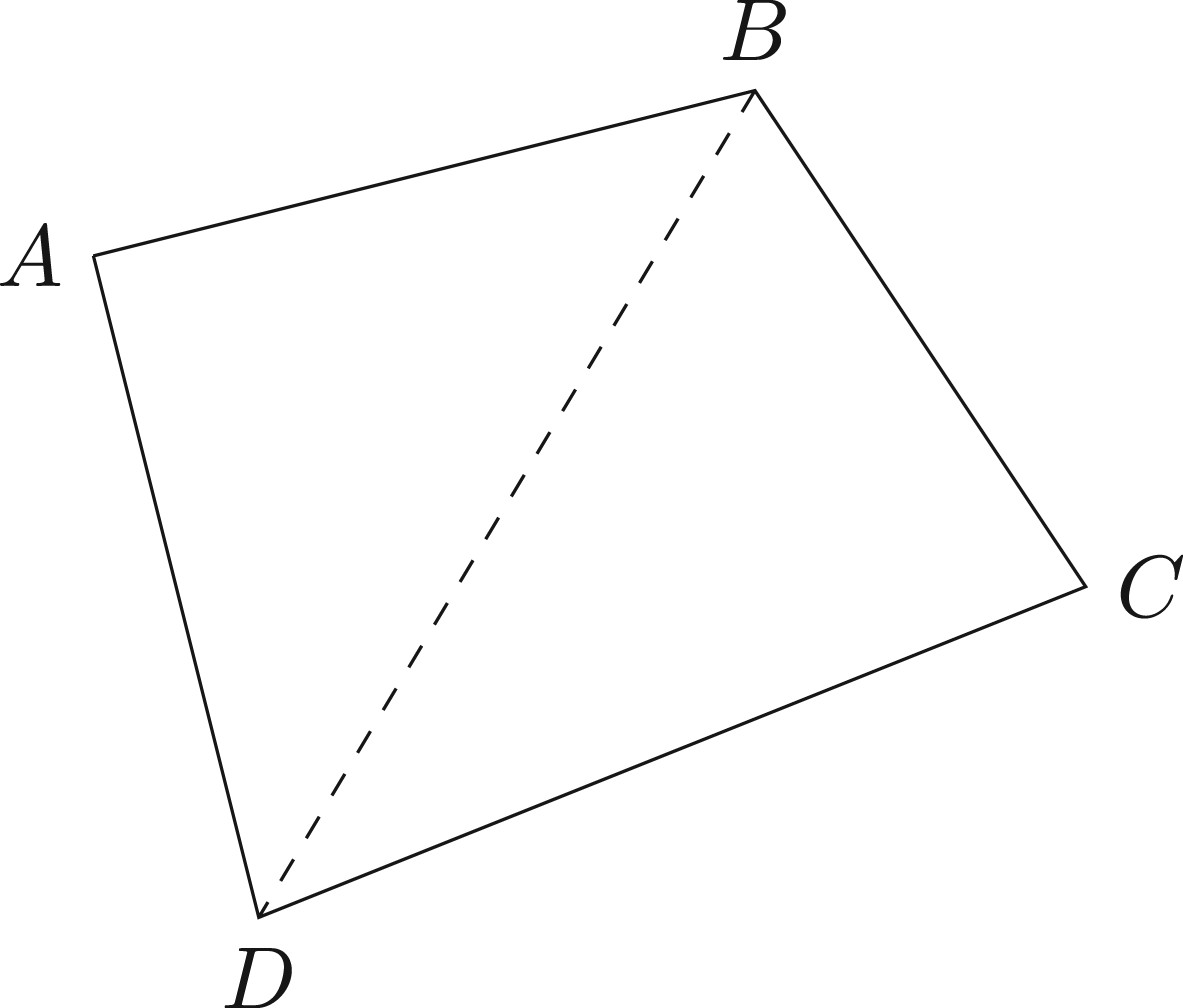This paper studies internal (or intra-)mathematical explanations, namely those proofs of mathematical theorems that seem to explain the theorem they prove. The goal of the paper is a rigorous analysis of these explanations. This will be done in two steps. First, we will show how to move from informal proofs of mathematical ...
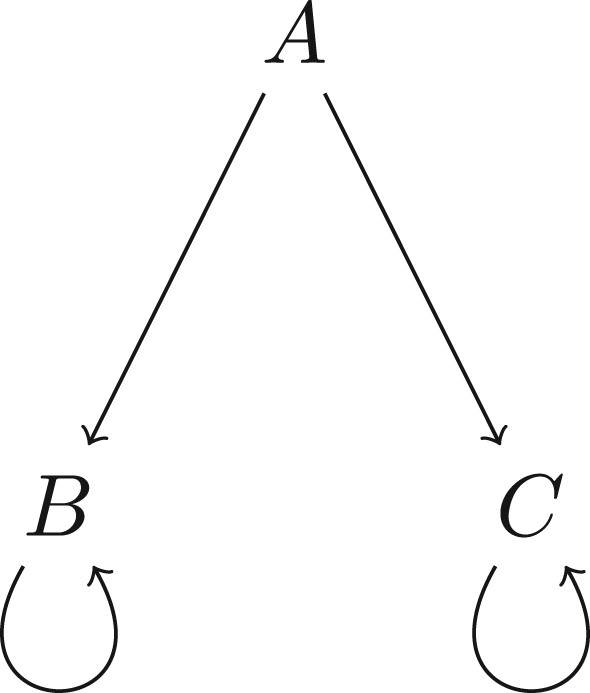Boffa non-well-founded set theory allows for several distinct sets equal to their respective singletons, the so-called ‘Quine atoms’. Rieger contends that this theory cannot be a faithful description of set-theoretic reality. He argues that, even after granting that there are non-well-founded sets, ‘the extensional nature ...
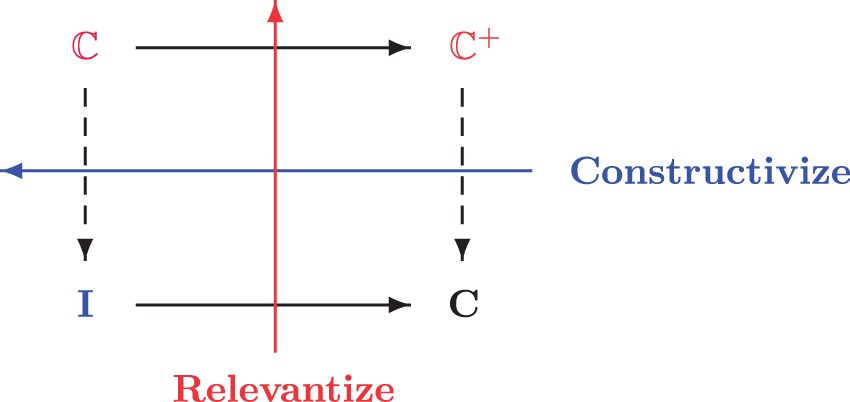Informally rigorous mathematical reasoning is relevant. So too should be the premises to the conclusions of formal proofs that regiment it. The rule Ex Falso Quodlibet induces spectacular irrelevance. We therefore drop it. The resulting systems of Core Logic $ \mathbb{C}$ and Classical Core Logic $ \mathbb{C}^{+}$ can ...
Most read
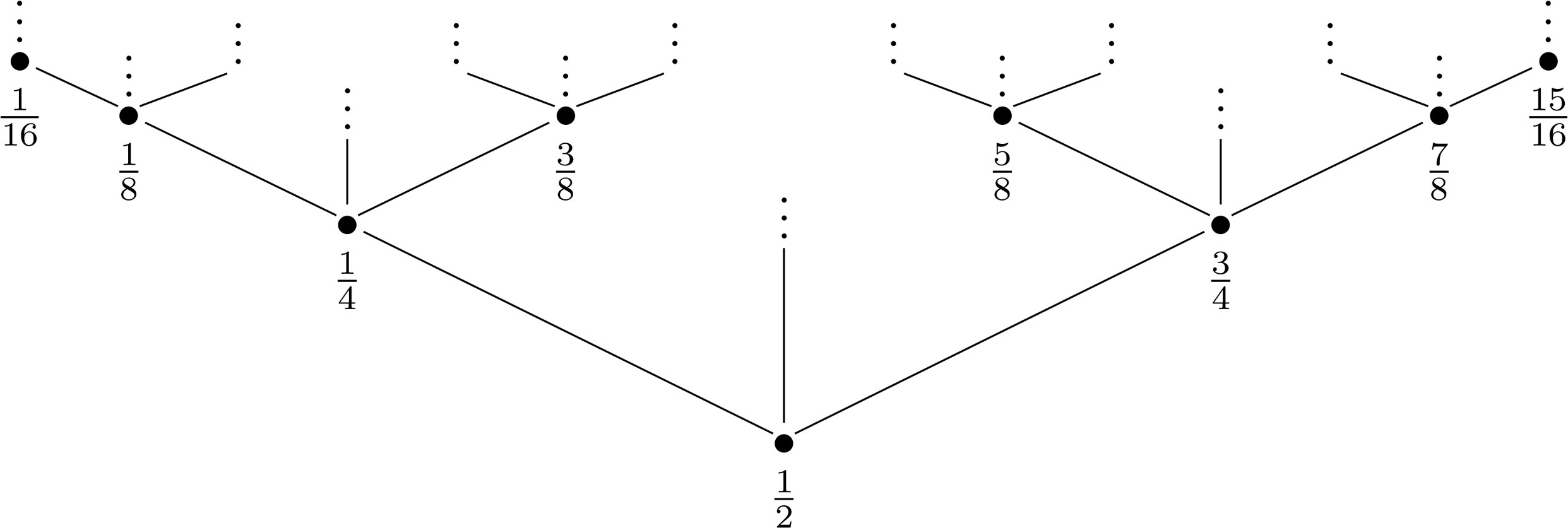Free choice sequences play a key role in the Brouwerian continuum. Using recent modal analysis of potential infinity, we can make sense of free choice sequences as potentially infinite sequences of natural numbers without adopting Brouwer’s distinctive idealistic metaphysics. This provides classicists with a means to make ...
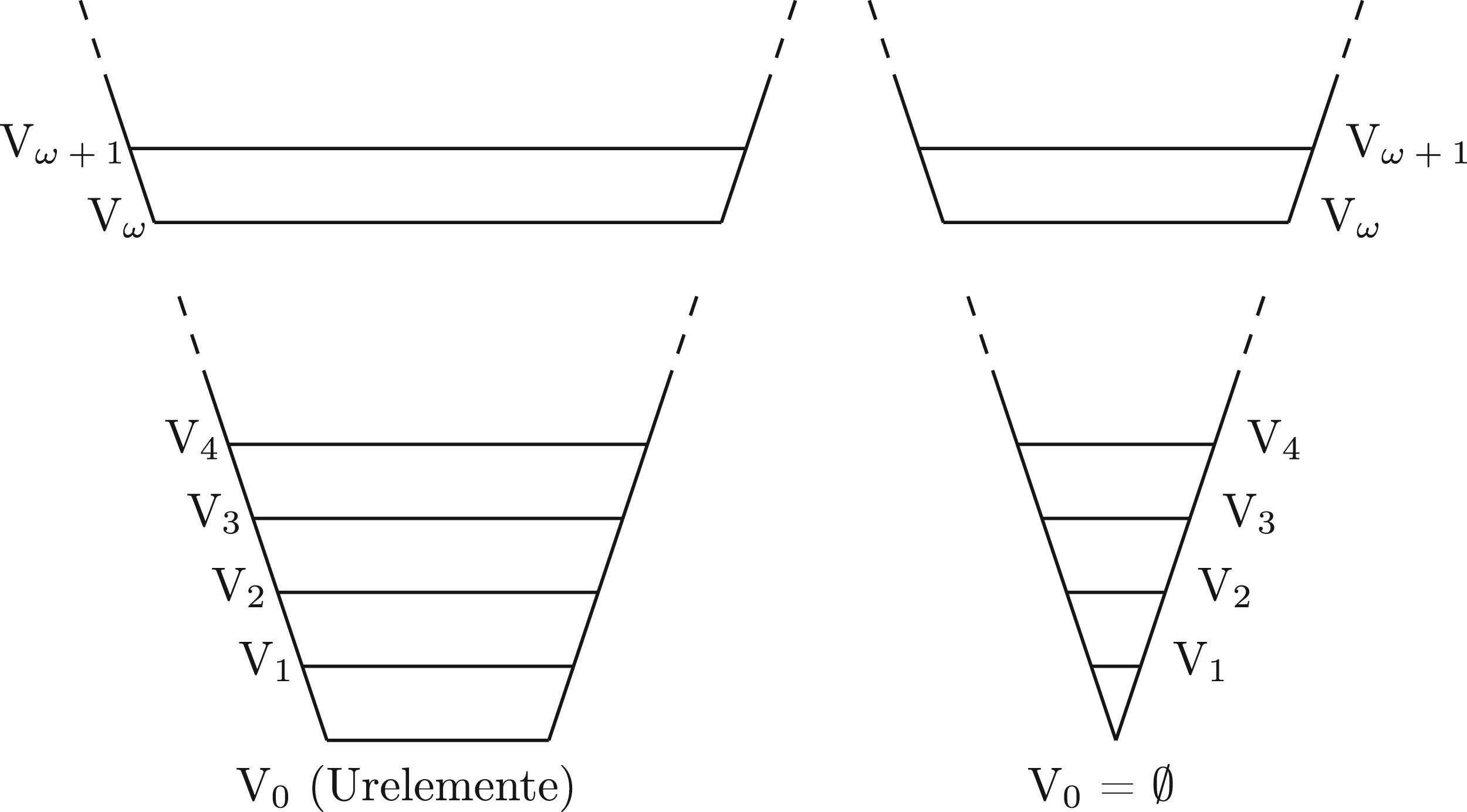Set-theoretic potentialism is one of the most lively trends in the philosophy of mathematics. Modal accounts of sets have been developed in two different ways. The first, initiated by Charles Parsons, focuses on sets as objects. The second, dating back to Hilary Putnam and Geoffrey Hellman, investigates set-theoretic ...
Boffa non-well-founded set theory allows for several distinct sets equal to their respective singletons, the so-called ‘Quine atoms’. Rieger contends that this theory cannot be a faithful description of set-theoretic reality. He argues that, even after granting that there are non-well-founded sets, ‘the extensional nature ...
Recognizing and Celebrating Women in Science
Oxford University Press is proud to support diverse voices across our publishing. In this collection, we shine a spotlight on the representation of women in scientific fields, the gains that have been made in their fields, from research and major discoveries to advocacy and outreach, and amplify the voices of women who have made a career in scientific research.
Delve into the Women in Science collection
