Design, expression and characterization of mutants of fasciculin optimized for interaction with its target, acetylcholinesterase

Abstract

Introduction

Computational protein design has been used frequently to predict stabilizing mutations (Malakauskas and Mayo, 1998), to repack protein cores and to redesign entire protein sequences (Dahiyat and Mayo, 1997). Design of protein–protein binding interactions is one of the directions in the field that presents particular interest. Indeed, the capability of creating a binding partner for any given protein would allow us to construct inhibitors for a specific disease-associated pathway, thus revolutionizing the pharmaceutical industry. However, to date, only relatively few studies have reported successful redesign of protein–protein interfaces. Computational methods have been used to substantially increase protein binding specificity in calmodulin-target complexes (Shifman and Mayo, 2002, 2003; Yosef et al., 2009) and to supply proteins with novel binding specificities (Reina et al., 2002; Kortemme et al., 2004; Joachimiak et al., 2006). Introduction of computationally designed mutations at protein–protein interfaces helped to convert a native homodimer to a heterodimer (Bolon et al., 2005), and to construct chimeric proteins with novel DNA-binding properties (Chevalier et al., 2002). Optimization of electrostatic potential between two proteins was shown to increase association rates significantly (Selzer et al., 2000; Kiel et al., 2004).

It remains difficult, however, to use existing protein design methodology to predict affinity-enhancing mutations of residues located at protein–protein binding interfaces. Computational design of point mutations intended to increase binding affinity have met with variable success, while redesign of entire binding interfaces was often found to result in reduced affinities (Shifman and Mayo, 2003; Clark et al., 2006; Palmer et al., 2006; Song et al., 2006). A recent study by Kuhlman and colleagues suggests an approach that predicts single affinity-enhancing mutations by substituting polar residues at the binding interface by hydrophobic residues, and hydrophobic residues by larger hydrophobic residues (Sammond et al., 2007). This approach, probably the most successful so far, cannot, however, be applied to the redesign of entire binding interfaces, since it is inherently bound to increase the hydrophobicity of the individual proteins, thus enhancing their propensity to aggregate. In addition, removal of polar residues at the binding interface is likely to reduce the binding specificity of the bio-molecular interaction, which is usually not desirable. We set as our goal the development of a more general strategy for predicting affinity-enhancing mutations in protein complexes. Such a strategy would allow for the improvement of both polar and hydrophobic interactions at protein–protein interfaces.

As our model system we chose a complex of the synaptic enzyme, acetylcholinesterase (AChE) with a polypeptide toxin present in the venom of the green mamba, fasciculin-2 (Fas). There were several reasons for this choice. First, the interaction displays a very high affinity (Karlsson et al., 1985; Eastman et al., 1995; Radic et al., 1995), thus making the Fas/AChE complex an excellent and challenging system for designing enhanced protein–protein interactions. Secondly, structural studies reveal that no substantial conformational change occurs upon binding (Bourne et al., 1995; Harel et al., 1995; Kryger et al., 2000), thus simplifying the design and the analysis procedures. Lastly, a convenient assay is available for assessing the changes in the affinity of Fas for AChE.

AChE is a synaptic enzyme that terminates impulse transmission at cholinergic synapses by rapid hydrolysis of the neurotransmitter, acetylcholine (Zimmerman and Soreq, 2006). Fas is a snake venom polypeptide toxin that is a very powerful reversible inhibitor of AChE (Karlsson et al., 1985); it belongs to the family of three-finger toxins that share a common structural motif: a β-sheet core stabilized by four disulfide bridges and three protruding loops that resemble human fingers (Kini, 2002). The crystal structure of the Fas/AChE complex has been solved for Torpedo californica AChE (TcAChE), mouse AChE (mAChE) and human AChE (hAChE) (Bourne et al., 1995; Harel et al., 1995; Kryger et al., 2000). The three structures are almost super-imposable, with Fas binding at the peripheral anionic site of the enzyme, thus sealing the narrow gorge that leads to the active site (Fig. 1B). Complexes of Fas with mammalian AChEs display very high affinities (K_d values of 10⁻¹¹–10⁻¹² M) (Karlsson et al., 1985; Eastman et al., 1995; Radic et al., 1995). A weaker, yet still high affinity (K_d of 4 × 10⁻¹⁰ M) was reported for the complex between Fas and TcAChE (Weiner et al., 2009). The tight binding between these two proteins has been attributed to several factors, including a remarkable surface complementarity, a large hydrophobic surface burial accompanying binding and formation of several inter-molecular hydrogen bonds (Harel et al., 1995). In addition, electrostatic interactions between cationic residues on the interaction surface of Fas and anionic residues on the interaction surface of AChE play an important role in the binding process (Radic et al., 1997).

Fig. 1

(A) The amino acid sequence of Fas, showing the four intra-chain disulphide bridges and the interfacial residues chosen for redesign. (B) The Fas/TcAChE binding interface before redesign; (C) The Fas/TcAChE binding interface after redesign. Fas (pink) sits at the entrance of the narrow gorge leading to the active site of TcAChE (gray). The side-chains on Fas and TcAChE selected for computational optimization are displayed as pink and blue sticks, respectively. The numbers are shown for the Fas residues for which affinity-enhancing mutations had been predicted.

Open in new tabDownload slide

A few studies have been performed to determine the contribution of individual amino acid residues of Fas to the interaction between the two proteins. Karlsson and coworkers neutralized positive charges on Fas by chemical modification of single lysines or arginines, and reported a substantial decrease in Fas activity (Cervenansky et al., 1994; Cervenansky et al., 1995). Marchot et al. used structural and kinetic data to construct 14 single and double Fas mutants (Marchot et al., 1997). They assayed these mutants on mouse AChE (mAChE), measuring inhibitory activity by an indirect assay based on titration of the mutants with a polyclonal anti-Fas serum. Seven of these mutants lost some or all their affinity for the enzyme compared to that of wild-type Fas (Fas^WT), while four mutants showed no change in affinity. The remaining three Fas mutants surprisingly exhibited an increased inhibitory activity against mAChE. However, the authors suggested that this may reflect immuno-dominant determinants in these regions or intra-molecular rearrangements in conformation that enhance the interaction (Marchot et al., 1997). In contrast to the earlier studies, we chose to develop a quantitative computational approach in attempt to optimize the Fas–AChE interaction. Mutations in Fas that were computationally predicted to stabilize the Fas/TcAChE complex were tested experimentally by expressing the Fas mutants and measuring their binding affinity for TcAChE. To this end, we developed a reproducible and efficient methodology for overexpression and refolding of WT and mutant forms of Fas in Escherichia coli. This was a challenging task due both to the small size of Fas (61 residues) and to the fact that it contains four intra-chain disulfides (Fig. 1A).

Materials and methods

Computational design

The protein redesign program ORBIT was used for Fas design (Dahiyat and Mayo, 1997). The residues on Fas that are within 4 Å of TcAChE in the Fas–TcAChE complex structure (Harel et al., 1995) were selected for optimization (positions 6, 8, 9, 11, 12, 27, 29, 32, 33, 34, 35, 37 and 61). All amino acids, except for Pro, Cys and Gly, were considered at all the design positions. The residues on TcAChE that are within 4 Å of Fas in the Fas–TcAChE complex structure were allowed to change their side-chain conformation. Rotamer libraries used for the Fas–TcAChE optimizations were based on the backbone-dependent library of Dunbrack and Karplus (Dunbrack and Karplus, 1993), with additional rotamers expanded by one standard deviation around their mean χ₁ and χ₂ values for all residues except Lys and Arg. A potential energy function that included terms for Van der Waals, electrostatic and hydrogen bonding interactions, and for surface area-based solvation, was used to calculate side chain/side chain and side chain/backbone pairwise interactions as described (Dahiyat and Mayo, 1997; Gordon et al., 1999; Street and Mayo, 1999). In the Fas design, we used the ORBIT energy function that was optimized to better reproduce the side-chain conformations in the data set of protein–protein interfaces (O. Sharabi and J. M. Shifman, in preparation). In this energy function, the value of the distance-dependent dielectric constant used to calculate the electrostatic interactions was set to 10r (where r is distance between two atoms) and the penalty for hydrophobic burial, σ_p, was set to 0.005 kcal mol⁻¹ Å⁻². The calculated energies served as input to a side-chain selection procedure that used the Dead-End Elimination theorem (Desmet et al., 1992; Gordon et al., 2003). All optimizations were performed using a cluster of Xeon computers.

Gene construction

The gene construct encoding Fas^WT was cloned into the bacterial expression vector pET-25b (Novagen). The pelB leader peptide was removed from the expression vector in the cloning process. The genes for the designed Fas mutants were constructed based on the skeleton of the WT Fas expression vector using the standard site-directed mutagenesis procedure. The full open reading frames of both Fas^WT and Fas mutants were encoded without additional residues.

Expression of Fas^WT and mutants

Fas^WT and Fas mutants were expressed using the E. coli BL21(DE3) cell line at 37°C. Induction was initiated by the addition of 0.1 mM isopropyl-D-thiogalactopyranoside (IPTG) when the optical density of the culture had reached 0.8 OD at 600 nm. 3.5 hours after induction, the cells were harvested by centrifugation, and resuspended in a lysis buffer containing 50 mM phosphate, 1% Triton X100, lysozyme (1 mg/L), 15 mM DNase I and 0.1 mM phenylmethylsulfonyl fluoride, pH 7.8. The cells were sonicated and centrifuged at 16 000 rpm for 20 min at 4°C. The pellets containing the inclusion bodies (IBs) were collected and stored at −20°C.

Refolding of Fas variants

The IBs were dissolved in the denaturing buffer (6 M GdHCl, 10 mM EDTA, 50 mM phosphate, pH 8.0) by sonicating the samples at 0°C. Reduction of the disulphide bonds of the protein samples was carried out by the addition of 0.1 M 1,4-dithiothreitol (DTT), followed by shaking at room temperature for 2 h. The non-soluble material was removed by ultracentrifugation of the sample at 35 000 rpm at 4°C. The denatured and reduced Fas samples were purified by reversed-phase HPLC using an acetonitrile/water gradient. The Fas samples eluted at ∼30% acetonitrile. The concentration of the purified protein was determined by measuring the absorption at 280 nm. The purified Fas samples were diluted in the denaturing buffer to a final concentration of ∼10 µM, and slowly dialyzed into the refolding buffer (0.5 M GdHCl, 0.3 M NaCl, 2 mM reduced glutathione, 1 mM oxidized glutathione, 5 mM EDTA, 100 mM Tris, pH 9.0). To remove the reducing agents, three more rounds of dialysis were performed against a buffer containing 0.3 M NaCl, 5 mM EDTA, 100 mM Tris, pH 9.0, at 4°C. The correct molecular mass of the refolded protein was confirmed by mass spectrometry, and the absence of free SH groups by use of the Ellman assay (Ellman, 1959).

AChE activity assays

Native, snake-derived fasciculin-II was purchased from Alomone Laboratories (Jerusalem, Israel). TcAChE was purified from electric organ tissue of T.californica (Sussman et al., 1988), and AChE activity essays were performed as previously described (Ellman et al., 1961). TcAChE at 0.04 nM concentration was pre-incubated for 20 min either alone or together with a Fas variant at the desired concentration in 50 mM phosphate, pH 8.0, containing 0.1 mg/ml BSA and 0.01% NaN₃. The same assay mixture without the enzyme was used as a control to monitor non-specific substrate hydrolysis and subtracted from the sample readings. A range of concentrations were explored for each Fas mutant. The reaction was started by the addition of the substrate acetylthiocholine iodide (ATC) at 0.8 mM and 5,5′-Dithiobis-2-nitro-benzoic acid (DTNB) at 0.4 mM. The increase in absorption at 412 nm was monitored over 1 min at 10 s intervals, and the initial velocity of the reaction was calculated from the slope of the line thus obtained. The fraction of TcAChE activity for a particular concentration of a Fas variant was calculated by dividing the initial velocity of the reaction by the initial velocity of the reaction in the absence of Fas. The experiment was repeated for a range of Fas concentrations to obtain a full inhibitory profile (Fig. 2). Each curve was fitted to determine the K_d of binding. To fit the data, we assumed that Fas is a non-competitive inhibitor of TcAChE (Weiner et al., 2009) that forms a 1:1 complex with the enzyme, whose affinity is not affected by binding of substrate to the enzyme. In this assumption, the binding could be described by a reaction: and the K_d of binding is:

(1)

where [Fas], [AChE] and [Fas · AChE] are the concentrations of the unbound Fas, free TcAChE and the inactive complex, respectively, when the system had reached equilibrium. [Fas]_tot and [AChE]_tot are the total concentration of Fas and TcAChE, respectively. The fraction of the residual active enzyme measured in Fig. 2 then becomes:

(2)

Fig. 2

Comparison of recombinant wild-type Fas expressed in E.coli to native Fas purified from mamba venom. Activity profiles of TcAChE when inhibited by recombinant wild-type Fas (closed triangle) and by native Fas (closed circle). [Fas] are plotted on a log scale. TcAChE activity is measured with an accuracy of ±0.05. An insert shows an SDS–PAGE gel for equal amounts of recombinant Fas (lane 1) and native Fas (lane 2). Molecular weight markers are shown in the leftmost lane.

Open in new tabDownload slide

Measurement of the kinetic parameters

To measure the association and the dissociation rates for interaction of a Fas mutant with TcAChE, we performed the TcAChE activity assays under conditions that allowed us to monitor the kinetics of approach to equilibrium. For this purpose, mixtures of TcAChE at 0.02 nM, and of a Fas variant in at least 10-fold excess over the TcAChE concentration were pre-incubated with 0.6 mM DTNB for a variable period of time (usually, 10–70 s). TcAChE activity was measured immediately after the addition of 1 mM ATC. The percent of TcAChE activity for the sample pre-incubated for a certain period of time was calculated by dividing the measured TcAChE activity of the sample by that of the sample containing TcAChE in the absence of Fas. To fit the data, we assumed that Fas binding to TcAChE could be described by the opposing association and dissociation reactions:

When the Fas concentration is much greater than that of TcAChE, the percentage of enzymatic activity can be described by the following expression that combines the k_on and k_off rate equations (Laidler, 1965):

(3)

where [Fas] is the total concentration of Fas at t = 0, and t is the time elapsed from the addition of Fas. The kinetic data were fitted using Eq. (3) in order to determine k_on and k_off.

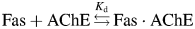
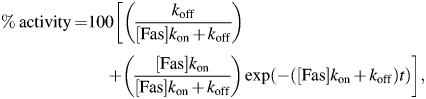
Results

We used the computational design program ORBIT (Dahiyat and Mayo, 1997) to optimize the Fas sequence for interaction with TcAChE. Starting from the X-ray structure of the Fas–TcAChE complex (Harel et al., 1995), we defined the Fas–TcAChE binding interface by selecting the residues on each protein that are within 4 Å of the second protein in the complex (Fig. 1B). The 13 Fas residues belonging to the binding interface were simultaneously redesigned, using all amino acids as possible candidates except for Pro, Cys and Gly. At the same time, the side chains of 28 residues on TcAChE were allowed to change their conformations (Fig. 1B). The optimal Fas sequence was selected by minimizing the total energy of the Fas–TcAChE complex. The calculation was performed using the energy function optimized for design of partially polar protein–protein interfaces (see Materials and methods). The optimization yielded a Fas mutant, Fas^des, with five interfacial mutations with respect to Fas^WT: T8V, T9N, R11K, H29R and K32R (Fig. 1C).

To access experimental parameters for the binding of Fas^des to TcAChE, we first had to develop a strategy for expression of Fas mutants. Fas^WT from the green mamba venom could be obtained from a commercial source, while recombinant Fas^WT and Fas mutants had been previously expressed only in mammalian cells (Marchot et al., 1997). We chose, however, to express Fas variants in E.coli. The main challenge in making this choice is the presence of four intra-chain disulfide bonds in a protein as small as Fas, making it prone to mis-folding when expressed in a prokaryotic host. Initially, we attempted to express Fas^WT in strains of E.coli in which disulfide bond formation is enhanced. Both periplasmic expression and expression in cells in which mutations had been introduced into the thioredoxin reductase (trxB) and glutathione reductase (gor) genes (e.g. Rosetta-Gami(DE3)) were unsuccessful. Although we were able to obtain some soluble Fas^WT, the protein displayed a large content of free thiol groups, and exhibited very weak inhibition of AChE, indicating that the Fas^WT produced was largely misfolded (data not shown). Hence, we decided to pursue an alternative strategy that involved expressing of the Fas^WT as IBs, followed by a refolding procedure. The gene corresponding to Fas^WT was cloned into the pET-25b vector and expressed in BL21(DE3) cells. A large amount of the Fas polypeptide indeed expressed as IBs. The IBs were denatured and reduced, the Fas was purified by reverse phase HPLC and was then slowly refolded making use of a GSH-GSSG redox buffer. The refolded Fas^WT migrated identically to commercially available Fas^WT on SDS–PAGE (insert to Fig. 2). The correct molecular mass of the refolded protein was confirmed by mass spectrometry, and the absence of free thiol groups by the Ellman assay (Ellman, 1959). Since the formation of all four disulphide bonds is highly unlikely to occur in a misfolded species, the absence of free SH groups in the purified protein provides strong evidence that the Fas^WT had indeed folded correctly. To further verify the correctness of the Fas fold, we compared the inhibitory activity of our refolded Fas^WT against TcAChE to that of the commercially available Fas^WT. Figure 2 shows that the inhibitory activities of the two Fas samples are equal within experimental error. The above experiments clearly demonstrate that our expression/refolding procedure yields the correctly folded and fully active Fas^WT in reasonable quantities (∼1 mg of protein from 1.5 l of E.coli culture). Next, we used the same procedure to obtain Fas^des. Less than 3% of free SH groups were detected in the protein sample after refolding, indicating that the correct Fas structure had been attained for the vast majority of the Fas^des molecules.

To measure the binding affinity of Fas^WT and Fas^des for TcAChE, we performed TcAChE activity assays in the presence of each Fas variant. A large range of Fas concentrations were explored to obtain a full TcAChE inhibition profile (Fig. 3A). Since binding of Fas to TcAChE inactivates the enzyme almost completely, the fractional enzymatic activity is inversely proportional to the Fas-bound enzyme species and can thus be used to calculate the binding affinity (K_d) of the Fas variant for TcAChE [see Eq. (2) in Materials and methods]. The K_d of Fas^WT for TcAChE was found to be 0.31 ± 0.07 nM, very similar to the value of 0.4 nM reported previously (Weiner et al., 2009). Fas^des bound to TcAChE with a K_d of 1.2 ± 0.2 nM, corresponding to a ∼0.8 kcal/mol increase in the free energy of binding, ΔΔG_bind, compared to Fas^WT (Fig. 3B).

Fig. 3

(A) Residual TcAChE activity in the presence of Fas variants (viz., T9N, K32R, Fas^des, R11K, T8V/T9N, Fas^WT, Fas^desR32K, T8V and H29R) is displayed as a function of their concentrations. TcAChE was maintained at a concentration of 0.04 nM in all experiments. A wide range of Fas concentrations were explored in order to encompass the entire activity profile for each mutant. The curves were fitted to a 1:1 binding model to determine the K_d values for interaction of TcAChE with the Fas mutants [See Eq. (2)]. Each experiment was repeated two to four times, and the average K_d and the standard deviation were calculated; (B) ΔΔG_bind values for interaction of the Fas mutants with TcAChE were calculated according to ΔΔG_bind=0.59 kcal/mol ln [K_d(Fas^mutant)/K_d(Fas^WT)]. The error bars were calculated from the standard deviations in the K_d values determined by repeating the experiments shown in (A).

Open in new tabDownload slide

To determine whether the increase in ΔΔG_bind displayed by Fas^des is due to a single mutation that is highly destabilizing for the Fas–TcAChE complex or to the sum of several slightly destabilizing mutations, we constructed all single mutants derived from the sequence of Fas^des. In addition, we made a double mutant, T8V/T9N, to explore the possibility that these two spatially proximal mutations are energetically coupled. TcAChE activity measurements in the presence of single and double Fas mutants are shown in Fig. 3A, while changes in binding affinity (K_d) and free energy of binding to TcAChE are summarized in Table I and Fig. 3B. Two mutations, K32R and T9N, proved to be rather deleterious for Fas binding to TcAChE, resulting in increases of 1.2 and 1.3 kcal/mol, respectively, in ΔΔG_bind. Mutation R11K destabilized the Fas–TcAChE complex very slightly, while mutation T8V was moderately stabilizing. Mutation H29R, however, improved the binding affinity for TcAChE considerably, producing a 1.1 kcal/mol decrease in ΔΔG_bind. The double mutant, T8V/T9N, exhibited a 0.4 kcal/mol increase in ΔΔG_bind. Simultaneous introduction of the T8V and T9N mutations destabilized the Fas–TcAChE complex by a smaller amount compared to the sum of ΔΔG_binds observed for the two individual mutations (0.75 kcal/mol). Hence, these two mutations are indeed energetically coupled. The rest of the single mutations were additive, producing a 0.84 kcal/mol increase in ΔΔG_bind for the sum of all the designed mutations in the Fas^des sequence (T8V/T9N+R11K+H29R+K32R) compared to 0.82 kcal/mol measured for Fas^des. In an attempt to obtain a multiple Fas mutant that would bind to TcAChE better than Fas^WT, we constructed the Fas^desR32K variant. In this variant, all the designed mutations were incorporated except for K32R, which had proved to be the most deleterious mutation. Fas^desR32K showed an enhanced binding affinity for TcAChE corresponding to a 0.4 kcal/mol decrease in ΔΔG_bind (Fig. 3B and Table I).

Our computational design procedure seeks to increase the overall stability of the Fas–TcAChE complex, but cannot make predictions with respect to changes in the rates of association and dissociation of the two proteins (k_on and k_off, respectively). Nevertheless, it is interesting to measure the effect of the predicted Fas mutations on the kinetics of the Fas–TcAChE interaction. To determine k_on and k_off for interaction of the Fas mutants with TcAChE, we performed the TcAChE activity assays under conditions in which the interaction of the two proteins approaches equilibrium. In these experiments, a Fas mutant was pre-incubated with TcAChE for various time intervals before the enzymatic activity was measured (Fig. 4A). At shorter incubation times, the system has not yet reached equilibrium and a number of the enzyme-bound Fas molecules depend on the association and the dissociation rates of this bio-molecular interaction. At longer incubation times, equilibrium is achieved and the fraction of the enzyme-bound Fas molecules is determined solely by the equilibrium binding affinity, K_d. The data were then analyzed using Eq. (3) (see Materials and methods) to obtain k_on and k_off (Fig. 4B and C and Table I). Most of the Fas mutants exhibited very slight changes in k_on, the exception being the H29R mutation, for which a ∼6-fold increase in k_on was observed. This substantial improvement in k_on is consistent with our computational prediction that H29R introduces a favorable electrostatic interaction of Fas with TcAChE Asp 285. A slight enhancement in k_on is also seen for the quintuple mutant Fas^des. k_off was unaltered for the H29R and R11K mutants. The rest of the Fas mutants (T8V/T9N, K32R and Fas^des) displayed a several-fold increase in k_off. The K_d values calculated from the kinetic constants are in good agreement with the K_d values obtained in the equilibrium experiments (Table I).

Fig. 4

(A) TcAChE activity in the presence of Fas mutants under conditions in which interaction between the two proteins approaches equilibrium. For clarity, the data for only three mutants are shown: K32R (closed square), Fas^des (closed circle) and H29R (closed diamond). TcAChE activity decreases with time until a plateau is reached. Slightly different concentrations were used for each Fas mutant so as to obtain optimal results. TcAChE at 0.025 nM was incubated with 0.75 nM Fas^des and 1.25 nM K32R; TcAChE at 0.006 nM was incubated with 0.15 nM H29R. The data were fitted to Eq. (3). (B) and (C) summarize the rates of association with TcAChE (B) and dissociation from the enzyme (C) of the various Fas mutants. Error bars represent the standard deviation obtained by repeating the experiments shown in (A). The experiment for K32R was performed only once.

Open in new tabDownload slide

Discussion

Our optimization produced a Fas mutant, Fas^des, with a binding interface composition 62% identical to that of Fas^WT. In this design procedure, we achieved a wild-type recovery rate higher than that observed on the average in protein design studies (51 and 27% in protein cores and surfaces, respectively) (Kuhlman and Baker, 2000). In addition, the optimization almost completely preserved the polar/hydrophobic content of the Fas^WT/TcAChE interface, although no hydrophobic patterning had been imposed during the design. These two results indicate that our energy function was able to reproduce successfully most of the favorable interactions in a high-affinity protein–protein complex. Nevertheless, Fas^des, with the five designed mutations, exhibited a ∼4-fold reduction in affinity for TcAChE compared to Fas^WT when measured experimentally. This reduction is attributed to an increase in k_off. Examination of single and double Fas mutants derived from the Fas^des sequence revealed that the reduced binding affinity is due primarily to one mutation, K32R, and removal of this mutation indeed resulted in a Fas mutant displaying increased affinity for TcAChE. At least one designed mutation, H29R, enhanced the affinity of the Fas–TcAChE complex significantly, due to enhancement of k_on. It should be noted that this mutation involves substitution of a polar residue by another polar residue, and does not increase the buried hydrophobic surface area of the Fas–TcAChE interface, in contrast to the strategy previously suggested for enhancing protein binding affinity (Sammond et al., 2007). A closer look at the design results revealed that our best Fas mutant, H29R, is predicted to considerably improve inter-molecular interactions between Fas and TcAChE. Our worst Fas mutant, K32R, in contrast, is predicted to improve interactions within Fas, while slightly destabilizing the Fas–TcAChE complex. To better understand the shortcomings of our computational procedure, we calculated the relative energetic contributions of inter- and intra-molecular interactions for each of the designed Fas mutations. In doing so, we summed all the molecular interactions considered in the ORBIT energy function, including van der Waals interactions, electrostatic interactions, hydrogen bonding and solvation. In addition, using the structure of the Fas–mAChE complex, we calculated the same energetic contributions for Fas mutants whose inhibitory activity towards mAChE had been reported previously (Marchot et al., 1997). For both Fas–AChE complexes, we observed only a weak correlation between the experimentally observed ΔΔG_bind and the change in the total calculated energy of the complex (ΔE_tot) that was used as a design criterion in this study (Fig. 5A). However, the correlation improved greatly when the inter-molecular energy term (ΔE_inter) alone was considered (Fig. 5B). A correlation coefficient of 0.80 was obtained for the single, double and quadruple Fas mutants reported in this study. This correlation coefficient was slightly reduced to 0.74 if the data for the previously reported Fas mutants were also incorporated. A slightly worse correlation between the experimental ΔΔG_bind and the calculated ΔE_inter was observed for the quintuple mutant Fas^des. One possible reason for this discrepancy is accumulation of errors in our predictions due to slight overestimation of ΔE_inter for each individual mutation (Fig. 5B). Another source of error might arise from slight changes in the backbone conformation of the Fas–TcAChE complex that is not modeled in our study. Such changes are much more likely to occur when multiple, rather than single, mutations are introduced into the Fas sequence.

Fig. 5

Correlation between the experimentally observed change in free energy of binding, ΔΔG_bind, and the change in the calculated energies for the Fas–TcAChE complex. (A) Correlation with the total energy change, ΔE_total. (B) Correlation with the inter-molecular energy change, ΔE_inter. (Closed circle) Fas mutants tested for binding to TcAChE in this study.(Closed inverted triangle) Fas mutants previously tested for binding to mAChE. We excluded Fas mutants with amino acid deletions or with mutations outside the Fas–mAChE interface, as well as mutants for which an exact value of K_d had not been reported. The lines represent the linear fitting of all the data points except for that for Fas^des.

Open in new tabDownload slide

In our recent study in which calmodulin (CaM) was optimized for interaction with a target peptide, a very strong correlation was observed between the experimental ΔΔG_bind and the calculated ΔE_tot, which is in contrast to our present findings (Yosef et al., 2009). This discrepancy can be explained easily if one takes into account that CaM undergoes a large conformational change upon binding. Hence, improvement in binding of CaM to its targets can be achieved not only by introduction of mutations that improve inter-molecular interactions, but also by introduction of mutations that stabilize CaM in its target-bound conformation [see also (Shimaoka et al., 2000)]. In the Fas/TcAChE complex, for which no substantial conformational change is believed to occur, mutations that stabilize Fas alone are thus not expected to improve its binding affinity for TcAChE.

In conclusion, using our computational design procedure, we were able to identify a single Fas mutant with a significantly enhanced binding affinity for TcAChE, and a quadruple Fas mutant with a slightly enhanced binding affinity for TcAChE. Inspection of our data revealed a better correlation of the experimental ΔΔG_bind with the calculated inter-molecular energy ΔE_inter than with ΔE_total. Thus, ΔE_inter may serve as a better predictive measure for redesign of protein–protein complexes in which no substantial conformational changes occur upon binding. A more extensive mutational study of the Fas–AChE binding interface is under way in order to test this prediction.

Funding

This study was supported by the Israeli Ministry of Health (J.M.S), by the Israel Science Foundation and by the Divadol Foundation (J.L.S.) J.L.S. is the Morton and Gladys Pickman Professor of Structural Biology. This work was in collaboration with the Israel Structural Proteomics Center (ISPC), supported by The Israel Ministry of Science, Culture, and Sport, the Divadol Foundation, the Neuman Foundation and the European Commission Sixth Framework Research and Technological Development Program ‘SPINE2-COMPLEXES’ Project Contract No. 031220. Funding to pay the Open Access publication charges for this article was provided by the Divadol Foundation.

References

Author notes