-
PDF
- Split View
-
Views
-
Cite
Cite
Kenji Eric Sadanari, Kazuyuki Omukai, Kazuyuki Sugimura, Tomoaki Matsumoto, Kengo Tomida, Impact of turbulent magnetic fields on disk formation and fragmentation in first star formation, Publications of the Astronomical Society of Japan, Volume 76, Issue 4, August 2024, Pages 823–840, https://doi.org/10.1093/pasj/psae051
Close - Share Icon Share
Abstract
Recent cosmological hydrodynamic simulations have suggested that the first stars in the Universe often form as binary or multiple systems. However, previous studies typically overlooked the potential influence of magnetic fields during this process, assuming them to be weak and minimally impactful. Emerging theoretical investigations, however, propose an alternative perspective, suggesting that turbulent dynamo effects within first-star forming clouds can generate strong magnetic fields. In this study, we perform three-dimensional ideal magnetohydrodynamics simulations, starting from the gravitational collapse of a turbulent cloud core to the early accretion phase, where disk fragmentation frequently occurs. Our findings reveal that turbulent magnetic fields, if they reach an equipartition level with turbulence energy across all scales during the collapse phase, can significantly affect the properties of the multiple systems. Specifically, both magnetic pressure and torques contribute to disk stabilization, leading to a reduction in the number of fragments, particularly for low-mass stars. Additionally, our observations indicate the launching of protostellar jets driven by magnetic pressure of toroidal fields, although their overall impact on star formation dynamics appears to be minor. Given the case with which seed magnetic fields amplify to the full equipartition level, our results suggest that magnetic fields likely play a significant role in shaping the initial mass function of the first stars, highlighting the importance of magnetic effects on star formation in the early Universe.
1 Introduction
The first stars in the Universe, formed from primordial hydrogen and helium gas and commonly referred to as Population III (Pop III) stars or metal-free stars, are believed to have emerged in the Universe around redshift |$z\sim 10\\!-\\!30$| according to the standard cosmology. Their appearance marks a significant change in the cosmic landscape, as they initiated the process of reionizing the Universe (e.g., Barkana & Loeb 2001). When these stars reached the end of their lives and exploded as supernovae, heavy elements synthesized within them were released into the interstellar medium, altering the thermal properties of the gas and triggering the transition to the next generation of star formation, namely Pop II/I stars (e.g., Heger et al. 2003; Umeda & Nomoto 2003; Greif et al. 2010; Chiaki et al. 2018).
Studies on the formation of the first stars have been actively pursued since the development of the Big Bang cosmology in the 1960s. Over the past few decades, significant advancements have been made in our theoretical understanding. According to the current understanding, the formation of the first stars occurs within so-called minihalos, which are dark matter halos with masses ranging from |$10^{5}\\!-\\!10^{6}\ M_{\odot }$| (e.g., Couchman & Rees 1986; Yoshida et al. 2003; Greif 2015). The star formation is triggered by |$\rm H_{2}$| cooling, which enables the baryonic gas to cool, leading to gravitational collapse. In the course of this, the cooling efficiency decreases as the |$\rm H_2$| rotational levels reach the local thermodynamic equilibrium at densities of around |$10^4\:\text{cm}^{-3}$|, causing the gas to enter a stage known as the “loitering stage” (e.g., Bromm et al. 2002), characterized by slow contraction, before eventually forming a cloud core in a state of quasi-hydrostatic equilibrium. As this cloud core grows and approaches the Jeans mass (|$M_{\rm J} \sim 10^{3}\ M_{\odot }$|) through gas accretion, it undergoes runaway collapse, leading to the birth of protostars at its center (e.g., Abel et al. 2002; Bromm et al. 2002; Yoshida et al. 2008).
After protostars are formed, they undergo a phase of mass growth through gas accretion from the surrounding envelope, known as the accretion phase. Due to the high temperatures, typically of the order of a few hundred K, the accretion rate can reach around |$\dot{M}\sim 10^{-3}\ M_{\rm \odot }\:\text{yr}^{-1}$| (e.g., Stahler et al. 1986; Omukai & Nishi 1998), significantly higher than in the case of present-day star formation. With such high accretion rates, the radiative feedback from the stars becomes inefficient, potentially allowing the first stars to grow to masses exceeding a few tens to even a few hundred solar masses if we assume minimal fragmentation and the formation of a single protostar (e.g., Omukai & Palla 2003; McKee & Tan 2008; Hosokawa et al. 2016)
However, a number of hydrodynamical simulations (e.g., Clark et al. 2011; Smith et al. 2011; Greif et al. 2012; Stacy & Bromm 2013; Susa 2019; Chon & Hosokawa 2019; Kimura et al. 2021; Park et al. 2021; Sugimura et al. 2020, 2023) have revealed that disk fragmentation due to gravitational instability tends to occur under conditions of high accretion rates. Susa (2019) have further shown that the number of fragments increases over time, resulting in highly multiple systems containing both massive and low-mass stars, with some even less than the solar mass. In these systems, low-mass stars can be easily ejected from the disk due to gravitational interactions within few-body systems (e.g., Clark et al. 2008; Greif et al. 2012; Susa et al. 2014). While low-mass first stars theoretically should still survive until the present-day Universe, they have yet to be detected despite concerted observational efforts (e.g., Hartwig et al. 2015; Ishiyama et al. 2016; Magg et al. 2018). Moreover, massive binary systems evolving into binary black holes (BHs) could potentially serve as sources of gravitational wave events (e.g., Kinugawa et al. 2014, 2016; Abbott et al. 2016; Hartwig et al. 2016). However, current simulations struggle to reproduce close binaries capable of merging within the age of the Universe, as accretion of high angular momentum gas causes the binary separation to expand to more than |$10^{3}\:\text{au}$| (e.g., Sugimura et al. 2020, 2023; Park et al. 2024).
Previous simulations, however, overlooked the influence of magnetic fields, which could potentially alter the characteristics of binary and multiple stellar systems. In the early Universe, theoretical investigations suggested the existence of minute seed magnetic fields generated from cosmological phenomena (e.g., Turner & Widrow 1988; Quashnock et al. 1989; Ratra 1992; Wagstaff et al. 2014; Saga et al. 2015; Subramanian 2016) and astrophysical processes, such as the Biermann battery mechanism (Biermann 1950; Biermann & Schlüter 1951) associated with supernova explosions (e.g,, Hanayama et al. 2005), radiation effects (e.g., Gnedin et al. 2000; Langer et al. 2003; Doi & Susa 2011; Attia et al. 2021), galaxy formation (e.g., Kulsrud et al. 1997), and the streaming of primordial cosmic rays (Ohira 2020, 2021). In particular, accretion shocks on to minihalos can generate weak magnetic fields in first star-forming regions, with field strengths ranging from |$10^{-20}$| to |$10^{-18}\:\text{G}$| (e.g., Xu et al. 2008; McKee et al. 2020).
Seed magnetic fields can be amplified further via a combined effect of global compression and dynamo action (e.g., Brandenburg & Subramanian 2005; Federrath 2016) during gravitational collapse. While compression alone might not suffice to generate magnetic fields that significantly influence gas dynamics, the turbulence naturally arising during gas accretion on to minihalos (e.g., Greif et al. 2012; Stacy & Bromm 2013; McKee et al. 2020) can drive a small-scale dynamo, thereby enhancing the amplification process (e.g., Batchelor 1950; Kazantsev 1968; Kulsrud & Anderson 1992; Schekochihin et al. 2004; Schleicher et al. 2010; Sur et al. 2010; Turk et al. 2012; Schober et al. 2012a; Xu & Lazarian 2016; McKee et al. 2020; Sadanari et al. 2023; Higashi et al. 2024). As a result, these fields can reach strengths comparable to turbulent energy levels before protostar formation (e.g., Schober et al. 2012a; McKee et al. 2020; Higashi et al. 2024). Hence, we can expect that the first star-forming clouds are magnetized close to the equipartition level, exhibiting a perturbed morphology as a result of turbulent motions, i.e., turbulent magnetic fields.
The impact of magnetic fields on star formation has been actively studied in the context of present-day star-forming regions, where strong and coherent magnetic fields have been observed (e.g., Crutcher 1999; Troland & Crutcher 2008; Pillai et al. 2015). According to magnetohydrodynamics (MHD) simulations, these coherent magnetic fields can efficiently transport angular momentum through processes such as magnetic braking (e.g., Gillis et al. 1974, 1979; Mouschovias & Paleologou 1979), MHD outflows (e.g., Blandford & Payne 1982; Tomisaka 2002; Banerjee & Pudritz 2006; Machida et al. 2008a; Tomida et al. 2010), and turbulence generation via magneto-rotational instability (MRI; e.g., Balbus & Hawley 1991; Bai & Stone 2013). These MHD phenomena result in the reduction of the disk size (e.g., Tomisaka 2000; Price & Bate 2007; Machida et al. 2011), suppression of fragmentation, decreased binary separation (e.g., Matsumoto 2024), and lower star formation efficiency (e.g., Padoan & Nordlund 2011; Federrath & Klessen 2012; Machida & Hosokawa 2013; Federrath 2015).
In turbulent magnetic fields, as expected in the first star-forming regions, numerical simulations suggest that the efficiency of magnetic braking tends to decrease due to the effects of the complex field structure (Hennebelle & Ciardi 2009; Seifried et al. 2012; Joos et al. 2012; Hirano et al. 2020) and magnetic dissipation via turbulent reconnection (e.g., Santos-Lima et al. 2012; Joos et al. 2013). Additionally, the power of MHD outflows is weaker in the presence of turbulent fields (e.g., Matsumoto et al. 2017; Lewis & Bate 2018; Hirano et al. 2020; Mignon-Risse et al. 2021; Takaishi et al. 2024). Gerrard, Federrath, and Kuruwita (2019) also pointed out that without a coherent magnetic field, outflows may not occur.
Several authors have performed MHD simulations of first-star formation during the accretion phase to investigate the impact of turbulent fields generated via dynamo on disk fragmentation and the initial mass function (IMF; e.g., Sharda et al. 2020, 2021; Stacy et al. 2022; Prole et al. 2022). However, these simulations yield conflicting results. Simulations which consider the magnetic field amplification from the collapse phase indicate that disk fragmentation is suppressed, resulting in a top-heavy IMF (Sharda et al. 2020, 2021; Stacy et al. 2022). Conversely, Prole et al. (2022) observed no magnetic effects on the fragmentation process when introducing random fields dominated by a small-scale power spectrum, as predicted by dynamo theory, at the end of collapse phase. The discrepancy may arise from different magnetic field structures at the beginning of the accretion phase, but this remains unclear.
Here, we perform the MHD simulations starting from the gravitational collapse of a turbulent gas cloud core, during which the magnetic fields are amplified via both dynamo and compression mechanisms. Subsequently, we simulate the ensuing evolution up to the accretion phase, where disk fragmentation occurs frequently, giving rise to the formation of multiple systems. Our investigation focuses on three key magnetic effects: magnetic pressure, previously demonstrated to stabilize the disk (e.g., Stacy et al. 2022); magnetic torques, responsible for angular momentum transport; and MHD outflows, capable of ejecting both mass and angular momentum. We investigate how these effects influence disk size, disk fragmentation, and binary properties such as separation, aiming to identify the conditions necessary for magnetic effects to impact the formation of first stars.
This paper is organized as follows: Section 2 outlines the numerical methods we used and the initial setup. In section 3, we present the results of our simulations. We first explain the magnetic amplification during the collapse in subsection 3.1. Subsequently, in subsection 3.2, we examine the evolution of the disk and its fragmentation during the accretion phase. Then, we examine how magnetic fields evolved within the disk and explore their effects on the system, focusing on magnetic pressure, magnetic torques, and MHD outflow, in subsection 3.3. In subsection 3.4, we discuss how these magnetic effects influenced the properties of binary and multiple systems. We summarize our findings and discuss their implications for the formation of first stars in section 4.
2 Numerical method
2.1 Code description
We perform three-dimensional ideal MHD simulations using the adaptive mesh refinement (AMR) code SFUMATO (Matsumoto 2007; Matsumoto et al. 2015). These simulations start with the collapse of a gas cloud core and extend though the accretion phase. To model the chemical and thermal evolution, we use the SFUMATO-RT module (Sugimura et al. 2020). The chemical network and the thermal process are described in detail in Sadanari et al. (2021). Since non-ideal MHD effects are expected to be negligible in primordial gas (e.g., Maki & Susa 2004, 2007; Machida et al. 2008b; Sadanari et al. 2023), we adopt ideal MHD assumptions in our simulations. We solve the same governing equations as in Sadanari et al. (2021), using the HLLD approximate Riemann solver (Miyoshi & Kusano 2005) for the MHD part with a divergence cleaning technique (Dedner et al. 2002) and the multi-grid method for the self-gravity part. Both parts are solved with a second-order accuracy in space and time.
We initially set the box size and the number of cells in each direction to |$L_{\rm box}=4\times 10^{6}\:\text{au}$| and |$N_{\rm base}=256$|, respectively. We employ a cell refinement condition, where the cells are divided if their size exceeds |$1/64$| of the local Jeans length, to ensure accurate representation of dynamo amplification during the collapse phase (e.g., Sur et al. 2010; Federrath et al. 2011b; Turk et al. 2012). The maximum refined level is limited to |$l_{\rm max}=15$|, and the minimum cell size is |$\Delta x_{\rm min}\simeq 4.7\times 10^{-1}\:\text{au}$|.
To simulate up to the accretion phase without employing the sink particle technique, we suspend cooling when the density reaches |$n_{\rm th}=10^{14}\:\text{cm}^{-3}$|. This prevents further collapse and results in the formation of artificial adiabatic gas cores with |$n\\gt n_{\rm th}$|. Although these cores are considerably larger than the radius of real protostars, we interpret their formation as indicative of protostar formation. Our simulations continue for at least |$3500\:\text{yr}$| after the formation of the primary protostar (adiabatic core) to observe the magnetic effects on disk fragmentation.
2.2 Initial properties of gas cloud cores
As in our previous paper (Sadanari et al. 2023), we consider a single gas cloud core in the loitering phase, on the verge of gravitational collapse. We vary the magnetic field strength as a parameter for each simulation run. We adopt a density distribution characterized by a gravitationally unstable Bonnor– Ebert sphere (Ebert 1955; Bonnor 1956), with a density profile enhanced by a factor of 1.4 to initiate collapse.
This core is initially endowed with rigid rotation and turbulence, characterized by a typical power spectrum indicative of supersonic and compressible turbulence, given by |$P(k)\propto k^{-4}$| (e.g., Federrath et al. 2021), where k denotes the wavenumber. The rotational and turbulent energies within the core amount to 1% and 3% of the gravitational energy |$|E_{\rm grav}|$|, respectively, consistent with typical energies anticipated from cosmological simulations (Greif et al. 2012; Stacy & Bromm 2013; Stacy et al. 2022). Note that the choice of initial turbulence energy does not significantly impact the simulation results because turbulence can be amplified during the gravitational collapse (e.g., Vázquez-Semadeni et al. 1998; Federrath et al. 2011b; Higashi et al. 2021, 2022). The various quantities characterizing the cloud core employed as the initial condition are summarized in table 1.
| Parameter . | Value . |
|---|---|
| Mass |$M_{\rm cl}$| | |$5.5\times 10^{3}\ M_{\odot }$| |
| Radius |$R_{\rm cl}$| | |$1.1\times 10^{6}\:\text{au}$| |
| Central number density |$n_{\rm c,0}$| | |$1.4\times 10^{3}\:\text{cm}^{-3}$| |
| Temperature |$T_{\rm init}$| | |$198\:\text{K}$| |
| Ratio of thermal to gravitational energies |$E_{\rm th}/|E_{\rm g}|$| | 0.6 |
| Ratio of rotational to gravitational energies |$E_{\rm rot}/|E_{\rm g}|$| | 0.01 |
| Ratio of turbulent to gravitational energies |$E_{\rm turb}/|E_{\rm g}|$| | 0.03 |
| Parameter . | Value . |
|---|---|
| Mass |$M_{\rm cl}$| | |$5.5\times 10^{3}\ M_{\odot }$| |
| Radius |$R_{\rm cl}$| | |$1.1\times 10^{6}\:\text{au}$| |
| Central number density |$n_{\rm c,0}$| | |$1.4\times 10^{3}\:\text{cm}^{-3}$| |
| Temperature |$T_{\rm init}$| | |$198\:\text{K}$| |
| Ratio of thermal to gravitational energies |$E_{\rm th}/|E_{\rm g}|$| | 0.6 |
| Ratio of rotational to gravitational energies |$E_{\rm rot}/|E_{\rm g}|$| | 0.01 |
| Ratio of turbulent to gravitational energies |$E_{\rm turb}/|E_{\rm g}|$| | 0.03 |
| Parameter . | Value . |
|---|---|
| Mass |$M_{\rm cl}$| | |$5.5\times 10^{3}\ M_{\odot }$| |
| Radius |$R_{\rm cl}$| | |$1.1\times 10^{6}\:\text{au}$| |
| Central number density |$n_{\rm c,0}$| | |$1.4\times 10^{3}\:\text{cm}^{-3}$| |
| Temperature |$T_{\rm init}$| | |$198\:\text{K}$| |
| Ratio of thermal to gravitational energies |$E_{\rm th}/|E_{\rm g}|$| | 0.6 |
| Ratio of rotational to gravitational energies |$E_{\rm rot}/|E_{\rm g}|$| | 0.01 |
| Ratio of turbulent to gravitational energies |$E_{\rm turb}/|E_{\rm g}|$| | 0.03 |
| Parameter . | Value . |
|---|---|
| Mass |$M_{\rm cl}$| | |$5.5\times 10^{3}\ M_{\odot }$| |
| Radius |$R_{\rm cl}$| | |$1.1\times 10^{6}\:\text{au}$| |
| Central number density |$n_{\rm c,0}$| | |$1.4\times 10^{3}\:\text{cm}^{-3}$| |
| Temperature |$T_{\rm init}$| | |$198\:\text{K}$| |
| Ratio of thermal to gravitational energies |$E_{\rm th}/|E_{\rm g}|$| | 0.6 |
| Ratio of rotational to gravitational energies |$E_{\rm rot}/|E_{\rm g}|$| | 0.01 |
| Ratio of turbulent to gravitational energies |$E_{\rm turb}/|E_{\rm g}|$| | 0.03 |
We introduce uniform magnetic fields aligned with the rotation axis, each possessing distinct levels of magnetic energy: |$E_{\rm mag}/|E_{\rm grav}| = 2\times 10^{-7}$|, |$2\times 10^{-5}$|, and |$2\times 10^{-4}$|. Correspondingly, the initial strengths of these magnetic fields are set to |$B_{\rm init} = 10^{-8}\:\text{G}$|, |$10^{-7}\:\text{G}$|, and |$5\times 10^{-7}\:\text{G}$|, respectively. In addition, for comparison, we conduct hydrodynamics simulations devoid of any magnetic field. These initial field strengths are chosen to allow for the dynamo process during collapse, ensuring that the magnetic energy remains lower than the turbulent energy. By adjusting the initial field strengths, we replicate various magnetic field strengths and structures at the epoch of the end of the collapse phase. This enables us to investigate the necessary conditions under which turbulent magnetic fields impact the formation of first stars.
3 Results
3.1 Magnetic amplification during the collapse phase
First, we investigate the evolution of magnetic fields during the collapse phase and analyze the field structure at the onset of the accretion phase in our simulations. According to theoretical prediction, when the initial magnetic energy is lower than the turbulent energy, a small-scale dynamo driven by turbulence can enhance the magnetic amplification rate.
The dynamo process during the collapse phase can be divided into three distinct stages (e.g., Xu & Lazarian 2016; McKee et al. 2020). Initially, during the kinematic stage, magnetic fields undergo exponential amplification on small scales, without encountering significant back reaction from magnetic forces. This stage is characterized by the prevalence of small-scale structures in the magnetic field configuration. Subsequently, in the nonlinear stage following equipartition on the smallest scales, further dynamo amplification on small scales is impeded by the back reaction. However, on larger scales, magnetic fields continue to amplify through dynamo action, eventually becoming dominant over the small-scale fields. In the final phase, once all scales, from the smallest scale to the driving scale corresponding to the Jeans scale, reach the equipartition level, the dynamo amplification halts. At this stage, the field strength approaches to the equipartition with turbulence, defined as
where |$V_{\rm turb}$| denotes turbulent velocity. Note that the saturation of the turbulent dynamo depends on the properties of turbulence, i.e., the Mach number and the driving mode (e.g., Federrath et al. 2011a) and on the plasma parameter, i.e., the Prandtl number (Federrath et al. 2014a). For subsonic turbulence, the magnetic fields typically saturate around |$0.7B_{\rm eq}$| (Haugen et al. 2004; Federrath et al. 2011a; Brandenburg 2014). During this phase, the magnetic energy becomes concentrated on the largest scales (Jeans scale) as the magnetic power spectrum follows the turbulent spectrum |$P(k) \propto k^{-4}$|. Additionally, Sadanari et al. (2023) observed a tendency for field lines to align due to the effects of the global compression of equipartition fields.
Figure 1 shows the configuration and strength of sliced magnetic field lines on the plane perpendicular to the rotation axis at the moment of first (primary) protostar formation for three magnetized cases. The field lines are 2D projection of the 3D magnetic fields on to the plane. These figures illustrate the generation of turbulent magnetic fields in all cases, attributable to dynamo action. We can also see that the surrounding field strength is greater in cases where the initial magnetization is higher.
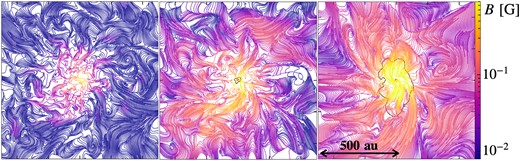
Configuration of sliced magnetic field lines on the face-on plane at the epoch of the formation of the primary protostar for the cases of |$B_{\rm init}=10^{-8}\:\text{G}$| (left), |$10^{-7}\:\text{G}$| (middle), and |$5\times 10^{-7}\:\text{G}$| (right). The field lines are the 2D projection of the 3D magnetic fields on to the plane. The protostar is located at the center of each panel. Line color indicates the field strength, and the areas enclosed by black lines in the middle and right-hand panels indicate the region where the fields reach a full equipartition state.
In the least magnetized case, with |$B_{\rm init} = 10^{-8}\:\text{G}$|, magnetic fields are amplified until their energy matches that of the turbulent energy on the smallest resolved scale, i.e., the cell scale, by this moment. At this stage, as magnetic fields on larger scales have not yet reached equipartition with the turbulent energy, the predominant field energy remains concentrated on smaller scales. Consequently, only turbulent motion on smaller scales is affected by the back reaction of magnetic forces.
In the cases with stronger initial magnetic fields, |$B_{\rm init} = 10^{-7}\:\text{G}$| and |$5\times 10^{-7}\:\text{G}$|, the magnetic fields achieve equipartition levels before the formation of the protostar. Consequently, the magnetic energy becomes concentrated on larger scales, specifically the Jeans scale. The density at which the magnetic fields reach equipartition is approximately |$10^{13}\:\text{cm}^{-3}$| for |$B_{\rm init} = 10^{-7}\:\text{G}$| and |$10^{11}\:\text{cm}^{-3}$| for |$B_{\rm init} = 5\times 10^{-7}\:\text{G}$|. Thus, the spatial extent where |$B\sim B_{\rm eq}$| is greater for the case of |$B_{\rm init} = 5\times 10^{-7}\:\text{G}$|. This region is illustrated in figure 1 by the enclosed area marked by black thin lines. The properties of each magnetized case are summarized in table 2.
| Model . | |$E_{\rm {rot}}/|E_{\rm g}|$| . | |$E_{\rm {turb}}/|E_{\rm g}|$| . | |$E_{\rm {mag}}/|E_{\rm g}|$| . | |$\mu _{0}$| . | |$B_{\rm init}\ \rm [G]$| . | B-field @ protostar formation . |
|---|---|---|---|---|---|---|
| T2M0... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$0$| | |$\infty$| | |$0$| | — |
| T2M7... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-7}$| | 27000 | |$10^{-8}$| | |$B \\lt B_{\rm eq}$| |
| T2M5... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-5}$| | 2700 | |$10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{13}\:\text{cm}^{-3}$|) |
| T2M4... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-4}$| | 100 | |$5\times 10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{11}\:\text{cm}^{-3}$|) |
| Model . | |$E_{\rm {rot}}/|E_{\rm g}|$| . | |$E_{\rm {turb}}/|E_{\rm g}|$| . | |$E_{\rm {mag}}/|E_{\rm g}|$| . | |$\mu _{0}$| . | |$B_{\rm init}\ \rm [G]$| . | B-field @ protostar formation . |
|---|---|---|---|---|---|---|
| T2M0... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$0$| | |$\infty$| | |$0$| | — |
| T2M7... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-7}$| | 27000 | |$10^{-8}$| | |$B \\lt B_{\rm eq}$| |
| T2M5... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-5}$| | 2700 | |$10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{13}\:\text{cm}^{-3}$|) |
| T2M4... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-4}$| | 100 | |$5\times 10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{11}\:\text{cm}^{-3}$|) |
The dimensionless parameter |$\mu _{\rm 0}$| indicates the mass-to-flux ratio normalized by the critical value |$(M/\Phi )_{\rm cr}$|.
| Model . | |$E_{\rm {rot}}/|E_{\rm g}|$| . | |$E_{\rm {turb}}/|E_{\rm g}|$| . | |$E_{\rm {mag}}/|E_{\rm g}|$| . | |$\mu _{0}$| . | |$B_{\rm init}\ \rm [G]$| . | B-field @ protostar formation . |
|---|---|---|---|---|---|---|
| T2M0... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$0$| | |$\infty$| | |$0$| | — |
| T2M7... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-7}$| | 27000 | |$10^{-8}$| | |$B \\lt B_{\rm eq}$| |
| T2M5... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-5}$| | 2700 | |$10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{13}\:\text{cm}^{-3}$|) |
| T2M4... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-4}$| | 100 | |$5\times 10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{11}\:\text{cm}^{-3}$|) |
| Model . | |$E_{\rm {rot}}/|E_{\rm g}|$| . | |$E_{\rm {turb}}/|E_{\rm g}|$| . | |$E_{\rm {mag}}/|E_{\rm g}|$| . | |$\mu _{0}$| . | |$B_{\rm init}\ \rm [G]$| . | B-field @ protostar formation . |
|---|---|---|---|---|---|---|
| T2M0... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$0$| | |$\infty$| | |$0$| | — |
| T2M7... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-7}$| | 27000 | |$10^{-8}$| | |$B \\lt B_{\rm eq}$| |
| T2M5... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-5}$| | 2700 | |$10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{13}\:\text{cm}^{-3}$|) |
| T2M4... | |$10^{-2}$| | |$3\times 10^{-2}$| | |$2\times 10^{-4}$| | 100 | |$5\times 10^{-7}$| | |$B\sim B_{\rm eq}$| (|$n_{\rm H}\gtrsim 10^{11}\:\text{cm}^{-3}$|) |
The dimensionless parameter |$\mu _{\rm 0}$| indicates the mass-to-flux ratio normalized by the critical value |$(M/\Phi )_{\rm cr}$|.
3.2 Disk evolution and fragmentation
Next, we investigate the gas dynamics during the accretion phase following the formation of the primary protostar. First, we focus on examining how circumstellar disks around primary protostars fragment to give rise to binary or multiple systems in the absence of an initial magnetic field (|$B_{\rm init}=0\:\text{G}$|). As we will see later, the fragmentation process of the disks proceeds similarly even in the magnetized cases.
Figure 2 presents a sequence of face-on density-weighted projections showing the evolution from the formation of a primary protostar to the emergence of a binary system. The enclosed area marked by black lines corresponds to the adiabatic core or protostar (|$n_{\rm H}\\gt 10^{14}\:\text{cm}^{-3}$|), with its center of gravity indicated by a red dot. Additionally, we show the disk region where rotational motion dominates over collapse motion with orange circles in each panel. These circles are determined based on the disk radius |$R_{\rm disk}$|, defined as the transition radius R where the azimuthally-averaged rotation speed |$v_{\phi }(R)$| surpasses three times the collapse speed |$v_{R}(R)$|. This empirical criterion effectively traces the disk region.
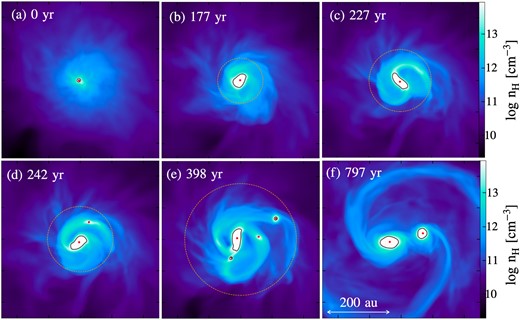
Sequence of face-on density-weighted projections illustrating the distribution of number density at six different time intervals, from the formation of a primary protostar (panel a) to the emergence of a binary system (panel f) in the unmagnetized case (|$B_{\rm init}=0\:\text{G}$|). The time elapsed from the formation of the primary protostar is indicated in the top left-hand corner of each panel. The regions enclosed by the black lines and the red points delineate the adiabatic regions, where |$n_{\rm H}\\gt 10^{14}\:\text{cm}^{-3}$| and their center of mass, respectively. The orange circles indicate the disk region, defined as the transition radius R where the azimuthally-averaged rotation speed |$v_{\phi }(R)$| exceeds three times the collapse speed |$v_{R}(R)$|. We do not draw the orange circle in panel (f) because |$R_{\rm disk}$| in that case is larger than one side of the snapshot.
Initially, a primary protostar emerges at the center of the collapsing gas cloud, as illustrated in figure 2a. Subsequently, it gains mass through the accretion of envelope gas. The envelope accretes on to the center along with the angular momentum inherited from the initial rotation and turbulence of the cloud core, leading to the spontaneous formation of a rotating disk around the protostar, as depicted by the orange circle in figure 2b.
As time elapses, the disk region continues to expand and gain mass, eventually becoming gravitationally unstable. This instability manifests in the emergence of two spiral arms within the disk, as shown in figure 2c. Quantitatively, the disk’s gravitational instability can be assessed using the Toomre Q parameter (Toomre 1964), defined as |$Q \equiv c_{\rm s}\Omega _{\rm epi}/(\pi G \Sigma )$|, where |$c_{\rm s}$|, |$\Omega _{\rm epi}$|, and |$\Sigma$| are the sound speed, epicyclic frequency, and surface density of the disk, respectively. When the Toomre Q parameter approaches unity, spiral arms begin to emerge within the disk (e.g., Laughlin & Bodenheimer 1994), a criterion we also confirm in our simulations. These arms play a crucial role in redistributing mass and angular momentum within the disk by generating non-axisymmetric gravitational torques, thereby aiding in disk stabilization.
However, in cases characterized by high accretion rates, such as in our case of first star formation, gravitational instability persists and intensifies as the disk accumulates mass more rapidly than it can be stabilized by the spiral arms. Consequently, the spiral arms continue to acquire mass, eventually becoming gravitationally unstable and undergoing fragmentation, as evidenced by the red point in figure 2d. As noted by Takahashi, Tsukamoto, and Inutsuka (2016), spiral arms become unstable when the Toomre Q parameter drops below approximately 0.6, as inferred from linear stability analyses. In most cases, this condition is met when the spiral arms are tightly wound and collide with each other, causing an increase in the surface density. Consequently, the spiral arms continue fragmenting further, resulting in the emergence of three protostars (fragments) surrounding the primary protostar, as depicted in figure 2e. However, gravitational torques exerted by the spiral arms cause most of the protostars to migrate towards the primary protostar. Eventually, only one companion protostar survives around the central protostar, resulting in the formation of a binary system, as illustrated in figure 2f.
Following the formation of binary or multiple systems, we can identify two distinct types of disks: circumstellar disks surrounding each individual protostar, and circum-binary or circum-multiple disks enveloping the entire binary or multiple systems. The circum-multiple disk primarily gains mass from the accreting envelope, whereas the circumstellar disk primarily receives gas from the spiral arms extending from each protostar, as depicted in figure 2f. As time elapses, the spiral arms in both types of disks will undergo further fragmentation, as detailed later.
Next, we also examine the magnetized cases. Figure 3 presents a face-on view of the density structure for cases with |$B_{\rm init}=0\:\text{G},\ 10^{-8}\:\text{G},\ 10^{-7}\:\text{G}$|, and |$5\times 10^{-7}\:\text{G}$|, spanning from |$\rm 500\:\text{yr}$| to |$\rm 3000\:\text{yr}$| at intervals of |$\rm 500\:\text{yr}$|. Additionally, the time evolution of the radial density profile for all these cases is depicted in figure 4. The horizontal axis represents the time after the formation of the primary protostar |$t_{\rm p}$|, while the vertical axis represents the radius from the center of mass R. The color scale represents the azimuthally-averaged density on the disk midplane. In figures 3 and 4, orange circles and dashed orange lines respectively denote the disk region, defined in the same manner as in figure 2. Additionally, in figure 4, yellow and red star symbols indicate the positions where fragmentation occurred in the circumstellar and circum-multiple disks, respectively.
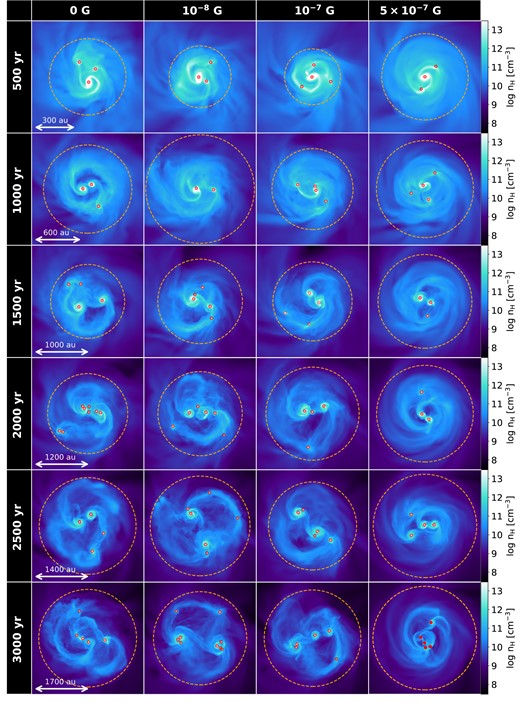
Face-on mass-weighted average density distribution at six different time intervals: |$\rm 500\:\text{yr},\ 1000\:\text{yr},\ 1500\:\text{yr},\ 2000\:\text{yr},\ 2500\:\text{yr}$|, and |$\rm 3000\:\text{yr}$| after the formation of the primary protostar, with four different initial magnetic field strengths: |$B_{\rm init}=0\:\text{G},\ 10^{-8}\:\text{G},\ 10^{-7}\:\text{G}$|, and |$5\times 10^{-7}\:\text{G}$| (columns from left to right). The center of each snapshot corresponds to the center of mass. Snapshots at the same epoch (row) share the same scale, as indicated by the white arrow in the left-hand panel. The orange circles indicate the radius of the disk region |$R_{\rm disk}$|.
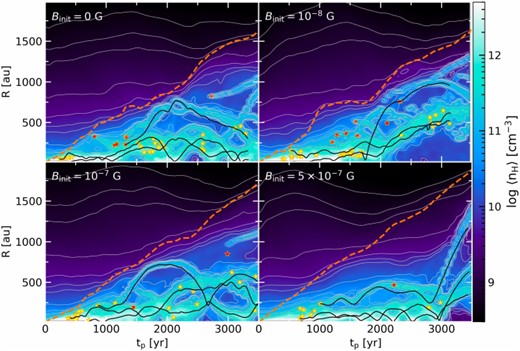
Time evolution of the radial profile of azimuthally-averaged density for four different cases: |$B_{\rm init}=0\:\text{G},\ 10^{-8}\:\text{G},\ 10^{-7}\:\text{G}$|, and |$5\times 10^{-7}\:\text{G}$|. Orange dashed lines represent the disk radius |$R_{\rm disk}$|, while black lines indicate the trajectories of three massive protostars. Yellow (red) stars indicate the radial positions at which protostars form through the fragmentation of spiral arms in circumstellar (circum-multiple/binary, respectively) disks.Thin lines represent the contours of the azimuthally-averaged density.
From figure 3, we can clearly see that the binary or multiple systems form in all cases, regardless of magnetized level. These systems form through the fragmentation process of the spiral arms, as seen in the unmagnetized case. Once multiple systems are established, fragmentation primarily occurs in two distinct regions: one involves the fragmentation of the spiral arms within the circumstellar disk (yellow stars in figure 4), while the other involves the fragmentation of the spiral arms extending outward from the binary systems (red stars in figure 4).
The former type of fragmentation primarily occurs across all the cases, albeit with a decreased frequency in more strongly magnetized cases, as evidenced by the diminishing number of yellow stars in figure 4. This reduction is mainly attributed to the stabilizing effect induced by magnetic pressure (sub-subsection 3.3.2). Protostars formed through this fragmentation process often merge with the central protostar due to their initial proximity.
In the latter type of fragmentation, fragmentation predominantly occurs in the relatively outer region of the disk (as indicated by the red stars in figure 4). In the weakly magnetized cases (|$B_{\rm init}=0\:\text{G}$| and |$10^{-8}\:\text{G}$|), the spiral arms extend outward to the outer region, facilitating fragmentation. However, in the case of |$B_{\rm init}=10^{-7}\:\text{G}$|, although prominent spiral arms are observed in the circum-multiple disk, fragmentation frequency is reduced, by the magnetic pressure effect, compared to the weakly magnetized cases, as evidenced by the smaller number of red stars in figure 4. In the strongest magnetized case (|$B_{\rm init}=5\times 10^{-7}\:\text{G}$|), prominent spirals are absent due to the angular momentum transport by magnetic torques (see sub-subsection 3.3.3), resulting in the suppression of fragmentation in the outer region. Consequently, both the gas and protostars tend to be more concentrated toward the center of the disk region compared to other weakly magnetized cases (|$B_{\rm init} \le 10^{-7} \:\text{G}$|), as illustrated in figures 3 and 4.
3.3 Magnetic field evolution and their impact on the disks
Although the formation of multiple systems occurs regardless of the initial magnetic field strength, differences arise in the evolution and structure of the disk, leading to variations in the frequency of fragmentation, as observed in the previous section. These differences stem from the influence of magnetic fields on the gas dynamics within the disk region. In this section, we first investigate the evolution of magnetic field strength and configuration within the disk region. Subsequently, we examine three magnetic effects: magnetic pressure, magnetic torques as a mechanism for angular momentum transport, and magnetically-driven outflows, in this order.
3.3.1 Magnetic evolution within the disk
Figure 5 shows the face-on density-weighted projection of magnetic field strength at |$t_{\rm p}=0$| (top) and |$t_{\rm p}=3500\:\text{yr}$| (middle). The left-hand column represents the case of |$B_{\rm init}=10^{-8}\:\text{G}$|, the middle column |$B_{\rm init}=10^{-7}\:\text{G}$|, and the right-hand column |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|. The orange circles and green points, respectively, indicate the disk region and the positions of protostars. The pattern of shadows in each snapshot represents the direction of the magnetic field lines sliced in the plane.
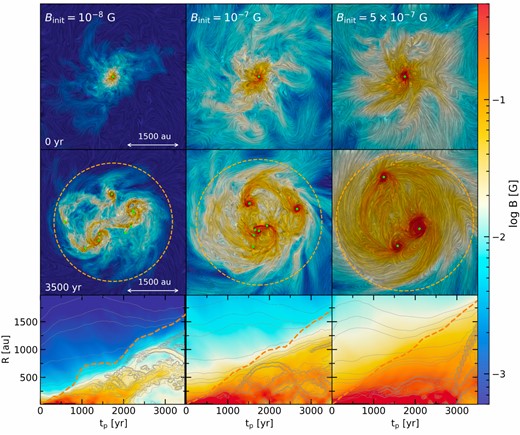
Face-on, mass-averaged magnetic field strength distribution at |$t_{\rm p}= 0\:\text{yr}$| (top) and |$3500\:\text{yr}$| (middle) for the three magnetized cases: |$B_{\rm init}=10^{-8}\:\text{G}$| (left-hand column), |$10^{-7}\:\text{G}$| (middle column), and |$5\times 10^{-7}\:\text{G}$| (right-hand column). The orange circles represent the radius of the disk region as defined in subsection 3.2. The positions of protostars in top and middle panels are indicated as green points. The shadow pattern represents the direction of magnetic field lines sliced in the plane. The bottom figures display the time evolution of the radial profile of azimuthally-averaged field strength, similar to figure 4. The orange dashed lines represent the radius of the disk region |$R_{\rm disk}$|. Thin gray lines in the bottom panels represent the density contour, as shown in figure 4.
As mentioned in subsection 3.1, the distribution of field strength at |$t_{\rm p}=0$| (top panels in figure 5) varies depending on the initial field strength |$B_{\rm init}$|. A stronger initial field results in a higher field strength at the beginning of the accretion phase. Moreover, the magnetic field lines have undergone significant disturbance due to the dynamo amplification process during the collapse (see also figure 1).
After the formation of the primary protostar, the rotational motion inside the disk region generates toroidal magnetic fields from poloidal fields, as illustrated in the shadow pattern in the middle panel in figure 5. Particularly, the differential rotation can amplify the toroidal fields, a phenomenon known as the |$\Omega$| effect (e.g., Babcock 1961).
Additionally, as the spiral arms extend outward, they gather toroidal fields along their trajectories, leading to the emergence of coherent toroidal fields within the arms. This is clearly seen in the middle top panel of figure 6, where a detailed view of the magnetic field structure around the spiral arm is depicted during its fragmentation into a new protostar for the magnetized case with |$B_{\rm init}=10^{-7}\:\text{G}$|. In this field configuration, the field strength within the arm experiences amplification due to compression along them, following a relation of |$B\propto \rho$| at maximum. This amplification rate surpasses that in the case of spherical compression (|$B\propto \rho ^{2/3}$|). Consequently, the average field strength within the disk is enhanced by compression along the arms after their emergence.
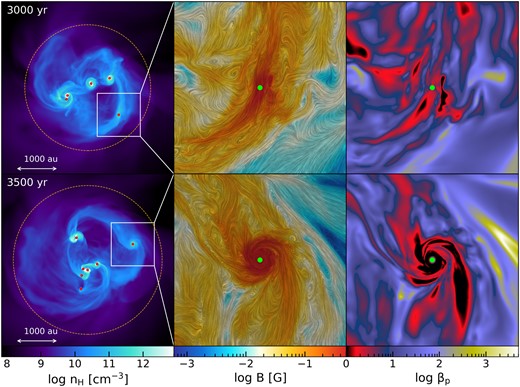
Close-up view of the magnetic field structure around a protostar in the case of |$B_{\rm init}=10^{-7}\:\text{G}$|. The left-hand panel displays the density distribution of the entire disk region, with the boxed area highlighted for enlargement in the middle and right-hand panels. The middle panel provides a close-up depiction of the magnetic field strength, while the right-hand panel illustrates the plasma beta |$\beta _{\rm p}\equiv P_{\rm th}/P_{\rm mag}$|, specifically focusing on a spiral arm within the circum-multiple disk. The upper panels correspond to the moment when the arm fragments into a new protostar (|$t_{\rm p}=3000\:\text{yr}$|), while the lower panels represent a later moment, |$500\:\text{yr}$| after the fragmentation. Shadow patterns in the field strength panel indicate the direction of field lines, as illustrated in figure 5.
Another possible mechanism for magnetic amplification is the |$\alpha$| dynamo process (e.g., Steenbeck et al. 1966; Brandenburg & Subramanian 2005). This process involves the generation of poloidal fields from toroidal fields due to helical motion inside the disk. Some studies (e.g., Liao et al. 2021) have argued that the |$\alpha$| dynamo significantly contributes to field amplification in accretion disks, a conclusion supported by MHD simulations performed by Sharda, Federrath, and Krumholz (2021). However, our simulations do not observe the growth of poloidal fields through this dynamo process, even in the outer region of the disk, where the required resolution is sufficient to capture the dynamo process (e.g., Federrath et al. 2011b). We infer that disk fragmentation disrupts the helical motion, thereby impeding the driving mechanism of the |$\alpha$| dynamo. Confirmation of this hypothesis will necessitate higher resolution in future numerical studies.
From the distribution of magnetic fields at |$t_{\rm p}=3500\:\text{yr}$| (middle panels of figure 5), we can find an increase in field strength within the disk region across the all magnetized cases. Comparing the magnetic field distribution with the density (figure 3), we observe a rough correlation between them. In the bottom panels of figure 5, we present the time evolution of the radial profile of field strength, overlaid with the density contour from figure 4 shown as thin gray lines. It appears that the field strength remains almost constant along the iso-density contour. This suggests that the amplification mechanisms shown above, i.e., the |$\Omega$| effect and |$\alpha$| dynamo, are not efficient within the disk.
While the magnetic field strength correlates well with the density, we also observe a slow amplification of the magnetic fields at a fixed density. To analyze the magnetic evolution qualitatively, we plot the time evolution of the average energy density of the magnetic field over the density range |$6 \times 10^9$| to |$8 \times 10^9 \:\text{cm}^{-3}$| for three magnetized cases in figure 7. Note that in this density regime, the field strength in none of these cases has reached the equipartition field |$B_{\rm eq}$| by the beginning of the accretion phase. For the case with |$B_{\rm init}=5\times 10^{-7}\:\text{G}$| (orange line), the magnetic field gradually amplifies initially and eventually reaches a level close to saturation, roughly equaling the thermal energy (indicated by the dashed line) within a factor of about 2. For less magnetized cases (|$B_{\rm init}\le 10^{-7}\:\text{G}$|), the field energies continue to increase slowly over time. This gradual amplification is caused by the combination of the |$\Omega$| effect and the compression by spiral arms, as mentioned before.
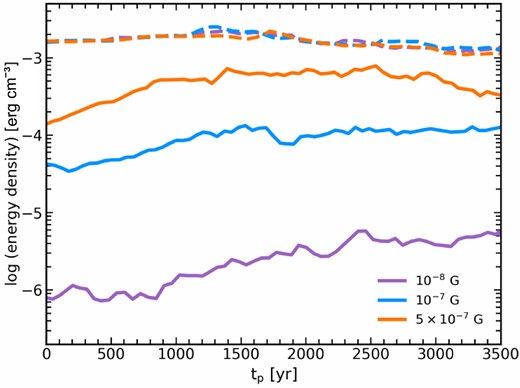
Time evolution following the formation of the primary protostar (|$t_{\rm p}$|) of the average magnetic energy density within a specific density range from |$6\times 10^{9}\:\text{cm}^{-3}$| to |$8\times 10^{9}\:\text{cm}^{-3}$| (solid line). The thermal energy density is represented by dashed lines.
We speculate that the diffusion process of magnetic turbulent reconnection, discussed in previous studies (e.g., Santos-Lima et al. 2012), slows down the amplification rates within the disk region. Additionally, disk fragmentation disturbs the magnetic field lines, further enhancing this diffusion mechanism (see figure 5). Consequently, the level of magnetization within the disk region during the early accretion phase, where the disk fragmentation frequently occurs, appears to depend on how strongly the magnetic fields are amplified during the collapse phase.
3.3.2 Effects of magnetic pressure
Magnetic pressure can stabilize the disks against gravitational instability by adding to thermal pressure. To investigate its impact on gas dynamics, we evaluate the plasma beta |$\beta _{\rm p}$|, which represents the ratio of thermal pressure (|$P_{\rm th}$|) to magnetic pressure (|$P_{\rm mag}=B^{2}/(8\pi )$|). As |$\beta _{\rm p}$| approaches unity, magnetic pressure can affect the gas dynamics. Since transonic turbulence is realized in our simulations, |$\beta _{\rm p}$| can be approximated as |$\beta _{\rm p} \sim (B_{\rm eq}/B)^{2}$|, where |$B_{\rm eq}$| denotes the fields strength at the equipartition with turbulent energy as defined in equation (1). Figure 8 shows the distribution of |$\beta _{\rm p}$| at |$t_{\rm p}=0\:\text{yr}$| (top) and |$3500\:\text{yr}$| (middle), similar to figure 5, along with the time evolution of radial profile (bottom). Roughly speaking, the regions colored from red to black are thought to be where magnetic pressure is likely to influence the gas dynamics.
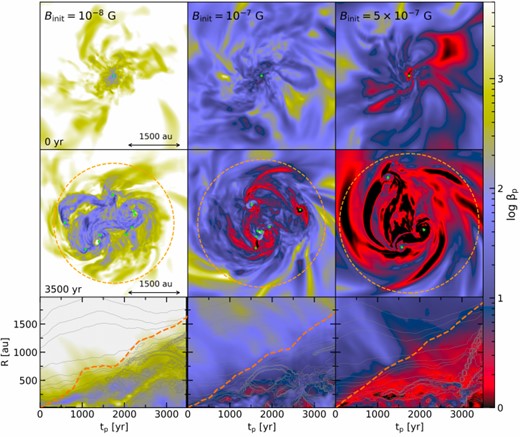
Same as figure 5, but for the plasma beta |$\beta _{\rm p}\equiv P_{\rm th}/P_{\rm mag}$|.
Given that the thermal structure remains independent of magnetization levels, differences in |$\beta _{\rm p}$| reflect variations in field strength. In the case of |$B_{\rm init} = 10^{-8}\:\text{G}$|, where the magnetic fields fail to reach |$B_{\rm eq}$| during the collapse, the central |$\beta _{\rm p}$| at |$t_{\rm p}=0$| (top left-hand panel in figure 8) drops to a maximum of |$\beta _{\rm p} \sim 10^2$|. This suggests that the magnetic pressure is insignificantly weak compared to the thermal pressure at the onset of the accretion phase. For the cases where the fields are amplified to |$B_{\rm eq}$| such as |$B_{\rm init} = 10^{-7}\:\text{G}$| and |$5\times 10^{-7}\:\text{G}$|, central |$\beta _{\rm p}$| approaches the magnetization level of |$\beta _{\rm p} \sim (B_{\rm eq}/B)^2\sim 1$| in both cases (top middle and top right-hand panels). Notably, in the case of |$B_{\rm init} = 5\times 10^{-7}\:\text{G}$|, the region where the magnetic pressure can affect the gas dynamics (colored from red to black) is broader due to the earlier amplification to |$B_{\rm eq}$|.
The magnetization level inside the disk region appears to remain relatively constant over time, as seen in the bottom panels of figure 8. Here, the azimuthally averaged |$\beta _{\rm p}$| below the orange dashed line persists at approximately |$\beta _{\rm p}\sim 10^{2}\\!-\\!10^{3}$| (|$B_{\rm init}=10^{-8}\:\text{G}$|), |$\beta _{\rm p} \sim 10\\!-\\!10^{2}$| (|$B_{\rm init}=10^{-7}\:\text{G}$|), and |$\beta _{\rm p} \sim 1\\!-\\!10$| (|$B_{\rm init}=5\times 10^{-7}\:\text{G}$|), respectively. This constancy arises because magnetic amplification within the disk is not notably efficient, as show in figure 7. Therefore, whether magnetic pressure can stabilize the disk during the earlier accretion phase depends on the magnetization level during the collapse phase. From the middle and top panels of figure 8, we can observe that only in the most magnetized case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$| can magnetic pressure stabilize the entire disk region.
However, when we focus on the magnetization levels within spiral arms, we notice a decrease in |$\beta _{\rm p}$|. For instance, the third column of figure 6 shows the distribution of |$\beta _{\rm p}$| around a single spiral arm in the case of |$B_{\rm init}=10^{-7}\:\text{G}$|. Initially, at the moment of a new protostar formation through fragmentation of the spiral arm, there is a clear decline in |$\beta _{\rm p}$| along the arm (top right-hand panel) attributed to the accumulation of toroidal fields generated by disk rotation (top middle panel). 500 years later, the coherent fields along the arm are effectively amplified by the rotation of a circumstellar disk (bottom middle panel), with minimal dissipation through magnetic reconnection. Consequently, |$\beta _{\rm p}$| within the circumstellar disk decreases further, dipping below 1 (black region in bottom right-hand panel), indicating the dominance of magnetic pressure, which stabilize the disk and inhibits further fragmentation. This suggests that there is a significant influence of magnetic pressure on the evolution of circumstellar disks and protostars originating from the fragmentation of spiral arms.
3.3.3 Effects of magnetic torques
Next, we will examine the impact of angular momentum transport caused by magnetic torques. The equation governing angular momentum conservation in cylindrical coordinates is given by (e.g., Joos et al. 2012):
where |$\rho$|, P, |$\boldsymbol {v}$|, |$\boldsymbol {B}$| and |$\boldsymbol {g}$| are the gas density, gas pressure, velocity, magnetic field, and gravitational acceleration, respectively. The terms |$R \rho v_{\rm \phi }\boldsymbol {v}$|, |$RB_{\phi }\boldsymbol {B}/(4\pi )$|, and |$R g_{\phi }\boldsymbol {g}/(4\pi G)$| in the equation represent the angular momentum flux due to gas advection, magnetic torques, and gravitational torques, respectively. In practice, while the advection term also includes transport due to turbulent torque, advection remains the dominant component in most cases here.
The angular momentum in the disk is primarily transported through the above three mechanisms. Angular momentum is brought into the disk region first by gas accretion from outside. This gas continues to move inward until it reaches the centrifugal radius, typically located inside the disk radius |$R_{\rm disk}$| defined in this study. Consequently, angular momentum flows inward between the centrifugal radius and the disk radius due to advection. Gravitational and magnetic torques can also play a role in transporting angular momentum brought in by advection. Gravitational torques primarily arise from the asymmetric structure of the spiral arms and transport angular momentum only in the radial (R) direction, along with the gas material. Conversely, magnetic torques have the ability to transport angular momentum in both the radial and vertical (z) directions of the disk, depending on the configuration of the magnetic field. In general, angular momentum tends to be transported along the field lines.
The structure of a disk undergoes changes depending on the direction of angular momentum transport. Vertical transport can result in the extraction of angular momentum from the disk, causing it to contract, while radial transport leads to the expansion of the disk radius as outer gas receives angular momentum from the inner region. Consequently, the surface density in the outer part of the disk decreases, stabilizing it against gravitational instability.
To investigate the direction of angular momentum transport by magnetic torques, we depict the streamlines of the 2D flux |$\boldsymbol {F}_{\rm mag} = [-R\\lesssimngle B_{\phi } B_{R}\rangle /(4\pi ) ,\ -R\\lesssimngle B_{\phi } B_{z} \rangle /(4\pi )]$| in the R–z plane for the most strongly magnetized case (|$B_{\rm init}=5\times 10^{-7}\:\text{G}$|) at |$t_{\rm p} = 800 \:\text{yr}$| in figure 9. Here, |$\\lesssimngle \cdots \rangle$| represents the volume average in the azimuthal (|$\phi$|) direction, and the color of the streamlines indicates the strength of the flux. The background color and red points denote the distribution of the azimuthal average of the number density and the radial position of the protostars, respectively. From this figure, we can see that the magnetic torques primarily transport angular momentum in the radial direction. This implies that when turbulent magnetic fields accrete on to the disk, angular momentum cannot be extracted from the disk region. Consequently, as shown in figure 3, the disk radius tends to expand compared to the weaker magnetized cases (|$B_{\rm init}\le 10^{-7}\:\text{G}$|).
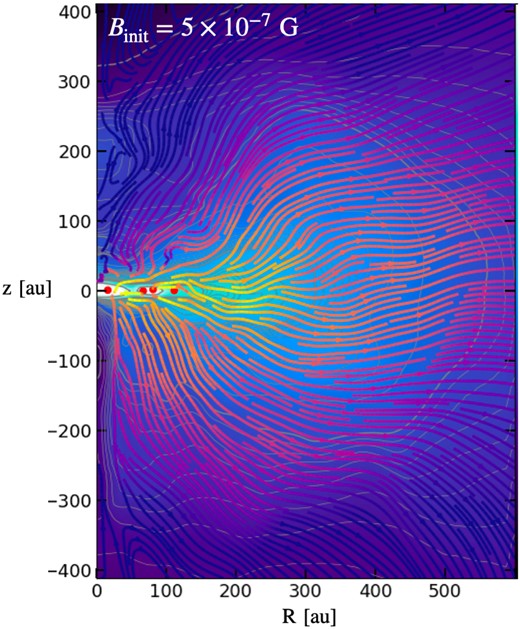
Angular momentum transport from the circumstellar disk. Streamlines of the 2D flux (|$\\lesssimngle R B_{\phi } B_{R}/(4\pi ) \rangle ,\ \\lesssimngle R B_{\phi } B_{z}/(4\pi ) \rangle$|) are illustrated in the R–z plane for the strongest magnetized case (|$B_{\rm init}=5\times 10^{-7}\:\text{G}$|) at |$t_{\rm p} = 800 \:\text{yr}$|. The color of the streamlines corresponds to the strength of the flux. The background color and red points denote the distribution of the azimuthal average of the number density and the radial position of protostars, respectively.
To analyze the contribution of magnetic torques as angular momentum transport, we evaluate the strength of the angular momentum flux due to the magnetic torques |$G_{R,\rm mag}$|, gravitational torques |$G_{R, \rm grav}$|, and advection induced by the gas accretion |$G_{R, \rm adv}$|. These fluxes are defined as
where h is set to |$300\:\text{au}$|, chosen to be larger than the disk height, although this choice does not significantly impact the flux strength.
In the top panels of figure 10, we present the temporal evolution of the radial profile of |$|G_{R,\rm mag}|$| (left) and |$|G_{R, \rm grav}|$| (right) in the case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|. When we compare these two panels, it becomes apparent that the flux of magnetic torques surpasses that of gravitational torques in the outer disk region. Conversely, the inner part is predominantly influenced by gravitational torques, where the spiral arms develop and the binary system is located. This region roughly corresponds to inside the centrifugal radius.
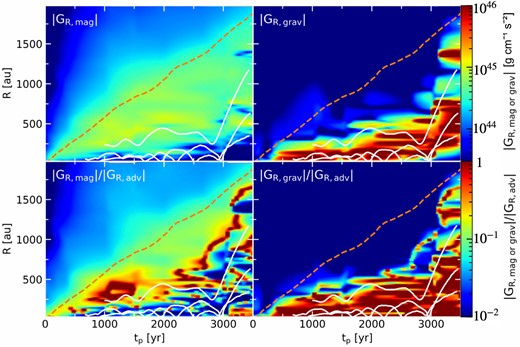
Time evolution of the radial profiles of the radial fluxes due to magnetic torques |$|G_{R,\rm mag}|$| (top left) and gravitational torques |$|G_{R,\rm grav}|$| (top right), along with the ratio with respect to the advection as |$|G_{R,\rm mag}|/|G_{R,\rm adv}|$| (bottom left) and |$|G_{R,\rm grav}|/|G_{R,\rm adv}|$| (bottom right) in the case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|. The orange dashed lines and white lines indicate the disk radius and the trajectories of protostars as shown in figure 4, respectively.
To compare these torques with advection, we present their ratios |$|G_{R, \rm mag}|/|G_{R, \rm adv}|$| (left) and |$|G_{R, \rm grav}|/|G_{R, \rm adv}|$| (right) in the bottom panel of figure 10. In the left-hand panel, we observe that magnetic torques are enhanced within the disk region due to the increased strength of |$B_{\rm \phi }$| resulting from disk rotation. Consequently, within the disk region (below the orange dashed line), magnetic torques can transport 10%–|$20\%$| of the angular momentum that is carried by advection outward (corresponding to green or yellow regions in the bottom left-hand panel). This leads to a decrease in surface density of the outer part of disk region, stabilizing the disk and suppressing the development of the spiral arms there. As a result, the density distribution within the disk is concentrated toward the center compared to the weaker field cases (see figure 4). For gravitational torques (bottom right-hand panel), they are comparable to advection in inner part.
For |$B_{\rm init}=10^{-8}\:\text{G}$| and |$10^{-7}\:\text{G}$|, the field strength across the entire circum-multiple disk is insufficient to produce noticeable magnetic torques for stabilizing it. However, in some circumstellar disks as shown in figure 6, the magnetic fields are amplified to approximately |$\beta _{\rm p} \sim 10$|, where the magnetic torques surpass gravitational torques.
3.3.4 MHD outflows
In general, magnetic fields can drive outflows or jets that expel gas with angular momentum, consequently reducing star formation efficiency. MHD outflows arise from two mechanisms: the magneto-centrifugal wind (e.g., Blandford & Payne 1982), driven by magnetic and centrifugal forces, and the magnetic pressure-driven wind (e.g., Tomisaka 2002; Banerjee & Pudritz 2006; Machida et al. 2008a), driven by the gradient of toroidal magnetic pressure. The former type of outflows initially require coherent magnetic fields with strengths around |$\beta _{\rm p}\\lt 1$| to permeate rotating objects like protostars or disks. On the other hand, for the latter type, initially uniform strong magnetic fields are not mandatory. This mechanism operates by twisting magnetic field lines through rotating objects, amplifying toroidal magnetic fields, and creating a gradient of magnetic pressure.
We observed the launching of outflows in the cases of |$B_{\rm init}=10^{-7}\:\text{G}$| and |$5\times 10^{-7}\:\text{G}$|, where magnetic fields reach equipartition during the collapse phase. In both cases, the outflows are driven as magnetic pressure-driven winds originating from the base of the artificial adiabatic cores (protostars), resembling certain types of “protostellar jets.” The outflows blow as a pressure-driven wind rather than a centrifugal wind because the field strength around the protostar before the jet formation is not as strong as |$\beta _{\rm p}\sim 1$|, and the configuration is disturbed by turbulence rather than being coherent. The rotation of a protostar swiftly twists the magnetic field lines, generating a strong toroidal magnetic pressure capable of overcoming gravity and the ram pressure of gas accretion.
Figure 11 shows the three-dimensional view of the protostellar jets under the case of |$B_{\rm init}=10^{-7}\:\text{G}$| at |$t_{\rm p}=3800\:\text{yr}$| (left-hand panel) and |$5\times 10^{-7}\:\text{G}$| at |$t_{\rm p}=700\:\text{yr}$| (right-hand panel). Solid lines denote magnetic field lines with their colors indicating field strength, while arrows represent the velocity field of gas being ejected outward against gravity. From these figures, we can clearly see that the fields lines inside the outflowing region are tightly twisted by the rotation of the protostar, generating a strong outward magnetic pressure gradient. This leads to a highly collimated jet structure, shaped by the pinch effect of the toroidal fields (e.g., Tomisaka 2002), forming a tower-like configuration. This type of jet resembles magnetic tower jets observed in MHD simulations around an accretion disk around a BH (e.g., Kato et al. 2004) which can be driven by various field structures. In addition, both jets exhibit a unipolar type. This result is consistent with findings from previous MHD simulations, indicating that unipolar outflows are likely to occur when the initial magnetic field’s energy is weaker than the turbulent energy (e.g., Mignon-Risse et al. 2021; Takaishi et al. 2024).
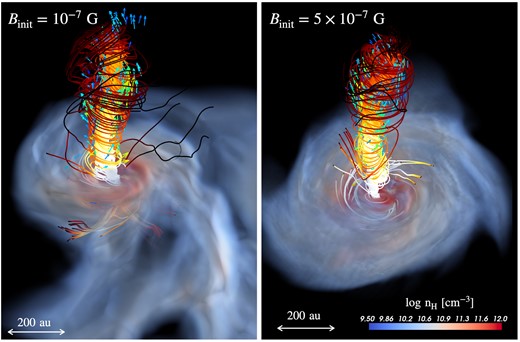
Bird’s-eye views of protostellar jets in the cases with |$B_{\rm init}=10^{-7}\:\text{G}$| at |$t_{\rm p}=3800\:\text{yr}$| (left) and |$B_{\rm init}=5\times 10^{-7}\:\text{G}$| at |$t_{\rm p}=700\:\text{yr}$| (right). In the case of |$B_{\rm init}=10^{-7}\:\text{G}$|, the jet is launched from a protostar formed by the fragmentation of a spiral arm in the circum-multiple disk, which is the same as shown in figure 6. In the case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|, the jet originates from the primary protostar. Solid lines depict magnetic field lines color-coded by their strength, while arrows indicate the direction of outflowing velocity fields. Gas distribution is visualized using volume rendering.
In the case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|, the protostellar jet appears from the primary protostar. Figure 12 shows the temporal evolution of the edge-on slice of the density structure (left-hand column) and velocity field (right-hand column) from the birth to extinction of the protostar jet. In the velocity map, the outflowing and inflowing region are depicted as red and blue, respectively. From this figure, we can observe that the jet begins to emerge from one side at around |$t_{\rm p} \simeq 300\:\text{yr}$| (second panel of figure 12). Although the jet maintains its collimation and continues to extend outward, its strength begins to decrease after about |$720\:\text{yr}$|. This weakening is attributed to the high ram pressure resulting from high accretion rates. As a consequence, the jet eventually halts around |$860\:\text{yr}$| (bottom panel of figure 12), causing the blown gas to fall back toward the protostar. This phenomenon resembles the so-called “failed outflows” observed in simulations of high-mass star formation within present-day environments (e.g., Matsushita et al. 2017; Machida & Hosokawa 2020). Consequently, the lifespan of the jet is very brief and its impact on gas ejection is minor. While some gas may be entrained by the recurrent generation and dissipation of the jet, no substantial contribution towards disk fragmentation was observed.
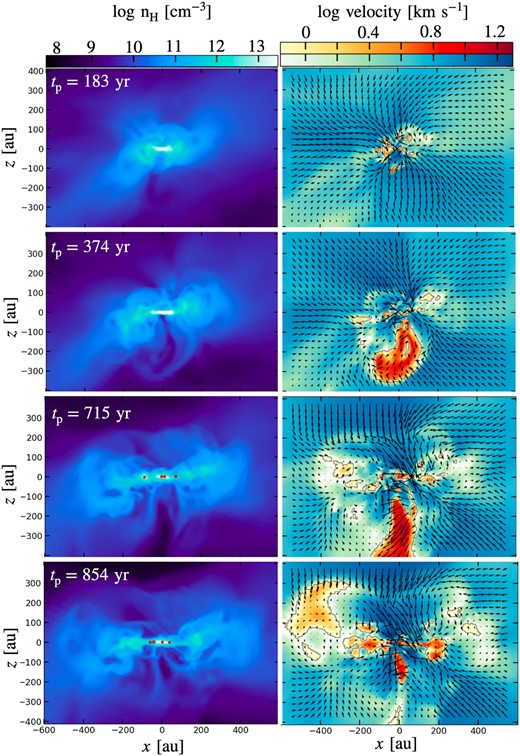
Series of edge-on slices depicting density (left) and radial velocity (right) structures in the case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|. The red and blue colors in the velocity panel represent outflowing and inflowing regions, respectively. Black arrows denote the direction of the velocity field sliced in the edge-on plane.
In the weaker field case of |$B_{\rm init}=10^{-7}\:\text{G}$|, a protostellar jet is observed only from the protostar presented in figure 6. This protostar forms as a result of the fragmentation of a spiral arm within the circum-multiple disk, as previously mentioned. Due to the combined effects of disk rotation and compression of the arm, the magnetic fields surrounding the protostar become intensified and coherent. Such a magnetic field configuration facilitates the generation of strong toroidal fields through its rotation, resulting in the initiation of the protostellar jet (figure 11). However, similar to the case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|, the lifespan of the jet is relatively short, and its impact on mass ejection remains small. Note that numerical simulations of the present-day star formation (e.g., Federrath et al. 2014b; Federrath 2015) have suggested that protostellar jets can influence the star formation rate and the IMF by driving turbulence within the parent gas cloud. Therefore, after longer-term evolution, these jets may affect the properties of first stars.
3.4 The properties of multiple systems
Based on our analysis presented above, we confirm that both magnetic pressure and magnetic torques play significant roles in suppressing disk fragmentation. To see the impact of magnetic effects on the fragmentation quantitatively, we plot the time evolution of the cumulative number of fragmentation events |$N_{\rm frag}$| in the top panel of figure 13. This figure clearly shows a trend of decreasing |$N_{\rm frag}$| with stronger magnetization within the disk region. In particular, we observe a notable decrease in |$N_{\rm frag}$| in the case of |$B_{\rm init} = 5\times 10^{-7}\:\text{G}$| compared to less magnetized cases (|$B_{\rm init}\le 10^{-7}\:\text{G}$|). While variations in |$N_{\rm frag}$| among simulations runs may stem from diverse realizations of the initial turbulence (e.g., Sharda et al. 2020), our detailed examination in subsection 3.3 conclusively verifies that this difference primarily originates from magnetic field effects.
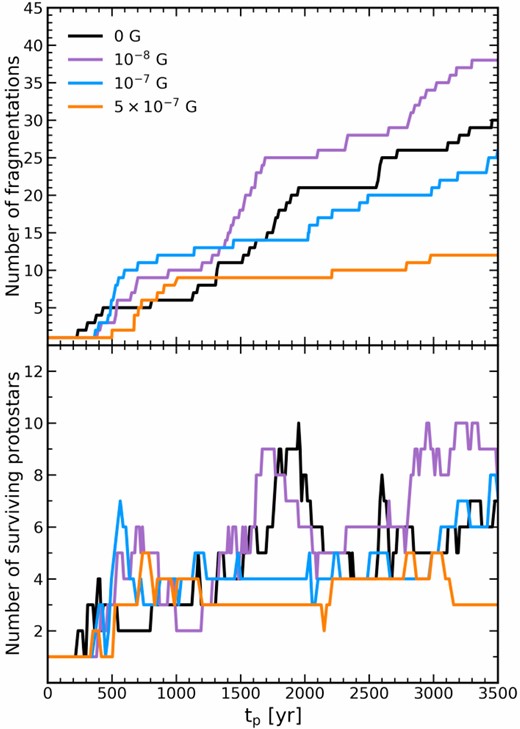
Time evolution of the cumulative number of fragments (top) and the number of surviving protostars (bottom) for four different cases: |$B_{\rm init}=0\:\text{G}$|, |$10^{-8}\:\text{G}$|, |$10^{-7}\:\text{G}$|, and |$5\times 10^{-7}\:\text{G}$|.
Interestingly, in the weakly magnetized case with |$B_{\rm init}=10^{-8}\:\text{G}$| (violet line), we observe that |$N_{\rm frag}$| exceeds that of the unmagnetized case (|$B_{\rm init}=0$|, black line). This could be partly due to different realizations of turbulence, but it could also be attributed to the so-called magneto-Jeans instability, by which weak toroidal fields render spiral arms gravitationally unstable, leading to increased fragmentation (e.g., Lynden-Bell 1966; Elmegreen 1987; Kim & Ostriker 2001; Inoue & Yoshida 2019). Additionally, toroidal fields along the arms can hinder vertical gas motion, effectively trapping gas within the arms and potentially promoting fragmentation. Our simulations reveal that the magnetic fields within the arms are coherent along the arms (figure 6), suggesting that such magnetic effects are indeed plausible.
In examining the number of surviving protostars in the bottom panel of figure 13, we find that the protostar count is less than half of the number of fragmentation events in all cases. This outcome arises primarily from the merging of multiple protostars. In weakly magnetized cases (|$B_{\rm init}\le 10^{-7}\:\text{G}$|), the protostar count exhibits episodic oscillations. Sharp spikes in the bottom panel of figure 13 correspond to circumstellar disk fragmentation events. However, such protostars often migrate towards the central protostar, leading to frequent mergers. Nevertheless, some protostars survive and their number gradually increases over time, consistent with previous studies (e.g., Susa 2019). On the other hand, in the strongly magnetized case (|$B_{\rm init}=5\times 10^{-7}\:\text{G}$|), such fragmentation itself is suppressed by magnetic effects. As a result, the protostar count remains low and relatively constant. This suggests that the influence of magnetic effects on the number of protostars may become more pronounced during later phases of accretion, allowing for clearer distinctions between them.
Furthermore, it should be noted that in our simulations protostars are more likely to merge with each other than in reality. This is because the adiabatic core is larger than the real protostar size. Therefore, in reality, we should expect that the protostars are not merging, but are instead being formed as closed binary systems or ejected out of the disk by gravitational interactions. The difference in the number of protostars due to magnetic effects may be clearly visible in reality, as shown in the top panel of figure 13. In particular, the ejected protostars can be expected to become low-mass first stars that are observable in the present-day Universe below |$0.8\ M_{\rm \odot }$|, as accretion stops halfway through. In other words, strong magnetic fields amplified to about equipartition suppress the formation of low-mass stars, consistent with the observed fact that they have not yet been found (e.g., Hartwig et al. 2015; Ishiyama et al. 2016; Magg et al. 2018).
The size of protostar can also influence the outflow velocity of protostellar jets. The larger protostellar radius in our simulations results in a shallower gravitational potential, leading to slower velocity. Conversely, when considering the actual radius, a stronger jet can blow, influencing the protostellar properties, such as their mass and spin.
Focusing on the separation of the most massive binary systems, we observe minimal changes across different magnetized cases (see the trajectories of black lines in figure 4). In the case of |$B_{\rm init}=5\times 10^{-7}\:\text{G}$|, the binary separation remains relatively small until |$t_{\rm p}\sim 3000\:\text{yr}$|, but it widens due to gravitational interactions with the third protostar. This suggests that in turbulent magnetic fields the efficiency of angular momentum transport within the disk via magnetic torques is not sufficient to reduce the separation. Instead, it indicates that gravitational interactions with other protostars play a more significant role in determining the separation. Considering that the orbital angular momentum of the binaries comes from the accreting angular momentum, the binary separation typically has the same order as the radius of a circum-multiple disk. This means that in order to reduce the separation effectively it is necessary to reduce the accreting angular momentum. This can be achieved by ensuring that magnetic fields reach equipartition level during the earlier collapse phase, facilitating the extraction of angular momentum from the envelope through magnetic torques.
4 Summary and discussion
We have performed 3D ideal MHD simulations, starting from the collapse of a turbulent primordial-gas cloud core with a density of approximately |$10^{3}\:\text{cm}^{-3}$|, extending up to the early accretion phase characterized by frequent disk fragmentation. Our objective was to investigate the impact of amplified turbulent magnetic fields on the first star formation process, focusing specifically on disk fragmentation. We paid special attention to three major magnetic effects: magnetic pressure, magnetic torques, and MHD outflows. Through systematic exploration, we analyzed how each of these effects influences gas dynamics during the accretion phase, in order to identify the necessary conditions for magnetic fields to affect the multiplicity and binary properties of the first stars.
Our findings are summarized as follows:
Initially disturbed by turbulence before the formation of the primary protostar, the magnetic field configuration gradually transitions to a toroidally dominated one due to rotational motion within the disk. Notably, coherent toroidal fields prevail within the spiral arms. The average field strength within the disk remains relatively constant due to turbulent magnetic reconnection, which dissipates magnetic energy, suggesting that the field strength is primarily determined by amplification during the collapse phase.
When magnetic fields reach equipartition fields (|$B_{\rm eq}$|), where the field strength on each scale is comparable to the turbulent energy, during collapse, magnetic pressure stabilizes both the disk and spiral arms against gravitational instability, leading to fewer fragmentation events.
Magnetic torques within the disk can stabilize it by radially transporting angular momentum, similar to magnetic viscosity, if the magnetic field reaches equipartition during collapse, reducing the formation of spiral arms and fragments. However, in environments with turbulent fields persisting around the disk, magnetic torques have minimal impact on disk size or binary separation.
Some protostars launch well-collimated MHD outflows, known as protostellar jets, driven by magnetic pressure winds when the magnetic field reaches equipartition during collapse. These jets, however, do not contribute significantly to disk fragmentation due to their short duration.
Magnetic effects, particularly magnetic pressure and magnetic torques, impact gas dynamics during the accretion phase when magnetic fields are amplified to equipartition strength during collapse. Large-scale (around the Jeans scale) magnetic fields must be comparable to turbulence energy to influence gas dynamics.
When magnetic fields meet this criterion at the onset of the accretion phase, both magnetic pressure and angular momentum transport via magnetic torques reduce the number of fragmentations, suggesting fewer low-mass stars and a top-heavy IMF.
In our simulations, we have varied the initial strength of magnetic fields to control the density at which |$B_{\rm eq}$| is reached during the collapse, i.e., |$10^{13}\:\text{cm}^{-3}$| for |$B_{\rm init}= 10^{-7}\:\text{G}$| and |$10^{11}\:\text{cm}^{-3}$| for |$B_{\rm init}= 10^{-7}\:\text{G}$|, respectively. This was necessary because current simulations cannot accurately capture the actual amplification rate of kinematic dynamo due to resolution constraints. Nonetheless, analytical considerations (e.g., McKee et al. 2020) and one-zone calculations (e.g., Schober et al. 2012b) suggest that the dynamo mechanism can amplify the seed field up to the equipartition level before the formation of a cloud core of |$n_{\rm H}\simeq 10^{3}\\!-\\!10^{4}\:\text{cm}^{-3}$|. Hence, we expect that the conditions mentioned here are easily satisfied in realistic first star-forming regions, suggesting a significant magnetic impact on circumstellar disk evolution.
As suggested in our previous study of Sadanari et al. (2023), turbulent fields reaching equipartition levels can undergo a transition into a more coherent configuration. Coherent fields enhance the efficiency of magnetic braking, facilitating efficient extraction of angular momentum from the collapsing cloud. As a result, the reduction in angular momentum accretion on to the disk leads to shrinkage in disk radius and binary separation. This is favorable for the formation of tight massive binary systems, which could serve as progenitors of gravitational wave events. The disc also becomes gravitationally stable, thereby suppressing disk fragmentation. Consequently, the formation of low-mass first stars is effectively inhibited, resulting in the predominance of massive first stars, consistent with the absence of observed low-mass first stars in the present Universe.
Furthermore, protostellar jets may persist over an extended duration, potentially exerting a substantial influence on the characteristics of protostars, including their mass and spin. Additionally, during later accretion phase, the radiative feedback from protostars becomes crucial in halting gas accretion. Therefore, it is imperative to perform radiative MHD simulations incorporating ionization feedback from protostars in future studies.
Acknowledgements
The authors would like to thank Drs. Gen Chiaki, Sunmyon Chon, Takashi Hosokawa, Ralf Klessen, Masahiro Machida, Hajime Susa and Benoit Commerçon for fruitful discussions and useful comments. The numerical simulations were carried out on XC50 Aterui II in Oshu City at the Center for Computational Astrophysics (CfCA) of the National Astronomical Observatory of Japan, the Cray XC40 at Yukawa Institute for Theoretical Physics in Kyoto University, and the computer cluster Draco at Frontier Research Institute for Interdiskiplinary Sciences of Tohoku University. This research is supported by Grants-in-Aid for Scientific Research (KO: 22H00149; KS: 21K20373; TM: 18H05437, 23K03464; KT: 21H04487, 22K0043) from the Japan Society for the Promotion of Science. KES acknowledges financial support from the Graduate Program on Physics for Universe of Tohoku University.



