-
PDF
- Split View
-
Views
-
Cite
Cite
Yoshiaki Ono, Yuichi Harikane, Masami Ouchi, Kimihiko Nakajima, Yuki Isobe, Takatoshi Shibuya, Minami Nakane, Hiroya Umeda, Yi Xu, Yechi Zhang, Census for the rest-frame optical and UV morphologies of galaxies at z = 4–10: First phase of inside-out galaxy formation, Publications of the Astronomical Society of Japan, Volume 76, Issue 2, April 2024, Pages 219–250, https://doi.org/10.1093/pasj/psae004
Close - Share Icon Share
Abstract
We present the rest-frame optical and UV surface brightness (SB) profiles for 149 galaxies with Mopt < −19.4 mag at z = 4–10 (29 of which are spectroscopically confirmed with JWST NIRSpec), securing high signal-to-noise ratios of 10–135 with deep JWST NIRCam 1–|$5\, \mu$|m images obtained by the CEERS survey. We derive morphologies of our high-z galaxies, carefully evaluating the systematics of SB profile measurements with Monte Carlo simulations as well as the impacts of a) AGNs, b) multiple clumps including galaxy mergers, c) spatial resolution differences with previous HST studies, and d) strong emission lines, e.g., Hα and [O iii], on optical morphologies with medium-band F410M images. Conducting Sérsic profile fitting for our high-z galaxy SBs with GALFIT, we obtain effective radius ranges for optical re,opt and UV re,UV wavelengths of re, opt = 0.05–1.6 kpc and re,UV = 0.03–1.7 kpc that are consistent with previous results within large scatters in the size–luminosity relations. However, we find that the effective radius ratio, re,opt|$/$|re,UV, is almost unity, |$1.01^{+0.35}_{-0.22}$|, over z = 4–10 with no signatures of past inside-out star formation such as found at z ∼ 0–2. There are no spatial offsets exceeding 3σ between the optical and UV morphology centers in cases of no mergers, indicative of major star-forming activity only being found near mass centers of galaxies at z ≳ 4 probably experiencing the first phase of inside-out galaxy formation.
1 Introduction
Investigating the evolution of galaxy morphologies over cosmic time offers valuable insights into the understanding of galaxy evolution (Conselice 2014). The launch of the James Webb Space Telescope (JWST; Gardner et al. 2023) has catalyzed significant advancements in characterizing the morphological properties of high-z star-forming galaxies (SFGs) predominantly selected based on the rest-frame UV spectral shapes (Yang et al. 2022; Treu et al. 2023; Ono et al. 2023; see also Langeroodi & Hjorth 2023). Several morphological studies have also been reported for other galaxy types including dusty SFGs and quiescent galaxies as well as galaxies selected more generally using photometric redshifts (Suess et al. 2022; Gillman et al. 2023; Ito et al. 2023; Le Bail et al. 2023; Yao et al. 2023; van der Wel et al. 2024). Furthermore, comprehensive morphological classifications have been conducted, encompassing visual classifications (Ferreira et al. 2022, 2023; Kartaltepe et al. 2023) and classifications employing machine-learning techniques (Robertson et al. 2023; Huertas-Company et al. 2023; Tohill et al. 2024).
To understand the evolution of galaxy morphologies, it is important to elucidate how galaxy sizes change across various wavelengths. In general, the rest-frame UV continuum predominantly traces young massive stars, whereas the rest-frame optical continuum captures even less massive stars. Notably, the rest-frame UV morphologies of nearby galaxies tend to be patchier compared to their rest-frame optical ones (e.g., Kuchinski et al. 2000, 2001; Windhorst et al. 2002). This trend extends to galaxies up to at least z ∼ 1 based on Hubble Space Telescope (HST) data (Papovich et al. 2005). Van der Wel et al. (2014) have investigated the wavelength dependence of SFG sizes up to z ∼ 2, finding that galaxy sizes decrease with longer wavelengths. Their results could be interpreted as a sign of inside-out growth, considering that longer wavelengths trace older less massive stars. However, some previous studies have reported little difference in morphologies in the rest-frame UV and optical for high-z galaxies (e.g., Dickinson 2000; Papovich et al. 2005; Shibuya et al. 2015). Nevertheless, it is worth noting that HST data probe the rest-frame optical morphologies of galaxies only up to z ∼ 3.
From a theoretical standpoint, the rest-frame UV and optical morphologies of higher-z galaxies have been investigated using cosmological simulations that properly take into account the baryonic physics including star formation and feedback processes. For instance, Ma et al. (2018) have used the results of the FIRE-2 cosmological simulations to study the rest-frame UV and optical sizes of z = 5–10 galaxies with halo masses of |$10^{8-12}\, M_{\odot }$| at z = 5. They have found that the rest-frame optical sizes are significantly larger compared to the rest-frame UV, because the rest-frame UV images are dominated by a limited number of bright clumps with young massive stars that are often not associated with a substantial stellar mass. Conversely, based on the results of the IllustrisTNG cosmological simulations, Costantin et al. (2023) have studied the morphologies of galaxies at z = 5–6 with stellar masses exceeding 109M⊙, and reported that their sizes in the rest-frame UV and optical are similar, probably due to their young ages. Similar results have also been obtained by Wu et al. (2020) based on the SIMBA cosmological hydrodynamic simulations.
Thanks to the near-infrared camera onboard JWST, NIRCam (Rieke et al. 2005), deep high-resolution images can now be obtained up to around |$5\, \mu$|m, allowing for the examination of galaxy morphologies in the rest-frame UV and optical up to z ≃ 9.5. Yang et al. (2022) have investigated the sizes of galaxies at z ∼ 7–10 in the rest-frame UV and optical based on the JWST GLASS data (Treu et al. 2022), and found that the average ratio of sizes in the rest-frame optical to UV is consistent with unity. Ono et al. (2023) have expanded individual high-z galaxy size measurements to faint galaxies by stacking their NIRCam images, thus further revealing that the size ratio is consistent with unity even down to fainter magnitudes. However, these studies have not covered a bright magnitude range exceeding −21 mag, which corresponds to the characteristic luminosity of z ∼ 3 galaxies, |$L^\ast _{z=3}$| (Steidel et al. 1999).
In this paper, we utilize JWST NIRCam images taken by the Cosmic Evolution Early Release Science (CEERS; Finkelstein et al. 2022) survey to determine the sizes of galaxies at z ≃ 4–10 in the rest-frame UV and optical across a broad luminosity range. We investigate sizes of spectroscopically identified galaxies at zspec > 4.5 in the CEERS fields compiled by Nakajima et al. (2023) as well as galaxy candidates at similar redshifts selected based on photometric redshifts or the dropout technique (Shibuya et al. 2015; Bouwens et al. 2015; Finkelstein et al. 2023).
This paper is structured as follows. In section 2, we introduce the CEERS NIRCam data used in this study, and compile samples of galaxies at z ≃ 4–10 found in the CEERS fields in previous studies. In section 3, we describe our methodology for two-dimensional (2D) surface brightness (SB) profile fitting and conduct Monte Carlo (MC) simulations to correct systematic uncertainties in size and total magnitude measurements and to estimate statistical uncertainties in these measurements. In addition, we investigate the impact of strong emission lines on the rest-frame optical size measurements and the effect of the spatial resolution difference between the rest-frame UV and optical on the size measurements. Section 4 presents the results of our SB profile fittings for the galaxies at z ≃ 4–10 in the rest-frame UV and optical, and compares our results with those in previous work such as the size–luminosity relation and size ratio between the rest-frame UV and optical. Finally, we summarize this study in section 5. Throughout this paper, we employ magnitudes in the AB system (Oke & Gunn 1983). A flat universe with Ωm = 0.3, |$\Omega _\Lambda = 0.7$|, and H0 = 70 km s−1 Mpc−1 is adopted. In this cosmological model, for instance, an angular dimension of |${1_{.}^{\prime \prime}0}$| corresponds to a physical dimension of 6.603 kpc at z = 4.5, 5.226 kpc at z = 7.0, and 4.463 kpc at z = 9.0 [equation (18) of Hogg 1999].
2 Data and samples
We investigate the sizes of galaxies at z ≃ 4–10 found in the CEERS fields. First, we use the spectroscopic sample of Nakajima et al. (2023), who have compiled spectroscopically identified galaxies in the CEERS fields (see also Arrabal Haro et al. 2023; Fujimoto et al. 2023; Tang et al. 2023). To increase the number of sources that we examine, we incorporate samples of galaxy candidates at similar redshifts selected based on photometric redshifts or the dropout technique. One is the Finkelstein et al. (2023) sample at z ∼ 9, which is selected from the JWST and HST data with photometric redshift values of zphoto ≃ 8–10. In addition, we include the Shibuya, Ouchi, and Harikane (2015) sample of dropout galaxies at z ∼ 5–7 selected in Harikane et al. (2016) from the HST data obtained by the Cosmic Assembly Near-IR Deep Extragalactic Legacy Survey (CANDELS; Grogin et al. 2011; Koekemoer et al. 2011). To compensate for the small number for z ∼ 7–8, we further add the z ∼ 7–8 samples from Bouwens et al. (2015), which are dropout galaxies selected based on the HST data. Note that there are overlaps between these samples; in this paper, we assign a unique ID to each source as listed in table 5 in appendix 1. The number of sources in each sample and the numbers of duplicated sources are summarized in table 1. Their redshift distributions are presented in figure 1.
Numbers of sources included in the samples and the numbers of duplicated sources between the samples.
| . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Shibuya, Ouchi, and Harikane (2015) . | Bouwens et al. (2015) . |
|---|---|---|---|---|
| Number of galaxies | 41 | 15 | 106 | 28 |
| Number of galaxies with S|$/$|N > 10 in F150W | 31 | 4 | 105 | 26 |
| Number of galaxies with S|$/$|N > 10 in F444W | 24 | 10 | 82 | 23 |
| Duplicate with Finkelstein et al. (2023) | 2 | — | — | — |
| Duplicate with Shibuya, Ouchi, and Harikane (2015) | 6 | 0 | — | — |
| Duplicate with Bouwens et al. (2015) | 0 | 0 | 5 | — |
| . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Shibuya, Ouchi, and Harikane (2015) . | Bouwens et al. (2015) . |
|---|---|---|---|---|
| Number of galaxies | 41 | 15 | 106 | 28 |
| Number of galaxies with S|$/$|N > 10 in F150W | 31 | 4 | 105 | 26 |
| Number of galaxies with S|$/$|N > 10 in F444W | 24 | 10 | 82 | 23 |
| Duplicate with Finkelstein et al. (2023) | 2 | — | — | — |
| Duplicate with Shibuya, Ouchi, and Harikane (2015) | 6 | 0 | — | — |
| Duplicate with Bouwens et al. (2015) | 0 | 0 | 5 | — |
Numbers of sources included in the samples and the numbers of duplicated sources between the samples.
| . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Shibuya, Ouchi, and Harikane (2015) . | Bouwens et al. (2015) . |
|---|---|---|---|---|
| Number of galaxies | 41 | 15 | 106 | 28 |
| Number of galaxies with S|$/$|N > 10 in F150W | 31 | 4 | 105 | 26 |
| Number of galaxies with S|$/$|N > 10 in F444W | 24 | 10 | 82 | 23 |
| Duplicate with Finkelstein et al. (2023) | 2 | — | — | — |
| Duplicate with Shibuya, Ouchi, and Harikane (2015) | 6 | 0 | — | — |
| Duplicate with Bouwens et al. (2015) | 0 | 0 | 5 | — |
| . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Shibuya, Ouchi, and Harikane (2015) . | Bouwens et al. (2015) . |
|---|---|---|---|---|
| Number of galaxies | 41 | 15 | 106 | 28 |
| Number of galaxies with S|$/$|N > 10 in F150W | 31 | 4 | 105 | 26 |
| Number of galaxies with S|$/$|N > 10 in F444W | 24 | 10 | 82 | 23 |
| Duplicate with Finkelstein et al. (2023) | 2 | — | — | — |
| Duplicate with Shibuya, Ouchi, and Harikane (2015) | 6 | 0 | — | — |
| Duplicate with Bouwens et al. (2015) | 0 | 0 | 5 | — |
To trace their rest-frame UV and optical continuum from galaxies at z ≃ 4–10, we make use of the JWST NIRCam F150W and F444W images, respectively (top panel of figure 2). We refer the reader to Harikane et al. (2023b) and Y. Harikane et al. (in preparation) for details about the imaging data sets. At the moment, our reduction of the F444W images for CEERS7 is suboptimal for reasons we do not yet fully understand; we therefore do not use it for our analyses. Although the wide wavelength coverage of F444W allows the capture of strong emission lines such as Hα and [O iii] 5008 at z ≳ 5 as demonstrated in the bottom panel of figure 2, this does not significantly affect measurements of galaxy sizes, as shown later in a comparison of measurements with F444W and F410M (subsection 3.3). The pixel scale of the NIRCam images is 0|${_{.}^{\prime\prime}}$|015 pix−1. Their 10σ limiting magnitudes are summarized in table 2. Following the previous work (Mosleh et al. 2012; Ono et al. 2023), we select sources with a signal-to-noise ratio (S|$/$|N) larger than 10 for individual analyses in each band based on their apparent magnitudes measured in 0|${_{.}^{\prime\prime}}$|2 diameter circular apertures. For instance, if a galaxy shows an S|$/$|N larger than 10 in the F150W (F444W) image, its F150W (F444W) image is used for analysis. In cases where a galaxy has an S|$/$|N larger than 10 in F150W but has an S|$/$|N below 10 in F444W, only the F150W image is utilized for analysis. The number of sources in each catalog that have an S|$/$|N larger than 10 in each band is presented in table 1.
![Top: Transmissions of two NIRCam broad-band filters (blue: F150W; red: F444W) and one NIRCam medium-band filter (orange: F410M) together with spectra of SFGs from the Bruzual and Charlot (2003) library at three example redshifts of z = 4.5, 7.0, and 9.0 (black lines). Bottom: Redshift ranges where the rest-frame strong emission lines of Hα (red), [O iii] (orange), and Hβ (green) enter the JWST NIRCam filters of F410M and F444W. For F444W, Hα and [O iii] are allowed to enter seamlessly because of the wide wavelength range, while, for F410M, there is a redshift gap between the redshift ranges where Hα and [O iii] enter, i.e., z ≃ 5.63–6.63.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/76/2/10.1093_pasj_psae004/1/m_psae004fig2.jpeg?Expires=1748712565&Signature=3noC4j2qe25aocOTQr3W3cBglHxrIG60R5apo2Wi9PAdqpy~azIvAHJRJzyWOF067LmkydcpFSMjjSl78UwTblAu2oh~ltNK1xysjEpK0cQFKJQ2-F~xi4aUYHx0LuuU7pplz-htObDJqR3Par~yWqAMF70Iz4v7XviQagTh52txmql8XZNJZCYA4tewz4dQWdcfWAID7yu4xmJh0~-b9OmNPkJutdUd84qmhZduoLFbXVrlry3VzS~r3XVxbYzkMru9GeBQ~4QqdRG9Y9Rdxzrgodbb92f-9m9R6a68pjHz3RXYvsaJiXfoVtk-K~cnqFWrTvkaEdKazgMFjzEw8A__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Top: Transmissions of two NIRCam broad-band filters (blue: F150W; red: F444W) and one NIRCam medium-band filter (orange: F410M) together with spectra of SFGs from the Bruzual and Charlot (2003) library at three example redshifts of z = 4.5, 7.0, and 9.0 (black lines). Bottom: Redshift ranges where the rest-frame strong emission lines of Hα (red), [O iii] (orange), and Hβ (green) enter the JWST NIRCam filters of F410M and F444W. For F444W, Hα and [O iii] are allowed to enter seamlessly because of the wide wavelength range, while, for F410M, there is a redshift gap between the redshift ranges where Hα and [O iii] enter, i.e., z ≃ 5.63–6.63.
Limiting magnitudes and PSF FWHMs of the JWST NIRCam images used for the present analysis of source sizes.
| . | 10σ depth / PSF FWHM . | ||
|---|---|---|---|
| Field . | F150W . | F410M . | F444W . |
| CEERS1 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.1 / 0|${_{.}^{\prime\prime}}$|154 | 28.3 / 0|${_{.}^{\prime\prime}}$|161 |
| CEERS2 | 28.2 / 0|${_{.}^{\prime\prime}}$|062 | 28.1 / 0|${_{.}^{\prime\prime}}$|170 | 28.6 / 0|${_{.}^{\prime\prime}}$|172 |
| CEERS3 | 28.4 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / 0|${_{.}^{\prime\prime}}$|155 | 28.4 / 0|${_{.}^{\prime\prime}}$|159 |
| CEERS4 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|164 |
| CEERS5 | 28.3 / 0|${_{.}^{\prime\prime}}$|066 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|169 |
| CEERS6 | 28.3 / 0|${_{.}^{\prime\prime}}$|059 | 28.2 / 0|${_{.}^{\prime\prime}}$|157 | 28.2 / 0|${_{.}^{\prime\prime}}$|166 |
| CEERS7 | 28.3 / 0|${_{.}^{\prime\prime}}$|062 | 28.2 / — | 28.2 / — |
| CEERS8 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|165 |
| CEERS9 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|157 |
| CEERS10 | 28.3 / 0|${_{.}^{\prime\prime}}$|064 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|162 |
| . | 10σ depth / PSF FWHM . | ||
|---|---|---|---|
| Field . | F150W . | F410M . | F444W . |
| CEERS1 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.1 / 0|${_{.}^{\prime\prime}}$|154 | 28.3 / 0|${_{.}^{\prime\prime}}$|161 |
| CEERS2 | 28.2 / 0|${_{.}^{\prime\prime}}$|062 | 28.1 / 0|${_{.}^{\prime\prime}}$|170 | 28.6 / 0|${_{.}^{\prime\prime}}$|172 |
| CEERS3 | 28.4 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / 0|${_{.}^{\prime\prime}}$|155 | 28.4 / 0|${_{.}^{\prime\prime}}$|159 |
| CEERS4 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|164 |
| CEERS5 | 28.3 / 0|${_{.}^{\prime\prime}}$|066 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|169 |
| CEERS6 | 28.3 / 0|${_{.}^{\prime\prime}}$|059 | 28.2 / 0|${_{.}^{\prime\prime}}$|157 | 28.2 / 0|${_{.}^{\prime\prime}}$|166 |
| CEERS7 | 28.3 / 0|${_{.}^{\prime\prime}}$|062 | 28.2 / — | 28.2 / — |
| CEERS8 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|165 |
| CEERS9 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|157 |
| CEERS10 | 28.3 / 0|${_{.}^{\prime\prime}}$|064 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|162 |
Limiting magnitudes and PSF FWHMs of the JWST NIRCam images used for the present analysis of source sizes.
| . | 10σ depth / PSF FWHM . | ||
|---|---|---|---|
| Field . | F150W . | F410M . | F444W . |
| CEERS1 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.1 / 0|${_{.}^{\prime\prime}}$|154 | 28.3 / 0|${_{.}^{\prime\prime}}$|161 |
| CEERS2 | 28.2 / 0|${_{.}^{\prime\prime}}$|062 | 28.1 / 0|${_{.}^{\prime\prime}}$|170 | 28.6 / 0|${_{.}^{\prime\prime}}$|172 |
| CEERS3 | 28.4 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / 0|${_{.}^{\prime\prime}}$|155 | 28.4 / 0|${_{.}^{\prime\prime}}$|159 |
| CEERS4 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|164 |
| CEERS5 | 28.3 / 0|${_{.}^{\prime\prime}}$|066 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|169 |
| CEERS6 | 28.3 / 0|${_{.}^{\prime\prime}}$|059 | 28.2 / 0|${_{.}^{\prime\prime}}$|157 | 28.2 / 0|${_{.}^{\prime\prime}}$|166 |
| CEERS7 | 28.3 / 0|${_{.}^{\prime\prime}}$|062 | 28.2 / — | 28.2 / — |
| CEERS8 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|165 |
| CEERS9 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|157 |
| CEERS10 | 28.3 / 0|${_{.}^{\prime\prime}}$|064 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|162 |
| . | 10σ depth / PSF FWHM . | ||
|---|---|---|---|
| Field . | F150W . | F410M . | F444W . |
| CEERS1 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.1 / 0|${_{.}^{\prime\prime}}$|154 | 28.3 / 0|${_{.}^{\prime\prime}}$|161 |
| CEERS2 | 28.2 / 0|${_{.}^{\prime\prime}}$|062 | 28.1 / 0|${_{.}^{\prime\prime}}$|170 | 28.6 / 0|${_{.}^{\prime\prime}}$|172 |
| CEERS3 | 28.4 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / 0|${_{.}^{\prime\prime}}$|155 | 28.4 / 0|${_{.}^{\prime\prime}}$|159 |
| CEERS4 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|164 |
| CEERS5 | 28.3 / 0|${_{.}^{\prime\prime}}$|066 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|169 |
| CEERS6 | 28.3 / 0|${_{.}^{\prime\prime}}$|059 | 28.2 / 0|${_{.}^{\prime\prime}}$|157 | 28.2 / 0|${_{.}^{\prime\prime}}$|166 |
| CEERS7 | 28.3 / 0|${_{.}^{\prime\prime}}$|062 | 28.2 / — | 28.2 / — |
| CEERS8 | 28.3 / 0|${_{.}^{\prime\prime}}$|061 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|165 |
| CEERS9 | 28.3 / 0|${_{.}^{\prime\prime}}$|065 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|157 |
| CEERS10 | 28.3 / 0|${_{.}^{\prime\prime}}$|064 | 28.2 / — | 28.2 / 0|${_{.}^{\prime\prime}}$|162 |
Median sizes and total magnitudes in the rest-frame UV and optical of the subsamples divided into three redshift bins.*
| Redshift . | Flag . | MUV . | re . | Mopt . | re, opt . |
|---|---|---|---|---|---|
| . | . | (mag) . | (kpc) . | (mag) . | (kpc) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| z = 4.5–5.5 | 1 | −19.89 | |$0.36^{+0.17}_{-0.11}$| | −20.58 | |$0.47^{+0.30}_{-0.15}$| |
| 2 | −19.83 | |$0.41^{+0.22}_{-0.15}$| | −20.35 | |$0.49^{+0.21}_{-0.15}$| | |
| 2 | −20.30 | |$0.55^{+0.27}_{-0.27}$| | −20.89 | |$0.59^{+0.23}_{-0.17}$| | |
| 2 | −20.95 | |$0.77^{+0.44}_{-0.41}$| | −21.72 | |$0.89^{+0.41}_{-0.39}$| | |
| z = 5.5–6.5 | 1 | −19.96 | |$0.40^{+0.09}_{-0.19}$| | −21.45 | |$0.36^{+0.29}_{-0.13}$| |
| 2 | −20.10 | |$0.41^{+0.13}_{-0.22}$| | −20.92 | |$0.56^{+0.23}_{-0.26}$| | |
| 2 | −20.69 | |$0.76^{+0.10}_{-0.39}$| | −22.20 | |$0.75^{+0.22}_{-0.16}$| | |
| z = 6.5–9.5 | 1 | −20.27 | |$0.13^{+0.10}_{-0.05}$| | −20.75 | |$0.24^{+0.04}_{-0.05}$| |
| 2 | −20.05 | |$0.22^{+0.11}_{-0.12}$| | −20.70 | |$0.28^{+0.24}_{-0.06}$| | |
| 2 | −20.73 | |$0.20^{+0.32}_{-0.05}$| | −21.63 | |$0.26^{+0.19}_{-0.11}$| |
| Redshift . | Flag . | MUV . | re . | Mopt . | re, opt . |
|---|---|---|---|---|---|
| . | . | (mag) . | (kpc) . | (mag) . | (kpc) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| z = 4.5–5.5 | 1 | −19.89 | |$0.36^{+0.17}_{-0.11}$| | −20.58 | |$0.47^{+0.30}_{-0.15}$| |
| 2 | −19.83 | |$0.41^{+0.22}_{-0.15}$| | −20.35 | |$0.49^{+0.21}_{-0.15}$| | |
| 2 | −20.30 | |$0.55^{+0.27}_{-0.27}$| | −20.89 | |$0.59^{+0.23}_{-0.17}$| | |
| 2 | −20.95 | |$0.77^{+0.44}_{-0.41}$| | −21.72 | |$0.89^{+0.41}_{-0.39}$| | |
| z = 5.5–6.5 | 1 | −19.96 | |$0.40^{+0.09}_{-0.19}$| | −21.45 | |$0.36^{+0.29}_{-0.13}$| |
| 2 | −20.10 | |$0.41^{+0.13}_{-0.22}$| | −20.92 | |$0.56^{+0.23}_{-0.26}$| | |
| 2 | −20.69 | |$0.76^{+0.10}_{-0.39}$| | −22.20 | |$0.75^{+0.22}_{-0.16}$| | |
| z = 6.5–9.5 | 1 | −20.27 | |$0.13^{+0.10}_{-0.05}$| | −20.75 | |$0.24^{+0.04}_{-0.05}$| |
| 2 | −20.05 | |$0.22^{+0.11}_{-0.12}$| | −20.70 | |$0.28^{+0.24}_{-0.06}$| | |
| 2 | −20.73 | |$0.20^{+0.32}_{-0.05}$| | −21.63 | |$0.26^{+0.19}_{-0.11}$| |
*(1) Redshift range. (2) Flag for spectroscopic redshifts: 1. galaxies with spectroscopic confirmation; 2. galaxies with and without spectroscopic confirmation. (3) Median rest-frame UV total magnitude. (4) Median size in the rest-frame UV and its 68th percentiles. (5) Median rest-frame optical total magnitude. (6) Median size in the rest-frame optical and its 68th percentiles.
Median sizes and total magnitudes in the rest-frame UV and optical of the subsamples divided into three redshift bins.*
| Redshift . | Flag . | MUV . | re . | Mopt . | re, opt . |
|---|---|---|---|---|---|
| . | . | (mag) . | (kpc) . | (mag) . | (kpc) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| z = 4.5–5.5 | 1 | −19.89 | |$0.36^{+0.17}_{-0.11}$| | −20.58 | |$0.47^{+0.30}_{-0.15}$| |
| 2 | −19.83 | |$0.41^{+0.22}_{-0.15}$| | −20.35 | |$0.49^{+0.21}_{-0.15}$| | |
| 2 | −20.30 | |$0.55^{+0.27}_{-0.27}$| | −20.89 | |$0.59^{+0.23}_{-0.17}$| | |
| 2 | −20.95 | |$0.77^{+0.44}_{-0.41}$| | −21.72 | |$0.89^{+0.41}_{-0.39}$| | |
| z = 5.5–6.5 | 1 | −19.96 | |$0.40^{+0.09}_{-0.19}$| | −21.45 | |$0.36^{+0.29}_{-0.13}$| |
| 2 | −20.10 | |$0.41^{+0.13}_{-0.22}$| | −20.92 | |$0.56^{+0.23}_{-0.26}$| | |
| 2 | −20.69 | |$0.76^{+0.10}_{-0.39}$| | −22.20 | |$0.75^{+0.22}_{-0.16}$| | |
| z = 6.5–9.5 | 1 | −20.27 | |$0.13^{+0.10}_{-0.05}$| | −20.75 | |$0.24^{+0.04}_{-0.05}$| |
| 2 | −20.05 | |$0.22^{+0.11}_{-0.12}$| | −20.70 | |$0.28^{+0.24}_{-0.06}$| | |
| 2 | −20.73 | |$0.20^{+0.32}_{-0.05}$| | −21.63 | |$0.26^{+0.19}_{-0.11}$| |
| Redshift . | Flag . | MUV . | re . | Mopt . | re, opt . |
|---|---|---|---|---|---|
| . | . | (mag) . | (kpc) . | (mag) . | (kpc) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| z = 4.5–5.5 | 1 | −19.89 | |$0.36^{+0.17}_{-0.11}$| | −20.58 | |$0.47^{+0.30}_{-0.15}$| |
| 2 | −19.83 | |$0.41^{+0.22}_{-0.15}$| | −20.35 | |$0.49^{+0.21}_{-0.15}$| | |
| 2 | −20.30 | |$0.55^{+0.27}_{-0.27}$| | −20.89 | |$0.59^{+0.23}_{-0.17}$| | |
| 2 | −20.95 | |$0.77^{+0.44}_{-0.41}$| | −21.72 | |$0.89^{+0.41}_{-0.39}$| | |
| z = 5.5–6.5 | 1 | −19.96 | |$0.40^{+0.09}_{-0.19}$| | −21.45 | |$0.36^{+0.29}_{-0.13}$| |
| 2 | −20.10 | |$0.41^{+0.13}_{-0.22}$| | −20.92 | |$0.56^{+0.23}_{-0.26}$| | |
| 2 | −20.69 | |$0.76^{+0.10}_{-0.39}$| | −22.20 | |$0.75^{+0.22}_{-0.16}$| | |
| z = 6.5–9.5 | 1 | −20.27 | |$0.13^{+0.10}_{-0.05}$| | −20.75 | |$0.24^{+0.04}_{-0.05}$| |
| 2 | −20.05 | |$0.22^{+0.11}_{-0.12}$| | −20.70 | |$0.28^{+0.24}_{-0.06}$| | |
| 2 | −20.73 | |$0.20^{+0.32}_{-0.05}$| | −21.63 | |$0.26^{+0.19}_{-0.11}$| |
*(1) Redshift range. (2) Flag for spectroscopic redshifts: 1. galaxies with spectroscopic confirmation; 2. galaxies with and without spectroscopic confirmation. (3) Median rest-frame UV total magnitude. (4) Median size in the rest-frame UV and its 68th percentiles. (5) Median rest-frame optical total magnitude. (6) Median size in the rest-frame optical and its 68th percentiles.
Median optical-to-UV size ratios and UV total magnitudes of the subsamples divided into two redshift bins.*
| Redshift . | Flag . | MUV . | re, opt|$/$|re, UV . |
|---|---|---|---|
| . | . | (mag) . | . |
| (1) . | (2) . | (3) . | (4) . |
| z = 4.5–5.5 | 1 | −20.24 | |$0.97^{+0.29}_{-0.22}$| |
| 2 | −20.17 | |$0.95^{+0.49}_{-0.17}$| | |
| 2 | −20.90 | |$1.00^{+0.25}_{-0.15}$| | |
| z = 5.5–6.5 | 1 | −20.42 | |$1.22^{+0.25}_{-0.35}$| |
| 2 | −21.36 | |$0.95^{+0.28}_{-0.10}$| | |
| 2 | −20.34 | |$1.08^{+0.48}_{-0.24}$| | |
| z = 6.5–9.5 | 1 | −20.69 | |$1.33^{+1.14}_{-0.36}$| |
| 2 | −20.93 | |$1.13^{+0.28}_{-0.53}$| | |
| 2 | −20.32 | |$1.20^{+0.18}_{-0.32}$| |
| Redshift . | Flag . | MUV . | re, opt|$/$|re, UV . |
|---|---|---|---|
| . | . | (mag) . | . |
| (1) . | (2) . | (3) . | (4) . |
| z = 4.5–5.5 | 1 | −20.24 | |$0.97^{+0.29}_{-0.22}$| |
| 2 | −20.17 | |$0.95^{+0.49}_{-0.17}$| | |
| 2 | −20.90 | |$1.00^{+0.25}_{-0.15}$| | |
| z = 5.5–6.5 | 1 | −20.42 | |$1.22^{+0.25}_{-0.35}$| |
| 2 | −21.36 | |$0.95^{+0.28}_{-0.10}$| | |
| 2 | −20.34 | |$1.08^{+0.48}_{-0.24}$| | |
| z = 6.5–9.5 | 1 | −20.69 | |$1.33^{+1.14}_{-0.36}$| |
| 2 | −20.93 | |$1.13^{+0.28}_{-0.53}$| | |
| 2 | −20.32 | |$1.20^{+0.18}_{-0.32}$| |
*(1) Redshift range. (2) Flag for spectroscopic redshifts: 1. galaxies with spectroscopic confirmation; 2. galaxies with and without spectroscopic confirmation. (3) Median rest-frame UV total magnitude. (4) Median ratio of the rest-frame optical size to the UV size and its 68th percentiles.
Median optical-to-UV size ratios and UV total magnitudes of the subsamples divided into two redshift bins.*
| Redshift . | Flag . | MUV . | re, opt|$/$|re, UV . |
|---|---|---|---|
| . | . | (mag) . | . |
| (1) . | (2) . | (3) . | (4) . |
| z = 4.5–5.5 | 1 | −20.24 | |$0.97^{+0.29}_{-0.22}$| |
| 2 | −20.17 | |$0.95^{+0.49}_{-0.17}$| | |
| 2 | −20.90 | |$1.00^{+0.25}_{-0.15}$| | |
| z = 5.5–6.5 | 1 | −20.42 | |$1.22^{+0.25}_{-0.35}$| |
| 2 | −21.36 | |$0.95^{+0.28}_{-0.10}$| | |
| 2 | −20.34 | |$1.08^{+0.48}_{-0.24}$| | |
| z = 6.5–9.5 | 1 | −20.69 | |$1.33^{+1.14}_{-0.36}$| |
| 2 | −20.93 | |$1.13^{+0.28}_{-0.53}$| | |
| 2 | −20.32 | |$1.20^{+0.18}_{-0.32}$| |
| Redshift . | Flag . | MUV . | re, opt|$/$|re, UV . |
|---|---|---|---|
| . | . | (mag) . | . |
| (1) . | (2) . | (3) . | (4) . |
| z = 4.5–5.5 | 1 | −20.24 | |$0.97^{+0.29}_{-0.22}$| |
| 2 | −20.17 | |$0.95^{+0.49}_{-0.17}$| | |
| 2 | −20.90 | |$1.00^{+0.25}_{-0.15}$| | |
| z = 5.5–6.5 | 1 | −20.42 | |$1.22^{+0.25}_{-0.35}$| |
| 2 | −21.36 | |$0.95^{+0.28}_{-0.10}$| | |
| 2 | −20.34 | |$1.08^{+0.48}_{-0.24}$| | |
| z = 6.5–9.5 | 1 | −20.69 | |$1.33^{+1.14}_{-0.36}$| |
| 2 | −20.93 | |$1.13^{+0.28}_{-0.53}$| | |
| 2 | −20.32 | |$1.20^{+0.18}_{-0.32}$| |
*(1) Redshift range. (2) Flag for spectroscopic redshifts: 1. galaxies with spectroscopic confirmation; 2. galaxies with and without spectroscopic confirmation. (3) Median rest-frame UV total magnitude. (4) Median ratio of the rest-frame optical size to the UV size and its 68th percentiles.
| . | . | . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Bouwens et al. (2015) . | Shibuya, Ouchi, and Harikane (2015) . | . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | |||||||||||
| ID . | RA (○) . | Dec (○) . | ID . | zspec . | ID . | zphoto . | ID . | zphoto . | ID . | zphoto . | Other references* . |
| C01_01 | 215.00522 | 52.99652 | P5P_00003 | 8.01 | 3908 | 9.04 | — | — | — | — | 2,4 |
| C01_02 | 215.01173 | 52.98822 | P5P_00007 | 8.87 | 6059 | 9.01 | — | — | — | — | 2,5 |
| C01_03 | 215.00117 | 53.01119 | P5P_00044 | 7.10 | — | — | — | — | — | — | 4 |
| C01_04 | 215.01562 | 53.01176 | P5P_00067 | 6.21 | — | — | — | — | — | — | — |
| C01_05 | 215.01090 | 53.01324 | P5P_01912 | 5.10 | — | — | — | — | — | — | — |
| C01_06 | 214.99828 | 52.99467 | P5P_01953 | 4.61 | — | — | — | — | — | — | — |
| C01_07 | 214.98878 | 52.99797 | P5P_03584 | 4.64 | — | — | — | — | — | — | — |
| C01_08 | 214.96063 | 52.94051 | — | — | — | — | — | — | 26647 | 5 | — |
| C01_09 | 215.01605 | 52.98248 | — | — | — | — | — | — | 27229 | 5 | — |
| C01_10 | 215.02613 | 52.99457 | — | — | — | — | — | — | 28414 | 5 | — |
| C01_11 | 215.01527 | 52.98672 | — | — | — | — | — | — | 28427 | 5 | — |
| C01_12 | 215.01114 | 52.98909 | — | — | — | — | — | — | 29656 | 5 | — |
| C01_13 | 214.97204 | 52.96254 | — | — | — | — | — | — | 29855 | 5 | — |
| C01_14 | 214.97481 | 52.96650 | — | — | — | — | — | — | 30425 | 5 | — |
| C01_15 | 214.99405 | 52.98085 | — | — | — | — | — | — | 30550 | 5 | — |
| C01_16 | 214.94419 | 52.96760 | — | — | — | — | — | — | 35779 | 5 | — |
| C01_17 | 214.93204 | 52.95899 | — | — | — | — | — | — | 35809 | 5 | — |
| C01_18 | 214.92475 | 52.95584 | — | — | — | — | — | — | 36262 | 5 | — |
| C01_19 | 215.00974 | 52.98144 | — | — | — | — | — | — | 28026 | 6 | — |
| C01_20 | 215.01415 | 53.01115 | — | — | — | — | — | — | 34318 | 6 | — |
| C01_21 | 214.95194 | 52.97174 | — | — | 1875 | 8.92 | — | — | — | — | — |
| C01_22 | 214.99440 | 52.98938 | — | — | 3858 | 8.95 | — | — | — | — | 2,3,5 |
| C01_23 | 215.00537 | 52.99670 | — | — | 3910 | 9.55 | — | — | — | — | 2,3 |
| C01_24 | 214.95008 | 52.94927 | — | — | 5534 | 8.62 | — | — | — | — | — |
| C01_25 | 214.96672 | 52.96829 | — | — | 4143 | 8.98 | — | — | — | — | — |
| C01_26 | 214.99475 | 53.00781 | — | — | — | — | EGSY-9587400281 | 7.58 | — | — | — |
| C02_01 | 214.87255 | 52.87595 | P4M_00323 | 5.67 | — | — | — | — | — | — | — |
| C02_02 | 214.88802 | 52.88826 | P4M_01465 | 5.27 | — | — | — | — | — | — | — |
| C02_03 | 214.85964 | 52.88814 | P4P_02000 | 4.81 | — | — | — | — | 31247 | 5 | — |
| C02_04 | 214.95381 | 52.93373 | — | — | — | — | — | — | 26115 | 5 | — |
| C02_05 | 214.94847 | 52.93859 | — | — | — | — | — | — | 28205 | 5 | — |
| C02_06 | 214.88124 | 52.89609 | — | — | — | — | — | — | 29440 | 5 | — |
| C02_07 | 214.85954 | 52.88801 | — | — | — | — | — | — | 31167 | 5 | — |
| C02_08 | 214.91837 | 52.93187 | — | — | — | — | — | — | 31703 | 5 | — |
| C02_09 | 214.91887 | 52.93921 | — | — | — | — | — | — | 33230 | 5 | — |
| C02_10 | 214.87215 | 52.90633 | — | — | — | — | — | — | 33438 | 5 | — |
| C02_11 | 214.91523 | 52.94503 | — | — | — | — | — | — | 35205 | 5 | — |
| C02_12 | 214.92457 | 52.91873 | — | — | — | — | EGSZ-9419055074 | 6.69 | 27521 | 6 | — |
| C02_13 | 214.93474 | 52.94714 | — | — | — | — | — | — | 32583 | 6 | — |
| C02_14 | 214.84477 | 52.89210 | — | — | 2402 | 8.71 | — | — | — | — | — |
| C02_15 | 214.87614 | 52.88083 | — | — | 7534 | 8.95 | — | — | — | — | — |
| C02_16 | 214.86160 | 52.90460 | — | — | 2324 | 9.58 | — | — | — | — | 1,5 |
| C02_17 | 214.90224 | 52.93937 | — | — | 1298 | 8.53 | — | — | — | — | — |
| C02_18 | 214.84617 | 52.89400 | — | — | 2274 | 8.62 | — | — | — | — | — |
| C02_19 | 214.90763 | 52.94461 | — | — | 1075 | 8.38 | — | — | — | — | — |
| C02_20 | 214.89087 | 52.89331 | — | — | — | — | EGSZ-9338153359 | 6.92 | — | — | — |
| C02_21 | 214.88100 | 52.89125 | — | — | — | — | EGSZ-9314453285 | 6.92 | — | — | — |
| C02_22 | 214.89608 | 52.92519 | — | — | — | — | EGSZ-9350655307 | 6.77 | — | — | — |
| C02_23 | 214.86304 | 52.88947 | — | — | — | — | EGSZ-9271353221 | 6.77 | — | — | — |
| C03_01 | 214.80652 | 52.87874 | P4M_00355 | 6.10 | — | — | — | — | — | — | — |
| C03_02 | 214.81273 | 52.88145 | P4P_00362 | 6.05 | — | — | — | — | — | — | — |
| C03_03 | 214.81970 | 52.87967 | P4M_00381 | 5.51 | — | — | — | — | — | — | — |
| C03_04 | 214.83622 | 52.88258 | P4M_00397 | 6.00 | — | — | — | — | — | — | — |
| C03_05 | 214.82900 | 52.87561 | P4M_00403 | 5.76 | — | — | — | — | — | — | — |
| C03_06 | 214.83935 | 52.88247 | P4M_00407 | 7.03 | — | — | — | — | — | — | 4 |
| C03_07 | 214.82538 | 52.86297 | P4P_00439 | 7.18 | — | — | — | — | — | — | — |
| C03_08 | 214.81304 | 52.83415 | P4P_00498 | 7.18 | — | — | — | — | — | — | 4 |
| C03_09 | 214.81168 | 52.83714 | P4P_02116 | 5.28 | — | — | — | — | — | — | — |
| C03_10 | 214.86453 | 52.87087 | P4P_02362 | 5.32 | — | — | — | — | — | — | — |
| C03_11 | 214.79396 | 52.82025 | — | — | — | — | — | — | 26215 | 5 | — |
| C03_12 | 214.81201 | 52.83682 | — | — | — | — | — | — | 27005 | 5 | — |
| C03_13 | 214.80701 | 52.83825 | — | — | — | — | — | — | 28123 | 5 | — |
| C03_14 | 214.80686 | 52.83829 | — | — | — | — | — | — | 28217 | 5 | — |
| C03_15 | 214.82586 | 52.85515 | — | — | — | — | — | — | 29028 | 5 | — |
| C03_16 | 214.82518 | 52.85907 | — | — | — | — | — | — | 30133 | 5 | — |
| C03_17 | 214.79000 | 52.83466 | — | — | — | — | — | — | 30300 | 5 | — |
| C03_18 | 214.77238 | 52.82342 | — | — | — | — | — | — | 30572 | 5 | — |
| C03_19 | 214.79449 | 52.83954 | — | — | — | — | — | — | 30668 | 5 | — |
| C03_20 | 214.76766 | 52.83329 | — | — | — | — | — | — | 33751 | 5 | — |
| C03_21 | 214.76385 | 52.83544 | — | — | — | — | — | — | 34851 | 5 | — |
| C03_22 | 214.83347 | 52.88902 | — | — | — | — | — | — | 35846 | 5 | — |
| C03_23 | 214.74571 | 52.83906 | — | — | — | — | — | — | 37651 | 5 | — |
| C03_24 | 214.83556 | 52.87748 | — | — | — | — | — | — | 32502 | 6 | — |
| C03_25 | 214.76480 | 52.82764 | — | — | — | — | — | — | 32881 | 6 | — |
| C03_26 | 214.83068 | 52.88777 | — | — | 1748 | 8.77 | — | — | — | — | 2 |
| C03_27 | 214.79396 | 52.84158 | — | — | — | — | EGSY-9105550297 | 8.11 | — | — | — |
| C04_01 | 214.74666 | 52.74776 | — | — | — | — | — | — | 17063 | 5 | — |
| C04_02 | 214.79050 | 52.78157 | — | — | — | — | — | — | 17722 | 5 | — |
| C04_03 | 214.80567 | 52.79693 | — | — | — | — | — | — | 18783 | 5 | — |
| C04_04 | 214.72571 | 52.76288 | — | — | — | — | — | — | 24140 | 5 | — |
| C04_05 | 214.78409 | 52.80859 | — | — | — | — | — | — | 25149 | 5 | — |
| C04_06 | 214.71657 | 52.76452 | — | — | — | — | — | — | 26086 | 5 | — |
| C04_07 | 214.75336 | 52.74102 | — | — | — | — | — | — | 14598 | 6 | — |
| C04_08 | 214.79315 | 52.77049 | — | — | — | — | — | — | 14850 | 6 | — |
| C04_09 | 214.78767 | 52.77317 | — | — | — | — | — | — | 16300 | 6 | — |
| C04_10 | 214.79033 | 52.77294 | — | — | — | — | EGSZ-9096846226 | 6.54 | — | — | — |
| C05_01 | 214.88608 | 52.87689 | P4P_01534 | 4.59 | — | — | — | — | 24123 | 5 | — |
| C05_02 | 214.96740 | 52.93296 | P9M_01025 | 8.71 | — | — | — | — | — | — | 4,5 |
| C05_03 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C05_04 | 214.92186 | 52.88563 | — | — | — | — | — | — | 20105 | 5 | — |
| C05_05 | 214.96585 | 52.93406 | — | — | — | — | — | — | 24219 | 7 | — |
| C05_06 | 214.98904 | 52.91969 | — | — | — | — | EGSZ-9573755109 | 6.69 | — | — | — |
| C05_07 | 214.94558 | 52.90025 | — | — | — | — | EGSZ-9469454009 | 6.92 | — | — | — |
| C05_08 | 214.94675 | 52.90056 | — | — | — | — | EGSZ-9472254020 | 7.24 | — | — | — |
| C05_09 | 214.97017 | 52.91647 | — | — | — | — | EGSZ-9528454593 | 6.46 | — | — | — |
| C06_01 | 214.86441 | 52.85366 | P4P_00545 | 5.67 | — | — | — | — | — | — | — |
| C06_02 | 214.86725 | 52.83674 | P4M_00603 | 6.06 | — | — | — | — | — | — | — |
| C06_03 | 214.87646 | 52.83942 | P4M_00618 | 6.05 | — | — | — | — | — | — | — |
| C06_04 | 214.87177 | 52.83317 | P4M_00792 | 6.26 | — | — | — | — | — | — | — |
| C06_05 | 214.88299 | 52.84042 | P4M_01027 | 7.82 | — | — | — | — | — | — | 4 |
| C06_06 | 214.82345 | 52.83028 | P4M_02782 | 5.24 | — | — | — | — | — | — | — |
| C06_07 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C06_08 | 214.90369 | 52.84492 | P10M_00670 | 5.80 | — | — | — | — | — | — | — |
| C06_09 | 214.85224 | 52.80917 | — | — | — | — | — | — | 13963 | 5 | — |
| C06_10 | 214.89508 | 52.84799 | — | — | — | — | — | — | 15866 | 5 | — |
| C06_11 | 214.84701 | 52.81407 | — | — | — | — | — | — | 15930 | 5 | — |
| C06_12 | 214.82490 | 52.83610 | — | — | — | — | — | — | 24754 | 5 | — |
| C06_13 | 214.85514 | 52.82081 | — | — | — | — | — | — | 16208 | 6 | — |
| C06_14 | 214.88813 | 52.85899 | — | — | 4012 | 8.89 | — | — | — | — | 2 |
| C06_15 | 214.80217 | 52.80589 | — | — | — | — | EGSZ-9125248212 | 6.54 | — | — | — |
| C06_16 | 214.80625 | 52.81275 | — | — | — | — | EGSZ-9135048459 | 6.77 | — | — | — |
| C06_17 | 214.85917 | 52.85364 | — | — | — | — | EGSZ-9262051131 | 6.39 | — | — | — |
| C07_01 | 215.09088 | 52.95152 | P8M_01358 | 5.50 | — | — | — | — | — | — | — |
| C07_02 | 215.07996 | 52.95677 | P8M_01449 | 4.75 | — | — | — | — | 10735 | 5 | — |
| C07_03 | 215.08602 | 52.95219 | P8P_11383 | 5.07 | — | — | — | — | — | — | — |
| C07_04 | 215.13529 | 52.99323 | — | — | — | — | — | — | 10203 | 5 | — |
| C07_05 | 215.14644 | 52.97027 | — | — | — | — | — | — | 3639 | 5 | — |
| C07_06 | 215.13511 | 52.96719 | — | — | — | — | — | — | 4678 | 5 | — |
| C07_07 | 215.14402 | 52.95935 | — | — | — | — | — | — | 1744 | 5 | — |
| C07_08 | 215.14620 | 52.95540 | — | — | — | — | — | — | 872 | 5 | — |
| C07_09 | 215.09061 | 52.95167 | — | — | — | — | — | — | 7923 | 5 | — |
| C07_10 | 215.10084 | 52.93848 | — | — | — | — | — | — | 3761 | 5 | — |
| C07_11 | 215.08727 | 52.94106 | — | — | — | — | — | — | 6407 | 5 | — |
| C07_12 | 215.10358 | 52.93191 | — | — | — | — | — | — | 1984 | 5 | — |
| C07_13 | 215.07971 | 52.93832 | — | — | — | — | — | — | 6795 | 5 | — |
| C07_14 | 215.08314 | 52.91996 | — | — | — | — | — | — | 2462 | 5 | — |
| C07_15 | 215.12673 | 52.98391 | — | — | — | — | — | — | 9529 | 6 | — |
| C07_16 | 215.07467 | 52.94472 | — | — | — | — | EGSZ-0179256410 | 6.69 | — | — | — |
| C08_01 | 215.03540 | 52.89067 | P9M_01019 | 8.68 | — | — | — | — | — | — | 4,5 |
| C08_02 | 215.03972 | 52.90160 | P9M_01038 | 7.19 | — | — | — | — | — | — | 4 |
| C08_03 | 215.03055 | 52.90259 | P9M_01324 | 5.01 | — | — | — | — | — | — | — |
| C08_04 | 215.03318 | 52.89002 | — | — | — | — | — | — | 3610 | 5 | — |
| C08_05 | 215.04419 | 52.89879 | — | — | — | — | — | — | 3733 | 5 | — |
| C08_06 | 215.00895 | 52.87673 | — | — | — | — | — | — | 4326 | 5 | — |
| C08_07 | 215.06373 | 52.91751 | — | — | — | — | — | — | 4736 | 5 | — |
| C08_08 | 214.97835 | 52.85675 | — | — | — | — | — | — | 4743 | 5 | — |
| C08_09 | 215.03308 | 52.89651 | — | — | — | — | — | — | 5021 | 5 | — |
| C08_10 | 214.98738 | 52.86896 | — | — | — | — | — | — | 6056 | 5 | — |
| C08_11 | 215.04264 | 52.91202 | — | — | — | — | — | — | 6813 | 5 | — |
| C08_12 | 215.01083 | 52.90101 | — | — | — | — | — | — | 9263 | 5 | — |
| C08_13 | 214.97813 | 52.87957 | — | — | — | — | — | — | 9635 | 5 | — |
| C08_14 | 215.00995 | 52.91071 | — | — | — | — | — | — | 11586 | 5 | — |
| C08_15 | 215.03564 | 52.89226 | — | — | — | — | EGSZ-0085553321 | 7.00 | 3320 | 6 | — |
| C08_16 | 215.04600 | 52.89818 | — | — | — | — | — | — | 3441 | 6 | — |
| C08_17 | 215.00943 | 52.87537 | — | — | — | — | — | — | 3989 | 6 | — |
| C08_18 | 215.00769 | 52.87418 | — | — | — | — | — | — | 4076 | 6 | — |
| C08_19 | 214.98723 | 52.87465 | — | — | — | — | — | — | 7282 | 6 | — |
| C08_20 | 214.98694 | 52.87462 | — | — | — | — | — | — | 7371 | 6 | — |
| C08_21 | 214.98797 | 52.87950 | — | — | — | — | EGSZ-9571152461 | 6.46 | 8177 | 6 | — |
| C08_22 | 215.03394 | 52.91384 | — | — | — | — | — | — | 8534 | 6 | — |
| C08_23 | 215.03210 | 52.91902 | — | — | — | — | — | — | 9935 | 6 | — |
| C08_24 | 214.95842 | 52.87517 | — | — | — | — | EGSZ-9500252305 | 6.54 | 11721 | 6 | — |
| C08_25 | 215.03721 | 52.90675 | — | — | — | — | EGSZ-0089354243 | 7.00 | — | — | — |
| C08_26 | 215.03704 | 52.89194 | — | — | — | — | EGSZ-0088953310 | 7.00 | — | — | — |
| C08_27 | 215.00600 | 52.90536 | — | — | — | — | EGSZ-0014454193 | 6.69 | — | — | — |
| C08_28 | 214.97996 | 52.86114 | — | — | — | — | EGSZ-9551951401 | 7.08 | — | — | — |
| C08_29 | 214.97192 | 52.86922 | — | — | — | — | EGSZ-9532652092 | 6.39 | — | — | — |
| C08_30 | 214.99875 | 52.85542 | — | — | — | — | EGSY-9597051195 | 8.38 | — | — | — |
| C08_31 | 214.98958 | 52.86658 | — | — | — | — | EGSY-9575051597 | 8.11 | — | — | — |
| C09_01 | 214.95990 | 52.83118 | P10M_01207 | 4.90 | — | — | — | — | 2131 | 5 | — |
| C09_02 | 214.94755 | 52.83709 | P10M_01289 | 4.88 | — | — | — | — | — | — | — |
| C09_03 | 214.95516 | 52.84290 | P10M_01294 | 5.00 | — | — | — | — | 5342 | 5 | — |
| C09_04 | 214.94379 | 52.85006 | P10M_01374 | 5.00 | — | — | — | — | 8518 | 5 | — |
| C09_05 | 214.92738 | 52.81349 | — | — | — | — | — | — | 3324 | 5 | — |
| C09_06 | 214.95796 | 52.83598 | — | — | — | — | — | — | 3426 | 5 | — |
| C09_07 | 214.93801 | 52.83249 | — | — | — | — | — | — | 5763 | 5 | — |
| C09_08 | 214.94369 | 52.85014 | — | — | — | — | — | — | 8598 | 5 | — |
| C10_01 | 214.83230 | 52.74412 | — | — | — | — | — | — | 2973 | 5 | — |
| C10_02 | 214.81900 | 52.75974 | — | — | — | — | — | — | 8275 | 5 | — |
| C10_03 | 214.80973 | 52.75440 | — | — | — | — | — | — | 8514 | 5 | — |
| C10_04 | 214.83919 | 52.77684 | — | — | — | — | — | — | 8846 | 5 | — |
| C10_05 | 214.84428 | 52.78964 | — | — | — | — | — | — | 10641 | 5 | — |
| C10_06 | 214.83044 | 52.78370 | — | — | — | — | — | — | 11720 | 5 | — |
| C10_07 | 214.83851 | 52.79330 | — | — | — | — | — | — | 12509 | 5 | — |
| C10_08 | 214.80272 | 52.76821 | — | — | — | — | — | — | 12664 | 5 | — |
| C10_09 | 214.85085 | 52.77673 | — | — | — | — | EGSZ-9242146357 | 6.84 | 7028 | 7 | — |
| C10_10 | 214.83100 | 52.74914 | — | — | — | — | EGSZ-9194444569 | 6.77 | — | — | — |
| . | . | . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Bouwens et al. (2015) . | Shibuya, Ouchi, and Harikane (2015) . | . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | |||||||||||
| ID . | RA (○) . | Dec (○) . | ID . | zspec . | ID . | zphoto . | ID . | zphoto . | ID . | zphoto . | Other references* . |
| C01_01 | 215.00522 | 52.99652 | P5P_00003 | 8.01 | 3908 | 9.04 | — | — | — | — | 2,4 |
| C01_02 | 215.01173 | 52.98822 | P5P_00007 | 8.87 | 6059 | 9.01 | — | — | — | — | 2,5 |
| C01_03 | 215.00117 | 53.01119 | P5P_00044 | 7.10 | — | — | — | — | — | — | 4 |
| C01_04 | 215.01562 | 53.01176 | P5P_00067 | 6.21 | — | — | — | — | — | — | — |
| C01_05 | 215.01090 | 53.01324 | P5P_01912 | 5.10 | — | — | — | — | — | — | — |
| C01_06 | 214.99828 | 52.99467 | P5P_01953 | 4.61 | — | — | — | — | — | — | — |
| C01_07 | 214.98878 | 52.99797 | P5P_03584 | 4.64 | — | — | — | — | — | — | — |
| C01_08 | 214.96063 | 52.94051 | — | — | — | — | — | — | 26647 | 5 | — |
| C01_09 | 215.01605 | 52.98248 | — | — | — | — | — | — | 27229 | 5 | — |
| C01_10 | 215.02613 | 52.99457 | — | — | — | — | — | — | 28414 | 5 | — |
| C01_11 | 215.01527 | 52.98672 | — | — | — | — | — | — | 28427 | 5 | — |
| C01_12 | 215.01114 | 52.98909 | — | — | — | — | — | — | 29656 | 5 | — |
| C01_13 | 214.97204 | 52.96254 | — | — | — | — | — | — | 29855 | 5 | — |
| C01_14 | 214.97481 | 52.96650 | — | — | — | — | — | — | 30425 | 5 | — |
| C01_15 | 214.99405 | 52.98085 | — | — | — | — | — | — | 30550 | 5 | — |
| C01_16 | 214.94419 | 52.96760 | — | — | — | — | — | — | 35779 | 5 | — |
| C01_17 | 214.93204 | 52.95899 | — | — | — | — | — | — | 35809 | 5 | — |
| C01_18 | 214.92475 | 52.95584 | — | — | — | — | — | — | 36262 | 5 | — |
| C01_19 | 215.00974 | 52.98144 | — | — | — | — | — | — | 28026 | 6 | — |
| C01_20 | 215.01415 | 53.01115 | — | — | — | — | — | — | 34318 | 6 | — |
| C01_21 | 214.95194 | 52.97174 | — | — | 1875 | 8.92 | — | — | — | — | — |
| C01_22 | 214.99440 | 52.98938 | — | — | 3858 | 8.95 | — | — | — | — | 2,3,5 |
| C01_23 | 215.00537 | 52.99670 | — | — | 3910 | 9.55 | — | — | — | — | 2,3 |
| C01_24 | 214.95008 | 52.94927 | — | — | 5534 | 8.62 | — | — | — | — | — |
| C01_25 | 214.96672 | 52.96829 | — | — | 4143 | 8.98 | — | — | — | — | — |
| C01_26 | 214.99475 | 53.00781 | — | — | — | — | EGSY-9587400281 | 7.58 | — | — | — |
| C02_01 | 214.87255 | 52.87595 | P4M_00323 | 5.67 | — | — | — | — | — | — | — |
| C02_02 | 214.88802 | 52.88826 | P4M_01465 | 5.27 | — | — | — | — | — | — | — |
| C02_03 | 214.85964 | 52.88814 | P4P_02000 | 4.81 | — | — | — | — | 31247 | 5 | — |
| C02_04 | 214.95381 | 52.93373 | — | — | — | — | — | — | 26115 | 5 | — |
| C02_05 | 214.94847 | 52.93859 | — | — | — | — | — | — | 28205 | 5 | — |
| C02_06 | 214.88124 | 52.89609 | — | — | — | — | — | — | 29440 | 5 | — |
| C02_07 | 214.85954 | 52.88801 | — | — | — | — | — | — | 31167 | 5 | — |
| C02_08 | 214.91837 | 52.93187 | — | — | — | — | — | — | 31703 | 5 | — |
| C02_09 | 214.91887 | 52.93921 | — | — | — | — | — | — | 33230 | 5 | — |
| C02_10 | 214.87215 | 52.90633 | — | — | — | — | — | — | 33438 | 5 | — |
| C02_11 | 214.91523 | 52.94503 | — | — | — | — | — | — | 35205 | 5 | — |
| C02_12 | 214.92457 | 52.91873 | — | — | — | — | EGSZ-9419055074 | 6.69 | 27521 | 6 | — |
| C02_13 | 214.93474 | 52.94714 | — | — | — | — | — | — | 32583 | 6 | — |
| C02_14 | 214.84477 | 52.89210 | — | — | 2402 | 8.71 | — | — | — | — | — |
| C02_15 | 214.87614 | 52.88083 | — | — | 7534 | 8.95 | — | — | — | — | — |
| C02_16 | 214.86160 | 52.90460 | — | — | 2324 | 9.58 | — | — | — | — | 1,5 |
| C02_17 | 214.90224 | 52.93937 | — | — | 1298 | 8.53 | — | — | — | — | — |
| C02_18 | 214.84617 | 52.89400 | — | — | 2274 | 8.62 | — | — | — | — | — |
| C02_19 | 214.90763 | 52.94461 | — | — | 1075 | 8.38 | — | — | — | — | — |
| C02_20 | 214.89087 | 52.89331 | — | — | — | — | EGSZ-9338153359 | 6.92 | — | — | — |
| C02_21 | 214.88100 | 52.89125 | — | — | — | — | EGSZ-9314453285 | 6.92 | — | — | — |
| C02_22 | 214.89608 | 52.92519 | — | — | — | — | EGSZ-9350655307 | 6.77 | — | — | — |
| C02_23 | 214.86304 | 52.88947 | — | — | — | — | EGSZ-9271353221 | 6.77 | — | — | — |
| C03_01 | 214.80652 | 52.87874 | P4M_00355 | 6.10 | — | — | — | — | — | — | — |
| C03_02 | 214.81273 | 52.88145 | P4P_00362 | 6.05 | — | — | — | — | — | — | — |
| C03_03 | 214.81970 | 52.87967 | P4M_00381 | 5.51 | — | — | — | — | — | — | — |
| C03_04 | 214.83622 | 52.88258 | P4M_00397 | 6.00 | — | — | — | — | — | — | — |
| C03_05 | 214.82900 | 52.87561 | P4M_00403 | 5.76 | — | — | — | — | — | — | — |
| C03_06 | 214.83935 | 52.88247 | P4M_00407 | 7.03 | — | — | — | — | — | — | 4 |
| C03_07 | 214.82538 | 52.86297 | P4P_00439 | 7.18 | — | — | — | — | — | — | — |
| C03_08 | 214.81304 | 52.83415 | P4P_00498 | 7.18 | — | — | — | — | — | — | 4 |
| C03_09 | 214.81168 | 52.83714 | P4P_02116 | 5.28 | — | — | — | — | — | — | — |
| C03_10 | 214.86453 | 52.87087 | P4P_02362 | 5.32 | — | — | — | — | — | — | — |
| C03_11 | 214.79396 | 52.82025 | — | — | — | — | — | — | 26215 | 5 | — |
| C03_12 | 214.81201 | 52.83682 | — | — | — | — | — | — | 27005 | 5 | — |
| C03_13 | 214.80701 | 52.83825 | — | — | — | — | — | — | 28123 | 5 | — |
| C03_14 | 214.80686 | 52.83829 | — | — | — | — | — | — | 28217 | 5 | — |
| C03_15 | 214.82586 | 52.85515 | — | — | — | — | — | — | 29028 | 5 | — |
| C03_16 | 214.82518 | 52.85907 | — | — | — | — | — | — | 30133 | 5 | — |
| C03_17 | 214.79000 | 52.83466 | — | — | — | — | — | — | 30300 | 5 | — |
| C03_18 | 214.77238 | 52.82342 | — | — | — | — | — | — | 30572 | 5 | — |
| C03_19 | 214.79449 | 52.83954 | — | — | — | — | — | — | 30668 | 5 | — |
| C03_20 | 214.76766 | 52.83329 | — | — | — | — | — | — | 33751 | 5 | — |
| C03_21 | 214.76385 | 52.83544 | — | — | — | — | — | — | 34851 | 5 | — |
| C03_22 | 214.83347 | 52.88902 | — | — | — | — | — | — | 35846 | 5 | — |
| C03_23 | 214.74571 | 52.83906 | — | — | — | — | — | — | 37651 | 5 | — |
| C03_24 | 214.83556 | 52.87748 | — | — | — | — | — | — | 32502 | 6 | — |
| C03_25 | 214.76480 | 52.82764 | — | — | — | — | — | — | 32881 | 6 | — |
| C03_26 | 214.83068 | 52.88777 | — | — | 1748 | 8.77 | — | — | — | — | 2 |
| C03_27 | 214.79396 | 52.84158 | — | — | — | — | EGSY-9105550297 | 8.11 | — | — | — |
| C04_01 | 214.74666 | 52.74776 | — | — | — | — | — | — | 17063 | 5 | — |
| C04_02 | 214.79050 | 52.78157 | — | — | — | — | — | — | 17722 | 5 | — |
| C04_03 | 214.80567 | 52.79693 | — | — | — | — | — | — | 18783 | 5 | — |
| C04_04 | 214.72571 | 52.76288 | — | — | — | — | — | — | 24140 | 5 | — |
| C04_05 | 214.78409 | 52.80859 | — | — | — | — | — | — | 25149 | 5 | — |
| C04_06 | 214.71657 | 52.76452 | — | — | — | — | — | — | 26086 | 5 | — |
| C04_07 | 214.75336 | 52.74102 | — | — | — | — | — | — | 14598 | 6 | — |
| C04_08 | 214.79315 | 52.77049 | — | — | — | — | — | — | 14850 | 6 | — |
| C04_09 | 214.78767 | 52.77317 | — | — | — | — | — | — | 16300 | 6 | — |
| C04_10 | 214.79033 | 52.77294 | — | — | — | — | EGSZ-9096846226 | 6.54 | — | — | — |
| C05_01 | 214.88608 | 52.87689 | P4P_01534 | 4.59 | — | — | — | — | 24123 | 5 | — |
| C05_02 | 214.96740 | 52.93296 | P9M_01025 | 8.71 | — | — | — | — | — | — | 4,5 |
| C05_03 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C05_04 | 214.92186 | 52.88563 | — | — | — | — | — | — | 20105 | 5 | — |
| C05_05 | 214.96585 | 52.93406 | — | — | — | — | — | — | 24219 | 7 | — |
| C05_06 | 214.98904 | 52.91969 | — | — | — | — | EGSZ-9573755109 | 6.69 | — | — | — |
| C05_07 | 214.94558 | 52.90025 | — | — | — | — | EGSZ-9469454009 | 6.92 | — | — | — |
| C05_08 | 214.94675 | 52.90056 | — | — | — | — | EGSZ-9472254020 | 7.24 | — | — | — |
| C05_09 | 214.97017 | 52.91647 | — | — | — | — | EGSZ-9528454593 | 6.46 | — | — | — |
| C06_01 | 214.86441 | 52.85366 | P4P_00545 | 5.67 | — | — | — | — | — | — | — |
| C06_02 | 214.86725 | 52.83674 | P4M_00603 | 6.06 | — | — | — | — | — | — | — |
| C06_03 | 214.87646 | 52.83942 | P4M_00618 | 6.05 | — | — | — | — | — | — | — |
| C06_04 | 214.87177 | 52.83317 | P4M_00792 | 6.26 | — | — | — | — | — | — | — |
| C06_05 | 214.88299 | 52.84042 | P4M_01027 | 7.82 | — | — | — | — | — | — | 4 |
| C06_06 | 214.82345 | 52.83028 | P4M_02782 | 5.24 | — | — | — | — | — | — | — |
| C06_07 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C06_08 | 214.90369 | 52.84492 | P10M_00670 | 5.80 | — | — | — | — | — | — | — |
| C06_09 | 214.85224 | 52.80917 | — | — | — | — | — | — | 13963 | 5 | — |
| C06_10 | 214.89508 | 52.84799 | — | — | — | — | — | — | 15866 | 5 | — |
| C06_11 | 214.84701 | 52.81407 | — | — | — | — | — | — | 15930 | 5 | — |
| C06_12 | 214.82490 | 52.83610 | — | — | — | — | — | — | 24754 | 5 | — |
| C06_13 | 214.85514 | 52.82081 | — | — | — | — | — | — | 16208 | 6 | — |
| C06_14 | 214.88813 | 52.85899 | — | — | 4012 | 8.89 | — | — | — | — | 2 |
| C06_15 | 214.80217 | 52.80589 | — | — | — | — | EGSZ-9125248212 | 6.54 | — | — | — |
| C06_16 | 214.80625 | 52.81275 | — | — | — | — | EGSZ-9135048459 | 6.77 | — | — | — |
| C06_17 | 214.85917 | 52.85364 | — | — | — | — | EGSZ-9262051131 | 6.39 | — | — | — |
| C07_01 | 215.09088 | 52.95152 | P8M_01358 | 5.50 | — | — | — | — | — | — | — |
| C07_02 | 215.07996 | 52.95677 | P8M_01449 | 4.75 | — | — | — | — | 10735 | 5 | — |
| C07_03 | 215.08602 | 52.95219 | P8P_11383 | 5.07 | — | — | — | — | — | — | — |
| C07_04 | 215.13529 | 52.99323 | — | — | — | — | — | — | 10203 | 5 | — |
| C07_05 | 215.14644 | 52.97027 | — | — | — | — | — | — | 3639 | 5 | — |
| C07_06 | 215.13511 | 52.96719 | — | — | — | — | — | — | 4678 | 5 | — |
| C07_07 | 215.14402 | 52.95935 | — | — | — | — | — | — | 1744 | 5 | — |
| C07_08 | 215.14620 | 52.95540 | — | — | — | — | — | — | 872 | 5 | — |
| C07_09 | 215.09061 | 52.95167 | — | — | — | — | — | — | 7923 | 5 | — |
| C07_10 | 215.10084 | 52.93848 | — | — | — | — | — | — | 3761 | 5 | — |
| C07_11 | 215.08727 | 52.94106 | — | — | — | — | — | — | 6407 | 5 | — |
| C07_12 | 215.10358 | 52.93191 | — | — | — | — | — | — | 1984 | 5 | — |
| C07_13 | 215.07971 | 52.93832 | — | — | — | — | — | — | 6795 | 5 | — |
| C07_14 | 215.08314 | 52.91996 | — | — | — | — | — | — | 2462 | 5 | — |
| C07_15 | 215.12673 | 52.98391 | — | — | — | — | — | — | 9529 | 6 | — |
| C07_16 | 215.07467 | 52.94472 | — | — | — | — | EGSZ-0179256410 | 6.69 | — | — | — |
| C08_01 | 215.03540 | 52.89067 | P9M_01019 | 8.68 | — | — | — | — | — | — | 4,5 |
| C08_02 | 215.03972 | 52.90160 | P9M_01038 | 7.19 | — | — | — | — | — | — | 4 |
| C08_03 | 215.03055 | 52.90259 | P9M_01324 | 5.01 | — | — | — | — | — | — | — |
| C08_04 | 215.03318 | 52.89002 | — | — | — | — | — | — | 3610 | 5 | — |
| C08_05 | 215.04419 | 52.89879 | — | — | — | — | — | — | 3733 | 5 | — |
| C08_06 | 215.00895 | 52.87673 | — | — | — | — | — | — | 4326 | 5 | — |
| C08_07 | 215.06373 | 52.91751 | — | — | — | — | — | — | 4736 | 5 | — |
| C08_08 | 214.97835 | 52.85675 | — | — | — | — | — | — | 4743 | 5 | — |
| C08_09 | 215.03308 | 52.89651 | — | — | — | — | — | — | 5021 | 5 | — |
| C08_10 | 214.98738 | 52.86896 | — | — | — | — | — | — | 6056 | 5 | — |
| C08_11 | 215.04264 | 52.91202 | — | — | — | — | — | — | 6813 | 5 | — |
| C08_12 | 215.01083 | 52.90101 | — | — | — | — | — | — | 9263 | 5 | — |
| C08_13 | 214.97813 | 52.87957 | — | — | — | — | — | — | 9635 | 5 | — |
| C08_14 | 215.00995 | 52.91071 | — | — | — | — | — | — | 11586 | 5 | — |
| C08_15 | 215.03564 | 52.89226 | — | — | — | — | EGSZ-0085553321 | 7.00 | 3320 | 6 | — |
| C08_16 | 215.04600 | 52.89818 | — | — | — | — | — | — | 3441 | 6 | — |
| C08_17 | 215.00943 | 52.87537 | — | — | — | — | — | — | 3989 | 6 | — |
| C08_18 | 215.00769 | 52.87418 | — | — | — | — | — | — | 4076 | 6 | — |
| C08_19 | 214.98723 | 52.87465 | — | — | — | — | — | — | 7282 | 6 | — |
| C08_20 | 214.98694 | 52.87462 | — | — | — | — | — | — | 7371 | 6 | — |
| C08_21 | 214.98797 | 52.87950 | — | — | — | — | EGSZ-9571152461 | 6.46 | 8177 | 6 | — |
| C08_22 | 215.03394 | 52.91384 | — | — | — | — | — | — | 8534 | 6 | — |
| C08_23 | 215.03210 | 52.91902 | — | — | — | — | — | — | 9935 | 6 | — |
| C08_24 | 214.95842 | 52.87517 | — | — | — | — | EGSZ-9500252305 | 6.54 | 11721 | 6 | — |
| C08_25 | 215.03721 | 52.90675 | — | — | — | — | EGSZ-0089354243 | 7.00 | — | — | — |
| C08_26 | 215.03704 | 52.89194 | — | — | — | — | EGSZ-0088953310 | 7.00 | — | — | — |
| C08_27 | 215.00600 | 52.90536 | — | — | — | — | EGSZ-0014454193 | 6.69 | — | — | — |
| C08_28 | 214.97996 | 52.86114 | — | — | — | — | EGSZ-9551951401 | 7.08 | — | — | — |
| C08_29 | 214.97192 | 52.86922 | — | — | — | — | EGSZ-9532652092 | 6.39 | — | — | — |
| C08_30 | 214.99875 | 52.85542 | — | — | — | — | EGSY-9597051195 | 8.38 | — | — | — |
| C08_31 | 214.98958 | 52.86658 | — | — | — | — | EGSY-9575051597 | 8.11 | — | — | — |
| C09_01 | 214.95990 | 52.83118 | P10M_01207 | 4.90 | — | — | — | — | 2131 | 5 | — |
| C09_02 | 214.94755 | 52.83709 | P10M_01289 | 4.88 | — | — | — | — | — | — | — |
| C09_03 | 214.95516 | 52.84290 | P10M_01294 | 5.00 | — | — | — | — | 5342 | 5 | — |
| C09_04 | 214.94379 | 52.85006 | P10M_01374 | 5.00 | — | — | — | — | 8518 | 5 | — |
| C09_05 | 214.92738 | 52.81349 | — | — | — | — | — | — | 3324 | 5 | — |
| C09_06 | 214.95796 | 52.83598 | — | — | — | — | — | — | 3426 | 5 | — |
| C09_07 | 214.93801 | 52.83249 | — | — | — | — | — | — | 5763 | 5 | — |
| C09_08 | 214.94369 | 52.85014 | — | — | — | — | — | — | 8598 | 5 | — |
| C10_01 | 214.83230 | 52.74412 | — | — | — | — | — | — | 2973 | 5 | — |
| C10_02 | 214.81900 | 52.75974 | — | — | — | — | — | — | 8275 | 5 | — |
| C10_03 | 214.80973 | 52.75440 | — | — | — | — | — | — | 8514 | 5 | — |
| C10_04 | 214.83919 | 52.77684 | — | — | — | — | — | — | 8846 | 5 | — |
| C10_05 | 214.84428 | 52.78964 | — | — | — | — | — | — | 10641 | 5 | — |
| C10_06 | 214.83044 | 52.78370 | — | — | — | — | — | — | 11720 | 5 | — |
| C10_07 | 214.83851 | 52.79330 | — | — | — | — | — | — | 12509 | 5 | — |
| C10_08 | 214.80272 | 52.76821 | — | — | — | — | — | — | 12664 | 5 | — |
| C10_09 | 214.85085 | 52.77673 | — | — | — | — | EGSZ-9242146357 | 6.84 | 7028 | 7 | — |
| C10_10 | 214.83100 | 52.74914 | — | — | — | — | EGSZ-9194444569 | 6.77 | — | — | — |
| . | . | . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Bouwens et al. (2015) . | Shibuya, Ouchi, and Harikane (2015) . | . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | |||||||||||
| ID . | RA (○) . | Dec (○) . | ID . | zspec . | ID . | zphoto . | ID . | zphoto . | ID . | zphoto . | Other references* . |
| C01_01 | 215.00522 | 52.99652 | P5P_00003 | 8.01 | 3908 | 9.04 | — | — | — | — | 2,4 |
| C01_02 | 215.01173 | 52.98822 | P5P_00007 | 8.87 | 6059 | 9.01 | — | — | — | — | 2,5 |
| C01_03 | 215.00117 | 53.01119 | P5P_00044 | 7.10 | — | — | — | — | — | — | 4 |
| C01_04 | 215.01562 | 53.01176 | P5P_00067 | 6.21 | — | — | — | — | — | — | — |
| C01_05 | 215.01090 | 53.01324 | P5P_01912 | 5.10 | — | — | — | — | — | — | — |
| C01_06 | 214.99828 | 52.99467 | P5P_01953 | 4.61 | — | — | — | — | — | — | — |
| C01_07 | 214.98878 | 52.99797 | P5P_03584 | 4.64 | — | — | — | — | — | — | — |
| C01_08 | 214.96063 | 52.94051 | — | — | — | — | — | — | 26647 | 5 | — |
| C01_09 | 215.01605 | 52.98248 | — | — | — | — | — | — | 27229 | 5 | — |
| C01_10 | 215.02613 | 52.99457 | — | — | — | — | — | — | 28414 | 5 | — |
| C01_11 | 215.01527 | 52.98672 | — | — | — | — | — | — | 28427 | 5 | — |
| C01_12 | 215.01114 | 52.98909 | — | — | — | — | — | — | 29656 | 5 | — |
| C01_13 | 214.97204 | 52.96254 | — | — | — | — | — | — | 29855 | 5 | — |
| C01_14 | 214.97481 | 52.96650 | — | — | — | — | — | — | 30425 | 5 | — |
| C01_15 | 214.99405 | 52.98085 | — | — | — | — | — | — | 30550 | 5 | — |
| C01_16 | 214.94419 | 52.96760 | — | — | — | — | — | — | 35779 | 5 | — |
| C01_17 | 214.93204 | 52.95899 | — | — | — | — | — | — | 35809 | 5 | — |
| C01_18 | 214.92475 | 52.95584 | — | — | — | — | — | — | 36262 | 5 | — |
| C01_19 | 215.00974 | 52.98144 | — | — | — | — | — | — | 28026 | 6 | — |
| C01_20 | 215.01415 | 53.01115 | — | — | — | — | — | — | 34318 | 6 | — |
| C01_21 | 214.95194 | 52.97174 | — | — | 1875 | 8.92 | — | — | — | — | — |
| C01_22 | 214.99440 | 52.98938 | — | — | 3858 | 8.95 | — | — | — | — | 2,3,5 |
| C01_23 | 215.00537 | 52.99670 | — | — | 3910 | 9.55 | — | — | — | — | 2,3 |
| C01_24 | 214.95008 | 52.94927 | — | — | 5534 | 8.62 | — | — | — | — | — |
| C01_25 | 214.96672 | 52.96829 | — | — | 4143 | 8.98 | — | — | — | — | — |
| C01_26 | 214.99475 | 53.00781 | — | — | — | — | EGSY-9587400281 | 7.58 | — | — | — |
| C02_01 | 214.87255 | 52.87595 | P4M_00323 | 5.67 | — | — | — | — | — | — | — |
| C02_02 | 214.88802 | 52.88826 | P4M_01465 | 5.27 | — | — | — | — | — | — | — |
| C02_03 | 214.85964 | 52.88814 | P4P_02000 | 4.81 | — | — | — | — | 31247 | 5 | — |
| C02_04 | 214.95381 | 52.93373 | — | — | — | — | — | — | 26115 | 5 | — |
| C02_05 | 214.94847 | 52.93859 | — | — | — | — | — | — | 28205 | 5 | — |
| C02_06 | 214.88124 | 52.89609 | — | — | — | — | — | — | 29440 | 5 | — |
| C02_07 | 214.85954 | 52.88801 | — | — | — | — | — | — | 31167 | 5 | — |
| C02_08 | 214.91837 | 52.93187 | — | — | — | — | — | — | 31703 | 5 | — |
| C02_09 | 214.91887 | 52.93921 | — | — | — | — | — | — | 33230 | 5 | — |
| C02_10 | 214.87215 | 52.90633 | — | — | — | — | — | — | 33438 | 5 | — |
| C02_11 | 214.91523 | 52.94503 | — | — | — | — | — | — | 35205 | 5 | — |
| C02_12 | 214.92457 | 52.91873 | — | — | — | — | EGSZ-9419055074 | 6.69 | 27521 | 6 | — |
| C02_13 | 214.93474 | 52.94714 | — | — | — | — | — | — | 32583 | 6 | — |
| C02_14 | 214.84477 | 52.89210 | — | — | 2402 | 8.71 | — | — | — | — | — |
| C02_15 | 214.87614 | 52.88083 | — | — | 7534 | 8.95 | — | — | — | — | — |
| C02_16 | 214.86160 | 52.90460 | — | — | 2324 | 9.58 | — | — | — | — | 1,5 |
| C02_17 | 214.90224 | 52.93937 | — | — | 1298 | 8.53 | — | — | — | — | — |
| C02_18 | 214.84617 | 52.89400 | — | — | 2274 | 8.62 | — | — | — | — | — |
| C02_19 | 214.90763 | 52.94461 | — | — | 1075 | 8.38 | — | — | — | — | — |
| C02_20 | 214.89087 | 52.89331 | — | — | — | — | EGSZ-9338153359 | 6.92 | — | — | — |
| C02_21 | 214.88100 | 52.89125 | — | — | — | — | EGSZ-9314453285 | 6.92 | — | — | — |
| C02_22 | 214.89608 | 52.92519 | — | — | — | — | EGSZ-9350655307 | 6.77 | — | — | — |
| C02_23 | 214.86304 | 52.88947 | — | — | — | — | EGSZ-9271353221 | 6.77 | — | — | — |
| C03_01 | 214.80652 | 52.87874 | P4M_00355 | 6.10 | — | — | — | — | — | — | — |
| C03_02 | 214.81273 | 52.88145 | P4P_00362 | 6.05 | — | — | — | — | — | — | — |
| C03_03 | 214.81970 | 52.87967 | P4M_00381 | 5.51 | — | — | — | — | — | — | — |
| C03_04 | 214.83622 | 52.88258 | P4M_00397 | 6.00 | — | — | — | — | — | — | — |
| C03_05 | 214.82900 | 52.87561 | P4M_00403 | 5.76 | — | — | — | — | — | — | — |
| C03_06 | 214.83935 | 52.88247 | P4M_00407 | 7.03 | — | — | — | — | — | — | 4 |
| C03_07 | 214.82538 | 52.86297 | P4P_00439 | 7.18 | — | — | — | — | — | — | — |
| C03_08 | 214.81304 | 52.83415 | P4P_00498 | 7.18 | — | — | — | — | — | — | 4 |
| C03_09 | 214.81168 | 52.83714 | P4P_02116 | 5.28 | — | — | — | — | — | — | — |
| C03_10 | 214.86453 | 52.87087 | P4P_02362 | 5.32 | — | — | — | — | — | — | — |
| C03_11 | 214.79396 | 52.82025 | — | — | — | — | — | — | 26215 | 5 | — |
| C03_12 | 214.81201 | 52.83682 | — | — | — | — | — | — | 27005 | 5 | — |
| C03_13 | 214.80701 | 52.83825 | — | — | — | — | — | — | 28123 | 5 | — |
| C03_14 | 214.80686 | 52.83829 | — | — | — | — | — | — | 28217 | 5 | — |
| C03_15 | 214.82586 | 52.85515 | — | — | — | — | — | — | 29028 | 5 | — |
| C03_16 | 214.82518 | 52.85907 | — | — | — | — | — | — | 30133 | 5 | — |
| C03_17 | 214.79000 | 52.83466 | — | — | — | — | — | — | 30300 | 5 | — |
| C03_18 | 214.77238 | 52.82342 | — | — | — | — | — | — | 30572 | 5 | — |
| C03_19 | 214.79449 | 52.83954 | — | — | — | — | — | — | 30668 | 5 | — |
| C03_20 | 214.76766 | 52.83329 | — | — | — | — | — | — | 33751 | 5 | — |
| C03_21 | 214.76385 | 52.83544 | — | — | — | — | — | — | 34851 | 5 | — |
| C03_22 | 214.83347 | 52.88902 | — | — | — | — | — | — | 35846 | 5 | — |
| C03_23 | 214.74571 | 52.83906 | — | — | — | — | — | — | 37651 | 5 | — |
| C03_24 | 214.83556 | 52.87748 | — | — | — | — | — | — | 32502 | 6 | — |
| C03_25 | 214.76480 | 52.82764 | — | — | — | — | — | — | 32881 | 6 | — |
| C03_26 | 214.83068 | 52.88777 | — | — | 1748 | 8.77 | — | — | — | — | 2 |
| C03_27 | 214.79396 | 52.84158 | — | — | — | — | EGSY-9105550297 | 8.11 | — | — | — |
| C04_01 | 214.74666 | 52.74776 | — | — | — | — | — | — | 17063 | 5 | — |
| C04_02 | 214.79050 | 52.78157 | — | — | — | — | — | — | 17722 | 5 | — |
| C04_03 | 214.80567 | 52.79693 | — | — | — | — | — | — | 18783 | 5 | — |
| C04_04 | 214.72571 | 52.76288 | — | — | — | — | — | — | 24140 | 5 | — |
| C04_05 | 214.78409 | 52.80859 | — | — | — | — | — | — | 25149 | 5 | — |
| C04_06 | 214.71657 | 52.76452 | — | — | — | — | — | — | 26086 | 5 | — |
| C04_07 | 214.75336 | 52.74102 | — | — | — | — | — | — | 14598 | 6 | — |
| C04_08 | 214.79315 | 52.77049 | — | — | — | — | — | — | 14850 | 6 | — |
| C04_09 | 214.78767 | 52.77317 | — | — | — | — | — | — | 16300 | 6 | — |
| C04_10 | 214.79033 | 52.77294 | — | — | — | — | EGSZ-9096846226 | 6.54 | — | — | — |
| C05_01 | 214.88608 | 52.87689 | P4P_01534 | 4.59 | — | — | — | — | 24123 | 5 | — |
| C05_02 | 214.96740 | 52.93296 | P9M_01025 | 8.71 | — | — | — | — | — | — | 4,5 |
| C05_03 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C05_04 | 214.92186 | 52.88563 | — | — | — | — | — | — | 20105 | 5 | — |
| C05_05 | 214.96585 | 52.93406 | — | — | — | — | — | — | 24219 | 7 | — |
| C05_06 | 214.98904 | 52.91969 | — | — | — | — | EGSZ-9573755109 | 6.69 | — | — | — |
| C05_07 | 214.94558 | 52.90025 | — | — | — | — | EGSZ-9469454009 | 6.92 | — | — | — |
| C05_08 | 214.94675 | 52.90056 | — | — | — | — | EGSZ-9472254020 | 7.24 | — | — | — |
| C05_09 | 214.97017 | 52.91647 | — | — | — | — | EGSZ-9528454593 | 6.46 | — | — | — |
| C06_01 | 214.86441 | 52.85366 | P4P_00545 | 5.67 | — | — | — | — | — | — | — |
| C06_02 | 214.86725 | 52.83674 | P4M_00603 | 6.06 | — | — | — | — | — | — | — |
| C06_03 | 214.87646 | 52.83942 | P4M_00618 | 6.05 | — | — | — | — | — | — | — |
| C06_04 | 214.87177 | 52.83317 | P4M_00792 | 6.26 | — | — | — | — | — | — | — |
| C06_05 | 214.88299 | 52.84042 | P4M_01027 | 7.82 | — | — | — | — | — | — | 4 |
| C06_06 | 214.82345 | 52.83028 | P4M_02782 | 5.24 | — | — | — | — | — | — | — |
| C06_07 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C06_08 | 214.90369 | 52.84492 | P10M_00670 | 5.80 | — | — | — | — | — | — | — |
| C06_09 | 214.85224 | 52.80917 | — | — | — | — | — | — | 13963 | 5 | — |
| C06_10 | 214.89508 | 52.84799 | — | — | — | — | — | — | 15866 | 5 | — |
| C06_11 | 214.84701 | 52.81407 | — | — | — | — | — | — | 15930 | 5 | — |
| C06_12 | 214.82490 | 52.83610 | — | — | — | — | — | — | 24754 | 5 | — |
| C06_13 | 214.85514 | 52.82081 | — | — | — | — | — | — | 16208 | 6 | — |
| C06_14 | 214.88813 | 52.85899 | — | — | 4012 | 8.89 | — | — | — | — | 2 |
| C06_15 | 214.80217 | 52.80589 | — | — | — | — | EGSZ-9125248212 | 6.54 | — | — | — |
| C06_16 | 214.80625 | 52.81275 | — | — | — | — | EGSZ-9135048459 | 6.77 | — | — | — |
| C06_17 | 214.85917 | 52.85364 | — | — | — | — | EGSZ-9262051131 | 6.39 | — | — | — |
| C07_01 | 215.09088 | 52.95152 | P8M_01358 | 5.50 | — | — | — | — | — | — | — |
| C07_02 | 215.07996 | 52.95677 | P8M_01449 | 4.75 | — | — | — | — | 10735 | 5 | — |
| C07_03 | 215.08602 | 52.95219 | P8P_11383 | 5.07 | — | — | — | — | — | — | — |
| C07_04 | 215.13529 | 52.99323 | — | — | — | — | — | — | 10203 | 5 | — |
| C07_05 | 215.14644 | 52.97027 | — | — | — | — | — | — | 3639 | 5 | — |
| C07_06 | 215.13511 | 52.96719 | — | — | — | — | — | — | 4678 | 5 | — |
| C07_07 | 215.14402 | 52.95935 | — | — | — | — | — | — | 1744 | 5 | — |
| C07_08 | 215.14620 | 52.95540 | — | — | — | — | — | — | 872 | 5 | — |
| C07_09 | 215.09061 | 52.95167 | — | — | — | — | — | — | 7923 | 5 | — |
| C07_10 | 215.10084 | 52.93848 | — | — | — | — | — | — | 3761 | 5 | — |
| C07_11 | 215.08727 | 52.94106 | — | — | — | — | — | — | 6407 | 5 | — |
| C07_12 | 215.10358 | 52.93191 | — | — | — | — | — | — | 1984 | 5 | — |
| C07_13 | 215.07971 | 52.93832 | — | — | — | — | — | — | 6795 | 5 | — |
| C07_14 | 215.08314 | 52.91996 | — | — | — | — | — | — | 2462 | 5 | — |
| C07_15 | 215.12673 | 52.98391 | — | — | — | — | — | — | 9529 | 6 | — |
| C07_16 | 215.07467 | 52.94472 | — | — | — | — | EGSZ-0179256410 | 6.69 | — | — | — |
| C08_01 | 215.03540 | 52.89067 | P9M_01019 | 8.68 | — | — | — | — | — | — | 4,5 |
| C08_02 | 215.03972 | 52.90160 | P9M_01038 | 7.19 | — | — | — | — | — | — | 4 |
| C08_03 | 215.03055 | 52.90259 | P9M_01324 | 5.01 | — | — | — | — | — | — | — |
| C08_04 | 215.03318 | 52.89002 | — | — | — | — | — | — | 3610 | 5 | — |
| C08_05 | 215.04419 | 52.89879 | — | — | — | — | — | — | 3733 | 5 | — |
| C08_06 | 215.00895 | 52.87673 | — | — | — | — | — | — | 4326 | 5 | — |
| C08_07 | 215.06373 | 52.91751 | — | — | — | — | — | — | 4736 | 5 | — |
| C08_08 | 214.97835 | 52.85675 | — | — | — | — | — | — | 4743 | 5 | — |
| C08_09 | 215.03308 | 52.89651 | — | — | — | — | — | — | 5021 | 5 | — |
| C08_10 | 214.98738 | 52.86896 | — | — | — | — | — | — | 6056 | 5 | — |
| C08_11 | 215.04264 | 52.91202 | — | — | — | — | — | — | 6813 | 5 | — |
| C08_12 | 215.01083 | 52.90101 | — | — | — | — | — | — | 9263 | 5 | — |
| C08_13 | 214.97813 | 52.87957 | — | — | — | — | — | — | 9635 | 5 | — |
| C08_14 | 215.00995 | 52.91071 | — | — | — | — | — | — | 11586 | 5 | — |
| C08_15 | 215.03564 | 52.89226 | — | — | — | — | EGSZ-0085553321 | 7.00 | 3320 | 6 | — |
| C08_16 | 215.04600 | 52.89818 | — | — | — | — | — | — | 3441 | 6 | — |
| C08_17 | 215.00943 | 52.87537 | — | — | — | — | — | — | 3989 | 6 | — |
| C08_18 | 215.00769 | 52.87418 | — | — | — | — | — | — | 4076 | 6 | — |
| C08_19 | 214.98723 | 52.87465 | — | — | — | — | — | — | 7282 | 6 | — |
| C08_20 | 214.98694 | 52.87462 | — | — | — | — | — | — | 7371 | 6 | — |
| C08_21 | 214.98797 | 52.87950 | — | — | — | — | EGSZ-9571152461 | 6.46 | 8177 | 6 | — |
| C08_22 | 215.03394 | 52.91384 | — | — | — | — | — | — | 8534 | 6 | — |
| C08_23 | 215.03210 | 52.91902 | — | — | — | — | — | — | 9935 | 6 | — |
| C08_24 | 214.95842 | 52.87517 | — | — | — | — | EGSZ-9500252305 | 6.54 | 11721 | 6 | — |
| C08_25 | 215.03721 | 52.90675 | — | — | — | — | EGSZ-0089354243 | 7.00 | — | — | — |
| C08_26 | 215.03704 | 52.89194 | — | — | — | — | EGSZ-0088953310 | 7.00 | — | — | — |
| C08_27 | 215.00600 | 52.90536 | — | — | — | — | EGSZ-0014454193 | 6.69 | — | — | — |
| C08_28 | 214.97996 | 52.86114 | — | — | — | — | EGSZ-9551951401 | 7.08 | — | — | — |
| C08_29 | 214.97192 | 52.86922 | — | — | — | — | EGSZ-9532652092 | 6.39 | — | — | — |
| C08_30 | 214.99875 | 52.85542 | — | — | — | — | EGSY-9597051195 | 8.38 | — | — | — |
| C08_31 | 214.98958 | 52.86658 | — | — | — | — | EGSY-9575051597 | 8.11 | — | — | — |
| C09_01 | 214.95990 | 52.83118 | P10M_01207 | 4.90 | — | — | — | — | 2131 | 5 | — |
| C09_02 | 214.94755 | 52.83709 | P10M_01289 | 4.88 | — | — | — | — | — | — | — |
| C09_03 | 214.95516 | 52.84290 | P10M_01294 | 5.00 | — | — | — | — | 5342 | 5 | — |
| C09_04 | 214.94379 | 52.85006 | P10M_01374 | 5.00 | — | — | — | — | 8518 | 5 | — |
| C09_05 | 214.92738 | 52.81349 | — | — | — | — | — | — | 3324 | 5 | — |
| C09_06 | 214.95796 | 52.83598 | — | — | — | — | — | — | 3426 | 5 | — |
| C09_07 | 214.93801 | 52.83249 | — | — | — | — | — | — | 5763 | 5 | — |
| C09_08 | 214.94369 | 52.85014 | — | — | — | — | — | — | 8598 | 5 | — |
| C10_01 | 214.83230 | 52.74412 | — | — | — | — | — | — | 2973 | 5 | — |
| C10_02 | 214.81900 | 52.75974 | — | — | — | — | — | — | 8275 | 5 | — |
| C10_03 | 214.80973 | 52.75440 | — | — | — | — | — | — | 8514 | 5 | — |
| C10_04 | 214.83919 | 52.77684 | — | — | — | — | — | — | 8846 | 5 | — |
| C10_05 | 214.84428 | 52.78964 | — | — | — | — | — | — | 10641 | 5 | — |
| C10_06 | 214.83044 | 52.78370 | — | — | — | — | — | — | 11720 | 5 | — |
| C10_07 | 214.83851 | 52.79330 | — | — | — | — | — | — | 12509 | 5 | — |
| C10_08 | 214.80272 | 52.76821 | — | — | — | — | — | — | 12664 | 5 | — |
| C10_09 | 214.85085 | 52.77673 | — | — | — | — | EGSZ-9242146357 | 6.84 | 7028 | 7 | — |
| C10_10 | 214.83100 | 52.74914 | — | — | — | — | EGSZ-9194444569 | 6.77 | — | — | — |
| . | . | . | Nakajima et al. (2023) . | Finkelstein et al. (2023) . | Bouwens et al. (2015) . | Shibuya, Ouchi, and Harikane (2015) . | . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | |||||||||||
| ID . | RA (○) . | Dec (○) . | ID . | zspec . | ID . | zphoto . | ID . | zphoto . | ID . | zphoto . | Other references* . |
| C01_01 | 215.00522 | 52.99652 | P5P_00003 | 8.01 | 3908 | 9.04 | — | — | — | — | 2,4 |
| C01_02 | 215.01173 | 52.98822 | P5P_00007 | 8.87 | 6059 | 9.01 | — | — | — | — | 2,5 |
| C01_03 | 215.00117 | 53.01119 | P5P_00044 | 7.10 | — | — | — | — | — | — | 4 |
| C01_04 | 215.01562 | 53.01176 | P5P_00067 | 6.21 | — | — | — | — | — | — | — |
| C01_05 | 215.01090 | 53.01324 | P5P_01912 | 5.10 | — | — | — | — | — | — | — |
| C01_06 | 214.99828 | 52.99467 | P5P_01953 | 4.61 | — | — | — | — | — | — | — |
| C01_07 | 214.98878 | 52.99797 | P5P_03584 | 4.64 | — | — | — | — | — | — | — |
| C01_08 | 214.96063 | 52.94051 | — | — | — | — | — | — | 26647 | 5 | — |
| C01_09 | 215.01605 | 52.98248 | — | — | — | — | — | — | 27229 | 5 | — |
| C01_10 | 215.02613 | 52.99457 | — | — | — | — | — | — | 28414 | 5 | — |
| C01_11 | 215.01527 | 52.98672 | — | — | — | — | — | — | 28427 | 5 | — |
| C01_12 | 215.01114 | 52.98909 | — | — | — | — | — | — | 29656 | 5 | — |
| C01_13 | 214.97204 | 52.96254 | — | — | — | — | — | — | 29855 | 5 | — |
| C01_14 | 214.97481 | 52.96650 | — | — | — | — | — | — | 30425 | 5 | — |
| C01_15 | 214.99405 | 52.98085 | — | — | — | — | — | — | 30550 | 5 | — |
| C01_16 | 214.94419 | 52.96760 | — | — | — | — | — | — | 35779 | 5 | — |
| C01_17 | 214.93204 | 52.95899 | — | — | — | — | — | — | 35809 | 5 | — |
| C01_18 | 214.92475 | 52.95584 | — | — | — | — | — | — | 36262 | 5 | — |
| C01_19 | 215.00974 | 52.98144 | — | — | — | — | — | — | 28026 | 6 | — |
| C01_20 | 215.01415 | 53.01115 | — | — | — | — | — | — | 34318 | 6 | — |
| C01_21 | 214.95194 | 52.97174 | — | — | 1875 | 8.92 | — | — | — | — | — |
| C01_22 | 214.99440 | 52.98938 | — | — | 3858 | 8.95 | — | — | — | — | 2,3,5 |
| C01_23 | 215.00537 | 52.99670 | — | — | 3910 | 9.55 | — | — | — | — | 2,3 |
| C01_24 | 214.95008 | 52.94927 | — | — | 5534 | 8.62 | — | — | — | — | — |
| C01_25 | 214.96672 | 52.96829 | — | — | 4143 | 8.98 | — | — | — | — | — |
| C01_26 | 214.99475 | 53.00781 | — | — | — | — | EGSY-9587400281 | 7.58 | — | — | — |
| C02_01 | 214.87255 | 52.87595 | P4M_00323 | 5.67 | — | — | — | — | — | — | — |
| C02_02 | 214.88802 | 52.88826 | P4M_01465 | 5.27 | — | — | — | — | — | — | — |
| C02_03 | 214.85964 | 52.88814 | P4P_02000 | 4.81 | — | — | — | — | 31247 | 5 | — |
| C02_04 | 214.95381 | 52.93373 | — | — | — | — | — | — | 26115 | 5 | — |
| C02_05 | 214.94847 | 52.93859 | — | — | — | — | — | — | 28205 | 5 | — |
| C02_06 | 214.88124 | 52.89609 | — | — | — | — | — | — | 29440 | 5 | — |
| C02_07 | 214.85954 | 52.88801 | — | — | — | — | — | — | 31167 | 5 | — |
| C02_08 | 214.91837 | 52.93187 | — | — | — | — | — | — | 31703 | 5 | — |
| C02_09 | 214.91887 | 52.93921 | — | — | — | — | — | — | 33230 | 5 | — |
| C02_10 | 214.87215 | 52.90633 | — | — | — | — | — | — | 33438 | 5 | — |
| C02_11 | 214.91523 | 52.94503 | — | — | — | — | — | — | 35205 | 5 | — |
| C02_12 | 214.92457 | 52.91873 | — | — | — | — | EGSZ-9419055074 | 6.69 | 27521 | 6 | — |
| C02_13 | 214.93474 | 52.94714 | — | — | — | — | — | — | 32583 | 6 | — |
| C02_14 | 214.84477 | 52.89210 | — | — | 2402 | 8.71 | — | — | — | — | — |
| C02_15 | 214.87614 | 52.88083 | — | — | 7534 | 8.95 | — | — | — | — | — |
| C02_16 | 214.86160 | 52.90460 | — | — | 2324 | 9.58 | — | — | — | — | 1,5 |
| C02_17 | 214.90224 | 52.93937 | — | — | 1298 | 8.53 | — | — | — | — | — |
| C02_18 | 214.84617 | 52.89400 | — | — | 2274 | 8.62 | — | — | — | — | — |
| C02_19 | 214.90763 | 52.94461 | — | — | 1075 | 8.38 | — | — | — | — | — |
| C02_20 | 214.89087 | 52.89331 | — | — | — | — | EGSZ-9338153359 | 6.92 | — | — | — |
| C02_21 | 214.88100 | 52.89125 | — | — | — | — | EGSZ-9314453285 | 6.92 | — | — | — |
| C02_22 | 214.89608 | 52.92519 | — | — | — | — | EGSZ-9350655307 | 6.77 | — | — | — |
| C02_23 | 214.86304 | 52.88947 | — | — | — | — | EGSZ-9271353221 | 6.77 | — | — | — |
| C03_01 | 214.80652 | 52.87874 | P4M_00355 | 6.10 | — | — | — | — | — | — | — |
| C03_02 | 214.81273 | 52.88145 | P4P_00362 | 6.05 | — | — | — | — | — | — | — |
| C03_03 | 214.81970 | 52.87967 | P4M_00381 | 5.51 | — | — | — | — | — | — | — |
| C03_04 | 214.83622 | 52.88258 | P4M_00397 | 6.00 | — | — | — | — | — | — | — |
| C03_05 | 214.82900 | 52.87561 | P4M_00403 | 5.76 | — | — | — | — | — | — | — |
| C03_06 | 214.83935 | 52.88247 | P4M_00407 | 7.03 | — | — | — | — | — | — | 4 |
| C03_07 | 214.82538 | 52.86297 | P4P_00439 | 7.18 | — | — | — | — | — | — | — |
| C03_08 | 214.81304 | 52.83415 | P4P_00498 | 7.18 | — | — | — | — | — | — | 4 |
| C03_09 | 214.81168 | 52.83714 | P4P_02116 | 5.28 | — | — | — | — | — | — | — |
| C03_10 | 214.86453 | 52.87087 | P4P_02362 | 5.32 | — | — | — | — | — | — | — |
| C03_11 | 214.79396 | 52.82025 | — | — | — | — | — | — | 26215 | 5 | — |
| C03_12 | 214.81201 | 52.83682 | — | — | — | — | — | — | 27005 | 5 | — |
| C03_13 | 214.80701 | 52.83825 | — | — | — | — | — | — | 28123 | 5 | — |
| C03_14 | 214.80686 | 52.83829 | — | — | — | — | — | — | 28217 | 5 | — |
| C03_15 | 214.82586 | 52.85515 | — | — | — | — | — | — | 29028 | 5 | — |
| C03_16 | 214.82518 | 52.85907 | — | — | — | — | — | — | 30133 | 5 | — |
| C03_17 | 214.79000 | 52.83466 | — | — | — | — | — | — | 30300 | 5 | — |
| C03_18 | 214.77238 | 52.82342 | — | — | — | — | — | — | 30572 | 5 | — |
| C03_19 | 214.79449 | 52.83954 | — | — | — | — | — | — | 30668 | 5 | — |
| C03_20 | 214.76766 | 52.83329 | — | — | — | — | — | — | 33751 | 5 | — |
| C03_21 | 214.76385 | 52.83544 | — | — | — | — | — | — | 34851 | 5 | — |
| C03_22 | 214.83347 | 52.88902 | — | — | — | — | — | — | 35846 | 5 | — |
| C03_23 | 214.74571 | 52.83906 | — | — | — | — | — | — | 37651 | 5 | — |
| C03_24 | 214.83556 | 52.87748 | — | — | — | — | — | — | 32502 | 6 | — |
| C03_25 | 214.76480 | 52.82764 | — | — | — | — | — | — | 32881 | 6 | — |
| C03_26 | 214.83068 | 52.88777 | — | — | 1748 | 8.77 | — | — | — | — | 2 |
| C03_27 | 214.79396 | 52.84158 | — | — | — | — | EGSY-9105550297 | 8.11 | — | — | — |
| C04_01 | 214.74666 | 52.74776 | — | — | — | — | — | — | 17063 | 5 | — |
| C04_02 | 214.79050 | 52.78157 | — | — | — | — | — | — | 17722 | 5 | — |
| C04_03 | 214.80567 | 52.79693 | — | — | — | — | — | — | 18783 | 5 | — |
| C04_04 | 214.72571 | 52.76288 | — | — | — | — | — | — | 24140 | 5 | — |
| C04_05 | 214.78409 | 52.80859 | — | — | — | — | — | — | 25149 | 5 | — |
| C04_06 | 214.71657 | 52.76452 | — | — | — | — | — | — | 26086 | 5 | — |
| C04_07 | 214.75336 | 52.74102 | — | — | — | — | — | — | 14598 | 6 | — |
| C04_08 | 214.79315 | 52.77049 | — | — | — | — | — | — | 14850 | 6 | — |
| C04_09 | 214.78767 | 52.77317 | — | — | — | — | — | — | 16300 | 6 | — |
| C04_10 | 214.79033 | 52.77294 | — | — | — | — | EGSZ-9096846226 | 6.54 | — | — | — |
| C05_01 | 214.88608 | 52.87689 | P4P_01534 | 4.59 | — | — | — | — | 24123 | 5 | — |
| C05_02 | 214.96740 | 52.93296 | P9M_01025 | 8.71 | — | — | — | — | — | — | 4,5 |
| C05_03 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C05_04 | 214.92186 | 52.88563 | — | — | — | — | — | — | 20105 | 5 | — |
| C05_05 | 214.96585 | 52.93406 | — | — | — | — | — | — | 24219 | 7 | — |
| C05_06 | 214.98904 | 52.91969 | — | — | — | — | EGSZ-9573755109 | 6.69 | — | — | — |
| C05_07 | 214.94558 | 52.90025 | — | — | — | — | EGSZ-9469454009 | 6.92 | — | — | — |
| C05_08 | 214.94675 | 52.90056 | — | — | — | — | EGSZ-9472254020 | 7.24 | — | — | — |
| C05_09 | 214.97017 | 52.91647 | — | — | — | — | EGSZ-9528454593 | 6.46 | — | — | — |
| C06_01 | 214.86441 | 52.85366 | P4P_00545 | 5.67 | — | — | — | — | — | — | — |
| C06_02 | 214.86725 | 52.83674 | P4M_00603 | 6.06 | — | — | — | — | — | — | — |
| C06_03 | 214.87646 | 52.83942 | P4M_00618 | 6.05 | — | — | — | — | — | — | — |
| C06_04 | 214.87177 | 52.83317 | P4M_00792 | 6.26 | — | — | — | — | — | — | — |
| C06_05 | 214.88299 | 52.84042 | P4M_01027 | 7.82 | — | — | — | — | — | — | 4 |
| C06_06 | 214.82345 | 52.83028 | P4M_02782 | 5.24 | — | — | — | — | — | — | — |
| C06_07 | 214.87854 | 52.87414 | P10M_00515 | 5.66 | — | — | — | — | — | — | — |
| C06_08 | 214.90369 | 52.84492 | P10M_00670 | 5.80 | — | — | — | — | — | — | — |
| C06_09 | 214.85224 | 52.80917 | — | — | — | — | — | — | 13963 | 5 | — |
| C06_10 | 214.89508 | 52.84799 | — | — | — | — | — | — | 15866 | 5 | — |
| C06_11 | 214.84701 | 52.81407 | — | — | — | — | — | — | 15930 | 5 | — |
| C06_12 | 214.82490 | 52.83610 | — | — | — | — | — | — | 24754 | 5 | — |
| C06_13 | 214.85514 | 52.82081 | — | — | — | — | — | — | 16208 | 6 | — |
| C06_14 | 214.88813 | 52.85899 | — | — | 4012 | 8.89 | — | — | — | — | 2 |
| C06_15 | 214.80217 | 52.80589 | — | — | — | — | EGSZ-9125248212 | 6.54 | — | — | — |
| C06_16 | 214.80625 | 52.81275 | — | — | — | — | EGSZ-9135048459 | 6.77 | — | — | — |
| C06_17 | 214.85917 | 52.85364 | — | — | — | — | EGSZ-9262051131 | 6.39 | — | — | — |
| C07_01 | 215.09088 | 52.95152 | P8M_01358 | 5.50 | — | — | — | — | — | — | — |
| C07_02 | 215.07996 | 52.95677 | P8M_01449 | 4.75 | — | — | — | — | 10735 | 5 | — |
| C07_03 | 215.08602 | 52.95219 | P8P_11383 | 5.07 | — | — | — | — | — | — | — |
| C07_04 | 215.13529 | 52.99323 | — | — | — | — | — | — | 10203 | 5 | — |
| C07_05 | 215.14644 | 52.97027 | — | — | — | — | — | — | 3639 | 5 | — |
| C07_06 | 215.13511 | 52.96719 | — | — | — | — | — | — | 4678 | 5 | — |
| C07_07 | 215.14402 | 52.95935 | — | — | — | — | — | — | 1744 | 5 | — |
| C07_08 | 215.14620 | 52.95540 | — | — | — | — | — | — | 872 | 5 | — |
| C07_09 | 215.09061 | 52.95167 | — | — | — | — | — | — | 7923 | 5 | — |
| C07_10 | 215.10084 | 52.93848 | — | — | — | — | — | — | 3761 | 5 | — |
| C07_11 | 215.08727 | 52.94106 | — | — | — | — | — | — | 6407 | 5 | — |
| C07_12 | 215.10358 | 52.93191 | — | — | — | — | — | — | 1984 | 5 | — |
| C07_13 | 215.07971 | 52.93832 | — | — | — | — | — | — | 6795 | 5 | — |
| C07_14 | 215.08314 | 52.91996 | — | — | — | — | — | — | 2462 | 5 | — |
| C07_15 | 215.12673 | 52.98391 | — | — | — | — | — | — | 9529 | 6 | — |
| C07_16 | 215.07467 | 52.94472 | — | — | — | — | EGSZ-0179256410 | 6.69 | — | — | — |
| C08_01 | 215.03540 | 52.89067 | P9M_01019 | 8.68 | — | — | — | — | — | — | 4,5 |
| C08_02 | 215.03972 | 52.90160 | P9M_01038 | 7.19 | — | — | — | — | — | — | 4 |
| C08_03 | 215.03055 | 52.90259 | P9M_01324 | 5.01 | — | — | — | — | — | — | — |
| C08_04 | 215.03318 | 52.89002 | — | — | — | — | — | — | 3610 | 5 | — |
| C08_05 | 215.04419 | 52.89879 | — | — | — | — | — | — | 3733 | 5 | — |
| C08_06 | 215.00895 | 52.87673 | — | — | — | — | — | — | 4326 | 5 | — |
| C08_07 | 215.06373 | 52.91751 | — | — | — | — | — | — | 4736 | 5 | — |
| C08_08 | 214.97835 | 52.85675 | — | — | — | — | — | — | 4743 | 5 | — |
| C08_09 | 215.03308 | 52.89651 | — | — | — | — | — | — | 5021 | 5 | — |
| C08_10 | 214.98738 | 52.86896 | — | — | — | — | — | — | 6056 | 5 | — |
| C08_11 | 215.04264 | 52.91202 | — | — | — | — | — | — | 6813 | 5 | — |
| C08_12 | 215.01083 | 52.90101 | — | — | — | — | — | — | 9263 | 5 | — |
| C08_13 | 214.97813 | 52.87957 | — | — | — | — | — | — | 9635 | 5 | — |
| C08_14 | 215.00995 | 52.91071 | — | — | — | — | — | — | 11586 | 5 | — |
| C08_15 | 215.03564 | 52.89226 | — | — | — | — | EGSZ-0085553321 | 7.00 | 3320 | 6 | — |
| C08_16 | 215.04600 | 52.89818 | — | — | — | — | — | — | 3441 | 6 | — |
| C08_17 | 215.00943 | 52.87537 | — | — | — | — | — | — | 3989 | 6 | — |
| C08_18 | 215.00769 | 52.87418 | — | — | — | — | — | — | 4076 | 6 | — |
| C08_19 | 214.98723 | 52.87465 | — | — | — | — | — | — | 7282 | 6 | — |
| C08_20 | 214.98694 | 52.87462 | — | — | — | — | — | — | 7371 | 6 | — |
| C08_21 | 214.98797 | 52.87950 | — | — | — | — | EGSZ-9571152461 | 6.46 | 8177 | 6 | — |
| C08_22 | 215.03394 | 52.91384 | — | — | — | — | — | — | 8534 | 6 | — |
| C08_23 | 215.03210 | 52.91902 | — | — | — | — | — | — | 9935 | 6 | — |
| C08_24 | 214.95842 | 52.87517 | — | — | — | — | EGSZ-9500252305 | 6.54 | 11721 | 6 | — |
| C08_25 | 215.03721 | 52.90675 | — | — | — | — | EGSZ-0089354243 | 7.00 | — | — | — |
| C08_26 | 215.03704 | 52.89194 | — | — | — | — | EGSZ-0088953310 | 7.00 | — | — | — |
| C08_27 | 215.00600 | 52.90536 | — | — | — | — | EGSZ-0014454193 | 6.69 | — | — | — |
| C08_28 | 214.97996 | 52.86114 | — | — | — | — | EGSZ-9551951401 | 7.08 | — | — | — |
| C08_29 | 214.97192 | 52.86922 | — | — | — | — | EGSZ-9532652092 | 6.39 | — | — | — |
| C08_30 | 214.99875 | 52.85542 | — | — | — | — | EGSY-9597051195 | 8.38 | — | — | — |
| C08_31 | 214.98958 | 52.86658 | — | — | — | — | EGSY-9575051597 | 8.11 | — | — | — |
| C09_01 | 214.95990 | 52.83118 | P10M_01207 | 4.90 | — | — | — | — | 2131 | 5 | — |
| C09_02 | 214.94755 | 52.83709 | P10M_01289 | 4.88 | — | — | — | — | — | — | — |
| C09_03 | 214.95516 | 52.84290 | P10M_01294 | 5.00 | — | — | — | — | 5342 | 5 | — |
| C09_04 | 214.94379 | 52.85006 | P10M_01374 | 5.00 | — | — | — | — | 8518 | 5 | — |
| C09_05 | 214.92738 | 52.81349 | — | — | — | — | — | — | 3324 | 5 | — |
| C09_06 | 214.95796 | 52.83598 | — | — | — | — | — | — | 3426 | 5 | — |
| C09_07 | 214.93801 | 52.83249 | — | — | — | — | — | — | 5763 | 5 | — |
| C09_08 | 214.94369 | 52.85014 | — | — | — | — | — | — | 8598 | 5 | — |
| C10_01 | 214.83230 | 52.74412 | — | — | — | — | — | — | 2973 | 5 | — |
| C10_02 | 214.81900 | 52.75974 | — | — | — | — | — | — | 8275 | 5 | — |
| C10_03 | 214.80973 | 52.75440 | — | — | — | — | — | — | 8514 | 5 | — |
| C10_04 | 214.83919 | 52.77684 | — | — | — | — | — | — | 8846 | 5 | — |
| C10_05 | 214.84428 | 52.78964 | — | — | — | — | — | — | 10641 | 5 | — |
| C10_06 | 214.83044 | 52.78370 | — | — | — | — | — | — | 11720 | 5 | — |
| C10_07 | 214.83851 | 52.79330 | — | — | — | — | — | — | 12509 | 5 | — |
| C10_08 | 214.80272 | 52.76821 | — | — | — | — | — | — | 12664 | 5 | — |
| C10_09 | 214.85085 | 52.77673 | — | — | — | — | EGSZ-9242146357 | 6.84 | 7028 | 7 | — |
| C10_10 | 214.83100 | 52.74914 | — | — | — | — | EGSZ-9194444569 | 6.77 | — | — | — |
When measuring galaxy sizes, it is imperative to consider image smearing by point spread functions (PSFs). To address this, we utilize empirical PSFs generated by stacking bright point sources in the actual NIRCam images. Within each field, we select four to nine unsaturated bright point sources with ≃22–24 mag. The PSF FWHM values are listed in table 2.
3 Analyses
3.1 Surface brightness profile fitting
We measure the half-light radii of the high-z galaxies in our compiled sample through fitting the Sérsic profile (Sersic 1968) to the observed 2D SB profiles. The Sérsic profile is defined as follows:
where Σe is the surface brightness at the half-light radius re, and n signifies the Sérsic index. The value of bn is specified such that re encapsulates half of the total flux.
We deploy GALFIT version 3 (Peng et al. 2002, 2010) for the profile fitting. This software convolves a galaxy surface brightness profile with a PSF profile and optimizes the fits using the Levenberg–Marquardt algorithm to minimize χ2. The resultant parameters from GALFIT comprise the centroid coordinates, total magnitude, radius along the semi-major axis (a), Sérsic index (n), axis ratio (b|$/$|a), and position angle of the fitted object. The circularized half-light radius, |$r_e = a \sqrt{b/a}$|, is calculated by utilizing the radius along the semi-major axis and the axis ratio, which is commonly used in galaxy size measurements in previous studies (e.g., Newman et al. 2012; Mosleh et al. 2012; Ono et al. 2013; Shibuya et al. 2015; Kawamata et al. 2018). SExtractor is deployed to obtain initial parameters for the GALFIT profile fitting. With the exception of the Sérsic index, all parameters are set to vary during the profile fitting. Noise images are derived from the inverse square root of the weight maps and employed to assign weights to individual pixels during the profile fitting. Segmentation images generated by SExtractor are used for masking extraneous objects around the sources of interest.
We fix the Sérsic index at n = 1.5, which corresponds to the median value of SFGs with similar UV luminosities to those of our sources reported in the previous work (Shibuya et al. 2015).1 In fact, when we run GALFIT with the Sérsic index left as a free parameter for 29 bright spectroscopically confirmed galaxies in our sample, the median values of the best-fitting Sérsic indices are 1.4 in F150W and 1.0 in F444W (see also Sun et al. 2024; for lower redshifts, see Martorano et al. 2023). However, the uncertainties of the Sérsic indices for individual sources would not be small. For illustration, figure 3 displays the observed radial profiles for C01_02, C01_06, and C03_04, together with the best-fitting results where the Sérsic index n is treated as a free parameter and where n is fixed at 1.5 or 4.0. All of these cases fit the observed data points well, suggesting that it is challenging to determine the Sérsic index simultaneously with the other parameters using the currently available data. Therefore, we fix the value of the Sérsic index in the SB profile fittings, consistent with the approach taken in the previous studies.
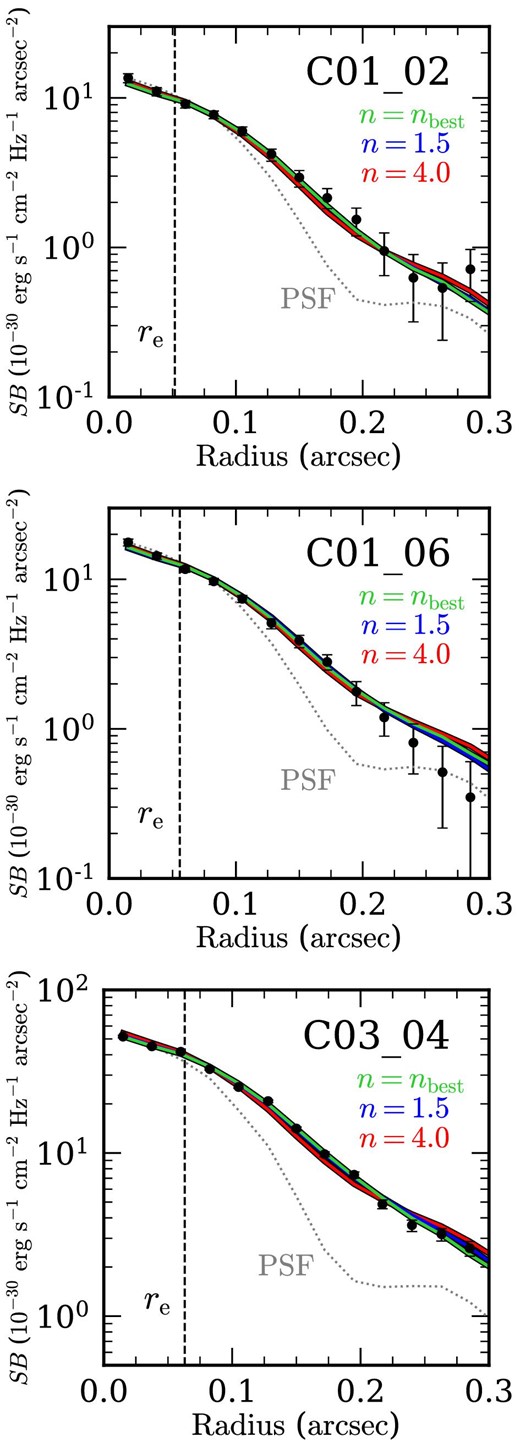
Examples of the rest-frame optical SB radial profiles: C01_02 (top), C01_06 (middle), and C03_04 (bottom). In each panel, the black circles represent the observed SB profile in F444W. The 1σ uncertainties are calculated from the 68th percentiles of radial profiles obtained at randomly selected positions in the F444W image. The green curve corresponds to the best-fitting Sérsic profile where the Sérsic index is allowed to vary as a free parameter (nbest = 1.4 for C01_02, nbest = 2.1 for C01_06, and nbest = 1.1 for C03_04). The blue and red curves denote the best-fitting Sérsic profiles with a fixed Sérsic index of n = 1.5 and n = 4.0, respectively. The gray dotted curve is the PSF profile whose peak is normalized by the peak of the observed profile. The black vertical dashed line represents the best-fitting half-light radius, re.
3.2 Monte Carlo simulations
Following previous work (e.g., Ono et al. 2013, 2023; Shibuya et al. 2015), we execute a series of MC simulations to quantify systematic and statistical uncertainties in the profile fitting with GALFIT. We use the F150W and F444W images, which probe the rest-frame UV and optical emission from our galaxies at z ≃ 4–10. In addition, we utilize the F410M images as detailed in subsection 3.3, as well as smoothed F150W images whose PSF sizes are comparable to those of the F444W images as described in subsection 3.4. As demonstrated in table 2, the depths and PSF FWHMs are almost the same across different pointings of CEERS. For simplicity, we conduct MC simulations for each band with respect to CEERS2 and apply the results to correct systematic uncertainties and estimate statistical uncertainties for all the pointings from CEERS1 to CEERS10. We use GALFIT to generate galaxy images with a fixed Sérsic index n of 1.5. The half-light radius re and total magnitude are randomly selected within ranges of 0.5–27.0 pixels and 24.5–30.0 mag, respectively. These galaxy images are then convolved with a PSF image, which is a composite of bright, unsaturated stars selected from each band. The PSF-convolved galaxy images are subsequently inserted into blank regions of the actual NIRCam images and analyzed in an identical manner to our high-z galaxies.
We present the results of size measurements for our MC simulated galaxies in figure 4, and those of total magnitude measurements in figure 5. The general trends seen in these figures are the same as those in our previous results of Ono et al. (2023). Our MC simulations confirm a systematic underestimation of half-light radii and overestimation of total magnitudes in GALFIT measurements for fainter objects. It is also found that the MC simulated galaxies with faint magnitudes and large sizes do not meet the S|$/$|N > 10 criterion for aperture magnitude. Since our sample is limited to those with an aperture magnitude S|$/$|N larger than 10, the systematic effects are not large.2 We rectify these systematic effects and also use statistical uncertainties in size and total magnitude measurements in the same manner as our previous work; briefly, we utilize the MC simulation outcomes within the same output magnitude (size) bins as our high-z galaxies to correct for the output sizes (magnitudes) by the median differences between the input and output values and to assign the 68th percentiles in these bins as statistical uncertainties [see section 3 of Ono et al. (2023) for details].
![Input circularized radius vs. output circularized radius for output total magnitudes of m(out) = 25–26, 26–27, and 27–28 mag from left to right, based on our GALFIT MC simulations for the CEERS2 field in F150W, F410M, F444W, and PSF-matched F150W [F150W(s)]. The red filled circles and error bars denote the median values of the differences between the input and output circularized radii and the corresponding 68 percentile ranges, respectively. Individual simulated objects are represented with gray dots, and those with an aperture magnitude S$/$N > 10 are marked with open pink circles. The blue dashed line illustrates the relationship where the input and output circularized radius are equivalent.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/76/2/10.1093_pasj_psae004/1/m_psae004fig4.jpeg?Expires=1748712566&Signature=AJIJm1duC1kRCLLqZ4L3up14STB0Cv73IBS-Lbc4FdSiDn9rsf76SHgjV~AfgvSJb5jyHnsmMFAWFlJehRFaGR3ZNflkAlAIsbUleZKvtMrrFGYU8AgDPBIfenv5I-O~JImn-NzU7wRez247NNFa-5us5dDuot1PqiOLgYrenkZrEF-QhWyVzjTfVgnpFBf1IZr56kD5qjhVKtQQzhO78qfsy1DkV-cAWnZB-yMhwuTHp-UdnDjovmApcx11bl8yW7Hp4FK0tbZsWxxeGVxgo-vEveF6WeiU6yO5bF0Fw7c17yAimrT8i1kgPF5Y8cbN6Z6clPD2oGIEdYqCEIpQ4w__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Input circularized radius vs. output circularized radius for output total magnitudes of m(out) = 25–26, 26–27, and 27–28 mag from left to right, based on our GALFIT MC simulations for the CEERS2 field in F150W, F410M, F444W, and PSF-matched F150W [F150W(s)]. The red filled circles and error bars denote the median values of the differences between the input and output circularized radii and the corresponding 68 percentile ranges, respectively. Individual simulated objects are represented with gray dots, and those with an aperture magnitude S|$/$|N > 10 are marked with open pink circles. The blue dashed line illustrates the relationship where the input and output circularized radius are equivalent.
![Input total magnitude vs. output total magnitude for output half-light radii of $r_{\rm e}^{\rm (out)} = 0$–5 pixels (left) and 5–10 pixels (right) based on our GALFIT MC simulations for the CEERS2 field in F150W, F410M, F444W, and PSF-matched F150W [F150W(s)]. The red filled circles and error bars denote the median values of the differences between the input and output magnitudes and the corresponding 68 percentile ranges, respectively. Individual simulated objects are represented by gray dots, with an additional open pink circle marking those having aperture magnitude S$/$N above 10. The blue dashed line corresponds to the relationship where the input and output magnitudes are equal.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/76/2/10.1093_pasj_psae004/1/m_psae004fig5.jpeg?Expires=1748712566&Signature=0Z8-E1ipPkLiAZdCxvn0IiC3BqlnaNqEqysjzbahBTbL0A4SMSpZ-lImDDC0pqHI1YxOhct4sezj7MsD8lt8JNOp~0YT8087lfaT2uyaDfiKEKg4LMZdblHj1craNY9MAkyPksioLMX0d0nLi8hHYv5V6iGC0LwPtqp4QgbZvIQuHiIKgAo4N2zx73x6M0q3T99NUg3tkYawDH3KosfsK0bDcGsvmh9Waga-ONNwOgI0g30qCNvGTe4EMfPekdL2~ABG6BFnmzQLUi1LM01V3wltEUZyNISSPwGMUmQgbhwvsRfEa8RVX3BTbYClh3p5hkY1rU7zuALj4LZhwJlNpQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Input total magnitude vs. output total magnitude for output half-light radii of |$r_{\rm e}^{\rm (out)} = 0$|–5 pixels (left) and 5–10 pixels (right) based on our GALFIT MC simulations for the CEERS2 field in F150W, F410M, F444W, and PSF-matched F150W [F150W(s)]. The red filled circles and error bars denote the median values of the differences between the input and output magnitudes and the corresponding 68 percentile ranges, respectively. Individual simulated objects are represented by gray dots, with an additional open pink circle marking those having aperture magnitude S|$/$|N above 10. The blue dashed line corresponds to the relationship where the input and output magnitudes are equal.
3.3 Impact of strong emission lines
As mentioned in section 2, strong emission lines such as Hα and [O iii] from galaxies at z ≳ 5 are included in F444W due to its wide wavelength coverage. To assess the impact of the strong emission lines on our galaxy size measurements, we use images with the medium-band filter F410M. As shown in the bottom panel of figure 2, for the redshift range of z ≃ 5.63–6.63, F410M does not encompass the strong emission lines, allowing us to primarily probe the rest-frame optical continuum.
We perform SB profile fittings for galaxies with spectroscopic redshifts of zspec = 5.63–6.63 in our sample using the F410M and F444W images. Although the number of sources with spectroscopic redshifts within this range is 13 regardless of their S|$/$|N values, successful convergence of the SB profile fitting is achieved for three sources each in the CEERS3 and CEERS6 fields. For the remaining sources, the SB profile fitting encounters numerical convergence issues probably due to the low S|$/$|N values (for details, see section 10 of the GALFIT user’s manual). Figure 6 displays the results of the SB profile fittings. Among them, C03_01, C06_02, and C06_07 are relatively faint, but still appear to fit well with the Sérsic profiles. Given the limited number of sources explored here, we include these faint ones in the plots as well.

Sérsic profile fitting results for the F410M and F444W images of spectroscopically confirmed galaxies within the redshift range zspec = 5.63–6.63, where strong emission lines do not enter the F410M band. From left to right, the 1|${_{.}^{\prime\prime}}$|5 × 1|${_{.}^{\prime\prime}}$|5 cutouts of the original images, the best-fitting Sérsic model profile images, and the residual images that are created by subtracting the best-fitting images from the original ones are presented.
The top and bottom panels of figure 7 compare the size and total magnitude measurement results, respectively. We confirm a broad agreement in sizes derived from F410M and F444W. While individual size measurements differ by about 1–4σ between F410M and F444W, suggesting that sizes may vary to this extent for individual sources, the overall average does not seem to be significantly impacted. Moreover, particularly for relatively brighter sources indicated with filled circles, the difference in size is within 20%. On the other hand, the total magnitudes measured with F444W are systematically brighter than those measured with F410M mostly by ≃ 0.2–0.4 mag, which is likely due to the strong Hα emission line probed with F444W. Indeed, since the FWHM of the F444W filter transmission3 is about |$1.1\, \mu$|m, these magnitude differences roughly correspond to rest-frame Hα emission line equivalent widths (EWs) of 320–700 Å for galaxies at z = 6. These values roughly align with the average EW values for high-z SFGs reported in previous studies: |$555^{+332}_{-311}$| Å for z = 4.9 galaxies with a median MUV = −21.4 mag (table 4 of Harikane et al. 2018) and 453 ± 84 Å for z = 3.8–5.3 galaxies with −20.5 < MUV < −19.5 mag (table 3 of Lam et al. 2019; see also Maseda et al. 2020; Prieto-Lyon et al. 2023).4 Because the Hβ + [O iii] EWs are not very different from that of Hα (the median Hβ + [O iii] EW value for galaxies at z ∼ 6.5–8 with slightly fainter magnitudes is 780 Å; Endsley et al. 2023), the impact of strong line emission from Hα and Hβ + [O iii] should be comparable.5 Since the size and magnitude differences due to the strong emission lines are not very large owing to the wide wavelength coverage of F444W, from the next subsection onwards, we utilize the F444W images to measure the rest-frame optical sizes and total magnitudes of our galaxies over a more extensive redshift range.
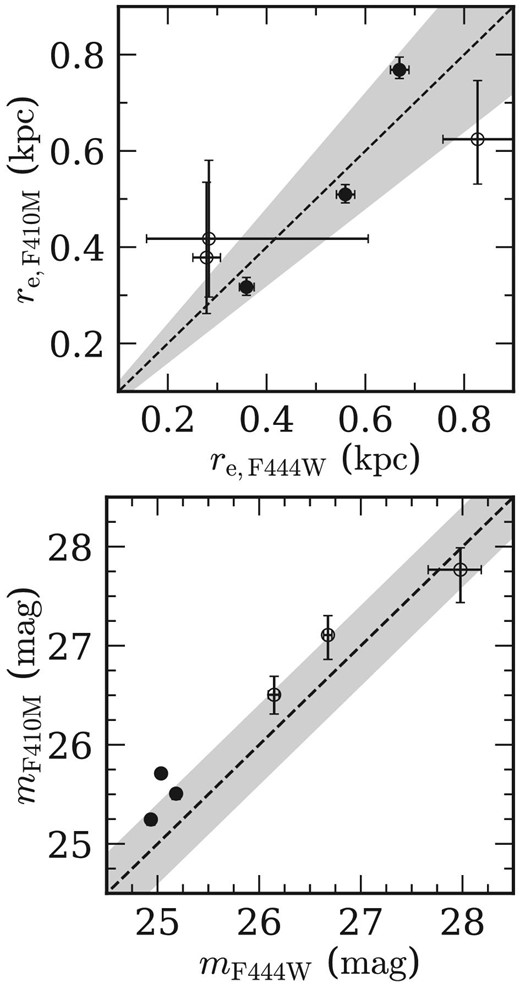
Comparison of SB profile fitting results for F410M and F444W images of galaxies with spectroscopic redshifts zspec = 5.63–6.63, where strong emission lines do not enter the F410M band. The top panel shows the size comparison, while the bottom panel illustrates the total magnitude comparison. The filled circles represent bright sources, while the open circles indicate faint sources. The dashed line denotes the case where the results from F410M and F444W are equal. The gray shade in the top (bottom) panel represents the range where the difference between these sizes (total magnitudes) is within ±20% (±0.4 mag).
Note that Zhang et al. (2023) have selected sources with spatially extended Hβ + [O iii] emission by combining two NIRCam broad-band filters, one of which incorporates the Hβ + [O iii] emission and the other does not. The focus of their study is primarily on the spatially extended SB distributions substantially beyond the effective radii. In contrast, our size measurements mainly rely on SB profiles within the effective radii with relatively high S|$/$|N values. Therefore, there is no conflict between our confirmation and the approach of Zhang et al. (2023). Moreover, it is worth noting that sources exhibiting spatially extended Hβ + [O iii] emission are rare, and hence unlikely to significantly impact our general measurements of high-z galaxy sizes.
3.4 Impact of different spatial resolutions in the rest-frame UV and optical
One of the primary topics of interest in this study is the comparison between the rest-frame UV and optical sizes. For this purpose, the difference in the spatial resolutions of the F150W and F444W images needs to be taken into account. For instance, as presented in figure 17 in appendix 2, C01_05 has two components near the center of the F150W cutout image, and the SB profile fitting is performed for one of the two components. However, in the F444W image, these two components are considered as one blended source, and the SB profile fitting is performed for the blended source accordingly. As such, for fair comparisons of the SB profile fitting results with the F150W and F444W images, we need to consider the difference in the spatial resolutions.
We create smoothed F150W images by applying Gaussian kernels to the original F150W images so that the PSF sizes of the smoothed F150W images match those of the F444W images. We then perform SB profile fittings using GALFIT on the PSF-matched F150W images. We also carry out MC simulations for the PSF-matched F150W images following the same methodology outlined in subsection 3.2. The results of size and total magnitude measurements for our MC simulated galaxies are shown in figures 4 and 5, respectively. Based on these MC simulation results, we correct systematic effects associated with the SB profile fittings and evaluate statistical uncertainties in the measurements.
By visually inspecting the output images of the SB profile fittings, we assign a flag about blendedness to each object as listed in table 6 in appendix 2. When the component fitted in the smoothed F150W image and/or the F444W image is a single component in the original F150W image, we set the flag to 1 (single). When the component fitted in the smoothed F150W image and/or the F444W image is multiple components in the original F150W image, we set the flag to 2 (multiple). In other words, we assign a multiple flag to a source if visual inspection of the residual image from a single component fit for it reveals the presence of additional components. These cases often show multiple segments in segmentation maps created by SExtractor. Typically, the centers of these multiple components are spatially offset from each other. For comparisons of the SB profile fitting results in the rest-frame UV and optical, we use the results from the original (PSF-matched) F150W images for the single (multiple) flagged sources. This approach ensures a fair comparison even for data with different spatial resolutions.
| . | F150W . | F150W (PSF matched) . | F444W . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | Flag . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mUV . | MUV . | re . | mUV . | MUV . | re . | mopt . | Mopt . | re, opt . | . | (PSF matched) . | . |
| ID . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . |
| C01_02 | |$26.57^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$26.62^{+0.05}_{-0.05}$| | |$-20.68^{+0.05}_{-0.05}$| | |$0.13^{+0.02}_{-0.02}$| | |$26.77^{+0.08}_{-0.12}$| | |$-20.53^{+0.08}_{-0.12}$| | |$0.23^{+0.02}_{-0.02}$| | |$1.36^{+0.15}_{-0.14}$| | |$1.77^{+0.28}_{-0.28}$| | 1 |
| C01_03 | |$27.68^{+0.20}_{-0.22}$| | |$-19.28^{+0.20}_{-0.22}$| | |$0.03^{+0.03}_{-0.02}$| | — | — | — | |$26.96^{+0.08}_{-0.12}$| | |$-20.00^{+0.08}_{-0.12}$| | |$0.12^{+0.12}_{-0.09}$| | |$4.44^{+7.25}_{-5.30}$| | — | 1 |
| C01_05 | |$26.42^{+0.04}_{-0.05}$| | |$-20.01^{+0.04}_{-0.05}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.65^{+0.04}_{-0.05}$| | |$-20.78^{+0.04}_{-0.05}$| | |$0.80^{+0.02}_{-0.02}$| | |$24.87^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$2.14^{+0.12}_{-0.10}$| | |$0.97^{+0.08}_{-0.07}$| | 2 |
| C01_06 | |$26.60^{+0.04}_{-0.05}$| | |$-19.67^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.01^{+0.09}_{-0.11}$| | |$0.49^{+0.04}_{-0.04}$| | |$26.45^{+0.04}_{-0.04}$| | |$-19.81^{+0.04}_{-0.04}$| | |$0.36^{+0.03}_{-0.03}$| | |$1.34^{+0.13}_{-0.13}$| | |$0.74^{+0.15}_{-0.16}$| | 1 |
| C01_07 | |$25.62^{+0.01}_{-0.02}$| | |$-20.66^{+0.01}_{-0.02}$| | |$0.26^{+0.00}_{-0.00}$| | |$25.55^{+0.02}_{-0.02}$| | |$-20.73^{+0.02}_{-0.02}$| | |$0.30^{+0.02}_{-0.02}$| | |$25.48^{+0.02}_{-0.03}$| | |$-20.79^{+0.02}_{-0.03}$| | |$0.29^{+0.02}_{-0.02}$| | |$1.13^{+0.08}_{-0.07}$| | |$0.97^{+0.10}_{-0.09}$| | 1 |
| C01_08 | |$25.78^{+0.05}_{-0.07}$| | |$-20.62^{+0.05}_{-0.07}$| | |$0.48^{+0.01}_{-0.01}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.54^{+0.03}_{-0.03}$| | |$0.42^{+0.02}_{-0.01}$| | |$25.46^{+0.04}_{-0.04}$| | |$-20.93^{+0.04}_{-0.04}$| | |$0.48^{+0.02}_{-0.02}$| | |$1.00^{+0.04}_{-0.03}$| | |$1.14^{+0.05}_{-0.05}$| | 1 |
| C01_09 | |$24.83^{+0.03}_{-0.04}$| | |$-21.57^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$24.75^{+0.04}_{-0.05}$| | |$-21.65^{+0.04}_{-0.05}$| | |$0.72^{+0.02}_{-0.02}$| | |$23.41^{+0.04}_{-0.04}$| | |$-22.99^{+0.04}_{-0.04}$| | |$0.75^{+0.02}_{-0.02}$| | |$1.26^{+0.04}_{-0.04}$| | |$1.04^{+0.05}_{-0.05}$| | 1 |
| C01_10 | |$25.94^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.37^{+0.01}_{-0.01}$| | |$25.67^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.55^{+0.02}_{-0.01}$| | |$25.38^{+0.04}_{-0.04}$| | |$-21.02^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$1.58^{+0.07}_{-0.06}$| | |$1.07^{+0.07}_{-0.07}$| | 2 |
| C01_11 | |$26.36^{+0.08}_{-0.11}$| | |$-20.04^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_12 | |$26.66^{+0.04}_{-0.05}$| | |$-19.74^{+0.04}_{-0.05}$| | |$0.37^{+0.02}_{-0.01}$| | |$26.44^{+0.05}_{-0.05}$| | |$-19.96^{+0.05}_{-0.05}$| | |$0.37^{+0.03}_{-0.04}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.50^{+0.03}_{-0.04}$| | |$1.35^{+0.11}_{-0.11}$| | |$1.35^{+0.15}_{-0.17}$| | 2 |
| C01_13 | |$26.33^{+0.15}_{-0.18}$| | |$-20.06^{+0.15}_{-0.18}$| | |$1.02^{+0.05}_{-0.04}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.15^{+0.09}_{-0.11}$| | |$0.81^{+0.05}_{-0.05}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.87^{+0.10}_{-0.06}$| | 2 |
| C01_14 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.20^{+0.01}_{-0.01}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.37^{+0.03}_{-0.03}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.22^{+0.03}_{-0.03}$| | |$-20.18^{+0.03}_{-0.03}$| | |$0.37^{+0.03}_{-0.04}$| | |$1.89^{+0.20}_{-0.20}$| | |$0.90^{+0.23}_{-0.26}$| | 2 |
| C01_15 | |$26.42^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.66^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_16 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.51^{+0.04}_{-0.05}$| | |$-20.89^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$24.56^{+0.05}_{-0.07}$| | |$-21.84^{+0.05}_{-0.07}$| | |$1.11^{+0.04}_{-0.03}$| | |$1.45^{+0.05}_{-0.04}$| | |$1.52^{+0.06}_{-0.06}$| | 1 |
| C01_17 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.50^{+0.03}_{-0.03}$| | |$0.39^{+0.02}_{-0.01}$| | |$25.37^{+0.02}_{-0.03}$| | |$-21.03^{+0.02}_{-0.03}$| | |$0.22^{+0.02}_{-0.02}$| | |$1.26^{+0.14}_{-0.11}$| | |$0.56^{+0.12}_{-0.10}$| | 2 |
| C01_18 | |$26.09^{+0.05}_{-0.07}$| | |$-20.30^{+0.05}_{-0.07}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.18^{+0.06}_{-0.07}$| | |$-20.22^{+0.06}_{-0.07}$| | |$0.49^{+0.03}_{-0.04}$| | |$25.97^{+0.05}_{-0.06}$| | |$-20.43^{+0.05}_{-0.06}$| | |$0.49^{+0.03}_{-0.04}$| | |$0.84^{+0.06}_{-0.06}$| | |$1.00^{+0.08}_{-0.09}$| | 2 |
| C01_19 | |$25.06^{+0.03}_{-0.04}$| | |$-21.63^{+0.03}_{-0.04}$| | |$0.78^{+0.02}_{-0.01}$| | |$24.71^{+0.05}_{-0.07}$| | |$-21.98^{+0.05}_{-0.07}$| | |$1.20^{+0.04}_{-0.03}$| | |$24.00^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$1.36^{+0.05}_{-0.04}$| | |$0.88^{+0.07}_{-0.05}$| | 2 |
| C01_20 | |$25.27^{+0.03}_{-0.04}$| | |$-21.43^{+0.03}_{-0.04}$| | |$0.75^{+0.01}_{-0.01}$| | |$25.25^{+0.04}_{-0.05}$| | |$-21.45^{+0.04}_{-0.05}$| | |$0.78^{+0.03}_{-0.02}$| | |$24.32^{+0.04}_{-0.04}$| | |$-22.37^{+0.04}_{-0.04}$| | |$0.70^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.89^{+0.04}_{-0.04}$| | 1 |
| C01_22 | |$27.22^{+0.06}_{-0.07}$| | |$-20.10^{+0.06}_{-0.07}$| | |$0.10^{+0.03}_{-0.02}$| | |$27.22^{+0.09}_{-0.08}$| | |$-20.09^{+0.09}_{-0.08}$| | |$0.11^{+0.07}_{-0.05}$| | — | — | — | — | — | 1 |
| C01_26 | |$26.38^{+0.08}_{-0.11}$| | |$-20.68^{+0.08}_{-0.11}$| | |$0.42^{+0.01}_{-0.01}$| | |$25.93^{+0.06}_{-0.07}$| | |$-21.13^{+0.06}_{-0.07}$| | |$0.65^{+0.02}_{-0.02}$| | |$25.45^{+0.05}_{-0.07}$| | |$-21.61^{+0.05}_{-0.07}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.89^{+0.09}_{-0.07}$| | |$1.21^{+0.07}_{-0.06}$| | 2 |
| C02_01 | |$27.82^{+0.20}_{-0.22}$| | |$-18.79^{+0.20}_{-0.22}$| | |$0.07^{+0.04}_{-0.03}$| | |$27.85^{+0.21}_{-0.27}$| | |$-18.76^{+0.21}_{-0.27}$| | |$0.10^{+0.09}_{-0.07}$| | |$27.20^{+0.16}_{-0.19}$| | |$-19.40^{+0.16}_{-0.19}$| | |$0.14^{+0.14}_{-0.10}$| | |$1.91^{+2.13}_{-1.60}$| | |$1.36^{+2.48}_{-1.92}$| | 1 |
| C02_02 | |$26.60^{+0.04}_{-0.05}$| | |$-19.89^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-19.79^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.99^{+0.03}_{-0.03}$| | |$-20.49^{+0.03}_{-0.03}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.78^{+0.08}_{-0.07}$| | |$0.86^{+0.10}_{-0.11}$| | 1 |
| C02_03 | |$26.67^{+0.08}_{-0.11}$| | |$-19.67^{+0.08}_{-0.11}$| | |$0.50^{+0.02}_{-0.01}$| | |$25.89^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.95^{+0.03}_{-0.03}$| | |$25.81^{+0.05}_{-0.06}$| | |$-20.53^{+0.05}_{-0.06}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.59^{+0.07}_{-0.06}$| | |$0.83^{+0.07}_{-0.06}$| | 2 |
| C02_04 | |$25.01^{+0.01}_{-0.02}$| | |$-21.39^{+0.01}_{-0.02}$| | |$0.35^{+0.00}_{-0.00}$| | |$24.97^{+0.02}_{-0.02}$| | |$-21.43^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.49^{+0.02}_{-0.03}$| | |$-21.91^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$1.18^{+0.05}_{-0.05}$| | |$1.01^{+0.07}_{-0.06}$| | 1 |
| C02_05 | |$26.43^{+0.08}_{-0.11}$| | |$-19.97^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | |$26.60^{+0.09}_{-0.11}$| | |$-19.79^{+0.09}_{-0.11}$| | |$0.63^{+0.05}_{-0.05}$| | |$25.61^{+0.04}_{-0.04}$| | |$-20.78^{+0.04}_{-0.04}$| | |$0.84^{+0.03}_{-0.02}$| | |$1.02^{+0.05}_{-0.04}$| | |$1.33^{+0.09}_{-0.09}$| | 1 |
| C02_06 | |$26.33^{+0.08}_{-0.11}$| | |$-20.07^{+0.08}_{-0.11}$| | |$0.70^{+0.03}_{-0.02}$| | |$26.31^{+0.09}_{-0.11}$| | |$-20.08^{+0.09}_{-0.11}$| | |$0.74^{+0.05}_{-0.05}$| | |$25.86^{+0.05}_{-0.06}$| | |$-20.54^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$0.89^{+0.05}_{-0.04}$| | |$0.85^{+0.07}_{-0.07}$| | 1 |
| C02_07 | |$25.71^{+0.05}_{-0.07}$| | |$-20.69^{+0.05}_{-0.07}$| | |$0.80^{+0.01}_{-0.01}$| | |$25.71^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.85^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$0.74^{+0.03}_{-0.03}$| | |$0.69^{+0.04}_{-0.03}$| | 1 |
| C02_08 | |$26.04^{+0.02}_{-0.03}$| | |$-20.35^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.05^{+0.03}_{-0.03}$| | |$-20.35^{+0.03}_{-0.03}$| | |$0.36^{+0.03}_{-0.04}$| | |$25.76^{+0.03}_{-0.03}$| | |$-20.64^{+0.03}_{-0.03}$| | |$0.32^{+0.02}_{-0.02}$| | |$0.94^{+0.07}_{-0.05}$| | |$0.88^{+0.11}_{-0.11}$| | 1 |
| C02_09 | |$25.28^{+0.06}_{-0.07}$| | |$-21.12^{+0.06}_{-0.07}$| | |$1.08^{+0.03}_{-0.02}$| | |$25.26^{+0.05}_{-0.07}$| | |$-21.14^{+0.05}_{-0.07}$| | |$1.13^{+0.04}_{-0.03}$| | |$24.31^{+0.05}_{-0.07}$| | |$-22.09^{+0.05}_{-0.07}$| | |$0.95^{+0.03}_{-0.02}$| | |$0.88^{+0.04}_{-0.03}$| | |$0.85^{+0.04}_{-0.03}$| | 1 |
| C02_10 | |$26.82^{+0.06}_{-0.07}$| | |$-19.58^{+0.06}_{-0.07}$| | |$0.28^{+0.01}_{-0.01}$| | |$26.37^{+0.09}_{-0.11}$| | |$-20.03^{+0.09}_{-0.11}$| | |$0.53^{+0.03}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.45^{+0.05}_{-0.06}$| | |$0.51^{+0.03}_{-0.04}$| | |$1.78^{+0.13}_{-0.14}$| | |$0.96^{+0.16}_{-0.18}$| | 2 |
| C02_12 | |$26.37^{+0.08}_{-0.11}$| | |$-20.33^{+0.08}_{-0.11}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.38^{+0.09}_{-0.11}$| | |$-20.31^{+0.09}_{-0.11}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.44^{+0.04}_{-0.04}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.08^{+0.05}_{-0.04}$| | |$1.05^{+0.07}_{-0.08}$| | 1 |
| C02_13 | |$26.77^{+0.13}_{-0.18}$| | |$-19.92^{+0.13}_{-0.18}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.83^{+0.15}_{-0.17}$| | |$-19.86^{+0.15}_{-0.17}$| | |$0.48^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C02_14 | |$27.34^{+0.11}_{-0.14}$| | |$-19.93^{+0.11}_{-0.14}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.84^{+0.09}_{-0.08}$| | |$-20.43^{+0.09}_{-0.08}$| | |$0.34^{+0.02}_{-0.03}$| | |$25.60^{+0.02}_{-0.03}$| | |$-21.68^{+0.02}_{-0.03}$| | |$0.13^{+0.01}_{-0.01}$| | |$0.52^{+0.08}_{-0.06}$| | |$0.39^{+0.07}_{-0.06}$| | 2 |
| C02_15 | |$27.57^{+0.11}_{-0.14}$| | |$-19.75^{+0.11}_{-0.14}$| | |$0.05^{+0.03}_{-0.02}$| | |$27.64^{+0.14}_{-0.17}$| | |$-19.68^{+0.14}_{-0.17}$| | |$0.09^{+0.07}_{-0.05}$| | |$25.67^{+0.02}_{-0.03}$| | |$-21.64^{+0.02}_{-0.03}$| | |$0.05^{+0.01}_{-0.01}$| | |$1.13^{+0.76}_{-0.55}$| | |$0.60^{+0.87}_{-0.69}$| | 1 |
| C02_20 | |$26.71^{+0.13}_{-0.18}$| | |$-20.21^{+0.13}_{-0.18}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.82^{+0.15}_{-0.17}$| | |$-20.10^{+0.15}_{-0.17}$| | |$0.40^{+0.03}_{-0.03}$| | |$25.90^{+0.05}_{-0.06}$| | |$-21.02^{+0.05}_{-0.06}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.25^{+0.06}_{-0.05}$| | |$1.36^{+0.10}_{-0.11}$| | 1 |
| C02_21 | |$27.16^{+0.06}_{-0.07}$| | |$-19.76^{+0.06}_{-0.07}$| | |$0.17^{+0.03}_{-0.02}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.44^{+0.09}_{-0.11}$| | |$0.50^{+0.04}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.97^{+0.05}_{-0.06}$| | |$0.59^{+0.07}_{-0.04}$| | |$3.56^{+0.86}_{-0.58}$| | |$1.19^{+0.53}_{-0.39}$| | 2 |
| C02_22 | |$26.12^{+0.02}_{-0.03}$| | |$-20.76^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.10^{+0.03}_{-0.03}$| | |$-20.79^{+0.03}_{-0.03}$| | |$0.25^{+0.03}_{-0.03}$| | |$25.63^{+0.02}_{-0.03}$| | |$-21.25^{+0.02}_{-0.03}$| | |$0.23^{+0.02}_{-0.01}$| | |$1.12^{+0.09}_{-0.08}$| | |$0.92^{+0.15}_{-0.14}$| | 1 |
| C02_23 | |$26.68^{+0.04}_{-0.05}$| | |$-20.21^{+0.04}_{-0.05}$| | |$0.22^{+0.01}_{-0.01}$| | |$26.54^{+0.05}_{-0.05}$| | |$-20.35^{+0.05}_{-0.05}$| | |$0.34^{+0.03}_{-0.03}$| | |$26.24^{+0.04}_{-0.04}$| | |$-20.65^{+0.04}_{-0.04}$| | |$0.25^{+0.03}_{-0.03}$| | |$1.10^{+0.13}_{-0.12}$| | |$0.73^{+0.15}_{-0.16}$| | 1 |
| C03_01 | |$26.89^{+0.06}_{-0.07}$| | |$-19.83^{+0.06}_{-0.07}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.91^{+0.09}_{-0.08}$| | |$-19.81^{+0.09}_{-0.08}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.67^{+0.04}_{-0.04}$| | |$-20.05^{+0.04}_{-0.04}$| | |$0.28^{+0.03}_{-0.03}$| | |$0.68^{+0.07}_{-0.07}$| | |$0.68^{+0.08}_{-0.09}$| | 1 |
| C03_04 | |$25.62^{+0.01}_{-0.02}$| | |$-21.08^{+0.01}_{-0.02}$| | |$0.30^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-21.09^{+0.02}_{-0.02}$| | |$0.28^{+0.01}_{-0.01}$| | |$25.03^{+0.02}_{-0.03}$| | |$-21.66^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$1.22^{+0.05}_{-0.05}$| | |$1.27^{+0.08}_{-0.08}$| | 1 |
| C03_05 | |$26.20^{+0.08}_{-0.11}$| | |$-20.42^{+0.08}_{-0.11}$| | |$0.46^{+0.02}_{-0.01}$| | |$26.22^{+0.09}_{-0.11}$| | |$-20.41^{+0.09}_{-0.11}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.45^{+0.04}_{-0.04}$| | |$0.56^{+0.02}_{-0.02}$| | |$1.23^{+0.06}_{-0.05}$| | |$1.25^{+0.10}_{-0.11}$| | 1 |
| C03_07 | |$27.76^{+0.20}_{-0.22}$| | |$-19.21^{+0.20}_{-0.22}$| | |$0.11^{+0.03}_{-0.02}$| | |$27.93^{+0.21}_{-0.27}$| | |$-19.04^{+0.21}_{-0.27}$| | |$0.05^{+0.08}_{-0.06}$| | — | — | — | — | — | 1 |
| C03_08 | |$26.71^{+0.04}_{-0.05}$| | |$-20.27^{+0.04}_{-0.05}$| | |$0.23^{+0.01}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-20.29^{+0.05}_{-0.05}$| | |$0.27^{+0.03}_{-0.03}$| | |$26.23^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$1.21^{+0.12}_{-0.12}$| | |$1.01^{+0.17}_{-0.16}$| | 1 |
| C03_09 | |$26.75^{+0.06}_{-0.07}$| | |$-19.74^{+0.06}_{-0.07}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.84^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.25^{+0.03}_{-0.03}$| | |$26.10^{+0.05}_{-0.06}$| | |$-20.39^{+0.05}_{-0.06}$| | |$0.48^{+0.03}_{-0.03}$| | |$1.58^{+0.12}_{-0.12}$| | |$1.89^{+0.23}_{-0.23}$| | 1 |
| C03_11 | |$25.57^{+0.06}_{-0.07}$| | |$-20.83^{+0.06}_{-0.07}$| | |$1.62^{+0.05}_{-0.04}$| | |$25.65^{+0.05}_{-0.07}$| | |$-20.75^{+0.05}_{-0.07}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C03_12 | |$25.23^{+0.03}_{-0.04}$| | |$-21.16^{+0.03}_{-0.04}$| | |$0.85^{+0.02}_{-0.01}$| | |$24.93^{+0.05}_{-0.07}$| | |$-21.46^{+0.05}_{-0.07}$| | |$1.04^{+0.03}_{-0.03}$| | |$23.76^{+0.04}_{-0.04}$| | |$-22.64^{+0.04}_{-0.04}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.07^{+0.04}_{-0.03}$| | |$0.87^{+0.05}_{-0.04}$| | 2 |
| C03_13 | |$25.29^{+0.06}_{-0.07}$| | |$-21.11^{+0.06}_{-0.07}$| | |$1.42^{+0.04}_{-0.03}$| | |$25.18^{+0.05}_{-0.07}$| | |$-21.22^{+0.05}_{-0.07}$| | |$1.44^{+0.05}_{-0.04}$| | |$24.29^{+0.05}_{-0.07}$| | |$-22.11^{+0.05}_{-0.07}$| | |$1.66^{+0.06}_{-0.05}$| | |$1.17^{+0.05}_{-0.04}$| | |$1.16^{+0.06}_{-0.04}$| | 2 |
| C03_14 | |$25.83^{+0.09}_{-0.11}$| | |$-20.57^{+0.09}_{-0.11}$| | |$0.96^{+0.02}_{-0.01}$| | |$25.62^{+0.05}_{-0.07}$| | |$-20.77^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$24.99^{+0.05}_{-0.07}$| | |$-21.41^{+0.05}_{-0.07}$| | |$1.41^{+0.05}_{-0.04}$| | |$1.48^{+0.06}_{-0.05}$| | |$1.35^{+0.07}_{-0.06}$| | 2 |
| C03_15 | |$26.46^{+0.04}_{-0.05}$| | |$-19.94^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.06^{+0.06}_{-0.07}$| | |$-20.34^{+0.06}_{-0.07}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.71^{+0.02}_{-0.03}$| | |$-20.69^{+0.02}_{-0.03}$| | |$0.45^{+0.02}_{-0.02}$| | |$1.76^{+0.10}_{-0.09}$| | |$0.87^{+0.13}_{-0.15}$| | 2 |
| C03_16 | |$26.57^{+0.04}_{-0.05}$| | |$-19.83^{+0.04}_{-0.05}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.69^{+0.05}_{-0.05}$| | |$26.32^{+0.04}_{-0.04}$| | |$-20.08^{+0.04}_{-0.04}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.09^{+0.09}_{-0.09}$| | |$0.64^{+0.11}_{-0.12}$| | 1 |
| C03_17 | |$26.64^{+0.13}_{-0.18}$| | |$-19.76^{+0.13}_{-0.18}$| | |$0.48^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.08^{+0.03}_{-0.03}$| | |$-20.32^{+0.03}_{-0.03}$| | |$0.39^{+0.03}_{-0.04}$| | |$0.80^{+0.07}_{-0.08}$| | |$0.72^{+0.08}_{-0.09}$| | 2 |
| C03_18 | |$26.12^{+0.02}_{-0.03}$| | |$-20.28^{+0.02}_{-0.03}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.97^{+0.03}_{-0.03}$| | |$-20.43^{+0.03}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$26.14^{+0.03}_{-0.03}$| | |$-20.26^{+0.03}_{-0.03}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.66^{+0.14}_{-0.14}$| | |$1.26^{+0.14}_{-0.15}$| | 2 |
| C03_19 | |$26.54^{+0.04}_{-0.05}$| | |$-19.86^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.99^{+0.06}_{-0.07}$| | |$-20.41^{+0.06}_{-0.07}$| | |$0.66^{+0.05}_{-0.05}$| | |$25.56^{+0.04}_{-0.04}$| | |$-20.84^{+0.04}_{-0.04}$| | |$0.92^{+0.03}_{-0.02}$| | |$3.42^{+0.19}_{-0.14}$| | |$1.40^{+0.28}_{-0.28}$| | 2 |
| C03_20 | |$26.70^{+0.13}_{-0.18}$| | |$-19.70^{+0.13}_{-0.18}$| | |$0.73^{+0.03}_{-0.02}$| | |$27.04^{+0.15}_{-0.17}$| | |$-19.36^{+0.15}_{-0.17}$| | |$0.64^{+0.20}_{-0.12}$| | — | — | — | — | — | 1 |
| C03_21 | |$26.62^{+0.04}_{-0.05}$| | |$-19.78^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.33^{+0.05}_{-0.05}$| | |$-20.07^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$24.89^{+0.05}_{-0.07}$| | |$-21.51^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.02}$| | |$3.98^{+0.21}_{-0.16}$| | |$2.34^{+0.32}_{-0.36}$| | 2 |
| C03_22 | |$25.88^{+0.09}_{-0.11}$| | |$-20.52^{+0.09}_{-0.11}$| | |$1.28^{+0.03}_{-0.02}$| | |$25.98^{+0.08}_{-0.10}$| | |$-20.42^{+0.08}_{-0.10}$| | |$1.19^{+0.11}_{-0.08}$| | — | — | — | — | — | 1 |
| C03_23 | |$26.31^{+0.08}_{-0.11}$| | |$-20.08^{+0.08}_{-0.11}$| | |$0.79^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C03_24 | |$24.71^{+0.01}_{-0.02}$| | |$-21.98^{+0.01}_{-0.02}$| | |$0.37^{+0.01}_{-0.00}$| | |$24.69^{+0.02}_{-0.02}$| | |$-22.00^{+0.02}_{-0.02}$| | |$0.37^{+0.01}_{-0.01}$| | |$24.37^{+0.04}_{-0.04}$| | |$-22.32^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.01}$| | |$1.39^{+0.05}_{-0.04}$| | |$1.38^{+0.07}_{-0.06}$| | 2 |
| C03_25 | |$26.13^{+0.05}_{-0.07}$| | |$-20.57^{+0.05}_{-0.07}$| | |$0.81^{+0.04}_{-0.03}$| | |$26.23^{+0.09}_{-0.11}$| | |$-20.46^{+0.09}_{-0.11}$| | |$0.76^{+0.07}_{-0.06}$| | |$26.18^{+0.09}_{-0.12}$| | |$-20.52^{+0.09}_{-0.12}$| | |$0.72^{+0.08}_{-0.04}$| | |$0.89^{+0.11}_{-0.07}$| | |$0.95^{+0.13}_{-0.09}$| | 1 |
| C03_27 | |$26.25^{+0.04}_{-0.05}$| | |$-20.91^{+0.04}_{-0.05}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.24^{+0.03}_{-0.03}$| | |$-20.92^{+0.03}_{-0.03}$| | |$0.21^{+0.03}_{-0.03}$| | |$25.36^{+0.02}_{-0.03}$| | |$-21.80^{+0.02}_{-0.03}$| | |$0.34^{+0.01}_{-0.01}$| | |$1.80^{+0.11}_{-0.09}$| | |$1.59^{+0.23}_{-0.22}$| | 1 |
| C04_02 | |$25.38^{+0.01}_{-0.02}$| | |$-21.02^{+0.01}_{-0.02}$| | |$0.19^{+0.00}_{-0.00}$| | |$25.24^{+0.02}_{-0.02}$| | |$-21.16^{+0.02}_{-0.02}$| | |$0.31^{+0.01}_{-0.02}$| | |$24.32^{+0.02}_{-0.03}$| | |$-22.08^{+0.02}_{-0.03}$| | |$0.46^{+0.02}_{-0.02}$| | |$2.42^{+0.11}_{-0.10}$| | |$1.46^{+0.15}_{-0.14}$| | 1 |
| C04_03 | |$26.15^{+0.05}_{-0.07}$| | |$-20.25^{+0.05}_{-0.07}$| | |$0.63^{+0.03}_{-0.02}$| | |$25.95^{+0.06}_{-0.07}$| | |$-20.45^{+0.06}_{-0.07}$| | |$0.71^{+0.02}_{-0.02}$| | |$25.30^{+0.04}_{-0.04}$| | |$-21.10^{+0.04}_{-0.04}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.78^{+0.05}_{-0.04}$| | |$0.69^{+0.04}_{-0.03}$| | 2 |
| C04_04 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-20.80^{+0.02}_{-0.02}$| | |$0.29^{+0.01}_{-0.02}$| | |$24.85^{+0.02}_{-0.03}$| | |$-21.55^{+0.02}_{-0.03}$| | |$0.30^{+0.02}_{-0.02}$| | |$1.25^{+0.08}_{-0.07}$| | |$1.02^{+0.10}_{-0.09}$| | 2 |
| C04_05 | |$25.68^{+0.03}_{-0.04}$| | |$-20.72^{+0.03}_{-0.04}$| | |$0.63^{+0.01}_{-0.01}$| | |$25.64^{+0.04}_{-0.05}$| | |$-20.76^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$25.07^{+0.04}_{-0.04}$| | |$-21.33^{+0.04}_{-0.04}$| | |$0.68^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.93^{+0.04}_{-0.04}$| | 1 |
| C04_06 | |$26.27^{+0.04}_{-0.05}$| | |$-20.13^{+0.04}_{-0.05}$| | |$0.46^{+0.02}_{-0.01}$| | — | — | — | |$24.85^{+0.05}_{-0.07}$| | |$-21.55^{+0.05}_{-0.07}$| | |$1.35^{+0.05}_{-0.04}$| | |$2.95^{+0.16}_{-0.12}$| | — | 2 |
| C04_07 | |$26.47^{+0.04}_{-0.05}$| | |$-20.22^{+0.04}_{-0.05}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.32^{+0.03}_{-0.04}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.83^{+0.03}_{-0.03}$| | |$0.35^{+0.02}_{-0.01}$| | |$1.16^{+0.07}_{-0.06}$| | |$1.08^{+0.12}_{-0.14}$| | 1 |
| C04_08 | |$26.48^{+0.08}_{-0.11}$| | |$-20.22^{+0.08}_{-0.11}$| | |$0.74^{+0.03}_{-0.02}$| | |$26.51^{+0.09}_{-0.11}$| | |$-20.18^{+0.09}_{-0.11}$| | |$0.70^{+0.04}_{-0.05}$| | |$26.24^{+0.09}_{-0.12}$| | |$-20.45^{+0.09}_{-0.12}$| | |$0.67^{+0.08}_{-0.04}$| | |$0.90^{+0.11}_{-0.06}$| | |$0.96^{+0.12}_{-0.08}$| | 1 |
| C04_09 | |$26.23^{+0.08}_{-0.11}$| | |$-20.46^{+0.08}_{-0.11}$| | |$0.85^{+0.04}_{-0.03}$| | |$26.32^{+0.09}_{-0.11}$| | |$-20.38^{+0.09}_{-0.11}$| | |$0.71^{+0.04}_{-0.05}$| | |$25.36^{+0.05}_{-0.07}$| | |$-21.33^{+0.05}_{-0.07}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.08^{+0.07}_{-0.05}$| | |$1.29^{+0.08}_{-0.08}$| | 1 |
| C04_10 | |$26.42^{+0.08}_{-0.11}$| | |$-20.41^{+0.08}_{-0.11}$| | |$0.76^{+0.04}_{-0.03}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.35^{+0.09}_{-0.11}$| | |$0.69^{+0.04}_{-0.04}$| | |$26.19^{+0.09}_{-0.12}$| | |$-20.64^{+0.09}_{-0.12}$| | |$0.52^{+0.08}_{-0.04}$| | |$0.68^{+0.11}_{-0.06}$| | |$0.75^{+0.11}_{-0.07}$| | 1 |
| C05_01 | |$26.94^{+0.06}_{-0.07}$| | |$-19.32^{+0.06}_{-0.07}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.50^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.58^{+0.02}_{-0.02}$| | |$2.17^{+0.12}_{-0.10}$| | — | 2 |
| C05_04 | |$25.74^{+0.09}_{-0.11}$| | |$-20.66^{+0.09}_{-0.11}$| | |$0.97^{+0.02}_{-0.01}$| | |$25.35^{+0.05}_{-0.07}$| | |$-21.05^{+0.05}_{-0.07}$| | |$1.00^{+0.03}_{-0.03}$| | |$24.80^{+0.04}_{-0.04}$| | |$-21.60^{+0.04}_{-0.04}$| | |$0.87^{+0.03}_{-0.02}$| | |$0.89^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C05_05 | |$26.49^{+0.04}_{-0.05}$| | |$-20.45^{+0.04}_{-0.05}$| | |$0.18^{+0.01}_{-0.01}$| | |$26.09^{+0.03}_{-0.03}$| | |$-20.85^{+0.03}_{-0.03}$| | |$0.31^{+0.03}_{-0.03}$| | |$25.68^{+0.02}_{-0.03}$| | |$-21.26^{+0.02}_{-0.03}$| | |$0.19^{+0.02}_{-0.01}$| | |$1.05^{+0.11}_{-0.08}$| | |$0.61^{+0.13}_{-0.13}$| | 2 |
| C05_06 | |$26.49^{+0.04}_{-0.05}$| | |$-20.37^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.45^{+0.05}_{-0.05}$| | |$-20.41^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.03}$| | |$26.65^{+0.04}_{-0.04}$| | |$-20.22^{+0.04}_{-0.04}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.94^{+0.09}_{-0.09}$| | |$0.94^{+0.11}_{-0.13}$| | 1 |
| C05_07 | |$25.96^{+0.02}_{-0.03}$| | |$-20.95^{+0.02}_{-0.03}$| | |$0.35^{+0.01}_{-0.00}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.89^{+0.03}_{-0.03}$| | |$0.30^{+0.03}_{-0.03}$| | |$25.82^{+0.03}_{-0.03}$| | |$-21.10^{+0.03}_{-0.03}$| | |$0.29^{+0.01}_{-0.01}$| | |$0.83^{+0.04}_{-0.04}$| | |$0.96^{+0.09}_{-0.10}$| | 1 |
| C05_08 | |$26.28^{+0.08}_{-0.11}$| | |$-20.71^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.02}$| | |$26.10^{+0.06}_{-0.07}$| | |$-20.89^{+0.06}_{-0.07}$| | |$0.73^{+0.06}_{-0.05}$| | |$25.99^{+0.05}_{-0.06}$| | |$-21.00^{+0.05}_{-0.06}$| | |$0.43^{+0.03}_{-0.03}$| | |$0.73^{+0.05}_{-0.05}$| | |$0.59^{+0.07}_{-0.07}$| | 2 |
| C05_09 | |$26.62^{+0.04}_{-0.05}$| | |$-20.19^{+0.04}_{-0.05}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.58^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.26^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C06_01 | |$26.15^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.38^{+0.02}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-21.13^{+0.04}_{-0.05}$| | |$0.81^{+0.03}_{-0.02}$| | |$24.75^{+0.04}_{-0.04}$| | |$-21.85^{+0.04}_{-0.04}$| | |$0.80^{+0.03}_{-0.02}$| | |$2.09^{+0.12}_{-0.09}$| | |$0.98^{+0.10}_{-0.08}$| | 2 |
| C06_02 | |$26.61^{+0.08}_{-0.11}$| | |$-20.10^{+0.08}_{-0.11}$| | |$0.55^{+0.03}_{-0.02}$| | |$26.77^{+0.09}_{-0.08}$| | |$-19.94^{+0.09}_{-0.08}$| | |$0.37^{+0.03}_{-0.04}$| | — | — | — | — | — | 2 |
| C06_03 | |$26.90^{+0.13}_{-0.18}$| | |$-19.81^{+0.13}_{-0.18}$| | |$0.49^{+0.07}_{-0.04}$| | |$26.95^{+0.09}_{-0.08}$| | |$-19.76^{+0.09}_{-0.08}$| | |$0.40^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C06_05 | |$26.61^{+0.04}_{-0.05}$| | |$-20.50^{+0.04}_{-0.05}$| | |$0.07^{+0.01}_{-0.01}$| | |$26.42^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.18^{+0.03}_{-0.03}$| | |$25.61^{+0.02}_{-0.03}$| | |$-21.50^{+0.02}_{-0.03}$| | |$0.24^{+0.02}_{-0.01}$| | |$3.21^{+0.44}_{-0.34}$| | |$1.33^{+0.51}_{-0.49}$| | 2 |
| C06_06 | |$26.63^{+0.04}_{-0.05}$| | |$-19.84^{+0.04}_{-0.05}$| | |$0.09^{+0.01}_{-0.01}$| | |$26.31^{+0.05}_{-0.05}$| | |$-20.17^{+0.05}_{-0.05}$| | |$0.25^{+0.03}_{-0.03}$| | — | — | — | — | — | 2 |
| C06_09 | |$26.21^{+0.08}_{-0.11}$| | |$-20.19^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.51^{+0.09}_{-0.12}$| | |$-19.89^{+0.09}_{-0.12}$| | |$0.55^{+0.03}_{-0.04}$| | |$0.92^{+0.06}_{-0.06}$| | |$1.02^{+0.08}_{-0.09}$| | 1 |
| C06_10 | |$25.46^{+0.06}_{-0.07}$| | |$-20.94^{+0.06}_{-0.07}$| | |$0.99^{+0.02}_{-0.01}$| | |$25.53^{+0.05}_{-0.07}$| | |$-20.87^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.03}$| | |$25.84^{+0.05}_{-0.06}$| | |$-20.56^{+0.05}_{-0.06}$| | |$0.92^{+0.03}_{-0.02}$| | |$0.93^{+0.04}_{-0.03}$| | |$0.96^{+0.04}_{-0.03}$| | 1 |
| C06_11 | |$25.34^{+0.03}_{-0.04}$| | |$-21.05^{+0.03}_{-0.04}$| | |$0.79^{+0.01}_{-0.01}$| | |$25.34^{+0.04}_{-0.05}$| | |$-21.06^{+0.04}_{-0.05}$| | |$0.81^{+0.02}_{-0.02}$| | |$25.69^{+0.05}_{-0.06}$| | |$-20.71^{+0.05}_{-0.06}$| | |$0.73^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.90^{+0.04}_{-0.03}$| | 1 |
| C06_12 | |$26.41^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.61^{+0.03}_{-0.02}$| | |$26.00^{+0.06}_{-0.07}$| | |$-20.40^{+0.06}_{-0.07}$| | |$0.93^{+0.07}_{-0.07}$| | |$25.52^{+0.05}_{-0.07}$| | |$-20.88^{+0.05}_{-0.07}$| | |$1.01^{+0.03}_{-0.02}$| | |$1.66^{+0.10}_{-0.07}$| | |$1.09^{+0.14}_{-0.12}$| | 2 |
| C06_13 | |$26.10^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.80^{+0.04}_{-0.03}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.73^{+0.06}_{-0.07}$| | |$0.83^{+0.03}_{-0.02}$| | |$25.68^{+0.07}_{-0.10}$| | |$-21.01^{+0.07}_{-0.10}$| | |$0.88^{+0.03}_{-0.02}$| | |$1.10^{+0.07}_{-0.05}$| | |$1.06^{+0.05}_{-0.04}$| | 2 |
| C06_15 | |$27.51^{+0.11}_{-0.14}$| | |$-19.32^{+0.11}_{-0.14}$| | |$0.14^{+0.04}_{-0.03}$| | |$27.18^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.30^{+0.08}_{-0.06}$| | — | — | — | — | — | 2 |
| C06_16 | |$26.50^{+0.04}_{-0.05}$| | |$-20.39^{+0.04}_{-0.05}$| | |$0.14^{+0.01}_{-0.01}$| | |$26.59^{+0.05}_{-0.05}$| | |$-20.30^{+0.05}_{-0.05}$| | |$0.10^{+0.03}_{-0.03}$| | |$26.64^{+0.04}_{-0.04}$| | |$-20.25^{+0.04}_{-0.04}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.25^{+0.20}_{-0.19}$| | |$1.80^{+0.41}_{-0.40}$| | 1 |
| C07_01 | |$26.90^{+0.06}_{-0.07}$| | |$-19.66^{+0.06}_{-0.07}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.70^{+0.09}_{-0.08}$| | |$0.23^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C07_02 | |$25.01^{+0.01}_{-0.02}$| | |$-21.31^{+0.01}_{-0.02}$| | |$0.32^{+0.00}_{-0.00}$| | |$25.02^{+0.02}_{-0.02}$| | |$-21.30^{+0.02}_{-0.02}$| | |$0.35^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_04 | |$25.61^{+0.06}_{-0.07}$| | |$-20.79^{+0.06}_{-0.07}$| | |$1.66^{+0.05}_{-0.04}$| | |$25.75^{+0.08}_{-0.10}$| | |$-20.65^{+0.08}_{-0.10}$| | |$1.45^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_06 | |$26.70^{+0.04}_{-0.05}$| | |$-19.70^{+0.04}_{-0.05}$| | |$0.24^{+0.01}_{-0.01}$| | |$25.70^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_07 | |$25.70^{+0.09}_{-0.11}$| | |$-20.70^{+0.09}_{-0.11}$| | |$1.49^{+0.04}_{-0.03}$| | |$25.76^{+0.08}_{-0.10}$| | |$-20.64^{+0.08}_{-0.10}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_08 | |$26.68^{+0.08}_{-0.11}$| | |$-19.72^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.54^{+0.09}_{-0.08}$| | |$0.44^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_09 | |$25.34^{+0.01}_{-0.02}$| | |$-21.06^{+0.01}_{-0.02}$| | |$0.40^{+0.01}_{-0.01}$| | |$25.39^{+0.02}_{-0.02}$| | |$-21.01^{+0.02}_{-0.02}$| | |$0.36^{+0.02}_{-0.01}$| | — | — | — | — | — | 1 |
| C07_10 | |$26.24^{+0.08}_{-0.11}$| | |$-20.16^{+0.08}_{-0.11}$| | |$0.68^{+0.03}_{-0.02}$| | |$26.21^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.60^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_12 | |$26.28^{+0.08}_{-0.11}$| | |$-20.12^{+0.08}_{-0.11}$| | |$0.58^{+0.02}_{-0.01}$| | |$26.20^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.63^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_13 | |$25.32^{+0.03}_{-0.04}$| | |$-21.08^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$24.53^{+0.05}_{-0.07}$| | |$-21.87^{+0.05}_{-0.07}$| | |$1.18^{+0.04}_{-0.03}$| | — | — | — | — | — | 2 |
| C07_14 | |$25.81^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.72^{+0.01}_{-0.01}$| | |$25.82^{+0.06}_{-0.07}$| | |$-20.58^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | — | — | — | — | — | 1 |
| C07_15 | |$26.95^{+0.06}_{-0.07}$| | |$-19.75^{+0.06}_{-0.07}$| | |$0.31^{+0.01}_{-0.01}$| | |$26.77^{+0.15}_{-0.17}$| | |$-19.93^{+0.15}_{-0.17}$| | |$0.43^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_16 | |$26.63^{+0.08}_{-0.11}$| | |$-20.23^{+0.08}_{-0.11}$| | |$0.65^{+0.03}_{-0.02}$| | |$25.82^{+0.08}_{-0.10}$| | |$-21.05^{+0.08}_{-0.10}$| | |$1.36^{+0.05}_{-0.04}$| | — | — | — | — | — | 2 |
| C08_01 | |$25.87^{+0.02}_{-0.03}$| | |$-21.40^{+0.02}_{-0.03}$| | |$0.13^{+0.00}_{-0.00}$| | |$24.89^{+0.04}_{-0.05}$| | |$-22.38^{+0.04}_{-0.05}$| | |$0.53^{+0.01}_{-0.01}$| | |$24.01^{+0.02}_{-0.03}$| | |$-23.25^{+0.02}_{-0.03}$| | |$0.28^{+0.01}_{-0.01}$| | |$2.21^{+0.11}_{-0.10}$| | |$0.53^{+0.12}_{-0.11}$| | 2 |
| C08_02 | |$27.52^{+0.11}_{-0.14}$| | |$-19.46^{+0.11}_{-0.14}$| | |$0.23^{+0.03}_{-0.02}$| | |$27.40^{+0.14}_{-0.17}$| | |$-19.57^{+0.14}_{-0.17}$| | |$0.35^{+0.13}_{-0.06}$| | — | — | — | — | — | 1 |
| C08_03 | |$27.02^{+0.06}_{-0.07}$| | |$-19.38^{+0.06}_{-0.07}$| | |$0.15^{+0.04}_{-0.03}$| | |$26.74^{+0.05}_{-0.05}$| | |$-19.66^{+0.05}_{-0.05}$| | |$0.30^{+0.03}_{-0.03}$| | |$26.87^{+0.08}_{-0.12}$| | |$-19.53^{+0.08}_{-0.12}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.22^{+0.40}_{-0.32}$| | |$0.60^{+0.25}_{-0.25}$| | 2 |
| C08_04 | |$26.55^{+0.04}_{-0.05}$| | |$-19.85^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.43^{+0.05}_{-0.07}$| | |$-20.97^{+0.05}_{-0.07}$| | |$1.02^{+0.03}_{-0.02}$| | |$3.84^{+0.20}_{-0.15}$| | — | 1 |
| C08_05 | |$24.75^{+0.06}_{-0.07}$| | |$-21.65^{+0.06}_{-0.07}$| | |$0.98^{+0.02}_{-0.01}$| | |$24.73^{+0.05}_{-0.07}$| | |$-21.67^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$23.11^{+0.04}_{-0.04}$| | |$-23.29^{+0.04}_{-0.04}$| | |$0.93^{+0.03}_{-0.02}$| | |$0.96^{+0.04}_{-0.03}$| | |$0.89^{+0.04}_{-0.03}$| | 2 |
| C08_06 | |$26.06^{+0.02}_{-0.03}$| | |$-20.34^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$24.84^{+0.05}_{-0.07}$| | |$-21.56^{+0.05}_{-0.07}$| | |$1.21^{+0.04}_{-0.03}$| | |$23.64^{+0.05}_{-0.07}$| | |$-22.76^{+0.05}_{-0.07}$| | |$1.29^{+0.04}_{-0.03}$| | |$6.15^{+0.38}_{-0.30}$| | |$1.07^{+0.26}_{-0.21}$| | 2 |
| C08_07 | |$25.37^{+0.03}_{-0.04}$| | |$-21.02^{+0.03}_{-0.04}$| | |$0.93^{+0.02}_{-0.01}$| | |$25.52^{+0.04}_{-0.05}$| | |$-20.88^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.22^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$0.85^{+0.03}_{-0.02}$| | |$1.00^{+0.03}_{-0.03}$| | 2 |
| C08_08 | |$25.72^{+0.03}_{-0.04}$| | |$-20.68^{+0.03}_{-0.04}$| | |$0.90^{+0.02}_{-0.01}$| | |$25.40^{+0.05}_{-0.07}$| | |$-21.00^{+0.05}_{-0.07}$| | |$1.17^{+0.04}_{-0.03}$| | |$23.71^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$0.97^{+0.03}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.83^{+0.05}_{-0.04}$| | 2 |
| C08_09 | |$25.79^{+0.09}_{-0.11}$| | |$-20.61^{+0.09}_{-0.11}$| | |$1.10^{+0.03}_{-0.02}$| | |$25.83^{+0.08}_{-0.10}$| | |$-20.57^{+0.08}_{-0.10}$| | |$1.12^{+0.04}_{-0.03}$| | |$25.09^{+0.04}_{-0.04}$| | |$-21.31^{+0.04}_{-0.04}$| | |$0.54^{+0.02}_{-0.02}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.48^{+0.02}_{-0.02}$| | 1 |
| C08_10 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.38^{+0.02}_{-0.01}$| | |$26.02^{+0.06}_{-0.07}$| | |$-20.38^{+0.06}_{-0.07}$| | |$0.55^{+0.03}_{-0.04}$| | |$25.49^{+0.04}_{-0.04}$| | |$-20.91^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$2.11^{+0.12}_{-0.09}$| | |$1.45^{+0.14}_{-0.16}$| | 2 |
| C08_11 | |$24.25^{+0.06}_{-0.07}$| | |$-22.15^{+0.06}_{-0.07}$| | |$1.28^{+0.03}_{-0.02}$| | |$24.16^{+0.05}_{-0.07}$| | |$-22.24^{+0.05}_{-0.07}$| | |$1.49^{+0.05}_{-0.04}$| | |$23.59^{+0.05}_{-0.07}$| | |$-22.81^{+0.05}_{-0.07}$| | |$1.30^{+0.04}_{-0.03}$| | |$1.01^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_12 | |$25.93^{+0.05}_{-0.07}$| | |$-20.47^{+0.05}_{-0.07}$| | |$0.84^{+0.02}_{-0.01}$| | |$25.45^{+0.05}_{-0.07}$| | |$-20.95^{+0.05}_{-0.07}$| | |$1.03^{+0.03}_{-0.03}$| | |$24.55^{+0.05}_{-0.07}$| | |$-21.85^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.02}$| | |$1.15^{+0.04}_{-0.03}$| | |$0.94^{+0.05}_{-0.04}$| | 2 |
| C08_13 | |$25.68^{+0.01}_{-0.02}$| | |$-20.71^{+0.01}_{-0.02}$| | |$0.20^{+0.00}_{-0.00}$| | |$25.50^{+0.02}_{-0.02}$| | |$-20.90^{+0.02}_{-0.02}$| | |$0.34^{+0.01}_{-0.02}$| | |$25.41^{+0.02}_{-0.03}$| | |$-20.99^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$2.09^{+0.09}_{-0.09}$| | |$1.25^{+0.12}_{-0.12}$| | 2 |
| C08_14 | |$26.11^{+0.05}_{-0.07}$| | |$-20.29^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.04^{+0.06}_{-0.07}$| | |$-20.36^{+0.06}_{-0.07}$| | |$0.61^{+0.05}_{-0.05}$| | |$24.84^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.52^{+0.02}_{-0.02}$| | |$0.99^{+0.05}_{-0.04}$| | |$0.85^{+0.09}_{-0.09}$| | 2 |
| C08_15 | |$25.20^{+0.06}_{-0.07}$| | |$-21.49^{+0.06}_{-0.07}$| | |$0.87^{+0.02}_{-0.01}$| | |$25.19^{+0.05}_{-0.07}$| | |$-21.50^{+0.05}_{-0.07}$| | |$0.90^{+0.03}_{-0.02}$| | |$24.61^{+0.04}_{-0.04}$| | |$-22.08^{+0.04}_{-0.04}$| | |$0.78^{+0.03}_{-0.02}$| | |$0.90^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_16 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.20^{+0.07}_{-0.05}$| | |$26.09^{+0.08}_{-0.10}$| | |$-20.61^{+0.08}_{-0.10}$| | |$1.29^{+0.12}_{-0.09}$| | — | — | — | — | — | 1 |
| C08_17 | |$25.19^{+0.03}_{-0.04}$| | |$-21.51^{+0.03}_{-0.04}$| | |$0.64^{+0.01}_{-0.01}$| | |$25.22^{+0.04}_{-0.05}$| | |$-21.48^{+0.04}_{-0.05}$| | |$0.66^{+0.02}_{-0.02}$| | |$24.17^{+0.04}_{-0.04}$| | |$-22.52^{+0.04}_{-0.04}$| | |$0.83^{+0.03}_{-0.02}$| | |$1.30^{+0.05}_{-0.04}$| | |$1.27^{+0.06}_{-0.05}$| | 2 |
| C08_18 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.08^{+0.07}_{-0.05}$| | |$25.88^{+0.08}_{-0.10}$| | |$-20.81^{+0.08}_{-0.10}$| | |$1.29^{+0.04}_{-0.03}$| | |$23.81^{+0.05}_{-0.07}$| | |$-22.88^{+0.05}_{-0.07}$| | |$1.28^{+0.04}_{-0.04}$| | |$1.18^{+0.09}_{-0.06}$| | |$0.99^{+0.06}_{-0.04}$| | 2 |
| C08_19 | |$26.08^{+0.05}_{-0.07}$| | |$-20.61^{+0.05}_{-0.07}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.98^{+0.06}_{-0.07}$| | |$-20.72^{+0.06}_{-0.07}$| | |$0.60^{+0.04}_{-0.05}$| | |$23.88^{+0.04}_{-0.04}$| | |$-22.82^{+0.04}_{-0.04}$| | |$0.71^{+0.02}_{-0.02}$| | |$1.45^{+0.06}_{-0.05}$| | |$1.19^{+0.11}_{-0.12}$| | 1 |
| C08_20 | |$26.65^{+0.04}_{-0.05}$| | |$-20.04^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.67^{+0.05}_{-0.05}$| | |$-20.03^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.04}$| | |$24.63^{+0.05}_{-0.07}$| | |$-22.06^{+0.05}_{-0.07}$| | |$0.94^{+0.03}_{-0.02}$| | |$2.72^{+0.15}_{-0.11}$| | |$2.68^{+0.25}_{-0.28}$| | 1 |
| C08_21 | |$25.93^{+0.02}_{-0.03}$| | |$-20.77^{+0.02}_{-0.03}$| | |$0.22^{+0.00}_{-0.00}$| | |$25.10^{+0.04}_{-0.05}$| | |$-21.59^{+0.04}_{-0.05}$| | |$0.57^{+0.02}_{-0.02}$| | |$24.78^{+0.04}_{-0.04}$| | |$-21.92^{+0.04}_{-0.04}$| | |$0.62^{+0.02}_{-0.02}$| | |$2.74^{+0.10}_{-0.09}$| | |$1.08^{+0.12}_{-0.12}$| | 2 |
| C08_22 | |$25.41^{+0.03}_{-0.04}$| | |$-21.28^{+0.03}_{-0.04}$| | |$0.83^{+0.02}_{-0.01}$| | |$25.32^{+0.05}_{-0.07}$| | |$-21.37^{+0.05}_{-0.07}$| | |$0.99^{+0.04}_{-0.03}$| | |$24.79^{+0.04}_{-0.04}$| | |$-21.90^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$0.73^{+0.03}_{-0.02}$| | |$0.61^{+0.03}_{-0.03}$| | 1 |
| C08_23 | |$26.35^{+0.08}_{-0.11}$| | |$-20.34^{+0.08}_{-0.11}$| | |$0.45^{+0.02}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.81^{+0.03}_{-0.03}$| | |$0.31^{+0.02}_{-0.01}$| | |$0.69^{+0.05}_{-0.04}$| | |$0.78^{+0.07}_{-0.07}$| | 1 |
| C08_24 | |$26.31^{+0.08}_{-0.11}$| | |$-20.38^{+0.08}_{-0.11}$| | |$0.57^{+0.03}_{-0.02}$| | |$25.77^{+0.08}_{-0.10}$| | |$-20.92^{+0.08}_{-0.10}$| | |$0.94^{+0.03}_{-0.02}$| | |$25.33^{+0.04}_{-0.04}$| | |$-21.36^{+0.04}_{-0.04}$| | |$0.76^{+0.03}_{-0.02}$| | |$1.34^{+0.08}_{-0.06}$| | |$0.81^{+0.06}_{-0.05}$| | 2 |
| C08_25 | |$26.89^{+0.06}_{-0.07}$| | |$-20.05^{+0.06}_{-0.07}$| | |$0.13^{+0.01}_{-0.01}$| | |$26.87^{+0.09}_{-0.08}$| | |$-20.07^{+0.09}_{-0.08}$| | |$0.19^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C08_27 | |$25.74^{+0.02}_{-0.03}$| | |$-21.12^{+0.02}_{-0.03}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.68^{+0.02}_{-0.02}$| | |$-21.18^{+0.02}_{-0.02}$| | |$0.32^{+0.01}_{-0.01}$| | |$24.61^{+0.02}_{-0.03}$| | |$-22.26^{+0.02}_{-0.03}$| | |$0.38^{+0.01}_{-0.01}$| | |$1.61^{+0.07}_{-0.06}$| | |$1.20^{+0.09}_{-0.09}$| | 1 |
| C08_28 | |$26.23^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.95^{+0.06}_{-0.07}$| | |$-21.01^{+0.06}_{-0.07}$| | |$0.52^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C08_29 | |$26.61^{+0.04}_{-0.05}$| | |$-20.18^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.91^{+0.06}_{-0.07}$| | |$-20.88^{+0.06}_{-0.07}$| | |$0.55^{+0.02}_{-0.02}$| | |$25.67^{+0.05}_{-0.06}$| | |$-21.12^{+0.05}_{-0.06}$| | |$0.49^{+0.02}_{-0.01}$| | |$2.82^{+0.19}_{-0.15}$| | |$0.89^{+0.13}_{-0.12}$| | 2 |
| C08_30 | |$26.48^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.16^{+0.01}_{-0.01}$| | |$26.52^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.17^{+0.03}_{-0.02}$| | |$25.64^{+0.02}_{-0.03}$| | |$-21.58^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$1.28^{+0.11}_{-0.09}$| | |$1.25^{+0.21}_{-0.20}$| | 1 |
| C08_31 | |$27.07^{+0.06}_{-0.07}$| | |$-20.09^{+0.06}_{-0.07}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.81^{+0.15}_{-0.17}$| | |$-20.35^{+0.15}_{-0.17}$| | |$0.38^{+0.03}_{-0.03}$| | |$25.55^{+0.04}_{-0.04}$| | |$-21.61^{+0.04}_{-0.04}$| | |$0.39^{+0.01}_{-0.01}$| | |$1.54^{+0.20}_{-0.14}$| | |$1.01^{+0.12}_{-0.13}$| | 1 |
| C09_01 | |$26.13^{+0.05}_{-0.07}$| | |$-20.24^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.16^{+0.06}_{-0.07}$| | |$-20.20^{+0.06}_{-0.07}$| | |$0.50^{+0.03}_{-0.04}$| | |$25.73^{+0.05}_{-0.06}$| | |$-20.64^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$1.21^{+0.06}_{-0.05}$| | |$1.27^{+0.09}_{-0.10}$| | 1 |
| C09_02 | |$26.82^{+0.13}_{-0.18}$| | |$-19.54^{+0.13}_{-0.18}$| | |$0.63^{+0.03}_{-0.02}$| | |$26.71^{+0.15}_{-0.17}$| | |$-19.65^{+0.15}_{-0.17}$| | |$0.66^{+0.05}_{-0.05}$| | |$26.46^{+0.04}_{-0.04}$| | |$-19.90^{+0.04}_{-0.04}$| | |$0.47^{+0.03}_{-0.04}$| | |$0.74^{+0.06}_{-0.06}$| | |$0.70^{+0.08}_{-0.08}$| | 2 |
| C09_03 | |$25.88^{+0.05}_{-0.07}$| | |$-20.51^{+0.05}_{-0.07}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.86^{+0.04}_{-0.04}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.13^{+0.04}_{-0.04}$| | 1 |
| C09_04 | |$25.58^{+0.03}_{-0.04}$| | |$-20.82^{+0.03}_{-0.04}$| | |$0.52^{+0.01}_{-0.01}$| | |$25.63^{+0.04}_{-0.05}$| | |$-20.77^{+0.04}_{-0.05}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.24^{+0.02}_{-0.03}$| | |$-21.16^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.78^{+0.04}_{-0.03}$| | |$0.84^{+0.04}_{-0.04}$| | 2 |
| C09_05 | |$26.46^{+0.08}_{-0.11}$| | |$-19.94^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.08^{+0.06}_{-0.07}$| | |$-20.32^{+0.06}_{-0.07}$| | |$0.67^{+0.05}_{-0.05}$| | |$25.90^{+0.05}_{-0.06}$| | |$-20.50^{+0.05}_{-0.06}$| | |$0.64^{+0.02}_{-0.02}$| | |$1.20^{+0.06}_{-0.05}$| | |$0.96^{+0.10}_{-0.10}$| | 2 |
| C09_06 | |$25.93^{+0.02}_{-0.03}$| | |$-20.47^{+0.02}_{-0.03}$| | |$0.21^{+0.00}_{-0.00}$| | |$25.66^{+0.02}_{-0.02}$| | |$-20.74^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.86^{+0.04}_{-0.04}$| | |$-21.54^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$2.89^{+0.11}_{-0.11}$| | |$1.48^{+0.15}_{-0.14}$| | 2 |
| C09_07 | |$27.17^{+0.06}_{-0.07}$| | |$-19.23^{+0.06}_{-0.07}$| | |$0.44^{+0.07}_{-0.05}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.90^{+0.07}_{-0.07}$| | |$26.16^{+0.05}_{-0.06}$| | |$-20.24^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$1.60^{+0.34}_{-0.20}$| | |$0.78^{+0.24}_{-0.16}$| | 2 |
| C09_08 | |$26.41^{+0.08}_{-0.11}$| | |$-19.99^{+0.08}_{-0.11}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.38^{+0.05}_{-0.05}$| | |$-20.02^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.15^{+0.04}_{-0.04}$| | |$0.72^{+0.02}_{-0.02}$| | |$1.29^{+0.06}_{-0.05}$| | |$1.58^{+0.10}_{-0.12}$| | 2 |
| C10_01 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.13^{+0.03}_{-0.03}$| | |$-20.27^{+0.03}_{-0.03}$| | |$0.40^{+0.03}_{-0.04}$| | |$25.59^{+0.04}_{-0.04}$| | |$-20.81^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.99^{+0.09}_{-0.08}$| | |$1.63^{+0.18}_{-0.21}$| | 2 |
| C10_02 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.44^{+0.01}_{-0.01}$| | |$25.53^{+0.04}_{-0.05}$| | |$-20.87^{+0.04}_{-0.05}$| | |$0.63^{+0.02}_{-0.02}$| | |$24.99^{+0.04}_{-0.04}$| | |$-21.41^{+0.04}_{-0.04}$| | |$0.47^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.04}$| | |$0.75^{+0.05}_{-0.05}$| | 1 |
| C10_03 | |$25.44^{+0.03}_{-0.04}$| | |$-20.96^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-20.93^{+0.04}_{-0.05}$| | |$0.58^{+0.02}_{-0.01}$| | |$24.89^{+0.04}_{-0.04}$| | |$-21.51^{+0.04}_{-0.04}$| | |$0.73^{+0.02}_{-0.02}$| | |$1.21^{+0.04}_{-0.04}$| | |$1.26^{+0.05}_{-0.04}$| | 2 |
| C10_04 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.15^{+0.06}_{-0.07}$| | |$-20.25^{+0.06}_{-0.07}$| | |$0.58^{+0.03}_{-0.04}$| | |$26.72^{+0.04}_{-0.04}$| | |$-19.68^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$0.62^{+0.08}_{-0.07}$| | |$0.47^{+0.08}_{-0.08}$| | 2 |
| C10_05 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.49^{+0.01}_{-0.01}$| | |$25.40^{+0.04}_{-0.05}$| | |$-21.00^{+0.04}_{-0.05}$| | |$0.59^{+0.02}_{-0.01}$| | |$25.67^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.84^{+0.04}_{-0.03}$| | |$0.70^{+0.04}_{-0.04}$| | 2 |
| C10_06 | |$26.40^{+0.15}_{-0.18}$| | |$-20.00^{+0.15}_{-0.18}$| | |$1.12^{+0.08}_{-0.05}$| | |$26.37^{+0.14}_{-0.15}$| | |$-20.03^{+0.14}_{-0.15}$| | |$0.96^{+0.07}_{-0.07}$| | |$26.22^{+0.09}_{-0.12}$| | |$-20.17^{+0.09}_{-0.12}$| | |$0.77^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.80^{+0.09}_{-0.06}$| | 2 |
| C10_07 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$25.72^{+0.04}_{-0.05}$| | |$-20.68^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.51^{+0.04}_{-0.04}$| | |$-20.89^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$1.79^{+0.09}_{-0.07}$| | |$0.89^{+0.08}_{-0.07}$| | 2 |
| C10_08 | |$26.03^{+0.05}_{-0.07}$| | |$-20.37^{+0.05}_{-0.07}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.12^{+0.06}_{-0.07}$| | |$-20.28^{+0.06}_{-0.07}$| | |$0.48^{+0.03}_{-0.04}$| | |$25.37^{+0.04}_{-0.04}$| | |$-21.03^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.02}$| | |$0.92^{+0.04}_{-0.04}$| | |$1.07^{+0.07}_{-0.08}$| | 1 |
| C10_09 | |$24.91^{+0.03}_{-0.04}$| | |$-22.03^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$25.00^{+0.04}_{-0.05}$| | |$-21.93^{+0.04}_{-0.05}$| | |$0.56^{+0.02}_{-0.02}$| | |$23.99^{+0.04}_{-0.04}$| | |$-22.95^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.15^{+0.04}_{-0.04}$| | 2 |
| C10_10 | |$25.41^{+0.01}_{-0.02}$| | |$-21.48^{+0.01}_{-0.02}$| | |$0.16^{+0.00}_{-0.00}$| | |$25.48^{+0.02}_{-0.02}$| | |$-21.41^{+0.02}_{-0.02}$| | |$0.14^{+0.01}_{-0.01}$| | |$25.42^{+0.02}_{-0.03}$| | |$-21.46^{+0.02}_{-0.03}$| | |$0.16^{+0.02}_{-0.01}$| | |$0.95^{+0.10}_{-0.08}$| | |$1.10^{+0.13}_{-0.12}$| | 1 |
| . | F150W . | F150W (PSF matched) . | F444W . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | Flag . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mUV . | MUV . | re . | mUV . | MUV . | re . | mopt . | Mopt . | re, opt . | . | (PSF matched) . | . |
| ID . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . |
| C01_02 | |$26.57^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$26.62^{+0.05}_{-0.05}$| | |$-20.68^{+0.05}_{-0.05}$| | |$0.13^{+0.02}_{-0.02}$| | |$26.77^{+0.08}_{-0.12}$| | |$-20.53^{+0.08}_{-0.12}$| | |$0.23^{+0.02}_{-0.02}$| | |$1.36^{+0.15}_{-0.14}$| | |$1.77^{+0.28}_{-0.28}$| | 1 |
| C01_03 | |$27.68^{+0.20}_{-0.22}$| | |$-19.28^{+0.20}_{-0.22}$| | |$0.03^{+0.03}_{-0.02}$| | — | — | — | |$26.96^{+0.08}_{-0.12}$| | |$-20.00^{+0.08}_{-0.12}$| | |$0.12^{+0.12}_{-0.09}$| | |$4.44^{+7.25}_{-5.30}$| | — | 1 |
| C01_05 | |$26.42^{+0.04}_{-0.05}$| | |$-20.01^{+0.04}_{-0.05}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.65^{+0.04}_{-0.05}$| | |$-20.78^{+0.04}_{-0.05}$| | |$0.80^{+0.02}_{-0.02}$| | |$24.87^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$2.14^{+0.12}_{-0.10}$| | |$0.97^{+0.08}_{-0.07}$| | 2 |
| C01_06 | |$26.60^{+0.04}_{-0.05}$| | |$-19.67^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.01^{+0.09}_{-0.11}$| | |$0.49^{+0.04}_{-0.04}$| | |$26.45^{+0.04}_{-0.04}$| | |$-19.81^{+0.04}_{-0.04}$| | |$0.36^{+0.03}_{-0.03}$| | |$1.34^{+0.13}_{-0.13}$| | |$0.74^{+0.15}_{-0.16}$| | 1 |
| C01_07 | |$25.62^{+0.01}_{-0.02}$| | |$-20.66^{+0.01}_{-0.02}$| | |$0.26^{+0.00}_{-0.00}$| | |$25.55^{+0.02}_{-0.02}$| | |$-20.73^{+0.02}_{-0.02}$| | |$0.30^{+0.02}_{-0.02}$| | |$25.48^{+0.02}_{-0.03}$| | |$-20.79^{+0.02}_{-0.03}$| | |$0.29^{+0.02}_{-0.02}$| | |$1.13^{+0.08}_{-0.07}$| | |$0.97^{+0.10}_{-0.09}$| | 1 |
| C01_08 | |$25.78^{+0.05}_{-0.07}$| | |$-20.62^{+0.05}_{-0.07}$| | |$0.48^{+0.01}_{-0.01}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.54^{+0.03}_{-0.03}$| | |$0.42^{+0.02}_{-0.01}$| | |$25.46^{+0.04}_{-0.04}$| | |$-20.93^{+0.04}_{-0.04}$| | |$0.48^{+0.02}_{-0.02}$| | |$1.00^{+0.04}_{-0.03}$| | |$1.14^{+0.05}_{-0.05}$| | 1 |
| C01_09 | |$24.83^{+0.03}_{-0.04}$| | |$-21.57^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$24.75^{+0.04}_{-0.05}$| | |$-21.65^{+0.04}_{-0.05}$| | |$0.72^{+0.02}_{-0.02}$| | |$23.41^{+0.04}_{-0.04}$| | |$-22.99^{+0.04}_{-0.04}$| | |$0.75^{+0.02}_{-0.02}$| | |$1.26^{+0.04}_{-0.04}$| | |$1.04^{+0.05}_{-0.05}$| | 1 |
| C01_10 | |$25.94^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.37^{+0.01}_{-0.01}$| | |$25.67^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.55^{+0.02}_{-0.01}$| | |$25.38^{+0.04}_{-0.04}$| | |$-21.02^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$1.58^{+0.07}_{-0.06}$| | |$1.07^{+0.07}_{-0.07}$| | 2 |
| C01_11 | |$26.36^{+0.08}_{-0.11}$| | |$-20.04^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_12 | |$26.66^{+0.04}_{-0.05}$| | |$-19.74^{+0.04}_{-0.05}$| | |$0.37^{+0.02}_{-0.01}$| | |$26.44^{+0.05}_{-0.05}$| | |$-19.96^{+0.05}_{-0.05}$| | |$0.37^{+0.03}_{-0.04}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.50^{+0.03}_{-0.04}$| | |$1.35^{+0.11}_{-0.11}$| | |$1.35^{+0.15}_{-0.17}$| | 2 |
| C01_13 | |$26.33^{+0.15}_{-0.18}$| | |$-20.06^{+0.15}_{-0.18}$| | |$1.02^{+0.05}_{-0.04}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.15^{+0.09}_{-0.11}$| | |$0.81^{+0.05}_{-0.05}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.87^{+0.10}_{-0.06}$| | 2 |
| C01_14 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.20^{+0.01}_{-0.01}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.37^{+0.03}_{-0.03}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.22^{+0.03}_{-0.03}$| | |$-20.18^{+0.03}_{-0.03}$| | |$0.37^{+0.03}_{-0.04}$| | |$1.89^{+0.20}_{-0.20}$| | |$0.90^{+0.23}_{-0.26}$| | 2 |
| C01_15 | |$26.42^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.66^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_16 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.51^{+0.04}_{-0.05}$| | |$-20.89^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$24.56^{+0.05}_{-0.07}$| | |$-21.84^{+0.05}_{-0.07}$| | |$1.11^{+0.04}_{-0.03}$| | |$1.45^{+0.05}_{-0.04}$| | |$1.52^{+0.06}_{-0.06}$| | 1 |
| C01_17 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.50^{+0.03}_{-0.03}$| | |$0.39^{+0.02}_{-0.01}$| | |$25.37^{+0.02}_{-0.03}$| | |$-21.03^{+0.02}_{-0.03}$| | |$0.22^{+0.02}_{-0.02}$| | |$1.26^{+0.14}_{-0.11}$| | |$0.56^{+0.12}_{-0.10}$| | 2 |
| C01_18 | |$26.09^{+0.05}_{-0.07}$| | |$-20.30^{+0.05}_{-0.07}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.18^{+0.06}_{-0.07}$| | |$-20.22^{+0.06}_{-0.07}$| | |$0.49^{+0.03}_{-0.04}$| | |$25.97^{+0.05}_{-0.06}$| | |$-20.43^{+0.05}_{-0.06}$| | |$0.49^{+0.03}_{-0.04}$| | |$0.84^{+0.06}_{-0.06}$| | |$1.00^{+0.08}_{-0.09}$| | 2 |
| C01_19 | |$25.06^{+0.03}_{-0.04}$| | |$-21.63^{+0.03}_{-0.04}$| | |$0.78^{+0.02}_{-0.01}$| | |$24.71^{+0.05}_{-0.07}$| | |$-21.98^{+0.05}_{-0.07}$| | |$1.20^{+0.04}_{-0.03}$| | |$24.00^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$1.36^{+0.05}_{-0.04}$| | |$0.88^{+0.07}_{-0.05}$| | 2 |
| C01_20 | |$25.27^{+0.03}_{-0.04}$| | |$-21.43^{+0.03}_{-0.04}$| | |$0.75^{+0.01}_{-0.01}$| | |$25.25^{+0.04}_{-0.05}$| | |$-21.45^{+0.04}_{-0.05}$| | |$0.78^{+0.03}_{-0.02}$| | |$24.32^{+0.04}_{-0.04}$| | |$-22.37^{+0.04}_{-0.04}$| | |$0.70^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.89^{+0.04}_{-0.04}$| | 1 |
| C01_22 | |$27.22^{+0.06}_{-0.07}$| | |$-20.10^{+0.06}_{-0.07}$| | |$0.10^{+0.03}_{-0.02}$| | |$27.22^{+0.09}_{-0.08}$| | |$-20.09^{+0.09}_{-0.08}$| | |$0.11^{+0.07}_{-0.05}$| | — | — | — | — | — | 1 |
| C01_26 | |$26.38^{+0.08}_{-0.11}$| | |$-20.68^{+0.08}_{-0.11}$| | |$0.42^{+0.01}_{-0.01}$| | |$25.93^{+0.06}_{-0.07}$| | |$-21.13^{+0.06}_{-0.07}$| | |$0.65^{+0.02}_{-0.02}$| | |$25.45^{+0.05}_{-0.07}$| | |$-21.61^{+0.05}_{-0.07}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.89^{+0.09}_{-0.07}$| | |$1.21^{+0.07}_{-0.06}$| | 2 |
| C02_01 | |$27.82^{+0.20}_{-0.22}$| | |$-18.79^{+0.20}_{-0.22}$| | |$0.07^{+0.04}_{-0.03}$| | |$27.85^{+0.21}_{-0.27}$| | |$-18.76^{+0.21}_{-0.27}$| | |$0.10^{+0.09}_{-0.07}$| | |$27.20^{+0.16}_{-0.19}$| | |$-19.40^{+0.16}_{-0.19}$| | |$0.14^{+0.14}_{-0.10}$| | |$1.91^{+2.13}_{-1.60}$| | |$1.36^{+2.48}_{-1.92}$| | 1 |
| C02_02 | |$26.60^{+0.04}_{-0.05}$| | |$-19.89^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-19.79^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.99^{+0.03}_{-0.03}$| | |$-20.49^{+0.03}_{-0.03}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.78^{+0.08}_{-0.07}$| | |$0.86^{+0.10}_{-0.11}$| | 1 |
| C02_03 | |$26.67^{+0.08}_{-0.11}$| | |$-19.67^{+0.08}_{-0.11}$| | |$0.50^{+0.02}_{-0.01}$| | |$25.89^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.95^{+0.03}_{-0.03}$| | |$25.81^{+0.05}_{-0.06}$| | |$-20.53^{+0.05}_{-0.06}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.59^{+0.07}_{-0.06}$| | |$0.83^{+0.07}_{-0.06}$| | 2 |
| C02_04 | |$25.01^{+0.01}_{-0.02}$| | |$-21.39^{+0.01}_{-0.02}$| | |$0.35^{+0.00}_{-0.00}$| | |$24.97^{+0.02}_{-0.02}$| | |$-21.43^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.49^{+0.02}_{-0.03}$| | |$-21.91^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$1.18^{+0.05}_{-0.05}$| | |$1.01^{+0.07}_{-0.06}$| | 1 |
| C02_05 | |$26.43^{+0.08}_{-0.11}$| | |$-19.97^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | |$26.60^{+0.09}_{-0.11}$| | |$-19.79^{+0.09}_{-0.11}$| | |$0.63^{+0.05}_{-0.05}$| | |$25.61^{+0.04}_{-0.04}$| | |$-20.78^{+0.04}_{-0.04}$| | |$0.84^{+0.03}_{-0.02}$| | |$1.02^{+0.05}_{-0.04}$| | |$1.33^{+0.09}_{-0.09}$| | 1 |
| C02_06 | |$26.33^{+0.08}_{-0.11}$| | |$-20.07^{+0.08}_{-0.11}$| | |$0.70^{+0.03}_{-0.02}$| | |$26.31^{+0.09}_{-0.11}$| | |$-20.08^{+0.09}_{-0.11}$| | |$0.74^{+0.05}_{-0.05}$| | |$25.86^{+0.05}_{-0.06}$| | |$-20.54^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$0.89^{+0.05}_{-0.04}$| | |$0.85^{+0.07}_{-0.07}$| | 1 |
| C02_07 | |$25.71^{+0.05}_{-0.07}$| | |$-20.69^{+0.05}_{-0.07}$| | |$0.80^{+0.01}_{-0.01}$| | |$25.71^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.85^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$0.74^{+0.03}_{-0.03}$| | |$0.69^{+0.04}_{-0.03}$| | 1 |
| C02_08 | |$26.04^{+0.02}_{-0.03}$| | |$-20.35^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.05^{+0.03}_{-0.03}$| | |$-20.35^{+0.03}_{-0.03}$| | |$0.36^{+0.03}_{-0.04}$| | |$25.76^{+0.03}_{-0.03}$| | |$-20.64^{+0.03}_{-0.03}$| | |$0.32^{+0.02}_{-0.02}$| | |$0.94^{+0.07}_{-0.05}$| | |$0.88^{+0.11}_{-0.11}$| | 1 |
| C02_09 | |$25.28^{+0.06}_{-0.07}$| | |$-21.12^{+0.06}_{-0.07}$| | |$1.08^{+0.03}_{-0.02}$| | |$25.26^{+0.05}_{-0.07}$| | |$-21.14^{+0.05}_{-0.07}$| | |$1.13^{+0.04}_{-0.03}$| | |$24.31^{+0.05}_{-0.07}$| | |$-22.09^{+0.05}_{-0.07}$| | |$0.95^{+0.03}_{-0.02}$| | |$0.88^{+0.04}_{-0.03}$| | |$0.85^{+0.04}_{-0.03}$| | 1 |
| C02_10 | |$26.82^{+0.06}_{-0.07}$| | |$-19.58^{+0.06}_{-0.07}$| | |$0.28^{+0.01}_{-0.01}$| | |$26.37^{+0.09}_{-0.11}$| | |$-20.03^{+0.09}_{-0.11}$| | |$0.53^{+0.03}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.45^{+0.05}_{-0.06}$| | |$0.51^{+0.03}_{-0.04}$| | |$1.78^{+0.13}_{-0.14}$| | |$0.96^{+0.16}_{-0.18}$| | 2 |
| C02_12 | |$26.37^{+0.08}_{-0.11}$| | |$-20.33^{+0.08}_{-0.11}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.38^{+0.09}_{-0.11}$| | |$-20.31^{+0.09}_{-0.11}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.44^{+0.04}_{-0.04}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.08^{+0.05}_{-0.04}$| | |$1.05^{+0.07}_{-0.08}$| | 1 |
| C02_13 | |$26.77^{+0.13}_{-0.18}$| | |$-19.92^{+0.13}_{-0.18}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.83^{+0.15}_{-0.17}$| | |$-19.86^{+0.15}_{-0.17}$| | |$0.48^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C02_14 | |$27.34^{+0.11}_{-0.14}$| | |$-19.93^{+0.11}_{-0.14}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.84^{+0.09}_{-0.08}$| | |$-20.43^{+0.09}_{-0.08}$| | |$0.34^{+0.02}_{-0.03}$| | |$25.60^{+0.02}_{-0.03}$| | |$-21.68^{+0.02}_{-0.03}$| | |$0.13^{+0.01}_{-0.01}$| | |$0.52^{+0.08}_{-0.06}$| | |$0.39^{+0.07}_{-0.06}$| | 2 |
| C02_15 | |$27.57^{+0.11}_{-0.14}$| | |$-19.75^{+0.11}_{-0.14}$| | |$0.05^{+0.03}_{-0.02}$| | |$27.64^{+0.14}_{-0.17}$| | |$-19.68^{+0.14}_{-0.17}$| | |$0.09^{+0.07}_{-0.05}$| | |$25.67^{+0.02}_{-0.03}$| | |$-21.64^{+0.02}_{-0.03}$| | |$0.05^{+0.01}_{-0.01}$| | |$1.13^{+0.76}_{-0.55}$| | |$0.60^{+0.87}_{-0.69}$| | 1 |
| C02_20 | |$26.71^{+0.13}_{-0.18}$| | |$-20.21^{+0.13}_{-0.18}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.82^{+0.15}_{-0.17}$| | |$-20.10^{+0.15}_{-0.17}$| | |$0.40^{+0.03}_{-0.03}$| | |$25.90^{+0.05}_{-0.06}$| | |$-21.02^{+0.05}_{-0.06}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.25^{+0.06}_{-0.05}$| | |$1.36^{+0.10}_{-0.11}$| | 1 |
| C02_21 | |$27.16^{+0.06}_{-0.07}$| | |$-19.76^{+0.06}_{-0.07}$| | |$0.17^{+0.03}_{-0.02}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.44^{+0.09}_{-0.11}$| | |$0.50^{+0.04}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.97^{+0.05}_{-0.06}$| | |$0.59^{+0.07}_{-0.04}$| | |$3.56^{+0.86}_{-0.58}$| | |$1.19^{+0.53}_{-0.39}$| | 2 |
| C02_22 | |$26.12^{+0.02}_{-0.03}$| | |$-20.76^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.10^{+0.03}_{-0.03}$| | |$-20.79^{+0.03}_{-0.03}$| | |$0.25^{+0.03}_{-0.03}$| | |$25.63^{+0.02}_{-0.03}$| | |$-21.25^{+0.02}_{-0.03}$| | |$0.23^{+0.02}_{-0.01}$| | |$1.12^{+0.09}_{-0.08}$| | |$0.92^{+0.15}_{-0.14}$| | 1 |
| C02_23 | |$26.68^{+0.04}_{-0.05}$| | |$-20.21^{+0.04}_{-0.05}$| | |$0.22^{+0.01}_{-0.01}$| | |$26.54^{+0.05}_{-0.05}$| | |$-20.35^{+0.05}_{-0.05}$| | |$0.34^{+0.03}_{-0.03}$| | |$26.24^{+0.04}_{-0.04}$| | |$-20.65^{+0.04}_{-0.04}$| | |$0.25^{+0.03}_{-0.03}$| | |$1.10^{+0.13}_{-0.12}$| | |$0.73^{+0.15}_{-0.16}$| | 1 |
| C03_01 | |$26.89^{+0.06}_{-0.07}$| | |$-19.83^{+0.06}_{-0.07}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.91^{+0.09}_{-0.08}$| | |$-19.81^{+0.09}_{-0.08}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.67^{+0.04}_{-0.04}$| | |$-20.05^{+0.04}_{-0.04}$| | |$0.28^{+0.03}_{-0.03}$| | |$0.68^{+0.07}_{-0.07}$| | |$0.68^{+0.08}_{-0.09}$| | 1 |
| C03_04 | |$25.62^{+0.01}_{-0.02}$| | |$-21.08^{+0.01}_{-0.02}$| | |$0.30^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-21.09^{+0.02}_{-0.02}$| | |$0.28^{+0.01}_{-0.01}$| | |$25.03^{+0.02}_{-0.03}$| | |$-21.66^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$1.22^{+0.05}_{-0.05}$| | |$1.27^{+0.08}_{-0.08}$| | 1 |
| C03_05 | |$26.20^{+0.08}_{-0.11}$| | |$-20.42^{+0.08}_{-0.11}$| | |$0.46^{+0.02}_{-0.01}$| | |$26.22^{+0.09}_{-0.11}$| | |$-20.41^{+0.09}_{-0.11}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.45^{+0.04}_{-0.04}$| | |$0.56^{+0.02}_{-0.02}$| | |$1.23^{+0.06}_{-0.05}$| | |$1.25^{+0.10}_{-0.11}$| | 1 |
| C03_07 | |$27.76^{+0.20}_{-0.22}$| | |$-19.21^{+0.20}_{-0.22}$| | |$0.11^{+0.03}_{-0.02}$| | |$27.93^{+0.21}_{-0.27}$| | |$-19.04^{+0.21}_{-0.27}$| | |$0.05^{+0.08}_{-0.06}$| | — | — | — | — | — | 1 |
| C03_08 | |$26.71^{+0.04}_{-0.05}$| | |$-20.27^{+0.04}_{-0.05}$| | |$0.23^{+0.01}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-20.29^{+0.05}_{-0.05}$| | |$0.27^{+0.03}_{-0.03}$| | |$26.23^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$1.21^{+0.12}_{-0.12}$| | |$1.01^{+0.17}_{-0.16}$| | 1 |
| C03_09 | |$26.75^{+0.06}_{-0.07}$| | |$-19.74^{+0.06}_{-0.07}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.84^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.25^{+0.03}_{-0.03}$| | |$26.10^{+0.05}_{-0.06}$| | |$-20.39^{+0.05}_{-0.06}$| | |$0.48^{+0.03}_{-0.03}$| | |$1.58^{+0.12}_{-0.12}$| | |$1.89^{+0.23}_{-0.23}$| | 1 |
| C03_11 | |$25.57^{+0.06}_{-0.07}$| | |$-20.83^{+0.06}_{-0.07}$| | |$1.62^{+0.05}_{-0.04}$| | |$25.65^{+0.05}_{-0.07}$| | |$-20.75^{+0.05}_{-0.07}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C03_12 | |$25.23^{+0.03}_{-0.04}$| | |$-21.16^{+0.03}_{-0.04}$| | |$0.85^{+0.02}_{-0.01}$| | |$24.93^{+0.05}_{-0.07}$| | |$-21.46^{+0.05}_{-0.07}$| | |$1.04^{+0.03}_{-0.03}$| | |$23.76^{+0.04}_{-0.04}$| | |$-22.64^{+0.04}_{-0.04}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.07^{+0.04}_{-0.03}$| | |$0.87^{+0.05}_{-0.04}$| | 2 |
| C03_13 | |$25.29^{+0.06}_{-0.07}$| | |$-21.11^{+0.06}_{-0.07}$| | |$1.42^{+0.04}_{-0.03}$| | |$25.18^{+0.05}_{-0.07}$| | |$-21.22^{+0.05}_{-0.07}$| | |$1.44^{+0.05}_{-0.04}$| | |$24.29^{+0.05}_{-0.07}$| | |$-22.11^{+0.05}_{-0.07}$| | |$1.66^{+0.06}_{-0.05}$| | |$1.17^{+0.05}_{-0.04}$| | |$1.16^{+0.06}_{-0.04}$| | 2 |
| C03_14 | |$25.83^{+0.09}_{-0.11}$| | |$-20.57^{+0.09}_{-0.11}$| | |$0.96^{+0.02}_{-0.01}$| | |$25.62^{+0.05}_{-0.07}$| | |$-20.77^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$24.99^{+0.05}_{-0.07}$| | |$-21.41^{+0.05}_{-0.07}$| | |$1.41^{+0.05}_{-0.04}$| | |$1.48^{+0.06}_{-0.05}$| | |$1.35^{+0.07}_{-0.06}$| | 2 |
| C03_15 | |$26.46^{+0.04}_{-0.05}$| | |$-19.94^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.06^{+0.06}_{-0.07}$| | |$-20.34^{+0.06}_{-0.07}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.71^{+0.02}_{-0.03}$| | |$-20.69^{+0.02}_{-0.03}$| | |$0.45^{+0.02}_{-0.02}$| | |$1.76^{+0.10}_{-0.09}$| | |$0.87^{+0.13}_{-0.15}$| | 2 |
| C03_16 | |$26.57^{+0.04}_{-0.05}$| | |$-19.83^{+0.04}_{-0.05}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.69^{+0.05}_{-0.05}$| | |$26.32^{+0.04}_{-0.04}$| | |$-20.08^{+0.04}_{-0.04}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.09^{+0.09}_{-0.09}$| | |$0.64^{+0.11}_{-0.12}$| | 1 |
| C03_17 | |$26.64^{+0.13}_{-0.18}$| | |$-19.76^{+0.13}_{-0.18}$| | |$0.48^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.08^{+0.03}_{-0.03}$| | |$-20.32^{+0.03}_{-0.03}$| | |$0.39^{+0.03}_{-0.04}$| | |$0.80^{+0.07}_{-0.08}$| | |$0.72^{+0.08}_{-0.09}$| | 2 |
| C03_18 | |$26.12^{+0.02}_{-0.03}$| | |$-20.28^{+0.02}_{-0.03}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.97^{+0.03}_{-0.03}$| | |$-20.43^{+0.03}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$26.14^{+0.03}_{-0.03}$| | |$-20.26^{+0.03}_{-0.03}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.66^{+0.14}_{-0.14}$| | |$1.26^{+0.14}_{-0.15}$| | 2 |
| C03_19 | |$26.54^{+0.04}_{-0.05}$| | |$-19.86^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.99^{+0.06}_{-0.07}$| | |$-20.41^{+0.06}_{-0.07}$| | |$0.66^{+0.05}_{-0.05}$| | |$25.56^{+0.04}_{-0.04}$| | |$-20.84^{+0.04}_{-0.04}$| | |$0.92^{+0.03}_{-0.02}$| | |$3.42^{+0.19}_{-0.14}$| | |$1.40^{+0.28}_{-0.28}$| | 2 |
| C03_20 | |$26.70^{+0.13}_{-0.18}$| | |$-19.70^{+0.13}_{-0.18}$| | |$0.73^{+0.03}_{-0.02}$| | |$27.04^{+0.15}_{-0.17}$| | |$-19.36^{+0.15}_{-0.17}$| | |$0.64^{+0.20}_{-0.12}$| | — | — | — | — | — | 1 |
| C03_21 | |$26.62^{+0.04}_{-0.05}$| | |$-19.78^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.33^{+0.05}_{-0.05}$| | |$-20.07^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$24.89^{+0.05}_{-0.07}$| | |$-21.51^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.02}$| | |$3.98^{+0.21}_{-0.16}$| | |$2.34^{+0.32}_{-0.36}$| | 2 |
| C03_22 | |$25.88^{+0.09}_{-0.11}$| | |$-20.52^{+0.09}_{-0.11}$| | |$1.28^{+0.03}_{-0.02}$| | |$25.98^{+0.08}_{-0.10}$| | |$-20.42^{+0.08}_{-0.10}$| | |$1.19^{+0.11}_{-0.08}$| | — | — | — | — | — | 1 |
| C03_23 | |$26.31^{+0.08}_{-0.11}$| | |$-20.08^{+0.08}_{-0.11}$| | |$0.79^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C03_24 | |$24.71^{+0.01}_{-0.02}$| | |$-21.98^{+0.01}_{-0.02}$| | |$0.37^{+0.01}_{-0.00}$| | |$24.69^{+0.02}_{-0.02}$| | |$-22.00^{+0.02}_{-0.02}$| | |$0.37^{+0.01}_{-0.01}$| | |$24.37^{+0.04}_{-0.04}$| | |$-22.32^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.01}$| | |$1.39^{+0.05}_{-0.04}$| | |$1.38^{+0.07}_{-0.06}$| | 2 |
| C03_25 | |$26.13^{+0.05}_{-0.07}$| | |$-20.57^{+0.05}_{-0.07}$| | |$0.81^{+0.04}_{-0.03}$| | |$26.23^{+0.09}_{-0.11}$| | |$-20.46^{+0.09}_{-0.11}$| | |$0.76^{+0.07}_{-0.06}$| | |$26.18^{+0.09}_{-0.12}$| | |$-20.52^{+0.09}_{-0.12}$| | |$0.72^{+0.08}_{-0.04}$| | |$0.89^{+0.11}_{-0.07}$| | |$0.95^{+0.13}_{-0.09}$| | 1 |
| C03_27 | |$26.25^{+0.04}_{-0.05}$| | |$-20.91^{+0.04}_{-0.05}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.24^{+0.03}_{-0.03}$| | |$-20.92^{+0.03}_{-0.03}$| | |$0.21^{+0.03}_{-0.03}$| | |$25.36^{+0.02}_{-0.03}$| | |$-21.80^{+0.02}_{-0.03}$| | |$0.34^{+0.01}_{-0.01}$| | |$1.80^{+0.11}_{-0.09}$| | |$1.59^{+0.23}_{-0.22}$| | 1 |
| C04_02 | |$25.38^{+0.01}_{-0.02}$| | |$-21.02^{+0.01}_{-0.02}$| | |$0.19^{+0.00}_{-0.00}$| | |$25.24^{+0.02}_{-0.02}$| | |$-21.16^{+0.02}_{-0.02}$| | |$0.31^{+0.01}_{-0.02}$| | |$24.32^{+0.02}_{-0.03}$| | |$-22.08^{+0.02}_{-0.03}$| | |$0.46^{+0.02}_{-0.02}$| | |$2.42^{+0.11}_{-0.10}$| | |$1.46^{+0.15}_{-0.14}$| | 1 |
| C04_03 | |$26.15^{+0.05}_{-0.07}$| | |$-20.25^{+0.05}_{-0.07}$| | |$0.63^{+0.03}_{-0.02}$| | |$25.95^{+0.06}_{-0.07}$| | |$-20.45^{+0.06}_{-0.07}$| | |$0.71^{+0.02}_{-0.02}$| | |$25.30^{+0.04}_{-0.04}$| | |$-21.10^{+0.04}_{-0.04}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.78^{+0.05}_{-0.04}$| | |$0.69^{+0.04}_{-0.03}$| | 2 |
| C04_04 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-20.80^{+0.02}_{-0.02}$| | |$0.29^{+0.01}_{-0.02}$| | |$24.85^{+0.02}_{-0.03}$| | |$-21.55^{+0.02}_{-0.03}$| | |$0.30^{+0.02}_{-0.02}$| | |$1.25^{+0.08}_{-0.07}$| | |$1.02^{+0.10}_{-0.09}$| | 2 |
| C04_05 | |$25.68^{+0.03}_{-0.04}$| | |$-20.72^{+0.03}_{-0.04}$| | |$0.63^{+0.01}_{-0.01}$| | |$25.64^{+0.04}_{-0.05}$| | |$-20.76^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$25.07^{+0.04}_{-0.04}$| | |$-21.33^{+0.04}_{-0.04}$| | |$0.68^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.93^{+0.04}_{-0.04}$| | 1 |
| C04_06 | |$26.27^{+0.04}_{-0.05}$| | |$-20.13^{+0.04}_{-0.05}$| | |$0.46^{+0.02}_{-0.01}$| | — | — | — | |$24.85^{+0.05}_{-0.07}$| | |$-21.55^{+0.05}_{-0.07}$| | |$1.35^{+0.05}_{-0.04}$| | |$2.95^{+0.16}_{-0.12}$| | — | 2 |
| C04_07 | |$26.47^{+0.04}_{-0.05}$| | |$-20.22^{+0.04}_{-0.05}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.32^{+0.03}_{-0.04}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.83^{+0.03}_{-0.03}$| | |$0.35^{+0.02}_{-0.01}$| | |$1.16^{+0.07}_{-0.06}$| | |$1.08^{+0.12}_{-0.14}$| | 1 |
| C04_08 | |$26.48^{+0.08}_{-0.11}$| | |$-20.22^{+0.08}_{-0.11}$| | |$0.74^{+0.03}_{-0.02}$| | |$26.51^{+0.09}_{-0.11}$| | |$-20.18^{+0.09}_{-0.11}$| | |$0.70^{+0.04}_{-0.05}$| | |$26.24^{+0.09}_{-0.12}$| | |$-20.45^{+0.09}_{-0.12}$| | |$0.67^{+0.08}_{-0.04}$| | |$0.90^{+0.11}_{-0.06}$| | |$0.96^{+0.12}_{-0.08}$| | 1 |
| C04_09 | |$26.23^{+0.08}_{-0.11}$| | |$-20.46^{+0.08}_{-0.11}$| | |$0.85^{+0.04}_{-0.03}$| | |$26.32^{+0.09}_{-0.11}$| | |$-20.38^{+0.09}_{-0.11}$| | |$0.71^{+0.04}_{-0.05}$| | |$25.36^{+0.05}_{-0.07}$| | |$-21.33^{+0.05}_{-0.07}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.08^{+0.07}_{-0.05}$| | |$1.29^{+0.08}_{-0.08}$| | 1 |
| C04_10 | |$26.42^{+0.08}_{-0.11}$| | |$-20.41^{+0.08}_{-0.11}$| | |$0.76^{+0.04}_{-0.03}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.35^{+0.09}_{-0.11}$| | |$0.69^{+0.04}_{-0.04}$| | |$26.19^{+0.09}_{-0.12}$| | |$-20.64^{+0.09}_{-0.12}$| | |$0.52^{+0.08}_{-0.04}$| | |$0.68^{+0.11}_{-0.06}$| | |$0.75^{+0.11}_{-0.07}$| | 1 |
| C05_01 | |$26.94^{+0.06}_{-0.07}$| | |$-19.32^{+0.06}_{-0.07}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.50^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.58^{+0.02}_{-0.02}$| | |$2.17^{+0.12}_{-0.10}$| | — | 2 |
| C05_04 | |$25.74^{+0.09}_{-0.11}$| | |$-20.66^{+0.09}_{-0.11}$| | |$0.97^{+0.02}_{-0.01}$| | |$25.35^{+0.05}_{-0.07}$| | |$-21.05^{+0.05}_{-0.07}$| | |$1.00^{+0.03}_{-0.03}$| | |$24.80^{+0.04}_{-0.04}$| | |$-21.60^{+0.04}_{-0.04}$| | |$0.87^{+0.03}_{-0.02}$| | |$0.89^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C05_05 | |$26.49^{+0.04}_{-0.05}$| | |$-20.45^{+0.04}_{-0.05}$| | |$0.18^{+0.01}_{-0.01}$| | |$26.09^{+0.03}_{-0.03}$| | |$-20.85^{+0.03}_{-0.03}$| | |$0.31^{+0.03}_{-0.03}$| | |$25.68^{+0.02}_{-0.03}$| | |$-21.26^{+0.02}_{-0.03}$| | |$0.19^{+0.02}_{-0.01}$| | |$1.05^{+0.11}_{-0.08}$| | |$0.61^{+0.13}_{-0.13}$| | 2 |
| C05_06 | |$26.49^{+0.04}_{-0.05}$| | |$-20.37^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.45^{+0.05}_{-0.05}$| | |$-20.41^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.03}$| | |$26.65^{+0.04}_{-0.04}$| | |$-20.22^{+0.04}_{-0.04}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.94^{+0.09}_{-0.09}$| | |$0.94^{+0.11}_{-0.13}$| | 1 |
| C05_07 | |$25.96^{+0.02}_{-0.03}$| | |$-20.95^{+0.02}_{-0.03}$| | |$0.35^{+0.01}_{-0.00}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.89^{+0.03}_{-0.03}$| | |$0.30^{+0.03}_{-0.03}$| | |$25.82^{+0.03}_{-0.03}$| | |$-21.10^{+0.03}_{-0.03}$| | |$0.29^{+0.01}_{-0.01}$| | |$0.83^{+0.04}_{-0.04}$| | |$0.96^{+0.09}_{-0.10}$| | 1 |
| C05_08 | |$26.28^{+0.08}_{-0.11}$| | |$-20.71^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.02}$| | |$26.10^{+0.06}_{-0.07}$| | |$-20.89^{+0.06}_{-0.07}$| | |$0.73^{+0.06}_{-0.05}$| | |$25.99^{+0.05}_{-0.06}$| | |$-21.00^{+0.05}_{-0.06}$| | |$0.43^{+0.03}_{-0.03}$| | |$0.73^{+0.05}_{-0.05}$| | |$0.59^{+0.07}_{-0.07}$| | 2 |
| C05_09 | |$26.62^{+0.04}_{-0.05}$| | |$-20.19^{+0.04}_{-0.05}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.58^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.26^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C06_01 | |$26.15^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.38^{+0.02}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-21.13^{+0.04}_{-0.05}$| | |$0.81^{+0.03}_{-0.02}$| | |$24.75^{+0.04}_{-0.04}$| | |$-21.85^{+0.04}_{-0.04}$| | |$0.80^{+0.03}_{-0.02}$| | |$2.09^{+0.12}_{-0.09}$| | |$0.98^{+0.10}_{-0.08}$| | 2 |
| C06_02 | |$26.61^{+0.08}_{-0.11}$| | |$-20.10^{+0.08}_{-0.11}$| | |$0.55^{+0.03}_{-0.02}$| | |$26.77^{+0.09}_{-0.08}$| | |$-19.94^{+0.09}_{-0.08}$| | |$0.37^{+0.03}_{-0.04}$| | — | — | — | — | — | 2 |
| C06_03 | |$26.90^{+0.13}_{-0.18}$| | |$-19.81^{+0.13}_{-0.18}$| | |$0.49^{+0.07}_{-0.04}$| | |$26.95^{+0.09}_{-0.08}$| | |$-19.76^{+0.09}_{-0.08}$| | |$0.40^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C06_05 | |$26.61^{+0.04}_{-0.05}$| | |$-20.50^{+0.04}_{-0.05}$| | |$0.07^{+0.01}_{-0.01}$| | |$26.42^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.18^{+0.03}_{-0.03}$| | |$25.61^{+0.02}_{-0.03}$| | |$-21.50^{+0.02}_{-0.03}$| | |$0.24^{+0.02}_{-0.01}$| | |$3.21^{+0.44}_{-0.34}$| | |$1.33^{+0.51}_{-0.49}$| | 2 |
| C06_06 | |$26.63^{+0.04}_{-0.05}$| | |$-19.84^{+0.04}_{-0.05}$| | |$0.09^{+0.01}_{-0.01}$| | |$26.31^{+0.05}_{-0.05}$| | |$-20.17^{+0.05}_{-0.05}$| | |$0.25^{+0.03}_{-0.03}$| | — | — | — | — | — | 2 |
| C06_09 | |$26.21^{+0.08}_{-0.11}$| | |$-20.19^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.51^{+0.09}_{-0.12}$| | |$-19.89^{+0.09}_{-0.12}$| | |$0.55^{+0.03}_{-0.04}$| | |$0.92^{+0.06}_{-0.06}$| | |$1.02^{+0.08}_{-0.09}$| | 1 |
| C06_10 | |$25.46^{+0.06}_{-0.07}$| | |$-20.94^{+0.06}_{-0.07}$| | |$0.99^{+0.02}_{-0.01}$| | |$25.53^{+0.05}_{-0.07}$| | |$-20.87^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.03}$| | |$25.84^{+0.05}_{-0.06}$| | |$-20.56^{+0.05}_{-0.06}$| | |$0.92^{+0.03}_{-0.02}$| | |$0.93^{+0.04}_{-0.03}$| | |$0.96^{+0.04}_{-0.03}$| | 1 |
| C06_11 | |$25.34^{+0.03}_{-0.04}$| | |$-21.05^{+0.03}_{-0.04}$| | |$0.79^{+0.01}_{-0.01}$| | |$25.34^{+0.04}_{-0.05}$| | |$-21.06^{+0.04}_{-0.05}$| | |$0.81^{+0.02}_{-0.02}$| | |$25.69^{+0.05}_{-0.06}$| | |$-20.71^{+0.05}_{-0.06}$| | |$0.73^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.90^{+0.04}_{-0.03}$| | 1 |
| C06_12 | |$26.41^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.61^{+0.03}_{-0.02}$| | |$26.00^{+0.06}_{-0.07}$| | |$-20.40^{+0.06}_{-0.07}$| | |$0.93^{+0.07}_{-0.07}$| | |$25.52^{+0.05}_{-0.07}$| | |$-20.88^{+0.05}_{-0.07}$| | |$1.01^{+0.03}_{-0.02}$| | |$1.66^{+0.10}_{-0.07}$| | |$1.09^{+0.14}_{-0.12}$| | 2 |
| C06_13 | |$26.10^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.80^{+0.04}_{-0.03}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.73^{+0.06}_{-0.07}$| | |$0.83^{+0.03}_{-0.02}$| | |$25.68^{+0.07}_{-0.10}$| | |$-21.01^{+0.07}_{-0.10}$| | |$0.88^{+0.03}_{-0.02}$| | |$1.10^{+0.07}_{-0.05}$| | |$1.06^{+0.05}_{-0.04}$| | 2 |
| C06_15 | |$27.51^{+0.11}_{-0.14}$| | |$-19.32^{+0.11}_{-0.14}$| | |$0.14^{+0.04}_{-0.03}$| | |$27.18^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.30^{+0.08}_{-0.06}$| | — | — | — | — | — | 2 |
| C06_16 | |$26.50^{+0.04}_{-0.05}$| | |$-20.39^{+0.04}_{-0.05}$| | |$0.14^{+0.01}_{-0.01}$| | |$26.59^{+0.05}_{-0.05}$| | |$-20.30^{+0.05}_{-0.05}$| | |$0.10^{+0.03}_{-0.03}$| | |$26.64^{+0.04}_{-0.04}$| | |$-20.25^{+0.04}_{-0.04}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.25^{+0.20}_{-0.19}$| | |$1.80^{+0.41}_{-0.40}$| | 1 |
| C07_01 | |$26.90^{+0.06}_{-0.07}$| | |$-19.66^{+0.06}_{-0.07}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.70^{+0.09}_{-0.08}$| | |$0.23^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C07_02 | |$25.01^{+0.01}_{-0.02}$| | |$-21.31^{+0.01}_{-0.02}$| | |$0.32^{+0.00}_{-0.00}$| | |$25.02^{+0.02}_{-0.02}$| | |$-21.30^{+0.02}_{-0.02}$| | |$0.35^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_04 | |$25.61^{+0.06}_{-0.07}$| | |$-20.79^{+0.06}_{-0.07}$| | |$1.66^{+0.05}_{-0.04}$| | |$25.75^{+0.08}_{-0.10}$| | |$-20.65^{+0.08}_{-0.10}$| | |$1.45^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_06 | |$26.70^{+0.04}_{-0.05}$| | |$-19.70^{+0.04}_{-0.05}$| | |$0.24^{+0.01}_{-0.01}$| | |$25.70^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_07 | |$25.70^{+0.09}_{-0.11}$| | |$-20.70^{+0.09}_{-0.11}$| | |$1.49^{+0.04}_{-0.03}$| | |$25.76^{+0.08}_{-0.10}$| | |$-20.64^{+0.08}_{-0.10}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_08 | |$26.68^{+0.08}_{-0.11}$| | |$-19.72^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.54^{+0.09}_{-0.08}$| | |$0.44^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_09 | |$25.34^{+0.01}_{-0.02}$| | |$-21.06^{+0.01}_{-0.02}$| | |$0.40^{+0.01}_{-0.01}$| | |$25.39^{+0.02}_{-0.02}$| | |$-21.01^{+0.02}_{-0.02}$| | |$0.36^{+0.02}_{-0.01}$| | — | — | — | — | — | 1 |
| C07_10 | |$26.24^{+0.08}_{-0.11}$| | |$-20.16^{+0.08}_{-0.11}$| | |$0.68^{+0.03}_{-0.02}$| | |$26.21^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.60^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_12 | |$26.28^{+0.08}_{-0.11}$| | |$-20.12^{+0.08}_{-0.11}$| | |$0.58^{+0.02}_{-0.01}$| | |$26.20^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.63^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_13 | |$25.32^{+0.03}_{-0.04}$| | |$-21.08^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$24.53^{+0.05}_{-0.07}$| | |$-21.87^{+0.05}_{-0.07}$| | |$1.18^{+0.04}_{-0.03}$| | — | — | — | — | — | 2 |
| C07_14 | |$25.81^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.72^{+0.01}_{-0.01}$| | |$25.82^{+0.06}_{-0.07}$| | |$-20.58^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | — | — | — | — | — | 1 |
| C07_15 | |$26.95^{+0.06}_{-0.07}$| | |$-19.75^{+0.06}_{-0.07}$| | |$0.31^{+0.01}_{-0.01}$| | |$26.77^{+0.15}_{-0.17}$| | |$-19.93^{+0.15}_{-0.17}$| | |$0.43^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_16 | |$26.63^{+0.08}_{-0.11}$| | |$-20.23^{+0.08}_{-0.11}$| | |$0.65^{+0.03}_{-0.02}$| | |$25.82^{+0.08}_{-0.10}$| | |$-21.05^{+0.08}_{-0.10}$| | |$1.36^{+0.05}_{-0.04}$| | — | — | — | — | — | 2 |
| C08_01 | |$25.87^{+0.02}_{-0.03}$| | |$-21.40^{+0.02}_{-0.03}$| | |$0.13^{+0.00}_{-0.00}$| | |$24.89^{+0.04}_{-0.05}$| | |$-22.38^{+0.04}_{-0.05}$| | |$0.53^{+0.01}_{-0.01}$| | |$24.01^{+0.02}_{-0.03}$| | |$-23.25^{+0.02}_{-0.03}$| | |$0.28^{+0.01}_{-0.01}$| | |$2.21^{+0.11}_{-0.10}$| | |$0.53^{+0.12}_{-0.11}$| | 2 |
| C08_02 | |$27.52^{+0.11}_{-0.14}$| | |$-19.46^{+0.11}_{-0.14}$| | |$0.23^{+0.03}_{-0.02}$| | |$27.40^{+0.14}_{-0.17}$| | |$-19.57^{+0.14}_{-0.17}$| | |$0.35^{+0.13}_{-0.06}$| | — | — | — | — | — | 1 |
| C08_03 | |$27.02^{+0.06}_{-0.07}$| | |$-19.38^{+0.06}_{-0.07}$| | |$0.15^{+0.04}_{-0.03}$| | |$26.74^{+0.05}_{-0.05}$| | |$-19.66^{+0.05}_{-0.05}$| | |$0.30^{+0.03}_{-0.03}$| | |$26.87^{+0.08}_{-0.12}$| | |$-19.53^{+0.08}_{-0.12}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.22^{+0.40}_{-0.32}$| | |$0.60^{+0.25}_{-0.25}$| | 2 |
| C08_04 | |$26.55^{+0.04}_{-0.05}$| | |$-19.85^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.43^{+0.05}_{-0.07}$| | |$-20.97^{+0.05}_{-0.07}$| | |$1.02^{+0.03}_{-0.02}$| | |$3.84^{+0.20}_{-0.15}$| | — | 1 |
| C08_05 | |$24.75^{+0.06}_{-0.07}$| | |$-21.65^{+0.06}_{-0.07}$| | |$0.98^{+0.02}_{-0.01}$| | |$24.73^{+0.05}_{-0.07}$| | |$-21.67^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$23.11^{+0.04}_{-0.04}$| | |$-23.29^{+0.04}_{-0.04}$| | |$0.93^{+0.03}_{-0.02}$| | |$0.96^{+0.04}_{-0.03}$| | |$0.89^{+0.04}_{-0.03}$| | 2 |
| C08_06 | |$26.06^{+0.02}_{-0.03}$| | |$-20.34^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$24.84^{+0.05}_{-0.07}$| | |$-21.56^{+0.05}_{-0.07}$| | |$1.21^{+0.04}_{-0.03}$| | |$23.64^{+0.05}_{-0.07}$| | |$-22.76^{+0.05}_{-0.07}$| | |$1.29^{+0.04}_{-0.03}$| | |$6.15^{+0.38}_{-0.30}$| | |$1.07^{+0.26}_{-0.21}$| | 2 |
| C08_07 | |$25.37^{+0.03}_{-0.04}$| | |$-21.02^{+0.03}_{-0.04}$| | |$0.93^{+0.02}_{-0.01}$| | |$25.52^{+0.04}_{-0.05}$| | |$-20.88^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.22^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$0.85^{+0.03}_{-0.02}$| | |$1.00^{+0.03}_{-0.03}$| | 2 |
| C08_08 | |$25.72^{+0.03}_{-0.04}$| | |$-20.68^{+0.03}_{-0.04}$| | |$0.90^{+0.02}_{-0.01}$| | |$25.40^{+0.05}_{-0.07}$| | |$-21.00^{+0.05}_{-0.07}$| | |$1.17^{+0.04}_{-0.03}$| | |$23.71^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$0.97^{+0.03}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.83^{+0.05}_{-0.04}$| | 2 |
| C08_09 | |$25.79^{+0.09}_{-0.11}$| | |$-20.61^{+0.09}_{-0.11}$| | |$1.10^{+0.03}_{-0.02}$| | |$25.83^{+0.08}_{-0.10}$| | |$-20.57^{+0.08}_{-0.10}$| | |$1.12^{+0.04}_{-0.03}$| | |$25.09^{+0.04}_{-0.04}$| | |$-21.31^{+0.04}_{-0.04}$| | |$0.54^{+0.02}_{-0.02}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.48^{+0.02}_{-0.02}$| | 1 |
| C08_10 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.38^{+0.02}_{-0.01}$| | |$26.02^{+0.06}_{-0.07}$| | |$-20.38^{+0.06}_{-0.07}$| | |$0.55^{+0.03}_{-0.04}$| | |$25.49^{+0.04}_{-0.04}$| | |$-20.91^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$2.11^{+0.12}_{-0.09}$| | |$1.45^{+0.14}_{-0.16}$| | 2 |
| C08_11 | |$24.25^{+0.06}_{-0.07}$| | |$-22.15^{+0.06}_{-0.07}$| | |$1.28^{+0.03}_{-0.02}$| | |$24.16^{+0.05}_{-0.07}$| | |$-22.24^{+0.05}_{-0.07}$| | |$1.49^{+0.05}_{-0.04}$| | |$23.59^{+0.05}_{-0.07}$| | |$-22.81^{+0.05}_{-0.07}$| | |$1.30^{+0.04}_{-0.03}$| | |$1.01^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_12 | |$25.93^{+0.05}_{-0.07}$| | |$-20.47^{+0.05}_{-0.07}$| | |$0.84^{+0.02}_{-0.01}$| | |$25.45^{+0.05}_{-0.07}$| | |$-20.95^{+0.05}_{-0.07}$| | |$1.03^{+0.03}_{-0.03}$| | |$24.55^{+0.05}_{-0.07}$| | |$-21.85^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.02}$| | |$1.15^{+0.04}_{-0.03}$| | |$0.94^{+0.05}_{-0.04}$| | 2 |
| C08_13 | |$25.68^{+0.01}_{-0.02}$| | |$-20.71^{+0.01}_{-0.02}$| | |$0.20^{+0.00}_{-0.00}$| | |$25.50^{+0.02}_{-0.02}$| | |$-20.90^{+0.02}_{-0.02}$| | |$0.34^{+0.01}_{-0.02}$| | |$25.41^{+0.02}_{-0.03}$| | |$-20.99^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$2.09^{+0.09}_{-0.09}$| | |$1.25^{+0.12}_{-0.12}$| | 2 |
| C08_14 | |$26.11^{+0.05}_{-0.07}$| | |$-20.29^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.04^{+0.06}_{-0.07}$| | |$-20.36^{+0.06}_{-0.07}$| | |$0.61^{+0.05}_{-0.05}$| | |$24.84^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.52^{+0.02}_{-0.02}$| | |$0.99^{+0.05}_{-0.04}$| | |$0.85^{+0.09}_{-0.09}$| | 2 |
| C08_15 | |$25.20^{+0.06}_{-0.07}$| | |$-21.49^{+0.06}_{-0.07}$| | |$0.87^{+0.02}_{-0.01}$| | |$25.19^{+0.05}_{-0.07}$| | |$-21.50^{+0.05}_{-0.07}$| | |$0.90^{+0.03}_{-0.02}$| | |$24.61^{+0.04}_{-0.04}$| | |$-22.08^{+0.04}_{-0.04}$| | |$0.78^{+0.03}_{-0.02}$| | |$0.90^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_16 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.20^{+0.07}_{-0.05}$| | |$26.09^{+0.08}_{-0.10}$| | |$-20.61^{+0.08}_{-0.10}$| | |$1.29^{+0.12}_{-0.09}$| | — | — | — | — | — | 1 |
| C08_17 | |$25.19^{+0.03}_{-0.04}$| | |$-21.51^{+0.03}_{-0.04}$| | |$0.64^{+0.01}_{-0.01}$| | |$25.22^{+0.04}_{-0.05}$| | |$-21.48^{+0.04}_{-0.05}$| | |$0.66^{+0.02}_{-0.02}$| | |$24.17^{+0.04}_{-0.04}$| | |$-22.52^{+0.04}_{-0.04}$| | |$0.83^{+0.03}_{-0.02}$| | |$1.30^{+0.05}_{-0.04}$| | |$1.27^{+0.06}_{-0.05}$| | 2 |
| C08_18 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.08^{+0.07}_{-0.05}$| | |$25.88^{+0.08}_{-0.10}$| | |$-20.81^{+0.08}_{-0.10}$| | |$1.29^{+0.04}_{-0.03}$| | |$23.81^{+0.05}_{-0.07}$| | |$-22.88^{+0.05}_{-0.07}$| | |$1.28^{+0.04}_{-0.04}$| | |$1.18^{+0.09}_{-0.06}$| | |$0.99^{+0.06}_{-0.04}$| | 2 |
| C08_19 | |$26.08^{+0.05}_{-0.07}$| | |$-20.61^{+0.05}_{-0.07}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.98^{+0.06}_{-0.07}$| | |$-20.72^{+0.06}_{-0.07}$| | |$0.60^{+0.04}_{-0.05}$| | |$23.88^{+0.04}_{-0.04}$| | |$-22.82^{+0.04}_{-0.04}$| | |$0.71^{+0.02}_{-0.02}$| | |$1.45^{+0.06}_{-0.05}$| | |$1.19^{+0.11}_{-0.12}$| | 1 |
| C08_20 | |$26.65^{+0.04}_{-0.05}$| | |$-20.04^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.67^{+0.05}_{-0.05}$| | |$-20.03^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.04}$| | |$24.63^{+0.05}_{-0.07}$| | |$-22.06^{+0.05}_{-0.07}$| | |$0.94^{+0.03}_{-0.02}$| | |$2.72^{+0.15}_{-0.11}$| | |$2.68^{+0.25}_{-0.28}$| | 1 |
| C08_21 | |$25.93^{+0.02}_{-0.03}$| | |$-20.77^{+0.02}_{-0.03}$| | |$0.22^{+0.00}_{-0.00}$| | |$25.10^{+0.04}_{-0.05}$| | |$-21.59^{+0.04}_{-0.05}$| | |$0.57^{+0.02}_{-0.02}$| | |$24.78^{+0.04}_{-0.04}$| | |$-21.92^{+0.04}_{-0.04}$| | |$0.62^{+0.02}_{-0.02}$| | |$2.74^{+0.10}_{-0.09}$| | |$1.08^{+0.12}_{-0.12}$| | 2 |
| C08_22 | |$25.41^{+0.03}_{-0.04}$| | |$-21.28^{+0.03}_{-0.04}$| | |$0.83^{+0.02}_{-0.01}$| | |$25.32^{+0.05}_{-0.07}$| | |$-21.37^{+0.05}_{-0.07}$| | |$0.99^{+0.04}_{-0.03}$| | |$24.79^{+0.04}_{-0.04}$| | |$-21.90^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$0.73^{+0.03}_{-0.02}$| | |$0.61^{+0.03}_{-0.03}$| | 1 |
| C08_23 | |$26.35^{+0.08}_{-0.11}$| | |$-20.34^{+0.08}_{-0.11}$| | |$0.45^{+0.02}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.81^{+0.03}_{-0.03}$| | |$0.31^{+0.02}_{-0.01}$| | |$0.69^{+0.05}_{-0.04}$| | |$0.78^{+0.07}_{-0.07}$| | 1 |
| C08_24 | |$26.31^{+0.08}_{-0.11}$| | |$-20.38^{+0.08}_{-0.11}$| | |$0.57^{+0.03}_{-0.02}$| | |$25.77^{+0.08}_{-0.10}$| | |$-20.92^{+0.08}_{-0.10}$| | |$0.94^{+0.03}_{-0.02}$| | |$25.33^{+0.04}_{-0.04}$| | |$-21.36^{+0.04}_{-0.04}$| | |$0.76^{+0.03}_{-0.02}$| | |$1.34^{+0.08}_{-0.06}$| | |$0.81^{+0.06}_{-0.05}$| | 2 |
| C08_25 | |$26.89^{+0.06}_{-0.07}$| | |$-20.05^{+0.06}_{-0.07}$| | |$0.13^{+0.01}_{-0.01}$| | |$26.87^{+0.09}_{-0.08}$| | |$-20.07^{+0.09}_{-0.08}$| | |$0.19^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C08_27 | |$25.74^{+0.02}_{-0.03}$| | |$-21.12^{+0.02}_{-0.03}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.68^{+0.02}_{-0.02}$| | |$-21.18^{+0.02}_{-0.02}$| | |$0.32^{+0.01}_{-0.01}$| | |$24.61^{+0.02}_{-0.03}$| | |$-22.26^{+0.02}_{-0.03}$| | |$0.38^{+0.01}_{-0.01}$| | |$1.61^{+0.07}_{-0.06}$| | |$1.20^{+0.09}_{-0.09}$| | 1 |
| C08_28 | |$26.23^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.95^{+0.06}_{-0.07}$| | |$-21.01^{+0.06}_{-0.07}$| | |$0.52^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C08_29 | |$26.61^{+0.04}_{-0.05}$| | |$-20.18^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.91^{+0.06}_{-0.07}$| | |$-20.88^{+0.06}_{-0.07}$| | |$0.55^{+0.02}_{-0.02}$| | |$25.67^{+0.05}_{-0.06}$| | |$-21.12^{+0.05}_{-0.06}$| | |$0.49^{+0.02}_{-0.01}$| | |$2.82^{+0.19}_{-0.15}$| | |$0.89^{+0.13}_{-0.12}$| | 2 |
| C08_30 | |$26.48^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.16^{+0.01}_{-0.01}$| | |$26.52^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.17^{+0.03}_{-0.02}$| | |$25.64^{+0.02}_{-0.03}$| | |$-21.58^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$1.28^{+0.11}_{-0.09}$| | |$1.25^{+0.21}_{-0.20}$| | 1 |
| C08_31 | |$27.07^{+0.06}_{-0.07}$| | |$-20.09^{+0.06}_{-0.07}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.81^{+0.15}_{-0.17}$| | |$-20.35^{+0.15}_{-0.17}$| | |$0.38^{+0.03}_{-0.03}$| | |$25.55^{+0.04}_{-0.04}$| | |$-21.61^{+0.04}_{-0.04}$| | |$0.39^{+0.01}_{-0.01}$| | |$1.54^{+0.20}_{-0.14}$| | |$1.01^{+0.12}_{-0.13}$| | 1 |
| C09_01 | |$26.13^{+0.05}_{-0.07}$| | |$-20.24^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.16^{+0.06}_{-0.07}$| | |$-20.20^{+0.06}_{-0.07}$| | |$0.50^{+0.03}_{-0.04}$| | |$25.73^{+0.05}_{-0.06}$| | |$-20.64^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$1.21^{+0.06}_{-0.05}$| | |$1.27^{+0.09}_{-0.10}$| | 1 |
| C09_02 | |$26.82^{+0.13}_{-0.18}$| | |$-19.54^{+0.13}_{-0.18}$| | |$0.63^{+0.03}_{-0.02}$| | |$26.71^{+0.15}_{-0.17}$| | |$-19.65^{+0.15}_{-0.17}$| | |$0.66^{+0.05}_{-0.05}$| | |$26.46^{+0.04}_{-0.04}$| | |$-19.90^{+0.04}_{-0.04}$| | |$0.47^{+0.03}_{-0.04}$| | |$0.74^{+0.06}_{-0.06}$| | |$0.70^{+0.08}_{-0.08}$| | 2 |
| C09_03 | |$25.88^{+0.05}_{-0.07}$| | |$-20.51^{+0.05}_{-0.07}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.86^{+0.04}_{-0.04}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.13^{+0.04}_{-0.04}$| | 1 |
| C09_04 | |$25.58^{+0.03}_{-0.04}$| | |$-20.82^{+0.03}_{-0.04}$| | |$0.52^{+0.01}_{-0.01}$| | |$25.63^{+0.04}_{-0.05}$| | |$-20.77^{+0.04}_{-0.05}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.24^{+0.02}_{-0.03}$| | |$-21.16^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.78^{+0.04}_{-0.03}$| | |$0.84^{+0.04}_{-0.04}$| | 2 |
| C09_05 | |$26.46^{+0.08}_{-0.11}$| | |$-19.94^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.08^{+0.06}_{-0.07}$| | |$-20.32^{+0.06}_{-0.07}$| | |$0.67^{+0.05}_{-0.05}$| | |$25.90^{+0.05}_{-0.06}$| | |$-20.50^{+0.05}_{-0.06}$| | |$0.64^{+0.02}_{-0.02}$| | |$1.20^{+0.06}_{-0.05}$| | |$0.96^{+0.10}_{-0.10}$| | 2 |
| C09_06 | |$25.93^{+0.02}_{-0.03}$| | |$-20.47^{+0.02}_{-0.03}$| | |$0.21^{+0.00}_{-0.00}$| | |$25.66^{+0.02}_{-0.02}$| | |$-20.74^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.86^{+0.04}_{-0.04}$| | |$-21.54^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$2.89^{+0.11}_{-0.11}$| | |$1.48^{+0.15}_{-0.14}$| | 2 |
| C09_07 | |$27.17^{+0.06}_{-0.07}$| | |$-19.23^{+0.06}_{-0.07}$| | |$0.44^{+0.07}_{-0.05}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.90^{+0.07}_{-0.07}$| | |$26.16^{+0.05}_{-0.06}$| | |$-20.24^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$1.60^{+0.34}_{-0.20}$| | |$0.78^{+0.24}_{-0.16}$| | 2 |
| C09_08 | |$26.41^{+0.08}_{-0.11}$| | |$-19.99^{+0.08}_{-0.11}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.38^{+0.05}_{-0.05}$| | |$-20.02^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.15^{+0.04}_{-0.04}$| | |$0.72^{+0.02}_{-0.02}$| | |$1.29^{+0.06}_{-0.05}$| | |$1.58^{+0.10}_{-0.12}$| | 2 |
| C10_01 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.13^{+0.03}_{-0.03}$| | |$-20.27^{+0.03}_{-0.03}$| | |$0.40^{+0.03}_{-0.04}$| | |$25.59^{+0.04}_{-0.04}$| | |$-20.81^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.99^{+0.09}_{-0.08}$| | |$1.63^{+0.18}_{-0.21}$| | 2 |
| C10_02 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.44^{+0.01}_{-0.01}$| | |$25.53^{+0.04}_{-0.05}$| | |$-20.87^{+0.04}_{-0.05}$| | |$0.63^{+0.02}_{-0.02}$| | |$24.99^{+0.04}_{-0.04}$| | |$-21.41^{+0.04}_{-0.04}$| | |$0.47^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.04}$| | |$0.75^{+0.05}_{-0.05}$| | 1 |
| C10_03 | |$25.44^{+0.03}_{-0.04}$| | |$-20.96^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-20.93^{+0.04}_{-0.05}$| | |$0.58^{+0.02}_{-0.01}$| | |$24.89^{+0.04}_{-0.04}$| | |$-21.51^{+0.04}_{-0.04}$| | |$0.73^{+0.02}_{-0.02}$| | |$1.21^{+0.04}_{-0.04}$| | |$1.26^{+0.05}_{-0.04}$| | 2 |
| C10_04 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.15^{+0.06}_{-0.07}$| | |$-20.25^{+0.06}_{-0.07}$| | |$0.58^{+0.03}_{-0.04}$| | |$26.72^{+0.04}_{-0.04}$| | |$-19.68^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$0.62^{+0.08}_{-0.07}$| | |$0.47^{+0.08}_{-0.08}$| | 2 |
| C10_05 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.49^{+0.01}_{-0.01}$| | |$25.40^{+0.04}_{-0.05}$| | |$-21.00^{+0.04}_{-0.05}$| | |$0.59^{+0.02}_{-0.01}$| | |$25.67^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.84^{+0.04}_{-0.03}$| | |$0.70^{+0.04}_{-0.04}$| | 2 |
| C10_06 | |$26.40^{+0.15}_{-0.18}$| | |$-20.00^{+0.15}_{-0.18}$| | |$1.12^{+0.08}_{-0.05}$| | |$26.37^{+0.14}_{-0.15}$| | |$-20.03^{+0.14}_{-0.15}$| | |$0.96^{+0.07}_{-0.07}$| | |$26.22^{+0.09}_{-0.12}$| | |$-20.17^{+0.09}_{-0.12}$| | |$0.77^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.80^{+0.09}_{-0.06}$| | 2 |
| C10_07 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$25.72^{+0.04}_{-0.05}$| | |$-20.68^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.51^{+0.04}_{-0.04}$| | |$-20.89^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$1.79^{+0.09}_{-0.07}$| | |$0.89^{+0.08}_{-0.07}$| | 2 |
| C10_08 | |$26.03^{+0.05}_{-0.07}$| | |$-20.37^{+0.05}_{-0.07}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.12^{+0.06}_{-0.07}$| | |$-20.28^{+0.06}_{-0.07}$| | |$0.48^{+0.03}_{-0.04}$| | |$25.37^{+0.04}_{-0.04}$| | |$-21.03^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.02}$| | |$0.92^{+0.04}_{-0.04}$| | |$1.07^{+0.07}_{-0.08}$| | 1 |
| C10_09 | |$24.91^{+0.03}_{-0.04}$| | |$-22.03^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$25.00^{+0.04}_{-0.05}$| | |$-21.93^{+0.04}_{-0.05}$| | |$0.56^{+0.02}_{-0.02}$| | |$23.99^{+0.04}_{-0.04}$| | |$-22.95^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.15^{+0.04}_{-0.04}$| | 2 |
| C10_10 | |$25.41^{+0.01}_{-0.02}$| | |$-21.48^{+0.01}_{-0.02}$| | |$0.16^{+0.00}_{-0.00}$| | |$25.48^{+0.02}_{-0.02}$| | |$-21.41^{+0.02}_{-0.02}$| | |$0.14^{+0.01}_{-0.01}$| | |$25.42^{+0.02}_{-0.03}$| | |$-21.46^{+0.02}_{-0.03}$| | |$0.16^{+0.02}_{-0.01}$| | |$0.95^{+0.10}_{-0.08}$| | |$1.10^{+0.13}_{-0.12}$| | 1 |
*(1) ID. (2) Total apparent UV magnitude in F150W. (3) Total absolute UV magnitude in F150W. (4) UV size measured in F150W. (5) Total apparent UV magnitude measured in the smoothed F150W images. (6) Total absolute UV magnitude measured in the smoothed F150W images. (7) UV size measured in the smoothed F150W images. (8) Total apparent optical magnitude in F444W. (9) Total absolute optical magnitude in F444W. (10) Optical size measured in F444W. (11) Optical-to-UV size ratio measured with the F150W and F444W images. (12) Optical-to-UV size ratio measured with the smoothed F150W and F444W images. (13) Flag about blendedness. 1: The component fitted in the smoothed F150W image and/or the F444W image is a single component in the original F150W image. 2: The component fitted in the smoothed F150W image and/or the F444W image consists of multiple components in the original F150W image. 0: Too faint or the SB profile fitting encounters numerical convergence issues.
| . | F150W . | F150W (PSF matched) . | F444W . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | Flag . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mUV . | MUV . | re . | mUV . | MUV . | re . | mopt . | Mopt . | re, opt . | . | (PSF matched) . | . |
| ID . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . |
| C01_02 | |$26.57^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$26.62^{+0.05}_{-0.05}$| | |$-20.68^{+0.05}_{-0.05}$| | |$0.13^{+0.02}_{-0.02}$| | |$26.77^{+0.08}_{-0.12}$| | |$-20.53^{+0.08}_{-0.12}$| | |$0.23^{+0.02}_{-0.02}$| | |$1.36^{+0.15}_{-0.14}$| | |$1.77^{+0.28}_{-0.28}$| | 1 |
| C01_03 | |$27.68^{+0.20}_{-0.22}$| | |$-19.28^{+0.20}_{-0.22}$| | |$0.03^{+0.03}_{-0.02}$| | — | — | — | |$26.96^{+0.08}_{-0.12}$| | |$-20.00^{+0.08}_{-0.12}$| | |$0.12^{+0.12}_{-0.09}$| | |$4.44^{+7.25}_{-5.30}$| | — | 1 |
| C01_05 | |$26.42^{+0.04}_{-0.05}$| | |$-20.01^{+0.04}_{-0.05}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.65^{+0.04}_{-0.05}$| | |$-20.78^{+0.04}_{-0.05}$| | |$0.80^{+0.02}_{-0.02}$| | |$24.87^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$2.14^{+0.12}_{-0.10}$| | |$0.97^{+0.08}_{-0.07}$| | 2 |
| C01_06 | |$26.60^{+0.04}_{-0.05}$| | |$-19.67^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.01^{+0.09}_{-0.11}$| | |$0.49^{+0.04}_{-0.04}$| | |$26.45^{+0.04}_{-0.04}$| | |$-19.81^{+0.04}_{-0.04}$| | |$0.36^{+0.03}_{-0.03}$| | |$1.34^{+0.13}_{-0.13}$| | |$0.74^{+0.15}_{-0.16}$| | 1 |
| C01_07 | |$25.62^{+0.01}_{-0.02}$| | |$-20.66^{+0.01}_{-0.02}$| | |$0.26^{+0.00}_{-0.00}$| | |$25.55^{+0.02}_{-0.02}$| | |$-20.73^{+0.02}_{-0.02}$| | |$0.30^{+0.02}_{-0.02}$| | |$25.48^{+0.02}_{-0.03}$| | |$-20.79^{+0.02}_{-0.03}$| | |$0.29^{+0.02}_{-0.02}$| | |$1.13^{+0.08}_{-0.07}$| | |$0.97^{+0.10}_{-0.09}$| | 1 |
| C01_08 | |$25.78^{+0.05}_{-0.07}$| | |$-20.62^{+0.05}_{-0.07}$| | |$0.48^{+0.01}_{-0.01}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.54^{+0.03}_{-0.03}$| | |$0.42^{+0.02}_{-0.01}$| | |$25.46^{+0.04}_{-0.04}$| | |$-20.93^{+0.04}_{-0.04}$| | |$0.48^{+0.02}_{-0.02}$| | |$1.00^{+0.04}_{-0.03}$| | |$1.14^{+0.05}_{-0.05}$| | 1 |
| C01_09 | |$24.83^{+0.03}_{-0.04}$| | |$-21.57^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$24.75^{+0.04}_{-0.05}$| | |$-21.65^{+0.04}_{-0.05}$| | |$0.72^{+0.02}_{-0.02}$| | |$23.41^{+0.04}_{-0.04}$| | |$-22.99^{+0.04}_{-0.04}$| | |$0.75^{+0.02}_{-0.02}$| | |$1.26^{+0.04}_{-0.04}$| | |$1.04^{+0.05}_{-0.05}$| | 1 |
| C01_10 | |$25.94^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.37^{+0.01}_{-0.01}$| | |$25.67^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.55^{+0.02}_{-0.01}$| | |$25.38^{+0.04}_{-0.04}$| | |$-21.02^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$1.58^{+0.07}_{-0.06}$| | |$1.07^{+0.07}_{-0.07}$| | 2 |
| C01_11 | |$26.36^{+0.08}_{-0.11}$| | |$-20.04^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_12 | |$26.66^{+0.04}_{-0.05}$| | |$-19.74^{+0.04}_{-0.05}$| | |$0.37^{+0.02}_{-0.01}$| | |$26.44^{+0.05}_{-0.05}$| | |$-19.96^{+0.05}_{-0.05}$| | |$0.37^{+0.03}_{-0.04}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.50^{+0.03}_{-0.04}$| | |$1.35^{+0.11}_{-0.11}$| | |$1.35^{+0.15}_{-0.17}$| | 2 |
| C01_13 | |$26.33^{+0.15}_{-0.18}$| | |$-20.06^{+0.15}_{-0.18}$| | |$1.02^{+0.05}_{-0.04}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.15^{+0.09}_{-0.11}$| | |$0.81^{+0.05}_{-0.05}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.87^{+0.10}_{-0.06}$| | 2 |
| C01_14 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.20^{+0.01}_{-0.01}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.37^{+0.03}_{-0.03}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.22^{+0.03}_{-0.03}$| | |$-20.18^{+0.03}_{-0.03}$| | |$0.37^{+0.03}_{-0.04}$| | |$1.89^{+0.20}_{-0.20}$| | |$0.90^{+0.23}_{-0.26}$| | 2 |
| C01_15 | |$26.42^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.66^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_16 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.51^{+0.04}_{-0.05}$| | |$-20.89^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$24.56^{+0.05}_{-0.07}$| | |$-21.84^{+0.05}_{-0.07}$| | |$1.11^{+0.04}_{-0.03}$| | |$1.45^{+0.05}_{-0.04}$| | |$1.52^{+0.06}_{-0.06}$| | 1 |
| C01_17 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.50^{+0.03}_{-0.03}$| | |$0.39^{+0.02}_{-0.01}$| | |$25.37^{+0.02}_{-0.03}$| | |$-21.03^{+0.02}_{-0.03}$| | |$0.22^{+0.02}_{-0.02}$| | |$1.26^{+0.14}_{-0.11}$| | |$0.56^{+0.12}_{-0.10}$| | 2 |
| C01_18 | |$26.09^{+0.05}_{-0.07}$| | |$-20.30^{+0.05}_{-0.07}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.18^{+0.06}_{-0.07}$| | |$-20.22^{+0.06}_{-0.07}$| | |$0.49^{+0.03}_{-0.04}$| | |$25.97^{+0.05}_{-0.06}$| | |$-20.43^{+0.05}_{-0.06}$| | |$0.49^{+0.03}_{-0.04}$| | |$0.84^{+0.06}_{-0.06}$| | |$1.00^{+0.08}_{-0.09}$| | 2 |
| C01_19 | |$25.06^{+0.03}_{-0.04}$| | |$-21.63^{+0.03}_{-0.04}$| | |$0.78^{+0.02}_{-0.01}$| | |$24.71^{+0.05}_{-0.07}$| | |$-21.98^{+0.05}_{-0.07}$| | |$1.20^{+0.04}_{-0.03}$| | |$24.00^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$1.36^{+0.05}_{-0.04}$| | |$0.88^{+0.07}_{-0.05}$| | 2 |
| C01_20 | |$25.27^{+0.03}_{-0.04}$| | |$-21.43^{+0.03}_{-0.04}$| | |$0.75^{+0.01}_{-0.01}$| | |$25.25^{+0.04}_{-0.05}$| | |$-21.45^{+0.04}_{-0.05}$| | |$0.78^{+0.03}_{-0.02}$| | |$24.32^{+0.04}_{-0.04}$| | |$-22.37^{+0.04}_{-0.04}$| | |$0.70^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.89^{+0.04}_{-0.04}$| | 1 |
| C01_22 | |$27.22^{+0.06}_{-0.07}$| | |$-20.10^{+0.06}_{-0.07}$| | |$0.10^{+0.03}_{-0.02}$| | |$27.22^{+0.09}_{-0.08}$| | |$-20.09^{+0.09}_{-0.08}$| | |$0.11^{+0.07}_{-0.05}$| | — | — | — | — | — | 1 |
| C01_26 | |$26.38^{+0.08}_{-0.11}$| | |$-20.68^{+0.08}_{-0.11}$| | |$0.42^{+0.01}_{-0.01}$| | |$25.93^{+0.06}_{-0.07}$| | |$-21.13^{+0.06}_{-0.07}$| | |$0.65^{+0.02}_{-0.02}$| | |$25.45^{+0.05}_{-0.07}$| | |$-21.61^{+0.05}_{-0.07}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.89^{+0.09}_{-0.07}$| | |$1.21^{+0.07}_{-0.06}$| | 2 |
| C02_01 | |$27.82^{+0.20}_{-0.22}$| | |$-18.79^{+0.20}_{-0.22}$| | |$0.07^{+0.04}_{-0.03}$| | |$27.85^{+0.21}_{-0.27}$| | |$-18.76^{+0.21}_{-0.27}$| | |$0.10^{+0.09}_{-0.07}$| | |$27.20^{+0.16}_{-0.19}$| | |$-19.40^{+0.16}_{-0.19}$| | |$0.14^{+0.14}_{-0.10}$| | |$1.91^{+2.13}_{-1.60}$| | |$1.36^{+2.48}_{-1.92}$| | 1 |
| C02_02 | |$26.60^{+0.04}_{-0.05}$| | |$-19.89^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-19.79^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.99^{+0.03}_{-0.03}$| | |$-20.49^{+0.03}_{-0.03}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.78^{+0.08}_{-0.07}$| | |$0.86^{+0.10}_{-0.11}$| | 1 |
| C02_03 | |$26.67^{+0.08}_{-0.11}$| | |$-19.67^{+0.08}_{-0.11}$| | |$0.50^{+0.02}_{-0.01}$| | |$25.89^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.95^{+0.03}_{-0.03}$| | |$25.81^{+0.05}_{-0.06}$| | |$-20.53^{+0.05}_{-0.06}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.59^{+0.07}_{-0.06}$| | |$0.83^{+0.07}_{-0.06}$| | 2 |
| C02_04 | |$25.01^{+0.01}_{-0.02}$| | |$-21.39^{+0.01}_{-0.02}$| | |$0.35^{+0.00}_{-0.00}$| | |$24.97^{+0.02}_{-0.02}$| | |$-21.43^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.49^{+0.02}_{-0.03}$| | |$-21.91^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$1.18^{+0.05}_{-0.05}$| | |$1.01^{+0.07}_{-0.06}$| | 1 |
| C02_05 | |$26.43^{+0.08}_{-0.11}$| | |$-19.97^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | |$26.60^{+0.09}_{-0.11}$| | |$-19.79^{+0.09}_{-0.11}$| | |$0.63^{+0.05}_{-0.05}$| | |$25.61^{+0.04}_{-0.04}$| | |$-20.78^{+0.04}_{-0.04}$| | |$0.84^{+0.03}_{-0.02}$| | |$1.02^{+0.05}_{-0.04}$| | |$1.33^{+0.09}_{-0.09}$| | 1 |
| C02_06 | |$26.33^{+0.08}_{-0.11}$| | |$-20.07^{+0.08}_{-0.11}$| | |$0.70^{+0.03}_{-0.02}$| | |$26.31^{+0.09}_{-0.11}$| | |$-20.08^{+0.09}_{-0.11}$| | |$0.74^{+0.05}_{-0.05}$| | |$25.86^{+0.05}_{-0.06}$| | |$-20.54^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$0.89^{+0.05}_{-0.04}$| | |$0.85^{+0.07}_{-0.07}$| | 1 |
| C02_07 | |$25.71^{+0.05}_{-0.07}$| | |$-20.69^{+0.05}_{-0.07}$| | |$0.80^{+0.01}_{-0.01}$| | |$25.71^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.85^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$0.74^{+0.03}_{-0.03}$| | |$0.69^{+0.04}_{-0.03}$| | 1 |
| C02_08 | |$26.04^{+0.02}_{-0.03}$| | |$-20.35^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.05^{+0.03}_{-0.03}$| | |$-20.35^{+0.03}_{-0.03}$| | |$0.36^{+0.03}_{-0.04}$| | |$25.76^{+0.03}_{-0.03}$| | |$-20.64^{+0.03}_{-0.03}$| | |$0.32^{+0.02}_{-0.02}$| | |$0.94^{+0.07}_{-0.05}$| | |$0.88^{+0.11}_{-0.11}$| | 1 |
| C02_09 | |$25.28^{+0.06}_{-0.07}$| | |$-21.12^{+0.06}_{-0.07}$| | |$1.08^{+0.03}_{-0.02}$| | |$25.26^{+0.05}_{-0.07}$| | |$-21.14^{+0.05}_{-0.07}$| | |$1.13^{+0.04}_{-0.03}$| | |$24.31^{+0.05}_{-0.07}$| | |$-22.09^{+0.05}_{-0.07}$| | |$0.95^{+0.03}_{-0.02}$| | |$0.88^{+0.04}_{-0.03}$| | |$0.85^{+0.04}_{-0.03}$| | 1 |
| C02_10 | |$26.82^{+0.06}_{-0.07}$| | |$-19.58^{+0.06}_{-0.07}$| | |$0.28^{+0.01}_{-0.01}$| | |$26.37^{+0.09}_{-0.11}$| | |$-20.03^{+0.09}_{-0.11}$| | |$0.53^{+0.03}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.45^{+0.05}_{-0.06}$| | |$0.51^{+0.03}_{-0.04}$| | |$1.78^{+0.13}_{-0.14}$| | |$0.96^{+0.16}_{-0.18}$| | 2 |
| C02_12 | |$26.37^{+0.08}_{-0.11}$| | |$-20.33^{+0.08}_{-0.11}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.38^{+0.09}_{-0.11}$| | |$-20.31^{+0.09}_{-0.11}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.44^{+0.04}_{-0.04}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.08^{+0.05}_{-0.04}$| | |$1.05^{+0.07}_{-0.08}$| | 1 |
| C02_13 | |$26.77^{+0.13}_{-0.18}$| | |$-19.92^{+0.13}_{-0.18}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.83^{+0.15}_{-0.17}$| | |$-19.86^{+0.15}_{-0.17}$| | |$0.48^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C02_14 | |$27.34^{+0.11}_{-0.14}$| | |$-19.93^{+0.11}_{-0.14}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.84^{+0.09}_{-0.08}$| | |$-20.43^{+0.09}_{-0.08}$| | |$0.34^{+0.02}_{-0.03}$| | |$25.60^{+0.02}_{-0.03}$| | |$-21.68^{+0.02}_{-0.03}$| | |$0.13^{+0.01}_{-0.01}$| | |$0.52^{+0.08}_{-0.06}$| | |$0.39^{+0.07}_{-0.06}$| | 2 |
| C02_15 | |$27.57^{+0.11}_{-0.14}$| | |$-19.75^{+0.11}_{-0.14}$| | |$0.05^{+0.03}_{-0.02}$| | |$27.64^{+0.14}_{-0.17}$| | |$-19.68^{+0.14}_{-0.17}$| | |$0.09^{+0.07}_{-0.05}$| | |$25.67^{+0.02}_{-0.03}$| | |$-21.64^{+0.02}_{-0.03}$| | |$0.05^{+0.01}_{-0.01}$| | |$1.13^{+0.76}_{-0.55}$| | |$0.60^{+0.87}_{-0.69}$| | 1 |
| C02_20 | |$26.71^{+0.13}_{-0.18}$| | |$-20.21^{+0.13}_{-0.18}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.82^{+0.15}_{-0.17}$| | |$-20.10^{+0.15}_{-0.17}$| | |$0.40^{+0.03}_{-0.03}$| | |$25.90^{+0.05}_{-0.06}$| | |$-21.02^{+0.05}_{-0.06}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.25^{+0.06}_{-0.05}$| | |$1.36^{+0.10}_{-0.11}$| | 1 |
| C02_21 | |$27.16^{+0.06}_{-0.07}$| | |$-19.76^{+0.06}_{-0.07}$| | |$0.17^{+0.03}_{-0.02}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.44^{+0.09}_{-0.11}$| | |$0.50^{+0.04}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.97^{+0.05}_{-0.06}$| | |$0.59^{+0.07}_{-0.04}$| | |$3.56^{+0.86}_{-0.58}$| | |$1.19^{+0.53}_{-0.39}$| | 2 |
| C02_22 | |$26.12^{+0.02}_{-0.03}$| | |$-20.76^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.10^{+0.03}_{-0.03}$| | |$-20.79^{+0.03}_{-0.03}$| | |$0.25^{+0.03}_{-0.03}$| | |$25.63^{+0.02}_{-0.03}$| | |$-21.25^{+0.02}_{-0.03}$| | |$0.23^{+0.02}_{-0.01}$| | |$1.12^{+0.09}_{-0.08}$| | |$0.92^{+0.15}_{-0.14}$| | 1 |
| C02_23 | |$26.68^{+0.04}_{-0.05}$| | |$-20.21^{+0.04}_{-0.05}$| | |$0.22^{+0.01}_{-0.01}$| | |$26.54^{+0.05}_{-0.05}$| | |$-20.35^{+0.05}_{-0.05}$| | |$0.34^{+0.03}_{-0.03}$| | |$26.24^{+0.04}_{-0.04}$| | |$-20.65^{+0.04}_{-0.04}$| | |$0.25^{+0.03}_{-0.03}$| | |$1.10^{+0.13}_{-0.12}$| | |$0.73^{+0.15}_{-0.16}$| | 1 |
| C03_01 | |$26.89^{+0.06}_{-0.07}$| | |$-19.83^{+0.06}_{-0.07}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.91^{+0.09}_{-0.08}$| | |$-19.81^{+0.09}_{-0.08}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.67^{+0.04}_{-0.04}$| | |$-20.05^{+0.04}_{-0.04}$| | |$0.28^{+0.03}_{-0.03}$| | |$0.68^{+0.07}_{-0.07}$| | |$0.68^{+0.08}_{-0.09}$| | 1 |
| C03_04 | |$25.62^{+0.01}_{-0.02}$| | |$-21.08^{+0.01}_{-0.02}$| | |$0.30^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-21.09^{+0.02}_{-0.02}$| | |$0.28^{+0.01}_{-0.01}$| | |$25.03^{+0.02}_{-0.03}$| | |$-21.66^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$1.22^{+0.05}_{-0.05}$| | |$1.27^{+0.08}_{-0.08}$| | 1 |
| C03_05 | |$26.20^{+0.08}_{-0.11}$| | |$-20.42^{+0.08}_{-0.11}$| | |$0.46^{+0.02}_{-0.01}$| | |$26.22^{+0.09}_{-0.11}$| | |$-20.41^{+0.09}_{-0.11}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.45^{+0.04}_{-0.04}$| | |$0.56^{+0.02}_{-0.02}$| | |$1.23^{+0.06}_{-0.05}$| | |$1.25^{+0.10}_{-0.11}$| | 1 |
| C03_07 | |$27.76^{+0.20}_{-0.22}$| | |$-19.21^{+0.20}_{-0.22}$| | |$0.11^{+0.03}_{-0.02}$| | |$27.93^{+0.21}_{-0.27}$| | |$-19.04^{+0.21}_{-0.27}$| | |$0.05^{+0.08}_{-0.06}$| | — | — | — | — | — | 1 |
| C03_08 | |$26.71^{+0.04}_{-0.05}$| | |$-20.27^{+0.04}_{-0.05}$| | |$0.23^{+0.01}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-20.29^{+0.05}_{-0.05}$| | |$0.27^{+0.03}_{-0.03}$| | |$26.23^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$1.21^{+0.12}_{-0.12}$| | |$1.01^{+0.17}_{-0.16}$| | 1 |
| C03_09 | |$26.75^{+0.06}_{-0.07}$| | |$-19.74^{+0.06}_{-0.07}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.84^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.25^{+0.03}_{-0.03}$| | |$26.10^{+0.05}_{-0.06}$| | |$-20.39^{+0.05}_{-0.06}$| | |$0.48^{+0.03}_{-0.03}$| | |$1.58^{+0.12}_{-0.12}$| | |$1.89^{+0.23}_{-0.23}$| | 1 |
| C03_11 | |$25.57^{+0.06}_{-0.07}$| | |$-20.83^{+0.06}_{-0.07}$| | |$1.62^{+0.05}_{-0.04}$| | |$25.65^{+0.05}_{-0.07}$| | |$-20.75^{+0.05}_{-0.07}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C03_12 | |$25.23^{+0.03}_{-0.04}$| | |$-21.16^{+0.03}_{-0.04}$| | |$0.85^{+0.02}_{-0.01}$| | |$24.93^{+0.05}_{-0.07}$| | |$-21.46^{+0.05}_{-0.07}$| | |$1.04^{+0.03}_{-0.03}$| | |$23.76^{+0.04}_{-0.04}$| | |$-22.64^{+0.04}_{-0.04}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.07^{+0.04}_{-0.03}$| | |$0.87^{+0.05}_{-0.04}$| | 2 |
| C03_13 | |$25.29^{+0.06}_{-0.07}$| | |$-21.11^{+0.06}_{-0.07}$| | |$1.42^{+0.04}_{-0.03}$| | |$25.18^{+0.05}_{-0.07}$| | |$-21.22^{+0.05}_{-0.07}$| | |$1.44^{+0.05}_{-0.04}$| | |$24.29^{+0.05}_{-0.07}$| | |$-22.11^{+0.05}_{-0.07}$| | |$1.66^{+0.06}_{-0.05}$| | |$1.17^{+0.05}_{-0.04}$| | |$1.16^{+0.06}_{-0.04}$| | 2 |
| C03_14 | |$25.83^{+0.09}_{-0.11}$| | |$-20.57^{+0.09}_{-0.11}$| | |$0.96^{+0.02}_{-0.01}$| | |$25.62^{+0.05}_{-0.07}$| | |$-20.77^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$24.99^{+0.05}_{-0.07}$| | |$-21.41^{+0.05}_{-0.07}$| | |$1.41^{+0.05}_{-0.04}$| | |$1.48^{+0.06}_{-0.05}$| | |$1.35^{+0.07}_{-0.06}$| | 2 |
| C03_15 | |$26.46^{+0.04}_{-0.05}$| | |$-19.94^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.06^{+0.06}_{-0.07}$| | |$-20.34^{+0.06}_{-0.07}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.71^{+0.02}_{-0.03}$| | |$-20.69^{+0.02}_{-0.03}$| | |$0.45^{+0.02}_{-0.02}$| | |$1.76^{+0.10}_{-0.09}$| | |$0.87^{+0.13}_{-0.15}$| | 2 |
| C03_16 | |$26.57^{+0.04}_{-0.05}$| | |$-19.83^{+0.04}_{-0.05}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.69^{+0.05}_{-0.05}$| | |$26.32^{+0.04}_{-0.04}$| | |$-20.08^{+0.04}_{-0.04}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.09^{+0.09}_{-0.09}$| | |$0.64^{+0.11}_{-0.12}$| | 1 |
| C03_17 | |$26.64^{+0.13}_{-0.18}$| | |$-19.76^{+0.13}_{-0.18}$| | |$0.48^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.08^{+0.03}_{-0.03}$| | |$-20.32^{+0.03}_{-0.03}$| | |$0.39^{+0.03}_{-0.04}$| | |$0.80^{+0.07}_{-0.08}$| | |$0.72^{+0.08}_{-0.09}$| | 2 |
| C03_18 | |$26.12^{+0.02}_{-0.03}$| | |$-20.28^{+0.02}_{-0.03}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.97^{+0.03}_{-0.03}$| | |$-20.43^{+0.03}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$26.14^{+0.03}_{-0.03}$| | |$-20.26^{+0.03}_{-0.03}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.66^{+0.14}_{-0.14}$| | |$1.26^{+0.14}_{-0.15}$| | 2 |
| C03_19 | |$26.54^{+0.04}_{-0.05}$| | |$-19.86^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.99^{+0.06}_{-0.07}$| | |$-20.41^{+0.06}_{-0.07}$| | |$0.66^{+0.05}_{-0.05}$| | |$25.56^{+0.04}_{-0.04}$| | |$-20.84^{+0.04}_{-0.04}$| | |$0.92^{+0.03}_{-0.02}$| | |$3.42^{+0.19}_{-0.14}$| | |$1.40^{+0.28}_{-0.28}$| | 2 |
| C03_20 | |$26.70^{+0.13}_{-0.18}$| | |$-19.70^{+0.13}_{-0.18}$| | |$0.73^{+0.03}_{-0.02}$| | |$27.04^{+0.15}_{-0.17}$| | |$-19.36^{+0.15}_{-0.17}$| | |$0.64^{+0.20}_{-0.12}$| | — | — | — | — | — | 1 |
| C03_21 | |$26.62^{+0.04}_{-0.05}$| | |$-19.78^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.33^{+0.05}_{-0.05}$| | |$-20.07^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$24.89^{+0.05}_{-0.07}$| | |$-21.51^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.02}$| | |$3.98^{+0.21}_{-0.16}$| | |$2.34^{+0.32}_{-0.36}$| | 2 |
| C03_22 | |$25.88^{+0.09}_{-0.11}$| | |$-20.52^{+0.09}_{-0.11}$| | |$1.28^{+0.03}_{-0.02}$| | |$25.98^{+0.08}_{-0.10}$| | |$-20.42^{+0.08}_{-0.10}$| | |$1.19^{+0.11}_{-0.08}$| | — | — | — | — | — | 1 |
| C03_23 | |$26.31^{+0.08}_{-0.11}$| | |$-20.08^{+0.08}_{-0.11}$| | |$0.79^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C03_24 | |$24.71^{+0.01}_{-0.02}$| | |$-21.98^{+0.01}_{-0.02}$| | |$0.37^{+0.01}_{-0.00}$| | |$24.69^{+0.02}_{-0.02}$| | |$-22.00^{+0.02}_{-0.02}$| | |$0.37^{+0.01}_{-0.01}$| | |$24.37^{+0.04}_{-0.04}$| | |$-22.32^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.01}$| | |$1.39^{+0.05}_{-0.04}$| | |$1.38^{+0.07}_{-0.06}$| | 2 |
| C03_25 | |$26.13^{+0.05}_{-0.07}$| | |$-20.57^{+0.05}_{-0.07}$| | |$0.81^{+0.04}_{-0.03}$| | |$26.23^{+0.09}_{-0.11}$| | |$-20.46^{+0.09}_{-0.11}$| | |$0.76^{+0.07}_{-0.06}$| | |$26.18^{+0.09}_{-0.12}$| | |$-20.52^{+0.09}_{-0.12}$| | |$0.72^{+0.08}_{-0.04}$| | |$0.89^{+0.11}_{-0.07}$| | |$0.95^{+0.13}_{-0.09}$| | 1 |
| C03_27 | |$26.25^{+0.04}_{-0.05}$| | |$-20.91^{+0.04}_{-0.05}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.24^{+0.03}_{-0.03}$| | |$-20.92^{+0.03}_{-0.03}$| | |$0.21^{+0.03}_{-0.03}$| | |$25.36^{+0.02}_{-0.03}$| | |$-21.80^{+0.02}_{-0.03}$| | |$0.34^{+0.01}_{-0.01}$| | |$1.80^{+0.11}_{-0.09}$| | |$1.59^{+0.23}_{-0.22}$| | 1 |
| C04_02 | |$25.38^{+0.01}_{-0.02}$| | |$-21.02^{+0.01}_{-0.02}$| | |$0.19^{+0.00}_{-0.00}$| | |$25.24^{+0.02}_{-0.02}$| | |$-21.16^{+0.02}_{-0.02}$| | |$0.31^{+0.01}_{-0.02}$| | |$24.32^{+0.02}_{-0.03}$| | |$-22.08^{+0.02}_{-0.03}$| | |$0.46^{+0.02}_{-0.02}$| | |$2.42^{+0.11}_{-0.10}$| | |$1.46^{+0.15}_{-0.14}$| | 1 |
| C04_03 | |$26.15^{+0.05}_{-0.07}$| | |$-20.25^{+0.05}_{-0.07}$| | |$0.63^{+0.03}_{-0.02}$| | |$25.95^{+0.06}_{-0.07}$| | |$-20.45^{+0.06}_{-0.07}$| | |$0.71^{+0.02}_{-0.02}$| | |$25.30^{+0.04}_{-0.04}$| | |$-21.10^{+0.04}_{-0.04}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.78^{+0.05}_{-0.04}$| | |$0.69^{+0.04}_{-0.03}$| | 2 |
| C04_04 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-20.80^{+0.02}_{-0.02}$| | |$0.29^{+0.01}_{-0.02}$| | |$24.85^{+0.02}_{-0.03}$| | |$-21.55^{+0.02}_{-0.03}$| | |$0.30^{+0.02}_{-0.02}$| | |$1.25^{+0.08}_{-0.07}$| | |$1.02^{+0.10}_{-0.09}$| | 2 |
| C04_05 | |$25.68^{+0.03}_{-0.04}$| | |$-20.72^{+0.03}_{-0.04}$| | |$0.63^{+0.01}_{-0.01}$| | |$25.64^{+0.04}_{-0.05}$| | |$-20.76^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$25.07^{+0.04}_{-0.04}$| | |$-21.33^{+0.04}_{-0.04}$| | |$0.68^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.93^{+0.04}_{-0.04}$| | 1 |
| C04_06 | |$26.27^{+0.04}_{-0.05}$| | |$-20.13^{+0.04}_{-0.05}$| | |$0.46^{+0.02}_{-0.01}$| | — | — | — | |$24.85^{+0.05}_{-0.07}$| | |$-21.55^{+0.05}_{-0.07}$| | |$1.35^{+0.05}_{-0.04}$| | |$2.95^{+0.16}_{-0.12}$| | — | 2 |
| C04_07 | |$26.47^{+0.04}_{-0.05}$| | |$-20.22^{+0.04}_{-0.05}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.32^{+0.03}_{-0.04}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.83^{+0.03}_{-0.03}$| | |$0.35^{+0.02}_{-0.01}$| | |$1.16^{+0.07}_{-0.06}$| | |$1.08^{+0.12}_{-0.14}$| | 1 |
| C04_08 | |$26.48^{+0.08}_{-0.11}$| | |$-20.22^{+0.08}_{-0.11}$| | |$0.74^{+0.03}_{-0.02}$| | |$26.51^{+0.09}_{-0.11}$| | |$-20.18^{+0.09}_{-0.11}$| | |$0.70^{+0.04}_{-0.05}$| | |$26.24^{+0.09}_{-0.12}$| | |$-20.45^{+0.09}_{-0.12}$| | |$0.67^{+0.08}_{-0.04}$| | |$0.90^{+0.11}_{-0.06}$| | |$0.96^{+0.12}_{-0.08}$| | 1 |
| C04_09 | |$26.23^{+0.08}_{-0.11}$| | |$-20.46^{+0.08}_{-0.11}$| | |$0.85^{+0.04}_{-0.03}$| | |$26.32^{+0.09}_{-0.11}$| | |$-20.38^{+0.09}_{-0.11}$| | |$0.71^{+0.04}_{-0.05}$| | |$25.36^{+0.05}_{-0.07}$| | |$-21.33^{+0.05}_{-0.07}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.08^{+0.07}_{-0.05}$| | |$1.29^{+0.08}_{-0.08}$| | 1 |
| C04_10 | |$26.42^{+0.08}_{-0.11}$| | |$-20.41^{+0.08}_{-0.11}$| | |$0.76^{+0.04}_{-0.03}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.35^{+0.09}_{-0.11}$| | |$0.69^{+0.04}_{-0.04}$| | |$26.19^{+0.09}_{-0.12}$| | |$-20.64^{+0.09}_{-0.12}$| | |$0.52^{+0.08}_{-0.04}$| | |$0.68^{+0.11}_{-0.06}$| | |$0.75^{+0.11}_{-0.07}$| | 1 |
| C05_01 | |$26.94^{+0.06}_{-0.07}$| | |$-19.32^{+0.06}_{-0.07}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.50^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.58^{+0.02}_{-0.02}$| | |$2.17^{+0.12}_{-0.10}$| | — | 2 |
| C05_04 | |$25.74^{+0.09}_{-0.11}$| | |$-20.66^{+0.09}_{-0.11}$| | |$0.97^{+0.02}_{-0.01}$| | |$25.35^{+0.05}_{-0.07}$| | |$-21.05^{+0.05}_{-0.07}$| | |$1.00^{+0.03}_{-0.03}$| | |$24.80^{+0.04}_{-0.04}$| | |$-21.60^{+0.04}_{-0.04}$| | |$0.87^{+0.03}_{-0.02}$| | |$0.89^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C05_05 | |$26.49^{+0.04}_{-0.05}$| | |$-20.45^{+0.04}_{-0.05}$| | |$0.18^{+0.01}_{-0.01}$| | |$26.09^{+0.03}_{-0.03}$| | |$-20.85^{+0.03}_{-0.03}$| | |$0.31^{+0.03}_{-0.03}$| | |$25.68^{+0.02}_{-0.03}$| | |$-21.26^{+0.02}_{-0.03}$| | |$0.19^{+0.02}_{-0.01}$| | |$1.05^{+0.11}_{-0.08}$| | |$0.61^{+0.13}_{-0.13}$| | 2 |
| C05_06 | |$26.49^{+0.04}_{-0.05}$| | |$-20.37^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.45^{+0.05}_{-0.05}$| | |$-20.41^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.03}$| | |$26.65^{+0.04}_{-0.04}$| | |$-20.22^{+0.04}_{-0.04}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.94^{+0.09}_{-0.09}$| | |$0.94^{+0.11}_{-0.13}$| | 1 |
| C05_07 | |$25.96^{+0.02}_{-0.03}$| | |$-20.95^{+0.02}_{-0.03}$| | |$0.35^{+0.01}_{-0.00}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.89^{+0.03}_{-0.03}$| | |$0.30^{+0.03}_{-0.03}$| | |$25.82^{+0.03}_{-0.03}$| | |$-21.10^{+0.03}_{-0.03}$| | |$0.29^{+0.01}_{-0.01}$| | |$0.83^{+0.04}_{-0.04}$| | |$0.96^{+0.09}_{-0.10}$| | 1 |
| C05_08 | |$26.28^{+0.08}_{-0.11}$| | |$-20.71^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.02}$| | |$26.10^{+0.06}_{-0.07}$| | |$-20.89^{+0.06}_{-0.07}$| | |$0.73^{+0.06}_{-0.05}$| | |$25.99^{+0.05}_{-0.06}$| | |$-21.00^{+0.05}_{-0.06}$| | |$0.43^{+0.03}_{-0.03}$| | |$0.73^{+0.05}_{-0.05}$| | |$0.59^{+0.07}_{-0.07}$| | 2 |
| C05_09 | |$26.62^{+0.04}_{-0.05}$| | |$-20.19^{+0.04}_{-0.05}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.58^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.26^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C06_01 | |$26.15^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.38^{+0.02}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-21.13^{+0.04}_{-0.05}$| | |$0.81^{+0.03}_{-0.02}$| | |$24.75^{+0.04}_{-0.04}$| | |$-21.85^{+0.04}_{-0.04}$| | |$0.80^{+0.03}_{-0.02}$| | |$2.09^{+0.12}_{-0.09}$| | |$0.98^{+0.10}_{-0.08}$| | 2 |
| C06_02 | |$26.61^{+0.08}_{-0.11}$| | |$-20.10^{+0.08}_{-0.11}$| | |$0.55^{+0.03}_{-0.02}$| | |$26.77^{+0.09}_{-0.08}$| | |$-19.94^{+0.09}_{-0.08}$| | |$0.37^{+0.03}_{-0.04}$| | — | — | — | — | — | 2 |
| C06_03 | |$26.90^{+0.13}_{-0.18}$| | |$-19.81^{+0.13}_{-0.18}$| | |$0.49^{+0.07}_{-0.04}$| | |$26.95^{+0.09}_{-0.08}$| | |$-19.76^{+0.09}_{-0.08}$| | |$0.40^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C06_05 | |$26.61^{+0.04}_{-0.05}$| | |$-20.50^{+0.04}_{-0.05}$| | |$0.07^{+0.01}_{-0.01}$| | |$26.42^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.18^{+0.03}_{-0.03}$| | |$25.61^{+0.02}_{-0.03}$| | |$-21.50^{+0.02}_{-0.03}$| | |$0.24^{+0.02}_{-0.01}$| | |$3.21^{+0.44}_{-0.34}$| | |$1.33^{+0.51}_{-0.49}$| | 2 |
| C06_06 | |$26.63^{+0.04}_{-0.05}$| | |$-19.84^{+0.04}_{-0.05}$| | |$0.09^{+0.01}_{-0.01}$| | |$26.31^{+0.05}_{-0.05}$| | |$-20.17^{+0.05}_{-0.05}$| | |$0.25^{+0.03}_{-0.03}$| | — | — | — | — | — | 2 |
| C06_09 | |$26.21^{+0.08}_{-0.11}$| | |$-20.19^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.51^{+0.09}_{-0.12}$| | |$-19.89^{+0.09}_{-0.12}$| | |$0.55^{+0.03}_{-0.04}$| | |$0.92^{+0.06}_{-0.06}$| | |$1.02^{+0.08}_{-0.09}$| | 1 |
| C06_10 | |$25.46^{+0.06}_{-0.07}$| | |$-20.94^{+0.06}_{-0.07}$| | |$0.99^{+0.02}_{-0.01}$| | |$25.53^{+0.05}_{-0.07}$| | |$-20.87^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.03}$| | |$25.84^{+0.05}_{-0.06}$| | |$-20.56^{+0.05}_{-0.06}$| | |$0.92^{+0.03}_{-0.02}$| | |$0.93^{+0.04}_{-0.03}$| | |$0.96^{+0.04}_{-0.03}$| | 1 |
| C06_11 | |$25.34^{+0.03}_{-0.04}$| | |$-21.05^{+0.03}_{-0.04}$| | |$0.79^{+0.01}_{-0.01}$| | |$25.34^{+0.04}_{-0.05}$| | |$-21.06^{+0.04}_{-0.05}$| | |$0.81^{+0.02}_{-0.02}$| | |$25.69^{+0.05}_{-0.06}$| | |$-20.71^{+0.05}_{-0.06}$| | |$0.73^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.90^{+0.04}_{-0.03}$| | 1 |
| C06_12 | |$26.41^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.61^{+0.03}_{-0.02}$| | |$26.00^{+0.06}_{-0.07}$| | |$-20.40^{+0.06}_{-0.07}$| | |$0.93^{+0.07}_{-0.07}$| | |$25.52^{+0.05}_{-0.07}$| | |$-20.88^{+0.05}_{-0.07}$| | |$1.01^{+0.03}_{-0.02}$| | |$1.66^{+0.10}_{-0.07}$| | |$1.09^{+0.14}_{-0.12}$| | 2 |
| C06_13 | |$26.10^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.80^{+0.04}_{-0.03}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.73^{+0.06}_{-0.07}$| | |$0.83^{+0.03}_{-0.02}$| | |$25.68^{+0.07}_{-0.10}$| | |$-21.01^{+0.07}_{-0.10}$| | |$0.88^{+0.03}_{-0.02}$| | |$1.10^{+0.07}_{-0.05}$| | |$1.06^{+0.05}_{-0.04}$| | 2 |
| C06_15 | |$27.51^{+0.11}_{-0.14}$| | |$-19.32^{+0.11}_{-0.14}$| | |$0.14^{+0.04}_{-0.03}$| | |$27.18^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.30^{+0.08}_{-0.06}$| | — | — | — | — | — | 2 |
| C06_16 | |$26.50^{+0.04}_{-0.05}$| | |$-20.39^{+0.04}_{-0.05}$| | |$0.14^{+0.01}_{-0.01}$| | |$26.59^{+0.05}_{-0.05}$| | |$-20.30^{+0.05}_{-0.05}$| | |$0.10^{+0.03}_{-0.03}$| | |$26.64^{+0.04}_{-0.04}$| | |$-20.25^{+0.04}_{-0.04}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.25^{+0.20}_{-0.19}$| | |$1.80^{+0.41}_{-0.40}$| | 1 |
| C07_01 | |$26.90^{+0.06}_{-0.07}$| | |$-19.66^{+0.06}_{-0.07}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.70^{+0.09}_{-0.08}$| | |$0.23^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C07_02 | |$25.01^{+0.01}_{-0.02}$| | |$-21.31^{+0.01}_{-0.02}$| | |$0.32^{+0.00}_{-0.00}$| | |$25.02^{+0.02}_{-0.02}$| | |$-21.30^{+0.02}_{-0.02}$| | |$0.35^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_04 | |$25.61^{+0.06}_{-0.07}$| | |$-20.79^{+0.06}_{-0.07}$| | |$1.66^{+0.05}_{-0.04}$| | |$25.75^{+0.08}_{-0.10}$| | |$-20.65^{+0.08}_{-0.10}$| | |$1.45^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_06 | |$26.70^{+0.04}_{-0.05}$| | |$-19.70^{+0.04}_{-0.05}$| | |$0.24^{+0.01}_{-0.01}$| | |$25.70^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_07 | |$25.70^{+0.09}_{-0.11}$| | |$-20.70^{+0.09}_{-0.11}$| | |$1.49^{+0.04}_{-0.03}$| | |$25.76^{+0.08}_{-0.10}$| | |$-20.64^{+0.08}_{-0.10}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_08 | |$26.68^{+0.08}_{-0.11}$| | |$-19.72^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.54^{+0.09}_{-0.08}$| | |$0.44^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_09 | |$25.34^{+0.01}_{-0.02}$| | |$-21.06^{+0.01}_{-0.02}$| | |$0.40^{+0.01}_{-0.01}$| | |$25.39^{+0.02}_{-0.02}$| | |$-21.01^{+0.02}_{-0.02}$| | |$0.36^{+0.02}_{-0.01}$| | — | — | — | — | — | 1 |
| C07_10 | |$26.24^{+0.08}_{-0.11}$| | |$-20.16^{+0.08}_{-0.11}$| | |$0.68^{+0.03}_{-0.02}$| | |$26.21^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.60^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_12 | |$26.28^{+0.08}_{-0.11}$| | |$-20.12^{+0.08}_{-0.11}$| | |$0.58^{+0.02}_{-0.01}$| | |$26.20^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.63^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_13 | |$25.32^{+0.03}_{-0.04}$| | |$-21.08^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$24.53^{+0.05}_{-0.07}$| | |$-21.87^{+0.05}_{-0.07}$| | |$1.18^{+0.04}_{-0.03}$| | — | — | — | — | — | 2 |
| C07_14 | |$25.81^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.72^{+0.01}_{-0.01}$| | |$25.82^{+0.06}_{-0.07}$| | |$-20.58^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | — | — | — | — | — | 1 |
| C07_15 | |$26.95^{+0.06}_{-0.07}$| | |$-19.75^{+0.06}_{-0.07}$| | |$0.31^{+0.01}_{-0.01}$| | |$26.77^{+0.15}_{-0.17}$| | |$-19.93^{+0.15}_{-0.17}$| | |$0.43^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_16 | |$26.63^{+0.08}_{-0.11}$| | |$-20.23^{+0.08}_{-0.11}$| | |$0.65^{+0.03}_{-0.02}$| | |$25.82^{+0.08}_{-0.10}$| | |$-21.05^{+0.08}_{-0.10}$| | |$1.36^{+0.05}_{-0.04}$| | — | — | — | — | — | 2 |
| C08_01 | |$25.87^{+0.02}_{-0.03}$| | |$-21.40^{+0.02}_{-0.03}$| | |$0.13^{+0.00}_{-0.00}$| | |$24.89^{+0.04}_{-0.05}$| | |$-22.38^{+0.04}_{-0.05}$| | |$0.53^{+0.01}_{-0.01}$| | |$24.01^{+0.02}_{-0.03}$| | |$-23.25^{+0.02}_{-0.03}$| | |$0.28^{+0.01}_{-0.01}$| | |$2.21^{+0.11}_{-0.10}$| | |$0.53^{+0.12}_{-0.11}$| | 2 |
| C08_02 | |$27.52^{+0.11}_{-0.14}$| | |$-19.46^{+0.11}_{-0.14}$| | |$0.23^{+0.03}_{-0.02}$| | |$27.40^{+0.14}_{-0.17}$| | |$-19.57^{+0.14}_{-0.17}$| | |$0.35^{+0.13}_{-0.06}$| | — | — | — | — | — | 1 |
| C08_03 | |$27.02^{+0.06}_{-0.07}$| | |$-19.38^{+0.06}_{-0.07}$| | |$0.15^{+0.04}_{-0.03}$| | |$26.74^{+0.05}_{-0.05}$| | |$-19.66^{+0.05}_{-0.05}$| | |$0.30^{+0.03}_{-0.03}$| | |$26.87^{+0.08}_{-0.12}$| | |$-19.53^{+0.08}_{-0.12}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.22^{+0.40}_{-0.32}$| | |$0.60^{+0.25}_{-0.25}$| | 2 |
| C08_04 | |$26.55^{+0.04}_{-0.05}$| | |$-19.85^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.43^{+0.05}_{-0.07}$| | |$-20.97^{+0.05}_{-0.07}$| | |$1.02^{+0.03}_{-0.02}$| | |$3.84^{+0.20}_{-0.15}$| | — | 1 |
| C08_05 | |$24.75^{+0.06}_{-0.07}$| | |$-21.65^{+0.06}_{-0.07}$| | |$0.98^{+0.02}_{-0.01}$| | |$24.73^{+0.05}_{-0.07}$| | |$-21.67^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$23.11^{+0.04}_{-0.04}$| | |$-23.29^{+0.04}_{-0.04}$| | |$0.93^{+0.03}_{-0.02}$| | |$0.96^{+0.04}_{-0.03}$| | |$0.89^{+0.04}_{-0.03}$| | 2 |
| C08_06 | |$26.06^{+0.02}_{-0.03}$| | |$-20.34^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$24.84^{+0.05}_{-0.07}$| | |$-21.56^{+0.05}_{-0.07}$| | |$1.21^{+0.04}_{-0.03}$| | |$23.64^{+0.05}_{-0.07}$| | |$-22.76^{+0.05}_{-0.07}$| | |$1.29^{+0.04}_{-0.03}$| | |$6.15^{+0.38}_{-0.30}$| | |$1.07^{+0.26}_{-0.21}$| | 2 |
| C08_07 | |$25.37^{+0.03}_{-0.04}$| | |$-21.02^{+0.03}_{-0.04}$| | |$0.93^{+0.02}_{-0.01}$| | |$25.52^{+0.04}_{-0.05}$| | |$-20.88^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.22^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$0.85^{+0.03}_{-0.02}$| | |$1.00^{+0.03}_{-0.03}$| | 2 |
| C08_08 | |$25.72^{+0.03}_{-0.04}$| | |$-20.68^{+0.03}_{-0.04}$| | |$0.90^{+0.02}_{-0.01}$| | |$25.40^{+0.05}_{-0.07}$| | |$-21.00^{+0.05}_{-0.07}$| | |$1.17^{+0.04}_{-0.03}$| | |$23.71^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$0.97^{+0.03}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.83^{+0.05}_{-0.04}$| | 2 |
| C08_09 | |$25.79^{+0.09}_{-0.11}$| | |$-20.61^{+0.09}_{-0.11}$| | |$1.10^{+0.03}_{-0.02}$| | |$25.83^{+0.08}_{-0.10}$| | |$-20.57^{+0.08}_{-0.10}$| | |$1.12^{+0.04}_{-0.03}$| | |$25.09^{+0.04}_{-0.04}$| | |$-21.31^{+0.04}_{-0.04}$| | |$0.54^{+0.02}_{-0.02}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.48^{+0.02}_{-0.02}$| | 1 |
| C08_10 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.38^{+0.02}_{-0.01}$| | |$26.02^{+0.06}_{-0.07}$| | |$-20.38^{+0.06}_{-0.07}$| | |$0.55^{+0.03}_{-0.04}$| | |$25.49^{+0.04}_{-0.04}$| | |$-20.91^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$2.11^{+0.12}_{-0.09}$| | |$1.45^{+0.14}_{-0.16}$| | 2 |
| C08_11 | |$24.25^{+0.06}_{-0.07}$| | |$-22.15^{+0.06}_{-0.07}$| | |$1.28^{+0.03}_{-0.02}$| | |$24.16^{+0.05}_{-0.07}$| | |$-22.24^{+0.05}_{-0.07}$| | |$1.49^{+0.05}_{-0.04}$| | |$23.59^{+0.05}_{-0.07}$| | |$-22.81^{+0.05}_{-0.07}$| | |$1.30^{+0.04}_{-0.03}$| | |$1.01^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_12 | |$25.93^{+0.05}_{-0.07}$| | |$-20.47^{+0.05}_{-0.07}$| | |$0.84^{+0.02}_{-0.01}$| | |$25.45^{+0.05}_{-0.07}$| | |$-20.95^{+0.05}_{-0.07}$| | |$1.03^{+0.03}_{-0.03}$| | |$24.55^{+0.05}_{-0.07}$| | |$-21.85^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.02}$| | |$1.15^{+0.04}_{-0.03}$| | |$0.94^{+0.05}_{-0.04}$| | 2 |
| C08_13 | |$25.68^{+0.01}_{-0.02}$| | |$-20.71^{+0.01}_{-0.02}$| | |$0.20^{+0.00}_{-0.00}$| | |$25.50^{+0.02}_{-0.02}$| | |$-20.90^{+0.02}_{-0.02}$| | |$0.34^{+0.01}_{-0.02}$| | |$25.41^{+0.02}_{-0.03}$| | |$-20.99^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$2.09^{+0.09}_{-0.09}$| | |$1.25^{+0.12}_{-0.12}$| | 2 |
| C08_14 | |$26.11^{+0.05}_{-0.07}$| | |$-20.29^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.04^{+0.06}_{-0.07}$| | |$-20.36^{+0.06}_{-0.07}$| | |$0.61^{+0.05}_{-0.05}$| | |$24.84^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.52^{+0.02}_{-0.02}$| | |$0.99^{+0.05}_{-0.04}$| | |$0.85^{+0.09}_{-0.09}$| | 2 |
| C08_15 | |$25.20^{+0.06}_{-0.07}$| | |$-21.49^{+0.06}_{-0.07}$| | |$0.87^{+0.02}_{-0.01}$| | |$25.19^{+0.05}_{-0.07}$| | |$-21.50^{+0.05}_{-0.07}$| | |$0.90^{+0.03}_{-0.02}$| | |$24.61^{+0.04}_{-0.04}$| | |$-22.08^{+0.04}_{-0.04}$| | |$0.78^{+0.03}_{-0.02}$| | |$0.90^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_16 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.20^{+0.07}_{-0.05}$| | |$26.09^{+0.08}_{-0.10}$| | |$-20.61^{+0.08}_{-0.10}$| | |$1.29^{+0.12}_{-0.09}$| | — | — | — | — | — | 1 |
| C08_17 | |$25.19^{+0.03}_{-0.04}$| | |$-21.51^{+0.03}_{-0.04}$| | |$0.64^{+0.01}_{-0.01}$| | |$25.22^{+0.04}_{-0.05}$| | |$-21.48^{+0.04}_{-0.05}$| | |$0.66^{+0.02}_{-0.02}$| | |$24.17^{+0.04}_{-0.04}$| | |$-22.52^{+0.04}_{-0.04}$| | |$0.83^{+0.03}_{-0.02}$| | |$1.30^{+0.05}_{-0.04}$| | |$1.27^{+0.06}_{-0.05}$| | 2 |
| C08_18 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.08^{+0.07}_{-0.05}$| | |$25.88^{+0.08}_{-0.10}$| | |$-20.81^{+0.08}_{-0.10}$| | |$1.29^{+0.04}_{-0.03}$| | |$23.81^{+0.05}_{-0.07}$| | |$-22.88^{+0.05}_{-0.07}$| | |$1.28^{+0.04}_{-0.04}$| | |$1.18^{+0.09}_{-0.06}$| | |$0.99^{+0.06}_{-0.04}$| | 2 |
| C08_19 | |$26.08^{+0.05}_{-0.07}$| | |$-20.61^{+0.05}_{-0.07}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.98^{+0.06}_{-0.07}$| | |$-20.72^{+0.06}_{-0.07}$| | |$0.60^{+0.04}_{-0.05}$| | |$23.88^{+0.04}_{-0.04}$| | |$-22.82^{+0.04}_{-0.04}$| | |$0.71^{+0.02}_{-0.02}$| | |$1.45^{+0.06}_{-0.05}$| | |$1.19^{+0.11}_{-0.12}$| | 1 |
| C08_20 | |$26.65^{+0.04}_{-0.05}$| | |$-20.04^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.67^{+0.05}_{-0.05}$| | |$-20.03^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.04}$| | |$24.63^{+0.05}_{-0.07}$| | |$-22.06^{+0.05}_{-0.07}$| | |$0.94^{+0.03}_{-0.02}$| | |$2.72^{+0.15}_{-0.11}$| | |$2.68^{+0.25}_{-0.28}$| | 1 |
| C08_21 | |$25.93^{+0.02}_{-0.03}$| | |$-20.77^{+0.02}_{-0.03}$| | |$0.22^{+0.00}_{-0.00}$| | |$25.10^{+0.04}_{-0.05}$| | |$-21.59^{+0.04}_{-0.05}$| | |$0.57^{+0.02}_{-0.02}$| | |$24.78^{+0.04}_{-0.04}$| | |$-21.92^{+0.04}_{-0.04}$| | |$0.62^{+0.02}_{-0.02}$| | |$2.74^{+0.10}_{-0.09}$| | |$1.08^{+0.12}_{-0.12}$| | 2 |
| C08_22 | |$25.41^{+0.03}_{-0.04}$| | |$-21.28^{+0.03}_{-0.04}$| | |$0.83^{+0.02}_{-0.01}$| | |$25.32^{+0.05}_{-0.07}$| | |$-21.37^{+0.05}_{-0.07}$| | |$0.99^{+0.04}_{-0.03}$| | |$24.79^{+0.04}_{-0.04}$| | |$-21.90^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$0.73^{+0.03}_{-0.02}$| | |$0.61^{+0.03}_{-0.03}$| | 1 |
| C08_23 | |$26.35^{+0.08}_{-0.11}$| | |$-20.34^{+0.08}_{-0.11}$| | |$0.45^{+0.02}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.81^{+0.03}_{-0.03}$| | |$0.31^{+0.02}_{-0.01}$| | |$0.69^{+0.05}_{-0.04}$| | |$0.78^{+0.07}_{-0.07}$| | 1 |
| C08_24 | |$26.31^{+0.08}_{-0.11}$| | |$-20.38^{+0.08}_{-0.11}$| | |$0.57^{+0.03}_{-0.02}$| | |$25.77^{+0.08}_{-0.10}$| | |$-20.92^{+0.08}_{-0.10}$| | |$0.94^{+0.03}_{-0.02}$| | |$25.33^{+0.04}_{-0.04}$| | |$-21.36^{+0.04}_{-0.04}$| | |$0.76^{+0.03}_{-0.02}$| | |$1.34^{+0.08}_{-0.06}$| | |$0.81^{+0.06}_{-0.05}$| | 2 |
| C08_25 | |$26.89^{+0.06}_{-0.07}$| | |$-20.05^{+0.06}_{-0.07}$| | |$0.13^{+0.01}_{-0.01}$| | |$26.87^{+0.09}_{-0.08}$| | |$-20.07^{+0.09}_{-0.08}$| | |$0.19^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C08_27 | |$25.74^{+0.02}_{-0.03}$| | |$-21.12^{+0.02}_{-0.03}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.68^{+0.02}_{-0.02}$| | |$-21.18^{+0.02}_{-0.02}$| | |$0.32^{+0.01}_{-0.01}$| | |$24.61^{+0.02}_{-0.03}$| | |$-22.26^{+0.02}_{-0.03}$| | |$0.38^{+0.01}_{-0.01}$| | |$1.61^{+0.07}_{-0.06}$| | |$1.20^{+0.09}_{-0.09}$| | 1 |
| C08_28 | |$26.23^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.95^{+0.06}_{-0.07}$| | |$-21.01^{+0.06}_{-0.07}$| | |$0.52^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C08_29 | |$26.61^{+0.04}_{-0.05}$| | |$-20.18^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.91^{+0.06}_{-0.07}$| | |$-20.88^{+0.06}_{-0.07}$| | |$0.55^{+0.02}_{-0.02}$| | |$25.67^{+0.05}_{-0.06}$| | |$-21.12^{+0.05}_{-0.06}$| | |$0.49^{+0.02}_{-0.01}$| | |$2.82^{+0.19}_{-0.15}$| | |$0.89^{+0.13}_{-0.12}$| | 2 |
| C08_30 | |$26.48^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.16^{+0.01}_{-0.01}$| | |$26.52^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.17^{+0.03}_{-0.02}$| | |$25.64^{+0.02}_{-0.03}$| | |$-21.58^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$1.28^{+0.11}_{-0.09}$| | |$1.25^{+0.21}_{-0.20}$| | 1 |
| C08_31 | |$27.07^{+0.06}_{-0.07}$| | |$-20.09^{+0.06}_{-0.07}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.81^{+0.15}_{-0.17}$| | |$-20.35^{+0.15}_{-0.17}$| | |$0.38^{+0.03}_{-0.03}$| | |$25.55^{+0.04}_{-0.04}$| | |$-21.61^{+0.04}_{-0.04}$| | |$0.39^{+0.01}_{-0.01}$| | |$1.54^{+0.20}_{-0.14}$| | |$1.01^{+0.12}_{-0.13}$| | 1 |
| C09_01 | |$26.13^{+0.05}_{-0.07}$| | |$-20.24^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.16^{+0.06}_{-0.07}$| | |$-20.20^{+0.06}_{-0.07}$| | |$0.50^{+0.03}_{-0.04}$| | |$25.73^{+0.05}_{-0.06}$| | |$-20.64^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$1.21^{+0.06}_{-0.05}$| | |$1.27^{+0.09}_{-0.10}$| | 1 |
| C09_02 | |$26.82^{+0.13}_{-0.18}$| | |$-19.54^{+0.13}_{-0.18}$| | |$0.63^{+0.03}_{-0.02}$| | |$26.71^{+0.15}_{-0.17}$| | |$-19.65^{+0.15}_{-0.17}$| | |$0.66^{+0.05}_{-0.05}$| | |$26.46^{+0.04}_{-0.04}$| | |$-19.90^{+0.04}_{-0.04}$| | |$0.47^{+0.03}_{-0.04}$| | |$0.74^{+0.06}_{-0.06}$| | |$0.70^{+0.08}_{-0.08}$| | 2 |
| C09_03 | |$25.88^{+0.05}_{-0.07}$| | |$-20.51^{+0.05}_{-0.07}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.86^{+0.04}_{-0.04}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.13^{+0.04}_{-0.04}$| | 1 |
| C09_04 | |$25.58^{+0.03}_{-0.04}$| | |$-20.82^{+0.03}_{-0.04}$| | |$0.52^{+0.01}_{-0.01}$| | |$25.63^{+0.04}_{-0.05}$| | |$-20.77^{+0.04}_{-0.05}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.24^{+0.02}_{-0.03}$| | |$-21.16^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.78^{+0.04}_{-0.03}$| | |$0.84^{+0.04}_{-0.04}$| | 2 |
| C09_05 | |$26.46^{+0.08}_{-0.11}$| | |$-19.94^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.08^{+0.06}_{-0.07}$| | |$-20.32^{+0.06}_{-0.07}$| | |$0.67^{+0.05}_{-0.05}$| | |$25.90^{+0.05}_{-0.06}$| | |$-20.50^{+0.05}_{-0.06}$| | |$0.64^{+0.02}_{-0.02}$| | |$1.20^{+0.06}_{-0.05}$| | |$0.96^{+0.10}_{-0.10}$| | 2 |
| C09_06 | |$25.93^{+0.02}_{-0.03}$| | |$-20.47^{+0.02}_{-0.03}$| | |$0.21^{+0.00}_{-0.00}$| | |$25.66^{+0.02}_{-0.02}$| | |$-20.74^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.86^{+0.04}_{-0.04}$| | |$-21.54^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$2.89^{+0.11}_{-0.11}$| | |$1.48^{+0.15}_{-0.14}$| | 2 |
| C09_07 | |$27.17^{+0.06}_{-0.07}$| | |$-19.23^{+0.06}_{-0.07}$| | |$0.44^{+0.07}_{-0.05}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.90^{+0.07}_{-0.07}$| | |$26.16^{+0.05}_{-0.06}$| | |$-20.24^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$1.60^{+0.34}_{-0.20}$| | |$0.78^{+0.24}_{-0.16}$| | 2 |
| C09_08 | |$26.41^{+0.08}_{-0.11}$| | |$-19.99^{+0.08}_{-0.11}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.38^{+0.05}_{-0.05}$| | |$-20.02^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.15^{+0.04}_{-0.04}$| | |$0.72^{+0.02}_{-0.02}$| | |$1.29^{+0.06}_{-0.05}$| | |$1.58^{+0.10}_{-0.12}$| | 2 |
| C10_01 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.13^{+0.03}_{-0.03}$| | |$-20.27^{+0.03}_{-0.03}$| | |$0.40^{+0.03}_{-0.04}$| | |$25.59^{+0.04}_{-0.04}$| | |$-20.81^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.99^{+0.09}_{-0.08}$| | |$1.63^{+0.18}_{-0.21}$| | 2 |
| C10_02 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.44^{+0.01}_{-0.01}$| | |$25.53^{+0.04}_{-0.05}$| | |$-20.87^{+0.04}_{-0.05}$| | |$0.63^{+0.02}_{-0.02}$| | |$24.99^{+0.04}_{-0.04}$| | |$-21.41^{+0.04}_{-0.04}$| | |$0.47^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.04}$| | |$0.75^{+0.05}_{-0.05}$| | 1 |
| C10_03 | |$25.44^{+0.03}_{-0.04}$| | |$-20.96^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-20.93^{+0.04}_{-0.05}$| | |$0.58^{+0.02}_{-0.01}$| | |$24.89^{+0.04}_{-0.04}$| | |$-21.51^{+0.04}_{-0.04}$| | |$0.73^{+0.02}_{-0.02}$| | |$1.21^{+0.04}_{-0.04}$| | |$1.26^{+0.05}_{-0.04}$| | 2 |
| C10_04 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.15^{+0.06}_{-0.07}$| | |$-20.25^{+0.06}_{-0.07}$| | |$0.58^{+0.03}_{-0.04}$| | |$26.72^{+0.04}_{-0.04}$| | |$-19.68^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$0.62^{+0.08}_{-0.07}$| | |$0.47^{+0.08}_{-0.08}$| | 2 |
| C10_05 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.49^{+0.01}_{-0.01}$| | |$25.40^{+0.04}_{-0.05}$| | |$-21.00^{+0.04}_{-0.05}$| | |$0.59^{+0.02}_{-0.01}$| | |$25.67^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.84^{+0.04}_{-0.03}$| | |$0.70^{+0.04}_{-0.04}$| | 2 |
| C10_06 | |$26.40^{+0.15}_{-0.18}$| | |$-20.00^{+0.15}_{-0.18}$| | |$1.12^{+0.08}_{-0.05}$| | |$26.37^{+0.14}_{-0.15}$| | |$-20.03^{+0.14}_{-0.15}$| | |$0.96^{+0.07}_{-0.07}$| | |$26.22^{+0.09}_{-0.12}$| | |$-20.17^{+0.09}_{-0.12}$| | |$0.77^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.80^{+0.09}_{-0.06}$| | 2 |
| C10_07 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$25.72^{+0.04}_{-0.05}$| | |$-20.68^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.51^{+0.04}_{-0.04}$| | |$-20.89^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$1.79^{+0.09}_{-0.07}$| | |$0.89^{+0.08}_{-0.07}$| | 2 |
| C10_08 | |$26.03^{+0.05}_{-0.07}$| | |$-20.37^{+0.05}_{-0.07}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.12^{+0.06}_{-0.07}$| | |$-20.28^{+0.06}_{-0.07}$| | |$0.48^{+0.03}_{-0.04}$| | |$25.37^{+0.04}_{-0.04}$| | |$-21.03^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.02}$| | |$0.92^{+0.04}_{-0.04}$| | |$1.07^{+0.07}_{-0.08}$| | 1 |
| C10_09 | |$24.91^{+0.03}_{-0.04}$| | |$-22.03^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$25.00^{+0.04}_{-0.05}$| | |$-21.93^{+0.04}_{-0.05}$| | |$0.56^{+0.02}_{-0.02}$| | |$23.99^{+0.04}_{-0.04}$| | |$-22.95^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.15^{+0.04}_{-0.04}$| | 2 |
| C10_10 | |$25.41^{+0.01}_{-0.02}$| | |$-21.48^{+0.01}_{-0.02}$| | |$0.16^{+0.00}_{-0.00}$| | |$25.48^{+0.02}_{-0.02}$| | |$-21.41^{+0.02}_{-0.02}$| | |$0.14^{+0.01}_{-0.01}$| | |$25.42^{+0.02}_{-0.03}$| | |$-21.46^{+0.02}_{-0.03}$| | |$0.16^{+0.02}_{-0.01}$| | |$0.95^{+0.10}_{-0.08}$| | |$1.10^{+0.13}_{-0.12}$| | 1 |
| . | F150W . | F150W (PSF matched) . | F444W . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | |$\displaystyle\frac{r_{\rm e,opt}}{r_{\rm e,UV}}$| . | Flag . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mUV . | MUV . | re . | mUV . | MUV . | re . | mopt . | Mopt . | re, opt . | . | (PSF matched) . | . |
| ID . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | (mag) . | (mag) . | (kpc) . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . | (13) . |
| C01_02 | |$26.57^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$26.62^{+0.05}_{-0.05}$| | |$-20.68^{+0.05}_{-0.05}$| | |$0.13^{+0.02}_{-0.02}$| | |$26.77^{+0.08}_{-0.12}$| | |$-20.53^{+0.08}_{-0.12}$| | |$0.23^{+0.02}_{-0.02}$| | |$1.36^{+0.15}_{-0.14}$| | |$1.77^{+0.28}_{-0.28}$| | 1 |
| C01_03 | |$27.68^{+0.20}_{-0.22}$| | |$-19.28^{+0.20}_{-0.22}$| | |$0.03^{+0.03}_{-0.02}$| | — | — | — | |$26.96^{+0.08}_{-0.12}$| | |$-20.00^{+0.08}_{-0.12}$| | |$0.12^{+0.12}_{-0.09}$| | |$4.44^{+7.25}_{-5.30}$| | — | 1 |
| C01_05 | |$26.42^{+0.04}_{-0.05}$| | |$-20.01^{+0.04}_{-0.05}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.65^{+0.04}_{-0.05}$| | |$-20.78^{+0.04}_{-0.05}$| | |$0.80^{+0.02}_{-0.02}$| | |$24.87^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$2.14^{+0.12}_{-0.10}$| | |$0.97^{+0.08}_{-0.07}$| | 2 |
| C01_06 | |$26.60^{+0.04}_{-0.05}$| | |$-19.67^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.01^{+0.09}_{-0.11}$| | |$0.49^{+0.04}_{-0.04}$| | |$26.45^{+0.04}_{-0.04}$| | |$-19.81^{+0.04}_{-0.04}$| | |$0.36^{+0.03}_{-0.03}$| | |$1.34^{+0.13}_{-0.13}$| | |$0.74^{+0.15}_{-0.16}$| | 1 |
| C01_07 | |$25.62^{+0.01}_{-0.02}$| | |$-20.66^{+0.01}_{-0.02}$| | |$0.26^{+0.00}_{-0.00}$| | |$25.55^{+0.02}_{-0.02}$| | |$-20.73^{+0.02}_{-0.02}$| | |$0.30^{+0.02}_{-0.02}$| | |$25.48^{+0.02}_{-0.03}$| | |$-20.79^{+0.02}_{-0.03}$| | |$0.29^{+0.02}_{-0.02}$| | |$1.13^{+0.08}_{-0.07}$| | |$0.97^{+0.10}_{-0.09}$| | 1 |
| C01_08 | |$25.78^{+0.05}_{-0.07}$| | |$-20.62^{+0.05}_{-0.07}$| | |$0.48^{+0.01}_{-0.01}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.54^{+0.03}_{-0.03}$| | |$0.42^{+0.02}_{-0.01}$| | |$25.46^{+0.04}_{-0.04}$| | |$-20.93^{+0.04}_{-0.04}$| | |$0.48^{+0.02}_{-0.02}$| | |$1.00^{+0.04}_{-0.03}$| | |$1.14^{+0.05}_{-0.05}$| | 1 |
| C01_09 | |$24.83^{+0.03}_{-0.04}$| | |$-21.57^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$24.75^{+0.04}_{-0.05}$| | |$-21.65^{+0.04}_{-0.05}$| | |$0.72^{+0.02}_{-0.02}$| | |$23.41^{+0.04}_{-0.04}$| | |$-22.99^{+0.04}_{-0.04}$| | |$0.75^{+0.02}_{-0.02}$| | |$1.26^{+0.04}_{-0.04}$| | |$1.04^{+0.05}_{-0.05}$| | 1 |
| C01_10 | |$25.94^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.37^{+0.01}_{-0.01}$| | |$25.67^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.55^{+0.02}_{-0.01}$| | |$25.38^{+0.04}_{-0.04}$| | |$-21.02^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$1.58^{+0.07}_{-0.06}$| | |$1.07^{+0.07}_{-0.07}$| | 2 |
| C01_11 | |$26.36^{+0.08}_{-0.11}$| | |$-20.04^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_12 | |$26.66^{+0.04}_{-0.05}$| | |$-19.74^{+0.04}_{-0.05}$| | |$0.37^{+0.02}_{-0.01}$| | |$26.44^{+0.05}_{-0.05}$| | |$-19.96^{+0.05}_{-0.05}$| | |$0.37^{+0.03}_{-0.04}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.50^{+0.03}_{-0.04}$| | |$1.35^{+0.11}_{-0.11}$| | |$1.35^{+0.15}_{-0.17}$| | 2 |
| C01_13 | |$26.33^{+0.15}_{-0.18}$| | |$-20.06^{+0.15}_{-0.18}$| | |$1.02^{+0.05}_{-0.04}$| | |$26.25^{+0.09}_{-0.11}$| | |$-20.15^{+0.09}_{-0.11}$| | |$0.81^{+0.05}_{-0.05}$| | |$26.05^{+0.05}_{-0.06}$| | |$-20.35^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.87^{+0.10}_{-0.06}$| | 2 |
| C01_14 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.20^{+0.01}_{-0.01}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.37^{+0.03}_{-0.03}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.22^{+0.03}_{-0.03}$| | |$-20.18^{+0.03}_{-0.03}$| | |$0.37^{+0.03}_{-0.04}$| | |$1.89^{+0.20}_{-0.20}$| | |$0.90^{+0.23}_{-0.26}$| | 2 |
| C01_15 | |$26.42^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.66^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C01_16 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.51^{+0.04}_{-0.05}$| | |$-20.89^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$24.56^{+0.05}_{-0.07}$| | |$-21.84^{+0.05}_{-0.07}$| | |$1.11^{+0.04}_{-0.03}$| | |$1.45^{+0.05}_{-0.04}$| | |$1.52^{+0.06}_{-0.06}$| | 1 |
| C01_17 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.50^{+0.03}_{-0.03}$| | |$0.39^{+0.02}_{-0.01}$| | |$25.37^{+0.02}_{-0.03}$| | |$-21.03^{+0.02}_{-0.03}$| | |$0.22^{+0.02}_{-0.02}$| | |$1.26^{+0.14}_{-0.11}$| | |$0.56^{+0.12}_{-0.10}$| | 2 |
| C01_18 | |$26.09^{+0.05}_{-0.07}$| | |$-20.30^{+0.05}_{-0.07}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.18^{+0.06}_{-0.07}$| | |$-20.22^{+0.06}_{-0.07}$| | |$0.49^{+0.03}_{-0.04}$| | |$25.97^{+0.05}_{-0.06}$| | |$-20.43^{+0.05}_{-0.06}$| | |$0.49^{+0.03}_{-0.04}$| | |$0.84^{+0.06}_{-0.06}$| | |$1.00^{+0.08}_{-0.09}$| | 2 |
| C01_19 | |$25.06^{+0.03}_{-0.04}$| | |$-21.63^{+0.03}_{-0.04}$| | |$0.78^{+0.02}_{-0.01}$| | |$24.71^{+0.05}_{-0.07}$| | |$-21.98^{+0.05}_{-0.07}$| | |$1.20^{+0.04}_{-0.03}$| | |$24.00^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$1.36^{+0.05}_{-0.04}$| | |$0.88^{+0.07}_{-0.05}$| | 2 |
| C01_20 | |$25.27^{+0.03}_{-0.04}$| | |$-21.43^{+0.03}_{-0.04}$| | |$0.75^{+0.01}_{-0.01}$| | |$25.25^{+0.04}_{-0.05}$| | |$-21.45^{+0.04}_{-0.05}$| | |$0.78^{+0.03}_{-0.02}$| | |$24.32^{+0.04}_{-0.04}$| | |$-22.37^{+0.04}_{-0.04}$| | |$0.70^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.89^{+0.04}_{-0.04}$| | 1 |
| C01_22 | |$27.22^{+0.06}_{-0.07}$| | |$-20.10^{+0.06}_{-0.07}$| | |$0.10^{+0.03}_{-0.02}$| | |$27.22^{+0.09}_{-0.08}$| | |$-20.09^{+0.09}_{-0.08}$| | |$0.11^{+0.07}_{-0.05}$| | — | — | — | — | — | 1 |
| C01_26 | |$26.38^{+0.08}_{-0.11}$| | |$-20.68^{+0.08}_{-0.11}$| | |$0.42^{+0.01}_{-0.01}$| | |$25.93^{+0.06}_{-0.07}$| | |$-21.13^{+0.06}_{-0.07}$| | |$0.65^{+0.02}_{-0.02}$| | |$25.45^{+0.05}_{-0.07}$| | |$-21.61^{+0.05}_{-0.07}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.89^{+0.09}_{-0.07}$| | |$1.21^{+0.07}_{-0.06}$| | 2 |
| C02_01 | |$27.82^{+0.20}_{-0.22}$| | |$-18.79^{+0.20}_{-0.22}$| | |$0.07^{+0.04}_{-0.03}$| | |$27.85^{+0.21}_{-0.27}$| | |$-18.76^{+0.21}_{-0.27}$| | |$0.10^{+0.09}_{-0.07}$| | |$27.20^{+0.16}_{-0.19}$| | |$-19.40^{+0.16}_{-0.19}$| | |$0.14^{+0.14}_{-0.10}$| | |$1.91^{+2.13}_{-1.60}$| | |$1.36^{+2.48}_{-1.92}$| | 1 |
| C02_02 | |$26.60^{+0.04}_{-0.05}$| | |$-19.89^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-19.79^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.99^{+0.03}_{-0.03}$| | |$-20.49^{+0.03}_{-0.03}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.78^{+0.08}_{-0.07}$| | |$0.86^{+0.10}_{-0.11}$| | 1 |
| C02_03 | |$26.67^{+0.08}_{-0.11}$| | |$-19.67^{+0.08}_{-0.11}$| | |$0.50^{+0.02}_{-0.01}$| | |$25.89^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.95^{+0.03}_{-0.03}$| | |$25.81^{+0.05}_{-0.06}$| | |$-20.53^{+0.05}_{-0.06}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.59^{+0.07}_{-0.06}$| | |$0.83^{+0.07}_{-0.06}$| | 2 |
| C02_04 | |$25.01^{+0.01}_{-0.02}$| | |$-21.39^{+0.01}_{-0.02}$| | |$0.35^{+0.00}_{-0.00}$| | |$24.97^{+0.02}_{-0.02}$| | |$-21.43^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.49^{+0.02}_{-0.03}$| | |$-21.91^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$1.18^{+0.05}_{-0.05}$| | |$1.01^{+0.07}_{-0.06}$| | 1 |
| C02_05 | |$26.43^{+0.08}_{-0.11}$| | |$-19.97^{+0.08}_{-0.11}$| | |$0.82^{+0.03}_{-0.02}$| | |$26.60^{+0.09}_{-0.11}$| | |$-19.79^{+0.09}_{-0.11}$| | |$0.63^{+0.05}_{-0.05}$| | |$25.61^{+0.04}_{-0.04}$| | |$-20.78^{+0.04}_{-0.04}$| | |$0.84^{+0.03}_{-0.02}$| | |$1.02^{+0.05}_{-0.04}$| | |$1.33^{+0.09}_{-0.09}$| | 1 |
| C02_06 | |$26.33^{+0.08}_{-0.11}$| | |$-20.07^{+0.08}_{-0.11}$| | |$0.70^{+0.03}_{-0.02}$| | |$26.31^{+0.09}_{-0.11}$| | |$-20.08^{+0.09}_{-0.11}$| | |$0.74^{+0.05}_{-0.05}$| | |$25.86^{+0.05}_{-0.06}$| | |$-20.54^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$0.89^{+0.05}_{-0.04}$| | |$0.85^{+0.07}_{-0.07}$| | 1 |
| C02_07 | |$25.71^{+0.05}_{-0.07}$| | |$-20.69^{+0.05}_{-0.07}$| | |$0.80^{+0.01}_{-0.01}$| | |$25.71^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.85^{+0.04}_{-0.04}$| | |$0.59^{+0.02}_{-0.02}$| | |$0.74^{+0.03}_{-0.03}$| | |$0.69^{+0.04}_{-0.03}$| | 1 |
| C02_08 | |$26.04^{+0.02}_{-0.03}$| | |$-20.35^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.05^{+0.03}_{-0.03}$| | |$-20.35^{+0.03}_{-0.03}$| | |$0.36^{+0.03}_{-0.04}$| | |$25.76^{+0.03}_{-0.03}$| | |$-20.64^{+0.03}_{-0.03}$| | |$0.32^{+0.02}_{-0.02}$| | |$0.94^{+0.07}_{-0.05}$| | |$0.88^{+0.11}_{-0.11}$| | 1 |
| C02_09 | |$25.28^{+0.06}_{-0.07}$| | |$-21.12^{+0.06}_{-0.07}$| | |$1.08^{+0.03}_{-0.02}$| | |$25.26^{+0.05}_{-0.07}$| | |$-21.14^{+0.05}_{-0.07}$| | |$1.13^{+0.04}_{-0.03}$| | |$24.31^{+0.05}_{-0.07}$| | |$-22.09^{+0.05}_{-0.07}$| | |$0.95^{+0.03}_{-0.02}$| | |$0.88^{+0.04}_{-0.03}$| | |$0.85^{+0.04}_{-0.03}$| | 1 |
| C02_10 | |$26.82^{+0.06}_{-0.07}$| | |$-19.58^{+0.06}_{-0.07}$| | |$0.28^{+0.01}_{-0.01}$| | |$26.37^{+0.09}_{-0.11}$| | |$-20.03^{+0.09}_{-0.11}$| | |$0.53^{+0.03}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.45^{+0.05}_{-0.06}$| | |$0.51^{+0.03}_{-0.04}$| | |$1.78^{+0.13}_{-0.14}$| | |$0.96^{+0.16}_{-0.18}$| | 2 |
| C02_12 | |$26.37^{+0.08}_{-0.11}$| | |$-20.33^{+0.08}_{-0.11}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.38^{+0.09}_{-0.11}$| | |$-20.31^{+0.09}_{-0.11}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.44^{+0.04}_{-0.04}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.08^{+0.05}_{-0.04}$| | |$1.05^{+0.07}_{-0.08}$| | 1 |
| C02_13 | |$26.77^{+0.13}_{-0.18}$| | |$-19.92^{+0.13}_{-0.18}$| | |$0.51^{+0.02}_{-0.01}$| | |$26.83^{+0.15}_{-0.17}$| | |$-19.86^{+0.15}_{-0.17}$| | |$0.48^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C02_14 | |$27.34^{+0.11}_{-0.14}$| | |$-19.93^{+0.11}_{-0.14}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.84^{+0.09}_{-0.08}$| | |$-20.43^{+0.09}_{-0.08}$| | |$0.34^{+0.02}_{-0.03}$| | |$25.60^{+0.02}_{-0.03}$| | |$-21.68^{+0.02}_{-0.03}$| | |$0.13^{+0.01}_{-0.01}$| | |$0.52^{+0.08}_{-0.06}$| | |$0.39^{+0.07}_{-0.06}$| | 2 |
| C02_15 | |$27.57^{+0.11}_{-0.14}$| | |$-19.75^{+0.11}_{-0.14}$| | |$0.05^{+0.03}_{-0.02}$| | |$27.64^{+0.14}_{-0.17}$| | |$-19.68^{+0.14}_{-0.17}$| | |$0.09^{+0.07}_{-0.05}$| | |$25.67^{+0.02}_{-0.03}$| | |$-21.64^{+0.02}_{-0.03}$| | |$0.05^{+0.01}_{-0.01}$| | |$1.13^{+0.76}_{-0.55}$| | |$0.60^{+0.87}_{-0.69}$| | 1 |
| C02_20 | |$26.71^{+0.13}_{-0.18}$| | |$-20.21^{+0.13}_{-0.18}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.82^{+0.15}_{-0.17}$| | |$-20.10^{+0.15}_{-0.17}$| | |$0.40^{+0.03}_{-0.03}$| | |$25.90^{+0.05}_{-0.06}$| | |$-21.02^{+0.05}_{-0.06}$| | |$0.55^{+0.02}_{-0.02}$| | |$1.25^{+0.06}_{-0.05}$| | |$1.36^{+0.10}_{-0.11}$| | 1 |
| C02_21 | |$27.16^{+0.06}_{-0.07}$| | |$-19.76^{+0.06}_{-0.07}$| | |$0.17^{+0.03}_{-0.02}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.44^{+0.09}_{-0.11}$| | |$0.50^{+0.04}_{-0.04}$| | |$25.95^{+0.05}_{-0.06}$| | |$-20.97^{+0.05}_{-0.06}$| | |$0.59^{+0.07}_{-0.04}$| | |$3.56^{+0.86}_{-0.58}$| | |$1.19^{+0.53}_{-0.39}$| | 2 |
| C02_22 | |$26.12^{+0.02}_{-0.03}$| | |$-20.76^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.10^{+0.03}_{-0.03}$| | |$-20.79^{+0.03}_{-0.03}$| | |$0.25^{+0.03}_{-0.03}$| | |$25.63^{+0.02}_{-0.03}$| | |$-21.25^{+0.02}_{-0.03}$| | |$0.23^{+0.02}_{-0.01}$| | |$1.12^{+0.09}_{-0.08}$| | |$0.92^{+0.15}_{-0.14}$| | 1 |
| C02_23 | |$26.68^{+0.04}_{-0.05}$| | |$-20.21^{+0.04}_{-0.05}$| | |$0.22^{+0.01}_{-0.01}$| | |$26.54^{+0.05}_{-0.05}$| | |$-20.35^{+0.05}_{-0.05}$| | |$0.34^{+0.03}_{-0.03}$| | |$26.24^{+0.04}_{-0.04}$| | |$-20.65^{+0.04}_{-0.04}$| | |$0.25^{+0.03}_{-0.03}$| | |$1.10^{+0.13}_{-0.12}$| | |$0.73^{+0.15}_{-0.16}$| | 1 |
| C03_01 | |$26.89^{+0.06}_{-0.07}$| | |$-19.83^{+0.06}_{-0.07}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.91^{+0.09}_{-0.08}$| | |$-19.81^{+0.09}_{-0.08}$| | |$0.41^{+0.03}_{-0.04}$| | |$26.67^{+0.04}_{-0.04}$| | |$-20.05^{+0.04}_{-0.04}$| | |$0.28^{+0.03}_{-0.03}$| | |$0.68^{+0.07}_{-0.07}$| | |$0.68^{+0.08}_{-0.09}$| | 1 |
| C03_04 | |$25.62^{+0.01}_{-0.02}$| | |$-21.08^{+0.01}_{-0.02}$| | |$0.30^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-21.09^{+0.02}_{-0.02}$| | |$0.28^{+0.01}_{-0.01}$| | |$25.03^{+0.02}_{-0.03}$| | |$-21.66^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$1.22^{+0.05}_{-0.05}$| | |$1.27^{+0.08}_{-0.08}$| | 1 |
| C03_05 | |$26.20^{+0.08}_{-0.11}$| | |$-20.42^{+0.08}_{-0.11}$| | |$0.46^{+0.02}_{-0.01}$| | |$26.22^{+0.09}_{-0.11}$| | |$-20.41^{+0.09}_{-0.11}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.45^{+0.04}_{-0.04}$| | |$0.56^{+0.02}_{-0.02}$| | |$1.23^{+0.06}_{-0.05}$| | |$1.25^{+0.10}_{-0.11}$| | 1 |
| C03_07 | |$27.76^{+0.20}_{-0.22}$| | |$-19.21^{+0.20}_{-0.22}$| | |$0.11^{+0.03}_{-0.02}$| | |$27.93^{+0.21}_{-0.27}$| | |$-19.04^{+0.21}_{-0.27}$| | |$0.05^{+0.08}_{-0.06}$| | — | — | — | — | — | 1 |
| C03_08 | |$26.71^{+0.04}_{-0.05}$| | |$-20.27^{+0.04}_{-0.05}$| | |$0.23^{+0.01}_{-0.01}$| | |$26.69^{+0.05}_{-0.05}$| | |$-20.29^{+0.05}_{-0.05}$| | |$0.27^{+0.03}_{-0.03}$| | |$26.23^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$1.21^{+0.12}_{-0.12}$| | |$1.01^{+0.17}_{-0.16}$| | 1 |
| C03_09 | |$26.75^{+0.06}_{-0.07}$| | |$-19.74^{+0.06}_{-0.07}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.84^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.25^{+0.03}_{-0.03}$| | |$26.10^{+0.05}_{-0.06}$| | |$-20.39^{+0.05}_{-0.06}$| | |$0.48^{+0.03}_{-0.03}$| | |$1.58^{+0.12}_{-0.12}$| | |$1.89^{+0.23}_{-0.23}$| | 1 |
| C03_11 | |$25.57^{+0.06}_{-0.07}$| | |$-20.83^{+0.06}_{-0.07}$| | |$1.62^{+0.05}_{-0.04}$| | |$25.65^{+0.05}_{-0.07}$| | |$-20.75^{+0.05}_{-0.07}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C03_12 | |$25.23^{+0.03}_{-0.04}$| | |$-21.16^{+0.03}_{-0.04}$| | |$0.85^{+0.02}_{-0.01}$| | |$24.93^{+0.05}_{-0.07}$| | |$-21.46^{+0.05}_{-0.07}$| | |$1.04^{+0.03}_{-0.03}$| | |$23.76^{+0.04}_{-0.04}$| | |$-22.64^{+0.04}_{-0.04}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.07^{+0.04}_{-0.03}$| | |$0.87^{+0.05}_{-0.04}$| | 2 |
| C03_13 | |$25.29^{+0.06}_{-0.07}$| | |$-21.11^{+0.06}_{-0.07}$| | |$1.42^{+0.04}_{-0.03}$| | |$25.18^{+0.05}_{-0.07}$| | |$-21.22^{+0.05}_{-0.07}$| | |$1.44^{+0.05}_{-0.04}$| | |$24.29^{+0.05}_{-0.07}$| | |$-22.11^{+0.05}_{-0.07}$| | |$1.66^{+0.06}_{-0.05}$| | |$1.17^{+0.05}_{-0.04}$| | |$1.16^{+0.06}_{-0.04}$| | 2 |
| C03_14 | |$25.83^{+0.09}_{-0.11}$| | |$-20.57^{+0.09}_{-0.11}$| | |$0.96^{+0.02}_{-0.01}$| | |$25.62^{+0.05}_{-0.07}$| | |$-20.77^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$24.99^{+0.05}_{-0.07}$| | |$-21.41^{+0.05}_{-0.07}$| | |$1.41^{+0.05}_{-0.04}$| | |$1.48^{+0.06}_{-0.05}$| | |$1.35^{+0.07}_{-0.06}$| | 2 |
| C03_15 | |$26.46^{+0.04}_{-0.05}$| | |$-19.94^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.06^{+0.06}_{-0.07}$| | |$-20.34^{+0.06}_{-0.07}$| | |$0.52^{+0.03}_{-0.04}$| | |$25.71^{+0.02}_{-0.03}$| | |$-20.69^{+0.02}_{-0.03}$| | |$0.45^{+0.02}_{-0.02}$| | |$1.76^{+0.10}_{-0.09}$| | |$0.87^{+0.13}_{-0.15}$| | 2 |
| C03_16 | |$26.57^{+0.04}_{-0.05}$| | |$-19.83^{+0.04}_{-0.05}$| | |$0.41^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.69^{+0.05}_{-0.05}$| | |$26.32^{+0.04}_{-0.04}$| | |$-20.08^{+0.04}_{-0.04}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.09^{+0.09}_{-0.09}$| | |$0.64^{+0.11}_{-0.12}$| | 1 |
| C03_17 | |$26.64^{+0.13}_{-0.18}$| | |$-19.76^{+0.13}_{-0.18}$| | |$0.48^{+0.02}_{-0.01}$| | |$26.33^{+0.09}_{-0.11}$| | |$-20.07^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.08^{+0.03}_{-0.03}$| | |$-20.32^{+0.03}_{-0.03}$| | |$0.39^{+0.03}_{-0.04}$| | |$0.80^{+0.07}_{-0.08}$| | |$0.72^{+0.08}_{-0.09}$| | 2 |
| C03_18 | |$26.12^{+0.02}_{-0.03}$| | |$-20.28^{+0.02}_{-0.03}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.97^{+0.03}_{-0.03}$| | |$-20.43^{+0.03}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$26.14^{+0.03}_{-0.03}$| | |$-20.26^{+0.03}_{-0.03}$| | |$0.45^{+0.03}_{-0.04}$| | |$1.66^{+0.14}_{-0.14}$| | |$1.26^{+0.14}_{-0.15}$| | 2 |
| C03_19 | |$26.54^{+0.04}_{-0.05}$| | |$-19.86^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | |$25.99^{+0.06}_{-0.07}$| | |$-20.41^{+0.06}_{-0.07}$| | |$0.66^{+0.05}_{-0.05}$| | |$25.56^{+0.04}_{-0.04}$| | |$-20.84^{+0.04}_{-0.04}$| | |$0.92^{+0.03}_{-0.02}$| | |$3.42^{+0.19}_{-0.14}$| | |$1.40^{+0.28}_{-0.28}$| | 2 |
| C03_20 | |$26.70^{+0.13}_{-0.18}$| | |$-19.70^{+0.13}_{-0.18}$| | |$0.73^{+0.03}_{-0.02}$| | |$27.04^{+0.15}_{-0.17}$| | |$-19.36^{+0.15}_{-0.17}$| | |$0.64^{+0.20}_{-0.12}$| | — | — | — | — | — | 1 |
| C03_21 | |$26.62^{+0.04}_{-0.05}$| | |$-19.78^{+0.04}_{-0.05}$| | |$0.26^{+0.01}_{-0.01}$| | |$26.33^{+0.05}_{-0.05}$| | |$-20.07^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$24.89^{+0.05}_{-0.07}$| | |$-21.51^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.02}$| | |$3.98^{+0.21}_{-0.16}$| | |$2.34^{+0.32}_{-0.36}$| | 2 |
| C03_22 | |$25.88^{+0.09}_{-0.11}$| | |$-20.52^{+0.09}_{-0.11}$| | |$1.28^{+0.03}_{-0.02}$| | |$25.98^{+0.08}_{-0.10}$| | |$-20.42^{+0.08}_{-0.10}$| | |$1.19^{+0.11}_{-0.08}$| | — | — | — | — | — | 1 |
| C03_23 | |$26.31^{+0.08}_{-0.11}$| | |$-20.08^{+0.08}_{-0.11}$| | |$0.79^{+0.03}_{-0.02}$| | — | — | — | — | — | — | — | — | 0 |
| C03_24 | |$24.71^{+0.01}_{-0.02}$| | |$-21.98^{+0.01}_{-0.02}$| | |$0.37^{+0.01}_{-0.00}$| | |$24.69^{+0.02}_{-0.02}$| | |$-22.00^{+0.02}_{-0.02}$| | |$0.37^{+0.01}_{-0.01}$| | |$24.37^{+0.04}_{-0.04}$| | |$-22.32^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.01}$| | |$1.39^{+0.05}_{-0.04}$| | |$1.38^{+0.07}_{-0.06}$| | 2 |
| C03_25 | |$26.13^{+0.05}_{-0.07}$| | |$-20.57^{+0.05}_{-0.07}$| | |$0.81^{+0.04}_{-0.03}$| | |$26.23^{+0.09}_{-0.11}$| | |$-20.46^{+0.09}_{-0.11}$| | |$0.76^{+0.07}_{-0.06}$| | |$26.18^{+0.09}_{-0.12}$| | |$-20.52^{+0.09}_{-0.12}$| | |$0.72^{+0.08}_{-0.04}$| | |$0.89^{+0.11}_{-0.07}$| | |$0.95^{+0.13}_{-0.09}$| | 1 |
| C03_27 | |$26.25^{+0.04}_{-0.05}$| | |$-20.91^{+0.04}_{-0.05}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.24^{+0.03}_{-0.03}$| | |$-20.92^{+0.03}_{-0.03}$| | |$0.21^{+0.03}_{-0.03}$| | |$25.36^{+0.02}_{-0.03}$| | |$-21.80^{+0.02}_{-0.03}$| | |$0.34^{+0.01}_{-0.01}$| | |$1.80^{+0.11}_{-0.09}$| | |$1.59^{+0.23}_{-0.22}$| | 1 |
| C04_02 | |$25.38^{+0.01}_{-0.02}$| | |$-21.02^{+0.01}_{-0.02}$| | |$0.19^{+0.00}_{-0.00}$| | |$25.24^{+0.02}_{-0.02}$| | |$-21.16^{+0.02}_{-0.02}$| | |$0.31^{+0.01}_{-0.02}$| | |$24.32^{+0.02}_{-0.03}$| | |$-22.08^{+0.02}_{-0.03}$| | |$0.46^{+0.02}_{-0.02}$| | |$2.42^{+0.11}_{-0.10}$| | |$1.46^{+0.15}_{-0.14}$| | 1 |
| C04_03 | |$26.15^{+0.05}_{-0.07}$| | |$-20.25^{+0.05}_{-0.07}$| | |$0.63^{+0.03}_{-0.02}$| | |$25.95^{+0.06}_{-0.07}$| | |$-20.45^{+0.06}_{-0.07}$| | |$0.71^{+0.02}_{-0.02}$| | |$25.30^{+0.04}_{-0.04}$| | |$-21.10^{+0.04}_{-0.04}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.78^{+0.05}_{-0.04}$| | |$0.69^{+0.04}_{-0.03}$| | 2 |
| C04_04 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.60^{+0.02}_{-0.02}$| | |$-20.80^{+0.02}_{-0.02}$| | |$0.29^{+0.01}_{-0.02}$| | |$24.85^{+0.02}_{-0.03}$| | |$-21.55^{+0.02}_{-0.03}$| | |$0.30^{+0.02}_{-0.02}$| | |$1.25^{+0.08}_{-0.07}$| | |$1.02^{+0.10}_{-0.09}$| | 2 |
| C04_05 | |$25.68^{+0.03}_{-0.04}$| | |$-20.72^{+0.03}_{-0.04}$| | |$0.63^{+0.01}_{-0.01}$| | |$25.64^{+0.04}_{-0.05}$| | |$-20.76^{+0.04}_{-0.05}$| | |$0.73^{+0.02}_{-0.02}$| | |$25.07^{+0.04}_{-0.04}$| | |$-21.33^{+0.04}_{-0.04}$| | |$0.68^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.93^{+0.04}_{-0.04}$| | 1 |
| C04_06 | |$26.27^{+0.04}_{-0.05}$| | |$-20.13^{+0.04}_{-0.05}$| | |$0.46^{+0.02}_{-0.01}$| | — | — | — | |$24.85^{+0.05}_{-0.07}$| | |$-21.55^{+0.05}_{-0.07}$| | |$1.35^{+0.05}_{-0.04}$| | |$2.95^{+0.16}_{-0.12}$| | — | 2 |
| C04_07 | |$26.47^{+0.04}_{-0.05}$| | |$-20.22^{+0.04}_{-0.05}$| | |$0.30^{+0.01}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.32^{+0.03}_{-0.04}$| | |$25.86^{+0.03}_{-0.03}$| | |$-20.83^{+0.03}_{-0.03}$| | |$0.35^{+0.02}_{-0.01}$| | |$1.16^{+0.07}_{-0.06}$| | |$1.08^{+0.12}_{-0.14}$| | 1 |
| C04_08 | |$26.48^{+0.08}_{-0.11}$| | |$-20.22^{+0.08}_{-0.11}$| | |$0.74^{+0.03}_{-0.02}$| | |$26.51^{+0.09}_{-0.11}$| | |$-20.18^{+0.09}_{-0.11}$| | |$0.70^{+0.04}_{-0.05}$| | |$26.24^{+0.09}_{-0.12}$| | |$-20.45^{+0.09}_{-0.12}$| | |$0.67^{+0.08}_{-0.04}$| | |$0.90^{+0.11}_{-0.06}$| | |$0.96^{+0.12}_{-0.08}$| | 1 |
| C04_09 | |$26.23^{+0.08}_{-0.11}$| | |$-20.46^{+0.08}_{-0.11}$| | |$0.85^{+0.04}_{-0.03}$| | |$26.32^{+0.09}_{-0.11}$| | |$-20.38^{+0.09}_{-0.11}$| | |$0.71^{+0.04}_{-0.05}$| | |$25.36^{+0.05}_{-0.07}$| | |$-21.33^{+0.05}_{-0.07}$| | |$0.91^{+0.03}_{-0.02}$| | |$1.08^{+0.07}_{-0.05}$| | |$1.29^{+0.08}_{-0.08}$| | 1 |
| C04_10 | |$26.42^{+0.08}_{-0.11}$| | |$-20.41^{+0.08}_{-0.11}$| | |$0.76^{+0.04}_{-0.03}$| | |$26.48^{+0.09}_{-0.11}$| | |$-20.35^{+0.09}_{-0.11}$| | |$0.69^{+0.04}_{-0.04}$| | |$26.19^{+0.09}_{-0.12}$| | |$-20.64^{+0.09}_{-0.12}$| | |$0.52^{+0.08}_{-0.04}$| | |$0.68^{+0.11}_{-0.06}$| | |$0.75^{+0.11}_{-0.07}$| | 1 |
| C05_01 | |$26.94^{+0.06}_{-0.07}$| | |$-19.32^{+0.06}_{-0.07}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.50^{+0.04}_{-0.04}$| | |$-20.75^{+0.04}_{-0.04}$| | |$0.58^{+0.02}_{-0.02}$| | |$2.17^{+0.12}_{-0.10}$| | — | 2 |
| C05_04 | |$25.74^{+0.09}_{-0.11}$| | |$-20.66^{+0.09}_{-0.11}$| | |$0.97^{+0.02}_{-0.01}$| | |$25.35^{+0.05}_{-0.07}$| | |$-21.05^{+0.05}_{-0.07}$| | |$1.00^{+0.03}_{-0.03}$| | |$24.80^{+0.04}_{-0.04}$| | |$-21.60^{+0.04}_{-0.04}$| | |$0.87^{+0.03}_{-0.02}$| | |$0.89^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C05_05 | |$26.49^{+0.04}_{-0.05}$| | |$-20.45^{+0.04}_{-0.05}$| | |$0.18^{+0.01}_{-0.01}$| | |$26.09^{+0.03}_{-0.03}$| | |$-20.85^{+0.03}_{-0.03}$| | |$0.31^{+0.03}_{-0.03}$| | |$25.68^{+0.02}_{-0.03}$| | |$-21.26^{+0.02}_{-0.03}$| | |$0.19^{+0.02}_{-0.01}$| | |$1.05^{+0.11}_{-0.08}$| | |$0.61^{+0.13}_{-0.13}$| | 2 |
| C05_06 | |$26.49^{+0.04}_{-0.05}$| | |$-20.37^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.45^{+0.05}_{-0.05}$| | |$-20.41^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.03}$| | |$26.65^{+0.04}_{-0.04}$| | |$-20.22^{+0.04}_{-0.04}$| | |$0.33^{+0.03}_{-0.03}$| | |$0.94^{+0.09}_{-0.09}$| | |$0.94^{+0.11}_{-0.13}$| | 1 |
| C05_07 | |$25.96^{+0.02}_{-0.03}$| | |$-20.95^{+0.02}_{-0.03}$| | |$0.35^{+0.01}_{-0.00}$| | |$26.03^{+0.03}_{-0.03}$| | |$-20.89^{+0.03}_{-0.03}$| | |$0.30^{+0.03}_{-0.03}$| | |$25.82^{+0.03}_{-0.03}$| | |$-21.10^{+0.03}_{-0.03}$| | |$0.29^{+0.01}_{-0.01}$| | |$0.83^{+0.04}_{-0.04}$| | |$0.96^{+0.09}_{-0.10}$| | 1 |
| C05_08 | |$26.28^{+0.08}_{-0.11}$| | |$-20.71^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.02}$| | |$26.10^{+0.06}_{-0.07}$| | |$-20.89^{+0.06}_{-0.07}$| | |$0.73^{+0.06}_{-0.05}$| | |$25.99^{+0.05}_{-0.06}$| | |$-21.00^{+0.05}_{-0.06}$| | |$0.43^{+0.03}_{-0.03}$| | |$0.73^{+0.05}_{-0.05}$| | |$0.59^{+0.07}_{-0.07}$| | 2 |
| C05_09 | |$26.62^{+0.04}_{-0.05}$| | |$-20.19^{+0.04}_{-0.05}$| | |$0.21^{+0.01}_{-0.01}$| | |$26.58^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.26^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C06_01 | |$26.15^{+0.02}_{-0.03}$| | |$-20.45^{+0.02}_{-0.03}$| | |$0.38^{+0.02}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-21.13^{+0.04}_{-0.05}$| | |$0.81^{+0.03}_{-0.02}$| | |$24.75^{+0.04}_{-0.04}$| | |$-21.85^{+0.04}_{-0.04}$| | |$0.80^{+0.03}_{-0.02}$| | |$2.09^{+0.12}_{-0.09}$| | |$0.98^{+0.10}_{-0.08}$| | 2 |
| C06_02 | |$26.61^{+0.08}_{-0.11}$| | |$-20.10^{+0.08}_{-0.11}$| | |$0.55^{+0.03}_{-0.02}$| | |$26.77^{+0.09}_{-0.08}$| | |$-19.94^{+0.09}_{-0.08}$| | |$0.37^{+0.03}_{-0.04}$| | — | — | — | — | — | 2 |
| C06_03 | |$26.90^{+0.13}_{-0.18}$| | |$-19.81^{+0.13}_{-0.18}$| | |$0.49^{+0.07}_{-0.04}$| | |$26.95^{+0.09}_{-0.08}$| | |$-19.76^{+0.09}_{-0.08}$| | |$0.40^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C06_05 | |$26.61^{+0.04}_{-0.05}$| | |$-20.50^{+0.04}_{-0.05}$| | |$0.07^{+0.01}_{-0.01}$| | |$26.42^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.18^{+0.03}_{-0.03}$| | |$25.61^{+0.02}_{-0.03}$| | |$-21.50^{+0.02}_{-0.03}$| | |$0.24^{+0.02}_{-0.01}$| | |$3.21^{+0.44}_{-0.34}$| | |$1.33^{+0.51}_{-0.49}$| | 2 |
| C06_06 | |$26.63^{+0.04}_{-0.05}$| | |$-19.84^{+0.04}_{-0.05}$| | |$0.09^{+0.01}_{-0.01}$| | |$26.31^{+0.05}_{-0.05}$| | |$-20.17^{+0.05}_{-0.05}$| | |$0.25^{+0.03}_{-0.03}$| | — | — | — | — | — | 2 |
| C06_09 | |$26.21^{+0.08}_{-0.11}$| | |$-20.19^{+0.08}_{-0.11}$| | |$0.59^{+0.02}_{-0.01}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.54^{+0.03}_{-0.04}$| | |$26.51^{+0.09}_{-0.12}$| | |$-19.89^{+0.09}_{-0.12}$| | |$0.55^{+0.03}_{-0.04}$| | |$0.92^{+0.06}_{-0.06}$| | |$1.02^{+0.08}_{-0.09}$| | 1 |
| C06_10 | |$25.46^{+0.06}_{-0.07}$| | |$-20.94^{+0.06}_{-0.07}$| | |$0.99^{+0.02}_{-0.01}$| | |$25.53^{+0.05}_{-0.07}$| | |$-20.87^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.03}$| | |$25.84^{+0.05}_{-0.06}$| | |$-20.56^{+0.05}_{-0.06}$| | |$0.92^{+0.03}_{-0.02}$| | |$0.93^{+0.04}_{-0.03}$| | |$0.96^{+0.04}_{-0.03}$| | 1 |
| C06_11 | |$25.34^{+0.03}_{-0.04}$| | |$-21.05^{+0.03}_{-0.04}$| | |$0.79^{+0.01}_{-0.01}$| | |$25.34^{+0.04}_{-0.05}$| | |$-21.06^{+0.04}_{-0.05}$| | |$0.81^{+0.02}_{-0.02}$| | |$25.69^{+0.05}_{-0.06}$| | |$-20.71^{+0.05}_{-0.06}$| | |$0.73^{+0.02}_{-0.02}$| | |$0.93^{+0.03}_{-0.03}$| | |$0.90^{+0.04}_{-0.03}$| | 1 |
| C06_12 | |$26.41^{+0.08}_{-0.11}$| | |$-19.98^{+0.08}_{-0.11}$| | |$0.61^{+0.03}_{-0.02}$| | |$26.00^{+0.06}_{-0.07}$| | |$-20.40^{+0.06}_{-0.07}$| | |$0.93^{+0.07}_{-0.07}$| | |$25.52^{+0.05}_{-0.07}$| | |$-20.88^{+0.05}_{-0.07}$| | |$1.01^{+0.03}_{-0.02}$| | |$1.66^{+0.10}_{-0.07}$| | |$1.09^{+0.14}_{-0.12}$| | 2 |
| C06_13 | |$26.10^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.80^{+0.04}_{-0.03}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.73^{+0.06}_{-0.07}$| | |$0.83^{+0.03}_{-0.02}$| | |$25.68^{+0.07}_{-0.10}$| | |$-21.01^{+0.07}_{-0.10}$| | |$0.88^{+0.03}_{-0.02}$| | |$1.10^{+0.07}_{-0.05}$| | |$1.06^{+0.05}_{-0.04}$| | 2 |
| C06_15 | |$27.51^{+0.11}_{-0.14}$| | |$-19.32^{+0.11}_{-0.14}$| | |$0.14^{+0.04}_{-0.03}$| | |$27.18^{+0.09}_{-0.08}$| | |$-19.65^{+0.09}_{-0.08}$| | |$0.30^{+0.08}_{-0.06}$| | — | — | — | — | — | 2 |
| C06_16 | |$26.50^{+0.04}_{-0.05}$| | |$-20.39^{+0.04}_{-0.05}$| | |$0.14^{+0.01}_{-0.01}$| | |$26.59^{+0.05}_{-0.05}$| | |$-20.30^{+0.05}_{-0.05}$| | |$0.10^{+0.03}_{-0.03}$| | |$26.64^{+0.04}_{-0.04}$| | |$-20.25^{+0.04}_{-0.04}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.25^{+0.20}_{-0.19}$| | |$1.80^{+0.41}_{-0.40}$| | 1 |
| C07_01 | |$26.90^{+0.06}_{-0.07}$| | |$-19.66^{+0.06}_{-0.07}$| | |$0.19^{+0.01}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.70^{+0.09}_{-0.08}$| | |$0.23^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C07_02 | |$25.01^{+0.01}_{-0.02}$| | |$-21.31^{+0.01}_{-0.02}$| | |$0.32^{+0.00}_{-0.00}$| | |$25.02^{+0.02}_{-0.02}$| | |$-21.30^{+0.02}_{-0.02}$| | |$0.35^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_04 | |$25.61^{+0.06}_{-0.07}$| | |$-20.79^{+0.06}_{-0.07}$| | |$1.66^{+0.05}_{-0.04}$| | |$25.75^{+0.08}_{-0.10}$| | |$-20.65^{+0.08}_{-0.10}$| | |$1.45^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_06 | |$26.70^{+0.04}_{-0.05}$| | |$-19.70^{+0.04}_{-0.05}$| | |$0.24^{+0.01}_{-0.01}$| | |$25.70^{+0.04}_{-0.05}$| | |$-20.69^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C07_07 | |$25.70^{+0.09}_{-0.11}$| | |$-20.70^{+0.09}_{-0.11}$| | |$1.49^{+0.04}_{-0.03}$| | |$25.76^{+0.08}_{-0.10}$| | |$-20.64^{+0.08}_{-0.10}$| | |$1.47^{+0.05}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_08 | |$26.68^{+0.08}_{-0.11}$| | |$-19.72^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.86^{+0.09}_{-0.08}$| | |$-19.54^{+0.09}_{-0.08}$| | |$0.44^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_09 | |$25.34^{+0.01}_{-0.02}$| | |$-21.06^{+0.01}_{-0.02}$| | |$0.40^{+0.01}_{-0.01}$| | |$25.39^{+0.02}_{-0.02}$| | |$-21.01^{+0.02}_{-0.02}$| | |$0.36^{+0.02}_{-0.01}$| | — | — | — | — | — | 1 |
| C07_10 | |$26.24^{+0.08}_{-0.11}$| | |$-20.16^{+0.08}_{-0.11}$| | |$0.68^{+0.03}_{-0.02}$| | |$26.21^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.60^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_12 | |$26.28^{+0.08}_{-0.11}$| | |$-20.12^{+0.08}_{-0.11}$| | |$0.58^{+0.02}_{-0.01}$| | |$26.20^{+0.06}_{-0.07}$| | |$-20.19^{+0.06}_{-0.07}$| | |$0.63^{+0.05}_{-0.05}$| | — | — | — | — | — | 2 |
| C07_13 | |$25.32^{+0.03}_{-0.04}$| | |$-21.08^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$24.53^{+0.05}_{-0.07}$| | |$-21.87^{+0.05}_{-0.07}$| | |$1.18^{+0.04}_{-0.03}$| | — | — | — | — | — | 2 |
| C07_14 | |$25.81^{+0.05}_{-0.07}$| | |$-20.59^{+0.05}_{-0.07}$| | |$0.72^{+0.01}_{-0.01}$| | |$25.82^{+0.06}_{-0.07}$| | |$-20.58^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | — | — | — | — | — | 1 |
| C07_15 | |$26.95^{+0.06}_{-0.07}$| | |$-19.75^{+0.06}_{-0.07}$| | |$0.31^{+0.01}_{-0.01}$| | |$26.77^{+0.15}_{-0.17}$| | |$-19.93^{+0.15}_{-0.17}$| | |$0.43^{+0.03}_{-0.04}$| | — | — | — | — | — | 1 |
| C07_16 | |$26.63^{+0.08}_{-0.11}$| | |$-20.23^{+0.08}_{-0.11}$| | |$0.65^{+0.03}_{-0.02}$| | |$25.82^{+0.08}_{-0.10}$| | |$-21.05^{+0.08}_{-0.10}$| | |$1.36^{+0.05}_{-0.04}$| | — | — | — | — | — | 2 |
| C08_01 | |$25.87^{+0.02}_{-0.03}$| | |$-21.40^{+0.02}_{-0.03}$| | |$0.13^{+0.00}_{-0.00}$| | |$24.89^{+0.04}_{-0.05}$| | |$-22.38^{+0.04}_{-0.05}$| | |$0.53^{+0.01}_{-0.01}$| | |$24.01^{+0.02}_{-0.03}$| | |$-23.25^{+0.02}_{-0.03}$| | |$0.28^{+0.01}_{-0.01}$| | |$2.21^{+0.11}_{-0.10}$| | |$0.53^{+0.12}_{-0.11}$| | 2 |
| C08_02 | |$27.52^{+0.11}_{-0.14}$| | |$-19.46^{+0.11}_{-0.14}$| | |$0.23^{+0.03}_{-0.02}$| | |$27.40^{+0.14}_{-0.17}$| | |$-19.57^{+0.14}_{-0.17}$| | |$0.35^{+0.13}_{-0.06}$| | — | — | — | — | — | 1 |
| C08_03 | |$27.02^{+0.06}_{-0.07}$| | |$-19.38^{+0.06}_{-0.07}$| | |$0.15^{+0.04}_{-0.03}$| | |$26.74^{+0.05}_{-0.05}$| | |$-19.66^{+0.05}_{-0.05}$| | |$0.30^{+0.03}_{-0.03}$| | |$26.87^{+0.08}_{-0.12}$| | |$-19.53^{+0.08}_{-0.12}$| | |$0.18^{+0.03}_{-0.03}$| | |$1.22^{+0.40}_{-0.32}$| | |$0.60^{+0.25}_{-0.25}$| | 2 |
| C08_04 | |$26.55^{+0.04}_{-0.05}$| | |$-19.85^{+0.04}_{-0.05}$| | |$0.27^{+0.01}_{-0.01}$| | — | — | — | |$25.43^{+0.05}_{-0.07}$| | |$-20.97^{+0.05}_{-0.07}$| | |$1.02^{+0.03}_{-0.02}$| | |$3.84^{+0.20}_{-0.15}$| | — | 1 |
| C08_05 | |$24.75^{+0.06}_{-0.07}$| | |$-21.65^{+0.06}_{-0.07}$| | |$0.98^{+0.02}_{-0.01}$| | |$24.73^{+0.05}_{-0.07}$| | |$-21.67^{+0.05}_{-0.07}$| | |$1.05^{+0.03}_{-0.03}$| | |$23.11^{+0.04}_{-0.04}$| | |$-23.29^{+0.04}_{-0.04}$| | |$0.93^{+0.03}_{-0.02}$| | |$0.96^{+0.04}_{-0.03}$| | |$0.89^{+0.04}_{-0.03}$| | 2 |
| C08_06 | |$26.06^{+0.02}_{-0.03}$| | |$-20.34^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$24.84^{+0.05}_{-0.07}$| | |$-21.56^{+0.05}_{-0.07}$| | |$1.21^{+0.04}_{-0.03}$| | |$23.64^{+0.05}_{-0.07}$| | |$-22.76^{+0.05}_{-0.07}$| | |$1.29^{+0.04}_{-0.03}$| | |$6.15^{+0.38}_{-0.30}$| | |$1.07^{+0.26}_{-0.21}$| | 2 |
| C08_07 | |$25.37^{+0.03}_{-0.04}$| | |$-21.02^{+0.03}_{-0.04}$| | |$0.93^{+0.02}_{-0.01}$| | |$25.52^{+0.04}_{-0.05}$| | |$-20.88^{+0.04}_{-0.05}$| | |$0.79^{+0.02}_{-0.02}$| | |$25.18^{+0.04}_{-0.04}$| | |$-21.22^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$0.85^{+0.03}_{-0.02}$| | |$1.00^{+0.03}_{-0.03}$| | 2 |
| C08_08 | |$25.72^{+0.03}_{-0.04}$| | |$-20.68^{+0.03}_{-0.04}$| | |$0.90^{+0.02}_{-0.01}$| | |$25.40^{+0.05}_{-0.07}$| | |$-21.00^{+0.05}_{-0.07}$| | |$1.17^{+0.04}_{-0.03}$| | |$23.71^{+0.05}_{-0.07}$| | |$-22.69^{+0.05}_{-0.07}$| | |$0.97^{+0.03}_{-0.02}$| | |$1.08^{+0.04}_{-0.03}$| | |$0.83^{+0.05}_{-0.04}$| | 2 |
| C08_09 | |$25.79^{+0.09}_{-0.11}$| | |$-20.61^{+0.09}_{-0.11}$| | |$1.10^{+0.03}_{-0.02}$| | |$25.83^{+0.08}_{-0.10}$| | |$-20.57^{+0.08}_{-0.10}$| | |$1.12^{+0.04}_{-0.03}$| | |$25.09^{+0.04}_{-0.04}$| | |$-21.31^{+0.04}_{-0.04}$| | |$0.54^{+0.02}_{-0.02}$| | |$0.49^{+0.02}_{-0.02}$| | |$0.48^{+0.02}_{-0.02}$| | 1 |
| C08_10 | |$26.35^{+0.04}_{-0.05}$| | |$-20.05^{+0.04}_{-0.05}$| | |$0.38^{+0.02}_{-0.01}$| | |$26.02^{+0.06}_{-0.07}$| | |$-20.38^{+0.06}_{-0.07}$| | |$0.55^{+0.03}_{-0.04}$| | |$25.49^{+0.04}_{-0.04}$| | |$-20.91^{+0.04}_{-0.04}$| | |$0.80^{+0.02}_{-0.02}$| | |$2.11^{+0.12}_{-0.09}$| | |$1.45^{+0.14}_{-0.16}$| | 2 |
| C08_11 | |$24.25^{+0.06}_{-0.07}$| | |$-22.15^{+0.06}_{-0.07}$| | |$1.28^{+0.03}_{-0.02}$| | |$24.16^{+0.05}_{-0.07}$| | |$-22.24^{+0.05}_{-0.07}$| | |$1.49^{+0.05}_{-0.04}$| | |$23.59^{+0.05}_{-0.07}$| | |$-22.81^{+0.05}_{-0.07}$| | |$1.30^{+0.04}_{-0.03}$| | |$1.01^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_12 | |$25.93^{+0.05}_{-0.07}$| | |$-20.47^{+0.05}_{-0.07}$| | |$0.84^{+0.02}_{-0.01}$| | |$25.45^{+0.05}_{-0.07}$| | |$-20.95^{+0.05}_{-0.07}$| | |$1.03^{+0.03}_{-0.03}$| | |$24.55^{+0.05}_{-0.07}$| | |$-21.85^{+0.05}_{-0.07}$| | |$0.96^{+0.03}_{-0.02}$| | |$1.15^{+0.04}_{-0.03}$| | |$0.94^{+0.05}_{-0.04}$| | 2 |
| C08_13 | |$25.68^{+0.01}_{-0.02}$| | |$-20.71^{+0.01}_{-0.02}$| | |$0.20^{+0.00}_{-0.00}$| | |$25.50^{+0.02}_{-0.02}$| | |$-20.90^{+0.02}_{-0.02}$| | |$0.34^{+0.01}_{-0.02}$| | |$25.41^{+0.02}_{-0.03}$| | |$-20.99^{+0.02}_{-0.03}$| | |$0.42^{+0.02}_{-0.02}$| | |$2.09^{+0.09}_{-0.09}$| | |$1.25^{+0.12}_{-0.12}$| | 2 |
| C08_14 | |$26.11^{+0.05}_{-0.07}$| | |$-20.29^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.04^{+0.06}_{-0.07}$| | |$-20.36^{+0.06}_{-0.07}$| | |$0.61^{+0.05}_{-0.05}$| | |$24.84^{+0.04}_{-0.04}$| | |$-21.56^{+0.04}_{-0.04}$| | |$0.52^{+0.02}_{-0.02}$| | |$0.99^{+0.05}_{-0.04}$| | |$0.85^{+0.09}_{-0.09}$| | 2 |
| C08_15 | |$25.20^{+0.06}_{-0.07}$| | |$-21.49^{+0.06}_{-0.07}$| | |$0.87^{+0.02}_{-0.01}$| | |$25.19^{+0.05}_{-0.07}$| | |$-21.50^{+0.05}_{-0.07}$| | |$0.90^{+0.03}_{-0.02}$| | |$24.61^{+0.04}_{-0.04}$| | |$-22.08^{+0.04}_{-0.04}$| | |$0.78^{+0.03}_{-0.02}$| | |$0.90^{+0.04}_{-0.03}$| | |$0.87^{+0.04}_{-0.03}$| | 2 |
| C08_16 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.20^{+0.07}_{-0.05}$| | |$26.09^{+0.08}_{-0.10}$| | |$-20.61^{+0.08}_{-0.10}$| | |$1.29^{+0.12}_{-0.09}$| | — | — | — | — | — | 1 |
| C08_17 | |$25.19^{+0.03}_{-0.04}$| | |$-21.51^{+0.03}_{-0.04}$| | |$0.64^{+0.01}_{-0.01}$| | |$25.22^{+0.04}_{-0.05}$| | |$-21.48^{+0.04}_{-0.05}$| | |$0.66^{+0.02}_{-0.02}$| | |$24.17^{+0.04}_{-0.04}$| | |$-22.52^{+0.04}_{-0.04}$| | |$0.83^{+0.03}_{-0.02}$| | |$1.30^{+0.05}_{-0.04}$| | |$1.27^{+0.06}_{-0.05}$| | 2 |
| C08_18 | |$26.13^{+0.09}_{-0.11}$| | |$-20.56^{+0.09}_{-0.11}$| | |$1.08^{+0.07}_{-0.05}$| | |$25.88^{+0.08}_{-0.10}$| | |$-20.81^{+0.08}_{-0.10}$| | |$1.29^{+0.04}_{-0.03}$| | |$23.81^{+0.05}_{-0.07}$| | |$-22.88^{+0.05}_{-0.07}$| | |$1.28^{+0.04}_{-0.04}$| | |$1.18^{+0.09}_{-0.06}$| | |$0.99^{+0.06}_{-0.04}$| | 2 |
| C08_19 | |$26.08^{+0.05}_{-0.07}$| | |$-20.61^{+0.05}_{-0.07}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.98^{+0.06}_{-0.07}$| | |$-20.72^{+0.06}_{-0.07}$| | |$0.60^{+0.04}_{-0.05}$| | |$23.88^{+0.04}_{-0.04}$| | |$-22.82^{+0.04}_{-0.04}$| | |$0.71^{+0.02}_{-0.02}$| | |$1.45^{+0.06}_{-0.05}$| | |$1.19^{+0.11}_{-0.12}$| | 1 |
| C08_20 | |$26.65^{+0.04}_{-0.05}$| | |$-20.04^{+0.04}_{-0.05}$| | |$0.35^{+0.02}_{-0.01}$| | |$26.67^{+0.05}_{-0.05}$| | |$-20.03^{+0.05}_{-0.05}$| | |$0.35^{+0.03}_{-0.04}$| | |$24.63^{+0.05}_{-0.07}$| | |$-22.06^{+0.05}_{-0.07}$| | |$0.94^{+0.03}_{-0.02}$| | |$2.72^{+0.15}_{-0.11}$| | |$2.68^{+0.25}_{-0.28}$| | 1 |
| C08_21 | |$25.93^{+0.02}_{-0.03}$| | |$-20.77^{+0.02}_{-0.03}$| | |$0.22^{+0.00}_{-0.00}$| | |$25.10^{+0.04}_{-0.05}$| | |$-21.59^{+0.04}_{-0.05}$| | |$0.57^{+0.02}_{-0.02}$| | |$24.78^{+0.04}_{-0.04}$| | |$-21.92^{+0.04}_{-0.04}$| | |$0.62^{+0.02}_{-0.02}$| | |$2.74^{+0.10}_{-0.09}$| | |$1.08^{+0.12}_{-0.12}$| | 2 |
| C08_22 | |$25.41^{+0.03}_{-0.04}$| | |$-21.28^{+0.03}_{-0.04}$| | |$0.83^{+0.02}_{-0.01}$| | |$25.32^{+0.05}_{-0.07}$| | |$-21.37^{+0.05}_{-0.07}$| | |$0.99^{+0.04}_{-0.03}$| | |$24.79^{+0.04}_{-0.04}$| | |$-21.90^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$0.73^{+0.03}_{-0.02}$| | |$0.61^{+0.03}_{-0.03}$| | 1 |
| C08_23 | |$26.35^{+0.08}_{-0.11}$| | |$-20.34^{+0.08}_{-0.11}$| | |$0.45^{+0.02}_{-0.01}$| | |$26.47^{+0.05}_{-0.05}$| | |$-20.23^{+0.05}_{-0.05}$| | |$0.39^{+0.03}_{-0.04}$| | |$25.89^{+0.03}_{-0.03}$| | |$-20.81^{+0.03}_{-0.03}$| | |$0.31^{+0.02}_{-0.01}$| | |$0.69^{+0.05}_{-0.04}$| | |$0.78^{+0.07}_{-0.07}$| | 1 |
| C08_24 | |$26.31^{+0.08}_{-0.11}$| | |$-20.38^{+0.08}_{-0.11}$| | |$0.57^{+0.03}_{-0.02}$| | |$25.77^{+0.08}_{-0.10}$| | |$-20.92^{+0.08}_{-0.10}$| | |$0.94^{+0.03}_{-0.02}$| | |$25.33^{+0.04}_{-0.04}$| | |$-21.36^{+0.04}_{-0.04}$| | |$0.76^{+0.03}_{-0.02}$| | |$1.34^{+0.08}_{-0.06}$| | |$0.81^{+0.06}_{-0.05}$| | 2 |
| C08_25 | |$26.89^{+0.06}_{-0.07}$| | |$-20.05^{+0.06}_{-0.07}$| | |$0.13^{+0.01}_{-0.01}$| | |$26.87^{+0.09}_{-0.08}$| | |$-20.07^{+0.09}_{-0.08}$| | |$0.19^{+0.03}_{-0.03}$| | — | — | — | — | — | 1 |
| C08_27 | |$25.74^{+0.02}_{-0.03}$| | |$-21.12^{+0.02}_{-0.03}$| | |$0.24^{+0.00}_{-0.00}$| | |$25.68^{+0.02}_{-0.02}$| | |$-21.18^{+0.02}_{-0.02}$| | |$0.32^{+0.01}_{-0.01}$| | |$24.61^{+0.02}_{-0.03}$| | |$-22.26^{+0.02}_{-0.03}$| | |$0.38^{+0.01}_{-0.01}$| | |$1.61^{+0.07}_{-0.06}$| | |$1.20^{+0.09}_{-0.09}$| | 1 |
| C08_28 | |$26.23^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.36^{+0.02}_{-0.01}$| | |$25.95^{+0.06}_{-0.07}$| | |$-21.01^{+0.06}_{-0.07}$| | |$0.52^{+0.02}_{-0.02}$| | — | — | — | — | — | 2 |
| C08_29 | |$26.61^{+0.04}_{-0.05}$| | |$-20.18^{+0.04}_{-0.05}$| | |$0.17^{+0.01}_{-0.01}$| | |$25.91^{+0.06}_{-0.07}$| | |$-20.88^{+0.06}_{-0.07}$| | |$0.55^{+0.02}_{-0.02}$| | |$25.67^{+0.05}_{-0.06}$| | |$-21.12^{+0.05}_{-0.06}$| | |$0.49^{+0.02}_{-0.01}$| | |$2.82^{+0.19}_{-0.15}$| | |$0.89^{+0.13}_{-0.12}$| | 2 |
| C08_30 | |$26.48^{+0.04}_{-0.05}$| | |$-20.73^{+0.04}_{-0.05}$| | |$0.16^{+0.01}_{-0.01}$| | |$26.52^{+0.05}_{-0.05}$| | |$-20.69^{+0.05}_{-0.05}$| | |$0.17^{+0.03}_{-0.02}$| | |$25.64^{+0.02}_{-0.03}$| | |$-21.58^{+0.02}_{-0.03}$| | |$0.21^{+0.01}_{-0.01}$| | |$1.28^{+0.11}_{-0.09}$| | |$1.25^{+0.21}_{-0.20}$| | 1 |
| C08_31 | |$27.07^{+0.06}_{-0.07}$| | |$-20.09^{+0.06}_{-0.07}$| | |$0.25^{+0.03}_{-0.02}$| | |$26.81^{+0.15}_{-0.17}$| | |$-20.35^{+0.15}_{-0.17}$| | |$0.38^{+0.03}_{-0.03}$| | |$25.55^{+0.04}_{-0.04}$| | |$-21.61^{+0.04}_{-0.04}$| | |$0.39^{+0.01}_{-0.01}$| | |$1.54^{+0.20}_{-0.14}$| | |$1.01^{+0.12}_{-0.13}$| | 1 |
| C09_01 | |$26.13^{+0.05}_{-0.07}$| | |$-20.24^{+0.05}_{-0.07}$| | |$0.52^{+0.02}_{-0.01}$| | |$26.16^{+0.06}_{-0.07}$| | |$-20.20^{+0.06}_{-0.07}$| | |$0.50^{+0.03}_{-0.04}$| | |$25.73^{+0.05}_{-0.06}$| | |$-20.64^{+0.05}_{-0.06}$| | |$0.63^{+0.02}_{-0.02}$| | |$1.21^{+0.06}_{-0.05}$| | |$1.27^{+0.09}_{-0.10}$| | 1 |
| C09_02 | |$26.82^{+0.13}_{-0.18}$| | |$-19.54^{+0.13}_{-0.18}$| | |$0.63^{+0.03}_{-0.02}$| | |$26.71^{+0.15}_{-0.17}$| | |$-19.65^{+0.15}_{-0.17}$| | |$0.66^{+0.05}_{-0.05}$| | |$26.46^{+0.04}_{-0.04}$| | |$-19.90^{+0.04}_{-0.04}$| | |$0.47^{+0.03}_{-0.04}$| | |$0.74^{+0.06}_{-0.06}$| | |$0.70^{+0.08}_{-0.08}$| | 2 |
| C09_03 | |$25.88^{+0.05}_{-0.07}$| | |$-20.51^{+0.05}_{-0.07}$| | |$0.76^{+0.01}_{-0.01}$| | |$25.96^{+0.06}_{-0.07}$| | |$-20.44^{+0.06}_{-0.07}$| | |$0.70^{+0.02}_{-0.02}$| | |$25.54^{+0.04}_{-0.04}$| | |$-20.86^{+0.04}_{-0.04}$| | |$0.79^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.13^{+0.04}_{-0.04}$| | 1 |
| C09_04 | |$25.58^{+0.03}_{-0.04}$| | |$-20.82^{+0.03}_{-0.04}$| | |$0.52^{+0.01}_{-0.01}$| | |$25.63^{+0.04}_{-0.05}$| | |$-20.77^{+0.04}_{-0.05}$| | |$0.49^{+0.02}_{-0.01}$| | |$25.24^{+0.02}_{-0.03}$| | |$-21.16^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.78^{+0.04}_{-0.03}$| | |$0.84^{+0.04}_{-0.04}$| | 2 |
| C09_05 | |$26.46^{+0.08}_{-0.11}$| | |$-19.94^{+0.08}_{-0.11}$| | |$0.54^{+0.02}_{-0.01}$| | |$26.08^{+0.06}_{-0.07}$| | |$-20.32^{+0.06}_{-0.07}$| | |$0.67^{+0.05}_{-0.05}$| | |$25.90^{+0.05}_{-0.06}$| | |$-20.50^{+0.05}_{-0.06}$| | |$0.64^{+0.02}_{-0.02}$| | |$1.20^{+0.06}_{-0.05}$| | |$0.96^{+0.10}_{-0.10}$| | 2 |
| C09_06 | |$25.93^{+0.02}_{-0.03}$| | |$-20.47^{+0.02}_{-0.03}$| | |$0.21^{+0.00}_{-0.00}$| | |$25.66^{+0.02}_{-0.02}$| | |$-20.74^{+0.02}_{-0.02}$| | |$0.41^{+0.02}_{-0.01}$| | |$24.86^{+0.04}_{-0.04}$| | |$-21.54^{+0.04}_{-0.04}$| | |$0.61^{+0.02}_{-0.02}$| | |$2.89^{+0.11}_{-0.11}$| | |$1.48^{+0.15}_{-0.14}$| | 2 |
| C09_07 | |$27.17^{+0.06}_{-0.07}$| | |$-19.23^{+0.06}_{-0.07}$| | |$0.44^{+0.07}_{-0.05}$| | |$26.29^{+0.09}_{-0.11}$| | |$-20.11^{+0.09}_{-0.11}$| | |$0.90^{+0.07}_{-0.07}$| | |$26.16^{+0.05}_{-0.06}$| | |$-20.24^{+0.05}_{-0.06}$| | |$0.70^{+0.09}_{-0.05}$| | |$1.60^{+0.34}_{-0.20}$| | |$0.78^{+0.24}_{-0.16}$| | 2 |
| C09_08 | |$26.41^{+0.08}_{-0.11}$| | |$-19.99^{+0.08}_{-0.11}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.38^{+0.05}_{-0.05}$| | |$-20.02^{+0.05}_{-0.05}$| | |$0.45^{+0.03}_{-0.04}$| | |$25.25^{+0.04}_{-0.04}$| | |$-21.15^{+0.04}_{-0.04}$| | |$0.72^{+0.02}_{-0.02}$| | |$1.29^{+0.06}_{-0.05}$| | |$1.58^{+0.10}_{-0.12}$| | 2 |
| C10_01 | |$26.21^{+0.02}_{-0.03}$| | |$-20.19^{+0.02}_{-0.03}$| | |$0.33^{+0.01}_{-0.01}$| | |$26.13^{+0.03}_{-0.03}$| | |$-20.27^{+0.03}_{-0.03}$| | |$0.40^{+0.03}_{-0.04}$| | |$25.59^{+0.04}_{-0.04}$| | |$-20.81^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.99^{+0.09}_{-0.08}$| | |$1.63^{+0.18}_{-0.21}$| | 2 |
| C10_02 | |$25.66^{+0.01}_{-0.02}$| | |$-20.74^{+0.01}_{-0.02}$| | |$0.44^{+0.01}_{-0.01}$| | |$25.53^{+0.04}_{-0.05}$| | |$-20.87^{+0.04}_{-0.05}$| | |$0.63^{+0.02}_{-0.02}$| | |$24.99^{+0.04}_{-0.04}$| | |$-21.41^{+0.04}_{-0.04}$| | |$0.47^{+0.02}_{-0.02}$| | |$1.08^{+0.04}_{-0.04}$| | |$0.75^{+0.05}_{-0.05}$| | 1 |
| C10_03 | |$25.44^{+0.03}_{-0.04}$| | |$-20.96^{+0.03}_{-0.04}$| | |$0.60^{+0.01}_{-0.01}$| | |$25.47^{+0.04}_{-0.05}$| | |$-20.93^{+0.04}_{-0.05}$| | |$0.58^{+0.02}_{-0.01}$| | |$24.89^{+0.04}_{-0.04}$| | |$-21.51^{+0.04}_{-0.04}$| | |$0.73^{+0.02}_{-0.02}$| | |$1.21^{+0.04}_{-0.04}$| | |$1.26^{+0.05}_{-0.04}$| | 2 |
| C10_04 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.44^{+0.02}_{-0.01}$| | |$26.15^{+0.06}_{-0.07}$| | |$-20.25^{+0.06}_{-0.07}$| | |$0.58^{+0.03}_{-0.04}$| | |$26.72^{+0.04}_{-0.04}$| | |$-19.68^{+0.04}_{-0.04}$| | |$0.27^{+0.03}_{-0.03}$| | |$0.62^{+0.08}_{-0.07}$| | |$0.47^{+0.08}_{-0.08}$| | 2 |
| C10_05 | |$25.49^{+0.03}_{-0.04}$| | |$-20.91^{+0.03}_{-0.04}$| | |$0.49^{+0.01}_{-0.01}$| | |$25.40^{+0.04}_{-0.05}$| | |$-21.00^{+0.04}_{-0.05}$| | |$0.59^{+0.02}_{-0.01}$| | |$25.67^{+0.02}_{-0.03}$| | |$-20.73^{+0.02}_{-0.03}$| | |$0.41^{+0.02}_{-0.02}$| | |$0.84^{+0.04}_{-0.03}$| | |$0.70^{+0.04}_{-0.04}$| | 2 |
| C10_06 | |$26.40^{+0.15}_{-0.18}$| | |$-20.00^{+0.15}_{-0.18}$| | |$1.12^{+0.08}_{-0.05}$| | |$26.37^{+0.14}_{-0.15}$| | |$-20.03^{+0.14}_{-0.15}$| | |$0.96^{+0.07}_{-0.07}$| | |$26.22^{+0.09}_{-0.12}$| | |$-20.17^{+0.09}_{-0.12}$| | |$0.77^{+0.09}_{-0.05}$| | |$0.69^{+0.09}_{-0.05}$| | |$0.80^{+0.09}_{-0.06}$| | 2 |
| C10_07 | |$26.31^{+0.04}_{-0.05}$| | |$-20.09^{+0.04}_{-0.05}$| | |$0.43^{+0.02}_{-0.01}$| | |$25.72^{+0.04}_{-0.05}$| | |$-20.68^{+0.04}_{-0.05}$| | |$0.86^{+0.03}_{-0.03}$| | |$25.51^{+0.04}_{-0.04}$| | |$-20.89^{+0.04}_{-0.04}$| | |$0.77^{+0.02}_{-0.02}$| | |$1.79^{+0.09}_{-0.07}$| | |$0.89^{+0.08}_{-0.07}$| | 2 |
| C10_08 | |$26.03^{+0.05}_{-0.07}$| | |$-20.37^{+0.05}_{-0.07}$| | |$0.55^{+0.02}_{-0.01}$| | |$26.12^{+0.06}_{-0.07}$| | |$-20.28^{+0.06}_{-0.07}$| | |$0.48^{+0.03}_{-0.04}$| | |$25.37^{+0.04}_{-0.04}$| | |$-21.03^{+0.04}_{-0.04}$| | |$0.51^{+0.02}_{-0.02}$| | |$0.92^{+0.04}_{-0.04}$| | |$1.07^{+0.07}_{-0.08}$| | 1 |
| C10_09 | |$24.91^{+0.03}_{-0.04}$| | |$-22.03^{+0.03}_{-0.04}$| | |$0.62^{+0.01}_{-0.01}$| | |$25.00^{+0.04}_{-0.05}$| | |$-21.93^{+0.04}_{-0.05}$| | |$0.56^{+0.02}_{-0.02}$| | |$23.99^{+0.04}_{-0.04}$| | |$-22.95^{+0.04}_{-0.04}$| | |$0.65^{+0.02}_{-0.02}$| | |$1.04^{+0.03}_{-0.03}$| | |$1.15^{+0.04}_{-0.04}$| | 2 |
| C10_10 | |$25.41^{+0.01}_{-0.02}$| | |$-21.48^{+0.01}_{-0.02}$| | |$0.16^{+0.00}_{-0.00}$| | |$25.48^{+0.02}_{-0.02}$| | |$-21.41^{+0.02}_{-0.02}$| | |$0.14^{+0.01}_{-0.01}$| | |$25.42^{+0.02}_{-0.03}$| | |$-21.46^{+0.02}_{-0.03}$| | |$0.16^{+0.02}_{-0.01}$| | |$0.95^{+0.10}_{-0.08}$| | |$1.10^{+0.13}_{-0.12}$| | 1 |
*(1) ID. (2) Total apparent UV magnitude in F150W. (3) Total absolute UV magnitude in F150W. (4) UV size measured in F150W. (5) Total apparent UV magnitude measured in the smoothed F150W images. (6) Total absolute UV magnitude measured in the smoothed F150W images. (7) UV size measured in the smoothed F150W images. (8) Total apparent optical magnitude in F444W. (9) Total absolute optical magnitude in F444W. (10) Optical size measured in F444W. (11) Optical-to-UV size ratio measured with the F150W and F444W images. (12) Optical-to-UV size ratio measured with the smoothed F150W and F444W images. (13) Flag about blendedness. 1: The component fitted in the smoothed F150W image and/or the F444W image is a single component in the original F150W image. 2: The component fitted in the smoothed F150W image and/or the F444W image consists of multiple components in the original F150W image. 0: Too faint or the SB profile fitting encounters numerical convergence issues.
The question of whether the sizes and total magnitudes obtained from the original F150W images can be reproduced when the spatial resolution is as low as that of the F444W images is intriguing. Figure 8 compares the size and total magnitude results derived for the original and PSF-matched F150W images. The top panel illustrates the comparison of the size measurements. For single sources, the results are in good agreement across a wide range of sizes. This indicates that, even when the spatial resolution is as large as in the F444W image, small sizes derived for the original F150W image can still be obtained in the PSF-matched F150W image. On the other hand, for multiple sources, the obtained sizes tend to be larger after PSF matching as expected, because more components are fitted in the SB profile fitting after PSF matching.
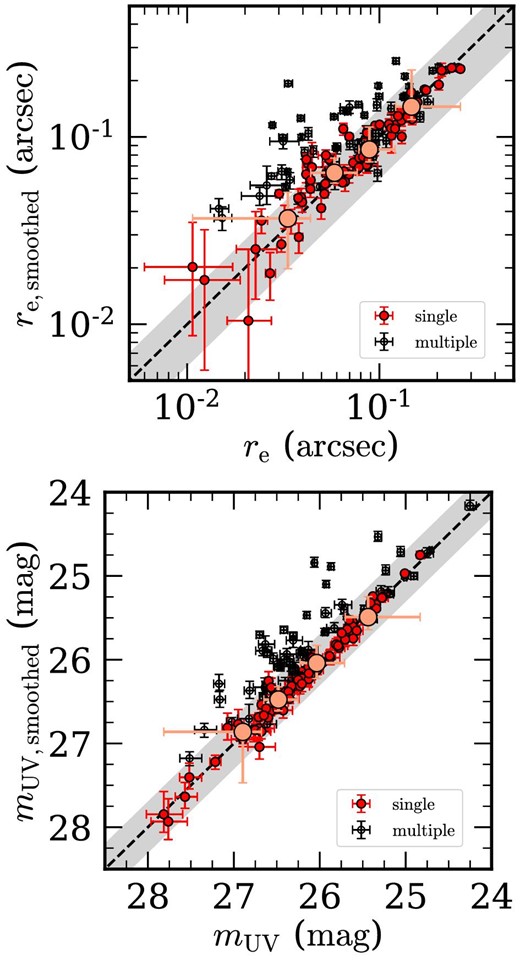
Comparison of SB profile fitting results for galaxies at z ≃ 4–10 with the F150W images before and after PSF matching. The top panel presents the results for size, while the bottom panel shows the results for total magnitude. The red filled circles represent sources where the component fitted with the smoothed F150W image and/or the F444W image is the same as the one fitted with the original F150W image (single). The black open circles indicate sources where the component fitted with the smoothed F150W image and/or the F444W image includes surrounding components not fitted in the original F150W image (multiple). The large orange filled circles and error bars along the y-axis represent the median values and 68th percentiles of the results from the PSF-matched images for the single sources, with the sample divided into quartiles based on the results from the images before PSF matching. The error bars along the x-axis represent the range of size or total magnitude values in each divided sample. The gray shade in the top (bottom) panel represents the range where the difference between the sizes (total magnitudes) is within ±40% (±0.3 mag).
The bottom panel of figure 8 demonstrates the magnitude measurements with the F150W images before and after PSF matching. As expected, the results for the single sources align well, while the multiple sources tend to be systematically brighter after PSF matching.
4 Results and discussion
4.1 SB profile fitting results for the rest-frame UV and optical continuum
We perform SB profile fittings for the galaxies at z ≃ 4–10 in the CEERS fields, which are compiled in section 2, to determine their sizes and total magnitudes in the rest-frame UV and optical. The F150W images are used to probe the rest-frame UV continuum, whereas the F444W images are used for the rest-frame optical. The SB profile fittings are conducted only for sources with S|$/$|N values exceeding 10 (section 2). Among them, the SB profile fittings with the F150W (F444W) images successfully converge for 29 and 120 (22 and 96) sources with and without spectroscopic confirmations, respectively. Their distributions on the rest-frame UV absolute magnitude (MUV) vs. redshift and the rest-frame optical absolute magnitude (Mopt) vs. redshift planes are presented in figure 9. The best-fitting parameters obtained from the SB profile fittings for the individual sources are summarized in table 6 and the individual fitting result images are shown in figure 17 in appendix 2. Pseudo-color cutout images of those galaxies whose spectroscopic redshifts have been compiled by Nakajima et al. (2023) are shown in figure 18 in appendix 2.6
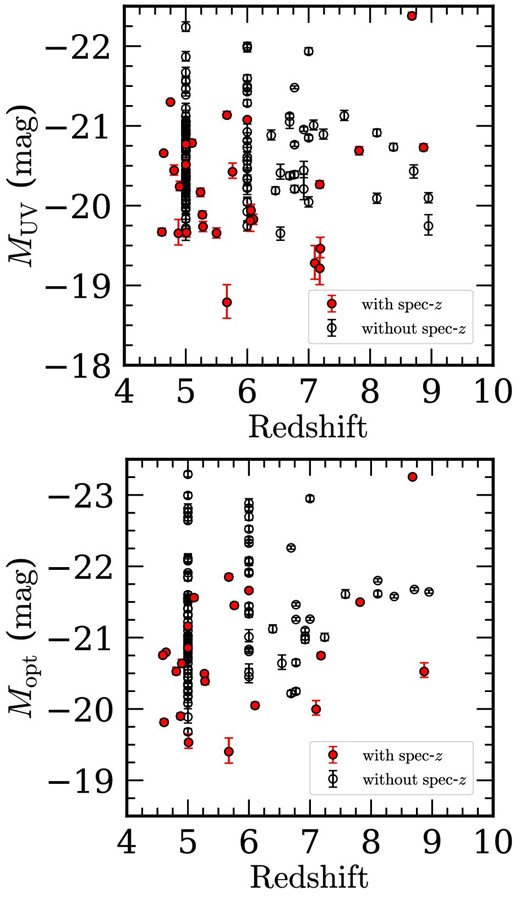
Top: Distribution of MUV and redshift for the galaxies at z ≃ 4–10 where the S|$/$|N values are larger than 10 in the F150W images and the SB profile fittings are successfully converged. The red filled circles represent spectroscopically confirmed sources, while the black open circles indicate sources without spectroscopic confirmation. Bottom: Same as the top panel but for Mopt obtained from the F444W images.
The morphologies of some of these sources have been investigated in previous work. C06_06 is the same as CEERS-AGN-z5-1 in Onoue et al. (2023) and CEERS 1670 in Kocevski et al. (2023), which is selected as an AGN candidate and confirmed by follow-up spectroscopy. Onoue et al. (2023) have reported that the central SB profile of C06_06 is dominated by the PSF in the F115W image, suggesting a size of less than 0.13 kpc. Our obtained size for this source in F150W is 0.09 ± 0.01 kpc, which is consistent with these previous results. Note that the other source reported in Kocevski et al. (2023), CEERS 3210, is too faint to be investigated in this study.
In addition to C06_06, C03_04 is selected as a broad-line AGN by Harikane et al. (2023a) based on the broad component detections only in the permitted Hα line.7 In addition, C02_02 (CEERS 1465) and C08_01 (CEERS 1019) are selected as possible broad-line AGN candidates in Harikane et al. (2023a) (see also Larson et al. 2023). Harikane et al. (2023a) have reported that C06_06 shows a compact morphology, while the other three sources have extended morphologies. In our SB profile fittings, although all of these sources are fitted with Sérsic profiles, C06_06 shows the smallest size.8 In this sense, our results are consistent with their findings. In what follows, we mark these AGNs and AGN candidates with a special symbol in the figures as necessary. As mentioned in subsection 4.3, these broad-line AGNs and AGN candidates tend to be more compact than normal SFGs. It should also be noted that the remaining sources at z > 4.5 in their study are not investigated in this paper due to their faintness or encountering numerical convergence issues in the SB profile fittings.
Very recently, based on the data from public extragalactic fields obtained in JWST Cycle 1, Morishita et al. (2024) have compiled a catalog of SFGs at z = 5–14 and measured their sizes in the rest-frame UV. Their catalog encompasses 20 of the galaxies that we investigate. A comparison of the size measurement results for these galaxies is shown in figure 10. Because they only provide the effective radius along the semi-major axis, our comparison here is also based on the effective radius along the semi-major axis. Based on the single or multiple flags established in subsection 3.4, we differentiate the symbols for the data points. As can be seen from figure 10, when considering only the galaxies labeled single, our results align well with theirs. However, there are some multiple flagged galaxies that deviate significantly. Specifically, for three objects, their results are larger by about 0.3–0.5 dex compared to ours; their IDs are C01_05, C06_01, and C08_01 (figure 17 in appendix 2). It is likely that Morishita et al. (2024) have treated them as a single blended source in their SB profile fittings, while we perform SB profile fittings for one of these components, which could explain the significant size discrepancy. Despite these exceptions, the results from both studies generally align well.
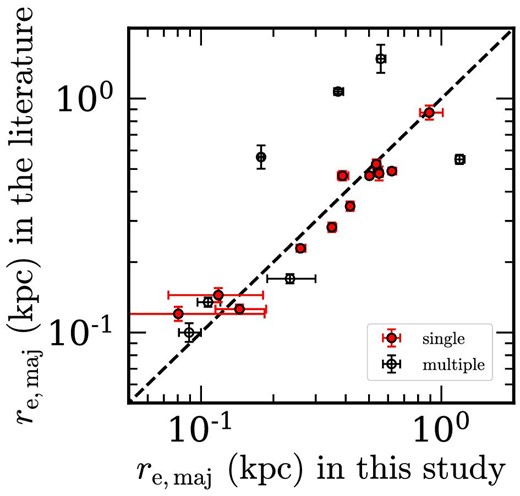
Comparison of size measurement results for individual galaxies in the rest-frame UV. The horizontal axis represents our size measurements and the vertical axis denotes those in Morishita et al. (2024). The red filled circles represent sources where the component fitted with JWST NIRCam F444W is the same as the one fitted with F150W (single). The black open circles indicate sources where the component fitted with F444W includes surrounding components not fitted in the F150W image (multiple). Given that Morishita et al. (2024) provide only the effective radius along the semi-major axis (re,maj), these comparisons are also based on the semi-major-axis effective radius. The black dashed line is the case where our estimates and those in the literature are equivalent.
In Zhang et al. (2023), galaxies with spatially extended Hβ + [O iii] emission are selected based on the emission line images created by subtracting NIRCam broad-band images with and without emission line contributions. Among the selected sources, CEERS 792 is the same as C06_04. However, due to the low S|$/$|N, we do not conduct SB profile fitting for this particular source in this study.
4.2 Comparisons between HST and JWST measurement results
Based on the HST WFC3 images, Shibuya, Ouchi, and Harikane (2015) have performed SB profile fittings for the galaxies in their sample and estimated their sizes and total magnitudes in the rest-frame UV. Because the spatial resolutions of HST and JWST are different, it raises a concern whether it is appropriate to compare these SB profile fitting results.
Figure 11 displays a comparison of the rest-frame UV sizes and total magnitudes for the galaxies in the Shibuya, Ouchi, and Harikane (2015) sample obtained with the HST and JWST images. Because of the difference in spatial resolution between HST and JWST, some galaxies appearing as single sources in the HST images are resolved into multiple components in the JWST images. Conveniently, the spatial resolution of HST WFC3 is similar to those of the red filters of JWST NIRCam. Therefore, for this comparison with the HST results, we use the JWST results from the original or PSF-matched F150W images depending on whether the sources are flagged as single or multiple in subsection 3.4.
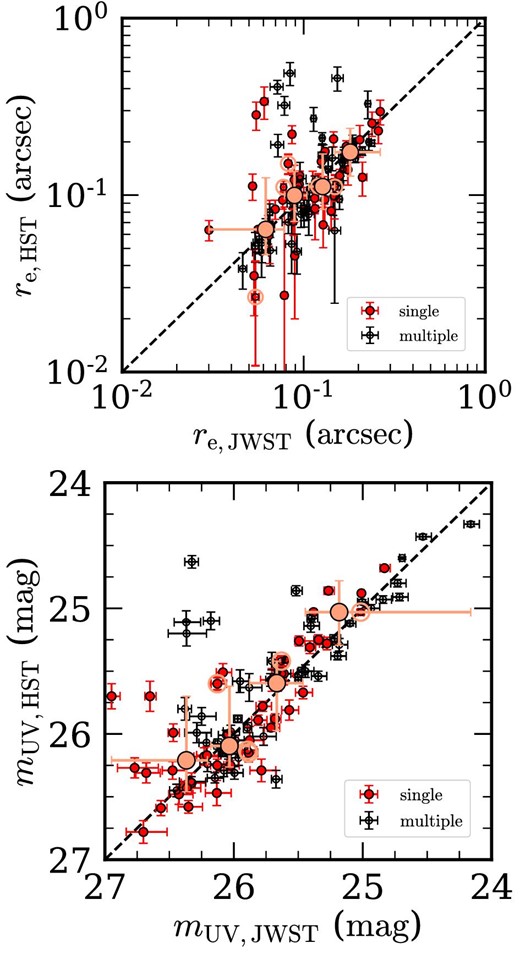
Comparison of SB profile fitting results for the galaxies at z ≃ 4–10 based on the rest-frame UV images obtained with HST and JWST. The top panel presents the results for size, while the bottom panel shows the results for total magnitude. The JWST results are obtained in this study, and the HST results are obtained by Shibuya, Ouchi, and Harikane (2015). The red filled circles represent sources where the component fitted with JWST NIRCam F444W, having a spatial resolution similar to HST, is the same as the one fitted with F150W (single). The black open circles indicate sources where the component fitted with F444W includes surrounding components not fitted in the F150W image (multiple). For the single (multiple) sources, the JWST results are based on the results from the original (PSF-matched) F150W images. The large orange open circles denote sources with spectroscopic redshifts. The large orange filled circles and error bars along the y-axis represent the median values and 68th percentiles of the HST results, with the sample divided into quartiles based on the results from JWST. The error bars along the x-axis represent the range of size or total magnitude values in each divided sample.
As depicted in the top panel of figure 11, the size results obtained from HST and JWST images roughly coincide. Likewise, as presented in the bottom panel of figure 11, the total magnitude results also largely agree. Although individual outliers exist that deviate significantly, such sources are rare, and on average the results show good agreement. In the following subsections, we compare our JWST results with previous results obtained from the HST images, along with previous JWST results.
4.3 Size–luminosity relation in the rest-frame UV and optical
We investigate the relationship between the size and luminosity of our galaxies. The top (bottom) panel of figure 12 shows the rest-frame UV (optical) sizes and total magnitudes for galaxies at z ≃ 4.5–9.5, which are estimated from our SB profile fittings with the F150W (F444W) images in this study. Here we directly use the optical total magnitudes obtained with the F444W images; these measurements are systematically brighter due to the influence of strong emission lines such as Hα and [O iii] as examined in subsection 3.3.
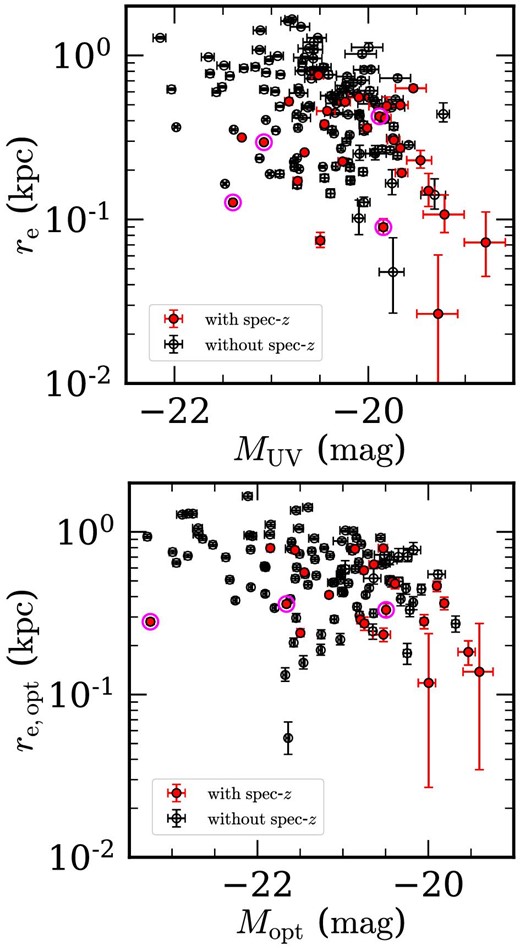
Top: Rest-frame UV size re vs. total magnitude MUV for galaxies at z ≃ 4–10. The red filled circles denote sources with spectroscopic redshifts, while the black open circles are those without spectroscopic confirmation. These sizes and total magnitudes are estimated from the F150W images. The large open magenta circles represent broad-line AGNs and AGN candidates identified in Kocevski et al. (2023) and Harikane et al. (2023a) (see also Onoue et al. 2023). Bottom: Same as the top panel but for the rest-frame optical size re, opt vs. total magnitude Mopt estimated from the F444W images.
Both panels confirm the trend that fainter sources tend to be smaller in size reported in the literature (Oesch et al. 2010; Grazian et al. 2012; Ono et al. 2013, 2023; Huang et al. 2013; Jiang et al. 2013; Kawamata et al. 2015, 2018; Holwerda et al. 2015, 2020; Shibuya et al. 2015; Curtis-Lake et al. 2016; Bowler et al. 2017; Bouwens et al. 2017, 2022; Bridge et al. 2019; Yang et al. 2022). Additionally, the spectroscopically confirmed sources appear to be more compact, probably because the more compact a source is, the easier it is to detect its emission lines by spectroscopy. The broad-line AGNs and AGN candidates except for C02_02 appear to be relatively compact, which can be attributed to the bright emission from the central core compared to the host galaxy components.
The previous work has shown that the sizes of galaxies decrease with increasing redshift on average (Ferguson et al. 2004; Bouwens et al. 2004, 2006, 2017, 2022; Hathi et al. 2008; Oesch et al. 2010; Grazian et al. 2012; Ono et al. 2013, 2023; Huang et al. 2013; Jiang et al. 2013; Kawamata et al. 2015, 2018; Holwerda et al. 2015, 2020; Shibuya et al. 2015; Curtis-Lake et al. 2016; Allen et al. 2017; Bowler et al. 2017). Thus, we show the rest-frame UV sizes and total magnitudes divided into three redshift ranges in figure 13. For each redshift bin, we split the samples into three or two groups based on the total magnitude and calculate the median sizes and its 68th percentiles. These values are plotted together and summarized in table 3. For all of these subsamples, we confirm the trend that fainter sources have smaller sizes, although this trend is not very apparent in the median values for the 6.5 < z < 9.5 subsample. For comparison, we also show the results of Shibuya, Ouchi, and Harikane (2015), who have investigated the rest-frame UV sizes of high-z galaxies using HST images, as well as the results of Yang et al. (2022) and Ono et al. (2023) based on JWST images. We find that our results are broadly consistent with these previous results when comparing at similar total magnitudes. Note that the results from Morishita et al. (2024) are not plotted here, because their measurements for the circularized radius are not available.
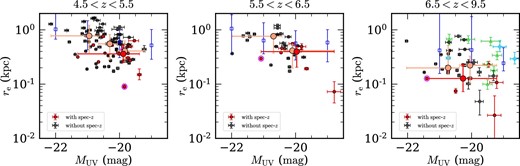
Same as the top panel of figure 12, but the data are divided into bins of redshift: from left to right, z = 4.5–5.5, 5.5–6.5, and 6.5–9.5. The large orange filled circles and error bars along the y-axis represent the median values and 68th percentiles of the subsamples, which are divided into two or three groups based on MUV. The large red filled circles and error bars along the y-axis denote the median values and 68th percentiles of the galaxies with spectroscopic redshifts. The error bars of the large symbols along the x-axis denote the range of total magnitude values in each sample. The blue open squares, cyan open diamonds, and green open triangles are previous results for galaxies at similar redshifts obtained by Shibuya, Ouchi, and Harikane (2015), Ono et al. (2023), and Yang et al. (2022), respectively.
In figure 14, we show the rest-frame optical sizes and total magnitudes divided into three redshift ranges in the same way as figure 13. For the 4.5 < z < 5.5 subsample, we confirm the trend that fainter sources are smaller in size. However, such a trend is not significantly seen in the remaining subsamples. For the 6.5 < z < 9.5 subsample, we find that our results are broadly consistent with the previous results of Yang et al. (2022) and Ono et al. (2023) at around Mopt ≃ −21 mag. It should be noted that, in these previous studies, SB profile fittings have been performed for galaxies fainter than those investigated in this study thanks to the GLASS data, which are deeper than the CEERS data used in this study. Additionally, we confirm that our results are on average in broad agreement with the very recent results of Sun et al. (2024).
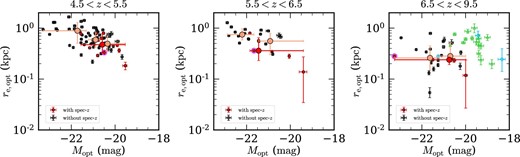
Same as the bottom panel of figure 12, but the data are divided into bins of redshift: from left to right, z = 4.5–5.5, 5.5–6.5, and 6.5–9.5. The large orange filled circles and error bars along the y-axis represent the median values and 68th percentiles of the subsamples, which are divided into two or three groups based on Mopt. The large red filled circles and error bars along the y-axis denote the median values and 68th percentiles of the galaxies with spectroscopic redshifts. The error bars of the large symbols along the x-axis denote the range of total magnitude values in each divided sample. The cyan open diamonds and green open triangles are previous results for galaxies at similar redshifts obtained by Ono et al. (2023) and Yang et al. (2022), respectively.
4.4 Size ratio and spatial offset between the rest-frame optical and UV
The main topic of this study is to compare the sizes of high-z galaxies in the rest-frame UV and optical. When comparing galaxy sizes in different wavelengths, it is necessary to properly consider the wavelength dependence of the spatial resolution.9 As described in subsection 3.4, to ensure a fair comparison of the SB profile fitting results in the rest-frame UV and optical, we use the results from the original (PSF-matched) F150W images for the single (multiple) flagged sources.
The top panels of figure 15 plot the sizes in the rest-frame UV and optical of the z ≃ 4–10 galaxies estimated from the SB profile fittings with the F150W and F444W images. The bottom panels of figure 15 present the size ratio against the total magnitude in the rest-frame UV for these galaxies. In these plots, we divide the sample into three redshift ranges to examine any difference due to redshift. Based on these panels, we find that the size ratio is around unity, with some galaxies being larger than 1 and others smaller. In a similar manner to figures 13 and 14, the sample is divided in half based on size or total magnitude, and their median sizes or median size ratios with its 68th percentiles are also shown in figure 15. The median size ratios and their corresponding total magnitudes are summarized in table 4. In these redshift ranges, we find that the average size ratios align with unity regardless of MUV. For the highest redshift range, our results are in agreement with the previous results obtained for galaxies at z ≃ 7–9 (Yang et al. 2022; Ono et al. 2023). Our results demonstrate that the average size ratios of galaxies at lower redshifts of z ≃ 4.5–6.5 are also unity. The median size ratio of all the galaxies at z ≃ 4–10 investigated in this study is |$r_{\rm e,opt}/r_{\rm e,UV} = 1.01^{+0.35}_{-0.22}$|.10 Very recently, Morishita et al. (2024) have reported that the sizes in the rest-frame UV and optical for z = 5–10 galaxies are comparable, which is consistent with our results.
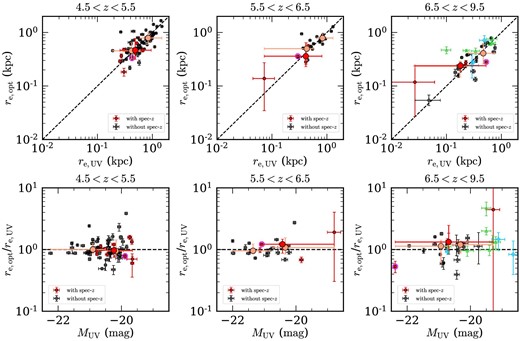
Top: Comparison of rest-frame UV and optical sizes for galaxies at z = 4.5–5.5, 5.5–6.5, and 6.5–9.5, from left to right. The red filled circles are spectroscopically confirmed sources, while the black open circles are not spectroscopically confirmed. Due to the different spatial resolutions, we use the values obtained from the original F150W images for sources flagged as single, and the values from the PSF - matched F150W images for sources flagged as multiple. The large orange filled circles and error bars along the y-axis denote the median values and 68th percentiles of the rest-frame optical sizes for the samples divided into two based on the UV size. The large red filled circles and error bars along the y-axis denote the median values and 68th percentiles of the galaxies with spectroscopic redshifts. The error bars of the large symbols along the x-axis represent the range of UV sizes in each subsample. The black dashed line corresponds to the unity size ratio. The large open magenta circles represent broad-line AGNs and AGN candidates identified in Harikane et al. (2023a). The cyan open diamonds and green open triangles are previous results for galaxies at similar redshifts obtained by Ono et al. (2023) and Yang et al. (2022), respectively. Bottom: Same as the top panel, but the x-axis represents the rest-frame UV magnitude, and the y-axis is the ratio of rest-frame optical to UV sizes.
Utilizing the HST CANDELS data, van der Wel et al. (2014) have demonstrated that the sizes of SFGs at z ∼ 0–2 decrease with increasing wavelength. Interestingly, the difference in size becomes smaller at higher redshifts. Their results can be attributed to younger average ages of SFGs at higher redshifts, resulting in a convergence of the spatial distributions of young massive stars traced in the UV and somewhat older less massive stars traced in the optical (see also Shibuya et al. 2015). The combination of our results with the previous JWST results indicate that there is no significant difference in the sizes of SFGs at z ≃ 4–10 in the rest-frame UV and optical across a wide magnitude range, which is in line with the idea of younger average ages of SFGs at higher redshifts. Indeed, recent spectral energy distribution (SED) analyses for SFGs at comparable redshifts have reported remarkably young ages (e.g., Papovich et al. 2023; Fujimoto et al. 2023).
Furthermore, figure 16 illustrates the spatial offsets between the positions of the rest-frame UV and optical emission of 45 galaxies in our sample for which sizes are successfully measured with both the F150W and F444W images showing no signs of merger activity (red filled circles). The determination of the presence of signs of mergers or tidal interactions is based on visual inspection. Primarily, sources flagged with the multiple component flag as presented in table 6 in appendix 2 are considered to show signs of mergers or tidal interactions. Additionally, sources that are also resolved into multiple components in the smoothed F150W images and/or F444W images are classified as exhibiting signs of mergers or tidal interactions as well, such as C2_20 and C09_01.11 We find that, although 16 sources exhibit spatial offsets exceeding 1σ, none surpass the 3σ threshold. If the positional offset follows a Gaussian distribution centered at zero, the expected numbers of sources within and outside the 1σ range are 45 × 0.683 = 30.735 and 45 × 0.317 = 14.265, respectively, resulting in a chi-squared goodness of fit of 0.309. Since the chi-squared value for a 95% confidence level with one degree of freedom is 3.84, our results do not contradict the assumption of a Gaussian distribution centered at zero, implying on average no significant spatial offset between the rest-frame UV and optical. This suggests that, for SFGs at z = 4–10 with no clear signs of galaxy merger, the primary star-forming activity occurs near the mass centers of the galaxies.
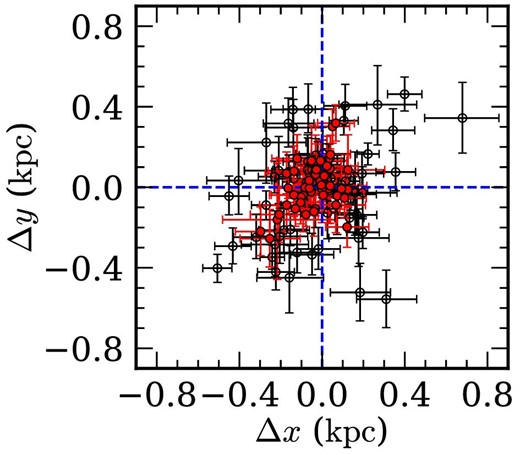
Spatial offsets between the rest-frame UV and optical emissions for SFGs at z = 4–10. The red filled (black open) circles represent the offsets between the F150W and F444W images along the xy-directions for individual galaxies without (with possible) signs of galaxy merger and/or tidal interactions. The horizontal and vertical blue dashed lines represent the cases where the offsets are zero.
Our results demonstrate that, for SFGs at z = 4–10, the sizes and positions traced in the rest-frame UV and optical continuum are not significantly different. This contrasts with observations at lower redshifts z ≲ 2, where galaxies exhibit smaller sizes at longer wavelengths, suggesting inside-out growth (e.g., van der Wel et al. 2014). Based on this concept, our results might imply that SFGs at z = 4–10 are in the early stages of inside-out galaxy formation, where the distribution of young massive and less massive stars is not yet differentiated, indicative of the first phase of this process. More precisely, future studies might offer clear insights through spatially resolved SED analyses (e.g., Giménez-Arteaga et al. 2023; Boyett et al. 2024) for galaxies over a wide range of magnitudes and redshifts.
In figure 16, we additionally present the results of the spatial offsets in the rest-frame UV and optical for sources whose sizes are measured with both the F150W and F444W images exhibiting possible signs of merger and/or tidal interactions (depicted as black open circles). Among the 67 sources that we analyze, 48 have an offset from the origin greater than 1σ, yielding a chi-squared goodness of fit of 49.4. This rejects the hypothesis that the data follow a Gaussian distribution centered at the origin at a confidence level of 95%, possibly implying that SFGs at z = 4–10 accompanied by multiple components on average show significant offsets between the positions in the rest-frame UV and optical. Although the observed offsets of these sources seem to be less conspicuous than those reported in the simulation results of Ma et al. (2018) (see their figure 2), a quantitative comparison in the future might provide valuable insights into the physical processes involved in galaxy formation.
5 Summary
In this study, we have performed SB profile fittings for the 149 galaxies at z ≃ 4–10 with S|$/$|N values exceeding 10, 29 of which have been spectroscopically confirmed, using the deep JWST NIRCam images obtained by the CEERS survey. The F150W and F444W images allow for probing their rest-frame UV and optical continuum emission. Although the Sérsic index is typically around 1.0–1.5 in the rest-frame UV and optical, we have fixed it in the SB profile fittings in the same manner as previous work due to the large uncertainties for individual galaxies. Following our previous approach (Ono et al. 2023), we have performed MC simulations to correct for the systematic underestimates of galaxy sizes and total luminosities, particularly for faint sources. Our primary results are as follows:
We have carefully examined the impact of strong emission lines on galaxy size measurements with galaxies at zspec = 5.63–6.63, utilizing images with the medium-band filter F410M and the broad-band filter F444W, one of which incorporates strong emission lines and the other does not. We have concluded that the size differences due to the effect of strong emission lines are minor, enabling the use of the F444W images to measure galaxy sizes across a more extensive redshift range.
We have also taken into account the difference in spatial resolutions between the F150W and F444W images for a fair comparison between the rest-frame UV and optical sizes of galaxies, by smoothing the F150W images to match the PSF sizes of the F444W images. The SB profile fitting results from the original F150W images and the PSF-matched F150W images have demonstrated that, even when the spatial resolution differs by a factor of about three, the size and total magnitude measurements are in good agreement.
Based on the comparisons between the rest-frame UV sizes and total magnitudes of galaxies observed by the HST and JWST, considering the difference of their spatial resolutions, these two measurements broadly align with each other with few outliers, confirming the availability of the previously obtained HST results (Shibuya et al. 2015) in comparison with JWST measurements.
We have investigated the relationship between the size and luminosity of galaxies at z = 4–10 both in the rest-frame UV and optical, confirming the trend that fainter sources are smaller in size on average as reported in the previous studies (e.g., Oesch et al. 2010; Grazian et al. 2012; Ono et al. 2013).
After careful consideration of the spatial resolution differences in the rest-frame UV and optical images, we have found that the optical-to-UV size ratios of galaxies at z = 4–10 are on average around unity across a wide range of magnitudes, likely because of the young average ages of SFGs at high redshifts.
We have found no significant spatial offsets between the rest-frame UV and optical for z = 4–10 SFGs with no clear signs of merger, implying that the primary star-forming activity in these galaxies is likely occurring near their mass centers, which can be explained by the possibility that these galaxies are experiencing the initial stages of inside-out galaxy formation.
Ackonowledgments
This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. This work was partially performed using the computer facilities of the Institute for Cosmic Ray Research, the University of Tokyo. This research made use of GALFIT (Peng et al. 2002, 2010), SExtractor (Bertin & Arnouts 1996), IRAF (Tody 1986, 1993),12 SAOImage DS9 (Joye & Mandel 2003), Numpy (Harris et al. 2020), Matplotlib (Hunter 2007), Scipy (Virtanen et al. 2020), Astropy (Astropy Collaboration 2013, 2018),13 and Ned Wright’s Javascript Cosmology Calculator (Wright 2006).14 This work was supported by the World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan, as well as KAKENHI Grant Numbers 15K17602, 15H02064, 17H01110, 17H01114, 19K14752, 20H00180, 21H04467, 21J20785, and 22K03670 through the Japan Society for the Promotion of Science (JSPS). This work was partially supported by the joint research program of the Institute for Cosmic Ray Research (ICRR), the University of Tokyo.
Appendix 1. IDs of the galaxies analyzed in this study
In section 2, we compiled galaxies with redshifts ranging from z ≃ 4 to 10 in the CEERS fields found in previous studies (Shibuya et al. 2015; Bouwens et al. 2015; Nakajima et al. 2023; Finkelstein et al. 2023). Table 5 summarizes their unique IDs assigned in this study, their original IDs in the previous catalogs, and their overlaps between the previous catalogs. Additionally, we include a flag in table 5 to indicate if these galaxies are also listed in catalogs from the following studies by different groups: Donnan et al. (2023), Fujimoto et al. (2023), Bouwens et al. (2023), Tang et al. (2023), Harikane et al. (2024). One should be aware that this additional flag is not comprehensive, as it does not cover all published literature to date. It should also be noted that these catalogs have a preference for focusing exclusively on higher-z (z ≳ 7) sources compared to the redshift range covered in our study.
Appendix 2. SB fitting results for individual galaxies
In section 4, we have performed SB profile fittings for the high-z galaxies in the CEERS fields. The sizes and total magnitudes obtained from the SB profile fittings for individual galaxies are summarized in table 6. In addition, the SB profile fitting result images for each object are presented in figure 17. Moreover, the pseudo-color images of those galaxies whose spectroscopic redshifts are compiled by Nakajima et al. (2023) are shown in figure 18.
Sérsic profile fitting results for bright sources in our sample. For each source, from top to bottom, the fitting results for F150W, PSF-matched F150W, and F444W are presented. From left to right, the 1|${_{.}^{\prime\prime}}$|5 × 1|${_{.}^{\prime\prime}}$|5 cutouts of the original image, the best-fitting Sérsic model profile images, and the residual images that are produced by subtracting the best-fitting images from the original ones are shown.

Pseudo-color images of spectroscopically confirmed galaxies in our sample whose sizes are measured in our SB profile fittings. The F150W image is assigned to blue, the F277W image to green, and the F444W image to red, after their PSFs are matched. The size of each image is 1|${_{.}^{\prime\prime}}$|5 × 1|${_{.}^{\prime\prime}}$|5.
Upon scrutinizing the output images of the SB profile fittings, we allocate a blendedness designation for each subject as listed in table 6. This process involves identifying whether the fitted component in either the smoothed F150W and/or the F444W image corresponds to a single source or multiple sources in the original F150W image. For instances where the fitted component in the F444W image is a single component in the original F150W image, we label it as “single” with a flag value of 1. In contrast, when the fitted component in the F444W image consists of multiple components in the original F150W image, the classification becomes “multiple,” marked by a flag value of 2. Essentially, this means that a source is marked as having multiple components if the residual image after a single component fit indicates the existence of other components. This approach ensures a fair comparison even for data with different spatial resolutions.
Footnotes
We confirm that the size and magnitude distribution of our high-z galaxies with S|$/$|N values larger than 10 nearly entirely falls within the range covered by the MC simulated galaxies with S|$/$|N > 10.
C03_04 shows a slightly larger magnitude difference of 0.68 mag. This might indicate that this source has a larger Hα EW experiencing a relatively young starburst compared to the others.
Note that the impact of Hβ + [O iii] line emission on the recovered size and magnitudes for sources will need to be investigated in future work.
As can be seen from this figure, sources at moderate redshifts often appear green, while those at relatively high redshifts often appear red. This is primarily due to the effect of strong emission lines in the rest-frame optical (subsection 3.3).
C03_04 is CEERS 397 and C06_06 is CEERS 2782 in Harikane et al. (2023a).
We exclude the F444W fitting results for C06_06 due to issues with SB profile fitting convergence.
As mentioned in subsection 3.4, some sources are resolved into multiple clumps in the rest-frame UV. To determine whether they appear clumpier in the rest-frame UV compared to the rest-frame optical, as seen in nearby galaxies (e.g., Kuchinski et al. 2000, 2001; Windhorst et al. 2002), or whether high-z galaxies have clumpy morphology in the rest-frame optical as well, higher spatial resolution imaging in the rest-frame optical is required.
If we do not consider the flag about blendedness, we obtain a median size ratio of |$r_{\rm e,opt}/r_{\rm e,UV} = 1.18^{+0.76}_{-0.33}$|. This value is still consistent with unity; however, because multiple components are only fitted in the rest-frame optical for about half of the sources, the size ratio on average becomes larger and its 68th percentile also increases.
Most of these multiple components are not spectroscopically confirmed yet, and therefore further verification is needed to ascertain whether they are physically associated or not.
IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.











