-
PDF
- Split View
-
Views
-
Cite
Cite
Jiro Shimoda, Shu-ichiro Inutsuka, Masahiro Nagashima, The history of the Milky Way: The evolution of star formation, cosmic rays, metallicity, and stellar dynamics over cosmic time, Publications of the Astronomical Society of Japan, Volume 76, Issue 1, February 2024, Pages 81–97, https://doi.org/10.1093/pasj/psad081
Close - Share Icon Share
Abstract
We study the long-term evolution of the Milky Way (MW) over cosmic time by modeling the star formation, cosmic rays, metallicity, stellar dynamics, outflows, and inflows of the galactic system to obtain various insights into the galactic evolution. The mass accretion is modeled by the results of cosmological N-body simulations for the cold dark matter. We find that the star formation rate is about half the mass accretion rate of the disk, given the consistency between observed Galactic diffuse X-ray emissions (GDXEs) and possible conditions driving the Galactic wind.Our model simultaneously reproduces the quantities of star formation rate, cosmic rays, metals, and the rotation curve of the current MW. The most important predictions of the model are that there is an unidentified accretion flow with a possible number density of ∼10−2 cm−3 and that part of the GDXEs originates from a hot, diffuse plasma which is formed by consuming about |$10\%$| of supernova explosion energy. The latter is the science case for future X-ray missions: XRISM, Athena, and so on. We also discuss further implications of our results for the planet formation and observations of external galaxies in terms of multi-messenger astronomy.
1 Introduction
The evolution of galaxies over cosmic time is related to many astrophysical subjects, such as the formation of stars, the origin of cosmic rays (CRs) and radiation, and the evolution of the environment for the life on the planets, and has been widely studied (e.g., van der Kruit & Freeman 2011; Putman et al. 2012; Naab & Ostriker 2017). Nevertheless, our current understanding is far from sufficient. The long-term star formation rate of the Milky Way (MW), which continues with an almost constant rate of several M⊙ yr−1 throughout the cosmic age (e.g., Haywood et al. 2016), is a representative puzzle; if the constant star formation resulted from the similar Galactic disk conditions during the cosmic age of 14 Gyr, the gaseous matter with a mass of |$\sim 10^9\, M_{\odot }$| would have been depleted within ∼1 Gyr. This puzzle can be translated by the cosmological context. Supposing the cosmic density ratio of the baryon to dark matter (DM) is ∼0.1 (Planck Collaboration 2020), the total baryon mass of the MW is estimated to be |$\sim 10^{11}\, M_{\odot }$|, while the total mass of stars is |$4\!-\!6\times 10^{10}\, M_{\odot }$| (Bland-Hawthorn & Gerhard 2016). Therefore, we need to find an explanation why half of the gaseous matter is converted into stars, leaving ∼1% of the mass in the galactic disk. In this paper, we construct the galactic evolution model to elucidate what could be the essence of this fine-tuning mechanism.
The galactic wind (outflow from the disk) is invoked to explain the observed metal absorption lines in the circumgalactic medium (CGM; Tumlinson et al. 2017). Shimoda and Inutsuka (2022) studied the galactic wind considering the effects of the radiative cooling and CR diffusion for the case of the MW. They found that the current conditions of the MW allow the existence of the wind with a mass transfer rate of several M⊙ yr−1 which is comparable to the star formation rate. Thus, the galactic wind is also important for the mass budget of the Galactic system. They also pointed out that the mass loss due to the wind and star formation should be balanced with the disk mass accretion to explain the constant star formation rate over cosmic time. In this paper, following their considerations, we commit to finding the possible gas accretion that would reproduce the current conditions of the MW.
Since we consider the CR-driven wind and the metal-polluted CGM, our model also predicts the amounts of CRs and metals, simultaneously. The combination of predictions on the star formation, the CRs, the metals, and the gaseous matter distribution can be useful for broad astrophysical subjects such as the planet formation (e.g., Tsukamoto & Okuzumi 2022; Tsukamoto et al. 2023) and particle astrophysics in terms of multi-messenger astronomy (e.g., Murase 2022). We also discuss our model predictions and the implications for various observations.
This paper is organized as follows. In section 2, we review the important physical processes through the construction of our model and present analytical estimates of the current star formation rate, metallicity, and CR energy density. The numerical results of our model are presented in section 3. We discuss the implications for observations and future prospects in section 4 and summarize our results in section 5. We will find that the origins of the outflow and inflow are controversially uncertain, although they are really important for understanding galactic evolution.
2 Model description
We model the galactic system under the assumption of axial symmetry. Figure 1 shows a schematic diagram of our model. The horizontal axis shows the radial distance R in cylindrical coordinates. The vertical axis shows the vertical distance z. Thus, the galactocentric radius is |$r=\sqrt{R^2+z^2}$|. The model consists of four parts: (1) the galactic disk, (2) the hot gas layer extending to z = zhl ∼ kpc which is responsible for the observed diffuse X-ray emission (e.g., Nakashima et al. 2018), (3) the galactic wind extending to around the DM core radius of r = 2 rcore(t), and (4) the CGM extending from r > 2 rcore(t). The upper arrows indicate the outflow. The SNe expel the diffuse gaseous matter from the disk into the hot gas layer. The CRs can drive the galactic wind from z = zhl = 2 kpc (Shimoda & Inutsuka 2022). We assume that the wind merges with the CGM at r = 2 rcore(t). The lower arrows indicate the inflow. We suppose that a fraction of the metal-polluted CGM condenses and falls to the disk due to the radiative cooling. The dynamics of the wind are estimated from the CR pressure gradient and the gravitational acceleration. There is also cosmological gas accretion from the intergalactic medium (IGM). We assume that a fraction of the accretion gas is expelled by the wind to remain in the CGM, and the other fraction falls on to the disk. In the following we describe basic equations of the model for each part respectively. The model parameters are obtained by following the various observations and theoretical studies for the MW.
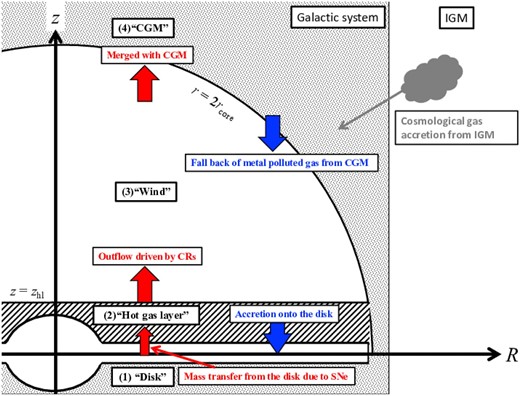
Schematic illustration of our model. The horizontal axis shows the radial distance R in cylindrical coordinates. The vertical axis shows the vertical distance z. The galactocentric radius is |$r=\sqrt{R^2+z^2}$|.
2.1 The cosmological accretion
The galaxy is considered to be formed and evolved with cosmological baryon accretion. In this paper, we presume that the baryon accretion rate to the galactic system, |$\dot{M}_{\rm b}(t)$|, is proportional to the DM accretion rate, |$\dot{M}_{\rm vir}$|, as |$\dot{M}_{\rm b}=f_{\rm cb}\dot{M}_{\rm vir}$|, where fcb = 0.156 is the cosmic baryon fraction. We follow the results of cosmological N-body simulations for the cold DM and their fitting functions given by Rodríguez-Puebla et al. (2016) (the “Instantaneous” model is used). The cosmological parameters are the same as in their settings. The fitting function of |$\dot{M}_{\rm vir}$| is parametrized by the current DM total mass Mvir, 0. We set |$M_{\rm vir,0}=10^{12}\, M_{\odot }$| (e.g., Sofue 2012; Posti & Helmi 2019). Figures 2a and 2b show |$\dot{M}_{\rm b}$| and Mvir, respectively.
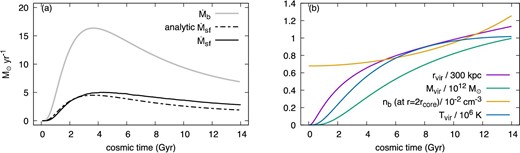
(a) The solid gray line is the baryon accretion rate |$\dot{M}_{\rm b}(t)$|. The broken black line is the analytical estimate of the star formation rate given by the equation (36) with setting fms = 0.22, ηw = 6.58, and |$\dot{\Sigma }_{\rm cl}=\dot{\Sigma }_{\rm fb}=0$| (see subsections 2.2 and 2.3). The black solid line shows the numerical results of the star formation rate for the fiducial model (see section 3). (b) The purple line shows the virial radius rvir(t), which becomes rvir ≃ 342 kpc at t = 14 Gyr. The green line shows the virial mass of the DM halo Mvir. The number density of the accreting baryon at r = 2rcore is shown by the orange line as nb(t, 2rcore) = fcbρdm(t, 2rcore)|$/$|mp. The blue line shows the virial temperature which is given by equation (1).
The mass density of the DM halo, ρdm(t, r), is assumed to be spherically symmetric with the NFW density profile (Navarro et al. 1996, 1997). We assume the core radius to be rcore(t) = rvir(t)|$/$|20, where rvir(t) is the virial radius defined in equation (1) of Rodríguez-Puebla et al. (2016). In this paper, we assume that the mass density of the accreting baryon is proportional to the DM mass density as ρb(t, r) = fcbρdm(t, r), which is shown in figure 2b in terms of the number density nb = ρb|$/$|mp at the radius of r = 2rcore, where mp is the proton mass. The virial temperature, defined as
is also shown, where kB is the Boltzmann constant.
2.2 The galactic disk and hot gas layer
The galactic gas disk can be modeled by a viscous accretion disk. The local turbulent viscosity leads to the transport of the angular momentum (Shakura & Sunyaev 1973). The disk wind and mass accretion are responsible for the change in total angular momentum (Suzuki & Inutsuka 2009; Suzuki et al. 2010, 2016). We apply this disk model to the Galactic gas disk following Suzuki et al. (2016).
Under the axisymmetric approximation, the equations of the continuity and the conservation of the angular momentum can be written as (Balbus & Hawley 1998)
and
respectively. ρ is the mass density and the other symbols have their usual meaning. The azimuthal velocity is decomposed into the mean galaxy rotation velocity |${\cal V}_\phi$| and the turbulent perturbation δvϕ as |$v_\phi = {\cal V}_\phi +\delta v_\phi$|. We assume that the rotation velocity of the gaseous matter is given by the equilibrium condition between the radial gravitational force, gR = ∂Φ|$/$|∂R, and centrifugal force |${\cal V}_\phi {}^2/R$|, where Φ is the gravitational potential and |${\cal V}_\phi =\sqrt{R\big |g_R\big |}$|. For the numerical calculation of Φ, we consider the mass components of the disk gas, stars, and the DM halo. The stars and the disk gas are approximated at the midplane (z = 0). In this case, the potential can be calculated as the sum of uniform rings of width ΔR at each discretized radius (see Krough et al. 1982; Lass & Blitzer 1983), where ΔR is the interval of radial coordinates. Then, from equation (3) and multiples of equation (2) and |$R {\cal V}_\phi$|, we obtain
where we approximate |$\partial (\rho R v_\phi )/\partial t\approx R{\cal V}_\phi \partial \rho / \partial t$| and use the α prescription (Shakura & Sunyaev 1973); αRϕ ≡ vRδvϕ − BRBϕ|$/$|4πρ and αRϕ ≡ vRδvϕ − BRBϕ|$/$|4πρ. When |$\partial (R{\cal V}_\phi )/\partial R=0$| (there is no radial gradient in the specific angular momentum), we regard ∂ρ|$/$|∂t = 0 from equation (3). For |$\partial (R{\cal V}_\phi )/\partial R\ne 0$|, substituting equation (4) to the equation of the continuity, we obtain
where |${\cal V}_\phi {}^{\prime }=\partial {\cal V}_\phi /\partial R$|. Integrating this equation along the vertical direction z from the bottom surface (z = −H|$/$|2) to the top surface (z = H|$/$|2), we can derive
where Σ = ∫ρdz is the surface mass density, |$\bar{\alpha }_{R \phi }\equiv \int \rho \alpha _{R \phi } dz/C_{\rm s}{}^2\Sigma$|, and |$\bar{\alpha }_{\phi z}\equiv \rho R \alpha _{\phi z}/C_{\rm s}{}^2\Sigma$|. Cs is the sound speed of the disk gas. In this paper, we approximate Σ = ρH and fix the disk thickness as H = 300 pc and Cs = 10 km s−1 for simplicity. The [ρRvz] term on the right-hand side represents the effects of outflow and accretion. We denote these two effects separately as |$-[\rho R v_z]= -R\dot{\Sigma }_{\rm blown}+ R\dot{\Sigma }_{\rm acc}$|. |$\dot{\Sigma }_{\rm blown}$| indicates the mass transfer rate from the disk to the hot gas layer due to the supernova explosions and |$\dot{\Sigma }_{\rm acc}$| indicates the net mass accretion rate. Adding the source terms due to the star formation (|$-\dot{\Sigma }_{\rm sf}$|) and mass ejection by supernovae (|$\dot{\Sigma _{\rm ej}}$|), we finally obtain the diffusion–convection type equation as
The coefficients |${\cal V}_\Sigma$|, |${\cal D}_\Sigma$|, and |${\cal Q}_\Sigma$| can be derived by simple algebra. We assume that the α-coefficients are constant; |$\bar{\alpha }_{R\phi }= \bar{\alpha }_{\phi z}=10^{-6}$|. In the realistic Galactic disk, the mass transfer speed may not exceed the typical sound velocity Cs ≈ 10 km s−1, which is a consequence of the very efficient Lyα cooling of the neutral hydrogen atoms. The sound crossing time of the galactic length scale is ∼10 kpc|$/$|Cs ∼ 1 Gyr, i.e., the radial mass transfer does not affect the evolution so much and the galactic radial profile depends strongly on the source terms. Therefore, we choose the small α-coefficients to reproduce the realistic situation safely.
The mass consumption rate due to the star formation is estimated as |$-\dot{\Sigma }_{\rm sf}= -\epsilon _{\rm sf}\Sigma /\tau _{\rm sf}$|, where τsf and ϵsf are the star formation time and efficiency, respectively. From the state-of-the-art studies, the present-day star formation rate is determined by the molecular cloud formation that is driven through multiple compressions of diffuse gas by supernovae (Inoue & Inutsuka 2009, 2012; Inutsuka et al. 2015; Hennebelle & Inutsuka 2019; Pineda et al. 2022). Thus, we set the star formation time as τsf = 100 pc|$/$|Cs ≃ 9.8 Myr, where the length scale of 100 pc is assumed to be a typical size of local bubbles [e.g., Zucker et al. 2022 in the solar neighborhood and Watkins et al. 2023 in NGC 628]. By simply adopting the Kennicutt–Schmidt law (Kennicutt & Evans 2012), we set the star formation efficiency as
which results in |$\dot{\Sigma }_{\rm sf}\propto \Sigma ^{1.4}$| and an effective star formation time-scale of |$\tau _{\rm sf}/\epsilon _{\rm sf}\simeq 1\,\,\mbox{Gyr}(\Sigma /10\, M_{\odot }\,\,\mbox{pc}^{-2})^{-0.4}$|. For the numerical calculation, we set a threshold mass density of |$R\Sigma \Delta R=10^3\, M_{\odot }$|, below which |$\dot{\Sigma }_{\rm sf}=0$|.
The surface mass density of long-lived low-mass stars and that of short-lived massive stars are calculated separately as
and
where Σ* and Σms are the surface mass densities of the low-mass stars and massive stars, respectively. We will discuss the treatments of the left-hand side terms, dΣ*|$/$|dt and dΣms|$/$|dt, later. fms is a mass fraction of the massive stars resulting in supernova explosions at the end of their life. |$\dot{\Sigma }_{\rm sn}$| is the supernova rate in terms of the surface mass density. The massive star fraction, fms, is estimated from the initial mass function by following the arguments of Inutsuka et al. (2015); |$f_{\rm ms} = \left(8\, M_{\odot } / m_{*,{\rm min}} \right)^{2-\beta }$|, where β = 2.35 corresponds to the Salpeter power-law index for a higher stellar mass part and m*,min is the effective minimum stellar mass parametrizing the shape of a lower stellar mass part. In this paper, we set |$m_{*,{\rm min}}=0.1\, M_{\odot }$| and thus fms ≃ 0.22. Note that the number fraction becomes |$(8\, M_{\odot }/m_{*,{\rm min}})^{1-\beta } \simeq 2.6\times 10^{-3}$|. Then, we set |$\dot{\Sigma }_{\rm sn}= \Sigma _{\rm ms} / \tau _{*,{\rm ms}}$|, where τ*,ms is a typical lifetime of the massive stars. The lifetime is estimated from the mass–luminosity relation, |$\tau _*=10\,\,\mbox{Gyr}(m_*/ 1\, M_{\odot })^{-2.5}$|, as
Note that the event rate of the supernova can be estimated as |$\dot{\Sigma }_{\rm sn}/\bar{m}_{*,{\rm ms}} \approx f_{\rm ms}\dot{\Sigma }_{\rm sf}/\bar{m}_{*,{\rm ms}}$|, where the average stellar mass of massive stars (the ratio of total mass to total number) is |$\bar{m}_{*,{\rm ms}}=(\beta -1)/(\beta -2) \times 8\, M_{\odot } \simeq 30.9\, M_{\odot }$| and the steady-state approximation dΣms|$/$|dt ≈ 0 is used. Then, the total event rate becomes |$\dot{N}_{\rm sn}=f_{\rm ms}\dot{M}_{\rm sf}/ \bar{m}_{*,{\rm ms}}\simeq 0.02\,\,{\mbox{yr}^{-1}} (\dot{M}_{\rm sf}/3\, M_{\odot }\,\,{\mbox{yr}^{-1}})(m_{*,{\rm min}}/0.1\, M_{\odot })^{\beta -2}$|, where |$\dot{M}_{\rm sf}= 2\pi \int \dot{\Sigma }_{\rm sf}R^2dR$| and β = 2.35 is used. This is consistent with the current state of the MW.
The supernova explosions result in the ejection of mass from Σms to Σ, the rate of which is given by |$\dot{\Sigma }_{\rm ej}$| in equation (7). We suppose that each of the massive stars leaves one neutron star with a mass of |$m_{*,{\rm ns}}=1.4\, M_{\odot }$| as a result of the supernova. The net mass ejected per one supernova event is |$m_{\rm ej}=\bar{m}_{*,{\rm ms}}-m_{*,{\rm ns}}$| and the mass ejection rate is |$\dot{\Sigma }_{\rm ej}=(m_{\rm ej}/\bar{m}_{*,{\rm ms}})\dot{\Sigma }_{\rm sn}$|. The surface mass density of the created neutron stars is given by
The treatment of the left-hand side term, dΣns|$/$|dt, will be discussed later.
The supernovae may also blow the gaseous matter off the disk. We suppose that some of the blown gas is responsible for the diffuse, X-ray emitting hot gas (e.g., Wada & Norman 2001; Girichidis et al. 2018). The current Galactic disk shows such diffuse X-ray emission, called the Galactic Diffuse X-ray Emissions (GDXEs). Their origin is still under debate (see, e.g., Koyama 2018, for reviews). Since the estimated temperature of the GDXE (>1 keV) is much higher than the virial temperature of the current MW (∼0.1 keV), we expect that such X-ray emitting gas goes to the Galactic halo region. Indeed, the extended soft-X-ray emission (∼0.1 keV) is observed at much higher latitudes than the case of GDXE (e.g., Nakashima et al. 2018; Predehl et al. 2020). Thus, we regard that the blown gas enters the hot gas layer which extends from z = H|$/$|2 to z = zhl = 2 kpc. The outflow rate from the disk into the layer, |$\dot{\Sigma }_{\rm blown}$|, in the right-hand side of equation (7) is estimated as
where Esn = 1051 erg and Thl = 3 × 106 K are the supernova explosion energy and the temperature of the hot gas layer, respectively. The conversion efficiency ηblown is treated as a free parameter in this paper. The effective outflow efficiency driven by the supernovae, ηw, becomes
Then, the surface mass density of the hot gas layer, Σhl, is given by
where |$C_{{\rm s},{\rm hl}} =\sqrt{k_{\rm B}T_{\rm hl}/(0.6m_{\rm p})}\simeq 200\,\,\mbox{km}\,\,\mbox{s}^{-1}(T_{\rm hl}/ 3\times 10^6\,\,\mbox{K})^{1/2}$|. The radial mass transfer in the hot gas layer is omitted for simplicity. The factor 1|$/$|2 of the first term on the right-hand side represents the existence of the layer on both the +z and −z sides. The second term represents the mass loss due to the Galactic wind (discussed later). The existence of the Galactic wind is supported by Shimoda and Inutsuka (2022) for the current condition of the MW.
We can find the importance of ηw from the steady-state approximation for equation (7),
and equation (10),
From these equations, we obtain |$\dot{\Sigma }_{\rm ej}\approx (m_{\rm ej}/\bar{m}_{*,{\rm ms}})f_{\rm ms}\dot{\Sigma }_{\rm sf}$|, |$- \dot{\Sigma }_{\rm blown}\approx -f_{\rm ms}\eta _{\rm w}\dot{\Sigma }_{\rm sf}$|, and
where we use |$m_{\rm ej}/\bar{m}_{*,{\rm ms}}\simeq 1$|. The denominator is about 2.2 for which fms ≃ 0.22 and ηw ≃ 6.58 (fmsηw ≃ 1.42). Shimoda and Inutsuka (2022) showed that the mass transfer rate by the wind is comparable to the current star formation rate of several M⊙ yr−1, which is consistent with the estimated |$\dot{\Sigma }_{\rm blown}\simeq 1.42\dot{\Sigma }_{\rm sf}$|. Thus, our choice of the conversion efficiency ηblown = 0.1 can be reasonable and the star formation rate can be about half of the net accretion rate |$\dot{\Sigma }_{\rm acc}$|. Note that the current cosmological accretion rate of baryons estimated from the N-body simulations by Rodríguez-Puebla et al. (2016) is about |$7\, M_{\odot }\,\,$|yr−1 (see figure 2a). Thus, the current star formation rate can be |$\sim 3\, M_{\odot }\,\,$|yr−1. Then, the total mass of the disk gas is |$M\approx 3\times 10^9\, M_{\odot }(\tau _{\rm sf}/10\,\,\mbox{Myr}) (\epsilon _{\rm sf}/0.01)^{-1}$| and the mass ratio of the hot gas layer to the disk gas is |$\approx \left( f_{\rm ms}\eta _{\rm w}z_{\rm hl}/C_{{\rm s},{\rm hl}} \right)\times 3\, M_{\odot }\,\,{\mbox{yr}^{-1}}/ M \approx 3\times 10^{-3}(z_{\rm hl}/2\,\,\mbox{kpc})$|, which is consistent with the typical number density of the extended soft X-ray emission, ∼10−3 cm−3.
We also calculate the metal surface mass density, ΣZ, to estimate the metal pollution of the CGM which is related to the net accretion rate |$\dot{\Sigma }_{\rm acc}$| (discussed later). The differential equation of the metal surface density is assumed to be the same form as equation (7), except for |$\dot{\Sigma }_{\rm ej}$| and |$\dot{\Sigma }_{\rm blown}$|. The other differential equations of the stellar surface mass densities have the same form as those of the total surface mass densities (Σ* → ΣZ, *, Σms → ΣZ, ms, etc.). We include the newly created metal mass in the mass ejection rate as
where |$\dot{\Sigma }_{Z,{\rm sn}}=\Sigma _{Z,{\rm ms}}/\tau _{*,{\rm ms}}$|. mco is the CO core mass in a massive star. The mass ratio of the massive star to the CO core is calculated as ∼1|$/$|6–1|$/$|4 (e.g., Sukhbold et al. 2018; Chieffi & Limongi 2020). In this paper, we fix |$\bar{m}_{\rm co}/ \bar{m}_{*,{\rm ms}}=1/6$| for simplicity. The metal outflow rate is set to |$\dot{\Sigma }_{Z, {\rm blown}} = (\Sigma _Z / \Sigma ) \dot{\Sigma }_{\rm blown}$|.
Here we describe the terms dΣ*|$/$|dt, dΣms|$/$|dt, and dΣns|$/$|dt. For the short-lived massive-stars, we approximate dΣms|$/$|dt = ∂Σms|$/$|∂t. Since the gravitational potential evolves with time, the long-lived low-mass stars and neutron stars can move away from their birthplace (Chandrasekhar 1943). In this paper, we omit the motion along the z-direction for simplicity. Then, for the numerical calculation, we introduce “parcels” consisting of the formed stars at each time step and each radial position (tn, Ri) and solve for their motion:
where R*,j and v*,ϕ,j are the position and rotation velocity of the parcel denoted by the subscript j, respectively. Note that R*,jv*,ϕ,j is constant. The net surface density of the mass is calculated as
where δm*,j is the line mass of parcel j. Let tbirth, j be the birthtime of the stellar objects in the parcel j at (tn, Ri). Then, the birthplace is written as Rbirth, j = R*,j(tbirth, j) = Ri. We assume the initial radial velocity as v*,R, j(tbirth, j) = dR*,j|$/$|dt = 0 and the initial rotation velocity as |$v_{*,\phi ,j}(t_{\rm birth})={\cal V}_\phi (t_{\rm birth}, R_{\rm birth})$|. The mass of parcel j is given by |$\delta m_{*,j}=R_{\rm birth}\dot{\Sigma }_{\rm sf}(t_{\rm birth},R_{\rm birth})\Delta t$| for the low-mass stars and |$\delta m_{*,j}=R_{\rm birth}\dot{\Sigma }_{\rm ns}(t_{\rm birth},R_{\rm birth})\Delta t$| for the neutron stars, respectively, where Δt is the time interval of the numerical calculation. To save the computation costs, we implement that parcels j and k are unified under the conditions of |R*,j − R*,k| < 10−2, |v*,ϕ,j − v*,ϕ,k| < 10−2, |v*,R, j − v*,R, k| < 10−2, and v*,R, jv*,R, k > 0. The mass of the unified parcel becomes δm*,j + δm*,k. The information of the birthtime and place are evaluated as (δm*,jtbirth, j + δm*,ktbirth, k)|$/$|(δm*,j + δm*,k) and (δm*,jRbirth, j + δm*,kRbirth, k)|$/$|(δm*,j + δm*,k), respectively. We set the inner and outer boundary conditions as follows. For R*,j < ΔR, we regard that the parcel is trapped at the galactic center and no longer calculate its motion. For R*,j > 3RB, where RB = 30 kpc is the outer boundary of the gas disk calculation, we regard the parcel as having escaped from the system.
We summarize the disk model thus:
The metal surface mass densities are denoted by replacing the symbols as Σ → ΣZ, Σ* → ΣZ, *, |$\dot{\Sigma }_{\rm sf}\rightarrow \dot{\Sigma }_{Z,{\rm sf}}=(\epsilon _{\rm sf}/\tau _{\rm sf})\Sigma _Z$| and so on, except for |$\dot{\Sigma }_{Z,{\rm ej}}$| and |$\dot{\Sigma }_{Z,{\rm blown}}$|. We find that Σ is conserved (take |$\dot{\Sigma }_{\rm blown}= \dot{\Sigma }_{\rm scc}=0$| and Σhl = 0), while ΣZ increases at a rate of |$(m_{\rm co}/\bar{m}_{*,{\rm ms}}) \dot{\Sigma }_{\rm sn}$|.
The estimation of the total mass of metal ejected by the supernovae clarifies the importance of the galactic wind (i.e. the role of the CRs). When the star formation continues with a constant rate of |$\sim 3\, M_{\odot }\,\,$|yr−1 throughout the cosmic age, the total metal mass ejected by supernovae becomes |$\sim (m_{\rm co}/\bar{m}_{*,{\rm ms}})f_{\rm ms}\times 3\, M_{\odot }\,\,\mbox{yr}^{-1}\times 14\,\,\mbox{Gyr} \sim 1.54\times 10^9\, M_{\odot }$|, where |$\dot{\Sigma }_{\rm sn}\approx f_{\rm ms}\dot{\Sigma }_{\rm sf}$| is used. The total mass of the disk gas, |$\sim 3\times 10^9\, M_{\odot }$|, which is comparable to the estimated metal mass, implies the existence of the wind; almost all the metals should be expelled from the disk in order to explain the total mass of the disk gas and the metallicity of Z⊙ ∼ 0.01 in the current Galactic disk simultaneously. If the metal-polluted gas is well-mixed with a primordial gas with mass of |$f_{\rm cb}M_{\rm vir,0}\sim 10^{11}\, M_{\odot }$|, the mean metallicity becomes |$\sim 10^9\, M_{\odot }/10^{11}_\odot \sim 0.01$|, which is consistent with the solar metallicity. Thus, the CRs also play a key role in controlling the amount of metals in the Galactic disk by driving the wind.
2.3 The galactic halo region; wind, CGM, and IGM
We suppose that the galactic wind is driven by CRs from the upper boundary of the hot gas layer, z = zhl = 2 kpc, with a rate of (Σhl|$/$|zhl)Cs, hl following Shimoda and Inutsuka (2022). The CRs are assumed to be accelerated by supernova remnant shocks. In the following, we discuss the CR energy density and describe the numerical modeling of the galactic halo gas. In our model, the disk accretion rate, |$R\dot{\Sigma }_{\rm acc}$|, is decomposed into three components as
where the |$\dot{\Sigma }_{\rm b,disk}$| is the cosmological baryon accretion rate on the disk, |$\dot{\Sigma }_{\rm fb}$| is the mass coming from the wind region, and |$\dot{\Sigma }_{\rm cl}$| is the mass accretion rate from the metal-polluted CGM, respectively. Note that our model calculation of the disk is carried out using the line mass of RΣ as shown in equation (20).
Shimoda et al. (2022) recently suggested that the energy injection rate of CRs at the shocks can be about 10% of the supernova explosion energy by modeling the ion heating process at the shock transition. We follow their results and set the CR energy injection rate (erg s−1 cm−3) as
where ηcr ∼ 0.1 is the injection efficiency. The energy loss rate of the CRs via the hadronic interactions (erg s−1 cm−3) can be approximated by
where Λh = 7.44 × 10−16 s−1 cm3 is the collision rate per particle (see Pfrommer et al. 2017 for details), and ecr (erg cm−3) is the energy density of the CRs. We presume that the acceleration time of CRs at each supernova remnant shock is quite short, at most ∼104 yr, which is a typical radiative cooling time of the shock-heated plasma for an ambient density of ∼1 cm−3 (e.g., Vink et al. 2006). Thus, we approximate the energy density of the CRs around their source as |$\dot{q}_{\rm cr}- {\cal L}_{\rm cr}\approx 0$|, i.e.,
Note that ecr, source is assumed to be uniform along the vertical direction z in the disk. The injected CRs will escape from the galaxy. In this paper, the escape flux is assumed to be dominated by the diffusion effect (the convection effect is omitted for simplicity). Then, we approximate the CR energy density released around the sources as
where |$\cal {D}_{\rm cr}$| and τcr,esc are the CR diffusion coefficient and the CR escape time from the galaxy, respectively. The escape time is estimated by the abundance of CR nuclei (e.g., the boron-to-carbon ratio) as ∼10 Myr. The diffusion coefficient is estimated from the abundance ratio with the assumption that the CR scale height is |$\sim \,$|kpc; |${\cal D}_{\rm cr}=3\times 10^{28}\,\,$|cm2 s−1 is frequently used (e.g., Gabici et al. 2019). In this paper, we parametrize the CR scale height, |$H_{\rm cr}=\sqrt{{\cal D}_{\rm cr}\tau _{\rm cr,esc}}$|. Then, the CR energy densities are estimated by using the steady-state approximation of |$\dot{\Sigma }_{\rm sn}\approx f_{\rm ms}\dot{\Sigma }_{\rm sf}$| and |$\Sigma \approx (\tau _{\rm sf}/\epsilon _{\rm sf})\dot{\Sigma }_{\rm sf}$| as
and by using |$\boldsymbol {\nabla }^2e_{\rm cr}\approx e_{\rm cr}/(\mbox{kpc})^2$| as
Thus, we can find that the CR energy density in the interstellar medium (ISM), which is expected to be a few eV cm−3, is given by |$\eta _{\rm cr}/ {\cal D}_{\rm cr}\tau _{\rm esc}=\eta _{\rm cr}/H_{\rm cr}{}^2$|. We treat the CR scale height Hcr as a free parameter to study the effects of CR and fix the injection efficiency as ηcr = 0.1. In the CR injection scenario proposed by Shimoda et al. (2022), the injection efficiency depends on the sonic Mach number of the collisionless shocks. Therefore, we regard that the efficiency ηcr is universally determined by the local physics. On the other hand, the diffusion coefficient may depend on the local magnetic field strength, the evolution of which over cosmic time may still be uncertain. Moreover, there is no consensus on the general expression of the CR diffusion coefficient. Note that the energy densities depend on the star formation rate via (τsf|$/$|ϵsf)−1∝Σ0.4; a larger Σ results in a larger star formation rate and a larger CR energy density. To estimate the CR energy density, we omit non-trivial numerical factors, so for simplicity we chose Hcr = 3 kpc. From the numerical results discussed later, we find that (ηcr, Hcr) = (0.1, 10 kpc) produces a reasonable result. The height of Hcr = 10 kpc is consistent with the recent theoretical model of CR transport (Evoli et al. 2020).
The galactic wind is driven by the CR pressure, Pcr = (γc − 1)ecr, where γc = 4|$/$|3, from the hot gas layer. Shimoda and Inutsuka (2022) showed that, for the current conditions of the MW, the wind density and temperature can be nearly constant at z ≲ 10 kpc due to the balance between the radiative cooling and effects of CR heating. The thermal gas pressure and the CR pressure are comparable to each other. From these results, we simplify the wind dynamics as
where we approximate the total pressure as P ≈ Pcr. ρw and |$\boldsymbol {v}_{\rm w}$| are the mass density and velocity of the wind, respectively. |$\boldsymbol {g}$| is the gravitational acceleration calculated from the Poisson equation with the DM component and the disk mass components (Σ, Σ*, Σms, and Σns). For numerical calculations of the wind, we treat the fluid parcel as a test particle denoted by the subscript k and adopt equation (28) as its equation of motion under the axisymmetric approximation. The density ρw, k is assumed to be constant. For each time step, new particles are newly introduced at each point of (Ri, zhl). The initial conditions of the particles are assumed to be ρw, k = Σhl(t, R)|$/$|zhl, vw, R, k = 0, |$v_{{\rm w},\phi ,k}=\sqrt{Rg_R(t,R,z_{\rm hl})}$|, and vw, z, k = Cs,hl, where gR is the radial component of |$\boldsymbol {g}$| and the centrifugal force equilibrium is assumed, vw, ϕ2|$/$|R = gR. The mass of each particle is assumed to be |$dm_{{\rm w},k}=\rho _{{\rm w},k}C_{{\rm s},{\rm hl}}R\Delta R\Delta t d\phi =\,$|constant. The infinitesimal azimuthal element vanishes by the axisymmetric integration. Using the particles located at |z| < H|$/$|2 and R < RB with a density of ρw, k ≤ Σ(t, Rk)|$/$|H, where RB = 30 kpc is the outer boundary of the disk region, we calculate the accretion rate component, |$R\dot{\Sigma }_{\rm fb}$|, as
where |$N_k=(\int _0^{R_{\rm B}} e^{- (R-R_k)^2 / 2H^2 } dR)^{-1}$| is the normalization factor. Note that the metal mass is calculated in the same manner as the total mass.
We regard that the particles located at rk > rcgm enter the CGM region, where |$r_k=\sqrt{R_k{}^2+z_k{}^2}$| and rcgm = 2 rcore(t) is the boundary galactocentric radius between the wind region and the CGM region. The total CGM mass, Mcgm(t), is calculated as
where
and |$\dot{M}_{\rm ex}$| represents the mass supply due to the interaction between the wind and the baryon accretion flow. Some of the accreting baryons from the IGM may be expelled by the wind entering the CGM region. For simplicity, we assume that |$\dot{M}_{\rm ex}= \dot{M}_{\rm w}$|. |$\dot{M}_{\rm cl}$| is the mass loss of the CGM due to the metal pollution which results in a large radiative cooling rate. For the CGM of external galaxies, absorption lines of lower ionized species such as H i, C ii, and Mg ii are observed (Tumlinson et al. 2017, and references therein). The existence of such lower ionized species implies the existence of condensation phenomena that shield the cool gas from ionizing photons (e.g., the metagalactic radiation field, see Gnat 2017). We assume that such cool, condensed gas leaves from the CGM by losing its angular momentum at a rate of
where ncgm is the mean number density estimated as
and the radiative cooling time is estimated as
The mean temperature of the CGM, Tcgm, is assumed to be equal to the virial temperature, Tvir(t), which is given by equation (1). Λrad, ⊙(Tcgm) is the radiative cooling rate for the solar abundance given by Shimoda and Inutsuka (2022). Zcgm is the metallicity of the CGM estimated as Zcgm = MZ, cgm|$/$|Mcgm and Z⊙ = 0.0134 is the solar metallicity (Asplund et al. 2009). ϵcgm represents the efficiency of the angular momentum loss which is required for both condensation and accretion phenomena. We fix the efficiency ϵcgm = 0.01 by analogy with ϵsf. The factor Zcgm|$/$|Z⊙ approximately reflects the metallicity dependence of Λrad.
The net baryon accretion rate on to the disk is given by |$\dot{M}_{\rm b}-\dot{M}_{\rm ex}+\dot{M}_{\rm cl}$|. The local accretion rate at R is assumed to be
where |$N_{\rm b,disk}=[\int _0^{R_{\rm B}} e^{-(R-r_{\rm core})^2/2r_{\rm core}{}^2}dR]^{-1}$| is the normalization factor. Here, the core radius rcore is assumed to reflect a small angular momentum of the accreting gas from the IGM so that the galactic disk is formed. The radial profile of the galactic disk depends strongly on the source terms, as we discussed in equation (7). Since the galactic wind acts after the mass supply at a local point, the radial profile is almost given by this assumed |$R\dot{\Sigma }_{\rm b.disk}$|.
The estimate of the star formation rate under the steady-state approximation discussed in equation (16) is rewritten as
where we use the total disk mass accretion rate |$\dot{\Sigma }_{\rm acc}=\dot{\Sigma }_{\rm b}-\dot{\Sigma }_{\rm w}+\dot{\Sigma }_{\rm cl}+ \dot{\Sigma }_{\rm fb}$| and approximate that |$\dot{\Sigma }_{\rm w}\approx \dot{\Sigma }_{\rm blown}$|. The dashed line in figure 2a shows the estimated total star formation rate with fms = 0.22, ηw = 6.58, and |$\dot{\Sigma }_{\rm cl}=\dot{\Sigma }_{\rm fb}=0$|. Since the total mass of stars at the current MW is |$\sim (4\!-\!6) \times 10^{10}\, M_{\odot }$| (Bland-Hawthorn & Gerhard 2016), and since the expected total baryon mass is |$M_{\rm b}\sim f_{\rm cb}M_{\rm vir,0}\sim 10^{11}\, M_{\odot }$|, a significant fraction of gaseous matter should be deposited in the galactic halo region (Tumlinson et al. 2017). The small |$\dot{\Sigma }_{\rm fb}$| and |$\dot{\Sigma }_{\rm cl}$| are preferred to realize such a situation under the assumed |$\dot{\Sigma }_{\rm b,disk}$| given by equation (35).
In this paper we focus on studying the effects of ηblown and Hcr. The conversion efficiency ηblown determines the relation between the star formation rate, |$\dot{\Sigma }_{\rm sf}$|, and the disk mass accretion rate, |$\dot{\Sigma }_{\rm acc}$|. The CR scale height Hcr determines the CR energy density, ecr. If the energy density is small, the galactic wind is unable to reach the CGM region; the wind gas falls back to the disk and the net mass accretion rate increases by the term of |$\dot{\Sigma }_{\rm fb}$|. Note that the CGM metal pollution by the galactic wind is required to explain the galactic halo observations and the typical metallicity of the current Galactic disk of Z ∼ Z⊙. ηblown also determines the mass transfer rate from the disk to the hot gas layer and Hcr determines that from the hot gas layer to the CGM region. The efficient metal pollution of the CGM can result in a large additional mass accretion rate |$\dot{\Sigma }_{\rm cl}$|. Thus, these two parameters ηblown and Hcr are important for the gas mass distribution and consequently for the star formation. We regard the case of ηblown = 0.1 and Hcr = 10 kpc as the fiducial model and summarize the other case in table 1. Note that the values of Hcr are chosen to be (10|$/$|7.07)2 ≃ 2 and (10|$/$|14.14)2 ≃ 0.5.
| Model . | ηblown . | Hcr . | Category . |
|---|---|---|---|
| 0 | 0.1 | 10 kpc | Fiducial model |
| 1 | 0.2 | 10 kpc | Massive wind |
| 2 | 0.05 | 10 kpc | Weak wind |
| 3 | 0.1 | 7.07 kpc | Large ecr |
| 4 | 0.1 | 14.14 kpc | Small ecr |
| Model . | ηblown . | Hcr . | Category . |
|---|---|---|---|
| 0 | 0.1 | 10 kpc | Fiducial model |
| 1 | 0.2 | 10 kpc | Massive wind |
| 2 | 0.05 | 10 kpc | Weak wind |
| 3 | 0.1 | 7.07 kpc | Large ecr |
| 4 | 0.1 | 14.14 kpc | Small ecr |
| Model . | ηblown . | Hcr . | Category . |
|---|---|---|---|
| 0 | 0.1 | 10 kpc | Fiducial model |
| 1 | 0.2 | 10 kpc | Massive wind |
| 2 | 0.05 | 10 kpc | Weak wind |
| 3 | 0.1 | 7.07 kpc | Large ecr |
| 4 | 0.1 | 14.14 kpc | Small ecr |
| Model . | ηblown . | Hcr . | Category . |
|---|---|---|---|
| 0 | 0.1 | 10 kpc | Fiducial model |
| 1 | 0.2 | 10 kpc | Massive wind |
| 2 | 0.05 | 10 kpc | Weak wind |
| 3 | 0.1 | 7.07 kpc | Large ecr |
| 4 | 0.1 | 14.14 kpc | Small ecr |
For the numerical calculations, we set the time interval as Δt = 0.85 Myr. Such small Δt is required to resolve the lifetime of massive stars, τ*,ms ≃ 24.2 Myr. The interval of the radial coordinate for the disk region is set to be ΔR = RB|$/$|128. The initial time is set to t0 = 0.1 Gyr, and the total baryon mass is given by the N-body simulation results. Then, we set Σ(t0, R) = constant with a total mass of fcbMvir(t0) × 10−2 ≃ 7.8 × M⊙. The initial mass of the CGM is Mcgm(t0) = 0.99fcbMvir(t0). The stellar objects and metal masses are initially zero. Note that the results are not affected by these assumed initial conditions.
3 Results
We display the numerical results of our model for the parameter sets summarized by table 1. First, we present the fiducial model, Model 0. We then discuss the difference between Model 0 and the others.
Figure 3a shows the results for the total star formation rate, |$\dot{M}_{\rm sf}$| (solid black line), the mass transfer rate given by the falling-back wind particles, |$\dot{M}_{\rm fb}$| (purple), and the disk outflow rate, |$\dot{M}_{\rm blown}$| (green). |$\dot{M}_{\rm sf}$| is in good agreement with the estimated star formation rate, for which |$\dot{\Sigma }_{\rm cl} =\dot{\Sigma }_{\rm fb}=0$| is given by equation (36). |$\dot{M}_{\rm fb}$| is small, although its contribution becomes large from t > 8 Gyr due to a combination of disk mass growth and CR pressure decrease. Figure 3b shows the time evolution of the total mass of the CGM, Mcgm, the total mass of low-mass stars, M*, the total mass of the disk gas, M, and the total mass of the wind, Mwind. |$M_*\simeq 4\times 10^{10}\, M_{\odot }$| at t = 14 Gyr is consistent with the current condition of our galaxy (Bland-Hawthorn & Gerhard 2016). The time evolution of M is almost the same as |$\dot{M}_{\rm sf}$| because of the assumed |$\dot{\Sigma }_{\rm sf}=(\epsilon _{\rm sf}/ \tau _{\rm sf})\Sigma$|. The wind mass Mwind is flattened from t ≃ 4 Gyr on, when the growth of virial radius rvir(t) almost finishes (see figure 2b). Since we regard the region within r < 2rcore(t) = rvir(t)|$/$|10 as the “wind” region, this feature may have no useful physical meaning. The mass of the CGM increases monotonically, reflecting the cosmological accretion rate |$\dot{M}_{\rm b}$| and the small mass loss rate of the CGM, |$\dot{M}_{\rm cl}$|.
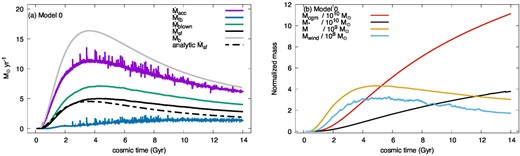
Numerical results of Model 0. (a) The baryon accretion rate |$\dot{M}_{\rm b}$| (solid grey line), the estimated star formation rate given by equation (36) with |$\dot{\Sigma }_{\rm cl}=\dot{\Sigma }_{\rm fb}=0$| (broken black line), and the calculated star formation rate |$\dot{M}_{\rm sf}$| (solid black line) are also shown in figure 2a. The solid purple line shows the net accretion rate |$\dot{M}_{\rm acc}$|. The solid green line is the outflow rate of the disk |$\dot{M}_{\rm blown}$|. (b) The results of total mass of the CGM (red), the stellar mass (black), the gaseous matter at the disk (orange), and the wind (light blue).
Figures 4a, 4b, and 4c show the radial profiles of the surface mass densities of the low-mass stars, Σ*(t, R), that of the gas, Σ(t, R), and the net accretion rate |$\dot{\Sigma }_{\rm acc}(t,R)$| for each time, respectively. The radial profiles of Σ* and Σ are nearly converged at t ∼ 8 Gyr, although Σ* is perturbed by the stellar dynamics. The accretion rate, |$\dot{\Sigma }_{\rm acc}$|, shows drastic variations at R ≲ 5 kpc from t ∼ 8 Gyr due to the falling-back of the wind, |$\dot{\Sigma }_{\rm fb}$|. Although our treatment of the wind dynamics is still not sufficient (the disk is axisymmetric and the vertical motion is omitted), this result implies that the inner region of the disk is more affected by the gas accretion from the galactic halo than the outer region. The variations of |$\dot{\Sigma }_{\rm acc}$| correspond to the perturbations of Σ which may have a three-dimensional, compact structure in reality (such as giant molecular clouds). If that is the case, the local perturbations of the gravitational potential would lead to the stellar migration phenomena (e.g., Fujimoto et al. 2023). It would be an interesting subject to investigate the birthplace of the solar system, the morphology of galaxies, especially for the formation and evolution of the Galactic bulge region, and so on. Figure 4d shows the number density profiles of the hot gas layer, nhl ≡ Σhl|$/$|(zhlmp), which can be responsible for the extended soft X-ray emission, as we discussed in subsection 2.2, and the steady-state solutions of the galactic wind derived by Shimoda and Inutsuka (2022).
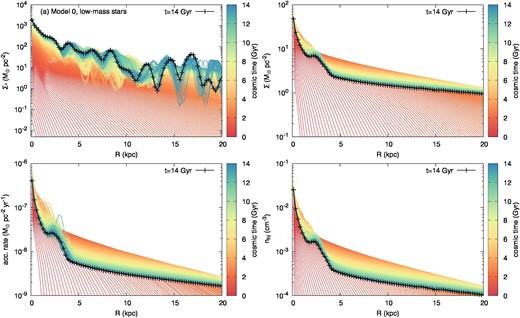
Radial profile of the disk and hot gas layer at each time for Model 0. (a) The surface mass density of the low-mass stars Σ*. (b) The surface mass density of the gas Σ. (c) The net accretion rate |$\dot{\Sigma }_{\rm acc}$|. (d) The number density of the hot gas layer nhl ≡ Σhl|$/$|(zhlmp).
Figures 5a and 5b are the snapshots at t = 14 Gyr showing the vertical velocity component of the wind, vw, z, and the number density of the wind, nw ≡ ρw|$/$|mp, respectively. The wind morphology is affected by the centrifugal force. Such a morphology is reported in the external galaxy of NGC 3079 by Hodges-Kluck et al. (2020), for example. As shown in figure 3a, most of the wind mass is transferred to the CGM region (|$\dot{M}_{\rm blown}\gt \dot{M}_{\rm fb}$|). A wind particle that leaves the radius of R ≲ 5 kpc eventually falls back to the disk. This results in the metal pollution of the inner disk region. The metallicity history of the disk will be discussed later.
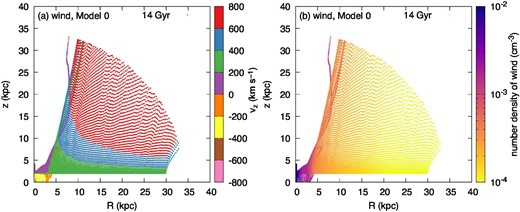
Numerical results of the galactic halo region for Model 0. (a) The wind profile of the vertical velocity component, vw,z, at t = 14 Gyr. (b) The wind profile of the number density, nw ≡ ρw|$/$|mp, at t = 14 Gyr.
Figure 6 shows the time evolution of the CGM number density, ncgm [equation (33)], the radiative cooling time, τcool [equation (34)], the mass depletion rate, |$\dot{M}_{\rm cl}$| [equation (32)], and the metallicity, MZ, cgm|$/$|Mcgm. At the very early stage t < 1 Gyr, the very small virial radius, rvir(t), results in a large ncgm. The large τcool is due to the small metallicity of the CGM. At t > 1 Gyr, rvir becomes ∼30 kpc (see figure 2b), and then the magnitudes of ncgm and τcool converge. The mass growth of the CGM due to the mass transfer by the wind is balanced with the growth of ∼rvir(t)3 as a result, leading to the almost constant ncgm(t) ∼ 10−5 cm−3. The cooling time becomes ∼1 Gyr, which is consistent with the steady-state solutions of the galactic wind studied by Shimoda and Inutsuka (2022). The small mass depletion rate of CGM, |$\dot{M}_{\rm cl}\sim 0.5\,\, {M_\odot }\,\,$|yr−1, is determined by the assumed efficiency of ϵcgm = 0.01. The CGM metallicity may be sufficient to reproduce the observed metal absorption lines (see Tumlinson et al. 2017 for a review).
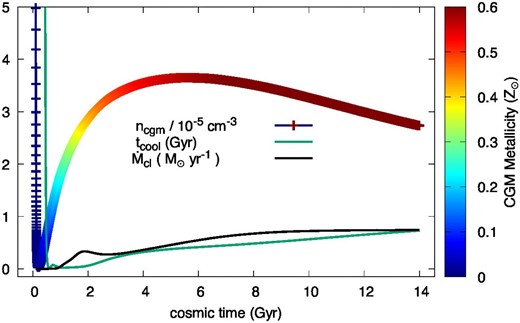
Numerical results of the galactic halo region for Model 0: The time evolution of the CGM number density, ncgm, radiative cooling time, τcool (green line), and the mass depletion rate of the CGM, |$\dot{M}_{\rm cl}$| (black line). The color bar indicates the metallicity of the CGM, |$M_{Z,{\rm cgm}/M_{\rm cgm}}$|.
The CR energy density, ecr, at t = 14 Gyr shown in figure 7 is 2–4 eV cm−3. The radial dependence of ecr reflects the star formation rate |$\dot{\Sigma }_{\rm sf}(R)$| [see equation (26)]. Although ecr is measured to be ≃1 eV cm−3 around the Earth, the actual ecr in the local ISM is still uncertain. To explain the CR ionization rates measured in the local molecular clouds, the higher energy density of 2–4 eV cm−3 may be preferred (e.g., Cummings et al. 2016).1 Note that our model is based on the long-term averaged argument of the star formation with a time scale of ∼1 Gyr. The CR energy density measured around the Earth reflects short-time, local variations of the ISM, such as the local star formation and local diffusion of the CRs. These possible variations occur on very short-time scales of τsf ∼ 100 pc|$/$|Cs ∼ 10 Myr and |$(1\,\,\rm{kpc})^2/{\cal D}_{\rm cr}\sim 10\,\,\rm{Myr}({\cal D}_{\rm cr}/3\times 10^{28}\,\,\rm{cm}^2\,\,\rm{s}^{-1})^{-1}$|, respectively.
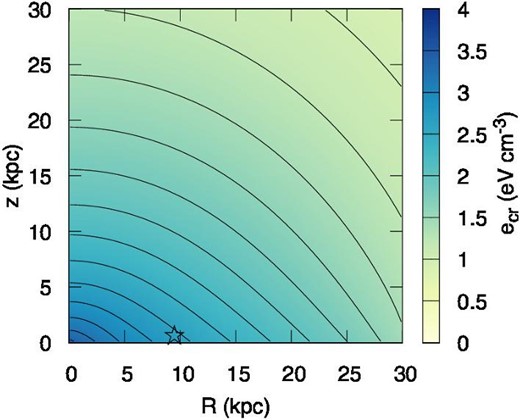
Numerical results of the galactic halo region for Model 0: The profile of the CR energy density, ecr, at t = 14 Gyr. The black contours show the density increasing by 0.2 eV cm−3 from 1 to 3.6 eV cm−3. The star symbol indicates R = 8.5 kpc.
Figures 8a and 8b show the spacetime diagrams of the radial star formation rate, |$\Delta \dot{M}_{\rm sf}=2\pi \dot{\Sigma }_{\rm sf}R\Delta R$|, and the disk gas metallicity, ΣZ|$/$|Σ, respectively. The star formation history follows the assumed |$\dot{\Sigma }_{\rm b,disk}$| given by equation (35). At the inner radius of R ≲ 3 kpc, the mass transfer via the falling-back wind particles leads to higher star formation rates. The metallicity of the disk gas becomes large at R ≲ 3 kpc due to the metal transfer by the falling-back wind particles. Note that the cosmological accretion gas does not contain the metals. The metallicity at R ≳ 5 kpc is almost constant with a value of ∼Z⊙ over the cosmic time because of the large mass transfer rate of wind, |$\dot{M}_{\rm w}\sim \dot{M}_{\rm b}$|, and the small mass depletion rate of the CGM, |$\dot{M}_{\rm cl}\ll \dot{M}_{\rm b}$|. Most of the created metals go to and stay in the CGM; |$M_{\rm cgm}\sim 10^{11}\, M_{\odot }$| (see figure 3b), and the CGM metallicity is ∼0.5 Z⊙ (see figure 5d). This trend of larger metallicity at the inner radius region is consistent with the current state of the Galactic disk. Figure 8c shows the age–metallicity distribution of the low-mass stars. The older stars tend to have smaller metallicities and the typical stellar metallicity is Z⊙, which reflects the metallicity of the disk gas. Note that our model result is based on the long-term averaged argument. The actual stellar metallicity may reflect local and short time-scale physical processes and conditions, which would produce a larger dispersion than our result. The mean behavior—rapid growth at t ≲ 2 Gyr and plateau distribution with Z ∼ Z⊙ at t ≳ 2 Gyr—is similar to that observed by the Gaia satellite (Xiang & Rix 2022). The CR energy density, ecr, shown in figure 8d also traces the mass accretion via the star formation rate, but the structures are smoothed out by the diffusion.
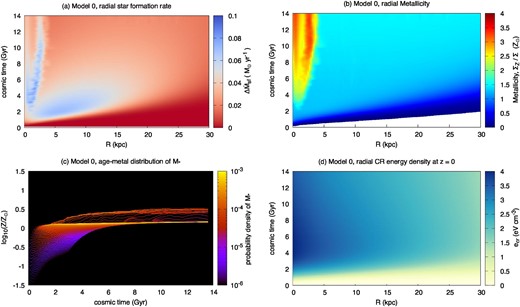
(a) Spacetime diagram of the radial star formation rate, |$\!\Delta \dot{M}_{\rm sf}\!$|. (b) Spacetime diagram of the disk gas metallicity, ΣZ|$/$|Σ for which |$\Delta \dot{M}_{\rm sf}\gt 10^{-8}\, M_{\odot }\,\,$|yr−1. (c) Probability density distribution of the stellar metallicity for the cosmic time, corresponding to the age–metal distribution of the low-mass stars. (d) Spacetime diagram of the CR energy density at z = 0 kpc.
Figure 9 shows the results of |$\dot{M}_{\rm sf}$| for each model summarized in table 1. The different conversion efficiency ηblown (Models 1 and 2) results in the different mass transfer rate of the outflow via |$\dot{\Sigma }_{\rm blown}=\eta _{\rm w}\dot{\Sigma }_{\rm sn}\propto \eta _{\rm blown}$| and the effects of Hcr (Models 3 and 4) appear via |$\dot{\Sigma }_{\rm fb}$|. In the case of larger ηblown (Model 1, the purple lines in figure 9a), the gaseous matter is efficiently removed by the wind and therefore the CGM mass becomes larger than in the case of Model 0. The opposite behavior is obtained in the case of smaller ηblown (Model 2, the green lines in figure 9a). Such simple interpretations can also be found from the fact that the calculated |$\dot{M}_{\rm sf}$| of each case is in good agreement with the estimated star formation rate given by equation (36) for which |$\dot{\Sigma }_{\rm cl}=\dot{\Sigma }_{\rm fb}=0$|. For Model 1 (ηblown = 0.05), the total mass of low-mass stars is |$M_*\simeq 6\times 10^{10}\, M_{\odot }$|. This is still consistent with the observationally estimated total stellar mass in the MW, |$4\!-\!6\times 10^{10}\, M_{\odot }$| (Bland-Hawthorn & Gerhard 2016). On the other hand, for Model 2 (ηblown = 0.2), the mass is |$M_*\simeq 2\times 10^{10}\, M_{\odot }$|, which is not likely. Figure 9b shows the larger ecr case (Model 3, the orange line) and the smaller ecr case (Model 4, the red line). Although the total star formation rate of each case may be acceptable, the CR energy density in the disk becomes ∼4–8 eV cm−3 for Model 3, which is a bit too large. In the case of Model 4, the energy density is ∼0.5–2 eV cm−3, which may still be acceptable. This weak dependence on Hcr implies that the Galactic evolution may be stable for variations in the CR energy density due to the uncertain magnetic field properties (or the diffusion coefficient). Note that the galactic wind solutions derived by Shimoda and Inutsuka (2022) exist in the range of ecr ∼ 0.1–10 eV cm−3. Thus, to reproduce the current MW, the parameter ranges of 0.05 ≲ ηblown ≲ 0.1 and 10 kpc ≲ Hcr ≲ 14 kpc with ηcr = 0.1 are favored.
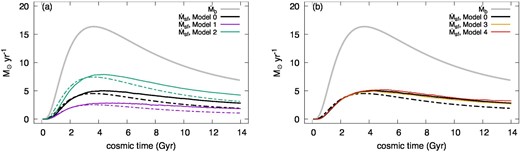
Results of star formation rate |$\dot{M}_{\rm sf}$| for the models summarized in table 1. The solid gray line, broken black line, and solid black lines are the same as in figures 2a and 3a. (a) The results of the strong wind case (Model 1, purple) and the weak wind case (Model 2, green). (b) The results of the large ecr case (Model 3, orange) and the small ecr case (Model 4, red).
To test the assumed |$\dot{\Sigma }_{\rm b,disk}$| given by equation (35), the rotation curve argument can be useful. Figure 10a shows the rotation velocity at t = 14 Gyr and z = 0 kpc. The rotation curve with a velocity of ∼200–250 km s−1 is well reproduced (e.g., Mróz et al. 2019, for the observed one).2 The dispersion of the rotation curve is due to the collisionless nature of the stars. For the other models, the curves are similar to each other. Thus, we regard that the assumptions in |$\dot{\Sigma }_{\rm b,disk}$| can be reasonable. Figure 10b shows the distribution of stellar parcels in the velocity space (see Belokurov et al. 2018, for the one observed by the Gaia satellite). Note that since our model does not account for perturbations from local objects such as giant molecular clouds, the result tends to have a smaller dispersion than the realistic one. The older stars tend to be at R ≲ 3 kpc and have a large radial velocity dispersion, reflecting the rapid growth of the gravitational potential in the early stage. The relatively younger stars have smaller radial velocities with smaller dispersion, corresponding to the Galactic stellar disk. The growth of gravitational potentail results in a systematic stellar migration which is indicated by figure 10c. This tendency may be an indication of the bulge formation process, which will be studied in our future work.
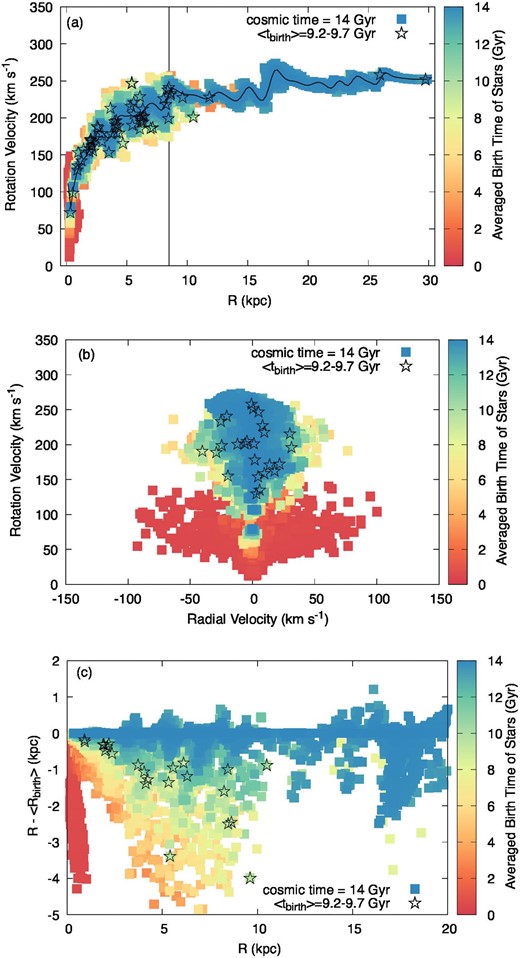
(a) Rotation curves at t = 14 Gyr and z = 0 kpc of Model 0. The gray line shows the rotation velocity calculated from the DM potential alone. The black curve shows the velocities calculated from the sum of the DM and mass components at the disk. The vertical black line indicates R = 8.5 kpc. The square boxes are the stellar parcels and their colors show the averaged birth time, 〈t〉birth. The star symbols indicate parcels with 9.2 Gyr < 〈t〉birth < 9.7 Gyr. Note that the points of the stellar parcels overlap. (b) Distribution of stellar parcels in the velocity space. (c) Relation of stellar parcels between the current place and averaged birth place 〈R〉birth.
4 Implication for observations
We discuss the implications of our model for various observations focusing on the assumed gas accretion, the origin of the outflowing hot X-ray emitting gas, and so on.
4.1 The dark accretion flow tested by the X-ray, ultraviolet, infrared and radio observations
Finding the gas accretion flow on to the disk is an important but unsettled issue in the MW. In our model, we assume that most of the cosmological accretion gas with a number density of ∼10−2 cm−3 falls directly on to the disk. Although the actual physical conditions of the cosmological accretion gas are non-trivial, the interactions between the dense, possibly low-temperature accretion gas and the diffuse gas in the galactic halo are important issues that may be similar to the cooling flow problem in the clusters of galaxies (Fabian 1994; Makishima et al. 2001; Peterson et al. 2003; Peterson & Fabian 2006). If this is the case, observations at the soft X-ray band may be important in finding the accretion flow in the analogue of the clusters of galaxies.
The high- and intermediate-velocity clouds observed at the Galactic halo region by the 21 cm line emission may be part of this expected accretion gas (Wakker & van Woerden 1997; Putman et al. 2012; Hayakawa & Fukui 2022). The estimated mass accretion rate of the observed H i components, ∼0.1–|$0.5\, M_{\odot }\,\,$|yr−1, is too small to be responsible for the star formation rate of |$\sim 3\, M_{\odot }\,\,$|yr−1, although the distance of these clouds are not tightly constrained [i.e., the total mass is uncertain; see Putman, Peek, and Joung (2012) and references therein]. In our model, the mass accretion from the CGM region occurs with an assumed efficiency of the angular momentum transfer in condensation processes (ϵcgm = 0.01). The accretion rate is |$\dot{M}_{\rm cl}\sim 0.5\, M_{\odot }{\rm yr^{-1}}$|, which can be consistent with the estimated accretion rate of the observed H i components. Hayakawa and Fukui (2022) argued the origin of the intermediate-velocity clouds and found that a picture of the external low-metallicity H i gas accretion is favored instead of the Galactic-fountain model (Shapiro & Field 1976). This scenario is consistent with our model results.
Thus, our model predicts the existence of dark accretion flows (DAFs) with a possible number density of ∼10−2 cm−3, corresponding to |$\dot{\Sigma }_{\rm b,disk}$| given by equation (35). The DAFs are expected to be responsible for the continuous star formation rate in the disk, and the galactic rotation curve reflects the accretion dynamics of the DAFs. When the temperature of the DAFs is comparable to the virial temperature (∼106 K), the DAFs are bright in the far ultraviolet and/or soft X-ray bands, which are actually obscured by the disk gas in the case of observations from the solar system. Investigating the dynamics of the gaseous matter including the DAFs, wind, H i clouds, and so on would be one of the most important issues. We will address this issue together with the study of the observational methods in future work.
It is worth emphasizing that an alternative scenario for the origin of DAFs is that most of the cosmological gas accretion remains in the Galactic halo or CGM region—not accreting directly on to the disk due to the uncertain angular momentum properties. In this case, the mass accretion responsible for sustaining the long-term star formation is invoked from the metal-polluted CGM with a larger ϵcgm, although most CGM gas should be virialized to explain the observed massive CGM. Then, the observational implications are changed as follows: the accretion gas consists of the metals and possibly dust grains produced during the gas condensation processes. The metals can produce the atomic line emissions in the ultraviolet band to the X-ray band, so the gas accretion motions can be identified by the detailed spectroscopy. The amount of dust grains is also an important predictable value that can be tested by the observations in the radio and infrared bands.
4.2 The accretaion history tested by the galactic archaeology
The relations between the stellar age, metallicity, and phase space distribution are important clues for investigating galactic evolution. In the case of the MW, sophisticated chemical abundance modeling favors much more episodic gas accretion on to the disk than that assumed in this paper to explain two clear, distinguished sequences in the [Mg|$/$|Fe] versus [Fe|$/$|H] relation (e.g., Spitoni et al. 2021; Sahlholdt et al. 2022). The interpretation and prediction of the two sequences are not so simple because: (i) the stars can move from their birthplace, (ii) most of the ejected metals should be removed from the disk by the wind, (iii) a fraction of the wind possibly falls back on to the inner disk, and (iv) (local) gas or dust migration/dynamics may have an effect (e.g., Chen et al. 2023). In particular, the formation condition and migration of white dwarf(s) in a close binary system, which results in the Fe pollution by type Ia supernovae, may be significantly uncertain. Thus, it would be worth considering another footprint for the accretion history.
To investigate the accretion history on to the disk, we adopt the episodic gas accretion scenario by replacing the term of exp [−(R − rcore)2|$/$|2rcore2] in equation (35) to exp [−(R − rcore)2|$/$|2(rcore|$/$|2)2] at t > 5 Gyr, i.e., the accretion gas is more concentrated. The other parameters are the same as Model 0.
Figures 11a and 11b are the resultant gas accretion rate on to the disk at R = 8 kpc (a) and R = 1 kpc (b). The concentrated accretion of the primordial gas dilutes the disk gas metallicity more at R ∼ rcore(t = 5 Gyr) ∼ 10 kpc, while the inner radius region is less diluted. Such accretion history forms high-metallicity stars at the inner galaxy which can be seen in the age–metallicity distribution (figure 11c). Future observations providing more complete stellar samples such as JASMINE (Gouda & Jasmine Team 2021) will constrain the actual gas accretion history.
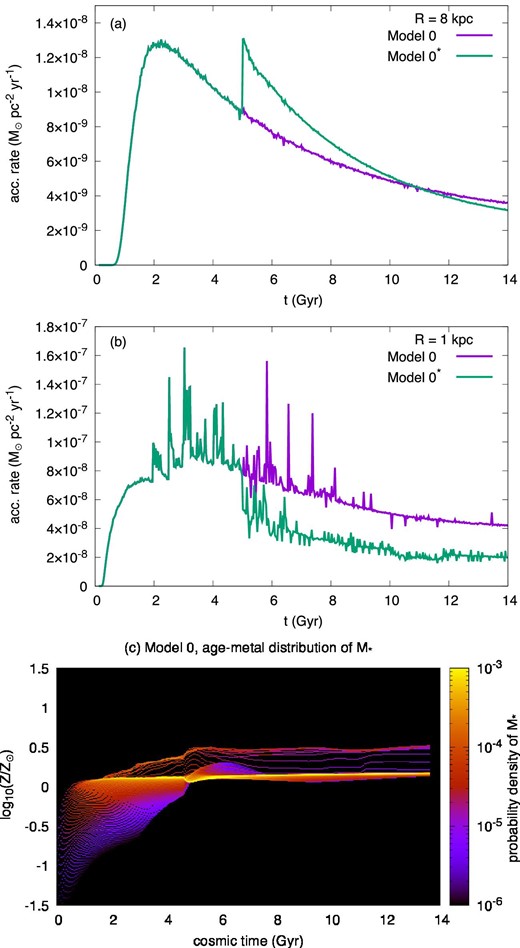
(a) Accretion rate on to the disk at R = 8 kpc. The purple line indicates Model 0. The green line indicates the case of the episodic accretion. (b) Rate at R = 1 kpc. (c) Age–metal distribution of the low-mass stars in the case of the episodic accretion. The other parameters are the same as Model 0.
4.3 The origin of outflowing gas tested by X-ray observations
A gas with virial temperature for the galactic mass scale |$kT_{\rm vir}\sim 0.1\,\,\mbox{keV}(M_{\rm vir}/10^{12}\, M_{\odot })$| is bright at the X-ray band. The X-ray observations play a key role in studying the outflow from the galactic system in general.
The origin and formation processes of the diffuse X-ray emission around the Galactic disk are currently controversial issues as reviewed by Koyama (2018) for the GDXE. Note that the outflow is alternatively responsible for removing the metals from the galactic disk. Thus, a fraction of the disk gas should have a temperature of T ≳ Tvir to transfer the metals from the disk to the Galactic halo region. In our model, we assume that the outflows are driven by consuming a tenth of the supernova explosion energy (ηblown ∼ 0.1). The proposed candidates for the GDXE origin(s) are the assembly of young–intermediate-aged supernova remnants and/or discrete, unresolved stellar objects. The former scenario is possibly consistent with the numerical simulation results of the local galactic disk performed by Girichidis et al. (2018), although the current computational resources are far from sufficient to resolve the energy injection processes by the supernovae in general. It is worth pointing out that the CRs are also able to heat the diffuse gas via the dissipation of self-excited Alfvén waves at a rate comparable to the radiative cooling rate as discussed by Shimoda and Inutsuka (2022). Note that Shimoda and Inutsuka (2022) assumed one of the simplest CR heating scenarios (e.g., Völk & McKenzie 1981; Zirakashvili et al. 1996), but the effects of the CR heating on the background plasma remain to be studied (e.g., Zweibel 2020; Yokoyama & Ohira 2023). Thus, further investigations on the origin of GDXE are necessary for the understanding of the Galactic long-term evolution, and these are the science cases of future X-ray observations such as XRISM (Tashiro et al. 2020) and Athena (Nandra et al. 2013).
Related to the origin of the GDXE, the galactic center activity is potentially important (e.g., Totani 2006; Koyama 2018). Note that the galactic center of our galaxy roughly corresponds to the region around Sgr A* within a radius of ∼300 pc. This region is not resolved by our model. The existence of such activities is also favored to explain the bubble-like structures seen in the soft X-ray sky (e.g., Predehl et al. 2020) and possibly smaller bubble structures bright at the γ-ray band [the so-called Fermi bubble (Su et al. 2010), but see also Crocker et al. (2022) who suggest the external galaxy scenario]. The effects of such activities are not considered in our model and are also important issues for the net gas accretion rate at the Galactic center, which is related to the formation and evolution process of the supermassive black hole.
The outflow that originated from the disk may explain the metal pollution of the CGM as we mentioned in this paper. The actual CGM temperature is also important to understand the observed “stable” CGM (e.g., Miller & Bregman 2015; Tumlinson et al. 2017; Nakashima et al. 2018; Das et al. 2019). If the temperature of CGM was much smaller than the virial temperature of ∼106 K, a significant gas accretion from the CGM would happen. In the case of the MW, the estimated mass and temperature are |$\sim 4\times 10^{10}\, M_{\odot }$| and ∼3 × 106 K, respectively (Miller & Bregman 2015). Das et al. 2019 reported that a very hot phase with temperature of ∼107 K is possibly co-spatial in the CGM. In the case of external galaxies, lower-ionized ions are also reported (Tumlinson et al. 2017). Shimoda and Inutsuka (2022) studied the Galactic wind theoretically and showed that the allowed wind solutions range from 104 to 107 K depending on the physical conditions (especially, the CR pressure) at the hot gas layer (z ∼ 2 kpc). Obviously, the angular momentum distribution is also important, however it is more uncertain than the thermal condition. Further theoretical and observational investigations of the thermal condition, chemical enrichment, and angular momentum distribution of the CGM are necessary.
4.4 Implication for the planet formation and cosmic life
The amounts of metals and CRs in the disk are important for the planet formation. The protoplanetary disk (PPD) can be dissipated quickly by too-efficient angular momentum transport in the ideal magnetohydrodynamics regime, so the effects of finite magnetic resistivity are invoked for long-lived PPDs (e.g., Inutsuka 2012; Tsukamoto et al. 2023, for reviews). The magnetic resistivity is, however, uncertain due to large uncertainties in the CR ionization rate, the amount of dust, and the dust size distributions (e.g., Tsukamoto & Okuzumi 2022). Further development along the lines of this study, such as the dust formation and detailed CR transport in the disk, would describe the change due to the Galactic evolution for the environment of PPDs in terms of the amount of dust and CRs over cosmic time as shown in figures 8b and 8d, and provide a useful step for investigations of the birthplace of the solar system. We will attempt to extend our model in future work.
The almost constant star formation rate of ∼M⊙ yr−1 corresponds to the almost constant supernova rates under the assumption of the universal initial mass function and star formation efficiency, ϵsf. In contrast, the size of the gas disk can evolve in time from the center outward, reflecting the gas accretion. Thus, the star and planet systems formed at a very early cosmic time, say t < 2 Gyr, are more frequently swept up by the supernova blast waves than those formed at later times. The irradiation of the CRs and high-energy photons is also strong at the early time. These may be more severe conditions for cosmic life to survive than the current condition. The frequent shock propagation may also affect the dust grains in the ISM. At t ∼ 4 Gyr, the size evolution of the gas disk almost converges (figure 4b), and the local star formation rate starts to increase at R ≲ 3 kpc (gradually decreasing at R ≳ 3 kpc, figure 8a). These are interesting clues to study the habitable region and time of the Galactic disk.
4.5 Further improvement by observations of external galaxies
Comparison with the observations of external galaxies will also provide improvement of our modeling. Since our model can simultaneously describe the star formation history, CR energy density, metallicity, and total baryon mass of a galactic halo, the correlations among the galaxy color–magnitude diagram, γ-ray luminosity, and neutrino luminosity can be studied in a self-consistent manner. The origin of high-energy cosmic neutrinos discovered by the IceCube Collaboration (Aartsen et al. 2013; IceCube Collaboration 2013) is considered as possible evidence for the existence of hidden CR accelerators (e.g., Murase 2022). Our model is also useful for studying such a big enigma in particle astrophysics.
The difference and relation between the host galaxy and its satellites would also be interesting subjects. Ruiz-Lara et al. (2020) suggested that repeated encounters of the Sagittarius dwarf galaxy with the MW result in star formation enhancements in the past, ∼5.7 Gyr, 1.9 Gyr, and 1.0 Gyr ago. We will investigate what insights can be obtained from such multi-messenger astronomy methods, including the effects from satellites, in future work.
Once we have a reasonable model for Galaxy evolution, we may predict the future of our Galaxy (see, e.g., Tutukov et al. 2000). For example, according to a simple extrapolation we need ∼100 Gyr to make the mean metallicity on the order of |$10\%$|, which might be too large to test observationally. However, it might not be impossible to study the effect of such a large metallicity by the systematic observation of the extreme regions in some external galaxies.
5 Summary
We have constructed a model of the Galactic system that describes the long-term evolution of the star formation, CRs, metallicity, and stellar dynamics over cosmic time. The Galactic gas disk can be modeled by the accretion disk with the α prescription, however the radial mass transfer is not so important for the surface mass density profiles due to the limited amount of turbulent radial excursion of the gas. This can be easily understood via α|$/$|Cs2 < 0.1 and 10 kpc|$/$|Cs ∼ 1 Gyr(Cs|$/$|10 km s−1) that corresponds to the sound crossing time of the gas at 104 K, which is essentially determined by the Lyα cooling. When the galactic wind is driven, the long-term star formation can be simply estimated by equation (16). Considering the consistency between the observed diffuse X-ray emission of the current MW (Koyama 2018; Nakashima et al. 2018; Predehl et al. 2020) and the steady-state wind solutions given by Shimoda and Inutsuka (2022), we have found that if about a tenth of the supernova explosion energy is consumed to form such diffuse, hot X-ray emitting gas (i.e., ηblown ∼ 0.1), the star formation rate of a few M⊙ yr−1 can be explained. This hypothesis will be investigated by future X-ray missions; XRISM, Athena, and so on. We have found that the acceptable CR energy density of a few eV cm−3 in the disk given by the CR scale height of Hcr ∼ 10 kpc can explain the long-term star formation rate. In our model, a fraction of the wind mass falls back to the disk. The mass transfer rate of the falling-back wind is a minor component of the net accretion rate of the total gas mass as a result, while it is responsible for the metallicity increase of the disk gas in the inner radius region (see figure 8b). To test the validity of our scenario, in particular the assumed accretion rate of the disk given by equation (35), we have estimated the rotation curves of low-mass stars and found that the parameter set of (ηblown; Hcr) = (0.1, 10 kpc) can simultaneously explain the star formation rate, metallicity in the disk, CR energy density in the disk, and the rotation curve.
Acknowledgments
We thank T. Ishiyama, S. Inoue, M. Nobukawa, K. Nobukawa, S. Yamauchi, T. G. Tsuru, D. Kashino, and S. Cooray, for useful discussions and suggestions. We are grateful to the anonymous referee, for his/her comments that further improved the paper. This work is partly supported by JSPS Grants-in-Aid for Scientific Research Nos. 20J01086 (JS), 18H05436, 18H05437 (SI), and 20H01950 (MN).
Footnotes
Cummings et al. (2016) reported the CR energy spectrum in the energy range from ∼3 MeV to ∼0.3 GeV by using the Voyager I data. These low-energy CRs are not expected to penetrate the heliopause. Voyager I, which crossed the solar wind termination shock, measured this energy band for the first time. They found that the amount of these low-energy CRs is too small to explain the ionization rate of the local molecular clouds. It is still an open question whether the local clouds consist of a significant fraction of the CRs with an energy of <0.3 MeV, or whether the CR energy density around the Earth is not representative of the ISM.
Recent analysis of Gaia-DR3 data reports the Keplerian decline at a range of |$R=19.5$| kpc and |$R=26.5$| (Jiao et al. 2023). This decline implies more compact DM halo than that assumed in this paper. We will study this new possibility in our future work.



