-
PDF
- Split View
-
Views
-
Cite
Cite
Pablo Villanueva-Domingo, Kiyotomo Ichiki, 21 cm forest constraints on primordial black holes, Publications of the Astronomical Society of Japan, Volume 75, Issue Supplement_1, February 2023, Pages S33–S49, https://doi.org/10.1093/pasj/psab119
Close - Share Icon Share
Abstract
Primordial black holes (PBHs) as part of the dark matter (DM) would modify the evolution of large-scale structures and the thermal history of the universe. Future 21 cm forest observations, sensitive to small scales and the thermal state of the intergalactic medium (IGM), could probe the existence of such PBHs. In this article, we show that the shot noise isocurvature mode on small scales induced by the presence of PBHs can enhance the amount of low-mass halos, or minihalos, and thus, the number of 21 cm absorption lines. However, if the mass of PBHs is as large as MPBH ≳ 10 |$M_\odot$|, with an abundant enough fraction of PBHs as DM, fPBH, the IGM heating due to accretion on to the PBHs counteracts the enhancement due to the isocurvature mode, reducing the number of absorption lines instead. The concurrence of both effects imprints distinctive signatures on the number of absorbers, allowing the abundance of PBHs to be bound. We compute the prospects for constraining PBHs with future 21 cm forest observations, finding achievable competitive upper limits on the abundance as low as fPBH ∼ 10−3 at MPBH = 100 |$M_\odot$|, or even lower at larger masses, in regions of the parameter space unexplored by current probes. The impact of astrophysical X-ray sources on the IGM temperature is also studied, which could potentially weaken the bounds.
1 Introduction
After the LIGO collaboration detected gravitational waves from the merging event of intermediate-mass black holes (Abbott et al. 2016), primordial black holes (PBHs) have attracted much attention again as the possible origin of those merger events (Sasaki et al. 2016). PBHs are interesting objects in cosmology because they can constitute part of the dark matter (DM) in the universe (Clesse & García-Bellido 2017; Carr et al. 2016). Furthermore, their abundance can be employed to investigate the amplitude of primordial density fluctuations on very small scales (Kalaja et al. 2019) responsible for the PBH formation. They could also act as seeds that form super massive black holes, the large masses of which are hardly explained by standard accretion mechanisms (Carr & Silk 2018). Many astronomical observations have placed stringent constraints on their abundance over extended ranges of their mass from different probes, including gravitational lensing, gamma-ray background, and cosmic microwave background (CMB) [see, e.g., Green & Kavanagh (2021), Carr et al. (2021), and Villanueva-Domingo et al. (2021) for recent reviews regarding the current constraints on PBHs].
Assuming that the primordial fluctuations are originally Gaussian-distributed, PBHs are expected to be initially randomly distributed on small scales, with no significant clustering (Ali-Haïmoud 2018; Desjacques & Riotto 2018). If the spatial distribution of PBHs in the universe follows the Poisson statistics, given that they behave as discrete objects, the existence of PBHs will enhance cosmological density fluctuations on small scales (Afshordi et al. 2003). Therefore, observations of small-scale structures can be used to constrain the PBH abundance in the universe, as done, e.g., via the Lyα forest (Murgia et al. 2019). A promising probe could be provided by observing the cosmological 21 cm line, one of the most propitious tools to study the intergalactic medium (IGM) from the Cosmic Dawn to the Epoch of Reionization (Pritchard & Loeb 2012; Furlanetto et al. 2006). The first claimed measurement of a global absorption signal by the EDGES collaboration (Bowman et al. 2018) has been employed to set competitive bounds on the PBH abundance, either from accretion processes (Hektor et al. 2018) or PBH evaporation (Clark et al. 2018; Halder & Banerjee 2021; Halder & Pandey 2021). Gong and Kitajima (2017, 2018) investigated the 21 cm line emission signal of the neutral hydrogen in low-mass halos, known as minihalos, from the density fluctuations enhanced by PBHs in the Reionization epoch. They found that future 21 cm line surveys such as Square Kilometre Array (SKA) can constrain the fraction to DM density to be less than 10−3 for 10 |$M_\odot$| mass PBHs (Gong & Kitajima 2017, 2018). On the other hand, Mena et al. (2019) further investigated the 21 cm signal in PBHs scenarios, emitted or absorbed in the IGM as well as in minihalos. They found that the enhancement of the signal present in Gong and Kitajima (2018) due to the shot noise power spectrum could be significantly diminished when taking into account the heating of the IGM, either from astrophysical sources or from accretion on to PBHs. The reason is that the minimum collapsed mass, which can be estimated as the Jeans mass, grows with the temperature. Hence, a hot IGM would increase the minimum mass of minihalos, suppressing their number and counteracting the enhancement of the power spectrum at small scales.
This paper investigates the prospect of constraining the mass and abundance of PBHs using 21 cm line observations. Unlike the references mentioned above, which accounted for the signal emitted (or absorbed) relative to the CMB from minihalos or in the IGM, we study the absorption lines that constitute the so-called 21 cm forest. The 21 cm forest is the absorption line system in the spectra of bright radio sources caused by the intervening neutral hydrogen atoms, in an analogous way to the Lyα forest (Carilli et al. 2002; Furlanetto & Loeb 2002; Xu et al. 2009, 2011; Mack & Wyithe 2012; Semelin 2016). Unlike observations of the 21 cm temperature from the IGM (either its global average or the power spectrum) with the CMB as the backlight, the 21 cm forest is observed against a bright radio source, allowing easy removal of foregrounds, which is the main problem of the IGM signal. Furthermore, it allows smaller scales to be reached since it only depends upon the frequency resolution of the observed spectra. Moreover, the 21 cm forest can probe earlier times and smaller scales than the Lyα forest can, owing to its smaller optical depth. Prospects for detecting the 21 cm forest with LOFAR and SKA have been examined in the literature (Ciardi et al. 2013, 2015). Several works have made use of the 21 cm forest in order to obtain constraints on decaying DM (Vasiliev & Shchekinov 2012), neutrino masses, running spectral index, or warm DM masses (Shimabukuro et al. 2014), ultra-light DM particles (Shimabukuro et al. 2020a; Kawasaki et al. 2021) or axion DM (Shimabukuro et al. 2020b). We compute the prospects for observing the 21 cm forest within a PBH scenario. We incorporate the enhancement at small scales from the Poisson shot noise power spectrum, as done in Gong and Kitajima (2017, 2018). Moreover, we consider the effect of gas accretion on to PBHs, as properly accounted in Mena et al. (2019), which was neglected in the former works.
This paper is organized as follows. In section 2, we briefly review the 21 cm forest methodology. In section 3, we discuss the effects of the PBHs on the matter power spectrum and the heating of the IGM. We present our results in section 4, while section 5 is devoted to the summary and discussion of the most relevant conclusions.
2 21 cm forest
During the Cosmic Dawn and the Epoch of Reionization, the neutral hydrogen atoms that create 21 cm absorption lines resided mostly in the IGM or the DM halos. In Furlanetto and Loeb (2002), the authors showed that distinctive absorption lines should be created due to neutral hydrogen atoms in the minihalos. In contrast, the IGM forms continuous absorptions with a small optical depth observed as an overall declination in the amplitude of the radio spectrum. Minihalos are those DM halos not massive enough to host star formation. They typically present virial temperatures below 104 K, which corresponds to the atomic cooling threshold for the production of effective star formation activity in Population (Pop) II stars (Barkana & Loeb 2001).1 Therefore, one can expect the abundant neutral hydrogen atoms existing in minihalos to create deep absorption lines. In this work, we only consider the absorption lines due to neutral hydrogen in minihalos, whose number density in the universe depends on the amplitude of cosmological density perturbations and hence on the number and mass of the PBHs. In this section, we show how to calculate the number of absorption lines due to minihalos. We mostly base our methodology on the seminal work by Furlanetto and Loeb (2002).
2.1 Minihalos
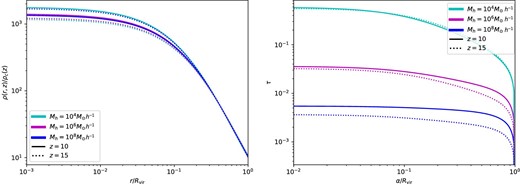
Left: Density profile of the gas as a function of radius. Right: 21 cm optical depth as a function of the impact parameter. Both panels show results for redshifts of 10 and 15, as well as for three different halo masses.
2.2 21 cm optical depth
2.3 Number of absorbers
It is worth noting that one could apply a version of equation (13) for other features of the 21 cm forest besides the optical depth, such as the intrinsic equivalent width (Furlanetto & Loeb 2002). For simplicity, here we focus only on τ as the characteristic quantity of the 21 cm forest.
2.4 Detectability of the 21 cm forest
How likely is it to observe the 21 cm forest in the future? Such detections may need relatively bright radio background fluxes to distinguish the absorption troughs in the spectra. In this section we estimate the required sources where 21 cm forest observations are feasible.
The main uncertainty regarding the 21 cm forest is whether there are such bright radio sources at high redshifts. There has been significant progress recently finding new radio bright sources at z ≳ 6, such as quasars (Bañados et al. 2015, 2018, 2021; Belladitta et al. 2020). Only four out of the ∼ 200 known quasars at z > 6 are known to be radio-loud (i.e., where radio emission is the dominant component in their spectra), with the farthest one recently discovered at z = 6.82 (Bañados et al. 2021). However, around |$10\%$| of all quasars could be radio-loud, nearly independently of redshift (Ivezic et al. 2002; Bañados et al. 2015). The brightest radio source known so far is a radio-loud quasar found at z = 5.84, with the flux 8–100 mJy from 3 GHz to 230 MHz, which could be bright enough for the 21 cm forest studies if its local dense gas environment is confirmed by the follow-up surveys (Bañados et al. 2018). The estimates based on extrapolations of the observed radio luminosity functions to the higher redshift indicate that there could be as many as ∼104–105 radio quasars with sufficient brightness at z ∼ 10 (Haiman et al. 2004; Xu et al. 2009).
Gamma-ray bursts (GRBs) may also present a radio afterglow where the 21 cm forest could be potentially identified (Ioka & Mészáros 2005; Ciardi et al. 2015). There are several known GRBs at high redshift (at least six at z > 6), such as the ones at z = 6.7 (Greiner et al. 2009), z = 8.2 (Tanvir et al. 2009), and z = 9.4 (Cucchiara et al. 2011). Pop III stars in metal-free environments may lead to the formation of GRBs that are much more energetic than the ordinary ones, being able to generate much brighter low-frequency radio afterglows, exceeding tens of mJy (Toma et al. 2011; de Souza et al. 2011). The claimed detection of the 21 cm global signal by EDGES (Bowman et al. 2018), if verified, would imply that Pop III stars should exist at z ≳ 17 (Madau 2018), as well as Pop III GRBs at z ≳ 10. Hence, all these findings and estimates present good prospects for observing the 21 cm forest in the future.
3 Effects of primordial black holes
In this section, two of the most relevant effects of solar mass PBHs on cosmology are discussed, namely the enhancement of fluctuations due to shot noise and the heating of the IGM due to accretion. Throughout this work, we assume a monochromatic distribution for the PBH mass at MPBH and write the fraction of PBHs that comprise DM as fPBH = ΩPBH/ΩDM, with ΩPBH and ΩDM the current energy density of PBHs and DM, respectively, relative to the critical density ρcrit, 0.
3.1 Shot noise
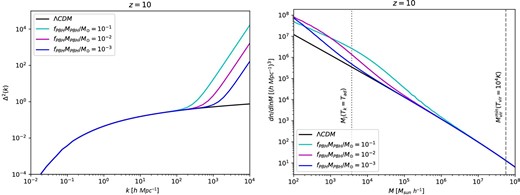
Matter power spectrum (left) and halo mass function (right) for several values of fPBHMPBH at z = 10. The vertical lines in the right-hand panel correspond to the Jeans mass evaluated at the adiabatic temperature (i.e., without considering IGM heating) and the mass relative to a virial temperature of 104 K, respectively. Note that when including the accretion effects outlined in subsection 3.2, the IGM is heated up and the Jeans mass becomes larger.
3.2 PBH accretion in the IGM
| |$10 \, \dot{M}_{\rm PBH} / L_{\rm Edd}$| . | ε0 . | a . |
|---|---|---|
| ≲ 9.4 × 10−5 | 0.12 | 0.59 |
| 9.4 × 10−5–5 × 10−3 | 0.026 | 0.27 |
| 5 × 10−3–6.6 × 10−3 | 0.50 | 4.53 |
| |$10 \, \dot{M}_{\rm PBH} / L_{\rm Edd}$| . | ε0 . | a . |
|---|---|---|
| ≲ 9.4 × 10−5 | 0.12 | 0.59 |
| 9.4 × 10−5–5 × 10−3 | 0.026 | 0.27 |
| 5 × 10−3–6.6 × 10−3 | 0.50 | 4.53 |
These values are taken from Xie & Yuan (2012), for the ADAF electron heating parameter δ = 0.1 and for the viscous parameter α = 0.1.
| |$10 \, \dot{M}_{\rm PBH} / L_{\rm Edd}$| . | ε0 . | a . |
|---|---|---|
| ≲ 9.4 × 10−5 | 0.12 | 0.59 |
| 9.4 × 10−5–5 × 10−3 | 0.026 | 0.27 |
| 5 × 10−3–6.6 × 10−3 | 0.50 | 4.53 |
| |$10 \, \dot{M}_{\rm PBH} / L_{\rm Edd}$| . | ε0 . | a . |
|---|---|---|
| ≲ 9.4 × 10−5 | 0.12 | 0.59 |
| 9.4 × 10−5–5 × 10−3 | 0.026 | 0.27 |
| 5 × 10−3–6.6 × 10−3 | 0.50 | 4.53 |
These values are taken from Xie & Yuan (2012), for the ADAF electron heating parameter δ = 0.1 and for the viscous parameter α = 0.1.
Finally, it is worth examining the scaling of the heating rate with the PBH parameters. From equation (27), one has |$\dot{M}_{\rm PBH}\propto M^2_{\rm PBH}$|. Noting that LEdd ∝ MPBH, the fit of equation (28) for the efficiency scales as |$\epsilon \propto (\dot{M}_{\rm PBH}/M_{\rm PBH})^a \propto M_{\rm PBH}^{a}$|. Hence, from equation (25), |$L_{\rm acc} \propto M_{\rm PBH}^{a+2}$|, and finally, the rate of energy injected from equation (26) goes as |$\left({dE_{\rm heat}}/{dV dt}\right)_{{\rm inj}} \propto f_{\rm PBH} M_{\rm PBH}^{a+1}$|. Taking into account that the accretion rates considered correspond to the fit for the efficiency given by the first row of table 1, the injection of energy depends upon the combination |$\sim f_{\rm PBH} M_{\rm PBH}^{1.59}$|. Given that the energy deposition fraction depends weakly on the mass, the heating term |$\mathcal {Q}_{\rm PBH}$| and the kinetic temperature should show the same scaling, as is explicitly checked in subsection 4.1.
4 Results and discussion
In this section, the main results of our computations are discussed in detail. The number of absorbers in PBH scenarios, taking into account shot noise and accretion effect, is calculated to estimate the possible limits on the PBH abundance that future observations could achieve. The codes to perform these computations have been released and are publicly available (P. Villanueva-Domingo 2021).6
4.1 Thermal evolution of the IGM
The thermal histories of the IGM for the PBH scenarios are computed with the publicly available code 21cmFAST (Mesinger et al. 2011), properly modifying equation (32) to include the heating from PBH accretion.7 We start the simulations at z = 30, when initial conditions of the gas temperature are computed with the recombination code CosmoRec (Chluba & Thomas 2011), also modified to include accretion effects. We show the evolution of Tk as a function of redshift for several PBH models in figure 3. For now, we focus on the thin lines of the figure, which omit any astrophysical heating in our calculation except for the one from PBH accretion, to perceive the PBH effect explicitly. Standard astrophysical heating effects will be discussed below. Two cases for the PBH fraction are considered, fPBH = 10−2 and 10−3, with three different PBH masses, MPBH = 1, 10, and 102 |$M_\odot$|. One can observe that larger PBH fractions give rise to a more pronounced heating effect and the IGM temperature remains higher compared to the case for the standard CDM model. With the PBH fraction fixed, PBHs with larger masses give rise to a higher temperature due to the larger mass accretion rate given by equation (27). Our calculation shows that the accretion effect becomes important if the PBH mass is ≳10 |$M_\odot$| for the PBH fraction of fPBH = 10−2. However, the heating effect is not significant if the fraction is as small as fPBH = 10−3 even for the PBH with mass as large as 10 |$M_\odot$|.
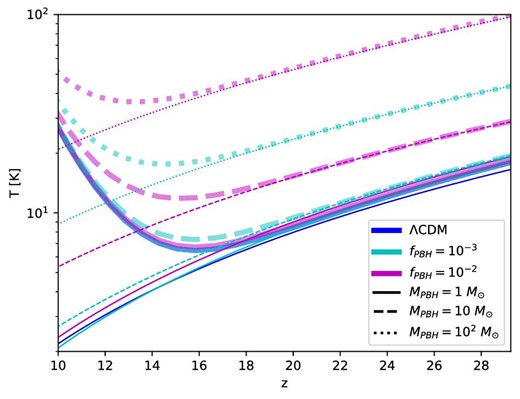
IGM temperature evolution with redshift for a CDM scenario and for several PBH models. Thin lines account for a scenario without astrophysical X-ray heating, presenting only heating by PBH accretion, while thick lines correspond to a model with |$L_{\rm X}/\mathit {SFR}= 10^{40}\:$|erg s−1.
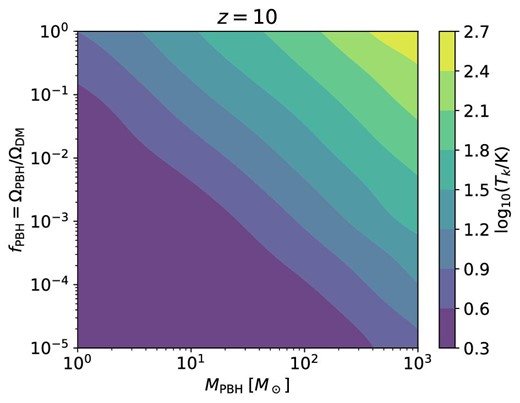
Values of the IGM temperature at z = 10 as a function of the mass MPBH and fraction as DM fPBH of PBHs.
There might be a possible enhancement of the gas accretion on to PBHs due to the cosmological accretion of DM halos around the PBHs, which we did not consider in this work. The additional gravitational potential due to a DM halo makes the effective Bondi radius larger, leading to a more significant accretion rate (Park et al. 2016). The authors of Serpico et al. (2020) investigated this effect in the context of the CMB constraint on fPBH from the CMB E-mode power spectrum and found that the constraints become significantly tighter for ≳102 |$M_\odot$|, while they do not alter very much for ≲101 |$M_\odot$|. Accordingly, the effect would impact our results for ≳102 |$M_\odot$| if we took it into account. Serpico et al. (2020) assumed spherically symmetric CDM halos around the PBHs that enhanced the gas accretion on to the PBH in high-redshift universes (z > 99) where the spherical symmetry is a good approximation. However, at the redshifts we are interested in, there were many structures both in baryons and CDM which break the assumption of the spherical symmetry. Therefore, to be conservative, we did not include the effect from the CDM halos around the PBHs.
A more realistic treatment requires the consideration of X-ray heating from different astrophysical sources, such as X-ray binaries. One could naively argue that the relevant quantity to constrain the abundance of PBHs is the difference between the number of absorbers in the PBH and the ΛCDM scenario, which would be both additionally suppressed in the same amount, and one would thus expect that X-ray heating would have little impact on this difference. However, as it will be explicitly shown, the number of absorbers can be significantly suppressed if astrophysical sources inject energetic radiation in the IGM, which affects our statistical approach based on the Poisson statistics, thus weakening the bounds. Actually, strong heating of the IGM can be a potential issue even in the standard ΛCDM scenario, worsening the prospects of observing the 21 cm forest (Mack & Wyithe 2012).
There are many uncertainties regarding X-ray sources in the pre-Reionization universe. Compact X-ray binaries in starburst galaxies are the most likely origin of energetic radiation if their emissivity in the Cosmic Dawn is similar to that currently observed. Therefore, as usually done in the literature for the fiducial astrophysical heating, we extrapolate to our redshifts of interest the estimated luminosity from nearby X-ray binaries. The X-ray luminosity per star formation rate, |$L_{\rm X}/\mathit {SFR}$|, integrated within the range 2–10 keV from X-ray compact binaries, lies between ∼1039 and ∼1040 erg s|$^{-1}\, M_{\odot }^{-1}\:$|yr between redshifts 0 and ∼4 (Madau & Fragos 2017). We thus consider two limiting fiducial values of the luminosity per star formation rate, 1039 and 1040 erg s|$^{-1}\, M_{\odot }^{-1}\:$|yr, corresponding to mild and high X-ray heating scenarios, in order to illustrate the impact of astrophysical heating on our results. For the ratio of baryons into stars, f*, we adopt a value of f* = 0.01, as suggested from radiation–hydrodynamic simulations of high-redshift galaxies (see, e.g., Wise et al. 2014), or from the comparison of the star formation rate with the one derived from measurements of the UV luminosity function (see, e.g., Leite et al. 2017; Lidz & Hui 2018, and references therein). The standard X-ray heating is already implemented in 21cmFAST; see Mesinger, Furlanetto, and Cen (2011) and Park et al. (2019) for more details. Figure 3 shows in thick lines examples of thermal histories for PBH scenarios including X-ray astrophysical heating with |$L_{\rm X}/\mathit {SFR}= 10^{40}\:$|erg s−1. Notice that, for that value, the onset of X-ray sources takes place at z ∼ 15, the astrophysical effects thus being still very moderate at that epoch. They become significant, however, at z ∼ 10. It is noteworthy that X-ray heating from astrophysical sources is more prominent for PBH scenarios with low accretion heating, increasing the temperature up to one order of magnitude in the limiting ΛCDM case. In contrast, the impact is reduced in PBH cases already substantially heated by accretion, increasing for instance by only a factor of ≃ 2.5 for MPBH = 102 |$M_\odot$| and fPBH = 10−2. Finally, the addition of the astrophysical X-ray heating does not change the dependence between fPBH and MPBH from equation (33) and shown in figure 4.
4.2 Number of absorber features
With the thermal history of the IGM and the mass function of the DM halos, we calculate the expected number of absorption lines due to minihalos following the method presented in section 2. To investigate the effects of heating and the enhancement of the power spectrum by PBHs separately, we first focus on the shot noise contribution. Figure 5 shows the number of absorption lines without the heating effect. Neglecting the heating by accretion (and by astrophysical heating), the change in the number of absorption lines due to minihalos simply reflects the change in the matter power spectrum. Because the power of the Poisson noise is proportional to |$P\propto f_{\rm PBH}^2/n_{\rm PBH} \propto f_{\rm PBH}M_{\rm PBH}$|, the effect depends on the combination of the parameters fPBHMPBH, and larger fPBHMPBH results in the larger number of absorption features. This behavior is shown in figure 5 for the cumulative number of absorbers above a certain optical depth τ, dN(>τ)/dz [as computed from equation (13)], and its logarithmic derivative with respect to τ, τd2N(>τ)/dz/dτ, in the top and bottom panels, respectively. Both quantities reflect an enhancement powered by fPBHMPBH, which is approximately equally distributed along τ.
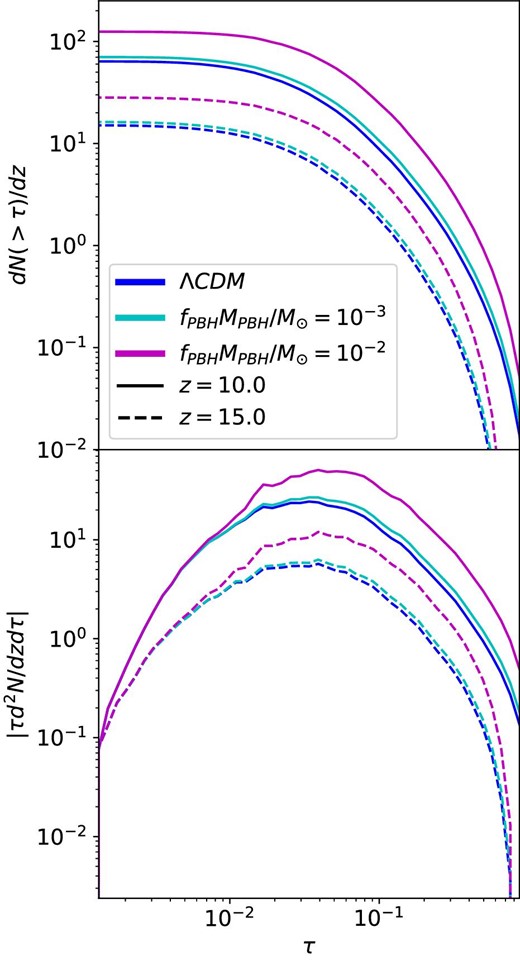
Number of absorbers and its derivative, neglecting the heating by accretion, for several values of fPBHMPBH at two different redshifts.
We now include the heating effect from PBH accretion, using the IGM temperature instead of the adiabatic one for computing the Jeans mass. Examples for four values of the PBH masses are shown in figure 6. Because the IGM temperature scales with the parameters fPBH and MPBH differently than it does with the shot noise contribution, the degeneracy between these two parameters found in the power spectrum is broken. The increase in the Jeans mass reduces the range of mass integration in equation (13), and therefore it counteracts the enhancement effect due to the additional contribution of the power spectrum. As can be seen in the right-hand panel of figure 1, the highest optical depths appear in low-mass minihalos, while the largest minihalos produce lower optical depths. Increasing the IGM temperature and the Jeans mass reduces the low-mass halos, where the highest values of τ are obtained. Hence, the accretion effect is more pronounced at large optical depths.
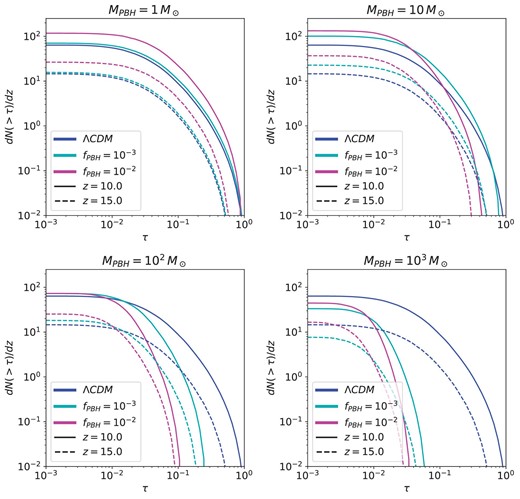
Number of absorbers and its derivative for four values of MPBH with an IGM heated only by accretion.
Comparing the first panel of figure 6 with figure 5, one can see that the accretion effect is mostly negligible at MPBH = |$M_\odot$| for the abundances assumed. At PBH masses ≲ 10 |$M_\odot$|, for relatively high fractions fPBH ≃ 10−2, the enhancement is still noticeable, especially for higher redshifts. Nonetheless, at MPBH = 10 |$M_\odot$|, the largest optical depths are already suppressed due to the accretion effect. For the cases with MPBH = 102 |$M_\odot$|, the number of absorption lines only slightly increases compared to the standard ΛCDM case (being more prominent at z = 15). On the other hand, the increase in the Jeans mass due to the extra heating overcomes the enhancement effect in the matter power spectrum, suppressing the number of absorption lines with respect to the CDM case, having the opposite effect. For MPBH = 103|$M_\odot$|, the accretion effect dominates, suppressing the number of absorbers along the τ range (except for fPBH = 10−2 at z = 15, which still shows a small enhancement at very low optical depths).
Number of absorbers at z = 10 computed using equation (34) assuming only heating by PBH accretion.
| (MPBH, fPBH) . | N(0.01 ≤ τ ≤ 0.03) . | N(τ > 0.03) . |
|---|---|---|
| (1, 10−2) | 34 | 74 |
| (1, 10−3) | 23 | 39 |
| (10, 10−2) | 54 | 65 |
| (10, 10−3) | 32 | 61 |
| (100, 10−2) | 42 | 9 |
| (100, 10−3) | 35 | 25 |
| ΛCDM (0,0) | 22 | 33 |
| (MPBH, fPBH) . | N(0.01 ≤ τ ≤ 0.03) . | N(τ > 0.03) . |
|---|---|---|
| (1, 10−2) | 34 | 74 |
| (1, 10−3) | 23 | 39 |
| (10, 10−2) | 54 | 65 |
| (10, 10−3) | 32 | 61 |
| (100, 10−2) | 42 | 9 |
| (100, 10−3) | 35 | 25 |
| ΛCDM (0,0) | 22 | 33 |
Number of absorbers at z = 10 computed using equation (34) assuming only heating by PBH accretion.
| (MPBH, fPBH) . | N(0.01 ≤ τ ≤ 0.03) . | N(τ > 0.03) . |
|---|---|---|
| (1, 10−2) | 34 | 74 |
| (1, 10−3) | 23 | 39 |
| (10, 10−2) | 54 | 65 |
| (10, 10−3) | 32 | 61 |
| (100, 10−2) | 42 | 9 |
| (100, 10−3) | 35 | 25 |
| ΛCDM (0,0) | 22 | 33 |
| (MPBH, fPBH) . | N(0.01 ≤ τ ≤ 0.03) . | N(τ > 0.03) . |
|---|---|---|
| (1, 10−2) | 34 | 74 |
| (1, 10−3) | 23 | 39 |
| (10, 10−2) | 54 | 65 |
| (10, 10−3) | 32 | 61 |
| (100, 10−2) | 42 | 9 |
| (100, 10−3) | 35 | 25 |
| ΛCDM (0,0) | 22 | 33 |
4.3 Bounds on the PBH abundance
Figure 7 shows a forecast of the upper bounds on the fraction of PBHs as DM as a function of their mass, based on the criterion from equation (35) for a hypothetical background source located at z = 10 (left) and z = 15 (right). The solid lines correspond to N(0.01 ≤ τ ≤ 0.03), while the dotted ones to N(τ > 0.03). Three heating scenarios are considered, one neglecting astrophysical X-ray heating, considering only heating by accretion (blue lines), and two fiducial values of the X-ray luminosity from X-ray binaries, accounting for mild (|$L_{\rm X}/\mathit {SFR}= 10^{39}\:$|erg s−1, purple lines) and high (|$L_{\rm X}/\mathit {SFR}= 10^{40}\:$|erg s−1, red lines) heating, as discussed in subsection 4.1.
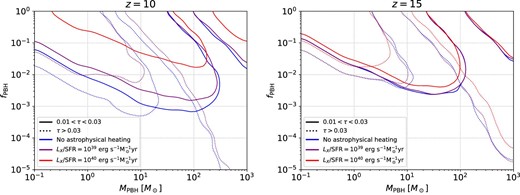
Constraints on the abundance of PBHs as a function of their mass applying the criterion form equation (35), for three astrophysical heating regimes and a background source located at z = 10 (left) and z = 15 (right). The solid line accounts for N(0.01 ≤ τ ≤ 0.03), while the dotted line is for N(τ > 0.03).
It is straightforward to understand the shape of these forecasted limits. Focusing now on the range 0.01 ≤ τ ≤ 0.03 (solid lines), one can distinguish two different regimes on the expected bounds, roughly the same at both redsfhits. At low masses, MPBH ≲ 100 |$M_\odot$|, and relatively low PBH fractions, fPBH < 10−1, the shot noise effect dominates, and allows that region of the parameter space to be probed. Given that the enhancement is powered by the product fPBHMPBH, the upper limit follows a line with the dependence |$f_{\rm PBH} \propto M_{\rm PBH}^{-1}$|. In the other extreme, at high masses, MPBH ≳ 100 |$M_\odot$|, and large PBH fractions, fPBH > 10−2, the number of absorbers is suppressed due to heating from accretion. This constraint depends upon the IGM temperature, which recalling from subsection 4.1, depends upon the joint product |$f_{\rm PBH} M_{\rm PBH}^{\beta }$|, with β ≃ 1.59. Hence, the shape of the upper limit reflects the isotherms of equation (33), shown in figure 4, scaling as |$f_{\rm PBH} \propto M_{\rm PBH}^{-\beta }$|.
Amidst these two regimes, both effects compensate, leading to a number of absorbers similar to those expected from the ΛCDM case. This trade-off leaves a window around ∼100 |$M_\odot$| where the possible bounds relax and even disappear. The analysis employing N(τ > 0.03) is qualitatively the same, albeit the ranges of masses delimiting the different regimes change. Larger optical depths are more sensitive to the drop in the number of minihalos due to the IGM heating, as is manifest in figure 6, and thus the accretion regime starts at a lower mass, roughly ∼10 |$M_\odot$| in this case. Note that measuring at different ranges of τ can probe distinct regions of the parameter space, and combining them, it would be possible to remove the windows with no bounds.
While the aforementioned dependences in figure 7 behave similarly at z = 10 and z = 15, astrophysical heating establishes a key difference between both redshifts. At z = 15, X-ray binaries and other sources are not abundant enough to impact the IGM temperature greatly, as seen in figure 3, and the bounds are not significantly modified for large astrophysical heating. However, at z = 10, X-ray background radiation could be important enough to increase the IGM temperature substantially, leaving a deep impact in our analysis. While the limits only worsen by a factor of a few in the mild heating scenario, the case with large X-ray luminosity reduces the bounds by more than an order of magnitude. Moreover, this weakening is not equal for all the ranges of optical depths, disappearing completely for τ > 0.03. These facts show the great dependence of the 21 cm forest results upon the IGM heating, becoming mandatory to understand the growth of X-ray sources during the Cosmic Dawn properly in order to infer robust bounds on PBHs.
In order to understand the strength of these forecasted bounds better, it is useful to compare them with the constraints from other studies. Figure 8 depicts a sample of our bounds together with the current constraints on the abundance on this range of masses extracted from different probes. The purple lines account for the case z = 10 and mild heating (|$L_{\rm X}/\mathit {SFR}= 10^{39}\:$|erg s−1), for both ranges of τ considered in figure 7. We opt to show this scenario since it is the intermediate case at z = 10, and roughly coincides with the bounds at z = 15 for mild and vanishing X-ray sources, being thus a representative example. The considered experiments include the non-observation of microlensing events (blue) from the MACHO (Alcock et al. 2001), EROS (Tisserand et al. 2007), Kepler (Griest et al. 2014) and Icarus (Oguri et al. 2018) collaborations; PBH accretion signatures on the CMB anisotropies with Planck data (orange) (Poulin et al. 2017); dynamical constraints, such as disruption of stellar systems by the presence of PBHs (green), on wide binaries (Monroy-Rodríguez & Allen 2014) and on ultra-faint dwarf galaxies (Brandt 2016); and the power spectrum from the Lyα forest enhanced by shot noise (cyan) (Murgia et al. 2019). Forecasted limits from the imprints of accretion in the IGM 21 cm power spectrum from future observations with SKA are also shown (dotted brown line) (Mena et al. 2019).
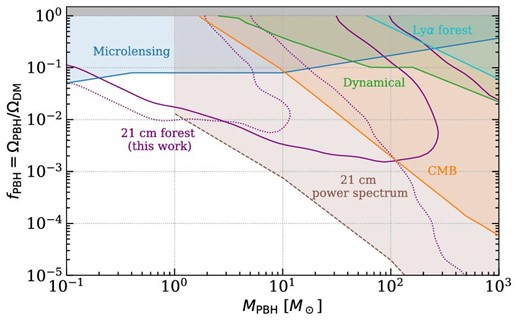
Constraints on the abundance of PBHs as a function of their mass. Purple lines denote the prospects from our analysis, employing the number of absorbers of the 21 cm forest at z = 10 with mild astrophysical heating, applying the criterion from equation (35). The solid line accounts for N(0.01 ≤ τ ≤ 0.03), the dotted line for N(τ > 0.03). For comparison, current bounds from other probes have been included, namely: non-observation of microlensing events (blue) from the MACHO (Alcock et al. 2001), EROS (Tisserand et al. 2007), Kepler (Griest et al. 2014), and Icarus (Oguri et al. 2018) collaborations; PBH accretion signatures on the CMB (orange), assuming disk ADAF accretion (Poulin et al. 2017); dynamical constraints, such as disruption of stellar systems by the presence of PBHs (green), on wide binaries (Monroy-Rodríguez & Allen 2014) and on ultra-faint dwarf galaxies (Brandt 2016); power spectrum from the Lyα forest (cyan) (Murgia et al. 2019). The dotted brown line corresponds to forecasts for SKA from the impact of accretion on the 21 cm power spectrum of the IGM (Mena et al. 2019). This figure was created with the publicly available Python code PBHbounds (B. J. Kavanagh 2019)9.
One can see that our estimate from future 21 cm forest observations at z ∼ 10 may be able to explore a broad region in the parameter space not yet covered by current probes, being sensitive to even small abundances of PBHs, and partly overlapping the prospects from the 21 cm power spectrum of the IGM. Note that Lyα forest bounds present the same scaling with MPBH as our predictions at masses ≲1 |$M_\odot$|. This is because both are based on the contribution from the shot noise power spectrum. However, the 21 cm forest may provide much more stringent constraints since it can probe smaller scales at higher redshifts. Similarly, both the 21 cm power spectrum prospects and the CMB bounds scale in a similar way to those from the accretion effect obtained here, because both bounds would depend on the IGM temperature, heated in the same way due to ADAF disk accretion. Other CMB bounds have been derived in the literature modifying the accretion modeling, e.g., assuming spherical accretion of PBHs within halos (Serpico et al. 2020), which present a different scaling. Finally, it is worth noting that observations of BH merger events from gravitational waves have been claimed to set stringent bounds in the range of masses from 10−2 to ∼102 |$M_\odot$|, by demanding that the predicted merger rates of PBH binaries cannot exceed the measured ones. This can be achieved either employing individual merger events (Kavanagh et al. 2018; Abbott et al. 2019; Hütsi et al. 2021b) or searches of a stochastic background of gravitational waves (Chen & Huang 2020). However, these limits assume PBHs as Schwarzschild BHs, while a cosmological BH solution embedded in the FLRW metric should be more appropriate. Properly accounting for a cosmological metric (specifically, the Thakurta metric: Thakurta 1981) may allow the avoidance of those bounds, getting merger rates compatible with the LIGO and VIRGO detections (Boehm et al. 2021b).10 For that reason, we exclude these bounds from figure 8.
5 Conclusions
In this article, we have investigated the effects of PBHs on the 21 cm forest due to minihalos in the Epoch of Reionization and the Cosmic Dawn. The 21 cm forest presents several advantages over other approaches to probe the IGM. It allows the study of earlier periods than the Lyα forest, previous to Reionization. Moreover, unlike the 21 cm signal from the IGM, it avoids the problem of foreground removal since backlit radio sources would be much brighter. Additionally, arbitrary small scales can be probed, relying on the frequency resolution. However, it also suffers from two main uncertainties and drawbacks.
On the one hand, it depends upon the existence of sufficiently bright radio sources at high redshift, none of which has been observed yet, although there are good prospects for discovering them in the future. On the other hand, it is strongly dependent on the heating state of the IGM. Since the number of minihalos is limited by the Jeans mass, a gas that is too hot would drastically reduce the number of absorbers, eventually spoiling the statistical power.
The presence of PBHs as DM may alter the number of 21 cm absorption lines in two ways. One is increasing their number through enhancing the mass function due to the newly induced Poisson shot-noise isocurvature mode on small scales. The other is further heating the IGM due to the gas accretion on to the PBHs, making the Jeans mass scale larger, reducing the number of absorbers. We estimate via a semianalytic approach the number of absorption lines for PBH masses of 0.1 ≤ MPBH/|$M_\odot$| ≤ 104 and abundances 10−5 ≤ fPBH ≤ 1. We find that the PBHs have a negligible impact on the number of absorption lines for fPBH ≲ 10−3 for their masses up to 100 |$M_\odot$|. If the mass of PBHs is smaller than ≲ 100 |$M_\odot$|, the heating effect is weak, and the number of absorption lines monotonically increases as fPBH increases. If the mass of PBHs is as large as 100 |$M_\odot$|, the heating effect can be significant, and the number of absorption lines becomes smaller compared to the standard ΛCDM case. However, this behavior depends on the range of optical depths considered. Absorbers with large values of τ are more affected by the suppression due to accretion than those with lower values. Hence the bounds on intervals of large optical depths are dominated by the accretion heating effect at large PBH masses.
We find that our results strongly rely on the assumed astrophysical X-ray heating. A IGM that is too hot can substantially reduce the number of absorbers in both PBH and CDM scenarios, weakening considerably the obtained bounds and even preventing us from reaching the statistical sensitivity required to discriminate between both models if large values of the optical depth are employed. However, mild heating scenarios may only feebly reduce the limits. Nevertheless, the presence and luminosity of X-ray sources during the Cosmic Dawn is quite unclear. It is customary to assume similar luminosities at high redshift to those existing in the nearby universe. However, the EDGES collaboration claimed a detection of the 21 cm global signal at z ≃ 17, which, if it is verified, would imply a cold IGM at z > 10 (Bowman et al. 2018). It is therefore not clear how hot the IGM may be, and further studies are mandatory for a proper determination of the possible bounds on the PBH abundance.
Our approach is based on a semianalytic framework, mainly following the formalism from Furlanetto and Loeb (2002), which significantly simplifies the extremely complex physics of the IGM. The virial characterization of minihalos, the computation of the gas density profile, or neglecting the Lyα coupling to compute the spin temperature inside minihalos are well motivated although oversimplistic approximations, which may have an impact on the final bounds. In order to obtain more reliable results, hydrodynamical simulations would be required. However, we have taken several conservative assumptions throughout our work to ensure the robustness of the results. For instance, for a background source located at redshift z, we have employed a range of integration of Δz = 1 in equation (34), while in general there should be contributions from lower redshifts <z, as long as neutral minihalos still exist. In addition, the Jeans mass has been taken as the minimal threshold for considering minihalos. This could be seen as a conservative hypothesis, since minihalos with lower masses formed previously in a colder IGM are thus excluded, which could contribute to the number of absorption features (Meiksin 2011). Relaxing some of these conditions may imply stronger bounds than obtained here.
The statistical test based on the criterion from equation (35) based on the Poisson statistics is considerably simple. Nevertheless, it suffices for providing a rough conservative estimate of the expected bounds, rather than a precise evaluation of the limits. Further rigorous approaches, involving Fisher matrix analyses or Monte Carlo methods, should be employed to ensure more robust constraints. Nonetheless, the approach followed here is enough for illustrating the power of the 21 cm forest for constraining the abundance of PBHs as DM.
Acknowledgements
PVD thanks the universities of Nagoya and Tokyo for their hospitality during the early stages of this work. We thank Masahiro Takada for insightful conversations in the first stages of the project, and Kyungjin Ahn, Kenji Hasegawa, Hayato Shimabukuro and Kenji Kadota for helpful discussions. We also thank Samuel J. Witte for his modified version of CosmoRec. This work was in part supported by the JSPS grant numbers 18K03616, 17H01110, 21H04467 and JST AIP Acceleration Research Grant JP20317829 and FOREST Program JPMJFR20352935. The work is also supported by JSPS Core- to-Core Program (JPJSCCA20200002). PVD is supported by the Spanish MINECO grants SEV-2014-0398 and FPA2017-85985-P, by the Generalitat Valenciana grant PROMETEO/2019/083, and by the European Union's Horizon 2020 research and innovation program under the Marie SkÅodowska-Curie grant agreements No. 690575 (InvisiblesPlus) and 674896 (Elusives). We have made use of the Python package Colossus (Diemer 2018). KI would like to thank the fruitful discussions in the YITP workshop “Brain-storming workshop on Primordial Black Holes and Gravitational Waves” (code No. YITP-X-21-02).
Footnotes
Note that early metal-free Pop III stars with molecular cooling could have lower virial temperatures, down to ∼103 K.
Note that some previous 21 cm forest calculations (Shimabukuro et al. 2014, 2020a, 2020b; Kawasaki et al. 2021) made use of the parameterization from Bullock et al. (2001), which shows a stronger dependence on redshift, and increases the optical depth at low impact parameters and halo masses. This thus provides an enhancement of the number of absorbers at large optical depths; see subsection 2.3.
Writing the cross-section in physical units gives the factor (1 + z)2 of Furlanetto and Loeb (2002).
Note that there are different conventions to define the Jeans mass, which differ by a factor of the order of |$\mathcal {O}(1)$|.
P. Villanueva-Domingo 2021, 21cmForest_PBH, doi:10.5281/zenodo.4707447 〈https://github.com/PabloVD/21cmForest_PBH〉.
Shot noise effects are also included for completeness in the initial linear power spectrum, but their effects are negligible since they affect scales smaller than the resolution of the simulations, 1.5 Mpc.
Kavanagh, B. J. 2019, bradkav/PBHbounds: Release version, doi:10.5281/zenodo.3538999 〈https://github.com/bradkav/PBHbounds〉.
Alternatively, one could also employ |$\sqrt{\Delta N^2_{\Lambda {\rm CDM}} + \Delta N^2_{\mathit{\rm PBH}}}$| instead of ΔNΛCDM + ΔNPBH, but since ΔNi are positive by definition, and the latter is always equal or larger than the former, we opt for equation (35) in order to be more conservative.



