-
PDF
- Split View
-
Views
-
Cite
Cite
Azizbek Matekov, Fangbin Meng, Shengbang Qian, Ildar Asfandiyarov, Linjia Li, Shuhrat Ehgamberdiev, Liying Zhu, New results on the two low-mass-ratio overcontact binaries V1309 Herculis and AS Coronae Borealis, Publications of the Astronomical Society of Japan, Volume 75, Issue 4, August 2023, Pages 701–712, https://doi.org/10.1093/pasj/psad030
Close - Share Icon Share
Abstract
We present new multi-color light curves of V1309 Her and AS CrB, which were observed by the 60 cm telescope located at the Maidanak Astronomical Observatory. Combined with the Large-Sky-Area Multi-Object Fiber Spectroscopic Telescope atmospheric parameters, we analyzed our BVRCIC light curves for both systems by employing the Wilson–Devinney program. Our results show that both systems are low-mass-ratio overcontact binaries (V1309 Her: q = 0.213, AS CrB: q = 0.16). AS CrB has a high fill-out factor, while that of V1309 Her is moderate. By adding our new times of minimum light, we found the periodic oscillations in their O − C curves, which could be explained by the light travel-time effect of the third bodies. The third lights detected during the light curve analysis support the existence of the third bodies in V1309 Her and AS CrB. Third bodies usually play an important role for the origin and evolution of the central pair by removing their angular momentum. With the angular momentum loss, a moderate-fill-out overcontact binary like V1309 Her will evolve to a deep one like AS CrB. AS CrB lies at the late evolutionary stage of contact binaries. A long-term period increase at a rate of dP/dt = 5.22(± 0.28) × 10−7 d yr−1 was detected in our O − C diagram analysis. When its orbital angular momentum is less than three times the total spin angular momentum, a system may finally evolve into a rapid-rotating single star.
1 Introduction
W UMa-type variables are contact binaries with both components filling their critical Roche lobes (Kopal 1955) and sharing a common convective envelope (Lucy 1968). Under the interaction, an EW-type light curve is generated, and the depths of the primary and secondary minima are usually equal because the temperatures of both components are relatively close due to their common convective envelope. Contact binaries are believed to be formed from detached binaries through the near-contact phase as the consequence of mass transfer and angular momentum loss, and will merge to form blue stragglers and FK Comae stars (Bradstreet & Guinan 1994; Qian et al. 2017, 2020). Therefore, contact binaries are natural laboratories for studying the mass and energy transfer, the system’s angular momentum loss, and the stars’ evolution and merging. This paper presents new results for the two contact binaries V1309 Her and AS CrB.
V1309 Her (=TIC193823999) is a totally eclipsing contact binary that was first discovered by the Robotic Optical Transient Search Experiment I (ROTSE-I; Akerlof et al. 2000). Its stellar atmospheric parameters and spectral type were given by the Large-Sky-Area Multi-Object Fiber Spectroscopic Telescope (LAMOST; Cui et al. 2012; Zhao et al. 2012) low-resolution spectrum observed on 2013 May 22, which is listed in table 1. The All-Sky Automated Survey for Supernovae (ASAS-SN; Jayasinghe et al. 2018) performed observations of V1309 Her during 2013–2018. Alton (2020) obtained light curves in the BVIC bands and analyzed the multi-color light curves using the Wilson–Devinney (W–D; Wilson & Devinney 1971; Wilson 1990, 2012; Wilson & Wyithe 2003) program. They concluded that the system is a W UMa-type binary with a mass ratio of q = 0.213, an overcontact degree of |$f = 23.4\%$|, and one dark spot for each component. In addition, the orbital period variation indicated the possible existence of a third body in the system.
| Name . | Teff . | log (g) . | [Fe/H] . | Type . | Date . |
|---|---|---|---|---|---|
| V1309 Her | 6237 K | 4.141 | −0.348 | F4 | 2013-05-22 |
| AS CrB | 6208 K | 4.190 | −0.541 | F0 | 2014-06-02 |
| 6166 K | 4.145 | −0.501 | F5 | 2019-05-30 |
| Name . | Teff . | log (g) . | [Fe/H] . | Type . | Date . |
|---|---|---|---|---|---|
| V1309 Her | 6237 K | 4.141 | −0.348 | F4 | 2013-05-22 |
| AS CrB | 6208 K | 4.190 | −0.541 | F0 | 2014-06-02 |
| 6166 K | 4.145 | −0.501 | F5 | 2019-05-30 |
| Name . | Teff . | log (g) . | [Fe/H] . | Type . | Date . |
|---|---|---|---|---|---|
| V1309 Her | 6237 K | 4.141 | −0.348 | F4 | 2013-05-22 |
| AS CrB | 6208 K | 4.190 | −0.541 | F0 | 2014-06-02 |
| 6166 K | 4.145 | −0.501 | F5 | 2019-05-30 |
| Name . | Teff . | log (g) . | [Fe/H] . | Type . | Date . |
|---|---|---|---|---|---|
| V1309 Her | 6237 K | 4.141 | −0.348 | F4 | 2013-05-22 |
| AS CrB | 6208 K | 4.190 | −0.541 | F0 | 2014-06-02 |
| 6166 K | 4.145 | −0.501 | F5 | 2019-05-30 |
AS CrB (=TIC458490358) was first discovered by ROTSE-I, and its charge-coupled device (CCD) light curve (without filter) was subsequently published by Blattler and Diethelm (2002), which showed that the system is a W UMa-type contact binary. They determined an orbital period of 0.380658 d and a number of times of minimum light. Liu et al. (2017) performed a multi-color light curve analysis and orbital period analysis of AS CrB. They found that the system is a low-mass-ratio deep-contact binary with a mass ratio of q = 0.172, an overcontact degree of |$f = 59.6\%$|, and a long-term increase in the orbital period. Its low-resolution spectra were observed by LAMOST on 2014 June 2 and 2019 May 30, and the relevant stellar atmospheric parameters are listed in table 1.
2 Observations and data reduction
New photometric observations of V1309 Her and AS CrB were carried out with the Carl Zeiss-600 (Southern) telescope in 2022 June at Maidanak Astronomical Observatory (MAO) of the Ulugh Beg Astronomical Institute of the Uzbekistan Academy of Science (Ehgamberdiev 2018). The optical system of the telescope is Cassegrain, and the focal length is 7200 mm. The Apogee Aspen CG230 2048 × 2048 CCD camera was used as the detector. The readout noise and gain of the CCD are 28.8 ADUs and 3.2e−, respectively, the effective field of view is |${14{^{\prime }_{.}}6} \times {14{^{\prime }_{.}}6}$|, and the pixel scale is |${0{^{\prime \prime}_{.}}429}$| per pixel. Image acquisition was done with MaxIm DL. The filter system was a standard Johnson–Cousins multi-color BVRCIC photometric system.
2.1 V1309 Her
We performed BVRCIC-band photometric observations of V1309 Her on 2022 July 1 and 2, with corresponding exposure times of 120, 90, 60, and 60 s. All CCD-observed images were processed by IRAF (Image Reduction and Analysis Facility) software, including flat-field, bias-field, dark current corrections, and aperture photometry processes. The coordinates of the variable star, the comparison star, and the check star are listed in table 2. Based on the photometric data, we obtained three new times of minimum light, which are listed in table 3. We converted time to phase with the linear ephemeris of |$\mathrm{Min.I(HJD)} = 2459762.42079 + {0{_{.}^{\circ}}3698847} \times E$|, and obtained a complete set of light curves. As can be seen in figure 1, V1309 Her is a totally eclipsing binary with an occultation time of about 41 min.
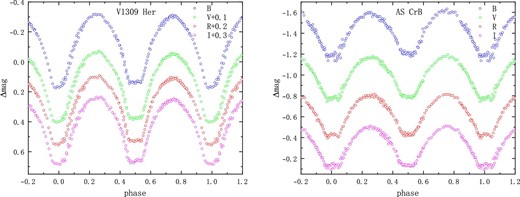
CCD photometric light curves in BVRCIC band for V1309 Her and AS CrB.
| Stars . | αJ2000.0 . | δJ2000.0 . |
|---|---|---|
| V1309 Her | |${17^{\rm h}55^{\rm m}35{^{\rm s}_{.}}84}$| | |$+43^{\circ }{48^{\prime}20{^{\prime \prime }_{.}}15}$| |
| Comparison | |${17^{\rm h}56^{\rm m}10{^{\rm s}_{.}}94}$| | |$+43^{\circ }{51^{\prime}14{^{\prime \prime }_{.}}38}$| |
| Check | |${17^{\rm h}56^{\rm m}12{^{\rm s}_{.}}48}$| | |$+43^{\circ }{52^{\prime}04{^{\prime \prime }_{.}}39}$| |
| AS CrB | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}50}$| | |$+35^{\circ }{12^{\prime}31{^{\prime \prime }_{.}}68}$| |
| Comparison | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}43}$| | |$+35^{\circ }{09^{\prime}48{^{\prime \prime }_{.}}59}$| |
| Check | |${16^{\rm h}00^{\rm m}34{^{\rm s}_{.}}73}$| | |$+35^{\circ }{11^{\prime}31{^{\prime \prime }_{.}}20}$| |
| Stars . | αJ2000.0 . | δJ2000.0 . |
|---|---|---|
| V1309 Her | |${17^{\rm h}55^{\rm m}35{^{\rm s}_{.}}84}$| | |$+43^{\circ }{48^{\prime}20{^{\prime \prime }_{.}}15}$| |
| Comparison | |${17^{\rm h}56^{\rm m}10{^{\rm s}_{.}}94}$| | |$+43^{\circ }{51^{\prime}14{^{\prime \prime }_{.}}38}$| |
| Check | |${17^{\rm h}56^{\rm m}12{^{\rm s}_{.}}48}$| | |$+43^{\circ }{52^{\prime}04{^{\prime \prime }_{.}}39}$| |
| AS CrB | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}50}$| | |$+35^{\circ }{12^{\prime}31{^{\prime \prime }_{.}}68}$| |
| Comparison | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}43}$| | |$+35^{\circ }{09^{\prime}48{^{\prime \prime }_{.}}59}$| |
| Check | |${16^{\rm h}00^{\rm m}34{^{\rm s}_{.}}73}$| | |$+35^{\circ }{11^{\prime}31{^{\prime \prime }_{.}}20}$| |
| Stars . | αJ2000.0 . | δJ2000.0 . |
|---|---|---|
| V1309 Her | |${17^{\rm h}55^{\rm m}35{^{\rm s}_{.}}84}$| | |$+43^{\circ }{48^{\prime}20{^{\prime \prime }_{.}}15}$| |
| Comparison | |${17^{\rm h}56^{\rm m}10{^{\rm s}_{.}}94}$| | |$+43^{\circ }{51^{\prime}14{^{\prime \prime }_{.}}38}$| |
| Check | |${17^{\rm h}56^{\rm m}12{^{\rm s}_{.}}48}$| | |$+43^{\circ }{52^{\prime}04{^{\prime \prime }_{.}}39}$| |
| AS CrB | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}50}$| | |$+35^{\circ }{12^{\prime}31{^{\prime \prime }_{.}}68}$| |
| Comparison | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}43}$| | |$+35^{\circ }{09^{\prime}48{^{\prime \prime }_{.}}59}$| |
| Check | |${16^{\rm h}00^{\rm m}34{^{\rm s}_{.}}73}$| | |$+35^{\circ }{11^{\prime}31{^{\prime \prime }_{.}}20}$| |
| Stars . | αJ2000.0 . | δJ2000.0 . |
|---|---|---|
| V1309 Her | |${17^{\rm h}55^{\rm m}35{^{\rm s}_{.}}84}$| | |$+43^{\circ }{48^{\prime}20{^{\prime \prime }_{.}}15}$| |
| Comparison | |${17^{\rm h}56^{\rm m}10{^{\rm s}_{.}}94}$| | |$+43^{\circ }{51^{\prime}14{^{\prime \prime }_{.}}38}$| |
| Check | |${17^{\rm h}56^{\rm m}12{^{\rm s}_{.}}48}$| | |$+43^{\circ }{52^{\prime}04{^{\prime \prime }_{.}}39}$| |
| AS CrB | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}50}$| | |$+35^{\circ }{12^{\prime}31{^{\prime \prime }_{.}}68}$| |
| Comparison | |${16^{\rm h}00^{\rm m}14{^{\rm s}_{.}}43}$| | |$+35^{\circ }{09^{\prime}48{^{\prime \prime }_{.}}59}$| |
| Check | |${16^{\rm h}00^{\rm m}34{^{\rm s}_{.}}73}$| | |$+35^{\circ }{11^{\prime}31{^{\prime \prime }_{.}}20}$| |
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51358.69650 | 0.00080 | P | −18752 | 0.036919 | (1) | 59001.76280 | 0.00019 | S | 1911.5 | −0.007213 | (15) | |
| 51364.79780 | 0.00090 | S | −18735.5 | 0.035123 | (1) | 59001.94850 | 0.00014 | P | 1912 | −0.006455 | (15) | |
| 53121.54670 | 0.00050 | P | −13986 | 0.017116 | (1) | 59002.13250 | 0.00018 | S | 1912.5 | −0.007397 | (15) | |
| 53143.37030 | 0.00190 | P | −13927 | 0.017524 | (1) | 59002.31850 | 0.00016 | P | 1913 | −0.006340 | (15) | |
| 53150.39810 | 0.00060 | P | −13908 | 0.017517 | (1) | 59002.50260 | 0.00018 | S | 1913.5 | −0.007182 | (15) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 59000.83880 | 0.00014 | P | 1909 | −0.006501 | (15) | 59035.05240 | 0.00018 | S | 2001.5 | −0.007227 | (15) | |
| 59001.02310 | 0.00018 | S | 1909.5 | −0.007144 | (15) | 59762.23647 | 0.00036 | S | 3967.5 | −0.016283 | (16) | |
| 59001.20870 | 0.00015 | P | 1910 | −0.006486 | (15) | 59762.42067 | 0.0003 | P | 3968 | −0.017025 | (16) | |
| 59001.39290 | 0.00019 | S | 1910.5 | −0.007228 | (15) | 59763.34532 | 0.00038 | S | 3970.5 | −0.017082 | (16) | |
| 59001.57870 | 0.00013 | P | 1911 | −0.006371 | (15) |
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51358.69650 | 0.00080 | P | −18752 | 0.036919 | (1) | 59001.76280 | 0.00019 | S | 1911.5 | −0.007213 | (15) | |
| 51364.79780 | 0.00090 | S | −18735.5 | 0.035123 | (1) | 59001.94850 | 0.00014 | P | 1912 | −0.006455 | (15) | |
| 53121.54670 | 0.00050 | P | −13986 | 0.017116 | (1) | 59002.13250 | 0.00018 | S | 1912.5 | −0.007397 | (15) | |
| 53143.37030 | 0.00190 | P | −13927 | 0.017524 | (1) | 59002.31850 | 0.00016 | P | 1913 | −0.006340 | (15) | |
| 53150.39810 | 0.00060 | P | −13908 | 0.017517 | (1) | 59002.50260 | 0.00018 | S | 1913.5 | −0.007182 | (15) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 59000.83880 | 0.00014 | P | 1909 | −0.006501 | (15) | 59035.05240 | 0.00018 | S | 2001.5 | −0.007227 | (15) | |
| 59001.02310 | 0.00018 | S | 1909.5 | −0.007144 | (15) | 59762.23647 | 0.00036 | S | 3967.5 | −0.016283 | (16) | |
| 59001.20870 | 0.00015 | P | 1910 | −0.006486 | (15) | 59762.42067 | 0.0003 | P | 3968 | −0.017025 | (16) | |
| 59001.39290 | 0.00019 | S | 1910.5 | −0.007228 | (15) | 59763.34532 | 0.00038 | S | 3970.5 | −0.017082 | (16) | |
| 59001.57870 | 0.00013 | P | 1911 | −0.006371 | (15) |
This is a sample of the full table, which can be obtained from 〈https://github.com/Fangbin-Meng/V1309-Her〉.
References: (1) Blattler and Diethelm (2004); (2) SuperWASP; (3) Diethelm (2006); (4) Diethelm (2007); (5) Diethelm (2008); (6) Nelson (2010); (7) Diethelm (2010); (8) Nelson (2011); (9) Hubscher (2014); (10) Hubscher and Lehmann (2015); (11) Hubscher (2017); (12) Lehký et al. (2021); (13) ASAS-SN; (14) Alton (2020); (15) TESS; (16) MAO.
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51358.69650 | 0.00080 | P | −18752 | 0.036919 | (1) | 59001.76280 | 0.00019 | S | 1911.5 | −0.007213 | (15) | |
| 51364.79780 | 0.00090 | S | −18735.5 | 0.035123 | (1) | 59001.94850 | 0.00014 | P | 1912 | −0.006455 | (15) | |
| 53121.54670 | 0.00050 | P | −13986 | 0.017116 | (1) | 59002.13250 | 0.00018 | S | 1912.5 | −0.007397 | (15) | |
| 53143.37030 | 0.00190 | P | −13927 | 0.017524 | (1) | 59002.31850 | 0.00016 | P | 1913 | −0.006340 | (15) | |
| 53150.39810 | 0.00060 | P | −13908 | 0.017517 | (1) | 59002.50260 | 0.00018 | S | 1913.5 | −0.007182 | (15) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 59000.83880 | 0.00014 | P | 1909 | −0.006501 | (15) | 59035.05240 | 0.00018 | S | 2001.5 | −0.007227 | (15) | |
| 59001.02310 | 0.00018 | S | 1909.5 | −0.007144 | (15) | 59762.23647 | 0.00036 | S | 3967.5 | −0.016283 | (16) | |
| 59001.20870 | 0.00015 | P | 1910 | −0.006486 | (15) | 59762.42067 | 0.0003 | P | 3968 | −0.017025 | (16) | |
| 59001.39290 | 0.00019 | S | 1910.5 | −0.007228 | (15) | 59763.34532 | 0.00038 | S | 3970.5 | −0.017082 | (16) | |
| 59001.57870 | 0.00013 | P | 1911 | −0.006371 | (15) |
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51358.69650 | 0.00080 | P | −18752 | 0.036919 | (1) | 59001.76280 | 0.00019 | S | 1911.5 | −0.007213 | (15) | |
| 51364.79780 | 0.00090 | S | −18735.5 | 0.035123 | (1) | 59001.94850 | 0.00014 | P | 1912 | −0.006455 | (15) | |
| 53121.54670 | 0.00050 | P | −13986 | 0.017116 | (1) | 59002.13250 | 0.00018 | S | 1912.5 | −0.007397 | (15) | |
| 53143.37030 | 0.00190 | P | −13927 | 0.017524 | (1) | 59002.31850 | 0.00016 | P | 1913 | −0.006340 | (15) | |
| 53150.39810 | 0.00060 | P | −13908 | 0.017517 | (1) | 59002.50260 | 0.00018 | S | 1913.5 | −0.007182 | (15) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 59000.83880 | 0.00014 | P | 1909 | −0.006501 | (15) | 59035.05240 | 0.00018 | S | 2001.5 | −0.007227 | (15) | |
| 59001.02310 | 0.00018 | S | 1909.5 | −0.007144 | (15) | 59762.23647 | 0.00036 | S | 3967.5 | −0.016283 | (16) | |
| 59001.20870 | 0.00015 | P | 1910 | −0.006486 | (15) | 59762.42067 | 0.0003 | P | 3968 | −0.017025 | (16) | |
| 59001.39290 | 0.00019 | S | 1910.5 | −0.007228 | (15) | 59763.34532 | 0.00038 | S | 3970.5 | −0.017082 | (16) | |
| 59001.57870 | 0.00013 | P | 1911 | −0.006371 | (15) |
This is a sample of the full table, which can be obtained from 〈https://github.com/Fangbin-Meng/V1309-Her〉.
References: (1) Blattler and Diethelm (2004); (2) SuperWASP; (3) Diethelm (2006); (4) Diethelm (2007); (5) Diethelm (2008); (6) Nelson (2010); (7) Diethelm (2010); (8) Nelson (2011); (9) Hubscher (2014); (10) Hubscher and Lehmann (2015); (11) Hubscher (2017); (12) Lehký et al. (2021); (13) ASAS-SN; (14) Alton (2020); (15) TESS; (16) MAO.
2.2 AS CrB
We conducted a three-day BVRCIC multi-band observation of AS CrB on 2022 June 7, 9, and 13, which finally formed a set of completed light curves. Four new CCD times of minimum light were obtained, as listed in table 4. The phase was calculated using the linear ephemeris formula of |$\mathrm{Min.I(HJD)} = 2459740.245785 + {0{_{.}^{\circ}}380662479}\times E$|. The complete light curves in the BVRCIC bands are shown in figure 1. The light curves show flat bottoms in the minima, indicating that AS CrB is a totally eclipsing system with a duration of about 43 min. The photometric data for V1309 Her and AS CrB can be accessed from GitHub.1
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51291.83390 | 0.00040 | P | −12398 | 0.024684 | (1) | 58977.76966 | 0.00012 | P | 7793 | 0.031371 | (28) | |
| 51305.73100 | 0.00020 | S | −12361.5 | 0.027652 | (1) | 58977.96056 | 0.00015 | S | 7793.5 | 0.031940 | (28) | |
| 52360.53210 | 0.00080 | S | −9590.5 | 0.016733 | (1) | 58978.15028 | 0.00011 | P | 7794 | 0.031330 | (28) | |
| 52365.47920 | 0.00090 | S | −9577.5 | 0.015238 | (1) | 58978.34114 | 0.00015 | S | 7794.5 | 0.031859 | (28) | |
| 52368.34100 | 0.00060 | P | −9570 | 0.022080 | (1) | 58978.53078 | 0.00012 | P | 7795 | 0.031168 | (28) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 58976.81866 | 0.00015 | S | 7790.5 | 0.032024 | (28) | 59328.55650 | 0.00100 | S | 8714.5 | 0.038965 | (30) | |
| 58977.00819 | 0.00013 | P | 7791 | 0.031223 | (28) | 59740.24578 | 0.00072 | P | 9796 | 0.043228 | (31) | |
| 58977.19936 | 0.00015 | S | 7791.5 | 0.032063 | (28) | 59740.43834 | 0.00049 | S | 9796.5 | 0.045449 | (31) | |
| 58977.38908 | 0.00012 | P | 7792 | 0.031452 | (28) | 59744.24177 | 0.00039 | S | 9806.5 | 0.042268 | (31) | |
| 58977.57980 | 0.00016 | S | 7792.5 | 0.031841 | (28) | 59744.43389 | 0.00037 | P | 9807 | 0.044063 | (31) |
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51291.83390 | 0.00040 | P | −12398 | 0.024684 | (1) | 58977.76966 | 0.00012 | P | 7793 | 0.031371 | (28) | |
| 51305.73100 | 0.00020 | S | −12361.5 | 0.027652 | (1) | 58977.96056 | 0.00015 | S | 7793.5 | 0.031940 | (28) | |
| 52360.53210 | 0.00080 | S | −9590.5 | 0.016733 | (1) | 58978.15028 | 0.00011 | P | 7794 | 0.031330 | (28) | |
| 52365.47920 | 0.00090 | S | −9577.5 | 0.015238 | (1) | 58978.34114 | 0.00015 | S | 7794.5 | 0.031859 | (28) | |
| 52368.34100 | 0.00060 | P | −9570 | 0.022080 | (1) | 58978.53078 | 0.00012 | P | 7795 | 0.031168 | (28) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 58976.81866 | 0.00015 | S | 7790.5 | 0.032024 | (28) | 59328.55650 | 0.00100 | S | 8714.5 | 0.038965 | (30) | |
| 58977.00819 | 0.00013 | P | 7791 | 0.031223 | (28) | 59740.24578 | 0.00072 | P | 9796 | 0.043228 | (31) | |
| 58977.19936 | 0.00015 | S | 7791.5 | 0.032063 | (28) | 59740.43834 | 0.00049 | S | 9796.5 | 0.045449 | (31) | |
| 58977.38908 | 0.00012 | P | 7792 | 0.031452 | (28) | 59744.24177 | 0.00039 | S | 9806.5 | 0.042268 | (31) | |
| 58977.57980 | 0.00016 | S | 7792.5 | 0.031841 | (28) | 59744.43389 | 0.00037 | P | 9807 | 0.044063 | (31) |
This is a sample of the full table, which can be obtained from 〈https://github.com/Fangbin-Meng/AS-CrB〉.
References: (1) Blattler and Diethelm (2002); (2) Diethelm (2004); (3) Diethelm (2005); (4) Diethelm (2006); (5) Diethelm (2007); (6) Nagai (2009); (7) Diethelm (2009); (8) Hubscher et al. (2010); (9) Nelson (2010); (10) Diethelm (2009); (11) Hubscher and Monninger (2011); (12) Diethelm (2010); (13) Diethelm (2010); (14) Nagai (2012); (15) Diethelm (2011); (16) Liu et al. (2017); (17) Nagai (2013); (18) Diethelm (2012); (19) Nelson (2014); (20) Hoňková et al. (2013); (21) Hubscher and Lehmann (2015); (22) Nelson (2016); (23) Hubscher (2017); (24) Nelson (2017); (25) Nagai (2018); (26) Paschke (2019); (27) Pagel (2021); (28) TESS; (29) Nagai (2022); (30) Pagel (2022); (31) MAO.
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51291.83390 | 0.00040 | P | −12398 | 0.024684 | (1) | 58977.76966 | 0.00012 | P | 7793 | 0.031371 | (28) | |
| 51305.73100 | 0.00020 | S | −12361.5 | 0.027652 | (1) | 58977.96056 | 0.00015 | S | 7793.5 | 0.031940 | (28) | |
| 52360.53210 | 0.00080 | S | −9590.5 | 0.016733 | (1) | 58978.15028 | 0.00011 | P | 7794 | 0.031330 | (28) | |
| 52365.47920 | 0.00090 | S | −9577.5 | 0.015238 | (1) | 58978.34114 | 0.00015 | S | 7794.5 | 0.031859 | (28) | |
| 52368.34100 | 0.00060 | P | −9570 | 0.022080 | (1) | 58978.53078 | 0.00012 | P | 7795 | 0.031168 | (28) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 58976.81866 | 0.00015 | S | 7790.5 | 0.032024 | (28) | 59328.55650 | 0.00100 | S | 8714.5 | 0.038965 | (30) | |
| 58977.00819 | 0.00013 | P | 7791 | 0.031223 | (28) | 59740.24578 | 0.00072 | P | 9796 | 0.043228 | (31) | |
| 58977.19936 | 0.00015 | S | 7791.5 | 0.032063 | (28) | 59740.43834 | 0.00049 | S | 9796.5 | 0.045449 | (31) | |
| 58977.38908 | 0.00012 | P | 7792 | 0.031452 | (28) | 59744.24177 | 0.00039 | S | 9806.5 | 0.042268 | (31) | |
| 58977.57980 | 0.00016 | S | 7792.5 | 0.031841 | (28) | 59744.43389 | 0.00037 | P | 9807 | 0.044063 | (31) |
| HJD . | Error . | Min. . | E . | O − C . | Ref.† . | . | HJD . | Error . | Min. . | E . | O − C . | Ref.† . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ . | (±d) . | P/S . | . | (d) . | . | . | 2400000+ . | (±d) . | P/S . | . | (d) . | . |
| 51291.83390 | 0.00040 | P | −12398 | 0.024684 | (1) | 58977.76966 | 0.00012 | P | 7793 | 0.031371 | (28) | |
| 51305.73100 | 0.00020 | S | −12361.5 | 0.027652 | (1) | 58977.96056 | 0.00015 | S | 7793.5 | 0.031940 | (28) | |
| 52360.53210 | 0.00080 | S | −9590.5 | 0.016733 | (1) | 58978.15028 | 0.00011 | P | 7794 | 0.031330 | (28) | |
| 52365.47920 | 0.00090 | S | −9577.5 | 0.015238 | (1) | 58978.34114 | 0.00015 | S | 7794.5 | 0.031859 | (28) | |
| 52368.34100 | 0.00060 | P | −9570 | 0.022080 | (1) | 58978.53078 | 0.00012 | P | 7795 | 0.031168 | (28) | |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | |
| 58976.81866 | 0.00015 | S | 7790.5 | 0.032024 | (28) | 59328.55650 | 0.00100 | S | 8714.5 | 0.038965 | (30) | |
| 58977.00819 | 0.00013 | P | 7791 | 0.031223 | (28) | 59740.24578 | 0.00072 | P | 9796 | 0.043228 | (31) | |
| 58977.19936 | 0.00015 | S | 7791.5 | 0.032063 | (28) | 59740.43834 | 0.00049 | S | 9796.5 | 0.045449 | (31) | |
| 58977.38908 | 0.00012 | P | 7792 | 0.031452 | (28) | 59744.24177 | 0.00039 | S | 9806.5 | 0.042268 | (31) | |
| 58977.57980 | 0.00016 | S | 7792.5 | 0.031841 | (28) | 59744.43389 | 0.00037 | P | 9807 | 0.044063 | (31) |
This is a sample of the full table, which can be obtained from 〈https://github.com/Fangbin-Meng/AS-CrB〉.
References: (1) Blattler and Diethelm (2002); (2) Diethelm (2004); (3) Diethelm (2005); (4) Diethelm (2006); (5) Diethelm (2007); (6) Nagai (2009); (7) Diethelm (2009); (8) Hubscher et al. (2010); (9) Nelson (2010); (10) Diethelm (2009); (11) Hubscher and Monninger (2011); (12) Diethelm (2010); (13) Diethelm (2010); (14) Nagai (2012); (15) Diethelm (2011); (16) Liu et al. (2017); (17) Nagai (2013); (18) Diethelm (2012); (19) Nelson (2014); (20) Hoňková et al. (2013); (21) Hubscher and Lehmann (2015); (22) Nelson (2016); (23) Hubscher (2017); (24) Nelson (2017); (25) Nagai (2018); (26) Paschke (2019); (27) Pagel (2021); (28) TESS; (29) Nagai (2022); (30) Pagel (2022); (31) MAO.
3 Orbital period variations
3.1 Orbital period analysis of V1309 Her
Alton (2020) collected the times of minima of V1309 Her up to the year 2018 and found a long-term increase and periodic oscillation in the orbital period. We obtained 273 new light minimum times by least squares parabolic fitting, of which 260 mid-eclipse times were from TESS, 3 eclipse times were from MAO, and 10 times of minima were from ASAS-SN. The new eclipse times extend the O − C curve of V1309 Her and reveal that the long-term increase in the orbital period discovered by Alton (2020) does not exist. All the times of minima, together with those collected in the literature, are listed in table 3. With the linear ephemeris from Alton (2020),
the O − C values were calculated and the corresponding O − C diagram is shown in the upper panel of figure 2. The O − C values derived from the new light minimum times are represented by red dots, while the others are represented by black squares. As shown in the figure, the O − C curve exhibits a linear variation coupled with a periodic variation. Periodic oscillation may be caused by the light-travel-time effect (LTTE) of the third body (Liao & Qian 2010). We fitted the periodic variation with a sine (i.e., circular orbit) and derived the following equation:
The sinusoidal term in equation (2) indicates the amplitude of the periodic oscillation A = 0.007258(±0.001494) d and the oscillation period P = 26.428(±2.677) yr. The fitting results and fitting residuals are shown in the middle and bottom panels of figure 2, respectively. As the residuals show some deviations, the case of eccentric orbits was also considered. We used the following general equation to fit the eccentric orbit (Irwin 1952):
Here, |$A=a_{12}\sin {i_3}/c$| is the semi-amplitude of the periodic oscillation, a12 is the orbital semi-major axis of the binary in the triple system, i3 is the orbital inclination of the third body, e3 is the orbital eccentricity of the third body, ω is the longitude of the periastron, ν is the true anomaly, and E* is the eccentric anomaly. The eccentric orbit fitting results are shown in figure 3, and the parameters for both cases (circular and eccentric orbits) are listed in table 5.
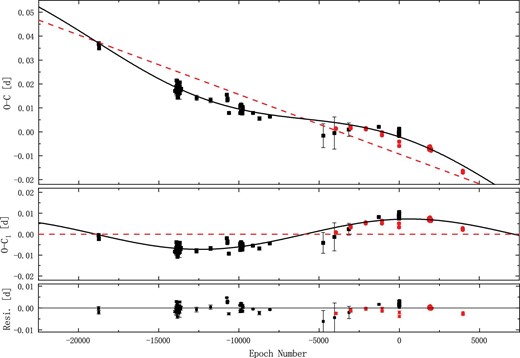
O − C diagram of V1309 Her (circular orbit). The red dots are the new eclipse times, and the black dots are the same as Alton (2020). The solid black line in the upper panel represents the linear fit (red dashed line) plus the sine fit. The solid black line in the middle panel represents the sine fit after removing the linear trend. The bottom panel shows the residuals after removing the two variations.
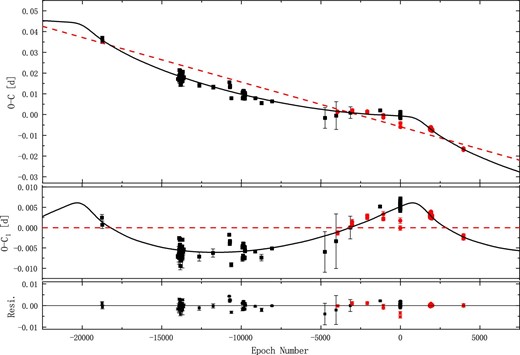
O − C diagram of V1309 Her (eccentric orbit). The Symbols are the same as figure 2. The solid black line in the upper panel represents the linear fit (red dashed line) plus the sine fit. The solid black line in the middle panel represents the eccentric orbit fit after removing the linear trend. The bottom panel shows the residuals after removing the two variations.
| . | V1309 Her . | AS CrB . | |
|---|---|---|---|
| Parameter . | Circular orbit . | Eccentric orbit . | Circular orbit . |
| Revised epoch, HJD0 (d) | 2458294.72631(146) | 2458294.72972(69) | 2456011.24856(34) |
| Revised period, P0 (d) | 0.3698821(3) | 0.3698824(7) | 0.380662479(13) |
| Eccentricity, e3 | 0 | 0.7297(±0.1123) | 0 |
| Amplitude, A (d) | 0.007258(±0.001494) | 0.0065693(±0.0005931) | 0.00343(31) |
| Orbital period, P3 (yr) | 26.428(±2.677) | 21.359(±0.588) | 18.031(±0.912) |
| Projected semi-major axis, a12sin (i3) (au) | 1.256(±0.257) | 1.137(±0.102) | 0.594(±0.053) |
| Longitude of periastron passage, ω (rad) | — | 2.11(±0.120) | — |
| Mass function, f (m) | 0.0028 M⊙ | 0.0032 M⊙ | 0.00064 M⊙ |
| . | V1309 Her . | AS CrB . | |
|---|---|---|---|
| Parameter . | Circular orbit . | Eccentric orbit . | Circular orbit . |
| Revised epoch, HJD0 (d) | 2458294.72631(146) | 2458294.72972(69) | 2456011.24856(34) |
| Revised period, P0 (d) | 0.3698821(3) | 0.3698824(7) | 0.380662479(13) |
| Eccentricity, e3 | 0 | 0.7297(±0.1123) | 0 |
| Amplitude, A (d) | 0.007258(±0.001494) | 0.0065693(±0.0005931) | 0.00343(31) |
| Orbital period, P3 (yr) | 26.428(±2.677) | 21.359(±0.588) | 18.031(±0.912) |
| Projected semi-major axis, a12sin (i3) (au) | 1.256(±0.257) | 1.137(±0.102) | 0.594(±0.053) |
| Longitude of periastron passage, ω (rad) | — | 2.11(±0.120) | — |
| Mass function, f (m) | 0.0028 M⊙ | 0.0032 M⊙ | 0.00064 M⊙ |
| . | V1309 Her . | AS CrB . | |
|---|---|---|---|
| Parameter . | Circular orbit . | Eccentric orbit . | Circular orbit . |
| Revised epoch, HJD0 (d) | 2458294.72631(146) | 2458294.72972(69) | 2456011.24856(34) |
| Revised period, P0 (d) | 0.3698821(3) | 0.3698824(7) | 0.380662479(13) |
| Eccentricity, e3 | 0 | 0.7297(±0.1123) | 0 |
| Amplitude, A (d) | 0.007258(±0.001494) | 0.0065693(±0.0005931) | 0.00343(31) |
| Orbital period, P3 (yr) | 26.428(±2.677) | 21.359(±0.588) | 18.031(±0.912) |
| Projected semi-major axis, a12sin (i3) (au) | 1.256(±0.257) | 1.137(±0.102) | 0.594(±0.053) |
| Longitude of periastron passage, ω (rad) | — | 2.11(±0.120) | — |
| Mass function, f (m) | 0.0028 M⊙ | 0.0032 M⊙ | 0.00064 M⊙ |
| . | V1309 Her . | AS CrB . | |
|---|---|---|---|
| Parameter . | Circular orbit . | Eccentric orbit . | Circular orbit . |
| Revised epoch, HJD0 (d) | 2458294.72631(146) | 2458294.72972(69) | 2456011.24856(34) |
| Revised period, P0 (d) | 0.3698821(3) | 0.3698824(7) | 0.380662479(13) |
| Eccentricity, e3 | 0 | 0.7297(±0.1123) | 0 |
| Amplitude, A (d) | 0.007258(±0.001494) | 0.0065693(±0.0005931) | 0.00343(31) |
| Orbital period, P3 (yr) | 26.428(±2.677) | 21.359(±0.588) | 18.031(±0.912) |
| Projected semi-major axis, a12sin (i3) (au) | 1.256(±0.257) | 1.137(±0.102) | 0.594(±0.053) |
| Longitude of periastron passage, ω (rad) | — | 2.11(±0.120) | — |
| Mass function, f (m) | 0.0028 M⊙ | 0.0032 M⊙ | 0.00064 M⊙ |
3.2 Orbital period analysis of AS CrB
For AS CrB, we collected 52 mid-eclipse times from the literature. In addition, we obtained 266 new eclipse times, with 262 from TESS and 4 from the MAO 60 cm telescope. All the light minimum times are listed in table 4. The initial linear ephemeris was from Liu et al. (2017),
The corresponding O − C curve is shown in the upper panel of figure 4. In figure 4, we can see that in addition to the upward parabolic trend, there is a periodic oscillation that was not found in the previous study. After removing the parabola and periodic variation, the final residuals are shown in the bottom panel of figure 4. A new ephemeris formula was obtained:
The quadratic term in equation (5) indicates that the orbital period is increasing at a rate of dP/dt = 5.22(±0.28) × 10−7 d yr−1, which may be due to the mass transfer from the less massive component to the more massive one. The sinusoidal term represents the periodic variation of the orbital period with amplitude A = 0.00343(±0.00031) d and period P = 18.031(±0.912) yr. The orbital parameters of the third body are listed in table 5.
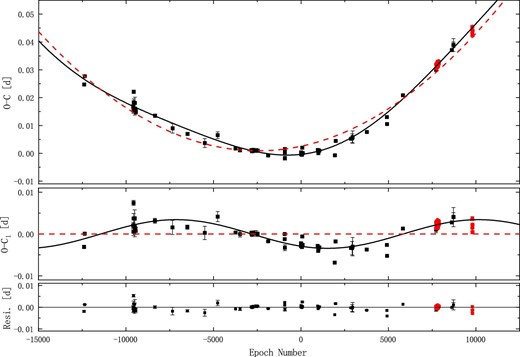
O − C diagram of AS CrB. The red dots represent the new eclipse times. The solid black line in the upper panel represents the parabolic fit (red dashed line) plus the sine fit. The solid black line in the middle panel represents the sine fit after removing the parabolic trend. The bottom panel shows the residuals after removing the two variations.
4 Light-curve solutions
We obtained new complete multi-filter light curves of V1309 Her and AS CrB. As shown in the previous section, the light curves of both systems display total eclipses, which enables us to determine reliable orbital parameters by photometric analysis (Terrell & Wilson 2005). Thus we analyzed these light curves with the W–D program. Before running the W–D program, we first need to determine several parameters.
4.1 V1309 Her
For V1309 Her, the temperature of star 1 (the star eclipsed at primary light minimum) was fixed at 6237 K according to the LAMOST spectrum. As V1309 Her is a late-type binary system, the gravity-darkening coefficients g1 = g2 = 0.32 (Lucy 1967) and the bolometric albedo A1 = A2 = 0.5 (Ruciński 1969) were applied for the convective envelopes. The bolometric and bandpass limb-darkening coefficients were derived from van Hamme (1993). Mode 3 (contact model) was selected. In addition, there are a number of adjustable parameters, including the orbital inclination i, the mass ratio q, the mean surface temperature T2 of star 2, the dimensionless surface potential (Ω1 = Ω2 for mode 3), and the monochromatic luminosity L1 of star 1. Due to the lack of a radial velocity curve, the q-search method was used to determine the mass ratio q. We set the search range of the mass ratio q between 0.1 and 0.5, and obtained the corresponding convergent solutions and the sum of weighted square deviations Σ. The q-search results are shown in figure 5, where the minimum value of Σ corresponds to a mass ratio of q = 0.213. We then adopted q = 0.213 as the initial value to obtain the photometric solution. The W–D-fitted theoretical light curves (solid line) are shown in the left panel of figure 6. The fitted curves deviate from the observed curves at the light maximum and minimum. One of the methods commonly used for the asymmetry of the light curve is the dark model. At the light minima, the theoretical light curves deviate differently in different bands, implying the possible existence of a third body. Therefore, we added a dark spot on star 1 to improve the fit at the maximum and applied the third light model to improve the fit at the minimum, as shown in the right panel of figure 6. The fitted parameters are listed in table 6.
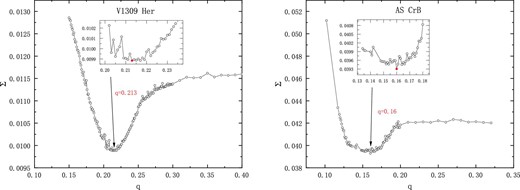
q-search curves for V1309 Her and AS CrB. Left panel: Lowest value of Σ for V1309 Her corresponds to q = 0.213. Right panel: Lowest value of Σ for AS CrB corresponds to q = 0.16.

Theoretical and observational light curves of V1309 Her. Left panel: Photometric solution wihtout spot and third light. Right panel: Photometric solution with a spot (star 1) and third light. The hollow circles represent the observed data and the multi-color curves represent the theoretical curves for the different bands.
| Parameters . | Without spot and L3 . | With spot and L3 . | Alton (2020) . |
|---|---|---|---|
| q | 0.2130(23) | 0.2713(48) | 0.213(1) |
| i |$(^{\circ})$| | 80.19(44) | 89.82(45) | 82.3(2) |
| T1 (K) | 6237 | 6237 | 6196 |
| T2/T1 | 1.0035(16) | 1.0199(17) | 1.02162(32) |
| Ω1 = Ω2 | 2.2167(63) | 2.3163(79) | 2.232(2) |
| L1B/(L1B + L2B) | 0.79019(48) | 0.7268(40) | 0.7780(2) |
| L1V/(L1V + L2V) | 0.79205(45) | 0.78751(30) | 0.7835(1) |
| |$L_{1 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}})$| | 0.79308(49) | 0.7406(39) | — |
| |$L_{1 I_{\rm C}} /(L_{1 I_{\rm C}}+L_{2 I_{\rm C}})$| | 0.79396(55) | 0.7446(41) | 0.7884(1) |
| r1 (pole) | 0.4939(11) | 0.4823(10) | 0.4899(3) |
| r1 (side) | 0.5401(15) | 0.5259(14) | 0.5343(5) |
| r1 (back) | 0.5667(16) | 0.5574(16) | 0.5596(5) |
| r2 (pole) | 0.2496(46) | 0.2760(64) | 0.2452(9) |
| r2 (side) | 0.2614(56) | 0.2907(80) | 0.2562(11) |
| r2 (back) | 0.307(12) | 0.347(20) | 0.2963(22) |
| f | 0.355(46) | 0.503(46) | 0.234 |
| ρ1 (g cm−3) | 0.748 | 0.758 | — |
| ρ2 (g cm−3) | 1.183 | 1.061 | — |
| Spot latitude ϕ (rad) | — | 1.58433 | 1.5184 |
| Spot longitude θ (rad) | — | 0.31769 | 3.0892 |
| Spot size rs (rad) | — | 0.26726 | 0.2443 |
| Ts/T* | — | 0.89026 | 0.83 |
| L3B/(L1B + L2B + L3B) | — | 0.1812(89) | — |
| L3V/(L1V + L2V + L3V) | — | 0.1421(99) | — |
| |$L_{3 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}})$| | — | 0.127(11) | — |
| |$L_{3 I_{\mathrm{C}}} /(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}})$| | — | 0.107(13) | — |
| Σ | 0.0093 | 0.00458 | 0.00808 |
| Parameters . | Without spot and L3 . | With spot and L3 . | Alton (2020) . |
|---|---|---|---|
| q | 0.2130(23) | 0.2713(48) | 0.213(1) |
| i |$(^{\circ})$| | 80.19(44) | 89.82(45) | 82.3(2) |
| T1 (K) | 6237 | 6237 | 6196 |
| T2/T1 | 1.0035(16) | 1.0199(17) | 1.02162(32) |
| Ω1 = Ω2 | 2.2167(63) | 2.3163(79) | 2.232(2) |
| L1B/(L1B + L2B) | 0.79019(48) | 0.7268(40) | 0.7780(2) |
| L1V/(L1V + L2V) | 0.79205(45) | 0.78751(30) | 0.7835(1) |
| |$L_{1 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}})$| | 0.79308(49) | 0.7406(39) | — |
| |$L_{1 I_{\rm C}} /(L_{1 I_{\rm C}}+L_{2 I_{\rm C}})$| | 0.79396(55) | 0.7446(41) | 0.7884(1) |
| r1 (pole) | 0.4939(11) | 0.4823(10) | 0.4899(3) |
| r1 (side) | 0.5401(15) | 0.5259(14) | 0.5343(5) |
| r1 (back) | 0.5667(16) | 0.5574(16) | 0.5596(5) |
| r2 (pole) | 0.2496(46) | 0.2760(64) | 0.2452(9) |
| r2 (side) | 0.2614(56) | 0.2907(80) | 0.2562(11) |
| r2 (back) | 0.307(12) | 0.347(20) | 0.2963(22) |
| f | 0.355(46) | 0.503(46) | 0.234 |
| ρ1 (g cm−3) | 0.748 | 0.758 | — |
| ρ2 (g cm−3) | 1.183 | 1.061 | — |
| Spot latitude ϕ (rad) | — | 1.58433 | 1.5184 |
| Spot longitude θ (rad) | — | 0.31769 | 3.0892 |
| Spot size rs (rad) | — | 0.26726 | 0.2443 |
| Ts/T* | — | 0.89026 | 0.83 |
| L3B/(L1B + L2B + L3B) | — | 0.1812(89) | — |
| L3V/(L1V + L2V + L3V) | — | 0.1421(99) | — |
| |$L_{3 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}})$| | — | 0.127(11) | — |
| |$L_{3 I_{\mathrm{C}}} /(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}})$| | — | 0.107(13) | — |
| Σ | 0.0093 | 0.00458 | 0.00808 |
| Parameters . | Without spot and L3 . | With spot and L3 . | Alton (2020) . |
|---|---|---|---|
| q | 0.2130(23) | 0.2713(48) | 0.213(1) |
| i |$(^{\circ})$| | 80.19(44) | 89.82(45) | 82.3(2) |
| T1 (K) | 6237 | 6237 | 6196 |
| T2/T1 | 1.0035(16) | 1.0199(17) | 1.02162(32) |
| Ω1 = Ω2 | 2.2167(63) | 2.3163(79) | 2.232(2) |
| L1B/(L1B + L2B) | 0.79019(48) | 0.7268(40) | 0.7780(2) |
| L1V/(L1V + L2V) | 0.79205(45) | 0.78751(30) | 0.7835(1) |
| |$L_{1 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}})$| | 0.79308(49) | 0.7406(39) | — |
| |$L_{1 I_{\rm C}} /(L_{1 I_{\rm C}}+L_{2 I_{\rm C}})$| | 0.79396(55) | 0.7446(41) | 0.7884(1) |
| r1 (pole) | 0.4939(11) | 0.4823(10) | 0.4899(3) |
| r1 (side) | 0.5401(15) | 0.5259(14) | 0.5343(5) |
| r1 (back) | 0.5667(16) | 0.5574(16) | 0.5596(5) |
| r2 (pole) | 0.2496(46) | 0.2760(64) | 0.2452(9) |
| r2 (side) | 0.2614(56) | 0.2907(80) | 0.2562(11) |
| r2 (back) | 0.307(12) | 0.347(20) | 0.2963(22) |
| f | 0.355(46) | 0.503(46) | 0.234 |
| ρ1 (g cm−3) | 0.748 | 0.758 | — |
| ρ2 (g cm−3) | 1.183 | 1.061 | — |
| Spot latitude ϕ (rad) | — | 1.58433 | 1.5184 |
| Spot longitude θ (rad) | — | 0.31769 | 3.0892 |
| Spot size rs (rad) | — | 0.26726 | 0.2443 |
| Ts/T* | — | 0.89026 | 0.83 |
| L3B/(L1B + L2B + L3B) | — | 0.1812(89) | — |
| L3V/(L1V + L2V + L3V) | — | 0.1421(99) | — |
| |$L_{3 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}})$| | — | 0.127(11) | — |
| |$L_{3 I_{\mathrm{C}}} /(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}})$| | — | 0.107(13) | — |
| Σ | 0.0093 | 0.00458 | 0.00808 |
| Parameters . | Without spot and L3 . | With spot and L3 . | Alton (2020) . |
|---|---|---|---|
| q | 0.2130(23) | 0.2713(48) | 0.213(1) |
| i |$(^{\circ})$| | 80.19(44) | 89.82(45) | 82.3(2) |
| T1 (K) | 6237 | 6237 | 6196 |
| T2/T1 | 1.0035(16) | 1.0199(17) | 1.02162(32) |
| Ω1 = Ω2 | 2.2167(63) | 2.3163(79) | 2.232(2) |
| L1B/(L1B + L2B) | 0.79019(48) | 0.7268(40) | 0.7780(2) |
| L1V/(L1V + L2V) | 0.79205(45) | 0.78751(30) | 0.7835(1) |
| |$L_{1 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}})$| | 0.79308(49) | 0.7406(39) | — |
| |$L_{1 I_{\rm C}} /(L_{1 I_{\rm C}}+L_{2 I_{\rm C}})$| | 0.79396(55) | 0.7446(41) | 0.7884(1) |
| r1 (pole) | 0.4939(11) | 0.4823(10) | 0.4899(3) |
| r1 (side) | 0.5401(15) | 0.5259(14) | 0.5343(5) |
| r1 (back) | 0.5667(16) | 0.5574(16) | 0.5596(5) |
| r2 (pole) | 0.2496(46) | 0.2760(64) | 0.2452(9) |
| r2 (side) | 0.2614(56) | 0.2907(80) | 0.2562(11) |
| r2 (back) | 0.307(12) | 0.347(20) | 0.2963(22) |
| f | 0.355(46) | 0.503(46) | 0.234 |
| ρ1 (g cm−3) | 0.748 | 0.758 | — |
| ρ2 (g cm−3) | 1.183 | 1.061 | — |
| Spot latitude ϕ (rad) | — | 1.58433 | 1.5184 |
| Spot longitude θ (rad) | — | 0.31769 | 3.0892 |
| Spot size rs (rad) | — | 0.26726 | 0.2443 |
| Ts/T* | — | 0.89026 | 0.83 |
| L3B/(L1B + L2B + L3B) | — | 0.1812(89) | — |
| L3V/(L1V + L2V + L3V) | — | 0.1421(99) | — |
| |$L_{3 R_{\rm C}} /(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}})$| | — | 0.127(11) | — |
| |$L_{3 I_{\mathrm{C}}} /(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}})$| | — | 0.107(13) | — |
| Σ | 0.0093 | 0.00458 | 0.00808 |
4.2 AS CrB
For AS CrB, the average temperature of LAMOST, 6187 K, was used for the temperature of star 1. For the convective envelope, the gravity-darkening coefficients g1 = g2 = 0.32 (Lucy 1967) and the bolometric albedo A1 = A2 = 0.5 (Ruciński 1969) are used to perform the W–D analysis. We chose a mass ratio search range from 0.05 to 0.32. The relationship between the mass ratio q and the sum of weighted square deviations Σ is plotted in figure 5, where the minimum value of Σ corresponds to a mass ratio of q = 0.16. According to the shape of the light curves, mode 3 was selected. We chose q = 0.16 as the initial value and set the mass ratio as an adjustable parameter. The photometric solution obtained is listed in table 7. The W–D-fitted light curves are shown as the multi-color solid lines in the left panel of figure 7. In addition, considering the existence of periodic change in the O − C curve, we also set L3 as an adjustable parameter. The corresponding photometric parameters are listed in table 7, and the W–D theoretical curves are shown as the multi-color dashed line in the right panel of figure 7.
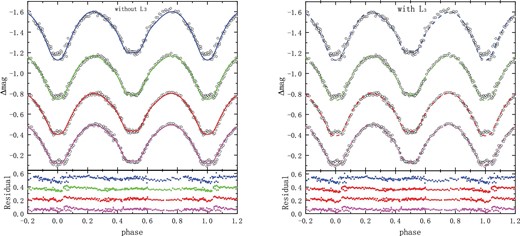
Theoretical and observational light curves of AS CrB. Left panel: Photometric solution wihtout third light. Right panel: Photometric solution with third light. The hollow circles represent the observed data and the multi-color curves represent the theoretical curves for the different bands.
| Parameters . | Without L3 . | With L3 . | Liu et al. (2017) . |
|---|---|---|---|
| q | 0.1600(34) | 0.183(12) | 0.172(8) |
| i (|$^{\circ} $|) | 77.88(69) | 79.1(13) | 78.4(2) |
| T1 (K) | 6187 | 6187 | 6500(376) |
| T2/T1 | 1.0061(26) | 1.00614 | 0.9997(811) |
| Ω1 = Ω2 | 2.055(12) | 2.092(26) | 2.0961(27) |
| L1B/(L1B + L2B) | 0.81790(49) | 0.7963(84) | 0.8176(10) |
| L1V/(L1V + L2V) | 0.81967(50) | 0.7983(86) | 0.8179(8) |
| |$L_{1 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}\right)$| | 0.82043(71) | 0.7991(97) | 0.8181(7) |
| |$L_{1 I_{\rm C}} /\left(L_{1 I_{\rm C}}+L_{2 I_{\rm C}}\right)$| | 0.8211(10) | 0.800(12)(38) | 0.8181(7) |
| r1 (pole) | 0.5228(24) | 0.5164(41) | 0.5147(7) |
| r1 (side) | 0.5813(35) | 0.5730(57) | 0.5693(11) |
| r1 (back) | 0.6087(37) | 0.6041(49) | 0.5962(14) |
| r2 (pole) | 0.242(11) | 0.263(30) | 0.2424(16) |
| r2 (side) | 0.255(14) | 0.279(39) | 0.2550(19) |
| r2 (back) | 0.323(49) | 0.38(29) | 0.3129(56) |
| f | 0.73(11) | 0.83(22) | 0.596(25) |
| ρ1 (g cm−3) | 0.605 | 0.919 | — |
| ρ2 (g cm−3) | 0.605 | 0.852 | — |
| L3B/(L1B + L2B + L3B) | — | 0.108(31) | — |
| L3V/(L1V + L2V + L3V) | — | 0.081(34) | — |
| |$L_{3 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}}\right)$| | — | 0.072(41) | — |
| |$L_{3 I_{\mathrm{C}}} /\left(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}}\right)$| | — | 0.066(52) | — |
| Σ | 0.037 | 0.0319 | — |
| Parameters . | Without L3 . | With L3 . | Liu et al. (2017) . |
|---|---|---|---|
| q | 0.1600(34) | 0.183(12) | 0.172(8) |
| i (|$^{\circ} $|) | 77.88(69) | 79.1(13) | 78.4(2) |
| T1 (K) | 6187 | 6187 | 6500(376) |
| T2/T1 | 1.0061(26) | 1.00614 | 0.9997(811) |
| Ω1 = Ω2 | 2.055(12) | 2.092(26) | 2.0961(27) |
| L1B/(L1B + L2B) | 0.81790(49) | 0.7963(84) | 0.8176(10) |
| L1V/(L1V + L2V) | 0.81967(50) | 0.7983(86) | 0.8179(8) |
| |$L_{1 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}\right)$| | 0.82043(71) | 0.7991(97) | 0.8181(7) |
| |$L_{1 I_{\rm C}} /\left(L_{1 I_{\rm C}}+L_{2 I_{\rm C}}\right)$| | 0.8211(10) | 0.800(12)(38) | 0.8181(7) |
| r1 (pole) | 0.5228(24) | 0.5164(41) | 0.5147(7) |
| r1 (side) | 0.5813(35) | 0.5730(57) | 0.5693(11) |
| r1 (back) | 0.6087(37) | 0.6041(49) | 0.5962(14) |
| r2 (pole) | 0.242(11) | 0.263(30) | 0.2424(16) |
| r2 (side) | 0.255(14) | 0.279(39) | 0.2550(19) |
| r2 (back) | 0.323(49) | 0.38(29) | 0.3129(56) |
| f | 0.73(11) | 0.83(22) | 0.596(25) |
| ρ1 (g cm−3) | 0.605 | 0.919 | — |
| ρ2 (g cm−3) | 0.605 | 0.852 | — |
| L3B/(L1B + L2B + L3B) | — | 0.108(31) | — |
| L3V/(L1V + L2V + L3V) | — | 0.081(34) | — |
| |$L_{3 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}}\right)$| | — | 0.072(41) | — |
| |$L_{3 I_{\mathrm{C}}} /\left(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}}\right)$| | — | 0.066(52) | — |
| Σ | 0.037 | 0.0319 | — |
| Parameters . | Without L3 . | With L3 . | Liu et al. (2017) . |
|---|---|---|---|
| q | 0.1600(34) | 0.183(12) | 0.172(8) |
| i (|$^{\circ} $|) | 77.88(69) | 79.1(13) | 78.4(2) |
| T1 (K) | 6187 | 6187 | 6500(376) |
| T2/T1 | 1.0061(26) | 1.00614 | 0.9997(811) |
| Ω1 = Ω2 | 2.055(12) | 2.092(26) | 2.0961(27) |
| L1B/(L1B + L2B) | 0.81790(49) | 0.7963(84) | 0.8176(10) |
| L1V/(L1V + L2V) | 0.81967(50) | 0.7983(86) | 0.8179(8) |
| |$L_{1 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}\right)$| | 0.82043(71) | 0.7991(97) | 0.8181(7) |
| |$L_{1 I_{\rm C}} /\left(L_{1 I_{\rm C}}+L_{2 I_{\rm C}}\right)$| | 0.8211(10) | 0.800(12)(38) | 0.8181(7) |
| r1 (pole) | 0.5228(24) | 0.5164(41) | 0.5147(7) |
| r1 (side) | 0.5813(35) | 0.5730(57) | 0.5693(11) |
| r1 (back) | 0.6087(37) | 0.6041(49) | 0.5962(14) |
| r2 (pole) | 0.242(11) | 0.263(30) | 0.2424(16) |
| r2 (side) | 0.255(14) | 0.279(39) | 0.2550(19) |
| r2 (back) | 0.323(49) | 0.38(29) | 0.3129(56) |
| f | 0.73(11) | 0.83(22) | 0.596(25) |
| ρ1 (g cm−3) | 0.605 | 0.919 | — |
| ρ2 (g cm−3) | 0.605 | 0.852 | — |
| L3B/(L1B + L2B + L3B) | — | 0.108(31) | — |
| L3V/(L1V + L2V + L3V) | — | 0.081(34) | — |
| |$L_{3 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}}\right)$| | — | 0.072(41) | — |
| |$L_{3 I_{\mathrm{C}}} /\left(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}}\right)$| | — | 0.066(52) | — |
| Σ | 0.037 | 0.0319 | — |
| Parameters . | Without L3 . | With L3 . | Liu et al. (2017) . |
|---|---|---|---|
| q | 0.1600(34) | 0.183(12) | 0.172(8) |
| i (|$^{\circ} $|) | 77.88(69) | 79.1(13) | 78.4(2) |
| T1 (K) | 6187 | 6187 | 6500(376) |
| T2/T1 | 1.0061(26) | 1.00614 | 0.9997(811) |
| Ω1 = Ω2 | 2.055(12) | 2.092(26) | 2.0961(27) |
| L1B/(L1B + L2B) | 0.81790(49) | 0.7963(84) | 0.8176(10) |
| L1V/(L1V + L2V) | 0.81967(50) | 0.7983(86) | 0.8179(8) |
| |$L_{1 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}\right)$| | 0.82043(71) | 0.7991(97) | 0.8181(7) |
| |$L_{1 I_{\rm C}} /\left(L_{1 I_{\rm C}}+L_{2 I_{\rm C}}\right)$| | 0.8211(10) | 0.800(12)(38) | 0.8181(7) |
| r1 (pole) | 0.5228(24) | 0.5164(41) | 0.5147(7) |
| r1 (side) | 0.5813(35) | 0.5730(57) | 0.5693(11) |
| r1 (back) | 0.6087(37) | 0.6041(49) | 0.5962(14) |
| r2 (pole) | 0.242(11) | 0.263(30) | 0.2424(16) |
| r2 (side) | 0.255(14) | 0.279(39) | 0.2550(19) |
| r2 (back) | 0.323(49) | 0.38(29) | 0.3129(56) |
| f | 0.73(11) | 0.83(22) | 0.596(25) |
| ρ1 (g cm−3) | 0.605 | 0.919 | — |
| ρ2 (g cm−3) | 0.605 | 0.852 | — |
| L3B/(L1B + L2B + L3B) | — | 0.108(31) | — |
| L3V/(L1V + L2V + L3V) | — | 0.081(34) | — |
| |$L_{3 R_{\rm C}} /\left(L_{1 R_{\rm C}}+L_{2 R_{\rm C}}+L_{3 R_{\rm C}}\right)$| | — | 0.072(41) | — |
| |$L_{3 I_{\mathrm{C}}} /\left(L_{1 I_{\mathrm{C}}}+L_{2 I_{\mathrm{C}}}+L_{3 I_{\mathrm{C}}}\right)$| | — | 0.066(52) | — |
| Σ | 0.037 | 0.0319 | — |
5 Remarks and discussions
5.1 W–D photometric solution
We observed V1309 Her and AS CrB with the MAO 60 cm telescope and obtained their multi-color light curves in the BVRCIC bands. From the shapes of the light curves, both V1309 Her and AS CrB are totally eclipsing systems, allowing us to obtain reliable photometric parameters (Terrell & Wilson 2005). Based on our new complete multi-filter photometric data, we analyzed the light curves with the W–D program. The W–D photometric solution indicates that V1309 Her is a low-mass-ratio median-contact binary with a mass ratio of q = 0.213 and a fill-out factor of |$f = 35.5\%$|. In order to resolve the fit bias at the maximum, we considered adding a spot to the primary star. In addition, the deviations of the theoretical and observed curves at the minima in different bands are different, implying the possible existence of a third body. We applied the L3 model, and appropriate (i.e., non-zero) third light contributions were found for each bandpass. The luminous contribution of the third light to the total luminosity is |$18.12\%$| in the B band, |$14.21\%$| in the V band, |$12.7\%$| in the RC band, and |$10.7\%$| in the IC band. For AS CrB, the light-curve analysis results reveal that it is a deep, low-mass-ratio overcontact binary with mass ratio q = 0.16 and fill-out factor |$f = 73\%$|. During our analysis, a third light was also found in AS CrB. The luminous contribution of the third light to the total luminosity is 10.8|$\%$|, 8.1|$\%$|, 7.2|$\%$|, and 6.6|$\%$| in the B, V, RC, and IC bands, respectively. Low-mass-ratio and deep-contact binaries are defined as contact binaries with mass ratios q < 0.25 and fill-out factor |$f > 50\%$|. They are in the final evolutionary stage of contact binaries and are considered to be the progenitors of merging stars (Qian et al. 2005, 2006, 2020).
Based on the photometric elements, we estimated the absolute parameters of V1309 Her and AS CrB using the same method as Li et al. (2021) and Xu et al. (2022). The absolute parameters of both systems are shown in table 8, where the maximum apparent magnitude mv max is from the ASAS-SN survey data, the parallax ϖ is from Gaia (Gaia Collaboration 2018), the extinction coefficient Av is from the NASA/IPAC Extragalactic Database,2 and the bolometric correction BC refers to the table provided by Worthey and Lee (2011). With these absolute parameters, the mean density of the two systems can be calculated using the relationship provided by Mochnacki (1981). For V1309 Her, the mean density of star 1 is ρ1 = 0.753 g cm−3, and that of star 2 is ρ2 = 1.212 g cm−3. For AS CrB, the mean density of star 1 is ρ1 = 0.607 g cm−3, and that of star 2 is ρ1 = 0.903 g cm−3. These values are very close to the densities calculated by the W–D method, as shown in tables 6 and 7.
| . | mv max . | ϖ . | Av . | MV . | BC . | Mbol . | a . | R1 . | R2 . | M1 . | M2 . | L1 . | L2 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mag . | mas . | mag . | mag . | mag . | mag . | R⊙ . | R⊙ . | R⊙ . | M⊙ . | M⊙ . | L⊙ . | L⊙ . |
| V1309 Her | 12.08 | 2.01 | 0.1 | 3.496 | 0.07 | 3.566 | 2.462 | 1.311 | 0.668 | 1.205 | 0.257 | 2.33 | 0.613 |
| AS CrB | 11.45 | 2.52 | 0.058 | 3.4 | 0.07 | 3.47 | 2.477 | 1.411 | 0.671 | 1.211 | 0.194 | 2.613 | 0.605 |
| . | mv max . | ϖ . | Av . | MV . | BC . | Mbol . | a . | R1 . | R2 . | M1 . | M2 . | L1 . | L2 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mag . | mas . | mag . | mag . | mag . | mag . | R⊙ . | R⊙ . | R⊙ . | M⊙ . | M⊙ . | L⊙ . | L⊙ . |
| V1309 Her | 12.08 | 2.01 | 0.1 | 3.496 | 0.07 | 3.566 | 2.462 | 1.311 | 0.668 | 1.205 | 0.257 | 2.33 | 0.613 |
| AS CrB | 11.45 | 2.52 | 0.058 | 3.4 | 0.07 | 3.47 | 2.477 | 1.411 | 0.671 | 1.211 | 0.194 | 2.613 | 0.605 |
| . | mv max . | ϖ . | Av . | MV . | BC . | Mbol . | a . | R1 . | R2 . | M1 . | M2 . | L1 . | L2 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mag . | mas . | mag . | mag . | mag . | mag . | R⊙ . | R⊙ . | R⊙ . | M⊙ . | M⊙ . | L⊙ . | L⊙ . |
| V1309 Her | 12.08 | 2.01 | 0.1 | 3.496 | 0.07 | 3.566 | 2.462 | 1.311 | 0.668 | 1.205 | 0.257 | 2.33 | 0.613 |
| AS CrB | 11.45 | 2.52 | 0.058 | 3.4 | 0.07 | 3.47 | 2.477 | 1.411 | 0.671 | 1.211 | 0.194 | 2.613 | 0.605 |
| . | mv max . | ϖ . | Av . | MV . | BC . | Mbol . | a . | R1 . | R2 . | M1 . | M2 . | L1 . | L2 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | mag . | mas . | mag . | mag . | mag . | mag . | R⊙ . | R⊙ . | R⊙ . | M⊙ . | M⊙ . | L⊙ . | L⊙ . |
| V1309 Her | 12.08 | 2.01 | 0.1 | 3.496 | 0.07 | 3.566 | 2.462 | 1.311 | 0.668 | 1.205 | 0.257 | 2.33 | 0.613 |
| AS CrB | 11.45 | 2.52 | 0.058 | 3.4 | 0.07 | 3.47 | 2.477 | 1.411 | 0.671 | 1.211 | 0.194 | 2.613 | 0.605 |
5.2 O − C curve and period variation
By using all the available light minimum times, we constructed O − C curves and carried out orbital period analysis for V1309 Her and AS CrB. The O − C curve of V1309 Her exhibits linear variation coupled with a periodic variation. The new O − C values change the original trend, indicating that the long-term increase in the orbital period found by Alton (2020) does not exist. Combined with the light curve analysis, the periodic oscillation is most likely caused by the LTTE of the third body. We fitted the O − C curve of V1309 Her in two ways, a circular orbit and an eccentric orbit. For the circular orbit, the amplitude and period of the cyclic variation are A = 0.007258(±0.00149) d and P = 26.42(±2.67) yr, respectively. For the eccentric orbit, the amplitude and period of the cyclic variation are A = 0.006569(±0.0005931) d and P = 21.359(±0.588) yr, respectively. Using the equation
the mass function of the system is f(m) = 0.0028 M⊙ for the circular orbit and f(m) = 0.0032 M⊙ for the eccentric orbit. When the orbital inclination i3 = 90°, the minimum masses of the third body are M3min, cir = 0.1987 M⊙ and M3min, ecc = 0.208 M⊙, respectively. This does not produce enough luminous contribution to make it consistent with the photometric solution, indicating that the third body is not coplanar with the binary pair.
For AS CrB, the O − C curve shows an upward parabolic trend combined with a periodic variation. The upward parabolic trend indicates that the binary orbital period is continuously increasing at a rate of dP/dt = 5.22(±0.28) × 10−7 d yr−1. The secular increase of the orbital period can be explained by mass transfer from the less massive component to the more massive one. As the mass is transferred, the primary component will become more massive and the mass ratio will decrease. Finally, AS CrB may merge into a rapidly rotating single star when its orbital angular momentum is less than three times the total spin angular momentum, i.e., Jorb < 3Jrot (Hut 1980). Assuming a conservative system, according to the equation
the mass transfer rate |$\dot{M}_2 = 1.056\times 10^{-7}\, M_{\odot }$| yr−1 can be obtained. For periodic variation, both circular and eccentric orbits were considered, but a convergent solution was generated only in the case of circular orbits. The amplitude and period of the cyclic variation are A = 0.00343(±0.0031) d and P = 18.03(±0.91) yr, respectively. According to equation (6), the mass function was calculated as f(m) = 0.00064 M⊙. The minimum mass of the additional body is M3min = 0.114 M⊙, which cannot provide a sufficient luminous contribution. Thus, if a third body exists, it should be non-coplanar with the inner pair.
In addition, magnetic activity cycles may also cause periodic changes in the orbital period (Applegate 1992). Using the finite-shell two-zone model provided by Völschow et al. (2016), we consider whether the magnetic activity can cause such periodic variation by calculating the ratio of the energy required to drive the Applegate mechanism to the available energy produced in the active star (ΔE/Esec). Völschow et al. (2016) provided an online site3 to calculate this value. For V1309 Her and AS CrB, ΔE−/Esec is 0.46 and 0.14 (both less than one), respectively, indicating that the periodic oscillation may also be caused by the magnetic activity cycle. Statistics reveal that a third object is very common in contact binaries (Tokovinin et al. 2006; Pribulla & Rucinski 2006; D’Angelo et al. 2006; Rucinski et al. 2007). The study of Liao and Qian (2010) found that the phenomenon of periodic oscillation of the orbital period in contact binaries is most likely due to a third body. Combined with the light curve analysis, although the periodic oscillations of V1309 Her and AS CrB are most likely caused by a third body, we cannot completely exclude the magnetic activity cycle. Therefore, longer periods of light minimum time data and spectral data are needed for further studies.
Acknowledgements
We are grateful to the referee for his/her valuable comments and suggestions, which have improved the manuscript greatly. This work is supported by the International Cooperation Projects of the National Key R&D Program (No. 2022YFE0127300) and the National Natural Science Foundation of China (Nos. 11933008 and 11922306). The CCD photometric data were obtained with the Maidanak Astronomical Observatory 60 cm telescope. This work has made use of data from the All-Sky Automated Survey for Supernovae (ASAS-SN), SuperWASP, the Large-Sky-Area Multi-Object Fibre Spectroscopic Telescope (LAMOST), the Transiting Exoplanet Survey Satellite (TESS), and Gaia. The authors thank the teams for providing open data.



