X-ray line diagnostics of ion temperature at cosmic ray accelerating collisionless shocks

Abstract

A novel collisionless shock jump condition is suggested by modeling the entropy production at the shock transition region. We also calculate downstream developments of the atomic ionization balance and the ion temperature relaxation in supernova remnants (SNRs). The injection process and subsequent acceleration of cosmic rays (CRs) in the SNR shocks are closely related to the formation process of the collisionless shocks. The formation of the shock is caused by wave–particle interactions. Since the wave–particle interactions result in energy exchanges between electromagnetic fields and charged particles, the randomization of particles associated with the shock transition may occur at a rate given by the scalar product of the electric field and current. We find that order-of-magnitude estimates of the randomization with reasonable strength of the electromagnetic fields in the SNR constrain the amount of CR nuclei and the ion temperatures. The constrained amount of CR nuclei can be sufficient to explain the Galactic CRs. The ion temperature becomes significantly lower than that in the case without CRs. To distinguish the case without CRs, we perform synthetic observations of atomic line emissions from the downstream region of the SNR RCW 86. Future observations by XRISM and Athena can distinguish whether the SNR shock accelerates the CRs or not from the ion temperatures.

1 Introduction

Collisionless shocks of supernova remnants (SNRs) are invoked as the primary sources of Galactic cosmic rays (CRs); however, the production process of CRs is an unsettled issue despite numerous studies reported. The most generally accepted and widely studied mechanism for CR acceleration is diffusive shock acceleration (Blandford & Ostriker 1978; DSA, Bell 1978). In the DSA mechanism, we assume energetic particles around the shock; the particles bounce back and forth between the upstream and downstream regions by scattering particles. The particle scattering results from interactions between plasma waves and the particles. The maximum energy of the accelerated particles depends on the magnetic-field strength and turbulence (e.g., Lagage & Cesarsky 1983a, 1983b). To explain the energy spectrum of the CR nuclei observed around the Earth, the maximum energy of the accelerated protons should be at least 10^15.5 eV (the so-called knee energy). The knee energy can be achieved in the DSA mechanism by a magnetic-field strength of ≳|$100\,\, {\mu \rm {G}}$|⁠, which is larger than the typical strength of ∼|$1\,\, {\mu \rm {G}}$| seen in the interstellar medium (ISM, Myers 1978; Beck 2001). Bell (2004) pointed out that the upstream magnetic field is amplified by the effects of a back reaction from the accelerated protons themselves. This amplification is called the Bell instability, whose growth rate is proportional to the CR energy density. Observations of nonthermal X-ray emissions around the SNR shocks imply the existence of amplified magnetic fields in the downstream region (e.g., Vink & Laming 2003; Bamba et al. 2005; Uchiyama et al. 2007). Hence, in a modern scenario of CR acceleration, the SNR shock is assumed to inject a considerably large amount of CRs (≳10% of the shock kinetic energy), and their effects on the background plasma are regarded as one of the most important issues. Since the wave–particle interactions also cause the formation of the collisionless shock, the injection of energetic particles, subsequent acceleration by the DSA mechanism, and the amplification of the magnetic field are closely related to the formation process. Although many kinetic simulations studying collisionless shock physics have been reported (e.g., Ohira 2013, 2016a, 2016b; Matsumoto et al. 2017; Caprioli et al. 2020; Marcowith et al. 2020), self-consistent treatment of the collisionless shock, including these effects, is currently incomplete due to the limitation of too-short simulation times compared to actual SNR shocks.

When the SNR shock consumes its kinetic energy to accelerate energetic, nonthermal particles, the downstream thermal energy can be lower than the case of adiabatic shock without CRs (e.g., Hughes et al. 2000; Helder et al. 2009; Morlino et al. 2013a, 2013b, 2014; Hovey et al. 2015, 2018; Shimoda et al. 2015, 2018b). Thus, we observe small downstream ion temperatures if the SNR shocks efficiently accelerate the CR nuclei (protons and heavier ions). In the near future, spatially resolved high-energy-resolution spectroscopy of the SNR shock regions will be achieved by the micro-calorimeter array with Resolve (Ishisaki et al. 2018) onboard XRISM (Tashiro et al. 2020) and with the X-IFU onboard Athena (Barret et al. 2018) providing precise line diagnostics of plasmas to represent the effect of the CR acceleration. Note that observations of γ-ray emissions possibly provide the amount of CR protons from the luminosities. However, it may be challenging to determine the amounts of CR nuclei individually. Thus, in this paper, we study the shock jump conditions of ions, including the effects of CR acceleration. To distinguish the case without CRs by future X-ray spectroscopy, we calculate the temporal evolutions of the downstream ionization structure and downstream ion temperatures resulting from the Coulomb interactions. From the calculations of the downstream values, we also perform synthetic observations of atomic lines, including the effects of downstream turbulence. Since the turbulence affects the line width by the Doppler effect, it is non-trivial whether the observed line width reflects the intrinsic ion temperature.

A typical example of the missing thermal energy measurement was provided by the SNR RCW 86 (Helder et al. 2009). RCW 86 is considered as the remnant of SN 185 (Vink et al. 2006), so its age is ∼2000 yr. The current radius is ∼15 pc, and the shock velocity is ∼3000 km s⁻¹ with an assumed distance of 2.5 kpc (Yamaguchi et al. 2016), where we estimate the angular size as ∼40″. Since 2000 yr × 3000 km s⁻¹ ≃ 6 pc < 15 pc, the blast wave has already decelerated. The mean expansion speed should be ∼10⁹ cm s⁻¹ if the radius becomes ∼10 pc within a time of ∼1 kyr. Such high expansion speed can be maintained for 1 kyr if the progenitor star explodes in a wind-blown cavity created by the progenitor system. Broersen et al. (2014) studied this scenario by comparing the X-ray observations and hydrodynamical simulations. They concluded that the progenitor star of SN 185 exploded as a Type-Ia supernova inside the wind cavity. The progenitor system could be a binary system consisting of a white dwarf and a donor star. In the present day, RCW 86 shows Hα filaments everywhere (Helder et al. 2013). The Hα emission means that the shock is now propagating into a partially ionized medium (Chevalier et al. 1980). In the case of a stellar wind from a massive star, the ionization front precedes the front of the swept-up matter (e.g., Arthur et al. 2011). Thus, the forward shock of RCW 86 may currently propagate in the medium not swept up by the wind. In this paper, we suppose such a scenario for RCW 86 and perform synthetic observations of the X-ray atomic lines.

This paper is organized as follows: In section 2, we review a physical model of the temporal evolutions of the downstream ionization balance and the ion internal energies. The ion temperatures are derived from the equation of state. Section 3 provides shock jump conditions as initial conditions for the downstream temporal evolution. We introduce shock jump conditions usually supposed in SNRs and a novel condition given by modeling the entropy productions of the ions due to the wave–particle interactions. The latter includes the effects of the CR acceleration, magnetic-field amplification, and ion heating balance. The results of the downstream temporal evolutions are summarized in section 4. In section 5, we perform synthetic observations of atomic lines, including the effects of the downstream turbulence. Finally, we summarize our results and future prospects.

2 Physical model of the downstream ionization balance and ion internal energies

Here we review a physical model of the temporal evolutions of the downstream ionization balance and ion internal energy. Let V be a fluid parcel volume. The parcel contains a mass of M. We assume that species within the parcel always have the Maxwell velocity distribution function with a temperature of T_j, where the subscript j indicates the species j. Then, the internal energy E_j and pressure P_j of the species j can be written as

$$\begin{eqnarray} E_j = \frac{N_j k T_j}{\gamma -1}, \end{eqnarray}$$

(1)

$$\begin{eqnarray} P_j = n_j k T_j, \end{eqnarray}$$

(2)

where N_j, n_j, and k are the total number of species j, the number density of species j (n_j = N_j/V), and the Boltzmann constant, respectively. The adiabatic index is γ = 5/3. From the first law of thermodynamics, we obtain

$$\begin{eqnarray} && \frac{d E_j}{dt} + P_j \frac{dV}{dt} = \frac{ d Q_j }{ dt }, \end{eqnarray}$$

(3)

where dQ_j/dt is the external energy gain or loss per unit time of the species j; we discuss this later. Defining the internal energy per unit volume ϵ_j ≡ E_j/V and the external energy gain or loss per unit time per unit volume |$\dot{q}_j\equiv V^{-1}dQ_j/dt$|⁠, we rewrite equation (3) as

$$\begin{eqnarray} \frac{d\varepsilon _j}{dt} = \dot{q_j} + \frac{\gamma \varepsilon _j}{\rho }\frac{d\rho }{dt}, \end{eqnarray}$$

(4)

where ρ ≡ M/V is the total mass density. In this paper, we suppose the case of young SNRs and approximate their dynamics by the Sedov–Taylor model (Sedov 1959; Vink 2012). Then, we approximate the downstream velocity profile as

$$\begin{eqnarray} v(r,t) = \left(1-\frac{1}{r_{\rm c}}\right)\frac{V_{\rm sh}(t)}{R_{\rm sh}(t)}r, \end{eqnarray}$$

(5)

where r is the radial distance from the explosion center and r_c is the compression ratio, respectively. The radius of the SNR and the shock velocity are given by, respectively,

$$\begin{eqnarray} && R_{\rm sh}(t) = R_0 \left( \frac{ t }{ t_0 } \right)^{2/5}, \end{eqnarray}$$

(6)

$$\begin{eqnarray} && V_{\rm sh}(t) = \frac{dR_{\rm sh}}{dt} = \frac{2}{5}\frac{R_0}{t_0}\left(\frac{t}{t_0}\right)^{-3/5}, \end{eqnarray}$$

(7)

where we have assumed that the ambient density structure around the SNR is uniform. The dimensional constants R₀ and t₀ are characterized by a combination of the explosion energy of the supernova, the structure of the ejecta, and the ambient density structure. The actual values of R₀ and t₀ are not used in our model calculation; we only use V_sh/R_sh = (2/5)t⁻¹. The temporal evolution of the mass density along the trajectory of the fluid parcel is derived from the continuous equation as

$$\begin{eqnarray} \frac{d\rho }{dt} = -\rho \frac{1}{r^2}\frac{ \partial }{ \partial r } \left(r^2 v\right) = - \frac{6}{5}\left(1-\frac{1}{r_{\rm c}}\right)\frac{ \rho }{ t }. \end{eqnarray}$$

(8)

To calculate ρ and ϵ_j along the trajectory of the fluid parcel, we introduce the position of the fluid parcel at |$\tilde{r}(t)$| that is derived from the differential equation of

$$\begin{eqnarray} \frac{d\tilde{r}}{dt} = v[\tilde{r}(t),t] = \frac{2}{5}\left(1-\frac{1}{r_{\rm c}}\right)\frac{\tilde{r}}{t}. \end{eqnarray}$$

(9)

Defining the time t_* when the fluid parcel currently at |$\tilde{r}(t)=r$| crosses the shock, i.e., |$\tilde{r}(t_*)=R_{\rm sh}(t_*)$|⁠, we obtain

$$\begin{eqnarray} \ln \frac{\tilde{r}(t)}{R_{\rm sh}(t_*)} =\frac{2}{5}\left(1-\frac{1}{r_{\rm c}}\right)\ln \frac{t}{t_*}, \end{eqnarray}$$

(10)

where we regard r_c = const. When we observe the atomic line emissions from the fluid parcel at |$r=\tilde{r}(t_{\rm age})$|⁠, where t_age is the age of the SNR, the crossing time is derived as¹

$$\begin{eqnarray} t_*(r) = \left[ \frac{r}{ R_{\rm sh}{ (t_{\rm age}) }} \right]^{r_{\rm c}} t_{\rm age}. \end{eqnarray}$$

(11)

Thus, by introducing t′ = t − t_*, the temporal evolution of the downstream internal energy and the mass density are written as, respectively,

$$\begin{eqnarray} && \frac{d\varepsilon _j}{dt^{\prime }} =\dot{q}_j - \frac{6\gamma }{5}\left(1-\frac{1}{r_{\rm c}}\right)\frac{\varepsilon _j}{t^{\prime }+t_*}, \end{eqnarray}$$

(12)

$$\begin{eqnarray} && \rho (t^{\prime }) = \rho (t_*)\left(1+\frac{t^{\prime }}{t_*}\right)^{-\frac{6}{5}\left(1-\frac{1}{r_{\rm c}}\right)}. \end{eqnarray}$$

(13)

Integrating the differential equation of ϵ_j from t′ = 0 to t′ = t_age − t_*(r) with the shock jump conditions given by V_sh(t_*), we obtain the spatial profile of the downstream internal energy at the observed time t = t_age. The age is known for a historical SNR (e.g., SNR RCW 86, SN 1006, Tycho’s SNR, Kepler’s SNR). The shock velocity at the current time can be estimated from the proper motion of the shock. To calculate the rate of the Coulomb interactions (see below), the number density is needed. The density is evaluated from the surface brightness of the X-ray or Hα emissions, for instance.

Here we consider the energy source or sink term |$\dot{q}_j$|⁠. The charged particles exchange their momenta and energies via Coulomb collision. Although the exchange is negligible during the shock transition, the effect becomes important for the long-time evolution in the downstream region. The energy exchange rate is given by (e.g., Spitzer 1962; Itoh 1984)

$$\begin{eqnarray} \dot{q}_{j,{\rm Col}} = \sum _{m} \frac{ \left( n_j\varepsilon _m - n_m\varepsilon _j \right)z_m{}^2 z_j{}^2\ln \Lambda }{5.87A_m A_j} \left(\frac{T_m}{A_m}+\frac{T_j}{A_j} \right)^{-3/2},\nonumber\\ \end{eqnarray}$$

(14)

where A_j and ln Λ are the particle mass in atomic mass units and the Coulomb logarithm. In this paper, we fix ln Λ = 30 for simplicity. For atoms, the energy transfer due to the ionization or recombination may be given by

$$\begin{eqnarray} \dot{q}_{Z,z} &=& n_{\rm e}\left[ R_{Z,z-1}\varepsilon _{Z,z-1} - \left( R_{Z,z}+K_{Z,z} \right)\varepsilon _{Z,z} +K_{Z,z+1}\varepsilon _{Z,z+1} \right], \nonumber\\ \end{eqnarray}$$

(15)

where we introduce the notation j = {Z, z} to represent the species with an atomic number Z and ionic charge state z, respectively (e.g., Z = 2 and z = 1 indicate He⁺¹ or He ii). The subscript “e” indicates the electron. The electron-impact ionization rate per unit time per particle (s⁻¹ cm³) is R_{Z, z}(T_e), and the recombination rate per unit time per particle is K_{Z, z}(T_e). In this paper, we omit the charge-exchange reactions and the ion impact ionization for simplicity and consider 10 atoms H, He, C, N, O, Ne, Mg, Si, S, and Fe with the solar abundance (Asplund et al. 2009). The atomic data used in this paper are the same as in Shimoda and Inutsuka (2022): The ionization cross-sections are given by Janev and Smith (1993) for H, and by Lennon et al. (1988) for the others. The fitting functions for those data are given by the International Atomic Energy Agency.² Table 1 summarizes the literature on the recombination rates. Those data are fitted by Chebyshev polynomials with 20 terms. For the hydrogen-like atoms, the fitting function is given by Kotelnikov and Milstein (2019). The electron number density is given by the charge neutrality condition as

$$\begin{eqnarray} n_{\rm e} = \sum _{Z}\sum _{z=1}^{z=Z} z n_{Z,z}, \end{eqnarray}$$

(16)

and the total number density n is given by

$$\begin{eqnarray} n = n_{\rm e} + \sum _{Z} \sum _{z=0}^{z=Z} n_{Z,z}. \end{eqnarray}$$

(17)

For electrons, by following Shimoda and Inutsuka (2022), the radiative and ionization losses are given by

$$\begin{eqnarray} \dot{q}_{\rm e} = - \sum _Z\sum _{z=0}^{Z-1} n_{\rm e}n_{Z,z}R_{Z,z}I_{Z,z} - n_{\rm e}\sum _{Z,z}n_{Z,z} W_{Z,z}, \end{eqnarray}$$

(18)

where I_{Z, z} is the first ionization potential of the species j = {Z, z} (we omit the inner shell ionization). The radiation power W_{Z, z} includes the bound–bound, free–bound, free–free, and two-photon decay. For the continuum components, the formula given by Gronenschild and Mewe (1978) (free–free and two-photon decays) and Mewe, Lemen, and van den Oord (1986) (free–bound) are used. For the bound–bound component, the radiation power per particle is given by

$$\begin{eqnarray} W_{Z,z}^{\rm ul} = E_{\rm ul}C_{\rm lu}, \end{eqnarray}$$

(19)

where the emitted photon energy is the subtraction of the upper energy level E_u and the lower energy level E_l, E_ul = E_u − E_l. The collisional excitation rate per unit time per particle (s⁻¹ cm³) is given by (e.g., Osterbrock & Ferland 2006)

$$\begin{eqnarray} && C_{\rm lu} = 8.629\times 10^{-6} \frac{ \Omega _{\rm lu} }{ g_{\rm l} } \frac{ {\rm e}^{-\frac{ E_{\rm ul} }{ kT_{\rm e} } } }{ \sqrt{ T_{\rm e} } }, \end{eqnarray}$$

(20)

where g_l is the statistical weight of the lower level. The collision strength is

$$\begin{eqnarray} && \Omega _{\rm lu} = \frac{ 8\pi }{ \sqrt{3} } \frac{ g_{\rm l} f_{\rm lu} }{ E_{\rm ul,Ryd} } \bar{g}(T_{\rm e}), \end{eqnarray}$$

(21)

where f_lu is the oscillator strength, and E_{ul, Ryd} is the photon energy given in Rydberg units. g_l is the statistical weight of the lower level. The averaged Gaunt factor is |$\bar{g}$|⁠. The value of the averaged Gaunt factor is around unity and determines the detailed temperature dependence of the excitation rate. The precise data of the excitation rate (or |$\bar{g}$|⁠) are, however, not available yet. The following fitting function (Mewe 1972),

$$\begin{eqnarray} \bar{g}(T_{\rm e}) = 0.15 + 0.28 \left[ \log \left( \frac{ \chi +1 }{\chi } \right) - \frac{ 0.4 }{ (1+\chi )^2 } \right], \end{eqnarray}$$

(22)

where χ = E_ul/kT_e, is used for the neutral atoms, while |$\bar{g}=1$| is assumed for the ionized atoms. Note that the cooling function mainly depends on the ionization structure rather than |$\bar{g}$|⁠. For the oscillator strength and energy levels, the data table given by the National Institute of Standards and Technology³ are used. For the calculation of the radiative cooling rate, it is sufficient to consider only the allowed transitions from the ground state. We obtain the net radiation power and thus the net radiative loss by integrating the photon frequency. Here is a summary of the energy source or sink term: |$\dot{q}_j=\dot{q}_{Z,0}$| for the neutral atoms, |$\dot{q}_j=\dot{q}_{j,{\rm Col}}+\dot{q}_{Z,z}$| for the ions, and |$\dot{q}_j=\dot{q}_{j,{\rm Col}}+\dot{q}_{\rm e}$| for the electrons.

Table 1.

Open in new tab

Literature on the recombition rate.

Ion	Literature	Ion	Literature	Ion	Literature
C⁺¹	Nahar and Pradhan (1999)	Mg⁺⁵	Arnaud and Rothenflug (1985)	S⁺¹²	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺²	Nahar and Pradhan (1999)	Mg⁺⁶	Zatsarinny et al. (2004)	S⁺¹³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺³	Nahar and Pradhan (1997)	Mg⁺⁷	Nahar (1995)	S⁺¹⁴	Arnaud and Rothenflug (1985)
C⁺⁴	Nahar and Pradhan (1997)	Mg⁺⁸	Arnaud and Rothenflug (1985)	S⁺¹⁵	Arnaud and Rothenflug (1985)
C⁺⁵	Nahar and Pradhan (1997)	Mg⁺⁹	Arnaud and Rothenflug (1985)	Fe⁺¹	Nahar and Pradhan (1997)
N⁺¹	Zatsarinny et al. (2004)	Mg⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺²	Nahar and Pradhan (1997)
N⁺²	Nahar and Pradhan (1997)	Mg⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺³	Nahar and Pradhan (1997)
N⁺³	Nahar and Pradhan (1997)	Si⁺¹	Nahar (2000)	Fe⁺⁴	Nahar (1998)
N⁺⁴	Nahar and Pradhan (1997)	Si⁺²	Altun et al. (2007)	Fe⁺⁵	Nahar and Pradhan (1999)
N⁺⁵	Nahar (2006)	Si⁺³	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺⁶	Arnaud and Rothenflug (1985)
N⁺⁶	Nahar (2006)	Si⁺⁴	Zatsarinny et al. (2003)	Fe⁺⁷	Nahar (2000)
O⁺¹	Nahar (1998)	Si⁺⁵	Zatsarinny et al. (2006)*	Fe⁺⁸	Arnaud and Rothenflug (1985)
O⁺²	Zatsarinny et al. (2004)	Si⁺⁶	Zatsarinny et al. (2003)	Fe⁺⁹	Arnaud and Rothenflug (1985)
O⁺³	Nahar (1998)	Si⁺⁷	Mitnik and Badnell (2004)*	Fe⁺¹⁰	Lestinsky et al. (2009)*
O⁺⁴	Nahar (1998)	Si⁺⁸	Zatsarinny et al. (2004)	Fe⁺¹¹	Novotný et al. (2012)*
O⁺⁵	Nahar (1998)	Si⁺⁹	Nahar (1995)	Fe⁺¹²	Hahn et al. (2014)*
O⁺⁶	Nahar (1998)	Si⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺¹³	Arnaud and Rothenflug (1985)
O⁺⁷	Nahar (1998)	Si⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺¹⁴	Altun et al. (2007)*
Ne⁺¹	Arnaud and Rothenflug (1985)	Si⁺¹²	Arnaud and Rothenflug (1985)	Fe⁺¹⁵	Murakami et al. (2006)*
Ne⁺²	Zatsarinny et al. (2003)	Si⁺¹³	Arnaud and Rothenflug (1985)	Fe⁺¹⁶	Zatsarinny et al. (2004)
Ne⁺³	Mitnik and Badnell (2004)*	S⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺¹⁷	Arnaud and Rothenflug (1985)
Ne⁺⁴	Zatsarinny et al. (2004)	S⁺²	Nahar (1995)	Fe⁺¹⁸	Zatsarinny et al. (2003)
Ne⁺⁵	Nahar (1995)	S⁺³	Nahar (2000)	Fe⁺¹⁹	Savin et al. (2002)*
Ne⁺⁶	Arnaud and Rothenflug (1985)	S⁺⁴	Altun et al. (2007)	Fe⁺²⁰	Zatsarinny et al. (2004)
Ne⁺⁷	Arnaud and Rothenflug (1985)	S⁺⁵	Arnaud and Rothenflug (1985)	Fe⁺²¹	Arnaud and Rothenflug (1985)
Ne⁺⁸	Nahar (2006)	S⁺⁶	Zatsarinny et al. (2004)	Fe⁺²²	Arnaud and Rothenflug (1985)
Ne⁺⁹	Nahar (2006)	S⁺⁷	Zatsarinny et al. (2006)*	Fe⁺²³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
Mg⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	S⁺⁸	Zatsarinny et al. (2003)	Fe⁺²⁴	Nahar, Pradhan, and Zhang (2001)
Mg⁺²	Zatsarinny et al. (2004)	S⁺⁹	Mitnik and Badnell (2004)*	Fe⁺²⁵	Nahar, Pradhan, and Zhang (2001)
Mg⁺³	Arnaud and Rothenflug (1985)	S⁺¹⁰	Zatsarinny et al. (2004)
Mg⁺⁴	Zatsarinny et al. (2004)	S⁺¹¹	Nahar (1995)

Ion	Literature	Ion	Literature	Ion	Literature
C⁺¹	Nahar and Pradhan (1999)	Mg⁺⁵	Arnaud and Rothenflug (1985)	S⁺¹²	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺²	Nahar and Pradhan (1999)	Mg⁺⁶	Zatsarinny et al. (2004)	S⁺¹³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺³	Nahar and Pradhan (1997)	Mg⁺⁷	Nahar (1995)	S⁺¹⁴	Arnaud and Rothenflug (1985)
C⁺⁴	Nahar and Pradhan (1997)	Mg⁺⁸	Arnaud and Rothenflug (1985)	S⁺¹⁵	Arnaud and Rothenflug (1985)
C⁺⁵	Nahar and Pradhan (1997)	Mg⁺⁹	Arnaud and Rothenflug (1985)	Fe⁺¹	Nahar and Pradhan (1997)
N⁺¹	Zatsarinny et al. (2004)	Mg⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺²	Nahar and Pradhan (1997)
N⁺²	Nahar and Pradhan (1997)	Mg⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺³	Nahar and Pradhan (1997)
N⁺³	Nahar and Pradhan (1997)	Si⁺¹	Nahar (2000)	Fe⁺⁴	Nahar (1998)
N⁺⁴	Nahar and Pradhan (1997)	Si⁺²	Altun et al. (2007)	Fe⁺⁵	Nahar and Pradhan (1999)
N⁺⁵	Nahar (2006)	Si⁺³	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺⁶	Arnaud and Rothenflug (1985)
N⁺⁶	Nahar (2006)	Si⁺⁴	Zatsarinny et al. (2003)	Fe⁺⁷	Nahar (2000)
O⁺¹	Nahar (1998)	Si⁺⁵	Zatsarinny et al. (2006)*	Fe⁺⁸	Arnaud and Rothenflug (1985)
O⁺²	Zatsarinny et al. (2004)	Si⁺⁶	Zatsarinny et al. (2003)	Fe⁺⁹	Arnaud and Rothenflug (1985)
O⁺³	Nahar (1998)	Si⁺⁷	Mitnik and Badnell (2004)*	Fe⁺¹⁰	Lestinsky et al. (2009)*
O⁺⁴	Nahar (1998)	Si⁺⁸	Zatsarinny et al. (2004)	Fe⁺¹¹	Novotný et al. (2012)*
O⁺⁵	Nahar (1998)	Si⁺⁹	Nahar (1995)	Fe⁺¹²	Hahn et al. (2014)*
O⁺⁶	Nahar (1998)	Si⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺¹³	Arnaud and Rothenflug (1985)
O⁺⁷	Nahar (1998)	Si⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺¹⁴	Altun et al. (2007)*
Ne⁺¹	Arnaud and Rothenflug (1985)	Si⁺¹²	Arnaud and Rothenflug (1985)	Fe⁺¹⁵	Murakami et al. (2006)*
Ne⁺²	Zatsarinny et al. (2003)	Si⁺¹³	Arnaud and Rothenflug (1985)	Fe⁺¹⁶	Zatsarinny et al. (2004)
Ne⁺³	Mitnik and Badnell (2004)*	S⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺¹⁷	Arnaud and Rothenflug (1985)
Ne⁺⁴	Zatsarinny et al. (2004)	S⁺²	Nahar (1995)	Fe⁺¹⁸	Zatsarinny et al. (2003)
Ne⁺⁵	Nahar (1995)	S⁺³	Nahar (2000)	Fe⁺¹⁹	Savin et al. (2002)*
Ne⁺⁶	Arnaud and Rothenflug (1985)	S⁺⁴	Altun et al. (2007)	Fe⁺²⁰	Zatsarinny et al. (2004)
Ne⁺⁷	Arnaud and Rothenflug (1985)	S⁺⁵	Arnaud and Rothenflug (1985)	Fe⁺²¹	Arnaud and Rothenflug (1985)
Ne⁺⁸	Nahar (2006)	S⁺⁶	Zatsarinny et al. (2004)	Fe⁺²²	Arnaud and Rothenflug (1985)
Ne⁺⁹	Nahar (2006)	S⁺⁷	Zatsarinny et al. (2006)*	Fe⁺²³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
Mg⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	S⁺⁸	Zatsarinny et al. (2003)	Fe⁺²⁴	Nahar, Pradhan, and Zhang (2001)
Mg⁺²	Zatsarinny et al. (2004)	S⁺⁹	Mitnik and Badnell (2004)*	Fe⁺²⁵	Nahar, Pradhan, and Zhang (2001)
Mg⁺³	Arnaud and Rothenflug (1985)	S⁺¹⁰	Zatsarinny et al. (2004)
Mg⁺⁴	Zatsarinny et al. (2004)	S⁺¹¹	Nahar (1995)

We use Mewe’s formula for the radiative recombination (Mewe et al. 1980a, 1980b).

Table 1.

Open in new tab

Literature on the recombition rate.

Ion	Literature	Ion	Literature	Ion	Literature
C⁺¹	Nahar and Pradhan (1999)	Mg⁺⁵	Arnaud and Rothenflug (1985)	S⁺¹²	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺²	Nahar and Pradhan (1999)	Mg⁺⁶	Zatsarinny et al. (2004)	S⁺¹³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺³	Nahar and Pradhan (1997)	Mg⁺⁷	Nahar (1995)	S⁺¹⁴	Arnaud and Rothenflug (1985)
C⁺⁴	Nahar and Pradhan (1997)	Mg⁺⁸	Arnaud and Rothenflug (1985)	S⁺¹⁵	Arnaud and Rothenflug (1985)
C⁺⁵	Nahar and Pradhan (1997)	Mg⁺⁹	Arnaud and Rothenflug (1985)	Fe⁺¹	Nahar and Pradhan (1997)
N⁺¹	Zatsarinny et al. (2004)	Mg⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺²	Nahar and Pradhan (1997)
N⁺²	Nahar and Pradhan (1997)	Mg⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺³	Nahar and Pradhan (1997)
N⁺³	Nahar and Pradhan (1997)	Si⁺¹	Nahar (2000)	Fe⁺⁴	Nahar (1998)
N⁺⁴	Nahar and Pradhan (1997)	Si⁺²	Altun et al. (2007)	Fe⁺⁵	Nahar and Pradhan (1999)
N⁺⁵	Nahar (2006)	Si⁺³	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺⁶	Arnaud and Rothenflug (1985)
N⁺⁶	Nahar (2006)	Si⁺⁴	Zatsarinny et al. (2003)	Fe⁺⁷	Nahar (2000)
O⁺¹	Nahar (1998)	Si⁺⁵	Zatsarinny et al. (2006)*	Fe⁺⁸	Arnaud and Rothenflug (1985)
O⁺²	Zatsarinny et al. (2004)	Si⁺⁶	Zatsarinny et al. (2003)	Fe⁺⁹	Arnaud and Rothenflug (1985)
O⁺³	Nahar (1998)	Si⁺⁷	Mitnik and Badnell (2004)*	Fe⁺¹⁰	Lestinsky et al. (2009)*
O⁺⁴	Nahar (1998)	Si⁺⁸	Zatsarinny et al. (2004)	Fe⁺¹¹	Novotný et al. (2012)*
O⁺⁵	Nahar (1998)	Si⁺⁹	Nahar (1995)	Fe⁺¹²	Hahn et al. (2014)*
O⁺⁶	Nahar (1998)	Si⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺¹³	Arnaud and Rothenflug (1985)
O⁺⁷	Nahar (1998)	Si⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺¹⁴	Altun et al. (2007)*
Ne⁺¹	Arnaud and Rothenflug (1985)	Si⁺¹²	Arnaud and Rothenflug (1985)	Fe⁺¹⁵	Murakami et al. (2006)*
Ne⁺²	Zatsarinny et al. (2003)	Si⁺¹³	Arnaud and Rothenflug (1985)	Fe⁺¹⁶	Zatsarinny et al. (2004)
Ne⁺³	Mitnik and Badnell (2004)*	S⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺¹⁷	Arnaud and Rothenflug (1985)
Ne⁺⁴	Zatsarinny et al. (2004)	S⁺²	Nahar (1995)	Fe⁺¹⁸	Zatsarinny et al. (2003)
Ne⁺⁵	Nahar (1995)	S⁺³	Nahar (2000)	Fe⁺¹⁹	Savin et al. (2002)*
Ne⁺⁶	Arnaud and Rothenflug (1985)	S⁺⁴	Altun et al. (2007)	Fe⁺²⁰	Zatsarinny et al. (2004)
Ne⁺⁷	Arnaud and Rothenflug (1985)	S⁺⁵	Arnaud and Rothenflug (1985)	Fe⁺²¹	Arnaud and Rothenflug (1985)
Ne⁺⁸	Nahar (2006)	S⁺⁶	Zatsarinny et al. (2004)	Fe⁺²²	Arnaud and Rothenflug (1985)
Ne⁺⁹	Nahar (2006)	S⁺⁷	Zatsarinny et al. (2006)*	Fe⁺²³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
Mg⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	S⁺⁸	Zatsarinny et al. (2003)	Fe⁺²⁴	Nahar, Pradhan, and Zhang (2001)
Mg⁺²	Zatsarinny et al. (2004)	S⁺⁹	Mitnik and Badnell (2004)*	Fe⁺²⁵	Nahar, Pradhan, and Zhang (2001)
Mg⁺³	Arnaud and Rothenflug (1985)	S⁺¹⁰	Zatsarinny et al. (2004)
Mg⁺⁴	Zatsarinny et al. (2004)	S⁺¹¹	Nahar (1995)

Ion	Literature	Ion	Literature	Ion	Literature
C⁺¹	Nahar and Pradhan (1999)	Mg⁺⁵	Arnaud and Rothenflug (1985)	S⁺¹²	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺²	Nahar and Pradhan (1999)	Mg⁺⁶	Zatsarinny et al. (2004)	S⁺¹³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
C⁺³	Nahar and Pradhan (1997)	Mg⁺⁷	Nahar (1995)	S⁺¹⁴	Arnaud and Rothenflug (1985)
C⁺⁴	Nahar and Pradhan (1997)	Mg⁺⁸	Arnaud and Rothenflug (1985)	S⁺¹⁵	Arnaud and Rothenflug (1985)
C⁺⁵	Nahar and Pradhan (1997)	Mg⁺⁹	Arnaud and Rothenflug (1985)	Fe⁺¹	Nahar and Pradhan (1997)
N⁺¹	Zatsarinny et al. (2004)	Mg⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺²	Nahar and Pradhan (1997)
N⁺²	Nahar and Pradhan (1997)	Mg⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺³	Nahar and Pradhan (1997)
N⁺³	Nahar and Pradhan (1997)	Si⁺¹	Nahar (2000)	Fe⁺⁴	Nahar (1998)
N⁺⁴	Nahar and Pradhan (1997)	Si⁺²	Altun et al. (2007)	Fe⁺⁵	Nahar and Pradhan (1999)
N⁺⁵	Nahar (2006)	Si⁺³	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺⁶	Arnaud and Rothenflug (1985)
N⁺⁶	Nahar (2006)	Si⁺⁴	Zatsarinny et al. (2003)	Fe⁺⁷	Nahar (2000)
O⁺¹	Nahar (1998)	Si⁺⁵	Zatsarinny et al. (2006)*	Fe⁺⁸	Arnaud and Rothenflug (1985)
O⁺²	Zatsarinny et al. (2004)	Si⁺⁶	Zatsarinny et al. (2003)	Fe⁺⁹	Arnaud and Rothenflug (1985)
O⁺³	Nahar (1998)	Si⁺⁷	Mitnik and Badnell (2004)*	Fe⁺¹⁰	Lestinsky et al. (2009)*
O⁺⁴	Nahar (1998)	Si⁺⁸	Zatsarinny et al. (2004)	Fe⁺¹¹	Novotný et al. (2012)*
O⁺⁵	Nahar (1998)	Si⁺⁹	Nahar (1995)	Fe⁺¹²	Hahn et al. (2014)*
O⁺⁶	Nahar (1998)	Si⁺¹⁰	Arnaud and Rothenflug (1985)	Fe⁺¹³	Arnaud and Rothenflug (1985)
O⁺⁷	Nahar (1998)	Si⁺¹¹	Arnaud and Rothenflug (1985)	Fe⁺¹⁴	Altun et al. (2007)*
Ne⁺¹	Arnaud and Rothenflug (1985)	Si⁺¹²	Arnaud and Rothenflug (1985)	Fe⁺¹⁵	Murakami et al. (2006)*
Ne⁺²	Zatsarinny et al. (2003)	Si⁺¹³	Arnaud and Rothenflug (1985)	Fe⁺¹⁶	Zatsarinny et al. (2004)
Ne⁺³	Mitnik and Badnell (2004)*	S⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	Fe⁺¹⁷	Arnaud and Rothenflug (1985)
Ne⁺⁴	Zatsarinny et al. (2004)	S⁺²	Nahar (1995)	Fe⁺¹⁸	Zatsarinny et al. (2003)
Ne⁺⁵	Nahar (1995)	S⁺³	Nahar (2000)	Fe⁺¹⁹	Savin et al. (2002)*
Ne⁺⁶	Arnaud and Rothenflug (1985)	S⁺⁴	Altun et al. (2007)	Fe⁺²⁰	Zatsarinny et al. (2004)
Ne⁺⁷	Arnaud and Rothenflug (1985)	S⁺⁵	Arnaud and Rothenflug (1985)	Fe⁺²¹	Arnaud and Rothenflug (1985)
Ne⁺⁸	Nahar (2006)	S⁺⁶	Zatsarinny et al. (2004)	Fe⁺²²	Arnaud and Rothenflug (1985)
Ne⁺⁹	Nahar (2006)	S⁺⁷	Zatsarinny et al. (2006)*	Fe⁺²³	Mewe, Schrijver, and Sylwester (1980a, 1980b)
Mg⁺¹	Mewe, Schrijver, and Sylwester (1980a, 1980b)	S⁺⁸	Zatsarinny et al. (2003)	Fe⁺²⁴	Nahar, Pradhan, and Zhang (2001)
Mg⁺²	Zatsarinny et al. (2004)	S⁺⁹	Mitnik and Badnell (2004)*	Fe⁺²⁵	Nahar, Pradhan, and Zhang (2001)
Mg⁺³	Arnaud and Rothenflug (1985)	S⁺¹⁰	Zatsarinny et al. (2004)
Mg⁺⁴	Zatsarinny et al. (2004)	S⁺¹¹	Nahar (1995)

We use Mewe’s formula for the radiative recombination (Mewe et al. 1980a, 1980b).

Since the SNR shock may heat the plasma faster than the Coulomb collisions due to the wave–particle interactions in the plasma, the ionization state of atoms can significantly deviate from the ionization equilibrium. Thus, we simultaneously solve the atomic rate equations:

$$\begin{eqnarray} \frac{d}{ dt^{\prime } }\left( \frac{ n_{Z,z} }{ \rho } \right) &=& n_{\rm e} \left[ R_{Z,z-1} \frac{ n_{Z,z-1} }{\rho } - \left( R_{Z,z} + K_{Z,z} \right) \frac{ n_{Z,z} }{\rho }\right.\nonumber\\ && \left. +\, K_{Z,z+1} \frac{ n_{Z,z+1} }{\rho } \right]. \end{eqnarray}$$

(23)

Note that, in our formulation, the velocity distribution function of the species is always assumed to be the Maxwellian.

3 Shock jump conditions

Here we give the initial conditions for the temporal developments of the downstream ionization balance and temperature relaxation by considering shock jump conditions. We introduce the conditions usually supposed in the SNR shocks from analogs of collisional shocks and the novel condition given by modeling the energy exchange between electromagnetic fields and particles.

3.1 Collisional shock model (Models 0, 1, and 2)

For the pre-shock gas (denoted by the subscript “0”), we set T_{j, 0} = T₀ = 3 × 10⁴ K assuming collisional ionization equilibrium and temperature equilibrium. In this condition, the fraction of the neutral atoms is ∼1.3 × 10⁻² in number. For the downstream values (denoted by the subscript “2”) of the charged particles, assuming a negligibly small magnetic field at the upstream region (or a parallel shock), we consider the total flux conservation laws as

$$\begin{eqnarray} && \rho _{0} v_{0} = \rho _{2} v_{2}, \end{eqnarray}$$

(24)

$$\begin{eqnarray} && \rho _{0}v_0{}^2+P_{0} = \rho _{2}v_{2}{}^2+P_{2}, \end{eqnarray}$$

(25)

$$\begin{eqnarray} && \frac{ \rho _0 v_0{}^3 }{2} + \left(\varepsilon _{0}+P_{0}\right)v_{0} = \frac{ \rho _2 v_{2}{}^3 }{2} + \left(\varepsilon _{2}+P_{2}\right)v_2, \end{eqnarray}$$

(26)

where the total pressure is P = ∑_jP_j and the total internal energy is ϵ = ∑_jϵ_j, respectively. The mass density of the species j is ρ_j = m_jn_j, where m_j is the particle mass, and the total mass density is ρ = ∑_jρ_j. The compression ratio r_c and total pressure jump x_c are derived as

$$\begin{eqnarray} && r_{\rm c} \equiv \frac{\rho _2}{\rho _0} = \frac{v_0}{v_2} = \frac{ \left(\gamma +1\right){\cal M}_{\rm s}{}^2 }{ \left(\gamma -1\right){\cal M}_{\rm s}{}^2+2 } \end{eqnarray}$$

(27)

$$\begin{eqnarray} && x_c \equiv \frac{ P_2 }{ P_0 } = \frac{ \varepsilon _2}{ \varepsilon _0 } = \frac{ 2\gamma {\cal M}_{\rm s}{}^2 - \left(\gamma -1\right) }{ \gamma +1 }, \end{eqnarray}$$

(28)

where |${\cal M}_{\rm s}\equiv v_0/\sqrt{\gamma P_0/\rho _0}$| is the sonic Mach number defined by the total pressure and mass density. For each species j, we assume the flux conservation laws as

$$\begin{eqnarray} && \rho _{j,0} v_{0} = \rho _{j,2} v_{2}, \end{eqnarray}$$

(29)

$$\begin{eqnarray} && \rho _{j,0}v_0{}^2+P_{j,0} = \rho _{j,2}v_{2}{}^2+P_{2}\frac{\rho _{j,0}}{\rho _0}, \end{eqnarray}$$

(30)

$$\begin{eqnarray} && \frac{ \rho _{j,0}v_0{}^3 }{2} + \left(\varepsilon _{j,0}+P_{j,0}\right)v_0\nonumber\\ && = \frac{ \rho _{j,2}v_{2}{}^3 }{2} + \left\lbrace \left(\varepsilon _{j,2}+P_{j,2}\right)\frac{\rho _{j,0}}{\rho _0}\right\rbrace v_2, \end{eqnarray}$$

(31)

where we have assumed that the downstream ion velocities are the same as each other (v_{j, 2} = v₂), and that the downstream internal energy ϵ_{j, 2} = (ρ_{j, 0}/ρ₀)ϵ₂ and pressure P_{j, 2} = (ρ_{j, 0}/ρ₀)P₂ are proportional to the upstream kinetic energy ρ_{j, 0}v₀²/2. The downstream temperature of the species j, kT_{j, 2} = P_{j, 2}/n_{j, 2} = (P₂/ρ₂)m_j, is derived as

$$\begin{eqnarray} kT_{j,2} &=&\frac{m_j v_0{}^2}{r_{\rm c}}\left(1-\frac{1}{r_{\rm c}}+\frac{1}{\gamma {\cal M}_{\rm s}{}^2}\right) \nonumber \\ &=&\frac{ \left(\gamma -1\right) m_j v_0^{\prime }{}^2 }{2} \frac{ \left( {\cal M}_{\rm s}{}^2+\frac{2 }{\gamma -1} \right) \left( {\cal M}_{\rm s}{}^2-\frac{\gamma -1}{2\gamma } \right) }{ \left( {\cal M}_{\rm s}{}^2 - 1 \right)^2 }, \end{eqnarray}$$

(32)

where |$v_0^{\prime }=v_0-v_2$| is the upstream velocity measured in the downstream rest. In the strong shock limit with γ = 5/3, we obtain the relation |$(3/2)kT_{j,2}=m_jv_0^{\prime }{}^2/2$|⁠, indicating that the upstream coherent motion of the particles is completely randomized due to the shock transition. The temperature ratio of the species j to k is equal to their ion mass ratio, T_j/T_k = m_j/m_k. This corresponds to the fact that the widths of the Maxwell velocity distribution function of each species are the same. The neutral particles do not form a shock structure because they do not interact with the electromagnetic fields. Thus, for the neutral particles, we approximately adopt ϵ_j,2 = ρ_j,0v₀²/2 + ϵ_j,0. We will refer to this collisional shock model as Model 0.

To investigate the effects of the electron heating around the shock transition region, we parametrize the energy exchange between protons and electrons as

$$\begin{eqnarray} && \varepsilon _{{\rm p},2} = \varepsilon _2 \frac{ \rho _{{\rm p},0} }{ \rho _0 } \left(1-f_{\rm eq}\right), \end{eqnarray}$$

(33)

$$\begin{eqnarray} && \varepsilon _{{\rm e},2} = \varepsilon _2 \left( \frac{ \rho _{{\rm e},0} }{ \rho _0} + \frac{ \rho _{{\rm p},0} }{ \rho _0}f_{\rm eq}\right) \end{eqnarray}$$

(34)

where the subscript “p” denotes the proton. The degree of equilibrium is represented by the parameter f_eq, which is related to the temperature ratio as follows:

$$\begin{eqnarray} \frac{ \varepsilon _{\rm e,2} }{ \varepsilon _{\rm p,2} } =\frac{ n_{\rm e,2} }{ n_{\rm p,2} } \frac{ T_{\rm e,2} }{ T_{\rm p,2} } =\frac{ (\rho _{\rm e,0}/\rho _{\rm p,0}) + f_{\rm eq}\,\, }{ 1-f_{\rm eq}}. \end{eqnarray}$$

(35)

Introducing β ≡ T_e,2/T_p,2, we obtain

$$\begin{eqnarray} f_{\rm eq}= \frac{ n_{\rm e,0} }{ n_{\rm p,0} } \frac{ \beta - ( m_{\rm e}/m_{\rm p} ) }{ 1 + ( n_{\rm e,0}/n_{\rm p,0} )\beta }. \end{eqnarray}$$

(36)

We consider the cases of β = 0.01 (Model 1) and β = 0.1 (Model 2). Although the electron might exchange its internal energy with other ions, we omit this possibility for simplicity. Complete treatments of the electron heating around the shock may be needed to solve the nature of electromagnetic fields and wave–particle interactions in detail, and this issue is as yet unsettled (e.g., Ohira & Takahara 2007, 2008; Rakowski et al. 2008; Laming et al. 2014).

3.2 Collisionless shock model (Models 3, 4, and 5)

Here we consider another way of giving a shock transition with the CR acceleration. We assume that part of the shock kinetic energy is consumed for the generation of CRs and amplification of the magnetic field. The generated magnetic field is assumed to be disturbed (not an ordered field). In this model, we consider the randomization of the particles incoming from the far-upstream region at the shock transition region. The randomization is quantified by the entropy. We notice that the “randomization” results in a more isotropic particle distribution downstream than the pre-shock one (measured in the shock rest frame). In the collisional shocks, this may be called “thermalization;” however, the particle distribution may deviate from the Maxwellian in the collisionless shocks. We use “randomization” for both collisional and collisionless shocks in the following.

The conservation laws of total mass and momentum flux can be written as

$$\begin{eqnarray} && \rho _0 v_0 = \rho _2 v_2, \end{eqnarray}$$

(37)

$$\begin{eqnarray} && \rho _0 v_0{}^2 + P_0 + F_{{\rm esc}} = \rho _2 v_2{}^2 + P_2 + \frac{\delta B^2}{4\pi } + P_{\rm cr}, \end{eqnarray}$$

(38)

where the generated (turbulent) magnetic-field strength is δB. We regard the field with δB as having a coherent length scale (injection scale of turbulence) much larger than the Larmor radius of the thermal particles with a velocity of ∼v₀ and that the turbulence cascades to the smaller scale. The disturbances associated with the field are assumed to randomize the thermal particles by the wave–particle interactions. The CR pressure of the species j is defined as P_{cr, j} and the total CR pressure is P_cr = ∑_jP_{cr, j}. The net momentum flux of escaping CRs is F_esc ≲ ρ₀v₀³/3c. We neglect the total flux and the flux of each species j in this article (F_esc = 0 and F_{esc, j} = 0). For each species denoted by the subscript j, we give the flux conservation laws as

$$\begin{eqnarray} && \rho _{j,0} v_0 = \rho _{j,2} v_2, \end{eqnarray}$$

(39)

$$\begin{eqnarray} && \rho _{j,0} v_0{}^2 + P_{j,0} = \rho _{j,2} v_2{}^2 + P_{j,2} +\left( \frac{\delta B^2}{4\pi }+P_{\rm cr} \right)\frac{\rho _{j,0}}{\rho _0} \end{eqnarray}$$

(40)

where we assume a contribution of the species j for the magnetic-field amplification and nonthermal pressure is proportional to the upstream kinetic energy ρ_{j, 0}v₀²/2. The compression ratios of the species j are equal (v_{2, j} = v₂). From these conservation laws, we can derive the relation between the compression ratio r_{c, j} = ρ_{j, 2}/ρ_{j, 0} = ρ₂/ρ₀ ≡ r_c and the jump of internal energy x_{c, j} ≡ ϵ_{j, 2}/ϵ_{j, 0} as

$$\begin{eqnarray} r_{\rm c} &=& \left[ 1 + \frac{1-x_{{\rm c},j}}{\gamma {\cal M}_{{\rm s},j}{}^2} - \xi _{\rm B} - \xi _{{\rm cr}} \right]^{-1}, \end{eqnarray}$$

(41)

$$\begin{eqnarray} x_{{\rm c},j} &=& 1 + \gamma {\cal M}_{{\rm s},j}{}^2\left( 1 - \frac{1}{r_{\rm c}} - \xi _{\rm B} - \xi _{{\rm cr}} \right), \end{eqnarray}$$

(42)

where ξ_B ≡ δB²/(4πρ₀v₀²), ξ_cr ≡ P_cr/(ρ₀v₀²), and |${\cal M}_{{\rm s},j}=v_0/\sqrt{\gamma P_{j,0}/\rho _{j,0}}$| is the sonic Mach number defined by the pressure and density of the species j. Thus, once another relation between r_c and x_{c, j} is found, we can derive the shock jump condition with given ξ_B and ξ_cr. As usual, the energy flux conservation is considered by modeling the magnetic-field amplification and the injection rate of nonthermal particles. Since we focus on the downstream ion temperature, we consider the randomization process of thermal ions rather than modeling the behavior of nonthermal particles. Thus, we consider the entropy production of the thermal particles explicitly.

The entropy of the species j per unit mass is defined as

$$\begin{eqnarray} ds_j = \frac{1}{M_j}\frac{ d\tilde{Q}_j }{ kT_j }, \end{eqnarray}$$

(43)

where |$d\tilde{Q}_j$| is the energy transferred from electromagnetic fields to the internal energy of the species j due to the shock transition, and M_j = N_jm_j is the total mass of the species j within the fluid parcel.⁴ Note that |$d\tilde{Q}_j=dE_j+P_jdV$| indicates only the increment of the internal energy rather than the total kinetic energy of the thermal particles (the sum of the bulk motion and the random motion). The upstream total kinetic energy of the thermal particles is divided into δB and P_cr. Substituting |$d\tilde{Q}_j=dE_j+P_jdV$| into equation (43) and using the relation dϵ_j = d(ρ_je_j) = e_jdρ_j + ρ_jde_j, where e_j ≡ E_j/M_j, we can derive the change of the internal energy per unit volume as

$$\begin{eqnarray} \frac{d\varepsilon _j}{\varepsilon _j} =\gamma \frac{d\rho _j}{\rho _j} +(\gamma -1)m_j ds_j. \end{eqnarray}$$

(44)

Note that we have presumed that N_j is constant during the shock transition. Thus, we obtain the entropy jump before and after the shock transition, Δs_j = s_{j, 2} − s_{j, 0} as

$$\begin{eqnarray} \left(\gamma -1\right)m_j\Delta s_j &=&\ln \left( \frac{ \varepsilon _{j,2} }{ \varepsilon _{j,0} } \right) -\gamma \ln \left( \frac{ \rho _{j,2} }{ \rho _{j,0} } \right) \nonumber \\ &=&\ln x_{{\rm c},j} - \gamma \ln \ r_{\rm c}. \end{eqnarray}$$

(45)

Then, the jump conditions are derived by estimating Δs_j independently of equation (45). Since the SNR shock is expected to be formed by the wave–particle interactions, the transferred energy in total |$\Delta \tilde{Q}_j$| may be around ∼|$\boldsymbol {J\!\!}_j\cdot \boldsymbol {E}\Delta t_j$|⁠, where |$\boldsymbol {J}_j$| is the electric current of species j. The electric field measured in the comoving frame of the ions is |$\boldsymbol {E}$|⁠. Δt_j is the time taken by the shock transition. We estimate each value as |$J_j\sim q_j N_j\langle \tilde{v}_j\rangle$|⁠, |$E\equiv |\boldsymbol {E}|\sim (\langle \tilde{v}_j\rangle /c)\delta B$|⁠, and Δt_j ∼ m_jc/q_jδB, where q_j is the electric charge of the species j, |$\langle \tilde{v}_j\rangle =v_0+\sqrt{2kT_0/m_j}$| is the mean kinetic velocity of the species j, and c is the speed of light, respectively. The transition timescale is assumed to be comparable with the inverse of the cyclotron frequency. In a hybrid simulation solving the particle acceleration (e.g., Ohira 2016b), the shock jump seems to occur at a very small length scale despite significant amplification of turbulent magnetic fields at the “upstream” region (this may correspond to the shock precursor region in our situation). We regard that the randomization of particles resulting in shock transition mainly occurs at such a very small length scale. Thus, we assume the entropy production due to the shock transition as

$$\begin{eqnarray} \Delta s_j &=& \frac{1}{M_j} \frac{ J_jE\Delta t_j }{ kT_j } \nonumber \\ &=& \frac{1}{M_j} \frac{q_jN_j\langle \tilde{v}_j\rangle }{kT_{j,2}} \frac{\langle \tilde{v}_j\rangle }{c}\delta B \frac{m_jc}{q_j\delta B} \nonumber \\ &=& \frac{\langle \tilde{v}_j\rangle ^2 }{ kT_0 } \frac{ r_{\rm c} }{ x_{{\rm c},j} }, \end{eqnarray}$$

(46)

where we suppose T_j ∼ T_{j, 2}. Substituting equation (46) into equation (45), we obtain the relation between r_c and x_{c, j} as

$$\begin{eqnarray} f\equiv \frac{ x_{{\rm c},j} }{ r_{\rm c} } \left( \ln x_{{\rm c},j} -\gamma \ln r_{\rm c} \right) -\gamma \left(\gamma -1\right) \left( \frac{ \langle \tilde{v}_j\rangle }{ v_0 } \right)^2 {\cal M}_{{\rm s},j}{}^2 = 0. \nonumber\\ \end{eqnarray}$$

(47)

We solve this equation setting P_cr, δB, and |${\cal M}_{{\rm s},j}=v_0/\sqrt{\gamma P_{j,0}/\rho _{j,0}}$| with equation (41) to derive x_{c, j} in the case of the proton by regarding that the most abundant ions form the shock structure. Then, the compression ratio r_c is derived from equation (41) by using the derived x_{c, p}. The downstream pressures of the other species j are derived from equation (42) by using the derived compression ratio r_c. Note that if we supposed small δB and P_cr, the resultant downstream values would be different from the case of the collisional shock (Model 0) reflecting the different randomization process. In this paper, we consider the most efficiently accelerating CR shock feasible. In such a situation, the CR pressure is a practical function of δB because of the energy budget of the shock. The upstream kinetic energy is divided into thermal energy, magnetic field, and CRs. The fraction of the thermal energy is given by the entropy production. The fraction of the magnetic field is treated as a free parameter. Thus, the remaining energy is divided into the CRs.

The left panel of figure 1 shows f = f(x_{c, j}) (upper part), r_c = r_c(x_{c, j}) (middle part), and Δs_j(x_{c, j})/Δs_{j, ncr} (lower part) for the proton with γ = 5/3. We set the parameters as ξ_cr = 0.5 (purple line), ξ_cr = 0.3 (black line), and ξ_cr = 0 (green line) with fixed values of v₀ = 4000 km s⁻¹, T₀ = 3 × 10⁴ K, and |$1/\sqrt{\xi }_{\rm B}=v_0/(\delta B/\sqrt{4\pi \rho _0})=3$|⁠. The entropy jump Δs_{j, ncr} for the case without the CRs (Model 0, and thus the case of the usual collisional shock) is derived from

$$\begin{eqnarray} \left(\gamma -1\right)m_j\Delta s_{j,{\rm ncr}} = \ln x_{{\rm c},j,{\rm ncr}} - \gamma \ln r_{\rm c,ncr}, \end{eqnarray}$$

(48)

where x_{c, j, ncr} and r_{c, ncr} are given by Model 0. The right panel of figure 1 shows the sets of ξ_cr, x_{c, j}, and r_c satisfying f = 0. The function f(x_{c, j}) shows two solutions for a given δB depending on P_cr. Although we do not have a precise explanation about these two solutions that may require a full understanding of the ion heating by the kinetics theory, we may be able to interpret them from resultant downstream values. Let us consider the case of ξ_cr = 0 in which Δs_j/Δs_{j, ncr} ≈ 1 around each solution. We will refer to the solution giving |$x_{{\rm c},j}/{\cal M}_{{\rm s},j}{}^2\approx 0.17$| and r_c ≈ 1.27 as “solution A,” while we will refer to the other solution giving |$x_{{\rm c},j}/{\cal M}_{{\rm s},j}{}^2\approx 1.28$| and r_c ≈ 8.31 as “solution B.” The resultant temperatures (T_{j, 2}/T₀ = x_{c, j}/r_c ≈ 0.1mv₀²/γkT₀) are almost the same as each other. This means that the speed of the particles’ random motion is almost the same as each solution. On the other hand, the difference in the compression ratios indicates that the speeds of the particles’ bulk motion are significantly different from each other. In a collisional shock in the strong shock limit, the downstream temperature satisfies |$(3/2)kT_2=m v^{\prime }_{0}{}^2/2$|⁠, where |$v^{\prime }_0=v_0-v_2$| is the upstream velocity measured in the downstream rest frame and we use γ = 5/3. This might mean that, since our shock consumes its energy for the generation of the nonthermal components, the random motion speed measured in the downstream rest frame |$\tilde{v}^{\prime }_{\rm R}\equiv \sqrt{3kT_{j,2}/m_j}$| should be equal to or smaller than |$v_0^{\prime }=v_0-v_2$| for the solution representing the shock transition (i.e., |$\tilde{v}^{\prime }_{\rm R}/v_0^{\prime }\le 1$|⁠). Solution A gives the speed as |$\tilde{v}^{\prime }_{{\rm R}}/v_0^{\prime }\simeq 2.3$|⁠, while solution B gives |$\tilde{v}^{\prime }_{{\rm R}}/v_0^{\prime }\simeq 0.6$|⁠. Hence, solution B may correspond to the shock transition. Solution A should be rejected because it does not satisfy the energy flux conservation law.

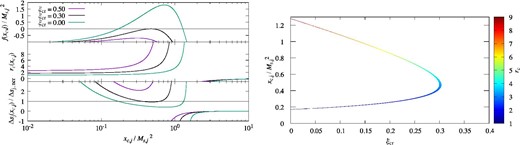
$Left: Function of f = f(xc, j) defined in equation (47) (upper part), the compression ratio rc = rc(xc, j) (middle part), and Δsj(xc, j)/Δsj, ncr (lower part) for the proton with γ = 5/3. We set the parameters as ξcr = 0.5 (purple line), ξcr = 0.3 (black line), and ξcr = 0 (green line) with fixed values of v0 = 4000 km s−1, T0 = 3 × 104 K, and $1/\sqrt{\xi }_{\rm B}=v_0/(\delta B/\sqrt{4\pi \rho _0})=3$. Note that ${\cal M}_{{\rm s},j}=197$. Right: Solutions of f = 0 with fixed $1/\sqrt{\xi }_{\rm B}=3$ and ${\cal M}_{{\rm s},j}=197$ for the proton. The horizontal axis shows the CR fraction ξcr and the vertical axis shows the pressure jump $x_{{\rm c},j}/{\cal M}_{{\rm s},j}{}^2$. The color indicates the compression ratio rc.$

Fig. 1.

Left: Function of f = f(x_{c, j}) defined in equation (47) (upper part), the compression ratio r_c = r_c(x_{c, j}) (middle part), and Δs_j(x_{c, j})/Δs_{j, ncr} (lower part) for the proton with γ = 5/3. We set the parameters as ξ_cr = 0.5 (purple line), ξ_cr = 0.3 (black line), and ξ_cr = 0 (green line) with fixed values of v₀ = 4000 km s⁻¹, T₀ = 3 × 10⁴ K, and |$1/\sqrt{\xi }_{\rm B}=v_0/(\delta B/\sqrt{4\pi \rho _0})=3$|⁠. Note that |${\cal M}_{{\rm s},j}=197$|⁠. Right: Solutions of f = 0 with fixed |$1/\sqrt{\xi }_{\rm B}=3$| and |${\cal M}_{{\rm s},j}=197$| for the proton. The horizontal axis shows the CR fraction ξ_cr and the vertical axis shows the pressure jump |$x_{{\rm c},j}/{\cal M}_{{\rm s},j}{}^2$|⁠. The color indicates the compression ratio r_c.

Open in new tab Download slide

When ξ_cr becomes large, the two solutions approach each other, coinciding at ξ_cr ≃ 0.3 (multiple roots) and, finally, the solution vanishes. The multiple roots (ξ_cr = 0.3) give |$\tilde{v}^{\prime }_{\rm R}/v_0^{\prime }\simeq 0.7$| and Δs_j/Δs_{j, ncr} ≃ 0.93. Thus, the multiple roots may represent the shock transition giving the maximum P_cr feasible in our shock model. In this article, we set the maximum ξ_cr to compare the no-CR cases with the case of extremely efficient CR acceleration. The maximum ξ_cr is derived from the multiple roots of f = 0 with a given ξ_B.

For the case of v₀ = 4000 km s⁻¹ and T₀ = 3 × 10⁴ K with given |$1/\sqrt{\xi _{\rm B}}=3$|⁠, we obtain the maximum acceptable CR production ξ_cr ≃ 0.3, Δs_j/Δs_{j, ncr} ≃ 0.92–0.95 depending on m_j, r_c ≃ 3.29, and kT_{p, 2} ≃ 14.4 keV. Note that in the case of Model 0 (the usual collisional shock case), we obtain r_c = 4.00 and kT_{p, 2} = 31.3 keV. The fraction of CRs ξ_cr = 0.3 seems to be reasonable for the SNR shocks as sources of Galactic CRs. From the subtraction of the energy fluxes of the thermal particles at the far upstream and downstream, we can regard that roughly 50% of the upstream energy flux is transferred to the nonthermal components. The fraction of magnetic pressure |$1/\sqrt{\xi _{\rm B}}=3$| corresponds to a magnetic-field strength of |$\delta B\simeq 611\,\, {\mu \rm {G}} ( v_0 /4000\,\, {\rm km\,\, s^{-1}} ) ( n_{\rm p,0}/1\,\, {\rm cm^{-3}})^{1/2}$|⁠, which is consistent with the estimated strength from X-ray observations of young SNRs (e.g., Vink & Laming 2003; Bamba et al. 2005; Uchiyama et al. 2007). Thus, our parameter choice of |$1/\sqrt{\xi _{\rm B}}=3$| can be reasonable to adopt our model to the young SNR shocks.

Here we consider the choice of the maximum ξ_cr. In the case of collisional shock formed by hard-sphere collisions, for example, the collisions result in one of the most efficient randomizations of particles. Thus, the collisional shock can “easily” dissipate its kinetic energy within the mean collision time. In the collisionless plasma, such an efficient randomization process is absent. The particles in the plasma tend to behave as “nonthermal” particles resulting in a generation of electromagnetic disturbances by themselves. The collisionless shock is formed by the self-generated disturbances so that almost all particles become thermal particles. Although the number of the nonthermal particles is much smaller than the number of thermal particles, efficient randomization caused by the nonthermal particles is required to form the collisionless shock. Our choice of the maximum ξ_cr corresponds with the effect being minimized per one nonthermal particle.

Figure 2 shows the maximum ξ_cr derived from f = 0 as a function of |$1/\sqrt{\xi _{\rm B}}$| for |${\cal M}_{\rm s,p}=197$|⁠. The fraction ξ_cr drops around |$1/\sqrt{\xi _{\rm B}}\lesssim 3$| but is flattened for |$1/\sqrt{ \xi _{\rm B} } $| ≳ 3. This depletion of the maximum ξ_cr is qualitatively obvious in terms of the energy budget of the shock; the upstream kinetic energy is divided into the thermal components, P_cr and δB. The fraction of δB is a given parameter. The fraction of the thermal components and the maximum fraction of P_cr are derived from the entropy production. We will refer to this model with |$1/\sqrt{\xi _{\rm B}}=3$| and the maximum ξ_cr as Model 3.

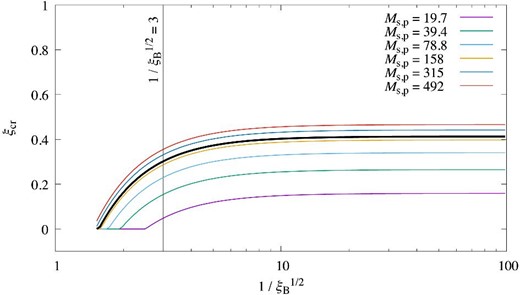
$Maximum ξcr derived from f = 0 as a function of $1/\sqrt{ \xi _{\rm B} }=v_0/(\delta B/\sqrt{4\pi \rho _0})$ for a given shock velocity v0 and T0 = 3 × 104 K. The heavy black solid line shows ${\cal M}_{\rm s,p}=197$ (v0 = 4000 km s−1). The vertical thin line indicates $1/\sqrt{ \xi _{\rm B} }=3$. For a comparison, we display ${\cal M}_{\rm s,p}=$ 19.7 (purple, v0 = 400 km s−1), 39.4 (green, v0 = 800 km s−1), 78.8 (light blue, v0 = 1600 km s−1), 158 (orange, v0 = 3200 km s−1), 315 (blue, v0 = 6400 km s−1), and 492 (red, v0 = 10000 km s−1).$

Fig. 2.

Maximum ξ_cr derived from f = 0 as a function of |$1/\sqrt{ \xi _{\rm B} }=v_0/(\delta B/\sqrt{4\pi \rho _0})$| for a given shock velocity v₀ and T₀ = 3 × 10⁴ K. The heavy black solid line shows |${\cal M}_{\rm s,p}=197$| (v₀ = 4000 km s⁻¹). The vertical thin line indicates |$1/\sqrt{ \xi _{\rm B} }=3$|⁠. For a comparison, we display |${\cal M}_{\rm s,p}=$| 19.7 (purple, v₀ = 400 km s⁻¹), 39.4 (green, v₀ = 800 km s⁻¹), 78.8 (light blue, v₀ = 1600 km s⁻¹), 158 (orange, v₀ = 3200 km s⁻¹), 315 (blue, v₀ = 6400 km s⁻¹), and 492 (red, v₀ = 10000 km s⁻¹).

Open in new tab Download slide

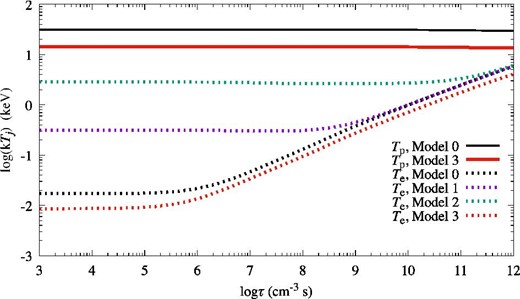
Figure 3 shows the results of downstream ion temperatures divided by 2Z (i.e., the particle mass in atomic units) for Model 0 and Model 3 with v₀ = 4000 km s⁻¹ and T₀ = 3 × 10⁴ K. The reduced temperatures kT_{Z, z}/2Z of Model 3 do not depend on the particle mass, indicating that the temperature ratios between the ions are equal to their ion mass ratio. Such mass-proportional ion temperatures are observed at SN 1987A (Miceli et al. 2019). The temperature jump T_{j, 2}/T₀ is given by |$x_{{\rm c},j}/r_{\rm c}\sim {\cal M}_{{\rm s},j}$|⁠. The relation of |$x_{{\rm c},j}/r_{\rm c}\sim {\cal M}_{{\rm s},j}$| is also implied by the condition of f = 0. Thus, Model 3 predicts that the ion temperature ratio is given by the mass ratio, similar to the case of Model 0. Note that Model 1 and Model 2 give ion temperatures almost the same as Model 0. On the other hand, kT_{Z, z}/2Z of Model 3 is smaller than the case of Model 0 by a factor of 2 due to the generation of nonthermal components.

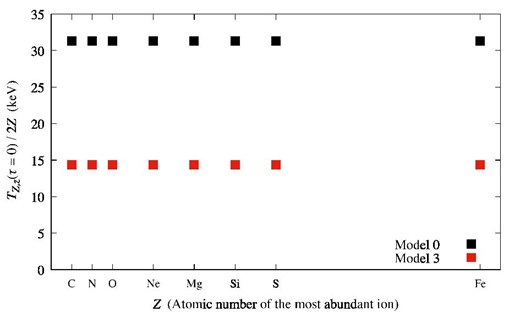
Initial downstream ion temperatures divided by 2Z (i.e., the particle mass in atomic mass units) for Model 0 and Model 3 with v0 = 4000 km s−1 and T0 = 3 × 104 K. The black square shows the results of Model 0, and the red square shows the results of Model 3. The results of Model 1 and Model 2 are the same as the results of Model 0, respectively. The horizontal axis shows the atomic number Z.

Fig. 3.

Initial downstream ion temperatures divided by 2Z (i.e., the particle mass in atomic mass units) for Model 0 and Model 3 with v₀ = 4000 km s⁻¹ and T₀ = 3 × 10⁴ K. The black square shows the results of Model 0, and the red square shows the results of Model 3. The results of Model 1 and Model 2 are the same as the results of Model 0, respectively. The horizontal axis shows the atomic number Z.

Open in new tab Download slide

The existence of more than two solutions is usually seen in the CR accelerating shock model (e.g., Drury & Voelk 1981; Vink et al. 2010; Vink & Yamazaki 2014, and references therein). The unphysical solution like Solution A of our model, which does not satisfy the energy flux conservation law, also exists in previous studies. The essential difference between our model and previous studies is the treatment of randomization in the shock transition. In the previous studies, the randomization process, which determines the downstream thermal energy, may be implicitly chosen to satisfy the flux conservation laws with assumed parameters (P_cr, energy flux of escaping CRs, etc.). Vink and Yamazaki (2014) also derived a critical sonic Mach number |${\cal M}_{\rm acc}=\sqrt{5}$| below which the particle acceleration should not occur. In our model, a similar sonic Mach number may be derived from conditions of Δs_j ≤ Δs_{j, ncr} and T_{j, 2} ≤ T_{j, 2, ncr}, where T_{j, 2, ncr} is given by Model 0 [equation (32)]. The former states that the entropy generated in the collisionless shock should be smaller than in the case of collisional shocks. The latter states that the downstream temperature should be smaller than the case of adiabatic collisional shocks without CRs. Note that the entropy and temperature must be determined independently to derive the density or pressure in thermodynamics. In other words, the conditions Δs_j ≤ Δs_{j, ncr} and T_{j, 2} ≤ T_{j, 2, ncr} are independent of each other. From equations (48) and (46), and using the relation of |$m_jv_0{}^2/kT_0=(\rho _{j,0}/\rho _0)\gamma {\cal M}_{\rm s}{}^2$|⁠, we can derive

$$\begin{eqnarray} \frac{ T_{j,2,{\rm ncr}} }{ T_0 } &\ge & \frac{ T_{j,2} }{ T_0 }\nonumber\\ & \ge & \frac{\rho _{j,0} }{\rho _0} \frac{ \gamma (\gamma -1) {\cal M}_{\rm s}{}^2 }{ \ln {\left(T_{j,2,{\rm ncr}}/T_0\right)} - \left(\gamma -1\right)\ln r_{ c,{\rm ncr}} } \left( \frac{\langle \tilde{v}_j\rangle }{v_0 } \right)^2, \nonumber\\ \end{eqnarray}$$

(49)

where

$$\begin{eqnarray} \frac{ T_{j,2,{\rm ncr}} }{ T_0 } =\frac{ \rho _{j,0} }{ \rho _0 } \frac{ \gamma {\cal M}_{\rm s}{}^2 }{ r_{\rm c,ncr} } \left( 1 - \frac{ 1 }{ r_{\rm c,ncr} } + \frac{1}{\gamma {\cal M}_{\rm s}{}^2 } \right), \end{eqnarray}$$

(50)

and r_{c, ncr} is given by equation (27). The critical Mach number |${\cal M}_{\rm s,acc}$| is given when the equals sign of the inequality holds. Regarding |$\langle \tilde{v}_j\rangle \simeq v_0$| and ρ_j/ρ₀ ≃ 1 for simplicity, we obtain the numerical value of |${\cal M}_{\rm s,acc}\simeq 16.34$| above which we can find sets of ξ_cr and ξ_B satisfying the inequality (49). The larger critical Mach number than that derived by Vink and Yamazaki (2014) may be due to the difference in the assumed randomization process. However, the value of |${\cal M}_{\rm s,acc}$| may also depend on the Alfvén Mach number, whose effects are not studied in this paper. When the sonic Mach number decreases due to shock deceleration, the effects of the mean magnetic field at the far-upstream region can be important. Shocks with a lower Mach number are seen in the solar wind at coronal mass ejection events, galaxy clusters, and so on. In predictions of the amount of accelerated particles in such cases, we shoud include the pre-existing ordered magnetic field with the flux conservation laws and evaluation of the |$\boldsymbol {J}\cdot \boldsymbol {E}$| term, differing from the current approach. We will study a general critical Mach number with more elaborate models in future work.

Finally, we parametrize the electron heating for the case of extremely efficient CR acceleration as

$$\begin{eqnarray} && \varepsilon _{\rm p,2} = \varepsilon _{{\rm p,2,Model3}}(1-f_{\rm eq}), \nonumber \\ && \varepsilon _{\rm e,2} = \varepsilon _{{\rm e,2,Model3}}+\varepsilon _{\rm p,2,Model3}f_{\rm eq}, \end{eqnarray}$$

(51)

where ϵ_{p, 2, Model3} and ϵ_{e, 2, Model3} are the internal energy calculated by Model 3. Here we have supposed an additional energy transfer: the internal energy of the thermal protons is transferred to the thermal electrons. The fraction of the transferred internal energy is written by the temperature ratio of β = T_{e, 2}/T_{p, 2} as

$$\begin{eqnarray} f_{\rm eq}\,\, = \frac{ \beta (n_{\rm e,0}/n_{\rm p,0})-(\varepsilon _{\rm e,2,Model3}/\varepsilon _{\rm p,2,Model3}) }{ \beta (n_{\rm e,0}/n_{\rm p,0}) + 1 }. \end{eqnarray}$$

(52)

Laming et al. (2014) pointed that the electron temperature can be significantly large (β ∼ 0.1) when the shock accelerates the CRs efficiently. We calculate the cases of β = 0.01 (Model 4) and β = 0.1 (Model 5) in this paper. Table 2 shows a summary of our shock models.

Table 2.

Open in new tab

Summary of the shock jump models.*

Model	r_c	kT_{p, 2}	kT_{e, 2} (β = T_{e, 2}/T_{p, 2})	ξ_B	ξ_cr
0	4	31.32 keV	17.1 eV (m_e/m_p)	0	0
1	4	31.01 keV	31.0 eV (0.01)	0	0
2	4	28.34 keV	2.83 keV (0.1)	0	0
3	3.29	14.38 keV	8.62 eV (1.1m_e/m_p)	1/9	0.30
4	3.29	14.23 keV	14.2 eV (0.01)	1/9	0.30
5	3.29	13.01 keV	1.30 keV (0.1)	1/9	0.30

Model	r_c	kT_{p, 2}	kT_{e, 2} (β = T_{e, 2}/T_{p, 2})	ξ_B	ξ_cr
0	4	31.32 keV	17.1 eV (m_e/m_p)	0	0
1	4	31.01 keV	31.0 eV (0.01)	0	0
2	4	28.34 keV	2.83 keV (0.1)	0	0
3	3.29	14.38 keV	8.62 eV (1.1m_e/m_p)	1/9	0.30
4	3.29	14.23 keV	14.2 eV (0.01)	1/9	0.30
5	3.29	13.01 keV	1.30 keV (0.1)	1/9	0.30

We set v₀ = 4000 km s⁻¹ and T₀ = 3 × 10⁴ K. From the left-hand side to the right-hand side, the columns indicate the model name, the compression ratio r_c, the downstream proton temperature kT_{p, 2}, the downstream electron temperature kT_{e, 2}, the fraction of the amplified magnetic field ξ_B = δB²/(4πρ₀v₀²), and the fraction of the CR pressure ξ_cr = P_cr/(ρ₀v₀²).

Table 2.

Open in new tab

Summary of the shock jump models.*

Model	r_c	kT_{p, 2}	kT_{e, 2} (β = T_{e, 2}/T_{p, 2})	ξ_B	ξ_cr
0	4	31.32 keV	17.1 eV (m_e/m_p)	0	0
1	4	31.01 keV	31.0 eV (0.01)	0	0
2	4	28.34 keV	2.83 keV (0.1)	0	0
3	3.29	14.38 keV	8.62 eV (1.1m_e/m_p)	1/9	0.30
4	3.29	14.23 keV	14.2 eV (0.01)	1/9	0.30
5	3.29	13.01 keV	1.30 keV (0.1)	1/9	0.30

Model	r_c	kT_{p, 2}	kT_{e, 2} (β = T_{e, 2}/T_{p, 2})	ξ_B	ξ_cr
0	4	31.32 keV	17.1 eV (m_e/m_p)	0	0
1	4	31.01 keV	31.0 eV (0.01)	0	0
2	4	28.34 keV	2.83 keV (0.1)	0	0
3	3.29	14.38 keV	8.62 eV (1.1m_e/m_p)	1/9	0.30
4	3.29	14.23 keV	14.2 eV (0.01)	1/9	0.30
5	3.29	13.01 keV	1.30 keV (0.1)	1/9	0.30

4 Evolution track of the downstream ionization balance and temperatures

Here we show the results of the ionization balance and temperature relaxation in the downstream region, omitting the effects of the expansion (dV/dt = 0) as a reference. For convenience, we introduce dτ = ndt, where n is the total number density, so that

$$\begin{eqnarray} && \frac{d\varepsilon _j}{d\tau } \approx \frac{\dot{q}_j}{n}, \end{eqnarray}$$

(53)

$$\begin{eqnarray} \frac{dn_{Z,z}}{d\tau } &=& \frac{ n_{\rm e} }{ n } [ R_{Z,z-1} n_{Z,z-1} - \left( R_{Z,z} + K_{Z,z} \right) n_{Z,z}\nonumber\\ && +\, K_{Z,z+1} n_{Z,z+1} ], \end{eqnarray}$$

(54)

where we use ρ = const. Figures 4 (for He, C, and N), 5 (for O, Ne, and Mg), and 6 (for Si, S, and Fe) show n_{Z, z}/n_Z and kT_{Z, z} for Model 0 with the shock velocity of v₀ = 4000 km s⁻¹, where |$n_Z=\sum _{z}^{}n_{Z,z}$| is the total number density of the atoms with the atomic number Z. Note that τ = ∫ndt ≃ nt because of the small neutral fraction. Here we display the ion temperatures for the most abundant species among its ionic charge.

Fig. 4.

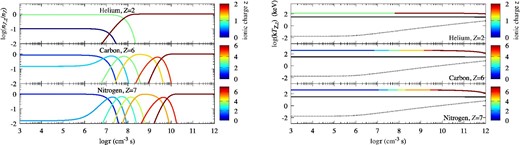
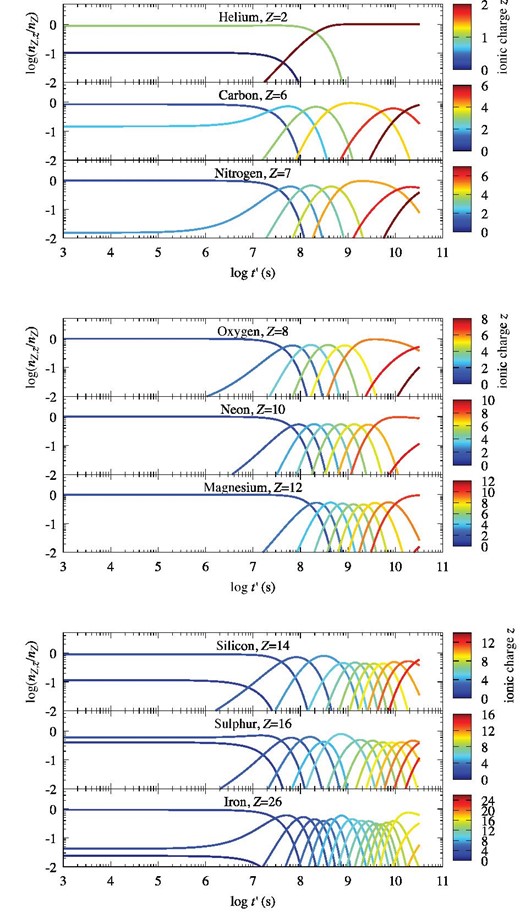
Ionization balance n_{Z, z}/n_Z (left) and temperature kT_{Z, z} of the most abundant species among its ionic charge (right) for Model 0 with a shock velocity of v₀ = 4000 km s⁻¹. We display the species He, C, and N. The color represents the ionic charge z of the ion. The solid black line and black dots are the temperatures of the proton and electron, respectively.

Open in new tab Download slide

Fig. 5.

Ionization balance n_{Z, z}/n_Z (left) and temperature kT_{Z, z} of the most abundant species among its ionic charge (right) for Model 0 with a shock velocity of v₀ = 4000 km s⁻¹. We display the species O, Ne, and Mg. The color represents the ionic charge z of the ion. The solid black line and black dots are the temperatures of the proton and electron, respectively.

Open in new tab Download slide

Fig. 6.

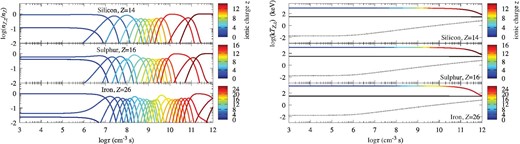
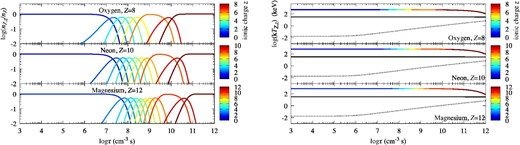
Ionization balance n_{Z, z}/n_Z (left) and temperature kT_{Z, z} of the most abundant species among its ionic charge (right) for Model 0 with a shock velocity of v₀ = 4000 km s⁻¹. We display the species Si, S, and Fe. The color represents the ionic charge z of the ion. The solid black line and black dots are the temperatures of the proton and electron, respectively.

Open in new tab Download slide

The evolution tracks of n_{Z, z}/n_Z and T_{Z, z} for other models are not so different from the case of Model 0. In the case of a higher electron temperature (Model 1 and Model 2), the ions are quickly ionized. Figure 7 shows the electron temperatures for Models 0, 1, 2, and 3 with v₀ = 4000 km s⁻¹. The relation between Model 4 and Model 1 (Model 5 and Model 2) is similar to that of Model 3 and Model 0. The ionization balance n_{Z, z}/n_Z becomes the same in each model after the electron temperature coincides. Note that the electron temperature increases within a column density scale of ntV_sh ∼ 10¹⁴ cm⁻²(nt/10⁶ cm⁻³ s)(V_sh/4000 km s⁻¹). This column density scale is comparable to the size of the Hα emission region (e.g., Shimoda & Laming 2019). Therefore, to study the electron heating at the shock, the Hα observation may be better than the X-ray line observations. In the case of a lower ion temperature due to the production of P_cr and δB (Model 3), the temperature equilibrium is achieved at a smaller nt (e.g., the temperature of Fe is equal to that of the proton at nt ≃ 2 × 10¹¹ cm⁻³ s) because the relaxation time of the Coulomb collision depends on T^3/2 (Spitzer 1962). Note that the lower electron temperature results in a lower ionization state at a given τ ≃ nt.

Electron temperatures for Models 0 (black dots), 1 (purple dots), and 2 (green dots) with v0 = 4000 km s−1. The solid black line shows the proton temperature for Model 0. The red solid line and red dots are the proton and electron temperatures of Model 3, respectively.

Fig. 7.

Electron temperatures for Models 0 (black dots), 1 (purple dots), and 2 (green dots) with v₀ = 4000 km s⁻¹. The solid black line shows the proton temperature for Model 0. The red solid line and red dots are the proton and electron temperatures of Model 3, respectively.

Open in new tab Download slide

When the effects of the expansion become important, we cannot characterize the evolution only by τ ≃ nt and we should introduce parameters to describe the expansion of SNRs and the observed position r/R_sh(t_age). Here we set ρ₀ = 4.08 × 10⁻²m_p, t_age = 1836 yr, and V_sh(t_age) = 3000 km s⁻¹ for example. This parameter set will be used in comparisons of our model to the SNR RCW 86 (discussed later in section 5). Figure 8 shows the downstream ionization structure of He, C, N (top); O, Ne, Mg (middle); and Si, S, and Fe (bottom). The fluid parcel currently at r/R_sh(t_age) = 0.8 crossed the shock at the time of t_* when the shock velocity was V_sh(t_*) = 5094 km s⁻¹ for Models 0, 1, and 2 (4565 km s⁻¹ for Models 3, 4, and 5). Since the compression ratio depends on whether the CRs exist, the shock transition time t_*, shock velocity V_sh(t_*), and T_e(t_*) are different for each model for the fluid parcel currently at r/R_sh(t_age). The evolution of the ionization balance is similar to the case of the plane-parallel shock until t′ ∼ 10⁹–10¹⁰ s ∼ t_age. Cooling due to expansion becomes important at t′ ∼ t_age. The ion temperatures decrease before the ions are well ionized due to the expansion (decreasing of the density, ion temperature, and electron temperature). Figure 9 shows the electron temperatures for Models 0 (black dots), 1 (purple dots), 2 (green dots), 3 (red dots), 4 (orange dots), and 5 (blue dots).

Ionization balance nZ, z/nZ for Model 0 with ρ0 = 4.08 × 10−2mp, tage = 1836 yr, Vsh(tage) = 3000 km s−1, and r/Rsh(tage) = 0.8. We display the species He, C, N (top); O, Ne, Mg (center); and Si, S, and Fe (bottom). The color represents the ionic charge z of the ion. The horizontal axis shows the time t′ = t − t*, where t* is the shock transition time of the fluid parcel currently at r/Rsh(tage) = 0.8.

Fig. 8.

Ionization balance n_{Z, z}/n_Z for Model 0 with ρ₀ = 4.08 × 10⁻²m_p, t_age = 1836 yr, V_sh(t_age) = 3000 km s⁻¹, and r/R_sh(t_age) = 0.8. We display the species He, C, N (top); O, Ne, Mg (center); and Si, S, and Fe (bottom). The color represents the ionic charge z of the ion. The horizontal axis shows the time t′ = t − t_*, where t_* is the shock transition time of the fluid parcel currently at r/R_sh(t_age) = 0.8.

Open in new tab Download slide

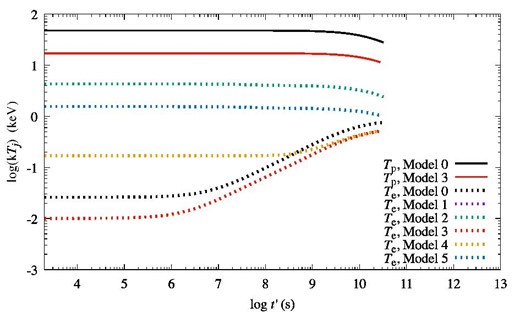
Electron temperatures for Models 0 (black dots), 1 (purple dots), 2 (green dots), 3 (red dots), 4 (orange dots), and 5 (blue dots) with ρ0 = 4.08 × 10−2mp, tage = 1836 yr, Vsh(tage) = 3000 km s−1, and r/Rsh(tage) = 0.8. The solid black (red) line shows the proton temperature for Model 0 (Model 3). The proton temperatures for Model 1 and Model 2 (Model 4 and Model 5) are almost the same as Model 0 (Model 3).

Fig. 9.

Electron temperatures for Models 0 (black dots), 1 (purple dots), 2 (green dots), 3 (red dots), 4 (orange dots), and 5 (blue dots) with ρ₀ = 4.08 × 10⁻²m_p, t_age = 1836 yr, V_sh(t_age) = 3000 km s⁻¹, and r/R_sh(t_age) = 0.8. The solid black (red) line shows the proton temperature for Model 0 (Model 3). The proton temperatures for Model 1 and Model 2 (Model 4 and Model 5) are almost the same as Model 0 (Model 3).

Open in new tab Download slide

5 Synthetic observations

In this section, we perform synthetic observations of the shocked plasma considering the effects of turbulence for the case of the SNR RCW 86. Since we do not calculate the overall spectrum of the emitted photons, which needs enormous calculations about emission lines, we mainly estimate the line shape.

The SNR RCW 86 is one of the best targets for the study of CR injection via ion temperatures because the shells of the SNR show different thermal/nonthermal features from position to position (Bamba et al. 2000; Borkowski et al. 2001; Tsubone et al. 2017). RCW 86 is considered as a historical SNR of SN 185 (Vink et al. 2006). Thus, we set t_age = 1836 yr. Along the north-eastern shell of RCW 86, the dominant X-ray radiation changes from thermal to synchrotron emission (Vink et al. 2006). The thermal emission-dominated region is referred to as the “E-bright” region, and the synchrotron one is referred to as the “NE” region. The ionization age at NE is estimated as τ = (2.25 ± 0.15) × 10⁹ cm⁻³ s though this estimate potentially contains errors due to the lack of thermal continuum emissions (Vink et al. 2006). The E-bright region is fitted by two plasma components: (i) τ = (6.7 ± 0.6) × 10⁹ cm⁻³ s, and (ii) τ = (17 ± 0.5) × 10⁹ cm⁻³ s. Both E-bright and NE show clear O vii Heα and Ne ix Heα line emissions. From the width of the synchrotron-emitting region (NE), the magnetic-field strength is estimated as |$\approx \! 24\pm 5\,\, {\mu \rm {G}}$| (Vink et al. 2006).

Yamaguchi et al. (2016) measured proper motions around these regions (not exactly the same regions) as v₀ = 720 ± 360 km s⁻¹ (E-bright), v₀ = 1780 ± 240 km s⁻¹ (upper part of NE referred to as “NE_b”), and v₀ = 3000 ± 340 km s⁻¹ (lower part of NE referred to as “NE_f”). In the case of Model 3, the fractions of CR pressure ξ_cr become ξ_cr,720 ≃ 0.14 for v₀ = 720 km s⁻¹, ξ_cr,1780 ≃ 0.24 for v₀ = 1780 km s⁻¹, and ξ_cr,3000 ≃ 0.28 for v₀ = 3000 km s⁻¹, respectively. If we simply suppose ρ₀ = (τ/t_age)m_p and adopt |$1/\sqrt{\xi _{\rm B}}=3$|⁠, the CR pressure and δB of each region become P_cr,720 ∼ 0.2 keV cm⁻³ and |$\delta B_{\rm 720}\sim 51\,\, {\mu \rm {G}}$|⁠, P_cr,1780 ∼ 0.3 keV cm⁻³ and |$\delta B_{\rm 1780}\sim 55\,\, {\mu \rm {G}}$|⁠, and P_cr,3000 ∼ 1.1 keV cm⁻³ and |$\delta B_{\rm 3000}\sim 93\,\, {\mu \rm {G}}$|⁠, where we adopt τ = 12.0 × 10⁹ cm⁻³ s for the E-bright region as an average of the two components and τ = 2.25 × 10⁹ cm⁻³ s for the NE region, respectively. If we adopt v₀ = 360 km s⁻¹ for the E-bright region, we obtain ξ_cr,360 ∼ 2.9 × 10⁻². The thermal-dominated E-bright region results from a higher density than the density at the NE region. The magnetic-field strengths δB are the almost the same as one another. Note that Vink et al. (2006) estimated the electron density at the E-bright region as ∼0.6–1.5 cm⁻³ from the emission measure assuming the volume of the emission region. Our model predicts the downstream density as r_cρ₀/m_p ≈ 0.55 cm⁻³ for the E-bright region with v₀ = 720 km s⁻¹, which is consistent with the previous estimate. For the NE region, the number density is not well constrained because of the lack of the thermal continuum component. Thus, our choice of model parameters can be consistent with the observations of RCW 86. In the following, we apply our model to the NE region, setting the parameters as t_age = 1836 yr, V_sh(t_age) = 3000 km s⁻¹, and ρ₀/m_p = τ/t_age = 4.08 × 10⁻² cm⁻³, where τ = 2.25 × 10⁹ cm⁻³ s is used. We suppose that the downstream region from r = R_obs = 0.8R_sh(t_age) to r = R_sh(t_age) is observed. Then, our model supposes that the expansion follows the Sedov–Taylor model during a time of |$\Delta t\ge t_{\rm age}-t_*(R_{\rm obs}) = \left[1 - (R_{\rm obs}/R_{\rm sh})^{r_{\rm c}} \right] t_{\rm age}\approx 0.6\, t_{\rm age}$|⁠, where r_c = 4 and equation (11) are used. If RCW 86 expands with a velocity of ∼10⁹ cm s⁻¹ on average before entering the Sedov–Taylor stage, we effectively assume the radius at the transition time of t₀ ≈ 0.6 t_age as R₀ ∼ 10⁹ cm s⁻¹ × 0.6 t_age ∼ 11 pc. Then, the radius at the current time is R_sh(t_age) ∼ R₀(1/0.6)^2/5 ∼ 13.5 pc, which can be consistent with the actual radius of ∼15 pc (the distance is assumed as 2.5 kpc).

Figure 10 shows the radial profile of the electron temperature at t = t_age for Model 0 (black solid line), Model 1 (purple dots), Model 2 (green broken line), Model 3 (red solid line), Model 4 (orange dots), and Model 5 (blue broken line). To reproduce the bright O vii Heα, a relatively high electron temperature is preferred in terms of the excitation (∼1 keV; see also Vink et al. 2006), though it degenerates by the number density uncertainty. Note that the excitation rate is |$C_{\rm l,u}\propto \exp (-E_{\rm ul}/kT_{\rm e})/\sqrt{T_{\rm e}}$| and E_{u, l} ≃ 0.574 keV for O vii Heα. Thus, we mainly consider Model 2 (β = T_{e, 2}/T_{p, 2} = 0.1 without the CRs) and Model 5 (β = 0.1 with the CRs). Model 5 predicts kT_e(r) ≃ 0.5 keV ≃ E_{u, l}; therefore the predicted O vii Heα line would be the brightest among the models.

Fig. 10.

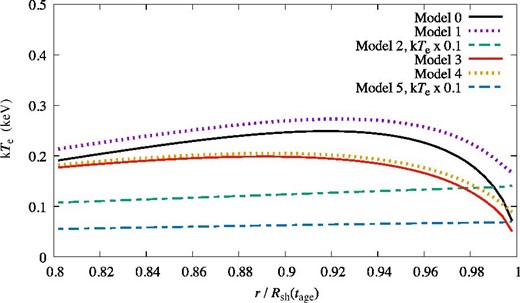
Radial profile of the electron temperature at t_age = 1826 yr for the NE region of RCW 86 with V_sh(t_age) = 3000 km s⁻¹ and ρ₀/m_p = 1.29 × 10⁻². We display the results of Model 0 (black solid line), Model 1 (purple dots), Model 2 (green broken line), Model 3 (red solid line), Model 4 (orange dots), and Model 5 (blue broken line).

Open in new tab Download slide

Figure 11 shows the radial profile of the oxygen abundance n_{Z, z}/n_Z for Model 2 (left) and Model 5 (right). The O vii abundance (orange) is large. Note that the other models (e.g., Model 0) also result in a large O vii abundance. Model 2 predicts a smaller abundance of O vii than the case of Model 5 because the higher electron temperature results in faster ionization. The temperature of O vii is approximately kT_{Z, z}(r) ≈ 250 keV × [r/R_sh(t_age)] for Model 2 and kT_{Z, z}(r) ≈ 140 keV × [r/R_sh(t_age)] for Model 5.

Fig. 11.

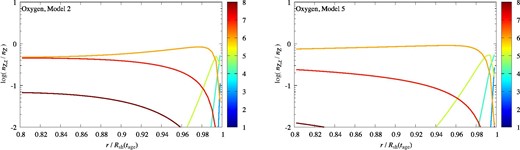
Radial profile of the oxygen abundance n_{Z, z}/n_Z at t_age = 1826 yr for the NE region of RCW 86 with V_sh(t_age) = 3000 km s⁻¹ and ρ₀/m_p = 1.29 × 10⁻². The left panel shows the results of Model 2 and the right panel shows Model 5. The color indicates the ionic charge z of the ion.

Open in new tab Download slide

We estimate the line emission as follows: the observed specific intensity per frequency I_ν at the sky position |${\cal X}$| from the center of the SNR is calculated as

$$\begin{eqnarray} I_\nu ({\cal X}) = \int _{-L}^{L} \left\lbrace \int _{-\infty }^{\infty }{\cal J}_\nu {\cal G}\left(w_t,v_{\cal Z}\right) dw_t \right\rbrace d{\cal Z}, \end{eqnarray}$$

(55)

where |$L=\sqrt{R_{\rm sh}-{\cal X}^2}$|⁠. The position along the line of sight is |${\cal Z}$| so that |$r=\sqrt{{\cal X}^2+{\cal Z}^2}$|⁠. |$v_{\cal Z}(r)=({\cal Z}/r)v(r)$| is the line-of-sight velocity. The probability distribution function of the turbulence |${\cal G}$| is assumed to be a Gaussian as

$$\begin{eqnarray} {\cal G}(w_t,v_{\cal Z}) =\frac{1}{\sqrt{\pi }v_{\rm turb}} \exp \left[-\frac{ m_Z\left( w_t - v_{\cal Z} \right)^2 }{ 2K_Z } \right], \end{eqnarray}$$

(56)

where v_turb is a typical turbulent velocity and K_Z ≡ (1/2)m_Zv_turb². Note that w_t is the variable for the integration. In this paper, we assume that the intensity of the turbulence is proportional to the proton sound speed as |$v_{\rm turb}(r)=\delta \sqrt{\gamma kT_{\rm p}(r)/m_{\rm p}}$|⁠. Supposing the incompressible turbulence is driven in the downstream region (see Shimoda et al. 2018a), we calculate the case of δ = 0.5 and the case without the turbulent Doppler broadening δ = 0 for a comparison. The emissivity of the line is given by

$$\begin{eqnarray} {\cal J}_\nu = \frac{W_{Z,z}^{\rm u,l}}{4\pi } n_{\rm e} n_{Z,z} \phi _\nu , \end{eqnarray}$$

(57)

where we have neglected the cascade from the higher excitation levels. The line profile function is defined as

$$\begin{eqnarray} && \phi _\nu \equiv \frac{1}{\sqrt{\pi }\Delta \nu }\exp \left[-\left(\frac{\nu -\nu _0}{\Delta \nu }\right)^2\right], \end{eqnarray}$$

(58)

$$\begin{eqnarray} && \Delta \nu = \nu _0^{\prime }\sqrt{ \frac{2kT_{Z,z}}{m_Zc^2} }, \end{eqnarray}$$

(59)

$$\begin{eqnarray} && \nu _0 = \nu _0^{\prime }\left( 1 + \frac{v_{\cal Z}}{c} \right), \end{eqnarray}$$

(60)

where |$\nu _0^{\prime }$| is the frequency of the line measured in the rest frame of the atom. Then, we obtain

$$\begin{eqnarray} I_\nu ({\cal X}) &=& \int _{-L}^{L} \frac{n_{\rm e}n_{Z,z}W_{Z,z}^{\rm u,l}}{4\pi \Delta \nu \sqrt{\pi \left(1+{\cal M}_{Z,z}{}^2\right)}}\nonumber\\ &&\times \exp \! \left\lbrace - \left[ \frac{ \nu - \nu _0^{\prime }\left(1+v_{\cal Z}/c\right) }{ \Delta \nu \sqrt{1+{\cal M}_{Z,z}{}^2} } \right]^2\right\rbrace d{\cal Z}, \end{eqnarray}$$

(61)

where |${\cal M}_{Z,z}{}^2\equiv K_Z/kT_{Z,z} = (\gamma \delta ^2/2)(m_Z/m_{\rm p})(T_{\rm p}/T_{Z,z})$|⁠. The line shape is broadened by the bulk Doppler effect |$(1+v_{\cal Z}/c$|⁠) and the turbulent Doppler effect |$\sqrt{1+{\cal M}_{Z,z}{}^2}$|⁠.

Figure 12 shows |$I_\nu ({\cal X})/I_\nu (0.8\, R_{\rm sh})$| at the line center for Model 5 (solid lines) and Model 2 (dots). We also display profiles of the column density of O vii (green). The difference between the column density profile and the intensity profile results from the excitation. The spatial variation of the electron temperature is relatively less important in this case because the excitation rate depends on |$\exp (-E_{\rm ul}/kT_{\rm e})/\sqrt{T_{\rm e}}$|⁠, which is not so sensitive to T_e unless kT_e ≪ E_ul.

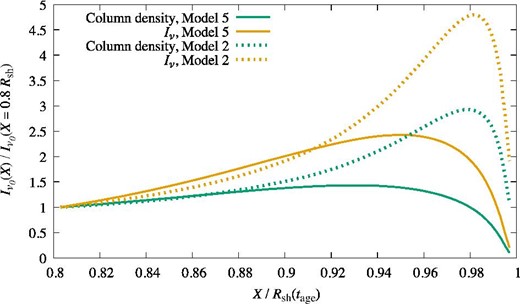
$Radial profile of the specific intensity $I_\nu ({\cal X})/I_\nu (0.8R_{\rm sh})$ at the line center for O vii Heα (orange). The solid lines show the results of Model 5 (multiplied by a factor of 10) and the dots show Model 2. We also display profiles of the column density (green) of O vii.$

Fig. 12.

Radial profile of the specific intensity |$I_\nu ({\cal X})/I_\nu (0.8R_{\rm sh})$| at the line center for O vii Heα (orange). The solid lines show the results of Model 5 (multiplied by a factor of 10) and the dots show Model 2. We also display profiles of the column density (green) of O vii.

Open in new tab Download slide

Figure 13 shows the calculated O vii Heα line for Model 5 (blue solid line) and Model 2 (green solid line) derived from |$\int I_\nu d{\cal X}$| with δ = 0.5. We assume the distance of RCW 86 as 2.5 kpc (Yamaguchi et al. 2016) and the observed area as 0.2R_sh × 0.2R_sh, where R_sh = 15.27 pc. We also display the results of Model 0 (black dots), Model 1 (purple dots), Model 3 (red dots), and Model 4 (orange dots). The results show a good agreement with the observed photon counts ∼0.15 counts s⁻¹ keV⁻¹ (Vink et al. 2006). Table 3 shows a summary of the calculated O vii Heα line. The derived temperatures reflect the effects of the efficient CR acceleration. From the comparison of δ = 0.5 to δ = 0, turbulent Doppler broadening results in higher observed temperatures by a factor of ∼1.05. The degree of broadening can be estimated as |$\sqrt{1+{\cal M}_{Z,z}{}^2}\approx 1.1$| for δ = 0.5 with approximating T_p/T_{Z, z} ≈ m_p/m_Z. Since the observed line consists of multiple temperature populations, and since a higher-temperature population contributes less around the line center, a lower-temperature population is accentuated around the line center. The contribution of the higher-temperature population appears far from the line center like a “wing.” If we measure the temperature using the full width at the e-folding scale, the difference in the derived temperatures becomes large. Hence the observed FWHM is smaller than that expected from |$\sqrt{1+{\cal M}_{Z,z}{}^2}$|⁠.

Fig. 13.

Calculated O vii Heα line with δ = 0.5 for Model 5 (blue solid line) and Model 2 (green solid line). We also display the results of Model 0 (black dots), Model 1 (purple dots), Model 3 (red dots), and Model 4 (orange dots). We assume that the distance of RCW 86 is 2.5 kpc and the observed area is 0.2R_sh × 0.2R_sh, where R_sh = 15.27 pc.

Open in new tab Download slide

Table 3.

Open in new tab

Summary of the calculated O vii Heα.

	kT_{Z, z} (kT_{Z, z}/2Z)*
Model	for δ = 0.5	for δ = 0
0	325.9 keV (20.4 keV)	312.3 keV (19.5 keV)
1	325.6 keV (20.3 keV)	312.4 keV (19.5 keV)
2	306.4 keV (19.2 keV)	296.5 keV (18.5 keV)
3	160.6 keV (10.0 keV)	153.8 keV (9.62 keV)
4	160.6 keV (10.0 keV)	154.2 keV (9.63 keV)
5	157.7 keV (9.85 keV)	152.5 keV (9.53 keV)

	kT_{Z, z} (kT_{Z, z}/2Z)*
Model	for δ = 0.5	for δ = 0
0	325.9 keV (20.4 keV)	312.3 keV (19.5 keV)
1	325.6 keV (20.3 keV)	312.4 keV (19.5 keV)
2	306.4 keV (19.2 keV)	296.5 keV (18.5 keV)
3	160.6 keV (10.0 keV)	153.8 keV (9.62 keV)
4	160.6 keV (10.0 keV)	154.2 keV (9.63 keV)
5	157.7 keV (9.85 keV)	152.5 keV (9.53 keV)

The O vii temperature derived from the FWHM of the line for the case of δ = 0.5 and δ = 0.

Table 3.

Open in new tab

Summary of the calculated O vii Heα.

	kT_{Z, z} (kT_{Z, z}/2Z)*
Model	for δ = 0.5	for δ = 0
0	325.9 keV (20.4 keV)	312.3 keV (19.5 keV)
1	325.6 keV (20.3 keV)	312.4 keV (19.5 keV)
2	306.4 keV (19.2 keV)	296.5 keV (18.5 keV)
3	160.6 keV (10.0 keV)	153.8 keV (9.62 keV)
4	160.6 keV (10.0 keV)	154.2 keV (9.63 keV)
5	157.7 keV (9.85 keV)	152.5 keV (9.53 keV)

	kT_{Z, z} (kT_{Z, z}/2Z)*
Model	for δ = 0.5	for δ = 0
0	325.9 keV (20.4 keV)	312.3 keV (19.5 keV)
1	325.6 keV (20.3 keV)	312.4 keV (19.5 keV)
2	306.4 keV (19.2 keV)	296.5 keV (18.5 keV)
3	160.6 keV (10.0 keV)	153.8 keV (9.62 keV)
4	160.6 keV (10.0 keV)	154.2 keV (9.63 keV)
5	157.7 keV (9.85 keV)	152.5 keV (9.53 keV)

The O vii temperature derived from the FWHM of the line for the case of δ = 0.5 and δ = 0.

RCW 86 also shows bright Ne ix Heα; however, our model predicts a faint Ne ix Heα emission (the intensity is smaller than a tenth of the O vii Heα intensity). The line intensity also depends on the ion abundance. In this paper, we use the solar abundance, which reflects the condition of our Galaxy ≃4.6 Gyr ago. Moreover, De Cia et al. (2021) found large variations in the chemical abundance of the neutral ISM in the vicinity of the Sun over a factor of 10 (they analyzed Si, Ti, Cr, Fe, Ni, and Zn). Their findings imply that the gaseous matter is not well mixed. The predicted faint Ne ix Heα might reflect a different abundance pattern from the solar abundance pattern.

Figure 14 represents the line shape with 5 eV resolution for δ = 0.5. We additionally show O vii Lyα, Ne ix Heα, and Ne x Lyα. Since the widths of the particle distribution function are almost the same as each other for nt ∼ 10⁹–10¹¹ cm⁻³ s, the observation of lines at higher photon energies is better to resolve the line width. Note that the observed O vii Heα and Ne ix Heα are bright compared to the continuum emission (Vink et al. 2006). The energy resolution of XRISM’s micro-calorimeter Resolve is sufficient to distinguish whether the SNR shock accelerates the CRs (Model 5) or not (Model 2).

Fig. 14.

Line profiles with 5 eV resolution for δ = 0.5. We display O vii Heα, O viii Lyα, Ne ix Heα, and Ne x Lyα for Model 5 (black solid line) and Model 2 (green solid line).

Open in new tab Download slide

6 Summary and discussion

We suggest a novel collisionless shock jump condition, which is given by modeling each ion species’ entropy production at the shock transition region. As a result, the amount of the downstream thermal energy is given. The magnetic-field amplification driven by the CRs is assumed. For a given strength of the amplified field, the amount of CRs is constrained by the energy conservation law. The constrained amount of CRs can be sufficiently large to explain the Galactic CRs. The ion temperature is lower than the case without CRs because the upstream kinetic energy is divided into CRs and the amplified field. The strength of the field around the shock transition region is assumed to be |$1/\sqrt{\xi _{\rm B}}=v_0/(\delta B/\sqrt{4\pi \rho _0})\simeq 3$|⁠. Downstream developments of the ionization balance and temperature relaxation are also calculated. Using the calculated downstream values, we perform synthetic observations of atomic lines for the SNR RCW 86, including Doppler broadening by turbulence. Our model predictions can be consistent with previous observations of the SNR RCW 86, and the predicted line widths are sufficiently broad to be resolved by XRISM’s micro-calorimeter. Future observations of the X-ray lines can distinguish whether the SNR shock accelerates the CRs or not from the ion temperatures.

Our shock model constrains the maximum fraction of the CRs depending on the shock velocity, the upstream density, and the sonic Mach number (see figure 2). Since the SNR shock decelerates gradually, we can predict the history of the CR injection and related nonthermal emissions, especially the hadronic γ-ray emissions. Although the injection history of the CRs is essential to estimate the intrinsic injection of the CRs into our Galaxy per one supernova explosion, this issue currently remains to be resolved (e.g., Ohira et al. 2010; Ohira & Ioka 2011). The injected CRs will contribute to the dynamics of the ISM as a pressure source, leading to a feedback effect on the star formation rate, for example (e.g., Girichidis et al. 2018; Hopkins et al. 2018; Shimoda & Inutsuka 2022). The origin of γ-ray emissions in the SNRs is also unsettled, whether of hadronic origin or leptonic origin (Abdo et al. 2011; but see also Fukui et al. 2021). We will study these in a forthcoming paper.

For distinguishing the case of extremely efficient CR acceleration (Model 3) from the case of no CRs (Model 0), a comparison of the FWHM to other values is required in general (e.g., the difference between the ionization states, the shock velocity, and so on). The FWHM of Model 3 becomes smaller than Model 0 at a given shock velocity and nt, and abundant ions of Model 3 tend to be less ionized than in the case of Model 0 because of the lower electron temperature. The lower electron temperature and lower ionization states of Model 3 may result in a different photon spectrum from the case of other models, especially the equivalent widths, recombination lines, Auger transitions due to inner shell ionization, and so on. We will attempt further investigations by calculating the overall photon spectrum in future work.

The line diagnostics of the thermal plasma of young SNRs on the effect of CR acceleration will be a good science objective for the XRISM mission (Tashiro et al. 2020), which will provide high-resolution X-ray spectroscopy. Since the micro-calorimeter array is not a distributed-type spectroscope like grating optics on Chandra and/or XMM–Newton, the Resolve onboard XRISM (Ishisaki et al. 2018) can accurately measure the atomic line profiles in the X-ray spectra from diffuse objects like SNRs. XRISM will have an energy resolution of 7 eV (as the design goal), and the calibration goals on the energy scale and resolution are 2 eV and 1 eV, respectively (Miller et al. 2020). Therefore, the line broadening values from multiple elements with/without CRs in figure 3 can be distinguished by XRISM. Another importance of XRISM is the wider energy coverage, with which atomic lines not only from light elements (C, N, O, etc.) but also from Fe will be measured. So, the intensity of the turbulence demonstrated in section 5 will be constrained with XRISM. The preparations for the instruments (Nakajima et al. 2020; Porter et al. 2020) and in-orbit operations (Loewenstein et al. 2020; Terada et al. 2021) are proceeding smoothly for the launch in 2022/2023, and several young SNRs, including RCW 86, are listed as targets during the performance verification phase of XRISM.⁵ We expect to verify our predictions observationally soon.

Acknowledgements

We thank K. Masai and G. Rigon for useful discussions. We are grateful to the anonymous referee for his/her comments, which further improved the paper. This work is partly supported by JSPS Grants-in-Aid for Scientific Research Nos. 20J01086 (JS), 19H01893 (YO), JP21H04487 (YO) 19K03908 (AB), 20K04009 (YT), 18H01232 (RY), 22H01251 (RY), and 20H01944 (TI). YO is supported by the Leading Initiative for Excellent Young Researchers, MEXT, Japan. RY and SJT deeply appreciate the Aoyama Gakuin University Research Institute for helping our research with the fund.

Footnotes

The compression ratio is strictly a function of the shock velocity. For the calculation of t_* only, we use the compression ratio given by V_sh(t_age) but, for the other cases, we calculate the shock jump conditions using V_sh(t_*) given by the calculated t_*.

〈https://www.iaea.org/resources/databases/aladdin〉.

〈https://www.nist.gov/pml/atomic-spectra-database〉.

This definition corresponds to a reversible process. The collisionless shock is formed by the wave–particle interaction, which might be a reversible process like a plasma echo, for example. Although this may be an unsettled issue, we apply this definition of entropy in this article. Note that the entropy is defined as a non-dimensional value differing from the usual dimensional definition in thermodynamics, dS = dQ/T.

〈https://xrism.isas.jaxa.jp/research/proposer/approved/pv/index.html〉.

References

Abdo

A. A.

et al.

2011

ApJ

736

131

Month:	Total Views:
July 2022	189
August 2022	197
September 2022	58
October 2022	130
November 2022	57
December 2022	37
January 2023	30
February 2023	26
March 2023	36
April 2023	22
May 2023	19
June 2023	16
July 2023	18
August 2023	13
September 2023	19
October 2023	10
November 2023	14
December 2023	16
January 2024	43
February 2024	16
March 2024	16
April 2024	55
May 2024	12
June 2024	21
July 2024	15
August 2024	17
September 2024	19
October 2024	13
November 2024	17
December 2024	8
January 2025	12
February 2025	8
March 2025	9
April 2025	11

Article Contents

X-ray line diagnostics of ion temperature at cosmic ray accelerating collisionless shocks

Abstract

1 Introduction

2 Physical model of the downstream ionization balance and ion internal energies

3 Shock jump conditions

3.1 Collisional shock model (Models 0, 1, and 2)

3.2 Collisionless shock model (Models 3, 4, and 5)

4 Evolution track of the downstream ionization balance and temperatures

5 Synthetic observations

6 Summary and discussion

Acknowledgements

Footnotes

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only