E/B mode decomposition of HSC-Y1 cosmic shear using COSEBIs: Cosmological constraints and comparison with other two-point statistics

Hamana, Takashi; Hikage, Chiaki; Oguri, Masamune; Shirasaki, Masato; More, Surhud

doi:10.1093/pasj/psac046

Abstract

We perform a cosmic shear analysis of Hyper Suprime-Cam Subaru Strategic Program first-year data (HSC-Y1) using complete orthogonal sets of E/B-integrals (COSEBIs) to derive cosmological constraints. We compute E/B-mode COSEBIs from cosmic shear two-point correlation functions measured on an angular range of 4^′ < θ < 180^′. We perform a standard Bayesian likelihood analysis for cosmological inference from the measured E-mode COSEBIs, including contributions from intrinsic alignments of galaxies as well as systematic effects from point spread function model errors, shear calibration uncertainties, and source redshift distribution errors. We adopt a covariance matrix derived from realistic mock catalogs constructed from full-sky gravitational lensing simulations that fully take account of the survey geometry and measurement noise. For a flat Λ cold dark matter model, we find |$S\,_8 \equiv \sigma _8\sqrt{\Omega _{\rm m}/0.3}=0.809_{-0.026}^{+0.036}$|⁠. We carefully check the robustness of the cosmological results against astrophysical modeling uncertainties and systematic uncertainties in measurements, and find that none of them has a significant impact on the cosmological constraints. We also find that the measured B-mode COSEBIs are consistent with zero. We examine, using mock HSC-Y1 data, the consistency of our S₈ constraints with those derived from the other cosmic shear two-point statistics, the power spectrum analysis by Hikage et al. (2019, PASJ, 71, 43) and the two-point correlation function analysis by Hamana et al. (2020, PASJ, 72, 16), which adopt the same HSC-Y1 shape catalog, and find that all the S₈ constraints are consistent with each other, although the expected correlations between derived S₈ constraints are weak.

1 Introduction

Cosmic shear is measured from the coherent distortion of the shapes of distant galaxies caused by gravitational lensing of intervening large-scale structures, and is one of the most powerful tools for cosmology, as it provides a unique means of studying the matter distribution in the Universe, including the dark matter component. Statistical measures of cosmic shear, such as the two-point correlation function (TPCF) or the power spectrum (PS), depend both on the time evolution of the cosmic structure and on the cosmic expansion history at relatively recent epochs (z < 1), and thus serve as a unique late-time cosmological probe. Aiming to place useful constraints on cosmological parameters independently from early-time probes, currently three weak lensing projects with wide-field imaging surveys are underway: the Dark Energy Survey (DES, Dark Energy Survey Collaboration 2016), the Kilo-Degree survey (KiDS, de Jong et al. 2013), and the Hyper Suprime-Cam Subaru Strategic Program (hereafter the HSC survey; Aihara et al. 2018a). All three projects have published initial/mid-term cosmic shear results from early data, yielding constraints with 2%–8% precision on S₈ = σ₈(Ω_m/0.3)^0.5, where σ₈ is the amplitude of matter fluctuations in scales of 8 Mpc/h and Ω_m is the mean matter density parameter (Hildebrandt et al. 2017, 2020; Köhlinger et al. 2017; Troxel et al. 2018; Hikage et al. 2019; Hamana et al. 2020; Asgari et al. 2021; Amon et al. 2022).

Cosmic shear analyses with the HSC survey first-year weak lensing shape catalog (HSC-Y1; Aihara et al. 2018b; Mandelbaum et al. 2018b) were conducted in Fourier space using the power spectra (PS; Hikage et al. 2019, hereafter H19), and in configuration space using the two-point correlation functions (TPCF; Hamana et al. 2020, hereafter H20). Although those two analyses are both based on two-point statistics with the same data set, they are complementary to each other for the following three reasons, among others. First, masking and finite-field effects affect PS/TPCF analyses in different ways: The Fourier space measurements are directly affected by those effects, although a technique aimed at correcting those effects (the pseudo-C_l method) was adopted in H19. The pseudo-C_l method was also adopted in Camacho et al. (2021), while Köhlinger et al. (2017) adopted the quadratic estimator. On the other hand, the configuration-space measurements are not affected by the effects, although the effects need to be taken into account in their covariance estimation.

Secondly, E/B-mode decomposition of cosmic shear is properly conducted in Fourier space PS measurements, but is not feasible for configuration-space TPCFs as it requires a measurement of TPCFs with angular separations ranging from zero to infinity. This is a disadvantage of TPCF analyses for the following reason: gravitational lensing by a scalar gravitational field generates only E-mode shear at a leading order, and the B-mode signal generated by lensing is expected to be very small unless there are any systematics in the measurements (see Kilbinger 2015, for a review and references therein). Therefore, null tests of B-mode signals can be used to verify a standard assumption of a scalar gravitational field, and to check systematics in cosmic shear measurements. Thus, a clean E/B-mode decomposition is of vital importance for cosmological analyses. Finally, the PS and TPCF probe different multipole ranges, as the kernels linking the TPCFs to the PS have very broad shapes. The HSC-Y1 PS analysis by H19 adopted a multipole range of 300 < ℓ < 1900, whereas a large part of the contribution to TPCFs on a range of angular separations adopted in H20 comes from ℓ < 300. Constraints on S₈ derived from those two studies appear to differ significantly (⁠|$S_8=0.780_{-0.033}^{+0.030}$| for PS, whereas |$S_8=0.823_{-0.028}^{+0.032}$| for TPCF). In order to check whether the difference can be explained simply by a statistical fluctuation, a cross-correlation analysis of realistic HSC mock catalogs was conducted: H19 and H20 performed a cosmological inference on the same 100 mock catalogs with software used in their cosmological analyses on the real HSC-Y1 data, and the derived constraints were used as a statistical sample of cross-correlation analysis of the differences in the derived S₈ values between PS and TPCF analyses. Then, it was found that the difference in the derived S₈ was explained by a statistical fluctuation at the ∼1.6σ level, and thus those S₈ constraints are consistent with each other (H20; see also subsection 6.6).

Complete orthogonal sets of E/B-integrals (COSEBIs: Schneider et al. 2010) are an another configuration-space measure of cosmic shear two-point statistics. COSEBIs are complementary to TPCFs in the sense that they eliminate the two disadvantages of the TPCF (see Asgari et al. 2021, for a closely related discussion): First, COSEBIs are defined by an integration of TPCFs weighted by kernel functions over finite angular separations, and COSEBI kernels linking to the PS have more compact shapes in multipole space than TPCF kernels. Accordingly, this offers better control over multipole ranges contributing to COSEBI signals. Notably, COSEBIs are less sensitive to low multipoles where only a few independent modes are available from finite-area survey data. Secondly, COSEBIs enable a clean E/B-mode separation over a range of finite angular separations available from a finite survey area.

In this paper, we present a cosmic shear analysis of the HSC-Y1 weak lensing shape catalog using E/B-mode COSEBIs. We use the same data set as used in H19 and H20 along with the same tomographic redshift binning (four bins with 0.3 < z < 0.6, 0.6 < z < 0.9, 0.9 < z < 1.2, and 1.2 < z < 1.5). We also use realistic HSC-Y1 mock catalogs constructed from full-sky gravitational lensing simulations (Takahashi et al. 2017) taking full account of the survey geometry and measurement noise (Shirasaki et al. 2019), from which we derive E/B-mode covariance matrices.

The structure of this paper is as follows. In section 2, we briefly summarize the HSC-Y1 shear catalog and the photometric redshift data used in this study. In section 3, we present an overview of the theoretical modeling of COSEBIs and define the scale-cut adopted in our analyses. In section 4, we describe the method to measure the cosmic shear COSEBIs and present our measurements. We also present covariance matrices derived from the realistic HSC-Y1 mock shape catalogs. The result of the B-mode null test is also presented. In section 5, we describe a method for cosmological inference along with methods to take into account various systematics in our cosmological analysis, for which we closely follow the analysis framework adopted in H20. In section 6, we present the results of our cosmological constraints and tests for systematics. We compare our cosmological constraints with other cosmic shear results and the Planck cosmic microwave background (CMB) result. We also compare our results with those from the HSC-Y1 cosmic shear PS and TPCF analyses, and examine the consistency among them using mock HSC-Y1 data. Finally, we summarize and discuss our results in section 7. In appendix 2, we examine COSEBIs expected from errors in measurements and modeling of the point spread functions (PSFs) and from constant shears over survey fields, and describe empirical models for those systematics. In appendix 3, we present supplementary figures.

Throughout this paper we quote 68% credible intervals for parameter uncertainties unless otherwise stated.

2 HSC-Y1 data set

We use the same HSC-Y1 data set as that used in H19 and H20, and thus here we focus on aspects that are directly relevant to this study. We refer the readers to those two papers and references therein for details.

We use the HSC first-year shape catalog (Mandelbaum et al. 2018b), which covers 136.9 deg² and contains ∼12.1M galaxies that pass the selection criteria; among others, the four major criteria are:

Full-color and full-depth cut: the object should be located in regions reaching approximately full survey depth in all five (grizy) broad-bands.
Magnitude cut: the i-band cmodel magnitude (corrected for extinction) should be brighter than 24.5 AB mag.
Resolution cut: the galaxy size normalized by the PSF size defined by the re-Gaussianization method should be larger than a given threshold of ishape_hsm_regauss_resolution ≥ 0.3.
Bright object mask cut: the object should not be located within the bright object masks.

See table 4 of Mandelbaum et al. (2018b) for a full description of the selection criteria. The shapes of galaxies are estimated on the i-band coadded image using the re-Gaussianization PSF correction method (Hirata & Seljak 2003). Following appendix A of Mandelbaum et al. (2018b), an estimator for the shear, denoted by |$\boldsymbol {\hat{\gamma }} = (\hat{\gamma }_1, \hat{\gamma }_2)$|⁠, is obtained for each galaxy as

$$\begin{equation} \hat{\gamma }_i = {1\over {1+\bar{m}}} \left( {{e_i}\over {2 \cal {R}}}-c_i\right), \end{equation} $$

(1)

where e_i is the two-component distortion representing the shape of each galaxy image, m is multiplicative bias, and c_i is additive bias. The multiplicative and additive biases of individual galaxy shapes are estimated using simulations of HSC images of the Hubble Space Telescope COSMOS galaxy sample (Mandelbaum et al. 2018b). In addition, we take into account two additional multiplicative biases arising from the tomographic redshift galaxy selection (to be specific m_sel and m_R in H19’s terminology) in the same manner used in H19 (see their subsection 5.7).

We use photometric redshift (hereafter photo-z) information to divide galaxies into tomographic redshift bins (see Tanaka et al. 2018, for details of the photo-z of the HSC-Y1 data). To do this, we adopt the same procedure as in H19 and H20: Adopting the best estimate of a neural network code Ephor AB (Tanaka et al. 2018) for the point estimator of the photo-z, we select galaxies with 0.3 < z_best < 1.5, and divide them into four tomographic redshift bins with equal redshift widths of Δz = 0.3. We choose the above redshift range because photo-z estimations with the HSC-Y1 data are most accurate in that redshift range (Tanaka et al. 2018). The final numbers of galaxies are 3.0M, 3.0M, 2.3M, and 1.3M galaxies respectively from the lowest to the highest redshift bins. We adopt the redshift distributions of galaxies in individual bins derived with the reweighting method based on the HSC’s five-band photometry and COSMOS 30-band photo-z catalog (Ilbert et al. 2009; Laigle et al. 2016). See figure 1 of H20 for the derived redshift distributions. We refer readers to subsection 5.2 of H19 and references therein for full details of the method.

Fig. 1.

Left: Cumulative contribution of power spectra to X from a limited range of ℓ < ℓ_max as a function of ℓ_max [to be specific, the upper limit of the ℓ-integration in equations (7) and (4) are truncated at ℓ_max], where X stands for TPCF ξ₊ (top panel), ξ₋ (middle panel), or COSEBI E_n (bottom panel). All the results are normalized by their unlimited value. Here a combination of tomographic redshift bins of z₃ × z₃ and the WMAP9 cosmological model (Hinshaw et al. 2013) are adopted, but the results are insensitive to those choices. For TPCFs, three angular scales roughly corresponding to the minimum, intermediate, and maximum scales of H20 are shown. Vertical dotted lines show the ℓ-range used in the Fourier space PS analysis by H19. Right: Integrands of the transformation between the power spectra to ξ_± [top and middle panels; see equation (7)] or E_n [bottom panel; see equation (4)]. All integrands are normalized by their maximum value. The same angular scales shown in the left panels are shown except for ξ_± where the intermediate case is omitted for clarity.

Open in new tab Download slide

3 Theoretical models

3.1 COSEBIs

The E/B-mode COSEBIs are defined as integrals over TPCFs on a finite range of angular separations θ_min < θ < θ_max (Schneider et al. 2010),

$$\begin{eqnarray} E_n^{ab} &=& {1\over 2} \int _{\theta _{\rm min}}^{\theta _{\rm max}} d\theta \theta \left[ T_{+n}(\theta ) \xi _+^{ab}(\theta ) + T_{-n}(\theta ) \xi _-^{ab}(\theta ) \right], \end{eqnarray} $$

(2)

$$\begin{eqnarray} B_n^{ab} &=& {1\over 2} \int _{\theta _{\rm min}}^{\theta _{\rm max}} d\theta \theta \left[ T_{+n}(\theta ) \xi _+^{ab}(\theta ) - T_{-n}(\theta ) \xi _-^{ab}(\theta ) \right], \end{eqnarray} $$

(3)

where |$\xi _{\pm }^{ab}(\theta )$| are TPCFs for two tomographic redshift bins a and b; a natural number n, starting from 1, is the order of the COSEBI modes; and T_±n are the COSEBI filter functions. Alternatively, the E/B-mode COSEBIs can be expressed as a function of E/B-mode cosmic shear PS denoted by |$P_{E/B}^{ab}(\ell )$|⁠,

$$\begin{eqnarray} E_n^{ab} &=& {1\over {2\pi }}\int _0^\infty d \ell \ell P_E^{ab}(\ell ) W_n(\ell ), \end{eqnarray} $$

(4)

$$\begin{eqnarray} B_n^{ab} &=& {1\over {2\pi }}\int _0^\infty d \ell \ell P_B^{ab}(\ell ) W_n(\ell ), \end{eqnarray} $$

(5)

where W_n(ℓ) are the Hankel transforms of T_±n(θ),

$$\begin{eqnarray} W_n &=& \int _{\theta _{\rm min}}^{\theta _{\rm max}} d\theta \theta T_{+n}(\theta ) J_0(\ell \theta ), \nonumber \\ {} &=& \int _{\theta _{\rm min}}^{\theta _{\rm max}} d\theta \theta T_{-n}(\theta ) J_4(\ell \theta ), \end{eqnarray} $$

(6)

with J_0/4 being the zeroth- or fourth-order Bessel functions of the first kind. Note that TPCFs are also related to power spectra but mix E- and B-modes:

$$\begin{equation} \xi _{\pm }^{ab}(\theta ) = {1\over {2\pi }}\int _0^\infty d\ell \ell J_{0/4} (\ell \theta ) \left[ P_E^{ab}(\ell ) \pm P_B^{ab}(\ell ) \right]. \end{equation} $$

(7)

Schneider, Eifler, and Krause (2010) introduced two sets of COSEBI filter functions, the Lin- and Log-COSEBIs, which are given in terms of polynomials in θ and ln θ, respectively (see section 3 of Schneider et al. 2010, for the explicit equations for those filter functions). It is found in Schneider, Eifler, and Krause (2010) that the Log-COSEBIs require the first five modes to essentially capture all the cosmological information, whereas the Lin-COSEBIs require ∼25 modes to capture the equivalent information. We adopt the Log-COSEBIs as they require far fewer modes compared to Lin-COSEBIs. Following previous studies (Asgari et al. 2020, 2021), we use the first five COSEBI modes (i.e., 1 ≤ n ≤ 5) in the following analyses.

3.2 Cosmic shear power spectra

In this study, we consider the standard cold dark matter (CDM) cosmological model and thus we assume that no B-mode shear is generated by gravitational lensing. Note that we find that the B-mode COSEBIs measured from the HSC-Y1 are consistent with zero as shown in subsection 4.3 below (see also H19 for the power spectrum analysis of the B-mode shear). Therefore, for theoretical model computations in this study, we set |$P_B^{ab}(\ell ) = 0$|⁠.

In computing theoretical models of cosmic shear power spectra, we follow the framework adopted in H20 and refer readers to section 4 of that paper and references therein for expressions and details. In short, for the computation of the shear–shear power spectrum (also known as the convergence power spectrum), |$P_{\rm GG}^{ab}(\ell )$|⁠, we adopt the standard expression which relates it to the matter power spectrum. For the computation of the linear matter power spectrum, we use CAMB (Challinor & Lewis 2011). In order to model the nonlinear matter power spectrum, we employ the fitting function by Bird, Viel, and Haehnelt (2012), which is based on the halofit model (Smith et al. 2003; Takahashi et al. 2012) but is modified so as to include the effect of non-zero neutrino mass. It is well known that the evolution of the nonlinear matter power spectrum, especially on small scales, is affected by baryon physics such as gas cooling, star formation, and supernova and active galactic nuclei (AGN) feedbacks (Schaye et al. 2010; van Daalen et al. 2011; Mead et al. 2015; Hellwing et al. 2016; McCarthy et al. 2017; Springel et al. 2018; Chisari et al. 2018). When we evaluate baryonic feedback effects on our analyses, we adopt an extreme model, the AGN feedback model by Harnois-Déraps et al. (2015), which is based on the OverWhelming Large Simulations project (Schaye et al. 2010; van Daalen et al. 2011). Our treatment of baryon feedback effects in our cosmological analyses is described in sub-subsection 5.1.2.

3.3 Scale-cut

We set the scale-cut of COSEBIs [see equation (2)] as θ_min = 4^′ and θ_max = 180^′ for the following reasons. First, to determine the minimum scale, we impose a requirement that changes of E-mode COSEBIs due to baryon feedback effects are less than 2%. In evaluating it, we adopt the AGN feedback model by Harnois-Déraps et al. (2015) as an extreme model, and find that θ_min > 4^′ meets the requirement. Secondly, for the large-scale cut, we follow the HSC-Y1 TPCF analysis (H20), and set θ_max = 180^′, which is the largest angular scale used in H20 determined based on the condition that the signal-to-noise ratio per individual angular bin of the measured TPCFs is greater than 1 (see subsection 5.1 of H20).

The right panels of figure 1 compare differential contributions of power spectra to three two-point statistics (ξ₊, ξ₋, and E_n from top to bottom) as a function of ℓ, to be specific, integrands of the relevant equations: equation (7) for ξ_± and equation (4) for E_n. The left panels of figure 1 compare cumulative contributions of power spectra to three two-point statistics (ξ₊, ξ₋, and E_n from top to bottom) from a limited range of ℓ < ℓ_max as a function of ℓ_max; to be specific, the upper limits of the ℓ-integration in the relevant equations [equations (7) and (4)] are truncated at ℓ_max. For TPCFs, the three angular scales shown in the plots roughly correspond to the minimum, intermediate, and maximum scales of H20. Vertical dotted lines show the ℓ-range (300 < ℓ < 1900) used in the Fourier space PS analysis by H19. One can see, from the figure, noticeable differences in ℓ-ranges contributing to each HSC-Y1 cosmic shear two-point statistics. Notably, ξ₊ has the broadest sensitivity range (non-zero ranges without the rapid oscillation in the differential contributions shown in the right panels of figure 1), especially toward very low-ℓ modes. Compared to the TPCFs’ broad sensitivity range, our scale-cut of COSEBIs suppresses the sensitivity on both low- and high-ℓ modes, but a large part of the contribution comes from modes with ℓ < 300. Therefore, we expect weak correlations in resulting cosmological parameter constraints between COSEBIs and TPCFs as well as between COSEBIs and PS, as in the case between PS and TPCFs found in H20, in which the two methods probe the different ℓ-ranges and a 1σ level difference in the resulting S₈ constraints between PS and TPCFs was found (H20).

4 Measurements

4.1 Measurements of COSEBIs from the HSC-Y1 data

The method of measuring COSEBIs precisely was developed and tested by Asgari et al. (2017, 2021). We confirmed the accuracy of the method adopted in Asgari et al. (2021) with HSC-Y1 mock catalogs (see appendix 1 for details of this test), and we adopt it in this study. We first measure the cosmic shear TPCFs for two tomographic redshift bins a and b taking the shape weight into account as

$$\begin{equation} \hat{\xi }_\pm ^{ab}(\theta )={ {\sum _{ij} w_i w_j \left[\hat{\gamma }_{i,t}^{a}(\vec{\theta }_i) \hat{\gamma }_{j,t}^{b}(\vec{\theta }_j) \pm \hat{\gamma }_{i,\times }^{a}(\vec{\theta }_i) \hat{\gamma }_{j,\times }^{b}(\vec{\theta }_j)\right]} \over {\sum _{ij} w_i w_j } }, \end{equation} $$

(8)

where the tangential (⁠|$\hat{\gamma }_{\rm t}$|⁠) and cross (⁠|$\hat{\gamma }_{\times }$|⁠) components of shear are defined with respect to the direction connecting the pair of galaxies under consideration (i and j), w_i is the shape weight for each galaxy, and the summation runs over pairs of galaxies with their angular separation |$\theta =|\vec{\theta }_i-\vec{\theta }_j|$| within an interval Δθ around θ. Following Asgari et al. (2021), we adopt a fine log θ-binning, to be specific, 4000 bins over |${0_{.}^{\prime }5}<\theta <300^{\prime }$| with an equal log θ-bin width, although we only use the limited range of 4^′ < θ < 180^′. For actual measurements of the TPCFs, we used the public software Athena¹(Schneider et al. 2002). We then perform linear transformations in equations (2) and (3) to compute E/B-mode COSEBIs. We use the first five COSEBI modes in the following analyses following the previous studies (Schneider et al. 2010; Asgari et al. 2012).

The measured signals are shown in figure 2 with error bars representing the square-root of the diagonal elements of the covariance matrix (see subsection 4.2). For comparison, the best-fitting theoretical model obtained from the cosmological inference of our fiducial ΛCDM model (described in subsection 6.1) is shown in the E-mode plots. The E-mode signals shown in figure 2 form the data vector of our cosmological inference (see section 5). We define the data vector as |$d_{E,i} = (E_1^{11},E_2^{11},\ldots ,E_5^{11},E_1^{12},\ldots ,E_5^{44})$|⁠. Since there are five modes for each of the 10 combinations of tomographic redshift bins, the data vector consists of 50 elements.

$Comparison of the HSC-Y1 tomographic cosmic shear COSEBIs with the best-fitting theoretical model for the fiducial flat ΛCDM model. Top and bottom triangular-tiled panels show $E_n^{ab}$ and $B_n^{ab}$, respectively. Error bars represent the square-root of the diagonal elements of the covariance matrix. The solid lines in the top panels correspond to the best-fitting (maximum likelihood) fiducial model.$

Fig. 2.

Comparison of the HSC-Y1 tomographic cosmic shear COSEBIs with the best-fitting theoretical model for the fiducial flat ΛCDM model. Top and bottom triangular-tiled panels show |$E_n^{ab}$| and |$B_n^{ab}$|⁠, respectively. Error bars represent the square-root of the diagonal elements of the covariance matrix. The solid lines in the top panels correspond to the best-fitting (maximum likelihood) fiducial model.

Open in new tab Download slide

4.2 Covariance from HSC-Y1 mock catalogs

Following the methodology of the HSC-Y1 cosmic shear TPCF analysis by H20, we derive covariance matrices of the COSEBI measurement using 2268 realizations of mock HSC-Y1 shape catalogs (see Shirasaki et al. 2019, for a detailed description of the mock catalogs). Since the HSC mock catalogs are constructed based on full-sky lensing simulation data with galaxy positions, intrinsic shape noise, and measurement noise taken from the real HSC-Y1 shape catalog, the mock data naturally have the same survey geometry and the same noise properties as the real catalog, and include super-survey cosmic shear signals from these full-sky lensing simulations. In addition, the effects of nonlinear structure formation on the lensing shear field are included in the mock data. Therefore the covariance matrix computed from the mock catalogs automatically includes all the contributions, namely, the shape noise, Gaussian, non-Gaussian, and super-survey covariance with the survey geometry being naturally taken into account.

We measure the cosmic shear COSEBIs for all 2268 mock catalogs in exactly the same manner as the real data measurement and derive covariances for E- and B-mode COSEBIs. The results are shown in figure 3, in which covariance matrices normalized by the diagonal components, i.e., |${\rm Cov}_{E,ij}/\sqrt{{\rm Cov}_{E,ii}{\rm Cov}_{E,jj}}$| are plotted. We show some diagonal components in figure 4 so that the readers can grasp absolute values of the covariance matrices. In that figure, for a rough comparison, approximate theoretical predictions of the covariance matrices are shown. To calculate them, we follow the prescription described in appendix A of Asgari et al. (2020), and we take only major components into account; the Gaussian and shape-noise terms for E-mode, and only the shape-noise term for B-mode (for contributions from the non-Gaussian term and super-sample covariance, see Barreira et al. 2018; Shirasaki et al. 2019). Overall, reasonably good agreement between mock measurements and theoretical predictions can be seen in figure 4. The disagreement between the mock covariance and the theoretical predictions presumably originates mainly from a simplified assumption to ignore the effect of survey geometry and masking in estimating the Gaussian and shape-noise terms in the theoretical predictions (see Asgari et al. 2020). We note that these effects are properly taken into account in the mock covariance, which will be used in our cosmological analysis throughout the paper.

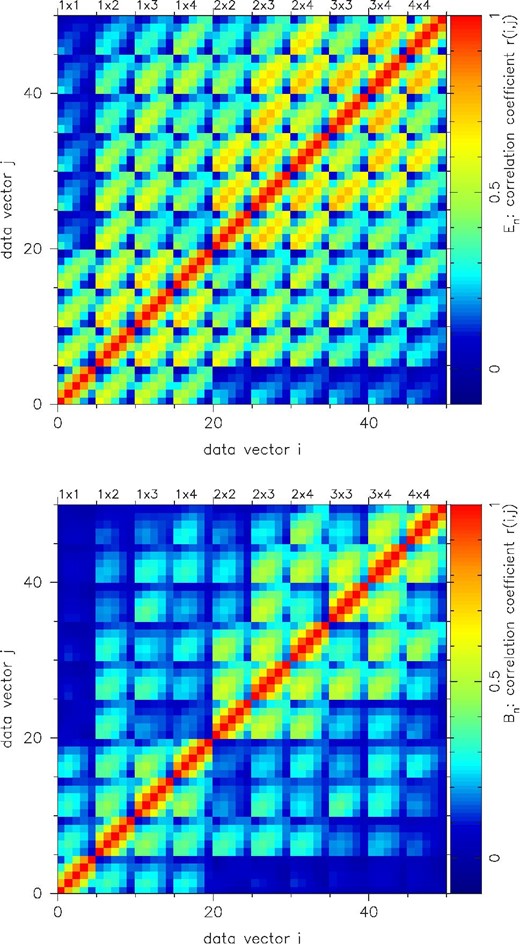
$Covariance matrices normalized by the diagonal components, i.e., ${\rm Cov}_{ij}/\sqrt{{\rm Cov}_{ii}{\rm Cov}_{jj}}$, are shown. Top: En, bottom: Bn. The x- and y-axes indicate elements of the data vector, which is defined as $d_{E,i} = (E_1^{11},E_2^{11},\ldots ,E_5^{11},E_1^{12},\ldots ,E_5^{44})$ and has 50 elements consisting of 10 tomographic combinations of COSEBIs (indicated as top label) each with five modes.$

Fig. 3.

Covariance matrices normalized by the diagonal components, i.e., |${\rm Cov}_{ij}/\sqrt{{\rm Cov}_{ii}{\rm Cov}_{jj}}$|⁠, are shown. Top: E_n, bottom: B_n. The x- and y-axes indicate elements of the data vector, which is defined as |$d_{E,i} = (E_1^{11},E_2^{11},\ldots ,E_5^{11},E_1^{12},\ldots ,E_5^{44})$| and has 50 elements consisting of 10 tomographic combinations of COSEBIs (indicated as top label) each with five modes.

Open in new tab Download slide

Fig. 4.

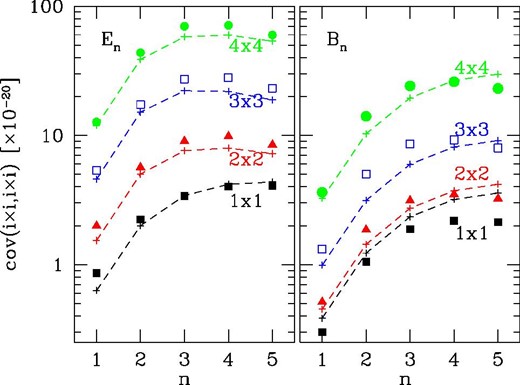
Diagonal components of covariance matrices of E_n (left) and B_n (right), to be specific 〈X_n(z_i × z_j)X_n(z_i × z_j)〉, are shown for four auto-correlation cases of tomographic redshift bins z₁ × z₁ (filled squares), z₂ × z₂ (filled triangles), z₃ × z₃ (open squares), and z₄ × z₄ (filled circles), from lowest to highest, respectively. Theoretical predictions (see text for details) are plotted with plus marks connected by dashed lines for visual help.

Open in new tab Download slide

Shirasaki et al. (2019) studied in detail the accuracy of the estimation of the covariance matrix of cosmic shear TPCFs from the HSC-Y1 mocks, and investigated the impact of various systematic effects in the cosmic shear analysis, including photo-z errors and the uncertainty in the multiplicative bias, on the covariance estimation. Based on their results, H20 concluded that the covariance matrix of TPCFs estimated from the mocks is calibrated with |$<\!10\%$| accuracy against various systematic effects in the cosmic shear analysis (see subsection 4.4 of H20). Since the COSEBIs are linearly related to TPCFs, a similar level of accuracy can be expected for the covariance matrix of COSEBI measurements. It should be noted that the cosmology dependence of the covariance cannot be included in our mock-based approach, because the HSC-Y1 mock catalogs are based on a set of full-sky gravitational lensing ray-tracing simulations that adopt a specific flat ΛCDM cosmology (Takahashi et al. 2017). In the HSC-Y1 cosmic shear PS analysis by H19, the effect of the cosmology dependence of the covariance on their cosmological inference was examined by comparing cosmological constraints derived using the cosmology-dependent covariance (which is their fiducial model) with those derived using a cosmology-independent one (fixed to the best-fitting cosmological model). They found that the best-fitting Ω_m and S₈ [=σ₈(Ω_m/0.3)^α with α = 0.45 or 0.5] values agree with each other within 20% of the statistical uncertainty. Based on this result, we assume that the cosmology dependence of the covariance matrix does not significantly impact our cosmological analysis.

Using the mock |$E_n^{ab}$| data vectors and their covariance matrix obtained above, we examine the Gaussianity of the likelihood function of cosmic shear COSEBIs as it is a basic assumption in the standard Bayesian likelihood analysis. Specifically, we check a necessary condition of the Gaussianity; whether a distribution of χ² measured from 2268 mock samples follows the theoretical χ² distribution with the same degrees of freedom. We compute, for each piece of mock data, the standard χ²,

$$\begin{equation} \chi _E^2 = \sum _{i,j} (d_{E,i}-\bar{d}_{E,i}) {\rm Cov}_{E,ij}^{-1} (d_{E,j}-\bar{d}_{E,i}), \end{equation} $$

(9)

where d_E,i is the E-mode data vector consisting of 10 tomographic combinations of |$E_n^{ab}$| each with five modes and thus having 50 elements, |$\bar{d}_{E,i}$| is its average among 2268 mock samples, and Cov_E,ij is the E-mode covariance matrix. We perform a Kolmogorov–Smirnov (KS) test for the distribution of mock |$\chi _E^2$| against the theoretical χ² distribution, and obtain a KS p-value of 0.11. Thus we conclude that the mock |$\chi _E^2$| distribution is in reasonable agreement with the theoretical one.

4.3 B-mode null test

Here, we quantitatively test the consistency of the B-mode COSEBIs signals with zero using the standard χ² statistics,

$$\begin{equation} \chi _B^2 = \sum _{i,j} d_{B,i} {\rm Cov}_{B,ij}^{-1} d_{B,j}, \end{equation} $$

(10)

where d_B,i is the B-mode data vector (presented in figure 2), and Cov_B,ij is the B-mode covariance matrix presented in figure 4. We find |$\chi _B^2=66.1$| for 50 degrees of freedom, corresponding to a p-value of 0.063. Therefore we conclude that no evidence for a significant B-mode signal is found.

We also compute the B-mode |$\chi _B^2$| for each of the 2268 mock catalogs. We compare the distribution of them with the theoretical χ² distribution, and find a good agreement between them. We find that 135 cases out of 2268 mock samples exceed the observed B-mode |$\chi _B^2$| values of 66.1, corresponding to a probability of 0.060, which is in good agreement with the p-value estimated above.

5 Cosmological analyses

We employ the standard Bayesian likelihood analysis for the cosmological inference of measured E-mode COSEBIs. The log-likelihood is given by

$$\begin{equation} -2 \ln {\cal L}(\boldsymbol {p}) = \sum _{i,j} [d_i-m_i(\boldsymbol {p})]{\mbox{Cov}}_{ij}^{-1} [d_j-m_j(\boldsymbol {p})], \end{equation} $$

(11)

where d_i is the E-mode data vector consisting of 10 tomographic combinations of |$E_n^{ab}$| each with five modes presented in subsection 4.1, |$m_i(\boldsymbol {p})$| is the theoretical model with |$\boldsymbol {p}$| being a set of parameters detailed in subsection 5.1, and Cov_ij is the covariance matrix presented in subsection 4.2. Since our covariance matrix is constructed from 2268 mock realizations, its inverse covariance is known to be biased high (see Anderson 2003; Hartlap et al. 2007, and references therein). When calculating the inverse covariance, we therefore include the so-called Anderson–Hartlap correction factor α = (N_mock − N_d − 2)/(N_mock − 1), where N_mock = 2268 is the number of mock realizations and N_d = 50 is the length of our data vector.

In order to sample the likelihood efficiently, we employ a multimodal nested sampling algorithm (Feroz & Hobson 2008; Feroz et al. 2009, 2019), as implemented in the public software MultiNest.

5.1 Model parameters

In this subsection, we summarize the model parameters and their prior ranges used in our cosmological analysis. Prior ranges and the choice of the parameter set for systematics tests are summarized in table 1.

Table 1.

Open in new tab

Summary of the cosmological, astrophysical, and systematics parameters used in our cosmological analysis.

	Prior range
Parameter^*	Fiducial ΛCDM^†	wCDM	Systematics tests	Section
Cosmological				5.1.1
Ω_c	flat[0.01, 0.9]
σ₈	flat[0.1, 2]
Ω_b	flat[0.038, 0.053]
n_s	flat[0.87, 1.07]
h	flat[0.64, 0.82]
∑m_ν [eV]	fixed at 0.06		flat[0, 0.5] for “∑m_ν varied“
w	fixed at −1	flat[−2, −1/3]
Astrophysical				5.1.2
A_IA	flat[−5, 5]		fixed at 0 for “w/o IA”
η_IA	flat[−5, 5]		fixed at 3 for “IA η_IA = 3”
A_B	fixed at 0		fixed at 1 for “A_B = 1” or flat[−5, 5] for “A_B varied”
Systematics				5.1.3
A_psf	Gauss(1, 1)		fixed at 0 for “w/o PSF error”	appendix 2.1
Δm	Gauss(0, 0.01)		fixed at 0 for “w/o Δm”
Δz₁	Gauss(0, 0.0374)		fixed at 0 for “w/o p(z) error”
Δz₂	Gauss(0, 0.0124)		fixed at 0 for “w/o p(z) error”
Δz₃	Gauss(0, 0.0326)		fixed at 0 for “w/o p(z) error”
Δz₄	Gauss(0, 0.0343)		fixed at 0 for “w/o p(z) error”
A_〈γ〉	fixed at 0		flat[−5, 5] for “w/ const-γ”	appendix 2.2

	Prior range
Parameter^*	Fiducial ΛCDM^†	wCDM	Systematics tests	Section
Cosmological				5.1.1
Ω_c	flat[0.01, 0.9]
σ₈	flat[0.1, 2]
Ω_b	flat[0.038, 0.053]
n_s	flat[0.87, 1.07]
h	flat[0.64, 0.82]
∑m_ν [eV]	fixed at 0.06		flat[0, 0.5] for “∑m_ν varied“
w	fixed at −1	flat[−2, −1/3]
Astrophysical				5.1.2
A_IA	flat[−5, 5]		fixed at 0 for “w/o IA”
η_IA	flat[−5, 5]		fixed at 3 for “IA η_IA = 3”
A_B	fixed at 0		fixed at 1 for “A_B = 1” or flat[−5, 5] for “A_B varied”
Systematics				5.1.3
A_psf	Gauss(1, 1)		fixed at 0 for “w/o PSF error”	appendix 2.1
Δm	Gauss(0, 0.01)		fixed at 0 for “w/o Δm”
Δz₁	Gauss(0, 0.0374)		fixed at 0 for “w/o p(z) error”
Δz₂	Gauss(0, 0.0124)		fixed at 0 for “w/o p(z) error”
Δz₃	Gauss(0, 0.0326)		fixed at 0 for “w/o p(z) error”
Δz₄	Gauss(0, 0.0343)		fixed at 0 for “w/o p(z) error”
A_〈γ〉	fixed at 0		flat[−5, 5] for “w/ const-γ”	appendix 2.2

*

For detailed descriptions of the parameters, see sub-subsections 5.1.1 for the cosmological parameters, 5.1.2 for the astrophysical nuisance parameters, and 5.1.3 for the systematics nuisance parameters.

†

“flat[x₁, x₂]” means a flat prior between x₁ and x₂, whereas “Gauss(⁠|$\bar{x}$|⁠, σ)” means a Gaussian prior with the mean |$\bar{x}$| and the standard deviation σ.

Table 1.

Open in new tab

Summary of the cosmological, astrophysical, and systematics parameters used in our cosmological analysis.

	Prior range
Parameter^*	Fiducial ΛCDM^†	wCDM	Systematics tests	Section
Cosmological				5.1.1
Ω_c	flat[0.01, 0.9]
σ₈	flat[0.1, 2]
Ω_b	flat[0.038, 0.053]
n_s	flat[0.87, 1.07]
h	flat[0.64, 0.82]
∑m_ν [eV]	fixed at 0.06		flat[0, 0.5] for “∑m_ν varied“
w	fixed at −1	flat[−2, −1/3]
Astrophysical				5.1.2
A_IA	flat[−5, 5]		fixed at 0 for “w/o IA”
η_IA	flat[−5, 5]		fixed at 3 for “IA η_IA = 3”
A_B	fixed at 0		fixed at 1 for “A_B = 1” or flat[−5, 5] for “A_B varied”
Systematics				5.1.3
A_psf	Gauss(1, 1)		fixed at 0 for “w/o PSF error”	appendix 2.1
Δm	Gauss(0, 0.01)		fixed at 0 for “w/o Δm”
Δz₁	Gauss(0, 0.0374)		fixed at 0 for “w/o p(z) error”
Δz₂	Gauss(0, 0.0124)		fixed at 0 for “w/o p(z) error”
Δz₃	Gauss(0, 0.0326)		fixed at 0 for “w/o p(z) error”
Δz₄	Gauss(0, 0.0343)		fixed at 0 for “w/o p(z) error”
A_〈γ〉	fixed at 0		flat[−5, 5] for “w/ const-γ”	appendix 2.2

	Prior range
Parameter^*	Fiducial ΛCDM^†	wCDM	Systematics tests	Section
Cosmological				5.1.1
Ω_c	flat[0.01, 0.9]
σ₈	flat[0.1, 2]
Ω_b	flat[0.038, 0.053]
n_s	flat[0.87, 1.07]
h	flat[0.64, 0.82]
∑m_ν [eV]	fixed at 0.06		flat[0, 0.5] for “∑m_ν varied“
w	fixed at −1	flat[−2, −1/3]
Astrophysical				5.1.2
A_IA	flat[−5, 5]		fixed at 0 for “w/o IA”
η_IA	flat[−5, 5]		fixed at 3 for “IA η_IA = 3”
A_B	fixed at 0		fixed at 1 for “A_B = 1” or flat[−5, 5] for “A_B varied”
Systematics				5.1.3
A_psf	Gauss(1, 1)		fixed at 0 for “w/o PSF error”	appendix 2.1
Δm	Gauss(0, 0.01)		fixed at 0 for “w/o Δm”
Δz₁	Gauss(0, 0.0374)		fixed at 0 for “w/o p(z) error”
Δz₂	Gauss(0, 0.0124)		fixed at 0 for “w/o p(z) error”
Δz₃	Gauss(0, 0.0326)		fixed at 0 for “w/o p(z) error”
Δz₄	Gauss(0, 0.0343)		fixed at 0 for “w/o p(z) error”
A_〈γ〉	fixed at 0		flat[−5, 5] for “w/ const-γ”	appendix 2.2

*

For detailed descriptions of the parameters, see sub-subsections 5.1.1 for the cosmological parameters, 5.1.2 for the astrophysical nuisance parameters, and 5.1.3 for the systematics nuisance parameters.

†

“flat[x₁, x₂]” means a flat prior between x₁ and x₂, whereas “Gauss(⁠|$\bar{x}$|⁠, σ)” means a Gaussian prior with the mean |$\bar{x}$| and the standard deviation σ.

5.1.1 Cosmological parameters

We focus on the flat ΛCDM cosmological model characterized by five parameters: the density parameter of CDM (Ω_c), the normalization of matter fluctuation (σ₈), the density parameter of baryons (Ω_b), the Hubble parameter (h), and the scalar spectrum index (n_s). Among those parameters, the cosmic shear COSEBIs are most sensitive to Ω_c and σ₈. Thus we adopt prior ranges that are sufficiently wide for these parameters (see table 1). Note that in contrast to H20, in which A_s (the scalar amplitude of the linear matter power spectrum on k = 0.05 Mpc⁻¹) was adopted for the amplitude parameter of the linear CDM power spectrum, we adopt σ₈ because, for the cosmic shear or more generally low-redshift probes of large-scale structure, observables are more directly sensitive to σ₈. We treat A_s as a derived parameter. For Ω_b, n_s, and h, which are only weakly constrained with cosmic shear COSEBIs, we set prior ranges which largely bracket allowed values from external experiments (see table 1). For the sum of the neutrino mass, we take ∑m_ν = 0.06 eV from the lower bound indicated by the neutrino oscillation experiments (see, e.g., Lesgourgues et al. 2013, for a review) for our fiducial choice. As a systematics test, we check the impact of neutrino mass on our conclusions by varying ∑m_ν.

In addition to the fiducial ΛCDM model, we consider an extended model by including the time-independent equation-of-state parameter for the dark energy (w), referred to as the wCDM model. We take a flat prior with −2 < w < −1/3, which excludes the non-accelerating expansion of the present day Universe, and brackets allowed values from external experiments.

5.1.2 Astrophysical parameters

In theoretical modeling of the COSEBI signal, we include two astrophysical effects; one is the effect of baryon physics on the nonlinear matter power spectrum (see subsection 3.2), and the other is the contribution of the intrinsic alignment (IA) of galaxy shapes (see Kirk et al. 2015; Troxel & Ishak 2015, for recent reviews). Below we summarize our treatment of those effects in our cosmological analyses.

In modeling the baryonic effect, we follow the methodology of Köhlinger et al. (2017), in which a modification of the dark matter power spectrum due to the AGN feedback is modeled by the fitting function derived by Harnois-Déraps et al. (2015), but an additional parameter (A_B) that controls the strength of the feedback is introduced (see sub-subsection 5.1.2 of Köhlinger et al. 2017, for the explicit expression). We note that H19 and H20 employed the same methodology. However, since we impose the scale-cut of cosmic shear COSEBIs conservatively so that the baryon effects do not have a significant impact on our analysis (see subsection 3.3), we do not include the baryon effect in our fiducial model, but check its impact in our systematics tests, one fixing A_B = 1 that corresponds to the original AGN feedback model, and the other in which A_B is a free parameter (see table 1).

The IA comes both from the correlation between intrinsic shapes of two physically associated galaxies in the same local field (referred to as the II-term) and from the cross-correlation between lensing shear of background galaxies and the intrinsic shape of foreground galaxies (referred to as the GI-term). We employ the standard theoretical framework for these terms, namely, the nonlinear modification of the tidal alignment model (Hirata & Seljak 2004; Bridle & King 2007; Joachimi et al. 2011). In this model, the E-mode COSEBIs originating from the II and GI terms are given in a similar manner as the cosmic shear COSEBIs, equation (4), but with IA power spectra |$P_{{\rm II}}^{ab}(\ell )$| and |$P_{{\rm GI}}^{ab}(\ell )$| [see equations (12) and (13) of H20 for explicit expressions for those terms]. Following H20, we adopt the standard parametric IA model with two parameters, the amplitude parameter A_IA and the power-law redshift dependence parameter η_IA that represents the effective redshift evolution of the IA amplitude. Following recent cosmic shear studies, e.g., Hildebrandt et al. (2017), Troxel et al. (2018), and H19, we adopt wide prior ranges for these parameters (see table 1).

5.1.3 Systematic parameters

Our treatment of systematic effects in the cosmological analysis largely follows that in H20. To summarize, in our fiducial model we take account of systematic effects from PSF leakage and PSF modeling errors, the uncertainty in the shear multiplicative bias correction, and uncertainties in the source galaxy redshift distributions. In addition, in systematics tests we check the impact of the uncertainty of the constant shear over fields. Below we summarize our modeling of those systematic effects, and choices for prior ranges on nuisance parameters in these models.

Our models for the PSF leakage and PSF modeling errors are described in appendix 2.1. We apply the correction for these systematics by equation (A7), which has one nuisance parameter A_psf. We adopt a Gaussian prior with (mean, σ) = (1, 1) for it and include them in our fiducial model.

Regarding the uncertainty in the shear multiplicative bias correction, we follow H20 (see sub-subsection 5.2.3 of H20). In short, we introduce the nuisance parameter Δm, which represents the residual multiplicative bias and modifies the theoretical prediction for the COSEBIs to

$$\begin{equation} E_n^{ab} \rightarrow (1+\Delta m)^2 E_n^{ab}. \end{equation} $$

(12)

A Gaussian prior with (mean, σ) = (0, 0.01) is taken for Δm based on the calibration of the HSC-Y1 shear catalog (Mandelbaum et al. 2018a).

Regarding uncertainties in the redshift distributions of source galaxies, we again follow H20. Introducing a nuisance parameter Δz_a for each tomographic redshift bin, the source redshift distribution, p^a(z), is shifted by p^a(z) → p^a(z + Δz_a). Gaussian priors are taken for Δz_a with the same mean and σ as those adopted in H20 (see table 1).

Finally, as described in appendix 2.2, we model a contribution to E-mode COSEBIs arising from a constant shear by equation (A9), which has one nuisance parameter A_〈γ〉. We assume a redshift-independent constant shear for simplicity. Given that we have not found strong evidence of the existence of the residual constant shear (see appendix 1 of H20), we do not include it in our fiducial model, but check its impact as a systematics test, in which we take a flat prior of −5 < A_〈γ〉 < 5.

6 Results

We first present cosmological constraints from our cosmic shear COSEBI analysis in the fiducial flat ΛCDM model. We then discuss the robustness of the results against various systematics, and present results from internal consistency checks among different choices of tomographic redshift bins and scale-cuts. We compare our cosmological constraints with other cosmic shear results and the Planck CMB result. We also compare our results with those from the HSC-Y1 cosmic shear PS and TPCF analyses, and examine the consistency among them using mock HSC-Y1 catalogs.

6.1 Cosmological constraints in the fiducial flat ΛCDM model

First, we present results for our fiducial flat ΛCDM model. Marginalized posterior contours in the Ω_m–σ₈ and Ω_m–S₈ planes are shown in figure 5, and marginalized one-dimensional posterior distributions of 13 model parameters and three derived parameters are shown in figure 6. We find marginalized 68% confidence intervals of 0.218 < Ω_m < 0.492, 0.576 < σ₈ < 0.883, and 0.783 < S₈ < 0.844 (see also table 2).

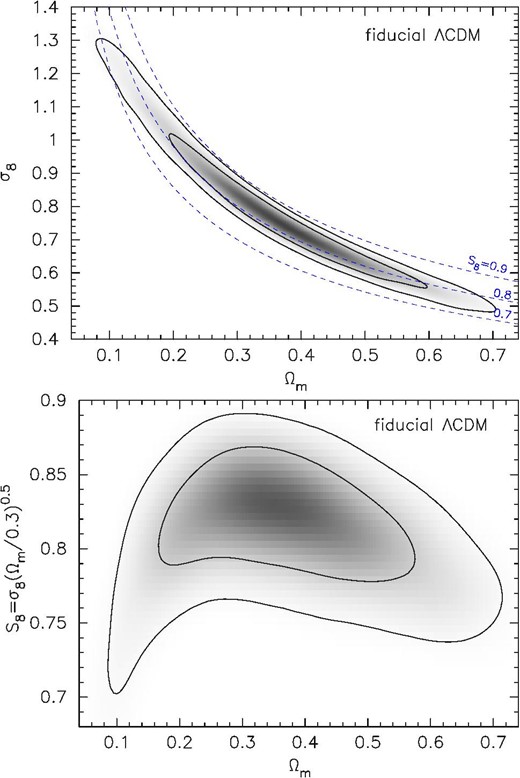
$Marginalized posterior contours (68% and 95% confidence levels) with a gray scale for a visual overview of the distribution (darker for higher posterior) in the Ωm–σ8 plane (top) and in the Ωm–S8 plane (bottom), where $S_8=\sigma _8\sqrt{\Omega _{\rm m}/0.3}$, in the fiducial flat ΛCDM model. In the Ωm–σ8 panel, three constant S8 loci (S8 = 0.7, 0.8, and 0.9 from bottom to top, respectively) are shown by dashed blue curves.$

Fig. 5.

Marginalized posterior contours (68% and 95% confidence levels) with a gray scale for a visual overview of the distribution (darker for higher posterior) in the Ω_m–σ₈ plane (top) and in the Ω_m–S₈ plane (bottom), where |$S_8=\sigma _8\sqrt{\Omega _{\rm m}/0.3}$|⁠, in the fiducial flat ΛCDM model. In the Ω_m–σ₈ panel, three constant S₈ loci (S₈ = 0.7, 0.8, and 0.9 from bottom to top, respectively) are shown by dashed blue curves.

Open in new tab Download slide

Fig. 6.

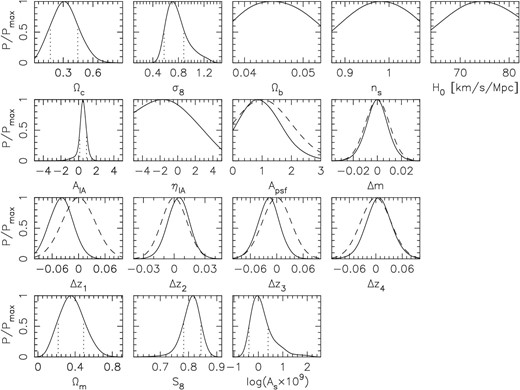
The upper three rows show the marginalized one-dimensional posterior distributions of model parameters in the fiducial flat ΛCDM model; the cosmological parameters are in the top row and the astrophysical and systematics parameters are in the two middle rows. The three panels in the bottom row are for the derived parameters. For parameters with flat prior ranges, the plotted range of the horizontal axis indicates its prior range. For parameters with Gaussian priors, the Gaussian priors are shown by the dashed curves. Dotted vertical lines represent the approximate 68% credible intervals, which are not shown for poorly constrained parameters.

Open in new tab Download slide

Table 2.

Open in new tab

Means and 68% confidence intervals of marginalized posterior distributions for well constrained cosmological parameters.

Parameter	Mean	68% confidence interval
Ω_c	0.319	0.169–0.447
Ω_m	0.365	0.218–0.492
A_s × 10⁹	1.46	0.411–2.50
σ₈	0.780	0.576–0.883
S₈	0.809	0.783–0.844

Parameter	Mean	68% confidence interval
Ω_c	0.319	0.169–0.447
Ω_m	0.365	0.218–0.492
A_s × 10⁹	1.46	0.411–2.50
σ₈	0.780	0.576–0.883
S₈	0.809	0.783–0.844

Table 2.

Open in new tab

Means and 68% confidence intervals of marginalized posterior distributions for well constrained cosmological parameters.

Parameter	Mean	68% confidence interval
Ω_c	0.319	0.169–0.447
Ω_m	0.365	0.218–0.492
A_s × 10⁹	1.46	0.411–2.50
σ₈	0.780	0.576–0.883
S₈	0.809	0.783–0.844

Parameter	Mean	68% confidence interval
Ω_c	0.319	0.169–0.447
Ω_m	0.365	0.218–0.492
A_s × 10⁹	1.46	0.411–2.50
σ₈	0.780	0.576–0.883
S₈	0.809	0.783–0.844

From the posterior distributions shown in figure 6, it can be seen that the HSC-Y1 cosmic shear COSEBIs alone cannot place useful constraints on three out of five input cosmological parameters (Ω_b, n_s, and H₀), but we confirm that the constraint on S₈ is not strongly affected by uncertainties in these parameters as long as they are restricted within the prior ranges considered in this study.

It is also found from the two middle rows of figure 6 that, except for A_IA, one-dimensional posteriors of astrophysical and systematics parameters are dominated by priors. In the following subsections, we discuss the effects of these nuisance parameters on the cosmological inference by changing the parameter setup.

In figure 2, we compare the measured cosmic shear COSEBI signals with the theoretical model with best-fitting parameter values for the fiducial flat ΛCDM model. In these plots, error bars represent the square-root of the diagonal elements of the covariance matrix. We find that our model with the fiducial parameter setup reproduces the observed signals quite well. The χ² value for the best-fitting parameter set is χ² = 40.7 for the effective degree of freedom² of 50 − 3 = 47, resulting in a p-value of 0.73.

6.2 Systematics tests

In our cosmological analysis, we have a number of astrophysical and systematics nuisance parameters that are marginalized over. Also, we have four model parameters that are fixed at the fiducial values in our fiducial setup (namely, ∑m_ν, w, A_B, and A_〈γ〉; see table 1), but may have, in principle, an impact on the cosmological inference. Below, we discuss the effects of these nuisance parameters on the cosmological inference by changing the parameter setup (see table 1 for parameter setups and the following subsections for details). In addition, we also perform an empirical test of the robustness of our cosmological constraints against possible uncertainties in the source redshift distributions by replacing the default ones derived from the COSMOS reweighted method with ones derived from stacked PDFs with three photo-z methods, DEmP, Ephor AB, and FRANKEN-Z (see sub-subsection 6.2.7, and also subsection 2.2 of H20, for details).

We focus on S₈ constraints to assess the impact of the nuisance parameters and source redshift distributions as it is a primary parameter to be constrained by cosmic shear two-point statistics. The results of these systematics tests are summarized in figure 7, in which credible intervals of marginalized one-dimensional posterior distributions of S₈ derived from systematics tests are compared with that of the fiducial setup. In this comparison, we use S₈ = σ₈(Ω_m/0.3)^α with α = 0.5. In appendix 3, we also present comparisons of marginalized posterior contours in the Ω_m–σ₈ plane because a single choice of α does not always provide an optimal description for the σ₈–Ω_m degeneracy, especially for cases with broad confidence contours such as ours. Overall, we find that no significant impact on our S₈ constraint is found from the systematics tests, as described in detail in the following subsections.

$Means and 68% credible intervals of marginalized one-dimensional constraints on $S\,_8=\sigma _8\sqrt{\Omega _{\rm m}/0.3}$. The fiducial case (top) is compared with different setups to check the robustness of our result. Vertical dotted lines show the 68% credible interval of the fiducial case. See figure 17 for comparisons of constraints in the Ωm–σ8 plane.$

Fig. 7.

Means and 68% credible intervals of marginalized one-dimensional constraints on |$S\,_8=\sigma _8\sqrt{\Omega _{\rm m}/0.3}$|⁠. The fiducial case (top) is compared with different setups to check the robustness of our result. Vertical dotted lines show the 68% credible interval of the fiducial case. See figure 17 for comparisons of constraints in the Ω_m–σ₈ plane.

Open in new tab Download slide

6.2.1 Intrinsic galaxy alignment

We find that the marginalized one-dimensional constraint on A_IA obtained from our fiducial cosmological inference is |$A_{\rm IA}=0.44_{-0.31}^{+0.46}$| , which is consistent with the results from the HSC-Y1 TPCF (⁠|$A_{\rm IA}=0.91_{-0.32}^{+0.27}$|⁠, H20) and PS analyses (A_IA = 0.38 ± 0.70, H19) for their fiducial setup.

In order to test the robustness of the cosmological constraints against the uncertainty of the intrinsic galaxy alignment, we perform two cosmological inferences with different IA modeling. In one case, the IA contribution is completely ignored; i.e., A_IA is fixed at 0 (“w/o IA” setup), and in the other case η_IA is fixed at 3 while A_IA is treated as a free parameter (“IA η_IA = 3” setup; see subsection 5.4 of H19 for the reasoning behind this choice). The results from these settings are compared with the fiducial one in figure 7 (see figures 17a and 17b for constraints in the σ₈–Ω_m plane). We find that in both cases the changes in cosmological constraints are not significant. On those grounds, we conclude that the effects of uncertainty in IA modeling on our fiducial cosmological constraints are insignificant.

6.2.2 Baryonic feedback

In our fiducial setup, we do not include the effect of baryonic feedback, but instead we impose a conservative scale-cut so that the baryon effects do not have a significant impact on our analysis (see subsection 3.3). It is therefore expected that the baryonic feedback effect does not strongly affect our cosmological constraints. We check this explicitly by employing an empirical model described in sub-subsection 5.1.2 (see sub-subsection 4.1.1 of H20 for details). Following H20, we consider two cases; the original AGN feedback model by Harnois-Déraps et al. (2015), which corresponds to fixing the baryon feedback parameter A_B = 1 (“A_B = 1” setup), and a more flexible model in which A_B is allowed to vary with a flat prior in the range −5 < A_B < 5 (“A_B varied” setup). From the results shown in figure 7 (and see figures 17c and 17d for constraints in the σ₈–Ω_m plane), we find that in both cases the changes in cosmological constraints are not significant. The marginalized one-dimensional posterior distribution of A_B obtained from the “A_B varied” setup is shown in figure 8, from which it is found that the constraint on A_B is very weak with A_B = 2.0 ± 1.2 (mean and σ). We also find that the correlation between A_B and S₈ is very weak. Based on these results, we conclude that the effect of baryonic feedback on our fiducial cosmological constraints is insignificant.

Fig. 8.

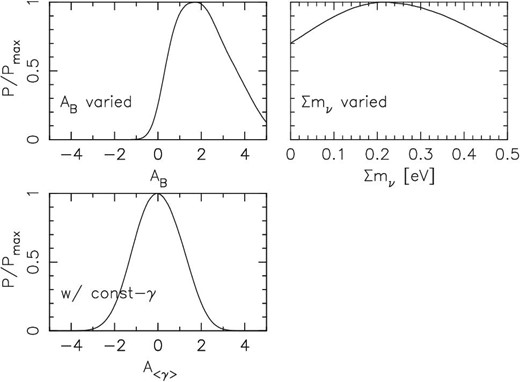
Marginalized one-dimensional posterior distributions of nuisance parameters derived from non-fiducial models. Top left: the baryon feedback model parameter from the “A_B varied” setup; top right: the neutrino mass from the “∑m_ν varied” setup; bottom: the residual constant shear A_〈γ〉 from the “w/const-γ” setup.

Open in new tab Download slide

6.2.3 Neutrino mass

In our fiducial setup, the neutrino mass is fixed at ∑m_ν = 0.06 eV. Since the non-zero neutrino mass leads to a redshift-dependent suppression of the matter power spectrum on small scales, it has, in principle, an impact on our cosmological inference. However, the HSC-Y1 cosmic shear analyses are expected to be insufficient to place a useful constraint on the neutrino mass due to the current measurement precision and the scale-cuts on small scales, and this is indeed the cases for HSC-Y1 PS (H19) and TPCF analyses (H20). We find that this is also the case for our COSEBI analysis; figure 8 shows the one-dimensional posterior distribution of ∑m_ν obtained from the “∑m_ν varied” setup in which the neutrino mass is allowed to vary with a flat prior in the range 0 < ∑m_ν < 0.5 eV. The credible interval on S₈ is compared with the fiducial case in figure 7 (see figure 17e for the σ₈–Ω_m constraints). It is found from this comparison result that the non-zero neutrino mass indeed has little impact on our cosmological constraints.

6.2.4 Residual constant shear

Here we check the robustness of our fiducial cosmological constraints against the residual constant shear that is not included in our fiducial model. To do so, we test the same setup as in the fiducial case but including a contribution from residual constant shear by equation (A9) with a nuisance parameter A_〈γ〉 that controls its amplitude (“w/ const-γ” setup; see appendix 2.2 for details). We adopt a flat prior in the range −5 < A_〈γ〉 < 5. The derived S₈ constraint is compared with the fiducial case in figure 7 (see also figure 17f). We find that the resulting changes in the cosmological constraints are very small. The marginalized one-dimensional posterior distribution of A_〈γ〉 is shown in figure 8, and its mean and σ are found to be A_〈γ〉 = 0.0 ± 1.1, which is consistent with the constant shear expected from the cosmic shear that is coherent over the field (see appendix 1 of H20).

6.2.5 PSF leakage and PSF modeling errors

Following the previous HSC-Y1 cosmic shear analyses (H19 and H20), we employ the conventional model for the PSF leakage and PSF modeling errors given by equation (A1). We then derive an empirical model for a contribution to the measured E-mode COSEBIs by equation (A7) with a nuisance parameter A_psf that controls its amplitude (see appendix 2.1 for details), for which we adopt a Gaussian prior of (mean, σ) = (1, 1). Marginalized one-dimensional posterior distributions of these parameters from our fiducial analysis are shown in figure 6. We find that the posterior is largely determined by the prior. We also find that the marginalized constraint on A_psf is not strongly correlated with either Ω_m, σ₈, or S₈.

In order to check the robustness of our cosmological constraints against these systematics, we test the same setup as the fiducial case but ignoring them, i.e., setting A_psf = 0 (“w/o PSF error” setup). The result is shown in figure 7 (see also figure 17g). We find that the changes in the cosmological constraints are very small as a natural consequence of PSF leakage and PSF modeling errors being smaller than the size of errors on the HSC-Y1 cosmic shear COSEBIs.

6.2.6 Shear calibration error

In our fiducial analysis we also take account of the uncertainty in the shear multiplicative bias correction using a simple model, equation (12), with a Gaussian prior corresponding to a 1% uncertainty (see sub-subsection 5.1.3). The marginalized one-dimensional posterior distribution of the model parameter Δm from our fiducial analysis is shown in figure 6, which indicates that the posterior is dominated by the prior.

In order to check the effect of this residual calibration bias on our cosmological constraints, we test the same setup as the fiducial case but ignoring the nuisance parameter, i.e., setting Δm = 0 (“w/o Δm” setup). The result is shown in figure 7 (see also figure 17h). We find that the changes in the cosmological constraints are very small.

6.2.7 Source redshift distribution errors

In our fiducial analysis, we introduce nuisance parameters Δz_a, which represent a shift of each of the source redshift distributions. To be specific, the source redshift distribution, p^a(z), is shifted by p^a(z) → p^a(z + Δz_a) (see sub-subsection 5.1.3). Marginalized one-dimensional posterior distributions of these parameters from our fiducial analysis are shown in figure 6. Although the peak positions of these posteriors show shifts from the peak prior distributions, the sizes of the shifts are within 1σ of the Gaussian priors, and thus are not statistically significant. We note that a relatively large shift seen for the lowest redshift bin is also seen in the HSC-Y1 TPCF analysis with a similar size and direction (H20), and thus it may indicate an unknown bias in estimation of the source redshift distribution that is not captured in the prior knowledge.

In order to check the robustness of our cosmological constraints against these uncertainties, we test the same setup as the fiducial analysis but ignoring these parameters [“w/o p(z) error” setup] The result is shown in figure 7 (see also figure 17i). We find that the changes in the cosmological constraints are very small.

In addition, following H20, we also perform an empirical test; we replace the default source redshift distributions derived from the COSMOS reweighted method with ones derived from stacked PDFs with three photo-z methods, DEmP, Ephor AB, and FRANKEN-Z (see subsection 2.2 of H20 for details). Other settings remain the same as the fiducial setup. The results are shown in figure 7 [labeled as “P(z) method”; see also figures 17j, 17k, and 17l]. Again, we find that the changes in the cosmological constraints are not significant, and thus we conclude that no additional systematics are identified from this test.

6.3 Internal consistency

Here we present the results of internal consistency checks in which we derive cosmological constraints from subsets of the data vector, and from data vectors generated with smaller-/larger-half scale-cuts than the original scale-cut range, and then we compare the derived cosmological constraints with the ones from a reference setup. In doing so, following H20, we do not use the fiducial results as the reference, but instead we adopt the results from the “cosmology alone” setup in which we include neither systematics nor astrophysical parameters; only five cosmological parameters are included as a baseline for comparison. The reason for this choice is to avoid undesirable changes in nuisance parameters, which may add or cancel out shifts in parameter constraints. Of course, for this test to be meaningful, the reference setup must provide cosmological constraints that are consistent with ones from the fiducial case, which we have explicitly confirmed.

6.3.1 Tomographic redshift bins

First, we exclude one of the four redshift bins, and perform the cosmological inference with the remaining three tomographic bins. The resulting marginalized constraints on S₈ are shown in figure 9 (see also figures 18a–18d for marginalized constraints in the Ω_m–σ₈ plane). We find that constraints on S₈ from test setups are consistent within 1σ of the reference result. Also, it is seen in figure 18 that the 68% credible contours in the Ω_m–σ₈ plane in these cases largely overlap with the reference contour. Thus we conclude that no significant internal inconsistency is found from this test.

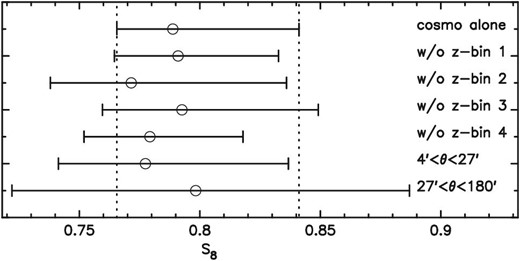
Means and 68% credible intervals of marginalized one-dimensional constraints on S8. The “cosmology alone” case (top) is compared with different setups for internal consistency checks. Vertical dotted lines show the 68% credible interval of the cosmology alone case. See figure 18 for comparisons of constraints in the Ωm–σ8 plane.

Fig. 9.

Means and 68% credible intervals of marginalized one-dimensional constraints on S₈. The “cosmology alone” case (top) is compared with different setups for internal consistency checks. Vertical dotted lines show the 68% credible interval of the cosmology alone case. See figure 18 for comparisons of constraints in the Ω_m–σ₈ plane.

Open in new tab Download slide

6.3.2 Different scale-cuts

Next, we check the internal consistency among different angular ranges by splitting the original scale-cut (4^′ < θ < 180^′) into two scale-cuts (4^′ < θ < 27^′ and 27^′ < θ < 180^′). We generate the data vectors and covariance matrices for these two scale-cuts following the same procedure as for the fiducial scale-cut. The resulting marginalized constraints on S₈ are shown in figure 9. As expected, the credible intervals are larger than the reference case. We see that the smaller-half scale-cut has more constraining power than the larger-half scale-cut. In addition, some more information on this can be seen in the comparison plots in the Ω_m–σ₈ plane (figures 18e and 18f): The smaller-half scale-cut places constraint contours which are as tight as the reference contours in the S₈ direction (perpendicular to the Ω_m–σ₈ degeneracy direction), but are very elongated in the degeneracy direction. Thus from these results we see that a wider angular range is effective in placing a tighter constraint in the Ω_m–σ₈ plane. Overall, the results from the larger/smaller-half scale-cuts are consistent with the reference results. Thus we again conclude that no significant internal inconsistency is found from this test.

6.4 wCDM model

In addition to the fiducial ΛCDM model, we test one extended model by including the time-independent dark energy equation of state parameter w, although it was found in H19 and H20 that HSC-Y1 cosmic shear two-point statistics alone cannot place a useful constraint on w. We allow w to vary with a flat prior in the range −2 < w < −1/3. The setup of the other parameters is the same as the fiducial ΛCDM model.

The marginalized constraints in the Ω_m–σ₈, Ω_m–w, and S₈–w planes are shown in figure 10, along with constraints from the fiducial ΛCDM model and the Planck 2018 results for the wCDM model (Planck Collaboration 2020a, TT+TE+EE+lowE). As can be seen from the figure, our constraints on those parameters are consistent with the Planck results, although the Planck constraints are much tighter than our constraints. The marginalized one-dimensional constraint range of S₈ is shown in figure 7. It is found that the derived two-dimensional marginalized posterior distributions are similar to those obtained from the HSC-Y1 cosmic shear TPCF (see figure 14 of H20) and PS (see figure 16 of H19) analyses, as expected.

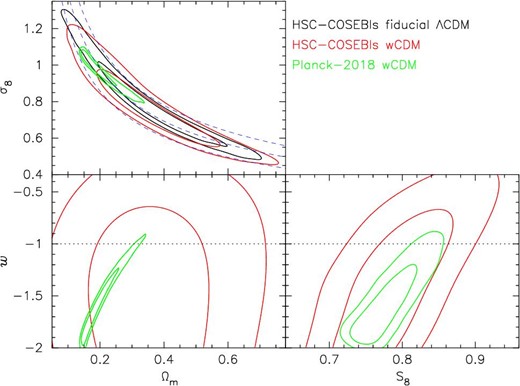
Marginalized posterior contours (68% and 95% confidence levels) in the Ωm–σ8 plane (top), the Ωm–w plane (bottom left), and the S8–w plane (bottom right) in the wCDM model are shown by red contours. Constraints from the fiducial ΛCDM model are shown by black contours, and Planck 2018 results for the wCDM model (Planck Collaboration 2020a, TT+TE+EE+lowE) are shown by green contours. In the Ωm–σ8 panel, three constant S8 loci (S8 = 0.7, 0.8, and 0.9 from bottom to top, respectively) are shown by dashed blue curves.

Fig. 10.

Marginalized posterior contours (68% and 95% confidence levels) in the Ω_m–σ₈ plane (top), the Ω_m–w plane (bottom left), and the S₈–w plane (bottom right) in the wCDM model are shown by red contours. Constraints from the fiducial ΛCDM model are shown by black contours, and Planck 2018 results for the wCDM model (Planck Collaboration 2020a, TT+TE+EE+lowE) are shown by green contours. In the Ω_m–σ₈ panel, three constant S₈ loci (S₈ = 0.7, 0.8, and 0.9 from bottom to top, respectively) are shown by dashed blue curves.

Open in new tab Download slide

6.5 Comparison to other constraints from the literature

Next, we compare the cosmological constraints from our fiducial ΛCDM model with results from other cosmic shear and CMB measurements. Figure 11 compares the 68% credible intervals of |$S_8=\sigma _8\sqrt{\Omega _{\rm m}/0.3}$|⁠, where the results of other projects are taken from the literature. See also figure 19 for the comparison to other results in the Ω_m–σ₈ plane.

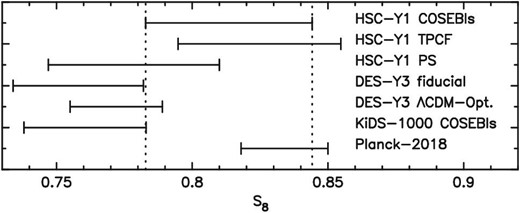
$68% credible intervals of marginalized posterior distributions of $S\,_8=\sigma _8\sqrt{\Omega _{\rm m}/0.3}$ or that of the projected joint highest posterior density (PJ-HPD) for KiDS-1000. Our result from the fiducial ΛCDM model is compared with other results in the literature, HSC first-year (HSC-Y1) cosmic shear TPCF (H20), PS (H19), DES-Y3 cosmic shear TPCFs (their fiducial and ΛCDM-Optimized models are shown; for details see Amon et al. 2022), KiDS-1000 cosmic shear COSEBIs (Asgari et al. 2021), and Planck 2018 CMB (Planck Collaboration 2020a, TT+TE+EE+lowE). Since different studies adopt different definitions of the central values (mean, median, or peak of the marginalized posterior distribution, or the multivariate maximum posterior), central values are not shown to avoid possible misunderstanding. Note that since different studies adopt different priors and modeling, some of the differences in the credible intervals may be due to the different choices of priors and modeling. See figure 19 for comparisons of constraints from studies in the Ωm–σ8 plane.$

Fig. 11.

68% credible intervals of marginalized posterior distributions of |$S\,_8=\sigma _8\sqrt{\Omega _{\rm m}/0.3}$| or that of the projected joint highest posterior density (PJ-HPD) for KiDS-1000. Our result from the fiducial ΛCDM model is compared with other results in the literature, HSC first-year (HSC-Y1) cosmic shear TPCF (H20), PS (H19), DES-Y3 cosmic shear TPCFs (their fiducial and ΛCDM-Optimized models are shown; for details see Amon et al. 2022), KiDS-1000 cosmic shear COSEBIs (Asgari et al. 2021), and Planck 2018 CMB (Planck Collaboration 2020a, TT+TE+EE+lowE). Since different studies adopt different definitions of the central values (mean, median, or peak of the marginalized posterior distribution, or the multivariate maximum posterior), central values are not shown to avoid possible misunderstanding. Note that since different studies adopt different priors and modeling, some of the differences in the credible intervals may be due to the different choices of priors and modeling. See figure 19 for comparisons of constraints from studies in the Ω_m–σ₈ plane.

Open in new tab Download slide

DES-Y3 (Amon et al. 2022) covers a much larger area (4143 deg²) than HSC-Y1, yielding tighter constraints than our fiducial results. Note that, in their cosmological analyses, the neutrino mass density is allowed to vary. They provide results from two models; their fiducial model adopts a very conservative small-scale cut yielding a broader constraint than the one from their ΛCDM-Optimized model in which smaller-scale information is used safely (see Amon et al. 2022). In both cases, their S₈ constraints are lower than ours, and their ΛCDM-Optimized model shows about 1.0σ difference³ from our fiducial result (see figure 11).

KiDS-1000 covers an effective area of 777.4 deg² (Asgari et al. 2021). They employed three two-points statistics, the TPCF, band power spectra, and COSEBIs, and found the cosmological results from these three to be in excellent agreement. Their S₈ value from a COSEBI analysis is lower than ours and shows about 1.4σ difference from our fiducial result (see figure 11).

The credible interval of S₈ from Planck 2018 (Planck Collaboration 2020a, we take TT+TE+EE+lowE without CMB lensing) is consistent with our result. It is also found from figure 19 that the credible contours in the Ω_m–σ₈ plane from the Planck 2018 CMB result overlap well with our result. We therefore conclude that there is no tension between the Planck 2018 constraints and the HSC-Y1 cosmic shear COSEBI constraints as far as S₈, Ω_m, and σ₈ are concerned.

6.6 Comparison with HSC-Y1 cosmic shear PS and TPCF results

Finally, we compare the cosmological constraints from our fiducial model with the HSC-Y1 cosmic shear PS (H19) and TPCF (H20) results. As seen in figure 11, our constraint on S₈ is in good agreement with the TPCF results (H20), and is in weak agreement with the PS results (H19). Similar comparison results are found for two-dimensional constraint contours in the Ω_m–σ₈ plane presented in figure 19a, although our contours are much broader than theirs. Although no strong evidence of inconsistency among these results is seen from those results, we examine the consistency between them, paying particular attention to the fact that those analyses share the same HSC-Y1 data set with the same tomographic redshift binning and adopt a similar analysis setup.

We perform the same cross-correlation analysis as one done in H20 (see subsection 6.7 of H20), in which cosmological inferences on the 100 realistic mock catalogs (see also Oguri et al. 2018) are performed with the same fiducial setups of HSC-Y1 PS and TPCF analyses except for ignoring PSF modeling errors because no PSF modeling error is added in the mock data, and then the derived cosmological constraints are compared. We apply our COSEBI analysis to the same mock catalogs but ignoring PSF modeling errors as well. We present the scatter plots comparing S₈ values (we take the median of a posterior distribution) derived from these three cosmological analyses on the same mock catalogs in figure 12. We compute the standard cross-correlation coefficient of those distributions,

$$\begin{equation} r(S_8)={ {\mbox{Cov}\left(S_8^A,S_8^B\right)} \over { {\mbox{Cov}\left(S_8^A,S_8^A\right)^{1/2}} {\mbox{Cov}\left(S_8^B,S_8^B\right)^{1/2}}}}, \end{equation} $$

(13)

where the superscripts A and B stand for an analysis method (i.e., PS, TPCF, or COSEBI). We show the results in each panel of figure 12. We find r(S₈) ∼ 0.5 for all the three cases, which indicates that the correlations between the derived cosmological constraints among the three analyses are weak. Although qualitative, this result can be intuitively understood as each analysis method is sensitive to different multipole ranges, as seen in figure 1. In figure 13, we present frequency distributions of the differences in the S₈ values (⁠|$\Delta S_8 = S_8^A-S_8^B$|⁠) derived from any pair of PS, TPCF, and COSEBI analyses along with corresponding results from the real HSC-Y1 cosmic shear analyses (shown by the vertical red dashed line). We also compute the root-mean-square values of these distributions (σ), which are denoted in each panel. We find that the derived σ values for ΔS₈ are only slightly smaller than those for the parent S₈ (0.022, 0.031, and 0.038 for PS, TPCF, and COSEBI, respectively), which confirms the weak correlations between the derived cosmological constraints among the three analyses. We note that similar results but for the COSEBIs, band power spectra, and TPCF analyses are found in the KiDS-1000 cosmic shear study by Asgari et al. (2021). It follows from the above results that the ΔS₈ values from the three real HSC-Y1 cosmic shear analyses are explained by statistical fluctuations below 1.5σ.

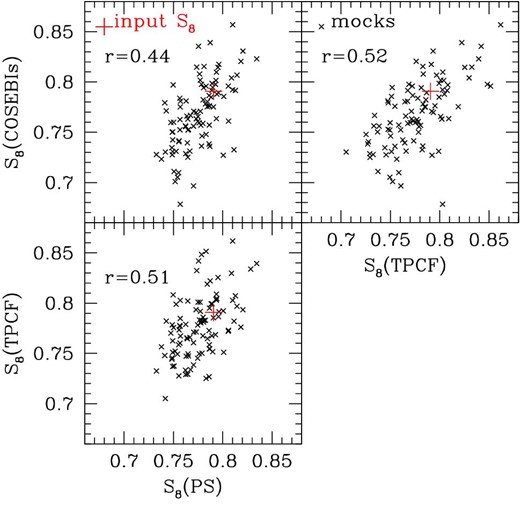
Scatter plots showing median values of marginalized one-dimensional posterior distributions of S8 derived from cosmological analyses on 100 mock catalogs. In each of the three panels, results from any one of the PS, TPCF, or COSEBI analyses are compared to those from either of the rest. The red cross shows the value of S8 adopted in generating the mock catalogs. The cross-correlation coefficient defined by equation (13) is denoted in each panel.

Fig. 12.

Scatter plots showing median values of marginalized one-dimensional posterior distributions of S₈ derived from cosmological analyses on 100 mock catalogs. In each of the three panels, results from any one of the PS, TPCF, or COSEBI analyses are compared to those from either of the rest. The red cross shows the value of S₈ adopted in generating the mock catalogs. The cross-correlation coefficient defined by equation (13) is denoted in each panel.

Open in new tab Download slide

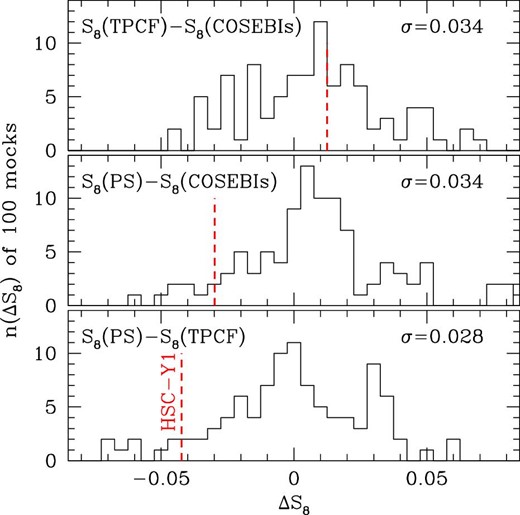
Frequency distributions of the differences in median S8 values derived from any two of the PS, TPCF, and COSEBI analyses on 100 mock catalogs. The root-mean-square value of the distribution (σ) is denoted in each panel. Corresponding results from the real HSC-Y1 cosmic shear analyses are shown by the vertical red dashed line in each panel.

Fig. 13.

Frequency distributions of the differences in median S₈ values derived from any two of the PS, TPCF, and COSEBI analyses on 100 mock catalogs. The root-mean-square value of the distribution (σ) is denoted in each panel. Corresponding results from the real HSC-Y1 cosmic shear analyses are shown by the vertical red dashed line in each panel.

Open in new tab Download slide

7 Summary and conclusions

We have presented a cosmological analysis of the cosmic shear COSEBIs measured from the HSC-Y1 data, covering 136.9 deg². Photometric redshifts derived from the HSC five-band photometry are adopted to select galaxies and divided into four tomographic redshift bins ranging from z = 0.3 to 1.5 with equal widths of Δz = 0.3. The total number of selected galaxies is 9.6 million. We compute tomographic E/B-mode COSEBIs from measured cosmic shear TPCFs on the angular range of 4^′ < θ < 180^′.

In addition to the HSC-Y1 data set, we have used HSC-Y1 mock shape catalogs constructed from full-sky gravitational lensing simulations (Takahashi et al. 2017) that fully take account of the survey geometry and measurement noise (Shirasaki et al. 2019). Using 2268 mock realizations, we have derived the E/B-mode covariance matrices adopted in our cosmological analysis. The mock catalogs are also used to assess the statistical significance of some of our results.

We have quantitatively tested the consistency of the B-mode COSEBI signals with zero using the standard χ² statistics, and found χ² = 66.1 for 50 degrees of freedom, corresponding to a p-value of 0.063. We thus conclude that no evidence of significant B-mode shear is found.

We have performed a standard Bayesian likelihood analysis for the cosmological inference of the measured E-mode COSEBIs. Our fiducial ΛCDM model consists of five cosmological parameters and includes contributions from the intrinsic alignment of galaxies (with two parameters for the nonlinear alignment IA model) as well as six nuisance parameters (one for PSF errors, one for shear calibration error, and four for source redshift distribution errors). We have found that our fiducial model fits the measured E-mode COSEBI signals very well with a minimum χ² of 40.7 for 47 effective degrees of freedom. The derived marginalized one-dimensional constraint on S₈ is |$S_8=0.809_{-0.026}^{+0.036}$| (mean and 68% credible interval).

We have carefully checked the robustness of our cosmological results against astrophysical uncertainties in modeling and systematics uncertainties in measurements. The former includes the intrinsic alignment of galaxies and the baryonic feedback effect on the nonlinear matter power spectrum, and the latter includes PSF errors, shear calibration error, errors in the estimation of source redshift distributions, and a residual constant shear over fields. We have tested the validity of our treatment of those uncertainties by changing parameter setups or by adopting empirical or extreme models for them. We have found that none of these uncertainties has a significant impact on the cosmological constraints. We have also confirmed the internal consistency of our results among different choices of tomographic redshift bins and different scale-cuts.

We have examined, using mock HSC-Y1 catalogs, the consistency in the S₈ constraints derived from the three HSC-Y1 cosmic shear two-point statistics, PS (H19), TPCF (H20), and COSEBIs (this study), which share the same HSC-Y1 data set with the same tomographic redshift binning and adopt a similar analysis setup. We have found that correlations between the derived S₈ constraints among the three analyses are weak, most likely because each analysis method is sensitive to different multipole ranges of cosmic shear power spectra. We have also found that differences in the derived S₈ values between different analyses are explained by statistical fluctuations below 1.5σ.

We have compared our S₈ constraint with those obtained from DES-Y3 (Amon et al. 2022) and KiDS-1000 (Asgari et al. 2021). We have found that our S₈ value is higher than theirs such that the 68% credible intervals only slightly overlap with each other at the edges. Quantitatively, the S₈ constraint from DES-Y3 (their ΛCDM-Optimized model) shows about 1.0σ difference, and that of KiDS-1000 (their COSEBI result) shows about 1.4σ difference from our fiducial result (see figure 11). We have also found that the S₈ constraint from Planck (Planck Collaboration 2020a) is consistent with our result.

Acknowledgements

We would like to thank the anonymous referee for many constructive comments on the earlier manuscript, which improved the paper. We would like to thank members of the HSC weak lensing working group for useful discussions. We would like to thank R. Takahashi for making full-sky gravitational lensing simulation data publicly available. We would like to thank Martin Kilbinger for making the software Athena publicly available, Antony Lewis and Anthony Challinor for making the software CAMB publicly available, the MultiNest developers for making MultiNest publicly available, the HEALPix team for making the HEALPix software publicly available, and Nick Kaiser for making the software imcat publicly available.

This work was supported in part by JSPS KAKENHI Grant Numbers JP15H05892, JP17K05457, JP20H05856, JP20H00181, and 22K03655.

Data analyses were in part carried out on the PC cluster at the Center for Computational Astrophysics, National Astronomical Observatory of Japan. Numerical computations were in part carried out on the Cray XC30 and XC50 at the Center for Computational Astrophysics, National Astronomical Observatory of Japan, and also on the Cray XC40 at YITP at Kyoto University.

The Hyper Suprime-Cam (HSC) Collaboration includes the astronomical communities of Japan and Taiwan, and Princeton University. The HSC instrumentation and software were developed by the National Astronomical Observatory of Japan (NAOJ), the Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU), the University of Tokyo, the High Energy Accelerator Research Organization (KEK), the Academia Sinica Institute for Astronomy and Astrophysics in Taiwan (ASIAA), and Princeton University. Funding was contributed by the FIRST program from the Japanese Cabinet Office, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), the Japan Society for the Promotion of Science (JSPS), the Japan Science and Technology Agency (JST), the Toray Science Foundation, NAOJ, Kavli IPMU, KEK, ASIAA, and Princeton University.

This paper is based on data collected at the Subaru Telescope and retrieved from the HSC data archive system, which is operated by the Subaru Telescope and Astronomy Data Center (ADC) at NAOJ. Data analysis was in part carried out with the cooperation of the Center for Computational Astrophysics (CfCA) at NAOJ. We are honored and grateful for the opportunity of observing the Universe from Mauna Kea, which has cultural, historical, and natural significance in Hawaii.

This paper makes use of software developed for the Vera C. Rubin Observatory. We thank the Rubin Observatory for making their code available as free software at 〈http://pipelines.lsst.io/〉.

The Pan-STARRS1 Surveys (PS1) and the PS1 public science archive have been made possible through contributions by the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg, and the Max Planck Institute for Extraterrestrial Physics, Garching, the Johns Hopkins University, Durham University, the University of Edinburgh, the Queen's University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration under grant No. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation grant No. AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), the Los Alamos National Laboratory, and the Gordon and Betty Moore Foundation.

Appendix 1 Test of the measurement method of COSEBIs using mock catalogs

Here we present the results of an accuracy test of our method of measuring COSEBI signals, which is described in subsection 4.1. To do this, we use 2268 HSC-Y1 mock catalogs but ignore shape noise (Shirasaki et al. 2019). We measure E/B-mode COSEBIs from each of the 2268 mock catalogs using the same method as the real HSC-Y1 COSEBI measurements (see subsection 4.1), and compute means and root-mean-squares (RMSs) of them. Since the shape noise is not included in this mock analysis, the RMSs represent an expected sample variance for the HSC-Y1 field. The results are shown in figure 14 along with the theoretical predictions of E-mode COSEBIs based on the WMAP9 cosmological model (Hinshaw et al. 2013), which is adopted in the ray-tracing simulation (Takahashi et al. 2017). It is seen from the figure that the averaged E_n signals agree with the theoretical predictions well within the RMSs, and the B_n signals are consistent with zero. Therefore we conclude that the measurement method is accurate enough for this study.

Fig. 14.

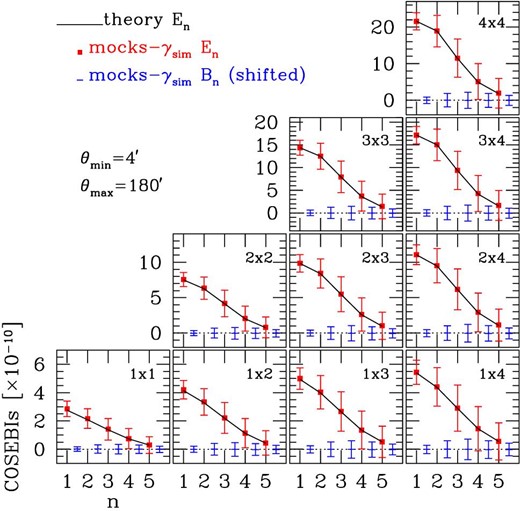
E/B-mode COSEBIs of the same redshift bin combinations as the HSC-Y1 measurements (shown in figure 2) measured from HSC-Y1 mock catalogs are compared with the theoretical predictions. In these mock measurements, the cosmic shear signals without shape-noise components are used. Means and root-mean-squares (RMSs) of COSEBI signals computed from 2268 HSC-Y1 mock catalogs are shown by red filled squares and blue bars for the E- and B-modes, respectively. B-mode signals are shifted to the right by 0.5 for clarity. The black lines show the theoretical predictions of E-mode COSEBIs based on the WMAP9 cosmological model (Hinshaw et al. 2013), which is adopted in the ray-tracing simulation (Takahashi et al. 2017).

Open in new tab Download slide

Appendix 2 Estimations of COSEBI signals from possible systematics

A.2.1 COSEBIs from shapes of PSFs and residuals

Here we describe our scheme to estimate COSEBI signals arising from residuals in the correction for the point spread function (PSF) anisotropy in galaxy shapes (see Mandelbaum 2018, for a review) and present the result. In fact, systematic tests of the HSC-Y1 shape catalog showed small residual correlations between galaxy shears and PSF shapes (Mandelbaum et al. 2018b; Oguri et al. 2018), which may bias the cosmic shear COSEBIs and our cosmological analysis.

We first estimate TPCFs arising from PSF residuals following the scheme adopted in H20, which is based on the simple model used by H19 (see also Troxel et al. 2018). The model assumes that PSF residuals are added to the shear linearly,

$$\begin{equation} \gamma ^{\mathrm{sys}} =\alpha _{{\rm psf}} \gamma ^p + \beta _{{\rm psf}} \gamma ^q, \end{equation} $$

(A1)

where γ^P is the shear⁴of the shape of the model PSF, and γ^q is the difference in shears between the PSF model and the true PSF, as estimated from the shapes of individual stars, γ^*, i.e., γ^q = γ^p − γ^*. The first and second terms of the right-hand side of equation (A1) represent the residual PSF effects from the deconvolution error and the imperfect PSF model, respectively. With these terms added to the measured shear |$\hat{\gamma }$|⁠, the contributions from these terms to the observed TPCFs are written as

$$\begin{equation} \xi _{{\rm psf},\pm }(\theta ) = \alpha _{{\rm psf}}^2 \xi _\pm ^{pp}(\theta ) +2 \alpha _{{\rm psf}}\beta _{{\rm psf}} \xi _\pm ^{pq}(\theta ) +\beta _{{\rm psf}}^2 \xi _\pm ^{qq}(\theta ), \end{equation} $$

(A2)

where |$\xi _\pm ^{pp}$| and |$\xi _\pm ^{qq}$| represent the auto-TPCFs of γ^p and γ^q, respectively, and |$\xi _\pm ^{pq}$| are the cross-TPCFs of γ^p and γ^q. Those TPCFs measured from HSC-Y1 data are presented in figures 20 and 23 of H20 for ξ₊ and ξ₋, respectively. The model parameters, α_psf and β_psf, can be estimated by the cross-correlation functions between γ^p,q and galaxy shears, |$\xi ^{gp,gq}=\langle \hat{\gamma } \gamma ^{p,q} \rangle$|⁠, which are related to |$\xi _\pm ^{pp,pq,qq}$| as

$$\begin{eqnarray} \xi _{\pm }^{gp}&=&\alpha _{{\rm psf}}\xi _\pm ^{pp}+\beta _{{\rm psf}}\xi _\pm ^{pq}, \end{eqnarray} $$

(A3)

$$\begin{eqnarray} \xi _{\pm }^{gq}&=&\alpha _{{\rm psf}}\xi _\pm ^{pq}+\beta _{{\rm psf}}\xi _\pm ^{qq}. \end{eqnarray} $$

(A4)

In measuring these quantities, we use the combined galaxy catalog of the four tomographic redshift bins, because the measurement of |$\xi _-^{gp,gq}$| is very noisy, as shown in figure 19 of H20. As a consequence, we do not take into account the possible redshift dependence of α_psf and β_psf. For the ξ₊ component, the derived α_psf and β_psf with equations (A3) and (A4) are shown in figure 21 of H20, and their means and standard deviations were found to be α_psf = 0.029 ± 0.010 and β_psf = −1.42 ± 1.11 (H20). For the ξ₋ component, due to the very poor signal-to-noise ratios of the TPCFs (see figures 19 and 23 of H20), useful estimated values of α_psf and β_psf could not be derived (see appendix 2 of H20), and thus in the following analysis we adopt the values obtained from the ξ₊ component for the ξ₋ component. In figure 15, ξ_{psf, ±} defined in equation (A2) with α_psf = 0.029 ± 0.010 and β_psf = −1.42 ± 1.11 are shown, where error bars are computed from those of α_psf and β_psf. We derived the fitting functions of those estimates over the θ-range of our interest as (plotted as solid curves in figure 15)

$$\begin{eqnarray} \xi _{{\rm psf},+}^{\rm fit}(\theta ) &=& 6\times 10^{-6} \left({\theta \over {1^{\prime }}}\right)^{-1} + 4\times 10^{-7}, \end{eqnarray} $$

(A5)

$$\begin{eqnarray} \xi _{{\rm psf},-}^{\rm fit}(\theta ) &=& -5\times 10^{-7} \left({\theta \over {1^{\prime }}}\right)^{-1} + 3\times 10^{-8} \left({\theta \over {100^{\prime }}}\right)^2. \end{eqnarray} $$

(A6)

Using the above fitting functions, we derived E-mode COSEBIs expected from PSF residuals using equation (2) with the same scale-cut (4^′ < θ < 180^′) as adopted in our cosmological analysis. The result is shown in figure 16 as filled squares. Although the derived E-mode COSEBI should be considered as a rough estimate because it is based on a simple linear model, equations (A1) and (A2) with α_psf and β_psf being not well determined, we may expect that it captures its characteristic shape. Therefore, in our cosmological analysis, we take this result as a reference model, |$E_n^{\rm psf-ref}$|⁠, and introduce an amplitude parameter as

$$\begin{equation} E_n^{\rm psf} = A_{\rm psf} E_n^{\rm psf-ref}. \end{equation} $$

(A7)

We add this term to the theoretical prediction for the E-mode COSEBIs. We treat A_psf as a nuisance parameter (see sub-subsection 5.1.3).

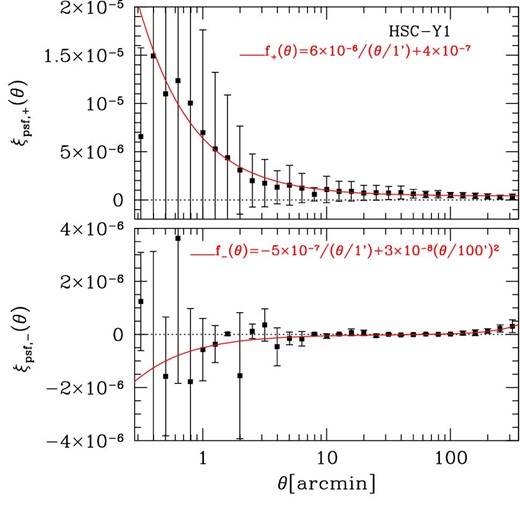
$Symbols with error bars show ξpsf, ± defined in equation (A2) with measured $\xi _\pm ^{pp}$, $\xi _\pm ^{pq}$, and $\xi _\pm ^{qq}$ from the HSC-Y1 data set (see appendix 2 of H20). Here αpsf = 0.029 ± 0.010 and βpsf = −1.42 ± 1.11 are adopted. The errors shown are computed from those of αpsf and βpsf. The solid curve show the fitting functions (see text for details).$

Fig. 15.

Symbols with error bars show ξ_{psf, ±} defined in equation (A2) with measured |$\xi _\pm ^{pp}$|⁠, |$\xi _\pm ^{pq}$|⁠, and |$\xi _\pm ^{qq}$| from the HSC-Y1 data set (see appendix 2 of H20). Here α_psf = 0.029 ± 0.010 and β_psf = −1.42 ± 1.11 are adopted. The errors shown are computed from those of α_psf and β_psf. The solid curve show the fitting functions (see text for details).

Open in new tab Download slide

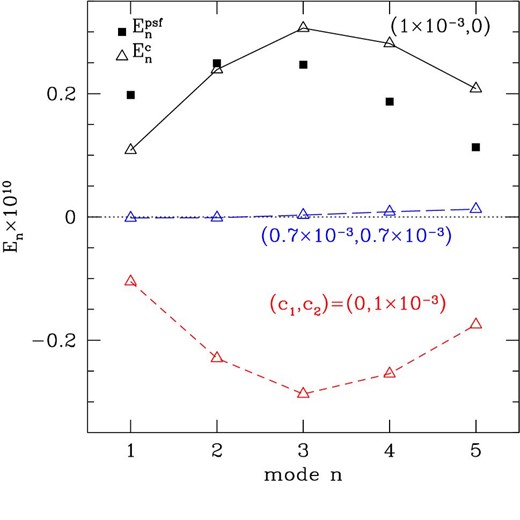
$Filled squares show E-mode COSEBI signals expected from PSF residuals in the HSC-Y1 shape catalog (see appendix 2.1 for details). Crosses show E-mode COSEBI signals arising from a constant shear of |c| = 10−3 on positions of galaxies used in this study (see appendix 2.2 for details). Results for three cases are plotted: (c1, c2) = (10−3, 0), (0, 10−3), and $(1/\sqrt{2}\times 10^{-3},1/\sqrt{2}\times 10^{-3})$ for the solid, dashed, and long-dashed lines, respectively. Here the results of tomographic redshift bins of z3 × z3 are shown, but the results are insensitive to the choice of bins.$

Fig. 16.

Filled squares show E-mode COSEBI signals expected from PSF residuals in the HSC-Y1 shape catalog (see appendix 2.1 for details). Crosses show E-mode COSEBI signals arising from a constant shear of |c| = 10⁻³ on positions of galaxies used in this study (see appendix 2.2 for details). Results for three cases are plotted: (c₁, c₂) = (10⁻³, 0), (0, 10⁻³), and |$(1/\sqrt{2}\times 10^{-3},1/\sqrt{2}\times 10^{-3})$| for the solid, dashed, and long-dashed lines, respectively. Here the results of tomographic redshift bins of z₃ × z₃ are shown, but the results are insensitive to the choice of bins.

Open in new tab Download slide

A.2.2 COSEBIs from the constant shear over a field

The value of the shear averaged over a field is not expected to be zero due to the presence of the cosmic shear signal on scales larger than a field. However, it could also be non-zero due to residual systematics in the shear estimation and/or data reduction process. The latter, if present, may bias the cosmological inference. Mandelbaum et al. (2018b) examined the mean shear of the HSC-Y1 shape catalog, and found no evidence of a mean shear above that expected from large-scale cosmic shear. H20 reexamined it for each tomographic galaxy sample and for each field, and found that the measured mean shears are consistent with that expected from large-scale cosmic shear (see appendix 1 of H20). Although, as mentioned above, no clear evidence of an excess mean shear was found, we check the impact of a constant shear over a field on our cosmological analysis by modeling it as a redshift-independent constant shear for simplicity, which we describe below.

COSEBI signals arising from a constant shear were studied in detail in appendix D of Asgari et al. (2021), which we follow here. We denote two components of a constant shear in Cartesian coordinates as (c₁, c₂). A constant shear generates a separation-independent constant ξ₊ term (to be specific, |$\xi _+^c=c_1^2+c_2^2$|⁠), and a separation-dependent |$\xi _-^c$| term, whose shape is determined by a field geometry and masks; see equation (D.3) of Asgari et al. (2021). In the transformation from TPCFs to COSEBIs, equation (2), the constant |$\xi _+^c$| term is filtered out, only the |$\xi _-^c$| term remains, and the E-mode COSEBI is given by equation (D.6) of Asgari et al. (2021),

$$\begin{eqnarray} E_n^c &=& {1\over 2}\left(c_1^2 - c_2^2\right) \int _{\theta _{\rm min}}^{\theta _{\rm max}} d\theta \theta T_{-n} \langle \cos (4\phi )\rangle (\theta )\nonumber \\ {}&& + c_1 c_2 \int _{\theta _{\rm min}}^{\theta _{\rm max}} d\theta \theta T_{-n} \langle \sin (4\phi )\rangle (\theta ), \end{eqnarray} $$

(A8)

where φ is the polar angle of the vector connecting two galaxies in Cartesian coordinates, and 〈⋅⋅⋅〉(θ) denotes the average taken over all pairs of galaxies with a separation θ.

We estimate actual |$E_n^c$| signals for the HSC-Y1 shear catalog with |c| = 10⁻³ (which is a typical value for the HSC-Y1 shear catalog; see figure 18 of H20) by artificially assigning a constant shear of (c₁, c₂) (but in the sky coordinates; see the discussion below on this point) to all the galaxies, and doing the same COSEBI measurement procedure as done for the real data. The results are shown in figure 16 for three cases; (c₁, c₂) = (10⁻³, 0), (0, 10⁻³), and |$(1/\sqrt{2}\times 10^{-3},1/\sqrt{2}\times 10^{-3})$| for the solid, dashed, and long-dashed line, respectively. In the plot, the results for tomographic redshift bins of z₃ × z₃ are shown, but are insensitive to a choice of bins. It is found from these results that the first term of equation (A8) is much larger than the second term except for cases of |c₁| ≃ |c₂|, though |$E_n^c$| itself is very small in such cases. Note that, from equation (A8), one may expect that |$|E_n^c|$| for cases of (c₁, c₂) = (10⁻³, 0) and (0, 10⁻³) should be equal, but not exactly in those actual measurements as can be seen in figure 16. The reason for this is our use of the sky coordinates, instead of Cartesian coordinates, in assigning a constant shear; we simply replace the shears of the HSC shape catalog that are defined in the sky coordinates with a constant shear (c₁, c₂). In this case, equation (A8) does not hold, but is still useful to understand a basic behavior of |$E_n^c$| as each of the six HSC-Y1 fields is not very wide, and five out of the six fields have a strip-shaped geometry on the equator (see figure 1 of Mandelbaum et al. 2018b).

Our modeling of E-mode COSEBIs arising from the constant shear, which we use to check the impact of a constant shear on our cosmological analysis, is as follows: We consider a redshift-independent constant shear for simplicity (see appendix 1 of H20 for a discussion on this point). From the above analysis, we find that the first term of equation (A8) dominates the |$E_n^c$| signals, and thus it may be reasonable to adopt the measured |$E_n^c$| for the case of (c₁, c₂) = (10⁻³, 0) as a reference for modeling. We denote this as |$E_n^{c-\rm ref}$| and introduce an amplitude parameter as

$$\begin{equation} E_n^{\langle \gamma \rangle } = A_{\langle \gamma \rangle } E_n^{c-\rm ref}. \end{equation} $$

(A9)

We add this term to the theoretical prediction for the E-mode COSEBIs. We treat A_〈γ〉 as a nuisance parameter (see sub-subsection 5.1.3).

Appendix 3 Supplementary figures

In this appendix, we present supplementary figures for systematics tests (subsection 6.2), internal consistency checks (subsection 6.3), and comparison of our cosmological constraints with ones from other projects (subsection 6.5). Although in those sections we use S₈ = σ₈(Ω_m/0.3)^α with α = 0.5 for a primary parameter to be constrained by cosmic shear two-point statistics, a single choice of α does not always provide an optimal description for the σ₈–Ω_m degeneracy, especially for cases with broad confidence contours such as ours. Therefore, in this appendix, we present marginalized posterior contours in the Ω_m–σ₈ plane.

In figure 17, we compare constraints from our fiducial setup with different setups for systematics tests (see subsection 6.2 for details). Figure 18 shows the same comparison but between the cosmology alone setup and different setups for internal consistency checks (see subsection 6.3).

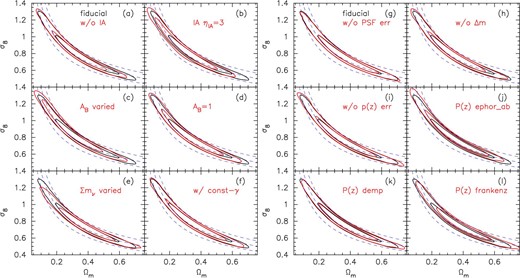
Comparison of constraints in the Ωm–σ8 plane between the fiducial setup (black contours) and different assumptions, as described in the text (red contours showing 68% and 95% credible levels). Dashed blue curves show constant S8 loci (S8 = 0.7, 0.8, and 0.9 from bottom to top, respectively).

Fig. 17.

Comparison of constraints in the Ω_m–σ₈ plane between the fiducial setup (black contours) and different assumptions, as described in the text (red contours showing 68% and 95% credible levels). Dashed blue curves show constant S₈ loci (S₈ = 0.7, 0.8, and 0.9 from bottom to top, respectively).

Open in new tab Download slide

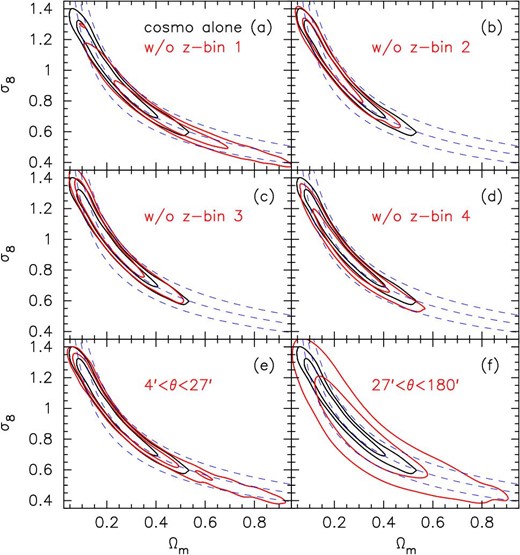
Comparison of constraints in the Ωm–σ8 plane from the cosmology alone setup (black contours) with different setups for internal consistency checks (red contours showing 68% and 95% credible levels). Dashed blue curves show constant S8 loci (S8 = 0.7, 0.8, and 0.9 from bottom to top, respectively).

Fig. 18.

Comparison of constraints in the Ω_m–σ₈ plane from the cosmology alone setup (black contours) with different setups for internal consistency checks (red contours showing 68% and 95% credible levels). Dashed blue curves show constant S₈ loci (S₈ = 0.7, 0.8, and 0.9 from bottom to top, respectively).

Open in new tab Download slide

In figure 19, we compare constraints from our fiducial ΛCDM model with other results in the literature (see subsection 6.5), where constraints from other studies are derived from publicly available chains. Note that although different studies adopt different priors, we do not adjust them to our fiducial setup, but rather use their original priors. Therefore, some of the difference in the posteriors may be due to the different choices of priors and modeling.

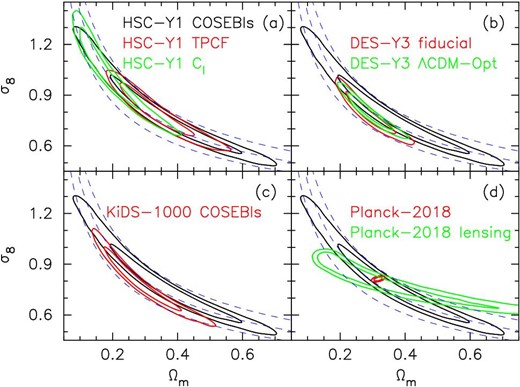
Marginalized posterior contours (68% and 95% credible levels) in the Ωm–σ8 plane. Our result from the fiducial ΛCDM model (black contours) is compared with results in the literature (red or green contours). (a) HSC-Y1 cosmic shear TPCF (red lines, H20) and PS results (green lines, H19). (b) Dark Energy Survey Year 1 (DES-Y1) cosmic shear TPCF result (Troxel et al. 2018). Note that, in subsection 6.5, we take the S8 constraint from the DES-Y3 result (Amon et al. 2022), but its chain is not yet available. (c) KiDS-1000 cosmic shear COSEBI result (Asgari et al. 2021). (d) Planck 2018 CMB result without CMB lensing (Planck Collaboration 2020a, TT+TE+EE+lowE, red lines), and Planck 2018 lensing result (Planck Collaboration 2020b, green lines). Dashed blue curves show constant S8 loci (S8 = 0.7, 0.8, and 0.9 from bottom to top, respectively).

Fig. 19.

Marginalized posterior contours (68% and 95% credible levels) in the Ω_m–σ₈ plane. Our result from the fiducial ΛCDM model (black contours) is compared with results in the literature (red or green contours). (a) HSC-Y1 cosmic shear TPCF (red lines, H20) and PS results (green lines, H19). (b) Dark Energy Survey Year 1 (DES-Y1) cosmic shear TPCF result (Troxel et al. 2018). Note that, in subsection 6.5, we take the S₈ constraint from the DES-Y3 result (Amon et al. 2022), but its chain is not yet available. (c) KiDS-1000 cosmic shear COSEBI result (Asgari et al. 2021). (d) Planck 2018 CMB result without CMB lensing (Planck Collaboration 2020a, TT+TE+EE+lowE, red lines), and Planck 2018 lensing result (Planck Collaboration 2020b, green lines). Dashed blue curves show constant S₈ loci (S₈ = 0.7, 0.8, and 0.9 from bottom to top, respectively).

Open in new tab Download slide

There is one thing to note about figure 19d; we compare our result with the Planck 2018 lensing result (Planck Collaboration 2020b), which is not discussed in the main text because it does not provide a useful constraint on S₈ = σ₈(Ω_m/0.3)^0.5 but provides a tight constraint on |$\sigma _8\Omega _{\rm m}^{0.25}$| due to a different degeneracy direction in the Ω_m–σ₈ plane, as can be seen from panel (d). The cosmic microwave background (CMB) lensing is a unique probe of the distribution of mass in the Universe at intermediate redshifts (typically z ∼ 2) and is thus complementary to cosmic shear statistics, as demonstrated by the Planck Collaboration (2020b). Such complementarity can also be seen in panel (d), although a combined cosmological inference with the Planck results is beyond the scope of this study.

Footnotes

1

〈http://www.cosmostat.org/software/athena〉.

2

Although the total number of model parameters is 13 for our fiducial case, only three of them (Ω_c, σ₈, and A_IA) are constrained by the data with much narrower posterior distributions than with priors. Therefore, the standard definition of the degree of freedom (N_d − N_p = 50 − 13 for our fiducial case) would most likely be underestimated. A conservative choice of the effective number of free parameters should account for only these three parameters. See Raveri and Hu (2019) and subsection 6.1 of H19 for a more mathematically robust way to define the effective number of free parameters.

3

In estimating the statistical significance of the difference between two measurements of S₈, we adopt a conventional method, |$\delta = (\bar{A}-\bar{B})/\sqrt{\sigma _A^2+\sigma _B^2})$|⁠.

4

“Shears” of stars and PSFs are converted from the measured distortion using the relation between them for intrinsically round objects (γ = e/2). See Mandelbaum et al. (2018b) for the definition of distortion of star images.

References

Aihara

H.

et al.

2018a

,

PASJ

,

70

,

S4

Aihara

H.

et al.

2018b

,

PASJ

,

70

,

S8

Amon

A.

et al.

2022

,

Phys. Rev. D

,

105

,

023514

Crossref

Search ADS

Anderson

T. W.

2003

,

An Introduction to Multivariate Statistical Analysis

, 3rd ed. (

New York

:

Wiley-Interscience

)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Asgari

M.

et al.

2020

,

A&A

,

634

,

A127

Crossref

Search ADS

Asgari

M.

et al.

2021

,

A&A

,

645

,

A104

Crossref

Search ADS

Asgari

M.

,

Heymans

C.

,

Blake

C.

,

Harnois-Deraps

J.

,

Schneider

P.

,

Van Waerbeke

L.

2017

,

MNRAS

,

464

,

1676

Crossref

Search ADS

Asgari

M.

,

Schneider

P.

,

Simon

P.

2012

,

A&A

,

542

,

A122

Crossref

Search ADS

Barreira

A.

,

Krause

E.

,

Schmidt

F.

2018

,

J. Cosmology Astroparticle Phys.

,

1810

,

053

Bird

S.

,

Viel

M.

,

Haehnelt

M. G.

2012

,

MNRAS

,

420

,

2551

Crossref

Search ADS

Bridle

S.

,

King

L.

2007

,

New J. Phys.

,

9

,

444

Crossref

Search ADS

Camacho

H.

et al.

2021

,

arXiv:2111.07203

Challinor

A.

,

Lewis

A.

2011

,

Phys. Rev. D

,

84

,

043516

Crossref

Search ADS

Chisari

N. E.

et al.

2018

,

MNRAS

,

480

,

3962

Crossref

Search ADS

Dark Energy Survey Collaboration

,

2016

,

MNRAS

,

460

,

1270

Crossref

Search ADS

de Jong

J. T. A.

,

Verdoes Kleijn

G. A.

,

Kuijken

K. H.

,

Valentijn

E. A.

2013

,

Exp. Astron.

,

35

,

25

Crossref

Search ADS

Feroz

F.

,

Hobson

M. P.

2008

,

MNRAS

,

384

,

449

Crossref

Search ADS

Feroz

F.

,

Hobson

M. P.

,

Bridges

M.

2009

,

MNRAS

,

398

,

1601

Crossref

Search ADS

Feroz

F.

,

Hobson

M. P.

,

Cameron

E.

,

Pettitt

A. N.

2019

,

Open J. Astrophys.

,

2

,

10

Crossref

Search ADS

Hamana

T.

et al.

2020

,

PASJ

,

72

,

16

(H20)

Crossref

Search ADS

Harnois-Déraps

J.

,

van Waerbeke

L.

,

Viola

M.

,

Heymans

C.

2015

,

MNRAS

,

450

,

1212

Crossref

Search ADS

Hartlap

J.

,

Simon

P.

,

Schneider

P.

2007

,

A&A

,

464

,

399

Crossref

Search ADS

Hellwing

W. A.

,

Schaller

M.

,

Frenk

C. S.

,

Theuns

T.

,

Schaye

J.

,

Bower

R. G.

,

Crain

R. A.

2016

,

MNRAS

,

461

,

L11

Crossref

Search ADS

Hikage

C.

et al.

2019

,

PASJ

,

71

,

43

(H19)

Crossref

Search ADS

Hildebrandt

H.

et al.

2017

,

MNRAS

,

465

,

1454

Crossref

Search ADS

Hildebrandt

H.

et al.

2020

,

A&A

,

633

,

A69

Crossref

Search ADS

Hinshaw

G.

et al.

2013

,

ApJS

,

208

,

19

Crossref

Search ADS

Hirata

C.

,

Seljak

U.

2003

,

MNRAS

,

343

,

459

Crossref

Search ADS

Hirata

C. M.

,

Seljak

U.

2004

,

Phys. Rev. D

,

70

,

063526

Crossref

Search ADS

Ilbert

O.

et al.

2009

,

ApJ

,

690

,

1236

Crossref

Search ADS

Joachimi

B.

,

Mandelbaum

R.

,

Abdalla

F. B.

,

Bridle

S. L.

2011

,

A&A

,

527

,

A26

Crossref

Search ADS

Kilbinger

M.

2015

,

Rep. Progress Phys.

,

78

,

086901

Crossref

Search ADS

Kirk

D.

et al.

2015

,

Space Sci. Rev.

,

193

,

139

Crossref

Search ADS

Köhlinger

F.

et al.

2017

,

MNRAS

,

471

,

4412

Crossref

Search ADS

Laigle

C.

et al.

2016

,

ApJS

,

224

,

24

Crossref

Search ADS

Lesgourgues

J.

,

Mangano

G.

,

Miele

G.

,

Pastor

S.

2013

,

Neutrino Cosmology

(

Cambridge

:

Cambridge University Press

)

Mandelbaum

R.

2018

,

ARA&A

,

56

,

393

Crossref

Search ADS

Mandelbaum

R.

et al.

2018a

,

MNRAS

,

481

,

3170

Crossref

Search ADS

Mandelbaum

R.

et al.

2018b

,

PASJ

,

70

,

S25

Crossref

Search ADS

McCarthy

I. G.

,

Schaye

J.

,

Bird

S.

,

Le Brun

A. M. C.

2017

,

MNRAS

,

465

,

2936

Crossref

Search ADS

Mead

A. J.

,

Peacock

J. A.

,

Heymans

C.

,

Joudaki

S.

,

Heavens

A. F.

2015

,

MNRAS

,

454

,

1958

Crossref

Search ADS

Oguri

M.

et al.

2018

,

PASJ

,

70

,

S26

Planck Collaboration

2020a

,

A&A

,

641

,

A6

Crossref

Search ADS

Planck Collaboration

2020b

,

A&A

,

641

,

A8

Crossref

Search ADS

Raveri

M.

,

Hu

W.

2019

,

Phys. Rev. D

,

99

,

043506

Crossref

Search ADS

Schaye

J.

et al.

2010

,

MNRAS

,

402

,

1536

Crossref

Search ADS

Schneider

P.

,

van Waerbeke

L.

,

Kilbinger

M.

,

Mellier

Y.

2002

,

A&A

,

396

,

1

Crossref

Search ADS

Schneider

P.

,

Eifler

T.

,

Krause

E.

2010

,

A&A

,

520

,

A116

Crossref

Search ADS

Shirasaki

M.

,

Hamana

T.

,

Takada

M.

,

Takahashi

R.

,

Miyatake

H.

2019

,

MNRAS

,

486

,

52

Crossref

Search ADS

Smith

R. E.

et al.

2003

,

MNRAS

,

341

,

1311

Crossref

Search ADS

Springel

V.

et al.

2018

,

MNRAS

,

475

,

676

Crossref

Search ADS

Takahashi

R.

,

Sato

M.

,

Nishimichi

T.

,

Taruya

A.

,

Oguri

M.

2012

,

ApJ

,

761

,

152

Crossref

Search ADS

Takahashi

R.

,

Hamana

T.

,

Shirasaki

M.

,

Namikawa

T.

,

Nishimichi

T.

,

Osato

K.

,

Shiroyama

K.

2017

,

ApJ

,

850

,

24

Crossref

Search ADS

Tanaka

M.

et al.

2018

,

PASJ

,

70

,

S9

Crossref

Search ADS

Troxel

M. A.

,

Ishak

M.

2015

,

Phys. Rep.

,

558

,

1

Crossref

Search ADS

Troxel

M. A.

et al.

2018

,

Phys. Rev. D

,

98

,

043528

Crossref

Search ADS

van Daalen

M. P.

,

Schaye

J.

,

Booth

C. M.

,

Dalla Vecchia

C.

2011

,

MNRAS

,

415

,

3649

Crossref

Search ADS

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
June 2022	6
July 2022	19
August 2022	19
September 2022	8
October 2022	7
November 2022	6
December 2022	3
January 2023	2
February 2023	12
March 2023	6
April 2023	4
May 2023	3
June 2023	4
July 2023	6
August 2023	8
September 2023	11
October 2023	8
November 2023	5
December 2023	16
January 2024	12
February 2024	7
March 2024	1
April 2024	2
May 2024	2
June 2024	1
July 2024	2
August 2024	14
September 2024	24
October 2024	15
November 2024	10
December 2024	2
January 2025	3
February 2025	2
March 2025	8
April 2025	8
May 2025	2

Article Contents

E/B mode decomposition of HSC-Y1 cosmic shear using COSEBIs: Cosmological constraints and comparison with other two-point statistics Free

Abstract

1 Introduction

2 HSC-Y1 data set

3 Theoretical models

3.1 COSEBIs

3.2 Cosmic shear power spectra

3.3 Scale-cut

4 Measurements

4.1 Measurements of COSEBIs from the HSC-Y1 data

4.2 Covariance from HSC-Y1 mock catalogs

4.3 B-mode null test

5 Cosmological analyses

5.1 Model parameters

5.1.1 Cosmological parameters

5.1.2 Astrophysical parameters

5.1.3 Systematic parameters

6 Results

6.1 Cosmological constraints in the fiducial flat ΛCDM model

6.2 Systematics tests

6.2.1 Intrinsic galaxy alignment

6.2.2 Baryonic feedback

6.2.3 Neutrino mass

6.2.4 Residual constant shear

6.2.5 PSF leakage and PSF modeling errors

6.2.6 Shear calibration error

6.2.7 Source redshift distribution errors

6.3 Internal consistency

6.3.1 Tomographic redshift bins

6.3.2 Different scale-cuts

6.4 wCDM model

6.5 Comparison to other constraints from the literature

6.6 Comparison with HSC-Y1 cosmic shear PS and TPCF results

7 Summary and conclusions

Acknowledgements

Appendix 1 Test of the measurement method of COSEBIs using mock catalogs

Appendix 2 Estimations of COSEBI signals from possible systematics

A.2.1 COSEBIs from shapes of PSFs and residuals

A.2.2 COSEBIs from the constant shear over a field

Appendix 3 Supplementary figures

Footnotes

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

E/B mode decomposition of HSC-Y1 cosmic shear using COSEBIs: Cosmological constraints and comparison with other two-point statistics