-
PDF
- Split View
-
Views
-
Cite
Cite
Shinichi W Kinoshita, Fumitaka Nakamura, Quang Nguyen-Luong, Benjamin Wu, Tomomi Shimoikura, Koji Sugitani, Kazuhito Dobashi, Hideaki Takemura, Patricio Sanhueza, Kee-Tae Kim, Hyunwoo Kang, Neal J Evans, Glenn J White, Cassandra Fallscheer, Cloud structures in M 17 SWex : Possible cloud–cloud collision, Publications of the Astronomical Society of Japan, Volume 73, Issue Supplement_1, January 2021, Pages S300–S320, https://doi.org/10.1093/pasj/psaa053
Close - Share Icon Share
Abstract
Using wide-field 13CO (J = 1−0) data taken with the Nobeyama 45 m telescope, we investigate cloud structures of the infrared dark cloud complex in M 17 with Spectral Clustering for Interstellar Molecular Emission Segmentation. In total, we identified 118 clouds that include 11 large clouds with radii larger than 1 pc. The clouds are mainly distributed in the two representative velocity ranges of 10–20 km s−1 and 30–40 km s−1. By comparing this with the ATLASGAL catalog, we found that the majority of the 13CO clouds with 10–20 km s−1 and 30–40 km s−1 are likely located at distances of 2 kpc (Sagittarius arm) and 3 kpc (Scutum arm), respectively. Analyzing the spatial configuration of the identified clouds and their velocity structures, we attempt to reveal the origin of the cloud structure in this region. Here we discuss three possibilities: (1) overlapping with different velocities, (2) cloud oscillation, and (3) cloud–cloud collision. In the position–velocity diagrams, we found spatially extended faint emission between ∼20 km s−1 and ∼35 km s−1, which is mainly distributed in the spatially overlapped areas of the clouds. Additionally, the cloud complex system is unlikely to be gravitationally bound. We also found that in some areas where clouds with different velocities overlapped, the magnetic field orientation changes abruptly. The distribution of the diffuse emission in the position–position–velocity space and the bending magnetic fields appear to favor the cloud–cloud collision scenario compared to other scenarios. In the cloud–cloud collision scenario, we propose that two ∼35 km s−1 foreground clouds are colliding with clouds at ∼20 km s−1 with a relative velocity of 15 km s−1. These clouds may be substructures of two larger clouds having velocities of ∼35 km s−1 (≳103 M⊙) and ∼20 km s−1 (≳104 M⊙), respectively.
1 Introduction
The high-mass stellar population dominates the energy budget of all forming stars; thus, they significantly influence the evolution of the Galaxy (Beuther et al. 2007; Zinnecker & Yorke 2007; Motte et al. 2018). Therefore, it is crucial to understand how high-mass stars form. However, the formation process of high-mass stars is still under debate (Bonnell et al. 1998, 2001; McKee & Tan 2003). Recent observations have suggested that very massive and dense clumps in large clouds or infrared dark clouds (IRDCs) are promising sites of ongoing or future high-mass star formation (Rathborne et al. 2006; Sakai et al. 2010; Sanhueza et al. 2012, 2017, 2019; Shimoikura et al. 2013; Contreras et al. 2018). Some theoretical and observational studies have proposed that collisions of clouds may trigger the formation of such massive and dense clumps and thus possibly trigger high-mass star formation (Scoville et al. 1986; Tan 2000; Fukui et al. 2014; Wu et al. 2017; Kohno et al. 2018; Dobashi et al. 2019; Montillaud et al. 2019). In this paper, we present recent observations of the M 17 region, focusing on the kinematics of the IRDC and potential scenarios that could explain them. We note that Nishimura et al. (2018) mentioned the possibility of a cloud–cloud collision around the M 17 H ii region, which is located next to the M 17 IRDC region, including other possibilities.
Povich and Whitney (2010) assumed that M 17 SWex is located in the Sagittarius arm at a distance of ∼2.0 kpc which is measured toward the M 17 H ii region based on the parallax observations by Xu et al. (2011), because the local standard of rest (LSR) velocity of M 17 SWex and the H ii region are almost the same (VLSR ≃ 20 km s−1). On the other hand, on the basis of the very long baseline interferometry (VLBI) observations toward a G14.33–0.64 core, located in the M 17 SWex region, Sato et al. (2010) derived a closer distance of 1.1 kpc ± 0.1 kpc. They argued that the core belongs to the Sagittarius arm, which is closer in the direction of M 17 SWex. In contrast, Povich et al. (2016)
interpreted that this core might be a foreground object and the main structure of M 17 SWex may be located at 2 kpc. Recently we analyzed the cloud structures in this area using the wide-field 12CO, 13CO, and C18O observations (Shimoikura et al. 2019; Nguyen-Luong et al. 2020), and found that the molecular gas in the M 17 and M 17 SWex regions is continuous in the position–position–velocity space, which is consistent with the argument of Povich et al. (2016). Thus, in this paper, we adopt a distance to M 17 SWex of 2 kpc.
The M 17 cluster has very high star density of >103 stars pc−2, which is 10–100 times higher than that of the Orion Nebula Cluster, the nearest high-mass star-forming region (Lada et al. 1991; Ando et al. 2002). Previous molecular line observations have revealed that the H ii region is surrounded by large molecular clouds which are also sites of active ongoing high-mass star formation (hereafter the M 17 H ii region). Elmegreen, Lada, and Dickinson (1979) discovered a significant amount of gas extending to the southwest from the M 17 H ii region, and Spitzer observations reveal that this cloud is dark in the mid-infrared. The dark infrared feature suggests that high-mass star formation is at a very early stage of evolution without significantly disrupting the cloud (hereafter M 17 SWex).
Recently, Povich and Whitney (2010) and Povich et al. (2016) found a very interesting characteristic of the protostellar populations in the M 17 region. From Spitzer observations, they discovered that the mass function of protostars around the M 17 H ii region seems consistent with the Salpeter initial mass function (IMF), whereas that in M 17 SWex is significantly steeper than the Salpeter IMF. In other words, the high-mass stellar population in M 17 SWex is significantly deficient compared to what the Salpeter IMF expects. It remains uncertain whether the future stellar mass function in the IRDC region will evolve into a Salpeter-like IMF, or if the high-mass stellar population will stay deficient. In either case, the M 17 region is a feature-rich region that may shed light on what triggers or initiates high-mass star formation processes [see also Ohashi et al. (2016) and Chen et al. (2019) for recent ALMA observations in M 17 SWex].
Recently, from wide field 12CO (J = 1−0), 13CO (J = 1−0), HCO+ (J = 1−0), and HCN+ (J = 1−0) observations, Nguyen-Luong et al. (2020) investigated the cloud structure in the M 17 region and found significant differences in dense gas distribution. In the M 17 H ii region, about |$27 \%$| of the molecular gas mass is concentrated in compact regions whose column densities are higher than 1023 cm−2, or ∼1 g cm−2, a theoretical threshold suggested for high-mass star formation proposed by Krumholz and McKee (2008). In contrast, in M 17 SWex, the column densities are significantly lower than the threshold for high-mass star formation. Only |$0.46\%$| of gas is denser than 1023 cm−3. In addition, the clumps in the M 17 H ii region are more massive than those in M 17 SWex, but have similar sizes and therefore higher densities. Thus, Nguyen-Luong et al. (2020) concluded that the deficiency in the high-mass stellar population in M 17 SWex presumably comes from the extremely low dense gas fraction. A similar trend is observed in other nearby star-forming regions such as Orion A and Aquila Rift (Nakamura et al. 2019). The IRDC also contains prominent filamentary structures, some of which appear to be parallel to one another (Busquet et al. 2013, 2016).
Sugitani et al. (2019) performed wide-field near-infrared (near-IR) polarization observations toward the M 17 SWex region and found that the magnetic field is globally well-ordered and perpendicular to the filamentary structures and the galactic plane. From the 12CO (J = 3–2) data, Sugitani et al. (2019) also found two cloud components with different line-of-sight velocities: one at ∼20 km s−1, and the other at ∼35 km s−1. Regarding the cloud morphology, they suggested that a cloud–cloud collision might have happened along the direction of the ordered magnetic field. The cloud–cloud collision is expected to promote the creation of high-density clouds and clumps and thus possibly trigger high mass star formation. One difficulty of this scenario is that the velocity of ∼35 km s−1 is coincidentally close to the representative velocity of the adjacent Galactic spiral arm, the Scutum arm, at a distance of ∼3 kpc. The representative velocity of the Scutum arm is estimated to be 40 km s−1 along the line of sight (Nguyen-Luong et al. 2020). Therefore, the ∼35 km s−1 molecular gas component might simply overlap with the ∼20 km s−1 component along the line of sight. In this paper, we attempt to constrain the cloud structure in a possible future high-mass star-forming region, M 17 SWex, and analyze the possibility of the cloud–cloud collision scenario proposed by Sugitani et al. (2019).
The paper is organized as follows. In section 2, we describe the details of the observations. We present the overall gas distribution in section 3. Then, in section 4 we decompose clouds in the M 17 SWex region with 13CO (J = 1−0) using Spectral Clustering for Interstellar Molecular Emission Segmentation (SCIMES), which identifies continuous gas structures in the position–position–velocity space within dendrograms of emission using the spectral clustering paradigm (Colombo et al. 2015). In section 5, we discuss some possible scenarios which can explain observational features in M 17 SWex. Finally, we summarize the main results in section 6.
2 Observations
2.1 12CO (J = 1–0) and 13CO (J = 1–0) observations
The details of the observations are described by Shimoikura et al. (2019), Nakamura et al. (2019), and Nguyen-Luong et al. (2020). In brief, we carried out mapping observations in 12CO (J = 1−0) and 13CO (J = 1−0) toward the M 17 region using the FOREST receiver (Minamidani et al. 2016) installed on the 45 m telescope of the Nobeyama Radio Observatory. See Nakamura et al. (2019) for the actual mapping area. In this paper, we focus on the IRDC region. The observations were done in an on-the-fly (OTF) mode (Sawada et al. 2008) in the period from 2016 December to 2017 March. As the backends, we used a digital spectrometer based on an FX-type correlator, SAM45, that consists of 16 sets of 4096-channel arrays. The frequency resolution of all spectrometer arrays is set at 15.26 kHz, which corresponds to 0.05 km s−1 at 110 GHz. The temperature scale was determined by the chopper-wheel method. The telescope pointing was checked every hour by observing the SiO maser line. The pointing accuracy was better than ∼3″ throughout the entire observation. The typical system noise temperature was in the range from 150 K to 200 K in the single sideband mode. The main beam efficiency at 110 GHz was ηmb = 0.435.
In order to minimize the OTF scanning effects, the data with orthogonal scanning directions along the RA and Dec. axes were combined into a single map. We chose a spheroidal function with a width of |${7{^{\prime\prime}_{.}}5}$| as a gridding convolution function to derive the intensity at each grid point of the final cube data with a spatial grid size of |${7{^{\prime\prime}_{.}}5}$|, about a third of the beam size. The resultant effective angular resolution is about 22″ at 110 GHz, corresponding to ∼0.25 pc at a distance of 2 kpc.
In this paper, we adopt the 12CO (J = 1−0) peak temperature to derive excitation temperatures of CO molecules, and use the 13CO (J = 1−0) emission to derive the column density at each pixel. See Nguyen-Luong et al. (2020) for the CO peak intensity map of M 17. We assume a fractional abundance of 13CO relative to H2 of 2 × 10−6 (Dickman 1978), similar to that assumed in Shimoikura et al. (2019) and Nguyen-Luong et al. (2020).
2.2 12CO (J = 3–2) observations
The 12CO (J = 3–2) data were obtained with the James Clerk Maxwell Telescope (JCMT) toward a much wider area than that of the 13CO (J = 1−0) observations. The OTF mapping technique was employed. The observations were carried out from 2013 to 2015. All of the observations were carried out with the Heterodyne Array Receiver Program (HARP; Buckle et al. 2009), consisting of 16 superconductor–insulator–superconductor detectors arranged in an array of 4 × 4 beams separated by 30″. At this frequency, the angular resolution of HARP is 14″ and the main-beam efficiency is ηmb = 0.61. The Auto-Correlation Spectral Imaging System (ACSIS; Buckle et al. 2009) was used as the backend with a different frequency resolution: ∼0.0305 MHz, ∼0.061 MHz, or ∼0.488 MHz. We reduced the data with different frequency resolutions separately. Data were reduced by the standard ORAC-DR pipeline on the Starlink package which contains various software for analyzing JCMT data (Jenness et al. 2015; Berry et al. 2007; Currie et al. 2008). For more details on the data reduction, see Dempsey, Thomas, and Currie (2013) and Rigby et al. (2016). For this paper, we combined all of the three data sets and binned them to the coarsest spectral resolution of 0.488 MHz, which is that of the CO high resolution (COHR) survey. Our final data for this paper have an angular resolution of 14″, a velocity resolution of 0.4 km s−1, and are resampled on to the 7″ × 7″ grid. See Nguyen-Luong et al. (2020) for details of the observations.
3 Overall structure from 13CO (J = 1–0) emission
Figure 1 shows the 13CO (J = 1–0) velocity-integrated intensity map of M 17 SWex. The contours of the H2 column density map, which was derived by the SED fitting (Sugitani et al. 2019) of the Herschel archival data (160, 250, 350, and 500 μm) are superimposed. The column density tends to be high in the areas with strong 13CO integrated intensities. This indicates that the 13CO emission traces the high-density molecular gas in this region. The molecular gas is roughly distributed from northeast to southwest.
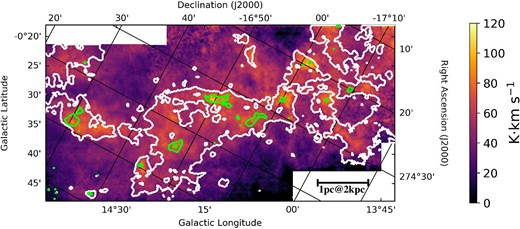
13CO(J = 1–0) intensity map of M 17 SWex, integrated over the velocity range from −10 km s−1 to 55 km s−1. Contours of the H2 column density map derived from the Herschel data are superimposed. Contours are drawn at 1.0 × 1022 cm−2 by white, and 3.0 × 1022 cm−2 by green. The label “00” on the galactic-longitude axis means |$14^{\circ}00'$|. The same applies in the following figures of this paper. (Color online)
Figure 2 shows the 13CO (J = 1–0) spectrum averaged over M 17 SWex. It has three major peaks over the velocity range from −18 km s−1 to 60 km s−1 (see also Nguyen-Luong et al. 2020). The red line shows the least-squares fit with three Gaussian components. Best-fitting Gaussian parameters of the averaged spectra are shown in table 1. These three components could correspond to the molecular gas and belong mainly to the Sagittarius, Scutum, and Norma arms, respectively (Nakamura et al. 2019). The strongest component of this region has a velocity of ∼21 km s−1, and represents the main part of M 17 SWex (Elmegreen et al. 1979; Nguyen-Luong et al. 2020). We did not fit a small spike to the velocity around 6 km s−1.
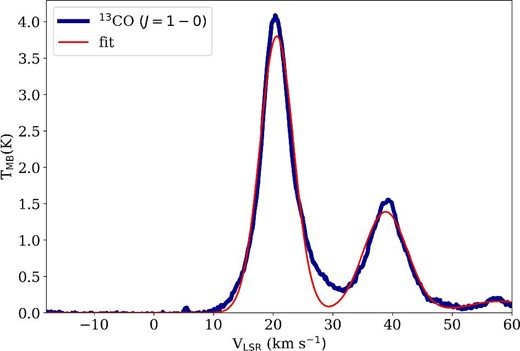
The 13CO(J = 1–0) spectra averaged over the entire M 17 SWex region (the deep blue thick line). The red line indicates the best-fitting three-Gaussian-component model, and the fitted parameters are listed in table 1. (Color online)
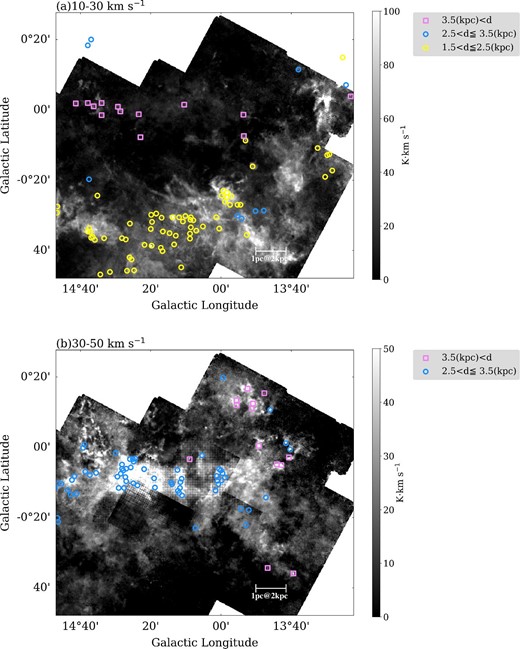
Figure 3 shows the 13CO (J = 1–0) intensity maps of M 17 SWex, integrated over the velocity ranges from 10 km s−1 to 30 km s−1, and from 30 km s−1 to 50 km s−1 (see also figure 18 in Nguyen-Luong et al. 2020). The bulk of the M 17 SWex emission is seen in the velocity range 10–30 km s−1. The emission in the velocity range 30–50 km s−1 is stronger toward the galactic plane [the upper area (around b = 0°) in each panel].
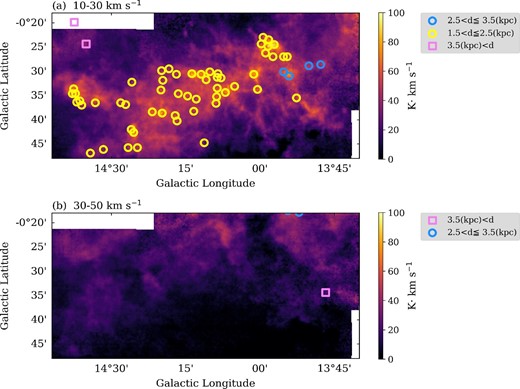
(a) 13CO(J = 1−0) intensity map integrated from 10 km s−1 to 30 km s−1. (b) Same as panel (a) but for the velocity range of 30 km s−1 < VLSR < 50 km s−1. In both panels, clumps cataloged by Urquhart et al. (2018) are presented, which have the mean velocity within the velocity range used for the integration. Shapes and colors of each mark represent the distances. (Color online)
For comparison, we also plotted clumps identified with ATLASGAL, an unbiased 870 micron submillimetre survey of the inner galactic plane which provides a large and systematic inventory of all massive (>1000 M⊙), dense clumps in the Galaxy (Schuller et al. 2009). Urquhart et al. (2018) derived the detailed properties (velocities, distances, luminosities, and masses) and spatial distribution of a complete sample of ∼ 8000 dense clumps detected with the ATLASGAL survey. The distances of the clumps are determined by using various data sets such as maser parallaxes and spectroscopic data of H i and molecular lines. The uncertainty in the distance estimation may be ∼0.3 kpc or more. Therefore, we expect that we can distinguish between the structures associated with different arms. In the following, we adopt the distances listed in Urquhart et al. (2018) (table 2, column 7) toward the clumps located in this area. The ATLASGAL clumps at ∼2 kpc are associated mainly with the cloud structure in the velocity range from 10 km s−1 to 30 km s−1. In the upper edge of figure 3b, there are two clumps at ∼3 kpc. As shown in figure 9b (appendix 1), the majority of the ATLASGAL clumps located near the Galactic plane have distances of ∼3 kpc, and are closely associated with 13CO structures within the 30–50 km s−1 velocity range toward the M 17 SWex cloud structure. Therefore, we infer that most of the 13CO emission in this velocity range is likely to originate from the Scutum arm in the background. However, as is discussed later (section 5), there may be some 30–50 km s−1 cloud structures located at the same distances as M 17 SWex (∼2 kpc).
| . | VLSR . | TMB . | σv . |
|---|---|---|---|
| . | (km s−1) . | (K) . | (km s−1) . |
| Gaussian 1 | 20.61 ± 0.02 | 3.80 ± 0.02 | 2.84 ± 0.02 |
| Gaussian 2 | 38.84 ± 0.06 | 1.39 ± 0.02 | 3.73 ± 0.07 |
| Gaussian 3 | 57.91 ± 2.15 | 0.16 ± 0.02 | 5.40 ± 1.86 |
| . | VLSR . | TMB . | σv . |
|---|---|---|---|
| . | (km s−1) . | (K) . | (km s−1) . |
| Gaussian 1 | 20.61 ± 0.02 | 3.80 ± 0.02 | 2.84 ± 0.02 |
| Gaussian 2 | 38.84 ± 0.06 | 1.39 ± 0.02 | 3.73 ± 0.07 |
| Gaussian 3 | 57.91 ± 2.15 | 0.16 ± 0.02 | 5.40 ± 1.86 |
| . | VLSR . | TMB . | σv . |
|---|---|---|---|
| . | (km s−1) . | (K) . | (km s−1) . |
| Gaussian 1 | 20.61 ± 0.02 | 3.80 ± 0.02 | 2.84 ± 0.02 |
| Gaussian 2 | 38.84 ± 0.06 | 1.39 ± 0.02 | 3.73 ± 0.07 |
| Gaussian 3 | 57.91 ± 2.15 | 0.16 ± 0.02 | 5.40 ± 1.86 |
| . | VLSR . | TMB . | σv . |
|---|---|---|---|
| . | (km s−1) . | (K) . | (km s−1) . |
| Gaussian 1 | 20.61 ± 0.02 | 3.80 ± 0.02 | 2.84 ± 0.02 |
| Gaussian 2 | 38.84 ± 0.06 | 1.39 ± 0.02 | 3.73 ± 0.07 |
| Gaussian 3 | 57.91 ± 2.15 | 0.16 ± 0.02 | 5.40 ± 1.86 |
Clouds identified with SCIMES whose radii are more than |${1{^{\prime }_{.}}7}$| (|$=\!{102{^{\prime\prime}_{.}}0}$|, 1 pc at the 2 kpc distance).
| No.* . | vcen† . | l‡ . | b§ . | R|| . | Rmajor♯ . | Rminor** . | Boundary†† . |
|---|---|---|---|---|---|---|---|
| . | (km s−1) . | (arcsec) . | (arcsec) . | (arcsec) . | |||
| 1 | 18.79 | 14°27′00″ | −0°36′36″ | 137.91 | 233.71 | 81.38 | |
| 2 | 20.50 | 13°40′12″ | −0°20′24″ | 102.48 | 138.72 | 75.71 | Y |
| 3 | 20.51 | 14°13′12″ | −0°31′12″ | 342.90 | 602.85 | 195.04 | Y |
| 4 | 20.59 | 13°40′12″ | −0°31′48″ | 130.63 | 227.00 | 75.17 | Y |
| 5 | 35.03 | 14°19′12″ | −0°30′00″ | 170.89 | 258.63 | 112.91 | |
| 6 | 36.21 | 14°38′24″ | −0°46′12″ | 188.21 | 265.48 | 133.43 | |
| 7 | 38.81 | 14°16′12″ | −0°19′12″ | 199.15 | 303.08 | 130.85 | Y |
| 8 | 39.82 | 13°55′12″ | −0°18′00″ | 239.44 | 299.28 | 191.57 | Y |
| 9 | 40.63 | 13°52′48″ | −0°36′36″ | 115.05 | 162.97 | 81.22 | |
| 10 | 41.70 | 14°33′36″ | −0°25′12″ | 158.51 | 226.20 | 111.07 | Y |
| 11 | 45.36 | 13°40′12″ | −0°37′48″ | 106.74 | 166.27 | 68.53 | Y |
| No.* . | vcen† . | l‡ . | b§ . | R|| . | Rmajor♯ . | Rminor** . | Boundary†† . |
|---|---|---|---|---|---|---|---|
| . | (km s−1) . | (arcsec) . | (arcsec) . | (arcsec) . | |||
| 1 | 18.79 | 14°27′00″ | −0°36′36″ | 137.91 | 233.71 | 81.38 | |
| 2 | 20.50 | 13°40′12″ | −0°20′24″ | 102.48 | 138.72 | 75.71 | Y |
| 3 | 20.51 | 14°13′12″ | −0°31′12″ | 342.90 | 602.85 | 195.04 | Y |
| 4 | 20.59 | 13°40′12″ | −0°31′48″ | 130.63 | 227.00 | 75.17 | Y |
| 5 | 35.03 | 14°19′12″ | −0°30′00″ | 170.89 | 258.63 | 112.91 | |
| 6 | 36.21 | 14°38′24″ | −0°46′12″ | 188.21 | 265.48 | 133.43 | |
| 7 | 38.81 | 14°16′12″ | −0°19′12″ | 199.15 | 303.08 | 130.85 | Y |
| 8 | 39.82 | 13°55′12″ | −0°18′00″ | 239.44 | 299.28 | 191.57 | Y |
| 9 | 40.63 | 13°52′48″ | −0°36′36″ | 115.05 | 162.97 | 81.22 | |
| 10 | 41.70 | 14°33′36″ | −0°25′12″ | 158.51 | 226.20 | 111.07 | Y |
| 11 | 45.36 | 13°40′12″ | −0°37′48″ | 106.74 | 166.27 | 68.53 | Y |
*ID of the identified structures.
†The mean velocity of the structures.
‡The intensity peak position of the structure in the longitude direction.
§The intensity peak position of the structure in the latitude direction.
||The size of the structure (Geometric mean of the major radius♯ and minor radius**).
♯Major radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment in the direction of the greatest elongation in the PP plane.
**Minor radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment perpendicular to the major axis in the PP plane.
††“Y” indicates clouds extending outside the mapped area.
Clouds identified with SCIMES whose radii are more than |${1{^{\prime }_{.}}7}$| (|$=\!{102{^{\prime\prime}_{.}}0}$|, 1 pc at the 2 kpc distance).
| No.* . | vcen† . | l‡ . | b§ . | R|| . | Rmajor♯ . | Rminor** . | Boundary†† . |
|---|---|---|---|---|---|---|---|
| . | (km s−1) . | (arcsec) . | (arcsec) . | (arcsec) . | |||
| 1 | 18.79 | 14°27′00″ | −0°36′36″ | 137.91 | 233.71 | 81.38 | |
| 2 | 20.50 | 13°40′12″ | −0°20′24″ | 102.48 | 138.72 | 75.71 | Y |
| 3 | 20.51 | 14°13′12″ | −0°31′12″ | 342.90 | 602.85 | 195.04 | Y |
| 4 | 20.59 | 13°40′12″ | −0°31′48″ | 130.63 | 227.00 | 75.17 | Y |
| 5 | 35.03 | 14°19′12″ | −0°30′00″ | 170.89 | 258.63 | 112.91 | |
| 6 | 36.21 | 14°38′24″ | −0°46′12″ | 188.21 | 265.48 | 133.43 | |
| 7 | 38.81 | 14°16′12″ | −0°19′12″ | 199.15 | 303.08 | 130.85 | Y |
| 8 | 39.82 | 13°55′12″ | −0°18′00″ | 239.44 | 299.28 | 191.57 | Y |
| 9 | 40.63 | 13°52′48″ | −0°36′36″ | 115.05 | 162.97 | 81.22 | |
| 10 | 41.70 | 14°33′36″ | −0°25′12″ | 158.51 | 226.20 | 111.07 | Y |
| 11 | 45.36 | 13°40′12″ | −0°37′48″ | 106.74 | 166.27 | 68.53 | Y |
| No.* . | vcen† . | l‡ . | b§ . | R|| . | Rmajor♯ . | Rminor** . | Boundary†† . |
|---|---|---|---|---|---|---|---|
| . | (km s−1) . | (arcsec) . | (arcsec) . | (arcsec) . | |||
| 1 | 18.79 | 14°27′00″ | −0°36′36″ | 137.91 | 233.71 | 81.38 | |
| 2 | 20.50 | 13°40′12″ | −0°20′24″ | 102.48 | 138.72 | 75.71 | Y |
| 3 | 20.51 | 14°13′12″ | −0°31′12″ | 342.90 | 602.85 | 195.04 | Y |
| 4 | 20.59 | 13°40′12″ | −0°31′48″ | 130.63 | 227.00 | 75.17 | Y |
| 5 | 35.03 | 14°19′12″ | −0°30′00″ | 170.89 | 258.63 | 112.91 | |
| 6 | 36.21 | 14°38′24″ | −0°46′12″ | 188.21 | 265.48 | 133.43 | |
| 7 | 38.81 | 14°16′12″ | −0°19′12″ | 199.15 | 303.08 | 130.85 | Y |
| 8 | 39.82 | 13°55′12″ | −0°18′00″ | 239.44 | 299.28 | 191.57 | Y |
| 9 | 40.63 | 13°52′48″ | −0°36′36″ | 115.05 | 162.97 | 81.22 | |
| 10 | 41.70 | 14°33′36″ | −0°25′12″ | 158.51 | 226.20 | 111.07 | Y |
| 11 | 45.36 | 13°40′12″ | −0°37′48″ | 106.74 | 166.27 | 68.53 | Y |
*ID of the identified structures.
†The mean velocity of the structures.
‡The intensity peak position of the structure in the longitude direction.
§The intensity peak position of the structure in the latitude direction.
||The size of the structure (Geometric mean of the major radius♯ and minor radius**).
♯Major radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment in the direction of the greatest elongation in the PP plane.
**Minor radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment perpendicular to the major axis in the PP plane.
††“Y” indicates clouds extending outside the mapped area.
4 Cloud identification with SCIMES
4.1 Structures identified with SCIMES
We identify the cloud structure in M 17 SWex by applying SCIMES (Spectral Clustering for Interstellar Molecular Emission Segmentation; Colombo et al. 2015) to the 13CO (J = 1–0) data cube. SCIMES is an algorithm based on graph theory and cluster analysis; it identifies relevant molecular gas structures within dendrograms (Rosolowsky et al. 2008) of emission using the spectral clustering paradigm.
First, we identify the cloud structures with dendrograms using the following three parameters min|$\_$|value =10σrms, min|$\_$|delta =3σrms, and min|$\_$|npix =30, where σrms = 0.38 K is the average rms noise level of the 13CO (J = 1–0) data. The first parameter, min|$\_$|value, represents the minimum value of the intensity used for analysis. Above this minimum, structures are identified. The second parameter, min|$\_$|delta, is the minimum step of intensity required for a structure to be identified, and it defines a minimum significance for structures. The third parameter, min|$\_$|npix, is the minimum number of pixels in the position–position–velocity space that structures must contain. Then, we applied SCIMES for the hierarchical structures specified by dendrograms. In total, we identified 118 individual structures. Hereafter, we call structures identified by SCIMES “clouds.”
Figure 4a shows the spatial distribution of clouds identified by SCIMES. The color represents the mean velocities of the clouds. In figure 4b, we show only the clouds whose radii are greater than |${1{^{\prime }_{.}}7}$| (equivalent to 1 pc at a distance of 2 kpc). Some properties of these large clouds are listed in table 2. Figure 5 represents the distribution of clouds with radii greater than |${1{^{\prime }_{.}}7}$| in a position–velocity (P–V) diagram which is integrated in the galactic latitude direction.
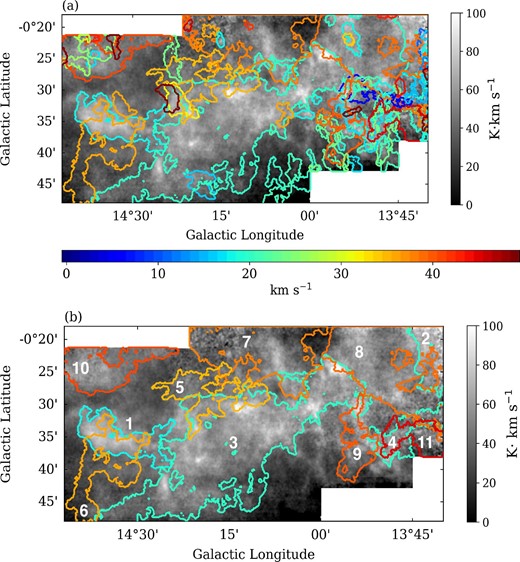
Structures identified by SCIMES. Contours represent the outline of every structure orthogonally projected on the plane of the sky. Each contour is colored depending on its mean velocity of the structure, according to the color bar at the bottom of this panel. The background image is the integrated intensity map of the 13CO(J = 1–0). The velocity range used for the integration is −18 km s−1 < VLSR < 60 km s−1. (a) All clouds identified by SCIMES are shown as contoured. (b) Only clouds with radii |$> {1{^{\prime }_{.}}7}$| (equivalent to 1 pc at a distance of 2 kpc) are shown. The labels denote the ID in table 2. (Color online)
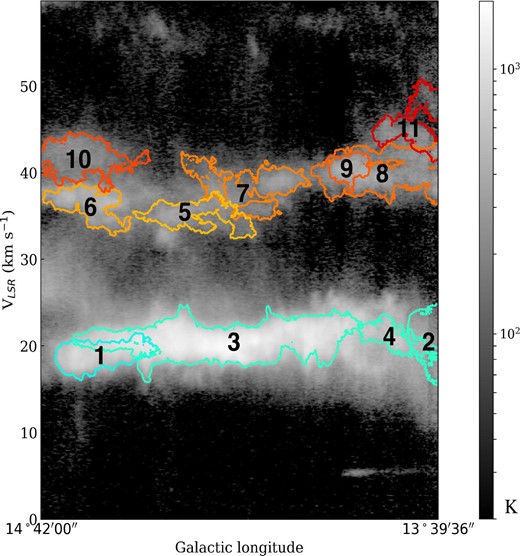
Structures identified by SCIMES with radii greater than |${1{^{\prime }_{.}}7}$| in the velocity–galactic latitude diagram. Each contour represents the identified structures projected on the velocity–galactic plane. Colors of the contours are the same as in figure 4. The background image is the 13CO(J = 1–0) data integrated in galactic-latitude direction. (Color online)
It is worth noting that the cloud identification depends on the dendrogram parameters. For example, if we adopt a smaller value of min|$\_$|value, the No. 5 and No. 6 clouds become a single structure. We discuss how the structure identification changes with other parameters in the appendix 2. In this paper, we adopt a relatively high min|$\_$|value of 10σ to inspect relatively high-density structure embedded in less-dense structure.
Figure 5 shows that mean velocities of most of the clouds are distributed around 20 km s−1 or 40 km s−1. The main component in M 17 SWex is shown in light green (around 20 km s−1), resembling a “flying dragon” in figure 4 (No. 3 in table 2). The cyan colored structure (No. 1 in table 2) touches this main component and has a mean velocity around 20 km s−1 too. These two clouds (Nos. 1 and 3) also become a single structure if we adopt a lower min|$\_$|value. Table 3 shows the properties of these clouds.
| No.† . | vcen‡ . | Rmajor§ . | Rminor|| . | Mass♯ . | vrms** . | Boundary†† . |
|---|---|---|---|---|---|---|
| . | (km s−1) . | (pc) . | (pc) . | (103|${M_{\odot}}$|) . | (km s−1) . | |
| 1 | 18.79 | 2.27 | 0.79 | 7.48 | 0.89 | |
| 3 | 20.51 | 5.85 | 1.89 | 37.21 | 1.16 | Y |
| 5 | 35.03 | 2.51 | 1.09 | 1.33 | 0.91 | |
| 6 | 36.21 | 2.57 | 1.29 | 1.65 | 2 1.17 | Y |
| No.† . | vcen‡ . | Rmajor§ . | Rminor|| . | Mass♯ . | vrms** . | Boundary†† . |
|---|---|---|---|---|---|---|
| . | (km s−1) . | (pc) . | (pc) . | (103|${M_{\odot}}$|) . | (km s−1) . | |
| 1 | 18.79 | 2.27 | 0.79 | 7.48 | 0.89 | |
| 3 | 20.51 | 5.85 | 1.89 | 37.21 | 1.16 | Y |
| 5 | 35.03 | 2.51 | 1.09 | 1.33 | 0.91 | |
| 6 | 36.21 | 2.57 | 1.29 | 1.65 | 2 1.17 | Y |
*The distances to all the clouds are assumed to be 2 kpc.
†Number of the identified structures (corresponding to table 2).
‡The mean velocity of the structures.
§Major radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment in the direction of the greatest elongation in the PP plane.
||Minor radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment perpendicular to the major axis in the PP plane.
♯Mass of the cloud.
** Intensity-weighted second moment of velocity.
††“Y” indicates clouds extending outside of the mapped area.
| No.† . | vcen‡ . | Rmajor§ . | Rminor|| . | Mass♯ . | vrms** . | Boundary†† . |
|---|---|---|---|---|---|---|
| . | (km s−1) . | (pc) . | (pc) . | (103|${M_{\odot}}$|) . | (km s−1) . | |
| 1 | 18.79 | 2.27 | 0.79 | 7.48 | 0.89 | |
| 3 | 20.51 | 5.85 | 1.89 | 37.21 | 1.16 | Y |
| 5 | 35.03 | 2.51 | 1.09 | 1.33 | 0.91 | |
| 6 | 36.21 | 2.57 | 1.29 | 1.65 | 2 1.17 | Y |
| No.† . | vcen‡ . | Rmajor§ . | Rminor|| . | Mass♯ . | vrms** . | Boundary†† . |
|---|---|---|---|---|---|---|
| . | (km s−1) . | (pc) . | (pc) . | (103|${M_{\odot}}$|) . | (km s−1) . | |
| 1 | 18.79 | 2.27 | 0.79 | 7.48 | 0.89 | |
| 3 | 20.51 | 5.85 | 1.89 | 37.21 | 1.16 | Y |
| 5 | 35.03 | 2.51 | 1.09 | 1.33 | 0.91 | |
| 6 | 36.21 | 2.57 | 1.29 | 1.65 | 2 1.17 | Y |
*The distances to all the clouds are assumed to be 2 kpc.
†Number of the identified structures (corresponding to table 2).
‡The mean velocity of the structures.
§Major radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment in the direction of the greatest elongation in the PP plane.
||Minor radius of the projection on to the position–position (PP) plane, computed from the intensity-weighted second moment perpendicular to the major axis in the PP plane.
♯Mass of the cloud.
** Intensity-weighted second moment of velocity.
††“Y” indicates clouds extending outside of the mapped area.
4.2 Comparison with the magnetic field directions
Sugitani et al. (2019) performed near-IR polarization observations toward the M 17 SWex area and revealed that the global magnetic fields are roughly perpendicular to the galactic plane and the dense filamentary structures. Figure 6 shows near-IR polarization H-band vector maps (Sugitani et al. 2019) superposed on the H2 column density map. The magnetic field is globally perpendicular to structure No. 3 extending from southeast to northwest. However, the magnetic fields suddenly change their directions at the intersection areas of the Nos. 1/6 and 3/5 clouds, and the field direction becomes preferentially parallel to the galactic plane. In other words, the magnetic field vectors appear to change their directions at the interface of the clouds.
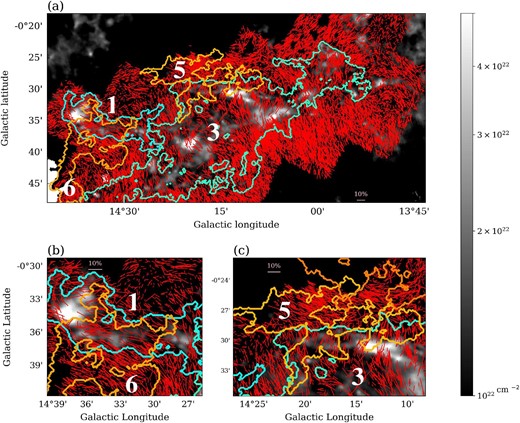
Near-IR polarization H-band vector maps (Sugitani et al. 2019) superposed on the H2 column density map derived from the Herschel data. The length of each vector is in proportion to its polarization degree and a vector of |$10\%$| polarization is shown. Colored contours represent the Nos. 1, 3, 5, and 6 cloud structures (see table 3). (a) Overall view of the M 17 SWex. (b) and (c) Enlarged views of interaction areas of the Nos. 1/6 and 3/5 clouds. (Color online)
4.3 Intermediate velocity components
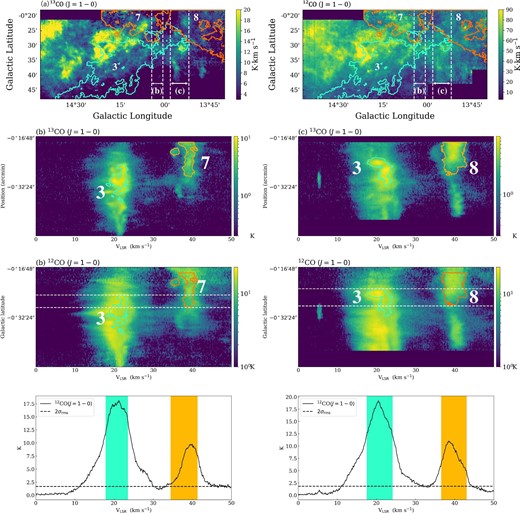
In figure 7a, we present the 12CO (J = 1–0)- and 13CO (J = 1–0)-intensity maps integrated in the range 24.6 km s−1 < VLSR < 32.5 km s−1 which corresponds to the intermediate velocity range between Nos. 1/3 and 5/6 clouds. For comparison, we show the boundaries of the Nos. 1, 3, 5 and 6 clouds by the contours. We focus on clouds Nos. 1 and 3 and Nos. 5 and 6 in table 2, because clouds Nos. 1 and 3 are main components of M 17 SWex, and clouds Nos. 5 and 6 are overlapped or close to these components.
(a) Integrated intensity maps of the 13CO(J = 1–0) and 12CO(J = 1–0) emission lines. Colored contours represent some 13CO structures identified by SCIMES (see figure 4). The labels denote the ID in table 3. The velocity range used for the integration is 24.6 km s−1 < VLSR < 32.5 km s−1, which is between the velocity ranges of the Nos. 1/3 and 5/6 structures. (b) The upper and middle panels show P–V diagrams of the 13CO(J = 1–0) and 12CO(J = 1–0) emission lines taken along the white solid line in panel (a). The bottom panel shows the mean 12CO spectra of the region within the two white dashed lines in the middle panel. Velocity ranges of the identified clouds are shaded in their respective colors. The 2σrms level is indicated, where σrms is the average rms noise level of the 12CO(J = 1–0) data within the range used for mean spectra. (c) and (d) Same as (b) except for the respective regions as indicated by dashed white lines in panel (a). (Color online)
In figure 7b, we show the P–V diagram along the white solid line indicated in panel (a). Figures 7c and 7d show the mean P–V (galactic latitude–velocity) diagrams within the range indicated by the respective white-dashed lines in panel (a). The 12CO emission is intense around the 20 km s−1 (Nos. 1 and 3) and 35 km s −1 (Nos. 5 and 6) components, and the faint emission is mainly distributed between these two velocities. In contrast, such faint emission is rarely found outside of the two components (>40 km s−1 and <15 km s−1).
5 Discussion and conclusions
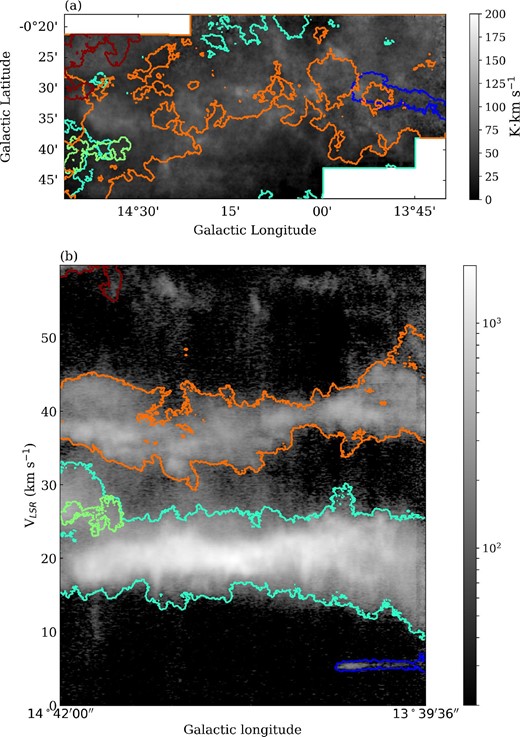
As mentioned above, clouds with different velocities appear to overlap along the line of sight. Figure 8 shows the 13CO (J = 1–0) contour plot of intensity integrated from 10 km s−1 to 30 km s−1 (green contours) and 30 km s−1 to 50 km s−1 (red map) (see also Sugitani et al. 2019). From the cloud morphology, Sugitani et al. (2019) pointed out that a couple of clouds with 30–50 km s−1 appears to physically interact with those with 10–30 km s−1. If this is the case, the 30–50 km s−1 component should be located at the same distance as the 10–30 km s−1 component, 2 kpc.
![13CO(J=1−0)-intensity map integrated from 10 km s−1 to 30 km s−1 (green contours) and from 30 km s−1 to 50 km s−1 (red map). Contours are drawn at 30, 40, and 50 K km s−1. Distributions of the 13CO components in the 10–30 km s−1 and 30–50 km s−1 ranges show an anticorrelation [see also Sugitani et al. (2019)]. (Color online)](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/73/Supplement_1/10.1093_pasj_psaa053/3/m_psaa053fig8.jpeg?Expires=1749378180&Signature=DQToc4WJ1fv-Bi-ySrZ6H7v0pnuCM-CpbI5E-8TbYbK3-eO-F3KjmxLHS2lMZojp-ttEXun-zvnhNs827I6QuSfz03qn3eYSc4S5sN0H9XTAIesp~s1KyVc4gD~wK2PrDGAkmHquPPkiTVNrN~C7z~-AOfM7Ldf-0LSiI33wLMOXYV9HUi10jIQ0aK579B~wxtXgPdhGSbnvUtKHCu1ENAckcbHr4e2hc9YYvJsYBxmHP0QUwa0jQYD~pJwLcU2oMHrKADCQYagkcgy0P4gGQ89SxExYJ-X560Z5UvlwzqqoAwTxOyksPtue-05UvmGm48tdn7hqBEJB65bc--4uKA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
13CO(J=1−0)-intensity map integrated from 10 km s−1 to 30 km s−1 (green contours) and from 30 km s−1 to 50 km s−1 (red map). Contours are drawn at 30, 40, and 50 K km s−1. Distributions of the 13CO components in the 10–30 km s−1 and 30–50 km s−1 ranges show an anticorrelation [see also Sugitani et al. (2019)]. (Color online)
Here, we discuss three possible scenarios that appear to be consistent with observational properties: (i) overlapped clouds with different distances, (ii) oscillation of a larger cloud, and (iii) cloud–cloud collision.
5.1 Case (i): A chance coincidence of clouds with different distances
As mentioned in section 3, some molecular clouds with >35 km s−1 are likely to belong mainly to the distant Scutum or Norma spiral arm and simply overlap with the main component with ∼20 km s−1 along the line-of-sight. This may be the case for clouds Nos. 5 and 6. In subsection 4.3, we presented the intermediate-velocity components in the P–V diagram. There is a possibility that this emission comes from the inter-arm region between the Sagittarius arm and the Scutum arm. The bending magnetic fields at
the intersection of the clouds may be consistent with the observed polarization pattern if the orientations of the magnetic fields associated with the individual clouds are different. For example, if the magnetic field orientations of the
Nos. 5/6 clouds are preferentially parallel to the Galactic plane, and if the magnetic fields of the Nos. 1/3 clouds are perpendicular to the Galactic plane, the observed polarization pattern would be achieved.
However, from our dendrogram/SCIMES analysis, we could not identify any outstanding clouds/clumps in the intermediate-velocity range (see figures 4 and 5). Even if we change the parameters of dendrogram/SCIMES, the diffuse emission is simply connected to the previously-identified clouds (see appendix 2). In other words, their distribution in the P–P–V space is very continuous in the intermediate velocity range. Such continuous diffuse emission is not distributed below 10 km s−1 or above 40 km s−1.
5.2 Case (ii): A larger cloud oscillation
One of the possible scenarios which can explain the existence of CO structures with a peak velocity of ∼35 km s−1 (clouds Nos. 5/6) and the spatial distribution of these structures with ∼20 km s−1 structures is that these structures are denser parts created by the oscillation of a single larger cloud. Such oscillation of clouds has been discussed for a Bok globule, B 68 (Redman et al. 2006). If a cloud is oscillating, the clouds identified should be gravitationally bound as a whole. Here we discuss the dynamical state of the two clouds with VLSR ∼ 20 km s−1 and ∼35 km s−1 using a simple analysis.
5.3 Case (iii): Cloud–cloud collision
Here, we discuss the possible collision of ∼20 km s−1 clouds and ∼35 km s−1 clouds. We provide two primary pieces of evidence supporting the cloud–cloud collision scenario. One is a bridge feature in the P–V diagram which often appears in the early stages of cloud–cloud collisions (Takahira et al. 2014; Haworth et al. 2015). The other is bent magnetic field structures which appear to be consistent with numerical simulation results of the colliding magnetized clouds (Wu et al. 2017, 2020).
The extended emission with the intermediate velocities shown in figure 7 implies that the two structures may be dynamically interacting. Haworth et al. (2015) demonstrated that the turbulent motion in the compressed layer of a cloud–cloud collision can be observed in a P–V diagram as “broad bridge features” connecting the two clouds. They produced synthetic P–V diagrams from a range of different simulations of molecular clouds, including cloud–cloud collisions and isolated clouds. They found that “broad bridge features” appeared in their cloud–cloud collision models, but did not appear in any of the simulations of isolated clouds (see also Takahira et al. 2014). Thus, the Nos. 5 and 6 clouds might lie at the same distance (2 kpc) as Nos. 1 and 3, and these four clouds might be colliding with each other.
Appendix 4 shows mean P–V (galactic latitude–velocity) diagrams measured in regions where Nos. 7 and 8 clouds overlap with No. 3. In these diagrams, emission at the intermediate velocities is very weak, and there are no bridge features detected. Thus, Nos. 7 and 8 clouds may be unrelated to the cloud–cloud collision.
Additionally, Nos. 7 and 8 clouds are closer to b = 0° than Nos. 1/3 clouds. Since the solar system is located several hundred pc above the midplane of our Galaxy, M 17 SWex should appear displaced toward more negative or positive latitudes, while distant clouds appear around b = 0° due to perspective effects. Hence, Nos. 7 and 8 clouds may be more distant clouds. While Nos. 5/6 clouds are actually at the similar latitudes to Nos. 1/3 clouds, this fact is consistent with the idea that Nos. 5/6 clouds are located at the same distance as Nos. 1/3 clouds.
We also found noteworthy features of the magnetic field orientation in some possible interacting parts. As discussed in subsection 4.2, the magnetic-field orientation changes abruptly at the intersection areas of the Nos. 1/6 and 3/5 clouds. Wu et al. (2017) indicate that when two clouds collide, magnetic fields become oriented preferentially parallel along the boundary of collision. The observed abrupt changes of the magnetic field seem qualitatively consistent with the cloud–cloud collision scenario.
Two clouds, Nos. 5 and 6, lie adjacent to each other and have similar velocities. Further inspection of the channel maps (see appendix 3) reveals weak emission connecting these two clouds Therefore, we can interpret that the Nos. 5 and 6 clouds may be connected and belong to a larger structure, but two dense parts within one structure may have been identified independently with SCIMES. The same goes for the Nos. 1 and 3 clouds. The masses of the Nos. 1 and 3 clouds are estimated to be 7.5 × 103 M⊙, and 3.7 × 104 M⊙, respectively (see table 3), while the masses of the Nos. 5 and 6 clouds are estimated to be 1.3 × 103 M⊙, and 1.7 × 103 M⊙, respectively. If the Nos. 1/3 clouds and the Nos. 5/6 clouds are single structures, those two large complexes have masses greater than 4.5 × 104 M⊙ and 3.0 × 103 M⊙, respectively. In summary, we propose that a ∼20 km s−1 cloud complex with mass ≳4.5 × 104 M⊙ and a ∼35 km s−1 cloud complex with mass ≳3.0 × 103 M⊙ may be colliding with a relative speed of ∼15 km s−1 for case (iii).
In summary, we think that the most plausible scenario is case (iii), the cloud–cloud collision, although we presented only circumstantial evidence such as the spatial configuration of the clouds, a bridge emission, and the bending magnetic field at the possible interacting areas. Further concrete evidence would be needed to prove the cloud–cloud collision scenario completely.
6 Summary
We analyzed the cloud structure of the M 17 SWex in 13CO (J = 1−0). Our main results are summarized as follows:
Our 13CO integrated intensity distribution in M 17 SWex closely follows the dense part traced by the Herschel column density map.
By applying SCIMES to the 13CO data cube, we identified 118 clouds in M 17 SWex.
We select six large (>|${1{^{\prime }_{.}}7}$|) clouds identified by SCIMES. At least two large clouds with ∼35 km s−1 seem to be located close to the main clouds at ∼20 km s−1 in the galactic longitude–galactic latitude plane.
We discussed three possibilities that appear to be consistent with the observed features. The first scenario is that clouds at different distances from the Sun are overlapped along the line of sight. The second scenario is that a large cloud is oscillating. The third scenario is that clouds located at the same distance are colliding.
Judging from (1) the existence of the bridge feature in the P–V map and from (2) the distortion of the magnetic field orientation at the intersections, we think that cloud–cloud collision is the most plausible scenario. However, it is very difficult to rule out other scenarios. Further concrete evidence would be needed to prove the cloud–cloud collision scenario.
Acknowledgements
This work was partly supported by JSPS KAKENHI Grant Numbers JP24540233, JP16H05730, and JP17H01118. This work was carried out as one of the large projects of the Nobeyama Radio Observatory (NRO), which is a branch of the National Astronomical Observatory of Japan, National Institute of Natural Sciences. We thank the NRO staff for both operating the 45 m and helping us with the data reduction. B.W. and P.S. were partly supported by a Grant-in-Aid for Scientific Research (KAKENHI Number 18H01259) of Japan Society for the Promotion of Science (JSPS). GJW expresses his grateful thanks to The Leverhulme Trust for an Emeritus Fellowship.
Appendix 1 Integrated intensity maps of 12CO(J = 3–2) with ATLASGAL clumps
Figure 9 shows the integrated intensity maps of the 12CO(J = 3–2) emission line. The velocity ranges used for the integration are (a) 10 km s−1 < VLSR < 30 km s−1 and (b) 30 km s−1 < VLSR < 50 km s−1. In both panels, we plot clumps cataloged by Urquhart et al. (2018).
Integrated intensity maps of the 12CO(J = 3–2) emission line. The velocity ranges used for the integration are (a) 10 km s−1 < VLSR < 30 km s−1 and (b) 30 km s−1 < VLSR < 50 km s−1. In both panels, we plot clumps cataloged by Urquhart et al. (2018), which fall in the velocity ranges used for the integration, by symbols of different colors. The shapes and colors of each symbol represent the distances. (Color online)
Appendix 2 Identified clouds with SCIMES for different parameters of dendrograms
Figure 10 shows clouds identified with SCIMES, when using the three parameters of min|$\_$|value =5σrms, min|$\_$|delta =3σrms, and min|$\_$|npix =30.
Clouds identified by SCIMES using three parameters of min|$\_$|value =5σrms, min|$\_$|delta =3σrms, and min|$\_$|npix =30. (a) Identified structures whose radii are larger than |${1{^{\prime }_{.}}7}$| by SCIMES. Contours represent the outline of every structure orthogonally projected on to the plane of the sky. Each contour is colored depending on the mean velocity of the structure, according to the color-bar at the bottom of this panel. The background image is the integrated intensity map of the 13CO(J = 1–0) emission. The velocity range used for the integration is −18 km s−1 < VLSR < 60 km s−1. (b) Structures identified by SCIMES with radii greater than |${1{^{\prime }_{.}}7}$| shown on the longitude–velocity diagram generated by integrating the spectra along the latitude direction. Colors of the contours are the same as in panel (a). The background image is the 13CO(J = 1−0) data integrated in galactic latitude direction. (Color online)
Appendix 3 Channel maps of 13CO (J = 1–0) of the M 17 SWex
Figure 11 shows the 13CO (J = 1–0) channel maps integrated over 1 km s−1 in the range 10–50 km s−1. For comparison, in each map, we show the boundaries of Nos. 1, 3, 5, and 6 clouds in the corresponding velocity ranges (see tables 2 and 3) by contours.
Intensity maps of M 17 SWex integrated for every 1 km s−1 within 10–50 km s−1. For comparison, the Nos. 1, 3, 5, and 6 clouds are shown by contours in some panels with the corresponding velocities. In the upper left-hand corner, the velocity range used for the integration is shown. (Color online)
Appendix 4 P–V diagram including No. 3 and Nos. 7/8 clouds
Figure 12a shows the |$^{13}{\rm CO}(J = 1-0)$| and 12CO(J = 1–0) integrated intensity map integrated over the range 24.6–36.4 km s−1. Colored contours represent some 13CO structures identified by SCIMES (see figure 4). In figures 12b and 12c, the upper and middle panels show the P–V diagrams of the |$^{13}{\rm CO}(J = 1-0)$| and 12CO(J = 1–0) emission line taken within the range of white broken lines indicated in panel (a). The bottom panel shows the mean |$^{12}{\rm CO}(J = 1-0)$| spectra within the range between the two white broken lines in the middle panel. Velocity ranges of the identified clouds are shaded in their respective colors.
(a) Integrated intensity maps of the 13CO(J = 1–0) and 12CO(J = 1–0) emission lines. Colored contours represent some 13CO structures identified by SCIMES (see figure 4). The labels denote the ID in table 3. The velocity range used for the integration is 24.6 km s−1 < VLSR < 36.4 km s−1, which is between the velocity ranges of the Nos. 1/3 and 7/8 structures. (b) and (c) The upper and middle panels show the mean P–V diagram of the 13CO(J = 1–0) and 12CO(J = 1–0) emission lines taken within the range of white broken lines indicate in panel (a). The bottom panel shows the mean 12CO spectra of the region within the two white dashed lines in the middle panel. Velocity ranges of the identified clouds are shaded in their respective colors. The 2σrms level is indicated, where σrms is the average rms noise level of the 12CO(J = 1–0) data within the range used for mean spectra. (Color online)
Appendix 5 Comparison with the N2H+ cores
Recently, Shimoikura et al. (2019) identified 46 dense cores and clumps in M 17 SWex by using the N2H+ (J = 1−0) line, and constrain their evolutionary times by comparing with the evolutionary stages of young stellar objects (YSOs) classified by Povich et al. (2016). Figure 13 shows the distribution of the dense cores and clumps identified by Shimoikura et al. (2019) with the stages classified. The background image shows the H2 column density distribution derived from the Herschel data. The dense cores and clumps are mainly distributed along the two large filamentary structures seen in the H2 column density map.

Distribution of the molecular cores identified by Shimoikura et al. (2019). Cores associated with stage |$\rm {II/III}$| YSOs are shown by the red filled circle. Cores unassociated with stage |$\rm {II/III}$| but stage |$\rm {0/I}$| YSOs or ambiguous stage YSOs are shown by the blue filled circle. Cores unassociated with YSOs are shown by the green filled circle. The background is the H2 column density map derived from the Herschel data. Colored contours represent the Nos. 1, 3, 5, and 6 cloud structures (see table 3). (Color online)
Here, we discuss whether a possible cloud–cloud collision triggered the formation of dense structures such as cores and clumps in this region. We define the cloud–cloud collision timescale as the time required for clouds with a relative velocity Vrel to cross each other. We adopt the typical diameter of the No 1/3 clouds (∼1.5–12 pc) and the relative velocity of 15 km s−1 (see table 2). The cloud–cloud collision timescale is roughly estimated to be ∼0.05–0.4 Myr. If the evolutionary times of the dense cores and clumps are shorter than the crossing time, there is a possibility that the formation of cores and clumps may have been triggered by the collision.
The collision timescale of <106 yr seems to be shorter than ages of stage |$\rm {II/III}$| stars (Schulz 2012). Thus, it is difficult to form protostellar cores associated with stage |$\rm {II/III}$| YSOs by the cloud–cloud collision we discussed here. However, several cores with stage |$\rm {0/I}$| YSOs and cores with no YSOs which seem to be distributed mainly in the overlapped areas of Nos. 1, 3, 5, and 6 clouds might be formed by the cloud–cloud collision.








