-
PDF
- Split View
-
Views
-
Cite
Cite
Sang-Hyeon Ahn, Revisiting the epoch of the earliest Chinese star catalog titled “Shi Shi Xing Jing”, Publications of the Astronomical Society of Japan, Volume 72, Issue 5, October 2020, 87, https://doi.org/10.1093/pasj/psaa080
Close - Share Icon Share
Abstract
The Shi Shi Xing Jing (SSXJ) is known to be the earliest star catalog in Chinese history. Its epoch of observation has long been a matter of debate. In recent studies, Sun Xiaochun pointed out that the observations must have been made using meridian instruments and developed a so-called Fourier method to determine the epoch, while Tsuko Nakamura developed a χ2 method to determine the epoch and showed that the measurement error can be estimated using bootstrap resamplings. However, they did not take both meridian measurements and bootstrap resamplings into consideration simultaneously. Hence, in this paper we determine the epoch and its uncertainty by applying the two methods and performing the bootstrap resamplings in a careful manner. We adopt identifications of the reference stars of 116 asterisms with stars in modern catalogs, including the determinative stars or the reference stars for the 28 lunar lodges. We find that the stars can be divided into four groups. Twenty-five of the 28 determinative stars are estimated to have been observed around 65 ± 28 BCE, corresponding to either Xianyu Wangren’s observation in 78–76 BCE or Geng Shouchang’s observation in 52 BCE. The other stars make three groups: the main group composed of 63 reference stars has an observation epoch of 108 ± 16 BCE corresponding to Luoxia Hong’s observation in 104 BCE; another group of eight reference stars including two determinative stars has an observation epoch of 200 ± 45 BCE, corresponding to the establishment of the Former Han dynasty; and the other group of 13 reference stars including one determinative star has an observation epoch of approximately 100 ± 35 CE, corresponding to the observations by ecliptic instruments in 103 CE following Gia Kui’s suggestion of 92 CE. In conclusion, the SSXJ has a few temporal strata of observations made through the Han dynasty.
1 Introduction
The observation of stellar positions in Chinese history traces back to 104 BCE, when a famous historian Sima Qian organized a group of astronomers including Luoxia Hong to measure the positions of major reference stars in order to make a calendar system of the Han dynasty’s own. A few decades later, around 77 BCE, another group of astronomers led by Xianyu Wangren made observations to verify the reliability of the calendar system. In 52 BCE, a minister called Geng Shouchang made new observations. These facts were summarized by the philosopher Yang Xiong (53 BCE–18 CE) in his book titled “Fa Yan,” and that Luoxia Hong constructed armillary spheres,1 Xianyu Wangren made observations with them, and the minister Geng Shouchang made a celestial globe with the observed data. Since these astronomers lived in the Former Han period, it is thought that meridian observations were first performed then (Sun & Kistemaker 1997).
The astronomers belonging to the so-called Shi Shi school attributed their achievements to the legendary figure Shi Shi. Hence, the information on stellar positions was handed down in the name of Shi Shi. Later they were compiled by Chen Zhuo, an astronomer of the Three Kingdoms period (220–280 CE) in Chinese history, into a book titled “Shi Shi Xing Jing” (“Shi Shen’s Astral Canon,” hereafter SSXJ), with supplementary information from the Gan De and Wuxian schools. 2 Chen Zhuo compiled 283 asterisms comprising 1464 stars in the Chinese sky.
The book of SSXJ itself was lost, but the coordinates of the reference stars for 118 asterisms including the 28 lunar lodges are preserved in an early Tang astrological compendium called “Kai Yuan Zhan Jing” (ca. 720 CE, hereafter KYZJ) or the “Treatise on Astrology of the Kai Yuan Era.” The coordinate values of the SSXJ stars are partially preserved in other material such as “San Jia Bu Zan” (“Records and Praise for the Three Schools’ Astral Canon”)3 and “Cheonji-Seosangji” (“Treatise on Auspicious Phenomena in Heaven and on Earth”).4 The configurations of the asterisms are depicted in the Dunhuang star chart, which dates back to 649–684 CE (Bonnet-Bidaud et al. 2009) and was discovered in 1907 at the Silk Road town of Dunhuang; it is now housed in the British Library. The configurations are also depicted on the Korean ancient star chart called “Cheonsang-Yeolcha-Bunyajido” (Ahn 2011). These data can be used to complement the KYZJ’s coordinate values.
Although SSXJ was named after an astronomer of the fourth century BCE called Shi Shen, its epoch of observation has been a matter of debate. The detailed history of researches on this topic was described in detail by Sun and Kistemaker (1997) and Nakamura (2018). The estimated epoch was first reported by Shinjo to be around 50 BCE, but he later published an article that reported his estimation of the observational epoch to be 360 BCE (Shinjo 1928). His opinions seemed to diverge. Hence, a mathematical verification was performed by Ueda (1929), who concluded that there exist two groups of stars in the determinative stars5 of 28 lunar lodges: three of them were observed around 300 BCE, while 18 of them were observed around 200 CE. More recently, Pan (2009) analyzed the whole SSXJ catalog, and reached a similar conclusion that the SSXJ stars are comprised of two groups of stars, observed around 450 BCE and 160 CE, respectively.
Yabuuchi (1937) and Qian (1983) undertook independent textual studies on Chinese classics to conclude that the SSXJ texts were composed during the Former Han dynasty. In particular, Yabuuchi (1937) claimed the epoch of observation to be approximately 70 BCE. Maeyama (1977) pointed out the existence of a misalignment error during the installation of meridian instruments, and performed analytic studies to obtain an epoch of 70 ± 30 BCE.
However, there have been only a couple of research works that gave the statistical uncertainty in the epoch of observation. Recently, Sun and Tian (1993), Sun (1994), and Sun and Kistemaker (1997) also considered the possiblity of meridian observations and a misalignment error. They developed a so-called Fourier analysis method. They analyzed all 120 stars, and concluded that all the stars in the SSXJ catalog were observed around 78 ± 20 BCE. They regarded the standard deviation of the mean for a finite sample of measurements as an estimator of uncertainty for the total population. This quantity will be fine when the number of samples is large, but it can be a rough estimator when the number is small. They did not perform a statistical estimation of the uncertainties by using methods such as bootstrap resamplings. On the other hand, Nakamura (2018) determined the epoch of observation by applying least-squares fitting and bootstrap resamplings to only the 28 determinative stars rather than the 120 stars to obtain the epoch of 54 ± 12 BCE. Moreover, he did not take into account the fact that the polar angles could have misalignment errors caused by measurement with a meridian instrument.
Thus, in this paper we will determine the epoch of observation for all the reference stars listed in SSXJ by using both least-squares fitting and the Fourier method, including instrumental misalignment. In order to estimate the uncertainty, we perform bootstrap samplings. In section 2 we introduce the data and the analysis methods. The results are given in section 3. In section 4 we discuss the statistical implications of the results by performing hypothesis tests.
2 Analysis of the data
2.1 Data
The positions of SSXJ stars are preserved in KYZJ. The original books of KYZJ had disappeared after the Song dynasty, but in 1616 CE a manuscript copy was recovered in the belly of the Buddha’s statue during its restoration (Sun & Kistemaker 1997). This copy was later inserted in Siku Quanshu, whose first workable drafts were completed in 1781 CE. We reference volumes 65–68 of KYZJ in the Wenyuan Library version, which contains the name, the number of constituent stars, a rough description of its location relative to other neighboring asterisms, the lodge angle, the polar angle, and the ecliptic angle for each asterism. For example, the first entry in volume 65 of KYZJ reads:
Shi Shi told that the asterism called Sheti [1] consisting of six stars embraces Dajiao [2] (α Boo). [Its lodge angle is 8 du (du is the Chinese degree) from the reference star of the lunar lodge Jiao [93] (α Vir); its polar angle is 59 and a half du from the north celestial pole; it is at 32.75 du inside of the ecliptic.]
First of all, the lodge angle is the eastward angular difference of a celestial object in right ascension from the reference star of its nearest-to-the-west lunar lodge. Hence, the reference star of Sheti [1] has a right ascension of 8 du plus the right ascension of α Vir. Second, the polar angle is simply the anglular distance from the north celestial pole to an object. We should not be confused that the polar anlges were measured from Polaris. Last of all, the so-called ecliptic angle, called huang dao nei wai du, is the angular distance from the object to the ecliptic along the hour circle that penetrates the object. This is not the ecliptic latitude of the object, which was also pointed out by Yabuuchi (1937) and demonstrated with astronomical calculations by Sun and Kistemaker (1995) and Sun (2000). These ecliptic angles are useful to crosscheck the polar angles.
The identification of stars is the first and crucial step in this analysis. In this paper we basically adopt the identifications made by Sun and Kistemaker (1997). However, we check their identifications one by one. We calculate the equatorial coordinates of the stars at the epoch of 104 BCE by using the PC planetarium software Stellarium. We find a number of exceptional cases, in which other identifications seem to be better. The details are shown in the Appendix. We present those exceptional cases in table 1, where a double dagger at the end of a name represents an exceptional case. A dagger at the end of a name means that the star is discarded during the analysis as an outlier due to its large deviation from the fitting curves.
| Id . | Names . | No. . | Bayer . | HR . | Xiu . | L.A. . | P.A. . | RA . | Dec . | Δi . |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sheti | 6 | η Boo | HR5235 | 1 | 8.25 | 59.50 | 183.23 | 29.61 | –1.75 |
| 2 | Dajiao† | 1 | α Boo | HR5340 | 2 | 2.50 | 58.00 | 189.01 | 30.05 | –2.79 |
| 3 | Genghe | 3 | ρ Boo | HR5429 | 2 | 8.00 | 48.00 | 194.81 | 40.83 | –1.86 |
| 4 | Zhaoyao | 1 | γ Boo | HR5435 | 3 | 2.50 | 40.75 | 196.21 | 48.70 | –1.13 |
| 5 | Xuange | 1 | λ Boo | HR5351 | 3 | 1.00 | 32.50 | 193.09 | 56.79 | –1.18 |
| 6 | Tianqiang†‡ | 3 | κ2 Boo | HR5329 | 3 | 0.75 | 28.75 | 193.73 | 62.50 | 0.84 |
| 7 | Tianpei‡ | 5 | ι Her | HR6588 | 7 | 8.50 | 42.00 | 250.39 | 48.54 | –0.07 |
| 8 | Nuchuang† | 3 | π Her | HR6418 | 7 | 1.00 | 50.00 | 240.74 | 40.88 | 0.16 |
| 9 | Qigong | 7 | β Boo | HR5602 | 3 | 4.50 | 39.25 | 205.44 | 49.92 | –1.40 |
| 10 | Guansuo†‡ | 9 | β CrB | HR5747 | 6 | 0.50 | 59.25 | 210.18 | 37.92 | 6.32 |
| 11 | Tianji | 9 | ξ CrB | HR6103 | 6 | 5.00 | 51.50 | 225.20 | 37.55 | –1.69 |
| 12 | Zhinu | 3 | α Lyr | HR7001 | 8 | 11.00 | 52.00 | 261.76 | 38.69 | –0.06 |
| 13 | Tianshi | 22 | ζ Oph | HR6175 | 6 | 0.75 | 94.25 | 221.21 | –3.90 | –1.01 |
| 14 | Dizuo | 1 | α1 Her | HR6406 | 6 | 15.50 | 71.25 | 235.02 | 19.00 | –0.78 |
| 15 | Hou | 1 | α Oph | HR6556 | 7 | 2.50 | 73.75 | 239.72 | 16.24 | –1.07 |
| 16 | Huanzhe | 4 | 60 Her | HR6355 | 6 | 12.00 | 72.50 | 232.36 | 17.81 | –0.73 |
| 17 | Dou†‡ | 5 | κ Oph | HR6299 | 6 | 10.25 | 75.00 | 229.77 | 14.85 | –4.18 |
| 18 | Zongzheng | 2 | γ Oph | HR6629 | 7 | 2.00 | 84.00 | 240.96 | 5.95 | –1.26 |
| 19 | Zongren† | 4 | 68 Oph | HR6723 | 7 | 7.50 | 85.00 | 244.09 | 3.89 | –2.33 |
| 20 | Zong | 2 | 71 Oph | HR6770 | 7 | 9.00 | 79.00 | 246.95 | 10.90 | –1.24 |
| 21 | Dongxian‡ | 8 | ψ Oph | HR6104 | 5 | 2.00 | 103.00 | 218.74 | –9.62 | 1.91 |
| 22 | Tianjiang | 4 | θ Oph | HR6453 | 6 | 6.25 | 111.00 | 229.25 | –20.03 | –0.62 |
| 23 | Jianxing† | 6 | ξ2 Sgr | HR7150 | 8 | 7.25 | 113.25 | 253.08 | –20.84 | 0.78 |
| 24 | Tianbian†‡ | 9 | 5 Aql | HR7059 | 8 | 6.75 | 90.75 | 254.99 | 1.32 | 0.76 |
| 25 | Hegu | 12 | α Aql | HR7557 | 8 | 22.75 | 85.00 | 272.29 | 5.85 | –0.37 |
| 26 | Lizhu† | 5 | 1 Aqr | HR7897 | 10 | 0.00 | 94.00 | 282.60 | –4.67 | –2.02 |
| 27 | Hugua | 5 | ζ Del | HR7871 | 10 | 0.25 | 81.50 | 284.20 | 9.47 | –0.21 |
| 28 | Tianjin‡ | 9 | δ Cyg | HR7528 | 8 | 2.00 | 49.00 | 279.88 | 41.50 | –0.20 |
| 29 | Dengshe† | 22 | α Lac | HR8585 | 13 | 1.50 | 51.00 | 317.32 | 40.43 | 0.69 |
| 30 | Wangliang | 5 | β Cas | HR0021 | 14 | 0.50 | 42.50 | 338.12 | 47.67 | –0.45 |
| 31 | Gedao | 6 | φ Cas | HR0382 | 15 | 5.00 | 43.25 | 351.63 | 46.64 | –0.74 |
| 32 | Fulu | 1 | υ1 Cas | HR0253 | 15 | 3.00 | 43.00 | 346.82 | 47.32 | –0.30 |
| 33 | Tianjiangjun† | 11 | γ1 And | HR0603 | 15 | 15.50 | 60.33 | 1.66 | 31.14 | 0.61 |
| 34 | Daling | 8 | 9 Per | HR0685 | 16 | 6.25 | 44.25 | 3.96 | 44.86 | –1.52 |
| 35 | Tianchuan | 9 | η Per | HR0834 | 16 | 9.00 | 43.50 | 9.54 | 45.40 | –1.72 |
| 36 | Juanshi | 6 | ν Per | HR1135 | 17 | 10.25 | 56.00 | 23.55 | 33.61 | –1.19 |
| 37 | Wuche | 14 | ι Aur | HR1577 | 19 | 3.00 | 63.00 | 41.65 | 26.95 | –0.95 |
| 38 | Tianguan | 1 | ζ Tau | HR1910 | 20 | 0.00 | 73.50 | 53.77 | 16.96 | –0.60 |
| 39 | Nanbeihe | 6 | β CMi | HR2845 | 22 | 17.25 | 80.00 | 83.08 | 9.79 | –1.36 |
| 40 | Wuzhuhou | 5 | θ Gem | HR2540 | 22 | 2.00 | 57.00 | 68.60 | 33.11 | –0.71 |
| 41 | Jisui† | 1 | o Gem | HR2930 | 22 | 13.00 | 55.00 | 79.70 | 36.05 | 0.26 |
| 42 | Jixin‡ | 1 | φ Gem | HR3067 | 22 | 21.50 | 61.50 | 85.43 | 29.17 | –0.21 |
| 43 | Suiwei | 4 | 68 Gem | HR2886 | 22 | 19.50 | 72.50 | 83.07 | 17.49 | –1.05 |
| 44 | Xuanyuan† | 17 | α Leo | HR3982 | 26 | 0.75 | 71.00 | 122.92 | 20.57 | 0.55 |
| 45 | Shaowei | 4 | 53 Leo | HR4227 | 26 | 10.50 | 70.50 | 133.73 | 20.44 | –0.08 |
| 46 | Taiwei | 10 | β Vir | HR4540 | 27 | 9.00 | 76.50 | 150.39 | 12.97 | –1.63 |
| 47 | Huangdizuo | 1 | β Leo | HR4534 | 27 | 9.50 | 63.50 | 149.16 | 25.73 | –1.68 |
| 48 | Shidizuo | 4 | ||||||||
| 49 | Neiping†‡ | 4 | ξ Vir | HR4515 | 28 | 0.00 | 72.50 | 148.59 | 19.37 | 0.83 |
| 50 | Langwei‡ | 15 | γ Com | HR4737 | 28 | 0.00 | 157.58 | |||
| 51 | Langjiang | 1 | α2 CVn | HR4915 | 28 | 8.00 | 39.25 | 167.26 | 49.97 | –1.34 |
| 52 | Changchen | 7 | 61 UMa | HR4496 | 28 | 5.00 | 45.00 | 145.10 | 45.17 | –0.48 |
| 53 | Santai | 6 | ι UMa | HR3569 | 22 | 30.75 | 36.25 | 95.03 | 52.99 | –1.28 |
| 54 | Xiang | 1 | χ UMa | HR4518 | 27 | 5.00 | 31.50 | 144.39 | 58.77 | –0.18 |
| 55 | Taiyangshou | 1 | ψ UMa | HR4335 | 26 | 13.25 | 35.50 | 133.80 | 54.67 | –0.34 |
| 56 | Tianlao† | 6 | 44 UMa | HR4246 | 26 | 1.25 | 26.50 | 124.95 | 64.09 | 0.21 |
| 57 | Wenchang | 6 | o UMa | HR3323 | 22 | 15.75 | 25.75 | 79.09 | 63.45 | –1.17 |
| 58 | Beidou | 8 | α UMa | HR4301 | 26 | 0.00 | 18.25 | 123.41 | 71.35 | –0.66 |
| 59 | Ziwei† | 15 | κ Dra | HR4787 | 28 | 10.00 | 9.50 | 154.83 | 81.33 | 0.70 |
| 60 | Beiji Gouchen | 11 | α UMi | HR0424 | 14 | 8.75 | 11.50 | 348.04 | 77.67 | –0.99 |
| 61 | Tianyi‡ | 1 | 7 Dra | HR4863 | 28 | 10.00 | 10.50 | 163.49 | 78.43 | –1.22 |
| 62 | Taiyi† | 1 | 8 Dra | HR4916 | 28 | 10.00 | 10.00 | 167.34 | 77.09 | –3.06 |
| 63 | Kulou†‡ | 29 | δ Cru | HR4656 | 28 | 0.25 | 140.00 | 159.22 | –47.22 | 0.77 |
| 64 | Nanmen | 2 | ξ2 Cen | HR4942 | 28 | 14.00 | 130.00 | 169.28 | –38.27 | –0.14 |
| 65 | Ping†‡ | 2 | γ Hya | HR5020 | 28 | 14.00 | 100.00 | 172.48 | –11.58 | –3.02 |
| 66 | Qiguan | 27 | c1 Cen | HR5485 | 2 | 4.75 | 115.50 | 191.10 | –24.69 | –0.85 |
| 67 | Jizu†‡ | 12 | η Lup | HR5948 | 3 | 13.75 | 124.25 | 207.67 | –29.96 | 2.50 |
| 68 | Gui‡ | 5 | 6 | 12.00 | 131.00 | |||||
| 69 | Fuyue†‡ | 1 | G Sco | HR6630 | 6 | 12.75 | 120.50 | 232.88 | –33.06 | –4.29 |
| 70 | Yu | 1 | M 7 | NGC6475 | 6 | 14.00 | 122.00 | 234.42 | –31.06 | –0.81 |
| 71 | Chu‡ | 3 | 7 | 1.75 | 132.50 | |||||
| 72 | Bie‡ | 14 | μ CrA | HR7050 | 8 | 1.00 | 129.50 | 245.39 | –39.10 | –1.46 |
| 73 | Jiukan† | 9 | ι Sgr | HR7581 | 8 | 14.50 | 136.00 | 261.24 | –43.90 | 0.14 |
| 74 | Baijiu | 4 | ι PsA | HR8305 | 10 | 10.00 | 131.25 | 292.62 | –40.45 | –1.08 |
| 75 | Yulin | 57 | υ Aqr | HR8592 | 12 | 4.75 | 120.75 | 308.51 | –30.09 | –1.08 |
| 76 | Beiluo | 1 | α PsA | HR8728 | 12 | 9.00 | 130.75 | 313.37 | –39.61 | –0.74 |
| 77 | Tusikong | 1 | β Cet | HR0188 | 14 | 7.75 | 120.25 | 343.79 | –29.63 | –1.11 |
| 78 | Tiangcang | 6 | η Cet | HR0334 | 15 | 4.75 | 112.00 | 350.50 | –21.81 | –1.42 |
| 79 | Tianqun | 13 | α Cet | HR0911 | 17 | 6.25 | 96.50 | 18.80 | –5.79 | –0.67 |
| 80 | Tianlin | 4 | o Tau | HR1030 | 17 | 11.25 | 90.00 | 23.79 | –0.23 | –1.53 |
| 81 | Tianyuan†‡ | 16 | γ Eri | HR1231 | 19 | 2.75 | 114.00 | 35.35 | –21.42 | 0.95 |
| 82 | Shenqi | 9 | π5 Ori | HR1567 | 19 | 9.50 | 93.00 | 46.78 | –3.38 | –1.72 |
| 83 | Yujing | 4 | β Eri | HR1666 | 19 | 12.25 | 100.75 | 51.51 | –10.17 | –0.87 |
| 84 | Ping | 2 | ε Lep | HR1654 | 20 | 0.75 | 118.00 | 54.41 | –27.25 | –0.95 |
| 85 | Ce | 4 | β Lep | HR1829 | 21 | 3.25 | 115.00 | 59.81 | –24.59 | –1.24 |
| 86 | Tianshi | 1 | ν2 Col | HR1935 | 21 | 7.00 | 123.00 | 64.14 | –31.87 | –0.64 |
| 87 | Junshi | 13 | 17 Lep | HR2148 | 22 | 3.25 | 110.00 | 68.02 | –18.60 | –0.18 |
| 88 | Yeji† | 1 | β CMa | HR2294 | 22 | 8.00 | 111.00 | 72.71 | –19.15 | 0.26 |
| 89 | Lang | 1 | α CMa | HR2491 | 22 | 13.00 | 106.75 | 77.94 | –16.80 | –1.58 |
| 90 | Hu‡ | 9 | κ CMa | HR2538 | 22 | 16.00 | 122.25 | 82.97 | –31.96 | –1.47 |
| 91 | Laoren | 1 | α Car | HR2326 | 22 | 19.00 | 143.50 | 84.50 | –52.66 | –1.22 |
| 92 | Ji† | 5 | δ Vel | HR3485 | 24 | 14.25 | 138.00 | 116.52 | –48.17 | –2.16 |
| 93 | Jiao | 2 | α Vir | HR5056 | 1 | 0.00 | 91.00 | 174.28 | 0.39 | 0.08 |
| 94 | Kang | 4 | κ Vir | HR5315 | 2 | 0.00 | 89.00 | 186.03 | 0.71 | –1.57 |
| 95 | Di† | 4 | α2 Lib | HR5531 | 3 | 0.00 | 94.00 | 194.77 | –5.81 | –3.16 |
| 96 | Fang | 4 | π Sco | HR5944 | 4 | 0.00 | 108.00 | 209.54 | –17.80 | –1.35 |
| 97 | Xin | 3 | σ Sco | HR6084 | 5 | 0.00 | 108.50 | 214.84 | –18.09 | –1.15 |
| 98 | Wei† | 9 | μ1 Sco | HR6247 | 6 | 0.00 | 120.00 | 219.36 | –31.52 | –3.25 |
| 99 | Ji | 4 | γ2 Sgr | HR6746 | 7 | 0.00 | 118.00 | 238.35 | –27.36 | –1.06 |
| 100 | Dou | 6 | φ Sgr | HR7039 | 8 | 0.00 | 116.00 | 248.74 | –25.98 | –1.64 |
| 101 | Niu | 6 | β Cap | HR7776 | 9 | 0.00 | 110.00 | 275.07 | –18.80 | –0.38 |
| 102 | Xu Nu | 4 | ε Aqr | HR7950 | 10 | 0.00 | 106.00 | 282.81 | –14.86 | –0.38 |
| 103 | Xu | 2 | β Aqr | HR8232 | 11 | 0.00 | 104.00 | 294.54 | –12.87 | –0.36 |
| 104 | Wei | 3 | α Aqr | HR8414 | 12 | 0.00 | 99.00 | 304.03 | –8.31 | –0.73 |
| 105 | Ying Shi | 2 | α Peg | HR8781 | 13 | 0.00 | 85.00 | 320.25 | 4.80 | –1.42 |
| 106 | Dong Bi | 2 | γ Peg | HR0039 | 14 | 0.00 | 86.00 | 336.78 | 3.71 | –1.53 |
| 107 | Kui | 16 | ζ And | HR0215 | 15 | 0.00 | 77.00 | 345.08 | 12.62 | –1.49 |
| 108 | Lou | 3 | β Ari | HR0553 | 16 | 0.00 | 80.00 | 0.99 | 9.54 | –1.61 |
| 109 | Wei | 3 | 35 Ari | HR0801 | 17 | 0.00 | 72.00 | 11.85 | 17.25 | –1.78 |
| 110 | Mao | 17 | 17 Tau | HR1142 | 18 | 0.00 | 74.00 | 26.58 | 15.35 | –1.71 |
| 111 | Bi | 8 | ε Tau | HR1409 | 19 | 0.00 | 78.00 | 37.70 | 12.05 | –1.07 |
| 112 | Zhi | 3 | φ1 Ori | HR1876 | 20 | 0.00 | 84.00 | 55.41 | 5.40 | –1.81 |
| 113 | Shen | 10 | δ Ori | HR1852 | 21 | 0.00 | 94.50 | 56.47 | –3.76 | –0.62 |
| 114 | Dong Jing | 8 | μ Gem | HR2286 | 22 | 0.00 | 70.00 | 64.34 | 20.48 | –0.53 |
| 115 | Gui | 5 | θ Cnc | HR3357 | 23 | 0.00 | 68.00 | 97.03 | 22.55 | –0.43 |
| 116 | Liu | 8 | δ Hya | HR3410 | 24 | 0.00 | 79.00 | 101.03 | 10.67 | –1.46 |
| 117 | 7 | α Hya | HR3748 | 25 | 0.00 | 91.00 | 115.83 | –1.34 | –1.65 | |
| 118 | Zhang | 6 | υ1 Hya | HR3903 | 26 | 0.00 | 97.00 | 122.56 | –6.57 | –0.96 |
| 119 | Yi | 22 | α Crt | HR4287 | 27 | 0.00 | 99.00 | 139.36 | –7.99 | –0.42 |
| 120 | Zhen† | 4 | γ Crv | HR4662 | 28 | 0.00 | 99.00 | 157.48 | –6.04 | 1.53 |
| Id . | Names . | No. . | Bayer . | HR . | Xiu . | L.A. . | P.A. . | RA . | Dec . | Δi . |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sheti | 6 | η Boo | HR5235 | 1 | 8.25 | 59.50 | 183.23 | 29.61 | –1.75 |
| 2 | Dajiao† | 1 | α Boo | HR5340 | 2 | 2.50 | 58.00 | 189.01 | 30.05 | –2.79 |
| 3 | Genghe | 3 | ρ Boo | HR5429 | 2 | 8.00 | 48.00 | 194.81 | 40.83 | –1.86 |
| 4 | Zhaoyao | 1 | γ Boo | HR5435 | 3 | 2.50 | 40.75 | 196.21 | 48.70 | –1.13 |
| 5 | Xuange | 1 | λ Boo | HR5351 | 3 | 1.00 | 32.50 | 193.09 | 56.79 | –1.18 |
| 6 | Tianqiang†‡ | 3 | κ2 Boo | HR5329 | 3 | 0.75 | 28.75 | 193.73 | 62.50 | 0.84 |
| 7 | Tianpei‡ | 5 | ι Her | HR6588 | 7 | 8.50 | 42.00 | 250.39 | 48.54 | –0.07 |
| 8 | Nuchuang† | 3 | π Her | HR6418 | 7 | 1.00 | 50.00 | 240.74 | 40.88 | 0.16 |
| 9 | Qigong | 7 | β Boo | HR5602 | 3 | 4.50 | 39.25 | 205.44 | 49.92 | –1.40 |
| 10 | Guansuo†‡ | 9 | β CrB | HR5747 | 6 | 0.50 | 59.25 | 210.18 | 37.92 | 6.32 |
| 11 | Tianji | 9 | ξ CrB | HR6103 | 6 | 5.00 | 51.50 | 225.20 | 37.55 | –1.69 |
| 12 | Zhinu | 3 | α Lyr | HR7001 | 8 | 11.00 | 52.00 | 261.76 | 38.69 | –0.06 |
| 13 | Tianshi | 22 | ζ Oph | HR6175 | 6 | 0.75 | 94.25 | 221.21 | –3.90 | –1.01 |
| 14 | Dizuo | 1 | α1 Her | HR6406 | 6 | 15.50 | 71.25 | 235.02 | 19.00 | –0.78 |
| 15 | Hou | 1 | α Oph | HR6556 | 7 | 2.50 | 73.75 | 239.72 | 16.24 | –1.07 |
| 16 | Huanzhe | 4 | 60 Her | HR6355 | 6 | 12.00 | 72.50 | 232.36 | 17.81 | –0.73 |
| 17 | Dou†‡ | 5 | κ Oph | HR6299 | 6 | 10.25 | 75.00 | 229.77 | 14.85 | –4.18 |
| 18 | Zongzheng | 2 | γ Oph | HR6629 | 7 | 2.00 | 84.00 | 240.96 | 5.95 | –1.26 |
| 19 | Zongren† | 4 | 68 Oph | HR6723 | 7 | 7.50 | 85.00 | 244.09 | 3.89 | –2.33 |
| 20 | Zong | 2 | 71 Oph | HR6770 | 7 | 9.00 | 79.00 | 246.95 | 10.90 | –1.24 |
| 21 | Dongxian‡ | 8 | ψ Oph | HR6104 | 5 | 2.00 | 103.00 | 218.74 | –9.62 | 1.91 |
| 22 | Tianjiang | 4 | θ Oph | HR6453 | 6 | 6.25 | 111.00 | 229.25 | –20.03 | –0.62 |
| 23 | Jianxing† | 6 | ξ2 Sgr | HR7150 | 8 | 7.25 | 113.25 | 253.08 | –20.84 | 0.78 |
| 24 | Tianbian†‡ | 9 | 5 Aql | HR7059 | 8 | 6.75 | 90.75 | 254.99 | 1.32 | 0.76 |
| 25 | Hegu | 12 | α Aql | HR7557 | 8 | 22.75 | 85.00 | 272.29 | 5.85 | –0.37 |
| 26 | Lizhu† | 5 | 1 Aqr | HR7897 | 10 | 0.00 | 94.00 | 282.60 | –4.67 | –2.02 |
| 27 | Hugua | 5 | ζ Del | HR7871 | 10 | 0.25 | 81.50 | 284.20 | 9.47 | –0.21 |
| 28 | Tianjin‡ | 9 | δ Cyg | HR7528 | 8 | 2.00 | 49.00 | 279.88 | 41.50 | –0.20 |
| 29 | Dengshe† | 22 | α Lac | HR8585 | 13 | 1.50 | 51.00 | 317.32 | 40.43 | 0.69 |
| 30 | Wangliang | 5 | β Cas | HR0021 | 14 | 0.50 | 42.50 | 338.12 | 47.67 | –0.45 |
| 31 | Gedao | 6 | φ Cas | HR0382 | 15 | 5.00 | 43.25 | 351.63 | 46.64 | –0.74 |
| 32 | Fulu | 1 | υ1 Cas | HR0253 | 15 | 3.00 | 43.00 | 346.82 | 47.32 | –0.30 |
| 33 | Tianjiangjun† | 11 | γ1 And | HR0603 | 15 | 15.50 | 60.33 | 1.66 | 31.14 | 0.61 |
| 34 | Daling | 8 | 9 Per | HR0685 | 16 | 6.25 | 44.25 | 3.96 | 44.86 | –1.52 |
| 35 | Tianchuan | 9 | η Per | HR0834 | 16 | 9.00 | 43.50 | 9.54 | 45.40 | –1.72 |
| 36 | Juanshi | 6 | ν Per | HR1135 | 17 | 10.25 | 56.00 | 23.55 | 33.61 | –1.19 |
| 37 | Wuche | 14 | ι Aur | HR1577 | 19 | 3.00 | 63.00 | 41.65 | 26.95 | –0.95 |
| 38 | Tianguan | 1 | ζ Tau | HR1910 | 20 | 0.00 | 73.50 | 53.77 | 16.96 | –0.60 |
| 39 | Nanbeihe | 6 | β CMi | HR2845 | 22 | 17.25 | 80.00 | 83.08 | 9.79 | –1.36 |
| 40 | Wuzhuhou | 5 | θ Gem | HR2540 | 22 | 2.00 | 57.00 | 68.60 | 33.11 | –0.71 |
| 41 | Jisui† | 1 | o Gem | HR2930 | 22 | 13.00 | 55.00 | 79.70 | 36.05 | 0.26 |
| 42 | Jixin‡ | 1 | φ Gem | HR3067 | 22 | 21.50 | 61.50 | 85.43 | 29.17 | –0.21 |
| 43 | Suiwei | 4 | 68 Gem | HR2886 | 22 | 19.50 | 72.50 | 83.07 | 17.49 | –1.05 |
| 44 | Xuanyuan† | 17 | α Leo | HR3982 | 26 | 0.75 | 71.00 | 122.92 | 20.57 | 0.55 |
| 45 | Shaowei | 4 | 53 Leo | HR4227 | 26 | 10.50 | 70.50 | 133.73 | 20.44 | –0.08 |
| 46 | Taiwei | 10 | β Vir | HR4540 | 27 | 9.00 | 76.50 | 150.39 | 12.97 | –1.63 |
| 47 | Huangdizuo | 1 | β Leo | HR4534 | 27 | 9.50 | 63.50 | 149.16 | 25.73 | –1.68 |
| 48 | Shidizuo | 4 | ||||||||
| 49 | Neiping†‡ | 4 | ξ Vir | HR4515 | 28 | 0.00 | 72.50 | 148.59 | 19.37 | 0.83 |
| 50 | Langwei‡ | 15 | γ Com | HR4737 | 28 | 0.00 | 157.58 | |||
| 51 | Langjiang | 1 | α2 CVn | HR4915 | 28 | 8.00 | 39.25 | 167.26 | 49.97 | –1.34 |
| 52 | Changchen | 7 | 61 UMa | HR4496 | 28 | 5.00 | 45.00 | 145.10 | 45.17 | –0.48 |
| 53 | Santai | 6 | ι UMa | HR3569 | 22 | 30.75 | 36.25 | 95.03 | 52.99 | –1.28 |
| 54 | Xiang | 1 | χ UMa | HR4518 | 27 | 5.00 | 31.50 | 144.39 | 58.77 | –0.18 |
| 55 | Taiyangshou | 1 | ψ UMa | HR4335 | 26 | 13.25 | 35.50 | 133.80 | 54.67 | –0.34 |
| 56 | Tianlao† | 6 | 44 UMa | HR4246 | 26 | 1.25 | 26.50 | 124.95 | 64.09 | 0.21 |
| 57 | Wenchang | 6 | o UMa | HR3323 | 22 | 15.75 | 25.75 | 79.09 | 63.45 | –1.17 |
| 58 | Beidou | 8 | α UMa | HR4301 | 26 | 0.00 | 18.25 | 123.41 | 71.35 | –0.66 |
| 59 | Ziwei† | 15 | κ Dra | HR4787 | 28 | 10.00 | 9.50 | 154.83 | 81.33 | 0.70 |
| 60 | Beiji Gouchen | 11 | α UMi | HR0424 | 14 | 8.75 | 11.50 | 348.04 | 77.67 | –0.99 |
| 61 | Tianyi‡ | 1 | 7 Dra | HR4863 | 28 | 10.00 | 10.50 | 163.49 | 78.43 | –1.22 |
| 62 | Taiyi† | 1 | 8 Dra | HR4916 | 28 | 10.00 | 10.00 | 167.34 | 77.09 | –3.06 |
| 63 | Kulou†‡ | 29 | δ Cru | HR4656 | 28 | 0.25 | 140.00 | 159.22 | –47.22 | 0.77 |
| 64 | Nanmen | 2 | ξ2 Cen | HR4942 | 28 | 14.00 | 130.00 | 169.28 | –38.27 | –0.14 |
| 65 | Ping†‡ | 2 | γ Hya | HR5020 | 28 | 14.00 | 100.00 | 172.48 | –11.58 | –3.02 |
| 66 | Qiguan | 27 | c1 Cen | HR5485 | 2 | 4.75 | 115.50 | 191.10 | –24.69 | –0.85 |
| 67 | Jizu†‡ | 12 | η Lup | HR5948 | 3 | 13.75 | 124.25 | 207.67 | –29.96 | 2.50 |
| 68 | Gui‡ | 5 | 6 | 12.00 | 131.00 | |||||
| 69 | Fuyue†‡ | 1 | G Sco | HR6630 | 6 | 12.75 | 120.50 | 232.88 | –33.06 | –4.29 |
| 70 | Yu | 1 | M 7 | NGC6475 | 6 | 14.00 | 122.00 | 234.42 | –31.06 | –0.81 |
| 71 | Chu‡ | 3 | 7 | 1.75 | 132.50 | |||||
| 72 | Bie‡ | 14 | μ CrA | HR7050 | 8 | 1.00 | 129.50 | 245.39 | –39.10 | –1.46 |
| 73 | Jiukan† | 9 | ι Sgr | HR7581 | 8 | 14.50 | 136.00 | 261.24 | –43.90 | 0.14 |
| 74 | Baijiu | 4 | ι PsA | HR8305 | 10 | 10.00 | 131.25 | 292.62 | –40.45 | –1.08 |
| 75 | Yulin | 57 | υ Aqr | HR8592 | 12 | 4.75 | 120.75 | 308.51 | –30.09 | –1.08 |
| 76 | Beiluo | 1 | α PsA | HR8728 | 12 | 9.00 | 130.75 | 313.37 | –39.61 | –0.74 |
| 77 | Tusikong | 1 | β Cet | HR0188 | 14 | 7.75 | 120.25 | 343.79 | –29.63 | –1.11 |
| 78 | Tiangcang | 6 | η Cet | HR0334 | 15 | 4.75 | 112.00 | 350.50 | –21.81 | –1.42 |
| 79 | Tianqun | 13 | α Cet | HR0911 | 17 | 6.25 | 96.50 | 18.80 | –5.79 | –0.67 |
| 80 | Tianlin | 4 | o Tau | HR1030 | 17 | 11.25 | 90.00 | 23.79 | –0.23 | –1.53 |
| 81 | Tianyuan†‡ | 16 | γ Eri | HR1231 | 19 | 2.75 | 114.00 | 35.35 | –21.42 | 0.95 |
| 82 | Shenqi | 9 | π5 Ori | HR1567 | 19 | 9.50 | 93.00 | 46.78 | –3.38 | –1.72 |
| 83 | Yujing | 4 | β Eri | HR1666 | 19 | 12.25 | 100.75 | 51.51 | –10.17 | –0.87 |
| 84 | Ping | 2 | ε Lep | HR1654 | 20 | 0.75 | 118.00 | 54.41 | –27.25 | –0.95 |
| 85 | Ce | 4 | β Lep | HR1829 | 21 | 3.25 | 115.00 | 59.81 | –24.59 | –1.24 |
| 86 | Tianshi | 1 | ν2 Col | HR1935 | 21 | 7.00 | 123.00 | 64.14 | –31.87 | –0.64 |
| 87 | Junshi | 13 | 17 Lep | HR2148 | 22 | 3.25 | 110.00 | 68.02 | –18.60 | –0.18 |
| 88 | Yeji† | 1 | β CMa | HR2294 | 22 | 8.00 | 111.00 | 72.71 | –19.15 | 0.26 |
| 89 | Lang | 1 | α CMa | HR2491 | 22 | 13.00 | 106.75 | 77.94 | –16.80 | –1.58 |
| 90 | Hu‡ | 9 | κ CMa | HR2538 | 22 | 16.00 | 122.25 | 82.97 | –31.96 | –1.47 |
| 91 | Laoren | 1 | α Car | HR2326 | 22 | 19.00 | 143.50 | 84.50 | –52.66 | –1.22 |
| 92 | Ji† | 5 | δ Vel | HR3485 | 24 | 14.25 | 138.00 | 116.52 | –48.17 | –2.16 |
| 93 | Jiao | 2 | α Vir | HR5056 | 1 | 0.00 | 91.00 | 174.28 | 0.39 | 0.08 |
| 94 | Kang | 4 | κ Vir | HR5315 | 2 | 0.00 | 89.00 | 186.03 | 0.71 | –1.57 |
| 95 | Di† | 4 | α2 Lib | HR5531 | 3 | 0.00 | 94.00 | 194.77 | –5.81 | –3.16 |
| 96 | Fang | 4 | π Sco | HR5944 | 4 | 0.00 | 108.00 | 209.54 | –17.80 | –1.35 |
| 97 | Xin | 3 | σ Sco | HR6084 | 5 | 0.00 | 108.50 | 214.84 | –18.09 | –1.15 |
| 98 | Wei† | 9 | μ1 Sco | HR6247 | 6 | 0.00 | 120.00 | 219.36 | –31.52 | –3.25 |
| 99 | Ji | 4 | γ2 Sgr | HR6746 | 7 | 0.00 | 118.00 | 238.35 | –27.36 | –1.06 |
| 100 | Dou | 6 | φ Sgr | HR7039 | 8 | 0.00 | 116.00 | 248.74 | –25.98 | –1.64 |
| 101 | Niu | 6 | β Cap | HR7776 | 9 | 0.00 | 110.00 | 275.07 | –18.80 | –0.38 |
| 102 | Xu Nu | 4 | ε Aqr | HR7950 | 10 | 0.00 | 106.00 | 282.81 | –14.86 | –0.38 |
| 103 | Xu | 2 | β Aqr | HR8232 | 11 | 0.00 | 104.00 | 294.54 | –12.87 | –0.36 |
| 104 | Wei | 3 | α Aqr | HR8414 | 12 | 0.00 | 99.00 | 304.03 | –8.31 | –0.73 |
| 105 | Ying Shi | 2 | α Peg | HR8781 | 13 | 0.00 | 85.00 | 320.25 | 4.80 | –1.42 |
| 106 | Dong Bi | 2 | γ Peg | HR0039 | 14 | 0.00 | 86.00 | 336.78 | 3.71 | –1.53 |
| 107 | Kui | 16 | ζ And | HR0215 | 15 | 0.00 | 77.00 | 345.08 | 12.62 | –1.49 |
| 108 | Lou | 3 | β Ari | HR0553 | 16 | 0.00 | 80.00 | 0.99 | 9.54 | –1.61 |
| 109 | Wei | 3 | 35 Ari | HR0801 | 17 | 0.00 | 72.00 | 11.85 | 17.25 | –1.78 |
| 110 | Mao | 17 | 17 Tau | HR1142 | 18 | 0.00 | 74.00 | 26.58 | 15.35 | –1.71 |
| 111 | Bi | 8 | ε Tau | HR1409 | 19 | 0.00 | 78.00 | 37.70 | 12.05 | –1.07 |
| 112 | Zhi | 3 | φ1 Ori | HR1876 | 20 | 0.00 | 84.00 | 55.41 | 5.40 | –1.81 |
| 113 | Shen | 10 | δ Ori | HR1852 | 21 | 0.00 | 94.50 | 56.47 | –3.76 | –0.62 |
| 114 | Dong Jing | 8 | μ Gem | HR2286 | 22 | 0.00 | 70.00 | 64.34 | 20.48 | –0.53 |
| 115 | Gui | 5 | θ Cnc | HR3357 | 23 | 0.00 | 68.00 | 97.03 | 22.55 | –0.43 |
| 116 | Liu | 8 | δ Hya | HR3410 | 24 | 0.00 | 79.00 | 101.03 | 10.67 | –1.46 |
| 117 | 7 | α Hya | HR3748 | 25 | 0.00 | 91.00 | 115.83 | –1.34 | –1.65 | |
| 118 | Zhang | 6 | υ1 Hya | HR3903 | 26 | 0.00 | 97.00 | 122.56 | –6.57 | –0.96 |
| 119 | Yi | 22 | α Crt | HR4287 | 27 | 0.00 | 99.00 | 139.36 | –7.99 | –0.42 |
| 120 | Zhen† | 4 | γ Crv | HR4662 | 28 | 0.00 | 99.00 | 157.48 | –6.04 | 1.53 |
The columns represent the entry number, the name of the asterism, the number of constituent stars, the identified stars in Bayer designation and HR-number, the determinative stars and the lodge angle (L.A.), the polar angle (P.A.), right ascension (RA) and the declination (Dec) of the identified star at the epoch of 104 BCE, and the residual in declination (Δi) at the epoch of 104 BCE. Identifications are adopted from Sun and Kistemaker (1997).
The stars eventually removed from the analysis due to their large deviations.
The stars identified differently from Sun and Kistemaker (1997), whose details are shown in the Appendix.
| Id . | Names . | No. . | Bayer . | HR . | Xiu . | L.A. . | P.A. . | RA . | Dec . | Δi . |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sheti | 6 | η Boo | HR5235 | 1 | 8.25 | 59.50 | 183.23 | 29.61 | –1.75 |
| 2 | Dajiao† | 1 | α Boo | HR5340 | 2 | 2.50 | 58.00 | 189.01 | 30.05 | –2.79 |
| 3 | Genghe | 3 | ρ Boo | HR5429 | 2 | 8.00 | 48.00 | 194.81 | 40.83 | –1.86 |
| 4 | Zhaoyao | 1 | γ Boo | HR5435 | 3 | 2.50 | 40.75 | 196.21 | 48.70 | –1.13 |
| 5 | Xuange | 1 | λ Boo | HR5351 | 3 | 1.00 | 32.50 | 193.09 | 56.79 | –1.18 |
| 6 | Tianqiang†‡ | 3 | κ2 Boo | HR5329 | 3 | 0.75 | 28.75 | 193.73 | 62.50 | 0.84 |
| 7 | Tianpei‡ | 5 | ι Her | HR6588 | 7 | 8.50 | 42.00 | 250.39 | 48.54 | –0.07 |
| 8 | Nuchuang† | 3 | π Her | HR6418 | 7 | 1.00 | 50.00 | 240.74 | 40.88 | 0.16 |
| 9 | Qigong | 7 | β Boo | HR5602 | 3 | 4.50 | 39.25 | 205.44 | 49.92 | –1.40 |
| 10 | Guansuo†‡ | 9 | β CrB | HR5747 | 6 | 0.50 | 59.25 | 210.18 | 37.92 | 6.32 |
| 11 | Tianji | 9 | ξ CrB | HR6103 | 6 | 5.00 | 51.50 | 225.20 | 37.55 | –1.69 |
| 12 | Zhinu | 3 | α Lyr | HR7001 | 8 | 11.00 | 52.00 | 261.76 | 38.69 | –0.06 |
| 13 | Tianshi | 22 | ζ Oph | HR6175 | 6 | 0.75 | 94.25 | 221.21 | –3.90 | –1.01 |
| 14 | Dizuo | 1 | α1 Her | HR6406 | 6 | 15.50 | 71.25 | 235.02 | 19.00 | –0.78 |
| 15 | Hou | 1 | α Oph | HR6556 | 7 | 2.50 | 73.75 | 239.72 | 16.24 | –1.07 |
| 16 | Huanzhe | 4 | 60 Her | HR6355 | 6 | 12.00 | 72.50 | 232.36 | 17.81 | –0.73 |
| 17 | Dou†‡ | 5 | κ Oph | HR6299 | 6 | 10.25 | 75.00 | 229.77 | 14.85 | –4.18 |
| 18 | Zongzheng | 2 | γ Oph | HR6629 | 7 | 2.00 | 84.00 | 240.96 | 5.95 | –1.26 |
| 19 | Zongren† | 4 | 68 Oph | HR6723 | 7 | 7.50 | 85.00 | 244.09 | 3.89 | –2.33 |
| 20 | Zong | 2 | 71 Oph | HR6770 | 7 | 9.00 | 79.00 | 246.95 | 10.90 | –1.24 |
| 21 | Dongxian‡ | 8 | ψ Oph | HR6104 | 5 | 2.00 | 103.00 | 218.74 | –9.62 | 1.91 |
| 22 | Tianjiang | 4 | θ Oph | HR6453 | 6 | 6.25 | 111.00 | 229.25 | –20.03 | –0.62 |
| 23 | Jianxing† | 6 | ξ2 Sgr | HR7150 | 8 | 7.25 | 113.25 | 253.08 | –20.84 | 0.78 |
| 24 | Tianbian†‡ | 9 | 5 Aql | HR7059 | 8 | 6.75 | 90.75 | 254.99 | 1.32 | 0.76 |
| 25 | Hegu | 12 | α Aql | HR7557 | 8 | 22.75 | 85.00 | 272.29 | 5.85 | –0.37 |
| 26 | Lizhu† | 5 | 1 Aqr | HR7897 | 10 | 0.00 | 94.00 | 282.60 | –4.67 | –2.02 |
| 27 | Hugua | 5 | ζ Del | HR7871 | 10 | 0.25 | 81.50 | 284.20 | 9.47 | –0.21 |
| 28 | Tianjin‡ | 9 | δ Cyg | HR7528 | 8 | 2.00 | 49.00 | 279.88 | 41.50 | –0.20 |
| 29 | Dengshe† | 22 | α Lac | HR8585 | 13 | 1.50 | 51.00 | 317.32 | 40.43 | 0.69 |
| 30 | Wangliang | 5 | β Cas | HR0021 | 14 | 0.50 | 42.50 | 338.12 | 47.67 | –0.45 |
| 31 | Gedao | 6 | φ Cas | HR0382 | 15 | 5.00 | 43.25 | 351.63 | 46.64 | –0.74 |
| 32 | Fulu | 1 | υ1 Cas | HR0253 | 15 | 3.00 | 43.00 | 346.82 | 47.32 | –0.30 |
| 33 | Tianjiangjun† | 11 | γ1 And | HR0603 | 15 | 15.50 | 60.33 | 1.66 | 31.14 | 0.61 |
| 34 | Daling | 8 | 9 Per | HR0685 | 16 | 6.25 | 44.25 | 3.96 | 44.86 | –1.52 |
| 35 | Tianchuan | 9 | η Per | HR0834 | 16 | 9.00 | 43.50 | 9.54 | 45.40 | –1.72 |
| 36 | Juanshi | 6 | ν Per | HR1135 | 17 | 10.25 | 56.00 | 23.55 | 33.61 | –1.19 |
| 37 | Wuche | 14 | ι Aur | HR1577 | 19 | 3.00 | 63.00 | 41.65 | 26.95 | –0.95 |
| 38 | Tianguan | 1 | ζ Tau | HR1910 | 20 | 0.00 | 73.50 | 53.77 | 16.96 | –0.60 |
| 39 | Nanbeihe | 6 | β CMi | HR2845 | 22 | 17.25 | 80.00 | 83.08 | 9.79 | –1.36 |
| 40 | Wuzhuhou | 5 | θ Gem | HR2540 | 22 | 2.00 | 57.00 | 68.60 | 33.11 | –0.71 |
| 41 | Jisui† | 1 | o Gem | HR2930 | 22 | 13.00 | 55.00 | 79.70 | 36.05 | 0.26 |
| 42 | Jixin‡ | 1 | φ Gem | HR3067 | 22 | 21.50 | 61.50 | 85.43 | 29.17 | –0.21 |
| 43 | Suiwei | 4 | 68 Gem | HR2886 | 22 | 19.50 | 72.50 | 83.07 | 17.49 | –1.05 |
| 44 | Xuanyuan† | 17 | α Leo | HR3982 | 26 | 0.75 | 71.00 | 122.92 | 20.57 | 0.55 |
| 45 | Shaowei | 4 | 53 Leo | HR4227 | 26 | 10.50 | 70.50 | 133.73 | 20.44 | –0.08 |
| 46 | Taiwei | 10 | β Vir | HR4540 | 27 | 9.00 | 76.50 | 150.39 | 12.97 | –1.63 |
| 47 | Huangdizuo | 1 | β Leo | HR4534 | 27 | 9.50 | 63.50 | 149.16 | 25.73 | –1.68 |
| 48 | Shidizuo | 4 | ||||||||
| 49 | Neiping†‡ | 4 | ξ Vir | HR4515 | 28 | 0.00 | 72.50 | 148.59 | 19.37 | 0.83 |
| 50 | Langwei‡ | 15 | γ Com | HR4737 | 28 | 0.00 | 157.58 | |||
| 51 | Langjiang | 1 | α2 CVn | HR4915 | 28 | 8.00 | 39.25 | 167.26 | 49.97 | –1.34 |
| 52 | Changchen | 7 | 61 UMa | HR4496 | 28 | 5.00 | 45.00 | 145.10 | 45.17 | –0.48 |
| 53 | Santai | 6 | ι UMa | HR3569 | 22 | 30.75 | 36.25 | 95.03 | 52.99 | –1.28 |
| 54 | Xiang | 1 | χ UMa | HR4518 | 27 | 5.00 | 31.50 | 144.39 | 58.77 | –0.18 |
| 55 | Taiyangshou | 1 | ψ UMa | HR4335 | 26 | 13.25 | 35.50 | 133.80 | 54.67 | –0.34 |
| 56 | Tianlao† | 6 | 44 UMa | HR4246 | 26 | 1.25 | 26.50 | 124.95 | 64.09 | 0.21 |
| 57 | Wenchang | 6 | o UMa | HR3323 | 22 | 15.75 | 25.75 | 79.09 | 63.45 | –1.17 |
| 58 | Beidou | 8 | α UMa | HR4301 | 26 | 0.00 | 18.25 | 123.41 | 71.35 | –0.66 |
| 59 | Ziwei† | 15 | κ Dra | HR4787 | 28 | 10.00 | 9.50 | 154.83 | 81.33 | 0.70 |
| 60 | Beiji Gouchen | 11 | α UMi | HR0424 | 14 | 8.75 | 11.50 | 348.04 | 77.67 | –0.99 |
| 61 | Tianyi‡ | 1 | 7 Dra | HR4863 | 28 | 10.00 | 10.50 | 163.49 | 78.43 | –1.22 |
| 62 | Taiyi† | 1 | 8 Dra | HR4916 | 28 | 10.00 | 10.00 | 167.34 | 77.09 | –3.06 |
| 63 | Kulou†‡ | 29 | δ Cru | HR4656 | 28 | 0.25 | 140.00 | 159.22 | –47.22 | 0.77 |
| 64 | Nanmen | 2 | ξ2 Cen | HR4942 | 28 | 14.00 | 130.00 | 169.28 | –38.27 | –0.14 |
| 65 | Ping†‡ | 2 | γ Hya | HR5020 | 28 | 14.00 | 100.00 | 172.48 | –11.58 | –3.02 |
| 66 | Qiguan | 27 | c1 Cen | HR5485 | 2 | 4.75 | 115.50 | 191.10 | –24.69 | –0.85 |
| 67 | Jizu†‡ | 12 | η Lup | HR5948 | 3 | 13.75 | 124.25 | 207.67 | –29.96 | 2.50 |
| 68 | Gui‡ | 5 | 6 | 12.00 | 131.00 | |||||
| 69 | Fuyue†‡ | 1 | G Sco | HR6630 | 6 | 12.75 | 120.50 | 232.88 | –33.06 | –4.29 |
| 70 | Yu | 1 | M 7 | NGC6475 | 6 | 14.00 | 122.00 | 234.42 | –31.06 | –0.81 |
| 71 | Chu‡ | 3 | 7 | 1.75 | 132.50 | |||||
| 72 | Bie‡ | 14 | μ CrA | HR7050 | 8 | 1.00 | 129.50 | 245.39 | –39.10 | –1.46 |
| 73 | Jiukan† | 9 | ι Sgr | HR7581 | 8 | 14.50 | 136.00 | 261.24 | –43.90 | 0.14 |
| 74 | Baijiu | 4 | ι PsA | HR8305 | 10 | 10.00 | 131.25 | 292.62 | –40.45 | –1.08 |
| 75 | Yulin | 57 | υ Aqr | HR8592 | 12 | 4.75 | 120.75 | 308.51 | –30.09 | –1.08 |
| 76 | Beiluo | 1 | α PsA | HR8728 | 12 | 9.00 | 130.75 | 313.37 | –39.61 | –0.74 |
| 77 | Tusikong | 1 | β Cet | HR0188 | 14 | 7.75 | 120.25 | 343.79 | –29.63 | –1.11 |
| 78 | Tiangcang | 6 | η Cet | HR0334 | 15 | 4.75 | 112.00 | 350.50 | –21.81 | –1.42 |
| 79 | Tianqun | 13 | α Cet | HR0911 | 17 | 6.25 | 96.50 | 18.80 | –5.79 | –0.67 |
| 80 | Tianlin | 4 | o Tau | HR1030 | 17 | 11.25 | 90.00 | 23.79 | –0.23 | –1.53 |
| 81 | Tianyuan†‡ | 16 | γ Eri | HR1231 | 19 | 2.75 | 114.00 | 35.35 | –21.42 | 0.95 |
| 82 | Shenqi | 9 | π5 Ori | HR1567 | 19 | 9.50 | 93.00 | 46.78 | –3.38 | –1.72 |
| 83 | Yujing | 4 | β Eri | HR1666 | 19 | 12.25 | 100.75 | 51.51 | –10.17 | –0.87 |
| 84 | Ping | 2 | ε Lep | HR1654 | 20 | 0.75 | 118.00 | 54.41 | –27.25 | –0.95 |
| 85 | Ce | 4 | β Lep | HR1829 | 21 | 3.25 | 115.00 | 59.81 | –24.59 | –1.24 |
| 86 | Tianshi | 1 | ν2 Col | HR1935 | 21 | 7.00 | 123.00 | 64.14 | –31.87 | –0.64 |
| 87 | Junshi | 13 | 17 Lep | HR2148 | 22 | 3.25 | 110.00 | 68.02 | –18.60 | –0.18 |
| 88 | Yeji† | 1 | β CMa | HR2294 | 22 | 8.00 | 111.00 | 72.71 | –19.15 | 0.26 |
| 89 | Lang | 1 | α CMa | HR2491 | 22 | 13.00 | 106.75 | 77.94 | –16.80 | –1.58 |
| 90 | Hu‡ | 9 | κ CMa | HR2538 | 22 | 16.00 | 122.25 | 82.97 | –31.96 | –1.47 |
| 91 | Laoren | 1 | α Car | HR2326 | 22 | 19.00 | 143.50 | 84.50 | –52.66 | –1.22 |
| 92 | Ji† | 5 | δ Vel | HR3485 | 24 | 14.25 | 138.00 | 116.52 | –48.17 | –2.16 |
| 93 | Jiao | 2 | α Vir | HR5056 | 1 | 0.00 | 91.00 | 174.28 | 0.39 | 0.08 |
| 94 | Kang | 4 | κ Vir | HR5315 | 2 | 0.00 | 89.00 | 186.03 | 0.71 | –1.57 |
| 95 | Di† | 4 | α2 Lib | HR5531 | 3 | 0.00 | 94.00 | 194.77 | –5.81 | –3.16 |
| 96 | Fang | 4 | π Sco | HR5944 | 4 | 0.00 | 108.00 | 209.54 | –17.80 | –1.35 |
| 97 | Xin | 3 | σ Sco | HR6084 | 5 | 0.00 | 108.50 | 214.84 | –18.09 | –1.15 |
| 98 | Wei† | 9 | μ1 Sco | HR6247 | 6 | 0.00 | 120.00 | 219.36 | –31.52 | –3.25 |
| 99 | Ji | 4 | γ2 Sgr | HR6746 | 7 | 0.00 | 118.00 | 238.35 | –27.36 | –1.06 |
| 100 | Dou | 6 | φ Sgr | HR7039 | 8 | 0.00 | 116.00 | 248.74 | –25.98 | –1.64 |
| 101 | Niu | 6 | β Cap | HR7776 | 9 | 0.00 | 110.00 | 275.07 | –18.80 | –0.38 |
| 102 | Xu Nu | 4 | ε Aqr | HR7950 | 10 | 0.00 | 106.00 | 282.81 | –14.86 | –0.38 |
| 103 | Xu | 2 | β Aqr | HR8232 | 11 | 0.00 | 104.00 | 294.54 | –12.87 | –0.36 |
| 104 | Wei | 3 | α Aqr | HR8414 | 12 | 0.00 | 99.00 | 304.03 | –8.31 | –0.73 |
| 105 | Ying Shi | 2 | α Peg | HR8781 | 13 | 0.00 | 85.00 | 320.25 | 4.80 | –1.42 |
| 106 | Dong Bi | 2 | γ Peg | HR0039 | 14 | 0.00 | 86.00 | 336.78 | 3.71 | –1.53 |
| 107 | Kui | 16 | ζ And | HR0215 | 15 | 0.00 | 77.00 | 345.08 | 12.62 | –1.49 |
| 108 | Lou | 3 | β Ari | HR0553 | 16 | 0.00 | 80.00 | 0.99 | 9.54 | –1.61 |
| 109 | Wei | 3 | 35 Ari | HR0801 | 17 | 0.00 | 72.00 | 11.85 | 17.25 | –1.78 |
| 110 | Mao | 17 | 17 Tau | HR1142 | 18 | 0.00 | 74.00 | 26.58 | 15.35 | –1.71 |
| 111 | Bi | 8 | ε Tau | HR1409 | 19 | 0.00 | 78.00 | 37.70 | 12.05 | –1.07 |
| 112 | Zhi | 3 | φ1 Ori | HR1876 | 20 | 0.00 | 84.00 | 55.41 | 5.40 | –1.81 |
| 113 | Shen | 10 | δ Ori | HR1852 | 21 | 0.00 | 94.50 | 56.47 | –3.76 | –0.62 |
| 114 | Dong Jing | 8 | μ Gem | HR2286 | 22 | 0.00 | 70.00 | 64.34 | 20.48 | –0.53 |
| 115 | Gui | 5 | θ Cnc | HR3357 | 23 | 0.00 | 68.00 | 97.03 | 22.55 | –0.43 |
| 116 | Liu | 8 | δ Hya | HR3410 | 24 | 0.00 | 79.00 | 101.03 | 10.67 | –1.46 |
| 117 | 7 | α Hya | HR3748 | 25 | 0.00 | 91.00 | 115.83 | –1.34 | –1.65 | |
| 118 | Zhang | 6 | υ1 Hya | HR3903 | 26 | 0.00 | 97.00 | 122.56 | –6.57 | –0.96 |
| 119 | Yi | 22 | α Crt | HR4287 | 27 | 0.00 | 99.00 | 139.36 | –7.99 | –0.42 |
| 120 | Zhen† | 4 | γ Crv | HR4662 | 28 | 0.00 | 99.00 | 157.48 | –6.04 | 1.53 |
| Id . | Names . | No. . | Bayer . | HR . | Xiu . | L.A. . | P.A. . | RA . | Dec . | Δi . |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sheti | 6 | η Boo | HR5235 | 1 | 8.25 | 59.50 | 183.23 | 29.61 | –1.75 |
| 2 | Dajiao† | 1 | α Boo | HR5340 | 2 | 2.50 | 58.00 | 189.01 | 30.05 | –2.79 |
| 3 | Genghe | 3 | ρ Boo | HR5429 | 2 | 8.00 | 48.00 | 194.81 | 40.83 | –1.86 |
| 4 | Zhaoyao | 1 | γ Boo | HR5435 | 3 | 2.50 | 40.75 | 196.21 | 48.70 | –1.13 |
| 5 | Xuange | 1 | λ Boo | HR5351 | 3 | 1.00 | 32.50 | 193.09 | 56.79 | –1.18 |
| 6 | Tianqiang†‡ | 3 | κ2 Boo | HR5329 | 3 | 0.75 | 28.75 | 193.73 | 62.50 | 0.84 |
| 7 | Tianpei‡ | 5 | ι Her | HR6588 | 7 | 8.50 | 42.00 | 250.39 | 48.54 | –0.07 |
| 8 | Nuchuang† | 3 | π Her | HR6418 | 7 | 1.00 | 50.00 | 240.74 | 40.88 | 0.16 |
| 9 | Qigong | 7 | β Boo | HR5602 | 3 | 4.50 | 39.25 | 205.44 | 49.92 | –1.40 |
| 10 | Guansuo†‡ | 9 | β CrB | HR5747 | 6 | 0.50 | 59.25 | 210.18 | 37.92 | 6.32 |
| 11 | Tianji | 9 | ξ CrB | HR6103 | 6 | 5.00 | 51.50 | 225.20 | 37.55 | –1.69 |
| 12 | Zhinu | 3 | α Lyr | HR7001 | 8 | 11.00 | 52.00 | 261.76 | 38.69 | –0.06 |
| 13 | Tianshi | 22 | ζ Oph | HR6175 | 6 | 0.75 | 94.25 | 221.21 | –3.90 | –1.01 |
| 14 | Dizuo | 1 | α1 Her | HR6406 | 6 | 15.50 | 71.25 | 235.02 | 19.00 | –0.78 |
| 15 | Hou | 1 | α Oph | HR6556 | 7 | 2.50 | 73.75 | 239.72 | 16.24 | –1.07 |
| 16 | Huanzhe | 4 | 60 Her | HR6355 | 6 | 12.00 | 72.50 | 232.36 | 17.81 | –0.73 |
| 17 | Dou†‡ | 5 | κ Oph | HR6299 | 6 | 10.25 | 75.00 | 229.77 | 14.85 | –4.18 |
| 18 | Zongzheng | 2 | γ Oph | HR6629 | 7 | 2.00 | 84.00 | 240.96 | 5.95 | –1.26 |
| 19 | Zongren† | 4 | 68 Oph | HR6723 | 7 | 7.50 | 85.00 | 244.09 | 3.89 | –2.33 |
| 20 | Zong | 2 | 71 Oph | HR6770 | 7 | 9.00 | 79.00 | 246.95 | 10.90 | –1.24 |
| 21 | Dongxian‡ | 8 | ψ Oph | HR6104 | 5 | 2.00 | 103.00 | 218.74 | –9.62 | 1.91 |
| 22 | Tianjiang | 4 | θ Oph | HR6453 | 6 | 6.25 | 111.00 | 229.25 | –20.03 | –0.62 |
| 23 | Jianxing† | 6 | ξ2 Sgr | HR7150 | 8 | 7.25 | 113.25 | 253.08 | –20.84 | 0.78 |
| 24 | Tianbian†‡ | 9 | 5 Aql | HR7059 | 8 | 6.75 | 90.75 | 254.99 | 1.32 | 0.76 |
| 25 | Hegu | 12 | α Aql | HR7557 | 8 | 22.75 | 85.00 | 272.29 | 5.85 | –0.37 |
| 26 | Lizhu† | 5 | 1 Aqr | HR7897 | 10 | 0.00 | 94.00 | 282.60 | –4.67 | –2.02 |
| 27 | Hugua | 5 | ζ Del | HR7871 | 10 | 0.25 | 81.50 | 284.20 | 9.47 | –0.21 |
| 28 | Tianjin‡ | 9 | δ Cyg | HR7528 | 8 | 2.00 | 49.00 | 279.88 | 41.50 | –0.20 |
| 29 | Dengshe† | 22 | α Lac | HR8585 | 13 | 1.50 | 51.00 | 317.32 | 40.43 | 0.69 |
| 30 | Wangliang | 5 | β Cas | HR0021 | 14 | 0.50 | 42.50 | 338.12 | 47.67 | –0.45 |
| 31 | Gedao | 6 | φ Cas | HR0382 | 15 | 5.00 | 43.25 | 351.63 | 46.64 | –0.74 |
| 32 | Fulu | 1 | υ1 Cas | HR0253 | 15 | 3.00 | 43.00 | 346.82 | 47.32 | –0.30 |
| 33 | Tianjiangjun† | 11 | γ1 And | HR0603 | 15 | 15.50 | 60.33 | 1.66 | 31.14 | 0.61 |
| 34 | Daling | 8 | 9 Per | HR0685 | 16 | 6.25 | 44.25 | 3.96 | 44.86 | –1.52 |
| 35 | Tianchuan | 9 | η Per | HR0834 | 16 | 9.00 | 43.50 | 9.54 | 45.40 | –1.72 |
| 36 | Juanshi | 6 | ν Per | HR1135 | 17 | 10.25 | 56.00 | 23.55 | 33.61 | –1.19 |
| 37 | Wuche | 14 | ι Aur | HR1577 | 19 | 3.00 | 63.00 | 41.65 | 26.95 | –0.95 |
| 38 | Tianguan | 1 | ζ Tau | HR1910 | 20 | 0.00 | 73.50 | 53.77 | 16.96 | –0.60 |
| 39 | Nanbeihe | 6 | β CMi | HR2845 | 22 | 17.25 | 80.00 | 83.08 | 9.79 | –1.36 |
| 40 | Wuzhuhou | 5 | θ Gem | HR2540 | 22 | 2.00 | 57.00 | 68.60 | 33.11 | –0.71 |
| 41 | Jisui† | 1 | o Gem | HR2930 | 22 | 13.00 | 55.00 | 79.70 | 36.05 | 0.26 |
| 42 | Jixin‡ | 1 | φ Gem | HR3067 | 22 | 21.50 | 61.50 | 85.43 | 29.17 | –0.21 |
| 43 | Suiwei | 4 | 68 Gem | HR2886 | 22 | 19.50 | 72.50 | 83.07 | 17.49 | –1.05 |
| 44 | Xuanyuan† | 17 | α Leo | HR3982 | 26 | 0.75 | 71.00 | 122.92 | 20.57 | 0.55 |
| 45 | Shaowei | 4 | 53 Leo | HR4227 | 26 | 10.50 | 70.50 | 133.73 | 20.44 | –0.08 |
| 46 | Taiwei | 10 | β Vir | HR4540 | 27 | 9.00 | 76.50 | 150.39 | 12.97 | –1.63 |
| 47 | Huangdizuo | 1 | β Leo | HR4534 | 27 | 9.50 | 63.50 | 149.16 | 25.73 | –1.68 |
| 48 | Shidizuo | 4 | ||||||||
| 49 | Neiping†‡ | 4 | ξ Vir | HR4515 | 28 | 0.00 | 72.50 | 148.59 | 19.37 | 0.83 |
| 50 | Langwei‡ | 15 | γ Com | HR4737 | 28 | 0.00 | 157.58 | |||
| 51 | Langjiang | 1 | α2 CVn | HR4915 | 28 | 8.00 | 39.25 | 167.26 | 49.97 | –1.34 |
| 52 | Changchen | 7 | 61 UMa | HR4496 | 28 | 5.00 | 45.00 | 145.10 | 45.17 | –0.48 |
| 53 | Santai | 6 | ι UMa | HR3569 | 22 | 30.75 | 36.25 | 95.03 | 52.99 | –1.28 |
| 54 | Xiang | 1 | χ UMa | HR4518 | 27 | 5.00 | 31.50 | 144.39 | 58.77 | –0.18 |
| 55 | Taiyangshou | 1 | ψ UMa | HR4335 | 26 | 13.25 | 35.50 | 133.80 | 54.67 | –0.34 |
| 56 | Tianlao† | 6 | 44 UMa | HR4246 | 26 | 1.25 | 26.50 | 124.95 | 64.09 | 0.21 |
| 57 | Wenchang | 6 | o UMa | HR3323 | 22 | 15.75 | 25.75 | 79.09 | 63.45 | –1.17 |
| 58 | Beidou | 8 | α UMa | HR4301 | 26 | 0.00 | 18.25 | 123.41 | 71.35 | –0.66 |
| 59 | Ziwei† | 15 | κ Dra | HR4787 | 28 | 10.00 | 9.50 | 154.83 | 81.33 | 0.70 |
| 60 | Beiji Gouchen | 11 | α UMi | HR0424 | 14 | 8.75 | 11.50 | 348.04 | 77.67 | –0.99 |
| 61 | Tianyi‡ | 1 | 7 Dra | HR4863 | 28 | 10.00 | 10.50 | 163.49 | 78.43 | –1.22 |
| 62 | Taiyi† | 1 | 8 Dra | HR4916 | 28 | 10.00 | 10.00 | 167.34 | 77.09 | –3.06 |
| 63 | Kulou†‡ | 29 | δ Cru | HR4656 | 28 | 0.25 | 140.00 | 159.22 | –47.22 | 0.77 |
| 64 | Nanmen | 2 | ξ2 Cen | HR4942 | 28 | 14.00 | 130.00 | 169.28 | –38.27 | –0.14 |
| 65 | Ping†‡ | 2 | γ Hya | HR5020 | 28 | 14.00 | 100.00 | 172.48 | –11.58 | –3.02 |
| 66 | Qiguan | 27 | c1 Cen | HR5485 | 2 | 4.75 | 115.50 | 191.10 | –24.69 | –0.85 |
| 67 | Jizu†‡ | 12 | η Lup | HR5948 | 3 | 13.75 | 124.25 | 207.67 | –29.96 | 2.50 |
| 68 | Gui‡ | 5 | 6 | 12.00 | 131.00 | |||||
| 69 | Fuyue†‡ | 1 | G Sco | HR6630 | 6 | 12.75 | 120.50 | 232.88 | –33.06 | –4.29 |
| 70 | Yu | 1 | M 7 | NGC6475 | 6 | 14.00 | 122.00 | 234.42 | –31.06 | –0.81 |
| 71 | Chu‡ | 3 | 7 | 1.75 | 132.50 | |||||
| 72 | Bie‡ | 14 | μ CrA | HR7050 | 8 | 1.00 | 129.50 | 245.39 | –39.10 | –1.46 |
| 73 | Jiukan† | 9 | ι Sgr | HR7581 | 8 | 14.50 | 136.00 | 261.24 | –43.90 | 0.14 |
| 74 | Baijiu | 4 | ι PsA | HR8305 | 10 | 10.00 | 131.25 | 292.62 | –40.45 | –1.08 |
| 75 | Yulin | 57 | υ Aqr | HR8592 | 12 | 4.75 | 120.75 | 308.51 | –30.09 | –1.08 |
| 76 | Beiluo | 1 | α PsA | HR8728 | 12 | 9.00 | 130.75 | 313.37 | –39.61 | –0.74 |
| 77 | Tusikong | 1 | β Cet | HR0188 | 14 | 7.75 | 120.25 | 343.79 | –29.63 | –1.11 |
| 78 | Tiangcang | 6 | η Cet | HR0334 | 15 | 4.75 | 112.00 | 350.50 | –21.81 | –1.42 |
| 79 | Tianqun | 13 | α Cet | HR0911 | 17 | 6.25 | 96.50 | 18.80 | –5.79 | –0.67 |
| 80 | Tianlin | 4 | o Tau | HR1030 | 17 | 11.25 | 90.00 | 23.79 | –0.23 | –1.53 |
| 81 | Tianyuan†‡ | 16 | γ Eri | HR1231 | 19 | 2.75 | 114.00 | 35.35 | –21.42 | 0.95 |
| 82 | Shenqi | 9 | π5 Ori | HR1567 | 19 | 9.50 | 93.00 | 46.78 | –3.38 | –1.72 |
| 83 | Yujing | 4 | β Eri | HR1666 | 19 | 12.25 | 100.75 | 51.51 | –10.17 | –0.87 |
| 84 | Ping | 2 | ε Lep | HR1654 | 20 | 0.75 | 118.00 | 54.41 | –27.25 | –0.95 |
| 85 | Ce | 4 | β Lep | HR1829 | 21 | 3.25 | 115.00 | 59.81 | –24.59 | –1.24 |
| 86 | Tianshi | 1 | ν2 Col | HR1935 | 21 | 7.00 | 123.00 | 64.14 | –31.87 | –0.64 |
| 87 | Junshi | 13 | 17 Lep | HR2148 | 22 | 3.25 | 110.00 | 68.02 | –18.60 | –0.18 |
| 88 | Yeji† | 1 | β CMa | HR2294 | 22 | 8.00 | 111.00 | 72.71 | –19.15 | 0.26 |
| 89 | Lang | 1 | α CMa | HR2491 | 22 | 13.00 | 106.75 | 77.94 | –16.80 | –1.58 |
| 90 | Hu‡ | 9 | κ CMa | HR2538 | 22 | 16.00 | 122.25 | 82.97 | –31.96 | –1.47 |
| 91 | Laoren | 1 | α Car | HR2326 | 22 | 19.00 | 143.50 | 84.50 | –52.66 | –1.22 |
| 92 | Ji† | 5 | δ Vel | HR3485 | 24 | 14.25 | 138.00 | 116.52 | –48.17 | –2.16 |
| 93 | Jiao | 2 | α Vir | HR5056 | 1 | 0.00 | 91.00 | 174.28 | 0.39 | 0.08 |
| 94 | Kang | 4 | κ Vir | HR5315 | 2 | 0.00 | 89.00 | 186.03 | 0.71 | –1.57 |
| 95 | Di† | 4 | α2 Lib | HR5531 | 3 | 0.00 | 94.00 | 194.77 | –5.81 | –3.16 |
| 96 | Fang | 4 | π Sco | HR5944 | 4 | 0.00 | 108.00 | 209.54 | –17.80 | –1.35 |
| 97 | Xin | 3 | σ Sco | HR6084 | 5 | 0.00 | 108.50 | 214.84 | –18.09 | –1.15 |
| 98 | Wei† | 9 | μ1 Sco | HR6247 | 6 | 0.00 | 120.00 | 219.36 | –31.52 | –3.25 |
| 99 | Ji | 4 | γ2 Sgr | HR6746 | 7 | 0.00 | 118.00 | 238.35 | –27.36 | –1.06 |
| 100 | Dou | 6 | φ Sgr | HR7039 | 8 | 0.00 | 116.00 | 248.74 | –25.98 | –1.64 |
| 101 | Niu | 6 | β Cap | HR7776 | 9 | 0.00 | 110.00 | 275.07 | –18.80 | –0.38 |
| 102 | Xu Nu | 4 | ε Aqr | HR7950 | 10 | 0.00 | 106.00 | 282.81 | –14.86 | –0.38 |
| 103 | Xu | 2 | β Aqr | HR8232 | 11 | 0.00 | 104.00 | 294.54 | –12.87 | –0.36 |
| 104 | Wei | 3 | α Aqr | HR8414 | 12 | 0.00 | 99.00 | 304.03 | –8.31 | –0.73 |
| 105 | Ying Shi | 2 | α Peg | HR8781 | 13 | 0.00 | 85.00 | 320.25 | 4.80 | –1.42 |
| 106 | Dong Bi | 2 | γ Peg | HR0039 | 14 | 0.00 | 86.00 | 336.78 | 3.71 | –1.53 |
| 107 | Kui | 16 | ζ And | HR0215 | 15 | 0.00 | 77.00 | 345.08 | 12.62 | –1.49 |
| 108 | Lou | 3 | β Ari | HR0553 | 16 | 0.00 | 80.00 | 0.99 | 9.54 | –1.61 |
| 109 | Wei | 3 | 35 Ari | HR0801 | 17 | 0.00 | 72.00 | 11.85 | 17.25 | –1.78 |
| 110 | Mao | 17 | 17 Tau | HR1142 | 18 | 0.00 | 74.00 | 26.58 | 15.35 | –1.71 |
| 111 | Bi | 8 | ε Tau | HR1409 | 19 | 0.00 | 78.00 | 37.70 | 12.05 | –1.07 |
| 112 | Zhi | 3 | φ1 Ori | HR1876 | 20 | 0.00 | 84.00 | 55.41 | 5.40 | –1.81 |
| 113 | Shen | 10 | δ Ori | HR1852 | 21 | 0.00 | 94.50 | 56.47 | –3.76 | –0.62 |
| 114 | Dong Jing | 8 | μ Gem | HR2286 | 22 | 0.00 | 70.00 | 64.34 | 20.48 | –0.53 |
| 115 | Gui | 5 | θ Cnc | HR3357 | 23 | 0.00 | 68.00 | 97.03 | 22.55 | –0.43 |
| 116 | Liu | 8 | δ Hya | HR3410 | 24 | 0.00 | 79.00 | 101.03 | 10.67 | –1.46 |
| 117 | 7 | α Hya | HR3748 | 25 | 0.00 | 91.00 | 115.83 | –1.34 | –1.65 | |
| 118 | Zhang | 6 | υ1 Hya | HR3903 | 26 | 0.00 | 97.00 | 122.56 | –6.57 | –0.96 |
| 119 | Yi | 22 | α Crt | HR4287 | 27 | 0.00 | 99.00 | 139.36 | –7.99 | –0.42 |
| 120 | Zhen† | 4 | γ Crv | HR4662 | 28 | 0.00 | 99.00 | 157.48 | –6.04 | 1.53 |
The columns represent the entry number, the name of the asterism, the number of constituent stars, the identified stars in Bayer designation and HR-number, the determinative stars and the lodge angle (L.A.), the polar angle (P.A.), right ascension (RA) and the declination (Dec) of the identified star at the epoch of 104 BCE, and the residual in declination (Δi) at the epoch of 104 BCE. Identifications are adopted from Sun and Kistemaker (1997).
The stars eventually removed from the analysis due to their large deviations.
The stars identified differently from Sun and Kistemaker (1997), whose details are shown in the Appendix.
The lodge angles are given in the seventh column of table 1, along with the reference stars denoted by the numbers of lunar lodges in the sixth column. Here, a number n in the sixth column means the determinative star of the nth lunar lodge. The lodge angles and polar angles are described in Chinese degrees or du, which can be converted into Babylonian degrees by multiplying by 360°/365.25 du. We will use the Babylonian degrees in the main text. We also note that the declination of a reference star, δc, is obtained from the polar angle, P, using the relationship δc = 90° − P. The right ascensions and the declinations are given in Babylonian degrees. The residuals in declination, Δi, are also given in Babylonian degrees for the epoch of 104 BCE.
2.2 Analysis methods
One can find the epoch of observation by finding the equatorial plane of a certain time that fits best to a set of positional data considering the precession of equinoxes. We make use of the fact that the polar angles observed at an epoch tr deviate from the polar angles at a certain epoch ts, which is not too far from tr, form a sinusoidal function of right ascension. The polar angles are assumed to have been measured with meridian instruments when the astronomical objects culminate on the meridian line. Meridian observations have systemic errors because the axis of the meridian instrument may not be aligned with the axis of the celestial poles. As such, we can analyze the observed coordinates of the stars as follows. A more comprehensive description of the methodology is given by Sun and Kistemaker (1997).
Let us denote the deviation of an observed declination |$\delta _i^{\rm obs}$| from the calculated value |$\delta _i^{\rm cal}$| for the ith reference star at a supposed epoch, ts, by Δi. In this paper we will analyze the polar angles of N reference stars, so i = 1, 2, …, N. The given polar angle of the ith reference star, Pi, is converted into the declination |$\delta _i^{\rm obs}$| by |$\delta _i^{\rm obs}=90^{\circ }-P_i$|. We obtain the calculated declination of the star, |$\delta _i^{\rm cal}$|, at the supposed epoch, ts, by converting the J2000.0 coordinates to the coordinates at the supposed epoch by considering the precession of equinoxes with the method described by Meeus (1998). For the J2000.0 coordinates, we adopt the ICRS J2000.0 coordinate obtained from the SIMBAD.6 Although they are small, we also take the proper motions into account. Then, we define the deviation |$\Delta _i\equiv \delta _i^{\rm cal}-\delta _i^{\rm obs}$| for the ith reference star.
These deviations can be fitted with a sinusoidal function f(α) = c + acos α, as suggested by Sun and Kistemaker (1997). Here, α is the right ascension of the reference star at the supposed time of observation ts. We see that the amplitude a = n × (ts − tr), where the rate of change of the declination due to the precession of equinoxes n = 0.°5567 per century, and (ts − tr) is the time difference between the epoch of observation tr and the supposed time ts. Thus, at the epoch of observation, the fitting parameter a = 0. In other words, in order to find the epoch of observation, we have only to find ts when a = 0. The coefficient c represents the misalignment angle of the instrument’s axis of rotation with respect to the direction of the north celestial pole in meridian observations.
Thereby, we know that [Δi] ≃ f(αi) = c + acos αi, where αi is the right ascension of the ith reference star at the trial epoch ts with the precessional effects corrected. Here, the coefficients can be obtained by |$a={1\over \pi }\int _{0}^{2\pi }f(\alpha )\cos \alpha \, d\alpha$| and |$c={1\over 2\pi }\int _{0}^{2\pi }f(\alpha )d\alpha$|, which are similar to Fourier analysis. In practice, we can obtain the amplitude a and the misalignment c by using the numerical integration of Δi. That is, |$a\simeq {1\over \pi }\sum _{i=1}^{N}[\Delta _i]\cos \alpha _i \, \delta \alpha _i$| and |$c\simeq {1\over 2\pi }\sum _{i=1}^{N}[\Delta _i]\delta \alpha _i$|, where |$\delta \alpha_{i}$| is the interval in right ascension between neighboring reference stars.
However, this numerical scheme is not useful for either highly sparse or highly uneven data sets. Thus, we devise a method to fit the data points with the same function f(α) = c + acos α by minimizing the weighted sum of squared residuals, |$\Phi ^2(c,a)\equiv \sum _{i=1}^{N}w_i r_i^2$|. Here, ri ≡ Δi(αi) − f(αi) is the residual for the ith data point, and |$w$|i is the weight given to that point. The best fit can be found by selecting parameters (c, a) that minimize this quantity Φ2(c, a). Thus, this method is a special case of generalized least squares called weighted least squares (Press et al. 1988; Bevington & Robinson 2003). This can be applied to samples of independent measurements, which is guaranteed by our assumption that all polar angles must have been measured independently with the same meridian instrument on the same occasion.
The weight |$w$|i for each point can be assumed to be inversely proportional to the variance of each data point. That is to say, |$w_i=1/\sigma _i^2$|. Here, σi can be approximated by the measurement error si for the ith star. However, no errors are given in the catalog. Thus, we assume that the measurement errors are constant or si = s, because they were measured with the same meridian instrument and method on the same occasion. Then, s is the sample standard error estimated from the entire measurement data for the N reference stars. If the number of stars is sufficiently large, σ ≃ s. Therefore, we have only to calculate a sort of merit function |$\phi (c,a)\equiv \Phi ^2(c,a)/w_i=\sum _{i=1}^{N}r_i^2$| to find the parameters (c, a) that minimize φ(c, a) for given data points. Then, we can estimate the measurement error, s, by calculating |$s^2=\sum _{i=1}^{N}r_i^2/(N-1)$| for the best-fitting parameters. If we approximate |$\sigma _i^2\simeq s^2$| or |$w_i=1/\sigma _i^2\simeq 1/s^2$|, then Φ2∝χ2. For this reason, this least squares method can also be called a χ2 method.
There are a number of extreme outliers whose residual is larger than 2 σ error bars. Hence, we remove them and make another best fit by minimizing their χ2 value with the procedure explained above. After a couple of iterations we get sufficiently accurate results. These are the basic procedures for analyzing the coordinates of the SSXJ reference stars.
Note that the uncertainty estimations in the above-mentioned two methods are just approximations. Hence, we make a more robust and sophisticated estimation by adopting a bootstrap method to calculate the confidence interval for the epoch of observation tr. The number of data points in our case is not large enough to confidently assume that the parent distribution of the residuals is Gaussian. In this case, the bootstrap method is useful for estimating standard errors and obtaining confidence intervals for tr. We apply Efron’s approach or residual resamplings only to the Δi values (Efron & Tibshirani 1993).
The bootstrap samplings are carried out as follows:
Make a best fit to the original data with either the Fourier method or the χ2 method to find the epoch ts = tr.
Obtain the residuals ri = Δi − f(αi) when ts = tr.
A set of resampled residuals |$\lbrace r_i^*\rbrace$|, i = 1, ⋅⋅⋅, N, of the same size is drawn with replacement from {ri}, i = 1, ⋅⋅⋅, N.
The resampled residuals |$\lbrace r_i^*\rbrace$| are added to the predicted values of the original fit. Here, the predicted values means the predicted declination |$(\delta _i^{\rm obs})^{\prime }=\delta _i^{\rm cal}-f(\alpha _i)$| or |$(\delta _i^{\rm obs})^{\prime }=\delta _i^{\rm cal}-c$| at ts = tr, which will yield the best-fitting parameters (c, a) at ts = tr. Hence, the resampled declinations are |$\delta _i^{\rm obs*}=(\delta _i^{\rm obs})^{\prime }+r_j$|, where the subscript j is an integer number j = R × N + 1 for a uniform random number 0 < R < 1.
Then, make a best fit to the resampled data set |$\lbrace \delta _i^{\rm obs*}\rbrace$| to obtain |$t_{\rm r}^*$|.
Repeat steps 3–5 a sufficiently large number of times.
We finally obtain statistics such as mean, median, percentiles, standard error, and confidence intervals for |$\lbrace t_{\rm r}^*\rbrace$|. In this paper we make 40000 bootstrap resamples. The 95% (90%) confidence intervals for tr can be obtained from the bootstrap results. For example, the 95% (90%) confidence interval [tA, tB] can be found by just reading off from the sorted epochs calculated for the resampled data sets. That is to say, tA is the tr value for the 2.5 (5) percentile and tB is the tr value for the 97.5 (95) percentile of the resultant tr values. We note that the distributions of |$t_{\rm r}^*$| values in this paper are usually normal. Note that the 1 σ, 2 σ, and 3 σ confidence levels correspond to the |$68.2689\%$|, |$95.4500\%$|, and |$99.7300\%$| confidence levels, respectively.
3 Results
3.1 Entire SSXJ stars
Assuming that both the polar angles and the lodge angles of all the SSXJ stars were measured on the same occasion, we apply the Fourier fit method to all 116 SSXJ stars given by Sun and Kistemaker (1997). As shown in table 2, we obtain the epoch of observation tr = 〈tr〉 ± Δt = −79 ± 21, the 1 σ measurement error s = 1.°24, and the misalignment angle c = −0.°82. The uncertainty in the epoch of observation is obtained by generating 40000 bootstrap resamples to obtain the normal distribution of the epoch with |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-78.8\pm 33.8\:$|yr (to 1 σ), which is equivalent to the bootstrap 95% confidence interval tr = [−145, −11] and the 90% confidence interval tr = [−134, −23]. We show these results in the upper part of table 2.
Epochs of observation and their uncertainties for the stars listed in the SSXJ catalog estimated using the Fourier and χ2 methods.*
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Whole SSXJ, Fourier method, NBS = 40000 | ||||||
| 116 | –0.82 | 1.24 | –79 ± 21 | –78.8 ± 33.8 | [−145, −11] | [−134, −23] |
| 115 | –0.88 | 1.05 | –96 ± 18 | –96.4 ± 28.6 | [−153, −40] | [−143, −49] |
| 111 | –0.86 | 0.89 | –94 ± 15 | –93.6 ± 24.5 | [−142, −46] | [−134, −53] |
| 105 | –0.86 | 0.74 | –72 ± 13 | –71.6 ± 21.3 | [−113, −29] | [−106, −36] |
| 98 | –0.91 | 0.64 | –70 ± 12 | –70.3 ± 18.9 | [−107, −33] | [−101, −39] |
| 94 | –0.96 | 0.58 | –86 ± 11 | –86.5 ± 17.7 | [−121, −52] | [−116, −57] |
| 92 | –0.98 | 0.56 | –84 ± 10 | –84.4 ± 16.9 | [−117, −51] | [−112, −57] |
| 91 | –1.00 | 0.55 | –87 ± 10 | –86.6 ± 16.8 | [−119, −54] | [−114, −59] |
| 89 | –1.00 | 0.53 | –87 ± 10 | –87.3 ± 16.2 | [−119, −55] | [−114, −60] |
| 110 | –0.86 | 1.05 | –77 ± 18 | Sun (1994) | ||
| 116 | –0.86 | 1.08 | –77 ± 20 | Sun and Kistemaker (1997) | ||
| Whole SSXJ, χ2 method, NBS = 40000 | ||||||
| 116 | –0.86 | 1.24 | –95 ± 21 | –95.1 ± 29.4 | [−152, −37] | [−143, −46] |
| 115 | –0.87 | 1.23 | –101 ± 21 | –101.3 ± 29.1 | [−158, −43] | [−149, −53] |
| 112 | –0.88 | 0.91 | –110 ± 15 | –110.2 ± 21.8 | [−153, −67] | [−146, −74] |
| 106 | –0.81 | 0.76 | –84 ± 13 | –83.5 ± 19.3 | [−121, −45] | [−115, −52] |
| 99 | –0.89 | 0.66 | –84 ± 12 | –84.0 ± 17.1 | [−117, −51] | [−112, −56] |
| 95 | –0.95 | 0.59 | –92 ± 11 | –91.8 ± 15.7 | [−123, −61] | [−118, −66] |
| 92 | –0.97 | 0.56 | –87 ± 10 | –87.2 ± 14.9 | [−116, −58] | [−111, −63] |
| 91 | –0.98 | 0.55 | –90 ± 10 | –89.8 ± 14.8 | [−119, −61] | [−114, −65] |
| 89 | –1.00 | 0.53 | –93 ± 10 | –92.9 ± 14.3 | [−121, −65] | [−116, −69] |
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Whole SSXJ, Fourier method, NBS = 40000 | ||||||
| 116 | –0.82 | 1.24 | –79 ± 21 | –78.8 ± 33.8 | [−145, −11] | [−134, −23] |
| 115 | –0.88 | 1.05 | –96 ± 18 | –96.4 ± 28.6 | [−153, −40] | [−143, −49] |
| 111 | –0.86 | 0.89 | –94 ± 15 | –93.6 ± 24.5 | [−142, −46] | [−134, −53] |
| 105 | –0.86 | 0.74 | –72 ± 13 | –71.6 ± 21.3 | [−113, −29] | [−106, −36] |
| 98 | –0.91 | 0.64 | –70 ± 12 | –70.3 ± 18.9 | [−107, −33] | [−101, −39] |
| 94 | –0.96 | 0.58 | –86 ± 11 | –86.5 ± 17.7 | [−121, −52] | [−116, −57] |
| 92 | –0.98 | 0.56 | –84 ± 10 | –84.4 ± 16.9 | [−117, −51] | [−112, −57] |
| 91 | –1.00 | 0.55 | –87 ± 10 | –86.6 ± 16.8 | [−119, −54] | [−114, −59] |
| 89 | –1.00 | 0.53 | –87 ± 10 | –87.3 ± 16.2 | [−119, −55] | [−114, −60] |
| 110 | –0.86 | 1.05 | –77 ± 18 | Sun (1994) | ||
| 116 | –0.86 | 1.08 | –77 ± 20 | Sun and Kistemaker (1997) | ||
| Whole SSXJ, χ2 method, NBS = 40000 | ||||||
| 116 | –0.86 | 1.24 | –95 ± 21 | –95.1 ± 29.4 | [−152, −37] | [−143, −46] |
| 115 | –0.87 | 1.23 | –101 ± 21 | –101.3 ± 29.1 | [−158, −43] | [−149, −53] |
| 112 | –0.88 | 0.91 | –110 ± 15 | –110.2 ± 21.8 | [−153, −67] | [−146, −74] |
| 106 | –0.81 | 0.76 | –84 ± 13 | –83.5 ± 19.3 | [−121, −45] | [−115, −52] |
| 99 | –0.89 | 0.66 | –84 ± 12 | –84.0 ± 17.1 | [−117, −51] | [−112, −56] |
| 95 | –0.95 | 0.59 | –92 ± 11 | –91.8 ± 15.7 | [−123, −61] | [−118, −66] |
| 92 | –0.97 | 0.56 | –87 ± 10 | –87.2 ± 14.9 | [−116, −58] | [−111, −63] |
| 91 | –0.98 | 0.55 | –90 ± 10 | –89.8 ± 14.8 | [−119, −61] | [−114, −65] |
| 89 | –1.00 | 0.53 | –93 ± 10 | –92.9 ± 14.3 | [−121, −65] | [−116, −69] |
The first column is the number of reference stars in the sample analyzed. The second column is the misalignment error c in Babylonian degrees. The third column is the measurement errors s in Babylonian degrees. The fourth column is the estimated epoch of observation tr with its uncertainty or the standard deviation of the mean Δt. The fifth to seventh columns represent the uncertainties estimated by bootstrap resamplings.
Epochs of observation and their uncertainties for the stars listed in the SSXJ catalog estimated using the Fourier and χ2 methods.*
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Whole SSXJ, Fourier method, NBS = 40000 | ||||||
| 116 | –0.82 | 1.24 | –79 ± 21 | –78.8 ± 33.8 | [−145, −11] | [−134, −23] |
| 115 | –0.88 | 1.05 | –96 ± 18 | –96.4 ± 28.6 | [−153, −40] | [−143, −49] |
| 111 | –0.86 | 0.89 | –94 ± 15 | –93.6 ± 24.5 | [−142, −46] | [−134, −53] |
| 105 | –0.86 | 0.74 | –72 ± 13 | –71.6 ± 21.3 | [−113, −29] | [−106, −36] |
| 98 | –0.91 | 0.64 | –70 ± 12 | –70.3 ± 18.9 | [−107, −33] | [−101, −39] |
| 94 | –0.96 | 0.58 | –86 ± 11 | –86.5 ± 17.7 | [−121, −52] | [−116, −57] |
| 92 | –0.98 | 0.56 | –84 ± 10 | –84.4 ± 16.9 | [−117, −51] | [−112, −57] |
| 91 | –1.00 | 0.55 | –87 ± 10 | –86.6 ± 16.8 | [−119, −54] | [−114, −59] |
| 89 | –1.00 | 0.53 | –87 ± 10 | –87.3 ± 16.2 | [−119, −55] | [−114, −60] |
| 110 | –0.86 | 1.05 | –77 ± 18 | Sun (1994) | ||
| 116 | –0.86 | 1.08 | –77 ± 20 | Sun and Kistemaker (1997) | ||
| Whole SSXJ, χ2 method, NBS = 40000 | ||||||
| 116 | –0.86 | 1.24 | –95 ± 21 | –95.1 ± 29.4 | [−152, −37] | [−143, −46] |
| 115 | –0.87 | 1.23 | –101 ± 21 | –101.3 ± 29.1 | [−158, −43] | [−149, −53] |
| 112 | –0.88 | 0.91 | –110 ± 15 | –110.2 ± 21.8 | [−153, −67] | [−146, −74] |
| 106 | –0.81 | 0.76 | –84 ± 13 | –83.5 ± 19.3 | [−121, −45] | [−115, −52] |
| 99 | –0.89 | 0.66 | –84 ± 12 | –84.0 ± 17.1 | [−117, −51] | [−112, −56] |
| 95 | –0.95 | 0.59 | –92 ± 11 | –91.8 ± 15.7 | [−123, −61] | [−118, −66] |
| 92 | –0.97 | 0.56 | –87 ± 10 | –87.2 ± 14.9 | [−116, −58] | [−111, −63] |
| 91 | –0.98 | 0.55 | –90 ± 10 | –89.8 ± 14.8 | [−119, −61] | [−114, −65] |
| 89 | –1.00 | 0.53 | –93 ± 10 | –92.9 ± 14.3 | [−121, −65] | [−116, −69] |
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Whole SSXJ, Fourier method, NBS = 40000 | ||||||
| 116 | –0.82 | 1.24 | –79 ± 21 | –78.8 ± 33.8 | [−145, −11] | [−134, −23] |
| 115 | –0.88 | 1.05 | –96 ± 18 | –96.4 ± 28.6 | [−153, −40] | [−143, −49] |
| 111 | –0.86 | 0.89 | –94 ± 15 | –93.6 ± 24.5 | [−142, −46] | [−134, −53] |
| 105 | –0.86 | 0.74 | –72 ± 13 | –71.6 ± 21.3 | [−113, −29] | [−106, −36] |
| 98 | –0.91 | 0.64 | –70 ± 12 | –70.3 ± 18.9 | [−107, −33] | [−101, −39] |
| 94 | –0.96 | 0.58 | –86 ± 11 | –86.5 ± 17.7 | [−121, −52] | [−116, −57] |
| 92 | –0.98 | 0.56 | –84 ± 10 | –84.4 ± 16.9 | [−117, −51] | [−112, −57] |
| 91 | –1.00 | 0.55 | –87 ± 10 | –86.6 ± 16.8 | [−119, −54] | [−114, −59] |
| 89 | –1.00 | 0.53 | –87 ± 10 | –87.3 ± 16.2 | [−119, −55] | [−114, −60] |
| 110 | –0.86 | 1.05 | –77 ± 18 | Sun (1994) | ||
| 116 | –0.86 | 1.08 | –77 ± 20 | Sun and Kistemaker (1997) | ||
| Whole SSXJ, χ2 method, NBS = 40000 | ||||||
| 116 | –0.86 | 1.24 | –95 ± 21 | –95.1 ± 29.4 | [−152, −37] | [−143, −46] |
| 115 | –0.87 | 1.23 | –101 ± 21 | –101.3 ± 29.1 | [−158, −43] | [−149, −53] |
| 112 | –0.88 | 0.91 | –110 ± 15 | –110.2 ± 21.8 | [−153, −67] | [−146, −74] |
| 106 | –0.81 | 0.76 | –84 ± 13 | –83.5 ± 19.3 | [−121, −45] | [−115, −52] |
| 99 | –0.89 | 0.66 | –84 ± 12 | –84.0 ± 17.1 | [−117, −51] | [−112, −56] |
| 95 | –0.95 | 0.59 | –92 ± 11 | –91.8 ± 15.7 | [−123, −61] | [−118, −66] |
| 92 | –0.97 | 0.56 | –87 ± 10 | –87.2 ± 14.9 | [−116, −58] | [−111, −63] |
| 91 | –0.98 | 0.55 | –90 ± 10 | –89.8 ± 14.8 | [−119, −61] | [−114, −65] |
| 89 | –1.00 | 0.53 | –93 ± 10 | –92.9 ± 14.3 | [−121, −65] | [−116, −69] |
The first column is the number of reference stars in the sample analyzed. The second column is the misalignment error c in Babylonian degrees. The third column is the measurement errors s in Babylonian degrees. The fourth column is the estimated epoch of observation tr with its uncertainty or the standard deviation of the mean Δt. The fifth to seventh columns represent the uncertainties estimated by bootstrap resamplings.
As can be seen in figure 1, the reference star of Guansuo [10] has an extremely large deviation from the other stars. We discard this extreme outlier and apply the Fourier method to the remaining 115 stars to obtain the results shown in table 2: the misalignment error c = −0.°88, the measurement error s = 1.°05, the epoch of observation tr ± Δt = −96 ± 18, and the epoch obtained by bootstrap resamplings |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-96.4\pm 28.6$|.
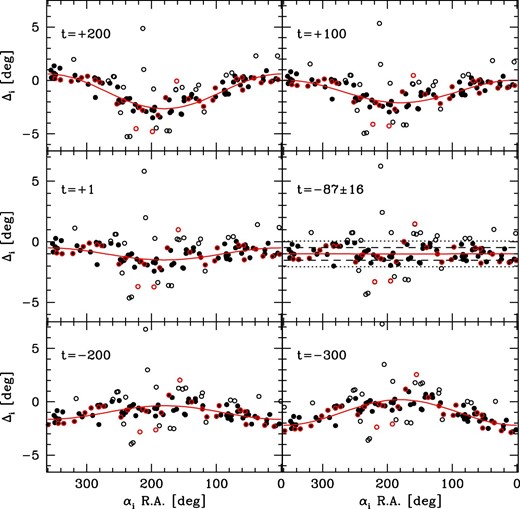
Fitting results obtained by applying the Fourier method to the polar angles in the entire N = 116 SSXJ catalog. Removing the outliers denoted by open dots, we obtain the epoch of observation and its bootstrap uncertainty for the N = 89 SSXJ stars to be |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-87\pm 16$|, and the meridian instrument was misaligned by −1.°00. The measurement error of the polar angle is estimated to be s = 0.°53. The ±1s error line and the ±2s error lines are drawn as dashed lines and dotted lines, respectively. The red dots represent the determinative stars or the reference stars of 28 lunar lodges. (Color online)
In the next step, we discard all the outliers whose absolute value of residual, |Δi|, is larger than twice the measurement error s, or |Δi| > 2s, and make a fitting for the remaining stars. When we make a fit for the N = 116 stars, we find five outliers that meet this criterion: Jizu [67], Guansuo [10], Wei [98], Dou [17], and Fuyue [69]. Such outliers are represented by open dots in figure 1. Subsequently, we make a new fit to the N = 111 stars. We repeat these procedures until there is no star that meets the outlier criterion and the relative decrement of the measurement error becomes sufficiently small, say 10%.
We thus obtain the final results for N = 89 stars: the misalignment of the meridian armillary c = −1.°00, the measurement error s = 0.°53, and the epoch of observation tr ± Δt = −87 ± 10. We generate 40000 bootstrap samples to obtain the normal distribution of tr with |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-87.3\pm 16.2$| (to 1 σ). This is equivalent to the bootstrap 95% confidence interval tr = [−119, −55] and the 90% confidence interval tr = [−114, −60].
We perform a similar analysis using the χ2 method. We do not describe the detailed procedures here, because it is similar to those using the Fourier method described above. We show the results in figure 2 and in the lower part of table 2. We obtain the final results for N = 89 stars: the misalignment of the meridian armillary c = −1.°00, the measurement error s = 0.°53, and the epoch of observation tr ± Δt = −93 ± 10. We generate 40000 bootstrap samples to obtain the normal distribution of tr with |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-92.9\pm 14.3$| (to 1 σ). This is equivalent to the bootstrap 95% confidence interval tr = [−121, −65] and the 90% confidence interval tr = [−116, −69].
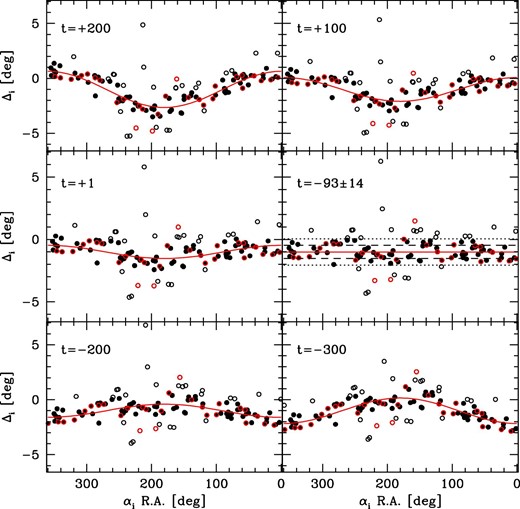
Fitting results obtained by applying the χ2 method to the polar angles in the entire N = 116 SSXJ catalog. Removing the outliers denoted by the open dots, we obtain the epoch of observation and its bootstrap uncertainty for the N = 89 SSXJ stars to be |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-93\pm 14$|, and the meridian instrument was misaligned by −1.°00. The measurement error of the polar angle is estimated to be s = 0.°53. The ±1s error line and the ±2s error lines are drawn as dashed lines and dotted lines, respectively. The red dots represent the determinative stars or the reference stars of 28 lunar lodges. (Color online)
In order to check the reliability of our results, we compare them with previous results given by Sun (1994) and Sun and Kistemaker (1997), who analyzed the same data with the same Fourier method. Sun (1994) reported the results for 117 of the 120 SSXJ stars. However, table 1 of Sun (1994) shows that only 116 stars could be used for the analysis. In fact, the 120 SSXJ stars were listed in the KYZJ. However, the polar angles for the reference stars of Shidizuo [48] and Liangwei [50] are not given in the SSXJ catalog, and the reference stars of Gui [68] and Chu [71] could not be identified by the author. In his table 1, we see that the reference star of Liangwei [50] is identified as γ Com. However, its polar angle is not given in the original literature. Hence, this star must have been regarded by mistake as a star that can be identified and analyzed. Thus, we think that he must have analyzed the polar angles of 110 of the 116 stars to obtain the epoch of observation tr ± Δt = −77 ± 18 and the misalignment error c = −0.°86. The measurement error s can be calculated from the uncertainty in the epoch of observation Δt = 18 yr, because Δt = SRV/0.5567 century and the square root variance (SRV) is calculated by |$\mathit {SRV}=s/\sqrt{N}$| for the N stars. This gives |$\mathit {SRV}=0.^{\!\!\!\circ }10$| for the N = 110 stars. Hence, the measurement error is calculated to be s = 1.°05. Sun and Kistemaker (1997) reported the results for all the SSXJ stars with the same analysis method to obtain the epoch of observation tr ± Δt = −77 ± 20 and the misalignment error c = −0.°86. It is not certain whether “all stars” means the N = 116 case.
We guess that the two papers reported the results obtained by applying the same method to samples which were extracted from the same catalog but whose sizes were different. Their epochs of observation and uncertainties seem to be estimated from the N = 116 case in our study, the misalignment error c from the N = 111 case in our study, and the measurement error s from the N = 115 case in our study. Hence, there must have been some confusion in their reports. When we take this confusion into account, we can conclude that our calculations reliably reproduce the previous research.
Conclusively, in both methods, the fitting parameters in our study converge to c ≃ −1.°00, s = 0.°53, |$t_{\rm r}\pm s/\sqrt{N}\simeq -90\pm 15$| yr. We note that the epoch of observation obtained for the N = 116 SSXJ stars lies between the two events of astronomical observation in 104 BCE and 78–76 BCE that are recorded in the history books of the early Han dynasty. The meaning of these results will become clear in the following sections.
3.2 SSXJ stars excluding determinative stars
So far we have assumed that all the SSXJ stars were measured on the same occasion. However, the reference stars for the 28 lunar lodges, which are also called determinative stars, had been more important than the other SSXJ stars in making calendars. Thus, it is probable that their polar angles had been frequently substituted whenever new observations were made. Furthermore, the SSXJ catalog was compiled much later than the period of the Han dynasty. Thus, we can assume that at least the 28 determinative stars can be separated from the other stars to form an independent group.
We plot the 28 determinative stars with red dots in figures 1 and 2. They seem to be uniformly mixed with the other SSXJ stars marked by black dots. We see in the figures that there are three extreme outliers among the determinative stars, plotted with open red dots, such as Di [95], Wei [98], and Zhen [120], which has been a well-known fact in previous researches (Sun & Kistemaker 1997). Their large deviations have been ascribed to the low declination of these stars. But this cannot be true, because there are many other stars whose polar angles are accurate even though their declinations are very low. Furthermore, we can see that the outliers marked by open dots in figures 1 and 2 are concentrated in the range of 120° < α < 260°, and that the three outlying determinative stars are also distributed in this range.
As such, we divide the SSXJ stars into two groups: one group is composed of the determinative stars and the other group is composed of the remaining SSXJ stars. Here, the former group is called the determinative group, and the latter is called the non-determinative group. We analyze the two independent samples by using the same methods explained above. We report the results of our analyses for the non-determinative group first; the results for the 28 determinative stars will be presented later.
We analyze the non-determinative group with the same methods applied to the full SSXJ data presented in the previous subsection. We show the results obtained using the Fourier method in figure 3, and the results obtained by the χ2 method in figure 4. We also show the epochs of observation and the fitting parameters for each step during the iterations in table 3. After successive iterations to remove outliers, we obtain the final results for the misalignment error c = −0.°92, the measurement error s = 0.°50, and the epoch of observation and its uncertainty obtained with bootstrap resamplings |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-103.9\pm 18.9$|, obtained using Fourier method for N = 63 stars; and c = −0.°96, s = 0.°50, and |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-106.5\pm 15.9$| obtained using the χ2 method for N = 63 stars. We will define the final N = 63 stars as the main group. The measurement error s = 0.°50 is reasonable, because the polar angles were measured up to a scale of 1/4 du. We also find that the outliers rejected during the analyses for the non-determinative group in this subsection coincide with those rejected during the analyses for all the SSXJ stars in the last subsection, whether we use the Fourier method or the χ2 method.
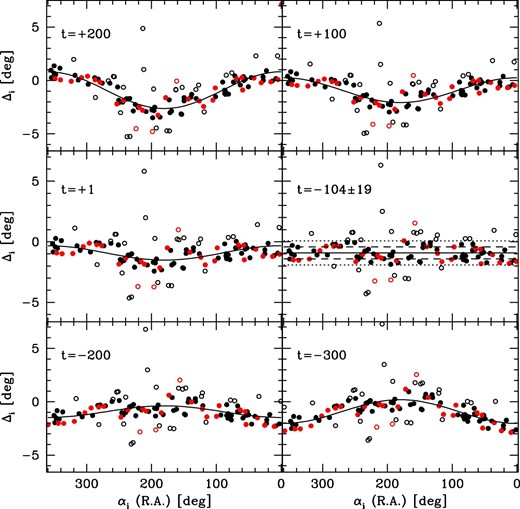
Fitting results obtained by applying the Fourier method to the polar angles of the SSXJ stars excluding the 28 determinative stars. Removing outliers (open dots), we obtain the epoch of observation and its bootstrap uncertainty for the N = 63 stars to be |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-104\pm 19$|, the misalignment of the meridian instrument c = −0.°92, and the measurement error of polar angles s = 0.°50. In the right middle panel, the ±1s error lines and the ±2s error lines are drawn as dashed lines and dotted lines, respectively. (Color online)

Fitting results obtained by applying the χ2 method to the polar angles of the SSXJ stars excluding the 28 determinative stars. Removing outliers (open dots), we obtain the epoch of observation and its bootstrap uncertainty for the N = 63 stars to be |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-107\pm 16$|, the misalignment of the meridian instrument c = −0.°96, and the measurement error of polar angles s = 0.°50. In the right middle panel, the ±1s error lines and the ±2s error lines are drawn as dashed lines and dotted lines, respectively. The blue dashed curves represent the fitting curves for group A, and the blue dotted curves represent the fitting curves for group B.
Epochs of observation and their uncertainties for the SSXJ stars excluding the 28 determinative stars.*
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Non-determinatives, Fourier method, NBS = 40000 | ||||||
| 88 | –0.70 | 1.32 | –120 ± 25 | –119.5 ± 43.1 | [−202, −31] | [−189, −48] |
| 84 | –0.80 | 0.90 | –153 ± 18 | –153.6 ± 29.8 | [−212, −95] | [−202, −105] |
| 79 | –0.77 | 0.78 | –144 ± 16 | –144.3 ± 26.9 | [−197, −92] | [−188, −100] |
| 75 | –0.81 | 0.71 | –151 ± 15 | –151.2 ± 24.8 | [−200, −102] | [−192, −110] |
| 73 | –0.86 | 0.66 | –137 ± 14 | –136.8 ± 23.5 | [−183, −90] | [−175, −98] |
| 71 | –0.91 | 0.62 | –124 ± 13 | –123.8 ± 22.8 | [−168, −79] | [−161, −86] |
| 70 | –0.94 | 0.60 | –112 ± 13 | –111.9 ± 22.3 | [−155, −68] | [−149, −75] |
| 68 | –0.90 | 0.57 | –102 ± 12 | –101.9 ± 21.3 | [−143, −60] | [−137, −67] |
| 67 | –0.92 | 0.56 | –100 ± 12 | –100.2 ± 20.8 | [−140, −59] | [−134, −66] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.3 ± 20.1 | [−143, −64] | [−136, −70] |
| 64 | –0.92 | 0.52 | –104 ± 12 | –103.9 ± 19.6 | [−142, −66] | [−136, −72] |
| 63 | –0.92 | 0.50 | –104 ± 11 | –103.9 ± 18.9 | [−141, −67] | [−135, −73] |
| Non-determinatives, χ2 method, NBS = 40000 | ||||||
| 88 | –0.76 | 1.32 | –103 ± 25 | –102.5 ± 36.4 | [−173, −30] | [−162, −42] |
| 84 | –0.79 | 0.89 | –122 ± 17 | –121.8 ± 24.8 | [−170, −73] | [−162, −81] |
| 81 | –0.72 | 0.80 | –95 ± 16 | –95.2 ± 23.2 | [−140, −49] | [−133, −57] |
| 79 | –0.73 | 0.77 | –85 ± 15 | –84.9 ± 22.4 | [−128, −41] | [−122, −48] |
| 77 | –0.77 | 0.74 | –80 ± 15 | –80.2 ± 21.8 | [−123, −38] | [−116, −45] |
| 73 | –0.85 | 0.66 | –86 ± 14 | –86.3 ± 20.4 | [−127, −47] | [−120, −53] |
| 69 | –0.89 | 0.58 | –102 ± 13 | –101.8 ± 18.4 | [−137, −66] | [−132, −72] |
| 66 | –0.91 | 0.54 | –100 ± 12 | –99.8 ± 17.2 | [−133, −66] | [−128, −71] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.0 ± 16.8 | [−136, −70] | [−131, −75] |
| 63 | –0.96 | 0.50 | –107 ± 11 | –106.5 ± 15.9 | [−138, −76] | [−133, −81] |
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Non-determinatives, Fourier method, NBS = 40000 | ||||||
| 88 | –0.70 | 1.32 | –120 ± 25 | –119.5 ± 43.1 | [−202, −31] | [−189, −48] |
| 84 | –0.80 | 0.90 | –153 ± 18 | –153.6 ± 29.8 | [−212, −95] | [−202, −105] |
| 79 | –0.77 | 0.78 | –144 ± 16 | –144.3 ± 26.9 | [−197, −92] | [−188, −100] |
| 75 | –0.81 | 0.71 | –151 ± 15 | –151.2 ± 24.8 | [−200, −102] | [−192, −110] |
| 73 | –0.86 | 0.66 | –137 ± 14 | –136.8 ± 23.5 | [−183, −90] | [−175, −98] |
| 71 | –0.91 | 0.62 | –124 ± 13 | –123.8 ± 22.8 | [−168, −79] | [−161, −86] |
| 70 | –0.94 | 0.60 | –112 ± 13 | –111.9 ± 22.3 | [−155, −68] | [−149, −75] |
| 68 | –0.90 | 0.57 | –102 ± 12 | –101.9 ± 21.3 | [−143, −60] | [−137, −67] |
| 67 | –0.92 | 0.56 | –100 ± 12 | –100.2 ± 20.8 | [−140, −59] | [−134, −66] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.3 ± 20.1 | [−143, −64] | [−136, −70] |
| 64 | –0.92 | 0.52 | –104 ± 12 | –103.9 ± 19.6 | [−142, −66] | [−136, −72] |
| 63 | –0.92 | 0.50 | –104 ± 11 | –103.9 ± 18.9 | [−141, −67] | [−135, −73] |
| Non-determinatives, χ2 method, NBS = 40000 | ||||||
| 88 | –0.76 | 1.32 | –103 ± 25 | –102.5 ± 36.4 | [−173, −30] | [−162, −42] |
| 84 | –0.79 | 0.89 | –122 ± 17 | –121.8 ± 24.8 | [−170, −73] | [−162, −81] |
| 81 | –0.72 | 0.80 | –95 ± 16 | –95.2 ± 23.2 | [−140, −49] | [−133, −57] |
| 79 | –0.73 | 0.77 | –85 ± 15 | –84.9 ± 22.4 | [−128, −41] | [−122, −48] |
| 77 | –0.77 | 0.74 | –80 ± 15 | –80.2 ± 21.8 | [−123, −38] | [−116, −45] |
| 73 | –0.85 | 0.66 | –86 ± 14 | –86.3 ± 20.4 | [−127, −47] | [−120, −53] |
| 69 | –0.89 | 0.58 | –102 ± 13 | –101.8 ± 18.4 | [−137, −66] | [−132, −72] |
| 66 | –0.91 | 0.54 | –100 ± 12 | –99.8 ± 17.2 | [−133, −66] | [−128, −71] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.0 ± 16.8 | [−136, −70] | [−131, −75] |
| 63 | –0.96 | 0.50 | –107 ± 11 | –106.5 ± 15.9 | [−138, −76] | [−133, −81] |
We use both Fourier and χ2 methods. The first column is the number of reference stars in the sample analyzed. The second column is the misalignment error c in Babylonian degrees. The third column is the measurement errors s in Babylonian degrees. The fourth column is the estimated epoch of observation tr with its uncertainty, or the standard deviation of the mean Δt. The fifth to seventh columns represent the uncertainties estimated by bootstrap resamplings.
Epochs of observation and their uncertainties for the SSXJ stars excluding the 28 determinative stars.*
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Non-determinatives, Fourier method, NBS = 40000 | ||||||
| 88 | –0.70 | 1.32 | –120 ± 25 | –119.5 ± 43.1 | [−202, −31] | [−189, −48] |
| 84 | –0.80 | 0.90 | –153 ± 18 | –153.6 ± 29.8 | [−212, −95] | [−202, −105] |
| 79 | –0.77 | 0.78 | –144 ± 16 | –144.3 ± 26.9 | [−197, −92] | [−188, −100] |
| 75 | –0.81 | 0.71 | –151 ± 15 | –151.2 ± 24.8 | [−200, −102] | [−192, −110] |
| 73 | –0.86 | 0.66 | –137 ± 14 | –136.8 ± 23.5 | [−183, −90] | [−175, −98] |
| 71 | –0.91 | 0.62 | –124 ± 13 | –123.8 ± 22.8 | [−168, −79] | [−161, −86] |
| 70 | –0.94 | 0.60 | –112 ± 13 | –111.9 ± 22.3 | [−155, −68] | [−149, −75] |
| 68 | –0.90 | 0.57 | –102 ± 12 | –101.9 ± 21.3 | [−143, −60] | [−137, −67] |
| 67 | –0.92 | 0.56 | –100 ± 12 | –100.2 ± 20.8 | [−140, −59] | [−134, −66] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.3 ± 20.1 | [−143, −64] | [−136, −70] |
| 64 | –0.92 | 0.52 | –104 ± 12 | –103.9 ± 19.6 | [−142, −66] | [−136, −72] |
| 63 | –0.92 | 0.50 | –104 ± 11 | –103.9 ± 18.9 | [−141, −67] | [−135, −73] |
| Non-determinatives, χ2 method, NBS = 40000 | ||||||
| 88 | –0.76 | 1.32 | –103 ± 25 | –102.5 ± 36.4 | [−173, −30] | [−162, −42] |
| 84 | –0.79 | 0.89 | –122 ± 17 | –121.8 ± 24.8 | [−170, −73] | [−162, −81] |
| 81 | –0.72 | 0.80 | –95 ± 16 | –95.2 ± 23.2 | [−140, −49] | [−133, −57] |
| 79 | –0.73 | 0.77 | –85 ± 15 | –84.9 ± 22.4 | [−128, −41] | [−122, −48] |
| 77 | –0.77 | 0.74 | –80 ± 15 | –80.2 ± 21.8 | [−123, −38] | [−116, −45] |
| 73 | –0.85 | 0.66 | –86 ± 14 | –86.3 ± 20.4 | [−127, −47] | [−120, −53] |
| 69 | –0.89 | 0.58 | –102 ± 13 | –101.8 ± 18.4 | [−137, −66] | [−132, −72] |
| 66 | –0.91 | 0.54 | –100 ± 12 | –99.8 ± 17.2 | [−133, −66] | [−128, −71] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.0 ± 16.8 | [−136, −70] | [−131, −75] |
| 63 | –0.96 | 0.50 | –107 ± 11 | –106.5 ± 15.9 | [−138, −76] | [−133, −81] |
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| Non-determinatives, Fourier method, NBS = 40000 | ||||||
| 88 | –0.70 | 1.32 | –120 ± 25 | –119.5 ± 43.1 | [−202, −31] | [−189, −48] |
| 84 | –0.80 | 0.90 | –153 ± 18 | –153.6 ± 29.8 | [−212, −95] | [−202, −105] |
| 79 | –0.77 | 0.78 | –144 ± 16 | –144.3 ± 26.9 | [−197, −92] | [−188, −100] |
| 75 | –0.81 | 0.71 | –151 ± 15 | –151.2 ± 24.8 | [−200, −102] | [−192, −110] |
| 73 | –0.86 | 0.66 | –137 ± 14 | –136.8 ± 23.5 | [−183, −90] | [−175, −98] |
| 71 | –0.91 | 0.62 | –124 ± 13 | –123.8 ± 22.8 | [−168, −79] | [−161, −86] |
| 70 | –0.94 | 0.60 | –112 ± 13 | –111.9 ± 22.3 | [−155, −68] | [−149, −75] |
| 68 | –0.90 | 0.57 | –102 ± 12 | –101.9 ± 21.3 | [−143, −60] | [−137, −67] |
| 67 | –0.92 | 0.56 | –100 ± 12 | –100.2 ± 20.8 | [−140, −59] | [−134, −66] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.3 ± 20.1 | [−143, −64] | [−136, −70] |
| 64 | –0.92 | 0.52 | –104 ± 12 | –103.9 ± 19.6 | [−142, −66] | [−136, −72] |
| 63 | –0.92 | 0.50 | –104 ± 11 | –103.9 ± 18.9 | [−141, −67] | [−135, −73] |
| Non-determinatives, χ2 method, NBS = 40000 | ||||||
| 88 | –0.76 | 1.32 | –103 ± 25 | –102.5 ± 36.4 | [−173, −30] | [−162, −42] |
| 84 | –0.79 | 0.89 | –122 ± 17 | –121.8 ± 24.8 | [−170, −73] | [−162, −81] |
| 81 | –0.72 | 0.80 | –95 ± 16 | –95.2 ± 23.2 | [−140, −49] | [−133, −57] |
| 79 | –0.73 | 0.77 | –85 ± 15 | –84.9 ± 22.4 | [−128, −41] | [−122, −48] |
| 77 | –0.77 | 0.74 | –80 ± 15 | –80.2 ± 21.8 | [−123, −38] | [−116, −45] |
| 73 | –0.85 | 0.66 | –86 ± 14 | –86.3 ± 20.4 | [−127, −47] | [−120, −53] |
| 69 | –0.89 | 0.58 | –102 ± 13 | –101.8 ± 18.4 | [−137, −66] | [−132, −72] |
| 66 | –0.91 | 0.54 | –100 ± 12 | –99.8 ± 17.2 | [−133, −66] | [−128, −71] |
| 65 | –0.92 | 0.53 | –103 ± 12 | –103.0 ± 16.8 | [−136, −70] | [−131, −75] |
| 63 | –0.96 | 0.50 | –107 ± 11 | –106.5 ± 15.9 | [−138, −76] | [−133, −81] |
We use both Fourier and χ2 methods. The first column is the number of reference stars in the sample analyzed. The second column is the misalignment error c in Babylonian degrees. The third column is the measurement errors s in Babylonian degrees. The fourth column is the estimated epoch of observation tr with its uncertainty, or the standard deviation of the mean Δt. The fifth to seventh columns represent the uncertainties estimated by bootstrap resamplings.
3.3 Two groups of outlying stars
In figures 3 and 4, the stars above the solid curve can be regarded as being observed later than the epoch tr, while those below the solid curve can be regarded as being observed ealier than the epoch tr. Interestingly, the outliers both above and below the solid curve seem to be aligned along single curves, respectively. This means that each group may have a different epoch of observation. So, we define the outliers below the fitting curve as “group A,” and those above the fitting curve as “group B.” Then we will estimate the epoch of observation for each group.
Both groups A and B are composed of small numbers of stars. Group A is composed of only 10 stars, including two determinative stars, and group B is composed of 18 stars, including one determinative star. We perform the fitting with both methods, but we cannot obtain any meaningful results. Hence, we do not fit the outliers with the two methods, and try to find another way.
It happens that we can find the approximate epochs of observations by eye in figures 3 and 4. The outliers below the fitting curve seem to become flat around tA ≈ −200, and the outliers above the fitting curve seems to become flat around tB ≈ +100, while they seem to be distributed together along curved lines in other epochs. Hence, we draw the fitting curves f(α) = c + acos α for the two groups, where the amplitude a = n × (ts − tr). Here, n is the rate of change of the declination due to the precession of equinoxes and is defined by n = 0.°5567 per century, and (ts − tr) is the time difference between the time of observation tr and the supposed time ts. Adopting the calculated values for a, we need to find the misalignment error c by trying a few values to minimize the fitting error. Excluding a number of extreme outliers (two for group A and five for group B), we find the misalignment error that makes the fitting curves pass through the outlying points with the numbers of points above and below the curve being equal.
As a result, we find that the misalignment error for group A is roughly cA ≃ −2.°5 for all the trial times, and for group B it is roughly cB ≃ 0.°0. Furthermore, we estimate the uncertainties of the epochs of observation by only considering the sizes of the samples. Since the uncertainty obtained by bootstrap resamplings from the N = 63 main group is |$s/\sqrt{N}=15.9$|, the uncertainty of the epoch of observation for group A (NA = 8) is |$s/\sqrt{N_{\rm A}}\sim 45\:$|yr, and the uncertainty for group B (NB = 13) is |$s/\sqrt{N_{\rm B}}\sim 35$|.
Thus, we obtain the fitting curves for the two groups of outliers and draw them in figure 4 with dashed and dotted curves. Satisfactorily, we see that each group seems to be fitted by each curve. This means that the epochs of observation we obtained are meaningful. As a result, we find that the rough epoch of observation for group A is tA ≈ −200 ± 45, and that for group B is tB ≈ +100 ± 35.
It is remarkable that the three outliers among the 28 determinative stars are fitted with the same fitting curves for groups A and B, as well. The two outliers Di [95] and Wei [98], the third and sixth lunar lodges, seem to belong to group A, while the outlier Zhen [120], the 28th lunar lodge, seems to belong to group B.
3.4 The 28 determinative stars
We determine the epoch of observation for the 28 determinative stars with the same methods and criterion for rejecting outliers. Excluding three outliers, the Fourier method gives us the epoch of observation for the 25 determinative stars as tr ± Δt = −53 ± 20, the misalignment error c = −1.°02, the measurement error s = 0.°55, and the bootstrap mean and uncertainty |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-52.0\pm 28.6$|, while the χ2 method gives the epoch of observation for the 25 determinative stars as tr ± Δt = −64 ± 20, the misalignment error c = −1.°01, the measurement error s = 0.°54, and the bootstrap mean and uncertainty |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-64.5\pm 27.7$|. We show the results in table 4. We note that the epochs of observation obtained by the two methods are a bit different from each other, even though the epochs agree with each other within the statistical uncertainties. We note that the χ2 method is a more reliable numerical integration scheme for sparse data. Hence, we place more trust in the results obtained by the χ2 method.
Epochs of observation and their uncertainties for the 28 determinative stars.*
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| 28 determinative stars, Fourier method, NBS = 40000 | ||||||
| 28 | –1.06 | 0.93 | –65 ± 32 | –64.4 ± 44.3 | [−151, 22] | [−137, 8] |
| 25 | –1.02 | 0.55 | –53 ± 20 | –52.0 ± 28.6 | [−108, 3] | [−99, −5] |
| 28 | –1.02 | 0.90 | –59 ± 30 | Sun and Kistemaker (1997) | ||
| 25 | –1.02 | 0.50 | –49 ± 18 | Sun and Kistemaker (1997) | ||
| 28 | –1.13 | 0.93 | –92 ± 32 | Lower rectangle | ||
| 28 | –0.99 | 0.95 | –37 ± 32 | Upper rectangle | ||
| 28 | –1.06 | 0.93 | –65 ± 32 | Triangle and trapezoid | ||
| 28 determinative stars, χ2 method, NBS = 40000 | ||||||
| 28 | –1.14 | 0.93 | –87 ± 32 | –86.5 ± 42.9 | [−171, −3] | [−157, −16] |
| 25 | –1.01 | 0.54 | –64 ± 20 | –64.5 ± 27.7 | [−119, −11] | [−110, −19] |
| 25 | –1.05 | 0.54 | –69 ± 20 | Lower rectangle | ||
| 25 | –0.99 | 0.55 | –37 ± 20 | Upper rectangle | ||
| 25 | –1.02 | 0.55 | –53 ± 20 | Triangle and trapezoid | ||
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| 28 determinative stars, Fourier method, NBS = 40000 | ||||||
| 28 | –1.06 | 0.93 | –65 ± 32 | –64.4 ± 44.3 | [−151, 22] | [−137, 8] |
| 25 | –1.02 | 0.55 | –53 ± 20 | –52.0 ± 28.6 | [−108, 3] | [−99, −5] |
| 28 | –1.02 | 0.90 | –59 ± 30 | Sun and Kistemaker (1997) | ||
| 25 | –1.02 | 0.50 | –49 ± 18 | Sun and Kistemaker (1997) | ||
| 28 | –1.13 | 0.93 | –92 ± 32 | Lower rectangle | ||
| 28 | –0.99 | 0.95 | –37 ± 32 | Upper rectangle | ||
| 28 | –1.06 | 0.93 | –65 ± 32 | Triangle and trapezoid | ||
| 28 determinative stars, χ2 method, NBS = 40000 | ||||||
| 28 | –1.14 | 0.93 | –87 ± 32 | –86.5 ± 42.9 | [−171, −3] | [−157, −16] |
| 25 | –1.01 | 0.54 | –64 ± 20 | –64.5 ± 27.7 | [−119, −11] | [−110, −19] |
| 25 | –1.05 | 0.54 | –69 ± 20 | Lower rectangle | ||
| 25 | –0.99 | 0.55 | –37 ± 20 | Upper rectangle | ||
| 25 | –1.02 | 0.55 | –53 ± 20 | Triangle and trapezoid | ||
We use both the Fourier and χ2 methods. We cite the corresponding results from previous research. We also show the results obtained by a few schemes for numerical integration. The first column is the number of reference stars in the sample analyzed. The second column is the misalignment error c in Babylonian degrees. The third column is the measurement error s in Babylonian degrees. The fourth column is the estimated epoch of observation and its uncertainty or the standard deviation of the mean tr ± Δt. The fifth to seventh columns represent the uncertainties estimated by bootstrap resamplings.
Epochs of observation and their uncertainties for the 28 determinative stars.*
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| 28 determinative stars, Fourier method, NBS = 40000 | ||||||
| 28 | –1.06 | 0.93 | –65 ± 32 | –64.4 ± 44.3 | [−151, 22] | [−137, 8] |
| 25 | –1.02 | 0.55 | –53 ± 20 | –52.0 ± 28.6 | [−108, 3] | [−99, −5] |
| 28 | –1.02 | 0.90 | –59 ± 30 | Sun and Kistemaker (1997) | ||
| 25 | –1.02 | 0.50 | –49 ± 18 | Sun and Kistemaker (1997) | ||
| 28 | –1.13 | 0.93 | –92 ± 32 | Lower rectangle | ||
| 28 | –0.99 | 0.95 | –37 ± 32 | Upper rectangle | ||
| 28 | –1.06 | 0.93 | –65 ± 32 | Triangle and trapezoid | ||
| 28 determinative stars, χ2 method, NBS = 40000 | ||||||
| 28 | –1.14 | 0.93 | –87 ± 32 | –86.5 ± 42.9 | [−171, −3] | [−157, −16] |
| 25 | –1.01 | 0.54 | –64 ± 20 | –64.5 ± 27.7 | [−119, −11] | [−110, −19] |
| 25 | –1.05 | 0.54 | –69 ± 20 | Lower rectangle | ||
| 25 | –0.99 | 0.55 | –37 ± 20 | Upper rectangle | ||
| 25 | –1.02 | 0.55 | –53 ± 20 | Triangle and trapezoid | ||
| No. . | c . | s . | t r ± Δt . | |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}$| . | 95% C.I. . | 90% C.I. . |
|---|---|---|---|---|---|---|
| 28 determinative stars, Fourier method, NBS = 40000 | ||||||
| 28 | –1.06 | 0.93 | –65 ± 32 | –64.4 ± 44.3 | [−151, 22] | [−137, 8] |
| 25 | –1.02 | 0.55 | –53 ± 20 | –52.0 ± 28.6 | [−108, 3] | [−99, −5] |
| 28 | –1.02 | 0.90 | –59 ± 30 | Sun and Kistemaker (1997) | ||
| 25 | –1.02 | 0.50 | –49 ± 18 | Sun and Kistemaker (1997) | ||
| 28 | –1.13 | 0.93 | –92 ± 32 | Lower rectangle | ||
| 28 | –0.99 | 0.95 | –37 ± 32 | Upper rectangle | ||
| 28 | –1.06 | 0.93 | –65 ± 32 | Triangle and trapezoid | ||
| 28 determinative stars, χ2 method, NBS = 40000 | ||||||
| 28 | –1.14 | 0.93 | –87 ± 32 | –86.5 ± 42.9 | [−171, −3] | [−157, −16] |
| 25 | –1.01 | 0.54 | –64 ± 20 | –64.5 ± 27.7 | [−119, −11] | [−110, −19] |
| 25 | –1.05 | 0.54 | –69 ± 20 | Lower rectangle | ||
| 25 | –0.99 | 0.55 | –37 ± 20 | Upper rectangle | ||
| 25 | –1.02 | 0.55 | –53 ± 20 | Triangle and trapezoid | ||
We use both the Fourier and χ2 methods. We cite the corresponding results from previous research. We also show the results obtained by a few schemes for numerical integration. The first column is the number of reference stars in the sample analyzed. The second column is the misalignment error c in Babylonian degrees. The third column is the measurement error s in Babylonian degrees. The fourth column is the estimated epoch of observation and its uncertainty or the standard deviation of the mean tr ± Δt. The fifth to seventh columns represent the uncertainties estimated by bootstrap resamplings.
Now, we compare our results for the polar angles of the 28 determinative stars in the SSXJ catalog with the previous research. Sun and Kistemaker (1997) applied the Fourier method to obtain the epoch tr ± Δt = 60 ± 30 BCE and the misalignment angle c = −1.°02 for the 28 determinative stars. When they removed the three determinative stars having obviously large deviations (Di [95], Wei [98], and Zhen [120], which are the same as in our results) they obtained the epoch tr ± Δt = 50 ± 18 BCE and the misalignment angle c = −1.°02. Comparing these with our results in table 3, we see that both results are in good agreement with each other.
Nakamura (2018) applied the χ2 method to the polar angles alone to obtain |$t_{\rm r}\pm s/\sqrt{N}=21\pm 250$| CE. His data for the SSXJ determinative stars has a number of polar angles that are different from those given in Sun and Kistemaker (1997). In particular, the polar angle of lunar lodge Kui [107] is different by 7 du. Certainly this abnormal polar angle might result in a large error in Nakamura’s result. Moreover, he did not take into account the fact that the polar angles were observed by using meridian instruments and so they have misalignment errors as large as −1°, which might cause serious errors in his results. Hence, we correct the polar angle of Kui [105] to be 77 in his catalog, and apply the same analyses to his star catalog. We obtain the epoch of observation tr ± Δt = −57 ± 35 (with measurement error s = 1.°03), the misalignment angle c = −1.°08, and the bootstrap mean and standard error |$\langle t_{\rm r}\rangle \pm s/\sqrt{N}=-57.0\pm 46.9$| (to 1 σ). We remove the five outliers Di [95], Wei [98], Liu [116], Xing [117], and Zhen [120], and analyze the polar angles of the remaining 23 determinative stars. We obtain the epoch of observations tr ± Δt = −51 ± 19, the misalignment angle c = −0.°96, and the measurement error s = 0.°51. We also make 40000 bootstrap resamplings to obtain the 95% confidence interval tr = [−102, 1] and the 90% confidence interval tr = [−94, −7]. These results are in good agreement with ours in table 4, as well as with Sun and Kistemaker (1997). Actually, the differences between his catalog and our catalog are not so large, with the exception of Kui [105]. Hence, we can expect similar results.
Lastly, we comment on the accuracy of the integration scheme in the Fourier method. We check the reliability of the numerical integration methods applied to the polar angles for the 28 determinative stars in SSXJ. As for the simplest integration scheme, the lower rectangle rule gives us a result of tr ± Δt = −92 ± 32, s = 0.°93, and c = −1.°13, while the upper rectangle rule gives us a result of tr ± Δt = −37 ± 32, s = 0.°95, and c = −0.°99. The trapezoid rule, thought to be more accurate than the rectangle rules, gives us results of tr ± Δt = −65 ± 32, s = 0.°93, and c = −1.°06, while the triangle rule gives the same results as the trapezoid rule. We also determine the epochs of observation by applying these various integration schemes to the 25 determinative stars excluding the three outliers. All the results are shown in table 4. We also note that the average value of the epochs obtained by the upper and lower rectagle rules is in agreement with the results made by the trapezoid or triangle rule. Of course, a more accurate quadrature rule can be made by using a quadratic interpolant function (Simpson’s rule). In a similar fashion, we can derive higher-order quadrature rules by using the Newton–Cotes rules. However, we do not use higher-order rules in this paper and apply only the trapezoid rule.
However, we confirm that, for a large set of data such as the the main group of SSXJ data, the Fourier method with the trapezoid rule gives the same results as those obtained by the χ2 method, while, for a smaller data set such as 25 determinative stars, the two methods give different results. Due to the limitations of the numerical integration scheme, we think that the Fourier method gives less accurate results when the number of points is small, uneven, and sparse. Thus, the χ2 method is thought to be more reliable in those cases.
4 Conclusions
In order to determine the epoch of observations for the stars in SSXJ, we have analyzed the polar angles of those stars by adopting a Fourier method devised by the previous researchers (Sun & Kistemaker 1997). However, in the case of sparse and uneven data, this method cannot give accurate results. Hence, we have also adopted another method of χ2 fitting. In addition, we have performed bootstrap samplings to estimate the uncertainties of the epochs derived from the analyses.
We have found that the SSXJ stars can be classified into a few groups whose epochs of observation are different from one another. To begin with, we assumed that the determinative stars of 28 lunar lodges were observed independently of the other SSXJ stars. The determinative stars were found to have been measured around 53 ± 29 BCE with the Fourier method and 65 ± 28 BCE with the χ2 method, where we have excluded three outliers in the analyses. The χ2 method is thought to be more reliable for cases when the sample is small, uneven, and sparse. While analyzing the 88 SSXJ stars excluding the 28 determinative stars, we have found that the 88 stars can be divided into three goups: the main group is composed of 63 stars whose polar angles are estimated to have been measured around 107 ± 16 BCE, a group of outliers denoted by “group A” is composed of six SSXJ stars and two determinative stars (plus two extreme outliers) whose polar angles are thought to have been measured around 200 ± 45 BCE, and another group, denoted by “group B,” composed of 12 SSXJ stars and one determinative star (plus five extreme outliers) whose polar angles were measured around 100 ± 35 CE. It is notable that the two outlying determinative stars Di [95] and Wei [98] belong to group A, and one outlying determinative star Zhen [120] belongs to group B. We summarize our results in table 5, where we see that both the misalignment and the measurement errors for the main group of stars are similar to those for the 28 determinative stars. It seems that the misalignment error had decreased as time went by. However, the numbers of groups and their sizes are too small to confirm this trend.
| Groups . | Size . | Epoch . | c . | s . | Possibly related occasions . |
|---|---|---|---|---|---|
| Group A | 8(2) | –200 ± 45 | –2.5 | 221–206 BCE, Qin empire | |
| 202 BCE, Establishment of the Former Han | |||||
| Main group | 63 | –107 ± 16 | –0.92 | 0.50 | 104 BCE, Tang Du and Luoxia Hong, |
| the Grand Inception system | |||||
| Determinatives | 25 | –64 ± 28 | –1.01 | 0.54 | 78–76 BCE, Xianyu Wangren’s observations |
| 52 BCE, Geng Shouchang, with circular instruments | |||||
| Group B | 13(1) | 100 ± 35 | 0.0 | 92 CE, Memorial of Gia Kui | |
| 103 CE, observations with ecliptic armillaries |
| Groups . | Size . | Epoch . | c . | s . | Possibly related occasions . |
|---|---|---|---|---|---|
| Group A | 8(2) | –200 ± 45 | –2.5 | 221–206 BCE, Qin empire | |
| 202 BCE, Establishment of the Former Han | |||||
| Main group | 63 | –107 ± 16 | –0.92 | 0.50 | 104 BCE, Tang Du and Luoxia Hong, |
| the Grand Inception system | |||||
| Determinatives | 25 | –64 ± 28 | –1.01 | 0.54 | 78–76 BCE, Xianyu Wangren’s observations |
| 52 BCE, Geng Shouchang, with circular instruments | |||||
| Group B | 13(1) | 100 ± 35 | 0.0 | 92 CE, Memorial of Gia Kui | |
| 103 CE, observations with ecliptic armillaries |
We can divide the SSXJ stars into at least four groups. The size of each group is shown in the second column. The figures in parentheses are the number of determinative stars included in the group. We show the epochs of observation in the third column, the misalignment errors c in the fourth column, the measurement errors s in the fifth column, and the historical events that may be related to the epochs in the sixth column.
| Groups . | Size . | Epoch . | c . | s . | Possibly related occasions . |
|---|---|---|---|---|---|
| Group A | 8(2) | –200 ± 45 | –2.5 | 221–206 BCE, Qin empire | |
| 202 BCE, Establishment of the Former Han | |||||
| Main group | 63 | –107 ± 16 | –0.92 | 0.50 | 104 BCE, Tang Du and Luoxia Hong, |
| the Grand Inception system | |||||
| Determinatives | 25 | –64 ± 28 | –1.01 | 0.54 | 78–76 BCE, Xianyu Wangren’s observations |
| 52 BCE, Geng Shouchang, with circular instruments | |||||
| Group B | 13(1) | 100 ± 35 | 0.0 | 92 CE, Memorial of Gia Kui | |
| 103 CE, observations with ecliptic armillaries |
| Groups . | Size . | Epoch . | c . | s . | Possibly related occasions . |
|---|---|---|---|---|---|
| Group A | 8(2) | –200 ± 45 | –2.5 | 221–206 BCE, Qin empire | |
| 202 BCE, Establishment of the Former Han | |||||
| Main group | 63 | –107 ± 16 | –0.92 | 0.50 | 104 BCE, Tang Du and Luoxia Hong, |
| the Grand Inception system | |||||
| Determinatives | 25 | –64 ± 28 | –1.01 | 0.54 | 78–76 BCE, Xianyu Wangren’s observations |
| 52 BCE, Geng Shouchang, with circular instruments | |||||
| Group B | 13(1) | 100 ± 35 | 0.0 | 92 CE, Memorial of Gia Kui | |
| 103 CE, observations with ecliptic armillaries |
We can divide the SSXJ stars into at least four groups. The size of each group is shown in the second column. The figures in parentheses are the number of determinative stars included in the group. We show the epochs of observation in the third column, the misalignment errors c in the fourth column, the measurement errors s in the fifth column, and the historical events that may be related to the epochs in the sixth column.
We have determined the epochs of observation for both the main-group stars and the 25 determinative stars by means of statistical analyses. Their sample means seem to be different from each other. However, they also have uncertainties. The uncertainty of epoch for the 25 determinative stars is larger, because the sample size is small. Hence, it is questionable if the main-group stars were measured simultaneously with the 25 determinative stars.
In order to answer this question, we perform a two-sample t-test that is usually used to test the difference d between two population means. To begin with, we define the hypotheses. Denoting the population mean of one sample by μ1 and the population mean of the other sample by μ2, we can set the null hypothesis as H0: μ1 − μ2 = d, and the alternative hypothesis H1: μ1 − μ2 ≠ d. Here we set d = 0, because we are to test if μ1 = μ2.
In our case of χ2 analyses, we have 〈t1〉 = −64.5, |$s_1/\sqrt{n_1}=27.7$|, and n1 = 25 obtained from the 25 determinative stars, and 〈t2〉 = −106.5, |$s_2/\sqrt{n_2}=15.9$|, and n2 = 63 for the main group. Substituting these values into equations (8) and (9), we have the statistic t0 = 1.315 and the degrees of freedom ν = 40.7099 ≃ 41. Thus, using a t40-score table or calculator, we obtain the probability that the absolute value of a statistic T is greater than or equal to t0 or P(|T| ≥ |t0|) = .196, because it is a two-sided test. Thus, we have obtained the p-value p = .196 for this case. We can do the same hypothesis test for the results obtained with the Fourier method, and obtain p = .137. We show our results in table 6. Since the p-vaues are higher than 0.05, we cannot reject the null hypothesis.
Results of hypothesis tests if the 25 determinative stars in SSXJ were measured at the same occasion as the 63 stars of the main group.
| Method . | |$\langle t_1\rangle \pm s_1/\sqrt{n_1}$| . | n 1 . | |$\langle t_2\rangle \pm s_2/\sqrt{n_2}$| . | n 2 . | t 0 . | ν . | p-value . |
|---|---|---|---|---|---|---|---|
| Main group vs. 28 determinative stars, NBS = 40000 | |||||||
| Fourier | –52.0 ± 28.6 | 25 | –103.9 ± 18.9 | 63 | 1.514 | 47 | .137 |
| χ2 | –64.5 ± 27.7 | 25 | –106.5 ± 15.9 | 63 | 1.315 | 41 | .196 |
| Method . | |$\langle t_1\rangle \pm s_1/\sqrt{n_1}$| . | n 1 . | |$\langle t_2\rangle \pm s_2/\sqrt{n_2}$| . | n 2 . | t 0 . | ν . | p-value . |
|---|---|---|---|---|---|---|---|
| Main group vs. 28 determinative stars, NBS = 40000 | |||||||
| Fourier | –52.0 ± 28.6 | 25 | –103.9 ± 18.9 | 63 | 1.514 | 47 | .137 |
| χ2 | –64.5 ± 27.7 | 25 | –106.5 ± 15.9 | 63 | 1.315 | 41 | .196 |
Results of hypothesis tests if the 25 determinative stars in SSXJ were measured at the same occasion as the 63 stars of the main group.
| Method . | |$\langle t_1\rangle \pm s_1/\sqrt{n_1}$| . | n 1 . | |$\langle t_2\rangle \pm s_2/\sqrt{n_2}$| . | n 2 . | t 0 . | ν . | p-value . |
|---|---|---|---|---|---|---|---|
| Main group vs. 28 determinative stars, NBS = 40000 | |||||||
| Fourier | –52.0 ± 28.6 | 25 | –103.9 ± 18.9 | 63 | 1.514 | 47 | .137 |
| χ2 | –64.5 ± 27.7 | 25 | –106.5 ± 15.9 | 63 | 1.315 | 41 | .196 |
| Method . | |$\langle t_1\rangle \pm s_1/\sqrt{n_1}$| . | n 1 . | |$\langle t_2\rangle \pm s_2/\sqrt{n_2}$| . | n 2 . | t 0 . | ν . | p-value . |
|---|---|---|---|---|---|---|---|
| Main group vs. 28 determinative stars, NBS = 40000 | |||||||
| Fourier | –52.0 ± 28.6 | 25 | –103.9 ± 18.9 | 63 | 1.514 | 47 | .137 |
| χ2 | –64.5 ± 27.7 | 25 | –106.5 ± 15.9 | 63 | 1.315 | 41 | .196 |
Subsequently, we test if the main-group sample was observed earlier than the 25 determinative stars. We set the null hypothesis H0: μ1 = μ2 and the alternative hypothesis H1: μ1 > μ2. Then, p-values can be calculated by the probability that the value of a statistic T is greater than or equal to t0. Hence, we obtain p = .079 and p = .098, respectively, for each method, because it is a one-sided test. We cannot reject the null hypothesis at the usual significance level of 0.05. However, at a significance level of 0.1, we can reject the null hypothesis and accept the alternative hypothesis. In other words, we have evidence at a significance level of 0.1 that the main-group sample was observed earlier than the 25 determinative stars.
We now determine if the epoch of observation derived for each group agrees with the events written in history books. In order to do that, we have to review the Chinese history of astronomical observation. The nominal author of SSXJ is Shi Shen, a figure of the period of Warring States (475–221 BCE). However, astrologers of later times often attributed their works to the legendary figure Shi Shen. Hence, the book titled SSXJ became a mixture of works from the descendants of Shi Shen. Thus, the astrologers are called the Shi Shi school, which was active during the Han times from 206 BCE to 220 CE (Sun & Kistemaker 1997). Their activities are written in a monograph on musical scales and astronomical systems (Lulizhi) in the “History of Han” (“Hou Han Shu”), whose English translation can be found in Cullen (2017). It is noteworthy that the book titled “Shi Shi Xing Jing” was mentioned for the first time in this history book.
According to the monograph, the Shi Shi school had played an important role in making calendars during the Han dynasty (Sun & Kistemaker 1997). In order to make calendars, we need to measure the positions of reference stars for major asterisms, because they become the references for the positions of the Sun, the Moon, the planets, and comets. In particular, the 28 determinative stars are crucial to measuring date and time. As time went by, Chinese astronomers became interested in making celestial globes and circular star charts. According to the method of making a star chart that was explained in the “Old Book of Tang” (“Jiu Tang Shu”) and the “New Book Of Tang” (“Xin Tang Shu”), the polar angles of stars are needed to make celestial globes and circular star charts (Ahn 2015). In order to measure polar angles, ancient Chinese astronomers devised meridian instruments such as armillary spheres (Sun & Kistemaker 1997).
The Han dynasty was established in 206 BCE. However, according to the monograph or Lulizhi of “Hou Han Shu,” the dynasty continued the calendar system, called the Zhuan Xu system, of the previous dynasty called Qin (221–206 BCE), and could not develop their own calendar system until 104 BCE, when calendar reform was achieved by more than 20 astronomers including Tang Du and Luoxia Hong. The new calendar system was called the Grand Inception system of the Han dynasty. It is possible that polar angles were measured at this time.
According to the same monograph, Zhang Shouwang sent a memorial in which he doubted the reliability of the Grand Inception system. Hence, Xianyu Wangren organized a group of astronomers to make observational tests for the system from 78 BCE to 76 BCE. Thanks to this verification, the revised system was regularized from 75 BCE. Here, we regard the year of 76 BCE as the epoch of observation.
According to the same monograph, there were a few occasions when officials proposed calendar modification. One of the proposals was made by Jia Kui, who sent a memorial to the throne in 92 CE. In that memorial, he mentioned that observations had been made in 52 BCE when Geng Shouchang, the Grand Director of Agriculture, suggested measuring the coordinates of celestial objects by using a circular instrument called Yuan Yi.8 We also comment that such knowledge as measurement by using circular instruments was something that everyone in the previous age had known about. In this memorial Gia Kui proposed that ecliptic armillaries (the “Yellow Road” instrument) should be used, because they are more precise than equatorial armillaries (the “Red Road” instrument). His proposal was realized in 103 CE, when the Yellow Road instrument was constructed at the emperor’s order.
During the Han dynasty, the Shi Shi school attributed their works to the legendary figure Shi Shi. Moreover, there were also other schools who attributed their works to other legendary figures such as Gan De and Wuxian. Such knowledge was gathered into a star chart and a book by Chen Zuo around 230 CE. He compiled 92 asterisms of the Shi Shi school, 112 asterims of the Gan Shi school, 44 asterisms of the Wuxian school, and one star called Shengong, 283 asterisms composed of 1464 stars in total. It is also notable that Qian Lezhi used solid red/white/black dots to depict the stars belonging to the Shi Shi/Wuxian Shi/Gan Shi schools when he constructed a sky globe. The coordinates of stars must have been passed down until they were recorded in KYZJ around 720 CE. However, only the coordinate values of the Shi Shi school were recorded in KYZJ.
We have proved that the polar angles of the reference stars in SSXJ were measured on a few occasions during the Han times. We are to match them with the historical occasions explained above. To do this we perform hypothesis tests regarding the epochs given in the history book, μi = −103, −75, −51, +103 as population means: μ1 = −103 for the epoch of the Grand Inception system, μ2 = −75 for Xianyu Wangren’s observation, μ3 = −51 for Geng Shouchang’s obervation, and μ4 = +103 for the observation with ecliptic instruments; the epochs obtained from our analyses 〈ti〉 = −200, −107(−104), −64(−53), +100 as sample means that have bootstrap errors of |$\sigma _i\simeq s_i/\sqrt{N_i}=45, 15.9(18.9), 27.7(28.6), 35$| for Ni = 8, 63, 25, 13, respectively. Here, the numbers in parentheses are obtained with the Fourier method. We state the null hypothesis H0: μ = μi and alternative hypothesis H1: μ ≠ μi. We use the test static of a |$t_{N_i-1}$|-distribution to obtain the standard statistic |$t_0=(\langle t_i\rangle -\mu _i)/(s_i/\sqrt{N_i})$|. Subsequently, we calculate the p-value or |$P(|t_{N_i-1}|>|t_0|)$|, because it is a two-sided test. Then, we decide whether we can reject the null hypothesis at a given significance level.
We show our results for the hypothesis tests in table 7. The p-values for the groups allow us to decide when each group was observed. The p-values for the main group composed of 63 stars indicate that its member stars were observed around 104 BCE when Tang Du and Luoxia Hong made observations to make the Grand Inception system.
Results of hypothesis tests if each group of stars in SSXJ was measured at an occasion recorded in history.*
| Data . | 〈ti〉 . | μi . | |$s_i/\sqrt{N_i}$| . | t 0 . | N i . | p-value . |
|---|---|---|---|---|---|---|
| Main group (63 stars) | ||||||
| Fourier | –104 | –103 | 18.9 | –0.053 | 63 | .958 |
| Fourier | –104 | –75 | 18.9 | –1.534 | 63 | .130 |
| Fourier | –104 | –51 | 18.9 | –2.804 | 63 | .007 |
| Fourier | –104 | +103 | 18.9 | +10.952 | 63 | <.001 |
| χ2 | –107 | –103 | 15.9 | –0.252 | 63 | .802 |
| χ2 | –107 | –75 | 15.9 | –2.013 | 63 | .048 |
| χ2 | –107 | –51 | 15.9 | –3.522 | 63 | .0008 |
| χ2 | –107 | +103 | 15.9 | –13.208 | 63 | <.001 |
| Determinative stars (25 stars) | ||||||
| Fourier | –53 | –103 | 28.6 | +1.748 | 25 | .093 |
| Fourier | –53 | –75 | 28.6 | +0.769 | 25 | .449 |
| Fourier | –53 | –51 | 28.6 | –0.070 | 25 | .945 |
| Fourier | –53 | +103 | 28.6 | –5.455 | 25 | <.001 |
| χ2 | –64 | –103 | 27.7 | +1.408 | 25 | .172 |
| χ2 | –64 | –75 | 27.7 | +0.397 | 25 | .695 |
| χ2 | –64 | –51 | 27.7 | –0.469 | 25 | .643 |
| χ2 | –64 | +103 | 27.7 | –6.029 | 25 | <.001 |
| Group A (6 outliers and two determinative stars) | ||||||
| –200 | –201 | 45 | 0.022 | 8 | .983 | |
| –200 | –103 | 45 | –2.156 | 8 | .068 | |
| –200 | –75 | 45 | –2.778 | 8 | .027 | |
| –200 | –51 | 45 | –3.311 | 8 | .013 | |
| –200 | +103 | 45 | –6.733 | 8 | <.001 | |
| Group B (12 outliers and one determinative star) | ||||||
| +100 | –103 | 35 | +5.8 | 13 | <.001 | |
| +100 | –75 | 35 | +5.0 | 13 | <.001 | |
| +100 | –51 | 35 | +4.3 | 13 | .001 | |
| +100 | +103 | 35 | –0.09 | 13 | .930 | |
| Data . | 〈ti〉 . | μi . | |$s_i/\sqrt{N_i}$| . | t 0 . | N i . | p-value . |
|---|---|---|---|---|---|---|
| Main group (63 stars) | ||||||
| Fourier | –104 | –103 | 18.9 | –0.053 | 63 | .958 |
| Fourier | –104 | –75 | 18.9 | –1.534 | 63 | .130 |
| Fourier | –104 | –51 | 18.9 | –2.804 | 63 | .007 |
| Fourier | –104 | +103 | 18.9 | +10.952 | 63 | <.001 |
| χ2 | –107 | –103 | 15.9 | –0.252 | 63 | .802 |
| χ2 | –107 | –75 | 15.9 | –2.013 | 63 | .048 |
| χ2 | –107 | –51 | 15.9 | –3.522 | 63 | .0008 |
| χ2 | –107 | +103 | 15.9 | –13.208 | 63 | <.001 |
| Determinative stars (25 stars) | ||||||
| Fourier | –53 | –103 | 28.6 | +1.748 | 25 | .093 |
| Fourier | –53 | –75 | 28.6 | +0.769 | 25 | .449 |
| Fourier | –53 | –51 | 28.6 | –0.070 | 25 | .945 |
| Fourier | –53 | +103 | 28.6 | –5.455 | 25 | <.001 |
| χ2 | –64 | –103 | 27.7 | +1.408 | 25 | .172 |
| χ2 | –64 | –75 | 27.7 | +0.397 | 25 | .695 |
| χ2 | –64 | –51 | 27.7 | –0.469 | 25 | .643 |
| χ2 | –64 | +103 | 27.7 | –6.029 | 25 | <.001 |
| Group A (6 outliers and two determinative stars) | ||||||
| –200 | –201 | 45 | 0.022 | 8 | .983 | |
| –200 | –103 | 45 | –2.156 | 8 | .068 | |
| –200 | –75 | 45 | –2.778 | 8 | .027 | |
| –200 | –51 | 45 | –3.311 | 8 | .013 | |
| –200 | +103 | 45 | –6.733 | 8 | <.001 | |
| Group B (12 outliers and one determinative star) | ||||||
| +100 | –103 | 35 | +5.8 | 13 | <.001 | |
| +100 | –75 | 35 | +5.0 | 13 | <.001 | |
| +100 | –51 | 35 | +4.3 | 13 | .001 | |
| +100 | +103 | 35 | –0.09 | 13 | .930 | |
According to “Han Shu” (the history of the Han dynasty) there were at least four observational campaigns, in 104 BCE, 78–76 BCE, 52 BCE, and 103 CE. In addition, we consider the establishment of the Han dynasty in 202 BCE.
Results of hypothesis tests if each group of stars in SSXJ was measured at an occasion recorded in history.*
| Data . | 〈ti〉 . | μi . | |$s_i/\sqrt{N_i}$| . | t 0 . | N i . | p-value . |
|---|---|---|---|---|---|---|
| Main group (63 stars) | ||||||
| Fourier | –104 | –103 | 18.9 | –0.053 | 63 | .958 |
| Fourier | –104 | –75 | 18.9 | –1.534 | 63 | .130 |
| Fourier | –104 | –51 | 18.9 | –2.804 | 63 | .007 |
| Fourier | –104 | +103 | 18.9 | +10.952 | 63 | <.001 |
| χ2 | –107 | –103 | 15.9 | –0.252 | 63 | .802 |
| χ2 | –107 | –75 | 15.9 | –2.013 | 63 | .048 |
| χ2 | –107 | –51 | 15.9 | –3.522 | 63 | .0008 |
| χ2 | –107 | +103 | 15.9 | –13.208 | 63 | <.001 |
| Determinative stars (25 stars) | ||||||
| Fourier | –53 | –103 | 28.6 | +1.748 | 25 | .093 |
| Fourier | –53 | –75 | 28.6 | +0.769 | 25 | .449 |
| Fourier | –53 | –51 | 28.6 | –0.070 | 25 | .945 |
| Fourier | –53 | +103 | 28.6 | –5.455 | 25 | <.001 |
| χ2 | –64 | –103 | 27.7 | +1.408 | 25 | .172 |
| χ2 | –64 | –75 | 27.7 | +0.397 | 25 | .695 |
| χ2 | –64 | –51 | 27.7 | –0.469 | 25 | .643 |
| χ2 | –64 | +103 | 27.7 | –6.029 | 25 | <.001 |
| Group A (6 outliers and two determinative stars) | ||||||
| –200 | –201 | 45 | 0.022 | 8 | .983 | |
| –200 | –103 | 45 | –2.156 | 8 | .068 | |
| –200 | –75 | 45 | –2.778 | 8 | .027 | |
| –200 | –51 | 45 | –3.311 | 8 | .013 | |
| –200 | +103 | 45 | –6.733 | 8 | <.001 | |
| Group B (12 outliers and one determinative star) | ||||||
| +100 | –103 | 35 | +5.8 | 13 | <.001 | |
| +100 | –75 | 35 | +5.0 | 13 | <.001 | |
| +100 | –51 | 35 | +4.3 | 13 | .001 | |
| +100 | +103 | 35 | –0.09 | 13 | .930 | |
| Data . | 〈ti〉 . | μi . | |$s_i/\sqrt{N_i}$| . | t 0 . | N i . | p-value . |
|---|---|---|---|---|---|---|
| Main group (63 stars) | ||||||
| Fourier | –104 | –103 | 18.9 | –0.053 | 63 | .958 |
| Fourier | –104 | –75 | 18.9 | –1.534 | 63 | .130 |
| Fourier | –104 | –51 | 18.9 | –2.804 | 63 | .007 |
| Fourier | –104 | +103 | 18.9 | +10.952 | 63 | <.001 |
| χ2 | –107 | –103 | 15.9 | –0.252 | 63 | .802 |
| χ2 | –107 | –75 | 15.9 | –2.013 | 63 | .048 |
| χ2 | –107 | –51 | 15.9 | –3.522 | 63 | .0008 |
| χ2 | –107 | +103 | 15.9 | –13.208 | 63 | <.001 |
| Determinative stars (25 stars) | ||||||
| Fourier | –53 | –103 | 28.6 | +1.748 | 25 | .093 |
| Fourier | –53 | –75 | 28.6 | +0.769 | 25 | .449 |
| Fourier | –53 | –51 | 28.6 | –0.070 | 25 | .945 |
| Fourier | –53 | +103 | 28.6 | –5.455 | 25 | <.001 |
| χ2 | –64 | –103 | 27.7 | +1.408 | 25 | .172 |
| χ2 | –64 | –75 | 27.7 | +0.397 | 25 | .695 |
| χ2 | –64 | –51 | 27.7 | –0.469 | 25 | .643 |
| χ2 | –64 | +103 | 27.7 | –6.029 | 25 | <.001 |
| Group A (6 outliers and two determinative stars) | ||||||
| –200 | –201 | 45 | 0.022 | 8 | .983 | |
| –200 | –103 | 45 | –2.156 | 8 | .068 | |
| –200 | –75 | 45 | –2.778 | 8 | .027 | |
| –200 | –51 | 45 | –3.311 | 8 | .013 | |
| –200 | +103 | 45 | –6.733 | 8 | <.001 | |
| Group B (12 outliers and one determinative star) | ||||||
| +100 | –103 | 35 | +5.8 | 13 | <.001 | |
| +100 | –75 | 35 | +5.0 | 13 | <.001 | |
| +100 | –51 | 35 | +4.3 | 13 | .001 | |
| +100 | +103 | 35 | –0.09 | 13 | .930 | |
According to “Han Shu” (the history of the Han dynasty) there were at least four observational campaigns, in 104 BCE, 78–76 BCE, 52 BCE, and 103 CE. In addition, we consider the establishment of the Han dynasty in 202 BCE.
The p-values for the 25 stars among the 28 determinative stars provide strong evidence that they were observed either in 76–78 BCE, when Xianyu Wangren’s team made observations, or in 52 BCE, during Geng Shouchang’s observations with circular instruments. This vagueness is caused by the relatively small size of the sample and poor observational precision, which we cannot overcome.
The p-values for group A, composed of only eight SSXJ stars, including the two determinative stars Di [95] and Wei [98], indicate that they were measured around 200 BCE, when the Former Han dynasty was established. The p-values for group B, composed of only 13 SSXJ stars, including one determinative star Zhen [120], indicate that they were probably observed around 103 CE, when new observations were made by means of ecliptic armillary instruments that had been proposed by Gia Kui in 92 CE. However, the conclusions for these two groups have limitations, because they are not based on robust statistical analyses but on rough eye-fits. This is inevitable because the samples are highly sparse and uneven, as well as small in sample number.
However, we have demonstrated that the SSXJ catalog has a number of temporal strata of astronomical observations made by astronomers of the Shi Shi school at different times, who were most active during the Han dynasty.
Acknowledgements
This work is supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2018R1D1A1B07050035).
Appendix. Identifications of stars
The first entry in the SSXJ catalog quoted in KYZJ is an asterism called Sheti [1], where the number in square brackets means the entry number in KYZJ as well as in table 1. The coordinate of its reference star is given by quoting the legendary astronomer Shi Shi as follows:
Shi Shi or Master Shi told that six stars of Sheti [1] embrace Dajiao [2]. The lodge angle of its reference star is 8 and a quarter du from the determinative star of Jiao [93]. Its polar angle is 59 and half du. It is located inside of the ecliptic by 32 and three quarters du.
Here, du is the Chinese degree that is equal to (365.25/360) times the Babylonian degree.
According to “Astrological Treatise of Shiji (Records of the Grand Historian),”
Dajiao [2] is the court of Heavenly Emperor. There are three stars in each of left and right sides to form three legs of Ding (Chinese ritual bronze vessel).
Since Dajiao [2] is a well-knwon bright star called Arcturus or α Boo, we can infer the relative location of Sheti [1]. The determinative star of lunar lodge Jiao [93] is well known to be a bright star called Spica or α Vir. The right ascension of α Vir at the epoch of 104 BCE is calculated to be |$\alpha ={11^{\rm h}37^{\rm m}16^{\rm s}}$|, and the lodge angle (hereafter, LA) given in units of Chinese degrees is converted to be |$\delta \alpha ={32^{\rm m}32^{\rm s}}$| in hour angles. Hence, the right ascension of the reference star of Sheti [1] in the catalog becomes |$\alpha _{\rm c}=\alpha +\delta \alpha ={12^{\rm h}09^{\rm m}48^{\rm s}}\simeq {12^{\rm h}10^{\rm m}}$|. The polar angle (hereafter, PA) can also be converted into an angle in Babylonian degrees, P, and the declination δ in the catalog can be calculated by δc = 90° − P. In the case of Sheti [1], P = 59.5 du = 59.5 du × (360°/365.25 du) = 58.°645, and so we obtain δc = +31.°355 = 31°21′19″ ≃ 31°21′. Thus, we obtain |$\alpha _{\rm c}={12^{\rm h}10^{\rm m}}$| and δc = 31°21′ for the reference star of the asterism called Sheti [1]. Here, the subscript “c” indicates that the values are calculated from the coordinates given in the SSXJ catalog quoted in KYZJ.
Then, we check whether there is any bright star near to the location indicated by this coordinate on the star chart obtained using PC planetarium software (we use Stellarium) with the epoch of observation set to be 104 BCE. For the case of Sheti [1], we find that η Boo had a right ascension of |$\alpha _{\rm s}={12^{\rm h}13^{\rm m}}$| and declination of δs = 29°50′ by considering the precession of equinoxes. Here, the subscript s indicates that the values are calculated from the modern star catalog. Hence, the difference in the right ascension is Δα ≡ αs − αc = 3′ and the difference in the declination is Δδ ≡ =δs − δc = −1.°5. Thus, the angular distance δr can be calculated with the Pythagorean theorem: (δr)2 ≃ (Δαcos δ)2 + Δδ2. In this case, we obtain δr ≃ 1.°5.
We can use similar procedures to check the validity of the identifications in Sun and Kistemaker (1997) (hereafter, SK97). Basically, we have adopted their identifications in this study. However, we will comment if there are other opinions to our own. Readers can also consult the comments tagged as footnotes in table 3.1 of SK97. In our verification we also consult two information sources: one is a Korean star chart called “Cheonsang-Yeolcha-Bunyajido” that was manufactured in 1396 CE based on a star chart of the previous dynasty Goryeo, but its star chart depicts the sky during the Han dynasty (Ahn 2011, 2013b, 2015). This star chart will be called “C-Map” hereafter. The coordinate values of the SSXJ stars are also quoted in a compendium of books called “Cheoji–Seosangji,” which was written by a Korean scholar called Sal Sujin in 666 CE (Ahn 2013a). This book will be called CJSSJ hereafter.
Genghe [3]: Its PA is recorded as 38 du in KYZJ, but it should be 48 du.
Tianqiang [6]: SK97 identified it as κ2 Boo. However, θ Boo can also be a good candidate.
Tianpei [7]: This asterism is well known to be formed of stars such as ξ Dra, ν1 Dra, β Dra, γ Dra, and ι Her that form the head of Draco. The westernmost star among them is ι Her. However, in order for this star to be the reference star, the PA in KYZJ should be corrected to 42 du instead of 32 du.
Guansuo [10]: This means the chain to link ancient coins with central holes that are the stars of Corona Borealis. SK97 identified this star as β CrB. According to KYZJ, the reference star is designated as a star in the right part of the asterism. When referring to the relative position of stars in ancient Chinese astronomy, the standard for determining the left and right directions is conventionally the Heavenly Emperor, who had been thought to be located around the north celestial pole. In this sense, the reference star should have been described as being on the left part of the asterism. The reason why KYZJ describes the reference star in the right direction is uncertain. If we just consider the angular distance, α CrB can also be a good candidate.
Dou [17]: SK97 identified its reference star as κ Her, but it should be κ Oph. This may be a typographical error.
Dongxian [21]: Sun (1994) identified its reference star as φ Oph, but SK97 identified the star as ψ Oph. We confirm that ψ Oph is correct. There must be a typographical error.
Tianbian [24]: SK97 identified its reference star as 5 Aql. However, this asterism is well known to form an ω shape composed of stars such as λ Aql, ι Aql, η Sct, β Sct, ε Sct, δ Sct, and α Sct. Since it was a convention that the westernmost star is designated as the reference star, we can identify α Sct as its reference star. However, the declination of α Sct at 104 BCE is about δs = −7°, while the declination calculated from the KYZJ record is δc = +0.°5. Considering the misalignment error of −1°, we guess that a number 9 is omitted in the KYZJ record of the polar angle 90.75 du. Hence, the correct polar angle should have been 99.75 du. However, we adopt the identification of SK97, because their identification is faithful to the numeric values.
Tianjin [28]: This is a well-known asterism composed of stars such as α Cyg, δ Cyg, γ Cyg, ε Cyg, ζ Cyg, and τ Cyg that forms the wings of the Swan. Its northwest star of δ Cyg should be designated as the reference star. SK97 identified this correctly. Accordingly, its lodge angle is provided as 2 du from Dou (φ Sgr) in KYZJ, but it should be 2 du from Niu (α Cap).
Jixin [42]: SK97 identified this as φ Gem, but ω1 Cnc can also be a good candidate due to its close distance from the position given in the catalog.
Shaowei [45]: SK97 identified its reference star as 53 Leo, whose position at the epoch of 104 BCE is far from the position indicated by the coordinate values given in KYZJ. However, there are no bright and close candidates around the position other than 53 Leo.
Neiping [49]: SK97 identified this as ξ Vir, but ν Vir can also be a good candidate. However, its LA is not given in KYZJ. The coordinate values are complemented by the values given in CJSSJ.
Langwei [50]: The LA and PA are not given in KYZJ. The LA is given in CJSSJ to be 0 du from Zhen [120], but the PA is not given in the literature. The determinative star of Zhen [120] is γ Crv, whose right ascension was |${10^{\rm h}30^{\rm m}19^{\rm s}}$| at the epoch of 104 BCE. Langwei is a well-known asterism. It means the chief officer leading a swarm of stars in the constellation Coma Berenices. Hence, it is identified as γ Com.
Santai [53]: The PA of its reference star is given to be 30.25 du in KYZJ, while it is given to be 36.25 du in CJSSJ. Santai [53] is a well-known asterism. It is feet of the big bear or Ursa Major. Hence, the westernmost star ι UMa should be the reference star, and so the PA value in CJSSJ is correct.
Beidou [58]: This is a well-known asterism called the North Dipper composed of seven stars. KYZJ mentions the positions of two stars in this asterism. The reference star called Jixing has an LA of 0 du from the determinative star of Zhang [118] or υ1 Hya, and a PA of 18.25 du. Hence, its right ascension is |$\alpha _{\rm c}={8^{\rm h}10^{\rm m}}$| and its declination is δc = +72°1′. The westernmost star is α UMa, a well-known reference star of this asterism. Its right ascension was |$\alpha _{\rm s}={8^{\rm h}14{^{\rm m}_{.}}5}$| and its declination was |$\delta _{\rm s}=+71^{\circ }{17{^{\prime }_{.}}5}$| at the epoch of 104 BCE. Thus, we confirm that the reference star of Beidou [58] is α UMa.
KYZJ gives the coordinate of another member star of this asterism: the fifth star of Beidou [58] had an LA of 13 du from Jing [106] and a PA of 11.75 du. The determinative star of Jing [106] is known to be μ Gem. Hence, according to the catalog coordinate values, the reference star has the right ascension |$\alpha _{\rm c}={5^{\rm h}8{^{\rm m}_{.}}5}$| and the declination δc = +78°25′. The fifth star is easily identified as ε UMa. Its right ascension and declination at the epoch of 104 BCE were |$\alpha _{\rm s}={11^{\rm h}6^{\rm m}}$| and |$\delta _{\rm s}=+67^{\circ }{35{^{\prime }_{.}}5}$|, respectively. They do not agree with each other. If the LA of the fifth star were 13 du from Zhen [120] (γ Crv) instead of 13 du from Jing [106], and the PA were 21.75 du instead of 11.75 du, then the catalog values would be |$\alpha _{\rm c}={11^{\rm h}21{^{\rm m}_{.}}5}$| and δs = 68°34′, which are in agreement with the position of ε UMa at the epoch of 103 BCE. We note that the pronunciation of Jing is similar to that of Zhen [120].
Ziwei [59]: This is well known as being identified with κ Dra. Its declination was δs = +81°22′. Hence, we see that the PA of 90.5 du is a transcription error of 9.5 du. The reference star was described as a star at the right side. It should have been described as a left star, because the left and right directions on the sky had been designated from the viewpoint of the Heavenly Emperor. Hence, the right side means that it was described from the viewpoint of observers on the ground. We have a similar case for Guansuo [10].
Tianyi [61] and Taiyi [62]: Their coordinates indicate that SK97’s identifications are correct. However, their locations differ from those depicted on the Korean star chart C-Map, in which both stars stick closely to κ Dra. Hence, 6‘Dra and 4 Dra can also be good candiates. We can identify 6 Dra as the reference star of Jiwei [59], κ Dra as the star called Tianyi [61], and 4 Dra as the star called Taiyi [62].
Kolou [63]: Both KYZJ and CJSSJ give the LA of its reference star to be 0.25 du of Zhen [120], which is equal to |$\alpha _{\rm c}\simeq {10^{\rm h}13^{\rm m}}$|. On the other hand, the PA in KYZJ is 140 du or δc ≃ −47°59′, while the PA in CJSSJ is 130.25 du or δc = −38°23′. SK97 adopted the KYZJ values and identified the reference star as δ Cru, which had |$\alpha _{\rm s}\simeq {10^{\rm h}37^{\rm m}}$| and |$\delta _{\rm s}=-47^{\circ }{13{^{\prime }_{.}}5}$| at the epoch of 104 BCE. However, when we adopt the CJSSJ values, we can identify the reference star as δ Cen, which had |$\alpha _{\rm s}\simeq {10^{\rm h}29^{\rm m}}$| and δs = −39°15′ at the epoch of 104 BCE. We note that both cases have an angular difference of about 1°, and that both stars have similar visual magnitudes: 2.75 for δ Cru and 2.55 for δ Cen. We prefer δ Cen, because it is the westernmost star. However, we adopt the identification of SK97 for consistency.
Ping[65]: SK97 identified this as γ Hya, but ψ Hya is also a good candidate. Ping [65] is identified to be composed of γ Hya and ψ Hya. By convention, the westernmost star is designated as the reference star, so ψ Hya should be identified as the reference star. Their relative distances to the catalog values are similar. However, we just adopt the identification of SK97.
Jizu [67]: SK97 identified this as η Lup, but HR5993 is also a good candidate. Both catalogs in Sun (1994) and SK97 have a typographical error in the PA: it should be 124.25 du instead of 124.5 du.
Gui[68]: SK97 could not identify this. The LA value in KYZJ is 12 du of Wei [98], corresponding to |$\alpha _{\rm c} \simeq {15^{\rm h}25^{\rm m}}$|. The PA in KYZJ is 131 du or δc = −39°7′. CJSSJ gives a slightly different PA value of 131.5 du, corresponding to |$\delta _{\rm c}\simeq -39^{\circ }{36{^{\prime }_{.}}5}$|. A star called HR6675 had |$\alpha _{\rm s}\simeq {15^{\rm h}29^{\rm m}}$| and δs = −40°27′ at the epoch of 104 BCE. Its visual magnitude is 4.85. So, we can identify HR6675 as the reference star. However, we just adopt the identification of SK97, and leave another possibility for future work.
Fuyue [69]: The LA and PA values written in KYZJ can be converted into |$\alpha _{\rm c}={15^{\rm h}28^{\rm m}}$| and δc = −28°46′. SK97 identified this as a star called G Sco (|$\alpha _{\rm s}={15^{\rm h}31^{\rm m}}$| and |$\delta _{\rm s}=-33^{\circ }{4{^{\rm m}_{.}}5}$|), which is a relatively bright star of visual magnitude 3.15. However, it can also be identified as the M 6 open cluster, also called NGC 6405 (|$\alpha _{\rm s}={15^{\rm h}37{^{\rm m}_{.}}5}$| and |$\delta _{\rm s}=-31^{\circ }{2{^{\prime }_{.}}5}$|). Note that M 6 is closer to (αc, δc) than G Sco.
Chu [71]: The PA of the reference star is 130 du or δc = −38°8′ in CJSSJ, and 132.5 du or δc = −40°36′ in KYZJ. The right ascension is calculated to be |$\alpha _{\rm c}={16^{\rm h}1^{\rm m}}$|. SK97 could not identify this star, but we identify it as δ1 Tel, which had |$\alpha _{\rm s}={15^{\rm h}59^{\rm m}}$| and |$\delta _{\rm s}=-43^{\circ }{36{^{\prime }_{.}}5}$| at the epoch of 104 BCE. The visual magnitude of δ1 Tel is 4.90. Thus, we prefer the CJSSJ value.
Bie [72]: According to KYZJ, the reference star had |$\alpha _{\rm c}={16^{\rm h}39^{\rm m}}$| and δc = −37°38′. SK97 identified it as μ CrA, which had |$\alpha _{\rm s}={16^{\rm h}21{^{\rm m}_{.}}5}$| and δs = −39°5′ at the epoch of 104 BCE, which is far from the location (αc, δc). The star called α CrA (|$\alpha _{\rm s}={16^{\rm h}45{^{\rm m}_{.}}5}$|, δs = −37°42′) can also be a good candidate. However, we adopt SK97.
Beiluo [76]: This asterism is composed of one star. It is well known to be α PsA, also called Fomalhaut. Its PA is given to be 130.75 du in KYZJ, which agrees with the position of α PsA at the epoch of 104 BCE. CJSSJ gives a different PA of 120.75 du, which is far from the star by about 10°. We select the PA value in KYZJ.
Tiancang [78]: Its PA is given to be 120 du in KYZJ, but 112 du in CJSSJ. CJSSJ is correct.
Tianyuan[81]: SK97 identified the reference star as γ Eri. The LA is 2.75 du of the lunar lodge Bi [111]; 2.75 du is equal to |$\Delta \alpha _{\rm c}= {10^{\rm m}51^{\rm s}}$| in RA. The right ascension of the determinative star for the lunar lodge, Bi [111] or ε Tau, is |$\alpha ={2^{\rm h}30^{\rm m}32^{\rm s}}$|. The right ascension of γ Eri was |$\alpha _{\rm s}={2^{\rm h}21^{\rm m}13^{\rm s}}$| at the epoch of 104 BCE. Usually the right ascension is calculated by |$\alpha _{\rm c}\equiv \alpha +\Delta \alpha _{\rm c}={2^{\rm h}41^{\rm m}23^{\rm s}}$|, but in this case |$\alpha _{\rm c}\equiv \alpha -\Delta \alpha _{\rm c}={2^{\rm h}19^{\rm m}41^{\rm s}}$| is much better.
Yujing [83]: Its PA is given to be 120.75 du in KYZJ, which is too low. The PA must be corrected to be 100.75 du.
Hu [90]: SK97 has a typographical error. The PA in their table is given to be 122.75 du. The PA should be 122.25 du as is written in KYZJ.
Laoren [91]: Its PA is 133.5 du in KYZJ. It is a well-known star called Canopus or α Car, so its PA should be 143.5 du.
Ji [92]: Its PA is 148 du in KYZJ, but 138 du in CJSSJ. CJSSJ is correct.
Footnotes
Here, armillary spheres are astronomical instruments in the form of a spherical framework of rings. In Chinese astronomy they are meridian instruments used for astronomical observations and calendrical computations.
Shi Shi or Master Shi is Shi Shen or Shi Shen Fu. According to Sima Qian, he was an astronomer of the Warring States period (475–221 BCE). Gan De was a rather vague figure and also called Gan Shi. It is said that he also lived during the Warring States period. Wuxian Shi was also a legendary figure and lived a longer time ago, during the Yin dynasty (1600 BCE–1046 BCE). These figures represent the three schools of astronomy in ancient China rather than the authors of astronomical books.
This consists of four documents: “Shi Shi Xingguan Buzan,” “Gan Shi Xingguan Buzan,” “Wuxian Shi Buzan,” and “Huangdi Xingguan Buzan.” It is now preserved in Kyoto Prefectural Library and Archives, Japan. These are thought to be a handwritten copy of some documents related to “San Jia Xing Jing” (“Astral Canon of the Three Schools”) that was written by Chen Zuo (230–320 CE) in third-century China.
This treatise has been called “Tiandi ruixiang zhi” in Chinese, because the author had been believed to be Chinese. However, recent studies revealed that the treatise was written by a Korean scholar called Sal Sujin during the Silla dynasty in 666 CE (Ahn 2013a).
The asterisms designated by the Shi Shi school have their own reference stars. In particular, the reference stars for the 28 lunar lodges are called determinative stars.
The Chinese character Yuan means a circle, and the character Yi means an instrument. However, in “Han Shu” the Chinese letter Tu, meaning a diagram or a chart, was used instead of Yuan. On the other hand, in the astronomical treatise chapter of “Jin Shu” (“History of the Jin dynasty”), we can find a sentence describing the same event, which states that Geng Shouchang and others made a circular instrument to measure the calendrical angles. We know that the Chinese character Tu has a similar shape to the character Yuan. Therefore, the character Tu in “Han Shu” must be a typographical error for the character Yuan.
References



