https://orcid.org/0000-0002-4383-0368
Abstract
Supernova remnants (SNRs) have been regarded as major acceleration sites of Galactic cosmic rays. Recent X-ray studies revealed neutral Fe Kα line emission from dense gas in the vicinity of some SNRs, which can be best interpreted as K-shell ionization of Fe atoms in the gas by sub-relativistic particles accelerated in the SNRs. In this Letter, we propose a novel method of constraining the composition of particles accelerated in SNRs, which is currently unknown. When energetic heavy ions collide with target atoms, their strong Coulomb field can easily cause simultaneous ejection of multiple inner-shell electrons of the target. This results in shifts in characteristic X-ray line energies, forming distinctive spectral structures. Detection of such structures in the neutral Fe Kα line strongly supports the particle ionization scenario, and furthermore provides direct evidence of heavy ions in the accelerated particles. We construct a model for the Fe Kα line structures by various projectile ions utilizing atomic-collision data.
1 Introduction
Supernova remnants (SNRs) have been regarded as major acceleration sites of Galactic cosmic rays (CRs). Radio, X-ray, and gamma-ray observations have been providing evidence that particles are indeed accelerated in expanding shells of SNRs via the diffusive shock acceleration mechanism (e.g., Koyama et al. 1995; Aharonian et al. 2007; Ackermann et al. 2013). However, the emission channels detected are all radiations from relativistic particles, and thus particles with lower energies were almost unexplored until recently.
Suzaku data recently revealed the presence of enhanced neutral Fe Kα (∼6.4 keV) line emission in some SNRs, where gamma-rays are detected and thus particle acceleration is expected to be at work (e.g., W 44: Nobukawa et al. 2018; W 28: Okon et al. 2018; G323.7−1.0: Saji et al. 2018). In most cases, the line emission spatially coincides with dense gas in the vicinity of the SNRs. Based on these results, the authors interpreted that the Fe line emission is due to K-shell ionization of Fe atoms in the gas by particles accelerated in the SNRs. If this interpretation is the case, sub-relativistic particles are mainly responsible for the Fe emission line since the production cross-sections of the line emission peak at ∼10 MeV and ∼20 keV for protons and electrons, respectively (Dogiel et al. 2011).
Information on accelerated sub-relativistic particles can be exploited using the neutral Fe line emission. Dogiel et al. (2011) proposed an idea that species of radiating particles can be distinguished based on the equivalent width of the Fe line with respect to a non-thermal bremsstrahlung continuum from the same population of particles. Using the idea, Nobukawa et al. (2018, 2019) and Saji et al. (2018) claimed that protons account for the majority of the Fe line emission in some SNRs. Makino et al. (2019) presented an analytical model in which they consider energy-dependent escape of CRs from an SNR shock into an interacting cloud, and calculated emission spectra from the cloud, i.e., Fe line emission from sub-relativistic protons and π0-decay emission from relativistic protons. Applying their model to W 44 and W 28, they successfully reproduced both the observed Fe line emission intensity and the gamma-ray spectra.
Fine structures of the Fe Kα line, if detected, can provide another step forward in the study of sub-relativistic particles accelerated in astrophysical objects. Tatischeff et al. (2012) pointed out that charge exchange between fast heavy ions and ambient neutral atoms can produce broad line structures accompanied with narrower K-shell lines. Detection of such structures would allow us to prove the presence of heavy ions in accelerated particles and to constrain their composition. Apart from charge exchange, multiple ionization, which is the topic of this Letter, is another potentially important process caused by accelerated heavy ions, and thus can be a powerful diagnostic tool to probe accelerated particles.
In the present work, we qualitatively estimate the effect of the multiple ionization process on the Fe Kα line emission. We calculate a model to predict line structures due to multiple ionization by using the knowledge from beam experiments. Based on our model, we show Fe Kα line structures expected to be detected in SNRs by high-resolution X-ray spectroscopy with X-Ray Imaging and Spectroscopy Mission (XRISM).
2 Kα line structures by impacts of mono-energetic ions
2.1 KαLi peaks due to multiple ionization process
Ionization process of target atoms by projectile ions have been widely studied through both experimental and theoretical approaches. Through studies using high-resolution crystal spectrometers, authors such as Burch, Richard, and Blake (1971) and Kauffman et al. (1973) found differences of line structures between proton- and ion-produced Kα spectra. Figure 1 shows spectra of Fe Kα line structures originally presented by Burch, Richard, and Blake (1971). The proton-produced spectrum has only the neutral Fe Kα1 and Fe Kα2 lines due to the K–L1 and K–L2 transitions, respectively. The O5 +-produced spectrum, on the other hand, has broad line-like structures in the 6350–6550 eV band. When projectile particles are heavy ions, their strong Coulomb field can easily cause simultaneous ejection of multiple inner-shell electrons of targets, resulting in the significant characteristic structures.
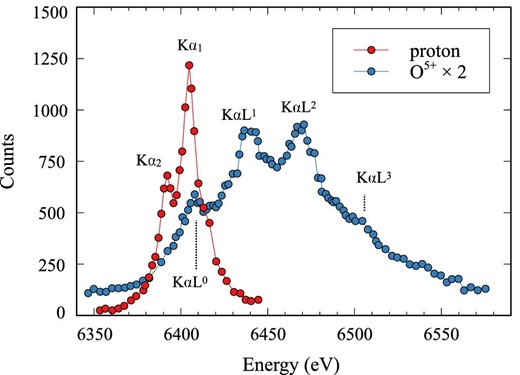
Fe Kα spectra produced by impacts of protons (red), and O5 + ions (blue) (Burch et al. 1971). For display purposes, the O5 + spectrum is scaled by a factor of two. (Color online)
The multiple ionization structures consist of peaks called KαLi (i = 0–7), each of which is a superposition of the K–L1 and the K–L2 transition lines from ionized Fe atoms with i L-shell vacancies. The center energies of the KαLi peaks are higher by ∼i × 20–30 eV than those of the Fe Kα1 and Kα2 lines. This is because the K–L1 (K–L2) transition lines shift upwards by ∼20–30 eV per L-shell electron ionization (=ΔEL) (e.g., Wang et al. 2012). The outer shell (M, N, ...) ionization is mainly manifested in broadenings of the KαLi peaks because the energy shift ΔEM (and ΔEN, ...) of the transition lines due to additional M-shell and outer shell vacancies is sufficiently smaller than ΔEL, and is equal to or smaller than the natural widths of the transition lines.
2.2 Modeling of KαLi peaks
The KαLi peaks are the sums of the Kα1Li and Kα2Li sub-peaks, which are superpositions of the K–L1 and K–L2 transition lines, respectively. The Kα1Li (Kα2Li) sub-peaks are expressed as superpositions of Lorentzians corresponding to transition lines. According to Horvat, Watson, and Peng (2006, 2009), KαLi spectra obtained in ion beam experiments can phenomenologically be reproduced by the sums of the Kα1Li and Kα2Li peaks described by Voigt functions, or a convolution of a Lorentzian and a Gaussian. Here, the Gaussian reflects broadening of the sub-peaks due to simultaneous ionization of electrons in outer shells. Taking the same approach, we modeled the Kα1Li and Kα2Li sub-peaks with the Voigt function.
The above scaling laws by Horvat, Watson, and Peng (2006) are derived from experimental data using a variety of solid targets with Z2 = 17–32 and projectile ions with Z1 = 6–83 at 2.5–25 MeV amu−1. The data cover impacts by various ions with ∼10 MeV amu−1, where the cross-sections for K-shell ionization of Fe atoms (Z2) peak. We applied the scaling laws to the calculation of the Fe line structures generated by impacts of various ions in the 0.5–1000 MeV amu−1 region, where collision nature is well-described by the perturbation theory and the scaling laws of Horvat, Watson, and Peng (2006) can be considered valid.
According to Horvat, Watson, and Peng (2009), intensities of the KαLi peaks are changed depending on the phase of the target, whether it is gas or solid. Compared to the solid target case, the Fe KαLi peaks become dominant with gaseous targets. Horvat, Watson, and Peng (2009) derived the scaling law of |$p_L^X$| similar to the equation (2) from atomic data of collisions between various ions at ∼10 MeV amu−1 and monoatomic Ar gas. The scaling law for gas is the same as equation (2), but with a′ = 0.856, b′ = 2.94, and c′ = 1.71.
2.3 Results
In figure 2a, we plot the models for the Kα line emitted by solid Fe bombarded by protons and fully ionized O and Fe ions. Figure 2b is the same but for gaseous Fe. The results clearly indicate that the intensities of the KαLi peaks depends on the charge state and kinetic energy of the projectiles. The larger charge the projectile has, the more significant the KαLi peaks become. This is naturally explained by a stronger Coulomb field of heavy ions. Regardless of the projectile species, the Fe KαLi peaks are the most significant when the projectile kinetic energy is ∼1.6 MeV amu−1. Electrons generally are ejected most efficiently when the projectile ion velocity matches the average velocity of electrons in orbit of an atom (Bohr 1948). Since the kinetic energy of ∼1.6 MeV amu−1 is translated into a projectile velocity close to that of Fe-L electrons, L-shell electrons are efficiently ionized around this energy.
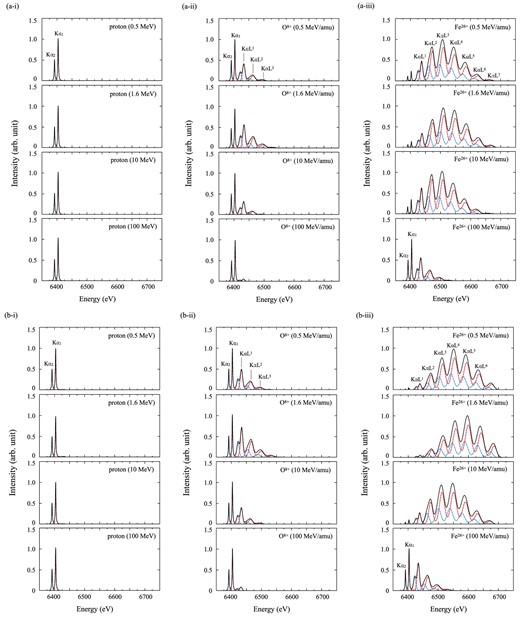
Fe Kα structures emitted from (a) solid and (b) gaseous Fe targets under bombardment by (i) protons, (ii) O8 +, and (iii) Fe26 + ions. The red and blue dashed curves denote the Fe Kα1 and Fe Kα2 structures, respectively. (Color online)
2.4 Assumptions
Figure 3 shows a comparison between the computed models and experimental data by Horvat, Watson, and Peng (2006, 2009). In the experimental data, the KαLi peaks (i = 0–7) are generated by impacts of projectile ions, while the Kα1 and Kα2 lines in figure 3a are mainly induced by secondary electrons and X-rays. Our model reproduces the overall KαLi peaks structures. However, we found some discrepancies of the line center energies and intensities. The contradiction about the center energy could be explained by the inaccuracy of equations (1), (2), and (4), which is estimated to be at a few percent level by Horvat, Watson, and Peng (2006). The discrepancy of the intensities could be brought about by continuous changes of energy and charge state of projectile ions in thick (∼mg cm−2) targets, which change the value of |$p_L^X$|. Another possibility would be contribution of electron captures from the L-shell of the target atoms in L-shell vacancy production, as Rymuza et al. (1989) and Kavčič et al. (2000) pointed out. Those effects are not included in the present model.
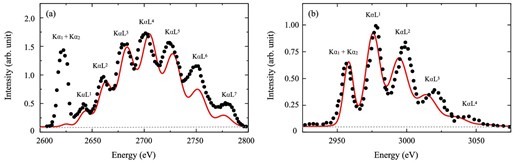
(a) Cl Kα spectrum from solid KCl targets under bombardment by 4 MeV amu−1 Kr36 + ions (Horvat et al. 2006) and (b) Ar Kα spectrum from a gaseous Ar target under bombardment by 9.4 MeV amu−1 Ne10 + ions (Horvat et al. 2009) from experiments (the black dots), compared with our model (the red curves). The gray dashed curves represent the background. (Color online)
3 Fe Kα structures produced by CRs
Using our model, we compute Fe Kα line spectra expected to be observed in SNRs. In SNR shocks, various ions would be accelerated at the same time, and thus the spectra would be superpositions of contributions from each ion species. Since the composition of CRs at acceleration sites is unknown, we here assume it is the same as that observed in the solar system by referring to Mewaldt (1994). We also assume that ions are fully ionized and that all ions follow a common spectrum. We take into account contributions from H, He, ..., Fe, Co, and Ni ions in an energy range of 0.5–1000 MeV amu−1.
3.1 Results and future observations
Figure 4 presents the result, where the models are folded with the response of the X-ray micro-calorimeter Resolve (Ishisaki et al. 2018) aboard XRISM (Tashiro et al. 2018). Accelerated ions have a power-law spectrum dN/dE ∝ E−s with s = 1 and s = 2 in the panels (a) and (b), respectively. The former is chosen referring to the measurement of non-thermal bremsstrahlung in W 49 B by Tanaka et al. (2018). The latter is the index expected in diffusive shock acceleration at a strong shock. In both cases, the KαLi (i = 1–7) peaks appear in the 6420–6700 eV band. The intensities of each KαLi peak strongly reflect the composition of the emitting particles. If particles accelerated in SNRs have a similar ion composition to CRs arriving at the solar system, the most significant peak is the KαL1 peak, which can be resolved into Kα1L1 and Kα2L1 with Resolve. The intensities of the two sub-peaks are ∼1/10 of those of Kα1 and Kα2. The Fe Kα1L1 and Kα2L1 sub-peaks are shifted by ∼30 eV with respect to the Fe Kα1 and Kα2.
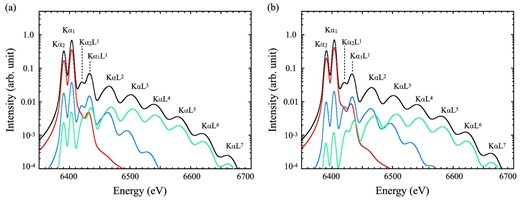
Fe Kα structures expected from Fe atoms bombarded by accelerated particles with spectral indices of (a) s = 1 and (b) s = 2 (black). The red, blue, and green curves represent contributions from protons, O ions, and Fe ions, respectively. (Color online)
A ∼eV energy resolution by X-ray micro-calorimeters would be necessary to resolve the structures. In addition to XRISM, future missions such as Athena (Barcons et al. 2017) and Super DIOS (Ohashi et al. 2018) with X-ray micro-calorimeters will able to detect the line structures. Such studies will play a complementary role to CR-ionization rate estimates based on H|$_3^{+}$| absorption lines (e.g., Indriolo et al. 2010). We finally note that potential targets would not be limited to SNRs, considering the recent claims of contribution of CR-ionization to the neutral Fe K line in the Arches cluster region (Tatischeff et al. 2012; Krivonos et al. 2017) and in the Galactic ridge (Nobukawa et al. 2015).
Acknowledgements
We thank T. Mukoyama, M. Pajek, B. Sulik, V. Tatischeff, and D. Banas for helpful discussion. This work is supported by JSPS/MEXT Scientific Research Grant Numbers JP19J14025 (H.O.), JP16K06937 (M.I.), JP19H01936 (T.T.), JP19K03915 (H.U.), and JP15H02090 (T.G.T.).
References
