X-ray emissions from magnetic polar regions of neutron stars

Inoue, Hajime

doi:10.1093/pasj/psz132

Abstract

Structures of X-ray emitting magnetic polar regions on neutron stars in X-ray pulsars are studied in the accretion rate range 10¹⁷ g s⁻¹–10¹⁸ g s⁻¹. It is shown that a thin but tall, radiation-energy-dominated, X-ray emitting polar cone appears at each of the polar regions. The height of the polar cone is several times as large as the neutron star radius. The energy gain due to the gravity of the neutron star in the polar cone exceeds the energy loss due to photon diffusion in the azimuthal direction of the cone, and a significant amount of energy is advected to the neutron star surface. Then, the radiation energy carried with the flow should become large enough for the radiation pressure to overcome the magnetic pressure at the bottom of the cone. As a result, the matter should expand in the tangential direction along the neutron star surface, dragging the magnetic lines of force, and form a mound-like structure. The advected energy to the bottom of the cone should finally be radiated away from the surface of the polar mound and the matter should be settled on the neutron star surface there. From such configurations, we can expect an X-ray spectrum composed of a multi-color blackbody spectrum from the polar cone region and a quasi-single blackbody spectrum from the polar mound region. These spectral properties agree with observations. A combination of a fairly sharp pencil beam and a broad fan beam is expected from the polar cone region, while a broad pencil beam is expected from the polar mound region. With these X-ray beam properties, basic patterns of pulse profiles of X-ray pulsars can be explained too.

1 Introduction

Soon after periodic X-ray variations were discovered from Cen X-3 (Giacconi et al. 1971) and Her X-1 (Tananbaum et al. 1972), accretion environments of such sources were theoretically discussed by Pringle and Rees (1972) and Lamb, Pethick, and Pines (1973). Since then, a large number of X-ray pulsars have been found and theoretical attempts have continuously been being done to explain the observational appearances of X-ray pulsars. We now have a general consensus on the situations of X-ray pulsars, the settings of which could sequentially be summarized as follows:

(1) a close binary of a strongly magnetized neutron star + a “normal” companion star,
(2) an accretion flow from the companion star to the neutron star,
(3) a magneto-boundary surface at ∼10⁸ cm from the neutron star where the magnetic pressure stops the accretion flow,
(4) two channeled flows along magnetic funnels towards the magnetic poles on the neutron star surface,
(5) very hot regions at the bottoms of the channeled flows, after energy conversions of the kinetic energies to thermal energies through standing shocks,
(6) X-ray emissions from the polar regions near the neutron star surface,
(7) an oblique rotation of the magnetic axis, causing X-ray pulsations.

Pioneer studies on the properties of the X-ray emitting regions had already done by some authors by the mid-1970s. Davidson (1973) proposed a situation that a hot, dense mound should be formed above each magnetic pole and that infalling material would be decelerated by the radiation pressure of photons trapped inside the mound. He further argued that energy released above the mound should diffuse out as moderately hard X-rays and that energy released within the mound should emerge as soft X-rays from the whole surface of the neutron star. By extending the idea of the radiation-pressure dominant polar mound to cases of high accretion rate, Inoue (1975) studied a structure of a radiation-pressure dominant polar cone above each magnetic pole by taking account of the effect of the gravity there. He discussed that the gravitational energy released in the polar cone should be radiated away from the surface of the cone as a multi-color blackbody emission. Basko and Sunyaev (1975), on the other hand, discussed the generation and diffusion of radiation in a plasma with a strong magnetic field at the bottom of a magnetic funnel, supposing a fairly low accretion rate corresponding to the X-ray luminosity ≪10³⁷ erg s⁻¹.

Even at this early stage in the middle of 1970’s, a general picture of X-ray emission regions on each magnetic pole of X-ray pulsars was suggested. It was that two regions should exist; the primary region where the kinematic energy of the infalling matter is converted to thermal energy and photons generated there or from the bottom side diffuse out upward suffering various interactions with matter in a magnetized plasma, and the secondary region where the accreted matter still gradually falls, being braked by the radiation pressure, and the gravitational energy gained there finally diffuses out from its surface and/or the adjacent neutron star surface as blackbody emissions. Studies on the primary region have since been done by several authors (e.g., Becker & Wolff 2007; Wolff et al. 2016) but the secondary region has not been studied in more detail than by the work of Inoue (1975).

Davidson (1973) first introduced the secondary region as the dense mound at the base of the magnetic funnel. This mound should be surrounded by the magnetic funnel, and the infalling matter through the magnetic funnel is considered to finally accumulate there. In the mound, a hydrostatic equilibrium should be established as

$$\begin{equation} \frac{dP}{dz} = \rho \frac{GM}{R^{2}}, \end{equation}$$

(1)

where P is the pressure at a position with a distance |$z$| from the mound bottom in the direction perpendicular to the stellar surface, ρ is the matter density, G is the gravitational constant, M is the neutron star mass, and R is the neutron star radius. Here, we have assumed the height of the mound, h_M, is sufficiently smaller than the stellar radius. Equation (1) can be solved as

$$\begin{equation} P_{*} = m \frac{GM}{R^{2}}, \end{equation}$$

(2)

where P_* is the pressure at the bottom of the mound and that at the top has been approximated to be zero. m is the column density of the accreted matter in the mound defined as

$$\begin{equation} m = \int _{0}^{h} \rho dz. \end{equation}$$

(3)

The total mass of the mound, M_M, is approximately given by introducing the average radius of the mound cross-section, x_M, as

$$\begin{equation} M_{\rm M} = \pi x_{\rm M}^{2} m. \end{equation}$$

(4)

Let t be time from the start of the accretion, then M_M should increase with t as

$$\begin{equation} M_{\rm M} = \frac{\dot{M}}{2} \,\, t. \end{equation}$$

(5)

|$\dot{M}$| is the total accretion rate on to the neutron star and the factor (1/2) comes from an assumption that the flow should be equally divided into the two funnel flows to the respective N or S magnetic poles. From these equations above, we see that the column density, m, should increase in time and the bottom pressure, P_*, should also do so. Then, at some moment, the pressure should overcome the magnetic pressure of the magnetic funnel and the matter should start to flow out from the mound bottom to the entire surface of the neutron star. Thus, a steady state of the mass flow in the mound should be realized when the bottom pressure slightly exceeds the magnetic pressure.

The column density in the steady state, m_M, is approximately achieved by equating the bottom pressure, P_*, to the bottom magnetic pressure, (B²/8π)_*, in equation (2) as

$$\begin{equation} m_{\rm M} = \frac{(B^{2}/8\pi )_{*}}{GM/R^{2}}, \end{equation}$$

(6)

and the accumulation time of the matter in the mound, t_A, is roughly estimated as

$$\begin{equation} t_{\rm A} = \frac{m_{\rm M} \pi x_{\rm M}^{2}}{\dot{M} /2}. \end{equation}$$

(7)

In the mound, the gravitational energy should still be released as the matter flows downwards and the energy generation rate should balance with the matter cooling rate in the steady state. The matter cooling rate should be given by the photon diffusion in the azimuthal direction of the mound as far as x_M ≪ h_M. The sideways diffusion time, t_{D, M}, is approximately given as

$$\begin{equation} t_{\rm D, M} = \frac{3\kappa _{\rm T} \rho _{\rm M} x_{\rm M}^{2}}{4c} \end{equation}$$

(8)

(see Inoue 1975), where κ_T is the Thomson scattering opacity, and c is the light velocity. ρ_M is the average density of the mound and can be approximated as

$$\begin{equation} \rho _{\rm M} \simeq \frac{m_{\rm M}}{h_{\rm M}}. \end{equation}$$

(9)

For the steady energy flow to realize, we set t_A = t_D and get, from equations (7), (8) and (9),

$$\begin{equation} h_{\rm M} \simeq \frac{3\kappa _{\rm T} }{8\pi c} \dot{M} = 1.4 \times 10^{5} \left( \frac{\dot{M}}{10^{17}\:\mbox{g}\:\mbox{s}^{-1}} \right) \:\mbox{cm}. \end{equation}$$

(10)

The simple considerations above indicate that the height of the mound, h_M, could increase as the accretion rate, |$\dot{M}$|⁠, increases and become comparable to or even larger than the stellar radius when |$\dot{M}$| approaches to 10¹⁸ g s⁻¹. If h_M gets larger than R, the X-ray luminosity from the secondary region could be dominant over that from the primary region, since the energy release rate from the primary region and that from the secondary region are approximately given as (⁠|$\dot{M}$|/2)GM/(R + h_M) and (⁠|$\dot{M}$|/2){(GM/R) − [GM/(R + h_M)]}, respectively.

In this paper, we study the nature and structure of the secondary region as a function of |$\dot{M}$| more precisely than such simple arguments given above. Based on the results, we then discuss observational appearances of X-ray emissions from there, focusing on cases of fairly high accretion rates corresponding to X-ray luminosities of 10³⁷–10³⁸ erg s⁻¹. In section 2, the basic assumptions of studying the accretion flow along the magnetic funnel are presented and structures of the X-ray emitting regions around the magnetic pole are solved through approximate equations. In section 3, we discuss observational appearances of X-ray spectra and pulse profiles expected from the magnetic polar regions as studied in section 2. Summary and discussions are given in section 4.

2 Structures of magnetic polar regions

2.1 Magneto-boundary surface

Following the general consensus summarized in the previous section, we consider a situation that matter flows from a companion star into a region governed by the gravitational field of a neutron star with magnetic field as strong as 10¹²–10¹³ gauss at its surface. The magnetic field halts the matter from further falling around the magneto-boundary surface at the distance ∼10⁸ cm from the neutron star. The matter then flows along the magneto-boundary surface towards the magnetic poler regions and falls on to the neutron star through two funnel-like tubes guided by the magnetic lines of force.

The picture of the magneto-boundary surface was historically first studied in the case of roughly spherical accretion by a strongly magnetized compact star (e.g., Lamb et al. 1973; Inoue & Hōshi 1975; Arons & Lea 1976; Elsner & Lamb 1977), where the magnetic field is considered to be confined inside the magneto-spheric cavity as a result of complete screening of the stellar magnetic field from the outside plasma by currents in the transition region between the magneto-boundary surface and the plasma.

In the case that a thin disk extends down to the magneto-bounding surface, which should be more realistic in most of X-ray pulsars than the spherical flow, the accretion flow from the disk to the neutron star surface was studied in detail by Ghosh, Lamb, and Pethick (1977) and Ghosh and Lamb (1978, 1979). It is shown that the stellar magnetic field penetrates the inner part of the disk through the Kelvin–Helmholtz instability, turbulent diffusion, and so on, and that a transition zone arises in which magnetic coupling between the star and the disk transfers the angular momentum from the disk to the star. The accreted matter is thus considered to flow from the innermost region of the disk along the lines of force of the stellar magnetic field on to the polar regions of the stellar surface by getting over the barrier of the centrifugal force through the angular momentum transfer.

In the scheme of Ghosh and Lamb (1978, 1979), only a thin disk is assumed to extend down to the magneto-boundary region and |$\sim 20\%$| of the stellar magnetic field is considered to remain outside the inner edge of the disk. Recent observations, however, indicate that a geometrically thick flow could exist in parallel to the thin disk from the outermost part of the accretion disk (Churazov et al. 2001; Sugimoto et al. 2016; H. Inoue in preparation). If so, the thick flow should completely screen the remaining magnetic field and thus such a configuration as is seen in figure 1 could be expected. As discussed by Ghosh and Lamb (1978, 1979), a fraction of the magnetic field should penetrate the inner part of the thin disk and the matter should flow along the lines of force of the field threaded in the disk by losing its angular momentum through the magnetic stress force. A small fraction of the magnetic field could remain outside the transition layer in which the matter is flowing from the thin disk but it should completely be compressed and screened by the plasma in the thick disk. The matter in the thick disk could go into the transition layer through instabilities such as the Reyleigh–Taylor instability (Arons & Lea 1976; Elsner & Lamb 1977), and flow together with the matter from the thick disk on to the neutron star surface. As a result, the outer surface of the transition layer could have a shape similar to those obtained by Arons and Lea (1976) and Elsner and Lamb (1977), as schematically drawn in figure 1, where two cusps appear on the magnetic axis. Here, we assume for simplicity that the magnetic axis and the rotational axis of the neutron star are aligned with each other and are perpendicular to the disk plane, as is done in the above literatures.

Fig. 1.

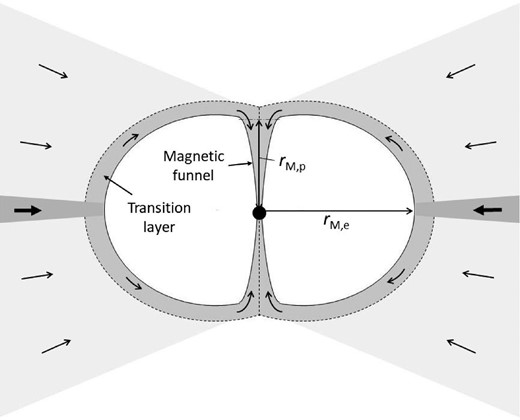
Schematic cross-section of the magneto-boundary surface considered in this paper.

Open in new tab Download slide

Let r_M,e and r_M,p be the distances of the inner surface of the transition layer in the magneto-boundary surface on the equatorial plane and on the magnetic axis, respectively. We assume

$$\begin{equation} r_{\rm {M,e}} = 0.4 \,\, r_{\rm {M,0}}, \end{equation}$$

(11)

adopting the result from Ghosh and Lamb (1978), where r_M,0 is the characteristic radius of the magneto-boundary surface for spherical accretion, and

$$\begin{eqnarray} r_{\rm {M,p}} &=& \!\!\!\!\!\!0.5 \,\, r_{\rm {M,e}} \nonumber \\ &\quad\simeq & 6.4 \times 10^{7} \left(\frac{\dot{M}}{10^{17} \,\, \mbox{g}\:\mbox{s}^{-1}} \right)^{-2/7} \left(\frac{M}{M_{\odot }} \right)^{-1/7} \nonumber\\ &&\times\,\left(\frac{\mu _{\rm M}}{10^{30} \:\mbox{gauss}\:\mbox{cm}^{3}} \right)^{4/7}, \end{eqnarray}$$

(12)

adopting the value used by Arons and Lea (1976). μ_M is the magnetic moment of the neutron star. Considering a situation where accreted matter with density ρ_T falls with velocity |$v$|_T in the transition layer with thickness h_T from the equatorial side to the polar side, the mass continuity is approximately expressed as

$$\begin{equation} \frac{\dot{M}}{2} \simeq \rho _{\rm T} v_{\rm T} h_{\rm T} 2\pi r \sin \theta , \end{equation}$$

(13)

where the factor of 1/2 comes from the presence of the two separate streams toward the two respective poles, and θ is the tangential angle of a relevant position from the polar axis. Here and hereafter, we assume that identical things happen in both sides of the magnetic poles.

The pressure of the matter in the transition layer, P_T, is expressed with help from equation (13) as

$$\begin{equation} P_{\rm T} = \frac{2 \rho _{\rm T}}{m_{\rm p}} kT_{\rm T} \simeq \frac{\dot{M} kT_{\rm T}}{m_{\rm p}v_{\rm T} h_{\rm T} 2 \pi r \sin \theta }, \end{equation}$$

(14)

where m_p is the proton mass, k is the Boltzmann constant, and T_T is the temperature of the flowing matter. The flow velocity, |$v$|_T, should be given as a result of the angular momentum transfer in the transition layer and thus be proportional to the Alfven velocity there. In the present situation, the Alfven velocity should roughly equal the sound velocity and hence |$v$|_T should be constant if the temperature is constant throughout the transition layer. Under the isothermal approximation, P_T can be written in terms of that around the equatorial plane, P_T,e, as

$$\begin{equation} P_{\rm T} \simeq P_{\rm T,e} \left( \frac{r}{r_{\rm M,e}} \right)^{-1} \sin ^{-1} \theta . \end{equation}$$

(15)

The magnetic pressure in the transition layer, P_B, is, on the other hand, governed mainly by the magnetic field in the θ direction, which could be proportional to r⁻³sin θ. Hence, P_B is approximately given, referring to the value around the equatorial plane, P_B,e, as

$$\begin{equation} P_{\rm B} \simeq P_{\rm B,e} \left(\frac{r}{r_{\rm M,e}}\right)^{-6} \sin ^{2} \theta . \end{equation}$$

(16)

Since P_T ≃ P_B and P_T,e ≃ P_B,e, we get an approximate relation between θ and r as

$$\begin{equation} \sin \theta \simeq \left( \frac{r}{r_{\rm M,e}} \right)^{5/3}. \end{equation}$$

(17)

From this relation, we can see that there should be no solution near the cusp, where r ≃ r_M,p and θ < 1, for the magnetic pressure of the magneto-boundary surface to balance with the matter pressure. The opening angle, Θ₀, of the region in which the matter tends to fall radially on to the stellar surface without being halted by the magnetic pressure is approximately calculated from equation (17) with the help of equation (12) as

$$\begin{equation} \Theta _{0} \simeq \left(\frac{r_{\rm M,p}}{r_{\rm M,e}}\right)^{5/3} \simeq 0.32. \end{equation}$$

(18)

We assume that the magnetic field tends to be dipole-like and the matter should infall to the stellar surface along the lines of force in this region with θ ≤ Θ₀, and we call this region the magnetic funnel hereafter. We then approximate the opening angle of the magnetic funnel, Θ, to be a function of r, as

$$\begin{equation} \Theta = \Theta _{0} \left(\frac{r}{r_{\rm M,p}} \right)^{1/2}, \end{equation}$$

(19)

guided by the dipole-field lines of force. This equation can be rewritten with the help of equations (11), (12), and (18) as

$$\begin{equation} \Theta = \Theta _{*} \left(\frac{r}{R} \right)^{1/2}, \end{equation}$$

(20)

where Θ_* is the opening angle of the funnel on the surface of the neutron star and is as

$$\begin{eqnarray} \Theta _{*} &=& 4.0 \times 10^{-2} \left(\frac{R}{10^{6} \:\mbox{cm}} \right)^{1/2} \left(\frac{\dot{M}}{10^{17} \:\mbox{g}\:\mbox{s}^{-1}} \right)^{1/7} \left(\frac{M}{M_{\odot }} \right)^{1/14} \nonumber\\ &&\times\,\left( \frac{\mu _{\rm M}}{10^{30} \:\mbox{gauss}\:\mbox{cm}^{3}} \right)^{-2/7}. \end{eqnarray}$$

(21)

2.2 Overall picture of the magnetic polar regions

As the matter falling in the magnetic funnel finally hits the neutron star surface, a standing shock should appear at a certain height from the stellar surface. The matter can be approximated to flow with the free-fall velocity on the upper-stream side of the shock. We call this region the free-fall region.

The kinetic energy of the inflowing matter should be converted to the thermal energy through the shock. Thermal emissions are expected mainly in the X-ray band from the region between the shock and the stellar surface. We call this X-ray emitting region the polar cone. The thermal pressure is lower than the magnetic pressure in the polar cone, and the matter falls inwards along the magnetic lines of force there.

At the bottom of the polar cone, however, the matter pressure comes to exceed the magnetic pressure and the matter flows out along the stellar surface from the polar cone by dragging the magnetic lines of force. A mound-like structure appears at each of the two polar surface regions and additional X-ray emissions are expected from there. We call these mound-like structures the polar mounds hereafter.

Figure 2 shows the schematic diagram of the magnetic polar regions considered in this paper.

Fig. 2.

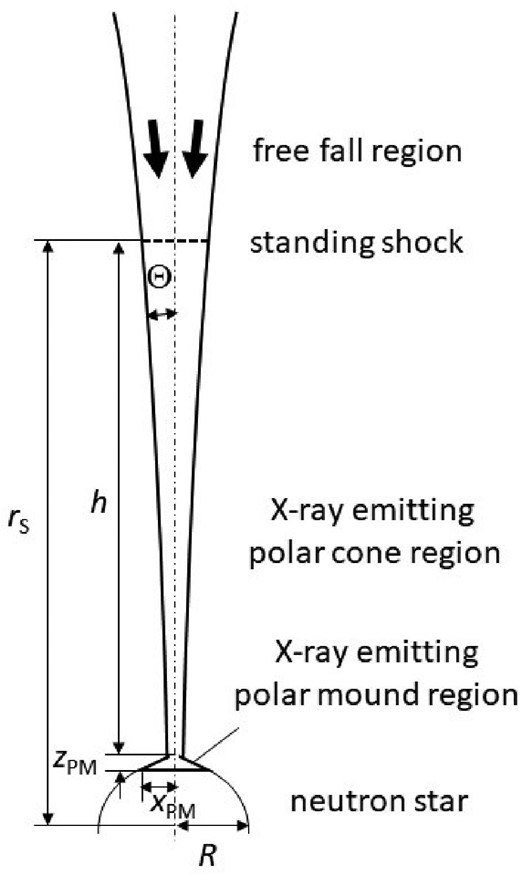
Schematic diagram of magnetic polar regions considered in this paper.

Open in new tab Download slide

2.3 Free-fall region

The matter is assumed to flow with the free-fall velocity in the free-fall region and then the radial inflow velocity |$v$|_F at a position with a distance r from the center of the neutron star is given as

$$\begin{equation} v_{\rm F} = \left(\frac{2GM}{r} \right)^{1/2}. \end{equation}$$

(22)

The continuity equation is written as

$$\begin{equation} \rho _{\rm F} v_{\rm r} \pi (r \Theta )^{2} = \frac{\dot{M}}{2}, \end{equation}$$

(23)

where ρ_F is the density of the matter in the free-fall region and is found to be

$$\begin{equation} \rho _{\rm F} = \frac{\dot{M}}{2\pi \Theta _{*}^{2} (2GM)^{1/2} R^{3/2}} \left(\frac{r}{R} \right)^{-5/2}. \end{equation}$$

(24)

The optical depth for Thomson scatterings, τ_F, in the azimuthal direction in the free-fall region is calculated with equations (20) and (24) as

$$\begin{eqnarray} \tau _{\rm F} &=& \kappa _{\rm T} \rho _{\rm F} r \Theta \nonumber \\ &\simeq & 9.9 \left( \frac{\dot{M}}{10^{17} \:\mbox{g}\:\mbox{s}^{-1}} \right)^{6/7} \left(\frac{M}{M_{\odot }} \right)^{-4/7} \left(\frac{\mu _{\rm M}}{10^{30} \:\mbox{gauss}\:\mbox{cm}^{3}} \right)^{-2/7}\nonumber \\ &&\times\, \left(\frac{r}{10^{6} \mbox{cm}} \right)^{-1}, \end{eqnarray}$$

(25)

where κ_T is the opacity of the Thomson scattering. From this equation, we see that the flow within the magnetic funnel above the shock front is optically thick for the Thomson scattering in the case of |$\dot{M} \gtrsim 10^{17}\:$|g s⁻¹ unless r ≫ 10⁷ cm.

2.4 X-ray emitting polar cone region

2.4.1 Dominance of the radiation energy in the polar cone

As shown in equation (25), the optical depth is larger than unity even in the free-fall region in front of the shock. The density behind the shock front must be larger than the density in the free-fall region and the density gets larger and larger as the matter infalls in the polar cone. Thus, we can say that polar cone is sufficiently optically thick.

The density behind the shock, ρ_S, is given as

$$\begin{equation} \rho _{\rm S} = \frac{\gamma +1}{\gamma -1} \rho _{\rm F} (r_{\rm S}), \end{equation}$$

(26)

where γ is the specific heat ratio. If we initially assume that the gaseous energy is dominant compared to the radiation energy, γ should be 5/3 and then ρ_S = 4ρ_F(r_S). The ion temperature behind the shock, T_i,S, is given as

$$\begin{equation} T_{\rm i, S} = \frac{3}{8} \frac{m_{\rm p}}{k} \frac{GM}{ r_{\rm S}}. \end{equation}$$

(27)

The electron temperature T_e,S should be determined by a balance between energy input through collisions with protons and energy loss through photon emissions and Compton scatterings. The energy input rate per mass, ϵ₊, is expressed as

$$\begin{equation} \dot{\varepsilon }_{+} = \frac{3 kT_{\rm i,S}/ 2m_{\rm p}}{t_{\rm ie}}, \end{equation}$$

(28)

when T_i,S ≫ T_e,S. t_ie is the ion–electron equipartition time and is given by Spitzer (1962) as

$$\begin{equation} t_{\rm ie} = 4.2 \times 10^{-22} (\ln \Lambda )^{-1} \rho _{\rm S}^{-1} T_{\rm e,S}^{3/2} \end{equation}$$

(29)

in cgs units, where ln Λ is the Coulomb logarithm. The energy loss rate per mass, |$\dot{\varepsilon }_{-}$| is, on the other hand, written as

$$\begin{equation} \dot{\varepsilon }_{-} = A \dot{\varepsilon }_{0} \rho _{\rm S} T_{\rm e, S}^{1/2}, \end{equation}$$

(30)

where |$\dot{\varepsilon }_{0} \rho _{\rm S} T_{\rm e, S}^{1/2}$| is the free–free emission rate per mass and A is an amplification factor through inverse Compton scatterings. From |$\dot{\varepsilon }_{+} = \dot{\varepsilon }_{-}$| and with the help of equations (27)–(30) we get, independently of the density,

$$\begin{equation} T_{\rm e,S} = 1.9 \times 10^{10} \left(\frac{M}{M_{\odot }}\right)^{1/2} \left(\frac{r_{\rm S}}{10^{6} \:\mbox{cm}}\right)^{-1/2}\:\mbox{K}, \end{equation}$$

(31)

where we have assumed ln Λ = 10 and A = 10 (Illarionov & Sunyaev 1972).

Since |$\dot{\varepsilon }_{-}$| is thought to be the radiation energy generation rate per mass, we can approximately calculate the radiation energy density per mass, ϵ_{Rad, S}, expected when the electron temperature is as in equation (31), as

$$\begin{equation} \varepsilon _{\rm Rad,S} \simeq \dot{\varepsilon }_{-} t_{\rm D,S}. \end{equation}$$

(32)

Here, t_D,S is a time scale, during which the generated photons diffuse out in the azimuthal direction of the polar cone, and is approximately represented as

$$\begin{equation} t_{\rm D, S} = \frac{3 \kappa _{\rm T} \rho _{\rm S} (r_{\rm S} \Theta _{\rm S})^{2}}{4 c}. \end{equation}$$

(33)

If ϵ_{Rad, S} is as large as or larger than the gaseous energy per mass behind the shock, which is given as

$$\begin{equation} \varepsilon _{\rm Gas, S} = \frac{9}{16} \frac{GM}{r_{\rm S}}, \end{equation}$$

(34)

with the specific heat ratio of 5/3, we can assure that the radiation energy is sufficiently established to be dominant compared to the gaseous energy in the polar cone.

Let ζ be the ratio of ϵ_{Rad, S} to ϵ_{Gas, S}, and given from the above equations as

$$\begin{eqnarray} \zeta &=& \frac{\varepsilon _{\rm Rad,S}}{\varepsilon _{\rm Gas,S}} \nonumber \\ &=& 0.9 \, \left(\frac{\dot{M}}{10^{17} \:\mbox{g}\:\mbox{s}^{-1}} \right)^{12/7} \left(\frac{\mu _{\rm M}}{10^{30} \:\mbox{gauss}\:\mbox{cm}^{3}} \right)^{4/7} \left(\frac{M}{M_{\odot }} \right)^{-53/28} \nonumber \\ &&\times\,\left(\frac{r_{\rm S}}{10^{6} \:\mbox{cm}} \right)^{-5/4}, \end{eqnarray}$$

(35)

where we have assumed A = 10 and ln Λ = 10 again. By using the r_S and |$\dot{M}$| relation for the polar cone as given in figure 6 in sub-subsection 2.4.3, we can calculate ζ as a function of |$\dot{M}$| for two cases of μ_M, and the result is shown in figure 3. We see that ζ ≳ 1 when |$\dot{M} \gtrsim 10^{17}\:$|g s⁻¹. Since our concern here mainly exists on the bright X-ray pulsars with |$\dot{M} \gtrsim 10^{17}\:$|g s⁻¹, we approximate the thermal energy as being governed by the radiation energy, and neglect the gaseous energy in the polar cone.

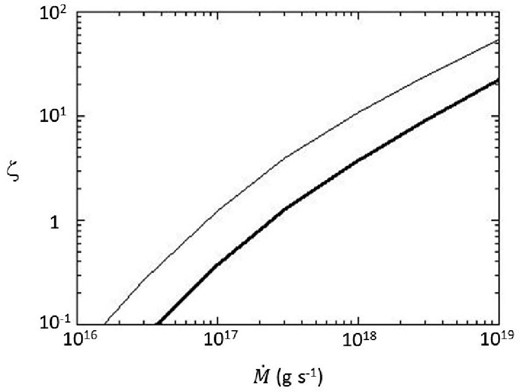
$ζ-value, which indicates the dominance of the radiation energy density behind the shock, as a function of $\dot{M}$. The thick and thin lines correspond to cases of μM = 1030 gauss cm3 and μM = 1031 gauss cm3, respectively.$

Fig. 3.

ζ-value, which indicates the dominance of the radiation energy density behind the shock, as a function of |$\dot{M}$|⁠. The thick and thin lines correspond to cases of μ_M = 10³⁰ gauss cm³ and μ_M = 10³¹ gauss cm³, respectively.

Open in new tab Download slide

2.4.2 Energy loss due to side-say diffusion of photons

Since Θ ≪ 1, photons in the polar cone tend to diffuse out in the azimuthal direction of the cone. Thus, we approximate that the energy loss of the inflowing matter in the polar cone is governed by the sideways diffusion of photons. In that case, the energy loss rate per unit volume, q, is approximately given as

$$\begin{equation} q = \frac{u}{t_{\rm D}}, \end{equation}$$

(36)

where u is the typical radiative energy density in the polar cone, and t_D is the diffusion time as in equation (33). The equation for the energy flow in the polar cone is then given as

$$\begin{eqnarray} \frac{\dot{M}}{2} \frac{d}{dr}\left(\frac{v^{2}}{2} + \frac{4}{3} \varepsilon - \frac{GM_{\rm X}}{r} \right) &=& \pi (r \Theta )^{2} q = \frac{4 \pi c}{3 \kappa _{\rm T}} \varepsilon , \end{eqnarray}$$

(37)

with the help of equation (36), equation u = ρϵ, and equation (33), where |$v$| and ϵ are, respectively, the inflow velocity and the radiative energy per unit mass in the polar cone.

2.4.3 Structure of the polar cone

Based on the above arguments, equations determining structures of the polar cone are as follows.

The first is the continuity equation which is given in equation (23) by replacing |$v$|_T with |$v$|⁠. Here, we assume for simplicity that ρ and |$v$| are uniform on a cross-section in the azimuthal direction of the polar cone.

The second is the dynamical equation, on an assumption that the flow in the polar cone is sufficiently subsonic to neglect the velocity gradient term;

$$\begin{equation} \frac{dP}{dr} = - \rho \frac{GM}{r^{2}}. \end{equation}$$

(38)

The third is the energy equation, modified from equation (37) by neglecting the kinetic energy of the matter flow, as

$$\begin{equation} \frac{d}{dr} \left(\frac{4}{3} \varepsilon - \frac{GM}{r} \right) = \frac{\varepsilon }{r_{\rm D}}, \end{equation}$$

(39)

where r_D is a parameter defined as

$$\begin{equation} r_{\rm D} = \frac{3 \kappa _{\rm T} \dot{M}}{8 \pi c} = 1.4 \times 10^{5} \left(\frac{\dot{M}}{10^{17} \mbox{g}\:\mbox{s}^{-1}} \right) \:\mbox{cm}. \end{equation}$$

(40)

In the above two equations, we have assumed that P and ϵ are radiation pressure and radiation energy per mass, neglecting gaseous pressure and energy, and that both are representative quantities over a cross-section of the polar cone. Then, we can set

$$\begin{equation} P = \frac{u}{3} = \frac{\rho \varepsilon }{3}. \end{equation}$$

(41)

From equations (38), (39), and (41), we get two equations to determine ϵ and ρ as functions of r as

$$\begin{equation} \frac{d\varepsilon }{dr} = \frac{3}{4} \left( \frac{\varepsilon }{r_{\rm D}} - \frac{GM}{r^{2}} \right), \end{equation}$$

(42)

and

$$\begin{equation} \frac{d\rho }{dr} = -\frac{3\rho }{4\varepsilon } \left( \frac{\varepsilon }{r_{\rm D}} + 3 \frac{GM}{r^{2}} \right). \end{equation}$$

(43)

The top boundary of the polar cone is the shock front. The density at the top boundary should be given by equation (26). Since the radiation energy density is considered to be dominant in the polar cone, we set γ = 4/3 in the polar cone and then ρ_S = 7ρ_F(r_S). By also approximating that the kinetic energy of the inflow matter in front of the shock is all converted to the radiative energy (enthalpy) behind the shock, ϵ_S is expressed as

$$\begin{equation} \varepsilon _{\rm S} = \frac{3}{4} \frac{GM}{r_{\rm S}}. \end{equation}$$

(44)

These boundary values are functions of r_S, and thus we numerically solve equations (42) and (43) from an assumed position, r_S, successively decreasing r inward to the bottom boundary at the neutron star surface where r = R. As shown later, the radiative pressure steeply increases as r decreases and comes to exceed the magnetic pressure of the funnel at some position. The magnetic funnel should be pushed out, when the radiative pressure exceeds the magnetic pressure, and the matter should flow out along the neutron star surface by dragging the magnetic lines of force from the funnel-like magnetic column. Thus, the following condition should be satisfied at the bottom of the polar cone as

$$\begin{equation} P_{*} = \frac{\rho _{*} \varepsilon _{*}}{3} = \frac{B_{r, *}^{2}}{8 \pi }, \end{equation}$$

(45)

where we represent the physical quantities at the bottom of the polar cone with the subscript *. The distance of the top boundary of the polar cone, r_S, has been searched to satisfy this bottom boundary condition.

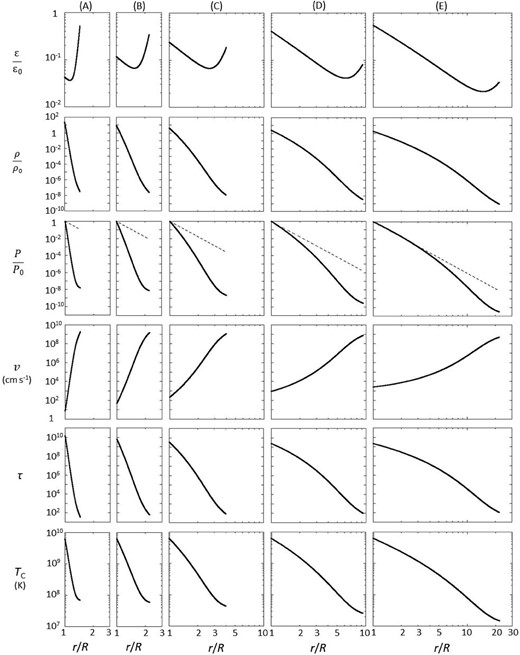
Solutions of equations (42) and (43) have been found with the procedures described above in various cases of |$\dot{M}$|⁠, where we have adopted M = M|$_{\odot}$|⁠, R = 10⁶ cm and two cases of B_r,* as 10¹² G and 10¹³ G. The obtained ϵ, ρ, P, |$v$|⁠, τ, and T_C as functions of r are shown for five cases of |$\dot{M}$| for B_r,* = 10¹² G in figure 4 and for B_r,* = 10¹³ G in figure 5, respectively. Here, |$v$| has been calculated from the continuity equation. τ is the optical depth for the Thomson scattering in the tangential direction of the polar cone. T_C is the typical temperature of the matter in the polar cone and has been calculated by an equation as T_C = (ρ ϵ/a)^1/4, where a is the first radiation constant. The normalization parameters in the figures are defined as ϵ₀ = GM/R, |$\rho _{0} = 3 B_{\rm r, *}^{2} R / (8 \pi GM) \sim 9 \times 10^{2} (B_{\rm r, *}/10^{12}\:$|G)²(M/M|$_{\odot}$|⁠)⁻¹(R/10⁶ cm) g cm⁻³, and P₀ = P_* in equation (45).

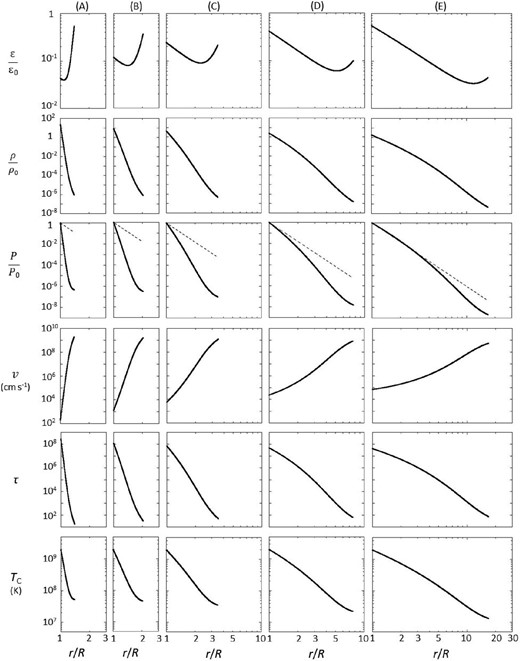
$Solved distributions of ϵ, ρ, P, $v$, τ, and TC as functions of r in five $\dot{M}$ cases for Br, * = 1012 G. Columns (A), (B), (C), (D), and (E) correspond to cases of $\dot{M} = 3 \times 10^{16}\:$g s−1, 1017 g s−1, 3 × 1017 g s−1, 1018 g s−1, and 3 × 1018 g s−1, respectively. Dashed lines in the row of P represent the r-dependence of the magnetic pressure as ∝ r−6.$

Fig. 4.

Solved distributions of ϵ, ρ, P, |$v$|⁠, τ, and T_C as functions of r in five |$\dot{M}$| cases for B_{r, *} = 10¹² G. Columns (A), (B), (C), (D), and (E) correspond to cases of |$\dot{M} = 3 \times 10^{16}\:$|g s⁻¹, 10¹⁷ g s⁻¹, 3 × 10¹⁷ g s⁻¹, 10¹⁸ g s⁻¹, and 3 × 10¹⁸ g s⁻¹, respectively. Dashed lines in the row of P represent the r-dependence of the magnetic pressure as ∝ r⁻⁶.

Open in new tab Download slide

Fig. 5.

Same as figure 4 but for B_r,* = 10¹³ G.

Open in new tab Download slide

The height of the polar cone, h, defined as

$$\begin{equation} h = r_{\rm S} - R, \end{equation}$$

(46)

is plotted as a function of |$\dot{M}$| in figure 6. As seen from this figure, h increases roughly in proportion to |$\dot{M}$|⁠. When |$\dot{M}$| is ∼10¹⁶ g s⁻¹, h is about a tenth as small as the neutron star radius. When |$\dot{M}$| is ∼10¹⁸ g s⁻¹, however, h gets about ten times as large as the neutron star radius.

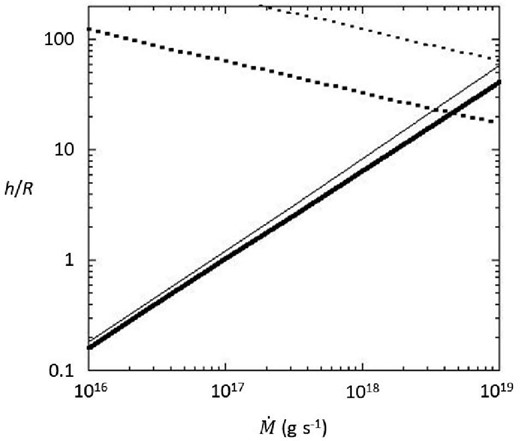
$Height of the polar cone region as a function of $\dot{M}$ (solid lines). Dotted lines indicate positions of rM,p. The thick and thin lines correspond to cases of Br,* = 1012 G and 1013 G. respectively.$

Fig. 6.

Height of the polar cone region as a function of |$\dot{M}$| (solid lines). Dotted lines indicate positions of r_M,p. The thick and thin lines correspond to cases of B_r,* = 10¹² G and 10¹³ G. respectively.

Open in new tab Download slide

2.4.4 Energy loss from the polar cone

From figures 4 and 5, we see, irrespectively of |$\dot{M}$|⁠, that ϵ decreases as r decreases from r_S but that it increases after r gets smaller than a certain value. The variation of ϵ is determined by equation (42), in which the first term and the second term on the right-hand side are the energy loss rate through the radiative diffusion and the energy gain rate from the gravitational energy, respectively. In the upper region near the shock, the radiative cooling rate is dominant compared to the energy gain rate and ϵ decreases as the matter flows downwards. The energy gain rate through the gravitational acceleration, however, becomes dominant compared to the energy-loss rate and ϵ starts increasing with r-decrease when r gets smaller than the boundary distance, r_B, where dϵ/dr = 0. Hereafter, the region where r > r_B and that where r < r_B are called as the upper polar cone region and the lower polar cone region respectively.

Let the total energy per mass of the inflow matter in the polar cone be u, it is expressed as

$$\begin{equation} u = \frac{4}{3} \,\, \varepsilon - \frac{GM}{r}, \end{equation}$$

(47)

where the first term on the right-hand side is the enthalpy per mass under the situation in which the radiative energy density is largely dominant to the gaseous energy density. Since the top boundary condition of ϵ is given as in equation (44), we have

$$\begin{equation} u_{\rm S} = 0, \end{equation}$$

(48)

just behind the shock front. This is the result from an approximation that the specific total energy u is just zero at infinity. Then, if u decreases to u_B as the matter falls down to the position r_B, the inflow matter should lose an amount of energy per mass, |$w$|_U, in the upper region as

$$\begin{equation} w_{\rm U} = u_{\rm S}-u_{\rm B}=-u_{\rm B}. \end{equation}$$

(49)

Similarly, another amount of energy per mass, |$w$|_L, which is lost from the inflow matter in the lower polar cone region, is given as

$$\begin{equation} w_{\rm L} = u_{\rm B}-u_{*}, \end{equation}$$

(50)

where u_* is the u value at the bottom of the polar cone. The inflow matter should finally spread over the neutron star surface and assimilate with the interior matter of the neutron star. In order to do that, however, the inflow matter should throw away the radiative thermal energy, ϵ_*, which has remained at the bottom of the polar cone. This ϵ_* should be conveyed to the polar mound region, as discussed in the next sub-section, and finally be radiated away from its surface. The amount of the thermal energy, |$w$|_*, which has been carried without being radiated away even to the bottom of the polar cone, is given as

$$\begin{equation} w_{*} = \frac{4}{3}\,\, \varepsilon _{*}. \end{equation}$$

(51)

Figure 7 shows respective portions of the three amounts of the energy |$w$|_U, |$w$|_L, and |$w$|_* to the sum of the three, as functions of |$\dot{M}$| in the case of B_r,* = 10¹² G. The result is about the same in the case of B_r,* = 10¹³ G. We see that |$w$|_H is dominant when |$\dot{M} \lesssim 10^{17}\:$|g s⁻¹, the three are comparable to one another when 10¹⁷ g s⁻¹|$\lesssim \dot{M} \lesssim 10^{18}\:$|g s⁻¹, and |$w$|_* is dominant when |$\dot{M} \gtrsim 10^{18}\:$|g s⁻¹.

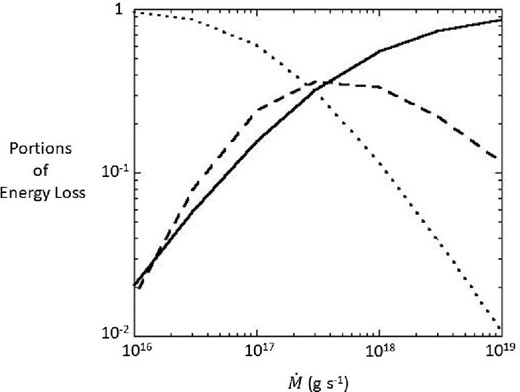
$Portions of energy loss in the upper polar cone region (dotted line), the lower polar cone region (dashed line) and in the mound region (thick line) as functions of $\dot{M}$ in the case of Br,* = 1012 G.$

Fig. 7.

Portions of energy loss in the upper polar cone region (dotted line), the lower polar cone region (dashed line) and in the mound region (thick line) as functions of |$\dot{M}$| in the case of B_r,* = 10¹² G.

Open in new tab Download slide

2.5 X-ray emitting polar mound region

The accreted matter still tends to flow downwards with a significant amount of the thermal energy at the bottom of the polar cone, but the thermal pressure should get stronger than the magnetic pressure of the surrounding magnetic funnel if the matter flows further below the bottom boundary. Thus, the matter should start expanding along the surface of neutron star, dragging the magnetic lines of force. We call this tangentially expanding region the polar mound region. The schematic cross-section of the polar mound is drawn in figure 8.

Fig. 8.

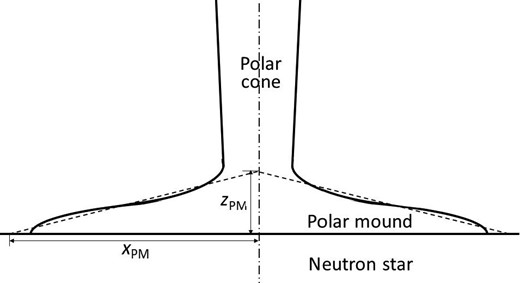
Schematic cross-section of the polar mound. The shape is approximated by a low cone, as indicated with dashed lines, with a radius x_PM of the base and a height |$z$|_PM at the center, in order to roughly estimate the sizes of the polar mound.

Open in new tab Download slide

The structure of the polar mound should be determined from the following two conditions.

The first is that the matter flowing in the polar mound should radiate away the residual thermal energy which has remained at the bottom of the polar cone before settling on the surface of the neutron star. This condition can be represented by a simple equation as

$$\begin{equation} \frac{\dot{M}}{2} = \frac{M_{\rm PM}}{t_{\rm D, PM}}. \end{equation}$$

(52)

M_PM is the total mass in the polar mound, approximately given as

$$\begin{equation} M_{\rm PM} = \frac{1}{3} \pi x_{\rm PM}^{2} z_{\rm PM} \rho _{\rm PM}, \end{equation}$$

(53)

and t_{D, PM} is the photon diffusion time in the direction perpendicular to the stellar surface, roughly written as

$$\begin{equation} t_{\rm D, PM} = \frac{\kappa _{\rm T} \rho _{\rm PM} z_{\rm PM}^{2}}{3c}. \end{equation}$$

(54)

Here, we have assumed the shape of the polar mound to be a very low cone with radius x_PM of the base and height |$z$|_PM. It is simply assumed that the density is uniform in the polar mound and that t_{D, PM} is represented by the value in the envelope of the cone with average thickness |$z$|_PM/3. From above three equations we get

$$\begin{equation} x_{\rm PM}^{2} = \frac{\dot{M} \kappa _{\rm T}}{2\pi c} z_{\rm PM}. \end{equation}$$

(55)

The second condition is a pressure balance between the radiation pressure pushing out the magnetic lines of force and the magnetic pressure intensified by being dragged by the expanding flow in the polar mound. The radiation pressure, P, could be approximately obtained by extending the P–r relation in the polar cone to a position slightly lower than the bottom of the polar cone. If we express it as P ∝ r^−α, P which pushes out the magnetic lines of force is roughly given as

$$\begin{equation} P = P_{*} \left( \frac{R}{R + z_{\rm PM}} \right)^{-\alpha }, \end{equation}$$

(56)

where P_* is the pressure at the bottom of the polar cone as is given in equation (45). The magnetic pressure which pushes back the matter pressure could be approximated as

$$\begin{eqnarray} \left( \frac{B^{2}}{8\pi } \right)_{\theta } &=& \left( \frac{B^{2}}{8\pi } \right) \frac{z_{\rm PM}}{\big(x_{\rm PM}^{2} + z_{\rm PM}^{2}\big)^{1/2}} \nonumber \\ &=& P_{*} \frac{\big(x_{\rm PM}^{2} + z_{\rm PM}^{2}\big)^{1/2}}{z_{\rm PM}}, \end{eqnarray}$$

(57)

where we have assumed

$$\begin{equation} B = B_{\rm r, *} \frac{\big(x_{\rm PM}^{2} + z_{\rm PM}^{2}\big)^{1/2}}{z_{\rm PM}}. \end{equation}$$

(58)

By equating two equations (56) and (57), we get

$$\begin{equation} \left( \frac{R}{R + z_{\rm PM}} \right)^{-\alpha } = \frac{(x_{\rm PM}^{2} + z_{\rm PM}^{2})^{1/2}}{z_{\rm PM}}. \end{equation}$$

(59)

By seeing α from the P distribution in the polar cone as a function of |$\dot{M}$|⁠, shown in figures 4 and 5, and solving simultaneous equations (55) and (59), we obtain x_PM and |$z$|_PM as functions of |$\dot{M}$| in two cases of B_*. The results in the case of B_* = 10¹² gauss are plotted in figure 9. Those in the case of B_* = 10¹³ gauss are almost identical. When |$\dot{M}$| becomes larger than 10¹⁸ g s⁻¹, x_PM comes to be as large as or even larger than R and simple arguments as done above become inapplicable.

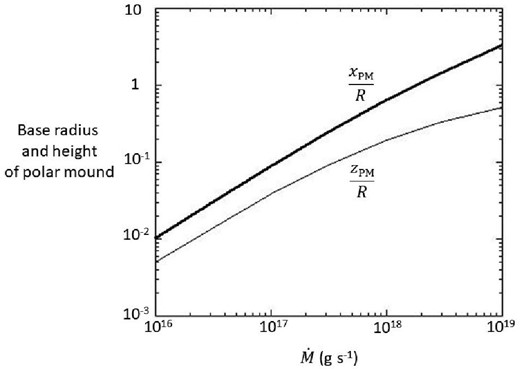
$Base radius (the thick line) and height (the thin line) of the polar mound, in units of stellar radius, as a function of $\dot{M}$.$

Fig. 9.

Base radius (the thick line) and height (the thin line) of the polar mound, in units of stellar radius, as a function of |$\dot{M}$|⁠.

Open in new tab Download slide

3 X-ray emissions from the magnetic polar regions

We have seen the portions of energy loss from the upper polar cone region, the lower polar cone region, and the polar mound region in sub-subsection 2.4.4. Since the energy lost from these regions should be emitted mainly in X-rays from their surfaces, the portions of the energy loss from the three regions as shown in figure 7 correspond to those of the local X-ray luminosities.

In the polar cone region, photons are considered to diffuse out from the side surface of the cone. The differential X-ray luminosity emitted from the polar cone surface per unit radial-length is given from equation (37) as

$$\begin{equation} \frac{dL}{dr} = \frac{4\pi c}{3 \kappa _{\rm T}} \varepsilon . \end{equation}$$

(60)

It should be noted that this quantity is proportional to ϵ and does not directly depend on |$\dot{M}$| nor Θ.

Since thermal equilibrium between matter and radiation is considered to be well established in the polar cone, emission from the surface of the polar cone should be basically blackbody emission. In that case, the effective temperature T_e of a surface of the polar cone at a distance r is estimated from the following equation as

$$\begin{equation} \frac{dL}{dr} = 2 \pi r \Theta \sigma T_{\rm e}^{4}, \end{equation}$$

(61)

where σ is the Stefan–Boltzmann constant.

However, we should take account of the dilution effect of the blackbody photons, since scattering is considered to be dominant to absorption in such an atmosphere with a temperature as high as 10⁷ K as the surface of the polar cone. In such a situation, we can approximate that the thermal equilibrium between matter and radiation is established within a region with an optical depth for the scattering, τ_a ≫ 1, and only elastic scattering takes place in the atmosphere with τ < τ_a. Under this approximation, the observed spectrum can be approximated with the blackbody spectrum with the apparent temperature, T_a, at the bottom of the scattering atmosphere with τ_a. In the atmosphere with τ ≲ τ_a, a radiation energy flux should be conserved, and we can approximate that

$$\begin{equation} \frac{T_{\rm a}^{4}}{\tau _{\rm a}} = T_{\rm e}^{4}. \end{equation}$$

(62)

From equations (60) and (61) with help from equation (62), the observed blackbody (apparent) temperature, T_a, is written as

$$\begin{equation} T_{\rm a} = \left( \frac{2c}{3\kappa _{\rm T} \sigma } \frac{\tau _{\rm a} \varepsilon }{r \Theta } \right)^{1/4}. \end{equation}$$

(63)

If we introduce the following relations in general as

$$\begin{equation} T_{\rm a} \propto r^{-p}, \end{equation}$$

(64)

$$\begin{equation} \varepsilon \propto r^{\nu }, \end{equation}$$

(65)

$$\begin{equation} \Theta \propto r^{\eta }, \end{equation}$$

(66)

$$\begin{equation} \tau _{\rm a} \propto T_{\rm a}^{\omega }, \end{equation}$$

(67)

we get

$$\begin{equation} p = \frac{-\nu + \eta + 1}{4 - \omega }. \end{equation}$$

(68)

Note that differential equations (42) and (43) in sub-subsection 2.4.3 do not include the parameter Θ. Thus, the solutions as shown in figures 4 and 5 allow such a freedom of r-dependence of Θ as in equation (66), as far as Θ ≪ 1. In this study, we have assumed η = 0.5, as in equation (20).

As seen in the top panels of figures 4 and 5, two local maxima of ϵ appear, and the locally most luminous positions in the polar cone are the top of the polar cone just behind the shock and the bottom of the polar cone just on the neutron star surface. The most luminous place, however, depends on |$\dot{M}$|⁠. When |$\dot{M} \lesssim 10^{17}\:$|g s⁻¹, the top of the polar cone is the most luminous, when |$\dot{M} \simeq 3 \times 10^{17}\:$|g s⁻¹, the top and the bottom of the polar cone are comparably luminous, and when |$\dot{M} \gtrsim 10^{18}\:$|g s⁻¹, the bottom is the most luminous.

The relative amount of the differential luminosity between the top and bottom of the polar cone is seen to depend on |$\dot{M}$| in figure 7 too. This figure further reminds us that the polar mound region is the most luminous when |$\dot{M} \gtrsim 3 \times 10^{17}\:$|g s⁻¹.

The X-ray luminosity from the polar mound region, L_PM, is given as

$$\begin{equation} L_{\rm PM} = \frac{\dot{M}}{2} w_{*}, \end{equation}$$

(69)

where |$w$|_* has been defined in sub-subsection 2.4.4. In the polar mound region, the matter should successively sink into the surface layer of the neutron star as it expands tangentially on the stellar surface. Because of the matter sinking and the area-extension, the column density should decrease and it should get easier for photons to diffuse out as the distance from the mound center increases. Furthermore, since the magnetic lines of force are dragged tangentially along the surface of the polar mound, photons easily go outward, without being scattered by ambient electrons which cannot move across the dragged lines of force. As a result, we can expect that the X-ray emission could be largely weighted on the outermost area of the polar mound and be approximated by a single blackbody emission with an apparent temperature, T_a,PM, which could be calculated from the following equation as

$$\begin{equation} L_{\rm PM} = \chi \pi x_{\rm PM}^{2} \sigma T_{\rm a, PM}^{4}. \end{equation}$$

(70)

Here, χ is a parameter which represents both a reducing factor of the effective emission area from the whole surface area of the mound and a dilution factor of the scattering dominant atmosphere, and should be ≪1.

3.1 Properties of X-ray spectrum

When |$\dot{M} \lesssim 10^{17}\:$|g s⁻¹, X-ray emission from the upper polar cone is the most luminous. As seen from the top panels of figures 4 and 5, the logarithmic slope of ϵ against r, ν, is much larger than unity, and thus a single blackbody spectrum is expected in this |$\dot{M}$| range within the simplified arguments in this study. Since the establishment of the radiation field is thought to be insufficient behind the shock as in figure 3, however, Comptonization of bremsstrahlung photons and blackbody photons produced around there should be taken into account to consider properties of X-ray spectrum from there; this was already studied by Becker and Wolff (2007) and Wolff et al. (2016). We do not go into detail on this low-|$\dot{M}$| range here.

When |$\dot{M} \gg 10^{17}\:$|g s⁻¹, on the other hand, the X-ray emissions from the upper polar cone region get less luminous than those from the lower polar cone region and the polar mound region. Furthermore, since the distance of the shock front, r_S, is several times as large as the neutron star radius in the case of |$\dot{M} \simeq 10^{18}\:$|g s⁻¹ (see figure 6), the temperature of the emission from the upper polar cone region should be much lower than those from the two regions near the neutron star surface. Thus, we neglect the contribution of the emission from the upper polar cone region here because our present concern focuses on the properties of the X-ray spectrum in the energy range above a few keV in the |$\dot{M}$| range around 10¹⁸ g s⁻¹.

From the lower polar cone region, we can expect a multi-color blackbody spectrum, which should be expressed with the p-free disk model (Kubota & Makishima 2004). This model was developed to reproduce X-ray spectra from accretion disks and the surface blackbody temperature is assumed to be distributed as a function of an orbital radius in a disk as in equation (64). In the present case considered here, the p parameter is given by equation (68). The value of ν, which is defined as the logarithmic slope of ϵ against r in equation (65), can be calculated from the radial distribution of ϵ solved in sub-subsection 2.4.3, and is ∼−1.3 near the bottom of the polar cone when |$\dot{M}$| is around 10¹⁸ g s⁻¹. Then, p is estimated to be ∼0.7, taking account of η = 0.5 as assumed in equation (20), and we set ω = 0 for simplicity. The highest apparent temperature in the multi-color component can be estimated from equation (63) by setting ϵ = ϵ_*, r = R, and Θ = Θ_*, and assuming |$\tau _{\rm a}^{1/4} \simeq 2$| (e.g., Shimura & Takahara 1995). Since ϵ_* ≃ 0.4ϵ₀ when |$\dot{M} = 10^{18}\:$|g s⁻¹, as seen both in figures 4 and 5, we get the highest apparent temperature (∼5 keV) around that accretion rate.

From the polar mound region, a quasi-single blackbody spectrum should be detected. The apparent temperature, T_a,PM, is calculated from equation (70) again to be ∼5 keV when L_PM ≃ 10³⁸ erg s⁻¹ and χ^−1/4(x_PM/R)^−1/2 ≃ 2.

According to the above arguments, we can expect a hybrid spectrum composed of the multi-color blackbody spectrum from the lower polar cone region and the quasi-single blackbody spectrum from the polar mound region, for X-ray emissions in the energy range above a few keV, in the case of |$\dot{M} \gg 10^{17}\:$|g s⁻¹.

Observationally, Makishima et al. (1999) showed that continuum X-ray spectra of X-ray pulsars in 2–50 keV can generally be reproduced with the Negative and Positive power laws with a common EXponential cutoff factor (NPEX) model, in which the model spectrum, F(E), is assumed as

$$\begin{equation} F(E) = ( G_{1} E^{-\lambda } + G_{2} E^{2} ) \exp \left( - \frac{E}{kT} \right), \end{equation}$$

(71)

where E is the photon energy and G₁ and G₂ are normalization factors. In the present framework, the first and second components could be understood to be the multi-color blackbody spectrum from the bottom polar cone region and the quasi-single blackbody spectrum from the polar mound region respectively. The multi-color blackbody spectrum from the polar cone has a power-law-like spectrum in the medium-energy range and an exponential decay determined by the highest surface temperature of the polar cone in the high-energy range. This could well be reproduced by the first component of the NPEX model. The second component of the NPEX model has the Rayleigh–Jeans spectrum in the low-energy range and the Wien spectrum in the high-energy range, and could be considered to represent the quasi-single blackbody spectrum from the polar mound surface. Although there is no reason why the first and second components have a common temperature in these considerations, the NPEX model is a phenomenological model that can reproduce the observed spectra and it would not be required to separate the common temperature into two in practical spectral fits.

From these considerations, the fact that an NPEX model consisting of two spectral components—the cut-off power law spectrum and the single blackbody-like spectrum—can reproduce the continuum spectra observed from many X-ray pulsars well could be considered to support strongly the present model, which predicts the presence of two other spectral components, the multi-color blackbody spectrum from the polar cone region and the quasi-single blackbody spectrum from the polar mound region. It should be noted that the temperatures obtained with the NPEX model fits to X-ray spectra observed from several sources by Makishima et al. (1999) are distributed around 5 keV, which agree to the values estimated above in the present study.

Furthermore, K. Kondo, T. Dotani, and H. Inoue (in preparation) have recently analyzed phase-resolved spectra observed from Her X-1 with Suzaku and have successfully resolved the continuum spectra into three components, each of which keeps its respective spectral shape constant and varies only its normalization factor in association with the pulse-phase change, independently of the other components. A remarkable thing is that the two components resolved in the energy range above ∼2 keV are well reproduced with the multi-color blackbody spectrum and the single blackbody spectrum respectively, although they have been obtained in a model-independent way.

3.2 Properties of X-ray pulse profile

Here, we discuss pulse profiles expected from the presently considered configurations in the magnetic polar regions in the case of |$\dot{M} \gg 10^{17}\:$|g s⁻¹.

As seen in figure 12c in Makishima et al. (1999), the crossover energy, where the two components in the NPEX model in equation (71) cross over, generally exists around 10 keV. Thus, we can consider that the multi-color blackbody component, identical to the first component in the NPEX model, from the lower polar cone should mainly govern the pulse profile in an energy range of, say, 2 to 6 or 7 keV. On the other hand, in an energy range above, say, 15 or 20 keV, the single blackbody component, identical to the second component in the NPEX model, from the polar mound region should be the main component in the pulse profile.

We discuss pulse profiles expected for X-rays from the polar cone and the polar mound below. In calculating the pulse profiles, we take into account two effects deforming the profiles; occultation of the emission regions by the neutron star body and influences of relativistic light bending. They are explained in the Appendix.

3.2.1 Directional distributions of X-ray emissions from the polar cone

X-rays from the polar cone mainly form the pulse profile in 2 to 6–7 keV.

Several X-ray pulsars exhibit absorption features at Cyclotron resonance energies around 20–40 keV in their X-ray spectra (e.g., Makishima et al. 1999). Since the X-ray energies of 2 to 6–7 keV now considered are significantly lower than these cyclotron energies, X-rays in this energy range cannot move electrons in the direction perpendicular to the magnetic lines of force. Hence, when X-rays diffuse out in the azimuthal direction of the polar cone, those with a linear polarization perpendicular to the magnetic lines of force (“ordinary photons”) can easily go out of the surface layer without suffering from electron scattering, but those that have another polarization in the direction towards the line of forces (“extraordinary photons”) cannot escape without a number of electron scatterings from the surface layer. Even the extraordinary photons, however, become free from electron scattering, if they are scattered in the direction towards the magnetic lines of force. Therefore, the extraordinary photons should gradually be focused in the direction to the magnetic lines of force through a number of electron scatterings. This beaming effect was first pointed out by Basko and Sunyaev (1975).

As a result, photons diffusing out in the azimuthal direction from the central region of the polar cone could be divided into two groups in the surface layer. One is the ordinary photon group and could be emitted with a constant intensity per a solid angle to every direction from the surface. Then, a differential flux per unit length of the polar cone, dF_O/dr, detected by an observer in a direction with an angle, φ, from the outward direction of the central axis of the polar cone at a distance of D can be expressed as

$$\begin{equation} \frac{dF_{\rm O}}{dr} = \frac{4}{\pi } \frac{dL_{\rm PC, O}/dr}{4\pi D^{2}} \,\, \sin \phi , \end{equation}$$

(72)

where dL_O/dr is a differential luminosity of this ordinary component emitted from the surface per unit length.

The other half is the extraordinary photon group and should be focused in the direction of the surface magnetic lines of force. If the beam pattern is assumed to have the form exp [− (φ/σ_E)²] with a parameter, σ_E, representing the beam width, the differential flux per unit length of the polar cone, dF_E/dr, can be approximated under a condition σ_E ≪ 1 as

$$\begin{equation} \frac{dF_{\rm E}}{dr} = \frac{dF_{\rm E, 0}}{dr} \,\, \exp \left[-\left(\frac{\phi }{\sigma _{\rm E}}\right)^{2}\right] \,\, \sin \phi , \end{equation}$$

(73)

where

$$\begin{equation} \frac{dF_{\rm E, 0}}{dr} = \frac{4}{\pi ^{1/2} \sigma _{\rm E}^{3}} \frac{dL_{\rm PC, E}/dr}{4 \pi D^{2}}. \end{equation}$$

(74)

dL_PC,E/dr is the differential luminosity of this extraordinary component. Calculated from equation (73), dF_E/dE has a peak at φ_P given as

$$\begin{equation} \phi _{\rm P} = \frac{\sigma _{\rm E}}{\pi ^{1/2}}. \end{equation}$$

(75)

Let us introduce dL_PC/dr as the total differential luminosity per unit length of the polar cone and set dL_{PC, O}/dr = dL_{PC, E}/dr = (dL_PC/dr)/2; we then get the total differential flux dF_PC/dr as

$$\begin{eqnarray} \frac{dF_{\rm PC}}{dr} = \frac{dL_{\rm PC}/dr}{4 \pi D^{2}} \left\lbrace \frac{2}{\pi ^{1/2} \sigma _{\rm E}^{3}} \,\, \exp \left[-\left(\frac{\phi }{\sigma _{\rm E}}\right)^{2}\right] \,\, + \,\, \frac{2}{\pi } \,\, \right\rbrace \,\, \sin \phi. \nonumber\\ \end{eqnarray}$$

(76)

3.2.2 Directional distributions of X-ray emissions from the polar mound

X-rays from the polar mound mainly form a pulse profile in the energy range above ∼20 keV.

In the polar mound, the accreted matter produces a mound-like structure by dragging the magnetic lines of force and finally lands on the stellar surface there. The remaining thermal energy at the bottom of the polar cone should be carried in the polar mound as radiation energy and the photons should diffuse out in the direction of the surface of the mound. The X-ray emission from the polar mound could be expected to be largely weighted on the outermost area, as discussed earlier in this section. Since magnetic lines of force cover this mound region, the same thing happens to the diffusing-out photons in the surface layer as in the polar cone. Namely, ordinary photons can easily go out in every direction without suffering from electron scattering, while extraordinary photons tend to escape, after a number of electron scatterings, in the direction along the magnetic lines of force. In the case of the polar mound, however, the surface magnetic lines of force should gradually curve to be normal to the stellar surface towards the outermost side of the polar mound (see figure 8) and the extraordinary photons should tend to go out in directions around the normal axis to the stellar surface. The ordinal photons should, on the other hand, be radiated away, independently of the directions of the magnetic lines of force, around the normal axis to the stellar surface simply by the projection effect. We approximate, therefore, that the intensity per solid angle from the polar mound surface is isotropic and that the observed flux, F_PM, is written as

$$\begin{equation} F_{\rm PM} = 4 \frac{L_{\rm PM}}{4 \pi D^{2}} \cos \phi , \end{equation}$$

(77)

where L_PM is the X-ray luminosity radiated from the polar mound and φ is an angle between the line of sight and the central axis of the mound.

3.2.3 Expected pulse profiles

The pulse profile of X-rays from the polar cone and the polar mound can be obtained from equation (76) and equation (77), respectively, by substituting φ derived from φ’, which periodically varies in association with the neutron star rotation, taking account of the light-bending effect as shown in the Appendix. φ’ is calculated with an inclination angle, i, of the line of sight to the rotational axis, an angle, θ_R, of the magnetic axis of the neutron star to the rotational axis, and a rotational angle, ψ, of the magnetic axis around the rotational axis. Figure 10 indicates (A) angular relations among the rotational axis, the magnetic axis, and the line of sight, and (B) a relation between φ and φ’ reflecting the light bending effect. Note that the opening angle of the polar cone and the height of the polar mound are both assumed to be negligibly small in the pulse-profile computations and that all the angular distributions of the emissions from them are given as functions of φ, referring to the magnetic axis.

Fig. 10.

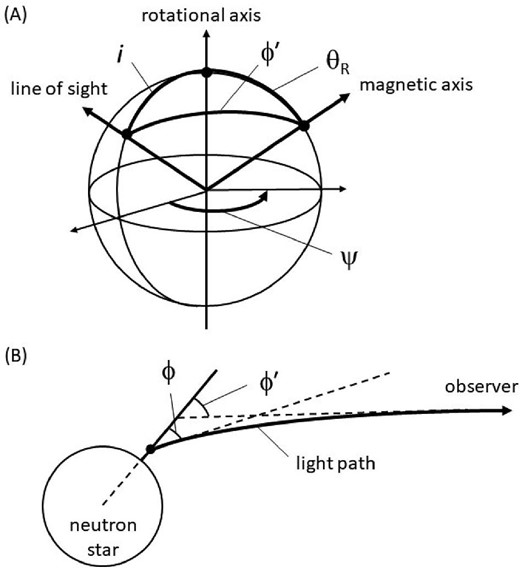
(A) Angular relations among the rotational axis, the magnetic axis and the line of sight, and (B) a relation between φ and φ’ reflecting the light-bending effect.

Open in new tab Download slide

Figure 11 show two-dimensional distributions of the flux from the polar cone and the polar mound, respectively, as functions of i and ψ, in three cases of θ_R. Fluxes in figures 11 through 15 are given as fluxes relative to those in cases of isotropic emission, by normalizing dF_PC/dr in equation (76) by (dL_PC/dr)/(4πD²) for the polar cone component, and F_PM in equation (77) by L_PM/(4πD²) for the polar mound component, respectively.

Fig. 11.

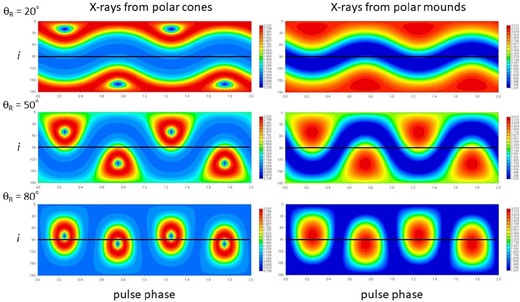
Two-dimensional distributions of flux from the polar cone (left) and the polar mound (right) on pulse phases and inclinations in three cases of θ_R. ξ = 5, θ_R = 30°, and φ_C = 60° are assumed. (Color online)

Open in new tab Download slide

Since emissions from both the polar cone and the polar mound are mainly focused in the directions of the two magnetic axes corresponding to the N and S poles, two enhancements of the flux appear in each of these maps. In case of emissions from the polar mound, each enhancement has a flux-peak at a position where the line of sight is only directed towards the N or S pole. In the case of those from the polar cone, however, each enhancement has a crator-like hole at its center surrounded by a circular wall with an angular radius of φ_P as defined in equation (75).

Hereafter, we discuss properties of the pulse profiles only in the range of i ≤ 90° and let the magnetic axis closer to the line of sight be the N pole.

In case of those from the polar mound, pulse profiles in terms of i are somewhat simpler than those of the polar cone. When i is larger than a boundary value, two peaks are exhibited; a stronger peak from the N-pole side and a weaker peak from the S-pole side. When i is smaller than the boundary value, on the other hand, we see only one peak from the N-pole side. The boundary i-value depends on θ_R and gets larger as θ_R gets smaller.

The similar trend of the overall flux-enhancements is seen in pulse profiles of X-rays from the polar cone. Sub-peaks, however, appear in some ranges of i in these cases.

Let us here introduce θ_{L, N} and θ_{L, S} as

$$\begin{equation} \theta _{\rm L, N} = |\theta _{\rm R}-i| \end{equation}$$

(78)

and

$$\begin{equation} \theta _{\rm L, S} = |\pi - \theta _{\rm R}-i|. \end{equation}$$

(79)

Then, we observe two sub-peaks around the top of the flux enhancement associated with the N pole, in the case of

$$\begin{equation} \theta _{\rm L,N} < \phi _{\rm P}, \end{equation}$$

(80)

while another couple of sub-peaks appear in the flux enhancement associated with the S pole, in the case of

$$\begin{equation} \theta _{\rm L,S} < \phi _{\rm P}. \end{equation}$$

(81)

From the above four equations (78)–(81), we see that both enhancements with N and S poles respectively exhibit two sub-peaks only when both i and θ_R are close to π/2 satisfying a condition i + θ_R < π − φ_R. In the other i–θ_R range, the enhancement with the S pole never show two sub-peaks, while that with the N pole exhibits two sub-peaks in a range of i as

$$\begin{equation} \theta _{\rm R} - \phi _{\rm P} < i < \theta _{\rm R} + \phi _{\rm P}, \end{equation}$$

(82)

calculated from equations (78) and (80).

Figure 12 shows some examples of pulse profiles of emissions expected from the present model configurations for different combinations of i and θ_R. Those of emissions from the polar cone and the polar mound are respectively presented in parallel there. In a relatively soft X-ray band, say, in 2–5 keV, X-rays from the polar cone are dominant, while those from the polar mound are thus in a relatively hard X-ray band, say, in 20–50 keV. Thus, the left- and right-hand panels in figure 12 can be considered to represent pulse profiles expected in the soft and hard bands, respectively.

Fig. 12.

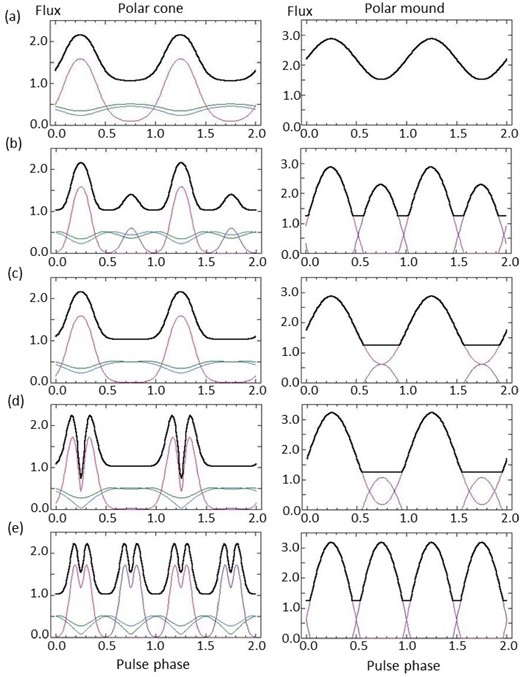
Pulse profiles of fluxes from the polar cone (left) and the polar mound (right) in five cases for the combination of i and θ_R. (a) through (e) corresponds to cases of (50°, 20°), (80°, 50°), (60°, 30°), (50°, 50°), and (90°, 80°), respectively. If we replace the values of i and θ_R with each other, the profile is the same. ξ = 5, σ_E = 30°, and φ_C = 60° are assumed. The red, purple, blue, and green lines in the polar cone component are profiles of the pencil beam component from the N pole, that from the S pole, the fan-beam component from the N pole, and that from the S pole, respectively. The red and purple lines in the polar mound component are the profiles from the N pole and S pole, respectively. (Color online)

Open in new tab Download slide

Pulse profiles observed from X-ray pulsars are classified into five groups by Nagase (1989). His classifications are shown (with slight changes to the original wording) as follows:

(a) single sinusoidal-like shapes both in the soft and hard bands,
(b) sinusoidal-like double peaks with little energy dependence, where the amplitudes of the two peaks are usually different,
(c) an asymmetric single peak with some features,
(d) a single sinusoidal-like peak in the high-energy band and close adjacent double peaks in the soft energy band, and
(d) double sinusoidal-like peaks in the high-energy band and complex five peaks in the soft energy band.

Although the sources on which the Nagase’s classifications are based have a wide range of X-ray luminosities, we can assign sources with X-ray luminosities ≳ 10³⁷ erg s⁻¹ to groups (a)–(d); LMC X-4 (e.g., Hung et al. 2010) to (a), SMC X-1 (e.g., Raichur & Paul 2010) to (b), Cen X-3 (e.g., Raichur & Paul 2010) to (c) and Her X-1 (e.g., Deeter et al. 1998) to (d). Vela X-1 (e.g., Makishima et al. 1999) is the representative source of group (e) but its luminosity is as low as ∼10³⁶ erg s⁻¹.

The present model can explain the basic features of the profiles (a) through (d), as seen from figure 12, where each pair of profiles (a) through (d) is shown as a typical example for the respective group (a) through (d). Even for the group (e), we see the presence of multiple peaks in the profile of the polar cone component in figure 12e, although the number of peaks is not five but four.

Even though the pulse profiles are mainly reproduced by adjusting two parameters, θ_R and i, simultaneous adjusting of the other model parameters should be necessary in order to have the model profile fit to the observed profile as accurately as possible.

The beam-width parameter, σ_E, determines the width of the main peak in the pulse profile of the polar cone component. Figure 13 shows the pulse profiles of the polar cone component when we change only the value of σ_E from 30° to 20° to 40° keeping the other parameters in the case of figure 12c. We can see that the peak profile gets significantly sharper with the σ_E decrease. In rough comparisons of the models with the observations, σ_E around 30° seems appropriate.

Fig. 13.

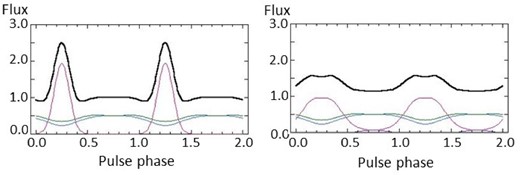
Examples of pulse profile variations in terms of σ_E. The pulse profile of the polar cone component in figure 12c in which σ_E = 30° changes to the left- and right-hand profiles in this figure by replacing σ_E with 20° and 40°, respectively. (Color online)

Open in new tab Download slide

The relative distance, ξ, of the X-ray emitting position, normalized by the Schwarzschild radius of the neutron star mass, determines the effects of the relativistic light-bending on pulse profiles. One of the effects appears in the depth of the hollows between pulse peaks of the polar mound component. Figure 14 shows respective pulse profiles of the polar mound component in cases of ξ = 10 and 2.5 when the other parameters are the same as those in figure 12e, in which ξ = 5. We see that the smaller ξ makes the hollow shallower, suffering the larger light bending.

Fig. 14.

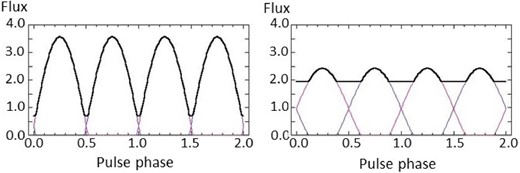
Examples of pulse profile variations in terms of ξ. The pulse profile of the polar cone component in figure 12e in which ξ = 5 changes to the left- and right-hand profiles in this figure by replacing ξ with 10 and 2.5, respectively. (Color online)

Open in new tab Download slide

The other effect produces small humps between main peaks in combination with the parameter φ_C, which expresses the degree of the obscuration of X-rays by the neutron star body, defined in the Appendix. Two examples are shown in figures 15. A low plateau begins to appear between two adjacent peaks when we change ξ from 5 to 10 for the profile of the polar cone component in figure 12c, as in figure 15A (left). It gets more significant if we add a change of φ_C from 60° to 30°, as in figure 15A (right). This feature could explain the presence of a small hump only in the soft band in the observed pulse profile of Cen X-3 (see figure 12 in Raichur & Paul 2009).

Fig. 15.

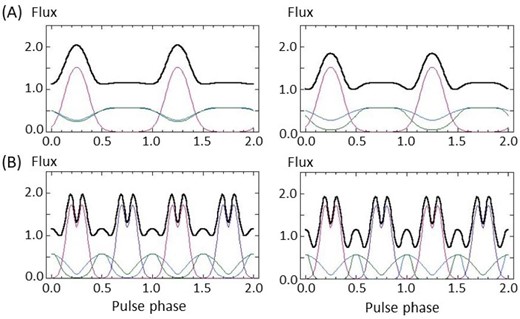
Two examples of pulse profile variations in terms of a combination of ξ_S and φ_C. (A) The pulse profile of the polar cone component in figure 12c in which ξ = 5 and φ_C = 60° changes to the left-hand profile by replacing ξ to 10, and further changes to the right profile by replacing φ_C to 30°. (B) The pulse profile of the polar cone component in figure 12e in which ξ = 5 and φ_C = 60° changes to the left- and right-hand profiles by replacing (ξ, φ_C) to (10, 30°) and further to (10, 15°), respectively. (Color online)

Open in new tab Download slide

If we change the combination of ξ and φ_C from (5, 60°) to (10, 30°), the pulse profile of the polar cone component in figure 12e also converts to that of figure 15B (left) and a small peak starts to appear. It gets higher when we further change φ_C to 15° as seen in figure 15B (right), where we can now present six peaks in the model pulse profile.

As seen above, various combinations of the model parameters can produce variety in the pulse profiles but cannot form an asymmetry of a pulse peak around the center of the peak. Such asymmetries are often seen in observed pulse profiles, and a typical example is the pulse profile of Cen X-3. A similar asymmetry is seen in the pulse profile of Her X-1. It is known, in the case of Her X-1, that the pulse profile changes between the main-on phase and the mid-on phase of the 35-day on–off cycles. Deeter et al. (1998) and Scott, Leahy, and Wilson (2000) propose that the central X-ray emission regions are periodically obscured by the outer boundary of the magnetic funnels located at the inner edge of a precessing accretion disk, and that the pulse phase of the obscuration varies in association with geometry changes due to the disk precession. By introducing such periodic obscuration by the outer boundaries of the magnetic funnels co-rotating with the central neutron star, we could interpret the asymmetries seen in the pulse profiles from Cen X-3 and Her X-1 in the present model frame.

Obscuration could be done even by matter flowing along the magnetic funnels toward the neutron star surface, since the optical depth for the electron scattering of the free-fall region in the magnetic funnel is calculated in equation (25) to be larger than unity unless r ≫ 10⁷ cm. In this case, the obscuration could be observed as an absorption dip in a pulse profile and could interpret some of the features in the complex multiple peaks as seen in the group (e).

4 Summary and discussions

Structures of X-ray emitting magnetic polar regions of neutron stars in X-ray pulsars are studied, and the expected properties of X-ray emissions from them are compared with observations.

The matter flow in the polar cone is solved on several such assumptions as follows:

(1) The flow is one-dimensional in the radial direction, steady and sufficiently subsonic.
(2) The opening angle of the cone is sufficiently smaller than unity and the physical quantities can be represented by respective typical values over the cross-section of the cone.
(3) The optical depth in the tangential direction of the cone is sufficiently large and the radiation energy density is greatly dominant compared to the gaseous one.
(4) The energy loss of the flow is governed by photon diffusion in the tangential direction of the cone.

We discuss the validity of these assumptions below.

Equations (42) and (43) do not include the opening angle parameter, Θ, and thus the solutions on the basic structure of the polar cone do not depend on the assumption of Θ in equation (20). That assumption is necessary only to calculate the inflow velocity and the optical depth in the azimuthal direction.

As seen in figure 6, the height of the polar cone is close to the position of the magneto-boundary surface with the distance of r_M,p, when |$\dot{M}$| gets as large as several times 10¹⁸ g s⁻¹. Since Θ = 0.32 at r_M,p, as obtained in equation (18), Θ ≪ 1 can be assured in the polar cone unless |$\dot{M}$| is close to 10¹⁹ g s⁻¹. The solved infall velocities are displayed in figures 4 and 5, while the sound velocities in the polar cones should be 10⁹–10¹⁰ cm s⁻¹. These confirm that the flow in the polar cone is sufficiently subsonic. The sufficiently large optical depth can be recognized in figures 4 and 5.

The radiation temperatures of the polar cone are plotted in figures 4 and 5, while the gaseous temperature should be 10¹¹–10¹² K in order for the gaseous energy density to comparable to the radiation energy density. Thus we see that the radiation energy is greatly dominant compared to the gaseous one in the polar cone. The establishment of the radiation field just behind the shock front (the upper boundary) has been discussed in sub-subsection 2.4.1.

The temperature at the bottom of the polar cone is simply calculated by the lower boundary condition as |$P = B_{\rm r, *}^{2} / 8\pi$| to be 2.0 × 10⁹ for B_{r, *} = 10¹² G, and the average energy of photons is ∼170 keV. Since this energy is much larger than the cyclotron energy, ∼12 keV for B_{r, *} = 10¹² G, the reduction of the electron-scattering opacity for photons passing along the magnetic lines’ force should not take place in the main part of the polar cone. Thus, we can say that the simple geometry with Θ ≪ 1 determines the direction of the photon diffusion, which should be the sideways direction.

Solutions show that the height of the polar cone has a large dependence on the accretion rate. When |$\dot{M} \simeq 10^{16}\:$|g s⁻¹, the height is a tenth as low as the neutron star radius. On the other hand, when |$\dot{M} \simeq 10^{18}\:$|g s⁻¹, the height is about 10 times as large as the neutron star radius. This large dependence of the height on the accretion rate originates from the proportionality of r_D to the accretion rate, |$\dot{M}$| as seen in equation (40). If we introduce the time scale for photons to diffuse out in the azimuthal direction, t_D, it is given by replacing r_S, ρ_S and Θ_s in equation (33) with r, ρ and Θ for a general position in the polar cone. Then, with the help of equation (23), the following relation is achieved:

$$\begin{equation} r_{\rm D} = v t_{\rm D}. \end{equation}$$

(83)

This means that r_D expresses the distance by which the infalling matter advances in the diffusion time. Since the photon diffusion time is considered to be the cooling time of the radiation energy in the polar cone, r_D represents the cooling length in which the infalling matter significantly loses its energy unless heating exists. In fact, if we neglect the heating term, GM/r², on the right-hand side of equation (42), we get such a solution as an exponential decay of ϵ with the scale length of (4/3)r_D. The rough proportionality of the height of the polar cone to |$\dot{M}$|⁠, as seen in figure 6, is basically explained by the proportionality of r_D to |$\dot{M}$|⁠.

In practice, however, the term of GM/r on the right-hand side of equation (42) cannot be neglected, and rather plays the more important role with the larger accretion rate. When |$\dot{M}$| is as low as 10¹⁶ g s⁻¹, the energy carried with the free-fall matter is almost released soon after the shock. However, when |$\dot{M}$| is as large as 10¹⁸ g s⁻¹ or larger, the gravitational energy gain exceeds the energy loss due to the photon diffusion and a significant amount of energy piles up on the bottom side of the polar cone. In section 1 it was mentioned that the presence of the two regions, the primary and secondary regions, were already introduced even in the middle of the 1970s. This paper quantitatively clarifies that X-ray emissions from the primary region is dominant when |$\dot{M} \lesssim 10^{17}\:$|g s⁻¹, and that those from the secondary region become dominant when |$\dot{M}$| exceeds 10¹⁷ g s⁻¹.

As the accretion rate increases to 10¹⁷–10¹⁸ g s⁻¹, the specific radiation energy remaining at the bottom of the polar cone increases. Then, the radiation pressure should increase and exceed the magnetic pressure which holds the flow within the polar cone. As a result, the matter should expand in the tangential direction along the neutron star surface, dragging the magnetic lines of force, and form a mound-like structure (the polar mound region). By assuming that the matter settles on the neutron star surface after losing its remaining energy through photon diffusion in the polar mound and the excess radiation pressure balances with magnetic pressure enhanced by dragging, the structure of the polar mound is simply calculated and the results are reasonable unless |$\dot{M} \gg 10^{18}\:$|g s⁻¹. Davidson (1973) originally introduced the concept of the mound as the optically thick region at the bottom of the magnetic funnel. It is here generalized to be composed of the polar cone and the polar mound, the structures of which vary with the accretion rate.

From such configurations as discussed above, we can expect an X-ray spectrum composed of a multi-color black-body spectrum from the polar cone region and a quasi-single black-body spectrum from the polar mound region from X-ray pulsars with |$\dot{M} \gtrsim 10^{17}\:$|g s⁻¹. These spectral properties basically agree with observations as discussed in subsection 3.1. For further confirmations of the validity of the present model, the following two analyses are expected. One is the analyses of spectral variations linked with the pulse phase, as done by Kondo, Dotani and Inoue (in preparation) for Her X-1. This could resolve the overall spectrum of an X-ray pulsar into several components, which keep a constant spectral shape but change their normalization factors with the pulse phase. The other is to see a spectral change of an X-ray pulsar associated with the flux. The spectrum should get harder as the accretion rate increases, since the relative flux of the quasi-single blackbody component to the multi-color blackbody component increases with the accretion rate.

A fairly sharp pencil beam is expected together with a broad fan beam from the polar cone region, while a broad pencil beam from the polar mound region is expected. With these X-ray beam properties, basic patterns in X-ray pulse profiles observed from X-ray pulsars can be explained too.

The fairly sharp pencil beam is formed when the emitted photon energy is considerably lower than the cyclotron energy at the surface of the pencil beam. The cyclotron energies observed from several X-ray pulsars are around 20 keV (e.g., Makishima et al. 2000), while the typical X-ray energies from the polar cone are around a few keV. This confirms the above condition for the fairly sharp pencil beam to appear. If we see softer X-rays from an X-ray emitting place in the polar cone far from the stellar surface, however, the cyclotron energy rapidly decreases in proportion to r⁻³ while the surface temperature largely does not. Hence, the beaming effect should tend to weaken in the spectral range below 1 keV.

We have a number of freedoms in the present phenomenological model for the pulse profiles in order to fine-tune the model pulse profile to reproduce an observed pulse profile. In particular, there could be large uncertainties in the periodic obscuration by the outer boundary and the lower side of the free-fall region of the magnetic funnel. The magnetic funnel should be bent in the rotational direction around the axis of the total angular momentum of the accreted matter at the magneto-boundary surface, since the angular momentum should be transferred though the magnetic stress to the neutron star within the magneto-boundary surface. The degree of the bend of the magnetic lines of force depends on the amount of the angular momentum to be transferred (see, e.g., Inoue 1976). Thus, if the amount of the angular momentum changes, the pulse phase at which obscuration by the magnetic funnel takes place should change. In fact, Her X-1 exhibits the pulse-profile change linked with the 35-day on-off cycle. The super-orbital modulation of the X-ray flux can be explained well by the precession of the accretion disk (Inoue 2019). If so, the angular momentum axis of the accreted matter changes with the precession, and the periodic phase-shift of the obscuration place in the pulse profile could be understandable. It could be possible to resolve the practical configurations of the magnetic funnel by changing the model pulse profile to an observed profile.

This model can explain basic features in the pulse-profiles of many X-ray pulsars, as discussed in sub-subsection 3.2.3, but it has not yet been done to show good evidence that the present model can reproduce an observed pulse profile precisely. This should be done in future.

In this paper, we have basically dealt with cases of the accretion rate in the range of 10¹⁷–10¹⁸ g s⁻¹. In this accretion rate range, we have seen that the fairly tall polar cone stand and the fairly wide polar mound extends from the bottom of the polar cone on each of the magnetic polar regions of the neutron star. The strength of the magnetic field of the neutron star has been assumed to be 10¹²–10¹³ gauss at its surface and the obtained configurations of the X-ray emitting polar region do not largely depend on it around this magnetic field range.

When the accretion rate is as low as 10¹⁶ g s⁻¹ or less, the height of the polar cone becomes as low as or lower than a tenth of the neutron star radius. Thus, such cases do not fit to the main assumption of the present study that the photon diffusion in the tangential direction plays the main role in constructing the polar cone. Several studies have, however, been done on this low accretion rate case by several authors (e.g., Becker & Wolff 2007; Wolff et al. 2016, and references therein) since the pioneer works of Davidson (1973) and Basko and Sunyaev (1975).

When the accretion rate is as high as 10¹⁹ g s⁻¹ or higher, on the other hand, the luminosity largely exceeds the Eddington luminosity of 1 M|$_{\odot}$|⁠. Although the solution can exist in the present scheme of the magnetic polar regions even in the case of |$\dot{M} \simeq 10^{19}\:$|g s⁻¹, some obtained parameters are inconsistent with the approximations in this study.

The first issue is on the base radius of the polar mound, x_PM, as shown in figure 9. We see that it exceeds the stellar radius when |$\dot{M}$| gets close to 10¹⁹ g s⁻¹. Although this is the result from the very simplified treatment, it could be understood as a tendency for the polar mound to extend over the entire surface of the neutron star as the accretion rate increases. Taking account of the fact that the portion of the energy loss rate from the polar mound gets close to unity when |$\dot{M}$| gets close to 10¹⁹ g s⁻¹, as seen in figure 7, most of the super-Eddington luminosity should quasi-spherically be emitted from the entire surface of the neutron star with this accretion rate. It could, therefore, be difficult for the polar mound to maintain the steady state under the super-Eddington radiation pressure. The effect of the radiation pressure might, however, be weakened due to the reduction of the Thomson scattering cross-section under the strong magnetic field on the surface of the neutron star.

The second issue is on the height of polar cone. It becomes as high as or higher than that of the magneto-boundary surface when |$\dot{M} \gtrsim 10^{19}\:$|g s⁻¹, as shown in figure 6. If the upper boundary of the polar cone reaches the magneto-boundary surface, the matter trying to flow into the magnetic funnel should flood over the magneto-boundary surface. In that case, the approximations around the upper boundary of the polar cone in the present study become inapplicable and we will need some new treatments for them.

In addition to them, the optical depth of the accreted matter surrounding the central X-ray source could be a problem. The optical depth of the transition layer of the magneto-boundary surface, τ_T, is roughly calculated from equation (13) as

$$\begin{eqnarray} \tau _{\rm T} &\simeq & \kappa _{\rm T} \rho _{\rm T} h_{\rm T} \nonumber \\ &\simeq & \frac{\dot{M}}{4\pi r v_{\rm T} \sin \theta } \nonumber \\ &=& 3.3 \,\, \beta ^{-1} \sin ^{-1} \theta \left(\frac{r}{r_{\rm M,e}}\right)^{-1/2} \left(\frac{\dot{M}}{10^{19}\:\mbox{g}\:\mbox{s}^{-1}}\right)^{8/7} \left(\frac{M}{M_{\odot }}\right)^{-1/14}\nonumber \\ &&\times\,\left(\frac{\mu _{\rm M}}{10^{30} \mbox{gauss}\:\mbox{cm}^{3}}\right)^{2/7}, \end{eqnarray}$$

(84)

where we have expressed |$v$|_T = β(2GM/r)^1/2. Since β must be significantly smaller than unity, the matter in the transition layer is considered to be optically thick everywhere in the case of |$\dot{M} \gtrsim 10^{19}\:$|g s⁻¹. If so, the super-Eddington radiation pressure should interfere with steady accretion.

This estimation is, however, made on the assumption that the magnetic axis aligns with the rotational axis of the neutron star and both axes are perpendicular to the equatorial plane of the accretion disk. In practical cases of X-ray pulsars, the magnetic axis must be oblique to the rotational axes, and thus the matter distribution in the transition layer should be biased to the equatorial plane of the disk. In those cases, a part of the transition layer could be optically thin and steady accretion, in which the matter inflow and the photon outflow segregate from each other, might be possible even if the luminosity exceeds the Eddington limit.

These issues in the case of |$\dot{M} \gtrsim 10^{19}\:$|g s⁻¹ as discussed above are quite interesting in relation to ultra-luminous X-ray pulsars recently discovered one after another (Bachetti et al. 2014; Fürst et al. 2016; Israel et al. 2017; Carpano et al. 2018), and await future studies.

This study presents several clues to resolve observational evidence of X-ray pulsars from various viewpoints, but is still based on several simplified assumptions and approximations. Further theoretical and observational studies of X-ray pulsars are largely expected.

Acknowledgements

The author greatly appreciates the referee for his or her critical comment on the original manuscript.

Appendix. Deformations of pulse profiles by the central neutron star

We discuss two effects deforming the pulse profile of X-ray pulsars owing to the central neutron star.

One is an occultation of X-rays emitted from the polar cone by the neutron star body. When the line of sight of those X-rays from the polar cone crosses the neutron star body, they cannot be observed. A critical direction within which emitted X-rays suffer from this effect depends on the height of the X-ray emitting position on the polar cone, but we simultaneously observe X-rays from the polar cone in a fairly wide range of height. Thus, we introduce the following deformation factor, A, in calculating expected pulse profiles as

$$\begin{equation} A = \left\lbrace \begin{array}{ll}1 & \rm {when} \,\, \,\, \phi \le \pi /2 \\ \exp \left(- \left[\frac{(\phi - \pi /2)}{\phi _{\rm c}} \right]^{2} \right) & \rm {when} \,\, \,\, \phi > \pi /2, \end{array} \right. \end{equation}$$

(A1)

where φ_C is the average critical angle over the region of the polar cone emitting relevant X-rays.

Another is the relativistic light bending effect by the gravitational field of the neutron star. To include this effect, we adopt the simple analytic formula to describe it which was introduced by Leahy and Li (1995). The applicable range of their original formula is limited to 2 ≤ ξ ≤ 5, supposing the photon-emitting place is on the surface of the neutron star. Here, ξ is the relative distance of a photon-emitting place to the Schwarzschild radius. In the present study, our interests are also in the emissions from fairly far places of the polar cone from the neutron star surface and thus we have expanded the applicable range of ξ up to ∼10 or more by recalculating the necessary parameters in the same way as used in Leahy and Li (1995). The formula we have used is as follows.

$$\begin{equation} \cos \phi ^{\prime } = a \cos \phi + b, \end{equation}$$

(A2)

where

$$\begin{equation} a = \frac{2.304}{\xi ^{2}} + \frac{0.653}{\xi } + 1.017, \end{equation}$$

(A3)

$$\begin{equation} b = -\frac{2.490}{\xi ^{2}} - \frac{0.584}{\xi } - 0.021. \end{equation}$$

(A4)

Here, φ is an angle, at which the light is emitted from a place with a relative distance, ξ, to the radial direction from the gravity center, and φ′ is an angle at which the light is observed at infinity, to the original radial direction.

References

Arons

J.

,

Lea

S. M.

1976

,

ApJ

,

207

,

914

Crossref

Search ADS

Bachetti

M.

et al. .

2014

,

Nature

,

514

,

202

Crossref

Search ADS

PubMed

Basko

M. M.

,

Sunyaev

R. A.

1975

,

A&A

,

42

,

311

Becker

P. A.

,

Wolff

M. T.

2007

,

ApJ

,

654

,

435

Crossref

Search ADS

Carpano

S.

,

Haberl

F.

,

Maitra

G.

,

Vasilopoulos

G.

2018

,

MNRAS

,

476

,

L45

Crossref

Search ADS

Churazov

E.

,

Gilfanov

M.

,

Revnivtsev

M.

2001

,

MNRAS

,

321

,

759

Crossref

Search ADS

Davidson

K.

1973

,

Nature Phys. Sci

.,

246

,

1

Crossref

Search ADS

Deeter

J. E.

,

Scott

D. M.

,

Boynton

P. E.

,

Miyamoto

S.

,

Kitamoto

S.

,

Takahama

S.

,

Nagase

F.

1998

,

ApJ

,

502

,

802

Crossref

Search ADS

Elsner

R. F.

,

Lamb

F. K.

1977

,

ApJ

,

215

,

897

Crossref

Search ADS

Fürst

F.

et al. .

2016

,

ApJ

,

831

,

L14

Crossref

Search ADS

Ghosh

P.

,

Lamb

F. K.

1978

,

ApJ

,

223

,

L83

Crossref

Search ADS

Ghosh

P.

,

Lamb

F. K.

1979

,

ApJ

,

232

,

259

Crossref

Search ADS

Ghosh

P.

,

Lamb

F. K.

,

Pethick

C. J.

1977

,

ApJ

,

217

,

578

Crossref

Search ADS

Giacconi

R.

,

Gursky

H.

,

Kellogg

E.

,

Schreier

E.

,

Tananbaum

H.

1971

,

ApJ

,

167

,

L67

Crossref

Search ADS

Hung

L.-W.

,

Hickox

R. C.

,

Boroson

B. S.

,

Vrtilek

S. D.

2010

,

ApJ

,

720

,

1202

Crossref

Search ADS

Illarionov

A. F.

,

Syunyaev

R. A.

1972

,

Soviet Astron.

,

16

,

45

Inoue

H.

1975

,

PASJ

,

27

,

311

Inoue

H.

1976

,

PASJ

,

28

,

293

Inoue

H.

2019

,

PASJ

,

71

,

36

Crossref

Search ADS

Inoue

H.

,

Hōshi

R.

,

1975

,

Prog. Theor. Phys

.,

54

,

415

Crossref

Search ADS

Israel

G. L.

et al. .

2017

,

Science

,

355

,

817

Crossref

Search ADS

PubMed

Kubota

A.

,

Makishima

K.

2004

,

ApJ

,

601

,

428

Crossref

Search ADS

Lamb

F. K.

,

Pethick

C. J.

,

Pines

D.

1973

,

ApJ

,

184

,

271

Crossref

Search ADS

Leahy

D. A.

,

Li

L.

1995

,

MNRAS

,

277

,

1177

Crossref

Search ADS

Makishima

K.

,

Mihara

T.

,

Nagase

F.

,

Tanaka

Y.

1999

,

ApJ

,

525

,

978

Crossref

Search ADS

Nagase

F.

1989

,

PASJ

,

41

,

1

Pringle

J. E.

,

Rees

M. J.

1972

,

A&A

,

21

,

1

Raichur

H.

,

Paul

B.

2010

,

MNRAS

,

401

,

1532

Crossref

Search ADS

Scott

D. M.

,

Leahy

D. A.

,

Wilson

R. B.

2000

,

ApJ

,

539

,

392

Crossref

Search ADS

Shimura

T.

,

Takahara

F.

1995

,

ApJ

,

445

,

780

Crossref

Search ADS

Spitzer

L.

Jr.

1962

,

Physics of Fully Ionized Gases

(

New York

:

John Wiley & Sons

)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Sugimoto

J.

,

Mihara

T.

,

Kitamoto

S.

,

Matsuoka

M.

,

Sugizaki

M.

,

Negoro

H.

,

Nakahira

S.

,

Makishima

K.

2016

,

PASJ

,

68

,

S17

Crossref

Search ADS

Tananbaum

H.

,

Gursky

H.

,

Kellogg

E. M.

,

Levinson

R.

,

Schreier

E.

,

Giacconi

R.

1972

,

ApJ

,

174

,

L143

Crossref

Search ADS

Wolff

M. T.

et al. .

2016

,

ApJ

,

831

,

194

Crossref

Search ADS

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
December 2019	12
January 2020	13
February 2020	14
April 2020	10
June 2020	7
July 2020	5
August 2020	2
September 2020	4
October 2020	1
November 2020	2
December 2020	4
January 2021	1
February 2021	5
March 2021	3
May 2021	4
August 2021	5
September 2021	3
October 2021	2
February 2022	9
March 2022	3
April 2022	1
May 2022	3
June 2022	11
July 2022	8
August 2022	9
September 2022	15
October 2022	2
November 2022	3
December 2022	4
January 2023	14
February 2023	6
March 2023	8
April 2023	7
May 2023	4
June 2023	11
July 2023	6
August 2023	11
September 2023	4
October 2023	6
November 2023	9
December 2023	14
January 2024	20
February 2024	4
March 2024	10
April 2024	17
May 2024	10
June 2024	6
July 2024	5
August 2024	11
September 2024	5
October 2024	3
December 2024	1
January 2025	4
February 2025	2
March 2025	5
May 2025	1

Article Contents

X-ray emissions from magnetic polar regions of neutron stars

Abstract

1 Introduction

2 Structures of magnetic polar regions

2.1 Magneto-boundary surface

2.2 Overall picture of the magnetic polar regions

2.3 Free-fall region

2.4 X-ray emitting polar cone region

2.4.1 Dominance of the radiation energy in the polar cone

2.4.2 Energy loss due to side-say diffusion of photons

2.4.3 Structure of the polar cone

2.4.4 Energy loss from the polar cone

2.5 X-ray emitting polar mound region

3 X-ray emissions from the magnetic polar regions

3.1 Properties of X-ray spectrum

3.2 Properties of X-ray pulse profile

3.2.1 Directional distributions of X-ray emissions from the polar cone

3.2.2 Directional distributions of X-ray emissions from the polar mound

3.2.3 Expected pulse profiles

4 Summary and discussions

Acknowledgements

Appendix. Deformations of pulse profiles by the central neutron star

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

X-ray emissions from magnetic polar regions of neutron stars

Abstract

1 Introduction

2 Structures of magnetic polar regions

2.1 Magneto-boundary surface

2.2 Overall picture of the magnetic polar regions

2.3 Free-fall region

2.4 X-ray emitting polar cone region

2.4.1 Dominance of the radiation energy in the polar cone

2.4.2 Energy loss due to side-say diffusion of photons

2.4.3 Structure of the polar cone

2.4.4 Energy loss from the polar cone

2.5 X-ray emitting polar mound region

3 X-ray emissions from the magnetic polar regions

3.1 Properties of X-ray spectrum

3.2 Properties of X-ray pulse profile

3.2.1 Directional distributions of X-ray emissions from the polar cone

3.2.2 Directional distributions of X-ray emissions from the polar mound

3.2.3 Expected pulse profiles

4 Summary and discussions

Acknowledgements

Appendix. Deformations of pulse profiles by the central neutron star

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only