-
PDF
- Split View
-
Views
-
Cite
Cite
Tomomi Shimoikura, Kazuhito Dobashi, Asha Hirose, Fumitaka Nakamura, Yoshito Shimajiri, Koji Sugitani, A survey of molecular cores in M 17 SWex, Publications of the Astronomical Society of Japan, Volume 71, Issue Supplement_1, December 2019, S6, https://doi.org/10.1093/pasj/psz061
Close - Share Icon Share
Abstract
A survey of molecular cores covering the infrared dark cloud known as the M 17 southwest extension (M 17 SWex) has been carried out with the 45 m Nobeyama Radio Telescope. Based on the N2H+ (J = 1–0) data obtained, we have identified 46 individual cores whose masses are in the range from 43 to |$3026\, {M}_{\odot }$|. We examined the relationship between the physical parameters of the cores and those of young stellar objects (YSOs) associated with the cores found in the literature. The comparison of the virial mass and the core mass indicates that most of the cores can be gravitationally stable if we assume a large external pressure. Among the 46 cores, we found four massive cores with YSOs. They have large masses of |$\gtrsim 1000\, M_{\odot }$| and line widths of |$\gtrsim 2.5\:$|km s−1 which are similar to those of clumps forming high-mass stars. However, previous studies have shown that there is no active massive star formation in this region. Recent measurements of near-infrared polarization imply that the magnetic field around M 17 SWex is likely to be strong enough to support the cores against self-gravity. We therefore suggest that the magnetic field may prevent the cores from collapsing, causing the low level of massive star formation in M 17 SWex.
1 Introduction
The infrared dark cloud M 17 southwest extension (M 17 SWex; Povich & Whitney 2010), which is shaped like a “flying dragon,” is located to the southwest of the M 17 H|$\,$|ii region. A huge (|${\sim }10^{6}\, M_{\odot }$|) molecular cloud was found through CO observations in the region using the Texas 5 m telescope with a beam size of ∼3′ (Elmegreen & Lada 1976). More recently, Busquet et al. (2013) conducted NH3 observations using the Very Large Array and Effelsberg 100 m telescope toward a part of the high density region in M 17 SWex, and they revealed a network of filaments constituting two hub-filament systems. The two hubs are dubbed “hub-N” and “hub-S.” Busquet et al. (2013) suggested that they are the main sites of stellar activity within the cloud.
Povich et al. (2016) suggested that M 17 SWex has been an active star-forming region for the past |$\gtrsim 1\:$|Myr. Povich and Whitney (2010) identified 488 young stellar objects (YSOs) in M 17 SWex, and about 200 of them are found to be stars with a mass greater than |$3\, M_{\odot }$| that will grow into B-type stars in the future. Povich and Whitney suggested that M 17 SWex probably has not yet formed its most massive star, predicted to be an early O-type star. From the 3 mm continuum emission observations toward the two hubs with ALMA, Ohashi et al. (2016) identified 48 cores and indicated that the internal turbulence is insufficient to prevent the gravitational collapse of the two hubs. They also suggested that clumps hosting the cores may be able to supply material to the cores. Povich et al. (2016) and Ohashi et al. (2016) speculate that mass accretion onto the cores via the hubs could produce massive star formation in the future. M 17 SWex is thus considered to be in the early stages of formation of a new OB association (e.g., Elmegreen & Lada 1976; Povich & Whitney 2010). Therefore, M 17 SWex is a molecular cloud suitable for study to explore the initial state of massive star formation. However, high-resolution observations of molecular emission lines in this region have been done only toward a limited area including hub-N and hub-S. The Millimeter Astronomy Legacy Team 90 GHz (MALT90) survey (Foster et al. 2011) revealed some dense cores in M 17. A comprehensive molecular core survey in the cloud to cover the entire M 17 SWex region is needed.
In other star-forming regions, Shimoikura et al. (2018) found massive (|${\sim }10^{3}\, M_{\odot }$|) and dense (∼105 cm−3) clumps with no massive stars. They suggested that such clumps are gravitationally stable without collapsing due to clump-supporting forces such as turbulence and magnetic fields. Sugitani et al. (2019) conducted near-infrared polarization observations toward M 17 SWex. They revealed filament-like structures in the H2 column density map, and found that the local magnetic field is perpendicular to most of the individual filamentary structures in high column density regions. They suggested that the magnetic field is likely to influence the formation and evolution of M 17 SWex. To understand the relationship between the cores and the magnetic field in M 17 SWex, it is necessary to identify dense cores in the region and to investigate the dynamical stability of the cores.
To search for dense cores in M 17 SWex and to study their dynamics, we observed the region using the 45 m radio telescope at Nobeyama Radio Observatory (NRO) in some molecular lines at 93–115 GHz. In this study, we aim to identify the molecular cores in M 17 SWex and catalog them using the N2H+ molecular emission line at 93 GHz, which is a good tracer of dense gas. We investigate physical parameters of the cores and examine the relationship between physical properties of the cores and those of YSOs associated with the cores.
Povich and Whitney (2010) assumed that M 17 SWex is at a distance of 2.0 kpc measured in the M 17 H|$\,$|ii region based on the parallax measurements by Xu et al. (2011), since the LSR velocity VLSR of M 17 SWex and the H|$\,$|ii region are the same (VLSR ≃ 20 km s−1). In our study, we also found that M 17 SWex is likely to be connected to the H|$\,$|ii region, and thus we adopt 2.0 kpc as the distance to M 17 SWex in this paper.
This study is based on “the Star Formation Legacy project” which is a large-scale survey of molecular gas in star-forming regions. The outline of the project is presented by Nakamura et al. (2019a). Results of other regions are given in separate articles (OrionA: Nakamura et al. 2019b; Ishii et al. 2019; Tanabe et al. 2018, Aquila Rift: Shimoikura et al. 2019; Kusune et al. 2019, M 17: Sugitani et al. 2019, NCS: Dobashi et al. 2019a, DR21: Dobashi et al. 2019b).
2 Observations
2.1 Observations with the NRO 45 m telescope
Observations of the 12CO, 13CO, C18O, CCS, and N2H+ emission lines were carried out with the 45 m telescope at NRO. We observed the 12CO and 13CO emission lines for 20 hours in the period between 2015 April and 2016 March, and the other emission lines for 50 hours in the period between 2016 April and 2017 March. We used an on-the-fly (OTF) observing technique that was implemented for the 45 m telescope by Sawada et al. (2008). We observed whole of the M 17 H|$\,$|ii region and M 17 SWex (|${\sim } {1{^{\circ}_{.}}5} \times {0{^{\circ}_{.}}5}$|) in the 12CO and 13CO lines. We also mapped an ∼1° × |${0{^{\circ}_{.}}5}$| area in M 17 SWex in the other lines. The beam size of the 45 m telescope is ∼15″ (HPBW) at 100 GHz. We used the multi-beam receiver “FOREST” (FOur beam REceiver System on the 45 m telescope; Minamidani et al. 2016) as the front end and the digital spectrometer SAM45 as the back end. The velocity resolution was set to 0.04 km s−1 for the observed emission lines. The receiver provided a typical system temperature of 170 K. The pointing was checked every two hours by observing the SiO maser source V1111-Oph and was accurate within 5″. The intensity calibration was made by observing a small region of ∼1′ × 1′ in hub-N every time we tuned the receiver, and we found that the intensity fluctuations for all of the lines are less than 10%.
The data reduction for baseline subtraction was carried out using the NOSTAR software package developed at NRO. The 3D fits data were generated by convolving the observed data with a spheroidal function and regridding them at |${7{^{\prime \prime}_{.}}5}$| per pixel, resulting in an effective angular resolution of 22″–24″, corresponding to a linear resolution 0.2 pc at a distance of 2.0 kpc. To increase the signal-to-noise ratios, we regridded the data to a velocity resolution of 0.1 km s−1. We converted the antenna temperature |$T_{\rm a}^{*}$| to the main beam temperature Tmb assuming that the main beam efficiency of the telescope is 0.416, 0.435, 0.437, 0.497, and 0.500 for the 12CO, 13CO, C18O, CCS, and N2H+ emission lines, respectively. The rms noise of the final data is ΔTmb = 0.4–1.0 K. We summarize the observed molecular lines and the resulting noise levels in table 1. More detailed descriptions of the data reduction are provided by Nakamura et al. (2019a) and Shimoikura et al. (2019).
2.2 Archival data
We used the Herschel archival data of 160, 250, 350, and |$500\, \mu \mathrm{m}$| toward M 17 SWex to construct an H2 column density N(H2) map and a dust temperature Tdust map which are derived by fitting the spectral energy distribution (SED) of the Herschel data. Details of the data analysis are described by Sugitani et al. (2019). We regridded the maps of N(H2) and Tdust on to the same grid as that of the molecular data obtained by the 45 m telescope.
3 Results
3.1 Spatial distributions of M 17 SWex
Figure 1 shows the integrated intensity maps of the 12CO and 13CO emission lines. As we show in panels (c) and (d) of the figure, we made position–velocity (PV) diagrams across the M 17 H|$\,$|ii region and M 17 SWex along the line in panel (b). As seen in the figure, the intense emission lines around VLSR = 20 km s−1 change smoothly from the M 17 H|$\,$|ii region to M 17 SWex in terms of the radial velocity, line width, and the brightness temperature. We therefore assume that M 17 SWex is physically connected with the M 17 H|$\,$|ii region.
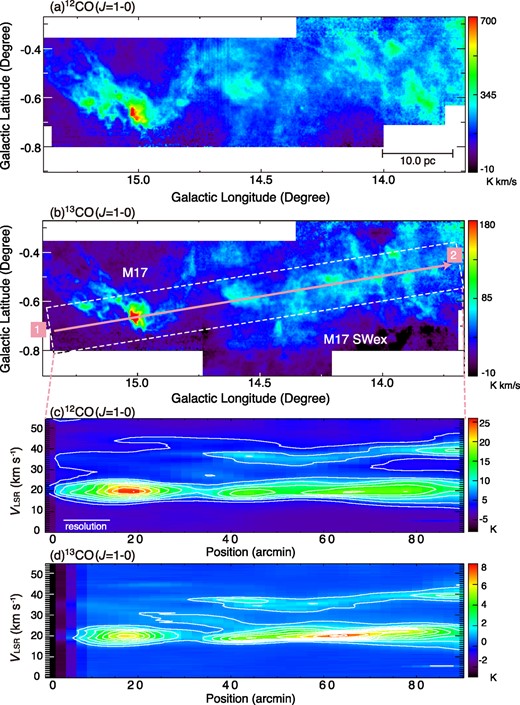
Integrated intensity maps of the (a) 12CO and (b) 13CO emission lines. The velocity range used for the integration is −10.0 ≲ VLSR ≲ 55.0 km s−1 for both of the emission lines. Position–velocity diagrams of the (c) 12CO and (d) 13CO emission lines are taken along the cut (1)–(2) in panel (b). The lowest contour and the contour interval are both 3.0 K for panel (c) and are both 1.0 K for panel (d). As indicated in panel (b) by the white broken line, the angular resolution of the position–velocity diagrams is set to 10′ to cover most of the cores identified in this study. The velocity resolution is set to 0.5 km s−1. (Color online)
Figure 2 shows the integrated intensity maps of the C18O and N2H+ emission lines. CCS emission was not detected at the present sensitivity. The N2H+ and C18O emission lines are distributed in the velocity range 6.0 ≲ VLSR ≲ 34.0 km s−1 and 15.0 ≲ VLSR ≲ 26.0 km s−1, respectively. The map of C18O traces the shape of the flying dragon of the infrared dark cloud well. Since the signal-to-noise ratio of the N2H+ map is poor at the edge, we analyzed the data within the area surrounded by the broken yellow line shown on the map for N2H+ in this study. For comparison, we also show the N(H2) map calculated using the Herschel data by Sugitani et al. (2019) in figure 2c. As seen in panels (a) and (c), the distributions of C18O and N(H2) show a good correlation. We also found that N2H+ is distributed in regions where the N(H2) density is relatively high (|$\gtrsim 10^{22}\:$|cm−2).
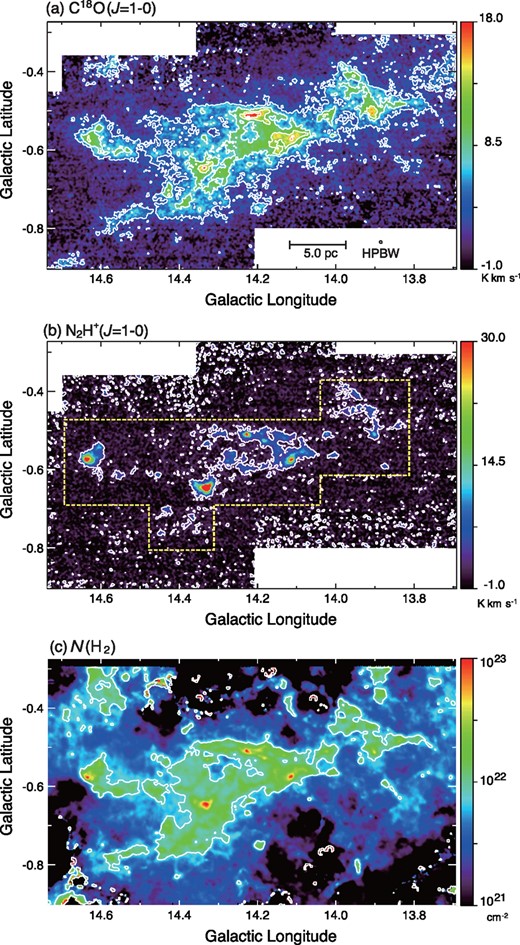
Integrated intensity maps of the (a) C18O and (b) N2H+ emission lines. The velocity ranges used for the integration are (a) 15.0 ≲ VLSR ≲ 26.0 km s−1 and (b) 6.0 ≲ VLSR ≲ 34.0 km s−1. (c) The H2 column density map derived from the Herschel data. The lowest contour and the contour interval for the C18O map are 4.0 K km s−1. Contours are drawn at 2.8 K km−1 and 1.0 × 1022 cm−2 in the N2H+ and N(H2) maps, respectively. (Color online)
Povich and Whitney (2010) made a YSOs survey around M 17 SWex. In the catalog they compiled, a total of 488 YSOs classified as Stage 0/I (YSOs accompanied by an infalling envelope), Stage II (YSOs with optically thick circumstellar disk), Stage III (YSOs with optically thin disk), and “Ambiguous stage” are listed. Povich et al. (2016) updated the catalog. In the catalog, 840 stars are classified as Stage 0/I, Stage II/III, and Ambiguous stage. We show the distributions of these YSOs associated with the observed region using the catalog of Povich et al. (2016) in figure 3. We found that the Stage 0/I YSOs are distributed in dense parts of the N2H+ emission whereas the Stage II and III YSOs are distributed more randomly throughout the M 17 SWex region.
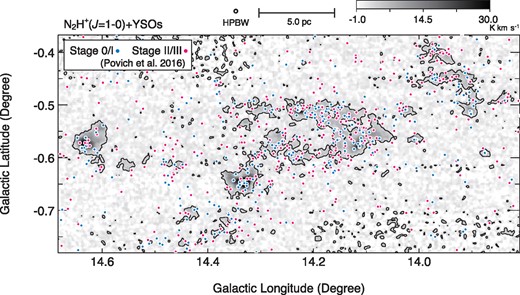
Distribution of YSOs associated with the M 17 SWex region reported by Povich et al. (2016). The contours denote the N2H+ integrated intensity map same as in figure 2 (b). Stage 0/I is the YSO accompanied by an infalling envelope, Stage II is the YSO with an optically thick circumstellar disk, and Stage III is the YSO with an optically thin disk (see Povich & Whitney 2010). (Color online)
3.2 Identification of cores
In order to identify cores based on the N2H+ emission, we apply the “dendrogram” algorithm (e.g., Rosolowsky et al. 2008) to the N2H+ integrated intensity map.1 The dendrogram identifies three hierarchical structures of “leaf,” “branch,” and “trunk.” We chose the minimum threshold intensity required to identify a parent tree structure to be |$4\, \sigma$| (= 2.8 K km s−1) and a splitting threshold intensity required to identify structures to be |$2\, \sigma$|. We only consider leaves with at least 25 pixels which are the equivalent area of the synthesized beam (0.39 arcmin2), and we refer to them as “cores.” As a result, a total of 46 cores are identified. We note that the results of the above core identification, e.g., the number and position of the cores, do not change significantly with other algorithms such as “clumpfind.”
Figure 4 shows the cores identified. We numbered the identified cores from No. 1 to No. 46 in the order of galactic longitude. We searched for YSOs in the catalog of Povich et al. (2016) within the boundary of the cores and found that there are 40 cores with YSOs and six cores without YSOs. We assume that the YSOs are associated with the cores. The peak position of the cores and the number of YSOs associated with each core are summarized in table 2. We found that four cores (Nos. 15, 23, 33, and 46) are especially large, having a size of ∼1 pc. These cores are accompanied by many YSOs. Among these, two cores correspond to the regions known as hub-N (= No. 33) and hub-S (= No. 15).
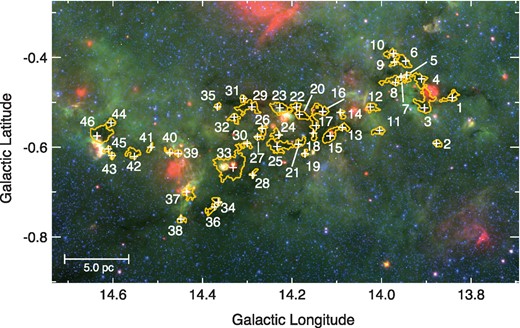
Distribution of the identified cores. The background is a Spitzer composite image made with the 24.0μm (red), 8.0μm (green) and 3.6μm (blue) data. The identified cores are numbered in the order of galactic longitude. The white plus sign is the peak position of the N2H+ integrated intensity of each core. Orange contours denote the surface area of the cores defined at 2.8 K km s−1 (= 4σ). (Color online)
The distances to some of the detected cores can be found in the literature, but there is an uncomfortable mismatch. Wu et al. (2014) determined the distance of G14.63−0.57 (= core No. 46) to be |$1.83 ^{+0.08}_{-0.07}\:$|kpc by a parallax measurement. On the other hand, Sato et al. (2010) reported a distance of 1.12 ± 0.13 kpc for G14.33−0.64 (= core No. 23) which is located not far from G14.63−0.57 on the plane of the sky. Povich et al. (2016) suggested that G14.63−0.57 is actually much closer than the other core. However, as can be seen in figure 1, the radial velocities, line widths, and intensities of the observed 12CO and 13CO lines change smoothly over the entire M 17 SWex region including cores Nos. 33 and 46, suggesting that they may belong to the same system. In this paper, we assume that all of the cores identified in this work are located at 2.0 kpc (Xu et al. 2011) for simplicity. Parameters of the cores derived in this paper should be rescaled when their distances are established precisely. The complexity of the distance measurements of the M 17 SWex region in the literature is summarized and discussed in detail by Povich et al. (2016).
3.3 Physical parameters derived from the molecular line data
Assuming local thermodynamic equilibrium (LTE), we estimated the physical parameters of the cores.
In order to derive the excitation temperature based on the 12CO data as well as to derive the column density of C18O, we followed the method described by Shimoikura et al. (2018). Using the optically thick 12CO line (τ ≫ 1), we estimated the excitation temperature |$T^{\rm {co}}_{\rm ex}$| at the individual positions in the observed region. The 12CO emission is widely distributed over the whole region in the observed velocity range (see figure 1). The peak intensity of the 12CO spectra was measured for M 17 SWex in the velocity range from 0 to 30 km s−1, and we determined |$T^{\rm {co}}_{\rm ex}$| by measuring the peak brightness temperature of the 12CO line in this velocity range. Finally, the C18O column density N(C18O) was calculated from the C18O intensity.
Next, we derived the physical parameters of the N2H+ molecular emission line. The procedure for the derivation is similar to that described by Shimoikura et al. (2019). We fitted the seven hyperfine components with multiple Gaussian functions under the assumption that all of the seven hyperfine lines have a single line width and excitation temperature. The fitting was performed on the spectra within the area where the cores were identified. We then derived the peak temperature Tmb, the centroid velocity VLSR, the line width ΔV, the excitation temperature |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$|, and the total optical depth τtot for all of the hyperfine components. When the emission line is optically thin, τtot and |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| cannot be estimated well simultaneously by the fitting. For such spectra, we estimated |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| by interpolating |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| at the neighboring positions with a weighted two-dimensional Gaussian function. We then estimated the N2H+ column density N(N2H+) using the line parameters derived above (see Shimoikura et al. 2019).
In figure 5, we present each parameter map obtained from the hyperfine spectra fitting. The line parameters of the peak positions of the cores are summarized in table 3. The distributions of the temperatures |$T^{\rm {co}}_{\rm ex}$|, |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$|, and Tdust are shown in figure 6.
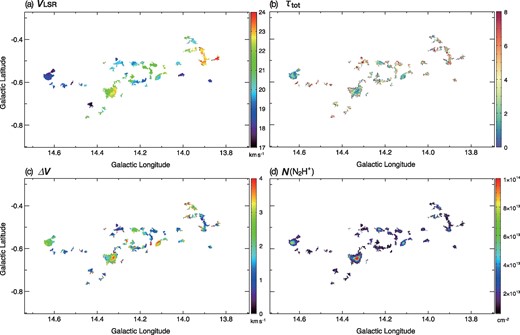
(a) Centroid velocity map, (b) total optical depth map, (c) line width map, and (d) column density map of the N2H+ emission line. These maps are obtained based on the hyperfine spectra fitting of the N2H+ data. (Color online)
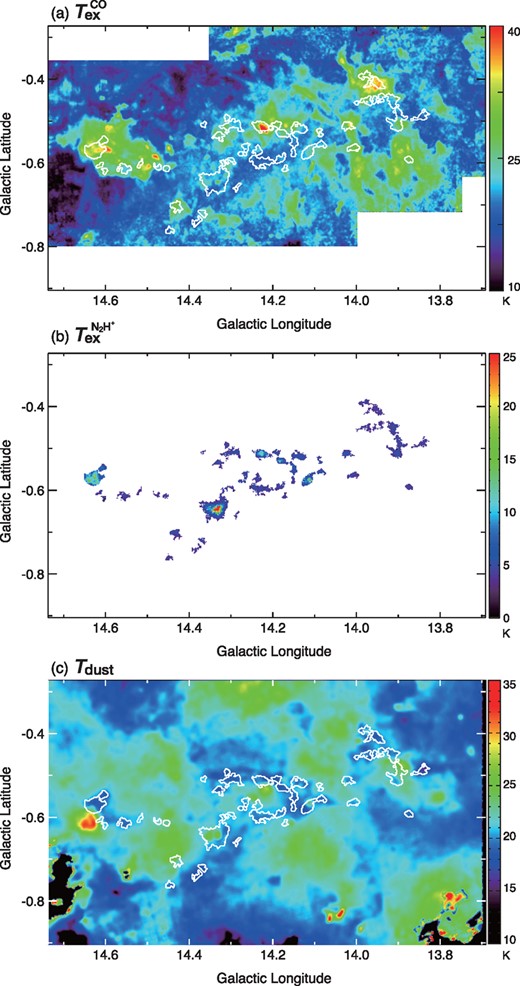
(a) Excitation temperature map derived from the 12CO data. (b) Excitation temperature map derived from the N2H+ data. (c) Dust temperature map derived from the Herschel data. The cores shown in figure 4 are overlaid in panels (a) and (c) by the white contours. (Color online)
Furthermore, the fractional abundances of C18O and N2H+, f(C18O) and f(N2H+), respectively, are directly derived from the ratios of each column density and N(H2).
The constants of the observed molecular lines used to derive the parameters in this section are summarized by Shimoikura et al. (2018, see their table 2). We found that the derived parameters are in the ranges 0.2 ≲ Rcore ≲ 1.0 pc, |$43 \lesssim M_{\rm core} \lesssim 3026\, {M}_{\odot }$|, |$3.00 \lesssim T^{\rm {N{_2}H^{+}}}_{\rm ex} \lesssim 31.68\:$|K, and 0.76 ≲ ΔV ≲ 4.00 km s−1. Among the 46 cores, we found four massive ones (Nos. 15, 23, 33, and 46) with a mass of more than |$1000\, M_{\odot }$|. These cores have larger ΔV (|$\gtrsim 2.5\:$|km s−1) and higher |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| (|$\gtrsim 10\:$|K) than the other cores. |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$|and ΔV of the other cores are <10 K and <2 km s−1, respectively, indicating that |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| and ΔV increase as Mcore increases.
Busquet et al. (2013) revealed that the velocity dispersion is locally enhanced (σ ∼ 1 km s−1) toward hub-N (No. 23) and hub-S (No. 15). Based on the SMA images, Busquet et al. (2016) show that the two hubs fragment into several dust condensations. The large ΔV of the four cores suggest that there are multiple unresolved sub-cores not only in cores Nos. 15 and 23 but also in cores Nos. 33 and 46. In figure 7, we show the parameter maps for the four cores. It seems that there is a correlation between the distributions of |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| and those of YSOs. In addition, it appears that there is an anti-correlation between the distributions of f(N2H+) and those of YSOs. For the relationships between the distribution of ΔV and those of YSOs, the correlation is not clear.
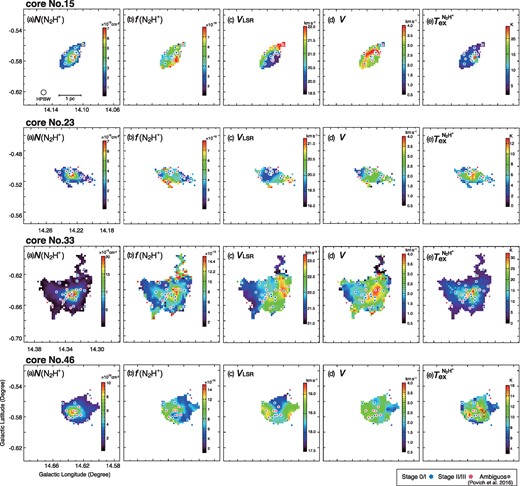
N2H+ parameter maps for cores Nos. 15, 23, 33, and 46. (a) N(N2H+) map. (b) f(N2H+) map. (c) VLSR map. (d) ΔV map. (e) |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| map. (Color online)
3.4 Correlation between N(N2H+) and N(H2) for the cores
To estimate the total masses of cores from N(N2H+), the abundance ratio of f(N2H+) = 3 × 10−10 reported by Caselli, Myers, and Thaddeus (1995) has widely been used in star-forming regions. However, as seen in figure 7, f(N2H+) varies even within a single core. In this study, we investigate the relationship between N(N2H+) and N(H2) of the identified cores.
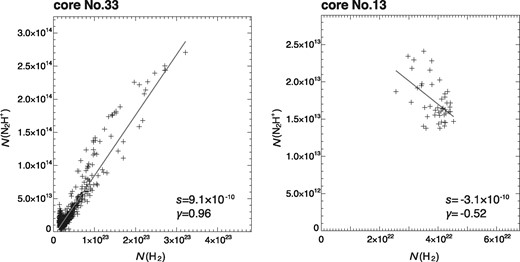
Relation between N(N2H+) and N(H2) for cores Nos. 33 (left) and 13 (right).
In table 5, we summarize the obtained values of s and i together with the correlation coefficients γ. As listed in the table, there is a large variation in s, and its median value is s = 3.5 × 10−10, which is consistent with that measured in other clouds (e.g., Tanaka et al. 2013; Shimoikura et al. 2019).
Among the detected 46 cores, there are 15 cores showing a good correlation with |$\gamma \gtrsim 0.6$|, and 14 cores showing almost no correlation (|$\gamma \lesssim 0.2$|). Most of the cores have a positive value of s(> 0), but there are some cores that have negative values (s < 0, e.g., core No. 13), suggesting that N2H+ is probably adsorbed onto dust in the densest part of the cores (e.g., Bergin et al. 2002; Belloche & André 2004).
3.5 Relationship between the cores and YSOs
We attempt to investigate the relationship between the mass of the cores and those of YSOs forming in the cores. For this, we estimated the total stellar mass ΣM⋆ associated with each core. The catalogue of Povich and Whitney (2010) contains a number of good candidate YSOs, but some of the estimated parameters such as the stellar mass could be erroneous due to ambiguities of the adopted model. We therefore made use of the newer catalog by Povich et al. (2016) which is more complete but does not present stellar masses, and we adopted the following rough method to estimate ΣM⋆: First, we counted the catalogued YSOs located within the extent of each core, and assumed that the median value of their masses is |$M_{\rm medi}=3\, {M}_{\odot }$| (M. S. Povich 2019, private communication). Secondly, we assumed the stellar initial mass function (IMF) by Kroupa (2001) and scaled the IMF to match the observed number of YSOs having a mass greater than Mmedi in each core. Finally, we estimated ΣM⋆ in the cores by integrating the scaled IMF. Resulting values of ΣM⋆ are summarized in the last column of table 4. The total stellar mass in the table amounts to |${\sim }2900\, {M}_{\odot }$|.
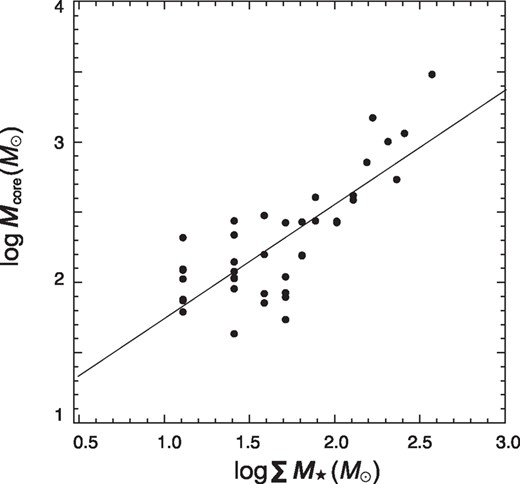
Core mass Mcore vs. the total stellar mass ΣM⋆. The solid line is the least-squares fit given in equation 5.
3.6 Star formation efficiency of M 17 SWex
We show a plot of ΣM⋆ vs. Mcore + ΣM⋆ in figure 10. Star formation efficiency (SFE) is a fundamental parameter of the cluster formation process (Lada & Lada 2003) and is calculated as ΣM⋆/(Mcore + ΣM⋆). We investigated the SFE of M 17 SWex by fitting the all of the data points in figure 10. The result is shown in the figure by the solid line which corresponds to SFE =13.7%. Many of the data points smaller than |$M_{\rm core}+\Sigma M_\star =2000\, M_{\odot }$| are above the solid line because of core No. 33, whose distance might be very different from the other cores (see subsection 3.2). We would obtain SFE = 17.0% if we exclude this core from the fit (the broken line in the figure). The total SFE obtained from the total stellar mass (|${\sim }2920\, M_{\odot }$|) and the total mass of the cores (|${\sim }14300\, M_{\odot }$|) is 16.9%.

Total stellar mass of YSOs associated with each core ΣM⋆ vs. the total mass of the system for each core (Mcore + ΣM⋆). The linear least-squares fit (SFE =13.7%) is shown by the solid line. The broken line denotes the best fit when we exclude core No. 33 from the fit.
As seen in figure 3, there are YSOs outside the extents of the detected cores. Povich and Whitney (2010) estimated ΣM⋆ for M 17 SWex to be |$8\times 10^{3}\, M_{\odot }$| by integrating the IMF of Kroupa (2001) over |$M_{\star }\gtrsim 0.1\, M_{\odot }$|. We estimated the total gas mass of the entire M 17 SWex region to be |$7.8\times 10^{4}\, M_{\odot }$| by integrating |$N(\rm {H}_2)$| within the area defined by the 1.0 × 1021 H2 cm−2 contour. These values infer an average SFE of 9.3% for the entire M 17 SWex region.
According to Lada and Lada (2003), who cataloged the SFEs for nearby embedded clusters, the SFEs range from approximately 10% to 30%. The values of 9.3% and ∼17% obtained in M 17 SWex is comparable to those of the cluster-forming regions.
4 Discussion
4.1 Dynamical state of the cores
We investigate the dynamical state of the cores. Figure 11a shows the relation between Mvir and Mcore. The solid line indicates Mcore = Mvir. Focusing on the relationship between Mcore and Mvir, the observed cores can be divided into the following three types, and we discuss their characteristics.
We found that many cores satisfy the condition of Mcore ≃ Mvir, indicating that the cores are dynamically stable if there is no external pressure (Pext = 0). More massive cores tend to be in the gravitational virial equilibrium.
Cores satisfying the condition of Mcore > Mvir may be contracting because they cannot prevent collapsing as a result of the internal pressure even when Pext = 0. The value of ΔV for such cores (e.g., cores Nos. 1 and 28) is relatively small, being less than 1 km s−1 (table 3).
- There are some cores under the condition of Mcore < Mvir (e.g., cores Nos. 10 and 35), and such cores will disperse under the condition Pext = 0. However, they can be confined in the pressure of the high-density gas surrounding the cores. We suggest that such cores are highly influenced by Pext in equation (2). Virial mass, taking into account Pext, can be expressed aswhere A and B are constants to relate Mcore and Rcore; |$R_{\rm {core}}= {\rm A} M^{\rm B}_{\rm core}$|. We derived A = 0.05 and B = 0.37 for Rcore and Mcore in units of pc and |${M}_{\odot }$|, respectively, by fitting the plot shown in figure 11b with the relation. In figure 11a, we show Mvir by the broken lines calculated based on equation (6) for various Pext(≠ 0). As seen in the figure, comparing the position of the plot with the lines, most of the cores can be dynamically stable under Pext/k = 105.0–105.5 K cm−3.(6)$$\begin{equation} {M_{\rm vir}}= {M_{\rm core}}+ \frac{20\pi }{3G} {\rm {A}}{M^{4{\rm B}-1}_{\rm core}} P_{\rm ext}\ , \end{equation}$$
In summary, we suggest that many of the cores can be dynamically stable if we assume a large external pressure. For cores under the condition Mcore > Mvir, the internal pressure due to turbulence is too small, and they should contract by the self-gravity if there is no magnetic field strong enough to support them. We will further discuss this point in subsection 4.3.
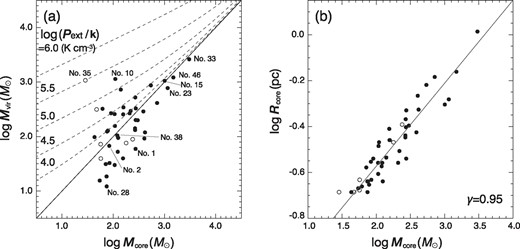
(a) Relationship between Mvir and Mcore. Filled and open circles represent the cores with and without YSOs, respectively. The solid line shows the external pressure Pext = 0 where Mcore = Mvir, and the dotted lines show the virial masses in equilibrium with the external pressure log (Pext/k) = 4.0, 4.5, 5.0, 5.5, 6.0 K cm−3. (b) Relationship between Rcore and Mcore. The black line shows the fitting result of the relation (|$R_{\rm core}=0.05\, M_{\,\rm core}^{\,0.37}$|; see text). (Color online)
4.2 Density structure of the cores
We investigate the distribution of N(H2) of the cores as a function of the projected distance R from the peak of N(H2). We found that profile of N(H2) for the cores are found to be different for each core. In the case of a spherical core, we assume that the number density of H2 molecules ρ is expressed as ρ(r) ∝ r−α, where r is the distance from the center of the sphere. The physical state of the cores can be estimated by examining the value of α. For example, a density profile of gravitationally stable cores and free-falling cores show α = 2.0 and 1.5, respectively (e.g., Shu 1977; Motte & André 2001; Shimoikura et al. 2016).
To investigate the density structure of the cores, we fitted the relations between N(H2) and R of the cores with N(H2) = N0(R/R0)−β + C where N0, R0, and C are constants. The obtained values of the index β are roughly divided into three types: (a) 0.7–1.2 for the four massive cores, (b) 0.3–0.6 for the smaller cores with YSOs, and (c) 0.1–0.3 for the cores without YSOs. Because β = α − 1, the values of β infer α = 1.7–2.2, 1.3–1.6, and 1.1–1.3 for the cases (a), (b), and (c) in the above, respectively. In figure 12, we show typical examples of the N(H2) vs. R relations for the three types. There are four, 28, and 14 cores belonging the types (a), (b), and (c), respectively.
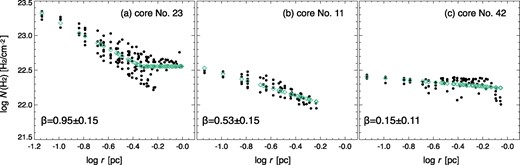
Distribution of N(H2) as a function of the projected distance from the peak of N(H2) for cores (a) No. 23, (b) No. 11, and (c) No. 42. Green diamonds represent fits (see text). (Color online)
The results suggest that the cores of (a) and (b) types are likely to be gravitationally stable and free-falling, respectively. Note that, in the case of the type (c) cores, they show a flat density profile and there is a possibility that the cores are not resolved at the present resolution due to their small size.
4.3 Star formation in M 17 SWex
As found in section 4.1, some of the cores satisfy the condition Mcore > Mvir, which means that the cores are contracting if we ignore the effects of the magnetic field. Ohashi et al. (2016) observed small cores in the two hubs identified with ALMA observations which correspond to the cores Nos. 12–23 in our work. They found that the small cores have viral parameters (defined as Mvir/Mcore) in the range 0.1–1.3, which is comparable to our results. Based on the analysis of the virial parameters, Ohashi et al. (2016) speculated that mass accretion onto the cores via the hubs could produce massive stars in the future. However, their values of the virial parameters do not take into account the effect of the magnetic field. In order to investigate whether the cores are really contracting or not, a quantitative estimate of the magnetic field is needed.
Recently, Sugitani et al. (2019) conducted near-infrared polarization observations toward M 17 SWex, and revealed the overall distribution of the magnetic field around the individual filamentary structures. They found that the magnetic field in M 17 SWex is mostly perpendicular to the elongation of the filamentary clouds, and they estimated the strength of the magnetic field to be 70–|$300\, \mu$|G using the Davis–Chandrasekhar–Fermi method. Based on these results, Sugitani et al. (2019) suggested that the clouds in M 17 SWex are likely to be magnetically critical or sub-critical, which may be responsible for the present low level of massive star formation in M 17 SWex.
The critical mass of the cores that can be supported by the magnetic field is expressed as Mcr/|${M}_{\odot }$| ≃ 2 × 102(B/30μG)(Rcore/1 pc)2 (e.g., Nakano & Yoshida 1986; Shu et al. 1987). Using Rcore and Mcore given in table 4, we found that a magnetic field of ∼100–|$600\, \mu$|G is necessary for these cores to be magnetically critical. The range of the magnetic field is consistent with or slightly larger than the values 70–|$300\, \mu$|G reported by Sugitani et al. (2019). We should note that Sugitani et al. (2019) measured the magnetic field at the periphery of M 17 SWex where the background stars were well detected in the near-infrared; the magnetic field inside the dense cores can be stronger than the values they obtained, if the magnetic field is frozen into the dense cores. In addition, their values are for the component projected on the plane of the sky but do not include the component parallel to the line-of-sight. As Sugitani et al. (2019) suggested, we conclude that the cores detected in this study are likely to be magnetically critical or sub-critical, and the magnetic field prevents the cores from collapsing, which may be the cause of the inactive massive star formation in M 17 SWex.
However, it is rather mysterious that the total SFE of M 17 SWex (∼9%–17%) is comparable to those of other cluster-forming clumps producing massive stars (subsection 3.6), indicating that low-mass (and intermediate-mass) stars are forming in spite of the magnetic fields. We imagine that the small cores producing the small stars, which may not be detected by our observations, can lose the supporting force of the magnetic field quickly via the ambipolar diffusion because of their small sizes. In addition, sporadic collisions of the internal substructures of the cores/clumps (such as “fibers”) may also induce formation of low-mass stars via a sudden increment of density (Dobashi et al. 2014; Matsumoto et al. 2015). These effects can help the formation of low-mass stars. For the massive cores we identified in M 17 SWex, we suggest that they are unlikely to collapse at the moment due to the support by the magnetic field, but they may eventually become supercritical to collapse and form massive stars if they lose the clump-supporting force of the magnetic field, or if they gain more mass via mass accretion from the surroundings.
5 Conclusions
An N2H+ survey for molecular cores was made toward the M 17 southwest extension (M 17 SWex) region. We identified 46 molecular cores. Among the 46 cores, 40 are associated with YSOs and the other six are not associated with any YSOs. Investigation of the core properties was also carried out by using the 12CO, 13CO, and C18O data as well as N(H2) the column density of H2 and the dust temperature derived from Herschel data. We also used physical properties of YSOs found in the literature.
We summarize the main findings of this study as follows:
We derived the masses of the individual cores from the N(H2) data assuming a distance of 2.0 kpc, and found that the core masses vary in the range from |$43\, M_{\odot }$| to |$3026\, M_{\odot }$|. Based on the N2H+ data, we derived the physical parameters of the cores and presented each parameter map. The derived excitation temperature and the line width range from 3.0 K to 31.7 K and from 0.8 km s−1 to 4.0 km s−1, respectively. Among the 46 cores, we found four massive cores associated with YSOs. The cores have a large mass of |$\gtrsim 1000\, M_{\odot }$|, a line width of |$\gtrsim 2.5\:$|km s−1, and an excitation temperature of |$\gtrsim 10\:$|K.
We investigated the fractional abundance of N2H+ for all of the cores. The values are estimated to be in the range (4–10) × 10−10, indicating that there is a large variation among the cores.
We estimated the average star formation efficiency of M 17 SWex to be ∼9%–17%.
Comparison of the virial mass and the core mass estimated from the Herschel data revealed that most of the cores can be dynamically stable if we assume a large external pressure. For some cores, the results of the comparison indicate that internal pressure due to turbulence is small, and they can collapse by the self-gravity if there is no internal supporting force by the magnetic field.
Assuming a radial density profile of spherical gas, we examined the N(H2) distribution to infer the index α of the density profile of the cores ρ(r) ∝ r−α. We found that 32 out of 46 cores have a value of α in the range 1.3–2.2, suggesting that the cores are gravitationally stable or free-falling.
We estimated that a magnetic field of ∼100–|$600\, \mu$|G is required for the cores to be critical. This value is comparable to the strength of the magnetic filed recently measured by Sugitani et al. (2019). Previous studies (e.g., Povich & Whitney 2010) have shown that there is no active massive star formation in M 17 SWex, and we suggest that it is due to the cloud-supporting force by the magnetic field which prevents the cores from collapsing.
| Molecule . | Transition . | Frequency* . | Beam . | ΔTmb . |
|---|---|---|---|---|
| . | . | (GHz) . | . | (K) . |
| N2H+ | J = 1–0 | 93.1737637 | |${17{^{\prime \prime}_{.}}9}$| | 0.44 |
| CCS | JN = 87–76 | 93.8700980 | |${17{^{\prime \prime}_{.}}8}$| | 0.42 |
| C18O | J = 1–0 | 109.7821760 | |${15{^{\prime \prime}_{.}}2}$| | 0.43 |
| 13CO | J = 1–0 | 110.2013540 | |${15{^{\prime \prime}_{.}}1}$| | 0.37 |
| 12CO | J = 1–0 | 115.2712040 | |${14{^{\prime \prime}_{.}}5}$| | 0.90 |
| Molecule . | Transition . | Frequency* . | Beam . | ΔTmb . |
|---|---|---|---|---|
| . | . | (GHz) . | . | (K) . |
| N2H+ | J = 1–0 | 93.1737637 | |${17{^{\prime \prime}_{.}}9}$| | 0.44 |
| CCS | JN = 87–76 | 93.8700980 | |${17{^{\prime \prime}_{.}}8}$| | 0.42 |
| C18O | J = 1–0 | 109.7821760 | |${15{^{\prime \prime}_{.}}2}$| | 0.43 |
| 13CO | J = 1–0 | 110.2013540 | |${15{^{\prime \prime}_{.}}1}$| | 0.37 |
| 12CO | J = 1–0 | 115.2712040 | |${14{^{\prime \prime}_{.}}5}$| | 0.90 |
| Molecule . | Transition . | Frequency* . | Beam . | ΔTmb . |
|---|---|---|---|---|
| . | . | (GHz) . | . | (K) . |
| N2H+ | J = 1–0 | 93.1737637 | |${17{^{\prime \prime}_{.}}9}$| | 0.44 |
| CCS | JN = 87–76 | 93.8700980 | |${17{^{\prime \prime}_{.}}8}$| | 0.42 |
| C18O | J = 1–0 | 109.7821760 | |${15{^{\prime \prime}_{.}}2}$| | 0.43 |
| 13CO | J = 1–0 | 110.2013540 | |${15{^{\prime \prime}_{.}}1}$| | 0.37 |
| 12CO | J = 1–0 | 115.2712040 | |${14{^{\prime \prime}_{.}}5}$| | 0.90 |
| Molecule . | Transition . | Frequency* . | Beam . | ΔTmb . |
|---|---|---|---|---|
| . | . | (GHz) . | . | (K) . |
| N2H+ | J = 1–0 | 93.1737637 | |${17{^{\prime \prime}_{.}}9}$| | 0.44 |
| CCS | JN = 87–76 | 93.8700980 | |${17{^{\prime \prime}_{.}}8}$| | 0.42 |
| C18O | J = 1–0 | 109.7821760 | |${15{^{\prime \prime}_{.}}2}$| | 0.43 |
| 13CO | J = 1–0 | 110.2013540 | |${15{^{\prime \prime}_{.}}1}$| | 0.37 |
| 12CO | J = 1–0 | 115.2712040 | |${14{^{\prime \prime}_{.}}5}$| | 0.90 |
| . | . | . | Number of YSOs* . | ||
|---|---|---|---|---|---|
| Core . | l . | b . | . | ||
| . | (°) . | (°) . | Stage 0/I . | Stage II/III . | A† . |
| 1 | 13.84 | −0.49 | 1 | 7 | 0 |
| 2 | 13.88 | −0.59 | 2 | 1 | 0 |
| 3 | 13.90 | −0.51 | 10 | 2 | 0 |
| 4 | 13.91 | −0.45 | 2 | 0 | 0 |
| 5 | 13.94 | −0.44 | 0 | 2 | 0 |
| 6 | 13.95 | −0.41 | 0 | 3 | 2 |
| 7 | 13.96 | −0.44 | 0 | 2 | 2 |
| 8 | 13.97 | −0.46 | 4 | 0 | 1 |
| 9 | 13.97 | −0.41 | 0 | 0 | 1 |
| 10 | 13.97 | −0.39 | 3 | 1 | 0 |
| 11 | 14.00 | −0.56 | 3 | 2 | 0 |
| 12 | 14.02 | −0.51 | 4 | 2 | 2 |
| 13 | 14.09 | −0.56 | 1 | 0 | 0 |
| 14 | 14.09 | −0.52 | 0 | 0 | 0 |
| 15 | 14.11 | −0.57 | 9 | 3 | 4 |
| 16 | 14.13 | −0.52 | 4 | 6 | 0 |
| 17 | 14.15 | −0.55 | 1 | 1 | 2 |
| 18 | 14.15 | −0.57 | 1 | 0 | 0 |
| 19 | 14.17 | −0.61 | 3 | 0 | 1 |
| 20 | 14.18 | −0.53 | 5 | 4 | 1 |
| 21 | 14.19 | −0.59 | 0 | 2 | 1 |
| 22 | 14.19 | −0.51 | 2 | 3 | 1 |
| 23 | 14.23 | −0.51 | 11 | 8 | 1 |
| 24 | 14.23 | −0.57 | 0 | 1 | 1 |
| 25 | 14.23 | −0.60 | 8 | 6 | 4 |
| 26 | 14.27 | −0.56 | 1 | 0 | 0 |
| 27 | 14.28 | −0.58 | 3 | 1 | 0 |
| 28 | 14.29 | −0.66 | 0 | 1 | 0 |
| 29 | 14.29 | −0.51 | 2 | 1 | 3 |
| 30 | 14.30 | −0.59 | 1 | 2 | 0 |
| 31 | 14.31 | −0.49 | 1 | 0 | 0 |
| 32 | 14.33 | −0.53 | 0 | 0 | 0 |
| 33 | 14.33 | −0.65 | 14 | 11 | 4 |
| 34 | 14.36 | −0.72 | 0 | 1 | 0 |
| 35 | 14.37 | −0.51 | 0 | 0 | 0 |
| 36 | 14.37 | −0.73 | 1 | 1 | 0 |
| 37 | 14.44 | −0.70 | 1 | 2 | 0 |
| 38 | 14.45 | −0.76 | 1 | 1 | 0 |
| 39 | 14.45 | −0.61 | 1 | 1 | 0 |
| 40 | 14.47 | −0.61 | 1 | 0 | 0 |
| 41 | 14.51 | −0.60 | 0 | 0 | 0 |
| 42 | 14.55 | −0.62 | 0 | 0 | 0 |
| 43 | 14.60 | −0.62 | 0 | 2 | 0 |
| 44 | 14.60 | −0.55 | 1 | 1 | 0 |
| 45 | 14.61 | −0.60 | 0 | 0 | 0 |
| 46 | 14.64 | −0.57 | 6 | 7 | 0 |
| . | . | . | Number of YSOs* . | ||
|---|---|---|---|---|---|
| Core . | l . | b . | . | ||
| . | (°) . | (°) . | Stage 0/I . | Stage II/III . | A† . |
| 1 | 13.84 | −0.49 | 1 | 7 | 0 |
| 2 | 13.88 | −0.59 | 2 | 1 | 0 |
| 3 | 13.90 | −0.51 | 10 | 2 | 0 |
| 4 | 13.91 | −0.45 | 2 | 0 | 0 |
| 5 | 13.94 | −0.44 | 0 | 2 | 0 |
| 6 | 13.95 | −0.41 | 0 | 3 | 2 |
| 7 | 13.96 | −0.44 | 0 | 2 | 2 |
| 8 | 13.97 | −0.46 | 4 | 0 | 1 |
| 9 | 13.97 | −0.41 | 0 | 0 | 1 |
| 10 | 13.97 | −0.39 | 3 | 1 | 0 |
| 11 | 14.00 | −0.56 | 3 | 2 | 0 |
| 12 | 14.02 | −0.51 | 4 | 2 | 2 |
| 13 | 14.09 | −0.56 | 1 | 0 | 0 |
| 14 | 14.09 | −0.52 | 0 | 0 | 0 |
| 15 | 14.11 | −0.57 | 9 | 3 | 4 |
| 16 | 14.13 | −0.52 | 4 | 6 | 0 |
| 17 | 14.15 | −0.55 | 1 | 1 | 2 |
| 18 | 14.15 | −0.57 | 1 | 0 | 0 |
| 19 | 14.17 | −0.61 | 3 | 0 | 1 |
| 20 | 14.18 | −0.53 | 5 | 4 | 1 |
| 21 | 14.19 | −0.59 | 0 | 2 | 1 |
| 22 | 14.19 | −0.51 | 2 | 3 | 1 |
| 23 | 14.23 | −0.51 | 11 | 8 | 1 |
| 24 | 14.23 | −0.57 | 0 | 1 | 1 |
| 25 | 14.23 | −0.60 | 8 | 6 | 4 |
| 26 | 14.27 | −0.56 | 1 | 0 | 0 |
| 27 | 14.28 | −0.58 | 3 | 1 | 0 |
| 28 | 14.29 | −0.66 | 0 | 1 | 0 |
| 29 | 14.29 | −0.51 | 2 | 1 | 3 |
| 30 | 14.30 | −0.59 | 1 | 2 | 0 |
| 31 | 14.31 | −0.49 | 1 | 0 | 0 |
| 32 | 14.33 | −0.53 | 0 | 0 | 0 |
| 33 | 14.33 | −0.65 | 14 | 11 | 4 |
| 34 | 14.36 | −0.72 | 0 | 1 | 0 |
| 35 | 14.37 | −0.51 | 0 | 0 | 0 |
| 36 | 14.37 | −0.73 | 1 | 1 | 0 |
| 37 | 14.44 | −0.70 | 1 | 2 | 0 |
| 38 | 14.45 | −0.76 | 1 | 1 | 0 |
| 39 | 14.45 | −0.61 | 1 | 1 | 0 |
| 40 | 14.47 | −0.61 | 1 | 0 | 0 |
| 41 | 14.51 | −0.60 | 0 | 0 | 0 |
| 42 | 14.55 | −0.62 | 0 | 0 | 0 |
| 43 | 14.60 | −0.62 | 0 | 2 | 0 |
| 44 | 14.60 | −0.55 | 1 | 1 | 0 |
| 45 | 14.61 | −0.60 | 0 | 0 | 0 |
| 46 | 14.64 | −0.57 | 6 | 7 | 0 |
*Povich et al. (2016).
†Ambiguous stage.
| . | . | . | Number of YSOs* . | ||
|---|---|---|---|---|---|
| Core . | l . | b . | . | ||
| . | (°) . | (°) . | Stage 0/I . | Stage II/III . | A† . |
| 1 | 13.84 | −0.49 | 1 | 7 | 0 |
| 2 | 13.88 | −0.59 | 2 | 1 | 0 |
| 3 | 13.90 | −0.51 | 10 | 2 | 0 |
| 4 | 13.91 | −0.45 | 2 | 0 | 0 |
| 5 | 13.94 | −0.44 | 0 | 2 | 0 |
| 6 | 13.95 | −0.41 | 0 | 3 | 2 |
| 7 | 13.96 | −0.44 | 0 | 2 | 2 |
| 8 | 13.97 | −0.46 | 4 | 0 | 1 |
| 9 | 13.97 | −0.41 | 0 | 0 | 1 |
| 10 | 13.97 | −0.39 | 3 | 1 | 0 |
| 11 | 14.00 | −0.56 | 3 | 2 | 0 |
| 12 | 14.02 | −0.51 | 4 | 2 | 2 |
| 13 | 14.09 | −0.56 | 1 | 0 | 0 |
| 14 | 14.09 | −0.52 | 0 | 0 | 0 |
| 15 | 14.11 | −0.57 | 9 | 3 | 4 |
| 16 | 14.13 | −0.52 | 4 | 6 | 0 |
| 17 | 14.15 | −0.55 | 1 | 1 | 2 |
| 18 | 14.15 | −0.57 | 1 | 0 | 0 |
| 19 | 14.17 | −0.61 | 3 | 0 | 1 |
| 20 | 14.18 | −0.53 | 5 | 4 | 1 |
| 21 | 14.19 | −0.59 | 0 | 2 | 1 |
| 22 | 14.19 | −0.51 | 2 | 3 | 1 |
| 23 | 14.23 | −0.51 | 11 | 8 | 1 |
| 24 | 14.23 | −0.57 | 0 | 1 | 1 |
| 25 | 14.23 | −0.60 | 8 | 6 | 4 |
| 26 | 14.27 | −0.56 | 1 | 0 | 0 |
| 27 | 14.28 | −0.58 | 3 | 1 | 0 |
| 28 | 14.29 | −0.66 | 0 | 1 | 0 |
| 29 | 14.29 | −0.51 | 2 | 1 | 3 |
| 30 | 14.30 | −0.59 | 1 | 2 | 0 |
| 31 | 14.31 | −0.49 | 1 | 0 | 0 |
| 32 | 14.33 | −0.53 | 0 | 0 | 0 |
| 33 | 14.33 | −0.65 | 14 | 11 | 4 |
| 34 | 14.36 | −0.72 | 0 | 1 | 0 |
| 35 | 14.37 | −0.51 | 0 | 0 | 0 |
| 36 | 14.37 | −0.73 | 1 | 1 | 0 |
| 37 | 14.44 | −0.70 | 1 | 2 | 0 |
| 38 | 14.45 | −0.76 | 1 | 1 | 0 |
| 39 | 14.45 | −0.61 | 1 | 1 | 0 |
| 40 | 14.47 | −0.61 | 1 | 0 | 0 |
| 41 | 14.51 | −0.60 | 0 | 0 | 0 |
| 42 | 14.55 | −0.62 | 0 | 0 | 0 |
| 43 | 14.60 | −0.62 | 0 | 2 | 0 |
| 44 | 14.60 | −0.55 | 1 | 1 | 0 |
| 45 | 14.61 | −0.60 | 0 | 0 | 0 |
| 46 | 14.64 | −0.57 | 6 | 7 | 0 |
| . | . | . | Number of YSOs* . | ||
|---|---|---|---|---|---|
| Core . | l . | b . | . | ||
| . | (°) . | (°) . | Stage 0/I . | Stage II/III . | A† . |
| 1 | 13.84 | −0.49 | 1 | 7 | 0 |
| 2 | 13.88 | −0.59 | 2 | 1 | 0 |
| 3 | 13.90 | −0.51 | 10 | 2 | 0 |
| 4 | 13.91 | −0.45 | 2 | 0 | 0 |
| 5 | 13.94 | −0.44 | 0 | 2 | 0 |
| 6 | 13.95 | −0.41 | 0 | 3 | 2 |
| 7 | 13.96 | −0.44 | 0 | 2 | 2 |
| 8 | 13.97 | −0.46 | 4 | 0 | 1 |
| 9 | 13.97 | −0.41 | 0 | 0 | 1 |
| 10 | 13.97 | −0.39 | 3 | 1 | 0 |
| 11 | 14.00 | −0.56 | 3 | 2 | 0 |
| 12 | 14.02 | −0.51 | 4 | 2 | 2 |
| 13 | 14.09 | −0.56 | 1 | 0 | 0 |
| 14 | 14.09 | −0.52 | 0 | 0 | 0 |
| 15 | 14.11 | −0.57 | 9 | 3 | 4 |
| 16 | 14.13 | −0.52 | 4 | 6 | 0 |
| 17 | 14.15 | −0.55 | 1 | 1 | 2 |
| 18 | 14.15 | −0.57 | 1 | 0 | 0 |
| 19 | 14.17 | −0.61 | 3 | 0 | 1 |
| 20 | 14.18 | −0.53 | 5 | 4 | 1 |
| 21 | 14.19 | −0.59 | 0 | 2 | 1 |
| 22 | 14.19 | −0.51 | 2 | 3 | 1 |
| 23 | 14.23 | −0.51 | 11 | 8 | 1 |
| 24 | 14.23 | −0.57 | 0 | 1 | 1 |
| 25 | 14.23 | −0.60 | 8 | 6 | 4 |
| 26 | 14.27 | −0.56 | 1 | 0 | 0 |
| 27 | 14.28 | −0.58 | 3 | 1 | 0 |
| 28 | 14.29 | −0.66 | 0 | 1 | 0 |
| 29 | 14.29 | −0.51 | 2 | 1 | 3 |
| 30 | 14.30 | −0.59 | 1 | 2 | 0 |
| 31 | 14.31 | −0.49 | 1 | 0 | 0 |
| 32 | 14.33 | −0.53 | 0 | 0 | 0 |
| 33 | 14.33 | −0.65 | 14 | 11 | 4 |
| 34 | 14.36 | −0.72 | 0 | 1 | 0 |
| 35 | 14.37 | −0.51 | 0 | 0 | 0 |
| 36 | 14.37 | −0.73 | 1 | 1 | 0 |
| 37 | 14.44 | −0.70 | 1 | 2 | 0 |
| 38 | 14.45 | −0.76 | 1 | 1 | 0 |
| 39 | 14.45 | −0.61 | 1 | 1 | 0 |
| 40 | 14.47 | −0.61 | 1 | 0 | 0 |
| 41 | 14.51 | −0.60 | 0 | 0 | 0 |
| 42 | 14.55 | −0.62 | 0 | 0 | 0 |
| 43 | 14.60 | −0.62 | 0 | 2 | 0 |
| 44 | 14.60 | −0.55 | 1 | 1 | 0 |
| 45 | 14.61 | −0.60 | 0 | 0 | 0 |
| 46 | 14.64 | −0.57 | 6 | 7 | 0 |
*Povich et al. (2016).
†Ambiguous stage.
| Core . | V LSR . | τtot . | ΔV . | |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| . | N(N2H+) . |
|---|---|---|---|---|---|
| . | (km−1) . | . | (km−1) . | (K) . | (cm−2) . |
| 1 | 24.40|$\, \pm \,$|0.04 | 5.7|$\, \pm \,$|3.0 | 0.85|$\, \pm \,$|0.10 | 4.39|$\, \pm \,$|0.44 | 1.29E+13 |
| 2 | 18.42|$\, \pm \,$|0.04 | 6.2|$\, \pm \,$|0.8 | 1.07|$\, \pm \,$|0.10 | 4.45 | 1.81E+13 |
| 3 | 22.86|$\, \pm \,$|0.03 | 4.7|$\, \pm \,$|0.9 | 1.74|$\, \pm \,$|0.09 | 5.72|$\, \pm \,$|0.26 | 3.23E+13 |
| 4 | 22.77|$\, \pm \,$|0.05 | 1.6|$\, \pm \,$|1.3 | 1.83|$\, \pm \,$|0.20 | 5.92|$\, \pm \,$|1.79 | 1.25E+13 |
| 5 | 22.30|$\, \pm \,$|0.11 | 5.4|$\, \pm \,$|3.3 | 2.11|$\, \pm \,$|0.37 | 3.58|$\, \pm \,$|0.20 | 2.27E+13 |
| 6 | 19.87|$\, \pm \,$|0.07 | 5.8|$\, \pm \,$|0.8 | 2.41|$\, \pm \,$|0.19 | 3.93 | 3.16E+13 |
| 7 | 22.97|$\, \pm \,$|0.04 | 13.2|$\, \pm \,$|6.6 | 0.82|$\, \pm \,$|0.13 | 3.86|$\, \pm \,$|0.15 | 2.39E+13 |
| 8 | 21.92|$\, \pm \,$|0.04 | 9.2|$\, \pm \,$|4.8 | 0.70|$\, \pm \,$|0.09 | 3.96|$\, \pm \,$|0.26 | 1.48E+13 |
| 9 | 19.64|$\, \pm \,$|0.14 | 8.1|$\, \pm \,$|3.9 | 2.66|$\, \pm \,$|0.38 | 3.31|$\, \pm \,$|0.08 | 3.90E+13 |
| 10 | 20.88|$\, \pm \,$|0.20 | 1.4|$\, \pm \,$|1.8 | 4.00|$\, \pm \,$|0.60 | 4.00|$\, \pm \,$|1.19 | 1.36E+13 |
| 11 | 18.18|$\, \pm \,$|0.04 | 4.7|$\, \pm \,$|1.1 | 1.87|$\, \pm \,$|0.12 | 4.52|$\, \pm \,$|0.19 | 2.43E+13 |
| 12 | 20.06|$\, \pm \,$|0.02 | 3.6|$\, \pm \,$|0.9 | 1.32|$\, \pm \,$|0.08 | 6.17|$\, \pm \,$|0.50 | 2.09E+13 |
| 13 | 22.08|$\, \pm \,$|0.03 | 1.7|$\, \pm \,$|0.7 | 2.15|$\, \pm \,$|0.13 | 6.32|$\, \pm \,$|1.02 | 1.72E+13 |
| 14 | 22.10|$\, \pm \,$|0.03 | 5.2|$\, \pm \,$|2.5 | 0.90|$\, \pm \,$|0.10 | 4.53|$\, \pm \,$|0.45 | 1.29E+13 |
| 15 | 19.90|$\, \pm \,$|0.02 | 1.9|$\, \pm \,$|0.2 | 3.19|$\, \pm \,$|0.05 | 10.49|$\, \pm \,$|0.58 | 6.36E+13 |
| 16 | 21.22|$\, \pm \,$|0.02 | 6.0|$\, \pm \,$|1.1 | 1.10|$\, \pm \,$|0.06 | 5.51|$\, \pm \,$|0.24 | 2.43E+13 |
| 17 | 21.30|$\, \pm \,$|0.03 | 2.2|$\, \pm \,$|1.0 | 1.38|$\, \pm \,$|0.09 | 6.39|$\, \pm \,$|1.05 | 1.44E+13 |
| 18 | 21.24|$\, \pm \,$|0.03 | 3.7|$\, \pm \,$|1.3 | 1.40|$\, \pm \,$|0.12 | 4.66|$\, \pm \,$|0.37 | 1.51E+13 |
| 19 | 20.14|$\, \pm \,$|0.03 | 8.3|$\, \pm \,$|5.5 | 0.59|$\, \pm \,$|0.09 | 3.94|$\, \pm \,$|0.37 | 1.11E+13 |
| 20 | 21.46|$\, \pm \,$|0.02 | 1.5|$\, \pm \,$|0.4 | 1.92|$\, \pm \,$|0.06 | 9.83|$\, \pm \,$|1.29 | 2.67E+13 |
| 21 | 19.02|$\, \pm \,$|0.07 | 3.6|$\, \pm \,$|1.7 | 2.17|$\, \pm \,$|0.25 | 3.93|$\, \pm \,$|0.29 | 1.78E+13 |
| 22 | 20.36|$\, \pm \,$|0.04 | 2.8|$\, \pm \,$|1.0 | 1.82|$\, \pm \,$|0.14 | 5.30|$\, \pm \,$|0.54 | 1.80E+13 |
| 23 | 19.55|$\, \pm \,$|0.01 | 2.3|$\, \pm \,$|0.2 | 2.66|$\, \pm \,$|0.05 | 11.34|$\, \pm \,$|0.56 | 7.51E+13 |
| 24 | 21.80|$\, \pm \,$|0.08 | 5.7|$\, \pm \,$|3.5 | 1.51|$\, \pm \,$|0.28 | 3.63|$\, \pm \,$|0.22 | 1.77E+13 |
| 25 | 19.87|$\, \pm \,$|0.06 | 1.6|$\, \pm \,$|1.0 | 2.62|$\, \pm \,$|0.23 | 4.97|$\, \pm \,$|0.96 | 1.37E+13 |
| 26 | 19.41|$\, \pm \,$|0.04 | 1.5|$\, \pm \,$|0.1 | 2.11|$\, \pm \,$|0.14 | 6.08 | 1.36E+13 |
| 27 | 20.85|$\, \pm \,$|0.04 | 2.3|$\, \pm \,$|1.0 | 1.66|$\, \pm \,$|0.13 | 6.06|$\, \pm \,$|0.96 | 1.64E+13 |
| 28 | 19.10|$\, \pm \,$|0.04 | 12.6|$\, \pm \,$|10.1 | 0.53|$\, \pm \,$|0.11 | 3.46|$\, \pm \,$|0.20 | 1.28E+13 |
| 29 | 19.77|$\, \pm \,$|0.03 | 5.6|$\, \pm \,$|2.0 | 0.90|$\, \pm \,$|0.08 | 4.81|$\, \pm \,$|0.36 | 1.54E+13 |
| 30 | 21.28|$\, \pm \,$|0.04 | 9.5|$\, \pm \,$|4.5 | 0.75|$\, \pm \,$|0.10 | 3.74|$\, \pm \,$|0.18 | 1.51E+13 |
| 31 | 18.33|$\, \pm \,$|0.02 | 3.4|$\, \pm \,$|2.5 | 0.62|$\, \pm \,$|0.06 | 5.53|$\, \pm \,$|1.38 | 7.94E+12 |
| 32 | 19.93|$\, \pm \,$|0.02 | 8.4|$\, \pm \,$|1.8 | 1.03|$\, \pm \,$|0.07 | 4.94|$\, \pm \,$|0.17 | 2.75E+13 |
| 33 | 22.32|$\, \pm \,$|0.01 | 1.0|$\, \pm \,$|0.1 | 3.48|$\, \pm \,$|0.03 | 31.68|$\, \pm \,$|2.50 | 2.71E+14 |
| 34 | 20.46|$\, \pm \,$|0.04 | 1.4|$\, \pm \,$|2.2 | 0.95|$\, \pm \,$|0.12 | 6.59|$\, \pm \,$|4.89 | 6.59E+12 |
| 35 | 15.30|$\, \pm \,$|0.96 | 16.2|$\, \pm \,$|49.0 | 0.96|$\, \pm \,$|0.35 | 3.00 | 9.59E+13 |
| 36 | 20.08|$\, \pm \,$|0.19 | 0.3|$\, \pm \,$|0.0 | 3.45|$\, \pm \,$|0.52 | 6.95 | 5.16E+12 |
| 37 | 17.58|$\, \pm \,$|0.04 | 3.2|$\, \pm \,$|1.3 | 1.54|$\, \pm \,$|0.14 | 5.08|$\, \pm \,$|0.54 | 1.63E+13 |
| 38 | 21.35|$\, \pm \,$|0.06 | 3.1|$\, \pm \,$|2.2 | 1.37|$\, \pm \,$|0.20 | 4.60|$\, \pm \,$|0.80 | 1.19E+13 |
| 39 | 20.35|$\, \pm \,$|0.02 | 9.6|$\, \pm \,$|2.6 | 0.76|$\, \pm \,$|0.06 | 4.80|$\, \pm \,$|0.21 | 2.21E+13 |
| 40 | 19.07|$\, \pm \,$|0.08 | 1.6|$\, \pm \,$|0.3 | 1.61|$\, \pm \,$|0.27 | 4.80 | 7.70E+12 |
| 41 | 17.51|$\, \pm \,$|0.12 | 1.2|$\, \pm \,$|0.1 | 2.70|$\, \pm \,$|0.36 | 4.56 | 8.69E+12 |
| 42 | 18.62|$\, \pm \,$|0.05 | 3.5|$\, \pm \,$|0.5 | 1.02|$\, \pm \,$|0.14 | 4.56 | 1.00E+13 |
| 43 | 19.15|$\, \pm \,$|0.07 | 2.6|$\, \pm \,$|2.2 | 1.51|$\, \pm \,$|0.24 | 4.55|$\, \pm \,$|0.95 | 1.10E+13 |
| 44 | 17.66|$\, \pm \,$|0.04 | 1.0|$\, \pm \,$|0.8 | 2.13|$\, \pm \,$|0.15 | 9.03|$\, \pm \,$|3.79 | 1.77E+13 |
| 45 | 19.32|$\, \pm \,$|0.05 | 2.8|$\, \pm \,$|0.4 | 1.28|$\, \pm \,$|0.17 | 4.56 | 1.00E+13 |
| 46 | 18.74|$\, \pm \,$|0.01 | 2.0|$\, \pm \,$|0.2 | 2.90|$\, \pm \,$|0.05 | 13.04|$\, \pm \,$|0.74 | 9.10E+13 |
| Core . | V LSR . | τtot . | ΔV . | |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| . | N(N2H+) . |
|---|---|---|---|---|---|
| . | (km−1) . | . | (km−1) . | (K) . | (cm−2) . |
| 1 | 24.40|$\, \pm \,$|0.04 | 5.7|$\, \pm \,$|3.0 | 0.85|$\, \pm \,$|0.10 | 4.39|$\, \pm \,$|0.44 | 1.29E+13 |
| 2 | 18.42|$\, \pm \,$|0.04 | 6.2|$\, \pm \,$|0.8 | 1.07|$\, \pm \,$|0.10 | 4.45 | 1.81E+13 |
| 3 | 22.86|$\, \pm \,$|0.03 | 4.7|$\, \pm \,$|0.9 | 1.74|$\, \pm \,$|0.09 | 5.72|$\, \pm \,$|0.26 | 3.23E+13 |
| 4 | 22.77|$\, \pm \,$|0.05 | 1.6|$\, \pm \,$|1.3 | 1.83|$\, \pm \,$|0.20 | 5.92|$\, \pm \,$|1.79 | 1.25E+13 |
| 5 | 22.30|$\, \pm \,$|0.11 | 5.4|$\, \pm \,$|3.3 | 2.11|$\, \pm \,$|0.37 | 3.58|$\, \pm \,$|0.20 | 2.27E+13 |
| 6 | 19.87|$\, \pm \,$|0.07 | 5.8|$\, \pm \,$|0.8 | 2.41|$\, \pm \,$|0.19 | 3.93 | 3.16E+13 |
| 7 | 22.97|$\, \pm \,$|0.04 | 13.2|$\, \pm \,$|6.6 | 0.82|$\, \pm \,$|0.13 | 3.86|$\, \pm \,$|0.15 | 2.39E+13 |
| 8 | 21.92|$\, \pm \,$|0.04 | 9.2|$\, \pm \,$|4.8 | 0.70|$\, \pm \,$|0.09 | 3.96|$\, \pm \,$|0.26 | 1.48E+13 |
| 9 | 19.64|$\, \pm \,$|0.14 | 8.1|$\, \pm \,$|3.9 | 2.66|$\, \pm \,$|0.38 | 3.31|$\, \pm \,$|0.08 | 3.90E+13 |
| 10 | 20.88|$\, \pm \,$|0.20 | 1.4|$\, \pm \,$|1.8 | 4.00|$\, \pm \,$|0.60 | 4.00|$\, \pm \,$|1.19 | 1.36E+13 |
| 11 | 18.18|$\, \pm \,$|0.04 | 4.7|$\, \pm \,$|1.1 | 1.87|$\, \pm \,$|0.12 | 4.52|$\, \pm \,$|0.19 | 2.43E+13 |
| 12 | 20.06|$\, \pm \,$|0.02 | 3.6|$\, \pm \,$|0.9 | 1.32|$\, \pm \,$|0.08 | 6.17|$\, \pm \,$|0.50 | 2.09E+13 |
| 13 | 22.08|$\, \pm \,$|0.03 | 1.7|$\, \pm \,$|0.7 | 2.15|$\, \pm \,$|0.13 | 6.32|$\, \pm \,$|1.02 | 1.72E+13 |
| 14 | 22.10|$\, \pm \,$|0.03 | 5.2|$\, \pm \,$|2.5 | 0.90|$\, \pm \,$|0.10 | 4.53|$\, \pm \,$|0.45 | 1.29E+13 |
| 15 | 19.90|$\, \pm \,$|0.02 | 1.9|$\, \pm \,$|0.2 | 3.19|$\, \pm \,$|0.05 | 10.49|$\, \pm \,$|0.58 | 6.36E+13 |
| 16 | 21.22|$\, \pm \,$|0.02 | 6.0|$\, \pm \,$|1.1 | 1.10|$\, \pm \,$|0.06 | 5.51|$\, \pm \,$|0.24 | 2.43E+13 |
| 17 | 21.30|$\, \pm \,$|0.03 | 2.2|$\, \pm \,$|1.0 | 1.38|$\, \pm \,$|0.09 | 6.39|$\, \pm \,$|1.05 | 1.44E+13 |
| 18 | 21.24|$\, \pm \,$|0.03 | 3.7|$\, \pm \,$|1.3 | 1.40|$\, \pm \,$|0.12 | 4.66|$\, \pm \,$|0.37 | 1.51E+13 |
| 19 | 20.14|$\, \pm \,$|0.03 | 8.3|$\, \pm \,$|5.5 | 0.59|$\, \pm \,$|0.09 | 3.94|$\, \pm \,$|0.37 | 1.11E+13 |
| 20 | 21.46|$\, \pm \,$|0.02 | 1.5|$\, \pm \,$|0.4 | 1.92|$\, \pm \,$|0.06 | 9.83|$\, \pm \,$|1.29 | 2.67E+13 |
| 21 | 19.02|$\, \pm \,$|0.07 | 3.6|$\, \pm \,$|1.7 | 2.17|$\, \pm \,$|0.25 | 3.93|$\, \pm \,$|0.29 | 1.78E+13 |
| 22 | 20.36|$\, \pm \,$|0.04 | 2.8|$\, \pm \,$|1.0 | 1.82|$\, \pm \,$|0.14 | 5.30|$\, \pm \,$|0.54 | 1.80E+13 |
| 23 | 19.55|$\, \pm \,$|0.01 | 2.3|$\, \pm \,$|0.2 | 2.66|$\, \pm \,$|0.05 | 11.34|$\, \pm \,$|0.56 | 7.51E+13 |
| 24 | 21.80|$\, \pm \,$|0.08 | 5.7|$\, \pm \,$|3.5 | 1.51|$\, \pm \,$|0.28 | 3.63|$\, \pm \,$|0.22 | 1.77E+13 |
| 25 | 19.87|$\, \pm \,$|0.06 | 1.6|$\, \pm \,$|1.0 | 2.62|$\, \pm \,$|0.23 | 4.97|$\, \pm \,$|0.96 | 1.37E+13 |
| 26 | 19.41|$\, \pm \,$|0.04 | 1.5|$\, \pm \,$|0.1 | 2.11|$\, \pm \,$|0.14 | 6.08 | 1.36E+13 |
| 27 | 20.85|$\, \pm \,$|0.04 | 2.3|$\, \pm \,$|1.0 | 1.66|$\, \pm \,$|0.13 | 6.06|$\, \pm \,$|0.96 | 1.64E+13 |
| 28 | 19.10|$\, \pm \,$|0.04 | 12.6|$\, \pm \,$|10.1 | 0.53|$\, \pm \,$|0.11 | 3.46|$\, \pm \,$|0.20 | 1.28E+13 |
| 29 | 19.77|$\, \pm \,$|0.03 | 5.6|$\, \pm \,$|2.0 | 0.90|$\, \pm \,$|0.08 | 4.81|$\, \pm \,$|0.36 | 1.54E+13 |
| 30 | 21.28|$\, \pm \,$|0.04 | 9.5|$\, \pm \,$|4.5 | 0.75|$\, \pm \,$|0.10 | 3.74|$\, \pm \,$|0.18 | 1.51E+13 |
| 31 | 18.33|$\, \pm \,$|0.02 | 3.4|$\, \pm \,$|2.5 | 0.62|$\, \pm \,$|0.06 | 5.53|$\, \pm \,$|1.38 | 7.94E+12 |
| 32 | 19.93|$\, \pm \,$|0.02 | 8.4|$\, \pm \,$|1.8 | 1.03|$\, \pm \,$|0.07 | 4.94|$\, \pm \,$|0.17 | 2.75E+13 |
| 33 | 22.32|$\, \pm \,$|0.01 | 1.0|$\, \pm \,$|0.1 | 3.48|$\, \pm \,$|0.03 | 31.68|$\, \pm \,$|2.50 | 2.71E+14 |
| 34 | 20.46|$\, \pm \,$|0.04 | 1.4|$\, \pm \,$|2.2 | 0.95|$\, \pm \,$|0.12 | 6.59|$\, \pm \,$|4.89 | 6.59E+12 |
| 35 | 15.30|$\, \pm \,$|0.96 | 16.2|$\, \pm \,$|49.0 | 0.96|$\, \pm \,$|0.35 | 3.00 | 9.59E+13 |
| 36 | 20.08|$\, \pm \,$|0.19 | 0.3|$\, \pm \,$|0.0 | 3.45|$\, \pm \,$|0.52 | 6.95 | 5.16E+12 |
| 37 | 17.58|$\, \pm \,$|0.04 | 3.2|$\, \pm \,$|1.3 | 1.54|$\, \pm \,$|0.14 | 5.08|$\, \pm \,$|0.54 | 1.63E+13 |
| 38 | 21.35|$\, \pm \,$|0.06 | 3.1|$\, \pm \,$|2.2 | 1.37|$\, \pm \,$|0.20 | 4.60|$\, \pm \,$|0.80 | 1.19E+13 |
| 39 | 20.35|$\, \pm \,$|0.02 | 9.6|$\, \pm \,$|2.6 | 0.76|$\, \pm \,$|0.06 | 4.80|$\, \pm \,$|0.21 | 2.21E+13 |
| 40 | 19.07|$\, \pm \,$|0.08 | 1.6|$\, \pm \,$|0.3 | 1.61|$\, \pm \,$|0.27 | 4.80 | 7.70E+12 |
| 41 | 17.51|$\, \pm \,$|0.12 | 1.2|$\, \pm \,$|0.1 | 2.70|$\, \pm \,$|0.36 | 4.56 | 8.69E+12 |
| 42 | 18.62|$\, \pm \,$|0.05 | 3.5|$\, \pm \,$|0.5 | 1.02|$\, \pm \,$|0.14 | 4.56 | 1.00E+13 |
| 43 | 19.15|$\, \pm \,$|0.07 | 2.6|$\, \pm \,$|2.2 | 1.51|$\, \pm \,$|0.24 | 4.55|$\, \pm \,$|0.95 | 1.10E+13 |
| 44 | 17.66|$\, \pm \,$|0.04 | 1.0|$\, \pm \,$|0.8 | 2.13|$\, \pm \,$|0.15 | 9.03|$\, \pm \,$|3.79 | 1.77E+13 |
| 45 | 19.32|$\, \pm \,$|0.05 | 2.8|$\, \pm \,$|0.4 | 1.28|$\, \pm \,$|0.17 | 4.56 | 1.00E+13 |
| 46 | 18.74|$\, \pm \,$|0.01 | 2.0|$\, \pm \,$|0.2 | 2.90|$\, \pm \,$|0.05 | 13.04|$\, \pm \,$|0.74 | 9.10E+13 |
*The parameters are measured toward the peak position of the cores (table 2). |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| values without an error are the values derived by interpolating the |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| values of the neighboring pixels.
| Core . | V LSR . | τtot . | ΔV . | |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| . | N(N2H+) . |
|---|---|---|---|---|---|
| . | (km−1) . | . | (km−1) . | (K) . | (cm−2) . |
| 1 | 24.40|$\, \pm \,$|0.04 | 5.7|$\, \pm \,$|3.0 | 0.85|$\, \pm \,$|0.10 | 4.39|$\, \pm \,$|0.44 | 1.29E+13 |
| 2 | 18.42|$\, \pm \,$|0.04 | 6.2|$\, \pm \,$|0.8 | 1.07|$\, \pm \,$|0.10 | 4.45 | 1.81E+13 |
| 3 | 22.86|$\, \pm \,$|0.03 | 4.7|$\, \pm \,$|0.9 | 1.74|$\, \pm \,$|0.09 | 5.72|$\, \pm \,$|0.26 | 3.23E+13 |
| 4 | 22.77|$\, \pm \,$|0.05 | 1.6|$\, \pm \,$|1.3 | 1.83|$\, \pm \,$|0.20 | 5.92|$\, \pm \,$|1.79 | 1.25E+13 |
| 5 | 22.30|$\, \pm \,$|0.11 | 5.4|$\, \pm \,$|3.3 | 2.11|$\, \pm \,$|0.37 | 3.58|$\, \pm \,$|0.20 | 2.27E+13 |
| 6 | 19.87|$\, \pm \,$|0.07 | 5.8|$\, \pm \,$|0.8 | 2.41|$\, \pm \,$|0.19 | 3.93 | 3.16E+13 |
| 7 | 22.97|$\, \pm \,$|0.04 | 13.2|$\, \pm \,$|6.6 | 0.82|$\, \pm \,$|0.13 | 3.86|$\, \pm \,$|0.15 | 2.39E+13 |
| 8 | 21.92|$\, \pm \,$|0.04 | 9.2|$\, \pm \,$|4.8 | 0.70|$\, \pm \,$|0.09 | 3.96|$\, \pm \,$|0.26 | 1.48E+13 |
| 9 | 19.64|$\, \pm \,$|0.14 | 8.1|$\, \pm \,$|3.9 | 2.66|$\, \pm \,$|0.38 | 3.31|$\, \pm \,$|0.08 | 3.90E+13 |
| 10 | 20.88|$\, \pm \,$|0.20 | 1.4|$\, \pm \,$|1.8 | 4.00|$\, \pm \,$|0.60 | 4.00|$\, \pm \,$|1.19 | 1.36E+13 |
| 11 | 18.18|$\, \pm \,$|0.04 | 4.7|$\, \pm \,$|1.1 | 1.87|$\, \pm \,$|0.12 | 4.52|$\, \pm \,$|0.19 | 2.43E+13 |
| 12 | 20.06|$\, \pm \,$|0.02 | 3.6|$\, \pm \,$|0.9 | 1.32|$\, \pm \,$|0.08 | 6.17|$\, \pm \,$|0.50 | 2.09E+13 |
| 13 | 22.08|$\, \pm \,$|0.03 | 1.7|$\, \pm \,$|0.7 | 2.15|$\, \pm \,$|0.13 | 6.32|$\, \pm \,$|1.02 | 1.72E+13 |
| 14 | 22.10|$\, \pm \,$|0.03 | 5.2|$\, \pm \,$|2.5 | 0.90|$\, \pm \,$|0.10 | 4.53|$\, \pm \,$|0.45 | 1.29E+13 |
| 15 | 19.90|$\, \pm \,$|0.02 | 1.9|$\, \pm \,$|0.2 | 3.19|$\, \pm \,$|0.05 | 10.49|$\, \pm \,$|0.58 | 6.36E+13 |
| 16 | 21.22|$\, \pm \,$|0.02 | 6.0|$\, \pm \,$|1.1 | 1.10|$\, \pm \,$|0.06 | 5.51|$\, \pm \,$|0.24 | 2.43E+13 |
| 17 | 21.30|$\, \pm \,$|0.03 | 2.2|$\, \pm \,$|1.0 | 1.38|$\, \pm \,$|0.09 | 6.39|$\, \pm \,$|1.05 | 1.44E+13 |
| 18 | 21.24|$\, \pm \,$|0.03 | 3.7|$\, \pm \,$|1.3 | 1.40|$\, \pm \,$|0.12 | 4.66|$\, \pm \,$|0.37 | 1.51E+13 |
| 19 | 20.14|$\, \pm \,$|0.03 | 8.3|$\, \pm \,$|5.5 | 0.59|$\, \pm \,$|0.09 | 3.94|$\, \pm \,$|0.37 | 1.11E+13 |
| 20 | 21.46|$\, \pm \,$|0.02 | 1.5|$\, \pm \,$|0.4 | 1.92|$\, \pm \,$|0.06 | 9.83|$\, \pm \,$|1.29 | 2.67E+13 |
| 21 | 19.02|$\, \pm \,$|0.07 | 3.6|$\, \pm \,$|1.7 | 2.17|$\, \pm \,$|0.25 | 3.93|$\, \pm \,$|0.29 | 1.78E+13 |
| 22 | 20.36|$\, \pm \,$|0.04 | 2.8|$\, \pm \,$|1.0 | 1.82|$\, \pm \,$|0.14 | 5.30|$\, \pm \,$|0.54 | 1.80E+13 |
| 23 | 19.55|$\, \pm \,$|0.01 | 2.3|$\, \pm \,$|0.2 | 2.66|$\, \pm \,$|0.05 | 11.34|$\, \pm \,$|0.56 | 7.51E+13 |
| 24 | 21.80|$\, \pm \,$|0.08 | 5.7|$\, \pm \,$|3.5 | 1.51|$\, \pm \,$|0.28 | 3.63|$\, \pm \,$|0.22 | 1.77E+13 |
| 25 | 19.87|$\, \pm \,$|0.06 | 1.6|$\, \pm \,$|1.0 | 2.62|$\, \pm \,$|0.23 | 4.97|$\, \pm \,$|0.96 | 1.37E+13 |
| 26 | 19.41|$\, \pm \,$|0.04 | 1.5|$\, \pm \,$|0.1 | 2.11|$\, \pm \,$|0.14 | 6.08 | 1.36E+13 |
| 27 | 20.85|$\, \pm \,$|0.04 | 2.3|$\, \pm \,$|1.0 | 1.66|$\, \pm \,$|0.13 | 6.06|$\, \pm \,$|0.96 | 1.64E+13 |
| 28 | 19.10|$\, \pm \,$|0.04 | 12.6|$\, \pm \,$|10.1 | 0.53|$\, \pm \,$|0.11 | 3.46|$\, \pm \,$|0.20 | 1.28E+13 |
| 29 | 19.77|$\, \pm \,$|0.03 | 5.6|$\, \pm \,$|2.0 | 0.90|$\, \pm \,$|0.08 | 4.81|$\, \pm \,$|0.36 | 1.54E+13 |
| 30 | 21.28|$\, \pm \,$|0.04 | 9.5|$\, \pm \,$|4.5 | 0.75|$\, \pm \,$|0.10 | 3.74|$\, \pm \,$|0.18 | 1.51E+13 |
| 31 | 18.33|$\, \pm \,$|0.02 | 3.4|$\, \pm \,$|2.5 | 0.62|$\, \pm \,$|0.06 | 5.53|$\, \pm \,$|1.38 | 7.94E+12 |
| 32 | 19.93|$\, \pm \,$|0.02 | 8.4|$\, \pm \,$|1.8 | 1.03|$\, \pm \,$|0.07 | 4.94|$\, \pm \,$|0.17 | 2.75E+13 |
| 33 | 22.32|$\, \pm \,$|0.01 | 1.0|$\, \pm \,$|0.1 | 3.48|$\, \pm \,$|0.03 | 31.68|$\, \pm \,$|2.50 | 2.71E+14 |
| 34 | 20.46|$\, \pm \,$|0.04 | 1.4|$\, \pm \,$|2.2 | 0.95|$\, \pm \,$|0.12 | 6.59|$\, \pm \,$|4.89 | 6.59E+12 |
| 35 | 15.30|$\, \pm \,$|0.96 | 16.2|$\, \pm \,$|49.0 | 0.96|$\, \pm \,$|0.35 | 3.00 | 9.59E+13 |
| 36 | 20.08|$\, \pm \,$|0.19 | 0.3|$\, \pm \,$|0.0 | 3.45|$\, \pm \,$|0.52 | 6.95 | 5.16E+12 |
| 37 | 17.58|$\, \pm \,$|0.04 | 3.2|$\, \pm \,$|1.3 | 1.54|$\, \pm \,$|0.14 | 5.08|$\, \pm \,$|0.54 | 1.63E+13 |
| 38 | 21.35|$\, \pm \,$|0.06 | 3.1|$\, \pm \,$|2.2 | 1.37|$\, \pm \,$|0.20 | 4.60|$\, \pm \,$|0.80 | 1.19E+13 |
| 39 | 20.35|$\, \pm \,$|0.02 | 9.6|$\, \pm \,$|2.6 | 0.76|$\, \pm \,$|0.06 | 4.80|$\, \pm \,$|0.21 | 2.21E+13 |
| 40 | 19.07|$\, \pm \,$|0.08 | 1.6|$\, \pm \,$|0.3 | 1.61|$\, \pm \,$|0.27 | 4.80 | 7.70E+12 |
| 41 | 17.51|$\, \pm \,$|0.12 | 1.2|$\, \pm \,$|0.1 | 2.70|$\, \pm \,$|0.36 | 4.56 | 8.69E+12 |
| 42 | 18.62|$\, \pm \,$|0.05 | 3.5|$\, \pm \,$|0.5 | 1.02|$\, \pm \,$|0.14 | 4.56 | 1.00E+13 |
| 43 | 19.15|$\, \pm \,$|0.07 | 2.6|$\, \pm \,$|2.2 | 1.51|$\, \pm \,$|0.24 | 4.55|$\, \pm \,$|0.95 | 1.10E+13 |
| 44 | 17.66|$\, \pm \,$|0.04 | 1.0|$\, \pm \,$|0.8 | 2.13|$\, \pm \,$|0.15 | 9.03|$\, \pm \,$|3.79 | 1.77E+13 |
| 45 | 19.32|$\, \pm \,$|0.05 | 2.8|$\, \pm \,$|0.4 | 1.28|$\, \pm \,$|0.17 | 4.56 | 1.00E+13 |
| 46 | 18.74|$\, \pm \,$|0.01 | 2.0|$\, \pm \,$|0.2 | 2.90|$\, \pm \,$|0.05 | 13.04|$\, \pm \,$|0.74 | 9.10E+13 |
| Core . | V LSR . | τtot . | ΔV . | |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| . | N(N2H+) . |
|---|---|---|---|---|---|
| . | (km−1) . | . | (km−1) . | (K) . | (cm−2) . |
| 1 | 24.40|$\, \pm \,$|0.04 | 5.7|$\, \pm \,$|3.0 | 0.85|$\, \pm \,$|0.10 | 4.39|$\, \pm \,$|0.44 | 1.29E+13 |
| 2 | 18.42|$\, \pm \,$|0.04 | 6.2|$\, \pm \,$|0.8 | 1.07|$\, \pm \,$|0.10 | 4.45 | 1.81E+13 |
| 3 | 22.86|$\, \pm \,$|0.03 | 4.7|$\, \pm \,$|0.9 | 1.74|$\, \pm \,$|0.09 | 5.72|$\, \pm \,$|0.26 | 3.23E+13 |
| 4 | 22.77|$\, \pm \,$|0.05 | 1.6|$\, \pm \,$|1.3 | 1.83|$\, \pm \,$|0.20 | 5.92|$\, \pm \,$|1.79 | 1.25E+13 |
| 5 | 22.30|$\, \pm \,$|0.11 | 5.4|$\, \pm \,$|3.3 | 2.11|$\, \pm \,$|0.37 | 3.58|$\, \pm \,$|0.20 | 2.27E+13 |
| 6 | 19.87|$\, \pm \,$|0.07 | 5.8|$\, \pm \,$|0.8 | 2.41|$\, \pm \,$|0.19 | 3.93 | 3.16E+13 |
| 7 | 22.97|$\, \pm \,$|0.04 | 13.2|$\, \pm \,$|6.6 | 0.82|$\, \pm \,$|0.13 | 3.86|$\, \pm \,$|0.15 | 2.39E+13 |
| 8 | 21.92|$\, \pm \,$|0.04 | 9.2|$\, \pm \,$|4.8 | 0.70|$\, \pm \,$|0.09 | 3.96|$\, \pm \,$|0.26 | 1.48E+13 |
| 9 | 19.64|$\, \pm \,$|0.14 | 8.1|$\, \pm \,$|3.9 | 2.66|$\, \pm \,$|0.38 | 3.31|$\, \pm \,$|0.08 | 3.90E+13 |
| 10 | 20.88|$\, \pm \,$|0.20 | 1.4|$\, \pm \,$|1.8 | 4.00|$\, \pm \,$|0.60 | 4.00|$\, \pm \,$|1.19 | 1.36E+13 |
| 11 | 18.18|$\, \pm \,$|0.04 | 4.7|$\, \pm \,$|1.1 | 1.87|$\, \pm \,$|0.12 | 4.52|$\, \pm \,$|0.19 | 2.43E+13 |
| 12 | 20.06|$\, \pm \,$|0.02 | 3.6|$\, \pm \,$|0.9 | 1.32|$\, \pm \,$|0.08 | 6.17|$\, \pm \,$|0.50 | 2.09E+13 |
| 13 | 22.08|$\, \pm \,$|0.03 | 1.7|$\, \pm \,$|0.7 | 2.15|$\, \pm \,$|0.13 | 6.32|$\, \pm \,$|1.02 | 1.72E+13 |
| 14 | 22.10|$\, \pm \,$|0.03 | 5.2|$\, \pm \,$|2.5 | 0.90|$\, \pm \,$|0.10 | 4.53|$\, \pm \,$|0.45 | 1.29E+13 |
| 15 | 19.90|$\, \pm \,$|0.02 | 1.9|$\, \pm \,$|0.2 | 3.19|$\, \pm \,$|0.05 | 10.49|$\, \pm \,$|0.58 | 6.36E+13 |
| 16 | 21.22|$\, \pm \,$|0.02 | 6.0|$\, \pm \,$|1.1 | 1.10|$\, \pm \,$|0.06 | 5.51|$\, \pm \,$|0.24 | 2.43E+13 |
| 17 | 21.30|$\, \pm \,$|0.03 | 2.2|$\, \pm \,$|1.0 | 1.38|$\, \pm \,$|0.09 | 6.39|$\, \pm \,$|1.05 | 1.44E+13 |
| 18 | 21.24|$\, \pm \,$|0.03 | 3.7|$\, \pm \,$|1.3 | 1.40|$\, \pm \,$|0.12 | 4.66|$\, \pm \,$|0.37 | 1.51E+13 |
| 19 | 20.14|$\, \pm \,$|0.03 | 8.3|$\, \pm \,$|5.5 | 0.59|$\, \pm \,$|0.09 | 3.94|$\, \pm \,$|0.37 | 1.11E+13 |
| 20 | 21.46|$\, \pm \,$|0.02 | 1.5|$\, \pm \,$|0.4 | 1.92|$\, \pm \,$|0.06 | 9.83|$\, \pm \,$|1.29 | 2.67E+13 |
| 21 | 19.02|$\, \pm \,$|0.07 | 3.6|$\, \pm \,$|1.7 | 2.17|$\, \pm \,$|0.25 | 3.93|$\, \pm \,$|0.29 | 1.78E+13 |
| 22 | 20.36|$\, \pm \,$|0.04 | 2.8|$\, \pm \,$|1.0 | 1.82|$\, \pm \,$|0.14 | 5.30|$\, \pm \,$|0.54 | 1.80E+13 |
| 23 | 19.55|$\, \pm \,$|0.01 | 2.3|$\, \pm \,$|0.2 | 2.66|$\, \pm \,$|0.05 | 11.34|$\, \pm \,$|0.56 | 7.51E+13 |
| 24 | 21.80|$\, \pm \,$|0.08 | 5.7|$\, \pm \,$|3.5 | 1.51|$\, \pm \,$|0.28 | 3.63|$\, \pm \,$|0.22 | 1.77E+13 |
| 25 | 19.87|$\, \pm \,$|0.06 | 1.6|$\, \pm \,$|1.0 | 2.62|$\, \pm \,$|0.23 | 4.97|$\, \pm \,$|0.96 | 1.37E+13 |
| 26 | 19.41|$\, \pm \,$|0.04 | 1.5|$\, \pm \,$|0.1 | 2.11|$\, \pm \,$|0.14 | 6.08 | 1.36E+13 |
| 27 | 20.85|$\, \pm \,$|0.04 | 2.3|$\, \pm \,$|1.0 | 1.66|$\, \pm \,$|0.13 | 6.06|$\, \pm \,$|0.96 | 1.64E+13 |
| 28 | 19.10|$\, \pm \,$|0.04 | 12.6|$\, \pm \,$|10.1 | 0.53|$\, \pm \,$|0.11 | 3.46|$\, \pm \,$|0.20 | 1.28E+13 |
| 29 | 19.77|$\, \pm \,$|0.03 | 5.6|$\, \pm \,$|2.0 | 0.90|$\, \pm \,$|0.08 | 4.81|$\, \pm \,$|0.36 | 1.54E+13 |
| 30 | 21.28|$\, \pm \,$|0.04 | 9.5|$\, \pm \,$|4.5 | 0.75|$\, \pm \,$|0.10 | 3.74|$\, \pm \,$|0.18 | 1.51E+13 |
| 31 | 18.33|$\, \pm \,$|0.02 | 3.4|$\, \pm \,$|2.5 | 0.62|$\, \pm \,$|0.06 | 5.53|$\, \pm \,$|1.38 | 7.94E+12 |
| 32 | 19.93|$\, \pm \,$|0.02 | 8.4|$\, \pm \,$|1.8 | 1.03|$\, \pm \,$|0.07 | 4.94|$\, \pm \,$|0.17 | 2.75E+13 |
| 33 | 22.32|$\, \pm \,$|0.01 | 1.0|$\, \pm \,$|0.1 | 3.48|$\, \pm \,$|0.03 | 31.68|$\, \pm \,$|2.50 | 2.71E+14 |
| 34 | 20.46|$\, \pm \,$|0.04 | 1.4|$\, \pm \,$|2.2 | 0.95|$\, \pm \,$|0.12 | 6.59|$\, \pm \,$|4.89 | 6.59E+12 |
| 35 | 15.30|$\, \pm \,$|0.96 | 16.2|$\, \pm \,$|49.0 | 0.96|$\, \pm \,$|0.35 | 3.00 | 9.59E+13 |
| 36 | 20.08|$\, \pm \,$|0.19 | 0.3|$\, \pm \,$|0.0 | 3.45|$\, \pm \,$|0.52 | 6.95 | 5.16E+12 |
| 37 | 17.58|$\, \pm \,$|0.04 | 3.2|$\, \pm \,$|1.3 | 1.54|$\, \pm \,$|0.14 | 5.08|$\, \pm \,$|0.54 | 1.63E+13 |
| 38 | 21.35|$\, \pm \,$|0.06 | 3.1|$\, \pm \,$|2.2 | 1.37|$\, \pm \,$|0.20 | 4.60|$\, \pm \,$|0.80 | 1.19E+13 |
| 39 | 20.35|$\, \pm \,$|0.02 | 9.6|$\, \pm \,$|2.6 | 0.76|$\, \pm \,$|0.06 | 4.80|$\, \pm \,$|0.21 | 2.21E+13 |
| 40 | 19.07|$\, \pm \,$|0.08 | 1.6|$\, \pm \,$|0.3 | 1.61|$\, \pm \,$|0.27 | 4.80 | 7.70E+12 |
| 41 | 17.51|$\, \pm \,$|0.12 | 1.2|$\, \pm \,$|0.1 | 2.70|$\, \pm \,$|0.36 | 4.56 | 8.69E+12 |
| 42 | 18.62|$\, \pm \,$|0.05 | 3.5|$\, \pm \,$|0.5 | 1.02|$\, \pm \,$|0.14 | 4.56 | 1.00E+13 |
| 43 | 19.15|$\, \pm \,$|0.07 | 2.6|$\, \pm \,$|2.2 | 1.51|$\, \pm \,$|0.24 | 4.55|$\, \pm \,$|0.95 | 1.10E+13 |
| 44 | 17.66|$\, \pm \,$|0.04 | 1.0|$\, \pm \,$|0.8 | 2.13|$\, \pm \,$|0.15 | 9.03|$\, \pm \,$|3.79 | 1.77E+13 |
| 45 | 19.32|$\, \pm \,$|0.05 | 2.8|$\, \pm \,$|0.4 | 1.28|$\, \pm \,$|0.17 | 4.56 | 1.00E+13 |
| 46 | 18.74|$\, \pm \,$|0.01 | 2.0|$\, \pm \,$|0.2 | 2.90|$\, \pm \,$|0.05 | 13.04|$\, \pm \,$|0.74 | 9.10E+13 |
*The parameters are measured toward the peak position of the cores (table 2). |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| values without an error are the values derived by interpolating the |$T^{\rm {N{_2}H^{+}}}_{\rm ex}$| values of the neighboring pixels.
| Core . | S . | R core . | M core . | M vir . | ΣM⋆ . |
|---|---|---|---|---|---|
| . | (arcmin2) . | (pc) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . |
| 1 | 1.44 | 0.40 | 272|$\, \pm \,$|2 | 59 | 103 |
| 2 | 0.72 | 0.28 | 83|$\, \pm \,$|2 | 67 | 39 |
| 3 | 3.94 | 0.65 | 717|$\, \pm \,$|4 | 412 | 154 |
| 4 | 2.02 | 0.47 | 275|$\, \pm \,$|3 | 328 | 26 |
| 5 | 0.77 | 0.29 | 90|$\, \pm \,$|2 | 268 | 26 |
| 6 | 1.69 | 0.43 | 269|$\, \pm \,$|2 | 522 | 64 |
| 7 | 0.50 | 0.23 | 85|$\, \pm \,$|1 | 33 | 51 |
| 8 | 1.39 | 0.39 | 155|$\, \pm \,$|2 | 40 | 64 |
| 9 | 0.44 | 0.22 | 62|$\, \pm \,$|1 | 323 | 13 |
| 10 | 1.06 | 0.34 | 110|$\, \pm \,$|2 | 1139 | 51 |
| 11 | 1.11 | 0.35 | 156|$\, \pm \,$|2 | 255 | 64 |
| 12 | 1.22 | 0.36 | 267|$\, \pm \,$|2 | 132 | 103 |
| 13 | 0.70 | 0.28 | 209|$\, \pm \,$|2 | 267 | 13 |
| 14 | 0.50 | 0.23 | 57|$\, \pm \,$|1 | 39 | 0 |
| 15 | 2.27 | 0.50 | 1007|$\, \pm \,$|3 | 1054 | 206 |
| 16 | 2.05 | 0.47 | 416|$\, \pm \,$|3 | 119 | 129 |
| 17 | 1.17 | 0.36 | 266|$\, \pm \,$|2 | 141 | 51 |
| 18 | 0.48 | 0.23 | 125|$\, \pm \,$|1 | 95 | 13 |
| 19 | 0.42 | 0.21 | 54|$\, \pm \,$|1 | 16 | 51 |
| 20 | 1.30 | 0.38 | 387|$\, \pm \,$|2 | 289 | 129 |
| 21 | 1.11 | 0.35 | 158|$\, \pm \,$|2 | 343 | 39 |
| 22 | 0.77 | 0.29 | 274|$\, \pm \,$|2 | 201 | 77 |
| 23 | 2.52 | 0.52 | 1152|$\, \pm \,$|3 | 774 | 257 |
| 24 | 0.98 | 0.33 | 108|$\, \pm \,$|2 | 157 | 26 |
| 25 | 3.36 | 0.60 | 541|$\, \pm \,$|3 | 869 | 232 |
| 26 | 0.70 | 0.28 | 106|$\, \pm \,$|2 | 258 | 13 |
| 27 | 0.45 | 0.22 | 79|$\, \pm \,$|1 | 128 | 51 |
| 28 | 0.39 | 0.21 | 74|$\, \pm \,$|1 | 12 | 13 |
| 29 | 2.70 | 0.54 | 405|$\, \pm \,$|3 | 92 | 77 |
| 30 | 0.64 | 0.26 | 71|$\, \pm \,$|1 | 31 | 39 |
| 31 | 0.48 | 0.23 | 74|$\, \pm \,$|1 | 19 | 13 |
| 32 | 1.06 | 0.34 | 179|$\, \pm \,$|2 | 76 | 0 |
| 33 | 9.80 | 1.03 | 3026|$\, \pm \,$|6 | 2617 | 373 |
| 34 | 0.70 | 0.28 | 122|$\, \pm \,$|2 | 53 | 13 |
| 35 | 0.39 | 0.21 | 29|$\, \pm \,$|1 | 1075 | 0 |
| 36 | 0.78 | 0.29 | 140|$\, \pm \,$|2 | 727 | 26 |
| 37 | 1.48 | 0.40 | 300|$\, \pm \,$|2 | 199 | 39 |
| 38 | 0.66 | 0.27 | 120|$\, \pm \,$|1 | 105 | 26 |
| 39 | 0.56 | 0.25 | 107|$\, \pm \,$|1 | 30 | 26 |
| 40 | 0.48 | 0.23 | 76|$\, \pm \,$|1 | 124 | 13 |
| 41 | 0.39 | 0.21 | 47|$\, \pm \,$|1 | 314 | 0 |
| 42 | 1.52 | 0.41 | 239|$\, \pm \,$|2 | 89 | 0 |
| 43 | 0.39 | 0.21 | 43|$\, \pm \,$|1 | 98 | 26 |
| 44 | 0.89 | 0.31 | 218|$\, \pm \,$|2 | 294 | 26 |
| 45 | 0.41 | 0.21 | 57|$\, \pm \,$|1 | 72 | 0 |
| 46 | 4.38 | 0.69 | 1488|$\, \pm \,$|4 | 1216 | 167 |
| Core . | S . | R core . | M core . | M vir . | ΣM⋆ . |
|---|---|---|---|---|---|
| . | (arcmin2) . | (pc) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . |
| 1 | 1.44 | 0.40 | 272|$\, \pm \,$|2 | 59 | 103 |
| 2 | 0.72 | 0.28 | 83|$\, \pm \,$|2 | 67 | 39 |
| 3 | 3.94 | 0.65 | 717|$\, \pm \,$|4 | 412 | 154 |
| 4 | 2.02 | 0.47 | 275|$\, \pm \,$|3 | 328 | 26 |
| 5 | 0.77 | 0.29 | 90|$\, \pm \,$|2 | 268 | 26 |
| 6 | 1.69 | 0.43 | 269|$\, \pm \,$|2 | 522 | 64 |
| 7 | 0.50 | 0.23 | 85|$\, \pm \,$|1 | 33 | 51 |
| 8 | 1.39 | 0.39 | 155|$\, \pm \,$|2 | 40 | 64 |
| 9 | 0.44 | 0.22 | 62|$\, \pm \,$|1 | 323 | 13 |
| 10 | 1.06 | 0.34 | 110|$\, \pm \,$|2 | 1139 | 51 |
| 11 | 1.11 | 0.35 | 156|$\, \pm \,$|2 | 255 | 64 |
| 12 | 1.22 | 0.36 | 267|$\, \pm \,$|2 | 132 | 103 |
| 13 | 0.70 | 0.28 | 209|$\, \pm \,$|2 | 267 | 13 |
| 14 | 0.50 | 0.23 | 57|$\, \pm \,$|1 | 39 | 0 |
| 15 | 2.27 | 0.50 | 1007|$\, \pm \,$|3 | 1054 | 206 |
| 16 | 2.05 | 0.47 | 416|$\, \pm \,$|3 | 119 | 129 |
| 17 | 1.17 | 0.36 | 266|$\, \pm \,$|2 | 141 | 51 |
| 18 | 0.48 | 0.23 | 125|$\, \pm \,$|1 | 95 | 13 |
| 19 | 0.42 | 0.21 | 54|$\, \pm \,$|1 | 16 | 51 |
| 20 | 1.30 | 0.38 | 387|$\, \pm \,$|2 | 289 | 129 |
| 21 | 1.11 | 0.35 | 158|$\, \pm \,$|2 | 343 | 39 |
| 22 | 0.77 | 0.29 | 274|$\, \pm \,$|2 | 201 | 77 |
| 23 | 2.52 | 0.52 | 1152|$\, \pm \,$|3 | 774 | 257 |
| 24 | 0.98 | 0.33 | 108|$\, \pm \,$|2 | 157 | 26 |
| 25 | 3.36 | 0.60 | 541|$\, \pm \,$|3 | 869 | 232 |
| 26 | 0.70 | 0.28 | 106|$\, \pm \,$|2 | 258 | 13 |
| 27 | 0.45 | 0.22 | 79|$\, \pm \,$|1 | 128 | 51 |
| 28 | 0.39 | 0.21 | 74|$\, \pm \,$|1 | 12 | 13 |
| 29 | 2.70 | 0.54 | 405|$\, \pm \,$|3 | 92 | 77 |
| 30 | 0.64 | 0.26 | 71|$\, \pm \,$|1 | 31 | 39 |
| 31 | 0.48 | 0.23 | 74|$\, \pm \,$|1 | 19 | 13 |
| 32 | 1.06 | 0.34 | 179|$\, \pm \,$|2 | 76 | 0 |
| 33 | 9.80 | 1.03 | 3026|$\, \pm \,$|6 | 2617 | 373 |
| 34 | 0.70 | 0.28 | 122|$\, \pm \,$|2 | 53 | 13 |
| 35 | 0.39 | 0.21 | 29|$\, \pm \,$|1 | 1075 | 0 |
| 36 | 0.78 | 0.29 | 140|$\, \pm \,$|2 | 727 | 26 |
| 37 | 1.48 | 0.40 | 300|$\, \pm \,$|2 | 199 | 39 |
| 38 | 0.66 | 0.27 | 120|$\, \pm \,$|1 | 105 | 26 |
| 39 | 0.56 | 0.25 | 107|$\, \pm \,$|1 | 30 | 26 |
| 40 | 0.48 | 0.23 | 76|$\, \pm \,$|1 | 124 | 13 |
| 41 | 0.39 | 0.21 | 47|$\, \pm \,$|1 | 314 | 0 |
| 42 | 1.52 | 0.41 | 239|$\, \pm \,$|2 | 89 | 0 |
| 43 | 0.39 | 0.21 | 43|$\, \pm \,$|1 | 98 | 26 |
| 44 | 0.89 | 0.31 | 218|$\, \pm \,$|2 | 294 | 26 |
| 45 | 0.41 | 0.21 | 57|$\, \pm \,$|1 | 72 | 0 |
| 46 | 4.38 | 0.69 | 1488|$\, \pm \,$|4 | 1216 | 167 |
*The parameters S, Rcore, Mcore, and Mvir are derived on the assumption of a uniform distance of 2.0 kpc.
| Core . | S . | R core . | M core . | M vir . | ΣM⋆ . |
|---|---|---|---|---|---|
| . | (arcmin2) . | (pc) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . |
| 1 | 1.44 | 0.40 | 272|$\, \pm \,$|2 | 59 | 103 |
| 2 | 0.72 | 0.28 | 83|$\, \pm \,$|2 | 67 | 39 |
| 3 | 3.94 | 0.65 | 717|$\, \pm \,$|4 | 412 | 154 |
| 4 | 2.02 | 0.47 | 275|$\, \pm \,$|3 | 328 | 26 |
| 5 | 0.77 | 0.29 | 90|$\, \pm \,$|2 | 268 | 26 |
| 6 | 1.69 | 0.43 | 269|$\, \pm \,$|2 | 522 | 64 |
| 7 | 0.50 | 0.23 | 85|$\, \pm \,$|1 | 33 | 51 |
| 8 | 1.39 | 0.39 | 155|$\, \pm \,$|2 | 40 | 64 |
| 9 | 0.44 | 0.22 | 62|$\, \pm \,$|1 | 323 | 13 |
| 10 | 1.06 | 0.34 | 110|$\, \pm \,$|2 | 1139 | 51 |
| 11 | 1.11 | 0.35 | 156|$\, \pm \,$|2 | 255 | 64 |
| 12 | 1.22 | 0.36 | 267|$\, \pm \,$|2 | 132 | 103 |
| 13 | 0.70 | 0.28 | 209|$\, \pm \,$|2 | 267 | 13 |
| 14 | 0.50 | 0.23 | 57|$\, \pm \,$|1 | 39 | 0 |
| 15 | 2.27 | 0.50 | 1007|$\, \pm \,$|3 | 1054 | 206 |
| 16 | 2.05 | 0.47 | 416|$\, \pm \,$|3 | 119 | 129 |
| 17 | 1.17 | 0.36 | 266|$\, \pm \,$|2 | 141 | 51 |
| 18 | 0.48 | 0.23 | 125|$\, \pm \,$|1 | 95 | 13 |
| 19 | 0.42 | 0.21 | 54|$\, \pm \,$|1 | 16 | 51 |
| 20 | 1.30 | 0.38 | 387|$\, \pm \,$|2 | 289 | 129 |
| 21 | 1.11 | 0.35 | 158|$\, \pm \,$|2 | 343 | 39 |
| 22 | 0.77 | 0.29 | 274|$\, \pm \,$|2 | 201 | 77 |
| 23 | 2.52 | 0.52 | 1152|$\, \pm \,$|3 | 774 | 257 |
| 24 | 0.98 | 0.33 | 108|$\, \pm \,$|2 | 157 | 26 |
| 25 | 3.36 | 0.60 | 541|$\, \pm \,$|3 | 869 | 232 |
| 26 | 0.70 | 0.28 | 106|$\, \pm \,$|2 | 258 | 13 |
| 27 | 0.45 | 0.22 | 79|$\, \pm \,$|1 | 128 | 51 |
| 28 | 0.39 | 0.21 | 74|$\, \pm \,$|1 | 12 | 13 |
| 29 | 2.70 | 0.54 | 405|$\, \pm \,$|3 | 92 | 77 |
| 30 | 0.64 | 0.26 | 71|$\, \pm \,$|1 | 31 | 39 |
| 31 | 0.48 | 0.23 | 74|$\, \pm \,$|1 | 19 | 13 |
| 32 | 1.06 | 0.34 | 179|$\, \pm \,$|2 | 76 | 0 |
| 33 | 9.80 | 1.03 | 3026|$\, \pm \,$|6 | 2617 | 373 |
| 34 | 0.70 | 0.28 | 122|$\, \pm \,$|2 | 53 | 13 |
| 35 | 0.39 | 0.21 | 29|$\, \pm \,$|1 | 1075 | 0 |
| 36 | 0.78 | 0.29 | 140|$\, \pm \,$|2 | 727 | 26 |
| 37 | 1.48 | 0.40 | 300|$\, \pm \,$|2 | 199 | 39 |
| 38 | 0.66 | 0.27 | 120|$\, \pm \,$|1 | 105 | 26 |
| 39 | 0.56 | 0.25 | 107|$\, \pm \,$|1 | 30 | 26 |
| 40 | 0.48 | 0.23 | 76|$\, \pm \,$|1 | 124 | 13 |
| 41 | 0.39 | 0.21 | 47|$\, \pm \,$|1 | 314 | 0 |
| 42 | 1.52 | 0.41 | 239|$\, \pm \,$|2 | 89 | 0 |
| 43 | 0.39 | 0.21 | 43|$\, \pm \,$|1 | 98 | 26 |
| 44 | 0.89 | 0.31 | 218|$\, \pm \,$|2 | 294 | 26 |
| 45 | 0.41 | 0.21 | 57|$\, \pm \,$|1 | 72 | 0 |
| 46 | 4.38 | 0.69 | 1488|$\, \pm \,$|4 | 1216 | 167 |
| Core . | S . | R core . | M core . | M vir . | ΣM⋆ . |
|---|---|---|---|---|---|
| . | (arcmin2) . | (pc) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . | (|${M}_{\odot }$|) . |
| 1 | 1.44 | 0.40 | 272|$\, \pm \,$|2 | 59 | 103 |
| 2 | 0.72 | 0.28 | 83|$\, \pm \,$|2 | 67 | 39 |
| 3 | 3.94 | 0.65 | 717|$\, \pm \,$|4 | 412 | 154 |
| 4 | 2.02 | 0.47 | 275|$\, \pm \,$|3 | 328 | 26 |
| 5 | 0.77 | 0.29 | 90|$\, \pm \,$|2 | 268 | 26 |
| 6 | 1.69 | 0.43 | 269|$\, \pm \,$|2 | 522 | 64 |
| 7 | 0.50 | 0.23 | 85|$\, \pm \,$|1 | 33 | 51 |
| 8 | 1.39 | 0.39 | 155|$\, \pm \,$|2 | 40 | 64 |
| 9 | 0.44 | 0.22 | 62|$\, \pm \,$|1 | 323 | 13 |
| 10 | 1.06 | 0.34 | 110|$\, \pm \,$|2 | 1139 | 51 |
| 11 | 1.11 | 0.35 | 156|$\, \pm \,$|2 | 255 | 64 |
| 12 | 1.22 | 0.36 | 267|$\, \pm \,$|2 | 132 | 103 |
| 13 | 0.70 | 0.28 | 209|$\, \pm \,$|2 | 267 | 13 |
| 14 | 0.50 | 0.23 | 57|$\, \pm \,$|1 | 39 | 0 |
| 15 | 2.27 | 0.50 | 1007|$\, \pm \,$|3 | 1054 | 206 |
| 16 | 2.05 | 0.47 | 416|$\, \pm \,$|3 | 119 | 129 |
| 17 | 1.17 | 0.36 | 266|$\, \pm \,$|2 | 141 | 51 |
| 18 | 0.48 | 0.23 | 125|$\, \pm \,$|1 | 95 | 13 |
| 19 | 0.42 | 0.21 | 54|$\, \pm \,$|1 | 16 | 51 |
| 20 | 1.30 | 0.38 | 387|$\, \pm \,$|2 | 289 | 129 |
| 21 | 1.11 | 0.35 | 158|$\, \pm \,$|2 | 343 | 39 |
| 22 | 0.77 | 0.29 | 274|$\, \pm \,$|2 | 201 | 77 |
| 23 | 2.52 | 0.52 | 1152|$\, \pm \,$|3 | 774 | 257 |
| 24 | 0.98 | 0.33 | 108|$\, \pm \,$|2 | 157 | 26 |
| 25 | 3.36 | 0.60 | 541|$\, \pm \,$|3 | 869 | 232 |
| 26 | 0.70 | 0.28 | 106|$\, \pm \,$|2 | 258 | 13 |
| 27 | 0.45 | 0.22 | 79|$\, \pm \,$|1 | 128 | 51 |
| 28 | 0.39 | 0.21 | 74|$\, \pm \,$|1 | 12 | 13 |
| 29 | 2.70 | 0.54 | 405|$\, \pm \,$|3 | 92 | 77 |
| 30 | 0.64 | 0.26 | 71|$\, \pm \,$|1 | 31 | 39 |
| 31 | 0.48 | 0.23 | 74|$\, \pm \,$|1 | 19 | 13 |
| 32 | 1.06 | 0.34 | 179|$\, \pm \,$|2 | 76 | 0 |
| 33 | 9.80 | 1.03 | 3026|$\, \pm \,$|6 | 2617 | 373 |
| 34 | 0.70 | 0.28 | 122|$\, \pm \,$|2 | 53 | 13 |
| 35 | 0.39 | 0.21 | 29|$\, \pm \,$|1 | 1075 | 0 |
| 36 | 0.78 | 0.29 | 140|$\, \pm \,$|2 | 727 | 26 |
| 37 | 1.48 | 0.40 | 300|$\, \pm \,$|2 | 199 | 39 |
| 38 | 0.66 | 0.27 | 120|$\, \pm \,$|1 | 105 | 26 |
| 39 | 0.56 | 0.25 | 107|$\, \pm \,$|1 | 30 | 26 |
| 40 | 0.48 | 0.23 | 76|$\, \pm \,$|1 | 124 | 13 |
| 41 | 0.39 | 0.21 | 47|$\, \pm \,$|1 | 314 | 0 |
| 42 | 1.52 | 0.41 | 239|$\, \pm \,$|2 | 89 | 0 |
| 43 | 0.39 | 0.21 | 43|$\, \pm \,$|1 | 98 | 26 |
| 44 | 0.89 | 0.31 | 218|$\, \pm \,$|2 | 294 | 26 |
| 45 | 0.41 | 0.21 | 57|$\, \pm \,$|1 | 72 | 0 |
| 46 | 4.38 | 0.69 | 1488|$\, \pm \,$|4 | 1216 | 167 |
*The parameters S, Rcore, Mcore, and Mvir are derived on the assumption of a uniform distance of 2.0 kpc.
| Core . | s . | i (cm−2) . | γ . |
|---|---|---|---|
| 1 | 1.7E|$-10\, \pm \,$|0.8E−10 | 7.66E|$+12\, \pm \,$|2.20E+12 | 0.23 |
| 2 | 6.0E|$-10\, \pm \,$|2.0E−10 | 4.43E|$+12\, \pm \,$|3.06E+12 | 0.42 |
| 3 | 4.1E|$-10\, \pm \,$|0.3E−10 | 6.85E|$+12\, \pm \,$|0.83E+12 | 0.65 |
| 4 | 3.6E|$-10\, \pm \,$|0.4E−10 | 4.30E|$+12\, \pm \,$|0.82E+12 | 0.63 |
| 5 | 1.7E|$-09\, \pm \,$|0.9E−09 | −9.49E|$+12\, \pm \,$|1.39E+13 | 0.30 |
| 6 | 1.0E|$-10\, \pm \,$|0.6E−10 | 9.80E|$+12\, \pm \,$|1.28E+12 | 0.20 |
| 7 | 3.0E|$-10\, \pm \,$|1.7E−10 | 6.49E|$+12\, \pm \,$|3.80E+12 | 0.32 |
| 8 | 1.8E|$-10\, \pm \,$|2.4E−10 | 1.08E|$+13\, \pm \,$|0.35E+13 | 0.10 |
| 9 | 1.8E|$-09\, \pm \,$|0.7E−09 | −1.42E|$+13\, \pm \,$|1.39E+13 | 0.52 |
| 10 | 9.9E|$-10\, \pm \,$|2.8E−10 | 5.65E|$+12\, \pm \,$|4.00E+12 | 0.43 |
| 11 | 1.9E|$-10\, \pm \,$|0.9E−10 | 1.15E|$+13\, \pm \,$|0.18E+13 | 0.27 |
| 12 | 3.2E|$-10\, \pm \,$|0.9E−10 | 4.91E|$+12\, \pm \,$|2.82E+12 | 0.40 |
| 13 | −3.1E|$-10\, \pm \,$|7.9E−11 | 2.95E|$+13\, \pm \,$|0.31E+13 | −0.52 |
| 14 | 9.1E|$-10\, \pm \,$|2.0E−10 | −2.75E|$+12\, \pm \,$|3.08E+12 | 0.63 |
| 15 | 3.6E|$-10\, \pm \,$|0.1E−10 | 7.78E|$+12\, \pm \,$|0.87E+12 | 0.92 |
| 16 | 4.2E|$-10\, \pm \,$|0.5E−10 | 5.74E|$+12\, \pm \,$|1.26E+12 | 0.63 |
| 17 | 4.8E|$-10\, \pm \,$|0.5E−10 | 4.75E|$+12\, \pm \,$|1.38E+12 | 0.63 |
| 18 | 2.7E|$-10\, \pm \,$|5.2E−10 | 0.89E|$+13\, \pm \,$|1.75E+13 | 0.10 |
| 19 | 0.8E|$-10\, \pm \,$|2.3E−10 | 9.48E|$+12\, \pm \,$|4.12E+12 | 0.08 |
| 20 | 2.9E|$-10\, \pm \,$|0.3E−10 | 4.87E|$+12\, \pm \,$|1.10E+12 | 0.79 |
| 21 | 2.2E|$-10\, \pm \,$|1.0E−10 | 5.56E|$+12\, \pm \,$|1.94E+12 | 0.27 |
| 22 | 3.9E|$-10\, \pm \,$|0.3E−10 | −1.75E|$+12\, \pm \,$|1.27E+12 | 0.91 |
| 23 | 3.4E|$-10\, \pm \,$|0.1E−10 | 5.06E|$+12\, \pm \,$|0.89E+12 | 0.91 |
| 24 | −1.1E|$-09\, \pm \,$|2.7E−10 | 2.72E|$+13\, \pm \,$|0.34E+13 | −0.46 |
| 25 | 5.6E|$-11\, \pm \,$|3.9E−11 | 9.45E|$+12\, \pm \,$|0.70E+12 | 0.11 |
| 26 | 4.1E|$-10\, \pm \,$|2.9E−10 | 1.00E|$+13\, \pm \,$|0.58E+13 | 0.21 |
| 27 | 1.3E|$-10\, \pm \,$|1.2E−10 | 1.25E|$+13\, \pm \,$|0.28E+13 | 0.19 |
| 28 | −2.0E|$-09\, \pm \,$|3.6E−09 | 7.16E|$+13\, \pm \,$|9.02E+13 | −0.12 |
| 29 | 1.8E|$-10\, \pm \,$|0.5E−10 | 6.38E|$+12\, \pm \,$|1.06E+12 | 0.33 |
| 30 | 5.0E|$-10\, \pm \,$|1.9E−10 | 1.99E|$+12\, \pm \,$|2.87E+12 | 0.40 |
| 31 | 6.8E|$-10\, \pm \,$|2.3E−10 | −1.04E|$+12\, \pm \,$|4.72E+12 | 0.42 |
| 32 | 4.8E|$-10\, \pm \,$|1.0E−10 | 5.83E|$+12\, \pm \,$|2.33E+12 | 0.54 |
| 33 | 9.1E|$-10\, \pm \,$|0.1E−10 | −6.41E|$+12\, \pm \,$|5.79E+11 | 0.96 |
| 34 | 4.9E|$-10\, \pm \,$|1.7E−10 | 1.27E|$+12\, \pm \,$|4.04E+12 | 0.40 |
| 35 | 9.4E|$-09\, \pm \,$|3.8E−09 | −8.23E|$+13\, \pm \,$|3.55E+13 | 0.62 |
| 36 | −1.2E|$-09\, \pm \,$|3.7E−10 | 4.27E|$+13\, \pm \,$|0.87E+13 | −0.45 |
| 37 | 8.8E|$-11\, \pm \,$|8.8E−11 | 1.06E|$+13\, \pm \,$|0.24E+13 | 0.11 |
| 38 | −3.3E|$-10\, \pm \,$|1.2E−10 | 2.44E|$+13\, \pm \,$|0.31E+13 | −0.41 |
| 39 | 1.3E|$-11\, \pm \,$|2.1E−10 | 1.68E|$+13\, \pm \,$|0.53E+13 | 0.01 |
| 40 | 1.8E|$-11\, \pm \,$|2.3E−10 | 1.22E|$+13\, \pm \,$|0.47E+13 | 0.01 |
| 41 | 1.5E|$-09\, \pm \,$|5.6E−10 | −1.15E|$+13\, \pm \,$|0.89E+13 | 0.53 |
| 42 | −2.5E|$-08\, \pm \,$|6.1E−09 | 5.83E|$+14\, \pm \,$|1.29E+14 | −0.41 |
| 43 | 7.0E|$-10\, \pm \,$|1.8E−10 | −1.02E|$+12\, \pm \,$|2.59E+12 | 0.65 |
| 44 | 6.8E|$-10\, \pm \,$|0.8E−10 | −3.84E|$+12\, \pm \,$|2.72E+12 | 0.74 |
| 45 | 5.7E|$-10\, \pm \,$|0.9E−10 | −9.70E|$+11\, \pm \,$|1.68E+12 | 0.79 |
| 46 | 6.0E|$-10\, \pm \,$|0.2E−10 | 3.54E|$+12\, \pm \,$|1.07E+12 | 0.86 |
| Core . | s . | i (cm−2) . | γ . |
|---|---|---|---|
| 1 | 1.7E|$-10\, \pm \,$|0.8E−10 | 7.66E|$+12\, \pm \,$|2.20E+12 | 0.23 |
| 2 | 6.0E|$-10\, \pm \,$|2.0E−10 | 4.43E|$+12\, \pm \,$|3.06E+12 | 0.42 |
| 3 | 4.1E|$-10\, \pm \,$|0.3E−10 | 6.85E|$+12\, \pm \,$|0.83E+12 | 0.65 |
| 4 | 3.6E|$-10\, \pm \,$|0.4E−10 | 4.30E|$+12\, \pm \,$|0.82E+12 | 0.63 |
| 5 | 1.7E|$-09\, \pm \,$|0.9E−09 | −9.49E|$+12\, \pm \,$|1.39E+13 | 0.30 |
| 6 | 1.0E|$-10\, \pm \,$|0.6E−10 | 9.80E|$+12\, \pm \,$|1.28E+12 | 0.20 |
| 7 | 3.0E|$-10\, \pm \,$|1.7E−10 | 6.49E|$+12\, \pm \,$|3.80E+12 | 0.32 |
| 8 | 1.8E|$-10\, \pm \,$|2.4E−10 | 1.08E|$+13\, \pm \,$|0.35E+13 | 0.10 |
| 9 | 1.8E|$-09\, \pm \,$|0.7E−09 | −1.42E|$+13\, \pm \,$|1.39E+13 | 0.52 |
| 10 | 9.9E|$-10\, \pm \,$|2.8E−10 | 5.65E|$+12\, \pm \,$|4.00E+12 | 0.43 |
| 11 | 1.9E|$-10\, \pm \,$|0.9E−10 | 1.15E|$+13\, \pm \,$|0.18E+13 | 0.27 |
| 12 | 3.2E|$-10\, \pm \,$|0.9E−10 | 4.91E|$+12\, \pm \,$|2.82E+12 | 0.40 |
| 13 | −3.1E|$-10\, \pm \,$|7.9E−11 | 2.95E|$+13\, \pm \,$|0.31E+13 | −0.52 |
| 14 | 9.1E|$-10\, \pm \,$|2.0E−10 | −2.75E|$+12\, \pm \,$|3.08E+12 | 0.63 |
| 15 | 3.6E|$-10\, \pm \,$|0.1E−10 | 7.78E|$+12\, \pm \,$|0.87E+12 | 0.92 |
| 16 | 4.2E|$-10\, \pm \,$|0.5E−10 | 5.74E|$+12\, \pm \,$|1.26E+12 | 0.63 |
| 17 | 4.8E|$-10\, \pm \,$|0.5E−10 | 4.75E|$+12\, \pm \,$|1.38E+12 | 0.63 |
| 18 | 2.7E|$-10\, \pm \,$|5.2E−10 | 0.89E|$+13\, \pm \,$|1.75E+13 | 0.10 |
| 19 | 0.8E|$-10\, \pm \,$|2.3E−10 | 9.48E|$+12\, \pm \,$|4.12E+12 | 0.08 |
| 20 | 2.9E|$-10\, \pm \,$|0.3E−10 | 4.87E|$+12\, \pm \,$|1.10E+12 | 0.79 |
| 21 | 2.2E|$-10\, \pm \,$|1.0E−10 | 5.56E|$+12\, \pm \,$|1.94E+12 | 0.27 |
| 22 | 3.9E|$-10\, \pm \,$|0.3E−10 | −1.75E|$+12\, \pm \,$|1.27E+12 | 0.91 |
| 23 | 3.4E|$-10\, \pm \,$|0.1E−10 | 5.06E|$+12\, \pm \,$|0.89E+12 | 0.91 |
| 24 | −1.1E|$-09\, \pm \,$|2.7E−10 | 2.72E|$+13\, \pm \,$|0.34E+13 | −0.46 |
| 25 | 5.6E|$-11\, \pm \,$|3.9E−11 | 9.45E|$+12\, \pm \,$|0.70E+12 | 0.11 |
| 26 | 4.1E|$-10\, \pm \,$|2.9E−10 | 1.00E|$+13\, \pm \,$|0.58E+13 | 0.21 |
| 27 | 1.3E|$-10\, \pm \,$|1.2E−10 | 1.25E|$+13\, \pm \,$|0.28E+13 | 0.19 |
| 28 | −2.0E|$-09\, \pm \,$|3.6E−09 | 7.16E|$+13\, \pm \,$|9.02E+13 | −0.12 |
| 29 | 1.8E|$-10\, \pm \,$|0.5E−10 | 6.38E|$+12\, \pm \,$|1.06E+12 | 0.33 |
| 30 | 5.0E|$-10\, \pm \,$|1.9E−10 | 1.99E|$+12\, \pm \,$|2.87E+12 | 0.40 |
| 31 | 6.8E|$-10\, \pm \,$|2.3E−10 | −1.04E|$+12\, \pm \,$|4.72E+12 | 0.42 |
| 32 | 4.8E|$-10\, \pm \,$|1.0E−10 | 5.83E|$+12\, \pm \,$|2.33E+12 | 0.54 |
| 33 | 9.1E|$-10\, \pm \,$|0.1E−10 | −6.41E|$+12\, \pm \,$|5.79E+11 | 0.96 |
| 34 | 4.9E|$-10\, \pm \,$|1.7E−10 | 1.27E|$+12\, \pm \,$|4.04E+12 | 0.40 |
| 35 | 9.4E|$-09\, \pm \,$|3.8E−09 | −8.23E|$+13\, \pm \,$|3.55E+13 | 0.62 |
| 36 | −1.2E|$-09\, \pm \,$|3.7E−10 | 4.27E|$+13\, \pm \,$|0.87E+13 | −0.45 |
| 37 | 8.8E|$-11\, \pm \,$|8.8E−11 | 1.06E|$+13\, \pm \,$|0.24E+13 | 0.11 |
| 38 | −3.3E|$-10\, \pm \,$|1.2E−10 | 2.44E|$+13\, \pm \,$|0.31E+13 | −0.41 |
| 39 | 1.3E|$-11\, \pm \,$|2.1E−10 | 1.68E|$+13\, \pm \,$|0.53E+13 | 0.01 |
| 40 | 1.8E|$-11\, \pm \,$|2.3E−10 | 1.22E|$+13\, \pm \,$|0.47E+13 | 0.01 |
| 41 | 1.5E|$-09\, \pm \,$|5.6E−10 | −1.15E|$+13\, \pm \,$|0.89E+13 | 0.53 |
| 42 | −2.5E|$-08\, \pm \,$|6.1E−09 | 5.83E|$+14\, \pm \,$|1.29E+14 | −0.41 |
| 43 | 7.0E|$-10\, \pm \,$|1.8E−10 | −1.02E|$+12\, \pm \,$|2.59E+12 | 0.65 |
| 44 | 6.8E|$-10\, \pm \,$|0.8E−10 | −3.84E|$+12\, \pm \,$|2.72E+12 | 0.74 |
| 45 | 5.7E|$-10\, \pm \,$|0.9E−10 | −9.70E|$+11\, \pm \,$|1.68E+12 | 0.79 |
| 46 | 6.0E|$-10\, \pm \,$|0.2E−10 | 3.54E|$+12\, \pm \,$|1.07E+12 | 0.86 |
| Core . | s . | i (cm−2) . | γ . |
|---|---|---|---|
| 1 | 1.7E|$-10\, \pm \,$|0.8E−10 | 7.66E|$+12\, \pm \,$|2.20E+12 | 0.23 |
| 2 | 6.0E|$-10\, \pm \,$|2.0E−10 | 4.43E|$+12\, \pm \,$|3.06E+12 | 0.42 |
| 3 | 4.1E|$-10\, \pm \,$|0.3E−10 | 6.85E|$+12\, \pm \,$|0.83E+12 | 0.65 |
| 4 | 3.6E|$-10\, \pm \,$|0.4E−10 | 4.30E|$+12\, \pm \,$|0.82E+12 | 0.63 |
| 5 | 1.7E|$-09\, \pm \,$|0.9E−09 | −9.49E|$+12\, \pm \,$|1.39E+13 | 0.30 |
| 6 | 1.0E|$-10\, \pm \,$|0.6E−10 | 9.80E|$+12\, \pm \,$|1.28E+12 | 0.20 |
| 7 | 3.0E|$-10\, \pm \,$|1.7E−10 | 6.49E|$+12\, \pm \,$|3.80E+12 | 0.32 |
| 8 | 1.8E|$-10\, \pm \,$|2.4E−10 | 1.08E|$+13\, \pm \,$|0.35E+13 | 0.10 |
| 9 | 1.8E|$-09\, \pm \,$|0.7E−09 | −1.42E|$+13\, \pm \,$|1.39E+13 | 0.52 |
| 10 | 9.9E|$-10\, \pm \,$|2.8E−10 | 5.65E|$+12\, \pm \,$|4.00E+12 | 0.43 |
| 11 | 1.9E|$-10\, \pm \,$|0.9E−10 | 1.15E|$+13\, \pm \,$|0.18E+13 | 0.27 |
| 12 | 3.2E|$-10\, \pm \,$|0.9E−10 | 4.91E|$+12\, \pm \,$|2.82E+12 | 0.40 |
| 13 | −3.1E|$-10\, \pm \,$|7.9E−11 | 2.95E|$+13\, \pm \,$|0.31E+13 | −0.52 |
| 14 | 9.1E|$-10\, \pm \,$|2.0E−10 | −2.75E|$+12\, \pm \,$|3.08E+12 | 0.63 |
| 15 | 3.6E|$-10\, \pm \,$|0.1E−10 | 7.78E|$+12\, \pm \,$|0.87E+12 | 0.92 |
| 16 | 4.2E|$-10\, \pm \,$|0.5E−10 | 5.74E|$+12\, \pm \,$|1.26E+12 | 0.63 |
| 17 | 4.8E|$-10\, \pm \,$|0.5E−10 | 4.75E|$+12\, \pm \,$|1.38E+12 | 0.63 |
| 18 | 2.7E|$-10\, \pm \,$|5.2E−10 | 0.89E|$+13\, \pm \,$|1.75E+13 | 0.10 |
| 19 | 0.8E|$-10\, \pm \,$|2.3E−10 | 9.48E|$+12\, \pm \,$|4.12E+12 | 0.08 |
| 20 | 2.9E|$-10\, \pm \,$|0.3E−10 | 4.87E|$+12\, \pm \,$|1.10E+12 | 0.79 |
| 21 | 2.2E|$-10\, \pm \,$|1.0E−10 | 5.56E|$+12\, \pm \,$|1.94E+12 | 0.27 |
| 22 | 3.9E|$-10\, \pm \,$|0.3E−10 | −1.75E|$+12\, \pm \,$|1.27E+12 | 0.91 |
| 23 | 3.4E|$-10\, \pm \,$|0.1E−10 | 5.06E|$+12\, \pm \,$|0.89E+12 | 0.91 |
| 24 | −1.1E|$-09\, \pm \,$|2.7E−10 | 2.72E|$+13\, \pm \,$|0.34E+13 | −0.46 |
| 25 | 5.6E|$-11\, \pm \,$|3.9E−11 | 9.45E|$+12\, \pm \,$|0.70E+12 | 0.11 |
| 26 | 4.1E|$-10\, \pm \,$|2.9E−10 | 1.00E|$+13\, \pm \,$|0.58E+13 | 0.21 |
| 27 | 1.3E|$-10\, \pm \,$|1.2E−10 | 1.25E|$+13\, \pm \,$|0.28E+13 | 0.19 |
| 28 | −2.0E|$-09\, \pm \,$|3.6E−09 | 7.16E|$+13\, \pm \,$|9.02E+13 | −0.12 |
| 29 | 1.8E|$-10\, \pm \,$|0.5E−10 | 6.38E|$+12\, \pm \,$|1.06E+12 | 0.33 |
| 30 | 5.0E|$-10\, \pm \,$|1.9E−10 | 1.99E|$+12\, \pm \,$|2.87E+12 | 0.40 |
| 31 | 6.8E|$-10\, \pm \,$|2.3E−10 | −1.04E|$+12\, \pm \,$|4.72E+12 | 0.42 |
| 32 | 4.8E|$-10\, \pm \,$|1.0E−10 | 5.83E|$+12\, \pm \,$|2.33E+12 | 0.54 |
| 33 | 9.1E|$-10\, \pm \,$|0.1E−10 | −6.41E|$+12\, \pm \,$|5.79E+11 | 0.96 |
| 34 | 4.9E|$-10\, \pm \,$|1.7E−10 | 1.27E|$+12\, \pm \,$|4.04E+12 | 0.40 |
| 35 | 9.4E|$-09\, \pm \,$|3.8E−09 | −8.23E|$+13\, \pm \,$|3.55E+13 | 0.62 |
| 36 | −1.2E|$-09\, \pm \,$|3.7E−10 | 4.27E|$+13\, \pm \,$|0.87E+13 | −0.45 |
| 37 | 8.8E|$-11\, \pm \,$|8.8E−11 | 1.06E|$+13\, \pm \,$|0.24E+13 | 0.11 |
| 38 | −3.3E|$-10\, \pm \,$|1.2E−10 | 2.44E|$+13\, \pm \,$|0.31E+13 | −0.41 |
| 39 | 1.3E|$-11\, \pm \,$|2.1E−10 | 1.68E|$+13\, \pm \,$|0.53E+13 | 0.01 |
| 40 | 1.8E|$-11\, \pm \,$|2.3E−10 | 1.22E|$+13\, \pm \,$|0.47E+13 | 0.01 |
| 41 | 1.5E|$-09\, \pm \,$|5.6E−10 | −1.15E|$+13\, \pm \,$|0.89E+13 | 0.53 |
| 42 | −2.5E|$-08\, \pm \,$|6.1E−09 | 5.83E|$+14\, \pm \,$|1.29E+14 | −0.41 |
| 43 | 7.0E|$-10\, \pm \,$|1.8E−10 | −1.02E|$+12\, \pm \,$|2.59E+12 | 0.65 |
| 44 | 6.8E|$-10\, \pm \,$|0.8E−10 | −3.84E|$+12\, \pm \,$|2.72E+12 | 0.74 |
| 45 | 5.7E|$-10\, \pm \,$|0.9E−10 | −9.70E|$+11\, \pm \,$|1.68E+12 | 0.79 |
| 46 | 6.0E|$-10\, \pm \,$|0.2E−10 | 3.54E|$+12\, \pm \,$|1.07E+12 | 0.86 |
| Core . | s . | i (cm−2) . | γ . |
|---|---|---|---|
| 1 | 1.7E|$-10\, \pm \,$|0.8E−10 | 7.66E|$+12\, \pm \,$|2.20E+12 | 0.23 |
| 2 | 6.0E|$-10\, \pm \,$|2.0E−10 | 4.43E|$+12\, \pm \,$|3.06E+12 | 0.42 |
| 3 | 4.1E|$-10\, \pm \,$|0.3E−10 | 6.85E|$+12\, \pm \,$|0.83E+12 | 0.65 |
| 4 | 3.6E|$-10\, \pm \,$|0.4E−10 | 4.30E|$+12\, \pm \,$|0.82E+12 | 0.63 |
| 5 | 1.7E|$-09\, \pm \,$|0.9E−09 | −9.49E|$+12\, \pm \,$|1.39E+13 | 0.30 |
| 6 | 1.0E|$-10\, \pm \,$|0.6E−10 | 9.80E|$+12\, \pm \,$|1.28E+12 | 0.20 |
| 7 | 3.0E|$-10\, \pm \,$|1.7E−10 | 6.49E|$+12\, \pm \,$|3.80E+12 | 0.32 |
| 8 | 1.8E|$-10\, \pm \,$|2.4E−10 | 1.08E|$+13\, \pm \,$|0.35E+13 | 0.10 |
| 9 | 1.8E|$-09\, \pm \,$|0.7E−09 | −1.42E|$+13\, \pm \,$|1.39E+13 | 0.52 |
| 10 | 9.9E|$-10\, \pm \,$|2.8E−10 | 5.65E|$+12\, \pm \,$|4.00E+12 | 0.43 |
| 11 | 1.9E|$-10\, \pm \,$|0.9E−10 | 1.15E|$+13\, \pm \,$|0.18E+13 | 0.27 |
| 12 | 3.2E|$-10\, \pm \,$|0.9E−10 | 4.91E|$+12\, \pm \,$|2.82E+12 | 0.40 |
| 13 | −3.1E|$-10\, \pm \,$|7.9E−11 | 2.95E|$+13\, \pm \,$|0.31E+13 | −0.52 |
| 14 | 9.1E|$-10\, \pm \,$|2.0E−10 | −2.75E|$+12\, \pm \,$|3.08E+12 | 0.63 |
| 15 | 3.6E|$-10\, \pm \,$|0.1E−10 | 7.78E|$+12\, \pm \,$|0.87E+12 | 0.92 |
| 16 | 4.2E|$-10\, \pm \,$|0.5E−10 | 5.74E|$+12\, \pm \,$|1.26E+12 | 0.63 |
| 17 | 4.8E|$-10\, \pm \,$|0.5E−10 | 4.75E|$+12\, \pm \,$|1.38E+12 | 0.63 |
| 18 | 2.7E|$-10\, \pm \,$|5.2E−10 | 0.89E|$+13\, \pm \,$|1.75E+13 | 0.10 |
| 19 | 0.8E|$-10\, \pm \,$|2.3E−10 | 9.48E|$+12\, \pm \,$|4.12E+12 | 0.08 |
| 20 | 2.9E|$-10\, \pm \,$|0.3E−10 | 4.87E|$+12\, \pm \,$|1.10E+12 | 0.79 |
| 21 | 2.2E|$-10\, \pm \,$|1.0E−10 | 5.56E|$+12\, \pm \,$|1.94E+12 | 0.27 |
| 22 | 3.9E|$-10\, \pm \,$|0.3E−10 | −1.75E|$+12\, \pm \,$|1.27E+12 | 0.91 |
| 23 | 3.4E|$-10\, \pm \,$|0.1E−10 | 5.06E|$+12\, \pm \,$|0.89E+12 | 0.91 |
| 24 | −1.1E|$-09\, \pm \,$|2.7E−10 | 2.72E|$+13\, \pm \,$|0.34E+13 | −0.46 |
| 25 | 5.6E|$-11\, \pm \,$|3.9E−11 | 9.45E|$+12\, \pm \,$|0.70E+12 | 0.11 |
| 26 | 4.1E|$-10\, \pm \,$|2.9E−10 | 1.00E|$+13\, \pm \,$|0.58E+13 | 0.21 |
| 27 | 1.3E|$-10\, \pm \,$|1.2E−10 | 1.25E|$+13\, \pm \,$|0.28E+13 | 0.19 |
| 28 | −2.0E|$-09\, \pm \,$|3.6E−09 | 7.16E|$+13\, \pm \,$|9.02E+13 | −0.12 |
| 29 | 1.8E|$-10\, \pm \,$|0.5E−10 | 6.38E|$+12\, \pm \,$|1.06E+12 | 0.33 |
| 30 | 5.0E|$-10\, \pm \,$|1.9E−10 | 1.99E|$+12\, \pm \,$|2.87E+12 | 0.40 |
| 31 | 6.8E|$-10\, \pm \,$|2.3E−10 | −1.04E|$+12\, \pm \,$|4.72E+12 | 0.42 |
| 32 | 4.8E|$-10\, \pm \,$|1.0E−10 | 5.83E|$+12\, \pm \,$|2.33E+12 | 0.54 |
| 33 | 9.1E|$-10\, \pm \,$|0.1E−10 | −6.41E|$+12\, \pm \,$|5.79E+11 | 0.96 |
| 34 | 4.9E|$-10\, \pm \,$|1.7E−10 | 1.27E|$+12\, \pm \,$|4.04E+12 | 0.40 |
| 35 | 9.4E|$-09\, \pm \,$|3.8E−09 | −8.23E|$+13\, \pm \,$|3.55E+13 | 0.62 |
| 36 | −1.2E|$-09\, \pm \,$|3.7E−10 | 4.27E|$+13\, \pm \,$|0.87E+13 | −0.45 |
| 37 | 8.8E|$-11\, \pm \,$|8.8E−11 | 1.06E|$+13\, \pm \,$|0.24E+13 | 0.11 |
| 38 | −3.3E|$-10\, \pm \,$|1.2E−10 | 2.44E|$+13\, \pm \,$|0.31E+13 | −0.41 |
| 39 | 1.3E|$-11\, \pm \,$|2.1E−10 | 1.68E|$+13\, \pm \,$|0.53E+13 | 0.01 |
| 40 | 1.8E|$-11\, \pm \,$|2.3E−10 | 1.22E|$+13\, \pm \,$|0.47E+13 | 0.01 |
| 41 | 1.5E|$-09\, \pm \,$|5.6E−10 | −1.15E|$+13\, \pm \,$|0.89E+13 | 0.53 |
| 42 | −2.5E|$-08\, \pm \,$|6.1E−09 | 5.83E|$+14\, \pm \,$|1.29E+14 | −0.41 |
| 43 | 7.0E|$-10\, \pm \,$|1.8E−10 | −1.02E|$+12\, \pm \,$|2.59E+12 | 0.65 |
| 44 | 6.8E|$-10\, \pm \,$|0.8E−10 | −3.84E|$+12\, \pm \,$|2.72E+12 | 0.74 |
| 45 | 5.7E|$-10\, \pm \,$|0.9E−10 | −9.70E|$+11\, \pm \,$|1.68E+12 | 0.79 |
| 46 | 6.0E|$-10\, \pm \,$|0.2E−10 | 3.54E|$+12\, \pm \,$|1.07E+12 | 0.86 |
Acknowledgments
We thank Dr. M. S. Povich for his reviewing this paper and for a number of useful comments. We are also grateful to the other members of Star Formation Legacy project for their support during the observations. This work was supported by JSPS KAKENHI Grant Numbers JP17K00963, JP17H02863, JP17H01118, JP16K12749, and NAOJ ALMA Scientific Research Grant Numbers 2017-04A. YS also received support from the ANR (project NIKA2SKY, grant agreement ANR-15-CE31-0017). The 45 m radio telescope is operated by NRO, a branch of NAOJ.
Footnotes
References



