The interstellar medium and star formation of galactic disks. I. Interstellar medium and giant molecular cloud properties with diffuse far-ultraviolet and cosmic-ray backgrounds

Configurations of simulations.

Run	Resolution (pc)	T _floor (K)	G ₀	ζ (s⁻¹)
I	8	300	4	10⁻¹⁶
II	8	300	1	10⁻¹⁶
III	8	300	Wolfire*	10⁻¹⁶
IV	8	10	Wolfire	10⁻¹⁶
V	8	10	Wolfire	ζ(r)^†
VI	4	10	Wolfire	10⁻¹⁶

Run	Resolution (pc)	T _floor (K)	G ₀	ζ (s⁻¹)
I	8	300	4	10⁻¹⁶
II	8	300	1	10⁻¹⁶
III	8	300	Wolfire*	10⁻¹⁶
IV	8	10	Wolfire	10⁻¹⁶
V	8	10	Wolfire	ζ(r)^†
VI	4	10	Wolfire	10⁻¹⁶

*FUV intensity radial profile from Wolfire et al. (2003).

^†Linear gradient from ζ = 5 × 10⁻¹⁶ s⁻¹ at r = 2 kpc to 5 × 10⁻¹⁷ s⁻¹ at r = 10 kpc.

Table 1.

Configurations of simulations.

Run	Resolution (pc)	T _floor (K)	G ₀	ζ (s⁻¹)
I	8	300	4	10⁻¹⁶
II	8	300	1	10⁻¹⁶
III	8	300	Wolfire*	10⁻¹⁶
IV	8	10	Wolfire	10⁻¹⁶
V	8	10	Wolfire	ζ(r)^†
VI	4	10	Wolfire	10⁻¹⁶

Run	Resolution (pc)	T _floor (K)	G ₀	ζ (s⁻¹)
I	8	300	4	10⁻¹⁶
II	8	300	1	10⁻¹⁶
III	8	300	Wolfire*	10⁻¹⁶
IV	8	10	Wolfire	10⁻¹⁶
V	8	10	Wolfire	ζ(r)^†
VI	4	10	Wolfire	10⁻¹⁶

*FUV intensity radial profile from Wolfire et al. (2003).

^†Linear gradient from ζ = 5 × 10⁻¹⁶ s⁻¹ at r = 2 kpc to 5 × 10⁻¹⁷ s⁻¹ at r = 10 kpc.

To better track the atomic to molecular transition, we then carry out several runs with a 10 K temperature floor. This also permits investigation of the effects of CR ionization, which mostly influences the chemistry and heating of cooler, denser (i.e., highly extinguished) molecular gas (i.e., T < 30 K, A_V > 10 mag)—n_H > 10³ cm⁻³ (see Bisbas et al. 2015). Note that the temperature floor is not necessarily reached in the simulations. In Run IV we use a CR ionization rate ζ = 1 × 10⁻¹⁶ s⁻¹, while Run V adopts a simple linear radial profile with maximum and minimum values being equal to 5 × 10⁻¹⁶ (at r = 2 kpc) and 5 × 10⁻¹⁷ s⁻¹ (at r = 10 kpc), respectively. Run VI uses the same constant value of ζ as in Run IV, but now introduces an extra level of AMR to yield 4 pc resolution.

2.2 Initial conditions

Following TT09, we initialize an isolated self-gravitating gas disk, rotating around the z-axis, in a static gravitational background potential. This potential is described by (Binney & Tremaine 1987)

\begin{equation} \phi _{\rm bg} = \frac{1}{2} v_{\rm c,0}^2 \ln \left[\frac{1}{r_{\rm c}^2}\left(r_{\rm c}^2+r^2+\frac{z^2}{q_\phi ^2}\right)\right], \end{equation}

(1)

i.e., identical to that adopted by TT09, which yields a flat rotation curve with v_c,0 = 200 km s⁻¹ at galactocentric radii r ≫ core radius (r_c = 0.5 kpc). The axial ratio of the potential field is q_φ = 0.7. The distribution of the background dark matter and stellar population would in reality evolve in response to the changing distribution of ISM gas mass (e.g., Read et al. 2016); however, this effect is not included here given our focus on determining ISM structure that occurs in a given galactic potential.

The initial density profile of the gas disk is set to be

\begin{equation} \rho (r,z) = \frac{\kappa c_{\rm s}}{2 \pi G Q\, z_{\rm h}} \mathrm{sech^2}\left(\frac{z}{z_{\rm h}}\right)\ (r<12\ \mathrm{kpc}), \end{equation}

(2)

where the scale height z_h is set to 290 pc, and for purposes of normalization of the initial condition, the sound speed c_s is set equal to 7.7 km s⁻¹. These choices are made so that the initial Toomre (1964) stability parameter, i.e., with input quantities averaged in annuli in the disk, is Q = 1.5 for 2 kpc < r < 10 kpc, which is our only region of interest, and Q = 20 at the same sound speed for r < 2 kpc or 10 kpc < r < 12 kpc, which are boundary regions. The epicyclic frequency κ is expressed by

\begin{equation} \kappa = \sqrt{2}\frac{v_{\rm circ}}{r}(1+\beta )^{\frac{1}{2}}, \end{equation}

(3)

where v_circ is the circular velocity, which is equal to |$v_{\rm c,0}r(r_{\rm c}^2+r^2)^{-1/2}$| set by the gravitational potential of equation (1), and β = d ln v_circ/d ln r. In total, the disk gas mass is ∼6 × 10⁹ M_⊙.

The disk is surrounded by a quasi-static, dynamically negligible ambient medium with the initial gas density:

\begin{equation} \rho _{\rm ambient} = \rho _0 {\rm exp}{\left(-\frac{\mu m_\mathrm{H}}{kT}\phi \right)}, \end{equation}

(4)

where the gravitational potential φ includes the contribution of background potential and the galactic gas disk. In our simulation, the maximum value of the initial ambient density is n_H = 10⁻⁴ cm⁻³ (approximately 10⁻⁴ of that in the main disk). We set its initial temperature to be 10⁶ K. The ambient density starts to dominate over that of the main disk component at several scale heights, e.g., at a height of ∼1.4 kpc at r ∼ 4 kpc.

As discussed below, the gas undergoes heating and cooling processes. The net effect of the evolution from the initial condition is cooling, which leads to a reduction of Q and thus fragmentation in the main disk region. Note, we adopt |$c_{\rm s}= \sqrt{\gamma k T / \mu }$| with a fixed adiabatic index γ = 5/3. In the limit of fully molecular |$\rm H_2$|⁠, the mean molecular weight μ = 2.33 m_H (i.e., we assume 0.1 He per H and ignore contributions from other species, including 1 × 10⁻⁴ C and 3 × 10⁻⁴ O per H). The true mean molecular weight μ varies based on thermal processes (determined in an iterative way, see subsection 2.3). We adopt the value of γ = 5/3 for the entire simulation domain. While this does not account for the excitation of rotational and vibrational modes of |$\rm H_2$| that would occur in shocks, we consider that this is the most appropriate single-valued choice of γ for our simulation setup, given our focus on the dynamics of the dense molecular gas and given the resolutions that are achieved in the models, including allowance for the fact that the Zeus solver itself does not allow for very accurate shock capturing.

2.3 Heating and cooling functions

To investigate the effects of diffuse FUV heating and CR ionization, we implement PDR-based heating and cooling functions. The method is based on that developed by Wu et al. (2015) in the context of simulations of GMC collisions and for the simple case of a fixed background FUV intensity (G₀ = 4) and CR ionization rate (ζ = 10⁻¹⁶ s⁻¹). For T < 10⁴ K, we use the Python-based PDR (PyPDR) code, which includes ∼30 species and performs well in producing results similar to larger PDR codes up to ∼10⁴ K (Röllig et al. 2007). PyPDR is also more flexible in being able to be adapted to calculate self-consistent grids of models at non-equilibrium conditions, including molecular self-shielding effects (see Wu et al. 2015). For T > 10⁴ K, we utilize the CLOUDY code (Ferland et al. 2013)—PyPDR is not designed to operate at these temperatures.

In each cell there are four parameters that are important for setting the chemical conditions and thus the (non-equilibrium) heating and cooling rates: gas number density of H nuclei (n_H), gas temperature (T), local FUV intensity (G₀), and CR ionization rate (ζ). The local FUV intensity is derived given G₀ (which may vary with a galactocentric radius) and the visual extinction, A_V, to a cell. The method of Wu et al. (2015) involves approximating A_V as a local, monotonically rising function of density n_H. The reliability of this approximation on the scales of GMCs has been investigated by comparison with full radiative transfer simulations of T. G. Bisbas et al. (in preparation) and found to be accurate to within ∼20% for heating and cooling rates at a typical density of n_H = 10³ cm⁻³ and the temperature of T = 100 K. More generally, on galactic scales, the validity of local approximations to account for FUV radiative shielding in multi-dimensional simulations has been studied by comparing it with a more accurate ray-tracing-based approach (Safranek-Shrader et al. 2017), and is reported to be physically appropriate to modeling the thermal impact of the H i–H₂ and C ii/C i/CO transitions.

In this paper we have extended the grid of heating and cooling functions to span extra dimensions of G₀ and ζ, i.e., up to a four-dimensional (4D) parameter space. The range of background diffuse FUV intensities and CR ionization rates are set as described in subsection 2.1. The heating/cooling functions span the density and temperature space of 10⁻⁴ cm⁻³ <n_H < 10⁶ cm⁻³ and 2.7 K < T < 10⁷ K, covering our regime of interest.

The resulting heating/cooling rates and corresponding mean molecular weights are incorporated into Enzo via the Grackle external chemistry and cooling library (Smith et al. 2017). The information is read in via the purely tabulated mode using quadrilinear interpolation to fill the entire 4D parameter space, and modifies the specific gas internal energy e = p/(γ − 1) of a given cell with a net heating/cooling rate calculated by

\begin{equation} H = n_\mathrm{H}(\Gamma -n_\mathrm{H}\Lambda )\ \mathrm{erg{\,\,}cm^{-3}{\,\,}s^{-1}}, \end{equation}

(5)

where Γ is the heating rate and Λ is the cooling rate. The species abundances and their line emissivities are also used to make predictions of emission line diagnostics (discussed in the next subsection).

2.4 Observational diagnostics

One important output of the PDR model described in subsection 2.3 is the detailed information about specific components that contribute to the radiative cooling rates. Given the local volume emissivities, j, of particular lines such as [C ii] emission at 158 |$\rm \mu m$| and rotational lines of ¹²CO and ¹³CO, we are able to create synthetic integrated intensity maps in post-processing.

We note that radiative transfer is incorporated, approximately, in each cell through implementation in the 1D PDR models, while (for the results presented in this paper) full line radiative transfer is not calculated during post-processing, i.e., we sum contributions along lines of sight, which is only fully valid in the optically thin limit.

Thus, we typically choose to study lines in which optical depths should be relatively small. The resulting intensities are simply integrated directly through the simulation domain. We also note that CO frozen onto dust grains is not yet treated in our PDR models. Following equation (6) in Wu et al. (2015), the integrated intensity is calculated through

\begin{equation} \int T_\mathrm{mb} {d}v = \frac{\lambda ^3}{2k_{\rm B}} I = \frac{\lambda ^3}{2\pi k_{\rm B}}\int _{\mathrm{LOS}} j {d}z, \end{equation}

(6)

where T_mb is the main-beam temperature, j is the emissivity (the output of PDR codes is 4πj), v is the line-of-sight velocity, dz is the line element along the line of sight, and λ is the chosen line centroid wavelength.

2.5 Cloud tracking

The clouds in the galactic disk were located using a number density of H nuclei threshold of |$n_{\rm \mathrm{H},GMC} = 100\:$|cm⁻³, i.e., the same value as used in the TT09 study and similar to the volume-averaged mean densities of typical Galactic GMCs. We will also justify this choice of density threshold based on the PDR models implemented in our simulations. When we refer to “clouds” or “GMCs,” we are describing the gas that has achieved densities of at least |$n_{\rm \mathrm{H},GMC}$|⁠.

Clouds are identified by utilizing a k-d tree, a binary-space-partitioning data structure especially effective in the proximity/clustering search, through the following loops, which achieve the same results as the method developed by TT09.

Loop 1: Local density peaks are identified within the cells with |$n_{\mathrm{H}}> n_{\rm \mathrm{H},GMC}$|⁠. If the distance between two peaks is smaller than the deblending length (here we set it to a fixed distance of 32 pc, including in the run with 4 pc resolution), then only the peak with the higher density is retained as a “peak.”
Loop 2: For every peak, adjacent cells with |$n_{\mathrm{H}} > n_{\rm \mathrm{H},GMC}$| are marked as “belonging to the peak,” and cells adjacent to these marked cells are recursively marked in the same way. Eventually, the cells that have continuous spatial connections with multiple peaks are assigned to the peak closest to them, i.e., each cell is only assigned to one peak. With this method, multiple clouds can exist in the same continuous density structure, if it contains more than one well-separated peak.

Once clouds are identified for each simulation output, we then calculate their physical properties and also track cloud evolution. The clouds at t₀ and those at t₁ (typically t₁ − t₀ = 1 Myr) are linked as parent–child pairs through the following steps.

Step 1: Assuming constant velocity within 1 Myr, a predicted center of mass at t₁ for each cloud found at t₀ is calculated.
Step 2: A volume of radius 50 pc, larger than the expected deviations due to typical accelerations, centered on the predicted position of each cloud is searched for clouds present at time t₁. If multiple clouds are found in this region at t₁, the nearest one is linked with the cloud at t₀.
Step 3: In the case that multiple t₀ clouds (parents) are linked to the same t₁ cloud (child) based on the previous step, the child will be assigned to the “parents” with the nearest predicted t₁ location. Other “parents” will repeat step 2 and search for alternative children excluding the assigned one until no conflict exists, or no alternative child exists so that the children defined in step 2 have to be linked to those “parents.”
Step 4: If no clouds at t₁ are linked with the t₀ cloud, then a volume with radius equal to 3× the average radius (defined as |$R_{\rm c}=\sqrt{A_{\rm c}/\pi }$|⁠, where A_c is the projected area of the cloud in the x–y plane) of the t₀ cloud is searched. This allows for large, extended clouds whose centers may have shifted due to external perturbations.
Step 5: If multiple clouds at t₀ are linked to one cloud at t₁, then the most massive t₀ cloud is claimed to survive while others are “destroyed” by merger. If one t₀ cloud has no child, then it is claimed to have been destroyed by non-merger processes. Cloud formation is claimed for each t₁ cloud without any parent.

This procedure tracks merger events accurately, but we caution that this simple prescription for identifying destruction events may have difficulties, particularly when strong feedback mechanisms are eventually included. Still, the prescription works well in the current simulation, since we have limited cloud destruction, i.e., the diffuse FUV radiation does not lead to significant GMC destruction.

3 Large-scale ISM properties

In the following sections, we restrict our analysis of ISM and GMC properties to galactocentric radii between 2.5 and 8.5 kpc in order to avoid structures affected by the boundaries of the main disk.

3.1 Global disk

The time evolutions of the galactic disks of Runs I–VI are shown in figures 1, 2, 3, 4, 5, and 6, respectively. At the beginning, with an initialized velocity dispersion of σ_g = c_s ≃ 8 km s⁻¹, the disks are marginally stable. As a result of radiative cooling, the disks become unstable and fragment into overdense structures, which increases the self-shielding from the diffuse FUV radiation, raises line cooling rates, thus leading to more rapid cooling and gathering of material from the surroundings. As overdense regions become denser than |$n_{\rm \mathrm{H},GMC} = 100\:$|cm⁻³, they are identified as components of GMCs. Similarly in the case of the results seen by TT09, this evolution, driven by cooling, occurs most rapidly in the denser inner regions and therefore the first structure to form is an overdense ring near the inner boundary due to the Toomre ring instability. The instability gathers material from a range of radii about equal to the Toomre length, λ_T = 2π²GΣ_g/κ². The instability then propagates to outer regions as radiative cooling continues. Overdense local spiral patterns form and fragment into clouds.

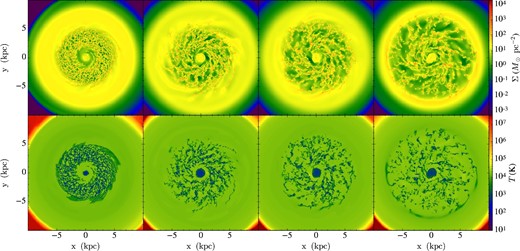
Evolution of the galactic disk for Run I (G0 = 4; 100, 200, 250, and 300 Myr from left to right). Images are 20 kpc across and show the disk gas mass surface density Σ (top row) and mass-weighted temperature T (bottom row), integrated vertically over the disk (over a range −1 kpc < z < +1 kpc).

Fig. 1.

Evolution of the galactic disk for Run I (G₀ = 4; 100, 200, 250, and 300 Myr from left to right). Images are 20 kpc across and show the disk gas mass surface density Σ (top row) and mass-weighted temperature T (bottom row), integrated vertically over the disk (over a range −1 kpc < z < +1 kpc).

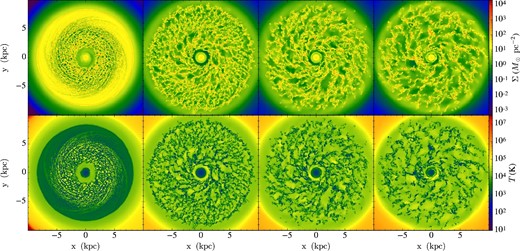
Same as figure 1, but for Run II (G0 = 1).

Fig. 2.

Same as figure 1, but for Run II (G₀ = 1).

Same as figure 1, but for Run III (radially variable G0).

Fig. 3.

Same as figure 1, but for Run III (radially variable G₀).

Same as figure 1, but for Run IV (radially variable G0 with 10 K temperature floor).

Fig. 4.

Same as figure 1, but for Run IV (radially variable G₀ with 10 K temperature floor).

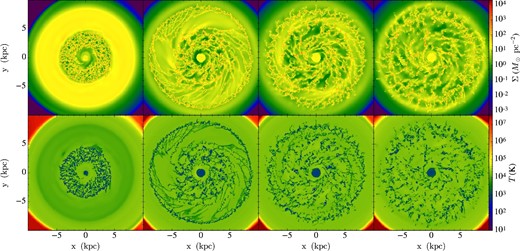
Same as figure 1, but for Run V (radially variable G0 and ζ with 10 K temperature floor).

Fig. 5.

Same as figure 1, but for Run V (radially variable G₀ and ζ with 10 K temperature floor).

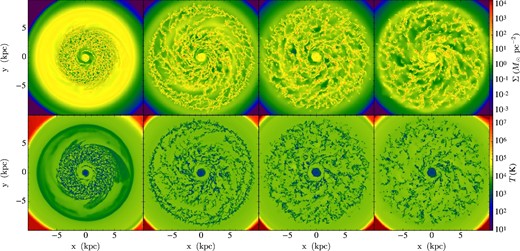
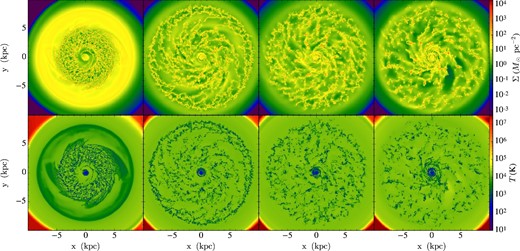
Same as figure 1, but for Run VI (radially variable G0 with 10 K temperature floor and 4 pc resolution).

Fig. 6.

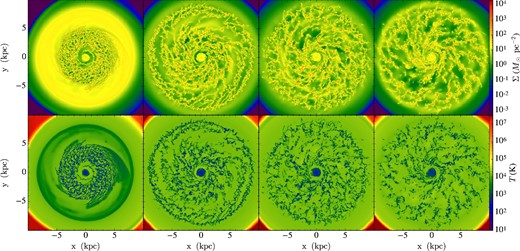
Same as figure 1, but for Run VI (radially variable G₀ with 10 K temperature floor and 4 pc resolution).

Since the early phase evolution is quite artificial, in figures 1–6 we focus on later stages from 100 to 300 Myr, also showing intermediate stages at 200 and 250 Myr. Later we will be focusing on the statistics of ISM and GMC properties from 200 to 300 Myr.

Comparing the first three runs (figures 1–3), which have different FUV intensities, we see that energy injection from FUV radiation suppresses the growth of gravitational instabilities, especially in the lower-density outer regions, thus shaping the spatial distribution as well as the global evolutionary history of GMCs. On the global scales viewed in figures 1–6, there appear to be only modest effects on the dense gas structures caused by lowering the temperature floor from 300 K to 10 K, i.e., comparing Run III and Run IV. Applying a radially variable ζ in Run V, which has overall stronger heating than the constant ζ case, we see that fragmentation is delayed to some extent. Cosmic-ray heating is of greater importance in the denser, molecular phase where FUV radiation is shielded and equilibrium temperatures are lower.

Figure 7 shows the time evolution of the radial profiles of Σ, azimuthally averaged in annuli, in these simulations. Fluctuations on the order of factors of a few are seen to develop due to gravitational instabilities. However, the average values overall remain similar to those of the initial conditions, with the exceptions being caused by modest amounts of radial accretion seen most obviously at the boundaries of the main disk region. These results are relatively insensitive to the choices of PDR-related parameters.

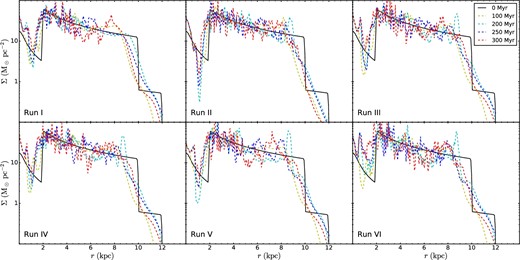
$The evolution of azimuthally averaged radial profiles of gas mass surface density $\Sigma =\int _{-1{\,\,}\mathrm{kpc}}^{+1{\,\,}\mathrm{kpc}}\rho dz$ for Run I (upper left, G0 = 4), II (upper middle, G0 = 1), III (upper right, radially variable G0), IV (lower left, radially variable G0, 10 K temperature floor), V (lower middle, radially variable G0 and ζ, 10 K temperature floor), and VI (lower right, radially variable G0, constant ζ, 10 K temperature floor with 4 pc resolution).$

Fig. 7.

The evolution of azimuthally averaged radial profiles of gas mass surface density |$\Sigma =\int _{-1{\,\,}\mathrm{kpc}}^{+1{\,\,}\mathrm{kpc}}\rho dz$| for Run I (upper left, G₀ = 4), II (upper middle, G₀ = 1), III (upper right, radially variable G₀), IV (lower left, radially variable G₀, 10 K temperature floor), V (lower middle, radially variable G₀ and ζ, 10 K temperature floor), and VI (lower right, radially variable G₀, constant ζ, 10 K temperature floor with 4 pc resolution).

The time evolution of the azimuthally averaged radial profiles (in range 2.5 kpc < r < 8.5 kpc, with annuli of width 0.5 kpc) of the Toomre Q parameter, the 1D gas velocity dispersion σ_g, and average gas temperature T for Run VI are shown in figure 8. Note that |$\sigma _{\rm g}=\sqrt{c_{\rm s}^2+\sigma ^2_{\rm nt}}$| is a mass-weighted average over −1 kpc < z < 1 kpc, where σ_nt is the 1D velocity dispersion of the gas motions in the plane of the disk after the subtraction of the local circular velocity, T is the mass-weighted average over −1 kpc < z < 1 kpc, and Q is calculated via

\begin{equation} Q = \frac{\kappa \sigma _{\rm g}}{\pi G \Sigma }. \end{equation}

(7)

During the early stage of the simulation, the gas cools rapidly, causing Q to drop and leading to gravitational instability. The inner region, where gas is denser, has faster cooling, so GMCs form earlier. We will see below that disk fragmentation eventually (by ∼200 Myr) reaches a relatively steady state, with the ISM existing in two main phases. The diffuse gas, being more exposed to the FUV field, retains a relatively high temperature and so the overall mass-weighted temperature is ≳2000 K, even though the majority (∼2/3) of the mass is in dense, “GMC”-like structures. However, σ_g is dominated by the random motions of GMCs in the disk, i.e., σ_nt. These are accelerated by mutual gravitational interactions between self-gravitating GMCs and are damped by cloud–cloud collisions (Gammie et al. 1991). Thus, at late times, Q, as defined by equation (7), rises to a value of ∼3; that is, it is already in a highly fragmented state due to gravitational instability, but then has the superficial appearance of being gravitationally stable.

Fig. 8.

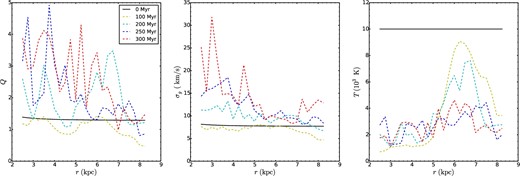
Galactic disk azimuthally averaged radial profiles (2.5 kpc < r < 8.5 kpc) and their evolution for Run VI; from left to right: (a) Toomre Q parameter, (b) one-dimensional gas velocity dispersion, σ_g (mass-weighted average over −1 kpc < z < 1 kpc), (c) gas temperature (mass-weighted average over −1 kpc < z < 1 kpc).

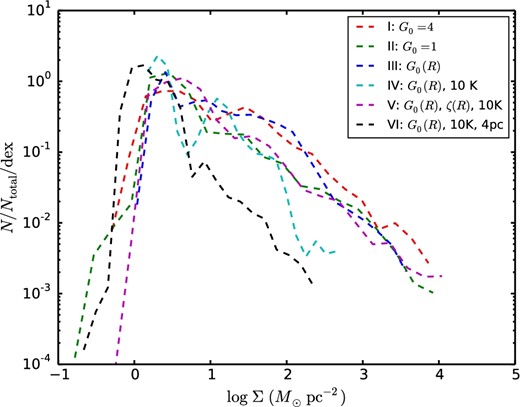
The top panel of figure 9 shows the evolution of the Σ probability density function (PDF) of Run I from 200 to 300 Myr. Overall, this PDF stays relatively constant during this period, implying that the ISM of the global disk is approaching a quasi-statistical equilibrium. However, there is a tendency seen for the mass fraction in the densest regions to be increasing. The effect of the final spreading of fragmentation to the outer disk by 300 Myr is also apparent in reducing the peak near Σ = 10 M_⊙ pc⁻². The middle panel shows equivalent results for Run VI, which is closer to full fragmentation during the period from 200 to 300 Myr. These PDFs show a greater degree of constancy, with just a minor enhancement in the fraction of material at the highest mass surface densities as the disk evolves. However, examining the morphologies shown in figure 6 we do see a trend for apparent agglomeration of clouds into larger structures. This is examined further in terms of GMC mass functions in the next section. Finally, the bottom panel of figure 9 compares the Σ PDFs of all six runs at 250 Myr. Overall, the results of the different runs are quite similar to each other, with the case of G₀ = 4 having the largest differences, as fragmentation in the outermost regions is still ongoing. The result of Run VI, which has the highest resolution, also shows a difference in being able to resolve a higher fraction of mass at the greatest mass surface densities.

Fig. 9.

Probability density functions of gas mass surface density, Σ, as viewed from above the disk, evaluated from 2.5 kpc < r < 8.5 kpc and projecting through −1 kpc < z < 1 kpc. Top panel: Results for Run I (G₀ = 4) at 200 (blue), 250 (green), and 300 Myr (red). Middle panel: Results for Run VI (variable G₀) at 200 (blue), 250 (green), and 300 Myr (red). Bottom panel: Results for Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black) at 250 Myr.

The density–temperature phase plots of the ISM at 300 Myr are shown in figure 10 for all runs. The solid curves delineate the equilibrium temperature as a function of density, set by the heating and cooling functions described in section 2. Much of the mass (especially the densest parts) of the simulated ISM is at a temperature close to that expected from thermal equilibrium. Some deviations are expected due to energy injection and dissipation via dynamical processes such as heating due to compressive motions (e.g., cloud–cloud collisions) and cooling due to rarefactions.

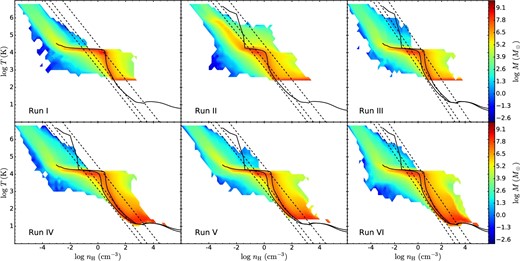
Density versus temperature phase plots showing the distribution of gas mass at 300 Myr for Runs I (G0 = 4), II (G0 = 1), III (radially variable G0), IV (radially variable G0 with 10 K temperature floor), V (radially variable G0 and ζ with 10 K temperature floor), and VI (radially variable G0 with 10 K temperature floor and 4 pc resolution). The mass scale indicates the total mass of gas within a given ΔlognH by ΔlogT interval. In each panel, the solid curves show the equilibrium temperature as a function of density. For Runs III–VI, the upper and lower solid curves at nH > 10−1.5 cm−3 represent the equilibrium temperatures for G0 = 4 and G0 = 1, respectively, both with ζ = 10−16 s−1. The dashed lines show estimates of the total pressure in the Milky Way (Boulares & Cox 1990), Ptot/k = 2.8 × 104 K cm−3 (top line), the total thermal pressure, Pth/k = 0.36 × 104 K cm−3 (middle line), and the thermal pressure excluding the hot gas component, Pth,nohot/k = 0.14 × 104 K cm−3 (bottom line).

Fig. 10.

Density versus temperature phase plots showing the distribution of gas mass at 300 Myr for Runs I (G₀ = 4), II (G₀ = 1), III (radially variable G₀), IV (radially variable G₀ with 10 K temperature floor), V (radially variable G₀ and ζ with 10 K temperature floor), and VI (radially variable G₀ with 10 K temperature floor and 4 pc resolution). The mass scale indicates the total mass of gas within a given Δlogn_H by ΔlogT interval. In each panel, the solid curves show the equilibrium temperature as a function of density. For Runs III–VI, the upper and lower solid curves at n_H > 10^−1.5 cm⁻³ represent the equilibrium temperatures for G₀ = 4 and G₀ = 1, respectively, both with ζ = 10⁻¹⁶ s⁻¹. The dashed lines show estimates of the total pressure in the Milky Way (Boulares & Cox 1990), P_tot/k = 2.8 × 10⁴ K cm⁻³ (top line), the total thermal pressure, P_th/k = 0.36 × 10⁴ K cm⁻³ (middle line), and the thermal pressure excluding the hot gas component, P_th,nohot/k = 0.14 × 10⁴ K cm⁻³ (bottom line).

Comparing Run IV to Run V, which has a radially variable and overall stronger ζ, we can see that CR ionization is an important heating source at low temperatures (≲30 K), which affects the lowest temperatures that the dense gas can reach. Additionally, comparing Runs IV and VI, one notices in the latter with its higher resolution a somewhat larger fraction of dense gas is seen to deviate from thermal equilibrium due to dynamical effects.

In the typical local Milky Way, the total diffuse ISM pressure is about 2.8 × 10⁴ K cm⁻³ and its thermal components are by about an order of magnitude smaller (Boulares & Cox 1990). These pressures are shown by straight lines in figure 10. Incorporating diffuse FUV feedback, our simulated diffuse ISM has comparable thermal pressures to the observed Milky Way thermal pressures at densities ≳ 10⁻¹ cm⁻³. At lower densities the simulation pressures are lower, which is most likely due to the lack of supernova feedback that would create a hot ionized medium with T ≳ 10⁶ K. At high densities, GMCs in the simulation are at much higher pressures than the diffuse ISM, mainly due to their self-gravity.

However, recall that in addition to the lack of SN feedback, the simulations also lack localized FUV, EUV, and wind momentum feedback from young stars. They also lack magnetic fields and the dynamical effects due to cosmic-ray pressure gradients. Both of them are important pressure components in the Milky Way. The inclusion of these physical processes is deferred to future papers in this series. Thus, when interpreting the results presented here, deviations from simulated and observed ISM properties may be due to the lack of these physical processes.

We evaluate gas density distributions and compositions for the main region of interest of the disk (2.5 kpc < r < 8.5 kpc and −1 kpc < z < 1 kpc). The mass fraction of gas that is in GMCs (i.e., with n_H ≥ 100 cm⁻³), f_GMC, is shown as a function of time in figure 11 (solid lines). These fractions rise for the first ∼150 Myr and then approximately stabilize. The case with G₀ = 4 has the smallest fraction of gas in GMCs, about 45% from 200 to 300 Myr. The other models have higher fractions, which are also very similar to each other, i.e., with about 67% of gas mass in GMCs. We note that this fraction is also very similar to that found by TT09, even though this simulation did not include FUV feedback. This tells us that the formation of dense gas, driven by gravitational instability, is not that sensitive to FUV feedback, until G₀ ∼ 4, when the outer disk begins to be stabilized.

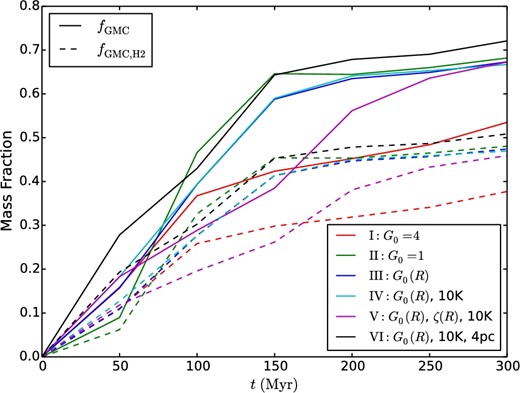
$Fraction of total disk mass in “GMCs,” i.e., with nH > 100 cm−3 (fGMC) as a function of simulation time (solid lines) for Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black). The dashed lines show the fraction of the total disk mass that is in “GMCs” and also in the $\rm H_2$ phase $(\!f_{\rm GMC,H_{2}}\!)$.$

Fig. 11.

Fraction of total disk mass in “GMCs,” i.e., with n_H > 100 cm⁻³ (f_GMC) as a function of simulation time (solid lines) for Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black). The dashed lines show the fraction of the total disk mass that is in “GMCs” and also in the |$\rm H_2$| phase |$(\!f_{\rm GMC,H_{2}}\!)$|⁠.

Figure 11 also shows the fraction of the total gas in the disk that is in GMCs and also in the |$\rm H_2$| phase, |$f_{\rm GMC,H_{2}}$| (dashed lines). This is the result of our PDR modeling of the gas with densities n_H ≥ 100 cm⁻³. This fraction rises with a similar time dependence to f_GMC. The ratio of the dashed line to solid line for a given simulation, i.e., |$f_{\rm GMC,H_{2}}/f_{\rm GMC}$|⁠, is the average |$\rm H_2$| mass fraction within our defined “GMCs.” We see that this ratio is close to 70%. This is broadly consistent with the fact that Galactic GMCs are known to have large mass fractions in atomic envelopes (Blitz 1990; Wannier et al. 1991). Thus, our choice of n_H = 100 cm⁻³ as a threshold density to define “GMCs” appears reasonable.

Figure 12a shows the radial profiles of f_GMC and |$f_{\rm GMC,H_{2}}$| at 250 Myr. These fractions decline gradually as one goes from the denser, inner regions to the lower-density, outer regions of the disk. In Run I, i.e., with high G₀, the transition from a gravitationally unstable inner (≲6.5 kpc) zone to a stable outer region is clearly seen in these profiles. The other simulation runs are seen to have radial profiles of these metrics that are quite similar to each other.

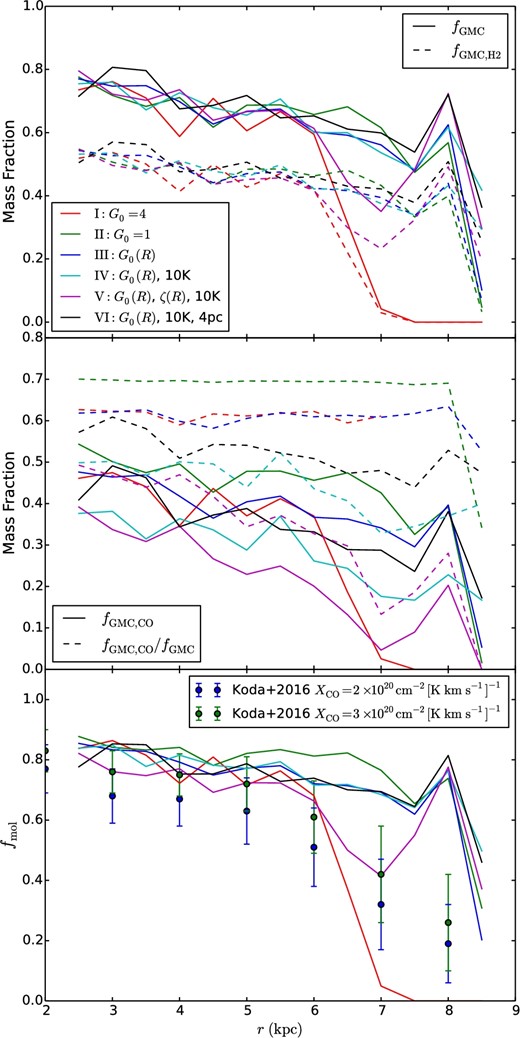
$(a) Top panel: Fraction of total disk gas mass in “GMCs” (fGMC), i.e., with nH > 100 cm−3, as a function of galactocentric radius (solid lines) for Runs I–VI as indicated in the legend, all evaluated at 250 Myr. The dashed lines show the fraction of the total disk gas mass in the “GMCs” that is also in the $\rm H_2$ phase ($f_{\rm GMC,H_{2}}$). (b) Middle panel: Fraction of total disk gas mass in GMCs that is also “CO-rich,” i.e., with nCO/nH > 10−5 (fGMC,CO, solid lines), with results shown for the runs at 250 Myr—see legend in panel (a). The ratio fGMC,CO/fGMC is also shown (dashed lines). (c) Bottom panel: Molecular fraction, $f_{\rm mol}\equiv \Sigma _{\rm H_{2}}/(\Sigma _{\rm H_{2}}+\Sigma _{\rm H\,{\small I}})$ for the different runs—see legend in panel (a)—compared to the Milky Way observed profile from the analysis of Koda, Scoville, and Heyer (2016) for two different values of XCO, as indicated.$

Fig. 12.

(a) Top panel: Fraction of total disk gas mass in “GMCs” (f_GMC), i.e., with n_H > 100 cm⁻³, as a function of galactocentric radius (solid lines) for Runs I–VI as indicated in the legend, all evaluated at 250 Myr. The dashed lines show the fraction of the total disk gas mass in the “GMCs” that is also in the |$\rm H_2$| phase (⁠|$f_{\rm GMC,H_{2}}$|⁠). (b) Middle panel: Fraction of total disk gas mass in GMCs that is also “CO-rich,” i.e., with n_CO/n_H > 10⁻⁵ (f_GMC,CO, solid lines), with results shown for the runs at 250 Myr—see legend in panel (a). The ratio f_GMC,CO/f_GMC is also shown (dashed lines). (c) Bottom panel: Molecular fraction, |$f_{\rm mol}\equiv \Sigma _{\rm H_{2}}/(\Sigma _{\rm H_{2}}+\Sigma _{\rm H\,{\small I}})$| for the different runs—see legend in panel (a)—compared to the Milky Way observed profile from the analysis of Koda, Scoville, and Heyer (2016) for two different values of X_CO, as indicated.

In figure 12b the solid lines show the galactic radial profiles at 250 Myr of the fraction, f_{GMC, CO}, of the total disk mass that is in “GMCs” and has a CO abundance n_CO/n_H > 10⁻⁵, i.e., within an order of magnitude of the maximal CO abundance of n_CO/n_H = 10⁻⁴, given our adopted total C and O abundances (i.e., n_C/n_H = 1 × 10⁻⁴). Like f_GMC and |$f_{\rm GMC,H_{2}}$|⁠, the profiles of f_{GMC, CO} show a general decrease with r, but now starting from values of ∼0.5 in the inner disk and reaching ∼0.1 (or less in the case of Run I) in the outer disk. As expected, Run II with a low value of G₀ = 1 has the highest values of f_GMC,CO. Run V, with the overall strongest CR ionization rate, generally shows the lowest f_{GMC, CO}, which we attribute to the fact that CO is efficiently destroyed indirectly by CRs via creation of He⁺ (Bisbas et al. 2015, 2017). Figure 12b also shows the ratio f_{GMC, CO}/f_GMC (dashed lines), which represents how well CO traces the defined “GMCs.” Comparing the first three runs, a stronger FUV radiation leads to slightly lower values of f_{GMC, CO}/f_GMC. Here, we again see that higher values of CRs in Run V compared to Run IV over most of the disk lead to a reduced fraction of the GMCs that are well traced by CO. In general, the structures identified as “GMCs” can have significant, ∼1/3 mass fractions in “CO-dark” regions (and even more in Run V), consistent with the properties of Milky Way GMCs (e.g., Wolfire et al. 2010).

Figure 12c shows the radial profile of |$f_{\rm mol}\equiv \Sigma _{\rm H_{2}}/(\Sigma _{\rm H_{2}}+\Sigma _{\rm H\,{\small I}})$| in the simulations and a comparison between our runs and its observed profile in the Milky Way from the analysis of Koda, Scoville, and Heyer (2016). We see that there is generally quite good agreement between the simulations and the observational data, indicating that, at least by this metric, the simulations are a reasonable representation of the Milky Way, and perhaps indicating that various physical effects that are not yet included (e.g., localized star formation feedback, including supernovae) are not important in regulating molecular mass fractions.

To gauge if the ISM of the main disk region achieves a quasi-statistical equilibrium state from 200 to 300 Myr, table 2 summarizes the values of f_GMC and |$f_{\rm GMC,H_{2}}$|⁠. We see that in most runs the ISM is in a relatively steady state during this period, with little (≲10%) change in these metrics. However, Runs I (G₀ = 4) and V (variable G₀ and ζ) are a little different, since the fragmentation of the outer disk regions is delayed and is continuing even after 200 Myr. Thus, from 200 to 300 Myr, f_GMC increases by about 20% in these runs. Table 2 also shows the fractions of the total H₂ mass in the main disk region that are contained in the defined GMCs, i.e., |$M_\mathrm{GMC,\mathrm{H_{2}}}/M_\mathrm{disk,\mathrm{H_{2}}}$|⁠. These fractions are typically >80%. We also list the fractions, f_{GMC, CO}, of the disk gas mass that is in “GMCs” and “CO-rich,” and f_{GMC, CO}/f_GMC. Again, these quantities are relatively stable, except for Runs I and V.

Table 2.

Properties of the ISM at 200 and 300 Myr for each simulation run.

Run time	f _GMC		\|$f_{\rm GMC,H_{2}}$\|		\|$f_{\rm GMC,H_{2}}/f_{\rm GMC}$\|		\|$M_\mathrm{GMC,\mathrm{H_{2}}}/M_\mathrm{disk,\mathrm{H_{2}}}$\|		f _{GMC, CO}		f _{GMC, CO}/f_GMC
(Myr)	200	300	200	300	200	300	200	300	200	300	200	300
I	0.452	0.535	0.319	0.377	0.706	0.705	0.857	0.859	0.395	0.468	0.874	0.875
II	0.644	0.682	0.467	0.478	0.706	0.714	0.791	0.814	0.634	0.673	0.984	0.987
III	0.634	0.673	0.447	0.474	0.705	0.704	0.844	0.847	0.547	0.597	0.863	0.887
IV	0.641	0.667	0.450	0.469	0.702	0.703	0.840	0.839	0.382	0.456	0.596	0.684
V	0.561	0.672	0.381	0.459	0.680	0.683	0.890	0.889	0.177	0.388	0.316	0.577
VI	0.678	0.721	0.479	0.509	0.706	0.706	0.897	0.901	0.500	0.576	0.737	0.799

Run time	f _GMC		\|$f_{\rm GMC,H_{2}}$\|		\|$f_{\rm GMC,H_{2}}/f_{\rm GMC}$\|		\|$M_\mathrm{GMC,\mathrm{H_{2}}}/M_\mathrm{disk,\mathrm{H_{2}}}$\|		f _{GMC, CO}		f _{GMC, CO}/f_GMC
(Myr)	200	300	200	300	200	300	200	300	200	300	200	300
I	0.452	0.535	0.319	0.377	0.706	0.705	0.857	0.859	0.395	0.468	0.874	0.875
II	0.644	0.682	0.467	0.478	0.706	0.714	0.791	0.814	0.634	0.673	0.984	0.987
III	0.634	0.673	0.447	0.474	0.705	0.704	0.844	0.847	0.547	0.597	0.863	0.887
IV	0.641	0.667	0.450	0.469	0.702	0.703	0.840	0.839	0.382	0.456	0.596	0.684
V	0.561	0.672	0.381	0.459	0.680	0.683	0.890	0.889	0.177	0.388	0.316	0.577
VI	0.678	0.721	0.479	0.509	0.706	0.706	0.897	0.901	0.500	0.576	0.737	0.799

*From left to right: mass fraction of total disk gas in GMCs (f_GMC); mass fraction of total disk gas in GMCs and in the H₂ phase (⁠|$f_{\rm GMC,H_{2}}$|⁠); |$f_{\rm GMC,H_{2}}/f_{\rm GMC}$|⁠; GMC H₂ phase mass compared to the whole disk’s H₂ mass; mass fraction of total disk gas in GMCs that is also “CO rich,” i.e., with n_CO/n_H > 10⁻⁵ (f_{GMC, CO}); mass fraction of GMC gas that is “CO rich,” i.e., f_GMC,CO/f_GMC.

Table 2.

Properties of the ISM at 200 and 300 Myr for each simulation run.

Run time	f _GMC		\|$f_{\rm GMC,H_{2}}$\|		\|$f_{\rm GMC,H_{2}}/f_{\rm GMC}$\|		\|$M_\mathrm{GMC,\mathrm{H_{2}}}/M_\mathrm{disk,\mathrm{H_{2}}}$\|		f _{GMC, CO}		f _{GMC, CO}/f_GMC
(Myr)	200	300	200	300	200	300	200	300	200	300	200	300
I	0.452	0.535	0.319	0.377	0.706	0.705	0.857	0.859	0.395	0.468	0.874	0.875
II	0.644	0.682	0.467	0.478	0.706	0.714	0.791	0.814	0.634	0.673	0.984	0.987
III	0.634	0.673	0.447	0.474	0.705	0.704	0.844	0.847	0.547	0.597	0.863	0.887
IV	0.641	0.667	0.450	0.469	0.702	0.703	0.840	0.839	0.382	0.456	0.596	0.684
V	0.561	0.672	0.381	0.459	0.680	0.683	0.890	0.889	0.177	0.388	0.316	0.577
VI	0.678	0.721	0.479	0.509	0.706	0.706	0.897	0.901	0.500	0.576	0.737	0.799

Run time	f _GMC		\|$f_{\rm GMC,H_{2}}$\|		\|$f_{\rm GMC,H_{2}}/f_{\rm GMC}$\|		\|$M_\mathrm{GMC,\mathrm{H_{2}}}/M_\mathrm{disk,\mathrm{H_{2}}}$\|		f _{GMC, CO}		f _{GMC, CO}/f_GMC
(Myr)	200	300	200	300	200	300	200	300	200	300	200	300
I	0.452	0.535	0.319	0.377	0.706	0.705	0.857	0.859	0.395	0.468	0.874	0.875
II	0.644	0.682	0.467	0.478	0.706	0.714	0.791	0.814	0.634	0.673	0.984	0.987
III	0.634	0.673	0.447	0.474	0.705	0.704	0.844	0.847	0.547	0.597	0.863	0.887
IV	0.641	0.667	0.450	0.469	0.702	0.703	0.840	0.839	0.382	0.456	0.596	0.684
V	0.561	0.672	0.381	0.459	0.680	0.683	0.890	0.889	0.177	0.388	0.316	0.577
VI	0.678	0.721	0.479	0.509	0.706	0.706	0.897	0.901	0.500	0.576	0.737	0.799

*From left to right: mass fraction of total disk gas in GMCs (f_GMC); mass fraction of total disk gas in GMCs and in the H₂ phase (⁠|$f_{\rm GMC,H_{2}}$|⁠); |$f_{\rm GMC,H_{2}}/f_{\rm GMC}$|⁠; GMC H₂ phase mass compared to the whole disk’s H₂ mass; mass fraction of total disk gas in GMCs that is also “CO rich,” i.e., with n_CO/n_H > 10⁻⁵ (f_{GMC, CO}); mass fraction of GMC gas that is “CO rich,” i.e., f_GMC,CO/f_GMC.

In figure 13 we show several diagnostic tracers of the global disk of Run VI at 250 Myr: [C ii] 158 μm, C i 609 μm, ¹²CO(J = 2–1), ¹³CO(J = 2–1), ¹³CO(J = 3–2), and ¹²CO(J = 8–7). Note that the adopted abundance ratio of ¹³C to ¹²C is 1/60. In constructing these maps we have simply summed the local emissivities and have not accounted for optical depth. However, such optical depth effects are partially accounted for in the local 1D PDR models. This will mostly affect the ¹²CO(2–1) results, which should be regarded as illustrative and should not be meant for quantitative assessment of line intensities. However, the other CO tracers are expected to be closer to being optically thin and thus more accurately represented by these maps.

Galactic disk for Run VI (radially variable G0, constant ζ, 4 pc resolution) at 250 Myr. Images are 20 kpc across. From top left to bottom right are shown integrated intensity maps of: (a) [C ii] 158 μm; (b) C i 609 μm; (c) 12CO(J = 2–1); (d) 13CO(J = 2–1); (e) 13CO(J = 3–2); (f) 12CO(J = 8–7).

Fig. 13.

Galactic disk for Run VI (radially variable G₀, constant ζ, 4 pc resolution) at 250 Myr. Images are 20 kpc across. From top left to bottom right are shown integrated intensity maps of: (a) [C ii] 158 μm; (b) C i 609 μm; (c) ¹²CO(J = 2–1); (d) ¹³CO(J = 2–1); (e) ¹³CO(J = 3–2); (f) ¹²CO(J = 8–7).

As expected, the [C ii] 158 μm emission is much more diffuse than the CO emission, i.e., tracing not only the cooler, denser structures, but also warmer and lower-density regions (n_H ∼ 10–100 cm⁻³) that are near the transition from the atomic to molecular phase. We see that CO emission lines are emitted from much more discrete, localized clouds. The ¹²CO(J = 2–1), ¹³CO(J = 2–1), and ¹³CO(J = 3–2) intensity maps show similar structures. On the scales shown in figure 13, ¹²CO(J = 8–7) also shows similar morphologies, but with lower overall intensities.

Figure 14 shows the area-weighted integrated [C ii] (top panel), ¹³CO(J = 2–1) (middle panel), and ¹²CO(J = 2–1) (bottom panel) line intensities along the line of sight as functions of galactocentric radii for face-on views of the disks at 250 Myr. Comparing runs with the same temperature floor we can see that, overall, a stronger FUV radiation field leads to higher [C ii] intensities, but has less influence on CO lines because it attenuates significantly through the dense regions where CO lines are strong.

Area-weighted integrated [C ii] 158 μm (top panel), 13CO(J = 2–1) (middle panel), and 12CO(J = 2–1) (bottom panel) emission line intensities along the line of sight as a function of galactocentric radii for face-on views of the disks of Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black)—all results for t = 250 Myr.

Fig. 14.

Area-weighted integrated [C ii] 158 μm (top panel), ¹³CO(J = 2–1) (middle panel), and ¹²CO(J = 2–1) (bottom panel) emission line intensities along the line of sight as a function of galactocentric radii for face-on views of the disks of Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black)—all results for t = 250 Myr.

3.2 Examples of kiloparsec patches

To examine the structure of the ISM on scales ≲ 1 kpc, we extract, as an example, 1 kpc disk patches from the simulations at galactocentric radius of 4.25 kpc and at 250 Myr, and visualize their mass surface density and temperature structures in figure 15. These are the locations and times extracted from the TT09 simulation and are used as initial conditions for higher-resolution simulations by Van Loo, Butler, and Tan (2013), Van Loo, Tan, and Falle (2015), Butler, Tan, and Van Loo (2015), and Butler et al. (2017).

Fig. 15.

(a) Top row: The mass surface density structures of 1 kpc-wide patches of the disks (averaged vertically over a 2 kpc vertical extent centered on the disk midplane) centered at (x, y) = (4.25, 0) kpc at 250 Myr, extracted from Runs I to VI (left to right). This part of the disk is in a quasi-steady state at this time with respect to the distribution of ISM phases for all these simulation runs, but large variations still occur on ∼kpc scales. (b) Bottom row: As (a), but now showing mass-weighted temperature structures.

The patches show large variations from run to run, which is caused by the chaotic nature of small-scale ISM, including GMC, evolution. General features include the presence of elongated, filamentary structures, some of which may be related to tidal tails around denser clouds. In the patches where there are high numbers of dense clouds, there is clear evidence for interactions.

The PDFs of mass surface density (calculated with a fixed linear resolution: 8 pc for Runs I–V and 4 pc for Run VI) are shown in figure 16. Again, these show a variety of shapes, but generally peak at a few M_⊙ pc⁻², with high-end power-law tails. A great deal of variation is due simply to stochastic sampling within a galaxy: for example, the region extracted from Run VI only has a couple of small GMCs and so has the smallest areal fraction of material above, e.g., 10 M_⊙ pc⁻².

Fig. 16.

Probability distribution function of gas mass surface density evaluated in the 1 kpc patch regions centered at (x, y) = (4.25, 0) pc at 250 Myr for Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black).

We also display a series of kiloparsec patches from Run VI, centering at r = 3, 4.25, 5.25, and 7 kpc (figure 17). These regions contain a great variety of structures, as seen in their mass surface densities, mass-weighted number densities, and temperatures, and integrated intensities of emission lines [C ii] 158 μm, ¹²CO(J = 2–1), ¹³CO(J = 2–1), ¹³CO(J = 3–2), and ¹²CO(J = 8–7) along the line of sight (z-direction). Here in the Σ maps, we also show the center of mass locations of identified “GMCs.” As noted earlier, [C ii] 158 μm line emission, tracing warmer and lower-density (n_H ∼ 10–100 cm⁻³) gas, is much more diffuse and extended than that of CO lines.

Fig. 17.

Examples of 1 kpc-sized patches (integrated over 2 kpc in the z-direction), extracted from the main disk of Run VI at 250 Myr, centering at r = 3, 4.25, 5.25, and 7 kpc (columns from left to right) in the midplane. The rows from top to bottom show the total gas mass surface density (Σ), mass-weighted number density of H nuclei (n_H), mass-weighted temperature (T), and integrated [C ii] 158 μm, ¹²CO(J = 2–1), ¹³CO(J = 2–1), ¹³CO(J = 3–2), and ¹²CO(J = 8–7) line intensities. The centers of mass of identified clouds are marked as white points in the top row, which also show the local velocity field, i.e., after subtracting the mean circular orbital velocity at each location.

In principle, the statistics of line and dust continuum emission from ensembles of such kpc patches, or whole galaxies, may be compared to observations of nearby galaxies, e.g., with ALMA or SOFIA. Such data could first be used to constrain a global model for a galactic disk [e.g., rotation curve, total gas Σ(r) profile], then allowing a tailored simulation of a particular system. Then the detailed statistics of the distributions of emissivities could be used to test the validity of the simulations, e.g., comparing the effects of including B-fields and/or methods of implementing feedback. Such comparisons are a longer-term goal of this project.

4 GMC physical properties

In this section we show the physical properties of the identified “GMCs,” which, recall, are connected, locally peaked structures identified by having n_H ≥ 100 cm⁻³ (see section 2). Our analysis methods follow those of TT09. We focus on GMC properties during the period from 200 to 300 Myr when the disks are in quasi-statistical equilibrium in terms of their global ISM properties, as shown in the previous section. Figure 18 compares the PDFs of several GMC properties for all six runs at 300 Myr. Figure 19 presents the time evolution of these PDFs from 200 to 300 Myr for Run VI.

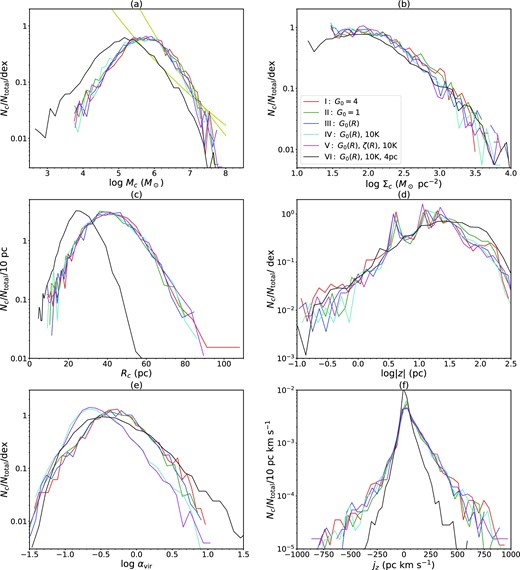
$Probability distribution functions of GMC properties for Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black) at 300 Myr (see legend). The panels show: (a) mass; (b) mass surface density; (c) average radius; (d) center-of-mass vertical position; (e) virial parameter; (f) specific angular momenta. The straight yellow lines in (a) show power-law fits to the high-end GMC mass spectra ${d}N_{\rm c}/{d}{\,\,} {\log }{\,\,} M_{\rm c} \propto M_{\rm c}^{-\alpha }$ with α = 1.43 ± 0.08 and 0.93 ± 0.03 for Runs IV and VI, respectively, at 300 Myr (see text).$

Fig. 18.

Probability distribution functions of GMC properties for Runs I (red), II (green), III (blue), IV (cyan), V (magenta), and VI (black) at 300 Myr (see legend). The panels show: (a) mass; (b) mass surface density; (c) average radius; (d) center-of-mass vertical position; (e) virial parameter; (f) specific angular momenta. The straight yellow lines in (a) show power-law fits to the high-end GMC mass spectra |${d}N_{\rm c}/{d}{\,\,} {\log }{\,\,} M_{\rm c} \propto M_{\rm c}^{-\alpha }$| with α = 1.43 ± 0.08 and 0.93 ± 0.03 for Runs IV and VI, respectively, at 300 Myr (see text).

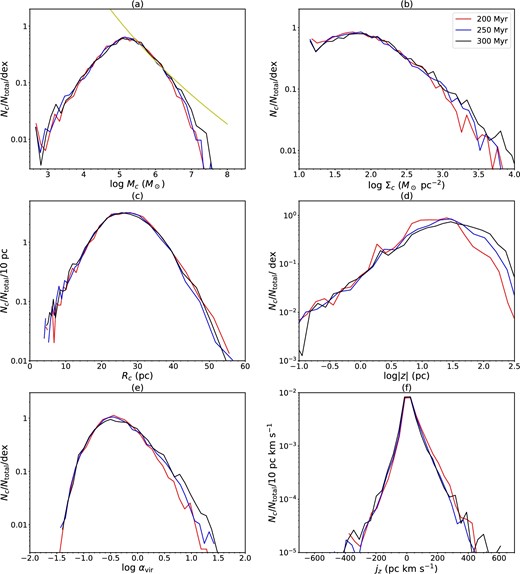
$Same as figure 18, but now showing results for Run VI at 200, 250, and 300 Myr. The panels show: (a) mass; (b) mass surface density; (c) average radius; (d) center-of-mass vertical position; (e) virial parameter; (f) specific angular momenta. The straight yellow line in (a) shows a power-law fit to the high-end GMC mass spectrum ${d}N_c/{d}{\,\,} {\log }{\,\,} M_{\rm c} \propto M_{\rm c}^{-\alpha }$ with α = 0.93 at 300 Myr.$

Fig. 19.

Same as figure 18, but now showing results for Run VI at 200, 250, and 300 Myr. The panels show: (a) mass; (b) mass surface density; (c) average radius; (d) center-of-mass vertical position; (e) virial parameter; (f) specific angular momenta. The straight yellow line in (a) shows a power-law fit to the high-end GMC mass spectrum |${d}N_c/{d}{\,\,} {\log }{\,\,} M_{\rm c} \propto M_{\rm c}^{-\alpha }$| with α = 0.93 at 300 Myr.

GMC mass (M_c) PDFs are shown in figure 18a. For Runs I to V (i.e., with 8 pc resolution), these PDFs show a broad peak near 5 × 10⁵ M_⊙, with clouds seen with masses from ∼10⁴ M_⊙ to ∼5 × 10⁷ M_⊙. We see that these GMC mass functions are fairly insensitive to the modeled PDR and CR physics. However, the linear resolution of the simulation has a significant effect; i.e., Run VI has a GMC mass function that peaks at lower masses. We fit power laws of the form |${d}N_{\rm c}/{d}{\,\,}{\log }{\,\,} M_{\rm c} \propto M_{\rm c}^{-\alpha }$| to the high-end range (>10⁶ M_⊙ for Runs I–V; >10^5.5 M_⊙ for Run VI), with errors set from Poisson counting statistics in each mass interval. Runs I–V have values of α ≃ 1.4, while Run VI has α ≃ 0.93 ± 0.03. Thus we see that the resolution of the simulation has a significant effect on the mass function of the GMCs, as defined as our selection criteria of section 2. Note that our selection of GMCs in Run VI uses the same deblending distance parameter of 32 pc as the other runs, so the difference in the mass function arises because of Run VI’s ability to better resolve fragmentation of the structures.

Figure 19a shows that the GMC mass function remains very constant from 200 to 300 Myr for Run VI, with the most noticeable evolution being a small increase in the number of the most massive clouds by the time of 300 Myr. As discussed earlier, detailed results of GMC mass functions are likely influenced by the lack of localized star formation and feedback in these simulations, since diffuse FUV feedback on its own is ineffective at destroying GMCs. However, since the mass fraction of gas in GMCs is quite stable (section 3), we hypothesize that in these simulations it is the process of GMC collisions that act to regulate the GMC population, i.e., keeping ∼1/3 of the gas in the diffuse intercloud medium.

We can compare the simulated GMC mass distributions to those observed in the Milky Way and M33, which can also be fitted with a power law at their high-mass end. In the Milky Way, α is estimated to be ∼0.6–0.8 (Williams & McKee 1997), based on analysis of ¹²CO(1–0) line survey data. In the inner (≤2 kpc) region of M 33, with ∼50 pc resolution, Gratier et al. (2012) measured α ≃ 0.6 ± 0.2 [assuming a one-to-one correspondence of CO(2–1) line luminosity with GMC mass]. At galactocentric distances >2 kpc, they measured α ≃ 1.3 ± 0.2. While the values of α seen in Run VI (i.e., α ≃ 0.93 ± 0.03) are similar to the above observed values, we caution that the numerical results are not converged (i.e., with the 4 pc resolution of Run VI, we see a much shallower high-end power-law slope). At the same time, one must recognize that observational results will also likely depend on the linear resolution achieved and the particular method of GMC identification and mass measurement. Most observational studies of GMC mass functions use ¹²CO line emission to identify the clouds, followed by empirical relations to convert line luminosities to mass. Since our PDR modeling does not yet include accurate treatment of the global radiative transfer effects that are important for the fluxes of optically thick lines, like ¹²CO(2–1), we defer more detailed comparisons of the GMC mass (and line luminosity) functions until a future paper.

Figure 18b shows the distributions of mass surface densities, |$\Sigma _{\rm c}\equiv M_{\rm c}/(\pi R_{\rm c}^2)$|⁠, of the clouds as viewed along the z-axis, perpendicular to the disk, at 300 Myr. Here, R_c is the average projected radius of the GMCs in the disk plane, discussed below. The distributions of mass surface densities are very similar to each other among the six runs, with a broad peak near ∼60 M_⊙ pc⁻² (the peak becomes the most apparent in Run VI), which falls off with a power-law tail at the high-Σ end. The minimum value of Σ_c can be understood as simply being related to that of a GMC which is only resolved with a single layer of grid cells in the vertical direction: i.e., ≃28 M_⊙ pc⁻² for an 8 pc-sided cell filled with gas at n_H = 100 cm⁻³, and half this value for the 4 pc resolution Run VI. On the other hand, a few, extreme “GMCs” have Σ ∼ 10⁴ M_⊙ pc⁻². Figure 19b shows that the PDFs of Σ for Run VI remain quite constant from 200 to 300 Myr. There is slight growth in the high-Σ tail of the distribution, but this involves only a relatively small number of clouds.

The mass surface density of the peak of the PDF of the Run VI GMCs is similar to the mean value of ∼200 M_⊙ pc⁻² derived by Solomon et al. (1987) from a ¹²CO(1–0) survey of the Galaxy. Heyer et al. (2009) have derived smaller values ∼100 M_⊙ pc⁻² based on better-sampled ¹³CO surveys (see discussion of Tan et al. 2013). Considering the difference in GMC identifications between observations based solely on molecular line (CO) emission and our simulated clouds, the Σ values of our simulated GMCs are broadly consistent with observations. Nevertheless, we again expect that additional physics of B-fields, star formation, and localized feedback all will act to reduce the Σ of the GMC population.

Figure 18c shows the PDFs of average GMC radius, R_c ≡ (A_c/π)^1/2, where A_c is the projected area viewed along the z-axis. Given the results for the PDFs of M_c and Σ_c, the similarity of the PDFs among Runs I to V is not surprising. Their PDFs peak at R_c ≃ 40 pc, and then extend up to ∼100 pc. For Run VI, the peak of the PDF is near 25 pc and the largest GMCs have radii of ∼50 pc. Figure 19c shows the constancy of the R_c distribution from 200 to 300 Myr for Run VI. These results show that the sizes of identified “GMCs” depend on the resolution of the simulation and are thus not numerically converged. Still, the sizes of the clouds in Run VI are comparable to those observed for GMCs in the Galaxy (e.g., Miville-Deschênes et al. 2017).

Figure 18d shows the distribution of the magnitudes of the vertical distances of GMC centers of mass from the disk midplane. Most clouds are located within a narrow range of ∼30 pc from the midplane. The vertical half-scale-height of the population of GMCs is |z|_1/2 = 26 pc, i.e., the median value of |z|. This half-scale-height is similar to the typical radii of the GMCs, demonstrating that the GMCs interact as part of a quasi-2D distribution, which is an assumption of the GMC–GMC collision models of Gammie, Ostriker, and Jog (1991) and Tan (2000), discussed below. A small number of GMCs are at relatively large vertical displacements from the midplane. Figure 19d shows that the numbers of these high-|z| GMCs increases moderately from 200 to 300 Myr in Run VI. All vertical displacements of the GMCs in these simulations are driven by gravitational forces acting between the self-gravitating clouds. Generally the largest velocities that will be achieved in such interactions will be approximately equal to the escape speed from the clouds. As shown in figure 8b, the gas velocity dispersion in the disk plane can reach 30 km s⁻¹ at late times in the inner region of the galaxy. A larger range of |z| at later times is consistent with the growth of some GMCs to larger masses and higher densities, as discussed above.

Figure 18e shows the distribution of GMC virial parameters, defined as (Bertoldi & McKee 1992)

\begin{equation} \alpha _{\rm vir} \equiv \frac{5\sigma _{\rm c}^2 R_{\rm c}}{G M_{\rm c}}, \end{equation}

(8)

where σ_c is the mass-averaged 1D velocity dispersion of the cloud, i.e., |$\sigma _{\rm c} \equiv (c_{\rm s}^2+\sigma ^2_{\mathrm{nt},\rm c})^{1/2}$| and |$\sigma ^2_{\mathrm{nt},\rm c}$| is the 1D velocity dispersion about the center-of-mass velocity of the cloud. A value of α_vir = 1 implies a spherical, uniform cloud with negligible surface pressure and magnetic fields virialized, while α_vir < 2 indicates this type of cloud is gravitationally bound. The PDFs of α_vir are relatively broad, but tending to peak at values <1. The effect of the 300 K temperature floor is clearly seen in Runs I, II, and III, since it sets an effective minimum velocity dispersion of about 1.6 km s⁻¹. Runs IV and V have PDFs of α_vir that peak at significantly lower values. Interestingly, the distribution of α_vir rises again in the GMCs in the higher-resolution simulation, Run VI. Figure 19 shows that this distribution remains nearly constant from 200 to 300 Myr. At 300 Myr, its median value is α_vir ≃ 0.45. Most (78%) of the GMCs are gravitationally bound, consistent with the observational results of Roman-Duval et al. (2010), as analyzed by Tan, Shaske, and Van Loo (2013). Giant molecular clouds that are unbound are likely due to the dynamical effects of strong gravitational interactions, including recent collisions, between GMCs.

Figure 18f shows the distribution of GMC-specific angular momenta about a rotation axis through the center of mass perpendicular to the disk plane, i.e., j_z. Positive values of j_z indicate prograde rotation, i.e., in the same sense as the orbital motion of the galaxy, while negative values indicate retrograde rotation. The distributions are similar to each other among Runs I–V, showing a modest excess of prograde over retrograde GMCs. The fraction of retrograde GMCs is f_retro ≃ 0.28 for these GMC populations. The distribution in Run VI is narrower, as expected since GMCs are smaller, and its value of f_retro ≃ 0.36 is slightly greater than the results of the other runs. Figure 19f shows that the Run VI PDF of j_z does not change significantly during the period from 200 to 300 Myr. As discussed by TT09 (see also Dobbs 2008; Dobbs et al. 2011), f_retro may be a useful diagnostic of the role of GMC–GMC collisions in a galaxy population. Large values of f_retro may indicate that GMCs are collisionally evolved. Our results are consistent with observations showing that retrograde clouds are nearly as common as prograde ones (Blitz 1993; Phillips 1999; Rosolowsky et al. 2003; Imara & Blitz 2011; Imara et al. 2011).

5 GMC collisions

Shear-driven GMC–GMC collisions have been proposed as a mechanism to trigger star cluster formation, which could then explain the SFRs of disk galaxies and circumnuclear starbursts (Tan 2000; see also TT09; Tan 2010; Tan et al. 2013; Suwannajak et al. 2014). This model assumes that the galactic disk has a Toomre parameter Q ∼ 1 and a significant fraction, f_GMC ∼ 0.5, of its gas mass in self-gravitating clouds, i.e., “GMCs,” which occupy an essentially 2D distribution in the disk plane (i.e., the scale height of the GMCs is similar to the size of the clouds). These conditions were met by the disk simulated by TT09 and are also achieved by the new disk simulations presented in this paper. Under such conditions, gravitational interactions between GMCs lead to an increase in the velocity dispersion of the clouds, which is eventually balanced by damping by GMC collisions (Gammie et al. 1991). These “peculiar motions” of GMCs with respect to their local circular velocity cause GMCs to interact with other clouds that are on orbits with slightly different mean galactocentric radii. For a population of equal-mass GMCs, typical collisions occur between clouds that have initial mean orbital separations, i.e., collision impact parameters, of b ∼ 1.6 r_t with a range of Δb ∼ r_t, where r_t = (1 − β)^−2/3(2M_c/M_gal)^1/3r is the tidal radius of the clouds, with β ≡ d ln v_circ/d ln r, and M_gal is the total galactic mass interior to the galactocentric radius r.

Under these conditions, the average rate of GMC–GMC collisions is estimated to be (Tan 2000; see also Tan et al. 2013):

\begin{eqnarray} t_{\rm coll} & \simeq & \frac{1}{2} \frac{\lambda _{\rm mfp}}{v_{\rm s}(b=1.6{\,\,}r_{\rm t})} \end{eqnarray}

(9)

\begin{eqnarray} & \simeq & \frac{1}{2 b^\prime (\Omega - {d}v_{\rm circ}/{d}r){\cal N}_{\rm A} r_{\rm t}^2 f_{\rm G}}, \end{eqnarray}

(10)

where λ_mfp is the mean free path between collisions, v_s is the shear velocity in the disk for orbits separated by a given initial impact parameter, i.e.,

\begin{equation} v_{\rm s} = b (\Omega - {d}v_{\rm circ} / {d}r), \end{equation}

(11)

b′ ≡ b/r_t ≃ 1.6, Ω = v_circ/r = 2π/t_orb, |${\cal N}_{\rm A}$| is the number of GMCs per unit area, and f_G ∼ 0.5 is the fraction of strong gravitational encounters that lead to collision. This fraction depends on the physical size of the GMCs and is somewhat uncertain. For |${\cal N}_{\rm A}\simeq f_{\rm GMC} \Sigma _{\rm g}/\bar{M}_{\rm c}$| and |$\sigma _{\rm g}\simeq (G\bar{M}_{\rm c}\kappa )^{1/3}(1.0-1.7\beta )$| (Gammie et al. 1991), we have

\begin{eqnarray} t_{\rm coll} & \simeq & \frac{0.15 Q t_{\rm orb}}{b^\prime f_{\rm GMC} f_{\rm G} (1.0-0.7\beta )}, \end{eqnarray}

(12)

\begin{eqnarray} & \rightarrow & 0.19 t_{\rm orb}/f_{\rm GMC}, \end{eqnarray}

(13)

where the last evaluation is for constant v_circ, i.e., β = 0, and for f_G = 0.5. If most star formation is initiated by GMC collisions, then this result predicts Σ_SFR ∝ Σ_gΩ(1.0 − 0.7β), i.e., a modification of the “dynamical” Kennicutt–Schmidt relation observed by Kennicutt (1998), and further tested in resolved nearby galaxies by Leroy et al. (2008, 2013), Momose et al. (2010), Tan (2010), and Suwannajak, Tan, and Leroy (2014).

By tracking GMCs in global galactic disk simulations, TT09 measured t_coll/t_orb as a function of r, finding typical values of ≃0.2, with a tendency for this ratio to decrease gradually with increasing r. Giant molecular clouds with M_c > 10⁶ M_⊙ had t_coll/t_orb ∼ 0.1; then, note that t_coll is the average time between collisions of these massive GMCs with all other GMCs. Note also that in the simulations there are effects of a range of GMC masses, as well as collective interactions, i.e., in and around GMC complexes, which are not accounted for in the simple analytic estimates that are based on idealized binary collision rates. There can also be systematic variations of |${\cal N}_{\rm A}$| and r_t with location in the simulated disk galaxy. To account for these, Tan, Shaske, and Van Loo (2013) tested the prediction of equation (10) directly in annuli in the TT09 disk, finding good agreement: in particular, the radial gradient in t_coll/t_orb was accounted for by systematic variations in |${\cal N}_{\rm A}$| and r_t (e.g., partly because of variations in the average GMC mass |$\bar{M}_{\rm c}$| with a galactocentric radius), and the faster collision rate of more massive clouds due to their larger tidal radii.

In this section we carry out a similar analysis of the GMC collisions in our simulated disks, as well as examining basic properties of the collisions, including mass ratios and relative velocities. We also examine the injection rate of “turbulent momentum” into GMCs that may help to explain the maintenance of their internal turbulence and thus their overall structural properties.

5.1 Mass ratios of colliding GMCs

We show the PDFs of mass ratios (M₂/M₁, where M₂ is defined as the smaller mass) of colliding GMCs in figure 20 for Runs I to VI during the simulation time 200–300 Myr. We see that the typical mass ratio of colliding GMCs peaks close to 1 in all the simulations; i.e., collisions can be described as “major mergers.” This PDF is not a natural result of the cloud mass functions shown in figure 18a, since the mass ratio of randomly selected pairs of GMCs is much broader (figure 20). Instead, it is caused by the collision rate being higher for more massive GMCs, given their larger tidal radii.

Fig. 20.

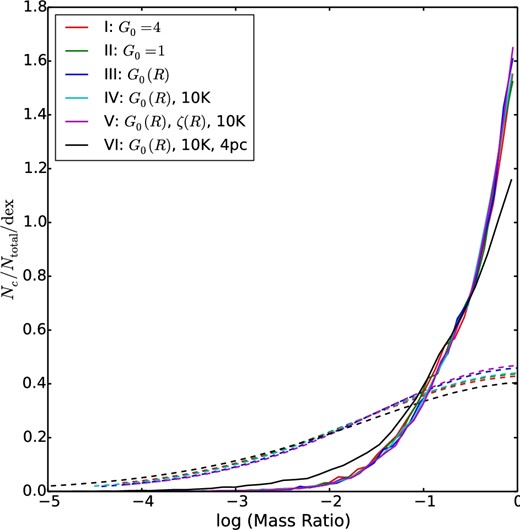
Probability density functions of mass ratios of colliding GMCs in Runs I–VI from 200 to 300 Myr (solid lines; see legend). The dashed lines with corresponding colors show the PDFs of mass ratios of randomly selected pairs of GMCs.

5.2 GMC collision speeds

The PDFs of the relative speeds v_coll of colliding GMCs are shown in figure 21. These distributions peak at ≃17 km s⁻¹ for Runs I–V and ≃13 km s⁻¹ for Run VI. These results are consistent with the collision speeds being set by the shear velocity from encounters with initial impact parameters of b ∼ (1–2 r_t), i.e., following equation (11). The smaller speeds in Run VI would then be caused by GMCs being of lower mass in this better-resolved simulation. Our results are comparable to recent observations on cloud collision (e.g., Fukui et al. 2015).

Fig. 21.

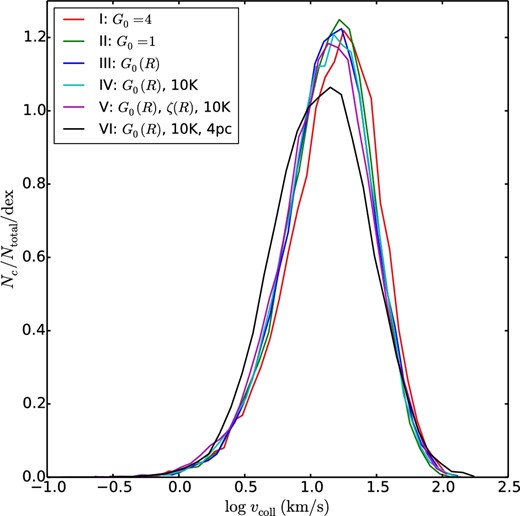
Probability desnity functions of relative speeds, v_coll, of colliding GMCs in Runs I–VI (see legend) evaluated from 200 to 300 Myr.

In figure 22 we show the mean relative speed of GMC collisions as a function of galactocentric radii, averaging in annuli. The relative speed is seen to be typically a slowly decreasing function of radius, with values of from ∼10 to 20 km s⁻¹ in Run VI when averaging over all GMCs, and from ∼15 to 30 km s⁻¹ for collisions involving the >10⁶ M_⊙ GMCs. These results, along with those of the colliding cloud mass ratios, can help to guide the initial conditions for numerical simulations of individual cases of GMC collisions (e.g., Wu et al. 2015, 2017a, 2017b).

$Average relative speeds of colliding GMCs in Runs I–VI from 200 to 300 Myr as a function of galactocentric radius. Blue solid lines show measured speeds in collisions of all GMCs; red solid lines show the speeds of collisions where one of the GMCs has a mass >106 M⊙. The diamonds show analytic estimates of the collision speeds following equation (14), which is based on the shear velocity at an impact parameter of b = 1.6 rt + $\bar{v}_{\rm ff}/6$ (see text), with the error bar showing 1 σ dispersion in these estimates based on GMC properties from 200 to 300 Myr.$

Fig. 22.

Average relative speeds of colliding GMCs in Runs I–VI from 200 to 300 Myr as a function of galactocentric radius. Blue solid lines show measured speeds in collisions of all GMCs; red solid lines show the speeds of collisions where one of the GMCs has a mass >10⁶ M_⊙. The diamonds show analytic estimates of the collision speeds following equation (14), which is based on the shear velocity at an impact parameter of b = 1.6 r_t + |$\bar{v}_{\rm ff}/6$| (see text), with the error bar showing 1 σ dispersion in these estimates based on GMC properties from 200 to 300 Myr.

We compare these speeds to the prediction of v_coll = v_s(b = 1.6 r_t), i.e., see equation (11). This is generally accurate to within ∼10%, but does systematically underestimate the collision speed. Gravitational acceleration is expected to boost the collision speed by an amount of up to the order of the free-fall speed, v_ff, though geometric effects and gas pressure gradients will lower the amount of the increase. We find that a collision speed given by

\begin{equation} v_{\rm coll} = v_{\rm s}(b=1.6{\,\,}r_{\rm t}) + (1/6) \bar{v}_{\rm ff}, \end{equation}

(14)

where |$\bar{v}_{\rm ff}=(2G\bar{M}_{\rm c}/\bar{R}_{\rm c})^{1/2}$|⁠, gives an accurate description of the mean collision speeds in Runs I–VI and for collisions between all GMCs and for those involving GMCs with >10⁶ M_⊙ (see figure 22).

5.3 GMC collision timescales

Figure 23 shows the ratio of mean GMC collision time to local orbital time, t_coll/t_orb, measured in simulation RunsI–VI from 200–300 Myr as a function of galactocentric radius averaged over all GMCs (blue lines) and for GMCs with >10⁶ M_⊙ (red lines). Note the local orbital time is given by

\begin{equation} t_\mathrm{orb} = 123(r/4 \mathrm{{\,\,}kpc})(v_{\rm circ}/200\:\mathrm{km\ s^{-1}})^{-1}\:\mathrm{Myr}. \end{equation}

(15)

The average values of t_coll/t_orb are measured by counting the total number of GMC collisions and the average total number of GMCs in annuli in the 200–300 Myr period, recognizing that each collision involves two GMCs, and using the value of t_orb appropriate for the middle of each annulus. We also calculate the theoretically expected value of t_coll/t_orb based on equation (10) for t_coll, which assumes f_G = 0.5 and uses the number of GMCs per unit area and the mean value of the GMC tidal radii, i.e., depending on M_c and r, as inputs. These estimates are made for the GMC populations measured in the simulation outputs every 1 Myr from 200 to 300 Myr, with the average results shown as diamond-shaped points for all GMCs (blue) and >10⁶ M_⊙ GMCs (red), with the vertical lines showing the 1 σ dispersions.

$Cloud collision timescales (measured from 200 to 300 Myr) relative to orbital timescale as a function of galactocentric radius for Runs I–VI (panels as labeled) averaged for all GMCs (blue solid lines) and for GMCs with Mc > 106 M$_{\odot}$ (red solid lines). Diamonds show the theoretical estimates from equation (10), averaged for GMC populations from 200 to 300 Myr, with the error bars showing the 1 σ standard deviation (see text).$

Fig. 23.

Cloud collision timescales (measured from 200 to 300 Myr) relative to orbital timescale as a function of galactocentric radius for Runs I–VI (panels as labeled) averaged for all GMCs (blue solid lines) and for GMCs with M_c > 10⁶ M|$_{\odot}$| (red solid lines). Diamonds show the theoretical estimates from equation (10), averaged for GMC populations from 200 to 300 Myr, with the error bars showing the 1 σ standard deviation (see text).

Similarly in the case of the results of TT09 and Tan, Shaske, and Van Loo (2013), the mean collision times averaged for all GMCs are seen to be a small fraction, ∼0.2, of an orbital time for Runs I–V, with a gradual decline in this ratio with increasing galactocentric radius. The more massive, >10⁶ M_⊙ GMCs also follow this trend, but have average values of t_coll/t_orb ∼ 0.1. In the higher-resolution Run VI these general results are also seen, but with collision timescales that are shorter by a factor of ∼0.5. The predictions of the two-body collision rate of GMCs in a shearing disk are quite accurate, especially for the more massive GMCs. The largest deviation is seen in Run VI for the “all GMC” case, where the observed timescale of collisions in the simulation can be about a factor of 0.5 shorter than the prediction. We suspect that this may be due to the GMCs being organized into larger complexes, where collisions are more frequent, with such collective effects being less apparent in the lower-resolution runs and when only considering the most massive GMCs.

In summary, at typical locations in the disk of ∼4 kpc, average times between GMC collisions are only ∼(10–20) Myr, with rates in approximate agreement with a simple model of two-body interactions set by shear in a thin disk (Gammie et al. 1991; Tan 2000). These values are relatively short compared to traditional estimates of cloud collision timescales of hundreds of Myr (e.g., McKee & Ostriker 2007). The difference arises because these traditional estimates consider a 3D (rather than 2D) geometry, invoke collision velocities set by GMC velocity dispersions (rather than shear velocities at one to two tidal radii), and have smaller collision cross sections using actual GMC sizes (rather than GMC tidal radii that result from gravitational focusing). The general implications of frequent GMC collisions are discussed below, starting with their ability to maintain turbulent motions within GMCs.

5.4 Maintenance of GMC turbulence

As reviewed by McKee and Ostriker (2007), observed GMC velocity dispersions are highly supersonic. However, from the results of numerical experiments, supersonic turbulence is expected to decay in ∼1 dynamical time, t_dyn = R_c/σ_c, where σ_c is the 1D internal velocity dispersion (Stone et al. 1998; Mac Low et al. 1998)—for α_vir ≃ 1, t_ff ≃ 0.5 t_dyn. Thus, maintenance of turbulence is a constraint on models of GMC formation and evolution.

McKee and Ostriker (2007) discussed two conceptual frameworks. First, GMCs are dynamic, transient, and largely unbound, with turbulence driven by large-scale colliding atomic flows that form the clouds (e.g., Heitsch et al. 2005; Vázquez-Semadeni et al. 2011; Inoue & Inutsuka 2012). These models do not naturally explain why most GMCs are bound with α_vir ∼ 1. More recent simulations with moderate strength B-fields show that it is difficult to compress the gas to observed GMC densities (e.g., Inoue & Inutsuka 2008; Körtgen & Banerjee 2015). Also, the required fast flows of H i around GMCs needed to form them quickly in ∼1t_dyn have not been observed. For example, Bihr et al. (2015) find approximately equal masses of H₂ and H i in the W 43 region out to radii of ∼140 pc. Thus, formation of the GMC in ∼1t_ff, i.e., ∼10 Myr, would require this H i to be converging radially on the W 43 GMC location at ∼10 km s⁻¹, which is an unlikely initial condition for the state of the gas before the GMC existed. Similarly, Rebolledo et al. (2017) find that the atomic mass around the Carina Nebula Gum 31 region (out to ∼70 pc) is only about 1/3 of the total (although optical depth corrections may provide a modest boost). In other words, locally, the mass fractions of gas that are in these GMCs are too large compared to the reservoir of H i, since in these scenarios one does not expect a very high efficiency of conversion of H i into a GMC. Similarly, it is unclear if such models are globally consistent with the relatively high mass fractions of gas in GMCs, at least inside the solar circle (e.g., Koda et al. 2016).

The second framework is that GMCs are formed by large-scale gravitational instabilities and are thus gravitationally bound with α_vir ∼ 1. Turbulence is maintained by contraction and then, later, star formation feedback (e.g., Goldbaum et al. 2011). While this paradigm may be relevant in regions of galaxies that are H i dominated, we argue below that in regions where a large fraction of gas is already organized into self-gravitating GMCs and their atomic envelopes, other processes become more important for controlling GMC dynamics and evolution.

A third paradigm of GMC evolution mediated by frequent GMC–GMC collisions has been presented by Tan (2000). The implications of this scenario for the maintenance of turbulence by frequent collisions have been discussed by Tan, Shaske, and Van Loo (2013). The rate of injection of “internal turbulent momentum” per GMC is |$\dot{p}_{\rm CC} = \bar{p}_{\rm CC}/\bar{t}_{\rm coll}$|⁠, where |$\bar{p}_{\rm CC}$| is the average internal turbulent momentum injected into a post-collision GMC. Note that |$\bar{p}_{\rm CC}$| is treated as a scalar quantity. It is evaluated by considering that each collision between two GMCs involves a certain amount of momentum being deposited into the resulting GMC, i.e., p_CC = M₁v₁ + M₂v₂, where v₁ and v₂ are the pre-collision velocities of the GMCs in the center of mass frame of the final cloud. Thus, in the case of equal-mass colliding GMCs, p_CC = 2 M_cv_coll/2 = M_cv_coll. Note that the pre-collision GMCs are expected to have a high degree of internal substructure, coupled together with moderately strong B-fields, and so we are assuming that the result of the collision is mostly a high degree of unbalanced shocks that generate internal turbulence in the post-collision cloud. Thus, in the limit of high efficiency of conversion of bulk collision momentum into internal turbulent momentum, we have

\begin{eqnarray} \dot{p}_{\rm CC} & = & \bar{M}_{\rm c} \bar{v}_{\rm coll}/ \bar{t}_{\rm coll}\nonumber \\ & = & \frac{b^\prime G^{1/3}}{2^{2/3}\pi \bar{f}_{\rm coll}}\left(\frac{\bar{M}_{\rm c} v_{\rm circ}}{r}\right)^{4/3}, \end{eqnarray}

(16)

where in the second line we have assumed the case of a flat rotation curve and where f_coll ≡ t_coll/t_orb.

In figure 24 we show the radial profiles of |$\dot{p}_{\rm CC}$| in the simulations, evaluated from 200 to 300 Myr and averaged over all GMCs. As expected from our previous results, the momentum injection rate per GMC is the highest in the inner galaxy. It is then seen to decline by a factor of ∼5 as one progresses outward to ∼8 kpc.

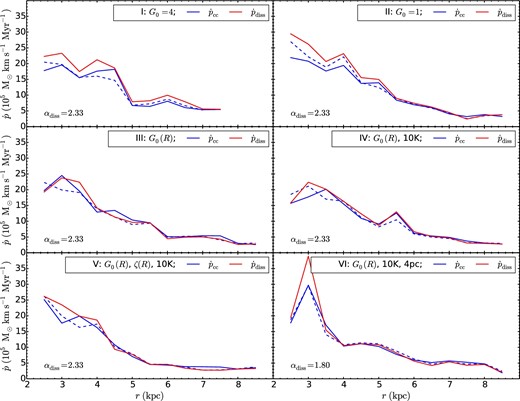
$Average rate of turbulent momentum injection per GMC, $\dot{p}\,_{\rm C\,C}$, as a function of galactocentric radius, measured from 200 to 300 Myr by summing over all recorded GMC collisions, for Runs I–VI (panels as labeled)—blue solid lines. The prediction from equation (16) is also indicated (blue dashed line). Also in the panels are shown estimates of the rate of dissipation of turbulent momentum per GMC, $\dot{p}_{\rm diss}$, due to internal shocks (red solid lines). The coefficient for this dissipation rate, αdiss, has been normalized separately for Runs I–V and for Run VI in order to give an approximate balance $\dot{p}_{\rm diss}\simeq \dot{p}_{\rm CC}$, with the values as indicated in the panels. The similarity of the radial profiles indicates that GMC collisions are driving internal turbulence in the GMCs, balancing the internal decay rate (see text).$

Fig. 24.

Average rate of turbulent momentum injection per GMC, |$\dot{p}\,_{\rm C\,C}$|⁠, as a function of galactocentric radius, measured from 200 to 300 Myr by summing over all recorded GMC collisions, for Runs I–VI (panels as labeled)—blue solid lines. The prediction from equation (16) is also indicated (blue dashed line). Also in the panels are shown estimates of the rate of dissipation of turbulent momentum per GMC, |$\dot{p}_{\rm diss}$|⁠, due to internal shocks (red solid lines). The coefficient for this dissipation rate, α_diss, has been normalized separately for Runs I–V and for Run VI in order to give an approximate balance |$\dot{p}_{\rm diss}\simeq \dot{p}_{\rm CC}$|⁠, with the values as indicated in the panels. The similarity of the radial profiles indicates that GMC collisions are driving internal turbulence in the GMCs, balancing the internal decay rate (see text).

The rate of dissipation of the total internal turbulent momentum, p_c, of a GMC can be expressed as (Tan et al. 2013):

\begin{eqnarray} \dot{p}_{\rm diss} & \equiv & - p_{\rm c}/(\alpha _{\rm diss}t_{\rm ff}) = -\sqrt{3}\bar{M}_{\rm c}\sigma _{\rm c}/(\alpha _{\rm diss}t_{\rm ff})\nonumber \\ & = & -2.19 \bar{\alpha }_{\rm vir}^{1/2}G\bar{M}_{\rm c}\bar{\Sigma }_{\rm c}/\alpha _{\rm diss}, \end{eqnarray}

(17)

where α_diss is a dimensionless constant. The turbulent energy dissipation rate has been measured in numerical simulations to be |$\epsilon _{\rm diss} = (1/2)(\dot{E}/{E})[l_0/(\sqrt{3}\sigma )]\simeq 0.6$| (see review by McKee & Ostriker 2007), so that α_diss ≃ 3.85 (in a cloud with α_vir ≃ 1 and l₀ = 2 R). Figure 24 also shows the radial profiles of |$\dot{p}_{\rm diss}$|⁠, but where we have allowed α_diss to vary (fixing a single value for Runs I–V, and another value for the higher-resolution Run VI) to obtain a close match between |$\dot{p}_{\rm diss}$| and |$\dot{p}_{\rm CC}$|⁠. This requires values of α_diss ≃ 2, i.e., a shorter dissipation timescale that is about half the theoretical expectation of ≃4 t_ff, which is not unexpected given the fact the GMCs in our simulations are only quite poorly resolved. Alternatively, agreement could be achieved at lower values of |$\dot{p}$| by reducing the efficiency of conversion of the bulk collision momentum to internal turbulent momentum to about 50% in equation (16). However, the most important point of figure 24 is that the radial profiles of |$\dot{p}_{\rm diss}$| and |$\dot{p}_{\rm CC}$| are very similar to each other, suggesting there is a physical link between them.

Finally, we balance the momentum injection rate due to cloud collisions, given by equation (16), with the dissipation rate within the clouds, given by equation (17), to predict typical GMC equilibrium mass surface density, |$\bar{\Sigma }_{\rm c, eq}$|⁠:

\begin{eqnarray} \bar{\Sigma }_{{\rm c, eq}} & = & 102 \bar{\alpha }_{\rm vir}^{-1/2} \frac{\alpha _{\rm diss}}{2} \frac{b^\prime }{1.6}\frac{0.2}{f_{\rm coll}} \left(\frac{\bar{M}_{\rm c}}{10^6{\,\,}M_{\odot }}\right)^{1/3}\nonumber \\ && \times \, \left(\frac{v_{\rm circ}}{200{\,\,}{\rm km{\,\,}s^{-1}}} \frac{4{\,\,}{\rm kpc}}{r} \right)^{4/3}{\,\,}M_{\odot }{\,\,}{\rm pc^{-2}}. \end{eqnarray}

(18)

Figure 25 shows the predicted radial dependence of |$\bar{\Sigma }_{\rm c,eq}$| from equation (18), which is calculated by assessing the values of |$\bar{M}_{\rm c}$|⁠, |$\bar{\alpha }_{\rm vir}$|⁠, and |$\bar{f}_{\rm coll}$| in each annulus. The figure also compares these estimates with the actual values of the mass surface densities of the GMCs in the simulations. Since the values of α_diss have been normalized so that |$\dot{p}_{\rm diss}\simeq \dot{p}_{\rm CC}$|⁠, we expect that |$\bar{\Sigma }_{\rm c,{\rm eq}}$| will on average be approximately equal to |$\bar{\Sigma }_{\rm c}$|⁠, as it is seen to be the case. Still, the close correspondence of the radial profiles of |$\bar{\Sigma }_{\rm c,eq}$| and |$\bar{\Sigma }_{\rm c}$|⁠, i.e., for a single value of α_diss, indicates that the average structural properties of these self-gravitating GMCs are being set by the injection of turbulent momentum from GMC collisions, balanced by its rate of decay at a rate inversely proportional to the local free-fall time.

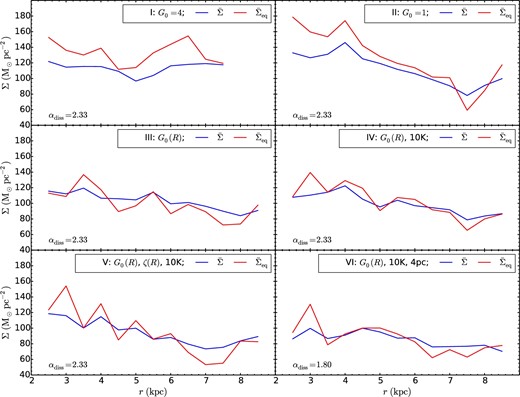
$Predicted mean GMC mass surface densities, $\bar{\Sigma }_{\rm eq}$ (red solid lines), measured from 200 to 300 Myr and shown as a function of galactocentric radius for Runs I–VI (panels as labelled). This estimate is based on a model of a balance between the momentum injection rate by GMC–GMC collisions and the internal dissipation rate resulting from supersonic turbulence, parameterized by αdiss (see text). The actual mean GMC mass surface densities, $\bar{\Sigma }_{\rm c}$ (blue solid lines), are also shown. The similarity between the radial profiles and Σ of the GMCs indicates that their structure can be explained by a simple model in which their internal turbulence is driven by GMC collisions and decays at a rate that is inversely proportional to the local free-fall time.$

Fig. 25.

Predicted mean GMC mass surface densities, |$\bar{\Sigma }_{\rm eq}$| (red solid lines), measured from 200 to 300 Myr and shown as a function of galactocentric radius for Runs I–VI (panels as labelled). This estimate is based on a model of a balance between the momentum injection rate by GMC–GMC collisions and the internal dissipation rate resulting from supersonic turbulence, parameterized by α_diss (see text). The actual mean GMC mass surface densities, |$\bar{\Sigma }_{\rm c}$| (blue solid lines), are also shown. The similarity between the radial profiles and Σ of the GMCs indicates that their structure can be explained by a simple model in which their internal turbulence is driven by GMC collisions and decays at a rate that is inversely proportional to the local free-fall time.

The equilibrium condition described by equation (18) is expected to be prone to instability, since as GMCs become denser and smaller, they dissipate their turbulent momentum at a faster absolute rate given their shorter free-fall times. At the same time, being smaller, they are expected to be less likely to undergo collisions. In reality, the processes of B-field support, star formation, and feedback are expected also to play a role in regulating the structure of these densest, collapsing GMCs. In the current simulations, lacking these processes, we expect that numerical diffusion and viscosity due to the fast, supersonic motion of the GMCs in their orbits in the galactic potential lead to some effective support of GMCs that become too small. In this way, a quasi-equilibrium distribution of GMC properties can still be established in these simulations (see also TT09).

5.5 General implications of short GMC collision timescales

Short GMC collision timescales have several important implications. First, we have already seen in subsection 5.4 that frequent GMC collisions could be an important driver of turbulence within the clouds. This mechanism could then regulate the structure of GMCs, i.e., setting their mass surface densities. The relative importance of GMC collisions and star formation feedback at driving internal turbulence needs to be assessed by future studies.

Second, GMC collisions may set the angular momentum distribution of the clouds, in particular helping to explain the relatively high fraction of retrograde rotation directions (Koda & Sofue 2006; Imara & Blitz 2011; Imara et al. 2011)—see also figures 18f and 19f.

Third, if t_coll is ≲30 Myr, then the collision time is shorter or similar to estimates of GMC lifetimes due to feedback (Williams & McKee 1997; Matzner 2002; Krumholz et al. 2006). This changes the nature of the lifecycle of GMCs, since they are continually changing and replenishing their gas content by collisions with other GMCs at rates similar to those at which they are losing gas by energy and momentum injection from massive stars. Thus, the “lifetime” of GMCs no longer has its traditional meaning, i.e., the time before the GMC is dispersed to the atomic or ionized phase of the ISM, since the clock is essentially “reset” after every major collision.

Fourth, GMC collisions may induce star formation, i.e., by compressing the gas that is already on the verge of gravitational instability in the pre-collision GMCs. The compressed region, with enhanced turbulence and large velocity gradients, may have its rates of ambipolar diffusion (e.g., Mouschovias 1991; Kunz & Mouschovias 2009) and/or reconnection diffusion (Lazarian & Vishniac 1999; Eyink et al. 2011) boosted, thus helping to remove magnetic flux and triggering gravitational instabilty and then star cluster formation. Shear-driven GMC collision is a process that naturally connects the kiloparsec scales of galactic orbital dynamics to the parsec scales of star cluster formation. There have been numerous claims of GMC collisions being the triggering agents of star cluster formation, e.g., Westerlund 2 (Furukawa et al. 2009; Ohama et al. 2010), M 20 (Torii et al. 2011), Cygnus OB 7 (Dobashi et al. 2014), and N 159 West (Fukui et al. 2015). GMC collisions are also a natural mechanism for creating the large observed dispersion in the star formation efficiencies in GMCs (e.g., Tan 2000; Lee et al. 2016).

6 Conclusions

We have simulated flat rotation curve galactic gas disks and investigated the dynamical evolution of their interstellar media and GMCs. Based on PDR models, we incorporated a self-consistent treatment of the ISM physics of the atomic to molecular phase transition under the influence of various background FUV radiation fields and CR ionization rates. We then explored the effects of different FUV intensities, including a model with a radial gradient designed to mimic the Milky Way galaxy. The effects of cosmic rays, including radial gradients in their heating and ionization rates, were also investigated. The final simulation in this series achieved 4 pc resolution across the ∼20 kpc global disk diameter, with heating and cooling followed down to ∼10 K temperatures. The galaxies were evolved for 300 Myr, i.e., long enough for ISM and GMC properties to achieve a quasi-steady state. We found that during the period of the simulations, the initially, marginally stable ISM fragmented into GMCs due to radiative cooling and gravitational instability. The GMC properties then became influenced by frequent interactions, including collisions.

We examined global ISM properties, including the mass surface density structures, thermal pressures, and the evolution and spatial distribution of GMC mass fractions, as well as the GMC mass traced by CO with n_CO/n_H > 10⁻⁵ cm⁻³. Our results show that strong FUV fields can suppress global GMC formation, especially in the outer regions where gas is more diffuse. Our fiducial model has a radial profile of molecular mass fraction that is quite similar to that observed in the Milky Way out to ∼6 kpc by Koda, Scoville, and Heyer (2016). The lack of the additional physics of localized star formation feedback is likely the main cause of the higher molecular fractions seen in our simulations at larger radii.

We also analyzed GMC properties, including distribution functions of mass, mass surface density, effective radii, vertical locations, virial parameters, and specific angular momenta. Though we only incorporated diffuse FUV heating and CR ionization, many observed GMC properties are approximately reproduced, including the mass spectrum, mass surface density distribution, and angular momentum distribution, which shows that retrograde clouds are relatively common. The distribution of virial parameters shows a large fraction of gravitationally bound clouds, along with a population of super-virial clouds potentially caused by strong and frequent cloud–cloud interactions. We notice that these GMC properties are relatively insensitive to our different implementations of diffuse FUV and CR heating, implying rather the important role of GMC interactions.

Finally, GMC collisions, which may be a means of triggering star cluster formation, were investigated and compared with analytic models of galactic shear-induced collisions. Our results show an approximate agreement with the models, and insensitivity to parameters related to the diffuse heating. The average collision timescale is relatively short, i.e., ∼0.1–0.2 times the local orbital time. Such frequent GMC collisions may be an important driver of turbulence in the clouds, potentially explaining their observed structural, kinematic, and dynamical properties.

The simulations so far presented lack several important pieces of physics, especially magnetic fields and localized star formation feedback. These aspects, along with the effects of different galactic dynamical environments, including spiral arms, will be studied in future papers in this series.

Acknowledgements

Computations described in this work were performed using the publicly available Enzo code http://enzo-project.org. This research also made use of the yt-project http://yt-project.org/, a toolkit for analyzing and visualizing quantitative data (Turk et al. 2011). These are products of collaborative efforts of many independent scientists from numerous institutions around the world. Their commitment to open science has helped make this work possible. The authors acknowledge University of Florida Research Computing www.rc.ufl.edu for providing computational resources and support that have contributed to the research results reported in this publication.

References

Agertz

O.

,

Kravtsov

A. V.

2015

,

ApJ

,

804

,

18

Agertz

O.

,

Kravtsov

A. V.

,

Leitner

S. N.

,

Gnedin

N. Y.

2013

,

ApJ

,

770

,

25

Bertoldi

F.

,

McKee

C. F.

1992

,

ApJ

,

395

,

140

Bigiel

F.

,

Leroy

A.

,

Walter

F.

,

Brinks

E.

,

de Blok

W. J. G.

,

Madore

B.

,

Thornley

M. D.

2008

,

AJ

,

136

,

2846

Bihr

S.

et al.

2015

,

A&A

,

580

,

A112

Binney

J.

,

Tremaine

S.

1987

,

Galactic Dynamics

(

Princeton, NJ

:

Princeton University Press

)

Bisbas

T. G.

,

Papadopoulos

P. P.

,

Viti

S.

2015

,

ApJ

,

803

,

37

Bisbas

T. G.

,

van Dishoeck

E. F.

,

Papadopoulos

P. P.

,

Szűcs

L.

,

Bialy

S.

,

Zhang

Z.-Y.

2017

,

ApJ

,

839

,

90

Blitz

L.

1990

, in

ASP Conf. Ser., 12, The Evolution of the Interstellar Medium

, ed.

Blitz

L.

(

San Francisco

:

ASP

),

273

Blitz

L.

1993

, in

Protostars and Planets III

, ed.

Levy

E. H.

,

Lunine

J. I.

(

Tucson

:

University of Arizona Press

),

125

Boulares

A.

,

Cox

D. P.

1990

,

ApJ

,

365

,

544

Bryan

G. L.

et al.

2014

,

ApJS

,

211

,

19

Butler

M. J.

,

Tan

J. C.

,

Teyssier

R.

,

Rosdahl

J.

,

Van Loo

S.

,

Nickerson

S.

2017

,

ApJ

,

841

,

82

Butler

M. J.

,

Tan

J. C.

,

Van Loo

S.

2015

,

ApJ

,

805

,

1

Dalgarno

A.

2006

,

Proc. Natl. Acad. Sci.

,

103

,

12269

Dobashi

K.

,

Matsumoto

T.

,

Shimoikura

T.

,

Saito

H.

,

Akisato

K.

,

Ohashi

K.

,

Nakagomi

K.

2014

,

ApJ

,

797

,

58

Dobbs

C. L.

2008

,

MNRAS

,

391

,

844

Dobbs

C. L.

et al.

2017

,

MNRAS

,

464

,

3580

Dobbs

C. L.

,

Burkert

A.

,

Pringle

J. E.

2011

,

MNRAS

,

417

,

1318

Draine

B. T.

1978

,

ApJS

,

36

,

595

Eyink

G. L.

,

Lazarian

A.

,

Vishniac

E. T.

2011

,

ApJ

,

743

,

51

Ferland

G. J.

et al.

2013

,

Rev. Mex. Astron. Astrophys.

,

49

,

137

Fujimoto

Y.

,

Bryan

G. L.

,

Tasker

E. J.

,

Habe

A.

,

Simpson

C. M.

2016

,

MNRAS

,

461

,

1684

Fujimoto

Y.

,

Tasker

E. J.

,

Wakayama

M.

,

Habe

A.

2014

,

MNRAS

,

439

,

936

Fukui

Y.

et al.

2015

,

ApJ

,

807

,

L4

Furukawa

N.

,

Dawson

J. R.

,

Ohama

A.

,

Kawamura

A.

,

Mizuno

N.

,

Onishi

T.

,

Fukui

Y.

2009

,

ApJ

,

696

,

L115

Gammie

C. F.

,

Ostriker

J. P.

,

Jog

C. J.

1991

,

ApJ

,

378

,

565

Genzel

R.

et al.

2010

,

MNRAS

,

407

,

2091

Goldbaum

N. J.

,

Krumholz

M. R.

,

Forbes

J. C.

2015

,

ApJ

,

814

,

131

Goldbaum

N. J.

,

Krumholz

M. R.

,

Forbes

J. C.

2016

,

ApJ

,

827

,

28

Goldbaum

N. J.

,

Krumholz

M. R.

,

Matzner

C. D.

,

McKee

C. F.

2011

,

ApJ

,

738

,

101

Gratier

P.

et al.

2012

,

A&A

,

542

,

A108

Habing

H. J.

1968

,

Bull. Astron. Inst. Netherlands

,

19

,

421

Heitsch

F.

,

Burkert

A.

,

Hartmann

L. W.

,

Slyz

A. D.

,

Devriendt

J. E. G.

2005

,

ApJ

,

633

,

L113

Heyer

M.

,

Krawczyk

C.

,

Duval

J.

,

Jackson

J. M.

2009

,

ApJ

,

699

,

1092

Hopkins

P. F.

,

Kereš

D.

,

Oñorbe

J.

,

Faucher-Giguère

C.-A.

,

Quataert

E.

,

Murray

N.

,

Bullock

J. S.

2014

,

MNRAS

,

445

,

581

Hopkins

P. F.

,

Narayanan

D.

,

Murray

N.

,

Quataert

E.

2013

,

MNRAS

,

433

,

69

Hopkins

P. F.

,

Quataert

E.

,

Murray

N.

2011

,

MNRAS

,

417

,

950

Hopkins

P. F.

,

Quataert

E.

,

Murray

N.

2012

,

MNRAS

,

421

,

3488

Imara

N.

,

Bigiel

F.

,

Blitz

L.

2011

,

ApJ

,

732

,

79

Imara

N.

,

Blitz

L.

2011

,

ApJ

,

732

,

78

Inoue

T.

,

Inutsuka

S.

2008

,

ApJ

,

687

,

303

Inoue

T.

,

Inutsuka

S.

2012

,

ApJ

,

759

,

35

Kennicutt

R. C., Jr.

1998

,

ApJ

,

498

,

541

Kennicutt

R. C., Jr

,

Evans

N. J.

2012

,

ARA&A

,

50

,

531

Koda

J.

,

Scoville

N.

,

Heyer

M.

2016

,

ApJ

,

823

,

76

Koda

J.

,

Sofue

Y.

2006

,

PASJ

,

58

,

299

König

S.

et al.

2017

,

A&A

,

602

,

A42

Körtgen

B.

,

Banerjee

R.

2015

,

MNRAS

,

451

,

3340

Krumholz

M. R.

,

McKee

C. F.

2005

,

ApJ

,

630

,

250

Krumholz

M. R.

,

Matzner

C. D.

,

McKee

C. F.

2006

,

ApJ

,

653

,

361

Krumholz

M. R.

,

Tan

J. C.

2007

,

ApJ

,

654

,

304

Kunz

M. W.

,

Mouschovias

T. Ch.

2009

,

MNRAS

,

399

,

L94

Lazarian

A.

,

Vishniac

E. T.

1999

,

ApJ

,

517

,

700

Lee

E. J.

,

Miville-Deschênes

M.-A.

,

Murray

N. W.

2016

,

ApJ

,

833

,

229

Leroy

A. K.

et al.

2013

,

AJ

,

146

,

19

Leroy

A. K.

,

Walter

F.

,

Brinks

E.

,

Bigiel

F.

,

de Blok

W. J. G.

,

Madore

B.

,

Thornley

M. D.

2008

,

AJ

,

136

,

2782

Mac Low

M.-M.

,

Klessen

R. S.

,

Burkert

A.

,

Smith

M. D.

1998

,

Phys. Rev. Lett.

,

80

,

2754

McKee

C. F.

,

Ostriker

E. C.

2007

,

ARA&A

,

45

,

565

Matzner

C. D.

2002

,

ApJ

,

566

,

302

Mayer

L.

,

Tamburello

V.

,

Lupi

A.

,

Keller

B.

,

Wadsley

J.

,

Madau

P.

2016

,

ApJ

,

830

,

L13

Miville-Deschênes

M.-A.

,

Murray

N.

,

Lee

E. J.

2017

,

ApJ

,

834

,

57

Momose

R.

,

Okumura

S. K.

,

Koda

J.

,

Sawada

T.

2010

,

ApJ

,

721

,

383

Mouschovias

T. Ch.

1991

,

ApJ

,

373

,

169

Ohama

A.

et al.

2010

,

ApJ

,

709

,

975

Padoan

P.

,

Nordlund

Å.

2002

,

ApJ

,

576

,

870

Phillips

J. P.

1999

,

A&AS

,

134

,

241

Read

J. I.

,

Agertz

O.

,

Collins

M. L. M.

2016

,

MNRAS

,

459

,

2573

Rebolledo

D.

et al.

2017

,

MNRAS

,

472

,

1685

Röllig

M.

et al.

2007

,

A&A

,

467

,

187

Roman-Duval

J.

,

Jackson

J. M.

,

Heyer

M.

,

Rathborne

J.

,

Simon

R.

2010

,

ApJ

,

723

,

492

Rosolowsky

E.

,

Engargiola

G.

,

Plambeck

R.

,

Blitz

L.

2003

,

ApJ

,

599

,

258

Safranek-Shrader

C.

,

Krumholz

M. R.

,

Kim

C.-G.

,

Ostriker

E. C.

,

Klein

R. I.

,

Li

S.

,

McKee

C. F.

,

Stone

J. M.

2017

,

MNRAS

,

465

,

885

Smith

B. D.

et al.

2017

,

MNRAS

,

466

,

2217

Sobolev

V. V.

1957

,

Soviet Ast.

,

1

,

678

Solomon

P. M.

,

Rivolo

A. R.

,

Barrett

J.

,

Yahil

A.

1987

,

ApJ

,

319

,

730

Stone

J. M.

,

Norman

M. L.

1992

,

ApJS

,

80

,

753

Stone

J. M.

,

Ostriker

E. C.

,

Gammie

C. F.

1998

,

ApJ

,

508

,

L99

Suwannajak

C.

,

Tan

J. C.

,

Leroy

A. K.

2014

,

ApJ

,

787

,

68

Tan

J. C.

2000

,

ApJ

,

536

,

173

Tan

J. C.

2010

,

ApJ

,

710

,

L88

Tan

J. C.

,

Shaske

S. N.

,

Van Loo

S.

2013

, in

IAU Symp. 292, Molecular Gas, Dust, and Star Formation in Galaxies

, ed.

Wong

T.

,

Ott

J.

(

Cambridge, UK

:

Cambridge University Press

),

19

Tasker

E. J.

2011

,

ApJ

,

730

,

11

Tasker

E. J.

,

Tan

J. C.

2009

,

ApJ

,

700

,

358

(TT09)

Tasker

E. J.

,

Wadsley

J.

,

Pudritz

R.

2015

,

ApJ

,

801

,

33

Toomre

A.

1964

,

ApJ

,

139

,

1217

Torii

K.

et al.

2011

,

ApJ

,

738

,

46

Truelove

J. K.

,

Klein

R. I.

,

McKee

C. F.

,

Holliman

J. H.

II,

Howell

L. H.

,

Greenough

J. A.

1997

,

ApJ

,

489

,

L179

Turk

M. J.

,

Smith

B. D.

,

Oishi

J. S.

,

Skory

S.

,

Skillman

S. W.

,

Abel

T.

,

Norman

M. L.

2011

,

ApJS

,

192

,

9

Van Loo

S.

,

Butler

M. J.

,

Tan

J. C.

2013

,

ApJ

,

764

,

36

Van Loo

S.

,

Tan

J. C.

,

Falle

S. A. E. G.

2015

,

ApJ

,

800

,

L11

Vázquez-Semadeni

E.

,

Banerjee

R.

,

Gómez

G. C.

,

Hennebelle

P.

,

Duffin

D.

,

Klessen

R. S.

2011

,

MNRAS

,

414

,

2511

von Neumann

J.

,

Richtmyer

R. D.

1950

,

J. Appl. Phys.

,

21

,

232

Wannier

P. G.

,

Lichten

S. M.

,

Andersson

B.-G.

,

Morris

M.

1991

,

ApJS

,

75

,

987

Williams

J. P.

,

McKee

C. F.

1997

,

ApJ

,

476

,

166

Wolfire

M. G.

,

Hollenbach

D.

,

McKee

C. F.

2010

,

ApJ

,

716

,

1191

Wolfire

M. G.

,

McKee

C. F.

,

Hollenbach

D.

,

Tielens

A. G. G. M.

2003

,

ApJ

,

587

,

278

Wu

B.

,

Tan

J. C.

,

Christie

D.

,

Nakamura

F.

,

Van Loo

S.

,

Collins

D.

2017a

,

ApJ

,

841

,

88

Wu

B.

,

Tan

J. C.

,

Nakamura

F.

,

Van Loo

S.

,

Christie

D.

,

Collins

D.

2017b

,

ApJ

,

835

,

137

Wu

B.

,

Van Loo

S.

,

Tan

J. C.

,

Bruderer

S.

2015

,

ApJ

,

811

,

56

Zuckerman

B.

,

Evans

N. J., II.

,

1974

,

ApJ

,

192

,

L14