-
PDF
- Split View
-
Views
-
Cite
Cite
Hsing-Wen Lin, Ying-Tung Chen, Jen-Hung Wang, Shiang-Yu Wang, Fumi Yoshida, Wing-Huen Ip, Satoshi Miyazaki, Tsuyoshi Terai, Machine-learning-based real–bogus system for the HSC-SSP moving object detection pipeline, Publications of the Astronomical Society of Japan, Volume 70, Issue SP1, January 2018, S39, https://doi.org/10.1093/pasj/psx082
Close - Share Icon Share
Abstract
Machine-learning techniques are widely applied in many modern optical sky surveys, e.g., Pan-STARRS1, PTF/iPTF, and the Subaru/Hyper Suprime-Cam survey, to reduce human intervention in data verification. In this study, we have established a machine-learning-based real–bogus system to reject false detections in the Subaru/Hyper-Suprime-Cam Strategic Survey Program (HSC-SSP) source catalog. Therefore, the HSC-SSP moving object detection pipeline can operate more effectively due to the reduction of false positives. To train the real–bogus system, we use stationary sources as the real training set and “flagged” data as the bogus set. The training set contains 47 features, most of which are photometric measurements and shape moments generated from the HSC image reduction pipeline (hscPipe). Our system can reach a true positive rate (tpr) ∼96% with a false positive rate (fpr) ∼1% or tpr ∼99% at fpr ∼5%. Therefore, we conclude that stationary sources are decent real training samples, and using photometry measurements and shape moments can reject false positives effectively.
1 Introduction
Synoptic optical sky surveys can generate huge amounts of imaging data every night and detect billions of astronomical sources. Along with the scientifically valuable sources such as stars, galaxies, supernovae, asteroids, etc., there are significant non-astrophysical detections in the data that require humans to inspect the images and look for new events.
Current modern sky survey data sets are too large to be examined only by humans without any computer intervention. Therefore, machine-learning (ML) techniques to automatically identify and classify astronomical sources have been introduced in many survey projects, e.g., Pan-STARRS1, PTF/iPTF, and the Dark Energy Survey. There are many applications for ML in astronomy, for example: (1) to identify real astronomical sources from artifacts (real–bogus system)—the process of image differencing introduces many of the artifacts that need to be removed using the ML software (Bailey et al. 2007; Bloom et al. 2012; Brink et al. 2013; Goldstein et al. 2015; Wright et al. 2015; Morii et al. 2016; Masci et al. 2017); (2) to classify the astronomical sources using multi-color photometry, spectrum (Bloom et al. 2012; du Buisson et al. 2015; Baron & Poznanski 2017; Miller et al. 2017), and/or lightcurves (Miller et al. 2015; Huppenkothen et al. 2017); (3) to estimate the photometry redshift (Gerdes et al. 2010; Zheng & Zhang 2012; Krone-Martins et al. 2014; Cavuoti et al. 2015, 2017; Sadeh et al. 2016; Samui & Samui Pal 2017; Wolf et al. 2017); and (4) to identify fast-moving near-Earth asteroids (Waszczak et al. 2017).
The Subaru/Hyper-Suprime-Cam (HSC: Kawanomoto et al. 2017; Komiyama et al. 2018; Miyazaki et al. 2018) Strategic Survey Program (SSP: R. Armstrong et al. in preparation; Bosch et al. 2018; T. Takata et al. in preparation) is one of the largest current optical surveys. It is planned to be executed over 6 yr from 2014, to mainly investigate the mystery of dark matter/dark energy as well as galaxy evolution, high-redshift AGNs, and other astrophysical topics. Undoubtedly, this survey will suffer the influences of many false positives. To conquer the problem, Morii et al. (2016) built a real–bogus system by training three different kinds of supervised learning mechanisms (AUC boosting, random forest, and deep neural network) with artificial objects. The system has been applied to select true optical transients in the differential images of the two HSC/SSP ultra-deep fields, COSMOS and SXDS, and it is able to reduce the false positive rate to 1.0%, reaching a true positive rate of 90% in the magnitude range from 22.0 to 25.0 mag.
This result looks promising. However, like all other real–bogus systems, this machine works for differential images (single-epoch “new” images have a “reference image” subtracted—the reference image is the deep co-add of many exposures) and is unsuitable in some cases. For example, if we need to process the survey data in real time, the difference images may be unavailable or not available in time. Searching for solar system moving objects in the HSC-SSP wide survey is one such case; the reference stacked images of HSC-SSP wide fields will not be made until the survey data is released, which has the timescale of about a year. However, even the slow-moving trans-Neptune objects (TNOs) need to be tracked within a few months. Therefore, the moving object detection pipeline has been developed to search for moving objects with single-exposure, non-differential source catalogs. The detailed algorithm of the pipeline is described in Chen et al. (2018).
Basically, the moving object pipeline detects moving objects by searching for sequences of detections within a few nights. Therefore, the total time span to finish the search is proportional to the number of sequence detections. It is roughly proportional to the square of the total non-stationary sources. Although false positives should be randomly distributed, they still have the chance to align in a row and become a moving-object-like sequence of detections. As a result, false positives can greatly decrease the search speed by producing too many possible false sequences, and reducing the number of false positives in the source catalogs is a major task to help complete moving object searches within reasonable computational time.
In this study, we seek an alternative real–bogus system that can work for the normal, non-differential source catalogs. In addition, to make this system easy to access, we will only use the features provided in the HSC image reduction pipeline (hscPipe) and avoid measuring extra moments of the objects from the images. This paper is structured as follows: In section 2, we explain how to collect the training data set and select the features. In section 3, we introduce the ML methods of the real–bogus system. In section 4, we evaluate the efficiency of the ML real–bogus system. A discussion and summary are in sections 5 and 6, respectively.
2 Training set and feature selection
A key point for building an effective, unbiased ML classifier is to collect an accurate, unbiased, and large training set. However, this is difficult in most cases. For example, human examination can provide accurate training samples, but this is time-consuming, and as a result can lead to limited sample sizes. By contrast, selecting the training sample using certain characteristics is very effective, but it could produce biased and inaccurate samples. To conquer this problem, Morii et al. (2016) trained the ML classifier with synthetic training samples that are both accurate and provide a large sample size. Still, the synthetic training set could be very biased, depending on the complexity of the synthetic models. For example, it is relatively easier to make synthetic stars than synthetic galaxies, because galaxies have significantly more complex shapes and features.
Here we propose a simple way to collect large training samples with high accuracy and small bias. The HSC data reduction pipeline (hscPipe) provides lots of features in the source catalogs, including all kinds of photometry measurements, position measurements, and shape moments. The software team of hscPipe has suggested some flags to use to filter the good and bad sources. However, it is possible that the “good flags” do not contain all of the faint real objects. On the other hand, the “bad flags” can be used for generating a set of “pure garbage,” which is an ideal bogus training set for ML. The “bad flags” consist of (1) centroid_sdss_flags == True and flux_aperture_flags == True (both object centroiding and aperture flux measurement failed), or (2) flags_pixel_saturated_any == True (any of the pixels in an object’s footprint is saturated). For detailed information on the HSC flags, please refer to R. Armstrong et al. (in preparation).
To collect a pure real training set, we use stationary sources to represent real astronomical sources. Each stationary source is identified from detections inside of a certain radius with sufficient duration (time span) in a single SSP observation run. The stationary selection criteria are:
Search radius ≤0|${^{\prime\prime}_{.}}$|5: A stationary source has to have corresponding detections in different exposures within a 0|${^{\prime\prime}_{.}}$|5 radius.
Lowest number of detections ≥2: A stationary source must have at least two corresponding detections within the search radius.
Time span ≥20 min: The two corresponding detections have to be separated by at least 20 min to avoid contamination from slow-moving solar system objects, because items such as distant TNOs could move less than 0|${^{\prime\prime}_{.}}$|5 within 20 min.
Here, we set the conditions of search radius and time span by calculating the expected movements of a slow-moving object at 100 au at opposition.
Comparing the two different selection criteria of bogus and real detections, the bogus training set selection may not be very uniform, because the “bad flags” could cause some bias in selecting the artifacts, e.g., some optical flares could be successfully centroided without any saturated pixels— they can pass thought the “bad flags” filter. On the other hand, the stationary sources collect almost all kinds of real detections with a whole range of brightness and shapes. These are closer to unbiased, uniform samples. An exception are the fast-moving asteroids, which have streak-like shapes. Fortunately, in our case of searching for distant moving objects, their movement rate is very slow and the shapes are very close to normal stars. In short, we have better confidence in our real training set than the bogus training set.
With both the real and bogus training samples, the next step is feature selection. Although artifacts are very likely to be location dependent (for example, they appear with higher frequency near bright stars and the edges of CCD chips), using a position-dependent feature to select artifacts will be very risky, since the ML may consider that every source around the edges of CCD chips should be bogus. Thus, we avoid the use of location-dependent features. The shape moments and photometry measurements are the ideal features for separating real and bogus sources, not only because the artifacts and real sources could have different shapes or brightness, but also because they are location-dependent features. Thus we mainly use the shape moments and photometry measurements to build our real–bogus system.
Table 1 shows all of the features we selected from the HSC source catalogs. The features are all related to shape and photometry, except parent and flux_aperture_nInterpolatedPixel. Four kinds of shape moments were selected in this study: shape_sdss, shape_hsm_moments, shape_sdss_psf, and shape_hsm_psf_moments. Of these, shape_sdss is a reimplementation of the algorithm used in the SDSS PHOTO pipeline, while shape_hsm_moments is a wrapper for HSM (Hirata & Seljak 2003) implemented in GalSim (Rowe et al. 2015). The fields shape_sdss_psf and shape_hsm_psf_moments are the same algorithms as shape_sdss and shape_hsm_moments, respectively, but measure the PSF model at the source position.
| Feature (# features if multiple) . | Description . |
|---|---|
| parent | Number of peaks within the footprint of the detection |
| shape_hsm_moments (3) | Source adaptive moments from HSM |
| shape_hsm_psf_moments (3) | PSF adaptive moments from HSM |
| shape_sdss (3) | Shape measured with SDSS adaptive moment algorithm |
| shape_sdss_psf (3) | Adaptive moments of the PSF model at the position |
| flux_aperture (6) | Sum of pixels in six different-sized apertures |
| flux_aperture_err (6) | Uncertainty for flux_apertures |
| flux_aperture_nInterpolatedPixel (6) | Number of interpolated pixels in apertures |
| flux_gaussian | Linear fit to elliptical Gaussian with shape parameters set by adaptive moments |
| flux_gaussian_err | Uncertainty for flux_gaussian |
| flux_kron | Kron photometry |
| flux_kron_err | Uncertainty for flux_kron |
| flux_kron_radius | Kron radius [|$\sqrt{(}a\times b)$|] |
| flux_kron_psfRadius | Radius of PSF |
| flux_psf | Flux measured by a fit to the PSF model |
| flux_psf_err | Uncertainty for flux_psf |
| flux_sinc | Elliptical aperture photometry using sinc interpolation |
| flux_sinc_err | Uncertainty for flux_sinc |
| flux_gaussian_apcorr | Aperture correction applied to flux_gaussian |
| flux_gaussian_apcorr_err | Error on aperture correction flux_gaussian_appcorr |
| flux_kron_apcorr | Aperture correction applied to flux_kron |
| flux_kron_apcorr_err | Error on aperture correction applied to flux_kron |
| flux_psf_apcorr | Aperture correction applied to flux_psf |
| flux_psf_apcorr_err | Error on aperture correction applied to flux_psf |
| Feature (# features if multiple) . | Description . |
|---|---|
| parent | Number of peaks within the footprint of the detection |
| shape_hsm_moments (3) | Source adaptive moments from HSM |
| shape_hsm_psf_moments (3) | PSF adaptive moments from HSM |
| shape_sdss (3) | Shape measured with SDSS adaptive moment algorithm |
| shape_sdss_psf (3) | Adaptive moments of the PSF model at the position |
| flux_aperture (6) | Sum of pixels in six different-sized apertures |
| flux_aperture_err (6) | Uncertainty for flux_apertures |
| flux_aperture_nInterpolatedPixel (6) | Number of interpolated pixels in apertures |
| flux_gaussian | Linear fit to elliptical Gaussian with shape parameters set by adaptive moments |
| flux_gaussian_err | Uncertainty for flux_gaussian |
| flux_kron | Kron photometry |
| flux_kron_err | Uncertainty for flux_kron |
| flux_kron_radius | Kron radius [|$\sqrt{(}a\times b)$|] |
| flux_kron_psfRadius | Radius of PSF |
| flux_psf | Flux measured by a fit to the PSF model |
| flux_psf_err | Uncertainty for flux_psf |
| flux_sinc | Elliptical aperture photometry using sinc interpolation |
| flux_sinc_err | Uncertainty for flux_sinc |
| flux_gaussian_apcorr | Aperture correction applied to flux_gaussian |
| flux_gaussian_apcorr_err | Error on aperture correction flux_gaussian_appcorr |
| flux_kron_apcorr | Aperture correction applied to flux_kron |
| flux_kron_apcorr_err | Error on aperture correction applied to flux_kron |
| flux_psf_apcorr | Aperture correction applied to flux_psf |
| flux_psf_apcorr_err | Error on aperture correction applied to flux_psf |
| Feature (# features if multiple) . | Description . |
|---|---|
| parent | Number of peaks within the footprint of the detection |
| shape_hsm_moments (3) | Source adaptive moments from HSM |
| shape_hsm_psf_moments (3) | PSF adaptive moments from HSM |
| shape_sdss (3) | Shape measured with SDSS adaptive moment algorithm |
| shape_sdss_psf (3) | Adaptive moments of the PSF model at the position |
| flux_aperture (6) | Sum of pixels in six different-sized apertures |
| flux_aperture_err (6) | Uncertainty for flux_apertures |
| flux_aperture_nInterpolatedPixel (6) | Number of interpolated pixels in apertures |
| flux_gaussian | Linear fit to elliptical Gaussian with shape parameters set by adaptive moments |
| flux_gaussian_err | Uncertainty for flux_gaussian |
| flux_kron | Kron photometry |
| flux_kron_err | Uncertainty for flux_kron |
| flux_kron_radius | Kron radius [|$\sqrt{(}a\times b)$|] |
| flux_kron_psfRadius | Radius of PSF |
| flux_psf | Flux measured by a fit to the PSF model |
| flux_psf_err | Uncertainty for flux_psf |
| flux_sinc | Elliptical aperture photometry using sinc interpolation |
| flux_sinc_err | Uncertainty for flux_sinc |
| flux_gaussian_apcorr | Aperture correction applied to flux_gaussian |
| flux_gaussian_apcorr_err | Error on aperture correction flux_gaussian_appcorr |
| flux_kron_apcorr | Aperture correction applied to flux_kron |
| flux_kron_apcorr_err | Error on aperture correction applied to flux_kron |
| flux_psf_apcorr | Aperture correction applied to flux_psf |
| flux_psf_apcorr_err | Error on aperture correction applied to flux_psf |
| Feature (# features if multiple) . | Description . |
|---|---|
| parent | Number of peaks within the footprint of the detection |
| shape_hsm_moments (3) | Source adaptive moments from HSM |
| shape_hsm_psf_moments (3) | PSF adaptive moments from HSM |
| shape_sdss (3) | Shape measured with SDSS adaptive moment algorithm |
| shape_sdss_psf (3) | Adaptive moments of the PSF model at the position |
| flux_aperture (6) | Sum of pixels in six different-sized apertures |
| flux_aperture_err (6) | Uncertainty for flux_apertures |
| flux_aperture_nInterpolatedPixel (6) | Number of interpolated pixels in apertures |
| flux_gaussian | Linear fit to elliptical Gaussian with shape parameters set by adaptive moments |
| flux_gaussian_err | Uncertainty for flux_gaussian |
| flux_kron | Kron photometry |
| flux_kron_err | Uncertainty for flux_kron |
| flux_kron_radius | Kron radius [|$\sqrt{(}a\times b)$|] |
| flux_kron_psfRadius | Radius of PSF |
| flux_psf | Flux measured by a fit to the PSF model |
| flux_psf_err | Uncertainty for flux_psf |
| flux_sinc | Elliptical aperture photometry using sinc interpolation |
| flux_sinc_err | Uncertainty for flux_sinc |
| flux_gaussian_apcorr | Aperture correction applied to flux_gaussian |
| flux_gaussian_apcorr_err | Error on aperture correction flux_gaussian_appcorr |
| flux_kron_apcorr | Aperture correction applied to flux_kron |
| flux_kron_apcorr_err | Error on aperture correction applied to flux_kron |
| flux_psf_apcorr | Aperture correction applied to flux_psf |
| flux_psf_apcorr_err | Error on aperture correction applied to flux_psf |
Both shape_sdss and shape_hsm_moments measure the shape with the adaptive moments, which are the second moments of the object intensity. They are measured by a particular scheme designed to have near-optimal signal-to-noise ratio. The three features provided by both algorithms are the sum of the second moments, the ellipticity (polarization) components, and a fourth-order moment. For details of adaptive moments, we refer to Bernstein and Jarvis (2002) and Hirata and Seljak (2003).
For the photometry measurements, there are 10 different aperture sizes (radius = 3, 4.5, 6, 9, 12, 17, 25, 35, 50, 70 pixel) included in hscPipe for the aperture photometry. Considering that the typical seeing size is about 3 pixel, we only select apertures with radius = 3, 4.5, 6, 9, 12, and 17 pixel as the six features of the aperture flux measurements. The flux_sinc is the elliptical aperture photometry using sinc interpolation. Finally, the only two features that are not photometry or shape moments are parent, which records the number of peaks within the footprint of the detections, and flux_aperture_nInterpolatedPixel, which is the number of interpolated pixels in an aperture. For detailed information on the hscPipe measurements, see Bosch et al. (2018).
3 Machine-learning algorithms for real–bogus classifier
Real–bogus separation is basically a two-class classification problem, and many of the “supervised learning” algorithms could be potentially useful in dealing with it. Supervised learning is teaching the computer using known-result training data to learn a general rule for mapping the input data to the output results. For example, in our case, we provide a set of detections to train the computer. Every detection has its own features and is labeled as “real” or “bogus.” After the training, the computer learns a general rule for distinguishing “real” and “bogus” by examining their features.
Alternatively, we may also treat real–bogus separation as a clustering problem, because the real and false detections can be potentially clustered into two different groups. In a clustering problem, the groups are unknown before training and make this an unsupervised task. Unlike supervised learning, unsupervised learning does not need any known results during the training, leaving the computer to figure out on its own the structure of the training data.
Since we have unbalanced training samples, with the real set much larger and possibly less biased than the bogus set, we also give unsupervised learning a try in building our real–bogus classifier. Here we selected random forest and isolation forest for the supervised and unsupervised learning algorithms, respectively.
3.1 Supervised learning: random forest
Random forest (RF: Breiman 2001), has been proved to be a very effective classifier for many kinds of data. It is a supervised ensemble method composed of multiple decision trees, which are trained by their own subsets of training data. These training data subsets are selected by bootstrap sampling (random sampling with replacement). The decision will be made by the majority voting of every tree to reduce the variance of the model predictions.
Random forest can process extremely high-dimensional data and evaluate the importance of each feature, which is suitable for our data. It also tends to produce less over-fitting than a single decision tree, although over-fitting is still possible.
Below is a short description of the RF algorithm:
Make a training subset by bootstrap sampling from the training set, which has a total of N detections, for growing the tree. Keep the unselected samples, a.k.a. “out-of-bag samples,” for the model evaluation.
If there are M features, randomly select m features from the M (m < M) at each node. Evaluate the optimal way for these m to split the samples. The value of m is held constant while we grow the forest.
Each tree is grown to the largest extent possible without pruning.
Repeat steps 1, 2, and 3 to build a forest of decision trees.
For more detailed descriptions of RF, we refer the reader to Breiman (2001).
3.2 Unsupervised learning: isolation forest
Isolation forest (IF: Liu et al. 2008) is an unsupervised learning method to search for anomaly detections or outliers in huge data sets. On one hand, IF is similar to RF, which is also constructed by multiple trees. On the other hand, unlike RF, which uses bootstrap sampling to select the training subsets for the decision trees, IF uses simple random sampling (without replacement) subsets to train the individual trees. The trees in IF are not decision trees; they do not make any decisions and are called isolation trees. Our motivation to use IF is that we have a better and larger real training set. Therefore, if we provide only the real set, we expect that the IF classifier will figure out how real detections look and reject the bogus. Below is a short description of the IF algorithm:
Randomly pick a feature as a node of the tree and randomly select a value (between maximum and minimum) of the feature to divide the training samples into two groups.
Repeat step 1 for each group, until the stop criterion is reached. This criterion can be either (a) every sample has been isolated, or (b) the bottom of the tree is reached. The count of the splittings required to isolate a sample is equivalent to the path length from the root node to the terminating node.
Repeat step 2 to generate a forest of isolation trees.
The mean path length, which is averaged over the path lengths of every tree in the forest, represents the normality of the training samples. If a data point produces a significantly longer path length than the mean path length, it is very likely an anomaly detection.
For the detailed algorithm of the IF method, we refer the reader to Liu, Ting, and Zhou (2008).
4 Implementation and evaluation of the real–bogus classifiers
We applied the RF and IF implementation in scikit-learn 0.181 (Pedregosa et al. 2011). The number of trees (n_estimators) in the classifiers can be specified in both RF and IF. With several tests we found that the out-of-bag error reaches a constant when n_estimators is larger than ∼140 to 160. Therefore, we set n_estimators = 160 for the duration of the study. Note that the out-of-bag error is the mean prediction error evaluated by using out-of-bag samples (see subsection 3.1).
We trained the RF and IF machines by inputting the HSC-SSP data from 2016 June. The data was processed using hscPipe version 4.0.5. First, we separated all data of the observing run in 2016 June into HEALPix (Górski et al. 2005) using the Python package healpy 1.9.12 with parameter nside = 32 [npix = 12288, mean spacing = 1.83 (r = 0.9), area = 3.34] and nest = True. Detections taken with all kind of filters in different weather and seeing conditions were all included. Then we picked the detections in one specific HEALPix, 6499, which has central coordinate RA and Dec of 208.1 and −001.2, respectively, as the training samples. The training samples contain 7265881 and 182218 real and bogus detections, respectively. Afterward, we randomly split the training samples into the training set and the test set with a ratio of 6 : 4. The test set is withheld from training the RF and IF models in order to assess their accuracy with an independent sample of sources. The RF classifier was trained by both the real and the bogus training sets. The IF classifier, based on unsupervised IF algorithms, was only trained with the real training set. Notice that some detections have feature values of nan, which are not readable by either of the classifiers; we use the value −999 instead of nan.
Both RF and IF classifiers were evaluated by the same test set, which includes both real and bogus detections. To test the efficiency consistency of the systems in different sky locations or with different SSP observing runs, we built two extra test sets. One used the data in HEALPix 6505, centered on RA = 206.7 and Dec = +000.0, to represent data taken in the same observing run but at a different sky location. The other used data in HEALPix 6491 (RA = 216.6 and Dec = +001.2), which was observed in 2015 May, to represent data taken in a different SSP observing run.
4.1 Receiver operating characteristic curves
Receiver operating characteristic curves (ROC curves) are created by plotting the true positive rate against the false positive rate at various threshold settings. The true positive rate (tpr) is the proportion of positives that are correctly identified as such. On the other hand, the false positive rate (fpr) is the proportion of negatives that are incorrectly identified as positives. The ROC curve is useful to demonstrate the performance of a binary classifier and select the optimal threshold for the data separation.
The performance of our real–bogus system is shown in figure 1 with ROC curves. The RF classifier can achieve a tpr of ∼99% at the point when the fpr = 5%. If we only allow less than 1% for the fpr, this classifier can still provide a tpr of more than 96%. The performance is similar if we apply the same RF classifier to identify detections in different HEALPix but in the same observing run (HEALPix 6505, the green curve). However, the performance decreases to tpr ∼97% at fpr = 5% (red curve) if we apply the same classifier to evaluate the data of a different SSP observing run (HEALPix 6491). Nevertheless, this result is still very good. Finally, we retrain the RF classifier using the 2015 SSP observing run data, the performance is back to normal (∼99% tpr at 5% fpr, the purple curve).
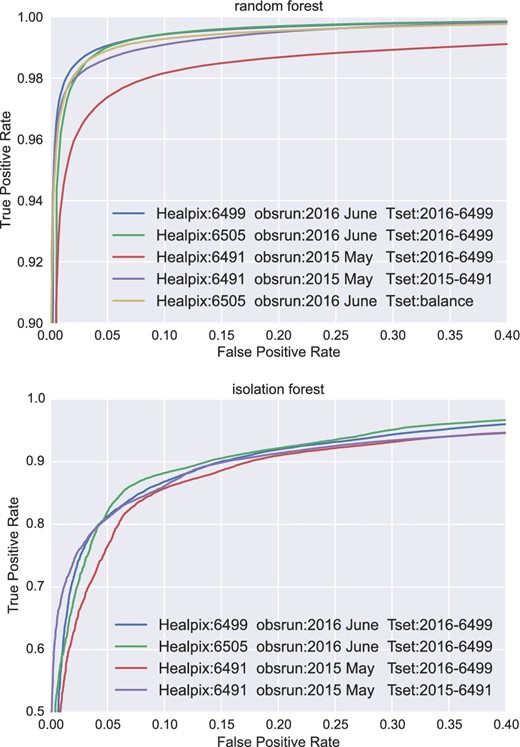
ROC curves of RF (top) and IF (bottom) classifiers. The blue, green, and red curves present the results of the same ML model applied to the same HEALPix in the same observation run, a different HEALPix but the same observation run, and a different HEALPix in different observation runs, respectively. The purple curve shows the result of retraining the ML model with the data used in the case of the red curve. The yellow curve in the RF plot presents the results of the model trained by a balanced training set. (Color online)
We noticed that the performance of the model on test data may be overstated due to the large imbalance in the training set. To test this issue, we randomly selected 2.5% of the real sample and made a balance training set with an equal number of “real” and “bogus” sources, and retrained the model. The new model with a balanced training set produced almost the same ROC curve as the origin model with the unbalanced training set (yellow curve). We conclude that using an unbalanced training set is appropriate in our case.
On the other hand, the unsupervised IF classifier did not perform as well as the RF classifier; it can only reach a tpr ∼90% at fpr = 15%. The performance of the IF classifier seems to be more independent of the different data; we tested it with data sets from both different HEALPix and different SSP runs, which resulted in very similar ROC curves.
4.2 Feature distributions
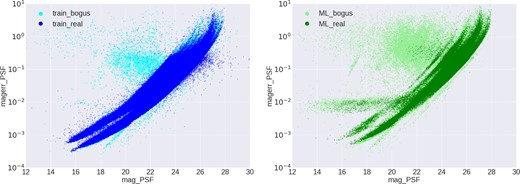
Based on the previous result, we chose the RF classifier to build our real–bogus system. To understand the brightness dependency of the real–bogus separation, we first examine the magnitude distribution of “real” and “bogus” sources for both training and ML selection samples. The results are shown in figure 2, in which “train_real” represents the sample of stationary sources, and “train_bogus” represents the “bad flags” sources. On the other hand, “ml_real” and “ml_bogus” are the non-stationary sources that were identified as “real” and “bogus” by the real–bogus system, respectively. Although “train_real” has fewer sources fainter than 26 mag, there is no evidence that all non-stationary sources with brightness fainter than 26 belong to “ml_bogus.” Furthermore, there is also no clear trend that “ml_bogus” sources are generally fainter than “ml_real.” This result suggests that the real–bogus separation is not a function of brightness, i.e., our system does not serve as a simple brightness cut.

PSF magnitude distribution of “real” and “bogus” sources for the training (left) and the ML selection samples (right). (Color online)
Figure 3 shows the distributions of magnitude versus magnitude error. The plots clearly show that the real sources follow a reasonable brightness–uncertainty relation (the fainter sources have larger uncertainties) for both the training and ML selection samples. By contrast, the bogus sources do not necessarily follow this relation, and almost all of the out-of-track sources (the sources with unreasonably large uncertainty) have been identified as “bogus” sources. Again, the plots show that our real–bogus system can select reasonable sources and reject the abnormal ones, and is not just a simple brightness cut. We notice that the three major different brightness–uncertainly relation curves in the plots should indicate the sources that were taken in three different filters.
PSF magnitude versus magnitude error of “real” and “bogus” sources for the training (left) and the ML selection samples (right). (Color online)
Figure 4 shows the distributions of the shape moments. The plots clearly show that “real” and “bogus” sources have different distributions in the training samples (blue), and our real–bogus selection results represent such distributions for both ML-selected real and bogus detections (green).
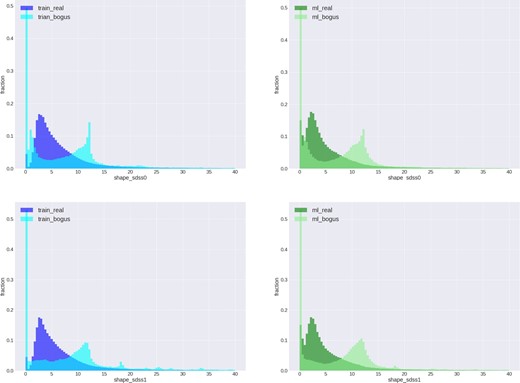
Shape moment distributions of “real” and “bogus” sources for the training (blue) and the ML selection samples (green). Here, shape_sdss0 is the sum of the second moments, and shape_sdss1 is the ellipticity component. (Color online)
4.3 Visual examination
The feature distributions suggest that our real–bogus system works properly. The next step is examining the detection images to understand whether the system can really separate real and bogus detections. Figure 5 shows the real and bogus detections selected by our system. The images with green frames represent the real detections. Many of the real detections have elongated shapes and are potentially asteroids. The images with blue frames are some samples of the bogus detections. They are cosmic rays, bright star spikes, pixels without interpretation or extremely low signal sources/non-detections.

Samples of real (green) and bogus (blue) detections that were identified by the real–bogus system. The size of each image is roughly consist with 17″ × 17″. (Color online)
We therefore examine the bogus sources without “bad flags.” The results are shown in figure 6. We found that the real–bogus system has higher sensitivity with (1) cosmic rays (blue), (2) non-detections (deep green), (3) bright star spikes (yellow), (4) optical effects (orange), (5) over-exposure bright sources (red), and (6) interpretation pixels (purple), but could misclassify (1) faint blurry sources (light green) and (2) extended sources in crowded fields (brown) as the bogus sources. The main purpose of our real–bogus system is to reduce the false positive rate for the HSC-SSP moving object detection pipeline (Chen et al. 2018). Therefore, it will be fine to exclude some extended real sources.

Samples of the real–bogus system identified bogus sources, but without “bad flags.” They can be classified as (1) cosmic rays (blue), (2) non-detections (deep green), (3) bright star spikes (yellow), (4) optical effect (orange), (5) over-exposure bright sources (red), (6) interpretation pixels (purple), (7) faint blurry sources (light green) and extended sources in crowded fields (brown). (Color online)
4.4 Real case evaluation
Finally, it is important to know how many sources will be input into the moving object detection pipeline with or without the real–bogus system. Here we use one HEALPix for evaluation. There are a total of 619207 non-stationary detections in the HEALPix for one SSP observation run. Without any false positive cut, the moving object detection pipeline has to process more than 0.6 million detections in the HEALPix. With the real–bogus system, 244407 potentially false detections are rejected, and 60% of the detections need to be processed. By comparison, using the “bad flags” we can only reject 126739 potentially false detections in this case.
We examined some of the remaining 0.24 million non-stationary detections and found that they are mainly very faint real stars and galaxies. Notice that our stationary source has to have corresponding detections in different exposures within a 0|${^{\prime\prime}_{.}}$|5 radius. Since the detectability of very faint objects is highly sensitive to image quality (e.g., seeing and transparency), some of them cannot be removed by the stationary selection criteria. Over-exposed bright stars also contribute some of the real non-stationary detections. This may be caused by the large centering error of the over-exposure sources. Apart from the stars and galaxies, the remaining non-stationary detections are dominated by asteroids and non-removed cosmic rays.
5 Discussion
The ROC curves show that our RF real–bogus system works very effectively, thanks to many features provided by hscPipe and the idea of using stationary sources as the real training set. Although using the stationary sources can easily produce a uniform, large-sized training data set, there is a known issue with this idea. Fast-moving asteroids do not have PSF-like shapes; they will make “streaks” in the images, and the profile should be a moving PSF. Vereš et al. (2012) and Lin et al. (2015) have more detailed descriptions of fast-moving asteroid profiles. As a result, fast-moving main-belt or near-Earth asteroids could be excluded by our real–bogus system. However, we also noticed that the moving object pipeline can find a lot of asteroids with short-streaked shapes, and this result implies that fast-moving asteroids will slip through the real–bogus system. Nevertheless, we have not currently tested the performance of the real–bogus system with streak-shaped detections. In the near future, once we tune the moving object pipeline to search for fast movers, testing of the real–bogus system for streak-shaped detections will be listed as the highest priority in our to-do list.
In general, the IF is not typically used for classification, therefore it is not surprising that the IF algorithm did not perform as well the RF classifier for real–bogus separation. However, IF still has an advantage. Using the IF classifier does not require any bogus training set; this could be very useful for some surveys for which false detections cannot be easily selected. Once the stationary sources can be identified, the IF classifier will work for the bogus rejection. In such a case, the bogus class must be only a small fraction of the total number of real sources, otherwise the IF algorithm for outlier rejection will not work.
Our concept in this paper, which is using stationary sources to produce a decent training sample and training an ML classifier to identify real and bogus detections, can be easily applied to any sky surveys. The widely used SEXtractor (Bertin & Arnouts 1996) can also provide all kinds of photometry and shape measurements, which is an ideal alternative to hscPipe for feature extraction. Therefore, the real–bogus systems can be applied widely in every asteroid survey and greatly reduce the computation time for asteroid discovery.
6 Summary
We built a real–bogus system to reduce the false positive rates for the non-differential source catalog based HSC-SSP moving object detection pipeline. The ML-classifier-based system was trained by stationary sources as the real data set. The bogus set was selected by the “bad flags” generated by hscPipe. We used 47 features, which are all provided by hscPipe, for the classifier to separate the real and bogus detections. Most of the features are correlated to photometry measurements and shape moments.
We tested two different machine-learning classifiers, the supervised random forest and the unsupervised isolation forest, both of which can result in decent separation of real and bogus detections. However, the RF classifier outperformed the IF classifier: the RF can reach 99% of tpr at 5% of fpr; by contrast, the IF can only reach a tpr ∼90% at fpr = 15%. Therefore, we use RF for the real–bogus separation.
Our real–bogus system is twice as effective as applying “bad flags” to reject the false positives; in our test the real–bogus system rejected more than 0.24 of 0.6 million non-stationary detections in a HEALPix, but the “bad flags” can only reject less than 0.12 million detections.
Finally, we suggest that the concept of a real–bogus system trained by stationary sources can be applied to any modern source-catalog-based asteroid surveys to reduce false positive rates and improve the system performance.
Acknowledgements
We are grateful to Paul Price and Hisanori Furusawa for kind suggestions and help in the data processing.
This work was supported in part by MOST Grant: MOST 104-2119-008-024 (TANGO II) and MOE under the Aim for Top University Program NCU, and Macau Technical Fund: 017/2014/A1 and 039/2013/A2. HWL acknowledges the support of the CAS Fellowship for Taiwan-Youth-Visiting-Scholars under grant no. 2015TW2JB0001.
The Hyper Suprime-Cam (HSC) collaboration includes the astronomical communities of Japan and Taiwan, and Princeton University. The HSC instrumentation and software were developed by the National Astronomical Observatory of Japan (NAOJ), the Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU), the University of Tokyo, the High Energy Accelerator Research Organization (KEK), the Academia Sinica Institute for Astronomy and Astrophysics in Taiwan (ASIAA), and Princeton University. Funding was contributed by the FIRST program from the Japanese Cabinet Office, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), the Japan Society for the Promotion of Science (JSPS), the Japan Science and Technology Agency (JST), the Toray Science Foundation, NAOJ, Kavli IPMU, KEK, ASIAA, and Princeton University.
This paper makes use of software developed for the Large Synoptic Survey Telescope. We thank the LSST Project for making their code available as free software at http://dm.lsst.org.
The Pan-STARRS1 Surveys (PS1) have been made possible through contributions of the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration under Grant No. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation under Grant No. AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), and the Los Alamos National Laboratory.
Based on data collected at the Subaru Telescope and retrieved from the HSC data archive system, which is operated by the Subaru Telescope and Astronomy Data Center, National Astronomical Observatory of Japan.
Footnotes
An open-source machine-learning library for Python 〈http://scikit-learn.org〉.
An open-source HEALPix tools package for Python 〈https://pypi.python.org/pypi/healpy〉.
References



