-
PDF
- Split View
-
Views
-
Cite
Cite
Keita Miyaoka, Nobuhiro Okabe, Takao Kitaguchi, Masamune Oguri, Yasushi Fukazawa, Rachel Mandelbaum, Elinor Medezinski, Yasunori Babazaki, Atsushi J Nishizawa, Takashi Hamana, Yen-Ting Lin, Hiroki Akamatsu, I-Non Chiu, Yutaka Fujita, Yuto Ichinohe, Yutaka Komiyama, Toru Sasaki, Motokazu Takizawa, Shutaro Ueda, Keiichi Umetsu, Jean Coupon, Chiaki Hikage, Akio Hoshino, Alexie Leauthaud, Kyoko Matsushita, Ikuyuki Mitsuishi, Hironao Miyatake, Satoshi Miyazaki, Surhud More, Kazuhiro Nakazawa, Naomi Ota, Kousuke Sato, David Spergel, Takayuki Tamura, Masayuki Tanaka, Manobu M Tanaka, Yousuke Utsumi, Multiwavelength study of X-ray luminous clusters in the Hyper Suprime-Cam Subaru Strategic Program S16A field, Publications of the Astronomical Society of Japan, Volume 70, Issue SP1, January 2018, S22, https://doi.org/10.1093/pasj/psx132
Close - Share Icon Share
Abstract
We present a joint X-ray, optical, and weak-lensing analysis for X-ray luminous galaxy clusters selected from the MCXC (Meta-Catalog of X-Ray Detected Clusters of Galaxies) cluster catalog in the Hyper Suprime-Cam Subaru Strategic Program (HSC-SSP) survey field with S16A data. As a pilot study for a series of papers, we measure hydrostatic equilibrium (HE) masses using XMM-Newton data for four clusters in the current coverage area out of a sample of 22 MCXC clusters. We additionally analyze a non-MCXC cluster associated with one MCXC cluster. We show that HE masses for the MCXC clusters are correlated with cluster richness from the CAMIRA catalog, while that for the non-MCXC cluster deviates from the scaling relation. The mass normalization of the relationship between cluster richness and HE mass is compatible with one inferred by matching CAMIRA cluster abundance with a theoretical halo mass function. The mean gas mass fraction based on HE masses for the MCXC clusters is 〈fgas〉 = 0.125 ± 0.012 at spherical overdensity Δ = 500, which is ∼80%–90% of the cosmic mean baryon fraction, Ωb/Ωm, measured by cosmic microwave background experiments. We find that the mean baryon fraction estimated from X-ray and HSC-SSP optical data is comparable to Ωb/Ωm. A weak-lensing shear catalog of background galaxies, combined with photometric redshifts, is currently available only for three clusters in our sample. Hydrostatic equilibrium masses roughly agree with weak-lensing masses, albeit with large uncertainty. This study demonstrates that further multiwavelength study for a large sample of clusters using X-ray, HSC-SSP optical, and weak-lensing data will enable us to understand cluster physics and utilize cluster-based cosmology.
1 Introduction
Galaxy clusters are the largest collapsed objects in the Universe, and the evolution of the dark halo mass is sensitive to the growth of matter density perturbations controlled by dark matter and dark energy. Thus, observations of the high-mass exponential tail of the mass function over wide redshift ranges can constrain cosmological parameters (e.g., Vikhlinin et al. 2009b; Mantz et al. 2016).
The anticipated wealth of data from both ongoing and upcoming multiwavelength galaxy cluster surveys like the Hyper Suprime-Cam Subaru Strategic Program (HSC-SSP: Miyazaki et al. 2012, 2015; Aihara et al. 2018a, 2018b), the Canada–France–Hawaii Telescope Legacy Survey (CFHTLS: Shan et al. 2012), the Dark Energy Survey (DES: Dark Energy Survey Collaboration 2016), XXL (Pierre et al. 2016), the Extended Roentgen Survey with an Imaging Telescope Array (eROSITA: Cappelluti et al. 2011), Planck (Planck Collaboration 2015b), the South Pole Telescope (SPT: Bleem et al. 2015) and South Pole Telescope Polarimeter (SPTPol: Austermann et al. 2012), and the Atacama Cosmology Telescope (ACT: Hasselfield et al. 2013) and Atacama Cosmology Telescope Polarimeter (ACTPol: Louis et al. 2017) now launches us into a new era of cluster-based cosmology and cluster study. A persistent challenge that affects the ultimate scientific impact of all of these surveys is the need for accurate measurements of mass for individual clusters.
In the last two decades, X-ray observations (e.g., Vikhlinin et al. 2006; Zhang et al. 2008; Sun et al. 2009; Mahdavi et al. 2013; Martino et al. 2014; Donahue et al. 2014) of the intracluster medium (ICM) have been used to measure gas temperature and density distributions and estimate the total mass under the assumption of hydrostatic equilibrium (HE). However, it is known that clusters are not exactly in HE because of some non-thermal phenomena in clusters such as radiative cooling and feedback from supernovae and active galactic nuclei (AGNs) in cluster central regions (e.g., Kravtsov et al. 2005; Pratt et al. 2010; Planelles et al. 2013). Also, the efficiency of accretion-shock heating of the infalling gas (e.g., Kawaharada et al. 2010; Lapi et al. 2010; Walker et al. 2012; Fujita et al. 2013; Okabe et al. 2014b; Avestruz et al. 2016) is still not well understood. The deviation between the HE mass and the actual total mass depends on the hydrodynamical states of individual clusters. The mean deviation among a cluster sample is called “mass bias.” Indeed, the mass bias may be one of the main causes of the tension in cosmological parameters obtained by the Planck cluster number counts (Planck Collaboration 2015b) and the Planck cosmic microwave background (CMB) analysis (Planck Collaboration 2015a). Therefore, X-ray observations have posed a challenge to this fundamental assumption.
On the other hand, weak-lensing (WL) distortions of background galaxy images provide us with a unique opportunity to reconstruct the mass distribution in clusters without any assumptions of dynamical states (Bartelmann & Schneider 2001), making WL complementary to X-ray analysis. In the past decade, tremendous progress in WL analysis was made by prime focus cameras at large ground-based telescopes like Subaru/Suprime-Cam (e.g., Okabe & Umetsu 2008; Okabe et al. 2010, 2013, 2016; Oguri et al. 2010, 2012; Umetsu et al. 2011, 2016; Miyatake et al. 2013; Medezinski et al. 2016), or wide-field surveys (e.g., Mandelbaum et al. 2006; Melchior et al. 2017; Simet et al. 2017). Weak-lensing mass estimates are, however, sensitive to assumptions about the 3D shapes, halo orientations (e.g., Oguri et al. 2005), and substructures (e.g., Okabe et al. 2014a) in the cluster gravitational potential, as well as any other large-scale structure between the lensed sources and the observer (e.g., Hoekstra 2003). Numerical simulations (e.g., Meneghetti et al. 2010; Becker & Kravtsov 2011) have shown that WL mass estimates have scatter caused by a combination of the above effects.
In order to constrain the HE mass bias and to test the validity of the HE assumption, which are of fundamental importance for cosmological applications, previous studies (e.g., Zhang et al. 2010; von der Linden et al. 2014; Okabe et al. 2014b; Donahue et al. 2014; Hoekstra et al. 2015; Smith et al. 2016) compiled a large number of clusters having both HE masses and WL masses. They compared the two masses to indirectly constrain the non-thermal pressure component involved in turbulence and/or bulk motions and its radial dependence, assuming a random orientation of halo asphericity. As before, joint studies based on complementary X-ray, optical, and WL datasets are definitely important in the new era of cluster physics and cluster-based cosmology.
The Hyper Suprime-Cam Subaru Strategic Program (HSC-SSP: Aihara et al. 2018a, 2018b) is an ongoing wide-field imaging survey using the HSC (Miyazaki et al. 2015), which is a new prime focus camera of the 8.2 m-aperture Subaru Telescope. The HSC-SSP survey is composed of three layers of different depths (Wide, Deep, and UltraDeep). The Wide layer is designed to obtain five-band (grizy) imaging over 1400 deg2. The HSC-SSP survey has both excellent imaging quality ( ∼ 0|${^{\prime\prime}_{.}}$|7 seeing in the i band) and deep observations (r ≲ 26 AB mag). The current status of the survey covers 456 deg2 with non-full depth and 178 deg2 with full depth and full color (Aihara et al. 2018b). The HSC-SSP survey enables optical detection of 2000 galaxy clusters (Oguri et al. 2018) in ∼232 deg2, and will reconstruct the mass distribution of clusters up to z ∼ 1 and beyond.
In this paper, we present HE mass measurements of galaxy clusters in the current HSC-SSP field using XMM-Newton X-ray data, and compare X-ray observables with optical and WL measurements. The HE mass measurement requires long integration times of an X-ray satellite and therefore we selected X-ray luminous galaxy clusters from an existing X-ray cluster catalog as a first study of the HSC-SSP survey.
The paper is organized as follows. We briefly summarize our target selection in section 2. The X-ray, optical, and WL measurements are described in sections 3, 4, and 5, respectively. The main results and discussion are presented in section 6. All results use a flat ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, Ωm0 = 0.3, and |$\Omega _\Lambda =0.7$|.
2 Target selection
With the aim of measuring HE masses, we select our sample of X-ray luminous clusters in the HSC-SSP field using the MCXC (Meta-Catalog of X-Ray Detected Clusters of Galaxies) cluster catalog (Piffaretti et al. 2011), which is a homogeneously measured cluster catalog derived from several public catalogs based on the ROSAT all-sky survey (RASS). The cluster selection from the MCXC catalog satisfies the following criteria: z < 0.4, LX(<r500)E(z)−7/3 > 1044 erg s−1, and fX > 10−12 erg s−1 cm−2 in the HSC-SSP survey region, where LX is the X-ray luminosity in the 0.1–2.4 keV energy band, fX is the X-ray flux, and |$E(z)=[\Omega _{{\rm m}0}(1+z)^3+\Omega _\Lambda ]^{1/2}$|. Adopting the mass–luminosity scaling relation (Piffaretti et al. 2011), the luminosity selection with the correction term E(z)−7/3 is equivalent to the mass selection |$M_{500}\gtrsim 2\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|. Here, M500 is the mass enclosed by the overdensity radius, r500, inside of which the mean mass density is 500 times the critical mass density, ρcr, at the redshift z. In the eventual full area of the HSC-SSP survey of ∼1400 deg2, 22 clusters can be selected from the MCXC all-sky X-ray survey (figure 1). To date, four X-ray luminous clusters (table 1) are in an area suitable for investigating cluster physics with the HSC-SSP S16A data (∼232 deg2: Oguri et al. 2018). We obtained XMM-Newton data for the three clusters through our own program (table 2). In the data analysis, we came across a companion cluster to the west of MCXC J1415.2−0030. As shown in table 1, its redshift is very close to that of MCXCJ1415, and its richness, Ncor, is higher than the originally selected cluster (Oguri et al. 2018). We cannot rule out the possibility that the companion cluster is the dominant component of the system. We additionally carry out X-ray analysis for this cluster, because it is important to precisely measure a gas density profile for MCXC1415 and the contamination of its companion cluster. The cluster is hereafter referred to as MCXC J1415.2−0030W. This paper compiles the analysis of the four MCXC clusters and the companion cluster in the S16A field. The details of the X-ray analysis for the full sample will appear in a future paper.
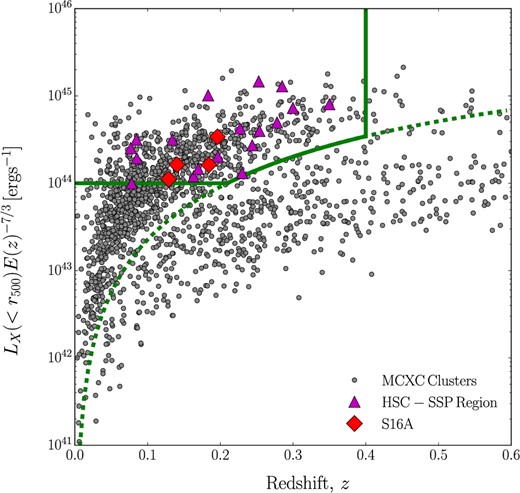
Target selection: X-ray luminosity versus redshift for the MCXC clusters based on the ROSAT all-sky survey. The green solid lines indicate our sample selection. The green dotted line is a flux threshold of 10−12 erg s−1 cm−2. Red diamonds and magenta triangles denote the targeting clusters in the paper and the full area (∼1400 deg2) of the HSC-SSP survey, respectively. (Color online)
| Cluster name . | Alternative name . | Redshift* . | (α, δ)XMM† . | (α, δ)BCG†,** . | (α, δ)CAMIRA§,** . | N cor ‖,** . | WL♯ . |
|---|---|---|---|---|---|---|---|
| MCXC J0157.4−0550 | Abell 281 | 0.12890 | (29.294, −5.869) | (29.279, −5.887) | (29.301, −5.918) | 41.3 | no |
| MCXC J0231.7−0451 | Abell 362 | 0.18430 | (37.927, −4.882) | (37.922, −4.882) | (37.922, −4.883) | 116.4 | yes |
| MCXC J0201.7−0212 | Abell 291 | 0.19600 | (30.429, −2.196) | (30.430, −2.197) | (30.445, −2.198) | 76.2 | no |
| MCXC J1415.2−0030 | Abell 1882A | 0.14030 | (213.785, −0.491) | (213.785, −0.494) | (213.785, −0.493) | 43.0 | yes |
| MCXC J1415.2−0030W | Abell 1882B | 0.14400** | (213.601, −0.377) | (213.600, −0.379) | (213.618, −0.330) | 68.8 | yes |
| Cluster name . | Alternative name . | Redshift* . | (α, δ)XMM† . | (α, δ)BCG†,** . | (α, δ)CAMIRA§,** . | N cor ‖,** . | WL♯ . |
|---|---|---|---|---|---|---|---|
| MCXC J0157.4−0550 | Abell 281 | 0.12890 | (29.294, −5.869) | (29.279, −5.887) | (29.301, −5.918) | 41.3 | no |
| MCXC J0231.7−0451 | Abell 362 | 0.18430 | (37.927, −4.882) | (37.922, −4.882) | (37.922, −4.883) | 116.4 | yes |
| MCXC J0201.7−0212 | Abell 291 | 0.19600 | (30.429, −2.196) | (30.430, −2.197) | (30.445, −2.198) | 76.2 | no |
| MCXC J1415.2−0030 | Abell 1882A | 0.14030 | (213.785, −0.491) | (213.785, −0.494) | (213.785, −0.493) | 43.0 | yes |
| MCXC J1415.2−0030W | Abell 1882B | 0.14400** | (213.601, −0.377) | (213.600, −0.379) | (213.618, −0.330) | 68.8 | yes |
*Cluster redshift from the MCXC catalog.
†X-ray centroid.
†BCG position.
§The center of the CAMIRA catalog.
‖Cluster optical richness.
♯Weak-lensing mass measurement satisfying the full-depth and full-color condition for the current HSC-SSP footprint.
**Data retrieved from the CAMIRA catalog (Oguri et al. 2018).
| Cluster name . | Alternative name . | Redshift* . | (α, δ)XMM† . | (α, δ)BCG†,** . | (α, δ)CAMIRA§,** . | N cor ‖,** . | WL♯ . |
|---|---|---|---|---|---|---|---|
| MCXC J0157.4−0550 | Abell 281 | 0.12890 | (29.294, −5.869) | (29.279, −5.887) | (29.301, −5.918) | 41.3 | no |
| MCXC J0231.7−0451 | Abell 362 | 0.18430 | (37.927, −4.882) | (37.922, −4.882) | (37.922, −4.883) | 116.4 | yes |
| MCXC J0201.7−0212 | Abell 291 | 0.19600 | (30.429, −2.196) | (30.430, −2.197) | (30.445, −2.198) | 76.2 | no |
| MCXC J1415.2−0030 | Abell 1882A | 0.14030 | (213.785, −0.491) | (213.785, −0.494) | (213.785, −0.493) | 43.0 | yes |
| MCXC J1415.2−0030W | Abell 1882B | 0.14400** | (213.601, −0.377) | (213.600, −0.379) | (213.618, −0.330) | 68.8 | yes |
| Cluster name . | Alternative name . | Redshift* . | (α, δ)XMM† . | (α, δ)BCG†,** . | (α, δ)CAMIRA§,** . | N cor ‖,** . | WL♯ . |
|---|---|---|---|---|---|---|---|
| MCXC J0157.4−0550 | Abell 281 | 0.12890 | (29.294, −5.869) | (29.279, −5.887) | (29.301, −5.918) | 41.3 | no |
| MCXC J0231.7−0451 | Abell 362 | 0.18430 | (37.927, −4.882) | (37.922, −4.882) | (37.922, −4.883) | 116.4 | yes |
| MCXC J0201.7−0212 | Abell 291 | 0.19600 | (30.429, −2.196) | (30.430, −2.197) | (30.445, −2.198) | 76.2 | no |
| MCXC J1415.2−0030 | Abell 1882A | 0.14030 | (213.785, −0.491) | (213.785, −0.494) | (213.785, −0.493) | 43.0 | yes |
| MCXC J1415.2−0030W | Abell 1882B | 0.14400** | (213.601, −0.377) | (213.600, −0.379) | (213.618, −0.330) | 68.8 | yes |
*Cluster redshift from the MCXC catalog.
†X-ray centroid.
†BCG position.
§The center of the CAMIRA catalog.
‖Cluster optical richness.
♯Weak-lensing mass measurement satisfying the full-depth and full-color condition for the current HSC-SSP footprint.
**Data retrieved from the CAMIRA catalog (Oguri et al. 2018).
| Cluster name . | Observational ID . | Net exposure (ks)* . | ||
|---|---|---|---|---|
| . | . | MOS1 . | MOS2 . | pn . |
| MCXC J0157.4−0550 | 0781200101† | 27.8 | 27.2 | 16.1 |
| MCXC J0231.7−0451 | 0762870201† | 22.5 | 22.3 | 15.5 |
| MCXC J0201.7−0212 | 0655343801† | 22.4 | 22.4 | 14.9 |
| MCXC J1415.2−0030 | 0762870501† | 19.3 | 19.0 | 13.0 |
| MCXC J1415.2−0030W | 0145480101† | 11.0 | 11.7 | 7.0 |
| Cluster name . | Observational ID . | Net exposure (ks)* . | ||
|---|---|---|---|---|
| . | . | MOS1 . | MOS2 . | pn . |
| MCXC J0157.4−0550 | 0781200101† | 27.8 | 27.2 | 16.1 |
| MCXC J0231.7−0451 | 0762870201† | 22.5 | 22.3 | 15.5 |
| MCXC J0201.7−0212 | 0655343801† | 22.4 | 22.4 | 14.9 |
| MCXC J1415.2−0030 | 0762870501† | 19.3 | 19.0 | 13.0 |
| MCXC J1415.2−0030W | 0145480101† | 11.0 | 11.7 | 7.0 |
*Net exposure time of each instrument after the data reduction.
†Data observed through our program.
†Archival data.
| Cluster name . | Observational ID . | Net exposure (ks)* . | ||
|---|---|---|---|---|
| . | . | MOS1 . | MOS2 . | pn . |
| MCXC J0157.4−0550 | 0781200101† | 27.8 | 27.2 | 16.1 |
| MCXC J0231.7−0451 | 0762870201† | 22.5 | 22.3 | 15.5 |
| MCXC J0201.7−0212 | 0655343801† | 22.4 | 22.4 | 14.9 |
| MCXC J1415.2−0030 | 0762870501† | 19.3 | 19.0 | 13.0 |
| MCXC J1415.2−0030W | 0145480101† | 11.0 | 11.7 | 7.0 |
| Cluster name . | Observational ID . | Net exposure (ks)* . | ||
|---|---|---|---|---|
| . | . | MOS1 . | MOS2 . | pn . |
| MCXC J0157.4−0550 | 0781200101† | 27.8 | 27.2 | 16.1 |
| MCXC J0231.7−0451 | 0762870201† | 22.5 | 22.3 | 15.5 |
| MCXC J0201.7−0212 | 0655343801† | 22.4 | 22.4 | 14.9 |
| MCXC J1415.2−0030 | 0762870501† | 19.3 | 19.0 | 13.0 |
| MCXC J1415.2−0030W | 0145480101† | 11.0 | 11.7 | 7.0 |
*Net exposure time of each instrument after the data reduction.
†Data observed through our program.
†Archival data.
3 X-ray analysis
In order to measure the total cluster mass with X-rays from the ICM gas, which is assumed to be in HE with the cluster gravitational potential, we need the gas density and temperature profiles. The European Photo Imaging Camera (EPIC: Turner et al. 2001; Strüder et al. 2001) on board the XMM-Newton satellite offers an opportunity to perform extremely sensitive imaging/spectroscopic observations for clusters. EPIC data were analyzed with the ESAS (Extended Source Analysis Software) package (Snowden et al. 2008). The details of the data analysis are described in the following sections. In this work, we used SAS version 16.0.0 and HEAsoft version 6.19 with the latest CALDB as of 2016 November.
3.1 Data reduction
The EPIC data were processed and screened in the standard way by using the ESAS pipeline. The data were filtered for intervals of high background due to soft proton flares, defined to be periods when the rates were outside the 2 σ range of a rate distribution. Point sources are removed from three EPIC (MOS1, MOS2, and pn) images with simultaneous maximum likelihood point spread function (PSF) fitting. The radius to mask a point source is chosen so that the surface brightness of the point source is one quarter of the surrounding background. If the radius is less than half of the power diameter (HPD ∼ 15″), we reset the radius to HPD. Table 2 summarizes the cluster data observed with XMM-Newton.
3.2 Spectral fit
In order to determine the gas temperature profile, a spectral fit is performed in the same way as in Snowden et al. (2008), where all spectra extracted from regions of interest are simultaneously fitted with a common model, including particle and cosmic background components that are assumed to be uniform across the detector except for instrumental lines. In this work, we used all three EPIC instruments of the MOS1, MOS2, and pn cameras. Three spectra, one from each instrument, are extracted from concentric annuli centered on an intensity-weighted centroid of the cluster (we first select an intensity peak and then iteratively determine intensity-weighted centroids within a radius of |$500\, h_{70}^{-1}\:$|kpc of the centroid). At each iteration, we exclude regions the sizes of which are the same as those of the excluded point sources (subsection 3.1) at their axially symmetric positions with respect to the centroid computed by the previous iteration. This process is important in order to avoid central shifts by the excluded point sources. The calculation converges within several iterations. Each spectrum is binned in energy to have at least 35 counts per spectral bin, including background. Since the finite PSF effect cannot be ignored for spectral fits of cluster diffuse emission, we consider contaminations from surrounding annuli using crosstalk auxiliary response files (ARFs) in the spectral fitting. The crosstalk contribution to the spectrum in a given annulus from a surrounding annulus is handled as an additional model component.
The instrumental background spectrum, which is stable with time, is modeled with data acquired with the filter wheel closed, available in ESAS CALDB, and is subtracted from the observed spectrum. The other particle backgrounds consisting of a continuum produced by soft protons and instrumental lines are determined by adding a power-law spectrum and narrow Gaussian lines with fixed central energies to the fitting model, respectively. The power-law model representing the soft proton background is added only for MCXC J0157.4−0550, because for the other clusters the spectrum in the outermost region of interest is not affected by the contamination of the soft proton background and therefore the corresponding model is negligible.
The cosmic diffuse background consists of the cosmic X-ray background (CXB), Galactic diffuse emission, and solar wind charge exchange (SWCX) emission lines, all of which are added to the fitting model. The CXB component is modeled with a power-law spectrum with a fixed index of 1.46 according to Snowden et al. (2008). The Galactic diffuse emission is fitted with the sum of absorbed and non-absorbed thermal plasma emission models, with temperatures ranging from 0.25 to 0.7 keV and from 0.1 to 0.3 keV, respectively. The SWCX lines are two narrow Gaussian models with fixed central energies of 0.56 and 0.65 keV, which correspond to O vii and O viii lines, respectively. The CXB and Galactic diffuse emission are constrained by simultaneously fitting a spectrum extracted from the 1°–2° annular region surrounding the cluster using the RASS data (Snowden et al. 1997).
The ICM emission spectrum is fitted by a thermal plasma emission model, APEC (Smith et al. 2001), with the Galactic photoelectric absorption model phabs (Balucinska-Church & McCammon 1992). In the identical annuli of the three EPIC detectors, each spectrum has common model parameters for ICM emission except for a normalization factor for cross-calibration. The metal abundance relative to solar from Anders and Grevesse (1989) in each annulus is co-varied among the three instruments. When the metallicity at large radii is not constrained, it is the same as the value determined in the adjacent inner annulus. The power-law indexes of the soft proton background are different free parameters in the MOS and pn, but are common in all annuli for each detector. The normalization for the soft proton background in individual annuli varies according to a scale factor computed from ESAS. Cluster redshift, the hydrogen column density for the Galactic absorption, and instrumental line center energies are also common but fixed. The hydrogen column densities use weighted averages from Kalberla et al. (2005) at cluster positions.
To properly treat the effect of the finite size of the PSF in XMM-Newton, we considered crosstalk ARFs Snowden et al. (2008) of three or fewer neighboring annuli in the spectral fit. A change of best-fit temperatures derived with and without crosstalk ARFs occurs at the very central region of radial width ∼1΄. We summarize the result of the spectral fit in table 4 in the Appendix. Figure 2 is a typical spectrum of MOS1 in the center region of MCXC J0157.4−0550.
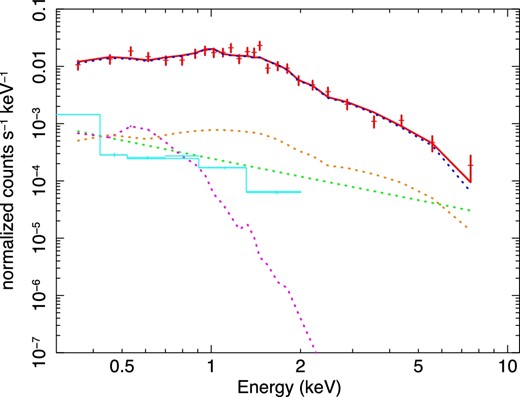
Observed MOS1 spectrum in the center region of MCXC J0157.4−0550 with various fitting model components. In the actual fitting, all 24 spectra are jointly fitted with the common model. The red points show the observed spectrum with the instrumental background subtracted. The red solid line is the sum of all the components. The blue, magenta, orange, and green dotted lines are the thermal emission spectrum of the cluster, Galactic diffuse emission, CXB, and the residual soft proton component, respectively. The light-blue line is the RASS spectrum. (Color online)
3.3 Surface brightness profile
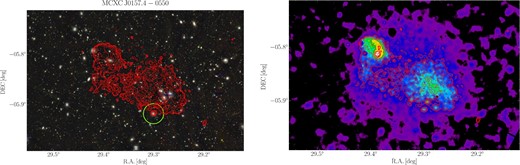
Left: HSC gri pseudocolor image for MCXC J0157.4−0550, overlaid with X-ray contours excluding point sources in red color. The green circle has a 1|${^{\prime}_{.}}$|2 radius and is centered on the CAMIRA cluster. The BCG is located at (α, δ) = (29.279, −5.887). Right: Adaptively smoothed image in 0.4–2.3 keV excluding point sources. The contours are logarithmically spaced from 10 to 1000 in units of cs−1 deg−2. The northeast gas substructure clearly shows a comma-shaped feature, suggesting ram-pressure stripping. (Color online)
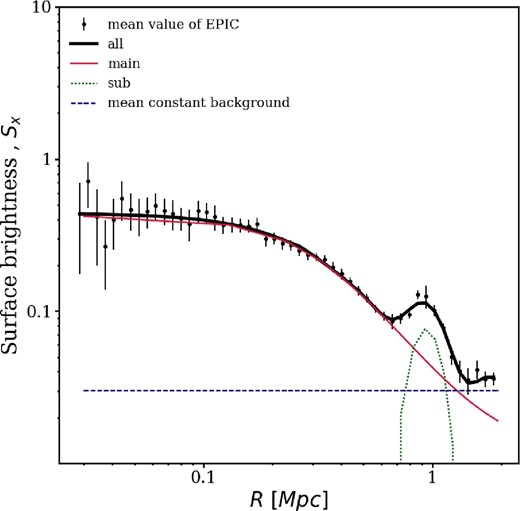
X-ray surface brightness profile for MCXC J0157.4−0550 in arbitrary units averaged over three instruments. The projected distance is described by R. The profile is corrected with different effective areas and background levels of MOS and pn. The center is the flux-weighted X-ray centroid of the western main cluster. Thin red solid, green dotted, and blue dashed lines show the model profile of the western main cluster, the off-centered subcluster, and the mean constant background, respectively. The thick black solid line is the sum over all components, which describes the observed profile very well. (Color online)
3.4 Temperature profile
3.5 HE mass profile
4 Optical catalog
We retrieved the cluster richness, Ncor, and the stellar masses, M*, from the CAMIRA cluster catalog (Oguri et al. 2018), which is constructed using the HSC-SSP Wide S16A data. The CAMIRA algorithm makes use of a stellar population synthesis model to predict colors of red-sequence galaxies at a given redshift for an arbitrary set of bandpass filters and a three-dimensional richness map with a compensated spatial filter. The details of the CAMIRA cluster algorithm are described in Oguri (2014) and Oguri et al. (2018). The smoothing scale for the compensated spatial filter is R0 = 0.8 h−1 Mpc in physical units. The total stellar mass for red galaxies of each cluster is estimated by convolution with the spatial filter. Since blue galaxies are a subdominant component in stellar mass at low redshifts, we estimate the stellar mass only using red galaxies. We confirmed that the photometric redshifts provided by the CAMIRA cluster catalog agree well with the spectroscopic redshifts.
5 Weak-lensing mass measurement
We carry out WL analysis using the WL shear data estimated by the re-Gaussianization method (Hirata & Seljak 2003) implemented in the HSC pipeline (see details in Mandelbaum et al. 2018). Both precise shape measurement and photometric redshift estimation are essential for WL-related studies, giving strict conditions on the depth of data and the availability of five-band photometry. For this reason, the WL shear catalog is restricted to the full-depth and full-color footprint. Three out of five clusters are located in the those regions, namely MCXC J0231.7−0451, MCXC J1415.2−0030, and MCXC J1415.2−0030W, for which we measure WL masses (table 1).
In cluster lensing, contamination of unlensed member galaxies in the source catalog significantly underestimates lensing signals at small radii, because a fraction of member and background galaxies is increasing with a decreasing radius. This is known as the dilution effect (Broadhurst et al. 2005). Previous studies (e.g., Okabe et al. 2013, 2014b; Okabe & Smith 2016) have shown that if there is no background selection, lensing signals for massive clusters at z ∼ 0.2 are underestimated by ∼40%. Previous studies (Okabe et al. 2013; Medezinski et al. 2010, 2016; Okabe & Smith 2016; Umetsu et al. 2016) securely selected background galaxies using color information and succeeded in keeping the level of contamination below a few percent. We briefly summarize the method here. It is very difficult to discriminate between faint members and background galaxies by magnitude information because of large photometric uncertainty and the intrinsic scatter of color distribution. We select a color-space region in which member galaxies are negligible by monitoring consistency among three independent items of information on color, lensing signal, and available, external photometric redshift catalog (Ilbert et al. 2013). Since passively evolving member galaxies are localized in color space, the mean tangential distortion strength in the color space close to the red sequence is significantly underestimated because member galaxies are not lensed. However, the mean lensing signals, which are computed by the ensemble shear and the photometric redshift, outside of red-sequence color space are flattened due to a reduction in contamination by member galaxies. By modeling the color distribution of faint member galaxies, we have succeeded in keeping the contamination limit at less than a few percent. In this procedure, we considered both shape noises and errors of photometric redshifts.
Based on a similar philosophy, Medezinski et al. (2018) developed a new scheme to make a secure selection of background galaxies. We utilized lensing signals and four-band magnitudes (griz) of the HSC-SSP survey, internal photometric redshifts (Tanaka et al. 2018) computed by machine learning (MLZ: Carrasco Kind & Brunner 2014) calibrated with spectroscopic data. We have succeeded in selecting background galaxies in the rz and gi color plane as the best combination for the HSC-SSP survey. Based on Medezinski et al. (2018), we select background galaxies for WL mass measurements (see also H. Miyatake et al. in preparation). The number of background galaxies after the color cuts is ≲11 arcmin−2.
Mass estimation at Δ = 500 in units of |$10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|.
| Name . | HE mass . | WL mass . |
|---|---|---|
| MCXC J0157.4−0550 | |$1.37_{-0.08}^{+0.09}$| | — |
| MCXC J0231.7−0451 | |$3.43_{-0.65}^{+0.77}$| | |$7.96_{-1.89}^{+2.58}$| |
| MCXC J0201.7−0212 | |$3.21_{-0.44}^{+0.51}$| | — |
| MCXC J1415.2−0030 | |$1.54_{-0.23}^{+0.34}$| | |$2.09_{-0.90}^{+1.43}$| |
| MCXC J1415.2−0030W | |$0.44^{+0.07}_{-0.07}$| | |$0.80_{-0.58}^{+0.87}$| |
| Name . | HE mass . | WL mass . |
|---|---|---|
| MCXC J0157.4−0550 | |$1.37_{-0.08}^{+0.09}$| | — |
| MCXC J0231.7−0451 | |$3.43_{-0.65}^{+0.77}$| | |$7.96_{-1.89}^{+2.58}$| |
| MCXC J0201.7−0212 | |$3.21_{-0.44}^{+0.51}$| | — |
| MCXC J1415.2−0030 | |$1.54_{-0.23}^{+0.34}$| | |$2.09_{-0.90}^{+1.43}$| |
| MCXC J1415.2−0030W | |$0.44^{+0.07}_{-0.07}$| | |$0.80_{-0.58}^{+0.87}$| |
Mass estimation at Δ = 500 in units of |$10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|.
| Name . | HE mass . | WL mass . |
|---|---|---|
| MCXC J0157.4−0550 | |$1.37_{-0.08}^{+0.09}$| | — |
| MCXC J0231.7−0451 | |$3.43_{-0.65}^{+0.77}$| | |$7.96_{-1.89}^{+2.58}$| |
| MCXC J0201.7−0212 | |$3.21_{-0.44}^{+0.51}$| | — |
| MCXC J1415.2−0030 | |$1.54_{-0.23}^{+0.34}$| | |$2.09_{-0.90}^{+1.43}$| |
| MCXC J1415.2−0030W | |$0.44^{+0.07}_{-0.07}$| | |$0.80_{-0.58}^{+0.87}$| |
| Name . | HE mass . | WL mass . |
|---|---|---|
| MCXC J0157.4−0550 | |$1.37_{-0.08}^{+0.09}$| | — |
| MCXC J0231.7−0451 | |$3.43_{-0.65}^{+0.77}$| | |$7.96_{-1.89}^{+2.58}$| |
| MCXC J0201.7−0212 | |$3.21_{-0.44}^{+0.51}$| | — |
| MCXC J1415.2−0030 | |$1.54_{-0.23}^{+0.34}$| | |$2.09_{-0.90}^{+1.43}$| |
| MCXC J1415.2−0030W | |$0.44^{+0.07}_{-0.07}$| | |$0.80_{-0.58}^{+0.87}$| |
| Cluster name . | Annulus* . | counts±error† . | Temperature‡ . | Abandance‡ . | ||
|---|---|---|---|---|---|---|
| . | (″) . | MOS1 . | MOS2 . | PN . | (keV) . | (Z⊙) . |
| MCXC J0157.4−0550 | 0–60 | 834 | 829 | 1400 | |$3.51 _{- 0.26 }^{+ 0.32 }$| | 0.26 |
| 60–100 | 1038 | 1163 | 1975 | |$3.02 _{- 0.22 }^{+ 0.27 }$| | 0.18 | |
| 100–140 | 1196 | 1267 | 1955 | |$3.28 _{- 0.25 }^{+ 0.33 }$| | 0.18 | |
| 140–180 | 1228 | 1303 | 2085 | |$2.84 _{- 0.23 }^{+ 0.30 }$| | 0.20 | |
| 180–270 | 2867 | 2732 | 4647 | |$2.73 _{- 0.13 }^{+ 0.28 }$| | 0.16 | |
| 270–360 | 2920 | 2640 | 5306 | |$2.54 _{- 0.10 }^{+ 0.31 }$| | 0.10 | |
| 360–600 | 7778 | 8959 | 17871 | — | ||
| 600–900 | 3117 | 5036 | 13795 | — | ||
| MCXC J0231.7−0451 | 0–40 | 1411 | 1355 | 3084 | |$5.64 _{- 0.34 }^{+ 0.40 }$| | 0.52 |
| 40–60 | 1381 | 1353 | 2739 | |$5.03 _{- 0.37 }^{+ 0.37 }$| | 0.12 | |
| 60–80 | 1339 | 1229 | 2492 | |$4.33 _{- 0.27 }^{+ 0.36 }$| | 0.46 | |
| 80–100 | 1182 | 1198 | 2455 | |$5.03 _{- 0.47 }^{+ 0.52 }$| | 0.33 | |
| 100–140 | 1936 | 1882 | 3737 | |$4.09 _{- 0.22 }^{+ 0.23 }$| | 0.20 | |
| 140–180 | 1155 | 1174 | 2052 | |$4.50 _{- 0.44 }^{+ 0.55 }$| | 0.20 | |
| 180–270 | 1665 | 1591 | 3373 | |$3.10 _{- 0.38 }^{+ 0.54 }$| | 0.20 | |
| 270–400 | 1633 | 1798 | 4002 | — | ||
| MCXC J0201.7−0212 | 0–40 | 7690 | 7369 | 16494 | |$3.30 _{- 0.05 }^{+ 0.05 }$| | 0.41 |
| 40–60 | 2617 | 2379 | 4139 | |$4.23 _{- 0.27 }^{+ 0.36 }$| | 0.28 | |
| 60–80 | 1649 | 1686 | 3218 | |$4.26 _{- 0.36 }^{+ 0.48 }$| | 0.14 | |
| 80–100 | 1157 | 1151 | 2440 | |$4.47 _{- 0.69 }^{+ 0.58 }$| | 0.14 | |
| 100–140 | 1667 | 1710 | 3198 | |$3.38 _{- 0.20 }^{+ 0.41 }$| | 0.17 | |
| 140–180 | 1044 | 1034 | 1750 | |$4.28 _{- 0.49 }^{+ 0.67 }$| | 0.17 | |
| 180–270 | 1596 | 1719 | 2486 | |$2.43 _{- 0.28 }^{+ 0.27 }$| | 0.17 | |
| 270–360 | 1324 | 1502 | 2463 | — | ||
| MCXC J1415.2−0030 | 0–50 | 509 | 519 | 889 | |$3.12 _{- 0.25 }^{+ 0.25 }$| | 0.22 |
| 50–90 | 690 | 683 | 1102 | |$3.99 _{- 0.41 }^{+ 0.46 }$| | 0.29 | |
| 90–140 | 761 | 736 | 1522 | |$3.00 _{- 0.34 }^{+ 0.31 }$| | 0.47 | |
| 140–180 | 481 | 444 | 890 | |$2.03 _{- 0.38 }^{+ 0.54 }$| | 0.21 | |
| 180–270 | 969 | 953 | 1984 | |$1.71 _{- 0.13 }^{+ 0.12 }$| | 0.12 | |
| 270–360 | 1302 | 1225 | 2653 | — | — | |
| MCXC J1415.2−0030W | 0–80 | 191 | 229 | 417 | |$2.06_{-0.22}^{+0.29}$| | 0.34 |
| 80–140 | 198 | 246 | 430 | |$1.80_{-0.28}^{+0.94}$| | 0.33 | |
| 140–270 | 772 | 803 | 1473 | — | ||
| Cluster name . | Annulus* . | counts±error† . | Temperature‡ . | Abandance‡ . | ||
|---|---|---|---|---|---|---|
| . | (″) . | MOS1 . | MOS2 . | PN . | (keV) . | (Z⊙) . |
| MCXC J0157.4−0550 | 0–60 | 834 | 829 | 1400 | |$3.51 _{- 0.26 }^{+ 0.32 }$| | 0.26 |
| 60–100 | 1038 | 1163 | 1975 | |$3.02 _{- 0.22 }^{+ 0.27 }$| | 0.18 | |
| 100–140 | 1196 | 1267 | 1955 | |$3.28 _{- 0.25 }^{+ 0.33 }$| | 0.18 | |
| 140–180 | 1228 | 1303 | 2085 | |$2.84 _{- 0.23 }^{+ 0.30 }$| | 0.20 | |
| 180–270 | 2867 | 2732 | 4647 | |$2.73 _{- 0.13 }^{+ 0.28 }$| | 0.16 | |
| 270–360 | 2920 | 2640 | 5306 | |$2.54 _{- 0.10 }^{+ 0.31 }$| | 0.10 | |
| 360–600 | 7778 | 8959 | 17871 | — | ||
| 600–900 | 3117 | 5036 | 13795 | — | ||
| MCXC J0231.7−0451 | 0–40 | 1411 | 1355 | 3084 | |$5.64 _{- 0.34 }^{+ 0.40 }$| | 0.52 |
| 40–60 | 1381 | 1353 | 2739 | |$5.03 _{- 0.37 }^{+ 0.37 }$| | 0.12 | |
| 60–80 | 1339 | 1229 | 2492 | |$4.33 _{- 0.27 }^{+ 0.36 }$| | 0.46 | |
| 80–100 | 1182 | 1198 | 2455 | |$5.03 _{- 0.47 }^{+ 0.52 }$| | 0.33 | |
| 100–140 | 1936 | 1882 | 3737 | |$4.09 _{- 0.22 }^{+ 0.23 }$| | 0.20 | |
| 140–180 | 1155 | 1174 | 2052 | |$4.50 _{- 0.44 }^{+ 0.55 }$| | 0.20 | |
| 180–270 | 1665 | 1591 | 3373 | |$3.10 _{- 0.38 }^{+ 0.54 }$| | 0.20 | |
| 270–400 | 1633 | 1798 | 4002 | — | ||
| MCXC J0201.7−0212 | 0–40 | 7690 | 7369 | 16494 | |$3.30 _{- 0.05 }^{+ 0.05 }$| | 0.41 |
| 40–60 | 2617 | 2379 | 4139 | |$4.23 _{- 0.27 }^{+ 0.36 }$| | 0.28 | |
| 60–80 | 1649 | 1686 | 3218 | |$4.26 _{- 0.36 }^{+ 0.48 }$| | 0.14 | |
| 80–100 | 1157 | 1151 | 2440 | |$4.47 _{- 0.69 }^{+ 0.58 }$| | 0.14 | |
| 100–140 | 1667 | 1710 | 3198 | |$3.38 _{- 0.20 }^{+ 0.41 }$| | 0.17 | |
| 140–180 | 1044 | 1034 | 1750 | |$4.28 _{- 0.49 }^{+ 0.67 }$| | 0.17 | |
| 180–270 | 1596 | 1719 | 2486 | |$2.43 _{- 0.28 }^{+ 0.27 }$| | 0.17 | |
| 270–360 | 1324 | 1502 | 2463 | — | ||
| MCXC J1415.2−0030 | 0–50 | 509 | 519 | 889 | |$3.12 _{- 0.25 }^{+ 0.25 }$| | 0.22 |
| 50–90 | 690 | 683 | 1102 | |$3.99 _{- 0.41 }^{+ 0.46 }$| | 0.29 | |
| 90–140 | 761 | 736 | 1522 | |$3.00 _{- 0.34 }^{+ 0.31 }$| | 0.47 | |
| 140–180 | 481 | 444 | 890 | |$2.03 _{- 0.38 }^{+ 0.54 }$| | 0.21 | |
| 180–270 | 969 | 953 | 1984 | |$1.71 _{- 0.13 }^{+ 0.12 }$| | 0.12 | |
| 270–360 | 1302 | 1225 | 2653 | — | — | |
| MCXC J1415.2−0030W | 0–80 | 191 | 229 | 417 | |$2.06_{-0.22}^{+0.29}$| | 0.34 |
| 80–140 | 198 | 246 | 430 | |$1.80_{-0.28}^{+0.94}$| | 0.33 | |
| 140–270 | 772 | 803 | 1473 | — | ||
*Cluster-centric annulus.
†Counts in the energy band of 0.3–11 keV of each instrument.
‡Best-fit temperature and abundance.
| Cluster name . | Annulus* . | counts±error† . | Temperature‡ . | Abandance‡ . | ||
|---|---|---|---|---|---|---|
| . | (″) . | MOS1 . | MOS2 . | PN . | (keV) . | (Z⊙) . |
| MCXC J0157.4−0550 | 0–60 | 834 | 829 | 1400 | |$3.51 _{- 0.26 }^{+ 0.32 }$| | 0.26 |
| 60–100 | 1038 | 1163 | 1975 | |$3.02 _{- 0.22 }^{+ 0.27 }$| | 0.18 | |
| 100–140 | 1196 | 1267 | 1955 | |$3.28 _{- 0.25 }^{+ 0.33 }$| | 0.18 | |
| 140–180 | 1228 | 1303 | 2085 | |$2.84 _{- 0.23 }^{+ 0.30 }$| | 0.20 | |
| 180–270 | 2867 | 2732 | 4647 | |$2.73 _{- 0.13 }^{+ 0.28 }$| | 0.16 | |
| 270–360 | 2920 | 2640 | 5306 | |$2.54 _{- 0.10 }^{+ 0.31 }$| | 0.10 | |
| 360–600 | 7778 | 8959 | 17871 | — | ||
| 600–900 | 3117 | 5036 | 13795 | — | ||
| MCXC J0231.7−0451 | 0–40 | 1411 | 1355 | 3084 | |$5.64 _{- 0.34 }^{+ 0.40 }$| | 0.52 |
| 40–60 | 1381 | 1353 | 2739 | |$5.03 _{- 0.37 }^{+ 0.37 }$| | 0.12 | |
| 60–80 | 1339 | 1229 | 2492 | |$4.33 _{- 0.27 }^{+ 0.36 }$| | 0.46 | |
| 80–100 | 1182 | 1198 | 2455 | |$5.03 _{- 0.47 }^{+ 0.52 }$| | 0.33 | |
| 100–140 | 1936 | 1882 | 3737 | |$4.09 _{- 0.22 }^{+ 0.23 }$| | 0.20 | |
| 140–180 | 1155 | 1174 | 2052 | |$4.50 _{- 0.44 }^{+ 0.55 }$| | 0.20 | |
| 180–270 | 1665 | 1591 | 3373 | |$3.10 _{- 0.38 }^{+ 0.54 }$| | 0.20 | |
| 270–400 | 1633 | 1798 | 4002 | — | ||
| MCXC J0201.7−0212 | 0–40 | 7690 | 7369 | 16494 | |$3.30 _{- 0.05 }^{+ 0.05 }$| | 0.41 |
| 40–60 | 2617 | 2379 | 4139 | |$4.23 _{- 0.27 }^{+ 0.36 }$| | 0.28 | |
| 60–80 | 1649 | 1686 | 3218 | |$4.26 _{- 0.36 }^{+ 0.48 }$| | 0.14 | |
| 80–100 | 1157 | 1151 | 2440 | |$4.47 _{- 0.69 }^{+ 0.58 }$| | 0.14 | |
| 100–140 | 1667 | 1710 | 3198 | |$3.38 _{- 0.20 }^{+ 0.41 }$| | 0.17 | |
| 140–180 | 1044 | 1034 | 1750 | |$4.28 _{- 0.49 }^{+ 0.67 }$| | 0.17 | |
| 180–270 | 1596 | 1719 | 2486 | |$2.43 _{- 0.28 }^{+ 0.27 }$| | 0.17 | |
| 270–360 | 1324 | 1502 | 2463 | — | ||
| MCXC J1415.2−0030 | 0–50 | 509 | 519 | 889 | |$3.12 _{- 0.25 }^{+ 0.25 }$| | 0.22 |
| 50–90 | 690 | 683 | 1102 | |$3.99 _{- 0.41 }^{+ 0.46 }$| | 0.29 | |
| 90–140 | 761 | 736 | 1522 | |$3.00 _{- 0.34 }^{+ 0.31 }$| | 0.47 | |
| 140–180 | 481 | 444 | 890 | |$2.03 _{- 0.38 }^{+ 0.54 }$| | 0.21 | |
| 180–270 | 969 | 953 | 1984 | |$1.71 _{- 0.13 }^{+ 0.12 }$| | 0.12 | |
| 270–360 | 1302 | 1225 | 2653 | — | — | |
| MCXC J1415.2−0030W | 0–80 | 191 | 229 | 417 | |$2.06_{-0.22}^{+0.29}$| | 0.34 |
| 80–140 | 198 | 246 | 430 | |$1.80_{-0.28}^{+0.94}$| | 0.33 | |
| 140–270 | 772 | 803 | 1473 | — | ||
| Cluster name . | Annulus* . | counts±error† . | Temperature‡ . | Abandance‡ . | ||
|---|---|---|---|---|---|---|
| . | (″) . | MOS1 . | MOS2 . | PN . | (keV) . | (Z⊙) . |
| MCXC J0157.4−0550 | 0–60 | 834 | 829 | 1400 | |$3.51 _{- 0.26 }^{+ 0.32 }$| | 0.26 |
| 60–100 | 1038 | 1163 | 1975 | |$3.02 _{- 0.22 }^{+ 0.27 }$| | 0.18 | |
| 100–140 | 1196 | 1267 | 1955 | |$3.28 _{- 0.25 }^{+ 0.33 }$| | 0.18 | |
| 140–180 | 1228 | 1303 | 2085 | |$2.84 _{- 0.23 }^{+ 0.30 }$| | 0.20 | |
| 180–270 | 2867 | 2732 | 4647 | |$2.73 _{- 0.13 }^{+ 0.28 }$| | 0.16 | |
| 270–360 | 2920 | 2640 | 5306 | |$2.54 _{- 0.10 }^{+ 0.31 }$| | 0.10 | |
| 360–600 | 7778 | 8959 | 17871 | — | ||
| 600–900 | 3117 | 5036 | 13795 | — | ||
| MCXC J0231.7−0451 | 0–40 | 1411 | 1355 | 3084 | |$5.64 _{- 0.34 }^{+ 0.40 }$| | 0.52 |
| 40–60 | 1381 | 1353 | 2739 | |$5.03 _{- 0.37 }^{+ 0.37 }$| | 0.12 | |
| 60–80 | 1339 | 1229 | 2492 | |$4.33 _{- 0.27 }^{+ 0.36 }$| | 0.46 | |
| 80–100 | 1182 | 1198 | 2455 | |$5.03 _{- 0.47 }^{+ 0.52 }$| | 0.33 | |
| 100–140 | 1936 | 1882 | 3737 | |$4.09 _{- 0.22 }^{+ 0.23 }$| | 0.20 | |
| 140–180 | 1155 | 1174 | 2052 | |$4.50 _{- 0.44 }^{+ 0.55 }$| | 0.20 | |
| 180–270 | 1665 | 1591 | 3373 | |$3.10 _{- 0.38 }^{+ 0.54 }$| | 0.20 | |
| 270–400 | 1633 | 1798 | 4002 | — | ||
| MCXC J0201.7−0212 | 0–40 | 7690 | 7369 | 16494 | |$3.30 _{- 0.05 }^{+ 0.05 }$| | 0.41 |
| 40–60 | 2617 | 2379 | 4139 | |$4.23 _{- 0.27 }^{+ 0.36 }$| | 0.28 | |
| 60–80 | 1649 | 1686 | 3218 | |$4.26 _{- 0.36 }^{+ 0.48 }$| | 0.14 | |
| 80–100 | 1157 | 1151 | 2440 | |$4.47 _{- 0.69 }^{+ 0.58 }$| | 0.14 | |
| 100–140 | 1667 | 1710 | 3198 | |$3.38 _{- 0.20 }^{+ 0.41 }$| | 0.17 | |
| 140–180 | 1044 | 1034 | 1750 | |$4.28 _{- 0.49 }^{+ 0.67 }$| | 0.17 | |
| 180–270 | 1596 | 1719 | 2486 | |$2.43 _{- 0.28 }^{+ 0.27 }$| | 0.17 | |
| 270–360 | 1324 | 1502 | 2463 | — | ||
| MCXC J1415.2−0030 | 0–50 | 509 | 519 | 889 | |$3.12 _{- 0.25 }^{+ 0.25 }$| | 0.22 |
| 50–90 | 690 | 683 | 1102 | |$3.99 _{- 0.41 }^{+ 0.46 }$| | 0.29 | |
| 90–140 | 761 | 736 | 1522 | |$3.00 _{- 0.34 }^{+ 0.31 }$| | 0.47 | |
| 140–180 | 481 | 444 | 890 | |$2.03 _{- 0.38 }^{+ 0.54 }$| | 0.21 | |
| 180–270 | 969 | 953 | 1984 | |$1.71 _{- 0.13 }^{+ 0.12 }$| | 0.12 | |
| 270–360 | 1302 | 1225 | 2653 | — | — | |
| MCXC J1415.2−0030W | 0–80 | 191 | 229 | 417 | |$2.06_{-0.22}^{+0.29}$| | 0.34 |
| 80–140 | 198 | 246 | 430 | |$1.80_{-0.28}^{+0.94}$| | 0.33 | |
| 140–270 | 772 | 803 | 1473 | — | ||
*Cluster-centric annulus.
†Counts in the energy band of 0.3–11 keV of each instrument.
‡Best-fit temperature and abundance.
6 Results and discussion
We carried out X-ray analysis and joint X-ray and optical analysis for the four MCXC clusters and the non-MCXC cluster (table 1) in the current coverage region for the HSC-SSP survey. As mentioned in section 5, the sample for WL mass measurement is only the three clusters (table 1) due to the full-color and full-depth condition. Thus, we shall use the WL mass estimates only for X-ray and WL mass comparisons.
Since this paper is a sort of pilot study to directly compare multiwavelength datasets, we shall first discuss results for individual clusters based on both X-ray and optical datasets. We then perform studies of a correlation between HE masses and richness, a mass comparison, and baryon fraction for the current sample of clusters.
6.1 MCXC J0157.4−0550
MCXC J0157.4−0550 is an ongoing cluster merger at z = 0.1289, as shown in figure 3. The system is composed of the western main gas halo and the northeast subhalo. Optically luminous galaxies are concentrated in the western region, where the X-ray morphology is highly elongated along the west–east direction. The CAMIRA center is slightly offset from both the X-ray and BCG centers, because some luminous galaxies are missing in the HSC CAMIRA catalog. A comma-shaped feature in the X-ray emission is discovered at ∼1.6 r500 ∼ r200 based on HE mass estimation (subsection 3.5), which suggests ram-pressure stripping of the subcluster. An optically luminous galaxy is located at the subcluster X-ray peak. The redshift retrieved from the SDSS, 0.1286, is very close to the cluster redshift, suggesting that the substructure is infalling in the plane of the sky. This is consistent with the fact that a prominent tail is observed. The comma-shaped feature also implies that the infalling gas observed in the X-ray has large angular momentum. If we improperly treat the substructure in the X-ray surface brightness (Sx) modeling, it may change the outer density slope [equation (2)] of the main halo and eventually affect the HE mass estimation. Furthermore, we cannot rule out the possibility that the slopes in the disturbed (east) and undisturbed (west) sectors are different. Since our analysis assumes spherical symmetry to measure spherical HE masses, it is not good to divide into azimuthally dependent subsectors. To solve these problems, we implement the subtraction using the off-centering effect [equation (4)] in a model of the azimuthally averaged surface brightness profile centering on the western gas halo. As a first approximation, we assume the β model for the western main gas halo and the northeast subhalo. The resulting profile describes well the observed surface brightness (figure 4).
The HE mass is estimated only for the main cluster. The total gas mass within ∼r200 computed for both the main gas and the gas substructure is ∼8% higher than that estimated by the main cluster component, while the gas mass within r500 does not change.
Unfortunately, this cluster is located outside of the full-depth and full-color region of the HSC-SSP S16A data, and thus the WL shape data are not available. A mass comparison for this cluster will be carried out in a future study.
6.2 MCXC J0231.7−0451
We present new observations of the cluster (z = 0.1843) located in the XXL survey region with XMM-Newton. An X-ray luminous point source at ∼ 3|${^{\prime}_{.}}$|5 east of the X-ray center is found. Faint X-ray emission from another CAMIRA cluster at z = 0.2760 is also detected around the edge of the X-ray detectors (figure 5). These X-ray sources are excluded in our analysis.
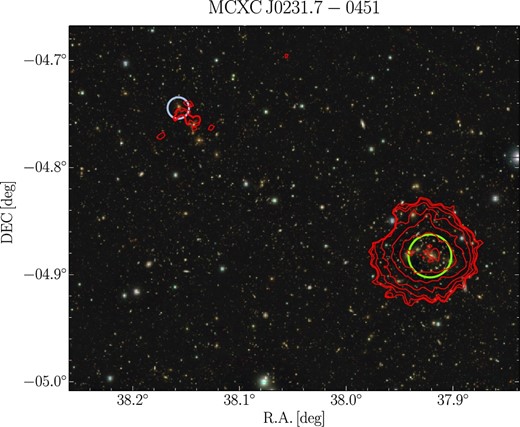
Optical image of MCXC J0231.7−0451, overlaid with X-ray contours in red color. Green circles show 1|${^{\prime}_{.}}$|2 radius centering CAMIRA clusters. The western diffuse X-ray emission is from the target cluster. Faint X-ray emission from another CAMIRA cluster with Ncor = 33.70 at (29.203, −6.119) and z = 0.2760, marked by a light-blue circle with 0|${^{\prime}_{.}}$|6 radius, is also detected around the edges of the instruments. The contours are the same as figure 3. (Color online)
The cluster is referred to as XXL091 in the XXL survey (Eckert et al. 2016), and has |$M_{\rm gas}=5.00^{+0.80}_{-0.83}\times 10^{13}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| within |$r_{500}^{\rm MT}=1149\pm 161\, h_{70}^{-1}\:$|kpc derived from a scaling relation between WL mass and X-ray temperature (Lieu et al. 2016). We find that our measurement |$M_{\rm gas}=5.10^{+0.85}_{-0.84}\times 10^{13}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| within the same radius is in good agreement with Eckert et al. (2016).
The mass estimation of the Planck SZ observation (Planck Collaboration 2015b) gives |$M_{500}^{\rm SZ}=3.96^{+0.49}_{-0.49}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|, which agrees with our HE mass estimate |$M_{500}^{\rm HE}=3.43^{+0.77}_{-0.65}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|.
Our WL mass measurement gives |$M_{500}^{\rm WL}=7.96_{-1.89}^{+2.58}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|, which agrees within errors with the CFHT WL mass measurement |$M_{500}^{{\rm WL}}=6.2^{+2.1}_{-1.8}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| (Lieu et al. 2016).
6.3 MCXC J0201.7−0212
This cluster is known as Abell 291, and has a cool core (Okabe et al. 2010, 2016; Martino et al. 2014). Since the HSC-SSP S16A data of the cluster do not satisfy the full-depth and full-color condition for WL mass measurement, we carry out X-ray and optical analysis.
We analyzed the same X-ray data used in Martino et al. (2014). The gas density profile is described well by a double β model. The CAMIRA center is slightly offset from the X-ray centroid and the BCG (figure 6), because a few bright galaxies are missing in the CAMIRA catalog. Our HE mass estimate, |$M_{500}^{\rm HE}=3.21_{-0.44}^{+0.51}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|, agrees with a previous X-ray study: |$M_{500}=2.92\pm 0.56\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| (Martino et al. 2014). They are slightly lower than the WL mass, |$M_{500}^{\rm WL}=4.46^{+1.01}_{-0.96}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| (Okabe & Smith 2016), but the difference is not statistically significant. A mass comparison using the HSC-SSP data is left for future work.
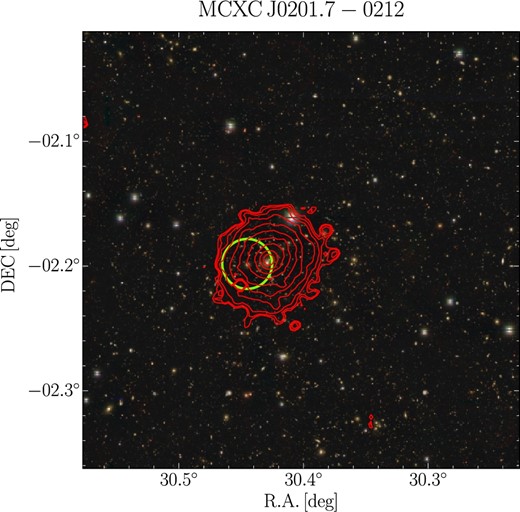
MCXC J0201.7−0212. The colors and contours are the same as those in figure 3. (Color online)
6.4 MCXC J1415.2−0030 and MCXC J1415.2−0030W
The system is mainly composed of the originally identified MCXC cluster MCXC J1415.2−0030 at the east and its companion cluster at ∼2 Mpc northwest of the MCXC cluster. We refer to the western cluster as MCXC J1415.2−0030W for convenience. The X-ray emission shows no evidence of disturbance due to merger activity. Besides the two clusters, two faint, diffuse X-ray emissions are found in the field (figure 7). The northern emission (α, δ) = (213.740, −0.350) and the north-western emission (α, δ) = (213.541, −0.272) are associated with galaxies at z = 0.1389 and z = 0.1398, respectively. These components of radii ∼ 0|${^{\prime}_{.}}$|7–0|${^{\prime}_{.}}$|8 are excluded in the following X-ray analysis. In the CAMIRA catalog, those galaxies are identified as a part of MCXC J1415.2−0030W, giving a large richness. The X-ray emission from the eastern MCXC cluster coincides with the CAMIRA center, while the western emission is ∼3΄ offset from the CAMIRA center. This is because the western CAMIRA cluster includes the northern and north-western groups. We find no evidence that the BCGs of the eastern and western clusters are significantly offset from the X-ray centroids. The X-ray luminosity of the eastern MCXC cluster is brighter than that of the western cluster, while the richness for the western cluster is higher. Owers et al. (2013, figure 4) have shown based on spectroscopic data that member galaxies of the eastern and western clusters are spread over ∼4 Mpc and ∼1 Mpc, respectively.
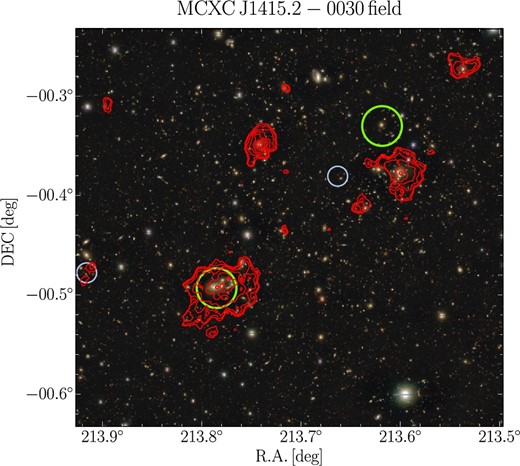
MCXC J1415.2−003 field, overlaid with X-ray contours in red color. Four diffuse X-ray sources are found in this field. MCXC J1415.2−0030 and MCXC J1415.2−0030W are at the middle left and middle right of the panel, respectively. The other two diffuse X-ray emissions surrounding the system are found at (α, δ) = (213.740, −0.350) and (α, δ) = (213.541, −0.272). The green circles have a 1|${^{\prime}_{.}}$|2 radius and are centered on the CAMIRA clusters. Two high-z CAMIRA clusters (z > 0.9 and Ncor ≳ 15) are found in the field, marked by light-blue circles with 0|${^{\prime}_{.}}$|6 radii. The contours are the same as figure 3. (Color online)
We analyzed X-ray data for these two clusters in order to measure gas temperatures and surface brightness profiles. To carefully estimate density outer slopes, we computed two surface brightness profiles centering on each of the two clusters and simultaneously fitted them with the two surface brightness models with the off-centering effect. We found that the observed profiles are described well by the sum of X-ray emission of the two clusters, requiring no extra component such as a filamentary gas component bridge between the two clusters. In the surface brightness profile centered on MCXC J1415.2−0030, the flux of the cluster, the other cluster, and the background at R ∼ 1 Mpc account for ∼1%, ∼13%, and ∼86%, respectively. In the temperature measurements for each cluster, we selected the background-dominated region for the annulus. Again, if we ignore the flux contamination from the other cluster in the surface brightness modeling, we overestimate the background component and eventually misestimate the outer slopes.
Based on the HE assumption, we estimate |$M_{500}^{\rm HE}=1.54_{-0.23}^{+0.34}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| for MCXC J1415.2−0030 and |$M_{500}^{\rm HE}=0.44_{-0.07}^{+0.07}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| for MCXC J1415.2−0030W (table 3), respectively. This suggests that the originally identified MCXC cluster is the main cluster.
We also carry out WL mass measurements for the two clusters. We adopt a maximum radius for each tangential shear profile centered on each BCG of ∼1.3 |$h_{70}^{-1}$| Mpc. Since the maximum radius is much less than the projected distance between the two clusters, the off-centering effect of the lensing signal is negligible, |$\sim {\mathcal {O}}(10^{-5})\times \langle \Sigma _{\rm cr}^{-1}\rangle ^{-1}$| (Yang et al. 2006), in contrast to X-ray analysis. This is caused by the fact that |$\Delta \Sigma _{+,\rm off}=\bar{\Sigma }_{\rm off}-{\Sigma }_{\rm off}$|, where the the surface mass density for the off-centering component at the measured radius, Σoff(R), is comparable to the mean surface mass density within the radius, |$\bar{\Sigma }_{\rm off}(<\!R)$|. The WL masses are |$M_{500}^{\rm WL}=2.09_{-0.90}^{+1.43}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| for MCXC J1415.2−0030 and |$M_{500}^{\rm WL}=0.80_{-0.58}^{+0.87}\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| for MCXC J1415.2−0030W (table 3). Since the signal-to-noise ratio of the tangential shear profile for MCXC J1415.2−0030W is small, we used one parameter, M500, assuming the halo concentration based on the median value of the mass versus concentration relation (Diemer & Kravtsov 2015). A sum of best-fit virial radii ∼2.6 Mpc is comparable to the projected separation ∼2 Mpc and non-disturbed gas distribution, suggesting that the two clusters are at an early phase of cluster merger. The HE mass for the western companion cluster is comparable to the WL mass.
Virial mass estimation (Owers et al. 2013) using spectroscopic data has shown that |$M_{500}^{\rm vir}=1.5\pm 0.3\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| for the main cluster (A1882A) and |$M_{500}^{\rm vir}=1.0\pm 0.5\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| for the companion cluster (A1882B), respectively. Dynamical mass estimates are in good agreement with our WL masses. Owers et al. (2013) also concluded, based on joint X-ray and kinematics analysis, that the system is likely to be before cluster merger. Our results agree with their conclusions.
6.5 Richness vs. MHE
We compare the HE masses for the MCXC clusters with the CAMIRA cluster richness. Since the cluster richness is generally proportional to the number of member galaxies, it is expected to be a good mass proxy. Indeed, Oguri et al. (2018) have compared public X-ray temperature and luminosity in the XXL and XMM-LSS fields with the CAMIRA cluster richness, and found good correlations. The slope in a richness and temperature scaling relation is found to be shallower than that predicted by a self-similar solution. The temperatures are measured within a fixed radius, 300 kpc, and thus are potentially and partially affected by baryonic physics. We study here a correlation between the HE masses and cluster richness.
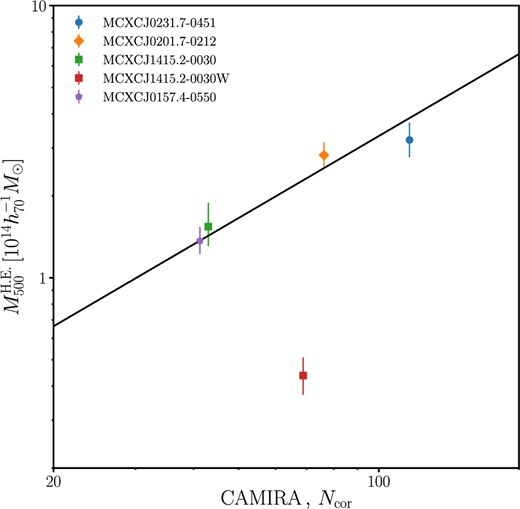
Comparison between CAMIRA richness (Oguri et al. 2018) and HE mass at Δ = 500. The solid line is the best fit for the four MCXC clusters. The HE mass for the non-MCXC cluster is significantly lower than the best-fit baseline. (Color online)
Interestingly, the HE mass for the non-MCXC cluster, MCXC J1415.2−0030W, is significantly lower than the best-fit baseline. The deviation might be explained by two possibilities or their combination. First, at the early stage of cluster merger, the ICM would strongly deviate from HE, consistent with our finding that the WL mass is higher (subsection 6.4). Second, the richness would be overestimated because the CAMIRA member galaxies of MCXC J1415.2−0030W include the other group components. We also fit the mass–richness scaling relation for the five clusters with a = 1 fixed, and confirm that the normalization, b = −3.74 ± 0.45, does not significantly change.
6.6 Mass comparison
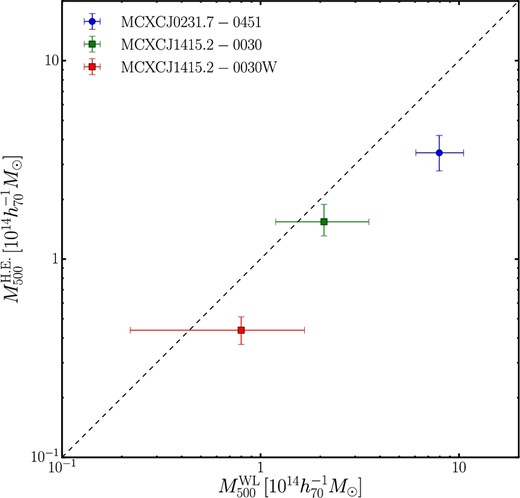
Mass comparison of WL and HE masses for the three clusters at Δ = 500. (Color online)
When we use the same radii determined by weak-lensing masses, we obtain |$b_{\rm m}=0.40_{-0.49}^{+0.39}$| for the three clusters and |$b_{\rm m}=0.34_{-0.41}^{+0.28}$| for the two clusters, respectively. Here we consider the error propagation of measurement uncertainties of the WL radii. The result does not significantly change. When we measure WL masses with X-ray centers, the best-fit WL masses are changed only by a few percent because the offset distances between X-ray centroids and BCG positions are very small.
Although our results are statistically poor because of a small sample of clusters, we compare them with the literature. Direct comparisons between weak-lensing masses and X-ray masses are not trivial, because previous studies applied their own methods: boost factor correction (e.g., von der Linden et al. 2014; Hoekstra et al. 2015) or no correction (e.g., Okabe et al. 2016; Umetsu et al. 2016) in WL analyses and emission-weighted temperatures (e.g., Zhang et al. 2008; Mahdavi et al. 2013) or spectroscopic-like temperature (e.g., Mazzotta et al. 2004; Martino et al. 2014) in X-ray analyses. Smith et al. 2016 obtained the average bias bm = 0.05 ± 0.05 for 50nclusters at z ∼ 0.2, and Mahdavi et al. (2013) computed bm = 0.12 ± 0.05 with their WL radii. Using the same sample between the two papers, the major difference (∼10%) would come from X-ray mass measurements (Smith et al. 2016). We assume here that the difference is mainly caused by temperature definitions and discuss this possibility. Mazzotta et al. (2004) discovered using realistic simulations that the HE mass estimations with emission-weighted temperatures would be underestimated by ∼10%, and those with spectroscopic-like temperature would recover the input mass. When we estimate the HE masses with emission-weighted temperatures, the masses are indeed lower by ∼10% than our results. Therefore, the possibility does not conflict with a difference between the two papers (Mahdavi et al. 2013; Smith et al. 2016). However, the current uncertainty in the averaged bias is too large to discuss the details. When we compile the full sample of 22 clusters, we expect that the uncertainty for the average bias will be comparable to those for previous studies for 50 clusters (Hoekstra et al. 2015; Smith et al. 2016). We will therefore compare WL and HE masses for the full sample, and investigate the redshift dependence and radial dependence of the mass bias.
6.7 Baryon fraction
The ratio of baryonic to total mass in massive clusters is expected to closely match the cosmic mean baryon fraction, Ωb/Ωm, measured from CMB experiments if baryons are trapped in potential wells (e.g., Evrard 1997; Kravtsov et al. 2005). However, the baryon budget in galaxy clusters is sensitive to non-gravitational processes; stars are formed from gas through radiative cooling, and AGN feedback may push the gas outside the potential well. Thus, measurements of the cluster baryon fraction are important to understand baryonic physics and the interplay between baryons and dark matter. Furthermore, assuming that the gas mass fraction is constant across redshifts, gas mass fraction measurements potentially provide a cosmological probe (e.g., Allen et al. 2008).
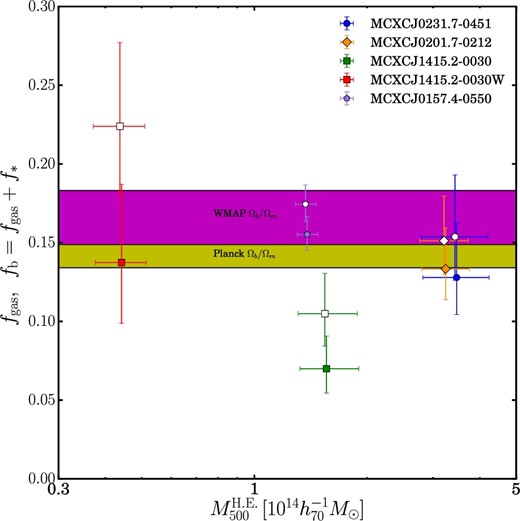
Gas fraction (filled symbols), fgas, and baryon fraction (opened symbols), fb, within r500 based on HE masses. The horizontal filled regions are the cosmic mean baryon fraction Ωb/Ωm for WMAP (Hinshaw et al. 2013) and Planck (Planck Collaboration 2015a) with their respective 1 σ uncertainties. For visual purposes, the HE masses of the gas fractions are multiplied by 1.01. (Color online)
We also investigate how much the stellar mass estimation is changed if blue galaxies are included. We select blue galaxies whose colors are bluer by 1–3 σ than those of the red-sequence galaxies within r500, and estimate their stellar mass in a cylinder volume subtracted by (2–3) r500 as the background region. The total stellar masses change only by sub-percent. Even if we neither subtract the background components nor change the background region, the result does not significantly change. This is not surprising because the faint and blue galaxies are not dominant in cluster central regions, in contrast to the bright and red galaxies. We note that the stellar mass estimation for blue galaxies is in the cylinder volume because the characteristic spatial distribution for the blue galaxies makes us to carry out the deprojection method. We stress that we estimated the total stellar mass using red galaxies in a spherical volume using the deprojection method (section 4).
In contrast to previous observational studies (e.g., Lin et al. 2003; Vikhlinin et al. 2009b) showing that gas mass fraction increases and stellar mass fraction decreases with increasing total mass, we find no significant evidence of a halo mass dependence of fgas and f* in the current sample. The relation might be difficult to measure given the intrinsic scatter and the small sample size. We therefore focus on a comparison between the averages for fgas and f* for the current sample and the literature. Based on the defined selection function of the MCXC clusters, we compute unweighted averages of gas and baryon fractions for the four MCXC clusters.
To investigate the mass dependence of fgas using the literature, we plot the averaged fraction enclosed within r500 and mass plane (left panel of figure 11). The average value is 〈fgas〉 = 0.125 ± 0.012, which is in agreement with previous studies based on HE mass or Sunyaev–Zel’dovich effect (SZE) mass (e.g., Vikhlinin et al. 2009a; Sun et al. 2009; Martino et al. 2014; Chiu et al. 2016) and based on WL masses (e.g., Zhang et al. 2010; Mahdavi et al. 2013; Okabe et al. 2014b). All points are unweighted averages from tables in the literature. Differences for those gas fractions at |$M_{500}\sim 2.4\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| and |$\sim\! 7\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| are ∼8% and ∼6%, respectively. However, the gas fraction of the XXL survey (Eckert et al. 2016) is systematically lower than in other studies in a wide mass range. The deviation is at the ∼5.3 σ level, where we use the 8% scatter. In our sample of the four MCXC clusters, the gas mass fraction is ∼0.8 ± 0.1 of the cosmic mean baryon fraction Ωb/Ωm for WMAP (Hinshaw et al. 2013) and ∼0.9 ± 0.1 for Planck (Planck Collaboration 2015a), though the two experiments have reported slightly discrepant results. The values are slightly higher than fgasΩm/Ωb ∼ 0.6 from numerical simulations (e.g., Kravtsov et al. 2005; Planelles et al. 2013; Battaglia et al. 2013).
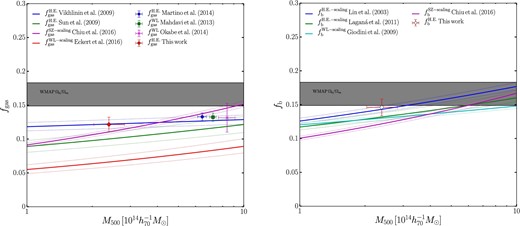
Comparison with the literature: gas fraction (left) and baryon fraction (right). Left: The red diamond is the average for fgas for the four MCXC clusters. The blue circle, green square, and magenta cross are 〈fgas〉 from Martino et al. (2014), Mahdavi et al. (2013), and Okabe et al. (2014b), respectively. The blue, green, magenta, and red solid lines are scaling functions between gas fraction and mass from Vikhlinin et al. (2009a), Sun et al. (2009), Chiu et al. (2016), and Eckert et al. (2016), respectively. The dotted lines are 1 σ uncertainties of the scaling functions. For simplicity, we plot Ωb/Ωm for WMAP (Hinshaw et al. 2013). Upper superscripts denote methods of total mass estimation. Right: The white diamond is the average for fb for the four MCXC clusters, derived by this study. The blue, green, cyan, and magenta solid lines are scaling functions between baryon fraction and mass from Lin, Mohr, and Stanford (2003), Laganá et al. (2011), Giodini et al. (2009), and Chiu et al. (2016) respectively. (Color online)
The average baryon fraction for the four MCXC clusters, 〈fb〉 = 0.146 ± 0.012, is comparable to Ωb/Ωm (right panel of figure 11). Our result is also comparable to previous observational studies (Lin et al. 2003, 2012; Giodini et al. 2009; Laganá et al. 2011; Chiu et al. 2016). The difference between those baryon fractions at |$M_{500}\sim 2.4\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$| is only ∼7%. There are some discrepancies in fb even between different numerical simulations. Kravtsov, Nagai, and Vikhlinin (2005) have shown that the total baryon fraction agrees with Ωb/Ωm, while Planelles et al. (2013) have pointed out that it accounts for ∼85% because some fraction of gas is displaced outside potential wells by AGN activities.
We also note that if there were HE mass bias then the gas and baryon fractions would be overestimated. Observations of baryon budget in galaxy clusters are still open questions. Since small clusters and groups are sensitive to baryonic physics (e.g., Kravtsov et al. 2005; Planelles et al. 2013; Battaglia et al. 2013), future progress of the HSC-SSP survey and future studies based on WL masses will play a key role in this subject.
7 Summary
We selected X-ray luminous clusters from the MCXC cluster catalog (Piffaretti et al. 2011) to measure HE masses for galaxy clusters in the HSC-SSP survey region. Based on the XMM-Newton and HSC-SSP datasets, we carried out a multiwavelength study of four MCXC clusters in the S16A field and a non-MCXC cluster associated with one MCXC cluster.
We found a correlation between cluster richness and HE mass for the MCXC clusters. The mass normalization agrees with expectations by comparing the CAMIRA cluster abundance with a theoretical prediction of cluster mass function with σ8 = 0.82 (Oguri et al. 2018). However, an infalling cluster to one MCXC cluster is highly deviant from the scaling relation, which could be caused by mass underestimation and/or richness overestimation. The average cluster gas mass fraction based on HE masses, 〈fb〉 = 0.146 ± 0.012, accounts for ∼80%–90% of the cosmic mean baryon fraction. In comparison with gas and baryon fractions from the literature based on various mass measurements (Vikhlinin et al. 2009a; Sun et al. 2009; Giodini et al. 2009; Mahdavi et al. 2013; Martino et al. 2014; Okabe et al. 2014b; Eckert et al. 2016; Chiu et al. 2016), our measurements are somewhat higher than previous studies but agree overall. Differences of gas and baryon fractions between these studies are ∼8% and ∼7% at |$M_{500}\sim 2.4\times 10^{14}{\, \mathrel {h_{70}^{-1}\, M_\odot }}$|, respectively. We also note the possibility that the average gas and baryon fraction is somehow overestimated if there were an HE mass bias. Therefore, future studies using WL masses for a large number of clusters/groups will be important to understand the baryon budgets and improve the current quality level.
The full-depth and full-color condition of the HSC-SSP survey allows us to compare HE mass with WL mass for the three clusters. The estimated mass bias, |$b_{\rm m}=0.44^{+0.31}_{-0.45}$|, allows for the possibility that the HE masses agree with the WL ones. In order to quantify the validity of the HE assumption, we need to carry out WL analysis for the full sample of clusters.
Further joint studies using a large number of clusters are vitally important to improve statistical uncertainty. Pointed X-ray observations with XMM-Newton and Chandra with sufficient integration times are essential to fairly compare X-ray observables with WL and optical measurements. The approach is complementary to the forthcoming X-ray survey from eROSITA, whose typical exposure in the HSC-SSP survey region is too shallow to estimate HE masses. A collaboration with the ongoing XXL survey is powerful for understanding cluster physics and carrying out cluster-based cosmology. In similar ways, joint studies with the ACTPol SZE observations (H. Miyatake et al. in preparation) provide us with a unique route for cluster studies. Future studies based on survey-type datasets will also reveal how much cluster properties are changed by cluster selection methods, like X-ray, SZE, optical, and WL techniques. The paper has demonstrated the power and impact of the HSC-SSP survey on other wavelengths and shown the first result of a series of multiwavelength studies.
Acknowledgements
The Hyper Suprime-Cam (HSC) collaboration includes the astronomical communities of Japan and Taiwan, and Princeton University. The HSC instrumentation and software were developed by the National Astronomical Observatory of Japan (NAOJ), the Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU), the University of Tokyo, the High Energy Accelerator Research Organization (KEK), the Academia Sinica Institute for Astronomy and Astrophysics in Taiwan (ASIAA), and Princeton University. Funding was contributed by the FIRST program from the Japanese Cabinet Office, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), the Japan Society for the Promotion of Science (JSPS), the Japan Science and Technology Agency (JST), the Toray Science Foundation, NAOJ, Kavli IPMU, KEK, ASIAA, and Princeton University.
This paper makes use of software developed for the Large Synoptic Survey Telescope. We thank the LSST Project for making their code available as free software at http://dm.lsst.org.
The Pan-STARRS1 Surveys (PS1) have been made possible through contributions of the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration under Grant No. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation under Grant No. AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), and the Los Alamos National Laboratory.
Based on data collected at the Subaru Telescope and retrieved from the HSC data archive system, which is operated by the Subaru Telescope and Astronomy Data Center at the National Astronomical Observatory of Japan.
This work was supported by the Funds for the Development of Human Resources in Science and Technology under MEXT, Japan and Core Research for Energetic Universe in Hiroshima University (the MEXT program for promoting the enhancement of research universities, Japan). This work was supported in part by World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan. This work was supported by MEXT KAKENHI Nos. 26800097 (NO), 26800093/15H05892 (MO), 15K05080 (YF), 26400218 (MT), and 15K17610 (SU). HM is supported by the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.
The paper is dedicated to the memory of our friend Dr. Yuying Zhang, who sadly passed away in 2016. She gave helpful suggestions on our X-ray analysis.
Appendix 1. Results of spectral fit
We summarize the results of the simultaneous fit for the spectrum in table 4. The techical details are described in section 3.
Footnotes
Based on data collected at the Subaru Telescope, which is operated by the National Astronomical Observatory of Japan. Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
References



