-
PDF
- Split View
-
Views
-
Cite
Cite
Yusuke Miyamoto, Masumichi Seta, Naomasa Nakai, Yoshimasa Watanabe, Dragan Salak, Shun Ishii, ALMA [C i] observations toward the central region of Seyfert galaxy NGC 613, Publications of the Astronomical Society of Japan, Volume 70, Issue 3, June 2018, L1, https://doi.org/10.1093/pasj/psy016
Close - Share Icon Share
Abstract
We report ALMA observations of [C i](3P1 − 3P0), 13CO, and C18O(J = 1–0) toward the central region of a nearby Seyfert galaxy NGC 613. The very high resolutions of 0|${^{\prime\prime}_{.}}$|26 × 0|${^{\prime\prime}_{.}}$|23 (=22 × 20 pc) for [C i] and 0|${^{\prime\prime}_{.}}$|42 × 0|${^{\prime\prime}_{.}}$|35 (=36 × 30 pc) for 13CO, and C18O resolve the circumnuclear disk (CND) and star-forming ring. The distribution of [C i] in the ring resembles that of the CO emission, although [C i] is prominent in the CND. This can be caused by the low intensities of the CO isotopes due to the low optical depths under the high temperature in the CND. We found that the intensity ratios of [C i] to 12CO(3–2) (|$R_{\rm C\,{\small I}/CO}$|) and to 13CO(1–0) (|$R_{\rm C\,{\small I}/^{13}CO}$|) are high at several positions around the edge of the ring. The spectral profiles of CO lines mostly correspond each other in the spots of the ring and high |$R_{\rm C\,{\small I}/CO}$|, but those of [C i] at spots of high |$R_{\rm C\,{\small I}/CO}$| are different from those of CO. These results indicate that [C i] at the high |$R_{\rm C\,{\small I}/CO}$| traces different gas from that traced by the CO lines. The [C i] kinematics along the minor axis of NGC 613 could be interpreted as a bubbly molecular outflow. The outflow rate of molecular gas is higher than star formation rate in the CND. The flow could be mainly boosted by the active galactic nucleus through its radio jets.
1 Introduction
Molecular hydrogen (H2) is a major component of the interstellar medium in galaxies. While the 12CO(J = 1–0) line has been used as a principal probe in tracing molecular gas and in studying dynamics and molecular gas distribution in galaxies, it is not easy to estimate the gas mass using 12CO due to the large optical depth. Recently, atomic carbon (C i) has attracted attention as a good tracer of the mass of the cold molecular gas, especially in high-redshift galaxies or metal-poor objects (e.g., Papadopoulos & Greve 2004; Papadopoulos et al. 2004).
It has been recognized that C i exists predominantly in the thin layer near the surface of molecular clouds exposed to UV radiation, which is called the photodissociation region (PDR: Tielens & Hollenbach 1985; Hollenbach et al. 1991). However, large-scale C i(3P1 − 3P0), hereafter simply referred as [C i], mapping of the Orion A and B molecular clouds revealed that [C i] coexists with 12CO and 13CO(1–0) and their intensities correlate with each other (Ikeda et al. 2002). Since the critical density of [C i] is similar to that of 12CO (n ≈ 103 cm−3), these findings indicate that the emission lines arise from the same volume and share similar excitation temperatures.
The global extent of the [C i] emission is similar to that of dense molecular gas traced by C18O, whereas the intensities of [C i] and C18O anti-correlate with each other (e.g., Maezawa et al. 1999). Oka et al. (2005) showed the distribution of the C i-to-12CO intensity ratio on the Galactic scale and suggested that the locations of the high-intensity ratio correspond to the upstream of spiral arms. These results indicate that [C i] abundance is high in the early stage of chemical evolution (within a timescale for conversion from C i to CO; ∼106 yr) and [C i] traces young clouds which are just forming dense cores (Suzuki et al. 1992; Maezawa et al. 1999).
A couple of dozen observations toward nearby galaxy centers with single-dish telescopes that have linear resolution of several 100 pc have revealed that the intensity ratio of [C i] to 13CO in most galaxy centers exceeds unity, which is rare for the Galactic molecular clouds, and is likely related with the central activities (Israel 2005). The central outflow or shock may enhance [C i] compared with CO(1–0) (Krips et al. 2016), indicating the possibility of [C i] being an outflow or shock tracer. On the other hand, the distribution of [C i] is still unclear due to a few mapping observations with the limited spatial resolution (e.g., Gerin & Phillips 2000). For characterizing molecular clouds traced by C i, it is necessary to clarify the distributions of C i and CO lines relative to energetic activities, such as star formation and central outflow.
Molecular gas in barred galaxies can be transported toward the galactic center, because the galactic bar can effectively drain the angular momentum of the gas (Binney & Tremaine 2008, and references therein). The gas gathers at the region of nearly circular orbits (x2 orbits) and forms a nuclear ring which is the site of vigorous star formation (r ∼ a few 100 pc; we refer to it as a star-forming ring). Star-forming rings are promising reservoirs of the gas that feeds to the accretion disks in active galactic nuclei (AGNs) via the circumnuclear disk (CND; r ∼ 1–100 pc).
The nearby galaxy NGC 613 hosts a low-luminosity AGN and prominent radio jets from the center (e.g., Goulding & Alexander 2009; Hummel & Jorsater 1992). The central CND of NGC 613 (r ≲ 90 pc) contains abundant molecular gas, while the star formation rate (SFR) in the CND is lower than that in its star-forming ring (250 ≲ r ≲ 340 pc), which is probably caused by the interaction between the jets and gas in the CND (Falcón-Barroso et al. 2014; Davies et al. 2017; Miyamoto et al. 2017). Comparisons between [C i] and CO lines in the energetic activities could provide clues to understanding what [C i] traces. This letter reports [C i] and CO observations with resolution high enough to resolve the central region of the galaxy, i.e., the CND and star-forming ring, for the first time as a galaxy.
2 Observations
NGC 613 was observed with the Atacama Large Millimeter/submillimeter Array (ALMA) using Band 3 and Band 8 receivers. For Band 8, the Atacama compact array (ACA) and total power array (TP) were used in addition to the 12 m array. The synthesized beams at Bands 3 and 8 were 0|${^{\prime\prime}_{.}}$|42 × 0|${^{\prime\prime}_{.}}$|35 (θ = −29°) and 0|${^{\prime\prime}_{.}}$|26 × 0|${^{\prime\prime}_{.}}$|23 (θ = −71°), corresponding to 36 × 30 and 22 × 20 pc, respectively, at the distance of the galaxy (17.5 Mpc; Tully 1988). Single-point observations and three-point mosaic observations were conducted for Band 3 and Band 8, respectively. The maximum recoverable scale for Band 3 is |$\sim\!{22^{\prime \prime }}$|. These setups allowed us to image the CND and star-forming ring of NGC 613. The phase reference center of (αJ2000.0, |$\delta _{\rm J2000.0})= ({1^{\rm h}34^{\rm m}18{^{\rm s}_{.}}19},\ {-29^{\circ}25^{\prime }06{^{\prime\prime}_{.}}60})$| was adopted (Miyamoto et al. 2017). The correlators for Band 3 were configured to set three spectral windows in the upper sideband to measure 13CO(1–0) (νrest = 110.201354 GHz) and C18O(1–0) (νrest = 109.782176 GHz) in the 2SB dual-polarization mode. The correlators for Band 8 were configured to set one spectral window in the upper sideband to cover C i(3P1 − 3P0) (νrest = 492.160651 GHz), in the dual-polarization mode. The flux density at the Band 3 was calibrated using J2357−5311 and J0334−4008, and at Band 8 using J0006−0623 and Uranus. The time variations of amplitude and phase were calibrated using J0106−2718 and J0145−2733 for Band 3 and by J0204−1701 and J0137−2430 for Band 8.
The data were processed using the Common Astronomy Software Application (CASA: McMullin et al. 2007). The velocity resolution of each line’s data obtained at different observing tracks with the 12 m array and ACA was separately rearranged to be 10 km s−1. Each line’s data were then combined after subtracting continuum emission determined via the channels that were free from spectral line emission. To image the continuum emission, we used the flux density at the emission-free channels. The imaging was performed using the CLEAN algorithm in CASA. CLEAN maps were obtained considering the Briggs weighting mode on the data with robustness of 0.5 for Band 3 and the natural weighting mode for Band 8. The resultant maps were 1500 × 1500 pixels with 0|${^{\prime\prime}_{.}}$|05 per pixel and 0|${^{\prime\prime}_{.}}$|02 per pixel for Bands 3 and 8, respectively. For the line emission of Band 8, TP data were calibrated through flagging and the system temperature correction, and imaged independently from the 12 m array and ACA data. By using the Feather algorithm in CASA, the low-resolution image obtained via the TP and high-resolution image obtained from the 12 m array and ACA were converted into the gridded visibility plane and combined. Finally, the data was reconverted into a combined image. The sensitivities in the resultant cube of [C i], 13CO, and C18O(J = 1–0) are 6 mJy beam−1 (∼0.5 K), 0.2 mJy beam−1 (∼0.1 K), and 0.2 mJy beam−1 (∼0.1 K), respectively, in channels of 10 km s−1 width.
We found that the peak position of the 100 GHz continuum corresponds to the phase center with an uncertainty of ∼0|${^{\prime\prime}_{.}}$|01, while the peak position of the 490 GHz continuum is offset from the phase center by ∼0|${^{\prime\prime}_{.}}$|07, which is caused by large separation of |${14.\!\!^{\circ}2}$| between NGC 613 and the phase calibrator (J0204−1701). We therefore shifted the position in Band 8 data so that the continuum position coincides with the center.
3 Results and discussion
3.1 Distributions of [C i] and CO lines
Figures 1a, 1c, and 1d show the integrated intensity maps of [C i], 13CO(J = 1–0), and C18O(J = 1–0), respectively, where pixel values <3σ in each velocity channel of the cube smoothed with twice the size of the beamwidth were masked to derive the integrated intensities of the weak emission accurately and enhance the contrasts, and figure 1b shows the intensity-weighted [C i] velocity field map. The [C i] line emission is detected both in the star-forming ring and CND, while C18O is faint in the CND. The velocity field of [C i] is consistent with that of 12CO(3–2) shown by Miyamoto et al. (2017), i.e., rigid rotation in the ring. The peak positions and distribution of the [C i] emission in the ring are consistent with those of the CO emission, but are inconsistent with them in the CND. In accordance with Ikeda et al. (2002), we calculated the optical depths of [C i], 13CO(1–0), and C18O(1–0) under a local thermodynamic equilibrium (LTE) assumption, where those excitation temperatures are similar, and we adopted the rotational temperatures of Trot ∼ 18 K in the CND and Trot ∼ 12 K in the ring as the excitation temperatures (Miyamoto et al. 2017). The optical depths of [C i] in the CND and in the ring are estimated to be |$\tau _{\rm C\,{\small I}}= 0.6\pm 0.3$| and ∼0.1–1.5, respectively, and those of 13CO(1–0) and C18O(1–0) are thin in both the CND and ring; |$\tau _{\rm ^{13}CO}= 0.06\pm 0.01$| (CND) and ∼0.1–0.4 (ring), and |$\tau _{\rm C^{18}O}\sim 0.02\pm 0.01$| (CND) and ∼0.02–0.08 (ring). The relatively high optical depth of [C i] in the ring can be caused by the underestimation of the excitation temperature. The corresponding distributions of [C i] and 13CO(1–0) in the ring are consistent with the previous studies about the Galactic components (e.g., Shimajiri et al. 2013), indicating a clumpy PDR model, in which UV radiation can penetrate deeper in a clumpy cloud (Spaans 1996), and/or a chemical evolution model (e.g., Oka et al. 2001; Ikeda et al. 2002).
![(a) Integrated intensity map of C i(3P1–3P0). The contours are 5, 10, 20, 30, 40, 50, 60, 70, and 80σ, where 1σ = 10 K km s−1. (b) [C i] velocity field map derived from intensity-weighted mean velocities. The velocity is in km s−1 with respect to LSR and the radio definition. (c) Integrated intensity map of 13CO(J = 1–0). The contours are 5, 15, 30, 40, 50, and 100σ, where 1σ = 2 K km s−1. (d) Integrated intensity map of C18O(J = 1–0). The contours are 5, 10, 15, 20, 35, 30, 35, 40, and 45σ where 1σ = 2 K km s−1. A cross in each map is the peak position of the continuum emission, i.e., the galactic center, (αJ2000.0, $\delta _{\rm J2000.0})=({1^{\rm h}34^{\rm m}18{^{\rm s}_{.}}19},\ {-29^{\circ}25^{\prime }06{^{\prime\prime}_{.}}60})$. The filled ellipse in the bottom right-hand corner of each map represents the beam size, 0${^{\prime\prime}_{.}}$26 × 0${^{\prime\prime}_{.}}$23 (θ = − 71°) for [C i] and 0${^{\prime\prime}_{.}}$42 × 0${^{\prime\prime}_{.}}$35 (θ = − 29°) for 13CO and C18O(1–0).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/70/3/10.1093_pasj_psy016/4/m_pasj_70_3_l1_f1.jpeg?Expires=1749540655&Signature=h85d1vV21gb5LUMe4PoDZZga9XF47Z3lCGo1-YrkRxEQm31M-ximlLayUiwBBqg2aQQ-1fn~AcrvxoTO894jd0zU1bL7ax6ylwlL6s91IR9JAbr0vTqFiS7Ue~Ox66Hig0YZrfCYSMqOc5W8hKqMT2rsCTsVpJtxnhIExfFwIRny3zo2Yck8pZjXqY5ulFSsAWvsp-rJUyZ-hBlatfU~A7UmVcUCmSMxUxHohofm8dRs61jNBoebwsg8dDUqu8uyIkMtut-dflWpZxbxZCryYg9HBTDyDUPMUxlxMTpIhjQ26cNTpppCT3R5oYIDDv6heDe2R--LRXgcKWoBRlzaVw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
(a) Integrated intensity map of C i(3P1–3P0). The contours are 5, 10, 20, 30, 40, 50, 60, 70, and 80σ, where 1σ = 10 K km s−1. (b) [C i] velocity field map derived from intensity-weighted mean velocities. The velocity is in km s−1 with respect to LSR and the radio definition. (c) Integrated intensity map of 13CO(J = 1–0). The contours are 5, 15, 30, 40, 50, and 100σ, where 1σ = 2 K km s−1. (d) Integrated intensity map of C18O(J = 1–0). The contours are 5, 10, 15, 20, 35, 30, 35, 40, and 45σ where 1σ = 2 K km s−1. A cross in each map is the peak position of the continuum emission, i.e., the galactic center, (αJ2000.0, |$\delta _{\rm J2000.0})=({1^{\rm h}34^{\rm m}18{^{\rm s}_{.}}19},\ {-29^{\circ}25^{\prime }06{^{\prime\prime}_{.}}60})$|. The filled ellipse in the bottom right-hand corner of each map represents the beam size, 0|${^{\prime\prime}_{.}}$|26 × 0|${^{\prime\prime}_{.}}$|23 (θ = − 71°) for [C i] and 0|${^{\prime\prime}_{.}}$|42 × 0|${^{\prime\prime}_{.}}$|35 (θ = − 29°) for 13CO and C18O(1–0).
Figures 2a and 2c show the integrated line ratios of [C i] to 12CO(3–2) (|$\equiv R_{\rm C\,{\small I}/CO}$|) and [C i] to 13CO(1–0) (|$\equiv R_{\rm C\,{\small I}/^{13}CO}$|), where the 12CO intensity map is from Miyamoto et al. (2017) and the beam size of [C i] is convolved with those of the CO. For comparison, the distribution of the 100 GHz continuum, the flux density of which can be dominated by free–free thermal emission from H ii regions followed by non-thermal emission, such as radio jets (e.g., Condon 1992; Salak et al. 2017), is superposed on the ratio map of |$R_{\rm C\,{\small I}/CO}$| in figure 2b. |$R_{\rm C\,{\small I}/CO}$| is in the range of 0.1–0.3 in both the CND and star-forming ring, and high at several spots on the edge of the ring. The temperature ratio of [C i] to CO at the spots, |$T_{\rm C\,{\small I}}/T_{\rm CO}\sim 0.6$|, is enhanced to more than double that in the ring, ∼0.1–0.3 (see channel map in supplementary material). The high |$R_{\rm C\,{\small I}/CO}$| is likely located around the bright spots in the 100 GHz continuum, although not always as in the southwest region. The |$R_{\rm C\,{\small I}/^{13}CO}$| is strikingly very high in the CND due to the low intensity of 13CO, although it is high at the edge of the ring, as is the case in |$R_{\rm C\,{\small I}/CO}$|. The low intensity of 13CO relative to 12CO (and C i) in the CND can be due to the low optical depth, not the extreme abundance of 13CO, which is caused by selective photo-dissociation, fractionation, or nucleosynthesis (e.g., Langer et al. 1984; van Dishoeck & Black 1988; Casoli et al. 1992). The selective photo-dissociation and nucleosynthesis are inconsistent with the lower rate of star formation activity in the CND than in the ring (Falcón-Barroso et al. 2014). In addition, the lower intensity ratio of C18O to 13CO in the CND than in the ring (figure 2d) cannot be explained by the fractionation, since the high temperature in the CND (e.g., Tk = 350–550 K; Miyamoto et al. 2017) makes the formation of 13CO ineffective, in contrast to C18O which does not undergo the fractionation. We found that an |$R_{\rm C\,{\small I}/^{13}CO}$| of ∼10 in the CND is consistent with the ratio of the optical depths of |$\tau _{\rm C\,{\small I}}=0.6\pm 0.3$| to |$\tau _{\rm ^{13}CO}=0.06\pm 0.01$|. In addition, it is expected that the low optical depth and high temperature in the CND cause the ratio of the fractions of the upper state level of 13CO (and C18O) to the J = 1 level. In NGC 1068, a case in which the intensities of CO isotopic species of the J = 1–0 transition in the CND were lower than the intensities in the ring and of the higher transition J = 3–2 in the CND was reported (Takano et al. 2014; Nakajima et al. 2015).
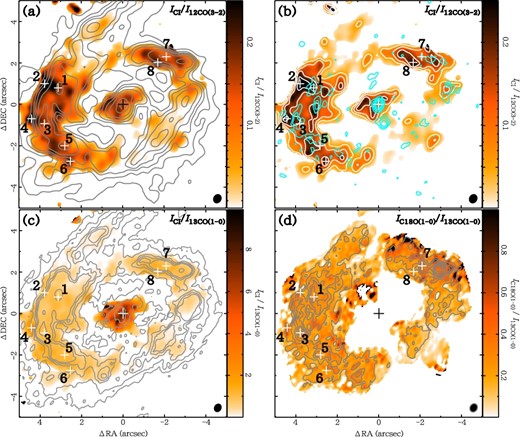
(a) Map (color) of the integrated intensity ratio of |$I_{\rm C\,{\small I}}$| to ICO(3–2), which is from Miyamoto et al. (2017), overlaid with ICO(3–2) contours of 5, 10, 15, 20, 30, 50, 100, 150, and 180σ where 1σ = 20 K km s−1. (b) Same as (a) but contours of the 100-GHz flux (cyan: 3, 5, 7, 9, 12, and 15σ where σ = 20 μJy beam−1). (c) Map (color) of the integrated intensity ratio of |$I_{\rm C\,{\small I}}$| to |$I_{\rm ^{13}CO(1-0)}$|, overlaid with |$I_{\rm ^{13}CO(1-0)}$| contours (same as figure 1c). (d) Map (color) of the integrated intensity ratio of |$I_{\rm C^{18}O(1-0)}$| to |$I_{\rm ^{13}CO(1-0)}$|, overlaid with |$I_{\rm C^{18}O(1-0)}$| contours (same as figure 1d).
Figure 3 shows the spectra of [C i], 12CO(3–2), 13CO(1–0), and C18O(1–0) at representative positions on the CND and ring. Spots 1, 3, 5, and 7 are peaks on the ring traced by CO(3–2) and 13CO(1–0) (see figures 2a and 2c), whereas spots 2, 4, 6, and 8 show the high intensity ratio of |$R_{\rm C\,{\small I}/CO}$| at the edge of the ring. The profiles of the CO lines mostly correspond to each other at all spots, but those of C i at spots of high |$R_{\rm C\,{\small I}/CO}$| have different velocity features from those of CO. The different spectral profiles at the high |$R_{\rm C\,{\small I}/CO}$| suggest that C i traces different gas from that traced by the CO lines. In the high |$R_{\rm C\,{\small I}/CO}$| at the edge of the ring, [C i] would trace dark CO, e.g., an early stage of chemical evolution (Tanaka et al. 2011), although other models, including the PDR model, cannot be excluded. In order to clarify the reason for the different spectral profiles, multi-wavelength observations with angular resolution high enough to resolve individual molecular clouds (≲10 pc) are needed, since PDR models are developed to represent the structure of an individual cloud.
![Spectra of [C i], CO(3–2), 13CO(1–0) and C18O(1–0) at the spots denoted in figure 2. The corresponding aperture is 0${^{\prime\prime}_{.}}$5 (42 pc).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/70/3/10.1093_pasj_psy016/4/m_pasj_70_3_l1_f3.jpeg?Expires=1749540655&Signature=YCkCAQAbUNtUsVlB5ciqbaHW1oKj-o0Udev1Eo5BC5jpRF~uOV-wAE7RJyyXFXXOGzg9DT2iJLHfOpzEAxJBIUZ3r3H3tPOTPV9seL0jbAP9i3vBCmCIpQubqhUOdWcMekKmXushT5kMEXYkOUBBWKhOzi67Q2iPQ6mf-~0mSGo6jeXADRp7DwTk37zYLn9hOBco~YHR3K0SVyPtVRJYnZkv3VcwcOKo3OzCLzP77ZmvFH7wXQGFXy6TZgUF1KsZ9Cf5Ib8Ry4JtV825ENgetv5VB~hjgq3LFKjEJBt7WsgCjYG0GRe5rD8cI1wQHYLj247O4cGydMcZ8p2WF~ooXA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Spectra of [C i], CO(3–2), 13CO(1–0) and C18O(1–0) at the spots denoted in figure 2. The corresponding aperture is 0|${^{\prime\prime}_{.}}$|5 (42 pc).
3.2 [C i] outflow in a circumnuclear disk (CND)
Figure 4b shows the position–velocity (PV) diagram of [C i] of NGC 613 along the minor axis with PA = 28° (figure 4a), superposed on the PV diagram of CO(3–2). The gas motion in NGC 613 is counterclockwise and the southern part of NGC 613 is on the near side (figure 1b; Burbidge et al. 1964). In the southern region (Y ∼ −1|${^{\prime\prime}_{.}}$|0), we found some compact components (A, B, and C) of size ∼0|${^{\prime\prime}_{.}}$|4(= 34 pc) and velocity width of ∼10 km s−1, consistent with those of giant molecular cloud (e.g., Sanders et al. 1985). Especially, the location of component B at Y ∼ −1|${^{\prime\prime}_{.}}$|0 (= 85 pc) is close to the peak of the southern bubble traced by the 4.9-GHz continuum, the flux density of which is dominated by synchrotron emission due to the nuclear jets (Hummel & Jorsater 1992). The [C i] intensities of 15.7, 44.0, and 14.7 K km s−1 of components A, B, and C correspond to the column densities of |$N_{\rm {\rm C\,{\small I}}} = 2.7$|, 7.6, and 2.5 × 1017 cm−2, respectively, according to Ikeda et al. (2002) and |$\tau _{\rm C\,{\small I}}\sim 0.6$| in the CND. The ratio of |$N({\rm C\,{\small I}})$| to N(CO) in the ring becomes ∼0.1, where we adopted |$N({\rm CO}) = 7.0 \times 10^{16} \int T_{\rm b}{\rm (^{13}CO)} dv \tau _{\rm ^{13}CO}/[1-\exp (-\tau _{\rm ^{13}CO})]$| [cm−2] by assuming Tex(ring) ∼ 12 K and [12CO]/[13CO] = 60 (cf. Ikeda et al. 2002). We estimated total (atomic and molecular) gas masses of components A, B, and C to be roughly 8.2, 63.0, and 3.6 × 104 M⊙, respectively, adopting a relation of total hydrogen carbon column density to that of carbon, |$N_{\rm H} \approx 2500 [N({\rm CO}) + N({\rm C})]$| (Israel & Baas 2001, 2003 and references therein), although these values can be underestimated since column density of the ionized carbon is not accounted here.
![(a) Enlarged view of the integrated intensity maps of [C i] in figure 1a (color) is overlaid with the 4.9-GHz continuum from Miyamoto et al. (2017) (contours). (b) Position–velocity (PV) diagram of [C i] along the minor axis of NGC 613; PA = 28° (Miyamoto et al. 2017) (Color image and white contours). The levels of the contours are 3, 4, 5, 7, 9, 11, 13, 15, and 17σ where σ = 0.5 K. Gray contours show the PV diagram of CO(3–2) from Miyamoto et al. (2017), and the levels are 5, 15, 20, 30, 50, 70, 90, and 100σ where σ = 0.25 K.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/70/3/10.1093_pasj_psy016/4/m_pasj_70_3_l1_f4.jpeg?Expires=1749540655&Signature=2YcseRKkSDykv8mkUygL8IRB2fEOoIpozn051~68koxrbAZXv~yqALPN5i8-D8nrL6V1jwr9jOrZ1yNw7R3qBUu0ytpdf5fxBzVOJa36wVyDhd7KGCs1AWQbaaF6uzrhRp0rKrb0mKy-lcPXCSy42t9QwRBhmvbInDxZsMjNQwJzBQJnaK22vNFeoGGRxyjgk7rihjA7qMEt~tIn1M9C3jbfpcpckb~DYrhLOmrXKR4fo5uy-4PYXRbsmh~RS5Rn155T6GRLCzI-yoHpaEsXEs9COzwa3f6qNiK-rxNvAa-1-OuUrrmONGqm1pVdp4NsIc5zMKfGzEkT0gNzrzonPQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
(a) Enlarged view of the integrated intensity maps of [C i] in figure 1a (color) is overlaid with the 4.9-GHz continuum from Miyamoto et al. (2017) (contours). (b) Position–velocity (PV) diagram of [C i] along the minor axis of NGC 613; PA = 28° (Miyamoto et al. 2017) (Color image and white contours). The levels of the contours are 3, 4, 5, 7, 9, 11, 13, 15, and 17σ where σ = 0.5 K. Gray contours show the PV diagram of CO(3–2) from Miyamoto et al. (2017), and the levels are 5, 15, 20, 30, 50, 70, 90, and 100σ where σ = 0.25 K.
The gas components may expand spherically because of the symmetric velocity patterns of the components and the edge relative to Vsys in figure 4b. We assumed that the velocity difference between the edge and Vsys is the same as the expanding velocities of all components, vexp ∼ 35[=(1510 − 1440)/2]/(cos iout) km s−1, where iout is an angle between a normal line to the bubble and the line of sight. The offset between the averaged velocity of the edge and Vsys could be caused by an inclination of the outflow to the line-of-sight, although the velocity resolution ΔV = 10 km s−1 is not good enough to permit further discussion. Taking the height of the component B to be ∼85 pc and the expanding velocity of vexp ∼ 35 km s−1 as a lower limit, the expanding time is texp ∼ 2.4 Myr, and the mass outflow rate of only component B becomes |$dM_{\rm H_2}/dt\sim 0.3\,M_\odot \:$|yr−1, which is higher than the SFR in the CND, 0.02 M⊙ yr−1 (Falcón-Barroso et al. 2014). It is noted that the mass outflow rate of nearby starburst galaxies, e.g., M 82 (Salak et al. 2013), NGC 253 (Bolatto et al. 2013), and NGC 1808 (Salak et al. 2016), is comparable to the SFR. The AGN bolometric luminosity of NGC 613 is a few 1042 erg s−1, accounting for ∼10% of total luminosity, including a contribution from shock excitation and star formation (Davies et al. 2017). In addition, the Eddington luminosity is Ledd = 1.3 × 1045 erg s−1, found by adopting an expected black hole mass of ∼107 M⊙ (Beifiori et al. 2012). The kinetic energy and luminosity of the outflowing component become |$1/2\,M_{\rm H_2} v^2_{\rm exp} \sim 7.7\times 10^{51}\:$|erg and |$1/2 dM_{\rm H_2}/dt v^2_{\rm exp} \sim 1.0\times 10^{38}\:$|erg s−1, respectively. The jet power Pjet = 1.5 × 1042 erg s−1, which can be estimated by adopting the central 1.4-GHz luminosity of 3.98 × 1037 W Hz−1 (Hummel et al. 1985) to a scaling relation suggested by Cavagnolo et al. (2010), is larger than the kinetic luminosity. The ratio of Pjet/Ledd = 1.2 × 10−3 is consistent with a value expected from a numerical simulation, within the range of which the jet can drive the interstellar medium efficiently (Wagner et al. 2012). These results indicate that the jet contributes towards driving the gas outflow, although the [C i] outflow is tentative. In order to confirm the outflow, more sensitive [C i] observations are needed.
Acknowledgments
We are grateful to the anonymous referee for insightful comments that improved this paper. This paper makes use of the following ALMA data: ADS/JAO. ALMA#2015.1.01487.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan) and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This work was financially supported by Grants-in-Aid for Scientific Research (KAKENHI) of the Japanese society for the Promotion of Science (JSPS, Grant No. 16H03961).
Supplementary data
Supplementary data are available at PASJ online.
CI_to_co.cube_2ch.ratio.eps
References



