Gravitational waves from an SMBH binary in M 87

Yonemaru, Naoyuki; Kumamoto, Hiroki; Kuroyanagi, Sachiko; Takahashi, Keitaro; Silk, Joseph

doi:10.1093/pasj/psw100

Abstract

We study gravitational-wave (GW) emission from a hypothetical supermassive black-hole (SMBH) binary at the center of M 87. The existence of an SMBH other than that usually identified with the central active galactic nucleus (AGN) is a possible explanation for the observed displacement [∼O(1) pc] between the AGN and the galactic centroid, and it is reasonable to assume considering the evolution of SMBHs through galaxy mergers. Because the period of the binary and the resulting GWs is much longer than the observational time-span, we calculate the variation of the GW amplitude, rather than the amplitude itself. We investigate its dependence on the orbital elements and the second BH mass, taking the observational constraints into account. The frequency of the GWs is too low to be detected with the conventional pulsar timing array and we propose a new method for detecting such low-frequency GWs with the distribution function of pulsar spin-down rates. Although the GWs from an SMBH binary that explains the observed displacement are extremely hard to detect even by the new method, GWs are still useful for probing the M 87 center.

1 Introduction

The giant elliptical galaxy M 87 (NGC 4486), located at 18.4 Mpc, hosts one of the nearest and best-studied active galactic nuclei (AGNs). A relativistic one-sided jet is ejected from the galactic center, where a supermassive black hole (SMBH) with a mass of (6.6 ± 0.4) × 10⁹ M_⊙ (Gebhardt et al. 2011) resides, and extends to hundreds of kiloparsecs.

It was reported in Batcheldor et al. (2010) that the luminous center of M 87 and the AGN are displaced significantly. The displacement was confirmed by Lena et al. (2014) and this fact suggests that the SMBH is not located at the center of mass of the galaxy, although there is a large uncertainty in the projected distance (∼1–7 pc). Several scenarios have been suggested to interpret this displacement: (1) acceleration by an asymmetric jet, (2) recoil due to gravitational-wave emission caused by a merger of two SMBHs, (3) binary motion with respect to another SMBH, and (4) gravitational perturbations from multiple massive objects at the galactic center. As a possible method of distinguishing among these scenarios, an observation of the proper motion of the SMBH (AGN) was suggested.

Here we focus on the latter two scenarios. Binary formation of two SMBHs through galaxy mergers is a basic process of SMBH evolution. The observed displacement can be explained if the center of mass of an SMBH binary is located at the galactic center and only one of the SMBHs has enough gas accretion to make it an AGN. On the other hand, there is a possibility that multiple intermediate mass BHs (IMBHs) or relatively small SMBHs reside at the galactic center through hierarchical galaxy merging (Islam et al. 2004; Rashkov & Madau 2014). The displacement can also be explained by gravitational perturbation of the main SMBH from these multiple BHs. In the scenario (4), the main SMBH can form a binary with one of the IMBHs or SMBHs, and the center of mass will not necessarily be located at the galactic center.

If the observed displacement is caused by these mechanisms, a substantial quantity of gravitational waves (GWs) is emitted by the SMBH binary. Thus, the observation of GWs from M 87 can probe the black hole population at the galactic center. In this paper, following these scenarios, we estimate the GWs under the constraints on the binary orbital elements from observations and discuss the detectability of GWs of pulsar timing arrays.

This paper is organized as follows. In section 2, we summarize the basic formulae of Keplerian motion. In section 3, we describe the formalism to calculate the amplitude of GWs from a binary and its time derivative. In section 4, we present our main results. In section 5, we discuss the detectability of the GWs and give a summary and discussion in section 6. For the rest of this paper we set c = G = 1, unless otherwise specified.

2 Orbital elements of an SMBH binary

The distance between the main SMBH and the barycenter of its host galaxy, r₁, is related to the projected displacement, r₀, as,

\begin{equation} r_1 = \frac{1}{\sin {\theta }} r_0, \end{equation}

(1)

where θ is the angle between the line of sight and the direction from the SMBH to the barycenter.

In the following, we discuss the orbital elements of the SMBH binary. The orbital motion is approximated to the Newtonian two-body problem since the binary has a typical separation of ≳1 pc so that gravity is sufficiently weak and the energy loss due to gravitational waves is negligible. The equation of motion for the relative motion of the SMBHs is given by

\begin{equation} \mu \,\frac{d^2\boldsymbol {r}}{dt^2} = -\frac{G m_1 m_2}{r^2}\frac{\boldsymbol {r}}{r}, \end{equation}

(2)

where r = r₁ − r₂, r = |r|, μ = m₁m₂/(m₁ + m₂) is the reduced mass, and m₁ = 6.6 × 10⁹ M_⊙ and m₂ are the masses of the main and second SMBHs, respectively.The orbital elements are described by

\begin{eqnarray} r = \frac{a(1 - e^{2})}{1 + e\,\cos {\phi }} \end{eqnarray}

(3)

\begin{eqnarray} r^{2} \frac{d\phi }{dt} = \left[Ma(1 - e^{2}) \right]^{1/2}, \end{eqnarray}

(4)

where e is the eccentricity (0 ≤ e < 1), a is the semi-major axis, ϕ is the orbital phase, and M = m₁ + m₂. Fixing the eccentricity, the semimajor axis is maximum (minimum) when the SMBH is located at the pericenter (apocenter) of the orbit. Therefore, the semimajor axis is constrained as

\begin{equation} \frac{r}{1+e}\ \le a \le \ \frac{r}{1-e} . \end{equation}

(5)

On the other hand, the orbital period is described by

\begin{equation} T = 2 \pi \sqrt{\frac{a^3}{M}} . \end{equation}

(6)

In the current case, the typical orbital period is 2 × 10³ yr for a₁ = 1 pc and m₂ = 6.6 × 10⁹ M_⊙(= m₁).

3 Gravitational waves from a binary

Gravitational waves are emitted from a binary and the waveforms of the plus and cross polarizations are given by

\begin{eqnarray} h_+(t) &=& \frac{1}{2}\,\left(p^ip^j - q^iq^j\right) h^{TT}_{ij} \end{eqnarray}

(7)

\begin{eqnarray} h_{\times }(t) &=& \frac{1}{2} \left(p^iq^j + p^jq^i\right)\ h^{TT}_{ij} . \end{eqnarray}

(8)

Here, p = (0, 1, 0) and q = (−cos ι, 0, sin ι) are the unit vectors of the gravitational wave principal axes, where ι is the inclination and |$h^{TT}_{ij} (i,j = 1,2,3)$| is the transverse-traceless part of the amplitude given by (Gopakumar & Iyer 2002)

\begin{equation} h^{TT}_{ij} = \frac{4\mu }{R}\ \left(v_iv_j - \frac{M}{r}n_in_j\right), \end{equation}

(9)

where n = (cos ϕ, sin ϕ, 0) and |$v = (\dot{r}\cos \phi - r\dot{\phi }\sin \phi$|⁠, |$\dot{r}\sin \phi + r\dot{\phi }\cos \phi , 0)$|⁠. Equations (7) and (8) can be rewritten as

\begin{eqnarray} h_+(t) &=& \frac{\mu }{R}\Biggl \lbrace (1+\cos ^2\iota ) \nonumber \\ &&\times \left[ \left(\frac{M}{r} + r^2\dot{\phi }^2 - \dot{r}^2\right) \cos 2\phi + 2r\dot{r}\dot{\phi }\ \sin 2\phi \right] \nonumber \\ &&+ \left[\frac{M}{r} - r^2\dot{\phi }^2 -\dot{r}^2\right]\sin ^2\iota \Biggr \rbrace, \end{eqnarray}

(10)

\begin{eqnarray} h_{\times }(t) &=& \frac{2\mu }{R}\cos \,\iota \nonumber \\ && \times \left[ \left( \frac{M}{r}+r^2\dot{\phi }^2 - \dot{r}^2 \right) \sin {2\phi } - 2 r \dot{r} \dot{\phi } \cos {2 \phi } \right] , \end{eqnarray}

(11)

where R = 18.4 Mpc is the distance to M 87.

Assuming the photocenter of the galaxy is on the orbital plane, the inclination is constrained as

\begin{eqnarray} 90^\circ -\theta \le \iota \le 90^\circ + \theta , \end{eqnarray}

(12)

\begin{eqnarray} \theta -90^\circ \le \iota \le 270^\circ - \theta , \end{eqnarray}

(13)

in the case where the main SMBH is located in front of (θ ≤ 90°) and behind (θ > 90°) the photocenter, respectively.

In the current situation, the period of gravitational waves is much longer than the observation time-span of pulsar timing arrays [O(10) years], so that the amplitude varies linearly with time on this time-scale. Thus, we consider the change in amplitude during the observational time-span, rather than the amplitude itself. To do this, we need the time derivative of the waveforms:

\begin{eqnarray} \frac{dh_+(t)}{dt} &=& \frac{\mu }{R}\ \Biggl \lbrace (1+\cos ^2\iota )\nonumber \\ &&\times \left[\left(\frac{M}{r^2}+2r\dot{\phi }^2\right) \dot{r} \cos 2\phi -4\frac{M}{r}\dot{\phi }\ \sin 2\phi \right] \nonumber \\ &&- \frac{M}{r^2}\dot{r}\ \sin ^2\iota \Biggr \rbrace, \end{eqnarray}

(14)

\begin{eqnarray} \frac{dh_{\times }(t)}{dt} &=& \frac{2 \mu }{R} \cos {\iota } \left\lbrace 4 \left(\frac{M}{r} - \dot{r}^2\right) \dot{\phi } \cos {2\phi } + \frac{M}{r^2} \dot{r} \sin {2 \phi } \right\rbrace .\nonumber\\ \end{eqnarray}

(15)

These time derivatives can be expressed in terms of r₁, e, a₁, and m₂ by substituting equations (3) and (4) for equations (14) and (15).

4 Results

First, we show the results in the case where the center of mass of two SMBHs is located at the photocenter of M 87. Figure 1 represents the absolute value of the time derivatives of the plus-mode and cross-mode amplitudes in a₁–e plane for r₁ = 3 pc and m₂ = m₁. Hereafter, the inclination is set to 0°, except for figure 4. The time derivative is of the order of 10⁻²⁵ s⁻¹ irrespective of the values of a₁ and e, although the ratio of the two polarization modes depends significantly on the phase of the orbital motion ϕ, which is uniquely determined by a₁ and e.

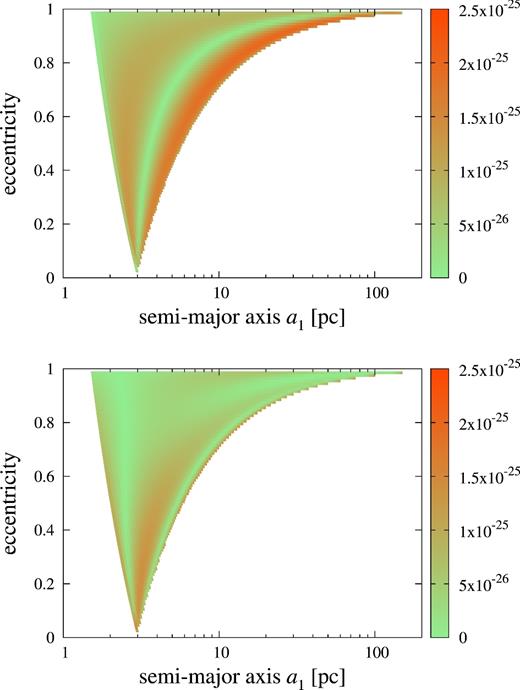
Absolute value of the time derivative of the plus-mode (top) and cross-mode (bottom) amplitudes for r1 = 3 pc and m2 = m1. (Color online)

Fig. 1.

Absolute value of the time derivative of the plus-mode (top) and cross-mode (bottom) amplitudes for r₁ = 3 pc and m₂ = m₁. (Color online)

Open in new tab Download slide

Figure 2 shows the dependence of the time derivative on the mass of the second SMBH for r₁ = 3 pc, e = 0.8, and a₁ = 10.0 pc. The dependence is strong (⁠|$\propto\! m_2^{3.5}$|⁠) for m₂ < m₁ and becomes relatively weak (∝ m₂) for m₂ > m₁.

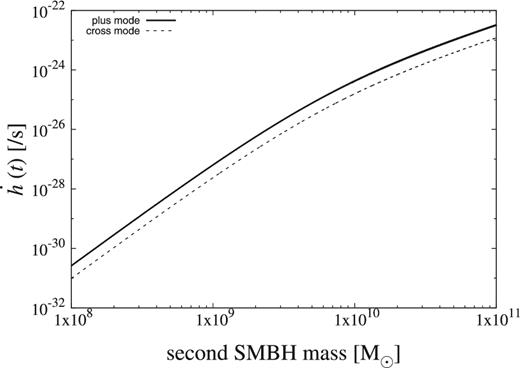
Dependence of the time derivative on the mass of the second SMBH for r1 = 3 pc, e = 0.8, and a1 = 10 pc.

Fig. 2.

Dependence of the time derivative on the mass of the second SMBH for r₁ = 3 pc, e = 0.8, and a₁ = 10 pc.

Open in new tab Download slide

Next, considering that the observed displacement has a large uncertainty, we show the dependence of the same quantity as figure 2 on the displacement in figure 3. The mass of the second SMBH is set to 3m₁, m₁, and 0.3m₁. From the figure, we see that the change of GW amplitude increases drastically as the displacement decreases. The current uncertainty in the displacement leads to the uncertainty in the change of about 4 orders of magnitude. It should be noted here that the correspondence between the displacement and the semimajor axis of the main SMBH, which is shown in the upper axis, depends on the eccentricity, which is set to 0.8 in this figure.

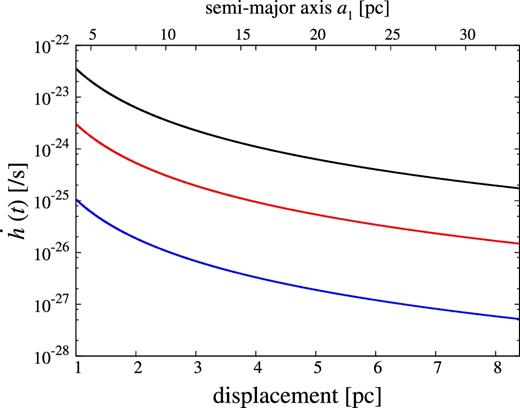
$Dependence of the time derivatives on the displacement (projected distance) for e = 0.8, ϕ = 56 $_{.}^{\circ}$6. The curves are for m2 = 3m1, m1, and 0.3m1 from top to bottom. The upper axis shows the semi-major axis of the main SMBH which corresponds to the displacement of the lower axis fixing eccentricity and the phase of the orbital motion. (Color online)$

Fig. 3.

Dependence of the time derivatives on the displacement (projected distance) for e = 0.8, ϕ = 56| $_{.}^{\circ}$|6. The curves are for m₂ = 3m₁, m₁, and 0.3m₁ from top to bottom. The upper axis shows the semi-major axis of the main SMBH which corresponds to the displacement of the lower axis fixing eccentricity and the phase of the orbital motion. (Color online)

Open in new tab Download slide

Figure 4 shows the inclination dependence with all the other parameters fixed. The inclination does not affect the overall amplitude so much, although the derivative of the cross-mode amplitude becomes zero at 90°.

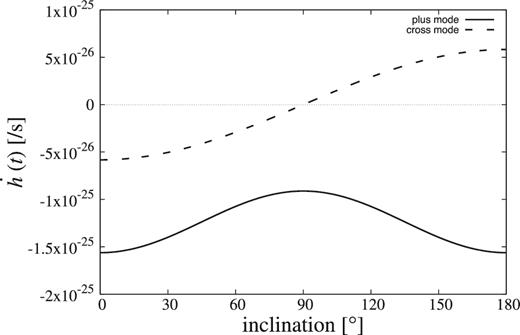
Inclination dependence of the time derivatives (change of the gravitational-wave amplitude in 10 years) for r1 = 3 pc, e = 0.8, a1 = 10.0 pc, and m2 = m1.

Fig. 4.

Inclination dependence of the time derivatives (change of the gravitational-wave amplitude in 10 years) for r₁ = 3 pc, e = 0.8, a₁ = 10.0 pc, and m₂ = m₁.

Open in new tab Download slide

Finally, we consider the scenario (4) where multiple BHs reside in the central region of M 87 and the main SMBH is forming a binary with a smaller BH. As remarked in section 1, the center of mass of the binary need not be located at the galactic center and the binary can have a much smaller semimajor axis compared with the previous cases. Because there is no constraint on the orbital elements, we compute the time derivative of GW amplitude for a number of random sets of orbital elements (semimajor axis, eccentricity, phase, and inclination), fixing the mass of the smaller BH. The results are shown as a function of the semimajor axis in figure 5 for m₂ = 0.1m₁, 0.01m₁, and 0.001m₁. Aside from m₂ and the semimajor axis, the time derivative of the GW amplitude has a strong dependence on the eccentricity and increases significantly for e ≳ 0.8.

Fig. 5.

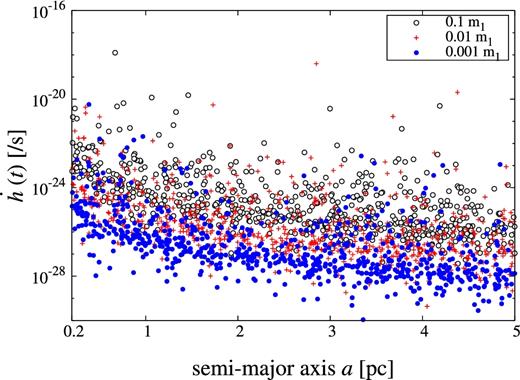
Time derivative of GW amplitude for random sets of orbital elements (semi-major axis, eccentricity, phase, and inclination), fixing the mass of the smaller BH. The results are shown as a function of the semi-major axis for m₂ = 0.1m₁, 0.01m₁, and 0.001m₁. (Color online)

Open in new tab Download slide

5 Detectability of gravitational waves

In this section, let us discuss the detectability of GWs from a possible SMBH binary at the center of M 87. Nano-Hertz GWs from SMBH binaries are targets of “pulsar timing arrays” (Sesana et al. 2008; Hobbs 2011; Lee et al. 2011; Mingarelli et al. 2013; Sesana 2013; Shannon et al. 2013; Taylor & Gair 2013; Burke-Spolaor 2015; Janssen et al. 2015). Because the arrival times of pulses are modulated by GWs, the time variation of timing residual—of a difference between the actual arrival time and the expectation in the absence of GWs—follows the wave form of the GWs crossing the earth. Thus, precise measurements of timing residuals can detect GWs with a long period comparable to the time span of observation, typically O(10) years.

In the current case with the linearly changing GWs, the situation is totally different, as we see below. The timing residual as a function of time, r_GW(t), induced by the GWs is generally described as

\begin{equation} r_{\rm GW}(t) = \frac{1}{2}\frac{\boldsymbol {p}^i\boldsymbol {p}^j}{1+\boldsymbol {\Omega }\cdot \boldsymbol {p}} \int ^{t} \Delta h_{ij}(t^{\prime },\boldsymbol {\Omega }) dt^{\prime } , \end{equation}

(16)

where Ω is the direction of the GW propagation, p is the unit vector of the direction of the pulsar, and Δh_ij(t, Ω) is the difference between the metric perturbation at Earth and the pulsar generated by GWs:

\begin{equation} \Delta h_{ij} = h_{+,\times }(t,\boldsymbol {\Omega }) - h_{+,\times }(t_p,\boldsymbol {\Omega }) , \end{equation}

(17)

where t_p = t − L/c and L is the distance to the pulsar. Below, we consider only the first term, the “Earth term,” and neglect the second term (the pulsar term), following previous works. Assuming that the GWs are linearly changing, that is, |$\dot{h}_{+,\times }$| are constant during an observation period, we have

\begin{equation} \Delta h_{ij} = \left(\dot{h}_+ \boldsymbol {e}^+_{ij} + \dot{h}_\times \boldsymbol {e}^\times _{ij} \right)t , \end{equation}

(18)

where |$\boldsymbol {e}^{+,\times }_{ij}$| are the polarization tensors. Then, equation (16) is written as

\begin{equation} r_{\rm GW}(t) = \frac{1}{2} \sum _{A=+,\times } F^A(\boldsymbol {\Omega }) \dot{h}_A t^2 , \end{equation}

(19)

where F^A(Ω) is the antenna beam pattern and is given by

\begin{equation} F^A(\boldsymbol {\Omega }) = \left[\frac{1}{2}\frac{\boldsymbol {p}^i\boldsymbol {p}^j}{1+\boldsymbol {\Omega }\cdot \boldsymbol {p}}e^A_{ij}(\boldsymbol {\Omega })\right] . \end{equation}

(20)

Thus, linearly changing GWs cause timing residuals which depend on squared time. However, this is exactly the same behavior as that due to the spin-down of the pulsar:

\begin{equation} r_{\dot{p}} = \frac{1}{2} \frac{\dot{p}}{p} t^2 , \end{equation}

(21)

where p is the pulse period and |$\dot{p}$| is the spin-down rate. Therefore, the linearly changing GWs are absorbed by the spin-down rate in the fitting of timing residual data with a timing model. In other words, the value of |$\dot{p}$| is biased by |$\alpha (\boldsymbol {\Omega }) \equiv \sum _A F^A(\boldsymbol {\Omega }) \dot{h}_A$|⁠, and the effects of GWs are absorbed as α(Ω)p.

It should be noted that α(Ω) can be positive or negative depending on the position of the pulsar and the GW polarization, while it is natural to consider an intrinsic |$\dot{p}$| should be positive. However, some of the observed pulsars have a negative |$\dot{p}$| value due to various effects, such as acceleration of the pulsar along the line of sight, the differential Galactic rotation, and the Shklovskii effect (Shklovskii 1970). Thus, we need to investigate the statistical feature of |$\dot{p}$| for many pulsars, rather than that of individual pulsars, in order to probe the existence of linearly changing GWs.

Here, we propose the distribution function of pulsar spin-down rate as a more robust method to detect linearly changing GWs. As noted above, the value of the bias α(Ω) depends on the pulsar position and the GW polarization. An example is shown in figure 6 for |$\dot{h}_+ = 0$| and |$\dot{h}_\times = 10^{-25}$|⁠, which shows the antenna beam pattern in the sky for the cross mode. As can be seen, the positive and negative areas appear as a quadrupole pattern. Thus, if we make histograms of |$\dot{p}$| of the pulsars in the positive and negative regions of the sky separately, a systematic difference between the two histograms would be seen for |$\dot{p} \lesssim |\alpha (\boldsymbol {\Omega })p|$|⁠. Practically, because we do not know the polarization of the GWs from M 87, we need to compare two histograms assuming any possible polarization and dividing the sky accordingly.

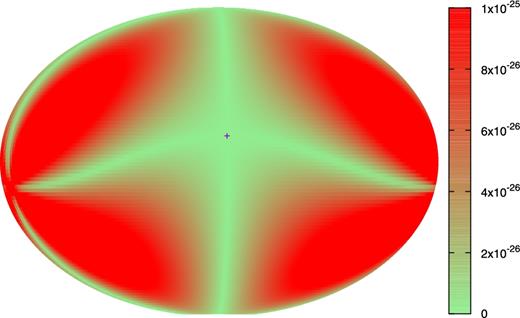
$Plot of the bias factor α(Ω) in the sky for $\dot{h}_+ = 0$ and $\dot{h}_\times = 10^{-25}$, which shows the antenna beam pattern for the cross mode. The symbol “+” in the figure represents the position of M 87. (Color online)$

Fig. 6.

Plot of the bias factor α(Ω) in the sky for |$\dot{h}_+ = 0$| and |$\dot{h}_\times = 10^{-25}$|⁠, which shows the antenna beam pattern for the cross mode. The symbol “+” in the figure represents the position of M 87. (Color online)

Open in new tab Download slide

The typical value of |$\dot{p}$| of the millisecond pulsars which have been found so far is about 10⁻²⁰, and |$\dot{p}/p$| can be as low as 10⁻¹⁹ (Ho et al. 2014). Therefore, linearly changing GWs with |$\dot{h} \gtrsim 10^{-19}$| could be, in principle, detected by the above method if we have a sufficiently large sample of millisecond pulsars. According to our calculation above, this level of GWs would not be generated in the scenario (3) (see figure 3), unless the second black-hole mass is extremely large (≫10m₁). On the other hand, there is a small chance in the scenario (4) (see figure 5), if the second BH mass is as large as 0.1m₁; besides, if the semimajor axis is relatively small ∼1 pc and the eccentricity is large.

In practice, due to the limited number of millisecond pulsars, the statistical errors in the histograms diminish the sensitivity of this method. The number of known millisecond pulsars is approximately 200 (the ATNF pulsar catalogue¹: Manchester et al. 2015), and this will reach 1400 via the planned SKA1 survey and 3000 via the SKA2 (Keane et al. 2015; Kramer & Stappers 2015). It is beyond the scope of the present paper to estimate the sensitivity quantitatively, taking the statistical errors and other observational systematics into account.

Let us comment on another aspect of this method which is significantly different from the conventional pulsar timing arrays. Pulsar timing arrays need a long-term observation of the order of O(10) years to follow the wave form of nano-Hertz GWs. Therefore, millisecond pulsars that have very stable periods through this time scale are necessary and only 5%–10% of millisecond pulsars satisfy this requirement. On the other hand, in this case, we do not need such a long-term observation, for the two reasons. One is that we do not need to follow the wave form of the GWs, and the other is that the relative importance of linearly changing GWs and pulsar spin-down in the timing residuals does not depend on the observation period [see equa-tions (19) and (21)]. Although the pulsars still need to be stable enough for a period of a few years in order to determine |$\dot{p}$| very precisely, the requirement on pulsar stability would be less strict. Thus, we expect that more millisecond pulsars could be used for this purpose compared with the conventional pulsar timing array, although it should be noted that only ∼30% of millisecond pulsars have |$\dot{p} < 10^{-20}$| and the increase would not be drastic.

6 Summary and discussion

In this paper, we estimated gravitational waves from a hypothetical SMBH binary at the center of M 87. This follows the scenario that the observed displacement between the AGN and the galactic center can be explained by the existence of another SMBH, or multiple IMBHs, or small SMBHs. Because the period of the binary and the resulting GWs is much longer than the observational time-span, the amplitude changes linearly with time and we calculated the time derivatives of the GW amplitudes. We investigated their dependence on the orbital elements and the second BH mass, taking the observational constraints into account.

We cannot detect GWs from a SMBH binary of the scenario (3) with pulsar timing arrays since the frequency of GWs in this case is too low to detect, or a new method since the time derivative of the amplitude of GWs is too small. In the scenario (4), where multiple IMBHs and small SMBHs reside and one of them is forming a binary with the main SMBH, there is a small chance of detecting the GWs with the new method. However, the detection of such GWs is not direct evidence of the existence of multiple BHs and, hence, does not give a decisive explanation of the AGN offset. Nevertheless, linearly changing GWs would still be a useful tool for probing the center of M 87.

If multiple BHs reside at the center of M 87, their gravitational perturbations will affect not only the main SMBH but also the distribution and velocity field of stars (Perets et al. 2007). This could be another probe of the M 87 center and will be studied in future.

Acknowledgments

KT is supported by Grand-in-Aid, from the Ministry of Education, Culture, Sports, and Science and Technology (MEXT) of Japan, No. 24340048, No. 26610048 and No. 15H05896. The research of JS has been supported at IAP and at CEA Saclay by the ERC Project No. 267117 (DARK) hosted by Université Pierre et Marie Curie (UPMC) - Paris 6 and at JHU by NSF Grant No. OIA-1124403.

1

〈http://www.atnf.csiro.au/people/pulsar/psrcat/〉.

References

Batcheldor

D.

,

Robinson

A.

,

Axon

D. J.

,

Perlman

E. S.

,

Merritt

D.

,

2010

,

ApJ

,

717

,

L6

Crossref

Search ADS

Burke-Spolaor

S.

,

2015

,

arXiv:1511.07869

Gebhardt

K.

,

Adams

J.

,

Richstone

D.

,

Lauer

T. R.

,

Faber

S. M.

,

Gültekin

K.

,

Murphy

J.

,

Tremaine

S.

,

2011

,

ApJ

,

729

,

119

Crossref

Search ADS

Gopakumar

A.

,

Iyer

B. R.

,

2002

,

Phys. Rev. D

,

65

,

084011

Crossref

Search ADS

Ho Wynn

C. G.

,

Klus

H.

,

Coe

M. J.

,

Andersson

N.

,

2014

,

MNRAS

,

437

,

3664

Crossref

Search ADS

Hobbs

G.

,

2011

, ,

High-Energy Emission from Pulsars and their Systems

,

Rea

N.

,

Torres

D. F.

Berlin

:

Springer-Verlag

229

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Islam

R. R.

,

Taylor

J. E.

,

Silk

J.

,

2004

,

MNRAS

,

354

,

427

Crossref

Search ADS

Janssen

G.

et al. ,

2015

, ,

Proc. Advancing Astrophysics with the Square Kilometre Array, PoS(AASKA14)

Trieste

:

SISSA

037

,

(arXiv:1501.00127)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Keane

E.

et al. ,

2015

, ,

Proc. Advancing Astrophysics with the Square Kilometre Array, PoS(AASKA14)

Trieste

:

SISSA

040

,

(arXiv:1501.00056)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Kramer

M.

,

Stappers

B.

,

2015

, ,

Proc. Advancing Astrophysics with the Square Kilometre Array, PoS(AASKA14)

Trieste

:

SISSA

036

,

(arXiv:1507.04423)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Lee

K. J.

,

Wex

N.

,

Kramer

M.

,

Stappers

B. W.

,

Bassa

C. G.

,

Janssen

G. H.

,

Karuppusamy

R.

,

Smits

R.

,

2011

,

MNRAS

,

414

,

3251

Crossref

Search ADS

Lena

D.

,

Robinson

A.

,

Marconi

A.

,

Axon

D. J.

,

Capetti

A.

,

Merritt

D.

,

Batcheldor

D.

,

2014

,

ApJ

,

795

,

146

Crossref

Search ADS

Manchester

R. N.

,

Hobbs

G. B.

,

Teoh

A.

,

Hobbs

M.

,

2005

,

AJ

,

129

,

1993

Crossref

Search ADS

Mingarelli

C. M. F.

,

Sidery

T.

,

Mandel

I.

,

Vecchio

A.

,

2013

,

Phys. Rev. D

,

88

,

062005

Crossref

Search ADS

Perets

H. B.

,

Hopman

C.

,

Alexander

T.

,

2007

,

ApJ

,

656

,

709

Crossref

Search ADS

Rashkov

V.

,

Madau

P.

,

2014

,

ApJ

,

780

,

187

Crossref

Search ADS

Sesana

A.

,

2013

,

Classical Quantum Gravity

,

30

,

244009

Crossref

Search ADS

Sesana

A.

,

Vecchio

A.

,

Colacino

C. N.

,

2008

,

MNRAS

,

390

,

192

Crossref

Search ADS

Shannon

R. M.

et al. ,

2013

,

ApJ

,

766

,

5

Crossref

Search ADS

Shklovskii

I. S.

,

1970

,

SvA

,

13

,

562

Taylor

S. R.

,

Gair

J. R.

,

2013

,

Phys. Rev. D

,

88

,

084001

Crossref

Search ADS

Download all slides

Month:	Total Views:
December 2016	1
February 2017	9
March 2017	7
April 2017	6
May 2017	5
June 2017	4
July 2017	6
August 2017	3
September 2017	7
October 2017	8
November 2017	3
December 2017	17
January 2018	20
February 2018	8
March 2018	12
April 2018	6
May 2018	12
June 2018	11
July 2018	10
August 2018	10
September 2018	11
October 2018	7
November 2018	6
December 2018	10
January 2019	7
February 2019	7
March 2019	18
April 2019	38
May 2019	21
June 2019	19
July 2019	8
August 2019	16
September 2019	12
October 2019	18
November 2019	12
December 2019	17
January 2020	5
February 2020	7
March 2020	11
April 2020	5
May 2020	10
June 2020	12
July 2020	7
August 2020	5
September 2020	3
October 2020	4
November 2020	4
December 2020	3
January 2021	3
February 2021	2
March 2021	7
April 2021	7
May 2021	3
June 2021	3
July 2021	1
August 2021	9
September 2021	3
October 2021	3
November 2021	9
December 2021	10
January 2022	5
February 2022	3
March 2022	2
May 2022	3
June 2022	9
July 2022	7
August 2022	12
September 2022	14
October 2022	6
November 2022	8
December 2022	7
January 2023	20
February 2023	4
March 2023	1
April 2023	4
May 2023	3
June 2023	1
July 2023	3
August 2023	2
September 2023	2
October 2023	5
November 2023	4
December 2023	6
January 2024	4
February 2024	5
March 2024	9
April 2024	5
May 2024	3
June 2024	5
July 2024	12
August 2024	3
September 2024	7
October 2024	4
November 2024	4
January 2025	2
February 2025	3
March 2025	3
April 2025	4
May 2025	1

Article Contents

Gravitational waves from an SMBH binary in M 87

Abstract

1 Introduction

2 Orbital elements of an SMBH binary

3 Gravitational waves from a binary

4 Results

5 Detectability of gravitational waves

6 Summary and discussion

Acknowledgments

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Gravitational waves from an SMBH binary in M 87

Abstract

1 Introduction

2 Orbital elements of an SMBH binary

3 Gravitational waves from a binary

4 Results

5 Detectability of gravitational waves

6 Summary and discussion

Acknowledgments

References

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only