-
PDF
- Split View
-
Views
-
Cite
Cite
Kotaro Moriyama, Shin Mineshige, New method for black-hole spin measurement based on flux variation from an infalling gas ring, Publications of the Astronomical Society of Japan, Volume 67, Issue 6, December 2015, 106, https://doi.org/10.1093/pasj/psv074
Close - Share Icon Share
Abstract
We propose a new method for black hole spin measurement. In this method, we consider a gas blob or ring falling onto a black hole from the marginally stable orbit, keeping its initial orbital angular momentum. We calculate the gas motion and photon trajectories in the Kerr space-time and, assuming that the gas blob or ring emits monochromatic radiation, carefully examine how it is observed by a distant observer. The light curve of the orbiting gas blob is composed of many peaks because of periodic enhancement of the flux due to the gravitational lensing and beaming effects. Further, the intensity of each peak first gradually increases with time due to the focusing effect around the photon circular orbit and then rapidly decreases due to the gravitational redshift, as the gas blob approaches the event horizon. The light curve of the gas ring is equivalent to a superposition of those of the blobs with various initial orbital phases, and so it is continuous and with no peaks. The flux first gradually increases and then rapidly decays, as in the blob model. The flux variation timescale depends on the black hole spin and is independent of the inclination angle, while time-averaged frequency shift has dependence on both effects. We can thus, in principle, determine spin and inclination angle from observations. The observational implications and future issues are briefly discussed.
1 Introduction
Observational proof of the black hole space-time is one of the most important outstanding issues in physics and astrophysics. This can lead to a proof of the existence of the event horizon and to a critical observational test of the general relativity theory proposed 100 years ago. It is known in general relativity that black hole space-time is uniquely described by a black hole mass, M, and a spin parameter, a (other than charges, which are never important in the astrophysical context). Masses can be relatively easily estimated by observing the motions of stars or gas (Shahbaz et al. 1999; Ghez et al. 2005; Orosz et al. 2011). The observed targets may not necessarily be close to the black hole, as long as they are bound to its gravitational potential. Black hole spins are, on the other hand, not easy to measure, since they only influence the space-time near to the black hole so that full consideration of general relativistic effects is necessary.
Until now, several methods have been proposed for the spin measurements. There are three major methods: (i) the continuum spectrum method (Hanawa 1989; Li et al. 2005; McClintock et al. 2011, 2014), (ii) the line spectrum method (Kojima 1991; Laor 1991; Tanaka et al. 1995; Duro et al. 2011; Steiner et al. 2011; Reynolds 2014), and (iii) the quasi-periodic oscillation (QPO) method (Kato 2001; Strohmayer 2001; Rezzolla et al. 2003; Remillard 2005; Kato et al. 2008).
We wish to note, however, that all of these methods have uncertainties and/or are based on critical assumptions that are not always easy to prove. The continuum spectrum method (i), for example, critically depends on the inclination angle. It also has an uncertainty in the spectral hardening factor in the emission from an accretion disk. The line spectrum method (ii) is sensitive to the emissivity profile assumed for the illuminated flux, as well as the iron ionization fraction as a function of radius. Further, it is not obvious how to separate line spectra from continuum ones. Moreover, it is assumed in both methods (i) and (ii) that the inner edge of the disk is at the radius of marginally stable orbit, but this remains a controversial issue (see Shidatsu et al. 2014). In the QPO method (iii), no widely accepted model is available for the origins of quasi periodic oscillations. Further, several different modes of QPOs are known and it is difficult to identify.
We should also point out that spins estimated by different methods are sometimes inconsistent. For example, the spin of GRO 1655−40 estimated by methods (i) and (iii) is 0.65 < a/M < 0.75 or 0.31 < a/M < 0.42, respectively (Shafee et al. 2006; Kato et al. 2008; McClintock et al. 2011). The spin of GRS 1915+105 is estimated to be a/M > 0.98 [method (i)], 0.54 < a/M < 0.58 or 0.97 < a/M < 0.99 [(ii)], and a/M < 0.44 [(iii)], respectively (Kato et al. 2008; Blum et al. 2009; McClintock et al. 2011). In short, all the existing methods are far from being complete. Therefore, it is required to construct new and independent methods for spin measurement to check the other methods.
We consider a gas blob or ring falling into the black hole from the marginally stable orbit (or the inner edge of an accretion disk) with a finite angular momentum and carefully examine how the gas blob or ring is observed by a distant observer. Radiation from the gas is known to undergo five relativistic effects which are summarized in table 1 (see Karas et al. 1992; Dovčiak et al. 2004a). We calculate the gas motion and photon trajectories in the Kerr space-time by a general relativistic ray-tracing method to seek good observational indicators of the black hole spin. Note that our approach is distinct from that of Dovčiak et al. (2004b), who were concerned with radiation from an accretion disk whose inner radius can be set below the marginally stable orbit, whereas we consider the gas blob or ring which is separated from an accretion disk and falls from the radius to the black hole.
| . | Relativistic effect . | Physical cause . | Remark (reference) . |
|---|---|---|---|
| (I) | Gravitational lensing | Focusing by light bending | (Karas et al. 1992) |
| towards a gravitating source | |||
| (II) | Beaming | Energy boost by relativistic | (Karas et al. 1992) |
| motion of particles | |||
| (III) | Photon circular orbit | Focusing around the | Key feature in the early stage |
| photon circular orbit, rph | |||
| (IV) | Focusing by | Focusing by frame dragging | Effective when a/M is high |
| frame dragging | due to black hole spin | ||
| (V) | Gravitational redshift | Energy loss by light travel | Key feature in the late stage |
| from deep potential well |
| . | Relativistic effect . | Physical cause . | Remark (reference) . |
|---|---|---|---|
| (I) | Gravitational lensing | Focusing by light bending | (Karas et al. 1992) |
| towards a gravitating source | |||
| (II) | Beaming | Energy boost by relativistic | (Karas et al. 1992) |
| motion of particles | |||
| (III) | Photon circular orbit | Focusing around the | Key feature in the early stage |
| photon circular orbit, rph | |||
| (IV) | Focusing by | Focusing by frame dragging | Effective when a/M is high |
| frame dragging | due to black hole spin | ||
| (V) | Gravitational redshift | Energy loss by light travel | Key feature in the late stage |
| from deep potential well |
| . | Relativistic effect . | Physical cause . | Remark (reference) . |
|---|---|---|---|
| (I) | Gravitational lensing | Focusing by light bending | (Karas et al. 1992) |
| towards a gravitating source | |||
| (II) | Beaming | Energy boost by relativistic | (Karas et al. 1992) |
| motion of particles | |||
| (III) | Photon circular orbit | Focusing around the | Key feature in the early stage |
| photon circular orbit, rph | |||
| (IV) | Focusing by | Focusing by frame dragging | Effective when a/M is high |
| frame dragging | due to black hole spin | ||
| (V) | Gravitational redshift | Energy loss by light travel | Key feature in the late stage |
| from deep potential well |
| . | Relativistic effect . | Physical cause . | Remark (reference) . |
|---|---|---|---|
| (I) | Gravitational lensing | Focusing by light bending | (Karas et al. 1992) |
| towards a gravitating source | |||
| (II) | Beaming | Energy boost by relativistic | (Karas et al. 1992) |
| motion of particles | |||
| (III) | Photon circular orbit | Focusing around the | Key feature in the early stage |
| photon circular orbit, rph | |||
| (IV) | Focusing by | Focusing by frame dragging | Effective when a/M is high |
| frame dragging | due to black hole spin | ||
| (V) | Gravitational redshift | Energy loss by light travel | Key feature in the late stage |
| from deep potential well |
The plan of this paper is as follows: in section 2, we introduce the basic equations to describe gas motions and ray trajectories, explain our models for the gas blob and ring, and describe methods of calculation. In section 3, we show numerical results and explain the physics underlying the key features of the light variations. On the basis of these simulation results we propose in section 4 our method for determining a spin a and inclination angle i. Section 5 is devoted to discussion of the distinctive features of our method, its observational implications, and future issues.
2 Models and methods of numerical calculation
In this section, we first introduce the basic equations (subsection 2.1). Next, we explain our models of an infalling gas blob (subsection 2.2) and ring (subsection 2.3). Finally, we describe the methods of numerical calculation (subsection 2.4).
2.1 Geodesic equations of gas particles and photons
As for a photon trajectory, we set μ = 0 in equations (3) and (4).
2.2 Gas blob model
We postulate the situation that a part of the innermost region of an accretion disk is stripped off, thus forming a gas blob, and that it starts to fall onto the black hole, keeping its original angular momentum. We assume that the gas blob has the following properties:
It has a spherical shape and its characteristic radius is Rblob, which has no time dependence.
We neglect self-gravity of the blob.
The gas blob emits radiation with monochromatic frequency ν0 in its inertial frame. This assumption is valid even in the case of multicolorwavelength radiation, such as the blackbody radiation, if the frequency width of the spectrum is sufficiently small. Its emissivity decreases with an increase in the distance from the center of the blob, obeying the Gaussian function.
We neglect self-absorption within the blob.
The initial position of the center of the gas blob is at (r, ϕ) = (0.98rms, 0). Here, rms is the radius of the marginally stable orbit.
The motion of the center of the blob follows the one-particle orbit given by equations (3) and (4). The blob falls onto the black hole on the equatorial plane, keeping constant energy, Ems, and angular momentum, Lms, where Ems and Lms are the energy and angular momentum of the particle rotating on the marginally stable orbit (figure 1).
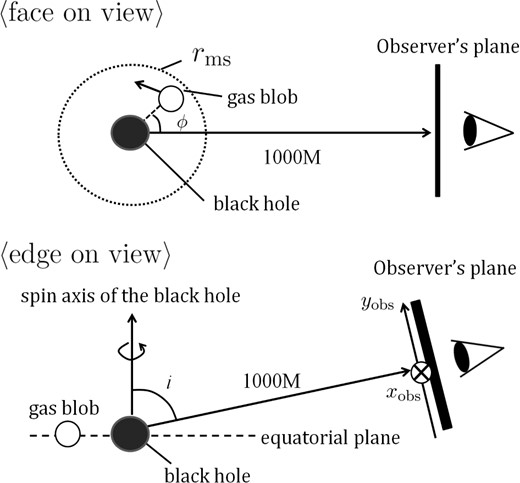
Schematic picture explaining the motion of the gas blob and the observer's plane. The xobs-axis is parallel to the equatorial plane of the black hole (⊗), and the yobs-axis is perpendicular to the xobs-axis.
2.3 Gas ring model
Next, we postulate the situation that the gas blob created in the innermost part of the disk is tidally disrupted and gets elongated by the rotational velocity differences in the azimuthal direction to form a rotating ring (figure 2). We assume that the gas ring has the following properties:
Its cross-section has a circular shape and its characteristic thickness is Rring, which has no time dependence.
We neglect self-gravity of the ring.
The gas ring emits radiation with monochromatic frequency ν0 in its inertial frame. Its emissivity decreases with increasing distance from the center of the cross-section of the ring (hereafter referred to as the center of the ring), obeying the Gaussian function.
We neglect self-absorption within the ring.
The initial position of the center of the ring is at r = 0.98rms.
The motion of the center of the ring follows the one-particle orbit given by equations (3) and (4). The ring falls to the black hole on the equatorial plane, keeping constant energy, Ems, and angular momentum, Lms.
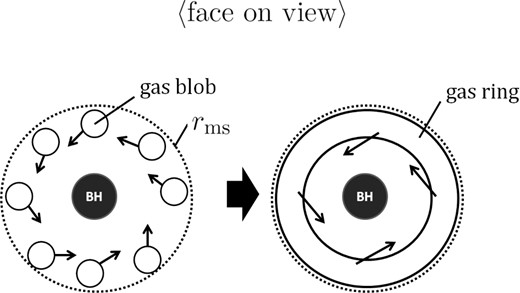
Schematic picture explaining the relationship between the blob model and the ring model.
2.4 Methods of numerical calculation
We divide the observer's plane into nr × nϕ cells. Here, the number of cells is nr × nϕ = 200 × 400, and spacings between each cell are drobs = 0.06M and robsdϕobs = robs × π/200. The distance between the center of the observer's plane and the black hole is set to be ro = 1000 M.
More detailed numerical procedures are as follows:
We calculate the ray trajectories which leave each cell of the observer's plane in the perpendicular direction to reach the vicinity of the black hole by applying the symplectic method (Yoshida 1993) obeying equations (3) and (4). Here the symplectic method is the numerical method to calculate test particle trajectories by solving Hamilton's canonical equation. We assume that a photon which enters within the radius r = rh + 10−4 M is captured by the black hole and thus cannot escape from there. Here, rh is the radius of the event horizon of the black hole.
Next, we calculate the trajectory of a test particle which falls to a rotating black hole from r = 0.98rms by the Runge–Kutta method. This is to describe the motion of the center of the gas blob or ring. We assume that a particle which enters within the radius r = rh + 10−4 M is captured by the black hole and thus cannot escape from there.
We choose one ray, which reaches a certain cell of the observer's plane at an observational time tobs. Any photons which reach the observer's plane at tobs after a traveling time of ttravel along this ray were radiated by the gas blob or ring at tem = tobs − ttravel. At tem, the position and the four-velocity of the center of the gas blob or ring are given by procedure 2. The emitted position of the photon which reaches the cell at tobs can be uniquely determined as a function of ttravel. Then by inserting the distance between the emitted position and the position of the center of the gas blob or ring into equations (5) and (6) we obtain the emissivity, jν, for each value of ttravel.
We assume the existence of an accretion disk, which is geometrically thin and optically thick, outside rms. That is, any photons that cross the disk surface should be absorbed by the disk and do not reach a distant observer.
By using jν calculated in procedure 3 and equations (7)– (11), we calculate the intensity of a ray which reaches one cell of the observer's plane at tobs for each value of ttravel. Here, we obtain Λ and q by inserting the position of the cell into equations (10) and (11).
We then sum all contributions by photons which were emitted at different times of tobs − ttravel and obtain the total intensity of rays, I, that reaches one cell at tobs.
- We finally integrate I over the entire observer's plane with the area, Sobs, and divide it by Sobs to calculate the flux, f(tobs), at each observational time, tobs,where dSobs is the area of the cell. We define tmax as the time when f(tobs) reaches its maximum; then, the normalized flux, F(tobs), is(12)\begin{equation} f(t_{\rm {obs}}) = \frac{1}{4\pi r_{\rm o}^{2}}\int I dS_{\rm {obs}}, \end{equation}Furthermore, by using jνdℓ at a radiative position, we calculate a photon number N(t, g)δg whose energy-shift factor is within g ∼ g + δg at time, tobs:(13)\begin{equation} F(t_{\rm {obs}}) = \frac{f(t_{\rm {obs}})}{f(t_{\rm {max}})}. \end{equation}where h is Planck's constant, and the integration is made to satisfy that the energy-shift factors of the rays reaching the observer are within a range between g ∼ g + δg.(14)\begin{equation} N(t_{\rm {obs}},g)\delta g =\frac{1}{h\nu _{0}}\int \int g^{3}j_{\rm {\nu }}d\ell dS_{\rm {obs}} \delta g, \end{equation}
Hereafter, we rewrite the observational time, tobs, simply as t.
3 Results
3.1 Blob model: typical case
We first show in figure 3 the results of a typical case in which we assign (a/M, i) = (0.0, 85°) and Rblob = 0.1 M. The detailed light curve around the first peak shown in panel (a) exhibits two peaks [see arrows in panel (a)]. The first peak appears when the blob is at the opposite side to the observer's position (phase ϕ = π, see figure 1), due to the gravitational lensing [effect (I) in table 1]. The second peak is due to the beaming occurring at ϕ = 1.5π [effect (II) in table 1]. After the second peak, the flux drops because of the redshift due to the motion of the blob moving away from the observer. At the time of the second peak, the centroid energy-shift factor reaches its maximum [see panel (c) of figure 3]. These properties are the same as the those studied for a rotating blob (cf. Karas et al. 1992; Dovčiak et al. 2004a).
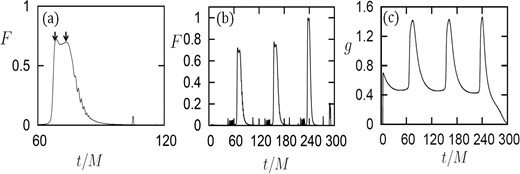
Typical results of the blob model for the case with (a/M, i) = (0.0, 85°) and Rblob = 0.1 M: (a) the detailed light curve around the first peak, (b) the entire light curve, and (c) the time variation of the centroid energy-shift, where contributions by the photons which reach the observer after crossing the equatorial plane are removed in this plot.
One might say, therefore, that the light variation in the first stage of evolution looks quite similar to that of a rotating blob at a fixed radius. Note, however, one important difference between them: the peak intensity gradually increases with time in our model (see figure 3b). Such an increase occurs when a blob approaches the radius of the photon circular orbit, rph, and this phenomenon is caused by the focusing effect around the photon circular orbit [effect (III) in table 1].
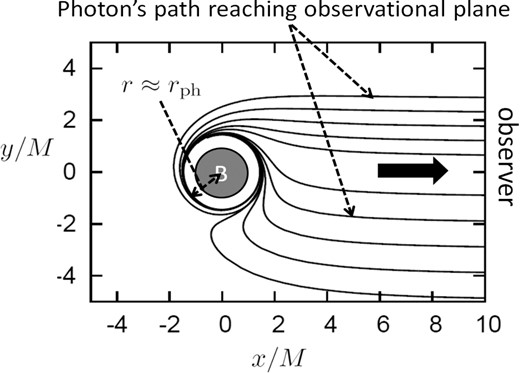
Schematic picture explaining the focusing around the photon circular orbit, rph (a/M = 0.9). Each line represents a ray that finally reaches the observer's plane.
Figures 3b and 3c clearly prove the existence of the focusing effect around rph. The flux reaches its maximum at tmax, and finally decreases with time, while the centroid energy-shift factor of the peak is nearly constant. That is, the peak flux increases in the first stage because of an increase of photon numbers, not because of an increase of mean photon energy, which provides support for the idea that flux increase is due to the focusing of rays. In the second stage (after tmax), the flux decays due to the gravitational redshift [effect (V) in table 1] and to an increase in the fraction of photons that are captured by the black hole.
3.2 Blob model: cases with various (a, i)
Next, the results of other cases with various combinations of spin parameters and inclination angles are shown in figure 5.
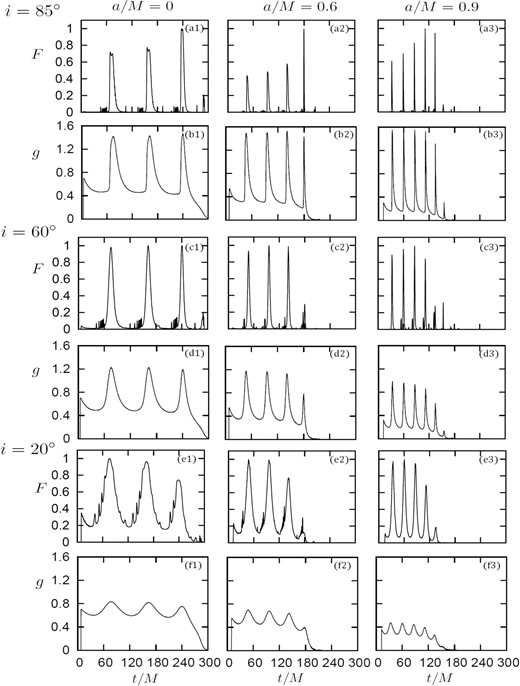
Time variations of the normalized flux F(t) (upper panels) and those of the centroid energy-shift factors g(t) (lower panels) for various combinations of a and i. The abscissa is observational time t normalized by the black hole mass M.
We first fix i, say, i = 85°; let us compare the non-spin case (a/M = 0.0; figure 5a1), a middle case (a/M = 0.6, figure 5a2), and a high-spin case (a/M = 0.9, figure 5a3). We immediately notice that the higher the spin is, the shorter the peak interval becomes. This is because as a increases, rms decreases, and hence the angular frequency (Ω) increases, whereas the orbital period (∝ Ω−1) decreases. One may think that we can easily estimate a by measuring peak intervals on the condition that we precisely know M. This is, however, not so feasible in practice, since it is hard to detect radiation from one separate, compact blob. Rather, it is more likely that an assembly of blobs (or a ring) falls together. Therefore, we had better pay more attention to the overall shape of the light curves. If we see how the maximum flux of each peak changes with time in figure 5, we find that the higher the spin is, the greater the number of peaks becomes, and the more rapidly the maximum flux of the peak grows. We also notice a similar tendency in the time variations of g displayed in the lower panels. These facts lead us to the conclusion that how the peak flux and the energy-shift factor vary with time can be good indicators of the black hole spin.
Next, we fix a and change i, finding that the flux peak increase is more appreciable in high-i systems. In fact, the first stage evolution (when the peak flux increases) is clear when i = 85°, while it is not when i = 20°. This is because the focusing effect around rph is more appreciable in nearly edge-on systems with smaller i values. Further, the higher i is, the sharper each peak in the g variation profile becomes (see lower panels). This can be naturally understood, since the beaming effect is more effective in higher-i systems.
In order to extract information regarding the spin (a/M) from the overall flux variations shown in figure 5, we next consider the cases in which numerous blobs fall together. We plot in figure 6a superposition of the light curves of numerous blobs rotating with different initial orbital phases for the cases of a/M = 0.0 (panel a1), 0.6 (a2), and 0.9 (a3), respectively. Here, we fix the inclination angle to be i = 85°. It is evident that the higher a is, the shorter the time to reach the flux maximum becomes. This is because the initial position of the blob (at ≈rms) is closer to the black hole with a higher a value.

Flux variations of numerous blobs for cases with different spin parameters, a/M = 0.0, 0.6, and 0.9. Panels (a) show superposition of light curves of numerous blobs rotating with different initial orbital phases. Panels (b) plot envelope curves connecting the peaks shown in panels (a). Panels (c) depict time developments of the peak areas, the time integral of the peaks shown in panels (a). Here we fix i = 85°. The abscissa is observational time t normalized by the black hole mass M, and the ordinate is the flux normalized by its maximum value in each panel.
In every case, two-stage evolution (rise and decay) is clear. Such a trend can be more clearly shown in panels b1–b3 in figure 6, in which envelope curves connecting each peak in panels a1–a3 are displayed. To be more precise, the first stage in figure 6b1 can be further divided into two sub-stages; that is, the flux first slowly increases (until t/M ∼ 220) and then starts to rapidly increase until the flux maximum at t/M ∼ 270, followed by a rapid decay at the end. Such sub-stages are not so clear in high-spin cases (see figure 6b3).
Further, we wish to draw attention to the a-dependence of the shape of the flux curve around its maximum; the peak is rather broad when a/M is high see panel b3), while it is sharp when a/M is low (see panel b1). That is, the region where focusing is prominent widens as a/M increases. This can be understood by the consequence of the frame dragging around a rotating black hole, by which photons are focused in the rotating direction [effect (IV) in table 1].
In the high-a case, the frame dragging effect plays an important role for flux peaks in panels 6b. The radius at which each flux peaks is r/M = (3, 2.9, 2.1) = (1, 1.32, 1.34)rph, for a/M = (0, 0.6, 0.9), respectively. In the case of a/M = 0, the emitting radius for the flux peak is equal to rph. In the case of a/M = 0.6 and 0.9, on the other hand, the radii of the flux peaks are outside rph. This can be understood by the consequence of frame dragging around a rotating black hole, by which photons are focused in the rotating direction.
We should be cautious here, however, since what is observed is not the envelope curve of the peaks but the total radiation energy received by an observer per unit time. We thus add three more panels as figures 6c1–6c3 displaying the time evolution of “peak area,” the time integral of the radiation energy of the peak. By comparing the bottom panels c1–c3 with the middle panels b1–b3, we understand that the sharp rises found in the middle panels are totally missing in the bottom panels and that such a distinction is clearer in the lower-spin cases. Since the bottom panels show the time integration of flux of each peak, while the middle panels show the maximum flux only, differences between them should mean differences in time width (i.e., duration) of each peak. We actually find that the time width of the peak significantly decreases with time because the Doppler beaming effect is more enhanced when gas moves nearer to the black hole. The bottom panels will be used for our method of spin measurements.
3.3 Results of ring model: light curves
We show the light curves of the ring for various combinations of a and i for a fixed value of Rring = 0.1 M in figure 7. The continuum curves are nothing but the superpositions of the light curves of numerous blobs with different initial orbital phases (cf. panels c of figure 6).
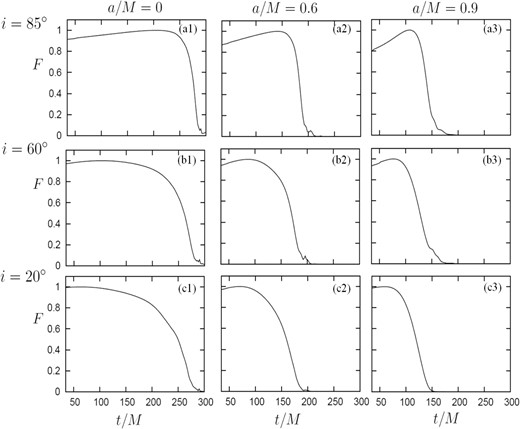
Light curves of the ring for the spins of a/M = 0.0 (left), 0.6 (middle), and 0.9 (right) and the inclination angles of i = 85° (upper), 60° (middle), and 20° (lower), respectively. The abscissa is observational time normalized by M, and the ordinate is the flux normalized by its maximum value, F(t). We fix Rring = 0.1 M.
There are several noteworthy features found in these light curves. First, the light curves have no peaks, unlike the case of the blob model. This is because a distant observer at any time receives the ray which is at the orbital phase of ϕ ∼ π (at which the gravitational lensing is most effective) or the one at ϕ ∼ 1.5π (at which the beaming is most effective). Next, the flux first increases due to the focusing effect around rph (in the first stage) and then decays due to the gravitational redshift and to the capture of rays by the black hole (in the second stage). These features are the same as those of the numerous blobs shown in figure 6.
Let us examine the (a, i)-dependence of the light curves. Let us first fix the inclination angle (i) and change the spin from a/M = 0.0 to a/M = 0.9 to see what changes do occur.
The higher a is, the shorter is the flux variation for all the values of i. This is because a ring falls to the black hole from smaller radii (recall that the initial position at r ≈ rms is smaller for a higher spin).
The higher a is, the steeper is the flux curve in the first stage. This feature is prominent for high-i cases, e.g., i = 85° and 60°. Note that the flux increase itself is not so appreciable when i is low. This is because the focusing effect around rph, which is responsible for the flux increase, is stronger when a is high and i is higher.
Next, we fix a/M and change the inclination angle from i = 20° to i = 85°. As stated above, the flux increases more rapidly in higher-i cases because of the enhanced focusing effect around rph. The same feature is seen in other spin cases.
3.4 Results of ring model: photon numbers
Although the flux variation contains useful information regarding the spin and the inclination angle, it is not sufficient to measure both quantities.
Other distinct information is needed. Since two pieces of independent information are mixed in the radiation flux, F(t) (photon energy and photon numbers), it may be useful to separate them. We next investigate the (a, i)-dependence of the energy-shift factor, g.
The time variation of the photon number is displayed in figure 8a. Here, the color represents the logarithm of the photon number normalized by its maximum value. Here we fix (a/M, i) = (0.0, 85°) and Rring = 0.1 M. Figure 8b shows the photon number profile (against g) at a fixed time of t/M = 50. Two peaks are prominent: one is the blue-shifted peak at g ∼ 1.4 and the other is the red-shifted peak at g ∼ 0.5 (see arrows). Hereafter, we call gblue (or gred) the g-value of the blue-shifted (red-shifted) component.
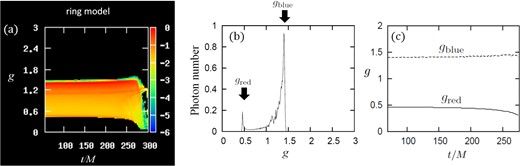
Time-dependent properties of the radiation emitted from a ring. We fix (a/M, i) = (0.0, 85°) and Rring = 0.1 M. Panel (a) shows the time variations of the photon numbers as a function of the energy-shift factor, g. The color represents the logarithm of the photon numbers normalized by their maximum value. Panel (b) shows the photon number distribution against g at the fixed time of t/M = 50. Two peaks are prominent, which are indicated by the two arrows. We call gblue (or gred) the g-value of the blue-shifted (red-shifted) component. Panel (c) shows the time variations of gblue and gred.
To consider the reason for the two peaks, let us look again at the time variation of the centroid energy-shift of an infalling blob shown in figure 3c. This panel exhibits two key features (or phases): (i) sharp peaks with large g-values (greater than 1.0), which occur due to the beaming, and (ii) long “quiescence” with low g-values (typically g ∼ 0.5), which occurs when the blob is moving away from the observer due to the Doppler effect and to the gravitational redshift. Now we understand that gblue (or gred) in figure 8b corresponds to the centroid energy-shift factor of the peaks (or of the quiescence) in figure 3c. Here, we wish to stress that figure 8b shows a local maximum at g ∼ gred, although the photon energy is low. This means that the area under the F(t) curve of the red-shifted component is larger than those of other energy-shift factors.
The double-horn profile displayed in figure 8b resembles that of the “disk line” Fe Kα emission line formed on a relativistic accretion disk around a black hole (Kojima 1991; Laor 1991). We wish to point out a big distinction, however, that our red peak is very narrow, while the red component of the disk line is usually broad, especially when a/M is large. This is because we are concerned with emission from a narrow ring (Rring ≪ r), while the disk line is produced on a disk with a large area. Superposition of emission lines from different radii produces the broad red wing of the disk line.
Finally, the time variations of these quantities are shown in figure 8c. The spin and inclination-angle dependence is expected, as will be shown in the next subsection.
3.5 Results of ring model: energy-shift factor
We show the time variations of gblue and gred for various combinations of a and i in figure 9. First, we immediately notice a clear trend that g-values depend more sensitively on i, rather than a, and that the higher i is, the longer the energy-shift interval between the two lines becomes. This can be easily understood, since the Doppler is more pronounced when i is higher. Let us next fix i and see how the results change by decreasing a from high a/M(= 0.9) values to lower ones. Here is a summary: (i) When i is low, e.g., i = 20°, both gblue and gred decrease with a at low i, since gravitational redshift is stronger in order that the initial position of the ring (≈ rms) is smaller (see figures 9c1 and 9c3). (ii) When i is large, say, e.g., i = 85°, gblue does not depend so much on a, while since the beaming effect is stronger than the gravitational redshift, gred is smaller due to the gravitational redshift and the redshift due to the motion of the ring fraction moving away from the observer.
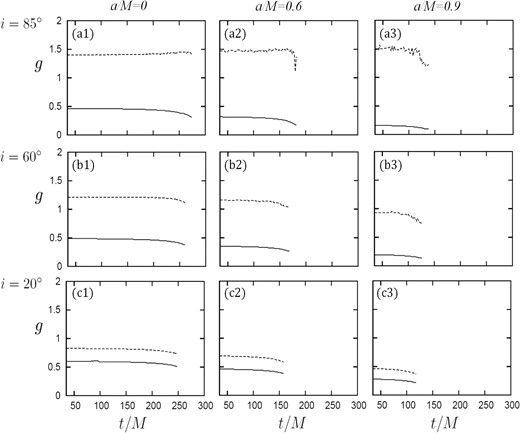
Time variations of gblue (dotted line) and gred (solid line) for a variety of a/M = 0.0 (left), 0.6 (middle), and 0.9 (right) and i = 85° (upper), 60° (middle), and 20° (bottom), respectively. Each curve is plotted until the time when the normalized flux decays to reach F = 1/2 (i.e., half of the maximum flux).
4 New method of black-hole spin measurement
4.1 Introduction of new quantities
In table 2 we summarize the physical meanings of the quantities A–D.
| Quantity . | Physical meaning . | Equation number . |
|---|---|---|
| A | Timescale of flux variation | (18) and (26) |
| B | Time-averaged gred(t) | (19) |
| C | Time-averaged gblue(t) | (20) |
| D | Relative difference between B and C | (21) |
| Quantity . | Physical meaning . | Equation number . |
|---|---|---|
| A | Timescale of flux variation | (18) and (26) |
| B | Time-averaged gred(t) | (19) |
| C | Time-averaged gblue(t) | (20) |
| D | Relative difference between B and C | (21) |
| Quantity . | Physical meaning . | Equation number . |
|---|---|---|
| A | Timescale of flux variation | (18) and (26) |
| B | Time-averaged gred(t) | (19) |
| C | Time-averaged gblue(t) | (20) |
| D | Relative difference between B and C | (21) |
| Quantity . | Physical meaning . | Equation number . |
|---|---|---|
| A | Timescale of flux variation | (18) and (26) |
| B | Time-averaged gred(t) | (19) |
| C | Time-averaged gblue(t) | (20) |
| D | Relative difference between B and C | (21) |
In the next section, we calculate A1–D for a variety of combinations of a, i, and Rring to seek the best combinations of the quantities for extracting information on the spin from observational data.
4.2 Dependence of A1–D on (a, i )
The calculation results are summarized in figures 10 and 11. It is important to note that all the curves in each panel do not cross each other; that is, we can, in principle, uniquely determine a and i, once the values of A1–D are specified.
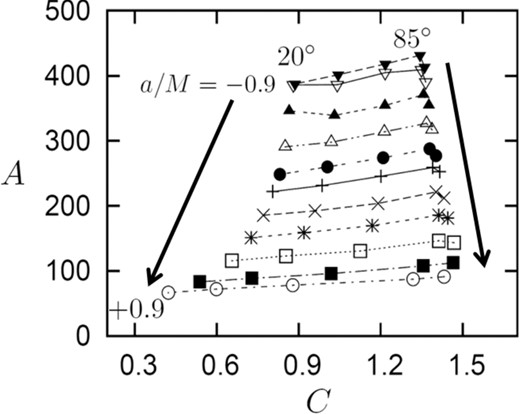
Relation between A and C for the inclination angles of i = 20°, 40°, 60°, 80°, and 85° and for the spin parameters of a/M = −0.9, −0.8, −0.6, −0.4, −0.2, 0, 0.2, 0.4, 0.6, 0.8, and 0.9. We fixed the ring width to be Rring = 0.1 M. The data points with the same a value are connected by lines. The two arrows indicate the direction of increasing a.
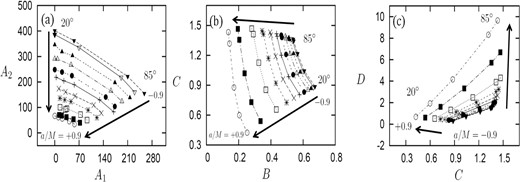
Relation between the quantities except for A and C for the same inclination angles, spin, and ring width as figure 10.
In particular, we notice that the lines (on which a is constant) are nearly horizontal; that is, A does not so much depend on i (figure 10). This fact leads to an important conclusion that we can roughly estimate a solely by A. We emphasize that it shows a way to break the classic a–i degeneracies of the spectral methods of measuring spin, and is not particularly model dependent like most QPO methods.
Let a/M increase from 0.0 to 0.9 for a fixed value of i to see how the key quantities of A1–D vary.
We find that all of the A values decrease with an increase of a/M. This is because the timescale of flux variation decreases with an increase of a/M both in the rise and decay phase for all i (see figure 7).
With an increase of a/M, both B (= 〈gred〉) and C (= 〈gblue〉) decrease, unless i is very high, because of the gravitational redshift (see figure 9). Since the decrease of C is slower than that of B, D[≡ (C/B) − 1] increases with an increase of a/M. When i is very high (e.g., i = 85°), conversely, C rather increases (while B still decreases) with an increase of a/M. This is due to the beaming effect, which is more effective for edge-on cases.
4.3 Dependence of A1–D on the thickness of the ring
In the previous subsection, we proposed a new method for the spin measurement. One may think, however, that the results may sensitively depend on the ring shape, such as the characteristic thickness of the ring. To demonstrate that this is not the case, we need to consider how the values of A1–D depend on the thickness of the ring. We will demonstrate that the results will not depend on Rring as long as we use A, instead of A1 or A2.
We display in figure 12 the relation between several quantities for Rring = 0.2 M (panels a1 and a2) and 0.3M (panels b1 and b2), respectively. By comparing these panels with figures 11a and 10, we understand that the relation between A and C does not critically depend on the thickness of the ring. Since we put the center of the ring (where the emissivity jν is maximum) at the same position for all the models, we can easily understand that B–D do not depend so much on the thickness of the ring. For low inclination angles (say, i = 20°), hence, we can determine a and i by using B, C, and D. For high inclination angles (say, i > 60°), however, the photon number of the red-shifted component is much less than that of the blue-shifted one so that precise measurements of gred from actual observations might be difficult. Henceforth, we mainly use the information A and C.
Figures 12a1 and 12b1 display how the relation between A1 and A2 depends on the thickness of the ring. Here, we fixed a and i. Comparing these with figure 9 a showing the case with Rring = 0.1 M, we see a clear tendency that the larger Rring is, the larger is A1 and the smaller is A2. This can be understood, since a larger thickness means a longer emission timescale, thereby increasing A1. (Note that the motion of the center of the ring is kept the same regardless of the ring thickness, but the epoch when the last tip of the ring material passes a certain radius (say, rph) is more and more delayed, as the ring thickness increases.) Since the decay timescale decreases, so does A2, as Rring increases.
To summarize, the thicker the ring is, the larger A1 is and the smaller A2 is, whereas A (=A1 + A2) does not critically depend on the ring thickness (see figures 10, 12b1, and 12b2). In fact, the relation between A and C shown in figures 12a1, 12b1, and 11a exhibits similar tendencies among different ring models.
Let us finally demonstrate that we can certainly have good guesses for a/M and i, by using the (A, C) diagram in figure 12. The results are summarized in table 3. We find that the differences in a/M and i among different models are within ranges of ∼ 0.01–0.1 and ∼ 1°, respectively. To conclude, we can measure the spin and inclination angle with good accuracy by using A and C.
| Quantities . | Thickness of the ring . | Spin . | Inclination angle . |
|---|---|---|---|
| (A, C) . | R ring/M . | a/M . | i° . |
| (100, 0.9) | 0.1 | 0.72 | 45 |
| 0.2 | 0.74 | 46 | |
| 0.3 | 0.76 | 46 | |
| (100, 1.2) | 0.1 | 0.78 | 69 |
| 0.2 | 0.77 | 70 | |
| 0.3 | 0.76 | 69 | |
| (300, 0.9) | 0.1 | −0.44 | 22 |
| 0.2 | −0.43 | 22 | |
| 0.3 | −0.44 | 23 | |
| (300, 1.2) | 0.1 | −0.27 | 64 |
| 0.2 | −0.27 | 64 | |
| 0.3 | −0.28 | 65 |
| Quantities . | Thickness of the ring . | Spin . | Inclination angle . |
|---|---|---|---|
| (A, C) . | R ring/M . | a/M . | i° . |
| (100, 0.9) | 0.1 | 0.72 | 45 |
| 0.2 | 0.74 | 46 | |
| 0.3 | 0.76 | 46 | |
| (100, 1.2) | 0.1 | 0.78 | 69 |
| 0.2 | 0.77 | 70 | |
| 0.3 | 0.76 | 69 | |
| (300, 0.9) | 0.1 | −0.44 | 22 |
| 0.2 | −0.43 | 22 | |
| 0.3 | −0.44 | 23 | |
| (300, 1.2) | 0.1 | −0.27 | 64 |
| 0.2 | −0.27 | 64 | |
| 0.3 | −0.28 | 65 |
| Quantities . | Thickness of the ring . | Spin . | Inclination angle . |
|---|---|---|---|
| (A, C) . | R ring/M . | a/M . | i° . |
| (100, 0.9) | 0.1 | 0.72 | 45 |
| 0.2 | 0.74 | 46 | |
| 0.3 | 0.76 | 46 | |
| (100, 1.2) | 0.1 | 0.78 | 69 |
| 0.2 | 0.77 | 70 | |
| 0.3 | 0.76 | 69 | |
| (300, 0.9) | 0.1 | −0.44 | 22 |
| 0.2 | −0.43 | 22 | |
| 0.3 | −0.44 | 23 | |
| (300, 1.2) | 0.1 | −0.27 | 64 |
| 0.2 | −0.27 | 64 | |
| 0.3 | −0.28 | 65 |
| Quantities . | Thickness of the ring . | Spin . | Inclination angle . |
|---|---|---|---|
| (A, C) . | R ring/M . | a/M . | i° . |
| (100, 0.9) | 0.1 | 0.72 | 45 |
| 0.2 | 0.74 | 46 | |
| 0.3 | 0.76 | 46 | |
| (100, 1.2) | 0.1 | 0.78 | 69 |
| 0.2 | 0.77 | 70 | |
| 0.3 | 0.76 | 69 | |
| (300, 0.9) | 0.1 | −0.44 | 22 |
| 0.2 | −0.43 | 22 | |
| 0.3 | −0.44 | 23 | |
| (300, 1.2) | 0.1 | −0.27 | 64 |
| 0.2 | −0.27 | 64 | |
| 0.3 | −0.28 | 65 |
5 Discussion
5.1 Brief summary
In this paper, we propose a new method for measuring a and i from observational data for a given mass M. In this method, we consider a gas cloud, which is assumed to have a ring shape, falling onto a black hole. Assuming that the gas ring emits monochromatic radiation, we calculated the flux variation and the time-averaged frequency shift of the radiation received by a distant observer for various combinations of a and i. We have demonstrated that we can uniquely determine a and i from observational data, not critically depending on the thickness of the ring.
The actual procedures of our method are in three steps:
Obtain time-sequence data of normalized flux F(t) and photon numbers N(t, g)δg as functions of frequency or g (frequency-shift factor).
Calculate the key quantities, A and C, by equations (16)–(18) and (20).
Estimate a and i by using figure 10.
In addition, we can also estimate the ring thickness from A1 and A2 by using figures 11a, 12a1, and 12b1. Even when the frequency information is not available, we still have a good guess on a solely from A, especially when the ring thickness is relatively large (∼ 0.3 M).
5.2 Distinctive features of the proposed method
The most distinctive feature of the proposed method is that we can directly measure black hole spin. This is made possible by focusing on non-periodic light variation events in the innermost region at r < rms. By contrast, the widely used methods are based on the steady or periodic phenomena occurring at r ≥ rms. In this respect our method is not only independent and complementary to other methods, but also advantageous in probing the innermost space-time structure around a black hole.
The most popular methods of spin measurements based on continuum or Fe Kα line spectra totally depend on the assumption that the inner edge of the disk is at rms (Duro et al. 2011; McClintock et al. 2011, 2014; Steiner et al. 2011; Reynolds 2014). We wish to point out that there is no solid physical reason for this assumption; i.e., the disk could be truncated at a radius greater than rms. It is of great importance to note the facts that line and continuum spectra are sensitive more to the radius of the inner edge of the emission region than to the spin values. This is obvious for the continuum spectra, since the smaller rms is, the higher is the maximum disk temperature (Tmax) and the smaller is the region emitting blackbody radiation with Tmax, while the shape of the gravitational potential at r > rms does not largely change with a change in a. This is also true for line spectra. Kojima (1991) compared two line profiles, one from a disk with the inner edge at 6M around a non-rotating black hole and another from a disk with the same radius of the inner edge but around a maximally rotating black hole, finding little difference between them (see his figure 2). In short, these major methods only indirectly measure spins.
One may think that our method might crucially depend how to take the initial time (ti) and radius, when and where a rotating ring starts to fall. This is not the case, however. We can arbitrarily choose the initial radius as long as r ≈ rms, as we have argued in subsection 4.1. This is because the gas ring is initially rotating on nearly a circular orbit and so its emitted flux is nearly constant at first, not contributing to A1. As a result, A does not critically depend on the initial position, nor on the time.
5.3 Observational implications: shot analysis
Our ring model may possibly be applied to the X-ray shots of black hole binaries. X-ray shots are flare-like light variations with sharp peaks (see Oda et al. 1971; Gierliňski & Zdziarski 2003; Focke et al. 2005) and are observed during the so-called low/hard state, which is characterized by power-law spectra and is associated with substantial variations (see, e.g., a review by Done et al. 2007).
Negoro et al. (1994) developed the technique of superposed shots, adding plenty of shot profiles (in X-ray bands) by aligning their peaks (called “superposed shot” analysis; see also Liu & Li 2004; Wu et al. 2007; Yamada et al. 2013). Furthermore Feng, Li, and Chen (1999) detected the shot profile with high time resolution, and found that (1) the time profile of the superposed shot is rather time symmetric with respect to its peak time, and that (2) it can be fitted well with the sum of two exponential functions: one with time constants of ∼ 0.01 [s] and another of ∼ 0.1 [s].
By means of global MHD simulations, Machida and Matsumoto (2003) studied the time evolution of a torus, which is initially threaded by a weak toroidal magnetic field, around a non-rotating black hole. They carefully analyzed the simulation results and found that gas clouds (or streams) with a spiral shape intermittently fall onto the black hole from the inner edge of the torus. These gas clouds are heated by dissipation of magnetic energy via magnetic reconnection and are thus expected to emit intense X-rays. This is exactly the situation that we have postulated in our blob or ring model.
We note, however, that the shape of accreting gas clouds is not a full ring but is a spiral according to the MHD simulation. It is thus necessary to check whether our proposed model based on full rings can apply to spiral-shaped gas clouds or not. We calculate a half-ring model as the intermediate case between the blob model and the ring model and show its light curves in figure 13. The light curves resemble those of the blob model in the sense that they have several peaks (or humps) due to the gravitational lensing and the beaming, but the duration of each peak is much longer in the half-ring model. We also confirm the tendency that the peak flux of the half-ring first increases by the focusing effect around rph and then decays due to gravitational redshift. Such overall variations are similar to those in the ring model. We thus expect that the superposed light curves of the half-rings (with different initial phases) are equivalent to those of a full ring (recall figure 6). In conclusion, we can use the ring model for spin measurements regardless of the precise shape of the gas cloud; it can be a blob, a half-ring, or a full ring.
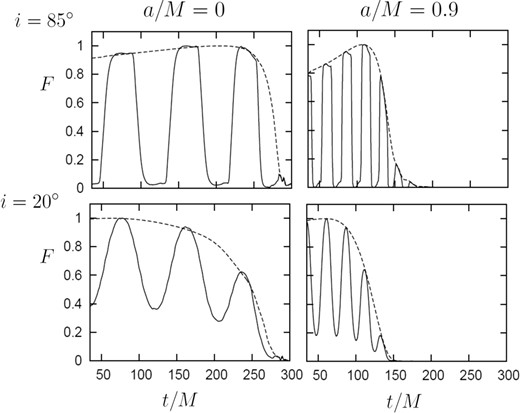
Light curves of a half-ring (the solid line) and those of a full ring (the dashed line) for a/M = 0 (left panels) and 0.9 (right panels), and for i = 85° (upper) and 20° (lower), respectively. We assumed Rring = 0.1 M in all models.
5.4 Observational implications: feasibility
How accurately can we measure the spin value when applying our method to the actual X-ray observational data? In subsection 4.3, we have demonstrated that we can estimate the spin value by measuring A. In this subsection, we evaluate the accuracy of the spin measurement by performing a Monte Carlo simulation for the light curve of the gas ring.
Let us first examine the case of observing Cyg X-1. The time resolution of the RXTE is 1 ms (Feng et al. 1999; Liu & Li 2004; Wu et al. 2007). This timescale corresponds to 0.07 tvar for a black hole mass of M = 14 M⊙ (Orosz et al. 2011), where tvar is the timescale of flux variation [see equation (27)]. Hereafter, we thus assign a constant time bin, Δt = 0.07 tvar. Suppose that we observe Cyg X-1 with the RXTE satellite. According to Feng, Li, and Chen (1999), however, the number of photons that are received during the time bin of 0.07 tvar is only 2 [counts keV−1] even at the peak. We thus give up using the RXTE data and calculate the cases of observations with future satellites, such as Athena (or LOFT). Since the effective area of these missions is about 10 (100) times as large as that of the RXTE, the average count rate around the peak is Nmax = 20 (200) [counts/(0.07tvar)/keV].
The actual procedures of evaluating the spin parameter ranges (aest) are as follows:
We first choose one value of the spin parameter (atrue) and, assuming the photon number at the flux maximum to be Nmax as given above, we calculate the expected (averaged) number of photons [N(t)] received per each time bin with a length of 0.07tvar, noting that N(t) ∝ F(t).
On the averaged photon number profile [N(t)] we superpose random errors [δNi(t)] (with i = 1, 2, …), assuming that the photon statistics obey a Poisson distribution [with a standard deviation of |$\sigma _N= \sqrt{N(t)}$|]. Figure 14 give one such example.
We superpose 500 such shot profiles, Ntot(t) ≡ ∑i[N(t) + δNi(t)].
We then normalize the time sequence of the number counts [Ntot(t)] of each run by their maximum value, and call it the redefined flux distribution, |$\tilde{F}(t)$|.
We calculate A by inserting |$\tilde{F}(t)$| into F(t) in equations (16)–(18) and estimate the spin parameter (aest) by using figure 10.
We repeat the same process 104 times, plot the distribution of the estimated spin, aest, and evaluate its 1 σ confidence range.
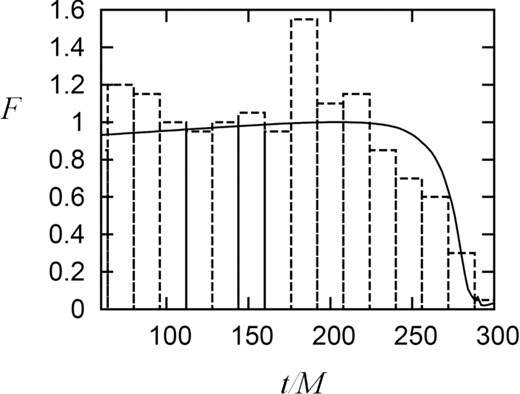
An example of the time profile of the observational flux, in which random errors are superposed by assuming Poisson statistics. The solid curve represents F(t), the result of figure 7, while the vertical bars represent one example of N(t) + δNi(t). Here, we postulate the case that we observe Cyg X-1 with Athena, and the model parameters are (atrue/M, i ) = (0, 85°). The time interval corresponds to 0.07tvar ≃ 14 M.
We summarize the results in table 4 for observations with each of Athena and LOFT, respectively. In the case of Athena (or LOFT), we can determine the spin value with following error, δa/M = 0.06–0.39 (0.03–0.14).
| . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.77–0.83 | 0.68–0.85 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.31–0.46 | 0.28–0.50 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.15–0.11 | −0.15–0.10 | −0.10–0.02 | −0.01–0.09 | |
| −0.4 | −0.54–−0.22 | −0.51–−0.31 | −0.48–−0.35 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.61 | −1.0−0.70 | −0.87–−0.74 | −0.88–−0.74 |
| . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.77–0.83 | 0.68–0.85 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.31–0.46 | 0.28–0.50 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.15–0.11 | −0.15–0.10 | −0.10–0.02 | −0.01–0.09 | |
| −0.4 | −0.54–−0.22 | −0.51–−0.31 | −0.48–−0.35 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.61 | −1.0−0.70 | −0.87–−0.74 | −0.88–−0.74 |
| . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.77–0.83 | 0.68–0.85 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.31–0.46 | 0.28–0.50 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.15–0.11 | −0.15–0.10 | −0.10–0.02 | −0.01–0.09 | |
| −0.4 | −0.54–−0.22 | −0.51–−0.31 | −0.48–−0.35 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.61 | −1.0−0.70 | −0.87–−0.74 | −0.88–−0.74 |
| . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.77–0.83 | 0.68–0.85 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.31–0.46 | 0.28–0.50 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.15–0.11 | −0.15–0.10 | −0.10–0.02 | −0.01–0.09 | |
| −0.4 | −0.54–−0.22 | −0.51–−0.31 | −0.48–−0.35 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.61 | −1.0−0.70 | −0.87–−0.74 | −0.88–−0.74 |
In a similar analysis to the case of Cyg X-1, we estimate the accuracy of spin in the case of MCG −6–30–15. The time resolution of RXTE is 102 [s] = 0.1 tvar, where we postulate the mass is 106 M⊙ (Lee et al. 2000; Reynolds 2000). Then we set to Δt = 0.1tvar. The averaged photon count rate of a one-shot peak is 100 [counts/(0.1 tvar)/keV]. Further, we set the number of superposed shots to 10 [shot], since the time interval between start and end time of the observation, 105 s, is about 10 times as large as the time duration of the shots (Lee et al. 2000; Reynolds 2000). In addition, since the effective area of Athena (or LOFT) is about 10 (100) times as large as that of the RXTE, the average count rate around the peak is Nmax = 103 (104) [counts/(0.1tvar)/keV].
The results for MCG −6–30–15 are summarized in table 5. By using Athena (or LOFT), we can estimate spin value with the error δa/M = 0.07–0.45 (δa/M = 0.03–0.14), while in the case of RXTE, we can scarcely detect the spin value with the rough accuracy δa/M = 0.13–0.78.
| . | RXTE . | . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.74–0.87 | 0.77–0.83 | 0.68–0.85 | 0.73–0.80 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.21–0.58 | 0.32–0.46 | 0.28–0.50 | 0.34–0.49 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.30–0.33 | −0.13–0.10 | −0.16–0.10 | −0.15–0.13 | −0.1–0.02 | −0.01–0.09 | |
| −0.4 | −0.70–0.08 | −0.53–−0.16 | −0.55–−0.22 | −0.51–−0.31 | −0.48–−0.34 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.25 | −1–−0.56 | −1.0–−0.55 | −1.0–−0.70 | −0.88–−0.74 | −0.88–−0.74 |
| . | RXTE . | . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.74–0.87 | 0.77–0.83 | 0.68–0.85 | 0.73–0.80 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.21–0.58 | 0.32–0.46 | 0.28–0.50 | 0.34–0.49 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.30–0.33 | −0.13–0.10 | −0.16–0.10 | −0.15–0.13 | −0.1–0.02 | −0.01–0.09 | |
| −0.4 | −0.70–0.08 | −0.53–−0.16 | −0.55–−0.22 | −0.51–−0.31 | −0.48–−0.34 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.25 | −1–−0.56 | −1.0–−0.55 | −1.0–−0.70 | −0.88–−0.74 | −0.88–−0.74 |
| . | RXTE . | . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.74–0.87 | 0.77–0.83 | 0.68–0.85 | 0.73–0.80 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.21–0.58 | 0.32–0.46 | 0.28–0.50 | 0.34–0.49 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.30–0.33 | −0.13–0.10 | −0.16–0.10 | −0.15–0.13 | −0.1–0.02 | −0.01–0.09 | |
| −0.4 | −0.70–0.08 | −0.53–−0.16 | −0.55–−0.22 | −0.51–−0.31 | −0.48–−0.34 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.25 | −1–−0.56 | −1.0–−0.55 | −1.0–−0.70 | −0.88–−0.74 | −0.88–−0.74 |
| . | RXTE . | . | Athena . | . | LOFT . | . | . |
|---|---|---|---|---|---|---|---|
| a true/M . | a est for i = 85° . | i = 40° . | i = 85° . | i = 40° . | i = 85° . | i = 40° . | . |
| 0.8 | 0.74–0.87 | 0.77–0.83 | 0.68–0.85 | 0.73–0.80 | 0.78– 0.81 | 0.79–0.85 | |
| 0.4 | 0.21–0.58 | 0.32–0.46 | 0.28–0.50 | 0.34–0.49 | 0.35–0.40 | 0.38–0.50 | |
| 0 | −0.30–0.33 | −0.13–0.10 | −0.16–0.10 | −0.15–0.13 | −0.1–0.02 | −0.01–0.09 | |
| −0.4 | −0.70–0.08 | −0.53–−0.16 | −0.55–−0.22 | −0.51–−0.31 | −0.48–−0.34 | −0.49–−0.35 | |
| −0.8 | −1.0–−0.25 | −1–−0.56 | −1.0–−0.55 | −1.0–−0.70 | −0.88–−0.74 | −0.88–−0.74 |
5.5 Remaining issues
We have so far argued that the proposed method should in principle work; however, we recognize a number of essential issues to be considered before applying this method to actual observational data. We first evaluate what resolutions are necessary for spin determination.
The first issue is time resolution. As we indicated by equation (27), the time resolution required by the ring model is less than 10(M/10M⊙) ms. This value itself is attainable but we need good photon statistics, which is another concern. Note that this timescale is much longer than the dynamical timescale (or the period of orbital motion), which is of the order of less than 1 ms. This is because we are considering gas falling while keeping a finite angular momentum.
The next issue is energy resolution. In order to estimate i from the C-value within an error of 20°, the required energy resolution is 0.1 × Eline, from figure 10, where Eline is the energy of the fluorescent Fe Kα line in the inertial frame of the emitting gas.
Relationship between the estimated and true spin for a given error in mass.
| Mass error . | True spin . | Estimated spin . |
|---|---|---|
| |δM|/M . | a true/M . | a est/M . |
| 0.1 | 0.8 | 0.74–0.85 |
| 0.4 | 0.30–0.49 | |
| 0 | −0.17–0.12 | |
| −0.4 | −0.55–−0.23 | |
| −0.8 | −1.0–−0.62 | |
| 0.2 | 0.8 | 0.69–0.92 |
| 0.4 | 0.21–0.60 | |
| 0 | −0.31–0.28 | |
| −0.4 | −0.68–−0.021 | |
| −0.8 | −1.0–−0.40 |
| Mass error . | True spin . | Estimated spin . |
|---|---|---|
| |δM|/M . | a true/M . | a est/M . |
| 0.1 | 0.8 | 0.74–0.85 |
| 0.4 | 0.30–0.49 | |
| 0 | −0.17–0.12 | |
| −0.4 | −0.55–−0.23 | |
| −0.8 | −1.0–−0.62 | |
| 0.2 | 0.8 | 0.69–0.92 |
| 0.4 | 0.21–0.60 | |
| 0 | −0.31–0.28 | |
| −0.4 | −0.68–−0.021 | |
| −0.8 | −1.0–−0.40 |
Relationship between the estimated and true spin for a given error in mass.
| Mass error . | True spin . | Estimated spin . |
|---|---|---|
| |δM|/M . | a true/M . | a est/M . |
| 0.1 | 0.8 | 0.74–0.85 |
| 0.4 | 0.30–0.49 | |
| 0 | −0.17–0.12 | |
| −0.4 | −0.55–−0.23 | |
| −0.8 | −1.0–−0.62 | |
| 0.2 | 0.8 | 0.69–0.92 |
| 0.4 | 0.21–0.60 | |
| 0 | −0.31–0.28 | |
| −0.4 | −0.68–−0.021 | |
| −0.8 | −1.0–−0.40 |
| Mass error . | True spin . | Estimated spin . |
|---|---|---|
| |δM|/M . | a true/M . | a est/M . |
| 0.1 | 0.8 | 0.74–0.85 |
| 0.4 | 0.30–0.49 | |
| 0 | −0.17–0.12 | |
| −0.4 | −0.55–−0.23 | |
| −0.8 | −1.0–−0.62 | |
| 0.2 | 0.8 | 0.69–0.92 |
| 0.4 | 0.21–0.60 | |
| 0 | −0.31–0.28 | |
| −0.4 | −0.68–−0.021 | |
| −0.8 | −1.0–−0.40 |
Finally, we give a summary of future issues.
We considered a particular shape of infalling gas cloud and assumed no changes of the shape with time. That is, a distortion of the ring shape in a deep potential well was not considered. We need to relax this assumption and improve the method by using, e.g., MHD simulation data.
The temperature and the emissivity (j0) of the ring is kept constant. This may not be realistic, since heating by magnetic energy release and/or radiative cooling should be effective.
We assumed monochromatic radiation from the gas clouds for the sake of simplicity. This is a critical assumption, on which the proposed method is constructed, but its physical reason is not yet clear. We need to expand our methodology so as to incorporate more general cases of continuum radiation, etc.
Actual correspondence with real observational data is under consideration. It will be important to identify which data really represent an infall of a gas ring in connection with real observational data and MHD simulation data.
We thank the referee for many constructive comments. We are also grateful to R. Takahashi for the simulation support.
References



![Panels (a1) and (b1) [or panels (a2) and (b2)] are the same as figure 11a (or figure 10) but for different values of the ring thickness: Rring = 0.2 M [(a1) and (a2)] and 0.3 M [(b1) and (b2)], respectively.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/67/6/10.1093_pasj_psv074/3/m_pasj_67_6_106_f4.jpeg?Expires=1749904891&Signature=HDsgeK4iZ1TN-4BqSupRqCF2pVYHSi~0QfO~EYYbyZ-sSHC03QsDIQ8TBgLQ9xk5gl7T9DPtUmOYm6LbGglOBRH~wc3rvXqUQaMvLqcskjWvx5XTI4RE1WfU3wi4vT1te1EF7MHQw2mI8M4ga~NhPGofryWc1yhbeuvI0vlIQmwIZohU0TT0LQ0Qv3gbsm1lO4SGKgzBYMzdEWFj3Wwf1Gyli078Sv4h8~MntJnrGZcDXCSD4BHMVkzsgyHCZiBfZNR-1qz1meGcb7ocdTKubbWNYwQv4VczwKNJGL1wxGYTC66h1pkeN71BvaAd5-5fsYIzPonlM9BaOr9yLiPBNg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
