-
PDF
- Split View
-
Views
-
Cite
Cite
Hiroshi Imai, Nobuyuki Sakai, Hiroyuki Nakanishi, Hirofumi Sakanoue, Mareki Honma, Takeshi Miyaji, Annual Parallax of the K-Type Star System IRAS 22480+6002 Measured with VERA, Publications of the Astronomical Society of Japan, Volume 64, Issue 6, 25 December 2012, 142, https://doi.org/10.1093/pasj/64.6.142
Close - Share Icon Share
Abstract
We present astrometric VLBI observations of H|$_2$| O masers associated with IRAS 22480|$+$| 6002 (|$=$| IRC|$+$| 60370, hereafter I22480) with the VLBI Exploration of Radio Astrometry (VERA). The stellar type of I22480 looks unusual in stellar maser sources, and has been debated since the 1970's. We successfully determined that an annual parallax of a group of H|$_2$| O maser spots is |$\pi$| |$=$| 0.400 |$\pm$| 0.025 mas, corresponding to a distance to I22480 of |$D$| |$=$| 2.50|$^{+0.17}_{-0.15}$| kpc. This suggests that an estimated bolometric luminosity of I22480 should be revised to 35000 |$L_{\odot}$| , preferring a K-type supergiant to an RV Tau-type variable star, previously suggested. Although its spectral type is unusual in stellar maser sources, internal motions of H|$_2$| O maser features suggest that the H|$_2$| O masers are associated with the circumstellar envelope of this star. We derived a secular proper motion of I22480, (|$\mu_{\alpha}$| , |$\mu_{\delta}$| ) |$=$| (|$-$| 2.58 |$\pm$| 0.33, |$-$| 1.91 |$\pm$| 0.17) [mas yr|$^{-1}$| ], from a possible stellar motion relative to the maser feature motion. The derived motion of I22480 in the Milky Way has a deviation of |$\sim-$| 30 km s|$^{-1}$| in the Galactic azimuthal direction from the circular motion, estimated from a galactocentric distance to I22480 and an assumption of a flat Galactic rotation curve. This peculiar motion is still comparable to those typically seen in H|$_2$| O maser sources located in the Perseus Arm. Taking into account its peculiar motion and proximity to the Galactic midplane (z |$\simeq$| 60 pc), I22480 may be a member of the Galactic thin disk.
1. Introduction
H|$_2$| O maser emission is observed in circumstellar envelopes of evolved stars, such as Mira variables, OH/IR stars, and red supergiants, which exhibit energetic stellar mass loss at a rate of |$\dot{M}$| |$\geq$| 10|$^{-7}$| |$M_{\odot}$| yr|$^{-1}$| (Elitzur 1992). Most of these stars with H|$_2$| O (and SiO) maser emission have the spectral type M, except for central stars of pre-planetary and planetary nebulae, whose circumstellar envelopes are destroyed (e.g., Miranda et al. 2001), or stars whose surfaces are still too hot, but that will become M-type stars.
IRAS 22480|$+$| 6002 (|$=$| AFGL 2968, IRC|$+$| 60370, hereafter abbreviated as I22480) has been classified as a K-type supergiant (Humphreys & Ney 1974, Fewley 1977). Although this star has a |$V$| magnitude of |$\sim$| 8.3 (Tycho Input Catalogue), it has not been reported as a variable star. The detection of H|$_2$| O and SiO masers was surprising for the above-mentioned reason (Han et al. 1998, Nyman et al. 1998). However, Winfrey et al. (1994) newly classified spectral type of I22480 as M01. CO emission was detected toward I22480, indicating that energetic mass loss still occurs or has already occurred. The systemic stellar velocity and the mass-loss flow velocity of I22480 are estimated to be |$V_{{\rm LSR}}$| |$=$| |$-$| 49.3 km s|$^{-1}$| and 26.4 km s|$^{-1}$| , respectively (Groenewegen et al. 1999), which are consistent with those estimated from the spatio-kinematics of H|$_2$| O masers in I22480 (Imai et al. 2008). The Two-Micron Sky Survey (2MASS) image shows a secondary star that is located only |$\sim$| 12 east of I22480, but this B5II star may have no physical association with the western K-type star. The distance to I22480 was estimated to be 5.0 kpc based on the kinematic distance method. This gives the K-type star an extremely high luminosity of |$L_{\ast}$| |$=$| 140000 |$L_{\odot}$| (Groenewegen et al. 1999). On the contrary, Imai et al. (2008) obtained a distance of |$\sim$| 1 kpc based on the basis of the statistical parallax method applied to the H|$_2$| O masers in I22480. If it is true, the stellar luminosity should be down to |$L_{\ast}$| |$=$| 5600 |$L_{\odot}$| , favoring an RV Tau-type variable star, or a population II low-mass post-AGB star.
In this paper, we report on new VLBI astrometric observations of H|$_2$| O masers associated with I22480 with the VLBI Exploration of Radio Astrometry (VERA), which yielded successful detection of the annual parallax of I22480.
2. Observations and Data Reduction
VERA observations of the I22480 H|$_2$| O (|$J_{\rm K_{-}K_{+}}$| |$=$| 6|$_{12}$| –5|$_{23}$| , 22.235080 GHz) masers were carried out at 16 epochs during the period from 2009 December to 2011 December. Table 1 gives the log of observations and their resulting performances. At each epoch, the observation was made for 8 hr in total. I22480 was scanned for |$\sim$| 4.5 hr together with the position-reference source, J225425.3|$+$| 620939 (hereafter abbreviated as J2254), simultaneously using the VERA's dual-beam system. I22480 and J2254 are separated by 1|$.^{\!\!\!\circ}$| 94. 3C 454.3 was also scanned in both of the dual beams for 5 min per beam every |$\sim$| 40 min for calibration of group-delay residuals. The received signals were digitized into four quantization levels, then divided into 16 base band channels (BBCs) with a bandwidth of 16 MHz each. The signals in one of the BBCs were obtained from scans on I22480 at the frequency band including the H|$_2$| O maser emission, while those in the other BBCs from scans on J2254 with a total frequency-band range of 480 MHz. The BBC outputs were recorded at a rate of 1024 Mbits s|$^{-1}$| . Data were analyzed using Mitaka FX correlator. The accumulation period of the correlation was set at 1 s. The correlation outputs consisted of 512 spectral channels for the H|$_2$| O maser and 32 for the continuum emission. The former corresponds to a velocity spacing of 0.42 km s|$^{-1}$| , which is narrow enough to resolve an H|$_2$| O maser feature (corresponding to a maser gas clump) consisting of two or more spectral channel components, called maser spots.
| Observation . | VERA . | Noise† . | Beam‡ . | |$N_{{\rm s}}$| § . | Astrometry . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Code . | Epoch . | Telescopes* . | [mas] . | . | . | Valid?‖ . | |$V_{\rm ref}$| ♯ . | |$F_{\rm ref}$| ** . | |$I_{\rm J2254}$| †† . | Note . |
| . | . | . | . | . | . | . | [km s|$^{-1}$|] . | [Jy] . | [mJy|$/$|b] . | . |
| r09346a | 2009 December 12 | MROS | 30 | 1.18 |$\times$| 0.93, |$-$| 50.|$^{\!\!\!\circ}$| 5 | 19 | Y | |$-$| 53.8 | 20 | 10.3 | |
| r10048b | 2010 February 18 | MROS | 30 | 1.20 |$\times$| 0.86, |$-$| 45.|$^{\!\!\!\circ}$| 8 | 14 | Y | |$-$| 53.9 | 24 | 8.3 | |
| r10139a | 2010 May 19 | MROS | 107 | 1.22 |$\times$| 0.80, |$-$| 28.|$^{\!\!\!\circ}$| 9 | 9 | Y | |$-$| 53.9 | 36 | 13.6 | |
| r10232a | 2010 August 10 | MROS | 80 | 1.19 |$\times$| 0.93, |$-$| 31.|$^{\!\!\!\circ}$| 6 | 9 | Y | |$-$| 53.9 | 24 | 13.5 | |
| r10316b | 2010 November 12 | MROS | 64 | 1.51 |$\times$| 0.91, |$-$| 45.|$^{\!\!\!\circ}$| 9 | 13 | Y | |$-$| 53.9 | 22 | 17.9 | |
| r10345a | 2010 December 11 | MROS | 44 | 1.23 |$\times$| 0.89, |$-$| 44.|$^{\!\!\!\circ}$| 5 | 17 | Y | |$-$| 53.8 | 19 | 16.1 | |
| r11060c | 2011 March 2 | MROS | 48 | 1.42 |$\times$| 0.86, |$-$| 46.|$^{\!\!\!\circ}$| 6 | 20 | Y | |$-$| 53.9 | 12 | 17.5 | |
| r11113b | 2011 April 23 | MROS | 46 | 1.38 |$\times$| 0.92, |$-$| 28.|$^{\!\!\!\circ}$| 1 | 7 | Y | |$-$| 54.1 | 6 | 16.0 | |
| r11215a | 2011 August 3 | (M)ROS | -- | -- | N | -- | -- | Bad recording in Mizusawa. | ||
| r11249b | 2011 September 6 | MROS | 80 | 1.42 |$\times$| 0.93, |$-$| 62.|$^{\!\!\!\circ}$| 4 | 7 | Y | |$-$| 51.0 | 6 | 13.7 | |
| r11344a | 2011 December 10 | MROS | 47 | 1.23 |$\times$| 1.05, |$-$| 55.|$^{\!\!\!\circ}$| 1 | 11 | Y | |$-$| 51.4 | 7 | 13.7 | |
| Observation . | VERA . | Noise† . | Beam‡ . | |$N_{{\rm s}}$| § . | Astrometry . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Code . | Epoch . | Telescopes* . | [mas] . | . | . | Valid?‖ . | |$V_{\rm ref}$| ♯ . | |$F_{\rm ref}$| ** . | |$I_{\rm J2254}$| †† . | Note . |
| . | . | . | . | . | . | . | [km s|$^{-1}$|] . | [Jy] . | [mJy|$/$|b] . | . |
| r09346a | 2009 December 12 | MROS | 30 | 1.18 |$\times$| 0.93, |$-$| 50.|$^{\!\!\!\circ}$| 5 | 19 | Y | |$-$| 53.8 | 20 | 10.3 | |
| r10048b | 2010 February 18 | MROS | 30 | 1.20 |$\times$| 0.86, |$-$| 45.|$^{\!\!\!\circ}$| 8 | 14 | Y | |$-$| 53.9 | 24 | 8.3 | |
| r10139a | 2010 May 19 | MROS | 107 | 1.22 |$\times$| 0.80, |$-$| 28.|$^{\!\!\!\circ}$| 9 | 9 | Y | |$-$| 53.9 | 36 | 13.6 | |
| r10232a | 2010 August 10 | MROS | 80 | 1.19 |$\times$| 0.93, |$-$| 31.|$^{\!\!\!\circ}$| 6 | 9 | Y | |$-$| 53.9 | 24 | 13.5 | |
| r10316b | 2010 November 12 | MROS | 64 | 1.51 |$\times$| 0.91, |$-$| 45.|$^{\!\!\!\circ}$| 9 | 13 | Y | |$-$| 53.9 | 22 | 17.9 | |
| r10345a | 2010 December 11 | MROS | 44 | 1.23 |$\times$| 0.89, |$-$| 44.|$^{\!\!\!\circ}$| 5 | 17 | Y | |$-$| 53.8 | 19 | 16.1 | |
| r11060c | 2011 March 2 | MROS | 48 | 1.42 |$\times$| 0.86, |$-$| 46.|$^{\!\!\!\circ}$| 6 | 20 | Y | |$-$| 53.9 | 12 | 17.5 | |
| r11113b | 2011 April 23 | MROS | 46 | 1.38 |$\times$| 0.92, |$-$| 28.|$^{\!\!\!\circ}$| 1 | 7 | Y | |$-$| 54.1 | 6 | 16.0 | |
| r11215a | 2011 August 3 | (M)ROS | -- | -- | N | -- | -- | Bad recording in Mizusawa. | ||
| r11249b | 2011 September 6 | MROS | 80 | 1.42 |$\times$| 0.93, |$-$| 62.|$^{\!\!\!\circ}$| 4 | 7 | Y | |$-$| 51.0 | 6 | 13.7 | |
| r11344a | 2011 December 10 | MROS | 47 | 1.23 |$\times$| 1.05, |$-$| 55.|$^{\!\!\!\circ}$| 1 | 11 | Y | |$-$| 51.4 | 7 | 13.7 | |
Telescopes whose data were valid for phase-referencing maser imaging. M, Mizusawa; R, Iriki; O, Ogasawara; S, Ishigakijima. The station in parentheses had its problems during the period of observation and affected the annual-parallax measurement.
Noise means rms one of the emission-free spectral channel image in units of mJy beam|$^{-1}$|.
Synthesized beam size resulting from natural weighted visibilities, i.e., major- and minor-axis lengths and position angle.
Number of identified maser features.
Y and N are valid and invalid data points for annual-parallax measurement, respectively.
LSR velocity of the spectral channel including the maser spot used for fringe-fitting, self-calibration, and the inverse phase referencing (see the main text).
Flux density of the maser spot used for fringe-fitting, self-calibration, and the inverse phase referencing.
Peak intensity of J225425.3|$+$| 620939 in units of mJy beam|$^{-1}$| on the phase-referenced image.
| Observation . | VERA . | Noise† . | Beam‡ . | |$N_{{\rm s}}$| § . | Astrometry . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Code . | Epoch . | Telescopes* . | [mas] . | . | . | Valid?‖ . | |$V_{\rm ref}$| ♯ . | |$F_{\rm ref}$| ** . | |$I_{\rm J2254}$| †† . | Note . |
| . | . | . | . | . | . | . | [km s|$^{-1}$|] . | [Jy] . | [mJy|$/$|b] . | . |
| r09346a | 2009 December 12 | MROS | 30 | 1.18 |$\times$| 0.93, |$-$| 50.|$^{\!\!\!\circ}$| 5 | 19 | Y | |$-$| 53.8 | 20 | 10.3 | |
| r10048b | 2010 February 18 | MROS | 30 | 1.20 |$\times$| 0.86, |$-$| 45.|$^{\!\!\!\circ}$| 8 | 14 | Y | |$-$| 53.9 | 24 | 8.3 | |
| r10139a | 2010 May 19 | MROS | 107 | 1.22 |$\times$| 0.80, |$-$| 28.|$^{\!\!\!\circ}$| 9 | 9 | Y | |$-$| 53.9 | 36 | 13.6 | |
| r10232a | 2010 August 10 | MROS | 80 | 1.19 |$\times$| 0.93, |$-$| 31.|$^{\!\!\!\circ}$| 6 | 9 | Y | |$-$| 53.9 | 24 | 13.5 | |
| r10316b | 2010 November 12 | MROS | 64 | 1.51 |$\times$| 0.91, |$-$| 45.|$^{\!\!\!\circ}$| 9 | 13 | Y | |$-$| 53.9 | 22 | 17.9 | |
| r10345a | 2010 December 11 | MROS | 44 | 1.23 |$\times$| 0.89, |$-$| 44.|$^{\!\!\!\circ}$| 5 | 17 | Y | |$-$| 53.8 | 19 | 16.1 | |
| r11060c | 2011 March 2 | MROS | 48 | 1.42 |$\times$| 0.86, |$-$| 46.|$^{\!\!\!\circ}$| 6 | 20 | Y | |$-$| 53.9 | 12 | 17.5 | |
| r11113b | 2011 April 23 | MROS | 46 | 1.38 |$\times$| 0.92, |$-$| 28.|$^{\!\!\!\circ}$| 1 | 7 | Y | |$-$| 54.1 | 6 | 16.0 | |
| r11215a | 2011 August 3 | (M)ROS | -- | -- | N | -- | -- | Bad recording in Mizusawa. | ||
| r11249b | 2011 September 6 | MROS | 80 | 1.42 |$\times$| 0.93, |$-$| 62.|$^{\!\!\!\circ}$| 4 | 7 | Y | |$-$| 51.0 | 6 | 13.7 | |
| r11344a | 2011 December 10 | MROS | 47 | 1.23 |$\times$| 1.05, |$-$| 55.|$^{\!\!\!\circ}$| 1 | 11 | Y | |$-$| 51.4 | 7 | 13.7 | |
| Observation . | VERA . | Noise† . | Beam‡ . | |$N_{{\rm s}}$| § . | Astrometry . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Code . | Epoch . | Telescopes* . | [mas] . | . | . | Valid?‖ . | |$V_{\rm ref}$| ♯ . | |$F_{\rm ref}$| ** . | |$I_{\rm J2254}$| †† . | Note . |
| . | . | . | . | . | . | . | [km s|$^{-1}$|] . | [Jy] . | [mJy|$/$|b] . | . |
| r09346a | 2009 December 12 | MROS | 30 | 1.18 |$\times$| 0.93, |$-$| 50.|$^{\!\!\!\circ}$| 5 | 19 | Y | |$-$| 53.8 | 20 | 10.3 | |
| r10048b | 2010 February 18 | MROS | 30 | 1.20 |$\times$| 0.86, |$-$| 45.|$^{\!\!\!\circ}$| 8 | 14 | Y | |$-$| 53.9 | 24 | 8.3 | |
| r10139a | 2010 May 19 | MROS | 107 | 1.22 |$\times$| 0.80, |$-$| 28.|$^{\!\!\!\circ}$| 9 | 9 | Y | |$-$| 53.9 | 36 | 13.6 | |
| r10232a | 2010 August 10 | MROS | 80 | 1.19 |$\times$| 0.93, |$-$| 31.|$^{\!\!\!\circ}$| 6 | 9 | Y | |$-$| 53.9 | 24 | 13.5 | |
| r10316b | 2010 November 12 | MROS | 64 | 1.51 |$\times$| 0.91, |$-$| 45.|$^{\!\!\!\circ}$| 9 | 13 | Y | |$-$| 53.9 | 22 | 17.9 | |
| r10345a | 2010 December 11 | MROS | 44 | 1.23 |$\times$| 0.89, |$-$| 44.|$^{\!\!\!\circ}$| 5 | 17 | Y | |$-$| 53.8 | 19 | 16.1 | |
| r11060c | 2011 March 2 | MROS | 48 | 1.42 |$\times$| 0.86, |$-$| 46.|$^{\!\!\!\circ}$| 6 | 20 | Y | |$-$| 53.9 | 12 | 17.5 | |
| r11113b | 2011 April 23 | MROS | 46 | 1.38 |$\times$| 0.92, |$-$| 28.|$^{\!\!\!\circ}$| 1 | 7 | Y | |$-$| 54.1 | 6 | 16.0 | |
| r11215a | 2011 August 3 | (M)ROS | -- | -- | N | -- | -- | Bad recording in Mizusawa. | ||
| r11249b | 2011 September 6 | MROS | 80 | 1.42 |$\times$| 0.93, |$-$| 62.|$^{\!\!\!\circ}$| 4 | 7 | Y | |$-$| 51.0 | 6 | 13.7 | |
| r11344a | 2011 December 10 | MROS | 47 | 1.23 |$\times$| 1.05, |$-$| 55.|$^{\!\!\!\circ}$| 1 | 11 | Y | |$-$| 51.4 | 7 | 13.7 | |
Telescopes whose data were valid for phase-referencing maser imaging. M, Mizusawa; R, Iriki; O, Ogasawara; S, Ishigakijima. The station in parentheses had its problems during the period of observation and affected the annual-parallax measurement.
Noise means rms one of the emission-free spectral channel image in units of mJy beam|$^{-1}$|.
Synthesized beam size resulting from natural weighted visibilities, i.e., major- and minor-axis lengths and position angle.
Number of identified maser features.
Y and N are valid and invalid data points for annual-parallax measurement, respectively.
LSR velocity of the spectral channel including the maser spot used for fringe-fitting, self-calibration, and the inverse phase referencing (see the main text).
Flux density of the maser spot used for fringe-fitting, self-calibration, and the inverse phase referencing.
Peak intensity of J225425.3|$+$| 620939 in units of mJy beam|$^{-1}$| on the phase-referenced image.
An analysis of data was mainly conducted using the National Radio Astronomy Observatory (NRAO) Astronomical Image Processing System (AIPS) package. For astrometry, we need special procedures, described in the following (see also, e.g., Honma et al. 2007, Imai et al. 2007). Firstly, delay-tracking was again performed on the correlated data using better delay-tracking models calculated by an original software equivalent to the CALC9 package developed by the Goddard Space Flight Center/NASA VLBI group. Throughout the whole data analysis, we adopted the following coordinates of the two delay-tracking centers: |$\alpha_{\rm J2000.0}$| |$=$| 22|$^{\rm h}$| 49|$^{\rm m}$| 58|$^{\rm s}\!\!\!.$| 876, |$\delta_{\rm J2000.0}$| |$=$| |$+$| 60|$^{\circ}$| 17|$'$| 56|$.\!\!\!''$| 65 of I22480; |$\alpha_{\rm J2000.0}$| |$=$| 22|$^{\rm h}$| 54|$^{\rm m}$| 25|$.\!\!\!^{\rm s}$| 293179, |$\delta_{\rm J2000.0}$| |$=$| |$+$| 62|$^{\circ}$| 09|$'$| 38|$.\!\!\!''$| 72393 of J2254. The delay-tracking solution includes delay residual contributions from the atmosphere, which were estimated using global positioning system (GPS) data (Honma et al. 2008). Secondly, the difference in the instrumental delay between two signal paths in the dual-beam system was calibrated using the differential delay, which was measured using artificial noise signals injected into the two receivers during the series of observations (Honma et al. 2008). Because J2254 was too faint (|$\sim$| 12 mJy) to detect in the normal fringe-fitting procedure, this should be detected through inverse phase-referencing to a bright H|$_2$| O maser spot in I22480, as will be mentioned later. Thirdly, fringe-fitting was performed using the data of 3C 454.3, whose solutions of the group delay, rate (fringe frequency), and phase residuals for the clock-parameter calibration were applied to the data calibrations of both I22480 and J2254. Fourthly, fringe-fitting and self-calibration were performed using the brightest H|$_2$| O maser spot in I22480, whose velocity with respect to the local standard of rest (LSR) is given in column 8 of table 1, without solving any group-delay residuals, in a solution interval of 2 min or shorter, whose solutions were applied to the data calibration of both I22480 and J2254. Before applying the second fringe-fitting solutions to the data calibration of J2254, the data of J2254 were averaged into a single spectral channel. The sequence of AIPS data reduction in the inverse phase-referencing part is described in appendix 1 in more detail. Finally, image cubes of the maser source and the image of J2254 were obtained in visibility deconvolution through the CLEAN algorithm in a typical synthesized beam of 1.3 |$\times$| 0.9 in mas. Each maser spot (or velocity component) was automatically identified as a Gaussian brightness component using the AIPS task SAD. The parameters of J2254 as a Gaussian component were obtained using AIPS task JMFIT.
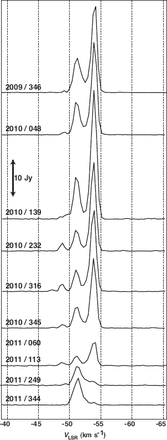
Scalar-averaged cross-power spectra of IRAS 22480|$+$| 6002, which were synthesized with the data obtained from all baselines. For clarity, these spectra are shifted in the vertical direction along with observation epochs. The dates of observation epochs (year / day of the year) are also displayed.
![Distribution of H$_2$O maser features in IRAS 22480$+$6002. The origin of coordinates is set at the maser feature that includes the $-$53.9 km s$^{-1}$ component in the maser feature IRAS 22480$+$6002:I2012-4. Colors of maser feature indicate LSR velocities. An arrow shows the relative proper motion of each maser feature. The root position of an arrow indicates the location of the maser feature at the first epoch when the feature was detected. The length and direction of an arrow indicate the speed and direction of the maser proper motion, respectively. The mean proper motion, ($\dot{X}$ , $\dot{Y}$ ) $=$ (7, $-$ 2) [km s$^{-1}$ ], is subtracted from individual proper motions. A cross indicates the location of the originating point of the outflow or that of the star itself, which is estimated in the model fitting by using the maser kinematical data. The size of the cross indicates its position error.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/64/6/10.1093_pasj_64.6.142/6/m_pasj64-0142-g002.gif?Expires=1750661973&Signature=aZvoRoW6xNgHqF9ib6yoVsGXFwfFqYfQOJ00q~r0CXnB25q-94oxk526eO4i~Mh3Mhgld7sP4IZIIImHWD64k-aD-~bHNQV4i7nrosbFYbwMuFXxY7KzXZJAiCh3YvDW1IyFLRQORv3sFeE8PpueRlmV-6vE4SwNgjSoGAQNZPjUncR2nzP6L1V1EwGY2~1dYEWrqmPitcEg4CV44dwtXxYkKv~KjYiW275hVbWFMDeOnHewYRDClbjT1Nc9IODVNVGBVkkEVULE1SGYRb7QO6udlOw-xwMvvx-zIQXfKkdMS~Fg9aG7sr3srgCFzLULqkSSfanN6c-z2mm~XTdTVQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distribution of H|$_2$|O maser features in IRAS 22480|$+$|6002. The origin of coordinates is set at the maser feature that includes the |$-$|53.9 km s|$^{-1}$| component in the maser feature IRAS 22480|$+$|6002:I2012-4. Colors of maser feature indicate LSR velocities. An arrow shows the relative proper motion of each maser feature. The root position of an arrow indicates the location of the maser feature at the first epoch when the feature was detected. The length and direction of an arrow indicate the speed and direction of the maser proper motion, respectively. The mean proper motion, (|$\dot{X}$| , |$\dot{Y}$| ) |$=$| (7, |$-$| 2) [km s|$^{-1}$| ], is subtracted from individual proper motions. A cross indicates the location of the originating point of the outflow or that of the star itself, which is estimated in the model fitting by using the maser kinematical data. The size of the cross indicates its position error.
3. Results
3.1. The Spatio-Kinematics in H2O O Masers in IRAS 22480+6002
Figure 1 shows the variation in the cross-power spectrum of the I22480 H|$_2$| O masers. The H|$_2$| O masers covered a velocity range of |$-$| 40 km s|$^{-1}$| |$\lt $| |$V_{{\rm LSR}}$| |$\lt $| |$-$| 60 km s|$^{-1}$| ; such a velocity width is typically seen in Mira-type AGB stars (e.g., Takaba et al. 1994). Imai et al. (2008) found five spectral peaks at intervals of 2–3 km s|$^{-1}$| . In the present spectra, only the middle three out of five peaks, |$V_{{\rm LSR}}$| |$\sim$| |$-$| 54, |$-$| 52, and |$-$| 48 km s|$^{-1}$| , were clearly seen. The |$-$| 53.9 km s|$^{-1}$| (or |$-$| 54.1 km s|$^{-1}$| ) component (maser spot) in the |$-$| 54 km s|$^{-1}$| peak was always visible through the observation epochs, and suitable for visibility phase calibration and position reference of the present VERA astrometry. At the latest two epochs when this component weakend, its position was determined relative to the |$-$| 51.0 km s|$^{-1}$| (or |$-$| 51.4 km s|$^{-1}$|) component that was used for the calibration. Although the phase-referencing velocity channel changed at different observing epochs, as shown in table 1, the positions of all maser spots in I22480 as well as that of J2254 were measured with respect to the phase center that was set after fringe-fitting and self-calibration using a specific brighter maser component in the phase-referencing velocity channel (column 8 of table 1).
Parameters of the H|$_2$|O maser features identified by the proper motion toward IRAS 22480|$+$|6002.
| Feature* . | Offset . | Proper motion† . | Radial motion‡ . | Detections at 10 epochs . | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mas) . | (mas yr|$^{-1}$|) . | (km s|$^{-1}$|) . | . | . | . | . | . | . | . | ||||||||
| . | |$\Delta\,\alpha$| . | |$\Delta\,\delta$| . | |$\mu_{x}$| . | |$\sigma \mu_{x}$| . | |$\mu_{y}$| . | |$\sigma \mu_{y}$| . | |$V_{{z}}$| . | |$\Delta{V}_{{z}}$| § . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | 10 . |
| 1 | 29.78 | 4.05 | 2.22 | 0.15 | |$-$| 0.96 | 0.24 | |$-$| 58.42 | 2.11 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 2 | 31.46 | 3.41 | 1.00 | 0.41 | |$-$| 0.20 | 0.37 | |$-$| 55.93 | 2.00 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 3 | |$-$| 1.42 | 3.02 | 0.19 | 0.29 | 0.36 | 0.22 | |$-$| 55.05 | 0.70 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 4 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.05 | |$-$| 54.04 | 2.95 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| |
| 5 | |$-$| 0.42 | 2.56 | |$-$| 0.12 | 0.42 | |$-$| 0.50 | 0.27 | |$-$| 53.36 | 0.21 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 6 | |$-$| 2.21 | |$-$| 2.01 | |$-$| 0.04 | 0.27 | |$-$| 0.27 | 0.16 | |$-$| 53.08 | 0.79 | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 7 | |$-$| 0.79 | 0.13 | |$-$| 0.03 | 0.05 | 0.08 | 0.02 | |$-$| 53.06 | 0.75 | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 8 | 0.28 | |$-$| 0.37 | 0.24 | 1.08 | |$-$| 0.21 | 1.17 | |$-$| 52.94 | 1.48 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 9 | 0.23 | 1.95 | 1.76 | 0.31 | 0.80 | 0.12 | |$-$| 52.10 | 0.98 | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 10 | 0.78 | |$-$| 0.44 | 0.37 | 0.13 | 0.03 | 0.02 | |$-$| 51.68 | 1.69 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 11 | 0.67 | |$-$| 0.58 | |$-$| 0.06 | 0.42 | |$-$| 0.15 | 0.58 | |$-$| 51.20 | 2.53 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 12 | 0.01 | |$-$| 0.73 | 0.31 | 0.08 | 0.00 | 0.06 | |$-$| 51.01 | 1.93 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 13 | 28.40 | 5.45 | 1.24 | 0.27 | 0.83 | 0.22 | |$-$| 50.83 | 0.49 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 14 | 32.28 | 5.20 | 0.92 | 0.23 | |$-$| 0.12 | 0.18 | |$-$| 50.55 | 0.42 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 15 | 29.74 | |$-$| 6.19 | 1.29 | 0.23 | |$-$| 1.36 | 0.26 | |$-$| 49.69 | 0.21 | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 16 | 29.34 | 3.65 | 0.22 | 0.46 | 0.10 | 0.12 | |$-$| 49.57 | 0.84 | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 17 | 30.38 | 6.39 | |$-$| 0.22 | 1.44 | |$-$| 0.12 | 0.56 | |$-$| 49.21 | 1.68 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 18 | 29.48 | 6.21 | 0.96 | 0.13 | 0.38 | 0.06 | |$-$| 49.17 | 2.39 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| |
| 19 | 4.77 | 8.05 | 0.28 | 0.03 | 0.15 | 0.03 | |$-$| 47.00 | 1.12 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\circ$| |
| 20 | 4.86 | 13.43 | |$-$| 0.08 | 1.41 | |$-$| 0.07 | 0.68 | |$-$| 44.94 | 0.84 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 21 | 29.55 | 11.67 | 0.38 | 0.33 | 0.06 | 0.27 | |$-$| 44.51 | 0.31 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 22 | 39.41 | |$-$| 47.15 | 1.12 | 0.33 | |$-$| 0.77 | 0.43 | |$-$| 43.67 | 1.05 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| Feature* . | Offset . | Proper motion† . | Radial motion‡ . | Detections at 10 epochs . | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mas) . | (mas yr|$^{-1}$|) . | (km s|$^{-1}$|) . | . | . | . | . | . | . | . | ||||||||
| . | |$\Delta\,\alpha$| . | |$\Delta\,\delta$| . | |$\mu_{x}$| . | |$\sigma \mu_{x}$| . | |$\mu_{y}$| . | |$\sigma \mu_{y}$| . | |$V_{{z}}$| . | |$\Delta{V}_{{z}}$| § . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | 10 . |
| 1 | 29.78 | 4.05 | 2.22 | 0.15 | |$-$| 0.96 | 0.24 | |$-$| 58.42 | 2.11 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 2 | 31.46 | 3.41 | 1.00 | 0.41 | |$-$| 0.20 | 0.37 | |$-$| 55.93 | 2.00 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 3 | |$-$| 1.42 | 3.02 | 0.19 | 0.29 | 0.36 | 0.22 | |$-$| 55.05 | 0.70 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 4 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.05 | |$-$| 54.04 | 2.95 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| |
| 5 | |$-$| 0.42 | 2.56 | |$-$| 0.12 | 0.42 | |$-$| 0.50 | 0.27 | |$-$| 53.36 | 0.21 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 6 | |$-$| 2.21 | |$-$| 2.01 | |$-$| 0.04 | 0.27 | |$-$| 0.27 | 0.16 | |$-$| 53.08 | 0.79 | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 7 | |$-$| 0.79 | 0.13 | |$-$| 0.03 | 0.05 | 0.08 | 0.02 | |$-$| 53.06 | 0.75 | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 8 | 0.28 | |$-$| 0.37 | 0.24 | 1.08 | |$-$| 0.21 | 1.17 | |$-$| 52.94 | 1.48 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 9 | 0.23 | 1.95 | 1.76 | 0.31 | 0.80 | 0.12 | |$-$| 52.10 | 0.98 | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 10 | 0.78 | |$-$| 0.44 | 0.37 | 0.13 | 0.03 | 0.02 | |$-$| 51.68 | 1.69 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 11 | 0.67 | |$-$| 0.58 | |$-$| 0.06 | 0.42 | |$-$| 0.15 | 0.58 | |$-$| 51.20 | 2.53 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 12 | 0.01 | |$-$| 0.73 | 0.31 | 0.08 | 0.00 | 0.06 | |$-$| 51.01 | 1.93 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 13 | 28.40 | 5.45 | 1.24 | 0.27 | 0.83 | 0.22 | |$-$| 50.83 | 0.49 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 14 | 32.28 | 5.20 | 0.92 | 0.23 | |$-$| 0.12 | 0.18 | |$-$| 50.55 | 0.42 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 15 | 29.74 | |$-$| 6.19 | 1.29 | 0.23 | |$-$| 1.36 | 0.26 | |$-$| 49.69 | 0.21 | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 16 | 29.34 | 3.65 | 0.22 | 0.46 | 0.10 | 0.12 | |$-$| 49.57 | 0.84 | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 17 | 30.38 | 6.39 | |$-$| 0.22 | 1.44 | |$-$| 0.12 | 0.56 | |$-$| 49.21 | 1.68 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 18 | 29.48 | 6.21 | 0.96 | 0.13 | 0.38 | 0.06 | |$-$| 49.17 | 2.39 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| |
| 19 | 4.77 | 8.05 | 0.28 | 0.03 | 0.15 | 0.03 | |$-$| 47.00 | 1.12 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\circ$| |
| 20 | 4.86 | 13.43 | |$-$| 0.08 | 1.41 | |$-$| 0.07 | 0.68 | |$-$| 44.94 | 0.84 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 21 | 29.55 | 11.67 | 0.38 | 0.33 | 0.06 | 0.27 | |$-$| 44.51 | 0.31 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 22 | 39.41 | |$-$| 47.15 | 1.12 | 0.33 | |$-$| 0.77 | 0.43 | |$-$| 43.67 | 1.05 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
H|$_2$| O maser features detected toward IRAS 22480|$+$| 6002. The feature is designated as IRAS 22480|$+$| 6002:I2012-N, where N is the ordinal source number given in this column (I2012 stands for sources found by H. Imai et al. and listed in 2012).
Value of proper motion relative to the position-reference maser feature: IRAS 22480|$+$| 6002:I2012-4.
Value of radial motion relative to the local standard of rest.
Mean full velocity width of a maser feature at half intensity.
Parameters of the H|$_2$|O maser features identified by the proper motion toward IRAS 22480|$+$|6002.
| Feature* . | Offset . | Proper motion† . | Radial motion‡ . | Detections at 10 epochs . | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mas) . | (mas yr|$^{-1}$|) . | (km s|$^{-1}$|) . | . | . | . | . | . | . | . | ||||||||
| . | |$\Delta\,\alpha$| . | |$\Delta\,\delta$| . | |$\mu_{x}$| . | |$\sigma \mu_{x}$| . | |$\mu_{y}$| . | |$\sigma \mu_{y}$| . | |$V_{{z}}$| . | |$\Delta{V}_{{z}}$| § . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | 10 . |
| 1 | 29.78 | 4.05 | 2.22 | 0.15 | |$-$| 0.96 | 0.24 | |$-$| 58.42 | 2.11 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 2 | 31.46 | 3.41 | 1.00 | 0.41 | |$-$| 0.20 | 0.37 | |$-$| 55.93 | 2.00 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 3 | |$-$| 1.42 | 3.02 | 0.19 | 0.29 | 0.36 | 0.22 | |$-$| 55.05 | 0.70 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 4 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.05 | |$-$| 54.04 | 2.95 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| |
| 5 | |$-$| 0.42 | 2.56 | |$-$| 0.12 | 0.42 | |$-$| 0.50 | 0.27 | |$-$| 53.36 | 0.21 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 6 | |$-$| 2.21 | |$-$| 2.01 | |$-$| 0.04 | 0.27 | |$-$| 0.27 | 0.16 | |$-$| 53.08 | 0.79 | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 7 | |$-$| 0.79 | 0.13 | |$-$| 0.03 | 0.05 | 0.08 | 0.02 | |$-$| 53.06 | 0.75 | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 8 | 0.28 | |$-$| 0.37 | 0.24 | 1.08 | |$-$| 0.21 | 1.17 | |$-$| 52.94 | 1.48 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 9 | 0.23 | 1.95 | 1.76 | 0.31 | 0.80 | 0.12 | |$-$| 52.10 | 0.98 | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 10 | 0.78 | |$-$| 0.44 | 0.37 | 0.13 | 0.03 | 0.02 | |$-$| 51.68 | 1.69 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 11 | 0.67 | |$-$| 0.58 | |$-$| 0.06 | 0.42 | |$-$| 0.15 | 0.58 | |$-$| 51.20 | 2.53 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 12 | 0.01 | |$-$| 0.73 | 0.31 | 0.08 | 0.00 | 0.06 | |$-$| 51.01 | 1.93 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 13 | 28.40 | 5.45 | 1.24 | 0.27 | 0.83 | 0.22 | |$-$| 50.83 | 0.49 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 14 | 32.28 | 5.20 | 0.92 | 0.23 | |$-$| 0.12 | 0.18 | |$-$| 50.55 | 0.42 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 15 | 29.74 | |$-$| 6.19 | 1.29 | 0.23 | |$-$| 1.36 | 0.26 | |$-$| 49.69 | 0.21 | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 16 | 29.34 | 3.65 | 0.22 | 0.46 | 0.10 | 0.12 | |$-$| 49.57 | 0.84 | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 17 | 30.38 | 6.39 | |$-$| 0.22 | 1.44 | |$-$| 0.12 | 0.56 | |$-$| 49.21 | 1.68 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 18 | 29.48 | 6.21 | 0.96 | 0.13 | 0.38 | 0.06 | |$-$| 49.17 | 2.39 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| |
| 19 | 4.77 | 8.05 | 0.28 | 0.03 | 0.15 | 0.03 | |$-$| 47.00 | 1.12 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\circ$| |
| 20 | 4.86 | 13.43 | |$-$| 0.08 | 1.41 | |$-$| 0.07 | 0.68 | |$-$| 44.94 | 0.84 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 21 | 29.55 | 11.67 | 0.38 | 0.33 | 0.06 | 0.27 | |$-$| 44.51 | 0.31 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 22 | 39.41 | |$-$| 47.15 | 1.12 | 0.33 | |$-$| 0.77 | 0.43 | |$-$| 43.67 | 1.05 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| Feature* . | Offset . | Proper motion† . | Radial motion‡ . | Detections at 10 epochs . | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mas) . | (mas yr|$^{-1}$|) . | (km s|$^{-1}$|) . | . | . | . | . | . | . | . | ||||||||
| . | |$\Delta\,\alpha$| . | |$\Delta\,\delta$| . | |$\mu_{x}$| . | |$\sigma \mu_{x}$| . | |$\mu_{y}$| . | |$\sigma \mu_{y}$| . | |$V_{{z}}$| . | |$\Delta{V}_{{z}}$| § . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | 10 . |
| 1 | 29.78 | 4.05 | 2.22 | 0.15 | |$-$| 0.96 | 0.24 | |$-$| 58.42 | 2.11 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 2 | 31.46 | 3.41 | 1.00 | 0.41 | |$-$| 0.20 | 0.37 | |$-$| 55.93 | 2.00 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 3 | |$-$| 1.42 | 3.02 | 0.19 | 0.29 | 0.36 | 0.22 | |$-$| 55.05 | 0.70 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 4 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.05 | |$-$| 54.04 | 2.95 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| |
| 5 | |$-$| 0.42 | 2.56 | |$-$| 0.12 | 0.42 | |$-$| 0.50 | 0.27 | |$-$| 53.36 | 0.21 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 6 | |$-$| 2.21 | |$-$| 2.01 | |$-$| 0.04 | 0.27 | |$-$| 0.27 | 0.16 | |$-$| 53.08 | 0.79 | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 7 | |$-$| 0.79 | 0.13 | |$-$| 0.03 | 0.05 | 0.08 | 0.02 | |$-$| 53.06 | 0.75 | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 8 | 0.28 | |$-$| 0.37 | 0.24 | 1.08 | |$-$| 0.21 | 1.17 | |$-$| 52.94 | 1.48 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 9 | 0.23 | 1.95 | 1.76 | 0.31 | 0.80 | 0.12 | |$-$| 52.10 | 0.98 | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 10 | 0.78 | |$-$| 0.44 | 0.37 | 0.13 | 0.03 | 0.02 | |$-$| 51.68 | 1.69 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 11 | 0.67 | |$-$| 0.58 | |$-$| 0.06 | 0.42 | |$-$| 0.15 | 0.58 | |$-$| 51.20 | 2.53 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 12 | 0.01 | |$-$| 0.73 | 0.31 | 0.08 | 0.00 | 0.06 | |$-$| 51.01 | 1.93 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 13 | 28.40 | 5.45 | 1.24 | 0.27 | 0.83 | 0.22 | |$-$| 50.83 | 0.49 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| |
| 14 | 32.28 | 5.20 | 0.92 | 0.23 | |$-$| 0.12 | 0.18 | |$-$| 50.55 | 0.42 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 15 | 29.74 | |$-$| 6.19 | 1.29 | 0.23 | |$-$| 1.36 | 0.26 | |$-$| 49.69 | 0.21 | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 16 | 29.34 | 3.65 | 0.22 | 0.46 | 0.10 | 0.12 | |$-$| 49.57 | 0.84 | |$\circ$| | |$\times$| | |$\times$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
| 17 | 30.38 | 6.39 | |$-$| 0.22 | 1.44 | |$-$| 0.12 | 0.56 | |$-$| 49.21 | 1.68 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| |
| 18 | 29.48 | 6.21 | 0.96 | 0.13 | 0.38 | 0.06 | |$-$| 49.17 | 2.39 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| |
| 19 | 4.77 | 8.05 | 0.28 | 0.03 | 0.15 | 0.03 | |$-$| 47.00 | 1.12 | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\circ$| | |$\times$| | |$\circ$| |
| 20 | 4.86 | 13.43 | |$-$| 0.08 | 1.41 | |$-$| 0.07 | 0.68 | |$-$| 44.94 | 0.84 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 21 | 29.55 | 11.67 | 0.38 | 0.33 | 0.06 | 0.27 | |$-$| 44.51 | 0.31 | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| |
| 22 | 39.41 | |$-$| 47.15 | 1.12 | 0.33 | |$-$| 0.77 | 0.43 | |$-$| 43.67 | 1.05 | |$\circ$| | |$\circ$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| | |$\times$| |
H|$_2$| O maser features detected toward IRAS 22480|$+$| 6002. The feature is designated as IRAS 22480|$+$| 6002:I2012-N, where N is the ordinal source number given in this column (I2012 stands for sources found by H. Imai et al. and listed in 2012).
Value of proper motion relative to the position-reference maser feature: IRAS 22480|$+$| 6002:I2012-4.
Value of radial motion relative to the local standard of rest.
Mean full velocity width of a maser feature at half intensity.
Figure 2 shows the distribution of the H|$_2$| O maser features and their relative proper motions. Table 2 gives the parameters of the maser features whose proper motions were identified. The angular extent of the maser distribution in the present work was up to |$\sim$| 70 mas, and larger than previously reported one (Imai et al. 2008). The difference in extent between the two works is attributed to a new maser feature found on the southeast side of the maser distribution. Two major clusters of maser features were always seen in the east–west direction with a separation of |$\sim$| 35 mas. One can roughly see outflow motions of maser features from a common originating point (the possible position of the central star). This may rule out the previously suggested possibility that the maser feature alignment in the north–south direction is attributed to the interaction of the circumstellar envelope harboring the H|$_2$| O masers with the wind from the eastern star (Imai et al. 2008).
Parameters of the best-fit 3D spatio-kinematical model of the H|$_2$|O masers in IRAS 22480|$+$|6002.
| Parameter . | Value . |
|---|---|
| |$\Delta X_{0}$| [mas]* | 22|$\pm$| 8 |
| |$\Delta Y_{0}$| [mas]* | 9|$\pm$| 6 |
| |$V_{0x}$| [km s|$^{-1}$| ]* | 7|$\pm$| 4 |
| |$V_{0y}$| [km s|$^{-1}$| ]* | 2|$\pm$| 2 |
| |$V_{0{z}}$| [km s|$^{-1}$| ]† | |$-$| 50 |
| |$D$| [kpc]† | 2.5 |
| |$\sqrt{\chi^{2}}$| ‡ | 2.08 |
| Parameter . | Value . |
|---|---|
| |$\Delta X_{0}$| [mas]* | 22|$\pm$| 8 |
| |$\Delta Y_{0}$| [mas]* | 9|$\pm$| 6 |
| |$V_{0x}$| [km s|$^{-1}$| ]* | 7|$\pm$| 4 |
| |$V_{0y}$| [km s|$^{-1}$| ]* | 2|$\pm$| 2 |
| |$V_{0{z}}$| [km s|$^{-1}$| ]† | |$-$| 50 |
| |$D$| [kpc]† | 2.5 |
| |$\sqrt{\chi^{2}}$| ‡ | 2.08 |
Value relative to the maser feature IRAS 22480|$+$| 6002:I2012-4.
Assumed value.
The |$\chi^{2}$|-square value was obtained in the model fitting by the least-squares method.
Parameters of the best-fit 3D spatio-kinematical model of the H|$_2$|O masers in IRAS 22480|$+$|6002.
| Parameter . | Value . |
|---|---|
| |$\Delta X_{0}$| [mas]* | 22|$\pm$| 8 |
| |$\Delta Y_{0}$| [mas]* | 9|$\pm$| 6 |
| |$V_{0x}$| [km s|$^{-1}$| ]* | 7|$\pm$| 4 |
| |$V_{0y}$| [km s|$^{-1}$| ]* | 2|$\pm$| 2 |
| |$V_{0{z}}$| [km s|$^{-1}$| ]† | |$-$| 50 |
| |$D$| [kpc]† | 2.5 |
| |$\sqrt{\chi^{2}}$| ‡ | 2.08 |
| Parameter . | Value . |
|---|---|
| |$\Delta X_{0}$| [mas]* | 22|$\pm$| 8 |
| |$\Delta Y_{0}$| [mas]* | 9|$\pm$| 6 |
| |$V_{0x}$| [km s|$^{-1}$| ]* | 7|$\pm$| 4 |
| |$V_{0y}$| [km s|$^{-1}$| ]* | 2|$\pm$| 2 |
| |$V_{0{z}}$| [km s|$^{-1}$| ]† | |$-$| 50 |
| |$D$| [kpc]† | 2.5 |
| |$\sqrt{\chi^{2}}$| ‡ | 2.08 |
Value relative to the maser feature IRAS 22480|$+$| 6002:I2012-4.
Assumed value.
The |$\chi^{2}$|-square value was obtained in the model fitting by the least-squares method.
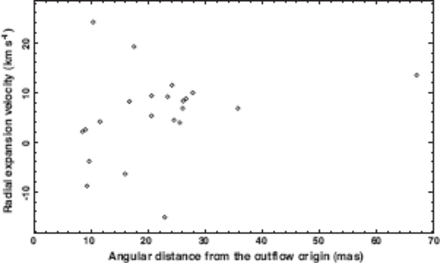
Distribution of the expansion velocities of individual maser features, which were derived from the model fitting.
The systemic LSR velocity of the central star, |$V_{{\rm0}{z}}$| |$=$| |$-$| 50 km s|$^{-1}$| , was adopted in this fitting. Table 3 gives the derived parameters of the fitting. A cross sign in figure 2 indicates the estimated location of the originating point of the outflow. The location appears to be biased toward the eastern maser feature cluster due to relatively high velocity components of its individual maser motions. We do not discuss the location of the central star in this paper. Radial expansion velocities of individual features were calculated after the model fitting [equation (7) of Imai et al. 2011a]. Figure 3 shows the distribution of expansion velocities. The data points seem to be concentrated around an expansion velocity of |$\sim$| 8 km s|$^{-1}$|.
3.2. Annual Parallax and Secular Motion of IRAS 22480+6002
As mentioned in subsection 3.1, at each observation epoch, we measured the position of all H|$_2$| O maser components (spots) in I22480 and J2254's one relative to the position reference where the brightest maser spot in the map was located. Assuming that J2254's position remains as a reference, we eventually measured positions of the maser spots relative to J2254. We estimate the intrinsic position error of J2254 to be |$\sigma_{\rm J2254}$| |$\simeq$| 0.03–0.07 mas, which is statistically determined by the signal-to-noise ratio of detection of J2254, |$\sigma$| |$\simeq$| 0.5 ( |${\theta_{\rm beam}}/{R_{\rm SN}}$| ). Here, |$\theta_{\rm beam}$| |$\simeq$| 1 mas is the synthesized beam size and 8 |$\leq$| |$R_{\rm SN}$| |$\leq$| 20 (for |$S_{\nu}$| |$\simeq$| 8–18 mJy) the range of signal-to-noise ratio (Moran & Reid 1993). The intrinsic position error of the position-reference maser spot is much smaller than that of J2254 because of the much higher signal-to-noise ratio. The systematic error in each astrometric measurement has been discussed in previous papers dealing with VERA astrometry (e.g., Honma et al. 2010 and references therein). One of the major factors in the systematic error is attributed to uncertain zenith delay residuals of VERA stations caused by the atmosphere [contributions from the troposphere and the ionosphere, |$\Delta\tau_{\rm atm}$| |$\simeq$| |$\surd(\Delta\tau^{2}_{\rm tropo}+\Delta\tau^{2}_{\rm iono})$| ], which are estimated to be |$\sigma_{\rm atm}$| |$\simeq$| |$\theta_{\rm beam}$| ( |${c\Delta\tau_{\rm atm}}/{\lambda}$| ) |$\simeq$| 0.027 |$\theta_{\rm beam}$| ( |${\theta_{\rm sep}}/$| 1|$^\circ$| ) |$\simeq$| 0.05 mas in the case of a typical zenith delay residual of |$\sim$| 2 cm (Honma et al. 2008) and a separation angle between I22480 and J2254 of 1 |$.^{\!\!\!\circ}$| 94. Thus, we estimate the position error to be typically |$\sigma_{\rm 1epoch}$| |$\simeq$| |$\surd$| ( |${\sigma^{2}_{\rm atm}+\sigma^{2}_{\rm J2254}}$| ) |$\simeq$| 0.08 mas by each measurement, which was actually dependent on the observation season.
We used the method of least-squares to fit modeled motions, each of which was composed of an annual parallax, a constant secular motion, and an position offset at the reference epoch (J2000.0),1 to the spot motions. We used all of the epoch points, except one without any valid astrometric result. Column 7 of table 1 shows a valid (Y) or invalid (N) astrometric observation epoch. In the model fitting, different weights were assigned to observed positions of spots. Errors of maser spot positions and those for the kinematic model fitting parameters were adjusted by using a constant factor, so that any residual of the model fitting |$\chi^{2}$| would be reduced to unity. In order to obtain an annual parallax common to these spots, we adopted the iterative procedure which is similar to that adopted by Sanna et al. (2012). At first, the model fitting to individual spot motions was begun independently (independent fitting). Then, a mean annual parallactic motion was subtracted from spot motions to estimate only the position offsets and linear motions of spots (proper-motion fitting). Further, the linear motions estimated here were subtracted from the original spot motions. Finally, the position residuals were used for estimating a parallax common to a position offset and proper-motion residuals (combined fitting). The proper-motion fitting was again performed using the estimated common parallax. Thus, a series of procedures were iterated until the estimated parameters had been converged. The left-hand panels of figure 4 show the motion of one of the target spots, the |$-$| 53.9 km s|$^{-1}$| component. The right-hand panel of figure 4 plots positions of five maser spots with their individual linear proper motions subtracted. The modeled annual parallax modulation is superposed on the maser positions. Table 4 gives results of the maser motion fitting.
Here, we consider a possible systematic error caused by a time variation of the brightness structures of J2254 and the H|$_2$| O maser spots in I22480. We found a simple, unresolved structure toward J2254, but this structure may be heavily affected by the synthesized beam pattern and low signal-to-noise ratio (column 5 of table 1). In fact, Gaussian brightness fitting errors for J2254 are larger than the intrinsic error mentioned above, and they are highly variable and dependent on observation conditions (see the relative variation of error-bar length in figure 4). This may be the largest contribution to the temporal fluctuation of the measured position (typically |$\sigma_{\rm J2254}$| |$\simeq$| 0.2 mas, up to 0.5 mas). The position of the position-reference maser spot is also fluctuated by any temporal structure variation of the associating maser-emitting gas clump (feature). As described in appendix 2, we estimated such an error contribution to be typically |$\sigma_{\rm maser}$| |$\simeq$| 0.05 mas. Thus, we estimated a typical value of the spot-position fluctuation (including a systematic position drift) to be |$\sigma$| |$\simeq$| |$\surd$| ( |${\sigma^{2}_{\rm 1epoch}}$| |$+$| |$\sigma^{2}_{\rm J2254}$| |$+$| |$\sigma^{2}_{\rm maser}$| ) |$\simeq$| 0.22 mas.
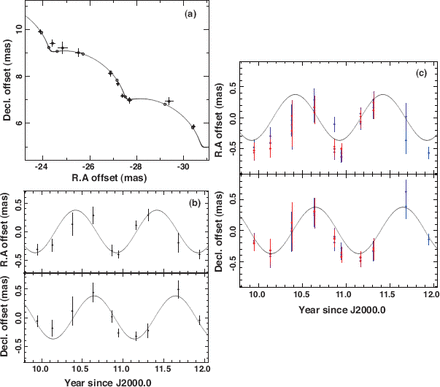
(a) Motion of the |$-$| 53.9 km s|$^{-1}$| component of H|$_2$| O maser emission in IRAS 22480|$+$| 6002 and the kinematical model fit to this motion. RA and Dec offsets with respect to the phase-tracking center of the |$-$| 53.9 km s|$^{-1}$| component. A filled circle shows the observed data point used for the annual parallax measurement. A solid curve shows the modeled motion including an annual parallax and a constant velocity proper motion. The length of the horizontal and vertical bars in each data point indicates the uncertainty of the spot position, which is adjusted so that a |$\chi^2$| value in the model fitting would be reduced to unity. An open circle indicates the spot position expected in the model at the observation epoch. (b) Same as (a), but right ascension- and declination-offset variation of the maser spot through the two years. The estimated linear proper motion is subtracted from the observed spot position. A solid curve shows the modeled annual parallactic motion. (c) Result of the combined annual parallax fitting using five maser spots at |$V_{{\rm LSR}}$| |$=$| |$-$| 53.9, |$-$| 52.7, |$-$| 51.0, |$-$| 48.9, and |$-$| 47.2 km s|$^{-1}$| in the maser features IRAS22480|$+$| 6002:I2012-4, 7, 12, 18, and 19. For clarity, data points in different spots are denoted by different colors and horizontally shifted slightly.
In the motion fitting of each maser spot with a position-fluctuation amplitude of |$\sim$| 0.22 mas to 10 data points (epochs), the accuracy of the annual parallax has increased to |$\sigma_{\pi}$| |$\simeq$| 0.05 mas, |$\sim$| 1|$/$| 4 of the position errors of individual data points. This is typically seen in previous VERA astrometry (e.g., Ando et al. 2011). Because some maser spots are associated with the same cluster including maser features, the position measurements of the five maser spots listed in table 4 are not completely independent. However, the fitting error contributed from the temporal (random) variation in maser-feature structure (see appendix 2) may be statistically mitigated. In fact, the final error of the annual parallax determined based on the result of the combined fitting was reduced to |$\sigma_{\pi}$| |$\simeq$| 0.025 mas, smaller by a factor of |$\sim$| 2 than the error in the independent fitting (|$\sim$| 0.05 mas). Finally, we obtained an annual parallax of |$\pi$| |$=$| 0.400 |$\pm$| 0.025 mas, corresponding to a distance to I22480 of |$D$| |$=$| 2.50 |$^{+0.17}_{-0.15}$| kpc.
| |$V_{{\rm LSR}}$| . | |$X_{0}$| * . | |$Y_{0}$| * . | |$\mu_{x}$| † . | |$\mu_{y}$| † . | |$\pi$| . | Deviation‡ . | |
|---|---|---|---|---|---|---|---|
| [km s|$^{-1}$|] . | [mas] . | [mas] . | [mas yr|$^{-1}$|] . | [mas yr|$^{-1}$|] . | [mas] . | |$\sigma_{x}$| . | |$\sigma_{y}$| . |
| Independent fitting | |||||||
| |$-$| 53.9 | 32.48|$\pm$| 0.56 | 20.33|$\pm$| 0.57 | |$-$| 3.23|$\pm$| 0.05 | |$-$| 2.04|$\pm$| 0.05 | 0.400|$\pm$| 0.040 | 0.13 | 0.11 |
| |$-$| 52.7 | 32.78|$\pm$| 1.72 | 19.99|$\pm$| 1.99 | |$-$| 3.23|$\pm$| 0.16 | |$-$| 1.95|$\pm$| 0.18 | 0.398|$\pm$| 0.071 | 0.25 | 0.17 |
| |$-$| 51.0 | 28.51|$\pm$| 1.01 | 22.28|$\pm$| 1.11 | |$-$| 2.84|$\pm$| 0.10 | |$-$| 2.23|$\pm$| 0.10 | 0.428|$\pm$| 0.059 | 0.17 | 0.09 |
| |$-$| 48.9 | 22.32|$\pm$| 0.69 | 18.76|$\pm$| 0.72 | |$-$| 2.22|$\pm$| 0.06 | |$-$| 1.87|$\pm$| 0.07 | 0.380|$\pm$| 0.038 | 0.12 | 0.08 |
| |$-$| 47.2 | 29.06|$\pm$| 0.94 | 20.75|$\pm$| 0.99 | |$-$| 2.90|$\pm$| 0.09 | |$-$| 2.01|$\pm$| 0.09 | 0.316|$\pm$| 0.052 | 0.14 | 0.14 |
| Proper motion fitting after subtracting the annual parallax§ | |||||||
| |$-$| 53.9 | 32.63|$\pm$| 1.45 | 20.71|$\pm$| 1.30 | |$-$| 3.23|$\pm$| 0.13 | |$-$| 2.06|$\pm$| 0.12 | -- | -- | |
| |$-$| 52.7 | 34.00|$\pm$| 3.45 | 20.92|$\pm$| 2.72 | |$-$| 3.33|$\pm$| 0.32 | |$-$| 2.03|$\pm$| 0.25 | -- | -- | |
| |$-$| 51.0 | 30.42|$\pm$| 1.85 | 21.54|$\pm$| 2.13 | |$-$| 3.01|$\pm$| 0.17 | |$-$| 2.15|$\pm$| 0.20 | -- | -- | |
| |$-$| 48.9 | 24.47|$\pm$| 2.09 | 17.93|$\pm$| 1.91 | |$-$| 2.40|$\pm$| 0.19 | |$-$| 1.78|$\pm$| 0.18 | -- | -- | |
| |$-$| 47.2 | 31.54|$\pm$| 2.48 | 19.12|$\pm$| 2.23 | |$-$| 3.11|$\pm$| 0.23 | |$-$| 1.90|$\pm$| 0.21 | -- | -- | |
| Combined fitting of an annual parallax | |||||||
| Combined | |$-$| 1.19|$\pm$| 0.43 | |$-$| 0.07|$\pm$| 0.45 | 0.10|$\pm$| 0.04 | |$-$| 0.02|$\pm$| 0.04 | 0.400|$\pm$| 0.025 | 0.18 | 0.13 |
| |$V_{{\rm LSR}}$| . | |$X_{0}$| * . | |$Y_{0}$| * . | |$\mu_{x}$| † . | |$\mu_{y}$| † . | |$\pi$| . | Deviation‡ . | |
|---|---|---|---|---|---|---|---|
| [km s|$^{-1}$|] . | [mas] . | [mas] . | [mas yr|$^{-1}$|] . | [mas yr|$^{-1}$|] . | [mas] . | |$\sigma_{x}$| . | |$\sigma_{y}$| . |
| Independent fitting | |||||||
| |$-$| 53.9 | 32.48|$\pm$| 0.56 | 20.33|$\pm$| 0.57 | |$-$| 3.23|$\pm$| 0.05 | |$-$| 2.04|$\pm$| 0.05 | 0.400|$\pm$| 0.040 | 0.13 | 0.11 |
| |$-$| 52.7 | 32.78|$\pm$| 1.72 | 19.99|$\pm$| 1.99 | |$-$| 3.23|$\pm$| 0.16 | |$-$| 1.95|$\pm$| 0.18 | 0.398|$\pm$| 0.071 | 0.25 | 0.17 |
| |$-$| 51.0 | 28.51|$\pm$| 1.01 | 22.28|$\pm$| 1.11 | |$-$| 2.84|$\pm$| 0.10 | |$-$| 2.23|$\pm$| 0.10 | 0.428|$\pm$| 0.059 | 0.17 | 0.09 |
| |$-$| 48.9 | 22.32|$\pm$| 0.69 | 18.76|$\pm$| 0.72 | |$-$| 2.22|$\pm$| 0.06 | |$-$| 1.87|$\pm$| 0.07 | 0.380|$\pm$| 0.038 | 0.12 | 0.08 |
| |$-$| 47.2 | 29.06|$\pm$| 0.94 | 20.75|$\pm$| 0.99 | |$-$| 2.90|$\pm$| 0.09 | |$-$| 2.01|$\pm$| 0.09 | 0.316|$\pm$| 0.052 | 0.14 | 0.14 |
| Proper motion fitting after subtracting the annual parallax§ | |||||||
| |$-$| 53.9 | 32.63|$\pm$| 1.45 | 20.71|$\pm$| 1.30 | |$-$| 3.23|$\pm$| 0.13 | |$-$| 2.06|$\pm$| 0.12 | -- | -- | |
| |$-$| 52.7 | 34.00|$\pm$| 3.45 | 20.92|$\pm$| 2.72 | |$-$| 3.33|$\pm$| 0.32 | |$-$| 2.03|$\pm$| 0.25 | -- | -- | |
| |$-$| 51.0 | 30.42|$\pm$| 1.85 | 21.54|$\pm$| 2.13 | |$-$| 3.01|$\pm$| 0.17 | |$-$| 2.15|$\pm$| 0.20 | -- | -- | |
| |$-$| 48.9 | 24.47|$\pm$| 2.09 | 17.93|$\pm$| 1.91 | |$-$| 2.40|$\pm$| 0.19 | |$-$| 1.78|$\pm$| 0.18 | -- | -- | |
| |$-$| 47.2 | 31.54|$\pm$| 2.48 | 19.12|$\pm$| 2.23 | |$-$| 3.11|$\pm$| 0.23 | |$-$| 1.90|$\pm$| 0.21 | -- | -- | |
| Combined fitting of an annual parallax | |||||||
| Combined | |$-$| 1.19|$\pm$| 0.43 | |$-$| 0.07|$\pm$| 0.45 | 0.10|$\pm$| 0.04 | |$-$| 0.02|$\pm$| 0.04 | 0.400|$\pm$| 0.025 | 0.18 | 0.13 |
Position at the epoch J2000.0 with respect to the delay-tracking center (see main text).
Secular motion of each component.
Mean deviation of the data points from the model-fit motion in units of mas.
The adopted annual parallax was given in the combined fitting in the converging phase of iterations.
| |$V_{{\rm LSR}}$| . | |$X_{0}$| * . | |$Y_{0}$| * . | |$\mu_{x}$| † . | |$\mu_{y}$| † . | |$\pi$| . | Deviation‡ . | |
|---|---|---|---|---|---|---|---|
| [km s|$^{-1}$|] . | [mas] . | [mas] . | [mas yr|$^{-1}$|] . | [mas yr|$^{-1}$|] . | [mas] . | |$\sigma_{x}$| . | |$\sigma_{y}$| . |
| Independent fitting | |||||||
| |$-$| 53.9 | 32.48|$\pm$| 0.56 | 20.33|$\pm$| 0.57 | |$-$| 3.23|$\pm$| 0.05 | |$-$| 2.04|$\pm$| 0.05 | 0.400|$\pm$| 0.040 | 0.13 | 0.11 |
| |$-$| 52.7 | 32.78|$\pm$| 1.72 | 19.99|$\pm$| 1.99 | |$-$| 3.23|$\pm$| 0.16 | |$-$| 1.95|$\pm$| 0.18 | 0.398|$\pm$| 0.071 | 0.25 | 0.17 |
| |$-$| 51.0 | 28.51|$\pm$| 1.01 | 22.28|$\pm$| 1.11 | |$-$| 2.84|$\pm$| 0.10 | |$-$| 2.23|$\pm$| 0.10 | 0.428|$\pm$| 0.059 | 0.17 | 0.09 |
| |$-$| 48.9 | 22.32|$\pm$| 0.69 | 18.76|$\pm$| 0.72 | |$-$| 2.22|$\pm$| 0.06 | |$-$| 1.87|$\pm$| 0.07 | 0.380|$\pm$| 0.038 | 0.12 | 0.08 |
| |$-$| 47.2 | 29.06|$\pm$| 0.94 | 20.75|$\pm$| 0.99 | |$-$| 2.90|$\pm$| 0.09 | |$-$| 2.01|$\pm$| 0.09 | 0.316|$\pm$| 0.052 | 0.14 | 0.14 |
| Proper motion fitting after subtracting the annual parallax§ | |||||||
| |$-$| 53.9 | 32.63|$\pm$| 1.45 | 20.71|$\pm$| 1.30 | |$-$| 3.23|$\pm$| 0.13 | |$-$| 2.06|$\pm$| 0.12 | -- | -- | |
| |$-$| 52.7 | 34.00|$\pm$| 3.45 | 20.92|$\pm$| 2.72 | |$-$| 3.33|$\pm$| 0.32 | |$-$| 2.03|$\pm$| 0.25 | -- | -- | |
| |$-$| 51.0 | 30.42|$\pm$| 1.85 | 21.54|$\pm$| 2.13 | |$-$| 3.01|$\pm$| 0.17 | |$-$| 2.15|$\pm$| 0.20 | -- | -- | |
| |$-$| 48.9 | 24.47|$\pm$| 2.09 | 17.93|$\pm$| 1.91 | |$-$| 2.40|$\pm$| 0.19 | |$-$| 1.78|$\pm$| 0.18 | -- | -- | |
| |$-$| 47.2 | 31.54|$\pm$| 2.48 | 19.12|$\pm$| 2.23 | |$-$| 3.11|$\pm$| 0.23 | |$-$| 1.90|$\pm$| 0.21 | -- | -- | |
| Combined fitting of an annual parallax | |||||||
| Combined | |$-$| 1.19|$\pm$| 0.43 | |$-$| 0.07|$\pm$| 0.45 | 0.10|$\pm$| 0.04 | |$-$| 0.02|$\pm$| 0.04 | 0.400|$\pm$| 0.025 | 0.18 | 0.13 |
| |$V_{{\rm LSR}}$| . | |$X_{0}$| * . | |$Y_{0}$| * . | |$\mu_{x}$| † . | |$\mu_{y}$| † . | |$\pi$| . | Deviation‡ . | |
|---|---|---|---|---|---|---|---|
| [km s|$^{-1}$|] . | [mas] . | [mas] . | [mas yr|$^{-1}$|] . | [mas yr|$^{-1}$|] . | [mas] . | |$\sigma_{x}$| . | |$\sigma_{y}$| . |
| Independent fitting | |||||||
| |$-$| 53.9 | 32.48|$\pm$| 0.56 | 20.33|$\pm$| 0.57 | |$-$| 3.23|$\pm$| 0.05 | |$-$| 2.04|$\pm$| 0.05 | 0.400|$\pm$| 0.040 | 0.13 | 0.11 |
| |$-$| 52.7 | 32.78|$\pm$| 1.72 | 19.99|$\pm$| 1.99 | |$-$| 3.23|$\pm$| 0.16 | |$-$| 1.95|$\pm$| 0.18 | 0.398|$\pm$| 0.071 | 0.25 | 0.17 |
| |$-$| 51.0 | 28.51|$\pm$| 1.01 | 22.28|$\pm$| 1.11 | |$-$| 2.84|$\pm$| 0.10 | |$-$| 2.23|$\pm$| 0.10 | 0.428|$\pm$| 0.059 | 0.17 | 0.09 |
| |$-$| 48.9 | 22.32|$\pm$| 0.69 | 18.76|$\pm$| 0.72 | |$-$| 2.22|$\pm$| 0.06 | |$-$| 1.87|$\pm$| 0.07 | 0.380|$\pm$| 0.038 | 0.12 | 0.08 |
| |$-$| 47.2 | 29.06|$\pm$| 0.94 | 20.75|$\pm$| 0.99 | |$-$| 2.90|$\pm$| 0.09 | |$-$| 2.01|$\pm$| 0.09 | 0.316|$\pm$| 0.052 | 0.14 | 0.14 |
| Proper motion fitting after subtracting the annual parallax§ | |||||||
| |$-$| 53.9 | 32.63|$\pm$| 1.45 | 20.71|$\pm$| 1.30 | |$-$| 3.23|$\pm$| 0.13 | |$-$| 2.06|$\pm$| 0.12 | -- | -- | |
| |$-$| 52.7 | 34.00|$\pm$| 3.45 | 20.92|$\pm$| 2.72 | |$-$| 3.33|$\pm$| 0.32 | |$-$| 2.03|$\pm$| 0.25 | -- | -- | |
| |$-$| 51.0 | 30.42|$\pm$| 1.85 | 21.54|$\pm$| 2.13 | |$-$| 3.01|$\pm$| 0.17 | |$-$| 2.15|$\pm$| 0.20 | -- | -- | |
| |$-$| 48.9 | 24.47|$\pm$| 2.09 | 17.93|$\pm$| 1.91 | |$-$| 2.40|$\pm$| 0.19 | |$-$| 1.78|$\pm$| 0.18 | -- | -- | |
| |$-$| 47.2 | 31.54|$\pm$| 2.48 | 19.12|$\pm$| 2.23 | |$-$| 3.11|$\pm$| 0.23 | |$-$| 1.90|$\pm$| 0.21 | -- | -- | |
| Combined fitting of an annual parallax | |||||||
| Combined | |$-$| 1.19|$\pm$| 0.43 | |$-$| 0.07|$\pm$| 0.45 | 0.10|$\pm$| 0.04 | |$-$| 0.02|$\pm$| 0.04 | 0.400|$\pm$| 0.025 | 0.18 | 0.13 |
Position at the epoch J2000.0 with respect to the delay-tracking center (see main text).
Secular motion of each component.
Mean deviation of the data points from the model-fit motion in units of mas.
The adopted annual parallax was given in the combined fitting in the converging phase of iterations.
We also estimated the secular motion of the star in I22480 to be (|$\mu_{\alpha}$| , |$\mu_{\delta}$| ) |$=$| (|$-$| 2.58 |$\pm$| 0.33, |$-$| 1.91 |$\pm$| 0.17) [mas yr|$^{-1}$| ], which was derived from a secular motion of the |$-$| 53.9 km s|$^{-1}$| component, (|$\mu_{\alpha}$| , |$\mu_{\delta}$| ) |$\equiv$| (|$\mu_{x}$| , |$\mu_{y}$| ) |$=$| (|$-$| 3.23 |$\pm$| 0.05, |$-$| 2.06 |$\pm$| 0.05) [mas yr|$^{-1}$| ] (see table 4), plus a relative motion of the star with respect to this maser spot (|$\dot{X}$| , |$\dot{Y}$| ) |$=$| (0.65, 0.15) [mas yr|$^{-1}$| ] [corresponding to (|$V_{{\rm0}x}$| , |$V_{{\rm0}y}$| ) |$=$| (7, 2) [km s|$^{-1}$| ], see subsection 3.1. The secular motion error is mainly attributed to an uncertainty of the stellar motion relative to the maser spot motion. The westerly proper motion of I22480 previously measured by using several literatures (Imai et al. 2008) is reconfirmed in this paper.
4. Discussion
As described in subsection 3.1, the spatio-kinematical structure of H|$_2$| O masers in I22480 is well modeled by an expanding outflow with an expansion velocity of |$\sim$| 8 km s|$^{-1}$| . Such a flow is typically seen in the circumstellar envelope around Mira variables (e.g., Bowers & Johnston 1994). On the other hand, the total extent of the maser-feature distribution is up to |$\sim$| 170 AU (|$D/$| 2.5 kpc), which is larger than those typically seen around Mira variables (up to 50 AU, e.g., Bowers & Johnston 1994) and comparable to, or a little smaller than, those seen around red supergiants (200–400 AU, e.g., Choi et al. 2008, Asaki et al. 2010). Therefore, these suggest that I22480 harbors an envelope seen in M-type supergiants and support the hypothesis that this star is a K-type supergiant or a post-AGB star harboring its ejected envelope. It has been suggested that I22480 is an RV Tau-type variable star (Imai et al. 2008). However, the revised distance gives a revised value of the stellar luminosity of 35000 |$L_{\odot}$| . Together with a negative confirmation of optical magnitude variability, this suggests again that I22480 should be a K-type supergiant rather than an RV Tau variable. Note that Winfrey et al. (1994) gave a new spectral classification of M0I for I22480.
Location and 3D motion of IRAS 22480|$+$|6002 in the Milky Way estimated from VERA astrometry.
| Parameter . | Value . |
|---|---|
| Galactic coordinates, (|$l$| ,|$b$| ) [|$^{\circ}$| ]|$^{*}$| | (108.43, 0.89) |
| Heliocentric distance, |$D$| [kpc]|$^{*}$| | 2.50|$\pm$| 0.16 |
| Systemic LSR velocity, |$V_{\rm sys}$| [km s|$^{-1}$| ]|$^{*}$| | |$-$| 50.8|$\pm$| 3.5 |
| Secular proper motion, |$\mu_{\alpha}$| [masyr|$^{-1}$|] | |$-$| 2.58|$\pm$| 0.33 |
| |$\mu_{\delta}$| [masyr|$^{-1}$|] | |$-$| 1.91|$\pm$| 0.17 |
| |$R_{\rm0}$| [kpc]|$^{\dagger}$| | 8.0 |
| |$\Theta_{\rm0}$| [km s|$^{-1}$| ]|$^{\dagger}$| | 220 |
| (|$U_{\odot}$| , |$V_{\odot}$| , |$W_{\odot}$| ) [km s|$^{-1}$| ]|$^{\ddagger}$| | (7.5, 13.5, 6.8) |
| |${z}_{\rm0}$| [pc]|$^{\S}$| | 16 |
| |$R_{\rm gal}$| [kpc] | 9.10|$\pm$| 0.09 |
| z [pc] | 55|$\pm$| 2 |
| |$V_{R}$| [km s|$^{-1}$|] | |$-$| 11|$\pm$| 4 |
| |$V_{\theta}$| [km s|$^{-1}$|] | 197|$\pm$| 4 |
| |$V_{{z}}$| [km s|$^{-1}$|] | 0|$\pm$| 3 |
| Parameter . | Value . |
|---|---|
| Galactic coordinates, (|$l$| ,|$b$| ) [|$^{\circ}$| ]|$^{*}$| | (108.43, 0.89) |
| Heliocentric distance, |$D$| [kpc]|$^{*}$| | 2.50|$\pm$| 0.16 |
| Systemic LSR velocity, |$V_{\rm sys}$| [km s|$^{-1}$| ]|$^{*}$| | |$-$| 50.8|$\pm$| 3.5 |
| Secular proper motion, |$\mu_{\alpha}$| [masyr|$^{-1}$|] | |$-$| 2.58|$\pm$| 0.33 |
| |$\mu_{\delta}$| [masyr|$^{-1}$|] | |$-$| 1.91|$\pm$| 0.17 |
| |$R_{\rm0}$| [kpc]|$^{\dagger}$| | 8.0 |
| |$\Theta_{\rm0}$| [km s|$^{-1}$| ]|$^{\dagger}$| | 220 |
| (|$U_{\odot}$| , |$V_{\odot}$| , |$W_{\odot}$| ) [km s|$^{-1}$| ]|$^{\ddagger}$| | (7.5, 13.5, 6.8) |
| |${z}_{\rm0}$| [pc]|$^{\S}$| | 16 |
| |$R_{\rm gal}$| [kpc] | 9.10|$\pm$| 0.09 |
| z [pc] | 55|$\pm$| 2 |
| |$V_{R}$| [km s|$^{-1}$|] | |$-$| 11|$\pm$| 4 |
| |$V_{\theta}$| [km s|$^{-1}$|] | 197|$\pm$| 4 |
| |$V_{{z}}$| [km s|$^{-1}$|] | 0|$\pm$| 3 |
Input value for IRAS 22480|$+$| 6002.
Input value for the Sun in the Milky Way.
Motion of the Sun with respect to the local standard of rest, cited from Francis and Anderson (2009) (cf. Dehnen & Binney 1998).
Height of the Sun from the Galactic midplane, cited from Hammersley et al. (1995).
Location and 3D motion of IRAS 22480|$+$|6002 in the Milky Way estimated from VERA astrometry.
| Parameter . | Value . |
|---|---|
| Galactic coordinates, (|$l$| ,|$b$| ) [|$^{\circ}$| ]|$^{*}$| | (108.43, 0.89) |
| Heliocentric distance, |$D$| [kpc]|$^{*}$| | 2.50|$\pm$| 0.16 |
| Systemic LSR velocity, |$V_{\rm sys}$| [km s|$^{-1}$| ]|$^{*}$| | |$-$| 50.8|$\pm$| 3.5 |
| Secular proper motion, |$\mu_{\alpha}$| [masyr|$^{-1}$|] | |$-$| 2.58|$\pm$| 0.33 |
| |$\mu_{\delta}$| [masyr|$^{-1}$|] | |$-$| 1.91|$\pm$| 0.17 |
| |$R_{\rm0}$| [kpc]|$^{\dagger}$| | 8.0 |
| |$\Theta_{\rm0}$| [km s|$^{-1}$| ]|$^{\dagger}$| | 220 |
| (|$U_{\odot}$| , |$V_{\odot}$| , |$W_{\odot}$| ) [km s|$^{-1}$| ]|$^{\ddagger}$| | (7.5, 13.5, 6.8) |
| |${z}_{\rm0}$| [pc]|$^{\S}$| | 16 |
| |$R_{\rm gal}$| [kpc] | 9.10|$\pm$| 0.09 |
| z [pc] | 55|$\pm$| 2 |
| |$V_{R}$| [km s|$^{-1}$|] | |$-$| 11|$\pm$| 4 |
| |$V_{\theta}$| [km s|$^{-1}$|] | 197|$\pm$| 4 |
| |$V_{{z}}$| [km s|$^{-1}$|] | 0|$\pm$| 3 |
| Parameter . | Value . |
|---|---|
| Galactic coordinates, (|$l$| ,|$b$| ) [|$^{\circ}$| ]|$^{*}$| | (108.43, 0.89) |
| Heliocentric distance, |$D$| [kpc]|$^{*}$| | 2.50|$\pm$| 0.16 |
| Systemic LSR velocity, |$V_{\rm sys}$| [km s|$^{-1}$| ]|$^{*}$| | |$-$| 50.8|$\pm$| 3.5 |
| Secular proper motion, |$\mu_{\alpha}$| [masyr|$^{-1}$|] | |$-$| 2.58|$\pm$| 0.33 |
| |$\mu_{\delta}$| [masyr|$^{-1}$|] | |$-$| 1.91|$\pm$| 0.17 |
| |$R_{\rm0}$| [kpc]|$^{\dagger}$| | 8.0 |
| |$\Theta_{\rm0}$| [km s|$^{-1}$| ]|$^{\dagger}$| | 220 |
| (|$U_{\odot}$| , |$V_{\odot}$| , |$W_{\odot}$| ) [km s|$^{-1}$| ]|$^{\ddagger}$| | (7.5, 13.5, 6.8) |
| |${z}_{\rm0}$| [pc]|$^{\S}$| | 16 |
| |$R_{\rm gal}$| [kpc] | 9.10|$\pm$| 0.09 |
| z [pc] | 55|$\pm$| 2 |
| |$V_{R}$| [km s|$^{-1}$|] | |$-$| 11|$\pm$| 4 |
| |$V_{\theta}$| [km s|$^{-1}$|] | 197|$\pm$| 4 |
| |$V_{{z}}$| [km s|$^{-1}$|] | 0|$\pm$| 3 |
Input value for IRAS 22480|$+$| 6002.
Input value for the Sun in the Milky Way.
Motion of the Sun with respect to the local standard of rest, cited from Francis and Anderson (2009) (cf. Dehnen & Binney 1998).
Height of the Sun from the Galactic midplane, cited from Hammersley et al. (1995).
Flow chart of the data reduction and image synthesis in the case of the inverse phase-referencing technique for VERA data. A round-square block denotes a visibility (UV) or image cube data set. A thick-black square block denotes a segment of process in AIPS. Setting of the essential parameters (adverbs) is described on the side. A thin-black square block denotes a file or solution (SN) table loaded or used for data calibration. The parts of calibration solution application (CLCAL in AIPS) are just expressed by crossing points of the lines that show the flows of data processing.
Obviously, the previous statistical parallax underestimated the distance to I22480 (|$\sim$| 1 kpc, Imai et al. 2008), in which only 13 proper motions were used for the estimation. Using the present data including 22 proper motions, we obtain a distance value of 2.9 |$\pm$| 0.4 kpc, in agreement with the distance (2.50 kpc) derived from an annual parallax. We have learned that the statistical parallax method is valid only with a sufficient number of maser-feature proper motions (|$\gt$| 20), that are uniformly and independently distributed (Moran & Reid 1993).
The location and velocity vector of I22480 in the Milky Way were also estimated in the same manner as that adopted in Imai et al. (2011b) from the derived secular motion shown in subsection 3.2. Table 5 gives derived parameters. Although the change of these values may depend on any assumption of the Galactic constants and the Solar motion relative to the LSR, it is clear that the secular motion of I22480 is slower by |$\sim$| 30 km s|$^{-1}$| than a circular motion estimated from the galactocentric distance to I22480 and from an assumption of flat Galactic rotation curve, as commonly found in maser sources in the Perseus Arm (Reid et al. 2009). Imai et al. (2008) reported a larger peculiar motion, |$U$| |$=$| |$-$| 71 km s|$^{-1}$| and |$V$| |$=$| |$-$| 29 km s|$^{-1}$| for I22480, where |$U$| and |$V$| indicate the peculiar-motion components in the antigalactic-center direction and the Galactic-rotation one, respectively. However, these components also should be revised from these values to the values determined in this paper (|$U$| |$=$| |$-$| 11 km s|$^{-1}$| and |$V$| |$=$| |$-$| 22 km s|$^{-1}$| ), because the distance and the secular motion of I22480 are now revised from 1.0 kpc to 2.5 kpc and from |$\sim$| 17 mas yr|$^{-1}$| in the westerly direction to |$\sim$| 3 mas yr|$^{-1}$| in the southwesterly one, respectively. In addition, I22480 is located close to the Galactic midplane (z |$\simeq$| 60 pc). They also support the hypothesis that I22480 is a (high-mass) K-type supergiant and a member of the Galactic thin disk. The discussion of the dynamics of the Galaxy to determine the Galactic rotation curve, itself, based on the peculiar motion of H|$_2$| O maser sources including I22480's motion, will be described in a separate paper.
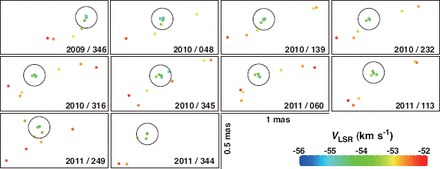
Maser spot distribution around the |$-$| 53.9-|$-$| 54.1 km s|$^{-1}$| components in the maser feature IRAS 22480|$+$| 6002:I2012-4, which was one of the maser spots used for the annual parallax measurement, at all observation epochs within a box of 1 mas |$\times$| 0.5 mas. An open circle with a radius of 0.1 mas is centered at the position-reference spot. The date of observation epoch is shown in the bottom-right corner of each subpanel.
We acknowledge all staff members and students who have helped us in array operation and in data correlation of the VERA. HI was supported by a Grant-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology (18740109) and the Strategic Young Researcher Overseas Visits Program for Accelerating Brain Circulation funded by Japan Society for the Promotion of Science.
Appendix 1. Inverse Phase-Referencing Method in VERA
As described in section 2, the present work adopted the inverse phase-referencing (IPR) technique for the first time throughout all observation epochs. This technique employs the transfer of fringe phase (and rate) calibration solutions from maser to continuum source data instead of that from the continuum to maser source data employed in the normal phase-referencing (PR) technique for maser source astrometry. The IPR technique has often been adopted in maser source astrometry with the Very Long Baseline Array (VLBA) (e.g., Reid et al. 2009, Sato et al. 2010). In the VLBA observation, a maser source and a position-reference continuum source are observed in the same signal-processing path and in the same frequency setup. In this case, the data from other scans on group-delay calibrators can commonly be used for calibrating both source data. Fringe fitting with the data of the maser scan is performed after this group-delay calibration in order to obtain only phase and rate residuals. These solutions are applied to the data of the position-reference source.
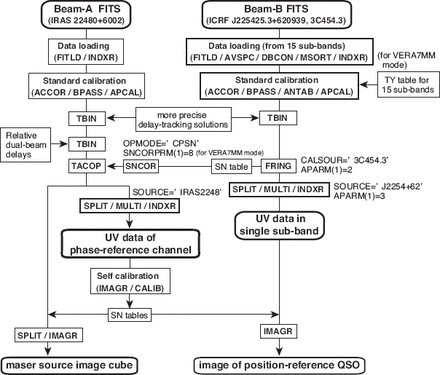
In the case of VERA, not only different signal processing paths, but also different frequency setups are used between the maser and continuum signals. Therefore, the sequence of data calibration steps is different from that in the VLBA data analysis. Figure 5 briefly shows the sequence of the whole data reduction in the IPR technique for VERA data. The essential and unique parts of the VERA IPR technique are summarized as follows:
The solutions for more precise delay tracking and those of the relative instrumental delays between Beam-A and Beam-B should be applied before any delay and phase calibration using the visibility data, themselves.
The group-delay calibration shall be made by using the data of another continuum calibrator, which should be brighter than the position-reference continuum source. The calibrator signals shall be recorded in Beam-B (15 BBCs), which has a much wider total bandwidth than Beam-A does (only one BBC). The group-delay calibration solutions shall be obtained by calculating multi-BBC group-delay residuals. The useful phase-calibration solutions shall be contained in the eighth BBC (in the digital filter mode of VERA7MM) of the solution (SN) table, whose base frequency is coincident with, or almost equal to if Beam-A data are filtered through a bandwidth of 8 MHz, that in Beam-A, and should be copied into the first subband. When they are copied to the data set of Beam-A, only those in the first subband are recognized in Beam-A.
The solutions of fringe-fitting and self-calibration using bright maser emission in Beam-A shall be applied to the data set of Beam-B after the Beam-B data are integrated into a single BBC.
The ParselTongue/python scripts for the PR/IPR calibration for VERA data in AIPS are now available in the wiki page.2 |$^{,}$| 3
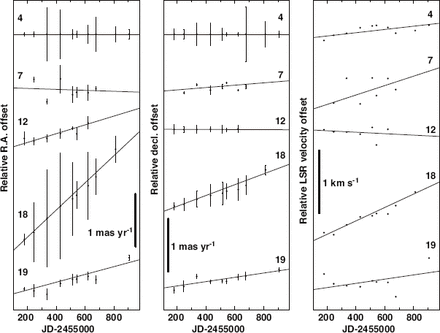
Observed relative proper motions and LSR velocity drifts of the H|$_2$| O maser features in IRAS 22480|$+$|6002, whose accompanying brightest maser spots were the targets of the annual parallax measurement. The number given to the proper motion of each maser feature means the assigned number added to the designated name ``IRAS 22480|$+$|6002:I2012.'' A thin solid line indicates a least-squares-fitted line assuming a constant velocity proper motion and a constant rate of the LSR velocity drift. A vertical bar for each data point in the left and middle panels indicates the defined size of the maser feature. For clarity, the velocity widths of maser features are not displayed.
Appendix 2. Contribution of Maser Structures to Accuracy of Absolute Astrometry
H|$_2$| O maser spots or features, as reference candles for VLBI astrometry, are time-variable. It is impossible to visualize the whole maser-feature structure in VLBI imaging and the locations of the individual maser spots in the feature, because we are always watching only the brightest parts of the feature structure in the spectral channel maps. Nevertheless, we can evaluate the stability of the structure and the accuracy of the astrometry described in this paper. Figure 6 shows the relative distribution of maser spots including one of the position-reference maser spots at all epochs. The position-reference spot was always located around the center of the whole distribution of maser spots (or a maser feature) whose spatial velocity pattern has persisted within |$\sim$| 0.1 mas. In particular, the locations of the position-reference spot and its velocity-adjacent spots (within 0.4 km s|$^{-1}$| ) were always concentrated within |$\sim$| 0.05 mas, corresponding to 0.6 km s|$^{-1}$| at 2.5 kpc from the Sun, although other spots exhibit relatively rapid variation in their locations. The latter scale may give the accuracy of our astrometry. Because the velocity spacing of VLBI spectroscopy itself was |$\sim$| 0.4 km s|$^{-1}$| (section 2), and the corresponding spectral channels covered slightly different velocity ranges among the observation epochs, we consider a group of maser spots within 1 km s|$^{-1}$| in our astrometry.
This is also supported by the deviations of the maser-feature positions from fitted ballistic motions (or constant proper motions) of the features. Figure 7 shows such deviations for the maser features whose accompanying brightest maser spots were the targets of the annual parallax measurement. The proper motions ralative to the reference feature IRAS 22480|$+$| 6002:I2012-4 (with zero relative proper motion) were measured. The displayed position and the size of maser feature were derived as shown in Imai, Deguchi, and Sasao (2002). Note that we suppose constant rates of the LSR velocity drifts of the maser features. Even the largest drift rate of |$\sim$| 0.4 km s|$^{-1}$| yr|$^{-1}$| , however, corresponds to only 0.03 mas yr|$^{-2}$| at the rate of the proper-motion variation per year. Except for a small number of large deviation cases (up to 0.3 mas), the position deviations from the expected ballistic feature motions are also within |$\sim$| 0.05 mas. The origins of the position deviation and the LSR velocity drifts are expected to be micro-turbulence in the feature (Imai et al. 2002).
References
In the model fitting, all spot positions were at first converted to the relative positions with respect to that at the first observation epoch for conserving the fitting accuracy.
See also the ParselTongue wiki page 〈http://www.jive.nl/dokuwiki/doku.php?id=parseltongue:parseltongue〉.



