-
PDF
- Split View
-
Views
-
Cite
Cite
Masaki Yoshida, Shunji Kitamoto, Hiroshi Murakami, Observation of the Cygnus OB2 Association with Suzaku and Long-Term Light Curves, Publications of the Astronomical Society of Japan, Volume 63, Issue sp3, 25 November 2011, Pages S717–S728, https://doi.org/10.1093/pasj/63.sp3.S717
Close - Share Icon Share
Abstract
We obtained a Suzaku 41-ks observation of the four brightest early type stars in the Cygnus OB2 association (Cyg OB2 Nos. 5, 8a, 9, and 12). The spectra of two of the stars, Nos. 9 and 12, could be fitted by a two-temperature thin-thermal collisional-ionization equilibrium model, while those of Nos. 5 and 8a required a three-temperature model. Star No. 8a showed a time variation both above 3 keV and below 1.5 keV. The time scale of the variation of the soft X-rays is |$\sim$| 8 |$\times$| 10 |$^{4}$| s, while that above 3 keV is |$\sim$| 2 |$\times$| 10 |$^{4}$| s. We found that the variation above 3 keV can be explained by temperature changes in the hottest plasma of the three-temperature model. This result restricts the size and density of the hottest component of the three-temperature model. We also produced long-term light curves of the four stars for over 30 yr. We confirmed the orbital modulation in the intensity of No. 8a, and discovered a possible orbital modulation of 2.35 yr in the light curve of No. 9.
1 Introduction
The detection of X-rays from five early-type stars in the Cygnus (Cyg) OB2 association Harnden et al. (1979) together with the Carinae stars Seward et al. (1979) by the Einstein observatory, led to early-type stars being known as X-ray emitters. Although various observations have been performed to date, the X-ray emission mechanisms of such stars are not well understood. A recent summary is provided by Waldron and Cassinelli (2007).
For single, isolated early-type stars, Lucy and White (1980) and Lucy (1982) have proposed an unstable line-driven wind model, where the stellar wind is heated by periodic unstable-wind-shocks and emits soft X-rays. This model has been extended by Owocki, Castor, and Rybicki (1988) and other subsequent studies (MacFarlane & Cassinelli (1989), Feldmeier et al. (1995), Feldmeier (1995)).
The collision of strong winds from early-type stars in binary systems (colliding wind binaries: CWBs) produces hot plasma, which emits X-rays Prilutskii & Usov (1976). Orbital modulation has been predicted by numerical simulations of CWBs (e.g., Stevens et al. (1992); Pittard & Stevens (1997)) and evidence of this has been reported by Pollock, Corcoran, and Stevens (2002).
If an early-type star, even a single isolated star, has a strong dipole magnetic field, its stellar wind is confined along the magnetic field lines. The confined winds collide at the equator and produce a shock (a magnetically channeled wind shock: MCWS) (ud-Doula & Owocki (2002), ud-Doula et al. (2006), ud-Doula et al. (2008)). The stellar wind in CWBs and/or at the MCWS is expected to heat the colliding gas more efficiently than the unstable-wind-shocks. Therefore, high-temperature and intense X-rays are expected from CWBs and/or in systems exhibiting MCWS. The detections of magnetic fields in some early-type stars have been reported, for example a 1-kG magnetic field in |$\theta^1$| Ori C Donati et al. (2002), a 500-G in |$\tau$| Sco Donati et al. (2006), and a 360-G in |$\beta$| Cep (Henrichs et al. (2000), Favata et al. (2009)).
Cyg OB2 includes over 2000 OB stars Knödlseder (2000) and Albacete Colombo et al. (2007) have detected 1003 X-ray sources. Among a number of early-type stars, four stars, Nos. 5, 8a, 9, and 12, have brighter X-ray emissions than the others. We summarize the spectral types and orbital periods of these four stars in table 1. They are also optically bright, and roughly follow the well-known |$L_{\rm X}/L_{\rm bol}$| relation Cassinelli et al. (1981), Waldron (1984). They are also known to be non-thermal radio emitters Abbott et al. (1984), Bieging et al. (1989). Nos. 5 and 8a are binaries. De Becker et al. (2006) found a phase-locked variability in the X-ray intensity of No. 8a, but No. 5 does not show any modulation with its orbital period Linder et al. (2009). van Loo et al. (2008) reported a variation in the radio emission from No. 9 with a period of 2.35 |$\ \pm\ $| 0.02 yr, and Nazé et al. (2010) confirmed an orbital period of |$\sim$| 2.4 yr by optical observation. No. 12 is possibly the most luminous star in the Galaxy, and is a candidate for a luminous blue variable Massey et al. (2001). It displays very high reddening Morgan et al. (1954), Sharpless (1957). Relatively high-temperature X-ray emissions from these stars were reported by Kitamoto and Mukai (1996) based on ASCA observations.
| Star . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| Spectral type | O6.5-7 |$+$| O fpe/WN9 |$^*$| | O6 If |$+$| O5.5 III |$^\ddagger$| | O5 If |$^\S$| | B3 Iae |$^\S$| |
| Orbital period | 6.6d |$^\dagger$| | 21.9d |$^\ddagger$| | |$\sim$| 850d |$^\Vert$| | — |
| Star . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| Spectral type | O6.5-7 |$+$| O fpe/WN9 |$^*$| | O6 If |$+$| O5.5 III |$^\ddagger$| | O5 If |$^\S$| | B3 Iae |$^\S$| |
| Orbital period | 6.6d |$^\dagger$| | 21.9d |$^\ddagger$| | |$\sim$| 850d |$^\Vert$| | — |
| Star . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| Spectral type | O6.5-7 |$+$| O fpe/WN9 |$^*$| | O6 If |$+$| O5.5 III |$^\ddagger$| | O5 If |$^\S$| | B3 Iae |$^\S$| |
| Orbital period | 6.6d |$^\dagger$| | 21.9d |$^\ddagger$| | |$\sim$| 850d |$^\Vert$| | — |
| Star . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| Spectral type | O6.5-7 |$+$| O fpe/WN9 |$^*$| | O6 If |$+$| O5.5 III |$^\ddagger$| | O5 If |$^\S$| | B3 Iae |$^\S$| |
| Orbital period | 6.6d |$^\dagger$| | 21.9d |$^\ddagger$| | |$\sim$| 850d |$^\Vert$| | — |
Recent high-resolution X-ray spectroscopy measurements have provided us with new insights into X-ray emission mechanisms of early type stars. Waldron et al. (2004) reported the results of these four Cyg OB2 stars obtained by the Chandra High Energy Transmission Grating Spectrometer (HETGS). Analyses of the He-like Fe lines of No. 8a give radial distances of their emission regions, and show that heavier ions have emission regions closer to the stellar surface than lighter ions. The emission regions are also consistent with their optical depth unity radii for their corresponding X-ray continuum. These results indicate the existence of high-temperature zones near the base of the wind. Waldron et al. (2004) reported that the |$\sim$| 19-MK component in No. 8a is located very close to the star, |$<$| 1.2 stellar radius. These results are found not only for No. 8a, but also for other typical early type stars, such as |$\zeta$| Ori (Waldron & Cassinelli (2001)), |$\zeta$| Pup (Cassinelli et al. (2001)), |$\delta$| Ori (Miller et al. (2002)), and many other OB stars (e.g., Waldron & Cassinelli (2007), 2009). In general, there is no evidence of any high-temperature ( |$>$| 5 MK) emission occurring above about 2 stellar radius.
High-resolution observations provide an opportunity to study line profiles. Some OB stars show broad, blue-shifted, and skewed line profiles, which agree with the prediction of emission from the stellar wind MacFarlane et al. (1991). However, many observations do not show the expected profile (Waldron & Cassinelli (2001), Miller et al. (2002), Leutenegger et al. (2006), Waldron & Cassinelli (2007)). To determine the cause of these observations, the effect of clumps in the wind has been discussed by Cassinelli et al. (2008) and a confined plasma on the stellar surface was suggested by Yamamoto et al. (2007).
Waldron et al. (1998) studied the long-term intensity-history of the four stars using the Einstein and the ROSAT data over 15 yr, and found that their intensities are relatively stable with a variability of less than |$\sim$| 20%, except for a flare-like event of star No. 5. De Becker et al. (2006) compiled ROSAT, Suzaku, and XMM-Newton data of No. 8a, which clearly show an orbital modulation of 21.908 d. Linder et al. (2009) made a multi-wavelength study of No. 5. Although the optical emission showed a 6.598-d periodicity, the X-rays did not show any phase-locked modulation. Such long-term variation may offer a clue concerning the emission mechanism.
In this paper, we report on results of analyses of the Suzaku data of these four bright and interesting stars in the Cyg OB2 association, while paying attention to their hard X-ray band property and variability. We also produce long-term light curves of the four stars, spanning 30 yr.
2 Observations with Suzaku
We observed the Cyg OB2 association with the fifth Japanese X-ray satellite, Suzaku Mitsuda et al. (2007), from 22:02:43 UT on 2007 December 18 to 20:15:14 UT on December 19, with a net exposure time of 41 ks. Suzaku has five X-ray telescope (XRT) modules Serlemitsos et al. (2007), each of which has an X-ray CCD camera, consisting an X-ray Imaging Spectrometer (XIS) system Koyama et al. (2007), at its focal plane. Three of the four XIS sensors (XIS 0, XIS 2, and XIS 3) use front-illuminated (FI) CCDs, while XIS 1 uses a back-illuminated (BI) CCD. The XIS covers an energy range from 0.2 to 10 keV with a large effective area and a low background. During the observation, three of the XIS sensors (XIS 0, XIS 1, and XIS 3) were operated in the normal-clocking mode, with a 5 |$\times$| 5- or a 3 |$\times$| 3-editing mode. Suzaku also has a Hard X-ray Detector (HXD) Takahashi et al. (2007), Kokubun et al. (2007) that consists of Si PIN-photo diodes and GSO scintillation counters, and covers an energy range from 12 keV to 600 keV. However, they were contaminated by a nearby strong hard X-ray source, Cyg X-3. Since the HXD is not an imaging detector, an estimation of contamination by a nearby source is difficult. Thus, we did not analyze the HXD data. The background of the XIS sensor, which is an imaging detector, is much smaller than that of the HXD, and can be estimated by using non-source areas in images.
We analyzed the cleaned event data of XIS 0, XIS 1, and XIS 3 prepared via version 1.2 processing. We further extracted data using xselect (version 2.4a).1 For the spectral analysis, we used xspec (version 12.5.0) and CALDB (2009-01-09).2
2.1 Image
Figure 1 shows an image compiled from the data obtained with XIS 0, XIS 1, and XIS 3 in the energy range from 0.5 to 10.0 keV, where events by calibration sources were excluded. We identified seven point sources (Nos. 5, 8a, 9, 12, CXO J203308.1 |$+$| 411304.0, J203231.53.1 |$+$| 411408.2, and J203234.33 |$+$| 411506.3), as indicated in the figure. Stray light from a nearby bright source, Cyg X-3, can be seen in the south–west and south–east regions.
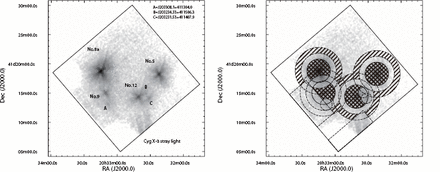
(Left) Image of Cyg OB2 obtained by XIS0, XIS1, and XIS3 in the energy range from 0.5 to 10keV. Events due to the calibration sources have been excluded. The identified sources are indicated; A, B, and C are CXO J203308.1 |$+$| 411304.0, J203231.53.1 |$+$| 411408.2, and J203234.33 |$+$| 411506.3, respectively. (Right) Regions of the extracted events. The source and background regions are hatched by meshes and lines, respectively. The details are described in the text.
We analyzed four statistically good stars (Nos. 5, 8a, 9, and 12). The extraction regions for the sources and their backgrounds were determined as follows. The source regions were determined to be circles with 2 |$'$| radius around the source positions. However, regions within 3 |$'$| of the three other bright sources and within 1 |$'$| of the three faint sources were excluded. The background events were extracted from an annulus region with a 4 |$'$| outer radius and a 3 |$'$| inner radius. However, the regions within 3 |$'$| circles from the three other sources and the region within 1 |$'$| of the three faint sources, were again excluded. Regions where stray light from Cyg X-3 was evident were also excluded.
2.2 Light Curves
We first applied a barycentric correction with aebarycen,3 and binned continuously obtained data into one data point; the time span of which was typically 3 |$\times$| 10 |$^{3}$| s. Light curves, combined from the three detectors, of the four sources in the energy ranges, 0.5–1.5 keV, 1.5–3.0 keV, and 3.0–10 keV, are plotted in figure 2. A |$\chi^2$| test was applied to test the statistical significance of the variation. The obtained |$\chi ^2_{\nu}$| values are given in the panels. The low and high energy bands of No. 8a show statistically significant variation with |$\chi ^2_{\nu}$| values greater than 2. The probabilities that the observed data are merely a statistical fluctuation from constant data are less than 5.8 |$\times$| 10 |$^{-2}$| % and 4.8 |$\times$| 10 |$^{-2}$| % for the 0.5–1.5 keV and for 3.0–10.0 keV bands of No. 8a, respectively. The time variation in the high-energy band seems to show a slow rise and a sharp decay (“saw”-like variation) with a decay time scale of |$\sim$| 3 |$\times$| 10 |$^{3}$| s (1 bin). On the other hand, the time variation in the low-energy band seems to be roughly sinusoidal. The amplitudes of the variations are |$\sim$| 6.0% and |$\sim$| 8.5% of the mean intensity for the 0.5–1.5 keV and 3.0–10.0 keV bands, respectively. The middle-energy band of No. 5 and the low-energy band of No. 9 show a marginal variation with |$\chi ^2_{\nu}$| values of 2.0, and 1.5. The corresponding probabilities of appearance within a statistical fluctuation are 1.7% and 11.5%. The |$\chi ^2_{\nu}$| values of the other light curves are equal to or less than 1.1.
Next, we constructed a history of the ratios of the count rates (hereafter CR), a softness ratio, CR(0.5–1.5 keV) |$/$| CR(1.5–3.0 keV) and a hardness ratio, CR(3.0–10.0 keV) |$/$| CR(1.5–3.0 keV) of No. 8a, as shown in figure 3. CR(3.0–10.0 keV) |$/$| CR(1.5–3.0 keV) shows a larger variation with a peak-to-bottom amplitude of |$\sim$| 18%, than CR(0.5–1.5 keV) |$/$| CR(1.5–3.0 keV) with |$\sim$| 10%. The saw-like variation with a slow rise and a sharp decay of CR(3.0–10.0 keV) |$/$| CR(1.5–3.0 keV) and a sinusoidal variation of CR(0.5–1.5 keV) |$/$| CR(1.5–3.0 keV) are clearly seen. We fitted the history of the ratios by sinusoidal curves, and obtained a sinusoidal period of |$\sim$| 20 ks and |$\sim$| 80 ks for the 3.0–10.0 keV and 0.5–1.5 keV bands, respectively.
2.3 Spectral Analysis
Spectra of the four stars are shown in figure 4. We calculated the XIS redistribution matrix files (RMFs) and ancillary response files (ARFs) for the extracted regions shown in figure 1 with xisrmfgen (ver. 2007-05-14) and xissimarfgen (ver. 2008-04-05) Ishisaki et al. (2007). We can recognize emission lines of Mg-K, Si-K, S-K, and Fe-K around 1.5, 1.9, 2.4, and 6.7 keV. Thus, we first fit the spectra by a one-temperature thin-thermal collisional-ionization equilibrium plasma model (mekal: Mewe et al. (1985)) (hereafter we call this the one-temperature CIE model), while taking interstellar and circumstellar absorptions (wabs) into account. The amount of interstellar medium (ISM) was taken from Waldron et al. (1998). The chemical abundance of He was fixed to be the solar value. The metal abundance was kept as a free parameter, where the relative abundances among metals were fixed to the solar value. This treatment of the abundance is not suitable in reality, especially for statistically better or high-resolution data. However, the line strength in our data does not allow us to accurately determine each abundance separately. The resultant abundance values should be considered to be weighted average values of the metals for a particular model used. The |$\chi^2/$| d.o.f. values are 3.07, 4.71, 2.00, and 1.78 for Nos. 5, 8a, 9, and 12, respectively. Positive residuals of the data from the best-fit models were found at both the low- and high-energy bands. This fact implies that there are other components.
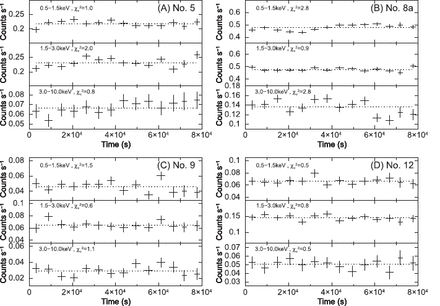
Light curves of the four stars in three energy bands (0.5-1.5keV, 1.5-3.0keV, and 3.0-10.0keV). The |$\chi ^2_{\nu}$| values obtained by a constant assumption are indicated in each panel.

(a) Hardness-ratio history of No. 8a, CR(3.0-10.0keV) |$/$| CR(1.5-3.0keV). (b) Softness-ratio history of No. 8a, CR(0.5-1.5keV) |$/$| CR(1.5-3.0keV). The |$\chi ^2_{\nu}$| values from a constant hypothesis are indicated in the panels. The broken lines are the best-fit sinusoidal curves.
We next fit the data by a two-temperature CIE model with interstellar and circumstellar absorptions. We assumed that the amount of circumstellar absorption and the metal abundances are the same for the two components. The best-fit parameters are listed in table 2. The two stars Nos. 9 and 12 were reasonably fitted by this model. However, for Nos. 5 and 8a, this model was formally rejected with a |$\chi^2/$| d.o.f. of 1.35 and 1.56, respectively. Therefore, we applied a three-temperature CIE model with absorptions for Nos. 5 and 8a. We restricted the amount of absorption of the three components to be the same. Although we also tried to fit the three-temperature CIE model to Nos. 9 and 12, the fits were not improved, and some of the resultant parameters were meaningless; for example, the normalization of the third component was consistent with zero. The results for Nos. 5 and 8a are given in table 3. The fits became slightly better, although the models were still unacceptable. Comparing the parameters in the two-temperature and the three-temperature models of Nos. 5 and 8a, we can recognize that the low-temperature component ( |$\sim$| 0.6 keV) in the two-temperature model was just an approximation of a more complex model (in this case, combination of a |$\sim$| 0.2 keV and a |$\sim$| 0.8 keV CIE model). Since the temperatures of the low-temperature component are 0.65 and 0.74 keV for Nos. 9 and 12 in the two-temperature model, we can speculate that the low-temperature components of Nos. 9 and 12 are also approximations of two-temperature or more complex plasma. On the other hand, the high-temperature components of Nos. 5 and 8a are |$\sim$| 2 keV in both of the two- and three-temperature CIE models. The metal abundance is roughly 0.58–0.75 in the two-temperature CIE model, but tends to be large in the three-temperature CIE model. The best fit three- or two-temperature CIE models and the residuals are shown in figure 4.
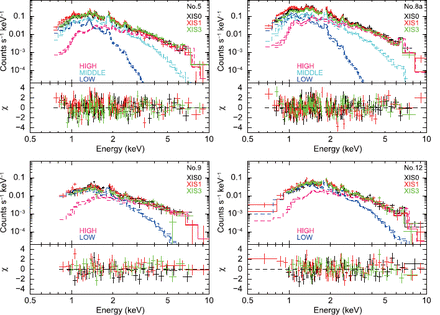
XIS spectra of the four stars: Nos. 5, 8a, 9, and 12. The best-fit model spectra for two- or three-temperature CIE models are also plotted. The lower panels show residuals of the data from the model, divided by the error of the data.
Best-fit parameters of spectral fitting by the two-temperature CIE model. |$^*$|
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${N_{\rm H}}\ (10^{22}$| Hcm |$^{-2}$| ) | 0.34 |$^{+0.04}_{\,-0.04}$| | 0.44 |$^{+0.03}_{\,-0.03}$| | 0.39 |$^{+0.13}_{\,-0.14}$| | 0.21 |$^{+0.08}_{\,-0.08}$| |
| |$Z_{\solar}$||$^\dag $| | 0.58 |$^{+0.11}_{\,-0.11}$| | 0.75 |$^{+0.10}_{\,-0.09}$| | 0.60 |$^{+0.41}_{\,-0.26}$| | 0.60 |$^{+0.17}_{\,-0.14}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.62 |$^{+0.02}_{\,-0.01}$| | 0.62 |$^{+0.01}_{\,-0.01}$| | 0.65 |$^{+0.19}_{\,-0.06}$| | 0.74 |$^{+0.07}_{\,-0.11}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.70 |$^{+0.13}_{\,-0.11}$| | 0.92 |$^{+0.11}_{\,-0.10}$| | 0.20 |$^{+0.12}_{\,-0.08}$| | 0.39 |$^{+0.11}_{\,-0.09}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.27 |$^{+0.27}_{\,-0.18}$| | 1.92 |$^{+0.07}_{\,-0.06}$| | 3.08 |$^{+1.57}_{\,-0.64}$| | 2.06 |$^{+0.48}_{\,-0.27}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.13 |$^{+0.02}_{\,-0.02}$| | 0.33 |$^{+0.02}_{\,-0.02}$| | 0.05 |$^{+0.01}_{\,-0.01}$| | 0.11 |$^{+0.04}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 376.13 |$/$| 279 (1.35) | 509.44 |$/$| 327 (1.56) | 115.31 |$/$| 102 (1.13) | 202.78 |$/$| 171 (1.19) |
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${N_{\rm H}}\ (10^{22}$| Hcm |$^{-2}$| ) | 0.34 |$^{+0.04}_{\,-0.04}$| | 0.44 |$^{+0.03}_{\,-0.03}$| | 0.39 |$^{+0.13}_{\,-0.14}$| | 0.21 |$^{+0.08}_{\,-0.08}$| |
| |$Z_{\solar}$||$^\dag $| | 0.58 |$^{+0.11}_{\,-0.11}$| | 0.75 |$^{+0.10}_{\,-0.09}$| | 0.60 |$^{+0.41}_{\,-0.26}$| | 0.60 |$^{+0.17}_{\,-0.14}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.62 |$^{+0.02}_{\,-0.01}$| | 0.62 |$^{+0.01}_{\,-0.01}$| | 0.65 |$^{+0.19}_{\,-0.06}$| | 0.74 |$^{+0.07}_{\,-0.11}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.70 |$^{+0.13}_{\,-0.11}$| | 0.92 |$^{+0.11}_{\,-0.10}$| | 0.20 |$^{+0.12}_{\,-0.08}$| | 0.39 |$^{+0.11}_{\,-0.09}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.27 |$^{+0.27}_{\,-0.18}$| | 1.92 |$^{+0.07}_{\,-0.06}$| | 3.08 |$^{+1.57}_{\,-0.64}$| | 2.06 |$^{+0.48}_{\,-0.27}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.13 |$^{+0.02}_{\,-0.02}$| | 0.33 |$^{+0.02}_{\,-0.02}$| | 0.05 |$^{+0.01}_{\,-0.01}$| | 0.11 |$^{+0.04}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 376.13 |$/$| 279 (1.35) | 509.44 |$/$| 327 (1.56) | 115.31 |$/$| 102 (1.13) | 202.78 |$/$| 171 (1.19) |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7kpc (Hanson (2003)).
Best-fit parameters of spectral fitting by the two-temperature CIE model. |$^*$|
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${N_{\rm H}}\ (10^{22}$| Hcm |$^{-2}$| ) | 0.34 |$^{+0.04}_{\,-0.04}$| | 0.44 |$^{+0.03}_{\,-0.03}$| | 0.39 |$^{+0.13}_{\,-0.14}$| | 0.21 |$^{+0.08}_{\,-0.08}$| |
| |$Z_{\solar}$||$^\dag $| | 0.58 |$^{+0.11}_{\,-0.11}$| | 0.75 |$^{+0.10}_{\,-0.09}$| | 0.60 |$^{+0.41}_{\,-0.26}$| | 0.60 |$^{+0.17}_{\,-0.14}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.62 |$^{+0.02}_{\,-0.01}$| | 0.62 |$^{+0.01}_{\,-0.01}$| | 0.65 |$^{+0.19}_{\,-0.06}$| | 0.74 |$^{+0.07}_{\,-0.11}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.70 |$^{+0.13}_{\,-0.11}$| | 0.92 |$^{+0.11}_{\,-0.10}$| | 0.20 |$^{+0.12}_{\,-0.08}$| | 0.39 |$^{+0.11}_{\,-0.09}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.27 |$^{+0.27}_{\,-0.18}$| | 1.92 |$^{+0.07}_{\,-0.06}$| | 3.08 |$^{+1.57}_{\,-0.64}$| | 2.06 |$^{+0.48}_{\,-0.27}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.13 |$^{+0.02}_{\,-0.02}$| | 0.33 |$^{+0.02}_{\,-0.02}$| | 0.05 |$^{+0.01}_{\,-0.01}$| | 0.11 |$^{+0.04}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 376.13 |$/$| 279 (1.35) | 509.44 |$/$| 327 (1.56) | 115.31 |$/$| 102 (1.13) | 202.78 |$/$| 171 (1.19) |
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${N_{\rm H}}\ (10^{22}$| Hcm |$^{-2}$| ) | 0.34 |$^{+0.04}_{\,-0.04}$| | 0.44 |$^{+0.03}_{\,-0.03}$| | 0.39 |$^{+0.13}_{\,-0.14}$| | 0.21 |$^{+0.08}_{\,-0.08}$| |
| |$Z_{\solar}$||$^\dag $| | 0.58 |$^{+0.11}_{\,-0.11}$| | 0.75 |$^{+0.10}_{\,-0.09}$| | 0.60 |$^{+0.41}_{\,-0.26}$| | 0.60 |$^{+0.17}_{\,-0.14}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.62 |$^{+0.02}_{\,-0.01}$| | 0.62 |$^{+0.01}_{\,-0.01}$| | 0.65 |$^{+0.19}_{\,-0.06}$| | 0.74 |$^{+0.07}_{\,-0.11}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.70 |$^{+0.13}_{\,-0.11}$| | 0.92 |$^{+0.11}_{\,-0.10}$| | 0.20 |$^{+0.12}_{\,-0.08}$| | 0.39 |$^{+0.11}_{\,-0.09}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.27 |$^{+0.27}_{\,-0.18}$| | 1.92 |$^{+0.07}_{\,-0.06}$| | 3.08 |$^{+1.57}_{\,-0.64}$| | 2.06 |$^{+0.48}_{\,-0.27}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.13 |$^{+0.02}_{\,-0.02}$| | 0.33 |$^{+0.02}_{\,-0.02}$| | 0.05 |$^{+0.01}_{\,-0.01}$| | 0.11 |$^{+0.04}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 376.13 |$/$| 279 (1.35) | 509.44 |$/$| 327 (1.56) | 115.31 |$/$| 102 (1.13) | 202.78 |$/$| 171 (1.19) |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7kpc (Hanson (2003)).
Best-fit parameters of spectral fitting by the three-temperature CIE model. |$^*$|
| . | No. 5 . | No. 8a . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.51 |$^{+0.06}_{\,-0.06}$| | 0.63 |$^{+0.04}_{\,-0.04}$| |
| |${Z_{}}$||$^\dag $| | 0.67 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.11}_{\,-0.10}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.24 |$^{+0.05}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 2.50 |$^{+2.00}_{\,-1.39}$| | 4.29 |$^{+1.65}_{\,-1.44}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.76 |$^{+0.05}_{\,-0.04}$| | 0.82 |$^{+0.04}_{\,-0.04}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.43 |$^{+0.10}_{\,-0.07}$| | 0.51 |$^{+0.07}_{\,-0.06}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.23 |$^{+0.39}_{\,-0.21}$| | 1.90 |$^{+0.08}_{\,-0.08}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.12 |$^{+0.02}_{\,-0.03}$| | 0.30 |$^{+0.03}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 359.66 |$/$| 277 (1.30) | 414.16 |$/$| 325 (1.27) |
| . | No. 5 . | No. 8a . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.51 |$^{+0.06}_{\,-0.06}$| | 0.63 |$^{+0.04}_{\,-0.04}$| |
| |${Z_{}}$||$^\dag $| | 0.67 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.11}_{\,-0.10}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.24 |$^{+0.05}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 2.50 |$^{+2.00}_{\,-1.39}$| | 4.29 |$^{+1.65}_{\,-1.44}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.76 |$^{+0.05}_{\,-0.04}$| | 0.82 |$^{+0.04}_{\,-0.04}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.43 |$^{+0.10}_{\,-0.07}$| | 0.51 |$^{+0.07}_{\,-0.06}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.23 |$^{+0.39}_{\,-0.21}$| | 1.90 |$^{+0.08}_{\,-0.08}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.12 |$^{+0.02}_{\,-0.03}$| | 0.30 |$^{+0.03}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 359.66 |$/$| 277 (1.30) | 414.16 |$/$| 325 (1.27) |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7kpc (Hanson (2003)).
Best-fit parameters of spectral fitting by the three-temperature CIE model. |$^*$|
| . | No. 5 . | No. 8a . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.51 |$^{+0.06}_{\,-0.06}$| | 0.63 |$^{+0.04}_{\,-0.04}$| |
| |${Z_{}}$||$^\dag $| | 0.67 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.11}_{\,-0.10}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.24 |$^{+0.05}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 2.50 |$^{+2.00}_{\,-1.39}$| | 4.29 |$^{+1.65}_{\,-1.44}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.76 |$^{+0.05}_{\,-0.04}$| | 0.82 |$^{+0.04}_{\,-0.04}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.43 |$^{+0.10}_{\,-0.07}$| | 0.51 |$^{+0.07}_{\,-0.06}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.23 |$^{+0.39}_{\,-0.21}$| | 1.90 |$^{+0.08}_{\,-0.08}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.12 |$^{+0.02}_{\,-0.03}$| | 0.30 |$^{+0.03}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 359.66 |$/$| 277 (1.30) | 414.16 |$/$| 325 (1.27) |
| . | No. 5 . | No. 8a . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.51 |$^{+0.06}_{\,-0.06}$| | 0.63 |$^{+0.04}_{\,-0.04}$| |
| |${Z_{}}$||$^\dag $| | 0.67 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.11}_{\,-0.10}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.24 |$^{+0.05}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 2.50 |$^{+2.00}_{\,-1.39}$| | 4.29 |$^{+1.65}_{\,-1.44}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.76 |$^{+0.05}_{\,-0.04}$| | 0.82 |$^{+0.04}_{\,-0.04}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.43 |$^{+0.10}_{\,-0.07}$| | 0.51 |$^{+0.07}_{\,-0.06}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.23 |$^{+0.39}_{\,-0.21}$| | 1.90 |$^{+0.08}_{\,-0.08}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddagger$| | 0.12 |$^{+0.02}_{\,-0.03}$| | 0.30 |$^{+0.03}_{\,-0.03}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 359.66 |$/$| 277 (1.30) | 414.16 |$/$| 325 (1.27) |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7kpc (Hanson (2003)).
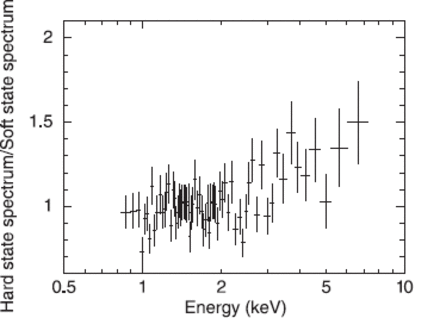
Spectral ratios of No. 8a: the hard-state spectrum divided by the soft-state spectrum.
If the emission regions of plasma of different temperature components are different from each other, the amount of circumstellar matter should be different. As suggested by high-resolution data (e.g., Waldron et al. (2004)), the high-temperature plasma possibly exists at the base of the stellar wind. Therefore, a relatively high column density of the high-temperature component would be expected. Thus, we tried to fit the spectra by the two- or three-temperature CIE model by keeping the amount of circumstellar absorption of each component as a free parameter. The resultant best-fit parameters are listed in table 4. However, the fittings for Nos. 8a, 9, and 12 were not improved, and the resultant amount of the absorption of components is the same within errors. Only the fitting of No. 5 slightly improved. Since the obtained circumstellar absorptions are smaller than the interstellar absorption, precise determinations of the amounts of the circumstellar absorptions are difficult.
As shown in figure 2 and figure 3, we already know that star No. 8a shows a variation in its intensity and hardness ratio. Therefore, we constructed two separate spectra of No. 8a using the hardness ratio CR(3.0–10 keV) |$/$| CR(1.5–3.0 keV). Data were extracted from bins harder than the mean hardness ratio in figure 3a, and one spectrum was constructed. We call this the “hard-state spectrum”. Similarly, data were extracted from bins softer, and another spectrum was constructed, which we call the “soft-state spectrum”. Figure 5 shows the ratios of the two spectra (“hard-state spectrum” |$/$| “soft-state spectrum”), after combining the XIS 0 and XIS 3 spectra. The ratios show clear hardening above 3 keV, while for energies below 3 keV they are nearly constant, suggesting that only the high-temperature component, obtained in the three-temperature CIE model fitting, changes.
The hard-state and soft-state spectra of No. 8a were fitted by the three-temperature CIE model with the same circumstellar absorptions. The best-fit parameters are listed in table 5. The highest temperature component changes in temperature, while its emission measure ( |$EM$||$=$||$\int n_{\rm {e}}n_{\rm {H}} dV$| ) is the same within the error. The other two components are consistently identical within their errors.
There is also a time variation in the low-energy band, as shown in figure 3b. Thus, we again extracted two spectra by selecting the soft intervals and the hard intervals separately for No. 8a, by using the softness ratio, CR(0.5–1.5 keV) |$/$| CR(1.5–3.0 keV). We fitted the two spectra by the three-temperature CIE model with the same circumstellar absorptions. We found that a change of any parameter among |$N_{\rm H}$| , |$k_{\rm B}T_{\rm low}$| , and |$EM_{\rm low}$| can explain the spectral variation. Hence, further information is required to distinguish them.
3 Long-Term History
Cyg OB2 has been observed for 30 yr. We analyzed the available archived data of various satellites, and investigated the flux variation in the energy ranges 0.5–4.0 keV (Low) and 4.0–10.0 keV (High). The data we analyzed are listed in table 6, including the observation date, satellite/instruments, and derived flux values. In the case of Einstein and ROSAT, their observable energy ranges are restricted to the low-energy band, less than |$\sim$| 4 or |$\sim$| 2 keV, respectively, and therefore we deduced only the low-energy fluxes for these two satellites.
The fluxes of the Einstein data were estimated using WebPIMMS4 with the count rate from Waldron et al. (1998), assuming that their spectra were the same as those published by Harnden et al. (1979). The ROSAT spectra were extracted using xselect (version 2.4a), and were fitted by a CIE model, where we fixed the absorption and temperature to the values from Waldron et al. (1998) and determined emission measures. The flux of each spectrum was calculated in the energy range 0.5–4.0 keV using WebPIMMS.
Best-fit parameters of the two- or three-temperature CIE model with free circumstellar absorptions. |$^*$|
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${Z_{}}$||$^\dag $| | 0.63 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.10}_{\,-0.11}$| | 0.55 |$^{+0.45}_{\,-0.29}$| | 0.59 |$^{+0.18}_{\,-0.15}$| |
| |$N_{\rm H(wind_{low})}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.38 |$^{+0.10}_{\,-0.11}$| | 0.57 |$^{+0.07}_{\,-0.07}$| | 0.39 |$^{+0.16}_{\,-0.14}$| | 0.19 |$^{+0.10}_{\,-0.12}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.04}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| | 0.64 |$^{+0.18}_{\,-0.05}$| | 0.67 |$^{+0.10}_{\,-0.05}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 2.60 |$^{+1.89}_{\,-1.36}$| | 3.91 |$^{+1.61}_{\,-1.36}$| | 0.23 |$^{+0.24}_{\,-0.10}$| | 0.44 |$^{+0.16}_{\,-0.12}$| |
| |$N_{\rm H(wind_{middle)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.70 |$^{+0.13}_{\,-0.12}$| | 0.71 |$^{+0.09}_{\,-0.08}$| | — | — |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.84 |$^{+0.13}_{\,-0.12}$| | 0.84 |$^{+0.06}_{\,-0.05}$| | — | — |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.52 |$^{+0.10}_{\,-0.09}$| | 0.55 |$^{+0.08}_{\,-0.08}$| | — | — |
| |$N_{\rm H(wind_{high)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.27 |$^{+0.69}_{\,-0.60}$| | 0.53 |$^{+0.19}_{\,-0.22}$| | 0.79 |$^{+5.38}_{\,-0.76}$| | 0.57 |$^{+0.57}_{\,-0.38}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.82 |$^{+0.92}_{\,-0.57}$| | 1.99 |$^{+0.21}_{\,-0.14}$| | 2.98 |$^{+1.52}_{\,-0.68}$| | 1.87 |$^{+0.24}_{\,-0.25}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.08 |$^{+0.04}_{\,-0.02}$| | 0.27 |$^{+0.05}_{\,-0.05}$| | 0.05 |$^{+0.07}_{\,-0.02}$| | 0.14 |$^{+0.05}_{\,-0.05}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 349.39 |$/$| 275 (1.27) | 410.90 |$/$| 323 (1.27) | 114.73 |$/$| 101 (1.14) | 200.34 |$/$| 170 (1.18) |
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${Z_{}}$||$^\dag $| | 0.63 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.10}_{\,-0.11}$| | 0.55 |$^{+0.45}_{\,-0.29}$| | 0.59 |$^{+0.18}_{\,-0.15}$| |
| |$N_{\rm H(wind_{low})}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.38 |$^{+0.10}_{\,-0.11}$| | 0.57 |$^{+0.07}_{\,-0.07}$| | 0.39 |$^{+0.16}_{\,-0.14}$| | 0.19 |$^{+0.10}_{\,-0.12}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.04}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| | 0.64 |$^{+0.18}_{\,-0.05}$| | 0.67 |$^{+0.10}_{\,-0.05}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 2.60 |$^{+1.89}_{\,-1.36}$| | 3.91 |$^{+1.61}_{\,-1.36}$| | 0.23 |$^{+0.24}_{\,-0.10}$| | 0.44 |$^{+0.16}_{\,-0.12}$| |
| |$N_{\rm H(wind_{middle)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.70 |$^{+0.13}_{\,-0.12}$| | 0.71 |$^{+0.09}_{\,-0.08}$| | — | — |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.84 |$^{+0.13}_{\,-0.12}$| | 0.84 |$^{+0.06}_{\,-0.05}$| | — | — |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.52 |$^{+0.10}_{\,-0.09}$| | 0.55 |$^{+0.08}_{\,-0.08}$| | — | — |
| |$N_{\rm H(wind_{high)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.27 |$^{+0.69}_{\,-0.60}$| | 0.53 |$^{+0.19}_{\,-0.22}$| | 0.79 |$^{+5.38}_{\,-0.76}$| | 0.57 |$^{+0.57}_{\,-0.38}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.82 |$^{+0.92}_{\,-0.57}$| | 1.99 |$^{+0.21}_{\,-0.14}$| | 2.98 |$^{+1.52}_{\,-0.68}$| | 1.87 |$^{+0.24}_{\,-0.25}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.08 |$^{+0.04}_{\,-0.02}$| | 0.27 |$^{+0.05}_{\,-0.05}$| | 0.05 |$^{+0.07}_{\,-0.02}$| | 0.14 |$^{+0.05}_{\,-0.05}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 349.39 |$/$| 275 (1.27) | 410.90 |$/$| 323 (1.27) | 114.73 |$/$| 101 (1.14) | 200.34 |$/$| 170 (1.18) |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7 kpc (Hanson (2003).
Best-fit parameters of the two- or three-temperature CIE model with free circumstellar absorptions. |$^*$|
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${Z_{}}$||$^\dag $| | 0.63 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.10}_{\,-0.11}$| | 0.55 |$^{+0.45}_{\,-0.29}$| | 0.59 |$^{+0.18}_{\,-0.15}$| |
| |$N_{\rm H(wind_{low})}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.38 |$^{+0.10}_{\,-0.11}$| | 0.57 |$^{+0.07}_{\,-0.07}$| | 0.39 |$^{+0.16}_{\,-0.14}$| | 0.19 |$^{+0.10}_{\,-0.12}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.04}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| | 0.64 |$^{+0.18}_{\,-0.05}$| | 0.67 |$^{+0.10}_{\,-0.05}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 2.60 |$^{+1.89}_{\,-1.36}$| | 3.91 |$^{+1.61}_{\,-1.36}$| | 0.23 |$^{+0.24}_{\,-0.10}$| | 0.44 |$^{+0.16}_{\,-0.12}$| |
| |$N_{\rm H(wind_{middle)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.70 |$^{+0.13}_{\,-0.12}$| | 0.71 |$^{+0.09}_{\,-0.08}$| | — | — |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.84 |$^{+0.13}_{\,-0.12}$| | 0.84 |$^{+0.06}_{\,-0.05}$| | — | — |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.52 |$^{+0.10}_{\,-0.09}$| | 0.55 |$^{+0.08}_{\,-0.08}$| | — | — |
| |$N_{\rm H(wind_{high)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.27 |$^{+0.69}_{\,-0.60}$| | 0.53 |$^{+0.19}_{\,-0.22}$| | 0.79 |$^{+5.38}_{\,-0.76}$| | 0.57 |$^{+0.57}_{\,-0.38}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.82 |$^{+0.92}_{\,-0.57}$| | 1.99 |$^{+0.21}_{\,-0.14}$| | 2.98 |$^{+1.52}_{\,-0.68}$| | 1.87 |$^{+0.24}_{\,-0.25}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.08 |$^{+0.04}_{\,-0.02}$| | 0.27 |$^{+0.05}_{\,-0.05}$| | 0.05 |$^{+0.07}_{\,-0.02}$| | 0.14 |$^{+0.05}_{\,-0.05}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 349.39 |$/$| 275 (1.27) | 410.90 |$/$| 323 (1.27) | 114.73 |$/$| 101 (1.14) | 200.34 |$/$| 170 (1.18) |
| . | No. 5 . | No. 8a . | No. 9 . | No. 12 . |
|---|---|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 1.047 . | 0.831 . | 1.148 . | 1.698 . |
| |${Z_{}}$||$^\dag $| | 0.63 |$^{+0.15}_{\,-0.13}$| | 0.87 |$^{+0.10}_{\,-0.11}$| | 0.55 |$^{+0.45}_{\,-0.29}$| | 0.59 |$^{+0.18}_{\,-0.15}$| |
| |$N_{\rm H(wind_{low})}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.38 |$^{+0.10}_{\,-0.11}$| | 0.57 |$^{+0.07}_{\,-0.07}$| | 0.39 |$^{+0.16}_{\,-0.14}$| | 0.19 |$^{+0.10}_{\,-0.12}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.04}_{\,-0.02}$| | 0.23 |$^{+0.02}_{\,-0.01}$| | 0.64 |$^{+0.18}_{\,-0.05}$| | 0.67 |$^{+0.10}_{\,-0.05}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 2.60 |$^{+1.89}_{\,-1.36}$| | 3.91 |$^{+1.61}_{\,-1.36}$| | 0.23 |$^{+0.24}_{\,-0.10}$| | 0.44 |$^{+0.16}_{\,-0.12}$| |
| |$N_{\rm H(wind_{middle)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.70 |$^{+0.13}_{\,-0.12}$| | 0.71 |$^{+0.09}_{\,-0.08}$| | — | — |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.84 |$^{+0.13}_{\,-0.12}$| | 0.84 |$^{+0.06}_{\,-0.05}$| | — | — |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.52 |$^{+0.10}_{\,-0.09}$| | 0.55 |$^{+0.08}_{\,-0.08}$| | — | — |
| |$N_{\rm H(wind_{high)}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.27 |$^{+0.69}_{\,-0.60}$| | 0.53 |$^{+0.19}_{\,-0.22}$| | 0.79 |$^{+5.38}_{\,-0.76}$| | 0.57 |$^{+0.57}_{\,-0.38}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.82 |$^{+0.92}_{\,-0.57}$| | 1.99 |$^{+0.21}_{\,-0.14}$| | 2.98 |$^{+1.52}_{\,-0.68}$| | 1.87 |$^{+0.24}_{\,-0.25}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3})$||$^\ddag $| | 0.08 |$^{+0.04}_{\,-0.02}$| | 0.27 |$^{+0.05}_{\,-0.05}$| | 0.05 |$^{+0.07}_{\,-0.02}$| | 0.14 |$^{+0.05}_{\,-0.05}$| |
| |$\chi^{2}/$| d.o.f. ( |$\chi^{2}_{\rm {red}}$| ) | 349.39 |$/$| 275 (1.27) | 410.90 |$/$| 323 (1.27) | 114.73 |$/$| 101 (1.14) | 200.34 |$/$| 170 (1.18) |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7 kpc (Hanson (2003).
Best-fit parameters of the hard-state spectrum and the soft-state spectrum of star No. 8a. |$^*$|
| . | No. 8a hard state . | No. 8a soft state . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 0.831 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.69 |$^{+0.07}_{\,-0.07}$| | 0.58 |$^{+0.07}_{\,-0.08}$| |
| |$^\dag $| | 1.13 |$^{+0.30}_{\,-0.23}$| | 0.85 |$^{+0.22}_{\,-0.17}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.03}_{\,-0.02}$| | 0.27 |$^{+0.07}_{\,-0.04}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 4.25 |$^{+3.11}_{\,-2.15}$| | 2.10 |$^{+2.74}_{\,-1.20}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.81 |$^{+0.08}_{\,-0.06}$| | 0.79 |$^{+0.08}_{\,-0.07}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.44 |$^{+0.11}_{\,-0.09}$| | 0.52 |$^{+0.13}_{\,-0.11}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.08 |$^{+0.18}_{\,-0.14}$| | 1.73 |$^{+0.15}_{\,-0.12}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.28 |$^{+0.05}_{\,-0.04}$| | 0.32 |$^{+0.07}_{\,-0.06}$| |
| . | No. 8a hard state . | No. 8a soft state . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 0.831 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.69 |$^{+0.07}_{\,-0.07}$| | 0.58 |$^{+0.07}_{\,-0.08}$| |
| |$^\dag $| | 1.13 |$^{+0.30}_{\,-0.23}$| | 0.85 |$^{+0.22}_{\,-0.17}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.03}_{\,-0.02}$| | 0.27 |$^{+0.07}_{\,-0.04}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 4.25 |$^{+3.11}_{\,-2.15}$| | 2.10 |$^{+2.74}_{\,-1.20}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.81 |$^{+0.08}_{\,-0.06}$| | 0.79 |$^{+0.08}_{\,-0.07}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.44 |$^{+0.11}_{\,-0.09}$| | 0.52 |$^{+0.13}_{\,-0.11}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.08 |$^{+0.18}_{\,-0.14}$| | 1.73 |$^{+0.15}_{\,-0.12}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.28 |$^{+0.05}_{\,-0.04}$| | 0.32 |$^{+0.07}_{\,-0.06}$| |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7 kpc (Hanson (2003).
Best-fit parameters of the hard-state spectrum and the soft-state spectrum of star No. 8a. |$^*$|
| . | No. 8a hard state . | No. 8a soft state . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 0.831 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.69 |$^{+0.07}_{\,-0.07}$| | 0.58 |$^{+0.07}_{\,-0.08}$| |
| |$^\dag $| | 1.13 |$^{+0.30}_{\,-0.23}$| | 0.85 |$^{+0.22}_{\,-0.17}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.03}_{\,-0.02}$| | 0.27 |$^{+0.07}_{\,-0.04}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 4.25 |$^{+3.11}_{\,-2.15}$| | 2.10 |$^{+2.74}_{\,-1.20}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.81 |$^{+0.08}_{\,-0.06}$| | 0.79 |$^{+0.08}_{\,-0.07}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.44 |$^{+0.11}_{\,-0.09}$| | 0.52 |$^{+0.13}_{\,-0.11}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.08 |$^{+0.18}_{\,-0.14}$| | 1.73 |$^{+0.15}_{\,-0.12}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.28 |$^{+0.05}_{\,-0.04}$| | 0.32 |$^{+0.07}_{\,-0.06}$| |
| . | No. 8a hard state . | No. 8a soft state . |
|---|---|---|
| |$N_{\rm H(ISM)}$| (10 |$^{22}$| Hcm |$^{-2}$| ) . | 0.831 . | 0.831 . |
| |${N_{\rm H}}$| (10 |$^{22}$| Hcm |$^{-2}$| ) | 0.69 |$^{+0.07}_{\,-0.07}$| | 0.58 |$^{+0.07}_{\,-0.08}$| |
| |$^\dag $| | 1.13 |$^{+0.30}_{\,-0.23}$| | 0.85 |$^{+0.22}_{\,-0.17}$| |
| |${k_{\rm {B}}T}_{\rm {low}}$| (keV) | 0.23 |$^{+0.03}_{\,-0.02}$| | 0.27 |$^{+0.07}_{\,-0.04}$| |
| |$EM_{\rm {low}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 4.25 |$^{+3.11}_{\,-2.15}$| | 2.10 |$^{+2.74}_{\,-1.20}$| |
| |${k_{\rm {B}}T}_{\rm {middle}}$| (keV) | 0.81 |$^{+0.08}_{\,-0.06}$| | 0.79 |$^{+0.08}_{\,-0.07}$| |
| |$EM_{\rm {middle}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.44 |$^{+0.11}_{\,-0.09}$| | 0.52 |$^{+0.13}_{\,-0.11}$| |
| |${k_{\rm {B}}T}_{\rm {high}}$| (keV) | 2.08 |$^{+0.18}_{\,-0.14}$| | 1.73 |$^{+0.15}_{\,-0.12}$| |
| |$EM_{\rm {high}}$| (10 |$^{57}$| cm |$^{-3}$| ) |$^\ddag $| | 0.28 |$^{+0.05}_{\,-0.04}$| | 0.32 |$^{+0.07}_{\,-0.06}$| |
The errors are 90% confidence level.
Values are ratios to the solar.
The distance to Cyg OB2 is assumed to be 1.7 kpc (Hanson (2003).
The ASCA/SIS, Chandra/ASIS-S, I, and XMM-Newton/ EPIC spectra of the four stars were extracted using xselect (version 2.4a), CIAO version 4.2, and SAS version 10.0.0, respectively. The obtained spectra were fitted with the same models as we used in the Suzaku analysis: the three-temperature CIE model for Nos. 5 and 8a and the two-temperature CIE model for Nos. 9 and 12. In figure 6, the obtained light curves for the four stars in the energy ranges 0.5–4.0 keV and 4.0–10 keV are plotted. All of the stars show a relatively large variation with a factor of more than 2.
Since we know that three stars (Nos. 5, 8a, and 9) have orbital periods, we folded the obtained light curves with the known periods (6.6 d, 21.9 d, and 2.35 yr for Nos. 5, 8a, and 9, respectively). We divided the ROSAT observation ID:900314 into four successive data-points for stars Nos. 5 and 8a, because its observation time was long. In figure 7, the folded light curves are plotted. No. 8a shows clear orbital modulation, which was previously pointed out by De Becker et al. (2006). No. 9 also shows a hint of orbital modulation in the low-energy band with a maximum around phase 0.0 and the minimum around phase 0.5.
4 Discussion
We analyzed Suzaku data of four stars (Nos. 5, 8a, 9, and 12) in the Cyg OB2 association. We found a statistically significant time variation in No. 8a, with time scales of |$\sim$| 20 ks in the high-energy band and of |$\sim$| 80 ks in the low-energy band. Although Albacete Colombo et al. (2007) reported the detection of an intensity decay of No. 12, a gradual decay of |$\sim$| 20% in 100 ks, we did not observe any time variation in this star during the Suzaku observation.
The energy spectra of the four stars, obtained by Suzaku, exhibit emission lines including Mg-K, Si-K, S-K, and Fe-K, suggesting a thin-thermal plasma origin. We fit the four spectra by multi-temperature CIE models. Nos. 9 and 12 could be fitted reasonably by a combination of emissions from 0.6–0.8 keV and |$\sim$| 2.0–3.0 keV CIE plasmas, while Nos. 5 and 8a require at least three CIE plasmas with temperatures of |$\sim$| 0.2 keV, |$\sim$| 0.8 keV, and |$\sim$| 2.0 keV, which are roughly consistent with those obtained by De Becker et al. (2006). This difference might arise from the fact that the spectra of Nos. 5 and 8a are statistically better than those of the other stars, which means that the 0.6–0.8 keV components obtained in the two-temperature model, in Nos. 9 and 12, are just rough approximations, and multiple-temperature components are inferred. In fact, recent high-resolution observations with the Chandra HETGS and XMM-Newton Reflection Grating Spectrometer clarify the existence of a gradual temperature distribution (e.g., Waldron & Cassinelli (2007)). Therefore, the three-component model should be considered to be still just an approximation of more complex plasmas. However, an approximation with a combination of several components is still useful for studying the rough structure of the temperature distribution of the X-ray emitting plasma. Especially, our finding of a short-term variation of the high-temperature component of No. 8a suggests that the high-temperature component could be independent from the other components.
| Observation start date/ID . | Satellite/Instrument . | No. 5 |$^*$| . | No. 8a |$^*$| . | No. 9 |$^*$| . | No. 12 |$^*$| . | ||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . |
| 1978-12-15 |$^\S$| / | Einstein/IPC | 1.10 |$^{+0.10}_{\,-0.10}$| | — | 3.10 |$^{+0.20}_{\,-0.20}$| | — | 1.50 |$^{+0.10}_{\,-0.10}$| | — | 0.89 |$^{+0.04}_{\,-0.04}$| | — |
| 1979-11-22/5219 | Einstein/IPC | 1.62 |$^{+0.12}_{\,-0.12}$| | — | 4.24 |$^{+0.22}_{\,-0.22}$| | — | 0.62 |$^{+0.11}_{\,-0.11}$| | — | 1.04 |$^{+0.12}_{\,-0.12}$| | — |
| 1980-06-09/4221 | Einstein/IPC | 2.16 |$^{+0.04}_{\,-0.04}$| | — | 3.81 |$^{+0.06}_{\,-0.06}$| | — | 0.84 |$^{+0.04}_{\,-0.04}$| | — | 1.09 |$^{+0.04}_{\,-0.04}$| | — |
| 1991-04-21/200109 | ROSAT/PSPC | 2.09 |$^{+0.18}_{\,-0.18}$| | — | 2.80 |$^{+0.19}_{\,-0.18}$| | — | 0.60 |$^{+0.09}_{\,-0.09}$| | — | 1.79 |$^{+0.19}_{\,-0.22}$| | — |
| 1993-04-29/20003000 | ASCA/SIS | 3.92 |$^{+0.02}_{\,-1.53}$| | 1.45 |$^{+0.64}_{\,-1.08}$| | 7.79 |$^{+0.09}_{\,-1.13}$| | 1.44 |$^{+0.17}_{\,-0.46}$| | 1.63 |$^{+0.13}_{\,-0.66}$| | 1.00 |$^{+0.19}_{\,-0.51}$| | 2.70 |$^{+0.21}_{\,-1.07}$| | 0.50 |$^{+0.18}_{\,-0.32}$| |
| 1993-04-29/900314 | ROSAT/PSPC | 2.38 |$^{+0.08}_{\,-0.08}$| | — | 4.14 |$^{+0.09}_{\,-0.10}$| | — | 0.76 |$^{+0.05}_{\,-0.05}$| | — | 1.79 |$^{+0.10}_{\,-0.11}$| | — |
| 2002-07-31/2572 | Chandra/ACIS-S | 2.12 |$^{+0.53}_{\,-0.77}$| | 0.25 |$^{+0.05}_{\,-0.13}$| | 3.16 |$^{+0.08}_{\,-0.60}$| | 0.65 |$^{+0.06}_{\,-0.20}$| | 0.99 |$^{+0.08}_{\,-0.29}$| | 0.41 |$^{+0.06}_{\,-0.20}$| | 1.16 |$^{+0.06}_{\,-0.45}$| | 0.22 |$^{+0.04}_{\,-0.20}$| |
| 2004-01-16/4511 | Chandra/ACIS-I | — | — | 3.32 |$^{+0.11}_{\,-0.08}$| | 2.17 |$^{+0.13}_{\,-1.04}$| | 0.96 |$^{+0.04}_{\,-0.07}$| | 0.77 |$^{+0.04}_{\,-0.12}$| | 1.72 |$^{+0.08}_{\,-0.13}$| | 0.36 |$^{+0.03}_{\,-0.09}$| |
| 2004-10-29/0200450201 | XMM-Newton /EPIC | 2.13 |$^{+0.06}_{\,-0.38}$| | 0.37 |$^{+0.05}_{\,-0.15}$| | 5.01 |$^{+0.05}_{\,-0.08}$| | 1.06 |$^{+0.03}_{\,-0.04}$| | 1.12 |$^{+0.04}_{\,-0.08}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.92 |$^{+0.09}_{\,-0.18}$| | 0.51 |$^{+0.03}_{\,-0.08}$| |
| 2004-11-08/0200450301 | XMM-Newton /EPIC | 2.47 |$^{+0.05}_{\,-0.33}$| | 0.38 |$^{+0.03}_{\,-0.06}$| | 4.16 |$^{+0.05}_{\,-0.11}$| | 0.66 |$^{+0.02}_{\,-0.03}$| | 1.19 |$^{+0.05}_{\,-0.08}$| | 0.45 |$^{+0.03}_{\,-0.04}$| | 2.18 |$^{+0.08}_{\,-0.10}$| | 0.62 |$^{+0.04}_{\,-0.05}$| |
| 2004-11-18/0200450401 | XMM-Newton /EPIC | 2.41 |$^{+0.07}_{\,-0.33}$| | 0.36 |$^{+0.04}_{\,-0.08}$| | 4.90 |$^{+0.04}_{\,-0.08}$| | 1.04 |$^{+0.03}_{\,-0.04}$| | 1.14 |$^{+0.05}_{\,-0.11}$| | 0.44 |$^{+0.03}_{\,-0.04}$| | 2.56 |$^{+0.08}_{\,-0.11}$| | 0.70 |$^{+0.04}_{\,-0.06}$| |
| 2004-11-28/0200450501 | XMM-Newton /EPIC | 2.48 |$^{+0.07}_{\,-0.48}$| | 0.29 |$^{+0.04}_{\,-0.08}$| | 4.76 |$^{+0.05}_{\,-0.30}$| | 0.80 |$^{+0.04}_{\,-0.05}$| | 1.16 |$^{+0.06}_{\,-0.22}$| | 0.43 |$^{+0.05}_{\,-0.09}$| | 2.17 |$^{+0.12}_{\,-0.22}$| | 0.45 |$^{+0.06}_{\,-0.14}$| |
| 2007-04-29/0505110301 | XMM-Newton /EPIC | 3.60 |$^{+0.05}_{\,-0.27}$| | 0.63 |$^{+0.05}_{\,-0.06}$| | 4.54 |$^{+0.03}_{\,-0.10}$| | 0.82 |$^{+0.03}_{\,-0.03}$| | 1.10 |$^{+0.05}_{\,-0.07}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.42 |$^{+0.07}_{\,-0.21}$| | 0.43 |$^{+0.06}_{\,-0.32}$| |
| 2007-05-03/0505110401 | XMM-Newton /EPIC | 4.65 |$^{+0.06}_{\,-0.23}$| | 0.90 |$^{+0.05}_{\,-0.08}$| | 5.13 |$^{+0.04}_{\,-0.07}$| | 0.97 |$^{+0.03}_{\,-0.04}$| | 1.09 |$^{+0.06}_{\,-0.10}$| | 0.41 |$^{+0.03}_{\,-0.04}$| | 1.52 |$^{+0.08}_{\,-0.13}$| | 0.39 |$^{+0.04}_{\,-0.07}$| |
| 2007-12-18/402030010 | Suzaku/XIS | 3.30 |$^{+0.07}_{\,-0.31}$| | 0.65 |$^{+0.05}_{\,-0.08}$| | 7.09 |$^{+0.04}_{\,-0.20}$| | 1.28 |$^{+0.06}_{\,-0.06}$| | 1.04 |$^{+0.06}_{\,-0.24}$| | 0.41 |$^{+0.05}_{\,-0.14}$| | 1.88 |$^{+0.11}_{\,-0.17}$| | 0.48 |$^{+0.05}_{\,-0.11}$| |
| 2010-02-11/10951 | Chandra/ACIS-I | 1.60 |$^{+0.06}_{\,-0.34}$| | 0.27 |$^{+0.05}_{\,-0.22}$| | — | — | — | — | — | — |
| 2010-02-11/10952 | Chandra/ACIS-I | 1.94 |$^{+0.07}_{\,-0.43}$| | 0.55 |$^{+0.06}_{\,-0.28}$| | — | — | — | — | 1.60 |$^{+0.11}_{\,-0.29}$| | 0.46 |$^{+0.04}_{\,-0.18}$| |
| 2010-02-12/10953 | Chandra/ACIS-I | — | — | — | — | — | — | 1.59 |$^{+0.11}_{\,-0.29}$| | 0.51 |$^{+0.07}_{\,-0.36}$| |
| 2010-02-14/10955 | Chandra/ACIS-I | — | — | 4.64 |$^{+0.04}_{\,-0.44}$| | 1.77 |$^{+0.09}_{\,-0.21}$| | 0.91 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.04}_{\,-0.12}$| | — | — |
| 2010-02-15/10956 | Chandra/ACIS-I | 2.27 |$^{+0.07}_{\,-0.37}$| | 0.42 |$^{+0.08}_{\,-0.34}$| | 5.28 |$^{+0.04}_{\,-0.62}$| | 1.40 |$^{+0.07}_{\,-0.42}$| | 0.63 |$^{+0.02}_{\,-0.18}$| | 0.42 |$^{+0.04}_{\,-0.34}$| | 1.42 |$^{+0.03}_{\,-0.17}$| | 0.64 |$^{+0.10}_{\,-0.49}$| |
| 2010-02-16/10957 | Chandra/ACIS-I | — | — | 4.60 |$^{+0.06}_{\,-0.36}$| | 1.45 |$^{+0.11}_{\,-0.55}$| | 0.77 |$^{+0.05}_{\,-0.11}$| | 0.32 |$^{+0.09}_{\,-0.20}$| | — | — |
| 2010-02-17/10958 | Chandra/ACIS-I | 2.10 |$^{+0.06}_{\,-0.31}$| | 0.45 |$^{+0.04}_{\,-0.16}$| | 4.35 |$^{+0.16}_{\,-0.47}$| | 1.01 |$^{+0.11}_{\,-0.58}$| | 0.77 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.06}_{\,-0.21}$| | 1.55 |$^{+0.07}_{\,-0.18}$| | 0.40 |$^{+0.03}_{\,-0.06}$| |
| 2010-02-22/10962 | Chandra/ACIS-I | 1.77 |$^{+0.06}_{\,-0.37}$| | 0.27 |$^{+0.05}_{\,-0.18}$| | — | — | — | — | — | — |
| Observation start date/ID . | Satellite/Instrument . | No. 5 |$^*$| . | No. 8a |$^*$| . | No. 9 |$^*$| . | No. 12 |$^*$| . | ||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . |
| 1978-12-15 |$^\S$| / | Einstein/IPC | 1.10 |$^{+0.10}_{\,-0.10}$| | — | 3.10 |$^{+0.20}_{\,-0.20}$| | — | 1.50 |$^{+0.10}_{\,-0.10}$| | — | 0.89 |$^{+0.04}_{\,-0.04}$| | — |
| 1979-11-22/5219 | Einstein/IPC | 1.62 |$^{+0.12}_{\,-0.12}$| | — | 4.24 |$^{+0.22}_{\,-0.22}$| | — | 0.62 |$^{+0.11}_{\,-0.11}$| | — | 1.04 |$^{+0.12}_{\,-0.12}$| | — |
| 1980-06-09/4221 | Einstein/IPC | 2.16 |$^{+0.04}_{\,-0.04}$| | — | 3.81 |$^{+0.06}_{\,-0.06}$| | — | 0.84 |$^{+0.04}_{\,-0.04}$| | — | 1.09 |$^{+0.04}_{\,-0.04}$| | — |
| 1991-04-21/200109 | ROSAT/PSPC | 2.09 |$^{+0.18}_{\,-0.18}$| | — | 2.80 |$^{+0.19}_{\,-0.18}$| | — | 0.60 |$^{+0.09}_{\,-0.09}$| | — | 1.79 |$^{+0.19}_{\,-0.22}$| | — |
| 1993-04-29/20003000 | ASCA/SIS | 3.92 |$^{+0.02}_{\,-1.53}$| | 1.45 |$^{+0.64}_{\,-1.08}$| | 7.79 |$^{+0.09}_{\,-1.13}$| | 1.44 |$^{+0.17}_{\,-0.46}$| | 1.63 |$^{+0.13}_{\,-0.66}$| | 1.00 |$^{+0.19}_{\,-0.51}$| | 2.70 |$^{+0.21}_{\,-1.07}$| | 0.50 |$^{+0.18}_{\,-0.32}$| |
| 1993-04-29/900314 | ROSAT/PSPC | 2.38 |$^{+0.08}_{\,-0.08}$| | — | 4.14 |$^{+0.09}_{\,-0.10}$| | — | 0.76 |$^{+0.05}_{\,-0.05}$| | — | 1.79 |$^{+0.10}_{\,-0.11}$| | — |
| 2002-07-31/2572 | Chandra/ACIS-S | 2.12 |$^{+0.53}_{\,-0.77}$| | 0.25 |$^{+0.05}_{\,-0.13}$| | 3.16 |$^{+0.08}_{\,-0.60}$| | 0.65 |$^{+0.06}_{\,-0.20}$| | 0.99 |$^{+0.08}_{\,-0.29}$| | 0.41 |$^{+0.06}_{\,-0.20}$| | 1.16 |$^{+0.06}_{\,-0.45}$| | 0.22 |$^{+0.04}_{\,-0.20}$| |
| 2004-01-16/4511 | Chandra/ACIS-I | — | — | 3.32 |$^{+0.11}_{\,-0.08}$| | 2.17 |$^{+0.13}_{\,-1.04}$| | 0.96 |$^{+0.04}_{\,-0.07}$| | 0.77 |$^{+0.04}_{\,-0.12}$| | 1.72 |$^{+0.08}_{\,-0.13}$| | 0.36 |$^{+0.03}_{\,-0.09}$| |
| 2004-10-29/0200450201 | XMM-Newton /EPIC | 2.13 |$^{+0.06}_{\,-0.38}$| | 0.37 |$^{+0.05}_{\,-0.15}$| | 5.01 |$^{+0.05}_{\,-0.08}$| | 1.06 |$^{+0.03}_{\,-0.04}$| | 1.12 |$^{+0.04}_{\,-0.08}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.92 |$^{+0.09}_{\,-0.18}$| | 0.51 |$^{+0.03}_{\,-0.08}$| |
| 2004-11-08/0200450301 | XMM-Newton /EPIC | 2.47 |$^{+0.05}_{\,-0.33}$| | 0.38 |$^{+0.03}_{\,-0.06}$| | 4.16 |$^{+0.05}_{\,-0.11}$| | 0.66 |$^{+0.02}_{\,-0.03}$| | 1.19 |$^{+0.05}_{\,-0.08}$| | 0.45 |$^{+0.03}_{\,-0.04}$| | 2.18 |$^{+0.08}_{\,-0.10}$| | 0.62 |$^{+0.04}_{\,-0.05}$| |
| 2004-11-18/0200450401 | XMM-Newton /EPIC | 2.41 |$^{+0.07}_{\,-0.33}$| | 0.36 |$^{+0.04}_{\,-0.08}$| | 4.90 |$^{+0.04}_{\,-0.08}$| | 1.04 |$^{+0.03}_{\,-0.04}$| | 1.14 |$^{+0.05}_{\,-0.11}$| | 0.44 |$^{+0.03}_{\,-0.04}$| | 2.56 |$^{+0.08}_{\,-0.11}$| | 0.70 |$^{+0.04}_{\,-0.06}$| |
| 2004-11-28/0200450501 | XMM-Newton /EPIC | 2.48 |$^{+0.07}_{\,-0.48}$| | 0.29 |$^{+0.04}_{\,-0.08}$| | 4.76 |$^{+0.05}_{\,-0.30}$| | 0.80 |$^{+0.04}_{\,-0.05}$| | 1.16 |$^{+0.06}_{\,-0.22}$| | 0.43 |$^{+0.05}_{\,-0.09}$| | 2.17 |$^{+0.12}_{\,-0.22}$| | 0.45 |$^{+0.06}_{\,-0.14}$| |
| 2007-04-29/0505110301 | XMM-Newton /EPIC | 3.60 |$^{+0.05}_{\,-0.27}$| | 0.63 |$^{+0.05}_{\,-0.06}$| | 4.54 |$^{+0.03}_{\,-0.10}$| | 0.82 |$^{+0.03}_{\,-0.03}$| | 1.10 |$^{+0.05}_{\,-0.07}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.42 |$^{+0.07}_{\,-0.21}$| | 0.43 |$^{+0.06}_{\,-0.32}$| |
| 2007-05-03/0505110401 | XMM-Newton /EPIC | 4.65 |$^{+0.06}_{\,-0.23}$| | 0.90 |$^{+0.05}_{\,-0.08}$| | 5.13 |$^{+0.04}_{\,-0.07}$| | 0.97 |$^{+0.03}_{\,-0.04}$| | 1.09 |$^{+0.06}_{\,-0.10}$| | 0.41 |$^{+0.03}_{\,-0.04}$| | 1.52 |$^{+0.08}_{\,-0.13}$| | 0.39 |$^{+0.04}_{\,-0.07}$| |
| 2007-12-18/402030010 | Suzaku/XIS | 3.30 |$^{+0.07}_{\,-0.31}$| | 0.65 |$^{+0.05}_{\,-0.08}$| | 7.09 |$^{+0.04}_{\,-0.20}$| | 1.28 |$^{+0.06}_{\,-0.06}$| | 1.04 |$^{+0.06}_{\,-0.24}$| | 0.41 |$^{+0.05}_{\,-0.14}$| | 1.88 |$^{+0.11}_{\,-0.17}$| | 0.48 |$^{+0.05}_{\,-0.11}$| |
| 2010-02-11/10951 | Chandra/ACIS-I | 1.60 |$^{+0.06}_{\,-0.34}$| | 0.27 |$^{+0.05}_{\,-0.22}$| | — | — | — | — | — | — |
| 2010-02-11/10952 | Chandra/ACIS-I | 1.94 |$^{+0.07}_{\,-0.43}$| | 0.55 |$^{+0.06}_{\,-0.28}$| | — | — | — | — | 1.60 |$^{+0.11}_{\,-0.29}$| | 0.46 |$^{+0.04}_{\,-0.18}$| |
| 2010-02-12/10953 | Chandra/ACIS-I | — | — | — | — | — | — | 1.59 |$^{+0.11}_{\,-0.29}$| | 0.51 |$^{+0.07}_{\,-0.36}$| |
| 2010-02-14/10955 | Chandra/ACIS-I | — | — | 4.64 |$^{+0.04}_{\,-0.44}$| | 1.77 |$^{+0.09}_{\,-0.21}$| | 0.91 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.04}_{\,-0.12}$| | — | — |
| 2010-02-15/10956 | Chandra/ACIS-I | 2.27 |$^{+0.07}_{\,-0.37}$| | 0.42 |$^{+0.08}_{\,-0.34}$| | 5.28 |$^{+0.04}_{\,-0.62}$| | 1.40 |$^{+0.07}_{\,-0.42}$| | 0.63 |$^{+0.02}_{\,-0.18}$| | 0.42 |$^{+0.04}_{\,-0.34}$| | 1.42 |$^{+0.03}_{\,-0.17}$| | 0.64 |$^{+0.10}_{\,-0.49}$| |
| 2010-02-16/10957 | Chandra/ACIS-I | — | — | 4.60 |$^{+0.06}_{\,-0.36}$| | 1.45 |$^{+0.11}_{\,-0.55}$| | 0.77 |$^{+0.05}_{\,-0.11}$| | 0.32 |$^{+0.09}_{\,-0.20}$| | — | — |
| 2010-02-17/10958 | Chandra/ACIS-I | 2.10 |$^{+0.06}_{\,-0.31}$| | 0.45 |$^{+0.04}_{\,-0.16}$| | 4.35 |$^{+0.16}_{\,-0.47}$| | 1.01 |$^{+0.11}_{\,-0.58}$| | 0.77 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.06}_{\,-0.21}$| | 1.55 |$^{+0.07}_{\,-0.18}$| | 0.40 |$^{+0.03}_{\,-0.06}$| |
| 2010-02-22/10962 | Chandra/ACIS-I | 1.77 |$^{+0.06}_{\,-0.37}$| | 0.27 |$^{+0.05}_{\,-0.18}$| | — | — | — | — | — | — |
The unit of flux is |$\times$| 10 |$^{-12}$| ergcm |$^{-2}$| s.
0.5-4.0keV.
4.0-10.0keV.
Harnden et al. (1979) is referred.
| Observation start date/ID . | Satellite/Instrument . | No. 5 |$^*$| . | No. 8a |$^*$| . | No. 9 |$^*$| . | No. 12 |$^*$| . | ||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . |
| 1978-12-15 |$^\S$| / | Einstein/IPC | 1.10 |$^{+0.10}_{\,-0.10}$| | — | 3.10 |$^{+0.20}_{\,-0.20}$| | — | 1.50 |$^{+0.10}_{\,-0.10}$| | — | 0.89 |$^{+0.04}_{\,-0.04}$| | — |
| 1979-11-22/5219 | Einstein/IPC | 1.62 |$^{+0.12}_{\,-0.12}$| | — | 4.24 |$^{+0.22}_{\,-0.22}$| | — | 0.62 |$^{+0.11}_{\,-0.11}$| | — | 1.04 |$^{+0.12}_{\,-0.12}$| | — |
| 1980-06-09/4221 | Einstein/IPC | 2.16 |$^{+0.04}_{\,-0.04}$| | — | 3.81 |$^{+0.06}_{\,-0.06}$| | — | 0.84 |$^{+0.04}_{\,-0.04}$| | — | 1.09 |$^{+0.04}_{\,-0.04}$| | — |
| 1991-04-21/200109 | ROSAT/PSPC | 2.09 |$^{+0.18}_{\,-0.18}$| | — | 2.80 |$^{+0.19}_{\,-0.18}$| | — | 0.60 |$^{+0.09}_{\,-0.09}$| | — | 1.79 |$^{+0.19}_{\,-0.22}$| | — |
| 1993-04-29/20003000 | ASCA/SIS | 3.92 |$^{+0.02}_{\,-1.53}$| | 1.45 |$^{+0.64}_{\,-1.08}$| | 7.79 |$^{+0.09}_{\,-1.13}$| | 1.44 |$^{+0.17}_{\,-0.46}$| | 1.63 |$^{+0.13}_{\,-0.66}$| | 1.00 |$^{+0.19}_{\,-0.51}$| | 2.70 |$^{+0.21}_{\,-1.07}$| | 0.50 |$^{+0.18}_{\,-0.32}$| |
| 1993-04-29/900314 | ROSAT/PSPC | 2.38 |$^{+0.08}_{\,-0.08}$| | — | 4.14 |$^{+0.09}_{\,-0.10}$| | — | 0.76 |$^{+0.05}_{\,-0.05}$| | — | 1.79 |$^{+0.10}_{\,-0.11}$| | — |
| 2002-07-31/2572 | Chandra/ACIS-S | 2.12 |$^{+0.53}_{\,-0.77}$| | 0.25 |$^{+0.05}_{\,-0.13}$| | 3.16 |$^{+0.08}_{\,-0.60}$| | 0.65 |$^{+0.06}_{\,-0.20}$| | 0.99 |$^{+0.08}_{\,-0.29}$| | 0.41 |$^{+0.06}_{\,-0.20}$| | 1.16 |$^{+0.06}_{\,-0.45}$| | 0.22 |$^{+0.04}_{\,-0.20}$| |
| 2004-01-16/4511 | Chandra/ACIS-I | — | — | 3.32 |$^{+0.11}_{\,-0.08}$| | 2.17 |$^{+0.13}_{\,-1.04}$| | 0.96 |$^{+0.04}_{\,-0.07}$| | 0.77 |$^{+0.04}_{\,-0.12}$| | 1.72 |$^{+0.08}_{\,-0.13}$| | 0.36 |$^{+0.03}_{\,-0.09}$| |
| 2004-10-29/0200450201 | XMM-Newton /EPIC | 2.13 |$^{+0.06}_{\,-0.38}$| | 0.37 |$^{+0.05}_{\,-0.15}$| | 5.01 |$^{+0.05}_{\,-0.08}$| | 1.06 |$^{+0.03}_{\,-0.04}$| | 1.12 |$^{+0.04}_{\,-0.08}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.92 |$^{+0.09}_{\,-0.18}$| | 0.51 |$^{+0.03}_{\,-0.08}$| |
| 2004-11-08/0200450301 | XMM-Newton /EPIC | 2.47 |$^{+0.05}_{\,-0.33}$| | 0.38 |$^{+0.03}_{\,-0.06}$| | 4.16 |$^{+0.05}_{\,-0.11}$| | 0.66 |$^{+0.02}_{\,-0.03}$| | 1.19 |$^{+0.05}_{\,-0.08}$| | 0.45 |$^{+0.03}_{\,-0.04}$| | 2.18 |$^{+0.08}_{\,-0.10}$| | 0.62 |$^{+0.04}_{\,-0.05}$| |
| 2004-11-18/0200450401 | XMM-Newton /EPIC | 2.41 |$^{+0.07}_{\,-0.33}$| | 0.36 |$^{+0.04}_{\,-0.08}$| | 4.90 |$^{+0.04}_{\,-0.08}$| | 1.04 |$^{+0.03}_{\,-0.04}$| | 1.14 |$^{+0.05}_{\,-0.11}$| | 0.44 |$^{+0.03}_{\,-0.04}$| | 2.56 |$^{+0.08}_{\,-0.11}$| | 0.70 |$^{+0.04}_{\,-0.06}$| |
| 2004-11-28/0200450501 | XMM-Newton /EPIC | 2.48 |$^{+0.07}_{\,-0.48}$| | 0.29 |$^{+0.04}_{\,-0.08}$| | 4.76 |$^{+0.05}_{\,-0.30}$| | 0.80 |$^{+0.04}_{\,-0.05}$| | 1.16 |$^{+0.06}_{\,-0.22}$| | 0.43 |$^{+0.05}_{\,-0.09}$| | 2.17 |$^{+0.12}_{\,-0.22}$| | 0.45 |$^{+0.06}_{\,-0.14}$| |
| 2007-04-29/0505110301 | XMM-Newton /EPIC | 3.60 |$^{+0.05}_{\,-0.27}$| | 0.63 |$^{+0.05}_{\,-0.06}$| | 4.54 |$^{+0.03}_{\,-0.10}$| | 0.82 |$^{+0.03}_{\,-0.03}$| | 1.10 |$^{+0.05}_{\,-0.07}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.42 |$^{+0.07}_{\,-0.21}$| | 0.43 |$^{+0.06}_{\,-0.32}$| |
| 2007-05-03/0505110401 | XMM-Newton /EPIC | 4.65 |$^{+0.06}_{\,-0.23}$| | 0.90 |$^{+0.05}_{\,-0.08}$| | 5.13 |$^{+0.04}_{\,-0.07}$| | 0.97 |$^{+0.03}_{\,-0.04}$| | 1.09 |$^{+0.06}_{\,-0.10}$| | 0.41 |$^{+0.03}_{\,-0.04}$| | 1.52 |$^{+0.08}_{\,-0.13}$| | 0.39 |$^{+0.04}_{\,-0.07}$| |
| 2007-12-18/402030010 | Suzaku/XIS | 3.30 |$^{+0.07}_{\,-0.31}$| | 0.65 |$^{+0.05}_{\,-0.08}$| | 7.09 |$^{+0.04}_{\,-0.20}$| | 1.28 |$^{+0.06}_{\,-0.06}$| | 1.04 |$^{+0.06}_{\,-0.24}$| | 0.41 |$^{+0.05}_{\,-0.14}$| | 1.88 |$^{+0.11}_{\,-0.17}$| | 0.48 |$^{+0.05}_{\,-0.11}$| |
| 2010-02-11/10951 | Chandra/ACIS-I | 1.60 |$^{+0.06}_{\,-0.34}$| | 0.27 |$^{+0.05}_{\,-0.22}$| | — | — | — | — | — | — |
| 2010-02-11/10952 | Chandra/ACIS-I | 1.94 |$^{+0.07}_{\,-0.43}$| | 0.55 |$^{+0.06}_{\,-0.28}$| | — | — | — | — | 1.60 |$^{+0.11}_{\,-0.29}$| | 0.46 |$^{+0.04}_{\,-0.18}$| |
| 2010-02-12/10953 | Chandra/ACIS-I | — | — | — | — | — | — | 1.59 |$^{+0.11}_{\,-0.29}$| | 0.51 |$^{+0.07}_{\,-0.36}$| |
| 2010-02-14/10955 | Chandra/ACIS-I | — | — | 4.64 |$^{+0.04}_{\,-0.44}$| | 1.77 |$^{+0.09}_{\,-0.21}$| | 0.91 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.04}_{\,-0.12}$| | — | — |
| 2010-02-15/10956 | Chandra/ACIS-I | 2.27 |$^{+0.07}_{\,-0.37}$| | 0.42 |$^{+0.08}_{\,-0.34}$| | 5.28 |$^{+0.04}_{\,-0.62}$| | 1.40 |$^{+0.07}_{\,-0.42}$| | 0.63 |$^{+0.02}_{\,-0.18}$| | 0.42 |$^{+0.04}_{\,-0.34}$| | 1.42 |$^{+0.03}_{\,-0.17}$| | 0.64 |$^{+0.10}_{\,-0.49}$| |
| 2010-02-16/10957 | Chandra/ACIS-I | — | — | 4.60 |$^{+0.06}_{\,-0.36}$| | 1.45 |$^{+0.11}_{\,-0.55}$| | 0.77 |$^{+0.05}_{\,-0.11}$| | 0.32 |$^{+0.09}_{\,-0.20}$| | — | — |
| 2010-02-17/10958 | Chandra/ACIS-I | 2.10 |$^{+0.06}_{\,-0.31}$| | 0.45 |$^{+0.04}_{\,-0.16}$| | 4.35 |$^{+0.16}_{\,-0.47}$| | 1.01 |$^{+0.11}_{\,-0.58}$| | 0.77 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.06}_{\,-0.21}$| | 1.55 |$^{+0.07}_{\,-0.18}$| | 0.40 |$^{+0.03}_{\,-0.06}$| |
| 2010-02-22/10962 | Chandra/ACIS-I | 1.77 |$^{+0.06}_{\,-0.37}$| | 0.27 |$^{+0.05}_{\,-0.18}$| | — | — | — | — | — | — |
| Observation start date/ID . | Satellite/Instrument . | No. 5 |$^*$| . | No. 8a |$^*$| . | No. 9 |$^*$| . | No. 12 |$^*$| . | ||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . | Low |$^\dagger$| . | High |$^\ddagger$| . |
| 1978-12-15 |$^\S$| / | Einstein/IPC | 1.10 |$^{+0.10}_{\,-0.10}$| | — | 3.10 |$^{+0.20}_{\,-0.20}$| | — | 1.50 |$^{+0.10}_{\,-0.10}$| | — | 0.89 |$^{+0.04}_{\,-0.04}$| | — |
| 1979-11-22/5219 | Einstein/IPC | 1.62 |$^{+0.12}_{\,-0.12}$| | — | 4.24 |$^{+0.22}_{\,-0.22}$| | — | 0.62 |$^{+0.11}_{\,-0.11}$| | — | 1.04 |$^{+0.12}_{\,-0.12}$| | — |
| 1980-06-09/4221 | Einstein/IPC | 2.16 |$^{+0.04}_{\,-0.04}$| | — | 3.81 |$^{+0.06}_{\,-0.06}$| | — | 0.84 |$^{+0.04}_{\,-0.04}$| | — | 1.09 |$^{+0.04}_{\,-0.04}$| | — |
| 1991-04-21/200109 | ROSAT/PSPC | 2.09 |$^{+0.18}_{\,-0.18}$| | — | 2.80 |$^{+0.19}_{\,-0.18}$| | — | 0.60 |$^{+0.09}_{\,-0.09}$| | — | 1.79 |$^{+0.19}_{\,-0.22}$| | — |
| 1993-04-29/20003000 | ASCA/SIS | 3.92 |$^{+0.02}_{\,-1.53}$| | 1.45 |$^{+0.64}_{\,-1.08}$| | 7.79 |$^{+0.09}_{\,-1.13}$| | 1.44 |$^{+0.17}_{\,-0.46}$| | 1.63 |$^{+0.13}_{\,-0.66}$| | 1.00 |$^{+0.19}_{\,-0.51}$| | 2.70 |$^{+0.21}_{\,-1.07}$| | 0.50 |$^{+0.18}_{\,-0.32}$| |
| 1993-04-29/900314 | ROSAT/PSPC | 2.38 |$^{+0.08}_{\,-0.08}$| | — | 4.14 |$^{+0.09}_{\,-0.10}$| | — | 0.76 |$^{+0.05}_{\,-0.05}$| | — | 1.79 |$^{+0.10}_{\,-0.11}$| | — |
| 2002-07-31/2572 | Chandra/ACIS-S | 2.12 |$^{+0.53}_{\,-0.77}$| | 0.25 |$^{+0.05}_{\,-0.13}$| | 3.16 |$^{+0.08}_{\,-0.60}$| | 0.65 |$^{+0.06}_{\,-0.20}$| | 0.99 |$^{+0.08}_{\,-0.29}$| | 0.41 |$^{+0.06}_{\,-0.20}$| | 1.16 |$^{+0.06}_{\,-0.45}$| | 0.22 |$^{+0.04}_{\,-0.20}$| |
| 2004-01-16/4511 | Chandra/ACIS-I | — | — | 3.32 |$^{+0.11}_{\,-0.08}$| | 2.17 |$^{+0.13}_{\,-1.04}$| | 0.96 |$^{+0.04}_{\,-0.07}$| | 0.77 |$^{+0.04}_{\,-0.12}$| | 1.72 |$^{+0.08}_{\,-0.13}$| | 0.36 |$^{+0.03}_{\,-0.09}$| |
| 2004-10-29/0200450201 | XMM-Newton /EPIC | 2.13 |$^{+0.06}_{\,-0.38}$| | 0.37 |$^{+0.05}_{\,-0.15}$| | 5.01 |$^{+0.05}_{\,-0.08}$| | 1.06 |$^{+0.03}_{\,-0.04}$| | 1.12 |$^{+0.04}_{\,-0.08}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.92 |$^{+0.09}_{\,-0.18}$| | 0.51 |$^{+0.03}_{\,-0.08}$| |
| 2004-11-08/0200450301 | XMM-Newton /EPIC | 2.47 |$^{+0.05}_{\,-0.33}$| | 0.38 |$^{+0.03}_{\,-0.06}$| | 4.16 |$^{+0.05}_{\,-0.11}$| | 0.66 |$^{+0.02}_{\,-0.03}$| | 1.19 |$^{+0.05}_{\,-0.08}$| | 0.45 |$^{+0.03}_{\,-0.04}$| | 2.18 |$^{+0.08}_{\,-0.10}$| | 0.62 |$^{+0.04}_{\,-0.05}$| |
| 2004-11-18/0200450401 | XMM-Newton /EPIC | 2.41 |$^{+0.07}_{\,-0.33}$| | 0.36 |$^{+0.04}_{\,-0.08}$| | 4.90 |$^{+0.04}_{\,-0.08}$| | 1.04 |$^{+0.03}_{\,-0.04}$| | 1.14 |$^{+0.05}_{\,-0.11}$| | 0.44 |$^{+0.03}_{\,-0.04}$| | 2.56 |$^{+0.08}_{\,-0.11}$| | 0.70 |$^{+0.04}_{\,-0.06}$| |
| 2004-11-28/0200450501 | XMM-Newton /EPIC | 2.48 |$^{+0.07}_{\,-0.48}$| | 0.29 |$^{+0.04}_{\,-0.08}$| | 4.76 |$^{+0.05}_{\,-0.30}$| | 0.80 |$^{+0.04}_{\,-0.05}$| | 1.16 |$^{+0.06}_{\,-0.22}$| | 0.43 |$^{+0.05}_{\,-0.09}$| | 2.17 |$^{+0.12}_{\,-0.22}$| | 0.45 |$^{+0.06}_{\,-0.14}$| |
| 2007-04-29/0505110301 | XMM-Newton /EPIC | 3.60 |$^{+0.05}_{\,-0.27}$| | 0.63 |$^{+0.05}_{\,-0.06}$| | 4.54 |$^{+0.03}_{\,-0.10}$| | 0.82 |$^{+0.03}_{\,-0.03}$| | 1.10 |$^{+0.05}_{\,-0.07}$| | 0.43 |$^{+0.03}_{\,-0.04}$| | 1.42 |$^{+0.07}_{\,-0.21}$| | 0.43 |$^{+0.06}_{\,-0.32}$| |
| 2007-05-03/0505110401 | XMM-Newton /EPIC | 4.65 |$^{+0.06}_{\,-0.23}$| | 0.90 |$^{+0.05}_{\,-0.08}$| | 5.13 |$^{+0.04}_{\,-0.07}$| | 0.97 |$^{+0.03}_{\,-0.04}$| | 1.09 |$^{+0.06}_{\,-0.10}$| | 0.41 |$^{+0.03}_{\,-0.04}$| | 1.52 |$^{+0.08}_{\,-0.13}$| | 0.39 |$^{+0.04}_{\,-0.07}$| |
| 2007-12-18/402030010 | Suzaku/XIS | 3.30 |$^{+0.07}_{\,-0.31}$| | 0.65 |$^{+0.05}_{\,-0.08}$| | 7.09 |$^{+0.04}_{\,-0.20}$| | 1.28 |$^{+0.06}_{\,-0.06}$| | 1.04 |$^{+0.06}_{\,-0.24}$| | 0.41 |$^{+0.05}_{\,-0.14}$| | 1.88 |$^{+0.11}_{\,-0.17}$| | 0.48 |$^{+0.05}_{\,-0.11}$| |
| 2010-02-11/10951 | Chandra/ACIS-I | 1.60 |$^{+0.06}_{\,-0.34}$| | 0.27 |$^{+0.05}_{\,-0.22}$| | — | — | — | — | — | — |
| 2010-02-11/10952 | Chandra/ACIS-I | 1.94 |$^{+0.07}_{\,-0.43}$| | 0.55 |$^{+0.06}_{\,-0.28}$| | — | — | — | — | 1.60 |$^{+0.11}_{\,-0.29}$| | 0.46 |$^{+0.04}_{\,-0.18}$| |
| 2010-02-12/10953 | Chandra/ACIS-I | — | — | — | — | — | — | 1.59 |$^{+0.11}_{\,-0.29}$| | 0.51 |$^{+0.07}_{\,-0.36}$| |
| 2010-02-14/10955 | Chandra/ACIS-I | — | — | 4.64 |$^{+0.04}_{\,-0.44}$| | 1.77 |$^{+0.09}_{\,-0.21}$| | 0.91 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.04}_{\,-0.12}$| | — | — |
| 2010-02-15/10956 | Chandra/ACIS-I | 2.27 |$^{+0.07}_{\,-0.37}$| | 0.42 |$^{+0.08}_{\,-0.34}$| | 5.28 |$^{+0.04}_{\,-0.62}$| | 1.40 |$^{+0.07}_{\,-0.42}$| | 0.63 |$^{+0.02}_{\,-0.18}$| | 0.42 |$^{+0.04}_{\,-0.34}$| | 1.42 |$^{+0.03}_{\,-0.17}$| | 0.64 |$^{+0.10}_{\,-0.49}$| |
| 2010-02-16/10957 | Chandra/ACIS-I | — | — | 4.60 |$^{+0.06}_{\,-0.36}$| | 1.45 |$^{+0.11}_{\,-0.55}$| | 0.77 |$^{+0.05}_{\,-0.11}$| | 0.32 |$^{+0.09}_{\,-0.20}$| | — | — |
| 2010-02-17/10958 | Chandra/ACIS-I | 2.10 |$^{+0.06}_{\,-0.31}$| | 0.45 |$^{+0.04}_{\,-0.16}$| | 4.35 |$^{+0.16}_{\,-0.47}$| | 1.01 |$^{+0.11}_{\,-0.58}$| | 0.77 |$^{+0.06}_{\,-0.16}$| | 0.29 |$^{+0.06}_{\,-0.21}$| | 1.55 |$^{+0.07}_{\,-0.18}$| | 0.40 |$^{+0.03}_{\,-0.06}$| |
| 2010-02-22/10962 | Chandra/ACIS-I | 1.77 |$^{+0.06}_{\,-0.37}$| | 0.27 |$^{+0.05}_{\,-0.18}$| | — | — | — | — | — | — |
The unit of flux is |$\times$| 10 |$^{-12}$| ergcm |$^{-2}$| s.
0.5-4.0keV.
4.0-10.0keV.
Harnden et al. (1979) is referred.
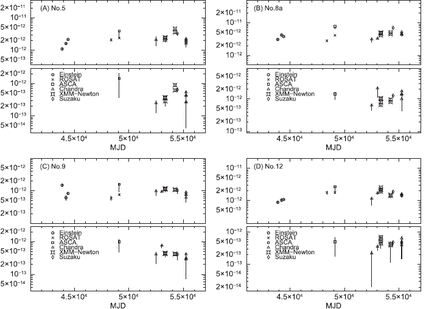
Long-term flux variation of the four stars. The upper and lower panels show the flux variation in the low-energy band (0.5-4.0keV) and high-energy band (4.0-10.0keV), respectively. The observatories of the data points are indicated by various marks shown in the bottom panels.
When we assume that all of the components have the same circumstellar absorption, the derived absorption is roughly 2–6 |$\times$| 10 |$^{21}$| H cm |$^{-2}$| . When we kept the circumstellar absorptions of the components to be free parameters in the fitting, the results did not improve. This was due to the difficulty of determining the absorption column for each component, because of the small amount of circumstellar absorption. Similar results were reported by De Becker et al. (2006) for star 8a. This does not necessarily rule out different circumstellar absorption components.
No. 12 is known to exhibit very high reddening Morgan et al. (1954), Sharpless (1957) due to the presence of circumstellar matter via its strong wind. The expected column density of the wind from the stellar surface can be calculated as 3.8 |$\times$| 10 |$^{22}$| H cm |$^{-2}$| , by assuming a mass-loss rate of 4 |$\times$| 10 |$^{-5}\ M_{\odot}$| yr |$^{-1}$|White & Becker (1983), a stellar radius of 338 |$\ R_{\odot}$|Bieging et al. (1989), and a wind velocity of |$\sim$| 1000 km s |$^{-1}$|White & Becker (1983). The calculated value is an order of magnitude larger than the observed column density. This discrepancy can be reconciled by two possibilities. One is that the X-ray emission region is far from the stellar surface, with a distance on an order of magnitude larger than the stellar radius. Another is that the absorbing matter is inhomogeneous Klochkova & Chentsov (2004), and we can see the X-ray emission region through the low column density region. Clumping of the stellar wind is indicated by observations: the observed line profiles Waldron & Cassinelli (2007) have smaller shifts and skews than expected MacFarlane et al. (1991). Unusual red-shifted absorption features also suggest in-falling matter observed in |$\tau$| Sco Howk et al. (2000). This clumping effect implies the production of bow shocks that can produce X-rays Cassinelli et al. (2008).
We observed No. 8a during an interval of only |$\sim$| 5% of its orbital period at around a phase of |$\sim$| 0.8. An orbital modulation of the X-ray intensity with a period of 21.9 d has been reported by De Becker et al. (2006). We found much shorter time variations. De Becker et al. (2006) analyzed the spectral variation of No. 8a with a three-temperature thin-thermal model, and reported that the orbital modulation is mainly due to a temperature change of the highest temperature component. We similarly found that the short time variation of No. 8a is due to a change in the temperature of the highest temperature component. De Becker et al. (2006) argued that this high-temperature component, |$\sim$| 2 keV, is dominated by colliding winds, because of its modulation with the orbital period. Although other possibilities for the origin of the |$\sim$| 2 keV component might be considered, such as magnetic activity, the |$\sim$| 20-ks time variability allows a further inspection of the colliding winds. Stevens, Blondin, and Pollock (1992) and Pittard and Stevens (1997) reported the X-ray properties of colliding stellar winds by a hydrodynamic simulation. They predicted an intrinsic variation of the X-ray luminosity from instabilities in the shocked wind as well as the primary orbital modulation. The time scale of the X-ray luminosity variation due to the instabilities is from minutes to several hours. This time scale is similar to the variation of |$\sim$| 20 ks ( |$\sim$| 6 hr) that we found. Hence, our finding could reasonably be considered to correspond to this variability. However, the conclusion that the high-temperature component originates in the colliding wind conflicts with the temperature distribution derived by the emission-line diagnostics using the high-resolution spectra obtained by Chandra HETGS, which suggests that the high-temperature plasma should exist near the stellar surface.
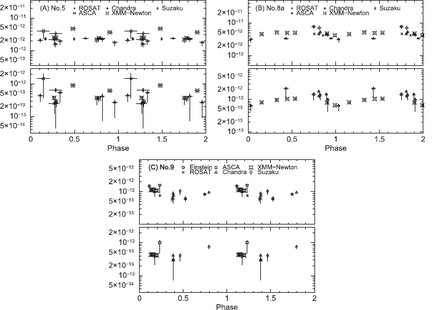
Folded light curves of three stars (Nos. 5, 8a, and 9). The periods are 6.6d, 21.9d, and 2.35yr. The ephemerides used are taken from Hall (1974), De Becker, Rauw, and Manfroid (2004), and van Loo et al. (2008).
Apart from a particular model, the short time scale of the temperature variation restricts the plasma properties. Suppose that the temperature decrease is by radiative cooling. We can then estimate a plasma density, and hence its volume. The energy in a unit volume of the plasma is |$E$||$=$||$n{{k_{\rm {B}}T}}$| , where |$n$| and |${{k_{\rm {B}}T}}$| are the number density and temperature of the plasma. The radiatively released energy is expressed as |$\epsilon$||$=$||$n^2\Lambda(T)$| , where |$\Lambda(T)$| is the emissivity of the plasma at temperature |$T$| . The time scale, |$\tau$| , of the temperature variation should be on the order of |$\tau$||$=$||$E/\epsilon$| . Our observations give |$\tau\sim$| 2 |$\times$| 10 |$^{4}$| s with the temperature of the time-variable component being |$\sim$| 2 keV. Since |$\Lambda$| (2 keV) |$\sim$| 2 |$\times$| 10 |$^{-23}$| erg s |$^{-1}$| cm |$^3$|Cox & Daltabuit (1971), we can calculate the density as |$\sim$| 0.8 |$\times$| 10 |$^{10}$| cm |$^{-3}$| . Assuming a filling factor of unity, the volume of the plasma is |$\sim$| 2.4 |$\times$| 10 |$^{36}$| cm |$^{3}$| . Since the separation of No. 8a is |$\sim$| 5.3 |$\times$| 10 |$^{12}$| cm De Becker et al. (2004), the derived volume is roughly the size of the colliding region of the winds. A number density of |$\sim$| 0.8 |$\times$| 10 |$^{10}$| cm |$^{-3}$| corresponds to a mass density of |$\sim$| 1.3 |$\times$| 10 |$^{-14}$| g cm |$^{-3}$| . This mass density is consistent with the numerical simulation by Pittard and Parkin (2010).
We should note that our finding of the variation time scale of |$\sim$| 2 |$\times$| 10 |$^{4}$| s does not exclude shorter time scales. Thus, the above volume and the densities should be an upper limit and a lower limit, respectively. Actually, the “saw”-like variation in the hardness ratio history (see figure 3a) showing sharp decays with a time scale of less than 3 |$\times$| 10 |$^{3}$| s, suggests a much shorter cooling time scale, and thus a small volume and high density. If the high-temperature plasma exists near the stellar surface, the size of the plasma should be at most the stellar radius, |$\sim$| 10 |$^{12}$| cm. In this case a short-term variation can be expected; otherwise, the average over a number of small emission regions would smear out the individual activity. Future observations with high statistics are required.
We produced 30-yr light curves for Nos. 5, 9, 8a, and 12. All of the stars show variations with factors of 2 or 3. This is the first time that light curves in a hard band above 4 keV have been obtained. We note a larger variation in No. 5 than in the others, especially in the hard band with a factor of |$\sim$| 5. The folded light curve of No. 5 does not show orbital modulation, as noted by Linder et al. (2009), showing that No. 5 exhibits a time variation that is independent of the orbital phase.
No. 8a shows clear orbital modulation with a gradual increase and sharp decay. This modulation pattern has been suggested by De Becker et al. (2006), and we confirmed it by compiling additional available data. The large amplitude of the hard band folded light curve compared to that of the low-energy band is also consistent with the results of De Becker et al. (2006). The Suzaku observation was performed around the brightest phase of the hard component. Thus, the hard component observed by Suzaku may be due to the hot plasma produced by wind collision. To explain the results of the high-resolution observations, the high-temperature plasma should exist both in the colliding wind region and around the stellar surface. We expect that a short-term variation around phase 0.0, where the hard component becomes faint, should represent a characteristics of the hot plasma around the stellar surface.
No. 9 is a strong radio emitter with a long orbital period. Our compiled data suggest a sinusoidal modulation with a maximum at around phase 0.0. The approximate periastron passage is at around 0 phase. Although our data are still sparse, a similar modulation pattern can be seen in both the low- and high-energy bands. Since the separation of this binary is large, |$\sim$| 10 |$^{3}\ R_{\odot}$| , and the eccentricity is also large Nazé et al. (2010), the interaction of the winds should be small, except around the phase 0.0. Therefore, the sinusoidal modulation cannot be simply explained by wind collision. In order to confirm this modulation, further long-term monitoring is required.
We acknowledge the reviewer for his/her valuable comments and suggestions, which significantly improved the quality of our work. This research was performed using data obtained from the Data Archives and Transmission System (DARTS), provided by Center for Science-satellite Operation and Data Archives (C-SODA) at ISAS/JAXA.
References
See |$\langle$|http://heasarc.gsfc.nasa.gov/docs/software/lheasoft/|$\rangle$| for details.
See |$\langle$|http://heasarc.gsfc.nasa.gov/docs/xanadu/xspec/index.html|$\rangle$| for details.
See |$\langle$|http://heasarc.gsfc.nasa.gov/docs/software/lheasoft/|$\rangle$| for details.
See |$\langle$|http://heasarc.gsfc.nasa.gov/Tools/w3pimms.html|$\rangle$| for details.



